正方体内切球、外接球、棱切球、图例演示(课堂PPT)
合集下载
正方体内切球、外接球、棱切球、图例演示

它包括球面和球面所包围的空间。
半径是R的球的体积:V 4R3
3
2、球的表面积
S 4πR2
练习一:
(1)球的半径伸长为原来的2倍,体积变为原 来的——8 倍.
(2)若球的表面积变为原来的2倍,则半径变 为原来的——2倍。
(3)若球半径变为原来的2倍,则表面积变
为原来的——4倍。
(4)若两球表面积之比为1:2,则其体积之 比是——1: 2—。2
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得 R 3a
2
S 4R2 3a 2
D A
D A11
D A
D A11
C B O
C1
B1
C B O
C1
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm,
这个球的体积为_32_3_ cm3.
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_1_:_2__2_: 3__3_.
例1.钢球直径是5cm,求它的体积.
B1
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
C1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,问球
O的表面积。
略 解 :RtB1D1D中 :
半径是R的球的体积:V 4R3
3
2、球的表面积
S 4πR2
练习一:
(1)球的半径伸长为原来的2倍,体积变为原 来的——8 倍.
(2)若球的表面积变为原来的2倍,则半径变 为原来的——2倍。
(3)若球半径变为原来的2倍,则表面积变
为原来的——4倍。
(4)若两球表面积之比为1:2,则其体积之 比是——1: 2—。2
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得 R 3a
2
S 4R2 3a 2
D A
D A11
D A
D A11
C B O
C1
B1
C B O
C1
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm,
这个球的体积为_32_3_ cm3.
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_1_:_2__2_: 3__3_.
例1.钢球直径是5cm,求它的体积.
B1
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
C1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,问球
O的表面积。
略 解 :RtB1D1D中 :
正方体内切球、外接球、棱切球、图例演示.

A1
C1
C1
B1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长为a, 它的各个顶点都在球O的球面上,问球O的表 面积。
D C B D1 A1
略解: RtB1 D1 D中 : ( 2 R ) a ( 2a ) , 得
2 2 2
A
O
C1 B1
3 R a 2 S 4R 2 3a 2
略解: RtB1 D1 D中 : ( 2 R ) a ( 2a ) , 得
2 2 2
D A D1 A1 B
C
O
C1 B1
3 R a 2 S 4R 2 3a 2
D
A D1 A1 B1 O B
C
C1
正方体的外接球
正方体的外接球
D A O D1 A1
C 对角面
B
ALeabharlann CODA D1 A1 B1 O B
C
C1
正方体的棱切球
正方体的棱切球直径是面对角线长
2.一个正方体的顶点都在球面上,它的棱长是4cm, 32 3 cm3. 这个球的体积为___ 3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 1: 2 2 : 3 3 个球的体积之比_________.
例1.钢球直径是5cm,求它的体积.
4 3 4 5 3 125 V R ( ) cm 3 3 3 2 6
变式1:把钢球放入一个正方体的有盖纸盒中, 至少要用多少纸?
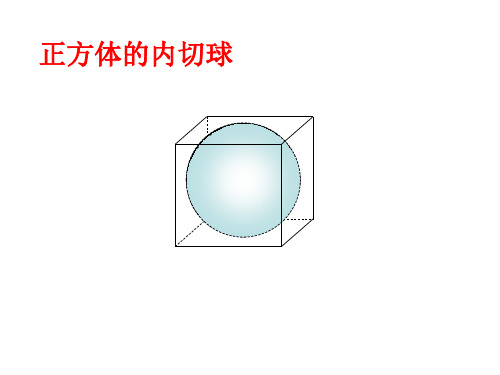
正方体的内切球
正方体的内切球的直径是棱长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各 个顶点都在球O的球面上,问球O的表面积。
C1
C1
B1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长为a, 它的各个顶点都在球O的球面上,问球O的表 面积。
D C B D1 A1
略解: RtB1 D1 D中 : ( 2 R ) a ( 2a ) , 得
2 2 2
A
O
C1 B1
3 R a 2 S 4R 2 3a 2
略解: RtB1 D1 D中 : ( 2 R ) a ( 2a ) , 得
2 2 2
D A D1 A1 B
C
O
C1 B1
3 R a 2 S 4R 2 3a 2
D
A D1 A1 B1 O B
C
C1
正方体的外接球
正方体的外接球
D A O D1 A1
C 对角面
B
ALeabharlann CODA D1 A1 B1 O B
C
C1
正方体的棱切球
正方体的棱切球直径是面对角线长
2.一个正方体的顶点都在球面上,它的棱长是4cm, 32 3 cm3. 这个球的体积为___ 3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 1: 2 2 : 3 3 个球的体积之比_________.
例1.钢球直径是5cm,求它的体积.
4 3 4 5 3 125 V R ( ) cm 3 3 3 2 6
变式1:把钢球放入一个正方体的有盖纸盒中, 至少要用多少纸?
正方体的内切球
正方体的内切球的直径是棱长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各 个顶点都在球O的球面上,问球O的表面积。
正方体内切球、外接球、棱切球、图例演示
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_________.
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各 个顶点都在球O的球面上,问球O的表面积。
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
正方体的内切球
正方体的内切球的直径是棱长
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 Aຫໍສະໝຸດ A1COC1
正方体的外接球直径是体对角线
正方体的棱切球
正方体的棱切球直径是面对角线长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a, 它的各个顶点都在球O的球面上,问球O的表
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得 R 3a
2
S 4R2 3a 2
D A
D1 A1
D A
D1 A1
C B O
C1
B1
C B O
C1
B1
面积。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得
R 3a 2
S 4R2 3a 2
D A
D1 A1
D A
C B
O C1
B1
C B
D1 A1
O C1
B1
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm, 这个球的体积为___cm3.
例2.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各 个顶点都在球O的球面上,问球O的表面积。
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
正方体的内切球
正方体的内切球的直径是棱长
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 Aຫໍສະໝຸດ A1COC1
正方体的外接球直径是体对角线
正方体的棱切球
正方体的棱切球直径是面对角线长
例2.如图,正方体ABCD-A1B1C1D1的棱长为a, 它的各个顶点都在球O的球面上,问球O的表
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得 R 3a
2
S 4R2 3a 2
D A
D1 A1
D A
D1 A1
C B O
C1
B1
C B O
C1
B1
面积。
略 解 :RtB1D1D中 :
(2R)2 a 2 ( 2a)2 , 得
R 3a 2
S 4R2 3a 2
D A
D1 A1
D A
C B
O C1
B1
C B
D1 A1
O C1
B1
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm, 这个球的体积为___cm3.
正方体内切球、外接球、棱切球、图例演示课件

感谢观看
THANKS
棱切球的半径与正方体的边长关系
半径公式
棱切球的半径r与正方体的边长a满足关系 r = a/2。
VS
几何解释
棱切球的球心位于正方体中心,且与正方 体的每个顶点距离为a/2,因此半径为 a/2。
棱切球的几何性质
相切性质
棱切球与正方体的所有棱都相切 ,与每个面都相切。
中心性质
棱切球的球心位于正方体的中心, 且与正方体的每个顶点距离相等。
半径与边长的关系
正方体的内切球半径r等于正方体边 长a的一半,即r = a/2。
证明方法
由于内切球与正方体的各面都相切, 其半径必然等于正方体中心到各面的 距离,即正方体边长的一半。
内切球的几何性质
01
02
03
04
性质1
内切球的直径等于正方体的对 角线长度。
性质2
内切球的表面积与正方体的表 面积之比为π:4。
外接球的半径R与正方体的边长a满足公式R = (√3/2)a。
推导过程
正方体的对角线长度等于外接球的直径,即2R,而正方体的对角线长度又等于空 间中两点(正方体的两个顶点)距离的最大值,即√(a^2 + a^2 + a^2) = √3a ,解得R = (√3/2)a。
外接球的几何性质
性质1
正方体的外接球与其六个 面都相切,且每个面上的 切点都是该面的中心。
性质3
内切球的体积与正方体的体积 之比为π:6。
证明方法
利用勾股定理和球的几何性质 ,可以推导出上述性质。
03
正方体的外接球
外接球的定义与特性
定义
外接球是指与正方体的八个顶点都相切的球。
特性
正方体内切球、外接球、棱切球、图例演示

2.一个正方体的顶点都在球面上,它的棱长是4cm, 这个球的体积为___cm3.
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_________.
3
32 6
变式1:把钢球放入一个正方体的有盖纸盒中, 至少要用多少纸?
正方体的内切球
正方体的内切球的直径是棱长
正方体的外接球
D1
A1
d
D
S
Aa
C1
c B1
C
b
B
d2 a2 b2 c2
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
ห้องสมุดไป่ตู้
A1
C
O
C1
正方体的外接球直径是正方体对角线
2
S 4R2 3a 2
D A
D1 A1
D A
D1 A1
C B O
C1
B1
C B O
C1
B1
练习:正方体的内切球和外接球的体积 之比为:
练习:用一个平面去截球,截得球所得的圆的半径为1
正方体的棱切球
正方体的棱切球直径是面对角线长
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
球的表面积和体积
球的体积
球面:半圆以它的直径为旋转轴,旋转所成的曲面。 球(即球体):球面所围成的几何体。
它包括球面和球面所包围的空间。
半径是R的球的体积:V 4R3
3
2、球的表面积
S 4πR2
例1.钢球直径是5cm,求它的体积.
V 4 R3 4 (5)3 125 cm3
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_________.
3
32 6
变式1:把钢球放入一个正方体的有盖纸盒中, 至少要用多少纸?
正方体的内切球
正方体的内切球的直径是棱长
正方体的外接球
D1
A1
d
D
S
Aa
C1
c B1
C
b
B
d2 a2 b2 c2
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
ห้องสมุดไป่ตู้
A1
C
O
C1
正方体的外接球直径是正方体对角线
2
S 4R2 3a 2
D A
D1 A1
D A
D1 A1
C B O
C1
B1
C B O
C1
B1
练习:正方体的内切球和外接球的体积 之比为:
练习:用一个平面去截球,截得球所得的圆的半径为1
正方体的棱切球
正方体的棱切球直径是面对角线长
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
球的表面积和体积
球的体积
球面:半圆以它的直径为旋转轴,旋转所成的曲面。 球(即球体):球面所围成的几何体。
它包括球面和球面所包围的空间。
半径是R的球的体积:V 4R3
3
2、球的表面积
S 4πR2
例1.钢球直径是5cm,求它的体积.
V 4 R3 4 (5)3 125 cm3
正方体内切球外接球棱切球图例演示

C1
B1
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
C1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,问球
O的表面积。
略解: Rt B 1 D 1 D 中 :
(2R )2 a 2 ( 2a)2,得
R
3 a
2
S 4R 2 3a 2
D A
D A11
D A
C B
O C1
B1
C B
D A11
O C1
B1
正方体的棱切球
正方体的棱切球直径是面对角线长
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
略解: Rt B 1 D 1 D 中 :
(2R )2 a 2 ( 2a)2,得 R 3a
2
S 4R 2 3a 2
D A
D A11
D A
D A11
C B O
C1
B1
C B O
1: 2 2
比是———。
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm, 这个球的体积为_32_3_ cm3.
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_1_:_2__2_:3__3_.
例1.钢球直径是5cm,求它的体积.
V4R34(5)312c5m 3 3 32 6
B1
正方体的外接球
正方体的外接球
D A
D1 A1
C
B O
C1 B1
对角面 A
A1
C
O
C1
正方体的外接球直径是体对角线
例2.如图,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,问球
O的表面积。
略解: Rt B 1 D 1 D 中 :
(2R )2 a 2 ( 2a)2,得
R
3 a
2
S 4R 2 3a 2
D A
D A11
D A
C B
O C1
B1
C B
D A11
O C1
B1
正方体的棱切球
正方体的棱切球直径是面对角线长
分析:正方体内接于球,则由球和正方 体都是中心对称图形可知,它们中心重 合,则正方体对角线与球的直径相等。
略解: Rt B 1 D 1 D 中 :
(2R )2 a 2 ( 2a)2,得 R 3a
2
S 4R 2 3a 2
D A
D A11
D A
D A11
C B O
C1
B1
C B O
1: 2 2
比是———。
练习一
1.球的半径伸长为原来的2倍,体积变为原来的_8 倍.
2.一个正方体的顶点都在球面上,它的棱长是4cm, 这个球的体积为_32_3_ cm3.
3.有三个球,一球切于正方体的各面,一球切于正 方体的各侧棱,一球过正方体的各顶点,求这三 个球的体积之比_1_:_2__2_:3__3_.
例1.钢球直径是5cm,求它的体积.
V4R34(5)312c5m 3 3 32 6
