qq图原理
统计图形

有时,人们也把统计图形与各种统计学表格统称为统计图表或统计学图表。
双标图可变量中的数据用图表表示出来。
类别)一类广义的双标图可箱形图(英文:Box-plot),又称为盒须图、盒式图、盒状图或箱线图,是一种用作显示一组数据分散情况资料的统计图。
因型状如箱子而得名。
在各种领域也经常被使用,常见于品质管理。
不过作法相对较较繁琐。
箱形图于1977年由美国著名统计学家约翰·图基(John Tukey)发明。
它能显示出一组数据的最大值、最小值、中位数、下四分位数及上四分位数。
[编辑]举例以下是箱形图的具体例子:+-----+-+* o |-------| + | |---|+-----+-++---+---+---+---+---+---+---+---+---+---+ 數線0 1 2 3 4 5 6 7 8 9 10这组数据显示出:Array最小值(min)=0.5。
下四分位数(Q1)=7。
中位数(Med)=8.5。
上四分位数(Q3)=9。
最大值(max)=10。
平均值=8。
四分位间距(interquartile range)==2 (即ΔQ)在区间 Q3+2(或3?)ΔQ, Q1-2(或3?)ΔQ 之外的值被视为应忽略(farout)。
farout: 在图上不予显示,仅标注一个符号∇。
最大值区间: Q3+1.5ΔQ最小值区间: Q1-1.5ΔQ最大值与最小值产生于这个区间。
区间外的值被视为outlier显示在图上.outlier = 3.5定义和构图:在构建的主要步骤是一个 QQ位数的计算或估计是威廉·普莱菲于1801年在他的《统计学摘要》Statistical Breviary中所作[7][5]。
编辑]示例示例数据的饼图示例数据的分裂式饼图,将最大的党派分离出来。
以下数据基于2004年欧洲议会选举的初步结果。
以下表格中列出了分配给各个党派的席位数量,并计算出了他们各自所占的百分比。
qq图原理

qq图原理
QQ图,又称为散点图,是一种用于描述两个变量之间关系的
图表。
它的原理是通过绘制一系列的散点,并利用空间位置来表示变量之间的关系和趋势。
在QQ图中,我们需要有两个变量,分别称为X变量和Y变量。
首先,将X变量进行排序,然后根据排序后的X变量值,找到对应的Y变量值,并将它们绘制在坐标系中。
X变量通常被称为自变量,而Y变量则被称为因变量。
通过
将X变量排序,并将它们与对应的Y变量值进行比较,我们
可以看出它们之间的关系。
如果X变量和Y变量之间存在某
种趋势或者规律,那么这种关系可以通过QQ图进行可视化展示。
通常情况下,QQ图会在坐标系中绘制一条直线,用于表示X
变量和Y变量之间的理论关系。
如果散点落在这条直线附近,并且比较均匀地分布在直线两侧,那么说明X变量和Y变量
之间存在着线性关系。
如果散点呈现出其他形状,比如曲线形状,那么说明X变量
和Y变量之间存在非线性关系。
通过观察散点的分布情况,
我们可以推断出X变量和Y变量之间的关系类型。
除了用于观察变量之间的关系,QQ图还可以用于检测数据是
否服从某种特定的分布。
通过将X变量的排序值与理论分布
的分位数进行比较,我们可以判断数据是否符合该分布。
总之,QQ图是一种简单而有效的数据可视化工具,它能够帮助我们理解变量之间的关系,并进行数据分布的检测。
它的原理就是通过绘制散点,并观察散点的分布情况,来揭示变量之间的关系和规律。
QQ图,柱状图分析方法

w<-c(21.4,20.3,22.4,21.4,21.8,20.9,17.2,25.3,20.2,19.6,23.1,19,22.6,21.9,19.2,24.5,22.1,22.5,18. 8,23.7,20.2,21.1,20.6,23.9,21.6,21.9,19.3,26.2,19.7,20.6,20.5,20.4,23,20.9,23.5,20.9,19.1,23.2,23 .4,23.7,20,20.1,22.3,18,24.1,21.7,23.8,20.8,19.3,21.5,22.2,21.3,19.2,25.6,19,23,23,23.6,19.9,25.4 ,20,20.7,22.3,22.9,22.3,24.3,20,23.2,17.7,22.7,21.3,22.7,22.5,22.5,22.5,20.3,27.1,18.7,25.2,18.9, 23.4,19.3,21.8,26.5,23.1,22.7,22.1,23.5,17.9,20.1,20.4,23.7,23.2,19.3,24.9,17.7,23,23.1,21,24.5,1 6.3,21.6,21.2,22.8,21.8,26.2,20.7,22.7,21,19.8,18.2,23,18.9,22,18.7,25.6,21.5,21.3,23.6,26.5,22.5 ,22.1,21,21.7,27.1,18.1,26.6,24.5,25.8,23.6,22.7,25.1,23.1,23.4,23.4,25.2,24.7,24,23.2,23.3,22.4, 22.8,24.2,22.7,20.6,23,23.6,23.4,25.2,23.7,26,23.5,26.4,21.2,25.2,24.8,25,23.2,22.9,24.5,23.8,24. 3,20.8,23.8,29.8,23.2,22.6,25.9,23.9,25,26.1,31.8,24.6,23.9,20.5,21.7,23.3,24,22.7,26.7,26.9,22,2 3.6,25.7,21.1,24.6,23.3,24.9,26.1,20,24.3,22.3,24.4,26.3,24.1,27.2,24.8,19.2,23,22.5,28.6,23.9,21 .6,25.6,25.3,24.1,24.5,24,25.8,23.8,21.3,24.9,25.2,21.8,23.7,26,24.4,26.1,23,25.8,19.8,24.3,24.1, 22.5,24.4,21.6,22.3,22.7,25.9,25.2,22.9,23.8,26.7,24.6,24,23.6,27.3,22.9,27.4,24,23.1,24.5,23.8,2 1.4,23.9,23.7,22.8,22.9,20,20.2,18.9,20.2,20.9,21.1,23.2,21.2,18.2,23.3,24,26.9,20.5,21.3,21,19.7 ,21.9,22.9,21.5,17.6,20,18.6,22.3,20.1,23,23,20.8,22.8,22.8,22.6,21.1,22.2,22.8,21.7,21.2,22,21.1 ,20.4,20.5,26.5,26,22.1,20.6,24.5,22.5,23.1,22,19.7,22.8,21,24.8,21.1,19.1,22.3,21.8,21.3,23.3,20 .3,21.3,20.4,22.9,23.4,23.8,24.9,21.7,21,20.4,23.1,21.5,23.7,18.9,24.9,20.6,20.4,21.8,21.5,20.5,1 7.4,19.2,23.5,25.1,20,22.4,23.3,24.4,28.8,26.1,26.4,21.1,23.9,23.9,23,21.7,21.9,25.5,25.5,22.9,23 .3,19.9,23.5,24.9,20.5,26.2,23.8,28,24.9,24.7,21.8,19.8,22.6,22.2,24.4,25.5,22.3,24.7,24.1,25.7,2 1.6,23.8,26.3,23.1,24,23.3,23,22.1,23.1,27.6,22.8,24.8,21.3,24.4,21.7,23.3,20.9,20.3,23.4,23.9,27 .9,24.3,24.2,22.7,21.2,23.7,25.1,22,27,21.3,23.4,23,23.8,22.4,23.3,21.2,23.2,21.7,21.8,25.6,23,23 .8,23.7,22.7,22.1,21.2,20.8,24.9,23.7,23.3,22.1,23.9,22.7,21.6,22,24.5,21.8,21.5,20.6,23.2,21.9,1 9.5,20.8,18.4,18.6,23.6,28.3,19.7,21.3,23.5,25.8,22.3,24.2,23.7,21.6,23.7,23.4,19.5,24.4,18,24.3, 20.1,25.1,19.3,23.5,24.2,24.4,22.4,22.2,23,24.8,18.5,17.9,24.1,24.7,19.8,23.1,21.4,22.6,23.7,19,1 6.5,23.4,20.9,20.3,18.5,22.7,24.4,20,22.4,24.6,24.3,24.7,21.3,19.5,22.3,24.3,22.1,19.5,18.9,21.3, 24.6,22.5,18.2,19.5,24.2,23,20.4,21.2)qqnorm(w); qqline(w)hist(w, freq = FALSE)lines(density(w), col = "blue")x <- 16.3:31.8lines(x, dnorm(x, mean(w), sd(w)), col = "red")w<-c(20.4,23,20.8,21.7,21.7,20.7,20.9,25.2,20,21.4,26.6,18.8,23,23.1,21.8,24.8,21.4,20.5,20.7,18 .6,25.6,23.5,18.9,19.9,18,23.4,22.3,21.6,23.4,18.2,22,19,23.6,22.4,21.9,20.6,21,19.2,21.5,23.1,22 .1,19.3,25.3,22.7,17.9,19.3,24.5,24.5,20.3,23.7,22.6,21.6,26.5,23.7,21.8,19.8,20.2,23,18.7,23,23. 1,26.2,20,24.9,20.9,21.1,26.9,22.9,21.5,20.6,23.2,20.9,18.2,20.4,21,21.3,22.6,22.8,23.7,21.7,21.8 ,19.3,21,20.8,24.5,18.9,23.3,18.9,22.4,22.2,21.8,24.9,20.2,21.2,21.4,24.4,27.7,25.1,23.8,23,23.8, 24.7,26.2,24,26.8,22.4,25.2,22.1,20.6,22.3,24.6,22,24,23.2,26.6,22.3,26,23.7,23,23.9,24,25.2,24, 23.5,21.6,24.8,24.8,21,22.7,22.6,19.8,21.1,25.9,21.3,24.6,25.2,24.5,21.8,22.4,24.5,24.5,25.7,24.9 ,24.9,22.7,23.8,22.7,23.3,27.2,25.2,24.4,20.6,23.7,23.6,23.9,26.4,24.3,24.2,24.1,27.1,23.1,23.3,2 4.5,23,21.3,23.9,23.8,23,24.4,22.9,22.6,23.9,23.3,24.4,22.1,21.7,27.9,23.9,21.2,22.4,25.1,23.3,21 .5,24,23.9,24.7,24.8,23.3,23.8,23.5,21.8,23.1,22.4,23.8,24.7,21.8,21.8,24.1,21.8,19.8,20,23,16.3, 23.3,20.1,21.6,21.5,22.1,19,22.7,22.5,23,18.6,21.5,23.4,21.1,26.5,20.4,22.2,21.8,21.3,21.2,20.1,2 2.3,19.9,23.1,21.7,22.1,22.2,22.9,20.3,20.8,23.1,25.4,25.5,22.4,25.6,20.9,26.4,23.3,25.7,22,23.2, 24.2,23.6,23.7,25.5,27.6,23.8,23.3,23.5,22.1,28.8,24.3,26.6,22.7,24.9,27,21.9,22.7,24.9,21.9,24.3 ,17.7,22.7,21.8,19.6,21.3,22.3,22.5,20.6,22.9,18.7,23.5,20.3,21.3,20.2,22.3,22.7,18.7,17.2,25.6,2 6.1,25.8,27.4,25.9,23.4,23.6,26.6,21.2,25,24.6,23,23.2,21.7,23.3,24.1,25.2,24.7,23.6,23.5,24.3,26 .7,23.1,21.2,23.2,24.6,23,23.4,23.1,23.2,20.5,22.8,21.6,23,23.5,22.2,17.6,23,22,21.1,22.9,20.5,21 .3,21.5,21,20.6,20.2,24.5,19.7,21,22.5,19.2,22,26,20.5,24.9,19.9,22,19.8,22.2,22.8,17.9,23.1,22.4 ,18.5,23.7,21.3,24.2,19,19.3,20.3,20,23.6,24.7,24.4,19.5,21.3,22.1,18,23.7,21.1,23.5,26.1,27,23.7 ,24,22.9,23.9,23.3,22.7,24.1,22.3,27.3,23.9,22.6,22.5,21.4,20.6,21.1,28,23.3,21.7,20.8,21.2,23,22 .4,21.6,20,21.2,27.1,24.2,23.7,20.8,23.3,21.8,21.2,22.4,22.3,23.2,22.9,21.6,22.8,25.5,26.3,20.5,22.3,23.1,26.1,22.7,20.3,23.1,21.6,21.7,21.2,25.5,24.9,24.1,23.7,23.4,21.3,20.9,23.4,22,23.7,24.1,.5,20.4,20.9,19.3,23.9,20.1,21,20.9,19.2,17.7,27.1,21.4,26.2,22.8,24.1,25,20.7,23.6,24,23.8,24.4, 29.9,23.6,25.8,24.9,24.8,25.8,26.3,24.5,23.9,26.3,22.2,23.2,28,25.6,31.8,25.2,26.9,23.8,24.9,23.4 ,26.1,24.3,26.6,26.8,21.4,24.1,21.7,20,21.7,21.1,19.7,20.6,20.5,19.2,22.8,17.4,18.9,22.8,22.8,24, 22,25.4,23.3,23.8,22.8,20.3,20.4,19.1,21.9,20.8,19.7,20,20.4,22.3,21.4,21,24.8,21.5,20,21.1,23.7, 23.1,22.4,23.4,22.2,22.9,19.5,25.2,23.4,24.3,24.7,20.4,22.3,20.8,22.5,26,24.3,19.7,24.4,20.9,25.5 ,23,19.4,24.3,22.7,19.5,18.6,21.5,18.9,20.3,21.9,17.2,28.3,20.8,22.2,29.3,23.6,22.5,26.1,24.6,22. 5,23.3,22.9,22.3,23.8,23.5,24.3,24.4,26,26.2,22.9,22.5,22.2,20.5,24.4,26.5,18.8,25.4,25.8,18.1,22 .8,24.2,21.3,22.5,21.3,24.2,18.4,20.1,22.2,20.4,19.2,18.2,19.5,18.5,19.5,23.5,16.5,21.6,25.1,22,1 9.8,21.9,24.6,24.6,28.6,24.1,27.1,25.1,26.7,22.7,29.8,24.4,22.5,24.1,25.3,22.5,21.6,23.7,22.1,25, 25.4,23)hist(w, freq = FALSE)lines(density(w), col = "blue")x <- 16.3:31.8lines(x, dnorm(x, mean(w), sd(w)), col = "red")w<-c(20.4,23,20.8,21.7,21.7,20.7,20.9,25.2,20,21.4,26.6,18.8,23,23.1,21.8,24.8,21.4,20.5,20.7,18 .6,25.6,23.5,18.9,19.9,18,23.4,22.3,21.6,23.4,18.2,22,19,23.6,22.4,21.9,20.6,21,19.2,21.5,23.1,221,26.2,20,24.9,20.9,21.1,26.9,22.9,21.5,20.6,23.2,20.9,18.2,20.4,21,21.3,22.6,22.8,23.7,21.7,21.8 ,19.3,21,20.8,24.5,18.9,23.3,18.9,22.4,22.2,21.8,24.9,20.2,21.2,21.4,24.4,27.7,25.1,23.8,23,23.8, 24.7,26.2,24,26.8,22.4,25.2,22.1,20.6,22.3,24.6,22,24,23.2,26.6,22.3,26,23.7,23,23.9,24,25.2,24, 23.5,21.6,24.8,24.8,21,22.7,22.6,19.8,21.1,25.9,21.3,24.6,25.2,24.5,21.8,22.4,24.5,24.5,25.7,24.9 ,24.9,22.7,23.8,22.7,23.3,27.2,25.2,24.4,20.6,23.7,23.6,23.9,26.4,24.3,24.2,24.1,27.1,23.1,23.3,2 4.5,23,21.3,23.9,23.8,23,24.4,22.9,22.6,23.9,23.3,24.4,22.1,21.7,27.9,23.9,21.2,22.4,25.1,23.3,21 .5,24,23.9,24.7,24.8,23.3,23.8,23.5,21.8,23.1,22.4,23.8,24.7,21.8,21.8,24.1,21.8,19.8,20,23,16.3, 23.3,20.1,21.6,21.5,22.1,19,22.7,22.5,23,18.6,21.5,23.4,21.1,26.5,20.4,22.2,21.8,21.3,21.2,20.1,2 2.3,19.9,23.1,21.7,22.1,22.2,22.9,20.3,20.8,23.1,25.4,25.5,22.4,25.6,20.9,26.4,23.3,25.7,22,23.2, 24.2,23.6,23.7,25.5,27.6,23.8,23.3,23.5,22.1,28.8,24.3,26.6,22.7,24.9,27,21.9,22.7,24.9,21.9,24.3 ,17.7,22.7,21.8,19.6,21.3,22.3,22.5,20.6,22.9,18.7,23.5,20.3,21.3,20.2,22.3,22.7,18.7,17.2,25.6,2 6.1,25.8,27.4,25.9,23.4,23.6,26.6,21.2,25,24.6,23,23.2,21.7,23.3,24.1,25.2,24.7,23.6,23.5,24.3,26 .7,23.1,21.2,23.2,24.6,23,23.4,23.1,23.2,20.5,22.8,21.6,23,23.5,22.2,17.6,23,22,21.1,22.9,20.5,21 .3,21.5,21,20.6,20.2,24.5,19.7,21,22.5,19.2,22,26,20.5,24.9,19.9,22,19.8,22.2,22.8,17.9,23.1,22.4 ,18.5,23.7,21.3,24.2,19,19.3,20.3,20,23.6,24.7,24.4,19.5,21.3,22.1,18,23.7,21.1,23.5,26.1,27,23.7 ,24,22.9,23.9,23.3,22.7,24.1,22.3,27.3,23.9,22.6,22.5,21.4,20.6,21.1,28,23.3,21.7,20.8,21.2,23,22 .4,21.6,20,21.2,27.1,24.2,23.7,20.8,23.3,21.8,21.2,22.4,22.3,23.2,22.9,21.6,22.8,25.5,26.3,20.5,2 2.3,23.1,26.1,22.7,20.3,23.1,21.6,21.7,21.2,25.5,24.9,24.1,23.7,23.4,21.3,20.9,23.4,22,23.7,24.1, 19.9,25.5,22.2,22.1,22.5,22.2,18.9,23.8,25.4,19.3,19.1,23.1,23.7,23.2,19.7,21.1,23.2,22.8,21.2,22 .5,20.4,20.9,19.3,23.9,20.1,21,20.9,19.2,17.7,27.1,21.4,26.2,22.8,24.1,25,20.7,23.6,24,23.8,24.4, 29.9,23.6,25.8,24.9,24.8,25.8,26.3,24.5,23.9,26.3,22.2,23.2,28,25.6,31.8,25.2,26.9,23.8,24.9,23.4 ,26.1,24.3,26.6,26.8,21.4,24.1,21.7,20,21.7,21.1,19.7,20.6,20.5,19.2,22.8,17.4,18.9,22.8,22.8,24, 22,25.4,23.3,23.8,22.8,20.3,20.4,19.1,21.9,20.8,19.7,20,20.4,22.3,21.4,21,24.8,21.5,20,21.1,23.7, 23.1,22.4,23.4,22.2,22.9,19.5,25.2,23.4,24.3,24.7,20.4,22.3,20.8,22.5,26,24.3,19.7,24.4,20.9,25.5 ,23,19.4,24.3,22.7,19.5,18.6,21.5,18.9,20.3,21.9,17.2,28.3,20.8,22.2,29.3,23.6,22.5,26.1,24.6,22. 5,23.3,22.9,22.3,23.8,23.5,24.3,24.4,26,26.2,22.9,22.5,22.2,20.5,24.4,26.5,18.8,25.4,25.8,18.1,22 .8,24.2,21.3,22.5,21.3,24.2,18.4,20.1,22.2,20.4,19.2,18.2,19.5,18.5,19.5,23.5,16.5,21.6,25.1,22,1 9.8,21.9,24.6,24.6,28.6,24.1,27.1,25.1,26.7,22.7,29.8,24.4,22.5,24.1,25.3,22.5,21.6,23.7,22.1,25, 25.4,23)plot(ecdf(w),verticals = TRUE, do.p = FALSE)x <- 16.3:31.8lines(x, pnorm(x, mean(w), sd(w)))X1<-c(7.33,6.33,9.04,7.13,6.62,8.9,8.37,6.53,9.11,7.7,7.66,7.36,8.46,8.16,9.37,7.2,8.04,7.2,7.22,6 .82,7.16,6.74,7.72,7.27,7.47,7.66,9.21,7.47,7.98,7.81,8.47,8.09,7.58,7.91,7.79,7.92,8.73,7.46,6.91 ,8.57,6.93,8.13,7.95,8.51,7.61,10.67,7.49,9.2,9.46,7.5,7.2,7.17,7.71,7,7.19,6.28,8.22,7.72,7.75,6. 11,7.82,7.46,7.64,9.06,8.8,7.89,7.5,6.34,7.16,6.69,8.81,9.02,8.67,8.68,7.6,5.89,8.32,7.62,9.02,6.9 ,8.43,7.14,10.41,9.19,7.37,8.34,7.44,6.86,8.29,6.6,6.43,6.39,7.41,8.76,7.79,8.6,6.84,5.92,6.86,8.0 8,7.73,7.73,6.63,7.32,7.1,6.75,8.39,8.51,7,7.52,8.06,7.65,6.71,7.99,9.66,5.95,7.85,8.01,5.79,6.01, 6.99,7.73,7.81,7.02,7.13,8.86,9.29,6.11,8.88,7.24,7.9,8.19,8.31,6.23,9.31,7.15,9.63,8.03,8.71,8.0 6,6.3,7.78,7.92,6.75,8.57,8.09,6.26,6.95,8.87,8.8,7.24,7.01,6.16,8.28,8.17,8.08,7.28,6.15,7.85,8.3 8,8.66,6.92,7.29,8.61,7.63,6.29,6.89,7.44,4.87,7.29,9.711,8.08,7.76,9.73,6.97,9.15,7.33,6.09,8.39 ,7.17,7.03,7.96,6.17,7.17,8.09,10.25,10.3,6.01,8.86,7.53,9.46,8.2,7.9,6.76,6.68,5.78,8.12,6.53,8.1 8,8.66,7.03,7.96,8.9,8.42,9.97,8.62,7.45,7.05,6.57,6.42,7.09,8.35,7.93,6.05,8.36,6.48,6.95,7.35,8. 13,6.54,7.28,7.66,6.2,7.2,8.29,7.5,7.73,7.86,7.72,8.23,6.75,7.69,7.68,8.52,8.04,9.44,7.94,6.95,6.2 2,7.8,7.62,8.715,8.78,5.99,8.07,6.99,8.08,8.18,7.3,7.65,7.86,7.48,7.88,8.67,7.99,6.42,6.46,6.87,7. 69,6.83,6.62,6.74,7.74,7.17,7.548,9.3,6.15,7.93,6.83,7.83,8.11,6.85,6.48,6.04,6.78,7.76,7.46,10.2 )X2<-c(8.91,9.17,8.59,9.8,9.32,10.85,9.02,9.16,9.28,8.35,8.28,9.02,8.83,9.17,8.21,8.47,8.72,10.2,8 .93,9.13,9.1,10.7,9.94,8.25,10.65,8.82,9.41,9.88,8.38,8.07,9.84,9.05,9.55,9.16,9.63,8.56,11.64,9. 45,10.8625,11.11,8.87,8.02,8.46,9.02,8.28,9.57,8.21,10.86,9.07,9.42,7.32,9.02,8.64,9.23,9.99,10. 61,9.44,9.57,7.51,8.79,8.26,10.19,9.31,10.85,10.06,8.81,7.05,9.65,8.95,10.55,9.02,10.3,8.14,11.8 ,10.32,8.56,9.99,9.72,8.72,9.58,7.43,8.27,8.21,9.29,10.81,8.82,9.76,8.51,7.55,8.17,9.24,9.35,8.95 ,8.19,8.64,8.18,8.34,9.87,10.53,8.5,9.14,8.96,9.62,7.68,9.01,11.08,7.32,9.05,9.19,7.5,6.74,8.92,8. 99,8.92,8.56,9.43,10.57,10.84,7.55,10.29,8.63,8.71,9,9.52,7.95,10.49,9.66,10.8,9.3,10.16,9.83,7. 51,9.04,10.05,8.63,10.01,9.58,8.01,8.05,9.92,9.5,9.65,8.8,8.25,10.43,9.844444444,9.38,9.49,6.62 ,9.16,10.31,9.92,8.15,8.47,9.35,8.83,7.68,8.71,8.97,6.72,8.3,11.09,9.23,8.72,10.78,8.14,10.62,8.1 6,8.2,9.55,9.55,7.96,9.05,7.58,8.27,9.27,12.36,11.64,7.33,11.89,9.5,11.11,10.051,8.16,8.41,8.37, 6.69,10.77,7.92,10.17,9.71,8.19,9.17,9.94,9.67,11.46,10,9.48,8.11,7.67,7.53,9.42,9.64,8.99,7.94, 9.42,7.95,9.18,8.46,9.13,8.19,8.37,9.32,7.79,8.87,10.24,9.622222222,10.04,9.66,8.95,9.55,8.54,8 .97,9.91,9.54,9.2,10.88,9.03,8.17,8.7,9.51,8.96,9.7,10.16,7.41,9.577777778,9.39,8.96,9.52,8.62,8 .79,9,8.92,9.28,10.63,10.5,7.26,7.68,7.83,9.722222222,8,8.4,8.15,8.82,9.48,9.04,10.89,7.85,9.42 2222222,7.86,9.67,8.79,8.01,7.96,7.16,9.01,10.62,9,11.82)plot(X1, X2)age <- c(1,3,5,2,11,9,3,9,12,3)weight <- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1)mean(weight)[1] 7.06sd(weight)[1] 2.077498cor(age,weight)[1] 0.9075655plot(age,weight)weight<- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1) demo(graphics)age <- c(1,3,5,2,11,9,3,9,12,3)weight <- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1) demo(Hershey)age <- c(1,3,5,2,11,9,3,9,12,3)weight <- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1) demo(persp)age <- c(1,3,5,2,11,9,3,9,12,3)weight <- c(4.4,5.3,7.2,5.2,8.5,7.3,6.0,10.4,10.2,6.1) demo(image)dose <- c(20, 30, 40, 45, 60)drugA<- c(16, 20, 27, 40, 60)drugB<- c(15, 18, 25, 31, 40)plot(dose, drugA,type="b")plot(dose, drugB, type="b")dose <- c(20, 30, 40, 45, 60)drugA<- c(16, 20, 27, 40, 60)opar<- par(no.readonly=TRUE)par(pin=c(2, 3))par(lwd=2, cex=1.5)par(cex.axis=.75, font.axis=3)plot(dose, drugA, type="b", pch=19, lty=2, col="red")plot(dose, drugB, type="b", pch=23, lty=6, col="blue", bg="green") par(opar)dose <- c(20, 30, 40, 45, 60)drugA<- c(16, 20, 27, 40, 60)drugB<- c(15, 18, 25, 31, 40)opar<- par(no.readonly=TRUE)par(lwd=2, cex=1.5, b=2)plot(dose, drugA, type="b",pch=15, lty=1, col="red", ylim=c(0, 60),main="Drug A vs. Drug B",xlab="Drug Dosage", ylab="Drug Response")lines(dose, drugB, type="b",pch=17, lty=2, col="blue")abline(h=c(30), lwd=1.5, lty=2, col="gray")library(Hmisc)minor.tick(nx=3, ny=3, tick.ratio=0.5)legend("topleft", inset=.05, title="Drug Type", c("A","B"),lty=c(1, 2), pch=c(15, 17), col=c("red", "blue"))par(opar)r22030405060Drug Dosagedose <- c(10,20,30,40,50,60,70,80,90,100,150,200,250,300,350,4000,450,500)drugA<-c(0.326234,0.282328,0.24779,0.22316,0.208824,0.196644,0.188323,0.181271,0.174908,0.16961 8,0.150605,0.13863,0.130229,0.124045,0.119344,0.115926,0.113623,0.112041689)drugB<-c(0.294204,0.244857,0.208469,0.181945,0.166209,0.153317,0.143793,0.136362,0.129652,0.123 988,0.103465,0.090991,0.082516,0.076451,0.072046,0.068799,0.066616,0.06523)opar<- par(no.readonly=TRUE)par(lwd=2, cex=1.5, b=2)plot(dose, drugA, type="b",pch=15, lty=1, col="red", xlim=c(10,500),ylim=c(0, 0.5),main="LD plot",xlab="Marker distance in kb", ylab="Average r2")lines(dose, drugB, type="b",pch=17, lty=2, col="blue")legend("topright", inset=.01, title="Two breeds", c("GM","CM"),lty=c(1, 2), pch=c(15, 17), col=c("red", "blue"))PEDpar(opar)。
多元数据的正态性检验

多元数据的正态性检验摘 要:本文对多元正态性检验的两种主要方法——2χ统计量的Q-Q 图检验法和主成分检验法进行了讨论,介绍其基本原理、具体实施步骤,通过实例分析进行应用研究,并比较它们的优劣,发现主成分检验法的实用性和应用价值更强. 关键词:多元正态性 2χ统计量 Q-Q 图检验法 主成分检验法The Normality Test for Multivariate DataAbstract: In this paper, we discuss two main methods of multiple normal tests, Q-Q chart test and principal component test, introduce the basic principle and the specific implementation steps, research through studying the case, and compare their advantages and disadvantages. We found that the principal component test is better than Q-Q chart test in practicality and applied value. Key words: Multivariate normality; Chi-square statistic; Q-Q char test; Principal component test引言正态分布在学习中是一种很重要的分布,在自然界中占据着很重要的位置,它能描述许多随机现象,从而充当一个真实的总体模型.尽管在学习中我们总是碰到很多问题的总体服从正态分布,然而,在一个实际问题中,总体一定是正态分布吗?一般的讲,所作统计推断的结论是否正确,取决于实际总体与正态总体接近的程度如何.因此,建立一些方法来检验多元观测数据与多元正态数据的差异是否显著是十分必要的.如今,一元数据的正态检验的理论已相当成熟,但对于多元数据的正态性检验问题还处在摸索前进的阶段,没有形成行之有效、有足够说服力的检验方法.本文将在第一节中介绍文中用到的一元正态性检验的两种基本方法:图方法和矩法;第二节中介绍2χ统计量的Q-Q 图检验法基本原理和检验步骤;第三节中介绍主成分正态检验法的基本原理和检验步骤;第四节中通过两个实例做应用分析;第五节中对这两种方法在应用中的优劣做比较分析.1 一元正态性检验的方法鉴于一元数据正态性检验的多样性,本文不一一介绍,只介绍本文中用到的2χ检验法和偏峰检验法.1.1 图方法设12,,...,n x x x 是来自总体的X 随机样本,检验),(~:20δμN X H .如果没有关于样本的附加信息可以利用,首选推荐的是利用正态概率纸画图.它让人们立即看到观测的分布是否接近正态分布.对于一张正态概率纸,它的横轴的刻度是均匀的,纵轴按标准正态分布的P 分位数均匀刻度,标上相应的P 值.正态概率纸上的坐标轴系统使正态分布的分布函数呈一条直线.利用正态概率纸检验一组观测值是否服从正态分布,可以按如下步骤进行: 把n 个观测值按非降次序排列成12n x x x ≤≤≤.然后把数对(3/8,1/4k k x n -+)(1,2,,k n =)点在正态概率纸上.如果所画的n 个点明显地不成一条直线,则拒绝原假设.如果这些点散布在一条直线附近,则可以粗略地说,样本来自正态分布.这时,可以凭直觉配一条直线,使它离各点的偏差尽可能地小,其中在纵轴刻度为50%附近各点离直线的偏差要优先照顾,使其尽可能地小,并且使直线两边的点数大致相等.如果发现得到的点系统地偏离一条直线,在拒绝原假设后,可以考虑备择假设的类型.特别,如果几个较大的值明显地倾向于由其它值确定的直线的下方,作log y x =或y 等变换可能使图形更符合一条直线.这种方法也就是人们常说的P-P 图法或Q-Q 图法. 1.2 矩法矩法,也称动差法、偏峰检验法,它是利用中心距的概念引入的两个量,正态分布的这两个量有着很好的特征,因此,常用这两个量进行正态性检验.总体X 的偏度是刻画X 分布的对称程度的量,记为31322()[()]E X EX G E X EX -=- , (1.2.1)10G =,X 的分布对称;10G >,称为正偏;10G <,称为负偏.总体X 的峰度是衡量X 的概率分布密度陡峭程度的量,记为4222()[()]E X EX G E X EX -=- , (1.2.2)正态分布的偏度为0,峰度为3.一个分布如果1G 远离0或2G 远离3,则可认为它与正态分布相差很大,为了检验样本12,,...,n x x x 是否来自正态总体,先计算偏度和峰度的估计量3113321()(())nii n i i xx g x x ==-=-∑∑,412321()(())nii n i i xx g x x ==-=-∑∑ .当总体服从正态分布且样本容量n 很大时,统计量1g 和2g 近似正态分布,且有1()0E g ≈,224()Var g n≈,如果以下不等式1g -≤23g --≤只要有一个不成立,就认为总体不服从正态分布[4].2 2χ统计量的Q-Q 图检验法2.1 2χ统计量的Q-Q 图检验法的原理为了充分解释2χ统计量的Q-Q 图检验法的基本原理,先引入分位数和经验分布函数的概念以及一个重要结论.定义2.1 对10<<p ,称满足不等式p x X P ≥≤)(,p x X P -≥≥1)(的x 值为随机变量X 的P 阶分位数.如果X 是连续型的,那么P 阶分位数就是满足方程p x F =)(的x 的值.如果X 是离散型的,那么,P 阶分位数存在唯一性的问题.因此采用以下定义更准确:设X 的分布函数为)(x F ,对10<<p ,定义x 的P 阶分位数为}{p x F x xp≥=)(:inf .所以)(1p F x p -=就是分布函数的反函数,且只存在唯一的P 阶分位数,即()x F 的左侧分位数.分位数是随机变量的重要数字特征,在描述数据的分布时非常有用.定义2.2 设()n x x x ,,21是总体X 的一组样本观察值,将它们按大小顺序排列为)()2()1(n x x x ≤≤≤ ,x 为任意实数,称函数(1)()()(1)()0,(),1,k n n k k n x x F x x x x x x +⎧<⎪=≤≤⎨⎪≥⎩, 为经验分布函数.经验分布函数的图像是一条阶梯曲线,若观察值不重复则阶梯的每一个跃度都是1n ,若重复,则按1n的倍数跳跃上升.对任意的实数x ,()n F x 的值等于样本的观察值12,,,n x x x 中不超过x 的频率,由频率与概率的关系,()n F x 可以作为总体X 的分布函数()F x 的一个近似值,随n 的增大,近似程度越好.结论2.1 设),(~∑μp N X ,0>∑,则),(~21δχp X X -∑',其中1'δμμ-=∑.证明:因为0∑>,由正定矩阵的分解可得'CC ∑=(C 为非退化方阵),令1Y C X -=,即X CY =,则),(~1p P I C N Y μ-,因'CC ∑=,所以()1,p p YN C I μ-,且有),(~211δχp Y Y CY C Y X X '=∑''=∑'--,其中()()111''C C δμμμμ---==∑.下面介绍2χ统计量的Q-Q 图检验法的原理,设()1(,...;)(1,,)p X X X a n ααα'==为来自p 元总体X 的随机样本,检验),(~:0∑μP N X H ,1:H X 不服从(,)p N μ∑.由上面的结论1可知在0H 成立时,)(~)()(21p X X χμμ-∑'--,所以将X 到总体中心μ的马氏距离2(,)D X μ=1()()X X μμ-'-∑-记为2D ,则有)(~22p Dχ.以下构造的检验方法是检验量2D 是否有)(~22P D χ成立.先由样品()a X 计算2(1,,)a D a n =,并对2a D 排序:222(1)(2)()...n D D D ≤≤;取统计量2D 的经验分布函数为2()0.5()n t t t F D p n-==,记2()(|)t H D p 表示2()p χ的分布函数在2()t D 的值,则在0H 下有2()(|)t t p H D p ≈;由经验分布得到样本的t p 分位数21()()t n t D F p -=,同时设2χ分布的tp 分位数为2t χ,若假设0H 成立,应有:22()t t D χ≈.然后绘制点22()(,)t t D χ的散点图,这些点应散布在一条过原点且斜率为1的直线上,如果存在明显的偏离,则可以拒绝原假设.这种检验法其实就是2χ分布的Q-Q 图检验法.如果不利用分位数,直接用概率散点2()(,(|))t t p H D p 绘图,就是2χ分布的P-P 图检验法.2.2 2χ统计量的Q-Q 图检验法一般步骤为了方便应用,将上述思路的具体实施步骤归纳如下:(1)由n 个p 维样品()()1,,a X a n =计算样本均值X 和样本协方差阵S :()()()()11'1na aa S X XX X n ==---∑; (2.2.1)(2)计算样品点()t X (1,2,,t n =)到X 的马氏距离:()()()()()21'1,,t t t D X X S X X t n -=--= ;(3)对马氏距离2t D 按从小到大的次序排序:()()()22212n D D D ≤≤≤;(4)计算()0.51,2,,t t p t n n-==以及2t χ,其中2t χ满足:()2t t H p p χ=(或计算()()2t H D p 的值);(5)以马氏距离为横坐标,2χ分位数为纵坐标作平面坐标系,用n 个点()()22,t t D χ绘制散布图,即得到2χ分布的Q-Q 图;或者用另n 个点()()()2,t t p H D p 绘制散布图,即得2χ分布的P-P 图;(6)考察这n 个点是否散布在一条通过原点,斜率为1的直线上,若是,接受数据来自p 元正态总体的假设;否则拒绝正态性假设.3 主成分检验法3.1 主成分检验法的基本原理目前,关于主成分的研究很多,但大多数集中在进行综合评价及回归分析,用来做检验的则几乎没有.主成分检验法是建立在主成分变量基础上的统计方法,基本思想是降维:将多元数据集转化为多个一元互相独立的数据集,通过检验一元数据集的正态性来判断原多元数据集的正态性.为充分解释这一思想,先引入主成分的定义.定义 3.1.1设X =12(,,,)'p X X X 是p 维随机向量,均值()E X μ=,协方差阵()D X =∑,称i i Z a X '=为X 的第i 主成分(1,2..i p =),如果:(1)1(1,2.,)i i a a i p '==;(2)当1i >时,0(1,2.,1)i j a a j i '∑==-; (3)1,0(1,2.,1)()max()i j i a a j i Var Z Var X ααα''=∑==-'=.若已知∑的特征值为 120p λλλ≥≥≥>,12,,,p a a a 为相应的单位正交特征向量,则X 的第i 主成分i i Z a X '=(1,2..i p =)具体的证明过程参见文献[1].如果可以证明:1Z ,…,p Z 是相互独立的,这时p 元数据的正态性检验可化为P 个相互独立的主成分的一元数据的正态性检验,这种检验方法称为主成分检验法.下面说明主成分的不相关性.设()D X =∑,如果∑是对角矩阵,即p 维向量的分量互不相关,这时可以直接把p 元正态性检验问题转化为p 个一元正态性检验问题.但一般∑不是对角矩阵,即分量间是相关的,利用主成分分析法,求得X 的p 个主成分1Z ,…,p Z .下证1Z ,…,p Z 是不相关的.令12(,,,)p Z Z Z Z =,由于1Z ,…,p Z 依次为X 的第i 主成分的充要条件是12()(,,,)p D Z diag λλλ=.即有(,)i j ii j Cov z z i jλ≠⎧=⎨=⎩,又1λ≥2λ≥……≥p λ>0 ,即说明任意两个不相同的主成分之间是不相关的,故12,,,p Z Z Z 不相关.文献[2]中给出了主成分数据处理的基本方法,并分析了方法的不足,提出了改进的方法.直接将标准化的数据代入*Tp n p n Z A X ⨯⨯=,则得到主成分得分.其中,系数矩阵p n A ⨯为对应特征向量组成的矩阵,*T p n X ⨯为标准化的数据集.从中我们看到,计算主成分得分实际上是将标准化后的原始数据投影到旋转后的坐标中. 结论3.1.1 若~(,)X N μ∑,则~(,)Z N A A A μ'∑;反之,若Z 服从多元正态分布,则X 也服从多元正态分布.证明:由主成分的定义知,Z A X '=,其中,12(,,,)p A a a a =且为正交矩阵.由于~(,)X N μ∑,则()()()E Z E AX AE X A μ===, ()()()D Z D A X A D X A A A '''===∑,从而,由多元正态分布的线性性质,~(,)Z N A A A μ'∑,反过来,由Z 服从正态分布,同理可知X 服从正态分布.结论3.1.2 若12,,,p Z Z Z 独立同正态分布,则Z 服从多元正态分布. 证明:此命题的结论可以直接从多元正态分布的定义得出.由主成分的理论特征知,主成分变量是新的互不相关的变量,因此,只要说明主成分变量12,,,p Z Z Z 分别服从一元正态分布,就可以说明Z 服从多元正态分布,从而由结论3.1.1知X 也服从多元正态分布. 3.2 主成分正态检验的一般步骤具体检验步骤如下:(1)由n 个p 维样品()()1,,a X a n =计算样本均值X 和样本协方差阵S ,计算公式同(2.2.1)式;(2)利用坐标变换计算每个样本点的主成分得分,得到新的主成分得分集12,,,p Z Z Z ;(3)对每个i Z (1,2,,i p =),求出其对应的偏度和峰度值;(4)考察偏度是否趋近0,峰度是否趋近3.若是,则接受X 来自于正态总体;若两个条件有一个不满足,则拒绝正态性假设.4 应用研究为了说明这两种方法具有很好的实用价值,并进行比较,本文给出两个实例研究.4.1 实例1对20 名健康成年女性的出汗(X1 ) ,钠的含量(X2) 和钾的含量(X3) 的数据进行正态性检验.本例数据与文献[4]中第45页例1的数据一样,文献[4]中是对样本数据进行均值向量的假设检验,检验方法是基于样本数据来自于3元正态分布的假设,但文献[4]并没有对样本数据进行正态性检验,现本文分别用2χ统计量的Q-Q图检验法和主成分检验法进行多元正态性检验.(1) 2χ统计量的Q-Q图检验法根据2.2节给出的一般步骤,结合数据集,首先利用SAS中主成分程序(程序同见附录3)计算出协方差阵S:X1 X2 X3X1 1.0000 0.4173 -.5597X2 0.4173 1.0000 -.2095X3 -.5597 -.2095 1.0000表4-1 协方差阵然后利用Matlab编程计算马氏距离(程序见附录1),并按升序排列;同时利用SAS软件计算出对应的2χ分位数(程序见附录2),结果见下表:序号马氏距离p分位数序号马氏距离p分位数1 0.003 0.2158 11 0.1096 2.50162 0.0061 0.472 12 0.123 2.79093 0.0064 0.6924 13 0.1446 3.10984 0.0179 0.9018 14 0.2238 3.46755 0.0296 1.1086 15 0.2241 3.87756 0.0355 1.3174 16 0.3571 4.36137 0.061 1.5316 17 0.455 4.95668 0.0885 1.754 18 0.4902 5.73949 0.0887 1.9875 19 0.8439 6.904610 0.0915 2.2354 20 1.1447 9.3484表4-2 马氏距离和p分位数最后以马氏距离为横坐标,以卡方分位数为纵坐标作散点图,见图4-1:χ统计量的Q-Q图图4-1 2从图中可以看出,这些点基本在一条直线的上下波动,偏离不是很大.因此,从直观上判断可以接受原多元数据集来自于多元正态分布的假设.(2) 主成分检验法obs Z1 Z2 Z3 obs Z1 Z2 Z31 -2.35056 -1.60948 -0.63809 11 -0.62827 0.3278 0.167342 1.28027 -1.57151 0.68293 12 -1.40979 0.37468 0.697083 0.29161 -1.15274 -0.44169 13 -0.54558 0.43448 -0.125834 -0.99597 -0.99533 -0.16326 14 1.68529 0.48243 -0.56935 5 0.24255 -0.76054 -0.42432 15 -0.1638 0.59492 -0.986336 0.34761 -0.48032 0.3077 16 0.68709 0.59525 0.94349 7 2.73671 -0.45672 0.58714 17 0.18684 0.85608 0.55041 8 1.30752 -0.44759 0.41891 18 1.38678 0.98895 -1.18331 9 -0.05272 0.03561 -0.68763 19 -0.90402 1.14607 -0.18851 10-2.800040.157190.6998620-0.301541.480770.35344表4-3 主成分得分集然后对主成分得分集进行分析,用SAS 中的UNIVARIATE 命令和SAS 中的分析家中的Q-Q 图分别对Z1、Z2、Z3做正态性检验.我们先看偏峰检验的结果表4-4:变量 偏度 峰度 均值 标准差 方差 Z1 -0.1509976 0.77631092 0.123713 1.259021 1.58513 Z2 -0.3508053 -0.6267268 0.084709 0.83305 0.69397 Z3-0.421413-0.89060520.0335830.623830.38916表4-4 偏峰度检验结果从表4-4中可以看出偏度是在0附近波动,但是峰度的波动很大,绝对值在0.7附近,结合2.2节中的结论可知,可以拒绝原数据集是来自3元正态分布的假设.我们再看图方法检验的结果,见图4-2:图4-2 QQ 图(依次为1Z 、2Z 、3Z )从图中左上角给出的拟合方差以及均值可以看出,直线的拟合度非常好,由此可以判断1Z 、2Z 、3Z 都服从一元正态分布,从而可以接受原数据集来自于3元正态分布的假设.从上面的分析我们看到一元正态检验的2 检验法和Q-Q 检验法得到了两种截然相反的结果,那哪个结果更可信呢?出现这样的情况也是正常的,最重要的原因是中心矩的结果很容易受到频数分布的影响.不同的分布可能计算出同样的中心矩,这样就造成检验误差增大.4.2 实例2本例选取我国2006年各地区城市设施水平数据作正态性检验,包含6个指标,1X :城市用水普及率;2X :城市燃气普及率;3X :每万人拥有公共交通车辆;4X :人均城市道路面积;5X :人均公园绿地面积;6X :每万人拥有公共厕所.用1~31依次表示北京、天津、河北、山西、内蒙古、辽宁、吉林,黑龙江,上海,江苏,浙江,安徽,福建,江西,山东,河南,湖北,湖南,广东,广西,海南,重庆,四川,贵州,云南,西藏,陕西,甘肃,青海,宁夏,新疆全国31个省、直辖市、自治区的名称.(1) 2χ统计量的Q-Q图检验法参照3.1.1中的步骤说明,可以得出相关的结果如下:X1 X2 X3 X4 X5 X6 X1 1 0.8212 0.3768 -0.1479 0.1356 -0.1812 X2 0.8212 1 0.5332 0.075 0.2839 -0.0797 X3 0.3768 0.5332 1 0.0923 0.2322 0.2216 X4 -0.1479 0.075 0.0923 1 0.5665 0.0193 X5 0.1356 0.2839 0.2322 0.5665 1 0.0371 X6 -0.1812 -0.0797 0.2216 0.0193 0.0371 1表4-5 相关阵obs 卡方分位数马氏距离obs 卡方分位数马氏距离1 1.043733 0.0421 17 5.614729 0.19162 1.613527 0.0569 18 5.891093 0.23813 2.003244 0.0579 19 6.181212 0.25574 2.328934 0.0659 20 6.48602 0.27525 2.62003 0.0713 21 6.810794 0.35716 2.889358 0.0725 22 7.157803 0.38767 3.146093 0.0767 23 7.534835 0.52228 3.393355 0.0774 24 7.948509 0.65179 3.635972 0.0783 25 8.408144 0.76210 3.875649 0.0849 26 8.932674 0.774411 4.113647 0.0889 27 9.544323 0.78612 4.353161 0.0919 28 10.29153 1.525313 4.59426 0.0939 29 11.26231 1.701614 4.83994 0.0943 30 12.68048 1.82515 5.09018 0.1127 31 15.59516 2.039316 5.348121 0.1665表4-6 马氏距离和2χ分位数最终得到2χ统计量的Q-Q图如下:图4-32χ统计量的Q-Q图从图4-3中可以看出,大部分数据呈抛物线分布,因此,拒绝原数据集来自于6元正态分布的假设.(2) 主成分检验法从表4-7中可以看出,1Z比较符合正态分布的特征,但从后面的方差以及标准差(根据Q-Q图拟合直线与点之间的关系得到的,方差和标准差越小说明Q-Q 图越接近于一条直线,也就说明该变量越服从正态分布)来看36X X拟合度比较好.无论怎样,从偏峰度和Q-Q图都可得出,原多元数据集不服从正态性检验.这个结果说明我国各省、直辖市、自治区在上面描述的六个指标中不存在都强或都弱的情况,都是此强彼弱,这很好的映证了目前我国各省、直辖市、自治区实际情况.5 两种方法的比较从上面的原理介绍和应用分析可以看出,多元数据正态性检验的2χ统计量的Q-Q图检验法和主成分检验法存在各自的优缺点.相对来说,主成分正态性检验法涉及到主成分的计算,较为麻烦,但容易在软件上实现,具有较强的实用性和应用价值.这也可以从主成分也能对一元变量进行检验可以看出来,但是需要注意的是一元检验的是新的主成分变量,并不是原始数据集的某一指标的一元检验.2χ统计量的Q-Q图检验法具有结论简单明了的直观效果,但是它没有现成的命令可以套用,对于专业知识不够的人是难以得出结果的.从理论上讲,主成分检验法是优于2χ统计量的Q-Q图检验法,这是因为相对来说一元数据的正态性检验理论已经相当成熟,在得出主成分变量后,就可以直接用相应的软件命令来实现,简单,但分析起来就相对麻烦些.结束语本文只是比较了多元数据正态性检验的两种常用方法的异同,对于其他分布的检验问题,由主成分的较好的特征,是否可以将主成分检验法推广到其他类型分布的检验上呢?本文受能力和时间限制没有研究.另外,主成分提出至今,通过大量的实践验证,发展形成了比较系统的体系.目前比较常见的有核主成分见文献[5]、灰(也称模糊)主成分见文献[6]、伪主成分见文献[7]、非线性主成分见文献[8]等分析方法,这些方法的提出弥补了主成分一般方法的不足.对于这些改进方法见文献[9],是否也可将之应用到本文中的主成分检验法中,使主成分检验法的结论更为准确,也没有研究.本文的创新之处在于通过了两个实例来衡量两种检验方法的优劣,这样做的好处是避免了以偏概全,而且很好的利用软件将2χ统计量的Q-Q图检验法的结果得出来了,并总结了两种检验方法的长处和短处.美中不足的是对于2χ统计量的Q-Q图检验法没有编写出一个完整的程序直接得出Q-Q图.限于作者的学术水平,文中难免有错误和不足,欢迎批评指正.致谢本论文选题及写作都是在徐伟老师的亲切关怀和细心指导下完成的.他的严肃的科学态度,严谨的治学精神,精益求精的工作作风,深深地感染和激励着我,使我不仅接受了全新的思想观念,树立了宏伟的学术目标,领会了基本的思考方式,掌握了通用的研究方法,而且还明白了许多为人处事的道理,在此,我对徐老师表示深深的感谢.与此同时,我还要感谢教过我的所有的老师,没有他们谆谆的教导就不会有我今天论文的完成,谢谢了老师,您们辛苦了.参考文献[1]高惠璇. 应用多元统计分析[M].北京:北京大学出版社,2005[2]A.H.Al-Ibrahim, Noriah M.Al-Kandari. Stability of principal components[J],Computational Statistics 23(8),2008.9[3]贾明辉,华志强.主成分分析数据处理方法探讨[J].内蒙古民族大学学报自然科学版,23(4),2008.7[4]Fabian Sinz, Sebastian Gerwinn, Matthias Bethge. Characterization of the p-generalized normal distribution。
PP图和QQ图

PP图和QQ图⼀. QQ图分位数图⽰法(Quantile Quantile Plot,简称 Q-Q 图)统计学⾥Q-Q图(Q代表分位数)是⼀个概率图,⽤图形的⽅式⽐较两个概率分布,把他们的两个分位数放在⼀起⽐较。
⾸先选好分位数间隔。
图上的点(x,y)反映出其中⼀个第⼆个分布(y坐标)的分位数和与之对应的第⼀分布(x坐标)的相同分位数。
因此,这条线是⼀条以分位数间隔为参数的曲线。
如果两个分布相似,则该Q-Q图趋近于落在y=x线上。
如果两分布线性相关,则点在Q-Q图上趋近于落在⼀条直线上,但不⼀定在y=x线上。
Q-Q图可以⽤来可在分布的位置-尺度范畴上可视化的评估参数。
从定义中可以看出Q-Q图主要⽤于检验数据分布的相似性,如果要利⽤Q-Q图来对数据进⾏正态分布的检验,则可以令x轴为正态分布的分位数,y轴为样本分位数,如果这两者构成的点分布在⼀条直线上,就证明样本数据与正态分布存在线性相关性,即服从正态分布。
⼆. PP图P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图,⽤于直观地检测样本数据是否符合某⼀概率分布。
如果被检验的数据符合所指定的分布,则代表样本数据的点应当基本在代表理论分布的对⾓线上。
由于P-P图和Q-Q图的⽤途完全相同,只是检验⽅法存在差异。
要利⽤QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在⼀条直线附近,⽽且该直线的斜率为标准差,截距为均值.⽤QQ图还可获得样本偏度和峰度的粗略信息.scipy 画Q-Q图fig = plt.figure()res = stats.probplot(train['SalePrice'], plot=plt)plt.show()scipy.stats ⽤法# -*- coding: utf-8 -*-from scipy import statsfrom numpy import random# Distributions# 常⽤分布可参考本⽂档结尾处# 分布可以使⽤的⽅法见下列清单data=random.normal(size=1000)stats.norm.rvs(loc=0,scale=1,size=10,random_state=None) # ⽣成随机数stats.norm.pdf(-1.96,loc=0,scale=1) # 密度分布函数,画密度分布图时使⽤stats.norm.cdf(-1.96,loc=0,scale=1) # 累计分布函数,-1.96对应2.5%stats.norm.sf(-1.96,loc=0,scale=1) # 残存函数(=1-cdf),-1.96对应97.5%stats.norm.ppf(0.025,loc=0,scale=1) # 累计分布函数反过来stats.norm.isf(0.975,loc=0,scale=1) # 残存函数反过来stats.norm.interval(0.95,loc=0,scale=1) # 置信度为95%的置信区间stats.norm.moment(n=2,loc=0,scale=1) # n阶⾮中⼼距,n=2时是⽅差stats.norm.median(loc=0,scale=1) # Median of the distribution.stats.norm.mean(loc=0,scale=1) # Mean of the distribution.stats.norm.var(loc=0,scale=1) # Variance of the distribution.stats.norm.std(loc=0,scale=1) # Standard deviation of the distribution.stats.norm.fit(data) # fit 估计潜在分布的参数# Statistical functionsstats.describe([1,2,3]) # 返回多个统计量stats.gmean([1,2,4]) # ⼏何平均数 n-th root of (x1 * x2 * ... * xn)stats.hmean([2,2,2]) # 调和平均数 n / (1/x1 + 1/x2 + ... + 1/xn)stats.trim_mean([1,2,3,5],0.25) # 砍头去尾均值,按⽐例砍stats.sem(data) # Calculates the standard error of the meanstats.mode([1,1,2]) # 众数stats.skew(data) # 偏度stats.kurtosis(data) # 峰度stats.moment(data,moment=3) # n阶中⼼矩,3阶就是偏度,4阶就是峰度stats.skewtest(data) # 检验偏度是否符合正态分布的偏度stats.kurtosistest(data) # 检验峰度是否符合正态分布的峰度stats.normaltest(data) # 检验是否符合正态分布stats.variation([1,2,3]) # 变异系数(=std/mean*100%)stats.find_repeats([1,1,2,2,3]) # 重复值查找stats.itemfreq([1,1,2,2,3]) # 频次统计stats.percentileofscore([1,2,3,4,5],2) # 返回数值的分位数stats.scoreatpercentile([1,2,3,4,5],80,interpolation_method="lower") # 返回分位数对应的数值stats.bayes_mvs(data) # 返回均值/⽅差/标准差的贝叶斯置信区间stats.iqr([1,2,3,4,5],rng=(25,75)) # 计算 IQRstats.zscore(data) # 计算 zscorestats.f_oneway(data,data+data,data+data+data) # 单因素⽅差分析,参数是(样本组1,样本组2,样本组3)stats.pearsonr(data,data+data) # ⽪尔森相关系数stats.spearmanr(data,data+data) # 斯⽪尔曼秩相关系数stats.kendalltau(data,data+data) # 肯德尔相关系数stats.pointbiserialr([1,1,1,0,0,0],[1,2,3,4,5,6]) # 点⼆系列相关,第⼀个变量需要是⼆分类变量stats.linregress(data,data+data) # 线性最⼩⼆乘回归stats.ttest_1samp(data,popmean=0) # 单样本 t-检验: 检验总体平均数的值stats.ttest_ind(data,data+data) # 双样本 t-检验: 检验不同总体的差异stats.ttest_rel(data,data+data) # 配对样本 t-检验stats.ttest_ind_from_stats(mean1=0,std1=1,nobs1=100,mean2=10,std2=1,nobs2=150,equal_var=True) # 根据统计量做 t-检验stats.wilcoxon(data,data+data) # ⼀种⾮参数的配对样本检验。
正态性检验几种方法

正态性检验的几种方法一、引言正态分布是自然界中一种最常见的也是最重要的分布。
因此,人们在实际使用统计分析时,总是乐于正态假定,但该假定是否成立,牵涉到正态性检验。
目前,正态性检验主要有三类方法:一是计算综合统计量,如动差法、Shapiro-Wilk 法(W 检验)、D ’Agostino 法(D 检验)、Shapiro-Francia 法(W ’检验)。
二是正态分布的拟合优度检验,如2χ检验、对数似然比检验、Kolmogorov-Smirov 检验。
三是图示法(正态概率图Normal Probability plot),如分位数图(Quantile Quantile plot ,简称QQ 图)、百分位数(Percent Percent plot ,简称PP 图)和稳定化概率图(Stablized Probability plot ,简称SP 图)等。
而本文从不同角度出发介绍正态性检验的几种常见的方法,并且就各种方法作了优劣比较,还进行了应用。
二、正态分布2.1 正态分布的概念定义1若随机变量X 的密度函数为()()()+∞∞-∈=--,,21222x e x f x σμπσ其中μ和σ为参数,且()0,,>+∞∞-∈σμ则称X 服从参数为μ和σ的正态分布,记为()2,~σμN X 。
另我们称1,0==σμ的正态分布为标准正态分布,记为()1,0~N X ,标准正态分布随机变量的密度函数和分布函数分别用()x ϕ和()x Φ表示。
引理1 若()2,~σμN X ,()x F 为X 的分布函数,则()⎪⎭⎫⎝⎛-Φ=σμx x F由引理可知,任何正态分布都可以通过标准正态分布表示。
2.2 正态分布的数字特征引理2 若()2,~σμN X ,则()()2,σμ==x D x E 引理3 若()2,~σμN X ,则X 的n 阶中心距为()()N k kn k k n kn ∈⎩⎨⎧=-+==2,!!1212,02σμ定义2 若随机变量的分布函数()x F 可表示为:()()()()x F x F x F 211εε+-= ()10<≤ε其中()x F 1为正态分布()21,σμN 的分布函数,()x F 2为正态分布()22,σμN 的分布函数,则称X 的分布为混合正态分布。
最新QQ登录界面因果图法设计测试用例

第二步:从因果图表导出测试用例:
附件(一):
附件(二):调查问卷设计大学生个性化消费增多是一种趋势。当前社会、经济飞速发展,各种新的消费品不断增多,流行文化时尚飞速变化,处于校园与社会两者之间的大学生肯定会受影响。目前在大学校园,电脑、手机、CD、MP3、录音笔被称为大学生的“五件武器”。除了实用,这也是一种表明自己生活优越的炫耀性的东西。现下很大一部分大学生中的“负债消费”表现的典型的超前享乐和及时行乐——其消费项目多半是用于奢侈浪费的非必要生活消耗。如举办生日宴会、打网球、保龄球、上舞厅跳舞、进夜总会唱“卡拉OK”等。“负债消费”使很多学生耽于物欲,发展严重者轻则引起经济纠纷,动武斗殴,影响同窗友谊,重则引发犯罪事件,于社会治安不利。
1、作者:蒋志华《市场调查与预测》,中国统计出版社2002年8月§11-2市场调查分析书面报告
2003年,上海市人均GDP按户籍人口计算就达到46700元,是1995年的2.5倍;居民家庭人均月可支配收入为14867元,是1995年的2.1倍。收入不断增加的同时,居民的消费支出也在增加。2003年上海居民人均消费支出为11040元,其中服务性消费支出为3369元,是1995年的3.6倍。
市场环境所提供的创业机会是客观的,但还必须具备自身的创业优势,才能使我们的创业项目成为可行。作为大学生的我们所具有的优势在于:
在上海,随着轨道交通的发展,地铁商铺应运而生,并且在重要商圈已经形成一定的气候,投资经营地铁商铺逐渐为一大热门。在人民广场地下的迪美购物中心,有一家DIY自制饰品店--“碧芝自制饰品店”
QQ登录界面因果图法设计测试用例
用因果图设计QQ登录界面的测试用例。我们看到有3个可以组合的项:QQ的帐号、QQ的密码、登录按钮。在测试的时候,要简化QQ的输入条件,这样才能有重点的去测试,也是主要关注用户的基本需求。
Normal Probability Plot+QQ Plot

右偏态
左偏态
Confidential
Page
Normal Probability Plot
正态概率图(Normal Probability Plot) • 概述:正态概率图用于检查一组数据是否服从正态分布,是实数与正态分布数据之间 函数关系的散点图。如果这组数据服从正态分布,正态概率图会是一条直线。 • 适用条件:(1)当你采用的工具或者方法需要使用服从正态分布的数据 (2)当有50个或更多数据点,为了获得更好的结果 • 计算原理:(1)将数据从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 (3)从正态分布概率表中找到各分位数对应的Z值 (4)将数据点作散点图:实际数据值对应Y轴,正态分位数Z值对应X轴 (5)画一条拟合大多数点的直线与点形成的图形相比较,判断拟合正态 分布的好坏
Confidential
Page
QQ-Plot
分位数-分位数图(quantile-quantile plot) • 概述:QQ图的主要作用是判断样本是否近似于某种类型的分布,或者验证两组数据是 否来自同一分布。这里的“QQ”是两个Quantiles的大写字母,即两个分位数。 • 适用条件:检验一组数据是否来自某个分布或者两组数据是否来自同一分布 • 计算原理:(1)将数据按照从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 ( 3 )将数据点作散点图:第一组数据的分位数对应 X 轴,另一组数据的 分位数对应Y轴 ( 4 )作 y=x 的直线,如果两个分布相似,则该 Q-Q 图趋近于落在 y=x 线上。 如果两分布线性相关,则点在Q-Q图上趋近于落在一条直线上,但不一定在y=x线上。
QQxml卡片的应用原理

QQxml卡片的应用原理什么是QQxml卡片QQxml卡片是一种在QQ聊天中常用的卡片样式,通常用于展示特定内容的卡片。
它可以在QQ聊天窗口中显示,包含标题、描述、封面图片等信息。
QQxml卡片的结构QQxml卡片是基于XML语法的,它以一对<xml></xml>标签包裹,内部包含多个标签组成,这些标签共同构成了卡片的结构。
卡片标签QQxml卡片的主要标签包括:1.<msg>标签:包裹所有卡片内容的最外层标签,表示一条聊天消息。
2.<item>标签:表示卡片内的一个条目,一个卡片可以包含多个条目。
3.<title>标签:用于显示条目的标题。
4.<description>标签:用于显示条目的描述内容。
5.<picture>标签:用于设置条目的封面图片,可以通过设置url属性来指定图片地址。
6.<url>标签:用于设置条目的点击跳转链接。
卡片样式QQxml卡片允许开发者自定义样式,可以通过设置标签的属性来实现。
常见的样式属性包括:1.color属性:用于设置标题和描述文字的颜色。
2.background属性:用于设置卡片的背景颜色。
3.align属性:用于设置文字的对齐方式,可以取值为left、center、right。
4.weight属性:用于设置文字的粗细,可以取值为bold、normal。
QQxml卡片的应用场景QQxml卡片广泛应用于QQ聊天中,主要用于展示一些重要信息,例如:1.商品展示:商家可以通过QQxml卡片的形式展示商品的标题、封面图片、价格等信息,吸引用户的注意。
2.资讯推送:媒体机构可以通过QQxml卡片的形式推送新闻、文章等内容,通过精美的封面图片和简洁的描述来吸引用户点击。
3.活动邀请:组织者可以通过QQxml卡片的形式邀请好友参加活动,包含活动的名称、时间、地点等信息。
4.个人名片:用户可以通过QQxml卡片来展示自己的个人信息,包括姓名、简介、联系方式等。
qq 原理

qq 原理
QQ是一种即时通讯软件,它通过互联网让用户可以实时地进行文本、语音、视频通话以及发送文件和图片等功能。
QQ的基本原理是通过建立服务器与客户端之间的连接,使用户可以通过服务器的中转来进行信息的发送和接收。
在实际使用中,QQ软件首先会通过用户输入的账号和密码来进行登录,验证账号和密码的正确性后,将用户的登录信息发送给服务器。
服务器接收到登录信息后会进行验证,验证成功后将与该账号对应的用户信息发送给用户的客户端。
客户端接收到用户信息后,即可与服务器保持长连接,以便进行后续的通讯。
当用户需要发送信息时,用户的客户端将信息内容发送给服务器,服务器将接收到的信息再转发给目标用户的客户端。
目标用户的客户端接收到消息后,将消息显示给用户。
这样,发送和接收消息的过程就完成了。
除了基本的文本信息,QQ还支持语音、视频通话以及发送文件和图片等功能。
其中,语音、视频通话功能的原理是将用户的语音或视频数据进行编码和解码,然后通过网络传输给接收方的客户端进行解码和播放;发送文件和图片的原理是将文件或图片数据进行传输和存储,并通过消息通知接收方的客户端进行接收和显示。
值得注意的是,QQ的通讯原理是基于客户端与服务器之间的连接,因此用户需要保持网络连接才能正常使用QQ的各项功
能。
另外,QQ的通讯过程也需要保障用户信息的安全性,所
以在数据传输过程中会使用加密技术来保护用户信息的机密性。
统计学中的正态性检验方法

统计学中的正态性检验方法统计学是一门研究数据收集、分析和解释的学科,它在各个领域都有广泛的应用。
正态性检验是统计学中的一个重要概念,用于判断数据是否服从正态分布。
本文将介绍统计学中的正态性检验方法,探讨其原理和应用。
一、正态分布的特征正态分布是统计学中最为常见的分布形式,也被称为高斯分布。
它具有以下特征:均值为μ,标准差为σ,对称分布,呈钟形曲线。
正态分布在自然界和社会科学中广泛存在,例如身高、体重、考试成绩等都可以近似看作服从正态分布。
二、为什么需要正态性检验正态性检验的目的是验证数据是否符合正态分布的假设。
在许多统计分析中,例如回归分析、方差分析等,都要求数据服从正态分布。
如果数据不满足正态性假设,可能会导致结果的偏差和误差。
因此,正态性检验是保证统计分析结果可靠性的重要步骤。
三、常见的正态性检验方法1. 直方图检验法直方图是一种常用的图形表示方法,可以用来观察数据的分布情况。
正态分布的直方图呈现出钟形曲线,而非正态分布的数据则会显示出不同的形状。
通过观察直方图的形状,可以初步判断数据是否服从正态分布。
2. QQ图检验法QQ图是一种用于检验数据是否服从某种分布的图形方法。
它将数据的分位数与理论分位数进行比较,如果数据点近似落在一条直线上,则说明数据近似服从正态分布。
如果数据点偏离直线,则说明数据不符合正态分布。
QQ图可以直观地展示数据的分布情况,是一种常用的正态性检验方法。
3. Shapiro-Wilk检验法Shapiro-Wilk检验是一种常用的正态性检验方法,它基于数据的偏度和峰度进行计算。
该检验方法的原假设是数据服从正态分布,备择假设是数据不服从正态分布。
通过计算统计量和对应的p值,可以判断数据是否符合正态分布。
如果p值小于显著性水平(通常为0.05),则拒绝原假设,即数据不服从正态分布。
四、正态性检验的应用正态性检验在统计学中有广泛的应用。
例如,在回归分析中,需要检验残差是否服从正态分布,以验证模型的合理性。
残差的正态性检验——概率图和QQ-plot图
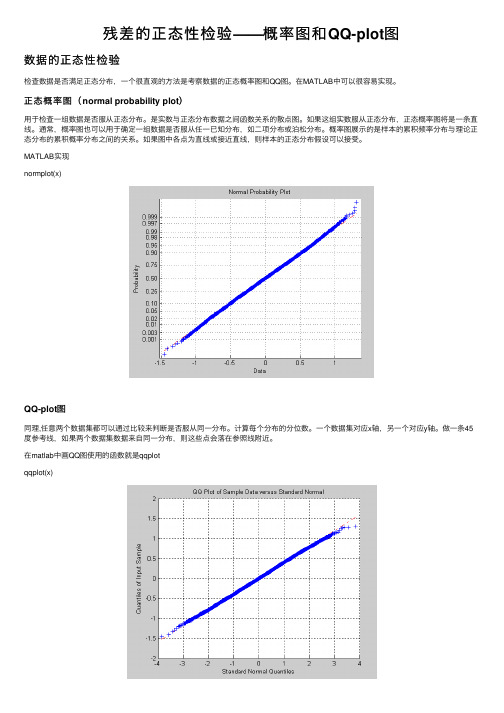
残差的正态性检验——概率图和QQ-plot图数据的正态性检验检查数据是否满⾜正态分布,⼀个很直观的⽅法是考察数据的正态概率图和QQ图。
在MATLAB中可以很容易实现。
正态概率图(normal probability plot)⽤于检查⼀组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是⼀条直线。
通常,概率图也可以⽤于确定⼀组数据是否服从任⼀已知分布,如⼆项分布或泊松分布。
概率图展⽰的是样本的累积频率分布与理论正态分布的累积概率分布之间的关系。
如果图中各点为直线或接近直线,则样本的正态分布假设可以接受。
MATLAB实现normplot(x)QQ-plot图同理,任意两个数据集都可以通过⽐较来判断是否服从同⼀分布。
计算每个分布的分位数。
⼀个数据集对应x轴,另⼀个对应y轴。
做⼀条45度参考线,如果两个数据集数据来⾃同⼀分布,则这些点会落在参照线附近。
在matlab中画QQ图使⽤的函数就是qqplotqqplot(x)The analysis of the AR(1) model residuals (Figure 71) shows that the residuals are normally distributed, zero centered and with a standard deviation equal to 0.764 °C.2019/5/27续。
之前看论⽂看到数据的正态性检验,不知道为啥这样能检验正态性。
这个好像是Q-Q plot图。
转⾃:QQ plot的全称是Quantile-Quantile Plot,即分位数-分位数图。
这个图形的形式⾮常简单,有点类似RNA-seq中评价两个样本相关性的散点图(图1)。
这类图形为什么那么相似呢?因为它们本质上就是做两组数据的⽐较,判断它们是否基本⼀致。
以样本重复性散点图为例(图1b),如果某个基因的表达量在样本C1和C2两个⽣物学重复中相同或相近,那么这个基因在这个散点图中X和Y轴坐标应该是相同或相近的,即这个点应该位于这个图形的45°对⾓线上。
(参考资料)QQ图法检验正态分布
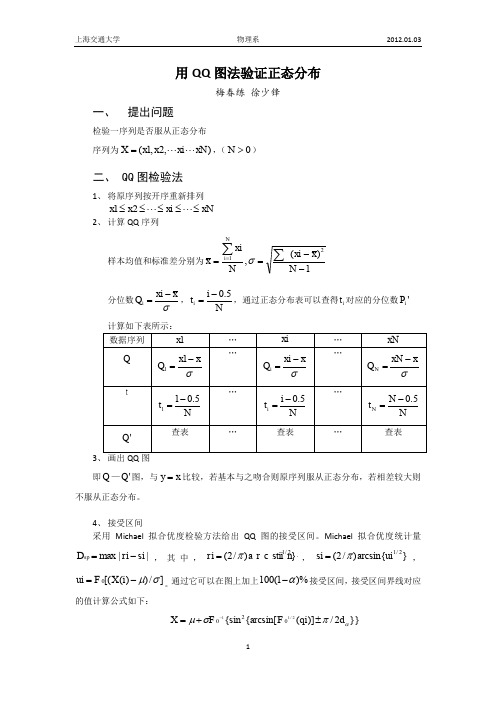
(xi x)2
N 1
分位数 Qi
xi
x
, ti
i 0.5 N
,通过正态分布表可以查得 ti 对应的分位数 Pi '
计算如下表所示:
数据序列
x1
Q
Q1
x1
x
…
xi
…
Qi
xi
x
…
xN
…
QN
xN x
t
…
…
t1
1 0.5 N
ti
i 0.5 N
tN
N
0.5 N
查表
…
查表
…
查表
Q'
3、 画出 QQ 图
x 62.4 , 11.0373,显著水平 0.10 ,Q1、Q2 及 Q’1、Q’2 为界值。
画出 Q — Q' 图及 y x ,如下所示
QQ图 法 验 证 正 态 分 布 ( α=0.10) 4
3
2
1
Q'
0-1-2来自-3-4-4-3
-2
-1
0
1
2
3
Q
从图中可以看出,Q — Q' 对应点较为均匀地分布在 y x 曲线附近,而且全部落在 90%
即 Q — Q' 图,与 y x 比较,若基本与之吻合则原序列服从正态分布,若相差较大则
不服从正态分布。
4、 接受区间 采用 Michael 拟合优度检验方法给出 QQ 图的接受区间。Michael 拟合优度统计量
Dsp max | ri si | , 其 中 , ri (2/ )a r c stii1/n2}{, si (2 / )arcsin{ui1/ 2} ,
统计学一些知识的总结:qq图,肥尾分布,置信区间

统计学⼀些知识的总结:qq图,肥尾分布,置信区间
Q-Q图: ⽐较已知样本的分布和猜测分布的图, 猜测的概率分布通常为正态分布。
⽐如猜测样本是正态分布的,则有:
假设样本有n个,则⽤标准正态分布函数获取n个分位值。
取法:
将样本和这个n个值都从⼩到⼤排列,⼀⼀对应。
这样就能获得n对坐标。
标准正态分布函数⽣成的值作x,样本值作y,则可在直⾓坐标系中绘制出n个点。
如果所有点连成的线越接近直线 y=x,那么就能说样本分布越近似猜测的分布。
参考链接:
/tag/qq图/
肥尾分布的q-q图如下:
置信区间: 值在某⼀个区间内的概率⼤于95%,就把这个区间叫作95%的置信区间,以此类推。
R的q-q图中虚线画出了95%的置信区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
qq 图原理
第一步,假设我们已经有数据 Height
[1] 72 66 61 63 71 76 67 70 73 64 66 62 69 69 72 71 65 75 63 67 71
第二步,我们看看R 语言中怎么来做qq 图 qqnorm(Height)
qqline(Height)
这样我们得到右图
第三步,分析,我们看到散点图近似均匀分布在红色直线的两侧,从而可以认为Height 近似服从正态分布
现在我们看这个图是怎么做出来的。
首先,对Height 排序 srt=sort(Height) n=length(Height) 其次,找出n 个分为点
> ct=seq(from=0.5/21,to=1-0.05/21,by=1/21) > ct
[1] 0.02380952 0.07142857 0.11904762 0.16666667 0.21428571 0.26190476 [7] 0.30952381 0.35714286 0.40476190 0.45238095 0.50000000 0.54761905 [13] 0.59523810 0.64285714 0.69047619 0.73809524 0.78571429 0.83333333 [19] 0.88095238 0.92857143 0.97619048
再次,求出这些分为点所对应的正态分位数 >norma=qnorm(ct,mean=0,sd=1) > norma
[1] -1.9807524 -1.4652338 -1.1797611 -0.9674216 -0.7916386 -0.6374842 [7] -0.4972006 -0.3661064 -0.2410404 -0.1196481 0.0000000 0.1196481 [13] 0.2410404 0.3661064 0.4972006 0.6374842 0.7916386 0.9674216 [19] 1.1797611 1.4652338 1.9807524
-2-1012
657075
Normal Q-Q Plot
Theoretical Quantiles S a m p l e Q u a n t i l e s
最后,用srt 关于norma 做散点图,结果如下 > plot(x=norma,y=srt)
再用,Height 的均值作为截距,标准差作为斜率做直线 > abline(a=mean(Height),b=sd(Height),col=2)
总结:qq 图的另外一个名称叫做分位数图,看来是有道理的,我们把这两个图放到一起对比一下
左边是标准qq 图,右边是我们自己做得qq 图。
-2-1012
657075
norma
s r t
-2
-1
1
2
65
7075
Normal Q-Q Plot
Theoretical Quantiles
S a m p l e Q u a n t i l e s
-2
-1012
65
7075
norma
s r t。
