2011年中考数学真题分类汇编:直线与圆的位置关系
直线与圆的位置关系知识点及例题

直线与圆的位置关系知识点及例题Prepared on 22 November 2020直线与圆的位置关系一、知识点梳理1、直线与圆的位置关系:图形名称相离相切相交判定d>r d=r d<r交点个数无1个2个例1、下列判断正确的是()①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,•则直线与圆相交.A.①②③ B.①② C.②③ D.③例2、过圆上一点可以作圆的______条切线;过圆外一点可以作圆的_____条切线;•过圆内一点的圆的切线______.例3、以三角形一边为直径的圆恰好与另一边相切,则此三角形是_______.例4、下列直线是圆的切线的是()A.与圆有公共点的直线 B.到圆心的距离等于半径的直线C.垂直于圆的半径的直线 D.过圆直径外端点的直线例5.如图所示,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r为多少时,⊙C与AB相切2、切线的判定:(1)根据切线的定义判定:即与圆有一个公共点的直线是圆的切线.(2)根据圆心到直线的距离来判定:即与圆心的距离等于半径的直线是圆的切线. (3)根据切线的判定定理来判定:即经过半径的外端并且垂直于这条半径的直线是圆的切线.判定切线时常用的辅助线作法:(1)若直线与圆有公共点时,辅助线的作法是“连结圆心和公共点”,再证明直线和半径垂直.(2)当直线与圆并没有明确有公共点时,辅助线的作法是“过圆心向直线作垂线”再证明圆心到直线的距离等于圆的半径.例6、判断下列命题是否正确(1)经过半径的外端的直线是圆的切线(2)垂直于半径的直线是圆的切线;(3)过直径的外端并且垂直于这条直径的直线是圆的切线;(4)和圆有一个公共点的直线是圆的切线;(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.例7.OA平分∠BOC,P是OA上任一点(O除外),若以P为圆心的⊙P与OC相离,•那么⊙P与OB的位置关系是()A.相离 B.相切 C.相交 D.相交或相切例8、如图所示,在直角坐标系中,⊙M的圆心坐标为(m,0),半径为2,•如果⊙M与y轴所在直线相切,那么m=______,如果⊙M与y轴所在直线相交,那么m•的取值范围是_______.例9、如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC•的延长线于点E,连结BC.(1)求证:BE为⊙O的切线;(2)如果CD=6,tan∠BCD=12,求⊙O的直径.例10、如图,已知:△ABC内接于⊙O,点D在OC的延长线上,sinB=12,∠D=30°.(1)求证:AD是⊙O的切线;(2)若AC=6,求AD的长.例11、如图,P为⊙O外一点,PO交⊙O于C,过⊙O上一点A作弦AB⊥PO于E,若∠EAC=∠CAP,求证:PA是⊙O的切线.3、切线的性质:1、经过切点的半径垂直于圆的切线,经过切点垂直于切线的直线必经过圆心对于切线的性质可分解为:过圆心、过切点、垂直于切线这三个条件中任意两个作为条件,就可以推出第三个作为结论4、切线长定理:切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角.例12、如图1,PA、PB是⊙O的两条切线、A、B为切点。
2011年中考数学试题汇编-直线与圆的位置关系

选择题(每小题x 分,共y 分)〔2011•日照市〕11.已知AC ⊥BC 于C ,BC =a ,CA =b ,AB =c ,下列选项中⊙O 的半径为ba ab +的是C〔2011•广州市〕10.如图,AB 切⊙O 于点B ,OA=23,AB=3,弦BC//OA ,则劣弧BC 的弧长为( A ) A.π33 B. π23 C. π D. π23 (2011•金华市)10.如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,点B 与下列格点的连线中,能够与该圆弧相切的是 ( C )A .点(0,3)B . 点(2,3)C .点(5,1)D . 点(6,1)〔2011•南京市〕6.如图,在平面直角坐标系中,⊙P 的圆心是(2,a )(a >2),半径为2,函数y =x 的图象被⊙P 的弦AB的长为a 的值是B A. B.2+C. D.2二、填空题(每小题x 分,共y 分)13、(2011·济宁)如图,在Rt △ABC 中,∠C=90°,BC=4cm ,以点C 为圆心,以3cm 长为半径作圆,则⊙C 与AB。
第10题图(2011•宿迁市)17.如图,从⊙O 外一点A 引圆的切线AB ,切点为B ,连接AO 并延长交圆于点C ,连接BC .若∠A =26°,则∠ACB 的度数为 32▲ .(2011•泰安市)23.如图,PA 与⊙O 相切,切点为A ,PO 交⊙O 于点C ,点B 是优弧CBA 上一点,若∠ABC=32°,则∠P 的度数为 26 。
〔2011•浙江省衢州〕16、木工师傅可以用角尺测量并计算出圆的半径r ,用角尺的较短边紧靠⊙O ,并使较长边与⊙O 相勤勤恳恳于点C ,假 设角尺的较长边足够多,角尺的顶点为B ,较短边AB=8cm , 若读得BC 长为acm ,则用含a 的代数式表示r为______当时8a 0≤<,a r =;时当8a >,4a 161r 2+=;或时8r 0≤<,a r =;时当8r >,4a 161r 2+=;___________________三、解答题:(共x 分)(2011•株洲市)22.(本题满分8分)如图,AB 为O 的直径,BC 为O 的切线,AC交O 于点E ,D 为AC 上一点,AOD C ∠=∠. (1)求证:OD AC ⊥;A (第17题)E DC(2)若8AE =,3tan 4A =,求OD 的长.22.(1)证明:BC 是O 的切线,AB 为O 的直径ABC=90∴∠︒,A+C=90∴∠∠︒ …… 2分又AOD=C ∠∠AOD+A=90∴∠∠︒ …… 3分90ADO ∴∠=︒OD AC ∴⊥ …… 4分(2)解:OD AE ⊥ ,O 为圆心D ∴为AE 中点 …… 6分1AD=AE=42∴ 又3tan 4A = OD=3∴ …… 8分〔2011•浙江省义乌〕21.如图,已知⊙O 的直径AB 与弦CD 互相垂直,垂足为点E . ⊙O的切线BF 与弦AD 的延长线相交于点F ,且AD =3,cos ∠BCD= . (1)求证:CD ∥BF ; (2)求⊙O 的半径; (3)求弦CD 的长.21.解:(1)∵BF 是⊙O 的切线 ∴AB ⊥BF …………………………………………1分∵AB ⊥CD∴CD ∥BF (2)分(2)连结BD∵AB 是直径 ∴∠ADB =90° (3)分∵∠BCD =∠BAD cos ∠BCD =43…………………4分 ∴cos ∠BAD =43=AB AD又∵AD =3 ∴AB =4∴⊙O 的半径为2 ……………………………………5分43A(3)∵cos ∠DAE =43=AD AE AD =3∴AE =49 (6)分∴ED =47349322=⎪⎭⎫ ⎝⎛- …………………………………………………7分∴CD =2ED =273 ………………………………………………………………8分〔2011•盐城市〕25.(本题满分10分)如图,在△ABC 中,∠C =90°,以AB 上一点O为圆心,OA 长为半径的圆与BC 相切于点D ,分别交AC 、AB 于点E 、F .(1)若AC =6,AB =10,求⊙O 的半径; (2)连接OE 、ED 、DF 、EF .若四边形BDEF 是平行四边形,试判断四边形OFDE 的形状, 并说明理由.25.解:(1)连接OD . 设⊙O 的半径为r . ∵BC 切⊙O 于点D ,∴OD ⊥BC .∵∠C =90°,∴OD ∥AC ,∴△OBD ∽△ABC .∴OD AC = OB AB ,即 r 6 = 10-r10. 解得r = 154, ∴⊙O 的半径为154.(2)四边形OFDE 是菱形.∵四边形BDEF 是平行四边形,∴∠DEF =∠B .∵∠DEF =12∠DOB ,∴∠B =12∠DOB .∵∠ODB =90°,∴∠DOB +∠B =90°,∴∠DOB =60°.∵DE ∥AB ,∴∠ODE =60°.∵OD =OE ,∴△ODE 是等边三角形. ∴OD =DE .∵OD =OF ,∴DE =OF .∴四边形OFDE 是平行四边形.∵OE =OF ,∴平行四边形OFDE 是菱形.〔2011•芜湖市〕23. (本小题满分12分)如图,已知直线PA 交⊙0于A 、B 两点,AE 是⊙0的直径.点C 为⊙0上一点,且AC 平分∠PAE ,过C 作CD ⊥PA ,垂足为D 。
直线与圆的位置关系典例+讲解+习题+答案

4.2.1 直线与圆的位置关系直线与圆的位置关系(典例)已知圆C:(x-a)2+(y-b)2=r2(r>0),直线L:Ax+By+C=01.位置关系的判定:判定方法1:联立方程组得到关于x(或y)的方程(1)△>0相交;(2)△=0相切;(3)△<0相离。
判定方法2:若圆心(a,b)到直线L的距离为d(1)d<r相交;(2)d=r相切;(3)d>r相离。
例1、判断直线L:(1+m)x+(1-m)y+2m-1=0与圆O:x2+y2=9的位置关系。
法一:直线L:m(x-y+2)+x+y-1=0恒过点,∵点P在圆O内,∴直线L与圆O相交。
法二:圆心O到直线L的距离为当d<3时,(2m-1)2<9(2m2+2),∴14m2+4m+17>0 ∴m∈R所以直线L与直线O相交。
2.切线问题:例3:已知点P(x0,y0)是圆C:x2+y2=r2上一点,求过点P的圆C的切线方程;(x0x+y0y=r2) 法一:∵点P(x0,y0)是圆C:x2+y2=r2上一点,∴当x0≠0且y0≠0时,∴切线方程为当P为(0,r)时,切线方程为y=r,满足方程(1);\当P为(0,-r)时,切线方程为t=-r,满足方程(1);当P为(r,0)时,切线方程为x=r,满足方程(1);当P为(-r,0)时,切线方程为x=-r,满足方程(1);综上,所求切线方程为x0x+y0y=r2法二:设M(x,y)为所求切线上除P点外的任一点,则由图知|OM|2=|OP|2+|PM|2,即x2+y2=r2+(x-x0)2+(y-y0)2∴x0x+y0y=r2且P(x0,y0)满足上面的方程。
综上,所求切线方程为x0x+y0y=r2。
(1)已知圆O:x2+y2=16,求过点P(4,6)的圆的切线PT的方程。
解:当PT方程为x=4时,为圆O的切线,满足题意:设PT的方程为y-6=k(x-4),即kx-y-4k+6=0则圆心O到PT的距离为所以PT的方程为综上,切线PT的方程为x=4,5x-12y+52=0 例4、求过下列各点的圆C:x2+y2-2x+4y-4=0的切线方程:(1);(2) B(4,5) 解: (1)圆C:(x-1)2+(y+2)2=9,圆心C(1,-2),r=3,且点A在圆C上,法一:设切线方程为,则圆心到切线的距离为,∴所求切线方程为法二:∵AC⊥l,∴所求切线方程为(2)点B在圆外,所以过B点的切线有两条设切线方程为y=k(x-4)+5,则圆心C到切线的距离为又直线x=4也是圆的切线方程,∴所求切线方程为例5、设点P(x,y)是圆x2+y2=1上任一点,求的取值范围。
(word完整版)直线与圆位置关系知识点及习题,文档
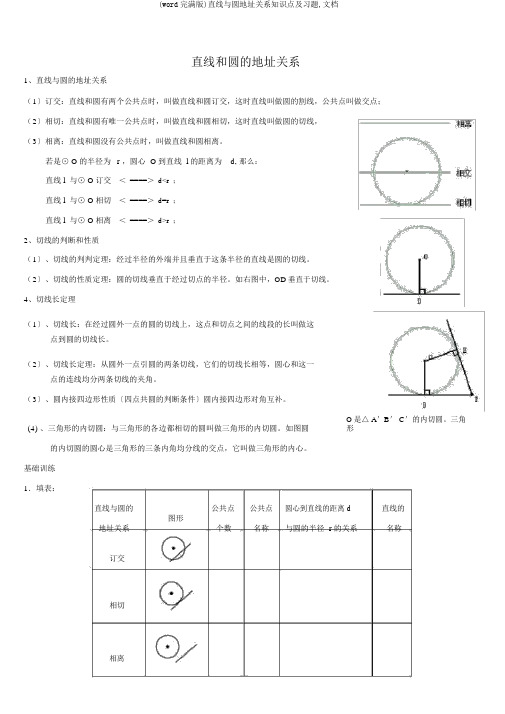
直线和圆的地址关系1、直线与圆的地址关系(1〕订交:直线和圆有两个公共点时,叫做直线和圆订交,这时直线叫做圆的割线,公共点叫做交点;(2〕相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,(3〕相离:直线和圆没有公共点时,叫做直线和圆相离。
若是⊙ O的半径为r ,圆心 O到直线 l 的距离为d, 那么:直线 l 与⊙ O订交<====>d<r;直线 l 与⊙ O相切<====>d=r;直线 l 与⊙ O相离<====>d>r;2、切线的判断和性质(1〕、切线的判判定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
(2〕、切线的性质定理:圆的切线垂直于经过切点的半径。
如右图中,OD垂直于切线。
4、切线长定理(1〕、切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长。
(2〕、切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线均分两条切线的夹角。
(3〕、圆内接四边形性质〔四点共圆的判断条件〕圆内接四边形对角互补。
(4) 、三角形的内切圆:与三角形的各边都相切的圆叫做三角形的内切圆。
如图圆O是△ A'B' C'的内切圆。
三角形的内切圆的圆心是三角形的三条内角均分线的交点,它叫做三角形的内心。
基础训练1.填表:直线与圆的公共点公共点圆心到直线的距离d直线的图形与圆的半径 r 的关系地址关系个数名称名称订交相切相离2.假设直线 a 与⊙ O交于 A, B 两点, O到直线 a?的距离为6, ?AB=?16, ?那么⊙ O?的半径为 _____.3.在△ ABC中,∠ ACB=90°, BC=AC=10,以 C 为圆心,分别以5,5 2 ,8为半径作图,那么直线AB与圆的地址关系分别是 ______, _______ ,_______.4.⊙ O的半径是6,点 O到直线 a 的距离为5,那么直线 a 与⊙ O的地址关系为〔〕A.相离B.相切C.订交D.内含5.以下判断正确的选项是〔〕①直线上一点到圆心的距离大于半径,那么直线与圆相离;②直线上一点到圆心的距离等于半径,那么直线与圆相切;③直线上一点到圆心的距离小于半径,?那么直线与圆订交.A.①②③B.①②C.②③D.③6. OA均分∠ BOC, P 是 OA上任一点〔 O除外〕,假设以 P 为圆心的⊙ P 与 OC相离, ?那么⊙ P 与 OB的地址关系是〔〕A.相离B.相切C.订交D.订交或相切7.以以下图, Rt△ ABC中,∠ ACB=90°, CA=6, CB=8,以 C 为圆心, r 为半径作⊙ C,当 r 为多少时,⊙ C 与 AB相切?8.如图,⊙ O的半径为3cm,弦 AC=4 2 cm, AB=4cm,假设以 O为圆心, ?再作一个圆与 AC相切,那么这个圆的半径为多少?这个圆与AB 的地址关系怎样?◆提高训练9.以以下图,在直角坐标系中,⊙M的圆心坐标为〔m,0〕,半径为 2, ?若是⊙ M与 y 轴所在直线相切,那么m=______,若是⊙ M与 y 轴所在直线订交,那么m?的取值范围是_______.10.如图,△ ABC中, AB=AC=5cm, BC=8cm,以 A 为圆心, 3cm?长为半径的圆与直线 BC的地址关系是_______.11.如图,正方形ABCD的边长为 2, AC和 BD订交于点O,过 O作 EF∥AB,交 BC于 E,交 AD于 F,那么以点B为圆心,2 长为半径的圆与直线AC, EF, CD的地址关系分别是什么?12.⊙ O的半径为5cm,点 O到直线 L 的距离 OP为 7cm,以以下图.(1〕怎样平移直线 L,才能使 L 与⊙ O相切?(2〕要使直线 L 与⊙ O订交,应把直线 L 向上平移多少 cm?13.如图, Rt △ ABC中,∠ C=90°, AC=3, AB=5,假设以 C 为圆心, r 为半径作圆,?那么 :(1〕当直线 AB 与⊙ C 相切时,求 r 的取值范围;(2〕当直线 AB 与⊙ C 相离时,求 r 的取值范围;(3〕当直线 AB与⊙ C 订交时,求 r 的取值范围.14.在南部沿海某气象站 A 测得一热带风暴从 A 的南偏东30?°的方向迎着气象站袭来,该风暴速度为每小时20千米,风暴周围50 千米范围内将碰到影响,?假设该风暴不改变速度与方向,问气象站正南方60 千米处的沿海城市B可否会受此次风暴的影响?假设不受影响,请说明原由;假设受影响,央求出受影响的时间.九年级下册直线和圆的地址关系练习题一、选择题:1.假设∠ OAB=30°, OA=10cm,那么以 O为圆心, 6cm 为半径的圆与射线 AB的地址关系是〔〕A.订交B.相切C.相离D.不能够确定2. Rt△ ABC中,∠ C=90°, AB=10, AC=6,以 C 为圆心作⊙ C和 AB 相切,那么⊙ C的半径长为〔〕A. 8B. 4C.9.6D. 4.83.⊙ O内最长弦长为m,直线l与⊙ O相离,设点 O到l的距离为d,那么d与m的关系是〔〕A.d = m B.d>m C.d>mD.d<m 224.以三角形的一边长为直径的圆切三角形的另一边,那么该三角形为〔〕A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形5.菱形对角线的交点为O,以 O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为〔〕A.订交B.相切C.相离D.不能够确定6.⊙ O的半径为 6,⊙ O的一条弦 AB为 6 3 ,以3为半径的同心圆与直线AB 的地址关系是〔〕A.相离B.订交C.相切D.不能够确定7.以下四边形中必然有内切圆的是〔〕A.直角梯形B.等腰梯形C.矩形D.菱形8.△ ABC的内切圆O与各边相切于 D、E、 F,那么点 O是△ DEF的〔〕A.三条中线交点B.三条高的交点 C .三条角均分线交点D.三条边的垂直均分线的交点9.给出以下命题:①任一个三角形必然有一个外接圆,并且只有一个外接圆;②任一个圆必然有一个内接三角形,并且只有一个内接三角形;③任一个三角形必然有一个内切圆,并且只有一个内切圆;④任一个圆必然有一个外切三角形,并且只有一个外切三角形.其中真命题共有〔〕A.1 个B.2个C.3 个D.4 个二、证明题1.如图,⊙ O中, AB是直径,过 B 点作⊙ O的切线 BC,连结 CO.假设 AD∥OC交⊙ O于 D.求证: CD是⊙ O的切线.2.:如图,同心圆O,大圆的弦AB=CD,且 AB是小圆的切线,切点为E.求证: CD是小圆的切线.3.如图,在Rt △ ABC中,∠ C=90°, AC=5, BC=12,⊙ O的半径为3.(1〕当圆心 O与 C 重合时,⊙ O与 AB的地址关系怎样?(2〕假设点 O沿 CA搬动时,当 OC为多少时?⊙ C与 AB相切?4.如图,直角梯形 ABCD中,∠ A=∠B=90°, AD∥ BC, E 为 AB上一点, DE均分∠ ADC,CE均分∠ BCD,以 AB 为直径的圆与边 CD有怎样的地址关系?5.设直线ι到⊙ O的圆心的距离为 d,半径为 R,并使 x2- 2 d x+ R=0,试由关于 x 的一元二次方程根的情况谈论ι与⊙O的地址关系.6.如图,AB是⊙ O直径,⊙ O过AC的中点D,DE⊥ BC,垂足为E.(1〕由这些条件,你能得出哪些结论?〔要求:严禁标其他字母,找结论过程中所连的辅助线不能够出现在结论中,不写推理过程,写出 4 个结论即可〕〔 2〕假设∠ ABC为直角,其他条件不变,除上述结论外你还能够推出哪些新的正确结论?并画出图形.〔要求:写出 6 个结论即可,其他要求同〔 1〕〕7.如图,在Rt △ABC中,∠ C=90°, AC=3,BC=4.假设以 C为圆心, R 为半径所作的圆与斜边AB只有一个公共点,那么R的取值范围是多少?8.如图,有一块锐角三角形木板,现在要把它截成半圆形板块〔圆心在BC上〕,问怎样截取才能使截出的半圆形面积最大?〔要求说明原由〕9.如图,直线ι1、ι2、ι3表示互订交织的公路.现要建一个货物中转站,要求它到三条公路的距离相等,那么可选择的地址有几处?答案 :一.1-5ADCBB;6-9CDDB二.1. 提示 : 连结 OC,证△ AOC与△ BOC全等2.作垂直证半径 , 弦心距相等3.①垂直三角形的高 , 用面积方法求 ; ②△ AOE∽△ ABC即可4.用角均分线定理证明 EF=EA=EB即可5.做三角形的内切圆6.222① DE与⊙ O相切 ,AB=BC,DE +CE=CD, ∠ C+∠CDE=90°② BC是⊙ O的切线 , 有 DE=1/2AB等 .7.R=2.4 或 3<R≤ 48.∠ A 角均分线与 BC的交点为圆心O,O到 AC的距离为半径做圆。
九年级数学直线与圆的位置关系

点和圆的位置关系有几种?
A B C
点到圆心的距离为d, 圆的半径为r,则: 点在圆外 点在圆上 点在圆内 d>r; d=r; d<r.
直线与圆的位置关系
(地平线)
● ● ●
O
● ●
O
O
a(地平线)
O
O
一、直线与圆的位置关系
(用公共点的个数来区分)
特点: 直线和圆没有公共点, 叫直线和圆相离 特点: 直线和圆有惟一的公共点, 叫做直线和圆相切。 C
C
x
A
图形 直线与圆的 位置关系
.O r d ┐ l
.o d r ┐ l .
A
. B
.O d r ┐ . lC
相离
0 d>r
相切
1 d=r
相交பைடு நூலகம்
2 d<r
公共点的个数
圆心到直线的距离 d 与半径 r 的关系
公共点的名称 直线名称
切点
切线
已知⊙O的半径r=7cm,直线l1 // l2, 且l1与⊙O相切,圆心O到l2的距离为9cm. 求l1与l2的距离m.
.A
.A
.B
这时的直线叫切线
惟一的公共点叫切点。 特点: 直线和圆有两个公共点, 叫做直线和圆相交。
a(地平线)
观察太阳落山的照片,在太阳落山的过程中,太阳与 地平线(直线a)经历了哪些位置关系的变化?
看图判断直线l与 ⊙O的位置关系
(1) (2)
· O · O
l
(3) l l
· O
相离
相交
相切
课堂练习:
2、已知⊙O的半径为5cm, 圆心O与直线AB的距 离为d, 根据条件填写d的范围: 1)若AB和⊙O相离, 则 d > 5cm ; ; 2)若AB和⊙O相切, 则 d = 5cm
直线与圆的位置关系(含答案)
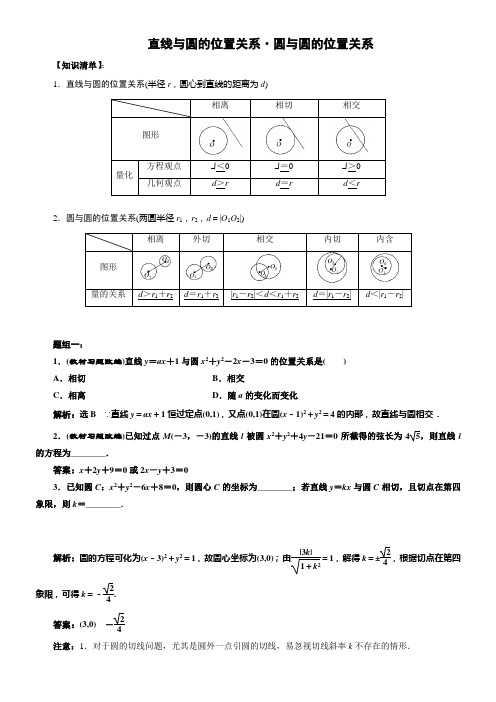
【知识清单】:
1.直线与圆的位置关系(半径r,圆心到直线的距离为d)
相离
相切
相交
图形
量化
方程观点
Δ<0
Δ=0
Δ>0
几何观点
d>r
d=r
d<r
2.圆与圆的位置关系(两圆半径r1,r2,d=|O1O2|)
相离
外切
相交
内切
内含
图形
量的关系
d>r1+r2
d=r1+r2
|r1-r2|<d<r1+r2
3.(2015·大连双基测试)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是________.
解析:法一:将直线方程代入圆方程,得(k2+1)x2+4kx+3=0,直线与圆没有公共点的充要条件是Δ=16k2-12(k2+1)<0,解得k∈(- , ).
法二:圆心(0,0)到直线y=kx+2的距离d= ,直线与圆没有公共点的充要条件是d>1,
即 >1,
解得k∈(- , ).
答案:k∈(- , )
[谨记通法]:判断直线与圆的位置关系的2大策略
(1)若两方程已知或圆心到直线的距离易表达,则用几何法.
(2)若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法.能用几何法,尽量不用代数法.
1.(2015·广东高考)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是()
A.x-y+5=0B.x+y-1=0
C.x-y-5=0D.2x+y+1=0
解析:选A由题意得圆的标准方程为(x+1)2+(y-2)2=5,则圆心C(-1,2).过圆心与点(-2,3)的直线l1的斜率为k= =-1.当直线l与l1垂直时,|AB|取得最小值,故直线l的斜率为1,所以直线l的方程为y-3=x-(-2),即x-y+5=0.
直线与圆的位置关系题型很全

注意:1.在求过一定点的圆的切线方程时,应首先判断这点与圆的位置关系,
2.设直线的方程时,切记千万要对直线的斜率存在与否进行讨论。
若存在,则经常设直线的方程为点斜式;若不存在,则特殊情况特殊对待。
小结:求圆的切线方程一般有两种方法:
(1)证明直线l与圆C相交;
(2)求直线l被圆C截得的弦长最小时, 直线l的方程.
题型五、判断点的个数问题
例1、圆x 2 + y 2 + 2 x + 4 y - 3 = 0上到直线x + y +1 = 0的 距离为 2的点共有几个.
练习1:已知圆
x y ,4
2 2
直线 l: y=x+b, 求b的取值范围,使
2 2
B
A
O
x
| AB | (1 k 2 )[( x1 x2 ) 2 4 x1 x2 ]
2.已知直线 y=x+1 与圆 x 2 y 2 4 相交于A,B两点,求
弦长|AB|的值
解三:解弦心距,半弦及半径构成的直角三角形) 设圆心O(0,0)到直线的距离为d,则 y
2 d 2 1 (1) 2 | AB | 2 r d 14
y y ,由直线 l 与圆的方程构造以 x x
为未知数的一元二次方程,由根与系数关系得出 kOP kOQ 的值,从而使问题得以解决.
解:设点 P 、 Q 的坐标为 ( x1 , y1 ) 、 ( x2 , y2 ) .一方面,由 OP OQ ,得
kOP kOQ 1 ,即
y1 y2 1 ,也即: x1 x2 y1 y2 0 . x1 x2
2011年中考数学试题汇编---圆与圆的位置关系

1.选择题(每小题x分,共y分)(2011•吉林省)15.如图,两个等圆⊙A⊙B分别与直线l相切于点C、D,连接AB,与直线l相交于点O ,∠AOC=300,连接AC.BC,若AB=4,则圆的半径为( B )lOA BCDA 错误!未找到引用源。
21B 1 C3 D 2 (2011•张家界)7、已知两圆相外切,连心线长度是10厘米,其中一圆的半径为6厘米,则另一圆的半径是(D )A、16厘米B、10厘米C、6厘米D、4厘米7、(2008•宁德)如图,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有(B)A、内切、相交B、外离、相交C、外切、外离D、外离、内切(2011•襄阳市)9.在△ABC中,∠C=90°.AC=3cm.BC=4cm,若⊙A.⊙B的半径分别为1cm,4cm.则⊙A与⊙B的位置关系是AA.外切B.内切C.相交D.外离(2011•扬州市)4.已知相交两圆的半径分别为4和7,则它们的圆心距可能是(C)A.2B.3 C.6D.11(2011•铜仁)6.已知⊙O1与⊙O2的半径分别为6cm、11cm,当两圆相切时,其圆心距d的值为( D )A、0cmB、5cmC、17cmD、5cm或17cm (2011•达州)7、如图4,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有BA.、内切、相交B、外离、相交C、外切、外离D、外离、内切(2011•陕西省)7.同一平面内的两个圆,他们的半径分别为2和3 ,圆心距为d,当51d 时,两圆的位置关系是【 B 】A、外离B、相交C、内切或外切D、内含(2011•天津)(6) 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是(A) 相交 (B) 相离 (C) 内切 (D) 外切〔2011•浙江省台州市〕8.如图是一个组合烟花的横截面,其中16个圆的半径相同,点A 、B 、C 、D 分别是四个角上的圆的圆心,且四边形ABCD 为正方形.若圆的半径为r ,组合烟花的高为h ,则组合烟花侧面包装纸的面积至少需要(接缝面积不计)【 D 】 A .rh π26 B .rh rh π+24 C .rh rh π212+ D .rh rh π224+3. (2011台湾台北,25)如图(九),圆A 、圆B 的半径分别为4、2,且AB =12。
中考数学直线与圆的位置关系专题含答案
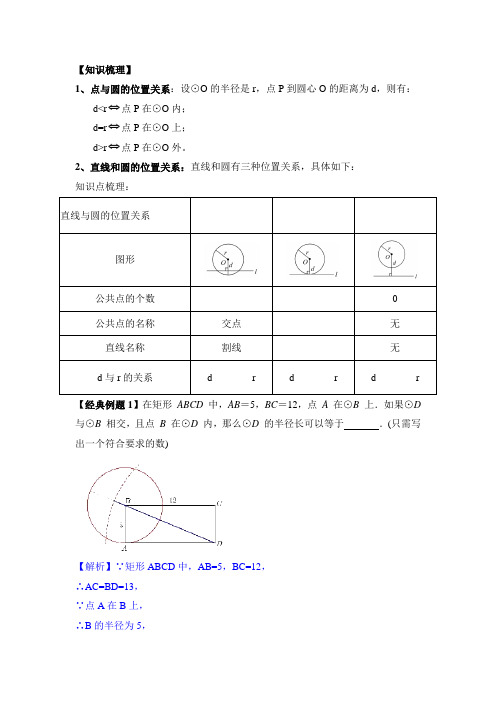
【知识梳理】1、点与圆的位置关系:设⊙O的半径是r,点P到圆心O的距离为d,则有:d<r⇔点P在⊙O内;d=r⇔点P在⊙O上;d>r⇔点P在⊙O外。
2、直线和圆的位置关系:直线和圆有三种位置关系,具体如下:知识点梳理:直线与圆的位置关系______ ______ ______ 图形公共点的个数______ ______ 0公共点的名称交点______ 无直线名称割线______ 无d与r的关系d________r d________r d________r 【经典例题1】在矩形ABCD 中,AB=5,BC=12,点 A 在⊙B 上.如果⊙D 与⊙B 相交,且点 B 在⊙D 内,那么⊙D 的半径长可以等于.(只需写出一个符合要求的数)【解析】∵矩形ABCD中,AB=5,BC=12,∴AC=BD=13,∵点A在B上,∴B的半径为5,∵如果D与B相交,∴D的半径R满足8∵点B在D内,∴R>13,∴14符合要求,故答案为:14(答案不唯一).练习1-1在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为 ()A.E,F,GB.F,G,HC.G,H,ED.H,E,F练习1-2已知☉O的直径等于12,圆心O到直线l的距离恰好为一元二次方程2x2-10x+3=0的两根的和,那么直线l和☉O的位置关系是.练习1-3如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=23.将⊙P沿着与y轴平行的方向平移,使⊙P与x轴相切,则平移距离为_____.练习1-4(20上海中考)如图,在矩形ABCD 中,AB=6,BC=8,点O 在对角线AC 上,⊙O 的半径为2,如果⊙O 与矩形ABCD 的各边都没有公共点,那么线段AO 长的取值范围是 .320310<<x练习1-5如图,已知矩形ABCD 中,AB=2,BC=32,O 是AC 上一点,AO=m ,且O 的半径长为1,求:(1)线段AB 与O 没有公共点时m 的取值范围。
专题07 直线与圆的位置关系(知识梳理+专题过关)(解析版)

专题07直线与圆的位置关系【知识梳理】1、直线与圆的位置关系:(1)直线与圆相交,有两个公共点;(2)直线与圆相切,只有一个公共点;(3)直线与圆相离,没有公共点.2、直线与圆的位置关系的判定:(1)代数法:判断直线l 与圆C 的方程组成的方程组是否有解.如果有解,直线l 与圆C 有公共点.有两组实数解时,直线l 与圆C 相交;有一组实数解时,直线l 与圆C 相切;无实数解时,直线l 与圆C 相离.(2)几何法:由圆C 的圆心到直线l 的距离d 与圆的半径r 的关系判断:当d r <时,直线l 与圆C 相交;当d r =时,直线l 与圆C 相切;当d r >时,直线l 与圆C 相离.3、圆的切线方程的求法(1)点M 在圆上,如图.法一:利用切线的斜率l k 与圆心和该点连线的斜率OM k 的乘积等于1-,即1OM l k k ⋅=-.法二:圆心O 到直线l 的距离等于半径r .(2)点()00,x y 在圆外,则设切线方程:00()y y k x x -=-,变成一般式:000kx y y kx -+-=,因为与圆相切,利用圆心到直线的距离等于半径,解出k .诠释:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.常见圆的切线方程:(1)过圆222x y r +=上一点()00,P x y 的切线方程是200x x y y r +=;(2)过圆()()222x a y b r -+-=上一点()00,P x y 的切线方程是()()()()200x a x a y b y b r --+--=.4、求直线被圆截得的弦长的方法(1)应用圆中直角三角形:半径r ,圆心到直线的距离d ,弦长l 具有的关系2222l r d ⎛⎫=+ ⎪⎝⎭,这也是求弦长最常用的方法.(2)利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.(3)利用弦长公式:设直线:l y kx b =+,与圆的两交点()()1122,,,x y x y ,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:12||l x x =-.【专题过关】【考点目录】考点1:直线与圆的位置关系考点2:直线与圆相交的性质——韦达定理及应用考点3:切线问题考点4:切点弦问题考点5:弦长问题考点6:面积问题考点7:直线与圆中的定点定值问题【典型例题】考点1:直线与圆的位置关系1.(2021·黑龙江·齐齐哈尔市恒昌中学校高二期中)直线43110x y -+=与圆()()22114x y +++=的位置关系是()A .相离B .相切C .相交D .不确定【答案】B【解析】圆心坐标为()1,1--,半径为2,圆心到直线的距离为341125-+=,所以直线43110x y -+=与圆()()22114x y +++=相切.故选:B2.(2020·四川·泸州老窖天府中学高二期中(理))已知点(,)P a b 在圆221x y +=上,则直线10ax by +-=与圆的位置关系是()A .相交B .相切C .相离D .无法判断【答案】B【解析】由题意得221a b +=,又1d r ===,即直线与圆相切故选:B3.(2021·黑龙江·牡丹江一中高二期中)直线:(1)(1)20()l a x a y a a R ++-+=∈与圆222270C x y x y +-+-=:的位置关系是()A .相切B .相交C .相离D .相交或相切【答案】B【解析】圆222270x y x y +-+-=,即22(1)(1)9x y -++=,表示以(1,1)-为圆心、半径等于3的圆.圆心到直线的距离d =再根据2222248474799221a a a a d a a ++-+-=-=++,而27470a a -+=的判别式∆161961800=-=-<,故有29d >,即3d <,故直线和圆相交,故选:B .4.(2022·上海市控江中学高二期中)若直线:3(1)l y k x -=-与曲线:C y =恰有两个不同公共点,则实数k 的取值范围是()A .4,3⎛⎫+∞ ⎪⎝⎭B .43,32⎛⎤⎥⎝⎦C .40,3⎛⎫ ⎪⎝⎭D .43,32⎛⎫ ⎪⎝⎭【答案】B【解析】直线:3(1)l y k x -=-过定点(1,3),曲线:C y 为以(0,0)为圆心,1为半径,且位于y 轴上半部分的半圆,如图所示当直线l 过点(1,0)-时,直线l 与曲线有两个不同的交点,此时03k k =-+-,解得32k =.当直线l 和曲线C 相切时,直线和半圆有一个交点,圆心(0,0)到直线:3(1)l y k x -=-的距离1d ==,解得43k =结合图像可知,当4332k <≤时,直线l 和曲线C 恰有两个交点故选:B5.(2021·浙江台州·高二期中)直线0x m +=与圆221x y +=有两个不同的交点,则实数m 的取值范围是()A .22m -≤≤B .22m -<<C .2m <-或2m >D .2m ≤-或2m ≥【答案】B【解析】因为直线0x m +=与圆221x y +=有两个不同的交点所以圆心到直线的距离小于圆的半径圆心为()0,0,半径1r =1<,整理得:2m <解得:22m -<<故选:B .6.(多选题)(2022·广东·汕头市潮南区陈店实验学校高二期中)已知直线:0l x y +=与圆22:(1)(1)4C x y -++=,则()A .直线l 与圆C 相离B .直线l 与圆C 相交C .圆C 上到直线l 的距离为1的点共有2个D .圆C 上到直线l 的距离为1的点共有3个【答案】BD【解析】由圆22:(1)(1)4C x y -++=,可知其圆心坐标为(1,1)-,半径为2,圆心(1,1)-到直线:0l x y +=的距离1d ==,所以可知选项B ,D 正确,选项A ,C 错误.故选:BD7.(2021·四川眉山·高二期中)圆222440x y x y +-+-=与直线2140()tx y t t R ---=∈的位置关系为__________.【答案】相交【解析】由2140()tx y t t R ---=∈得(24)10()x t y t R ---=∈,令240,10,2, 1.x y x y -=--=∴==-所以直线过定点(2,1)P -.把(2,1)P -的坐标代入圆的方程的左边得到414440+---<,所以点(2,1)P -在圆内,所以直线和圆相交.故答案为:相交8.(2021·辽宁实验中学高二期中)已知圆22:4C x y +=上至少存在两点......到直线0x y b +-=的距离为1,则实数b 的取值范围是___________.【答案】(-【解析】根据题意得圆C 的圆心为()0,0,半径为2r =,因为圆22:4C x y +=上至少存在两点......到直线0x y b +-=的距离为1,1r <+3<,解得b -<<所以实数b 的取值范围是(-故答案为:(-9.(2022·全国·高二课时练习)已知圆224x y +=上有且仅有四个点到直线1250x y c -+=的距离为1,则实数c 的取值范围是______.【答案】()13,13-【解析】由圆的方程知其圆心为()0,0,半径2r =,设圆心到直线1250x y c -+=的距离为d ,则13c d =;圆上有且仅有四个点到直线1250x y c -+=的距离为1,则1cd =<,解得:1313c -<<,所以实数c 的取值范围是()13,13-.故答案为:()13,13-.考点2:直线与圆相交的性质——韦达定理及应用10.(2021·安徽·马鞍山二中高二期中)已知一个动点P 在圆220432x y y -+=+上移动,它与定点(6,0)Q 所连线段的中点为M .(1)求点M 的轨迹方程;(2)是否存在过定点(0,3)-的直线l 与点M 的轨迹方程交于不同的两点()11,A x y ,()22,B x y ,且满足12212x x x x +=,若存在,求直线l 的方程;若不存在,说明理由.【解析】(1)设(,)M x y ,因M 是线段PQ 的中点,而点(6,0)Q ,则有点(26,2)P x y -,因P 在圆:22(2)36x y ++=上,于是得:22(26)(22)36x y -++=,化简得:22(3)(1)9x y -++=,所以点M 的轨迹方程是:22(3)(1)9x y -++=.(2)假定存在符合条件的直线l ,当l 斜率不存在时,直线:0l x =与圆M 相切,不符合题意,当直线l 斜率存在时,设直线l 方程为:3y kx =-,由223(3)(1)9y kx x y =-⎧⎨-++=⎩消去y 并整理得:22(1(64))40k x k x +-++=,则()22(64)1610k k ∆=+-+>,解得512k >-,122641kx x k ++=+,12241x x k =+,由2121212212()4x x x x x x x x +=⇔+=,得2226416()11k k k +=++,解得512k =-,与512k >-矛盾,所以不存在过定点(0,3)-的直线l 与点M 的轨迹方程交于不同的两点()11,A x y ,()22,B x y ,且满足12212x x x x +=.11.(2021·云南大理·高二期中)已知圆C 的圆心C 在直线40x y +-=上,且圆C 经过()2,0M ,()0,2N 两点.(1)求圆C 的方程;(2)已知点()0,P m ,过原点的直线l 与圆C 交于A ,B 两点,且PA PB ⊥.若13m <<,求直线l 的斜率k 的取值范围.【解析】(1)设(),C a b ,则222240(2)(2)a b a b a b +-=⎧⎨-+=+-⎩,解得2a =,2b =.从而圆C 的半径2r ==,故圆C 的方程为22(2)(2)4x y -+-=(或224440x y x y +--+=).(2)设直线l :y kx =,()11,A x y ,()22,B x y .联立224440y kx x y x y =⎧⎨+--+=⎩,整理得()2214(1)40k x k x +-++=,则1224(1)1k x x k ++=+,12241x x k =+.因为A ,B 两点在直线l 上,所以11y kx =,22y kx =,所以212241ky y k =+,1224(1)1k k y y k ++=+.因为PA PB ⊥,所以1PA PB k k ⋅=-,所以12121y m y mx x --⋅=-,即()21212120x x y y m y y m +-++=,则22222444(1)0111k mk k m k k k ++-+=+++,即24(1)41k k m k m+=++.因为()1,3m ∈,所以[)44,5m m+∈,所以24(1)451k k k +≤<+,解得1k ³.12.(2021·浙江省象山县第二中学高二期中)已知圆G 过点()1,3M -,()6,4N 且圆心G 在x 轴.(1)求圆G 的标准方程;(2)圆G 与x 轴的负半轴的交点为A ,过点A 作两条直线分别交圆于B ,C 两点,且5AB AC k k ⋅=-,求证:直线BC 恒过定点.【解析】(1)由题意设圆心为(,0)G a=3a =,5r ==,所以圆G 方程为22(3)25x y -+=;(2)在圆方程中令0y =得2x =-或8x =,所以(2,0)A -,BC 斜率存在时,设BC 方程为y kx m =+,设1122(,),(,)B x y C x y ,由()22x 325y kx m y =+⎧⎪⎨-+=⎪⎩得222(1)2(3)160k x km x m ++-+-=,2224(3)4(1)(16)0km k m ∆=--+->,即22166250k m lm --+>(*),1222(3)1km x x k -+=-+,2122161m x x k -=+,12121212()()22(2)(2)AB ACy y kx m kx m k k x x x x ++=⨯=++++2212121212()52()4k x x km x x m x x x x +++==-+++,22222222(16)2(3)5(16)20(3)201111k m km km m km m k k k k ------+=+-++++,化简得223720m km k -+=,(2)(3)0m k m k --=,所以2m k =或3k m =,都满足(*)式.2m k =时,方程为2y kx k =+,过定点(2,0)-,舍去,3k m =时,方程为3y mx m =+,过定点1(,0)3-,BC 斜率不存在时,1111(,),(,)B x y C x y -,21152AB ACy k k x ⎛⎫=-=- ⎪+⎝⎭,22115(2)y x =+,又2211(3)25x y -+=,12x ≠-,解得113x =-,因此BC 也过点1(,0)3-.综上,直线过定点1(,0)3-.13.(2021·广东外语外贸大学实验中学高二期中)已知过点(0,2)A 且斜率为k 的直线l 与圆22:(2)(3)1C x y -+-=交于M ,N 两点.(1)求k 的取值范围;(2)若12OM ON ⋅=,其中O 为坐标原点,求||MN .【解析】(1)圆22:(2)(3)1C x y -+-=,圆心(2,3),半径1r =设直线l 的方程为2y kx =+,即20kx y -+=因为直线l 与圆C 1<,解得403k <<.所以k 的取值范围为40,3⎛⎫ ⎪⎝⎭.(2)设()11,M x y ,()22,N x y .联立()()222231y kx x y =+⎧⎪⎨-+-=⎪⎩,整理得()()2212440k x k x +-++=,所以122241k x x k ++=+,12241x x k =+,所以()()()21212121224212481k k OM ON x x y y k x x k x x k +⋅=+=++++=++uuu r uuu r .由题设得()2428121k k k ++=+,解得12k =,所以直线l 的方程为122y x =+,所以圆心(2,3)C 在直线l 上,所以2MN =.14.(2021·广东·广州市第七十五中学高二期中)已知圆C 经过两点A (2,2),B (3,3),且圆心C 在直线x -y +1=0上.(1)求圆C 的标准方程;(2)设直线l :y =kx +1与圆C 相交于M ,N 两点,O 为坐标原点,若645OM ON ⋅=,求|MN |的值.【解析】(1)设所求圆C 的标准方程为()222()()0x a y b r r -+->=,由题意,有222222(2)(2)(3)(3)10a b r a b r a b ⎧-+-=⎪-+-=⎨⎪-+=⎩,解得231a b r =⎧⎪=⎨⎪=⎩,所以圆C 的标准方程为22(2)(3)1x y -+-=;(2)设1(M x ,1)y ,2(N x ,2)y ,将1y kx =+代入22(2)(3)1x y -+-=,整理得22(1)4(1)70k x k x +-++=,所以1224(1)1k x x k ++=+,12271x x k =+,0∆>,所以21212121224(1)64(1)()1851k k OM ON x x y y k x x k x x k+⋅=+=++++=+=+,解得2k =或3k =,检验3k =时,∆<0不合题意,所以2k =,所以12125x x +=,1275x x =,所以||MN 考点3:切线问题15.(2021·安徽·合肥市第六中学高二期中(理))圆心为C 的圆经过点(4,1)A -和(3,2)B -,且圆心C 在直线:20l x y --=上(1)求圆心为C 的圆的方程;(2)过点(5,8)P 作圆C 的切线,求切线的方程.【解析】(1)因圆心C 在直线:20l x y --=上,则设(,2)C a a -,由||||CA CB =得:,解得0a =,因此,圆心(0,2)C -,半径||5r CA ==,所以圆C 的方程为:22(2)25x y ++=.(2)设过点(5,8)P 的圆C 的切线方程为:(5)(8)0m x n y -+-=,220m n +≠,5=,整理得:2430mn n +=,解得0n =或34m n =-,当0n =时,切线方程为:50x -=,当34m n =-时,切线方程为:34170x y -+=,所以过点(5,8)P 的圆C 的切线方程为50x -=或34170x y -+=.16.(多选题)(2021·湖北·高二期中)设有一组圆()()()22:4k C x k y k k R -+-=∈,下列命题正确的是()A .不论k 如何变化,圆心k C 始终在一条直线上B .存在圆kC 经过点()3,0C .存在定直线与圆k C 都相切D .经过点()2,2的圆k C 有且只有一个【答案】AC【解析】根据题意,圆22:()()4()k C x k y k k R -+-=∈,其圆心为(,)k k ,半径为2;依次分析选项:对于A ,圆心为(,)k k ,其圆心在直线y x =上,A 正确;对于B ,圆22:()()4k C x k y k -+-=,将(3,0)代入圆的方程可得22(3)(0)4k k -+-=,化简得22650k k -+=,364040=-=-<,方程无解,B 错误;对于C ,存在直线y x =±0x y -+=或0x y --=,圆心(,)k k 到直线0x y -+=或0x y --=的距离2d =,这两条直线始终与圆k C 相切,C 正确,对于D ,将(2,2)代入圆的方程可得22(2)()42k k -+=-,解得2k =D 错误;故选:AC .17.(2021·安徽滁州·高二期中)过圆22:4O x y +=上一点(P -作圆O 的切线l ,则直线l 的方程是()A .40x -=B .20x +-=C .20x +=D .40x +=【答案】D【解析】由题意点(P -为切点,所以1OP l k k ⋅=-,又OP k =l k =因此直线l 的方程为40x +=.故选:D18.(2021·天津市咸水沽第二中学高二期中)过点(3,1)M 作圆222620x y x y +--+=的切线l ,则l 的方程为()A .40x y +-=B .40x y +-=或3x =C .20x y --=D .20x y +-=或3x =【答案】C【解析】根据题意,设圆x 2+y 2﹣2x ﹣6y +2=0的圆心为C ,圆x 2+y 2﹣2x ﹣6y +2=0,即()()22138-+-=x y ,其圆心为(1,3),又由点M 的坐标为(3,1),有()()2231138-+-=,即点M 在圆上,则13131-==--MC k ,则切线的斜率k =1,则切线的方程为y ﹣1=(x ﹣3),即x ﹣y ﹣2=0;故选:C .19.(2021·山东济宁·高二期中)过点()2,3P -的直线l 与圆222230x y x y ++--=相切,则直线l 的方程是()A .2x =-或280x y -+=B .280x y -+=C .2x =-或210x y ++=D .210x y ++=【答案】B【解析】把圆222230x y x y ++--=化为标准方程得:()()22115x y ++-=.因为()2,3P -在圆上,所以过P 的切线有且只有一条.显然过点()2,3P -且斜率不存在的直线:2x =-与圆相交,所以过P 的切线的斜率为k .因为切线与过切点的半径垂直,所以()13112k -=----,解得:12k =,所以切线方程为:()1322y x -=+,即280x y -+=.故选:B20.(2022·四川·泸县五中高二期中(文))已知直线()10ax y a R -+=∈是圆()()22:124C x y -+-=的一条对称轴,过点()2,A a --向圆C 作切线,切点为B ,则AB =()AB C D .【答案】C【解析】由圆()()22:124C x y -+-=,可知该圆的圆心坐标为()1,2C ,半径为2,因为直线10ax y -+=是圆()()22:124C x y -+-=的一条对称轴,所以圆心()1,2在直线10ax y -+=上,所以有2101a a -+=⇒=,因为过点()2,1A --向圆C 作切线,切点为B ,所以AC ==所以AB ==故选:C21.(2022·甘肃·临泽县第一中学高二期中(理))直线40x y +-=平分圆222:2250C x y bx by b +---+=的周长,过点()1,P b --作圆C 的一条切线,切点为Q ,则PQ =()A .5B .4C .3D .2【答案】B【解析】圆222:2250C x y bx by b +---+=的圆心为(,)C b b ,半径为r =因为直线40x y +-=平分圆222:2250C x y bx by b +---+=的周长,所以直线40x y +-=经过(,)C b b ,所以40b b +-=,故2b =,由已知()1,2P --,(2,2)C ,||PC ,圆的半径为3,所以4PQ ==,故选:B .22.(2022·上海·华东师范大学附属东昌中学高二期中)经过圆22:25C x y +=上一点()4,3A -且与圆相切的直线的一般式方程为__________.【答案】43250x y --=【解析】由题意,圆22:25C x y +=,可得圆心坐标为(0,0)C ,因为()4,3A -,则303404CA k --==--,则过点()4,3A -且与圆相切的直线的斜率为43k =,根据直线的点斜式方程,可得直线的方程为4(3)(4)3y x --=-,即43250x y --=,即点()4,3A -且与圆相切的直线的一般式方程为43250x y --=.故答案为:43250x y --=23.(2021·湖南·常德市第二中学高二期中)已知圆C :x 2+y 2=20,则过点P (4,2)的圆的切线方程是________.【答案】2100x y +-=【解析】由224220+=知P 在圆C 上,而(0,0)C ,2142PC k ==,所以所求切线斜率为2k =-,方程为22(4)y x -=--,即2100x y +-=.故答案为:2100x y +-=.24.(2022·上海理工大学附属中学高二期中)过点()1,2且与圆221x y +=相切的直线的方程是______.【答案】1x =或3450x y -+=【解析】当直线l 的斜率不存在时,因为过点()1,2,所以直线:1l x =,此时圆心(0,0)到直线1x =的距离为1=r ,此时直线:1l x =与圆221x y +=相切,满足题意;当直线l 的斜率存在时,设斜率为k ,所以:l 2(1)y k x -=-,即20kx y k --+=,因为直线l 与圆相切,所以圆心到直线的距离1d r ===,解得34k =,所以直线l 的方程为3450x y -+=.综上:直线的方程为1x =或3450x y -+=故答案为:1x =或3450x y -+=25.(2021·四川省叙永第一中学校高二期中(文))过直线34140x y ++=上的动点P 作圆22(1)(2)4x y -+-=的切线,切点为A ,则切线长PA 的最小值为____________.【解析】根据题意,圆的方程为22(1)(2)4x y -+-=,其圆心(1,2),半径2r =;设圆心为C ,即(1,2)C ;则有2222||||||||4PA PC AC PC =-=-,当||PC 取得最小值时,切线长||PA 最小,因为||PC 5=,则||PA=26.(2021·黑龙江·齐齐哈尔市恒昌中学校高二期中)已知圆224470x y x y +-++=与直线20x ay --=相切,则=a ___________.【答案】33【解析】()()22224470221x y x y x y +-++=⇒-++=,圆的圆心为(2,-2),半径r =1,()()2222311a a a -⋅--=⇒=+-故答案为:33±.考点4:切点弦问题27.(2021·福建宁德·高二期中)过圆221x y +=外一点(2,1)P -引圆的两条切线,则经过两切点的直线方程是________.【答案】210x y --=【解析】设切点分别为()()1122,,,A x y B x y ,因为点,A B 在圆221x y +=上,所以以,A B 为切点的切线方程分别为:11221,1x x y y x x y y +=+=,而点()2,1P -在两条切线上,所以112221,21x y x y -=-=,即点P 满足直线21210x y x y -=⇒--=.故答案为:210x y --=.28.(2021·广东·广州市第六十五中学高二期中)过点()5,3P 作圆229x y +=的两条切线,设两切点分别为A 、B ,则直线AB 的方程为_________.【答案】5390x y +-=【解析】根据题意,过点(5,3)P 作圆229x y +=的两条切线,设两切点分别为A 、B ,则2||||95PA PO =-,则以P 为圆心,PA 为半径为圆为22(5)(3)25x y -+-=,即圆2210690x y x y +--+=,AB 为两圆的公共弦所在的直线,则有2222910690x y x y x y ⎧+=⎨+--+=⎩,变形可得:5390x y +-=;即直线AB 的方程为5390x y +-=,故答案为:5390x y +-=29.(2021·安徽·合肥一中高二期中)已知圆22:4O x y +=,过动点(),4P a a +分别做直线PM 、PN 与圆O 相切,切点为M 、N ,设经过M 、N 两点的直线为l ,则动直线l 恒过的定点坐标为__________.【答案】()1,1-【解析】设点()00,Q x y 为圆O 上一点,当OQ 的斜率存在且不为零时,直线OQ 的斜率为0y x ,此时,圆O 在点()00,Q x y 处的切线方程为()0000x y y x x y -=--,即2200004x x y y x y +=+=,当OQ 与x 轴重合时,00y =,204x =,此时切线方程为0x x =,满足004x x y y +=,当OQ 与y 轴重合时,00x =,204y =,此时切线方程为0y y =,满足004x x y y +=.综上所述,圆O 在其上一点()00,Q x y 处的切线方程为004x x y y +=.设点()11,M x y 、()22,N x y ,则直线PM 的方程为114x x y y +=,直线PN 的方程为224x x y y +=,由题意可得()()11224444ax a y ax a y ⎧++=⎪⎨++=⎪⎩,所以,点M 、N 的坐标满足方程()440ax a y ++-=,故直线MN 的方程为()440ax a y ++-=,即()()440a x y y ++-=,由0440x y y +=⎧⎨-=⎩,解得11x y =-⎧⎨=⎩,因此,直线l 恒过的定点坐标为()1,1-.故答案为:()1,1-.30.(2021·安徽·屯溪一中高二期中)已知直线:10()l x ay a +-=∈R 是圆22:4210C x y x y +--+=的对称轴.过点(4,)A a -作圆C 的两条切线,切点分别为B 、D ,则直线BD 的方程为()A .350x y +-=B .250x y +-=C .350x y -+=D .250x y +-=【答案】A【解析】根据题意,圆C 的标准方程为()()22214x y -+-=,即圆心为C (2,1),半径为2.∴点(2,1)在直线10x ay +-=上,即2101a a +-=∴=-∴点A 的坐标为(-4,-1)AC ∴==∴过点A 作圆C 的切线所得切线长为6=∴以点A 为圆心,6为半径的圆A 的方程为()()224136x y +++=圆A 与圆C 的方程作差得350x y +-=,即直线BD 的方程为350x y +-=故选:A .31.(2021·四川省绵阳第一中学高二期中)过点()1,1P 作圆C :224470x y x y +--+=的两条切线,切点分别为A ,B ,则直线AB 的方程为()A .30x y +-=B .10x y --=C .10x y -+=D .10x y +-=【答案】A【解析】224470x y x y +--+=,即()()22221x y -+-=,圆心为()2,2,半径1r =.当斜率不存在时,直线1x =与圆相切,切点为()1,2;当斜率为0时,直线1y =与圆相切,切点为()2,1.故直线方程为斜率21112k -==--,直线方程为()12y x =--+,即30x y +-=.故选:A .32.(2020·安徽·六安市城南中学高二期中(理))过原点 O 作圆2268200x y x y +--+=的两条切线,设切点分别为P 、 Q ,则线段PQ 的长为()A .3B .4C .5D .6【答案】B【解析】由题意,2268200x y x y +--+=可化为22(3)(4)5x y -+-=,∴圆心(3,4)C ,半径r =,则有5OC =,故切线段长l ==若线段PQ 的长为x ,则2xOC l r ⋅=⋅,得4x =.故选:B .考点5:弦长问题33.(2021·广东·化州市第三中学高二期中)过点M (2,2)的直线l 与圆x 2+y 2﹣2x ﹣8=0相交于A ,B 两点,则|AB |的最小值为_____;此时直线l 的方程为_______.【答案】4260x y +-=【解析】∵圆x 2+y 2﹣2x ﹣8=0,即(x ﹣1)2+y 2=9,圆心C (1,0),半径为3,点M (2,2)在圆内,20221MC k -==-,要使|AB |的值最小,则MC ⊥AB ,此时|MC |=|AB |=4=;直线l 的斜率为12-,则直线l 的方程为y ﹣2=12-(x ﹣2),即x +2y ﹣6=0.故答案为:4;260x y +-=.34.(2021·湖北黄冈·高二期中)已知直线x y t +=与圆()2222x y t t t R +=-∈有公共点,则t 的取值范围为______,所有的弦中,最长的弦的长度为______.【答案】403t <≤【解析】由于直线x y t +=与圆()2222x y t t t R +=-∈有公共点,所以220403t t t ⎧->⇒<≤≤;又弦长==23t =时,有最大值,其最大值为故答案为:403t <≤35.(2021·广东·潮州市湘桥区南春中学高二期中)已知三点(2,0),(1,3),(2,2)A B C 在圆C 上,直线:360l x y +-=,(1)求圆C 的方程;(2)判断直线l 与圆C 的位置关系;若相交,求直线l 被圆C 截得的弦长.【解析】(1)设圆C 的方程为:220x y Dx Ey F ++++=,由题意得:24031002280D F DEF D E F ++=⎧⎪+++=⎨⎪+++=⎩,消去F 得:362D E D E -=⎧⎨-+=-⎩,解得:02D E =⎧⎨=-⎩,∴F =-4,∴圆C 的方程为:22240x y y +--=.(2)由(1)知:圆C 的标准方程为:22(1)5x y +-=,圆心(0,1)C,半径r =;点(0,1)C 到直线l的距离2d r ==<,故直线l 与圆C 相交,故直线l 被圆C截得的弦长为=36.(2021·广东·新会陈经纶中学高二期中)已知圆22:240C x y y +--=,直线()10l mx y m m -+-∈R :=.(1)写出圆C 的圆心坐标和半径,并判断直线l 与圆C 的位置关系;(2)设直线l 与圆C 交于A 、B 两点,若直线l 的倾斜角为120°,求弦AB 的长.【解析】(1)由题设知圆C :()2215x y +-=,∴圆C 的圆心坐标为C ()0,1,半径为r 又直线l 可变形为:()11y m x -=-,则直线恒过定点()1,1M ,∵()2211115+-=<,∴点M 在圆C 内,故直线l 必定与圆相交.(2)由题意知0m ≠,∴直线l 的斜率k m =tan120=︒=,∴圆心C ()0,1到直线l 10y +=的距离d ==,∴||AB ===.37.(2022·山东·济南外国语学校高二期中)已知圆C 的圆心在x 轴上,且经过点1,0,()(,2)1A B -.(1)求线段AB 的垂直平分线方程;(2)求圆C 的标准方程;(3)若过点(0,2)P 的直线l 与圆C 相交于M N 、两点,且MN =,求直线l 的方程.【解析】(1)设AB 的中点为D ,则(0,1)D .由圆的性质,得CD AB ⊥,所以1CD AB k k ⨯=-,得1CD k =-.所以线段AB 的垂直平分线的方程是1y x =-+.(2)设圆C 的标准方程为222()x a y r -+=,其中(,0)C a ,半径为()0r r >,由(1)得直线CD 的方程为1y x =-+,由圆的性质,圆心(,0)C a 在直线CD 上,化简得1a =,所以圆心()1,0C ,||2r CA ==,所以圆C 的标准方程为22(1)4x y -+=.(3)由(1)设F 为MN 中点,则CF l ⊥,得||||FM FN ==圆心C 到直线l的距离||1d CF ==,当直线l 的斜率不存在时,l 的方程0x =,此时||1CF =,符合题意;当直线l 的斜率存在时,设l 的方程2y kx =+,即20kx y -+=,由题意得d =34k =-;故直线l 的方程为324y x =-+,即3480x y +-=;综上直线l 的方程为0x =或3480x y +-=.38.(2021·湖北宜昌·高二期中)已知圆M 过点(1,2),(1,4),(3,2)A B C -.(1)求圆M 的方程;(2)若直线:340l x y b +-=与圆M相交所得的弦长为b 的值.【解析】(1)设圆M 的方程为220x y Dx Ey F ++++=,因为圆M 过(1,2),(1,4),(3,2)A B C -三点,则1420,11640,94320,D E F D E F D E F +-++=⎧⎪++++=⎨⎪++++=⎩解得2,4,1D E F =-=-=,所以圆M 的方程为222410x y x y +--+=,即22(1)(2)4x y -+-=;(2)由题意,得圆心(1,2)到直线l的距离1d =,1=,即|11|5b -=,解得6b =或16.故所求b 的值为6或16.39.(2022·上海·华东师范大学附属东昌中学高二期中)直线10x y +-=被圆()()229114x y -+-=所截得的弦长为__________【解析】圆()()229114x y -+-=的圆心为()1,1,半径为32圆心()1,1到直线10x y +-=2=则直线10x y +-=被圆()()229112x y -+-=所截得的弦长为40.(2021·福建·晋江市第一中学高二期中)已知()3,0M 是圆228280x y x y +--+=内一点,则过点M 最短的弦长为()A .B C .6D .8【答案】A【解析】圆228280x y x y +--+=,即()()22419x y -+-=,则该圆的半径为3,圆心为()4,1,M∴过点M 最短的弦长为.故选:A41.(2022·全国·高二期中)若直线20x y --=与圆()224x a y -+=所截得的弦长为则实数a 为().A .1-B .1或3C .3或6D .0或4【答案】D【解析】圆()224x a y -+=的圆心坐标为(,0)a ,半径为2,圆心(,0)a 到直线20x y --=的距离为d =,又直线20x y --=被圆()224x a y -+=所截的弦长为故,即2(2)4a -=,解得0a =或4a =.故选:D .42.(2022·江苏·淮阴中学高二期中)已知直线0x y m -+=与圆22:40C x y y ++=相交于A 、B 两点,若CA CB ⊥,则实数m 的值为()A .4-或0B .4-或4C .0或4D .4-或2【答案】A【解析】圆C 的标准方程为()2224x y ++=,圆心为()0,2C -,半径为2r =,因为CA CB ⊥且2CA CB ==,故ABC 为等腰直角三角形,且AB ==则圆心C 到直线AB 的距离为12d AB ==由点到直线的距离公式可为d ==4m =-或0.故选:A .43.(2022·广东·仲元中学高二期中)已知直线l :y kx =与圆22:20C x y y +--=相交于M ,N两点,若MN =k 的值为()AB .2CD .3【答案】C【解析】圆22:20C x y y +--=,可化为(()2214x y -+-=,∴圆心C的坐标),半径为21=,又圆心到直线的距离d =1=,解得0k =(舍去)或k 故选:C考点6:面积问题44.(2021·广东·汕头市潮阳区棉城中学高二期中)过直线:2l y x =-上任意点P 作圆22:1C x y +=的两条切线,切点分别为,A B ,当切线长最小时,切线长为_________;同时PAB △的面积为_______.【答案】112【解析】依据题意,作出图形,如下图:因为直线l 过点P 且与圆221x y +=相切于点A ,所以PA OA ⊥,所以PA ==要使得PA 最小,则OP 要最小,由题可得:OP 的最小值就是点O 到直线:2l y x =-的距离d ==此时,min 1PA =,所以4OPA π∠=由切线的对称性可得:,12BPA PB π∠==所以PAB △的面积为111122PABS =⨯⨯=,故答案为:1;12.45.(2021·广西·防城港市防城中学高二期中)已知点()3,2A ,点()3,6B ,直线l 过定点()1,0.(1)求以线段AB 为直径的圆的标准方程;(2)记(1)中求得的圆的圆心为C ,(i )若直线l 与圆C 相切,求直线l 的方程;(ii )若直线l 与圆C 交于,PQ 两点,求CPQ 面积的最大值,并求此时直线l 的方程.【解析】(1)依题可知线段AB 的中点为()3,4是圆心,半径122r AB ===.∴所求圆的标准方程为:()()22344x y -+-=;(2)(i )由(1)知:圆心()3,4C ,半径2r =,当直线l 斜率不存在时,方程为1x =,是圆的切线,满足题意;当直线l 斜率存在时,设其方程为()1y k x =-,即kx y k 0--=,∴圆心到直线l 距离2d =,解得:34k =,∴l :3430x y --=;综上所述:直线l 的方程为1x =或3430x y --=;(ii )由直线l 与圆C 交于P ,Q 两点知:直线l 斜率存在且不为0,设其方程为:()1y k x =-,即kx y k 0--=,∴圆心到直线l 距离d ==,∵()2222222144222CPQd d S PQ d d r d d d⎡⎤-+=⋅=-=-≤=⎢⎥⎣⎦△(当且仅当224d d -=,即22d =时取等号),由22d=得:()222421k k -=+,解得:1k =或7k =,∴CPQ 面积的最大值为2,此时l 方程为:10x y --=或770x y --=.46.(2020·四川省成都高新实验中学高二期中)已知直线:250l x y --=与圆22:50C x y +=相交于A ,B 两点,求:(1)交点A ,B 的坐标(2)AOB 的面积.【解析】(1)直线:250l x y --=与圆22:50C x y +=的交点,由2225050x y x y --=⎧⎨+=⎩,可得55x y =-⎧⎨=-⎩,71x y =⎧⎨=⎩所以交点A ,B 的坐标为()5,5--,()7,1(2)设直线:250l x y --=与x 轴的交点为E ,则()5,0E 所以AOBAOEEOBSSS=+11||22A B y OE y OE =+‖()1||2A B y y OE =+1652=⨯⨯15=47.(2020·湖北·高二期中)直线:1l y x =+与圆22:430C x y y +-+=交于A 、B 两点,则ABC 的面积是_________.【答案】12【解析】圆()22:21C x y +-=,()0,2C 到直线l 的距离021222d -+=,∴22122AB ⎛⎫=-= ⎪ ⎪⎝⎭∴111222ABC S AB d =⋅==△故答案为:1248.(2021·广东·佛山一中高二期中)已知圆的方程为222440x y x y +---=,设该圆过点()2,3M 的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 面积为()A .6B .C .D .【答案】C【解析】圆的标准方程为()()22129x y -+-=,圆心为()1,2E ,半径为3r =,()()2221329-+-<,故点M 在圆()()22129x y -+-=内,如下图所示:则ME 过点M 的弦过圆心时,弦长取最大值,即26AC r ==,当过M 的弦与ME 垂直时,弦长取最小值,即BD =此时AC BD ⊥,此时,四边形ABCD 的面积为11622S AC BD =⋅=⨯⨯=故选:C .49.(2021·福建龙岩·高二期中)设直线20ax y ++=与圆()22:24C x y +-=相交于A 、B 两点,且ABC 的面积为2,则=a ()A .B .C .D .【答案】D【解析】由三角形的面积公式可得212sin 22ABC S ACB =⨯⨯∠=△,可得sin 1ACB ∠=,0ACB π<∠<,故2ACB π∠=,则ABC 为等腰直角三角形,所以,圆心C 到直线20ax y ++=的距离为2sin4d π==由点到直线的距离公式可得d=,解得a=故选:D.50.(2021·江西南昌·高二期中(理))已知圆的方程为222440x y x y+---=,设该圆过点()1,3M的最长弦和最短弦分别为AC和BD,则四边形ABCD面积为()AB.C.8D.13【答案】B【解析】圆的方程为222440x y x y+---=,化为标准方程:()()22129x y-+-=,圆心为()1,2N,半径为3r=,当过点()1,3M的直线与NM垂直时,弦长最短,且AC==当过点()1,3M的直线且过圆心时,弦长最长,且26BD r==,此时,AC BD⊥,所以四边形ABCD面积为11622S AC BD=⋅=⨯=故选:B考点7:直线与圆中的定点定值问题51.(2021·山东潍坊·高二期中)已知圆M的圆心与点()1,4N-关于直线10x y-+=对称,且圆M与y轴相切于原点O.(1)求圆M的方程;(2)过原点O的两条直线与圆M分别交于,A B两点,直线,OA OB的斜率之积为12-,,OD AB D⊥为垂足,是否存在定点P,使得DP为定值,若存在,求出P点坐标;若不存在,说明理由.【解析】(1)(1)设M(a,b).则411141022baa b-⎧=-⎪⎪+⎨-+⎪-+=⎪⎩.解得3ab=⎧⎨=⎩.所以该圆的半径为3,.所以圆M的方程为()2239x y-+=;(2)设OA所在直线方程为()0y kx k=≠,联立()2239x y y kx ⎧-+=⎪⎨=⎪⎩得226611A Ak x y k k =⋅=++,同理把k 换做-12k ,可得222412,1414B Bk kx y k k-==++所以AB 所在直线方程为222636(1121k k y x k k k -=-+-+).当0y =时,可得4x =,故直线AB 过定点C (4,0).由于OC 为定值,且△ODC 为直角三角形,OC 为斜边,所以OC 中点P 满足22OC DP ==为定值,由于O (0,0),C (4,0),故由中点坐标公式可得P (2,0),故存在点P (2,0),使得|DP |为定值.52.(2021·全国·高二期中)已知圆C经过点(0,,(及()3,0.经过坐标原点O 的斜率为k 的直线l 与圆C 交于M ,N 两点.(1)求圆C 的标准方程;(2)若点()3,0P -,分别记直线PM 、直线PN 的斜率为1k 、2k ,求12k k +的值.【解析】(1)设圆C 的方程为:220x y Dx Ey F ++++=,由圆C过(0,,(及()3,0.∴23030330F F D F ⎧+=⎪⎪++=⎨⎪++=⎪⎩可得203D E F =-⎧⎪=⎨⎪=-⎩,∴圆C 的方程为:22230x y x +--=,其标准方程为()2214x y -+=;(2)设()11,M x y ,()22,N x y ,直线l 为y kx =,与圆C :()2214x y -+=联立得:()221230k x x +--=,∴()22443112160k k ∆=+⨯⨯+=+>,则12221x x k +=+,12231x x k =-+,∴12121212123333y y kx kx k k x x x x +=+=+++++()()()1212122333k x x x x x x ++⎡⎤⎣⎦=++()()22126611033k k k x x -⎛⎫+ ⎪++⎝⎭==++.53.(2020·浙江温州·高二期中)已知圆C :2280x x y ++=,直线l :20mx y m ++=.(1)当直线l 与圆C 相交于A ,B两点,且AB =l 的方程.(2)已知点P 是圆C 上任意一点,在x 轴上是否存在两个定点M ,N ,使得12PM PN=?若存在,求出点M ,N 的坐标;若不存在,说明理由.【解析】(1)由已知可得圆心()4,0C -,4r =.圆心C 到直线l的距离d =因此AB ===.22421m m =+,解得1m =±,直线l 的方程为2y x =+或2y x =--.(2)设(),P x y ,()1,0M x ,()2,0N x 由已知可得228x y x +=-12=,化简得211222821824x x x x x x x x -+-=-+-.即()()221221241240x x x x x -++-=恒成立所以122221412040x x x x -+=⎧⎨-=⎩,解得12612x x =-⎧⎨=-⎩,或1224x x =-⎧⎨=⎩所以满足题意的定点M ,N 存在,其坐标为()6,0M -,()12,0N -或()2,0M -,()4,0N .54.(2020·辽宁·大连八中高二期中)已知圆22:1O x y +=与x 轴的正半轴交于点P ,直线:30l kx y k --+=与圆O 交于不同的两点A ,B .(1)求实数k 的取值范围;(2)设直线PA ,PB 的斜率分别是12,k k ,试问12k k +是否为定值?若是定值,求出该定值;若不是定值,请说明理由;【解析】∵圆221O x y +=:与x 轴的正半轴交于点P ,∴圆心00O (,),半径1r =,()10,P .(1)∵直线30l kx y k --+=:与圆O 交于不同的两点,A B ,∴圆心O 到直线l 的距离1d =<,即3k -43k >.(2)设11(,)A x y ,22(,)B x y 联立22301kx y k x y --+=⎧⎨+=⎩,可得2222(1)(26)680k x k k x k k +--+-+=,∴2122261k k x x k -+=+,2122681k k x x k-+=+,∴121212121212(1)3(1)3332111111y y k x k x k k k x x x x x x -+-++=+=+=++------221222212123(2)3[262(1)]22()168(26)1x x k k k k k x x x x k k k k k +---+=+=+-++-+--++1862293k k --=+=-为定值.∴12k k +是定值,定值为23-.55.(2021·吉林·长春外国语学校高二期中)已知圆1O过点P ,且与圆2222:(2)(2)(0)O x y r r ++-=>关于直线20x y -+=对称.(1)求圆1O 、圆2O 的方程;(2)过点Q 向圆1O 和圆2O 各引一条切线,切点分别为C ,D ,且2QD QC =,则是否存在一定点M ,使得Q 到M 的距离为定值λ?若存在,求出M 的坐标,并求出λ的值;若不存在,请说明理由.【解析】(1)设圆1O 的圆心1(,)O a b ,因为圆1O 与圆2222:(2)(2)O x y r ++-=关于直线20x y -+=对称,可得2112222022b a a b -⎧⋅=-⎪⎪+⎨-+⎪-+=⎪⎩,解得0,0a b ==,设圆1O 的方程为222x y r +=,将点P ,代入可得2r =,所以圆1O 的方程为224x y +=,圆2O 的方程为22(2)(2)4x y ++-=.(2)由2QD QC ==设()00,Q x y ,则()()()2222000022444x y x y ++--=+-,化简得22002268339x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭,所以存在定点22,33M ⎛⎫- ⎪⎝⎭使得Q 到M.56.(2021·湖南·怀化五中高二期中)已知圆C 的圆心坐标为(3,0)C ,且该圆经过点(0,4)A .(1)求圆C 的标准方程;(2)直线n 交圆C 于M ,N 两点,若直线AM ,AN 的斜率之积为2,求证:直线n 过一个定点,并求出该定点坐标.(3)直线m 交圆C 于M ,N 两点,若直线AM ,AN 的斜率之和为0,求证:直线m 的斜率是定值,并求出该定值.【解析】(1)依题意,圆C 的半径22||345CA =+,所以圆C 的标准方程是:()22325x y -+=.(2)当直线n 的斜率不存在时,设(,),(,)M a b N a b -,由直线AM ,AN 的斜率之积为2,得442b b a a ---⋅=,即22162b a =-,又由点M ,N 在圆C 上得()22325a b -+=,消去b 得:260a a +=,而0a ≠,则6a =-,此时20b <,因此,无解,当直线n 的斜率存在时,设其方程为y kx t =+,由22(3)25y kx t x y =+⎧⎨-+=⎩消去y 并整理得:222(1)2(3)160k x kt x t ++-+-=,设1122(,),(,)M x y N x y ,则1222(3)1kt x x k --+=+,2122161t x x k -=+,直线AM 斜率114AM y k x -=,直线AN 斜率224AN y k x -=,则()()221212121212444·4AM ANt kx t kx t x xk k k k t x x x x x x -+-+-+==+-⋅+2222222226(1)(4)(4)26(1)(4)(4)16164kt k t k t k t k k t k k t t t t -++-+-+++-=+-⋅+=--+6424k t t +-==+,整理得612t k =-,此时直线n :(6)12y k x =+-过定点()6,12--,所以直线n 过一个定点,该定点坐标是()6,12--.(3)设直线AM 方程为:4y rx =+,由224(3)25y rx x y =+⎧⎨-+=⎩消去y 并整理得:22(1)2(43)0 r x r x++-=,则有点22268464(,)11r r rMr r--++++,而直线AN:4y rx=-+,同理22268464(,)11r r rNr r+--+++,于是得直线MN的斜率2222224644643116868411MNr r r rr rk r rr r-++--+-++==--+-++,所以直线m的斜率是定值,该定值为3 4-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年全国各地100份中考数学试卷分类汇编第33章直线与圆的位置关系一、选择题1. (2011宁波市,11,3分)如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB与P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现A.3次B.5次C.6次D.7次【答案】B2. (2011浙江台州,10,4分)如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切⊙O于点B,则PB的最小值是()A.13B.5C. 3D.2【答案】B3. (2011浙江温州,10,4分)如图,O是正方形ABCD的对角线BD上一点,⊙O边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF对折,折痕EF与⊙O相切,此时点D恰好落在圆心O处.若DE=2,则正方形ABCD的边长是( )A.3 B.4 C.2 D.【答案】C4. (2011浙江丽水,10,3分)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是()A .点(0,3)B .点(2,3)C .点(5,1)D .点(6,1)【答案】C5. (2011浙江金华,10,3分)如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,点B 与下列格点的连线中,能够与该圆弧相切的是( )A .点(0,3)B .点(2,3)C .点(5,1)D .点(6,1) 【答案】C6. (2011山东日照,11,4分)已知AC ⊥BC 于C ,BC =a ,CA =b ,AB =c ,下列选项中⊙O 的半径为ba ab 的是( )【答案】C7. (2011湖北鄂州,13,3分)如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,交AB 的延长线于D ,且CO=CD ,则∠PCA=( )A .30°B .45°C .60°D .67.5°【答案】D8. (2011 浙江湖州,9,3)如图,已知AB 是⊙O 的直径,C 是AB 延长线上一点,BC =OB ,A第13题图CE 是⊙O 的切线,切点为D ,过点A 作AE ⊥CE ,垂足为E ,则CD :DE 的值是 A .12B .1C .2D .3【答案】C9. (2011台湾全区,33)如图(十五),AB 为圆O 的直径,在圆O 上取异于A 、B 的一点C ,并连接BC 、AC .若想在AB 上取一点P ,使得P 与直线BC 的距离等于AP 长,判断下列四个作法何者正确?A .作AC 的中垂线,交AB 于P 点 B .作∠ACB 的角平分线,交AB 于P 点C .作∠ABC 的角平分线,交AC 于D 点,过D 作直线BC 的并行线,交AB 于P 点 D .过A 作圆O 的切线,交直线BC 于D 点,作∠ADC 的角平分线,交AB 于P 点 【答案】D10.(2011甘肃兰州,3,4分)如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于点C ,若∠A=25°,则∠D 等于A .20°B .30°C .40°D .50°【答案】C11. (2011四川成都,10,3分)已知⊙O 的面积为29cm π,若点0到直线l 的距离为cm π,则直线l 与⊙O 的位置关系是C(A)相交 (B)相切 (C)相离 (D)无法确定 【答案】CABDOC12. (2011重庆綦江,7,4分) 如图,PA 、PB 是⊙O 的切线,切点是A 、B ,已知∠P =60°,OA =3,那么∠AOB 所对弧的长度为( )A .6лB .5лC .3лD .2л【答案】:D13. (2011湖北黄冈,13,3分)如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,交AB 的延长线于D ,且CO=CD ,则∠PCA=( )[来源:学,科,网Z,X,X,K] A .30° B .45° C .60° D .67.5°【答案】D14. (2011山东东营,12,3分)如图,直线3y x =+与x 轴、y 分别相交与A 、B 两点,圆心P 的坐标为(1,0),圆P 与y 轴相切与点O 。
若将圆P 沿x 轴向左移动,当圆P 与该直线相交时,横坐标为整数的点P ′的个数是( )A .2B .3C .4D . 5【答案】B15. (2011浙江杭州,5,3)在平面直角坐标系xOy 中,以点(-3,4)为圆心,4为半径的圆( )A .与x 轴相交,与y 轴相切B .与x 轴相离,与y 轴相交C .与x 轴相切,与y 轴相交D .与x 轴相切,与y 轴相离A第13题图【答案】C16. (2011山东枣庄,7,3分)如图,P A 是O ⊙的切线,切点为A ,PA,∠APO =30°,)A .1BC .2D .4【答案】C 二、填空题1. (2011广东东莞,9,4分)如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点,连结BC.若∠A =40°,则∠C = °[来源:]【答案】0252. (2011四川南充市,13,3分)如图,PA ,PB 是⊙O 是切线,A ,B 为切点, AC 是⊙O 的直径,若∠BAC=25°,则∠P= __________度.【答案】503. (2011浙江衢州,16,4分)木工师傅可以用角尺测量并计算出圆的半径r .用角尺的较短边紧靠O ,并使较长边与O 相切于点C .假设角尺的较长边足够长,角尺的顶点B ,较短边8cm AB .若读得B C 长为cm a ,则用含a 的代数式表示r 为 .A【答案】当08a <≤时,r a =;当22118 4.08,;41616a r a r r a r a >=+<≤==+时,或当当.4. (2011浙江绍兴,16,5分) 如图,相距2cm 的两个点,A B 在在线l 上,它们分别以2 cm/s 和1 cm/s 的速度在l 上同时向右平移,当点,A B 分别平移到点11,A B 的位置时,半径为1 cm 的1A 与半径为1B B 的B 相切,则点A 平移到点1A 的所用时间为 s.lA【答案】33或5. (2011江苏苏州,16,3分)如图,已知AB 是⊙O 的一条直径,延长AB 至C 点,使得AC=3BC ,CD 与⊙O 相切,切点为D.若CD=3,则线段BC 的长度等于__________.【答案】16. (2011江苏宿迁,17,3分)如图,从⊙O 外一点A 引圆的切线AB ,切点为B ,连接AO 并延长交圆于点C ,连接BC .若∠A =26°,则∠ACB 的度数为 ▲.【答案】327. (2011山东济宁,13,3分)如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm,以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是.【答案】相交8. (2011广东汕头,9,4分)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点,连结BC.若∠A=40°,则∠C=°【答案】0259. (2011山东威海,17,3分)如图①,将一个量角器与一张等腰直角三角形(△ABC)纸片放置成轴对称图形,∠ACB=90°,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,没得CE=5cm,将量角器沿DC方向平移2cm,半圆(量角器)恰与△ABC的边AC、BC相切,如图②,则AB的长为cm.(精确到0.1cm)图①(第17题)图②[来源:学+科+网Z+X+X+K]【答案】24.510.(2011四川宜宾,11,3分)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC=_____.(第11题图)C第13题【答案】20°11. (2010湖北孝感,18,3分)如图,直径分别为CD 、CE 的两个半圆相切于点C ,大半圆M 的弦AB 与小半圆N 相切于点F ,且AB ∥CD ,AB=4,设 CD 、 CE 的长分别为x 、y ,线 段ED 的长为z ,则z (x+y )= .【答案】8π12. (2011广东省,9,4分)如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点,连结BC.若∠A =40°,则∠C = °[来源:学*科*网]【答案】025 三、解答题1. (2011浙江义乌,21,8分)如图,已知⊙O 的直径AB 与弦CD 互相垂直,垂足为点E . ⊙O 的切线BF 与弦AD 的延长线相交于点F ,且AD =3,cos ∠BCD= . (1)求证:CD ∥BF ; (2)求⊙O 的半径; (3)求弦CD 的长.的切线 ∴AB ⊥BFAB 是直径 ∴∠ADB =90° ∠BAD cos ∠BCD =43AC B∴cos ∠BAD =43=ABAD又∵AD =3 ∴AB =4 ∴⊙O 的半径为2(3)∵cos ∠DAE =43=ADAE AD =3∴AE =49∴ED =47349322=⎪⎭⎫⎝⎛-∴CD =2ED =3722. (2011浙江省舟山,22,10分)如图,△ABC 中,以BC 为直径的圆交AB 于点D ,∠ACD =∠ABC .(1)求证:CA 是圆的切线;(2)若点E 是BC 上一点,已知BE =6,tan ∠ABC =32,tan ∠AEC =35,求圆的直径.【答案】(1)∵BC 是直径,∴∠BDC =90°,∴∠ABC +∠DCB=90°,∵∠ACD =∠ABC , ∴∠ACD +∠DCB=90°,∴BC ⊥CA ,∴CA 是圆的切线. (2)在Rt △AEC 中,tan ∠AEC=53,∴53A C E C =,35E C A C =;在Rt △ABC 中,tan ∠ABC=23,∴23A CB C=,32B C A C =; ∵BC -EC=BE ,BE =6,∴33625AC AC -=,解得AC =203,A(第22题)BC∴BC=3201023⨯=.即圆的直径为10.3. (2011安徽芜湖,23,12分)如图,已知直线P A 交⊙O 于A 、B 两点,AE 是⊙O 的直径,点C 为⊙O 上一点,且AC 平分∠PAE ,过C 作C D P A ⊥,垂足为D .(1) 求证:CD 为⊙O 的切线;(2) 若DC +DA =6,⊙O 的直径为10,求AB 的长度.【答案】(1)证明:连接OC , ……………………………………1分 因为点C 在⊙O 上,OA =OC ,所以.O C A O AC ∠=∠ 因为C D P A ⊥,所以90CDA ∠= ,有90CAD DCA ∠+∠= .因为AC 平分∠PAE ,所以.D A C C A O ∠=∠……………3分 所以90.DCO DCA ACO DCA CAO DCA DAC ∠=∠+∠=∠+∠=∠+∠= ……4分 又因为点C 在⊙O 上,OC 为⊙O 的半径,所以CD 为⊙O 的切线. ………………5分 (2)解:过O 作O F AB ⊥,垂足为F ,所以90OCD CDA OFD ∠=∠=∠= , 所以四边形OC DF 为矩形,所以,.OC FD OF CD == ……………………………7分 因为DC +DA =6,设A D x =,则6.O F C D x ==-因为⊙O 的直径为10,所以5D F O C ==,所以5A F x =-. 在R t AO F △中,由勾股定理知222.AF OF OA +=即()()225625.x x -+-=化简得211180x x -+=,解得2x =或x=9. ………………9分 由AD D F <,知05x <<,故2x =. ………10分 从而AD =2,52 3.A F =-= …………………11分因为O F AB ⊥,由垂径定理知F 为AB 的中点,所以2 6.A B A F ==…………12分4. (2011山东滨州,22,8分)如图,直线PM 切⊙O 于点M ,直线PO 交⊙O 于A 、B 两点,弦AC ∥PM , 连接OM 、BC . 求证:(1)△ABC ∽△POM ;(2)2OA 2=OP ·BC .【答案】证明:(1)∵直线PM 切⊙O 于点M ,∴∠PMO=90°………………1分∵弦AB 是直径,∴∠ACB=90°………………2分∴∠ACB=∠PMO ………………3分∵AC ∥PM, ∴∠CAB=∠P ………………4分∴△ABC ∽△POM ………………5分 (2) ∵ △ABC ∽△POM, ∴A B B C P O O M=………………6分又AB=2OA,OA=OM, ∴2O A B C P OO A=………………7分∴2OA 2=OP ·BC ………………8分 5. (2011山东菏泽,18,10分)如图,BD 为⊙O 的直径,AB =AC ,AD 交B C 于点E ,AE =2,ED =4,(1)求证:△ABE ∽△ADB ;(2)求AB 的长;(3)延长DB 到F ,使得BF =BO ,连接FA ,试判断直线FA 与⊙O 的位置关系,并说明理由.解:(1)证明:∵AB =AC ,∴∠ABC =∠C ,∵∠C =∠D ,∴∠ABC =∠D ,又∵∠BAE =∠EAB ,∴△ABE ∽△ADB ,(2) ∵△ABE ∽△ADB ,∴AB AE ADAB=,(第22题图)PMO CBA∴AB 2=AD ·AE =(AE +ED )·AE =(2+4)×2=12∴AB =(3) 直线FA 与⊙O 相切,理由如下: 连接OA ,∵BD 为⊙O 的直径,∴∠BAD =90°,∴BD ==BF =BO =12BD =∵AB =,∴BF =BO =AB ,可证∠OAF =90°,∴直线FA 与⊙O 相切.6. (2011山东日照,21,9分)如图,AB 是⊙O 的直径,AC 是弦,CD 是⊙O 的切线,C为切点,AD ⊥CD 于点D . 求证:(1)∠AOC =2∠ACD ;(2)AC 2=AB ·AD .【答案】证明:(1)∵CD 是⊙O 的切线,∴∠OCD =90°,即∠ACD +∠ACO =90°.…① ∵OC=OA ,∴∠ACO =∠CAO , ∴∠AOC =180°-2∠ACO ,即21∠AOC +∠ACO =90°. ② 由①,②,得:∠ACD -21∠AOC =0,即∠AOC =2∠ACD ;(2)如图,连接BC .∵AB 是直径,∴∠ACB =90°. 在Rt △ACD 与△Rt ACD 中, ∵∠AOC =2∠B ,∴∠B =∠ACD , ∴△ACD ∽△ABC ,∴ACAD ABAC =,即AC 2=AB ·AD .7. (2011浙江温州,20,8分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,过点B 作⊙O 的切线,交AC 的延长线于点F .已知OA =3,AE =2, (1)求CD 的长; (2)求BF 的长.【答案】解:(1)连结OC ,在Rt △OCE中,C E ==.∵CD ⊥AB ,∴3CD CE ==(2) ∵BF 是⊙O 的切线, ∴FB ⊥AB , ∴CE ∥FB , ∴△ACE ∽△AFB , ∴C E AE BFAB=,26B F=,∴BF =8. (2011浙江省嘉兴,22,12分)如图,△ABC 中,以BC 为直径的圆交AB 于点D ,∠ACD =∠ABC .(1)求证:CA 是圆的切线;(2)若点E 是BC 上一点,已知BE =6,tan ∠ABC =32,tan ∠AEC =35,求圆的直径.[来源:学_科_网](第22题)BC【答案】(1)∵BC 是直径,∴∠BDC =90°,∴∠ABC +∠DCB=90°,∵∠ACD =∠ABC , ∴∠ACD +∠DCB=90°,∴BC ⊥CA ,∴CA 是圆的切线. (2)在Rt △AEC 中,tan ∠AEC=53,∴53A C E C =,35E C A C =;在Rt △ABC 中,tan ∠ABC=23,∴23A CB C=,32B C A C =; ∵BC -EC=BE ,BE =6,∴33625AC AC -=,解得AC =203,∴BC=3201023⨯=.即圆的直径为10.9. (2011广东株洲,22,8分)如图,AB 为⊙O 的直径,BC 为⊙O 的切线,AC 交⊙O 于点E ,D 为AC 上一点,∠AOD=∠C . (1)求证:OD ⊥AC ; (2)若AE=8,3tan 4A =,求OD 的长.【答案】(1)证明:∵BC 是⊙O 的切线,AB 为⊙O 的直径 ∴∠ABC=90°,∠A+∠C=90°, 又∵∠AOD=∠C , ∴∠AOD+∠A=90°, ∴∠ADO=90°, ∴OD ⊥AC.(2)解:∵OD ⊥AE ,O 为圆心, ∴D 为AE 中点 , ∴1AD =AE=42, 又3tan 4A = ,∴ OD=3.10.(2011山东济宁,20,7分)如图,AB 是⊙O 的直径,AM 和BN 是它的两条切线,DE 切⊙O 于点E ,交AM 于点D ,交BN 于点C ,F 是CD 的中点,连接OF ,(1)求证:OD ∥BE ;(2)猜想:OF 与CD 有何数量关系?并说明理由.【答案】(1)证明:连接OE ,∵AM 、DE 是⊙O 的切线,OA 、OE 是⊙O 的半径,∴∠ADO=∠EDO ,∠DAO=∠DEO =90°, ∴∠AOD=∠EOD=12∠AOE ,∵∠ABE=12∠AOE ,∴∠AOD=∠ABE ,∴OD ∥BE (2)OF =12CD ,理由:连接OC ,∵BC 、CE 是⊙O 的切线, ∴∠OCB=∠OCE∵AM ∥BN ,∴∠ADO+∠EDO+∠OCB+∠OCE=180° 由(1)得∠ADO=∠EDO , ∴2∠EDO+2∠OCE=180°,即∠EDO+∠OCE=90°在Rt △DOC 中,∵F 是DC 的中点,∴OF=12CD .11. (2011山东聊城,23,8分)如图,AB 是半圆的直径,点O 是圆心,点C 是OA 的中第20题B第20题点,CD ⊥OA 交半圆于点D ,点E 是 BD的中点,连接OD 、AE ,过点D 作D P ∥AE 交BA 的延长线于点P ,(1)求∠AOD 的度数;(2)求证:P D 是半圆O 的切线;【答案】(1)∵点C 是OA 的中点,∴OC =21OA =21OD ,∵CD ⊥OA ,∴∠OCD =90°,在Rt △OCD 中,cos ∠COD =21 ODOC ,∴∠COD =60°,即∠AOD =60°,(2)证明:连接OC ,点E 是BD 弧的中点,DE 弧=BE 弧,∴∠BOE =∠DOE =21∠DOB=21 (180°-∠COD )=60°,∵OA =OE ,∴∠EAO =∠AEO ,又∠EAO +∠AEO =∠EOB=60°,∴∠EAO =30°,∵P D ∥AE ,∴∠P =∠EAO =30°,由(1)知∠AOD =60°,∴∠P DO =180°-(∠P +∠P OD )=180°-(30°+60°)=90°,∴P D 是圆O 的切线12. (2011山东潍坊,23,11分)如图,AB 是半圆O 的直径,AB =2.射线AM 、BN 为半圆的切线.在AM 上取一点D ,连接BD 交半圆于点C ,连接AC .过O 点作BC 的垂线OE ,垂足为点E ,与BN 相交于点F .过D 点做半圆的切线DP ,切点为P ,与BN 相交于点Q .(1)求证:△ABC ∽ΔOFB ;(2)当ΔABD 与△BFO 的面积相等时,求BQ 的长;(3)求证:当D 在AM 上移动时(A 点除外),点Q 始终是线段BF 的中点.【解】(1)证明:∵AB 为直径, ∴∠ACB =90°,即AC ⊥BC .又∵OE ⊥BC ,∴OE //AC ,∴∠BAC =∠FOB .∵BN 是半圆的切线,故∠BCA =∠OBF =90°.∴△ACB ∽△OBF .(2)由△ACB ∽△OBF ,得∠OFB =∠DBA ,∠DAB =∠OBF =90°, ∴△ABD ∽△BFO ,当△ABD 与△BFO 的面积相等时,△ABD ≌△BFO . ∴AD =BO=12AB =1.∵DA ⊥AB ,∴DA 为⊙O 的切线. 连接OP ,∵DP 是半圆O 的切线, ∴DA=DP=1,∴DA=AO=OP=DP=1, ∴四边形ADPO 为正方形.∴DP//AB ,∴四边形DABQ 为矩形. ∴BQ =AD =1.(3)由(2)知,△ABD ∽△BFO , ∴B F A B O BA D=,∴2B F A D=.∵DPQ 是半圆O 的切线,∴AD =DP ,QB =QP .过点Q 作AM 的垂线QK ,垂足为K ,在Rt △DQK 中,222D Q Q K D K =+, ∴()()2222AD BQ AD BQ +=-+,∴1B Q A D=,∴BF =2BQ ,∴Q 为BF 的中点.13. (2011四川广安,29,10分)如图8所示.P 是⊙O 外一点.PA 是⊙O 的切线.A 是切点.B 是⊙O 上一点.且PA =PB ,连接AO 、BO 、AB ,并延长BO 与切线PA 相交于点Q .(1)求证:PB 是⊙O 的切线; (2)求证: AQ ·PQ = OQ ·BQ ; (3)设∠AOQ =α.若cos α=45.OQ = 15.求AB 的长【答案】(1)证明:如图,连结OP∵PA=PB ,AO=BO ,PO=PO∴△APO ≌△BPO ∴∠PBO=∠PAO=90° ∴PB 是⊙O 的切线 (2)证明:∵∠OAQ=∠PBQ=90° ∴△QPB ∽∆QOA∴PQ BQ O QAQ = 即AQ ·PQ = OQ ·BQ(3)解:cos α=AO OQ=45∴AO =12[来源:]∵△QPB ∽∆QOA ∠BPQ=∠AOQ=α ∴tan ∠BPQ=B Q P B=34∴PB =36∵12AB ·PO = OB ·BP ∴AB14. (2011江苏淮安,25,10分)如图,AD 是⊙O 的弦,AB 经过圆心O ,交⊙O 于点C ,∠DAB=∠B=30°. (1)直线BD 是否与⊙O 相切?为什么?(2)连接CD ,若CD=5,求AB 的长._ P_ B图8_ P_ B图8A【答案】(1)答:直线BD 与⊙O 相切.理由如下: 如图,连接OD ,∵∠ODA=∠DAB=∠B=30°,∴∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°, 即OD ⊥BD, ∴直线BD 与⊙O 相切.(2)解:由(1)知,∠ODA=∠DAB=30°, ∴∠DOB=∠ODA+∠DAB=60°, 又∵OC=OD ,∴△DOB 是等边三角形, ∴OA=OD=CD=5.又∵∠B=30°,∠ODB=30°, ∴OB=2OD=10.∴AB=OA+OB=5+10=15.[来源:学科网][来源:学。
