北京市朝阳区2018届高三3月综合练习一模数学文
北京市朝阳区2018届高三数学3月综合练习(一模)试题理

(A)甲
(B)乙
(C)丙
(D)丁
【答案】 A
【解析】本题考查学生的逻辑推理能力.
由四人的预测可得下表:
预测结果
中奖人
甲
乙
丙
丁
甲பைடு நூலகம்
✔
✖
✖
✖
乙
✔
✖
✔
✔
丙
✖
✖
✔
✔
-4-
如果您喜欢这份文档,欢迎下载! 来源网络,造福学生
———————欢迎下载,祝您学习进步,成绩提升———————
丁
✖
✔
✖
✔
1. 若甲中奖,仅有甲预测正确,符合题意 2. 若乙中奖,甲、丙、丁预测正确,不符合题意 3. 若丙中奖,丙、丁预测正确,不符合题意 4. 若丁中奖,乙、丁预测正确,不符合题意
65
4
第四次时, 65 50,所以输出 k 4
10.若三个点 (2,1),(2,3),(2, 1) 中恰有两个点在双曲线 C :
x2 a2
y2
1(a
0)
上,则
双曲线 C 的渐近线方程为 ______ .
【答案】 y 2 x 2
【解析】本题考查双曲线图象与渐近线方程.
由于双曲线关于原点对称,故 (2,1),(2, 1) 在双曲线上,代入方程解得 a 2 ,又因为
2. 复数 z 满足 (1 i) z i ,则在复平面内复数 z 所对应的点位于
(A)第一象限 (C)第三象限
(B)第二象限 (D)第四象限
【答案】 A
【解析】本题考查复数的运算与坐标表示.
-1-
如果您喜欢这份文档,欢迎下载! 来源网络,造福学生
———————欢迎下载,祝您学习进步,成绩提升———————
2018年高三最新 北京市朝阳区高三第三次统一考试数学(理科)试卷 精品

北京市朝阳区2018-2018学年综合练习(三)高三数学综合练习(理科)第Ⅰ卷 (选择题共40分)参考公式:如果事件A 、B 互斥,那么 球的表面积公式P(A+B)=P(A)+P(B) S =4πR 2如果事件A 、B 相互独立,那么 其中R 表示球的半径P(A·B)=P(A)·P(B)如果事件A 在一次试验中发生的 球的体积公式 概率是P,那么n 次独立重复试验 V =43πR 3 中恰好发生k 次的概率 其中R 表示球的半径k n kk n n P P C k P --=)1()(.一、选择题:本大题共8小题,每小题5分,共40分. 在每小题的 4个选项中,只有一项是符合题目要求的.(1) 若复数z 满足z (1-2i )=3+4i ,则z 等于(A )-1+2i (B )2+4i (C )2+i (D )-1+4i(2) 已知直线n m l 、、及平面α,下列命题中的假命题是 (A )若//l m ,//m n ,则//l n (B )若l α⊥,//n α,则l n ⊥ (C )若l m ⊥,//m n ,则l n ⊥ (D )若//l α,//n α,则//l n (3) 给定性质:①最小正周期为π,②图象关于直线3x π=对称,则下列函数中同时具有性质①、②的是 (A) sin()26x y π=+(B) sin(2)6y x π=- (C) sin y x = (D) sin(2)6y x π=+(4) 设函数f (x )在定义域内可导,y= f (x )的图象如右图所示,则导函数y= f ′(x )的图象可能为(5) 从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有(A )140种 (B )120种 (C )35种 (D )34种(6) 以椭圆221169144x y +=的右焦点为圆心,且与双曲线221916x y -=的渐近线相切的圆的方程是(A )221090x y x +-+= (B )221090x y x +--= (C )221090x y x +++= (D )221090x y x ++-= (7) 已知O 、A 、M 、B 为平面上四点,且)1(λλ-+=,)2,1(∈λ,则(A) 点M 在线段AB 上 (B) 点B 在线段AM 上 (C) 点A 在线段BM 上 (D) O 、A 、M 、B 四点一定共线(8) 已知函数y =f (x )(0≤x ≤1)的图象是如图所示的一段圆弧,若1201x x <<<,则 ( ) (A )1212()()f x f x x x < (B )1212()()f x f x x x = (C )1212()()f x f x x x > (D )11()f x x 与22()f x x 的大小关系不确定 第II 卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.将答案填在题中横线上.(9) 若函数y =2x 2+4x +3的图象按向量a 平移后,得到函数y =2x 2的图象,则a = .(10)点M (1,2) 到圆A :()9222=+-y x 的圆心距离是 ,过点M 的直线l 将圆A分成两段弧,其中劣弧最短时,l 的方程为 . (11)已知二项式72-展开式的第4项与第5项之和为零,那么x 等于 .( )( ) ( ) ( )(12)设地球的半径为R ,P 和Q 是地球上两地,P 在北纬45o ,东经20o ,Q 在北纬45o ,东经110o ,则P 、Q 两地的直线距离是 ,两地的球面距离是 . (13)已知f (x )是定义在R 上的奇函数,且当x <0时,f (x )=2x ,则11()4f--的值为 . (14)在等比数列}{n a 中,若19=a ,则有等式n n a a a a a a -=172121 ,),17(*∈<N n n 成立. 类比上述性质,相应的在等差数列}{n b 中,若09=b ,则有等式 成立.三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.(15)(本小题满分13分)在ABC ∆中 ,a 、b 、c 分别是角A 、B 、C 的对边,2C A =,3cos 4A =. (Ⅰ)求cosC ,cosB 的值;(Ⅱ)若272BA BC ⋅= ,求边AC 的长.(16)(本小题满分13分){a n }是公差为1的等差数列,{b n }是公比为2的等比数列,P n ,Q n 分别是{a n },{b n }的前n 项和,且a 6=b 3, P 10=Q 4+45. (I )求{a n }的通项公式;(II )若P n > b 6,求n 的取值范围.(17)(本小题满分13分)甲、乙两人参加一项智力测试.已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题. 规定每位参赛者都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过.(I )求甲答对试题数 的概率分布及数学期望; (II )求甲、乙两人至少有一人通过测试的概率.(18)(本小题满分13分)已知:在正三棱柱ABC —A 1B 1C 1中,AB = a ,AA 1 = 2a , D 、E 分别是侧棱BB 1和AC 1的中点.(Ⅰ)求异面直线AD 与A 1C 1所成角的余弦值;(Ⅱ)求证:ED ⊥平面ACC 1A 1;(Ⅲ)求平面ADC 1与平面ABC 所成二面角的大小.ABCA 1B 1C 1 DE(19)(本小题满分14分)设函数(1)()(1)x x a a -->.(Ⅰ)求()f x 的导函数/()f x,并证明()f x 有两个不同的极值点x 1、x 2;(Ⅱ)若对于(Ⅰ)中的x 1、x 2,不等式12()()0f x f x +≤ 成立,求a 的取值范围.(20)(本小题满分14分)在平面直角坐标系中,已知向量(,0)(,0)OF c c c => 为常数且,(,)(),OG x x x R =∈|2|1,(,)a FG OE t c = 的最小值为(a 为常数,且a>c ,t ∈R). 动点P 同时满足下列三个条件:(1)||||c PF PE a= ; (2)PE λ= (,0)OF R λλ∈≠且; (3) 动点P 的轨迹C经过点B(0,-1).(Ⅰ)求曲线C 的方程;(Ⅱ)是否存在方向向量为m = (1,k ) (k ≠ 0) 的直线l ,l 与曲线C 相交于M 、N 两点,使||||,BM BN BN =且BM 与的夹角为60°?若存在,求出k 值,并写出直线l的方程;若不存在,请说明理由.2018-2018高三数学综合练习(三)参考答案及评分标准(理科)一.选择题(本大题共8小题,每小题5分,共40分)(1)A (2)D (3) B (4) D (5)D (6)A (7) B (8) C二.填空题(本大题共6小题,每小题5分,共30分)(9) (1,-1) (10032=+-y x (11) 2 (12)R ,3πR (13) 2 (14) 121217,(17,)n n b b b b b b n n N *-+++=+++<∈ 三.解答题(本大题共6小题,共80分) 15. 解:(Ⅰ)21cos cos 22cos 18C A A ==-=. ………………………………3分 又3cos 04A =>,cosC=18>0, 故在ABC ∆中,A 、C 是锐角.∴sin 4A =,sin 8C =. ∴9cos cos()sin sin cos cos 16B AC A C A C =-+=-=. ……………………7分 (Ⅱ) 2727cos 2422BA BC ac B ac ⋅=⇒=⇒= . ……………………10分 由正弦定理32cos sin 2sin 2c a c A A A a =⇒==. 解得4a =,c =6. ∴2222cos 25b a c ac B =+-=. ∴5b =,即AC=5 . ……………………13分16. 解:(I )依条件得11115410910452a b b a +=⎧⎪⎨⨯+=+⎪⎩4(1-2)1-2, ……………………2分 解得1132a b =⎧⎨=⎩. …………………………………………4分 所以a n =3+(n -1)=n +2. …………………………………………6分(II )P n =2+2+3522n n n n+=(), b 6=2×26-1=64,由252n n+>64得n 2+5n -128>0. ………………………………9分所以n (n +5)>128.因为n 是正整数,且n =9时,n (n +5)=126,且n (n +5)是递增的, 所以当n ≥10时,n (n +5)>128.即n ≥10时,P n > b 6. …………………………………………………13分17. 解:(I )甲答对试题数ξ的可能取值为=ξ0、1、2、3.∵343101(0)30C P C ξ===,12643103(1)10C C P C ξ⋅===, 21643101(2)2C C P C ξ⋅===,363101(3)6C P C ξ===, …………………………4分 ∴ 甲答对试题数ξ的概率分布如下:故甲答对试题数ξ的数学期望为5961321210313010=⨯+⨯+⨯+⨯=ξE . …………………………7分 (II )设甲、乙两人通过测试的事件分别为A 、B ,则32)(310361426=+⋅=C C C C A P , 1514)(310381228=+⋅=C C C C B P . …………………………………………9分 A 、B 相互独立,∵甲、乙两人都未通过测试的概率为451)15141)(321()()()(=--=⋅=⋅B P A P B A P . ……………………………11分∴甲、乙两人至少有一个通过测试的概率为45444511)(1=-=⋅-=B A PP . ………………………………………13分18. (Ⅰ)解:∵正三棱柱中AC ∥A 1C 1,∴∠CAD 是异面直线AD 与A 1C 1所成的角. …………………………2分 连结CD ,易知,AC= a ,在△ACD 中易求出cos ∠CAD=4. 因此异面直线AD 与A 1C 1所成的角的余弦值为4. …………………………4分 (Ⅱ)证明:∵D 是B 1B 的中点,∴△C 1B 1D ≌△ABD . ∴AD= C 1D .于是△ADC 1是等腰三角形. ∵E 是AC 1的中点,∴DE ⊥AC 1. ……………………6分 设AC 的中点为G , ∴EG ∥C 1C ∥DB ,EG=12C 1C= DB . ∴四边形EGBD 是平行四边形. ∴ED ∥GB . ∵G 是AC 的中点,且AB=BC ,∴GB ⊥AC .∴ED ⊥AC .∵AC ∩AC 1=A ,∴ED ⊥平面ACC 1A 1. …………………………………………………8分 (或证ED ∥GB ,GB ⊥平面ACC 1A 1得到ED ⊥平面ACC 1A 1.)(Ⅲ)解:∵C 1D ,CB 共面,故C 1D ,CB 必相交,设交点为F ,连结AF .∴平面ADC 1与平面ABC 所成二面角是C-AF-C 1. ………………………………10分 ∵DB=12C 1C ,DB ∥C 1C , ∴B 是CF 的中点. ∴AC=CB=BF= a .在△ACF 中,由余弦定理可求出.∴易判断出△ACF 是直角三角形,即AC ⊥AF . ∵C 1C ⊥面ACF , ∴AC 1⊥AF .∴∠C 1AC 是所求二面角的平面角. …………………………………………12分 ∵tan ∠C 1AC=1C CAC=2, ∴平面ADC 1与平面ABC 所成二面角的大小是arctan2(或arccos 55). …………13分19. 解:(Ⅰ)∵32()(1)f x x a x ax =-++,∴'2()32(1)f x x a x a =-++. ……………………………………3分 令'()0f x =得,232(1)x a x a -++=0(*) .24(1)0a a ∆=-+> ,∴(*)方程有两个不同的实根1x 、2x .AB C A 1B 1C 1DFEG令12x x <,由'12()3()()f x x x x x =--可知: 当1x x <时,'()0f x >; 当'12()0x x x f x <<<时,; 当'2()0x x f x >>时,;∴1x 是极大值点,2x 是极小值点. ……………………………………7分 (Ⅱ)12()()0f x f x +≤ ,所以得不等式3322121212(1)()()0x x a x x a x x +-++++≤.即22121212121212()[()3](1)[()2]()0x x x x x x a x x x x a x x ++--++-++≤. ………10分又由(Ⅰ)知12122(1)33x x a a x x ⎧+=+⎪⎪⎨⎪=⎪⎩,代入前面的不等式,两边除以(1+a ),并化简得22520a a -+≥,解之得:2a ≥,或12a ≤(舍去). 所以当2a ≥时,不等式12()()0f x f x +≤成立. …………………………14分20. 解:(Ⅰ)∵||,2FG c ==∴1,2c ==即…………………………………………………2分 由2(,)()a OE t t R c =∈ , a x c2可知点E在直线=上.由(1)、(2)可知点P 到直线x =2(0)a aF a c c c>>距离与到点的距离之比为, 再由椭圆的第二定义可知,点P 的轨迹C 是椭圆. …………………………4分设椭圆C 的方程为:22221x y a b+=,222b ac 其中=-.由(3)可知b =1,∴a 2=b 2+c 2=1+2=3.∴椭圆C 的方程为: 2213x y +=. …………………………………5分 (Ⅱ)假设存在符合条件的直线l ,并设l 的方程为:y =kx+m ,M(x 1,y 1)、N(x 2,y 2),22222,,(13)633033y kx my k x kmx m x y =+⎧+++-=⎨+=⎩消去得. 则x 1+x 2= -21222633,1313km m x x k k -=++. ………………7分Δ=36 k 2m 2-12(m 2-1)(1+3k 2)=12[3k 2-m 2+1]>0 ①设线段MN 的中点G(x 0,y 0),x 0=2120022233,2131313x x km k m my kx m m k k k +=-=+=-+=+++, 线段MN 的垂直平分线的方程为:y -2213()1313m kmx k k k=-+++. ∵||||BM BN =, ∴线段MN 的垂直平分线过B (0,-1)点.∴-1-222133131313m km m k k k k =-⋅=-+++. ∴m=2132k +. ② ………9分②代入①,得3k 2-(2213)10,11,02k k k ++>-<<≠解得且. ③ ∵||||,BM BN BM BN =且与的夹角为60°,∴△BMN 为等边三角形.∴点B 到直线MN 的距离d=||2MN . …………………………10分∵213|1|k d ++===又∵12|x x -===2=. …………………………13分解得k2=1,33k=±即,满足③式. 代入②,得m=21311122k++==.直线l的方程为:y=1x+. ……………………………………………14分。
2018年北京市朝阳区高考一模数学试卷(文科)【解析版】

2018年北京市朝阳区高考数学一模试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集为实数集R,集合A={x|x2﹣3x<0},B={x|log2x>0},则(∁R A)∩B=()A.(﹣∞,0]∪(1,+∞)B.(0,1]C.[3,+∞)D.∅2.(5分)在复平面内,复数所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)已知平面向量=(x,1),=(2,x﹣1),且∥,则实数x的值是()A.﹣1B.1C.2D.﹣1或2 4.(5分)已知直线m⊥平面α,则“直线n⊥m”是“n∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(5分)已知F为抛物线C:y2=4x的焦点,过点F的直线l交抛物线C于A,B两点,若|AB|=8,则线段AB的中点M到直线x+1=0的距离为()A.2B.4C.8D.166.(5分)某四棱锥的三视图如图所示,则该四棱锥的体积等于()A.B.C.D.7.(5分)函数的零点个数为()A.0B.1C.2D.48.(5分)某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖.在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:小张说:“甲或乙团队获得一等奖”;小王说:“丁团队获得一等奖”;小李说:“乙、丙两个团队均未获得一等奖”;小赵说:“甲团队获得一等奖”.若这四位同学中只有两位预测结果是对的,则获得一等奖的团队是()A.甲B.乙C.丙D.丁二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)执行如图所示的程序框图,若输入m=5,则输出k的值为.10.(5分)双曲线的焦距为;渐近线方程为.11.(5分)已知圆C:x2+y2﹣2x﹣4y+1=0内有一点P(2,1),经过点P的直线l与圆C交于A,B两点,当弦AB恰被点P平分时,直线l的方程为.12.(5分)已知实数x,y满足,若z=mx+y(m>0)取得最小值的最优解有无数多个,则m的值为.13.(5分)函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则φ=;ω=.14.(5分)许多建筑物的地板是用正多边形的砖板铺成的(可以是多种正多边形).如果要求用这些正多边形的砖板铺满地面,在地面某一点(不在边界上)有k块砖板拼在一起,则k的所有可能取值为.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(13分)已知数列{a n}的前n项和S n满足S n=2a n﹣1(n∈N*).(Ⅰ)求a1,a2,a3的值;(Ⅱ)若数列{b n}满足b1=2,b n+1=a n+b n,求数列{b n}的通项公式.16.(13分)在△ABC中,已知,b=2a cos A.(Ⅰ)若ac=5,求△ABC的面积;(Ⅱ)若B为锐角,求sin C的值.17.(13分)某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如表:(Ⅰ)试估计该学校高一年级确定选考生物的学生有多少人?(Ⅱ)写出选考方案确定的男生中选择“物理、化学和地理”的人数.(直接写出结果)(Ⅲ)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.18.(14分)如图1,在梯形ABCD中,BC∥AD,BC=1,AD=3,BE⊥AD于E,BE=AE=1.将△ABE沿BE折起至△A'BE,使得平面A'BE⊥平面BCDE (如图2),M为线段A'D上一点.(Ⅰ)求证:A'E⊥CD;(Ⅱ)若M为线段A'D中点,求多面体A'BCME与多面体MCDE的体积之比;(Ⅲ)是否存在一点M,使得A'B∥平面MCE?若存在,求A'M的长.若不存在,请说明理由.19.(14分)已知椭圆的离心率为,且过点.(Ⅰ)求椭圆C的方程;(Ⅱ)过椭圆C的左焦点的直线l1与椭圆C交于A,B两点,直线l2过坐标原点且直线l1与l2的斜率互为相反数,直线l2与椭圆交于E,F两点且均不与点A,B重合,设直线AE的斜率为k1,直线BF的斜率为k2,证明:k1+k2为定值.20.(13分)已知函数.(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若a<﹣1,求函数f(x)的单调区间;(Ⅲ)若1<a<2,求证:f(x)<﹣1.2018年北京市朝阳区高考数学一模试卷(文科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集为实数集R,集合A={x|x2﹣3x<0},B={x|log2x>0},则(∁R A)∩B=()A.(﹣∞,0]∪(1,+∞)B.(0,1]C.[3,+∞)D.∅【解答】解:A={x|x2﹣3x<0}={x|x(x﹣3)<0}={x|0<x<3},B={x|log2x>0}={x|log2x>log21}={x|x>1};∴∁R A={x|x≤0,或x≥3};∴(∁R A)∩B={x|x≥3}=[3,+∞).故选:C.2.(5分)在复平面内,复数所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵复数===,∴复数对应的点的坐标是(,)∴复数在复平面内对应的点位于第一象限,故选:A.3.(5分)已知平面向量=(x,1),=(2,x﹣1),且∥,则实数x的值是()A.﹣1B.1C.2D.﹣1或2【解答】解:根据题意,向量=(x,1),=(2,x﹣1),若∥,则有x(x﹣1)=2,即x2﹣x﹣2=0,所以x=﹣1或x=2,故选:D.4.(5分)已知直线m⊥平面α,则“直线n⊥m”是“n∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:当m⊥α时,若m⊥n,则n∥α或n⊂平面α,则充分性不成立,若n∥α,则m⊥n成立,即必要性成立,则“m⊥n”是“n∥α”的必要不充分条件,故选:B.5.(5分)已知F为抛物线C:y2=4x的焦点,过点F的直线l交抛物线C于A,B两点,若|AB|=8,则线段AB的中点M到直线x+1=0的距离为()A.2B.4C.8D.16【解答】解:如图,抛物线y2=4x的焦点为F(1,0),准线为x=﹣1,即x+1=0.分别过A,B作准线的垂线,垂足为C,D,则有|AB|=|AF|+|BF|=|AC|+|BD|=8.过AB的中点M作准线的垂线,垂足为N,则MN为直角梯形ABDC中位线,则,即M到准线x=﹣1的距离为4.故选:B.6.(5分)某四棱锥的三视图如图所示,则该四棱锥的体积等于()A.B.C.D.【解答】解:抠点法:在长方体ABCD﹣A1B1C1D1中抠点,1)由正视图可知:C1D1上没有点;2)由侧视图可知:B1C1上没有点;3)由俯视图可知:CC1上没有点;4)由正(俯)视图可知:D,E处有点,由虚线可知B,F处有点,A点排除.由上述可还原出四棱锥A1﹣BEDF,=1×1=1,.如右图所示,S四边形BEDF故选:D.7.(5分)函数的零点个数为()A.0B.1C.2D.4【解答】解:,定义域为(﹣∞,0)∪(0,+∞),令f(x)=0可得2x sin x=x2+1,设,,画出f1(x),f2(x)在(0,+∞)上的大致图象如下:显然f1(1)=f2(1)=2,即f1(x)与f2(x)交于点A(1,2),又∵,f'2(x)=2x,∴f'1(1)=f'2(1)=2,即点A为公切点,∴点A为(0,+∞)内唯一交点,又∵f1(x),f2(x)均为偶函数,∴点B(﹣1,2)也为公切点,∴f1(x),f2(x)有两个公共点,即f(x)有两个零点.故选:C.8.(5分)某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖.在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:小张说:“甲或乙团队获得一等奖”;小王说:“丁团队获得一等奖”;小李说:“乙、丙两个团队均未获得一等奖”;小赵说:“甲团队获得一等奖”.若这四位同学中只有两位预测结果是对的,则获得一等奖的团队是()A.甲B.乙C.丙D.丁【解答】解:(1)若甲获得一等奖,则小张、小李、小赵的预测都正确,与题意不符;(2)若乙获得一等奖,则只有小张的预测正确,与题意不符;(3)若丙获得一等奖,则四人的预测都错误,与题意不符;(4)若丁获得一等奖,则小王、小李的预测正确,小张、小赵的预测错误,符合题意.故选:D.二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)执行如图所示的程序框图,若输入m=5,则输出k的值为4.【解答】解:模拟程序的运行,可得:第四次时,65>50,满足判断框内的条件,退出循环,输出k的值为4.故答案为:4.10.(5分)双曲线的焦距为;渐近线方程为y=.【解答】解:由题知,a2=4,b2=1,故c2=a2+b2=5,∴双曲线的焦距为:,渐近线方程为:.故答案为:;.11.(5分)已知圆C:x2+y2﹣2x﹣4y+1=0内有一点P(2,1),经过点P的直线l与圆C交于A,B两点,当弦AB恰被点P平分时,直线l的方程为y =x﹣1.【解答】解:根据直线与圆的位置关系.圆C:(x﹣1)2+(y﹣2)2=4,弦AB被P平分,故PC⊥AB,由P(2,1),C(1,2)得k pc•k l=﹣1,即:k l=1,所以直线方程为y=x﹣1.故答案为:y=x﹣1.12.(5分)已知实数x,y满足,若z=mx+y(m>0)取得最小值的最优解有无数多个,则m的值为1.【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由z=mx+y(m>0)得y=﹣mx+z,∵m>0,∴目标函数的斜率k=﹣m<0.平移直线y=﹣mx+z,由图象可知当直线y=﹣mx+z和直线x+y+1=0平行时,此时目标函数取得最小值时最优解有无数多个,∴m=1,故答案为:1.13.(5分)函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则φ=﹣;ω=.【解答】解:由图可知,A=2,根据f(x)的图象经过点(0,﹣1),可得2sinφ=﹣1,sinφ=﹣,∴φ=﹣.根据五点法作图可得ω×+(﹣)=,∴ω=,故答案为:﹣;.14.(5分)许多建筑物的地板是用正多边形的砖板铺成的(可以是多种正多边形).如果要求用这些正多边形的砖板铺满地面,在地面某一点(不在边界上)有k块砖板拼在一起,则k的所有可能取值为3,4,5,6.【解答】解:由题意知只需这k块砖板的角度之和为360°即可.显然k≥3,因为任意正多边形内角小于180°;且k≤6,因为角度最小的正多边形为正三角形,.当k=3时,3个正六边形满足题意;当k=4时,4个正方形满足题意;当k=5时,3个正三角形与2个正方形满足题意;当k=6时,6个正三角形满足题意.综上,所以k可能为3,4,5,6.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(13分)已知数列{a n}的前n项和S n满足S n=2a n﹣1(n∈N*).(Ⅰ)求a1,a2,a3的值;(Ⅱ)若数列{b n }满足b 1=2,b n +1=a n +b n ,求数列{b n }的通项公式. 【解答】解:(Ⅰ)由题知S 1=a 1=2a 1﹣1,得a 1=1, S 2=2a 2﹣1=a 1+a 2, 得a 2=a 1+1=2, S 3=2a 3﹣1=a 1+a 2+a 3, 得a 3=a 1+a 2+1=4,(Ⅱ)当n ≥2时,S n ﹣1=2a n ﹣1﹣1,S n =2a n ﹣1, 所以a n =S n ﹣S n ﹣1=2a n ﹣1﹣(2a n ﹣1﹣1), 得a n =2a n ﹣2a n ﹣1, 即a n =2a n ﹣1,{a n }是以a 1=1为首项,2为公比的等比数列, 则.当n ≥2时,b n =b 1+(b 2﹣b 1)+…+(b n ﹣b n ﹣1), =2+a 1+a 2+…+a n ﹣1, =,经验证:,综上:.16.(13分)在△ABC 中,已知,b =2a cos A .(Ⅰ)若ac =5,求△ABC 的面积; (Ⅱ)若B 为锐角,求sin C 的值.【解答】解:(Ⅰ)根据题意,若b =2a cos A ,由正弦定理得,则sin B=2sin A cos A ,, 因为,所以,所以,所以.(Ⅱ)由(Ⅰ)知,因为B为锐角,所以.所以sin C=sin(π﹣A﹣B)=sin(A+B)=sin A cos B+cos A sin B==17.(13分)某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如表:(Ⅰ)试估计该学校高一年级确定选考生物的学生有多少人?(Ⅱ)写出选考方案确定的男生中选择“物理、化学和地理”的人数.(直接写出结果)(Ⅲ)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.【解答】解:(Ⅰ)设该学校选考方案确定的学生中选考生物的学生为x,因为在选考方案确定的学生的人中,选生物的频率为,所以选择生物的概率约为,所以选择生物的人数约为人.(Ⅱ)2人.(Ⅲ)设选择物理、生物、化学的学生分别为A1,A2,A3,选择物理、化学、历史的学生为B1,选择物理、化学、地理的学生分别为C1,C2,所以任取2名男生的基本事件有:(A1,A2),(A2,A3),(A3,B1),(B1,C1),(C1,C2)(A1,A3),(A2,B1),(A3,C2),(B1,C2)(A1,B1),(A2,C1),(A3,C1)(A1,C1),(A2,C2)(A1,C2)所以两名男生所学科目相同的基本事件共有四个,分别为(A1,A2),(A2,A3),(C1,C2),(A1,A3),∴这2名学生选考科目完全相同的概率为p=.18.(14分)如图1,在梯形ABCD中,BC∥AD,BC=1,AD=3,BE⊥AD于E,BE=AE=1.将△ABE沿BE折起至△A'BE,使得平面A'BE⊥平面BCDE (如图2),M为线段A'D上一点.(Ⅰ)求证:A'E⊥CD;(Ⅱ)若M为线段A'D中点,求多面体A'BCME与多面体MCDE的体积之比;(Ⅲ)是否存在一点M,使得A'B∥平面MCE?若存在,求A'M的长.若不存在,请说明理由.【解答】证明:(Ⅰ)在梯形ABCD中,∵BE⊥AE,∴A'E⊥BE,∵平面A'BE⊥平面BCDE,BE=平面A'BE∩平面BCDE,A'E⊂平面A'BE,∴A'E⊥平面BCDE,∵CD⊂平面BCDE,∴A'E⊥CD.解:(Ⅱ)∵M为A'D中点,∴M到底面BCDE的距离为,在梯形ABCD中,,,.∵A'E⊥DE,∴在Rt△A'DE中,,∵A'E⊥平面BCDE,A'E⊂平面A'DE,∴平面A'DE⊥平面BCDE,∵BE⊥ED,平面A'DE∩平面BCDE=ED,∵BC∥AD,∴C到平面A'DE的距离为BE=1.∴,.∴V多面体A'BCME :V多面体MCDE=2:1.(Ⅲ)连结BD交CE于O,连结OM,在四边形BCDE中,∵BC∥DE,∴△BOC∽△DOE,∴,∵A'B∥平面CME,平面A'BD∩平面CEM=OM,∴A'B∥OM,在△A'BD中,OM∥A'B,∴,∵A'E=1,DE=2,A'E⊥ED,∴在Rt△A'ED中,,∴.19.(14分)已知椭圆的离心率为,且过点.(Ⅰ)求椭圆C的方程;(Ⅱ)过椭圆C的左焦点的直线l1与椭圆C交于A,B两点,直线l2过坐标原点且直线l1与l2的斜率互为相反数,直线l2与椭圆交于E,F两点且均不与点A,B重合,设直线AE的斜率为k1,直线BF的斜率为k2,证明:k1+k2为定值.【解答】解:(Ⅰ)由题可得,解得.所以椭圆C的方程为.(Ⅱ)由题知直线l1斜率存在,设l1:y=k(x+1),A(x1,y1),B(x2,y2).联立,消去y得(1+2k2)x2+4k2x+2k2﹣2=0,由题易知△>0恒成立,由韦达定理得,因为l2与l1斜率相反且过原点,设l2:y=﹣kx,E(x3,y3),F(﹣x3,﹣y3),联立,消去y得(1+2k2)x2﹣2=0,由题易知△>0恒成立,由韦达定理得,则=====0所以k1+k2为定值0.20.(13分)已知函数.(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若a<﹣1,求函数f(x)的单调区间;(Ⅲ)若1<a<2,求证:f(x)<﹣1.【解答】解:(Ⅰ)函数,若a=0,f(x)=,则f(1)=﹣1,切点坐标为(1,﹣1),,切线斜率k=2,所以f(x)在点(1,﹣1)处的切线方程为2x﹣y﹣3=0.(Ⅱ)根据题意,f(x)=﹣ax,则f′(x)=﹣a=,(x>0)令g(x)=2﹣ax2﹣lnx,则.令g'(x)=0,得(依题意)由g'(x)>0,得;由g'(x)<0,得.所以,g(x)在区间上单调递减,在区间上单调递增所以,.因为a<﹣1,所以.所以g(x)>0,即f'(x)>0.所以函数f(x)的单调递增区间为(0,+∞).(Ⅲ)证明:由x>0,f(x)<﹣1,即,等价于ax2﹣x+1﹣lnx >0.设h(x)=ax2﹣x+1﹣lnx,只须证h(x)>0成立.因为,由h'(x)=0,得2ax2﹣x﹣1=0有异号两根.令其正根为x0,则.在(0,x0)上h'(x)<0,在(x0,+∞)上h'(x)>0则h(x)的最小值为h(x0),且=﹣x0+1﹣lnx0=﹣lnx0,又,所以.则.因此,即h(x0)>0.所以h(x)>0.所以f(x)<﹣1.。
北京市朝阳区2018届高三---高考模拟数学试题

6理科数学2018年高三北京市朝阳区2018届高三(一模)数学(理)试题理科数学考试时间: _____ 钟题型单选题填空题总分得分单选题(本大题共8小题,每小题―,共—。
)1. 已知全集为实数集 R ,集合/ = {XH '—3H <0},B = {H 2‘〉1}, 则(卜伽二 A. (一讪]U 氏十对 B. 0UJ C •卜+讪 D.比+曲)2. 复数2满足(I i )z = i ,则在复平面内复数 Z 所对应的点位于 A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限i 厂 _3.直线/的参数方程为 d 为参数,则/的倾斜角大小为2TTC.3D.A. B.4•已知也」为非零向量则“”是“ Q与&夹角为锐角”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5•某单位安排甲、乙、丙、丁4名工作人员从周一到周五值班,每天有且只有1人值班, 每人至少安排一天且甲连续两天值班,则不同的安排方法种数为A. 18B. 24C. 48D. 96积等于A.-42 B.-31 C. 一6 .某四棱锥的三视图如图所示,则该四棱锥的体1 * 1 —H1 —H 侧视图217•庙会是我国古老的传统民俗文化活动,又称“庙市”或“节场” •庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”)•今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会•游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:甲说:“我或乙能中奖”;乙说:“丁能中奖”;丙说:“我或乙能中奖”;丁说:“甲不能中奖”.游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是A.甲B.乙C.丙D.丁&在平面直角坐标系xOy中,已知点丸无),陀2),动点P满足OP-AOA+flOli , 其中 .,则所有点P 构成的图形面积为A.1B.2C.总D.2鳥填空题(本大题共12小题,每小题― ,共―。
2018朝阳高三一模理科答案

10 18 420=140 人. 18 30
……….3 分
(Ⅱ)由数据可知,选考方案确定的 8 位男生中选出 1 人选考方案中含有历史学科的概率 为
2 1 = ; 8 4
选考方案确定的 10 位女生中选出 1 人选考方案中含有历史学科的概率为 所以该男生和该女生的选考方案中都含有历史学科的概率为
3 . 10
1 3 3 .…….8 分 4 10 40
(Ⅲ)由数据可知,选考方案确定的男生中有 4 人选择物理、化学和生物;有 2 人选择 物理、化学和历史;有 1 人选择物理、化学和地理;有 1 人选择物理、化学和政 治. 由已知得 的取值为 1, 2 .
P( 1)
2 2 C4 C2 1 , 2 C8 4
z z A X E O F C G D y z X
m AD 0, 所以 m DE 0,
即
x1 3 y1 2 z1 0, 2 y1 0.
取 z1 1 ,得 m ( 2, 0, 1) . 而 AC 1,3, 2 . 所以直线 AC 与平面 ADE 所成角的正弦值 sin
z z A X E O F x z X P G C D y z X
AP 1 时, OP // 平面 ADE . AC 2
1 [0,1] , 2
B
……….14 分
2
17.(本小题满分 13 分) 解:(Ⅰ)由题可知,选考方案确定的男生中确定选考生物的学生有 4 人,选考方案确定 的女生中确定选考生物的学生有 6 人, 该学校高一年级选考方案确定的学生中选考生物的学生有
因为 A(0,,,, 0 2), C (1 3 0) ,所以 ( x0 , y0 , z0 2) ( ,3 , 2 ) , 所以 x0 , y0 3 , z0
2018年高三北京市朝阳区2018届高三(一模)数学

理科数学 2018年高三北京市朝阳区2018届高三(一模)数学(理)试题解析单选题略略略略略略略略填空题略略略略略略略略略略略略单选题(本大题共8小题,每小题____分,共____分。
)1.已知全集为实数集,集合,,则A.B.C.D.2.复数满足,则在复平面内复数所对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.直线的参数方程为(为参数),则的倾斜角大小为A.C.D.4.已知为非零向量,则“”是“与夹角为锐角”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件5.某单位安排甲、乙、丙、丁4名工作人员从周一到周五值班,每天有且只有1人值班,每人至少安排一天且甲连续两天值班,则不同的安排方法种数为A.B.C.D.6.某四棱锥的三视图如图所示,则该四棱锥的体积等于A.C.D.7.庙会是我国古老的传统民俗文化活动,又称“庙市”或“节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:甲说:“我或乙能中奖”;乙说:“丁能中奖”;丙说:“我或乙能中奖”;丁说:“甲不能中奖”.游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是A. 甲B. 乙C. 丙D. 丁8.在平面直角坐标系xOy中,已知点,,动点满足,其中,则所有点构成的图形面积为A.B.C.D.填空题(本大题共12小题,每小题____分,共____分。
)9.执行如图所示的程序框图,若输入,则输出的值为________.10.若三个点中恰有两个点在双曲线上,则双曲线的渐近线方程为_____________.11.函数()的部分图象如图所示,则____;函数在区间上的零点为____.12.已知点,若点是圆上的动点,则面积的最小值为____.13.等比数列满足如下条件:①;②数列的前项和.试写出满足上述所有条件的一个数列的通项公式____.14.已知,函数当时,函数的最大值是____;若函数的图象上有且只有两对点关于轴对称,则的取值范围是____.15. (本小题满分13分)在中,已知,.(Ⅰ)若,求的面积;(Ⅱ)若为锐角,求的值.16.(本小题满分14分)如图1,在矩形中,,,为的中点,为中点.将沿折起到,使得平面平面(如图2).(Ⅰ)求证:;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)在线段上是否存在点,使得平面若存在,求出的值;若不存在,请说明理由.17.(本小题满分13分)某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生中随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史学科的概率;(Ⅲ)从选考方案确定的8名男生中随机选出2名,设随机变量求的分布列及数学期望.18. (本小题满分13分)已知函数.(Ⅰ)当时,(ⅰ)求曲线在点处的切线方程;(ⅱ)求函数的单调区间;(Ⅱ)若,求证:.19. (本小题满分14分)已知椭圆的离心率为,且过点.(Ⅰ)求椭圆的方程;(Ⅱ)过椭圆的左焦点的直线与椭圆交于两点,直线过坐标原点且与直线的斜率互为相反数.若直线与椭圆交于两点且均不与点重合,设直线与轴所成的锐角为,直线与轴所成的锐角为,判断与大小关系并加以证明.20. (本小题满分13分)已知集合是集合的一个含有8个元素的子集.(Ⅰ)当时,设,(i)写出方程的解;(ii)若方程至少有三组不同的解,写出的所有可能取值;(Ⅱ)证明:对任意一个,存在正整数,使得方程至少有三组不同的解.答案单选题1. C2. A3. C4. B5. B6. D7. A8. C 填空题9.410.11.12.213.14.15.(Ⅰ)由,得,因为,所以.因为,所以.故的面积.………………….7分(Ⅱ)因为,且为锐角,所以.所以.………….13分16.(Ⅰ)由已知,因为为中点,所以.因为平面平面,且平面平面,平面,所以平面.又因为平面,所以.………….5分(Ⅱ)设为线段上靠近点的四等分点,为中点.由已知易得.由(Ⅰ)可知,平面,所以,.以为原点,所在直线分别为轴建立空间直角坐标系(如图).因为,,所以.设平面的一个法向量为,因为,所以即取,得.而.所以直线与平面所成角的正弦值……….10分(Ⅲ)在线段上存在点,使得平面.设,且,则,.因为,所以,所以,所以,.若平面,则.即.由(Ⅱ)可知,平面的一个法向量,即,解得,所以当时,平面.……….14分17.(Ⅰ)由题可知,选考方案确定的男生中确定选考生物的学生有4人,选考方案确定的女生中确定选考生物的学生有6人,该学校高一年级选考方案确定的学生中选考生物的学生有人.……….3分(Ⅱ)由数据可知,选考方案确定的8位男生中选出1人选考方案中含有历史学科的概率为;选考方案确定的10位女生中选出1人选考方案中含有历史学科的概率为.所以该男生和该女生的选考方案中都含有历史学科的概率为.…….8分(Ⅲ)由数据可知,选考方案确定的男生中有4人选择物理、化学和生物;有2人选择物理、化学和历史;有1人选择物理、化学和地理;有1人选择物理、化学和政治.由已知得的取值为.,,或.所以的分布列为12所以.…….13分18.当时,..(ⅰ)可得,又,所以在点()处的切线方程为. ….3分(ⅱ)在区间()上,且,则.在区间()上,且,则.所以的单调递增区间为(),单调递减区间为(). ….8分(Ⅱ)由,,等价于,等价于. 设,只须证成立.因为,,由,得有异号两根.令其正根为,则.在上,在上.则的最小值为.又,,所以.则.因此,即.所以所以.….….13分19.Ⅰ)由题意得解得,,.故椭圆的方程为.….….5分(Ⅱ).证明如下:由题意可设直线的方程为,直线的方程为,设点,,,.要证,即证直线与直线的斜率之和为零,即.因为.由得,所以,.由得,所以.所以..所以.….….14分20.(Ⅰ)(ⅰ)方程的解有:. (2)分(ii)以下规定两数的差均为正,则:列出集合的从小到大8个数中相邻两数的差:1,3,2,4,2,3,1;中间隔一数的两数差(即上一列差数中相邻两数和):4,5,6,6,5,4;中间相隔二数的两数差:6,9,8,9,6;中间相隔三数的两数差:10,11,11,10;中间相隔四数的两数差:12,14,12;中间相隔五数的两数差:15,15;中间相隔六数的两数差:16这28个差数中,只有4出现3次、6出现4次,其余都不超过2次,所以的可能取值有4,6.…………………………………………………………6分(Ⅱ)证明:不妨设,记,,共13个差数.假设不存在满足条件的,则这13个数中至多两个1、两个2、两个3、两个4、两个5、两个6,从而. …………①又,这与①矛盾!所以结论成立.……………………………………………………………………13分解析单选题略略略略略略略略填空题略略略略略略略略略略略略。
北京朝阳区届高三年级第一次(3月)综合练习(一模)数学理试卷Word版含答案解析

北京市朝阳区届高三第一次(3月)综合练习(一模)数学理试卷
Word版含解析
北京市朝阳区高三年级第一次综合练习
数学(理)
).3
第一部分(选择题共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知集合,集合,则()
A. B. C. D.
【答案】B
【解析】
【分析】
解一元二次不等式求得集合,由此求得两个集合的交集.
【详解】由解得,故,故选B.
【点睛】本小题主要考查集合的交集,考查一元二次不等式的解法,属于基础题.
2.在复平面内,复数对应的点位于()
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
【答案】D
【解析】
【分析】
由题意可得:,据此确定复数所在的象限即可.
【详解】由题意可得:,
则复数z 对应的点为,位于第四象限.
本题选择D选项.
【点睛】本题主要考查复数的运算法则,各个象限内复数的特征等知识,意在考查学生的转化能力和计算求解能力.
1 / 1。
北京四中2018届高三第一次模拟考试(一模)仿真卷(A卷)文科数学试卷(含答案)

2018届高三第一次模拟考试仿真卷理科数学(A )注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·马鞍山一模]已知复数z 满足()1i 2i z -=+,则z 的共轭复数在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限2.[2018·承德期末]设集合{}2=36M x x <,{}2,4,6,8N =,则M N =I ( ) A .{}24,B .{}46,C .{}26,D .{}246,,3.[2018·亳州期末]下图中的图案是我国古代建筑中的一种装饰图案,形若铜钱,寓意富贵吉祥.在圆内随机取一点,则该点取自阴影区域内(阴影部分由四条四分之一圆弧围成)的概率是( ) A .12B .13C .41-πD .42-π4.[2018·泰安期末]函数()cos sin x f x x x =-,33,00,22x ππ⎡⎫⎛⎤∈-⎪ ⎢⎥⎣⎭⎝⎦U 的图象大致是( )班级 姓名 准考证号 考场号 座位号A .B .C .D .5.[2018·汕头期末]如图所示是一个几何体的三视图,则这个几何体外接球的体积为( )A .323π B .643π C .32πD .642π 6.[2018·遵义一模]数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后入称之为三角形的欧拉线.已知ABC △的顶点()2,0A ,()0,4B ,AC BC =,则ABC △的欧拉线方程为( ) A .230x y +-=B .230x y -+=C .230x y --=D .230x y -+=7.[2018·乌鲁木齐一模]执行如图所示的程序框图,则输出S 的值为( ) A .4097 B .9217 C .9729D .204818.[2018·承德期末]已知函数()()sin (0,)2f x x ωϕωϕπ=+><的最小正周期为6π,且其图象向右平移23π个单位后得到函数()sin g x x ω=的图象,则ϕ等于( )A .49πB .29πC .6πD .3π9.[2018·中山期末]已知实数ln22a =,ln33b =,ln55c =,则,,a b c 的大小关系是( ) A .a b c <<B .c a b <<C .c b a <<D .b a c <<10.[2018·佛山一模]如图所示,在正方体1111ABCD A B C D -中,,E F 分别为1111,B C C D 的中点,点P 是底面1111A B C D 内一点,且AP ∥平面EFDB ,则1tan APA ∠的最大值是( ) A.2B .1 CD.11.[2018·亳州一模]经过双曲线2222:1(0,0)x y M a b a b-=>>的左焦点作倾斜角为60︒的直线l ,若l 交双曲线M 的左支于,A B ,则双曲线M 离心率的取值范围是( ) A .()2,+∞B .()1,2C.(D.)+∞12.[2018·乌鲁木齐一模]设函数()3e 3x af x x x x⎛⎫=+-- ⎪⎝⎭,若不等式()0f x ≤有正实数解,则实数a 的最小值为( ) A .3B .2C .2eD .e第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·赣州期末]已知向量()12,a k =v ,()1,14b k =-v ,若a b ⊥vv ,则实数k =__________. 14.[2018·福州质检]ABC △的内角,,A B C 的对边分别为,,a b c ,已知)cos cos a C c A b -=,60B =︒,则A 的大小为__________.15.[2018·黄山一模]已知直线:l (0)x my n n =+>过点()A,若可行域00x my nx y +⎧⎪⎨⎪⎩≤≥≥的外接圆直径为20,则n =_____.16.[2018·沙市中学]“求方程341 55x x⎛⎫⎛⎫+=⎪ ⎪⎝⎭⎝⎭的解”有如下解题思路:设()3455x xf x⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭,则()f x在R上单调递减,且()21f=,所以原方程有唯一解2x=.类比上述解题思路,不等式()()63222x x x x-+>+-的解集是__________.三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答.(一)必考题:60分,每个试题12分.17.[2018·梅河口五中]已知数列{}n a的前n项和2nS n pn=+,且2a,5a,10a成等比数列.(1)求数列{}n a的通项公式;(2)若151nn nba a+=+⋅,求数列{}n b的前n项和n T.18.[2018·育才中学]某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.(1)根据频率分布直方图计算图中各小长方形的宽度;(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:由表中的数据显示,x 与y 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出y 关于x 的回归直线方程.(参考公式:1221 ˆˆˆni i i ni i x y nxy b x nx a y bx ==⎧-=-=⎪-⎪⎨⎪⎪⎩∑∑)19.[2018·淮南一模]如图所示,正四棱椎P ABCD -中,底面ABCD 的边长为2,侧棱长为22,E 为PD 的中点. (1)求证:PB ∥平面AEC ; (2)若F 为PA 上的一点,且3PFFA=, 求三棱椎A BDF -的体积.20.[2018·乌鲁木齐一模]椭圆()2222:10x y C a b a b+=>>的右焦点是(),0F c ,(),0A a ,()0,B b ,点P 是平行四边形FAPB 的一个顶点,PF x ⊥轴.(1)求椭圆C 的离心率;(2)过F 作直线l 交椭圆C 于,M N 两点,PM PN ⊥,求直线l 的斜率.21.[2018·石家庄一检]已知函数()()()ln f x x x ax a =-∈R . (1)若1a =,求函数()f x 的图像在点()()1,1f 处的切线方程;(2)若函数()f x 有两个极值点1x ,2x ,且12x x <,求证:()212f x >-.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做第一题计分)22.[2018·皖西质检]在平面直角坐标系中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l的参数方程为12 (x t t y =-⎪=⎧⎪⎨⎪⎪⎩为参数),曲线C 的极坐标方程为4cos ρθ=;(1)求直线l 的直角坐标方程和曲线C 的直角坐标方程; (2)若直线l 与曲线C 交点分别为,A B ,点()1,0P ,求11PA PB+的值.23.[2018·湖北联考]已知函数()2121f x x x =-++. (1)求函数()f x 的最小值m ; (2)若正实数,a b满足11a b +=,求证:2212m a b+≥.2018届高三第一次模拟考试仿真卷理科数学(A )答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】D【解析】Q ()1i 2i z -=+,()()()()1i 1i 2+i 1i z ∴-+=+,213i z =+,13i 22z =+,13i 22z =-,z 的共轭复数在复平面内对应点坐标为13,22⎛⎫- ⎪⎝⎭,z 的共轭复数在复平面内对应的点在第四象限,故选D . 2.【答案】A【解析】()6,6M =-,故{}2,4M N =I . 3.【答案】C【解析】令圆的半径为1,则()22'41S P S π-π-===-ππ,故选C . 4.【答案】C【解析】由()()f x f x -=-可得函数()f x 为奇函数,图像关于原点对称,可排除A ,B ,∵0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x >,故选C .5.【答案】D【解析】由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,故该四棱锥的外接球,与以俯视图为底面,以4为高的直三棱柱的外接球相同. 由底面底边长为4,高为2,故底面为等腰直角三角形,可得底面三角形外接圆的半径为2r =, 由棱柱高为4,可得22OO =,故外接球半径为R ==故外接球的体积为(3433V =π⨯=π.选D . 6.【答案】D【解析】线段AB 的中点为M (1,2),k AB =﹣2, ∴线段AB 的垂直平分线为:y ﹣2=12(x ﹣1),即x ﹣2y +3=0. ∵AC =BC ,∴△ABC 的外心、重心、垂心都位于线段AB 的垂直平分线上, 因此△ABC 的欧拉线的方程为:x ﹣2y +3=0.故选:D . 7.【答案】B【解析】阅读流程图可知,该流程图的功能是计算:0129122232102S =⨯+⨯+⨯++⨯L , 则123102122232102S =⨯+⨯+⨯++⨯L ,以上两式作差可得:10191012012222210210212S --=++++-⨯=-⨯-L , 则:109219217S =⨯+=.本题选择B 选项. 8.【答案】B【解析】由最小正周期公式可得:26ωπ=π,13ω∴=,函数的解析式为:()1sin 3f x x ϕ⎛⎫=+ ⎪⎝⎭,将函数图像向右平移23π个单位后得到的函数图像为:()12121sin sin sin 33393g x x x x ϕϕ⎡⎤ππ⎛⎫⎛⎫=-+=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,据此可得:229k ϕπ-=π,()229k k ϕπ∴=π+∈Z , 令0k =可得29ϕπ=.本题选择B 选项.9.【答案】B【解析】∵ln3ln22ln33ln2ln9ln803266b a ---=-==>,∴b a >; 又ln2ln55ln22ln5ln32ln250251010a c ---=-==>,∴a c >,∴b a c >>,即c a b <<.选B . 10.【答案】D【解析】由题意可得,点P 位于过点A 且与平面EFDB 平行的平面上, 如图所示,取1111,A D A B 的中点,G H ,连结,,,GH AH AG GE ,由正方形的性质可知:EF GH ∥,由ABEG 为平行四边形可知AG BE ∥, 由面面平行的判定定理可得:平面AGH ∥平面BEFD , 据此可得,点P 位于直线GH 上,如图所示,由1AA ⊥平面1111A B C D 可得11AA A P ⊥, 则111tan AA APA A P∠=,当1tan APA ∠有最大值时,1A P 取得最小值, 即点P 是GH 的中点时满足题意,结合正方体的性质可得此时1tan APA ∠的值是22.本题选择D 选项.11.【答案】B 【解析】由题意,3b a <22223b c a a =-<,所以2ca<,即离心率的范围是()1,2,故选B . 12.【答案】D【解析】原问题等价于()2e 33x a x x -+≥,令()()2e 33x g x x x =-+,则()min a g x ⎡⎤⎣⎦≥,而()()2'e x g x x x =-,由()'0g x >可得:()(),01,x ∈-∞+∞U , 由()'0g x <可得:()0,1x ∈,据此可知,函数()g x 在区间()0,+∞上的最小值为()1e g =,综上可得:实数a 的最小值为e .本题选择D 选项.第Ⅱ卷二、填空题:本大题共4小题,每小题5分. 13.【答案】6-【解析】由题意,()121140k k -+=,则6k =-. 14.【答案】75︒【解析】)cos cos a C c A b -=)sin cos sin cos sin A C C A B -=,即()A C -=,()1sin 2A C -=,1306A C -=π=︒,又180120A CB ︒-=︒+=Q ,2150A ∴=︒,75A =︒,故答案为75︒.15.【答案】【解析】由题意知可行域为图中△OAB 及其内部,解得(),0,B n AB =,又tan AOB ∠=AOB =30°,由正弦定理得2sin 20sin3010AB R AOB =∠=⨯︒=,解得n =16.【答案】()(),12,-∞-⋃+∞【解析】不等式x 6﹣(x +2)>(x +2)3﹣x 2变形为, x 6+x 2>(x +2)3+(x +2); 令u =x 2,v =x+2,则x 6+x 2>(x +2)3+(x+2)⇔u 3+u >v 3+v ; 考查函数f (x )=x 3+x ,知f (x )在R 上为增函数, ∴f (u )>f (v ),∴u >v ;不等式x 6+x 2>(x +2)3+(x +2)可化为x 2>x +2,解得x <﹣1或x >2; ∴不等式的解集为:(﹣∞,﹣1)∪(2,+∞). 故答案为:(﹣∞,﹣1)∪(2,+∞).三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答. (一)必考题:60分,每个试题12分.17.【答案】(1)25n a n =+;(2)214541449n n nT n +=+.【解析】(1)当2n ≥时,121n n n a S S n p -=-=-+,当1n =时,111a S p ==+,也满足21n a n p =-+,故21n a n p =-+, ∵2510,,a a a 成等比数列,∴()()()23199p p p ++=+, ∴6p =.∴25n a n =+.(2)由(1)可得()()155511111252722527n n n b a a n n n n +⎛⎫=+=+=+- ⎪⋅++++⎝⎭,∴2511111151454279911252714491449n n n nT n n n n n n +⎛⎫=+-+-+⋯+-=+= ⎪++++⎝⎭. 18.【答案】(1)2;(2)5;(3)答案见解析. 【解析】(1)设各小长方形的宽度为m .由频率分布直方图中各小长方形的面积总和为1,可知()0.080.10.140.120.040.02m +++++⋅0.51m ==,解得2m =.故图中各小长方形的宽度为2.(2)由(1)知各小组依次是[)0,2,[)2,4,[)4,6,[)6,8,[)8,10,[]10,12,其中点分别为1,3,5,7,9,11对应的频率分别为0.16,0.20,0.28,0.24,0.08,0.04 故可估计平均值为10.1630.250.28⨯+⨯+⨯+70.2490.08110.045⨯+⨯+⨯=. (3)由(2)可知空白栏中填5. 由题意可知1234535x ++++==,232573.85y ++++==,51i ii x y =∑1223324557=⨯+⨯+⨯+⨯+⨯69=,522232211234555i i x ==++++=∑, 根据公式,可求得26953 3.85553ˆb -⨯⨯=-⨯12 1.210==, 3.8 1.230ˆ.2a =-⨯=. 所以所求的回归直线方程为 1.20.2y x =+. 19.【答案】(1)见解析;(2)6. 【解析】(1)设BD 交AC 于O ,连接OE ,则在BDP △中,,O E 分别为,BD PD 的中点,∴OE PB ∥,又OE ⊂平面AEC ,PB ⊄平面AEC , ∴PB ∥平面AEC .(2)易知226PO PD OD =-=PO ⊥平面ABCD ,∴111116226343246A BDF F ABD ABD V V S PO --⎛⎫==⨯⨯=⨯⨯⨯⨯= ⎪⎝⎭△.20.【答案】(1)12;(2)0k =或23k =-【解析】(1)∵四边形FAPB 是平行四边形,∴BP FA =且BP FA ∥, 又∵PF ⊥ x 轴,∴BP OF =,∴2a c =,则12e =. (2)由(1)得2a c =,∴223b a c c -=,∴椭圆方程为2222143x y c c+=,设直线():l y k x c =-,代入椭圆方程,得:()2222223484120k x k cx k c c +-+-=,设()11,M x y ,()22,N x y ,则2122834k cx x k +=+,22212241234k c c x x k -⋅=+, 由于()11y k x c =-,()22y k x c =-,∴122634kcy y k -+=+,22122934k c y y k -⋅=+,根据题意得()3P c c ,且0PM PN ⋅=u u u u v u u u v,代入点坐标得:()()2212121212330x x c x x c y y c y y c -+++++=, 即2222222222222412896330343434k c c k c k c kc c c k k k --+-+=+++,化简得20k +=,解得0k =或k =- 21.【答案】(1) 0x y += (2)见解析【解析】(1)由已知条件,()()ln f x x x x =-,当1x =时,()1f x =-,()ln 12f x x x +'=-,当1x =时,()1f x '=-,所以所求切线方程为0x y +=(2)由已知条件可得()ln 12f x x ax +'=-有两个相异实根1x ,2x , 令()()'f x h x =,则()1'2h x a x=-, 1)若0a ≤,则()'0h x >,()h x 单调递增,()'f x 不可能有两根; 2)若0a >, 令()'0h x =得12x a =,可知()h x 在10,2a ⎛⎫ ⎪⎝⎭上单调递增,在1,2a ⎛⎫+∞ ⎪⎝⎭上单调递减, 令1'02f a ⎛⎫> ⎪⎝⎭解得102a <<,由11e 2a <有120e e a f ⎛⎫=-< ⎪⎝⎭', 由2112a a >有2122ln 10f a a a ⎛⎫=-'+-< ⎪⎝⎭, 从而102a <<时函数()f x 有两个极值点, 当x 变化时,()f x ',()f x 的变化情况如下表因为()1120f a =->',所以121x x <<,()f x 在区间[]21,x 上单调递增,()()2112f x f a ∴>=->-.另解:由已知可得()ln 12f x x ax +'=-,则1ln 2x a x +=,令()1ln xg x x+=, 则()2ln 'xg x x-=,可知函数()g x 在()0,1单调递增,在()1,+∞单调递减, 若()'f x 有两个根,则可得121x x <<, 当()21,x x ∈时,1ln 2,xa x+> ()ln 120f x x ax =+->', 所以()f x 在区间[]21,x 上单调递增,所以()()2112f x f a >=->-.(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做第一题计分)22.【答案】(1):10l x y +-=,曲线22:40C x y x +-=;(2)3. 【解析】(1):10l x y +-=,曲线22:40C x y x +-=;(2)将122x t y t ⎧⎪==⎨-⎪⎪⎪⎩(t 为参数)代入曲线C的方程,得23=0t -,12t t ∴-==,1212113t t PA PB t t -∴+==. 23.【答案】(1)2;(2)见解析.【解析】(1)()()212121212x x x x -++--+=≥当且仅当1122x -≤≤时,等式成立.(2)2221211112a b a b ⎛⎫⎛⎫⎛⎫+⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭≥则22122a b +≥,当且仅当2b a =时取,等号成立.。
2018年高三最新 北京朝阳区2018届高三文科数学一模试卷 精品

朝阳区高三数学第一次统一练习试卷(文史类) 2018.4(考试时间120分钟,满分150分)成绩_____________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题共60分) 参考公式:三角函数积化和差公式)]sin()[sin(21cos sin β-α+β+α=βα)]sin()[sin(21sin cos β-α-β+α=βα)]cos()[cos(21cos cos β-α+β+α=βα)]cos()[cos(21sin sin β-α-β+α-=βα正棱台、圆台侧面积公式:l )c 'c (21S +=台侧其中c ′、c 分别表示上、下底面周长,l 表示斜高或母线长。
台体的体积公式:h )s s 's 's (31V ++=台体其中s ′、s 分别表示上、下底面积,h 表示高。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡上将该选项涂黑。
(1)已知函数x 21x )x (f --+=的定义域为M ,1x )x (g +=的值域为N ,则( ) A .)1,1[N M -= B .]1,1[N M -= C .]2,(N M -∞= D .N M ⊆(2)直线1l :ax+2y-1=0与直线2l :0a y )1a (x 2=+-+平行,则a 的值为( ) A .-1 B .2 C .-1或2 D .0或1 (3)已知α、β是两个不同的平面,在下列条件中,可判断平面α与平面β平行的是( ) A .α、β都垂直于平面yB .a 、b 是α内两条直线,且a//β,b//βC .α内不共线的三个点到β的距离相等D .a 、b 为异面直线,且a//α,b//α,a//β,b//β(4)若直线y=2x+b 与圆0y 2y x 2=-+相切,则b 的值为( ) A .51+ B .51- C .51+,51- D .5,5-(5)不等式x 2x >+的解集为( ) A .{x|-2≤x<2} B .{x|-1<x<2} C .{x|0≤x<2} D .{x|x<2}(6)函数x cos 2x cos x sin 2)x (f 2+=的最小正周期为( ) A .3π B .2π C .π D .2π (7)某房地产开发商在销售一幢23层的商品楼之前接下列方法确定房价:由于首层与顶层均为复式结构,因此首层价格为21m /a 元,顶层由于景观好价格为22m /a 元,第二层价格为2m /a 元,从第三层开始每层在前一层价格上加价2m /100a元,则该商品房各层的平均价格为( )A .a 1.23a a 21=+B .)a 1.23a a (23121=+ C .)a 31.23a a (23121=+ D .)a 9.22a a (23121=+(8)若奇函数⎩⎨⎧<>-=)1x (,x )1x (,2x )x (f ,则不等式f(x)<0的解集为( )A .{x|x<0或1<x<2}B .{x|x<-1或0<x<1}C .{x|x<-2或-1<x<0}D .{x|x<0}(9)高中一年级8个班协商级建年级篮球队,共需10名队员,若每个班至少出一名,则不同的名额分配方式有( )A .224种B .62种C .36种D .28种 (10)如图,三棱台111C B A ABC -中,上底面111C B A 面积为41,侧面11A ACC 面积为2,点B 到上底面111C B A 及侧面11A ACC 的距离均为1,则三棱台111C B A ABC -的体积为( )A .21 B .43 C .23D .2(11)若复数不胜数z 适合2|1z ||i z |=-+-,则|z|的最小值为( )A .2B .1C .22 D .42 (12)设)0,c (F 1-,)0,c (F 2-(c>0)是椭圆)0b a (1by a x 2222>>=+的两个焦点,P 是以|F F |21为直径的圆与椭圆的一个交点,且1221F PF 5F PF ∠=∠,则该椭圆的离心率为( ) A .36 B .23 C .22 D .32第Ⅱ卷(非选择题共90分)二、填空题:本大题共4个小题,每小题4分,共16分,把答案填在题中横线上。
2018年高三最新 北京市朝阳区2018学年综合练习高三数学(文科) 精品

朝阳区高三第一次统一考试数学试卷(文科)一、选择题:(1) 设全集I={a,b,c,d,e},集合M={ a,b,d },N={ b,c,e },则下列关系中正确的是()A.M∩N∈M B.M∪N⊆MC.(C I M)∪N=φD.(C I N)∩M⊆M(2)在△ABC中,sin2A=sin2B是A=B的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件(3) 已知a、b是两条不重合的直线,α、β是两个不重合的平面,给出四个命题:①a∥b,b∥α,则a∥α;②a、b⊂α,a∥β,b∥β,则α∥β;③a与α成30°的角,a⊥b,则b与α成60°的角;④a⊥α,b∥α,则a⊥b.其中正确命题的个数是()A.4个B.3个C.2个D.1个(4)已知等比数列{a n}的前n项和为S n,S3=3,S6=27,则此等比数列的公比q等于()A. 2B.-2C.12D. -12(5)从4位男教师和3位女教师中选出3位教师,派往郊区3所学校支教,每校1人.要求这3位教师中男、女教师都要有,则不同的选派方案共有()A.210种B.186种C.180种D.90种(6) 已知函数f(x)=x∈[-2,0],则f(x)的反函数是()A.f(x)=x∈[0,2] B.f(x)=x∈[-2,0]C.f(x x∈[0,2] D.f(x x∈[-2,0](7) 已知椭圆焦点是F1、F2,P是椭圆上的一个动点,过点F2向∠F1PF2的外角平分线作垂线,垂线交F1P的延长线于点N,则点N的轨迹是()A. 圆B.椭圆C. 直线D.双曲线的一支(8) 已知计算机中的某些存储器有如下特性:若存储器中原有数据个数为m个,则从存储器中取出n个数据后,此存储器中的数据个数为m-n个;若存储器中原有数据为m个,则将n个数据存入存储器后,此存储器中的数据个数为m+n 个.现已知计算机中A、B、C三个存储器中的数据个数均为0,计算机有如下操作:第一次运算:在每个存储器中都存入个数相同且个数不小于2的数据;第二次运算:从A存储器中取出2个数据,将这2个数据存入B存储器中;第三次运算:从C存储器中取出1个数据,将这1个数据存入B存储器中;第四次运算:从B存储器中取出与A存储器中个数相同的数据,将取出的数据存入A存储器,则这时B存储器中的数据个数是()A. 8B. 7C. 6D. 5二、填空题:(9) 某市三所学校共有高三学生8000人,其中A校2520人;B校3280人;C校2200人.现在采用分层抽样方法从所有学生中抽取200人进行高考前心理测试.上述三个学校分别应该抽取人.(10) 若(1-ax)6的展开式中x4的系数是240,则实数a的值是 .(11)圆x2+y2+4x-2y+4=0上的点到直线x-y-1=0的最大距离与最小距离的差为.(12)已知一个球与一个二面角的两个半平面都相切,若球心到二面角棱的距离是5,切点到二面角棱的距离是1,则球的表面积是,球的体积是.(13)已知向量a = (2,3),|b|a∥b,则|a|= ,b的坐标是.(14)已知函数f(x)=|1|(1),3(1),x xx x+<⎧⎨-+⎩≥则不等式f (x)≥1的解集是.三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.(15)(本小题满分13分)已知a = (cos x,sin x),b = (-cos x,cos x),函数f (x)=2a·b +1.(Ⅰ)求函数f (x)的最小正周期;(Ⅱ)当x∈[0,2π]时,求f(x)的单调减区间.(16)(本小题满分13分)甲、乙两支篮球队进行比赛,已知每一场甲队获胜的概率为0.6,乙队获胜的概率为0.4,每场比赛均要分出胜负. 比赛时采用三场两胜制,即先取得两场胜利的球队胜出.(Ⅰ)求甲队以二比一获胜的概率;(Ⅱ)求乙队获胜的概率. (17)(本小题满分13分)如图,棱长为1的正四面体ABCD 中,E 、F 分别是棱AD 、CD 的中点,O 是点A 在平面BCD 内的射影.(Ⅰ)求直线EF 与直线BC 所成角的大小; (Ⅱ)求点O 到平面ACD 的距离; (Ⅲ) 求二面角C-BF-E 的大小.(18)(本小题满分13分) 已知函数f (x )= x 3+ax 2+bx +c 在x =1处有极值,f (x )在x =2处的切线l 不过第四象限且斜率为1,坐标原点到切线l的距离为2. (Ⅰ) 求a 、b 、c 的值; (Ⅱ) 求函数y = f (x )在区间[-1,32]上的最大值和最小值.(19)(本小题满分14分)已知数列{}n a 的前n 项和为n S ,点, n S n n⎛⎫⎪⎝⎭在直线11122y x =+上.数列{}n b 满足2120n n n b b b ++-+=*()n N ∈,且311b =,前9项和为153.(Ⅰ)求数列{}n a 、{}n b 的通项公式;· ABCDEFO(Ⅱ)设3(211)(21)n n n c a b =--,数列{}n c 的前n 项和为n T ,求使不等式57n k T >对一切*n N ∈都成立的最大正整数k 的值.(20)(本小题满分14分)已知双曲线的中心在原点O ,右焦点为(,0)F c ,P 是双曲线右支上任意一点,且OFP∆(Ⅰ)若点P 的坐标为(2,求此双曲线的离心率;(Ⅱ)若26(1)OF FP c ⋅=,当OP 取得最小值时,求此双曲线的方程. 朝阳区高三第一次统一考试数学试卷答案(文科) 2018.4一.选择题(1)D (2)B (3)D (4)A (5)C (6) B (7)A (8)D 二.填空题(9)63,82,55 (10)±2 (11)2 (12)16π323π(13(-4,-6)或(4,6) (14)(]2-∞-,∪[0,2]三.解答题(15) 解:(Ⅰ)因为f (x )= 2a ·b +1 = 2(cos x ,sin x )·(-cos x ,cos x )+1=2(-cos 2x + sin x cos x ) +1 ……………………………………2分 =1-2cos 2x + 2sin x cos x=sin2x -cos2x ……………………………………4分x -4π) ……………………………………6分所以f (x )的最小正周期是T=22π= π. ……………………………………7分 (Ⅱ)依条件得2k π+2π≤2x -4π≤2k π+32π(k ∈Z). ………………………………9分解得k π+38π≤x ≤k π+78π(k ∈Z). ……………………………………11分又x ∈[0,2π],所以38π≤x ≤78π,118π≤x ≤158π.即当x ∈[0,2π]时,f (x )的单调减区间是[38π,78π],[118π,158π]. ……13分(16) 解: (Ⅰ)甲队以二比一获胜,即前两场中甲胜1场,第三场甲获胜,其概率为P 1=12C ×0.6×0.4×0.6=0.288. ……………………………………6分(Ⅱ)乙队以2:0获胜的概率为 20.40.40.16P '=⨯=;乙队以2:1获胜的概率为 1220.40.60.40.192P C ''=⨯⨯=∴乙队获胜的概率为 P 2=0.42+12C ×0.4×0.6×0.4=0.16+0.192=0.352. ………………13分(17) 方法一:(Ⅰ)因为E 、F 分别是棱AD 、CD 的中点,所以EF ∥AC .所以∠BCA 是EF 与BC 所成角. ……………………………………2分 因为正四面体的面ABC 为正三角形, 所以∠BCA=60°.即EF 与BC 所成角的大小是60°. ……………………………………3分 (Ⅱ)解法1:如图,连结AO ,AF , 因为F 是CD 的中点,且△ACD ,△BCD 均为正三角形, 所以BF ⊥CD ,AF ⊥CD . 因为BF ∩AF=F ,所以CD ⊥面AFB . ………………4分因为CD ⊂面ACD , 所以面AFB ⊥面ACD . ……………5分因为ABCD 是正四面体,且O 是点A 在面BCD 内的射影,所以点O 必在正三角形BCD 的中线BF 上.在面ABF 中,过O 作OG ⊥AF ,垂足为G ,所以OG ⊥面ACD .· A B C D E FO G即OG 的长为点O 到面ACD 的距离. …………………………6分 因为正四面体ABCD 的棱长为1, 在△ABF 容易求出,因为△AOF ∽△OGF ,故由相似比易求出所以点O 到平面ACD………8分解法2:如图,连结AO ,CO ,DO , 所以点O 到平面ACD 的距离就是三棱锥 O-ACD 底面ACD 上的高h . 与解法1同理容易求出OF=6,AO=34分 所以V A -COD =13·312·6·1)=36.因为V O -ACD =V A -COD , ………………………………5分 = V O -ACD =13·h ·(121) . …………………………………6分解得h =9………………………………………8分 (Ⅲ) (文科)连结OD ,设OD 的中点为K ,连结EK , 则EK ∥AO .因为AO ⊥面BCD , 所以EK ⊥面BCD .在平面BCD 内,过点K 作KN ∥CD , KN 交BF 于M ,交BC 于N , 因为BF ⊥CD , 所以KN ⊥BF . 连结EM , 所以EM ⊥BF .· ABCDEFOKM· ABCDEFON所以∠NME 是所求二面角的平面角. ……………………………10分 因为EK=12AO=12MK=12FD=14CD=14, 所以tan ∠EMK=EK MK. …………………………………………12分 所以tan ∠NME=tan (π-∠EMK)=. 所以所求二面角的大小为π-. ………………………13分方法二:如图,以点A 在面BCD 的射影O 为坐标原点, 有向直线OA 为z 轴,有向直线BF 为y 轴,x 轴为过点O 与DC 平行方向.因为正四面体ABCD 的棱长为1,所以可以求出各点的坐标依次为: O(0,0,0),A(0,0,B(0,C(120),D(-12,,0), E(-14,F(0,,0).(Ⅰ)因为EF =(14,12,-6,BC =(12,2,0), 又EF ·BC =14×12+12×2-60=18+18=14,且|EF |=12|AC |=12,|BC |=1,CD所以cos 〈EF ,BC 〉=14112⨯=12.所以EF 与BC 所成角的大小是60°. ……………………………………3分(Ⅱ) 因为AC =(12,), AD =(-12,…5分 设平面ACD 的一个法向量为F ACD = (x 1,y 1,z 1),由AC ·F ACD =0,·F ACD =0,可得平面ACD 的一个法向量F ACD = (0,2,22). ………………………………………6分因为OF =(00),OF ·F ACD =33,| F ACD…………7分 所以点O 到平面ACD 的距离等于d =ACD ACD OF ⋅F F =33×3=9……8分(Ⅲ)因为EF =(14,12,-6,OF =(0,6,0), 设平面BEF 的一个法向量为F BEF = (x 2,y 2,z 2),由EF ·F BEF =0,OF ·F BEF =0,可得平面BEF 的一个法向量F BEF =0,3).……………………………………10分容易得到平面BCF 的一个法向量F BCF = (0,0,-1). 因为F BEF · F BCF =-3,|F BEF|F BCF |=1, 所以co s β=BEF BCF BEF BCF ⋅F F F F=-11. …………………………………12分所以二面角C-BF-E 的大小为arccos (-11)=π-arccos 11.……13分 (18) 解:(I) 由f (x )= x 3+ax 2+bx +c ,得f ′(x )= 3x 2+2ax +b . ………………………2分∵x =1时f (x )有极值,∴f ′(1)= 3+2a +b =0. ① ∵f (x )在x =2处的切线l 的斜率为1,∴f ′(2)= 12+4a +b =1. ②由①②可解得a = -4,b =5. ……………………………………4分设切线l 的方程为y =x + m ,由坐标原点(0,0)到切线l 的距离为2,可得m =±1, 又切线不过第四象限,所以m =1,切线方程为y =x +1. ……………………………6分 ∴ 切点坐标为(2,3),∴f (2)=8-16+10+c =3,所以c =1.故a = -4,b =5,c =1. ……………………………………7分(Ⅱ)由(Ⅰ)知f (x )= x 3-4x 2+5x +1,f ′(x )= 3x 2-8x +5=(x -1)(3x -5).∵x ∈[-1,32],∴ 函数f (x )在区间[-1,1]上递增,在3(1,]2上递减 . ………9分又f (-1)=-9,f (1)=3,f (32)=238, ……………………………………12分∴f (x )在区间[-1,32]上的最大值为3,最小值为-9. ……………………………13分(19) 解:(Ⅰ)由题意,得11122n S n n =+,即211122n S n n =+.故当2n ≥时,1n n n a S S -=-=2111()22n n +2111[(1)(1)]22n n --+-5n =+.…2分注意到1n =时,116a S ==,而当1n =时,56n += , …………………3分所以, *5 ()n a n n N =+∈. ……………………………………4分 又2120n n n b b b ++-+=,即211n n n n b b b b +++-=-*()n N ∈,所以{}n b 为等差数列. ……………………………………5分 于是379()1532b b +=. 而311b =,故723b =,2311373d -==-. …………………………………7分 因此,33(3)32n b b n n =+-=+,即32n b n =+*()n N ∈.………………8分 (Ⅱ)3(211)(21)n n n c a b =--3[2(5)11][2(32)1]n n =+-+-1111(21)(21)22121n n n n ⎛⎫==- ⎪-+-+⎝⎭. ………………………10分所以,12n n T c c c =+++1111111112335572121n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦11122121nn n ⎛⎫=-= ⎪++⎝⎭. ……………………………………12分 由于112321n n n n T T n n ++-=-++10(23)(21)n n =>++, 因此n T 单调递增,故min 1()3n T =. ……………………………………13分 令1357k >,得19k <,所以 max 18k =. …………………………………14分 (20)解:(Ⅰ)设所求的双曲线的方程为22221(0,0)x y a b a b-=>>,则1||2OF =,∴ c = ……………………………………1分 ∴ 22222b c a a =-=-. ……………………………………2分由点P 在双曲线上,∴224312a a-=-,解得21a =, ………………5分∴ 离心率ce a== ……………………………………6分 (Ⅱ)设所求的双曲线的方程为22221(0,0)x y a b a b-=>>,11(,)P x y ,则11(,)FP x c y =-. ……………………………………7分∵OFP ∆的面积为21122OF y =.∴1y c=…………8分∵26(1)3OF FP c ⋅=-, ∴21()(1)3OF FP x c c c ⋅=-=-.解得1x =……………………………………9分∵22OP x=, …………………………10分当且仅当c =. …………………………………11分 此时P .由此得2222221,3a b a b ⎧-=⎪⎨⎪+=⎩解得2212a b ⎧=⎨=⎩或2263a b ⎧=⎨=-⎩(舍).……13分 则所求双曲线的方程为2212y x -=. ………………………………14分 注:(1)2个空的填空题,第一个空给3分,第二个空给2分.(2)如有不同解法,请阅卷老师酌情给分.。
2018北京六区高三一模数学(文)汇编--立体几何

2018北京六区高三一模数学(文)汇编--立体几何【海淀一模】(18)(本小题14分)如图,四棱锥E ABCD -中,1//,12AD BC AD Ab AE BC ====,且BC ⊥平面ABE ,M 为棱CE 的中点.(I)求证:DM ∥平面ABE ; (Ⅱ)求证:平面CDE ⊥平面CBE ;(Ⅲ)当四面体D ABE -的体积最大时,判断直线AE 与直线CD 是 否垂直,并说明理由.18.(Ⅰ)证明:取线段EB 的中点N ,连接,MN AN .DABCMEN因为M 为棱CE 的中点,所以在CBE ∆中//MN BC ,12MN BC =. 又//AD BC ,12AD BC =, 所以//,MN AD MN AD =.所以四边形DMNA 是平行四边形, 所以//DM AN . 又DM ⊄平面ABE , AN ⊂平面ABE ,所以//DM 平面ABE . (Ⅱ)因为AE AB =,N 为EB 中点,所以AN BE ⊥. 又BC ⊥平面ABE ,AN ⊂平面ABE ,所以BC AN ⊥ 又BCBE B =,所以AN ⊥平面BCE . 又//DM AN , 所以DM ⊥平面BCE . 因为DM⊂平面CDE ,所以平面CDE ⊥平面CBE . .…………………….…9分 (Ⅲ)AE CD ⊥. 设EAB θ∠=,1AD AB AE ===则四面体D ABE -的体积 sin V AE AB AD θ⨯⋅⋅⋅11=321sin 6θ=. 当90θ=︒,即AE AB ⊥时体积最大. 又BC ⊥平面ABE ,AE ⊂平面ABE ,所以AE BC ⊥. 因为BCAB B =,所以AE ⊥平面ABC . 因为CD ⊂平面ABCD ,所以AE CD ⊥. .…………………….…14分 【西城一模】18.(本小题满分14分)如图1,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB AC ==,4BC =.将△ADE 沿DE 折起到△1A DE 的位置,使得平面1A DE ⊥平面BCED ,F 为1A C 的中点,如图2.(Ⅰ)求证://EF 平面1A BD ; (Ⅱ)求证:平面1A OB ⊥平面1A OC ;(Ⅲ)线段OC 上是否存在点G ,使得OC ⊥平面EFG ?说明理由.图1 图218.(本小题满分14分)解:(Ⅰ)取线段1A B 的中点H ,连接HD ,HF .[1分]因为在△ABC 中,D ,E 分别为AB ,AC 的中点, 所以 //DE BC ,12DE BC =.因为 H ,F 分别为1A B ,1A C 的中点,所以 //HF BC ,12HF BC =,所以 //HF DE ,HF DE =,所以 四边形DEFH 为平行四边形,[3分] 所以 //EF HD .[ 4分]因为 EF ⊄平面1A BD , HD ⊂平面1A BD , 所以 //EF 平面1A BD .[ 5分](Ⅱ)因为在△ABC 中,D ,E 分别为AB ,AC 的中点, 所以 AD AE =.所以11A D A E =,又O 为DE 的中点, 所以 1A O DE ⊥.[ 6分]因为平面1A DE ⊥平面BCED ,且1A O ⊂平面1A DE , 所以 1A O ⊥平面BCED ,[ 7分] 所以 1CO A O ⊥.[ 8分]在△OBC 中,4BC =,易知 OB OC == 所以 CO BO ⊥,所以 CO ⊥平面1A OB ,[ 9分] 所以 平面1A OB ⊥平面1A OC .[10分](Ⅲ)线段OC 上不存在点G ,使得OC ⊥平面EFG .[11分] 否则,假设线段OC 上存在点G ,使得OC ⊥平面EFG , 连接 GE ,GF ,则必有 OC GF ⊥,且OC GE ⊥.A在Rt △1A OC 中,由F 为1A C 的中点,OC GF ⊥, 得G 为OC 的中点.[12分] 在△EOC 中,因为OC GE ⊥, 所以EO EC =,这显然与1EO =,EC 矛盾!所以线段OC 上不存在点G ,使得OC ⊥平面EFG .[14分]【东城一模】(18)(本小题14分)如图,四边形ABCD 为菱形,60DAB ∠=o ,ED ⊥平面ABCD ,22ED AD EF ===,EF ∥AB ,M 为BC 中点.(Ⅰ)求证:FM ∥平面BDE ; (Ⅱ)求证:AC BE ⊥;(Ⅲ)若G 为线段BE 上的点,当三棱锥G BCD -的体积为9时,求BGBE的值.(18)(共14分)解:(Ⅰ) 设,连结.因为分别是的中点,因为EF //AB ,且12EF=AB , 因为OM //AB ,且12OM=AB , AC BD O =I ,EO MO ,M O ,BC BD所以EF //OM ,且EF=OM . 所以四边形EOMF 为平行四边形. 所以∥.又因为平面,平南,所以FM ∥平面BDE . ………5分 (Ⅱ)因为ABCD 为菱形, 所以.因为平面ABCD , 所以. 因为, 所以平面. 又因为平面,所以AC BE ⊥. ………10分 (Ⅲ)过作ED 的平行线交BD 于. 由已知ED ⊥平面ABCD , 所以平面ABCD .所以为三棱锥的高.因为三棱锥G BCD -的体积为9, 所以三棱锥G BCD -的体积11sin 6032V BD BC GH =⨯⋅⋅⋅⋅=o .所以. FM EO EO ⊂BDE FM ⊄BDE AC BD ⊥ED ⊥ED AC ⊥BD ED D =I AC ⊥BDE BE ⊂BDE G H GH ⊥GH G BCD -23GH =A所以21323GH BG ED BE ===.所以13BG =BE . ………14分 【朝阳一模】18.(本小题满分14分)如图1,在梯形ABCD 中,//BC AD ,1BC =,3AD =,BE AD ⊥于E ,1BE AE ==.将ABE ∆沿BE 折起至A BE '∆,使得平面A BE '⊥平面BCDE (如图2),M 为线段A D '上一点. (Ⅰ)求证:A E CD '⊥;(Ⅱ)若M 为线段A D '中点,求多面体A BCME '与多面体MCDE 的体积之比;(Ⅲ)是否存在一点M ,使得A B '//平面MCE ?若存在,求A M '的长.若不存在,请说明理由.18. (本小题满分14分)证明:(Ⅰ)如图1,在梯形中,因为,所以(如图2). 因为平面平面,且平面平面,所以平面.又因为平面,所以. ……………… 4分 (Ⅱ)解:由(Ⅰ)可知平面,所以,.过点作于,则, 所以平面.因为为中点,,所以. ABCD BE AD ⊥BE A E '⊥A BE '⊥BCDE A BE 'BCDE BE =A E '⊥BCDE CD ⊂BCDE A E CD '⊥A E '⊥BCDE A E BE '⊥A E DE '⊥M MH DE ⊥H //MH A E 'MH ⊥BCDE M A D '1A E '=12MH =图1EABC D图2C BMDA 'ECBMDA ′EH设四棱锥的体积为,则. 设三棱锥的体积为,则. 所以12111263A BCME V V V '=-=-=多面体 所以11::2:136A BCME MCDE V V '==多面体多面体. ……………… 9分 (Ⅲ)解:存在一点M ,使得平面MCE .理由如下:连结交于,连结,则 平面平面.由平面,得. 所以. 在梯形中,因为,所以∽.又因为,,所以.于是12A M MD '=,所以13A M AD '=. 又因为1A E '=,,所以A D '=.故A M '…………14分 【丰台一模】(17)(本小题共14分)如图所示,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,//AD BC ,=2AD BC ,90DAB ABP ∠=∠=︒. (Ⅰ)求证:AD ⊥平面PAB ; (Ⅱ)求证:AB ⊥PC ;A BCDE '-1V 111111()(12)1133262BCDE V S A E BC DE BE A E ''=⋅⋅=⨯+⋅⋅=+⨯⨯=四边形M CDE -2V 211111121332626CDE V S MH DE BE MH ∆=⋅⋅=⨯⋅⋅=⨯⨯⨯=//A B 'BD CE N MN A BD'MCE MN =//A B 'MCE //A B MN '::A M MD BN ND '=BCDE //BC DE BNC ∆DNE ∆1BC =2DE =::1:2BN ND BC DE ==2DE =(Ⅲ)若点E 在棱PD 上,且CE ∥平面PAB ,求PEPD的值.(17)(本小题共14分)(Ⅰ)证明:因为90DAB ∠=︒,所以AD ⊥AB . ……………………1分因为平面PAB ⊥平面ABCD , ……………………2分 且平面PAB I 平面=ABCD AB , ……………………3分所以AD ⊥平面PAB . ……………………4分(Ⅱ)证明:由已知得AD ⊥AB因为AD BC ∥,所以BC ⊥AB . ……………………5分 又因为90ABP ∠=︒,所以PB ⊥AB . ……………………6分因为=PB BC B I ……………………7分 所以AB ⊥平面PBC ……………………8分 所以AB ⊥PC . ……………………9分(Ⅲ)解:过E 作EF AD ∥交PA 于F ,连接BF . ……………………10分因为AD BC ∥, 所以EF BC ∥.所以E ,F ,B ,C 四点共面. ……………………11分 又因为CE ∥平面PAB , 且CE ⊂平面BCEF ,且平面BCEF I 平面=PAB BF ,所以CE BF ∥, ……………………13分 所以四边形BCEF 为平行四边形, 所以=EF BC .在△PAD 中,因为//EF AD ,所以1===2PE EF BC PD AD AD , ……………………14分 即1=2PE PD . 【石景山一模】18.(本小题共14分)如图,在三棱锥D ABC -中,已知BCD △是正三角形,AB ⊥平面BCD ,AB BC a ==,E 为BC 的中点,F 在棱AC 上,且3AF FC =.(Ⅰ)求三棱锥D ABC -的体积; (Ⅱ)求证:AC ⊥平面DEF ;(Ⅲ)若M 为DB 中点,N 在棱AC 上,且38CN CA =,求证:MN //平面DEF . 18.(本小题14分)解:(Ⅰ)因为BCD △是正三角形,且AB BC a ==,所以24BCD S =△.………………2分 又AB ⊥平面BCD ,………………3分故13D ABC A BCD V V AB --==⋅⋅S △BCD 2134a =⋅312a =.………………4分 (Ⅱ)在底面ABC 中,取AC 的中点H ,连接BH ,因AB BC =,故BH AC ⊥.因3AF FC =,故F 为CH 的中点. 又E 为BC 的中点,故EF ∥BH ,ABCDNFM EABDN M E HO故EF AC ⊥.……5分因AB ⊥平面BCD ,AB ⊂平面ABC , 故平面ABC ⊥平面BCD .BCD △是正三角形,E 为BC 的中点,故DE BC ⊥,故DE ⊥平面ABC .………………7分AC ⊂平面ABC ,故DE ⊥AC .………………8分又DE EF E ⋂=,故AC ⊥平面DEF .………………9分(Ⅲ)当38CN CA =时,连CM ,设CM DE O ⋂=,连OF .因E 为BC 的中点,M 为DB 中点,故O 为△BCD 的重心,23CO CM =.………………10分因3AF FC =,38CN CA =,故23CF CN =,所以MN ∥OF .………………12分又OF ⊂平面DEF ,MN ⊄平面DEF ,所以MN ∥平面DEF .……14分。
2018年北京市朝阳区高考一模数学试卷(理科)【解析版】

2018年北京市朝阳区高考数学一模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集为实数集R,集合A={x|x2﹣3x<0},B={x|2x>1},则(∁R A)∩B=()A.(﹣∞,0]∪[3,+∞)B.(0,1]C.[3,+∞)D.[1,+∞)2.(5分)复数z满足(1+i)z=i,则在复平面内复数z所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)直线l的参数方程为(t为参数),则l的倾斜角大小为()A.B.C.D.4.(5分)设,是单位向量,则“•>0”是“和的夹角为锐角”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.(5分)某单位安排甲、乙、丙、丁4名工作人员从周一到周五值班,每天有且只有1人值班,每人至少安排一天且甲连续两天值班,则不同的安排方法种数为()A.18B.24C.48D.966.(5分)某四棱锥的三视图如图所示,则该四棱锥的体积等于()A.B.C.D.7.(5分)庙会是我国古老的传统民俗文化活动,又称“庙市”或“节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:甲说:“我或乙能中奖”;乙说:“丁能中奖”;丙说:“我或乙能中奖”;丁说:“甲不能中奖”.游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是()A.甲B.乙C.丙D.丁8.(5分)在平面直角坐标系xOy中,已知点A(,0),B(1,2).动点P 满足=+,其中λ,μ∈[0,1],λ+μ∈[1,2],则所有点P构成的图形面积为()A.1B.2C.D.2二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)执行如图所示的程序框图,若输入m=5,则输出k的值为.10.(5分)若三个点(﹣2,1),(﹣2,3),(2,﹣1)中恰有两个点在双曲线上,则双曲线C的渐近线方程为.11.(5分)函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则ω=;函数f(x)在区间上的零点为.12.(5分)已知两点A(﹣2,0),B(0,2),点C是圆x2+y2﹣2x+2y=0上任意点,则△ABC面积的最小值是.13.(5分)等比数列{a n}满足如下条件:①a1>0;②数列{a n}的前n项和S n<1.试写出满足上述所有条件的一个数列的通项公式.14.(5分)已知a∈R,函数当x>0时,函数f(x)的最大值是;若函数f(x)的图象上有且只有两对点关于y轴对称,则a的取值范围是.三、解答题(共6小题,共80分,解答应写出文字说明,演算步骤或证明过程)15.(13分)在△ABC中,已知,b=2a cos A.(Ⅰ)若ac=5,求△ABC的面积;(Ⅱ)若B为锐角,求sin C的值.16.(14分)如图1,在矩形ABCD中,AB=2,BC=4,E为AD的中点,O为BE的中点.将△ABE沿BE折起到A'BE,使得平面A'BE⊥平面BCDE(如图2)(Ⅰ)求证:A'O⊥CD;(Ⅱ)求直线A'C与平面A'DE所成角的正弦值;(Ⅲ)在线段A'C上是否存在点P,使得OP∥平面A'DE?若存在,求出的值;若不存在,请说明理由.17.(13分)某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量求ξ的分布列及数学期望Eξ.18.(13分)已知函数.(Ⅰ)当a=2时,(i)求曲线y=f(x)在点(1,f(1))处的切线方程;(ii)求函数f(x)的单调区间;(Ⅱ)若1<a<2,求证:f(x)<﹣1.19.(14分)已知椭圆的离心率为,且过点.(Ⅰ)求椭圆C的方程;(Ⅱ)过椭圆C的左焦点的直线l1与椭圆C交于A,B两点,直线l2过坐标原点且与直线l1的斜率互为相反数.若直线l2与椭圆交于E,F两点且均不与点A,B重合,设直线AE与x轴所成的锐角为θ1,直线BF与x轴所成的锐角为θ2,判断θ1与θ2的大小关系并加以证明.20.(13分)已知集合X={x1,x2,…,x8}是集合S={2001,2002,2003,…,2016,2017}的一个含有8个元素的子集.(Ⅰ)当X={2001,2002,2005,2007,2011,2013,2016,2017}时,设x i,x j∈X(1≤i,j≤8),(i)写出方程x i﹣x j=2的解(x i,x j);(ii)若方程x i﹣x j=k(k>0)至少有三组不同的解,写出k的所有可能取值.(Ⅱ)证明:对任意一个X,存在正整数k,使得方程x i﹣x j=k(1≤i,j≤8)至少有三组不同的解.2018年北京市朝阳区高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集为实数集R,集合A={x|x2﹣3x<0},B={x|2x>1},则(∁R A)∩B=()A.(﹣∞,0]∪[3,+∞)B.(0,1]C.[3,+∞)D.[1,+∞)【解答】解:集合A={x|x2﹣3x<0}={x|x(x﹣3)<0}={x|0<x<3},集合B={x|2x>1}={x|2x>20}={x|x>0};所以∁R A={x|x≤0或x≥3},所以(∁R A)∩B={x|x≥3}=[3,+∞).故选:C.2.(5分)复数z满足(1+i)z=i,则在复平面内复数z所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:由(1+i)z=i,得,∴z在复平面内对应的点为,在第一象限,故选:A.3.(5分)直线l的参数方程为(t为参数),则l的倾斜角大小为()A.B.C.D.【解答】解:根据题意,直线l的参数方程为(t为参数),则到直线的方程为,所以直线的斜率为,倾斜角为,故选:C.4.(5分)设,是单位向量,则“•>0”是“和的夹角为锐角”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:设与的夹角是θ,因为,是单位向量,所以•>0等价于cosθ>0,由0≤θ≤π得,0≤θ<,所以“•>0”推不出“和的夹角为锐角”;反之,和的夹角为锐角得cosθ>0,即得•>0,所以“和的夹角为锐角”推出“•>0”,综上可得,“•>0”是“和的夹角为锐角”的必要不充分条件,故选:B.5.(5分)某单位安排甲、乙、丙、丁4名工作人员从周一到周五值班,每天有且只有1人值班,每人至少安排一天且甲连续两天值班,则不同的安排方法种数为()A.18B.24C.48D.96【解答】解:根据题意,分2步进行分析:①,甲连续2天上班,共有(周一,周二),(周二,周三),(周三,周四),(周四,周五)四种情况,②,剩下三个人进行全排列,有种排法,因此共有4×6=24种排法,故选:B.6.(5分)某四棱锥的三视图如图所示,则该四棱锥的体积等于()A.B.C.D.【解答】解:抠点法:在长方体ABCD﹣A1B1C1D1中抠点,1)由正视图可知:C1D1上没有点;2)由侧视图可知:B1C1上没有点;3)由俯视图可知:CC1上没有点;4)由正(俯)视图可知:D,E处有点,由虚线可知B,F处有点,A点排除.由上述可还原出四棱锥A1﹣BEDF,=1×1=1,.如右图所示,S四边形BEDF故选:D.7.(5分)庙会是我国古老的传统民俗文化活动,又称“庙市”或“节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:甲说:“我或乙能中奖”;乙说:“丁能中奖”;丙说:“我或乙能中奖”;丁说:“甲不能中奖”.游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是()A.甲B.乙C.丙D.丁【解答】解:由四人的预测可得下表:1)若甲中奖,仅有甲预测正确,符合题意2)若乙中奖,甲、丙、丁预测正确,不符合题意3)若丙中奖,丙、丁预测正确,不符合题意4)若丁中奖,乙、丁预测正确,不符合题意故只有当甲中奖时,仅有甲一人预测正确.故选:A.8.(5分)在平面直角坐标系xOy中,已知点A(,0),B(1,2).动点P 满足=+,其中λ,μ∈[0,1],λ+μ∈[1,2],则所有点P构成的图形面积为()A.1B.2C.D.2【解答】解:以OA,OB为邻边作平行四边形OACB,∵=+,且λ,μ∈[0,1],λ+μ∈[1,2],∴P点位于△ABC内部(包含边界).==.∴所有点P构成的图形面积为S△ABC故选:C.二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)执行如图所示的程序框图,若输入m=5,则输出k的值为4.【解答】解:模拟程序的运行,可得:第四次时,65>50,满足判断框内的条件,退出循环,输出k的值为4.故答案为:4.10.(5分)若三个点(﹣2,1),(﹣2,3),(2,﹣1)中恰有两个点在双曲线上,则双曲线C的渐近线方程为.【解答】解:根据题意,若三个点(﹣2,1),(﹣2,3),(2,﹣1)中恰有两个点在双曲线上,又由双曲线的图象关于原点对称,故(﹣2,1),(2,﹣1)在双曲线上,则有,解可得a=,则双曲线的方程为﹣y2=1,所以渐近线方程为;故答案为:11.(5分)函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则ω=2;函数f(x)在区间上的零点为.【解答】解:由函数f(x)=A sin(ωx+φ)的部分图象得,即最小正周期T=π;又因为,且ω>0,解得ω=2;由图得时,,又因为,所以;函数f(x)的零点即的图象与x轴交点的横坐标,令,解得;因为,得,所以函数的零点为.故答案为:.12.(5分)已知两点A(﹣2,0),B(0,2),点C是圆x2+y2﹣2x+2y=0上任意点,则△ABC面积的最小值是2.【解答】解:圆x2+y2﹣2x+2y=0化为(x2﹣2x+1)+(y2+2y+1)=2,即(x﹣1)2+(y+1)2=2,由题意即为在圆上找一点到线段AB的距离最小即可,直线,y﹣2=x,∴线段AB:y=x+2(﹣2≤x≤0),圆心(1,﹣1)到其距离,∴圆上某点到线段AB的距离最小值为,=2.故答案为:2.13.(5分)等比数列{a n}满足如下条件:①a1>0;②数列{a n}的前n项和S n<1.试写出满足上述所有条件的一个数列的通项公式(答案不唯一).【解答】解:根据题意,等比数列{a n}满足如下条件:①a1>0;②数列{a n}的前n项和S n<1,则有0<a1<1,0<q<1,据此满足条件的一个数列的通项公式为(答案不唯一);故答案为:(答案不唯一)14.(5分)已知a∈R,函数当x>0时,函数f(x)的最大值是;若函数f(x)的图象上有且只有两对点关于y轴对称,则a的取值范围是(﹣1,).【解答】解:(1)当x>0时,,令,当,即x=1时取等号,即当x=1时,f1(x)min=2,令,又因为,则;(2)f(x)图象仅有两对点关于y轴对称,即f(x)(x<0)的图象关于y轴对称的函数图象与f(x)(x>0)仅有两个交点,当x<0时,f(x)=(x+1)2+a.设其关于y轴对称的函数为g(x),∴g(x)=f(﹣x)=(x﹣1)2+a(x>0)∵,由(1)可知近似图象如图所示:当g(x)与f(x)仅有两个交点时,,综上,a的取值范围是(﹣1,),故答案为:,(﹣1,).三、解答题(共6小题,共80分,解答应写出文字说明,演算步骤或证明过程)15.(13分)在△ABC中,已知,b=2a cos A.(Ⅰ)若ac=5,求△ABC的面积;(Ⅱ)若B为锐角,求sin C的值.【解答】解:(Ⅰ)根据题意,若b=2a cos A,由正弦定理得,则sin B =2sin A cos A,,因为,所以,所以,所以.(Ⅱ)由(Ⅰ)知,因为B为锐角,所以.所以sin C=sin(π﹣A﹣B)=sin(A+B)=sin A cos B+cos A sin B==16.(14分)如图1,在矩形ABCD中,AB=2,BC=4,E为AD的中点,O为BE的中点.将△ABE沿BE折起到A'BE,使得平面A'BE⊥平面BCDE(如图2)(Ⅰ)求证:A'O⊥CD;(Ⅱ)求直线A'C与平面A'DE所成角的正弦值;(Ⅲ)在线段A'C上是否存在点P,使得OP∥平面A'DE?若存在,求出的值;若不存在,请说明理由.【解答】证明:(Ⅰ)如图,在矩形ABCD中,∵AB=2,BC=4,E为AD中点,∴AB=AE=2,∵O为BE的中点,∴AO⊥BE,由题意可知,A'O⊥BE,∵平面A'BE⊥平面BCDE,平面A'BE∩平面BCDE=BE,A'O⊂平面A'BE,∴A'O⊥平面BCDE,∵CD⊂平面BCDE,∴A'O⊥CD.解:(Ⅱ)取BC中点为F,连结OF,由矩形ABCD性质,AB=2,BC=4,可知OF⊥BE,由(Ⅰ)可知,A'O⊥BE,A'O⊥OF,以O为原点,OA'为z轴,OF为x轴,OE为y轴建立坐标系,在Rt△BAE中,由AB=2,AE=2,则,∴,,,,,设平面A'DE的一个法向量为则,,令y=z=1,则x=﹣1,∴,设直线A'C与平面A'DE所成角为θ,,∴直线A'C与平面A'DE所成角的正弦值为.(Ⅲ)假设在线段A'C上存在点P,满足OP∥平面A'DE,设由,∴,,若OP∥平面A'DE,则,∴,解得,所以.17.(13分)某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量求ξ的分布列及数学期望Eξ.【解答】解:(Ⅰ)设该学校选考方案确定的学生中选考生物的学生为x,则(人),所以该学校选考方案确定的学生中选考生物的学生为140人;(Ⅱ)该男生和该女生的选考方案中都含有历史科目的概率为P=;(Ⅲ)由题意知ξ的所有可能取值为1,2,,P(ξ=2)===;所以ξ的分布列为:ξ的数学期望为.18.(13分)已知函数.(Ⅰ)当a=2时,(i)求曲线y=f(x)在点(1,f(1))处的切线方程;(ii)求函数f(x)的单调区间;(Ⅱ)若1<a<2,求证:f(x)<﹣1.【解答】解:(Ⅰ)当a=2时,,定义域为(0,+∞),,f′(1)=﹣1﹣2=﹣3,f'(1)=2﹣2=0;所以切点坐标为(1,﹣3),切线斜率为0所以切线方程为y=﹣3;(ii)令g(x)=2﹣lnx﹣2x2,所以g(x)在(0,+∞)上单调递减,且g(1)=0所以当x∈(0,1)时,g(x)>0即f'(x)>0所以当x∈(1,+∞)时,g(x)<0即f'(x)<0综上所述,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).(Ⅱ)证明:f(x)<﹣1,即设,,设φ(x)=﹣ax2﹣lnx+2所以φ'(x)在(0,+∞)小于零恒成立即h'(x)在(0,+∞)上单调递减因为1<a<2,所以h'(1)=2﹣a>0,h'(e2)=﹣a<0,所以在(1,e2)上必存在一个x0使得,即,所以当x∈(0,x0)时,h'(x)>0,h(x)单调递增,当x∈(x0,+∞)时,h'(x)<0,h(x)单调递减,所以,因为,所以,令h(x0)=0得,因为1<a<2,所以,,因为,所以h(x0)<0恒成立,即h(x)<0恒成立,综上所述,当1<a<2时,f(x)<﹣1.19.(14分)已知椭圆的离心率为,且过点.(Ⅰ)求椭圆C的方程;(Ⅱ)过椭圆C的左焦点的直线l1与椭圆C交于A,B两点,直线l2过坐标原点且与直线l1的斜率互为相反数.若直线l2与椭圆交于E,F两点且均不与点A,B重合,设直线AE与x轴所成的锐角为θ1,直线BF与x轴所成的锐角为θ2,判断θ1与θ2的大小关系并加以证明.【解答】解:(Ⅰ)由题可得,解得.所以椭圆C的方程为.(Ⅱ)结论:θ1=θ2,理由如下:由题知直线l1斜率存在,设l1:y=k(x+1),A(x1,y1),B(x2,y2).联立,消去y得(1+2k2)x2+4k2x+2k2﹣2=0,由题易知△>0恒成立,由韦达定理得,因为l2与l1斜率相反且过原点,设l2:y=﹣kx,E(x3,y3),F(x4,y4),联立消去y得(1+2k2)x2﹣2=0,由题易知△>0恒成立,由韦达定理得,因为E,F两点不与A,B重合,所以直线AE,BF存在斜率k AE,k BF,则=====0所以直线AE,BF的倾斜角互补,所以θ1=θ2.20.(13分)已知集合X={x1,x2,…,x8}是集合S={2001,2002,2003,…,2016,2017}的一个含有8个元素的子集.(Ⅰ)当X={2001,2002,2005,2007,2011,2013,2016,2017}时,设x i,x j∈X(1≤i,j≤8),(i)写出方程x i﹣x j=2的解(x i,x j);(ii)若方程x i﹣x j=k(k>0)至少有三组不同的解,写出k的所有可能取值.(Ⅱ)证明:对任意一个X,存在正整数k,使得方程x i﹣x j=k(1≤i,j≤8)至少有三组不同的解.【解答】解:(Ⅰ)(i)方程x i﹣x j=2的解有:(x i,x j)=(2007,2005),(2013,2011)(ii)以下规定两数的差均为正,则:列出集合X的从小到大8个数中相邻两数的差:1,3,2,4,2,3,1;中间隔一数的两数差(即上一列差数中相邻两数和):4,5,6,6,5,4;中间相隔二数的两数差:6,9,8,9,6;中间相隔三数的两数差:10,11,11,10;中间相隔四数的两数差:12,14,12;中间相隔五数的两数差:15,15;中间相隔六数的两数差:16.这28个差数中,只有4出现3次,6出现4次,其余都不超过2次,所以k的可能取值有4,6(Ⅱ)证明:不妨设2001≤x1<x2<…<x8≤2017记a i=x i+1﹣x i(i=1,2,…,7),b i=x i+1﹣x i(i=1,2,…,6),共13个差数.假设不存在满足条件的k,则这13个数中至多两个1、两个2、两个3、两个4、两个5、两个6,从而(a1+a2+…+a7)+(b1+b2+…+b6)≥2(1+2+…+6)+7=49①这与①矛盾,所以结论成立.。
北京市朝阳区2018年一模数学理科试题
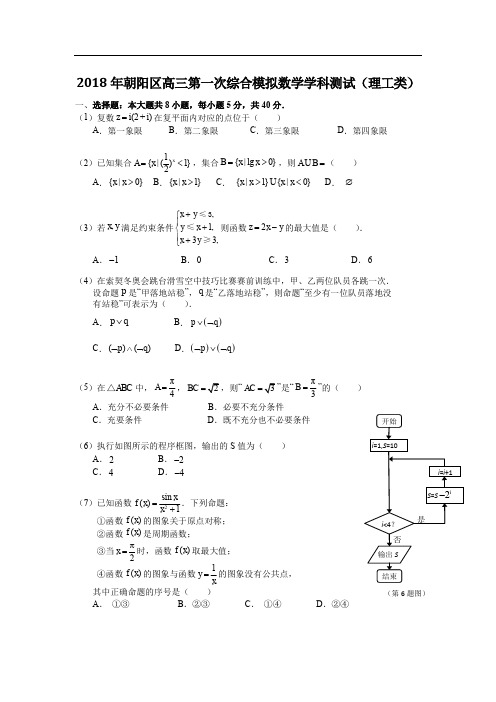
(第6题图)2018年朝阳区高三第一次综合模拟数学学科测试(理工类)一、选择题:本大题共8小题,每小题5分,共40分. (1)复数i(2+i)z =在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限(2)已知集合1{|(1}2xA x =<,集合{|lg 0}B x x =>,则A B =U ( )A .{|0}x x >B .{|1}x x >C . {|1}{|0}x x x x ><UD . ∅(3)若,x y 满足约束条件,1,33,x y y x x y +⎧⎪+⎨⎪+⎩≤3≤≥则函数2z x y =-的最大值是( ).A .1-B .0C .3D .6(4)在索契冬奥会跳台滑雪空中技巧比赛赛前训练中,甲、乙两位队员各跳一次.设命题p 是“甲落地站稳”,q 是“乙落地站稳”,则命题“至少有一位队员落地没 有站稳”可表示为( ).A .p q ∨B .()p q ∨⌝ C .()()p q ⌝∧⌝ D .()()p q ⌝∨⌝(5)在ABC △中,π4A =,BC ,则“AC ”是“π3B =”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件(6)执行如图所示的程序框图,输出的S 值为( )A .2B .2-C .4D .4-(7)已知函数2sin ()1xf x x =+.下列命题:①函数()f x 的图象关于原点对称; ②函数()f x 是周期函数;③当2x π=时,函数()f x 取最大值;④函数()f x 的图象与函数1y x=的图象没有公共点,其中正确命题的序号是( )A . ①③B .②③C . ①④D .②④(8)直线y x m =+与圆2216x y +=交于不同的两点M ,N,且MN ON ≥+uuu r r uuu r,其中O 是坐标原点,则实数m 的取值范围是( )A .(-U B.(⎡--⎣UC . [2,2]-D .[-二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.(9)抛物线28y x =的准线方程是 .(10)在一次选秀比赛中,五位评委为一位表演者打分,若去掉一个最低分后平均分为90分,去掉一个最高分后平均分为86分.那么最高分比最低分高 分.(11)某三棱锥的三视图如图所示,则这个三棱锥的体积为 ;表面积为 .(12)双曲线2221(0)y x b b-=>的一个焦点到其渐近线的距离是2,则b = ;此双曲线的离心率为 .(13)有标号分别为1,2,3的红色卡片3张,标号分别为1,2,3的蓝色卡片3张,现将全部的6张卡片放在2行3列的格内(如 图).若颜色相同的卡片在同一行, 则不同的放法种数为 .(用数字作答)(14)如图,在四棱锥S ABCD -中,SB ⊥底面ABCD .底面ABCD 为梯形,AB AD ⊥,AB ∥CD ,1,3AB AD ==,2CD =.若点E 是线段AD 上的 动点,则满足90SEC ∠=︒的点E 的个数是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分)已知函数22()2sin()cos sin cos f x x x x x =π-⋅+-,x ∈R .俯视图BC DESA(Ⅰ)求()2f π的值及函数()f x 的最小正周期;(Ⅱ)求函数()f x 在[]0,π上的单调减区间.(16)(本小题满分13分)某单位从一所学校招收某类特殊人才.对20位已经选拔入围的学生进行运动协调能力和逻辑思维能力只知道从这20位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为25.(I)求a,ξ的值;(II)从参加测试的20位学生中任意抽取2位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;(III)从参加测试的20位学生中任意抽取2位,设运动协调能力或逻辑思维能力优秀的学生人数为ξ,求随机变量ξ的分布列及其数学期望Eξ.(17)(本小题满分14分)如图,四棱锥P ABCD -的底面为正方形,侧面PAD ⊥底面ABCD .PAD △为等腰直角三角形,且PA AD ⊥. E ,F 分别为底边AB 和侧棱PC 的中点. (Ⅰ)求证:EF ∥平面PAD ; (Ⅱ)求证:EF ⊥平面PCD ; (Ⅲ)求二面角E PD C --的余弦值.A E BCDP F(18)(本小题满分13分)已知函数21()ln 2f x ax x =-,a ∈R .(Ⅰ)求函数()f x 的单调区间;(Ⅱ)若函数()f x 在区间[1,e]的最小值为1,求a 的值.(19)(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>经过点.(Ⅰ)求椭圆C 的方程;(Ⅱ)直线(1)(0)y k x k =-≠与椭圆C 交于,A B 两点,点M 是椭圆C 的右顶点.直线AM 与直线BM 分别与y 轴交于点,P Q ,试问以线段PQ 为直径的圆是否过x 轴上的定点?若是,求出定点坐标;若不是,说明理由.(20)(本小题满分13分)从1,2,3,,n L 中这n 个数中取m (,m n *∈N ,3m n ≤≤)个数组成递增等差数列,所有可能的递增等差数列的个数记为(,)f n m .(Ⅰ)当5,3n m ==时,写出所有可能的递增等差数列及(5,3)f 的值; (Ⅱ)求(100,10)f ;(Ⅲ)求证:()(1)(,)2(1)n m n f n m m -+>-.。
2018年高三最新 北京市朝阳区2018年高三第三次统一考

北京市朝阳区2018年高三第三次统一考试卷数学(文史类)2018.5本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
第I 卷1至2页。
第II 卷3至8页。
共150分。
考试时间120分钟。
第I 卷(选择题共40分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
3. 考试结束,监考人将本试卷和答题卡一并收回。
参考公式:三角函数的和差化积公式sin sin sincosαβαβαβ+=+-222sin sin cossinαβαβαβ-=+-222cos cos coscosαβαβαβ+=+-222cos cos sinsinαβαβαβ-=-+-222正棱台、圆台的侧面积公式:S c c l 台侧=+12(')其中c c '、分别表示上、下底面周长,l 表示斜高或母线长 台体的体积公式V S S S S h 台体=++13('')其中S S '、分别表示上、下底面面积,h 表示高一. 选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知全集{}I R M x x x ==<>,或|01,N x x x =-<⎧⎨⎩⎫⎬⎭10,则( ) A . M N R =B . M N =φC . M N =D . N M =2. 将函数y f x x x R =∈()cos ,的图象向右平移π4个单位长度,再作关于x 轴的对称变换,得到y x x R =∈cos2,的图象,则f x ()可以是( )A . sin xB . cos xC . 2sin xD . 2cos x3. 设l m n 、、表示三条直线,αβγ、、表示三个平面,则下列命题中不成立的是( )A . 若l m l m ⊥⊥αα,,则//B . 若m n l m l m n ⊂⊥⊥ββ,是在内的射影,,则C . 若m n m n n ⊂⊄ααα,,,则////D . 若αγβγαβ⊥⊥,,则//4. 抛物线C y ax x :=-2的顶点在直线y x =2的下方时,实数a 的取值范围是( )A . a>0B . a<4C . 0<a<4D . a<0或a>4 5. 已知复数z 满足||||z z i =+1,则的最大值是( ) A . 0 B . 1 C . 2 D . 36. 05<<x 是不等式||x -<24成立的( ) A . 充分不必要条件 B . 必要不充分条件 C . 充要条件D . 既不充分也不必要条件7. 直线x y x y sin cos sin ()θθθ+=+-+=21422与圆的位置关系是( ) A . 相离 B . 相切 C . 相交 D . 以上都可以8. 如图所示∠=ACB 90°,平面ACB 外有一点P ,PC=4cm ,点P 到角两边CA 、CB 的距离都等于23cm ,那么PC 与平面ABC 所成角的大小为( )A . 30°B . 45°C . 60°D . 75°第II卷(非选择题共110分)注意事项:1.第II卷共6页,用钢笔或圆珠笔直接答在试卷中。
2018-2019朝阳区一模数学文科答案

北京市朝阳区高三年级第一次综合练习数学(文)参考答案2019.3一、选择题(40分)二、填空题(30分)15. (本小题满分13分) 解:(Ⅰ)由已知2()coscos 3333f ππππ=+13144=+=. 因为()f x 1cos 2sin 222x x +=+π1sin(2)62x =++, 所以函数()f x 的最小正周期为π.………………………..7分(II )由πππ2π22π262k x k -++≤≤得,ππππ36k x k -+≤≤,k ∈Z .所以,函数()f x 的单调增区间为πππ,π36k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z . 当0k =时, 函数()f x 的单调增区间为ππ,36⎡⎤-⎢⎥⎣⎦, 若函数()f x 在区间[0,]m 上单调递增,则ππ[0,],36m ⎡⎤⊆-⎢⎥⎣⎦, 所以实数m 的最大值为π6. ………………………..13分16. (本小题满分13分) 解:(I )由数列{}n a 为等比数列,且112a =,44a =,得3414a a q ==,解得2q =.则数列{}n a 的通项公式1212n n n a a q --==,n *∈N . ………………..5分(II ) 2662n n n b a n n -=+-=-+102(546)(222)n n S n --=--++-++++L L(11)2122n n n --=+.当5n ≥时,(11)152n n -≥-,213122n -≥,所以0n S >; 当4n =时,44472102S -⨯+-=<; 当3n =时,33382102S -⨯+-=<; 当2n =时,22292102S -⨯+-=<; 当1n =时,111102102S -⨯+-=<. 所以,n 的最小值为5 .………………………..13分 17. (本小题满分13分)(Ⅰ)因为0.012530.040520.048551a ⨯⨯+⨯⨯+⨯+⨯=, 所以0.036=a .………………………..4分 (Ⅱ)由题意知,该乘客在甲站平均等待时间少于20分钟的频率为0.0120.0400.048)50.5(++⨯=,故()P A 的估计值为0.5 .…………..8分(Ⅲ)1=X 0.012⨯5+0.040⨯10+0.048⨯15+0.040⨯20+0.036⨯25+0.012⨯30+0.012⨯35⨯5() =18.3.由直方图知:12X X < ………………………..13分 18. (本小题满分14分)解:(Ⅰ)证明:因为四边形ADEF 为正方形,所以AF AD ⊥.又因为平面ADEF ⊥平面ABCD ,且平面ADEF I 平面ABCD AD =,AF ⊂平面ADEF , 所以AF ⊥平面ABCD .又CD ⊂平面ABCD ,所以AF CD ⊥. ……………………….4分 (Ⅱ)延长AM 交BC 于点G ,因为//AD BC ,M 为BD 中点, 所以BGM ∆≌DAM ∆, 所以1BG AD ==. 因为2BC =,所以1GC =. 由已知1FE AD ==,且//FE AD ,又因为//AD GC ,所以//FE GC ,且FE GC =, 所以四边形GCEF 为平行四边形,所以//CE GF . 因为CE ⊄平面AMF ,GF ⊂平面AMF ,所以//CE 平面AMF . ……………………….9分 (Ⅲ)设G 为BC 中点,连接DG ,EG .由已知//DG AB ,所以//DG 平面AFB . 又因为//DE AF ,所以//DE 平面AFB , 所以平面//DEG 平面AFB .因为AD AB ⊥,AD AF ⊥,所以AD ⊥平面ABF , 所以多面体AFB DEG -为直三棱柱. 因为1AB AF AD ===,且90BAF ∠=︒, 所以11111122AFB AFB DEG V V S AD ∆-==⋅=⨯⨯⨯=三棱柱. 由已知//DG AB ,且DG AB =, 所以DG GC ⊥,且1DG GC ==. 又因为//DE AF ,AF ⊥平面CDG , 所以DE ⊥平面CDG . 因为1DE AF ==,EDCBAFMG所以211111113326CDG E CDG V V S DE ∆-==⋅=⨯⨯⨯⨯=三棱锥, 所以12112263ABCDEFV V V =+=+=多面体. ……………………….14分19. (本小题满分13分)解:(Ⅰ)求导得()e 4xf x a '=-.定义域x ∈R .当0a ≤时,()0f x '<,函数()f x 在R 上为减函数. 当0a >时,令()0f x '>得4lnx a >,()f x 为增函数; 令()0f x '<得4ln x a<,()f x 为减函数.所以0a ≤时,函数()f x 减区间是(,)-∞+∞. 当0a >时,函数()f x 增区间是 4(ln,)a +∞;减区间是4(,ln )a-∞. ………5分 (Ⅱ)依题意,只需证2e 410x x x -++>.设2()e 41xF x x x =-++.则()e 42xF x x '=-+,设()()G x F x '=.因为()e 20xG x '=+>,所以()G x 在(,)-∞+∞上单调递增.又因为(0)30,(1)e 20G G =-<=->,所以()0G x =在(0,1)内有唯一解,记为0x 即00e42x x =-.当0x x <时,()0F x '<,()F x 单调递减;当0x x >时,()0F x '>,()F x 单调递增;所以022min 000000()()e 4165,(0,1)xF x F x x x x x x ==-++=-+∈.设22()65(3)4g x x x x =-+=--,(0,1)x ∈.则()(1)0g x g >=.所以0()0F x >.所以()0F x >,即曲线()y f x =在抛物线21y x =--上方.………13分20. (本小题满分14分)(Ⅰ)由题意a ,1b =,1c ==所以离心率c e a ==,左焦点(1,0)F -. …………4分(Ⅱ)由题知,220012x y +=,即220022x y +=. 当00y =时直线l方程为x或x =l 与椭圆C 相切. 当00y ≠时,由22001,222x y x x y y ⎧+=⎪⎨⎪+=⎩得2222000(2)4440y x x x x y +-+-=, 即22002220x x x y -+-= 所以 2200(2)4(22)x y ∆=---22004+880x y =-= 故直线l 与椭圆C 相切. …………8分 (Ⅲ)设11(,)A x y ,22(,)B x y ,当00y =时,12x x =,12y y =-,1x =2211(1)FA FB x y ⋅=+-u u u r u u u r 2211(1)6(1)x x =+-+-21240x =-=,所以FA FB ⊥u u u r u u u r,即90AFB ∠=o .当00y ≠时,由2200(1)6,22x y x x y y ⎧-+=⎪⎨+=⎪⎩ 得2222000(1)2(2)2100y x y x x y +-++-=, 则20012202(2)1y x x x y ++=+,21222101y x x y -=+, 2001212122220001()42x x y y x x x x y y y =-++200254422x x y --+=+. 因为1122(1,)(1,)FA FB x y x y ⋅=+⋅+u u u r u u u r1212121x x x x y y =++++2222000000220042084225442222y y x y x x y y -++++--+=+++ 220025(2)10022x y y -++==+. 所以FA FB ⊥u u u r u u u r,即90AFB ∠=o .故AFB ∠为定值90o . …………14分。
2018年高三最新 北京市朝阳区2018年高三第一次统一考试数学文试卷 精品

朝阳区2018年高三第一次统一考试数学试卷(文史类)本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至2页。
第II卷3至8页。
共150分,考试时间120分钟。
第I卷(选择题,共40分)注意事项:1. 答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
3. 考试结束,监考人将本试卷和答题卡一并收回。
参考公式:三角函数的和差化积公式:正棱台、圆台的侧面积公式:其中分别表示上、下底面周长,l表示斜高或母线长台体的体积公式其中分别表示上、下底面面积,h表示高一. 选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设,集合,则A与B的关系是()A. B.C. D.2. 已知图中曲线是函数的图象,则曲线对应的a的值依次为()A. B. C. D.3. 将函数图象上所有点向左平行移动个单位长度,再把所得图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为()A. B.C. D.4. 过双曲线的右焦点作直线l交双曲线于A、B两点,如果,则这样的直线的条数为()A. 1条B. 2条C. 3条D. 4条5. 山坡与水平面成角,坡面上有一条与山底坡脚的水平线成角的直线小路,某人沿小路上坡走了一段路后升高了100米,则此人行走的路程为()A. 300米B. 400米C. 200米D. 米6. ,则有()A. B. C. D.7. 若三棱锥S—ABC的顶点S在底面上的射影H在的内部,且是的垂心,则()A. 三条侧棱长相等B. 三个侧面与底面所成的角相等C. H到三边的距离相等D. 点A在平面SBC上的射影是的垂心8. 已知:,则使成立的充要条件是()A. B. C. D.第II卷(非选择题共110分)注意事项:1. 第II卷共6页,用钢笔或圆珠笔直接答在试卷中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年北京市朝阳区高三一模数学(文)考试
第I 卷(选择题爱共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1. 已知全集为实数集R ,集合2
2{|30},{|log 0}A x x x B x x , 则()A B
R e (A )(,0](1,)(B )(0,1]
(C )[3,)(D )
【答案】C
【解析】本题考查集合的运算.
集合2{|30}{|(3)0}{|03}A x x x x x x x x ,
集合222{|log 0}{|log log 1}{|1}B x x x x x x .
所以{|0A x x R e 或3}x ,所以(){|3}A B x x R e ,故选C .
2. 在复平面内,复数i
1i z 所对应的点位于
(A )第一象限(B )第二象限
(C )第三象限(D )第四象限
【答案】A
【解析】本题考查复数的运算与坐标表示.
i i(1i)1i
1i (1i)(1i)2z ,在复平面内对应的点为1
1
(,)22,在第一象限
,
故选A .
3. 已知平面向量(,1),(2,1)x x a b ,且//a b ,则实数x 的值是
(A )1(B )1(C )2(D )1或2
【答案】D
【解析】本题考查平面向量的平行的坐标运算
. 由(,1),(2,1)x x a b ,且//a b ,可以得到(1)2x x ,
即22(2)(1)0x x x x ,所以1x
或2x ,故选D . 4. 已知直线m 平面,则“直线n m ”是“//n ”的
(A )充分但不必要条件
(B )必要但不充分条件(C )充要条件(D )既不充分又不必要条件
【答案】B
【解析】本题考查线面位置关系的判定、性质与充分必要条件.
(充分性)当m 且n m 时,我们可以得到//n 或n (因为直线n 与平面的位置关系不确定),所以充分性不成立;
(必要性)当//n 时,过直线n 可做平面与平面交于直线a ,则有//n a .又有m ,则有m a ,即m n .所以必要性成立,故选B .
5. 已知F 为抛物线2:4C y
x 的焦点,过点F 的直线l 交抛物线C 于,A B 两点,若||8AB ,则线段AB 的中点M 到直线10x 的距离为
(A )2(B )4(C )8(D )16
【答案】B
【解析】本题考查抛物线的定义
. 如图,抛物线24y
x 的焦点为(1,0)F ,准线为1x ,即10x . 分别过,A B 作准线的垂线,垂足为,C D ,
则有||||||||||8AB AF BF AC BD .
过AB 的中点M 作准线的垂线,垂足为N ,
则MN 为直角梯形ABDC 中位线,
则1||(||||)42MN AC BD ,即M 到准线
1x 的距离为4.故选B .
6. 某四棱锥的三视图如图所示,则该四棱
锥的。
