2019朝阳区高三一模有答案(数学理)

合集下载

北京市朝阳区2019届高三一模数学(理)试题及答案

北京市朝阳区高三年级第一次综合练习数学（理） 2019.3本试卷共4页。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1.已知集合A={x︳x>1},集合B={ x︳x²<4},则A∩B=A. {x︳x>-2}B. {x︳1<x<2}C. {x︳1≤x<2}D. R2. 在复平面内，复数z=对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. （）的展开式中的常数项为A. -12B. -6C. 6D. 124. 若函数f(x)=则函数f(x)的值域是A. (-∞,2)B. (-∞,2]C. [0,+ ∞)D. (-∞,0)∪(0,2)5. 如图，函数f(x)的图像是由正弦曲线或余弦曲线经过变换得到的，则f(x)的解析式可以是A. f(x)=sin(2x+)B. f(x)=sin(4x+)C. f(x)=cos(2x+)D. f(x)=cos(4x+)6. 记不等式组,所表示的平面区域为D,“点（-1，1）∈D”是“k”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 某三棱锥的三视图如图所示（网格纸上小正方形的边长为1），则该三棱锥的体积为A. 4B. 2C.D.8. 某单位周一、周二、周三开车上班的职工人数分别是14、10、8，若这三天中至少有一天开车上班的职工人数是20，则这三天都开车上班的职工人数至多是A. 5B. 6C. 7D. 8第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

9. 双曲线-=1的右焦点到其一条渐近线的距离是10. 执行如图所示的程序框图，输出的x值为11.在极坐标系中，直线cosθ=1与圆cosθ交于A,B两点，则=12.能说明“函数f(x)的图像在区间[0,2]上是一条连续不断的曲线，若f(0), f(2)>0则f(x)在（0，2）内无零点”为假命题的一个函数是13.天坛公园是明、清两代皇帝“祭天”“祈谷”的场所，天坛公园中的圜丘台共有三层（如下页本题图1所示）上层坛的中心是一块呈圆形的大理石板，从中心向外围以扇面形石铺成（如下页本题图2所示），上层从第一环至第九还共有九环，中层坛从第十环至第十八环共有九环，下层坛从第十九环至第二十七环共有九环；第一环的扇面形石有9块，从第二环起，每环的扇面形石块数比前一环多9块，则第二十七环的扇面形石块数是；上、中、下三层坛所有的扇面形石块数是14.在平面内，点A是定点，动点B,C满足==1,·=0,则集合=+,1≤≤2｜所表示的区域面积是三、解答题共6小题，共80分，解答应写出文字说明，演算步骤或证明过程15.（本小题满分13分）在△ABC中，a=,∠A=120°，△ABC的面积等于，且b<c,（I）求b的值；（II）求cos2B的值16.（本小题满分13分）某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客。

北京各区2019-2021年高三年级数学模拟试题汇编-两角和与差的三角函数

北京各区2019-2021年高三年级数学一模二模试题汇编两角和与差的三角函数一．选择题（共11小题） 1．（2019•西城区模拟）已知12cos 13α=，(,0)2πα∈−，则cos()(4πα−= )A B C D 2．（2019•北京模拟）如图，在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，终边分别是射线OA 和射线OB ．射线OA ，OC 与单位圆的交点分别为34(,)55A ，(1,0)C −．若6BOC π∠=，则cos()βα−的值是( )A B C D3．（2019•丰台区二模）已知3(,)22ππα∈，且tan αsin (α= )A ．B ．C D4．（2019•延庆区一模）函数()sin 22f x x x =在区间[,]22ππ−上的零点之和是( )A ．3π−B ．6π−C ．6πD ．3π5．（2019•西城区模拟）sincos1212ππ+的值为( )A B C D ．126．（2019•北京模拟）已知tan()16πα+=，则tan()(6πα−= )A ．2B ．2C ．2−D ．2−+7．（2020•海淀区校级模拟）若()sin cos f x x x =−在[a −，]a 上是增函数，则a 的最大值是( )A ．6πB ．4πC ．3πD ．2π8．（2020•北京模拟）函数()sin 2cos 2f x x x =+的最小正周期是( ) A ．2πB ．πC ．2πD ．4π9．（2021•丰台区模拟）sin 69cos9sin 21sin 9(︒︒−︒︒= )A ．B ．12−C D ．1210．（2021•门头沟区一模）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于x 轴对称．若cos α=cos()(αβ−= ) A ．35−B ．35C ．1D ．3411．（2021•北京模拟）cos24cos36sin 24cos54︒︒−︒︒的值等于( )A ．0B ．12C D ．12−二．填空题（共8小题）12．（2019•海淀区校级模拟）若角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线3y x =上，则tan()4πθ−=13．（2019•北京模拟）已知3cos 5α=，(0,)2πα∈，则cos()3πα+=14．（2021•北京模拟）设θ为第二象限角，若1tan()42πθ+=，则sin cos θθ+= ．15．（2020•北京模拟）已知函数()sin f x a x x =−的一条对称轴为12,()()06x f x f x π=−+=，且函数()f x 在1(x ，2)x 上具有单调性，则12||x x +的最小值为．16．（2020•北京模拟）已知(2πα∈，)π，4sin 5α=，则tan()4πα+= ． 17．（2021•丰台区二模）函数()sin cos f x x x =+的值域为．18．（2021•顺义区二模）已知α是任意角，且满足cos()sin 6k παα+⋅=，则常数k 的一个取值为．19．（2021•海淀区校级三模）已知()sin())f x x x θθ=−++是偶函数，且[0θ∈，]π，则θ= ．三．解答题（共1小题）20．（2021•丰台区一模）已知函数()sin (0)f x x x ωωω=>．（Ⅰ）当1ω=时，求()6f π的值；（Ⅱ）当函数()f x 图象的两条相邻对称轴之间的距离是2π时，______．从①②③中任选一个，补充到上面空格处并作答．①求()f x 在区间[0,]2π上的最小值；②求()f x 的单调递增区间； ③若()0f x ，求x 的取值范围．参考答案与试题解析一．选择题（共11小题）1．【分析】由已知结合同角平方关系可求sin α，然后结合两角差的余弦公式可求．【解答】解：12cos 13α=，(,0)2πα∈−， 5sin 13α∴=−，则7cos()sin )413πααα−+=故选：D ．【点评】本题主要考查了同角平方关系及两角和的余弦公式在求解三角函数值中的简单应用，属于基础试题． 2．【分析】由三角函数的定义可知，3cos 5α=，4sin 5α=，56πβ=，然后结合两角差的余弦公式即可求解【解答】解：由三角函数的定义可知，3cos 5α=，4sin 5α=，56πβ=，55314cos()cos cos sin sin 66525ππβααα∴−=+=+⨯=故选：C ．【点评】本题主要考查了三角函数的定义及两角差的余弦公式的简单应用，属于基础试题 3．【分析】直接利用三角函数的定义的应用求出结果．【解答】解：已知3(,)22ππα∈，且tan α则：sin3α==−．故选：B ．【点评】本题考查的知识要点：三角函数关系式的变换，主要考查学生的运算能力和转换能力，属于基础题题型．4．【分析】利用两角和差的三角公式化简函数的解析式，再根据函数零点的定义、正弦函数的零点，求出在区间[,]22ππ−上的零点，可得结论．【解答】解：令函数()sin 222sin(2)03f x x x x π=−=−=，可得23x k ππ−=，求得26k x ππ=+，k Z ∈．根据x ∈区间[,]22ππ−，可得3x π=−，6π，故函数在区间[,]22ππ− 上的零点之和为366πππ−+=−，故选：B ．【点评】本题主要考查函数零点的定义，两角和差的三角公式，正弦函数的零点，属于基础题． 5．【分析】可利用辅助角公式将sincos1212ππ+sin()1243πππ+=，从而可得答案．【解答】解：sin cos2())121221221212432πππππππ++=+==， sincos1212ππ∴+．故选：A ．【点评】本题考查两角和与差的正弦函数，关键是辅助角公式的熟练应用及逆用两角和的正弦，属于中档题． 6．【分析】由题意利用两角和差的正切公式求得tan α的值，再利用两角和差的正切公式求得要求式子的值．【解答】解：已知tan tantan 6tan()1631tan tan 163πααπαπαα++===−−，tan 2α∴==则tan tantan()2633παπαα−−==，故选：D ．【点评】本题主要考查两角和差的正切公式的应用，属于基础题．7．【分析】由辅助角公式可得())4f x x π−，再根据正弦函数的单调性，即可得解．【解答】解：()sin cos )4f x x x x π=−=−，令[242x k πππ−∈−+,2]2k ππ+,k Z ∈，则[24x k ππ∈−+,32]4k ππ+,k Z ∈， ∴函数()f x 的单调递增区间为[24k ππ−+,32]4k ππ+,k Z ∈，又()f x 在[a −，]a 上是增函数,∴取0k =，()f x 的单调递增区间为[4π−,3]4π,此时对应的a 的最大值为4π．故选：B ．【点评】本题考查三角恒等变换与三角函数的综合，熟练掌握辅助角公式、正弦函数的单调性是解题的关键，考查逻辑推理能力和运算能力，属于基础题．8．【分析】函数y 变形，利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值代入周期公式即可求出最小正周期．【解答】解：函数sin 2cos22y x x x =++， 2ω=，T π∴=．故选：B ．【点评】此题考查了两角和与差的正弦函数公式，以及三角函数的周期性及其求法，将函数解析式化为一个角的正弦函数是解本题的关键．9．【分析】直接利用三角函数的关系式的变换求出结果．【解答】解：sin 69cos9sin 21sin9cos21cos9sin 21sin9cos30︒︒−︒︒=︒︒−︒︒=︒ 故选：C ．【点评】本题考查的知识要点：三角函数的关系式的变换，主要考查学生的运算能力和数学思维能力，属于基础题．10．【分析】由任意角的三角函数知cos cos αβ=，sin sin αβ=−，再根据两角差的余弦公式，即可得解．【解答】解：由题意得，cos cos αβ=，sin sin αβ=−， 2223cos()cos cos sin sin cos sin 2cos 15αβαβαβααα∴−=+=−=−=．故选：B ．【点评】本题考查两角和差的余弦公式，同角三角函数的平方关系，考查学生的逻辑推理能力和运算能力，属于基础题．11．【分析】由题意利用诱导公式、两角和的余弦公式，计算求得结果．【解答】解：cos24cos36sin24cos54cos24cos36sin24sin36︒︒−︒︒=︒︒−︒︒ 1cos(2436)cos602=︒+︒=︒=，故选：B ．【点评】本题主要考查诱导公式、两角和的余弦公式，属于基础题．二．填空题（共8小题）12．【分析】利用任意角的三角函数的定义求得tan θ的值，再利用两角和差的正切公式求得要求式子的值．【解答】解：角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线3y x =上，tan 3θ∴=，则tan 11tan()41tan 2πθθθ−−==+，故答案为：12．【点评】本题主要考查任意角的三角函数的定义，两角和差的正切公式的应用，属于基础题．13．【分析】利用同角三角函数的基本关系求得sin α的值，再利用两角和的余弦公式求得cos()3πα+的值．【解答】解：3cos 5α=，(0,)2πα∈，4sin 5α∴=，则1334343cos()cos cos sin sin 333252510πππααα−+=−=−=，故答案为：310−．【点评】本题主要考查同角三角函数的基本关系，两角和的余弦公式的应用，属于基础题．14．【分析】已知等式利用两角和与差的正切函数公式及特殊角的三角函数值化简，求出tan θ的值，再根据θ为第二象限角，利用同角三角函数间的基本关系求出sin θ与cos θ的值，即可求出sin cos θθ+的值．【解答】解：tan 11tan()41tan 2πθθθ++==−，1tan 3θ∴=−，而222221cos 1cos sin cos tan θθθθθ==++，θ为第二象限角，cos θ∴==，sin θ则sin cos θθ+==．故答案为：【点评】此题考查了两角和与差的正切函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．15．【分析】利用辅助角公式化简，对称为6x π=−，12()()0f x f x +=，且函数()f x 在1(x ，2)x 上具有单调性，可得对称中心，即可求出最小值．【解答】解：函数()(),f x asinx x tan θθ=−+=其中，函数()f x 的一条对称轴为6x π=−，可得1()62f a π−=−−=2a =． ∴3πθ=−；对称中心横坐标由()(),33x k k z x k k z ππππ−=∈=+∈可得；又12()()0f x f x +=，且函数()f x 在1(x ，2)x 上具有单调性，∴12||2||3x x k π+=+，当0k =时，可得122||3x x π+=．故答案为：23π．【点评】本题考查了正弦函数的最值和单调性的综合应用，属于中档题． 16．【分析】直接利用三角函数关系式的定义和和角公式的应用求出结果．【解答】解：4(,),sin 25παπα∈=，则：3cos 5α=−，所以：4tan 3α=−，则：41tan tan134tan()4471tan tan 143παπαπα−+++===−−+，故答案为：17−．【点评】本题考查的知识要点：三角函数关系式的变换，和角公式的应用，主要考查学生的运算能力和转换能力，属于基础题型．17．【分析】利用辅助角公式，化简函数的解析式，然后求解即可．【解答】解：函数()sin cos )[4f x x x x π=+=+∈．故答案为：[．【点评】本题考查了辅助角公式和三角函数的值域的求法，是基础题．18．【分析】由已知结合诱导公式进行化简即可求解．【解答】解：因为cos()sin 6k παα+⋅=，令62k ππ⋅=−，则3k =−．故答案为：3−（答案不唯一）．【点评】本题主要考查了诱导公式，属于基础题．19．【分析】正弦函数的图象关于y 轴对称，从而当0x =时，函数取得最值，代入函数后，结合正弦函数对称轴处取得函数最值可求．【解答】解()sin())f x x x θθ=−+是偶函数，故函数的图象关于y 轴对称，根据正弦函数的对称性可知，当0x =时，()f x 取得最值，故sin 2θθ−=±，所以sin 2θθ=±，即12(sin )22θθ=±，所以sin()13πθ−=±，因为[0θ∈，]π，则56πθ=，故答案为：56π．【点评】本题主要考查了正弦函数对称性的应用，解题的关键是正弦函数在对称轴处取得最值条件的应用．三．解答题（共1小题）20．【分析】()I 把1ω=代入可求()f x ，即可求解()6f π，()II 由已知先求出()2sin(2)3f x x π=+，选①：由02x π得42333x πππ+，然后结合正弦函数的性质可求； ②令222232k x k πππππ−++，解不等式可求函数的单调递增区间；③若()0f x ，结合正弦函数的图象及性质可求．【解答】解：()1I ω=时，()sin f x x x =+，故1()262f π=+=，()()2sin()3II f x x πω=+，由函数()f x 图象的两条相邻对称轴之间的距离是2π得T π=，2ω=，故()2sin(2)3f x x π=+，选①：由02x π得42333x πππ+，所以sin(2)13x π+，所以()f x 在区间[0,]2π上的最小值②求()f x 的单调递增区间，令222232k x k πππππ−++，得51212k x k ππππ−+，k Z ∈，故函数()f x 的单调递增区间5[12k ππ−，]12k ππ+，k Z ∈， ③若()0f x ，则2223k x k ππππ++，k Z ∈，解得63k x k ππππ−+，k Z ∈，故x 的取值范围[6k ππ−，]3k ππ+，k Z ∈．【点评】本题主要考查了正弦函数的周期性，单调性，最值求解，解题的关键是正弦函数性质的灵活应用．。

数学理Z

1.北京市宣武区高三第一次质量检测数学(理科)(本试卷满分150分，考试时间120分钟)第Ⅰ卷(选择题共40分)一、选择题(本大题共有8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合M＝{x|x2－2x－3≤0，x∈R}，N＝{x||x|<2，x∈R}，则M∩N等于( )A.∅B.{x|－1≤x<2}C.{x|－2≤x<－1}D.{x|2≤x<3}2.若a，b是空间两条不同的直线，α，β是空间的两个不同的平面，则a⊥α的一个充分不必要条件是( )A.a∥β，α⊥βB.a⊂β，α⊥βC.a⊥b，b∥αD.a⊥β，α∥β3.函数y＝3x＋1(－1≤x<0)的反函数是( )A.y＝1＋log3x(x>0)B.y＝－1＋log3x(x>0)C.y＝－1＋log3x(1≤x<3)D.y＝－1＋log3x(－1≤x<3)4.已知两个向量a＝(1,2)，b＝(x,1)，若(a＋2b)//(2a－2b)，则x 的值是( )A.1B.2C.12D.135.已知x ，y 满足条件⎩⎪⎨⎪⎧x ≤2，y ≤1，x ＋2y －2≥0，则x －y 的取值范围是( )A.[1,2]B.[－1,2]C.[－2,1]D.[－2，－1]6.一次演出，原计划要排4个节目，因临时有变化，拟再添加2个小品节目，若保持原有4个节目的相对顺序不变，则这6个节目不同的排列方法有( )A.30种B.25种C.24种D.20种7.已知{a n }是等比数列，a 2＝2，a 5＝14，则a 1a 2＋a 2a 3＋…＋a n a n＋1(n ∈N )的取值范围是( )A.[12,16]B.[8，323]C.[8，323)D.[163，323]8.已知定义域是全体实数的函数y ＝f (x )满足f (x ＋2π)＝f (x )，且函数g (x )＝f (x )＋f (－x )2，函数h (x )＝f (x )－f (－x )2.现定义函数p (x )，q (x )为：p (x )＝⎩⎪⎨⎪⎧g (x )－g (x ＋π)2cos x (x ≠k π＋π2)0 (x ＝k π＋π2)，q (x )＝⎩⎪⎨⎪⎧h (x )＋h (x ＋π)2sin2x (x ≠k π2)0 (x ＝k π2)，其中k ∈Z ，那么下列关于p (x )，q (x )叙述正确的是( )A.都是奇函数且周期为πB.都是偶函数且周期为πC.均无奇偶性但都有周期性D.均无周期性但都有奇偶性第Ⅱ卷(非选择题共110分)二、填空题(本大题共6个小题，每小题5分，共30分.把答案填在题中的横线上)9.设i 为虚数单位，则复数(1＋i)21－i＝ .10.若⎝ ⎛⎭⎪⎫x ＋1x n 展开式的二项式系数之和为256，则n ＝，其展开式的常数项等于 .(用数字作答)11.在等差数列{a n }中，已知a 1＋2a 8＋a 15＝96，则2a 9－a 10＝ .12.设函数y ＝2sin(2x ＋π3)的图象关于点P (x 0,0)成中心对称，若x 0∈[－π2，0]，则x 0＝ .13.以双曲线x 24－y 2m ＝1的离心率为半径，以右焦点为圆心的圆与该双曲线的渐近线相切，则m ＝ .14.连接球面上两点的线段称为球的弦，半径为4的球的两条弦AB 、CD 的长度分别为27和43，M 、N 分别是AB 、CD 的中点，两条弦的两端都在球面上运动，有下面四个命题：①弦AB 、CD 可能相交于点M ； ②弦AB 、CD 可能相交于点N ； ③MN 的最大值是5； ④MN 的最小值是1；其中所有正确命题的序号为 .三、解答题(本大题共6个小题，共80分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分13分) 已知函数f (x )＝3sin ωx ·cos ωx －cos 2ωx (ω>0)的最小正周期为π2. (Ⅰ)求ω的值；(Ⅱ)设△ABC 的三边a 、b 、c 满足b 2＝ac ，且边b 所对的角为x ，求此时f (x )的值域.16.(本小题满分13分)将3封不同的信投进A、B、C、D这4个不同的信箱、假设每封信投入每个信箱的可能性相等.(Ⅰ)求这3封信分别被投进3个信箱的概率；(Ⅱ)求恰有2个信箱没有信的概率；(Ⅲ)求A信箱中的信封数量的分布列和数学期望.17.(本小题满分13分)如图，已知四棱锥P－ABCD的底面是菱形，∠BCD＝60°，点E 是BC边的中点，AC与DE交于点O，PO⊥平面ABCD.(Ⅰ)求证：PD⊥BC；(Ⅱ)若AB＝63，PC＝62，求二面角P－AD－C的大小；(Ⅲ)在(Ⅱ)的条件下，求异面直线PB与DE所成角的余弦值.18.(本小题满分13分)设定义在R 上的函数f (x )＝a 0x 4＋a 1x 3＋a 2x 2＋a 3x ＋a 4(a 0，a 1，a 2，a 3，a 4∈R)当x ＝－1时，f (x )取得极大值23，且函数y ＝f (x ＋1)的图象关于点(－1,0)对称.(Ⅰ)求函数f (x )的表达式；(Ⅱ)试在函数y ＝f (x )的图象上求两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在区间[－2，2]上；(Ⅲ)设x n ＝2n －12n，y m ＝2(1－3m )3m(m ，n ∈N )，求证：|f (x n )－f (y m )|<43.19.(本小题满分14分)已知F 1，F 2分别是椭圆x 24＋y 23＝1的左、右焦点，曲线C 是以坐标原点为顶点，以F 2为焦点的抛物线，自点F 1引直线交曲线C 于P 、Q 两个不同的交点，点P 关于x 轴的对称点记为M .设F 1P ＝λF 1Q .(Ⅰ)求曲线C 的方程；(Ⅱ)证明：F 2M ＝－λF 2Q ； (Ⅲ)若λ∈[2,3]，求|PQ |的取值范围.20.(本小题满分14分)已知数列{a n }中，a 1＝t (t ∈R ，且t ≠0,1)，a 2＝t 2，且当x ＝t 时，函数f (x )＝12(a n －a n －1)x 2－(a n ＋1－a n )x (n ≥2，n ∈N )取得极值.(Ⅰ)求证：数列{a n ＋1－a n }是等比数列；(Ⅱ)若b n ＝a n ln|a n |(n ∈N )，求数列{b n }的前n 项和S n ； (Ⅲ)当t ＝－710时，数列{b n }中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由.2.北京市顺义区高三第一次统练数学(理科)(本试卷满分150分，考试时间120分钟)第Ⅰ卷(选择题共40分)一、选择题(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ x －x 2>0，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪－2<x <2，则( )A.M ∩N ＝ΦB.M ∪N ＝MC.M ∪N ＝RD.M ∩N ＝M 2.已知△ABC 中，AB ＝6＋22，AC ＝3，C ＝75°，那么角B等于( )A.120°B.60°C.45°D.30° 3.k ∈(33，＋∞)是“直线kx －y －4k ＝0与圆(x －2)2＋y 2＝1无公共点”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 4.函数y ＝log 2x 的图象与函数y ＝－log 2(－x )的图象( ) A.关于x 轴对称 B.关于y 轴对称 C.关于坐标原点对称 D.关于直线y ＝x 对称 5.已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点分别为F 1、F 2，点P 是双曲线右支上的一个动点，点Q 在线段F 1P 上，满足⎪⎪⎪⎪PQ ＝⎪⎪⎪⎪PF 2，那么动点Q 的轨迹是( )A.圆B.椭圆C.双曲线的一支D.抛物线6.若实数x ，y 满足⎩⎪⎨⎪⎧x －2≤0y －1≤0x ＋2y －2≥0，则z ＝2x －y 的取值范围是( )A.⎣⎢⎡⎦⎥⎤14，12B.⎣⎢⎡⎦⎥⎤14，2C.⎣⎢⎡⎦⎥⎤12，4 D.⎣⎡⎦⎤2，4 7.设函数f (x )定义在实数集上，它的图象关于直线x ＝2对称，且当x ≥2时，f (x )＝3x －1，则有( )A.f (43)<f (52)<f (53)B.f (52)<f (53)<f (43)C.f (53)<f (43)<f (52)D.f (53)<f (52)<f (43)8.数列⎩⎨⎧⎭⎬⎫a n 中，⎩⎨⎧⎭⎬⎫a n ＝⎩⎪⎨⎪⎧1n 2(1≤n ≤1 000)n2n 2－2n (n ≥1 001)则lim n →∞a n的值( ) A.等于0 B.等于1 C.等于0或1 D.不存在第Ⅱ卷(非选择题共110分)二、填空题(本大题共6小题，每小题5分，共30分.把答案填在题中横线上)9.已知(1＋a i)2＝2i ，其中i 是i 虚数单位，那么实数a ＝ .10.已知向量a 与b 的夹角为135°，且⎪⎪⎪⎪a ＝2，⎪⎪⎪⎪b ＝1.那么a·(a－b)的值为 .11.设α是第四象限的角，且tan α＝－43，则sin(α＋π4)＝ .12.已知等差数列⎩⎨⎧⎭⎬⎫an 中，a 1＝3，a 4＝12，若b n ＝a2n ，则数列⎩⎨⎧⎭⎬⎫bn 的前n 项的和S n ＝ .13.已知函数f (x )＝x 2＋2x ＋a ，f (bx )＝9x 2－6x ＋2，其中x ∈R ，a ，b 为常数，则方程f (ax ＋b )＝1的解集为 .14.已知点P 是抛物线x 2＝2y 上的一个动点，则点P 到点(2,0)的距离与点P 到该抛物线准线的距离之和的最小值为 .三、解答题(本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分13分)已知函数f (x )＝3－2sin 2ωx －2cos(ωx ＋π2)cos ωx (0<ω≤2)的图象过点(π16，2＋2).(Ⅰ)求ω的值及使f (x )取得最小值的x 的集合； (Ⅱ)该函数的图象可由函数y ＝2sin4x (x ∈R)的图象经过怎样的变换得出？16.(本小题满分13分)某项考试按科目A 、科目B 依次进行，只有当科目A 成绩合格时，才可继续参加科目B 的考试.已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书，现某考生参加这项考试，科目A 每次考试成绩合格的概率为p ，科目B 每次考试成绩合格的概率为12.假设各次考试成绩合格与否均互不影响.若该考生不需要补考就可以获得证书的概率为13.(Ⅰ)求p 的值；(Ⅱ)在这项考试过程中，假设该考生不放弃所有的考试机会，记他参加考试的次数为ξ，求ξ的数学期望Eξ.17.(本小题满分13分)直线l ：bx ＋ay ＝ab (a >0，b >0)与x 轴，y 轴的交点分别为A 、B ，O 为坐标原点，△OAB 的面积为233，直线l 的倾斜角为150°，A ，B 两点是中心在坐标原点的椭圆C 的两个顶点.(Ⅰ)求椭圆C 的标准方程；(Ⅱ)若直线l 1：y ＝x ＋m 与椭圆C 相交于M 、N 两点，求△OMN 面积的最大值.18.(本小题满分13分)已知函数f(x)＝ax3＋mx2＋nx－2在点x＝－2处取得极值，且曲线y＝f(x)在点x＝－1处的切线与直线3x＋y－3＝0平行，又函数g(x)＝f′(x)－6x是偶函数.(Ⅰ)求a、m、n的值及y＝f(x)的单调区间；(Ⅱ)若t<0，求函数y＝f(x)在区间(t－1，t＋1)内的极值.19.(本小题满分14分)设数列⎩⎨⎧⎭⎬⎫an 满足a 1＝1，a 2＝2，a n ＝(1＋q )a n －1－qa n －2(q ≠0，n＝3,4，…)(Ⅰ)设b n －1＝a n －a n －1(n≥2)，求数列⎩⎨⎧⎭⎬⎫b n ，⎩⎨⎧⎭⎬⎫an 的通项公式；(Ⅱ)在(Ⅰ)的条件下，设c n ＝b n ＋2－32b n ＋1，记数列⎩⎨⎧⎭⎬⎫b n ，⎩⎨⎧⎭⎬⎫c n 的前n项和分别为S n ，T n .当q >－1时，试比较S n 和T n 的大小.20.(本小题满分为14分)已知函数y ＝f (x )是函数y ＝log 4(1x－2)的反函数，点P 1(x 1，y 1)、P 2(x 2，y 2)是函数y ＝f (x )图象上两点，且线段P 1P 2中点P 的纵坐标是14. (Ⅰ)求点P 的横坐标；(Ⅱ)若数列⎩⎨⎧⎭⎬⎫an 的通项公式是a n ＝f (nm)(m ∈N *，n ＝1,2，…，m )，求数列⎩⎨⎧⎭⎬⎫a n 的前m 项的和S m ；(Ⅲ)在(Ⅱ)的条件下，若对任意的m ∈N *，不等式a m S m <a m ＋1S m ＋1恒成立，求实数a 的取值范围.3.北京市朝阳区高三统一练习(一)数学(理科)(本试卷满分150分，考试时间120分钟)第Ⅰ卷(选择题共40分) 一、选择题(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合P ＝{x ||x －2|≤1，x ∈R}，Q ＝{x |x ∈N}，则P ∩Q 等于( ) A.[1,3] B.{1,2} C.{2,3} D.{1,2,3}2.下列函数中，在区间(1，＋∞)上为增函数的是( ) A.y ＝－2x ＋1 B.y ＝x1－xC.y ＝－(x －1)2D.y ＝log 12(x －1)3.复数z ＝2－i1＋i (i 为虚数单位)在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限4.从6名女生，4名男生中，按性别采用分层抽样的方法抽取5名学生组成课外小组，则不同的抽取方法种数为( )A.C 36·C 24B.C 26·C 34C.C 510D.A 36·A 24 5.用一平面去截体积为43π的球，所得截面的面积为π，则球心到截面的距离为( )A.2B.3 C.2 D.16.各项均不为零的等差数列{a n }中，若a 2n －a n －1－a n ＋1＝0(n ∈N *且n ≥2)，则S 2 009等于( )A.0B.2C.2 009D.4 018 7.已知函数f (x )＝|x －1|－|x ＋1| .如果f (f (a ))＝f (9)＋1，则实数a 等于( )A.－14B.－1C.1D.328.蔬菜价格随着季节的变化而有所变化.根据对农贸市场蔬菜价格的调查得知，购买2千克甲种蔬菜与1千克乙种蔬菜所需费用之和大于8元，而购买4千克甲种蔬菜与5千克乙种蔬菜所需费用之和小于22元.设购买2千克甲种蔬菜所需费用为A 元，购买3千克乙种蔬菜所需费用为B 元，则( )A.A ＞BB.A ＜BC.A ＝BD.A ，B 大小不确定第Ⅱ卷(非选择题共110分)二、填空题(本大题共6小题，每小题5分，共30分.把答案填在题中的横线上)9.lim2x →- x 2＋3x ＋2x ＋2＝ .10.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c . 若∠B ＝45°，b ＝2，a ＝1，则∠C 等于 .11.若(x 2＋1x)n 展开式中的二项式系数和为512，则n 等于；该展开式中的常数项为 .12.已知动直线l 平分圆C ：(x －2)2＋(y －1)2＝1，则直线l 与圆O ：⎩⎨⎧x ＝3cos θy ＝3sin θ(θ为参数)的位置关系是 .13.过抛物线y 2＝2px (p ＞0)的焦点F 作直线l ，交抛物线于A ，B 两点，交其准线于C 点.若CB ＝3BF ，则直线l 的斜率为 .14.定义映射f ：A →B ，其中A ＝{(m ，n )|m ，n ∈R}，B ＝R.已知对所有的有序正整数对(m ，n )满足下述条件：①f (m,1)＝1；②若m <n ，f (m ，n )＝0；③f (m ＋1，n )＝n [f (m ，n )＋f (m ，n －1)]，则f (3,2)的值是；f (n ，n )的表达式为 (用含n 的代数式表示).三、解答题(本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分13分) 已知函数f (x )＝sin x 2·cos x2＋3sin 2x2＋32.(Ⅰ)求函数f (x )的最小正周期，并写出函数f (x )图象的对称轴方程； (Ⅱ)若x ∈[0，π]，求函数f (x )的值域.16.(本小题满分13分)在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较.在试制某种牙膏新品种时，需要选用两种不同的添加剂.现在可供选用的不同添加剂有6种，其中芳香度为1的添加剂1种，芳香度为2的添加剂2种，芳香度为3的添加剂3种.根据试验设计原理，通常要随机选取两种不同的添加剂进行搭配试验.(Ⅰ)求所选用的两种不同的添加剂的芳香度之和为3的概率；(Ⅱ)求所选用的两种不同的添加剂的芳香度之和为偶数的概率；(Ⅲ)用ξ表示所选用的两种不同的添加剂的芳香度之和，写出ξ的分布列，并求ξ的数学期望Eξ.17.(本小题满分14分)如图，在直三棱柱ABC－A′B′C′中，已知AA′＝4，AC＝BC＝2，∠ACB＝90°，D是AB的中点.(Ⅰ)求证：CD⊥AB′；(Ⅱ)求二面角A′－AB′－C的大小；(Ⅲ)求直线B′D与平面AB′C所成角的正弦值.18.(本小题满分13分) 已知函数f (x )＝124－x 2.(Ⅰ)写出函数f (x )的定义域，并求函数f (x )的单调区间；(Ⅱ)设过曲线y ＝f (x )上的点P 的切线l 与x 轴、y 轴所围成的三角形的面积为S ，求S 的最小值，并求此时点P 的坐标.19.(本小题满分13分)已知△ABC的三边长|CB|，|AB|，|CA|成等差数列，若点A，B的坐标分别为(－1,0)，(1,0).(Ⅰ)求顶点C的轨迹W的方程；(Ⅱ)若线段CA的延长线交轨迹W于点D，当2≤|CB|＜52时，求线段CD的垂直平分线l与x轴交点的横坐标的取值范围.20.(本小题满分14分)已知数列{a n }的前n 项和为S n ，且S n a n ＝12a n ＋1(n ∈N *)，其中a 1＝1，a n ≠0.(Ⅰ)求数列{a n }的通项公式；(Ⅱ)设数列{b n }满足(2a n －1)(2b n －1)＝1，T n 为{b n }的前n 项和，求证：2T n ＞log 2(2a n ＋1)，n ∈N *；(Ⅲ)是否存在正整数m ，d ，使得limn →∞ [(13)m ＋(13)m ＋d ＋(13)m ＋2d＋…＋(13)m ＋(n －1)d ]＝1a 8成立？若存在，请求出m 和d 的值；若不存在，请说明理由.4.湖北省八市3月高三调考数学(理科)(本试卷满分150分，考试时间120分钟)第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.设集合M ＝{x |x ≥2}，P ＝{x |x ＞1}，那么“x ∈M ∪P ”是“x ∈M ∩P ”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.若(1＋5x )n 的展开式中各项系数之和为a n ，(7x 2＋1)n 的展开式中各项的二项式系数之和为b n ，则lim n →∞a n －2b n3a n ＋4b n的值是( )A.13B.14C.1D.－12 3.S n 为等差数列{a n }的前n 项和，S 9＝－36，S 13＝－104，等比数列{b n}中，b5＝a5，b7＝a7，则b6等于( )A.4 2B.±2 2C.±4 2D.324.给出下列四个命题：①若直线l⊥平面α，l∥平面β，则α⊥β；②各侧面都是正方形的棱柱一定是正棱柱；③一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面，则这两个二面角的平面角互为补角；④过空间任意一点一定可以作一个和两条异面直线都平行的平面.其中正确的命题的个数有( )A.1B.2C.3D.45.某一批袋装大米，质量服从正态分布N(10,0.01)(单位：kg)，任选一袋大米，它的质量是9.8～10.2 kg内的概率为(已知Φ(1)＝0.841 3，Φ(2)＝0.977 2)( )A.0.841 3B.0.954 4C.0.977 2D.0.682 66.已知正数x、y满足等式x＋y－2xy＋4＝0，则( )A.xy的最大值是2，且x＋y的最小值为4B.xy的最小值是4，且x＋y的最大值为4C.xy的最大值是2，且x＋y的最大值为4D.xy的最小值是4，且x＋y的最小值为47.在航天员进行的一项太空实验中，先后要实施6个程序，其中程序A只能出现在第一步或最后一步，程序B和C实施时必须相邻，请问实验顺序的编排方法共有( )A.24种B.48种C.96种D.144种8.已知函数f(x)＝x ln(ax)＋e x－1在点(1,0)处切线经过椭圆4x2＋my2＝4m的右焦点，则椭圆两准线间的距离为( )A.6B.8C.10D.18 9.已知点F 1、F 2分别是双曲线x 2a 2－y 2b 2＝1的左、右焦点，过F 1且垂直于x 轴的直线与双曲线交于A 、B 两点，若A 、B 和双曲线的一个顶点构成的三角形为锐角三角形，则该双曲线的离心率e 的取值范围是( )A.(1,1＋2)B.(1，3)C.(2－1,1＋2) D.(1,2)10.已知函数f (x )＝⎩⎨⎧2－x －1(x ≤0)f (x －1)(x >0)，若方程f (x )＝x ＋a 有且只有两个不相等的实数根，则实数a 的取值范围是( )A.(－∞，1)B.(0,1)C.(－∞，1]D.[0，＋∞)第Ⅱ卷(非选择题共100分)二、填空题(本大题共5小题，每小题5分，共25分.把答案填在题中的横线上)11.已知复数z 1＝3－i ，z 2＝2i －1，z 是z 的共轭复数，则复数iz 1－z 24的虚部等于 .12.一个半径为1的球内切于正三棱柱，则该正三棱柱的体积为 .13.已知x 、y 满足条件⎩⎪⎨⎪⎧x ≥0y ≤x2x ＋y ＋k ≤0( k 为常数)，若z ＝x ＋3y 的最大值为8，则k ＝ .14.在三角形ABC 中，AB ·AC＝AB AC ＝6，M 为BC 边的中点，则中线AM 的长为，△ABC 的面积的最大值为 .15.在数列{a n }中，都有a 2n －a 2n －1＝p (n ≥2，n ∈N *)( p 为常数)，则称{a n }为“等方差数列”.下列是对“等方差数列”的判断：(1)数列{a n }是等方差数列，则数列{a 2n }是等差数列； (2)数列{(－1)n }是等方差数列；(3)若数列{a n }既是等方差数列，又是等差数列，则该数列必为常数列；(4)若数列{a n }是等方差数列，则数列{a kn }( k 为常数，k ∈N *)也是等方差数列，则正确命题序号为 .三、解答题(本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分12分)已知向量a ＝(cos 32x ，sin 32x )，b ＝(cos x 2，－sin x 2)，且x ∈[0，π2]；(Ⅰ)求a ·b 及|a ＋b |； (Ⅱ)若f (x )＝a ·b －3a b +sin x ，求f (x )的最大值与最小值.17.(本小题满分12分)下面玩掷骰子放球游戏，若掷出1点或6点，甲盒放一球；若掷出2点，3点，4点或5点，乙盒放一球，设掷n 次后，甲、乙盒内的球数分别为x 、y .(Ⅰ)当n ＝3时，设x ＝3，y ＝0的概率；(Ⅱ)当n ＝4时，设⎪⎪⎪⎪x －y ＝ξ，求ξ的分布列及数学期望Eξ.18.(本小题满分12分)四棱锥P －ABCD 中，底面ABCD 是边长为2的正方形，PB ⊥BC ，PD ⊥CD ，且PA ＝2，E 点满足PE ＝13PD .(Ⅰ)求证：PA ⊥平面ABCD ； (Ⅱ)求二面角E －AC －D 的大小；(Ⅲ)在线段BC 上是否存在点F 使得PF ∥面EAC ？若存在，确定F 的位置；若不存在，请说明理由.19.(本小题满分12分)某种商品的成本为5元/件，开始按8元/件销售，销售量为50件，为了获取最大利润，商家先后采取了提价与降价两种措施进行试销.经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q (件)与实际销售价x (元)满足关系：Q ＝⎩⎪⎨⎪⎧39(2x 2－29x ＋107)(5<x <7)198－6xx －5(7≤x <8)(Ⅰ)求总利润(利润＝销售额－成本) y (元)与实际销售价x (件)的函数关系式；(Ⅱ)试问：当实际销售价为多少元时，总利润最大.20.(本小题满分13分)已知A (－1,0)、B (3,0)，M 、N 是圆O ：x 2＋y 2＝1上的两个动点，且M 、N 关于x 轴对称，直线AM 与BN 交于P 点.(Ⅰ)求P 点的轨迹C 的方程；(Ⅱ)设动直线l ：y ＝k (x ＋32)与曲线C 交于S 、T 两点.求证：无论k为何值时，以动弦ST 为直径的圆总与定直线x ＝－12相切.21.(本小题满分14分)已知数列{a n }满足：a 1＝1，a n ＋1＝12a n ＋n2n ＋1(n ∈N *).(Ⅰ)求数列{a n }的通项公式； (Ⅱ)证明：12n －1≤a n ≤1；(Ⅲ)设T n ＝2nn 2－n ＋4a n ，且k n ＝ln(1＋T n )＋12T 2n ，证明：2T n ＋2<T nk n .5.长沙市4月高考模拟考试数学(理科)(本试卷满分150分，考试时间120分钟)参考公式：如果事件A 、B 互斥，那么P (A ＋B )＝P (A )＋P (B )；如果事件A 、B 相互独立，那么P (A ·B )＝P (A )·P (B )；如果事件A 在一次试验中发生的概率是P ，那么它在n 次独立重复试验中恰好发生k 次的概率P n (k )＝C k nP k (1－P )n －k ；球的表面积公式S 球＝4πR 2，其中R 表示球的半径；球的体积公式V 球＝43πR 3，其中R 表示球的半径.第Ⅰ卷(选择题共40分)一、选择题(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.设复数z 满足1－2iz＝i ，则z 等于( )A.－2＋iB.－2－iC.2－iD.2＋i2.下列函数中既是奇函数，又在区间(0,1)上单调递减的是( )A.y ＝(12)x B.12log y x C.y ＝sin xD.y ＝1x3.已知sin(2π－α)＝45，α∈(3π2，2π)，则tan(π－α)等于( )A.34 B.－43 C.－34 D.434.设等差数列{a n }的公差d 不为零，a 1＝9d ，若a k 是a 1和a 2k 的等比中项，则k 的值为( ) A.2 B.4 C.6D.85.已知A 、B 为球面上的两点，O 为球心，且AB ＝3，∠AOB ＝120°，则球的体积为( )A.9π2B.43π C.36πD.323π6.从5种不同的水果和4种不同的糖果中各选出3种，放入如图所示的6个不同区域(用数字表示)中拼盘，每个区域只放一种，且水果不能放在有公共边的相邻区域内，则不同的放法有( )A.2 880种B.2 160种C.1 440种D.720种7.设点P 是△ABC 内一点(不包括边界)，且AP ＝m AB＋n AC (m ，n ∈R)，则(m －1)2＋(n －1)2的取值范围是( )A.(0,1)B.⎝ ⎛⎭⎪⎫12，1C.⎝ ⎛⎭⎪⎫12，2D.⎝ ⎛⎭⎪⎫22，2 8.椭圆C 1：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左准线为l ，左右焦点分别为F 1、F 2，抛物线C 2的准线为l ，一个焦点为F 2，C 1与C 2的一个交点为P ，则|F 1F 2||PF 1|－|PF 1||PF 2|等于( )A.－1B.12 C.－12D.1第Ⅱ卷(非选择题共110分)二、填空题(本大题共7小题，每小题5分，共35分.把答案填在题中的横线上)9.已知公差不为0的等差数列{a n }中，有2a 3－a 27＋2a 11＝0，数列{b n }是等比数列，且b 7＝a 7，则b 6b 8＝ .10.已知OA ＝(3,1)，OB ＝(2,4)，|BC|＝1，点C 在直线OA 上的射影为点D ，则|OD|的最大值为 .11.若(x 2＋1ax )6的二项展开式中x 3的系数为52，则a ＝ .(用数字作答).12.函数y ＝a x ＋1－2(a ＞0，a ≠1)的图象恒过定点A ，若点A 在直线mx ＋ny ＋1＝0上，其中m 、n ＞0，则1m ＋2n的最小值为 .13.已知x 、y 满足条件⎩⎪⎨⎪⎧x ≥0y ≤x2x ＋y ＋k ≤0，(k 为常数)，若z ＝x ＋3y 的最大值为8，则k ＝ .14.关于x 的不等式2－x 2＞|x －a |至少有一个负数解，则a 的取值范围是 .15.在三角形ABC中，AB ·AC＝|AB AC - |＝6，M 为BC 边的中点，则中线AM 的长为，△ABC 的面积的最大值为 .三、解答题(本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤)16.(本小题满分12分)甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子，乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.(Ⅰ)若甲在自己的箱子里任意取球，取后不放回，每次只取一球，直到取得红球为止，求甲取球次数ξ的数学期望；(Ⅱ)若甲、乙两人各自从自己的箱子里任取一球比颜色，规定同色时为甲胜，异色时为乙胜，这个游戏规则公平吗？请说明理由.17.(本小题满分12分)设数列{x n }各项为正，且满足x 21＋x 22＋…＋x 2n ＝2n 2＋2n ， (Ⅰ)求x n ； (Ⅱ)已知1x 1＋x 2＋1x 2＋x 3＋…＋1x n ＋x n ＋1＝3，求n ；(Ⅲ)证明：x 1x 2＋x 2x 3＋…＋x n x n ＋1＜2[(n ＋1)2－1]18.(本小题满分12分)如图，四棱锥S －ABCD 的底面ABCD 是正方形，侧面SAB 是等腰三角形且垂直于底面，SA ＝SB ＝5，AB ＝2，E 、F 分别是AB 、SD 的中点.(Ⅰ)求证：EF ∥平面SBC ； (Ⅱ)求二面角F －CE －A 的大小.19.(本小题满分13分)为保增长、促发展，某地计划投资甲、乙两项目，市场调研得知，甲项目每投资100万元需要配套电能2万千瓦，可提供就业岗位24个，增加GDP260万元；乙项目每投资100万元需要配套电能4万千瓦，可提供就业岗位36个，增加GDP200万元，已知该地为甲、乙两项目最多可投资3 000万元，配套电能100万千瓦，并要求它们提供的就业岗位不少于840个.如何安排甲、乙两项目的投资额，增加的GDP最大？20.(本小题满分13分)已知定点A(a,0)(a＞0)，B为x轴负半轴上的动点.以AB为边作菱形ABCD，使其两对角线的交点恰好落在y轴上.(Ⅰ)求动点D的轨迹E的方程；(Ⅱ)过点A作直线l与轨迹E交于P、Q两点，设点R(－a,0)，问当l绕点A转动时，∠PRQ是否可以为钝角？请给出结论，并加以证明.21.(本小题满分13分)设函数f (x )＝x 2＋b ln(x ＋1)，其中b ≠0. (Ⅰ)若b ＝－12，求f (x )的单调递增区间；(Ⅱ)如果函数f (x )在定义域内既有极大值又有极小值，求实数b 的取值范围；(Ⅲ)求证对任意的n ∈N *，不等式ln n ＋1n＞n －1n3恒成立.6.山西省临汾市高中三年级第一次模拟测试数学(理科)(本试卷满分150分，时间120分钟)第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.设集合A ＝⎩⎨⎧⎭⎬⎫x ∈Z ⎪⎪0≤x ≤5，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ＝k 2，k ∈A ，则A ∩B＝( )A.⎩⎨⎧⎭⎬⎫0，1，2 B.⎩⎨⎧⎭⎬⎫0，1，2，3 C.⎩⎨⎧⎭⎬⎫0，1，3D.⎩⎨⎧⎭⎬⎫1，2，3 2.已知向量a ＝(cos x ，－2)，b ＝(1，sin x )，且a ⊥b ，则tan(x －π4)＝( )A.3B.13C.－ 13 D.－33.若a,2a ＋2,3a ＋3，…为等比数列，则a ＋2＝( )A.1B.－2C.1或－2D.64.函数y ＝xx －2(x >2)的反函数是( ) A. y ＝2x x －1(x >1) B. y ＝x2x －1(x >1)C. y ＝2xx －1(0<x <1) D. y ＝x2x －1(0<x <1) 5.已知双曲线kx 2－y 2＝1的一条渐近线与直线2x ＋y －1＝0垂直，则双曲线的离心率是( )A.62 B. 52 C. 32D.56.已知函数f (x )＝x 3＋sin x ＋1(x ∈R)，若f (m )＝2，则f (－m )的值为( )A.3B.0C.－1D.－27.若直线ax ＋by ＝1与圆x 2＋y 2＝1相切，且M ＝a cos θ＋b sin θ，θ∈⎣⎡⎭⎫0，2π，则M 的取值范围是( )A.⎣⎡⎦⎤0，1B.(0,1)C. ⎣⎡⎦⎤－1，1D.(－1,1)8.如图，函数f (x )的图象是锯齿形折线段，f ′(x )是函数f (x )的导函数，则f (f ′(5))＝( )A.32 B.2 C.1D.749.把函数y ＝cos(x ＋4π3)的图象沿x 轴平移⎪⎪⎪⎪φ个单位，所得图象关于原点对称，则⎪⎪⎪⎪φ的最小值是( )A.π6B. 2π3C. 5π6 D. 4π310.关于x 的方程x 2－⎪⎪⎪⎪x －a ＝0有三个不同的实根，则实数a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－14，14B. ⎣⎢⎡⎭⎪⎫－14，0∪⎝ ⎛⎦⎥⎤0，14C. ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫－14，14D. ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫－14，0，14 11.已知不等式组⎩⎪⎨⎪⎧x ＋y ≤2x －y ≤2x ≥03x －y ≤a表示的平面区域是四边形，则实数a 的取值范围是( )A.(－∞，－2)B.(2,6)C.(0,6)D.(0，＋∞)12.从双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点F 引圆x 2＋y 2＝a 2的切线l ，切点为T ，且l 交双曲线的右支于P ，若点M 是线段FP 的中点，O 为坐标原点，则⎪⎪⎪⎪OM －⎪⎪⎪⎪TM ＝( )A.b －a2B.b －aC.a ＋b2D.a＋b2第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中的横线上)13.等差数列⎩⎨⎧⎭⎬⎫an 的前n 项和为S n ，若S 3＝－6，S 18－S 15＝18，则S 18＝ .14.在△AOB 中，M 是OB 中点，N 是AB 中点，ON ，AM 交于点P ，若AP＝m OA ＋n OB (m ，n ∈R)，则n －m ＝ .15.已知抛物线y 2＝mx (m ≠0)的准线与椭圆x 26＋y 22＝1的右准线重合，则实数m 的值是 .16.如图，宽度为1.5米的胡同有一直角拐角，有三个物体试图通过拐角到达目的地①长4米的铝合金杆②棱长为1.4米的正方体电视机包装箱 ③长为2.2米，宽为1米的平板车；请你算一算，哪些物体可以通过拐角： (写上序号即可) 三、解答题(本大题6个小题，共70分.解答应写出文字说明，证明过程或演算步骤)17.(本小题满分10分) 解关于x 的不等式a x <a －1x －1(a >0)18.(本小题满分12分)设锐角三角形ABC 的角A 、B 、C 所对的边分别为a ，b ，c ，若m ＝(b,2c sin B )，n ＝(cos B ，sin C )，且m ∥n.(Ⅰ)求B 的大小；(Ⅱ)求sin A＋sin C的取值范围.19.(本小题满分12分)将圆x2＋y2＋2x－2y＝0按向量a平移得到圆O(O为坐标原点)，直线l与圆O相交于A、B两点，若在圆O上存在点C，使得OA＋OB＋OC＝0，且OC＝λa，求直线l的方程.20. (本小题满分12分)已知函数f(x)＝x2＋a ln x的图象与直线l：y＝－2x＋c相切，切点横坐标为1.(Ⅰ)求函数f(x)的解析式和直线l的方程；(Ⅱ)求函数f(x)的单调区间；(Ⅲ)若不等式f(x)≥2x＋m对f(x)定义域内的任意x恒成立，求m 的取值范围.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝32，左、右焦点分别为F 1、F 2， ⎪⎪⎪⎪⎪⎪F 1F 2＝23，设M (x 1，y 1)，N (x 2，y 2)(x 1≠x 2)是椭圆上不同的两点，且x 1x 2＋4y 1y 2＝0.(Ⅰ)求椭圆C 的方程； (Ⅱ)证明：x 21 ＋ x 22 为常数；(Ⅲ)在x 轴上有一点P ，使得⎪⎪⎪⎪⎪⎪PM ＝⎪⎪⎪⎪⎪⎪PN ，求△PMN 面积的最大值.已知数列⎩⎨⎧⎭⎬⎫an 满足：首项a 1＝35，3a n ＝2a n a n ＋1＋a n ＋1(n ＝1,2,3，…).(Ⅰ)若b n ＝a n1－a n，证明数列⎩⎨⎧⎭⎬⎫b n 为等比数列；(Ⅱ)求数列⎩⎨⎧⎭⎬⎫a n 的通项公式；(Ⅲ)证明n <a 1＋a 2＋a 3＋…＋a n ＋1<n ＋1(n ＝1,2,3，…).。

2019年北京市高考数学一模试卷(理科)(解析版)

2019年北京市高考数学一模试卷(理科)(解析版)2019年北京市高考数学一模试卷（理科）一、选择题共8个小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知复数z=i（1+i），则|z|等于（）A。

2B。

√2C。

1D。

2√22.在方程r=2cosθ+3sinθ（θ为参数）所表示的曲线上的点是（）A。

(2.-7)B。

(3.1)C。

(1.5)D。

(2.1)3.设公差不为零的等差数列{an}的前n项和为Sn，若a4=2(a2+a3)，则Sn=（）A。

5anB。

6anC。

7anD。

14an4.将函数y=sin2x的图象向左平移π/4个单位后得到函数y=g(x)的图象。

则函数g(x)的一个增区间是（）A。

(π/4.3π/4)B。

(3π/4.5π/4)C。

(5π/4.7π/4)D。

(7π/4.9π/4)5.使“a>b”成立的一个充分不必要条件是（）A。

a>b+1B。

a>b-1C。

a^2>b^2D。

a^3>b^36.下列函数：①y=-|x|；②y=(x-1)^3；③y=log2(x-1)；④y=-6.在x中，在(1.+∞)上是增函数且不存在零点的函数的序号是（）A。

①④B。

②③C。

②④D。

①③④7.某三棱锥的正视图和侧视图如图所示，则该三棱锥的俯视图的面积为（）A。

6B。

8C。

10D。

128.远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图所示的是一位母亲记录的孩子自出生后的天数，在从右向左依次排列的不同绳子上打结，满七进一，根据图示可知，孩子已经出生的天数是（）A。

336B。

510C。

1326D。

3603二、填空题共6小题，每小题5分，共30分。

9.在(1-x)^5的展开式中，x^2的系数为______（用数字作答）。

答案：1010.已知向量a=(1.b)。

b=(-2.-1)，且向量a+b的模长为√10.则实数x=______。

频率分布直方图-高中数学知识点讲解(含答案)

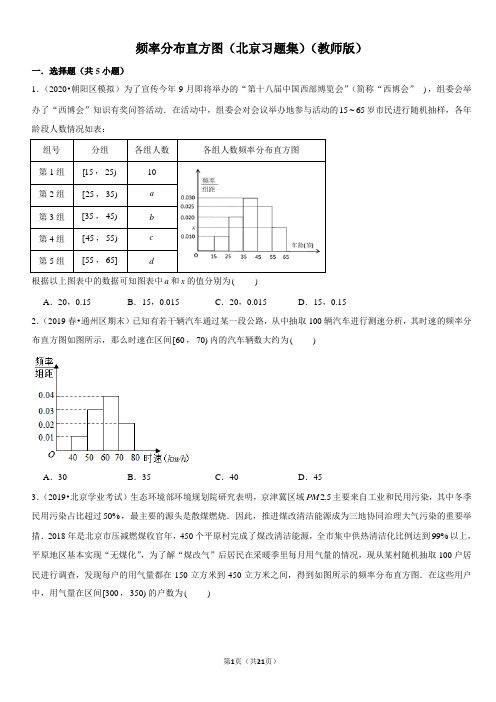
频率分布直方图（北京习题集）（教师版）一．选择题（共5小题）1．（2020•朝阳区模拟）为了宣传今年9月即将举办的“第十八届中国西部博览会”（简称“西博会”)，组委会举办了“西博会”知识有奖问答活动．在活动中，组委会对会议举办地参与活动的15~65岁市民进行随机抽样，各年龄段人数情况如表：组号分组各组人数各组人数频率分布直方图第1组[15，25)10第2组[25，35)a第3组[35，45)b第4组[45，55)c第5组[55，65]d根据以上图表中的数据可知图表中a和x的值分别为()A．20，0.15B．15，0.015C．20，0.015D．15，0.152．（2019春•通州区期末）已知有若干辆汽车通过某一段公路，从中抽取100辆汽车进行测速分析，其时速的频率分布直方图如图所示，那么时速在区间[60，70)内的汽车辆数大约为()A．30B．35C．40D．453．（2019•北京学业考试）生态环境部环境规划院研究表明，京津冀区域 2.5PM主要来自工业和民用污染，其中冬季民用污染占比超过50%，最主要的源头是散煤燃烧．因此，推进煤改清洁能源成为三地协同治理大气污染的重要举措．2018年是北京市压减燃煤收官年，450个平原村完成了煤改清洁能源，全市集中供热清洁化比例达到99%以上，平原地区基本实现“无煤化”，为了解“煤改气”后居民在采暖季里每月用气量的情况，现从某村随机抽取100户居民进行调查，发现每户的用气量都在150立方米到450立方米之间，得到如图所示的频率分布直方图．在这些用户中，用气量在区间[300，350)的户数为()A．5B．15C．20D．254．（2018•西城区模拟）某车站在春运期间为了改进服务，随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t（以下简称购票用时，单位：)min．下面是这次抽样的频率分布表和频率分布直方图，则旅客购票用时的平均数可能落在哪一个小组()分组频数频率t<00一组05t<10二组510t<100.10三组1015t<四组1520t<300.30五组2025合计100 1.00A．第二组B．第三组C．第四组D．第五组5．（2016春•西城区期末）如图是100名学生某次数学测试成绩（单位：分）的频率分布直方图，则测试成绩在区间[50，70)中的学生人数是()A．30B．25C．22D．20二．填空题（共7小题）6．（2019秋•房山区期末）为了解中学生课外阅读情况，现从某中学随机抽取200名学生，收集了他们一年内的课外阅读量（单位：本）等数据，以下是根据数据绘制的统计图表的一部分．阅读量人数学生类别[0，10)[10，20)[20，30)[30，40)[40，)性别男73125304女82926328学段初中25364411高中下面有四个推断：①这200名学生阅读量的平均数可能是26本；②这200名学生阅读量的75%分位数在区间[30，40)内；③这200名学生中的初中生阅读量的中位数一定在区间[20，30)内；④这200名学生中的初中生阅读量的25%分位数可能在区间[20，30)内．所有合理推断的序号是．7．（2019春•通州区期末）已知某地区中小学学生人数和近视情况分别如图1和图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取20%的近视学生进行调查，则样本容量为，从中抽取的高中生近视人数为．小学初中高中人数9000700040008．（2019春•西城区期末）从某校3000名学生中随机抽取若干学生，获得了他们一天课外阅读时间（单位：分钟）的数据，整理得到频率分布直方图如下．则估计该校学生中每天阅读时间在[70，80)的学生人数为．9．（2018秋•昌平区期末）为调查某校学生每天用于课外阅读的时间，现从该校3000名学生中随机抽取100名学生进行问卷调查，所得数据均在区间[50，100]上，其频率分布直方图如图所示，则估计该校学生中每天用于阅读的时间在[70，80)（单位：分钟）内的学生人数为．10．（2018秋•丰台区期末）某校为了解学生对本校食堂的满意度，随机抽取部分学生进行调查．根据学生的满意度评分，得到如图所示的频率分布直方图，其中a=，若这次满意度评分的中位数为b，根据频率分布直方图，估计b65（填“>”，“<”或“=”)11．（2017秋•海淀区校级期末）如图，从参加环保知识竞赛的学生中抽出80名，将其成绩（均为整数）整理后画出的频率分布直方图如图：观察图形，回答下列问题：（1）[79.5，89.5)这一组的频率是．（2）估计这次环保知识竞赛的及格率(60分以上为及格）为．12．（2018春•西城区校级期中）为了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁18岁的男生体重()kg，得到频率分布直方图如图，根据如图可得这100名学生中体重在(56.5,64.5)的学生人数是．三．解答题（共3小题）13．（2019秋•房山区期末）中学生研学旅行是通过集体旅行、集中食宿方式开展的研究性学习和旅行体验相结合的校外教育活动，是学校教育和校外教育衔接的创新形式，是综合实践育人的有效途径，每年暑期都会有大量中学生参加研学旅行活动．为了解某地区中学生暑期研学旅行支出情况，在该地区各个中学随机抽取了部分中学生进行问卷调查，从中统计得到中学生暑期研学旅行支出（单位：百元）频率分布直方图如图所示．（Ⅰ）利用分层抽样在[40，45)，[45，50)，[50，55]三组中抽取5人，应从这三组中各抽取几人？（Ⅱ）从（Ⅰ）抽取的5人中随机选出2人，对其消费情况进行进一步分析，求这2人不在同一组的概率；（Ⅲ）假设同组中的每个数据都用该区间的左端点值代替，估计该地区中学生暑期研学旅行支出的平均值．14．（2019•大兴区一模）随着智能手机的发展，各种“APP”（英文单词Application的缩写，一般指手机软件）应运而生．某机构欲对A市居民手机内安装的APP的个数和用途进行调研，在使用智能手机的居民中随机抽取100人，获得了他们手机内安装APP的个数，整理得到如图所示频率分布直方图．（Ⅰ）求a的值；（Ⅱ）从被抽取安装APP的个数不低于50的居民中，随机抽取2人进一步调研，求这2人安装APP的个数都低于60的概率；（Ⅲ）假设同组中的数据用该组区间的右端点值代替，以本次被抽取的居民情况为参考，试估计A市使用智能手机的居民手机内安装APP的平均个数在第几组（只需写出结论）．15．（2019•山东模拟）某快餐连锁店招聘外卖骑手，该快餐连锁店提供了两种日工资方案：方案（1）规定每日底薪50元，快递业务每完成一单提成3元；方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快餐连锁店记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35)，[35，45)，[45，55)，[55，65)，[65，75)，[75，85)，[85，95]七组，整理得到如图所示的频率分布直方图．（Ⅰ）随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率；（Ⅱ）若骑手甲、乙选择了日工资方案（1），丙、丁选择了日工资方案（2）．现从上述4名骑手中随机选取2人，求至少有1名骑手选择方案（1）的概率；（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由．（同组中的每个数据用该组区间的中点值代替）频率分布直方图（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2020•朝阳区模拟）为了宣传今年9月即将举办的“第十八届中国西部博览会”（简称“西博会”)，组委会举办了“西博会”知识有奖问答活动．在活动中，组委会对会议举办地参与活动的15~65岁市民进行随机抽样，各年龄段人数情况如表：组号分组各组人数各组人数频率分布直方图第1组[15，25)10第2组[25，35)a第3组[35，45)b第4组[45，55)c第5组[55，65]d根据以上图表中的数据可知图表中a和x的值分别为()A．20，0.15B．15，0.015C．20，0.015D．15，0.15【分析】由频率分布直方图可知第一组的频率，再根据第一组的人数求出总人数，从而由第二组的频率求出a的值，由频率分布直方图中各小长方体的面积之和为1，即可求出x的值．【解答】解：由频率分布直方图可知，第一组的频率为：0.010100.1⨯=，又第一组的人数为10，∴总人数为：10100 0,1=，第二组的频率为：0.020100.2⨯=，∴第二组的人数0.210020a=⨯=，由频率分布直方图可知，1[1(0.010.020.030.025)10]0.015 10x=⨯-+++⨯=，故选：C．【点评】本题主要考查了频率分布直方图的应用，是基础题．2．（2019春•通州区期末）已知有若干辆汽车通过某一段公路，从中抽取100辆汽车进行测速分析，其时速的频率分布直方图如图所示，那么时速在区间[60，70)内的汽车辆数大约为()A．30B．35C．40D．45【分析】由频率分布直方图求出时速在区间[60，70)内的频率，由此能求出时速在区间[60，70)内的汽车辆数．【解答】解：由频率分布直方图得：时速在区间[60，70)内的频率为：0.04100.4⨯=，∴时速在区间[60，70)内的汽车辆数大约为：⨯=．0.410040故选：C．【点评】本题考查时速在区间[60，70)内的汽车辆数的求法，考查频率分布直方图的性质等基础知识，考查运算求解能力，是基础题．3．（2019•北京学业考试）生态环境部环境规划院研究表明，京津冀区域 2.5PM主要来自工业和民用污染，其中冬季民用污染占比超过50%，最主要的源头是散煤燃烧．因此，推进煤改清洁能源成为三地协同治理大气污染的重要举措．2018年是北京市压减燃煤收官年，450个平原村完成了煤改清洁能源，全市集中供热清洁化比例达到99%以上，平原地区基本实现“无煤化”，为了解“煤改气”后居民在采暖季里每月用气量的情况，现从某村随机抽取100户居民进行调查，发现每户的用气量都在150立方米到450立方米之间，得到如图所示的频率分布直方图．在这些用户中，用气量在区间[300，350)的户数为()A．5B．15C．20D．25【分析】根据频率分布直方图求出用气量在区间[300，350)的频率，用样本容量与频率相乘即可得到用气量在区间[300，350)的户数．【解答】解：依题意，由频率分布直方图可知，用气量在[300，350)的频率为：0.005500.25⨯=，所以100户居民中用气量在区间[300，350)的户数为：1000.2525⨯=．故选：D．【点评】本题考查了频率分布直方图的应用，考查了考查数据分析处理、运算求解能力，属于基础题．4．（2018•西城区模拟）某车站在春运期间为了改进服务，随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t（以下简称购票用时，单位：)min．下面是这次抽样的频率分布表和频率分布直方图，则旅客购票用时的平均数可能落在哪一个小组()分组频数频率t<00一组05t<10二组510t<100.10三组1015t<四组1520t<300.30五组2025合计100 1.00A．第二组B．第三组C．第四组D．第五组【分析】由频率分布表和频率分布直方图得第四组的频率为0.5，从而求得旅客购票用时的平均数，由此得到旅客购票用时的平均数落第四小组．【解答】解：由频率分布表和频率分布直方图得第四组的频率为：---=，10.10.10.30.5由频率分布表和频率分布直方图得旅客购票用时的平均数为：7.50.1012.50.1017.50.5022.50.317.5⨯+⨯+⨯+⨯=，∴旅客购票用时的平均数落第四小组．故选：C．【点评】本题考查平均数、频率的求法及应用，考查频率分布表和频率分布直方图等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．5．（2016春•西城区期末）如图是100名学生某次数学测试成绩（单位：分）的频率分布直方图，则测试成绩在区间[50，70)中的学生人数是()A ．30B ．25C ．22D ．20【分析】根据频率分布直方图中频率和为1，求出a 的值，计算模块测试成绩落在[50，70)中的频率以及频数即可．【解答】解：根据频率分布直方图中频率和为1，得： 10(23762)1a a a a a ++++=，解得1200a =； ∴模块测试成绩落在[50，70)中的频率是1110(23)50502004a a a +==⨯=， ∴对应的学生人数是1100254⨯=．故选：B ．【点评】本题考查了频率分布直方图的应用问题，也考查了频率的计算问题，是基础题目．二．填空题（共7小题）6．（2019秋•房山区期末）为了解中学生课外阅读情况，现从某中学随机抽取200名学生，收集了他们一年内的课外阅读量（单位：本）等数据，以下是根据数据绘制的统计图表的一部分．阅读量人数学生类别 [0，10) [10，20) [20，30) [30，40) [40，)+∞性别男 7 31 25 30 4 女8 29 26 32 8 学段初中 25 36 44 11 高中下面有四个推断：①这200名学生阅读量的平均数可能是26本；②这200名学生阅读量的75%分位数在区间[30，40)内；③这200名学生中的初中生阅读量的中位数一定在区间[20，30)内；④这200名学生中的初中生阅读量的25%分位数可能在区间[20，30)内．所有合理推断的序号是①②③．【分析】利用频率分布直方图、平均数、75%分位数、中位数、25%分位数直接求解．【解答】解：在①中，这200名学生阅读量的平均数为：1x>⨯+⨯+⨯+⨯+⨯=．(5151560255235624512)24.93200∴这200名学生阅读量的平均数可能是26本，故①正确；在②中，20075%150⨯=，阅读量在[0，30)中有：156052117++=名学生，阅读量在[30，40)中有62名学生，∴这200名学生阅读量的75%分位数在区间[30，40)内，故②正确；在③中，阅读量在[0，20)中有：156065+=名学生，阅读量在[20，30)中有51名学生，∴这200名学生中的初中生阅读量的中位数一定在区间[20，30)内，故③正确；在④中，20025%50⨯=，阅读量在[0，10)中有15名学生，阅读量在[10，20)中有60名学生，∴这200名学生中的初中生阅读量的25%分位数可能在区间[10，20)内．故④错误．故答案为：①②③．【点评】本题考查命题真假的判断，考查频率分布直方图、平均数、75%分位数、中位数、25%分位数等基础知识，考查运算求解能力，是基础题．7．（2019春•通州区期末）已知某地区中小学学生人数和近视情况分别如图1和图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取20%的近视学生进行调查，则样本容量为4000，从中抽取的高中生近视人数为．小学初中高中人数900070004000【分析】用分层抽样的方法抽取20%的近视学生进行调查，利用分层抽样、频数分布表、条形图的性质求出样本容量和从中抽取的高中生近视人数．【解答】解：由题意得：用分层抽样的方法抽取20%的近视学生进行调查，则样本容量为：(900070004000)20%4000++⨯=．从中抽取的高中生近视人数为：⨯⨯=．400020%50%400故答案为：4000，400．【点评】本题考查样本容量、频率的求法，考查分层抽样、频数分布表、条形图的性质等基础知识，考查运算求解能力，是基础题．8．（2019春•西城区期末）从某校3000名学生中随机抽取若干学生，获得了他们一天课外阅读时间（单位：分钟）的数据，整理得到频率分布直方图如下．则估计该校学生中每天阅读时间在[70，80)的学生人数为900．【分析】求出a的值，根据[70，80)的概率求出在此区间的人数即可．【解答】解：由10.050.350.20.10.3----=，故0.03a=，故阅读的时间在[70，80)（单位：分钟）内的学生人数为：0.33000900⨯=，故答案为：900．【点评】本题考查了直方图问题，考查概率问题，是一道常规题．9．（2018秋•昌平区期末）为调查某校学生每天用于课外阅读的时间，现从该校3000名学生中随机抽取100名学生进行问卷调查，所得数据均在区间[50，100]上，其频率分布直方图如图所示，则估计该校学生中每天用于阅读的时间在[70，80)（单位：分钟）内的学生人数为900．【分析】求出a的值，根据[70，80)的概率求出在此区间的人数即可．【解答】解：由10.050.350.20.10.3----=，故0.03a=，故阅读的时间在[70，80)（单位：分钟）内的学生人数为：0.33000900⨯=，故答案为：900．【点评】本题考查了直方图问题，考查概率问题，是一道常规题．10．（2018秋•丰台区期末）某校为了解学生对本校食堂的满意度，随机抽取部分学生进行调查．根据学生的满意度评分，得到如图所示的频率分布直方图，其中a=0.005，若这次满意度评分的中位数为b，根据频率分布直方图，估计b65（填“>”，“<”或“=”)【分析】由频率分布直方图列方程能求出a；评分在[50，70)的频率为0.45，评分为[70，80)的频率为0.3，由此能求出中位数．【解答】解：由频率分布直方图得：a a++++⨯=，(0.040.030.02)101解得0.005a=．评分在[50，70)的频率为：(0.0050.04)100.45+⨯=，评分为[70，80)的频率为：0.03100.3⨯=，∴中位数0.50.452157010650.33b-=+⨯=>．故答案为：0.005，>．【点评】本题考查频率的求法、中位数的求法，考查频率分布直方图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题．11．（2017秋•海淀区校级期末）如图，从参加环保知识竞赛的学生中抽出80名，将其成绩（均为整数）整理后画出的频率分布直方图如图：观察图形，回答下列问题：（1）[79.5，89.5)这一组的频率是0.25．（2）估计这次环保知识竞赛的及格率(60分以上为及格）为．【分析】（1）由频率分布直方图能求出[79.5，89.5)这一组的频率．（2）由频率分布直方图能估计这次环保知识竞赛的及格率(60分以上为及格）．【解答】解：（1）由频率分布直方图得[79.5，89.5)这一组的频率是0.025100.25⨯=．故答案为：0.25．（2）由频率分布直方图估计这次环保知识竞赛的及格率(60分以上为及格）为：(0.0150.030.0250.005)10100%75%+++⨯⨯=．故答案为：75%．【点评】本题考查频率、及格率的求法，考查频率分布直方图的性质等基础知识，考查运算求出能力，考查函数与方程思想，是基础题．12．（2018春•西城区校级期中）为了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁18-岁的男生体重()kg，得到频率分布直方图如图，根据如图可得这100名学生中体重在(56.5,64.5)的学生人数是40．【分析】由频率分布直方图求出体重在(56.5,64.5)的频率为0.4，由此能求出这100名学生中体重在(56.5,64.5)的学生人数．【解答】解：由频率分布直方图得：体重在(56.5,64.5)的频率为：(0.030.050.050.07)20.4+++⨯=，∴这100名学生中体重在(56.5,64.5)的学生人数是：0.410040⨯=．故答案为：40．【点评】本题考查频数的求法，考查频率分布直方图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题．三．解答题（共3小题）13．（2019秋•房山区期末）中学生研学旅行是通过集体旅行、集中食宿方式开展的研究性学习和旅行体验相结合的校外教育活动，是学校教育和校外教育衔接的创新形式，是综合实践育人的有效途径，每年暑期都会有大量中学生参加研学旅行活动．为了解某地区中学生暑期研学旅行支出情况，在该地区各个中学随机抽取了部分中学生进行问卷调查，从中统计得到中学生暑期研学旅行支出（单位：百元）频率分布直方图如图所示．（Ⅰ）利用分层抽样在[40，45)，[45，50)，[50，55]三组中抽取5人，应从这三组中各抽取几人？（Ⅱ）从（Ⅰ）抽取的5人中随机选出2人，对其消费情况进行进一步分析，求这2人不在同一组的概率；（Ⅲ）假设同组中的每个数据都用该区间的左端点值代替，估计该地区中学生暑期研学旅行支出的平均值．【分析】（Ⅰ）利用分层抽样和频率分布直方图能求出在[40，45)，[45，50)，[50，55]三组中分别抽取的人数．（Ⅱ）从抽取的5人中随机选出2人，基本事件总数2510n C==，这2人不在同一组包含的基本事件个数112 3227m C C C=+=，由此能求出这2人不在同一组的概率．（Ⅲ）假设同组中的每个数据都用该区间的左端点值代替，利用频率分布直方图的性质能求出估计该地区中学生暑期研学旅行支出的平均值．【解答】解：（Ⅰ）分层抽样在[40，45)，[45，50)，[50，55]三组中抽取5人，应从[40，45)中抽取：0.06530.060.020.02⨯=++人，从[45，50)中抽取：0.02510.060.020.02⨯=++人，从[50，55)中抽取：0.02510.060.020.02⨯=++人．（Ⅱ）从（Ⅰ）抽取的5人中随机选出2人，对其消费情况进行进一步分析，基本事件总数2510n C==，这2人不在同一组包含的基本事件个数1123227m C C C=+=，∴这2人不在同一组的概率710mpn==．（Ⅲ）假设同组中的每个数据都用该区间的左端点值代替，估计该地区中学生暑期研学旅行支出的平均值为：32.50.04537.50.06542.50.06547.50.02552.50.02540.5x=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=．【点评】本题考查频数、概率、平均数的求法，考查频率分布直方图的性质、分层抽样、古典概型等基础知识，考查运算求解能力，是基础题．14．（2019•大兴区一模）随着智能手机的发展，各种“APP”（英文单词Application的缩写，一般指手机软件）应运而生．某机构欲对A市居民手机内安装的APP的个数和用途进行调研，在使用智能手机的居民中随机抽取100人，获得了他们手机内安装APP的个数，整理得到如图所示频率分布直方图．（Ⅰ）求a的值；（Ⅱ）从被抽取安装APP的个数不低于50的居民中，随机抽取2人进一步调研，求这2人安装APP的个数都低于60的概率；（Ⅲ）假设同组中的数据用该组区间的右端点值代替，以本次被抽取的居民情况为参考，试估计A市使用智能手机的居民手机内安装APP的平均个数在第几组（只需写出结论）．【分析】（Ⅰ）由频率分布直方图的性质能求出a ．（Ⅱ）设事件A 为“这2人手机内安装“APP ”的数量都低于60”．被抽取的智能手机内安装“APP ”的数量在[50，60)的有4人，分别记为1a ，2a ，3a ，4a ，被抽取的智能手机内安装“APP ”的数量在[60，70]的有1人，记为1b ，从被抽取的智能手机内安装“APP ”的数量不低于50的居民中随机抽取2人进一步调研，利用列举法能求出这2人安装APP 的个数都低于60的概率．（Ⅲ）第4组（或者写成[30，40))．【解答】（共13分）解：（Ⅰ）由(0.0110.0160.0180.0040.001)101a a ++++++⨯=，⋯⋯（2分）得0.025a =．⋯⋯（3分）（Ⅱ）设事件A 为“这2人手机内安装“APP ”的数量都低于60”． ⋯⋯（1分）被抽取的智能手机内安装“APP ”的数量在[50，60)的有0.004101004⨯⨯=人，分别记为1a ，2a ，3a ，4a ，⋯⋯（2分）被抽取的智能手机内安装“APP ”的数量在[60，70]的有0.001101001⨯⨯=人，记为1b ，⋯⋯（3分）从被抽取的智能手机内安装“APP ”的数量不低于50的居民中随机抽取2人进一步调研，共包含10个基本事件，分别为12a a ，13a a ，14a a ，11a b ，23a a ，24a a ，21a b ，34a a ，31a b ，41a b ，⋯⋯（5分）事件A 包含6个基本事件，分别为12a a ，13a a ，14a a ，23a a ，24a a ，34a a ，⋯⋯（6分）则这2人安装APP 的个数都低于60的概率63()105P A ==．⋯⋯（7分）（Ⅲ）第4组（或者写成[30，40))．⋯⋯（3分）【点评】本题考查频率、概率的求法，考查频率分布直方图的应用，考查用数学知识解决实际生活问题的能力，考查运算求解能力，是基础题．15．（2019•山东模拟）某快餐连锁店招聘外卖骑手，该快餐连锁店提供了两种日工资方案：方案（1）规定每日底薪50元，快递业务每完成一单提成3元；方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快餐连锁店记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35)，[35，45)，[45，55)，[55，65)，[65，75)，[75，85)，[85，95]七组，整理得到如图所示的频率分布直方图．（Ⅰ）随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率；（Ⅱ）若骑手甲、乙选择了日工资方案（1），丙、丁选择了日工资方案（2）．现从上述4名骑手中随机选取2人，求至少有1名骑手选择方案（1）的概率；（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由．（同组中的每个数据用该组区间的中点值代替）【分析】（Ⅰ）设事件A 为“随机选取一天，这一天该连锁店的骑手的人均日快递业务量不少于65单”依题意，连锁店的人均日快递业务量不少于65单的频率分别为：0.2，0.15，0.05，由此能估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率．（Ⅱ）设事件B 为“从四名骑手中随机选取2人，至少有1名骑手选择方案（1）”从四名新聘骑手中随机选取2名骑手，利用列举法能求出至少有1名骑手选择方案（1）的概率．（Ⅲ）方法1：求出快餐店人均日快递量的平均数，从而方案（1）日工资约为50623236+⨯=，方案2日工资约为100(6244)5190236+-⨯=<，由此得到骑手应选择方案（1）．方法2：设骑手每日完成快递业务量为n 件，分别求出方案（1）的日工资和方案（2）的日工资，从而建议骑手应选择方案（1）．方法3：设骑手每日完成快递业务量为n 单，方案（1）的日工资*1503()y n n N =+∈，方案（2）的日工资*2*100,44,1005(44),44,n n N y n n n N ⎧∈=⎨+->∈⎩求出结果，建议骑手选择方案（1）．【解答】解：（Ⅰ）设事件A 为“随机选取一天，这一天该连锁店的骑手的人均日快递业务量不少于65单” 依题意，连锁店的人均日快递业务量不少于65单的频率分别为：0.2，0.15，0.05因为0.20.150.050.4++=所以估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率P （A ）0.4=．（Ⅱ）设事件B 为“从四名骑手中随机选取2人，至少有1名骑手选择方案（1）” 从四名新聘骑手中随机选取2名骑手，有6种情况，即{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}，{丙，丁}，其中至少有1名骑手选择方案（1）的情况为：{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁} 所以至少有1名骑手选择方案（1）的概率5()6P B = （Ⅲ）方法1：快餐店人均日快递量的平均数是：300.05400.05500.2600.3700.2800.15900.0562⨯+⨯+⨯+⨯+⨯+⨯+⨯=因此，方案（1）日工资约为50623236+⨯= 方案2日工资约为100(6244)5190236+-⨯=< 故骑手应选择方案（1）方法2：设骑手每日完成快递业务量为n 件方案（1）的日工资*1503()y n n N =+∈，方案（2）的日工资*2*100,44,1005(44),44,n n N y n n n N ⎧∈=⎨+->∈⎩当17n <时，12y y <依题意，可以知道25n ，所以这种情况不予考虑当25n 时，令5031005(44)n n +>+-，则85n <，即若骑手每日完成快递业务量在85件以下，则方案（1）日工资大于方案（2）日工资，而依题中数据，每日完成快递业务量超过85件的频率是0.05，较低，故建议骑手应选择方案（1）方法3：设骑手每日完成快递业务量为n 单，方案（1）的日工资*1503()y n n N =+∈，方案（2）的日工资*2*100,44,1005(44),44,n n N y n n n N ⎧∈=⎨+->∈⎩所以方案（1）日工资约为1400.051700.052000.22300.32600.22900.153200.05236⨯+⨯+⨯+⨯+⨯+⨯+⨯= 方案（2）日工资约为1000.051000.051300.21800.32300.22800.153300.05194.5⨯+⨯+⨯+⨯+⨯+⨯+⨯= 因为236194.5>，所以建议骑手选择方案（1）．。

(高考题模拟题)高考数学素养提升练(一)理(含解析)-人教版高三全册数学试题

素养提升练(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷 (选择题，共60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2019·某某长郡中学一模)已知集合A ＝{x |x >a }，B ＝{x |x 2－4x ＋3≤0}，若A ∩B ＝B ，则实数a 的取值X 围是( )A ．a >3B ．a ≥3 C．a ≤1 D．a <1 答案 D解析因为B ＝{x |1≤x ≤3}，A ∩B ＝B ，所以a <1.故选D. 2．(2019·某某某某二模)若复数a －2i1＋i(a ∈R )为纯虚数，则|3－a i|＝( )A.13 B ．13 C ．10 D.10 答案 A 解析a －2i1＋i＝a －2i1－i 1＋i 1－i ＝a －2＋－a －2i2，因为复数a －2i1＋i (a ∈R )为纯虚数，所以⎩⎪⎨⎪⎧a －22＝0，－a －22≠0.即⎩⎪⎨⎪⎧a －2＝0，a ＋2≠0.解得a ＝2，所以|3－a i|＝|3－2i|＝32＋－22＝13.故选A.3．(2019·江淮十校模拟)为了解户籍、性别对生育二胎选择倾向的影响，某地从育龄人群中随机抽取了容量为200的调查样本，其中城镇户籍与农村户籍各100人；男性120人，女性80人，绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示)，其中阴影部分表示倾向选择生育二胎的对应比例，则下列叙述中错误的是( )A ．是否倾向选择生育二胎与户籍有关B ．是否倾向选择生育二胎与性别有关C ．倾向选择生育二胎的人群中，男性人数与女性人数相同D ．倾向选择不生育二胎的人群中，农村户籍人数少于城镇户籍人数答案 C解析由比例图可知，是否倾向选择生育二胎与户籍、性别有关，倾向选择不生育二胎的人员中，农村户籍人数少于城镇户籍人数，倾向选择生育二胎的人员中，男性人数为0.8×120＝96人，女性人数为0.6×80＝48人，男性人数与女性人数不相同，故C 错误，故选C.4．(2019·某某模拟)设等差数列{a n }的前n 项和为S n ，若a 4＝4，S 9＝72，则a 10＝( ) A ．20 B ．23 C ．24 D ．28 答案 D解析由于数列是等差数列，故⎩⎪⎨⎪⎧a 4＝a 1＋3d ＝4，S 9＝9a 1＋36d ＝72，解得a 1＝－8，d ＝4，故a 10＝a 1＋9d ＝－8＋36＝28.故选D.5．(2019·某某一模)已知函数f (x )＝x ln x ，若直线l 过点(0，－e)，且与曲线y ＝f (x )相切，则直线l 的斜率为( )A ．－2B ．2C ．－eD ．e 答案 B解析函数f (x )＝x ln x 的导数为f ′(x )＝ln x ＋1，设切点为(m ，n )，则n ＝m ln m ，可得切线的斜率为k ＝1＋ln m ，∴1＋ln m ＝n ＋e m ＝m ln m ＋e m，解得m ＝e ，k ＝1＋ln e ＝2，故选B.6．(2019·某某质检)如图，在△ABC 中，AN →＝23NC →，P 是BN 上一点，若AP →＝tAB →＋13AC →，则实数t 的值为( )A.23B.25C.16D.34 答案 C解析由题意及图，AP →＝AB →＋BP →＝AB →＋mBN →＝AB →＋m (AN →－AB →)＝mAN →＋(1－m )AB →，又AN →＝23NC →，∴AN →＝25AC →，∴AP →＝25mAC →＋(1－m )AB →，又AP →＝tAB →＋13AC →，∴⎩⎪⎨⎪⎧1－m ＝t ，25m ＝13，解得m ＝56，t ＝16，故选C.7．(2019·某某某某一模)如图是某几何体的三视图，其中网格纸上小正方形的边长为1，则该几何体的体积为( )A ．12B ．15 C.403 D.503答案 D解析其直观图为四棱锥E －ABCD ，由题意得V ＝13×⎝ ⎛⎭⎪⎫12×4×4＋12×2×2×5＝503.故选D.8．(2019·华师附中模拟)设F 1，F 2分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，若在直线x ＝a 2c(其中c 2＋b 2＝a 2)上存在点P ，使线段PF 1的垂直平分线经过点F 2，则椭圆离心率的取值X 围是( )A.⎝ ⎛⎦⎥⎤0，22 B.⎝ ⎛⎦⎥⎤0，33 C.⎣⎢⎡⎭⎪⎫33，1 D.⎣⎢⎡⎭⎪⎫22，1 答案 C解析由题意得F 1(－c,0)，F 2(c,0)，设点P ⎝ ⎛⎭⎪⎫a 2c ，m ，则由中点公式可得线段PF 1的中点K ⎝ ⎛⎭⎪⎫a 2－c 22c，12m ，∵线段PF 1的斜率与KF 2的斜率之积等于－1，即m －0a 2c ＋c ·12m －0a 2－c 22c－c ＝－1，∴m 2＝－⎝ ⎛⎭⎪⎫a 2c ＋c ·⎝ ⎛⎭⎪⎫a 2c －3c ≥0，∴a 4－2a 2c 2－3c 4≤0，∴3e 4＋2e 2－1≥0，∴e 2≥13或e 2≤－1(舍去)，∴e ≥33.又椭圆的离心率0<e <1，故33≤e <1，故选C. 9．(2019·某某模拟)已知函数f (x )＝⎩⎪⎨⎪⎧x e x，x ≤0，2－|x －1|，x >0，若函数g (x )＝f (x )－m 有两个零点x 1，x 2，则x 1＋x 2＝( ) A ．2 B ．2或2＋1eC ．2或3D ．2或3或2＋1e答案 D解析当x ≤0时，f ′(x )＝(x ＋1)e x，当x <－1时，f ′(x )<0，故f (x )在(－∞，－1)上为减函数，当－1<x <0时，f ′(x )>0，故f (x )在(－1,0)上为增函数，所以当x ≤0时，f (x )的最小值为f (－1)＝－1e.又在R 上，f (x )的图象如图所示，因为g (x )有两个不同的零点，所以方程f (x )＝m 有两个不同的解，即直线y ＝m 与y ＝f (x )有两个不同交点且交点的横坐标分别为x 1，x 2，故1<m <2或m ＝0或m ＝－1e.若1<m <2，则x 1＋x 2＝2；若m ＝0，则x 1＋x 2＝3；若m ＝－1e ，则x 1＋x 2＝－1＋3＋1e ＝2＋1e.综上，x 1＋x 2的值为2或3或2＋1e，故选D.10．(2019·某某模拟)如图，若在矩形OABC 中随机撒一粒豆子，则豆子落在图中阴影部分的概率为( )A ．1－2πB ．2πC ．2π2D ．1－2π2 答案 A解析 S 矩形＝π×1＝π，又⎠⎛0πsin x d x ＝－cos x ⎪⎪⎪π0＝－(cosπ－cos0)＝2，∴S 阴影＝π－2，∴豆子落在图中阴影部分的概率为π－2π＝1－2π.故选A .11．(2019·昌平期末)设点F 1，F 2分别为椭圆C ：x 29＋y 25＝1的左、右焦点，点P 是椭圆C 上任意一点，若使得PF 1→·PF 2→＝m 成立的点恰好是4个，则实数m 的值可以是( )A.12 B ．3 C ．5 D ．8 答案 B解析 ∵点F 1，F 2分别为椭圆C ：x 29＋y 25＝1的左、右焦点，即F 1(－2,0)，F 2(2,0)，a2＝9，b 2＝5，c 2＝4，c ＝2，设P (x 0，y 0)，PF 1→＝(－2－x 0，－y 0)，PF 2→＝(2－x 0，－y 0)，由PF 1→·PF 2→＝m 可得x 2＋y 20＝m ＋4，又∵P 在椭圆上，即x 209＋y 205＝1，∴x 20＝9m －94，要使得PF 1→·PF 2→＝m 成立的点恰好是4个，则0<9m －94<9，解得1<m <5，∴m 的值可以是3.故选B.12．(2019·某某某某、某某二模)已知正四面体的中心与球心O 重合，正四面体的棱长为26，球的半径为5，则正四面体表面与球面的交线的总长度为( )A ．4π B．82π C．122π D．12π 答案 A解析 ∵正四面体A －BCD 的中心与球心O 重合，正四面体的棱长为26，取CD 的中点E ，连接BE ，AE ，过A 作AF ⊥底面BCD ，交BE 于F ，则BE ＝AE ＝262－62＝32，BF ＝23BE ＝22，AF ＝262－222＝4，设正四面体内切球半径为r ，则(4－r )2＝(22)2＋r 2，解得正四面体内切球半径为r ＝1，∵球的半径为5，∴由球的半径知球被平面截得小圆半径为r 1＝5－1＝2，故球被正四面体一个平面截曲线为三段圆弧，且每段弧所对中心角为30°，∴正四面体表面与球面的交线的总长度为4×⎝ ⎛⎭⎪⎫3×30°360°×2π×2＝4π.故选A . 第Ⅱ卷 (非选择题，共90分)二、填空题：本大题共4小题，每小题5分，共20分．13．(2019·某某质检)设x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ＋1≤0，2x －y ≥0，x ≤2，则z ＝2x ＋3y 的最小值为________．答案 8解析画出不等式组⎩⎪⎨⎪⎧x －y ＋1≤0，2x －y ≥0，x ≤2表示的平面区域，如图阴影部分所示，由图形知，当目标函数z ＝2x ＋3y 过点A 时，z 取得最小值．由⎩⎪⎨⎪⎧x －y ＋1＝0，2x －y ＝0，求得A (1,2)，所以z ＝2x ＋3y 的最小值是2×1＋3×2＝8. 14．(2019·金山中学模拟)数列{a n }且a n ＝⎩⎪⎨⎪⎧1n 2＋2n ，n 为奇数，sin n π4，n 为偶数，若S n 为数列{a n }的前n 项和，则S 2018＝________.答案30282019解析数列{a n}且a n＝⎩⎪⎨⎪⎧1n 2＋2n ，n 为奇数，sin n π4，n 为偶数，①当n 为奇数时，a n ＝1n 2＋2n ＝12⎝ ⎛⎭⎪⎫1n －1n ＋2； ②当n 为偶数时，a n ＝sinn π4，所以S 2018＝(a 1＋a 3＋a 5＋…＋a 2017)＋(a 2＋a 4＋a 6＋…＋a 2018)＝12⎝⎛⎭⎪⎫1－13＋13－15＋…＋12017－12019＋(1＋0－1＋…＋0)＝10092019＋1＝30282019. 15．(2019·某某二模)将多项式a 6x 6＋a 5x 5＋…＋a 1x ＋a 0分解因式得(x －2)(x ＋2)5，则a 5＝________.答案 8解析 (x －2)(x ＋2)5＝(x 2－4)(x ＋2)4，(x ＋2)4展开式中的x 3系数为C 14·21＝8.所以a 5＝8.16．(2019·某某期末)已知函数f (x )＝sin x ·cos2x (x ∈R )，则f (x )的最小值为________．答案－1解析函数f (x )＝sin x ·cos2x ＝sin x (1－2sin 2x )＝sin x －2sin 3x ，令t ＝sin x ∈[－1,1]，则h (t )＝t －2t 3，h ′(t )＝1－6t 2，当－1≤t <－66时，h ′(t )<0，h (t )在⎣⎢⎡⎭⎪⎫－1，－66上单调递减；当－66≤t <66时，h ′(t )≥0，h (t )在⎣⎢⎡⎭⎪⎫－66，66上单调递增；当66≤t ≤1时，h ′(t )≤0，h (t )在⎣⎢⎡⎦⎥⎤66，1上单调递减．所以函数的最小值是h ⎝ ⎛⎭⎪⎫－66或h (1)，h (1)＝－1<h ⎝ ⎛⎭⎪⎫－66＝－66－2⎝ ⎛⎭⎪⎫－663＝－69，故函数f (x )的最小值为－1.三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．(一)必考题：60分．17．(本小题满分12分)(2019·全国卷Ⅰ)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .设(sin B －sin C )2＝sin 2A －sin B sin C .(1)求A ；(2)若2a ＋b ＝2c ，求sin C .解 (1)由已知得sin 2B ＋sin 2C －sin 2A ＝sinB sinC ，故由正弦定理得b 2＋c 2－a 2＝bc .由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12.因为0°<A <180°，所以A ＝60°. (2)由(1)知B ＝120°－C ，由题设及正弦定理得2sin A ＋sin(120°－C )＝2sin C ，即62＋32cos C ＋12sin C ＝2sin C ，可得cos(C ＋60°)＝－22. 因为0°<C <120°，所以sin(C ＋60°)＝22，故sin C ＝sin(C ＋60°－60°)＝sin(C ＋60°)cos60°－cos(C ＋60°)sin60°＝6＋24. 18．(本小题满分12分)(2019·某某一模)小明在某某市某物流公司找到了一份派送员的工作，该公司给出了甲、乙两种日薪薪酬方案，其中甲方案：底薪100元，每派送一单奖励1元；乙方案：底薪140元，每日前55单没有奖励，超过55单的部分每单奖励12元．(1)请分别求出甲、乙两种薪酬方案中日薪y (单位：元)与派送单数n 的函数关系式；(2)根据该公司所有派送员100天的派送记录，得到了如图所示的派送量指标的频率分布直方图，并发现每名派送员的日平均派送单数满足以下条件：当某天的派送量指标在⎝ ⎛⎦⎥⎤2n －110，n 5(n ＝1,2,3,4,5)时，日平均派送量为(50＋2n )单．若将频率视为概率，回答下列问题：①根据以上数据，设一名派送员的日薪为Y (单位：元)，试分别求出甲、乙两种方案中日薪Y 的分布列、数学期望及方差；②结合①中的数据，利用统计的知识，帮助小明分析，他选择哪种薪酬方案比较合适，并说明你的理由．(参考数据：0.62＝0.36,1.42＝1.96,2.62＝6.76,3.42＝11.56,3.62＝12.96,4.62＝21.16,15.62＝243.36,20.42＝416.16,44.42＝1971.36)解 (1)甲方案中派送员日薪y (单位：元)与派送单数n 的函数关系式为y ＝100＋n ，n ∈N .乙方案中派送员日薪y (单位：元)与派送单数n 的函数关系式为y ＝⎩⎪⎨⎪⎧140n ≤55，n ∈N ，12n －520n >55，n ∈N .(2)①由已知，在这100天中，该公司的一名派送员的日平均派送单数满足下表：派送单数 52 54 56 58 60 频率0.20.30.20.20.1所以Y 甲Y 甲 152 154 156 158 160 P0.20.30.20.20.1所以E (Y 甲)155.4，s 2甲＝0.2×(152－155.4)2＋0.3×(154－155.4)2＋0.2×(156－155.4)2＋0.2×(158－155.4)2＋0.1×(160－155.4)2＝6.44；Y 乙的分布列为Y 乙 140 152 176 200 P0.50.20.20.1所以E (Y 乙)，s 2乙＝0.5×(140－155.6)2＋0.2×(152－155.6)2＋0.2×(176－155.6)2＋0.1×(200－155.6)2＝404.64.②答案一：由①可知，E (Y 甲)<E (Y 乙)，但两者相关不大，且s 2甲远小于s 2乙，即甲方案中日薪的波动相对较小，所以小明选择甲方案比较合适．答案二：由①可知，E (Y 甲)<E (Y 乙)，即甲方案中日薪的期望小于乙方案中日薪的期望，所以小明选择乙方案比较合适．19．(本小题满分12分)(2019·某某调研)如图1，梯形ABCD 中，AB ∥CD ，过A ，B 分别作AE ⊥CD ，BF ⊥CD ，垂足分别为E ，F .AB ＝AE ＝2，CD ＝5，已知DE ＝1，将梯形ABCD 沿AE ，BF 同侧折起，得空间几何体ADE －BCF ，如图2.(1)若AF ⊥BD ，证明：DE ⊥平面ABFE ；(2)若DE ∥CF ，CD ＝3，线段AB 上存在一点P ，满足CP 与平面ACD 所成角的正弦值为520，求AP 的长．解 (1)证明：由已知得四边形ABFE 是正方形，且边长为2，在题图2中，AF ⊥BE ，由已知得AF ⊥BD ，BE ∩BD ＝B ，∴AF ⊥平面BDE ，又DE ⊂平面BDE ，∴AF ⊥DE ，又AE ⊥DE ，AE ∩AF ＝A ，∴DE ⊥平面ABFE .(2)在题图2中，AE ⊥DE ，AE ⊥EF ，DE ∩EF ＝E ，即AE ⊥平面DEFC ，在梯形DEFC 中，过点D 作DM ∥EF 交CF 于点M ，连接CE ，由题意得DM ＝2，CM ＝1，由勾股定理可得DC ⊥CF ，则∠CDM ＝π6，CE ＝2，过E 作EG ⊥EF 交DC 于点G ，可知GE ，EA ，EF 两两垂直，以E 为坐标原点，以EA →，EF →，EG →分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则A (2,0,0)，B (2,2,0)，C (0,1，3)，D ⎝ ⎛⎭⎪⎫0，－12，32，AC →＝(－2,1，3)，AD →＝⎝⎛⎭⎪⎫－2，－12，32. 设平面ACD 的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD →＝0，得⎩⎪⎨⎪⎧－2x ＋y ＋3z ＝0，－2x －12y ＋32z ＝0，取x ＝1得n ＝(1，－1，3)，设AP ＝m ，则P (2，m,0)(0≤m ≤2)，得CP →＝(2，m －1，－3)，设CP 与平面ACD 所成的角为θ， sin θ＝|cos 〈CP →，n 〉|＝|m |5·7＋m －12＝520⇒m ＝23. ∴AP ＝23.20．(本小题满分12分)(2019·某某高考)如图，已知点F (1,0)为抛物线y 2＝2px (p >0)的焦点．过点F 的直线交抛物线于A ，B 两点，点C 在抛物线上，使得△ABC 的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 的右侧．记△AFG ，△CQG 的面积分别为S 1，S 2.(1)求p 的值及抛物线的准线方程； (2)求S 1S 2的最小值及此时点G 的坐标．解 (1)由题意得p2＝1，即p ＝2.所以抛物线的准线方程为x ＝－1.(2)设A (x A ，y A )，B (x B ，y B )，C (x C ，y C )，重心G (x G ，y G )．令y A ＝2t ，t ≠0，则x A ＝t 2.由于直线AB 过F ，故直线AB 的方程为x ＝t 2－12ty ＋1，代入y 2＝4x ，得y 2－2t 2－1ty －4＝0，故2ty B ＝－4，即y B ＝－2t，所以B ⎝ ⎛⎭⎪⎫1t 2，－2t .又x G ＝13(x A ＋x B ＋x C )，y G ＝13(y A ＋y B ＋y C )及重心G 在x 轴上，得2t －2t ＋y C ＝0，得C ⎝ ⎛⎭⎪⎫⎝ ⎛⎭⎪⎫1t －t 2，2⎝ ⎛⎭⎪⎫1t －t ，G ⎝ ⎛⎭⎪⎫2t 4－2t 2＋23t 2，0.所以直线AC 的方程为y －2t ＝2t (x －t 2)，得Q (t 2－1,0)．由于Q 在焦点F 的右侧，故t 2>2.从而 S 1S 2＝12|FG |·|y A |12|QG |·|y C | ＝⎪⎪⎪⎪⎪⎪2t 4－2t 2＋23t 2－1·|2t |⎪⎪⎪⎪⎪⎪t 2－1－2t 4－2t 2＋23t 2·⎪⎪⎪⎪⎪⎪2t －2t ＝2t 4－t 2t 4－1＝2－t 2－2t 4－1. 令m ＝t 2－2，则m >0，S 1S 2＝2－m m 2＋4m ＋3＝2－1m ＋3m＋4≥2－12 m ·3m＋4＝1＋32. 当m ＝3时，S 1S 2取得最小值1＋32，此时G (2,0)． 21．(本小题满分12分)(2019·某某某某一模)已知函数f (x )＝ln x －ax 2＋(2－a )x ，a ∈R .(1)讨论函数f (x )的单调性；(2)当a <－12时，若对于任意x 1，x 2∈(1，＋∞)(x 1<x 2)，都存在x 0∈(x 1，x 2)，使得f ′(x 0)＝f x 2－f x 1x 2－x 1，证明：x 1＋x 22<x 0.解 (1)由题意得f ′(x )＝1x－2ax ＋(2－a )＝－2x ＋1ax －1x，x >0，当a ≤0时，f ′(x )>0在(0，＋∞)上恒成立，∴f (x )在(0，＋∞)上单调递增；当a >0时，令f ′(x )>0，则0<x <1a ；令f ′(x )<0，则x >1a.∴f (x )在⎝⎛⎭⎪⎫0，1a 上单调递增，在⎝ ⎛⎭⎪⎫1a ，＋∞上单调递减．(2)证明：∵当a <－12时，f x 2－f x 1x 2－x 1＝1x 2－x 1ln x 2x 1－a (x 2＋x 1)＋(2－a )，f ′(x 0)＝1x 0－2ax 0＋(2－a )，∴1x 2－x 1ln x 2x 1－a (x 2＋x 1)＝1x 0－2ax 0， ∴f ′⎝ ⎛⎭⎪⎫x 1＋x 22－f ′(x 0)＝2x 2＋x 1－a (x 2＋x 1)－⎝ ⎛⎭⎪⎫1x 0－2ax 0＝2x 2＋x 1－1x 2－x1ln x 2x 1＝1x 2－x 12x 2－x 1x 2＋x 1－ln x 2x 1＝1x 2－x 1⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x 2x 1－1x2x 1＋1－ln x 2x 1，令t ＝x 2x 1，g (t )＝2t －1t ＋1－ln t ，t >1，则g ′(t )＝－t －12t t ＋12<0，∴g (t )<g (1)＝0，∴f ′⎝ ⎛⎭⎪⎫x 1＋x 22－f ′(x 0)<0，∴f ′⎝⎛⎭⎪⎫x 1＋x 22<f ′(x 0)，设h (x )＝f ′(x )＝1x－2ax ＋(2－a )，x >1，则h ′(x )＝－1x2－2a >－1＋1＝0，∴h (x )＝f ′(x )在(1，＋∞)上单调递增， ∴x 1＋x 22<x 0.(二)选考题：10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．22．(本小题满分10分)[选修4－4：坐标系与参数方程](2019·某某某某一中三模)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos α，y ＝t sin α(其中t 为参数)．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ(1－cos2θ)＝8cos θ.(1)求l 和C 的直角坐标方程；(2)若l 与C 相交于A ，B 两点，且|AB |＝8，求α.解 (1)当α＝π2时，l ：x ＝1.当α≠π2时，l ：y ＝tan α·(x －1)．由ρ(1－cos2θ)＝8cos θ得2ρ2sin 2θ＝8ρcos θ，因为x ＝ρcos θ，y ＝ρsin θ，所以C 的直角坐标方程为y 2＝4x .(2)将直线l 的参数方程代入曲线C 的直角坐标方程，得(sin 2α)t 2－(4cos α)t －4＝0，则t 1＋t 2＝4cos αsin 2α，t 1t 2＝－4sin 2α，因为|AB |＝|t 1－t 2|＝t 1＋t 22－4t 1t 2＝4sin 2α＝8，所以sin α＝22或－22，因为0<α<π，所以sin α＝22，故α＝π4或3π4. 23．(本小题满分10分)[选修4－5：不等式选讲](2019·某某某某一中三模)设函数f (x )＝|2x ＋a |－|x －2|(a ∈R ，x ∈R )． (1)当a ＝－1时，求不等式f (x )>0的解集；(2)若在x ∈R 上f (x )≥－1恒成立，某某数a 的取值X 围．解 (1)a ＝－1时，f (x )>0可得|2x －1|>|x －2|，即(2x －1)2>(x －2)2，化简得(3x －3)(x ＋1)>0，所以不等式f (x )>0的解集为(－∞，－1)∪(1，＋∞)． (2)①当a <－4时，f (x )＝⎩⎪⎨⎪⎧－x －a －2，x <2，－3x －a ＋2，2≤x ≤－a 2，x ＋a ＋2，x >－a2，由函数单调性可得f (x )min ＝f ⎝ ⎛⎭⎪⎫－a 2＝a2＋2≥－1，解得－6≤a <－4；②当a ＝－4时，f (x )＝|x －2|，f (x )min ＝0≥－1，所以a ＝－4符合题意；③当a >－4时，f (x )＝⎩⎪⎨⎪⎧－x －a －2，x <－a2，3x ＋a －2，－a 2≤x ≤2，x ＋a ＋2，x >2，由函数单调性可得，f (x )min＝f ⎝ ⎛⎭⎪⎫－a 2＝－a 2－2≥－1，解得－4<a ≤－2.综上，实数a 的取值X 围为[－6，－2]．。

(完整)2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)

2019届全国高考高三模拟考试卷数学（理）试题（二）（解析版）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．[2019·南昌一模]已知复数()i2ia z a +=∈R 的实部等于虚部，则a =（） A ．12-B ．12C ．1-D ．12．[2019·梅州质检]已知集合{}31,A x x n n ==-∈N ，{}6,8,10,12,14B =，则集合A B I 中元素的个数为（） A ．2B ．3C ．4D ．53．[2019·菏泽一模]已知向量()1,1=-a ，()2,3=-b ，且()m ⊥+a a b ，则m =（） A ．25B ．25-C ．0D ．154．[2019·台州期末]已知圆C ：()()22128x y -+-=，则过点()3,0P 的圆C 的切线方程为（） A ．30x y +-=B ．30x y --=C ．230x y --=D ．230x y +-=5．[2019·东北三校]中国有十二生肖，又叫十二属相，每一个人的出生年份对应了十二种动物（鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪）中的一种，现有十二生肖的吉祥物各一个，三位同学依次选一个作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学哪个吉祥物都喜欢，如果让三位同学选取礼物都满意，则选法有（） A ．30种B ．50种C ．60种D ．90种6．[2019·汕尾质检]边长为1的等腰直角三角形，俯视图是扇形，则该几何体的体积为（）A ．π9B ．π3C ．π6D ．π187．[2019合肥质检]将函数()π2sin 16f x x ⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12（纵坐标不变）得到函数()g x 的图象，则下列说法正确的是（） A ．函数()g x 的图象关于点π,012⎛⎫- ⎪⎝⎭对称B ．函数()g x 的周期是π2C ．函数()g x 在π0,6⎛⎫⎪⎝⎭上单调递增D ．函数()g x 在π0,6⎛⎫⎪⎝⎭上最大值是18．[2019·临沂质检]执行如图所示的程序框图，输出的值为（）A ．0B ．12C ．1D ．1-9．[2019·重庆一中]2sin80cos70cos20︒︒-=︒（）A ．3B ．1C 3D ．210．[2019·揭阳一模]函数()f x 在[)0,+∞单调递减，且为偶函数．若()21f =-，则满足()31f x -≥-的x 的取值范围是（） A ．[]1,5B ．[]1,3C ．[]3,5D ．[]2,2-11．[2019·陕西联考]已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为2F ，若C 的左支上存在点M ，使得直线0bx ay -=是线段2MF 的垂直平分线，则C 的离心率为（）AB ．2CD ．512．[2019·临川一中]若函数()f x 在其图象上存在不同的两点()11,A x y ，()22,B x y ，其坐标满足条件：1212x x y y +0，则称()f x 为“柯西函数”，则下列函数：①()()10f x x x x=+>；②()()ln 0e f x x x =<<；③()cos f x x =；④()21f x x =-．其中为“柯西函数”的个数为（） A ．1 B ．2 C ．3 D ．4二、填空题：本大题共4小题，每小题5分，共20分．13．[2019·江门一模]已知a 、b 、c 是锐角ABC △内角A 、B 、C 的对边，S 是ABC △的面积，若8a =，5b =，S =，则c =_________．14．[2019·景山中学]已知a ，b 表示直线，α，β，γ表示不重合平面． ①若a αβ=I ，b α⊂，a b ⊥，则αβ⊥；②若a α⊂，a 垂直于β内任意一条直线，则αβ⊥； ③若αβ⊥，a αβ=I ，b αγ=I ，则a b ⊥；④若a α⊥，b β⊥，a b ∥，则αβ∥．上述命题中，正确命题的序号是__________．15．[2019·林芝二中]某传媒大学的甲、乙、丙、丁四位同学分别从影视配音、广播电视、公共演讲、播音主持四门课程中选修一门，且这四位同学选修的课程互不相同．下面是关于他们选课的一些信息：①甲同学和丙同学均不选播音主持，也不选广播电视；②乙同学不选广播电视，也不选公共演讲；③如果甲同学不选公共演讲，那么丁同学就不选广播电视．若这些信息都是正确的，依据以上信息可推断丙同学选修的课程是_______（填影视配音、广播电视、公共演讲、播音主持）16．[2019·河南联考]若一直线与曲线eln y x =和曲线2y mx =相切于同一点P ，则实数m =________．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．（12分）[2019·长郡中学]设正项数列{}n a 的前n 项和为n S n a 与1n a +的等比中项，其中*n ∈N ．（1）求数列{}n a 的通项公式；（2）设()11211n n n n n a b a a +++=-⋅，记数列{}n b 的前n 项和为n T ，求证：21n T <．18．（12分）[2019·维吾尔一模]港珠澳大桥是中国建设史上里程最长，投资最多，难度最大的跨海桥梁项目，大桥建设需要许多桥梁构件．从某企业生产的桥梁构件中抽取100件，测量这些桥梁构件的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[)55,65，[)65,75，[]75,85内的频率之比为4:2:1．（1）求这些桥梁构件质量指标值落在区间[]75,85内的频率；（2）若将频率视为概率，从该企业生产的这种桥梁构件中随机抽取3件，记这3件桥梁构件中质量指标值位于区间[)45,75内的桥梁构件件数为X ，求X 的分布列与数学期望．19．（12分）[2019·淄博模拟]如图，在四棱锥P ABCD -中，AB CD ∥，1AB =，3CD =，2AP =，23DP =，60PAD ∠=︒，AB ⊥平面PAD ，点M 在棱PC 上．（1）求证：平面PAB ⊥平面PCD ；（2）若直线PA ∥平面MBD ，求此时直线BP 与平面MBD 所成角的正弦值．20．（12分）[2019·泰安期末]已知椭圆()22122:10x y C a b a b+=>>的离心率为2，抛物线22:4C y x =-的准线被椭圆1C 截得的线段长为2．（1）求椭圆1C 的方程；（2）如图，点A 、F 分别是椭圆1C 的左顶点、左焦点直线l 与椭圆1C 交于不同的两点M 、N （M 、N 都在x 轴上方）．且AFM OFN ∠=∠．证明：直线l 过定点，并求出该定点的坐标．21．（12分）[2019·衡水中学]已知函数()23ln f x x ax x =+-，a ∈R ．（1）当13a =-时，求函数()f x 的单调区间；（2）令函数()()2x x f x ϕ'=，若函数()x ϕ的最小值为32-，求实数a 的值．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】[2019·揭阳一模]以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为22cos 2a ρθ=（a ∈R ，a 为常数）），过点()2,1P 、倾斜角为30︒的直线l 的参数方程满足32x t =+，（t 为参数）．（1）求曲线C 的普通方程和直线l 的参数方程；（2）若直线l 与曲线C 相交于A 、B 两点（点P 在A 、B 之间），且2PA PB ⋅=，求a 和PA PB -的值．23．（10分）【选修4-5：不等式选讲】[2019·汕尾质检]已知()221f x x x =++-的最小值为t ．求t 的值；若实数a ，b 满足2222a b t +=，求221112a b +++的最小值．2019届高三第三次模拟考试卷理科数学（二）答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】C 【解析】∵()2i i i 1i 2i 2i 22a a a z -++===--的实部等于虚部，∴122a=-，即1a =-．故选C ． 2．【答案】A【解析】由题意，集合{}31,A x x n n ==-∈N ，{}6,8,10,12,14B =， ∴{}8,14A B =I ，∴集合A B I 中元素的个数为2．故选A ． 3．【答案】A【解析】()()()1,12,312,31m m m m m +=-+-=--a b ，结合向量垂直判定，建立方程，可得12310m m --+=，解得25m =，故选A ． 4．【答案】B【解析】根据题意，圆C ：()()22128x y -+-=，P 的坐标为()3,0，则有()()2231028-+-=，则P 在圆C 上，此时20113CP K -==--，则切线的斜率1k =，则切线的方程为3y x =-，即30x y --=，故选B ． 5．【答案】B【解析】若同学甲选牛，那么同学乙只能选狗和羊中的一种，丙同学可以从剩下的10中任意选，∴共有11210C C 20⋅=，若同学甲选马，那么同学乙能选牛、狗和羊中的一种，丙同学可以从剩下的10中任意选，∴共有11310C C 30⋅=，∴共有203050+=种．故选B ． 6．【答案】A【解析】侧视图是直角边长为1的等腰直角三角形，圆锥的高为1，底面半径为1，俯视图是扇形，圆心角为2π3，几何体的体积为112ππ113239⨯⨯⨯⨯=．故选A ．7．【答案】C【解析】将函数()f x 横坐标缩短到原来的12后，得到()π2sin 216g x x ⎛⎫=+- ⎪⎝⎭，当π12x =-时，π112f ⎛⎫-=- ⎪⎝⎭，即函数()g x 的图象关于点π,112⎛⎫-- ⎪⎝⎭对称，故选项A 错误；周期2ππ2T ==，故选项B 错误；当π0,6x ⎛⎫∈ ⎪⎝⎭时，πππ2662x ⎛⎫+∈ ⎪⎝⎭,，∴函数()g x 在π0,6⎛⎫⎪⎝⎭上单调递增，故选项C 正确；∵函数()g x 在π0,6⎛⎫ ⎪⎝⎭上单调递增，∴()π16g x g ⎛⎫<= ⎪⎝⎭，即函数()g x 在π0,6⎛⎫⎪⎝⎭上没有最大值，故选项D 错误．故选C ．8．【答案】A【解析】第一次循环，1k =，cos01S ==，112k =+=，4k >不成立；第二次循环，2k =，π131cos 1322S =+=+=，213k =+=，4k >不成立；第三次循环，3k =，32π31cos 12322S =+=-=，314k =+=，4k >不成立；第四次循环，4k =，1cos π110S =+=-=，415k =+=，4k >成立，退出循环，输出0S =，故选A ． 9．【答案】C 【解析】∵()2sin 6020cos702sin80cos70cos20cos20︒+︒︒-︒-︒=︒︒2sin 60cos202cos60sin 20cos70cos20︒︒+︒︒-︒=︒2sin 60cos20sin 20cos70cos20︒︒+︒-︒=︒2sin 60cos202sin 603cos20︒︒==︒=︒．故选C ．10．【答案】A【解析】∵函数()f x 为偶函数，∴()()312f x f -≥-=等价于()()32f x f -≥， ∵函数()f x 在[)0,+∞单调递减，∴32x -≤，232x -≤-≤，15x ≤≤，故选A ． 11．【答案】C【解析】()2,0F c ，直线0bx ay -=是线段2MF 的垂直平分线，可得2F 到渐近线的距离为222F P b b a ==+，即有22OP c b a =-=，由OP 为12MF F △的中位线，可得122MF OP a ==，22MF b =，可得212MF MF a -=，即为222b a a -=，即2b a =，可得221145c b e a a==+=+=．故选C ．12．【答案】B【解析】由柯西不等式得：对任意实数1x ，1y ，2x ，2y ，2222121211220x x y y x y x y +-+⋅+≤恒成立，（当且仅当1221x y x y =取等号）若函数()f x 在其图象上存在不同的两点()11,A x y ，()22,B x y ，其坐标满足条件：222212121122x x y y x y x y +-+⋅+的最大值为0，则函数()f x 在其图象上存在不同的两点()11,A x y ，()22,B x y ，使得OA u u u r，OB u u u r 共线，即存在过原点的直线y kx =与()y f x =的图象有两个不同的交点：对于①，方程()10kx x x x=+>，即()211k x -=，不可能有两个正根，故不存在；对于②，，由图可知不存在；对于③，，由图可知存在；对于④，，由图可知存在，∴“柯西函数”的个数为2，故选B ．二、填空题：本大题共4小题，每小题5分，共20分． 13．【答案】7【解析】根据三角形面积公式得到1sin sin 2S ab C C =⨯⇒=∵三角形为锐角三角形，故得到角C 为π3，再由余弦定理得到222π1cos 7322a b c c ab+-==⇒=．故答案为7．14．【答案】②④【解析】对于①，根据线面垂直的判定定理，需要一条直线垂直于两条相交的直线，故不正确，对于②，a α⊂，a 垂直于β内任意一条直线，满足线面垂直的定理，即可得到αβ⊥，又a α⊂，则αβ⊥，故正确，对于③，αβ⊥，a αβ=I ，b αγ=I ，则a b ⊥或a b ∥，或相交，故不正确，对于④，可以证明αβ∥，故正确．故答案为②④． 15．【答案】影视配音【解析】由①知甲和丙均不选播音主持，也不选广播电视；由②知乙不选广播电视，也不选公共演讲；由③知如果甲不选公共演讲，那么丁就不选广播电视，综上得甲、乙、丙均不选广播电视，故丁选广播电视，从而甲选公共演讲，丙选影视配音，故答案为影视配音． 16．【答案】12【解析】曲线eln y x =的导数为e'y x=，曲线2y mx =的导数为2y mx '=，由e2mx x =，0x >且0m >，得x =e 2⎫⎪⎪⎭，代入eln y x =得e 2=，解得12m =，故答案为12．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤． 17．【答案】（1）n a n =；（2）见解析．【解析】（1）∵2n S 是n a 与1n a +的等比中项，∴()221n n n n n S a a a a =+=+，当1n =时，21112a a a =+，∴11a =．当2n ≥时，22111222n n n n n n n a S S a a a a ---=-=+--，整理得()()1110n n n n a a a a --+--=．又0n a >，∴()112n n a a n --=≥，即数列{}n a 是首项为1，公差为1的等差数列． ∴()()1111n a a n d n n =+-=+-=．（2）()()()1121111111n n n n b n n n n +++⎛⎫=-⋅=-+ ⎪++⎝⎭，∴21232111111111122334212221n n T b b b b n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++=+-+++-++-+ ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭L L11121n =-<+． 18．【答案】（1）0.05；（2）见解析．【解析】（1）设区间[]75,85内的频率为x ，则区间[)55,65，[)65,75内的频率分别为4x 和2x ．依题意得()0.0040.0120.0190.0310421x x x +++⨯+++=，解得0.05x =． ∴这些桥梁构件质量指标值落在区间[]75,85内的频率为0.05．（2）从该企业生产的该种桥梁构件中随机抽取3件，相当于进行了3次独立重复实验， ∴X 服从二项分布(),B n p ，其中3n =．由（1）得，区间[]45,75内的频率为0.30.20.10.6++=，将频率视为概率得0.6p =．∵X 的所有可能取值为0，1，2，3，且()00330C 0.60.40.064P X ==⨯⨯=，()11231C 0.60.40.288P X ==⨯⨯=，()22132C 0.60.40.432P X ==⨯⨯=，()33033C 0.60.40.216P X ==⨯⨯=．∴X 的分布列为：X P0.0640.2880.4320.216X 服从二项分布(),B n p ，∴X 的数学期望为30.6 1.8EX =⨯=．19．【答案】（1）见解析；（2219565【解析】（1）∵AB ⊥平面PAD ，∴AB DP ⊥，又∵23DP=，2AP=，60PAD∠=︒，由sin sinPD PAPAD PDA=∠∠，可得1sin2PDA∠=，∴30PDA∠=︒，90APD∠=︒，即DP AP⊥，∵AB AP A=I，∴DP⊥平面PAB，∵DP⊂平面PCD，∴平面PAB⊥平面PCD；（2）以点A为坐标原点，AD所在的直线为y轴，AB所在的直线为z轴，如图所示，建立空间直角坐标系，其中()0,0,0A，()0,0,1B，()0,4,3C，()0,4,0D，)3,1,0P．从而()0,4,1BD=-u u u r，)3,1,0AP=u u u r，()3,3,3PC=-u u u r，设PM PCλ=u u u u r u u u r，从而得()33,31,3Mλλλ+，()33,31,31BMλλλ=+-u u u u r，设平面MBD的法向量为(),,x y z=n，若直线PA∥平面MBD，满足BMBDAP⎧⋅=⎪⎪⋅=⎨⎪⋅=⎪⎩u u u u ru u u ru u u rnnn，即)()()31313104030x y zy zx yλλλ-+++-=-=⎨+=，得14λ=，取()3,3,12=--n，且()3,1,1BP=-u u u r，直线BP与平面MBD所成角的正弦值等于33122sin195651565BPBPθ⋅-+===⨯⋅u u u ru u u rnn20．【答案】（1）2212xy+=；（2）直线l过定点()2,0．【解析】（1）由题意可知，抛物线2C的准线方程为1x=，又椭圆1C2，∴点2⎛⎝⎭在椭圆上，∴221112a b+=，①又2cea==，∴222212a bea-==，∴222a b=，②，由①②联立，解得22a=，21b=，∴椭圆1C的标准方程为2212xy+=．（2）设直线:l y kx m =+，设()11,M x y ，()22,N x y ，把直线l 代入椭圆方程，整理可得()222214220k x km m +++-=，()()222222164212216880k m k m k m ∆=-+-=-+>，即22210k m -+>，∴122421kmx x k +=-+，21222221m x x k -=+，∵111FM y k x =+，221FN yk x =+，M 、N 都在x 轴上方，且AFM OFN ∠=∠，∴FM FN k k =-，∴121211y yx x =-++，即()()()()122111kx m x kx m x ++=-++，整理可得()()1212220kx x k m x x m ++++=，∴()2222242202121m km k k m m k k -⎛⎫⋅++-+= ⎪++⎝⎭，即22224444420km k k m km k m m ---++=，整理可得2m k =， ∴直线l 为()22y kx k k x =+=+，∴直线l 过定点()2,0． 21．【答案】（1）见解析；（2）56-．【解析】（1）13a =-时，()2ln f x x x x =--，则()()()221121x x x x f x x x +---'==，令()'0f x =，解得12x =-或1x =，而0x >，故1x =，则当()0,1x ∈时，()0f x '<，即()f x 在区间内递减，当()1,x ∈+∞时，()0f x '>，即()f x 在区间内递增．（2）由()23ln f x x ax x =+-，()123f x x a x'=+-，则()()23223x x f x x ax x ϕ'==+-，故()2661x x ax ϕ'=+-，又()()264610a ∆=-⨯⨯->，故方程()0x ϕ'=有2个不同的实根，不妨记为1x ，2x ，且12x x <，又∵12106x x =-<，故120x x <<，当()20,x x ∈时，()0x ϕ'<，()x ϕ递减，当()2,x x ∈+∞时，()0x ϕ'>，()x ϕ递增，故()()322222min 23x x x ax x ϕϕ==+-，①又()20x ϕ'=，∴2226610x ax +-=，即222166x a x -=，②将222166x a x -=代入式，得2222222222222233316112323622x x x x x x x x x x x -+⋅⋅-=+--=--，由题意得3221322x x --=-，即322230x x +-=，即()()222212230x x x -++=，解得21x =，将21x =代入式中，得56a =-．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．【答案】（1）222x y a -=，3212x t y =+=+⎧⎪⎪⎨⎪⎪⎩（t 为参数）；（2）2a =±，432．【解析】（1）由22cos 2a ρθ=得()2222cos sin a ρθθ-=，又cos x ρθ=，sin y ρθ=，得222x y a -=，∴C 的普通方程为222x y a -=， ∵过点()2,1P 、倾斜角为30︒的直线l 的普通方程为)321y x =-+，由32x =得112y t =+，∴直线l 的参数方程为3212x t y =+=+⎧⎪⎪⎨⎪⎪⎩（t 为参数）．（2）将3212x t y ==+⎧⎪⎪⎨⎪⎪⎩代入222x y a -=，得()()222231230t t a ++-=，依题意知()()222231830a ∆⎡⎤=-->⎣⎦，则上方程的根1t 、2t 就是交点A 、对应的参数，∵()21223t t a ⋅=-，由参数t 的几何意义知1212PA PB t t t t ⋅=⋅=⋅，得122t t ⋅=， ∵点P 在A 、B 之间，∴120t t ⋅<，∴122t t ⋅=-，即()2232a -=-，解得24a =（满足0∆>），∴2a =±， ∵1212PA PB t t t t -=-=+，又()122231t t +=-， ∴432PA PB -=． 23．【答案】（1）2；（2）1．【解析】（1）()31,12213,1131,1x x f x x x x x x x +≥⎧⎪=++-=+-<<⎨⎪--≤-⎩，故当1x =-时，函数()f x 有最小值2，∴2t =．（2）由（1）可知22222a b +=，故22124a b +++=，∴2222222222212111112121121244b a a b a b a b a b +++++++⎛⎫+++=+⋅=≥ ⎪++++⎝⎭，当且仅当22122a b +=+=，即21a =，20b =时等号成立，故221112a b +++的最小值为1．。

2020届高考数学(理)一轮必刷题专题32 数列的综合问题(解析版)

考点32 数列的综合问题1．（北京市房山区2019年高考第一次模拟测试理）《九章算术》中有如下问题：今有蒲生一日，长三尺，莞生一日，长1尺．蒲生日自半，莞生日自倍．问几何日而长等？意思是：今有蒲第一天长高3尺，莞第一天长高1尺，以后蒲每天长高前一天的一半，莞每天长高前一天的2倍．若蒲、莞长度相等，则所需时间为（）（结果精确到0.1．参考数据：lg2=0.3010，lg3=0.4771．）A．天B．天C．天D．天【答案】C【解析】设蒲的长度组成等比数列{a n}，其a1=3，公比为，其前n项和为A n，则A n=.莞的长度组成等比数列{b n}，其b1=1，公比为2，其前n项和为B n．则B n，由题意可得：，整理得：2n+=7，解得2n=6，或2n=1（舍去）．∴n=≈2.6．∴估计2.6日蒲、莞长度相等.故选：C．2．（新疆乌鲁木齐市2018届高三第三次诊断性测验）已知数列，满足，，，则数列的前10项的和为A．B．C．D．【答案】D【解析】由a n+1﹣a n2，所以数列{a n}是等差数列，且公差是2，{b n}是等比数列，且公比是2．又因为＝1，所以a n ＝+（n ﹣1）d ＝2n ﹣1．所以b 2n ﹣1＝•22n ﹣2＝22n ﹣2．设，所以＝22n ﹣2，所以4，所以数列{∁n }是等比数列，且公比为4，首项为1．由等比数列的前n 项和的公式得：其前10项的和为（410﹣1）．故选：D ．3．（安徽省“皖南八校”2018届高三第三次（4月)联考）删去正整数数列中的所有完全平方数，得到一个新数列，这个数列的第2018项是（） A ．B ．C ．D ．【答案】B 【解析】由题意可得，这些数可以写为：，第个平方数与第个平方数之间有个正整数，而数列共有项，去掉个平方数后，还剩余个数，所以去掉平方数后第项应在后的第个数，即是原来数列的第项，即为，故选B.4．（华大新高考联盟2018届高三上学期11月教学质量测评理）已知等比数列{}n a 的前n 项和为n S ,3123S a a =+，则42S S =（） A ．2 B ．3C ．4D ．5【答案】B 【解析】由3123S a a =+可得312a a =，所以22q =，又因为2123434421212113a a a a a a S q S a a a a ++++==+=+=++，所以选B.5．（湖南省2017届高三高考冲刺预测卷六理）最近各大城市美食街火爆热开，某美食店特定在2017年元旦期间举行特大优惠活动，凡消费达到88元以上者，可获得一次抽奖机会.已知抽奖工具是一个圆面转盘，被分为6个扇形块，分别记为1，2，3，4，5，6，其面积成公比为3的等比数列（即扇形块2是扇形块1面积的3倍），指针箭头指在最小的1区域内时，就中“一等奖”，则一次抽奖抽中一等奖的概率是（） A ．140B ．1121C ．1364D ．11093【答案】C 【解析】由题意，可设1,2,3,4,5,6 扇形区域的面积分别为,3,9,27,81,243x x x x x x ，则由几何概型得，消费88 元以上者抽中一等奖的概率1392781243364x P x x x x x x ==+++++ ，故选C. 6．（湖北省钟祥市2019届高三高考第一次模拟考试理）对于实数x ，[x]表示不超过x 的最大整数，已知正数列{a n }满足S n =12（a n n 1a +），n ∈N*，其中S n 为数列{a n }的前n 项的和，则[12121111S S S ++⋯+]=______．【答案】20 【解析】由题可知0n S >，当1n >时，1111[()]2n n n n n S S S S S --=-+-化简可得2211n n S S --=，当22111,1n S a === 所以数列2{}n S 是以首项和公差都是1的等差数列，即2n n S n S =∴=又1n >时，22nS =<<=记12121111S S S S =++一方面21]1)20S >-=>另一方面1(21)]11)21S <+++-=+=所以2021S << 即[]20S = 故答案为207．（北京市朝阳区2019届高三第一次（3月)综合练习一模）天坛公园是明、清两代皇帝“祭天”“祈谷”的场所．天坛公园中的圜丘台共有三层（如图1所示），上层坛的中心是一块呈圆形的大理石板，从中心向外围以扇面形石（如图2所示）．上层坛从第一环至第九环共有九环，中层坛从第十环至第十八环共有九环，下层坛从第十九环至第二十七环共有九环；第一环的扇面形石有9块，从第二环起，每环的扇面形石块数比前一环多9块，则第二十七环的扇面形石块数是______；上、中、下三层坛所有的扇面形石块数是_______．【答案】243 3402 【解析】第一环的扇面形石有9块，从第二环起，每环的扇面形石块数比前一环多9块，则依题意得：每环的扇面形石块数是一个以9为首项，9为公差的等差数列，所以，a n ＝9＋（n －1）×9＝9n ，所以，a 27＝9×27＝243，前27项和为：1272727()27(9243)22a a S ++==＝3402.格谦教育收集整理，更多优惠资料请搜索淘宝店铺：格谦教育 https://8．（江苏省南京师大附中2018届高三高考考前模拟考试）在数列{a n }中，若a 4＝1，a 12＝5，且任意连续三项的和都是15，则a 2018＝______．【答案】9【解析】分析：将a n +a n+1+a n+2=15中n 换为n+1，可得数列{a n }是周期为3的数列．求出a 2，a 1，即可得到a 2018详解：由题意可得a n +a n+1+a n+2=15，将n 换为a n+1+a n+2+a n+3=15，可得a n+3=a n ，可得数列{a n 是周期为3的数列．故，由a n +a n+1+a n+2=15，n 取1可得，故，故答案为9.9．（湖北省武昌2018届元月调研考试）对任一实数序列，定义新序列，它的第项为，假设序列的所有项都是，且，则__________．【答案】100. 【解析】设序列的首项为，则序列，则它的第n 项为，因此序列A 的第项，则是关于的二次多项式，其中的系数为，因为，所以必有，故。

北京市朝阳区2018-2019学年度第一学期期末质量检测高三年级数学试卷(理工类)

三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．
15.（本小题满分13分）
在中，已知，
（Ⅰ）求的长；
（Ⅱ）求边上的中线的长.
16.（本小题满分13分）
某日A,B,C三个城市18个销售点的小麦价格如下表：
销售点序号
所属城市
小麦价格（元/吨）
销售点序号
所属城市
小麦价格（元/吨）
所以，且 .
所以四边形是平行四边形.
所以 .
又因为平面，平面，
所以平面 .…………………4分
（Ⅱ）因为侧面是正方形，所以 .
又因为平面平面，且平面平面，
所以平面 .所以 .
又因为，以为原点建立空间直角坐标系，如图所示.
设，则，
.
（ⅰ）设平面的一个法向量为 .
由得即令，所以 .
1.已知集合，，则
A. B. C. D.
2.设复数满足，则 =
A. B. C.2D.
3.执行如图所示的程序框图，若输入的，则输出的 =
A. B. C. D.
4.在平面直角坐标系中，过三点的圆被轴
截得的弦长为
A. B. C. D.
5.将函数的图象向右平移个单位后，图象经过
点，则的最小值为
（Ⅰ）求点坐标和直线的方程；
（Ⅱ）求证： .
20.（本小题满分13分）
已知是由正整数组成的无穷数列，对任意，满足如下两个条件：
① 是的倍数；
② .
（Ⅰ）若，，写出满足条件的所有的值；
（Ⅱ）求证：当时，；
（Ⅲ）求所有可能取值中的最大值.

2020届高考数学(理)一轮必刷题专题47 两直线的位置关系、距离公式(解析版)

考点47 两直线的位置关系、距离公式1．（湖南省师范大学附属中学2019届高三下学期模拟三理）长方体1111ABCD A B C D -中，1AB BC ==，1BB ，设点A 关于直线1BD 的对称点为P ，则P 与1C 两点之间的距离为（）A ．2BC ．1D ．12【答案】C 【解析】将长方体中含有1ABD 的平面取出，过点A 作1AM BD ⊥，垂足为M ，延长AM 到AP ，使M P AM =，则P 是A 关于1BD 的对称点，如图所示，过P 作1PE BC ⊥，垂足为E ，连接PB ，1PC ，依题意1AB =，1AD ，12BD =，160ABD ∠=︒，30BAM ∠=︒，30PBE ∠=︒，12PE =，2BE =，所以11PC =. 故选C .2．（四川省宜宾市2019届高三第三次诊断性考试数学理）已知双曲线的左右焦点分别为，以它的一个焦点为圆心，半径为的圆恰好与双曲线的两条渐近线分别切于两点，则四边形的面积为（） A ．3 B ．4C ．5D ．6【答案】D 【解析】因为双曲线的左右焦点分别为双曲线的渐近线方程为，即其中一条渐近线方程为以它的一个焦点为圆心，半径为的圆恰好与双曲线的两条渐近线分别切于A ，B 两点根据焦点到渐近线的距离及双曲线中的关系可得所以解得，进而可求得切点则四边形的面积为故选：D3．（河北省保定市2019年高三第二次模拟考试理）设点P 为直线l ：40x y +-=上的动点，点(2,0)A -，()2,0B ，则||||PA PB +的最小值为（）A． BC．D【答案】A 【解析】依据题意作出图像如下：设点()2,0B 关于直线l 的对称点为()1,B a b ，则它们的中点坐标为：2,22a b +⎛⎫⎪⎝⎭，且1PB PB = 由对称性可得：()011224022b a a b -⎧⨯-=-⎪⎪-⎨+⎪+-=⎪⎩，解得：4a =，2b =所以()14,2B因为1||||||||PA PB PA PB +=+，所以当1,,A P B 三点共线时，||||PA PB +最大此时最大值为1AB ==故选：A4．（贵州省贵阳市2019年高三5月适应性考试二理）双曲线的两条渐近线分别为，，为其一个焦点，若关于的对称点在上，则双曲线的渐近线方程为（） A ．B ．C ．D ．【答案】D 【解析】不妨取，设其对称点在，由对称性可得：，解得：，点在，则：，整理可得：，双曲线的渐近线方程为：.故选：D .5．（广东省广州市普通高中毕业班2019届高三综合测试二理）已知点A 与点(1,2)B 关于直线30x y ++=对称，则点A 的坐标为（） A ．(3,4) B ．(4,5)C ．(4,3)--D ．(5,4)--【答案】D 【解析】设(),A x y ,则123052224(1)11x y x y y x ++⎧++=⎪=-⎧⎪∴⎨⎨-=-⎩⎪⋅-=-⎪-⎩，选D.6．（甘肃省2019届高三第一次高考诊断考试理）抛物线28y x =的焦点到双曲线2214y x -=的渐近线的距离是（） ABC．5D【答案】C 【解析】依题意，抛物线的焦点为()2,0，双曲线的渐近线为2y x =±，其中一条为20x y -=，由点到直线的距离公式得5d ==.故选C. 7．（黑龙江省齐齐哈尔市2019届高三第二次模拟考试数学理）已知椭圆2222:1(0)x y E a b a b+=>>的左，右焦点分别为1F ，2F ，过1F 作垂直x 轴的直线交椭圆E 于,A B 两点，点A 在x 轴上方.若3AB =，2ABF ∆的内切圆的面积为916π，则直线2AF 的方程是（） A ．ln()x a <- B ．2320x y +-=C ．4340x y +-=D ．3430x y +-=【答案】D 【解析】设内切圆半径为r ，则2916r ππ=，∴34r =，()1,0F c -，∴内切圆圆心为3,04c ⎛⎫-+ ⎪⎝⎭，由3AB =知3,2A c ⎛⎫- ⎪⎝⎭，又()2,0F c ，所以2AF 方程为3430x cy +-=，由内切圆圆心到直线2AF 距离为r ，34=得1c =，所以2AF 方程为3430x y +-=. 故选D 项8．（辽宁省丹东市2019届高三总复习质量测试一理）已知F是椭圆22:196x yC+=的右焦点，直线0x-=与C相交于,M N两点，则MNF∆的面积为（）AB．CD．【答案】C【解析】22196x yx⎧+=⎪⎨⎪+=⎩解得223xxy y⎧=⎪⎧=⎪⎪⎨⎨=⎪⎩⎪=-⎪⎩，即)22,,33M N⎛⎫--⎪⎪⎝⎭163MN∴==右焦点)F到直线0x+=11623ABCS∴=⨯=故选C项.9．（广西壮族自治区柳州市2019届高三毕业班3月模拟考试数学理）圆22430x y x+-+=关于直线3y x=对称的圆的方程是（）A．(()2211x y+-=B．()2221x y+-=C．()2211x y+-=D．()(2211x y-+-=【答案】D【解析】由题意得，圆22430x y x+-+=方程即为()2221x y-+=，∴圆心坐标为()2,0，半径为1．设圆心()2,0关于直线y x =的对称点的坐标为(),a b ，则1232232b a b a ⎧⋅=-⎪⎪-⎨+⎪=⋅⎪⎩，解得1a b =⎧⎪⎨=⎪⎩∴所求圆的圆心坐标为(， ∴所求圆的方程为()(2211x y -+=．故选D ．10．（湖南省三湘名校（五市十校)2019届高三下学期第一次联考数学理）如图，O 是坐标原点，过(,0)E p 的直线分别交抛物线22(0)y px p =>于A 、B 两点，直线BO 与过点A 平行于x 轴的直线相交于点M ，过点M 与此抛物线相切的直线与直线x p =相交于点N .则22||ME NE -=（）A ．2pB ．2pC ．22pD ．24p【答案】C 【解析】过E （p ，0）的直线分别交抛物线y 2＝2px （p ＞0）于A 、B ，两点为任意的，不妨设直线AB 为x ＝p ，由2y 2pxx p⎧=⎨=⎩，解得y ＝，则A （p），B （p），∵直线BM 的方程为y，直线AM 的方程为y ＝x ，解得M （﹣p），∴|ME |2＝（2p ）2+2p 2＝6p 2，设过点M 与此抛物线相切的直线为y＝k （x +p ），由()2y 2=k px x p ⎧=⎪⎨+⎪⎩，消x 整理可得ky 2﹣2py ﹣+2p 2k ＝0， ∴△＝4p 2﹣4k （﹣+2p 2k ）＝0，解得k＝2， ∴过点M 与此抛物线相切的直线为yp＝2（x +p ），由()=2x p x p =⎧⎪⎨+⎪⎩，解得N （p ，2p ）， ∴|NE |2＝4p 2，∴|ME |2﹣|NE |2＝6p 2﹣4p 2＝2p 2，故选：C ．11．（江西省南昌市2019届高三第一次模拟考试数学理）已知(A，B ，P 为圆221x y +=上的动点，AP PQ =，过点P 作与AP 垂直的直线l 交直线QB 于点M ，则M 的横坐标范围是( ) A ．||1x ≥ B ．||1x >C ．||2x ≥D．||2x ≥【答案】A 【解析】设P （00x ,y ），则Q （20x ，20y ），当0y ≠0时， kAP =kPM 00x y =-，直线PM ：y﹣000x y y +=-x ﹣0x ），①直线QB ：y ﹣002y 2x =（x ，② 联立①②消去y 得x =，∴x =，由|0x |＜1得x 2＞1，得|x|＞1，当0y ＝0时，易求得|x|＝1，故选：A ．12．（辽宁省沈阳市东北育才学校2019届高三第五次模拟数学理）若双曲线222:14x y C m-=的焦距为则C 的一个焦点到一条渐近线的距离为 ( ) A ．2 B ．4CD．【答案】B 【解析】因为双曲线222:14x y C m-=的焦距为所以2420m +=，即216m =；所以其中一个焦点坐标为()，渐近线方程为2y x =，所以焦点到渐近线的距离为d 4==.故选B13．（安徽省黄山市2019届高三第一次质量检测一模数学理）直线与轴的交点为,点把圆的直径分为两段，则较长一段比上较短一段的值等于 ( )A ．2B ．3C ．4D ．5 【答案】A 【解析】令代入可得，圆心坐标为，则与圆心的距离为，半径为6，可知较长一段为8，较短一段4，则较长一段比上较短一段的值等于2。

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试(数学理)

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷（理工类） 2012.1（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）注意事项：考生务必将答案答在答题卡上，在试卷上答无效。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. 1.已知平面向量(3,1)=a ，(,3)x =b ，且a ⊥b ，则实数x 的值为（） A ．9 B ．1 C ．1- D ． 9-2.设集合{}U =1,2,3,4，{}25M =x U x x+p =0∈-，若{}2,3U C M =，则实数p 的值为 ( ) A ．4- B ． 4 C ．6- D ．63. 设数列{}n a 是公差不为0的等差数列，11a =且136,,a a a 成等比数列，则{}n a 的前n 项和n S 等于（）A ． 2788n n +B ．2744n n + C ．2324n n+D ．2n n +4.执行如图所示的程序框图，输出的S 值为（） A ．1 B ．1- C ． 2- D ．05.已知函数()sin f x x x =，设()7a f π=，()6b f π=，()3c f π=，则,,a b c 的大小关系是（）A. a b c <<B.c a b <<C.b a c <<D.b c a << 6.函数2()2xf x a x=--的一个零点在区间(1,2)内，则实数a 的取值范围是（） A ．(1,3) B ．(1,2) C ．(0,3) D ． (0,2)7. 已知正方形ABCD的边长为ABC ∆沿对角线AC 折起，使平面ABC ⊥平面ACD ，得到如图所示的三棱锥B ACD -．若O 为AC 边的中点，M ，N 分别为线段DC ，BO 上的动点（不包括端点），且BN CM =.设BN x =，则三棱锥N AMC-ADBNMOC的体积()y f x =的函数图象大致是（）A ．B ．C ．D ．8.已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+ m ∈Z }.若存在实数,a b 使得A B ≠∅ 成立,称点(,)a b 为“￡”点，则“￡”点在平面区域22{(,)|108}C x y x y =+≤内的个数是( )A. 0B. 1C. 2D. 无数个第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分. 把答案填在答题卡上. 9.已知有若干辆汽车通过某一段公路，从中抽取200辆汽车进行测速分析，其时速的频率分布直方图如图所示，则时速在区间[60,70)上的汽车大约有辆.10．某几何体的三视图如图所示，则这个几何体的体积是 .11. 在平面直角坐标系中,不等式组0,40,x y x y x a +≥⎧⎪-+≥⎨⎪≤⎩所表示的平面区域的面积是9,则实数a 的值为 .12. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ，B 两点，且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润y （万元）与机器运转时间x （年数，x *∈N ）的关系为21825y x x =-+-.则当每台机器运转年时，年平均利润最大，最大值是万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作. （1）若1,3a b ==,按上述规则操作三次,扩充所得的数是__________；时速（km/h ）01002 003 004 40 50 60 70 80（2）若0p q >>，经过6次操作后扩充所得的数为(1)(1)1m n q p ++-（,m n 为正整数），则,m n 的值分别为______________.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本题满分13分）在锐角ABC ∆中，a ，b ，c 分别为内角A ，B ，C2sin 0b A -=．（Ⅰ）求角B 的大小；（Ⅱ）若5a c +=，且a c >，b =AB AC的值．16. （本题满分13分）如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转转盘，转盘停止转动时，箭头A 所指区域的数字就是每次游戏所得的分数（箭头指向两个区域的边界时重新转动），且箭头A 指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘，得分情况记为(,)a b （假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）．（Ⅰ）求某个家庭得分为(5,3)的概率？（Ⅱ）若游戏规定：一个家庭的得分为参与游戏的两人得分之和，且得分大于等于8的家庭可以获得一份奖品．请问某个家庭获奖的概率为多少？（Ⅲ）若共有5个家庭参加家庭抽奖活动．在（Ⅱ）的条件下，记获奖的家庭数为X ，求X 的分布列及数学期望．17. （本题满分13分）如图，在四棱锥S ABCD -中，平面SAD ⊥平面ABCD ．底面ABCD 为矩形，,AD AB =，SA SD a ==．（Ⅰ）求证：CD SA ⊥；（Ⅱ）求二面角C SA D --的大小.18. （本题满分13分）已知函数1()ln(1)1xf x ax x-=+++（0x ≥，a 为正实数）. （Ⅰ）若1a =，求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）若函数()f x 的最小值为1，求a 的取值范围.19. （本题满分14分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12，直线l 过点(4,0)A ，(0,2)B ，且与椭圆C 相切于点P .（Ⅰ）求椭圆C 的方程；（Ⅱ）是否存在过点(4,0)A 的直线m 与椭圆C 相交于不同的两点M 、N ，使得23635AP AM AN =⋅?若存在，试求出直线m 的方程；若不存在,请说明理由.20. （本题满分14分）数列{}n a ，{}n b （1,2,3,n = ）由下列条件确定：①110,0a b <>；②当2k ≥时，k a 与k b 满足：当011≥+--k k b a 时，1-=k k a a ,211--+=k k k b a b ；当011<+--k k b a 时，211--+=k k k b a a ，1-=k k b b . （Ⅰ）若11a =-，11b =，写出234,,a a a ，并求数列}{n a 的通项公式；（Ⅱ）在数列}{n b 中，若s b b b >>> 21(3s ≥,且*s ∈N )，试用11,b a 表示k b },,2,1{s k ∈；（Ⅲ）在（Ⅰ）的条件下，设数列}{n c (*)n ∈N 满足211=c ，0n c ≠， 2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数)，求证：当m n ≤时，恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷答案（理工类） 2012.1一、选择题：二、填空题：三、解答题：（15）（本小题满分13分）解：2sin 0b A -=，2sin sin 0A B A -=， ……………………………………………… 2分因为sin 0A ≠，所以23sin =B . …………………………………………………3分又B 为锐角，则3B π=. …………………………………………… 5分（Ⅱ）由（Ⅰ）可知，3B π=．因为b =根据余弦定理，得 2272cos3a c ac π=+-，………………………………………7分整理，得2()37a c ac +-=．由已知 5a c +=，则6ac =．又a c >，可得 3a =，2c =． ……………………………………… 9分于是222cos2b c a A bc +-===， ………………………… 11分所以cos cos 21AB AC AB AC A cb A ==== ． …………… 13分（16）（本小题满分13分）解：（Ⅰ）记事件A ：某个家庭得分情况为(5,3)．111()339P A =⨯=．所以某个家庭得分情况为(5,3)的概率为19．……………………………… 4分（Ⅱ）记事件B ：某个家庭在游戏中获奖，则符合获奖条件的得分包括(5,3),(5,5),(3,5) 共3类情况．所以1111111()3333333P B =⨯+⨯+⨯=．所以某个家庭获奖的概率为13． ………………………………………… 8分（Ⅲ）由（Ⅱ）可知，每个家庭获奖的概率都是13，所以1~(5,)3X B ．00551232(0)()()33243P X C ==⋅=，11451280(1)()()33243P X C ==⋅=，22351280(2)()()33243P X C ==⋅=，33251240(3)()()33243P X C ==⋅=，44151210(4)()()33243P X C ==⋅=，5505121(5)()()33243P X C ==⋅=. ………………………………… 11分所以X所以533EX np ==⨯=．所以X 的数学期望为53． ……………………………………………… 13分（17）（本小题满分13分）证明：（Ⅰ）因为平面SAD ⊥平面ABCD ， CD AD ⊥，且面SAD 面ABCD AD =，所以CD ⊥平面SAD . 又因为SA ⊂平面SAD所以CD SA ⊥． …………………………………………… 6分（Ⅱ）由（Ⅰ）可知，CD SA ⊥.在SAD ∆中，SA SD a ==，AD =，所以SA SD ⊥，所以SA ⊥平面SDC . 即SA SD ⊥，SA SC ⊥,所以CSD ∠为二面角C SA D --的平面角．在Rt CDS ∆中，tan CDCSD SD ∠===所以二面角C SA D --的大小3π． …………………………………… 13分法二：取BC 的中点E , AD 的中点P ．在SAD ∆中，SA SD a ==，P 为AD 的中点，所以，SP AD ⊥．又因为平面SAD ⊥平面ABCD ，且平面SAD 平面ABCD AD =所以，SP ⊥平面ABCD ．显然，有PE AD ⊥． ……………………………… 1分如图，以P 为坐标原点，P A 为x 轴，PE 为y 轴，PS为z 轴建立空间直角坐标系，则)S，,0,0)A ，,0)B，(,0)C ，(,0,0)D ． ………………………………………………………………3分（Ⅰ）易知(0,,0),,0,)CD SA ==因为0CD SA ⋅=，所以CD SA ⊥． …………………………………………………………… 6分（Ⅱ）设(,,)x y z =n 为平面CSA 的一个法向量，则有0SA CA ⎧⋅=⎪⎨⋅=⎪⎩n n ，即00=⎪-=⎩，所以=n ． ……………………………… 7分显然，EP ⊥平面SAD ，所以PE为平面SAD 的一个法向量，所以(0,1,0)=m 为平面SAD 的一个法向量．……………………………………… 9分所以1cos ,2<>==n m ，所以二面角C SA D --的大小为3π． ………………………………………… 13分（18）（本小题满分13分）解：（Ⅰ）当1a =时，1()ln(1)1xf x x x-=+++，则212()1(1)f x x x -'=+++. ………………………………………………… 2分所以(1)0f '=.又(1)ln 2f =，因此所求的切线方程为ln 2y =. ………… 4分（Ⅱ）22222()1(1)(1)(1)a ax a f x ax x ax x -+-'=+=++++. ………………………… 5分（1）当20a -≥，即2a ≥时，因为0x ≥，所以()0f x '>，所以函数()f x 在[)0,+∞上单调递增.…… 6分（2）当20a -<，即02a <<时，令()0f x '=，则220ax a +-=（0x ≥），所以x =.因此，当x ∈时，()0f x '<，当)x ∈+∞时，()0f x '>. 所以函数()f x的单调递增区间为)+∞，函数()f x的单调递减区间为. …… 10分（Ⅲ）当2a ≥时，函数()f x 在[)0,+∞上单调递增，则()f x 的最小值为(0)1f =，满足题意.……… 11分当02a <<时，由（Ⅱ）知函数()f x的单调递增区间为)+∞，函数()f x的单调递减区间为，则()f x的最小值为f ，而(0)1f =，不合题意. 所以a 的取值范围是[)2,+∞. ………………………………………………… 13分（19）（本小题满分14分）解: （Ⅰ）由题得过两点(4,0)A ，(0,2)B 直线l 的方程为240x y +-=.………… 1分因为12c a =，所以2a c =，b =. 设椭圆方程为2222143x y c c+=,由2222240,1,43x y x y c c+-=⎧⎪⎨+=⎪⎩消去x 得，224121230y y c -+-=. 又因为直线l 与椭圆C 相切,所以221244(123)0c ∆=-⨯-=,解得21c =.所以椭圆方程为22143x y +=. ……………………………………………… 5分（Ⅱ）易知直线m 的斜率存在,设直线m 的方程为(4)y k x =-，…………………… 6分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y ，整理得2222(34)3264120k x k x k +-+-=. ………… 7分由题意知2222(32)4(34)(6412)0k k k ∆=-+->，解得1122k -<<. ……………………………………………………………… 8分设11(,)M x y ，22(,)N x y ，则21223234k x x k +=+，2122641234k x x k -=+. …… 9分又直线:240l x y +-=与椭圆22:143x y C +=相切，由22240,1,43x y x y +-=⎧⎪⎨+=⎪⎩解得31,2x y ==，所以3(1,)2P . ……………………………10分则2454AP =. 所以3645813547AM AN ⋅=⨯=.又AM AN ⋅==212(1)(4)(4)k x x =+--21212(1)(4()16)k x x x x =+-++22222641232(1)(416)3434k k k k k -=+-⨯+++2236(1).34k k =++ 所以223681(1)347k k +=+，解得4k =±.经检验成立. …………………… 13分所以直线m的方程为(4)4y x =±-. …………………………………… 14分（20）（本小题满分14分）（Ⅰ）解：因为011=+b a ，所以112-==a a ,02112=+=b a b . 因为0122<-=+b a ,所以212223-=+=b a a ,023==b b . 因为33102a b +=-<,所以334124a b a +==-,430b b ==.所以1234111,1,,24a a a a =-=-=-=-. …………………………………… 2分由此猜想，当2≥k 时,011<+--k k b a ，则22111---=+=k k k k a b a a ，10k k b b -==.… 3分下面用数学归纳法证明：①当2k =时，已证成立.②假设当k l =（l *∈N ，且2l ≥）猜想成立，即110l l a b --+<，10l l b b -==，102l l a a -=<. 当1k l =+时，由102l l a a -=<， 10l l b b -==得0l l a b +<，则10l l b b +==，1022l l ll a b a a ++==<.综上所述，猜想成立.所以22221111(2)222n n n n a a n ---⎛⎫⎛⎫=⨯=-⋅=-≥ ⎪⎪⎝⎭⎝⎭.故211,12.2n n n a n --=⎧⎪=⎨-≥⎪⎩. ……………………………………………… 6分（Ⅱ）解：当s k ≤≤2时，假设110k k a b --+<，根据已知条件则有1-=k k b b ，与s b b b >>> 21矛盾，因此110k k a b --+<不成立， …………… 7分所以有110k k a b --+≥，从而有1k k a a -=，所以1a a k =. 当011≥+--k k b a 时，1-=k k a a ，211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………… 8分当s k ≤≤2时，总有111()2k k k k b a b a ---=-成立.又110b a -≠，所以数列}{k k a b -(s k ,,2,1 =)是首项为11b a -，公比为12的等比数列, 11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ，1,2,,k s = ,又因为1a a k =，所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………… 10分（Ⅲ）证明：由题意得2212m n n n mc c c ma -+=-+n n c c m +=21.因为211n n n c c c m +=+，所以2110n n n c c c m+-=>. 所以数列{}n c 是单调递增数列. …………………………………… 11分因此要证)(1m n c n ≤<,只须证1<m c . 由2≥m ，则n n n c c m c +=+211<n n n c c c m ++11，即1111n n c c m+->-.…… 12分因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->.所以11m mc m <<+. 故当m n ≤,恒有1<n c . …………………………………………………14分。

2019年高考理科数学全国2卷(附答案)

12B-SX-0000020-绝密★启用前__2019 年普通高等学校招生全国统一考试_ -__-理科数学全国 II 卷__- 本试卷共 23 小题，满分 150 分，考试用时 120 分钟：号 -(适用地区：内蒙古 / 黑龙江 /辽宁 /吉林 /重庆 /陕西 / 甘肃 /宁夏 /青海 /新疆 / 西藏 /海南 )学 -注意事项：_-__1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

_-__2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

__-如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在___答题卡上。

写在本试卷上无效。

_ 线__ 封_ 3．考试结束后，将本试卷和答题卡一并交回。

_密__ -__12 小题，每小题 5 分，共 60 分。

在每个小题给出的四个选：-一、选择题：本题共名 -项中，只有一项是符合题目要求的。

姓-2- 1．设集合 A={ x|x -5x+6>0} ， B={ x|x-1<0} ，则 A ∩B=班-A ． (-∞， 1)B ． (-2， 1)C ．(-3 ， -1)D ． (3， +∞)___ -_ 2 ．设 z=-3+2i ，则在复平面内 z 对应的点位于_-__A ．第一象限B ．第二象限C ．第三象限D ．第四象限年-____ 线 3 ．已知 AB =(2,3)，AC =(3，t)，BC =1，则AB BC= _ _ 封_A ．-3B ．-2C ． 2D ． 3_密_-__4． 2019 年 1 月 3 日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，_- ___ -我国航天事业取得又一重大成就，实现月球背面软着陆需要解决的一个关键___-_ 技术问题是地面与探测器的通讯联系．为解决这个问题，发射了嫦娥四号中__ -___ -继星 “鹊桥 ”，鹊桥沿着围绕地月拉格朗日 L 2点的轨道运行． L 2点是平衡点，__ -_M １，月球质量为 M ２，地月距离为： - 位于地月连线的延长线上．设地球质量为校学 -R ，L 2点到月球的距离为r ，根据牛顿运动定律和万有引力定律，地月连线的延长线上．设地球质量为M １，月球质量为 M ２，地月距离为R， L 2点到月球的距离为 r ，根据牛顿运动定律和万有引力定律，r 满足方程：M 1M 2M 1 (R r) 2r 2(R r ) 3.R设r ，由于的值很小，因此在近似计算中3 33 45 3 3，则R(1 ) 2r 的近似值为A ．M2RB ．M2RC ．33M2RD ．3M2RM 12M 1M 13M 15．演讲比赛共有 9 位评委分别给出某选手的原始评分，评定该选手的成绩时，从9 个原始评分中去掉 1 个最高分、 1 个最低分，得到 7 个有效评分 .7 个有效评分与 9 个原始评分相比，不变的数字特征是 A ．中位数B ．平均数C ．方差D ．极差6．若 a>b ，则A ． ln(a- b)>0B ．3a <3 bC ． a 3- b 3>0D ． │a │ >│b │7．设 α， β为两个平面，则α∥ β的充要条件是A ． α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ． α， β平行于同一条直线D ．α，β垂直于同一平面2x 2 y 2 p=8．若抛物线 y =2px(p>0) 的焦点是椭圆1 的一个焦点，则3pp12B-SX-0000020A ．2B． 3C． 4D． 89．下列函数中，以为周期且在区间(，)单调递增的是242A ．f(x)= │ cos x2│B ． f(x)= │ sin 2x│C．f(x)=cos │x│ D ． f(x)= sin x│10．已知α∈ (0，)， 2sin 2α=cos 2α+1，则 sin α=21B ．5A ．5 5C．3 D ．2535x2y21(a0,b0)的右焦点， O 为坐标原点，以 OF 11．设 F 为双曲线 C：b2a2为直径的圆与圆x2y2 a2交于P，Q两点.若PQ OF ，则C的离心率为A ．2B ．3C． 2 D ．512．设函数 f ( x) 的定义域为R，满足 f (x1) 2 f ( x) ，且当x(0,1] 时，f (x )x(x 1) .若对任意 x (, m]，都有 f ( x)8，则 m 的9取值范围是A ．9B ．7 ,, 43C．5D ．8,,23二、填空题：本题共 4 小题，每小题 5 分，共 20 分。

精品2019届高三数学上学期第一次教学质量检查考试试题理(含解析)

蚌埠市2019届高三年级第一次教学质量检查考试数学（理工类）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设集合，，若，则（）A. B. C. D.【答案】A【解析】依题意可知是集合的元素，即，解得，由，解得.2. 设是复数的共轭复数，且，则（）A. 3B. 5C.D.【答案】D【解析】，故.3. 若满足约束条件则的最小值为（）A. -3B. 0C. -4D. 1【答案】A【解析】画出可行域如下图所示，由图可知目标函数在点处取得最小值为.4. “直线不相交”是“直线为异面直线”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B5. 已知等差数列的前项和为，且满足，，则（）A. 4B. 5C. 6D. 7【答案】B【解析】设等差数列的公差为,,联立解得，则，故选B.6. 已知，且，则（）A. B. C. D.【答案】A【解析】，由于角为第三象限角，故，.7. 已知，则（）A. 18B. 24C. 36D. 56【答案】B【解析】，故，.8. 已知，下列程序框图设计的是求的值，在“”中应填的执行语句是（）A. B. C. D.【答案】A【解析】不妨设，要计算，首先，下一个应该加，再接着是加，故应填.9. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则它的体积可能为（）A. B. C. D.【答案】A【解析】由三视图可知，该几何体由半个圆锥和一个三棱锥组合而成.故体积为.10. 已知为双曲线的左焦点，直线经过点，若点，关于直线对称，则双曲线的离心率为（）A. B. C. D.【答案】C【解析】∵点，关于直线对称，，又∵直线经过点，∴直线的方程为，的中点坐标为，∴，化简整理得，即，，解得，（舍去），故选C.11. 已知，顺次连接函数与的任意三个相邻的交点都构成一个等边三角形，则（）A. B. C. D.【答案】B【解析】当正弦值等于余弦值时，函数值为，故等边三角形的高为，由此得到边长为，边长即为函数的周期，故.【点睛】本题主要考查三角函数的图像与性质.首先大致画出正弦函数图像和余弦函数图像，通过观察可知可知，三角形左右两个顶点之间为一个周期，故只需求出等边三角形的边长即可.再根据可知等边三角形的高，由此求得边长即函数的周期，再由周期公式求得的值.12. 定义在上的奇函数满足：当时，（其中为的导函数）.则在上零点的个数为（）A. 4B. 3C. 2D. 1【答案】D【解析】构造函数，，由于当时，，故当时，为增函数.又，所以当时，成立，由于，所以，由于为奇函数，故当时，，即只有一个根就是.【点睛】本题考查了零点的判断，考查了函数的奇偶性，和利用导数来研究函数的单调性.本题的难点在于构造新函数，然后利用导数来判断新函数的最值，进而判断出的取值.如何构造函数，主要靠平时积累，解题时要多尝试.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知，是两个不同的平面向量，满足：，则__________．【答案】【解析】，，解得，当时，两个是相同的向量，故舍去，所以.14. 已知函数图象关于原点对称.则实数的值为__________．【答案】【解析】依题意有，，，故.15. 已知是抛物线的焦点，是上一点，是坐标原点，的延长线交轴于点，若，则点的纵坐标为__________．【答案】【解析】由于三角形为直角三角形，而，即为中点，设，而，故，代入抛物线方程得，即点的纵坐标为.【点睛】本题主要考查直线和抛物线的位置关系，考查直角三角形斜边的中线等于斜边一半这一几何性质.首先根据题目所给的条件画出图像，突破口就在题目所给条件，这就联想到直角三角形斜边中线等于斜边一半这一几何性质，可得是的中点，设出坐标，代入抛物线方程即可得到所求的结果.16. 已知满足，，，则__________．（用表示）【答案】【解析】依题意，与已知条件相加可得.....................三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17. 在中，角的对边分别为，且，（1）求的面积；（2）若，求的周长.【答案】(1) （2）的周长为【解析】【试题分析】（1）根据余弦定理，由得到，，在利用三角形面积公式可求得面积.（2）利用三角形内角和定理，有,展开后结合已知条件可求得.利用正弦定理求得，利用配方法可求得由此求得周长为.【试题解析】（1）∵，∴，即，∴；（2）∵，∴由题意，∴，∵，∴，∴∵，∴．∴的周长为．18. 如图，在四棱锥中，是等边三角形，，.（1）求证：平面平面；（2）若直线与所成角的大小为60°，求二面角的大小.【答案】(1)见解析（2）90°【解析】【试题分析】（1）由于是等边三角形，结合勾股定理，可计算证明三条直线两两垂直，由此证得平面，进而得到平面平面.（2）根据（1）证明三条直线两两垂直，以为空间坐标原点建立空间直角坐标系，利用和所成角为计算出点的坐标，然后通过平面和平面的法向量计算二面角的余弦值并求得大小.【试题解析】（1）∵，且是等边三角形∴，，均为直角三角形，即，，∴平面∵平面∴平面平面（2）以为单位正交基底，建立如图所示的空间直角坐标系．令，，∴，，，．设，则，．∵直线与所成角大小为60°，所以，即，解得或（舍），∴，设平面的一个法向量为．∵，，则即令，则，所以．∵平面的一个法向量为，∵，，则即令，则，，∴．∴，故二面角的大小为90°．19. 为监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取10件零件，度量其内径尺寸（单位：）.根据长期生产经验，可以认为这条生产线正常状态下生产的零件的内径尺寸服从正态分布. （1）假设生产状态正常，记表示某一天内抽取的10个零件中其尺寸在之外的零件数，求及的数学期望；（2）某天正常工作的一条生产线数据记录的茎叶图如下图所示：①计算这一天平均值与标准差；②一家公司引进了一条这种生产线，为了检查这条生产线是否正常，用这条生产线试生产了5个零件，度量其内径分别为（单位：）：85,95,103,109,119，试问此条生产线是否需要进一步调试，为什么？参考数据：，，，，，，，.【答案】(1) （2）①②生产线异常，需要进一步调试【解析】【试题分析】（1）依题意可知满足二项分布，根据二项分布的公式计算出，然后用减去这个值记得到的值.利用二项分布的期望公式，直接计算出的值.（2）分别计算出均值和标准差，计算的范围，发现不在这个范围内，根据原理可知需要进一步调试.【试题解析】（1）由题意知：或，，∵，∴；（2）①所以②结论：需要进一步调试．理由如下：如果生产线正常工作，则服从正态分布，零件内径在之外的概率只有0.0026，而根据原则，知生产线异常，需要进一步调试．20. 已知椭圆经过点，离心率.（1）求的方程；（2）设直线经过点且与相交于两点（异于点），记直线的斜率为，直线的斜率为，证明：为定值.【答案】(1) （2）见解析【解析】【试题分析】（1）依题意可知，解方程组可求得椭圆的标准方程.（2）当直线斜率斜率不存在时，不符合题意.当斜率存在时，设出直线的方程，联立直线的方程和椭圆的方程，写出韦达定理，计算的值，化简后结果为，由此证明结论成立.【试题解析】（1）因为椭圆，经过点，所以．又，所以，解得．故而可得椭圆的标准方程为：．（2）若直线的斜率不存在，则直线的方程为，此时直线与椭圆相切，不符合题意．设直线的方程为，即，联立，得．设，，则所以为定值，且定值为-1．【点睛】本题主要考查椭圆标准方程的求法，考查直线与圆锥曲线位置关系，考查一元二次方程根与系数关系.椭圆标准方程的参数有两个，要确定这两个参数，需要有两个条件，结合恒等式，列方程组来求的椭圆的标准方程.考查直线和圆锥曲线位置关系，要注意直线斜率不存在的情况.21. 已知函数，（其中为自然对数的底数，）.（1）若函数的图象与函数的图象相切于处，求的值；（2）当时，若不等式恒成立，求的最小值.【答案】(1) ，（2）【解析】【试题分析】（1）依题意求得切点为，斜率为，由此列方程组可求得的值.（2）将原不等式等价变形为，构造函数，利用导数求得的最大值为，由此求得的最小值. 【试题解析】（1），．（过程略）（2）令，则，当时，单调递增，而，∴时，不合题意当时，令，则，∵为减函数，∴时，，单调递增，时，，单调递减，∴，即．（△）但，等号成立当且仅当且．故（△）式成立只能即．【点睛】本题主要考查导数与切线有关的知识.考查利用导数解不等式恒成立问题.解决导数与切线有关的问题，关键点在于切点和斜率，联络点在于切点的横坐标，以此建立方程组，求得未知参数的值.不等式恒成立问题往往可以考虑构造函数法，利用函数的最值来求解.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22. 选修4-4：坐标系与参数方程已知曲线的极坐标方程为，的参数方程为（为参数）.（1）将曲线与的方程化为直角坐标系下的普通方程；（2）若与相交于两点，求.【答案】(1) （2）【解析】【试题分析】（1）对方程两边乘以，由此求得曲线的普通方程.对的参数方程利用加减消元法可求得的普通方程.（2）将的参数方程代入，利用韦达定理和直线参数的几何意义，来求的弦长的值. 【试题解析】（1）曲线的普通方程为，曲线的普通方程为（2）将的参数方程代入的方程，得，得：解得，∴．23. 选修4-5：不等式选讲已知.（1）当时，求不等式的解集；（2）若函数与的图象恒有公共点，求实数的取值范围.【答案】(1) （2）【解析】【试题分析】（1）利用零点分段法，去绝对值，分别求解每一段的解集.由此计算不等式的解集.（2）先求得函数的最小值，求得函数的最大值，比较这两个数值的大小，即可求得有公共点时，实数的取值范围. 【试题解析】（1）当时，，由得，；（2），该二次函数在处取得最小值，因为函数，在处取得最大值故要使函数与的图象恒有公共点，只需要，即．。

2020届高考数学(理)一轮必刷题专题62 离散型随机变量均值与方差、正态分布(解析版)

考点62 离散型随机变量均值与方差、正态分布1．（广东省潮州市2019届高三第二次模拟考试数学理）一试验田某种作物一株生长果个数x 服从正态分布()290,N σ，且()700.2P x <=，从试验田中随机抽取10株，果实个数在[]90,110的株数记作随机变量X ，且X 服从二项分布，则X 的方差为（）A ．3B ．2.1C ．0.3D ．0.21【答案】B 【解析】∵290(),x N δ～，且()700.2P x <=，所以()1100.2P x >=∴()901100.50.20.3P x <<=-=， ∴()10,0.3X B ～，X 的方差为()100.310.3 2.1⨯⨯-=．故选B ．2．（湖北省钟祥市2019届高三高考第一次模拟考试理）某班有50名学生，一次数学考试的成绩ξ服从正态分布N （105，102），已知P （95≤ξ≤105）=0.32，估计该班学生数学成绩在115分以上的人数为（）A ．10B ．9C ．8D ．7【答案】B 【解析】∵考试的成绩ξ服从正态分布N （105，102）． ∴考试的成绩ξ关于ξ=105对称， ∵P （95≤ξ≤105）=0.32， ∴P （ξ≥115）=12（1-0.64）=0.18， ∴该班数学成绩在115分以上的人数为0.18×50=9 故选：B ．3．（辽宁省丹东市2019届高三总复习质量测试理）某种种子每粒发芽的概率都为0.85，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X ，则X 的数学期望()E X =_______．【答案】300【解析】设没有发芽的种子数为Y ,则有2X Y =,由题意可知Y 服从二项分布，即Y(1000,0.15)B ,()10000.15150E Y =⨯=,()2()300E X E Y ==.4．（河北省石家庄市2019届高三毕业班模拟考试一A 卷理）已知随机变量X 服从正态分布()2,1N ，若()()223P X a P X a ≤-=≥+，则a =__________．【答案】1 【解析】由正态分布的性质可得正态分布的图像对称轴为2X =，结合题意有：()()2232,12a a a -++=⇒=.故答案为：1．5．（湖南省益阳市2019届高三4月模拟考试数学理）某市高三年级26000名学生参加了2019年3月模拟考试，已知数学考试成绩2(100,)XN σ.统计结果显示数学考试成绩X 在80分到120分之间的人数约为总人数的34，则数学成绩不低于120分的学生人数约为__________．【答案】3250 【解析】因为成绩()2100,X N σ~，所以正态分布曲线关于100X =对称，又成绩在80分到120分之间的人数约占总人数的34，由对称性知：成绩不低于120分的学生约为总人数的1311248⎛⎫⨯-= ⎪⎝⎭，所以此次考试成绩不低于120分的学生约有12600032508⨯=.6．（2019届湘赣十四校高三联考第二次考试理）我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注，受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为23，女性观众认为《流浪地球》好看的概率为12.某机构就《流浪地球》是否好看的问题随机采访了4名观众（其中2男2女）. （1）求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率；（2）设ξ表示这4名观众中认为《流浪地球》好看的人数，求ξ的分布列与数学期望. 【答案】（1）736（2）见解析【解析】设X 表示2名女性观众中认为好看的人数，Y 表示2名男性观众中认为好看的人数，则12,2X B ⎛⎫~ ⎪⎝⎭，22,3Y B ⎛⎫~ ⎪⎝⎭. （1）设事件A 表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”，则()()()()2,12,01,0P A P X Y P X Y P X Y ===+==+==,222212022221211123323C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 21022111722336C C ⎛⎫⎛⎫⎛⎫+⋅= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. （2）ξ的可能取值为0，1，2，3，4，()()00,0P P X Y ξ==== 2200221112336C C ⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭， ()()()11,00,1P P X Y P X Y ξ====+==，= 2210012222111121223233C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⋅+⋅ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭16=， ()()()()22,01,10,2P P X Y P X Y P X Y ξ====+==+==,2220112222111121232233C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 22022*********C C ⎛⎫⎛⎫+⋅= ⎪ ⎪⎝⎭⎝⎭， ()()()31,22,1P P X Y P X Y ξ====+==,2212212222112*********C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭13=， ()()42,2P P X Y ξ==== 222222121239C C ⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭， ∴ξ的分布列为∴11131170123436636393E ξ=⨯+⨯+⨯+⨯+⨯=. 7．（天津市耀华中学2019届高三第一次模拟考试数学理）在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球4个，白球3个，蓝球3个。

2019年高考北京卷理科数学真题(含答案)

绝密★启用前2019年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1.已知复数z=2+i，则A. B. C. 3D. 5【答案】D【解析】【分析】题先求得，然后根据复数的乘法运算法则即得.【详解】∵故选D.【点睛】本容易题，注重了基础知识、基本计算能力的考查.2.执行如图所示的程序框图，输出的s值为A. 1B. 2C. 3D. 4【答案】B【解析】【分析】根据程序框图中的条件逐次运算即可.【详解】运行第一次，，，运行第二次，，，运行第三次，，，结束循环，输出，故选B.【点睛】本题考查程序框图，属于容易题，注重基础知识、基本运算能力的考查.3.已知直线l的参数方程为（t为参数），则点（1,0）到直线l的距离是A. B. C. D.【答案】D【分析】首先将参数方程化为直角坐标方程，然后利用点到直线距离公式求解距离即可.【详解】直线的普通方程为,即,点到直线的距离,故选D.【点睛】本题考查直线参数方程与普通方程转化,点到直线的距离,属于容易题,注重基础知识､基本运算能力的考查.4.已知椭圆（a＞b＞0）的离心率为，则A. a2=2b2B. 3a2=4b2C. a=2bD. 3a=4b【答案】B【解析】【分析】由题意利用离心率的定义和的关系可得满足题意的等式.【详解】椭圆的离心率,化简得,故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识､基本运算能力的考查.5.若x，y满足，且y≥−1，则3x+y的最大值为A. −7B. 1C. 5D. 7【答案】C【解析】首先画出可行域，然后结合目标函数的几何意义确定其最值即可.【详解】由题意作出可行域如图阴影部分所示.设,当直线经过点时,取最大值5.故选C.【点睛】本题是简单线性规划问题的基本题型,根据“画､移､解”等步骤可得解.题目难度不大题,注重了基础知识､基本技能的考查.6.在天文学中，天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足，其中星等为m1的星的亮度为E2（k=1,2）.已知太阳的星等是–26.7，天狼星的星等是–1.45，则太阳与天狼星的亮度的比值为A. 1010.1B. 10.1C. lg10.1D. 10–10.1【答案】D【解析】【分析】先求出，然后将对数式换为指数式求再求【详解】两颗星的星等与亮度满足,令，，，，故选D.【点睛】考查考生的数学应用意识、信息处理能力、阅读理解能力以及指数对数运算.7.设点A，B，C不共线，则“与的夹角为锐角”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】【分析】由题意结合向量的减法公式和向量的运算法则考查充分性和必要性是否成立即可.【详解】∵A､B､C三点不共线,∴|+|>|||+|>|-||+|2>|-|2•>0与的夹角为锐角.故“与的夹角为锐角”是“|+|>||”的充分必要条件,故选C. 【点睛】本题考查充要条件的概念与判断､平面向量的模､夹角与数量积,同时考查了转化与化归数学思想.8.数学中有许多形状优美、寓意美好的曲线，曲线C：就是其中之一（如图）.给出下列三个结论：①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C上任意一点到原点的距离都不超过；③曲线C所围成的“心形”区域的面积小于3.其中，所有正确结论的序号是A. ①B. ②C. ①②D. ①②③【答案】C【解析】【分析】将所给方程进行等价变形确定x的范围可得整点坐标和个数，结合均值不等式可得曲线上的点到坐标原点距离的最值和范围，利用图形的对称性和整点的坐标可确定图形面积的范围.详解】由得,,,所以可为的整数有0,-1,1,从而曲线恰好经过(0,1),(0,-1),(1,0),(1,1),(-1,0),(-1,1)六个整点,结论①正确.由得,,解得,所以曲线上任意一点到原点的距离都不超过. 结论②正确.如图所示,易知,四边形的面积,很明显“心形”区域的面积大于,即“心形”区域的面积大于3,说法③错误.故选C.【点睛】本题考查曲线与方程､曲线的几何性质，基本不等式及其应用,属于难题,注重基础知识､基本运算能力及分析问题解决问题的能力考查,渗透“美育思想”.第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

北京市朝阳区高三年级第一次综合练习数学试卷（理工类）（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）注意事项：考生务必将答案答在答题卡上，在试卷上答无效。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. 1. 复数10i12i=- A. 42i -+ B. 42i - C. 24i - D. 24i +2. 已知平面向量,a b 满足()=3a a +b ⋅，且2,1==a b ，则向量a 与b 的夹角为A.6π B. 3π C. 32π D. 65π 3.已知数列{}n a 的前n 项和为n S ，且21()n n S a n N *=-∈，则5a =A. 16-B. 16C. 31D. 324. 已知平面α，直线,,a b l ，且,a b αα⊂⊂，则“l a ⊥且l b ⊥”是“l α⊥”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5. 有10件不同的电子产品，其中有2件产品运行不稳定.技术人员对它们进行一一测试，直到2件不稳定的产品全部找出后测试结束，则恰好3次就结束测试的方法种数是（）A. 16B. 24C. 32D. 486.已知函数()f x 是定义在R 上的偶函数，且对任意的x ∈R ，都有(2)()f x f x +=.当01x ≤≤时，2()f x x =.若直线y x a =+与函数()y f x =的图象在[0,2]内恰有两个不同的公共点，则实数a 的值是 A.0 B. 0或12-C. 14-或12-D. 0或14- 7. 某工厂生产的A 种产品进入某商场销售，商场为吸引厂家第一年免收管理费，因此第一年A 种产品定价为每件70元，年销售量为11.8万件. 从第二年开始，商场对A 种产品征收销售额的%x 的管理费（即销售100元要征收x 元），于是该产品定价每件比第一年增加了70%1%x x ⋅-元，预计年销售量减少x 万件，要使第二年商场在A 种产品经营中收取的管理费不少于14万元，则x 的取值范围是A. 2B. 6.5C. 8.8D. 10 8.已知点集{}22(,)48160A x y x y x y =+--+≤，{}(,)4,B x y y x m m 是常数=≥-+，点集A 所表示的平面区域与点集B 所表示的平面区域的边界的交点为,M N .若点(,4)D m 在点集A 所表示的平面区域内（不在边界上），则△DMN 的面积的最大值是A. 1B. 2C.D. 4第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分. 把答案填在答题卡上.9. 已知双曲线的方程为2213x y -=，则此双曲线的离心率为，其焦点到渐近线的距离为 .10. 已知某几何体的三视图如图所示，则该几何体的体积为 .（第10题图）（第11题图）11. 执行如图所示的程序框图，若输入k 的值是4，则输出S 的值是 .12.在极坐标系中，曲线ρθ=和cos 1ρθ=相交于点,A B ，则线段AB 的中点E 到极点的距离是 .13.已知函数213(),2,()24log ,0 2.x x f x x x ⎧+≥⎪=⎨⎪<<⎩若函数()()g x f x k =-有两个不同的零点，则实数k 的取值范围是 .14.已知△ABC 中， 90,3,4C AC BC ∠=︒==.一个圆心为M ，半径为14的圆在△ABC 内，沿着△ABC 的边滚动一周回到原位. 在滚动过程中，圆M 至少与△ABC 的一边相切，则点M 到△ABC 顶点的最短距离是，点M的运动轨迹的周长正视图侧视图俯视图是 .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.把答案答在答题卡上. 15. （本小题满分13分）已知函数π()cos()4f x x =-.（Ⅰ）若()10f α=，求sin 2α的值；（II ）设()()2g x f x f x π⎛⎫=⋅+⎪⎝⎭，求函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上的最大值和最小值.16. （本小题满分13分）某次有1000人参加的数学摸底考试，其成绩的频率分布直方图如图所示，规定85分及其以上为优秀.（II ）现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析，求其中成绩为优秀的学生人数；（Ⅲ）在（II ）中抽取的40名学生中，要随机选取2名学生参加座谈会，记“其中成绩为优秀的人数”为X ，求X 的分布列与数学期望.17. （本小题满分14分）在如图所示的几何体中，四边形ABCD 为平行四边形，=90ABD ∠︒，EB ⊥平面ABCD ，EF//AB ，=2AB ，==1EB EF ，=BC ，且M 是BD 的中点.（Ⅰ）求证：EM//平面ADF ；（Ⅱ）求二面角D-AF-B 的大小；（Ⅲ）在线段EB 上是否存在一点P，使得CP 与AF 所成的角为30︒？若存在，求出BP 的长度；若不存在，请说明理由.18. （本小题满分13分）设函数2e (),1axf x a x R =∈+. （Ⅰ）当1a =时，求曲线()y f x =在点(0,(0))f 处的切线方程；（Ⅱ）求函数)(x f 单调区间.CA FEBMD19. （本小题满分14分）已知椭圆2222:1(0)x y C a b a b +=>>的两个焦点分别为1(0)F ，2F .点(1,0)M 与椭圆短轴的两个端点的连线相互垂直.（Ⅰ）求椭圆C 的方程；（Ⅱ）已知点N 的坐标为(3,2)，点P 的坐标为(,)(3)m n m ≠.过点M 任作直线l 与椭圆 C 相交于A ，B 两点，设直线AN ，NP ，BN 的斜率分别为1k ，2k ，3k ，若 1322k k k +=，试求,m n 满足的关系式.20．（本小题满分13分）已知各项均为非负整数的数列001:,,,n A a a a ()n *∈N ，满足00a =，1n a a n ++=．若存在最小的正整数k ，使得(1)k a k k =≥，则可定义变换T ，变换T 将数列0A 变为数列00111():1,1,,1,0,,,k k n T A a a a a a -++++．设1()i i A T A +=，0,1,2i =．（Ⅰ）若数列0:0,1,1,3,0,0A ，试写出数列5A ；若数列4:4,0,0,0,0A ，试写出数列0A ；（Ⅱ）证明存在唯一的数列0A ，经过有限次T 变换，可将数列0A 变为数列,0,0,,0n n 个；（Ⅲ）若数列0A ，经过有限次T 变换，可变为数列,0,0,,0n n 个．设1m m m n S a a a +=+++，1,2,,m n =，求证[](1)1mm m S a S m m =-++，其中[]1m S m +表示不超过1m Sm +的最大整数．北京市朝阳区高三年级第一次综合练习数学试卷（理工类）三、解答题：（15）（本小题满分13分）解：（Ⅰ）因为π()cos()4f αα=-=，所以(cos sin )210αα+=，所以 7cos sin 5αα+=. 平方得，22sin 2sin cos cos αααα++=4925，所以 24sin 225α=. ……………6分（II ）因为()π()2g x f x f x ⎛⎫=⋅+⎪⎝⎭=ππcos()cos()44x x -⋅+sin )sin )x x x x +- =221(cos sin )2x x - =1cos 22x . ……………10分当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2,33x ⎡⎤∈-⎢⎥⎣⎦. 所以，当0x =时，()g x 的最大值为12；当π3x =时，()g x 的最小值为14-. ……………13分（16）（本小题满分13分）解：（Ⅰ）依题意，0.0451000200,0.025*******a b =⨯⨯==⨯⨯=. ……………4分（Ⅱ）设其中成绩为优秀的学生人数为x ，则350300100401000x ++=，解得：x =30，即其中成绩为优秀的学生人数为30名. ……………7分（Ⅲ）依题意，X 的取值为0，1，2，2102403(0)52C P X C ===，1110302405(1)13C C P X C ===，23024029(2)52C P X C ===，所以X 的分布列为350125213522EX =⨯+⨯+⨯=，所以X 的数学期望为2. ……………13分（17）（本小题满分14分）证明：（Ⅰ）取AD 的中点N ，连接MN,NF .在△DAB 中，M 是BD 的中点，N 是AD 的中点，所以1=2MN//AB,MN AB ，又因为1=2EF//AB,EF AB ，所以MN//EF 且MN =EF .所以四边形MNFE 为平行四边形，所以EM//FN .又因为FN ⊂平面ADF ，⊄EM 平面ADF ，故EM//平面ADF . …………… 4分解法二：因为EB ⊥平面ABD ，AB BD ⊥，故以B 为原点，建立如图所示的空间直角坐标系-B xyz . ……………1分由已知可得 (0,0,0),(0,2,0),(3,0,0),B A D3(3,-2,0),(,0,0)2C E F M （Ⅰ）3=(,0,-3)(3,-2,0)2EM ,AD=，设平面ADF 的一个法向量是()x,y,z n =. 由0,0,AD AF n n ⎧⋅=⎪⎨⋅=⎪⎩得32x -y =0,=0.⎧⎪⎨⎪⎩令y=3，则n =. 又因为3(=3+0-3=02EM n ⋅=⋅，所以EM n ⊥，又EM ⊄平面ADF ，所以//EM 平面ADF . ……………4分NCA F EBMD（Ⅱ）由（Ⅰ）可知平面ADF的一个法向量是n =. 因为EB ⊥平面ABD ，所以EB BD ⊥.又因为AB BD ⊥，所以BD ⊥平面EBAF . 故(3,0,0)BD =是平面EBAF 的一个法向量. 所以1cos <=2BD BD,BD n n n⋅>=⋅，又二面角D-AF -B 为锐角，故二面角D-AF -B 的大小为60︒. ……………10分（Ⅲ）假设在线段EB 上存在一点P ，使得CP 与AF 所成的角为30︒. 不妨设(0,0,t)P（0t ≤≤，则=(3,-2,-),=PC AF t .所以2cos <2PC AF PC,AF PC AF ⋅>==⋅，=，化简得35-=，解得0t =<.所以在线段EB 上不存在点P ，使得CP 与AF 所成的角为30︒.…………14分（18）（本小题满分13分）解：因为2e (),1ax f x x =+所以222e (2)()(1)ax ax x a f x x -+'=+.（Ⅰ）当1a =时, 2e ()1xf x x =+,222e (21)()(1)x x xf x x -+'=+, 所以(0)1,f = (0)1f '=.所以曲线()y f x =在点(0,(0))f 处的切线方程为10x y -+=. ……………4分（Ⅱ）因为222222e (2)e ()(2)(1)(1)ax ax ax x a f x ax x a x x -+'==-+++， ……………5分（1）当0a =时,由()0f x '>得0x <；由()0f x '<得0x >.所以函数()f x 在区间(,0)-∞单调递增, 在区间(0,)+∞单调递减. ……………6分（2）当0a ≠时, 设2()2g x ax x a =-+，方程2()20g x ax x a =-+=的判别式2444(1)(1),a a a ∆=-=-+ ……………7分①当01a <<时，此时0∆>.由()0f x '>得x <,或x >；由()0f x '<得11x a a-+<<.所以函数()f x 单调递增区间是1(,a -∞和1()a ++∞,单调递减区间11(,a a +. ……………9分②当1a ≥时，此时0∆≤.所以()0f x '≥，所以函数()f x 单调递增区间是(,)-∞+∞. ……………10分 ③当10a -<<时，此时0∆>.由()0f x '>x <<；由()0f x '<得x <,或x >.所以当10a -<<时,函数()f x 单调递减区间是1(,a +-∞和1()a +∞,单调递增区间11(a a +-. ……………12分④当1a ≤-时, 此时0∆≤，()0f x '≤，所以函数()f x 单调递减区间是(,)-∞+∞. …………13分（19）（本小题满分14分）解: （Ⅰ）依题意，c =1b =，所以a == 故椭圆C 的方程为2213x y +=. ……………4分（Ⅱ）①当直线l 的斜率不存在时，由221,13x x y =⎧⎪⎨+=⎪⎩解得1,3x y ==±.不妨设(1,3A ，(1,)3B -，因为132233222k k +=+=，又1322k k k +=，所以21k =，所以,m n 的关系式为213n m -=-，即10m n --=. ………7分 ②当直线l 的斜率存在时，设直线l 的方程为(1)y k x =-.将(1)y k x =-代入2213x y +=整理化简得，2222(31)6330k x k x k +-+-=. 设11(,)A x y ，22(,)B x y ，则2122631k x x k +=+,21223331k x x k -=+. ………9分又11(1)y k x =-，22(1)y k x =-. 所以12122113121222(2)(3)(2)(3)33(3)(3)y y y x y x k k x x x x ----+--+=+=---- 12211212[2(1)](3)[2(1)](3)3()9k x x k x x x x x x ---+---=-++121212122(42)()6123()9kx x k x x k x x x x -++++=-++222222223362(42)6123131336393131k k k k k k k k k k k -⨯-+⨯++++=--⨯+++ 222(126)2.126k k +==+………12分所以222k =，所以2213n k m -==-，所以,m n 的关系式为10m n --=.………13分综上所述，,m n 的关系式为10m n --=. ………14分（20）（本小题满分13分）解：（Ⅰ）若0:0,1,1,3,0,0A ，则1:1,0,1,3,0,0A ；2:2,1,2,0,0,0A ； 3:3,0,2,0,0,0A ； 4:4,1,0,0,0,0A ； 5:5,0,0,0,0,0A ．若4:4,0,0,0,0A ，则 3:3,1,0,0,0A ； 2:2,0,2,0,0A ； 1:1,1,2,0,0A ；0:0,0,1,3,0A ． ………4分（Ⅱ）先证存在性，若数列001:,,,n A a a a 满足0k a =及0(01)i a i k >≤≤-，则定义变换1T -，变换1T -将数列0A 变为数列10()T A -：01111,1,,1,,,,k k n a a a k a a -+---．易知1T -和T 是互逆变换． ………5分对于数列,0,0,,0n 连续实施变换1T -（一直不能再作1T -变换为止）得,0,0,,0n 1T-−−→1,1,0,,0n -1T-−−→2,0,2,0,,0n -1T-−−→3,1,2,0,,0n -1T-−−→1T-−−→01,,,n a a a ，则必有00a =（若00a ≠，则还可作变换1T -）．反过来对01,,,n a a a 作有限次变换T ，即可还原为数列,0,0,,0n ，因此存在数列0A 满足条件．下用数学归纳法证唯一性：当1,2n =是显然的，假设唯一性对1n -成立，考虑n 的情形．假设存在两个数列01,,,n a a a 及01,,,n b b b 均可经过有限次T 变换，变为,0,,0n ，这里000a b ==，1212n n a a a b b b n +++=+++=若0n a n <<，则由变换T 的定义，不能变为,0,,0n ；若n a n =，则120n a a a ====，经过一次T 变换，有0,0,,0,n T−−→1,1,,1,0由于3n ≥，可知1,1,,1,0（至少3个1）不可能变为,0,,0n ．所以0n a =，同理0n b =令01,,,n a a a T−−→121,,,,na a a '''，01,,,n b b b T−−→121,,,,nb b b '''，则0n n a b ''==，所以1211n a a a n -'''+++=-，1211nb b b n -'''+++=-．因为110,,,n a a -''T−−−−→有限次-1,0,,0n ，110,,,n b b -''T −−−−→有限次-1,0,,0n ，故由归纳假设，有i i a b ''=，1,2,,1i n =-．再由T 与1T -互逆，有01,,,n a a a T −−→111,,,,0n a a -''， 01,,,n b b b T −−→111,,,,0n b b -''，所以i i a b =，1,2,,i n =，从而唯一性得证． ………9分（Ⅲ）显然i a i ≤(1,2,,)i n =，这是由于若对某个0i ，00i a i >，则由变换的定义可知，0i a 通过变换，不能变为0．由变换T 的定义可知数列0A 每经过一次变换，k S 的值或者不变，或者减少k ，由于数列0A 经有限次变换T ，变为数列,0,,0n 时，有0m S =，1,2,,m n =，所以m m S mt =(m t 为整数)，于是1m m m S a S +=+1(1)m m a m t +=++，0m a m ≤≤，所以m a 为m S 除以1m +后所得的余数，即[](1)1m m m S a S m m =-++．………13分。

2019朝阳区高三一模有答案(数学理)

北京市朝阳区2019届高三一模数学(理)试题及答案

北京各区2019-2021年高三年级数学模拟试题汇编-两角和与差的三角函数

数学理Z

2019年北京市高考数学一模试卷(理科)(解析版)

频率分布直方图-高中数学知识点讲解(含答案)

(高考题 模拟题)高考数学 素养提升练(一)理(含解析)-人教版高三全册数学试题

(完整)2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)

2020届高考数学(理)一轮必刷题 专题32 数列的综合问题(解析版)

北京市朝阳区2018-2019学年度第一学期期末质量检测高三年级数学试卷(理工类)

2020届高考数学(理)一轮必刷题 专题47 两直线的位置关系、距离公式(解析版)

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试(数学理)

2019年高考理科数学全国2卷(附答案)

精品2019届高三数学上学期第一次教学质量检查考试试题 理(含解析)

2020届高考数学(理)一轮必刷题 专题62 离散型随机变量均值与方差、正态分布(解析版)

2019年高考北京卷理科数学真题(含答案)

(高考题模拟题)高考数学素养提升练(一)理(含解析)-人教版高三全册数学试题

2020届高考数学(理)一轮必刷题专题32 数列的综合问题(解析版)

2020届高考数学(理)一轮必刷题专题47 两直线的位置关系、距离公式(解析版)

精品2019届高三数学上学期第一次教学质量检查考试试题理(含解析)

2020届高考数学(理)一轮必刷题专题62 离散型随机变量均值与方差、正态分布(解析版)