美国数学竞赛2016AMCAIME获奖喜报

合集下载

aime获奖规则

aime获奖规则第一部分：赛事介绍美国数学竞赛(AIME)是美国数学协会(AMA)主办的一项致力于挖掘和培养高中生数学天才的竞赛。

AIME是美国联邦政府底下的一个部门，也是世界数学联合会、国际数学联盟(IMU)的会员。

AIME的主要目的是培养和发现高中生中的数学天才，激发他们对数学的兴趣，提高他们的数学水平。

第二部分：AIME获奖规则AIME的获奖规则非常严格，只有符合以下要求的参赛者才能获得奖项：1. 参赛年龄AIME面向美国9年级至12年级的学生，以及留学生。

所有参赛者必须在比赛当年的2月1日至2月15日之间年满13岁。

2. 参赛资格AIME的参赛者必须在AMC 10或AMC 12中取得了相应的成绩。

AMC 10和AMC 12是美国数学协会所主办的高中生数学竞赛，分别面向高中10年级以下和高中12年级以下的学生。

3. 申请资格AIME的参赛者必须在规定的时间内向美国数学协会提交参赛申请，并缴纳相应的参赛费用。

参赛费用将用于奖金的设定以及赛事的举办和运营费用。

4. 参赛成绩AIME的获奖标准基于考试成绩的排名。

AIME的考试共有15道数学问题，时间限制为三小时。

在考试结束后，参赛者的成绩将由专业的评分人员进行评定和排名。

只有成绩在一定范围内的参赛者才有资格获奖。

5. 获奖类别AIME的获奖类别包括金奖、银奖和铜奖。

金奖为成绩排名前5%的参赛者，银奖为成绩排名前10%的参赛者，铜奖为成绩排名前15%的参赛者。

6. 奖金设置AIME的金奖获得者将获得高额的奖金，同时还有机会获得美国数学奥林匹克(AIMO)的资格。

银奖和铜奖获得者也将分别获得一定数额的奖金。

第三部分：AIME获奖的意义AIME的获奖者不仅仅是在数学方面有极高天赋的学生，更代表着他们在数学竞赛中的出色成绩。

获奖者将受到社会的高度赞扬和肯定，这将对他们今后的学术和职业发展产生积极的影响。

同时，AIME的获奖者还将有机会参与更高级别的数学竞赛，拓展自己的学术领域。

美国数学竞赛

• 我国数学竞赛题目多以理论题为主．这与美国中学数学竞赛题目恰恰相反，美国注重与生活联系在一起，题目多以实际应用题为主，也会有理论题目，但是相对来说数量较少．
竞赛题目的难度分布及运算量的不同
•我国数学竞赛题目缺乏应用性和技巧性，运算量较大，并且一个题目的内容比较单一．美国数学竞赛题目应用性很强，技巧性也较高，运算量比较小，同时能够够将多个知识点融合到一个题目当中． •竞赛时间的不同 •我国中学数学竞赛由于题目较难，运算量较大，导致考试时间较长．而美国题目难度稍低，运算量不大，同时有的竞赛允许使用计算器，这样就减少了很多的竞赛时间．
IMO选拔
• • • • • 初中数学联赛高中数学联赛 AMC8:11月中举行。 AMC10:2月初 AMC12:2月中。美国数学邀请赛:3月底。美国数学奥林匹克：4月的最后一周。数学奥林匹克夏令营（MOSP）国际数学奥林匹克（IMO)：7月
AMC通过其完善的测试体系一直承担着为美国培育世界数学奥林匹克IMO选手的重任。AMC的研究人员透过AMC8、AMC 10、AMC12、AIME等一系列测验,找出绩优生参加USJMO和 USAMO，再从全美数十州筛选出12位精英，成立美国数学奥林匹克夏令营（MOSP），最终从中选出美国参加IMO的6名选手，组成IMO美国国家队。
美国中学数学竞赛的特点
• 1）组织者广泛、参赛者自愿 • 2）竞赛目的多样化 • 3）普及与选拔两项功能有机结合
• 4）竞赛形式多样化,评分规则多元化
中美数学竞赛的比较
•竞赛考察知识点的不同 •首先,美国考察的内容比我国考察的内容更接近实际生活。 •其次,由于美国高中阶段就已经讲解了我们在大学阶段学习的内容，比如微积分、极限、级数等等，而我国高中只简单的涉及一点微积分的知识，故在一些中学数学竞赛中，美国考察的知识范围是大于同等级别中国数学竞赛考察知识的范围的.美国中学数学教学的特点是广而浅，我国则是窄而深．

2015美国大学生数学建模竞赛获奖名单

陆震宇林哲明王欣月侯顶顶赵清王琼瑶张鹏飞万冬梅王豪陈屹杨燕姚睿宏王致仪朱司雨庞培川郭林崔梦瑶周峻民林松王江北毛子豪徐云帆白云洁陈君麟曾维群郭晋岑韩升黄敏叶昊灵郑梓豪张荣王舜垚王逸群张旭韦金香池慧利
20124755 20124900 20122150 20122057 20122062 20123819 20123736 20123820 20123737 20123715 20124182 20135067 20130220 20132067 20124177 20123940 20123938 20122971 20124988 20122831 20120282 20123458 20124122 20124634 20121967 20120574 20124042 20125937 20126037 20135497 20135832 20132215 20122891 20122285 20122045 20121853
自动化自动化数统数统数统动力动力动力动力动力电气计算机弘深经管数统电气电气电气光电计算机机械经管材料电气自动化软件建管电气城环城环弘深弘深弘深光电机械数统软件
李
东
博雅
李曼曼
数统
刘朝林
数统
刘朝林
数统
刘朝林
数统
刘琼芳
数统
刘琼芳
数统
刘琼芳
董方亮徐达梁王哲王恩照张磊刘维维党丹丹周瑾张阳阳汪杨陈权刘金典孟祥义彭诗渊赵娟任婕张骜桀陈康达黄松渝孟维李小刚龚煜廉肖彤伍圣超安子轩李露贺志广徐雪萍李杰肖垚宁布潘丽娜詹国锋陈鹏

2016大英赛获奖名单

何益
省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖省奖
77 万洁雅 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
2014级本科电子信息工程1班
李娜
15级会计学本科8班
119 贺丽娟 2014级本科工程造价1班 120 彭少霞 2014级本科工程造价1班 121 姜阿婷 2014级本科工程造价1班 122 123 124
周赛群应学强张琪琪 2014级工商管理本科1班 2014级工商管理本科1班 2014级工商管理本科3班
伍施姣
14级商务英语本科（1）班 14级商务英语本科（1）班 14级商务英语本科（1）班 14级商务英语本科（1）班
张亦楠 15级飞行器制造本科班吴云飞 15级飞行器制造本科班周维车燕
15级工管金融方向1班 15级工管金融方向1班
14级商务专科班
施钰杰 15级工管金融方向1班
黎人根魏晔康雨萱黄佳乐李玲红 15级工商管理学本科1班 15级工商管理学本科1班 15级工商管理学本科2班 15级工商管理学本科2班 15级工商管理学本科2班
陈晓春
14商务英语本科2班 14商务英语本科2班
2015级本科服装设计班
卢旭瑶 2015级财经学院会计学5班徐丹
竺宁钱莎莹 2015级工程造价本科3班
2015级国际经济与贸易专科班 2015级国际经济与贸易专科班
叶赛花 14商务英语本科2班肖霄
14商务英语本科2班
15级本科播音与主持艺术1班 15级本科播音与主持艺术2班

【免费下载】华南师范大学参加美国数学建模竞赛获奖成绩

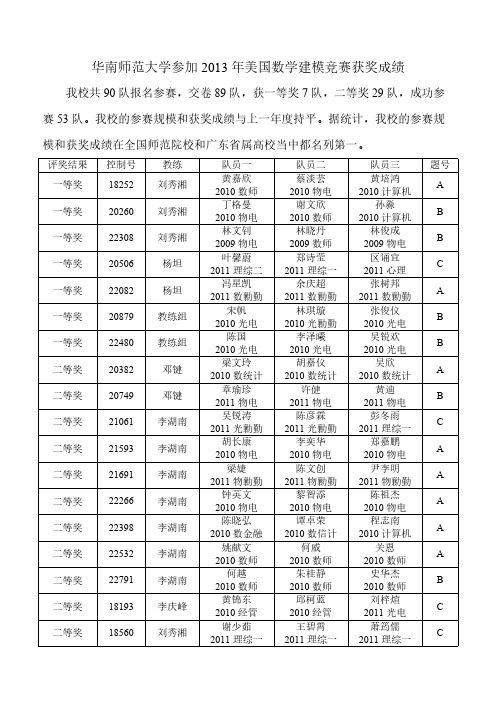
题号 A B B C A B B A B C A A A A A B C C
二等奖 20797 刘秀湘
二等奖
20853
二等奖 21820 刘秀湘
二等奖 23312 刘秀湘
二等奖 23232 苏洪雨
二等奖 20767
二等奖 21708
二等奖 22535
二等奖 22753
二等奖 19695 王明兰
二等奖
一等奖 22308
一等奖 20506
一等奖 22082
一等奖 20879
一等奖 22480
二等奖 20382
二等奖 20749
二等奖 21061
二等奖 21593
二等奖 21691
二等奖 22266
Hale Waihona Puke 二等奖 22398二等奖 22532
二等奖 22791
二等奖 18193
二等奖 18560
控制号 18252
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

2016年美国大学生数学建模大赛A题获奖论文A Hot Bath

Part II Finding the best strategy ...................................................................12 VI. Results ........................................................................................................ 12
The first part has five sections: air’s heat radiation, bathtub wall’s heat radiation, person in, hot water in, bubble existed. We discuss some factors that affect water temperature, such as the shape and the volume of the bathtub and person, especially the motions made by the person in the bathtub because the temperature in the bathtub has a great connection with person. Finally, we get the water temperature variation and distribution model.
In this article, we establish two models. One is water temperature variation and distr one is finding best strategy model. We put forward some acceptable hypothesis to simplify the model. What’s more, we clear the meaning of the word “noticeably”.

2016美国大学生数学建模大赛C题特等奖(原版论文)C42939Tsinghua University, China

For ofﬁce use only T1T2T3T4T eam Control Number42939Problem ChosenCFor ofﬁce use onlyF1F2F3F42016Mathematical Contest in Modeling(MCM)Summary Sheet (Attach a copy of this page to each copy of your solution paper.)SummaryIn order to determine the optimal donation strategy,this paper proposes a data-motivated model based on an original deﬁnition of return on investment(ROI) appropriate for charitable organizations.First,after addressing missing data,we develop a composite index,called the performance index,to quantify students’educational performance.The perfor-mance index is a linear composition of several commonly used performance indi-cators,like graduation rate and graduates’earnings.And their weights are deter-mined by principal component analysis.Next,to deal with problems caused by high-dimensional data,we employ a lin-ear model and a selection method called post-LASSO to select variables that statis-tically signiﬁcantly affect the performance index and determine their effects(coef-ﬁcients).We call them performance contributing variables.In this case,5variables are selected.Among them,tuition&fees in2010and Carnegie High-Research-Activity classiﬁcation are insusceptible to donation amount.Thus we only con-sider percentage of students who receive a Pell Grant,share of students who are part-time and student-to-faculty ratio.Then,a generalized adaptive model is adopted to estimate the relation between these3variables and donation amount.Weﬁt the relation across all institutions and get aﬁtted function from donation amount to values of performance contributing variables.Then we divide the impact of donation amount into2parts:homogenous and heterogenous one.The homogenous inﬂuence is modeled as the change inﬁt-ted values of performance contributing variables over increase in donation amount, which can be predicted from theﬁtted curve.The heterogenous one is modeled as a tuning parameter which adjusts the homogenous inﬂuence based on deviation from theﬁtted curve.And their product is increase in true values of performance over increase in donation amount.Finally,we calculate ROI,deﬁned as increase in performance index over in-crease in donation amount.This ROI is institution-speciﬁc and dependent on in-crease in donation amount.By adopting a two-step ROI maximization algorithm, we determine the optimal investment strategy.Also,we propose an extended model to handle problems caused by time dura-tion and geographical distribution of donations.A Letter to the CFO of the Goodgrant FoundationDear Chiang,Our team has proposed a performance index quantifying the students’educational per-formance of each institution and deﬁned the return of investment(ROI)appropriately for a charitable organization like Goodgrant Foundation.A mathematical model is built to help predict the return of investment after identifying the mechanism through which the donation generates its impact on the performance.The optimal investment strategy is determined by maximizing the estimated return of investment.More speciﬁcally,the composite performance index is developed after taking all the pos-sible performance indicators into consideration,like graduation rate and graduates’earnings. The performance index is constructed to represents the performance of the school as well as the positive effect that a college brings to students and the community.From this point of view, our deﬁnition manages to capture social beneﬁts of donation.And then we adopt a variable selection method toﬁnd out performance contributing vari-ables,which are variables that strongly affect the performance index.Among all the perfor-mance contributing variables we select,three variables which can be directly affected by your generous donation are kept to predict ROI:percentage of students who receive a Pell Grant, share of students who are part-time and student-to-faculty ratio.Weﬁtted a relation between these three variables and the donation amount to predict change in value of each performance contributing variable over your donation amount.And we calculate ROI,deﬁned as increase in the performance index over your donation amount, by multiplying change in value of each performance contributing variable over your donation amount and each performance contributing variable’s effect on performance index,and then summing up the products of all performance contributing variables.The optimal investment strategy is decided after maximizing the return of investment according to an algorithm for selection.In conclusion,our model successfully produced an investment strategy including a list of target institutions and investment amount for each institution.(The list of year1is attached at the end of the letter).The time duration for the investment could also be determined based on our model.Since the model as well as the evaluation approach is fully data-motivated with no arbitrary criterion included,it is rather adaptable for solving future philanthropic educational investment problems.We have a strong belief that our model can effectively enhance the efﬁciency of philan-thropic educational investment and provides an appropriate as well as feasible way to best improve the educational performance of students.UNITID names ROI donation 197027United States Merchant Marine Academy21.85%2500000 102711AVTEC-Alaska’s Institute of Technology21.26%7500000 187745Institute of American Indian and Alaska Native Culture20.99%2000000 262129New College of Florida20.69%6500000 216296Thaddeus Stevens College of Technology20.66%3000000 229832Western Texas College20.26%10000000 196158SUNY at Fredonia20.24%5500000 234155Virginia State University20.04%10000000 196200SUNY College at Potsdam19.75%5000000 178615Truman State University19.60%3000000 199120University of North Carolina at Chapel Hill19.51%3000000 101648Marion Military Institute19.48%2500000187912New Mexico Military Institute19.31%500000 227386Panola College19.28%10000000 434584Ilisagvik College19.19%4500000 199184University of North Carolina School of the Arts19.15%500000 413802East San Gabriel Valley Regional Occupational Program19.09%6000000 174251University of Minnesota-Morris19.09%8000000 159391Louisiana State University and Agricultural&Mechanical Col-19.07%8500000lege403487Wabash Valley College19.05%1500000 Yours Sincerely,Team#42939An Optimal Strategy of Donation for Educational PurposeControl Number:#42939February,2016Contents1Introduction51.1Statement of the Problem (5)1.2Baseline Model (5)1.3Detailed Deﬁnitions&Assumptions (8)1.3.1Detailed Deﬁnitions: (8)1.3.2Assumptions: (9)1.4The Advantages of Our Model (9)2Addressing the Missing Values93Determining the Performance Index103.1Performance Indicators (10)3.2Performance Index via Principal-Component Factors (10)4Identifying Performance Contributing Variables via post-LASSO115Determining Investment Strategy based on ROI135.1Fitted Curve between Performance Contributing Variables and Donation Amount145.2ROI(Return on Investment) (15)5.2.1Model of Fitted ROIs of Performance Contributing Variables fROI i (15)5.2.2Model of the tuning parameter P i (16)5.2.3Calculation of ROI (17)5.3School Selection&Investment Strategy (18)6Extended Model186.1Time Duration (18)6.2Geographical Distribution (22)7Conclusions and Discussion22 8Reference23 9Appendix241Introduction1.1Statement of the ProblemThere exists no doubt in the signiﬁcance of postsecondary education to the development of society,especially with the ascending need for skilled employees capable of complex work. Nevertheless,U.S.ranks only11th in the higher education attachment worldwide,which makes theﬁnancial support from large charitable organizations necessary.As it’s essential for charitable organizations to maximize the effectiveness of donations,an objective and systematic assessment model is in demand to develop appropriate investment strategies.To achieve this goal,several large foundations like Gates Foundation and Lumina Foundation have developed different evaluation approaches,where they mainly focus on spe-ciﬁc indexes like attendance and graduation rate.In other empirical literature,a Forbes ap-proach(Shifrin and Chen,2015)proposes a new indicator called the Grateful Graduates Index, using the median amount of private donations per student over a10-year period to measure the return on investment.Also,performance funding indicators(Burke,2002,Cave,1997,Ser-ban and Burke,1998,Banta et al,1996),which include but are not limited to external indicators like graduates’employment rate and internal indicators like teaching quality,are one of the most prevailing methods to evaluate effectiveness of educational donations.However,those methods also arise with widely acknowledged concerns(Burke,1998).Most of them require subjective choice of indexes and are rather arbitrary than data-based.And they perform badly in a data environment where there is miscellaneous cross-section data but scarce time-series data.Besides,they lack quantiﬁed analysis in precisely predicting or measuring the social beneﬁts and the positive effect that the investment can generate,which serves as one of the targets for the Goodgrant Foundation.In accordance with Goodgrant Foundation’s request,this paper provides a prudent def-inition of return on investment(ROI)for charitable organizations,and develops an original data-motivated model,which is feasible even faced with tangled cross-section data and absent time-series data,to determine the optimal strategy for funding.The strategy contains selection of institutions and distribution of investment across institutions,time and regions.1.2Baseline ModelOur deﬁnition of ROI is similar to its usual meaning,which is the increase in students’educational performance over the amount Goodgrant Foundation donates(assuming other donationsﬁxed,it’s also the increase in total donation amount).First we cope with data missingness.Then,to quantify students’educational performance, we develop an index called performance index,which is a linear composition of commonly used performance indicators.Our major task is to build a model to predict the change of this index given a distribution of Goodgrant Foundation$100m donation.However,donation does not directly affect the performance index and we would encounter endogeneity problem or neglect effects of other variables if we solely focus on the relation between performance index and donation amount. Instead,we select several variables that are pivotal in predicting the performance index from many potential candidates,and determine their coefﬁcients/effects on the performance index. We call these variables performance contributing variables.Due to absence of time-series data,it becomes difﬁcult toﬁgure out how performance con-tributing variables are affected by donation amount for each institution respectively.Instead, weﬁt the relation between performance contributing variables and donation amount across all institutions and get aﬁtted function from donation amount to values of performance contribut-ing variables.Then we divide the impact of donation amount into2parts:homogenous and heteroge-nous one.The homogenous inﬂuence is modeled as the change inﬁtted values of performance contributing variables over increase in donation amount(We call these quotientsﬁtted ROI of performance contributing variable).The heterogenous one is modeled as a tuning parameter, which adjusts the homogenous inﬂuence based on deviation from theﬁtted function.And their product is the institution-speciﬁc increase in true values of performance contributing variables over increase in donation amount(We call these values ROI of performance contributing vari-able).The next step is to calculate the ROI of the performance index by adding the products of ROIs of performance contributing variables and their coefﬁcients on the performance index. This ROI is institution-speciﬁc and dependent on increase in donation amount.By adopting a two-step ROI maximization algorithm,we determine the optimal investment strategy.Also,we propose an extended model to handle problems caused by time duration and geographical distribution of donations.Note:we only use data from the provided excel table and that mentioned in the pdfﬁle.Table1:Data SourceVariable DatasetPerformance index Excel tablePerformance contributing variables Excel table and pdfﬁleDonation amount PdfﬁleTheﬂow chart of the whole model is presented below in Fig1:Figure1:Flow Chart Demonstration of the Model1.3Detailed Deﬁnitions&Assumptions 1.3.1Detailed Deﬁnitions:1.3.2Assumptions:A1.Stability.We assume data of any institution should be stable without the impact from outside.To be speciﬁc,the key factors like the donation amount and the performance index should remain unchanged if the college does not receive new donations.A2.Goodgrant Foundation’s donation(Increase in donation amount)is discrete rather than continuous.This is reasonable because each donation is usually an integer multiple of a minimum amount,like$1m.After referring to the data of other foundations like Lumina Foundation,we recommend donation amount should be one value in the set below:{500000,1000000,1500000, (10000000)A3.The performance index is a linear composition of all given performance indicators.A4.Performance contributing variables linearly affect the performance index.A5.Increase in donation amount affects the performance index through performance con-tributing variables.A6.The impact of increase in donation amount on performance contributing variables con-tains2parts:homogenous one and heterogenous one.The homogenous inﬂuence is repre-sented by a smooth function from donation amount to performance contributing variables.And the heterogenous one is represented by deviation from the function.1.4The Advantages of Our ModelOur model exhibits many advantages in application:•The evaluation model is fully data based with few subjective or arbitrary decision rules.•Our model successfully identiﬁes the underlying mechanism instead of merely focusing on the relation between donation amount and the performance index.•Our model takes both homogeneity and heterogeneity into consideration.•Our model makes full use of the cross-section data and does not need time-series data to produce reasonable outcomes.2Addressing the Missing ValuesThe provided datasets suffer from severe data missing,which could undermine the reliabil-ity and interpretability of any results.To cope with this problem,we adopt several different methods for data with varied missing rate.For data with missing rate over50%,any current prevailing method would fall victim to under-or over-randomization.As a result,we omit this kind of data for simplicity’s sake.For variables with missing rate between10%-50%,we use imputation techniques(Little and Rubin,2014)where a missing value was imputed from a randomly selected similar record,and model-based analysis where missing values are substituted with distribution diagrams.For variables with missing rate under10%,we address missingness by simply replace miss-ing value with mean of existing values.3Determining the Performance IndexIn this section,we derive a composite index,called the performance index,to evaluate the educational performance of students at every institution.3.1Performance IndicatorsFirst,we need to determine which variables from various institutional performance data are direct indicators of Goodgrant Foundation’s major concern–to enhance students’educational performance.In practice,other charitable foundations such as Gates Foundation place their focus on core indexes like attendance and graduation rate.Logically,we select performance indicators on the basis of its correlation with these core indexes.With this method,miscellaneous performance data from the excel table boils down to4crucial variables.C150_4_P OOLED_SUP P and C200_L4_P OOLED_SUP P,as completion rates for different types of institutions,are directly correlated with graduation rate.We combine them into one variable.Md_earn_wne_p10and gt_25k_p6,as different measures of graduates’earnings,are proved in empirical studies(Ehren-berg,2004)to be highly dependent on educational performance.And RP Y_3Y R_RT_SUP P, as repayment rate,is also considered valid in the same sense.Let them be Y1,Y2,Y3and Y4.For easy calculation and interpretation of the performance index,we apply uniformization to all4variables,as to make sure they’re on the same scale(from0to100).3.2Performance Index via Principal-Component FactorsAs the model assumes the performance index is a linear composition of all performance indicators,all we need to do is determine the weights of these variables.Here we apply the method of Customer Satisfaction Index model(Rogg et al,2001),where principal-component factors(pcf)are employed to determine weights of all aspects.The pcf procedure uses an orthogonal transformation to convert a set of observations of pos-sibly correlated variables into a set of values of linearly uncorrelated variables called principal-component factors,each of which carries part of the total variance.If the cumulative proportion of the variance exceeds80%,it’s viable to use corresponding pcfs(usually theﬁrst two pcfs)to determine weights of original variables.In this case,we’ll get4pcfs(named P CF1,P CF2,P CF3and P CF4).First,the procedure provides the linear coefﬁcients of Y m in the expression of P CF1and P CF2.We getP CF1=a11Y1+a12Y2+a13Y3+a14Y4P CF2=a21Y1+a22Y2+a23Y3+a24Y4(a km calculated as corresponding factor loadings over square root of factor k’s eigenvalue) Then,we calculate the rough weights c m for Y m.Let the variance proportions P CF1and P CF2 represent be N1and N2.We get c m=(a1m N1+a2m N2)/(N1+N2)(This formulation is justiﬁedbecause the variance proportions can be viewed as the signiﬁcance of pcfs).If we let perfor-mance index=(P CF 1N 1+P CF 2N 2)/(N 1+N 2),c m is indeed the rough weight of Y m in terms of variance)Next,we get the weights by adjusting the sum of rough weights to 1:c m =c m /(c 1+c 2+c 3+c 4)Finally,we get the performance index,which is the weighted sum of the 4performance indicator.Performance index= m (c m Y m )Table 2presents the 10institutions with largest values of the performance index.This rank-ing is highly consistent with widely acknowledged rankings,like QS ranking,which indicates the validity of the performance index.Table 2:The Top 10Institutions in Terms of Performance IndexInstitutionPerformance index Los Angeles County College of Nursing and Allied Health79.60372162Massachusetts Institute of Technology79.06066895University of Pennsylvania79.05044556Babson College78.99269867Georgetown University78.90468597Stanford University78.70586395Duke University78.27719116University of Notre Dame78.15843964Weill Cornell Medical College 78.143341064Identifying Performance Contributing Variables via post-LASSO The next step of our model requires identifying the factors that may exert an inﬂuence on the students’educational performance from a variety of variables mentioned in the excel table and the pdf ﬁle (108in total,some of which are dummy variables converted from categorical variables).To achieve this purpose,we used a model called LASSO.A linear model is adopted to describe the relationship between the endogenous variable –performance index –and all variables that are potentially inﬂuential to it.We assign appropriate coefﬁcient to each variable to minimize the square error between our model prediction and the actual value when ﬁtting the data.min β1J J j =1(y j −x T j β)2where J =2881,x j =(1,x 1j ,x 2j ,...,x pj )THowever,as the amount of the variables included in the model is increasing,the cost func-tion will naturally decrease.So the problem of over ﬁtting the data will arise,which make the model we come up with hard to predict the future performance of the students.Also,since there are hundreds of potential variables as candidates.We need a method to identify the variables that truly matter and have a strong effect on the performance index.Here we take the advantage of a method named post-LASSO (Tibshirani,1996).LASSO,also known as the least absolute shrinkage and selection operator,is a method used for variableselection and shrinkage in medium-or high-dimensional environment.And post-LASSO is to apply ordinary least squares(OLS)to the model selected byﬁrst-step LASSO procedure.In LASSO procedure,instead of using the cost function that merely focusing on the square error between the prediction and the actual value,a penalty term is also included into the objective function.We wish to minimize:min β1JJj=1(y j−x T jβ)2+λ||β||1whereλ||β||1is the penalty term.The penalty term takes the number of variables into con-sideration by penalizing on the absolute value of the coefﬁcients and forcing the coefﬁcients of many variables shrink to zero if this variable is of less importance.The penalty coefﬁcient lambda determines the degree of penalty for including variables into the model.After min-imizing the cost function plus the penalty term,we couldﬁgure out the variables of larger essence to include in the model.We utilize the LARS algorithm to implement the LASSO procedure and cross-validation MSE minimization(Usai et al,2009)to determine the optimal penalty coefﬁcient(represented by shrinkage factor in LARS algorithm).And then OLS is employed to complete the post-LASSO method.Figure2:LASSO path-coefﬁcients as a function of shrinkage factor sFigure3:Cross-validated MSEFig2.displays the results of LASSO procedure and Fig3displays the cross-validated MSE for different shrinkage factors.As speciﬁed above,the cross-validated MSE reaches minimum with shrinkage factor between0.4-0.8.We choose0.6andﬁnd in Fig2that6variables have nonzero coefﬁcients via the LASSO procedure,thus being selected as the performance con-tributing variables.Table3is a demonstration of these6variables and corresponding post-LASSO results.Table3:Post-LASSO resultsDependent variable:performance_indexPCTPELL−26.453∗∗∗(0.872)PPTUG_EF−14.819∗∗∗(0.781)StudentToFaculty_ratio−0.231∗∗∗(0.025)Tuition&Fees20100.0003∗∗∗(0.00002)Carnegie_HighResearchActivity 5.667∗∗∗(0.775)Constant61.326∗∗∗(0.783)Observations2,880R20.610Adjusted R20.609Note:PCTPELL is percentage of students who receive aPell Grant;PPTUG_EF is share of students who are part-time;Carnegie_HighResearchActivity is Carnegie classiﬁca-tion basic:High Research ActivityThe results presented in Table3are consistent with common sense.For instance,the pos-itive coefﬁcient of High Research Activity Carnegie classiﬁcation implies that active research activity helps student’s educational performance;and the negative coefﬁcient of Student-to-Faculty ratio suggests that decrease in faculty quantity undermines students’educational per-formance.Along with the large R square value and small p-value for each coefﬁcient,the post-LASSO procedure proves to select a valid set of performance contributing variables and describe well their contribution to the performance index.5Determining Investment Strategy based on ROIWe’ve identiﬁed5performance contributing variables via post-LASSO.Among them,tu-ition&fees in2010and Carnegie High-Research-Activity classiﬁcation are quite insusceptible to donation amount.So we only consider the effects of increase in donation amount on per-centage of students who receive a Pell Grant,share of students who are part-time and student-to-faculty ratio.We denote them with F1,F2and F3,their post-LASSO coefﬁcients withβ1,β2andβ3.In this section,weﬁrst introduce the procedure used toﬁt the relation between performance contributing variables and donation amount.Then we provide the model employed to calcu-lateﬁtted ROIs of performance contributing variables(the homogenous inﬂuence of increase in donation amount)and the tuning parameter(the heterogenous inﬂuence of increase in dona-tion amount).Next,we introduce how to determine stly,we show how the maximiza-tion determines the investment strategy,including selection of institutions and distribution of investments.5.1Fitted Curve between Performance Contributing Variables and Donation AmountSince we have already approximated the linear relation between the performance index with the3performance contributing variables,we want to know how increase in donation changes them.In this paper,we use Generalized Adaptive Model(GAM)to smoothlyﬁt the relations. Generalized Adaptive Model is a generalized linear model in which the dependent variable depends linearly on unknown smooth functions of independent variables.Theﬁtted curve of percentage of students who receive a Pell Grant is depicted below in Fig4(see the other two ﬁtted curves in Appendix):Figure4:GAM ApproximationA Pell Grant is money the U.S.federal government provides directly for students who needit to pay for college.Intuitively,if the amount of donation an institution receives from other sources such as private donation increases,the institution is likely to use these donations to alleviate students’ﬁnancial stress,resulting in percentage of students who receive a Pell Grant. Thus it is reasonable to see aﬁtted curve downward sloping at most part.Also,in commonsense,an increase in donation amount would lead to increase in the performance index.This downward sloping curve is consistent with the negative post-LASSO coefﬁcient of percentage of students who receive a Pell Grant(as two negatives make a positive).5.2ROI(Return on Investment)5.2.1Model of Fitted ROIs of Performance Contributing Variables fROI iFigure5:Demonstration of fROI1Again,we useﬁtted curve of percentage of students who receive a Pell Grant as an example. We modeled the blueﬁtted curve to represent the homogeneous relation between percentage of students who receive a Pell Grant and donation amount.Recallﬁtted ROI of percentage of students who receive a Pell Grant(fROI1)is change in ﬁtted values(∆f)over increase in donation amount(∆X).SofROI1=∆f/∆XAccording to assumption A2,the amount of each Goodgrant Foundation’s donation falls into a pre-speciﬁed set,namely,{500000,1000000,1500000,...,10000000}.So we get a set of possible ﬁtted ROI of percentage of students who receive a Pell Grant(fROI1).Clearly,fROI1is de-pendent on both donation amount(X)and increase in donation amount(∆X).Calculation of ﬁtted ROIs of other performance contributing variables is similar.5.2.2Model of the tuning parameter P iAlthough we’ve identiﬁed the homogenous inﬂuence of increase in donation amount,we shall not neglect the fact that institutions utilize donations differently.A proportion of do-nations might be appropriated by the university’s administration and different institutions allocate the donation differently.For example,university with a more convenient and well-maintained system of identifying students who needﬁnancial aid might be willing to use a larger portion of donations to directly aid students,resulting in a lower percentage of under-graduate students receiving Pell grant.Also,university facing lower cost of identifying and hiring suitable faculty members might be inclined to use a larger portion of donations in this direction,resulting in a lower student-to-faculty ratio.These above mentioned reasons make institutions deviate from the homogenousﬁtted func-tion and presents heterogeneous inﬂuence of increase in donation amount.Thus,while the homogenous inﬂuence only depends on donation amount and increase in donation amount, the heterogeneous inﬂuence is institution-speciﬁc.To account for this heterogeneous inﬂuence,we utilize a tuning parameter P i to adjust the homogenous inﬂuence.By multiplying the tuning parameter,ﬁtted ROIs of performance con-tributing variables(ﬁtted value changes)convert into ROI of performance contributing variable (true value changes).ROI i=fROI i·P iWe then argue that P i can be summarized by a function of deviation from theﬁtted curve (∆h),and the function has the shape shown in Fig6.The value of P i ranges from0to2,because P i can be viewed as an ampliﬁcation or shrinkage of the homogenous inﬂuence.For example,P i=2means that the homogeneous inﬂuence is ampliﬁed greatly.P i=0means that this homogeneous inﬂuence would be entirely wiped out. The shape of the function is as shown in Fig6because of the following reasons.Intuitively,if one institution locates above theﬁtted line,when deviation is small,the larger it is,the larger P i is.This is because the institution might be more inclined to utilize donations to change that factor.However,when deviation becomes even larger,the institution grows less willing to invest on this factor.This is because marginal utility decreases.The discussion is similar if one institution initially lies under theﬁtted line.Thus,we assume the function mapping deviation to P i is similar to Fig6.deviation is on the x-axis while P i is on the y-axis.Figure6:Function from Deviation to P iIn order to simplify calculation and without loss of generality,we approximate the function。

amc获奖规则

amc获奖规则
AMC（美国数学竞赛）是由美国数学协会（MAA）主办的一
项全国性数学竞赛。

以下是AMC获奖的一般规则：
1. AMC 10/12奖项规则：AMC 10和AMC 12是两个不同水平
的竞赛，因此设有不同的获奖等级。

- 每个竞赛等级分为三个层次的奖项：优异奖（AIME资格奖）、荣誉奖和优胜奖。

- 在AMC 10中，获得120分及以上的学生可以获得优异奖，100分及以上获得荣誉奖，85分及以上获得优胜奖。

- 在AMC 12中，获得100分及以上的学生可以获得优异奖，90分及以上获得荣誉奖，80分及以上获得优胜奖。

- 在AMC 10和AMC 12中，获得竞赛分数最高者将获得冠
军奖。

2. AIME（美国数学邀请赛）获奖规则：AIME是AMC竞赛
的下一轮，只有获得AMC特定分数线上的学生才能参加。

- AIME竞赛获得者根据分数可以获得一个分数等级的奖项。

- AIME成绩相对于全国参赛者进行排名，最高分者获得冠
军奖。

3. 数学奥林匹克竞赛获奖规则：数学奥林匹克竞赛是AMC的
最高级别竞赛，只有获得AIME高分的学生才有机会参加。

- 数学奥林匹克竞赛获奖者根据分数可以获得金、银、铜牌
奖项。

- 数学奥林匹克竞赛根据分数进行排名，最高分者获得金牌奖。

以上是AMC获奖的一般规则，具体规则可能有细微的变化，可以参考美国数学协会（MAA）的官方规定了解更详细的信息。

美国数学竞赛(2016AMC-AIME)获奖喜报

美国数学竞赛（2016AMC-AIME）获奖喜报在2016年2-3月进行的美国数学竞赛（AMC-AIME）中，我校参赛同学成绩突出，共获得8个特优奖（Distinction Honor Roll，全球前1%）和22个优胜奖（Honor Roll，全球前5%）。

获奖名单：班级中文姓名AMC级别评奖评奖(中文)指导老师E4樊骅12Distinction Honor Roll特优奖(全球前1%)郭卫东DNS1李心宓10Distinction Honor Roll特优奖(全球前1%)伍毅东E1梁济凡12Distinction Honor Roll特优奖(全球前1%)周映平、刘军凤E8麦子涛12Distinction Honor Roll特优奖(全球前1%)先开萍DNS1翁一平12Distinction Honor Roll特优奖(全球前1%)伍毅东E3吴溥樾12Distinction Honor Roll特优奖(全球前1%)许作舟E19旋璇12Distinction Honor Roll特优奖(全球前1%)翁文ENS2周前12Distinction Honor Roll特优奖(全球前1%)梁万峰E8陈锦河12Honor Roll优胜奖(全球前5%)先开萍E8李城坚12Honor Roll优胜奖(全球前5%)先开萍E18方星棉12Honor Roll优胜奖(全球前5%)周若鸿DNS2庞颢然12Honor Roll优胜奖(全球前5%)伍毅东ENS1黄家和12Honor Roll优胜奖(全球前5%)梁万峰FAP黄敬乐12Honor Roll优胜奖(全球前5%)ENS2赵婧彤12Honor Roll优胜奖(全球前5%)梁万峰ENS1陶凯雯12Honor Roll优胜奖(全球前5%)梁万峰DNS1刘子欣10Honor Roll优胜奖(全球前5%)伍毅东E8劳雅静12Honor Roll优胜奖(全球前5%)先开萍E8李俊辉12Honor Roll优胜奖(全球前5%)先开萍E3林郁东12Honor Roll优胜奖(全球前5%)许作舟E14刘懿德12Honor Roll优胜奖(全球前5%)戴应超ENS2刘煜12Honor Roll优胜奖(全球前5%)梁万峰ENS1栾昊12Honor Roll优胜奖(全球前5%)梁万峰DNS1区子锐12Honor Roll优胜奖(全球前5%)伍毅东E8冉双璇12Honor Roll优胜奖(全球前5%)先开萍ENS1宋世健12Honor Roll优胜奖(全球前5%)梁万峰E10谭钰千12Honor Roll优胜奖(全球前5%)杨淑苹D6吴俊禄10Honor Roll优胜奖(全球前5%)许瑞蓉E6薛又天12Honor Roll优胜奖(全球前5%)宋沙沙ENS1曾子灏12Honor Roll优胜奖(全球前5%)梁万峰在此特向获奖的同学及指导老师表示祝贺！广东实验中学数学科2016年6月。

美国数学竞赛AMC1012简介

美国数学竞赛AMC1012简介AMC系列AMC系列的全称American Mathematics Competitions是由美国数学协会举办的，是美国最⽼的（1950年开始举办）的和最负盛名的初⾼中⽣数学竞赛。

AMC系列⽐赛⼀共有以下⼏个⽐赛：American Mathematics Competition 8 - AMC 8American Mathematics Competition 10/12 - AMC 10/12American Invitational Mathematics Exam - AIMEUnited States Mathematical Olympiad and Junior Mathematical Olympiad - USA(J)MOAMC10/12AMC10和12是AMC⽐赛系列中层次较⾼的，相⽐AMC8来说，这个⽐赛就是玩真格的了，难度也是提升了不少。

官⽹上是这么说的“The AMC 10/12 is the first in a series of competitions that eventually lead all the way to the International Mathematical Olympiad”。

翻译成⼤⽩话就是想去国际数学奥赛？那咱们从AMC10/12起步吧。

1、题型：共25道选择题，计时75分钟，总分150分。

包含⼏何，代数，基础数论，排列组合以及概率统计知识。

答对⼀题得六分，不答得1.5分，答错得0分。

AMC10 参赛年级：10年级及以下的美国，美属领地，加拿⼤和国际学⽣都可报名参加。

10年级以下的学⽣可以选择AMC10或12，或在不同⽇期参加AMC10和12。

（年龄要求：截⽌⽐赛当天17.5岁及以下）AMC12 参赛年级：12年级及以下的美国，美属领地，加拿⼤和国际学⽣都可报名参加。

11-12年级的学⽣只能参加AMC12。

重庆大学2016年美国大学生数学建模竞赛获奖名单(一等奖以上)

领取美国竞赛报名费的通知2016/6/13请通过了2016美国竞赛校内选拔赛并获得2016年美国数学建模竞赛一等奖及其以上的下列同学于6月17日(星期五)晚7:30带上你们的学生证到A区八教教员休息室领取竞赛报名费.请同学们互相转告.1 2053，方筑，张福，赵广特等奖2 2048，刘栋，雷凯民，薛艺鹏特等奖3 2062 张子祥梁蕾袁野一等奖4 2270，王芷晴，许日能，刘云龙一等奖5 2140，陈靖熙，秦雪梅，屈仁浩一等奖6 2212吴家豪，陈立庚，杨曼琳一等奖7 2036 王智，张彪，张翔一等奖8 2095 陈强张后谊陈道远一等奖9 2142 覃嘉乐罗永红刘礼恺一等奖10 2226 贺春旺，杨航，邓诗圆一等奖11 2083 甘健权，麦永锋，傅子安一等奖12 2119，陈洋，唐韬，杨莹一等奖13 2164 刘凯，张壮壮，汤秀洁一等奖14 2054，娄子屹，宫邦润，王浩欢一等奖15 2141尹旭阳曾查斯马晓晨一等奖16 2072，陈明，张悦，杨沐一等奖17 2110 张姬一哲韩晨阳张鹏一等奖18 2213 刘珉珂陶文轩刘硕一等奖19 2288，崔轩阁，张建功，毛浩一等奖20 2126，刘欣，陈诗颖，吴鸿燕一等奖21 2215 董靖严晗袁晨曦一等奖22 1439 王磊杨志勇赵中华一等奖23 2051-叶隆业-陶鑫-张昊一一等奖24 2027：王鹏博，李晓彤，严梓铭一等奖25 2086 张阳阳，伍圣超，张术雄一等奖26 2085 赵庭玉陈帮枫张强一等奖27 2149张尧钧彭丽杨栋钧一等奖28 2225，赵家俊，刘欢，姚嘉瑜一等奖29 2038 张超，王帆，杨丹宁一等奖30 2200，朱硕，熊光启，郭胜辉一等奖31 2267，胡奇强，王俊杰，徐军军一等奖重庆大学数学建模教练组。

比赛,更是磨砺!

比赛，更是磨砺——会话美国大学生数学建模大赛一等奖李珍珍团队已有几十年历史的美国大学生数学建模大赛（下文简称美赛）是全世界含金量最大的数学建模比赛。

来自全球的参赛队伍需先在各自的国家内角逐出一、二、三等奖，随后各国的评审团再从获得一等奖的作品中选取更为出众的几份作品送至美国，最终这些来自世界各地的佼佼者们将在同一舞台上竞争outstanding奖，其余被选送但未评上outstanding的作品则授予outstanding提名奖。

中国的参赛选手是这项比赛的主力军，每年都会有几支队伍凭着出色发挥拿下outstanding奖，今年更是包揽了全球13个中的6个。

四川大学也曾有一支队伍获得过这项殊荣，现任四川大学数学学院的王皓老师就是当时团队中的一员。

今年，四川大学同样有着不错的表现。

来自数学学院2010级的李珍珍、电子信息学院2011级的周龙和李高磊三位同学经过四天四夜的艰苦奋战取取了一等奖（M奖）。

“你要能熬夜，才能参加建模比赛”春节一过方才初几，李珍珍一行人就早早辞别家人来到学校，在她们租的小屋里一干就是四天四夜。

时间紧、任务重，熬夜是在所难免的，老师曾告诫过李珍珍那样：“你要能熬夜，才能参加建模比赛。

”所幸的是在她们参加美赛之前已有参加中国大学生数学建模比赛（后简称国赛）的经验。

国赛是由国外引进的中国大学生自己的数学建模比赛，在每年的九月份进行，赛程为三天。

为此，四川大学也会在暑期国际实践周专门开设“数学建模实践”的选修课程。

课程为期两周，将笼统介绍有关数学建模比赛中各个方面的知识。

但不给予大量的练习，仅为一入门引导课程，有广度没深度，以拓宽学生的知识面为主。

说起国赛，周龙与李高磊两位同学显得有些兴奋。

国赛时他们与另一位同学，在一间空寝室里奋战了三天三夜。

可是再看看这次美赛，李珍珍向我们爆料，“到了最后一天的时候周龙这家伙还给自己放假。

”一旁的周龙笑了笑，“也是因为之前参加国赛的经历，这次美赛的时间弹性就有了一些弹性时间，所以最后还剩下排版的时候我还忙里偷闲看了集《爱情公寓》”。

美国大学生数学建模竞赛赛20160719

美国大学生数学建模竞赛的命题与评阅
天津大学边馥萍 fpbian@
美国大学生数学建模竞赛
热烈祝贺山东大学荣获2016年美赛O奖
参赛命题评阅获奖培训
1. MCM/ICM 简介
美国大学生数学建模竞赛创始人 Ben Fusaro 1984年向美国教育部申请到一笔为期三年的基金，并于1985年开始正式举办。竞赛由COMAP组织和管理竞赛的命题、组织形式、宗旨、评审原则 MCM参赛情况：第1届：1985年参赛队158个队（美国），交卷90队，70所大学第32届：2016年参赛队7421个队，919所大学， 12个国家及地区，中国学生参赛队超过93.5%
初评标准
对题目的解读，赛题中没有明确给出的模糊概念是否澄清。建模所需的前提条件及假设及其合理性的说明。通过对赛题的分析论证建模的合理性。建立有效解答赛题的模型。对模型的稳定性、敏感性进行测试，检验。讨论模型的优缺点，给出清晰的结论。符合要求的摘要：应包含以下内容用自己的语言描述要解决的问题，强调建模所用的假设，指出所用的模型类型或构造的新模型，模型检验及误差分析和优缺点讨论。
2016 ICM Contest Outstanding Teams
2训资料（高教出版社出版）
美国大学生数学建模竞赛题解析与研究 2007-2008 第一册 2005-2006 第二册 Mathematical Modeling for the MCM/ICM Contest , Volume 1, 2 正确写作美国大学生数学建模竞赛论文 …..
UMAP数学建模案例精选1、2册，3册即将出版
UMAP 案例精选—1、2测已出版，3册即将出版特点：案例及习题有具体解法，有些适合做教学案例配套PPT正在制作中

西北工业大学竞赛获奖推荐免试名单

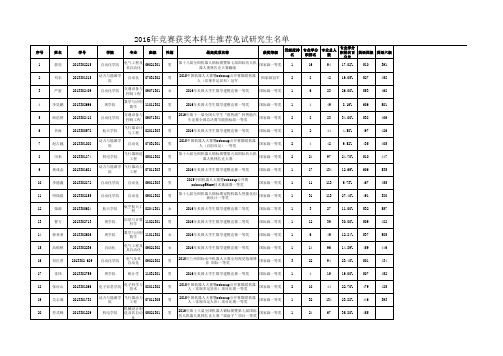
17
134
12.69%
606
535
10
11
113
9.73%
467
455
11 12 13
明瑞晨柴源
2013302155 2013300684
自动化学院航天学院
自动化
09011302
男女
第十七届全国机器人锦标赛宠物机器人智能化创国家级一等奖新设计一等奖 2016年美国大学生数学建模竞赛二等奖国际级二等奖
2
7 32 34
27 68 134
25.92% 47.00% 25.37%
565 500 590
457 413 548
郭靖韩昌富
2013300611 2013301659
航天学院
男男
1 2
41 42
动力与能源学飞行器动力 07011302 院工程电子信息学院电磁场与无 08051302 线技术
37
杨鸿杰苏秀中
2013300576 2012301054
航天学院机电学院
男男
1 3
14 47
44 97
31.80% 48.50%
476 525
437 464
38 39 40
张茜
2013300384
航空学院
女
中国国际飞行器设计挑战赛暨科研类全国航空航国家级一等奖天模型锦标赛限时载运空投项目 15、16年美国大学生数学建模竞赛二等奖 2015中国机器人大赛暨robocup公开赛（自创异形）一等奖冠军 2015中国机器人大赛暨robocup公开舞蹈机器人（自创多足异形）冠军国际级二等奖国家级冠军
6
27
22.20%

申请 mit 本科的 amc 和 aime

申请 MIT 本科的AMC和本人ME在申请美国麻省理工学院（MIT）本科项目时，AMC（American Mathematics Competitions）和本人ME（American Invitational Mathematics Examination）成绩是非常重要的参考因素。

AMC和本人ME分别是美国数学协会（MAA）举办的数学竞赛，涵盖了高中水平的数学知识和解题能力。

申请者需要通过这些竞赛考试来展现自己的数学天赋和学术能力。

申请MIT本科的AMC和本人ME考试是如何进行的？在申请过程中，AMC和本人ME成绩对申请者的影响有多大？对于MIT本科申请者来说，如何准备AMC和本人ME考试才能取得理想的成绩？本文将围绕这些问题展开讨论。

1. AMC和本人ME考试的重要性AMC是美国数学协会举办的数学竞赛，分为AMC 10和AMC 12两个等级，分别面向10年级和12年级以及以下的学生。

本人ME是AMC比赛中表现优异的学生可以参加的资格赛，是进入美国数学奥林匹克竞赛（USAMO）的关键一步。

这些竞赛不仅在美国范围内具有重要意义，对于申请MIT等顶尖大学的国际学生来说，也是非常重要的参考因素。

在MIT的冠方招生要求中，高度重视数学能力与成就。

MIT的招生官们看重数学竞赛的成绩，认为这是申请者具备数学才能和潜力的重要证明。

取得优异的AMC和本人ME成绩可以在申请MIT时起到加分的作用，有助于提升申请者的竞争力。

2. AMC和本人ME考试的准备准备AMC和本人ME考试需要良好的数学基础和解题能力。

申请MIT的学生通常需要在高中数学课程中表现出色，具备扎实的数学基础知识。

还需要掌握一定的数学解题技巧和思维能力，能够灵活运用所学知识解决复杂的数学问题。

为了取得理想的成绩，申请者可以通过以下几种途径来准备AMC和本人ME考试：参加数学竞赛培训班：有针对性地选择一些专业的数学竞赛培训班，接受系统的数学竞赛训练，提升解题能力和技巧。

amc数学竞赛成绩划分

amc数学竞赛成绩划分摘要：一、前言二、AMC 数学竞赛简介1.竞赛背景2.竞赛级别与分类三、AMC 数学竞赛成绩划分1.等级划分2.评分标准四、成绩划分的影响1.对参赛者的影响2.对数学教育的影响五、总结正文：一、前言近年来，AMC 数学竞赛在我国逐渐受到关注，吸引了大量学生参与。

对于这样一项具有国际影响力的数学竞赛，了解其成绩划分规则具有重要意义。

本文将对AMC 数学竞赛成绩划分的相关内容进行详细介绍。

二、AMC 数学竞赛简介AMC，全称American Mathematics Competitions，是美国数学竞赛的简称。

该竞赛起源于1950 年，目前已经成为全球范围内最具影响力的数学竞赛之一。

AMC 竞赛分为多个级别，包括AMC8、AMC10、AMC12、AIME （美国数学邀请赛）等，分别针对不同年龄段的学生。

三、AMC 数学竞赛成绩划分1.等级划分AMC 数学竞赛的成绩主要分为以下几个等级：（1）杰出奖（Distinction）：成绩在前1% 的考生；（2）优秀奖（Merit）：成绩在前10% 的考生；（3）达标奖（Pass）：成绩在参赛者总数的50% 之前的考生；（4）未达标（Fail）：成绩在参赛者总数的50% 之后的考生。

2.评分标准AMC 数学竞赛的评分标准主要依据考生的答题正确率。

在竞赛中，每道题目分值不同，难度也有所区别。

考生在规定时间内完成答题后，根据答对的题目数量和题目难度计算得分。

最终，根据得分情况对考生进行等级划分。

四、成绩划分的影响1.对参赛者的影响AMC 数学竞赛成绩的划分对参赛者具有激励作用，能够激发学生的学习兴趣和竞争意识。

同时，成绩划分也为参赛者提供了自我评价和定位的依据，有助于他们明确自己的优势和不足，调整学习策略。

2.对数学教育的影响AMC 数学竞赛成绩的划分对我国数学教育产生了一定的影响。

一方面，AMC 竞赛的成绩可以作为选拔优秀学生的参考依据；另一方面，AMC 竞赛的题目和理念对课堂教学具有启示作用，有助于提高数学教育的质量。

amc8相当于国内数学什么水平

amc8相当于国内数学什么水平amc8其实是跟国内的小学杯赛的这个水平比较相近，培养学生的数学兴趣，但没有后续的一个进阶比赛。

amc8所谓的这个8指的是指8年级及8年级以下的学生，可以参与到这样的一个比赛当中。

amc10和amc12是指10年级及10年以下或12年级及12年级以下的学生可以参与。

经过这个10和12，取得了amc10前2.5%或amc12前5%的学生才有资格受邀参加aime数学邀请赛。

再往上就amcmo，这就有一定的要求，只有美国籍的学生才能够参加这个比赛。

amc比赛的规定是由美国数学协会于1950年正式成立的。

它的试题由简单到难，一点点的让学生感觉到具有挑战性，可以让所有喜欢数学或者是热爱数学的学生都能参与其中。

同时，在这个过程中也可以让学生感受到某种挑战。

目前，amc是世界上可信度和效度最高的一个数学比赛，普及程度非常广，在全球有近百个国家的孩子热衷于这个比赛，在各个国家甚至达到了几千所学校，会参与到这样的一个比赛当中。

在美国上千种各类数学比赛当中，它是唯一的国际数学奥林匹克国家队的选拔体系从最底层开始的是amc8，然后往上进阶到amc10、amc12，再往上到aime美国数学邀请赛，再往上就是usamo和imo。

imo最后选出来的几位选手，就跟世界各个国家的奥林匹克竞赛选手进行角逐。

去年在罗马尼亚的比赛，美国是冠军，中国是亚军。

amc8所谓的这个8指的是指8年级及8年级以下的学生，可以参与到这样的一个比赛当中。

amc10和amc12是指10年级及10年以下或12年级及12年级以下的学生可以参与。

经过这个10和12，取得了amc10前2.5%或amc12前5%的学生才有资格受邀参加aime数学邀请赛。

再往上就amcmo，这就有一定的要求，只有美国籍的学生才能够参加这个比赛。

amc数学竞赛证书

**AMC数学竞赛证书**
AMC数学竞赛的证书不仅仅是一纸证明，它更是一份对参赛者能力的认可。

当参赛者拿到一张金色的杰出荣誉证书（DH奖）时，那份沉甸甸的荣誉感足以让他们在未来的日子里都为之骄傲。

DH奖证书，是AMC数学竞赛中的最高荣誉，它代表了参赛者在竞赛中展现出了卓越的数学才华和非凡的思维能力。

获得荣誉证书（H奖）的参赛者同样值得称赞。

他们在竞赛中表现优异，展现出了扎实的基础和出色的解题技巧。

这份证书不仅是对他们个人能力的肯定，更是对他们努力和付出的最好回报。

当然，成就证书（A奖）也是一份非常有分量的证书。

它代表了参赛者在竞赛中达到了较高的水平，是一份非常有价值的荣誉。

除了个人证书外，参赛者还有机会获得AIME参赛资格证书。

这张证书是进入AIME数学竞赛的通行证，代表了参赛者在数学领域的实力和潜力。

当然，要获得这张证书并非易事，需要达到一定的分数线才能获得。

另外，对于那些在竞赛中表现出色的参赛者，他们还有机会获得AMC10/12全球荣誉奖Certificate of Achievement。

这是一份非常珍贵的证书，是对他们在竞赛中的突出表现和卓越成绩的最高褒奖。

这些证书不仅仅是纸上的文字和图案，它们更是一份对参赛者汗水和智慧的肯定。

无论是在升学、求职或是未来的人生道路上，这些证书都会成为他们宝贵的财富和难忘的回忆。

在面对挫折和困难时，这些证书更是一份无形的力量和激励，鞭策他们勇往直前，追求更高
的目标。

amc数学竞赛区区分

amc数学竞赛区区分
AMC数学竞赛主要分为以下几个级别：
1.AMC8：由8年级和8年级以下学生参加。

2.AMC10：由10年级和10年级以下的学生参加。

3.AMC12：由12年级和12年级以下的学生参加。

4.AIME：在AMC10和AMC12测试中成绩达到要求的学生可以参加。

JMO：由AMC10的约前230名美国学生参加。

AMO：由AMC10的约前270名美国学生参加。

其中，AMC8、AMC10、AMC12、AIME、USJMO、USAMO这六个级别比赛组成了AMC系列赛。

AMC数学竞赛的参赛对象和举办时间也不同，具体如下：
1.AMC8：8年级或以下并且挑战当天未满14.5岁的学生可以参加，比赛在每年的11月中举行。

2.AMC10和AMC12：AMC10涵盖9-10年级相关数学内容，包括但不限于基础代数、基础几何、排列组合、初等数论和初等概率等；AMC12
涵盖了整个高中数学课程，包括代数、平面几何、数论证明、排列组合、三角函数、数列和级数、复数和图论等，但不包括微积分。

比赛时间相同，分A、B两次在每年的2月初和2月中举行。

3.AIME：在AMC10和AMC12测试中成绩达到要求的学生可以参加，比赛在每年的3月底举行。

JMO和USAMO：USJMO由AMC10的约前230名美国学生参加，USAMO由AMC10的约前270名美国学生参加，比赛在每年4月的最后一周举行。

总的来说，AMC数学竞赛是一个系列性的数学竞赛，不同级别的比赛难度和参赛对象不同，旨在激发学生对数学的兴趣和才能。