高考数学总复习(讲+练+测)：专题2.7 对数与对数函数(讲)

高考数学专题《对数与对数函数》习题含答案解析

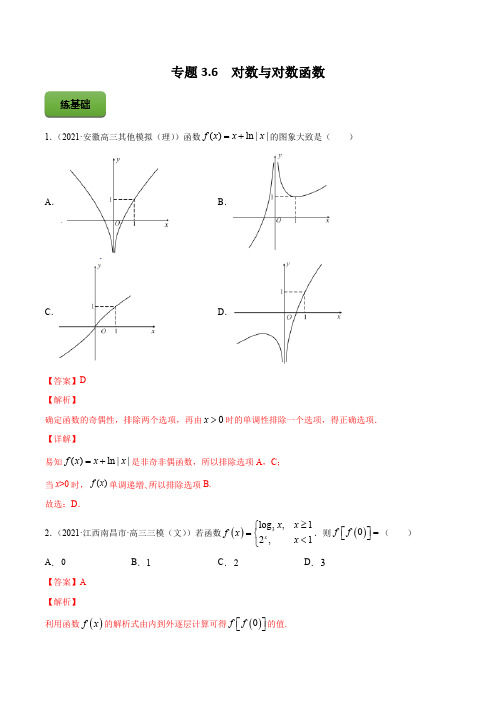
专题3.6 对数与对数函数1．（2021·安徽高三其他模拟（理））函数()ln ||f x x x =+的图象大致是（）A ．B ．C ．D ．【答案】D 【解析】确定函数的奇偶性，排除两个选项，再由0x >时的单调性排除一个选项，得正确选项．【详解】易知()ln ||f x x x =+是非奇非偶函数，所以排除选项A ，C ；当x >0时，()f x 单调递増､所以排除选项B.故选：D ．2．（2021·江西南昌市·高三三模（文））若函数()3log ,12,1x x x f x x ≥⎧=⎨<⎩．则()0f f ⎡⎤=⎣⎦（）A ．0B ．1C ．2D ．3【答案】A 【解析】利用函数()f x 的解析式由内到外逐层计算可得()0f f ⎡⎤⎣⎦的值.练基础()3log ,12,1x x x f x x ≥⎧=⎨<⎩，则()0021f ==，因此，()()301log 10f f f ===⎡⎤⎣⎦.故选：A.3．（2021·浙江高三其他模拟）已知a 为正实数，则“1a >”是“32212log log a a ->”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】C 【解析】利用充分、必要条件的定义，即可推出“1a >”与“32212log log a a ->”的充分、必要关系.【详解】因为32212log log a a ->等价于3222log log a a >，由a 为正实数且1a >，故有32a a >，所以3222log log a a >成立；由a 为正实数，3222log log a a >且函数2log y x =是增函数，有32a a >，故()210aa ->，所以1a >成立.故选：C ．4．（2021·浙江高三专题练习）已知函数f (x )＝1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y ＝f (1－x )的大致图象是（）A ．B ．C ．D ．【答案】D 【解析】由()f x 得到()1f x -的解析式，根据函数的特殊点和正负判断即可.因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩，所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩，当x ＝0时，y ＝f (1)＝3，即y ＝f (1－x )的图象过点(0，3)，排除A ；当x ＝－2时，y ＝f (3)＝－1，即y ＝f (1－x )的图象过点(－2，－1)，排除B ；当0x <时，()1311,(1)log 10x f x x ->-=-<，排除C ，故选：D ．5．（2021·江苏南通市·高三三模）已知1331311log 5,,log 26a b c ⎛⎫=== ⎪⎝⎭，则a ，b ，c 的大小关系为（）A ．a b c >>B ．b a c >>C ．c b a>>D ．c a b>>【答案】D 【解析】由于1331log g 66lo c ==，再借助函数3log y x =的单调性与中间值1比较即可.【详解】1331log g 66lo c ==，因为函数3log y x =在()0,∞上单调递增，所以333131log 31log 5log 6log 6a c =<=<<=，因为函数12xy ⎛⎫= ⎪⎝⎭在R 上单调递减，所以10312112b <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭，所以c a b >>故选：D6．（2021·辽宁高三月考）某果农借助一平台出售水果，为了适当地给鲜杏保留空气呼吸，还会在装杏用的泡沫箱用牙签戳上几个小洞，同时还要在鲜杏中间放上冰袋，来保持泡沫箱内部的温度稳定，这样可以有效延长水果的保鲜时间．若水果失去的新鲜度h 与其采摘后时间t （小时）满足的函数关系式为t h m a =⋅．若采摘后20小时，这种杏子失去的新鲜度为10%，采摘后40小时，这种杏子失去的新鲜度为20%．在这种条件下，杏子约在多长时间后会失去一半的新鲜度（）（已知lg 20.3≈，结果取整数）A ．42小时B ．53小时C ．56小时D ．67小时【答案】D 【解析】利用指数的运算得出1202a =，再利用对数的运算即可求解.【详解】由题意可得200010m a =⋅，①400020m a =⋅，②②÷①可得202a =，解得1202a =，所以0050t m a =⋅，③ ③÷①可得205t a -=，所以202025t -=，即20lg 2lg 51lg 20.720t -==-=，解得67t ≈（小时）.故选：D7．【多选题】（2021·辽宁高三月考）已知2log 3a =，34b =，22log 31c =+，则下列结论正确的是（）A ．a c ，即可判断A ；利用222log 3b a==判断B ；利用B 的结论判断C ；利用C 的结论判断D.【详解】因为2log 31a =>，所以22log 3112c a a c a =+=+<⇒<，即A 不正确；因为33222log 42log 2log 3b a====，所以2ab =，即B 正确；由2ab =可知，21abc c a ==+，C 正确；由1abc a =+可知，2ab c ab b =+，则22bc b =+，即D 正确．故选：BCD.8．【多选题】（2021·山东日照市·高三一模）已知113log 0x x +=，222log 0xx +=，则（）A ．2101x x <<【答案】BC 【解析】根据对数函数的性质可判断AB 正误，由不等式的基本性质可判断CD 正误.【详解】由131log 0x x =->可得101x <<，同理可得201x <<，因为(0,1)x ∈时，恒有23log log x x<所以122231log log 0x x x x -=-<，即12x x <，故A 错误B 正确；因为1201x x <<<，所以12lg lg 0x x <<，即210lg lg x x <-<-，由不等式性质可得1221lg lg x x x x -<-，即2112lg lg 0x x x x -<，故C 正确D 错误.故选：BC9．（2021·浙江高三期末）已知2log 3a =，则4a =________．【答案】9【解析】把2log 3a =代入4a 可得答案.【详解】因为2log 3a =，所以222log 3log 34429a ===.故答案为：9.10．（2021·河南高三月考（理））若41log 32a =，则39a a +=___________；【答案】6【解析】首先利用换底公式表示3log 2a =，再代入39a a +求值.【详解】由条件得331log 4log 22a ==，所以3333log 2log 2log 2log 4393933246a a +=+=+=+=.故答案为：61．（2021·浙江高三专题练习）如图，直线x t =与函数()3log f x x =和()3log 1g x x =-的图象分别交于点A ，B ，若函数()y f x =的图象上存在一点C ，使得ABC V 为等边三角形，则t 的值为（）ABCD．3+【答案】C 【解析】由题意得()3,log A t t ，()3,log 1B t t -，1AB =，根据等边三角形的性质求得C点的横坐标x t =-，结合A ，B两点的纵坐标和中点坐标公式列方程t =，解方程即可求得t 的值.【详解】由題意()3,log A t t ，()3,log 1B t t -，1AB =.设()3,log C x x ，因为ABC V 是等边三角形，所以点C 到直线AB所以t x -=，x t =-根据中点坐标公式可得练提升33333log log 11log log log 22t t t t ⎛+-==-= ⎝，所以t -=，解得t =故选：C2．（2021·安徽高三其他模拟（文））已知函数()()14,12ln 1,1xx f x x x ⎧⎛⎫-≤-⎪ ⎪=⎨⎝⎭⎪+>-⎩，若()0f f x <⎡⎤⎣⎦，则x 的取值范围为（）A ．()2,0-B ．21,1e ⎛⎫-∞- ⎪⎝⎭C ．212,1e ⎛⎫-- ⎪⎝⎭D ．()212,11,0e ⎛⎫--⋃-⎪⎝⎭【答案】D 【解析】先由()0f f x <⎡⎤⎣⎦可得出()20f x -<<，然后再分1x ≤-、1x >-两种情况解不等式()20f x -<<，即可得解.【详解】若()1f x ≤-，则()()1402f x f f x ⎛⎫=-<⎡⎤ ⎪⎣⎦⎝⎭，解得()2f x >-，此时，()21f x -<≤-；若()1f x >-，则()()ln 10f f x f x =+<⎡⎤⎡⎤⎣⎦⎣⎦，可得()011f x <+<，解得()10f x -<<.综上，()20f x -<<.若1x ≤-，由()20f x -<<可得12402x ⎛⎫-<-< ⎪⎝⎭，可得1242x⎛⎫<< ⎪⎝⎭，解得21x -<<-，此时21x -<<-；若1x >-，由()20f x -<<可得()2ln 10x -<+<，可得2111x e <+<，解得2110x e -<<，此时，2110x e -<<.综上，满足()0f f x <⎡⎤⎣⎦的x 的取值范围为()212,11,0e ⎛⎫--⋃- ⎪⎝⎭.故选：D.3．（2021·全国高三三模）已知函数()xxf x e e-=+，若()()4561log ,log 6,log 45a f b f c f ⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系正确的是（）A ．b a c >>B ．a b c >>C ．c b a >>D ．c a b>>【答案】B 【解析】先判断函数的奇偶性，再利用导数判断函数的单调性，最后根据对数函数的性质，结合基本不等式、比较法进行判断即可.【详解】因为()()xx f x ee f x --=+=，所以()f x 为偶函数，()21x xxxe x ee f e --=='-，当0x >时，()0f x '>，函数单调递增，当0x <时，()0f x '<，函数单调递减，()()()()444561log log 5log 5,log 6,log 45a f f f b f c f ⎛⎫==-=== ⎪⎝⎭，因为lg4lg6+>故2222lg4lg6lg 24lg25lg4lg6(lg5)242+⎛⎫⎛⎫⋅<=<= ⎪ ⎪⎝⎭⎝⎭245lg5lg6lg 5lg4lg6log 5log 60lg4lg5lg4lg5-⋅-=-=>⋅所以456log 5log 61log 40>>>>，则.a b c >>故选：B.4．【多选题】（2021·辽宁高三月考）若1a b >>，则（）A ．log 3log 3a b >，则333311log log 0log log a b a b>>⇒<，即log 3log 3a b <，A 正确；对于B 选项：函数y =x 3在R 上递增，则33a b >，B 错误；对于C 选项：1a b >>，则ab >1，a +b >2，11log ()log log ()1ab ab ab a ba b a b ab++==+-log 21ab >-，有11log (log 21ab ab a b+≥-成立，即C 正确；对于D 选项：1112a b a b >>⇒+>+>，而函数1y x =在(0,+∞)上递减，则有11+11a b <+，即D 正确.故选：ACD5．【多选题】（2021·全国高三专题练习（理））已知0a b >>，且4ab =，则（）A ．21a b ->B ．22log log 1a b ->C ．228a b +>D ．22log log 1a b ⋅<【答案】ACD 【解析】利用不等式的性质和基本不等式的应用，结合指数函数与对数函数的单调性，对选项逐一分析判断.【详解】因为0a b >>，且4ab =，对A ，0a b ->，所以0221a b ->=，故A 正确；对B ，取83,32a b ==，所以2222216log log log log log 219a ab b -==<=，故B 错误；对C，22a b ≥+，当且仅当a b =取等号，又因为4a b +≥=，当且仅当a b =取等号，所以228a b ≥≥=+，当且仅当a b =取等号，因为0a b >>，所以不能取等号，故C 正确；对D ，当10>>>a b ，22log 0,log 0a b ><，所以22log log 1a b ⋅<；当1a b >>，22log 0,log 0a b >>，所以()()2222222log log log log log 144a b ab a b +⋅≤==，当且仅当a b =取等号，因为0a b >>，所以不能取等号，故D 正确.故选：ACD.6．【多选题】（2021·湖南高三二模）若正实数a ，b 满足a b >且ln ln 0a b ⋅>，下列不等式恒成立的是（）A ．log 2log 2a b >B ．ln ln a a b b ⋅>⋅C ．122ab a b ++>D ．log 0a b >【答案】CD 【解析】由已知不等式，求出,a b 之间的关系，结合选项一一判断即可．【详解】由ln ln 0a b ⋅>有01b a <<< 或1a b >> ，对于选项A ，当01b a <<<或1a b >>都有log 2log 2a b < ，选项A 错误；对于选项B ，比如当11,24a b == 时，有211111111ln ln 2ln ln 44424222⎛⎫==⨯= ⎪⎝⎭故ln ln a a b b ⋅>⋅不成立，选项B 错误；对于C ，因为()()1110ab a b a b +--=-->，所以1ab a b +>+ ，则122ab a b ++> ，选项C 正确；对于选项D ，因为ln ln 0a b ⋅>，所以ln log 0ln a bb a=>，选项D 正确，故选：CD ．7．【多选题】（2021·山东临沂市·高三二模）若5log 2a =，1ln 22b =，1ln 55c =，则（）A ．a b >B ．b c>C ．c a>D ．2a b>【答案】AB 【解析】对四个选项一一验证：对于A ：利用换底公式，化为同底结构，利用函数的单调性比较大小；对于B ：利用换底公式，化为同底结构，利用函数的单调性比较大小；对于C ：利用不等式的传递性比较大小；对于D ：利用换底公式，化为同底结构，利用函数的单调性比较大小；【详解】对于A ：522221111ln o 21l g 2,log 522log log a b e e ====⨯=，又25e >，且2log y x =为增函数，所以222l l g 5og o e <，所以22251l og 1l og e <，即a b >.故A 正确；对于B：1ln 22b ==，1ln 55c ==因为101052232,525,ln y x =====为增函数，所以b c >；故B 正确；对于C ：因为a b >，b c >，所以a c >，故C 错误；对于D ：因为1ln 22b =，所以212ln 2log b e ==，而521log 2,log 5a ==又5e <，所以22log log 5e <，所以2211log log 5e >，所以2b a >，故D 错误.故选：AB.8．（2021·浙江高三专题练习）已知函数()f x 满足()(1)f x f x =-+，当(0,1)x ∈时，函数()3x f x =，则13(log 19)f =__________．【答案】2719-【解析】由()(1)f x f x =-+得函数的周期为2，然后利用周期和()(1)f x f x =-+对13(log 19)f 化简可得13(log 19)f 33927(log 1)(log 1919f f =-+=-，从而可求得结果【详解】解：由题意，函数()f x 满足()(1)f x f x =-+，化简可得()(2)f x f x =+，所以函数()f x 是以2为周期的周期函数，又由(0,1)x ∈时，函数()3x f x =，且()(1)f x f x =-+，则133339(log 19)(log 19)(log 192)(log 19f f f f =-=-+=327log 193392727(log 1)(log 3191919f f =-+=-=-=-．故答案为：2719-．9．（2021·千阳县中学高三其他模拟（文））已知函数()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩，则不等式()1f x >的解集为___________.【答案】11,3⎛⎫- ⎪⎝⎭【解析】根据分段函数的定义，分段讨论即可求解.【详解】解：()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩ ，()10131x x f x +≤⎧∴>⇔⎨>⎩或130log 1x x >⎧⎪⎨>⎪⎩，解得10-<≤x 或103x <<，即113x -<<，∴不等式()1f x >的解集为11,3⎛⎫- ⎪⎝⎭.故答案为：11,3⎛⎫- ⎪⎝⎭.10．（2021·浙江丽水市·高三期末）已知()()()1log 1log 01a a a a a ++<<<，则a 的取值范围是__________.【答案】⎫⎪⎪⎭【解析】通过作差将()()()1log 1log 01a a a a a ++<<<转化为(1)log (1)log 0++-<a a a a ，利用换底公式计算可得[][](1)lg(1)lg lg(1)lg log (1)log lg lg(1)++-+++-=+a a a a a a a a a a ，分别判断每个因式的正负，最终转化为211()124+->a 成立，结合二次函数图像，即可求得a 的取值范围.【详解】∵(1)lg(1)lg log (1)log lg lg(1)a a a aa a a a +++-=-+22lg (1)lg lg (1)a aalg a +-=+[][]lg(1)lg lg(1)lg lg lg(1)a a a a a a +-++=+而当01a <<时，lg 0a <，g(0)l 1a +>，1lg(1)lg lglg10a a a a++-=>=211lg(1)lg lg (1)lg (24a a a a a ⎡⎤++=+=+-⎢⎥⎣⎦，所以()()()1log 1log 01a a a a a ++<<<即为211lg ()024⎡⎤+->⎢⎥⎣⎦a ，由于lg u 单调递增，所以211(124+->a .211()24u a =+-的图象如图，当1u =时，0a =，1a <<时，12u <<，lg 0u >，可得()()log 1log 10a a a a a +-+<.故答案为：⎫⎪⎪⎭1.（2020·全国高考真题（文））设3log 42a =，则4a-=（）练真题A ．116B ．19C ．18D ．16【答案】B 【解析】由3log 42a =可得3log 42a=，所以49a =，所以有149a-=，故选：B.2.（2020·全国高考真题（理））设函数()ln |21|ln |21|f x x x =+--，则f (x )（）A ．是偶函数，且在1(,)2+∞单调递增B ．是奇函数，且在11(,22-单调递减C ．是偶函数，且在1(,)2-∞-单调递增D ．是奇函数，且在1(,2-∞-单调递减【答案】D 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-，()f x ∴为定义域上的奇函数，可排除AC ；当11,22x ⎛⎫∈-⎪⎝⎭时，()()()ln 21ln 12f x x x =+--，()ln 21y x =+Q 在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，()f x ∴在11,22⎛⎫- ⎪⎝⎭上单调递增，排除B ；当1,2x ⎛⎫∈-∞-⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭，2121x μ=+- 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，D 正确.故选：D.3．（2020·天津高考真题）设0.80.70.713,,log 0.83a b c -⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c <，0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<.故选：D.4.（2019年高考全国Ⅲ卷理）设是定义域为R 的偶函数，且在单调递减，则A ．（log 3）＞（）＞（）B ．（log 3）＞（）＞（）C ．（）＞（）＞（log 3）D ．（）＞（）＞（log 3）【答案】C【解析】是定义域为的偶函数，．，又在(0，+∞)上单调递减，∴，即.故选C ．5.（2020·全国高考真题（理））若2233x y x y ---<-，则（）()f x ()0,+∞f 14f 322-f 232-f 14f 232-f 322-f 322-f 232-f 14f 232-f 322-f 14()f x R 331(log (log 4)4f f ∴=223303322333log 4log 31,1222,log 422---->==>>∴>> ()f x 23323(log 4)22f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A ．ln(1)0y x -+>B ．ln(1)0y x -+<C ．ln ||0x y ->D ．ln ||0x y -<【答案】A 【解析】由2233x y x y ---<-得：2323x x y y ---<-，令()23t t f t -=-，2x y = 为R 上的增函数，3x y -=为R 上的减函数，()f t ∴为R 上的增函数，x y ∴<，0y x ->Q ，11y x ∴-+>，()ln 10y x ∴-+>，则A 正确，B 错误；x y -Q 与1的大小不确定，故CD 无法确定.故选：A.6.（2019·天津高考真题（文））已知a =log 27，b =log 38，c =0.30.2，则a ,b ,c 的大小关系为（）A.c log 24=2；1<log 38<log 39=2.故c <b <a .故选A.。

对数及对数函数要点及解题技巧讲解

的最大值与最小值之差为12，则 a 等于( )
人
A. 2
B．2 或12
教
B
版
C．2 2
D．4 或14
分析：∵a>1 与 0<a<1 时，f(x)的单调性不同，∴最
小值、最大值也不同，故需分类讨论．
第2章函数
高考数学总复习
解析：当 0<a<1 时，f(x)在[a,2a]上单调递减，由题意
得，logaa－loga2a＝12，∴loga2＝－12，∴a＝14.
人教
B
当 a>1 时，∴f(x)＝logax 在[a,2a]上为增函数，
版
∴loga2a－logaa＝12，解得 a＝4，故选 D.
答案：D
第2章函数
(2011·江苏四市联考)已知函数 f(x)＝|log2x|，正实数 m、n 满足 m<n，且 f(m)＝f(n)，若 f(x)在区间[m2，
高考数学总复习
二、对数函数的图象与性质
定义
y＝logax(a>0，a≠1)
人教
B
版
图象
第2章函数
高考数学总复习
(1)定义域：(0，＋∞) (2)值域：R
(3)过点(1,0)，即当 x＝1 时，y＝0.
人
性质 (4)当 a>1 时，在(0，＋∞)是增函数；
教
B
当 0<a<1 时，在(0，＋∞)上是减函数．
B
版
(2)原式＝llgg23＋llgg29·llgg34＋llgg38
＝llgg23＋2llgg23·2llgg32＋3llgg32＝32llgg23·56llgg32＝54.
答案：(1)2

高考数学总复习第2单元第7节对数与对数函数课件文新人教A

12(log23)1 1
8
24
4. 若y=log56log67log78log89log910，则有( )
A. y∈(0,1)
B. y∈(1,2)
C. y∈(2,3)
D. y∈{1}
B 解析：
yllg g6 5llg g7 6llg g7 8llg g8 9llg g 1 9 0llg g 1 5 0log510
的取值范围
错解 ∵函数y=log2 ax2 a1x的14 值域为R，
∴ 对任意实数 ax2+(a-1)x+
1 4
恒0 成立．
a=0时不成立
若a≠0时，则
a
即00
a 0 (a 1)2 a 0
解得 3 5 a3 5
2
2
错解分析 ∵函数y=log2 ax2 a1x的14值域为R， ∴(0，+∞)必须是u=ax2+(a-1)x+ 值14 域的子集．
值域：
R
过定点
(1,0)
当x>1时，__y_>_0__；当0<x<1时，__y_<_0__
当x>1时，_y_<_0___；当0<x<1时，_y_>_0___
在(0，+∞)上是 _增__函__数___
在(0，+∞)上是 __减__函__数__
函数y=logax与y=logx的图象关于__x轴____对称
∴log55＜log510＜log552， ∴1＜log510＜2，∴y∈(1,2)．
经典例题
题型一对数的运算
【例1】求下列各式的值．
(1)已知lg x+lg y=2lg(x-2y)，求l o g

高考数学一轮复习讲义对数与对数函数专题

第六讲对数及对数函数一．对数的概念 (1)对数的定义①一般地，如果a (a >0，a ≠1)的b 次幂等于N ，即a b＝N ，那么称b 是以a 为底N 的对数，记作b ＝log a N ，其中，a 叫做对数的底数，N 叫做真数．②底数的对数是1，即log a a ＝1,1的对数是0，即log a 1＝0. (2)几种常见对数4.对数的性质与运算法则 (1)对数的性质 ①log a Na＝N (a >0且a ≠1，N >0)；②log a a N＝N (a >0且a ≠1)． (2)对数的重要公式①换底公式：log b N ＝log a Nlog a b (a ，b 均大于零且不等于1，N >0)；②log a b ＝1log b a (a ，b 均大于零且不等于1)．(3)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么 ①log a (MN )＝log a M ＋log a N ； ②log a M N＝log a M －log a N ； ③log a M n＝n log a M (n ∈R )； ④log m na M ＝n mlog a M . 二．对数函数的定义1.形如y ＝log a x (a >0，a ≠1)的函数叫作对数函数，其中x 是自变量，函数的定义域是(0，＋∞)．2．对数函数的图象与性质定义域：(0，＋∞)3.反函数指数函数y ＝a x(a >0且a ≠1)与对数函数y ＝log a x (a >0且a ≠1)互为反函数，它们的图象关于直线y ＝x 对称．考向一对数的运算【例1】（1）lg 22·lg 250＋lg 25·lg 40＝ . （2）若3a=5b=225，则1a +1b = 。

（4）若log a 2=m ，log a 5=n ，则a 3m+n =( 。

【答案】（1）1 （2）12 （3）40【解析】（1）lg 22·lg 250＋lg 25·lg 40＝lg 22·⎝ ⎛⎭⎪⎫lg1 0004＋(1－lg 2)2·(2lg 2＋1) ＝lg 22·(3－2lg 2)＋(lg 22－2lg 2＋1)·(2lg 2＋1)＝1.（2）∵3a =5b =225∴a =log 3225, b =log 5225则1a+1b=log 2253+log 2255=log 22515=12（3）∵log a 2=m ，log a 5=n ，∴a m =2，a n =5 ∴a 3m+n =a 3m ⋅a n =23⋅5=40【举一反三】1．已知a ＝log 32，那么log 38－2log 36用a 表示为．【答案】 a －2【解析】 log 38－2log 36＝log 323－2(log 32＋log 33) ＝3log 32－2(log 32＋1)＝3a －2(a ＋1)＝a －2. 2．若3x ＝4y＝36，则2x ＋1y＝ .【答案】 1【解析】 3x＝4y＝36，两边取以6为底的对数，得x log 63＝y log 64＝2， ∴2x ＝log 63，2y ＝log 64，即1y ＝log 62，故2x ＋1y＝log 63＋log 62＝1.3．设2a ＝5b＝m ，且1a ＋1b＝2，则m ＝ .【答案】 10【解析】由已知，得a ＝log 2m ，b ＝log 5m ，则1a ＋1b ＝1log 2m ＋1log 5m ＝log m 2＋log m 5＝log m 10＝2.解得m ＝10.4．计算：(1－log 63)2＋log 62·log 618log 64＝ .【答案】 1【解析】原式＝1－2log 63＋(log 63)2＋log 663·log 6(6×3)log 64＝1－2log 63＋(log 63)2＋1－(log 63)2log 64＝2(1－log 63)2log 62＝log 66－log 63log 62＝log 62log 62＝1.5.已知均不为1的正数a ，b ，c 满足a x ＝b y ＝c z，且1x ＋1y ＋1z＝0，求abc 的值．【答案】1【解析】令a x ＝b y ＝c z＝k .由已知k >0且k ≠1，于是x lg a ＝y lg b ＝z lg c ＝lg k ，故1x ＝lg a lg k ，1y ＝lg b lg k ，1z ＝lg c lg k .因为1x ＋1y ＋1z ＝0，所以lg a ＋lg b ＋lg c lg k ＝0，即lg (abc )lg k ＝0.故lg(abc )＝0，得abc ＝1.6.设log a C ，log b C 是方程x 2－3x ＋1＝0的两根，求log a bC 的值．【答案】±55.【解析】由题意，得⎩⎪⎨⎪⎧log a C ＋log b C ＝3，log a C ·log b C ＝1，即⎩⎪⎨⎪⎧1log Ca ＋1log Cb ＝3，1log Ca ·log Cb ＝1，于是有⎩⎪⎨⎪⎧log C a ＋log C b ＝3，log C a ·log C b ＝1，(log C a －log C b )2＝(log C a ＋log C b )2－4log C a ·log C b ＝32－4＝5，故log C a －log C b ＝± 5.于是log a bC ＝⎝⎛⎭⎪⎫log C a b －1＝1log C a －log C b ＝±55.7.方程33x －56＝3x －1的实数解为．【答案】 x ＝log 32【解析】原方程可化为2(3x )2＋5·3x－18＝0，即(3x－2)(2·3x＋9)＝0,3x＝2(2·3x＝－9舍去)，得x ＝log 32.考向二对数函数的判断【例2】函数f(x)=(a 2+a −5)log a x 为对数函数，则f(18)等于( ) A ．3 B ．−3 C ．−log 36 D ．−log 38 【答案】B【解析】因为函数f(x) 为对数函数，所以函数f(x)系数为1，即a 2+a −5=1，即a =2或−3，因为对数函数底数大于0，所以a =2，f(x)=log 2x ，所以f (18)=−3。

对数与对数函数-高考数学复习课件

> 1，
故有ቊ
解得1＜ a ≤3.
6 − 2≥0，
(2)(2024·河南郑州模拟)设函数 f ( x )＝ln｜ x ＋3｜＋ln｜ x －3｜，则
f ( x )( A
)
A. 是偶函数，且在(－∞，－3)上单调递减
B. 是奇函数，且在(－3，3)上单调递减
C. 是奇函数，且在(3，＋∞)上单调递增
因为0＜ a ＜ b ，所以ln a ＜0，ln b ＞0，
所以0＜ a ＜1， b ＞1，
所以－ln a ＝ln b ，所以ln a ＋ln b ＝ln( ab )＝0，
1
所以 ab ＝1，则 b ＝，

2
所以 a ＋2 b ＝ a ＋ .

2
令 g ( x )＝ x ＋ (0＜ x ＜1)，
a ＞1
0＜ a ＜1
图象
定义域
(0，＋∞)
⁠
值域
性质
R
过定点 (1，0)
，即 x ＝ 1
时， y ＝ 0
⁠
a ＞1
0＜ a ＜1
当 x ＞1时， y ＞0 ；
当0＜ x ＜1时， y ＜0
⁠
性质
在(0，＋∞)上是增
数
函
当 x ＞1时， y ＜0 ；
当0＜ x ＜1时， y ＞0
⁠
⁠
⁠
⁠
在(0，＋∞)上是减
内容索引
必备知识
自主梳理
关键能力
重点探究
课时作业
巩固提升
必备知识自主梳理
[知识梳理]
知识点一对数与对数运算
1. 对数的概念
如果 ax ＝ N ( a ＞0，且 a ≠1)，那么数 x 叫做以 a 为底 N 的对数，记作

2024年高考数学专题复习第7讲对数与对数函数

2
-10-
第7讲
考点一
对数与对数函数
课标导引
知识聚焦
核心考点
核心考点
考点二
例2-2已知log89=m,log35=n,试用m,n表示log512.
2
3
2 lg3
3 lg2
解 ∵m=log89= log23= · ,
2
lg
3
∴lg 2=
又
则
=
=
3,
lg5ห้องสมุดไป่ตู้
n=log35= ,∴lg 5=nlg
lg3
其中a叫作对数的底数,N叫作真数.
(2)几种常见对数
对数形式
特点
记法
logaN
一般对数
底数为a(a>0,且a≠1)
lg N
常用对数
底数为10
ln N
自然对数
底数为e
-3-
第7讲
对数与对数函数
课标导引
知识聚焦
知识聚焦
核心考点
2.对数的性质与运算法则
(1)对数的性质
lo g =N(a>0,a≠1,N>0).
知识聚焦
核心考点
4.y=ax与y=logax(a>0,且a≠1)的关系
指数函数y=ax与对数函数y=logax互为反函数,它们的图象关于直线
y=x对称.
-7-
第7讲
考点一
对数与对数函数
课标导引
知识聚焦
核心考点
核心考点
考点二
对数运算
◆角度1.对数化简求值
例1-1计算lg 4+lg 25=(
A.2
B.3
3
3
1

【K12教育学习资料】高考数学总复习(讲+练+测)：专题2.7 对数与对数函数(讲)

第07节对数与对数函数【考纲解读】【知识清单】1. 对数的概念如果a x＝N (a >0，且a ≠1)，那么x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数. 对点练习设2a ＝5b＝m ，且1a ＋1b＝2，则m 等于( )A.10B.10C.20D.100【答案】A则251111a b log m log m+=+=25102m m m log log log ＋＝＝.解得m =2.对数的性质、换底公式与运算性质 (1)对数的性质：①a log aN＝N ；②log a a b＝b (a >0，且a ≠1)(2)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么 ①log a (MN )＝log a M ＋log a N ； ②log a M N＝log a M －log a N ； ③log a M n＝n log a M (n ∈R )；④log a m M n＝n mlog a M (m ，n ∈R ，且m ≠0). (3)对数的重要公式①换底公式：log b N ＝log a Nlog a b (a ，b 均大于零且不等于1)；②log a b ＝1log b a ，推广log a b ·log b c ·log c d ＝log a d .对点练习【2017浙江台州中学月考】25532lg2lglg 16981-+等于（） A.lg2 B.lg3 C.4 D.lg5 【答案】A.3.对数函数及其性质(1)概念：函数y ＝log a x (a >0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是(0，＋∞).(2)对数函数的图象与性质对点练习【2017天津，理6】已知奇函数()f x 在R 上是增函数，()()g x xf x =.若2(log 5.1)a g =-，0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为（A ）a b c << （B ）c b a <<（C ）b a c <<（D ）b c a <<【答案】C所以b a c <<，故选C ．【考点深度剖析】从近几年的高考试题来看，对数运算、对数函数的图象和性质及其应用是高考的热点，题型多以选择题、填空题为主，偶尔有以大题中关键一步的形式出现，主要考查视图用图能力、数形结合思想的应用、函数单调性的应用、运算能力等. 另外底数多含参数、考查分类讨论．常常以分段函数的形式与指数函数综合考查.【重点难点突破】考点1 对数的化简、求值【1-1【答案】-4()lg1000lg1041lg10lg102-==-⨯-；【1-2】已知()lg lg 2lg 23x y x y +=-，求32log xy的值. 【答案】233229log log 24x y ==. 【1-3】若log 2,log 3,a a m n ==则2m n a +=________,用,m n 表示4log 6为________. 【答案】 12 ，2m nm+. 【解析】∵log a 2=m ,log a 3=n ,∴a m=2,a n=3，a 2m +n =(a m )2×a n =22×3=12，4log 6log 2log 3log 6log 42log 22a a a a a m nm++===. 【领悟技法】1.对数运算法则是在化为同底的情况下进行的，因此，经常会用到换底公式及其推论；在对含有字母的对数式化简时，必须保证恒等变形．2. ba N ⇔＝ ab log N ＝ (a>0且a≠1)是解决有关指数、对数问题的有效方法，在运算中要注意灵活运用．3.利用对数运算法则，在真数的积、商、幂与对数的和、差、倍之间进行转化．4.有限制条件的对数化简、求值问题，往往要化简已知和所求，利用“代入法”. 【触类旁通】【变式一】【2017江西百所重点高中模拟】设函数()39xxf x =+，则()3l o g2f =__________．【答案】6【解析】()2233log log 23log 39246f =+=+=【变式二】【2017北京】根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是（参考数据：lg3≈0.48）（A ）1033 （B ）1053 （C ）1073 （D ）1093 【答案】D 【解析】设36180310M x N == ，两边取对数，36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=，所以93.2810x =，即MN最接近9310，故选D. 考点2 对数函数的图象及其应用【2-1】【2017河南郑州一模】若函数01()xy a a a >≠＝，且的值域为{}1|y y ≥，则函数a y log x ＝的图象大致是( )【答案】B【2-2】【2017河北衡水调研】已知函数2log ,0()3,0x x x f x x >⎧=⎨≤⎩，且关于x 的方程()0f x x a ＋－＝有且只有一个实根，则实数a 的取值范围是________.【答案】1a >【解析】如图，在同一坐标系中分别作出()y f x ＝与y x a ＝－＋的图象，其中a 表示直线在y 轴上截距.由图可知，当1a >时，直线y x a ＝－＋与2y log x ＝只有一个交点.【2-3】当0＜x ≤12时，4x＜log a x ，则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，22 B.⎝ ⎛⎭⎪⎫22，1 C ．(1，2) D ．(2，2) 【答案】B综上，可得a 的取值范围是⎝⎛⎭⎪⎫22，1. 【2-4】已知函数12log ,0,()2,0,x x x f x x >⎧⎪=⎨⎪≤⎩若关于的方程()f x k =有两个不等的实根，则实数的取值范围是 ( )A ．(0,)+∞B ．(,1)-∞C ．(1,)+∞D ．(0,1] 【答案】D【解析】在(,0]x ∈-∞时，()f x 是增函数，值域为(0,1]，在(0,)x ∈+∞时，()f x 是减函数，值域是(,)-∞+∞，因此方程()f x k =有两个不等实根，则有(0,1]k ∈. 【领悟技法】1. log a y x =的底数变化，其图象具有如下变化规律：（1）上下比较：在直线1x =的右侧，1a >时，底大图低（靠近x 轴）；01a <<时，底大图高（靠近x 轴）．（2）左右比较（比较图象与1y =的交点）：交点横坐标越大，对应的对数函数的底数越大.2. 涉及对数函数的定义域问题，要考虑底数大于零且不为1，真数大于零．3.涉及对数函数单调性问题，要注意底数的不同取值情况．【触类旁通】【变式一】【2017河南（中原名校）模拟】若函数()log 2(0,1)xa f x x a a -=->≠的两个零点是,m n ，则（）A. 1mn =B. 1mn >C. 1mn <D. 以上都不对【答案】C【解析】()11log 022n ma mn ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭，所以01mn <<，应选答案C 。

高考数学复习讲义：对数与对数函数

[答案] C
返回
[易错提醒] 应用对数函数图象求解问题时易出现作图失误导致求解错误，要记准记牢图象的变换规律．
返回
[集训冲关]
1.[考法一]函数 f(x)＝loga|x|＋1(0<a<1)的图象大致为 ( )
返回
解析：由函数 f(x)的解析式可确定该函数为偶函数，图象关于 y 轴对称．设 g(x)＝loga|x|，先画出 x>0 时，g(x)的图象，然后根据 g(x)的图象关于 y 轴对称画出 x<0 时 g(x)的图象，最后由函数 g(x)的图象向上整体平移一个单位即得 f(x)的图象，结合图象知选 A. 答案：A
() ()
(3)存在这样的 M，N 使得 log2(MN)＝log2M·log2N.( )
答案：(1)× (2)× (3)√
返回
二、填空题
1．已知 log62＝p，log65＝q，则 lg 5＝________(用 p，q 表示)．
解析：lg 5＝lloogg66150＝log62＋q log65＝p＋q q. 答案：p＋q q
抓牢双基·自学回扣
返回
对数函数的性质
[基本知识]
函数
y＝logax(a>0，且 a≠1)
a>1
0<a<1
定义域
(0，＋∞)
值域
R
性单调性在(0，＋∞)上是_增__函__数_ 在(0，＋∞)上是_减__函__数_
质函数值
当 x＝1 时， y＝0
变化规当 x>1 时， y>0 ；当 x>1 时， y<0 ；
N 叫做真数，logaN 叫做对数式
性质
对数式与指数式的互化：ax＝N⇔ x＝logaN loga1＝0，logaa＝1，alogaN＝ N

2020年高考数学一轮复习讲练测专题2.7函数的图象(讲)(含解析)(2021-2022学年)

第0７讲函数的图象－--讲1. 会运用函数图象理解和研究函数的性质.2。

高考预测:(1）函数图象的辨识(2）函数图象的变换（3）主要有由函数的性质及解析式选图;由函数的图象来研究函数的性质、图象的变换、数形结合解决不等式、方程等问题.常常与导数结合考查。

3．备考重点(1）基本初等函数的图象(2）两图象交点、函数性质、方程解的个数、不等式的解集等方面的应用知识点1.利用描点法作函数的图象步骤：(1）确定函数的定义域；(2)化简函数解析式;（3)讨论函数的性质（奇偶性、单调性、周期性、对称性等)；（４）列表（尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等），描点，连线．【典例1】【20１８年全国卷Ⅲ理】设函数．（1)画出的图象;（2)当，,求的最小值.【答案】(1)见解析;（２)ﻬ【解析】（1）的图象如图所示.(2）由（1）知,的图像与轴交点的纵坐标为,且各部分所在直线斜率的最大值为,故当且仅当且时,在成立，因此的最小值为．【规律方法】函数图象的画法(1）直接法：当函数表达式(或变形后的表达式)是熟悉的基本函数时，就可根据这些函数的特征描出图象的关键点直接作出．（2）转化法：含有绝对值符号的函数，可去掉绝对值符号,转化为分段函数来画图象．【变式1】【北京海淀十一学校2０1７—２018学年高一上期中】对、,记,函数.(1)求,.（２）写出函数的解析式，并作出图像．ﻬ（3)若关于的方程有且仅有个不等的解,求实数的取值范围.(只需写出结论)【答案】见解析．ab ∈R (0)f (4)f -()f x x()f x m =3m【解析】解：(1)∵，函数，∴，．(2）（3)或．知识点２.利用图象变换法作函数的图象 (1)平移变换（２)对称变换5m=mｙ=f(ｘ)的图象错误!ｙ＝-f（x)的图象；y＝f(x)的图象错误!y＝ｆ（－ｘ)的图象;y＝ｆ（ｘ）的图象错误!y＝-f(-ｘ)的图象；y＝a x(a＞0,且a≠1）的图象错误!y＝log a x（ａ〉0,且a≠１)的图象．(3）伸缩变换y＝f(x)错误!未定义书签。

高三总复习数学课件对数与对数函数

一般地，如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底N的对概念数，记作 x＝logaN ，其中 a 叫做对数的底数， N 叫做真数
基本性质
loga1＝ 0 ， logaa＝ 1 ， alogaN＝ N (N>0)， logaax＝ x ，其中a>0，且a≠1
2．对数的运算
运算法则
()
解析：由题意知，m1＝－26.7，m2＝－1.45，代入所给公式得－1.45－(－26.7) ＝52lgEE12，所以 lgEE12＝10.1，所以EE12＝1010.1. 答案：A
3．计算下列各式： (1)lg 500＋lg85－12lg 64＋50(lg 2＋lg 5)2＝________. (2)(1－log63)2＋loglo64g62×log618＝________.
3
(3)原式＝log5554 ＋31＋log36＋lg(102×2)－lg 2＝－14＋6＋2＋lg 2－lg 2＝341.
则有
()
A．a<b<c B．a<c<b C．c<a<b D．c<b<a
答案：A
4．(湘教版必修第一册 P123·T19)下列函数中，其定义域和值域分别与函数 y＝
10lg x 的定义域和值域相同的是
()
A．y＝x
B．y＝lg x
C．y＝2x
D．y＝
1 x
答案：D
5．已知函数y＝loga(x－3)－1的图象恒过定点P，则点P的坐标是________．答案：(4，－1)
＝llooggaaMN ＝llooggbbMN ；logab·logbc·logcd＝logad
3．对数函数的图象与性质

[高考总复习资料]数学总复习(讲+练+测)：专题2.7 对数与对数函数(讲)

第07节对数与对数函数【考纲解读】【知识清单】1. 对数的概念如果a x＝N (a >0，且a ≠1)，那么x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数. 对点练习设2a ＝5b＝m ，且1a ＋1b＝2，则m 等于( )A.10B.10C.20D.100【答案】A则251111a b log m log m+=+=25102m m m log log log ＋＝＝.解得m =2.对数的性质、换底公式与运算性质 (1)对数的性质：①a log aN＝N ；②log a a b＝b (a >0，且a ≠1)(2)对数的运算法则如果a >0且a ≠1，M >0，N >0，那么 ①log a (MN )＝log a M ＋log a N ； ②log a M N＝log a M －log a N ； ③log a M n＝n log a M (n ∈R )；④log a m M n＝n mlog a M (m ，n ∈R ，且m ≠0). (3)对数的重要公式①换底公式：log b N ＝log a Nlog a b (a ，b 均大于零且不等于1)；②log a b ＝1log b a ，推广log a b ·log b c ·log c d ＝log a d .对点练习【2017浙江台州中学月考】25532lg2lglg 16981-+等于（） A.lg2 B.lg3 C.4 D.lg5 【答案】A.3.对数函数及其性质(1)概念：函数y ＝log a x (a >0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是(0，＋∞).(2)对数函数的图象与性质对点练习【2017天津，理6】已知奇函数()f x 在R 上是增函数，()()g x xf x =.若2(log 5.1)a g =-，0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为（A ）a b c << （B ）c b a <<（C ）b a c <<（D ）b c a <<【答案】C所以b a c <<，故选C ．【考点深度剖析】从近几年的高考试题来看，对数运算、对数函数的图象和性质及其应用是高考的热点，题型多以选择题、填空题为主，偶尔有以大题中关键一步的形式出现，主要考查视图用图能力、数形结合思想的应用、函数单调性的应用、运算能力等. 另外底数多含参数、考查分类讨论．常常以分段函数的形式与指数函数综合考查.【重点难点突破】考点1 对数的化简、求值【1-1【答案】-4()lg1000lg1041lg10lg102-==-⨯-；【1-2】已知()lg lg 2lg 23x y x y +=-，求32log xy的值. 【答案】233229log log 24x y ==. 【1-3】若log 2,log 3,a a m n ==则2m n a +=________,用,m n 表示4log 6为________. 【答案】 12 ，2m nm+. 【解析】∵log a 2=m ,log a 3=n ,∴a m=2,a n=3，a 2m +n =(a m )2×a n =22×3=12，4log 6log 2log 3log 6log 42log 22a a a a a m nm++===. 【领悟技法】1.对数运算法则是在化为同底的情况下进行的，因此，经常会用到换底公式及其推论；在对含有字母的对数式化简时，必须保证恒等变形．2. ba N ⇔＝ ab log N ＝ (a>0且a≠1)是解决有关指数、对数问题的有效方法，在运算中要注意灵活运用．3.利用对数运算法则，在真数的积、商、幂与对数的和、差、倍之间进行转化．4.有限制条件的对数化简、求值问题，往往要化简已知和所求，利用“代入法”. 【触类旁通】【变式一】【2017江西百所重点高中模拟】设函数()39xxf x =+，则()3l o g2f =__________．【答案】6【解析】()2233log log 23log 39246f =+=+=【变式二】【2017北京】根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是（参考数据：lg3≈0.48）（A ）1033 （B ）1053 （C ）1073 （D ）1093 【答案】D 【解析】设36180310M x N == ，两边取对数，36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=，所以93.2810x =，即MN最接近9310，故选D. 考点2 对数函数的图象及其应用【2-1】【2017河南郑州一模】若函数01()xy a a a >≠＝，且的值域为{}1|y y ≥，则函数a y log x ＝的图象大致是( )【答案】B【2-2】【2017河北衡水调研】已知函数2log ,0()3,0x x x f x x >⎧=⎨≤⎩，且关于x 的方程()0f x x a ＋－＝有且只有一个实根，则实数a 的取值范围是________.【答案】1a >【解析】如图，在同一坐标系中分别作出()y f x ＝与y x a ＝－＋的图象，其中a 表示直线在y 轴上截距.由图可知，当1a >时，直线y x a ＝－＋与2y log x ＝只有一个交点.【2-3】当0＜x ≤12时，4x＜log a x ，则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，22 B.⎝ ⎛⎭⎪⎫22，1 C ．(1，2) D ．(2，2) 【答案】B综上，可得a 的取值范围是⎝⎛⎭⎪⎫22，1. 【2-4】已知函数12log ,0,()2,0,x x x f x x >⎧⎪=⎨⎪≤⎩若关于的方程()f x k =有两个不等的实根，则实数的取值范围是 ( )A ．(0,)+∞B ．(,1)-∞C ．(1,)+∞D ．(0,1] 【答案】D【解析】在(,0]x ∈-∞时，()f x 是增函数，值域为(0,1]，在(0,)x ∈+∞时，()f x 是减函数，值域是(,)-∞+∞，因此方程()f x k =有两个不等实根，则有(0,1]k ∈. 【领悟技法】1. log a y x =的底数变化，其图象具有如下变化规律：（1）上下比较：在直线1x =的右侧，1a >时，底大图低（靠近x 轴）；01a <<时，底大图高（靠近x 轴）．（2）左右比较（比较图象与1y =的交点）：交点横坐标越大，对应的对数函数的底数越大.2. 涉及对数函数的定义域问题，要考虑底数大于零且不为1，真数大于零．3.涉及对数函数单调性问题，要注意底数的不同取值情况．【触类旁通】【变式一】【2017河南（中原名校）模拟】若函数()log 2(0,1)xa f x x a a -=->≠的两个零点是,m n ，则（）A. 1mn =B. 1mn >C. 1mn <D. 以上都不对【答案】C【解析】()11log 022n ma mn ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭，所以01mn <<，应选答案C 。

2024年高考数学一轮复习讲练测(新教材新高考)第05讲对数与对数函数(课件)

以e为底的对数叫做自然对数，记作__l_n_N_.
2.对数的性质与运算性质
(1)对数的性质：loga1＝_0__，logaa＝1 ，aloga N ＝_N__(a>0，且a≠1，N>0). (2)对数的运算性质
如果a>0，且a≠1，M>0，N>0，那么：
①loga(MN)＝_lo_g_a_M__＋__lo_g_a_N_；
常用结论
1.如图给出4个对数函数的图象则b>a>1>d>c>0，即在第一象限，不同的对数函数图象从左到右底数逐渐增大.
题型一：对数运算及对数方程、对数不等式
题型一：对数运算及对数方程、对数不等式
题型一：对数运算及对数方程、对数不等式
题型一：对数运算及对数方程、对数不等式
题型一：对数运算及对数方程、对数不等式
题型三：对数函数的性质（单调性、最值（值域））
题型三：对数函数的性质（单调性、最值（值域））
题型四：对数函数中的恒成立问题
题型四：对数函数中的恒成立问题
题型五：对数函数的综合问题
题型五：对数函数的综合问题
题型五：对数函数的综合问题
04
真题感悟
B C C
感谢观看 THANK
稿定PPT，海量素材持续更
(，且)互为反函数．
新，上千款模板选择总有一
款适合你
02
网络构建
03
知识梳理题型归纳
1.对数的概念一般地，如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底N的对数，记作__x_＝__lo_g_a_N_，其中_a__叫做对数
的底数，_N__叫做真数. 以10为底的对数叫做常用对数，记作_l_g_N_.

高考数学一轮复习专题2.7对数与对数函数(测)(2021年整理)

（江苏专版）2019年高考数学一轮复习专题2.7 对数与对数函数（测）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（江苏专版）2019年高考数学一轮复习专题2.7 对数与对数函数（测））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（江苏专版）2019年高考数学一轮复习专题2.7 对数与对数函数（测）的全部内容。

专题2。

7 对数与对数函数班级__________ 姓名_____________ 学号___________ 得分__________(满分100分，测试时间50分钟)一、填空题：请把答案直接填写在答题卡相应的位置．．．．．．．．上(共10题，每小题6分，共计60分)．1．函数f（x）＝log错误!（x2－4）的单调递增区间为________．【答案】（－∞,－2）【解析】因为y＝log 12t在定义域上是减函数，所以求原函数的单调递增区间，即求函数t＝x2－4的单调递减区间，结合函数的定义域，可知所求区间为(－∞，－2)．2．已知f（x）是定义在R上的奇函数，当x≥0时，f（x)＝3x＋m(m为常数），则f(－log35）＝________.【答案】－4【解析】因为函数f(x)是定义在R上的奇函数,所以f（0)＝0，即30＋m＝0,解得m＝－1,所以f(log35）＝3log35－1＝4,所以f(－log35)＝－f（log35)＝－4.3．计算log23 log34＋（错误!)log34＝______.【答案】4【解析】log23 log34＋(错误!)log34＝错误!·错误!＋3错误!log34＝2＋3log32＝2＋2＝4.4．已知函数f(x)＝lg错误!，若f（a）＝错误!，则f(－a）＝________.【答案】－错误!5．函数f(x）＝4－|x｜＋lg错误!的定义域为__________．【答案】（2,3）∪（3,4］【解析】由错误!得错误!故函数定义域为（2，3)∪(3，4］．6．计算：lg 0.001＋ln 错误!＋2－1＋log23＝________。

高考数学总复习(讲+练+测)： 专题2.7 对数与对数函数(讲)