1.1 空间几何体的结构特征(3)
高一数学知识点总结_空间几何体的结构知识点

⾼⼀数学知识点总结_空间⼏何体的结构知识点⾼⼀数学怎么学? 学⽣学习期间,在课堂的时间占了⼀⼤部分。
因此听课的效率如何,决定着学习的基本状况,今天⼩编在这给⼤家整理了⾼⼀数学知识点总结,接下来随着⼩编⼀起来看看吧!⾼⼀数学知识点总结(⼀)空间⼏何体的结构知识点1、静态的观点有两个平⾏的平⾯,其他的⾯是曲⾯;动态的观点:矩形绕其⼀边旋转形成的⾯围成的旋转体,象这样的旋转体称为圆柱。
2、定义:以矩形的⼀边所在直线为旋转轴,其余各边旋转⽽形成的的曲⾯所围成的旋转体叫做圆柱,旋转轴叫圆柱的轴;垂直于旋转轴的边旋转⽽成的圆⾯叫做圆柱的底⾯;平⾏于圆柱轴的边旋转⽽成的⾯叫圆柱的侧⾯,圆柱的侧⾯⼜称圆柱的⾯。
⽆论转到什么位置,不垂直于轴的边都叫圆柱侧⾯的母线。
表⽰:圆柱⽤表⽰轴的字母表⽰。
规定:圆柱和棱柱统称为柱体。
3、静态观点:有⼀平⾯,其他的⾯是曲⾯;动态的观点:直⾓三⾓形绕其⼀直⾓旋转形成的⾯围成的旋转体,像这样的旋转体称为圆锥。
4、定义:以直⾓三⾓形的⼀条直⾓边所在的直线为旋转轴,其余两边旋转⽽形成的⾯所围成的旋转体叫做圆锥。
旋转轴叫圆锥的轴;垂直于旋转轴的边旋转⽽成的圆⾯成为圆锥的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫圆锥的侧⾯,圆锥的侧⾯⼜称圆锥的⾯,⽆论旋转到什么位置,这条边都叫做圆锥侧⾯的母线。
表⽰:圆锥⽤表⽰轴的字母表⽰。
规定:圆锥和棱锥统称为锥体。
5、定义:以半直⾓梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转⽽形成的曲⾯所围成的⼏何体叫圆台。
还可以看成⽤平⾏于圆锥底⾯的平⾯截这个圆锥,截⾯于底⾯之间的部分。
旋转轴叫圆台的轴。
垂直于旋转轴的边旋转⽽形成的圆⾯称为圆台的底⾯;不垂直于旋转轴的边旋转⽽成的曲⾯叫做圆台的侧⾯,⽆论转到什么位置,这条边都叫圆台侧⾯的母线。
表⽰:圆台⽤表⽰轴的字母表⽰。
规定:圆台和棱台统称为台体。
6、定义:以半圆的直径所在的直线为旋转轴,将半圆旋转⼀周所形成的曲⾯称为球⾯,球⾯所围成的旋转体称为球体,简称为球。
江苏省盐城中学高中数学立体几何知识点总结

高一立体几何知识梳理盐城中学高一数学组一、空间几何体(一)空间几何体的类型多面体:由若干个平面多边形围成的几何体.围成多面体的各个多边形叫做多面体的相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体.其这条直线称为旋转体的轴.(二)几种空间几何体的结构特征1 、棱柱的结构特征1.1 棱柱的定义:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.1.2 棱柱的分类图1-1棱柱①棱柱,械垂直于底面》直棱柱 底山是多形)正棱柱其他棱柱…底面是四边形 棱柱 底面是平行四边形 四棱柱平行六面体 侧棱垂直于底面直平行底面是矩形底面是正方形 六面体长方体 性质:棱长都相等 正四棱柱正方体I 、II 、m 、1.3 侧面都是平行四边形,且各侧棱互相平行且相等;两底面是全等多边形且互相平行;平行于底面的截面和底面全等;棱柱的面积和体积公式s 二ch (c 是底周长,h 是高) 直棱柱侧S 直棱柱表面=C ・h+2S 底2.1(V 棱柱=S 底•h棱锥的结构特征棱锥的定义)棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥.()正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底f斜棱柱面的中心,这样的棱锥叫做正棱锥.2.2正棱锥的结构特征I、平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;II、正棱锥的各侧棱相等,各侧面是全等的等腰三角形;III、两个特征三角形:()A POH(包含棱锥的高、斜高和底面内切圆半径);()A POB(包含棱锥的高、侧棱和底面外接圆半径)正棱锥侧面积:S=1ch'(c为底周长,h,为斜高)P正棱椎2体积:V=1Sh(S为底面积,h为高)DC棱椎3OHAB正四面体:各条棱长都相等的三棱锥叫正四面体2对于棱长为a正四面体的问题可将它补成一个边长为—a的正方体问题.211正四面体的中心到底面与顶点的距离之比为1:3(=-/』舟3:/十6正方体体对角线2正方体体对角线3、棱台的结构特征3.1棱台的定义:用一个平行于底面的平面去截棱锥,我们把截面和底面之间的部分称为棱台.3.2正棱台的结构特征(1)各侧棱相等,各侧面都是全等的等腰梯形;(2)正棱台的两个底面和平行于底面的截面都是正多边形;(3)正棱台的对角面也是等腰梯形;(4)各侧棱的延长线交于一点.4、圆柱的结构特征4.1圆柱的定义:以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.4.2圆柱的性质(1)上、下底及平行于底面的截面都是等圆;(2)过轴的截面(轴截面)是全等的矩形.4.3圆柱的侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.4.4圆柱的面积和体积公式S圆柱侧面=2n•r•h(r为底面半径,h为圆柱的高)V圆、=S h=nr2h5、圆锥的结构特征5.1圆锥的定义:以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆锥.5.2圆锥的结构特征(1)平行于底面的截面都是圆,截面直径与底面直径之比等于顶点到截面的距离与顶点到底面的距离之比;(2)轴截面是等腰三角形;(3)母线的平方等于底面半径与高的平方和:l2=r2+h25.3圆锥的侧面展开图:圆锥的侧面展开图是以顶点为圆心,以母线长为半径的扇形.6、圆台的结构特征6.1圆台的定义:用一个平行于底面的平面去截圆锥,我们把截面和底面之间的部分称为圆台.6.2圆台的结构特征⑴圆台的上下底面和平行于底面的截面都是圆;⑵圆台的截面是等腰梯形;⑶圆台经常补成圆锥,然后利用相似三角形进行研究.6.3圆台的面积和体积公式S圆台侧=n•(R+r)•l(r、R为上下底面半径)V1=1/3(n r2+n R2+n rR)h(h为圆台的高)7球的结构特征7.1球的定义:以半圆的直径所在的直线为旋转轴,半圆旋转一周形成的旋转体叫做球体.空间中,与定点距离等于定长的点的集合叫做球面,球面所围成的几何体称为球体.7-2球的结构特征⑴球心与截面圆心的连线垂直于截面;⑵截面半径等于球半径与截面和球心的距离的平方差:r2=R2-d2⑶注意圆与正方体的两个关系:球内接正方体,球直径等于正方体对角线;球外切正方体,球直径等于正方体的边长.7-3球的面积和体积公式S=4nR2(R为球半径);V=4/3nR3(三)空球面间几何体的表面积与体积球空间几何体的表面积棱柱、棱锥的表面积:各个面面积之和圆柱的表面积:S=2兀rl+2兀r2圆锥的表面积:S=兀rl+兀丫2圆台的表面积:S=兀r1+兀丫*兀Rl+兀R2球的表面积:S=4兀R2空间几何体的体积柱体的体积:V=S L X h;锥体的体积:v=1S X h底,3底1.T74〜台体的体积:V=-(S+JSS+S)X h;球体的体积:V二万兀R33上%’上下下3斜二测画法:(1)平行于坐标轴的线依然平行于坐标轴;(2)平行于y轴的线长度变半,平行于x,z轴的线长度不变;二、点、直线、平面之间的关系(一)、立体几何网络图:1、线线平行的判断:(1)平行于同一直线的两直线平行.(3)如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(6)如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(12)垂直于同一平面的两直线平行.2、线线垂直的判断:(7)三垂线定理:在平面内的一条直线,如果和这个平面7的一条斜线的射影垂直,那么它也和这条斜线垂直.(8)三垂线逆定理:在平面内的一条直线,如果和这个平/:□力面的一条斜线垂直,那么它和这条斜线的射影垂直.人二L如图,已知PO ±a ,斜线PA 在平面a 内的射影为OA ,a 是平面a 内一条直线. ①三垂线定理:若a ^OA ,则a ^PA .即垂直射影则垂直斜线.②三垂线定理逆定理:若a ^PA ,则a ^OA .即垂直斜线则垂直射影.(10)若一直线垂直于一个平面,则这条直线垂直于平面内所有直线.补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条.3、线面平行的判断:(2)如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.(5)两个平面平行,其中一个平面内的直线必平行于另一个平面.判定定理:allb[线线平行n 线面平行)性质定理:aliauu/i〔线面平行n线线平行)CK H p-b★判断或证明线面平行的方法⑴利用定义(反证法):/I a=0,则l〃a(用于判断);⑵利用判定定理:线线平行0线面平行(用于证明);⑶利用平面的平行:面面平行n线面平行(用于证明);⑷利用垂直于同一条直线的直线和平面平行(用于判断).2线面斜交和线面角:/Aa=A2.1直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角0.2.2线面角的范围:0£[0°,90°]注意:当直线在平面内或者直线平行于平面时,0=0°;当直线垂直于平面时,0=90°4、线面垂直的判断:(9)如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面.(11)如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面.(14)一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.(16)如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面.判定定理:。
空间几何体的结构1.1第1课时 棱柱、棱锥、棱台的结构特征

1.空间几何体的定义
空间中的物体都占据着空间的一部分, 若只考虑这些物体的_形__状___和_大__小___,
而不考虑其他因素,那么由这些物体抽 象出来的空间图形就叫做空间几何体.
[问题1] 图片(1)(2)(3)中的物体的形状有何特点? [提示] 由若干个平面多边形围成. [问题2] 图片(4)(5)(6)(7)的物体的形状与(1)(2)(3) 中有何不同?图片(4)(5)(6)(7)中的几何体可否看作 平面图形绕某定直线旋转而成? [提示] 表面是由平面与曲面围成.可以。
DCFD′. 其中四边形ABEA′和四边形DCFD′是底面, A′D′,EF,BC,AD为侧棱.
8.如 图 , 已 知 长 方 体 ABCD- A1B1C1D1,过 BC 和 AD 分别作 一 个 平 面 交 底 面 A1B1C1D1 于 EF、PQ,则长方体被分成的三 个几何体中,棱柱的个数是________.
答案: D
下列的几何体是多面体吗?
答:这些不但是多面体,他们还是多面体 当中的一种,叫做棱锥。
你们思考一下这些棱锥有什么共同特点?
2.棱锥的结构特征
什么是棱锥? 一般地,有一 个面是多边形,其余 各面都是有一个公共 点的三角形,由这些 面围成的多面体叫做 棱锥. 记为:棱锥S-ABCD
多边形 三角形
D'
E'
C'
D A'
B'
S A'B'C'D'E' S ABCDE
S' H '2 SH 2
E
O
C
AB
3. 棱台的结构特征
什么是棱台? 一般地,用一个平行于棱锥底面的平面去截 棱锥,底面和截面中间的部分的多面体叫做棱台.
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
高中《空间几何体的结构》知识点总结详解

间的部分是圆台.
想一想:圆台能否用 旋转的方法得到?若 能,请指出用什么图 形?怎样旋转?
思考:圆柱、圆锥和圆台都是旋转体,当 底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
定义:以半圆的
半径
直径所在直线为
O
旋转轴,半圆面
旋转一周形成的
球心
几何体.
球的表示方法:用表示球 心的字母表示,如:“球O”
S
A
BC
D
棱锥的性质:
侧面、对角面都是三角形;平行于底面的截面与底 面相似,其相似比等于顶点到截面距离与高的比。
用一个平行于棱 锥底面的平面去截棱 锥,底面与截面之间 的部分是棱台.
棱台的有关概念:
D’
D A’
C’
B’
C
A
B
棱台的分类: 由三棱锥、四棱锥、五棱锥…截
得的棱台,分别叫做三棱台,四棱台, 五棱台…
侧棱
F A
E
D
B
底面
侧 面
C
顶点
棱柱的分类:棱柱的底面可以是三角形、 四边形、五边形、 …… 我们把这样的棱柱 分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
1. 侧棱不垂直于底的棱柱叫做斜棱柱. 2.侧棱垂直于底的棱柱叫做直棱柱.
3. 底面是正多边形的直棱柱叫做正棱柱.
问:1.正棱柱一定是直棱柱? 2. 长方体一定是直四棱柱?长方体一定是正四棱柱? 3. 正方体一定是正四棱柱?正四棱柱一定是正方体?
棱柱的表示 用底面各顶点的字母表示棱柱,
E′ F′ A′
如图所示的六棱柱表示为:
“棱柱ABCDEF—A'B'C'D'E'F'” E
1.1.1空间几何体的结构特征

.
(1)
.
定义 表示方法 棱柱ABCD A1 B1C1 D1 棱柱AC1 斜棱柱 侧棱与底面是否垂直 直棱柱—正棱柱 三棱柱 分类 棱柱 四棱柱 底面边数 五棱柱 侧棱都相等,侧面都是平行四边形 性质 两个底面与平行于底面的截面是全等多边形 过不相邻的两条侧棱的截面是平行四边形
思考题2:
1、侧棱不垂直于底面且底面为三角形 斜三棱柱 的棱柱叫做___________; 2、侧棱垂直于底面且底面为四边形的 直四棱柱 棱柱叫做____________; 3、侧棱垂直于底面且底面为正五边形 正五棱柱 的棱柱叫做____________。
练习.在球内有相距14cm 的两个平行截面,它们的面 积分别是 64πcm2 和 36πcm2,求球的表面积。
1.1.1空间几何体的结构特征
简单几何体
简单多面体
简单旋转体
棱 柱
棱ห้องสมุดไป่ตู้锥
棱 台
球
圆 柱
圆 锥
圆 台
思考题1 例1:下列命题中正确的是( D ) A、有两个面平行,其余各面都是四 边形的几何体叫棱柱。 B、有两个面平行,其余各面都是平 行四边形的几何体叫棱柱。(举例) C、有两个侧面是矩形的棱柱是直棱 柱。(举例) D、有两个相邻侧面垂直与底面的棱 柱是直棱柱。
高中数学立体几何知识点总结
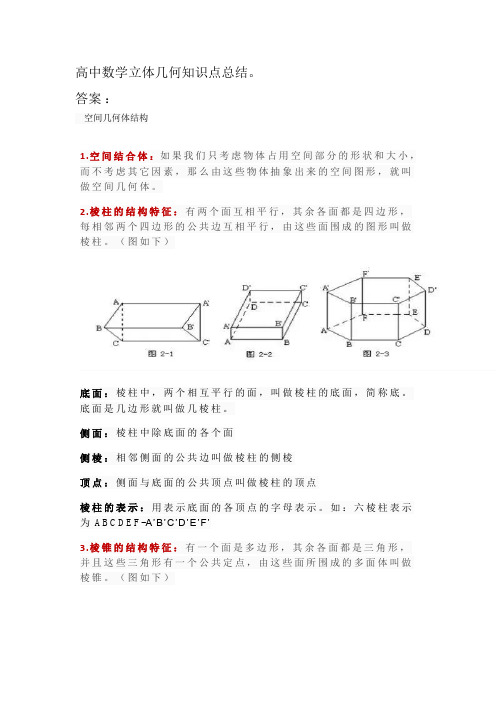
高中数学立体几何知识点总结。
答案:空间几何体结构1.空间结合体:如果我们只考虑物体占用空间部分的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形,就叫做空间几何体。
2.棱柱的结构特征:有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边互相平行,由这些面围成的图形叫做棱柱。
(图如下)底面:棱柱中,两个相互平行的面,叫做棱柱的底面,简称底。
底面是几边形就叫做几棱柱。
侧面:棱柱中除底面的各个面侧棱:相邻侧面的公共边叫做棱柱的侧棱顶点:侧面与底面的公共顶点叫做棱柱的顶点棱柱的表示:用表示底面的各顶点的字母表示。
如:六棱柱表示为ABCDEF-A’B’C’D’E’F’3.棱锥的结构特征:有一个面是多边形,其余各面都是三角形,并且这些三角形有一个公共定点,由这些面所围成的多面体叫做棱锥。
(图如下)4.圆柱的结构特征:以矩形的一边所在直线为旋转轴,其余边旋转形成的面所围成的旋转体叫做圆柱。
圆柱的轴:旋转轴叫做圆柱的轴圆柱的底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面圆柱的侧面:平行于轴的边旋转而成的曲面叫做圆柱的侧面圆柱侧面的母线:无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示,如:圆柱O’O注:棱柱与圆柱统称为柱体5.圆锥的结构特征:以直角三角形的一条直角边所在直线为旋转轴, 两余边旋转形成的面所围成的旋转体叫做圆锥。
轴:作为旋转轴的直角边叫做圆锥的轴底面:另外一条直角边旋转形成的圆面叫做圆锥的底面侧面:直角三角形斜边旋转形成的曲面叫做圆锥的侧面顶点:作为旋转轴的直角边与斜边的交点母线:无论旋转到什么位置,直角三角形的斜边叫做圆锥的母线。
圆锥可以用它的轴来表示。
如:圆锥SO注:棱锥与圆锥统称为锥体6.棱台和圆台的结构特征(1)棱台的结构特征:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台。
下底面和上底面:原棱锥的底面和截面分别叫做棱台的下底面和上底面。
高中数学必修2知识点总结:第一章-空间几何体

高中数学必修2知识点总结:第一章-空间几何体(总11页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征1.2空间几何体的三视图和直观图1 三视图:正视图:从前往后 侧视图:从左往右 俯视图:从上往下 2 画三视图的原则:长对齐、高对齐、宽相等3直观图:斜二测画法4斜二测画法的步骤:(1).平行于坐标轴的线依然平行于坐标轴;(2).平行于y 轴的线长度变半,平行于x ,z 轴的线长度不变;(3).画法要写好。
5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图1.3 空间几何体的表面积与体积(一 )空间几何体的表面积1棱柱、棱锥的表面积: 各个面面积之和2 圆柱的表面积3 圆锥的表面积2r rl S ππ+=4 圆台的表面积22R Rl r rl S ππππ+++=5 球的表面积24R S π=(二)空间几何体的体积1柱体的体积 h S V ⨯=底 2锥体的体积 h S V ⨯=底31 3台体的体积 h S S S S V ⨯++=)31下下上上( 4球体的体积 334R V π=222r rl S ππ+=第一章空间几何体1.1 空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是()A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是()A 有一个面是多边形,其余各面是三角形的多面体是棱锥B 有两个面互相平行,其余各面均为梯形的多面体是棱台C 有两个面互相平行,其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行,侧面均为平行四边形3、下面多面体是五面体的是()A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是()A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是()A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中,直角三角形最多可有几个()A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面,面数最少的棱柱有————————个顶点,有—————————个棱。
第一节 空间几何体的结构特征及三视图与直观图

图1
首页 上一页 下一页 末页
图2
第一节
空间几何体的结构特征及三视图与直观图
结束
3.解析:命题①符合平行六面体的定义,故命题①是正确的; 底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题 ②是错误的;因为直四棱柱的底面不一定是平行四边形,故 命题③是错误的;命题④由棱台的定义知是正确的. 答案:①④ 考点二 [典例] 故选 D. 答案:D
2
2 1 = ,∴直观图 A′B′C′D′的面积为 S′= × 4 2 2 2 (1+3)× = . 4 2 2 答案: 2
数学
首页
上一页
下一页
末页
第一节
空间几何体的结构特征及三视图与直观图
结束
迁移应用· 练透 1.解析:从俯视图来看,上、下底面都是正方形,但大小不 一样,可以判断是棱台. 答案:A 2.解析:当几何体是一个长方体,其中一个侧面为正方形时 A 可能;当几何体是横放的一个圆柱时,B 可能;当几何 体是横放的三棱柱时,C 可能;只有 D 不可能,故选 D. 答案:D
上一页
下一页
末页
第一节
空间几何体的结构特征及三视图与直观图
结束
4.解析:由题意知,正视图就是如图所示的截面 PEF,其中 E, F 分别是 AD,BC 的中点,则 BF=1, 在 Rt△PBF 中,BF=1, PB= 3,于是 PF= 2,同理 PE= 2, 故其正视图的周长为 2+2 2. 答案:2+2 2 5.解:由三视图知该几何体为
答案:①②③④
数学
首页
上一页
下一页
末页
第一节
空间几何体的结构特征及三视图与直观图
结束
考点三
[典例]
解 : 建 立 如 图 所 示 的 坐 标 系 xOy″ ,
高一数学人教A版必修二课件:1.1.1.1 棱柱、棱锥、棱台的结构特征

解:所截两部分分别是四棱柱和三棱柱.几何体ABCD-
一二三
知识精要 思考探究 典题例解 迁移应用
三、简单几何体的表面展开与折叠问题 1.绘制展开图
(1)绘制多面体的表面展开图要结合多面体的几何特征,发 挥空间想象能力或者是亲手制作多面体模型.
(2)在解题过程中,常常给多面体的顶点标上字母,先把多面 体的底面画出来,然后依次画出各侧面,便可得到其表面展开
图
示
底面:两个互相平行的面
及
侧面:底面以外的其余各面
相
侧棱:相邻侧面的公共边
关
顶点:侧面与底面的公共顶
概
点
念
记 法
棱柱 ABCDEF-A'B'C'D'E'F'
分 类
按底面多边形的边数分为三棱柱、四棱柱…
目标导航 预习导引
12
(2)棱锥的结构特征:
定 有一个面是多边形,其余各面都是有一个公共顶
义 点的三角形,由这些面所围成的多面体叫做棱锥
紧扣概念解题 在解答关于空间几何体概念的判断题时,要注意紧扣定义 判断,这就要求熟悉各种空间几何体的概念的内涵和外延,切 忌只凭图形主观臆断,如本例若意识不到棱台各侧棱延长后
交于一点则会致错.
多个梯形相连.
一二三
知识精要 思考探究 典题例解 迁移应用
【例3】 (1)请画出如图所示的几何体的表面展开图.
(2)根据下面所给的平面图形,画出立体图形.
一二三
知识精要 思考探究 典题例解 迁移应用
思路分析:由题意首先弄清几何体的侧面各是什么形状,然 后再通过空间想象或动手实践进行展开或折叠. 解:(1)展开图如图所示
A1B1C1平行于平面ABC,
立体几何知识点总结手写笔记

立体几何知识点总结手写笔记以下是立体几何知识点总结手写笔记:
1. 空间几何体的结构特征
柱体:两个平行的多边形面,一个矩形面。
锥体:一个顶点,一个圆面,一个多边形面。
球体:一个曲面,一个点。
2. 空间几何体的表面积和体积
柱体的表面积:两个底面面积 + 一个侧面面积。
锥体的表面积:底面面积 + 一个侧面面积。
球体的表面积:4πr^2。
柱体的体积:底面面积高。
锥体的体积:1/3 底面面积高。
球体的体积:4/3πr^3。
3. 点、直线、平面的位置关系
点在直线上:点在直线上或直线外。
点在平面上:点在平面上或平面外。
直线在平面内:直线与平面相交或平行。
4. 空间向量的加法、数乘和向量的模
向量加法:平行四边形法则或三角形法则。
数乘:向量与实数相乘得到新的向量。
向量的模:向量的长度或大小。
5. 向量的数量积、向量的向量积和向量的混合积
数量积:两个向量的点乘得到一个实数。
向量积:两个向量的叉乘得到一个新的向量。
混合积:三个向量的点乘得到一个实数。
6. 空间直角坐标系和点的坐标
空间直角坐标系:三个互相垂直的数轴。
点的坐标:在空间直角坐标系中表示点的位置。
7. 向量的坐标表示和运算
向量的坐标表示:通过起点和终点的坐标表示向量。
向量的运算:通过坐标进行向量的加法、数乘、点乘和叉乘。
8. 平面的方程
点法式方程:通过一个点和法线方向表示平面。
一般式方程:Ax + By + Cz + D = 0。
高中数学复习:空间几何体及其三视图、直观图

教材研读 栏目索引
答案 B 该几何体是组合体,上面的几何体是一个五面体,下面是一个 长方体,且五面体的一个面即为长方体的一个面,五面体最上面的棱的 两端点在底面的射影距左右两边距离相等,因此选B.
6.利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
4
教材研读 栏目索引
1.判断正误(正确的打“√”,错误的打“✕”) (1)有两个面平行,其余各面都是平行四边形的几何体是棱柱. ( ✕ ) (2)有一个面是多边形,其余各面都是三角形的几何体是棱锥. ( ✕ ) (3)夹在两个平行的平面之间,其余的面都是梯形,这样的几何体一定是 棱台. ( ✕ )
A.棱台 B.四棱柱 答案 C
C.五棱柱
D.简单组合体
教材研读 栏目索引
3.(教材习题改编)如图所示,在三棱台A'B'C'-ABC中,沿A'BC截去三棱锥 A'-ABC,则剩余的部分是 ( B )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
答案 B 如图所示,
教材研读 栏目索引
在三棱台A'B'C'-ABC中,沿A'BC截去三棱锥A'-ABC,剩余部分是四棱锥A' -BCC'B'.
多面体 结构特征
棱柱
棱锥 棱台
有两个面① 互相平行 ,其余各面都是四边形且每相邻的两个四边形的公共边都 互相平行 有一个面是多边形,而其余各面都是有一个② 公共顶点 的三角形 棱锥被③ 平行于 底面的平面所截,截面和底面之间的部分叫做棱台
(2)旋转体的形成
几何体 旋转图形
第1讲 空间几何体的结构特征及三视图和直观图

上一页
返回导航
下一页
第八章 立体几何
7
常用结论 1.常见旋转体的三视图 (1)球的三视图都是半径相等的圆. (2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形. (3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形. (4)水平放置的圆柱的正视图和侧视图均为全等的矩形.
上一页
返回导航
下一页
5
2.三视图 (1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的_正__前______方、 __正__左_____方、___正__上____方观察几何体画出的轮廓线. (2)三视图的画法 ①基本要求:_长__对__正____,_高__平__齐____,__宽__相__等___. ②画法规则:__正__侧_____一样高,__正__俯_____一样长,__侧__俯_____一样宽;看不到的线画 __虚_______线.
第八章 立体几何
8
2.斜二测画法中的“三变”与“三不变”
坐标轴的夹角改变 “三变”与y轴平行的线段的长度变为原来的一半
图形改变
“三不变”平 与行x,性z轴不平改行变的线段的长度不改变 相对位置不改变
上一页
返回导航
下一页
第八章 立体几何
9
二、习题改编 1.(必修 2P19 练习 T2 改编)下列说法正确的是 ( ) A.相等的角在直观图中仍然相等 B.相等的线段在直观图中仍然相等 C.正方形的直观图是正方形 D.若两条线段平行,则在直观图中对应的两条线段仍然平行 解析:选 D.由直观图的画法规则知,角度、长度都有可能改变,而线段的平行性不变.
解析:由斜二测画法的特点,知该平面图形的直观图的原图,即在平面直角坐标系 xOy 中,四边形 ABCO 是一个长为 4 cm,宽为 2 cm 的矩形,所以四边形 ABCO 的面积为 8 cm2.
高中数学立体几何知识点归纳总结
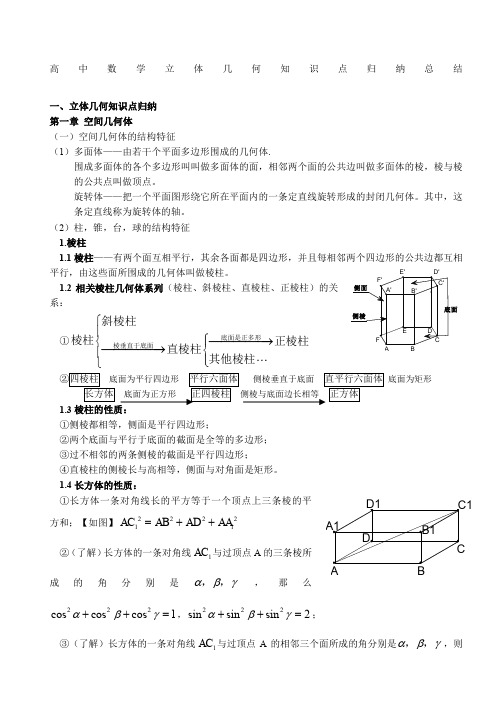
高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为矩形1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形; ③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222cos cos cos 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h 为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形.2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S =2rh π;S=222rh r ππ+,V=Sh=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
高二数学立体几何教案

高二数学立体几何教案【篇一:高中立体几何新课教案】第1章立体几何初步1.1.1 空间几何体得结构重难点:让学生感受大量空间实物及模型、概括出柱、锥、台、球的结构特征;柱、锥、台、球的结构特征的概括.考纲要求:认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.棱柱的结构特点:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边的都互相平行,由这些面说围成的几何体叫做棱柱。
棱锥的结构特点:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
圆柱:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱体。
圆锥,棱台,圆台经典例题:如图,长方体abcd-a1b1c1d1的长、宽、高分别是5cm、4cm、3cm,一只蚂蚁从a到c1点,沿着表面爬行的最短距离是多少.当堂练习:1.由平面六边形沿某一方向平移形成的空间几何体是()a.六棱锥 b.六棱台 c.六棱柱 d.非棱柱、棱锥、棱台的一个几何体 2下列说法中,正确的是()a.棱柱的侧面可以是三角形 b.由六个大小一样的正方形所组成的图形是正方体的展开图c.正方体的各条棱都相等 d.棱柱的各条棱都相等3.一个骰子由1~6六个数字组成,请你根据图中三种状态所显示的数字,推出“?”处的数字是()a. 6b. 3 c. 1d. 24.有两个面互相平行, 其余各面都是梯形的多面体是()a.棱柱 b.棱锥 c.棱台 d.可能是棱台, 也可能不是棱台, 但一定不是棱柱或棱锥5.构成多面体的面最少是()a.三个 b.四个 c.五个 d.六个6.用一个平面去截棱锥, 得到两个几何体, 下列说法正确的是() a.一个几何体是棱锥, 另一个几何体是棱台b.一个几何体是棱锥, 另一个几何体不一定是棱台c.一个几何体不一定是棱锥, 另一个几何体是棱台d.一个几何体不一定是棱锥, 另一个几何体不一定是棱台7.甲:“用一个平面去截一个长方体, 截面一定是长方形”;乙:“有一个面是多边形,其余各面都是三角形的几何体是棱锥”.这两种说法()a.甲正确乙不正确 b.甲不正确乙正确 c.甲正确乙正确 d.不正确乙不正确8.圆锥的侧面展开图是()a.三角形 b.长方形 c. d.形9.将直角三角形绕它的一边旋转一周, 形成的几何体一定是() a.圆锥b.圆柱 c.圆台 d.上均不正确10.下列说法中正确的是()a.半圆可以分割成若干个扇形b.面是八边形的棱柱共有8个面 c.直角梯形绕它的一条腰旋转一周形成的几何体是圆台d.截面是圆的几何体,不是圆柱,就是圆锥11.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是()a.圆锥 b.圆柱c.球体 d.以上都可能12.a、b为球面上相异两点, 则通过a、b可作球的大圆有()a.一个 b.无穷多个 c.零个 d.一个或无穷多个13.一个正方体内接于一个球,过球心作一个截面,下面的几个截面图中,必定错误的是()a. b. c. d.14.用一个平行于棱锥底面的平面去截棱锥, 得到两个几何体, 一个是________,另一个是.15. 如右图, 四面体p-abc中, pa=pb=pc=2,∠apb=∠bpc=∠apc=300. 一只蚂蚁从a点出发沿四面体的表面绕一周, 再回到a点, 问蚂蚁经过的最短路程是_________.16.如右图将直角梯形abcd绕ab边所在的直线旋转一周,由此形成的几何体是由简单几何体是___________________.17.边长为5cm的正方形efgh是圆柱的轴截面, 则从e点沿圆柱的侧面到相对顶点g的最短距离是_______________.18.只有3个面的几何体能构成多面体吗?4面体的棱台吗?棱台至少几个面.19.棱柱的特点是:(1)两个底面是全等的多边形,(2)多边形的对应边互相平行,(3)棱柱的侧面都是平行四边形.反过来,若一个几何体,具备上面三条,能构成棱柱吗?或者说,上面三条能作为棱柱的定义吗?20.如下图几何体是由哪些简单几何体构成的?21.(1)圆柱、圆锥、圆台可以看成以矩形的一边、直角三角形的一直角边、直角梯形中垂直于底边的腰所在直线为旋转轴,将矩形、直角三角形、直角梯形旋转一周而形成的曲面围成的几何体,三个图形之间的什么联系?(2)一个含有300的直角三角板绕其一条边旋转一周所得几何体是圆锥吗?如果以底边上的高所在直线为轴旋转1800得到什么几何体?旋转3600又如何?1.1.2 空间几何体的三视图和直观图重难点:理解中心投影、平行投影的概念,掌握三视图的画法规则及能画空间几何体的三视图并能根据三视图判断空间几何体的形状和结构,了解球、棱柱、棱锥、台的表面积和体积公式的推理过程.三视图包含正视图,测试图和俯视图。
立体几何与空间向量

空间几何体的结构、三视图和直观图1.空间几何体的结构特征(1)多面体①棱柱的侧棱都平行且相等,上、下底面是全等的多边形.②棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.③棱台可由平行于底面的平面截棱锥得到,其上、下底面是相似多边形.(2)旋转体①圆柱可以由矩形绕其一边所在直线旋转得到.②圆锥可以由直角三角形绕其直角边所在直线旋转得到.③圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上、下底中点连线所在直线旋转得到,也可由平行于底面的平面截圆锥得到.④球可以由半圆或圆绕直径所在直线旋转得到.2.空间几何体的三视图空间几何体的三视图是正投影得到,这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是完全相同的,三视图包括正视图、侧视图、俯视图.3.空间几何体的直观图画空间几何体的直观图常用斜二测画法,其规则是:(1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴、y′轴所在平面垂直.(2)原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.4.常用结论(1)常见旋转体的三视图①球的三视图都是半径相等的圆.②水平放置的圆锥的正视图和侧视图均为全等的等腰三角形.③水平放置的圆台的正视图和侧视图均为全等的等腰梯形.④水平放置的圆柱的正视图和侧视图均为全等的矩形.(2)斜二测画法中的“三变”与“三不变”“三变”⎩⎪⎨⎪⎧坐标轴的夹角改变,与y 轴平行的线段的长度变为原来的一半,图形改变.“三不变”⎩⎪⎨⎪⎧平行性不改变,与x ,z 轴平行的线段的长度不改变,相对位置不改变.空间几何体的表面积和体积1.多面体的表(侧)面积因为多面体的各个面都是平面,所以多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l3.柱、锥、台和球的表面积和体积名称 几何体表面积体积柱体 (棱柱和圆柱)S 表面积=S 侧+2S 底 V =Sh锥体 (棱锥和圆锥)S 表面积=S 侧+S 底V =13Sh台体 (棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 34.常用结论(1)与体积有关的几个结论①一个组合体的体积等于它的各部分体积的和或差. ②底面面积及高都相等的两个同类几何体的体积相等. (2)几个与球有关的切、接常用结论 a .正方体的棱长为a ,球的半径为R , ①若球为正方体的外接球,则2R =3a ; ②若球为正方体的内切球,则2R =a ; ③若球与正方体的各棱相切,则2R =2a .b .若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. c .正四面体的外接球与内切球的半径之比为3∶1.空间点、线、面位置关系1.四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 公理4:平行于同一条直线的两条直线平行. 2.直线与直线的位置关系 (1)位置关系的分类⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行直线相交直线异面直线:不同在任何一个平面内,没有公共点(2)异面直线所成的角①定义:设a ,b 是两条异面直线,经过空间任一点O 作直线a ′∥a ,b ′∥b ,把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角). ②范围:⎝⎛⎦⎤0,π2. 3.直线与平面的位置关系有平行、相交、在平面内三种情况. 4.平面与平面的位置关系有平行、相交两种情况. 5.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.直线、平面平行判定与性质1.直线与平面平行的判定与性质判定性质定义定理图形条件a∩α=∅a⊂α,b⊄α,a∥b a∥αa∥α,a⊂β,α∩β=b结论a∥αb∥αa∩α=∅a∥b2.面面平行的判定与性质判定性质定义定理图形条件α∩β=∅a⊂β,b⊂β,a∩b=P,a∥α,b∥αα∥β,α∩γ=a,β∩γ=bα∥β,a⊂β结论α∥βα∥βa∥b a∥α直线、平面垂直的判定与性质1.直线与平面垂直2.平面与平面垂直(1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理与性质定理图形条件结论判定a⊥b,b⊂α(b为α内的任意一条直线)a⊥αa⊥m,a⊥n,m、n⊂α,m∩n=O a⊥αa∥b,a⊥αb⊥α性质a⊥α,b⊂αa⊥ba⊥α,b⊥αa∥b空间向量及其运算1.空间向量的有关概念名称概念表示零向量模为0的向量0单位向量长度(模)为1的向量相等向量方向相同且模相等的向量a=b相反向量方向相反且模相等的向量a的相反向量为-a 共线向量表示空间向量的有向线段所在的直线互相平行或重合的向量a∥b共面向量平行于同一个平面的向量2.空间向量中的有关定理(1)共线向量定理空间两个向量a (a ≠0)与b 共线的充要条件是存在实数λ,使得b =λa . 推论如图所示,点P 在l 上的充要条件是OP →=OA →+t a ①其中a 叫直线l 的方向向量,t ∈R ,在l 上取AB →=a ,则①可化为OP →=OA →+tAB →或OP →=(1-t )OA →+tOB →.(2)共面向量定理共面向量定理的向量表达式:p =x a +y b ,其中x ,y ∈R ,a ,b 为不共线向量,推论的表达式为MP →=xMA →+yMB →或对空间任意一点O ,有OP →=OM →+xMA →+yMB →或OP →=xOM →+yOA →+zOB →,其中x +y +z = 1 . (3)空间向量基本定理如果向量e 1,e 2,e 3是空间三个不共面的向量,a 是空间任一向量,那么存在唯一一组实数λ1,λ2,λ3,使得a =λ1e 1+λ2e 2+λ3e 3,空间中不共面的三个向量e 1,e 2,e 3叫作这个空间的一个基底.3.空间向量的数量积及运算律 (1)数量积及相关概念 ①两向量的夹角已知两个非零向量a ,b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∠AOB 叫做向量a 与b 的夹角,记作〈a ,b 〉,其范围是0≤〈a ,b 〉≤π,若〈a ,b 〉=π2,则称a 与b 互相垂直,记作a ⊥b . ②两向量的数量积已知空间两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做向量a ,b 的数量积,记作a ·b ,即a ·b =|a ||b |cos 〈a ,b 〉. (2)空间向量数量积的运算律 ①结合律:(λa )·b =λ(a ·b ); ②交换律:a ·b =b ·a ; ③分配律:a ·(b +c )=a ·b +a ·c . 4.空间向量的坐标表示及其应用设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3).向量表示 坐标表示 数量积 a·ba 1b 1+a 2b 2+a 3b 3 共线 a =λb (b ≠0,λ∈R ) a 1=λb 1,a 2=λb 2,a 3=λb 3 垂直 a ·b =0(a ≠0,b ≠0)a 1b 1+a 2b 2+a 3b 3=0模|a |a 21+a 22+a 23夹角〈a ,b 〉(a ≠0,b ≠0)cos 〈a ,b 〉=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 23立体几何中的向量方法-证明平行与垂直1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:在直线上任取一非零向量作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎪⎨⎪⎧n ·a =0,n ·b =0. 2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数x ,y ,使v =x v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u . (4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1 ∥u 2. 3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0. (2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u . (3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0.立体几何中的向量方法-求空间角和距离1.两条异面直线所成角的求法设a ,b 分别是两异面直线l 1,l 2的方向向量,则l 1与l 2所成的角θa 与b 的夹角β范围 (0,π2][0,π] 求法cos θ=|a ·b ||a ||b |cos β=a ·b|a ||b |2.直线与平面所成角的求法设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,a 与n 的夹角为β,则sin θ=|cos β|=|a ·n ||a ||n |. 3.求二面角的大小(1)如图①,AB ,CD 分别是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.(2)如图②③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos 〈n 1,n 2〉|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角). 4.利用空间向量求距离(供选用) (1)两点间的距离设点A (x 1,y 1,z 1),点B (x 2,y 2,z 2),则|AB |=|AB →|=(x 1-x 2)2+(y 1-y 2)2+(z 1-z 2)2.(2)点到平面的距离如图所示,已知AB 为平面α的一条斜线段,n 为平面α的法向量,则B 到平面α的距离为|BO→|=|AB →·n ||n |.。
空间体定义

数学必修二
1.1空间几何体的结构
1、柱、锥、台、球的结构特征
(1)棱柱:
几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.
(2)棱锥
几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
其中,三棱锥也叫做四面体。
(3)棱台:
几何特征:上下底面是相似的平行多边形,侧面是梯形,侧棱交于原棱锥的顶点。
(4)圆柱:
定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成
(5)圆锥:
定义:以直角三角形的一条直角边为旋转轴,旋转一周所成
(6)圆台:
定义:以直角梯形的垂直与底边的腰为旋转轴,旋转一周所成
(7)球体:
定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体
几何特征:球的截面是圆;球面上任意一点到球心的距离等于半径.。
空间几何体的结构特征(浦仕国)

旋转体
由一个平面图形围绕其一 边或一点旋转而成,如圆 柱、圆锥、球等。
组合体
由两个或多个几何体组合 而成的立体图形,如金字 塔、连体双球等。
2023
PART 02
空间几何体的结构特征概 述
REPORTING
结构特征的定义
结构特征是指空间几何体的形状、 大小、位置和方向等属性,是描 述几何体外观和内部结构的特征。
PART 03
空间几何体的基本结构特 征
REPORTING
点、线、面的关系
点是几何体的基本元素,通过点可以 确定位置和方向。
面是由无数条线组成,表示二维平面 和形状。
线是由无数个点组成,表示方向和连 续性。
点、线、面之间的关系是几何体构成 的基础,它们之间的位置和数量关系 决定了几何体的形状和性质。
随着数学和其他学科的发展,空间几何体的结构特征将得到更深入的研究和应 用,这将有助于解决一些重要的数学和物理问题。
2023
THANKS
感谢观看
https://
REPORTING
REPORTING
空间几何体结构特征的未来发展
1 2 3
深入研究空间几何体的内在结构
随着数学和物理学的发展,未来将进一步揭示空 间几何体的内在结构,包括它们的对称性、维度 和拓扑性质。
探索更高维度的空间几何体
随着高维几何学的发展,未来将探索更高维度的 空间几何体,这将有助于理解宇宙的更高维度和 解决一些物理问题。
发现和应用新的几何结构
随着数学和其他学科的发展,未来将发现和应用 新的几何结构,这些结构可能会在解决实际问题 中发挥重要作用。
对空间几何体结构特征的总结与展望
空间几何体结构特征的总结
几何体的结构特征

几何体的结构特征几何体是具有三维形状的物体,其结构特征包括形状、边、顶点、面以及其他属性。
在几何体的研究中,我们常常关注其形状和各种特征之间的关系,以及如何描述和分类不同的几何体。
首先,几何体的形状是指其外部的轮廓或者内部的结构。
常见的几何体形状包括球体、立方体、圆柱体、圆锥体和棱柱体等。
其次,几何体的边是指连接两个顶点的线段,用来衡量几何体的长度。
例如,在立方体中,每个面上有四个边。
几何体的顶点是指几何体边的交点,也可理解为几何体的角。
例如,在正五边形棱柱体中,每个面上有一个顶点。
几何体的面是指平面区域,由一系列线段连接而成。
几何体的面是三维空间中的二维对象,它们可以是平坦的,也可以是弯曲的。
在立方体中,有六个面。
除了上述基本特征外,几何体还具有其他一些属性。
其中之一是体积,即几何体所占据的空间大小。
体积可以通过测量几何体的长度、宽度和高度来计算。
例如,球体的体积可以通过计算其半径来获得。
另一个属性是表面积,即几何体外部表面的总面积。
表面积可以通过测量几何体的各个面的面积并求和来计算。
例如,立方体的表面积可以通过计算每个面的面积并求和而得到。
几何体还具有性质,例如平行关系、垂直关系和对称性。
平行关系表明两条线或两个面在空间中始终平行。
垂直关系表示两条线或两个面在空间中始终垂直相交。
对称性是指几何体的一部分或整个几何体在一些轴或平面上对称。
此外,几何体还可以通过旋转、平移和缩放来改变其位置和大小。
旋转是指以一个中心为基准,沿着一个轴旋转几何体。
平移是指将几何体沿着平行于一些轴的方向移动。
缩放是指改变几何体的大小,使其更大或更小。
总体而言,几何体的结构特征包括形状、边、顶点、面以及其他属性。
这些特征能够帮助我们描述和分类不同的几何体,并研究它们之间的关系和性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A’
B’
D D C
C
A
B
A
B
1
2
问题1:观察下面的实物图片, 这些图片中的物 体具有怎样的形状?属于哪种空间几何体?
问题2:观察上述空间几何体,分析它的结构特征, 打算把上述几何体分成几类?
问题3:如何定义多面体与旋转体呢?
多面体
由若干个平面多 边形围成的几何体.
顶点 棱
A D1 A1 B1
E1 F1 A 1 B1
D1 C1
侧 面
用表示底面各顶点字母 表示棱柱,如: 棱柱ABCDE- A1B1C1D1E1 。
E
侧棱 F
D
C B
底面
A
顶点
棱柱的分类:棱柱的底面可以是三角 形、四边形、五边形、 …… 我们把这样的 棱柱分别叫做三棱柱、四棱柱、五棱 柱、……
三棱柱
四棱柱
五棱柱
理解棱柱的定义
①过BC的截面截去长方体的一角, 截去的几何体是不是棱柱,余下的几 何体是不是棱柱?
答:都是棱柱.
理解棱柱的定义
②观察右边的棱柱,共有多少对平 行平面?能作为棱柱的底面的有几对?
答:四对平行平面;只有一对可以作为棱柱的底 面.
理解棱柱的定义
③为什么定义中要说“其余各面都是平行四边形,
并且相邻两个四边形的公共边都互相平行,”而不简 单的只说“其余各面是平行四边形呢”?
一个数字的世界,我时时需要你. 一个形的世界,我处处离不开你.
一个美丽的世界,我欣赏你的韵律.
一个理想的世界,我探索你的奥秘.
几何学的简洁美却又正是几何学之所以完美的核心所在. ——牛顿
从航空测绘到土木建筑以至家居装潢,——空间图形与 我们的生活息息相关.
请观察:哪个更像长方体?
• .
D’ C’ D’ C’ A’ B’
课堂练习:
1. 下面的几何体中,哪些是棱柱?
棱锥的结构特征
如何描述下图的几何结构特征?
S 顶点
棱锥
侧面
有一个面是多边形,其余 各面都是有一个公共顶点的三 角形所围成的几何体叫棱锥.
侧棱
D
C 底面
B
A
S A
B
D C
2、棱锥的分类: 按底面多边形的边数,可以分为三 棱锥、四棱锥、五棱锥、……
3、棱锥的表示方法:用表示顶点和底面 的字母表示,如四棱锥S-ABCD。
练习1:下面图形中为棱锥的是
(1)
(3)
(2)
练习2:判断下列几何体是不是棱 台,并说明为什么.
现代汉语词典解释:
• 结构:各个组成部分的搭配和排列 • 特征:可以作为事物特点的征象、标志 • 结构特征:作为事物各个组成部分搭配 和排列特点的标志。
观察下列几何体的特征,它们与棱锥有何关系?
上底面
D1 A1
C1
B1
侧 棱
A1
D1
C1 侧
B1
面
下底面
顶 点
2.棱台的分类: 由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三 棱台、四棱台、五棱台…… 3.棱台的表示: 用各底面各顶点的字母表示
开普勒说:“我珍视类比胜过任何别的东西,它是我最 信赖的老师,它能揭示自然界的秘密”。
答:满的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
理解棱柱的定义
③为什么定义中要说“其余各面都是
四边形,并且相邻两个四边形的公共边 都互相平行,”而不简单的只说“其余 各面是平行四边形呢”?
答:满足“有两个面互相平行,其 余各面都是平行四边形的几何体”这样 说法的还有右图情况,如图所示.所以 定义中不能简单描述成“其余各面都是 平行四边形”.
C1
D B
面
C
A′
O′
A
O
多面体
由若干个平面多 边形围成的几何体.
顶点 棱
A D1 A1 B1
C1
旋转体
由一个平面图形 绕它所在平面内的一 条直线旋转所形成的 旋转轴 封闭几何体.
A' O'
D B
面
C
O A
合作探究
下图中的物体具有什么样的共同的结构特 征?
棱柱的结构特征
有两个面互相平行,其余各面 都是平行四边形,并且每相邻两个 四边形的公共边都互相平行,由这 些面所围成的多面体叫棱柱.
