空间几何体的结构以及特性
高一数学知识点整理:空间几何体的结构

高一数学知识点整理:空间几何体的结构高一数学知识点整理:空间几何体的结构几何体由平面和曲面所围成。
一般来说一个几何体是由面、交线、而构成的。
下面整理了一些空间几何体的结构的知识点,一起来看看!1.多面体的结构特征(1)棱柱有两个面相互平行,其余各面都是平行四边形,每相邻两个四边形的公共边平行。
正棱柱:侧棱垂直于底面的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱.反之,正棱柱的底面是正多边形,侧棱垂直于底面,侧面是矩形.(2)棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.正棱锥:底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥.特别地,各棱均相等的正三棱锥叫正四面体.反过来,正棱锥的底面是正多边形,且顶点在底面的射影是底面正多边形的中心.(3)棱台可由平行于底面的平面截棱锥得到,其上下底面是相似多边形.2.旋转体的结构特征(1)圆柱可以由矩形绕一边所在直线旋转一周得到.(2)圆锥可以由直角三角形绕一条直角边所在直线旋转一周得到.(3)圆台可以由直角梯形绕直角腰所在直线旋转一周或等腰梯形绕上下底面中心所在直线旋转半周得到,也可由平行于底面的平面截圆锥得到.(4)球可以由半圆面绕直径旋转一周或圆面绕直径旋转半周得到.3.空间几何体的三视图空间几何体的三视图是用平行投影得到,这种投影下,与投影面平行的平面图形留下的影子,与平面图形的形状和大小是全等和相等的,三视图包括正视图、侧视图、俯视图.三视图的.长度特征:“长对正,宽相等,高平齐”,即正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.4.空间几何体的直观图空间几何体的直观图常用斜二测画法来画,基本步骤是:(1)画几何体的底面在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=45°或135°,已知图形中平行于x轴、y轴的线段,在直观图中平行于x′轴、y′轴.已知图形中平行于x轴的线段,在直观图中长度不变,平行于y轴的线段,长度变为原来的一半.(2)画几何体的高在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的z′轴,也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直观图中仍平行于z′轴且长度不变.。
空间几何和结构特征以及三视图和直观图(1)

(3)长方体是正四棱柱
2、棱锥:底面任意多边形; 侧面都是有一个公共点的三角形
V Sh;(h为体高)
正棱锥:底面正多边形; 3
顶点在底面射影为底面中心的棱锥
S侧
1 2
Ch'; (h'为斜高)
正2四021/4面/10 体:各条棱都相等的正三棱锥
2
A
F
S 所有棱长都相等的空间四边形结论
E 设棱长为1
【答案】 C
2021/4/10
35
2.(2009·广州模拟)如图所示的图形是由若干个小正方体所叠
成的几何体的侧视图与俯视图,其中俯视图的小正方形中
的数字表示该几何体在同一位置上叠放的小正方体的个数,
则这个几何体的正视图是
()
2021/4/10
36
解析:从俯视图可看出,该几何体从右到左能分别看到3、 2、1块小正方体. 答案:A
27
【解】 ①两组相对侧面分别平行 ②一组相对侧面平行且全等 ③对角线交于一点且互相平分 ④底面是平行四边形. 任选两个即可.
2021/4/10
28
1.设有四个命题:
①底面是矩形的平行六面体是长方体;
②棱长相等的直四棱柱是正方体;
③有两条侧棱都垂直于底面一边的平行六面体是直平行
六面体;
④对角线相等的平行六面体是直平行六面体.
轴截面是等腰梯形
S侧 (R r)l; (l为母线长 )
V h (S ' S S 'S ) h (R2 r 2 Rr)
3
3
7、球:由圆或半圆绕直径旋转得到。 即
截面都是圆;过球心的圆最大叫球大圆
时 (1)
2021/4/10
7
(完整版)高中立体几何知识点总结
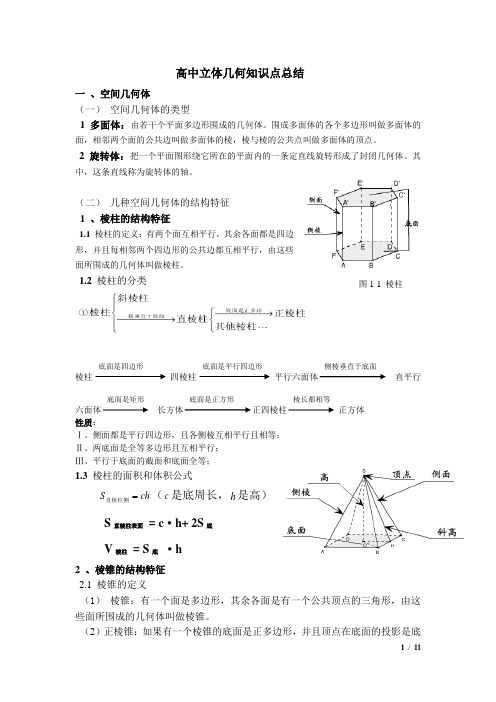
高中立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体 性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;1.3 棱柱的面积和体积公式ch S 直棱柱侧(c 是底周长,h 是高)S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱柱面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
空间立体几何知识点归纳

第一章 空间几何体知识点归纳1、空间几何体的结构:空间几何体分为多面体和旋转体和简单组合体⑴常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。
简单组合体的构成形式:⑵棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
⑶棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
1、空间几何体的三视图和直观图投影:中心投影 平行投影(1)定义:几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(2)三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”2、空间几何体的直观图(表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形.3、斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上)②建立斜坐标系'''x O y ∠,使'''x O y ∠=450(或1350),注意它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X 轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半;4、空间几何体的表面积与体积⑴圆柱侧面积;l r S ⋅⋅=π2侧面⑵圆锥侧面积:l r S ⋅⋅=π侧面 ⑶圆台侧面积:()S r R l π=+侧面⑷体积公式:h S V ⋅=柱体;h S V ⋅=31锥体; ()13V h S S =+下台体上⑸球的表面积和体积:32344R V R S ππ==球球,.一般地,面积比等于相似比的平方,体积比等于相似比的立方。
第二章 点、直线、平面之间的位置关系及其论证1,,A l B ll A B ααα∈∈⎧⇒⊂⎨∈∈⎩ 公理1的作用:判断直线是否在平面内2、公理2:过不在一条直线上的三点,有且只有一个平面。
《空间几何体》基础的知识点

《空间几何体》知识点总结一、 空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体旋转体一一把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其 中,这条定直线称为旋转体的轴。
(2 )柱,锥,台,球的结构特征1.1棱柱一一有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都 互相平行,由这些面所围成的几何体叫做棱柱。
1.2圆柱一一以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何 体叫圆柱.2.1棱锥一一有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的 几何体叫做棱锥。
2.2圆锥一一以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所 围成的几何体叫圆锥。
3.1棱台——用一个平行于底面的平面去截棱锥,我们把截面与底面之间的部分称为棱台 3.2圆台一一用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台4.1球一一以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球二、 空间几何体的三视图与直观图1. 投影:区分中心投影与平行投影。
平行投影分为正投影和斜投影。
2. 三视图一一正视图;侧视图;俯视图;是观察者从三个不同位置观察同一个空间几何体而 画出的图形;画三视图的原则: 长对齐、高对齐、宽相等3. 直观图:直观图通常是在平行投影下画出的空间图形。
4. 斜二测法:在坐标系 x'o'y'中画直观图时,已知图形中平行于坐标轴的线段保持平行性 不变,平行于x 轴(或在x 轴上)的线段保持长度不变,平行于y 轴(或在y 轴上)的线 段长度减半。
三、空间几何体的表面积与体积1、空间几何体的表面积① 棱柱、棱锥的表面积: 各个面面积之和2② 圆柱的表面积S = 2二「I • 2二r 2 ③圆锥的表面积 S =理「I •二r 2、空间几何体的体积 ④圆台的表面积S 二rl + Tt r 2 2 2 R ⑤球的表面积S = 4二R ⑥扇形的面积公式s 扇形 360^1|r (其中I 表示弧长,r 表示半径) ①柱体的体积 v = s 底②锥体的体积 1 VjS 底 h③台体的体积 v =丄(S 上S 上 S 下 • S 下)h ④球体的体积v3 知识赠送以下资料英语万能作文(模板型)Along with the adva nee of the society more and more problems arebrought to our atte nti on, one of which is that....随着社会的不断发展,出现了越来越多的问题,其中之一便是As to whether it is a blessing or a curse, however, people take differe nt attitudes.然而,对于此类问题,人们持不同的看法。
高中《空间几何体的结构》知识点总结详解

间的部分是圆台.
想一想:圆台能否用 旋转的方法得到?若 能,请指出用什么图 形?怎样旋转?
思考:圆柱、圆锥和圆台都是旋转体,当 底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
定义:以半圆的
半径
直径所在直线为
O
旋转轴,半圆面
旋转一周形成的
球心
几何体.
球的表示方法:用表示球 心的字母表示,如:“球O”
S
A
BC
D
棱锥的性质:
侧面、对角面都是三角形;平行于底面的截面与底 面相似,其相似比等于顶点到截面距离与高的比。
用一个平行于棱 锥底面的平面去截棱 锥,底面与截面之间 的部分是棱台.
棱台的有关概念:
D’
D A’
C’
B’
C
A
B
棱台的分类: 由三棱锥、四棱锥、五棱锥…截
得的棱台,分别叫做三棱台,四棱台, 五棱台…
侧棱
F A
E
D
B
底面
侧 面
C
顶点
棱柱的分类:棱柱的底面可以是三角形、 四边形、五边形、 …… 我们把这样的棱柱 分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
1. 侧棱不垂直于底的棱柱叫做斜棱柱. 2.侧棱垂直于底的棱柱叫做直棱柱.
3. 底面是正多边形的直棱柱叫做正棱柱.
问:1.正棱柱一定是直棱柱? 2. 长方体一定是直四棱柱?长方体一定是正四棱柱? 3. 正方体一定是正四棱柱?正四棱柱一定是正方体?
棱柱的表示 用底面各顶点的字母表示棱柱,
E′ F′ A′
如图所示的六棱柱表示为:
“棱柱ABCDEF—A'B'C'D'E'F'” E
空间几何体的结构要点知识汇总

【知识要点】几何体基本概念正棱锥底面是正多面形,并且顶点在底面的射影是底面的中心正棱台正棱锥被平行于底面的平面所截,截面与底面间的几何体是正棱台圆柱以矩形的一边所在的直线为轴,将矩形旋转一周形成的曲面围成的几何体圆锥以直角三角形的一边所在的直线为轴,将直角三角形旋转一周形成的曲面围成的几何体圆台以直角梯形中垂直于底边的腰所在的直线为轴,将直角梯形旋转一周形成的曲面围成的几何体球面半圆以它的直径为轴旋转,旋转而成的曲面球球面所围成的几何体几何体性质补充说明棱柱(1)侧棱都相等,侧面是平行四边形(2)两个底面与平行于底面的截面是全等的多边形(3)过不相邻的两条侧棱的截面(对角面)是平行四边形(1)直棱柱的侧棱长与高相等,侧面及对角面都是矩形(2)长方体一条对角线的平方等于一个顶点上三条棱长的平方和正棱锥(1)侧棱都相等,侧面是全等的等腰三角形(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形球(1)球心和球的截面圆心的连线垂直于截面(2)球心到截面的距离d,球的半径R,截面圆的半径r满足22dRr-=(1)过球心的截面叫球的大圆,不过球心的截面叫球的小圆(2)在球面上,两点之间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度(两点的球面距离) 3.简单几何体的三视图与直观图:(1)平行投影:①概念:如图,已知图形F,直线l与平面α 相交,过F上任意一点M作直线MM1平行于l,交平面α 于点M1,则点M1叫做点M在平面α 内关于直线l的平行投影.如果图形F上的所有点在平面α 内关于直线l的平行投影构成图形F1,则F1叫图形F在α 内关于直线l的平行投影.平面α 叫投射面,直线l叫投射线.②平行投影的性质:性质1.直线或线段的平行投影仍是直线或线段; 性质2.平行直线的平行投影是平行或重合的直线;性质3.平行于投射面的线段,它的投影与这条线段平行且等长; 性质4.与投射面平行的平面图形,它的投影与这个图形全等;性质5.在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比. (2)直观图:斜二侧画法画简单空间图形的直观图. (3)三视图:①正投影:在平行投影中,如果投射线与投射面垂直,这样的平行投影叫做正投影. ②三视图:选取三个两两垂直的平面作为投射面.若投射面水平放置,叫做水平投射面,投射到这个平面内的图形叫做俯视图;若投射面放置在正前方,叫做直立投射面,投射到这个平面内的图形叫做主视图;和直立、水平两个投射面都垂直的投射面叫做侧立投射面,投射到这个平面内的图形叫做左视图.将空间图形向这三个平面做正投影,然后把三个投影按右图所示的布局放在一个水平面内,这样构成的图形叫空间图形的三视图.③画三视图的基本原则是“主左一样高,主俯一样长,俯左一样宽”. 4.简单几何体的表面积与体积: (1)柱体、锥体、台体和球的表面积:①S 直棱柱侧面积=ch ,其中c 为底面多边形的周长,h 为直棱柱的高.②'=ch S 21正棱锥形面积,其中c 为底面多边形的周长,h '为正棱锥的斜高. ③''+=h c c S )(21正棱台侧面积,其中c ',c 分别是棱台的上、下底面周长,h '为正棱台的斜高.④S 圆柱侧面积=2πRh ,其中R 是圆柱的底面半径,h 是圆柱的高. ⑤S 圆锥侧面积=πRl ,其中R 是圆锥的底面半径,l 是圆锥的母线长. ⑥S 球=4πR 2,其中R 是球的半径. (2)柱体、锥体、台体和球的体积:①V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高. ②Sh V 31=锥体,其中S 是锥体的底面积,h 是锥体的高. ③)(31'+'+=S SS S h V 台体,其中S ',S 分别是台体的上、下底面的面积,h 为台体的高. ④3π34R V =球,其中R 是球的半径. 【复习要求】1.了解柱、锥、台、球及其简单组合体的结构特征;2.会画出简单几何体的三视图,会用斜二侧法画简单空间图形的直观图; 3.理解球、棱柱、棱锥、台的表面积与体积的计算公式. 【例题分析】例1 如图,正三棱锥P -ABC 的底面边长为a ,侧棱长为b .(Ⅰ)证明:P A ⊥BC ;(Ⅱ)求三棱锥P -ABC 的表面积; (Ⅲ)求三棱锥P -ABC 的体积.【分析】对于(Ⅰ)只要证明BC (P A )垂直于经过P A (BC )的平面即可;对于(Ⅱ)则要根据正三棱锥的基本性质进行求解.证明:(Ⅰ)取BC 中点D ,连接AD ,PD . ∵P -ABC 是正三棱锥,∴△ABC 是正三角形,三个侧面P AB ,PBC ,P AC 是全等的等腰三角形. ∵D 是BC 的中点,∴BC ⊥AD ,且BC ⊥PD , ∴BC ⊥平面P AD ,∴P A ⊥BC .(Ⅱ)解:在Rt △PBD 中,,4212222a b BD PB PD -=-= ∴.442122a b a PD BC S PBC -==⋅∆ ∵三个侧面P AB ,PBC ,P AC 是全等的等腰三角形, ∴三棱锥P -ABC 的侧面积是.44322a b a- ∴△ABC 是边长为a 的正三角形,∴三棱锥P -ABC 的底面积是,432a ∴三棱锥P -ABC 的表面积为⋅-+=-+)312(434434322222a b a aa b a a (Ⅲ)解:过点P 作PO ⊥平面ABC 于点O ,则点O 是正△ABC 的中心, ∴,63233131aa AD OD =⨯==在Rt △POD 中,,3332222a b OD PD PO -=-=∴三棱锥P -ABC 的体积为.3123334331222222a b a a b a -=-⨯⨯【评述】1、解决此问题要求同学们熟悉正棱锥中的几个直角三角形,如本题中的Rt △POD ,其中含有棱锥的高PO ;如Rt △PBD ,其中含有侧面三角形的高PD ,即正棱锥的斜高;如果连接OC ,则在Rt △POC 中含有侧棱.熟练运用这几个直角三角形,对解决正棱锥的有关问题很有帮助.正三角形正方形 正六边形边长 a aa对角线长a 2长:2a ;短:a 3边心距 a 63 2a a 23 面积 243a a 22233a 外接圆半径a 33 a 22 a例2 如图,正三棱柱ABC -A 1B 1C 1中,E 是AC 的中点.(Ⅰ)求证:平面BEC 1⊥平面ACC 1A 1;(Ⅱ)求证:AB 1∥平面BEC 1. 【分析】本题给出的三棱柱不是直立形式的直观图,这种情况下对空间想象能力提出了更高的要求,可以根据几何体自身的性质,适当添加辅助线帮助思考.证明:(Ⅰ)∵ABC -A 1B 1C 1是正三棱柱,∴AA 1⊥平面ABC , ∴BE ⊥AA 1.∵△ABC 是正三角形,E 是AC 的中点,∴BE ⊥AC ,∴BE ⊥平面ACC 1A 1,又BE ⊂平面BEC 1,∴平面BEC 1⊥平面ACC 1A 1.(Ⅱ)证明:连接B 1C ,设BC 1∩B 1C =D .∵BCC 1B 1是矩形,D 是B 1C 的中点, ∴DE ∥AB 1. 又DE ⊂平面BEC 1,AB 1⊄平面BEC 1, ∴AB 1∥平面BEC 1.例3 在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,AB ∥DC ,△P AD 是等边三角形,已知BD =2AD =8,542==DC AB .(Ⅰ)设M 是PC 上的一点,证明:平面MBD ⊥平面P AD ; (Ⅱ)求四棱锥P -ABCD 的体积.【分析】本题中的数量关系较多,可考虑从“算”的角度入手分析,如从M 是PC 上的动点分析知,MB ,MD 随点M 的变动而运动,因此可考虑平面MBD 内“不动”的直线BD 是否垂直平面P AD .证明:(Ⅰ)在△ABD 中,由于AD =4,BD =8,54=AB ,所以AD 2+BD 2=AB 2. 故AD ⊥BD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,BD ⊂平面ABCD , 所以BD ⊥平面P AD ,又BD ⊂平面MBD ,故平面MBD ⊥平面P AD . (Ⅱ)解:过P 作PO ⊥AD 交AD 于O ,由于平面P AD ⊥平面ABCD ,所以PO ⊥平面ABCD . 因此PO 为四棱锥P -ABCD 的高,又△P AD 是边长为4的等边三角形.因此.32423=⨯=PO 在底面四边形ABCD 中,AB ∥DC ,AB =2DC ,所以四边形ABCD 是梯形,在Rt △ADB 中,斜边AB 边上的高为5585484=⨯,即为梯形ABCD 的高,所以四边形ABCD 的面积为.2455825452=⨯+=S 故.316322431=⨯⨯=-ABCD P V例4 如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的主视图和左视图在下面画出(单位:cm)(Ⅰ)画出该多面体的俯视图;(Ⅱ)按照给出的尺寸,求该多面体的体积; (Ⅲ)在所给直观图中连结BC ',证明:BC '∥平面EFG .【分析】画三视图的基本原则是“主左一样高,主俯一样长,俯左一样宽”,根据此原则及相关数据可以画出三视图.证明:(Ⅰ)该几何体三视图如下图:(Ⅱ)所求多面体体积).cm (32842)2221(316442=⨯⨯⨯⨯-⨯⨯=-=正三棱锥长方体V V V (Ⅲ)证明:在长方体ABCD -A'B'C'D'中,连结AD',则AD'∥BC'. 因为E ,G 分别为AA',A'D'中点, 所以AD'∥EG ,从而EG ∥BC '.又BC'⊄平面EFG , 所以BC'∥平面EFG .例5 有两个相同的直三棱柱,底面三角形的三边长分别是3a ,4a ,5a ,高为a2,其中a >0.用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的一个是四棱柱,求a 的取值范围.解:直三棱柱ABC -A 1B 1C 1的三个侧面的面积分别是6,8,10,底面积是6a 2,因此每个三棱柱的表面积均是2×6a 2+6+8+10=12a 2+24.情形①:将两个直三棱柱的底面重合拼在一起,只能拼成三棱柱,其表面积为:2×(12a 2+24)-2×6a 2=12a 2+48.情形②:将两个直三棱柱的侧面ABB 1A 1重合拼在一起,结果可能拼成三棱柱,也可能拼成四棱柱,但表面积一定是:2×(12a 2+24)-2×8=24a 2+32.情形③:将两个直三棱柱的侧面ACC 1A 1重合拼在一起,结果可能拼成三棱柱,也可能拼成四棱柱,但表面积一定是:2×(12a 2+24)-2×6=24a 2+36.情形④:将两个直三棱柱的侧面BCC 1B 1重合拼在一起,只能拼成四棱柱,其表面积为:2×(12a 2+24)-2×10=24a 2+28在以上四种情形中,②、③的结果都比④大,所以表面积最小的情形只能在①、④中产生.依题意“表面积最小的一个是四棱柱”,得24a 2+28<12a 2+48,解得,352<a 所以a 的取值范围是⋅)315,0( 例6 在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点,求三棱锥F -A 1ED 1的体积.【分析】计算三棱锥F -A 1ED 1的体积时,需要确定锥体的高,即点F 到平面A 1ED 1的距离,直接求解比较困难.利用等积的方法,调换顶点与底面的方式,如1111EFD A ED A F V V --=,也不易计算,因此可以考虑使用等价转化的方法求解.解法1:取AB 中点G ,连接FG ,EG ,A 1G . ∵GF ∥AD ∥A 1D 1,∴GF ∥平面A 1ED 1,∴F 到平面A 1ED 1的距离等于点G 到平面A 1ED 1的距离.∴.8183313132111111111a a a D A S V V V EG A EG A D ED A G ED A F =⨯⨯====⋅∆---解法2:取CC 1中点H ,连接F A 1,FD 1,FH ,FC 1,D 1H ,并记FC 1∩D 1H =K .∵A 1D 1∥EH , A 1D 1=EH ,∴A 1,D 1,H ,E 四点共面.∵A 1D 1⊥平面C 1CDD 1,∴FC ⊥A 1D 1.又由平面几何知识可得FC 1⊥D 1H ,∴FC ⊥平面A 1D 1HE . ∴FK 的长度是点F 到平面A 1D 1HE (A 1ED 1)的距离. 容易求得.811053453131,1053321111a a a FK S V a FK ED A ED A F =⨯⨯===⋅∴∆-练习1-2一、选择题:1.将棱长为2的正方体木块削成一个体积最大的球,则这个球的表面积为( ) (A)2π (B)4π (C)8π (D)16π2.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )(A)9π(B)10π(C)11π(D)12π3.有一种圆柱体形状的笔筒,底面半径为4 cm ,高为12 cm .现要为100个这种相同规格的笔筒涂色(笔筒内外均要涂色,笔筒厚度忽略不计).如果所用涂料每0.5 kg 可以涂1 m 2,那么为这批笔筒涂色约需涂料( ) (A)1.23 kg (B)1.76 kg (C)2.46 kg (D)3.52 kg 4.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为( ) (A)22(B)32(C)4(D)52二、填空题:5.如图,正三棱柱ABC -A 1B 1C 1的每条棱长均为2,E 、F 分别是BC 、A 1C 1的中点,则EF 的长等于______.6.将边长为1的正方形ABCD 沿对角线AC 折起,使得BD =1,则三棱锥D -ABC 的体积是______.7.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为3,底面周长为3,则这个球的体积为______.8.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件①:_______________________________________________________________; 充要条件②:_______________________________________________________________. (写出你认为正确的两个充要条件) 三、解答题:9.如图,在正四棱柱ABCD -A 1B 1C 1D 1中,E 是DD 1的中点.(Ⅰ)求证:BD 1∥平面ACE ;(Ⅱ)求证:平面ACE ⊥平面B 1BDD 1.10.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(Ⅰ)求该几何体的体积V ; (Ⅱ)求该几何体的侧面积S .11.如图,已知ABCD -A 1B 1C 1D 1是棱长为3的正方体,点E 在AA 1上,点F 在CC 1上,且AE =FC 1=1.(Ⅰ)求证:E ,B ,F ,D 1四点共面; (Ⅱ)若点G 在BC 上,32BG ,点M 在BB 1上,GM ⊥BF ,求证:EM ⊥面BCC 1B 1.。
空间几何体的结构

空间几何体的结构空间几何体是指在三维空间中具有一定形状和特征的几何体。
它们广泛应用于建筑、工程、物理学、数学等领域,并且对于人们的日常生活也有着重要的影响。
空间几何体的结构包括点、线、面、体以及它们之间的关系和性质。
1.点:点是空间中最基本的几何结构,它没有大小和形状,只有位置。
点用坐标表示,通常用三维坐标系的(x,y,z)来表示。
2.线:线是由无限多个点连接而成的一维结构,它没有宽度和厚度,只有长度。
线用于连接两个点,表示直线的两个端点,也可以用于表示线段,即直线的一部分。
3.面:面是由无限多个线连接而成的二维结构,它具有宽度和长度,但没有厚度。
面用于表示平面或曲面,可以是多边形、圆形、椭圆等形状。
4.体:体是由无限多个面连接而成的三维结构,它具有长度、宽度和厚度。
常见的体包括立方体、圆柱体、球体等,它们具有不同的形状和特征。
在空间几何体中,还存在很多重要的关系和性质,如:1.位置关系:点与点之间可以有相对位置的关系,如点在直线上、点在平面上、点在体内等。
线与线、面与面之间也可以有相对位置的关系,如平行、垂直、相交等。
2.夹角关系:夹角是两条线相交时形成的角。
根据夹角的大小和形状,可以分为锐角、直角、钝角等,夹角的度数可以通过三角函数进行计算。
3.长度、面积和体积:空间几何体的长度、面积和体积是表征其大小的重要性质。
长度是线的特征,可以通过测量直线的长度得到。
面积是面的特征,可以通过测量平面图形的面积得到。
体积是体的特征,可以通过测量三维空间物体的体积得到。
4.对称关系:对称是指一个几何体在一些中心或条轴线下具有镜像关系。
常见的对称关系有轴对称和面对称,通过对称关系可以研究几何体的性质和变化。
总的来说,空间几何体的结构包括点、线、面、体以及它们之间的关系和性质。
了解和掌握这些结构和关系对于理解和应用空间几何体具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三棱柱
四棱柱
五棱柱
1. 侧棱不垂直于底的棱柱叫做斜棱柱. 2.侧棱垂直于底的棱柱叫做直棱柱. 3. 底面是正多边形的直棱柱叫做正棱柱.
棱柱的表示
E′
F′ A′
用底面各顶点的字母表示棱柱,
如图所示的六棱柱表示为:
“棱柱ABCDEF—A'B'C'D'E'F'”
E
理解棱柱
F
A
探究1:
一个长方体,能作为 棱柱底面的有几对?
D’GG’C’A’FF’
B’
H
D
H’
E
C
E’
A
B
答:都是棱柱.
探究4:
观察右边的棱柱,共有多少 对平行平面?能作为棱柱的 底面的有几对?
答:四对平行平面;只有一 对可以作为棱柱的底面.
棱柱的任何两个平行平面都可以作为棱柱 的底面吗?
答:不是.
练习1.在棱柱中………………..( D )
A . 只有两个面平行 B . 所有的棱都相等 C . 所有的面都是平行四边形 D . 两底面平行,并且各侧棱也平行
如果我们只考虑物体的形状和大小,而不考 虑其它因素,那么由这些物体抽象出来的空 间图形就叫做空间几何体。 请观察下图中的物体
提出问题
观察下面的图片, 这些图片中的物体具有什么几何结 构特征?你能对它们进行分类吗?分类依据是什么?
提出问题
观察下面的图片, 这些图片中的物体具有什么几何结 构特征?你能对它们进行分类吗?分类依据是什么?
棱台的特点:两个底面是相似多边形, 侧面都是梯形;侧棱延长后交于一点。
练习:下列几何体是不是棱台,为什么?
(1)
(2)
想一想,怎样给多面体分类呢?
答:可以按面数分类,多面体有几个面就 称为几面体。如:三棱锥是四面体,四棱柱 是六面体.
练习:见P8页A组第1题的(1),(2),(3)小题. 思考:棱柱、棱锥和棱台都是多面体,当 底面发生变化时,它们能否互相转化?
(1),(3),(4),(6),(8),(10),(11),(12)
具有相同的特点:组成它们的面不全是平面图形.
想一想?
我们应该给上述两大类几何 体取个什么名字才好呢?
定义:
1.由若干个平面多边形围成的几何体 叫做多面体。围成多面体的各个多 边形叫做多面体的面,相邻两个面的 公共边叫做多面体的棱,棱与棱的公 共点叫做多面体的顶点。
D′ C′
B′
D C
B
答:长方体有三对 平行平面;这三对都可 以作为棱柱的底面.
探究2: 有两个面互相平行,其余各面都是平行四 边形的几何体是棱柱吗?
答:不一定是. 如图所示的几何体, 不是棱柱.
探究3:
长方体按如图截去一角后所得的两部分还是棱柱吗?
D’ C’
A’
B’
D A
C B
探究3:
长方体按如图截去一角后所得的两部分还是棱柱吗?
O B
底面
圆柱的表示方法:用表示它的轴的字母表
示,如:“圆柱OO'”
5.圆锥的结构特征
定义:以直角三角形的
一条直角边所在直线为
母
旋转轴,其余两边旋转
线
形成的曲面所围成的几
想一想:
用一个平行于棱锥底面的平面去截棱锥, 得到怎样的两个几何体?
3.棱台的结构特征
用一个平行于棱 锥底面的平面去截棱 锥,底面与截面之间 的部分是棱台.
棱台的有关概念:
D’
D A’
C’
B’
C
A
B
棱台的分类: 由三棱锥、四棱锥、五棱锥…截
得的棱台,分别叫做三棱台,四棱台, 五棱台…
棱台的表示方法:“棱台ABCD—A'B'C'D'”
2.下图中不可能围成正方体的是( B )
A
B
C
D
2.棱锥的结构特征 请仔细观察下列几何体,说说它们的共同特点.
定义:有一个面是多边形,其余各面都是 有一个公共顶点的三角形,由这些面 所围成的几何体叫做棱锥。
棱锥的有关概念
顶点
棱锥中,这个多边形面
S
叫做棱锥的底面或底,有
侧面
公共顶点的各个三角形
面叫做棱锥的侧面,各侧 侧棱 D
棱柱的有关概念
棱柱中,两个互相平行的面 叫棱柱的底面(简称底), 其余各面叫棱柱的侧面, 相邻侧面的公共边叫侧棱, 侧面与底面的公共顶点叫 棱柱的顶点。
(1)底面互相平行.
(2)侧面都是 平行四边形. (3)侧棱平行且相等.
E′ F′ A′
D′
C′ B′
侧棱
F A
E
D
B
底面
侧 面
C
顶点
棱柱的分类:棱柱的底面可以是三角形、 四边形、五边形、 …… 我们把这样的棱柱 分别叫做三棱柱、四棱柱、五棱柱、……
提出问题
如何依据一定的标准,把前面的物体的 几何结构特征表示出来?
我要问
这些图片中的物体具有什么样的几何 结构特征?你能对它们进行分类吗?
我来答
上图中的物体大体可分为两大类.
其中(2),(5),(7),(9),(13),(14),(15),(16)
具有相同的特点:组成几何体的每个面都是平面图
形,并且都是平面多边形;
2.由一个平面图形绕它所在的平 面内的一条定直线旋转所形成 的封闭几何体,叫做旋转体,这条 定直线叫做旋转体的轴。
下面我们来探究柱,锥,台,球的结构特征
1.棱柱的结构特征 请仔细观察下列几何体,说说它们的共同特点.
定义:有两个面互相平行,其余各面都是 四边形,并且每相邻两个四边形的公共边
都互相平行,由这些面围成的几何体 叫做棱柱。
C
面的公共顶点叫做棱锥
底面
的顶点,相邻侧面的公共 A
B
边叫做棱锥的侧棱。
棱锥的表示
用表示顶点和底面各顶点的字母表示,如图所 示的棱锥表示为:“棱锥S—ABCD”
棱锥的分类:
按底面多边形的边数,可以分为三 棱锥、四棱锥、五棱锥、……
S
A
BC
D
棱锥的性质:
侧面、对角面都是三角形;平行于底面的截面与底 面相似,其相似比等于顶点到截面距离与高的比。
空间几何体的结构以 及特性
1.1空间几何体的结构
教学目标: 1.能根据几何结构特征对空间物体进行分类; 2.掌握棱柱、棱锥、圆柱、圆锥、棱台、圆 台、球的结构特征; 3.会表示有关几何体; 4.能判断组合体是由哪些简单几何体构成的。
空间几何体
在现实生活中,我们的周围存在着各种各样的 物体,它们具有不同的几何形状。
上底扩大
上底缩小
4.圆柱的结构特征
定义:以矩形的一边所在直线为 旋转轴,其余边旋转形成的曲面所
围成的几何体叫做圆柱。
(1)圆柱的轴——旋转轴.
A’
O’
(2)圆柱的底面——垂直于轴
的边旋转而成的圆面。
母 线
(3)圆柱的侧面——平行于轴
B’
轴
侧 面
的边旋转而成的曲面。
(4)圆柱侧面的母线——无论 旋转到什么位置,不垂直于轴的 A 边。
