工程力学公式大全修订版

合集下载

工程力学公式整理

工程力学公式整理工程力学（Engineering Mechanics）是一门研究力学原理在工程中的应用的学科。

它主要研究物体在受力作用下的运动和变形规律。

在工程学中，力学公式是进行分析和计算的基础。

下面是一些常见的工程力学公式整理。

1.力的合成与分解公式：力的合成公式：F = √(F₁² + F₂² + 2F₁F₂cosθ)力的分解公式：F₁ = Fcosθ, F₂ = Fsinθ其中，F为施于物体的合力，F₁、F₂为分解后的力，θ为施力与横坐标方向的夹角。

2.矩形截面惯性矩和抗弯应力公式：惯性矩公式：I=(b*h³)/12抗弯应力公式：σ=(M*y)/I其中，b和h分别为矩形截面的宽度和高度，I为截面的惯性矩，M 为弯矩，y为截面内其中一点的纵坐标。

3.应力和变形的关系公式：胡克定律公式：σ=Ee弹性模量公式：E=(F/A)/(ΔL/L₀)其中，σ为应力，E为弹性模量，F为受力，A为受力面积，ΔL为长度变化量，L₀为初始长度。

4.摩擦力公式：滑动摩擦力公式：F=μN滚动摩擦力公式：F=RμN其中，F为摩擦力，μ为摩擦系数，N为垂直于接触面的力，R为滚动半径。

5.动量和能量守恒公式：动量守恒公式：m₁v₁+m₂v₂=m₁v₁'+m₂v₂'动能公式：K = (1/2)mv²其中，m为物体的质量，v为物体的速度，v'为受撞物体的速度。

6.应力和应变的关系公式：杨氏模量公式：E=(σ/ε)横向收缩率公式：μ=-(ε₁/ε₂)泊松比公式：μ=-(ε₁/ε₂)其中，E为杨氏模量，σ为应力，ε为应变，μ为泊松比，ε₁为纵向应变，ε₂为横向应变。

这些力学公式是工程力学中常用的基本公式，用于解决各种工程问题。

通过运用这些公式，我们可以计算结构的受力情况、变形情况，进行力学分析和设计，保证工程的稳定性和安全性。

当然，工程力学的应用还远不止于此，还包括静力学、动力学、流体力学等等。

工程力学常用公式

工程力学常用公式3、伸长率：* 1。

％断面收缩率：字100%5、扭转切应力表达式：^，最大切应力：maxTP RW p ， d 44I P ”（1），W P d'(1 4)，强度校核： 16max TmaxW P[]6、单位扭转角：d—，刚度校核：maxTmax[]，长度为1dx Gl pGI P的一段轴两截面之间的相对扭转角證，扭转外力偶的计算公式: Me 9549P（KWLn（r/m in ）8平面应力状态下斜截面应力的一般公式:最大切应力max -'' - ( x y )22，最大正应力方位2 Y 21、轴向拉压杆件截面正应力牛，强度校核max2、轴向拉压杆件变形IFi Ni l i 4、胡克定律： E ，泊松比:，剪切胡克定律：G7、薄壁圆管的扭转切应力:T 2 R 29、 x yx ycos22 2 xsin 2-sin 2 x cos2平面应力状态三个主应力:II「（ x 2y）2X， ''' 01、100%tan2 0 2xx y10、第三和第四强度理论: r3 X 24 2， r4211、平面弯曲杆件正应力:M ，截面上下对称时，MW Z矩形的惯性矩表达式：I Z兽圆形的惯性矩表达式:I ZV(1 644)矩形的抗扭截面系数：W Z £圆形的抗扭截面系数:W Z 4)13、平面弯曲杆件横截面上的最大切应力:F s S max* zmaxbi z14、平面弯曲杆件的强度校核：（1）弯曲正应力tmax [t ]， cmaxc]（2）弯曲切应力max []（3）第三类危险点：第三和第四强度理论 16、（ 1）轴向载荷与横向载荷联合作用强度： ()FN M maxmax (min 丿15、平面弯曲杆件刚度校核：叠加法严 [f]， max []（2）偏心拉伸（偏心压缩）:max ( min)A（3）弯扭变形杆件的强度计算:工程力学常用公式伸长率: F N ； A ；FA ；泊松比E 2(1 )，l bI 0l 0100%，断面收缩率:A o A b A 02、扭转: { M }N gm9549 {P}kW ,{ n} r/ min,W p max TW p，3、4、ddxTGIP，TloGI P弯曲:MdxEl应力状态:MET Z，MyIT，maxMy maxIlMW zd 2wdx2MEIM , xdx)dx CxEIx sin2i2cos 2；x y )22tg2 o拉压强度条件：max(F N)[\ 八/max L扭转强度条件：max(T)[]W p扭转刚度条件：(T)max []GI P梁的弯曲强度条件M maxmaxW.梁弯曲的刚度条件:V V max[]-欧拉公式：F c r -2EIl2，2Ecr 2柔度：-惯性半径:max(min][],maxi x y2max,max . [](丿max [],I zi'■ A。

工程力学常用主要公式

∫
M z (x) 2 dx + li EI z
∫
M x (x) 2 dx + li GI p
∫
1 FR 2 k S FS (x) 2 ⎞ ⎟ dx + ⎟ 2 k li GA ⎠
单位载荷法
Δ=
∑ ∫
[
l
0
FN o ( x) FN ( x) dx + EA
+
∫
k S FS o ( x) FS ( x) dx 0 GA
σ r3 = σ 1 − σ 3 ≤ [σ ]
σ r4 =
1 [(σ 1 − σ 2 ) 2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 ] ≤ [σ ] 2
圆轴扭转
Δϕ = ∫
0
l
M x ( x) dx GI p
Δϕ =
Tl GI p
Ip =
π
32
D4
τ max =
Wp =
Mx Wp
τ I ,II = ± (
应变变换
σ x −σ y
2
)2 + τ xy 2
εx' =
εx + ε y 2
+
εx − ε y 2
cos 2α +
γ xy 2
sin 2α
γx' y' 2
=−
εx − ε y 2
sin 2α +
γ xy 2
cos 2α
εy' =
εx + ε y 2
−
εx − ε y 2
σ r3 = (
M Mz 2 ) + 4( x ) 2 = Wz Wp

工程力学公式大全-精选.pdf

wmax l
[ w] ， l
max
[]
16、（ 1）轴向载荷与横向载荷联合作用强度：
max ( min )
FN
M ห้องสมุดไป่ตู้ax
A WZ
（ 2）偏心拉伸 (偏心压缩 )： max ( min ) FN F A WZ
（ 3）弯扭变形杆件的强度计算：
r3
1 M 2 T2
1
M y2
M
2 z
T2
[]
WZ
WZ
r4
1 M 2 0.75T 2
6
32
13、平面弯曲杆件横截面上的最大切应力：
max
FS S * zmax
K FS
bI Z
A
14、平面弯曲杆件的强度校核：（ 1）弯曲正应力 t max [ t ] ， cmax [ c ]
（ 2）弯曲切应力 max [ ] （ 3）第三类危险点：第三和第四强度理论
15、平面弯曲杆件刚度校核：叠加法
R
， IP
I
IP
WP
d4 (1
32
4) ，
WP
d3 (1
4 ) ，强度校核： max Tmax [ ]
16
WP
6、单位扭转角：
d dx
T
，刚度校核： max
GI P
T max
GI P
[ ] ，长度为 l 的一段轴两截
面之间的相对扭转角
Tl
，扭转外力偶的计算公式：
GI P
Me 9549 p( KW ) n( r /min)
tan 2 0
10、第三和第四强度理论： 11、平面弯曲杆件正应力：
r3
2 4 2 ， r4

常用工程力学公式

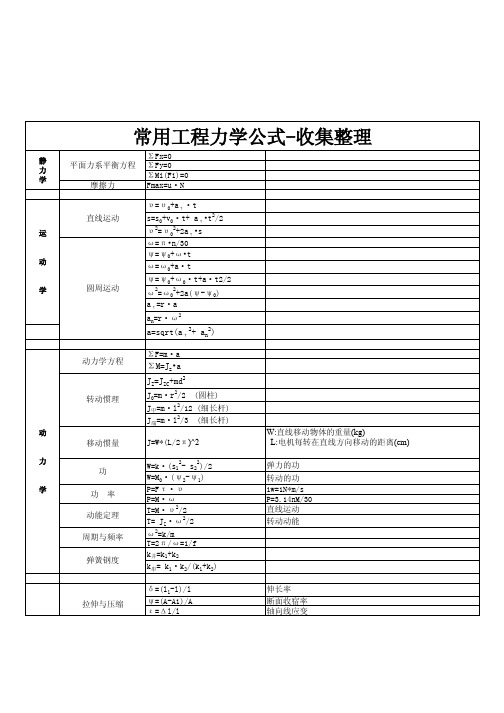
ω2=ω02+2a(ψ-ψ0)
aτ=r·a
an=r·ω2
a=sqrt(aτ2+ an2)
动力学方程
ΣF=m·a ΣM=Jz•a
JZ=JZC+md2
转动惯理
J0=m·r2/2 (圆柱) )
动
W:直线移动物体的重量(kg)
移动惯量
J=W*(L/2π)^2
θ=180T/（πG·IP）≤[θ]
[θ]：0.5～1.0度/米 [θ]：1.0～2.5度/米
一般传动精度不高传动
[θ]：2.0～4.0度/米
精度低传动
力
τmax＝MT/WT
WT——抗扭截面模量，WT=αhb2，方形截面扭转，系数
见右表
学
WZ=bh2/6
抗弯截面系数矩形截面
弯曲
WZ=πD3/32 或πD3(1-a4)/32 抗弯截面系数圆形或环形截面
L:电机每转在直线方向移动的距离(cm)
力
功
W=k·(s12- s22)/2
W=M0·(ψ2-ψ1)
学
功率
P=Fτ·υ P=M·ω
动能定理周期与频率
T=M·υ2/2 T= JZ·ω2/2 ω2=k/m T=2π/ω=1/f
弹簧钢度
k并=k1+k2 k串= k1·k2/(k1+k2)
弹力的功
转动的功 1w=1N*m/s P=3.14nM/30 直线运动转动动能
拉伸与压缩
δ=(l1-l)/l ψ=(A-A1)/A ε=Δl/l
伸长率
断面收宿率轴向线应变
胡克定律材料特性
u=ε|/ε σ=E·ε Δl=FN•l/(E•A)
塑性: 碳钢黄铜铝合金

工程力学(静力学与材料力学)公式整理

平面一般力系的平衡方程■ IFLm r∑ F=O (力平衡）投影方程J Z=I«简写I 工Ffo ---- ►2 ∑ F=Ot=l力矩(平衡〉方程Σ ^O(F i）=O J Σ^O(F）=O■ Σ平衢方程的”'二矩式” Y ∑ MΛ（^)=θ仙两点的连线不能垂直于耳.∑ M B(F)—O「Σ X, （HM）平衝方程的三矩式”YΣ¼(F)=O ABC^-点的不英线L ∑ M^F）=（}E：弹性（柿氏)4＊*胡克定律∆w=Illn —∖x→9 AX正应变①校垓强度：∕τnu LX ≤ ［σ]② 截面设计[步十Q ］=八啬 ③ 许可载荷:①皿=今≤Q］ l=〉 ∕7v < A ［σ］OMM ⅛⅛⅛ σ= IinIg〈7 = O ⅛⅛JiΔ/1 FJ σ = Eε正应变：/”E Ai 正应变轴向拉压杆件的强度条件F.（强度设计准则)σ=（川）≤［crl InaJC V λ 71TlaXIA4、泊松比(攻横向变形系数）1=—（TEV =切应力以绕研究对象顺时针转为正,逆时针转为负JI 1τ^τ^PV 柱体半径。

圆半径；D ：外圆半径扭转强度条件: f ∙=金^兰M ］ ①校核强度：q≡< =冷汙冬［门②设计截面尺寸：Fr Z 如LJt1叮③计算许可義荷:M nlM "卩；［打手螺旋法则 y 左=Qd^"CtV\羊任长上老相艮寸扌玄⅛ ⅛i单位：P 掾或MP i l （怕斯卡或兆帕）IPa=IN∕πι2-Fτrd'KX_* PP p—32鼻尸厂-~ 1 <⅛空心柱:Jr ^P4(l-α4)f P — P 32 1% "Af(Ow→o Λ√4实心柱:dCL ——D单位长度的相对扭转角TIGfP—扭转刚度寻島§7-2剪力方程与肆方程⅞X’lllllllHIIIIl ⅜lll,il∣π≡^MfIMf JkdzZrrTr_ L I 丨Tl車：在集中力偶M 作用处M 图突变(从左向右,谴顺时■针方向的力偶向上突变，喪变量为M)。

工程力学公式总概括

工程力学公式：1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤ 2、轴向拉压杆件变形Ni i i F l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯ 4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ=5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P P T T R I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：max max []P T W ττ=≤ 6、单位扭转角：P d T dx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角P Tl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202T R τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=，''2x y σσσ+='''0σ= 最大切应力max '''2σστ-=±=，最大正应力方位02tan 2x x yτασσ=-- 10、第三和第四强度理论：3r σ=，4r σ=11、平面弯曲杆件正应力：Z My I σ=，截面上下对称时，ZM W σ= 矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=- 矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=- 13、平面弯曲杆件横截面上的最大切应力：max max *S z S Z F S F K bI Aτ== 14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w w l l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： max max min ()N Z F M A W σσ=± （2）偏心拉伸(偏心压缩)：max min ()N Z F F A W δσσ=± （3）弯扭变形杆件的强度计算：3[]r Zσσ==4[]r Z σσ==≤简支梁在各种荷载作用下跨中最大挠度计算公式：均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式: Ymax = 8pl^3/(384EI)=1pl^3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 6.81pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式:Ymax = 6.33pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).悬臂梁受均布荷载或自由端受集中荷载作用时，自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).你可以根据最大挠度控制1/400，荷载条件25kn/m以及一些其他荷载条件进行反算，看能满足的上部荷载要求！机械零件和构件的一种截面几何参量，旧称截面模量。

工程力学公式

公式：1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤2、轴向拉压杆件变形Ni i iF l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯ 4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ=5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P P T TR I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：maxmax []PT W ττ=≤ 6、单位扭转角：Pd Tdx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角PTl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202T R τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=+''2x yσσσ+=，'''0σ=最大切应力max '''2σστ-=±=，最大正应力方位02tan 2x x yτασσ=--10、第三和第四强度理论：3r σ=，4r σ= 11、平面弯曲杆件正应力：ZMyI σ=，截面上下对称时，Z M W σ=矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=-矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=-13、平面弯曲杆件横截面上的最大切应力：max max *S z SZ F S FK bI Aτ==14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w wl l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： maxmax min ()N ZF M A W σσ=±（2）偏心拉伸(偏心压缩)：max min ()N ZF F A W δσσ=±（3）弯扭变形杆件的强度计算：3[]r Z σσ==≤4[]r Zσσ==≤。

工程力学公式大全

工程力学公式胡克定律：- E ■:，泊松比：；'--：；，剪切胡克定律：.=G最大切应力.max 二 £ 二■- C x^ "）22，最大正应力方位tan2〉°二10、第三和第四强度理论：；「r3二■2' 4 ■2，二r4=；42,3.1、轴向拉压杆件截面正应力 c=F N，强度校核 A二max -［二］2、轴向拉压杆件变形，計八詈. L 一 I伸长率： -- I 100%断面收缩率:A A 、A100%扭转切应力表达式：，最大切应力：-max R = — ， I pII P " W P二 d 4(1_G 432二d 34W p（1 -〉），强度校核：max16Tmaxk 二【］d 甲 T单位扭转角：，刚度校核：^maxmaxdx Gl PGl P乞口］，长度为I 的一段轴两截面之间的相对扭转角IL ，扭转外力偶的计算公式: GIMe 二 9549P (KW)n(r/m in)薄壁圆管的扭转切应力：•-22 兀 R0§8、平面应力状态下斜截面应力的一般公式: CL =cr +cr cr -<yxyx ycos2： - x sin2：，sin 2： x cos2-29、平面应力状态三个主应力:CT +CF 丄__y ■1 a -cr cc(x2丫，匚''CF一(X2CTy )2，二'''=02x14、平面弯曲杆件的强度校核：（1 ）弯曲正应力二tmax乞［G］，二cmax乞［二c］（2 ）弯曲切应力gax乞［J（3 ）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法W p aX- ［W］，二max -［二］（2 ）偏心拉伸（偏心压缩）:二max （二min）=旦，二匸一A W z（3）弯扭变形杆件的强度计算:1 .M2 T2M y2 Mz2T2逬二］W Z W Z 1 y表1杆件基本变形部分主要公式基本变形应力公式变形公成轴向拉压F N= ----AA/ =EA扭转Tn^甲=TlJ max —GIP弯曲0 —Mlmax -—-..i I El.11、平面弯曲杆件正应力: —My，截面上下对称时,IZMCT = ----------W Z矩形的惯性矩表达式: bh3——圆形的惯性矩表达式:124I z （1）矩形的抗扭截面系数:bh?叫盲，圆形的抗扭截面系数:3WZ 甘一4）13、平面弯曲杆件横截面上的最大切应力:FSS * zmaxmaxbi z= K F SAmax16、（1 ）轴向载荷与横向载荷联合作用强度: faxUmint^ -仏A W Z-r4 W z、nW z「M 2 2 2y M z 0.75T 打二］表3杆在简单载荷作用下的变形简團瓦载荷“2内容半面应力状态中任意斜截面 sin 2a 十 T xy cos 2A上的应力 *而应变狀态中任总方向h2的应变截面儿何性质的转轴公犬16£7yo=2El+■_L ■卩.4-- --F*] ■ \仁公式2_切 ~2~F0&A =~6D =X6E11G, 3B =TTcos 2a - s sin 2ticos 一 sin 2ft2 2 sin 2a 十世比 cos 2a-cns2n — sin 2n2 { 2--- »JH 2<t + cxjb 2u2谢谢观看! 欢迎您的下载，资料仅供参考，如有雷同纯属意外。

工程常用计算资料及公式

工程常用计算资料及公式在工程领域，常用计算资料及公式非常重要，它们可以帮助工程师解决各种问题和优化设计。

以下是一些常用的计算资料及公式。

1.工程力学-力等于质量乘以加速度：F = ma-力矩等于力乘以力臂：M=Fd-应力等于力除以面积：σ=F/A-应变等于变形除以初始尺寸：ε=ΔL/L-杨氏模量等于应力除以应变：E=σ/ε-密度等于质量除以体积：ρ=m/V2.静力学-万有引力定律：F=G(m1m2/r^2)-压力等于力除以面积：P=F/A-浮力等于体积乘以液体密度乘以重力加速度：F=ρVg3.材料力学-杨氏模量（弹性模量）：E=σ/ε-屈服应力：σy-断裂应力：σf-断裂伸长率：A%-泊松比：v4.流体力学-连续性方程：A1v1=A2v2-质量流率：ṁ=ρAv-动量守恒定律：F=Δp/Δt=ṁ(v2-v1)-伯努利方程：P + 0.5ρv^2 + ρgh = 常数5.热力学-热传导定律：Q=kA(ΔT/Δx)-热功公式：W=PΔV-理想气体状态方程：PV=nRT-热效率：η=W/Q6.电学-欧姆定律：V=IR-功率公式：P=IV-电阻公式：R=ρL/A-电容公式：C=Q/V7.结构力学-弯曲力矩：M=FL-悬臂梁最大弯曲应力：σmax = 3FL/2bd^28.照明工程-照度公式：E = F/(Acosθ)-灯具功率计算：P=E×A/η9.水力学-窄缝流量公式：Q = (2gh)^0.5×b×L/12-斜坡水射流距离：D=(K×Q^2/g)^0.33310.传热-对流传热公式：Q=hA(Ts-T∞)-热导率公式：Q=kA(ΔT/ΔX)以上是一些常用的计算资料及公式，用于解决和优化各种工程问题。

这些公式和资料在工程实践中非常有用，可以帮助工程师进行设计、分析和优化。

工程师应始终熟悉这些公式，并根据具体情况进行适当的应用。

工程力学公式总概括

工程力学公式:3、伸长率：¥ 1。

％断面收缩率:5、扭转切应力表达式：r，最大切应力：max ^R Wp，d4 4I p ”（1）W P叭1 4），强度校核:16 maxT maxW p[]6、单位扭转角： d 亠，刚度校核：max - T max[]，长度为1dx V G I p Gl P式：Me 9549P（KW1n（r/min）8平面应力状态下斜截面应力的一般公式:9、- -—-cos2 x sin22 2-- sin 2 x cos22平面应力状态三个主应力:II 「（x2y）22，''' 0最大切应力IImax （七丄）22，最大正应力方位1、轴向拉压杆件截面正应力A，强度校核max2、轴向拉压杆件变形I F Nil i4、胡克定律：E，泊松比: ，剪切胡克定律：G的一段轴两截面之间的相对扭转角TIGl扭转外力偶的计算公7、薄壁圆管的扭转切应力: T2 R2tan210、第三和第四强度理论:r3 .2 4 2，「4 、•211、平面弯曲杆件正应力: M '截面上下对称时'W Z矩形的惯性矩表达式：i Z兽圆形的惯性矩表达式:I zV(164矩形的抗扭截面系数：W Z竽，圆形的抗扭截面系数: WZ4)13、平面弯曲杆件横截面上的最大切应力:maxS*zmaxbi z14、平面弯曲杆件的强度校核：（1）弯曲正应力t max [ t]，cmax c] （2）弯曲切应力max[]（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法竽 [w]，max []16、（1）轴向载荷与横向载荷联合作用强度:( ) F N M maxmax ( min 丿A W z（2）偏心拉伸（偏心压缩）:max ( min )F NA W z（3）弯扭变形杆件的强度计算:W z"0柯2 2y2 2M z 0.75T简支梁在各种荷载作用下跨中最大挠度计算公式:均布荷载下的最大挠度在梁的跨中，其计算公式:Ymax = 5ql八4/(384EI).式中:Ymax为梁跨中的最大挠度(mm).q为均布线荷载标准值(kn/m).E为钢的弹性模量，对于工程用结构钢，E = 2100000 N/mm八2.I为钢的截面惯矩，可在型钢表中查得(mm A4).跨中一个集中荷载下的最大挠度在梁的跨中，其计算公式: Ymax = 8pl A3/(384EI)=1pl A3/(48EI).式中:Ymax为梁跨中的最大挠度(mm).p为各个集中荷载标准值之和(kn).E为钢的弹性模量，对于工程用结构钢，E = 2100000 N/mmA2.I为钢的截面惯矩，可在型钢表中查得(mmA4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中其计算公式:Y max = 6.81p|A3/(384EI).式中:Ymax为梁跨中的最大挠度(mm).p为各个集中荷载标准值之和(kn).E为钢的弹性模量，对于工程用结构钢，E = 2100000 N/mmA2.I为钢的截面惯矩，可在型钢表中查得(mmA4).跨间等间距布置三个相等的集中荷载下的最大挠度，其计算公式:Y max = 6.33pl八3/(384EI).式中:Ymax为梁跨中的最大挠度(mm).p为各个集中荷载标准值之和(kn).E为钢的弹性模量，对于工程用结构钢，E = 2100000 N/mm八2.I为钢的截面惯矩，可在型钢表中查得(mm A4).悬臂梁受均布荷载或自由端受集中荷载作用时，自由端最大挠度分别为的，其计算公式:Ymax =1ql A4/(8EI). ;Ymax =1pl A3/(3EI).q为均布线荷载标准值(kn/m). ;p为各个集中荷载标准值之和(kn).你可以根据最大挠度控制1/400,荷载条件25kn/m以及一些其他荷载条件进行反算，看能满足的上部荷载要求！机械零件和构件的一种截面几何参量，旧称截面模量。

工程力学公式复习大全

工程力学公式复习大全第一章静力学的基本概念和公理及受力图P2 刚体力的三要素：大小、方向、作用点静力学公理：1力的平行四边形法则2二力平衡条件3加减平衡力系原理（1）力的可传性原理（2）三力平衡汇交定理4作用与反作用定律P7 约束：柔索约束；光滑面约束；光滑圆柱（圆柱、固定铰链、向心轴承、辊轴支座）；链杆约束（二力杆）第二章平面汇交力系P16 平面汇交力系平衡几何条件：力多边形自行封闭P19 合力投影定理P20平面汇交力系平衡条件：∑F ix=0；∑F iy=0。

2个独立平衡方程第三章力矩平面力偶系P24 力矩M0(F)=±Fh(逆时针为正) P25 合力矩定理P26力偶；力偶矩M=±Fd(逆时针为正)P27力偶的性质：力偶只能用力偶平衡P28 平面力偶系平衡条件第四章平面任意力系P33 力的平移定理 P34 平面力向力系一点简化P36 平面任意力系平衡条件：∑F ix =0；∑F iy =0，∑M 0(Fi)=0。

3个独立方程 P38平面平行力系平衡条件：2个独立方程P39 静定，超静定P43 摩擦，静摩擦力，动摩擦力第五章空间力系重心P53 空间力系平衡条件：6个方程；空间汇交力系：3个方程；空间平行力系：3个方程第六章点的运动P64 质点 P65 点的速度dtds v =，加速度：切向加速度dtdv a =τ，速度大小变化；法向加速度ρ2v a n =，速度方向变化，加速度22n a a a +=τ第七章刚体的基本运动P73 平动 P74转动，角速度dt d ϕω=，角加速度dtd ωα=，角速度n πω2=(n 是转速，r/s)P76 转动刚体内各点的速度ωR v =，加速度2ωατR a R a n ==，第九章刚体动力学基础P87 质心运动定理：e F ma ∑=P88转动定理z z M J ∑=α，转动惯量：圆环2mR J z =；圆盘2/2mR J z =；细杆12/2ml J z =。

工程力学公式概括

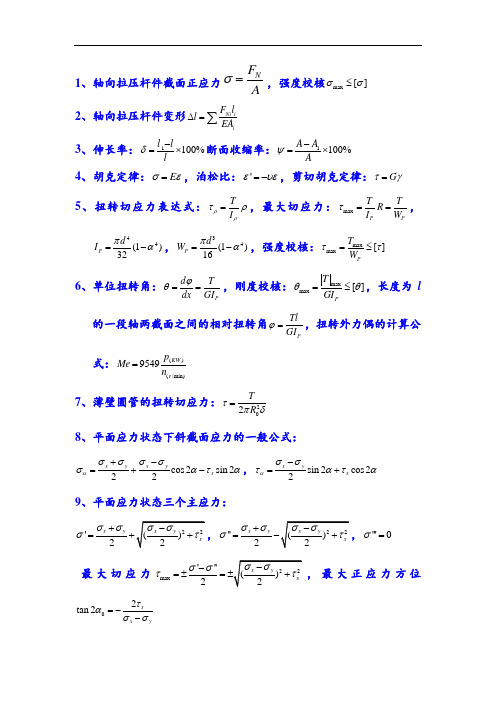
1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤ 2、轴向拉压杆件变形Ni i i F l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯ 4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ=5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P P T T R I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：max max []PT W ττ=≤ 6、单位扭转角：P d T dx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角P Tl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202T R τπδ=8、平面应力状态下斜截面应力的一般公式： cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=+''2x y σσσ+='''0σ= 最大切应力max '''2σστ-=±=，最大正应力方位02tan 2x x y τασσ=--10、第三和第四强度理论：3r σ=，4r σ=11、平面弯曲杆件正应力：Z My I σ=，截面上下对称时，ZM W σ= 矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=- 矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=- 13、平面弯曲杆件横截面上的最大切应力：max max *S z S Z F S F K bI Aτ== 14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w w l l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： max max min ()N Z F M A W σσ=± （2）偏心拉伸(偏心压缩)：max min ()N Z F F A W δσσ=± （3）弯扭变形杆件的强度计算：3[]r Zσσ==≤4[]r Z σσ==≤。

工程力学单位换算公式大全

工程力学单位换算公式大全
工程力学中常见的单位包括长度单位（米、厘米、毫米等）、质量单位（千克、克等）、力单位（牛顿、千克力等）等。

下面我会列举一些常见的工程力学中的单位换算公式，希望能对你有所帮助。

1. 长度单位换算公式：
1米 = 100厘米。

1米 = 1000毫米。

1千米 = 1000米。

2. 质量单位换算公式：
1千克 = 1000克。

1千克 = 2.20462磅。

1克 = 0.001千克。

3. 力单位换算公式：
1牛顿 = 1千克·米/秒^2。

1牛顿 = 0.22481磅力。

1千克力 = 9.80665牛顿。

以上是一些工程力学中常见的单位换算公式，希望对你有所帮助。

如果你需要更多单位的换算公式或者其他方面的帮助，请随时告诉我。

工程力学公式总结

工程力学公式总结工程力学是物理学的一个分支，研究物体在受力作用下的运动、变形和它们之间的关系。

它是工程学科中不可或缺的基础课程，应用广泛，涉及到力学、材料力学、结构力学、固体力学等领域。

在学习工程力学过程中，我们会遇到许多公式，这些公式是我们解决工程力学问题的重要工具。

下面我来总结一些常用的工程力学公式，希望能对大家的学习有所帮助。

1. 牛顿第二定律：F = ma牛顿第二定律描述了物体在外力作用下的加速度与力的关系。

其中，F代表力，m代表物体的质量，a代表物体的加速度。

这个公式在力学问题的求解中经常使用。

2. 力的合成与分解：当一个物体受到多个力的作用时，可以将这些力合成为一个合力。

合力的大小等于各个力的矢量和。

同时，也可以将一个力分解为两个或多个分力，分力的矢量和等于原力。

3. 力矩与力矩平衡条件：力矩是力对物体转动产生的影响。

力矩等于力的大小与力臂的乘积。

力矩的方向符合右手螺旋定则。

力矩平衡条件要求物体受到的所有力矩的矢量和为零，即力矩的代数和为零。

4. 刚体静力平衡条件：刚体静力平衡要求物体受到的所有力的矢量和为零，即力的代数和为零。

这个条件可以用于解决静力学问题，确定物体的受力情况。

5. 牛顿万有引力定律：F = G * (m1 * m2) / r^2牛顿万有引力定律描述了两个物体之间的引力的大小与它们之间的距离和质量有关。

其中，F代表引力，G为引力常数，m1和m2分别为两个物体的质量，r为它们之间的距离。

6. 弹性力学公式：弹性力学公式用于描述物体在受力下的弹性变形。

其中，Hooke定律描述了弹性材料的应力与应变之间的关系，即σ = E * ε。

这里，σ代表应力，E为杨氏模量，ε代表应变。

7. 杆件受拉伸或压缩的应力公式：当杆件受拉伸或压缩时，应力的大小与外力、截面积和材料性质有关。

受拉伸时，应力的大小等于外力除以截面积；受压缩时，应力的大小等于外力除以截面积的负值。

8. 曲杆弯曲公式：曲杆弯曲公式描述了杆件在受弯矩作用下的弯曲变形。

工程力学重点公式

刚体：在力的作用下不会发生形变的物体。

合力投影定理：合力在任一轴上的投影，等于各分力在该轴上投影的代数和。

力矩M 0(F)=±Fh(逆时针为正)，点O 为矩心，垂直距离h 为力臂，力使物体逆时针转动为正。

合力矩定理：平面汇交力系的合力对平面内任一点的矩，等于所有各分力对同一点的矩的代数和。

力偶：大小相等、方向相反，作用线平行且不共线的两个力组成的力系称为力偶；平面力偶系：作用在刚体上同一平面内的多个力偶，称为平面力偶系。

力的平移定理：作用于刚体上的力可以平行移动到刚体内的任意一点，但必须附加一个力偶，该附加力偶的力偶矩等于原力对指定点的矩。

平面任意力系中各力的矢量和F R `称为该力系的主矢量，简称主矢；力系各力对简化中心O 的矩的代数和Mo 称为该力系对简化中心O 的主矩。

平面任意力系平衡的必要和充分条件是：力系的主矢和对任意一点的主矩都等于零。

地心对物体的吸引力称为物体的重力，其大小就是物体的重量。

物体重力的作用点称为物体的重心。

由物体的几何形状和尺寸所决定的点是物体的几何中心，称为物体的形心。

强度（构件抵抗破坏的能力刚度（构件抵抗变形的能力稳定性（构件保持原有平衡形式的能力连续性假设（认为组成变形固体的物质毫无间隙地充满了它的整个几何空间，而且变形后仍保持这种连续性。

）、均匀性假设（认为整个物体是由同一材料组成。

）、各向同性假设（认为物体在各个方向具有相同的物理性质）、内力：因外力作用而引起构件内各部分之间相互作用力的改变量，称为附加内力，简称内力。

全应力：dAdF=P ，通常把全应力p 分解为垂直于截面的分量σ（正应力）和与截面相切的分量τ（切应力）。

第十二章轴向拉伸与压缩一、拉伸与压缩的概念：杆件所受外力（或外力的合力）作用线与杆轴线重合；杆件的变形为轴线方向的伸长或缩短。

这种变形形式称为轴向拉伸或轴向压缩。

线应变：l l∆=ε，胡克定律εσE =或EAl F l N =∆，E 是材料拉压弹性模量，E A 是材料抗拉压刚度横向线应变μεε-=`，μ是泊松比1、低碳钢在拉伸时四个阶段（1）弹性阶段（2）屈服阶段（3）强化阶段（4）局部变形阶段%1001⨯-=lll δ，衡量材料塑性的另一指标是断面收缩率ψ，%1001⨯-=AA A ψ塑性材料（如低碳钢）通常以屈服极限为其极限应力。

工程力学公式大全

扬州科技学院工程力学资料工程力学公式：1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤2、轴向拉压杆件变形Ni i iF l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯ 4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ= 5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P PT TR I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：maxmax []PT W ττ=≤ 6、单位扭转角：Pd Tdx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角PTl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202TR τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=，''2x yσσσ+='''0σ=最大切应力max '''2σστ-=±=，最大正应力方位02tan 2x x yτασσ=--10、第三和第四强度理论：3r σ=4r σ=11、平面弯曲杆件正应力：ZMy I σ=，截面上下对称时，ZM W σ=矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=-矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=-13、平面弯曲杆件横截面上的最大切应力：max max *S z SZ F S FK bI Aτ==14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w wl l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： maxmax min ()N ZF M A W σσ=±（2）偏心拉伸(偏心压缩)：max min ()N ZF F A W δσσ=±（3）弯扭变形杆件的强度计算：22222311[]r y z Z M T M M T W W σσ=+=++≤222224110.750.75[]r y z ZZM T M M T W W σσ=+=++≤机械制图方面=>齿轮计算公式1 齿轮模数：m=p/π齿轮模数m=齿距p 除以 3.14测绘时的简易计算m=齿顶圆直径（外径）d 除以（齿数z+2）2 齿轮分度圆直径：d=mz分度圆直径d=模数m 乘以齿数z3 齿轮压力角：标准齿轮的压力角为20度压力角标准为20度其他还有14.5度17.5度15度25度和28度4 齿轮变位系数：用范成法加工齿轮时，刀具中心线不与齿轮的分度圆相切，刀具中心与齿轮的分度圆的距离除以模数所得的商就是齿轮的变位系数。

工程力学公式

（压）扭转平面弯曲应力xsAx N )(=s Ot rpI T r r t =)(zx I My =s s txy zzy bI QS *=t Q][m ax m axs s ≤=AN ][m ax m axt t ≤=tW T ][m ax m axs s ≤=ZW M ][m ax t t ≤332016D.D R I W p t ≈==π16)1(43απ-==D R I W p t 324dI p π=对于实心圆截面：dO对于空心圆截面：)1(32)(32 4444αππ-=-=D d D I p )(Dd =αdD644dI I y z π==323dW W y z π==)1(3243απ-=DW z ybh123bh I z =62bh W z =Aa I I yC y 2+=平行移軸公式：nn （合力）（合力）P PP c n nQ剪切与挤压的实用计算[]t t ≤=AQ[]jyjyjy jy A F s s ≤=⎪⎪⎩⎪⎪⎨⎧+-=--++=αt αs s t αt αs s s s s αα2cos 2sin 22sin 2cos 22xy y x xy y x y x xy s xt xys y Os αt αα平面内的主应力yx xys s t α--=22tg 0xys xt xy s yO主单元体1s '2s '）2222xyy x y x minmax t s s s s s s +-±+=⎩⎨⎧（或3s t222x y y x minmax t s s t t +-±=⎩⎨⎧''）（045成最大剪应力面与主平面拉压扭转平面弯曲变形Lxx EA x F L L N d )()(⎰=∆ABpABGI Tl =ϕq= f ´y=fEIx M x y )()(=''qyx y∑=∆EALF L N ][m ax m axq q ≤=pGI T []njxs s=:1、容许应力},,2.0{ :2b s jx s s s s =、极限应力）εεμ'=γt =G εs =E Gijij t γ=()[]k j i i Es s μs ε+-=1),,,,(z y x k j i =（广义虎克定律）AP crcr =s 1.临界力和临界应力3.其中：2.压杆的临界应力：—惯性半径。