【2021高考数学】第2节 简单几何体的表面积和体积
立体几何的表面积和体积

立体几何的表面积和体积立体几何是数学的一个分支,研究物体在三维空间中的形状、大小等性质。
其中,表面积和体积是两个重要的概念。
表面积指的是物体表面所覆盖的面积,而体积则是物体所占据的空间大小。
本文将详细探讨立体几何中表面积和体积的计算方法及其应用。
一、表面积的计算方法表面积是指立体物体表面所覆盖的总面积。
不同形状的物体有不同的计算方法,下面将分别介绍常见几何体的表面积计算方法。
1. 立方体的表面积计算立方体是最简单的几何体之一,其六个面都是相等的正方形。
因此,立方体的表面积可以通过计算一个面的面积,并乘以六来得到。
设立方体的边长为a,则其表面积S可以表示为S = 6a^2。
2. 正方体的表面积计算正方体是特殊的立方体,其六个面也都是正方形。
同样地,正方体的表面积可以通过计算一个面的面积,并乘以六来得到。
设正方体的边长为a,则其表面积S = 6a^2。
3. 圆柱体的表面积计算圆柱体由一个长方形的侧面和两个圆形的底面组成。
要计算圆柱体的表面积,需要先计算侧面的面积,然后再加上两个底面的面积。
设圆柱体的底面半径为r,高为h,则侧面的面积可以表示为A = 2πrh,底面的面积表示为B = πr^2。
因此,圆柱体的表面积S = A + 2B = 2πrh + 2πr^2。
4. 球体的表面积计算球体是具有最大体积的几何形状,其表面积的计算稍微复杂一些。
设球体的半径为r,则球体的表面积S = 4πr^2。
二、体积的计算方法体积是指立体物体所占据的空间大小。
与表面积类似,不同几何体有不同的计算方法。
1. 立方体的体积计算立方体的体积可以通过计算边长的立方来得到,即V = a^3。
2. 正方体的体积计算正方体的体积与立方体的计算方法相同,也是通过计算边长的立方来得到。
设正方体的边长为a,则它的体积V = a^3。
3. 圆柱体的体积计算圆柱体的体积可以通过计算底面的面积,并乘以高来得到。
设圆柱体的底面半径为r,高为h,则它的体积V = πr^2h。
2021高考数学复习专题 空间几何体的表面积和体积(文 精讲)

专题8.2 空间几何体的表面积和体积【考情分析】1. 了解球、棱柱、棱锥、台的表面积和体积的计算公式. 【重点知识梳理】知识点一 圆柱、圆锥、圆台的侧面展开图及侧面积公式知识点二 柱、锥、台、球的表面积和体积【知识必备】1.设正方体的棱长为a ,则它的内切球半径r =a 2,外接球半径R =32a .2.设长方体的长、宽、高分别为a ,b ,c ,则它的外接球半径R =a 2+b 2+c 22.3.设正四面体的棱长为a ,则它的高为63a ,内切球半径r =612a ,外接球半径R =64a . 4.直棱柱的外接球半径可利用棱柱的上下底面平行,借助球的对称性,可知球心为上下底面外接圆圆心连线的中点,再根据勾股定理求球的半径.【典型题分析】高频考点一 空间几何体的的表面积【例1】(2020·新课标Ⅰ)已知A 、B 、C 为球O球面上的三个点,Ⅰ1O 为ABC 的外接圆,若Ⅰ1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π【变式探究】(2020·北京卷)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A 63+ B. 623+C. 123+D. 1223+【方法技巧】求空间几何体表面积的常见类型及思路【变式探究】(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .122πB .12πC .82πD .10π高频考点二 空间几何体的体积的.【例2】(2020·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A. 73B.143C. 3D. 6【变式探究】【2019·北京卷】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【变式探究】(2018·天津卷)已知正方体ABCD -A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M -EFGH 的体积为________.高频考点三 割补法求体积【例3】(2017·全国卷Ⅰ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π【方法技巧】把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积。
2021人教A版高考数学总复习《空间几何体的表面积和体积》

∴V 多面体=VE-ADG+VF-BHC+VAGD-BHC=2VE-ADG+VAGD-BHC=13
×
42×12×2+
42×1=
2 3.
答案
2 3
规律方法 1.(直接法)规则几何体:对于规则几何体,直接利用公式计算即可.若已 知三视图求体积,应注意三视图中的垂直关系在几何体中的位置,确定几何体中的 线面垂直等关系,进而利用公式求解. 2.(割补法)不规则几何体:当一个几何体的形状不规则时,常通过分割或者补形的手 段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.经常考虑将 三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体. 3.(等积法)三棱锥:利用三棱锥的“等积性”可以把任一个面作为三棱锥的底面. (1)求体积时,可选择“容易计算”的方式来计算;(2)利用“等积性”可求“点到面 的距离”,关键是在面中选取三个点,与已知点构成三棱锥.
面正方形对角线的一半.因为四棱锥的底面正方形的边长为 2,所以底面正方形对角
线长为 2,所以圆柱的底面半径为12.又因为四棱锥的侧棱长均为 5,所以四棱锥的
高为 ( 5)2-12=2,所以圆柱的高为 1.所以圆柱的体积 V=π122×1=π4.
答案
π 4
角度3 不规则几何体的体积 【例2-3】 如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且
角度2 简单几何体的体积 【例 2-2】 (2019·天津卷)已知四棱锥的底面是边长为 2的正方形,侧棱长均为 5.
若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱
锥底面的中心,则该圆柱的体积为________. 解析 由题意知圆柱的高恰为四棱锥的高的一半,圆柱的底面直径恰为四棱锥的底
高中数学必修二 8 简单几何体的表面积与体积(精讲)(含答案)

8.3 简单几何体的表面积与体积(精讲)考点一 旋转体的体积【例1】(2021·山东莱西·高一期末)在ABC 中,2AB =,32BC =,120ABC ∠=︒,若将ABC 绕BC 边所在的直线旋转一周,则所形成的面围成的旋转体的体积是______. 【答案】32π 【解析】依题意可知,旋转体是一个大圆锥去掉一个小圆锥,所以sin 602OA AB =︒==,1cos60212OB AB =︒=⨯=,所以旋转体的体积:()21332V OC OB ππ=⋅⋅-=故答案为:32π. 【一隅三反】1.(2021·湖南省邵东市第三中学高一期中)圆台上、下底面面积分别是π、4π积是( )A B .C D 【答案】D【解析】由题意1(4)3V ππ=+=.故选:D .2.(2021·山东任城·高一期中)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周六尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为6尺,米堆的高为5尺,问堆放的米有多少斛?”已知1斛米的体积约为1.6立方尺,圆周率约为3,估算出堆放的米约有_______斛.【答案】12.5【解析】设圆柱的底面半径为r 尺,则14⨯2πr =6,∴r ≈4,∴圆锥的体积V =21134543⨯⨯⨯⨯=20立方尺,∴堆放的米约有201.6=12.5斛. 故答案为:12.5.3.(2021·上海市七宝中学)已知圆锥的侧面展开图是半径为2的半圆,则圆锥的体积为________.【解析】由题意圆锥的母线长为2l =,设圆锥底面半径为r ,则22r ππ=,1r =,所以高为h体积为2211133V r h ππ==⨯=..考点二 旋转体的表面积【例2】(2021·吉林·延边二中高一期中)如图,圆锥的底面直径和高均是4,过PO 的中点O '作平行于底面的截面,以该截面为底面挖去一个圆柱,(1)求剩余几何体的体积 (2)求剩余几何体的表面积【答案】(1)103π;(2)8π+. 【解析】(1)由题意知,因为O '为PO 的中点,所以挖去圆柱的半径为1,高为2,剩下几何体的体积为圆锥的体积减去挖去小圆柱的体积, 所以22110241233V πππ=⋅⨯⨯-⨯⨯=.(2)因为圆锥的底面直径和高均是4,所以半径为2,母线l =所以圆锥的表面积为2122(4S πππ=⨯+⨯⨯+, 挖去的圆柱的侧面积为:22124S ππ=⨯⨯=,所以剩余几何体的表面积为12(4+4+8S S S πππ==+=+. 【一隅三反】1.(2021·广东·仲元中学高一期中)已知一个母线长为1的圆锥的侧面展开图的圆心角等于240︒,则该圆锥的侧面积为( )A B .881πCD .23π【答案】D【解析】将圆心角240︒化为弧度为:43π,设圆锥底面圆的半径为r 由圆心角、弧长和半径的公式得:4213r ππ=⨯,即23r = 由扇形面积公式得:22133S ππ=⨯⨯=所以圆锥的侧面积为23π.故选:D.2.(2021·全国·高一课时练习)已知圆台的上、下底面半径分别为10和20,它的侧面展开图的扇环的圆心角为180°,则这个圆台的侧面积为( ) A .600π B .300π C .900π D .450π【答案】A【解析】圆台的上底面圆半径10r '=,下底面圆半径20r =,设圆台的母线长为l ,扇环所在的小圆的半径为x ,依题意有:220()210l x x ππππ⨯=+⎧⎨⨯=⎩,解得2020x l =⎧⎨=⎩,所以圆台的侧面积20()()1020600+S r r l πππ'=⨯=+=. 故选:A3(2021·全国·高一课时练习)圆台的上、下底面半径和高的比为1:4:4,若母线长为10,则圆台的表面积为________. 【答案】168π【解析】圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,高为h 则4h R r ==,则它的母线长为510l r =, 所以2r,8R =.故()(82)10100S R r l πππ=+=+⨯=侧,22100464168S S r R ππππππ=++=++=表侧.故答案为:168π考点三 多面体的体积【例3-1】(2021·全国·高一课时练习)如图所示,正方体ABCD-A 1B 1C 1D 1的棱长为1,则三棱锥D-ACD 1的体积是( )A .16B .13C .1 2D .1【答案】A【解析】三棱锥D-ACD 1的体积等于三棱锥D 1-ACD 的体积,三棱锥D 1-ACD 的底面ACD 是直角边长为1的等腰直角三角形,高D 1D=1,∴三棱锥D-ACD 1的体积为V=1132⨯×1×1×1=16.故选:A【例3-2】(2021·全国·高一课时练习)若正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14,则棱台的高度为( ) A .8 B .4C .2D .【答案】C【解析】如图,设棱台的上、下底面边长分别为2x ,8x ,斜高h '为5x ,则棱台的高h x ,由棱台的体积公式1()3V S S h '=得:2224161)31(6444++x x x x ⋅=,解得12x =,棱台的高为h =4x =2. 故选:C 【一隅三反】1.(2021·全国·高一课时练习)设四棱锥的底面是对角线长分别为2和4的菱形,四棱锥的高为3,则该四棱锥的体积为( ) A .12 B .24 C .4 D .30【答案】C【解析】所求的体积为11324432⨯⨯⨯⨯=,故选:C.2.(2021·全国·高一课时练习)棱台的上、下底面面积分别是2,4,高为3,则棱台的体积等于( )A .6B .3+C .6+D .6【答案】C【解析】依题意,棱台的上底面面积2S '=,下底面面积4S =,高为3h =,故由公式可知,棱台的体积是()()11243633V S S h '==⨯⨯=+ 故选:C.3.(2021·全国·高一课时练习)若一个四棱锥的底面的面积为3,体积为9,则其高为( ) A .13B .1C .3D .9【答案】D【解析】设四棱锥的高为h ,则由锥体的体积公式得:13×3h =9,解得h =9,所以所求高为9. 故选:D4.(2021·广东·仲元中学高一期中)如图所示,在长方体ABCD A B C D ''''-中,用截面截下一个棱锥C A DD '''-则棱锥C A DD '''-的体积与剩余部分的体积之比为( )A .1:5B .1:4C .1:3D .1:2【答案】A【解析】由图知:13C A DD A DD V C D S'''''-''=⋅⋅,ABCD A B C D A D DA V C D S ''''''-''=⋅,而2A D DA A DD S S''''=,∴剩余部分的体积为53ABCD A B C D C A DD A DD V V C D S'''''''''--''-=⋅,∴棱锥C A DD '''-的体积与剩余部分的体积之比为1:5.故选:A考点四 多面体的表面积【例4】(2021·全国·高一课时练习)正六棱柱的底面边长为2,最长的一条对角线长为积为()A .4)B .2)C .1)D .8)【答案】B【解析】正六棱柱的底面边长为2,最长的一条对角线长为12BB =,它的表面积为)16=2622sin 6222412223S S S π=+⨯⨯⨯⨯⨯+⨯⨯==表面积底面积矩形.故选:B. 【一隅三反】1.(2021·全国·高一课时练习)若六棱柱的底面是边长为3的正六边形,侧面为矩形,侧棱长为4,则其侧面积等于( ) A .12 B .48 C .64 D .72【答案】D【解析】六棱柱的底面是边长为3的正六边形, 故底面周长6318C =⨯=, 又侧面是矩形,侧棱长为4, 故棱柱的高4h =,∴棱柱的侧面积72S Ch ==,故选:D2.(2021·全国·高一课时练习)如图,在正方体ABCD -A 1B 1C 1D 1中,三棱锥D 1AB 1C 的表面积与正方体的表面积的比为( )A .1∶1B .1C .1D .1∶2【答案】C【解析】设正方体的边长为a ,则表面积216S a =,因为三棱锥11D AB C -的各面均是正三角形,其边长为正方体侧面对角线.,三棱锥D 1AB 1C 的表面积)222142S =⨯⨯=,所以2221::6S S a ==故选:C3(2021·全国·高一课时练习)长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( ) A .12,32 B .12,24 C .22,12 D .12,11【答案】A【解析】长方体的体积为22312⨯⨯=,表面积为()222+23+2332⨯⨯⨯=, 故选:A.4.(2021·全国·高一课时练习)(多选)正三棱锥底面边长为3,侧棱长为则下列叙述正确的是( )A .正三棱锥高为3 BC D 【答案】ABD【解析】设E 为等边三角形ADC 的中心,F 为CD 的中点,连接,,PF EF PE , 则PE 为正三棱锥的高,PF 为斜高,又PF ==32EF ==,故3PE ==, 故AB 正确.而正三棱锥的体积为1393⨯=,侧面积为1332⨯⨯=故C 错误,D 正确. 故选:ABD.5(2021·全国·高一课时练习)(多选)在正方体1111ABCD A B C D -中,三棱锥11D AB C -的表面积与正方体的表面积的比不可能是( )A .1:1B .C .D .1:2【答案】ABD【解析】设正方体1111ABCD A B C D -的棱长为a ,则正方体1111ABCD A B C D -的表面积为226S a =.三棱锥11D AB C -的正四面体,其中一个面的面积为212S ==,则三棱锥11D AB C -的表面积为2214S ==所以三棱锥11D AB C -的表面积与正方体的表面积的比为22126S S a ==::故选:ABD.考点五 有关球的计算【例5-1】(2021·全国·高一课时练习)长方体的三个相邻面的面积分别是2,3,6,这个长方体的顶点都在同一个球面上,则这个球的表面积为( ) A .72π B .56π C .14π D .16π【答案】C【解析】设长方体的三条棱长分别为a ,b ,c ,由题意得236ab ac bc =⎧⎪=⎨⎪=⎩,得123a b c =⎧⎪=⎨⎪=⎩∴2414S R ππ球==. 故选:C【例5-2】(2021·广东高州·高一期末)已知正四面体ABCD的表面积为A 、B 、C ,D 四点都在球O 的球面上,则球O 的体积为( ) A. BCD .3π【答案】C【解析】正四面体各面都是全等的等边三角形,设正四面体的棱长为a ,所以该正四面体的表面积为2142S a =⨯⨯=,所以a =1, 所以正方体的外接球即为该正四面体的外接球,O 的体积为343π⨯=⎝⎭. 故选:C. 【一隅三反】1.(2021·全国·高一课时练习)表面积为16π的球的内接轴截面为正方形的圆柱的体积为( )A .B .C .16πD .8π【答案】A【解析】由题意可知,4πR 2=16π,所以R =2,即球的半径R =2.设圆柱的底面圆半径为r 2R =,即2816r =,所以r ,∴V 圆柱=πr 2·2r =2π·π.故选:A.2.(2021·全国·高一课时练习)若一个正方体内接于表面积为4π的球,则正方体的表面积等于( )A .B .8C .D .【答案】B【解析】设正方体棱长为x ,球半径为R ,则24π4πS R ==球,解得1R =,22R ==,解得x =所以该正方体的表面积为22668S x ==⨯=正.故选:B.3.(2021·全国·高一课时练习)(多选)我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知半球内有一个方锥,方锥的底面内接于半球的底面,方锥的顶点在半球的球面上,若方锥的体积为18,则半球的说法正确的是( ) A .半径是3 B .体积为18π C .表面积为27π D .表面积为18π【答案】ABC【解析】如图,PAC △是正四棱锥的对角面,设球半径为r ,AC 是半圆的直径,,棱锥体积为2312)1833V r r =⨯⨯==,3r =,半球体积为332231833V r πππ==⨯=,表面积为2223327S πππ=⨯+⨯=, 故选:ABC .4.(2021·全国·高一课时练习)一个球内有相距9cm 的两个平行截面,它们的面积分别为249cm π和2400cm π2,求球的体积和表面积.【答案】球的表面积为22500cm π,球的体积为362500cm 3π. 【解析】(1)当截面在球心的同侧时,如图①所示为球的轴截面,由截面性质知12AO //BO ,1O ,2O 为两截面圆的圆心,且11OO AO ⊥,22OO BO ⊥,①设球的半径为R ,因为2249O B ππ=,所以27cm O B =,同理得120cm O A =.设1cm OO x =,则2(9)cm OO x =+, 在1Rt O OA 中,22220R x =+,① 在2Rt OO B 中,2227(9)R x =++,② 联立①②可得15x =,25R =.所以2242500cm S R ππ==球,33462500cm 33V R ππ==球.(2)当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,12O A//O B ,1O ,2O 分别为两截面圆的圆心,且11OO O A ⊥,22OO O B ⊥.②设球的半径为R ,因为2249O B ππ⋅=,所以27cm O B =.因为21400O A ππ⋅=,所以120cm O A =.设1cm O O x =,则2(9)cm OO x =-. 在1Rt OO A △中,22400R x =+,在2Rt OO B 中,22(9)49R x =-+, 所以22400(9)49x x +=-+, 解得15x =-(不合题意,舍去) 综上所述,球的表面积为22500cm π. 球的体积为362500cm 3π. 考点六 综合运用【例6】(2021·全国·高一课时练习)一块边长为12cm 的正三角形薄铁片,按如图所示设计方案,裁剪下三个全等的四边形(每个四边形中有且只有一组对角为直角),然后用余下的部分加工制作成一个“无盖”的正三棱柱(底面是正三角形的直棱柱)形容器.(1)请将加工制作出来的这个“无盖”的正三棱柱形容器的容积V 表示为关于x 的函数,并标明其定义域; (2)若加工人员为了充分利用边角料,考虑在加工过程中,使用裁剪下的三个四边形材料恰好拼接成这个正三棱柱形容器的“顶盖”.请指出此时x 的值(不用说明理由),并求出这个封闭的正三棱柱形容器的侧面积S .【答案】(1)323(012)82x V x x =-+<<;(2)6cm x =,2S =侧.【解析】(1)结合平面图形数据及三棱柱直观图,求得三棱柱的高6cm 2x h ⎫=-⎪⎝⎭,其底面积22cm S =,则三棱柱容器的容积232236624282x x x x V Sh x x ⎫⎛⎫==-=-=-+⎪ ⎪⎝⎭⎝⎭, 即所求函数关系式为323(012)82x V x x =-+<<;(2)此时6cm x =,而相应棱柱的高h ,故侧面积为236S =⨯=. 【一隅三反】1.(2021·安徽镜湖·高一期中)如图所示,在边长为5的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥的底面,围成一个圆锥,求该圆锥的表面积与体积.【答案】表面积10π. 【解析】设圆的半径为r ,扇形的半径为R ,由题意,得(522R r Rr ππ⎧+=⎪⎨=⎪⎩,解得r R ⎧=⎪⎨=⎪⎩所以围成的圆锥的母线长为l =r =h ∴圆锥的表面积210S rl r πππ=+=;∴圆锥的体积为213V r h π==.2.(2021·全国·高一课时练习)有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,求该塔形的表面积(含最底层正方体的底面面积).【答案】36【解析】易知由下向上三个正方体的棱长依次为2,1.考虑该几何体在水平面的投影,可知其水平投影面积等于下底面最大正方体的底面面积.∴S 表=2S 下+S 侧=2×22+4×[22+2+12]=36, ∴该几何体的表面积为36.3.(2021·全国·高一课时练习)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m ,高为4 m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大4 m (高不变);二是高度增加4 m (底面直径不变). (1)分别计算按这两种方案所建的仓库的体积; (2)分别计算按这两种方案所建的仓库的表面积; (3)哪个方案更经济些?【答案】(1)2563π(m 3),96π(m 3);(m 2),60π(m 2);(3)方案二比方案一更加经济. 【解析】(1)若按方案一,仓库的底面直径变成16 m ,则仓库的体积为V 1=13S ·h=13×π×2162⎛⎫⎪⎝⎭×4=2563π(m 3).若按方案二,仓库的高变成8 m ,则仓库的体积为V 2=13S ·h=13×π×2122⎛⎫⎪⎝⎭×8=96π(m 3).(2)若按方案一,仓库的底面直径变成16 m ,半径为8 m.圆锥的母线长为l 1m ),则仓库的表面积为S 1=π×8×(m 2). 若按方案二,仓库的高变成8 m.圆锥的母线长为l 210(m ), 则仓库的表面积为S 2=π×6×10=60π(m 2).(3)由(1)、(2)知,V 1<V 2,S 2<S 1,故方案二体积更大,表面积更小,所需耗材更少,即方案二比方案一更加经济.。
高中数学高考第2节 空间几何体的表面积与体积 课件

自
素
主 回
H,连接
DG,CH,则原几何体分割为两个三棱锥和一个直三棱柱,
养 提
顾
升
课课ຫໍສະໝຸດ 后堂限考
时
点
集
探
训
究
返 首 页
42
课 前 自
因为三棱锥高为12,直三棱柱高为 1,AG= 12-122= 23,
前
外
自 主
线画出的是某多面体的三视图,则该多面体的表面积为(
)
素 养
回
提
顾
升
课
课
后
堂
限
考
A.18+36 5
点
B.54+18 5
时 集
探 究
C.90
D.81
训
返 首 页
28
课
课
前
外
自
素
主
养
回 顾
B
[由三视图可知该几何体是底面为正方形的斜四棱柱,其中
提 升
有两个侧面为矩形,另两个侧面为平行四边形,则表面积为(3×3+
前
外
自 主 回
故其体积 V=13×12×π×12×3+13×12×2×1×3=π2+1.故选 A.
素 养 提
顾
升
(2)四棱锥 A1-BB1D1D 的底面 BB1D1D 为矩形,其面积 S=1× 2
课
课 堂
=
2,又四棱锥的高为点 A1 到平面 BB1D1D 的距离,即 h=12A1C1=
后 限
考
时
点
集
3×3=3
3.]
后 限 时
点
集
探
训
究
返 首 页
16
课件1:简单几何体的表面积和体积

S 表面积=S 侧+2S 底 S 表面积=S 侧+S 底
V= Sh 1
V= 3Sh
台体 (棱台和圆台)
球
S 表面积=S 侧+S 上+S 下 V=13(S 上+S 下+ S上S下)h
S= 4πR2
V= 43πR3
1.求组合体的表面积时:组合体的衔接部分的面积问 题易出错.
2.易混侧面积与表面积的概念.
的体积,三棱锥 A -B1BC1 的高为 23,底面积为12,故其体
积为13×12×
23=
3 12 .
[答案]
3 12
(2)如图,在长方体 ABCD-A1B1C1D1 中,AB=AD=3 cm, AA1=2 cm,则三棱锥 A-B1D1D 的体积为________ cm3.
[解析] 因为长方体 ABCD-A1B1C1D1 的底面 ABCD 为正方形,
[针对训练] (2013·苏北四市二模)如图,已知正方体 ABCD-A1B1C1D1 的棱长为 2,O 为底面正方 形 ABCD 的中心,则三棱锥 B1-BCO 的体积 为________. 解析:由题意可得 VB1-BCO=13S△BCO×BB1=13×12S△BCD×2=13
×12×2×2×2=43. 答案:43
点都在一个球面上,则球的体积为________.
解析:依题意可知,球心到平面 ABC 的距离为12AA′=1,
平面 ABC 所在圆的半径为12BC= 3,则球的半径为
12+ 3 答案:323π
2=2,则球的体积为43×π×23=323π.
1.(2013·南通三模)底面边长为 2 m,高为 1 m 的正三棱锥的
2R=
OA2+OB2+OC2=
1 2×
2
高考数学高中复习8.2《简单几何体的表面积与体积》知识点讲解PPT课件

【教材回扣】
1.简单几何体的表面积 (1)棱柱、棱锥、棱台的表面积就是各个面的面积的和. (2)圆柱、圆锥、圆台的侧面展开图分别是 矩形 、 扇形 、 扇环 (3)若圆柱、圆锥的底面半径为 r,母线长 l,则其表面积为
S 柱=2πr2+2πrl,S 锥=πr2+πrl (4)若圆台的上下底面半径为 r1,r2,母线长为 l,则圆台的表面 积为 S= π(r12+r22)+π(r1+r2)l (5)球的表面积为 4πR2 (球半径是 R).
二、易错易混 3.圆柱的侧面展开图是边长为 6π 和 4π 的矩形,则圆柱的表面 积为( ) A.6π(4π+3) B.8π(3π+1) C.6π(4π+3)或 8π(3π+1) D.6π( 解析:设圆柱的底面半径为 r,分两种情况.①若 6π=2πr,r =3,∴圆柱的表面积为:4π×6π+2πr2=24π2+18π=6π(4π+3). ②若 4π=2πr,r=2,∴圆柱的表面积为:4π×6π+2×πr2=24π2 +8π=8π(3π+1),故选 C.
三、走进高考 5.[2018·全国Ⅰ卷]已知圆柱的上、下底面的中心分别为 O1、 O2,过直线 O1O2 的平面截该圆柱所得的截面是面积为 8 的正方形, 则该圆柱的表面积为( ) A.12 2π B.12π C.8 2π D.10π
答案:B 解析:设圆柱的底面半径为 r,高为 h,由题意可知 2r=h=2 2, ∴圆柱的表面积 S=2πr2+2πr·h=4π+8π=12π,故选 B.
答案:C 2
解析:底面半径 r=32ππl=13l,故圆锥中 S 侧=13πl2,S 表=13πl2+π13l 2=49πl2,所以表面积与侧面积的比为 4:3.
2.[2019·江苏卷]如图,长方体 ABCD-A1B1C1D1 的体积是 120, E 为 CC1 的中点,则三棱锥 E-BCD 的体积是________.
2021高考数学课件8.2简单几何体的表面积与体积

二、易错易混 3.圆柱的侧面展开图是边长为 6π 和 4π 的矩形,则圆柱的表面 积为( ) A.6π(4π+3) B.8π(3π+1) C.6π(4π+3)或 8π(3π+1) D.6π(4π+1)或 8π(3π+2)
答案:C 解析:设圆柱的底面半径为 r,分两种情况.①若 6π=2πr,r =3,∴圆柱的表面积为:4π×6π+2πr2=24π2+18π=6π(4π+3). ②若 4π=2πr,r=2,∴圆柱的表面积为:4π×6π+2×πr2=24π2 +8π=8π(3π+1),故选 C.
三角形,∴PA、PB、PC 两两垂直,故球 O 是棱长为 2的正方体的
外接球,设球 O 的半径为 R,则 2R= 3× 2,R= 26,∴球 O 的体 积 V=43πR3= 6π,故选 D.
题型一 简单几何体的表面积与体积[自主练透] 1.若圆锥的侧面展开图是圆心角为 120°,半径为 l 的扇形,则 这个圆锥的表面积与侧面积的比是( ) A.3:2 B.2:1 C.4:3 D.5:3
答案:10
解析:因为长方体的体积是 120,所以 2S△BCD·CC1=120,
则
S△BCD·CC1=60.所以
VE-
=13S△BCD·EC=13
2.简单几何体的体积
(1)V 柱体= Sh 1
(2)V 锥体= 3Sh (3)V 台体=13(S′+ SS′+S)h,V 圆台=13π(r21+r1r2+r22)·h, V 球= 43πR3 (球半径是 R).
【教材提炼】
一、教材改编 1.[必修二·P119 习题 8.3 T1]如图,八面体的每一个面都是正三角 形,并且 4 个顶点 A,B,C,D 在同一个平面内.如果四边形 ABCD 是边长为 30 cm 的正方形,那么这个八面体的表面积为( ) A.225 3 B.1 000 3 C.1 800 3 D.900+2 000 3
高考数学技巧如何快速计算几何体的表面积和体积

高考数学技巧如何快速计算几何体的表面积和体积几何体的表面积和体积是高考数学中的重要考点,掌握快速计算的技巧对于提高解题效率和得分至关重要。
本文将介绍几种常用的数学技巧,帮助考生们在高考数学中快速计算几何体的表面积和体积。
一、计算长方体的表面积和体积长方体是一种最基本的几何体,计算其表面积和体积是高考中常见的考题。
首先,我们来介绍如何计算长方体的表面积。
长方体具有六个面,即前后面、上下面和左右面。
每个面的面积都等于其对应边长的乘积。
因此,长方体的表面积等于每个面积的和。
具体计算步骤如下:1. 首先,计算前后面的面积,即长乘以高;2. 接着,计算上下面的面积,即宽乘以高;3. 最后,计算左右面的面积,即长乘以宽。
将上述三个面积相加,即可得到长方体的表面积。
下面,我们来介绍如何计算长方体的体积。
长方体的体积等于底面积乘以高度。
具体计算步骤如下:1. 首先,计算底面的面积,即长乘以宽;2. 接着,将底面积乘以高度,即可得到长方体的体积。
二、计算圆柱的表面积和体积圆柱也是高考数学中常见的几何体之一。
计算圆柱的表面积和体积同样需要掌握一些技巧。
先来介绍计算圆柱的表面积的方法。
圆柱的表面积由三部分组成,即上下底面积和侧面积。
具体计算步骤如下:1. 首先,计算上下底面的面积,即底面的面积乘以2;2. 接着,计算侧面的面积。
侧面是一个矩形,其长等于底边的周长,宽等于圆柱的高度。
因此,侧面的面积等于底边周长乘以高度;3. 最后,将上下底面积和侧面积相加,即可得到圆柱的表面积。
接下来,我们来介绍计算圆柱的体积的方法。
圆柱的体积由底面积和高度决定。
具体计算步骤如下:1. 首先,计算底面的面积,即底面的半径的平方乘以π;2. 接着,将底面积乘以高度,即可得到圆柱的体积。
三、计算球体的表面积和体积球体是一种特殊的几何体,其计算方法与其他几何体略有不同。
首先,我们来介绍计算球体的表面积的方法。
球体的表面积等于其半径的平方乘以4π。
几何体的体积与表面积

几何体的体积与表面积几何体是指具有一定形状和空间的物体,常见的几何体包括球体、立方体、圆柱体、锥体和棱柱体等。
在几何学中,我们常常需要计算几何体的体积和表面积来解决各种问题。
一、球体的体积与表面积球体是一种最简单的几何体,表面上呈现出完全圆滑的形状。
球体的体积和表面积的计算公式如下:1. 球体的体积公式:V = (4/3)πr³,其中V表示体积,π表示圆周率,r表示球的半径。
2. 球体的表面积公式:S = 4πr²,其中S表示表面积,π表示圆周率,r表示球的半径。
二、立方体的体积与表面积立方体是一种六个面都呈正方形的几何体,具有均匀分布的表面和体积。
立方体的体积和表面积的计算公式如下:1. 立方体的体积公式:V = a³,其中V表示体积,a表示立方体的边长。
2. 立方体的表面积公式:S = 6a²,其中S表示表面积,a表示立方体的边长。
三、圆柱体的体积与表面积圆柱体是由两个平行的圆底和一个侧面围成的几何体。
圆柱体的体积和表面积的计算公式如下:1. 圆柱体的体积公式:V = πr²h,其中V表示体积,π表示圆周率,r表示圆底的半径,h表示圆柱体的高度。
2. 圆柱体的表面积公式:S = 2πrh + 2πr²,其中S表示表面积,π表示圆周率,r表示圆底的半径,h表示圆柱体的高度。
四、锥体的体积与表面积锥体是由一个圆底和一个侧面围成的几何体,侧面呈三角形形状。
锥体的体积和表面积的计算公式如下:1. 锥体的体积公式:V = (1/3)πr²h,其中V表示体积,π表示圆周率,r表示圆底的半径,h表示锥体的高度。
2. 锥体的表面积公式:S = πrl + πr²,其中S表示表面积,π表示圆周率,r表示圆底的半径,l表示锥体的斜高。
五、棱柱体的体积与表面积棱柱体是由两个并列的多边形底面和若干个连接底面的长方形侧面围成的几何体。
棱柱体的体积和表面积的计算公式如下:1. 棱柱体的体积公式:V = Bh,其中V表示体积,B表示底面积,h表示棱柱体的高度。
高考数学空间几何体的表面积和体积知识点讲解

高考数学空间几何体的表面积和体积知识点讲解也许同学们正迷茫于该怎样复习,查字典数学网为大家带来空间几何体的表面积和体积知识点,供大家参考!1、圆柱体:表面积:2πRr+2πRh 体积:πR2h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根] 体积:πR2h/3 (r为圆锥体低圆半径,h为其高,3、正方体a-边长,S=6a2 ,V=a34、长方体a-长 ,b-宽 ,c-高 S=2(ab+ac+bc) V=abc5、棱柱S-底面积 h-高 V=Sh6、棱锥S-底面积 h-高 V=Sh/37、棱台S1和S2-上、下底面积 h-高 V=h[S1+S2+(S1S2)^1/2]/3 8、拟柱体S1-上底面积 ,S2-下底面积 ,S0-中截面积h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径 ,h-高 ,C—底面周长S底—底面积 ,S侧—侧面积 ,S表—表面积C=2πrS底=πr2,S侧=Ch ,S表=Ch+2S底 ,V=S底h=πr2h10、空心圆柱R-外圆半径 ,r-内圆半径 h-高V=πh(R^2-r^2)11、直圆锥r-底半径 h-高V=πr^2h/312、圆台r-上底半径 ,R-下底半径 ,h-高V=πh(R2+Rr+r2)/313、球r-半径 d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a2+h2)/6=πh2(3r-h)/315、球台r1和r2-球台上、下底半径 h-高V=πh[3(r12+r22)+h2]/6 16、圆环体R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径V=2π2Rr2 =π2Dd2/417、桶状体D-桶腹直径 d-桶底直径 h-桶高V=πh(2D2+d2)/12 ,(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)小编为大家提供的高考数学空间几何体的表面积和体积知识点讲解就到这里了,愿大家都能努力复习,丰富自己,锻炼自己。
新课程2021高考数学一轮复习第七章立体几何第2讲空间几何体的表面积与体积课件

面在距平面 β 任意高度 d 处可横截得到 S 圆及 S 环两截面,可以证明 S 圆=S 环总成立,据此,短轴长为 4 cm,长轴长为 6 cm 的椭球体的体积是__1_6_π__cm3.
解析 因为总有 S 圆=S 环,所以半椭球体的体积为 V 圆柱-V 圆锥=πb2a -13πb2a=23πb2a.又 2a=6,2b=4,即 a=3,b=2,所以椭球体的体积 V=43πb2a =43π×22×3=16π(cm3).
第七章 立体几何
第2讲 空间几何体的表面积与体积
[考纲解读] 1.掌握球、棱柱、棱锥、台的表面积和体积的计算公式.(重 点)
2.会处理空间几何体的“切”“接”问题.(难点) [考向预测] 从近三年高考情况来看,本讲内容属于高考的热点.预测 2021 年会对本讲内容进行考查,命题方式为:①求几何体的表面积或体积; ②涉及与球有关的几何体的外接与内切问题.题型以客观题为主,且试题难 度不会太大,属中档题型.
求体积的常用方法
直接法 对于规则的几何体,利用相关公式直接计算
首先把不规则的几何体分割成规则的几何体,然后进行
割补法 体积计算;或者把不规则的几何体补成规则的几何体,
不熟悉的几何体补成熟悉的几何体,便于计算
等体 积法
选择合适的底面来求几何体体积,常用于求三棱锥的体 积,即利用三棱锥的任一个面可作为三棱锥的底面进行 等体积变换
() A.6π(4π+3)
B.8π(3π+1)
C.6π(4π+3)或 8π(3π+1)
D.6π(4π+1)或 8π(3π+2)
答案 C
解析 分两种情况:①以长为 6π 的边为高时,4π 为圆柱底面周长,则
2πr=4π,r=2,所以 S 底=4π,S 侧=6π×4π=24π2,S 表=2S 底+S 侧=8π+ 24π2=8π(3π+1);②以长为 4π 的边为高时,6π 为圆柱底面周长,则 2πr=6π,
高考数学科学复习创新方案:简单几何体的表面积与体积
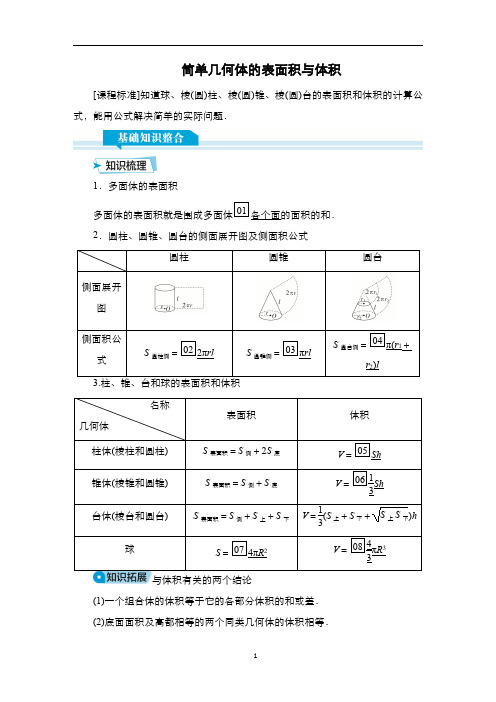
简单几何体的表面积与体积[课程标准]知道球、棱(圆)柱、棱(圆)锥、棱(圆)台的表面积和体积的计算公式,能用公式解决简单的实际问题.1.多面体的表面积多面体的表面积就是围成多面体01各个面的面积的和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧=022πrl S圆锥侧=03πrlS圆台侧=04π(r1+r2)l3.柱、锥、台和球的表面积和体积名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=05Sh锥体(棱锥和圆锥)S表面积=S侧+S底V=0613Sh台体(棱台和圆台)S表面积=S侧+S上+S下V=13(S上+S下+S上S下)h球S=074πR2V=0843πR3与体积有关的两个结论(1)一个组合体的体积等于它的各部分体积的和或差.(2)底面面积及高都相等的两个同类几何体的体积相等.1.(人教B必修第四册习题11-1A T6改编)棱长为2的正四面体的表面积是()A.3B.4C.43D.16答案C解析每个面的面积为12×2×2×32=3,所以正四面体的表面积为43.故选C.2.(人教B必修第四册11.1.4例1改编)设正六棱锥的底面边长为1,侧棱长为5,那么它的体积为()A.63 B.3C.23D.2答案B解析由正六棱锥底面边长为1和侧棱长为5,可知高h=2,又因为底面积S=332,所以体积V=13Sh=13×332×2=3.故选B.3.设一个球形西瓜,切下一刀后所得切面圆的半径为4,球心到切面圆心的距离为3,则该西瓜的表面积为()A.100π B.256π3C.400π D.500π3答案A解析由题意知切面圆的半径r=4,球心到切面圆心的距离d=3,所以球的半径R=r2+d2=42+32=5,故球的表面积为4πR2=4π×52=100π.故选A.4.(2023·新课标Ⅰ卷)在正四棱台ABCD-A1B1C1D1中,AB=2,A1B1=1,AA1=2,则该棱台的体积为________.答案766解析如图,过A1作A 1M ⊥AC ,垂足为M ,易知A 1M为正四棱台ABCD -A 1B 1C 1D 1的高.因为AB =2,A 1B 1=1,AA 1=2,则A 1O 1=12A 1C 1=12×2A 1B 1=22,AO =12AC =12×2AB =2,故AM =AO -A 1O 1=22,则A 1M =A 1A 2-AM 2=2-12=62,所以所求棱台的体积V =13×(4+1+4×1)×62=766.5.如图所示,在上、下底面对应边的比为1∶2的三棱台中,过上底面一边A 1B 1作一个平行于棱C 1C 的平面A 1B 1EF ,记平面分三棱台两部分的体积为V 1(三棱柱A 1B 1C 1-FEC ),V 2,那么V 1∶V 2=________.答案3∶4解析设三棱台的高为h ,上底面的面积是S ,则下底面的面积是4S ,∴V 三棱台=13h (S +4S +2S )=73,又V 1=Sh ,∴V 1V 2=Sh 73Sh -Sh =34.例1(1)(2023·襄阳四中模拟)如图,圆锥PO 的底面直径和高均是2,过PO 的中点O ′作平行于底面的截面,以该截面为底面挖去一个圆柱,则剩下的几何体的表面积为()A .(1+5)πB .(2+5)π答案B解析设圆柱的底面半径为r ,高为h ,则r =12×1=12,h =12=1,圆锥的母线长为22+12=5,过PO 的中点O ′作平行于底面的截面,以该截面为底面挖去一个圆柱,则剩下的几何体的表面积为π×1×5+2π×12×1+π×12=(2+5)π.故选B.(2)圆台的上、下底面半径分别是10cm 和20cm ,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积为________cm 2(结果中保留π).答案1100π解析如图所示,设圆台的上底周长为C ,因为扇环的圆心角是180°,所以C =π·SA .又C =2π×10=20π,所以SA =20cm.同理SB =40cm ,所以AB =SB -SA =20(cm).S 表=S 侧+S 上底+S 下底=π×(10+20)×20+π×102+π×202=1100π(cm 2).故圆台的表面积为1100πcm 2.求空间几何体表面积的类型及方法多面体的表面积只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表面积旋转体的表面积可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系不规则几何体的表面积通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积注意:(1)组合体的表面积注意衔接部分的处理.(2)灵活运用直角三角形与直角梯形,如圆锥(台)中的高、母线、底面半径;棱锥(台)中的高、棱长、底面边长.1.若正四棱锥的底面边长和高都为2,则其表面积为________.答案4+45解析如图,由题意知底面正方形的边长为2,正四棱锥的高为2,则正四棱锥的斜高PE =22+12=5,所以该四棱锥的侧面积S =4×12×2×5=45,所以S 表=2×2+45=4+45.2.(2024·南充诊断)如图,四边形OABC 是边长为1的正方形,AC ︵是四分之一圆,则图中阴影部分以OC 所在直线为旋转轴旋转一周得到的旋转体的表面积为________.答案5π解析该旋转体是一个圆柱挖去一个半球后剩余的部分,且圆柱的底面半径是1,高是1,球的半径是1,所以该旋转体的表面积为π×12+2π×1×1+12×4π×12=5π.多角度探究突破角度直接法求体积例2(2023·全国甲卷)在三棱锥P -ABC 中,△ABC 是边长为2的等边三角形,PA =PB =2,PC =6,则该棱锥的体积为()A .1 B.3C .2D .3答案A解析取AB 的中点E ,连接PE ,CE ,如图,∵△ABC是边长为2的等边三角形,PA =PB =2,∴PE ⊥AB ,CE ⊥AB ,∴PE =CE =2×32=3,又PC =6,故PC 2=PE 2+CE 2,即PE ⊥CE ,又AB ∩CE =E ,AB ,CE ⊂平面ABC ,∴PE ⊥平面ABC ,∴V P -ABC =13S △ABC ·PE =13×12×2×3×3=1.故选A.角度补形法求体积例3如图,一个底面半径为3的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为4和10,则该几何体的体积为()A .90πB .63πC .42πD .36π答案B解析由几何体的直观图可知,该几何体是一个圆柱截去上面虚线部分所得,如图所示.将圆柱补全,并将圆柱从点A 处水平分成上、下两部分.由图可知,该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V =π×32×4+π×32×6×12=63π.故选B.角度分割法求体积例4我国古代数学名著《九章算术》中记载:“刍薨者,下有袤有广,而上有袤无广,刍,草也,薨,屋盖也”.今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱EF =32,EF ∥平面ABCD ,EF 与平面ABCD 的距离为2,该刍薨的体积为()A .6 B.113C.314D .12答案B解析如图,作FN ∥AE ,FM ∥ED ,分别交AB ,CD于点N ,M ,连接MN ,则多面体被分割为棱柱与棱锥两个部分,则该刍薨的体积为V F -MNBC +V ADE -NMF =13S 四边形MNBC ·2+S 直截面·32=13×2×2-32×2+2×22×32=113.故选B.角度转化法求体积例5如图所示,在正三棱柱ABC -A1B 1C 1中,AB =4,AA 1=6.若E ,F 分别是棱BB 1,CC 1上的点,则三棱锥A -A 1EF 的体积是________.答案83解析由正三棱柱的底面边长为4,得点F 到平面A 1AE 的距离(等于点C 到平面A 1ABB 1的距离)为32×4=23,则VA -A 1EF =VF -A 1AE =13S △A 1AE ×23=13×12×6×4×23=83.1.处理体积问题的思路2.求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体、不熟悉的几何体补成熟悉的几何体,便于计算等体积法选择合适的底面来求几何体的体积,常用于求三棱锥的体积,即利用三棱锥的任何一个面可作为三棱锥的底面进行等体积变换1.(2023·佛山二模)极目一号(如图1)是中国科学院空天信息研究院自主研发的系留浮空器.“极目一号”Ⅲ型浮空艇长55m ,高19m ,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图2所示(单位:m),则“极目一号”Ⅲ型浮空艇的体积约为(参考数据:9.52≈90,9.53≈857,315×1005≈316600,π≈3.14)()A.9064m3B.9004m3C.8944m3D.8884m3答案A解析由图2得半球、圆柱底面和圆台一个底面的半径为R=192=9.5(m),而圆台另一个底面的半径为r=1(m),则V半球=12×43π×9.53≈1714π3(m3),V圆柱=π×9.52×14≈1260π(m3),V圆台=13×(9.52π+9.52π×π+π)×31.5≈3166π3(m3),所以V=V半球+V圆柱+V圆台≈1714π3+1260π+3166π3≈9064(m3).故选A.2.已知正方体ABCD-A1B1C1D1的棱长为2,则三棱锥A-B1CD1的体积为()A.43B.83C.4D.6答案B解析如图,三棱锥A-B1CD1是由正方体ABCD-A1B1C1D1截去四个小三棱锥A-A1B1D1,C-B1C1D1,B1-ABC,D1-ACD得到的,又VABCD-A1B1C1D1=23=8,VA-A1B1D1=VC-B1C1D1=VB1-ABC=VD1-ACD=13×12×23=43,所以VA-B1CD1=8-4×43=8 3.3.如图所示,已知多面体ABCDEFG中,AB,AC,AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为________.答案4解析解法一(分割法):因为几何体有两对相对面互相平行,如图所示,过点C作CH⊥DG于H,连接EH,即把多面体分割成一个直三棱柱DEH -ABC 和一个斜三棱柱BEF -CHG .由题意,知V 三棱柱DEH -ABC =S △DEH ·AD =2,V三棱柱BEF -CHG =S △BEF ·DE =2.故所求几何体的体积为V 多面体ABCDEFG =2+2=4.解法二(补形法):因为几何体有两对相对面互相平行,如图所示,将多面体补成棱长为2的正方体,显然所求多面体的体积为该正方体体积的一半.又正方体的体积V 正方体ABHI -DEKG =23=8,故所求几何体的体积为V多面体ABCDEFG=12×8=4.课时作业一、单项选择题1.(2023·锦州二模)已知某圆锥的高为22cm ,体积为22π3cm 3,则该圆锥的侧面积为()A.3π2cm 2B .3πcm 2C .6πcm 2D .12πcm 2答案B解析设该圆锥的底面半径与母线长分别为r ,l ,由V =13πr 2×22=22π3,得r =1cm ,所以l =12+(22)2=3(cm),所以该圆锥的侧面积S =πrl =3π(cm 2).故选B.2.张衡是中国东汉时期伟大的天文学家、数学家,他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥A -BCD 的每个顶点都在球O 的球面上,AB ⊥底面BCD ,BC ⊥CD ,且AB =CD =3,BC =2,利用张衡的结论可得球O 的表面积为()A .30B .1010C .33D .1210答案B解析因为BC⊥CD,所以BD=7,又AB⊥底面BCD,所以球O的球心为侧棱AD的中点,从而球O的直径为AD=10.利用张衡的结论可得π216=58,则π=10,所以球O的表面积为=10π=1010.故选B.3.(2024·合肥模拟)长方体的体对角线长为1,表面积为1,有一面为正方形,则其体积为()A.2 108B.2 27C.2 9D.2 6答案B解析不妨设长方体的底面为正方形,边长为a,高为b,则底面的对角线为a2+a2=2a,∵长方体的体对角线长为1,表面积为1,ab+2a2=1,(2a)2+b2=1,=26,=223,∴长方体的体积为a2b=227.故选B.4.(2023·河源模拟)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”“圆罂测雨”“峻积验雪”和“竹器验雪”.“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度=器皿中积雪体积除以器皿口面积),已知数据如图(单位:cm),则平地降雪厚度的近似值为()A.9112cm B.314cmC.9512cm D.9712cm答案C解析器皿中雪表面的半径为20+404=15(cm),所以平地降雪厚度的近似值为13π×20×(102+152+10×15)π×202=9512(cm).故选C.5.(2024·武汉模拟)已知一个圆柱的侧面积等于表面积的23,且其轴截面的周长是16,则该圆柱的体积是()A.54πB.36πC.27πD.16π答案D解析设圆柱的底面半径为r,高为h,rh=23(2πrh+2πr2),r+2h=16,=2,=4,∴该圆柱的体积是πr2h=16π.故选D.6.(2023·常州模拟)如图,圆锥的底面半径为1,侧面展开图是一个圆心角为60°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为13,则圆台的侧面积为()A.8π3B.35π2C.16π3D.8π答案C解析假设圆锥的半径为R,母线长为l,则R=1.设圆台的上底面半径为r,母线长为l1,则r=13.由已知可得,π3=2πRl=2πl,所以l=6.如图,作出圆锥、圆台的轴截面,则l-l1l=rR=13,所以l1=4.所以圆台的侧面积为π(R+r)l1==16π3.故选C.7.(2023·天津高考)在三棱锥P -ABC 中,线段PC 上的点M 满足PM =13PC ,线段PB 上的点N 满足PN =23PB ,则三棱锥P -AMN 和三棱锥P -ABC 的体积之比为()A.19B.29C.13D.49答案B解析如图,因为PM =13PC ,PN =23PB ,所以S △PMN S △PBC=12PM ·PN sin ∠BPC12PC ·PB sin ∠BPC =PM ·PN PC ·PB =13×23=29,所以V P -AMN V P -ABC =V A -PMN V A -PBC=13S △PMN ·d13S △PBC ·d =S △PMN S △PBC =29(其中d 为点A 到平面PBC 的距离,因为平面PMN 和平面PBC重合,所以点A 到平面PMN 的距离也为d ).故选B.8.中国南北朝时期数学家、天文学家祖冲之、祖暅父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.详细点说就是,界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.上述原理在中国被称为祖暅原理.一个上底面边长为1,下底面边长为2,高为23的正六棱台与一个不规则几何体满足“幂势既同”,则该不规则几何体的体积为()A .16B .163C .183D .21答案D解析由祖暅原理可知,该不规则几何体的体积与正六棱台的体积相等,∵正六棱台的上、下底面边长分别为1和2,则S 1=6×12×1×1×32=332,S 2=6×12×2×2×32=63,故V =13(S 1+S 1S 2+S 2)h =13×33+×23=21.故选D.二、多项选择题9.(2023·黄冈模拟)如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等,下列结论正确的是()A .圆柱的侧面积为2πR 2B .圆锥的侧面积为2πR 2C .圆柱的侧面积与球的表面积相等D .圆柱、圆锥、球的体积之比为3∶1∶2答案CD解析∵圆柱和圆锥的底面直径和它们的高都与一个球的直径2R 相等,∴圆柱的侧面积为2πR ·2R =4πR 2,A 错误;圆锥的母线长l =R 2+(2R )2=5R ,侧面积为πRl =5πR 2,B 错误;球的表面积为4πR 2,∴圆柱的侧面积与球的表面积相等,C 正确;∵V 圆柱=πR 2·2R =2πR 3,V 圆锥=13πR 2·2R =23πR 3,V 球=43πR 3,∴V 圆柱∶V 圆锥∶V 球=2πR 3∶23πR 3∶43πR 3=3∶1∶2,D 正确.故选CD.10.(2023·新课标Ⅱ卷)已知圆锥的顶点为P ,底面圆心为O ,AB 为底面直径,∠APB =120°,PA =2,点C 在底面圆周上,且二面角P -AC -O 为45°,则()A .该圆锥的体积为πB .该圆锥的侧面积为43πC .AC =22D .△P AC 的面积为3答案AC解析依题意,∠APB =120°,PA =2,所以OP =1,OA =OB =3,对于A ,圆锥的体积为13×π×(3)2×1=π,A正确;对于B ,圆锥的侧面积为π×3×2=23π,B 错误;对于C ,设D 是AC 的中点,连接OD ,PD ,则AC ⊥OD ,AC ⊥PD ,所以∠PDO 是二面角P -AC -O 的平面角,则∠PDO =45°,所以OP =OD =1,故AD =CD =3-1=2,则AC =22,C 正确;对于D ,PD =12+12=2,所以S △P AC =12×22×2=2,D 错误.故选AC.11.(2022·新高考Ⅱ卷)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,FB ∥ED ,AB =ED =2FB ,记三棱锥E -ACD ,F -ABC ,F -ACE 的体积分别为V 1,V 2,V 3,则()A .V 3=2V 2B .V 3=V 1C .V 3=V 1+V 2D .2V 3=3V 1答案CD解析设AB =ED =2FB =2a ,因为ED ⊥平面ABCD ,FB ∥ED ,则V 1=13ED ·S △ACD =13·2a ·12·(2a )2=43a 3,V 2=13FB ·S △ABC =13·a ·12·(2a )2=23a 3,连接BD 交AC 于点M ,连接EM ,FM ,易得BD ⊥AC ,又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED ⊥AC ,又ED ∩BD =D ,ED ,BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又BM =DM =12BD =2a ,过F 作FG ⊥DE 于点G ,易得四边形BDGF 为矩形,则FG =BD =22a ,EG =a ,则EM =(2a )2+(2a )2=6a ,FM =a 2+(2a )2=3a ,EF =a 2+(22a )2=3a ,EM 2+FM 2=EF 2,则EM ⊥FM ,S △EFM =12EM ·FM =322a 2,AC =22a ,则V 3=V A -EFM +V C -EFM =13AC ·S △EFM =2a 3,则2V 3=3V 1,V 3=3V 2,V 3=V 1+V 2.故选CD.三、填空题12.(2023·新课标Ⅱ卷)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为________.答案28解析解法一:由于24=12,而截去的正四棱锥的高为3,所以原正四棱锥的高为6,所以原正四棱锥的体积为13×(4×4)×6=32,截去的正四棱锥的体积为13×(2×2)×3=4,所以棱台的体积为32-4=28.解法二:棱台的体积为13×3×(16+4+16×4)=28.13.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形的边长为2cm ,高为2cm ,内孔半径为0.5cm ,则此六角螺帽毛坯的体积是________cm 3.答案123-π2解析正六棱柱的体积为6×34×22×2=123(cm 3),挖去的圆柱的体积为×2=π2(cm 3)1233).14.学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得的几何体.其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6cm ,AA 1=4cm.3D 打印所用原料密度为0.9g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为________g.答案118.8解析由题知挖去的四棱锥的底面是一个菱形,对角线长分别为6cm和4cm,故V挖去的四棱锥=13×12×4×6×3=12(cm3).又V长方体=6×6×4=144(cm3),所以模型的体积为V长方体-V挖去的四棱锥=144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g).四、解答题15.在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠CAB=120°.(1)求直三棱柱ABC-A1B1C1的体积;(2)求直三棱柱ABC-A1B1C1的表面积.解(1)AB=AC=1,AA1=2,∠CAB=120°,则直三棱柱ABC-A1B1C1的体积为S△ABC·AA1=12AB·AC sin∠CAB·AA1=1 2×1×1×32×2=64.(2)AB=AC=1,∠CAB=120°,则BC2=AB2+AC2-2AB·AC cos∠CAB=3,解得BC=3.故直三棱柱ABC-A1B1C1的表面积为2×12×1×1×32+2×(1+1+3)=22+6+32.16.如图,在△ABC中,AB=8,BC=10,AC=6,BD⊥平面ABC,且AE∥FC∥BD,BD=3,FC=4,AE=5.求此几何体的体积.解解法一(分割法):由AB=8,AC=6,BC=10,得AB2+AC2=BC2,所以AB⊥AC.因为BD⊥平面ABC,AE∥BD,所以AE ⊥平面ABC ,又AB ⊂平面ABC ,所以AE ⊥AB ,又AB ⊥AC ,AE ∩AC =A ,AE ,AC ⊂平面ACFE ,所以AB ⊥平面ACFE .如图,取CM =AN =BD ,连接DM ,MN ,DN ,用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥,则V 几何体=V 三棱柱+V 四棱锥.由题意知三棱柱ABC -NDM 的体积为V 1=12×8×6×3=72,四棱锥D -MNEF 的体积为V 2=13S 梯形MNEF ·DN =13×12×(1+2)×6×8=24,则此几何体的体积为V =V 1+V 2=72+24=96.解法二(补形法):用“补形法”把原几何体补成一个直三棱柱,使AA ′=BB ′=CC ′=8,所以V 几何体=12V 三棱柱=12S △ABC ·AA ′=12×24×8=96.17.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P -A 1B 1C 1D 1,下部的形状是正四棱柱ABCD -A 1B 1C 1D 1(如图所示),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍.(1)若AB =6m ,PO 1=2m ,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m ,则当PO 1为多少时,仓库的容积最大?解(1)由PO 1=2m 知O 1O =4PO 1=8m.因为A 1B 1=AB =6m ,所以正四棱锥P -A 1B 1C 1D 1的体积V 锥=13A 1B 21·PO 1=13×62×2=24(m 3).正四棱柱ABCD -A 1B 1C 1D 1的体积V 柱=AB 2·O 1O =62×8=288(m 3).所以仓库的容积V =V 锥+V 柱=24+288=312(m 3).(2)设A 1B 1=a m ,PO 1=h m ,则0<h <6,O 1O =4h m .连接O 1B 1.因为在Rt △PO 1B 1中,O 1B 21+PO 21=PB 21,+h 2=36,即a 2=2(36-h 2).于是仓库的容积V =V 柱+V 锥=a 2·4h +13a 2·h =133a 2h =263(36h -h 3),0<h <6,从而V ′=263(36-3h 2)=26(12-h 2).令V ′=0,得h =23或h =-23(舍去).当0<h <23时,V ′>0,V 是增函数;当23<h <6时,V ′<0,V 是减函数.故当h =23时,V 取得极大值,也是最大值.因此当PO 1=23m 时,仓库的容积最大.。
几何体的表面积与体积

几何体的表面积与体积几何体是我们在数学学习中常常遇到的概念,它包括了我们生活中的各种立体图形,例如立方体、圆柱体、球体等等。
在几何学中,我们经常需要计算几何体的表面积和体积,这两个概念是我们理解几何体性质和应用的重要基础。
本文将详细探讨几何体的表面积和体积的计算方法。
1. 立方体的表面积与体积立方体是最简单的几何体之一,基本特征是六个相等的正方形面。
我们通过边长的计算可以得出立方体的表面积和体积。
设立方体的边长为a,则立方体的表面积S和体积V的计算公式如下:表面积S = 6a²体积V = a³2. 圆柱体的表面积与体积圆柱体是另一种常见的几何体,它由两个平行的圆底和一个连接两个底的侧面组成。
我们可以通过底圆的半径和圆柱体的高来计算表面积和体积。
设圆柱体的底圆半径为r,高为h,则圆柱体的表面积S和体积V 的计算公式如下:表面积S = 2πr² + 2πrh体积V = πr²h3. 球体的表面积与体积球体是一个完全由一条曲线围成的几何体,它具有球心和半径。
计算球体的表面积和体积需要半径的信息。
设球体的半径为r,则球体的表面积S和体积V的计算公式如下:表面积S = 4πr²体积V = (4/3)πr³4. 其他几何体的表面积与体积除了上述的立方体、圆柱体和球体,还有许多其他常见的几何体,例如锥体、棱柱等。
它们的表面积和体积的计算方法也是有规律可循的。
以锥体为例,设锥体的底面积为B,高为h,则锥体的表面积S和体积V的计算公式如下:表面积S = B + (1/2)pl体积V = (1/3)Bh其中,p为锥体的斜高,l为锥体的侧棱长。
综上所述,几何体的表面积和体积可通过不同的计算公式得出。
对于不同的几何体,我们需要根据其特征确定哪些参数是需要计算的,然后代入相应的公式进行计算。
准确计算几何体的表面积和体积可以帮助我们更好地理解其性质和应用,为我们的数学学习和实际问题解决提供基础。
高中数学几何体表面积和体积

高中数学几何体表面积和体积
一、数学几何体的表面积和体积
1、正多面体
正多面体是由同一材料制成的,其面是同一材质形成的多个相互平行的多边形组成的几何体,也叫多面体,通常为平面多边形(三角形和四边形)。
正多面体的表面积称为外接球表面积,体积称为外接球体积。
外接球表面积S:
S = 4πr
外接球体积V:
V = 4/3πr
其中,r 代表正多面体的半径。
2、圆柱体
圆柱体是一个圆形柱体,由一个圆底面和一个圆顶面,以及靠近圆底面和圆顶面之间的圆柱侧面组成,它具有对称性和稳定性。
圆柱体表面积S:
S = 2πr (r+h)
其中,r 代表圆柱体的底面半径,h 代表圆柱体的高度。
圆柱体体积V:
V = πrh
其中,r 代表圆柱体的底面半径,h 代表圆柱体的高度。
3、圆锥体
圆锥体是一个有一个圆锥底和一个尖锥面组成的几何体,它们在一定比例下具有一定的对称性。
圆锥体表面积S:
S = πr (l+r)
其中,r 代表圆锥体的底面半径,l 代表圆锥体的高度。
圆锥体体积V:
V = 1/3πrh
其中,r 代表圆锥体的底面半径,h 代表圆锥体的高度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2节简单几何体的表面积和体积
.
考试要求了解球、棱柱、棱锥、台的表面积和体积的计算公式
知识梳理
1.多面体的表(侧)面积
多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.
2.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱圆锥圆台侧面展开图
侧面积公式S圆柱侧=2πrl S圆锥侧=πrl S圆台侧=π(r1+r2)l 3.简单几何体的表面积与体积公式
名称
表面积体积
几何体
1
柱体
(棱柱和圆柱)S表面积=S侧+2S底V=S底h
锥体(棱锥和圆锥)S表面积=S侧+S底V=1
3
S底h
台体(棱台和圆台)
S表面积=S侧+S上+S
下V=
1
3
(S上+S下+
S上S下)h
球S=4πR2V=4
3
πR3
[常用结论与微点提醒]
1.正方体与球的切、接常用结论
正方体的棱长为a,球的半径为R,
(1)若球为正方体的外接球,则2R=3a;
(2)若球为正方体的内切球,则2R=a;
(3)若球与正方体的各棱相切,则2R=2a.
2.长方体的共顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a2+b2+c2.
3.正四面体的外接球与内切球的半径之比为3∶1.
诊断自测
1.判断下列结论正误(在括号内打“√”或“×”)
(1)锥体的体积等于底面面积与高之积.( )
(2)两个球的体积之比等于它们的半径比的平方.( )
1
1
(3)台体的体积可转化为两个锥体的体积之差.( ) (4)已知球O 的半径为R ,其内接正方体的边长为a ,则R
=
32
a .( )
解析 (1)锥体的体积等于底面面积与高之积的三分之一,故不正确. (2)球的体积之比等于半径比的立方,故不正确. 答案 (1)× (2)× (3)√ (4)√
2.(新教材必修第二册P253A8改编)一个正方体的顶点都在球面上,若球的表面积为4π,则正方体的棱长为( ) A.
33
B.
233
C.
63
D.
3
解析 由S =4πR 2=4π,得R =1,故2×1=3a ,得a =
233. 答案 B
3.(老教材必修2P51A6改编)如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________.
解析 设长方体的相邻三条棱长分别为a ,b ,c ,它截出棱锥的体积为V 1=13×
1
2×12a ×12b ×12c =148abc ,剩下的几何体的体积V 2=abc -148abc =47
48
abc ,所以V 1∶V 2=1∶47. 答案 1∶47
4.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π
B.
3π
4
C.
π
2
D.
π
4
解析如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA
=1,球心到底面圆的距离为OM=1 2 .
∴底面圆半径r=OA2-OM2=
3
2
,故圆柱体积V=π·r2·h=π·
⎝
⎛
⎭
⎪
⎪
⎫3
2
2
×1=
3π
4
.
答案 B
5.(2018·浙江卷改编)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)为________.
解析由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何
体的体积V=1
2
×(1+2)×2×2=6.
答案 6
1。
