几何体的表面积和体积公式
常见几何体面积体积公式

常见几何体面积体积公式咱们从小学到高中,数学里那常见的几何体面积体积公式可真是重要得很呐!就拿我曾经遇到的一件小事儿来说吧。
有一次我去朋友家做客,他家孩子正为数学作业发愁呢,作业里就有不少关于几何体面积体积计算的题目。
那孩子一脸苦相,抓耳挠腮的,我就凑过去瞧了瞧。
嘿,这不就是咱们熟悉的那些几何体嘛!先来说说正方体。
正方体的表面积公式那就是 6a²,其中 a 是正方体的棱长;体积公式则是 a³。
想象一下,一个边长为 5 厘米的正方体盒子,它的表面积就是 6×5×5 = 150 平方厘米,能装的东西的体积就是5×5×5 = 125 立方厘米。
这就好像是在做一个精致的小盒子,你得清楚它的外表能占多大地方,里面又能装多少宝贝。
再说说长方体。
长方体表面积是 2(ab + ah + bh),体积是 abh 。
假设一个长方体,长 8 厘米,宽 6 厘米,高 4 厘米。
那它的表面积就是2×(8×6 + 8×4 + 6×4) = 208 平方厘米,体积就是 8×6×4 = 192 立方厘米。
这就好比是在给一个大柜子量尺寸,算能占多少空间。
圆柱也常见得很。
圆柱的表面积由侧面积和两个底面积组成,公式是2πr² + 2πrh ,体积是πr²h 。
比如说有个底面半径是 3 厘米,高是 10厘米的圆柱,表面积算下来大约是 244.92 平方厘米,体积大约是 282.6 立方厘米。
这就像在算一个大水桶能装多少水,外面的铁皮又得用多少。
圆锥呢,表面积的计算相对复杂点,咱重点说体积,公式是1/3πr²h 。
想象一下,一个圆锥形的冰淇淋甜筒,底面半径 2 厘米,高6 厘米,体积大约就是 25.12 立方厘米。
球就更有趣啦,表面积是4πr²,体积是4/3πr³ 。
就好像是个足球,知道半径就能算出它的大小和外表面积。
空间几何体的表面积及体积公式大全

空间⼏何体的表⾯积及体积公式⼤全空间⼏何体的表⾯积与体积公式⼤全⼀、全(表)⾯积(含侧⾯积) 1、柱体①棱柱②圆柱 2、锥体①棱锥:h c S ‘底棱锥侧21=②圆锥:l c S 底圆锥侧213、台体①棱台:h c c S )(21‘下底上底棱台侧+=②圆台:l c c S )(21下底上底棱台侧+=4、球体①球:r S 24π=球②球冠:略③球缺:略⼆、体积 1、柱体①棱柱②圆柱 2、①棱锥②圆锥3、①棱台②圆台 4、球体①球:rV 334π=球②球冠:略③球缺:略说明:棱锥、棱台计算侧⾯积时使⽤侧⾯的斜⾼h '计算;⽽圆锥、圆台的侧⾯积计算时使⽤母线l 计算。
三、拓展提⾼ 1、祖暅原理:(祖暅:祖冲之的⼉⼦)夹在两个平⾏平⾯间的两个⼏何体,如果它们在任意⾼度上的平⾏截⾯⾯积都相等,那么这两个⼏何体的体积相等。
最早推导出球体体积的祖冲之⽗⼦便是运⽤这个原理实现的。
2、阿基⽶德原理:(圆柱容球)圆柱容球原理:在⼀个⾼和底⾯直径都是r 2的圆柱形容器内装⼀个最⼤的球体,则该球体的全⾯积等于圆柱的侧⾯积,体积等于圆柱体积的32。
分析:圆柱体积:r r h S V r 3222)(ππ=?==圆柱圆柱侧⾯积:r h cS r r 242)2(ππ=?==圆柱侧因此:球体体积:r r V 3334232ππ=?=球球体表⾯积:r S 24π=球通过上述分析,我们可以得到⼀个很重要的关系(如图)+ =即底⾯直径和⾼相等的圆柱体积等于与它等底等⾼的圆锥与同直径的球体积之和 3、台体体积公式公式: )(31S SS S h V 下下上上台++=证明:如图过台体的上下两底⾯中⼼连线的纵切⾯为梯形ABCD 。
延长两侧棱相交于⼀点P 。
设台体上底⾯积为S 上,下底⾯积为S 下⾼为h 。
易知:PDC ?∽PAB ?,设h PE 1=,则h h PF +=1由相似三⾓形的性质得:PFPEAB CD =即:hh hSS +=11下上(相似⽐等于⾯积⽐的算术平⽅根)整理得:SS h S h 上下上-=1⼜因为台体的体积=⼤锥体体积—⼩锥体体积∴h S S S h h S h h S V 下上下上下台)(31)(313131111+-=-+=代⼊:SS h S h 上下上-=1得:h S S S SS h S V 下上下上下上台31)(31+--=即:)(3131)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(3S S h V 下下上上台++=4、球体体积公式推导分析:将半球平⾏分成相同⾼度的若⼲层(层n ),n 越⼤,每⼀层越近似于圆柱,+∞→n 时,每⼀层都可以看作是⼀个圆柱。
体积和表面积的关系与运算

体积和表面积的关系与运算一、体积与表面积的定义1.体积:物体所占空间的大小。
2.表面积:物体表面的总面积。
二、体积与表面积的计算公式1.立方体的体积公式:V = a³(a为立方体的边长)2.立方体的表面积公式:S = 6a²三、体积与表面积的运算关系1.体积与边长的关系:体积随边长的增加而增加。
2.表面积与边长的关系:表面积随边长的增加而增加。
四、体积与表面积的单位1.体积的单位:立方米(m³)、立方分米(dm³)、立方厘米(cm³)等。
2.表面积的单位:平方米(m²)、平方分米(dm²)、平方厘米(cm²)等。
五、体积与表面积的换算1.1立方米(m³)= 1000立方分米(dm³)2.1立方米(m³)= 1000000立方厘米(cm³)3.1平方米(m²)= 100平方分米(dm²)4.1平方米(m²)= 10000平方厘米(cm²)六、常见几何体的体积与表面积公式1.圆柱体的体积公式:V = πr²h(r为圆柱的底面半径,h为圆柱的高)2.圆柱体的表面积公式:S = 2πrh + 2πr²3.圆锥体的体积公式:V = (1/3)πr²h(r为圆锥的底面半径,h为圆锥的高)4.圆锥体的表面积公式:S = πr² + πrl(l为圆锥的母线长)5.球的体积公式:V = (4/3)πr³(r为球的半径)6.球的表面积公式:S = 4πr²七、体积与表面积的实际应用1.计算物体的体积和表面积,以便了解物体的大小和形状。
2.在制作和包装物体时,计算体积和表面积,以节省材料和空间。
3.在建筑设计中,计算建筑物的体积和表面积,以确定建筑材料的需求量和建筑物的外观。
八、体积与表面积的拓展1.立体图形的体积和表面积的计算。
长方体正方体面积体积公式

长方体正方体面积体积公式长方体公式
长方体是一种具有六个面的三维物体,每个面都是矩形。
其表面积和体积公式如下:
表面积:2(长 x 宽 + 宽 x 高 + 高 x 长)
体积:长 x 宽 x 高
正方体公式
正方体是一种特殊的长方体,其所有边长相等。
其表面积和体积公式如下:
表面积:6(边长)²
体积:边长³
具体实例
假设有一个长方体,其长为 5 cm,宽为 3 cm,高为 2 cm。
表面积:2(5 cm x 3 cm + 3 cm x 2 cm + 2 cm x 5 cm) = 56 cm²
体积:5 cm x 3 cm x 2 cm = 30 cm³
假设有一个正方体,其边长为 4 cm。
表面积:6(4 cm)² = 96 cm²
体积:4 cm³ = 64 cm³
其他公式
除了基本公式外,还有一些适用于特殊情况的附加公式:
侧表面积(长方体):2(长 + 宽) x 高
底面积(长方体):长 x 宽
对角线长度(长方体):√(长² + 宽² + 高²)
对角线面积(正方体):√(3) x 边长
内切球半径(正方体):边长 / 2
应用场景
这些公式在解决涉及长方体和正方体的几何问题时至关重要。
它们可用于计算包装、建筑和工程中的表面积和体积。
棱柱、棱锥、棱台和球的表面积和体积

7、如图所示正四棱锥的侧面都是等边三角形,它的斜高为 ,
则这个正四棱锥的体积是_________________.
8、已知圆锥的母线长为 高为 ,则这个圆锥的体积是
______________________.
7.球的体积公式
三:讨论与交流
1已知正三棱锥的底面周长为9,侧棱长为2,则此棱锥的高是()
2底面为正方形的直棱柱,它的底面对角线的长为 ,体对角线长为 ,则这个棱柱的侧面积是()
3若球的大圆周长为C,则这个球的表面积是()
4设长方体的长、宽、高分别为 q其顶点都在一个球面上,则该球的表面积为()
5、已知长方体形的铜块长、宽、高分别是2,4,8,将它熔化后铸成一个正方体形的铜块(不计损耗),则铸成的铜块的棱长是__________________;
9、一个球的大圆的面积增加为原来的100倍,则这个球的体积是原
来球体积的_______________倍.
10、正六棱柱的底面边长为10cm,高为15cm,则这个正六棱柱的体积是____________
11、正三棱台的上下底面边长分别为2、4,斜高为 ,则这个正三棱台的体积是_______
12、正方体的内切球与外接球的体积比是___________
名称
侧面积(Sห้องสมุดไป่ตู้)
表面积(S表)
圆柱
圆锥
球
3,体积公式:
1.柱体(棱柱、圆柱)的体积等于它的底面积S和高h的积.即
2.底面半径是r,高是h的圆柱体的体积的计算公式是
3.如果一个椎体(棱锥、圆锥)的底面积是S,高是h,那么它的体积是
空间几何体的表面积与体积公式记忆大全

空间几何体的表面积与体积公式记忆大全(总1页)
-CAL-FENGHAI.-(YICAI)-Company One1
-CAL-本页仅作为文档封面,使用请直接删
除
空间几何体的表面积与体积公式记忆大全(17公式)
1.几何体的表面积=几何体各个面的面积的和=展开图的面积.
2.特殊几何体表面积公式(c 为底面周长,h 为高,'
h 为斜高,l 为母线) ch
S =直棱柱侧面积 '21ch S =
正棱锥侧面积 ')(2121h c c S +=正棱台侧面积
rh S π2=圆柱侧 , ()l r r S +=π2圆柱表
rl S π=圆锥侧面积, ()
l r r S +=π圆锥表 ()S r R l π=+圆台侧面积, ()22R Rl rl r S +++=π圆台表
3.柱体、锥体、台体的体积公式:
V Sh =柱 13V Sh =锥 '1()3V S S h =台
2V Sh r h
π==圆柱 h r V 231π=圆锥
'2211()()33
V S S h r rR R h π==++圆台 4.球体的表面积和体积公式:34V 3
R π=球 ; S 球面=24R π。
长方体正方体表面积和体积公式

长方体正方体表面积和体积公式
长方体和正方体是几何学中常见的几何体,它们的表面积和体积是通过一些简单的公式来计算的。
首先来看长方体。
长方体是一种有六个矩形面的立体图形,其中每个面都是相对的两个相等的矩形。
我们可以使用以下公式来计算长方体的表面积和体积。
长方体的表面积等于所有面的面积之和。
假设长方体的长、宽、高分别为L、W、H,则长方体的表面积S可以用下面的公式表示:
S = 2LW + 2LH + 2WH
长方体的体积等于底面积乘以高。
长方体的体积V可以用下面的公式表示:
V = LWH
接下来我们来看正方体。
正方体是一种特殊的长方体,它的六个面都是正方形。
正方体的边长为a。
正方体的表面积和体积公式与长方体类似。
正方体的表面积等于所有面的面积之和。
正方体的表面积S可以用下面的公式表示:
S = 6a^2
正方体的体积等于边长的立方。
正方体的体积V可以用下面的公式表示:
V = a^3
长方体和正方体的表面积和体积公式是非常有用的,它们可以帮助我们计算这些几何体的重要属性。
无论是在日常生活中还是在工程领域,我们都经常需要使用这些公式来解决问题。
希望通过这篇文章的介绍,读者能更好地理解长方体和正方体的表面积和体积公式,并能灵活应用它们解决实际问题。
第二节 简单几何体的表面积和体积(知识梳理)
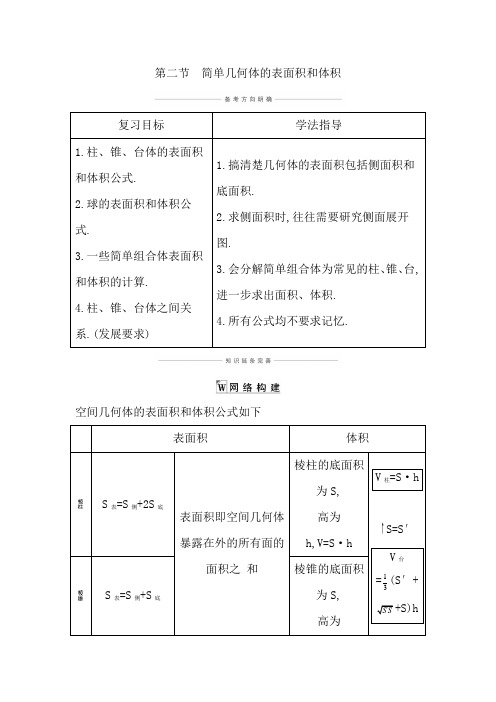
第二节简单几何体的表面积和体积复习目标学法指导1.柱、锥、台体的表面积和体积公式.2.球的表面积和体积公式.3.一些简单组合体表面积和体积的计算.4.柱、锥、台体之间关系.(发展要求)1.搞清楚几何体的表面积包括侧面积和底面积.2.求侧面积时,往往需要研究侧面展开图.3.会分解简单组合体为常见的柱、锥、台,进一步求出面积、体积.4.所有公式均不要求记忆.空间几何体的表面积和体积公式如下表面积体积S表=S侧+2S底表面积即空间几何体暴露在外的所有面的面积之和棱柱的底面积为S,高为h,V=S·hV柱=S·hS=S′V台=13(S′+S S +S)h S表=S侧+S底棱锥的底面积为S,高为h,V=13S ·h S ′=0 V 锥=13S ·hS 表=S 侧+ S 上底+S 下底棱台的上、下底面 面积分别为S ′,S,高为h, V=13(S ′+ S S+S)h圆柱的底面半径和母线长分别为r,lS 表=2πr 2+2πrl 圆柱的高为h,V=πr 2h圆锥的底面半径和母线长分别为r,l S 表=πr 2+πrl 圆锥的高为h,V=13πr 2h圆台的上、下底面半 径和母线长分圆台的高为h,V=13π(r ′2+别为r,r′,l,S表=π(r′2+r2+r′l+rl)r′r+r2)h球球半径为R,S球=4πR2V球=43πR31.概念理解(1)表面积应为侧面积和底面积的和,要注意组合体中哪些部分暴露或遮挡.(2)求空间几何体体积的常用方法①公式法:直接根据相关的体积公式计算.②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.2.求面积或体积中相关联的结论几个与球有关的切、接常用结论(1)正方体的棱长为a,球的半径为R,①正方体的外接球,则3②正方体的内切球,则2R=a;③球与正方体的各棱相切,则2(2)长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=222a b c ++.(3)正四面体的外接球与内切球的半径之比为3∶1.1.圆柱的底面积为S,侧面展开图是一个正方形,那么圆柱的侧面积是( A )(A)4πS (B)2πS (C)πS (D)23πS 解析:由πr 2=S 得圆柱的底面半径是πS , 故侧面展开图的边长为2π·πS =2πS,所以圆柱的侧面积是4πS.故选A.2.正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为3,D为BC 的中点,则三棱锥A-B 1DC 1的体积为 . 解析:如图,在正三棱柱ABC-A 1B 1C 1中, 因为AD ⊥BC,AD ⊥BB 1, BB 1∩BC=B,所以AD ⊥平面B 1DC 1. 所以11A B DC V-=1113B DC S ∆·AD=13×12×233=1. 答案:13.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 cm 3,表面积为 cm 2.解析:由三视图可得该几何体为二分之一圆锥, 圆锥的底面半径为1,高为2,所以可得该几何体的体积为12×13×π×12×2=π3, 该几何体的表面积为12×π×12+12π×114++12×2×2=)51π2+2.答案: π3)51π2+24.已知正四棱锥O-ABCD 32,3,则以O 为球心,OA 为半径的球的表面积是 . 解析:设O 到底面的距离为h,则13×3×32,解得32()()2233+62262h ⎛⎫+ ⎪ ⎪⎝⎭6故球的表面积为4π×62=24π.答案:24π5.(2019·浙江宁波模拟)已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为,该三棱锥的外接球体积为.解析:由三视图得几何体的直观图如图.所以S表=2×12×2×2+12×3512×3 1153如图,作DE⊥DB,以D为原点,DB所在直线为x轴,DE所在直线为y 轴,DA所在直线为z轴,建立空间直角坐标系,则3设球心坐标为(x,y,z),因为(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)23)2+z2=x2+y2+z2,③所以x=1,y=3,z=1,所以球心的坐标是(1,3,1), 所以球的半径是()222131++=5.所以球的体积是43π×(5)3=2053π.答案:4+15+32053π考点一几何体的表面积[例1] (1)(2018·金丽衢十二校联考)某四面体的三视图如图所示,正视图、侧视图都是腰长为2的等腰直角三角形,俯视图是边长为2的正方形,则此四面体的最大面的面积是( )(A)2 23(D)4(2)(2019·湖州模拟)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )(A)4π3(B)5π3(C)4π3(D)5π3(3)若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为;(4)四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若四棱锥S-ABCD的体积取值范围为4383],则该四棱锥外接球表面积的取值范围是.解析:(1)因为几何体为一个四面体,六条棱长分别为2223所以四面体的四个面的面积分别为12×2×2=2,12×2×2212×2×221 2×22sin π33因此四面体的最大面的面积是3.故选C.(2)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.(3)设圆锥底面半径为r,母线长为l,母线与轴夹角为θ, 则=22π122rl r l r⋅-2π,r l=3,即sin θ=3,θ=π3. 解析:(4)四棱锥S-ABCD 中,可得AD ⊥SA,AD ⊥AB ⇒AD ⊥平面SAB ⇒平面SAB ⊥平面ABCD,过S 作SO ⊥AB 于O,则SO ⊥平面ABCD, 设∠SAB=θ, 故S ABCDV-=13S 四边形ABCD ·SO=83sin θ, 所以sin θ∈[3,1]⇒θ∈[π3,2π3]⇒-12≤cos θ≤12, 在△SAB 中,SA=AB=2, 则有SB=221cos θ-,所以△SAB 的外接圆半径r=2sin SBθ=21cos θ-,将该四棱锥补成一个以SAB 为一个底面的直三棱柱,得外接球的半径R=21r +⇒S=4πR2=4π(21cos θ++1), 所以S ∈[28π3,20π]. 答案:(1)C (2)D (3)π3答案:(4)[28π3,20π] (1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.1.(2019·浙江十校联盟)如图所示,已知某几何体的三视图及其尺寸(单位:cm),则该几何体的表面积为( C )(A)15π cm2(B)21π cm2(C)24π cm2(D)33π cm2解析:由三视图可知,则该几何体是一个圆锥,圆锥的底面半径为3,母线长为5,故该几何体的表面积为S表=πr2+πrl=π×32+π×3×5=24π(cm2).故选C.2.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )(A)81π4(B)16π(C)9π(D)27π4解析:易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+(2)2=R2, 解得R=94,所以球的表面积为4π×(94)2=814π.故选A.考点二几何体的体积[例2] (1)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )(A)12cm3(B)1 cm3(C)16 cm3 (D)13cm3(2)(2018·天津卷)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H, M(如图),则四棱锥M-EFGH的体积为.解析:(1)由题意,根据给定的三视图可知,该几何体表示一个底面为腰长为1的等腰直角三角形,高为1的三棱锥, 如图所示,所以该三棱锥的体积为V=13×12×1×1×1=16(cm 3),故选C.解析:(2)依题意,易知四棱锥M-EFGH 是一个正四棱锥,且底面边长为2,高为12. 故M EFGHV=13×(2)2×12=112. 答案:(1)C 答案:(2)112(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解,其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.某三棱锥的三视图如图所示,则该三棱锥的体积为( D )(A)60 (B)30 (C)20 (D)10解析:如图,把三棱锥A-BCD 放到长方体中,长方体的长、宽、高分别为5,3,4,△BCD 为直角三角形,直角边分别为5和3,三棱锥A-BCD 的高为4,故该三棱锥的体积V=13×12×5×3×4=10.故选D.考点三 与面积、体积相关的综合问题[例3] (1)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则12S S = ;(2)将边长为a 的正方形ABCD 沿对角线AC 折起,点A,B,C,D 折叠后对应点为A ′,B ′,C ′,D ′,使B ′D ′=a,则三棱锥D ′-A ′B ′C ′的体积为 .解析:(1)设正四面体棱长为a,则正四面体的表面积为 S 1=43a 23a2,正四面体的高2233a a ⎛⎫- ⎪ ⎪⎝⎭6a,由13r ·S 1=1332·h 知r=146a. 因此内切球的表面积为S 2=4πr 2=2π6a,则12S S 2236a a 63.解析:(2)如图所示,正方形ABCD 及折叠后的直观图.易知在直观图中,A ′B ′=B ′C ′=C ′D ′=D ′A ′=a, 且A ′D ′⊥D ′C ′,A ′B ′⊥B ′C ′, 取A ′C ′的中点E,连接D ′E,B ′E, 则D ′E ⊥A ′C ′,D ′E=EB ′=2a,所以D ′E ⊥EB ′,所以D ′E ⊥平面A ′B ′C ′. D ′E 即为三棱锥D ′-A ′B ′C ′的高. 故D A B C V''''-=13S △A ′B ′C ′·D ′E =13×12×a ×a ×2a=2a 3.答案:(1)63 答案:(2)2a 3(1)①解决与球有关问题的关键是球心及球的半径,在球中球心与截面圆圆心的连线、截面圆圆心与截面圆周上一点、该点与球心的连线构成一个直角三角形.②解决多面体(或旋转体)的外接球、内切球问题的关键是确定球心在多面体(或旋转体)中的位置,找到球半径(或直径)与几何体相关元素之间的关系.有时将多面体补形为正(长)方体再求解.(2)求几何体表面上两点间的最短距离的常用方法是选择恰当的母线或棱将几何体展开,转化为求平面上两点间的最短距离.1.已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( C ) (A)3172 (B)210(C)132(D)310解析:如图,由球心作平面ABC 的垂线, 则垂足为BC 的中点M.又AM=12BC=52,OM=12AA 1=6, 所以球O 的半径 R=OA=22562⎛⎫+ ⎪⎝⎭=132. 故选C.2.已知某几何体的三视图如图所示,则该几何体的表面积是 ,体积是 .解析:本题考查空间几何体的三视图、体积和表面积的计算.由三视图得该几何体为底面是以上底为1,下底为3,高为3的直角梯形,高为3的直四棱柱,则其表面积为2×3×1+32+3×3+1×3+3×3+3×13=33+313,体积为3×3×1+32=18.答案:33+31318考点四易错辨析[例4] (2019·浙江绍兴模拟)如图是由半球和圆柱组合而成的几何体的三视图,则该几何体的体积为( )(A)5π3 (B)8π3(C)10π3(D)12+2π3解析:由题得,几何体是水平放置的一个圆柱和半个球,所以该几何体的体积为V=43π×13×12+π×12×2=83π,故选B.正确解决此类问题应注意确认几何体的形状时,要紧扣三视图,不能凭感觉去确定.已知直三棱柱ABC-A1B1C1的侧棱长为4,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( C ) 2(B)3 3(D)4解析:如图,不妨设N在B处,AM=h,CQ=m,则有MB2=h2+4,BQ2=m2+4,MQ2=(h-m)2+4,由MB2=BQ2+MQ2,得m2-hm+2=0.则Δ=h2-8≥0,即h2≥8,所以该直角三角形的斜边MB≥23.故选C.类型一几何体的表面积1.如图是一个封闭几何体的三视图,则该几何体的表面积为( C )(A)7π cm2(B)8π cm2(C)9π cm2(D)11π cm2解析:依题意,题中的几何体是从一个圆柱中挖去一个半球后所剩余的部分,其中圆柱的底面半径是1 cm、高是 3 cm,球的半径是1 cm,因此该几何体表面积等于12×(4π×12)+π×12+2π×1×3=9π(cm2).故选C.2.某三棱锥的三视图如图所示,该三棱锥的表面积是( B )(A)28+65(B)30+65(C)56+125(D)60+125解析:根据三棱锥的三视图可还原此几何体的直观图如图,此几何体为一个底面为直角三角形,高为4的三棱锥,因此表面积为S=12×(2+3)×4+12×4×5+12×4×(2+3)+12×5415 5故选B.类型二几何体的体积3.某几何体的三视图如图所示,它的体积为( C )(A)72π(B)48π(C)30π(D)24π解析:由三视图知该几何体是由一个半球和一个圆锥构成的组合体,所以其体积为V=12×43π×33+13π×32×4=30π.故选C.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A)π2(B)1+π2(C)1+π(D)2+π解析:由三视图可得,该几何体是一个长方体和半个圆柱的组合体,则该几何体的体积为V=12×2+12×π×12×2=2+π,故选D.5.(2018·全国Ⅲ卷)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为3则三棱锥D-ABC体积的最大值为( B )3333解析:由等边△ABC的面积为3323,所以AB=6,所以等边△ABC的外接圆的半径为r=33AB=23.设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则d=22R r-=1612-=2.所以三棱锥D-ABC高的最大值为2+4=6,所以三棱锥D-ABC体积的最大值为13×93×6=183.故选B.6.(2019·名校协作体模拟)某几何体的三视图(单位:mm)如图所示,则它的体积是cm3,表面积是cm2.解析:由三视图得该几何体底面是一个以上底为2,下底为4,高为3的直角梯形,高为33的四棱锥,则其体积为13×33×2+42×3=93(cm3),表面积为1 2×3×33+2+42×3+12×3×2+12×3×4+12×5×33=(18+63)(cm2).答案:93(18+63)7.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.解析:由题意知所给的几何体是棱长均为2的八面体,它是由两个有公共底面的正四棱锥组合而成的,正四棱锥的高为1,所以这个八面体的体积为2V 正四棱锥=2×13×(2)2×1=43.答案:43类型三 面积、体积综合问题8.(2018·浙江绍兴质量调测)已知一个几何体的三视图如图所示,则该几何体的体积是( A )(A)83 (B)8 (C)203(D)6 解析:如图所示,在棱长为2的正方体中,题中的三视图对应的几何体为四棱锥P-ADC 1B 1,其中P 为棱A 1D 1的中点,则该几何体的体积11P ADC B V -=211P DB C V -=211D PB C V-=2×13×11PB C S∆×DD 1=83. 故选A.9.已知球的直径SC=4,A,B是该球球面上的两点,AB=3,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( C )(A)33(B)23(C)3 (D)1解析:由题意知,如图所示,在棱锥S-ABC中,△SAC,△SBC都是有一个角为30°的直角三角形,且3,SC=4,所以3作BD⊥3×3)2×3. SC于D点,连接AD,易证SC⊥平面ABD,因此V=13故选C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S
Sr2r lr(rl)
l
2r
O
圆台的展开图是一个扇环,它的表面积等于上、下 两个底面和加上侧面的面积,即
S(r'2r2r'lr)l
2r 、 2r
O`
O
O S 、 A A E AB B 即 S A E A B B O 、 Arr 、 lr、
C
SБайду номын сангаас
2r 、
o、
A
r、
l
D
S扇 SA Cr、 SA r( 、rr、 lr、 )
S扇SBDrSBr(SAl) 2r r(rr、 lr、l)r(rrlr、)
S 扇 环 S 扇 SB -S 扇 D SA C l(r r、 )
o r E
B
S 表 S 上 面 S 下 底 S 侧 底 面 ( r 、 2 r 2 r 、 l r )
思考:圆柱、圆锥、圆台的侧面积公 式间的联系与区别
V螺帽 21630785295
V总 /V螺帽 743.25.9526 ( 52个
练习 1 . 若一个圆柱的侧面展开图是一个正方形, 则这个圆柱的全面积与侧面积的比是( A )
A . 1 2 2
1 4
B . 4
C . 1 2
1 4 D.
2
2 . 已知圆锥的全面积是底面积的3倍,那么这个 圆锥的侧面积展开图----扇形的圆心角为____
__1_8_0__度
B
D
C
S4SSBC4
3a2 4
3a2
圆柱的展开图是一个矩形:
如果圆柱的底面半径为 r,母线为 l,那么圆柱
的底面积为 r 2,侧面积为 2rl 。因此圆柱的
表面积为
S 2 r2 2 r l2 r(r l)
O`
l
Or
2r
圆锥的展开图是一个扇形:
如果圆柱的底面半径为 r,母线为 l
那么圆锥的侧面积为: S侧122rlrl
3
S h
O S
棱锥的体积公式也是 V 1 Sh 3
h C
A
B
探究
探究棱锥与同底等高的棱柱体积之间的关系? 它也是同底同高的棱柱的体积的 1
3
体台
圆台(棱台)的体积可以利用两个锥体 的体积差,得到台体体积公式:
V1(S` S`SS)h 3
其是S‘,S分别为上底面面积,h为圆台(棱台)高。
例3 有一堆规格相同的(铁铁的制密度7是 .8g/cm3) 六角螺(帽 如下图 )共重5.8kg,已知底面是正六, 边 边长为 12mm,内孔直1径0mm,高为10mm,问这堆螺帽
1. 柱体、锥体、台体的表面积
正方体、长方体的表面积就是各个面的面积之和。
探究
棱柱、棱锥、棱台也是由多个平面图形 围成的几何体,它们的展开图是什么?如 何计算它们的表面积?
棱柱的侧面展开图是由平行四边形组成的平面图形 棱锥的侧面展开图是由三角形组成的平面图形
棱台的侧面展开图是由梯形组成的平面图形
7.5cm
2、柱体、锥体、台体的体积
体柱
正方体、长方体,以及圆柱的体积公式可以统 一为:
V = Sh(S为底面面积,h为高)
一般棱柱的体积公式也是V = Sh,其中S为 底面面积,h为高(即上下底面的距离)
h s
锥 圆锥的体积公式是 V 1 Sh
3
(其中S为底面面积,h为高) 它是同底同高的圆柱的体积的 1
这样,求它们的表面积的问题就可转化为求平行四边形、 三角形、梯形的面积问题。
例1、已知棱长 a,各 为面均为等边三角 四形 面体SABC(如下图 ),求它的表面 . 积
S
SD SB 2BD 2 a2(a)2 3a 22
A
S SB C 1 2B• C SD 1 2a2 3a4 3a2
四面S体-ABC 的表面积
S圆锥侧= πrl r1=0
S圆台侧=π(r1+r2)l
r1=r2 S圆柱侧= 2πrl
例2 如下,图 一个圆台形花盆2直 0cm径 ,盆为底 直径1为5cm,底部渗水圆孔1直.5c径 m,盆 为壁长
15cm.那么花盆的表面多 积少 约平 是方厘 (取米
3.14,结果精确 1c到 m)?
10cm
15cm
大约有多少(取 个3.14)?
个数 V总/V每个螺帽
V螺帽 V棱柱 -V圆柱
V 总 m / 5 .8 10 7 .8 0 7 0 .5 4 c9 3 3m
S三角 1 212 2312363 V 棱柱 sh 63631 0216 3
h V 圆 柱 r2h3.1 4 52 1 078
12
