第3讲 三角函数的图象与性质
2015高考数学一轮课件:第3篇 第3讲 三角函数的图象与性质

因为
f(x)=sin
x-cos xsin sin x
(1)(教材习题改编)由 sin(30°+120°)=sin 30°知,120°是正
弦函数 y=sin x(x∈R)的一个周期.
(×)
(2)函数 y=tan2x+3π的最小正周期为2π. 2.判断奇偶性与对称性
(√)
(3)函数 y=sin2x+32π是奇函数.
(×)
(4)函数 y=sin x 的对称轴方程为 x=2kπ+π2(k∈Z).( × )
第3讲 三角函数的图像与性质
[最新考纲] 1.能画出 y=sin x,y=cos x,y=tan x 的图像,了解三角函
数的周期性. 2.借助图像理解正弦函数、余弦函数在[0,2π],正切函数在
-2π,π2上的性质.
诊断基础知识
突破高频考第点一页,编辑于星培期五养:解十三题点能四十力五分。
知识梳理 正弦、余弦、正切函数的图象与性质 (下表中k∈Z).
诊断基础知识
突破高频考第点四页,编辑于星培期五养:解十三题点能四十力五分。
3.求三角函数的单调区间
(5)函数 f(x)=sin(-2x)与 f(x)=sin 2x 的单调增区间都是
kπ-π4,kπ+π4(k∈Z). (6)函数 y=tan x 在整个定义域上是增函数.
( ×) (× )
4.求三角函数的最值
二是对于 y=tan x 不能认为其在定义域上为增函数,应在 每个区间kπ-π2,kπ+π2(k∈Z)内为增函数,如(6). 三是函数 y=sin x 与 y=cos x 的最大值为 1,最小值为-1, 不存在一个值使 sin x=32,如(7).
诊断基础知识
突破高频考第点七页,编辑于星培期五养:解十三题点能四十力五分。
三角函数的图像与性质

三角函数的图像与性质三角函数的图像与性质在数学中,三角函数是一种基本的函数类型,其中的很多图像和性质对理解数学十分重要。
它们有助于理解各种模型的表示和应用,增强数学思维的能力和加深数学知识。
本文就三角函数的图像与性质做一些简单的介绍。
I、三角函数图像1、正弦曲线:正弦曲线是由参数从0到2π(2π是将一个周期跨越两次)形成的空间曲线。
它是圆的切线,有一定的规律性,并且把圆分为一个完整的一个周期,表现的曲线是一个“s”字形,形成有节奏的变化形式。
2、余弦曲线:余弦曲线是一条由参数从0到2π(2π是将一个周期跨越两次)形成的空间曲线,它也是圆的切线,有一定的规律性,但是它把圆分为两个半周期,比较起来更加缓和,表现的曲线是一个“v”字形,形成有节奏的变化形式。
3、正切曲线:正切曲线可以由参数0到π(π是将一个周期跨越一次)形成的曲线。
它也是一个椭圆的切线,有一定的规律性,把椭圆分为一完整周期,表现的曲线是一个“z”字形,形成有节奏的变化形式。
II、三角函数的性质1、周期性:三角函数的周期性就是说其值的变化是有如左图5000式的一个循环周期,在实际应用中可以利用该性质进行参数估计。
2、增减性:三角函数具有明显的增减性,具体表现为当参数逐渐增加时,函数值会自动增大,而当参数逐渐减小时,函数值则会自动减小。
3、几何性:三角函数有一个令人惊讶的性质,即在几何上其值就等于一定参数的弧度,而且参数的变化也不会影响该弧度。
4、极限性:参数π/2处的正切函数的值无穷大,表示非常接近的范围内函数的变化是接近无穷大的,而参数为0处的余弦函数为1,表示函数在某一点的取值趋势没有了变化,变成一个规定值。
总结来说,三角函数可以说是数学之中一个基本的概念,其图形和性质极其重要,可以帮助我们更深入的理解数学,增进数学的应用能力,因此,值得我们认真好好的学习。
三角函数图像及性质的总结
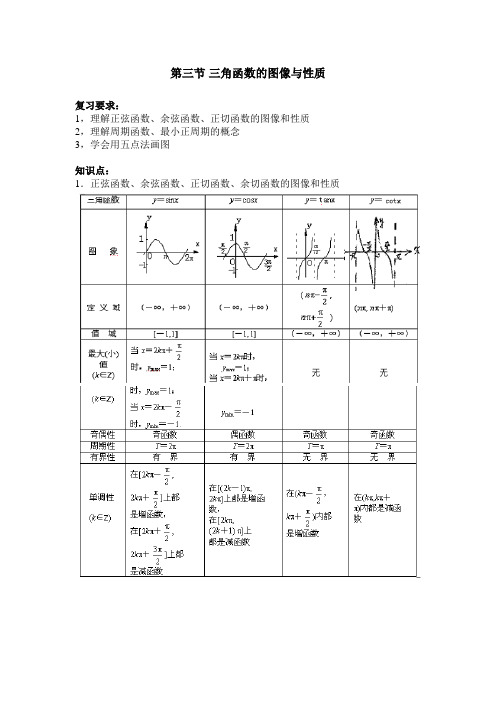
第三节三角函数的图像与性质复习要求:1,理解正弦函数、余弦函数、正切函数的图像和性质2,理解周期函数、最小正周期的概念3,学会用五点法画图知识点:1.正弦函数、余弦函数、正切函数、余切函数的图像和性质3.函数B x A y ++=)sin(ϕω),(其中00>>ωA最大值是B A +,最小值是A B -,周期是ωπ2=T ,频率是πω2=f ,相位是ϕω+x ,初相是ϕ;其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω,凡是该图象与直线B y =的交点都是该图象的对称中心。
4.由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换。
先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
5.由y =A sin(ωx +ϕ)的图象求其函数式:给出图象确定解析式y =A sin (ωx +ϕ)的题型,有时从寻找“五点”中的第一零点(-ωϕ,0)作为突破口,要从图象的升降情况找准..第一个零点的位置。
6.对称轴与对称中心: sin y x =的对称轴为2x k ππ=+,对称中心为(,0) k k Z π∈; cos y x =的对称轴为x k π=,对称中心为2(,0)k ππ+; 对于sin()y A x ωφ=+和cos()y A x ωφ=+来说,对称中心与零点相联系,对称轴与最值点联系。
《三角函数的图象与性质》PPT教学课件(第三课时正、余弦函数的单调性与最值)

栏目导航
12
(1)B
(2)xx≠-4kπ-43π,k∈Z
(3)x-π4+kπ≤x<π4+kπ,k∈Z
[(1)当-π4<x<0时,-1<tan x
<0,∴ta1n x≤-1;
当0<x<π4时,0<tan x<1,∴ta1n x≥1.
即当x∈-π4,0∪0,π4时,函数y=ta1n x的值域是(-∞,-1) ∪(1,+∞).
[提示] 由正切函数图象可知(1)×,(2)√,(3)×,(4)×. [答案] (1)× (2)√ (3)× (4)×
第五章 三角函数
5.4 三角函数的图象与性质 第4课时 正切函数的性质与图象
2
学习目标
核心素养
1.能画出正切函数的图象.(重点)
1.借助正切函数的图象研究问
2.掌握正切函数的性质.(重点、难点) 题,培养直观想象素养.
3.掌握正切函数的定义域及正切曲线的 2.通过正切函数的性质的应
渐近线.(易错点)
28
栏目导航
(2)函数定义域为 xx≠kπ-π4且x≠kπ+π4,k∈Z , 关于原点对称, 又f(-x)=tan-x-π4+tan-x+π4 =-tanx+π4-tanx-π4 =-f(x), 所以函数f(x)是奇函数.
29
栏目导航
30
正切函数单调性的应用 [探究问题] 1.正切函数y=tan x在其定义域内是否为增函数? 提示:不是.正切函数的图象被直线x=kπ+π2(k∈Z)隔开,所以它的 单调区间只在kπ-π2,kπ+π2(k∈Z)内,而不能说它在定义域内是增函 数.假设x1=π4,x2=54π,x1<x2,但tan x1=tan x2.
用,提升逻辑推理素养.
栏目导航
三角函数图像与性质

三角函数图像与性质在数学中,三角函数是研究角与角度关系的一类函数。
其中最重要的三角函数包括正弦函数、余弦函数和正切函数。
这些函数在数学和科学领域中有着广泛的应用,尤其是在研究周期性现象时起到了关键作用。
本文将详细介绍三角函数的图像特征和性质。
正弦函数的图像与性质正弦函数是最基本的三角函数之一,通常用符号$\\sin$表示。
它的图像是一条连续的波浪线,呈现出周期性的特点。
正弦函数的定义域为整个实数集$\\mathbb{R}$,值域为闭区间[−1,1]。
在0度、90度、180度、270度和360度等特殊角度上,正弦函数的取值分别为0、1、0、-1和0。
正弦函数是奇函数,即$\\sin(-x)=-\\sin(x)$,具有对称性。
余弦函数的图像与性质余弦函数是另一个重要的三角函数,通常用符号$\\cos$表示。
它的图像类似于正弦函数,也是一条连续的波浪线,同样呈现周期性。
余弦函数的定义域为整个实数集$\\mathbb{R}$,值域为闭区间[−1,1]。
在0度、90度、180度、270度和360度等特殊角度上,余弦函数的取值分别为1、0、-1、0和1。
余弦函数是偶函数,即$\\cos(-x)=\\cos(x)$,具有对称性。
正切函数的图像与性质正切函数是三角函数中的另一个重要函数,通常用符号$\\tan$表示。
它的图像是一组相互平行的直线,具有间断点。
正切函数的定义域为整个实数集$\\mathbb{R}$,在某些特殊角度上可能不存在定义,例如在90度和270度时。
正切函数的值域为整个实数集$\\mathbb{R}$。
正切函数是奇函数,即$\\tan(-x)=-\\tan(x)$。
三角函数的性质除了上述基本性质外,三角函数还有一些重要的性质:1.周期性:正弦函数和余弦函数的周期为$2\\pi$,即在$[0, 2\\pi]$范围内图像重复;2.奇偶性:正弦函数和正切函数是奇函数,余弦函数是偶函数;3.最值:正弦函数和余弦函数的最大值为1,最小值为-1;正切函数在定义域内取值范围较广;4.单调性:正弦函数、余弦函数和正切函数在各自的定义域上具有不同的单调性特点。
三角函数的图像与性质

三角函数的图像与性质三角函数是数学中的一类重要函数,由于其广泛应用于物理、工程和计算机科学等领域,对三角函数的图像和性质进行了深入的研究。
本文将就三角函数的图像和性质展开讨论。
一、正弦函数(Sine Function)正弦函数是最基本的三角函数之一,用sin(x)表示,其中x是一个实数。
正弦函数的图像可以通过绘制函数y = sin(x)来得到,横坐标x 表示角度(以弧度为单位),纵坐标y表示sin(x)的值。
正弦函数的图像具有以下性质:1. 周期性:正弦函数是周期性函数,其周期是2π(360度)。
2. 对称性:正弦函数是奇函数,即满足sin(-x) = -sin(x)。
3. 定义域和值域:正弦函数的定义域是整个实数集,值域在闭区间[-1, 1]内。
4. 最值:正弦函数在区间[0, 2π]取得最大值1和最小值-1。
二、余弦函数(Cosine Function)余弦函数是三角函数的另一个重要代表,用cos(x)表示,其中x是一个实数。
余弦函数的图像可以通过绘制函数y = cos(x)来得到,横坐标x表示角度(以弧度为单位),纵坐标y表示cos(x)的值。
余弦函数的图像具有以下性质:1. 周期性:余弦函数也是周期性函数,其周期是2π(360度)。
2. 对称性:余弦函数是偶函数,即满足cos(-x) = cos(x)。
3. 定义域和值域:余弦函数的定义域是整个实数集,值域在闭区间[-1, 1]内。
4. 最值:余弦函数在区间[0, 2π]取得最大值1和最小值-1。
三、正切函数(Tangent Function)正切函数是三角函数中的另一种形式,用tan(x)表示,其中x是一个实数。
正切函数的图像可以通过绘制函数y = tan(x)来得到,横坐标x表示角度(以弧度为单位),纵坐标y表示tan(x)的值。
正切函数的图像具有以下性质:1. 周期性:正切函数是周期性函数,其周期是π(180度)。
2. 对称性:正切函数是奇函数,即满足tan(-x) = -tan(x)。
【金版教程】届高考数学总复习 第3章 第3讲 三角函数的图象与性质课件 理 新人教A版

求形如y=Asin(ωx+φ)(A>0,ω>0)的函数的单调区间,基
本思路是把ωx+φ看作一个整体,由-
π 2
+2kπ≤ωx+φ≤
π 2
+
2kπ(k∈Z)求得函数的增区间,由
π 2
+2kπ≤ωx+φ≤
3π 2
+2kπ(k
∈Z)求得函数的减区间.若在y=Asin(ωx+φ)中,ω<0,则应
先利用诱导公式将解析式转化,使x的系数变为正数,再进行
(1)y=cos(x+π3)(x∈[0,π])的值域________. (2)y=tan(4π-x)的单调递减区间__________.
1.f(x+T)=f(x) 最小 最小正周期
想一想:提示:f[(x+2)+2]=-f(x+2)=f(x),即f(x+4)
=f(x),所以f(x)是周期为4的函数.
____
________
________
____
y=tanx
无最值
____ ________ 无对称轴
____
判断以下命题的正误. ①y=sinx在第一象限是增函数.( ) ②y=cosx在[0,π]上是减函数.( ) ③y=tanx在定义域上为增函数.( ) ④y=|sinx|的周期为2π.( ) ⑤y=ksinx+1,x∈R则y的最大值为k+1.( )
Z)
π+2kπ(k∈Z)
奇
偶
奇
(kπ,0),k∈Z
(kπ+
π 2
,
0),k∈Z
(
kπ 2
,0),k∈Z
x=kπ+
π 2
,k∈Z
x=kπ,k∈Z
2π 2π π
判一判:①× ②√ ③× ④× ⑤×
数学(浙江专用)总复习教师用书:第四章 三角函数、解三角形 第讲 三角函数的图象与性质

第3讲三角函数的图象与性质最新考纲 1.能画出y=sin x,y=cos x,y=tan x的图象,了解三角函数的周期性;2。
理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在区间错误!内的单调性。
知识梳理1。
用五点法作正弦函数和余弦函数的简图(1)正弦函数y=sin x,x∈[0,2π]的图象中,五个关键点是:(0,0),错误!,(π,0),错误!,(2π,0).(2)余弦函数y=cos x,x∈[0,2π]的图象中,五个关键点是:(0,1),错误!,(π,-1),错误!,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k∈Z)函数y=sin x y=cos x y=tan x图象定义域R R{x错误!错误!值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数1。
判断正误(在括号内打“√”或“×")(1)由sin错误!=sin 错误!知,错误!是正弦函数y=sin x(x∈R)的一个周期。
( )(2)余弦函数y=cos x的对称轴是y轴.()(3)正切函数y=tan x在定义域内是增函数.( )(4)已知y=k sin x+1,x∈R,则y的最大值为k+1。
( )(5)y=sin|x|是偶函数。
()解析(1)函数y=sin x的周期是2kπ(k∈Z).(2)余弦函数y=cos x的对称轴有无穷多条,y轴只是其中的一条.(3)正切函数y=tan x在每一个区间错误!(k∈Z)上都是增函数,但在定义域内不是单调函数,故不是增函数。
(4)当k〉0时,y max=k+1;当k<0时,y max=-k+1.答案(1)×(2)×(3)×(4)×(5)√2。
(2015·四川卷)下列函数中,最小正周期为π的奇函数是( )A。
y=sin错误!B。
y=cos错误!C.y=sin 2x+cos 2xD.y=sin x+cos x解析y=sin错误!=cos 2x是最小正周期为π的偶函数;y=cos错误!=-sin 2x是最小正周期为π的奇函数;y=sin 2x+cos 2x=2sin错误!是最小正周期为π的非奇非偶函数;y=sin x+cos x=错误!sin错误!是最小正周期为2π的非奇非偶函数.答案B3。
第3讲 三角函数的图象与性质

第3讲三角函数的图象与性质一、选择题1.函数f (x )=2sin x cos x 是( ).答案 CA .最小正周期为2 π的奇函数B .最小正周期为2 π的偶函数C .最小正周期为π的奇函数D .最小正周期为π的偶函数2.已知函数f (x )=sin(x +θ)+3cos(x +θ)⎝⎛⎭⎫θ∈⎣⎡⎦⎤-π2,π2是偶函数,则θ的值为( ). A .0 B.π6 C.π4 D.π3解析 据已知可得f (x )=2sin ⎝⎛⎭⎫x +θ+π3,若函数为偶函数,则必有θ+π3=k π+π2(k ∈Z ),又由于θ∈⎣⎡⎦⎤-π2,π2,故有θ+π3=π2,解得θ=π6,经代入检验符合题意.答案 B3.函数y =2sin ⎝⎛⎭⎫π6x -π3(0≤x ≤9)的最大值与最小值之和为 ( ). A .2- 3 B .0 C .-1 D .-1- 3解析 ∵0≤x ≤9,∴-π3≤π6x -π3≤7π6,∴-32≤sin ⎝⎛⎭⎫π6x -π3≤1,∴-3≤2sin ⎝⎛⎭⎫π6x -π3≤2.∴函数y =2sin ⎝⎛⎭⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为2- 3.答案 A4.函数f (x )=(1+3tan x )cos x 的最小正周期为( ).答案 AA .2π B.3π2C .π D.π25.函数y =sin 2x +sin x -1的值域为( ).A .[-1,1] B.⎣⎢⎡⎦⎥⎤-54,-1 C.⎣⎢⎡⎦⎥⎤-54,1 D.⎣⎢⎡⎦⎥⎤-1,54 解析 (数形结合法)y =sin 2x +sin x -1,令sin x =t ,则有y =t 2+t -1,t ∈[-1,1],画出函数图像如图所示,从图像可以看出,当t =-12及t =1时,函数取最值,代入y =t 2+t -1可得y ∈⎣⎢⎡⎦⎥⎤-54,1.答案 C6.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴,则φ= ( ).A.π4B.π3C.π2D.3π4解析 由题意可知函数f (x )的周期T =2×⎝⎛⎭⎫5π4-π4=2π,故ω=1,∴f (x )=sin(x +φ),令x +φ=k π+π2(k ∈Z ),将x =π4代入可得φ=k π+π4(k ∈Z ),∵0<φ<π,∴φ=π4.答案 A 二、填空题7.定义在R 上的函数f (x )既是偶函数又是周期函数,若f (x )的最小正周期是π,且当x ∈⎣⎡⎦⎤0,π2时,f (x )=sin x ,则f ⎝⎛⎭⎫5π3的值为________.解析 f ⎝⎛⎭⎫5π3=f ⎝⎛⎭⎫-π3=f ⎝⎛⎭⎫π3=sin π3=32.答案 328.函数f (x )=2sin ⎝⎛⎭⎪⎫x +π4+2x 2+x2x 2+cos x的最大值为M ,最小值为m ,则M +m =________. 解析 (构造法)根据分子和分母同次的特点,把分子展开,得到部分分式,f (x )=1+x +sin x2x 2+cos x,f (x )-1为奇函数,则m -1=-(M -1),所以M +m =2.答案 29.已知函数f (x )=12(sin x +cos x )-12|sin x -cos x |,则f (x )的值域是________.解析 f (x )=12(sin x +cos x )-12|sin x -cos x |=⎩⎪⎨⎪⎧cos x (sin x ≥cos x ),sin x (sin x <cos x ).画出函数f (x )的图象,可得函数的最小值为-1,最大值为22,故值域为⎣⎡⎦⎤-1,22.答案 ⎣⎡⎦⎤-1,2210.下列命题中:①α=2k π+π3(k ∈Z )是tan α=3的充分不必要条件;②函数f (x )=|2cos x -1|的最小正周期是π;③在△ABC 中,若cos A cos B >sin A sin B ,则△ABC 为钝角三角形;④若a +b =0,则函数y =a sin x -b cos x 的图象的一条对称轴方程为x =π4.其中是真命题的序号为________.解析 ①∵α=2k π+π3(k ∈Z )⇒tan α=3,而tan α=3⇒/ α=2k π+π3(k ∈Z ),∴①正确.②∵f (x +π)=|2cos(x +π)-1|=|-2cos x -1|=|2cos x +1|≠f (x ),∴②错误.③∵cos A cos B >sin A sin B ,∴cos A cos B -sin A sin B >0,即cos(A +B )>0,∵0<A +B <π,∴0<A +B <π2,∴C 为钝角,∴③正确.④∵a +b =0,∴b =-a ,y =a sin x -b cos x =a sin x +a cos x =2a sin ⎝⎛⎭⎫x +π4,∴x =π4是它的一条对称轴,∴④正确.答案 ①③④ 三、解答题11. 已知函数f (x )=2sin x cos x -2sin 2x +1.(1)求函数f (x )的最小正周期及值域;(2)求f (x )的单调递增区间.解 (1)f (x )=sin2x +cos2x =2sin ⎝ ⎛⎭⎪⎫2x +π4, 则函数f (x )的最小正周期是π,函数f (x )的值域是[]-2,2.(2)依题意得2k π-π2≤2x +π4≤2k π+π2(k ∈Z),则k π-3π8≤x ≤k π+π8(k ∈Z),即f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8(k ∈Z). 12.已知函数f (x )=cos ⎝⎛⎭⎫2x -π3+2sin ⎝⎛⎭⎫x -π4sin ⎝⎛⎭⎫x +π4. (1)求函数f (x )的最小正周期和图象的对称轴;(2)求函数f (x )在区间⎣⎡⎦⎤-π12,π2上的值域. 解 (1)f (x )=cos ⎝⎛⎭⎫2x -π3+2sin ⎝⎛⎭⎫x -π4sin ⎝⎛⎭⎫x +π4=12cos 2x +32sin 2x +(sin x -cos x )(sin x +cos x ) =12cos 2x +32sin 2x +sin 2x -cos 2x =12cos 2x +32sin 2x -cos 2x =sin ⎝⎛⎭⎫2x -π6. ∴最小正周期T =2π2=π,由2x -π6=k π+π2(k ∈Z ),得x =k π2+π3(k ∈Z ).∴函数图象的对称轴为x =k π2+π3(k ∈Z ).(2)∵x ∈⎣⎡⎦⎤-π12,π2,∴2x -π6∈⎣⎡⎦⎤-π3,5π6,∴-32≤sin ⎝⎛⎭⎫2x -π6≤1. 即函数f (x )在区间⎣⎡⎦⎤-π12,π2上的值域为⎣⎡⎦⎤-32,1. 函数y =A sin(ωx +φ)的图象及性质一、选择题1.已知函数f (x )=sin ⎝⎛⎭⎪⎫ωx +π3(ω>0)的最小正周期为π,则该函数的图像( ) 答案AA .关于点⎝ ⎛⎭⎪⎫π3,0对称B .关于直线x =π4对称C .关于点⎝ ⎛⎭⎪⎫π4,0对称 D .关于直线x =π3对称 2.要得到函数的图像,只要将函数的图像( )答案 C A. 向左平移1个单位 B. 向右平移1个单位C. 向左平移个单位 D.向右平移 个单位 3.函数f (x )=A sin(ωx +φ)A >0,ω>0,|φ|<π2的部分图象如图所示,则将y =f (x )的图象向右cos(21)y x =+cos 2y x =1212平移π6个单位后,得到的图象对应的函数解析式为( ). A .y =sin 2xB .y =cos 2xC .y =sin ⎝⎛⎭⎫2x +2π3D .y =sin ⎝⎛⎭⎫2x -π6 解析 由所给图象知A =1,34T =11π12-π6=3π4,T =π,所以ω=2πT =2,由sin ⎝⎛⎭⎫2×π6+φ=1,|φ|<π2得π3+φ=π2,解得φ=π6,所以f (x )=sin ⎝⎛⎭⎫2x +π6,则f (x )=sin ⎝⎛⎭⎫2x +π6的图象向右平移π6个单位后得到的图象对应的函数解析式为y =sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π6+π6=sin ⎝⎛⎭⎫2x -π6,故选D.答案 D 4.将函数y =sin 2x 的图象向左平移φ(φ>0)个单位,所得图象对应的函数为偶函数,则φ的最小值为 ( ).A.π6B.π3C.π4D.π12解析 将函数y =sin 2x 的图象向左平移φ个单位,得到函数y =sin 2(x +φ)=sin(2x +2φ)的图象,由题意得2φ=π2+k π(k ∈Z ),故φ的最小值为π4.答案 C5.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P (x ,y ).若初始位置为P 0⎝⎛⎭⎫32,12,当秒针从P 0(注:此时t =0)正常开始走时,那么点P的纵坐标y 与时间t 的函数关系为 ( ).A .y =sin ⎝⎛⎭⎫π30t +π6B .y =sin ⎝⎛⎭⎫-π60t -π6C .y =sin ⎝⎛⎭⎫-π30t +π6D .y =sin ⎝⎛⎭⎫-π30t -π3 解析 由题意可得,函数的初相位是π6,排除B ,D.又函数周期是60(秒)且秒针按顺时针旋转,即T =⎪⎪⎪⎪2πω=60,所以|ω|=π30,即ω=-π30,故选C.答案 C 6.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图像如图所示,则当t =1100秒时,电流强度是( )A .-5安B .5安C .53安D .10安解析由函数图像知A =10,T 2=4300-1300=1100.∴T =150=2πω,∴ω=100π.∴I =10sin(100πt +φ).又∵点⎝ ⎛⎭⎪⎫1300,10在图像上,∴10=10sin ⎝ ⎛⎭⎪⎫100π×1300+φ∴π3+φ=π2,∴φ=π6,∴I =10sin ⎝ ⎛⎭⎪⎫100πt +π6.当t =1100时,I =10sin ⎝⎛⎭⎪⎫100π×1100+π6=-5.答案A二、填空题7.已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图像上的两个相邻的最高点和最低点的距离为22,则ω=________. 解析由已知两相邻最高点和最低点的距离为22,而f (x )max -f (x )min =2,由勾股定理可得T2= 22 2-22=2,∴T =4,∴ω=2πT =π2.答案π28.已知函数f (x )=3sin ⎝⎛⎫ωx -π6(ω>0)和g (x )=2cos(2x +φ)+1的图象的对称轴完全相同,若x ∈⎣⎡⎤0,π2,则f (x )的取值范围是________.解析 ∵f (x )与g (x )的图象的对称轴完全相同,∴f (x )与g (x )的最小正周期相等,∵ω>0,∴ω=2,∴f (x )=3sin ⎝⎛⎭⎫2x -π6,∵0≤x ≤π2,∴-π6≤2x -π6≤5π6,∴-12≤sin ⎝⎛⎭⎫2x -π6≤1,∴-32≤3sin ⎝⎛⎭⎫2x -π6≤3,即f (x )的取值范围是⎣⎡⎦⎤-32,3.答案 ⎣⎡⎦⎤-32,39.已知函数f (x )=-2sin(2x +φ)(|φ|<π),若⎝⎛⎭⎫π8,5π8是f (x )的一个单调递增区间,则φ的值为________.解析 令π2+2k π≤2x +φ≤3π2+2k π,k ∈Z ,k =0时,有π4-φ2≤x ≤3π4-φ2,此时函数单调递增,若⎝⎛⎭⎫π8,5π8是f (x )的一个单调递增区间,则必有⎩⎨⎧π4-φ2≤π8,3π4-φ2≥5π8,解得⎩⎨⎧φ≥π4,φ≤π4,故φ=π4.答案 π410.在函数f (x )=A sin(ωx +φ)(A >0,ω>0)的一个周期内,当x =π9时有最大值12,当x =4π9时有最小值-12,若φ∈⎝⎛⎭⎪⎫0,π2,则函数解析式f (x )=________.解析 首先易知A =12,由于x =π9时f (x )有最大值12,当x =4π9时f (x )有最小值-12,所以T =⎝ ⎛⎭⎪⎫4π9-π9×2=2π3,ω=3.又12sin ⎝ ⎛⎭⎪⎫3×π9+φ=12,φ∈⎝⎛⎭⎪⎫0,π2,解得φ=π6,故f (x )=12sin ⎝ ⎛⎭⎪⎫3x +π6.答案 12sin ⎝ ⎛⎭⎪⎫3x +π6三、解答题11.已知函数f (x )=3sin2x +2cos 2x .(1)将f (x )的图像向右平移π12个单位长度,再将周期扩大一倍,得到函数g (x )的图像,求g (x )的解析式;(2)求函数f (x )的最小正周期和单调递增区间.解 (1)依题意f (x )=3sin2x +2·cos2x +12=3sin2x +cos2x +1=2sin ⎝⎛⎭⎪⎫2x +π6+1, 将f (x )的图像向右平移π12个单位长度,得到函数f 1(x )=2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π12+π6+1=2sin2x +1的图像,该函数的周期为π,若将其周期变为2π,则得g (x )=2sin x +1. (2)函数f (x )的最小正周期为T =π,当2k π-π2≤2x +π6≤2k π+π2(k ∈Z)时,函数单调递增,解得k π-π3≤x ≤k π+π6(k ∈Z),∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z). 12.已知向量m =(sin x,1),n =(3A cos x ,A2cos 2x )(A >0),函数f (x )=m ·n 的最大值为6.(1)求A ;(2)将函数y =f (x )的图象向左平移π12个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )在⎣⎡⎦⎤0,5π24上的值域. 解 (1)f (x )=m ·n =3A sin x cos x +A 2cos 2x =A ⎝⎛⎭⎫32sin 2x +12cos 2x =A sin ⎝⎛⎭⎫2x +π6. 因为A >0,由题意知A =6.(2)由(1)知f (x )=6sin ⎝⎛⎭⎫2x +π6. 将函数y =f (x )的图象向左平移π12个单位后得到y =6sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π12+π6=6sin ⎝⎛⎭⎫2x +π3的图象; 再将得到图象上各点横坐标缩短为原来的12倍,纵坐标不变,得到y =6sin ⎝⎛⎭⎫4x +π3的图象. 因此g (x )=6sin ⎝⎛⎭⎫4x +π3. 因为x ∈⎣⎡⎦⎤0,5π24,所以4x +π3∈⎣⎡⎦⎤π3,7π6,故g (x )在⎣⎡⎦⎤0,5π24上的值域为[-3,6].。
第三节 三角函数的图象与性质

题点(一) 求单调区间
[逐点例析]
[例 1] (1)函数 y=log12cos32π-2x的单调递增区间是 A.kπ-π4,kπ+π4 (k∈Z )
()
B.kπ-π4,kπ (k∈Z )
C.kπ-kπ+π4,kπ+34π (k∈Z )
D.kπ+π4,kπ+34π (k∈Z )
(2)函数 y=|tan x|的单调递增区间为________,单调递减区间为_______.
2.三角函数值域或最值的3种求法 形如y=asin x+k或y=acos x+k的三角函数,直接利用sin
直接法 x,cos x的值域求出 形如y=asin x+bcos x+k的三角函数,化为y=Asin(ωx+φ)+
化一法 k的形式,确定ωx+φ的范围,根据正弦函数单调性写出函数 的值域(最值) 形如y=asin2x+bsin x+k的三角函数,可先设sin x=t,化为 关于t的二次函数求值域(最值);形如y=asin xcos x+b(sin
[解析]
(1)y=log
1 2
cosπ3-2x=log
1 2
(-sin 2x),
由-sin 2x>0 得 sin 2x<0,即 2kπ-π<2x<2kπ,k∈Z ,
即 kπ-π2<x<kπ,k∈Z ,
设 t=-sin 2x,则 y=log 1 t 为减函数, 2
要求
y=log
1 2
cosπ3-2x的递增区间,
二、“基本技能”运用好 1.y=|tan x|·cos x0≤x<32π,x≠π2的图象是
答案:D
()
2.已知函数 f(x)=cosωx+π4 (ω>0)的最小正周期为 π,则 ω=________. 答案:2
三角函数的图像与性质

三角函数的图像与性质引言三角函数在数学中起着非常重要的作用,它们的图像与性质也是数学学习过程中的基础内容。
本文将介绍三角函数的图像和常见性质,包括正弦函数、余弦函数和正切函数。
正弦函数的图像与性质正弦函数是三角函数中最常见的函数之一,它的图像呈现周期性的波动。
正弦函数的定义域为实数集,值域为[-1, 1]。
正弦函数的图像可以用下面的公式表示:$$y = \\sin(x)$$正弦函数的图像在周期范围内呈现上升和下降的特点,其中最高点和最低点的纵坐标分别为1和-1。
正弦函数的图像以曲线方式连续无间断地进行。
正弦函数的性质包括: - 正弦函数的周期为$2\\pi$,即在每个周期内,正弦函数的图像完整地重复一次。
- 正弦函数的对称轴为x轴。
- 正弦函数的图像在$[\frac{\pi}{2},\frac{3\pi}{2}] $ 上是增函数,在$[0, \frac{\pi}{2}] $ 和$[\frac{3\pi}{2}, 2\pi] $ 上是减函数。
余弦函数的图像与性质余弦函数也是三角函数中常见的函数,它的图像与正弦函数非常相似,但是相位不同。
余弦函数的定义域为实数集,值域为[-1, 1]。
余弦函数的图像可以用下面的公式表示:$$y = \\cos(x)$$余弦函数的图像在周期范围内呈现上升和下降的特点,其中最高点和最低点的纵坐标分别为1和-1。
余弦函数的图像以曲线方式连续无间断地进行。
余弦函数的性质包括: - 余弦函数的周期为$2\\pi$,即在每个周期内,余弦函数的图像完整地重复一次。
- 余弦函数的对称轴为y轴。
- 余弦函数的图像在$[\pi, 2\pi] $ 上是增函数,在$[0, \pi] $ 上是减函数。
正切函数的图像与性质正切函数是另一个重要的三角函数,它的图像在不同的区间内有不同的特点。
正切函数的定义域是除了$\\frac{\\pi}{2} + k\\pi$(其中k是整数)的所有实数,值域是整个实数集。
高考数学第3章三角函数、解三角形第3讲三角函数的图象与性质创高三全册数学

第四页,共七十六页。
2.正弦函数、余弦函数、正切函数的图象和性质
函数 y=sinx
y=cosx
y=tanx
图象
定义 域 值域
xx∈R,且 x≠
R
R
kπ+π2,k∈Z
01 _[-___1_,1__] 02 _[-___1_,1_]_ 03 _R_
12/12/2021
第五页,共七十六页。
续表
函数
y=sinx
y=cosx
y=tanx
最值
当 x=π2+2kπ
当 x=2kπ(k∈Z)时,ymax
x∈
(k∈Z)时,ymax=1;
=1;
-π2+kπ, π2+kπ
当 x=32π+2kπ (k∈Z)时,ymin=-1
当 x=π+2kπ (k∈Z)时,ymin=-1
,k∈Z,无最大值, 也无最小值
12/12/2021
第二十四页,共七十六页。
解析
2.已知π3为函数 f(x)=sin(2x+φ)0<φ<π2的零点,则函数 f(x)的单调递 增区间是( )
A.2kπ-152π,2kπ+1π2(k∈Z) B.2kπ+1π2,2kπ+71π2(k∈Z) C.kπ-51π2,kπ+1π2(k∈Z) D.kπ+1π2,kπ+71π2(k∈Z)
第二十页,共七十六页。
1.函数 y= tanx+ -cosx的定义域为{__x_2_k_π_+__π_≤__x_<__2_kπ_+__3_2π_,__k_∈__Z_.
解析
tanx≥0, 由
-cosx≥0,
得
tanx≥0,
cosx≤0.
所以 2kπ+π≤x<2kπ+32π,k∈
三角函数的图像与性质

三角函数的图像与性质三角函数是数学中重要的概念,对描述周期性变化具有广泛应用。
本文将探讨三角函数的图像及其性质,包括正弦函数、余弦函数和正切函数。
一、正弦函数的图像与性质正弦函数是一种周期性的函数,用于描述角度和长度的关系。
正弦函数的图像呈现出一条连续的波浪线,具有以下性质:1. 定义域和值域:正弦函数的定义域为实数集,值域为闭区间[-1,1]。
2. 奇偶性:正弦函数是奇函数,即满足f(-x) = -f(x),图像关于y轴对称。
3. 周期性:正弦函数的周期为2π,即f(x + 2π) = f(x)。
4. 对称性:正弦函数关于直线x = π的中心对称。
二、余弦函数的图像与性质余弦函数也是一种周期性的函数,常用于描述角度和长度的关系。
余弦函数的图像呈现出一条连续的波浪线,具有以下性质:1. 定义域和值域:余弦函数的定义域为实数集,值域为闭区间[-1, 1]。
2. 奇偶性:余弦函数是偶函数,即满足f(-x) = f(x),图像关于y轴对称。
3. 周期性:余弦函数的周期为2π,即f(x + 2π) = f(x)。
4. 对称性:余弦函数关于直线x = π/2的中心对称。
三、正切函数的图像与性质正切函数是一种周期性的函数,用于描述角度和斜率的关系。
正切函数的图像呈现出一条连续的曲线,具有以下性质:1. 定义域和值域:正切函数的定义域为实数集,值域为整个实数集。
2. 奇偶性:正切函数是奇函数,即满足f(-x) = -f(x),图像关于原点对称。
3. 周期性:正切函数的周期为π,即f(x + π) = f(x)。
4. 渐近线:正切函数有两条水平渐近线,分别为y = π/2和y = -π/2。
总结:正弦函数、余弦函数和正切函数是三角函数中最常见的函数,它们的图像及性质对理解角度和长度、角度和斜率的关系有着重要的意义。
熟练掌握它们的图像和性质,能够帮助我们更好地解决与周期性变化相关的问题。
通过本文的探讨,我们了解到了正弦函数、余弦函数和正切函数的图像特点以及几个基本性质,包括定义域和值域、奇偶性、周期性和对称性等。
三角函数的图像与性质

三角函数的图像与性质三角函数是数学中的重要概念,涉及到三角比例和角度,广泛应用于几何、物理、工程等领域。
在本文中,我们将讨论三角函数的图像以及其性质。
一、正弦函数(sin)正弦函数是最基本的三角函数之一,用sin表示。
正弦函数的图像为一条连续不断的曲线,其横坐标表示角度(以弧度为单位),纵坐标表示正弦值。
正弦函数的周期是2π,即在区间[0, 2π]内,正弦函数的图像会完整地重复出现。
正弦函数的图像特点如下:1. 在0度(或0弧度)和180度(或π弧度)处,正弦函数的值为0;2. 在90度(或π/2弧度)处,正弦函数的值最大,为1;3. 在270度(或3π/2弧度)处,正弦函数的值最小,为-1;4. 在其他角度处,正弦函数的值位于-1和1之间,根据角度的大小而变化。
二、余弦函数(cos)余弦函数是另一个常见的三角函数,用cos表示。
余弦函数的图像也是一条连续曲线,其横坐标为角度,纵坐标为余弦值。
余弦函数的周期也是2π,即在区间[0, 2π]内,余弦函数的图像会一次完整地重复。
余弦函数的图像特点如下:1. 在0度(或0弧度)和360度(或2π弧度)处,余弦函数的值为1;2. 在180度(或π弧度)处,余弦函数的值最小,为-1;3. 在其他角度处,余弦函数的值位于-1和1之间,根据角度的大小而变化。
三、正切函数(tan)正切函数是三角函数中的第三个重要函数,用tan表示。
正切函数的图像也是一条光滑的曲线,以角度为横坐标,正切值为纵坐标。
正切函数的周期是π,即在区间[0, π]内,正切函数的图像会完整地重复。
正切函数的图像特点如下:1. 在0度(或0弧度)和180度(或π弧度)处,正切函数的值为0;2. 在90度(或π/2弧度)处,正切函数的值不存在,即为无穷大(正无穷或负无穷);3. 在其他角度处,正切函数的值在正无穷和负无穷之间变化。
四、其他三角函数除了正弦、余弦和正切函数外,还有一些相关的三角函数,如余割函数(cosec)、正割函数(sec)和余切函数(cot)等。
三角函数的图象和性质

三角函数定义域、值域的求解策略 (1)求与三角函数有关的定义域问题实际上是解简单的三角不等式,也可借助三角函数线或三角函数图 象来求解. (2)求解三角函数的值域(最值),首先把三角函数化为 y=Asin(ωx+φ)+k 的形式,再求最值(值域),或 用换元法(令 t=sinx,或 t=sinx±cosx)化为关于 t 的二次函数求值域(最值). (3)换元法的应用:把 sinx 或 cosx 看作一个整体,转化为二次函数,求给定区间上的值域(最值)问题.此 时注意所换元的取值范围.
第3讲 三角函数的图象和性质
1.能画出 y=sinx,y=cosx,y=tanx 的图象,了解三角函数的周期性. 2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值,图象 与 x 轴的交点等),理解正切函数在区间-π2,2π内的单调性.
板块一 知识梳理·自主学习
考点 1 周期函数和最小正周期
递增;π 在 2
+2kπ,32π+2kπ]
,k∈Z 上 ,k∈Z 上
在 [(2k-1)π,2kπ] k∈Z 上递增;
,在-π2
+kπ,
在 [2kπ,(2k+1)π],k∈Z 上递增
π2+kπ,
递减
k∈Z 上递减
-xπ2=+π22+kπ2(kkπ∈Z(k)∈时Z),时y,miny=max-=11;x=
[必备知识]
考点 2 正弦函数、余弦函数、正切函数的图象和性质
函数
y=sinx
y=cosx
y=tanx
图象
定义 域
值域
x∈R [-1,1]
x∈R [-1,1]
{ x|x∈R 且 x≠π2+kπ,k∈Z } R
续表 函数
单调性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 三角函数的图象与性质A 级 基础演练(时间:30分钟 满分:55分)一、选择题(每小题5分,共20分)1.(2011·山东)若函数f (x )=sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=( ).A.23B.32C .2D .3解析 由题意知f (x )的一条对称轴为x =π3,和它相邻的一个对称中心为原点,则f (x )的周期T =4π3,从而ω=32. 答案 B2.已知函数f (x )=sin(x +θ)+3cos(x +θ)⎝ ⎛⎭⎪⎫θ∈⎣⎢⎡⎦⎥⎤-π2,π2是偶函数,则θ的值为( ).A .0B.π6C.π4D.π3解析 据已知可得f (x )=2sin ⎝ ⎛⎭⎪⎫x +θ+π3,若函数为偶函数,则必有θ+π3=k π+π2(k ∈Z ),又由于θ∈⎣⎢⎡⎦⎥⎤-π2,π2,故有θ+π3=π2,解得θ=π6,经代入检验符合题意. 答案 B3.函数y =2sin ⎝ ⎛⎭⎪⎫π6x -π3(0≤x ≤9)的最大值与最小值之和为( ).A .2- 3B .0C .-1D .-1- 3解析 ∵0≤x ≤9,∴-π3≤π6x -π3≤7π6,∴-32≤sin ⎝ ⎛⎭⎪⎫π6x -π3≤1,∴-3≤2sin ⎝ ⎛⎭⎪⎫π6x -π3≤2.∴函数y =2sin ⎝ ⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为2- 3. 答案 A4.(2011·安徽)已知函数f (x )=sin(2x +φ),其中φ为实数.若f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对x ∈R恒成立,且f ⎝ ⎛⎭⎪⎫π2>f (π),则f (x )的单调递增区间是( ).A.⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z )B.⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z ) C.⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ) D.⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ) 解析 由f (x )=sin(2x +φ),且f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对x ∈R 恒成立,∴f ⎝ ⎛⎭⎪⎫π6=±1,即sin ⎝ ⎛⎭⎪⎫2×π6+φ=±1. ∴π3+φ=k π+π2(k ∈Z ).∴φ=k π+π6(k ∈Z ). 又f ⎝ ⎛⎭⎪⎫π2>f (π),即sin(π+φ)>sin(2π+φ),∴-sin φ>sin φ.∴sin φ<0.∴对于φ=k π+π6(k ∈Z ),k 为奇数.∴f (x )=sin(2x +φ)=sin ⎝ ⎛⎭⎪⎫2x +k π+π6=-sin ⎝ ⎛⎭⎪⎫2x +π6.∴由2m π+π2≤2x +π6≤2m π+3π2(m ∈Z ), 得m π+π6≤x ≤m π+2π3(m ∈Z ),∴f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤m π+π6,m π+2π3(m ∈Z ).答案 C二、填空题(每小题5分,共10分)5.定义在R 上的函数f (x )既是偶函数又是周期函数,若f (x )的最小正周期是π,且当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )=sin x ,则f ⎝ ⎛⎭⎪⎫5π3的值为________. 解析 f ⎝ ⎛⎭⎪⎫5π3=f ⎝ ⎛⎭⎪⎫-π3=f ⎝ ⎛⎭⎪⎫π3=sin π3=32.答案 326.若f (x )=2sin ωx (0<ω<1)在区间⎣⎢⎡⎦⎥⎤0,π3上的最大值是2,则ω=________.解析 由0≤x ≤π3,得0≤ωx ≤ωπ3<π3,则f (x )在⎣⎢⎡⎦⎥⎤0,π3上单调递增,且在这个区间上的最大值是2,所以2sin ωπ3=2,且0<ωπ3<π3, 所以ωπ3=π4,解得ω=34. 答案 34三、解答题(共25分) 7.(12分)设f (x )=1-2sin x . (1)求f (x )的定义域;(2)求f (x )的值域及取最大值时x 的值.解 (1)由1-2sin x ≥0,根据正弦函数图象知: 定义域为{x |2k π+56π≤x ≤2k π+13π6,k ∈Z }. (2)∵-1≤sin x ≤1,∴-1≤1-2sin x ≤3, ∵1-2sin x ≥0,∴0≤1-2sin x ≤3, ∴f (x )的值域为[0,3],当x =2k π+3π2,k ∈Z 时,f (x )取得最大值.8.(13分)(2013·东营模拟)已知函数f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3+2sin ⎝ ⎛⎭⎪⎫x -π4sin ⎝ ⎛⎭⎪⎫x +π4.(1)求函数f (x )的最小正周期和图象的对称轴; (2)求函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π2上的值域.解 (1)f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3+2sin ⎝ ⎛⎭⎪⎫x -π4sin ⎝ ⎛⎭⎪⎫x +π4=12cos 2x +32sin 2x +(sin x -cos x )(sin x +cos x ) =12cos 2x +32sin 2x +sin 2x -cos 2x =12cos 2x +32sin 2x -cos 2x =sin ⎝ ⎛⎭⎪⎫2x -π6.∴最小正周期T =2π2=π,由2x -π6=k π+π2(k ∈Z ), 得x =k π2+π3(k ∈Z ).∴函数图象的对称轴为x =k π2+π3(k ∈Z ). (2)∵x ∈⎣⎢⎡⎦⎥⎤-π12,π2,∴2x -π6∈⎣⎢⎡⎦⎥⎤-π3,5π6,∴-32≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1.即函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π2上的值域为⎣⎢⎡⎦⎥⎤-32,1.B 级 能力突破(时间:30分钟 满分:45分)一、选择题(每小题5分,共10分)1.(2012·新课标全国)已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π单调递减,则ω的取值范围是( ).A.⎣⎢⎡⎦⎥⎤12,54 B.⎣⎢⎡⎦⎥⎤12,34 C.⎝ ⎛⎦⎥⎤0,12 D .(0,2]解析 取ω=54,f (x )=sin ⎝ ⎛⎭⎪⎫54x +π4,其减区间为⎣⎢⎡⎦⎥⎤85k π+π5,85k π+π,k ∈Z ,显然⎝ ⎛⎭⎪⎫π2,π⊆85k π+π5,85k π+π,k ∈Z ,排除B ,C.取ω=2,f (x )=sin ⎝ ⎛⎭⎪⎫2x +π4,其减区间为⎣⎢⎡⎦⎥⎤k π+π8,k π+58π,k ∈Z ,显然⎝ ⎛⎭⎪⎫π2,π⃘⎣⎢⎡⎦⎥⎤k π+π8,k π+58π,k ∈Z ,排除D. 答案 A2.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴,则φ=( ).A.π4B.π3C.π2 D.3π4解析 由题意可知函数f (x )的周期T =2×⎝ ⎛⎭⎪⎫5π4-π4=2π,故ω=1,∴f (x )=sin(x+φ),令x +φ=k π+π2(k ∈Z ),将x =π4代入可得φ=k π+π4(k ∈Z ),∵0<φ<π,∴φ=π4. 答案 A二、填空题(每小题5分,共10分)3.(2013·徐州模拟)已知函数f (x )=12(sin x +cos x )-12|sin x -cos x |,则f (x )的值域是________.解析 f (x )=12(sin x +cos x )-12|sin x -cos x | =⎩⎨⎧cos x (sin x ≥cos x ),sin x (sin x <cos x ).画出函数f (x )的图象,可得函数的最小值为-1,最大值为22,故值域为⎣⎢⎡⎦⎥⎤-1,22.答案 ⎣⎢⎡⎦⎥⎤-1,224.(2012·西安模拟)下列命题中:①α=2k π+π3(k ∈Z )是tan α=3的充分不必要条件; ②函数f (x )=|2cos x -1|的最小正周期是π;③在△ABC 中,若cos A cos B >sin A sin B ,则△ABC 为钝角三角形; ④若a +b =0,则函数y =a sin x -b cos x 的图象的一条对称轴方程为x =π4. 其中是真命题的序号为________. 解析 ①∵α=2k π+π3(k ∈Z )⇒tan α=3, 而tan α=3⇒/ α=2k π+π3(k ∈Z ),∴①正确. ②∵f (x +π)=|2cos(x +π)-1|=|-2cos x -1|=|2cos x +1|≠f (x ),∴②错误.③∵cos A cos B >sin A sin B ,∴cos A cos B -sin A sin B >0, 即cos(A +B )>0,∵0<A +B <π,∴0<A +B <π2,∴C 为钝角,∴③正确. ④∵a +b =0,∴b =-a ,y =a sin x -b cos x =a sin x +a cos x =2a sin ⎝ ⎛⎭⎪⎫x +π4,∴x =π4是它的一条对称轴,∴④正确. 答案 ①③④ 三、解答题(共25分)5.(12分)已知函数f (x )=cos ⎝ ⎛⎭⎪⎫π3+x cos ⎝ ⎛⎭⎪⎫π3-x ,g (x )=12sin 2x -14.(1)求函数f (x )的最小正周期;(2)求函数h (x )=f (x )-g (x )的最大值,并求使h (x )取得最大值的x 的集合. 解 (1)∵f (x )=cos ⎝ ⎛⎭⎪⎫π3+x cos ⎝ ⎛⎭⎪⎫π3-x=⎝ ⎛⎭⎪⎫12cos x -32sin x ·⎝ ⎛⎭⎪⎫12cos x +32sin x =14cos 2x -34sin 2x =1+cos 2x 8-3-3cos 2x 8=12cos 2x -14,∴f (x )的最小正周期为2π2=π. (2)由(1)知h (x )=f (x )-g (x )=12cos 2x -12sin 2x =22cos ⎝ ⎛⎭⎪⎫2x +π4, 当2x +π4=2k π(k ∈Z ),即x =k π-π8(k ∈Z )时,h (x )取得最大值22.故h (x )取得最大值时,对应的x 的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k π-π8,k ∈Z.6.(13分)已知a >0,函数f (x )=-2a sin ⎝ ⎛⎭⎪⎫2x +π6+2a +b ,当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ⎝ ⎛⎭⎪⎫x +π2且lg g (x )>0,求g (x )的单调区间.解 (1)∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴2x +π6∈⎣⎢⎡⎦⎥⎤π6,7π6.∴sin ⎝ ⎛⎭⎪⎫2x +π6∈⎣⎢⎡⎦⎥⎤-12,1,又∵a >0, ∴-2a sin ⎝ ⎛⎭⎪⎫2x +π6∈[-2a ,a ].∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1,∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得a =2,b =-5,∴f (x )=-4sin ⎝ ⎛⎭⎪⎫2x +π6-1,g (x )=f ⎝ ⎛⎭⎪⎫x +π2=-4sin ⎝ ⎛⎭⎪⎫2x +7π6-1=4sin ⎝ ⎛⎭⎪⎫2x +π6-1,又由lg g (x )>0,得g (x )>1,∴4sin ⎝ ⎛⎭⎪⎫2x +π6-1>1,∴sin ⎝ ⎛⎭⎪⎫2x +π6>12,∴2k π+π6<2x +π6<2k π+5π6,k ∈Z ,其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为⎝ ⎛⎦⎥⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z .∴g (x )的单调减区间为⎝ ⎛⎭⎪⎫k π+π6,k π+π3,k ∈Z . 综上,g (x )的递增区间为⎝ ⎛⎦⎥⎤k π,k π+π6(k ∈Z );递减区间为⎝ ⎛⎭⎪⎫k π+π6,k π+π3(k ∈Z ).。
