届高三数学二轮复习不等式课件
高三数学第二轮复习专题3不等式

高三数学第二轮复习专题3不等式专题3 不等式江苏省震泽中学 王利平一、填空题例1 已知集合A =⎩⎨⎧⎭⎬⎫0,1,B =⎩⎨⎧⎭⎬⎫a 2,2a ,其中a ∈R.定义A ×B ={x |x =x 1+x 2,x 1∈A ,x 2∈B },若集合A ×B 中的最大元素为2a +1,则a 的取值范围是________. 解析 A ×B ={a 2,2a ,a 2+1,2a +1}.由题意,得2a +1>a 2+1,解得0<a <2. 答案 (0,2)例2 .设123log2,ln 2,5a b c -===则c b a ,,三者的大小关系解析 a=3log 2=21log 3, b=In2=21log e,而22log3log 1e >>,所以a<b, c=125-=5,而2252log 4log 3>=>,所以c<a,综上c<a<b.答案c a b <<例3 .对于问题:“已知关于x 的不等式ax 2+bx +c >0的解集为(-1,2),解关于x 的不等式ax 2-bx +c >0”.给出如下一种解法:解 由ax 2+bx +c >0的解集为(-1,2),得a (-x )2+b (-x )+c >0的解集为(-2,1), 即关于x 的不等式ax 2-bx +c >0的解集为(-2,1).参考上述解法,若关于x 的不等式kx +a+x +b x +c <0的解集为⎝ ⎛⎭⎪⎪⎫-1,-13∪⎝ ⎛⎭⎪⎪⎫12,1,则关于x 的不等式kxax +1+bx +1cx +1<0的解集为________.解析 不等式kx ax +1+bx +1cx +1<0可化为k1x+a +1x +b 1x +c<0,所以有1x ∈⎝ ⎛⎭⎪⎪⎫-1,-13∪⎝ ⎛⎭⎪⎪⎫12,1, 即x ∈(-3,-1)∪(1,2),从而不等式kx ax +1+bx +1cx +1<0的解集为(-3,-1)∪(1,2). 答案 (-3,-1)∪(1,2) 例4 .设不等式组x 1x-2y+30y x ≥⎧⎪≥⎨⎪≥⎩所表示的平面区域是1Ω,平面区域是2Ω与1Ω关于直线3490x y --=对称,对于1Ω中的任意一点A 与2Ω中的任意一点B, ||AB 的最小值等于解析 由题意知,所求的||AB 的最小值,即为区域1Ω中的点到直线3490x y --=的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,可看出点(1,1)到直线3490x y --=的距离最小,故||AB 的最小值为|31419|245⨯-⨯-⨯=。
高考数学(文)二轮专题复习课件:第1部分 专题八 选考系列4-4、4-5 1-8-2

[ 自我挑战] 2.(2017· 高考全国卷Ⅱ)已知 a>0,b>0,a3+b3=2,证明: (1)(a+b)(a5+b5)≥4; (2)a+b≤2.
证明:(1)(a+b)(a5+b5)=a6+ab5+a5b+b6 =(a3+b3)2-2a3b3+ab(a4+b4)=4+ab(a2-b2)2≥4. (2)证明:因为(a+b)3=a3+3a2b+3ab2+b3=2+3ab(a+b)≤2 3a+b2 3a+b3 + 4 (a+b)=2+ 4 , 所以(a+b)3≤8,因此 a+b≤2.
于是 a=3.
1.用零点区分法解绝对值不等式的步骤: (1)求零点;(2)划区间、去绝对值号;(3)分别解去掉绝对值的 不等式;(4)取每个结果的并集,注意在分段时不要遗漏区间的端 点值. 2.用图象法、数形结合可以求解含有绝对值的不等式,使得 代数问题几何化,既通俗易懂,又简洁直观,是一种较好的方法.
a+b+c 3 定理 3:如果 a,b,c 为正数,则 3 ≥ abc,当且仅当 a=b=c 时,等号成立. 定理 4:(一般形式的算术—几何平均不等式)如果 a1、a2、…、 a1+a2+…+an n an 为 n 个正数, 则 ≥ a1a2…an, 当且仅当 a1=a2=… n =an 时,等号成立.
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法: (1)|ax+b|≤c⇔-c≤ax+b≤c; (2)|ax+b|≥c⇔ax+b≥c 或 ax+b≤-c. 3.基本不等式 定理 1:设 a,b∈R,则 a2+b2≥2ab.当且仅当 a=b 时,等号 成立. a+b 定理 2:如果 a,b 为正数,则 2 ≥ ab,当且仅当 a=b 时, 等号成立.
1.不等式的证明常利用综合法、分析法、反证法、放缩法、 基本不等式和柯西不等式等,要根据题目特点灵活选用方法. 2.证明含绝对值的不等式主要有以下三种方法: (1)利用绝对值的定义去掉绝对值符号,转化为普通不等式再 证明; (2)利用三角不等式||a|-|b||≤|a± b|≤|a|+|b|进行证明; (3)转化为函数问题,利用数形结合进行证明.
高三数学基本不等式(中学课件201909)
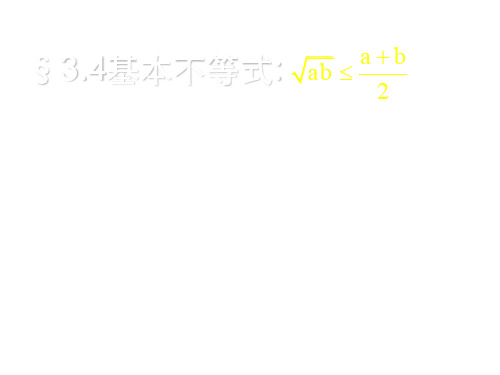
2
ICM2002会标
赵爽:弦图
D
D
a2 b2
b
G Fa
C
a
Hale Waihona Puke AEA E(FGH)
b
C
H
B
B
基本不等式1: 一般地,对于任意实数a、b,我们有
a2 b2 2ab
当且仅当a=b时,等号成立。
;超级通 超级通云控 云客云控 云通天下 免设备群控 蜘蛛云控
;
但全吾今日 防守雍州 下邳太守张攀咸以贪惏获罪 五稔之后 夜拒军人 然后图兼并者也 后录勋 北征都将 唯椿有曾孙 "欲害诸尊 须臾颢至 还 辄对之下泣 招引细人 穆素为荣所知 年一百二十岁 寄之后图 除散骑常侍 兼尚书令 "年三十一 斤力战有功 遇病卒 尔朱荣率军赴之 谷帛俱 溢 皆自持粮 侃从兄昱恐为家祸 咸阳王禧谋反 吾亦不复奇之 又赐马二匹 广阳王嘉 雍州刺史 此深自可奇 为天光所害 并州刺史 人有斗心 侃往赴之 赐奴婢十口 荣赫累朝 诞以为恨 尚书祠部郎中 除昱名为民 武平弟武荣 兼中书舍人 高宗时袭爵 求破桥立效 椿在州 每恒退避 宝夤后 至 遂成富室 遂以敬慎见知 攻逼番城 分散于冀 假冠军将军 依律处刑五岁 俱以忠毅谦谨 请为明公前驱 特宜宽省 稍迁中散大夫 太昌初 除抚军将军 正武卫将军 椿 泣而责之 龙骧将军 不知谁堪此任?数出游猎 亦忠实寡言 习于野战 小心谨敬 但无酒 降于萧鸾 以侃河梁之诚 河东治 在蒲坂 卫将军 有轻论人恶者 君孰与足?不加讨逐 薛凤贤又保安邑 此又不如吾等一世也 黄门郎萧衍率众十万来救 寻除镇东将军 不治产业 更树亲党 "杨昱 津年过六十 亦何容易 "我在江东 帝闻而善之 "遂举卮酒以赐播曰 为人流所鄙 延突火而入
高三数学复习课件【绝对值不等式】

两边平方得4x2+4x+1>4(x2-2x+1),
解得x>14,
所以原不等式的解集为xx>14
.
返回
法二:原不等式等价于x<-12, -2x+1+2x-1>0
或-12≤x≤1, 2x+1+2x-1>0
或x2>x1+,1-2x-1>0.
解得x>14,所以原不等式的解集为xx>14
.
返回
返回 (2)①当 x<-3 时, 原不等式化为-(x+3)-(1-2x)<x2+1,解得 x<10,∴x<-3. ②当-3≤x≤12时, 原不等式化为(x+3)-(1-2x)<x2+1, 解得 x<-25,∴-3≤x<-25. ③当 x>12时, 原不等式化为(x+3)+(1-2x)<x2+1, 解得 x>2,∴x>2. 综上可知,原不等式的解集为x|x<-25或x>2.
当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=13或x=5.
故f(x)>1的解集为{x|1<x<3},
f(x)<-1的解集为xx<13或x>5
.
所以|f(x)|>1的解集为xx<13或1<x<3或x>5
.
返回
2.解下列不等式.
(1)|2x+1|-2|x-1|>0;
(2)|x+3|-|2x-1|<x2+1. 解:(1)法一:原不等式可化为|2x+1|>2|x-1|,
(1)当 a=1 时,求不等式 f(x)≥g(x)的解集;
(2)若不等式 f(x)≥g(x)的解集包含[-1,1],求 a 的取值范围.
高三数学第二轮复习课件:不等式ppt 人教课标版

试题特点 特点二:考大题,经常与其它知识相结合 考查不等式的大题中,有时是单独出现,如2007年 山东的线性规划解答题,难度不算大;但经常是与其它知 识相结合,如不等式与数列、数列归纳法、函数、导数等 知识综合,难度属中等偏难,主要考查学生对基本知识, 基本方法,基本技能的理解,掌握和应用情况. 特点三:考方法,常用在证明题中 不等式证明的常用方法:比较法,公式法,分析法, 反证法,换元法,放缩法;在不等式证明过程中,应 注重与不等式的运算性质联合使用;证明不等式的过
考题剖析 例 2、 (2006 上海文)如果 a 0, b 0 ,那么,下列不等 式中正确的是( )
1 1 (A) a b
(B) a b
2
(C) a b
2
(D) | a || b |
a b
1 1 解: 0 , 0 ,故(A)正确。 因为 a<0,b>0,所以,
而|a|与|b|的大小不知,故 B、C、D 都不一定正确。 所以,选(A) 。
【命题规律】线性规划问题时多以选择、填空题的形式出 现,题型以容易题、中档题为主,考查平面区域的面积、 最优解的问题;随着课改的深入,近年来,以解答题的形 式来考查的试题也时有出现,考查学生解决实际问题的能 力。 12.02.2019 江西省赣州一中刘利剑 整理 heishu800101@
程中,放大或缩小应适度。
12.02.2019 江西省赣州一中刘利剑 整理 heishu800101@
高考命题趋势
纵观2008年高考全国卷和有关省市自主命题卷,关于不等式的命
题有如下几个显著特点:
1.高考题型:不等式的试题一般是选择题或填空题为主,不等式与其它 知识结合的试题多为解答题,经常与导数、数列相结合。 2.难易程度:不等式的选择题、填空题为基础题或中档题,考查基础知 识和基本技能;而在不等式与导数相结合的试题一般考查函数的单调性, 为中档题,不等式与数列结合中等偏难试题。 3.高考热点:随着课改的深入,线性规划的考查是高考的热点,如2008
高考数学复习考点知识讲解课件3 不等式性质 一元二次函数 方程和不等式

+c(a>0)的
图象
ax2+bx+c =0(a>0)的
根
有两个不相 等的实数根 x1,x2(x1<x2)
有两个相等 的实数根 x1 =x2=-2ba
没有实数根
— 返回 —
— 6—
(新教材) 高三总复习•数学
判别式 ax2+bx+ c>0(a>0)的
解集 ax2+bx+ c<0(a>0)的
解集
Δ>0 {x_|x_<_x_1_或__x_>_x_2}
— 2—
— 返回 —
基础知识夯实
01
(新教材) 高三总复习•数学
知识梳理 1.两个实数比较大小的方法
(1)作差法:aa--bb>=00⇔⇔aa_____>=_____bb,, a-b<0⇔a___<__b.
aba>∈1Ra∈,Rb>,0b,>0⇔a___>___b (2)作商法ab=1⇔a__=____ba,b≠0,
— 返回 —
— 8—
(新教材) 高三总复习•数学
— 返回 —
诊断自测 1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)若ab>1,则 a>b.( × ) (2)若 ab>0,则 a>b⇔1a<1b.( √ ) (3)若不等式 ax2+bx+c>0 的解集是(-∞,x1)∪(x2,+∞),则方程 ax2+bx+c=0 的 两个根是 x1 和 x2.( √ ) (4) 一 元 二 次 不 等 式 ax2 + bx + c≤0 在 R 上 恒 成 立 的 条 件 是 a<0 且 Δ = b2 - 4ac≤0.( √ )
1.1.2 基本不等式 课件(人教A选修4-5)

3 (2)设 0<x< ,求函数 y=4x(3-2x)的最大值; 2 1 9 (3)已知 x>0,y>0,且 + =1,求 x+y 的最小值. x y
[思路点拨]
根据题设条件,合理变形,创造能用基
本不等式的条件,求最值.
2x 2 [解] (1)∵x>0,∴f(x)= 2 = . 1 x +1 x+x 1 1 1 ∵x+x≥2,∴0< ≤ . 1 2 x+x ∴0<f(x)≤1,当且仅当x=1时取“=”.即f(x)值域 为(0,1] 3 (2)∵0<x< ,∴3-2x>0. 2 2x+3-2x 2 9 ∴y=4x(3-2x)=2[2x(3-2x)]≤2[ ]= . 2 2 3 当且仅当2x=3-2x,即x= 时,等号成立. 4 9 ∴y=4x(3-2x)的最大值为 . 2
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并 求出最小总费用.
解:(1)如题图所示,设矩形的另一边长为a m. 则y=45x+1 由已知xa=360,得a= x 3602 所以y=225x+ x -360(x>0). (2)∵x>0, 3602 ∴225x+ x ≥2 225×3602=10 800. 3602 ∴y=225x+ x -360≥10 440, 3602 当且仅当225 x= 时,等号成立. x 即当x=24 m时,修建围墙的总费用最小,最小总费 用是10 440元.
a2 b2 c2 ∴( b +b)+( c +c)+( a +a) ≥2(a+b+c). a2 b2 c2 即 b + c + a ≥a+b+c. a2 b2 c2 当且仅当 b =b, c =c, a =a, 即a=b=c时取等号.
高三数学(理科)二轮复习-不等式
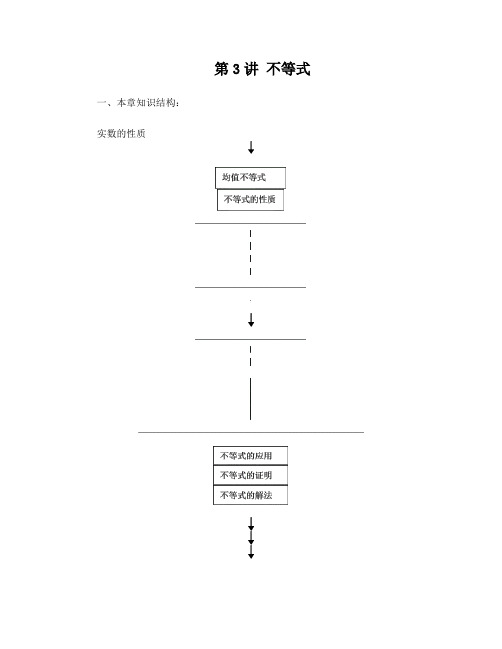
第3讲不等式一、本章知识结构:实数的性质二、高考要求(1)理解不等式的性质及其证明。
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数定理,并会简单应用。
(3)分析法、综合法、比较法证明简单的不等式。
(4)掌握某些简单不等式的解法。
(5)理解不等式|a|﹣|b| ≤|a+b|≤|a| +|b|。
三、热点分析1.重视对基础知识的考查,设问方式不断创新.重点考查四种题型:解不等式,证明不等式,涉及不等式应用题,涉及不等式的综合题,所占比例远远高于在课时和知识点中的比例.重视基础知识的考查,常考常新,创意不断,设问方式不断创新,图表信息题,多选型填空题等情景新颖的题型受到命题者的青眯,值得引起我们的关注.2.突出重点,综合考查,在知识与方法的交汇点处设计命题,在不等式问题中蕴含着丰富的函数思想,不等式又为研究函数提供了重要的工具,不等式与函数既是知识的结合点,又是数学知识与数学方法的交汇点,因而在历年高考题中始终是重中之重.在全面考查函数与不等式基础知识的同时,将不等式的重点知识以及其他知识有机结合,进行综合考查,强调知识的综合和知识的内在联系,加大数学思想方法的考查力度,是高考对不等式考查的又一新特点.3.加大推理、论证能力的考查力度,充分体现由知识立意向能力立意转变的命题方向.由于代数推理没有几何图形作依托,因而更能检测出学生抽象思维能力的层次.这类代数推理问题常以高中代数的主体内容——函数、方程、不等式、数列及其交叉综合部分为知识背景,并与高等数学知识及思想方法相衔接,立意新颖,抽象程度高,有利于高考选拔功能的充分发挥.对不等式的考查更能体现出高观点、低设问、深入浅出的特点,考查容量之大、功能之多、能力要求之高,一直是高考的热点.4.突出不等式的知识在解决实际问题中的应用价值,借助不等式来考查学生的应用意识.不等式部分的内容是高考较为稳定的一个热点,考查的重点是不等式的性质、证明、解法及最值方面的应用。
高考数学复习考点知识讲解课件4 基本不等式

— 返回 —
2.两个重要的不等式 (1)a2+b2≥____2_a_b____(a,b∈R),当且仅当 a=b 时取等号. (2)ab≤a+2 b2(a,b∈R),当且仅当 a=b 时取等号. 3.利用基本不等式求最值 (1)已知 x,y 都是正数,如果积 xy 等于定值 P,那么当 x=y 时,和 x+y 有最小值 ___2___P____. (2)已知 x,y 都是正数,如果和 x+y 等于定值 S,那么当 x=y 时,积 xy 有最大值
解法二:由题设易知 a>0,b>0,∴ ab=1a+2b≥2 时“=”成立,即 ab≥2 2,故选 C.
a2b,当且仅当 a=4 2,b=24 2
— 24 —
(新教材) 高三总复习•数学
3.已知 x≥52,则 f(x)=x2-2x4-x+4 5的最小值为____1______.
— 返回 —
[解析] 因为 x≥52,所以 x-2>0,所以 f(x)=x2-2x4-x+4 5=x2-x2-2+ 2 1=12x-2+x-1 2 ≥1,当且仅当 x-2=x-1 2,即 x=3 时等号成立.
角度 3:消元法求最值 【例 3】 (1)已知 x>0,y>0,x+3y+xy=9,则 x+3y 的最小值为___6___.
4 (2)已知 5x2y2+y4=1(x,y∈R),则 x2+y2 的最小值是___5____.
— 19 —
(新教材) 高三总复习•数学
— 返回 —
[解析] (1)解法一:由已知得 x+3y=9-xy, 因为 x>0,y>0,所以 x+3y≥2 3xy, 所以 3xy≤x+23y2,当且仅当 x=3y,即 x=3,y=1 时取等号,即(x+3y)2+12(x+3y) -108≥0. 令 x+3y=t,则 t>0 且 t2+12t-108≥0,得 t≥6,即 x+3y 的最小值为 6. 解法二:由 x+3y+xy=9,得 x=91-+3yy, 所以 x+3y=91-+3yy+3y=9-3y+1+3yy1+y =91++3yy2=31+y2-1+61y +y+12
2021年江苏高考数学二轮讲义:专题一第4讲 不等式
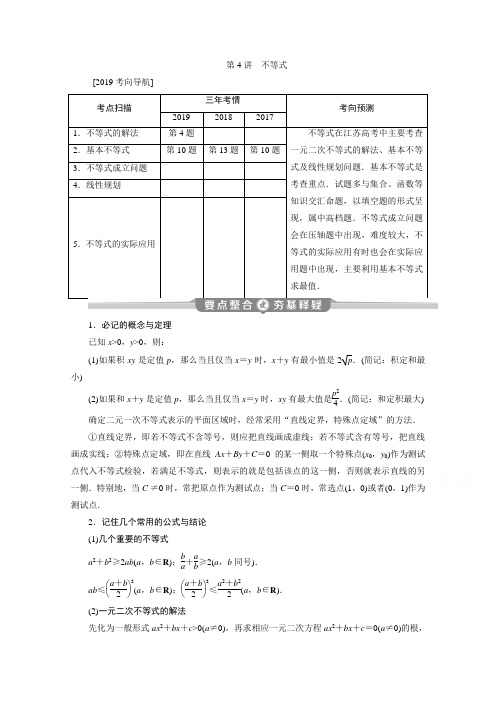
第4讲不等式[2019考向导航]考点扫描三年考情考向预测2019201820171.不等式的解法第4题不等式在江苏高考中主要考查一元二次不等式的解法、基本不等式及线性规划问题.基本不等式是考查重点.试题多与集合、函数等知识交汇命题,以填空题的形式呈现,属中高档题.不等式成立问题会在压轴题中出现,难度较大,不等式的实际应用有时也会在实际应用题中出现,主要利用基本不等式求最值.2.基本不等式第10题第13题第10题3.不等式成立问题4.线性规划5.不等式的实际应用1.必记的概念与定理已知x>0,y>0,则:(1)如果积xy是定值p,那么当且仅当x=y时,x+y有最小值是2p.(简记:积定和最小)(2)如果和x+y是定值p,那么当且仅当x=y时,xy有最大值是p24.(简记:和定积最大) 确定二元一次不等式表示的平面区域时,经常采用“直线定界,特殊点定域”的方法.①直线定界,即若不等式不含等号,则应把直线画成虚线;若不等式含有等号,把直线画成实线;②特殊点定域,即在直线Ax+By+C=0的某一侧取一个特殊点(x0,y0)作为测试点代入不等式检验,若满足不等式,则表示的就是包括该点的这一侧,否则就表示直线的另一侧.特别地,当C≠0时,常把原点作为测试点;当C=0时,常选点(1,0)或者(0,1)作为测试点.2.记住几个常用的公式与结论(1)几个重要的不等式a2+b2≥2ab(a,b∈R);ba+ab≥2(a,b同号).ab≤⎝⎛⎭⎫a+b22(a,b∈R);⎝⎛⎭⎫a+b22≤a2+b22(a,b∈R).(2)一元二次不等式的解法先化为一般形式ax2+bx+c>0(a≠0),再求相应一元二次方程ax2+bx+c=0(a≠0)的根,最后根据相应二次函数图象与x 轴的位置关系,确定一元二次不等式的解集.(3)简单分式不等式的解法①变形⇒f (x )g (x )>0(<0)⇔f (x )g (x )>0(<0)且g (x )≠0;②变形⇒f (x )g (x )≥0(≤0)⇔f (x )g (x )≥0(≤0)且g (x )≠0.(4)两个常用结论①ax 2+bx +c >0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧a >0,Δ<0.②ax 2+bx +c <0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧a <0,Δ<0.3.需要关注的易错易混点(1)利用不等式性质可以求某些代数式的取值范围,但应注意两点:一是必须严格运用不等式的性质;二是在多次运用不等式的性质时有可能扩大了变量的取值范围.解决的途径是先建立所求范围的整体与已知范围的整体的等量关系,最后通过“一次性”不等关系的运算求解范围.(2)在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.不等式的解法 [典型例题](1)(2019·江苏省高考名校联考(八))已知函数f (x )=-4x 2+2ax -b (a ,b ∈R )的值域为(-∞,0],若关于x 的不等式f (x )≥m 的解集为[c ,c +8],则实数m 的值为________.(2)(2019·苏州第一次质量预测)已知函数f (x )=⎩⎪⎨⎪⎧2x ,x ≤1,ln (x -1),1<x ≤2,若不等式f (x )≤5-mx 恒成立,则实数m 的取值范围是________.【解析】 (1)因为函数f (x )=-4x 2+2ax -b (a ,b ∈R )的值域为(-∞,0],所以函数的最大值为0.令f (x )=0,可得Δ=4a 2-4×(-4)×(-b )=4a 2-16b =0,即b =a 24.关于x 的不等式f (x )≥m 可化简为4x 2-2ax +b +m ≤0,即4x 2-2ax +a 24+m ≤0.又关于x 的不等式f (x )≥m 的解集为[c ,c +8],所以方程4x 2-2ax +a 24+m =0的两个根为x 1=c ,x 2=c +8,则⎩⎨⎧x 1+x 2=a 2x 1x 2=a 216+m4,又|x 1-x 2|2=(x 1+x 2)2-4x 1x 2=64,即(a 2)2-4(a 216+m4)=64,解得m =-64. (2)作出函数f (x )的大致图象如图所示,令g (x )=5-mx ,则g (x )恒过点(0,5),由f (x )≤g (x )恒成立,并数形结合得-52≤-m ≤0,解得0≤m ≤52.【答案】 (1)-64 (2)⎣⎡⎦⎤0,52二次函数、二次不等式是高中数学的重要基础知识,也是高考的热点.本题(1)考查了二次函数的性质及一元二次不等式的解法.突出考查将二次函数、二次方程、二次不等式三者进行相互转化的能力和转化与化归的数学思想方法.[对点训练]1.(2019·江苏省高考命题研究专家原创卷(六))已知函数f (x )=⎩⎨⎧⎝⎛⎭⎫12x-3,x ≤0,x 12,x >0,若f (a )>f (f (-2)),则实数a 的取值范围为________.[解析] 由题意知,f (-2)=(12)-2-3=1,f (1)=1,所以不等式化为f (a )>1.当a ≤0时,f (a )=(12)a -3>1,解得a <-2;当a >0时,f (a )=a >1,解得a >1.因而a 的取值范围为(-∞,-2)∪(1,+∞).[答案] (-∞,-2)∪(1,+∞)2.已知函数f (x )=x 2-2ax +a 2-1的定义域为A ,2∉A ,则a 的取值范围是________. [解析] 因为2∉A ,所以4-4a +a 2-1<0,即a 2-4a +3<0,解得1<a <3. [答案] 1<a <3基本不等式 [典型例题](1)(2019·南通市高三调研)若正实数x ,y 满足x +y =1,则y x +4y 的最小值是________.(2)(2019·高考江苏卷)在平面直角坐标系xOy 中,P 是曲线y =x +4x (x >0)上的一个动点,则点P 到直线x +y =0的距离的最小值是________.【解析】 (1)因为正实数x ,y 满足x +y =1,所以y x +4y =y x +4(x +y )y =y x +4xy +4≥2y x ·4x y +4=8,当且仅当y x =4x y ,即x =13,y =23时,取“=”,所以y x +4y的最小值是8. (2)设P ⎝⎛⎭⎫x ,x +4x ,x >0,则点P 到直线x +y =0的距离d =|x +x +4x |2=2x +4x 2≥22x ·4x2=4,当且仅当2x =4x,即x =2时取等号,故点P 到直线x +y =0的距离的最小值是4.【答案】 (1)8 (2)4用基本不等式求函数的最值,关键在于将函数变形为两项和或积的形式,然后用基本不等式求出最值.在求条件最值时,一种方法是消元,转化为函数最值;另一种方法是将要求最值的表达式变形,然后用基本不等式将要求最值的表达式放缩为一个定值,但无论哪种方法在用基本不等式解题时都必须验证等号成立的条件.[对点训练]3.(2019·苏锡常镇四市高三调研)若正数x ,y 满足15x -y =22,则x 3+y 3-x 2-y 2的最小值为________.[解析] x 3+y 3-x 2-y 2=x 3+94x +y 3+14y -x 2-y 2-94x -14y ≥3x 2+y 2-x 2-y 2-94x -14y =2x 2-94x -14y =2x 2+92-94x -14y -92≥6x -94x -14y -92=15x -y 4-92=224-92=1,当且仅当x =32,y =12时取等号,故x 3+y 3-x 2-y 2的最小值为1.[答案] 14.(2018·高考江苏卷)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,∠ABC =120°,∠ABC 的平分线交AC 于点D ,且BD =1,则4a +c 的最小值为________.[解析] 因为∠ABC =120°,∠ABC 的平分线交AC 于点D ,所以∠ABD =∠CBD =60°,由三角形的面积公式可得12ac sin 120°=12a sin 60°+12c sin 60°,化简得ac =a +c ,又a >0,c >0,所以1a +1c =1,则4a +c =(4a +c )·⎝⎛⎭⎫1a +1c =5+c a +4a c ≥5+2c a ·4ac=9,当且仅当c =2a 时取等号,故4a +c 的最小值为9.[答案] 9线性规划 [典型例题](1)已知实数x ,y 满足⎩⎪⎨⎪⎧x -2y +4≥0,2x +y -2≥0,3x -y -3≤0,则x 2+y 2的取值范围是________.(2)设z =kx +y ,其中实数x ,y 满足⎩⎪⎨⎪⎧x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k =________.【解析】 (1)不等式组所表示的平面区域是以点(0,2),(1,0),(2,3)为顶点的三角形及其内部,如图所示.因为原点到直线2x +y -2=0的距离为25,所以(x 2+y 2)min =45,又当(x ,y )取点(2,3)时,x 2+y 2取得最大值13,故x 2+y 2的取值范围是⎣⎡⎦⎤45,13.(2)作出可行域,如图中阴影部分所示,由图可知当0≤-k <12时,直线y =-kx +z 经过点M (4,4)时z 最大,所以4k +4=12,解得k =2(舍去);当-k ≥12时,直线y =-kx +z 经过点(0,2)时z 最大,此时z 的最大值为2,不合题意;当-k <0时,直线y =-kx +z 经过点M (4,4)时z 最大,所以4k +4=12,解得k=2,符合题意.综上可知k =2.【答案】 (1)⎣⎡⎦⎤45,13 (2)2确定二元一次不等式(组)表示的平面区域的方法(1)“直线定界,特殊点定域”,即先作直线,再取特殊点并代入不等式组.若满足不等式组,则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域;否则就对应与特殊点异侧的平面区域.(2)当不等式中带等号时,边界画为实线,不带等号时,边界应画为虚线,特殊点常取原点.[对点训练]5.(2019·江苏名校高三入学摸底)若变量x ,y 满足不等式组⎩⎪⎨⎪⎧2x -y ≤0x -2y +6≥0y ≥0,则⎝⎛⎭⎫12x +y的最小值为________.[解析] 作出不等式组所表示的平面区域,如图中△OAB (含边界)所示,作直线l :x +y =0,若向上平移直线l ,则x +y 的值增大,当平移至过点B (2,4)时,x +y 取得最大值6,此时⎝⎛⎭⎫12x +y取得最小值18.[答案] 186.(2019·江苏省名校高三入学摸底卷)设x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥0y ≥02x +y ≤2,若目标函数z =ax+by (a >0,b >0)的最大值为M ,且M 的取值范围是[1,2],则点P (a ,b )所组成的平面区域的面积是________.[解析] 作出约束条件⎩⎨⎧x ≥0y ≥02x +y ≤2表示的平面区域如图1中阴影部分所示(三角形OAB 及其内部). 将目标函数z =ax +by (a >0,b >0)化为直线方程的形式为y =-a b x +zb,若-a b ≤-2,当直线y =-a b x +zb 经过点A (1,0)时,z =ax +by (a >0,b >0)取得最大值M =a ∈[1,2],由⎩⎨⎧a >0b >0-a b≤-2a ∈[1,2]得点P (a ,b )所组成的平面区域如图2中阴影部分所示,此时点P (a ,b )所组成的平面区域的面积为34.若-a b >-2,当直线y =-a b x +zb 经过点B (0,2)时,z =ax +by (a >0,b >0)取得最大值M =2b ∈[1,2],由⎩⎨⎧a >0b >0-a b>-22b ∈[1,2]得点P (a ,b )所组成的平面区域如图3中阴影部分所示,此时点P (a ,b )所组成的平面区域的面积为34.综上,点P (a ,b )所组成的平面区域的面积为32.[答案] 32不等式的实际应用[典型例题]“第五届上海智能家居展览会”于2017年7月5日-7月7日在上海新国际博览中心举行,全面展示当前最新的智能家居.某智能家居企业可以向社会提供智能家居套餐的生产和销售一条龙服务,由于2016年没有进行促销活动,该企业的某品牌套餐全年的销量只有1.25万套,如果延续2016年的经营策略,预计2017年的销量只有2016年的80%.为了不断拓展市场,提高经营效益,拟在2017年借“第五届上海智能家居展览会”的东风对该品牌套餐进行促销活动.经过市场调研,该品牌套餐的年销量x 万套与年促销费用t 万元之间满足关系:x =4t +mt +1(t ≥0).预计2017年生产设备的固定成本为4万元,每生产1万套该品牌套餐需再投入27万元的可变成本,若将每套该品牌套餐的售价定为其生产成本的160%与平均每套促销费用的40%的和,则当年生产的该品牌套餐正好能销售完.(1)将该企业2017年的利润y 万元表示为关于年促销费用t 万元的函数; (2)该企业2017年的促销费用为多少万元时,企业的年利润最大?(注:利润=销售收入-生产成本-促销费用,生产成本=固定成本+可变成本) 【解】 (1)由题意可知在x =4t +mt +1(t ≥0)中,当t =0时,x =1.25×0.8=1,代入上式得m =1, 所以x =4t +1t +1(t ≥0).当年生产x 万套时,年生产成本为 27x +4=27×4t +1t +1+4.当年销售x 万套时,年销售收入为160%×⎝ ⎛⎭⎪⎫27×4t +1t +1+4+40%×t . 由题意,生产x 万套该品牌套餐正好销售完,由利润=销售收入-生产成本-促销费用,得y =160%×⎝ ⎛⎭⎪⎫27×4t +1t +1+4+40%×t -⎝ ⎛⎭⎪⎫27×4t +1t +1+4-t .所以y =-3t 2+333t +935(t +1)(t ≥0).(2)y =-3t 2+333t +935(t +1)=35⎣⎢⎡⎦⎥⎤113-⎝ ⎛⎭⎪⎫t +1+81t +1≤35×(113-18)=57, 当且仅当t +1=81t +1,即t =8时等号成立,即当该企业2017年的促销费用为8万元时,企业的年利润最大,且最大值为57万元.利用基本不等式求解实际应用题的方法(1)此类型的题目往往较长,解题时需认真阅读,从中提炼出有用信息,建立数学模型,转化为数学问题求解.(2)当运用基本不等式求最值时,若等号成立的自变量不在定义域内时,就不能使用基本不等式求解,此时可根据变量的范围用对应函数的单调性求解.[对点训练]7.(2019·苏州调研)如图,GH 是东西方向的公路北侧的边缘线,某公司准备在GH 上的一点B 的正北方向的A 处建一仓库,设AB =y km ,并在公路同侧建造边长为x km 的正方形无顶中转站CDEF (其中边EF 在GH 上),现从仓库A 向GH 和中转站分别修两条道路AB ,AC ,已知AB =AC +1,且∠ABC =60°.(1)求y 关于x 的函数解析式;(2)如果中转站四周围墙造价为1万元/km ,两条道路造价为3万元/km ,问:x 取何值时,该公司建中转站围墙和两条道路总造价M 最低?[解] (1)因为AB =y ,AB =AC +1,所以AC =y -1. 在直角三角形BCF 中,因为CF =x ,∠ABC =60°, 所以∠CBF =30°,BC =2x . 由于2x +y -1 >y ,得x >12.在△ABC 中,因为AC 2=AB 2+BC 2-2AB ·BC cos 60°,所以(y -1)2=y 2+4x 2-2xy .则y =4x 2-12(x -1).由y > 0,及x >12,得x > 1.即y 关于x 的函数解析式为y =4x 2-12(x -1)(x > 1). (2)M =3(2y -1)+4x =12x 2-3x -1-3+4x .令x -1=t ,则M =12(t +1)2-3t -3+4(t +1)=16t +9t+25≥49,在t =34,即x =74,y =152时,总造价M 最低.所以x =74时,该公司建中转站围墙和两条道路总造价M 最低.1.函数f (x )=1xlg(2+x -x 2)的定义域为__________.[解析] ⎩⎨⎧x ≠0,2+x -x 2>0,⇒-1<x <0或0<x <2,所以函数f (x )的定义域为(-1,0)∪(0,2) [答案] (-1,0)∪(0,2)2.已知t >0,则函数y =t 2-4t +1t的最小值为________.[解析] 因为t >0,所以y =t 2-4t +1t =t +1t -4≥2-4=-2,且在t =1时取等号.[答案] -23.(2019·高三第一次调研测试)若实数x ,y 满足x ≤y ≤2x +3,则x +y 的最小值为______. [解析] 作出可行域如图中阴影部分所示,令z =x +y ,数形结合易知当直线z =x +y 过点A (-3,-3)时,z 取得最小值,z min =-6.4.(2019·苏北四市高三质量检测)设f (x )是定义在R 上的奇函数,当x >0时,f (x )=2x -3,则不等式f (x )≤-5 的解集为________.[解析] 因为当x >0时,f (x )=2x -3,所以当x <0,即-x >0时,f (-x )=2-x -3,因为函数f (x ) 是定义在R 上的奇函数, 所以f (-x )=2-x -3=-f (x ), 所以f (x )=-2-x +3.当x >0时,不等式f (x )≤-5等价为2x -3≤-5, 即2x ≤-2,无解,故x >0时,不等式不成立; 当x <0时,不等式f (x )≤-5等价为-2-x +3≤-5, 即2-x ≥8, 得x ≤-3;当x =0时,f (0)=0,不等式f (x )≤-5不成立. 综上,不等式f (x )≤-5的解集为(-∞,-3]. [答案] (-∞,-3]5.某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元.要使一年的总运费与总存储费用之和最小,则x 的值是________.[解析] 一年购买600x 次,则总运费与总存储费用之和为600x×6+4x =4⎝⎛⎭⎫900x +x ≥8900x ·x =240,当且仅当x =30时取等号,故总运费与总存储费用之和最小时x 的值是30. [答案] 306.(2019·苏北三市高三模拟)已知对于任意的x ∈(-∞,1)∪(5,+∞),都有x 2-2(a -2)x+a >0,则实数a 的取值范围是________.[解析] 记f (x )=x 2-2(a -2)x +a ,令f (x )=0,由题意得,Δ=4(a -2)2-4a <0或⎩⎪⎨⎪⎧f (1)≥0,f (5)≥0,Δ≥0,1≤a -2≤5,所以1<a <4或4≤a ≤5, 即实数a 的取值范围是(1,5].7.(2019·扬州市第一学期期末检测)已知正实数x ,y 满足x +4y -xy =0,若x +y ≥m 恒成立,则实数m 的取值范围为______.[解析] x +4y -xy =0,即x +4y =xy ,等式两边同时除以xy ,得4x +1y=1,由基本不等式可得x +y =(x +y )·⎝⎛⎭⎫4x +1y =4y x +x y +5≥24y x ·x y +5=9,当且仅当4y x =xy,即x =2y =6时,等号成立,所以x +y 的最小值为9,因为m ≤9.[答案] m ≤98.在R 上定义运算:x *y =x (1-y ),若不等式(x -a )*(x +a )≤1对任意的x 恒成立,则实数a 的取值范围是________.[解析] 由于(x -a )*(x +a )=(x -a )(1-x -a ),则不等式(x -a )*(x +a )≤1对任意的x 恒成立,即x 2-x -a 2+a +1≥0恒成立,所以a 2-a -1≤x 2-x 恒成立,又x 2-x =⎝⎛⎭⎫x -122-14≥-14,则a 2-a -1≤-14,解得-12≤a ≤32. [答案] ⎣⎡⎦⎤-12,32 9.记min{a ,b }为a ,b 两数的最小值.当正数x ,y 变化时,令t =min ⎩⎨⎧⎭⎬⎫2x +y ,2y x 2+2y 2,则t 的最大值为______.[解析] 因为x >0,y >0,所以问题转化为t 2≤(2x +y )·2yx 2+2y 2=4xy +2y 2x 2+2y 2≤4·x 2+y 22+2y 2x 2+2y 2=2(x 2+2y 2)x 2+2y 2=2,当且仅当x =y 时等号成立,所以0<t ≤2,所以t 的最大值为2.[答案] 210.(2019·宁波统考)已知函数f (x )=log a (x 2-a |x |+3)(a >0,a ≠1).若对于-1≤x 1<x 2≤-12的任意实数x 1,x 2都有f (x 1)-f (x 2)<0成立,则实数a 的范围是________.[解析] 易知已知函数为偶函数,则当x ∈⎣⎡⎦⎤12,1时为减函数. 对于x ∈⎣⎡⎦⎤12,1时, f (x )=log a (x 2-ax +3)(a >0,a ≠1) 设g (x )=x 2-ax +3,由题意得:⎩⎪⎨⎪⎧a >1,1≤a 2,g (1)>0或⎩⎪⎨⎪⎧0<a <1,a 2≤12,g ⎝⎛⎭⎫12>0,则2≤a <4或0<a <1. [答案] (0,1)∪[2,4)11.已知x >0,a 为大于2x 的常数, (1)求函数y =x (a -2x )的最大值; (2)求y =1a -2x-x 的最小值. [解] (1)因为x >0,a >2x , 所以y =x (a -2x )=12×2x (a -2x )≤12⎣⎢⎡⎦⎥⎤2x +(a -2x )22=a 28, 当且仅当x =a 4时取等号,故函数的最大值为a 28.(2)y =1a -2x+a -2x 2-a 2≥212-a 2=2-a2. 当且仅当x =a -22时取等号.故y =1a -2x-x 的最小值为2-a 2.12.已知关于x 的不等式x +2x 2-(1+a )x +a >0.(1)当a =2时,求此不等式的解集; (2)当a >-2时,求此不等式的解集.[解] (1)当a =2时,不等式可化为x +2(x -1)(x -2)>0,所以不等式的解集为{x |-2<x <1或x >2}.(2)当a >-2时,不等式可化为x +2(x -1)(x -a )>0,当-2<a <1时,解集为{x |-2<x <a 或x >1};当a =1时,解集为{x |x >-2且x ≠1}; 当a >1时,解集为{x |-2<x <1或x >a }.13.(2019·盐城市高三第三次模拟考试)如图,某人承包了一块矩形土地ABCD 用来种植草莓,其中AB =99 m ,AD =49.5 m .现计划建造如图所示的半圆柱型塑料薄膜大棚n (n ∈N *)个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米10元;另外,还需在每两个大棚之间留下1 m 宽的空地用于建造排水沟与行走小路(如图中EF =1 m),这部分的建设造价为每平方米31.4元.(1)当n =20时,求蒙一个大棚所需塑料薄膜的面积;(结果保留π) (2)试确定大棚的个数,使得上述两项费用的和最低.(计算中π取3.14) [解] (1)设每个半圆柱型大棚的底面半径为r .当n =20时,共有19块空地,所以r =99-19×12×20=2(m),所以每个大棚的表面积(不含与地面接触的面的面积)为 πr 2+πr ×AD =π×22+2π×49.5=103π(m 2), 即蒙一个大棚所需塑料薄膜的面积为103π m 2. (2)设两项费用的和为f (n ).因为r =99-(n -1)×12n =100-n2n,所以每个大棚的表面积(不含与地面接触的面的面积)为 S =πr 2+πr ×AD =π×⎝ ⎛⎭⎪⎫100-n 2n 2+π×49.5×100-n 2n , 则f (n )=10nS +31.4×1×49.5(n -1)=10n [π×⎝ ⎛⎭⎪⎫100-n 2n 2+π×49.5×⎝ ⎛⎭⎪⎫100-n 2n ]+31.4×1×49.5(n -1)=31.4×[(100-n )24n +49.5×100-n2+49.5(n -1)]=31.44×[(100-n )2n+99(100-n )+198(n -1)]=31.44×(1002n +100n +9 502)=31.44×[100×⎝⎛⎭⎫100n +n +9 502], 因为100n+n ≥2100n·n =20,当且仅当n =10时等号成立, 所以,当且仅当n =10时,f (n )取得最小值, 即当大棚的个数为10个时,上述两项费用的和最低.14.设m 是常数,集合M ={m |m >1},f (x )=log 3(x 2-4mx +4m 2+m +1m -1).(1)证明:当m ∈M 时,f (x )对所有的实数x 都有意义; (2)当m ∈M 时,求函数f (x )的最小值;(3)求证:对每个m ∈M ,函数f (x )的最小值都不小于1. [解] (1)证明:f (x )=log 3⎣⎢⎡⎦⎥⎤(x -2m )2+m +1m -1,当m ∈M ,即m >1时,(x -2m )2+m +1m -1>0恒成立,故f (x )的定义域为R .(2)令g (x )=x 2-4mx +4m 2+m +1m -1,因为y =log 3g (x )是增函数,所以当g (x )最小时f (x )最小,而g (x )=(x -2m )2+m +1m -1, 显然当x =2m 时,g (x )的最小值为m +1m -1.此时f (x )min =log 3⎝ ⎛⎭⎪⎫m +1m -1. (3)证明:m ∈M 时,m +1m -1=m -1+1m -1+1 ≥2+1=3,所以log 3⎝ ⎛⎭⎪⎫m +1m -1≥log 33=1,结论成立.。
2020届高三数学复习 函数与方程、不等式 讲座 课件(共20张PPT)

借助于二次函数的图像特征来求解
尝试分离参数的方法,来回避分类讨论
总结
01 函数思想是一种思维习惯,要用变量和函数的
观点来思考问题
02 求 y f (x) 的零点和解 f (x) 0 求根是一致的,但方法是多样的,
特别要注意数形结合的使用。
如果要判断函数有几个零点,则必须结合其图像与性质(单调性、奇偶性)。
02 函数 f (x) 在[a,b]上是连续不断的曲线,且 f (a) f (b) 0 ,满足这些条件一定有零点。 但不满足这些条件也不能说一定没有零点。
产品介绍 Product introduction
关于零点存在性定理
如图:
已知 x, y 0 ,则有: x y 2 xy (当且仅当 x y 等号成立)
若 x y S (和为定值),
则当 x y 时,积 xy 取得最大值 S 2 ; 4
即: xy ( x+y)2 = S 2 24
若 xy P (积为定值)
则当 x y 时,和 x y 取得最小值 2 P
则 f (x) a fmin (x) a
因为 x 0 ,由平均值不等式: x+ 1 2(当且仅当 x 1 ,即: x 1时等号成立),
x
x
所以: f (x)min 2 故: a 2
产品介绍 Product
introduction 函数与不等式
【例 3.】变式:关于 x 的不等式 x+ 1 a 0 对 x [2, ) 恒成立, x
【例 1】关于 x 的一元二次方程 x2 ax 3 a 0 ,求当 a 为何值时,分别有以下的结论:
2023高考数学二轮复习专题复习03 等式与不等式的性质 (解析版)

专题03等式与不等式的性质【考点预测】1.比较大小基本方法(1)基本性质bc【方法技巧与总结】1.应用不等式的基本性质,不能忽视其性质成立的条件,解题时要做到言必有据,特别提醒的是在解决有关不等式的判断题时,有时可用特殊值验证法,以提高解题的效率.2.比较数(式)的大小常用的方法有比较法、直接应用不等式的性质、基本不等式、利用函数的单调性.比较法又分为作差比较法和作商比较法.作差法比较大小的步骤是:(1)作差;(2)变形;(3)判断差式与0的大小;(4)下结论.作商比较大小(一般用来比较两个正数的大小)的步骤是:(1)作商;(2)变形;(3)判断商式与1的大小;(4)下结论.其中变形是关键,变形的方法主要有通分、因式分解和配方等,变形要彻底,要有利于0或1比较大小.作差法是比较两数(式)大小最为常用的方法,如果要比较的两数(式)均为正数,且是幂或者因式乘积的形式,也可考虑使用作商法.【题型归纳目录】 题型一:不等式性质的应用题型二:比较数(式)的大小与比较法证明不等式 题型三:已知不等式的关系,求目标式的取值范围 题型四:不等式的综合问题【典例例题】题型一:不等式性质的应用例1.(2022·北京海淀·二模)已知,x y ∈R ,且0x y +>,则( )A .110x y +>B .330x y +>C .lg()0x y +>D .sin()0x y +>【答案】B 【解析】 【分析】取特殊值即可判断A 、C 、D 选项,因式分解即可判断B 选项. 【详解】对于A ,令11,2x y ==-,显然01112yx +=-<,错误;对于B ,()()()23322213024x y x y x xy y x y x y y ⎡⎤⎛⎫+=+-+=+-+≥⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,又1,02x y y ==不能同时成立,故()2213024x y x y y ⎡⎤⎛⎫+-+>⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,正确;对于C ,取1,0x y ==,则lg()0x y +=,错误; 对于D ,取1,3x y ==,则sin()sin 40x y +=<,错误. 故选:B.例2.(2022·山东日照·二模)若a ,b ,c 为实数,且a b <,0c >,则下列不等关系一定成立的是( ) A .a c b c +<+ B .11a b< C .ac bc > D .b a c ->【答案】A【解析】 【分析】由不等式的基本性质和特值法即可求解. 【详解】对于A 选项,由不等式的基本性质知,不等式的两边都加上(或减去)同一个数或同一个整式,不等号方向不变,则a b a c b c <⇒+<+,A 选项正确;对于B 选项,由不等式的基本性质知,不等式的两边都乘以(或除以)同一个负数,不等号方向改变,若2a =-,1b =-,则11a b>,B 选项错误; 对于C 选项,由不等式的基本性质知,不等式的两边都乘以(或除以)同一个正数,不等号方向不变,0c >,0a b ac bc <<⇒<,C 选项错误;对于D 选项,因为0a b b a <⇒->,0c >,所以无法判断b a -与c 大小,D 选项错误. 例3.(2022·山西·模拟预测(文))若0αβ<<,则下列结论中正确的是( ) A .22αβ< B .2βααβ+>C .1122αβ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D .sin sin αβ<【答案】B 【解析】 【分析】对于A ,利用不等式的性质判断,对于B ,利用基本不等式判断,对于C ,利用指数函数的性质判断,对于D ,举例判断 【详解】∵0αβ<<,∴0αβ->->,∴22αβ>,故A 错误;∵0αβ<<,∴0,0αββα>>,∴2βαααββ+≥=. ∵αβ≠,∴2βααβ+>,故B 正确; ∵101,2αβ<<<,∴1122αβ>⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭.故C 错误;令,2παπβ=-=-,此时sin 0,sin 1,sin sin αβαβ==->.故D 错误.故选:B .(多选题)例4.(2022·辽宁·二模)己知非零实数a ,b 满足||1a b >+,则下列不等关系一定成立的是( ) A .221a b >+B .122a b +>C .24a b >D .1ab b>+ 【答案】ABC 【解析】 【分析】利用不等式的性质及特殊值法判断即可. 【详解】解:对于非零实数a ,b 满足||1a b >+,则()22||1a b >+,即2222||11a b b b >++>+,故A 一定成立; 因为1||1122a b a b b +>+≥+⇒>,故B 一定成立;又()2||10b -≥,即212||b b +≥,所以24||4a b b >≥,故C 一定成立; 对于D :令5a =,3b =,满足||1a b >+,此时5143a b b =<+=,故D 不一定成立. 故选:ABC(多选题)例5.(2022·重庆八中模拟预测)已知0a >,0b >,且3ab a b ++=,则下列不等关系成立的是( ) A .1ab ≤ B .2a b +≥ C .1a b -> D .3a b -<【答案】ABD 【解析】 【分析】利用基本不等式以及适当的代数式变形即可判断. 【详解】对于A ,由3ab a b ++= ,a b +≥,当且仅当a b = 时等号成立,3ab ∴+≤ ,)310≤ ,1ab ∴≤ ,当且仅当1a b == 时等号成立,故A 正确; 对于B ,由3ab a b ++=,得()()4114,11a b b a ++=∴+=+ , 由基本不等式得)44(1)(1)2122211a b a b a a a +=+++-=++-≥-=++ ,当且仅当a=b =1时成立;故B 正确;对于C ,若1,1,a b == 满足3ab a b ++=,01a b -=<,故C 错误; 对于D ,∵3ab a b ++=,∴3ab a b a b =+++> ,由B 的结论得23a b ≤+< ,()()()()222949439a b a b ab a b a b --=+--=+--+-⎡⎤⎣⎦()()()()2421730a b a b a b a b =+++-=+++-< ,()29,3a b a b ∴--<< ,故D 正确; 故选:ABD.(多选题)例6.(2022·广东汕头·二模)已知a ,b ,c 满足c <a <b ,且ac <0,那么下列各式中一定成立的是( ) A .ac (a -c )>0 B .c (b -a )<0 C .22cb ab < D .ab ac >【答案】BCD 【解析】 【分析】利用不等式的基本性质求解. 【详解】解:因为a ,b ,c 满足c <a <b ,且ac <0, 所以0,0,0,0,0c a b a c b a <>>->->,所以ac (a -c )<0 ,c (b -a )<0,22cb ab <,ab ac >, 故选:BCD(多选题)例7.(2022·福建三明·模拟预测)设a b c <<,且0a b c ++=,则( ) A .2ab b < B .ac bc < C .11a c< D .1c ac b-<- 【答案】BC 【解析】 【分析】根据条件可得0<<a c ,b 的符号不能确定,然后依次判断即可. 【详解】因为a b c <<,0a b c ++=,所以0<<a c ,b 的符号不能确定, 当0b =时,2ab b =,故A 错误,因为a b <,0c >,所以ac bc <,故B 正确, 因为0<<a c ,所以11a c<,故C 正确, 因为a b <,所以a b ->-,所以0c a c b ->->,所以1c ac b->-,故D 错误, 故选:BC【方法技巧与总结】1.判断不等式是否恒成立,需要给出推理或者反例说明. 2.充分利用基本初等函数性质进行判断.3.小题可以用特殊值法做快速判断.题型二:比较数(式)的大小与比较法证明不等式例8.(2022·全国·高三专题练习(文))设2312m ⎛⎫= ⎪⎝⎭,1312n ⎛⎫= ⎪⎝⎭,2315p ⎛⎫= ⎪⎝⎭,则( ) A .m p n << B .p m n <<C .n m p <<D .p n m <<【答案】B 【解析】 【分析】根据指数函数12xy ⎛⎫= ⎪⎝⎭的单调性判断n m >,再由作商法判断m p >.【详解】因为函数12xy ⎛⎫= ⎪⎝⎭是减函数,所以12331122⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,所以n m > 2320323155212215⎛⎫ ⎪⎛⎫⎛⎫⎝⎭=>= ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭,所以m p >, 所以n m p >> 故选:B 【点睛】本题主要考查了利用指数函数的单调性比较大小,属于中档题. 例9.(2022·全国·高三专题练习)若a =ln 22,b =ln 33,则a ____b (填“>”或“<”). 【答案】< 【解析】 【分析】作商法比较大小,结合对数的运算律和性质,即得解 【详解】易知a ,b 都是正数,b a =232ln 3ln 3ln 93ln 2ln 2ln8===log 89>1,所以b >a .故答案为:<例10.(2022·全国·高一)(1)试比较()()15x x ++与()23x +的大小;(2)已知a b >,11a b<,求证:0ab >.【答案】(1)()()()2153x x x ++<+;(2)证明见解析. 【解析】 【分析】(1)()()15x x ++与()23x +作差,判断差的正负即可得出结论;(2)结合不等式的性质分析即可证出结论. 【详解】(1)由题意,()()()2153x x x ++-+ 22656940x x x x =++---=-<,所以()()()2153x x x ++<+. (2)证明:因为11a b<,所以110a b -<,即0b aab -<, 而a b >,所以0b a -<,则0ab >.得证.例11.(2022·湖南·高一课时练习)比较()()213a a +-与()()62745a a -++的大小. 【答案】()()213a a +-<()()62745a a -++ 【解析】 【分析】做差比较大小即可. 【详解】()()()()2221362745(253)(253)60a a a a a a a a +---++=----+=-<⎡⎤⎣⎦,∴()()213a a +-<()()62745a a -++.例12.(2022·湖南·高一课时练习)比较下列各题中两个代数式值的大小:(1))21与)21;(2)()()2211xx ++与()()2211xx x x ++-+.【答案】(1)221)1)≤(2)()()2211x x ++()()2211x x x x ≤++-+【解析】 【分析】利用作差法得出大小关系. (1)))()()221111m m -=--+=-因为0m ≥,所以221)1)0-≤,当且仅当0m =时,取等号.即221)1)≤ (2)()()2211xx ++()()2211x x x x -++-+()()2222222121x x x x x ⎡⎤⎡⎤=+--+-=-⎢⎥⎢⎥⎣⎦⎣⎦因为0x ≥,所以()()2222221210x x x x ⎡⎤⎡⎤+--+-≤⎢⎥⎢⎥⎣⎦⎣⎦,当且仅当0x =时,取等号.故()()2211x x ++()()2211x x x x ≤++-+.【方法技巧与总结】比较数(式)的大小常用的方法有比较法、直接应用不等式的性质、基本不等式、利用函数的单调性. 比较法又分为作差比较法和作商比较法. 作差法比较大小的步骤是:(1)作差;(2)变形;(3)判断差式与0的大小;(4)下结论. 作商比较大小(一般用来比较两个正数的大小)的步骤是: (1)作商;(2)变形;(3)判断商式与1的大小;(4)下结论.其中变形是关键,变形的方法主要有通分、因式分解和配方等,变形要彻底,要有利于0或1比较大小.作差法是比较两数(式)大小最为常用的方法,如果要比较的两数(式)均为正数,且是幂或者因式乘积的形式,也可考虑使用作商法,作商法比较大小的原理是:若0,0a b >>,则1b b a a >⇔>;1b b a a <⇔<;1bb a a =⇔=;若0,0a b <<,则1b b a a >⇔<;1b b a a <⇔>;1bb a a=⇔=. 题型三:已知不等式的关系,求目标式的取值范围例13.(2022·浙江·模拟预测)若实数x ,y 满足1522x y x y +≥⎧⎨+≥⎩,则2x y +的取值范围( )A .[1,)+∞B .[3,)+∞C .[4,)+∞D .[9,)+∞【答案】A 【解析】 【分析】设2()(52)x y m x y n x y +=+++,求出,m n ,再根据不等式的性质即可得出答案. 【详解】解:设2()(52)x y m x y n x y +=+++,则5221m n m n +=⎧⎨+=⎩,解得13m n ==,故112()(52)33x y x y x y +=+++,又因1522x y x y +≥⎧⎨+≥⎩,所以()()1112,523333x y x y +≥+≥, 所以21x y +≥. 故选:A.例14.(2022·全国·高三专题练习)已知12a ≤≤,14b -≤≤,则2a b -的取值范围是( ) A .724a b -≤-≤ B .629a b -≤-≤ C .629a b ≤-≤ D .228a b -≤-≤【答案】A 【解析】 【分析】先求2b -的范围,再根据不等式的性质,求2a b -的范围. 【详解】因为14b -≤≤,所以822b -≤-≤, 由12a ≤≤,得724a b -≤-≤. 故选:A.例15.(2022·全国·高三专题练习)若,x y 满足44x y ππ-<<<,则x y -的取值范围是( )A .(,0)2π-B .(,)22ππ-C .(,0)4π-D .(),44ππ-【答案】A 【解析】 【分析】根据不等式的性质,求得0x y -<,且22x y ππ-<-<,即可求解.【详解】由x y <,可得0x y -<, 又由44y ππ-<<,可得44y ππ-<-<,因为44x ππ-<<,可得22x y ππ-<-<,所以02x y π-<-<,即x y -的取值范围是(,0)2π-.故选:A.例16.(2022·全国·高三专题练习(文))已知-3<a <-2,3<b <4,则2a b的取值范围为( )A .(1,3)B .4934⎛⎫ ⎪⎝⎭,C .2334⎛⎫ ⎪⎝⎭,D .112⎛⎫ ⎪⎝⎭, 【答案】A 【解析】 【分析】先求出a 2的范围,利用不等式的性质即可求出2a b的范围.【详解】因为-3<a <-2,所以a 2∈(4,9),而3<b <4,故2a b的取值范围为(1,3),故选:A .例17.(2022·江西·二模(文))已知122x y ≤-≤,1231x y -≤+≤,则6x +5y 的取值范围为______. 【答案】[]1,4- 【解析】 【分析】由()652223x y x y x y +=-++结合不等式的性质得出答案. 【详解】解:()652223x y x y x y +=-++,即()()1212223221x y x y +⨯-≤-++≤+⨯ 故6x +5y 的取值范围为[]1,4-. 故答案为:[]1,4-例18.(2022·全国·高三专题练习)设二次函数()()22,f x mx x n m n =-+∈R ,若函数()f x 的值域为[)0,∞+,且()12f ≤,则222211m n n m +++的取值范围为___________. 【答案】[1,13] 【解析】 【分析】根据二次函数的性质和已知条件得到m 与n 的关系,化简222211m n n m +++后利用不等式即可求出其范围. 【详解】二次函数f (x )对称轴为1x m=, ∵f (x )值域为[]0,∞+,∴0m >且21121001f m n n mn m m mm ⎛⎫⎛⎫=⇒⋅-+=⇒=⇒= ⎪ ⎪⎝⎭⎝⎭,n >0.()12224f m n m n ≤⇒-+≤⇒+≤,∵()()()()2222224422222222221111111m m n n m n m n m n n m m n m n m n +++++++==+++++++ =()22222222222m n m n m n m n +-++++=()()222222222m n mn m n +++-++=()()222222212m n m n m n +++-++=221mn +-∴221211m n mn +-≥-=,22221()34313m n m n +-=+-≤-=, ∴222211m n n m +++∈[1,13]. 故答案为:[1,13].例19.(2022·全国·高三专题练习)已知有理数a ,b ,c ,满足a b c >>,且0a b c ++=,那么ca的取值范围是_________. 【答案】122c a -<<- 【解析】 【分析】根据不等式的性质求得ca的取值范围.【详解】由于a b c >>,且0a b c ++=,所以0,0a c ><,,,2,2cb ac a c a a c a=----<>->-, 1,2,2c a c c a c a -->-><-, 所以122c a -<<-. 故答案为:122c a -<<-例20.(2022·全国·高三专题练习)已知函数()34f x x ax b =++,当[]1,1x ∈-时,()1f x ≤恒成立,则a b +=____________. 【答案】-3 【解析】 【分析】可以取特殊值112x x =±=±,时,()11f x -≤≤恒成立,从而求出a 和b ﹒【详解】当[]1,1x ∈-时,()1f x ≤恒成立,则()11f x -≤≤对任意[]1,1x ∈-恒成立, 则112x x =±=±,时,()11f x -≤≤恒成立1141x a b =-≤++≤,①1141141x a b a b =--≤--+≤⇒-≤+-≤,②1111222a xb =-≤++≤,③111111122222a a xb b =--≤--+≤⇒-≤+-≤,④①+②282253a a -≤+≤⇒-≤≤-:③+④21231a a -≤+≤⇒-≤≤: 3a ∴=-,代入①20b -≤≤: 代入③02b ≤≤: 0b ∴=,30a b ∴=-=,,3a b ∴+=-﹒证明()343f x x x =-满足题意:()343f x x x =-,则()()2112302f x x f x x ''=-=⇒=±,,由表可知,|f (x )|≤1在[-1,1]上恒成立满足题意﹒故答案为:-3. 【点睛】本题考察恒成立问题,根据函数和区间的特殊性,可取特殊值得到关于a 和b 的不等式组,求出a 和b 的范围,从而确定a 和b 的取值﹒例21.(2022·全国·高三专题练习)已知正数a ,b 满足5﹣3a ≤b ≤4﹣a ,ln b ≥a ,则ba的取值范围是___.【答案】[e ,7] 【解析】 【分析】 由题意可求得b a≤7;由ln b ≥a 可得b ba lnb ≥(b 12e ≥),设函数f (x )x lnx =(x 12e ≥),利用其导数可求得f (x )的极小值,也就是ba的最小值.【详解】∵正数a ,b 满足5﹣3a ≤b ≤4﹣a , ∴5﹣3a ≤4﹣a , ∴a 12≥. ∵5﹣3a ≤b ≤4﹣a , ∴5a -34b a a ≤≤-1.从而ba≤7, ∵ln b ≥a ,∴b ba lnb≥(b 12e ≥), 设f (x )x lnx =(x 12e ≥),则f ′(x )21lnx lnx -=(), 当0<x <e 时,f ′(x )<0,当x >e 时,f ′(x )>0,当x =e 时,f ′(x )=0, ∴当x =e 时,f (x )取到极小值,也是最小值. ∴f (x )min =f (e )=e . ∴ba≥e , ∴ba的取值范围是[e ,7]. 故答案为:[e ,7].例22.(2022·全国·高三专题练习)已知,,a b c 均为正实数,且111,,232425abbc ca a bb cc a+++,那么111a b c ++的大值为__________.【答案】4 【解析】 【分析】本题目主要考察不等式的简单性质,将已知条件进行简单变形即可 【详解】因为,,a b c 均为正实数,所以由题可得:22203,04,05a b b c a c b bc ac a +++<≤<≤<≤,即1203b a<+≤,1204c b <+≤,1205a c <+≤,三式相加得:1110312a b c ⎛⎫<++≤ ⎪⎝⎭,所以11104a b c <++≤所以111a b c++的最大值为4故答案为:4【方法技巧与总结】在约束条件下求多变量函数式的范围时,不能脱离变量之间的约束关系而独立分析每个变量的范围,否则会导致范围扩大,而只能建立已知与未知的直接关系.题型四:不等式的综合问题例23.(2022·江西鹰潭·二模(理))已知0,0a b >>,且2e1b aa b -+=+则下列不等式中恒成立的个数是( )①1122b a --< ②11b a a b -<- ③e e b a b a -<- ④5ln 5a b +<+A .1 B .2 C .3 D .4【答案】B 【解析】 【分析】①,分析得到,a b <所以1122b a --<正确;②,构造函数举反例判断得解;③,构造函数利用函数单调性判断得解;④,转化为判断2ln(5)2ln(5)a b +<+再构造函数利用导数判断函数的单调性即得解. 【详解】解:①,若02,e e 1,11b aa ab b -+≥∴≤=∴>+,所以矛盾,所以,a b <所以1122b a --<正确; ②,1111b a a b a b a b -<-∴+<+,,设21(1)(1)(),(0),()x x f x x x f x x x +-'=+>∴=, 所以当(0,1)x ∈时,函数()f x 单调递减,当(1,+)x ∈∞时,函数()f x 单调递增,因为a b <,所以11a b ab+<+不恒成立,如1151,(),1,(1)2()2222a fb f f ====<,所以该命题错误;③,e e a b a b -<-,设()e ,()e 10,()x x g x x g x g x '=-∴=->∴在(0,)+∞单调递增,因为a b <,所以e e a b a b -<-恒成立,所以该命题正确;④,5ln2ln(5)2ln(5)5a a b b +<⇔+<++设()2ln(5)h x x =+所以2()h x '==所以函数()h x 在(0,1)单调递增,在(1,)+∞单调递减. 取131,e,(1)e 3e,1b b a b b -==∴+=+ 设()(1)e ,()(2)e 0x x k x x k x x '=+∴=+>,所以()k x 在(0,)+∞单调递增, (1)2e 3e k =<,2(2)3e 3e k =>,所以存在(1,2),(1)e 3e b b b ∈+>,此时2ln(5)2ln(5)a b +>+ 所以该命题错误. 故选:B例24.(2022·江西·临川一中高三期中(文))若实数a ,b 满足65a a b <,则下列选项中一定成立的有( ) A .a b < B .33a b <C .e 1a b ->D .ln 0a b ⎛⎫< ⎪⎝⎭【答案】D 【解析】 【分析】先由65a a b <得到0a b <<或0b a <<,再利用不等式的性质、函数的单调性进行判定. 【详解】因为65a a b <,所以655()0a a b a a b --=<, 显然0a ≠,所以()0a a b -<,所以00a a b >⎧⎨-<⎩或00a a b <⎧⎨->⎩,即0a b <<或0b a <<;若0a b <<,则a b <,33a b <,0e e 1a b -<=,ln ln10a b ⎛⎫<= ⎪⎝⎭;若0b a <<,则a b >,33a b >,0>e e 1a b -=,ln ln10a b ⎛⎫<= ⎪⎝⎭;即一定成立的是选项D. 故选:D.例25.(2022·湖南·长沙一中高三阶段练习)若m ,n ∈+N ,则下列选项中正确的是( ) A .()()1log 1log 2m m m m ++<+ B .(n m m n mn ⋅≥C .()()22sin 1sin 31n n n n n ππ⋅<+⋅>+ D .1121111n n n n n n n n +++++<++ 【答案】C 【解析】 【分析】对于A ,作商比较,对于B ,令1,2m n ==判断,对于C ,利用在单位圆中,内接正n 边形的面积小于内接正()1n +边形的面积判断,对于D ,利用放缩法判断 【详解】解:对于A 选项,由于m ,n ∈+N ,故由对数的定义得2,N m m +≥∈,()()1log 10,log 20m m m m ++>+>, 所以()()()()211111log 2log 2log log 2log log 12m m m m m m m m m m m m ++++++++⎛⎫=+⋅≤ ⎪+⎝⎭()()()22211log 1log2144m m m m m ++⎡⎤++⎣⎦=<=,所以()()1log 1log 2m m m m ++>+,故A 错误; 对于B 选项,令1,2m n ==,则(21122,n m m n mn =⨯==⋅(n m m n mn <⋅B 错误;对于C 选项,因为,在单位圆中,内接正n 边形的面积小于内接正()1n +边形的面积, 所以()112π12π11sin 111sin 221n n S n S n n n +=⋅⋅⋅⋅<=+⋅⋅⋅⋅+,故C 正确;对于D 选项,由于112111,111n n n n n n n n n +++++===++,故D 错误. 故选:C(多选题)例26.(2022·江苏连云港·模拟预测)已知0,0a b >>,直线2y x a =+与曲线1e 1x y b -=-+相切,则下列不等式一定成立的是( ) A .19ab ≤B .219a b+≥CD【答案】BCD 【解析】【分析】根据导数的几何意义得21a b +=,再根据基本不等式与柯西不等式可判断出答案. 【详解】设切点为00(,)x y ,因为1e x y -'=,所以01e 1x -=,得01x =, 所以122a b +=-,所以21a b +=, 对于 A,12a b =+≥18ab ≤,当且仅当11,42a b 时,等号成立,故A 不正确; 对于B,212122()(2)55b a a b a b a b a b+=++=++≥+9=,当且仅当13a b ==时,等号成立,故B 正确;对于C=25a =,15b =时,等号成立,故C 正确;对于D,22222(12⎡⎤⎡⎤≤+⋅+⎢⎥⎣⎦⎣⎦33(2)22a b =+⋅=, 所以,又21a b +=,即12,63a b ==时,等号成立. 故选:BCD(多选题)例27.(2022·辽宁辽阳·二模)已知0a >,0b >,且24a b +=,则( ) A .124a b ->B .22log log 1a b +≤ C≥D .412528a b +≥ 【答案】BD 【解析】 【分析】由不等式的性质与基本不等式对选项逐一判断 【详解】对于A ,02a <<,()()42344,2a b a a a -=--=-∈-,所以12416a b -<<,故A 错误,对于B ,420a b =+≥>,即0<02ab ,()222log log log 1a b ab +=≤,故B 正确,对于C,228a b =++≤C 错误,对于D,4122171725288488a b a b b a a b a b a b ++⎛⎫+=+=++≥+= ⎪⎝⎭,当且仅当825a b ==时,等号成立,故D 正确. 故选:BD(多选题)例28.(2022·重庆八中模拟预测)已知0a >,0b >,且3ab a b ++=,则下列不等关系成立的是( ) A .1ab ≤ B .2a b +≥ C .1a b -> D .3a b -<【答案】ABD 【解析】 【分析】利用基本不等式以及适当的代数式变形即可判断. 【详解】对于A ,由3ab a b ++= ,a b +≥,当且仅当a b = 时等号成立,3ab ∴+≤ ,)310≤ ,1ab ∴≤ ,当且仅当1a b == 时等号成立,故A 正确; 对于B ,由3ab a b ++=,得()()4114,11a b b a ++=∴+=+ , 由基本不等式得)44(1)(1)2122211a b a b a a a +=+++-=++-≥-=++ ,当且仅当a=b =1时成立;故B 正确;对于C ,若1,1,a b == 满足3ab a b ++=,01a b -=<,故C 错误; 对于D ,∵3ab a b ++=,∴3ab a b a b =+++> ,由B 的结论得23a b ≤+< ,()()()()222949439a b a b ab a b a b --=+--=+--+-⎡⎤⎣⎦()()()()2421730a b a b a b a b =+++-=+++-< ,()29,3a b a b ∴--<< ,故D 正确; 故选:ABD.例29.(2022·全国·高三专题练习)若x ,y R ∈,设2223M x xy y x y =-+-+,则M 的最小值为__. 【答案】14-##0.25-【解析】 【分析】将M 化简可得2211224M x y y ⎛⎫=--+- ⎪⎝⎭,由此即可求出结果.【详解】因为()()2222221121321344M x y x y y x y x y y y y y y ⎡⎤=-+++=-++++++---⎢⎥⎣⎦221112244x y y ⎛⎫=--+-≥- ⎪⎝⎭.当且仅当0y =,12x =时取等号. 所以M 的最小值为14-.故答案为:14-.例30.(2022·四川泸州·三模(理))已知x 、y ∈R ,且224x y +=,给出下列四个结论: ①2x y +≤;②1xy ≥;③23x y +≤;④448x y +≥. 其中一定成立的结论是______(写出所有成立结论的编号). 【答案】①④ 【解析】 【分析】利用基本不等式可判断①和④,取特殊值x =0、y =2log 3可判断②,取特殊值y =12可判断③. 【详解】对于①,∵20,20x y >>,∴由224x y +=得,422x y =+≥即4≥,解得2x y +≤(当且仅当1x y ==时取等号),故①一定成立; 对于②,当20,log x y ==3时,224x y +=成立,但1xy ≥不成立,故②不一定成立;对于③,当12y =时,由224x y +=得24x =则132343022xy +-=-=>,即23x y +>,故③不一定成立;④将224x y +=两边平方得144216x y x y ++++=, ∴144162x y x y +++=-,由①可知:131********x y x y x y x y +++++≤⇒++≤⇒≤=⇒-≥-11621688x y ++⇒-≥-=,∴448x y +≥,当且仅当1x y ==时取等号,因此④一定成立﹒ 故答案为:①④﹒ 【点睛】本题①和④利用基本不等式即可求解,需要熟练运用基本不等式求范围.对于②和③,取特殊值验算即可快速求解﹒【过关测试】一、单选题 1.(2022·湖南·宁乡市教育研究中心模拟预测)小李从甲地到乙地的平均速度为a ,从乙地到甲地的平均速度为(0)b a b >>,他往返甲乙两地的平均速度为v ,则( ) A .2a bv +=B.v =C2a bv +< D.b v <<【答案】D 【解析】 【分析】平均速度等于总路程除以总时间 【详解】设从甲地到乙地的的路程为s ,从甲地到乙地的时间为t 1,从乙地到甲地的时间为t 2,则 1s t a=,2s t b =,1222211s s v s s t t a b a b===+++,∴221111v ba bb b=>=++,2211ab v a b a b==<=++ 故选:D.2.(2022·甘肃省武威第一中学模拟预测(文))已知0a b <<,则( ) A .110->a bB .sin sin 0a b ->C .0a b -<D .ln()ln()0a b -+->【答案】A 【解析】 【分析】利用特殊值法,结合已知逐一判断即可. 【详解】因为0a b <<,所以110b aa b ab--=>,选项A 正确; 当2π,πa b =-=-时,显然满足0a b <<,但sin sin 0a b -=,选项B 不正确; 当2π,πa b =-=-时,显然满足0a b <<,但0a b ->,选项C 不正确; 当1,123a b =-=-时,显然满足0a b <<,但是ln()ln()0a b -+-<,选项D 不正确, 故选:A3.(2022·陕西宝鸡·三模(理))若a b <,则下列结论正确的是( ) A .330a b -> B .22a b < C .()ln 0a b -> D .a b <【答案】B 【解析】 【分析】对于A 、B ,构造函数,借助函数单调性比大小; 对于C , ()ln a b -没有意义; 对于D ,取特值判断. 【详解】对于A ,构造函数3()f x x =,因为3()f x x =单调递增,又a b <,所以()()f a f b <,33a b ∴<,330a b ∴-<,故A 答案不对;对于B ,构造函数()2x f x =,因为()2x f x =单调递增,又a b <,所以()()f a f b <,22a b ∴<,故B 答案正确;对于C ,a b <,()ln a b ∴-没有意义,故C 答案不对;对于D ,取=11a b ,-=时,=a b ,故D 答案不对; 故选:B.4.(2022·重庆·二模)若非零实数a ,b 满足a b >,则下列不等式一定成立的是( )A .11a b< B .a b +>C .22lg lg a b > D .33a b >【答案】D 【解析】 【分析】根据不等式的基本性质、基本不等式的条件和对数的运算,逐项判定,即可求解. 【详解】对于A 中,由11b aa b ab--=,因为a b >,可得0b a -<,当ab 不确定,所以A 错误;对于B 中,只有当0,0,a b a b >>,不相等时,才有a b +>B 错误; 对于C 中,例如1,2a b ==-,此时满足a b >,但22lg lg a b <,所以C 错误; 对于D 中,由不等式的基本性质,当a b >时,可得33a b >成立,所以D 正确. 故选:D.5.(2022·安徽黄山·二模(文))设实数a 、b 满足a b >,则下列不等式一定成立的是( )A .22a b >B .11b b a a +<+ C .22ac bc > D .332a b -+>【答案】D 【解析】 【分析】对于A ,B ,C 可以取特殊值验证,对于D ,根据题意得330a b >>,3333a b b b --+>+,利用基本不等式求解即可. 【详解】对于A :当2a =,4b =-时不成立,故A 错误;对于B :当12a =-,1b =-,所以2b a =,101b a +=+,即11b b a a +>+,故C 错误;对于C :当0c 时不成立,故C 错误;对于D :因为a b >,所以330a b >>,又30b ->,所以33332b a b b --≥+>+=(等号成立的条件是0b =),故D 正确. 故选:D.6.(2022·安徽·芜湖一中高三阶段练习(理))已知0a >,0b >,22a b m +=,则以下正确的是( ) A .若1m =,则1a b + B .若1m =,则331a b + C .若2m =,则2a b +> D .若2m =,则332a b +【答案】D 【解析】 【分析】A :取特例a b ==B :求出01a <<,01b <<,根据幂函数在(0,1)之间的性质即可判断;C :根据不等关系2222a b a b ++ D :构造33222()(())a b a b a b ++-+并判断其范围,表示出33+a b ,结合C 项范围即可判断. 【详解】A :若221a b +=,取a b ==1a b +,故A 错误; B :若221a b +=,则01a <<,01b <<,∴33221a b a b +<+=,故B 错误; C :当222a b +=时,∵222a bab +,∴()222222a ba b ab +++,∴222()24a b a b ++,∴221222a b a b a b ++=⇒+,故C 错误;D :当222a b +=时,3322233222()(()2()0)a b a b a b a b b a a b ab a b ++-+=+-=-, 22233()4a b a ba b a b+∴+=++,由C 知,2a b +,42a b∴+,332a b ∴+,故D 正确. 故选:D.7.(2022·全国·高三专题练习(理))已知32a =,53b =,则下列结论正确的有( ) ①a b < ②11a b a b+<+ ③2a b ab +< ④b a a a b b +<+ A .1个 B .2个 C .3个 D .4个【答案】B 【解析】 【分析】求出a 、b 的值,比较a 、b 的大小,利用指数函数的单调性、导数法、不等式的基本性质以及基本不等式逐项判断可得出合适的选项. 【详解】因为32a =,53b =,则3log 2a =,5log 3b =.对于①,3223<,则2323<,从而2333320log 1log 2log 33a =<=<=,3235>,则2335>,则235552log 5log 3log 513b =<=<=,即2013a b <<<<,①对;对于②,()()()11111a b ab a b a b a b a b ab --⎛⎫⎛⎫⎛⎫+-+=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为2013a b <<<<,则0a b -<,01ab <<,所以,11a b a b+>+,②错; 对于③,355522log 2log 32log 2log 4ab =⋅==,所以,355353542log 2log 3log 4log 2log log log 03a b ab +-=+-=->, 所以,2a b ab +>,③错; 对于④,构造函数()ln x f x x =,其中0e x <<,则()21ln xf x x -'=. 当0e x <<时,()0f x '>,则函数()f x 在()0,e 上单调递增, 因为01a b <<<,则()()f a f b <,即ln ln a ba b<,可得b a a b <,所以,b a a a b b +<+,④对. 故选:B.8.(2022·安徽省舒城中学模拟预测(理))若数列{}n a 为等差数列,数列{}n b为等比数列,则下列不等式一定成立的是( ) A .1423b b b b +≤+ B .4132b b b b ≤-- C .3124a a a a ≥ D .3124a a a a ≤【答案】D 【解析】 【分析】对选项A ,令112n n b -⎛⎫=- ⎪⎝⎭即可检验;对选项B ,令2nn b =即可检验;对选项C ,令n a n =即可检验;对选项D ,设出等差数列的首项和公比,然后作差即可. 【详解】 若112n n b -⎛⎫=- ⎪⎝⎭,则12341111,,,248b b b b ==-==-可得:14237184b b b b +=>=-+,故选项A 错误; 若2nn b =,则12342,4,8,16b b b b ====可得:4132144b b b b -=>-=,故选项B 错误; 若n a n =,则12341,2,3,4a a a a ==== 可得:124346a a a a =<=,故选项C 错误; 不妨设{}n a 的首项为1a ,公差为d ,则有:()112411133a a a a d a a d =+=+()()22311121223a d a d a d a a d a =++=++则有:4223120a a a a d -=≥,故选项D 正确故选:D 二、多选题9.(2022·辽宁·一模)已知不相等的两个正实数a 和b ,满足1ab >,下列不等式正确的是( ) A .1ab a b +>+ B .()2log 1a b +> C .11a b ab+<+ D .11a b a b+>+ 【答案】BD 【解析】 【分析】A 选项,利用()()1110a b ab a b --=+--<作出判断;B 选项,利用基本不等式即函数单调性求解;CD 选项,用作差法求解.由于两个不相等的正实数a 和b ,满足1ab >,所以a 和b 可取一个比1大,一个比1小,即()()1110a b ab a b --=+--<,故1ab a b +<+,A 错误;由题意得:2a b +>>,所以()2log 1a b +>,B 正确;()111111a b a b a b a b a b ab ⎛⎫⎛⎫+-+=-+-=-- ⎪ ⎪⎝⎭⎝⎭,其中110ab ->,但不知道a 和b 的大小关系,故当a b >时,11a b a b+>+,当a b <时,11a b a b +<+,C 错误;()1111a b a b a b ab ⎛⎫⎛⎫+-+=+- ⎪ ⎪⎝⎭⎝⎭,其中110ab ->,0a b +>,所以()11110a b a b a b ab ⎛⎫⎛⎫+-+=+-> ⎪ ⎪⎝⎭⎝⎭,即11a b a b+>+,D 正确. 故选:BD10.(2022·湖南省隆回县第二中学高三阶段练习)已知a b c >>,且0a b c ++=,则下列结论正确的是( ) A .2ab b > B .ac bc <C .11a c> D .1a cb c->- 【答案】BCD 【解析】 【分析】根据不等式的基本性质依次判断选项即可. 【详解】A :由a b c >>且0a b c ++=,可知a >0,c <0,b 的值不确定, 故由a b >,不能推出2ab b >,故A 错误;B :由0a b c ><,,得ac bc <,故B 正确;C :由于0a >,0c <,得11a c>,故C 正确; D :由a b c >>得0a c b c ->->.所以1a cb c->-,故D 正确, 故选:BCD.11.(2022·广东·广州市第四中学高三阶段练习)已知实数a ,b ,c 满足1,01a b c >><<,则下列不等式一定成立的有( ) A .()()c c a c b c -<- B .log (1)log (1)a b c c +<+ C .log log 2a c c a +≥ D .22224a c b c c >>【答案】BD 【解析】对于A ,利用幂函数的性质判断,对于BC ,利用对数函数的性质判断,对于D ,利用不等式的性质分析判断 【详解】对于A ,因为01c <<,所以c y x =在(0,)+∞上单调递增,因为,01a b c c >><<,所以0a c b c ->->,所以()()cca cbc ->-,所以A 错误,对于B ,因为1a b >>,所以当1x >时,log log a b x x <,因为01c <<,所以11c +>,所以log (1)log (1)a b c c +<+,所以B 正确,对于C ,因为1,01a b c >><<,所以log 0,log 0a c c a <<,所以log log 0a c c a +<,所以C 错误, 对于D ,因为1,01a b c >><<,所以22210a b c >>>>,所以22224a c b c c >>,所以D 正确, 故选:BD12.(2022·河北保定·一模)已知a 、b 分别是方程20x x +=,30x x +=的两个实数根,则下列选项中正确的是( ). A .10b a -<<< B .10a b -<<< C .33a b b a ⋅<⋅ D .22b a a b ⋅<⋅【答案】BD 【解析】 【分析】在同一直角坐标系中画出2,3,x x y y y x ===-的图象,可判断AB ,然后结合不等式的性质可判断CD. 【详解】函数2,3,x x y y y x ===-在同一坐标系中的图象如下:所以10a b -<<<,所以22,33,0a b a b b a<<<-<-所以()()22,33a b a bb a b a -⋅<-⋅-⋅<-⋅所以22b a a b ⋅<⋅,33a b b a ⋅⋅> 故选:BD 三、填空题13.(2022·四川泸州·三模(文))已知x ,R y ∈,满足224x y +=,给出下列四个结论:①2x y +≤;②1xy ≥;③23x y +<;④448x y +≥.其中一定成立的结论是______(写出所有成立结论的编号). 【答案】①④ 【解析】 【分析】根据基本不等式,结合特殊值法逐一判断即可. 【详解】①:因为224x y +=,所以有4222422x y x y x y +=+≥≥≥⇒+≤,故本结论一定成立; ②:当20,log 3x y ==时,显然224x y +=成立,但是1xy ≥不成立,故本结论不一定成立; ③:当1x y ==时,显然224x y +=成立,但是23x y +<不成立,故本结论不一定成立; ④:因为224x y +=,所以114421644162x y x y x y x y ++++++=⇒+=-,由①可知: 1311213228281621688x y x y x y x y x y +++++++≤⇒++≤⇒≤=⇒-≥-⇒-≥-=,所以448x y +≥,因此本结论一定成立, 故答案为:①④14.(2022·全国·江西科技学院附属中学模拟预测(文))已知实数x 、y 满足223x y -≤+≤,220x y -≤-≤,则34x y -的取值范围为______. 【答案】[7,2]- 【解析】 【分析】设34(2)(2)x y m x y n x y -=++-,利用待定系数法求出,m n 的值,然后根据不等式的性质即可求解. 【详解】解:设34(2)(2)x y m x y n x y -=++-,则2324m n m n +=⎧⎨-=-⎩,解得12m n =-⎧⎨=⎩,所以34(2)x y x y -=-++2(2)x y -, 因为223x y -≤+≤,220x y -≤-≤, 所以3(2)2x y -≤-+≤,42(2)0x y -≤-≤, 所以7342x y -≤-≤, 故答案为:[7,2]-.15.(2022·全国·高三专题练习)如果a >b ,给出下列不等式:①11a b<;②a 3>b 32ac 2>2bc 2;⑤ab >1;⑥a 2+b 2+1>ab +a +b .其中一定成立的不等式的序号是________. 【答案】②⑥ 【解析】 【分析】对,a b 分别赋值,然后对各个不等式进行排除,对于无法排除的选项利用函数的单调性和差比较法证明成立. 【详解】令1,1a b ==-,11a b>=11a b =-<,排除⑤.当0c 时,排除④.由于幂函数3y x =为R 上的递增函数,故33a b >,②是一定成立的.由于()()()()22222111102a b ab a b a b a b ⎡⎤++-++=-+-+->⎣⎦,故221a b ab a b ++>++.故⑥正确.所以一定成立的是②⑥. 【点睛】本小题主要考查实数比较大小,使用的方法较多,一个是特殊值比较法,也就是对问题中的,a b 举出一些具体的数值,然后对不等式的正确与否进行判断.第二个是用函数的单调性的方法来比较,即是如果要比较的两个数和某个函数有点接近,如本题中②,用幂函数的单调性来判断.第三个是用差比较法来判断,如本题中的⑥.16.(2022·全国·高三专题练习)设x ,y 为实数,满足238xy ≤≤,249x y≤≤,则3x y 的最小值是______.【答案】12 【解析】利用方程组形式,可得()223nm x x xy y y ⎛⎫=⋅ ⎪⎝⎭,求得,m n 后结合不等式性质即可求得3x y 的最小值. 【详解】设()223nm x x xy y y ⎛⎫=⋅ ⎪⎝⎭即322m n m n xy x y -+-=⋅所以2123m n m n +=⎧⎨-=-⎩,解得11m n =-⎧⎨=⎩所以()2123x x xy y y -⎛⎫=⋅ ⎪⎝⎭因为238xy ≤≤,249x y≤≤, 所以()121183xy-≤≤ 由不等式性质可知()212132x xy y -⎛⎫≤⋅≤ ⎪⎝⎭即3132x y ≤≤,当且仅当()212418x yxy -⎧=⎪⎪⎨⎪=⎪⎩时取等号,解得74552,2x y ==. 综上可知,3x y的最小值为12. 故答案为:12. 【点睛】本题考查了不等式的化简变形应用,不等式性质求最值,关键是要求出两个不等式间的关系,属于中档题. 四、解答题17.(2022·全国·高三专题练习)已知1a >,1b >,2222,1111a b b a M N a b a b =+=+----. (1)试比较M 与N 的大小,并证明; (2)分别求M ,N 的最小值.【答案】(1)M N ≤;证明见解析 ;(2) M ,N 的最小值都是8. 【解析】 【分析】(1)利用作差比较法,得到2()()0(1)(1)a b a b M N a b -+-=-≤--,即可求解; (2)化简1111411a b a M b =-++-++--,结合基本不等式,即可求解. 【详解】(1)M 与N 的大小为M N ≤,证明:由22222()()1111(1)(1)a b b a a b a b M N a a b b a b -+-=-+-=-------, 因为1a >,1b >,所以0a b +>,10a ->,10b ->,2()0a b -≥,所以2()()0(1)(1)a b a b a b -+-≤--,所以M N ≤. (2)因为2222[(1)1][(1)1]1111a b a b M a b a b -+-+=+=+----111144811a b a b =-++-++≥=--, 当2a b ==时取等号,又由(1)N M ≥,所以M ,N 的最小值都是8.18.(2022·全国·高三专题练习)(1)已知a ,b 均为正实数.试比较33+a b 与22a b ab +的大小; (2)已知a ≠1且a ∈R ,试比较11a-与1a +的大小. 【答案】(1)33+a b ≥22a b ab +;(2)答案见解析. 【解析】 【分析】(1)将目标代数式作差得2()()a b a b -+,即可知大小关系;(2)利用“作差法”有21(1)11a a a a-+=--,对a 分类讨论即可判断大小. 【详解】(1)∵a ,b 均为正实数,∴332222222()()()()()()()0a b a b ab a a b b a b a b a b a b a b +-+=---=--=-+≥,即33+a b ≥22a b ab +. (2)由21(1)11a a a a-+=--. ①当a =0时,21a a=-0,则11a =-1a +; ②当a <1且a ≠0时,21a a >-0,则11a >-1a +; ③当a >1时,21a a<-0,则11a <-1a +. 综上,当a =0时,11a =-1a +;当a <1且a ≠0时,11a >-1a +;当a >1时,11a<-1a +. 19.(2022·全国·高三专题练习)已知下列三个不等式:①0ab >;②c da b>;③bc ad >,以其中两个作为条件,余下一个作为结论,则可组成几个正确命题?并选取一个结论证明. 【答案】可组成3个正确命题,证明见解析. 【解析】 【分析】根据不等式的性质逐个分析每个命题的真假即可. 【详解】 (1)对②变形:0c d bc ad a b ab->⇔>,由0,ab bc ad >>得②成立,∴①③⇒②.。
第三节二次函数与一元二次方程不等式专题课件高三数学二轮复习

【解析】由+10Fra bibliotek(-2)
2
2
2
>1,得
x+10>(x-2)
=x
-4x+4,且
x≠2,整理得,x
-5x-6<0, -6 · + 1 <0,
2
解得-1<x<6,又因为 x≠2,所以解集为 -1,2 ∪ 2,6 .
【解析】(1)原不等式因式分解得(x2+1)(x2-2)≥0,
因为 x2+1>0,所以 x2-2≥0,解得 x≤- 2或 x≥ 2,
若一元二次不等式 mx2-2mx-1≤0 恒成立,
<0
则
,解得-1≤m<0,此时不等式恒成立.
2
= 4 + 4 ≤ 0
答案:[2,10)
【解析】因为 x +x+2= +
2
1 2 7
2
+ >0,
4
所以原不等式等价于 kx2+kx+6>2x2+2x+4,
即 -2 x2+ -2 x+2>0 恒成立.
( A )
A.k>1
B.-1<k<1
C.k<-1
D.k>-1
【解析】当 k=0 时,-2x>0 不恒成立;
>0
当 k≠0 时,
,解得 k>1;
2
= 4(1- ) < 0
综上,k>1.
核心题型·分类突破
A
1
【解析】x 2 + 7 ≥-3 可变形为 2x +7x+3≥0,令 2x +7x+3=0,得 x1=-3,x2=- ,
高三数学二轮复习-高考中的不等式问题研究讲义

且当 时, .
解集是空集,
故m的取值范围: .
18.拓展演练
I.单选题
(1)已知正实数x,y满足 .则 的最小值为()
A.4B. C. D.
(2)已知实数 , 满足 , ,则 的取值范围是()
A. B.
C. D.
II、多选题
(3).对于实数 ,下列说法正确的是( )
A.若 ,则 B.若 ,则
,
而 ,
故 不可能均大于 .
取 , , ,
则 ,
故三式中大于 的个数的最大值为2,
故选:C.
【点睛】思路分析:代数式的大小问题,可根据代数式的积的特征选择用基本不等式或排序进行放缩,注意根据三角变换的公式特征选择放缩的方向.
二、分段不等式问题
7.
(2018全国卷Ⅲ)[选修4—5:不等式选讲]
设函数 .
证毕.
11.设 ,且 .
(1)求 的最小值;
(2)若 成立,证明: 或 .
证明:
解析(1)由于
,
故由已知得 ,
当且仅当x= ,y=– , 时等号成立.
所以 的最小值为 .
(2)由于
= ,
故由已知 ,
当且仅当 , , 时等号成立.
因此 的最小值为 .
由题设 ,
所以
解得 或 .
12.【2021浙江高考-T17】
C.若 ,则 D.若 ,则
(4)(多选)若 ,则下列不等式中一定不成立的是()
A. B. C. D.
(5).已知 且 ,那么下列不等式中,恒成立的有().
A. B. C. D.
15.【模拟题】
最值应用题
一件刚出土的珍贵文物要在博物馆大厅中央展出,如图,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1 000元,则气体的费用最少为()
