《菱形》性质练习题
《菱形的性质》同步练习题

《菱形的性质》同步练习题菱形的性质同步练题
一、选择题
1. 菱形是指四个边相等的四边形。
下面哪个图形是菱形?
2. 菱形的对角线相等。
已知菱形的一条对角线长度为d,那么另一条对角线的长度应为:
A. d
B. 2d
C. √2d
3. 已知菱形的一条对角线长度为10cm,那么另一条对角线的长度应为:
A. 5cm
B. 10cm
C. 15cm
二、填空题
1. 菱形是特殊的\_\_\_\_\_\_\_\_\_。
2. 菱形的一大特点是它的\_\_\_\_\_\_\_\_\_相等。
3. 菱形的两条对角线相等,且相交于\_\_\_\_\_\_\_\_\_点。
4. 菱形的周长等于\_\_\_\_\_\_\_\_\_个边的长之和。
5. 菱形的面积等于\_\_\_\_\_\_\_\_\_。
三、解答题
1. 画一个菱形,标注出它的对角线和重心。
2. 已知菱形的一条边长为6cm,求它的周长和面积。
3. 若两个菱形的边长分别为a和b,其中a>b,则这两个菱形的周长之差为多少?
4. 证明:菱形的两个内角的和为180度。
四、应用题
1. 小明画了一个菱形,已知它的一条边长为4cm,求它的对角线长度、周长和面积。
2. 一块田地呈正菱形,已知它的面积为144平方米,求它的边长。
3. 小红拿到一张纸,发现它是一个正菱形,已知纸的一个内角为60度,求这张纸的周长。
以上是《菱形的性质》的同步练习题,希望能帮助加深对菱形性质的理解和应用。
人教版八年级数学下册 18.2.2.1菱形的性质 同步练习(包含答案)

人教版八年级数学下册18.2.2.1 菱形的性质同步练习一、选择题(共10小题,3*10=30)1.菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直2.(2019·贵阳)如图,菱形ABCD的周长是4 cm,∠ABC=60°,那么这个菱形的对角线AC的长是( ) A.1 cm B.2 cm C.3 cm D.4 cm3. 如图,在△ABC中,AB≠AC,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,要使四边形AEDF是菱形,只需添加的条件是()A.AD⊥BC B.∠BAD=∠CAD C.BD=DC D.AD=BD4. 如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是()A.4 3 B.3 3 C.2 3 D. 35. 如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′. 当CA′的长度最小时,CQ的长为()A.5 B.7 C.8 D. 106.如图,在菱形ABCD中,对角线AC,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于点F,则AE的长为()A.4B.4.8 C.2.4D.3.27. 已知菱形的周长为4 5 ,两条对角线的和为6,则菱形的面积为( )A .2 B. 5 C .3 D .48. 如图,菱形ABCD 的对角线AC ,BD 交于点O ,AC =4,BD =16,将△ABO 沿点A 到点C 的方向平移,得到△A′B′O′.当点A′与点C 重合时,点A 与点B′之间的距离为( )A .6B .8C .10D .129. 如图,四边形ABCD 是菱形,AC =8,DB =6,DH ⊥AB 于H ,则DH 等于( )A .245B .125C .5D .410.如图,在周长为12的菱形ABCD 中,AE =1,AF =2,若P 为对角线BD 上一动点,则EP +FP 的最小值为( )A .1B .2C .3D .4二.填空题(共8小题,3*8=24)11. 菱形的两条对角线长分别是5和12,则此菱形的边长是_______,面积是_______.12.在菱形ABCD 中,对角线AC 、BD 相交于点O ,若AB =7 cm ,则周长是________cm.13. 如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,若∠ABC =110°,则∠BAD =________°, ∠ABD =________°,∠BCA =________°.14.如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为_______.15.如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为________.16.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为6和8时,阴影部分的面积为_______.17. 如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于________.18. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD 的周长为________.三.解答题(共7小题,46分)19.(6分) 如图,已知菱形的周长为40 cm,两邻角度数之比为1∶2.(1)求菱形的两条对角线的长;(2)求菱形的面积.20.(6分) 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:OE=BC.21.(6分) 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE,若∠E=50°,求∠BAO的大小.22.(6分) 已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.23.(6分) 如图,在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:(1)△ABF≌△DAE;(2)DE=BF+EF.24.(8分) 如图,菱形ABCD的两条对角线相交于点O,∠DAC=30°,BD=12(1)求∠ABC的度数;(2)求菱形ABCD的面积.25.(8分) 在菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.参考答案1-5DABBB 6-10 DDCAC11. 6.5,3012. 2813. 70,55,3514. 24 15. 2 316. 1217.4518.2419. 解:(1) ∵四边形ABCD 是菱形,两邻角度数之比为1∶2, ∴∠ABC=∠BAC=60°又∵菱形的周长为40 cm ,AC =AB=10 cm ,BD =2BO=2×AB 2-AO 2 =2×102-52 =10 3 cm(2)S 菱形=12BD·AC =50 3 cm 2 20. 解:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形, ∵四边形ABCD 是菱形,∴AC ⊥BD ,∴∠DOC =90°,∴四边形OCED 是矩形,∴OE =CD ,∵四边形ABCD 是菱形,∴CD =BC ,∴OE =BC21. 解:菱形ABCD 中,AB =BC ,∵BE =AB ,∴BC =BE ,∴∠BCE =∠E =50°,∴∠CBE =180°-50°×2=80°,∵AD ∥BC ,∴∠BAD =∠CBE =80°,∴∠BAO =12×80°=40°. 22. 证明:∵四边形ABCD 是菱形,∴AD =CD ,∵点E 、F 分别为边CD 、AD 的中点,∴AD =2DF ,CD =2DE ,∴DE =DF ,在△ADE 和△CDF 中,⎩⎪⎨⎪⎧AD =CD ,∠ADE =∠CDF ,DE =DF ,∴△ADE ≌△CDF(SAS).23. 证明:(1)∵四边形ABCD 是菱形,∴AB =AD ,AD ∥BC , ∴∠BPA =∠DAE ,∵∠ABC =∠AED ,∴∠BAF =∠ADE ,∵∠ABF =∠BPF ,∠BPA =∠DAE ,∴∠ABF =∠DAE , ∵AB =DA ,∴△ABF ≌△DAE(ASA)(2)∵△ABF ≌△DAE ,∴AE =BF ,DE =AF ,∵AF =AE +EF =BF +EF ,∴DE =BF +EF24. 解:(1)∵菱形ABCD 的两条对角线相交于点O ,∠DAC =30°, ∴∠BAD =2∠DAC =60°,∵AD ∥BC ,∴∠ABC =180°-60°=120°;(2)∵菱形ABCD 的两条对角线相交于点O ,BD =12,∴AC ⊥BD ,DO =12BD =6, 又∵∠DAC =30°,∴AD =2DO =12,∴Rt △AOD 中,AO =122-62=63,∴AC =2AO =123,∴菱形ABCD 的面积=12×AC×BD =12×12×123=72 3. 25. 解:(1)连接AC ,∵四边形ABCD 是菱形,∴AB =BC ,∵∠B =60°,∴△ABC 是等边三角形,∵点E 为BC 的中点,∴AE ⊥BC ,∴∠AEC =90°,∵∠AEF =60°,∴∠FEC =90°-60°=30°,∵∠C =180°-∠B =120°,∠C +∠EFC +∠FEC =180°, ∴∠EFC =30°,∴∠FEC =∠EFC ,∴CE =CF ,∵BC =CD ,∴BC -CE =CD -CF ,即BE =DF(2)连接AC ,由(1)得△ABC 是等边三角形,∴AB =AC , ∵∠BAE +∠EAC =60°,∠EAF =∠CAF +∠EAC =60°,∴∠BAE =∠CAF ,∵四边形ABCD 是菱形,∠B =60°,∴∠ACF =12∠BCD =∠B =60°, ∴△ABE ≌△ACF(ASA),∴AE =AF , 又∵∠EAF =60°,∴△AEF 是等边三角形。
菱形性质习题

菱形性质:1.对边平行,四边相等;2对角相等,邻角互补。
3对角线互相垂直平分且平分每一组对角,菱形判定:1四条边都相等的四边形是菱形.2一组邻边相等的平行四边形是菱形。
3.对角线相互垂直的平行四边形是菱形。
(2013•滨州)(2013•淄博)(2013•梧州)(2013•随州)(2013•河北)1.(2013•滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是()2.(2013•淄博)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()3.(2013•梧州)如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是()4.(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是()5.(2013•河北)如图,菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB.若NF=NM=2,ME=3,则AN=()(2013•泉州)(2013•南京)(2013•内江)(2013•临沂)(2012•沈阳)6.(2013•泉州)如图,菱形ABCD的周长为8√(5),对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=,菱形ABCD的面积S=7.(2013•南京)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF= cm.8. (2013•内江)已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=9.(2013•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是 cm2.10.(2012•沈阳)如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为11.(2013•雅安)在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.(1)求证:△ADE≌△CBF;(2)若DF=BF,求证:四边形DEBF为菱形.12.(2013•乌鲁木齐)如图.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,分别于BC、CD交于E、F,EH⊥AB于H.连接FH,求证:四边形CFHE是菱形.13.(2012•柳州)如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个特殊的四边形.(1)这个特殊的四边形形状(2)请证明你的结论.14.(2011•湖州)如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.15.(2013•昭通)已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.。
菱形的性质专项练习30题(有答案)ok

菱形的性质专项练习30题(有答案)1.如图,菱形ABCD中,对角线AC、BD交于点O,过点A作AH⊥BC,交BD于E,垂足为H,已知CH=4,AH=8(1)求菱形的周长;(2)求OE的长度.2.如图,菱形ABCD中,两条对角线AC和BD相交于点O,AC=6cm,BD=8cm.(1)求菱形ABCD的面积;(2)求菱形ABCD的周长.3.如图,菱形对角线AC,BD相交于一点O,且AC=12cm,BD=16cm.求这个菱形的周长和面积.4.如图,已知菱形ABCD的边长是2cm,BAD=120°.(1)试说明:△ABC是等边三角形;(2)求菱形两条对角线的长.5.如图,菱形ABCD的两条对角线AC与BD相交于点O,AB=5,OA=3.(1)求菱形ABCD的周长;(2)求菱形ABCD的面积.6.如图,菱形ABCD的周长为200cm,对角AC与BD交于点O,且AC=60cm,试求菱形ABCD的面积.7.已知:菱形ABCD的两条对角线AC与BD相交于点O,且AC=6,BD=8,求菱形的周长和面积.8.如图,菱形ABCD的对角线AC、BD相交于点O,DE∥AC,AE∥BD.试判断四边形AODE的形状,并说明理由.9.如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AC=6,BD=8,求线段OE的长.10.如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.(1)证明:AM=DM;(2)若DF=2,求菱形ABCD的周长;(3)在没有辅助线的前提下,图中共有_________对相似三角形.11.菱形ABCD中,∠B=60°,一块三角板的60°角的顶点绕点A转动,两边分别交BC、CD于点E、F.(1)说明△ABC、△ACD都是等边三角形.(2)判断△AEF的形状,说明理由?(3)如果AB=2,写出△CEF的周长的最小值.12.如图,O是菱形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE,CE交于点E.(1)求证:四边形OCED是矩形;(2)若菱形ABCD的周长为20,矩形OCED的周长为14,求菱形ABCD的面积.13.如图,点E、F分别在菱形ABCD的边BC、AD上,且AF=CE,∠BAE=25°,∠BCD=130°,求∠AFC的度数.14.如图,平行四边形ABCD中,AE是BC边上的高,AE是BC沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG:(2)若四边形ABFG是菱形,且AB:BC=2:3,求∠B的度数.15.如图,菱形ABCD中,AE⊥BC,垂足为点E,BE=CE,求∠BAD的度数.16.如图,已知一四边形菜地ABCD为菱形,点E,F分别位于边AB,BC上,AD=6,AE=5BE,BF=5CF,若△DEF 为等边三角形.(1)求∠A的度数;(2)求菱形ABCD的面积.17.如图,已知菱形ABCD,∠B=60°,△ADC内一点M满足∠AMC=120°,若直线BA与CM交于点P,直线BC 与AM交于点Q,求证:P,D,Q三点共线.18.已知:如图,菱形ABCD的对角线交于点O,且AO、BO的长分别是方程x2﹣(2m﹣1)x+4(m﹣1)=0的两根,菱形ABCD的周长为20,求m的值.19.如图所示,在菱形ABCD中,点E,F分别在CD,BC上,且CE=CF,求证:AE=AF.20.已知:菱形ABCD中,对角线AC=16cm,BD=12cm,BE⊥DC于点E,求菱形ABCD的面积和BE的长.21.如图,菱形ABCD中,E是AD中点,EF⊥AC交CB的延长线于点F.(1)DE和BF相等吗?请说明理由.(2)连接AF、BE,四边形AFBE是平行四边形吗?说明理由.22.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,BE=DF.若AE垂直平分BC,AF垂直平分CD.求证:(1)AE=AF;(2)△AEF为等边三角形.23.如图,在菱形ABCD中,过点A作AE⊥BC,垂足E为BC的中点,连接DE,F为DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;(2)若AB=4,求DE和AF的长.24.如图,边长为a的菱形ABCD中,∠A=60°,过C任作直线分别交AB、AD的延长线于E、F,连接DE、BF 交于M,若△BEM和△DFM外接圆的半径分别是R1、R2,求证:R1•R2为定值,并求这个定值.25.如图,四边形ABCD为菱形,已知A(0,6),D(﹣8,0).(1)求点C的坐标;(2)设菱形ABCD对角线AC、BD相交于点E,求经过点E的反比例函数解析式.26.如图,菱形ABCD中,点P是AB的中点,延长DP交CB的延长线于E点.求证:BE=CD.27.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,BE=DF.(1)求证:AE=AF;(2)若AE垂直平分BC,AF垂直平分CD,求证:△AEF为等边三角形.28.如图,在菱形ABCD中,P是AB上的一个动点(不与A,B重合),连接DP交对角线AC于E,连接EB.求证:∠APD=∠EBC.29.如图,在菱形ABCD中,E是BC延长线上一点,连接AE,使得∠E=∠B,过D作DH⊥AE于H.(1)若AB=10,DH=6,求HE的长;(2)求证:AH=CE+EH.30.如图,已知点O在菱形ABCD内,过点O分别作OE⊥AB于E,OF⊥AD于F,且OE=OF.(1)求证:OB=OD;(2)把菱形换成矩形、平行四边形、等腰三角形,上述结论仍成立吗?(写出结论,不证明)参考答案:1.(1)设AB=x,则BC=x,BH=BC﹣CH=x﹣4,在Rt△ABH中,AH2+BH2=AB2,∴82+(x﹣4)2=x2,解得x=10,∴菱形周长为40.(2)∵AH=8,CH=4,∴AC==4,∴CO=AO=AC=2,∵BC=10,CO=2,∴BO==4∵∠BHE=∠BOC=90°,∠EBH=∠CBO,∴△BHE∽△BOC,∴,∴,∴EH=3,∴AE=AH﹣EH=8﹣3=5,∴OE==2.(1)菱形的对角线为AC=6cm,BD=8cm,则菱形的面积为AC•BD=×6×8=24cm2;(2)菱形对角线互相垂直平分,∴BO=OD=4cm,AO=OC=3cm,∴AB==5cm,故菱形的周长为20cm,答:菱形的周长为20cm,面积为24cm2.3.∵在菱形ABCD中,AC=12cm,BD=16cm,∴S菱形ABCD =×AC×BD=×12×16=96(cm2).∵四边形ABCD是菱形,∴AC⊥BD,OA=AC=6cm,OB=BD=8cm,∴AB==10cm,∴菱形ABCD的周长为:4×10=40(cm).故这个菱形的周长为40cm,面积为96cm24.(1)∵四边形ABCD是菱形,∠BAD=120°,∴AB=BC,∠BAC=∠BAD=60°,∴△ABC是等边三角形;(2)∵四边形ABCD是菱形,∴AC⊥BD,∵∠BAC=60°,AB=2cm,∴∠ABO=30°,∴OA AB=1(cm),∴OD==(cm),∴AC=2OA=2cm,BD=2OD=2cm.5.(1)∵四边形ABCD是菱形,AB=5,∴菱形ABCD的周长等于5×4=20;(2)∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,在Rt△AOB中,∠AOB=90°,根据勾股定理,得:OB=,==4,∴AC=2OA=6,BD=2OB=8,∴S菱形ABCD=×AC×BD=×6×8=246.菱形周长为200cm,则AB=50cm,∵AC=60cm,∴AO=30cm,菱形对角线互相垂直,∴△AOB为直角三角形,在Rt△AOB中,BO==40cm,∴BD=2BO=80cm,∴菱形ABCD的面积为S=×60cm×80cm=2400cm2,答:菱形ABCD的面积为2400cm2.7.由菱形对角线性质知,AO=AC=3,BO=BD=4,且AO⊥BO,∴AB=5,∴周长L=4AB=20;∵菱形对角线相互垂直,∴菱形面积是S=AC×BD=24.综上可得菱形的周长为20、面积为24.8.四边形AODE是矩形.∵DE∥AC,AE∥BD,∴四边形AODE是平行四边形,∵四边形ABCD是菱形,∴AC⊥BD∴∠AOD=90°,∴四边形AODE是矩形9.(1)四边形OCED是矩形.理由如下:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,∵四边形ABCD是菱形,∴∠COD=90°,∴四边形OCED是矩形;(2)在菱形ABCD中,∵AC=6,BD=8,∴OC=AC=×6=3,OD=BD=×8=4,∴CD===5,在矩形OCED中,OE=CD=510.1)证明:连接BD,∵四边形ABCD是菱形,∴AC⊥BD,∵EM⊥AC,∴EM∥BD,∵E为AB的中点,∴M为AD的中点,∴AM=DM;(2)解:∵EB∥FD,EM∥BD,∴四边形FDBE是平行四边形,∴FD=BD,∵DF=2,∴BE=2,∴AB=2BE=2×2=4,∴菱形ABCD的周长=4AB=4×4=16;(3)设ME与AC的交点为G,相似三角形有:△AGE∽△AGM,△AGE∽△CGF,△AGM∽△CGF,△AEM∽△DFM,△ABC∽△ADC共5对.11.(1)∵菱形ABCD中,AB=BC,AD=CD,∠B=∠D=60°,∴△ABC和△ACD都是等边三角形.(2)∵∠B=∠ACD=60°,AB=AC,∴△ABC是等边三角形,∴∠BAC=∠EAF=60°,∴∠BAE=∠CAF,∴△ABE≌△ACF,∴AE=AF,又∠EAF=60°,∴△AEF是等边三角形;(3)∵EC+CF=BE+EC=BC=2,△AEF是等边三角形,∴EF=AE,∴△CEF的周长=2+AE,由“垂线段最短”,当AE⊥BC时,AE最短,AE=,∴△CEF的周长=2+12.(1)∵DE∥AC,CE∥BD∴四边形OCED为平行四边形,∵AC,BD为菱形的对角线,∴AC⊥BD,即∠COD=90°,∴平行四边形OCED为矩形.(2)菱形ABCD的周长为20,则菱形的边长为5,即=5,矩形OCED的周长为14,则OC+OD=7,解题OC=3,OD=4,∴AC=6,BD=8,∴菱形的面积为×6×8=24.答:菱形ABCD的面积为2413.由菱形ABCD,得∠BAD=∠BCD=130°,∠BAE=25°,∴∠EAF=105°,又∵AF=CE,AD∥BC,∴四边形AECF是平行四边形,则∠AFC=180°﹣∠EAF=180°﹣105°=75°.14.(1)∵∠ABE=∠CDG,∠AEB=∠CGD,AE=CG,∴△ABE≌△CDG,∴BE=DG,(2)四边形ABFG是菱形,则BF=AB,∵AB:BC=2:3∴FC=AB,∵AE是BC沿BC方向平移,使点E与点C重合,得△GFC.∴BE=FC,∴AB=2BE,∴直角△ABE中,∠BAE=30°,∴∠ABE=60°15.∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∵AE⊥BC,BE=CE,∴AB=AC,∴AB=AC=BC,即△ABC是等边三角形,∴∠B=60°,又∵AD∥BC,∴∠BAD=180°﹣∠B=120°16.(1)如图,过E作AD,BC的垂线交AD和CB的延长线于H,G.∵AD∥CB,∴△BGE∽△AHE,∵AB=AD=6,∴AE=BF=5,CF﹣BE=1,令BG=x,GE=y,则EH=5y,AH=5x,在△FGE 中,,在△DEH 中,,根据EF=ED,BE=1,易得EF2=ED2,即有,解得,,∴tan∠A=,∴∠A=60°;(2)由以上求得知,EH=AEsin60°=,,故.17.连接PD,DQ,由已知∠PAC=120°,∠QCA=120°,∴△PAC∽△AMC,△AMC∽△ACQ.∴,.∴AC2=PA•QC,又AC=AD=DC.∴,又∠PAD=∠DCQ=60°,∴△PAD∽△DCQ,∴∠APD=∠CDQ.∴∠PDA+∠ADC+∠CDQ=180°,∴P,D,Q三点共线.18.∵菱形ABCD的周长为20,∴菱形的边长AB=5,由直角三角形的三边关系可得:AO2+BO2=25,又有根与系数的关系可得:AO+BO=2m﹣1,AO•BO=4(m﹣1),∴AO2+BO2=(AO+BO)2﹣2AO•BO=(2m﹣1)2﹣2×4(m﹣1)=25,整理得:4m2﹣12m+9=25,解得:m=4或﹣1(舍去).故m=419.∵四边形ABCD为菱形,∴AD=AB=CD=CB,∠B=∠D.又∵CE=CF,∴CD﹣CE=CB﹣CF,即DE=BF.∴△ADE≌△ABF.∴AE=AF20.菱形ABCD的面积S=×16×12=96,∵AC⊥BD,∴AB=10,∴CD=AB=10,∴×CD×BE=48,∴BE=cm,所以菱形ABCD的面积为96cm2,BE 的长为cm21.(1)DE=BF.理由如下:如图,设AB、EF相交于G,连接BD,在菱形ABCD中,BD⊥AC,∵EF⊥AC,∴EG∥BD,∵E是AD中点,∴EG是△ABD的中位线,∴AG=BG,又∵AD∥BC,∴∠AEG=∠BFG,在△AEG和△BFG 中,,∴△AEG≌△BFG(AAS),∴AE=BF,∵E是AD中点,∴AE=DE,∴DE=BF;(2)四边形AFBE是平行四边形.理由如下:∵四边形ABCD是菱形,∴AD∥BC,∴AE∥BF,又∵AE=BF,∴四边形AFBE是平行四边形22.(1)∵四边形ABCD是菱形,∴AB=CB=CD=AD,∠B=∠D,∵BE=DF∴△ABE≌△ADF(SAS),∴AE=AF;(2)连接AC,∵AE垂直平分BC,AF垂直平分CD.∴AB=AC=AD,∴AB=AD=BC=CD=AC,∴∠B=60°,∴∠BCD=120°,∴∠EAF=60°,∴△AEF为等边三角形.23.(1)证明:∵∠B+∠C=180°,∠AFE+∠AFD=180°,∠AFE=∠B,∴∠C=∠AFD.∵AD∥BC,∴∠ADF=∠DEC.∵AD=DC,∴△ADF∽△DEC.(2)解:∵AB=4,E为BC的中点,∴BE=2,AE=,DE=.∵△ADF∽△DEC,∴.∴AF=.24.△BEC∽△DCF,∴.∴△BED∽△DBF.∴∠BED=∠DBM.∴∠BME=∠BDM+∠DBM=∠BDM+∠BED=∠ABD= 60°.∴由正弦定理得:2R1=,2R2=.∴R1•R2=•==.25.(1)∵A(0,6),D(﹣8,0),∴OA=6,OD=8,∴由勾股定理可得AD=10,∵四边形ABCD为菱形∴CD=AD=10,∴OC=2,∴C(2,0),(2)∵A(0,6)C(2,0),∴E(1,3),设经过点E 的反比例函数解析式为,将E(1,3)代入求得k=3∴反比例函数解析式为:26.∵点P是AB的中点,∴AP=BP,∵四边形ABCD是菱形,∴AD=DC,AD∥BC,∴∠A=∠PBE,∵在△ADP和△BEP中,,∴△ADP≌△BEP(ASA),∴BE=AD,∵AD=CD,∴BE=CD27.(1)∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,又∵BE=DF,∴△ABE≌△ADF,∴AE=AF;(2)连接AC,∵AE垂直平分BC,AF垂直平分CD,∴AB=AC=AD.∵AB=BC=CD=DA,∴△ABC和△ACD都是等边三角形.∴∠CAE=∠BAE=30°,∠CAF=∠DAF=30°.∴∠EAF=∠CAE+∠CAF=60°又∵AE=AF,∴△AEF是等边三角形.28.∵四边形ABCD是菱形,∴BC=CD,AC平分∠BCD,在△BCE和△DCE 中,,∴△BCE≌△DCE(SAS),∴∠EBC=∠EDC,又AB∥DC,∴∠APD=∠EDC,∴∠EBC=∠APD29.(1)∵四边形ABCD是菱形,∴AD=AB=10,∵DH⊥AE,∴∠AHD=90°,在Rt△ADH中,AH===8,∵∠E=∠B,∴AE=AB=10,∴HE=AE﹣AH=10﹣8=2;证明:(2)过点D作DF⊥BC的延长线于点F,连接DE,∵四边形ABCD是菱形,∴AB∥CD,AD∥BC,AD=CD,∴∠1=∠B,∠2=∠3,∵∠B=∠2,∴∠1=∠3,∵DH⊥AE,DF⊥CF,∴∠4=∠F,在△ADH和△CDF中,,∴△ADH≌△CDF(AAS),∴AH=CF,DH=DF,∴在Rt△DEH和Rt△DEF中,,∴Rt△DEH≌Rt△DEF(HL),∴EH=EF,∵CF=CE+EF,∴AH=CE+EH30.(1)证明:连接OA、AC、BD,∵OE⊥AB,OF⊥AD,且OE=OF,∴∠BAO=∠DAO,∵菱形ABCD,∴AC⊥BD,MB=MD,∠BAC=∠DAC,∴O在AC上,∴OB=OD.(2)解:矩形和平行四边形时,结论不成立,等腰三角形时,结论成立,因为:矩形和平行四边形的对角线不一定平分对角,而等腰三角形的三线合一性质,能得出结论成立菱形的性质--11。
菱形性质习题精选(含答案)

菱形性质习题精选(含答案)菱形性质习题精选一.填空题(共26小题)1.(2015?模拟)如图,在菱形ABCD中,点E是AB上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO=度.2.(2015?模拟)如图,在四边形ABCD中,AB=6,∠ABC=90°,E在CD上,连接AE,BE,∠DAE=75°,若四边形ABED 是菱形,则EC的长度为.3.(2015?模拟)如图,菱形ABCD的对角线AC、BD交于点O,其中AC=8,BD=6,以OC、OB为边作矩形OBEC,矩形OBEC 的对角线OE、BC交于点F,再以CF、FE为边作第一个菱形CFEG,菱形CFEG的对角线FG、CE交于点H,如此继续,得到第n个菱形的周长等于.4.(2015?州市校级模拟)己知菱形相邻两角的度数比为1:5,且它的面积为8,则这个菱形的周长为.5.(2015?模拟)如图,在菱形ABCD中,∠A=45°,DE⊥AB,垂足为E,若CD=4cm,则菱形ABCD的面积是.6.(2015?模拟)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为40,则OH的长等于.7.(2014?)菱形ABCD中,若对角线长AC=8cm,BD=6cm,则边长AB=cm.8.(2014?)菱形的周长为20cm,两个相邻的角的度数之比为1:2,则较长的对角线长度是cm.9.(2014?)如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO=.10.(2014?宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y 轴上,则点C的坐标是.11.(2014?眉山)如图,菱形ABCD中,E、F分别是BC、CD 的中点,过点E作EG⊥AD 于G,连接GF.若∠A=80°,则∠DGF的度数为.12.(2014春?期末)如图在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的大小为.13.(2014?模拟)如图,在菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为.14.(2014?江都市二模)已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为cm.15.(2014?简阳市模拟)如图,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,记=k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k=.16.(2014?淮区一模)如图,在菱形ABCD中,∠ABC=60°,BC=1cm,以DC为边在菱形的外部作正三角形CDE,连接AE,则AE=cm.17.(2014?惠安县二模)如图,菱形ABCD的边长是2cm,∠A=60°,点E、F分别是边AB、CD上的动点,则线段EF的最小值为cm.18.(2013秋?海陵区期末)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为4cm,∠A=120°,则EF=cm.19.(2014春?仙游县校级期末)如图,以菱形AOBC的顶点O 为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB=,点C的坐标为(4,0),则点A的坐标为.20.(2014春?期末)如图,在菱形ABCD中,AB=13cm,BC 边上的高AH=5cm,那么对角线AC的长为cm.21.(2014春?泰兴市校级期末)如图,菱形ABCD的周长为16cm,BC的垂直平分线EF 经过点A,则对角线BD长为cm.22.(2014春?建湖县期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形,若AC=8,AB=5,则ED的长等于.23.(2014春?玄武区期末)如图,在菱形ABCD中,BE⊥AD,垂足为E,且E为AD为中点.则∠ADC=°.24.(2014春?定县期末)如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P 是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是.25.(2014春?顺义区期末)如图,菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC=度.26.(2014秋?武进区期中)如图,依次连结第一个矩形各边的中点得到第一个菱形,再依次连结所得菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为2,则第2013个菱形的面积为.二.解答题27.(2014?县模拟)如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,求证:CE=CF.28.(2014?江都市模拟)如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.(1)求证:∠1=∠2;(2)若DF⊥BC,求证:点F是边BC的中点.29.(2014春?期末)如图,在Rt△ABC中,∠B=90°,BC=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.30.(2014春?高淳县校级期末)如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.31.(2013秋?东海县月考)如图,在菱形ABCD中,点E是AD 边的中点,点M是AB边上的一个动点(不与点A重合),延长ME 交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)若∠DAB=60°,当点M位于何处时,四边形AMDN是矩形?并说明理由.(请在备用图中画出符合题意的图形)32.(2012秋?鼓楼区校级期末)如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B 出发向点C运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.参考答案1.50 2.3 3. 4.16 5.8cm 2 6.5 7.5 8.5 9.35° 10.(5,4) 11.50° 12.20°13.3 14.4.8 15. 16.17. 18.2 19.(2,1)20. 21.4 22.4-3 23.120 24.2 25.105 26.27、证明:四边形ABCD 是菱形CE ⊥AE,CF ⊥AF∠DAB=∠CBB,∠DAB=∠FDC,∴∠CBE=∠FDC又 BC=DC,∴Rt △BEC ≌Rt △DFC,∴CE=CF.28、证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,∴∠1=∠ACD ,∵MC=MD ,∴∠ACD=∠2,∴∠1=∠2;(2)连接BD ,∵四边形ABCD 是菱形,∴∠ACB=∠ACD ,BC=CD ,∵∠ACD=∠2,∴∠ACB=∠ACD=∠2,∵DF ⊥BC ,∴3∠2=90°,∴∠2=30°,∴∠BCD=∠ACB+∠ACD=60°,∴△BCD 是等边三角形,∴BF=CF ,即点F 是边BC 的中点.29、(1)在△DFC 中,∠DFC =90°,∠C =30°,DC =2t ,∴DF =t .又∵AE=t ,∴AE=DF(2)能.理由如下:∵AB ⊥BC ,DF ⊥BC ,∴AE ∥DF .又AE =DF ,∴四边形AEFD 为平行四边形.∵AB =21AC BC=35 222AC BC AB =+∴()2223521AC AC =+??? ?? ∴AC=1010 2.AD AC DC t ∴=-=-若使AEFD 为菱形,则需10.102,.3AE AD t t t ==-=即即当103t =时,四边形AEFD 为菱形30、(1)△ABP ≌△ACQ ,△APC ≌△AQD ;(2)∵△ACP ≌△ADQ ,∴S △ACP =S △ADQ ,即S 四边形APCQ =S △ACD =3221??;(3为菱形的高) (3)∵△PAQ 是等边三角形,点P 是BC 的中点时,AP 垂直于BC ,AP 最小,∴当AP ⊥BC 时,三角形APQ 的面积最小,故在四边形APCQ 的面积一定,△APQ 面积最小时,△PCQ 的面积最大. 此时BP=1,31、证明:∵四边形ABCD 是菱形∴∠DNM=∠AMN又∵DE=AE ,∠NDE=∠MAE∴△NDE=△MAE∴ND=AM∴ND ∥AM∴四边形ANDM 是平行四边形(2)当点M 是AB 的中点时,四边形AMDN 是矩形证明:如图所示∵四边形AMDN 是矩形,∠DAB=60o∴∠ADM=30o∴AM=AD 21 ∵AD=AB ∴AM=AB 21 即M 是AB 的中点32、解:(1)经过x 秒后,四边形AQCP 是菱形∴DP=X cm AP=CP=AD-DP=(8-X)cm∵DP 2+CD 2=PC 2∴16+X 2=(8-X) 2 解得x=3即经过3秒后四边形是菱形(2)由(1)得菱形的边长为5∴菱形AQCP的周长=5×4=20(㎝)菱形AQCP的面积=5×4=20(㎝2)。
22.3菱形的性质常考题(含详细的解析)

22.3菱形的性质常考题一、选择题(共18小题)1、(2009•长春)菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=,则点B的坐标为()A、(,1)B、(1,)C、(+1,1)D、(1,+1)2、(2010•盐城)如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为()A、5B、10C、6D、83、(2010•南通)如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于()A、20B、15C、10D、54、(2010•北京)菱形的两条对角线的长分别是6和8,则这个菱形的周长是()A、24B、20C、10D、55、(2009•河池)已知菱形的边长和一条对角线的长均为2cm,则菱形的面积为()A、3cm2B、4cm2C、cm2D、2cm26、(2009•杭州)如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=()A、35°B、45°C、50°D、55°7、(2008•台州)如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为()A、16aB、12aC、8aD、4a8、(2008•江汉区)如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是()A、DA=DEB、BD=CEC、∠EAC=90°D、∠ABC=2∠E9、(2007•嘉兴)如图,在菱形ABCD中,不一定成立的是()A、四边形ABCD是平行四边形B、AC⊥BDC、△ABD是等边三角形D、∠CAB=∠CAD10、(2005•扬州)如图是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉A、B之间的距离为20cm,则∠1等于()A、90°B、60°C、45°D、30°11、(2005•济宁)已知菱形的边长为6cm,一个内角为60°,则菱形较短的对角线长是()A、6cmB、cmC、3cmD、cm12、(2004•重庆)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为()A、80°B、70°C、65°D、60°13、在菱形ABCD中,AE⊥BC,AF⊥CD,且E,F分别为BC,CD的中点,那么∠EAF的度数为()A、75°B、60°C、45°D、30°14、菱形的周长等于高的8倍,则此菱形的较大内角是()A、60°B、90°C、120°D、150°15、在菱形ABCD中,AC与BD相交于点O,则下列说法不正确的是()A、AO⊥BOB、∠ABD=∠CBDC、AO=BOD、AD=CD16、菱形的周长为20cm,两邻角的比为1:2,则较长的对角线长为()A、4.5cmB、4cmC、5cmD、4cm17、已知菱形的两条对角线长分别为4cm和10cm,则菱形的边长为()A、116cmB、29cmC、cmD、cm18、菱形的周长为20cm,两邻角的比为1:3,则菱形的面积为()A、25cm2B、16cm2C、cm2D、cm2二、填空题(共12小题)19、(2006•泉州)菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为_________.20、(2008•陕西)如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为_________.21、(2009•临沂)如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB=_________度.22、(2008•肇庆)边长为5cm的菱形,一条对角线长是6cm,则另一条对角线的长是_________cm.23、(2003•盐城)已知菱形ABCD的对角线AC=6cm,BD=8cm,则菱形的边长是_________cm.24、如图,在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中,点P是其中的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长_________.25、(2011•长沙)已知菱形的两条对角线长分别是6cm和8cm,则周长是_________cm.26、(2009•江西)如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1= _________度.27、(2009•本溪)如图所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为24,则OH的长等于_________.28、(2008•镇江)如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2008厘米后停下,则这只蚂蚁停在_________点.29、(2008•温州)如图,菱形ABCD中,∠A=60°,对角线BD=8,则菱形ABCD的周长等于_________.30、(2008•恩施州)已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为_________cm2.答案与评分标准一、选择题(共18小题)1、(2009•长春)菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=,则点B的坐标为()A、(,1)B、(1,)C、(+1,1)D、(1,+1)考点:坐标与图形性质;菱形的性质。
菱形的性质与判定练习

菱形的性质与判定练习1、一个菱形的周长为52cm,一条对角线长为10cm,则其面积为 cm2.2、已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为______________cm2.3、如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO= ,菱形ABCD的面积S= .4、如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为_______.5、如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB= .6、如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长.7、已知菱形的周长为 40 cm ,两条对角线之比为3:4,则菱形的面积为_________.8、如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为24,则OH的长等于 .9、如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是____________(写出一个即可).10、如图,菱形ABCD中,对角线AC交BD于O, E是CD的中点,且OE=2,则菱形ABCD的周长等于.11、如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6 cm,则AB=________cm.12、两对角线分别是6cm和8cm的菱形面积是 cm2,周长是 cm.13、如图,在RtΔABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 时,平行四边形CDEB为菱形。
14、如图,在菱形ABCD中,∠B=60°,对角线BD=22,则点D到直线AB的距离DE= ,点D到直线BC的距离等于.15、如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为.16、如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加条件,就能保证四边形EFGH是菱形.17、如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD.DA的中点,则四边形EFGH的周长等于 cm.18、如图,在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于.19、如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE ⊥BC,垂足为点E,则OE= .20、.如图,菱形ABCD中,E、F分别是BC、CD的中点,过点E作EG⊥AD 于G,连接GF.若∠A=80°,则∠DGF的度数为.21、如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=120°,则∠AOE= .22、如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D 的坐标为(0,2),则点C的坐标为.23、如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE= 度.24、在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则该菱形的面积为.25、如图,已知菱形ABCD的对角线AC、BD的长分别为10cm,24cm,AE⊥BC于点E,则AE的长是 cm.26、将矩形纸片ABCD,按如图所示的方式折叠,点A、点C恰好落在对角线BD上,得到菱形BEDF.若BC=6,则AB的长为.27、如图,在菱形ABCD中,AB=4,线段AD的垂直平分线交AC于点N,△CND的周长是10,则AC的长为.28、如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为.29、如图,在菱形ABCD中,∠BAD=80º,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于.30、如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B 为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2 cm,四边形OACB的面积为4 cm2.则OC的长为________cm.31、把两张宽为2 cm的矩形纸片重叠在一起,然后将其中的一张任意旋转一个角度,则重叠部分(图中的阴影部分)的四边形ABCD的形状为________,其面积的最小值为________cm2.32、如图,将两张长为9,宽为3的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的面积有最小值9,那么菱形面积的最大值是.33、如图,菱形ABCD周长为16,∠ADC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是.34、如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=60°,连接EF,则△AEF的面积最小值是.35、已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .36、如图,菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.37、如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是_________.38、如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y 轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3……,连续翻转2017次,则B2017的坐标为__ ______.39、如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…依此类推,这样做的第n个菱形AB n C n D n的边AD n的长是.40、已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第4个图形中直角三角形的个数有_____________个;第2014个图形中直角三角形的个数有_____________个.参考答案1、答案为:120.2、答案为:243、答案为:1:2,.4、答案为:96.°.6、答案为:16.7、答案为:96 cm 28、答案为:3;9、答案为:AB=AD(答案不唯一)10、答案为:1611、答案为:1212、答案为:24,20.13、答案为:1.4;14、答案为:11,11.15、答案为:4.8;16、答案为:AC=BD.17、答案为:16.18、答案为:3.5;19、答案为:2.4.20、答案为:50°.21、答案为:60°.22、答案为:(4,4);23、答案为:45;24、答案为:12.25、答案为:.26、答案为:2.27、答案为:6.28、答案为:2.5;29、答案为:60度30、答案为:431、答案为:菱形,432、答案为:15.33、答案为:2.34、答案为:.35、答案为:5.36、答案为:2.37、答案为:38、答案为:(1345.5,)39、答案为:()n﹣1.40、答案为:8, 4028。
新人教版菱形的性质与判定经典例题练习

一.菱形的性质:例1.如图,在菱形ABCD 中,P 是AB 上的一个动点(不与A 、B 重合),连接DP 交对角线AC 于E ,连接EB 。
(1)求证:APD EBC ∠=∠;(2)若60DAB ∠=︒,试问:P 点运动到什么位置时,ADP V 的面积等于菱形ABCD 面积的14?为什么?1.菱形具有而一般平行四边形不具有的性质是( )A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等2.菱形ABCD 中,AC 、BD 相交于O 点,若∠OBC =21∠BAC ,则菱形的四个内角的度数为_______. 3、.若菱形的两条对角线的比为3∶4,且周长为20 cm,则它的一组对边的距离等于_____ cm,它的面积等于______ cm 2.4.菱形的周长为100 cm ,一条对角线长为14 cm ,它的面积是( )A.168 cm 2 B.336 cm 2 C.672 cm 2 D.84 cm 25.菱形的周长为16,两邻角度数的比为1∶2,此菱形的面积为( )A.43 B.83 C.103 D.1236.菱形的面积为83平方厘米,两条对角线的比为1∶3,那么菱形的边长为_______.7.在菱形ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,且E 、F 分别为BC 、CD 的中点,则∠EAF 等于( )A.75° B.60°C.45°D.30°7题 9题 10题8.菱形的边长是2 cm ,一条对角线的长是23 cm,则另一条对角线的长是( )A4 cm B 3 cm C2 cm D23 cm9.如图,将两张长为8,宽为2的矩形纸片交叉,使重叠部分是一个菱形,则菱形周长最小值是 ,最大值是 。
10.如图,菱形ABCD 的对角线AC 、BD 交于点O ,且AC =16 cm ,BD =12 cm ,求菱形ABCD 的高DH .11..如图,在菱形ABCD 中,AB=4a ,E 在BC 上,BE=2a ,120BAD ∠=︒,P 点在BD 上,求PE+PC 的最小值。
菱形的性质与判定经典例题练习

1、叫菱形2、菱形的性质1)边2)角3)对角线4)对称性5)菱形的面积计算方法:练一练:、1菱形具有而矩形不一定具有的性质是().A.对边相等 B.对角相等 C.对角线互相垂直 D.对角线相等2、能够找到一点使该点到各边距离相等的图形为().A.平行四边形 B.菱形 C.矩形 D.不存在3、如图所示,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于()A.80°B.70°C.65°D.60°3.如在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=AB2其中正确的结论有()A.1个B.2个C.3个D.4个4、菱形的周长为12 cm,相邻两角之比为5∶1,那么菱形对边间的距离是()A.6 cmB.1.5 cmC.3 cmD.0.75 cm5.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于()A.75° B.60° C.45° D.30°6、菱形的边长是2 cm,一条对角线的长是23 cm,则另一条对角线的长是()A.4 cmB.3 cmC.2 cmD.23 cm例1、如图,菱形ABCD的对角线AC、BD交于点O,且AC=16 cm,BD=12 cm,求菱形ABCD的高DH.2、如图,菱形ABCD的对角线AC、BD交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离为_______.3、如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.12. 如图,菱形OABC 在直角坐标系中,点A 的坐标为(5,0),对角线OB =45,反比 例函数xky(k ≠0,x >0)经过点C .则k 的值等于( ) A .12 B .8 C .15 D .94变式:菱形ABCD 的周长为20 cm ,两条对角线的比为3∶4,求菱形的面积.5如图,在菱形ABCD 中,∠BAD=60°,BD=4,则菱形ABCD 的周长是_________.6、如图,菱形ABCD 中,E 是AB 中点,DE ⊥AB ,AB=4.求(1)∠ABC 的度数; (2)AC 的长; (3)菱形ABCD 的面积.例7:如图,在菱形ABCD 中,AB=4,E 在BC 上,BE=2,角ABC=120度,P 点在AC 上,求PE+PC 的最小值。
菱形性质经典练习题(详细答案)

菱形性质经典练习题一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4)D.M(4,0),N(7,4)2.(2010•肇庆)菱形的周长为4,一个内角为60°,则较短的对角线长为()A.2 B.C.1 D.3.(2010•襄阳)菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A.3:1 B.4:1 C.5:1 D.6:14.(2010•宜昌)如图,菱形ABCD中,AB=15,∠ADC=120°,则B、D两点之间的距离为()A.15 B.C.7.5 D.二.填空题(共15小题)5.(2011•铜仁地区)已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_________cm2.6.(2011•綦江县)如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_________.7.(2011•南京)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.6题图7题图8题图9题图8.(2011•鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_________.9.(2010•嘉兴)如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_________度.10.(2009•江西)如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1= _________度.10题图12题13题图14题图11.(2009•朝阳)已知菱形的一个内角为60°,一条对角线的长为,则另一条对角线的长为_________.12.(2009•安顺)如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按A﹣>B﹣>C﹣>D﹣>E﹣>F﹣>C﹣>G﹣>A的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在_________点.13.(2008•长沙)如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则P点到AB的距离是_________cm.14.(2006•云南)已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________.15.(2005•黄石)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为_________cm2.16.(2005•新疆)已知菱形的周长是52cm,一条对角线长是24cm,则它的面积是_________cm2.17.(2004•贵阳)如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_________.17题图18题图19题图18.(2003•温州)如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________.19.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_________度.三.解答题(共7小题)20.(2011•南昌)如图,四边形ABCD为菱形,已知A(0,4),B(﹣3,0).(1)求点D的坐标;(2)求经过点C的反比例函数解析式.21.(2011•广安)如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线于点E.求证:DE=BE.22.(2010•益阳)如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23.(2010•宁洱县)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.24.(2009•贵阳)如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合),连接DP交对角线AC于E 连接BE.(1)证明:∠APD=∠CBE;(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?25.(2006•大连)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连接_________;(2)猜想:_________=_________;(3)证明:(说明:写出证明过程的重要依据)26.如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C 运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.答案与评分标准一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4) D.M(4,0),N(7,4)考点:菱形的性质;坐标与图形性质。
菱形性质测试题及答案

菱形性质测试题及答案
一、选择题
1. 下列哪个选项不是菱形的性质?
A. 对角线互相垂直
B. 四边相等
C. 对角线平分每一组对角
D. 内角和为180°
2. 菱形的对角线将菱形分成几个全等的三角形?
A. 1
B. 2
C. 3
D. 4
3. 如果菱形的一条对角线长为10,另一条对角线长为8,那么菱形的边长是多少?
A. 4√2
B. 6√2
C. 8√2
D. 10√2
二、填空题
4. 菱形的对角线互相________。
5. 菱形的面积可以通过________来计算。
三、简答题
6. 请简述菱形的判定定理。
四、计算题
7. 已知菱形ABCD的对角线AC=8cm,BD=6cm,求菱形ABCD的边长。
五、证明题
8. 已知菱形ABCD中,E、F分别是边AB和CD上的点,且AE=CF,证明:△AED≅△CFB。
答案:
一、选择题
1. D
2. D
3. A
二、填空题
4. 垂直且平分
5. 对角线乘积的一半
三、简答题
6. 菱形的判定定理包括:四边相等的四边形是菱形;对角线互相垂直且平分的四边形是菱形。
四、计算题
7. 根据菱形的性质,对角线互相平分,所以AO=CO=4cm,BO=DO=3cm。
根据勾股定理,边长AB=√(AO²+BO²)=√(4²+3²)=5cm。
五、证明题
8. 证明:由于AE=CF,且AD=CD(菱形的四边相等),根据SAS(边角边)相似定理,我们可以得出△AED≅△CFB。
菱形的性质和判定练习题

菱形检测题二1.菱形的两条对角线长分别为16cm ,12cm ,那么这个菱形的高是_______. 2.已知菱形两邻角的比是1:2,周长是40cm,则较短对角线长是________. 3.菱形的面积为50cm2,一个内角为30°,则其边长为______.4.菱形一边与两条对角线所构成两角之比为2:7,则它的各角为______. 5。
如图,在四边形ABCD 中,AB=CD ,AD=BC ,添加一个条件使四边形ABCD 是菱形,那么所添加的条件可以是__________(写出一个即可). 6、已知在菱形ABCD 中,下列说法错误的是( ).A. 两组对边分别平行B. 菱形对角线互相平分C. 菱形的对边相等 D 。
菱形的对角线相等 7、菱形具有而矩形不一定具有的性质是( ).A .对边相等B .对角相等C .对角线互相垂直D .对角线相等 8、能够找到一点使该点到各边距离相等的图形为( ). A .平行四边形 B .菱形 C .矩形 D .不存在 9、下列说法不正确的是( ).A .菱形的对角线互相垂直B .菱形的对角线平分各内角C .菱形的对角线相等D .菱形的对角线交点到各边等距离 10、菱形的两条对角线分别是12cm 、16cm,则菱形的周长是( ). A .24cm B .32cm C .40 cm D .60cm11.菱形ABCD ,若∠A :∠B=2:1,∠CAD 的平分线AE 和边CD 之间的关系是( ). A .相等 B .互相垂直且不平分 C .互相平分且不垂直 D .垂直且平分12.在菱形ABCD 中,AE ⊥BC 于E ,菱形ABCD 面积等于24cm2,AE=6cm ,则AB 长为( ). A .12cm B .8cm C .4cm D .2cm13.如图,在菱形ABCD 中,E 是AB 的中点,作EF ∥BC ,交AC•于点F,如果EF=4,那么CD 的长为( ). A .2 B .4 C .6 D .814.如图,已知菱形ABCD 的边长为2,∠DAB =60°,则对角线BD 的长是( ) A 。
完整版)菱形的性质和判定练习题

完整版)菱形的性质和判定练习题1.这个菱形的高为9cm。
2.较短对角线长为10cm。
3.边长为5cm。
4.各角分别为72°和108°。
5.添加的条件可以是AB=AD或BC=CD。
6.错误的说法是A,即两组对边分别平行。
7.对角线互相垂直。
8.菱形。
9.不正确的说法是B,即菱形的对角线平分各内角。
10.周长为40cm。
11.互相垂直且不平分。
12.AB长为8cm。
13.CD的长为4.14.对角线BD的长为2.15.边长为5.16.OH的长为7.17.若菱形的周长为20cm,则它的边长为4cm。
18.在菱形ABCD中,由对角线AC和BD相交于点O可知,菱形的对角线相等,即AC=BD。
又已知BD=6,则AC=6.设菱形ABCD的边长为a,则2a=20,即a=10.由菱形对角线的长度公式可得。
$AC=\sqrt{a^2+a^2}=a\sqrt{2}$,代入AC=6可得a=6/$\sqrt{2}$,因此菱形ABCD的面积为36.19.在菱形ABCD中,由$\angle ADC=120^\circ$可知,$\angle ADB=60^\circ$。
设$\angle ABD=\theta$,则$\angle ADB=120^\circ-\theta$。
由余弦定理可得,$BD^2=15^2+15^2-2\times15\times15\times\cos\theta$,化简可得$\cos\theta=1/2$,因此$\sin\theta=\sqrt{3}/2$。
由正弦定理可得,$BD/\sin\theta=2a$,其中a为菱形的边长。
又已知BD=15,代入可得$a=15\sqrt{3}/4$。
设B、D两点之间的距离为h,则$h=\sqrt{(15\sqrt{3}/4)^2-(15/2)^2}=15\sqrt{3}/4$,因此选项D 正确。
20.设菱形的较长对角线为2x,较短对角线为x,则菱形的面积为$x^2$。
(完整版)菱形性质经典练习题(详细答案)

菱形性质经典练习题一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是( )A.M(5,0),N(8,4)B.M(4,0),N(8,4)C.M(5,0),N(7,4)D.M(4,0),N(7,4)2.(2010•肇庆)菱形的周长为4,一个内角为60°,则较短的对角线长为()A.2 B.C.1 D.3.(2010•襄阳)菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )A.3:1 B.4:1 C.5:1 D.6:14.(2010•宜昌)如图,菱形ABCD中,AB=15,∠ADC=120°,则B、D两点之间的距离为()A.15 B.C.7。
5 D.二.填空题(共15小题)5.(2011•铜仁地区)已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_________ cm2.6.(2011•綦江县)如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH= _________ .7.(2011•南京)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.6题图 7题图 8题图 9题图8.(2011•鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_________ .9.(2010•嘉兴)如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_________ 度.10.(2009•江西)如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1=_________ 度.10题图12题 13题图 14题图11.(2009•朝阳)已知菱形的一个内角为60°,一条对角线的长为,则另一条对角线的长为_________ .12.(2009•安顺)如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按A﹣>B﹣>C﹣>D ﹣>E﹣>F﹣>C﹣>G﹣>A的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在_________ 点.13.(2008•长沙)如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则P点到AB的距离是_________ cm.14.(2006•云南)已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________ .15.(2005•黄石)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为_________ cm2.16.(2005•新疆)已知菱形的周长是52cm,一条对角线长是24cm,则它的面积是_________ cm2.17.(2004•贵阳)如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C 重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_________ .17题图18题图19题图18.(2003•温州)如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________ .19.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_________ 度.三.解答题(共7小题)20.(2011•南昌)如图,四边形ABCD为菱形,已知A(0,4),B(﹣3,0).(1)求点D的坐标;(2)求经过点C的反比例函数解析式.21.(2011•广安)如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线于点E.求证:DE=BE.22.(2010•益阳)如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23.(2010•宁洱县)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.24.(2009•贵阳)如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合),连接DP交对角线AC于E连接BE.(1)证明:∠APD=∠CBE;(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?25.(2006•大连)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连接_________ ;(2)猜想:_________ = _________ ;(3)证明:(说明:写出证明过程的重要依据)26.如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C 运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.答案与评分标准一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4)C.M(5,0),N(7,4)D.M(4,0),N(7,4)考点:菱形的性质;坐标与图形性质.专题:数形结合。
菱形的性质和判定(含解析)
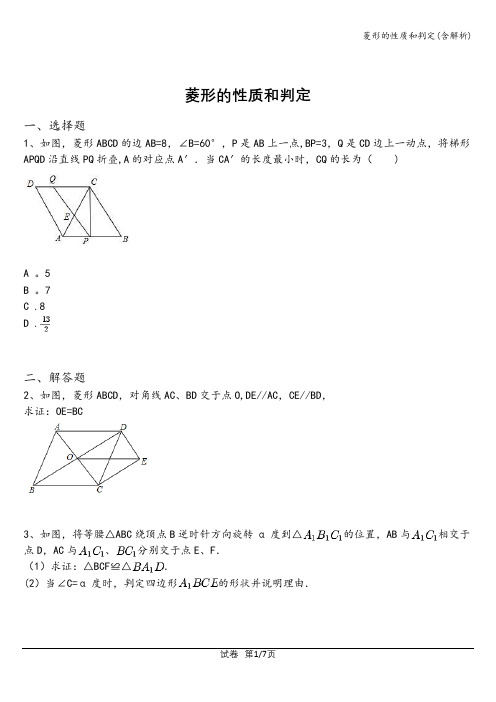
菱形的性质和判定一、选择题1、如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )A 。
5B 。
7C .8D .二、解答题2、如图,菱形ABCD,对角线AC、BD交于点O,DE//AC,CE//BD,求证:OE=BC3、如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△的位置,AB与相交于点D,AC与、分别交于点E、F.(1)求证:△BCF≌△.(2)当∠C=α度时,判定四边形的形状并说明理由.4、如图,矩形ABCD 中,对角线AC 的垂直平分线交AD 、BC 于点E 、F,AC 与EF 交于点O ,连结AF 、CE .(1)求证:四边形AFCE 是菱形;(2)若AB=3,AD=4,求菱形AFCE 的边长。
5、如图,CD 是△ABC 的中线,点E 是AF 的中点,CF∥AB. (1)求证:CF=AD ;(2)若∠ACB=90°,试判断四边形BFCD 的形状,并说明理由.6、如图,将矩形A 1B 1C 1D 1沿EF 折叠,使B 1点落在A 1D 1边上的B 点处;再将矩形A 1B 1C 1D 1沿BG 折叠,使D 1点落在D 点处且BD 过F 点.(1)求证:四边形BEFG 是平行四边形;(2)当∠B 1FE 是多少度时,四边形BEFG 为菱形?试说明理由.菱形的性质和判定的答案和解析一、选择题1、答案:B试题分析:作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH=AB=4,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可。
解:作CH⊥AB于H,如图,∵菱形ABCD的边AB=8,∠B=60°,∴△ABC为等边三角形,∴CH=AB=4,AH=BH=4,∵PB=3,∴HP=1,在Rt△CHP中,CP= =7,∵梯形APQD沿直线PQ折叠,A的对应点A′,∴点A′在以P点为圆心,PA为半径的弧上,∴当点A′在PC上时,CA′的值最小,∴∠APQ=∠CPQ,而CD∥AB,∴∠APQ=∠CQP,∴∠CQP=∠CPQ,∴CQ=CP=7.故选:B.二、解答题2、答案:证明见解析试题分析:先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED 是矩形,利用勾股定理即可求出BC=OE.证明:∵DE∥AC,CE∥BD,∴四边形OCED是平行四边形,∵四边形ABCD是菱形,∴∠COD=90°,∴四边形OCED是矩形,∴DE=OC,∵OB=OD,∠BOC=∠ODE=90°,∴BC===OE3、答案:(1)见解答过程(2)见解答过程试题分析:(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到=AB=BC,∠A=∠=∠C,∠BD=∠,根据全等三角形的判定定理得到△BCF≌△(2)由旋转的性质得到∠=∠A,根据平角的定义得到∠DEC=180°-α,根据四边形的内角和得到∠ABC=360°—∠—∠C—∠=180°-α,证的四边形是平行四边形,由于=BC,即可得到四边形是菱形。
(完整版)菱形性质经典练习题(详细答案)

菱形性质经典练习题一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4)D.M(4,0),N(7,4)2.(2010•肇庆)菱形的周长为4,一个内角为60°,则较短的对角线长为()A.2 B.C.1 D.3.(2010•襄阳)菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A.3:1 B.4:1 C.5:1 D.6:14.(2010•宜昌)如图,菱形ABCD中,AB=15,∠ADC=120°,则B、D两点之间的距离为()A.15 B.C.7.5 D.二.填空题(共15小题)5.(2011•铜仁地区)已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_________cm2.6.(2011•綦江县)如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_________.7.(2011•南京)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.6题图7题图8题图9题图8.(2011•鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_________.9.(2010•嘉兴)如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_________度.10.(2009•江西)如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1= _________度.10题图12题13题图14题图11.(2009•朝阳)已知菱形的一个内角为60°,一条对角线的长为,则另一条对角线的长为_________.12.(2009•安顺)如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按A﹣>B﹣>C﹣>D﹣>E﹣>F﹣>C﹣>G﹣>A的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在_________点.13.(2008•长沙)如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则P点到AB的距离是_________cm.14.(2006•云南)已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________.15.(2005•黄石)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为_________cm2.16.(2005•新疆)已知菱形的周长是52cm,一条对角线长是24cm,则它的面积是_________cm2.17.(2004•贵阳)如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_________.17题图18题图19题图18.(2003•温州)如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________.19.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_________度.三.解答题(共7小题)20.(2011•南昌)如图,四边形ABCD为菱形,已知A(0,4),B(﹣3,0).(1)求点D的坐标;(2)求经过点C的反比例函数解析式.21.(2011•广安)如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线于点E.求证:DE=BE.22.(2010•益阳)如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23.(2010•宁洱县)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.24.(2009•贵阳)如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合),连接DP交对角线AC于E 连接BE.(1)证明:∠APD=∠CBE;(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?25.(2006•大连)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连接_________;(2)猜想:_________=_________;(3)证明:(说明:写出证明过程的重要依据)26.如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C 运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.答案与评分标准一.选择题(共4小题)1.(2011•衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4) D.M(4,0),N(7,4)考点:菱形的性质;坐标与图形性质。
菱形的性质练习题

菱形的性质练习题菱形是一种特殊的四边形,它具有一些独特的性质。
在这篇文章中,我们将通过练习题来深入探讨菱形的性质。
练习题1:证明一个四边形是菱形的条件是什么?解答:一个四边形是菱形的条件有两个:首先,它的四条边都相等;其次,其中的两条对角线相互垂直。
练习题2:如果ABCD是一个菱形,证明ABCD的对角线相互平分。
解答:已知ABCD是一个菱形,即AB=BC=CD=DA。
我们需要证明对角线AC和BD相互平分。
根据菱形的性质,对角线AC和BD相互垂直,所以它们交于一点O。
我们需要证明AO=CO和BO=DO。
由于ABCD是一个菱形,所以AB=BC,结合直角三角形AOC,可以得出AO=CO。
同理,由于ABCD是一个菱形,所以AD=CD,结合直角三角形BOD,可以得出BO=DO。
因此,对角线AC和BD相互平分。
练习题3:如果ABCD是一个菱形,证明菱形内角的度数是多少?解答:已知ABCD是一个菱形,我们需要证明菱形的内角的度数。
由于菱形的性质,对角线AC和BD相互垂直,所以它们所夹的角是直角。
又因为菱形的四条边相等,我们可以得知菱形的四个内角都是90度。
练习题4:如果ABCD是一个菱形,证明菱形的内角和外角的关系。
解答:已知ABCD是一个菱形,我们需要证明菱形的内角和外角的关系。
菱形的四个内角都是90度,而外角则等于相邻的内角的补角。
所以,每个外角都等于90度减去相邻的内角的度数。
练习题5:如果E是菱形ABCD的一个顶点,证明AE、BE、CE和DE都是相等的。
解答:已知菱形ABCD,我们需要证明AE、BE、CE和DE都是相等的。
根据菱形的性质,AB=BC=CD=DA。
又因为AE是菱形的边,所以AE=AB。
同理,可以得出BE=BC、CE=CD和DE=DA。
因此,AE、BE、CE和DE都是相等的。
通过以上练习题的解答,我们深入了解了菱形的性质。
菱形具有四条相等的边和相互垂直的对角线,内角都是90度,外角等于相邻内角的补角,并且以任意一个顶点为中心的线段都相等。
菱形性质练习题

菱形性质练习题一、选择题1. 菱形的对角线互相垂直平分,以下哪个选项不是菱形的性质?A. 四边相等B. 对角线互相平分C. 对角线垂直D. 对角线长度相等2. 如果一个四边形的对角线互相垂直,那么这个四边形一定是:A. 矩形B. 菱形C. 平行四边形D. 梯形3. 菱形的面积可以通过以下哪种方式计算?A. 边长乘以边长B. 对角线乘积的一半C. 对角线长度的平方D. 对角线长度的立方4. 在菱形ABCD中,若AB=5,AC=6,BD=8,以下哪个选项是错误的?A. BC=5B. AD=5C. CD=5D. AB垂直于BC5. 菱形的内角和是多少度?A. 360度B. 180度C. 540度D. 720度二、填空题6. 菱形的对角线将菱形分为四个全等的_________。
7. 如果菱形的一条对角线长度为10,另一条对角线长度为8,那么菱形的面积是_________。
8. 菱形的四边中,任意两边所夹的角称为_________。
9. 菱形的对角线_________。
10. 菱形的四个角中,相邻角的度数之和为_________。
三、计算题11. 在菱形ABCD中,已知AB=6,AC=8,求菱形的面积。
12. 菱形EFGH的对角线EF和GH的长度分别为10和6,求菱形的边长。
四、证明题13. 已知四边形PQRS是菱形,且PS=QR,证明∠PQR=90°。
14. 在菱形LMNO中,MN=10,NO=8,求证对角线LM和ON互相垂直。
五、简答题15. 简述菱形的判定定理。
16. 菱形的对角线有哪些作用?六、应用题17. 一个菱形的花园,其对角线长度分别为15米和20米,求这个花园的面积。
18. 在菱形ABCD中,如果AB=10,且∠A=60°,求菱形的面积。
七、拓展题19. 如果菱形的对角线长度分别为a和b,求菱形的内切圆半径。
20. 菱形ABCD的对角线AC和BD互相垂直,且AC=8,BD=6,求菱形的边长。
菱形性质练习题-中考题集

菱形性质中考题一.选择题(共4小题)1.(2011?衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4) D.M(4,0),N(7,4)2.(2010?肇庆)菱形的周长为4,一个内角为60°,则较短的对角线长为()A.2 B.C.1 D.3.(2010?襄阳)菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A.3:1 B.4:1 C.5:1 D.6:14.(2010?宜昌)如图,菱形ABCD中,AB=15,∠ADC=120°,则B、D两点之间的距离为()A.15 B.C.7.5 D.二.填空题(共15小题)5.(2011?铜仁地区)已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_________ cm2.6.(2011?綦江县)如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=_________ .7.(2011?南京)如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为 cm2.6题图 7题图 8题图 9题图8.(2011?鞍山)如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_________ .9.(2010?嘉兴)如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_________ 度.10.(2009?江西)如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1=_________ 度.10题图 12题 13题图 14题图11.(2009?朝阳)已知菱形的一个内角为60°,一条对角线的长为,则另一条对角线的长为_________ .12.(2009?安顺)如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按A﹣>B﹣>C﹣>D﹣>E﹣>F﹣>C﹣>G﹣>A的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在_________ 点.13.(2008?长沙)如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则P点到AB的距离是_________ cm.14.(2006?云南)已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________ .15.(2005?黄石)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为_________ cm2.16.(2005?新疆)已知菱形的周长是52cm,一条对角线长是24cm,则它的面积是_________ cm2.17.(2004?贵阳)如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_________ .17题图 18题图 19题图18.(2003?温州)如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________ .19.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_________ 度.三.解答题(共7小题)20.(2011?南昌)如图,四边形ABCD为菱形,已知A(0,4),B(﹣3,0).(1)求点D的坐标;(2)求经过点C的反比例函数解析式.21.(2011?广安)如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC 的延长线于点E.求证:DE=BE.22.(2010?益阳)如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD 的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23.(2010?宁洱县)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.24.(2009?贵阳)如图,在菱形ABCD中,P是AB上的一个动点(不与A、B 重合),连接DP交对角线AC于E连接BE.(1)证明:∠APD=∠CBE;(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?25.(2006?大连)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连接_________ ;(2)猜想:_________ = _________ ;(3)证明:(说明:写出证明过程的重要依据)26.如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.答案与评分标准一.选择题(共4小题)1.(2011?衡阳)如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4) C.M(5,0),N(7,4) D.M(4,0),N(7,4)考点:菱形的性质;坐标与图形性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《菱形》性质练习题
一.选择题
1.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是()A.M(5,0),N(8,4) B.M(4,0),N(8,4)
C.M(5,0),N(7,4) D.M(4,0),N(7,4)
2.菱形的周长为4,一个内角为60°,则较短的对角线长为()
A.2 B. C.1 D.
3.菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()
A.3:1 B.4:1 C.5:1 D.6:1
4.如图,菱形ABCD中,AB=15,∠ADC=120°,则B、D两点之间的距离为()
A.15 B.C.7.5 D.
二.填空题
5.已知菱形的两条对角线长分别为2cm,3cm,则它的面积是_________ cm2.
6.如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB 的距离OH= _________ .
7.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.
6题图 7题图 8题图 9题图
8.如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_________ .
9.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_________ 度.
10.如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1=_________ 度.
10题图12题图 13题图 14题图
11.已知菱形的一个内角为60°,一条对角线的长为,则另一条对角线的长为_________ .
12.如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按A﹣>B﹣>C﹣>D﹣>E﹣>F﹣>C﹣>G﹣>A的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在_________ 点.
13.如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,PF=3cm,则P点到AB的距离是______cm.
14.已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________ .
15.已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为_________ cm2.
16.已知菱形的周长是52cm,一条对角线长是24cm,则它的面积是_________ cm2.
17.如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_________ .
17题图 18题图
18.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CF E= _________ 度.
三.解答题
19.如图,四边形ABCD为菱形,已知A(0,4),B(﹣3,0).
(1)求点D的坐标;
(2)求经过点C的反比例函数解析式.
20.如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线于点E.
求证:DE=BE.
21.如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.
22.如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.
(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.
23.如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
(1)在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?
(2)分别求出菱形AQCP的周长、面积.。
