山东省济宁市邹城四中2017-2018学年第二学期八年级第二次阶段检测试题(列答案)
山东省邹城市2017-2018学年度第二学期期中考试英语试题(word版,含听力、答案)

2017-2018学年度第二学期期中检测八年级英语试题注意事项:1.本试卷分第1卷和第Ⅱ卷两部分,第[卷为选择题,45分;第Ⅱ卷为非选择题,55分;共100分。
考试时间为100分钟(含听力20分钟)。
2.答题前,考生务必先核对条形码上的姓名、准考证号和座号,然后用0.5毫米黑色墨水签字笔将本人的姓名、准考证号和座号写在答题卡的相应位置。
3.答第1卷时,必须使用2B铅笔填涂答题卡上相应题目的答案标号,如如需改动,必须先用橡皮擦干净,再改涂其它答案。
4.答第Ⅱ卷时,必须使用0.5毫米黑色墨水签字笔在答题卡上书写。
务必在题号所指示的答题区域内作答。
若需改动,先划掉原来的答案,然后再写上新的答案。
不准使用涂改液、胶带纸、修正带,否则,答案无效。
第I卷(选择题共45分)ー、听力选择(共15小题,计15分)(一)请听录音中八组短对话。
每组对话后有一个小题,从题中所给的A、B、C三个选项中,选出与对话内容相符的图片或能回答所给问题的最佳答案。
(每组对话读两遍)八年级英语试题第1页(共10页)4. How long are they staying in the hotel?A. A weekB. Three daysC. Five days5. What must Tom do?A Sweep the floor B. Fold the clothes C. Do the dishes6. What will Jack do?A Put up some signs.B Care for the oldC Fix up his bike7. What happened to Gina?A. She got into a fight with her friendB. She had too much homeworkC. She lost his book8. What kind of music does the girl like now?A. Pop music.B. Country musicC. Rock music(二)请听录音中两段较长的对话。
山东省邹城市第四中学2017--2018学年八年级下学期期中考试物理试题(扫描版)

2017-2018 学年度第二学期期中检测八年级物理试题注意事项:本套试题分“试题卷”和“答题卡”两部分,请将“试题卷”中试题的答案填写到“答题卡”中对应的位置: 本套试题共60 分; 考试时间共60分钟。
g取10N/kg. 一、选择题(每小题2 分,共20 分,请把唯一正确答案的序号填在答题卡的表格中) 1.关于交通规则中的系安全带的理由,你认为正确的是A.系安全带是为了减小汽车和车内人员的惯性B.系安全带是为了增大汽车和车内人员的惯性林公服出C.系安全带可减小因汽车突然加速造成的人员伤害D.系安全带可诚小因汽车突然减速造成的人员伤害2.如图所示,下列物体受力示意图中,处于平衡的物体是3.如图,教室里悬挂的电灯处于静止状态,下列说法正确的是A.电灯受到的重力与电灯对绳的拉力是一对平衡力B.电灯受到力的合力为零C.假如悬挂它的绳子突然断了,由于惯性,它将仍然保持静止D.假如悬挂它的绳子突然断了,由于惯性,它将做匀速直线运动4.下列事例中利用大气压强的是A.护士给病人输液B.医生用听诊器给病人听诊C.用压力锅蒸煮进行医用消毒D.护士给病人注射肌肉针5.关于运动和力,以下说法中正确的是A .给正在运动的物体再施加一个力,物体一定比原来运动得更快B .做匀速直线运动的物体一定不受力的作用C .匀速转弯的物体,可能不受力的作用D .只受重力作用的物体也可能向上运动6.如图,在做托里拆利实验时,若将玻璃管由坚直变成倾斜,则管内真空部 分的长度A.变大B.变小C.不变D.无法判定八年级物理试题第1页(共6页)7.在如图所示的装置中,不是..利用连通器原理工作的是( )A .①②B .③④C .②③D .②④8.同一个小球,先后放入四个盛有不同液体的容器中,静止时的位置如图所示,四个容器中的液面到容器底面的距离相等,则容器底面受到液体压强最大的是( )A .B .C .D .①牲畜自动饮水机 ②托里拆利实验装置 ③洗手盆的下水管 ④液压机模型9.一个小球,在水中悬浮。
2017-2018学年济宁市邹城市八年级下期中数学试卷(有答案)-精

2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣15.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.47.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米8.已知m﹣=,则+m的值为()A.±B.C.±D.119.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3 B.C.D.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围.12.在▱ABCD中,∠A=70°,则∠C=度.13.化简:=.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为.15.方程3x2﹣6=0的解是.16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH 的长是.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA >PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P 点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.【分析】根据最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是进行判断即可.【解答】解:A、是最简二次根式,正确;B、不是最简二次根式,错误;C、不是最简二次根式,错误;D、不是最简二次根式,错误;故选:A.【点评】本题考查最简二次根式的定义.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD【分析】根据对角线相等的平行四边形是矩形得出即可.【解答】解:添加AO=BO,理由是:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴▱ABCD为矩形,故选:C.【点评】本题考查矩形的判定、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣1【分析】根据各个选项中的式子,可以计算出正确的结果,本题得以解决.【解答】解:∵不能合并,故选项A错误;∵3+不能合并,故选项B错误;∵,故选项C正确;∵,故选项D错误;故选:C.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形【分析】根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.【解答】解:四边形EFGH是菱形.理由是:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,∴AC=BD,∵EF为△ABD的中位线,∴EF=BD,又GH为△BCD的中位线,∴GH=BD,∴GH=EF=BD,同理FG=EH=AC,∴EF=GH=FG=EH,∴四边形EFGH是菱形.故选:B.【点评】此题主要考查学生对菱形的判定、三角形中位线定理和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.4【分析】直接利用偶次方的性质以及二次根式的性质得出m,n的值,进而得出答案.【解答】解:∵(m+3)2+=0,∴m=﹣3,n=﹣4,∴则==2.故选:C.【点评】此题主要考查了非负数的性质,正确得出m,n的值是解题关键.7.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米【分析】根据题意画出图形,构造出直角三角形,利用勾股定理求解.【解答】解:如图所示,过D点作DE⊥AB,垂足为E,∵AB=13,CD=8,又∵BE=CD,DE=BC,∴AE=AB﹣BE=AB﹣CD=13﹣8=5,∴在Rt△ADE中,DE=BC=12,∴AD2=AE2+DE2=122+52=144+25=169,∴AD=13(负值舍去),答:小鸟飞行的最短路程为13m.故选:A.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.8.已知m﹣=,则+m的值为()A.±B.C.±D.11【分析】把已知等式两边平方,利用完全平方公式化简,整理后利用平方根定义求出所求即可.【解答】解:把已知等式两边平方得:(m﹣)2=7,即m2+=9,∴(m+)2=m2++2=9+2=11,则+m=±,故选:A.【点评】此题考查了分式的加减法,平方根,以及算术平方根,熟练掌握运算法则是解本题的关键.9.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3 B.C.D.【分析】在Rt△BAN中,根据勾股定理可求AN,进一步得到DN,再在Rt△MDN中,根据勾股定理可求CM的长.【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,BC=AD=10cm,在Rt△BAN中,AN==8cm,DN=10﹣8=2cm,在Rt△MDN中,CM2=22+(6﹣CM)2,解得CM=cm.故选:D.【点评】本题考查了矩形的性质、勾股定理、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)【分析】先找出被开方数的规律,然后再求得的位置即可.【解答】解:这组数据可表示为:①,,,,,②,,,,;…∵19×2=38,∴19÷5=3…4,∴为第4行,第4个数字.故选:B.【点评】本题主要考查的是数字的变化规律,找出其中的规律是解题的关键.二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围x≤.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得1﹣2x≥0,解得:x≤,故答案为:x≤.【点评】本题考查了二次根式的性质,二次根式中的被开方数必须是非负数,否则二次根式无意义.12.在▱ABCD中,∠A=70°,则∠C=70 度.【分析】根据平行四边形的对角相等得出∠A=∠C,代入求出即可.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A=70°,∴∠C=70°,故答案为70.【点评】本题考查了平行四边形的性质,注意:平行四边形的对角相等.13.化简:=.【分析】根据二次根式化简解答即可.【解答】解:=,故答案为:.【点评】此题考查二次根式问题,关键是根据分母有理化解答.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为12.【分析】要求平行四边形的面积,只要根据勾股定理得出对角线垂直,进而解答即可.【解答】解:因为一个平行四边形的两邻边长分别为6和2,一条对角线长为8,因为:, 所以此平行四边形为矩形,这个平行四边形的面积为6×,故答案为:12. 【点评】本题考查了平行四边形的性质以及平行四边形的面积的求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S =a •h .其中a 可以是平行四边形的任何一边,h 必须是a 边与其对边的距离,即对应的高.15.方程3x 2﹣6=0的解是 x 1=,x 2=﹣ .【分析】利用直接开平方法解方程.【解答】解:3x 2﹣6=0,x 2=2,x =±,所以x 1=,x 2=﹣.故答案为x 1=,x 2=﹣. 【点评】本题考查了解一元二次方程﹣直接开平方法:形如x 2=p 或(nx +m )2=p (p ≥0)的一元二次方程可采用直接开平方的方法解一元二次方程16.如图,已知菱形OABC 的边OA 在x 轴上,∠AOC =60°,点A 的坐标为(0,6),则点B 的坐标为 (9,3) .【分析】过点B 作BD ⊥OA 于点D ,由菱形的性质可求AB =OA =6,∠BAD =60°,利用锐角三角函数解直角三角形,可求AD ,BD 的长,即可求点B 的坐标.【解答】解:如图:过点B 作BD ⊥OA 于点D∵点A的坐标为(0,6),∴OA=6∵四边形OABC是菱形∴OA=AB=6,AB∥OC∴∠BAD=∠AOC=60°∵∠BAD=60°,BD⊥AO∴∠ABD=30°∴AD=AB=3,BD=AD=3∴OD=OA+AD=9∴点B坐标(9,3)故答案为:(9,3)【点评】本题考查了菱形的性质,坐标与图形的性质,添加恰当的辅助线构造直角三角形是本题的关键.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.【分析】利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.【解答】解:如图,过点A作AD⊥BC于点D,∵△ABC边AB=AC=5,BC=6,∴BD=DC=3,∴AD=4,如图①所示:四边形ACBD是矩形,则其对角线AB的长为5;如图②所示:AD=4,连接BC,过点C作CE⊥BD于点E,则EC=4,BE=2BD=6,∴BC=2;如图③所示:BD=3,由题意可得:AE=3,EC=2BE=8,∴AC==,其中最长的对角线的值为.故答案为.【点评】此题主要考查了图形的剪拼以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).【分析】(1)直接利用二次根式的乘除运算法则计算得出答案;(2)利用二次根式混合运算法则计算得出答案.【解答】解:(1)2×÷5=4×÷5=3÷5=;(2)(﹣2)2+2×(﹣)=6+12﹣12+10﹣=18﹣3.【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.【分析】根据题意可求OA=OB=DO,∠AOB=60°,可得∠BAD=90°,即结论可得.【解答】解:∵△AOB为等边三角形,∴∠BAO=60°=∠AOB,OA=OB,∵四边形ABCD是平行四边形,∴OB=OD,∴OA=OD,∴∠OAD=30°,∴∠BAD=30°+60°=90°,∴平行四边形ABCD为矩形.【点评】本题考查了矩形的性质,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.【分析】先计算x、y两个数的和、差、积;(1)利用平方差公式进行因式分解,然后代入求值;(2)变形为完全平方公式与积的差(或和)的形式,整体代入求值.【解答】解:由已知可得:x+y=4,x﹣y=2,xy=1(1)x2﹣y2=(x+y)(x﹣y)=4×2=8;(2)x2﹣2xy+y2﹣xy=(x﹣y)2﹣xy=(2)2﹣1=12﹣1=11.【点评】本题考查了二次根式的运算,完全平方公式的变形、平方差公式等知识点.题目难度不大,注意整体代入思想的运用.22.如图,矩形ABCD 中,∠BAD 的平分线AE 与BC 边交于点E ,点P 是线段AE 上一定点(其中PA >PE ),过点P 作AE 的垂线与AD 边交于点F (不与D 重合).一直角三角形的直角顶点落在P 点处,两直角边分别交AB 边,AD 边于点M ,N .(1)求证:△PAM ≌△PFN ;(2)若PA =3,求AM +AN 的长.【分析】(1)由题意可证AP =PF ,∠MAP =∠PAF =∠PFA =45°,即可证△PAM ≌△PFN ;(2)由勾股定理可求AF =3,由△PAM ≌△PFN ,可得AM =NF ,即可得AM +AN =AF =3.【解答】证明:(1)∵四边形ABCD 是矩形∴∠BAD =90°∵∠BAD 的平分线AE 与BC 边交于点E ,∴∠BAE =∠EAD =45°∵PF ⊥AP∴∠PAF =∠PFA =45°∴AP =PF∵∠MPN =90°,∠APF =90°∴∠MPN ﹣∠APN =∠APF ﹣∠APN∴∠MPA =∠FPN ,且AP =PF ,∠MAP =∠PFA =45°∴△PAM ≌△PFN (ASA )(2)∵PA =3∴PA =PF =3,且∠APF =90°∴AF ==3∵△PAM ≌△PFN ;∴AM =NF∴AM +AN =AN +NF =AF =3 【点评】本题考查了矩形的性质,全等三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.【分析】(1)根据=,利用数形结合的思想解决问题即可;(2)作边长为的正方形ABCD即可;(3)根据线段的垂直平分线的判定定理,先作出垂直平分线上的两点,构造直线即可【解答】解:(1)线段MN如图所示;(2)正方形ABCD如图所示;(3)线段EF的垂直平分线l如图所示;【点评】本题考查作图﹣应用与设计、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.【分析】(1)连接AC交BD于O,根据正方形的性质得到BD⊥AC,BO=DO,AO=CO,根据菱形的判定定理即可得到结论;(2)根据勾股定理得到BD=AC=,根据菱形的面积公式即可得到结论;(3)根据菱形的性质得到点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM 最小,过C作CN⊥AF于N,根据勾股定理列方程即可得到结论.【解答】(1)证明:连接AC交BD于O,∵四边形ABCD是正方形,∴BD⊥AC,BO=DO,AO=CO,∵BF=DE=,∴OE=OF,∴四边形AECF是菱形;(2)解:∵四边形ABCD是边长为1的正方形,∴AB=AD=1,∴BD=AC=,∴EF=3,∴四边形AECF的面积=AC•EF=×3=3;(3)解:∵四边形AFCE是菱形,∴点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,则AC2﹣AN2=CN2=CF2﹣NF2,设AN=x,∴()2﹣x2=()2﹣(﹣x)2,解得:x=,∴MN=,∵CM2﹣MN2=AC2﹣AN2,∴CM2﹣()2=12﹣()2,解得:CM=,故PA+PM的最小值=.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,菱形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.。
2018山东邹城八年级下物理期末试题

2017- 2018 学年第二学期期末教学质量调研八年级物理试题注意事项:1,本试题分第I卷和第Ⅱ卷两部分。
第I卷为选样题,20分;第Ⅱ卷为非选择题,40分,共60分。
考试时间共60分钟。
2.答第I卷前务必将自己的姓名考号涂写在等题卡上,第I卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号( ABCD)徐黑,如需改动,必须用橡皮擦干净,再改除其他答案;答第Ⅱ卷时务必将答案填至相应题目规定区城内。
第I卷(选择题共20 分)一、选择题(下列各题的4个选项中,只有1项符合题意,请将正确选项填写在答案框内,每题2分,共20分)1.人类对力与运动关系的认识经历了漫长曲折的过程,下面是三位不同时代科学家的主要观点,下列说法正确的是A.①观点的提出是意大利科学家伽利略。
B.②观点是由牛顿在总结前人经验的基础上得出的。
C.这三种观点形成的先后顺序是③②①D.以上说法都不正确2. 如图1所示,用力将图钉按在墙壁上,下列说法正确的是A.手指对钉帽的压力小于墙壁对钉尖的压力B.手指对钉帽的压力等于钉尖对墙壁的压力C.手指对钉帽的压强等于钉尖对墙壁的压强D.钉尖对墙壁的压力和墙壁对钉尖的压力是平衡力图1八年级物理试题第1页(共6页)3.在探究实践创新大赛中,小明同学展示了他的“液体压强演示仪”,胶管其主要部件是一根两端开口且用橡皮膜扎紧的玻璃管(如图2),将橡皮膜此装置放于水中,通过橡皮膜的凹凸程度变化,探究液体压强规律.如图描述的几种橡皮膜的变化情况,其中正确的是A. B. C. D.4.如下图,下列用矿泉水瓶所做的实验中,能探究压力的作用效果与受力面积的关系的是A.两次海绵形变程度不同B. 从三孔流出水的喷射距离不同C. 用纸片盖住装满水的瓶口,倒立后纸片不下落D. 向两空瓶中间吹气,两瓶向中间靠拢5.在一密闭的真空玻璃罩里挂着一个弹簧秤,秤下挂个体积较大的物体,物体静止现将玻璃罩下的开关打开,让空气进人,则此时A.弹簧测力计的示数仍不变B.弹簧测力计的示数将增大C.弹簧测力计的示数将减小D.弹簧测力计的示数可能增大也可能减小6.小明用矿泉水瓶和小玻璃瓶制作了一个“浮沉子”(如图3).他将装有适量水的小玻璃瓶瓶口朝下,使其漂浮在矿泉水瓶内的水面上,矿泉水瓶内留有少量空气,拧紧瓶盖使其密封,用力挤压矿泉水瓶侧面时“浮沉子”下沉,松手后“浮沉子”即上浮,下列说法错误的是A.“浮沉子”下沉时,所受重力大于它受到的浮力B.无沦怎样挤压矿泉水瓶侧面,“浮沉子”不可能悬浮在水中图3C.“浮沉子”上浮时,小瓶内的压缩空气会将内部的水压出D.潜水艇与“浮沉子”浮沉的原理相同7.到野外郊游时,小明和爸爸喜欢钓鱼。
2017-2018学年济宁市邹城市八年级下期中数学试卷(有答案)-精选

2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣15.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.47.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米8.已知m﹣=,则+m的值为()A.±B.C.±D.119.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C 点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3 B.C.D.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围.12.在▱ABCD中,∠A=70°,则∠C=度.13.化简:=.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为.15.方程3x2﹣6=0的解是.16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B 的坐标为.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.【分析】根据最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是进行判断即可.【解答】解:A、是最简二次根式,正确;B、不是最简二次根式,错误;C、不是最简二次根式,错误;D、不是最简二次根式,错误;故选:A.【点评】本题考查最简二次根式的定义.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD【分析】根据对角线相等的平行四边形是矩形得出即可.【解答】解:添加AO=BO,理由是:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴▱ABCD为矩形,故选:C.【点评】本题考查矩形的判定、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣1【分析】根据各个选项中的式子,可以计算出正确的结果,本题得以解决.【解答】解:∵不能合并,故选项A错误;∵3+不能合并,故选项B错误;∵,故选项C正确;∵,故选项D错误;故选:C.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形【分析】根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.【解答】解:四边形EFGH是菱形.理由是:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,∴AC=BD,∵EF为△ABD的中位线,∴EF=BD,又GH为△BCD的中位线,∴GH=BD,∴GH=EF=BD,同理FG=EH=AC,∴EF=GH=FG=EH,∴四边形EFGH是菱形.故选:B.【点评】此题主要考查学生对菱形的判定、三角形中位线定理和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.4【分析】直接利用偶次方的性质以及二次根式的性质得出m,n的值,进而得出答案.【解答】解:∵(m+3)2+=0,∴m=﹣3,n=﹣4,∴则==2.故选:C.【点评】此题主要考查了非负数的性质,正确得出m,n的值是解题关键.7.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米【分析】根据题意画出图形,构造出直角三角形,利用勾股定理求解.【解答】解:如图所示,过D点作DE⊥AB,垂足为E,∵AB=13,CD=8,又∵BE=CD,DE=BC,∴AE=AB﹣BE=AB﹣CD=13﹣8=5,∴在Rt△ADE中,DE=BC=12,∴AD2=AE2+DE2=122+52=144+25=169,∴AD=13(负值舍去),答:小鸟飞行的最短路程为13m.故选:A.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.8.已知m﹣=,则+m的值为()A.±B.C.±D.11【分析】把已知等式两边平方,利用完全平方公式化简,整理后利用平方根定义求出所求即可.【解答】解:把已知等式两边平方得:(m﹣)2=7,即m2+=9,∴(m+)2=m2++2=9+2=11,则+m=±,故选:A.【点评】此题考查了分式的加减法,平方根,以及算术平方根,熟练掌握运算法则是解本题的关键.9.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C 点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3 B.C.D.【分析】在Rt△BAN中,根据勾股定理可求AN,进一步得到DN,再在Rt△MDN中,根据勾股定理可求CM的长.【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,BC=AD=10cm,在Rt△BAN中,AN==8cm,DN=10﹣8=2cm,在Rt△MDN中,CM2=22+(6﹣CM)2,解得CM=cm.故选:D.【点评】本题考查了矩形的性质、勾股定理、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)【分析】先找出被开方数的规律,然后再求得的位置即可.【解答】解:这组数据可表示为:①,,,,,②,,,,;…∵19×2=38,∴19÷5=3…4,∴为第4行,第4个数字.故选:B.【点评】本题主要考查的是数字的变化规律,找出其中的规律是解题的关键.二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围x≤.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得1﹣2x≥0,解得:x≤,故答案为:x≤.【点评】本题考查了二次根式的性质,二次根式中的被开方数必须是非负数,否则二次根式无意义.12.在▱ABCD中,∠A=70°,则∠C=70 度.【分析】根据平行四边形的对角相等得出∠A=∠C,代入求出即可.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A=70°,∴∠C=70°,故答案为70.【点评】本题考查了平行四边形的性质,注意:平行四边形的对角相等.13.化简:=.【分析】根据二次根式化简解答即可.【解答】解:=,故答案为:.【点评】此题考查二次根式问题,关键是根据分母有理化解答.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为12.【分析】要求平行四边形的面积,只要根据勾股定理得出对角线垂直,进而解答即可.【解答】解:因为一个平行四边形的两邻边长分别为6和2,一条对角线长为8,因为:,所以此平行四边形为矩形,这个平行四边形的面积为6×,故答案为:12.【点评】本题考查了平行四边形的性质以及平行四边形的面积的求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.=,x2=﹣.15.方程3x2﹣6=0的解是x【分析】利用直接开平方法解方程.【解答】解:3x2﹣6=0,x2=2,x=±,=,x2=﹣.所以x=,x2=﹣.故答案为x【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B 的坐标为(9,3).【分析】过点B作BD⊥OA于点D,由菱形的性质可求AB=OA=6,∠BAD=60°,利用锐角三角函数解直角三角形,可求AD,BD的长,即可求点B的坐标.【解答】解:如图:过点B作BD⊥OA于点D∵点A的坐标为(0,6),∴OA=6∵四边形OABC是菱形∴OA=AB=6,AB∥OC∴∠BAD=∠AOC=60°∵∠BAD=60°,BD⊥AO∴∠ABD=30°∴AD=AB=3,BD=AD=3∴OD=OA+AD=9∴点B坐标(9,3)故答案为:(9,3)【点评】本题考查了菱形的性质,坐标与图形的性质,添加恰当的辅助线构造直角三角形是本题的关键.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.【分析】利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.【解答】解:如图,过点A作AD⊥BC于点D,∵△ABC边AB=AC=5,BC=6,∴BD=DC=3,∴AD=4,如图①所示:四边形ACBD是矩形,则其对角线AB的长为5;如图②所示:AD=4,连接BC,过点C作CE⊥BD于点E,则EC=4,BE=2BD=6,∴BC=2;如图③所示:BD=3,由题意可得:AE=3,EC=2BE=8,∴AC==,其中最长的对角线的值为.故答案为.【点评】此题主要考查了图形的剪拼以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).【分析】(1)直接利用二次根式的乘除运算法则计算得出答案;(2)利用二次根式混合运算法则计算得出答案.【解答】解:(1)2×÷5=4×÷5=3÷5=;(2)(﹣2)2+2×(﹣)=6+12﹣12+10﹣=18﹣3.【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.【分析】根据题意可求OA=OB=DO,∠AOB=60°,可得∠BAD=90°,即结论可得.【解答】解:∵△AOB为等边三角形,∴∠BAO=60°=∠AOB,OA=OB,∵四边形ABCD是平行四边形,∴OB=OD,∴OA=OD,∴∠OAD=30°,∴∠BAD=30°+60°=90°,∴平行四边形ABCD为矩形.【点评】本题考查了矩形的性质,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.【分析】先计算x、y两个数的和、差、积;(1)利用平方差公式进行因式分解,然后代入求值;(2)变形为完全平方公式与积的差(或和)的形式,整体代入求值.【解答】解:由已知可得:x+y=4,x﹣y=2,xy=1(1)x2﹣y2=(x+y)(x﹣y)=4×2=8;(2)x2﹣2xy+y2﹣xy=(x﹣y)2﹣xy=(2)2﹣1=12﹣1=11.【点评】本题考查了二次根式的运算,完全平方公式的变形、平方差公式等知识点.题目难度不大,注意整体代入思想的运用.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.【分析】(1)由题意可证AP=PF,∠MAP=∠PAF=∠PFA=45°,即可证△PAM≌△PFN;(2)由勾股定理可求AF=3,由△PAM≌△PFN,可得AM=NF,即可得AM+AN=AF=3.【解答】证明:(1)∵四边形ABCD是矩形∴∠BAD=90°∵∠BAD的平分线AE与BC边交于点E,∴∠BAE=∠EAD=45°∵PF⊥AP∴∠PAF=∠PFA=45°∴AP=PF∵∠MPN=90°,∠APF=90°∴∠MPN﹣∠APN=∠APF﹣∠APN∴∠MPA=∠FPN,且AP=PF,∠MAP=∠PFA=45°∴△PAM≌△PFN(ASA)(2)∵PA=3∴PA=PF=3,且∠APF=90°∴AF==3∵△PAM≌△PFN;∴AM=NF∴AM+AN=AN+NF=AF=3【点评】本题考查了矩形的性质,全等三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.【分析】(1)根据=,利用数形结合的思想解决问题即可;(2)作边长为的正方形ABCD即可;(3)根据线段的垂直平分线的判定定理,先作出垂直平分线上的两点,构造直线即可【解答】解:(1)线段MN如图所示;(2)正方形ABCD如图所示;(3)线段EF的垂直平分线l如图所示;【点评】本题考查作图﹣应用与设计、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.【分析】(1)连接AC交BD于O,根据正方形的性质得到BD⊥AC,BO=DO,AO=CO,根据菱形的判定定理即可得到结论;(2)根据勾股定理得到BD=AC=,根据菱形的面积公式即可得到结论;(3)根据菱形的性质得到点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM =CM最小,过C作CN⊥AF于N,根据勾股定理列方程即可得到结论.【解答】(1)证明:连接AC交BD于O,∵四边形ABCD是正方形,∴BD⊥AC,BO=DO,AO=CO,∵BF=DE=,∴OE=OF,∴四边形AECF是菱形;(2)解:∵四边形ABCD是边长为1的正方形,∴AB=AD=1,∴BD=AC=,∴EF=3,∴四边形AECF的面积=AC•EF=×3=3;(3)解:∵四边形AFCE是菱形,∴点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,则AC2﹣AN2=CN2=CF2﹣NF2,设AN=x,∴()2﹣x2=()2﹣(﹣x)2,解得:x=,∴MN=,∵CM2﹣MN2=AC2﹣AN2,∴CM2﹣()2=12﹣()2,解得:CM=,故PA+PM的最小值=.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,菱形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.。
2017-2018学年济宁市邹城市八年级下期中数学试卷(含答案解析)

2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣15.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.47.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米8.已知m﹣=,则+m的值为()A.±B.C.±D.119.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD 上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围.12.在▱ABCD中,∠A=70°,则∠C=度.13.化简:=.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为.15.方程3x2﹣6=0的解是.16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.【分析】根据最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是进行判断即可.【解答】解:A、是最简二次根式,正确;B、不是最简二次根式,错误;C、不是最简二次根式,错误;D、不是最简二次根式,错误;故选:A.【点评】本题考查最简二次根式的定义.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD【分析】根据对角线相等的平行四边形是矩形得出即可.【解答】解:添加AO=BO,理由是:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴▱ABCD为矩形,故选:C.【点评】本题考查矩形的判定、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣1【分析】根据各个选项中的式子,可以计算出正确的结果,本题得以解决.【解答】解:∵不能合并,故选项A错误;∵3+不能合并,故选项B错误;∵,故选项C正确;∵,故选项D错误;故选:C.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形【分析】根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.【解答】解:四边形EFGH是菱形.理由是:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,∴AC=BD,∵EF为△ABD的中位线,∴EF=BD,又GH为△BCD的中位线,∴GH=BD,∴GH=EF=BD,同理FG=EH=AC,∴EF=GH=FG=EH,∴四边形EFGH是菱形.故选:B.【点评】此题主要考查学生对菱形的判定、三角形中位线定理和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.4【分析】直接利用偶次方的性质以及二次根式的性质得出m,n的值,进而得出答案.【解答】解:∵(m+3)2+=0,∴m=﹣3,n=﹣4,∴则==2.故选:C.【点评】此题主要考查了非负数的性质,正确得出m,n的值是解题关键.7.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米【分析】根据题意画出图形,构造出直角三角形,利用勾股定理求解.【解答】解:如图所示,过D点作DE⊥AB,垂足为E,∵AB=13,CD=8,又∵BE=CD,DE=BC,∴AE=AB﹣BE=AB﹣CD=13﹣8=5,∴在Rt△ADE中,DE=BC=12,∴AD2=AE2+DE2=122+52=144+25=169,∴AD=13(负值舍去),答:小鸟飞行的最短路程为13m.故选:A.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.8.已知m﹣=,则+m的值为()A.±B.C.±D.11【分析】把已知等式两边平方,利用完全平方公式化简,整理后利用平方根定义求出所求即可.【解答】解:把已知等式两边平方得:(m﹣)2=7,即m2+=9,∴(m+)2=m2++2=9+2=11,则+m=±,故选:A.【点评】此题考查了分式的加减法,平方根,以及算术平方根,熟练掌握运算法则是解本题的关键.9.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD 上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.【分析】在Rt△BAN中,根据勾股定理可求AN,进一步得到DN,再在Rt△MDN中,根据勾股定理可求CM的长.【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,BC=AD=10cm,在Rt△BAN中,AN==8cm,DN=10﹣8=2cm,在Rt△MDN中,CM2=22+(6﹣CM)2,解得CM=cm.故选:D.【点评】本题考查了矩形的性质、勾股定理、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)【分析】先找出被开方数的规律,然后再求得的位置即可.【解答】解:这组数据可表示为:①,,,,,②,,,,;…∵19×2=38,∴19÷5=3…4,∴为第4行,第4个数字.故选:B.【点评】本题主要考查的是数字的变化规律,找出其中的规律是解题的关键.二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围x≤.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得1﹣2x≥0,解得:x≤,故答案为:x≤.【点评】本题考查了二次根式的性质,二次根式中的被开方数必须是非负数,否则二次根式无意义.12.在▱ABCD中,∠A=70°,则∠C=70度.【分析】根据平行四边形的对角相等得出∠A=∠C,代入求出即可.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A=70°,∴∠C=70°,故答案为70.【点评】本题考查了平行四边形的性质,注意:平行四边形的对角相等.13.化简:=.【分析】根据二次根式化简解答即可.【解答】解:=,故答案为:.【点评】此题考查二次根式问题,关键是根据分母有理化解答.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为12.【分析】要求平行四边形的面积,只要根据勾股定理得出对角线垂直,进而解答即可.【解答】解:因为一个平行四边形的两邻边长分别为6和2,一条对角线长为8,因为:,所以此平行四边形为矩形,这个平行四边形的面积为6×,故答案为:12.【点评】本题考查了平行四边形的性质以及平行四边形的面积的求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.15.方程3x2﹣6=0的解是1=,2=﹣.【分析】利用直接开平方法解方程.【解答】解:3x2﹣6=0,x2=2,x=±,所以x1=,x2=﹣.故答案为x1=,x2=﹣.【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为(9,3).【分析】过点B作BD⊥OA于点D,由菱形的性质可求AB=OA=6,∠BAD=60°,利用锐角三角函数解直角三角形,可求AD,BD的长,即可求点B的坐标.【解答】解:如图:过点B作BD⊥OA于点D∵点A的坐标为(0,6),∴OA=6∵四边形OABC是菱形∴OA=AB=6,AB∥OC∴∠BAD=∠AOC=60°∵∠BAD=60°,BD⊥AO∴∠ABD=30°∴AD=AB=3,BD=AD=3∴OD=OA+AD=9∴点B坐标(9,3)故答案为:(9,3)【点评】本题考查了菱形的性质,坐标与图形的性质,添加恰当的辅助线构造直角三角形是本题的关键.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.【分析】利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.【解答】解:如图,过点A作AD⊥BC于点D,∵△ABC边AB=AC=5,BC=6,∴BD=DC=3,∴AD=4,如图①所示:四边形ACBD是矩形,则其对角线AB的长为5;如图②所示:AD=4,连接BC,过点C作CE⊥BD于点E,则EC=4,BE=2BD=6,∴BC=2;如图③所示:BD=3,由题意可得:AE =3,EC =2BE =8,∴AC ==,其中最长的对角线的值为.故答案为.【点评】此题主要考查了图形的剪拼以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.三、解答题(本大题共6个小题,共46分) 19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).【分析】(1)直接利用二次根式的乘除运算法则计算得出答案; (2)利用二次根式混合运算法则计算得出答案.【解答】解:(1)2×÷5=4×÷5=3÷5=;(2)(﹣2)2+2×(﹣)=6+12﹣12+10﹣=18﹣3.【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.【分析】根据题意可求OA=OB=DO,∠AOB=60°,可得∠BAD=90°,即结论可得.【解答】解:∵△AOB为等边三角形,∴∠BAO=60°=∠AOB,OA=OB,∵四边形ABCD是平行四边形,∴OB=OD,∴OA=OD,∴∠OAD=30°,∴∠BAD=30°+60°=90°,∴平行四边形ABCD为矩形.【点评】本题考查了矩形的性质,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.【分析】先计算x、y两个数的和、差、积;(1)利用平方差公式进行因式分解,然后代入求值;(2)变形为完全平方公式与积的差(或和)的形式,整体代入求值.【解答】解:由已知可得:x+y=4,x﹣y=2,xy=1(1)x2﹣y2=(x+y)(x﹣y)=4×2=8;(2)x2﹣2xy+y2﹣xy=(x﹣y)2﹣xy=(2)2﹣1=12﹣1=11.【点评】本题考查了二次根式的运算,完全平方公式的变形、平方差公式等知识点.题目难度不大,注意整体代入思想的运用.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.【分析】(1)由题意可证AP=PF,∠MAP=∠PAF=∠PFA=45°,即可证△PAM≌△PFN;(2)由勾股定理可求AF=3,由△PAM≌△PFN,可得AM=NF,即可得AM+AN=AF=3.【解答】证明:(1)∵四边形ABCD是矩形∴∠BAD=90°∵∠BAD的平分线AE与BC边交于点E,∴∠BAE=∠EAD=45°∵PF⊥AP∴∠PAF=∠PFA=45°∴AP=PF∵∠MPN=90°,∠APF=90°∴∠MPN﹣∠APN=∠APF﹣∠APN∴∠MPA=∠FPN,且AP=PF,∠MAP=∠PFA=45°∴△PAM≌△PFN(ASA)(2)∵PA=3∴PA=PF=3,且∠APF=90°∴AF==3∵△PAM≌△PFN;∴AM=NF∴AM+AN=AN+NF=AF=3【点评】本题考查了矩形的性质,全等三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.【分析】(1)根据=,利用数形结合的思想解决问题即可;(2)作边长为的正方形ABCD即可;(3)根据线段的垂直平分线的判定定理,先作出垂直平分线上的两点,构造直线即可【解答】解:(1)线段MN如图所示;(2)正方形ABCD如图所示;(3)线段EF的垂直平分线l如图所示;【点评】本题考查作图﹣应用与设计、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.【分析】(1)连接AC交BD于O,根据正方形的性质得到BD⊥AC,BO=DO,AO=CO,根据菱形的判定定理即可得到结论;(2)根据勾股定理得到BD=AC=,根据菱形的面积公式即可得到结论;(3)根据菱形的性质得到点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,根据勾股定理列方程即可得到结论.【解答】(1)证明:连接AC交BD于O,∵四边形ABCD是正方形,∴BD⊥AC,BO=DO,AO=CO,∵BF=DE=,∴OE=OF,∴四边形AECF是菱形;(2)解:∵四边形ABCD是边长为1的正方形,∴AB=AD=1,∴BD=AC=,∴EF=3,∴四边形AECF的面积=AC•EF=×3=3;(3)解:∵四边形AFCE是菱形,∴点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,则AC2﹣AN2=CN2=CF2﹣NF2,设AN=x,∴()2﹣x2=()2﹣(﹣x)2,解得:x=,∴MN=,∵CM2﹣MN2=AC2﹣AN2,∴CM2﹣()2=12﹣()2,解得:CM=,故PA+PM的最小值=.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,菱形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.。
2017-2018学年济宁市邹城市八年级下期中数学试卷(含答案解析)

2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣15.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.47.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米8.已知m﹣=,则+m的值为()A.±B.C.±D.119.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围.12.在▱ABCD中,∠A=70°,则∠C=度.13.化简:=.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为.15.方程3x2﹣6=0的解是.16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.【分析】根据最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是进行判断即可.【解答】解:A、是最简二次根式,正确;B、不是最简二次根式,错误;C、不是最简二次根式,错误;D、不是最简二次根式,错误;故选:A.【点评】本题考查最简二次根式的定义.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD【分析】根据对角线相等的平行四边形是矩形得出即可.【解答】解:添加AO=BO,理由是:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴▱ABCD为矩形,故选:C.【点评】本题考查矩形的判定、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣1【分析】根据各个选项中的式子,可以计算出正确的结果,本题得以解决.【解答】解:∵不能合并,故选项A错误;∵3+不能合并,故选项B错误;∵,故选项C正确;∵,故选项D错误;故选:C.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形【分析】根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF =GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.【解答】解:四边形EFGH是菱形.理由是:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,∴AC=BD,∵EF为△ABD的中位线,∴EF=BD,又GH为△BCD的中位线,∴GH=BD,∴GH=EF=BD,同理FG=EH=AC,∴EF=GH=FG=EH,∴四边形EFGH是菱形.故选:B.【点评】此题主要考查学生对菱形的判定、三角形中位线定理和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.4【分析】直接利用偶次方的性质以及二次根式的性质得出m,n的值,进而得出答案.【解答】解:∵(m+3)2+=0,∴m=﹣3,n=﹣4,∴则==2.故选:C.【点评】此题主要考查了非负数的性质,正确得出m,n的值是解题关键.7.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米【分析】根据题意画出图形,构造出直角三角形,利用勾股定理求解.【解答】解:如图所示,过D点作DE⊥AB,垂足为E,∵AB=13,CD=8,又∵BE=CD,DE=BC,∴AE=AB﹣BE=AB﹣CD=13﹣8=5,∴在Rt△ADE中,DE=BC=12,∴AD2=AE2+DE2=122+52=144+25=169,∴AD=13(负值舍去),答:小鸟飞行的最短路程为13m.故选:A.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.8.已知m﹣=,则+m的值为()A.±B.C.±D.11【分析】把已知等式两边平方,利用完全平方公式化简,整理后利用平方根定义求出所求即可.【解答】解:把已知等式两边平方得:(m﹣)2=7,即m2+=9,∴(m+)2=m2++2=9+2=11,则+m=±,故选:A.【点评】此题考查了分式的加减法,平方根,以及算术平方根,熟练掌握运算法则是解本题的关键.9.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.【分析】在Rt△BAN中,根据勾股定理可求AN,进一步得到DN,再在Rt△MDN中,根据勾股定理可求CM 的长.【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,BC=AD=10cm,在Rt△BAN中,AN==8cm,DN=10﹣8=2cm,在Rt△MDN中,CM2=22+(6﹣CM)2,解得CM=cm.故选:D.【点评】本题考查了矩形的性质、勾股定理、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)【分析】先找出被开方数的规律,然后再求得的位置即可.【解答】解:这组数据可表示为:①,,,,,②,,,,;…∵19×2=38,∴19÷5=3…4,∴为第4行,第4个数字.故选:B.【点评】本题主要考查的是数字的变化规律,找出其中的规律是解题的关键.二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围x≤.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得1﹣2x≥0,解得:x≤,故答案为:x≤.【点评】本题考查了二次根式的性质,二次根式中的被开方数必须是非负数,否则二次根式无意义.12.在▱ABCD中,∠A=70°,则∠C=70度.【分析】根据平行四边形的对角相等得出∠A=∠C,代入求出即可.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A=70°,∴∠C=70°,故答案为70.【点评】本题考查了平行四边形的性质,注意:平行四边形的对角相等.13.化简:=.【分析】根据二次根式化简解答即可.【解答】解:=,故答案为:.【点评】此题考查二次根式问题,关键是根据分母有理化解答.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为12.【分析】要求平行四边形的面积,只要根据勾股定理得出对角线垂直,进而解答即可.【解答】解:因为一个平行四边形的两邻边长分别为6和2,一条对角线长为8,因为:,所以此平行四边形为矩形,这个平行四边形的面积为6×,故答案为:12.【点评】本题考查了平行四边形的性质以及平行四边形的面积的求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.15.方程3x2﹣6=0的解是1=,2=﹣.【分析】利用直接开平方法解方程.【解答】解:3x2﹣6=0,x2=2,x=±,所以x1=,x2=﹣.故答案为x1=,x2=﹣.【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为(9,3).【分析】过点B作BD⊥OA于点D,由菱形的性质可求AB=OA=6,∠BAD=60°,利用锐角三角函数解直角三角形,可求AD,BD的长,即可求点B的坐标.【解答】解:如图:过点B作BD⊥OA于点D∵点A的坐标为(0,6),∴OA=6∵四边形OABC是菱形∴OA=AB=6,AB∥OC∴∠BAD=∠AOC=60°∵∠BAD=60°,BD⊥AO∴∠ABD=30°∴AD=AB=3,BD=AD=3∴OD=OA+AD=9∴点B坐标(9,3)故答案为:(9,3)【点评】本题考查了菱形的性质,坐标与图形的性质,添加恰当的辅助线构造直角三角形是本题的关键.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.【分析】利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.【解答】解:如图,过点A作AD⊥BC于点D,∵△ABC边AB=AC=5,BC=6,∴BD=DC=3,∴AD=4,如图①所示:四边形ACBD是矩形,则其对角线AB的长为5;如图②所示:AD=4,连接BC,过点C作CE⊥BD于点E,则EC=4,BE=2BD=6,∴BC=2;如图③所示:BD=3,由题意可得:AE=3,EC=2BE=8,∴AC==,其中最长的对角线的值为.故答案为.【点评】此题主要考查了图形的剪拼以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).【分析】(1)直接利用二次根式的乘除运算法则计算得出答案;(2)利用二次根式混合运算法则计算得出答案.【解答】解:(1)2×÷5=4×÷5=3÷5=;(2)(﹣2)2+2×(﹣)=6+12﹣12+10﹣=18﹣3.【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.【分析】根据题意可求OA=OB=DO,∠AOB=60°,可得∠BAD=90°,即结论可得.【解答】解:∵△AOB为等边三角形,∴∠BAO=60°=∠AOB,OA=OB,∵四边形ABCD是平行四边形,∴OB=OD,∴OA=OD,∴∠OAD=30°,∴∠BAD=30°+60°=90°,∴平行四边形ABCD为矩形.【点评】本题考查了矩形的性质,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.【分析】先计算x、y两个数的和、差、积;(1)利用平方差公式进行因式分解,然后代入求值;(2)变形为完全平方公式与积的差(或和)的形式,整体代入求值.【解答】解:由已知可得:x+y=4,x﹣y=2,xy=1(1)x2﹣y2=(x+y)(x﹣y)=4×2=8;(2)x2﹣2xy+y2﹣xy=(x﹣y)2﹣xy=(2)2﹣1=12﹣1=11.【点评】本题考查了二次根式的运算,完全平方公式的变形、平方差公式等知识点.题目难度不大,注意整体代入思想的运用.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.【分析】(1)由题意可证AP=PF,∠MAP=∠PAF=∠PFA=45°,即可证△PAM≌△PFN;(2)由勾股定理可求AF=3,由△PAM≌△PFN,可得AM=NF,即可得AM+AN=AF=3.【解答】证明:(1)∵四边形ABCD是矩形∴∠BAD=90°∵∠BAD的平分线AE与BC边交于点E,∴∠BAE=∠EAD=45°∵PF⊥AP∴∠PAF=∠PFA=45°∴AP=PF∵∠MPN=90°,∠APF=90°∴∠MPN﹣∠APN=∠APF﹣∠APN∴∠MPA=∠FPN,且AP=PF,∠MAP=∠PFA=45°∴△PAM≌△PFN(ASA)(2)∵PA=3∴PA=PF=3,且∠APF=90°∴AF==3∵△PAM≌△PFN;∴AM=NF∴AM+AN=AN+NF=AF=3【点评】本题考查了矩形的性质,全等三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.【分析】(1)根据=,利用数形结合的思想解决问题即可;(2)作边长为的正方形ABCD即可;(3)根据线段的垂直平分线的判定定理,先作出垂直平分线上的两点,构造直线即可【解答】解:(1)线段MN如图所示;(2)正方形ABCD如图所示;(3)线段EF的垂直平分线l如图所示;【点评】本题考查作图﹣应用与设计、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.【分析】(1)连接AC交BD于O,根据正方形的性质得到BD⊥AC,BO=DO,AO=CO,根据菱形的判定定理即可得到结论;(2)根据勾股定理得到BD=AC=,根据菱形的面积公式即可得到结论;(3)根据菱形的性质得到点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,根据勾股定理列方程即可得到结论.【解答】(1)证明:连接AC交BD于O,∵四边形ABCD是正方形,∴BD⊥AC,BO=DO,AO=CO,∵BF=DE=,∴OE=OF,∴四边形AECF是菱形;(2)解:∵四边形ABCD是边长为1的正方形,∴AB=AD=1,∴BD=AC=,∴EF=3,∴四边形AECF的面积=AC•EF=×3=3;(3)解:∵四边形AFCE是菱形,∴点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,则AC2﹣AN2=CN2=CF2﹣NF2,设AN=x,∴()2﹣x2=()2﹣(﹣x)2,解得:x=,∴MN=,∵CM2﹣MN2=AC2﹣AN2,∴CM2﹣()2=12﹣()2,解得:CM=,故PA+PM的最小值=.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,菱形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.。
山东省邹城市第四中学2017--2018学年八年级下学期期中考试语文试题(扫描版)

答案二、基础积累(12分)1.A .2.C.3.B. 4B5.(1)D.(2)略(印象1分,感受1分)三、古诗文积累与阅读(20分)6.D.7.B.8.(1) 小溪像北斗七星一样曲折,像蛇爬行那样弯曲,望过去一段看的见,一段看不见。
9.游人坐欹岩下望/以面受沫/乍若披丝。
10.乙文中作者用正、侧描写相结合的方法写出了瀑布的宏大雄伟(1分)。
“闻疾雷声,心悸”是侧面描写,“瀑行青壁间,撼山掉谷,喷雪直下”是正面描写。
11.示例: 绵绵春雨中,棟树开出淡紫色的花,格外娇艳。
(1分)南风轻轻吹拂,金黄的枇杷颗颗地满,挂在枝头(1分)12示例:“送”字运用拟人修辞,形象生动地写出了回家路上“莺啼”相伴的情景(1分),表达了诗人闲适愉悦的心情(1分)。
13.(1)窃究淑女,君子好逑。
(2) 白露未晞(3) 芳草鲜美(4)悠悠我心(5)气蒸云梦泽四、语言运用(4分)14 (1) 示例: 老字号迎来新的发展机遇。
(2) 示例: 尝一尝一品香的包子,那剔透的外形,鲜香的味道,让人垂涎欲滴。
五、现代文阅读(24 分)(一)15.本文主要从塞腰鼓表演的场面、声响、后生(表演人)、舞姿(每点1分,共4分) 四方面写出了安塞腰鼓的粗犷豪放、刚健雄浑的特点(1分)。
16.重读:“有力”“疾速”“大起大落”17.(1)江南流水更多地表现为柔媚的风格(1分),用江南的水更能衬托黄土高原的粗犷豪放,蕴含着无穷无尽的力量<1分)。
(2)“好一个安塞腰鼓”多次运用,形成反复咏叹,层层都有变化,把对腰鼓的赞颂之情步步推向高峰(1分),同时加强了散文的诗意美,使通篇具有形式的回环美和音乐的节奏美(1分)。
18.当鼓声停止后,人们仍沉浸在激情中,好像炽热后的沉寂,这时以“鸡啼”反衬(1分) 寂静,余音袅袅,给人留下无限的回味。
(1分)。
(二)19.文章通过描述西安植物园向日葵的美景和年轻爸妈向孩子讲向日葵名字的由来(1分),引出说明对象一一向口葵始终向阳的说法是错的。
邹城市2017-2018学年下学期八年级数学期中试卷及解析

邹城市2017-2018学年八年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.)1.下列二次根式是最简二次根式的是()A.B.C.D.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣15.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.47.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米8.已知m﹣=,则+m的值为()A.±B.C.±D.119.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围.12.在▱ABCD中,∠A=70°,则∠C=度.13.化简:=.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为.15.方程3x2﹣6=0的解是.16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.2017-2018学年山东省济宁市邹城市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中只有一项符合题目要求)1.下列二次根式是最简二次根式的是()A.B.C.D.【分析】根据最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是进行判断即可.【解答】解:A、是最简二次根式,正确;B、不是最简二次根式,错误;C、不是最简二次根式,错误;D、不是最简二次根式,错误;故选:A.【点评】本题考查最简二次根式的定义.最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等D.邻角互补【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.3.已知▱ABCD中,对角线AC,BD交于O点,如果能够判断▱ABCD为矩形,还需添加的条件是()A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD【分析】根据对角线相等的平行四边形是矩形得出即可.【解答】解:添加AO=BO,理由是:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴▱ABCD为矩形,故选:C.【点评】本题考查矩形的判定、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.4.下列计算正确的是()A.﹣=B.3+=3C.•=ab D.=﹣1【分析】根据各个选项中的式子,可以计算出正确的结果,本题得以解决.【解答】解:∵不能合并,故选项A错误;∵3+不能合并,故选项B错误;∵,故选项C正确;∵,故选项D错误;故选:C.【点评】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.E,F,G,H分别为矩形ABCD四边的中点,则四边形EFGH一定是()A.矩形B.菱形C.正方形D.非特殊的平行四边形【分析】根据矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,利用三角形中位线定理求证EF=GH=FG=EH,然后利用四条边都相等的平行四边形是菱形即可判定.【解答】解:四边形EFGH是菱形.理由是:连接BD,AC.∵矩形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,∴AC=BD,∵EF为△ABD的中位线,∴EF=BD,又GH为△BCD的中位线,∴GH=BD,∴GH=EF=BD,同理FG=EH=AC,∴EF=GH=FG=EH,∴四边形EFGH是菱形.故选:B.【点评】此题主要考查学生对菱形的判定、三角形中位线定理和矩形的性质的理解和掌握,证明此题的关键是熟练的利用三角形中位线定理,难度不大.6.若m,n为实数,(m+3)2+=0,则的值为()A.B.C.2D.4【分析】直接利用偶次方的性质以及二次根式的性质得出m,n的值,进而得出答案.【解答】解:∵(m+3)2+=0,∴m=﹣3,n=﹣4,∴则==2.故选:C.【点评】此题主要考查了非负数的性质,正确得出m,n的值是解题关键.7.如图,有一只小鸟从小树顶飞到大树顶上,它飞行的最短路程是()A.13米B.12米C.5米D.米【分析】根据题意画出图形,构造出直角三角形,利用勾股定理求解.【解答】解:如图所示,过D点作DE⊥AB,垂足为E,∵AB=13,CD=8,又∵BE=CD,DE=BC,∴AE=AB﹣BE=AB﹣CD=13﹣8=5,∴在Rt△ADE中,DE=BC=12,∴AD2=AE2+DE2=122+52=144+25=169,∴AD=13(负值舍去),答:小鸟飞行的最短路程为13m.故选:A.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.8.已知m﹣=,则+m的值为()A.±B.C.±D.11【分析】把已知等式两边平方,利用完全平方公式化简,整理后利用平方根定义求出所求即可.【解答】解:把已知等式两边平方得:(m﹣)2=7,即m2+=9,∴(m+)2=m2++2=9+2=11,则+m=±,故选:A.【点评】此题考查了分式的加减法,平方根,以及算术平方根,熟练掌握运算法则是解本题的关键.9.如图,把矩形纸片ABCD进行折叠,已知该纸片的长BC为10cm,宽AB为6cm,若折叠后C点落在边AD上的N点处,折痕为BM(M为折痕与CD边的交点),则CM的长为()A.3B.C.D.【分析】在Rt△BAN中,根据勾股定理可求AN,进一步得到DN,再在Rt△MDN中,根据勾股定理可求CM的长.【解答】解:∵四边形ABCD是矩形,∴AB=CD=6cm,BC=AD=10cm,在Rt△BAN中,AN==8cm,DN=10﹣8=2cm,在Rt△MDN中,CM2=22+(6﹣CM)2,解得CM=cm.故选:D.【点评】本题考查了矩形的性质、勾股定理、翻折变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.将一组数,2,,2,,…,2,按下列方式进行排列:①,2,,2,②2,,4,3,2…若的位置记为(1,3),2的位置记为(2,1),则这个数的位置记为()A.(5,4)B.(4,4)C.(4,5)D.(3,5)【分析】先找出被开方数的规律,然后再求得的位置即可.【解答】解:这组数据可表示为:①,,,,,②,,,,;…∵19×2=38,∴19÷5=3…4,∴为第4行,第4个数字.故选:B.【点评】本题主要考查的是数字的变化规律,找出其中的规律是解题的关键.二、填空题(本大题共8个小题,每小题3分,共24分)11.在实数范围内,若有意义,则x的取值范围x≤.【分析】根据二次根式的性质,被开方数大于或等于0,可以求出x的范围.【解答】解:根据题意得1﹣2x≥0,解得:x≤,故答案为:x≤.【点评】本题考查了二次根式的性质,二次根式中的被开方数必须是非负数,否则二次根式无意义.12.在▱ABCD中,∠A=70°,则∠C=70度.【分析】根据平行四边形的对角相等得出∠A=∠C,代入求出即可.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A=70°,∴∠C=70°,故答案为70.【点评】本题考查了平行四边形的性质,注意:平行四边形的对角相等.13.化简:=.【分析】根据二次根式化简解答即可.【解答】解:=,故答案为:.【点评】此题考查二次根式问题,关键是根据分母有理化解答.14.如果一个平行四边形的两邻边长分别为6和2,一条对角线长为8,则这个平行四边形的面积为12.【分析】要求平行四边形的面积,只要根据勾股定理得出对角线垂直,进而解答即可.【解答】解:因为一个平行四边形的两邻边长分别为6和2,一条对角线长为8,因为:,所以此平行四边形为矩形,这个平行四边形的面积为6×,故答案为:12.【点评】本题考查了平行四边形的性质以及平行四边形的面积的求法,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.15.方程3x2﹣6=0的解是x1=,x2=﹣.【分析】利用直接开平方法解方程.【解答】解:3x2﹣6=0,x2=2,x=±,所以x1=,x2=﹣.故答案为x1=,x2=﹣.【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程16.如图,已知菱形OABC的边OA在x轴上,∠AOC=60°,点A的坐标为(0,6),则点B的坐标为(9,3).【分析】过点B作BD⊥OA于点D,由菱形的性质可求AB=OA=6,∠BAD=60°,利用锐角三角函数解直角三角形,可求AD,BD的长,即可求点B的坐标.【解答】解:如图:过点B作BD⊥OA于点D∵点A的坐标为(0,6),∴OA=6∵四边形OABC是菱形∴OA=AB=6,AB∥OC∴∠BAD=∠AOC=60°∵∠BAD=60°,BD⊥AO∴∠ABD=30°∴AD=AB=3,BD=AD=3∴OD=OA+AD=9∴点B坐标(9,3)故答案为:(9,3)【点评】本题考查了菱形的性质,坐标与图形的性质,添加恰当的辅助线构造直角三角形是本题的关键.17.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是.【分析】根据正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,∴AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF===2,∴CH=,故答案为:.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.18.如图,在等腰三角形纸片ABC中,AB=AC=5,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则拼成的各种平行四边形中,其中最长的对角线的值为.【分析】利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.【解答】解:如图,过点A作AD⊥BC于点D,∵△ABC边AB=AC=5,BC=6,∴BD=DC=3,∴AD=4,如图①所示:四边形ACBD是矩形,则其对角线AB的长为5;如图②所示:AD=4,连接BC,过点C作CE⊥BD于点E,则EC=4,BE=2BD=6,∴BC=2;如图③所示:BD=3,由题意可得:AE=3,EC=2BE=8,∴AC==,其中最长的对角线的值为.故答案为.【点评】此题主要考查了图形的剪拼以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.三、解答题(本大题共6个小题,共46分)19.计算下列各题:(1)2×÷5;(2)(﹣2)2+2×(﹣).【分析】(1)直接利用二次根式的乘除运算法则计算得出答案;(2)利用二次根式混合运算法则计算得出答案.【解答】解:(1)2×÷5=4×÷5=3÷5=;(2)(﹣2)2+2×(﹣)=6+12﹣12+10﹣=18﹣3.【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.20.如图,▱ABCD的对角线AC和BD相交于点O,△OAB是等边三角形.求证:▱ABCD是矩形.【分析】根据题意可求OA=OB=DO,∠AOB=60°,可得∠BAD=90°,即结论可得.【解答】解:∵△AOB为等边三角形,∴∠BAO=60°=∠AOB,OA=OB,∵四边形ABCD是平行四边形,∴OB=OD,∴OA=OD,∴∠OAD=30°,∴∠BAD=30°+60°=90°,∴平行四边形ABCD为矩形.【点评】本题考查了矩形的性质,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.21.已知x=2+,y=2﹣,求下列各式的值:(1)x2﹣y2;(2)x2+y2﹣3xy.【分析】先计算x、y两个数的和、差、积;(1)利用平方差公式进行因式分解,然后代入求值;(2)变形为完全平方公式与积的差(或和)的形式,整体代入求值.【解答】解:由已知可得:x+y=4,x﹣y=2,xy=1(1)x2﹣y2=(x+y)(x﹣y)=4×2=8;(2)x2﹣2xy+y2﹣xy=(x﹣y)2﹣xy=(2)2﹣1=12﹣1=11.【点评】本题考查了二次根式的运算,完全平方公式的变形、平方差公式等知识点.题目难度不大,注意整体代入思想的运用.22.如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.(1)求证:△PAM≌△PFN;(2)若PA=3,求AM+AN的长.【分析】(1)由题意可证AP=PF,∠MAP=∠PAF=∠PFA=45°,即可证△PAM≌△PFN;(2)由勾股定理可求AF=3,由△PAM≌△PFN,可得AM=NF,即可得AM+AN=AF=3.【解答】证明:(1)∵四边形ABCD是矩形∴∠BAD=90°∵∠BAD的平分线AE与BC边交于点E,∴∠BAE=∠EAD=45°∵PF⊥AP∴∠PAF=∠PFA=45°∴AP=PF∵∠MPN=90°,∠APF=90°∴∠MPN﹣∠APN=∠APF﹣∠APN∴∠MPA=∠FPN,且AP=PF,∠MAP=∠PFA=45°∴△PAM≌△PFN(ASA)(2)∵PA=3∴PA=PF=3,且∠APF=90°∴AF==3∵△PAM≌△PFN;∴AM=NF∴AM+AN=AN+NF=AF=3【点评】本题考查了矩形的性质,全等三角形的性质和判定,勾股定理,熟练运用这些性质解决问题是本题的关键.23.如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点.请完成如图所示的画图,要求:①仅用无刻度的直尺,②不写画法,保留必要的画图痕迹.(1)在图1中画出一条长为的线段MN(M,N分别为格点)(2)在图2中画出一个以格点为顶点,以AB为一边的正方形ABCD;(3)在图3中,E,F分别为格点,画出线段EF的垂直平分线l.【分析】(1)根据=,利用数形结合的思想解决问题即可;(2)作边长为的正方形ABCD即可;(3)根据线段的垂直平分线的判定定理,先作出垂直平分线上的两点,构造直线即可【解答】解:(1)线段MN如图所示;(2)正方形ABCD如图所示;(3)线段EF的垂直平分线l如图所示;【点评】本题考查作图﹣应用与设计、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,且BF=DE=.连接AE,AF,CE,CF.(1)求证:四边形AECF是菱形;(2)求四边形AECF的面积;(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.【分析】(1)连接AC交BD于O,根据正方形的性质得到BD⊥AC,BO=DO,AO=CO,根据菱形的判定定理即可得到结论;(2)根据勾股定理得到BD=AC=,根据菱形的面积公式即可得到结论;(3)根据菱形的性质得到点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM =CM最小,过C作CN⊥AF于N,根据勾股定理列方程即可得到结论.【解答】(1)证明:连接AC交BD于O,∵四边形ABCD是正方形,∴BD⊥AC,BO=DO,AO=CO,∵BF=DE=,∴OE=OF,∴四边形AECF是菱形;(2)解:∵四边形ABCD是边长为1的正方形,∴AB=AD=1,∴BD=AC=,∴EF=3,∴四边形AECF的面积=AC•EF=×3=3;(3)解:∵四边形AFCE是菱形,∴点A与点C关于直线EF对称,连接CM交EF于P,则此时,PA+PM=CM最小,过C作CN⊥AF于N,则AC2﹣AN2=CN2=CF2﹣NF2,设AN=x,∴()2﹣x2=()2﹣(﹣x)2,解得:x=,∴MN=,∵CM2﹣MN2=AC2﹣AN2,∴CM2﹣()2=12﹣()2,解得:CM=,故PA+PM的最小值=.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,菱形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.。
山东省济宁市邹城四中八年级(下)期中物理试卷(2卷
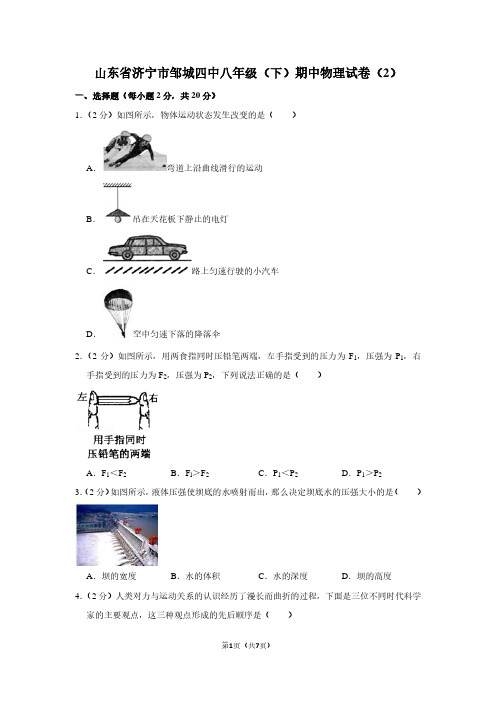
A.F1<F2
B.Fl>F2
C.P1<P2
D.P1>P2
3.(2 分)如图所示,液体压强使坝底的水喷射而出,那么决定坝底水的压强大小的是( )
A.坝的宽度
B.水的体积
C.水的深度
D.坝的高度
4.(2 分)人类对力与运动关系的认识经历了漫长而曲折的过程,下面是三位不同时代科学
家的主要观点,这三种观点形成的先后顺序是( )
聚乙烯
尼龙 66
塑料王
密度( kg/m3) 0.8×103
0.9×103
0.95×103
1.1×103
2.2×103
为了鉴别该小球究竟是由其中哪一种塑料制成的,某同学设计并进行了以下实验:
(1)把该小球放入盛有足够多酒精的量杯中,松手后,当小球处于平衡状态时,发现量杯
内的液面由 60ml 处升高到 90ml 处(已知酒精的密度是 0.8×103kg/m3),可知该小球的
D.用吸盘能将玻璃板提起是万有引力的作用
二、填空题(每空 1 分,共 12 分)
11.(4 分)停止蹬车后,行驶在水平路面上的自行车仍继续向前运动一段距离,这是因为
自行车具有
,自行车最后还会停下来,这是因为它受到
的缘故。若路面
光滑,自行车将一直做
运动,牛顿曾对此做过研究,并总结出
。
第3页(共7页)
12.(2 分)利用 U 形管液面高度差的大小关系,可以帮助我们比较一些物理量的大小。
C.B 球所受浮力大于 C 球所受浮力
D.三球所受浮力相等
10.(2 分)大气压与生产、生活、科研紧密相连,下面选项中,正确的是( )
A.做托里拆利实验,若有空气进入管内,则测出的大气压值比实际值大
山东省济宁市邹城县2017-2018学年八年级生物下学期期中试题(扫描版) 新人教版

山东省济宁市邹城县2017-2018学年八年级生物下学期期中试题
百度文库是百度发布的供网友在线分享文档的平台。
百度文库的文档由百度用户上传,需要经过百度的审核才能发布,百度自身不编辑或修改用户上传的文档内容。
网友可以在线阅读和下载这些文档。
百度文库的文档包括教学资料、考试题库、专业资料、公文写作、法律文件等多个领域的资料。
百度用户上传文档可以得到一定的积分,下载有标价的文档则需要消耗积分。
当前平台支持主流的doc(.docx)、.ppt(.pptx)、.xls(.xlsx)、.pot、.pps、.vsd、.rtf、.wps、.et、.dps、.pdf、.txt文件格式。
本文档仅用于百度文库的上传使用。
2017-2018学年山东省济宁市邹城市八年级(下)期中物理试卷(解析版)

2017-2018学年山东省济宁市邹城市八年级(下)期中物理试卷一、选择题(每小题2分,共20分,请把唯一正确答案的序号填在答题卡的表格中)1.(2分)关于交通规则中的系安全带的理由,你认为正确的是()A.系安全带是为了减小汽车和车内人员的惯性B.系安全带是为了增大汽车和车内人员的惯性C.系安全带可减小因汽车突然加速造成的人员伤害D.系安全带可减小因汽车突然减速造成的人员伤害2.(2分)如图所示,下列物体受力示意图中,处于平衡的物体是()A.B.C.D.3.(2分)如图,教室里悬挂的电灯处于静止状态,下列说法正确的是()A.电灯受到的重力与电灯对绳的拉力是一对平衡力B.电灯受到力的合力为零C.假如悬挂它的绳子突然断了,由于惯性,它将仍然保持静止D.假如悬挂它的绳子突然断了,由于惯性,它将做匀速直线运动4.(2分)下列事例中利用大气压强的是()A.护士给病人输液B.医生用听诊器给病人听诊C.用压力锅蒸煮进行医用消毒D.护士给病人注射肌肉针5.(2分)关于运动和力,以下说法中正确的是()A.给正在运动的物体再施加一个力,物体一定比原来运动得更快B.做匀速直线运动的物体一定不受力的作用C.匀速转弯的物体,可能不受力的作用D.只受重力作用的物体也可能向上运动6.(2分)如图,在做托里拆利实验时,若将玻璃管由竖直变成倾斜,则管内真空部分的长度()A.变大B.变小C.不变D.无法判定7.(2分)在图所示的装置中,不是利用连通器原理工作的是()A.①②B.③④C.②③D.②④8.(2分)同一个小球,先后放入四个盛有不同液体的容器中,静止时的位置如图所示,四个容器中的液面到容器底面的距离相等,则容器底面受到液体压强最小的是()A.B.C.D.9.(2分)一个小球,在水中悬浮。
如果把它放入酒精中,小球()A.一定会下沉B.一定会悬浮C.一定会漂浮D.条件不足,无法判断沉浮10.(2分)如图所示,三个完全相同的玻璃缸装满了水,其中(a)中只有水,(b)水中漂浮着只小鸭子,(c)水中漂浮着一只大鸭子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
邹城四中八年级下物理第二次阶段检测
(时间60分钟,共60分)
一、选择题 (每题2分,共20分)
1.如图所示的工具中,属于费力杠杆的是( )
2.如图所示,人对绳的自由端拉力F 都相等,且物体处于静止状态,不计滑轮重和摩擦,比较四个物体重力最大的是 ( ) A 、G 1 B 、G 2 C 、G 3 D 、G 4
3.如图所示,一个质量为50kg 的人,在10s 内连续向上跳12个台阶,已知每个台阶的高度为0.2m ,则这个人在这段时间内的功率是(g 取10N/kg
) ( )
A. 1200W
B. 10W
C. 12W
D. 120W
4.
下列说法正确的是 ( )
A .效率高的机械,功率一定大
B .做功时间长的机械,功率一定大
C .所有机械的机械效率都小于l
D .功率大的机械.做功一定多
5.放学后,某同学背着重40N 的书包沿水平路面走了200m ,又登上大约10m 高的四楼才回到家,则他在回家的过程中对书包所做的功约为( )
A 0J
B 400J
C 2019J
D 2400J
6题
6.如图所示,用力F 拉杠杆的A 点使它处在平衡状态。
图中F 1、F 2、 F 3、F 4表示力F 的四种不同方向,其中能使杠杆保持平衡的最小拉力为 ( )
A .F 1
B .F 2
C .F 3
D .F 4
7.用滑轮或滑轮组提起同一重物如图所示,其中 机械效率最高的是( )
8.在土耳其举行的举重世锦赛男子69公斤级比赛
中,我国选手廖辉最后一举顺利地举起了
198㎏的杠铃夺得冠军,如图所示是他在举重时的情形。
下列说法中正确的是( ) A .他将杠铃举高1.7m 做的功约为336.6J
B .他将杠铃举过头顶后静止了3s ,此过程中做的功约为3366J
C .他用3s 的时间将杠铃举高1.7m ,做功的功率约为1122W
D .不论是在举起杠铃的过程还是杠铃静止在头顶,他都做了功
9.如图所示,用动滑轮把一个物体匀速拉起,不计摩擦,则下列说法中正 确的( )
A .动滑轮的质量越大,机械效率越高
B .拉起的物体质量越大,机械效率越高
C .拉起物体的速度越大,机械效率越高
D .物体被拉起的越高,机械效率越高
10.某同学用自制的滑轮组来提起450N 的重物,如图,绳子自由端拉力F=200N ,重物以0.2m/s 的速度匀速上升10s ,不考虑绳重和摩擦,则拉力做功功率和该滑轮组的机械效率分别等于( )
A.120W, 80%
B.100W, 75%
C.120W, 75%
D.100W, 80% 二、填空题(每空1分,共10分)
11.“糖枣”是邹城的美食。
图示筷子夹“糖枣”的情景,此时筷子是
杠杆(填“省力”、“费力”或“等臂”)。
12.用如图所示的滑轮组提起重力为1200N 的物体,若不考虑摩擦、绳和动滑轮的重力,则拉力F 是_________N ;若实际作用在绳端的拉力是500N ,此时滑轮组的机械效率是_________。
13.上海自主研发了一种氢燃料汽车,它使用氢气代替汽油。
在一次测试中,汽车 在水平路面受到2400N 的水平牵引力,5min 内匀速直线行驶了9000m 。
这段时 间汽车牵引力所做的功为 J ,牵引力的功率是 W 。
14.起重机将重为N 1063
⨯的货物匀速提升10m ,它的电动机做的总功J 1025.15⨯,
起重机匀速提升货物做的有用功为 J ,机械效率为 .对于实际机械,机 械效率总小于100%的原因是 . 15. 小柯积极参加体育锻炼。
图甲所示为小柯初学俯卧撑时的姿势,他
的身体可作为一个杠杆,O 点是支点。
他的质量为60 kg ,所受重力 可视为集中在A 点。
将身体撑起时,地面对双手的支持力至少 N 。
若撑起时肩部上升0.4 m ,他至少要做功 J 。
(取g=10N/kg )
三、作图与实验题(16题3分,17题3分,18题10分,19题8分,共24分)
16.如图,O 点为直杠杆AB 的支点,要求在A 点用一个最小的力F 使杠杆处于静止状态,请画出该力F ,并做出阻力臂。
17.用滑轮组提升重物,请在下图中画出绳子的绕法,使提升重物最省力,。
18.在“研究杠杆平衡条件”的实验中。
(1)把杠杆挂在支架上,实验前没有挂钩码时,发现杠杆右端下倾,可将右端螺母向_____边旋转,使杠杆在水平位置平衡.(填“左”或“右”) (2)杠杆上每格距离相等,调节好杠杆后,在杠杆左边离支点2格的A 处挂了3个钩码,如图所示,为使杠杆在水平位置平衡,请你在杠杆右边挂上钩码(用一种方法).你的方法是__________________________。
(3)实验中得到两组数据如表所示:
实验序号 动力1F /N
动力臂
1l /m
阻力2F /N
阻力臂
2l /m
A. 钢丝钳
B. 起子 C 羊角锤. D.镊子
7题
10题
1 1 0.
2 6 0.1
2 2 0.4 4 0.2
这两组数据中,实验序号为__________的一组数据肯定有错误。
经检查,发现是测量动力臂时读错了,动力臂应该是___________ m。
(4)通过实验探究应该得出的结论是________________________________。
19.在“测定动滑轮机械效率”的实验中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,正确操作,实验数据如下:
(1)实验时,用手拉动弹簧测力计,使持在动滑轮下的钩码缓缓上升.
(2)第①次实验时测得动滑轮的机械效率为.
(3)第③次实验时,钩码上升的速度为0.05m/s,则拉力的功率为 W.
(4)由表中实验数据分析可知,同一动滑轮,所提升物重增大,机械效率
将(选填“增大”、“减小”或“不变”)
四、计算题(共6分)
20.邹城市在城市环境治理工程中,推土机发挥了重要作用.如图是某型号履带式推土机,其发动机的额定功率为15kW,质量为2.0×104kg,履带与地面的总接触面积为2.5m2.
(取g = 10N/kg)求:
(1)推土机静止时对水平地面的压强;
(2)若推土机在平直场地上以额定功率作业,在其以1.5m/s的速度
匀速前进15m的过程中,牵引力所做的功和它受到的阻力.。
