2020年八下平行四边形1.2平行四边形的判定复习
数学 八下 平行四边形的性质和判定

3.如图,在三角形ABC中,BD平分角ABC,DE平行于BC 交AB于点E,EF平行于AC于点F。试说明BE和CF的数量 关系,并说明理由。
4. 如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在 CD,AB的延长线上,且AE=AD,CF=CB . (1)求证:四边形AFCE是平行四边: (2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗? 若成立,请写出证明,若不成立,请说明理由。
初中数学八年级下册
平行四边形的性质和判定
习课
一、平行四边形知识结构及要点小结 平行四边形定义:有两组对边分别平行的四边形是平行四边 形。 性质:
1.平行四边形的两组对边分别平行。(定义) 2.平行四边形的两组对边分别相等。 3.平行四边形的两组对角分别相等。 4.平行四边形的两条对角线互相平分。
5.把两个全等的不等边三角形拼成平行四边形,可拼成的不同的
平行四边形的个数是
个。
6.平面上有不在同一直线上的三个点A、B、C,以这三个点为
顶点的平行四边形有
个。
7.如图,AD是△ABC的中线,求证:AB+AC>2AD
A
B
C
D
8.如图,在等腰△ABC中,AB=AC,点D是BC上一点,DE∥AC交AB于 点E,DF∥AB交AC于点F,解答下列问题: ①如图1,当点D在BC上时,有DE+DF=AB,请你说明理由。 ②如图2,当点D在BC的延长线上时,请你参考图1画出正确的图形, 写出DE,DF,AB之间的关系,并写出证明过程。
二、习题讲解
1.如图,四边形ABCD是平行四边形过点A的直线分别交 CD,CB的延长线于E,F点,且∠EAD=∠BAF. (1)判断△CEF的形状,并说明理由; (2)△CEF的哪两条边之和恰好等于平行四边形ABCD的周 长?为什么?
人教版八年级下册18.1.2平行四边形的判定(教案)

2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如使用直尺和量角器测量图形,以演示平行四边形判定方法的基本原理。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
在讲授过程中,我尽量用生动的语言和实际案例来解释抽象的判定方法,希望能让学生更好地理解。通过分组讨论和实验操作,我看到了学生们积极参与的热情,他们在交流中碰撞出思维的火花,这让我感到很欣慰。但同时,我也注意到有些学生在面对复杂问题时还是显得有些迷茫,这说明我在教学中还需要更加细致和耐心。
我意识到,在今后的教学中,应该更加注重以下几个方面:
此外,我还发现有些学生在小组讨论中表现较为内向,不善于表达自己的观点。在今后的教学中,我会更多地关注这些学生,鼓励他们大胆地说出自己的想法,提高他们的自信心。
三、教学难点与重点
1.教学重点
-核心内容:平行四边形的判定方法及其应用。
-重点讲解:
a.有一组对边平行且相等的四边形是平行四边形。
b.有两组对边分别平行的四边形是平行四边形。
c.有两组对角分别相等的四边形是平行四边形。
d.对角线互相平分的四边形是平行四边形。
-举例:通过图形示例,强调在给定条件下如何识别平行四边形,如在一个四边形中,若能证明一组对边平行且相等,即可判定该四边形为平行四边形。
-举例解释:
-难点a:在讲解“对角线互相平分的四边形是平行四边形”这一判定方法时,学生可能难以理解对角线平分与平行四边形之间的关系。教师可以通过画图或动画演示,让学生直观看到对角线平分后的四边形如何满足平行四边形的性质。
-难点b:学生在面对复杂图形时,可能难以找到合适的判定方法。例如,一个四边形给定了多个角度或边长信息,学生需要识别哪些信息是有用的,哪些是干扰项。教师可以通过典型例题的讲解,指导学生如何筛选信息,如何选择合适的判定方法。
最新八下平行四边形所有知识点总结和常考题型练习题

平行四边形知识点一、四边形相关1、四边形的内角和定理及外角和定理四边形的内角和定理:四边形的内角和等于360°。
四边形的外角和定理:四边形的外角和等于360°。
推论:多边形的内角和定理:n 边形的内角和等于∙-)2(n 180°; 多边形的外角和定理:任意多边形的外角和等于360°。
2、多边形的对角线条数的计算公式设多边形的边数为n ,则多边形的对角线条数为2)3(-n n 。
3.三角形中位线定理:三角形的中位线平行第三边,并且等于它的一半. 二、平行四边形1.定义:两组对边分别平行的四边形是平行四边形.平行四边形的定义既是平行四边形的一条性质,又是一个判定方法.2.平行四边形的性质:平行四边形的有关性质和判定都是从 边、角、对角线 三个方面的特征进行简述的.(1)角:平行四边形的对角相等,邻角互补; (2)边:平行四边形两组对边分别平行且相等; (3)对角线:平行四边形的对角线互相平分;(4)面积:①S ==⨯底高ah ; ②平行四边形的对角线将四边形分成4个面积相等的三角形. 3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形 ②方法1:两组对边分别相等的四边形是平行四边形 ③方法2:一组对边平行且相等的四边形是平行四边形 ④方法3:两组对角分别相等的四边形是平行四边形 ⑤方法4: 对角线互相平分的四边形是平行四边形 三、矩形1. 矩形定义:有一个角是直角的平行四边形是矩形。
2. 矩形性质①边:对边平行且相等; ②角:对角相等、邻角互补,矩形的四个角都是直角; ③对角线:对角线互相平分且相等; ④对称性:轴对称图形(对边中点连线所在直线,2条). 3. 矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形; ②对角线相等的平行四边形; ③四个角都相等 识别矩形的常用方法① 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的任意一个角为直角. ② 先说明四边形ABCD 为平行四边形,再说明平行四边形ABCD 的对角线相等. ③ 说明四边形ABCD 的三个角是直角. 4. 矩形的面积① 设矩形ABCD 的两邻边长分别为a,b ,则S 矩形=ab . 四、菱形1. 菱形定义:有一组邻边相等的平行四边形是菱形。
专题03《平行四边形》期末挑重点之2020-2021下学期年八年级数学(人教版)(原卷版)
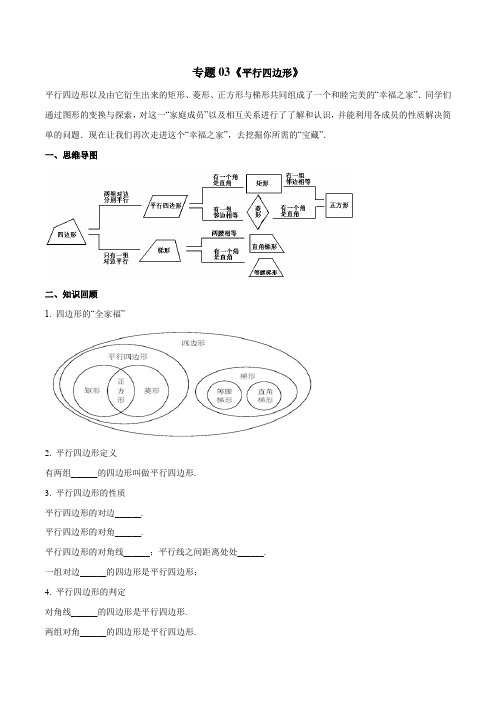
专题03《平行四边形》平行四边形以及由它衍生出来的矩形、菱形、正方形与梯形共同组成了一个和睦完美的“幸福之家”.同学们通过图形的变换与探索,对这一“家庭成员”以及相互关系进行了了解和认识,并能利用各成员的性质解决简单的问题.现在让我们再次走进这个“幸福之家”,去挖掘你所需的“宝藏”.一、思维导图二、知识回顾1. 四边形的“全家福”2. 平行四边形定义有两组______的四边形叫做平行四边形.3. 平行四边形的性质平行四边形的对边______.平行四边形的对角______.平行四边形的对角线______;平行线之间距离处处______.一组对边______的四边形是平行四边形;4. 平行四边形的判定对角线______的四边形是平行四边形.两组对角______的四边形是平行四边形.一组对边______的四边形是平行四边形.两组对边______的四边形是平行四边形.连接三角形两边中点的线段,叫做三角形的______.三角形的中位线平行于______,并且等于它的______.5. 矩形有一个角是______的平行四边形是矩形.矩形的四个内角都是______,对角线______且______;直角三角形斜边上的中线等于斜边的___. 对角线______的平行四边形是矩形,有三个角是______的四边形是矩形.6. 菱形有一组邻边______的平行四边形,叫做菱形.菱形的四条边都______,菱形的两条对角线______,并且每一条对角线平分每一组______.四条边______的四边形是菱形.7. 正方形正方形是______的菱形;正方形是______的矩形.三、中考链接考点1:平行四边形的性质例1(2020·湖南邵阳)如图,四边形ABCD 是平行四边形,点E ,B ,D ,F 在同一条直线上,请添加一个条件使得ABE CDF △≌△,下列不正确...的是( )A .AE CF =B .AEB CFD ∠=∠C .EAB FCD ∠=∠ D .BE DF =【答案】A 【分析】根据平行四边形的性质结合全等三角形的判定,逐项进行判断即可.【解析】∵四边形ABCD 是平行四边形,∴AB=CD ,AB ∥CD ,∴∠ABD=∠BDC ,∵∠ABE+∠ABD=∠BDC+∠CDF ,∴∠ABE=∠CDF ,A.若添加AE CF =,则无法证明ABE CDF △≌△,故A 错误;B.若添加AEB CFD ∠=∠,运用AAS 可以证明ABE CDF △≌△,故选项B 正确;C.若添加EAB FCD ∠=∠,运用ASA 可以证明ABE CDF △≌△,故选项C 正确;D.若添加BE DF =,运用SAS 可以证明ABE CDF △≌△,故选项D 正确.故选:A .【名师点睛】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是准确寻找全等三角形解决问题,属于中考常考题型.考点2:平行四边形的判定例2(2020·湖南衡阳)如图,在四边形ABCD 中,AC 与BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是( )A .AB ∥DC ,AB =DC B .AB =DC ,AD =BC C .AB ∥DC ,AD =BC D .OA=OC ,OB =OD【答案】C【分析】根据平行四边形的判定方法逐项分析即可.【解析】A. ∵ AB ∥DC ,AB =DC ,∴四边形ABCD 是平行四边形;B. ∵ AB =DC ,AD =BC ,∴四边形ABCD 是平行四边形;C.等腰梯形ABCD 满足 AB ∥DC ,AD =BC ,但四边形ABCD 是平行四边形;D. OA=OC ,OB =OD ,∴四边形ABCD 是平行四边形;故选C.【名师点睛】本题主要考查了平行四边形的判定,平行四边形的判定方法有:①两组对边分别平行的四边形是平行四边形;②一组对边平行且相等的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤.两组对角分别相等的四边形是平行四边形. 考点3:三角形中位线定理例3(2020·内蒙古赤峰)如图,在△ABC 中,点D ,E 分别是边AB ,AC 的中点,点F 是线段DE 上的一点连接AF ,BF ,∠AFB =90°,且AB=8,BC= 14,则EF 的长是 ( )A .2B .3C .4D .5【答案】B【分析】根据直角三角形的性质得到DF=4,根据BC= 14,由三角形中位线定理得到DE=7,解答即可.【解析】∵∠AFB=90°,点D 是AB 的中点,∴DF=12AB=4, ∵BC= 14,D 、E 分别是AB ,AC 的中点,∴DE=12BC=7,∴EF=DE -DF=3,故选:B 【名师点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.考点4:矩形的性质例4(2020·贵州毕节)如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别是AO ,AD 的中点,连接EF ,若6AB cm =,8BC cm =,则EF 的长是( )A .2.2cmB .2.3cmC .2.4cmD .2.5cm【答案】D 【分析】由勾股定理求出BD 的长,根据矩形的性质求出OD 的长,最后根据三角形中位线定理得出EF 的长即可.【解析】∵四边形ABCD 是矩形,∴∠ABC=90°,AC=BD ,OA=OC=OD=OB ,∵6AB cm =,8BC cm =,∴10cm = ∴BD=10cm ,∴152OD BD cm ==, ∵点E ,F 分别是AO ,AD 的中点,∴115 2.522EF OD cm ==⨯=.故选:D . 【名师点睛】本题考查矩形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握基本知识. 考点5:菱形的性质例5(2020·江苏无锡)如图,在菱形ABCD 中,50B ∠=︒,点E 在CD 上,若AE AC =,则BAE ∠=__________.【答案】115°【分析】先根据菱形性质求出∠BCD ,∠ACE ,再根据AE AC =求出∠AEC ,最后根据两直线平行,同旁内角互补解题即可.【解析】四边形ABCD 是菱形,50B ∠=︒,∴AB ∥CD ,∴∠BCD=180°-∠B=130°,∠ACE=12∠BCD=65°, ∵ AE AC =,∴∠ACE=∠AEC=65°,∴∠BAE=180°-∠AEC=115°.【名师点睛】本题考查了菱形性质,等腰三角形性质,解题方法较多,根据菱形性质求解∠ACE 是解题关键.考点6:菱形的判定例6(2020·内蒙古通辽)如图,AD 是ABC 的中线,四边形ADCE 是平行四边形,增加下列条件,能判断ADCE 是菱形的是( )A .90BAC ∠=︒B .90DAE ∠=︒C .AB AC =D .AB AE =【答案】A 【分析】根据菱形的判定方法逐一分析即可.【解析】A 、若90BAC ∠=︒,则AD=BD=CD=AE ,∵四边形ADCE 是平行四边形,则此时四边形ADCE 为菱形,故选项正确;B 、若90DAE ∠=︒,则四边形ADCE 是矩形,故选项错误;C 、若AB AC =,则∠ADC=90°,则四边形ADCE 是矩形,故选项错误;D 、若AB AE =,而AB >AD ,则AE≠AD ,无法判断四边形ADCE 为菱形,故选项错误.故选A.【名师点睛】本题考查了菱形的判定,还涉及到平行四边形的性质,矩形的判定,等腰三角形的性质,解题的关键是掌握判定定理.考点7:正方形的性质例7(2020·内蒙古呼和浩特)如图,正方形ABCD ,G 是BC 边上任意一点(不与B 、C 重合),DE AG ⊥于点E ,//BF DE ,且交AG 于点F .(1)求证:;(2)四边形BFDE 是否可能是平行四边形,如果可能请指出此时点G 的位置,如不可能请说明理由.AF BF EF -=【答案】(1)见解析;(2)不可能,理由见解析.【分析】(1)证明△ABF≌△DAE,从而得到AF=DE,AE=BF,可得结果;(2)若要四边形BFDE是平行四边形,则DE=BF,则∠BAF=45°,再证明∠BAF≠45°即可.【解析】(1)证明:∵正方形ABCD,∴AB=AD,∠BAF+∠DAE=90°,∵DE⊥AG,∴∠DAE+∠ADE=90°,∴∠ADE=∠BAF,BF DE,∴∠BFA=90°=∠AED,∴△ABF≌△DAE(AAS),又∵//-=-=;∴AF=DE,AE=BF,∴AF BF AF AE EF(2)不可能,理由是:如图,若要四边形BFDE是平行四边形,已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,∵DE=AF,∴BF=AF,即此时∠BAF=45°,而点G不与B和C重合,∴∠BAF≠45°,矛盾,∴四边形BFDE不能是平行四边形.【名师点睛】本题考查了全等三角形的判定和性质,正方形的性质,平行四边形的性质,解题的关键是找到三角形全等的条件.第18章平行四边形达标检测一、选择题(每题3分,共30分)1.下列条件中,不能判定四边形为平行四边形是()A. 一组对边平行,另一组对边相等B. 一组对边平行且相等C. 两组对边分别平行D. 对角线互相平分2.给出平面上不在同一直线上的三个点,则以此三点为顶点的平行四边形有()A.1个B.2个C.3个D4个3. 已知□ABCD中,∠A+∠C=200°,则∠B的度数是()A.100° B.160° C.80° D.60°4.(2020·湖南湘西)下列说法中,不正确...是()A.对角线互相平分的四边形是平行四边形B.两组对角分别相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.一组对边平行另一组对边相等的四边形是平行四边形5.(2020·江苏南通)下列条件中,能判定▱ABCD是菱形的是()A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD6.如图,如果□ABCD的对角线AC和BD相交于点O,那么图中全等的三角形共有()A.1对B.2对C.3对D.4对7.(2020·山东滨州)下列命题是假命题的是()A.对角线互相垂直且相等的平行四边形是正方形.B.对角线互相垂直的矩形是正方形.C.对角线相等的菱形是正方形.D.对角线互相垂直平分的四边形是正方形.8.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则DAE等于()A. 15°B. 30°C. 45°D. 60°9.如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为()A.20 B.18 C.16 D.1510.(2020·山东菏泽)如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A .互相平分B .相等C .互相垂直D .互相垂直平分二、填空题(每题3分,共30分)11.已知在□ABCD 中,AB =14cm ,BC =16cm ,则此平行四边形的周长为 cm .12.(2020·黑龙江)如图,在四边形ABCD 中,AD//BC ,在不添加任何辅助线的情况下,请你添加一个条件____,使四边形ABCD 是平行四边形(填一个即可).13.如图,正方形ABCD 的对线AC 、BD 相交于点O .那么图中共有 个等腰直角三角形.14. (2020·内蒙古)如图,在平行四边形ABCD 中,2,AB ABC =∠的平分线与BCD ∠的平分线交于点E ,若点E 恰好在边AD 上,则22BE CE +的值为______.15. (2020•无锡)如图,在菱形ABCD 中,∠B =50°,点E 在CD 上,若AE =AC ,则∠BAE = °.16.如图,□ABCD 中,AE 平分∠BAD ,AD =6cm,AB =9cm,则CE =________cm .17. (2020·江苏徐州)如图,在Rt ABC ∆中,90ABC ∠=︒,D 、E 、F 分别为AB 、BC 、CA 的中点,若5BF =,则DE =_______.18. 我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形......现有一个对角线分别为6cm 和8cm 的菱形,它的中点四边形的对角线长是 .19. (2020·浙江金华)如图,平移图形M ,与图形N 可以拼成一个平行四边形,则图中α的度数是______°.20.如图,l 是四边形ABCD 的对称轴,如果AD ∥BC ,有下列结论: (1)AB ∥CD ;(2)AB=CD ;(3)AB ⊥BC ;(4)AO=OC .其中正确的结论是 .(把你认为正确的结论的序号都填上)三、解答题(共60)21. (6分)(2020·山东济南)如图,在▱ABCD 中,对角线 AC ,BD 相交于点 O ,过点 O 的一条直线分别交 AD ,BC 于点 E ,F .求证:AE=CF .22. (6分)(2020·四川自贡)如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.求证: .23. (6分)如图12, □ABCD 中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG ,∠DGE =100°.(1)试说明DF=BG ;(2)试求AFD ∠的度数.24. (6分)(2020·湖南娄底)如图,ABCD 中,2BC AB =,AB AC ⊥,分别在边BC 、AD 上的点E 与点F 关于AC 对称,连接EF 、AE 、CF 、DE .(1)试判定四边形AECF 的形状,并说明理由;(2)求证:AE DE ⊥25. (8分)先阅读下面的题目及解题过程,再根据要求回答问题.如图,在□ABCD 中,∠BAD 的平分线与BC 边相交于点E ,∠ABC 的平分线与AD 边相交于点F ,AE 与BF 相交于O ,试说明四边形ABEF 是菱形.解:①∵四边形ABCD 是平行四边形,ABCD E BC F CD CE DF =AE BF M AE BF=A BC D 图1 ②∴AD ∥BC ,③∠ABE +∠BAF =1800,④∵AE ,BF 分别是∠BAF ,∠ABE 的平分线,⑤∴∠1=∠2=∠BAF ,∠3=∠4=∠ABE , ⑥∴∠1+∠3=(∠BAF +∠ABE )=900 ⑦∴∠AOB =900⑧∴AE ⊥BF⑨∴四边形ABEF 是菱形.(1)上述解题过程是 否正确?________.(2)如有错误,在第___步到第___步推理错误,应在第_____步后添加如下步骤:________.26. (8分)如图1,有一张菱形纸片ABCD ,AC =8,BD =6.(1)请沿着AC 剪一刀,把它分成两部分,把剪开的两部分分拼成一个平行四边形,在图2中用实线画出你所拼成的平行四边形;若沿着BD 剪开,请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边形的周长.(2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4中用实线画出拼成的平行四边形.(注:上述所画的平行四边形都不能与原菱形全等)27.(10分)(2020·四川遂宁)如图,在△ABC 中,AB =AC ,点D 、E 分别是线段BC 、AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:△BDE ≌△F AE ;(2)求证:四边形ADCF 为矩形.212121 A B C D 图3 周长________ A B C D 图4 A B C D 图2周长________28.(10分)(2020·浙江嘉兴)在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF 拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE (如图4).(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.。
2020--2021学年人教版八年级数学下册第18章:平行四边形的性质与判定 (1)

平行四边形(第一讲:性质与判定)[知识点梳理与例题讲解]一、平行四边形定义1、平行四边形:两组对边分别平行的四边形叫做平行四边形(如图),记作“□ABCD ”。
2、平行四边形的表示:一般按一定的方向依次 表示各顶点,如上图的平行四边形不能表示成□ACBD ,也不能表示成□ADBC 。
二、平行四边形的性质1、平行四边形的对边平行且相等;2、平行四边形相邻的角互补,对角相等;3、平行四边形的对角线互相平分;4、平行四边形是中心对称图形,对称中心是对角线的交点;5、四个相等,四组全等:DOA DOC BOC AOB S S S S ∆∆∆∆===COD AOB ∆≅∆;COB AOD ∆≅∆;CDA ABC ∆≅∆;DAB BCD ∆≅∆. 常用点:(1)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段的中点是对角线 的交点,并且这条直线二等分此平行四边形的面积。
(2)推论:夹在两条平行线间的平行线段相等。
[例1]如图,在□ABCD 中,已知AD =8cm ,AB =6cm ,DE 平分∠ADC 交BC 边于点E ,则BE 等于_________cm 。
[例2]如图,□ABCD 中,AC ,BD 为对角线,BC =6,BC 边上的高为4,则阴影部分的面积为________.[例3](1)已知□ABCD 的周长为60cm,对角线AC、BD 相交于O 点,△AOB 的周长比△BOC 的周长多8cm,则AB 的长度为_________cm。
⑵已知△ABC,若存在点D 使得以A、B、C、D 为顶点的四边形是平行四边形,这样的点D 有______个。
⑶接上题,若已知△ABC 的周长为3,则以所有D 点围成的多边形周长为________。
[例4]如图,在□ABCD 中,E、F 是对角线BD 上的两个点且DF=BE,试猜想AE 与CF 有何数量关系及位置关系并加以证明。
[例5]如图,当点 E、F 分别在线段BD、DB 的延长线上时,仍有DF=BE,此时AE 与CF 的数量关系及位置关系有变化吗?[例6](1)如图,□ABCD 中,平行于边的两条线段EF,GH 把□ABCD 分成四部分,分别记这四部分的面积为S1、S2、S3 和S4,这下列等式一定成立的是( )A.S1=S3 B.S1+S3=S2+S4C.S3-S1=S2-S4 D.S1×S3=S2×S4(2)如图,□ABCD 中,P 是中间任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1、S2、S3、S4,则一定成立的是( )A.S1+S2>S3+S4 B.S1+S2=S3+S4C.S1+S2<S3+S4 D.S1+S3=S2+S4三、平行四边形的判定(1)定义:两组对边分别平行的四边形是平行四边形;(2)定理1:两组对角分别相等的四边形是平行四边形;(3)定理2:两组对边分别相等的四边形是平行四边形;(4)定理3:对角线互相平分的四边形是平行四边形;(5)定理4:一组对边平行且相等的四边形是平行四边形。
期末考前复习第六章《平行四边形》高频考点分类精准练2020-2021学年北师大版八年级下册数学

北师大版八年级下册数学期末考前复习《平行四边形》高频考点分类精准练题型一:平行四边形的性质和判定1.如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )A.∠B=∠FB.∠B=∠BCFC.AC=CFD.AD=CF2.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )A.6B.8C.10D.123.如图,在▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=度.4.如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是.5.平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.6.如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为S,四边形AEDF的面积为T,求的值.题型二:三角形中位线定理1.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50 m,则AB的长是m.2.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC 的周长是 ( )A.6B.12C.18D.243.如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E,F分别为MB,BC 的中点,若EF=1,则AB=.4.如图,▱ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为.题型三:多边形的内角和与外角和1.下列图形为正多边形的是( )2.正十边形的外角和为 ( )A.180°B.360°C.720°D.1 440°3.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是 ( )A.12B.13C.14D.154.八边形的内角和为°.5.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是.6.乐乐和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中!请仔细观察下面的图形和表格,并回答下列问题:(1)观察探究.请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①;②.(2)实际应用.数学社团共分为6个小组,每组有3名同学.同学们约定,大年初一时不同组的两位同学之间要打一个电话拜年,请问,按照此约定,数学社团的同学们一共将拨打电话多少个?(3)类比归纳.乐乐认为(1),(2)之间存在某种联系,你能找到这两个问题之间的联系吗?请用语言描述你的发现.7.已知如图,四边形ABCD中,BE,DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.(1)如图1,说明∠MBC+∠NDC=α+β.(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α,β所满足的等量关系式.(3)如图2,若α=β,判断BE,DF的位置关系,并说明理由.北师大版八年级下册数学期末考前复习《平行四边形》高频考点分类精准练(解析版)题型一:平行四边形的性质和判定1.如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( B)A.∠B=∠FB.∠B=∠BCFC.AC=CFD.AD=CF2.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 ( B)A.6B.8C.10D.123.如图,在▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=61度.4.如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是10或4或2.5.平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.证明:连接AC,如图所示:在△ABC和△CDA中,∴△ABC≌△CDA(SSS),∴∠BAC=∠DCA,∠ACB=∠CAD,∴AB∥CD,BC∥AD,∴四边形ABCD是平行四边形. 6.如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为S,四边形AEDF的面积为T,求的值.略题型二:三角形中位线定理1.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50 m,则AB的长是100m.2.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC 的周长是 ( B)A.6B.12C.18D.243.如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E,F分别为MB,BC 的中点,若EF=1,则AB=4.4.如图,▱ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为16.题型三:多边形的内角和与外角和1.下列图形为正多边形的是( D)2.正十边形的外角和为 ( B )A.180°B.360°C.720°D.1 440°3.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是 ( C)A.12B.13C.14D.154.八边形的内角和为 1 080°.5.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是 5 .6.乐乐和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中!请仔细观察下面的图形和表格,并回答下列问题:(1)观察探究.请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①;②.(2)实际应用.数学社团共分为6个小组,每组有3名同学.同学们约定,大年初一时不同组的两位同学之间要打一个电话拜年,请问,按照此约定,数学社团的同学们一共将拨打电话多少个?(3)类比归纳.乐乐认为(1),(2)之间存在某种联系,你能找到这两个问题之间的联系吗?请用语言描述你的发现.解:(1)由题可得,当多边形的顶点数为n时,从一个顶点出发的对角线的条数为n-3,多边形对角线的总条数为n(n-3).答案:n-3 n(n-3)(2)∵3×6=18,∴数学社团的同学们一共将拨打电话×18×(18-3)=135(个).(3)每个同学相当于多边形的一个顶点,则共有n个顶点;每人要给不同组的同学打一个电话,则每人要打(n-3)个电话;两人之间不需要重复拨打电话,故拨打电话的总数为n(n-3);数学社团有18名同学,当n=18时,×18×(18-3)=135.7.已知如图,四边形ABCD中,BE,DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.(1)如图1,说明∠MBC+∠NDC=α+β.(2)如图1,若BE与DF相交于点G,∠BGD=45°,请写出α,β所满足的等量关系式.(3)如图2,若α=β,判断BE,DF的位置关系,并说明理由.答案:略.。
湘教版八年级数学下册平行四边形的判定定理1,2同步练习题

2.2.2 平行四边形的判定第1课时平行四边形的判定定理1,2要点感知1一组对边平行且__________的四边形是平行四边形.预习练习1-1如果□ABCD和□ABEF有公共边AB,那么四边形DCEF是__________.要点感知2两组对边分别相等的四边形是__________四边形.预习练习2-1如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=110°,则∠C=__________.知识点1 一组对边平行且相等的四边形是平行四边形1.如图,在四边形ABCD中,点E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.AD=BCB.CD=BFC.∠A=∠CD.∠F=∠CDE第1题图第2题图第3题图2.如图,□ABCD中,点E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是( )A.3B.4C.5D.63.如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是__________(只填写一个条件,不使用图形以外的字母和线段).4.如图,已知四边形ABCD中,AB=CD,∠BAC=∠DCA,求证:四边形ABCD 是平行四边形.5.已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.知识点2 两组对边分别相等的四边形是平行四边形6.四边形ABCD中,AB=CD,AD=BC,∠B=50°,则∠A=__________.7.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD、CD.若∠B=65°,则∠ADC的大小为__________.8.已知四边形ABCD的四条边长满足(AB-CD)2+(AD-BC)2=0,求证:AB∥CD.9.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD 这四个条件中任意选两个,能使四边形ABCD是平行四边形的有( )A.3种B.4种C.5种D.6种10.如图,□ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是__________.11.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.12.如图,在□ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.13.如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.(1)求证:四边形MNCD是平行四边形;(2)求证:BD=3MN.14.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,点E是BC的中点.点P 以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.求当运动时间t为多少秒时,以点P、Q、E、D为顶点的四边形是平行四边形?参考答案要点感知1相等预习练习1-1平行四边形要点感知2平行预习练习2-1110°1.D2.B3.答案不唯一,如AB=CD或BC∥AD4.证明:∵∠BAC=∠DCA,∴AB∥CD.又∵AB=CD,∴四边形ABCD是平行四边形.5.证明:∵AB∥CD,∴∠ABO=∠CDO,∠BAO=∠DCO.又∵BO=DO,∴△AOB≌△COD(AAS).∴AB=CD.∴四边形ABCD是平行四边形.6.130°7.65°8.证明:∵(AB-CD)2+(AD-BC)2=0,∴AB-CD=0,AD-BC=0.∴AB=CD,AD=BC.∴四边形ABCD是平行四边形.∴AB∥CD.9.B 10.111.证明:∵BE∥DF,∴∠AFD=∠CEB.又∵∠ADF=∠CBE,AF=CE,∴△ADF≌△CBE(AAS).∴DF=BE.又∵BE∥DF,∴四边形DEBF是平行四边形.12.证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF,∠DAE=∠BCF=60°.∴∠BCD-∠BCF=∠DAB-∠DAE,即∠DCF=∠BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.13.证明:(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC.∵M、N分别是AD、BC的中点,∴MD=NC,MD∥NC.∴MNCD是平行四边形;(2)连接ND,∵MNCD是平行四边形,∴MN=DC.∵N是BC的中点,∴BN=CN.∵BC=2CD ,∠C=60°, ∴△NCD 是等边三角形. ∴ND=NC ,∠DNC=60°. ∵∠DNC 是△BND 的外角, ∴∠NBD+∠NDB=∠DNC. ∵DN=NC=NB ,∴∠DBN=∠BDN=12∠DNC=30°.∴∠BDC=90°.∴BC=2DC ,BD=22BC CD -=()222CD CD -=3DC.又DC=MN ,∴BD=3MN.14.由题意可知,AP=t ,CQ=2t ,CE=12BC=8.∵AD ∥BC ,∴当PD =EQ 时,以点P 、Q 、E 、D 为顶点的四边形是平行四边形. 当2t <8即t <4时,点Q 在C 、E 之间,如图甲.此时,PD =AD-AP =6-t ,EQ =CE-CQ =8-2t ,由6-t =8-2t 得t =2. 当8<2t<16即4<t<8时,点Q 在B 、E 之间,如图乙.此时,PD=AD-AP=6-t,EQ=CQ-CE=2t-8,由6-t=2t-8得t=14 3.∴当运动时间为2或143时,以点P、Q、E、D为顶点的四边形是平行四边形.考点综合专题:一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1.(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.(广安中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的根,则该等腰三角形的周长是()A.12 B.9C.13 D.12或93.(罗田县期中)菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x +12=0的一个根,则菱形ABCD的周长为()A.16 B.12 C.16或12 D.244.(烟台中考)等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为()A.9 B.10C.9或10 D.8或105.(齐齐哈尔中考)△ABC的两边长分别为2和3,第三边的长是方程x2-8x +15=0的根,则△ABC的周长是.6.(西宁中考)若矩形的长和宽是方程2x2-16x+m=0(0<m≤32)的两根,则矩形的周长为.【方法8】7.已知一直角三角形的两条直角边是关于x的一元二次方程x2+(2k-1)x +k2+3=0的两个不相等的实数根,如果此直角三角形的斜边是5,求它的两条直角边分别是多少.【易错4】◆类型二一元二次方程与函数的综合8.(泸州中考)若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是()9.(安顺中考)若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m +1)x+m-1的图象不经过()A.第四象限B.第三象限C .第二象限D .第一象限10.(葫芦岛中考)已知k 、b 是一元二次方程(2x +1)(3x -1)=0的两个根,且k >b ,则函数y =kx +b 的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限11.(广元中考)从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y =(5-m 2)x 和关于x 的一元二次方程(m +1)x 2+mx +1=0中m 的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m 的值是 .12.(甘孜州中考)若函数y =-kx +2k +2与y =k x(k ≠0)的图象有两个不同的交点,则k 的取值范围是 . .◆类型三 一元二次方程与二次根式的综合13.(达州中考)方程(m -2)x 2-3-mx +14=0有两个实数根,则m 的取值范围为( )A .m >52B .m ≤52且m ≠2 C .m ≥3 D .m ≤3且m ≠214.(包头中考)已知关于x 的一元二次方程x 2+k -1x -1=0有两个不相等的实数根,则k 的取值范围是 .考点综合专题:一元二次方程与其他知识的综合1.B 2.A 3.A 4.B 5.86.16 解析:设矩形的长和宽分别为x 、y ,根据题意得x +y =8,所以矩形的周长为2(x +y)=16.7.解:∵一元二次方程x 2+(2k -1)x +k 2+3=0有两个不相等的实数根,∴Δ>0,∴(2k -1)2-4(k 2+3)>0,即-4k -11>0,∴k<-114,令其两根分别为x 1,x 2,则有x 1+x 2=1-2k ,x 1·x 2=k 2+3,∵此方程的两个根分别是一直角三角形的两条直角边,且此直角三角形的斜边长为5,∴x 21+x 22=52,∴(x 1+x 2)2-2x 1·x 2=25,∴(1-2k)2-2(k 2+3)=25,∴k 2-2k -15=0,∴k 1=5,k 2=-3,∵k<-114,∴k =-3, ∴把k =-3代入原方程得到x 2-7x +12=0,解得x 1=3,x 2=4,∴直角三角形的两直角边分别为3和4.8.B9.D 解析:∵一元二次方程x 2-2x -m =0无实数根,∴Δ<0,∴Δ=4-4×1×(-m)=4+4m <0,∴m <-1,∴m +1<1-1,即m +1<0,m -1<-1-1,即m -1<-2,∴一次函数y =(m +1)x +m -1的图象不经过第一象限.故选D.10.B 11.-2 12.k>-12且k ≠0 13.B 14.k ≥1。
2020年中考数学必考34个考点专题19:平行四边形(含答案解析)

专题19 平行四边形专题知识回顾1.平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2.平行四边形的性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分。
3.平行四边形的判定:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)对角线互相平分的四边形是平行四边形;(5)两组对角分别相等的四边形是平行四边形。
4.平行四边形的面积:S平行四边形=底边长×高=ah专题典型题考法及解析【例题1】(2019▪广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是()A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF【答案】B.【解析】利用三角形中位线定理得到DE AC,结合平行四边形的判定定理进行选择.∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE A C.A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.【例题2】(2018湖北黄石)如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.【答案】看解析。
人教版数学八年级下册第十八章平行四边形性质与判定专题复习辅导讲义

辅导讲义学员编号:年级:课时数:学员姓名:辅导科目:学科老师:授课类型T 平行四边形的概念、性质T 平行四边形的断定C中位线定理授课日期时段教学内容一、同步学问梳理学问点1:平行四边形的定义:两组对边分别平行的四边形是平行四边形.表示:平行四边形用符号“”来表示.如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD,记作ABCD”,读作“平行四边形ABCD”.留意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.学问点2:平行四边形的性质:(1)边:平行四边形的对边平行且相等.(2)角:平行四边形的对角相等.邻角互补(3)对角线:平行四边形的对角线相互平分对称性:平行四边形是中心对称图形,两条对角线的交点是对称中心;二、同步题型分析题型1:平行四边形的边、角例1:已知,如图1,四边形ABCD为平行四边形,∠A+∠C=80°,平行四边形ABCD的周长为46 cm,且AB-BC=3 cm,求平行四边形ABCD的各边长和各内角的度数.分析:由平行四边形的对角相等,邻角互补可求得各内角的度数;由平行四边形的对边相等,得AB+BC=23 cm,解方程组即可求出各边的长.解:由平行四边形的对角相等,∠A+∠C=80°,得∠A=∠C=40°又DC∥AB,∠D及∠A为同旁内角互补,∴∠D=180°-∠A=180°-40°=140°.∴∠B=140°.由平行四边形对边相等,得AB=CD,AD=BC.因周长为46 am,因此AB+BC=23 cm,而AB-BC=3 cm,得AB=13 cm,BC=10 cm,∴CD=13 am.AD=10 cm.题后反思:留意充分利用性质解题.例2:如图2,在平行四边形ABCD中,E、F是直线BD上的两点,且DE=BF,你认为AE=CF吗?试说明理由.分析:本题主要考察平行四边形的性质.要证明AE=CF,可以把两线段分别放在两个三角形里,然后证明两三角形全等.解:AE=CF.理由:在平行四边形ABCD中,∵AB=CD且AB∥CD.∴∠ABE=∠CDF.∵DE=BF,∴ DE+BD=BF+BD,即BE=DF:∴△ABE≌△CDF ∴ AE=CF题后反思:利用平行四边形的性质解题时,一般要用到三角形全等学问,此题还可以证明其他三角形全等来证明两线段相等.题型2:平行四边形的周长例1:如图3,在平行四边形ABCD中,AC、BD相交于点O,作OE⊥BD于O,交CD于E,连接BE,若△BCE的周长为6,则平行四边形ABCD的周长为( B )图3A. 6B. 12C. 18D. 不确定分析:本题主要考察平行四边形的性质:对角线相互平分。
最新人教版初中数学八年级下册-第18章《平行四边形》复习课件-

第 1 题图
第 2 题图
2.(4分)如图,在四边形ABCD中,E是BC边的中点,
连接DE并延长,交AB的延长线于F点,AB=BF.添
加一个条件,使四边形ABCD是平行四边形.你认为
下面四个条件中可选择的是( D )
A.AD=BC;
B.CD=BF;
C.∠A=∠C;
D.∠F=∠CDE。
3.(8分)(2013·镇江)如图,AB∥CD,AB=CD,点
6.(5分)小玲的爸爸在钉制平行四边形框架时,采用了
一种方法:如图所示,将两根木条AC,BD的中点
重叠,并用钉子固定,则四边形ABCD就是平行四
边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形 7.(8分)如图,在▱ABCD中,点E,F是对角线AC上两
四边形的个数为( ) A.4个; B.3个; C.2个; D.1个
9.已知三条线段的长分别为10 cm, 14 cm和8 cm, 如 果以其中的两条为对角线, 另一条为边, 那么可以 画出所有不同形状的平行四边形的个数为( ) A. 1个; B. 2个; C. 3个; D. 4个.
10.如图, 在▱ABCD中, 对角线AC, BD相交于点O, E,
∠CFD+∠DFE=180°,∴∠AEF=∠DFE.∴AE∥DF.∴四边形 AFDE 为平行四边形
4.(4分)如图,在▱ABCD中,点E,F分别在AD,BC
上,且BE∥DF,若∠EBF=45°,则∠EDF的度数
为 45 。
5.(A41第B分8C2.)1D如课.2为图时平,平行四行平四边边四行形形边四A,B形边C则D形的可中的判添,性定加AB的质∥条与C件D判,是定要的使四综边合形应用
2023年人教版八年级下册数学_ 平行四边形的判定1 第1课时 同步典型例题精讲课件

6
C.1∶2∶1∶2
D.1∶1∶2∶2
7
解析:由题意,得∠A与∠C是对角,∠B与∠D是对角.当∠A=∠C,
8
∠B=∠D时,四边形ABCD是平行四边形,故选项A,B,D不符合
9
题意,选项C符合题意.
第1课时 平行四边形的判定1
STEP1 知识理解与运用
返回目录
1
7.在下列条件中,不能确定四边形ABCD为平行四边形的是( D )
1
2.小红同学周末在家做家务,不慎把家里的一块
2
平行四边形玻璃打碎成如图所示的四块,为了
3
能从玻璃店配到一块与原来相同的玻璃,他应
4
该带去玻璃店的是( B )
5
A.①② B.②④ C.②③ D.①③
返回目录
6
7
解析:只有②④两块角的两边互相平行,且中间部分相连,角的两边
8
的延长线的交点就是平行四边形的顶点.
STEP1 知识理解与运用
返回目录
1
知识点四 对角线互相平分
2
8.如图,四边形ABCD的对角线AC和BD相交于点O,下列能判定四边
3
形ABCD是平行四边形的是( D )
4
A.AO=OC,AC=BD
5
B.BO=OD,AC=BD
6
C.AO=BO,CO=DO
D.AO=OC,BO=OD
7
8
解析:∵AC,BD是四边形ABCD的对角线,AO=OC,BO=OD,
6
∴四边形为平行四边形.
7
8
9
第1课时 平行四边形的判定1
STEP1 知识理解与运用
返回目录
1
知识点三 两组对角分别相等
平行四边形的判定及综合(八年级下)

专题09 平行四边形的判定及综合(八年级下)知识网络重难突破知识点一平行四边形的判定1.两组对边分别平行的四边形是平行四边形.2.一组对边平行且相等的四边形是平行四边形.3.两组对边分别相等的四边形是平行四边形.4.对角线互相平分的四边形是平行四边形.5.两组对角分别相等.则四边形是平行四边形.【典例1】(2020春•鹿城区校级期中)从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD,这四个条件中选取两个,使四边形ABCD成为平行四边形,下面不能说明是平行四边形的是()A.①②B.①③C.②④D.①④【点拨】根据平行四边形的判定方法中,①②、③④、①③、②④均可判定是平行四边形.【解析】解:根据平行四边形的判定,符合条件的有4种,分别是:①②、③④、①③、②④.故选:D.【点睛】本题考查了平行四边形的判定,平行四边形的判定方法共有五种,在四边形中如果有:①四边形的两组对边分别平行;②一组对边平行且相等;③两组对边分别相等;④对角线互相平分;⑤两组对角分别相等.则四边形是平行四边形.本题利用了第1,2,3种来判定.【变式训练】1.(2019秋•海曙区校级月考)下列说法不能判断平行四边形是()A.一组对边平行且相等B.一组对边平行,一组对角相等C.一组对边相等,一组对角相等D.两组对边相等【点拨】根据平行四边形的判定进行判断即可.【解析】解:A、一组对边平行且相等的四边形是平行四边形,不符合题意;B、一组对边平行,一组对角相等是平行四边形,不符合题意;C、一组对边相等且一组对角相等的四边形不一定是平行四边形,符合题意;D、两组对边分别相等的四边形是平行四边形,不符合题意;故选:C.【点睛】本题考查了平行四边形的判定方法;熟练掌握平行四边形的判定方法,并能进行推理论证是解决问题的关键.2.(2019春•嘉兴期末)如图,四边形ABCD中,已知AD∥BC,AC与BD相交于点O,则添加下列一个条件后,不能判定该四边形为平行四边形的是()A.AD=BC B.OA=OC C.OD=OB D.AB=DC【点拨】根据平行四边形的判定定理:有一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;分别进行推理即可.【解析】解:A.∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形;选项A正确;B.∵AD∥BC,∴∠OAD=∠OCB,在△AOD和△COB中,,∴△AOD≌△COB(ASA),∴OD=OB,又∵OA=OC,∴四边形ABCD是平行四边形;选项B正确;C.∵AD∥BC,∴∠OAD=∠OCB,在△AOD和△COB中,,∴△AOD≌△COB(AAS),又∵OD=OB,∴四边形ABCD是平行四边形;选项C正确;D.∵AD∥BC,AB=CD,∴四边形ABCD可能为等腰梯形,不一定是平行四边形,选项D不正确;故选:D.【点睛】此题主要考查了平行四边形的判定、全等三角形的判定与性质,关键是熟练掌握平行四边形的判定定理.3.(2018春•嘉兴期末)如图,已知BD是平行四边形ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.(1)求证:△ADE≌△CBF;(2)连结CE,AF,求证:四边形AFCE为平行四边形.【点拨】(1)利用平行四边形的性质,根据ASA即可证明;(2)首先证明四边形AECF是平行四边形.【解析】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠CBD,∵AE⊥AD,∴∠EAD=90°,同理∠BCF=90°.∴∠EAD=∠BCF.在△AED和△CFB中∠ADB=∠CBD,AD=BC,∠EAD=∠BCF,∴△ADE≌△CBF.(2)结论:四边形AECF是平行四边形.理由:连接AC,∵四边形ABCD是平行四边形,∴AC平分BD,由(1)△ADE≌△CBF,∴AE=CF,∠AED=∠BFC,∴四边形AECF是平行四边形【点睛】本题考查平行四边形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.4.(2019秋•垦利区期末)已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.【点拨】(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;(2)根据平行四边形的性质及(1)的结论可得BM=DN,BM∥DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.【解析】证明:(1)四边形ABCD是平行四边形,∴∠DAB=∠BCD,∴∠EAM=∠FCN,又∵AD∥BC,∴∠E=∠F.∵在△AEM与△CFN中,,∴△AEM≌△CFN(ASA);(2)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD又由(1)得AM=CN,∴BM=DN,BM∥DN,∴四边形BMDN是平行四边形.【点睛】本题考查了平行四边形的判定及性质,全等三角形的判定,解题的关键是准确寻找全等三角形解决问题,属于中考常考题型.知识点二三角形的中位线1.连结三角形两边中点的线段叫做三角形的中位线。
平行四边形的判定复习课

义务教育课程标准实验教科书
八年级 下册
数 学
SHU XUE
中川中心学校
侯建昌
19.1.2平行四边形的判定
平行四边形的定义:
两组对边分别平行的四边形叫 做平行四边形.
有两组对边分别平行的四边形 叫做 平行四边形
A D
如果
B
A C ABCD
D
A B O
D C
小锋提议:我们可以度量它的角,如果它的两组对 角分别相等,那么它就是一个平行四边形。 已知:四边形ABCD,
A D
∠A=∠C,∠B=∠D
求证:四边形ABCD是 平行四边形
B C
∠A+ ∠B +∠C+ ∠D =360 ° ∠A+ ∠D=180 ° ∠A+ ∠B=180 °
AB∥CD AD∥BC
ABCD
D
平行四边形判定
平行四边形的判定定理2:
两组对角分别相等的四边形是平行 四边形。
A B C
D
∵ ∠A=∠C, ∠B=∠D (已知) ∴四边形ABCD是平行四边形(两 组对角分别相等的四边形是平行四 边形。)
小丽却说:“我可以不用任何作图工具, 只要两条细绳就能判断它是不是平行四边形。” 只见小丽用两条细绳做四边形的对角线, 并在两条对角线的交点处作了个记号。然后分 别把两条对角线沿记号点对折,发现它们被记 号点分成的两段线段都能重合,小丽高兴地说: “这的确是个平行四边形!”
开心一练:
1.根据下列条件,不能判定一个四边形为平行 四边形的是( C ) (A)两组对边分别相等 (B)两条对角线互相平分 (C)两条对角线相等 (D)两组对边分别平行
北师大版数学八年级下册期末复习(六) 平行四边形

期末复习(六) 平行四边形01 各个击破)命题点1 平行四边形的性质与判定【例1】 (桂林中考)如图,在▱ABCD 中,E ,F 分别是AB ,CD 的中点. (1)求证:四边形EBFD 为平行四边形;(2)对角线AC 分别与DE ,BF 交于点M ,N ,求证:△ABN≌△CDM.【思路点拨】 (1)先根据平行四边形的性质得AB∥CD,AB =CD ,再根据一组对边平行且相等的四边形是平行四边形即可得证;(2)因为AB =CD ,∠CAB =∠ACD 已知,则只需要再证明一组对应角相等即可. 【解答】 证明:(1)∵四边形ABCD 是平行四边形, ∴ABCD.∵E ,F 分别是AB ,CD 的中点, ∴BE =12AB ,DF =12DC. ∴BEDF.∴四边形EBFD 为平行四边形. (2)∵四边形ABCD 是平行四边形, ∴ABCD.∴∠CAB =∠ACD.∵四边形EBFD 为平行四边形, ∴∠ABN =∠CDM. 又∵AB=CD ,∴△ABN ≌△CDM(ASA).【方法归纳】 1.判定平行四边形的基本思路:(1)若已知一组对边平行,可以证这一组对边相等或另一组对边平行;(2)若已知一组对边相等,可以证这一组对边平行或另一组对边相等;(3)若已知一组对角相等,可以证另一组对角相等;(4)若已知条件与对角线有关,可以证明对角线互相平分. 2.利用平行四边形的性质进行计算的方法:(1)利用平行四边形的性质,通过角度或线段之间的等量转化进行相应的计算;(2)找出所求线段或角所在的三角形,若三角形为直角三角形,通过直角三角形的性质或勾股定理求解;若三角形为任意三角形,可通过三角形全等的性质进行求解.1.如图,在四边形ABCD 中,已知AB =CD ,AD =BC ,AC ,BD 相交于点O ,若AC =6,则AO 的长度等于3.2.如图,已知D 是△ABC 的边AB 上一点,CE ∥AB ,DE 交AC 于点O ,且OA =OC ,猜想线段CD 与线段AE 的大小关系和位置关系,并说明理由.解:线段CD 与线段AE 的大小关系和位置关系是相等且平行. 理由:∵CE∥AB, ∴∠DAO =∠ECO.∵OA =OC ,∠AOD =∠COE, ∴△ADO ≌△CEO.∴AD =CE. 又∵AD∥CE,∴四边形ADCE 是平行四边形. ∴CD ∥AE ,CD =AE.3.如图,E 是▱ABCD 的边CD 的中点,延长AE 交BC 的延长线于点F. (1)求证:△ADE≌△FCE;(2)若∠BAF=90°,BC =5,EF =3,求CD 的长.解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB ∥CD.∴∠DAE =∠F,∠D =∠ECF. ∵E 是▱ABCD 的边CD 的中点, ∴DE =CE.在△ADE 和△FCE 中,⎩⎨⎧∠DAF=∠F,∠D =∠ECF,DE =CE ,∴△ADE ≌△FCE(AAS). (2)∵△ADE≌△FCE, ∴AE =EF =3. ∵AB ∥CD ,∴∠AED =∠BAF=90°. 在▱ABCD 中,AD =BC =5, ∴DE =AD 2-AE 2=52-32=4. ∴CD =2DE =8.命题点2 三角形的中位线【例2】 (邵阳中考)如图,等边三角形ABC 的边长是2,D ,E 分别为AB ,AC 的中点,延长BC 至点F ,使CF =12BC ,连接CD 和EF. (1)求证:DE =CF ; (2)求EF 的长.【思路点拨】 (1)欲证DE =CF ,由三角形中位线定理可知DE =12BC ,而条件中有CF =12BC 故易证得;(2)欲求EF 的长,可证四边形DEFC 是平行四边形,因此只需求出CD 的长.在等边三角形ABC 中,点D 是AB 的中点,因此运用勾股定理可求出,问题获解.【解答】 (1)证明:∵D,E 分别为AB ,AC 的中点,∴DE =12BC ,且DE∥BC. ∵点F 在BC 的延长线上,且CF =12BC ,∴DE ∥CF ,且DE =CF.(2)由(1)知DE∥CF,且DE =CF , ∴四边形DEFC 为平行四边形.∵△ABC 是等边三角形,边长是2,点D 是AB 的中点,AB =BC =2, ∴CD ⊥AB ,∠BDC =90°,BD =12AB =1. ∴CD =BC 2-BD 2=22-12= 3. ∵四边形DEFC 为平行四边形, ∴EF =CD = 3.【方法归纳】 若题中有中点通常考虑到三角形的中线和中位线,而在等边三角形(等腰三角形)中,中线同时也是高和角平分线.4.如图,CD 是△ABC 的中线,点E ,F 分别是AC ,DC 的中点,EF =2,则BD =4.5.如图所示,在四边形ABCD 中,AB =CD ,M ,N ,P 分别是AD ,BC ,BD 的中点,∠ABD =20°,∠BDC =70°,求∠PMN 的度数.解:∵M,N ,P 分别是AD ,BC ,BD 的中点,∴MP ,PN 分别是△ABD,△BCD 的中位线, ∴MP12AB, PN12CD.∴∠MPD =∠ABD=20°,∠BPN =∠BDC=70°. ∴∠DPN =110°.∴∠MPN =∠MPD+∠DPN=20°+110°=130°. 又∵AB=CD ,∴MP =PN. ∴∠PMN =∠PNM. ∴∠PMN =25°.命题点3 多边形的内角和与外角和【例3】(泰安中考)如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3等于(B)A.90°B.180°C.210°D.270°【思路点拨】由AB∥CD,推导∠B+∠C=180°,故∠B,∠C两角的外角和是180°,根据多边形外角和等于360°可计算∠1+∠2+∠3度数.【方法归纳】对于求多边形的外角和或部分外角的和的问题,都要根据任意多边形的外角和是360°以及邻角和其补角的互补关系这两个知识点,来解决问题.6.正多边形的一个内角的度数恰好等于它的外角的度数的3倍,则这个多边形的边数为8.7.如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和α+β的度数.解:∵AB⊥AF,BC⊥DC,∴∠A=∠C=90°.又∵∠E+∠F=260°,∴∠EDC+∠ABC=(6-2)×180°-90°×2-260°=280°.∴β+α=(180°-∠EDC)+(180°-∠ABC)=360°-(∠EDC+∠ABC)=80°.故两外角和α+β的度数为80°.02整合集训一、选择题(每小题3分,共24分)1.已知平行四边形ABCD的周长为32 cm,AB=4 cm,则BC的长为(B)A.4 cm B.12 cmD.16 cm D.24 cm2.(西宁中考)如果等边三角形的边长为4,那么等边三角形的中位线长为(A)A.2 B.4 C.6 D.83.(临沂中考)将一个n边形变成n+1边形,内角和将(C)A.减少180°B.增加90°C.增加180°D.增加360°4.(乐山中考)如图,点E是▱ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则▱ABCD 的周长为(D)A.5B.7C.10D.145.某平行四边形的对角线长为x,y,一边长为6,则x与y的值可能是(C)A.4和7 B.5和7C.5和8 D.4和176.(葫芦岛中考)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P 的度数是(A)A.60°B.65°C.55°D.50°7.如图,在▱ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为(B)A.2 3 B.43C.4 D.88.已知在正方形的网格中,每个小方格的边长都相等,A,B两点在小方格的顶点上,位置如图所示,则以A,B 为顶点的网格平行四边形的个数为(D)A.6个B.8个C.10个D.12个二、填空题(每小题4分,共24分)9.(陕西中考)一个正多边形的外角为45°,则这个正多边形的边数是8.10.如图所示,在▱ABCD中,E,F分别为AD,BC边上的一点,若添加一个条件AE=FC或∠ABE=∠CDF,则四边形EBFD为平行四边形.11.(娄底中考)如图,▱ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO 的周长是9.12.(泉州中考)如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是平行四边形.13.如图,在▱ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC,CF=3,则AB 的长为3.14.在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去两个三角形,剩下的部分就是如图所示的四边形;经测量这个四边形的相邻两边长为10 cm ,6 cm ,一条对角线的长为8 cm ;则原三角形纸片的周长是48_cm 或(32+813)cm .三、解答题(共52分)15.(6分)一个多边形的内角和与外角和的差为1 260度,求它的边数. 解:设多边形的边数是n ,则(n -2)·180-360=1 260.解得n =11. 答:它的边数为11.16.(8分)(陕西中考)如图,在▱ABCD 中,连接BD ,在BD 的延长线上取一点E ,在DB 的延长线上取一点F ,使BF =DE ,连接AF ,CE ,求证:AF∥CE.证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC. ∴∠ADB =∠CBD. ∵BF =DE ,∴BF +BD =DE +BD , 即DF =BE.在△ADF 和△CBE 中,⎩⎨⎧AD =CB ,∠ADF =∠CBE,DF =BE ,∴△ADF ≌△CBE(SAS). ∴∠AFD =∠CEB. ∴AF ∥CE.17.(8分)(永州中考)如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC,BN ⊥AN 于点N ,延长BN 交AC 于点D ,已知AB =10,BC =15,MN =3. (1)求证:BN =DN ; (2)求△ABC 的周长.解:(1)证明:∵AN 平分∠BAC, ∴∠BAN =∠DAN. ∵BN ⊥AN ,∴∠ANB =∠AND=90°. 又∵AN=AN ,∴△ABN ≌△ADN(ASA).∴BN=DN. (2)∵△ABN≌△ADN, ∴AD =AB =10,DN =NB. 又∵点M 是BC 中点,∴MN 是△BDC 的中位线. ∴CD =2MN =6.∴△ABC 的周长为AB +AC +BC =AB +AD +CD +BC =10+10+6+15=41.18.(10分)如图,在△ABC 中,点D ,E 分别是AB ,AC 的中点,连接DE 并延长到点F ,使EF =ED ,连接CF.(1)四边形DBCF 是平行四边形吗?说明理由;(2)DE 与BC 有什么样的位置关系和数量关系?说明理由. 解:(1)四边形DBCF 是平行四边形. 理由:∵E 是AC 的中点, ∴AE =CE.又∵EF=ED ,∠CEF =∠AED, ∴△AED ≌△CEF(SAS). ∴AD =CF ,∠A =∠ECF. ∴AD ∥CF ,即CF∥BD.又∵D 为AB 的中点,∴BD =AD.∴BD=CF. ∴四边形DBCF 是平行四边形. (2)DE∥BC,DE =12BC. 理由:∵EF=ED ,∴DE =12DF. 又∵四边形DBCF 是平行四边形, ∴DF =BC ,DF ∥BC. ∴DE ∥BC ,DE =12BC.19.(10分)(怀化中考)已知:如图,在△ABC 中,DE ,DF 是△ABC 的中位线,连接EF ,AD ,其交点为点O.求证: (1)△CDE≌△DBF; (2)OA =OD.证明:(1)∵DE,DF 是△ABC 的中位线, ∴DF =CE ,DF ∥CE ,DB =DC. ∵DF ∥CE , ∴∠C =∠BDF.在△CDE 和△DBF 中,⎩⎨⎧DC =BD ,∠C =∠BDF,CE =DF ,∴△CDE ≌△DBF(SAS).(2)∵DE,DF 是△ABC 的中位线, ∴DF =AE ,DF ∥AE.∴四边形DEAF 是平行四边形. ∵EF 与AD 交于点O , ∴OA =OD.20.(10分)(扬州中考改编)如图,AC 为长方形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处. (1)求证:四边形AECF 是平行四边形;(2)若AB =6,AC =10,求四边形AECF 的面积.解:(1)证明:由折叠的性质可知:AM =AB ,CN =CD ,∠FNC =∠D=90°,∠AME =∠B=90°, ∴∠ANF =90°,∠CME =90°. ∵四边形ABCD 为长方形, ∴AB =CD ,AD ∥BC.∴AM =CN ,∠FAN =∠ECM. ∴AM -MN =CN -MN , 即AN =CM.在△ANF 和△CME 中,∠FAN =∠ECM,AN =CM ,∠ANF =∠CME, ∴△ANF ≌△CME(ASA). ∴AF =CE. 又∵AF∥CE,∴四边形AECF 是平行四边形. (2)∵AB=6,AC =10,∴BC =8.设CE =x ,则EM =8-x ,CM =10-6=4. 在Rt △CEM 中,(8-x)2+42=x 2, 解得x =5.∴S 四边形AECF =EC·AB=5×6=30.。
人教版八年级下册数学 第18章《平行四边形》讲义 第12讲 平行四边形-复习训练(有答案)

第12讲平行四边形复习训练考点一、平行四边形的性质及判定 【知识要点】(1)、平行四边形的边、角、对角线性质, 对称性 (2)、平行四边形判定方法 (3)、三角形中位线【典型例题】例1、下列图形中是中心对称图形,但不是轴对称图形的是( ) A 、菱形 B 、矩形 C 、正方形 D 、平行四边形例2、如图,□ABCD 与□DCFE 的周长相等,且∠BAD=60°,∠F=110°,则∠DAE 的度数为 例3、如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延长线交于点E,与DC 交于点F,且点F 为边DC 的中点,DG ⊥AE,垂足为G,若DG=1,则AE 的长为( ) A 、2B 、4C 、4D 、8例4、平面直角坐标系中,□ABCD 的顶点,A ,B ,D 的坐标分别是(0,0)(5,0),(2,3),则顶点C 的坐标是( )A 、(3,7)B 、(5,3)C 、(7,3)D 、 (8,2)(例2) (例3) (例4) 例5、如图,E 是平行四边形内任一点, 若S 平行四边形ABCD=8,则图中阴影部分的面积是( ) A 、3B 、4C 、5D 、6例6、如图,将平行四边形ABCD 纸片沿EF 折叠,使点C 与点A 重合,点D 落在点G 处。
(1)求证:AE =AF (2)求证:△ABE ≌△AGF例7、如图所示:四边形ABCD 是平行四边形,DE 平分BF ADC ,∠平分ABC ∠.试证明四边形BFDE 是平行四边形.例8、如图,在△ABC 中,AB =4,AC =3,BC =5,以三边为边,在BC 的同侧分别作三个等边三角形即△ABD、△BCE、△ACF。
(1)求证:四边形EFAD是平行四边形;(2)求四边形EFAD的面积。
1、在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是()A、1:2:3:4B、2:2:3:3C、2:3:2:3D、2:3:3:22、顺次连结四边形各边的中点,所成的四边形必定是()A、等腰梯形B、直角梯形C、矩形D、平行四边形3、如图,在ABCD中,AB=5,AD=8,∠BAD、∠ADC的平分线分别交BC于E、F,则EF的长为()A、1B、2C、3D、44、如图,在□ABCD中,EF∥AD, GH∥AB,EF、GH相交于点O,则图中共有个平行四边形.(3)(4)5、如图,△ABC 中,∠ACB=90°,点D、E分别为AC,AB中点,点F在BC延长线上,且∠CDF=∠A。
2020年八年级数学下册 期中复习卷 平行四边形性质与判定(含答案)

2020年八年级数学下册期中复习卷平行四边形性质与判定一、选择题1.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为().A.4,4,8,8B.5,5,7,7C.5.5,5.5,6.5,6.5D.3,3,9,92.平行四边形ABCD中,如果∠B=100°,那么∠A、∠D的值分别是()A.∠A=80°,∠D=100°B.∠A=100°,∠D=80°C.∠B=80°,∠D=80°D.∠A=100°,∠D=100°3.在平行四边形ABCD中,∠A的平分线交DC于E,若∠DEA=30°,则∠B=().A100° B.120° C.135° D.150°4.如图,平行四边形ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为()A.8.3B.9.6C.12.6D.13.65.平行四边形的周长为25cm,对边的距离分别为2cm、3cm,则这个平行四边形的面积为()A.15cm2B.25cm2C.30cm2D.50cm26.已知O为平行四边形ABCD对角线的交点,△AOB的面积为1,则平行四边形的面积为()A.1B.2C.3D.47.如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )A.AD=BCB.OA=OCC.AB=CDD.∠ABC+∠BCD=180°8.下列条件中,不能判定四边形是平行四边形的是( )A.两组对边分别平行B.一组对边平行,另一组对边相等C.两组对边分别相等D.一组对边平行且相等9.如图,在平面直角坐标系中,以A(﹣1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()A.(3,1)B.(﹣4,1)C.(1,﹣1)D.(﹣3,1)10.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若BD、AC的和为18cm,CD:DA=2:3,△AOB的周长为13cm,那么BC的长是()A.6cm B.9cm C.3cm D.12cm11.如图,在▱ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为()A.4cm B.5cm C.6cm D.8cm12.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为()A.4s B.3s C.2s D.1s二、填空题13.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.14..E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=______15.如图,▱ABCD中,AC、BD为对角线,BC=6,BC边上的高为4,则阴影部分面积为.16.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,图中全等三角形共有________对17.如图,□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是.18.如图,第1个图形中一共有1个平行四边形,第2个图形中一共有5个平行四边形,第3个图形中一共有11个平行四边形,…则第n个图形中平行四边形的个数是.三、解答题19.如图,已知在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.求证:四边形ABCD为平行四边形.20.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.21.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
初二数学八下平行四边形所有知识点总结和常考题型练习题

平行四邊形知識點一、四邊形相關1、四邊形的內角和定理及外角和定理四邊形的內角和定理:四邊形的內角和等于360°。
四邊形的外角和定理:四邊形的外角和等于360°。
推論:多邊形的內角和定理:n 邊形的內角和等于•-)2(n 180°; 多邊形的外角和定理:任意多邊形的外角和等于360°。
2、多邊形的對角線條數的計算公式設多邊形的邊數為n ,則多邊形的對角線條數為2)3(-n n 。
二、平行四邊形1.定義:兩組對邊分別平行的四邊形是平行四邊形. 平行四邊形的定義既是平行四邊形的一條性質,又是一個判定方法.2.平行四邊形的性質:平行四邊形的有關性質和判定都是從 邊、角、對角線 三個方面的特征進行簡述的.(1)角:平行四邊形的對角相等,鄰角互補;(2)邊:平行四邊形兩組對邊分別平行且相等;ABDO C(3)對角線:平行四邊形的對角線互相平分;(4)面積:①S ==⨯底高ah ; ②平行四邊形的對角線將四邊形分成4個面積相等的三角形.3.平行四邊形的判別方法①定義:兩組對邊分別平行的四邊形是平行四邊形 ②方法1:兩組對邊分別相等的四邊形是平行四邊形③方法2:一組對邊平行且相等的四邊形是平行四邊形 ④方法3:兩組對角分別相等的四邊形是平行四邊形⑤方法4: 對角線互相平分的四邊形是平行四邊形三、矩形1. 矩形定義:有一個角是直角的平行四邊形是矩形。
2. 矩形性質①邊:對邊平行且相等; ②角:對角相等、鄰角互補,矩形的四個角都是直角;③對角線:對角線互相平分且相等; ④對稱性:軸對稱圖形(對邊中點連線所在直線,2條).3. 矩形的判定:滿足下列條件之一的四邊形是矩形①有一個角是直角的平行四邊形; ②對角線相等的平行四邊A DB CO形; ③四個角都相等識別矩形的常用方法① 先說明四邊形ABCD 為平行四邊形,再說明平行四邊形ABCD 的任意一個角為直角.② 先說明四邊形ABCD 為平行四邊形,再說明平行四邊形ABCD 的對角線相等.③ 說明四邊形ABCD 的三個角是直角.4. 矩形的面積① 設矩形ABCD 的兩鄰邊長分別為a,b ,則S 矩形=ab .四、菱形1. 菱形定義:有一組鄰邊相等的平行四邊形是菱形。
平行四边形判定与性质知识总结

平行四边形判定与性质知识总结平行四边形:在同一平面内有两组对边分别平行的四边形叫做平行四边形判定前提:在同一平面内(1)两组对边分别相等的四边形是平行四边形;(2)一组对边平行且相等的四边形是平行四边形;(3)两组对边分别平行的四边形是平行四边形;(4)两条对角线互相平分的四边形是平行四边形;性质(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
( 3)如果一个四边形是平行四边形,那么这个四边形的邻角互补(4)夹在两条平行线间的平行线段相等。
(5)如果一个四边形是平行四边形,那么这个四边形两条对角线互相平分。
(6)连接任意四边形各边的中点所得图形是平行四边形。
(推论)(7)平行四边形的面积等于底和高的积。
(可视为矩形)(8)过平行四边形对角线交点的直线,将平行四边形分成全等两部分图形。
(9)平行四边形是中心对称图形,对称中心是两对角线的交点.(10)平行四边形不是轴对称图形,矩形和菱形是轴对称图形。
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质。
(11)平行四边形ABCD中(如图)E为AB的中点,则AC和DE互相三等分,一般地,若E为AB上靠近A的n等分点,则AC和DE互相(n+1)等分。
(12)平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和。
(13)平行四边形对角线把平行四边形面积分成四等分。
(14)平行四边形中,两条在不同对边上的高所组成的夹角,较小的角等于平行四边形中较小的角,较大的角等于平行四边形中较大的角。
(15)平行四边形中,一个角的顶点向他对角的两边所做的高,与这个角的两边组成的夹角相等。
初二数学八下平行四边形所有知识点总结和常考题型练习题

平行四边形知识点一、四边形相关1 、四边形的内角和定理及外角和定理四边形的内角和定理:四边形的内角和等于360°。
四边形的外角和定理:四边形的外角和等于360°。
推论:多边形的内角和定理: n 边形的内角和等于( n2) ? 180°;多边形的外角和定理:任意多边形的外角和等于360°。
2、多边形的对角线条数的计算公式设多边形的边数为 n,则多边形的对角线条数为n(n3) 。
2二、平行四边形1.定义:两组对边分别平行的四边形是平行四边形.D C 平行四边形的定义既是平行四边形的一条性质,又是一个判定方法.O 2.平行四边形的性质:平行四边形的有关性质和判定都是从边、角、对角线三个方面的特征进行简述的.( 1)角:平行四边形的对角相等,邻角互补;A B ( 2)边:平行四边形两组对边分别平行且相等;( 3)对角线:平行四边形的对角线互相平分;( 4)面积:①S底高= ah;②平行四边形的对角线将四边形分成 4 个面积相等的三角形.3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形②方法 1:两组对边分别相等的四边形是平行四边形③方法 2:一组对边平行且相等的四边形是平行四边形④方法 3:两组对角分别相等的四边形是平行四边形D C⑤方法 4:对角线互相平分的四边形是平行四边形三、矩形O1.矩形定义:有一个角是直角的平行四边形是矩形。
A B2.矩形性质①边:对边平行且相等;②角:对角相等、邻角互补,矩形的四个角都是直角;③对角线:对角线互相平分且相等;④对称性:轴对称图形(对边中点连线所在直线, 2 条).3.矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形;②对角线相等的平行四边形;③四个角都相等识别矩形的常用方法①先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任意一个角为直角.②先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的对角线相等.③说明四边形ABCD的三个角是直角.4.矩形的面积①设矩形 ABCD的两邻边长分别为a,b ,则 S 矩形 =ab.四、菱形1.菱形定义:有一组邻边相等的平行四边形是菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.在四边形 ABCD 中,对角线 AC,BD 相交于点 O,给出下列四个
条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两
个条件,能使四边形 ABCD 为平行四边形的选法有( B )
A.3 种
B.4 种
C.5 种
归纳:判定四边形是平行四边形的思路:
从角来考虑: 证明两组对角分别相等; 从对角线考虑:证明两条对角线互相平分.
例1、如图,将平行四边形ABCD的对角线BD向两个方向延长至 点E和点F,使BE=DF,求证四边形AECF是平行四边形.
证法一:∵ 四边形ABCD是平行四边形, ∴AD=CB,AD//CB,
9.如图,已知四边形 ABCD 中,AC 与 BD 相交于点 O,若 AC=10, BD=6,则当 AO= 5 ,DO= 3 时,四边形 ABCD 是平行四边形.
Q 2t
12 t 2t
t 4
当t 4s时,四边形 PDCQ是平行四边形
课堂练习
1.如图,在四边形 ABCD 中,AB=CD,BC=AD.若∠B=110°,则 ∠A 的度数为( C)
A.110° B.80° C.70° D.90°
2.(2019·泸州)四边形 ABCD 的对角线 AC 与 BD 相交于点 O,下列四
当AP BQ时, 四边形APQB是平行四边形
t •P 12-t
• 15-2t
2t
Q
t 15 2t
t 5
当t 5s时,四边形 APQB是平行四边形
3)当t为何值时,
四边形PDCQ是平行四边形?
解:∵ AD∥ BC
当PD CQ时, 四边形PDCQ是平行四边形
t •P 12-t • 15-2t
4.(2018·东营)如图,在四边形 ABCD 中,E 是 BC 边的中点,连接 DE 并延长,交 AB 的延长线于点 F,AB=BF.添加一个条件,使四边 形 ABCD 是平行四边形.你认为下面四个条件中可选择的是( D)
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDE
5.如图,在平面直角坐标系中,以 A(-1,0),B(2,0),C(0,1)为顶 点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的是 ( B)
组条件中,一定能判定四边形 ABCD 为平行四边形的是( B )
A.AD∥BC
B.OA=OC,OB=OD
C.AD∥BC,AB=DC
D.AC⊥BD
3.如图,在▱ABCD 中,E,F 分别是 AB,CD 的中点,连接 DE,EF, BF,则图中平行四边形共有( B )
A.2 个 B.4 个 C.6 个 D.8 个
③∵_______∥_______,_______=_______, ∴四边形ABCD是平行四边形. ④∵∠A=_______,∠B=_______, ∴四边形ABCD是平行四边形. ⑤如图,对角线AC,BD相交于点O, ∵AO=_______,BO=_______, ∴四边形ABCD是平行四边形.
(1)用含t的代数式表示AP=t_,DP=_1_2_-_t,BQ=1_ 5_-2__t,CQ=_2__t.
(2)当t为何值时,四边形APQB Nhomakorabea平行四边形? (3)当t为何值时,四边形PDCQ是平行四边形?
t 12-t 12
15-2t 15 2t
(2)当t为何值时, 四边形APQB是平行四边形?
解:∵ AD∥ BC
证明:连接DE,BF
∵ 四边形ABCD是平行四边形,
AB∥CD,AB CD
∴BE//DF
又∵ AE CF AB AE CD CF即BE DF 四边形BEDF中,BE DF,BE∥DF 四边形BEDF是平行四边形 BD与EF互相平分
例3.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向 点D以1cm/s的速度运动,到D点即停止.点Q自点C向点B以2cm/s的 速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
人教版八年级数学下册 第十八章 平行四边形
18.1 平行四边形
1.2 平行四边形的判定复习(3)
1
知识提要
知识点平行四边形的判定方法 试一试: 1.如图,已知四边形ABCD.
①∵AB=_______,BC=_______, ∴四边形ABCD是平行四边形. ②∵AB∥_______,BC∥_______, ∴四边形ABCD是平行四边形.
D.6 种
7.如图,在四边形 ABCD 中,对角线 AC,BD 相交于点 E,∠CBD =90°,BC=4,BE=ED=3,AC=10,则四边形 ABCD 的面积为( D )
A.6 B.12 C.20 D.24
8.如图,△ABC≌△A′B′C′,点 B,C′,C,B′在同一直线上,且 B 与 B′ 不 重 合 , 则 以 点 A , B , A′ , B′ 为 顶 点 的 四 边 形 一 定 是 平行四边形 .(填某种特殊四边形的名称)
例1、如图,将平行四边形ABCD的对角线BD向两个方向延长至点 E和点F,使BE=DF,求证四边形AECF是平行四边形.
证法三:连接AC,交BD于O点
∵ 四边形ABCD是平行四边形,
O
∴ AO=CO,BO=DO 又∵ BE=DF ∴ BO+BE= DO+DF
∴EO=FO,
∴四边形AECF是平行四边形
∴ ∠ADB = ∠DBC,
∴ ∠ADF = ∠CBE,
在△ADF 和△CBE中,
AD=CB
∠ADF=∠CBE
BE=DF ∴△ADF ≌△CBE.(SAS)
同理可得:△ABE ≌△CDF. ∴AE=CF. ∴四边形AECF是平行四边形
∴AF=CE.
例1、如图,将平行四边形ABCD的对角线BD向两个方向延长至 点E和点F,使BE=DF,求证四边形AECF是平行四边形.
证法二:∵ 四边形ABCD是平行四边形, ∴AD=CB,AD//CB, ∴ ∠ADB = ∠DBC, ∴ ∠ADF = ∠EBC,
在△ADF 和△CBE中, AD=CB
∠ADF=∠CBE
∴AF//CE.
BE=DF ∴△ADF ≌△CBE.(SAS)
∴AF=CE. ∠AFD= ∠CEB,
∴四边形AECF是平行四边形
