苏教版八年级上期末复习3
苏教版八年级上册数学期末复习知识点+常考题型

苏教版八年级上册期末复习(知识点+考试热点题型)汇总第一章全等三角形知识点梳理1、全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转后得到的三角形,与原三角形仍然全等..;③三角形全等不因位置发生变化而改变。
2、全等三角形的性质:⑴全等三角形的对应边相等、对应角相等。
理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
⑵全等三角形的周长相等、面积相等。
⑶全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3、全等三角形的判定:①边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等。
②角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等。
③推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等。
④边边边公理(SSS) 有三边对应相等的两个三角形全等。
⑤斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等。
4、证明两个三角形全等的基本思路:⑴已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL).⑵已知一边一角:①找一角(AAS或ASA);②找夹边(SAS).⑶已知两角:①找夹边(ASA);②找其它边(AAS).常考题型汇总一、选择题1.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE 的是()A、∠A=∠CB、AD=CBC、BE='DF'D、AD∥BC2.如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列条件后,不能判定△ABE≌△ACD 的是( )A、AD=AEB、BE=CDC、∠AEB=∠ADCD、AB=AC3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是()A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBDD.AD∥BC,且AD=BC4.如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=ACB.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CADD.∠B=∠C,BD=DC5.已知图中的两个三角形全等,则∠1等于()A.72°B.60°C.50°D.58°6.在△ABC中和△DEF中,已知AC=DF,∠C= ∠F,增加下列条件后还不能判定△ABC≌△DEF 的是()A.BC=EF B.AB=DE C.∠A= ∠D D.∠B= ∠E7.(3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA二、填空题1.如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED=________°.2.如图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD,则另外两组对应边为________,另外两组对应角为________.3.如图,△ACE≌△DBF,点A、B、C、D共线,若AC=5,BC=2,则CD的长度等于________.4.如图,AB=AD,只需添加一个条件________,就可以判定△ABC≌△ADE.5.△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________.三、解答题1.如图,已知△ABC≌△BAD,AC与BD相交于点O,求证:OC=OD.2.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.3. 已知:如图,点D、E在BC上,且BD=CE,AD=AE,求证:AB=AC.4 已知:如图,A、C、F、D在同一直线上,AF=D C,AB=DE,BC=EF,求证:△ABC≌△DEF.5.已知:BE⊥CD,BE=DE,BC=DA,求证:①△BEC≌△DEA;②DF⊥BC.BCDEFABC EF AACD E6.如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O.求证:(1) △ABC ≌△AED ; (2) OB =OE .第二章 轴对称知识点梳理1、 轴对称图形相对一个图形的对称而言;轴对称是关于直线对称的两个图形而言。
苏教版八年级数学上册期末复习

八年级数学上册期末复习1班级姓名学号一、选择题1. 下列说法正确的是( )A. 0的平方根是0B. 9的立方根是3C. 是无理数D. 比小2.如果点在第四象限, 那么的取值范围是( )A. B. C. D.3. 等腰三角形两边分别为5cm和2cm, 则它的第三边长为( )A.2cmB.5cmC.2c m或5cmD.4cm4. 点(2, -3)关于坐标原点的对称点是( )A.(-2,-3)B.(2,-3)C. (2.3)D.(-2,3)5.小明骑自行车上学,开始以正常速度匀速行驶, 但行至途中因车出了毛病,只好停下修车,车修好后,怕耽误上课,他比修车前加快了骑车速度继续匀速行驶.下面是行驶路程关于行驶时间的函数图象,那么符合这个同学行驶情况的图象大致是( )A B C D二、填空题(本大题共10小题, 每小题2分, 共20分)1. 计算: = .2. 式子中x的取值范围是 .3. 在十八大精神的鼓舞下, 东台市的财政总收入超百亿元, 达110.6亿元, 这个数据用科学计数法表示为(精确到个位)元.4. 已知点在一次函数的图象上, 则= .5. 如图, 学校有一块长方形花铺, 有极少数人为了避开拐角走“捷径”, 在花铺内踩出了一条“路”. 他们仅仅少走了步路(假设2步为1米), 却踩伤了花草.6.若不等式组的解集为, 那么的值等于 .7. 如图, 已知矩形ABCD, AB在y轴上, AB=2, BC=3, 点A的坐标为(0, 1), 在AD边上有一点E(1, 1), 过点E的直线平分矩形ABCD的面积, 则此直线的解析式为 .第5题图第7题图三、解答题1. 计算:2. 求不等式组的整数解.3. (本题满分7分)12月份文化艺术节成功演出后, 实验中学决定将演出节目刻录成电脑光盘, 若到电脑公司刻录, 每张需8元(包括空白光盘费);如果学校自刻, 除租用刻录机需120元外, 每张光盘还需要成本4元(包括空白光盘), 问至少刻录电脑光盘多少张时学校自己刻录的费用较省?。
苏教版八年级物理上册复习资料及试题

第一章声现象复习教学设计一、知识网络二、识记巩固 1.声音是由于物体的 振动 产生的,正在发声的物体叫做 声源 。
2.声音的传播是以 声波 的形式进行的。
声音的传播需要 介质 , 真空 不能传声。
一般情况下,声音在固体中传播的速度 最大 ,在空气中的传播速度 最小 。
空气中的速度大约是 340m/s 。
3.在物理学中,把声音的 高低 叫做音调, 声源每秒内振动的次数 叫做频率,单位是赫兹 ,符号H z。
振动的频率 越高 ,声音的音调 越高 。
4.物理学中,把人耳感觉到的声音的 强弱 叫做响度,声源 振动的幅度 越大,声音的响度 越大 ,它还跟距声源的 距离 有关,它的计量单位是 分贝 ,符号 dB 。
5.声音的三个特征是 音调、响度、音色 。
音色 反映的是声音的品质。
6.控制噪声主要着眼于 在声源处减弱 、 在传播中减弱 、 在入耳处减弱 这三个环节。
7. 15~40 dB 是较好的生活环境,超过 70 dB 就难以长时间忍受了。
8.一般只有在 20~20000Hz 范围内的声音才能引起人的听觉; 高于20000Hz 的声波称为超声波;而低于20Hz 的声波叫做 次声波 。
三、《声现象》问题梳理1.产生声音和听到声音的区别。
物体只要振动就一定能够产生声音,但是这个声音,人不一定能够听到。
主要可能的原因有:(1)此声音属次声波或超声波;(2)此声音响度太弱或人距发声体太远;(3)没有传声的介质;(4)非正常的听觉。
2.产生回声和听到回声是否是一回事情?产生回声的条件很简单,只要有障碍物就存在回声。
但是,有回声时我们不一定能够听到。
由于人耳只能区分相隔0.1s 以上时间的两个声音,所以当回声返回的时间不到0.1s 时,人就无法听到回声,回声和原声混合在一起,使原声加强。
3.音调和响度的区别。
这是两个容易混淆的概念:音调指声音的高低,也就是日常生活中所说的声音的粗细,它是由声源振动的频率决定的;而响度是指声音强弱,也就是日常生活中所说的声音的大小,它是由声源振动的幅度决定的,响度越大具有的声能越多。
苏教版八年级(上)期末复习资料汇编

一、注音写字:池沼( ) 重峦叠嶂( ) 镂( )空斟酌( ) ( ) 琢( )磨栖( )息硕( )大老鸹( ) 肆无忌惮( ) 鹈鹕( ) ( )抿( )嘴懦( )弱抖擞( ) 摇曳( ) 虬( )干万斛( )闲愁惊悚( ) 霓( )虹灯倏( )然耽( )搁悖( )论温馨( ) 咆哮( ) 潴( ) 胼胝( ) ( ) 丘hâ( )lín xún( ) ( ) 房yán( ) jiàn( )赏玲lïng( ) 喜quâ( )围jiǎo( ) xī( )戏xuān( )闹mì( )食bà( )道guǎ( )人荒dàn( ) wānyán( ) ( ) liàn( )滟荆jí( )fù( )盖xiāo( )索wâi( )集pān( )附chïuchàng( )( ) 闲情yì( )致nân( )绿fū( )卵喧xiāo( ) 山岚( )辉huáng( ) mùyù( ) ( ) pán shān( ) ( ) 咨xún( )wàng( )意远嫌避yuàn( ) 坻( ) 屿( ) 堪( ) 悄怆( )佁( )然就寝( ) 藻荇( ) 风靡( ) 骤( )然傣( )族山寨( ) 船舷( ) 瑰( )丽鳞次栉( )比器皿( ) 啄( )眦( ) 堤( )岸脸颊( ) 靴( )子稠( )密椽( )子xī()忽深suì( ) tíng( )院朝tíng( ) huáng( )竹翠màn( ) 寂liáo( ) lì( )而从者yìn( )蔽suì( )道静mì( ) 盘jù( ) 迁x?( ) rïng( )会hu?ng ( )如隔世一hïng( )秋水dì( )听波lán( ) juã( )类植物miâ( )条zhēng( )汽jìsì( ) ( ) mïgu( ) ( ) huìlù( ) ( )wǔ( )媚qídǎo( ) ( ) 保yîu( ) d?ng( )立huī( )章cān( )厅船t?ng( ) tiào( )望nián( )土绿yīn( ) yàn( )会kūlong( ) ( ) dūnang( ) ( ) 狼藉( ) 蹒跚( ) ( )箸( ) 呼啸( ) 停滞( ) 磨蹭( ) 吮( )吸瞅( )馍( ) 病笃( ) 恸( ) 瞥( ) 憧憬( ) ( )脸颊( ) 歉疚( ) 褴褛( ) ( ) 妥( )帖城阙( )歧( )路簌簌( ) 交xiâ( ) chïuchú( ) ( ) àn( )然行náng( ) shuàn( )羊肉yú( )论jì( )然元xiāo( )惺sōng( ) zhì( )嫩犹yù( ) chïu( )谢qīqiāo()()yān()红山ào ()郝sǒu()fēng()火hān()然入梦xuàn()丽广mào()měng()懂jiǎo()健玛nǎo()裤dōu()dàn()生ào()悔kuǎn()待贫jí()mù()集卫shù()区diāo()零wùxū()()变法祈()祷捂()挟()持惩()罚眷()恋卓()越萌()发诬()陷月笼()沙寂寥()造诣()倔()强官huàn( )yín( )唱fù( )闲zhǔ( )托tuí( )唐琐xiâ( )diàn( )记缝rân( ) 唏xū( ) 吩fu( ) 岷()山蓦()地泥泞()猝()然抽噎()愠()怒焦灼()湿漉漉()pãng()勃帐pãng()精cuì()niān()巴yǎng()望wēi yí()()pãng pài()()白雪ái ái()()咀juã()liàng qiàng()()gōu()火qián()之驴群英huìcuì()()拖zhuài()T恤()如火如荼()多音字注音组词:龟( )_______ 恶( )_______ 翘( )_______ 教?( )_______ 朝( )_______ ( )_______ ( )_______ ( )_______ ?( )_______ ?( )_______夫( )_______ 劲?( )_______ 更( )_______ 强?( )_______ 泊?( )_______( )_______ ( )_______ ( )_______ ( )_______ ?( )_______?中( )_______ 量( )_______ 氓?( )_______ 应?( )_______ 朝?( )_______?( )?_______ ?( )_______ ?( )_______ ?( )_______ ?( )_______ ?辟?( )_______ 禁?( )_______ 度?( )_______相( )_______ 给( )_______ ? ( )_______ ?( )_______ ?( )_______ ( )_______ ( )_______帖( )_______ 吓( )_______ 奔( )_______ 晕( )_______ 吓( )_______ ( )_______ ?( )_______ ( )_______ ( )_______ ?( )_______蔚?( )_______ 尽?( )_______ 为?( )_______ 勾?( )_______ 查( )_______( )_______ ?( )_______ ?( )_______ ? ( )_______ ?( )_______幢( )_______ 乐( )_______ 传?( )_______ 悄?( )_______ 栅( )_______ ?( )_______ ( )?_______ ?( )_______ ( )_______ ( )_______背?( )_______ 丧?( )_______没?( )_______俶( )_______?( )?_______ ?( )_______ ( )_______ ( )_______解?( )_______ ?数?( )_______蒙?( )_______晃?( )_______? ( )_______ ? ?( )_______ ? ?( )?_______ ( )?_______( )_______ ?( )________ ( )_______ ( )_______差( )_______ 行?( )_______ 参( )?_______?( )_______ ( )_______ ( )_______( )_______ ( )_______ ( )_______( )_______ ( )_______ ( )______( )_______?重:重叠______ 量:打量______ 骨:骨头______ 盛:盛大______ 燎:燎原______ 重兵______ 测量______ 骨碌______ 盛饭______ 火烧火燎______磅:磅bï______ 咽:狼吞虎咽______ 扎:挣扎______ 宿:三天两宿______ 磅秤______ 呜咽______ 扎营盘______ 宿营______咽喉______ 扎辫子______ 星宿______注释:因地制宜:自出心裁:别具匠心:司空见惯:鲁殿灵光:毛骨悚然:林林总总:好逸恶劳:dì听:鳞次栉比:接风洗尘:瑰丽:风靡:qīqiāo:宛转:诧异:泛舟:汗青:寥落:瞭望:风烛残年:如火如荼:喧嚣:退避三舍:无所事事:诸如此类:斟酌:胸中有丘壑:山岚:失魂落魄:万籁俱寂:辗转反侧:歉疚:饮泣吞声:娓娓动听:循循善诱:触目伤怀:情郁于中:蹒跚:狼藉:修改下列词语中的错别字(在错别字下画线,括号内订正)悲喜交积()无瑕顾及()令人作欧()臭气薰天()如火如茶()受益非浅()图文并貌()布袍绶带()好益恶劳()见利忘益()事必恭亲()千锤百练()择无旁带()气势磅薄()万籁具寂()苛绢杂税()不宿之客()自济自足()毛骨竦然()闲情逸志()史无前列()十年浩疾()自之知明()月白风青()禄禄无为()因地治宜()亭台楦榭()重峦叠障()别俱匠心()自出新栽()肆无悸弹()旁惹无人()退辟三舍()司空见贯()杯盘狼藉()习已为常()风糜一时()接风洗程()晃如隔世()心弛神往()人迹罕致()轻瞄淡写()雄居一方()可见一般()鳞次节比()俯仰生恣()衣衫监娄()无精打采()失魂落魅()如数俸还()悄疮幽隧()碾转反侧()饮气吞声()莫明其妙()微微动听()热泪吟眶()前世怨家()徇徇善诱()一保眼福()情寓于中()夺框而出()不能自己()气势凶凶()情不自尽()摄手摄脚()璧垒森严()无与论比()晶花水月()陷指一算()居理力争()吊虎离山()千锤百练()珂捐杂税()憾然入梦()万赖俱寂()快致人口()良师亦友()梦昧以求()草毯泥粘()火急火撩()泥泞不勘()偏偏起舞()徇丽多姿()感概良深()曲指数算()姹紫艳红()萌懂少年()促目伤怀()痛绝良久()当面筹谢()云涯暖()莫然()渲闹()呆稚()荒涎()折分()徒峭()枯躁()孕藏()隔核()邪渎()康乃罄()文学常识填空1.古时行军打仗中的“三军”指、、;《七律长征》描绘了、、、、五幅图;《最后一课》作者是(国名)的,小说以为背景,着重表现了和等人物的爱国情怀。
苏教版八年级数学上册 压轴题 期末复习试卷(Word版 含解析)

苏教版八年级数学上册 压轴题 期末复习试卷(Word 版 含解析)一、压轴题1.如图1所示,直线:5L y mx m =+与x 轴负半轴,y 轴正半轴分别交于A 、B 两点.(1)当OA OB =时,求点A 坐标及直线L 的解析式.(2)在(1)的条件下,如图2所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM OQ ⊥于M ,BN OQ ⊥于N ,若17AM =,求BN 的长. (3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角OBF ∆和等腰直角ABE ∆,连接EF 交y 轴于P 点,如图3.问:当点B 在y 轴正半轴上运动时,试猜想PB 的长是否为定值?若是,请求出其值;若不是,说明理由.2.(1)探索发现:如图1,已知Rt △ABC 中,∠ACB =90°,AC =BC ,直线l 过点C ,过点A 作AD ⊥l ,过点B 作BE ⊥l ,垂足分别为D 、E .求证:AD =CE ,CD =BE .(2)迁移应用:如图2,将一块等腰直角的三角板MON 放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O 重合,另两个顶点均落在第一象限内,已知点M 的坐标为(1,3),求点N 的坐标.(3)拓展应用:如图3,在平面直角坐标系内,已知直线y =﹣3x+3与y 轴交于点P ,与x 轴交于点Q ,将直线PQ 绕P 点沿逆时针方向旋转45°后,所得的直线交x 轴于点R .求点R 的坐标.3.已知ABC 是等腰直角三角形,∠C=90°,点M 是AC 的中点,延长BM 至点D ,使DM =BM ,连接AD .(1)如图①,求证:DAM ≌BCM ;(2)已知点N 是BC 的中点,连接AN .①如图②,求证:ACN≌BCM;②如图③,延长NA至点E,使AE=NA,连接,求证:BD⊥DE.4.如图,已知等腰△ABC 中,AB=AC,∠A<90°,CD 是△ABC 的高,BE 是△ABC 的角平分线,CD 与BE 交于点P.当∠A 的大小变化时,△EPC 的形状也随之改变.(1)当∠A=44°时,求∠BPD 的度数;(2)设∠A=x°,∠EPC=y°,求变量y 与x 的关系式;(3)当△EPC 是等腰三角形时,请直接写出∠A 的度数.5.如图1.在△ABC中,∠ACB=90°,AC=BC=10,直线DE经过点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足分别为点D和E,AD=8,BE=6.(1)①求证:△ADC≌△CEB;②求DE的长;(2)如图2,点M以3个单位长度/秒的速度从点C出发沿着边CA运动,到终点A,点N 以8个单位长度/秒的速度从点B出发沿着线BC—CA运动,到终点A.M,N两点同时出发,运动时间为t秒(t>0),当点N到达终点时,两点同时停止运动,过点M作PM⊥DE 于点P,过点N作QN⊥DE于点Q;①当点N在线段CA上时,用含有t的代数式表示线段CN的长度;②当t为何值时,点M与点N重合;③当△PCM与△QCN全等时,则t=.6.已知三角形ABC 中,∠ACB =90°,点D (0,-4),M (4,-4).(1)如图1,若点C 与点O 重合,A (-2,2)、B (4,4),求△ABC 的面积;(2)如图2,AC 经过坐标原点O ,点C 在第三象限且点C 在直线DM 与x 轴之间,AB 分别与x 轴,直线DM 交于点G ,F ,BC 交DM 于点E ,若∠AOG =55°,求∠CEF 的度数;(3)如图3,AC 经过坐标原点O ,点C 在第三象限且点C 在直线DM 与x 轴之间,N 为AC 上一点,AB 分别与x 轴,直线DM 交于点G ,F ,BC 交DM 于点E ,∠NEC+∠CEF =180°,求证∠NEF =2∠AOG .7.已知:ABC 中,过B 点作BE ⊥AD ,=90=,∠︒ACB AC BC .(1)如图1,点D 在BC 的延长线上,连AD ,作BE AD ⊥于E ,交AC 于点F .求证:=AD BF ;(2)如图2,点D 在线段BC 上,连AD ,过A 作AE AD ⊥,且=AE AD ,连BE 交AC 于F ,连DE ,问BD 与CF 有何数量关系,并加以证明;(3)如图3,点D 在CB 延长线上,=AE AD 且AE AD ⊥,连接BE 、AC 的延长线交BE 于点M ,若=3AC MC ,请直接写出DB BC的值.8.如图,以直角△AOC 的直角顶点O 为原点,以OC ,OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足280a b b -++-=.(1)点A 的坐标为________;点C 的坐标为________.(2)已知坐标轴上有两动点P ,Q 同时出发,P 点从C 点出发沿x 轴负方向以每秒2个单位长度的速度匀速移动,Q 点从O 点出发沿y 轴正方向以每秒1个单位长度的速度匀速移动,点P 到达O 点整个运动随之结束.AC 的中点D 的坐标是(4,3),设运动时间为t 秒.问:是否存在这样的t ,使得△ODP 与△ODQ 的面积相等?若存在,请求出t 的值;若不存在,请说明理由.(3)在(2)的条件下,若∠DOC=∠DCO ,点G 是第二象限中一点,并且y 轴平分∠GOD .点E 是线段OA 上一动点,连接接CE 交OD 于点H ,当点E 在线段OA 上运动的过程中,探究∠GOA ,∠OHC ,∠ACE 之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).9.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.10.如图,已知直线l 1:y 1=2x +1与坐标轴交于A 、C 两点,直线l 2:y 2=﹣x ﹣2与坐标轴交于B 、D 两点,两直线的交点为P 点.(1)求P 点的坐标;(2)求△APB 的面积;(3)x 轴上存在点T ,使得S △ATP =S △APB ,求出此时点T 的坐标.11.在ABC 中,AB AC =,D 是直线AB 上一点,E 在直线BC 上,且DE DC =. (1)如图1,当D 在AB 上,E 在CB 延长线上时,求证:EDB ACD ∠=∠;(2)如图2,当ABC 为等边三角形时,D 是BA 的延长线上一点,E 在BC 上时,作//EF AC ,求证:BE AD =;(3)在(2)的条件下,ABC ∠的平分线BF 交CD 于点F ,连AF ,过A 点作AH CD ⊥于点H ,当30EDC ∠=︒,6CF =时,求DH 的长度.12.已知,在平面直角坐标系中,(42,0)A ,(0,42)B ,C 为AB 的中点,P 是线段AB 上一动点,D 是线段OA 上一点,且PO PD =,DE AB ⊥于E .(1)求OAB ∠的度数;(2)当点P 运动时,PE 的值是否变化?若变化,说明理由;若不变,请求PE 的值. (3)若45OPD ∠=︒,求点D 的坐标.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)5y x =+;(2)223)PB 的长为定值52 【解析】【分析】(1)先求出A 、B 两点坐标,求出OA 与OB ,由OA= OB ,求出m 即可;(2)用勾股定理求AB ,再证AMO OBN ∆≅∆,BN=OM ,由勾股定理求OM 即可; (3)先确定答案定值,如图引辅助线EG ⊥y 轴于G ,先证AOB EBG ∆≅∆,求BG 再证BFP GEP ∆≅∆,可确定BP 的定值即可.【详解】(1)对于直线:5L y mx m =+.当0y =时,5x =-.当0x =时,5y m =.()5,0A ∴-,()0,5B m .OA OB =.55m ∴=.解得1m =.∴直线L 的解析式为5y x =+.(2)5OA =,17AM =.∴由勾股定理,2222OM OA AM =-=.180AOM AOB BON ∠+∠+∠=︒.90AOB ∠=︒.90AOM BON ∴∠+∠=︒.90AOM OAM ∠+∠=︒.BON OAM ∴∠=∠.在AMO ∆与OBN ∆中,90BON OAM AMO BNO OA OB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩.()AMO OBN AAS ∴∆≅∆.22BN OM ∴==..(3)如图所示:过点E 作EG y ⊥轴于G 点.AEB ∆为等腰直角三角形,AB EB ∴=90ABO EBG ∠+∠=︒.EG BG ⊥,90GEB EBG ∴∠+∠=︒.ABO GEB ∴∠=∠.AOB EBG ∴∆≅∆.5BG AO ∴==,OB EG =OBF ∆为等腰直角三角形,OB BF ∴=BF EG ∴=.BFP GEP ∴∆≅∆.1522BP GP BG ∴===. 【点睛】本题考查求解析式,线段的长,判断定值问题,关键是掌握求坐标,利用条件OA= OB ,求OM ,用勾股定理求AB ,再证AMO OBN ∆≅∆,构造 AOB EBG ∆≅∆,求BG ,再证BFP GEP ∆≅∆.2.(1)见解析(2)(4,2)(3)(6,0)【解析】【分析】(1)先判断出∠ACB=∠ADC ,再判断出∠CAD=∠BCE ,进而判断出△ACD ≌△CBE ,即可得出结论;(2)先判断出MF=NG ,OF=MG ,进而得出MF=1,OF=3,即可求出FG=MF+MG=1+3=4,即可得出结论;(3)先求出OP=3,由y=0得x=1,进而得出Q (1,0),OQ=1,再判断出PQ=SQ ,即可判断出OH=4,SH=0Q=1,进而求出直线PR 的解析式,即可得出结论.【详解】证明:∵∠ACB =90°,AD ⊥l∴∠ACB =∠ADC∵∠ACE =∠ADC+∠CAD ,∠ACE =∠ACB+∠BCE∴∠CAD =∠BCE ,∵∠ADC =∠CEB =90°,AC =BC∴△ACD ≌△CBE ,∴AD =CE ,CD =BE ,(2)解:如图2,过点M 作MF ⊥y 轴,垂足为F ,过点N 作NG ⊥MF ,交FM 的延长线于G ,由已知得OM =ON ,且∠OMN =90°∴由(1)得MF =NG ,OF =MG ,∵M (1,3)∴MF =1,OF =3∴MG =3,NG =1∴FG =MF+MG =1+3=4,∴OF﹣NG=3﹣1=2,∴点N的坐标为(4,2),(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,对于直线y=﹣3x+3,由x=0得y=3∴P(0,3),∴OP=3由y=0得x=1,∴Q(1,0),OQ=1,∵∠QPR=45°∴∠PSQ=45°=∠QPS∴PQ=SQ∴由(1)得SH=OQ,QH=OP∴OH=OQ+QH=OQ+OP=3+1=4,SH=OQ=1∴S(4,1),设直线PR为y=kx+b,则341bk b=⎧⎨+=⎩,解得1k2b3⎧=-⎪⎨⎪=⎩∴直线PR为y=﹣12x+3由y=0得,x=6∴R(6,0).【点睛】本题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,构造出全等三角形是解本题的关键.3.(1)见解析;(2)①见解析;②见解析【解析】【分析】(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC 即可得证;②取AD中点F,连接EF,先证△EAF≌△ANC得∠NAC=∠AEF,∠C=∠AFE=90°,据此知∠AFE=∠DFE=90°,再证△AFE≌△DFE得∠EAD=∠EDA=∠ANC,从而由∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM即可得证.【详解】解:(1)∵点M是AC中点,∴AM=CM,在△DAM和△BCM中,∵AM CMAMD CMBDM BM=⎧⎪∠=∠⎨⎪=⎩,∴△DAM≌△BCM(SAS);(2)①∵点M是AC中点,点N是BC中点,∴CM=12AC,CN=12BC,∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,在△BCM和△ACN中,∵CM CNC CBC AC=⎧⎪∠=∠⎨⎪=⎩,∴△BCM≌△ACN(SAS);②证明:取AD中点F,连接EF,则AD=2AF,∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,由(1)知,△DAM≌△BCM,∴∠DBC=∠ADB,∴AD∥BC,∴∠EAF=∠ANC,在△EAF和△ANC中,AE AN EAF ANC AF NC =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△ANC (SAS ),∴∠NAC=∠AEF ,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,∵F 为AD 中点,∴AF=DF ,在△AFE 和△DFE 中,AF DF AFE DFE EF EF =⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFE (SAS ),∴∠EAD=∠EDA=∠ANC ,∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM=180°-90°=90°,∴BD ⊥DE .【点睛】本题是三角形的综合问题,解题的关键是掌握中点的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识点.4.(1)56°;(2)y=454x +;(3)36°或1807°. 【解析】【分析】(1)根据等边对等角求出等腰△ABC 的底角度数,再根据角平分线的定义得到∠ABE 的度数,再根据高的定义得到∠BDC=90°,从而可得∠BPD ;(2)按照(1)中计算过程,即可得到∠A 与∠EPC 的关系,即可得到结果;(3)分①若EP=EC ,②若PC=PE ,③若CP=CE ,三种情况,利用∠ABC+∠BCD=90°,以及y=454x +解出x 即可. 【详解】 解:(1)∵AB=AC ,∠A=44°,∴∠ABC=∠ACB=(180-44)÷2=68°,∵CD ⊥AB ,∴∠BDC=90°,∵BE 平分∠ABC ,∴∠ABE=∠CBE=34°,∴∠BPD =90-34=56°;(2)∵∠A =x °,∴∠ABC=(180°-x°)÷2=(902x -)°, 由(1)可得:∠ABP=12∠ABC=(454x -)°,∠BDC=90°, ∴∠EPC =y °=∠BPD=90°-(454x -)°=(454x +)°, 即y 与 x 的关系式为y=454x +; (3)①若EP=EC ,则∠ECP=∠EPC=y , 而∠ABC=∠ACB=902x -,∠ABC+∠BCD=90°, 则有:902x -+(902x --y )=90°,又y=454x +, ∴902x -+902x --(454x +)=90°, 解得:x=36°;②若PC=PE ,则∠PCE=∠PEC=(180-y )÷2=902y -, 由①得:∠ABC+∠BCD=90°, ∴902x -+[902x --(902y -)]=90,又y=454x +, 解得:x=1807°; ③若CP=CE , 则∠EPC=∠PEC=y ,∠PCE=180-2y ,由①得:∠ABC+∠BCD=90°, ∴902x -+902x --(180-2y )=90,又y=454x +, 解得:x=0,不符合, 综上:当△EPC 是等腰三角形时,∠A 的度数为36°或1807°. 【点睛】本题考查了等腰三角形的性质,二元一次方程组的应用,高与角平分线的定义,有一定难度,关键是找到角之间的等量关系.5.(1)①证明见解析;②DE =14;(2)①8t -10;②t =2;③t =10,211【解析】【分析】(1)①先证明∠DAC=∠ECB,由AAS即可得出△ADC≌△CEB;②由全等三角形的性质得出AD=CE=8,CD=BE=6,即可得出DE=CD+CE=14;(2)①当点N在线段CA上时,根据CN=CN−BC即可得出答案;②点M与点N重合时,CM=CN,即3t=8t−10,解得t=2即可;③分两种情况:当点N在线段BC上时,△PCM≌△QNC,则CM=CN,得3t=10−8t,解得t=1011;当点N在线段CA上时,△PCM≌△QCN,则3t=8t−10,解得t=2;即可得出答案.【详解】(1)①证明:∵AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∵∠ACB=90°,∴∠DAC+∠DCA=∠DCA+∠BCE=90°,∴∠DAC=∠ECB,在△ADC和△CEB中ADC CEBDAC ECBAC CB∠∠∠∠⎧⎪⎨⎪⎩===,∴△ADC≌△CEB(AAS);②由①得:△ADC≌△CEB,∴AD=CE=8,CD=BE=6,∴DE=CD+CE=6+8=14;(2)解:①当点N在线段CA上时,如图3所示:CN=CN−BC=8t−10;②点M与点N重合时,CM=CN,即3t=8t−10,解得:t=2,∴当t为2秒时,点M与点N重合;③分两种情况:当点N在线段BC上时,△PCM≌△QNC,∴CM=CN,∴3t=10−8t,解得:t=10 11;当点N在线段CA上时,△PCM≌△QCN,点M与N重合,CM=CN,则3t=8t−10,解得:t=2;综上所述,当△PCM与△QCN全等时,则t等于1011s或2s,故答案为:1011s或2s.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识;本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键.6.(1)8;(2)145°;(3)详见解析.【解析】【分析】(1)作AD⊥ x轴于D,BE⊥x轴于E,由点A,B的坐标可得出AD=OD=2,BE=EO=4,DE=6,由面积公式可求出答案;(2)作CH∥x轴,如图2,由平行线的性质可得出∠AOG=∠ACH,∠DEC=∠HCE,求出∠DEC+∠AOG=∠ACB=90°,可求出∠DEC=35°,则可得出答案;(3)证得∠NEC=∠HEC,则∠NEF=180°-∠NEH=180°-2∠HEC,可得出结论.【详解】解:(1)作AD⊥x轴于D,BE⊥x轴于E,如图1,∵A(﹣2,2)、B(4,4),∴AD=OD=2,BE=OE=4,DE=6,∴S△ABC=S梯形ABED﹣S△AOD﹣S△AOE=12×(2+4)×6﹣12×2×2﹣12×4×4=8;(2)作CH // x轴,如图2,∵D (0,﹣4),M (4,﹣4),∴DM // x 轴,∴CH // OG // DM,∴∠AOG =∠ACH,∠DEC =∠HCE,∴∠DEC+∠AOG =∠ACB =90°,∴∠DEC =90°﹣55°=35°,∴∠CEF =180°﹣∠DEC =145°;(3)证明:由(2)得∠AOG+∠HEC =∠ACB =90°,而∠HEC+∠CEF =180°,∠NEC+∠CEF =180°,∴∠NEC =∠HEC,∴∠NEF =180°﹣∠NEH =180°﹣2∠HEC,∵∠HEC =90°﹣∠AOG,∴∠NEF =180°﹣2(90°﹣∠AOG )=2∠AOG .【点睛】本题是三角形综合题,考查了坐标与图形的性质,三角形的面积,平行线的性质,三角形内角和定理,熟练掌握平行的性质及三角形内角和定理是解题的关键.7.(1)见详解,(2)2BD CF =,证明见详解,(3)23. 【解析】【分析】(1)欲证明BF AD =,只要证明BCF ACD ∆≅∆即可;(2)结论:2BD CF =.如图2中,作EH AC ⊥于H .只要证明ACD EHA ∆≅∆,推出CD AH =,EH AC BC ==,由EHF BCF ∆≅∆,推出CH CF =即可解决问题; (3)利用(2)中结论即可解决问题;【详解】(1)证明:如图1中,BE AD ⊥于E ,90AEF BCF ∴∠=∠=︒,AFE CFB ∠=∠,DAC CBF ∴∠=∠,BC AC =,BCF ACD ∴∆≅∆(AAS ),BF AD ∴=.(2)结论:2BD CF =.理由:如图2中,作EH AC ⊥于H .90AHE ACD DAE ∠=∠=∠=︒,90DAC ADC ∴∠+∠=︒,90DAC EAH ∠+∠=︒,ADC EAH ∴∠=∠,AD AE =,ACD EHA ∴∆≅∆,CD AH ∴=,EH AC BC ==,CB CA =,BD CH ∴=,90EHF BCF ∠=∠=︒,EFH BFC ∠=∠,EH BC =,EHF BCF ∴∆≅∆,FH FC ∴=,2BD CH CF ∴==.(3)如图3中,作EH AC ⊥于交AC 延长线于H .90AHE ACD DAE ∠=∠=∠=︒,90DAC ADC ∴∠+∠=︒,90DAC EAH ∠+∠=︒,ADC EAH ∴∠=∠,AD AE =,ACD EHA ∴∆≅∆,CD AH ∴=,EH AC BC ==,CB CA =,BD CH ∴=,90EHM BCM ∠=∠=︒,EMH BMC ∠=∠,EH BC =,EHM BCM ∴∆≅∆,MH MC ∴=,2BD CH CM ∴==.3AC CM =,设CM a =,则3AC CB a ==,2BD a =,∴2233DB a BC a ==.【点睛】本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.另外对于类似连续几步的综合题,一般前一步为后一步提供解题的条件或方法.8.(1)(0,6),(8,0);(2)存在t=2.4时,使得△ODP 与△ODQ 的面积相等;(3)2∠GOA+∠ACE=∠OHC ,理由见解析.【解析】【分析】(1)根据算术平方根的非负性,绝对值的非负性即可求解;(2)根据运动速度得到OQ=t ,OP=8-2t ,根据△ODP 与△ODQ 的面积相等列方程求解即可;(3)由∠AOC=90°,y 轴平分∠GOD 证得OG ∥AC ,过点H 作HF ∥OG 交x 轴于F ,得到∠FHC=∠ACE ,∠FHO=∠GOD ,从而∠GOD+∠ACE=∠FHO+∠FHC ,即可证得2∠GOA+∠ACE=∠OHC.【详解】(1280a b b -+-=,∴a-b+2=0,b-8=0,∴a=6,b=8,∴A (0,6),C (8,0);故答案为:(0,6),(8,0);(2)由(1)知,A (0,6),C (8,0),∴OA=6,OB=8,由运动知,OQ=t ,PC=2t ,∴OP=8-2t ,∵D (4,3),∴114222ODQ DS OQ x t t=⨯=⨯=△,11823123 22ODP DS OP y t t=⨯=-⨯=-△(),∵△ODP与△ODQ的面积相等,∴2t=12-3t,∴t=2.4,∴存在t=2.4时,使得△ODP与△ODQ的面积相等;(3)2∠GOA+∠ACE=∠OHC,理由如下:∵x轴⊥y轴,∴∠AOC=∠DOC+∠AOD=90°,∴∠OAC+∠ACO=90°.又∵∠DOC=∠DCO,∴∠OAC=∠AOD.∵x轴平分∠GOD,∴∠GOA=∠AOD.∴∠GOA=∠OAC.∴OG∥AC,如图,过点H作HF∥OG交x轴于F,∴HF∥AC,∴∠FHC=∠ACE.∵OG∥FH,∴∠GOD=∠FHO,∴∠GOD+∠ACE=∠FHO+∠FHC,即∠GOD+∠ACE=∠OHC,∴2∠GOA+∠ACE=∠OHC.【点睛】此题考查算术平方根的非负性,绝对值的非负性,坐标系中的动点问题,平行线的判定及性质定理,是一道较为综合的题型.9.(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析【解析】【分析】(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH=2EF,CH=2CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.【详解】解:(1)∵AB=AC,AE=AB,∴AB=AC=AE,∴∠ABE=∠AEB,∠ACE=∠AEC,∵∠AED=20°,∴∠ABE=∠AED=20°,∴∠BAE=140°,且∠BAC=90°∴∠CAE=50°,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=∠ACE=65°,∴∠DEC=∠AEC﹣∠AED=45°,故答案为:45;(2)猜想:∠AEC﹣∠AED=45°,理由如下:∵∠AED=∠ABE=α,∴∠BAE=180°﹣2α,∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=45°+α,∴∠AEC﹣∠AED=45°;(3)如图,过点C作CG⊥AH于G,∵∠AEC﹣∠AED=45°,∴∠FEH=45°,∵AH⊥BE,∴∠FHE=∠FEH=45°,∴EF=FH,且∠EFH=90°,∴EH2EF,∵∠FHE=45°,CG⊥FH,∴∠GCH=∠FHE=45°,∴GC=GH,∴CH2CG,∵∠BAC=∠CGA=90°,∴∠BAF+∠CAG=90°,∠CAG+∠ACG=90°,∴∠BAF=∠ACG,且AB=AC,∠AFB=∠AGC,∴△AFB≌△CGA(AAS)∴AF=CG,∴CH AF,∵在Rt△AEF中,AE2=AF2+EF2,AF)2+EF)2=2AE2,∴EH2+CH2=2AE2.【点睛】本题是综合了等腰直角三角形的性质,全等三角形的性质与判定的动点问题,三个问题由易到难,在熟练掌握各个相关知识的基础上找到问题之间的内部联系,层层推进去解答是关键.10.(1)P(﹣1,﹣1);(2)32;(3)T(1,0)或(﹣2,0).【解析】【分析】(1)解析式联立构成方程组,该方程组的解就是交点坐标;(2)利用三角形的面积公式解答;(3)求得C的坐标,因为S△ATP=S△APB,S△ATP=S△ATC+S△PTC=|x+12|,所以|x+12|=32,解得即可.【详解】解:(1)由212y xy x=+⎧⎨=--⎩,解得11xy=-⎧⎨=-⎩,所以P(﹣1,﹣1);(2)令x=0,得y1=1,y2=﹣2∴A(0,1),B(0,﹣2),则S△APB=12×(1+2)×1=32;(3)在直线l1:y1=2x+1中,令y=0,解得x=﹣12,∴C(﹣12,0),设T(x,0),∴CT=|x+12 |,∵S△ATP=S△APB,S△ATP=S△ATC+S△PTC=12•|x+12|•(1+1)=|x+12|,∴|x +12|=32, 解得x =1或﹣2,∴T (1,0)或(﹣2,0).【点睛】本题考查一次函数与二元一次方程组,解题的关键是准确将条件转化为二元一次方程组,并求出各点的坐标.11.(1)见解析;(2)见解析;(3)3【解析】【分析】(1)根据等腰三角形的性质和外角的性质即可得到结论;(2)过E 作EF ∥AC 交AB 于F ,根据已知条件得到△ABC 是等边三角形,推出△BEF 是等边三角形,得到BE=EF ,∠BFE=60°,根据全等三角形的性质即可得到结论; (3)连接AF ,证明△ABF ≌△CBF ,得AF=CF ,再证明DH=AH=12CF=3. 【详解】解:(1)∵AB=AC ,∴∠ABC=∠ACB ,∵DE=DC ,∴∠E=∠DCE ,∴∠ABC-∠E=∠ACB-∠DCB ,即∠EDB=∠ACD ;(2)∵△ABC 是等边三角形,∴∠B=60°,∴△BEF 是等边三角形,∴BE=EF ,∠BFE=60°,∴∠DFE=120°,∴∠DFE=∠CAD ,在△DEF 与△CAD 中, EDF DCA DFE CAD DE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF ≌△CAD (AAS ),∴EF=AD ,∴AD=BE ;(3)连接AF,如图3所示:∵DE=DC,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°,∵BF平分∠ABC,∴∠ABF=∠CBF,在△ABF和△CBF中,AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩,△ABF≌△CBF(SAS),∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°,∵AH⊥CD,∴AH=12AF=12CF=3,∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=3.【点睛】本题考查了全等三角形的判定与性质,等腰三角形和直角三角形的性质,三角形的外角的性质,等边三角形的判定和性质,证明三角形全等是解决问题的关键.12.(1)45°;(2)PE 的值不变,PE=4,理由见详解;(3)D(8-,0).【解析】【分析】(1)根据A,(0,B ,得△AOB 为等腰直角三角形,根据等腰直角三角形的性质,即可求出∠OAB 的度数;(2)根据等腰直角三角形的性质得到∠AOC=∠BOC=45°,OC ⊥AB ,再证明△POC ≌△DPE ,根据全等三角形的性质得到OC=PE ,即可得到答案;(3)证明△POB ≌△DPA ,得到PA=OB=,DA=PB ,进而得OD 的值,即可求出点D 的坐标.【详解】(1)A,(0,B ,∴OA=OB=∵∠AOB=90°,∴△AOB 为等腰直角三角形,∴∠OAB=45°;(2)PE 的值不变,理由如下:∵△AOB 为等腰直角三角形,C 为AB 的中点,∴∠AOC=∠BOC=45°,OC ⊥AB ,∵PO=PD ,∴∠POD=∠PDO ,∵D 是线段OA 上一点,∴点P 在线段BC 上,∵∠POD=45°+∠POC ,∠PDO=45°+∠DPE ,∴∠POC=∠DPE ,在△POC 和△DPE 中,90POC DPE OCP PED PO PD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△POC ≅△DPE(AAS),∴OC=PE ,∵OC=12AB=12××=4, ∴PE=4;(3)∵OP=PD ,∴∠POD=∠PDO=(180°−45°)÷2=67.5°,∴∠APD=∠PDO−∠A=22.5°,∠BOP=90°−∠POD=22.5°,∴∠APD=∠BOP ,在△POB 和△DPA 中,OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS),∴PA=OB=DA=PB ,∴DA=PB=-,∴OD=OA−DA=8-,∴点D 的坐标为(8,0).【点睛】本题主要考查等腰直角三角形的性质,三角形全等的判定与性质定理,图形与坐标,掌握等腰直角三角形的性质,是解题的关键.。
2010-2023历年初中数学苏教版八年级上册期末复习练习卷(带解析)

2010-2023历年初中数学苏教版八年级上册期末复习练习卷(带解析)第1卷一.参考题库(共10题)1.如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.2.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于B C,分别交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和的大小关系是()A. B.C. D.不能确定3.已知一次函数的图象经过第一、二、三象限,则b的值可以是()A.-1B.0C.2D.任意实数4.已知一次函数y=+m和y=+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是()A.2B.3C.4D.65.“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?6.若一组数据15,,11,,7的平均数为6,则的值是 .7.若点在第四象限,则点在()A.第一象限B.第二象限C.第三象限D.第四象限8.在直角坐标系中,用线段顺次连接点(,0),(0,3),(3,3),(4,0).(1)这是一个什么图形;(2)求出它的面积;(3)求出它的周长.9.有一数值转换器,原理如图所示,若开始输入的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2 011次输出的结果是___ .10.如图,△ABC中,AB=AC,BD是角平分线,BE=BD,∠A=72°,则∠DEC=" _______."第1卷参考答案一.参考题库1.参考答案:见解析2.参考答案:B3.参考答案:C4.参考答案:C5.参考答案:小麦11.2吨,玉米8.8吨6.参考答案:37.参考答案:B8.参考答案:(1)梯形(2)(3)9.参考答案:110.参考答案:103.5°。
苏教版八年级上学期期末复习数学试题
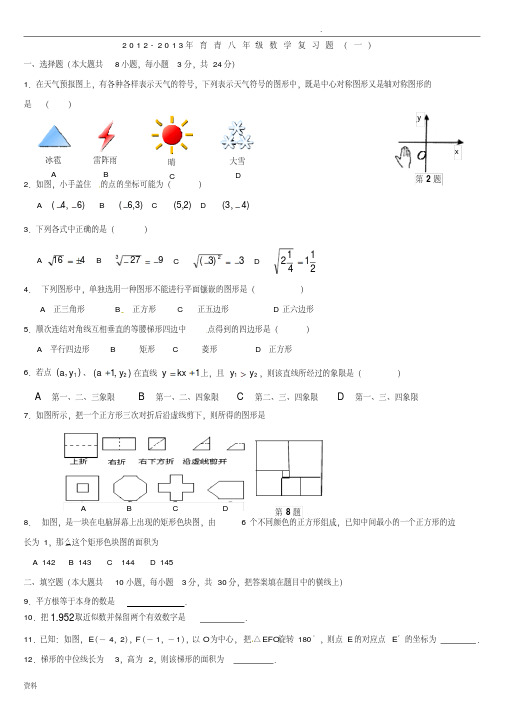
m) . 求: ( 1) m的值;
( 2)一次函数 y= kx +b 的解析式;( 3)这两个函数图像与 x 轴所围成的三角形面积 .
资料
.
24.(本题满分 10 分)甲、乙两人在相同条件下各射靶 10 次,每次射靶的成绩情况如左图所示:
环数 环数
10 9 8
7 6 5 4 3 2 1
一二 三 四五
∴ AC=DF ∠ ACB=∠ F ∴ AC∥ DF
………… 7 分 ………… 9 分
∴四边形 ACFD是平行四边形.……… 10 分
23、解:( 1)把点( 2, m)代入 y 1 x 得, m=1 2
……… 2 分
( 2)把点(- 1,- 5)、( 2, 1)代入 y= kx+ b 得,
kb 5
由题意知: AD∥ BC, AB∥CD
∴四边形 ABCD是平行四边形 …… 2 分
∵两个矩形全等
∴ AP=AQ
…… 3 分
10 分。
资料
∵ AP·BC=AQ· CD
∴ BC=CD
∴平行四边形 ABCD是菱形 H
…… 5 分
E
A
N D
E
A
.
…… 4 分
H D
KB
Q C
G
P
L
F
图甲
B
C
G
F 图乙
( 2)设 BC=x,则 CG=6-x , CD=BC=x
x4
15 、
y2
16、 6
17、 40°、 70°或 100° 18、- 3≤ b≤ 0
三、解答题 (本大题共 10 小题,共 96 分 . )
19、( 1)解:原式 =- 2- 1+ 2 ……… 3 分
【江苏省通用】江苏省苏科版初二数学第一学期期末复习要点(附练习及答案)

°.
19.如图,在△ABC 中,AB=AC,点 D 在 BC 上,且 AD=BD,∠ADB=100,则∠BAC
的度数为
°.
(第 18 题)
20.如图,已知△ABC 和△ADE 均为等腰直角三角形,∠BAC=∠DAE=90°,且 D、E、
C 三点在一直线上.若 AD=AE=1,DE=2E③④
C.②③④
D.①②④
2.如左图,以图形的右边缘所在的直线为轴将该图形向右翻折,再按顺时针方向旋转 1800,
所得的图形是( )
3.下面四个图形分别是节能、节水、低碳和绿色食品标志。在这四个标志中,是轴对称图形
的是(
)
A.
B.
C.
D.
4. 如图,在 Rt ABC 中, A 90 , D 是 BC 的中点, DE BC ,垂足为 D ,
25. 如图,已知∠EAC 是△ABC 的外角,AD 平分∠EAC,AB=AC.求证:AD∥BC.
26. 如图,在 Rt△ABC 中,∠C=90°,AB 的垂直平分线分别交 AB、AC 于点 D、E.m (1)若 AC=12,BC=9,求 AE 的长; (2)过点 D 作 DF⊥BC,垂足为 F,则△ADE 与△DFB 是否全等?请说明理由.
三角形能画( )
A. 1 个 B. 2 个
C. 3 个
D. 4 个
6.如图,在△ABC 中,AD⊥BC,垂足为 D,若 AD=3,∠B=45°,△ABC 的面积为 6,
则 AC 边的长是 ( )
A. 6
B.2 2
C. 10
D.3 2
(第 6 题)
(第 7 题)
7. 如图,已知 AD AB , C E , CDE 55 ,则 ABE 的度数为
苏教版八年级上册数学 压轴题 期末复习试卷复习练习(Word版 含答案)
苏教版八年级上册数学压轴题期末复习试卷复习练习(Word版含答案)一、压轴题1.已知ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM =BM,连接AD.(1)如图①,求证:DAM≌BCM;(2)已知点N是BC的中点,连接AN.①如图②,求证:ACN≌BCM;②如图③,延长NA至点E,使AE=NA,连接,求证:BD⊥DE.2.(1)在等边三角形ABC中,①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是度;②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是度;(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).3.如图,A点的坐标为(0,3),B点的坐标为(﹣3,0),D为x轴上的一个动点且不与B,O重合,将线段AD绕点A逆时针旋转90°得线段AE,使得AE⊥AD,且AE=AD,连接BE交y轴于点M.(1)如图,当点D在线段OB的延长线上时,①若D点的坐标为(﹣5,0),求点E的坐标.②求证:M为BE的中点.③探究:若在点D运动的过程中,OMBD的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.(2)请直接写出三条线段AO ,DO ,AM 之间的数量关系(不需要说明理由).4.如图①,在ABC ∆中,12AB =cm ,20BC =cm ,过点C 作射线//CD AB .点M 从点B 出发,以3 cm/s 的速度沿BC 匀速移动;点N 从点C 出发,以a cm/s 的速度沿CD 匀速移动.点M 、N 同时出发,当点M 到达点C 时,点M 、N 同时停止移动.连接AM 、MN ,设移动时间为t (s).(1)点M 、N 从移动开始到停止,所用时间为 s ;(2)当ABM ∆与MCN ∆全等时,①若点M 、N 的移动速度相同,求t 的值;②若点M 、N 的移动速度不同,求a 的值;(3)如图②,当点M 、N 开始移动时,点P 同时从点A 出发,以2 cm/s 的速度沿AB 向点B 匀速移动,到达点B 后立刻以原速度沿BA 返回.当点M 到达点C 时,点M 、N 、P 同时停止移动.在移动的过程中,是否存在PBM ∆与MCN ∆全等的情形?若存在,求出t 的值;若不存在,说明理由.5.如图,已知△ABC 中,AB=AC=10cm ,BC=8cm ,点D 为AB 的中点.如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. (1)若点Q 的运动速度与点P 的运动速度相等,经过1s 后,BP= cm ,CQ= cm . (2)若点Q 的运动速度与点P 的运动速度相等,经过1s 后,△BPD 与△CQP 是否全等,请说明理由;(3)若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?(4)若点Q 以(3)中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次相遇?6.在等边△ABC 的顶点A 、C 处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A 向B 和由C 向A 爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t 分钟后,它们分别爬行到D 、E 处,请问:(1)如图1,在爬行过程中,CD 和BE 始终相等吗,请证明?(2)如果将原题中的“由A 向B 和由C 向A 爬行”,改为“沿着AB 和CA 的延长线爬行”,EB 与CD 交于点Q ,其他条件不变,蜗牛爬行过程中∠CQE 的大小保持不变,请利用图2说明:∠CQE =60°;(3)如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行,连接DE 交AC 于F ”,其他条件不变,如图3,则爬行过程中,证明:DF =EF7.如图所示,在平面直角坐标系xOy 中,已知点A 的坐标(3,2)-,过A 点作AB x ⊥轴,垂足为点B ,过点(2,0)C 作直线l x ⊥轴,点P 从点B 出发在x 轴上沿着轴的正方向运动.(1)当点P 运动到点O 处,过点P 作AP 的垂线交直线l 于点D ,证明AP DP =,并求此时点D 的坐标;(2)点Q 是直线l 上的动点,问是否存在点P ,使得以P C Q 、、为顶点的三角形和ABP ∆全等,若存在求点P 的坐标以及此时对应的点Q 的坐标,若不存在,请说明理由.8.如图,在平面直角坐标系中,直线334y x =-+分别交,x y 轴于A B ,两点,C 为线段AB 的中点,(,0)D t 是线段OA 上一动点(不与A 点重合),射线//BF x 轴,延长DC 交BF 于点E .(1)求证:AD BE =;(2)连接BD ,记BDE 的面积为S ,求S 关于t 的函数关系式;(3)是否存在t 的值,使得BDE 是以BD 为腰的等腰三角形?若存在,求出所有符合条件的t 的值;若不存在,请说明理由.9.如图,以直角△AOC 的直角顶点O 为原点,以OC ,OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足280a b b -++-=.(1)点A 的坐标为________;点C 的坐标为________.(2)已知坐标轴上有两动点P ,Q 同时出发,P 点从C 点出发沿x 轴负方向以每秒2个单位长度的速度匀速移动,Q 点从O 点出发沿y 轴正方向以每秒1个单位长度的速度匀速移动,点P 到达O 点整个运动随之结束.AC 的中点D 的坐标是(4,3),设运动时间为t 秒.问:是否存在这样的t ,使得△ODP 与△ODQ 的面积相等?若存在,请求出t 的值;若不存在,请说明理由.(3)在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且y轴平分∠GOD.点E是线段OA上一动点,连接接CE交OD于点H,当点E在线段OA上运动的过程中,探究∠GOA,∠OHC,∠ACE之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).10.已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求ABFACFSS的值.11.如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.(1)求证:DG=BC;(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.12.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.(1)求证:AE=BD;(2)试探究线段AD、BD与CD之间的数量关系;(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:,CD,求线段AB的长.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)见解析;(2)①见解析;②见解析【解析】【分析】(1)由点M是AC中点知AM=CM,结合∠AMD=∠CMB和DM=BM即可得证;(2)①由点M,N分别是AC,BC的中点及AC=BC可得CM=CN,结合∠C=∠C和BC=AC 即可得证;②取AD中点F,连接EF,先证△EAF≌△ANC得∠NAC=∠AEF,∠C=∠AFE=90°,据此知∠AFE=∠DFE=90°,再证△AFE≌△DFE得∠EAD=∠EDA=∠ANC,从而由∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM即可得证.【详解】解:(1)∵点M是AC中点,∴AM=CM,在△DAM和△BCM中,∵AM CMAMD CMBDM BM=⎧⎪∠=∠⎨⎪=⎩,∴△DAM≌△BCM(SAS);(2)①∵点M是AC中点,点N是BC中点,∴CM=12AC,CN=12BC,∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,在△BCM和△ACN中,∵CM CNC C BC AC=⎧⎪∠=∠⎨⎪=⎩,∴△BCM≌△ACN(SAS);②证明:取AD中点F,连接EF,则AD=2AF ,∵△BCM ≌△ACN ,∴AN=BM ,∠CBM=∠CAN ,∵△DAM ≌△BCM ,∴∠CBM=∠ADM ,AD=BC=2CN ,∴AF=CN ,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC ,由(1)知,△DAM ≌△BCM ,∴∠DBC=∠ADB ,∴AD ∥BC ,∴∠EAF=∠ANC ,在△EAF 和△ANC 中,AE AN EAF ANC AF NC =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△ANC (SAS ),∴∠NAC=∠AEF ,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,∵F 为AD 中点,∴AF=DF ,在△AFE 和△DFE 中,AF DF AFE DFE EF EF =⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFE (SAS ),∴∠EAD=∠EDA=∠ANC ,∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM=180°-90°=90°,∴BD ⊥DE .【点睛】本题是三角形的综合问题,解题的关键是掌握中点的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识点.2.(1)①60°;②60°;(2)∠BFE =α.【解析】【分析】(1)①先证明△ACE≌△CBD得到∠ACE=∠CBD,再由三角形外角和定理可得∠BFE=∠CBD+∠BCF;②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF,再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA;(2)证明△AEC≌△CDB得到∠E=∠D,则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【详解】(1)如图①中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD,∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°.故答案为60.(2)如图②中,∵△ABC是等边三角形,∴AC=CB,∠A=∠BCD=60°,∴∠CAE=∠BCD=′120°∵AE=CD,∴△ACE≌△CBD,∴∠ACE=∠CBD=∠DCF,∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°.故答案为60.(3)如图③中,∵点O是AC边的垂直平分线与BC的交点,∴OC=OA,∴∠EAC=∠DCB=α,∵AC=BC,AE=CD,∴△AEC≌△CDB,∴∠E=∠D,∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α.【点睛】本题综合考查了三角形全等以及三角形外角和定理.3.(1)①E(3,﹣2)②见解析;③12OMBD,理由见解析;(2)OD+OA=2AM或OA﹣OD=2AM【解析】【分析】(1)①过点E作EH⊥y轴于H.证明△DOA≌△AHE(AAS)可得结论.②证明△BOM≌△EHM(AAS)可得结论.③是定值,证明△BOM≌△EHM可得结论.(2)根据点D在点B左侧和右侧分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可分别求出结论.【详解】解:(1)①过点E作EH⊥y轴于H.∵A(0,3),B(﹣3,0),D(﹣5,0),∴OA=OB=3,OD=5,∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∴△DOA≌△AHE(AAS),∴AH=OD=5,EH=OA=3,∴OH=AH﹣OA=2,∴E(3,﹣2).②∵EH⊥y轴,∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴BM=EM.③结论:OMBD=12.理由:∵△DOA≌△AHE,∴OD=AH,∵OA=OB,∴BD=OH,∵△BOM≌△EHM,∴OM=MH,∴OM=12OH=12BD.(2)结论:OA+OD=2AM或OA﹣OD=2AM.理由:当点D在点B左侧时,∵△BOM≌△EHM,△DOA≌△AHE∴OM=MH,OD=AH∴OH=2OM,OD-OB=AH-OA∴BD=OH∴BD=2OM,∴OD﹣OA=2(AM﹣AO),∴OD+OA=2AM.当点D在点B右侧时,过点E作EH⊥y轴于点H∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∵AD=AE∴△DOA≌△AHE(AAS),∴EH=AO=3=OB,OD=AH∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴OM=MH∴OA+OD= OA+AH=OH=OM+MH=2MH=2(AM+AH)=2(AM+OD)整理可得OA﹣OD=2AM.综上:OA+OD=2AM或OA﹣OD=2AM.【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系,掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键.4.(1)203;(2)①t=83;②a=185;(3)t=6.4或t=103【解析】【分析】(1)根据时间=路程÷速度即可求得答案;(2)①由题意得:BM=CN=3t,则只可以是△CMN≌△BAM,AB=CM,由此列出方程求解即可;②由题意得:CN≠BM,则只可以是△CMN≌△BMA,AB=CN=12,CM=BM,进而可得3t=10,求解即可;(3)分情况讨论,当△CMN≌△BPM时,BP=CM,若此时P由A向B运动,则12-2t=20-3t,但t=8不符合实际,舍去,若此时P由B向A运动,则2t-12=20-3t,求得t=6.4;当△CMN≌△BMP时,则BP=CN,CM=BM,可得3t=10,t=103,再将t=103代入分别求得AP,BP的长及a的值验证即可.【详解】解:(1)20÷3=203,故答案为:203;(2)∵CD∥AB,∴∠B=∠DCB,∵△CNM与△ABM全等,∴△CMN≌△BAM或△CMN≌△BMA,①由题意得:BM=CN=3t,∴△CMN≌△BAM∴AB=CM,∴12=20-3t,解得:t=83;②由题意得:CN≠BM,∴△CMN≌△BMA,∴AB=CN=12,CM=BM,∴CM=BM=12 BC,∴3t=10,解得:t=10 3∵CN=at,∴103a=12解得:a=185;(3)存在∵CD∥AB,∴∠B=∠DCB,∵△CNM与△PBM全等,∴△CMN≌△BPM或△CMN≌△BMP,当△CMN≌△BPM时,则BP=CM,若此时P由A向B运动,则BP=12-2t,CM=20-3t,∵BP=CM,∴12-2t=20-3t,解得:t=8 (舍去)若此时P由B向A运动,则BP=2t-12,CM=20-3t,∵BP=CM,∴2t-12=20-3t,解得:t=6.4,当△CMN≌△BMP时,则BP=CN,CM=BM,∴CM=BM=12 BC∴3t=10,解得:t=10 3当t=103时,点P的路程为AP=2t=203,此时BP=AB-AP=12-203=163,则CN=BP=16 3即at=163,∵t=103,∴a=1.6符合题意综上所述,满足条件的t的值有:t=6.4或t=10 3【点睛】本题考查了全等三角形的判定及性质的综合运用,解决本题的关键就是用方程思想及分类讨论思想解决问题,把实际问题转化为方程是常用的手段.5.(1)BP=3cm ,CQ=3cm ;(2)全等,理由详见解析;(3)154;(4)经过803s 点P 与点Q 第一次相遇.【解析】【分析】(1)速度和时间相乘可得BP 、CQ 的长;(2)利用SAS 可证三角形全等; (3)三角形全等,则可得出BP=PC ,CQ=BD ,从而求出t 的值;(4)第一次相遇,即点Q 第一次追上点P ,即点Q 的运动的路程比点P 运动的路程多10+10=20cm 的长度.【详解】解:(1)BP=3×1=3㎝,CQ=3×1=3㎝(2)∵t=1s ,点Q 的运动速度与点P 的运动速度相等∴BP=CQ=3×1=3cm ,∵AB=10cm ,点D 为AB 的中点,∴BD=5cm .又∵PC=BC ﹣BP ,BC=8cm ,∴PC=8﹣3=5cm ,∴PC=BD又∵AB=AC ,∴∠B=∠C ,在△BPD 和△CQP 中,PC BD B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP(SAS)(3)∵点Q 的运动速度与点P 的运动速度不相等,∴BP 与CQ 不是对应边,即BP≠CQ∴若△BPD ≌△CPQ ,且∠B=∠C ,则BP=PC=4cm ,CQ=BD=5cm ,∴点P ,点Q 运动的时间t=433BP =s , ∴154Q CQ V t ==cm/s ; (4)设经过x 秒后点P 与点Q 第一次相遇. 由题意,得154x=3x+2×10,解得80 x=3∴经过803s点P与点Q第一次相遇.【点睛】本题考查动点问题,解题关键还是全等的证明和利用,将动点问题视为定点问题来分析可简化思考过程.6.(1)相等,证明见解析;(2)证明见解析;(3)证明见解析.【解析】【分析】(1)先证明△ACD≌△CBE,再由全等三角形的性质即可证得CD=BE;(2)先证明△BCD≌△ABE,得到∠BCD=∠ABE,求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC,∠CQE=180°-∠DQB,即可解答;(3)如图3,过点D作DG∥BC交AC于点G,根据等边三角形的三边相等,可以证得AD=DG=CE;进而证明△DGF和△ECF全等,最后根据全等三角形的性质即可证明.【详解】(1)解:CD和BE始终相等,理由如下:如图1,AB=BC=CA,两只蜗牛速度相同,且同时出发,∴CE=AD,∠A=∠BCE=60°在△ACD与△CBE中,AC=CB,∠A=∠BCE,AD=CE∴△ACD≌△CBE(SAS),∴CD=BE,即CD和BE始终相等;(2)证明:根据题意得:CE=AD,∵AB=AC,∴AE=BD,∴△ABC是等边三角形,∴AB=BC,∠BAC=∠ACB=60°,∵∠EAB+∠ABC=180°,∠DBC+∠ABC=180°,∴∠EAB=∠DBC,在△BCD和△ABE中,BC=AB,∠DBC=∠EAB,BD=AE∴△BCD≌△ABE(SAS),∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°,∴∠CQE=180°-∠DQB=60°,即CQE=60°;(3)解:爬行过程中,DF始终等于EF是正确的,理由如下:如图,过点D作DG∥BC交AC于点G,∴∠ADG=∠B=∠AGD=60°,∠GDF=∠E,∴△ADG为等边三角形,∴AD=DG=CE,在△DGF和△ECF中,∠GFD=∠CFE,∠GDF=∠E,DG=EC∴△DGF≌△EDF(AAS),∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质;题弄懂题中所给的信息,再根据所提供的思路寻找证明条件是解答本题的关键.7.(1)证明见解析;(2,3)D;(2)存在,(0,0)P,(2,3)Q或(0,0)P,(2,3)Q-或(4,0)P,(2,7)Q或(4,0)P,(2,7)Q-或1(,0)2P-,(2,2)Q-或1(,0)2P-,(2,2)Q-.【解析】【分析】(1)通过全等三角形的判定定理ASA证得△ABP≌△PCD,由全等三角形的对应边相等证得AP=DP,DC=PB=3,易得点D的坐标;(2)设P(a,0),Q(2,b).需要分类讨论:①AB=PC,BP=CQ;②AB=CQ,BP=PC .结合两点间的距离公式列出方程组,通过解方程组求得a、b的值,得解.【详解】(1)AP PD⊥90APB DPC∴∠+∠=AB x⊥轴90A APB∴∠+∠=A DPC∴∠=∠在ABP∆和PCD∆中A DPCAB PCABP PCD∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA∴∆≅∆AP DP∴=,3DC PB==(2,3)D∴(2)设(,0)P a ,(2,)Q b①AB PC =,BP CQ =223a a b ⎧-=⎪⎨+=⎪⎩,解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴,(2,3)Q 或(0,0)P ,(2,3)Q -或(4,0)P ,(2,7)Q 或(4,0)P ,(2,7)Q - ②AB CQ =,BP PC =,322a a b +=-⎧⎨=⎩,解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-,(2,2)Q -或1(,0)2P -,(2,2)Q - 综上:(0,0)P ,(2,3)Q 或(0,0)P ,(2,3)Q -或(4,0)P ,(2,7)Q 或(4,0)P ,(2,7)Q -或1(,0)2P -,(2,2)Q -或1(,0)2P -,(2,2)Q - 【点睛】 考查了三角形综合题.涉及到了全等三角形的判定与性质,两点间的距离公式,一元一次绝对值方程组的解法等知识点.解答(2)题时,由于没有指明全等三角形的对应边(角),所以需要分类讨论,以防漏解.8.(1)详见解析;(2)36(04)2BDE t t S -+≤<=;(3)存在,当78t =或43时,使得BDE 是以BD 为腰的等腰三角形.【解析】【分析】(1)先判断出EBC DAC ∠=∠,CEB CDA ∠=∠,再判断出BC AC =,进而判断出△BCE ≌△ACD ,即可得出结论;(2)先确定出点A ,B 坐标,再表示出AD ,即可得出结论;(3)分两种情况:当BD BE =时,利用勾股定理建立方程2223(4)t t +=-,即可得出结论;当BD DE =时,先判断出Rt △OBD ≌Rt △MED ,得出DM OD t ==,再用OM BE =建立方程求解即可得出结论.【详解】解:(1)证明:射线//BF x 轴, EBC DAC ∴∠=∠,CEB CDA ∠=∠, 又C 为线段AB 的中点,BC AC ∴=,在△BCE 和△ACD 中,CEB CDAEBC DACBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△ACD(AAS),BE AD∴=;(2)解:在直线334y x=-+中,令0x=,则3y=,令0y=,则4x=,A∴点坐标为(4,0),B点坐标为(0,3),D点坐标为(,0)t,4AD t BE∴=-=,113(4)36(04)222BDE ABD BS S AD y t t t∴==⋅=-⨯=-+<;(3)当BD BE=时,在Rt OBD∆中,90BOD∠=︒,由勾股定理得:222OB OD DB+=,即2223(4)t t+=-解得:78t=;当BD DE=时,过点E作EM x⊥轴于M,90BOD EMD∴∠=∠=︒,//BF OA,OB ME∴=在Rt△OBD和Rt△MED中,==BD DEOB ME⎧⎨⎩,∴Rt△OBD≌Rt△MED(HL),OD DM t∴==,由OM BE=得:24t t=-解得:43t=,综上所述,当78t =或43时,使得△BDE 是以BD 为腰的等腰三角形.【点睛】本题是一次函数综合题,主要考查了平行线的性质,全等三角形的判定和性质,勾股定理,用方程的思想解决问题是解本题的关键.9.(1)(0,6),(8,0);(2)存在t=2.4时,使得△ODP 与△ODQ 的面积相等;(3)2∠GOA+∠ACE=∠OHC ,理由见解析.【解析】【分析】(1)根据算术平方根的非负性,绝对值的非负性即可求解;(2)根据运动速度得到OQ=t ,OP=8-2t ,根据△ODP 与△ODQ 的面积相等列方程求解即可;(3)由∠AOC=90°,y 轴平分∠GOD 证得OG ∥AC ,过点H 作HF ∥OG 交x 轴于F ,得到∠FHC=∠ACE ,∠FHO=∠GOD ,从而∠GOD+∠ACE=∠FHO+∠FHC ,即可证得2∠GOA+∠ACE=∠OHC.【详解】(1280a b b -+-=,∴a-b+2=0,b-8=0,∴a=6,b=8,∴A (0,6),C (8,0);故答案为:(0,6),(8,0);(2)由(1)知,A (0,6),C (8,0),∴OA=6,OB=8,由运动知,OQ=t ,PC=2t ,∴OP=8-2t ,∵D (4,3),∴114222ODQ D S OQ x t t =⨯=⨯=△, 1182312322ODP D S OP y t t =⨯=-⨯=-△(), ∵△ODP 与△ODQ 的面积相等,∴2t=12-3t ,∴t=2.4,∴存在t=2.4时,使得△ODP与△ODQ的面积相等;(3)2∠GOA+∠ACE=∠OHC,理由如下:∵x轴⊥y轴,∴∠AOC=∠DOC+∠AOD=90°,∴∠OAC+∠ACO=90°.又∵∠DOC=∠DCO,∴∠OAC=∠AOD.∵x轴平分∠GOD,∴∠GOA=∠AOD.∴∠GOA=∠OAC.∴OG∥AC,如图,过点H作HF∥OG交x轴于F,∴HF∥AC,∴∠FHC=∠ACE.∵OG∥FH,∴∠GOD=∠FHO,∴∠GOD+∠ACE=∠FHO+∠FHC,即∠GOD+∠ACE=∠OHC,∴2∠GOA+∠ACE=∠OHC.【点睛】此题考查算术平方根的非负性,绝对值的非负性,坐标系中的动点问题,平行线的判定及性质定理,是一道较为综合的题型.10.(1)①见解析;②见解析;(2)2【解析】【分析】(1)①只要证明∠2+∠BAF=∠1+∠BAF=60°即可解决问题;②只要证明△BFC≌△ADB,即可推出∠BFC=∠ADB=90°;(2)在BF上截取BK=AF,连接AK.只要证明△ABK≌CAF,可得S△ABK=S△AFC,再证明AF=FK=BK,可得S△ABK=S△AFK,即可解决问题;【详解】(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB =∠2+∠4+∠BAC ,∵∠BFE =∠BAC =2∠EFC ,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB =AC ,∴△ABK ≌CAF ,∴∠3=∠4,S △ABK =S △AFC ,∵∠1+∠3=∠2+∠3=∠CFE =∠AKB ,∠BAC =2∠CEF ,∴∠KAF =∠1+∠3=∠AKF ,∴AF =FK =BK ,∴S △ABK =S △AFK , ∴ABF AFCS 2S ∆∆=. 【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是能够正确添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.11.(1)见解析;(2)当F 运动到AF =AD 时,FD ∥BG ,理由见解析;(3)FH =HD ,理由见解析【解析】【分析】(1)证明△DEG ≌△CEB (AAS )即可解决问题.(2)想办法证明∠AFD =∠ABG =45°可得结论.(3)结论:FH =HD .利用等腰直角三角形的性质即可解决问题.【详解】(1)证明:∵AD ∥BC ,∴∠DGE =∠CBE ,∠GDE =∠BCE ,∵E 是DC 的中点,即 DE =CE ,∴△DEG ≌△CEB (AAS ),∴DG =BC ;(2)解:当F 运动到AF =AD 时,FD ∥BG .理由:由(1)知DG =BC ,∵AB =AD +BC ,AF =AD ,∴BF =BC =DG ,∴AB =AG ,∵∠BAG =90°,∴∠AFD =∠ABG =45°,∴FD ∥BG ,故答案为:F 运动到AF =AD 时,FD ∥BG ;(3)解:结论:FH =HD .理由:由(1)知GE=BE,又由(2)知△ABG为等腰直角三角形,所以AE⊥BG,∵FD∥BG,∴AE⊥FD,∵△AFD为等腰直角三角形,∴FH=HD,故答案为:FH=HD.【点睛】本题考查了全等三角形的判定和性质,平行线的判定,等腰直角三角形的性质,掌握三角形全等的判定和性质是解题的关键.12.(1)见解析;(2)BD2+AD2=2CD2;(3)AB=2+4.【解析】【分析】(1)根据等腰直角三角形的性质证明△ACE≌△BCD即可得到结论;(2)利用全等三角形的性质及勾股定理即可证得结论;(3)连接EF,设BD=x,利用(1)、(2)求出EF=3x,再利用勾股定理求出x,即可得到答案.【详解】(1)证明:∵△ACB和△ECD都是等腰直角三角形∴AC=BC,EC=DC,∠ACB=∠ECD=90°∴∠ACB﹣∠ACD=∠ECD﹣∠ACD∴∠ACE=∠BCD,∴△ACE≌△BCD(SAS),∴AE=BD.(2)解:由(1)得△ACE≌△BCD,∴∠CAE=∠CBD,又∵△ABC是等腰直角三角形,∴∠CAB=∠CBA=∠CAE=45°,∴∠EAD=90°,在Rt△ADE中,AE2+AD2=ED2,且AE=BD,∴BD2+AD2=ED2,∵ED2CD,∴BD2+AD2=2CD2,(3)解:连接EF,设BD=x,∵BD :AF =1:2AF =2x ,∵△ECD 都是等腰直角三角形,CF ⊥DE ,∴DF =EF ,由 (1)、(2)可得,在Rt △FAE 中,EF 22AF AE +22(22)x x +3x ,∵AE 2+AD 2=2CD 2, ∴222(223)2(36)x x x ++=,解得x =1,∴AB =2+4.【点睛】此题考查三角形全等的判定及性质,等腰直角三角形的性质,勾股定理.。
苏教版八年级上期末物理试卷3

苏教版八年级(上)期末物理试卷一、选择题:(本题共12小题,每小题2分,共24分.每小题给出的选项中只有一个选项符合题意)1.(2分)下列数据中最接近事实的是()A.成年人的拇指宽度约为1dmB.普通人的洗澡水温度约为40℃C.人步行的正常速度约为1.4km/hD.健康人的脉搏跳动频率约为75次/秒2.(2分)如图所示,改变试管中的水量,用同样大小的力吹气时会发出不同的声音。
这“不同的声音”主要是指声音的()A.音调B.响度C.音色D.振幅3.(2分)现在城市建设越来越注重以人为本,如:城区汽车禁止鸣笛,主干道路面铺设沥青,住宅区道路两旁安装隔音板等。
这些措施的共同点是()A.绿化居住环境B.缓解“热岛效应”C.降低噪声污染D.减少大气污染4.(2分)下列物理知识与实际应用对应关系中正确的是()A.红外线﹣验钞机B.次声波﹣B超C.超声波﹣声呐D.紫外线﹣夜视仪5.(2分)如图所示是小明观看国庆70周年阅兵式中的一个场景,有关光现象的说法,正确的是()A.旗手帽子上的军徽闪闪发光,因为军徽是光源B.五星红旗呈现红色是因为吸收了太阳光中的红光C.电视机画面的颜色由红、黄、蓝三种色光混合而成D.整个队伍整齐划一,现场观众是通过光的直线传播来判断的6.(2分)下列有关“二十四节气”的谚语,分析正确的是()A.“小寒冻土,大寒冻河”,河水结冰是熔化现象B.“霜降有霜,米谷满仓”,霜的形成是凝华现象C.“伏天三场雨,薄地长好麻”,雨的形成是凝固现象D.“惊蛰云不停,寒到五月中”,云的形成是升华现象7.(2分)下列图示的光现象中,由于光的折射形成的是()A.雨后彩虹B.水中倒影C.树荫下的光斑D.汽车后视镜8.(2分)如图所示,早期照相馆里摄影师取景时看到的像是倒立的。
在图示场景中,下列说法正确的是()A.摄影师面前所成的是倒立缩小的虚像B.两位照相的人站在照相机镜头的二倍焦距以外C.若要改拍全身像,应减小相机和两位照相的人之间的距离D.要使人像更亮,必须在两位照相的人身后进行“补光”9.(2分)如图所示,两列火车并排停在站台上,小明坐在车厢中向另一列车厢观望,突然,他觉得自己的列车开始缓缓地前进了,但是,“驶过”了旁边列车的车尾才发现,实际上他乘坐的列车还停在站台上。
苏教版八年级上数学期末复习知识点总结+例题(完美版)(3)(K12教育文档)

苏教版八年级上数学期末复习知识点总结+例题(完美版)(3)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(苏教版八年级上数学期末复习知识点总结+例题(完美版)(3)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为苏教版八年级上数学期末复习知识点总结+例题(完美版)(3)(word版可编辑修改)的全部内容。
八年级数学(上)期末复习+例题解析第一章三角形全等1、全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转后得到的三角形,与原三角形仍然全等..;③三角形全等不因位置发生变化而改变。
2、全等三角形的性质:⑴全等三角形的对应边相等、对应角相等.理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角.⑵全等三角形的周长相等、面积相等。
⑶全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3、全等三角形的判定:①边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等.②角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等。
③推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等。
④边边边公理(SSS)有三边对应相等的两个三角形全等。
⑤斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等。
4、证明两个三角形全等的基本思路:⑴已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL)。
⑵已知一边一角:①找一角(AAS或ASA);②找夹边(SAS).⑶已知两角:①找夹边(ASA);②找其它边(AAS)。
苏科版八年级数学上期末复习与强化提优(三)

苏科版八年级数学上期末复习与强化提优(三)《第三章勾股定理》期末专题复习重点知识扫描一:勾股定理——(揭示的是平面几何图形本身所蕴含的代数关系):如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2(勾三、股四、弦五)(1)重视勾股定理的叙述形式:①直角三角形直角边上的两个正方形的面积之和等于斜边上的正方形的面积.②斜边的平方等于两直角边的平方和.从这两种形式来看,有“形的勾股定理”和“数的勾股定理”之分。
(2)勾股定理的证明勾股定理的证明方法很多,教科书正文中介绍了赵爽弦图,这是一种面积证法.常见的是拼图的方法,用拼图的方法验证勾股定理的思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.常见方法如下:方法一:(赵爽弦图/毕达哥拉斯证法)方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形方法三:(美国第20任总统詹姆斯·加菲尔德)二:勾股定理的逆定理——如果三角形的三边长a、b、c满足a2+b2=c2;那么这个三角形是直角三角形.(1)勾股定理的逆定理的证明方法,通过构造一个三角形与直角三角形全等,达到证明某个角为直角的目的。
(2)逆定理的作用:判定一个三角形是否为直角三角形。
步骤: 找出最长边‚计算两短边的平方和是否与最长边的平方相等(3)直角三角形的判定:①有一个角是直角的三角形是直角三角形。
②有两个角互余的三角形是直角三角形。
③两短边的平方和等于最长边的平方的三角形是直角三角形。
(4)勾股数:能够成为直角三角形三条边长的三个正整数如:3,4,5; 5,12,13; 6,8,10; 7,24,25; 8,15,17; 9,12,15; 9,40,41;……以及这些数组的倍数组成的数组。
1)确定勾股数: 三个数都是正整数‚两个较小数的平方和等于最大数的平方2)如果a,b,c是一组勾股数,那么na,nb,nc(n为正整数)也是一组勾股数.经典例题例1 .已知,在△ABC中,△ACB=90°,CD△AB垂足为D,BC=6,AC=8,求AB与CD的长.例2.如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?例3.如图,在ABC 中,△ACB=90°,AC=BC,P、Q在斜边上,且△PCQ=45°,求证:PQ2=AP2+BQ2。
苏教版八年级上册复习课件(第3课时)

3、右图是某农业生态系统的食物网。在该食物网中,人 们合理利用了自然资源,将鸡、猪、人的粪便以及玉米 秸秆放入沼气池发酵,产生的沼气用于照明和做饭,沼 渣用来做肥料,从而建立起了一种多层次、多功能的生 态农业系统。
请据图回答以下问题:
玉米光合作用固
(1)该生态系统中能量流动是从 定太阳能
开始。
(2)该生态系统中的生物通过
活的行为 4、典型代表动物:蜜蜂、蚂蚁、狒狒等。
• 第十八章:动物行为的生理基础(第二节) • 1、先天性行为:
动物生来就有的、由遗传物质所决定的行为,又称本能 行为。
• 2、学习行为: • 经过学习才能形成的行为。 • 注意:学习行为是建立在先天性行为基础之上的。 • 3、大脑皮层越发达,动物的学习能力越强。 • 4、意义: • 先天性行为奠定了动物生存和繁衍的基础,但还不足以
(6)倡导低碳生活
减少 CO2 排放,是每位
公民应尽的义务。
及时练:
• 1、流入生态系统的总能量是( C )
A.照射到生态系统中的全部太阳能
B.照射到绿色植物上的全部太阳能
C.生产者通过光合作用固定的太阳能
D.流入消费者体内的太阳能。
2、下列关于生态系统中能量流动的叙述,正确的是( A)
A.单方向 B.可循环 C.逐级增加 D.与光合作用无关
八上期末复习
第3课时
第十七章:(一)动物运动的形式和能量供应
•1.动物的运动形式: 飞行 、 奔跑 、 游泳 、
和 爬行 、 行走 、 跳跃 等。
2.动物通过运动可以适应 环境,提高生存能力。
3.动物运动消耗能量来源于 细胞呼吸 作用所
释放的能量。
食物
4.能量的直接来源是 ATP 。
苏教版八年级物理上册期末总复习(带答案)

苏教版八年级物理上册期末总复习(带答案)(时间:60分钟分数:100分)班级:姓名:分数:一、选择题(每题2分,共30分)1、对于图中所示的四幅图,下列说法中正确的是()A.甲图中软木塞飞出时,管内水蒸气的内能增加B.乙图中两个压紧的铅块能吊起钩码,主要是因为分子间存在引力C.丙图中活塞向下运动是内燃机的做功冲程D.丁图中小朋友下滑时,内能转化为机械能2、近年来中国航天事业获得蓬勃发展,某位航天员在太空飞船演示了在“失重”状态下奇特的物理现象。
以下哪个实验不能在太空飞船中进行()A.用弹簧握力计测握力B.用手表测时间C.用温度计测温度D.用弹簧测力计测重力3、如图所示,用大小为8N的水平拉力F拉上表面粗糙程度各处相同的物体A,使其在水平地面上以1m/s匀速运动,当物体B静止不动时,与水平绳相连的弹簧测力计的示数为3N保持不变(不计绳和弹簧测力计重),下列说法正确的是()A.水平拉力F与地面对A的摩擦力是一对平衡力B.A对B的摩擦力方向水平向右,大小为8NC.若A以2m/s匀速运动,拉力F将变大D.地对A的摩擦力方向水平向左,大小为5N4、下列物体重力约为1N的是()A.一枚大头针 B.两个鸡蛋C.一头奶牛D.一个篮球5、班级大扫除时,小天发现许多现象与摩擦有关,其中减小摩擦的措施是()A.擦玻璃时把抹布压紧在玻璃上去擦B.书柜下装有滚轮便于移动位置C.黑板刷的刷面选用更粗糙的材料制成D.水桶的手柄上刻有凹凸不平的花纹6、下列叙述主要说明力能改变物体的形状的是()A.用力蹬车,车加速前进B.用力垫球,球飞出去C.用力拉弓,弓弯了D.瞄准射击,子弹飞出7、平直公路上并排停放着两辆汽车,一段时间后,坐在甲车上的小明感觉乙车向北运动,关于两辆汽车的运动情况,下列说法正确的是()A.以乙车为参照物,甲车一定向南运动B.以甲车为参照物,地面一定是静止的C.以地面为参照物,甲车一定是向南运动D.以地面为参照物,乙车一定向北运动8、如图所示,静止在水平桌面上的玻璃瓶,水中有个气泡和金属球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
礼物灯光很暗,女儿在母亲的床边站了一会儿,然后轻轻地把一个包装很精致的工艺品盒放在母亲的身边。
那是女儿送给母亲的生日礼物。
母亲依旧香甜地睡着,不时地发出轻微的酣声,借着不很明亮的灯光,女儿发现母亲又瘦了许多。
挂钟轻轻地敲了几下,女儿便背起了书包和画夹,蹑手蹑脚地退出了房门。
天边还没有露出鱼肚白,朦朦胧胧的月色里,小星星还在不停地眨着眼,借着月光,女儿欢快地朝一所很远的学校走去。
那是一所新校舍。
是一幢很高很高的大楼。
尽管路途遥远,但那是女儿心中向往已久的艺术殿堂。
没入学那会儿,女儿常常做梦。
梦见高耸的大楼和大楼里辉煌的一切。
接到录取通知书的那天,女儿高兴地依偎在母亲的怀里,母亲欣喜地流了泪。
可是,入学要交纳1万元,建校费,1万元呀,到哪去弄呢?入学的日子一天天地逼近,女儿也在这忐忑不安的焦灼..中等待。
终于有一天,母亲颤抖着双手把一叠大小不一的纸币小山似地....堆在了女儿的面前,数数,整整1万元人民币。
母亲病倒了。
夜里不断剧烈地咳嗽。
失去光泽的面孔,常常现出疲惫不堪的样子。
在女儿的眼里,母亲好久没有睡上一个完整的觉了。
母亲不很老,却有了白发。
女儿流泪了,她在心里暗暗发誓,有朝一日,一定要加倍回报母亲的爱!放学归来的路上,女儿一脸的阳光灿烂,思绪里不断勾勒着母亲看见她的礼物时欣喜、激动的样子。
要知道,这件小小的礼物是她用画笔辛勤勾勒了近一个月才换来的。
为了买下它,女儿在那家工艺品店的橱窗前踌躇过多次。
女儿特别欣赏雕像中的女孩和女孩旁慈祥的母亲,仿佛那就是她与母亲的化身。
推开房门,女儿呆住了。
母亲眼角挂着泪痕,脸上现出难以掩饰的失望..与愠怒。
她刚想问,就见母亲转身从里屋捧出那个包装很精致的盒,走到女儿身边,“慧慧,你怎么学会乱花钱啦,看看你买的是什么玩艺儿,袒胸露背的,连件衣服都没穿,多寒碜人哪。
”?“妈,这是一座母女雕像,是送给您的……”“好了,好了,就算是你有这份孝心,可买这能顶什么用啊,怎么摆得出呀!”母亲把工艺品盒朝女儿怀里一推,“去,跟人家好好说说,退了吧。
”“不,我不退。
”“那就换成别的什么吧,袜子或手套都行。
”母亲说完,扎上围裙进了厨房。
女儿愣愣地站着没动,随着一声很清脆的响声,工艺品盒重重地滑落在地。
望着支离破碎的母女雕像,两行泪水终于从女儿的脸上流落下来。
1.本文记叙了女儿送给母亲一座“雕像”的故事,请写出故事的梗概。
故事梗概:_________________________________________________________________ 2.按要求分析下列句子中加点的词语。
(1)“入学的日子一天天地逼近,女儿也在这忐忑不安的焦灼..中等待。
”“焦灼”表现了女儿怎样的心情?(2)“终于有一天,母亲颤抖着双手把一叠大小不一的纸币小山似地....堆在了女儿的面前,数数,整整1万元人民币。
”“小山似的”这个词语蕴含着丰富的情感,说说你的理解。
(3)“母亲眼角挂着泪痕,脸上现出难以掩饰的失望与愠怒。
”说说母亲为什么“失望”。
(2分)3.填空。
文中两次写到女儿流泪,第一次因为____________________________而流泪。
第二次因为____________________________而流泪。
4.文章结尾写饱含着女儿爱与深惰的“雕像”破碎了,事情为什么是这样的结局?谈谈你的理解。
多年父子成兄弟①这是我父亲的一句名言。
②父亲是个绝顶聪明的人。
他是画家,会刻图章,画写意花卉。
他会摆弄各种乐器,弹琵琶,拉胡琴,笙萧管笛,无一不通。
③父亲是个很随和的人,我很少见他发过脾气,对待子女,从无疾言厉色。
他爱孩子,喜欢孩子,爱跟孩子玩,带着孩子玩。
我的姑妈称他为“孩子头”。
春天,不到清明,他领一群孩子到麦田里放风筝,放的是他自己糊的蜈蚣。
放风筝的钱是胡琴的老弦。
老弦结实而轻,这样风筝可笔直的飞上去,没有“肚儿”。
他会做各种灯。
用浅绿透明的“鱼鳞纸”扎了一只纺织娘,栩栩如生。
在小西瓜上开小口挖净瓜瓤,在瓜皮上雕镂由极细的花纹,做成西瓜灯。
④父亲对我的学业是关心的,但不强求。
我小时上学,国文成绩一直是全班第一。
我的作文,时得佳评,他就拿出去到处给人看。
我的数学不好,他也不责怪,只要能及格,就行了。
我小时字写得不错,他倒是待我出过一点主意。
在我写过一阵《圭峰碑》和《多宝塔》以后,他建议我写写《张猛龙》。
我初中时爱唱戏,唱青衣,在家里,他拉胡琴,我唱。
学校开同乐会,他应我的邀请,到学校给我去伴奏。
父亲那么大的人陪着几个孩子玩了一下午,还挺高兴。
我十七岁初恋,暑假里,在家写情书,他在一旁瞎出主意。
我十几岁就学会了抽烟喝酒。
他喝酒,给我也倒一杯。
抽烟,一次抽出两根他一根我一根。
他还总是先给我点上火。
我们的这种关系,他人或以为怪。
父亲说:“我们是多年父子成兄弟。
”⑤我和儿子的关系也是不错的。
我戴了“右派分子”的帽子下放张家口农村劳动,儿子那时从幼儿园刚毕业,刚刚学会汉语拼音,用汉语拼音给我写了第一封信。
我也只好赶紧学会汉语拼音,好给他回信。
“文化大革命”期间,我被打成“黑帮”,送进“牛棚”。
偶尔回家,孩子们对我还是很亲热。
我的老伴告诉他们:“你们要和爸爸‘划清界限’。
”儿子反问母亲:“那你怎么还给他打酒?”只有一件事,两代之间,曾有分歧。
他下放山西忻县“插队落户”,按规定,春节可以回京探亲。
不料他带回了一个同学。
他这个同学的父亲是一位正受林彪迫害,搞得人囚家破的空军将领。
这个同学在北京已经没有家,按照规定是不能回北京的。
但是这孩子很想回北京,在一伙同学的秘密帮助下,我的儿子就偷偷地把他带回来了。
他连“临时户口”也不能上,是个“黑人”。
我们留他在家住,等于“窝藏”了他,公安局随时可以来查户口,街道办事处的大妈也可能举报。
当时人人自危,自顾不暇,惹了这么一个麻烦,使我们非常为难。
我和老伴把他叫到我们的卧室,对他的冒失行为表示很不满。
我的儿子哭了,哭得很委屈,很伤心。
我们当时立刻明白了:他是对的,我们是错的。
我们这种怕担干系的思想是庸俗的。
我们对儿子和同学之间的义气缺乏理解,对他的感情不够尊重。
他的同学在我们家一直住了四十多天,才离去。
⑤对儿子的几次恋爱,我采取的态度是“闻而不问”。
了解,但不干涉。
⑦我的孩子有时叫我“爸”,有时叫我“老头子”!连我的孙女也跟着叫。
我的亲家母说这孩子“没大没小....”。
父....”。
我觉得一个现代化的、充满人情味的家庭,首先必须做到“没大没小母叫人敬畏,儿女“笔管条直”,最没有意思。
⑧儿女是属于他们自己的。
他们的现在,和他们的未来,都应由他们自己来设计。
一个想用自己理想的模式塑造自己的孩子的父亲是愚蠢的,而且,可恶!另外,作为一个父亲,应该尽量保持一点童心。
1.文章开头“这是我父亲的一句名言”中的“这”指的是_________________________。
2.文中的“我”有双重身分,既是_________________,又是__________________。
据此,文章主体可分为两个部分,连接两部分的一个重要的词是________________。
3.文章从______________、______________、______________三个方面表现了“父亲”的性格特征。
4.文章第⑤段中略写了________件事,详写了________件事;该段中“使我们非常为难”的原因是________________________________________________。
(末一空用文中词语回答)5.第⑦段中两次写到“没大没小”,第一处的意思是____________________________,第二处的意思是_________________________________________。
6.第③段主要用了_______________________________的表达方式,从全文看,它的作用是_______________________________________________。
8.认真品味,第③段中“而且,可恶!”一句中的逗号不能去掉,原因是______________ _________________________________________________。
9.从文章选材的角度看,第④段中画线部分似乎有损于“父亲”的完美,作者为什么还要写这些内容?谈谈你的理解。
《钱塘湖春行》按要求填空1、诗中描述诗人游览行踪和西湖春来水涨的秀美景色诗句:2、描写春到西湖,以禽鸟的活跃突出盎然春意的两句诗:3、写西湖花草生气勃勃,妩媚动人的两句:4、写诗人被西湖美景所深深吸引而留恋忘返不愿离开句:5、点明春临西湖,并交待诗人行踪的两句:6、抓住早春特点,从而视角度描写禽鸟优美的诗句:7、诗中蕴含哲理,表现事物正在发展变化,花草勃勃生机的两句:8、诗中表现诗人愉悦自得的情趣的两句:9、诗人从两处名胜入手,形象描绘水天相接,天空中重重叠叠的白云与湖面的波澜连成一片的西湖早春宏伟轮廓的句子:10、采用问春的手法,渲染早春西湖美景的两句:11、诗中描写花草饰春的诗句:12、表明作者最爱的景致,看不够,赏不够,乐而忘返的留恋之情句:13、运用动态描写,以拟人的手法表现西湖美景让人观赏不够,并顿觉春意盎然,生机无限的两句:《登飞来峰》1对王安石的《登飞来峰》赏析不正确的一项是(3分)()飞来山上千寻塔,闻说鸡鸣见日升。
不畏浮云遮望眼,自缘身在最高层。
A.“不畏”显示出作者的自信,表达了作者不怕一切邪恶势力阻挠的豪情壮志。
B.“浮云”指眼前的困难、障碍,比喻阻挠变法的小人或一切阻碍历史前进的势力。
C.诗人登高远望,似觉天地万物皆可尽收眼底,“不畏浮云遮望眼,自缘身在最高层”,与杜甫的“会当凌绝顶,一览众山小”有异曲同工之妙。
D.这首诗借景说理,语意双关,既抒发了作者革新政治的雄心壮志,又表现出作者归隐山野的矛盾心理。
2这首诗揭示了怎样的人生哲理?已亥杂诗1、对这首诗的分析有误的一项是:()(3分)A.头两句叙事抒情,在辞官离京时的无限感慨中表现了豪放洒脱的气概。
B.后两句以落花为喻,表明自己的心志,在形象的比喻中,融入议论。
C.诗人说“落红”实际上是自吐心曲,诗人辞官归隐,是为了给年轻的更有才华的人提供更多的升迁机会。
D.这首诗反映了诗人辞官后不甘消沉,决心继续关心国家大事的积极向上的人生态度。
2、“落红不是无情物,化作春泥更护花”一句表达了作者怎样的感情?《钢铁是怎样炼成的》1.你知道《钢铁是怎样炼成的》这一题目的含义吗?2.我们生活在这样的一个年代,可以从保尔身上汲取到什么精神?3.用一句话评价《钢铁是怎样炼成的》这部小说。
4.《钢铁是怎样炼成的》这部小说给你印象最深的故事是哪一个?用简短的语言概括出来。
