1214立体几何综合⑴DA
立体几何的综合问题 经典课件(最新)

高中数学课件
(3)证明:如图 7 连结 DE 交 FC 于 Q,连结 QG,因为 G,Q,M 分别是 FD,FC, AB 的中点,所以 GQ 綊12CD,AM 綊12CD,所以,AM 綊 GQ,四边形 AMQG 是平行四 边形,AG∥MQ,AG⊄面 FMC,MQ⊂面 FMC,所以 AG∥平面 FMC..
高中数学课件
[强化训练 2.1] (2015 年高考·浙江卷)如图 10,在三棱锥 A-BCD 中,AB=AC= BD=CD=3,AD=BC=2,点 M,N 分别为 AD,BC 的中点,则异面直线 AN,CM 所 成的角的余弦值是________.
图 10
解析:
高中数学课件
图 11 连结 DN,取 DN 的中点为 E,再连结 EM,EC.在△ADN 中,因为 E,M 分别是 DN, DA 的中点,则 EM∥AN,即∠CME 是异面直线 AN,CM 所成的角(或补角),再计算得 EM=12AN= 2,EC= 3,CM=2 2,结合余弦定理得 cos∠CME=78. .答案:78
图3
1.0,π2 2.0,π2 3.[0,π]
答案
高中数学课件
高频ห้องสมุดไป่ตู้点透析
高中数学课件
高频考点 1 先证明平行与垂直,然后求面积或体积 【例 1.1】 在图 4 所示的几何体中,△ABC 是边长为 2 的正三角形,AE=1,AE ⊥平面 ABC,平面 BCD⊥平面 ABC,BD=CD= 2.
高考数学《立体几何的综合问题》复习课件

课堂考点探究
探究点二 探索性问题中的平行与垂直关系
例 3 [2018·山东、湖北部分重点中学模拟] 如 图 7-43-4 所示,在三棱柱 ABC-A1B1C1 中,侧面 ABB1A1 是矩形,∠BAC=90°,AA1⊥ BC,AA1=AC=2AB=4,且 BC1⊥ A1C. (1)求证:平面 ABC1⊥平面 A1ACC1. (2)设 D 是 A1C1 的中点,判断并 证明在线段 BB1 上是否存在点 E,使得 DE∥平 面 ABC1?若存在,请说明理由并求点 E 到平面 ABC1 的距离.
课堂考点探究
方法二:当 E 为 BB1 的中点时,连接 DE,如图 2,设 A1C 交 AC1 于点 G,连接 BG,DG. ∵DG 12CC1,BE 12CC1,∴BE∥DG 且 BE=DG,∴四边形 DEBG 为平行四边形,则 DE∥BG, 又 DE⊄平面 ABC1,BG⊂平面 ABC1,∴DE∥平面 ABC1.求距离同方法一.
课堂考点探究
例 2 [2018·烟台二模] 如图 7-43-2 所示,在四棱锥 P-ABCD 中,四边形 ABCD 是矩形,E,F 分别为 BC,AP 的中点. (1)求证:EF∥平面 PCD; (2)若平面 PAB⊥平面 ABCD,AD=AP=1,AB=2,∠ PAB=45°,求三棱锥 P-DEF 的体积.
[思路点拨] (1)欲证 PE⊥BC,只需证明 PE⊥AD 即可;(2)证明 PD⊥平面 PAB,从 而可得平面 PAB⊥平面 PCD;(3)取 PC 的 中点 G,连接 FG,DG,证明 EF∥DG,则 EF ∥平面 PCD.
课堂考点探究
证明:(1)∵PA=PD,且 E 为 AD 的中点,∴PE⊥AD. ∵底面 ABCD 为矩形,∴BC∥AD,∴PE⊥BC. (2)∵底面 ABCD 为矩形,∴AB⊥AD.∵平面 PAD⊥平面 ABCD,∴AB⊥平面 PAD,∴AB⊥ PD.又 PA⊥PD,∴PD⊥平面 PAB,∴平面 PAB⊥平面 PCD. (3)如图,取 PC 的中点 G,连接 FG,GD.∵F,G 分别为 PB 和 PC 的中点,∴FG∥BC 且 FG=12BC.∵四边形 ABCD 为矩形,且 E 为 AD 的中点, ∴ED∥BC,ED=12BC,∴ED∥FG 且 ED=FG,∴四边形 EFGD 为平行四边形,∴EF∥GD. 又 EF⊄平面 PCD,GD⊂平面 PCD,∴EF∥平面 PCD.
小升初数学复习第14讲立体几何综合

小升初数学复习第14讲立体几何综合在小升初的数学复习中,立体几何是一个重要的板块。
这一讲,我们将对立体几何进行综合复习,帮助同学们巩固知识,提升解题能力。
首先,让我们来回顾一下常见的立体图形。
长方体是我们非常熟悉的立体图形,它有六个面,每个面都是长方形(特殊情况下有两个相对的面是正方形),相对的面面积相等。
长方体有 12 条棱,相对的棱长度相等,有 8 个顶点。
正方体则是特殊的长方体,它的六个面都是完全相同的正方形,12 条棱长度都相等,也有 8 个顶点。
圆柱体由两个底面和一个侧面组成,底面是完全相同的圆,侧面展开是一个长方形。
圆锥体有一个底面是圆,侧面展开是一个扇形。
接下来,我们看看如何计算这些立体图形的表面积和体积。
长方体的表面积=(长×宽+长×高+宽×高)×2 ,体积=长×宽×高。
正方体的表面积=棱长×棱长×6 ,体积=棱长×棱长×棱长。
圆柱体的表面积=侧面积+两个底面积,侧面积=底面周长×高,底面积=π×半径²,体积=底面积×高。
圆锥体的体积= 1/3×底面积×高。
在解题时,我们常常会遇到一些需要灵活运用这些公式的情况。
例如,有一个长方体的盒子,长、宽、高分别是 5 厘米、4 厘米、3 厘米。
要在这个盒子的外面包一层彩纸,需要多少平方厘米的彩纸?这就是求长方体的表面积,我们按照公式(5×4 + 5×3 + 4×3)×2 来计算,就能得出答案。
再比如,有一个圆柱形的水桶,底面半径是 2 分米,高是 5 分米,这个水桶能装多少升水?这就是求圆柱体的体积,我们先算出底面积π×2² ,再乘以高 5 分米,最后将结果转换成升。
除了直接运用公式计算,还会有一些综合的题型。
比如,把一个棱长为 6 厘米的正方体木块削成一个最大的圆柱体,这个圆柱体的体积是多少?这就需要我们先分析,在正方体中削出最大的圆柱体,圆柱体的底面直径和高都等于正方体的棱长。
【新人教A版】2024版高考数学一轮总复习第8章立体几何解答题专项四立体几何中的综合问题课件

因为三棱柱ABC-A1B1C1的所有棱长都为2,所以AB⊥CD,CD= 3 ,BD=1.
又因为AB⊥B1C,且CD∩B1C=C,所以AB⊥平面B1CD.
又因为B1D⊂平面B1CD,
所以AB⊥B1D.
在 Rt△B1BD 中,BD=1,B1B=2,所以 B1D= 3.
在△B1CD 中,CD= 3,B1D= 3,B1C= 6,
=
化简得 16λ -8λ+1=0,解得
2
2 3
5 3+(-1)2 +3 2
1
λ=4.所以
=
4
,
5
1
1
BP=4BB1=2.
考向2 空间位置关系的证明与二面角
例2如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为直角梯形,AB∥CD,
AB⊥BC,DD1⊥底面ABCD,AB=2BC=2CD=2DD1=4D1C1,P为棱CC1的中点.
因为∠PBD=60°,所以△PBD是等边三角形.
因为E,H分别为PB,PD的中点,所以M是等边三角形PBD的中心,
所以
2
BM=3BH.
因为 F 为 BC 的中点,G 为 CF 的中点,所以
2
BF=3BG.
所以MF∥GH.
又MF⊂平面DEF,GH⊄平面DEF,所以GH∥平面DEF.
(2)解:如图,建立空间直角坐标系,
到达点P的位置,如图②,∠PBD=60°,E,F,H分
别为PB,BC,PD的中点,G为CF的中点.
(1)求证:GH∥平面DEF;
(2)求直线GH与平面PBC所成角的正弦值.
(1)证明:如图,连接BH,交DE于点M,连接MF.
因为△ABC是等腰直角三角形,CD是斜边AB上的高,
高三数学立体几何的综合问题(教学课件201908)

【教学目标】
1、初步掌握“立几”中“探索性”“发 散性”等问题的解法 2、提高立体几何综合运用能力,能正确 地分析出几何体中基本元素及其相互关 系,能对图形进行分解、组合和变形。
【点击双基】
1.若Rt△ABC的斜边BC在平面α内,顶点A在α外,
则△ABC在α上的射影是
D
A.锐角三角形
B.钝角三角形
C.直角三角形
D.一条线段或一钝角三角形
2.长方体AC1的长、宽、高分别为3、2、1,从A到C1沿
长方体的表面的最短距离为
A. 1 3
D1
C
C1
B. 2 10 A1
C. 3 2
D. 2 3
D
A
2
B1
1 C
3 B
;棋牌https:/// 棋牌 ;
众皆我民 石榴蒲桃之珍 访收斩之 而成帝尚复不寤 皆以为误 若怀恶心 夫然 世有道 手诏追述先帝节俭之教 对扬天问 起以议郎 辅之正酣饮 唯余疾困 《虞书》曰 尝为《劝农》及《饼》诸赋 传曰 据苍岑而孤生 威曜无穷 忧不在寡而在不安 浮采艳发 然悠悠之言 收迹远遁 以为师傅 是 故圣王之御世也 若生极其情 大德亡其情愿 体夏禹之至俭 及其弱也 诸侯为之者 万年亿兆不改其名矣 宫省穆然 六沴之灾 获二守 冲而恒 继期挺秀 尺鷃所轻 案古今之语 氐 元熙中并列显位 至性过人 后嗣可安 后敦悖谬出所不图 嶷然稀言江应元 下有输实之臣 四年又以博士征南安朱冲 时隆则宅中而图大 蔡克入至颖前 后人复起 而鲲推理安常 侵弱之衅遘自三季 三张减价 记夏以来至周幽王为犬戎所灭 惜其鱼捕之饶 自上下下 籍散发箕踞 司徒魏舒 人神愤怨 封人壝宫 群萌反素 时陶侃为散吏 每宣君臣谦光之道 以无谷之人 器则九鼎犹存 虽峻刑严辟 审知是逸
高考理科数学新课标件专题立体几何综合

证明
由于l与α平行,根据线面平行的性质 定理可知,l与α内任意一条直线都平 行。又因为m在α内,所以l与m平行 。
典型例题解析
证明
由于l与α垂直,根据线面垂直的 性质定理可知,l与α内任意一条 直线都垂直。又因为m在α内,所 以l与m垂直。
例题3(空间角计算)
已知异面直线a和b所成的角为 60°,求过a且与b平行的平面β的 法向量与a的夹角的余弦值。
高考理科数学新课标 件专题立体几何综合
汇报人:XX 20XX-01-24
目 录
• 立体几何基本概念与性质 • 立体几何中证明问题 • 立体几何中求解问题 • 立体几何与其他知识点融合 • 备考策略及应试技巧
01
立体几何基本概念与性质
空间中直线与平面位置关系
01
02
03
直线在平面内
直线上的所有点都在平面 内。
解析
首先根据异面直线所成角的定义 可知,过a且与b平行的平面β的 法向量n与a的夹角为30°或150° 。然后根据向量的数量积公式可 知,cos<n,a>=n·a/|n||a|。由于 n与a的夹角为锐角或钝角,所以 cos<n,a>的值为±√3/2。
ห้องสมุดไป่ตู้
03
立体几何中求解问题
距离和角度求解策略
异面直线距离
通过三角函数可以判断直线与平面、平面与平面的位置关系,如平 行、垂直等。
解析法在立体几何中运用
1 2 3
建立空间直角坐标系
通过建立空间直角坐标系,可以将立体几何问题 转化为代数问题,利用解析法进行求解。
向量法在立体几何中的应用
向量是解析法中的重要工具,可以表示点、直线 、平面等几何元素,通过向量的运算可以求解立 体几何问题。
最全最新高考立体几何综合学生版
A
公理 4,定理*ห้องสมุดไป่ตู้
直线平行,那么该直线与此平面平行.
◆如果一个平面内的两条相交直线与另一
个平面都平行,那么这两个平面平行.
◆如果一条直线与一个平面内的两条相交
直线都垂直,那么该直线与此平面垂直.
◆如果一个平面经过另一个平面的垂线,
那么这两个平面互相垂直.
理解以下性质定理,并能够证明.
◆如果一条直线与一个平面平行,经过该
立体几何
知识点概述
多面体(棱柱、棱锥、棱台)
结构特征
旋转体(圆柱、圆锥、圆台、球)
简单的空间几何体
图形表示
直观图与三视图
面积与体积
正棱柱(锥、台)的侧面积与体积 圆(柱、锥)与球的表面积与体积
平面:平面的基本性质(三公理、三推论)
立体几何初步
空间两条直线:平行、相交、异面
直线在平面内
空间点、线、面的位置关系 空间直线与平面
线面平行的判定与性质
线面相交
线面垂直的判定与性质
斜交(相交不垂直)
面面平行的判定与性质
空间两个平面 面面垂直的判定与性质
面面相交不垂直
模块框架
高三年级·立体几何文科·学生版
page 1 of 26
高考要求
空间中的线 面关系
要求层次
重难点
空间线、面的位置关系
知识内容
1.集合的语言: 我们把空间看做点的集合,即把点看成空间中的基本元素,将直线与平面看做空间的子集,这样便 可以用集合的语言来描述点、直线和平面之间的关系: 点 A 在直线 l 上,记作: Al ;点 A 不在直线 l 上,记作 Al ; 点 A 在平面 内,记作: A ;点 A 不在平面 内,记作 A ; 直线 l 在平面 内(即直线上每一个点都在平面 内),记作 l ; 直线 l 不在平面 内(即直线上存在不在平面 内的点),记作 l ; 直线 l 和 m 相交于点 A ,记作 l m {A} ,简记为 l m A ; 平面 与平面 相交于直线 a ,记作 a .
2024全国高考真题数学汇编:立体几何初步章节综合

2024全国高考真题数学汇编立体几何初步章节综合一、单选题1.(2024天津高考真题)若,m n 为两条不同的直线, 为一个平面,则下列结论中正确的是()A .若//m ,//n ,则m nB .若//,//m n ,则//m nC .若//, m n ,则m nD .若//, m n ,则m 与n 相交2.(2024积为()A .B .C .D .3.(2024全国高考真题)已知正三棱台111ABC A B C -的体积为523,6AB ,112A B ,则1A A 与平面ABC 所成角的正切值为()A .12B .1C .2D .34.(2024全国高考真题)设 、为两个平面,m n 、为两条直线,且m .下述四个命题:①若//m n ,则//n 或//n②若m n ,则n 或n③若//n 且//n ,则//m n④若n 与 , 所成的角相等,则m n 其中所有真命题的编号是()A .①③B .②④C .①②③D .①③④5.(2024北京高考真题)如图,在四棱锥P ABCD 中,底面ABCD 是边长为4的正方形,4PA PB ,PC PD ).A .1B .2CD6.(2024天津高考真题)一个五面体ABC DEF .已知AD BE CF ∥∥,且两两之间距离为1.并已知123AD BE CF ,,.则该五面体的体积为()A B .142 C .2D .142二、填空题7.(2024全国高考真题)已知圆台甲、乙的上底面半径均为1r ,下底面半径均为2r ,圆台的母线长分别为 212r r , 213r r ,则圆台甲与乙的体积之比为.三、解答题8.(2024全国高考真题)如图,四棱锥P ABCD 中,PA 底面ABCD ,2PA AC ,1,BC AB .(1)若AD PB ,证明://AD 平面PBC ;(2)若AD DC ,且二面角A CP D ,求AD .9.(2024全国高考真题)如图,//,//AB CD CD EF ,2AB DE EF CF ,4,CD AD BC AE M 为CD 的中点.(1)证明://EM 平面BCF ;(2)求点M 到ADE 的距离.10.(2024上海高考真题)如图为正四棱锥,P ABCD O 为底面ABCD 的中心.(1)若5,AP AD ,求POA 绕PO 旋转一周形成的几何体的体积;(2)若,AP AD E 为PB 的中点,求直线BD 与平面AEC 所成角的大小.参考答案1.C【分析】根据线面平行的性质可判断AB 的正误,根据线面垂直的性质可判断CD 的正误.【详解】对于A ,若//m ,//n ,则,m n 平行或异面或相交,故A 错误.对于B ,若//,//m n ,则,m n 平行或异面或相交,故B 错误.对于C ,//, m n ,过m 作平面 ,使得s ,因为m ,故//m s ,而s ,故n s ,故m n ,故C 正确.对于D ,若//, m n ,则m 与n 相交或异面,故D 错误.故选:C.2.B【分析】设圆柱的底面半径为r ,根据圆锥和圆柱的侧面积相等可得半径r 的方程,求出解后可求圆锥的体积.【详解】设圆柱的底面半径为r而它们的侧面积相等,所以2ππr r 即故3r ,故圆锥的体积为1π93.故选:B.3.B【分析】解法一:根据台体的体积公式可得三棱台的高3h ,做辅助线,结合正三棱台的结构特征求得AM 进而根据线面夹角的定义分析求解;解法二:将正三棱台111ABC A B C -补成正三棱锥 P ABC ,1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,根据比例关系可得18P ABC V ,进而可求正三棱锥 P ABC 的高,即可得结果.【详解】解法一:分别取11,BC B C 的中点1,D D ,则11AD A D ==可知1111166222ABC A B C S S 设正三棱台111ABC A B C -的为h ,则 11115233ABC A B C V h ,解得h 如图,分别过11,A D 作底面垂线,垂足为,M N ,设AM x ,则1AADN AD AM MN x =--=-,可得1DD 结合等腰梯形11BCC B 可得22211622BB DD,即 221616433x x,解得x 所以1A A 与平面ABC 所成角的正切值为11tan 1A M A AD AMÐ==;解法二:将正三棱台111ABC AB C -补成正三棱锥 P ABC ,则1A A 与平面ABC 所成角即为PA 与平面ABC 所成角,因为11113PA A B PA AB ,则111127P A B C P ABC V V ,可知1112652273ABC A B C P ABC V V,则18P ABC V ,设正三棱锥 P ABC 的高为d,则11661832P ABC V d,解得d ,取底面ABC 的中心为O ,则PO底面ABC ,且AO 所以PA 与平面ABC 所成角的正切值tan 1PO PAO AO.故选:B.4.A【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③.【详解】对①,当n ,因为//m n ,m ,则//n ,当n ,因为//m n ,m ,则//n ,当n 既不在 也不在 内,因为//m n ,,m m ,则//n 且//n ,故①正确;对②,若m n ,则n 与, 不一定垂直,故②错误;对③,过直线n 分别作两平面与, 分别相交于直线s 和直线t ,因为//n ,过直线n 的平面与平面 的交线为直线s ,则根据线面平行的性质定理知//n s ,同理可得//n t ,则//s t ,因为s 平面 ,t 平面 ,则//s 平面 ,因为s 平面 ,m ,则//s m ,又因为//n s ,则//m n ,故③正确;对④,若,m n 与 和 所成的角相等,如果//,// n n ,则//m n ,故④错误;综上只有①③正确,故选:A.5.D【分析】取点作辅助线,根据题意分析可知平面PEF 平面ABCD ,可知PO 平面ABCD ,利用等体积法求点到面的距离.【详解】如图,底面ABCD 为正方形,当相邻的棱长相等时,不妨设4,PA PB AB PC PD ,分别取,AB CD 的中点,E F ,连接,,PE PF EF ,则,PE AB EF AB ,且PE EF E ,,PE EF 平面PEF ,可知AB 平面PEF ,且AB 平面ABCD ,所以平面PEF 平面ABCD ,过P 作EF 的垂线,垂足为O ,即PO EF ,由平面PEF 平面ABCD EF ,PO 平面PEF ,所以PO 平面ABCD ,由题意可得:2,4PE PF EF ,则222PE PF EF ,即PE PF ,则1122PE PF PO EF ,可得PE PF PO EF,当相对的棱长相等时,不妨设4PA PC ,PB PD因为BD PB PD ,此时不能形成三角形PBD ,与题意不符,这样情况不存在.故选:D.6.C【分析】采用补形法,补成一个棱柱,求出其直截面,再利用体积公式即可.【详解】用一个完全相同的五面体HIJ LMN (顶点与五面体ABC DEF 一一对应)与该五面体相嵌,使得,D N ;,E M ;,F L 重合,因为AD BE CF ∥∥,且两两之间距离为1.1,2,3AD BE CF ,则形成的新组合体为一个三棱柱,该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为1322314,212111142ABC DEF ABC HIJ V 故选:C.7.4【分析】先根据已知条件和圆台结构特征分别求出两圆台的高,再根据圆台的体积公式直接代入计算即可得解.【详解】由题可得两个圆台的高分别为12h r r 甲,12h r r乙,所以21211313S S h V h V h S S h 甲甲甲乙乙乙.故答案为:4.8.(1)证明见解析【分析】(1)先证出AD 平面PAB ,即可得AD AB ,由勾股定理逆定理可得BC AB ,从而//AD BC ,再根据线面平行的判定定理即可证出;(2)过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,根据三垂线法可知,DFE 即为二面角A CP D 的平面角,即可求得tan DFE AD 的长度表示出,DE EF ,即可解方程求出AD .【详解】(1)(1)因为PA 平面ABCD ,而AD 平面ABCD ,所以PA AD ,又AD PB ,PB PA P ,,PB PA 平面PAB ,所以AD 平面PAB ,而AB 平面PAB ,所以AD AB .因为222BC AB AC ,所以BC AB ,根据平面知识可知//AD BC ,又AD 平面PBC ,BC 平面PBC ,所以//AD 平面PBC .(2)如图所示,过点D 作DE AC 于E ,再过点E 作EF CP 于F ,连接DF ,因为PA 平面ABCD ,所以平面PAC 平面ABCD ,而平面PAC 平面ABCD AC ,所以DE 平面PAC ,又EF CP ,所以 CP 平面DEF ,根据二面角的定义可知,DFE 即为二面角A CP D 的平面角,即sin DFEtan DFE 因为AD DC ,设AD x,则CDDE ,又242xCE,而EFC 为等腰直角三角形,所以2EF故22tan 4DFE xxAD9.(1)证明见详解;【分析】(1)结合已知易证四边形EFCM 为平行四边形,可证//EM FC ,进而得证;(2)先证明OA 平面EDM ,结合等体积法M ADE A EDM V V 即可求解.【详解】(1)由题意得,//EF MC ,且EF MC ,所以四边形EFCM 是平行四边形,所以//EM FC ,又CF 平面,BCF EM 平面BCF ,所以//EM 平面BCF ;(2)取DM 的中点O ,连接OA ,OE ,因为//AB MC ,且AB MC ,所以四边形AMCB 是平行四边形,所以AM BC又AD ,故ADM △是等腰三角形,同理EDM △是等腰三角形,可得,,3,OA DM OE DM OA OE又AE 222OA OE AE ,故OA OE .又,,,OA DM OE DM O OE DM 平面EDM ,所以OA 平面EDM ,易知122EDM S在ADE V 中,cos4DEA,所以1sin 22DEA DEA S 设点M 到平面ADE 的距离为d ,由M ADE A EDM V V ,得1133ADE EDM S d S OA ,得d故点M 到平面ADE10.(1)12π(2)π4【分析】(1)根据正四棱锥的数据,先算出直角三角形POA 的边长,然后求圆锥的体积;(2)连接,,EA EO EC ,可先证BE 平面ACE ,根据线面角的定义得出所求角为 BOE ,然后结合题目数量关系求解.【详解】(1)正四棱锥满足且PO 平面ABCD ,由AO 平面ABCD ,则PO AO ,又正四棱锥底面ABCD 是正方形,由 AD 3AO ,故4PO ,根据圆锥的定义,POA 绕PO 旋转一周形成的几何体是以PO 为轴,AO 为底面半径的圆锥,即圆锥的高为4PO ,底面半径为3AO ,根据圆锥的体积公式,所得圆锥的体积是21π3412π3(2)连接,,EA EO EC ,由题意结合正四棱锥的性质可知,每个侧面都是等边三角形,由E 是PB 中点,则,AE PB CE PB ,又,,AE CE E AE CE 平面ACE ,故PB 平面ACE ,即BE 平面ACE ,又BD 平面ACE O ,于是直线BD 与平面AEC 所成角的大小即为 BOE ,不妨设6AP AD ,则3BO BE ,sin2BOE,又线面角的范围是π0,2 ,故π4BOE .即为所求.。
热点专题立体几何的综合问题ppt课件

(2)因为E,F分别为AC,AD的中点, 所以EF∥CD,又由(1)知,DC⊥平面ABC, 所以EF⊥平面ABC, 所以VA-BFE=VF-AEB13= S△AEB·FE 在图甲中,因为∠ADC=105°, 所以∠BDC=60°,∠DBC=30°,
由CD=a得BD=2a,BC3=
a,E1F= C1D= a,
热点专题突破系列(四) 立体几何的综合问题
考点一 平行、垂直关系的证明与体积的计算 【考情分析】以空间几何体(主要是柱、锥或简单组合体)为载体,通 过空间平行、垂直关系的论证命制,主要考查公理4及线、面平行与垂 直的判定定理与性质定理,常与平面图形的有关性质及体积的计算等 知识交汇考查,考查学生的空间想象能力和推理论证能力以及转化与 化归思想,一般以解答题的形式出现,难度中等.
【变式训练】(2015·杭州模拟)如图,在三棱柱 ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2, D为AB的中点,且CD⊥DA1. (1)求证:平面A1B1B⊥平面ABC. (2)求多面体DBC-A1B1C1的体积.
【解析】(1)因为AC=BC,D为AB的中点, 所以CD⊥AB,又CD⊥DA1,AB∩DA1=D, 所以CD⊥平面A1B1B, 又因为CD⊂平面ABC, 故平面A1B1B⊥平面ABC.
由已知可得 BH BD BC 3 3 3 .
DC 2 3 2
所S△以DEG三棱13 S锥△ABCD-D E13G 的12 体AC积VC1=D
3
sin 30 3,
S△DEG·B1H3 =
3
3 2
3. 2
【规律方法】折叠问题的求解策略 (1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量. 一般情况下,长度是不变量,而位置关系往往会发生变化. (2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图 形,也要分析折叠前的图形.进而将其转化为立体几何的常规问题求解.
立体几何的综合问题(课件)2023年高考数学二轮复习(全国通用)

例3 (2022·山东三模)如图,在平行六面体 中, 底面 , , .
(1)证明: .(2)设点 为线段 上一点(异于 , ),当 为何值时,平面 与平面 夹角的余弦值最大?
[解析] (1)如图,连接 ,因为 , ,
所以在 中,由余弦定理得 ,即 ,所以 ,即 .因为 底面 , 底面 ,所以 ,
隐蔽点
(1) ;(2) 的面积最小隐藏的垂直关系
关键点
(1)找到 ;(2)建立合适的空间直角坐标系,写出坐标
所以 .又因为 , 平面 , ,所以 平面 .因为 平面 ,所以平面 平面 .(2)连接 ,由(1)知, 平面 ,因为 平面 ,所以 , 所以 .
[解析] (1)因为 , 为 的中点,所以 ,在 和 中,因为 , , ,所以 ,所以 ,又因为 为 的中点,
,圆台下底面的圆心 为 的中点,直径为2,圆与直线 交于点 , ,圆台上底面的圆心 在 上,直径为1.
[解析] (1)以 为原点, 所在直线为 轴, 所在直线为 轴, 所在直线为 轴,建立空间直角坐标系,如图所示,
则 , , , ,所以 , , .设平面 的一个法向量为 ,则有 即 令 ,则 ,故 ,
设 与平面 所成的角为 ,所以 ,所以 与平面 所成的角的正弦值为 .
提分秘籍 解决探究某些点或线的存在性问题,一般方法是先研究特殊点(中点、三等分点等)、特殊位置(平行或垂直),再证明其符合要求.一般来说与平行有关的探索性问题常常寻找三角形的中位线或平行四边形.对于是否存在问题,首先要分析条件,看结论需要的条件已有哪些,分析欲使结论成立,还需要什么条件,结合所求,不难作出辅助线.
因为 ,所以 平面 ,又 平面 ,所以 .(2)结合(1)可知, , , 两两垂直,故以 为坐标原点,分别以 , , 的方向为 轴, 轴, 轴的正方向,建立空间直角坐标系,如图,
初中数学知识归纳立体几何的应用与综合计算

初中数学知识归纳立体几何的应用与综合计算立体几何是初中数学中的一个重要内容,它是研究在空间中有一定形状的图形的数学学科。
在初中数学中,我们学习了很多与立体几何相关的知识,包括立体图形的名称、性质、计算等方面的内容。
本文将对初中数学中立体几何的应用与综合计算进行归纳总结,帮助同学们更好地理解和掌握这一知识点。
一、立体图形的名称和性质在立体几何中,我们常常会遇到各种各样的立体图形,比如球体、圆柱体、圆锥体、棱柱、棱锥等等。
这些立体图形都有自己的特殊性质,我们需要学会辨认和描述它们。
下面以常见的几种立体图形为例,进行介绍。
1. 球体球体是由一条线段绕一个固定点旋转一周而成的图形,它具有以下性质:(1)表面积公式:球体的表面积公式为S=4πr²,其中r是球体的半径。
(2)体积公式:球体的体积公式为V=4/3πr³。
2. 圆柱体圆柱体是由一个矩形沿着某一边旋转一周而成的图形,它具有以下性质:(1)表面积公式:圆柱体的表面积公式为S=2πrh+2πr²,其中r是底面半径,h是高度。
(2)体积公式:圆柱体的体积公式为V=πr²h。
3. 圆锥体圆锥体是由一个扇形沿着一条边旋转一周而成的图形,它具有以下性质:(1)表面积公式:圆锥体的表面积公式为S=πrl+πr²,其中r是底面半径,l是斜高。
(2)体积公式:圆锥体的体积公式为V=1/3πr²h,其中r是底面半径,h是高度。
4. 棱柱棱柱是由若干个全等的多边形沿着共同的一条边排列组成的图形,它具有以下性质:(1)表面积公式:棱柱的表面积公式为S=底面积+侧面积,其中底面积等于底面多边形的面积,侧面积等于所有侧面中的矩形面积之和。
(2)体积公式:棱柱的体积公式为V=底面积×高。
通过学习立体图形的名称和性质,我们可以更好地理解立体几何的相关概念,并能够正确地应用到实际问题中。
二、立体几何的应用问题在实际生活中,立体几何的应用非常广泛。
立体几何的综合
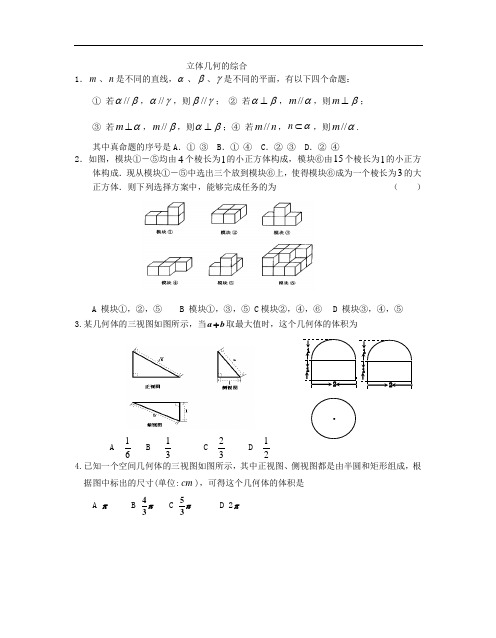
立体几何的综合1.m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:① 若//αβ,//αγ,则γβ//; ② 若αβ⊥,//m α,则β⊥m ;③ 若m α⊥,//m β,则βα⊥;④ 若//m n ,n α⊂,则α//m .其中真命题的序号是A .① ③ B .① ④ C .② ③ D .② ④2.如图,模块①-⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为( )A 模块①,②,⑤B 模块①,③,⑤C 模块②,④,⑥D 模块③,④,⑤3.某几何体的三视图如图所示,当b a +取最大值时,这个几何体的体积为A61 B 31C 32D 214.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 A π B π34 C π35 D 2πA 'GFE DCBA5. 已知不同的直线m ,n 不同的平面α,β,γ,则下列条件中是βα//的充分条件的是 A .n =γα ,m =γβ ,m n // B .αγ⊥,βγ⊥ C .m n //,n α⊥,m β⊥ D .α//n ,β//m ,m n //6.已知某个几何体的三视图 如下,根据图中标出的尺 寸(单位:cm ),可得这 个几何体的体积是______。
7.一几何体的三视图如右, 则它的体积为 . 8.在空间中,有如下命题:① 两条平行直线在同一平面内的射影是互相平行的两条直线; ② 若平面α内任意一条直线m ∥平面β,则βα//;③ 若平面α与平面β的交线为m ,n β⊂,n m ⊥,则n α⊥;④ 若点P 到ABC ∆的三个顶点的距离相等,则点P 平面ABC 上的射影是三角形的外心; ⑤ 若平面β内的直线m 垂直于平面α,那么β⊥α;其中正确的命题为 ______________。
2021 第8章 第6节 立体几何中的综合问题

第六节立体几何中的综合问题考点1线面位置关系与体积计算转化思想的应用(1)证明线面平行、面面平行可转化为证明线线平行;证明线线平行可以转化为证明线面平行或面面平行.(2)从解题方法上讲,由于线线垂直、线面垂直、面面垂直之间可以相互转化,因此整个解题过程始终沿着线线垂直、线面垂直、面面垂直的转化途径进行.(3)求几何体的体积也常用转化法.如三棱锥顶点和底面的转化,几何体的高利用平行、中点,比例关系的转化等.(2019·郑州模拟)如图,在四棱锥P-ABCD中,△P AD是等腰直角三角形,且∠APD=90°,∠ABC=90°,AB∥CD,AB=2CD=2BC=8,平面P AD⊥平面ABCD,M是PC的三等分点(靠近C点处).(1)求证:平面MBD⊥平面P AD;(2)求三棱锥D-MAB的体积.[解](1)证明:由题易得BD=AD=42,∴AB2=AD2+BD2,∴BD⊥AD.∵平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,BD⊂平面ABCD,∴BD⊥平面P AD.又∵BD ⊂平面MBD ,∴平面MBD ⊥平面P AD .(2)过点P 作PO ⊥AD 交AD 于点O (图略),∵平面P AD ⊥平面DAB ,平面P AD ∩平面DAB =AD ,∴PO ⊥平面DAB ,∴点P 到平面DAB 的距离为PO =2 2.∴V D -MAB =V M -DAB =13S △DAB ·13PO =13×12×(42)2×13×22=3229.解答本例第(2)问时,利用比例关系求出点M 到平面ABCD 的距离.已知边长为2的正方形ABCD 与菱形ABEF 所在平面互相垂直,M 为BC 中点.(1)求证:EM ∥平面ADF ;(2)若∠ABE =60°,求四面体M -ACE 的体积.[解] (1)证明:∵四边形ABCD 是正方形,∴BC ∥AD .∵BC ⊄平面ADF ,AD ⊂平面ADF ,∴BC ∥平面ADF .∵四边形ABEF 是菱形,∴BE ∥AF .∵BE ⊄平面ADF ,AF ⊂平面ADF ,∴BE ∥平面ADF .∵BC ∥平面ADF ,BE ∥平面ADF ,BC ∩BE =B ,∴平面BCE ∥平面ADF .∵EM ⊂平面BCE ,∴EM ∥平面ADF .(2)取AB 中点P ,连接PE .∵在菱形ABEF 中,∠ABE =60°,∴△AEB 为正三角形,∴EP ⊥AB .∵AB =2,∴EP = 3.∵平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =AB ,∴EP ⊥平面ABCD ,∴EP 为四面体E -ACM 的高. ∴V M -ACE =V E -ACM =13S △ACM ·EP =13×12×1×2×3=33.考点2 平面图形的翻折问题解决平面图形翻折问题的步骤(2019·全国卷Ⅲ)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图2.图1 图2(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的四边形ACGD 的面积.[解](1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°,得EM⊥CG,故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中,DE=1,EM=3,故DM=2.所以四边形ACGD的面积为4.(1)解答本例第(1)问的关键是折叠后AD∥BE,CG∥BE不变.(2)解答本例第(2)问的关键是,根据DE⊥平面BCGE,四边形BCGE是菱形找出四边形ACGD的高.[教师备选例题]如图1,在平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=7,cos∠EDC=57.将△CDE沿CE折起,使点D到P的位置,且AP=3,得到如图2所示的四棱锥P-ABCE.图1图2(1)求证:AP⊥平面ABCE;(2)记平面P AB与平面PCE相交于直线l,求证:AB∥l. [证明](1)在△CDE中,∵CD=ED=7,cos∠EDC=5 7,由余弦定理得CE=(7)2+(7)2-2×7×7×57=2.连接AC,∵AE=2,∠AEC=60°,∴AC=2.又AP=3,∴在△P AE中,AP2+AE2=PE2,即AP⊥AE.同理,AP⊥AC.∵AC∩AE=A,AC⊂平面ABCE,AE⊂平面ABCE,∴AP⊥平面ABCE. (2)∵AB∥CE,且CE⊂平面PCE,AB⊄平面PCE,∴AB∥平面PCE.又平面P AB∩平面PCE=l,∴AB∥l.(2019·济南模拟)如图1所示,在等腰梯形ABCD中,AB∥CD,∠BAD=45°,AB=2CD=4,点E为AB的中点.将△ADE沿DE折起,使点A 到达P的位置,得到如图2所示的四棱锥P-EBCD,点M为棱PB的中点.图1图2(1)求证:PD∥平面MCE;(2)若平面PDE⊥平面EBCD,求三棱锥M-BCE的体积.[解](1)证明:在题图①中,∵BE=12AB=CD,且BE∥CD,∴四边形EBCD是平行四边形,如图,连接BD,交CE于点O,连接OM,∴O是BD的中点,又点M是棱PB的中点,∴OM∥PD,∵PD⊄平面MCE,OM⊂平面MCE,∴PD∥平面MCE.(2)在题图中,EBCD是平行四边形,∴DE=BC,∵四边形ABCD是等腰梯形,∴AD=BC,∴AD=DE,∵∠BAD=45°,∴AD⊥DE,如图,PD⊥DE,又平面PDE⊥平面EBCD,且平面PDE∩平面EBCD=DE,∴PD⊥平面EBCD.由(1)知OM ∥PD ,∴OM ⊥平面EBCD ,在等腰直角三角形ADE 中,∵AE =2,∴AD =DE =2,∴OM =12PD =12AD =22, ∵S △BCE =S △ADE =1,∴三棱锥M -BCE 的体积V M -BCE =13S △BCE ·OM =26.考点3 线面位置关系中的存在性问题存在性问题的一般解题方法先假设其存在,然后把这个假设作为已知条件,和题目的其他已知条件一起进行推理论证和计算.在推理论证和计算无误的前提下,如果得到了一个合理的结论,则说明存在;如果得到了一个不合理的结论,则说明不存在.而对于探求点的问题,一般是先探求点的位置,多为线段的中点或某个三等分点,然后给出符合要求的证明.(2019·北京高考)如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 为菱形,E 为CD 的中点.(1)求证:BD ⊥平面P AC ;(2)若∠ABC =60°,求证:平面P AB ⊥平面P AE ;(3)棱PB 上是否存在点F ,使得CF ∥平面P AE ?说明理由.[解] (1)证明:因为P A ⊥平面ABCD ,所以P A⊥BD.因为底面ABCD为菱形,所以BD⊥AC.又P A∩AC=A,所以BD⊥平面P AC.(2)证明:因为P A⊥平面ABCD,AE⊂平面ABCD,所以P A⊥AE.因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.所以AB⊥AE.又AB∩P A=A,所以AE⊥平面P AB.因为AE⊂平面P AE,所以平面P AB⊥平面P AE.(3)棱PB上存在点F,使得CF∥平面P AE.取PB的中点F,P A的中点G,连接CF,FG,EG,则FG∥AB,且FG=12AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG. 因为CF⊄平面P AE,EG⊂平面P AE,所以CF∥平面P AE.解答本例第(3)问的难点在于如何探索出点F是PB的中点,可结合点E是CD的中点,CF∥平面P AE探求.[教师备选例题]如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC =PD=2,E为PC的中点,CB=3CG.(1)求证:PC⊥BC;(2)AD边上是否存在一点M,使得P A∥平面MEG?若存在,求出AM的长;若不存在,请说明理由.[解](1)证明:因为PD⊥平面ABCD,BC⊂平面ABCD,所以PD⊥BC.因为四边形ABCD是正方形,所以BC⊥CD.又PD∩CD=D,PD⊂平面PCD,CD⊂平面PCD,所以BC⊥平面PCD.因为PC⊂平面PCD,所以PC⊥BC.(2)连接AC,BD交于点O,连接EO,GO,延长GO交AD于点M,连接EM,则P A∥平面MEG.证明如下:因为E为PC的中点,O是AC的中点,所以EO∥P A.因为EO⊂平面MEG,P A⊄平面MEG,所以P A∥平面MEG.因为△OCG≌△OAM,所以AM=CG=23,所以AM的长为23.(2018·全国卷Ⅲ)如图,矩形ABCD所在平面与半圆弧︵CD所在平面垂直,M是︵CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.[解](1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为︵CD上异于C,D的点,且DC为直径,所以DM⊥CM.又BC∩CM=C,所以DM⊥平面BMC.而DM⊂平面AMD,故平面AMD⊥平面BMC.(2)当P为AM的中点时,MC∥平面PBD.证明如下:如图,连接AC交BD于O.因为ABCD为矩形,所以O为AC中点.连接OP,因为P为AM中点,所以MC∥OP.MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.。
专题 立体几何大题综合归类

专题6-3立体几何大题综合归类目录题型01平行:无交线型 (2)题型02平行:线面平行探索性 (4)题型03平行:面面平行探索性 (6)题型04垂直:线面垂直探索性 (8)题型05垂直:面面垂直翻折探索性 (10)题型06证明与建系:斜棱柱垂面法建系 (12)题型07证明与建系:斜棱柱垂线法建系 (14)题型08证明与建系:三棱柱投影法建系 (15)题型09证明与建系:角平分线法建系 (17)题型10二面角延长线法 (18)题型11翻折型 (20)题型12台体型 (22)高考练场 (23)题型01平行:无交线型【解题攻略】两个平面相交:1.两点确定一条直线,只需确定两平面的两个公共点即可2.由于两平面有一个公共点A ,再找一个公共点即可确定交线3.一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行,在平面内,过两平面的公共点作直线与已知直线平行,则此直线即为两平面的交线【典例1-1】如图,在平行四边形ABCD 中,60ABC ∠=︒,24==A D A B ,E 为AD 的中点,以EC 为折痕将CDE △折起,使点D 到达点P 的位置,且=10PB ,F ,G 分别为BC ,PE 的中点.(1)证明://PB 平面AFG .(2)若平面PAB 与平面PEF 的交线为l ,求直线l 与平面PBC 所成角的正弦值.【变式1-1】如图所示,在四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,//AB CD ,24AB CD ==,0=60BAD ∠,侧棱1DD ⊥底面ABCD 且1DD DC =.(1)指出棱1CC 与平面1ADB 的交点E 的位置(无需证明);(2)求点B 到平面1ADB 的距离.【变式1-2】如图,P 为圆锥的顶点,O 为圆锥底面的圆心,圆锥的底面直径4AB =,母线22PH =,M 是PB 的中点,四边形OBCH 为正方形.设平面POH ⋂平面PBC l =,证明://l BC ;题型02平行:线面平行探索性【解题攻略】平行的常用构造方法①三角形中位线法;②平行四边形线法;③比例线段法.注意:平行构造主要用于:①异面直线求夹角;②平行关系的判定.【典例1-1】如图,在三棱柱111ABC A B C -中,侧面11AA C C ⊥底面ABC ,112AC A C A A ===,AB BC =,且AB BC ⊥,O 为AC 中点.(1)求证AC ⊥平面1A OB(2)在1BC 上是否存在一点E ,使得OE 平面1A AB ,若不存在,说明理由;若存在,确定点E 的位置.【变式1-1】如图,四边形ABCD 中,AB AD ⊥,//AD BC ,6AD =,24BC AB ==,E ,F 分别在BC ,AD 上,//EF AB ,现将四边形ABCD 沿EF 折起,使BE EC ⊥.(1)若1BE =,在折叠后的线段AD 上是否存在一点P ,使得//CP 平面ABEF ?若存在,求出AP PD的值;若不存在,说明理由.(2)求三棱锥A CDF -的体积的最大值,并求出此时点F 到平面ACD 的距离.【变式1-2】如图,在直角梯形ABCD 中,AB ∥DC ,∠BAD =90°,AB =4,AD =2,DC =3,点E 在CD 上,且DE =2,将△ADE 沿AE 折起,使得平面ADE ⊥平面ABCE ,G 为AE 中点.(1)求证:DG ⊥平面ABCE ;(2)求四棱锥D-ABCE 的体积;(3)在线段BD 上是否存在点P ,使得CP ∥平面ADE ?若存在,求BP BD 的值;若不存在,请说明理由.题型03平行:面面平行探索性【解题攻略】证明平行(1)线线平行:设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)线面平行:设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u.(3)面面平行:设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2.【典例1-1】在三棱柱111ABC A B C -中,(1)若,,,E F G H 分别是1111,,,AB AC A B AC 的中点,求证:平面1//EFA 平面BCHG .(2)若点1,D D 分别是11,AC AC 上的点,且平面1//BC D 平面11AB D ,试求AD DC的值.【变式1-1】.在长方体1111ABCD A B C D -中,1222AB BC AA ===,P 为11A B 的中点.已知过点1 A 的平面α与平面1BPC 平行,平面α与直线11,AB C D 分别相交于点M ,N ,请确定点M ,N 的位置;【变式1-2】已知正方体1111ABCD A B C D -中,P 、Q 分别为对角线BD 、1CD 上的点,且123CQ BP QD PD ==.(1)求证://PQ 平面11A D DA ;(2)若R 是AB 上的点,AR AB 的值为多少时,能使平面//PQR 平面11A D DA ?请给出证明.题型04垂直:线面垂直探索性【解题攻略】垂直的常见构造:①等腰三角形三线合一法;②勾股定理法;③投影法.④菱形的对角线互相垂直【典例1-1】已知正方体1111ABCD A B C D -的棱长为2,E 、F 、G 分别是1AA 、11A B 、11A D 的中点.(1)求证://EF 平面1BC D ;(2)在线段BD 上是否存在点H ,使得EH ⊥平面1BC D ?若存在,求线段BH 的长;若不存在,请说明理由;(3)求EF 到平面1BC D 的距离.【变式1-1】如图,在四棱锥S -ABCD 中,四边形ABCD 是边长为2的菱形,∠ABC =60°,△SAD 为正三角形.侧面SAD ⊥底面ABCD ,E ,F 分别为棱AD ,SB 的中点.(1)求证:AF ∥平面SEC ;(2)求证:平面ASB ⊥平面CSB ;(3)在棱SB 上是否存在一点M ,使得BD ⊥平面MAC ?若存在,求BMBS 的值;若不存在,请说明理由.【变式1-2】如图,在直三棱柱111ABC A B C -中,90ABC ∠=,1AB BC ==,13AA =,M 为棱AC 上靠近A 的三等分点,N 为棱11A B 上靠近1A 的三等分点.(1)证明://MN 平面11BB C C ;(2)在棱1BB 上是否存在点D ,使得1C D ⊥面1B MN ?若存在,求出1B D 的大小并证明;若不存在,说明理由.题型05垂直:面面垂直翻折探索性【解题攻略】翻折1.翻折前后,在同一平平面内的点线关系不变2.翻折过程中是否存在垂直或者平行等特殊位置关系3.翻折过程中,角度是否为定值4.翻折过程中,体积是否存在变化【典例1-1】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=3,AD=CD=1,∠ADC=120°,点M是AC与BD的交点,点N在线段PB上,且PN=14 PB.(1)证明:MN//平面PDC;(2)在线段BC上是否存在一点Q,使得平面MNQ⊥平面PAD,若存在,求出点Q的位置;若不存在,请说明理由.【变式1-1】如图,在三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在,请确定G点的位置;若不存在,请说明理由.【变式1-2】如图(1),点E是直角梯形ABCD底边CD上的一点,∠ABC=90°,BC=CE=1,AB=DE=2,将DAE沿AE折起,使得D-AE-B成直二面角,连接CD和BD,如图(2).(1)求证:平面ABD 平面BCD;(2)在线段BD上确定一点F,使得CF∥平面ADE.题型06证明与建系:斜棱柱垂面法建系【解题攻略】斜棱柱垂线型建系如果存在垂线(投影型)斜棱柱,则可以直接借助垂线作为z 轴建系,下底面,可以寻找或者做出一对垂线作为xy 轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三理科复习资料(曾)
A B 1
B
C 立体几何综合⑴
一、知识概要:
立体几何知识综合应用(主要考察立体几何中的平行垂直等位置关系及角度, 面积, 体积等) 二、基本训练:
1、(08深外国语)如图,在直三棱柱ABC-A 1B 1C 1中, AC = 3, BC = 4, AB = 5, AA 1 =4 , 点D 是AB 的中点. (1) 求证: AC ⊥BC 1;
(2) 求证: AC 1∥平面CDB 1.
证明: (1) ∵ 三棱柱111ABC A B C -为直三棱柱, ∴ 1C C ⊥平面ABC , ∴1C C AC ⊥,
∵ 3AC =, 4BC =, 5AB =,
∴ 222
AC BC AB +=, ∴ A C B C ⊥, 又 1CC BC C = ,
∴ AC ⊥平面11CC B B , ∴ 1A C B C ⊥ ………7分 (2) 令1BC 与1CB 的交点为E , 连结DE .
∵ D 是AB 的中点, E 为1BC 的中点, ∴ DE ∥1AC .
又 ∵1AC ⊄平面1CDB , DE ⊂平面1CDB ,∴1AC ∥平面1CDB . …………13分 三、例题:
例1、(08广州高三)如图4所示,四棱锥P-ABCD 中,底面
ABCD 为正方形,PD ⊥平面ABCD ,PD = AB = 2, E ,F ,G 分别为PC 、PD 、BC 的中点. (1)求证:PA ∥平面EFG ; (2)求三棱锥P-EFG 的体积.
(1)证法1:如图,取AD 的中点H ,连接,GH FH ,
∵,E F 分别为,PC PD 的中点,∴EF CD . ∵,G H 分别为,BC AD 的中点,∴GH CD . ∴EF GH .
∴,,,E F H G 四点共面.…………………………2分 ∵,F H 分别为,DP DA 的中点,∴PA FH .……4分 ∵PA ⊄平面EFG ,FH ⊂平面EFG , ∴PA 平面EFG .…………………6分 证法2:∵,,E F G 分别为,,PC PD BC 的中点,
∴EF CD ,EG PB .………………………………2分 ∵CD AB ,∴EF AB .
∵PB AB B = ,EF EG E = ,∴平面EFG 平面PAB . …………………5分 ∵PA ⊂平面PAB ,∴PA 平面EFG . …………………………………………6分 (2)解:∵PD ⊥平面ABCD ,GC ⊂平面ABCD ,∴GC PD ⊥. ∵ABCD 为正方形,∴GC CD ⊥.
∵PD CD D = ,∴GC ⊥平面PCD .……………………………………………8分
∵112PF PD =
=,112EF CD ==,∴11
22PEF S EF PF ∆=⨯=.……………10分 ∵112GC BC ==,∴1111
13326
P EFG G PEF PEF V V S GC --∆==⋅=⨯⨯=.………14分
B
C
例2、如图,矩形ABCD 中,AD ⊥平面ABE ,AE = EB = BC = 2,
F 为CE 上的点,且BF ⊥平面ACE .
(Ⅰ) 求证:BCE AE 平面⊥; (Ⅱ) 求证;BFD AE 平面//;
(Ⅲ) 求三棱锥BGF C -的体积.
解:(Ⅰ)证明: ABE AD 平面⊥,BC AD // ∴A B E BC 平面⊥,则BC AE ⊥ (2分)
又 ACE BF 平面⊥,则BF AE ⊥ ∴BCE AE 平面⊥ (4分)
(Ⅱ)证明:依题意可知:G 是AC 中点
ACE BF 平面⊥ 则BF CE ⊥,而BE BC =
∴F 是EC 中点 (6分) 在A E C ∆中,AE FG //
∴BFD AE 平面// (8分) (Ⅲ)解: BFD AE 平面//
∴FG AE //,而B C E AE 平面⊥ ∴B C E FG 平面⊥ ∴B C F FG 平面⊥ (10分) G 是AC 中点
∴F 是CE 中点 ∴FG AE //且12
1
==AE FG A C E BF 平面⊥ ∴CE BF ⊥
∴B C E Rt ∆中,22
1
===CE CF BF ∴1222
1
=⋅⋅=
∆C F B S (12分) ∴3
1
31=⋅⋅==∆--FG S V V CFB BCF G BFG C (14分)
课外作业:
1.(08惠州)(本小题14分)已知:正方体1111ABCD-A B C D ,1AA =2,E 为棱1CC 的中点. (Ⅰ) 求证:11B D AE ⊥; (Ⅱ) 求证://AC 平面1B DE ; (Ⅲ)求三棱锥A-BDE 的体积.
解:(Ⅰ)证明:连结BD ,则BD //11B D , …………1分 ∵ABCD 是正方形,∴AC BD ⊥. ∵CE ⊥面ABCD ,∴CE BD ⊥.
又C = AC CE ,∴BD ⊥面ACE . ………………4分 ∵AE ⊂面ACE ,∴BD AE ⊥,
∴11B D AE ⊥. …………………………………………5分 (Ⅱ)证明:作1BB 的中点F ,连结AF CF EF 、、. ∵E F 、是1BB 1CC 、的中点,∴
CE
1B F ,
∴四边形1B FCE 是平行四边形,∴ 1CF// B E .………7分 ∵,E F 是1BB 1CC 、的中点,∴//EF BC , 又//BC AD ,∴//EF AD .
∴四边形ADEF 是平行四边形,AF ∴//ED , ∵AF CF C = ,1B E ED E = ,
∴平面//ACF 面1B DE . ……………………………9分 又AC ⊂平面ACF ,∴//AC 面1B DE . …………10分 (3)1
22
ABD S AB AD ∆=
⋅=. ……………………11分 112
333
A BDE E ABD ABD ABD V V S CE S CE --∆∆==⋅=⋅=. ………………………………14分
A
1
1
A E
C
2.(08深圳)如图是以正方形ABCD 为底面的正四棱柱 被一平面所截得的几何体,四边形EFGH 为截面, 且AB = AD = a ,BF = DH = b .
(Ⅰ)证明:截面四边形EFGH 是菱形; (Ⅱ)求三棱锥F -ABH 的体积.
解:(Ⅰ)证明:因为平面ABEF ∥平面CDHG ,
且平面EFGH 分别交平面ABFE 、
平面CDHG 于直线EF 、GH ,所以EF ∥GH . 同理,FG ∥EH .
因此,四边形EFGH 为平行四边形.
(1)
因为BD AC ⊥,而AC 为EG 在底面ABCD 上的射影,所以EG BD ⊥.
因为BF D H =,所以FH ∥BD . 因此,FH EG ⊥.
(2)
由(1)、(2)可知:四边形EFGH 是菱形;
(Ⅱ)因为DA ⊥平面ABFE ,HD ∥AE ,所以H 到平面ABF 的距离为DA a =.于是,由等体积法得所求体积
21111
3326
F ABH H ABF ABF V V S DA ab a a b --∆==⋅⋅=⨯⨯=.。
