弹簧扭矩计算
弹簧公差对照表
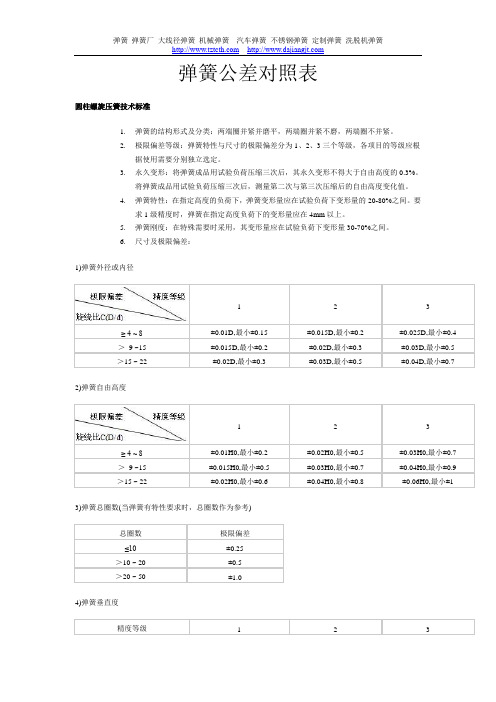
弹簧公差对照表圆柱螺旋压簧技术标准1.弹簧的结构形式及分类:两端圈并紧并磨平,两端圈并紧不磨,两端圈不并紧。
2.极限偏差等级:弹簧特性与尺寸的极限偏差分为1、2、3三个等级,各项目的等级应根据使用需要分别独立选定。
3.永久变形:将弹簧成品用试验负荷压缩三次后,其永久变形不得大于自由高度的0.3%。
将弹簧成品用试验负荷压缩三次后,测量第二次与第三次压缩后的自由高度变化值。
4.弹簧特性:在指定高度的负荷下,弹簧变形量应在试验负荷下变形量的20-80%之间。
要求1级精度时,弹簧在指定高度负荷下的变形量应在4mm以上。
5.弹簧刚度:在特殊需要时采用,其变形量应在试验负荷下变形量30-70%之间。
6.尺寸及极限偏差:1)弹簧外径或内径1 2 3≥ 4 ~ 8±0.01D,最小±0.15 ±0.015D,最小±0.2 ±0.025D,最小±0.4>9 ~15 ±0.015D,最小±0.2 ±0.02D,最小±0.3 ±0.03D,最小±0.5>15 ~ 22 ±0.02D,最小±0.3 ±0.03D,最小±0.5 ±0.04D,最小±0.7 2)弹簧自由高度1 2 3≥ 4 ~ 8±0.01H0,最小±0.2 ±0.02H0,最小±0.5 ±0.03H0,最小±0.7>9 ~15 ±0.015H0,最小±0.5 ±0.03H0,最小±0.7 ±0.04H0,最小±0.9>15 ~ 22 ±0.02H0,最小±0.6 ±0.04H0,最小±0.8 ±0.06H0,最小±1 3)弹簧总圈数(当弹簧有特性要求时,总圈数作为参考)总圈数极限偏差≤10±0.25>10 ~ 20 ±0.5>20 ~ 50 ±1.04)弹簧垂直度精度等级 1 2 3垂直度0.02H0(1°26′)0.05H0(2°52′)0.08H0(4°34′) 5)指定高度时的负荷P的极限偏差1 2 3≥ 3 ~ 10±0.05P ±0.10P ±0.15P>10 ±0.04P ±0.08P ±0.12P6)弹簧刚度P′的极限偏差1 2 3≥ 3 ~ 10±0.05P′±0.10P′±0.15P′>10 ±0.04P′±0.08P′±0.12P′7)节距:等节距的弹簧在压缩到全变形量的80%时,其正常节距圈不得接触。
弹簧的强度计算 1、弹簧的受力 图示的压缩弹簧,当弹簧受轴向压力
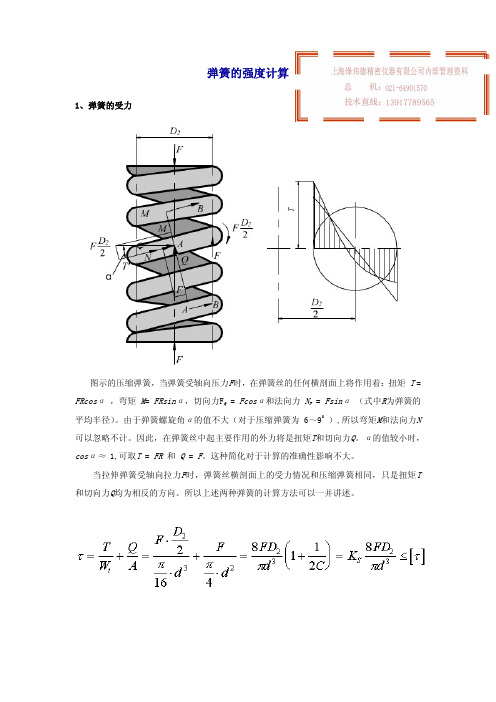
弹簧的强度计算1、弹簧的受力图示的压缩弹簧,当弹簧受轴向压力F时,在弹簧丝的任何横剖面上将作用着:扭矩 T= FRcosα ,弯矩 M= FRsinα,切向力F Q = Fcosα和法向力 N F = Fsinα (式中R为弹簧的平均半径)。
由于弹簧螺旋角α的值不大(对于压缩弹簧为6~90 ),所以弯矩M和法向力N 可以忽略不计。
因此,在弹簧丝中起主要作用的外力将是扭矩T和切向力Q。
α的值较小时,cosα≈ 1,可取T = FR 和 Q = F。
这种简化对于计算的准确性影响不大。
当拉伸弹簧受轴向拉力F时,弹簧丝横剖面上的受力情况和压缩弹簧相同,只是扭矩T 和切向力Q均为相反的方向。
所以上述两种弹簧的计算方法可以一并讲述。
2、弹簧的强度从受力分析可见,弹簧受到的应力主要为扭矩和横向力引起的剪应力,对于圆形弹簧丝系数K s可以理解为切向力作用时对扭应力的修正系数,进一步考虑到弹簧丝曲率的影响,可得到扭应力式中K为曲度系数。
它考虑了弹簧丝曲率和切向力对扭应力的影响。
一定条件下钢丝直径3、弹簧的刚度圆柱弹簧受载后的轴向变形量式中n为弹簧的有效圈数;G为弹簧的切变模量。
这样弹簧的圈数及刚度分别为对于拉伸弹簧,n>20时,一般圆整为整圈数,n<20时,可圆整为1/2圈;对于压缩弹簧总圈数n的尾数宜取1/4、1/2或整圈数,常用1/2圈。
为了保证弹簧具有稳定的性能,通常弹簧的有效圈数最少为2圈。
C值大小对弹簧刚度影响很大。
若其它条件相同时,C值愈小的弹簧,刚度愈大,弹簧也就愈硬;反之则愈软。
不过,C值愈小的弹簧卷制愈困难,且在工作时会引起较大的切应力。
此外,k值还和G、d、n有关,在调整弹簧刚度时,应综合考虑这些因素的影响。
4、稳定性计算压缩弹簧的长度较大时,受载后容易发生图a)所示的失稳现象,所以还应进行稳定性的验算。
为了便于制造和避免失稳现象出现,通常建议弹簧的长径比 b =H0/D2 按下列情况取为:弹簧两端均为回转端时,b≤2.6;弹簧两端均为固定端时,b≤5.3 ;弹簧两端一端固定而另一端回转时,b≤3.7。
圆柱螺旋弹簧一般计算公式

1. 弹簧刚度:
2. 力值: 其中:G 为材料剪切模量,一般不锈钢取71500Mpa,碳钢取
78500Mpa ;
d 为材料直径;
D 为弹簧中径;
n 为弹簧有效圈数;
f 为变形量(拉压行程)。
3. 应力: K 为曲度系数,公式为: 其中C 为弹簧旋绕比,是弹簧中径与线径的比值,即
4. 下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力,加上初拉力就行。
初拉力: 其中初拉力τ0按初切应力图选取,见下图。
三.扭簧:
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径;
E---材料的弹性模量,一般不锈钢丝取188000Mpa ,碳素钢丝
取206000Mpa ;
D---弹簧外径;
ϕ---弹簧的扭转行程(角度);
4. 应力: K1为曲度系数,顺旋向扭转取1,逆旋向扭转时按下式:
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。
弹簧设计计算软件
L=n*l+钩 mm 316.44 环展开尺
寸
计算
公式
661.5 N/mm2
78500 N/mm2 203000 N/mm2
备注
2.16 mm
Mn'>Mn
合理
8
n)/(3667* Mn*D)= φn/Ψn=
23 工作极限扭矩 Mj
N.mm
787.5
Mj=(d^3* [σ BP])/(10* K)
24 最小工作扭矩 M1 25 工作极限扭矩下扭转角 φj
N.mm (°)
295
M1=φ 1/(Ψ'*n)
88 φj=Ψ '*n*Mj
步骤 原始条件
选材
系数选取
序号 1 2 3 4 5 6 7 8
9 10 11 12 13
14
15 16
17
18
19
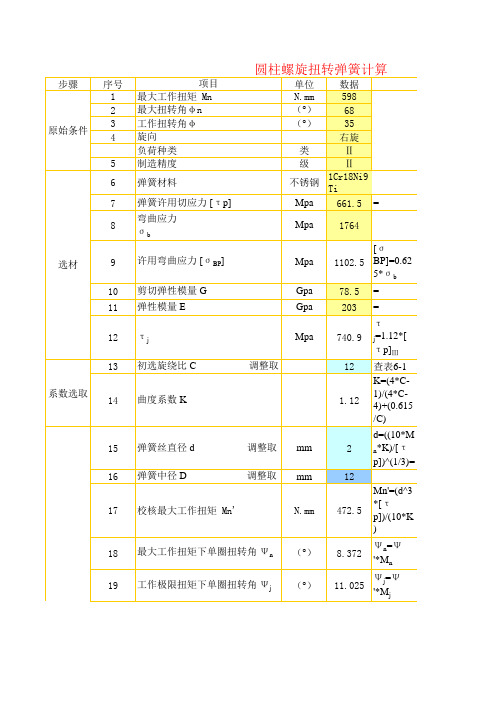
项目 最大工作扭矩 Mn 最大扭转角φn 工作扭转角φ 旋向 负荷种类 制造精度
弹簧材料
弹簧许用切应力 [τp] 弯曲应力 σb
许用弯曲应力 [σBP]
剪切弹性模量 G 弹性模量 E
圆柱螺旋扭转弹簧计算
(°) (°)
8.372 11.025
Ψn=Ψ '*Mn
Ψj=Ψ '*Mj
公式
Ψ
'=(3667*
20 在1N.mm扭矩作用下单圈扭转角Ψ' (°) 0.014 D)/(E*d^ 4)=Ψ
n/Mn l=((π
21 弹簧单圈展开长度 l
mm
37.68
*D)^2*t^ 2)^(1/2)
≈π*D
参数计算 22 有效圈数 n
26 最小工作扭矩下扭转角 φ1
弹簧的计算公式

線徑d(mm)中徑D(mm)有效圈數n 材质G/(Kg/mm )许用剪切应力[τ](Mpa)最大许用压力Ps(Kg.f)20110560Si2Mn 80007402154.368弹簧丝直径d (mm )0.2~0.40.5~1 1.1~2.2 2.5~67~1618~40C 7~145~125~104~104~84~6,通常α取5~90 。
弹簧丝材料的长度: δ=t-d ;弹簧的自由长度: H=n·δ+(n0-0.5)d (两端并紧磨平); H=n·δ+(n0+1)d (两端并紧,但不磨平)。
弹簧螺旋升角:t=d (对拉伸弹簧);式中:λmax --- 弹簧的最大变形量;Δ --- 最大变形时相邻两弹簧丝间的最小距离,一般不小于0.1d 。
弹簧钢丝间距:弹簧节距t 一般按下式取:(对压缩弹簧);弹簧设计中,旋绕比(或称弹簧指数)C 是最重要的参数之一。
C=D2/d ,弹簧指数愈小,其刚度愈大,弹簧愈硬,弹簧内外侧的应力相差愈大,材料利用率低;反之弹簧愈软。
常用弹簧指数的选取参见表。
弹簧总圈数与其工作圈数间的关系为:如图所示,圆柱弹簧的主要尺寸有:弹簧丝直径d 、弹簧圈外径D 、弹簧圈内径D1,弹簧圈中径D2,节距t 、螺旋升角a 、自由长度H0等。
2、弹簧参数的计算压缩弹簧参数计算圆柱螺旋压缩与拉伸弹簧的设计1 圆柱弹簧的参数及几何尺寸1、弹簧的主要尺寸(见右图)式中n 为弹簧的有效圈数;G 为弹簧的切变模量。
这样弹簧的圈数及刚度分别为3、弹簧的刚度圆柱弹簧受载后的轴向变形量式中K 为曲度系数。
它考虑了弹簧丝曲率和切向力对扭应力的影响。
一定条件下钢丝直径系数Ks 可以理解为切向力作用时对扭应力的修正系数,进一步考虑到弹簧丝曲率的影响,可得从受力分析可见,弹簧受到的应力主要为扭矩和横向力引起的剪应力,对于圆形弹簧丝当拉伸弹簧受轴向拉力F 时,弹簧丝槽剖面上的受力情况和压缩弹簧相同,只是扭矩T 和切向力Q 均为相反的方向。
弹簧选材及计算公式

弹簧的材料、选材与制造newmaker1 弹簧材料为了保障弹簧能够可靠地工作,其材料除应满足具有较高的强度极限和屈服极限外,还必须具有较高的弹性极限、疲劳极限、冲击韧性、塑性和良好的热处理工艺性等。
表20-2列出了几种主要弹簧材料及其使用性能。
实践中应用最广泛的就是弹簧钢,其品种又有碳素弹簧钢、低锰弹簧钢、硅锰弹簧钢和铬钒钢等。
图20-2给出了碳素弹簧钢丝的抗拉强度极限。
图20-2 碳素钢丝直径与强度的关系表20-2 主要弹簧材料及其许用应力类别代号许用扭应力[t T]许用弯曲应力[σb]/MPa 切变模量G/GPa弹性模量E/GPa推荐硬度范围HRC推荐使用温度°C特性及用途Ⅰ类弹簧Ⅱ类弹簧Ⅲ类弹簧Ⅰ类弹簧Ⅱ类弹簧钢丝碳素弹簧钢丝Ⅰ,Ⅱ,Ⅱa,Ⅲ0.3σb0.4σb0.5σb0.5σb0.625σb81.5~78.5204~202--40~120强度高,性能好,适于做小弹簧60Si2Mn60Si2MnA471 627 785 785 98178.5 19745~50-40~200弹性好,回火稳定,易脱碳,适于做受大载荷的弹簧65Si2MnWA60Si2CrVA560 745 931 931 1167 47~52-40~250强度好,耐高温,弹性好注:1.按受力循环次数N不同,弹簧分为三类:Ⅰ类N>106;Ⅱ类N=103~105以及受冲击载荷的场合;Ⅲ类N<103。
2.碳素弹簧钢丝按机械性能不同分为Ⅰ、Ⅱ、Ⅱa、Ⅲ四组,Ⅰ组强度最高,依次为Ⅱ、Ⅱa、Ⅲ组。
3.弹簧的工作极限应力tlim:Ⅰ类£1.67[t];Ⅱ类£1.25[t];Ⅲ类£1.12[t]。
4.轧制钢材的机械性能与钢丝相同。
5.碳素钢丝的切变模量和弹性模量对0.5~4mm直径有效,>4mm取下限。
2 材料选择弹簧材料选择必须充分考虑到弹簧的用途、重要程度与所受的载荷性质、大小、循环特性、工作温度、周围介质等使用条件,以及加工、热处理和经济性等因素,以便使选择结果与实际要求相吻合。
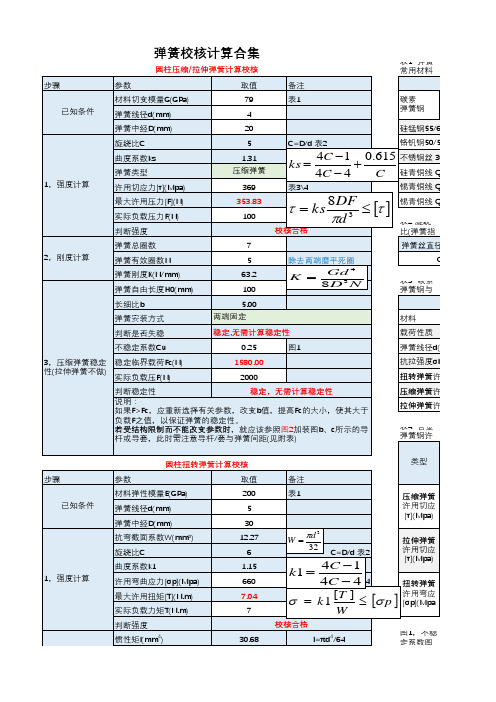
弹簧校核计算 计算表
校核合格
比(弹簧指
2,刚度计算
弹簧总圈数 弹簧有效圈数N 弹簧刚度K(N/磨平死圈
63.2
K Gd 4
100
8D3 N
弹簧丝直径d(mm) C
表3 碳素 弹簧钢与
长细比b 弹簧安装方式
5.00 两端固定
材料
参数
判断是否失稳
稳定,无需计算稳定性
载荷性质
不稳定系数Cu
295.68
载荷性质: I=无限疲劳寿命,交变载荷次数 >106,如内燃机气门弹簧、电磁 制动器弹簧;
附表 弹簧 钢抗拉强
II=有限疲劳寿命,交变载荷次数 103~105,如一般车辆弹簧
III=静载荷,交变载荷次数 <103,如安全阀弹簧
材料
I类弹簧 II类弹簧 III类弹簧 I类弹簧 II类弹簧 III类弹簧 I类弹簧 II类弹簧 III类弹簧
0.25
图1
弹簧线径d(mm)
3,压缩弹簧稳定 稳定临界载荷Fc(N) 性(拉伸弹簧不做) 实际负载压F(N)
1580.00 2000
抗拉强度σb(MPa)(右表) 扭转弹簧许用弯应[σp](MPa
判断稳定性
稳定,无需计算稳定性
说明:
如果F>Fc,应重新选择有关参数,改变b值,提高Fc的大小,使其大于
65Mn
340 455 570 285 325 380 455 570 710
硅锰,铬钒
55Si2Mn(B 铬锰钢
60Si2Mn( 55CrMnA
A
60CrMnA
50CrVA
445
430
590
570
740
710
370
360
弹簧的计算公式

線徑d(mm)中徑D(mm)有效圈數n 材质G/(Kg/mm )许用剪切应力[τ](Mpa)最大许用压力Ps(Kg.f)20110560Si2Mn 80007402154.368弹簧丝直径d (mm )0.2~0.40.5~1 1.1~2.2 2.5~67~1618~40C 7~145~125~104~104~84~6,通常α取5~90 。
弹簧丝材料的长度:(对压缩弹簧); δ=t-d ;弹簧的自由长度: H=n·δ+(n0-0.5)d (两端并紧磨平); H=n·δ+(n0+1)d (两端并紧,但不磨平)。
弹簧螺旋升角:t=d (对拉伸弹簧);式中:λmax --- 弹簧的最大变形量;Δ --- 最大变形时相邻两弹簧丝间的最小距离,一般不小于0.1d 。
弹簧钢丝间距:弹簧节距t 一般按下式取:(对压缩弹簧);弹簧设计中,旋绕比(或称弹簧指数)C 是最重要的参数之一。
C=D2/d ,弹簧指数愈小,其刚度愈大,弹簧愈硬,弹簧内外侧的应力相差愈大,材料利用率低;反之弹簧愈软。
常用弹簧指数的选取参见表。
弹簧总圈数与其工作圈数间的关系为:如图所示,圆柱弹簧的主要尺寸有:弹簧丝直径d 、弹簧圈外径D 、弹簧圈内径D1,弹簧圈中径D2,节距t 、螺旋升角a 、自由长度H0等。
2、弹簧参数的计算压缩弹簧参数计算圆柱螺旋压缩与拉伸弹簧的设计1 圆柱弹簧的参数及几何尺寸1、弹簧的主要尺寸(见右图)式中n 为弹簧的有效圈数;G 为弹簧的切变模量。
这样弹簧的圈数及刚度分别为3、弹簧的刚度圆柱弹簧受载后的轴向变形量式中K 为曲度系数。
它考虑了弹簧丝曲率和切向力对扭应力的影响。
一定条件下钢丝直径系数Ks 可以理解为切向力作用时对扭应力的修正系数,进一步考虑到弹簧丝曲率的影响,可得从受力分析可见,弹簧受到的应力主要为扭矩和横向力引起的剪应力,对于圆形弹簧丝当拉伸弹簧受轴向拉力F 时,弹簧丝槽剖面上的受力情况和压缩弹簧相同,只是扭矩T 和切向力Q 均为相反的方向。
扭簧设计计算表格

弹簧弹性模量
弹簧材料 不锈钢A组 不锈钢B组 不锈钢C组 琴钢丝E组 琴钢丝F组 琴钢丝G组
弹性模量 试验弯曲
E(MPa)
应力系数
185000 0.75
195000 0.75
195000 0.75
206000 0.78
206000 0.78
206000 0.78
受力侧力臂l2(mm)
7
负荷类型
静负荷
扭簧材料选择
不锈钢A组
以下为自动计算
项目
公式
弹簧弹性模量
Hale Waihona Puke 系统查表扭簧内径D1(mm)
D1=D-d
扭转变形角φ(°)
φ=φ2-φ1
内径减小量△D
△D=φ2*D/(360*n)
请输入 请输入 请输入 请输入 请选择 请选择
计算结果 185000
11 80 0.36
设计计算 强度校核
0.68 1400 952 790.58 158.12
上限应力系数
σmax/Rm
0.565
下限应力系数
σmin/Rm
0.11
循环特征系数γ
γ=σmin/σmax
0.2
强度校核要求:从上述计算中取坐标点(下限应力系数,上限应
力系数),若该点在γ=σmin/σmax与要求达到的寿命次数斜线
的交点以下,则说明此扭簧的疲劳寿命N大于寿命次数,符合寿命
扭矩T2 (N.mm)
T2=T´*φ2
620.92
曲度系数Kb
顺向扭转时为1
1
弯曲应力系数K1´ 材料抗拉强度Rm
(N/mm²) 许用弯曲应力σ
扭转弹簧设计计算
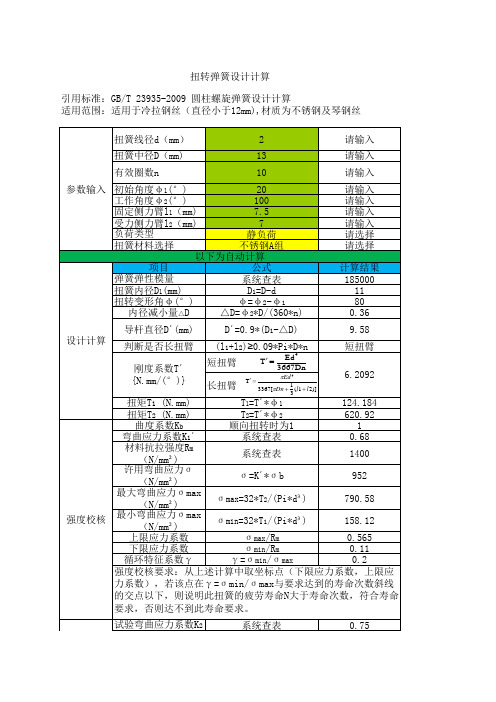
导杆直径D´(mm)
D´=0.9*(D1-△D)
9.58
判断是否长扭臂 (l1+l2)≥0.09*Pi*D*n
短扭臂
刚度系数T´ {N.mm/(°)}
扭矩T1 (N.mm)
短扭臂
T′ Ed4 3667Dn
长扭臂
T′
Ed 4 3367[Dn 1
(l1
l 2)]
3
T1=T´*φ1
6.2092 124.184
扭转弹簧设计计算
引用标准:GB/T 23935-2009 圆柱螺旋弹簧设计计算 适用范围:适用于冷拉钢丝(直径小于12mm),材质为不锈钢及琴钢丝
扭簧线径d(mm)
2
请输入
扭簧中径D(mm)
13
请输入
有效圈数n
10
请输入
参数输入 初始角度φ1(°)
20
工作角度φ2(°)
100
固定侧力臂l1(mm)
7.5
0.68
0.68
0.55
0.55
0.45
0.45
琴钢丝E组 0.7 0.58 0.49
琴钢丝F组 0.7 0.58 0.49
T′ Ed4 3667Dn
Ed 4 367[Dn 1 (l1 l2)]
3
6.2092 6.1366
琴钢丝G组 0.7 0.58 0.49
负荷类型 静负荷 动负荷有限疲劳 动负荷无限疲劳
弹簧弹性模量
弹簧材料 不锈钢A组 不锈钢B组 不锈钢C组 琴钢丝E组 琴钢丝F组 琴钢丝G组
弹性模量 试验弯曲
E(MPa)
应力系数
185000 0.75
195000 0.75
195000 0.75
两个弹簧扭转刚度

两个弹簧扭转刚度
弹簧的扭转刚度是指单位角度变化下的恢复力大小。
对于一个简单的弹簧系统,扭转刚度可以通过弹簧的扭转系数来描述。
扭转系数可以表示为弹簧扭矩与单位角度变化之间的比率。
对于两个弹簧的组合,可以分为串联和并联两种情况。
1. 串联弹簧:
串联弹簧是指将两个弹簧依次连接起来,其总的扭转刚度等于两个弹簧的扭转刚度之和。
即:
总扭转刚度 = 扭转刚度1 + 扭转刚度2
2. 并联弹簧:
并联弹簧是指将两个弹簧同时连接到同一个支点上,其总的扭转刚度等于两个弹簧扭转刚度之和的倒数。
即:
总扭转刚度 = (1/扭转刚度1 + 1/扭转刚度2)^-1
需要注意的是,以上公式适用于弹簧扭转刚度为线性的情况。
如果弹簧扭转刚度为非线性,公式可能会有所不同。
弹簧h的计算公式为

弹簧h的计算公式为弹簧的计算公式。
弹簧是一种常见的机械零件,广泛应用于各种机械设备中。
它的主要作用是储存和释放机械能,起到减震、缓冲和支撑的作用。
在设计和制造弹簧时,需要考虑到其弹性特性和力学性能,以确保其在使用过程中能够稳定可靠地工作。
而弹簧的计算公式则是设计和分析弹簧性能的重要工具。
弹簧的计算公式涉及到弹簧的材料、几何形状、载荷和变形等因素,通过这些公式可以得到弹簧的刚度、变形量、应力分布等关键参数,为弹簧的设计和选型提供重要参考。
在本文中,我们将介绍弹簧的计算公式及其应用。
弹簧的基本类型。
在介绍弹簧的计算公式之前,我们先来了解一下弹簧的基本类型。
根据其形状和用途,弹簧可以分为压缩弹簧、拉伸弹簧和扭转弹簧三种基本类型。
压缩弹簧主要用于承受压缩载荷,拉伸弹簧主要用于承受拉伸载荷,而扭转弹簧则主要用于扭转载荷。
不同类型的弹簧在计算公式和设计方法上会有所差异,需要根据具体情况进行选择和应用。
弹簧的计算公式。
1. 弹簧的刚度计算公式。
弹簧的刚度是衡量其弹性特性的重要参数,通常用弹簧常数K来表示。
对于压缩弹簧和拉伸弹簧,其刚度可以通过以下公式计算:K = F / δ。
其中,K为弹簧常数,F为载荷,δ为弹簧的变形量。
而对于扭转弹簧,其刚度的计算公式为:K = T / φ。
其中,T为扭矩,φ为扭转角度。
通过这些公式可以得到弹簧的刚度,为后续的设计和分析提供基础数据。
2. 弹簧的变形量计算公式。
弹簧的变形量是指在受载荷作用下,弹簧发生的变形量。
对于压缩弹簧和拉伸弹簧,其变形量可以通过以下公式计算:δ = F / K。
其中,δ为弹簧的变形量,F为载荷,K为弹簧常数。
而对于扭转弹簧,其变形量的计算公式为:φ = T / K。
其中,φ为扭转角度,T为扭矩,K为弹簧常数。
通过这些公式可以得到弹簧在受载荷作用下的变形量,为弹簧的设计和分析提供重要参考。
3. 弹簧的应力计算公式。
弹簧在受载荷作用下会产生应力,为了确保弹簧在使用过程中不会发生破坏,需要对其应力进行计算和分析。
弹簧公差对照表

弹簧公差对照表圆柱螺旋压簧技术标准1.弹簧的结构形式及分类:两端圈并紧并磨平,两端圈并紧不磨,两端圈不并紧。
2.极限偏差等级:弹簧特性与尺寸的极限偏差分为1、2、3三个等级,各项目的等级应根据使用需要分别独立选定。
3.永久变形:将弹簧成品用试验负荷压缩三次后,其永久变形不得大于自由高度的0.3%。
将弹簧成品用试验负荷压缩三次后,测量第二次与第三次压缩后的自由高度变化值。
4.弹簧特性:在指定高度的负荷下,弹簧变形量应在试验负荷下变形量的20-80%之间。
要求1级精度时,弹簧在指定高度负荷下的变形量应在4mm以上。
5.弹簧刚度:在特殊需要时采用,其变形量应在试验负荷下变形量30-70%之间。
6.尺寸及极限偏差:1)弹簧外径或内径1 2 3≥ 4 ~ 8±0.01D,最小±0.15 ±0.015D,最小±0.2 ±0.025D,最小±0.4>9 ~15 ±0.015D,最小±0.2 ±0.02D,最小±0.3 ±0.03D,最小±0.5>15 ~ 22 ±0.02D,最小±0.3 ±0.03D,最小±0.5 ±0.04D,最小±0.7 2)弹簧自由高度1 2 3≥ 4 ~ 8±0.01H0,最小±0.2 ±0.02H0,最小±0.5 ±0.03H0,最小±0.7>9 ~15 ±0.015H0,最小±0.5 ±0.03H0,最小±0.7 ±0.04H0,最小±0.9>15 ~ 22 ±0.02H0,最小±0.6 ±0.04H0,最小±0.8 ±0.06H0,最小±1 3)弹簧总圈数(当弹簧有特性要求时,总圈数作为参考)总圈数极限偏差≤10±0.25>10 ~ 20 ±0.5>20 ~ 50 ±1.04)弹簧垂直度精度等级 1 2 3垂直度0.02H0(1°26′)0.05H0(2°52′)0.08H0(4°34′) 5)指定高度时的负荷P的极限偏差1 2 3≥ 3 ~ 10±0.05P ±0.10P ±0.15P>10 ±0.04P ±0.08P ±0.12P6)弹簧刚度P′的极限偏差1 2 3≥ 3 ~ 10±0.05P′±0.10P′±0.15P′>10 ±0.04P′±0.08P′±0.12P′7)节距:等节距的弹簧在压缩到全变形量的80%时,其正常节距圈不得接触。
扭杆弹簧系数

扭杆弹簧系数
扭杆弹簧系数是指在单位扭转角度下,扭杆所产生的扭转弹簧力与扭转角度之间的比例关系。
它也被称为扭转刚度。
扭杆弹簧系数的单位是牛顿·米/弧度(N·m/rad),代表单位弧度下扭杆所能承受的扭矩大小。
扭杆弹簧系数的计算可以通过实验测定,即在已知扭杆长度、直径和材料的情况下,施加不同扭转角度后测量相应的扭转力或扭矩,然后计算得到。
在实际工程中,扭杆弹簧系数的大小决定了扭杆的刚度,对于扭转传递、扭转振动控制等方面具有重要的意义。
技术培训--旋扭转弹簧参数.doc
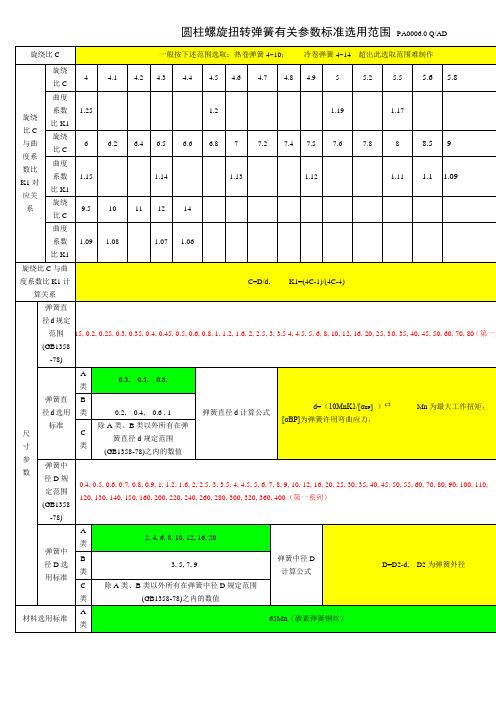
圆柱螺旋扭转弹簧有关参数标准选用范围PA0006.0 Q/ADB类65Mn(琴钢丝) 、黄铜H62C类1Cr18Ni9、55Si2Mn、QSn3-1、QBe2等表面处理A类镀镍(热处理RHC45~50)B类镀白锌(热处理RHC45~50)C类发兰、、发黑、镀彩锌(热处理RHC45~50)标记示例:215000系列产品扭转弹簧d=0.5,D=8,H0=15,n=5,β=120°,材料为65Mn,表面镀镍:扭转弹簧215000 65Mn 镀镍(0.5*8*15*5 β=120°)弹簧类别产品编号材料表面处理主要尺寸参数(d*D*H0*n β=)备注扭转弹簧****** 65Mn 镀镍0.5*8*15*5 β=120°注明:表中A类标准为优先选用标准,B类选用时需经标准化组审核后才能选用,C类原则上不选用,若有特殊情况需要选用时,需经研发部经理审批后方可选用。
美文欣赏1、走过春的田野,趟过夏的激流,来到秋天就是安静祥和的世界。
秋天,虽没有玫瑰的芳香,却有秋菊的淡雅,没有繁花似锦,却有硕果累累。
秋天,没有夏日的激情,却有浪漫的温情,没有春的奔放,却有收获的喜悦。
清风落叶舞秋韵,枝头硕果醉秋容。
秋天是甘美的酒,秋天是壮丽的诗,秋天是动人的歌。
2、人的一生就是一个储蓄的过程,在奋斗的时候储存了希望;在耕耘的时候储存了一粒种子;在旅行的时候储存了风景;在微笑的时候储存了快乐。
聪明的人善于储蓄,在漫长而短暂的人生旅途中,学会储蓄每一个闪光的瞬间,然后用它们酿成一杯美好的回忆,在四季的变幻与交替之间,散发浓香,珍藏一生!3、春天来了,我要把心灵放回萦绕柔肠的远方。
让心灵长出北归大雁的翅膀,乘着吹动彩云的熏风,捧着湿润江南的霡霂,唱着荡漾晨舟的渔歌,沾着充盈夜窗的芬芳,回到久别的家乡。
我翻开解冻的泥土,挖出埋藏在这里的梦,让她沐浴灿烂的阳光,期待她慢慢长出枝蔓,结下向往已久的真爱的果实。
