求等价函数最小依赖集数的方法(一)
最小函数依赖集的求法

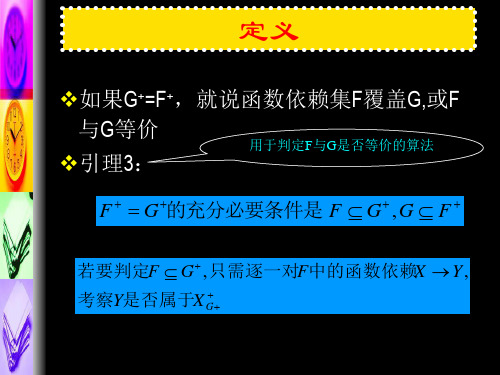
一、等价和覆盖定义:关系模式R<U,F>上的两个依赖集F和G,如果F+=G+,则称F和G是等价的,记做F≡G。
若F≡G,则称G是F的一个覆盖,反之亦然。
两个等价的函数依赖集在表达能力上是完全相同的。
二、最小函数依赖集定义:如果函数依赖集F满足下列条件,则称F为最小函数依赖集或最小覆盖。
① F中的任何一个函数依赖的右部仅含有一个属性;② F中不存在这样一个函数依赖X→A,使得F与F-{X→A}等价;③ F中不存在这样一个函数依赖X→A,X有真子集Z使得F-{X→A}∪{Z→A}与F等价。
算法:计算最小函数依赖集。
输入一个函数依赖集输出 F的一个等价的最小函数依赖集G步骤:① 用分解的法则,使F中的任何一个函数依赖的右部仅含有一个属性;② 去掉多余的函数依赖:从第一个函数依赖X→Y开始将其从F中去掉,然后在剩下的函数依赖中求X的闭包X+,看X+是否包含Y,若是,则去掉X→Y;否则不能去掉,依次做下去。
直到找不到冗余的函数依赖;③ 去掉各依赖左部多余的属性。
一个一个地检查函数依赖左部非单个属性的依赖。
例如XY→A,若要判Y为多余的,则以X→A代替XY→A是否等价?若A (X)+,则Y是多余属性,可以去掉。
举例:已知关系模式R<U,F>,U={A,B,C,D,E,G},F={AB→C,D→EG,C→A,BE→C,BC→D,CG→BD,ACD→B,CE→AG},求F的最小函数依赖集。
解1:利用算法求解,使得其满足三个条件① 利用分解规则,将所有的函数依赖变成右边都是单个属性的函数依赖,得F为:F={AB→C,D→E,D→G,C→A,BE→C,BC→D,CG→B,CG→D,ACD→B,CE→A,CE→G}② 去掉F中多余的函数依赖A.设AB→C为冗余的函数依赖,则去掉AB→C,得:F1={D→E,D→G,C→A,BE→C,BC→D,CG→B,CG→D,ACD→B,CE→A,CE→G}计算(AB)F1+:设X(0)=AB计算X(1):扫描F1中各个函数依赖,找到左部为AB或AB子集的函数依赖,因为找不到这样的函数依赖。
数据库之函数依赖公理体系

DE,DG,BEC,CGB , CGD,CEA,CEG
① F1=
ABC,CA,BCD,ACDB, DE,DG,BEC,CGB , CGD,CEA,CEG
② F21=
ABC,CA,BCD,ACDB, DE , DG , BEC , CGD , CEA,CEG
③ 对F中的任何FD:XA和X的任何真子集Z,
(F-{XA})∪{ZA}不等价于F。
每个FD左端无多余 的属性
F没有 多余的
FD
求解方法
(1)用分解规则将F中的所有函数依赖分解成右 端为单个属性的函数依赖;
Armstrong公理的推论 分解规则:若XY,且ZY,则XZ
(2)去掉F中冗余的函数依赖
(1)若X是L类属性,则X必为R的某一候选键的成 员;
(2)若X是L类属性,且X+包含了R的全部属性, 则X必为R的唯一候选键;
(3)若X是R类属性,则X不是任一候选键的成员; (4)若X是N类属性,则X必包含在R的某一候选键
中; (5)若X是R的N类属性和L类属性组成的属性集,
且X+包含了R的全部属性,则X是R的唯一候选键。
CGB,CEG
四、候选键的求解方法
1、属性分类 对于给定的关系R(U)和函数依赖集F,可将
其属性分为4类: ① L类:仅出现在F的函数依赖左部的属性; ② R类:仅出现在F的函数依赖右部的属性; ③ N类:在F的FD左右两边均未出现的属性; ④ LR类:在F的FD左右两边均出现的属性。
2、快速求解候选键的一个充分条件
对于F中任一FD:XY
① G = F-{XY};
② 求X关于G的闭包XG+; ③ 看XG+是否包含Y。如果XG+包含Y,则在G 中逻辑蕴涵XY,说明XY是多余的函数依赖, 所以F=G;如果X+不包含Y,则保留XY。
函数依赖集

函数依赖集这里,我想从函数依赖性质谈起。
从函数依赖的定义我们可以知道,一个函数在A上有依赖关系的话,那么它在B上也必定有依赖关系,就像两个多面体的棱互相依靠一样。
如果把这种函数依赖的现象叫做函数依赖性质的话,我认为是恰当不过的了。
但我要纠正一下,函数依赖性质并不是说函数具有依赖性质就叫函数依赖性质,函数依赖性质也不能保证函数在其他集合上也存在依赖性质,只能说明函数在A和B上都有依赖关系。
考虑一个由三元组构成的集合,其中每一个元素分别是三个函数的定义域,则该集合是否满足函数依赖呢?我们来看看下面的集合:①=0;② =1;③=2;④=3。
那么,以上四个集合中的函数是否满足函数依赖呢?我们来看看下面的集合:①=1;②=2;③=4;④=5。
那么,以上四个集合中的函数是否满足函数依赖呢?答案肯定是否定的。
因为函数依赖性质并不是说函数在其他集合上也存在依赖性质,而仅仅是说函数在这两个集合上都有依赖性质。
上面两个集合中的函数虽然在第三个集合中满足函数依赖性质,但是却在第二个集合中不满足函数依赖性质。
我认为,函数依赖性质应该指出在这些集合中某个集合中的函数,必须满足这个集合中的函数才能满足函数依赖性质。
也就是说,函数依赖性质是指出在A和B中都有函数依赖关系的时候,一定在A中和B中都存在这个函数依赖关系,并不需要再去说明这个函数在A和B上都有依赖性质。
(1)(3)(一)。
在A中的满足函数依赖性质的数有4个:x=x^3;y=y^3;z=z^3;则它们分别在A的四个象限中。
例:两个函数a、 b,若a可导则b也可导,如果a和b分别可导且分别连续,那么一定也可导,这种函数称为无穷依赖;如果a和b同时可导,则称a和b为无穷连续,如果a和b可导且不连续,那么称a和b为无穷间断。
其实函数依赖的重点不在于有无依赖性,而在于函数在依赖的集合中是否存在。
对于这样的集合,可以用排除法。
可以用函数a-1=1代入集合:(2)(1)。
得到函数y=1^3, x=0;可以用函数b-1=-2代入集合:(3)(1)。
数据库范式与关系模式示例

补充讲义一、范式举例BCNF.如:课程号与学号)例4:R(X,Y,Z),F={XY->Z},R为几范式?BCNF。
例5:R(X,Y,Z),F={Y->Z,XZ->Y},R为几范式?3NF。
R的候选码为{XZ,XY},(R中所有属性都是主属性,无传递依赖)二、求闭包数据库设计人员在对实际应用问题调查中,得到的结论往往是零散的、不规范的(直观问题好办,复杂问题难办了),所以,这对分析数据模型,达到规范化设计要求,还有差距,为此,从规范数据依赖集合的角度入手,找到正确分析数据模型的方法,以确定关系模式的规范化程度。
例1.已知关系模式R(U、F),其中,U={A,B,C,D,E}; F={AB→ C, B→ D, EC → B , AC→B} ,求(AB)+F.解:设X(0)=AB○1计算X(1),在F中找出左边为AB子集的FD,其结果是:AB→C,B→D∴X(1)=X(0)UB=ABUCD=ABCD 显然,X(1)≠X(0)○2计算X(2),在F中找出左边为ABCD子集的FD,其结果是:C→E,AC→B∴X(2)=X(1)UB=ABCDUBE=ABCDE 显然,X(2)=U所以,(AB)+ F=ABCDE.(等于U,所以AB是唯一候选关键字)例2.设有关系模式R(U、F),其中U={A,B,C,D,E,I};F={A→D,AB→E,B→E,CD→I,E→C},计算(AE)+解:令X={AE},X(0)=AE○1在F中找出左边是AE子集的FD,其结果是:A→D,E→C∴X(1)=X(0)UB=X(0)UDC=ACDE 显然,X(1)≠X(0)○2在F中找出左边是ACDE子集的FD,其结果是:CD→I∴X(2)=X(1)UI=ACDEI显然,X(2)≠X(1),但F中未用过的函数依赖的左边属性已含有X(2)的子集,所以不必再计算下去,即(AE)+=ACDEI.因为,X(3)=X(2),所以,算法结束。
关系数据理论练习题及答案详细

第一部分:一、求最小依赖集例:设有依赖集:F={AB-C, C-A, BC—D, ACD-B, D—EG, BE—C, CG—BD, CE f AG},计算与其等价的最小依赖集。
解:1、将依赖右边属性单一化,结果为:F1={AB—C, C—A, BC—D, ACD—B, D—E, D—G, BE—C, CG—B, CG—D CE―A, CE—G}2、在F1中去掉依赖左部多余的属性。
对于CE—A,由于C—A成立,故E是多余的;对于ACD—B,由于(CD) +=48。
£»6,故A是多余的。
删除依赖左部多余的依赖后:F2={AB—C, C—A, BC—D, CD—B, D—E, D—G, BE—C, CG—B, CG—D, CE—G }3、在F2中去掉多余的依赖。
对于CG—B,由于(CG) +=ABCEDG,故CG—B是多余的。
删除依赖左部多余的依赖后:F3={AB—C, C—A, BC—D, CD—B, D—E, D—G, BE—C, CG—D, CE—G }CG—B与CD—B不能同时存在,但去掉任何一个都可以,说明最小依赖集不唯一。
二、求闭包例:关系模式R (U, F),其中U={A, B, C, D, E, I}, F={A—D, AB—E, BI—E, CD—I, E—C},计算(AE) +。
解:令X={AE}, X (0) =AE;计算X(1);逐一扫描F集合中各个函数依赖,在F中找出左边是AE子集的函数依赖,其结果是:A—D, E—C。
于是X (1) =AE U DC=ACDE;因为X (0)W X (1),且X (1)WU,所以在F中找出左边是ACDE子集的函数依赖,其结果是:CD—I。
于是X (2) =ACDE UI=ACDEI。
虽然X (2)W X (1),但在F中未用过的函数依赖的左边属性已没有X (2) 的子集,所以不必再计算下去,即(AE) +=ACDEI。
数据库系统概论(第4版)相关考试题目 附带答案

数据库系统概论(第4版)考试复习题目)一、单项选择题(每小题2分,共30分)1.数据库系统的三级模式是指C。
A.外模式、模式、子模式B.子模式、模式、概念模式C.模式(逻辑模式)、外模式(子模式/用户模式)、存储模式(内模式)D.逻辑模式、子模式、模式2.数据库系统的数据独立性是指B。
A.不会因为数据的变化而影响应用程序B.不会因为系统数据存储结构与数据逻辑结构的变化而影响应用程序C.不会因为存储策略的变化而影响存储结构D.不会因为某些存储结构的变化而影响其他的存储结构3.数据模型的主要组成要素中,用于描述系统静态特征的是A。
A.数据结构B.数据操作C.数据完整性约束D.数据联系4.关于关系数据库系统叙述错误的是D。
A.关系模型给出了关系操作的能力和特点,关系操作通过关系语言实现B.关系语言的特点是高度的非过程化C.SQL语言介于关系代数和关系演算之间D.关系操作能力可以用三种方式来表示:关系代数、元组关系演算和域关系演算5.要求关系中的元组在组成主键的属性上不能为空,这是B。
A.参照完整性规则B.实体完整性规则C.用户定义完整性规则D.域完整性规则6.在关系代数运算中,五种基本运算为D。
A.并、差、选择、投影、自然连接B.并、差、交、选择、投影C.并、差、交、选择、笛卡尔积D.并、差、选择、投影、笛卡尔积7.在R(U)中,如果X→Y,并且对于X的任何一个真子集X’,都有X’→Y,则C。
A.Y函数决定X B.Y对X完全函数依赖C.X为关系R的候选码D.关系R属于2NF8.在关系数据库中,任何二元关系模式的最高范式必定是A。
A.BCNF B.3NF C.2NF D.1NF9.需求分析阶段得到的结果是D。
A.包括存储结构和存取方法的物理结构B.某个DBMS所支持的数据模型C.E-R图表示的概念模型D.数据字典描述的数据需求10.下面的选项中,哪些是数据库管理员的职责A。
①决定数据库中的信息内容和结构②定义数据的安全性要求和完整性约束③应用系统的需求分析和规范说明④确定系统的硬件配置并参与数据库系统的概要设计⑤决定数据库的存储结构和存取策略⑥负责设计应用系统的程序模块⑦数据库中数据的确定、数据库各级模式的设计A.①、②、⑤B.①、②、④、⑤C.①、④、⑤D.②、③、⑥、⑦11.设有两个事务T1、T2,其并发操作如下图所示,下面评价正确的是D。
最小函数依赖集F‘的最优算法

2 属性闭包 . 2
设有 关 系模式R u ( ,F) A U, ,r _ C
一 能 由 F根 据 A ms o g 理 导 出 } r tn 公 r
= I 似
则 函数 依 赖 W - WY是冗 余 的 .在 关 系 数 X-  ̄
据 库 的设 计 中 , 多 设 计 算 法 都 是基 于一 个 无 冗 许 余 的 函数 依 赖 集 ,尤 其 是 关 系设 计 的属 性综 合 法 , 基 本 思 想 是将 具 有 相 同决 定 子 的所 有 函数 其 依 赖 中 的属 性 构 成 一个 关 系模 式 , 就要 求 给 出 这
由 函数 依 赖 的定 义 及 函数 依 赖 的 公 理 系统 ( r tn A mso g公 理 ) r ,我 们 能 由已 知 的 函数 依 赖 推 导 出新 的 函数 依 赖 ,则 在一 个 函数 依 赖集 F 中 , 可 能 会 有 冗 余 的 函数 依 赖 .例 如 :给定 关 系 模 式 R u, ( 及 函数 依 赖集 F= { 一y , z , , wY} 由 —y及 u中 , 推 出函数 依 赖 , 可
依 赖 是 现 实 世 界 属性 间相 互 联 系 的抽 象 , 数 据 是 的 内在 性 质 , 是语 义 的 体 现 , 数依 赖 的确 定 决 函 定 于 设 计 者 对 相 关语 义 的理 解 .
21 函数依赖集的闭包 .
设 有 函数依 赖集 F,它 的闭 包 就 是 能够 和用 J 推 导规 则 由 F推 导 出来 的所 有 函数 依 赖 的集 合 .
收 稿 日期 : 2 0 0 0 2— 3—2 5
称 为属 性 关 于 函数 依 赖集 F的 闭 包 .
由属 性 闭包 的定 义 可 以证 明 判 断 y 是用 A m— r
SQL Server——SQLServer中最小函数依赖集

今天小编要和大家分享的是SQLServer中的最小函数依赖集,假设S 1和S 2是两个函数依赖集,如果所有为S 1所蕴涵的函数依赖都为S 2所蕴涵,—即S 1+是S 2+的子集,则S 2是S 1的覆盖,D B M S只要实现了S 2中的函数依赖,就自动实现S 1中的函数依赖。
如果S 2是S 1的覆盖,同时S 1是S 2的覆盖—则S 1和S 2等价,即S 1+=S 2+。
很显然,如果S 1和S 2等价,则D B M S只要实现S 1中的函数依赖,就自动实现S 2中的函数依赖,反之亦然。
当且仅当函数依赖集满足以下条件时,该函数依赖集为最小函数依赖集:1) 每个函数依赖的右边(应变量)只含有一个属性(即它是单元素集合)。
2) 每个函数依赖的左边(自变量)是不可约的—删除自变量的任何一个属性都将改变闭包S+(即会使S转变为一个不等价于原来的S的集合)。
这种函数依赖被称为左部不可约的函数依赖。
3) 删除S中任何一个函数依赖都将改变它的闭包S+,即使S转变为一个不等价于原来的S的集合。
关于第2点和第3点,在这里要指出的是,为了知道如果删除某些元素是否会改变闭包,不必要清楚地知道闭包的内容。
例如:观察大家熟悉的零件关系变量P,有下列函数依赖:P #→P N A M EP #→C O L O RP #→W E I G H TP #→C I T Y显而易见,该函数依赖集是最小依赖集:每个函数依赖中右边只含有一个属性,同样,左边也是不可约的,且任何一个函数依赖都不能被删除而不改变闭包(即不丢失信息)。
相反,下面的函数依赖集不是最小依赖集。
1 ) P #→{ P N A M E,COLOR} :第一个函数依赖的右边不是单属性集P #→W E I G H TP #→C I T Y2 ) { P #,P N A M E }→COLOR :第一个函数依赖左边的P N A M E可以删P #→PNAME 除而不改变闭包(即左边是可约的)P #→W E I G H TP #→C I T Y3 ) P #→P# :第一个函数可以删除而不改变闭包P #→P N A M EP #→C O L O RP #→W E I G H TP #→C I T Y任何一个函数依赖集至少存在一个最小函数依赖集。
函数依赖(理论及举例)

函数依赖(理论及举例)教你如何理解函数依赖一、函数依赖的概念函数依赖:函数依赖就是讨论一个数据表(关系)中属性值之间所存在的函数关系。
函数是一种数学中的概念,被引入到数据库中对数据的联系进行分析。
在一个关系中,属性相当于数学上的变量,属性的域相当于变量的取值范围,属性在一个元组上的取值相当于属性变量的当前值。
例如:在下面的这个职工关系中,职工号、姓名、性别、年龄、职务等属性都相当于变量;职工号属性的域,即四位十进制数字,就是取值范围,性别属性的域:{男、女},就是性别属性的取值范围。
此关系中包含有6个元组,如第2个元组为{3051、刘平、男、48、副处},其中的每个属性值都是对应属性在该元组上的当前值。
单值函数和多值函数:元组中一个属性或一些属性值对另一个属性值的影响相当于自变量值对函数值的影响。
当给定一个自变量值能求出唯一的一个函数值时,称此为单值函数或单映射函数,否则为多值函数。
在单值函数中由自变量的一个值确定函数的一个值,但不同的自变量值允许具有相同的函数值。
如f(x)=2x, f(n)=(-1)^n, f(x)=x^3+1等都是单值函数,由自变量x或n的值能够唯一确定f(x)或f(n)的值。
属性的单值函数决定(依赖):在一个关系中,若一个或一组属性的值对另一个或一组属性值起到决定性的作用,则称为单值函数决定(依赖)。
如上表中职工号的值就能够函数决定其余每个属性的值,也就是说,当职工号给定后,其他每个属性的值就跟着唯一地确定了。
如假定职工号为3074,则他的姓名必定是王海,性别必定为男,年龄必定为32岁,职务必定为正科。
这就叫做职工号能够分别单值函数决定姓名、性别和年龄属性,反过来,可以说姓名、性别和年龄等属性单值函数依赖于职工号属性。
二、函数依赖的定义定义:设一个关系为R(U),X和Y为属性集U上的子集,若对于X上的每个值都有Y上的一个唯一值与之对应,则称X和Y具有函数依赖关系,并称X 函数决定Y,或称Y函数依赖于X,记作X→Y,称X为决定因素。
ww就说函数依赖集F覆盖G
码的成员
如果X是R类属性,则X必不在任何候选码中பைடு நூலகம்如果X是L和N类组成的属性组,且X+包含了
全部属性,则X是R的唯一候选码
算法:对左边为单属性的函数依赖集求所 有候选码
• 单属性下求解候选码的充要条件
(1) 求F的最小依赖集F’ (2) 作出函数依赖图FDG (3) 从FDG图中找出无入边的属性集X (4) 察看FDG图中有无回路,若无,则输出X并结 束,否则 进行下一步 (5) 从各独立回路中各取一个结点的属性与X组成一个候选 码,重复取得所有可能的组合,即R的全部候选码
(1) F 中任一函数依赖的右部 ( 2 ) F 中不存在这样的函数依 F 与 F { X A}等价 ( 3 ) F 中不存在这样的函数依 赖 X A, X 有 真子集 Z 使得 F { X A} { Z A}与 F 等价 仅含一个属性 赖 X A , 使得
性质:函数依赖集F的最小函数依赖集不一定唯一,它与 求解的次序有关
已知 R ( XYWZ ), F {W Y , Y W , X WY , Z WY , XZ W }, 求 F ' 和所有的候选码 F ' {W Y , Y W , X Y , Z W }, 唯一的候选码为 ZX
Z
W
X
Y
已知 R ( SDBIOQ ), F { S D , I B , B O , O Q , Q I }, 求 F ' 和所有的候选码
包含 Y , 若是则去掉 X Y , 否则不去掉 的属性:逐个检查 XY A , 看 Y 是否多余,即考 Y 多余,否则不多余
察 X 是否包含 A ,若包含则表示
求最小值的方法

求最小值的方法
首先,我们来介绍一种常用的方法——暴力搜索法。
暴力搜索法是一种简单直接的方法,它通过遍历所有可能的解来寻找最小值。
虽然这种方法在理论上是可行的,但是在实际应用中往往效率较低,特别是当问题规模较大时,暴力搜索法的时间复杂度会非常高。
因此,我们通常只在问题规模较小的情况下才会使用暴力搜索法。
除了暴力搜索法之外,我们还可以利用数学分析的方法来求解函数的最小值。
对于一元函数,我们可以通过求导的方法来找到函数的驻点,然后通过二阶导数的符号来判断这些驻点是极小值还是极大值。
这种方法在理论上非常有效,但是在实际应用中,我们往往需要面对复杂的函数形式和多变的约束条件,这就需要我们结合数值计算的方法来求解最小值。
在数值计算中,最常用的方法之一就是梯度下降法。
梯度下降法是一种迭代的优化算法,它通过不断地沿着函数梯度的反方向更新参数,从而逐渐逼近函数的最小值。
梯度下降法在机器学习和深度学习等领域被广泛应用,它不仅可以用来求解无约束优化问题,还可以通过引入约束条件来求解约束优化问题。
除了梯度下降法之外,我们还可以利用其他优化算法来求解最小值,比如牛顿法、拟牛顿法、共轭梯度法等。
这些方法在不同的问题领域有着不同的优势和适用性,我们可以根据具体的问题特点来选择合适的优化算法。
总之,求最小值是一个非常重要的问题,它涉及到数学、计算机科学、优化理论等多个领域。
在实际应用中,我们需要根据具体的问题特点来选择合适的方法,有时甚至需要结合多种方法来求解最小值。
希望本文介绍的方法能够帮助读者更好地理解和应用求最小值的方法。
求最小值的方法

求最小值的方法一、穷举法。
穷举法是最直观、最简单的一种方法,它通过遍历所有可能的取值来找到最小值。
在一些情况下,穷举法是非常有效的,尤其是当问题规模较小、搜索空间较小的时候。
但是,穷举法的时间复杂度通常较高,当问题规模较大时,它的效率会变得很低。
二、贪心算法。
贪心算法是一种在每一步选择中都采取当前状态下最好或最优的选择,从而希望最终能够达到全局最优的算法。
在某些问题中,贪心算法可以很快地找到最小值,但是在一些情况下,贪心算法得到的结果并不一定是最优的。
三、动态规划。
动态规划是一种将原问题分解为若干个子问题,通过求解子问题的最优解来求得原问题的最优解的方法。
动态规划通常适用于具有重叠子问题和最优子结构性质的问题。
通过存储子问题的解,动态规划可以避免重复计算,从而提高求解效率。
四、二分法。
二分法是一种非常高效的求最小值的方法,它通常适用于在有序数组中查找特定元素的问题。
通过比较中间元素和目标值的大小关系,二分法可以将搜索空间缩小一半,从而快速地找到最小值。
二分法的时间复杂度为O(logn),因此在大规模问题中具有较高的效率。
五、数学优化方法。
在一些数学问题中,我们可以通过对函数进行求导,找到函数的极值点来求得最小值。
数学优化方法通常需要一定的数学知识和技巧,但是它可以提供精确的最小值结果。
总结。
在实际问题中,我们可以根据具体情况选择合适的方法来求最小值。
穷举法适用于规模较小的问题;贪心算法适用于一些特定的问题;动态规划适用于具有重叠子问题和最优子结构性质的问题;二分法适用于有序数组中的查找问题;数学优化方法适用于一些数学问题。
希望本文介绍的方法能够帮助读者更好地理解和应用求最小值的方法。
极小函数依赖

极小函数依赖
极小函数依赖是指在关系模式中,存在一个或多个属性集合 X,满足以下两个条件:
1. X 是候选键(即唯一标识关系中元组的属性集合)或超键(即包含候选键的属性集合)的真子集。
2. 对于 X 的任何一个真子集 Y,都有 Y 不是候选键或超键。
这个定义可以被表述为:如果一个属性集合 X 满足以上两个
条件,那么 X 对于关系模式 R 中的任意一个函数依赖来说都
是极小的。
从这个定义可以看出,一个关系模式可以有多个极小函数依赖,这些函数依赖描述了不同的属性间约束关系。
极小函数依赖是数据库设计中的一个重要概念,它可以用来优化数据库的性能和减少数据冗余。
函数依赖及范式

函数依赖及范式函数依赖基本概念:•函数依赖:FD(function dependency),设有关系模式R(U),X,Y是U的子集,r 是R的任一具体关系,如果对r的任意两个元组t1,t2,由t1[X]=t2[X]导致t1[Y]=t2[Y], 则称X 函数决定Y,或Y函数依赖于X,记为X→Y。
X→Y为模式R的一个函数依赖。
•部分函数依赖:即局部依赖,对于一个函数依赖W→A,如果存在X W(X包含于W)有X→A成立,那么称W→A是局部依赖,否则称W→A为完全函数依赖。
•传递依赖:在关系模式中,如果Y→X,X→A,且X Y(X不决定Y),A X(A不属于X),那么称Y→A是传递依赖。
•函数依赖集F的闭包F+: 被逻辑蕴涵的函数依赖的全体构成的集合,称为F的闭包(clo sure),记为F+。
•最小依赖集:如果函数集合F满足以下三个条件(1)F中每个函数依赖的右部都是单属性;(2) F中的任一函数依赖X→A,其F-{X→A}与F是不等价的;(3)F中的任一函数依赖X→A,Z为X的子集,(F-{X→A})∪{Z→A}与F不等价。
则称F为最小函数依赖集合,记为Fmin。
函数依赖的公理系统:设有关系模式R(U),X,Y,Z,W均是U的子集,F是R上只涉及到U中属性的函数依赖集,推理规则如下:•自反律:如果Y X U,则X→Y在R上成立。
•增广律:如果X→Y为F所蕴涵,Z U,则XZ→YZ在R上成立。
(XZ表示X∪Z,下同) •传递律:如果X→Y和Y→Z在R上成立,则X→Z在R上成立。
以上三条为Armstrong公理系统•合并律:如果X→Y和X→Z成立,那么X→YZ成立。
•伪传递律:如果X→Y和WY→Z成立,那么WX→Z成立。
•分解律:如果X→Y和Z Y成立,那么X→Z成立。
这三条为引理注意:•函数依赖推理规则系统(自反律、增广律和传递律)是完备的。
•由自反律所得到的函数依赖均是平凡的函数依赖。
四种范式的含义:•如果某个数据库模式都是第一范式的,则称该数据库模式是属于第一范式的数据库模式。
最小函数依赖集F‘的最优算法

作者: 徐爱芸
作者机构: 江汉大学数学与计算机科学学院,湖北武汉430056
出版物刊名: 江汉大学学报:社会科学版
页码: 20-22页
主题词: 最优算法;属性集;函数依赖集闭包;属性集闭包;逻辑蕴含;最小函数依赖集;数据库原理
摘要:在数据库设计中,依据函数依赖集的定义及Armstrong公理,求出的是一个可能存在冗余的函数依赖集。
为了判断一个函数依赖是否为某一函数依赖集逻辑蕴含,只要用求属性闭包的方法求出函数依赖中决定子的属性闭包,判断依赖子是否包含在属性闭包中即可。
本文从求属性闭包的角度出发,给出一个求最小函数依赖集的算法。
一个用于求解关系模式上最小函数依赖集合(F)min的算法

一个用于求解关系模式上最小函数依赖集合(F)min的算法庆振树;chen,PP
【期刊名称】《计算机工程》
【年(卷),期】1989(000)006
【摘要】本文介绍一个采用DDHD技术求解关系模式上最小函数依赖集合(F)min 的算法,采用这种方法可以方便地从任意给定的函数依赖集合F直接求得相应的最小函数依赖集合,这种方法是关系数据库设计和规范化的有用工具。
【总页数】11页(P32-42)
【作者】庆振树;chen,PP
【作者单位】不详;不详
【正文语种】中文
【中图分类】TP311.13
【相关文献】
1.关系模式最小函数依赖集的求解与应用 [J], 裴祥喜;李珉;赵福伟
2.最小函数依赖集Fmin求解算法研究及实现 [J], 邸振山
3.函数依赖最小覆盖集求解算法——在数据库设计中的应用 [J], 邹炜;周定康
4.用最小不动点理论求解最小函数依赖集 [J], 谢宝永;李磊
5.大型Petri网模型最小trap (siphon)集合的快速求解算法 [J], 廖晶静;王明哲;倪枫;郭法滨
因版权原因,仅展示原文概要,查看原文内容请购买。
02-6章-习题课-习题

习题课1.设有函数依赖集F = { D→G,C→A,CD→E,A→B},计算闭包D+,(AC)+,(ACD)+。
2.设有关系模式R(U,F),其中:U={A,B,C,D,E},F = { A→BC,CD→E,B→D,E→A}。
求R的所有候选码。
3.设有关系模式R(U,F),其中:U={E,F,G,H},F={E→G,G→E,F→EG,H→EG,FH →E},求F的最小依赖集。
4.设有关系R和函数依赖F:R(W,X,Y,Z),F = { X→Z,WX→Y }。
试求下列问题:(1)关系R属于第几范式?(2)如果关系R不属于BCNF,请将关系R逐步分解为BCNF。
要求:写出分解过程。
候选键:WZ部分函数依赖:Z部分函数依赖于WX存在部分函数依赖,不是2NF,是1NF分解结果为:R1(X,Z)R2(W,X,Y)5.设有关系模式R(U,F),其中U=ABCDE,F = { A→B,BC→E ,ED→AB }。
①计算A F+、(AB)F+、(ABC)F+及(BCD)F+;②求R的所有候选码,并说明理由;③R最高满足第几范式?为什么?④若R不属于BCNF,试改进该关系数据库设计,使它满足BCNF。
6.设有关系模式R(U,F),其中U={A,B,C,D,E},F = { A→D,E→D,D→B,BC→D ,DC→A }。
①计算D F+、(DC)F+、(BC)F+及(CE)F+;②求R的所有候选码,并说明理由;③R最高满足第几范式?为什么?④若R不属于BCNF,试改进该关系数据库设计,使它满足BCNF。
主属性CE;非主属性ABD由于D对于CE的部分函数依赖,只是1NF1)候选键CE,唯一1.最小化函数依赖集1)A F+=A; E F+=E; D F+=D; BC F+=BC; DC F+=BCD(出现在右侧的)2)B F+=B; C F+=C; D F+=BD(未出现在右侧的)F为最小化函数依赖集2.求候选键为CE3.不存在不在F中出现的属性4.不存在函数依赖X→Y,满足XY=U5.按左部相同的原则分组,得到ρ={R1(A,D),R2(E,D),R3(D,B),R4(B,C,D),R5(D,C,A)}6.考虑候选键CE,ρ*=Ρu R6(C,E)7.已知R<U,F>,U={ A,B,C,D,E },F={AB →C, C →D,D →E},R的一个分解ρ={ R1( A,B,C ),R2(C,D),R3(D,E) }判断ρ是否为无损连接?8.设有关系模式R(A,B,C,D),其上的函数依赖集:F={A→C,C→A,B→AC,D→AC}(1)求F的最小等价依赖集F C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求等价函数最小依赖集数的方法(一)
求等价函数最小依赖集数
介绍
在数据库设计中,等价函数最小依赖集数是指在给定一个关系模
式R的属性集合X和Y,找到R的最小依赖集合的个数,使得X完全决定Y。
方法一:函数依赖理论
1.首先,根据函数依赖理论,我们可以得到给定的属性集合X中的
属性与Y之间的依赖关系。
2.然后,根据函数依赖关系,我们可以找到Y中不依赖于X的属性,
将它们从Y中剔除,得到新的Y。
3.接着,我们可以继续找到Y中不依赖于X的属性,并剔除,直到
Y中的属性完全依赖于X为止。
4.最后,我们得到的Y即为最小依赖集合。
方法二:覆盖迭代法
1.首先,将属性集合X和Y分别作为开始的覆盖集C,即C = {X,
Y}。
2.然后,遍历所有的函数依赖关系,并判断是否可以通过合并覆盖
集C中的某些元素来得到新的覆盖集。
3.如果可以得到新的覆盖集,将其替换原有的覆盖集C,并继续遍
历直到无法得到新的覆盖集为止。
4.最后,得到的C即为最小依赖集合。
方法三:消除冗余法
1.首先,根据函数依赖理论,我们可以得到给定的属性集合X中的
属性与Y之间的依赖关系。
2.然后,对于每个函数依赖关系,我们可以尝试从Y中剔除某个属
性,看是否仍然能够完全决定X。
3.如果剔除某个属性后仍然能够完全决定X,说明该属性是冗余的,
可以将其从Y中剔除。
4.重复上述步骤,直到Y中的属性不能再剔除为止。
5.最后,得到的Y即为最小依赖集合。
总结
求等价函数最小依赖集数是数据库设计中的重要步骤,可以通过
函数依赖理论、覆盖迭代法和消除冗余法来实现。
选择合适的方法应
根据具体情况来考虑,以得到最优的结果。
以上三种方法均可以帮助
我们找到最小的依赖集合,进而优化数据库的设计和性能。
希望本文对您了解求等价函数最小依赖集数有所帮助!
方法四:逻辑推演法
1.首先,根据给定的属性集合X和Y以及函数依赖理论,我们可以
列出所有可能的依赖关系。
2.然后,根据Y中的属性,在X中逐个推演出能够完全决定X的属
性集合。
3.对于每个推演出的属性集合,检查是否存在其他更小的依赖集合
能够完全决定X。
4.如果存在更小的依赖集合,将该推演出的属性集合剔除,并继续
推演。
5.重复上述步骤,直到无法进行推演为止。
6.最后,得到的依赖集合即为最小依赖集合。
方法五:贪心算法
1.首先,将属性集合X和Y分别作为初始的依赖集合。
2.遍历Y中的每个属性,将其移除,并检查依赖集合是否仍然能够
完全决定X。
3.如果能够完全决定X,将该属性从Y中剔除,继续处理下一个属
性。
4.如果无法完全决定X,将该属性重新加入Y中。
5.重复上述步骤,直到遍历完所有属性。
6.最后,得到的Y即为最小依赖集合。
方法六:基于属性覆盖的启发式算法
1.首先,将属性集合X和Y分别作为初始的依赖集合。
2.根据函数依赖理论,找出使得X完全决定Y的最小依赖集合。
3.遍历Y中的每个属性,从Y中剔除该属性,并检查是否还存在其
他属性能够完全决定X。
4.如果存在,将该属性加入到依赖集合中,并继续遍历剩余属性。
5.如果不存在,将该属性加入到依赖集合中,并将剩余属性从Y中
剔除。
6.重复上述步骤,直到遍历完所有属性。
7.最后,得到的依赖集合即为最小依赖集合。
总结
上述方法各有特点,可以根据具体需求和场景选择合适的方法来
求解等价函数最小依赖集数问题。
通过合理的方法选择和运用,可以
帮助我们简化数据库设计,提高数据库的性能和查询效率。
希望本文对您理解求等价函数最小依赖集数的不同方法有所帮助!。
