2017-2018学年江苏省南京市高二上学期期末考试数学理试题
2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)

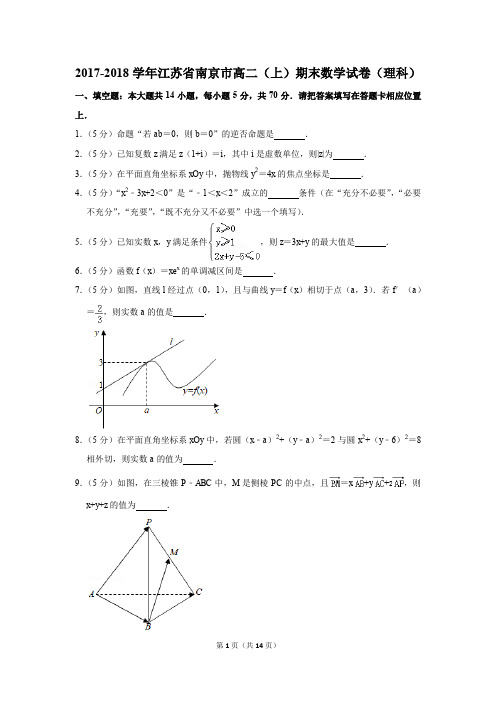
2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b,则|a|=|b|”的逆否命题是.2.(5分)双曲线=1的渐近线方程是.3.(5分)已知复数为纯虚数,其中i是虚数单位,则实数a的值是.4.(5分)在平面直角坐标系xOy中,点(4,3)到直线3x﹣4y+a=0的距离为1,则实数a的值是.5.(5分)曲线y=x4与直线y=4x+b相切,则实数b的值是.6.(5分)已知实数x,y满足条件则z=2x+y的最大值是.7.(5分)在平面直角坐标系xOy中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是.8.(5分)在平面直角坐标系xOy中,圆O:x2+y2=r2(r>0)与圆M:(x﹣3)2+(y+4)2=4相交,则r的取值范围是.9.(5分)观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=.10.(5分)若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是.11.(5分)已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是.12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是.13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是.14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b,则|a|=|b|”的逆否命题是若|a|≠|b|,则a≠b.【解答】解:命题“若a=b,则|a|=|b|”的逆否命题是命题“若|a|≠|b|,则a≠b”,故答案为:“若|a|≠|b|,则a≠b”2.(5分)双曲线=1的渐近线方程是y=±2x.【解答】解:∵双曲线标准方程为=1,其渐近线方程是=0,整理得y=±2x.故答案为y=±2x.3.(5分)已知复数为纯虚数,其中i是虚数单位,则实数a的值是2.【解答】解:==,∵复数为纯虚数,∴,解得a=2.故答案为:2.4.(5分)在平面直角坐标系xOy中,点(4,3)到直线3x﹣4y+a=0的距离为1,则实数a的值是±5.【解答】解:由题意,=1,∴a=±5.故答案为±5.5.(5分)曲线y=x4与直线y=4x+b相切,则实数b的值是﹣3.【解答】解:设直线与曲线的切点为P(m,n)则有:⇒,化简求:m=1,b=n﹣4;又因为点P满足曲线y=x4,所以:n=1;则:b=n﹣4=﹣3;故答案为:﹣3.6.(5分)已知实数x,y满足条件则z=2x+y的最大值是9.【解答】解:实数x,y满足条件作出不等式组对应的平面区域如图:由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,则当直线y=﹣2x+z经过点A时,直线的截距最大,此时z最大,由可得A(3,3).此时z=9,故答案为:9.7.(5分)在平面直角坐标系xOy中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是4.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=5,∴x=4,故答案为:48.(5分)在平面直角坐标系xOy中,圆O:x2+y2=r2(r>0)与圆M:(x﹣3)2+(y+4)2=4相交,则r的取值范围是3<r<7.【解答】解:由题意,圆心距为5,∴|r﹣2|<5<r+2,∴3<r<7.故答案为3<r<7.9.(5分)观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=n(n+1).【解答】解:观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=×n (n+1),故答案为:n(n+1)10.(5分)若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是(﹣∞,0]∪[4,+∞).【解答】解:若“∃x∈R,x2+ax+a=0”是真命题,则△=a2﹣4a≥0,解得:a∈(﹣∞,0]∪[4,+∞),故答案为:(﹣∞,0]∪[4,+∞)11.(5分)已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是﹣1.【解答】解:f(x)=(x2+x+m)e x,f′(x)=(x2+3x+m+1)e x,若f(x)在x=﹣3处函数f (x)有极大值,则f′(﹣3)=0,解得:m=﹣1,故f(x)=(x2+x﹣1)e x,f′(x)=(x2+3x)e x,令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<﹣3,故f(x)在(﹣∞,﹣3)递增,在(﹣3,0)递减,在(0,+∞)递增,=f(0)=﹣1,故f(x)极小值故答案为:﹣1.12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是②④.【解答】解:对于①,当m=1时,方程x2+my2=1表示圆,故错;对于②,∵a=±1时,直线l1与直线l2都平行,故正确;对于③,若函数f (x)=x3+mx单调递增⇒m≥0,故错;对于④,p或q是真命题⇒p且q不一定是真命题;⇒p且q是真命题⇒p或q 一定是真命题,故正确;故答案为:②④13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是[] .【解答】解:设P(x,y),由PM=PF⇒PM2=2PF2⇒(x+2c)2+y2=2(x+c)2+2y2⇒x2+y2=2c2,椭圆E上存在点P,使得PM=PF,则圆x2+y2=2c2与椭圆E:+=1(a>b >0)有公共点,∴b≤≤a⇒⇒.故答案为:[]14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是(3,4).【解答】解:∵函数f(x)=,∴函数f′(x)=,当x<,或x<t时,f′(x)>0,函数为增函数,当<x<t时,f′(x)<0,函数为减函数,故当x=时,函数f(x)取极大值,函数f(x)有两个零点0和t,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则方程f(x)﹣1=0和f(x)﹣1=t各有三个解,即函数f(x)的图象与y=1和y=t+1各有三个零点,由y|x=t==,故,=(t﹣3)(2t+3)2>0得:t>3,故不等式的解集为:t∈(3,4),故答案为:(3,4)二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.【解答】解:(1)由B(10,4),C(2,﹣4),得BC中点D的坐标为(6,0),…(2分)所以AD的斜率为k==8,…(5分)所以BC边上的中线AD所在直线的方程为y﹣0=8(x﹣6),即8x﹣y﹣48=0.…(7分)(2)由B(10,4),C(2,﹣4),得BC所在直线的斜率为k==1,…(9分)所以BC边上的高所在直线的斜率为﹣1,…(12分)所以BC边上的高所在直线的方程为y﹣8=﹣1(x﹣7),即x+y﹣15=0.…(14分)16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.【解答】解:(1)令n=1,﹣2a2+3=0,a2=,令n=2,﹣a3﹣+4=0,a3=,令n=3,﹣a4﹣+4=0,a4=.(2)猜想a n=(n∈N*).证明:当n=1时,a1=1=,所以a n=成立,假设当n=k时,a n=成立,即a k=,则(a k﹣3)a k+1﹣a k+4=0,即(﹣3)a k+1﹣+4=0,所以a k+1=,即a k+1==,所以当n=k+1时,结论a n=成立.综上,对任意的n∈N*,a n=成立.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.【解答】解:(1)过点(2,﹣1)且与直线x+y﹣1=0垂直的直线方程为x﹣y﹣3=0,…(2分)由解得,所以圆心M的坐标为(1,﹣2),…(4分)所以圆M的半径为r=,…(6分)所以圆M的方程为(x﹣1)2+(y+2)2=2.…(7分)(2)因为直线l被圆M截得的弦长为,所以圆心M到直线l的距离为d==,…(9分)若直线l的斜率不存在,则l为x=0,此时,圆心M到l的距离为1,不符合题意.若直线l的斜率存在,设直线l的方程为y=kx,即kx﹣y=0,由d==,…(11分)整理得k2+8k+7=0,解得k=﹣1或﹣7,…(13分)所以直线l的方程为x+y=0或7x+y=0.…(14分)18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.【解答】(本题满分16分)解:(1)作AH⊥CF于H,则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,…(2分)则六边形的面积为f (θ)=2×(AB+CF)×AH=(2cosθ+2)sinθ=2(cosθ+1)sinθ,θ∈(0,).…(6分)(2)f′(θ)=2[﹣sinθsinθ+(cosθ+1)cosθ]=2(2cos2θ+cosθ﹣1)=2(2cosθ﹣1)(cosθ+1).…(10分)令f′(θ)=0,因为θ∈(0,),所以cosθ=,即θ=,…(12分)当θ∈(0,)时,f′(θ)>0,所以f (θ)在(0,)上单调递增;当θ∈(,)时,f′(θ)<0,所以f (θ)在(,)上单调递减,…(14分)所以当θ=时,f (θ)取最大值f ()=2(cos+1)sin=.…(15分)答:当θ=时,可使得六边形区域面积达到最大,最大面积为平方百米.…(16分)19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.【解答】解:(1)因为3=,所以3(﹣1+a,0)=(a+1,0),解得a=2.…(2分)又因为=,所以c=,所以b2=a2﹣c2=1,所以椭圆E的方程为+y2=1.…(4分)(2)设点C的坐标为(x0,y0),y0>0,则=(﹣1﹣x0,﹣y0),=(2﹣x0,﹣y0).因为BC⊥CD,所以(﹣1﹣x0)(2﹣x0)+y02=0.①…(6分)又因为+y02=1,②联立①②,解得x0=﹣,y0=,…(8分)所以k==2.…(10分)(3),设C(x0,y0),则CD:y=(x+1)(﹣2<x0<2且x0≠﹣1),由消去y,得x2+8y02x+4y02﹣4(x0+1)2=0.…(12分)又因为+y02=1,所以得D(,),…(14分)所以===3,所以为定值.…(16分)20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.【解答】解:(1)f(x)=x﹣lnx(x>0)的导数为f′(x)=1﹣=,当x>1时,f′(x)>0,f(x)递增;当0<x<1时,f′(x)>0,f(x)递减.即有f(x)在x=1处取得极小值,也为最小值,且为1;(2)存在x∈[1,3],使+lnx=2成立,即为=2﹣lnx,即有a=,设g(x)=,x∈[1,3],则g′(x)=(1﹣lnx)(1+),当1<x<e时,g′(x)>0,g(x)递增;当e<x<3时,g′(x)<0,g(x)递减.则g(x)在x=e处取得极大值,且为最大值e+;努力的你,未来可期!g(1)=2,g(3)=3(2﹣ln3)+>2,则a的取值范围是[2,e+];(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,即为ax﹣lnx≥﹣ln,即有a(x﹣)≥2lnx,x≥1,令F(x)=a(x﹣)﹣2lnx,x≥1,F′(x)=a(1+)﹣,当x=1时,原不等式显然成立;当x>1时,由题意可得F′(x)≥0在(1,+∞)恒成立,即有a(1+)﹣≥0,即a≥,由=<=1,则a≥1.综上可得a的取值范围是[1,+∞).。
江苏省南京市2017-2018学年高二上学期期末数学试卷(理科) Word版含解析

2017-2018学年江苏省南京市高二(上)期末数学试卷(理科)一、填空题:本大题共14小题,每小题3分,共42分.1.:“∃x∈Q,x2﹣8=0”的否定是______.2.在平面直角坐标系xOy中,若抛物线y2=2px经过点(4,2),则实数p=______.3.在平面直角坐标系xOy中,双曲线x2﹣y2=1的渐近线方程是______.4.已知p:0<m<1,q:椭圆+y2=1的焦点在y轴上,则p是q的______条件.(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”填空)5.函数f(x)=x+sinx的图象在点O(0,0)处的切线方程是______.6.在空间直角坐标系中,已知A(1,0,0),B(4,﹣3,0),且=2,则点P的坐标是______.7.已知实数x,y满足,则z=x﹣2y的最大值是______.8.如图,在平面直角坐标系xOy中,以正方形ABCD的两个顶点A,B为焦点,且过点C,D的双曲线的离心率是______.9.函数f(x)=(e为自然对数的底数)的最大值是______.10.在平面直角坐标系xOy中,已知点O(0,0),A(3,0),动点P满足2PO=PA,则点P的轨迹方程是______.11.在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到点A(3,0)的距离等于它到准线的距离,则PA=______.12.如图,在平面直角坐标系xOy中,直线y=x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是______.13.在平面直角坐标系xOy中,已知直l:x+y﹣3=0和圆M:x2+(y﹣m)2=8,若圆M上存在点P,使得P到直线l的距离为3,则实数m的取值范围是______.14.已知函数y=x3﹣3x在区间[a,a+1](a≥0)上的最大值和最小值的差为2,则满足条件的实数a的所有值是______.二、解答题:本大题共6小题,共计58分.解答应写出文字说明、证明过程或演算步骤.15.在平面直角坐标系xOy中,已知椭圆C过点(0,2),其焦点为F1(﹣,0),F2(,0).(1)求椭圆C的标准方程;(2)已知点P在椭圆C上,且PF1=4,求△PF1F2的面积.16.在平面直角坐标系xOy中,已知圆M经过点A(1,0),B(3,0),C(0,1).(1)求圆M的方程;(2)若直线l“mx﹣2y﹣(2m+1)=0与圆M交于点P,Q,且=0,求实数m的值.17.如图,在直三棱柱ABC﹣A1B1C1中,AB=2,AC=2,AA1=1,∠BAC=90°,D 为线段BC的中点.(1)求异面直线B1D与AC所成角的大小;(2)求二面角D﹣A1B1﹣A的大小.18.A,B两地相距300km,汽车从A地以vkm/h的速度匀速行驶到B地(速度不得超过60km/h).已知汽车每小时的运输成本由固定成本和可变成本组成,固定成本为250元,可变成本(单位:元)与速度v的立方成正比,比例系数,设全程的运输成本为y元.(1)求y关于v的函数关系;(2)为使全程运输成本最小,汽车应以多大速度行驶?19.在平面直角坐标系xOy中,已知椭圆C: +=1(m>0)的离心率为.(1)求m的值;(2)设点A为椭圆C的上顶点,问是否存在椭圆C的一条弦AB,使直线AB与圆(x﹣1)2+y2=r2(r>0)相切,且切点P恰好为线段AB的中点?若存在,其满足条件的所有直线AB的方程和对应的r的值?若不存在,说明理由.20.已知函数f(x)=lnx.(1)若直线y=2x+p(p∈R)是函数y=f(x)图象的一条切线,求实数p的值;(2)若函数g(x)=x﹣﹣2f(x)(m∈R)有两个极值点x1,x2,且x1<x2.①求实数m的取值范围;②证明:g(x2)<x2﹣1.2015-2016学年江苏省南京市高二(上)期末数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题3分,共42分.1.:“∃x∈Q,x2﹣8=0”的否定是∀x∈Q,x2﹣8≠0.【考点】的否定.【分析】利用特称的否定是全称写出结果即可.【解答】解:因为特称的否定是全称,所以:“∃x∈Q,x2﹣8=0”的否定是:∀x∈Q,x2﹣8≠0.故答案为:∀x∈Q,x2﹣8≠0.【点评】本题考查的否定全称与特称的否定关系,是基础题.2.在平面直角坐标系xOy中,若抛物线y2=2px经过点(4,2),则实数p=1.【考点】抛物线的标准方程.【分析】利用抛物线经过的点,求解即可.【解答】解:抛物线y2=2px经过点(4,2),可得4=4P,解得p=1.故答案为:1.【点评】本题考查抛物线才的应用,基本知识考查.3.在平面直角坐标系xOy中,双曲线x2﹣y2=1的渐近线方程是y=±x.【考点】双曲线的简单性质;双曲线的标准方程.【分析】直接利用双曲线的标准方程求出渐近线方程即可.【解答】解:双曲线x2﹣y2=1的渐近线方程:y=±x.故答案为:y=±x.【点评】本题考查双曲线的简单性质的应用,是基础题.4.已知p:0<m<1,q:椭圆+y2=1的焦点在y轴上,则p是q的充要条件.(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”填空)【考点】必要条件、充分条件与充要条件的判断.【分析】q:椭圆+y2=1的焦点在y轴上,可得0<m<1.即可判断出结论.【解答】解:p:0<m<1,q:椭圆+y2=1的焦点在y轴上,∴0<m<1.则p是q的充要条件.故答案为:充要.【点评】本题考查了椭圆的标准方程、充要条件的判定、不等式的性质,考查了推理能力与计算能力,属于中档题.5.函数f(x)=x+sinx的图象在点O(0,0)处的切线方程是y=2x.【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求得切线的斜率,由点斜式方程可得切线的方程.【解答】解:函数f(x)=x+sinx的导数为f′(x)=1+cosx,即有图象在点O(0,0)处的切线斜率为k=1+cos0=2,则图象在点O(0,0)处的切线方程为y=2x.故答案为:y=2x.【点评】本题考查导数的运用:求切线的方程,考查直线方程的运用,正确求导是解题的关键.6.在空间直角坐标系中,已知A(1,0,0),B(4,﹣3,0),且=2,则点P的坐标是(3,﹣2,0).【考点】空间向量运算的坐标表示.【分析】设出点P的坐标,用坐标表示出与,根据=2列出方程组,求出点P的坐标.【解答】解:设点P(x,y,z),又点A(1,0,0),B(4,﹣3,0),∴=(x﹣1,y,z),=(4﹣x,﹣3﹣y,﹣z);又=2,∴,解得,∴点P的坐标是(3,﹣2,0).故答案为:(3,﹣2,0).【点评】本题考查了空间向量的坐标表示与应用问题,也考查了方程组的解法与应用问题,是基础题目.7.已知实数x,y满足,则z=x﹣2y的最大值是2.【考点】简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:化目标函数z=x﹣2y为,由图可知,当直线过A(2,2)时,直线在y轴上的截距最小,z有最大值为2.故答案为:2.【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.8.如图,在平面直角坐标系xOy中,以正方形ABCD的两个顶点A,B为焦点,且过点C,D的双曲线的离心率是.【考点】双曲线的简单性质.【分析】设出双曲线方程求出C的坐标,代入化简求解双曲线的离心率即可.【解答】解:设双曲线方程为:,以正方形ABCD的两个顶点A,B为焦点,且过点C,D的双曲线,可得C(c,2c),代入双曲线方程:,即.可得,解得e2=3+2,∴e=.故答案为:.【点评】本题考查双曲线的简单性质的应用,考查计算能力.9.函数f(x)=(e为自然对数的底数)的最大值是.【考点】函数的最值及其几何意义.【分析】求出函数的导数,求出单调区间,可得极大值,也为最大值,计算即可得到所求值.【解答】解:函数f(x)=的导数为f′(x)==,当x>1时,f′(x)<0,f(x)递减;当x<1时,f′(x)>0,f(x)递增.即有x=1处取得极大值,且为最大值.故答案为:.【点评】本题考查函数的最值的求法,注意运用导数,判断单调性,考查运算能力,属于中档题.10.在平面直角坐标系xOy中,已知点O(0,0),A(3,0),动点P满足2PO=PA,则点P的轨迹方程是x2+y2+2x﹣3=0.【考点】轨迹方程.【分析】利用点O(0,0),A(3,0),动点P满足2PO=PA,直接计算,即可求出点P 的轨迹方程.【解答】解:设P(x,y),则∵点O(0,0),A(3,0),动点P满足2PO=PA,∴4x2+4y2=(x﹣3)2+y2,∴x2+y2+2x﹣3=0.故答案为:x2+y2+2x﹣3=0.【点评】本题考查点P的轨迹方程,考查直接法的运用,比较基础.11.在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到点A(3,0)的距离等于它到准线的距离,则PA=3.【考点】抛物线的简单性质.【分析】由抛物线的定义,可得PA=PF,准线方程为x=﹣1,求出P的横坐标,即可得出结论.【解答】解:由抛物线的定义,可得PA=PF,准线方程为x=﹣1∵A(3,0),F(1,0),∴P的横坐标为2,∴PA=2+1=3,故答案为:3.【点评】本题考查抛物线的定义,考查学生的计算能力,正确运用抛物线的定义是关键.12.如图,在平面直角坐标系xOy中,直线y=x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2.【考点】变化的快慢与变化率.【分析】先用t表示出三角形的面积,再求导,代值计算即可.【解答】解:由|AB|==t,∴S(t)=|OA||OB|=tt=t2,∴S′(t)=t,∴S′(2)=2,故答案为:2.【点评】本题考查了三角形的面积公式和导数瞬时变化率的几合意义,属于基础题.13.在平面直角坐标系xOy中,已知直l:x+y﹣3=0和圆M:x2+(y﹣m)2=8,若圆M上存在点P,使得P到直线l的距离为3,则实数m的取值范围是[﹣7,1]∪[5,13] .【考点】直线与圆的位置关系.【分析】设P(2cosθ,m+2sinθ),由P到直线l:x+y﹣3=0的距离为3,得=6,由此利用三角函数性质能求出实数m的取值范围.【解答】解:∵圆M:x2+(y﹣m)2=8,圆M上存在点P,∴设P(2cosθ,m+2sinθ),∵P到直线l:x+y﹣3=0的距离为3,∴=3,即=6,∵,∴﹣7≤m≤1或5≤m≤13,∴实数m的取值范围是[﹣7,1]∪[5,13].【点评】本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意点到直线距离公式和三角函数性质的合理运用.14.已知函数y=x3﹣3x在区间[a,a+1](a≥0)上的最大值和最小值的差为2,则满足条件的实数a的所有值是a=﹣1或0.【考点】利用导数求闭区间上函数的最值.【分析】求出函数的导数,通过讨论a的范围,确定函数的单调区间,求出最大值和最小值,得到关于a的方程,解出即可.【解答】解:y′=f′(x)=3(x+1)(x﹣1),∴函数在在(﹣∞,﹣1)递增,在(﹣1,1)递减,在(1,+∞)递增,①a=0时,函数在[0,1]递减,函数的最大值是f(0)=0,函数的最小值是f(1)=﹣2,∴f(0)﹣f(1)=0﹣(﹣2)=2,故a=0符合题意;②0<a<1时,1<a+1<2,∴函数在[a,1)递减,在(1,a+1]递增,函数的最小值是f(1)=﹣2,由f(a)=f(a+1),得3a2+3a﹣2=0,解得:a=,(i)∴0≤a<时,f(x)的最大值是f(a),∴a3﹣3a﹣(﹣2)=2,解得a=0或或﹣,不合题意,舍,(ii)≤a<1时,f(x)的最大值是f(a+1),∴(a+1)3﹣3(a+1)﹣(﹣2)=2,解得a=﹣1,符合题意,③a≥1时,f(x)在[a,a+1]递增,∴f(x)min=f(a),f(x)max=f(a+1),∴(a+1)3﹣3(a+1)﹣a3+3a=2,解得:a=<1,舍,综上:a=﹣1或0.【点评】本题考查了函数的单调性、最值问题,考查导数的应用,分类讨论思想,是一道中档题.二、解答题:本大题共6小题,共计58分.解答应写出文字说明、证明过程或演算步骤.15.在平面直角坐标系xOy中,已知椭圆C过点(0,2),其焦点为F1(﹣,0),F2(,0).(1)求椭圆C的标准方程;(2)已知点P在椭圆C上,且PF1=4,求△PF1F2的面积.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(1)设椭圆方程为=1,(a>b>0),由椭圆C过点(0,2),其焦点为F2(﹣,0),F2(,0),求出a,b,c,由此能求出椭圆C的标准方程.(2)由点P在椭圆C上,且PF1=4,求出PF2,|F1F2|,由此能求出△PF1F2的面积.【解答】解:(1)∵椭圆C过点(0,2),其焦点为F2(﹣,0),F2(,0),∴设椭圆方程为=1,(a>b>0),则,∴=3,∴椭圆C的标准方程为=1.(2)∵点P在椭圆C上,且PF1=4,∴PF2=2×3﹣4=2,∵F1(﹣,0),F2(,0),∴|F1F2|=2,∴.∴PF1⊥PF2,∴△PF1F2的面积S===4.【点评】本题考查椭圆方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.16.在平面直角坐标系xOy中,已知圆M经过点A(1,0),B(3,0),C(0,1).(1)求圆M的方程;(2)若直线l“mx﹣2y﹣(2m+1)=0与圆M交于点P,Q,且=0,求实数m的值.【考点】平面向量数量积的运算;圆的一般方程.【分析】(1)由点的坐标求出弦的中垂线方程,联立求得圆心坐标,再求出半径,则圆的方程可求;(2)由题意可知∠PMQ=90°,结合圆的半径求出圆心到直线的距离,再由点到直线的距离公式求解.【解答】解:(1)如图,AB所在直线方程为x=2,AC所在直线方程为y=x,联立,解得M(2,2),又|MA|=,∴圆M的方程为(x﹣2)2+(y﹣2)2=5;(2)∵=0,∴∠PMQ=90°,则|PQ|=,∴M到直线mx﹣2y﹣(2m+1)=0的距离为.由,解得:m=.【点评】本题考查圆的方程的求法,考查了平面向量的数量积运算,考查了数学转化思想方法,是中档题.17.如图,在直三棱柱ABC﹣A1B1C1中,AB=2,AC=2,AA1=1,∠BAC=90°,D 为线段BC的中点.(1)求异面直线B1D与AC所成角的大小;(2)求二面角D﹣A1B1﹣A的大小.【考点】二面角的平面角及求法;异面直线及其所成的角.【分析】(1)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出异面直线B1D与AC所成角的大小.(2)求出平面A1B1D的法向量和平面A1B1A的法向量,利用向量法能求出二面角D﹣A1B1﹣A的大小.【解答】解:(1)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(0,2,0),B1(2,0,1),D(),=(﹣,,﹣1),=(0,2,0),设异面直线B1D与AC所成角为θ,则cosθ===,∴θ=.∴异面直线B1D与AC所成角的大小为.(2)==(2,0,0),=(﹣),设平面A1B1D的法向量=(x,y,z),则,取y=,得=(0,,3),又平面A1B1A的法向量=(0,1,0),设二面角D﹣A1B1﹣A的平面角为α,则cosα===,∴α=,∴二面角D﹣A1B1﹣A的大小为.【点评】本题考查异面直线所成角的大小的求法,考查二面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.18.A,B两地相距300km,汽车从A地以vkm/h的速度匀速行驶到B地(速度不得超过60km/h).已知汽车每小时的运输成本由固定成本和可变成本组成,固定成本为250元,可变成本(单位:元)与速度v的立方成正比,比例系数,设全程的运输成本为y元.(1)求y关于v的函数关系;(2)为使全程运输成本最小,汽车应以多大速度行驶?【考点】函数模型的选择与应用.【分析】(1)求出汽车从A地匀速行驶到B地所用时间,根据汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可得全程运输成本,及函数的定义域;(2)利用基本不等式可得结论.【解答】解:(1)依题意知汽车从A地匀速行驶到B地所用时间为,全程运输成本为y=(250+),即y=300(+),定义域为(0,60],(2)y=300(+)=300(++)≥300×3=2250,当且仅当=,即v=50km/h时,全程运输成本最小,最小为2250元.【点评】本题考查函数模型的构建,考查基本不等式的运用,解题的关键是构建函数模型,利用基本不等式求最值.19.在平面直角坐标系xOy中,已知椭圆C: +=1(m>0)的离心率为.(1)求m的值;(2)设点A为椭圆C的上顶点,问是否存在椭圆C的一条弦AB,使直线AB与圆(x﹣1)2+y2=r2(r>0)相切,且切点P恰好为线段AB的中点?若存在,其满足条件的所有直线AB的方程和对应的r的值?若不存在,说明理由.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(1)由已知得a2=m+8,b2=m,c2=a2﹣b2=8,=,由此能求出m的值.(2)椭圆C的方程为=1,A(0,2),线AB的斜率不存在时,直线AB的直线为x=0,符合题意.当直线AB斜率存在时,设直线AB的方程为y=kx+2,P(x0,y0),代入椭圆方程.得整理,得:(1+3k2)x2+12kx=0,由此利用直线方程、点到直线的距离公式,能求出结果.【解答】解:(1)∵椭圆C: +=1(m>0)的离心率为,∴a2=m+8,b2=m,c2=a2﹣b2=8,∵离心率为,∴=,解得m=4.(2)由(1)知椭圆C的方程为=1,∴A(0,2),假设存在椭圆C的一条弦AB满足条件,当直线AB的斜率不存在时,直线AB的直线为x=0,符合题意,此时,P(0,0),r=1.当直线AB斜率存在时,设直线AB的方程为y=kx+2,P(x0,y0),由,消去y,整理,得:(1+3k2)x2+12kx=0,解得x=0,或x=﹣,∴,,由×k=﹣1,得3k2+4k+1=0,解得k=﹣1或k=﹣.∴直线AB:y=﹣x+2,r=,或直线AB:y=﹣,r=.综上,存在这样的弦AB,直线AB:x=0,r=1,或直线AB:y=﹣x+2,r=,或直线AB:y=﹣,r=.【点评】本题考查实数值的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意直线方程的性质的合理运用.20.已知函数f(x)=lnx.(1)若直线y=2x+p(p∈R)是函数y=f(x)图象的一条切线,求实数p的值;(2)若函数g(x)=x﹣﹣2f(x)(m∈R)有两个极值点x1,x2,且x1<x2.①求实数m的取值范围;②证明:g(x2)<x2﹣1.【考点】利用导数研究函数的极值;利用导数研究曲线上某点切线方程.【分析】(1)求出f(x)的导数,求出切点的坐标,代入切线方程求出p的值即可;(2)①求出函数f(x)有两个极值点x1,x2,等价于方程x2﹣2x+m=0在(0,+∞),直接推出结果.通过①,推出0<m<1,构造新函数g(t)=t﹣2lnt﹣1,1<t<2,利用新函数的单调性证明,求解即可.【解答】解:(1)f(x)=lnx的定义域是(0,+∞),f′(x)=,若直线y=2x+p(p∈R)是函数y=f(x)图象的一条切线,∴=2,解得:x=,y=f(x)=ln=﹣ln2,将(,﹣ln2)代入y=2x+p,得:p=y﹣2x=﹣ln2﹣1;(2)①函数g(x)=x﹣﹣2lnx的定义域为(0,+∞),f′(x)=,令g′(x)=0,得x2﹣2x+m=0,其判别式△=4﹣4m,当△≤0,即m≥1时,x2﹣2x+m≥0,g′(x)≥0,此时,g(x)在(0,+∞)上单调递增,函数g(x)无极值点;②当△>0,即m<1时,方程x2﹣2x+a=0的两根为x1=1﹣,x2=1+>1,若m≤0,则x1≤0,则x∈(0,x2)时,g′(x)<0,x∈(x2,+∞)时,g′(x)>0,此时,g(x)在(0,x2)上单调递减,在(x2,+∞)上单调递增,函数g(x)有1个极值点;若m>0,则x1>0,则x∈(0,x1)时,g′(x)>0,x∈(x1,x2)时,g′(x)<0,x∈(x2,+∞)时,g′(x)>0,此时,g(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增,函数g(x)有2个极值点;综上,0<m<1;②证明:由①得0<m<1,x2=1+,且1<x2<2,m=﹣+2x2,g(x2)﹣x2+1=x2﹣﹣2lnx2﹣x2+1=x2﹣2lnx2﹣1,令h(t)=t﹣2lnt﹣1,1<t<2,则h′(t)=1﹣=,由于1<t<2,则h′(t)<0,故h(t)在(1,2)上单调递减,故h(t)<h(1)=1﹣2ln1﹣1=0,∴g(x2)﹣x2+1=h(x2)<0,∴g(x2)<x2﹣1.【点评】本题考查函数的导数的应用,函数的极值以及函数的单调性的应用,考查分析问题解决问题的能力,转化思想的应用.。
2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)

2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、填空题(本大题共14小题,共70.0分)1.命题“若a=b,则|a|=|b|”的逆否命题是______ .【答案】若|a|≠|b|,则a≠b【解析】解:命题“若a=b,则|a|=|b|”的逆否命题是命题“若|a|≠|b|,则a≠b”,故答案为:“若|a|≠|b|,则a≠b”根据已知中的原命题,结合逆否命题的定义,可得答案.本题考查的知识点是四种命题,难度不大,属于基础题.2.双曲线=1的渐近线方程是______ .【答案】y=±2x【解析】解:∵双曲线标准方程为=1,其渐近线方程是=0,整理得y=±2x.故答案为y=±2x.渐近线方程是=0,整理后就得到双曲线的渐近线方程.本题考查双曲线的简单性质的应用,令标准方程中的“1”为“0”即可求出渐近线方程.属于基础题.3.已知复数为纯虚数,其中i是虚数单位,则实数a的值是______ .【答案】2【解析】解:==,∵复数为纯虚数,∴,解得a=2.故答案为:2.直接由复数代数形式的乘除运算化简复数,再根据已知条件列出方程组,求解即可得答案.本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.4.在平面直角坐标系x O y中,点(4,3)到直线3x-4y+a=0的距离为1,则实数a的值是______ .【答案】±5【解析】解:由题意,=1,∴a=±5.故答案为±5.直接利用点到直线的距离公式,建立方程,即可求出实数a的值.本题考查求实数a的值,正确运用点到直线的距离公式是关键.5.曲线y=x4与直线y=4x+b相切,则实数b的值是______ .【答案】-3【解析】解:设直线与曲线的切点为P(m,n)则有:⇒,化简求:m=1,b=n-4;又因为点P满足曲线y=x4,所以:n=1;则:b=n-4=-3;故答案为:-3.设直线与曲线的切点为P(m,n),点P分别满足直线方程与曲线方程,同时y'(m)=4即可求出b值本题主要考察了点满足曲线,以及利用导数研究曲线上某点切线方程,属中等题.6.已知实数x,y满足条件,则z=2x+y的最大值是______ .【答案】9【解析】解:实数x,y满足条件,作出不等式组对应的平面区域如图:由z=2x+y得y=-2x+z,平移直线y=-2x+z,则当直线y=-2x+z经过点A时,直线的截距最大,此时z最大,由可得A(3,3).此时z=9,故答案为:9.作出不等式组对应的平面区域,利用线性规划的知识即可得到结论.本题主要考查线性规划的应用,利用数形结合是解决本题的关键.7.在平面直角坐标系x O y中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是______ .【答案】4【解析】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=5,∴x=4,故答案为:4由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,已知|PF|=5,则P到准线的距离也为5,即x+1=5,将p的值代入,进而求出x.活用抛物线的定义是解决抛物线问题最基本的方法.抛物线上的点到焦点的距离,叫焦半径.到焦点的距离常转化为到准线的距离求解.8.在平面直角坐标系x O y中,圆O:x2+y2=r2(r>0)与圆M:(x-3)2+(y+4)2=4相交,则r的取值范围是______ .【答案】3<r<7【解析】解:由题意,圆心距为5,∴|r-2|<5<r+2,∴3<r<7.故答案为3<r<7.由题意,圆心距为5,圆O:x2+y2=r2(r>0)与圆M:(x-3)2+(y+4)2=4相交,可得|r-2|<5<r+2,即可求出r的取值范围.本题考查圆与圆的位置关系,考查学生的计算能力,比较基础.9.观察下列等式:(sin)-2+(sin)-2=×1×2;(sin)-2+(sin)-2+(sin)-2+sin()-2=×2×3;(sin)-2+(sin)-2+(sin)-2+…+sin()-2=×3×4;(sin)-2+(sin)-2+(sin)-2+…+sin()-2=×4×5;…照此规律,(sin)-2+(sin)-2+(sin)-2+…+(sin)-2= ______ .【答案】n(n+1)【解析】解:观察下列等式:(sin)-2+(sin)-2=×1×2;(sin)-2+(sin)-2+(sin)-2+sin()-2=×2×3;(sin)-2+(sin)-2+(sin)-2+…+sin()-2=×3×4;(sin)-2+(sin)-2+(sin)-2+…+sin()-2=×4×5;…照此规律(sin)-2+(sin)-2+(sin)-2+…+(sin)-2=×n(n+1),故答案为:n(n+1)由题意可以直接得到答案.本题考查了归纳推理的问题,关键是找到相对应的规律,属于基础题.10.若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是______ .【答案】(-∞,0]∪[4,+∞)【解析】解:若“∃x∈R,x2+ax+a=0”是真命题,则△=a2-4a≥0,解得:a∈(-∞,0]∪[4,+∞),故答案为:(-∞,0]∪[4,+∞)若“∃x∈R,x2+ax+a=0”是真命题,则△=a2-4a≥0,解得实数a的取值范围.本题以命题的真假判断与应用为载体,考查了方程根的存在性与个数判断,特称命题,难度基础.11.已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=-3处函数f(x)有极大值,则函数f(x)的极小值是______ .【答案】-1【解析】解:f(x)=(x2+x+m)e x,f (x)=(x2+3x+m+1)e x,若f(x)在x=-3处函数f(x)有极大值,则f (-3)=0,解得:m=-1,故f(x)=(x2+x-1)e x,f (x)=(x2+3x)e x,令f (x)>0,解得:x>0,令f (x)<0,解得:x<-3,故f(x)在(-∞,-3)递增,在(-3,0)递减,在(0,+∞)递增,故f(x)极小值=f(0)=-1,故答案为:-1.求出函数f(x)的导数,根据f (-3)=0,求出m的值,从而求出函数f(x)的单调区间,求出函数的极小值即可.本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.12.有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y-1=0与直线l2:x+ay-2=0平行”的充分不必要条件;③“函数f(x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是______ .【答案】②④【解析】解:对于①,当m=1时,方程x2+my2=1表示圆,故错;对于②,∵a=±1时,直线l1与直线l2都平行,故正确;对于③,若函数f(x)=x3+mx单调递增⇒m≥0,故错;对于④,p或q是真命题⇒p且q不一定是真命题;⇒p且q是真命题⇒p或q一定是真命题,故正确;故答案为:②④①,当m=1时,方程x2+my2=1表示圆;②,∵a=±1时,直线l1与直线l2都平行;③,若函数f(x)=x3+mx单调递增⇒m≥0;④,p或q是真命题⇒p且q不一定是真命题;⇒p且q是真命题⇒p或q一定是真命题;本题考查了命题的真假,属于基础题.13.已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(-2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E离心率的取值范围是______ .【答案】[,]【解析】解:设P(x,y),由PM=PF⇒PM2=2PF2⇒(x+2c)2+y2=2(x+c)2+2y2⇒x2+y2=2c2,椭圆E上存在点P,使得PM=PF,则圆x2+y2=2c2与椭圆E:+=1(a>b>0)由公共点,∴b≤≤a⇒⇒.故答案为:[,]设P(x,y),由PM=PF⇒x2+y2=2c2.只需x2+y2=2c2与椭圆E:+=1(a>b>0)由公共点,即b≤≤a,可求离心率的取值范围.本题考查了椭圆的离心率,关键是要结合图形,属于中档题.14.已知t>0,函数f(x)=,,>,若函数g(x)=f(f(x)-1)恰有6个不同的零点,则实数t的取值范围是______ .【答案】(3,4)【解析】解:∵函数f(x)=,,>,∴函数f (x)=,,>,当x<,或x<t时,f (x)>0,函数为增函数,当<x<t时,f (x)<0,函数为减函数,故当x=时,函数f(x)取极大值,函数f(x)有两个零点0和t,若函数g(x)=f(f(x)-1)恰有6个不同的零点,则方程f(x)-1=0和f(x)-1=t各有三个解,即函数f(x)的图象与y=1和y=t+1各有三个零点,由y|x=t==,故<<<<,=(t-3)(2t+3)2>0得:t>3,故不等式的解集为:t∈(3,4),故答案为:(3,4)若函数g(x)=f(f(x)-1)恰有6个不同的零点,则方程f(x)-1=0和f(x)-1=t 各有三个解,即函数f(x)的图象与y=1和y=t+1各有三个零点,进而得到答案.本题考查的知识点是函数的零点个数的判定定理,分段函数的应用,难度中档.二、解答题(本大题共6小题,共90.0分)15.在平面直角坐标系x O y中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C (2,-4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.【答案】解:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),…(2分)所以AD的斜率为k==8,…(5分)所以BC边上的中线AD所在直线的方程为y-0=8(x-6),即8x-y-48=0.…(7分)(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k==1,…(9分)所以BC边上的高所在直线的斜率为-1,…(12分)所以BC边上的高所在直线的方程为y-8=-1(x-7),即x+y-15=0.…(14分)【解析】(1)求出BC中点D的坐标,AD的斜率,即可求BC边上的中线所在直线的方程;(2)求出BC边上的高所在直线的斜率为,即可求BC边上的高所在直线的方程.本题考查直线方程,考查学生的计算能力,正确求出直线的斜率是关键.16.已知数列{a n}满足a1=1,(a n-3)a n+1-a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.【答案】解:(1)令n=1,-2a2+3=0,a2=,令n=2,-a3-+4=0,a3=,令n=3,-a4-+4=0,a4=.(2)猜想a n=(n∈N*).证明:当n=1时,a1=1=,所以a n=成立,假设当n=k时,a n=成立,即a k=,则(a k-3)a k+1-a k+4=0,即(-3)a k+1-+4=0,所以a k+1=,即a k+1==,所以当n=k+1时,结论a n=成立.综上,对任意的n∈N*,a n=成立.【解析】(1)由数列{a n}的递推公式依次求出a2,a3,a4;(2)根据a2,a3,a4值的结构特点猜想{a n}的通项公式,再用数学归纳法①验证n=1成立,②假设n=k时命题成立,证明当n=k+1时命题也成立本题考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式,属于中档题.17.在平面直角坐标系x O y中,已知圆M的圆心在直线y=-2x上,且圆M与直线x+y-1=0相切于点P(2,-1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.【答案】解:(1)过点(2,-1)且与直线x+y-1=0垂直的直线方程为x-y-3=0,…(2分)由解得,所以圆心M的坐标为(1,-2),…(4分)所以圆M的半径为r=,…(6分)所以圆M的方程为(x-1)2+(y+2)2=2.…(7分)(2)因为直线l被圆M截得的弦长为,所以圆心M到直线l的距离为d==,…(9分)若直线l的斜率不存在,则l为x=0,此时,圆心M到l的距离为1,不符合题意.若直线l的斜率存在,设直线l的方程为y=kx,即kx-y=0,由d==,…(11分)整理得k2+8k+7=0,解得k=-1或-7,…(13分)所以直线l的方程为x+y=0或7x+y=0.…(14分)【解析】(1)求求出圆心坐标与半径,即可求出圆M的方程;(2)分类讨论,利用点到直线的距离公式,结合过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.本题考查圆的方程,考查直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.18.某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.【答案】(本题满分16分)解:(1)作AH⊥CF于H,则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,…(2分)则六边形的面积为f(θ)=2×(AB+CF)×AH=(2cosθ+2)sinθ=2(cosθ+1)sinθ,θ∈(0,).…(6分)(2)f (θ)=2[-sinθsinθ+(cosθ+1)cosθ]=2(2cos2θ+cosθ-1)=2(2cosθ-1)(cosθ+1).…(10分)令f (θ)=0,因为θ∈(0,),所以cosθ=,即θ=,…(12分)当θ∈(0,)时,f (θ)>0,所以f(θ)在(0,)上单调递增;当θ∈(,)时,f (θ)<0,所以f(θ)在(,)上单调递减,…(14分)所以当θ=时,f(θ)取最大值f()=2(cos+1)sin=.…(15分)答:当θ=时,可使得六边形区域面积达到最大,最大面积为平方百米.…(16分)【解析】(1)作AH⊥CF于H,则六边形的面积为f(θ)=2(cosθ+1)sinθ,θ∈(0,).(2)求导,分析函数的单调性,进而可得θ=时,f(θ)取最大值.本题考查的知识点是三角函数的实际应用,利用导数研究函数的最大值,难度中档.19.在平面直角坐标系x O y中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(-a,0),B(a,0),点M(-1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.【答案】解:(1)因为3=,所以3(-1+a,0)=(a+1,0),解得a=2.…(2分)又因为=,所以c=,所以b2=a2-c2=1,所以椭圆E的方程为+y2=1.…(4分)(2)设点C的坐标为(x0,y0),y0>0,则=(-1-x0,-y0),=(2-x0,-y0).因为BC⊥CD,所以(-1-x0)(2-x0)+y02=0.①…(6分)又因为+y02=1,②联立①②,解得x0=-,y0=,…(8分)所以k==2.…(10分)(3),设C(x0,y0),则CD:y=(x+1)(-2<x0<2且x0≠-1),由消去y,得x2+8y02x+4y02-4(x0+1)2=0.…(12分)又因为+y02=1,所以得D(,),…(14分)所以===3,所以为定值.…(16分)【解析】(1)由3=,得a即可;(2)设点C的坐标为(x0,y0),y0>0,由BC⊥CD,得(-1-x0)(2-x0)+y02=0.解得x0=-,y0=,即可.(3),设C(x0,y0),则CD:y=(x+1)(-2<x0<2且x0≠-1),由消去y,得x2+8y02x+4y02-4(x0+1)2=0,得D(,),可求本题考查了直线椭圆的位置关系,对计算能力的要求较高,设而不求、方程的思想贯穿整个解题过程,属于中档题.20.已知函数f(x)=ax-lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.【答案】解:(1)f(x)=x-lnx(x>0)的导数为f (x)=1-=,当x>1时,f (x)>0,f(x)递增;当0<x<1时,f (x)>0,f(x)递减.即有f(x)在x=1处取得极小值,也为最小值,且为1;(2)存在x∈[1,3],使+lnx=2成立,即为=2-lnx,即有a=,设g(x)=,x∈[1,3],则g (x)=(1-lnx)(1+),当1<x<e时,g (x)>0,g(x)递增;当e<x<3时,g (x)<0,g(x)递减.则g(x)在x=e处取得极大值,且为最大值e+;g(1)=2,g(3)=3(2-ln3)+>2,则a的取值范围是[2,e+];(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,即为ax-lnx≥-ln,即有a(x-)≥2lnx,x≥1,高中数学试卷第11页,共12页令F(x)=a(x-)-2lnx,x≥1,F (x)=a(1+)-,当x=1时,原不等式显然成立;当x>1时,由题意可得F (x)≥0在(1,+∞)恒成立,即有a(1+)-≥0,即a≥,由=<=1,则a≥1.综上可得a的取值范围是[1,+∞).【解析】(1)求得f(x)的导数,求得单调区间,可得f(x)的极小值,也为最小值;(2)由题意可得a=,设g(x)=,x∈[1,3],求出导数和单调区间,极值和最值,即可得到所求a的范围;(3)由题意可得ax-lnx≥-ln,即有a(x-)≥2lnx,x≥1,令F(x)=a(x-)-2lnx,x≥1,求出导数,讨论x=1,x>1时,F(x)递增,运用分离参数和基本不等式,即可得到a的范围.本题考查导数的运用:求单调区间和极值、最值,考查构造函数法和分类讨论思想方法的运用,考查运算能力,属于难题.高中数学试卷第12页,共12页。
2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)

2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b,则|a|=|b|”的逆否命题是.2.(5分)双曲线=1的渐近线方程是.3.(5分)已知复数为纯虚数,其中i是虚数单位,则实数a的值是.4.(5分)在平面直角坐标系xOy中,点(4,3)到直线3x﹣4y+a=0的距离为1,则实数a的值是.5.(5分)曲线y=x4与直线y=4x+b相切,则实数b的值是.6.(5分)已知实数x,y满足条件则z=2x+y的最大值是.7.(5分)在平面直角坐标系xOy中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是.8.(5分)在平面直角坐标系xOy中,圆O:x2+y2=r2(r>0)与圆M:(x﹣3)2+(y+4)2=4相交,则r的取值范围是.9.(5分)观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=.10.(5分)若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是.11.(5分)已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是.12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是.13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是.14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b,则|a|=|b|”的逆否命题是若|a|≠|b|,则a≠b.【解答】解:命题“若a=b,则|a|=|b|”的逆否命题是命题“若|a|≠|b|,则a≠b”,故答案为:“若|a|≠|b|,则a≠b”2.(5分)双曲线=1的渐近线方程是y=±2x.【解答】解:∵双曲线标准方程为=1,其渐近线方程是=0,整理得y=±2x.故答案为y=±2x.3.(5分)已知复数为纯虚数,其中i是虚数单位,则实数a的值是2.【解答】解:==,∵复数为纯虚数,∴,解得a=2.故答案为:2.4.(5分)在平面直角坐标系xOy中,点(4,3)到直线3x﹣4y+a=0的距离为1,则实数a的值是±5.【解答】解:由题意,=1,∴a=±5.故答案为±5.5.(5分)曲线y=x4与直线y=4x+b相切,则实数b的值是﹣3.【解答】解:设直线与曲线的切点为P(m,n)则有:⇒,化简求:m=1,b=n﹣4;又因为点P满足曲线y=x4,所以:n=1;则:b=n﹣4=﹣3;故答案为:﹣3.6.(5分)已知实数x,y满足条件则z=2x+y的最大值是9.【解答】解:实数x,y满足条件作出不等式组对应的平面区域如图:由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,则当直线y=﹣2x+z经过点A时,直线的截距最大,此时z最大,由可得A(3,3).此时z=9,故答案为:9.7.(5分)在平面直角坐标系xOy中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是4.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=5,∴x=4,故答案为:48.(5分)在平面直角坐标系xOy中,圆O:x2+y2=r2(r>0)与圆M:(x﹣3)2+(y+4)2=4相交,则r的取值范围是3<r<7.【解答】解:由题意,圆心距为5,∴|r﹣2|<5<r+2,∴3<r<7.故答案为3<r<7.9.(5分)观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=n(n+1).【解答】解:观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=×n (n+1),故答案为:n(n+1)10.(5分)若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是(﹣∞,0]∪[4,+∞).【解答】解:若“∃x∈R,x2+ax+a=0”是真命题,则△=a2﹣4a≥0,解得:a∈(﹣∞,0]∪[4,+∞),故答案为:(﹣∞,0]∪[4,+∞)11.(5分)已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是﹣1.【解答】解:f(x)=(x2+x+m)e x,f′(x)=(x2+3x+m+1)e x,若f(x)在x=﹣3处函数f (x)有极大值,则f′(﹣3)=0,解得:m=﹣1,故f(x)=(x2+x﹣1)e x,f′(x)=(x2+3x)e x,令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<﹣3,故f(x)在(﹣∞,﹣3)递增,在(﹣3,0)递减,在(0,+∞)递增,=f(0)=﹣1,故f(x)极小值故答案为:﹣1.12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是②④.【解答】解:对于①,当m=1时,方程x2+my2=1表示圆,故错;对于②,∵a=±1时,直线l1与直线l2都平行,故正确;对于③,若函数f (x)=x3+mx单调递增⇒m≥0,故错;对于④,p或q是真命题⇒p且q不一定是真命题;⇒p且q是真命题⇒p或q 一定是真命题,故正确;故答案为:②④13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是[] .【解答】解:设P(x,y),由PM=PF⇒PM2=2PF2⇒(x+2c)2+y2=2(x+c)2+2y2⇒x2+y2=2c2,椭圆E上存在点P,使得PM=PF,则圆x2+y2=2c2与椭圆E:+=1(a>b >0)有公共点,∴b≤≤a⇒⇒.故答案为:[]14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是(3,4).【解答】解:∵函数f(x)=,∴函数f′(x)=,当x<,或x<t时,f′(x)>0,函数为增函数,当<x<t时,f′(x)<0,函数为减函数,故当x=时,函数f(x)取极大值,函数f(x)有两个零点0和t,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则方程f(x)﹣1=0和f(x)﹣1=t各有三个解,即函数f(x)的图象与y=1和y=t+1各有三个零点,由y|x=t==,故,=(t﹣3)(2t+3)2>0得:t>3,故不等式的解集为:t∈(3,4),故答案为:(3,4)二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.【解答】解:(1)由B(10,4),C(2,﹣4),得BC中点D的坐标为(6,0),…(2分)所以AD的斜率为k==8,…(5分)所以BC边上的中线AD所在直线的方程为y﹣0=8(x﹣6),即8x﹣y﹣48=0.…(7分)(2)由B(10,4),C(2,﹣4),得BC所在直线的斜率为k==1,…(9分)所以BC边上的高所在直线的斜率为﹣1,…(12分)所以BC边上的高所在直线的方程为y﹣8=﹣1(x﹣7),即x+y﹣15=0.…(14分)16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.【解答】解:(1)令n=1,﹣2a2+3=0,a2=,令n=2,﹣a3﹣+4=0,a3=,令n=3,﹣a4﹣+4=0,a4=.(2)猜想a n=(n∈N*).证明:当n=1时,a1=1=,所以a n=成立,假设当n=k时,a n=成立,即a k=,则(a k﹣3)a k+1﹣a k+4=0,即(﹣3)a k+1﹣+4=0,=,即a k+1==,所以a k+1所以当n=k+1时,结论a n=成立.综上,对任意的n∈N*,a n=成立.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.【解答】解:(1)过点(2,﹣1)且与直线x+y﹣1=0垂直的直线方程为x﹣y﹣3=0,…(2分)由解得,所以圆心M的坐标为(1,﹣2),…(4分)所以圆M的半径为r=,…(6分)所以圆M的方程为(x﹣1)2+(y+2)2=2.…(7分)(2)因为直线l被圆M截得的弦长为,所以圆心M到直线l的距离为d==,…(9分)若直线l的斜率不存在,则l为x=0,此时,圆心M到l的距离为1,不符合题意.若直线l的斜率存在,设直线l的方程为y=kx,即kx﹣y=0,由d==,…(11分)整理得k2+8k+7=0,解得k=﹣1或﹣7,…(13分)所以直线l的方程为x+y=0或7x+y=0.…(14分)18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.【解答】(本题满分16分)解:(1)作AH⊥CF于H,则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,…(2分)则六边形的面积为f (θ)=2×(AB+CF)×AH=(2cosθ+2)sinθ=2(cosθ+1)sinθ,θ∈(0,).…(6分)(2)f′(θ)=2[﹣sinθsinθ+(cosθ+1)cosθ]=2(2cos2θ+cosθ﹣1)=2(2cosθ﹣1)(cosθ+1).…(10分)令f′(θ)=0,因为θ∈(0,),所以cosθ=,即θ=,…(12分)当θ∈(0,)时,f′(θ)>0,所以f (θ)在(0,)上单调递增;当θ∈(,)时,f′(θ)<0,所以f (θ)在(,)上单调递减,…(14分)所以当θ=时,f (θ)取最大值f ()=2(cos+1)sin=.…(15分)答:当θ=时,可使得六边形区域面积达到最大,最大面积为平方百米.…(16分)19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.【解答】解:(1)因为3=,所以3(﹣1+a,0)=(a+1,0),解得a=2.…(2分)又因为=,所以c=,所以b2=a2﹣c2=1,所以椭圆E的方程为+y2=1.…(4分)(2)设点C的坐标为(x0,y0),y0>0,则=(﹣1﹣x0,﹣y0),=(2﹣x0,﹣y0).因为BC⊥CD,所以(﹣1﹣x0)(2﹣x0)+y02=0.①…(6分)又因为+y02=1,②联立①②,解得x0=﹣,y0=,…(8分)所以k==2.…(10分)(3),设C(x0,y0),则CD:y=(x+1)(﹣2<x0<2且x0≠﹣1),由消去y,得x2+8y02x+4y02﹣4(x0+1)2=0.…(12分)又因为+y02=1,所以得D(,),…(14分)所以===3,所以为定值.…(16分)20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.【解答】解:(1)f(x)=x﹣lnx(x>0)的导数为f′(x)=1﹣=,当x>1时,f′(x)>0,f(x)递增;当0<x<1时,f′(x)>0,f(x)递减.即有f(x)在x=1处取得极小值,也为最小值,且为1;(2)存在x∈[1,3],使+lnx=2成立,即为=2﹣lnx,即有a=,设g(x)=,x∈[1,3],则g′(x)=(1﹣lnx)(1+),当1<x<e时,g′(x)>0,g(x)递增;当e<x<3时,g′(x)<0,g(x)递减.则g(x)在x=e处取得极大值,且为最大值e+;g(1)=2,g(3)=3(2﹣ln3)+>2,则a的取值范围是[2,e+];(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,即为ax﹣lnx≥﹣ln,即有a(x﹣)≥2lnx,x≥1,令F(x)=a(x﹣)﹣2lnx,x≥1,F′(x)=a(1+)﹣,当x=1时,原不等式显然成立;当x>1时,由题意可得F′(x)≥0在(1,+∞)恒成立,即有a(1+)﹣≥0,即a≥,由=<=1,则a≥1.综上可得a的取值范围是[1,+∞).。
江苏省南京市2018-2019学年高二上学期期末考试 数学(理) Word版含答案

南京市2018—2019学年度第一学期期末调研高二数学(理科) 2019.01注意事项:1.本试卷共4页,包括填空题(第1题〜第14题)、解答题(第15题〜第20题)两部分。
本试卷满分为160分,考试时间为120分钟。
2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内,试题的答案写在答题卡上对应题目的答案空格内。
考试结束后,交回答题卡。
一、填空题:本大题共14小题,每题5分,共70分。
请把答案填写在答题卡相应位置上。
1.已知命题ex e x p x ≥∀,0>:,写出命题p 的否定: ▲ . 2.在平面直角坐标系xOy 中,抛物线x y 22=的准线方程为 ▲ . 3.己知x e x f x sin )(⋅=,则)0('f 的值为 ▲ .4.已知复数z 满足(z-2)i=l+i (i 为虚数单位),则z 的实部为 ▲ .5.在平面直角坐标系xOy 中,P 是椭圆C: 1422=+y x 上一点,若点P 到椭圆C 的右焦点的距离为2,则它到椭圆C 的右准线的距离为 ▲ 。
6.已知实数y x ,满足⎪⎩⎪⎨⎧≥+≤-≤,2,3,1y x x x y ,则y x z 2+=的最小值为▲ 。
7.在平面直角坐标系xOy 中,“m >0”是“方程122=+my x 表示椭圆”的 条件。
(填 “充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”) 8.在平面角坐标系xOy 中,双曲线的顶点到它的渐近线的距离为▲ 。
9. 在平面角坐标系xOy 中,点A(4,0),点B(0,2),平面内点P 满足15=⋅,则 PO 的最大值是▲ 。
10.在平面直角坐标系xOy 中,点F 1,F 2分别是椭圆12222=+by a x (a>b>0)的左、右焦点,过点F 2且与x 轴垂直的直线与椭圆交于A ,B 两点。
若∠AF 1B 为锐角,则该椭圆的离心率的取值范围是 ▲ .11.在平面直角坐标系 xOy 中,圆 C 1: 1)()(22=-+-b y a x 与圆 C 2:03222=--+x y x 有公共点,则实数a 的取值范围是 ▲.12.如图,在正四棱锥P —ABCD 中,PA=AB ,点M 为的中点,BN BD λ=,若MN⊥AD , 则实数=λ ▲ .13.在平面直角坐标系xOy 中,圆M: 1)1(22=+-y x ,点A3,1),P 为抛物线上任意一点(异于原点),过点P 作圆M 的切线PB, B 为切点,则PA+PB 的最小值是 ▲ .14.已知函数a a x a x x f 463)(223+--= (a>0)只有一个零点,且这个零点为正数,则头数a 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
南京市2016-2017学年度第一学期期末检测卷(高二数学理)参考答案终稿

南京市2016-2017学年度第一学期期末检测卷 高二数学(理科)参考答案及评分标准 2017.01 说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,共70分)1.若|a |≠|b |,则a ≠b 2.y =±2x 3.2 4.±5 5.-3 6.9 7.48.(3,7) 9.4n (n +1)310.(-∞,0]∪[4,+∞) 11.-1 12. ②④ 13.[33,22] 14.(3,4) 二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤) 15.(本题满分14分)解:(1)由B (10,4),C (2,-4),得BC 中点D 的坐标为(6,0), ………………2分所以AD 的斜率为k =8-07-6=8, ……………… 5分 所以BC 边上的中线AD 所在直线的方程为y -0=8(x -6),即8x -y -48=0. ……………… 7分(2)由B (10,4),C (2,-4),得BC 所在直线的斜率为k =4-(-4)10-2=1,…… 9分 所以BC 边上的高所在直线的斜率为-1, ………………… 12分 所以BC 边上的高所在直线的方程为y -8=-(x -7),即x +y -15=0. ………………………… 14分16.(本题满分14分)解:(1)令n =1,-2a 2+3=0,a 2=32, ………………1分 令n =2,-32a 3-32+4=0,a 3=53, ………………2分 令n =3,-43a 4-53+4=0,a 4=74. ………………3分(2)猜想a n =2n -1n(n ∈N *). ………………5分 证明:当n =1时,a 1=1=2-11,所以a n =2n -1n成立, ……………… 6分 假设当n =k 时,a n =2n -1n 成立,即a k =2k -1k, ………………8分 则(a k -3)a k +1-a k +4=0,即(2k -1k -3)a k +1-2k -1k+4=0, 所以k +1k a k +1=2k +1k ,即a k +1=2k +1k +1=2(k +1)-1k +1, ………………12分 所以当n =k +1时,结论a n =2n -1n 成立. 综上,对任意的n ∈N *,a n =2n -1n成立. ………………14分 17.(本题满分14分)解:(1)过点(2,-1)且与直线x +y -1=0垂直的直线方程为x -y -3=0, ……2分由⎩⎨⎧y =-2x ,x -y -3=0, 解得⎩⎨⎧x =1,y =-2.所以圆心M 的坐标为(1,-2), ………………4分 所以圆M 的半径为r =(2-1)2+[-1-(-2)]2=2, ………………6分 所以圆M 的方程为 (x -1)2+(y +2)2=2. ………………7分(2)因为直线l 被圆M 截得的弦长为6,所以圆心M 到直线l 的距离为d =2-(62)2=22, ……………9分 若直线l 的斜率不存在,则l 为x =0,此时,圆心M 到l 的距离为1,则弦长为2,不符合题意.若直线l 的斜率存在,设直线l 的方程为y =kx ,即kx -y =0,由d =|k +2|k 2+(-1)2=22, ………………11分 整理得k 2+8k +7=0,解得k =-1或-7, ………………13分所以直线l 的方程为x +y =0或7x +y =0. ………………14分18.(本题满分16分)解:(1)作AH ⊥CF 于H ,则OH =cos θ,AB =2OH =2cos θ,AH =sin θ, ……………2分则六边形的面积为f (θ)=2×12(AB +CF )×AH =(2cos θ+2)sin θ =2(cos θ+1)sin θ,θ∈(0,π2). ………………6分 (2)f ′(θ)=2[-sin θsin θ+(cos θ+1)cos θ]=2(2cos 2θ+cos θ-1)=2(2cos θ-1)(cos θ+1). ………………10分令 f ′(θ)=0,因为θ∈(0,π2),所以cos θ=12,即θ=π3, ……………………12分 当θ∈(0,π3)时,f ′(θ)>0,所以f (θ)在(0,π3)上单调递增; 当θ∈(π3,π2)时,f ′(θ)<0,所以f (θ)在(π3,π2)上单调递减, …………14分 所以当θ=π3时,f (θ)取最大值f (π3)=2(cos π3+1)sin π3=323. …………15分 答:当θ=π3时,可使得六边形区域面积达到最大,最大面积为323平方百米. …………………………16分19.(本题满分16分)解:(1)因为3AM →=MB →,所以3(-1+a ,0)=(a +1,0),解得a =2. ………………2分又因为c a = 3 2,所以c =3,所以b 2=a 2-c 2=1, 所以椭圆E 的方程为x 24+y 2=1. ………………4分 (2)方法1设点C 的坐标为(x 0,y 0),y 0>0,则CM →=(-1-x 0,-y 0),CB →=(2-x 0,-y 0).因为BC ⊥CD ,所以(-1-x 0)( 2-x 0)+y 02=0. ① ……………6分 又因为x 024+y 02=1, ② 联立①②,解得x 0=-23,y 0=223, ………………8分 所以k =223-23+1=22. ………………10分 方法2因为CD 的方程为y =k (x +1),且BC ⊥CD ,所以BC 的方程为y =-1k(x -2), ………………6分 联立方程组,可得点C 的坐标为(2-k 21+k 2,3k 1+k 2), ………………8分 代入椭圆方程,得(2-k 21+k 2)24+(3k 1+k 2)2=1, 解得k =±22.又因为点C 在x 轴上方,所以3k 1+k 2>0,所以k >0,所以k =2 2 ………………10分(3)方法1因为直线CD 的方程为y =k (x +1),由⎩⎪⎨⎪⎧y =k (x +1),x 24+y 2=1,消去y ,得(1+4k 2)x 2+8k 2x +4k 2-4=0, 设C (x 1,y 1),D (x 2,y 2),则x 1+x 2=-8k 21+4k 2,x 1x 2=4k 2-4 1+4k 2. …………………12分 所以k 1k 2=y 2x 2+2 y 1x 1-2 =k (x 2+1)x 2+2 k (x 1+1)x 1-2 =(x 2+1)(x 1-2)(x 2+2)(x 1+1) =x 1x 2-2(x 1+x 2)+3x 1-2 x 1x 2+(x 1+x 2)+x 1+2…………………14分 =4k 2-4 1+4k 2-2×(-8k 21+4k 2)+3x 1-2 4k 2-4 1+4k 2+(-8k 21+4k 2)+x 1+2=12k 2-6 1+4k 2+3x 1 4k 2-2 1+4k 2+x 1=3, 所以k 1k 2为定值. ………………………16分 方法2因为直线AD 的方程为y =k 1(x +2),由⎩⎪⎨⎪⎧y =k 1(x +2),x 24+y 2=1,解得D (2-8k 12 1+4k 12,4k 1 1+4k 12), ………………………12分 因为直线BC 的方程为y =k 2(x -2),由⎩⎪⎨⎪⎧y =k 2(x -2),x 24+y 2=1,解得C (8k 22-2 1+4k 22,-4k 2 1+4k 22), 由于C ,M ,D 三点共线,故MC →,MD →共线,又MC →=(8k 22-2 1+4k 22+1,-4k 2 1+4k 22)=(12k 22-1 1+4k 22,-4k 2 1+4k 22), MD →=(2-8k 12 1+4k 12+1,4k 1 1+4k 12)=(3-4k 12 1+4k 12,4k 1 1+4k 12), 所以12k 22-1 1+4k 22·4k 1 1+4k 12=-4k 2 1+4k 22·3-4k 121+4k 12, ……………14分 化简得12k 22k 1-k 1=4k 12k 2-3k 2,即(4k 1k 2+1)(k 1-3k 2)=0,若4k 1k 2+1=0,则k 2=-14k 1代入C (8k 22-2 1+4k 22,-4k 2 1+4k 22), 化简得C (2-8k 12 1+4k 12,4k 1 1+4k 12), 此时C 与D 重合,于是4k 1k 2+1≠0,从而k 1-3k 2=0,所以k 1 k 2=3,即k 1k 2为定值. ………………………16分方法3设C (x 0,y 0),则CD :y =y 0 x 0+1(x +1)(-2<x 0<2且x 0≠-1), 由⎩⎨⎧y =y 0 x 0+1(x +1),x 24+y 2=1,消去y , 得[(x 0+1)2+4y 02]x 2+8y 02x +4y 02-4(x 0+1)2=0. ………………12分又因为x 024+y 02=1,所以得D (-8-5x 05+2x 0,-3y 05+2x 0), ………………14分 所以k 1k 2=-3y 05+2x 0-8-5x 05+2x 0+2·x 0-2 y 0 =-3y 0-x 0+2·x 0-2 y 0=3, 所以k 1k 2为定值. ……………………16分 方法4设D (x 0,y 0),y 0≠0,则k 1k BD =y 0 x 0+2·y 0 x 0-2=y 02x 02-4=1-x 024 x 02-4=-14. …………………12分 因为CD 的方程为y =k (x +1),设C (x 1,y 1),D (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x +1),x 24+y 2=1,消去y ,得(1+4k 2)x 2+8k 2x +4k 2-4=0, 则x 1+x 2=-8k 21+4k 2,x 1x 2=4k 2-4 1+4k 2, 所以k 2k BD =y 1x 1-2×y 2x 2-2=k 2(x 1+1) (x 2+1) (x 1-2)(x 2-2)=k 2(x 1 x 2+x 1+x 2+1) x 1 x 2-2 (x 1+x 2)+4=k 2(4k 2-4 1+4k 2-8k 21+4k 2+1) 4k 2-4 1+4k 2+2×8k 2 1+4k 2+4=-3k 236k 2=-112. …………………14分 又因为k 1k BD =-14, 所以k 1 k 2=3,即k 1k 2为定值. ………………………16分 20.(本题满分16分)解:(1)a =1时,f (x )=x -ln x , 则f '(x )=1-1x =x -1x,令f '(x )=0,则x =1. ……………………2分 当0<x <1时,f '(x )<0,所以f (x )在(0,1)上单调递减;当x >1时,f '(x )>0,所以f (x )在(1,+∞)上单调递增, ………………3分 所以当x =1时,f (x )取到最小值,最小值为1. …………………4分(2)因为 f (x )x 2+ln x =2(x >0), 所以ax -ln x =(2-ln x )x 2,即a =2x -x ln x +ln x x, …………………6分 设g (x )=2x -x ln x +ln x x,x ∈[1,3], 则g '(x )=2-(1+ln x )+1-ln x x 2=(1-ln x )(1+1x 2), 令g '(x )=0,解得x =e ,当1<x <e 时,g '(x )>0,所以g (x )在(1,e)上单调递增;当e <x <3时,g '(x )<0,所以g (x )在(e ,3)上单调递减, ………………8分因为g (1)=2,g (e)=e +1e ,g (3)=6-83ln3, 因为6-83ln3>2,所以函数g (x )的值域是[2,e +1e], 所以a 的取值范围是[2,e +1e]. ………………10分 (3)对任意的x ∈[1,+∞),有f (x )≥f (1x)成立, 则ax -ln x ≥a x +ln x ,即a (x -1x)-2ln x ≥0. 令h (x )=a (x -1x )-2ln x ,则h '(x )=a (1+1x 2)-2x =ax 2-2x +a x 2, ①当a ≥1时,ax 2-2x +a =a (x -1a )2+a 2-1a ≥0, 所以h '(x )≥0,因此h (x )在[1,+∞)上单调递增,所以x ∈[1,+∞)时,恒有h (x )≥h (1)=0成立,所以a ≥1满足条件. ………………12分②当0<a <1时,有1a >1,若x ∈[1,1a],则ax 2-2x +a <0, 此时h '(x )=ax 2-2x +a x 2<0, 所以h (x )在[1,1a ]上单调递减,所以h (1a)<h (1)=0, 即存在x =1a>1,使得h (x )<0,所以0<a <1不满足条件.……………14分 ③当a ≤0时,因为x ≥1,所以h '(x )=ax 2-2x +a x 2<0,所以h (x )在[1,+∞)上单调递减, 所以当x >1时,h (x )<h (1)=0,所以a ≤0不满足条件.综上, a 的取值范围为[1,+∞). ………………16分。
2017-2018学年高二年级数学期末试卷(理数)含答案

2.若 x 2m2 3 是 1 x 4 的必要不充分条件,则实数 m 的取值范围是( )
10.已知函数 f x 1 x3 1 mx2 4x 3 在区间 1,2上是增函数,则实数 m 的取值范围是(
32
A . 3,3
B . ,3 3, C . ,1 1,
,则满足
11.已知函数
f
x
3|x1| , x2 2x
x 1,
0, x
0
若关于
x
的方程 f
x2
a
1f
x
a
0有
7
个不
等实根,则实数 a 的取值范围是(
)
A . 2,1
B .2,4
C . 2,1
D . ,4
12.
已知函数
A . loga c logb c B . logc a logc b C . a c bc
D . ca cb
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是 9.已知函数 f x 2 xm 1 为偶函数,记 a f log0.5 3 , b f log2 5 , c f 2m,则
由题设知
,
则
解得 的横坐标分别是 则 有 又
,又 于是
, ,
,
,即 l 与直线 平行, 一定相交,分别联立方
设
是平面
的法向量,则
,即
。
对任意
,要使
与
的面积之比是常数,只需 t 满足
可取
,故,所以 与平面
20. (1)依题意可得
所成角的正弦值为 ---------12 分 ,
2017年江苏省南京市高二(上)期末数学试卷(含答案解析).doc

2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b ,则|a |=|b |”的逆否命题是 . 2.(5分)双曲线=1的渐近线方程是 .3.(5分)已知复数为纯虚数,其中i 是虚数单位,则实数a 的值是 .4.(5分)在平面直角坐标系xOy 中,点(4,3)到直线3x ﹣4y +a=0的距离为1,则实数a 的值是 .5.(5分)曲线y=x 4与直线y=4x +b 相切,则实数b 的值是 . 6.(5分)已知实数x ,y 满足条件则z=2x +y 的最大值是 .7.(5分)在平面直角坐标系xOy 中,抛物线C :y 2=4x 的焦点为F ,P 为抛物线C 上一点,且PF=5,则点P 的横坐标是 .8.(5分)在平面直角坐标系xOy 中,圆O :x 2+y 2=r 2(r >0)与圆M :(x ﹣3)2+(y +4)2=4相交,则r 的取值范围是 .9.(5分)观察下列等式:(sin )﹣2+(sin )﹣2=×1×2;(sin )﹣2+(sin )﹣2+(sin )﹣2+sin ()﹣2=×2×3;(sin )﹣2+(sin )﹣2+(sin )﹣2+…+sin ()﹣2=×3×4;(sin )﹣2+(sin)﹣2+(sin)﹣2+…+sin ()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2= .10.(5分)若“∃x ∈R ,x 2+ax +a=0”是真命题,则实数a 的取值范围是 . 11.(5分)已知函数f (x )=(x 2+x +m )e x (其中m ∈R ,e 为自然对数的底数).若在x=﹣3处函数f (x )有极大值,则函数f (x )的极小值是 .12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是.13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是.14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.2016-2017学年江苏省南京市高二(上)期末数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上1.(5分)命题“若a=b,则|a|=|b|”的逆否命题是若|a|≠|b|,则a≠b.【解答】解:命题“若a=b,则|a|=|b|”的逆否命题是命题“若|a|≠|b|,则a≠b”,故答案为:“若|a|≠|b|,则a≠b”2.(5分)双曲线=1的渐近线方程是y=±2x.【解答】解:∵双曲线标准方程为=1,其渐近线方程是=0,整理得y=±2x.故答案为y=±2x.3.(5分)已知复数为纯虚数,其中i是虚数单位,则实数a的值是2.【解答】解:==,∵复数为纯虚数,∴,解得a=2.故答案为:2.4.(5分)在平面直角坐标系xOy中,点(4,3)到直线3x﹣4y+a=0的距离为1,则实数a的值是±5.【解答】解:由题意,=1,∴a=±5.故答案为±5.5.(5分)曲线y=x4与直线y=4x+b相切,则实数b的值是﹣3.【解答】解:设直线与曲线的切点为P(m,n)则有:⇒,化简求:m=1,b=n﹣4;又因为点P满足曲线y=x4,所以:n=1;则:b=n﹣4=﹣3;故答案为:﹣3.6.(5分)已知实数x,y满足条件则z=2x+y的最大值是9.【解答】解:实数x,y满足条件作出不等式组对应的平面区域如图:由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,则当直线y=﹣2x+z经过点A时,直线的截距最大,此时z最大,由可得A(3,3).此时z=9,故答案为:9.7.(5分)在平面直角坐标系xOy中,抛物线C:y2=4x的焦点为F,P为抛物线C上一点,且PF=5,则点P的横坐标是4.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=5,∴x=4,故答案为:48.(5分)在平面直角坐标系xOy中,圆O:x2+y2=r2(r>0)与圆M:(x﹣3)2+(y+4)2=4相交,则r的取值范围是3<r<7.【解答】解:由题意,圆心距为5,∴|r﹣2|<5<r+2,∴3<r<7.故答案为3<r<7.9.(5分)观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律,(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=n(n+1).【解答】解:观察下列等式:(sin)﹣2+(sin)﹣2=×1×2;(sin)﹣2+(sin)﹣2+(sin)﹣2+sin()﹣2=×2×3;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×3×4;(sin)﹣2+(sin)﹣2+(sin)﹣2+…+sin()﹣2=×4×5;…照此规律(sin)﹣2+(sin)﹣2+(sin)﹣2+…+(sin)﹣2=×n (n+1),故答案为:n(n+1)10.(5分)若“∃x∈R,x2+ax+a=0”是真命题,则实数a的取值范围是(﹣∞,0]∪[4,+∞).【解答】解:若“∃x∈R,x2+ax+a=0”是真命题,则△=a2﹣4a≥0,解得:a∈(﹣∞,0]∪[4,+∞),故答案为:(﹣∞,0]∪[4,+∞)11.(5分)已知函数f(x)=(x2+x+m)e x(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是﹣1.【解答】解:f(x)=(x2+x+m)e x,f′(x)=(x2+3x+m+1)e x,若f(x)在x=﹣3处函数f (x)有极大值,则f′(﹣3)=0,解得:m=﹣1,故f(x)=(x2+x﹣1)e x,f′(x)=(x2+3x)e x,令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<﹣3,故f(x)在(﹣∞,﹣3)递增,在(﹣3,0)递减,在(0,+∞)递增,=f(0)=﹣1,故f(x)极小值故答案为:﹣1.12.(5分)有下列命题:①“m>0”是“方程x2+my2=1表示椭圆”的充要条件;②“a=1”是“直线l1:ax+y﹣1=0与直线l2:x+ay﹣2=0平行”的充分不必要条件;③“函数f (x)=x3+mx单调递增”是“m>0”的充要条件;④已知p,q是两个不等价命题,则“p或q是真命题”是“p且q是真命题”的必要不充分条件.其中所有真命题的序号是②④.【解答】解:对于①,当m=1时,方程x2+my2=1表示圆,故错;对于②,∵a=±1时,直线l1与直线l2都平行,故正确;对于③,若函数f (x)=x3+mx单调递增⇒m≥0,故错;对于④,p或q是真命题⇒p且q不一定是真命题;⇒p且q是真命题⇒p或q 一定是真命题,故正确;故答案为:②④13.(5分)已知椭圆E:+=1(a>b>0)的焦距为2c(c>0),左焦点为F,点M的坐标为(﹣2c,0).若椭圆E上存在点P,使得PM=PF,则椭圆E 离心率的取值范围是[] .【解答】解:设P(x,y),由PM=PF⇒PM2=2PF2⇒(x+2c)2+y2=2(x+c)2+2y2⇒x2+y2=2c2,椭圆E上存在点P,使得PM=PF,则圆x2+y2=2c2与椭圆E:+=1(a>b >0)有公共点,∴b≤≤a⇒⇒.故答案为:[]14.(5分)已知t>0,函数f(x)=,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是(3,4).【解答】解:∵函数f(x)=,∴函数f′(x)=,当x<,或x<t时,f′(x)>0,函数为增函数,当<x<t时,f′(x)<0,函数为减函数,故当x=时,函数f(x)取极大值,函数f(x)有两个零点0和t,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则方程f(x)﹣1=0和f(x)﹣1=t各有三个解,即函数f(x)的图象与y=1和y=t+1各有三个零点,由y|x=t==,故,=(t﹣3)(2t+3)2>0得:t>3,故不等式的解集为:t∈(3,4),故答案为:(3,4)二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).(1)求BC边上的中线所在直线的方程;(2)求BC边上的高所在直线的方程.【解答】解:(1)由B(10,4),C(2,﹣4),得BC中点D的坐标为(6,0),…(2分)所以AD的斜率为k==8,…(5分)所以BC边上的中线AD所在直线的方程为y﹣0=8(x﹣6),即8x﹣y﹣48=0.…(7分)(2)由B(10,4),C(2,﹣4),得BC所在直线的斜率为k==1,…(9分)所以BC边上的高所在直线的斜率为﹣1,…(12分)所以BC边上的高所在直线的方程为y﹣8=﹣1(x﹣7),即x+y﹣15=0.…(14分)16.(14分)已知数列{a n}满足a1=1,(a n﹣3)a n+1﹣a n+4=0(n∈N*).(1)求a2,a3,a4;(2)猜想{a n}的通项公式,并用数学归纳法证明.【解答】解:(1)令n=1,﹣2a2+3=0,a2=,令n=2,﹣a3﹣+4=0,a3=,令n=3,﹣a4﹣+4=0,a4=.(2)猜想a n=(n∈N*).证明:当n=1时,a1=1=,所以a n=成立,假设当n=k时,a n=成立,即a k=,则(a k﹣3)a k+1﹣a k+4=0,即(﹣3)a k+1﹣+4=0,所以a k+1=,即a k+1==,所以当n=k+1时,结论a n=成立.综上,对任意的n∈N*,a n=成立.17.(14分)在平面直角坐标系xOy中,已知圆M的圆心在直线y=﹣2x上,且圆M与直线x+y﹣1=0相切于点P(2,﹣1).(1)求圆M的方程;(2)过坐标原点O的直线l被圆M截得的弦长为,求直线l的方程.【解答】解:(1)过点(2,﹣1)且与直线x+y﹣1=0垂直的直线方程为x﹣y﹣3=0,…(2分)由解得,所以圆心M的坐标为(1,﹣2),…(4分)所以圆M的半径为r=,…(6分)所以圆M的方程为(x﹣1)2+(y+2)2=2.…(7分)(2)因为直线l被圆M截得的弦长为,所以圆心M到直线l的距离为d==,…(9分)若直线l的斜率不存在,则l为x=0,此时,圆心M到l的距离为1,不符合题意.若直线l的斜率存在,设直线l的方程为y=kx,即kx﹣y=0,由d==,…(11分)整理得k2+8k+7=0,解得k=﹣1或﹣7,…(13分)所以直线l的方程为x+y=0或7x+y=0.…(14分)18.(16分)某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF 和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.【解答】(本题满分16分)解:(1)作AH⊥CF于H,则OH=cosθ,AB=2OH=2cosθ,AH=sinθ,…(2分)则六边形的面积为f (θ)=2×(AB+CF)×AH=(2cosθ+2)sinθ=2(cosθ+1)sinθ,θ∈(0,).…(6分)(2)f′(θ)=2[﹣sinθsinθ+(cosθ+1)cosθ]=2(2cos2θ+cosθ﹣1)=2(2cosθ﹣1)(cosθ+1).…(10分)令f′(θ)=0,因为θ∈(0,),所以cosθ=,即θ=,…(12分)当θ∈(0,)时,f′(θ)>0,所以f (θ)在(0,)上单调递增;当θ∈(,)时,f′(θ)<0,所以f (θ)在(,)上单调递减,…(14分)所以当θ=时,f (θ)取最大值f ()=2(cos+1)sin=.…(15分)答:当θ=时,可使得六边形区域面积达到最大,最大面积为平方百米.…(16分)19.(16分)在平面直角坐标系xOy中,椭圆E:+=1(a>b>0)的离心率为,两个顶点分别为A(﹣a,0),B(a,0),点M(﹣1,0),且3=,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.(1)求椭圆E的方程;(2)若BC⊥CD,求k的值;(3)记直线AD,BC的斜率分别为k1,k2,求证:为定值.【解答】解:(1)因为3=,所以3(﹣1+a,0)=(a+1,0),解得a=2.…(2分)又因为=,所以c=,所以b2=a2﹣c2=1,所以椭圆E的方程为+y2=1.…(4分)(2)设点C的坐标为(x0,y0),y0>0,则=(﹣1﹣x0,﹣y0),=(2﹣x0,﹣y0).因为BC⊥CD,所以(﹣1﹣x0)(2﹣x0)+y02=0.①…(6分)又因为+y02=1,②联立①②,解得x0=﹣,y0=,…(8分)所以k==2.…(10分)(3),设C(x0,y0),则CD:y=(x+1)(﹣2<x0<2且x0≠﹣1),由消去y,得x2+8y02x+4y02﹣4(x0+1)2=0.…(12分)又因为+y02=1,所以得D(,),…(14分)所以===3,所以为定值.…(16分)20.(16分)已知函数f(x)=ax﹣lnx(a∈R).(1)当a=1时,求f(x)的最小值;(2)若存在x∈[1,3],使+lnx=2成立,求a的取值范围;(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,求a的取值范围.【解答】解:(1)f(x)=x﹣lnx(x>0)的导数为f′(x)=1﹣=,当x>1时,f′(x)>0,f(x)递增;当0<x<1时,f′(x)>0,f(x)递减.即有f(x)在x=1处取得极小值,也为最小值,且为1;(2)存在x∈[1,3],使+lnx=2成立,即为=2﹣lnx,即有a=,设g(x)=,x∈[1,3],则g′(x)=(1﹣lnx)(1+),当1<x<e时,g′(x)>0,g(x)递增;当e<x<3时,g′(x)<0,g(x)递减.则g(x)在x=e处取得极大值,且为最大值e+;g(1)=2,g(3)=3(2﹣ln3)+>2,则a的取值范围是[2,e+];(3)若对任意的x∈[1,+∞),有f(x)≥f()成立,即为ax﹣lnx≥﹣ln,即有a(x﹣)≥2lnx,x≥1,令F(x)=a(x﹣)﹣2lnx,x≥1,F′(x)=a(1+)﹣,当x=1时,原不等式显然成立;当x>1时,由题意可得F′(x)≥0在(1,+∞)恒成立,即有a(1+)﹣≥0,即a≥,由=<=1,则a≥1.综上可得a的取值范围是[1,+∞).。
江苏省南京市2018-2019学年高二上学期期末考试数学(理)(含答案)

南京市2018—2019学年度第一学期期末调研高二数学(理科)注意事项:1.本试卷共4页,包括填空题(第1题〜第14题)、解答题(第15题〜第20题)两部分。
本试卷满分为160分,考试时间为120分钟。
2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内,试题的答案写在答题卡上对应题目的答案空格内。
考试结束后,交回答题卡。
一、填空题:本大题共14小题,每题5分,共70分。
请把答案填写在答题卡相应位置上。
1.已知命题 2019.01p :∀x >0,e x ≥ex ,写出命题p 的否定:2▲.2.在平面直角坐标系xOy 中,抛物线y =2x 的准线方程为▲ .3.己知f (x )=e ⋅sin x ,则f '(0)的值为▲ .4.已知复数z 满足(z-2)i=l+i (i 为虚数单位),则z 的实部为▲ .x x 2+y 2=1上一点,若点P 到椭圆C 的右焦点的距离为2,则它到5.在平面直角坐标系xOy 中,P 是椭圆C:4椭圆C 的右准线的距离为▲。
⎧y ≤x -1,⎪6.已知实数x ,y 满足⎨x ≤3,,则z =x +2y 的最小值为⎪x +y ≥2,⎩22▲。
7.在平面直角坐标系xOy 中,“m >0”是“方程x +my =1表示椭圆”的条件。
(填“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”)8.在平面角坐标系xOy 中,双曲线的顶点到它的渐近线的距离为▲。
9.在平面角坐标系xOy 中,点A(4,0),点B(0,2),平面内点P 满足PA ⋅PB =15,则 PO 的最大值是▲。
x 2y 210.在平面直角坐标系xOy 中,点F 1,F 2分别是椭圆2+2=1 (a>b>0)的左、右焦点,过点F 2且与x 轴垂直a b 的直线与椭圆交于A ,B 两点。
若∠AF 1B 为锐角,则该椭圆的离心率的取值范围是▲ .11.在平面直角坐标系xOy 中,圆 C :(x -a )+(y -b )=1与圆 C :x +y -2x -3=0有公共点,则实2222数a 的取值范围是▲.12.如图,在正四棱锥P —ABCD 中,PA=AB ,点M 为的中点,BD =λBN ,若MN⊥AD,则实数λ=▲ .13.在平面直角坐标系xOy 中,圆M:(x -1)+y =1 ,点22A3,1),P 为抛物线上任意一点(异于原点),过点P 作圆M 的切线PB, B 为切点,则PA+PB 的最小值是▲ .14.已知函数f (x )=x -3a x -6a +4a (a>0)只有一个零点,且这个零点为正数,则头数a 的取值范围是▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
2017-2018学年江苏省南京市高二(上)期末数学试卷(理科)(解析版)
2017-2018学年江苏省南京市高二(上)期末数学试卷(理科)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1.(5分)命题“若ab=0,则b=0”的逆否命题是.2.(5分)已知复数z满足z(1+i)=i,其中i是虚数单位,则|z|为.3.(5分)在平面直角坐标系xOy中,抛物线y2=4x的焦点坐标是.4.(5分)“x2﹣3x+2<0”是“﹣1<x<2”成立的条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).5.(5分)已知实数x,y满足条件,则z=3x+y的最大值是.6.(5分)函数f(x)=xe x的单调减区间是.7.(5分)如图,直线l经过点(0,1),且与曲线y=f(x)相切于点(a,3).若f′(a)=,则实数a的值是.8.(5分)在平面直角坐标系xOy中,若圆(x﹣a)2+(y﹣a)2=2与圆x2+(y﹣6)2=8相外切,则实数a的值为.9.(5分)如图,在三棱锥P﹣ABC中,M是侧棱PC的中点,且=x+y+z,则x+y+z的值为.10.(5分)在平面直角坐标系xOy中,若双曲线﹣y2=1的渐近线与抛物线x2=4y 的准线相交于A,B两点,则三角形OAB的面积为.11.(5分)在平面直角坐标系xOy中,若点A到原点的距离为2,到直线x+y﹣2=0的距离为1,则满足条件的点A的个数为.12.(5分)若函数f(x)=x3﹣3x2+mx在区间(0,3)内有极值,则实数m的取值范围是.13.(5分)在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A,B两点,直线AF2与椭圆的另一个交点为C.若=2,则该椭圆的离心率为.14.(5分)已知函数f(x)=x|x2﹣3|.若存在实数m,m∈(0,],使得当x∈[0,m]时,f(x)的取值范围是[0,am],则实数a的取值范围是.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)已知复数z=,(m∈R,i是虚数单位).(1)若z是纯虚数,求m的值;(2)设是z的共轭复数,复数+2z在复平面上对应的点在第一象限,求m的取值范围.16.(14分)如图,在正方体ABCD﹣A1B1C1D1中,点E,F,G分别是棱BC,A1B1,B1C1的中点.(1)求异面直线EF与DG所成角的余弦值;(2)设二面角A﹣BD﹣G的大小为θ,求|cosθ|的值.17.(14分)如图,圆锥OO1的体积为π.设它的底面半径为x,侧面积为S.(1)试写出S关于x的函数关系式;(2)当圆锥底面半径x为多少时,圆锥的侧面积最小?18.(16分)在平面直角坐标系xOy中,已知圆C经过点A(1,3),B(4,2),且圆心在直线l:x﹣y﹣1=0上.(1)求圆C的方程;(2)设P是圆D:x2+y2+8x﹣2y+16=0上任意一点,过点P作圆C的两条切线PM,PN,M,N为切点,试求四边形PMCN面积S的最小值及对应的点P坐标.19.(16分)在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的一条准线方程为x=,离心率为.(1)求椭圆C的方程;(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.①设直线AM,AN的斜率分别是k1,k2,求k1k2的值;②过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.20.(16分)设函数f(x)=ax2﹣1﹣lnx,其中a∈R.(1)若a=0,求过点(0,﹣1)且与曲线y=f(x)相切的直线方程;(2)若函数f(x)有两个零点x1,x2,①求a的取值范围;②求证:f′(x1)+f′(x2)<0.2017-2018学年江苏省南京市高二(上)期末数学试卷(理科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1.【解答】解:根据原命题与逆否命题的关系,知:命题“若ab=0,则b=0”的逆否命题是“若b≠0,则ab≠0”.故答案为:若b≠0,则ab≠0.2.【解答】解:由z(1+i)=i,得z=,∴|z|=.故答案为:.3.【解答】解:抛物线y2=4x开口向右,p=2,所以抛物线的焦点坐标是(1,0).故答案为:(1,0).4.【解答】解:∵x2﹣3x+2<0⇔1<x<2,∵{x|1<x<2}⊊{x|﹣1<x<2},∴“x2﹣3x+2<0”是“﹣1<x<2”成立的充分不必要,故答案为:充分不必要.5.【解答】解:由题意,实数x,y满足条件表示一个三角形区域(包含边界),三角形的三个顶点的坐标分别为A(0,5),B(2,1),C(0,1)目标函数z=3x+y的几何意义是直线的纵截距由线性规划知识可得,在点(2,1)处取得最大值7.故答案为:76.【解答】解:函数f(x)=xe x,可得f′(x)=(1+x)e x,当f′(x)=(1+x)e x≤0,解得x≤﹣1,此时函数f(x)=xe x是单调减函数,函数的单调减区间(﹣∞,﹣1].故答案为:(﹣∞,﹣1].[或(﹣∞,﹣1)].7.【解答】解:直线l经过点(0,1),且与曲线y=f(x)相切于点(a,3).若f′(a)=,切线的斜率为,切线方程为:y﹣1=x,所以3﹣1=,解得a=3.故答案为:3.8.【解答】解:根据题意,圆(x﹣a)2+(y﹣a)2=2的圆心为(a,a),半径r1=,圆x2+(y﹣6)2=8的圆心为(0,6),半径r2=2,若圆(x﹣a)2+(y﹣a)2=2与圆x2+(y﹣6)2=8相外切,则有a2+(a﹣6)2=(+2)2,解可得:a=3;故答案为:3.9.【解答】解:∵M是侧棱PC的中点,∴=,又=,=.∴=()=﹣++,又=x+y+z,∴x=﹣1,y=z=.则x+y+z=0.故答案为:0.10.【解答】解:双曲线﹣y2=1的渐近线:x=y,抛物线x2=4y的准线y=﹣,双曲线﹣y2=1的渐近线与抛物线x2=4y的准线相交于A,B两点,所以A(3,﹣),(﹣3,﹣),则三角形OAB的面积为:=3.故答案为:3.11.【解答】解:如图,作出直线x+y﹣2=0,作出以原点为圆心,以2为半径的圆,∵原点O到直线x+y﹣2=0的距离为1,∴在直线x+y﹣2=0的右上方有一点满足到原点的距离为2,到直线x+y﹣2=0的距离为1,过原点作直线x+y﹣2=0的平行线,交圆于两点,则交点满足到原点的距离为2,到直线x+y﹣2=0的距离为1.∴到原点的距离为2,到直线x+y﹣2=0的距离为1的点A共3个.故答案为:3.12.【解答】解:∵函数f(x)=x3﹣3x2+mx.∴f′(x)=3x2﹣6x+m,若函数f(x)=x3﹣3x2+mx在区间(0,3)内有极值,则f′(x)=3x2﹣6x+m在区间(0,3)内有零点,导函数的对称轴为x=1,可得△=36﹣12m>0,解得m<3.并且f′(3)>0.即27﹣18+m>0.解得m∈(﹣9,3).故答案为:(﹣9,3).13.【解答】解:F1(﹣c,0),F2(c,0),直线AB的方程为x=﹣c,不妨设A在第二象限,把x=﹣c代入椭圆方程得A(﹣c,),过C作CD⊥x轴,垂足为D,则Rt△AF1F2∽Rt△CDF2,∴==,∴C(2c,﹣),代入椭圆方程得:+=1,即4e2+(1﹣e2)=1,解得e=.故答案为:.14.【解答】解:f(x)=x|x2﹣3|=,作出函数图象如图所示:根据题意知,m∈[0,],x∈[0,m],当m∈[0,1]时,f(x)在[0,m]上单调递增,此时f(x)的取值范围是[0,f(m)],所以f(m)=am,即m(3﹣m2)=am,得a=3﹣m2∈[[2,3);当m∈(1,2]时,此时f(x)的取值范围是[0,2],所以am=2,得a=∈[1,2),当m∈(2,]时,此时f(x)的取值范围是[0,f(m)],所以f(m)=am,即m(m2﹣3)=am,即a=m2﹣3∈(1,2],综上:实数a的取值范围是[1,3).故答案为:[1,3)二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.【解答】解:z==.(1)∵z是纯虚数,∴,即m=;(2)∵=(1﹣2m)﹣(1+2m)i,∴+2z=(1﹣2m)﹣(1+2m)i+2(1﹣2m)+2(1+2m)i=(3﹣6m)+(1+2m)i,由复数+2z在复平面上对应的点在第一象限,得,解得.∴m的取值范围是().16.【解答】(本题满分14分)解:如图,以{,,}为正交基底建立坐标系D﹣xyz.设正方体的边长为2,则D(0,0,0),A(2,0,0),B(2,2,0),E(1,2,0),F(2,1,2),G(1,2,2).(1)因为=(2,1,2)﹣(1,2,0)=(1,﹣1,2),=(1,2,2),…(2分)所以•=1×1+(﹣1)×2+2×2=3,||==,||=3.…(4分)从而cos<,>===,即向量与的夹角的余弦为,从而异面直线EF与DG所成角的余弦值为.…(7分)(2)=(2,2,0),=(1,2,2),设平面DBG的一个法向量为=(x,y,z).由题意,得,取x=2,可得y=﹣2,z=1.所以=(2,﹣2,1).…(11分)又平面ABD的一个法向量==(0,0,2),所以cos<,>===.因此|cosθ|=.…(14分)17.【解答】解:(1)设圆锥OO1的高为h,母线长为l.∵圆锥的体积为π,即πx2h=π,∴h=.因此l=,从而S=πxl=πx•=π,(x>0).(2)令f(x)=x4+,则f′(x)=4x3﹣,(x>0).由f′(x)=0,解得x=.当0<x<时,f′(x)<0,即函数f(x)在区间(0,)上单调递减;当x>时,f′(x)>0,即函数f(x)在区间(,+∞)上单调递增.∴当x=时,f(x)取得极小值也是最小值.答:当圆锥底面半径为时,圆锥的侧面积最小.18.【解答】解:(1)设圆C的方程为x2+y2+Dx+Ey+F=0,其圆心为(﹣,﹣).∵圆C经过点A(1,3),B(4,2),且圆心在直线l:x﹣y﹣1=0上,∴,解得.∴所求圆C的方程为x2+y2﹣4x﹣2y=0;(2)由(1)知,圆C的方程为(x﹣2)2+(y﹣1)2=5.依题意,S=2S△PMC=PM×MC=.∴当PC最小时,S最小.∵圆D:x2+y2+8x﹣2y+16=0,∴D(﹣4,1),半径为1.∵C(2,1),∴两个圆的圆心距DC=6.∵点P在圆D上,且圆D的半径为1,∴PC min=6﹣1=5.∴S min=×=10.此时直线PC:y=1,从而P(﹣3,1).19.【解答】解:(1)设椭圆C::+=1的半焦距为c.由题意,得解得从而b=1.所以椭圆C的方程为+y2=1.(2)①根据椭圆的性质,M,N两点关于x轴对称,故可设M(x0,y0),N(x0,﹣y0)(x0≠0,y0≠0),从而k1k2=•=.因为点M在椭圆C上,所以+y02=1,所以1﹣y02=,所以k1k2==.②设Q(x1,y1),依题意A(0,1).因为l1⊥AM,所以•=﹣1,即(y0﹣1)(y1﹣y0)=﹣x0(x1﹣x0);因为l2⊥AN,所以•=﹣1,即(﹣y0﹣1)(y1+y0)=﹣x0(x1﹣x0),故(y0﹣1)(y1﹣y0)﹣(﹣y0﹣1)(y1+y0)=0,化得(y1+1)y0=0.从而必有y1+1=0,即y1=﹣1.即点Q在一条定直线y=﹣1上.20.【解答】(本题满分16分)解(1)当a=0时,f(x)=﹣1﹣lnx,f′(x)=﹣.设切点为T(x0,﹣1﹣lnx0),则切线方程为:y+1+lnx0=﹣(x﹣x0).…(2分)因为切线过点(0,﹣1),所以﹣1+1+ln x0=﹣(0﹣x0),解得x0=e.所以所求切线方程为y=﹣x﹣1.…(4分)(2)①f′(x)=ax﹣=,x>0.(i)若a≤0,则f′(x)<0,所以函数f(x)在(0,+∞)上单调递减,从而函数f(x)在(0,+∞)上至多有1个零点,不合题意.…(5分)(ii)若a>0,由f′(x)=0,解得x=.当0<x<时,f′(x)<0,函数f(x)单调递减;当x>时,f′(x)>0,f(x)单调递增,所以f(x)min=f()=﹣ln﹣1=﹣﹣ln.要使函数f(x)有两个零点,首先﹣﹣ln<0,解得0<a<e.…(7分)当0<a<e时,>>.因为f()=>0,故f()•f()<0.又函数f(x)在(0,)上单调递减,且其图象在(0,)上不间断,所以函数f(x)在区间(0,)内恰有1个零点.…(9分)考察函数g(x)=x﹣1﹣lnx,则g′(x)=1﹣=.当x∈(0,1)时,g′(x)<0,函数g(x)在(0,1)上单调递减;当x∈(1,+∞)时,g′(x)>0,函数g(x)在(1,+∞)上单调递增,所以g(x)≥g(1)=0,故f()=﹣1﹣ln≥0.因为﹣=>0,故>.因为f()•f()≤0,且f(x)在(,+∞)上单调递增,其图象在(,+∞)上不间断,所以函数f(x)在区间(,]上恰有1个零点,即在(,+∞)上恰有1个零点.综上所述,a的取值范围是(0,e).…(11分)②由x1,x2是函数f(x)的两个零点(不妨设x1<x2),得两式相减,得a(x12﹣x22)﹣ln=0,即a(x1+x2)(x1﹣x2)﹣ln=0,所以a(x1+x2)=.…(13分)f′(x1)+f′(x2)<0等价于ax1﹣+ax2﹣<0,即a(x1+x2)﹣﹣<0,即:﹣﹣<0,即2ln+﹣>0.设h(x)=2lnx+﹣x,x∈(0,1).则h′(x)=﹣﹣1=﹣<0,所以函数h(x)在(0,1)单调递减,所以h(x)>h(1)=0.因为∈(0,1),所以2ln+﹣>0,即f′(x1)+f′(x2)<0成立.…(16分)。
2017—2018学年度第二学期期末考试高二数学理科(带答案

2017—2018学年度第二学期期末考试高二数学(理)试题一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合A={4,5,7,9},B={3,4,7,8,9},全集U A B =U ,则集合)(B A C U I 中的元素共有( ) A .3个 B. 4个C.5个D.6个2. 复数3223ii+=-( ) A.1 B.1-C.iD.i -3.已知)1,1(),2,(a n a m -=-=,且n m //,则a=( ) A .﹣1B .2或﹣1C .2D .﹣24. 在区间[]1,1-上随机选取一个实数x ,则事件"210"x -< 的概率为( )A .12B .34C .23D .145. 已知tan a =4,cot β=13,则tan(a+β)=( )A.711B.711-C. 713D.713-6.在6)2(y x -的展开式中,含24y x 的项的系数是( ) A .15 B .-15C .60D . -607.执行如图所示的程序框图,若输入的a 为2,则输出 的a 值是( )A. 2B. 1C.21D.1-8. 设非零向量a 、b 、c 满足c b a c b a =+==|,|||||,则>=<b a ,( ) A.150°B.120°C.60°D.30°9. 甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( ) A.150种B.180种C.300种D.345种10.下列四个结论中正确的个数是(1)对于命题,:0R x p ∈∃使得0120≤-x ,则,:R x p ∈∀⌝都有012>-x ; (2)已知),2(~2σN X ,则 (2)0.5P X >=(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为32ˆ-=x y; (4)“1≥x ”是“21≥+xx ”的充分不必要条件. A .1B .2C .3D .411.正方体1111ABCD A B C D -中,若1D AC △外接圆半径为26,则该正方体外接球的表面积为( ) A.2πB.8πC.12πD.16π12.已知奇函数()f x 的导函数为()f x ',当0x ≠时,()()0f x f x x'+>,若11(),()a f b ef e e e==--,()1c f =,则,,a b c 的大小关系正确的是( ) A .a b c << B .b c a << C .c a b << D .a c b <<二、填空题:本题共4小题,每小题5分,共20分。
南京市20172018学年度第一学期期末高二数学调研测试卷(2018年1月文科)

南京市2017-2018学年度第一学期期末调研测试卷高二数学(文科)注意事项:1.本试卷共3页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡. 参考公式:圆锥的体积公式:V =13πr 2h ,侧面积公式:S =πrl ,其中r ,h 和l 分别为圆锥的底面半径,高和母线长.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上.1.命题“若ab =0,则b =0”的逆否命题是 ▲ .2.已知复数z 满足 z (1+i)=i ,其中i 是虚数单位,则 |z | 为 ▲ . 3.在平面直角坐标系xOy 中,抛物线y 2=4x 的焦点坐标是 ▲ .4.“x 2-3x +2<0”是“-1<x <2”成立的 ▲ 条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).5.已知实数x ,y 满足条件 ⎩⎪⎨⎪⎧x ≥0,y ≥1,2x +y -5≤0,则z =3x +y 的最大值是 ▲ .6.函数 f (x )=x e x 的单调减区间是 ▲ .7.在平面直角坐标系xOy 中,直线x +2y =0与圆 (x -3)2+(y -1)2=25相交于A ,B 两点,则线段AB 的长为 ▲ .8.如图,直线l 经过点(0,1),且与曲线y =f (x ) 相切 于点(a ,3).若f ′(a )=23,则实数a 的值是 ▲ .9.在平面直角坐标系xOy 中,若圆 (x -a )2+(y -a )2=2 与圆 x 2+(y -6)2=8相外切,则实数a 的值为 ▲ .10.在平面直角坐标系xOy 中,若双曲线 x 23-y 2=1的渐近线与抛物线x 2=43y 的准线相交于A ,B 两点,则三角形OAB 的面积为 ▲ .11.若函数f (x )=x 3-3x 2+mx 在区间 (0,1) 内有极值,则实数m 的取值范围是 ▲ . 12.在平面直角坐标系xOy 中,若点A 到原点的距离为2,到直线 3x +y -2=0的距离为1,则满足条件的点A 的个数为 ▲ .13.在平面直角坐标系xOy 中,已知椭圆 x 2a 2+y 2b 2=1(a >b >0) 的左、右焦点分别为F 1,F 2,过F 1且与x 轴垂直的直线交椭圆于A ,B 两点,直线AF 2与椭圆的另一个交点为C . 若AF 2→=2F 2C →,则该椭圆的离心率为 ▲ .14.若对任意的x ∈[ 1e ,+∞),都有 12x 2-a ln x ≥0 成立,则实数a 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)已知复数z =2+4m i1-i ,(m ∈R ,i 是虚数单位).(1)若z 是纯虚数,求m 的值;(2)设—z 是z 的共轭复数,复数—z +2z 在复平面上对应的点在第一象限,求m 的取值范围.16.(本题满分14分)已知p :方程x 2+(m 2-6m )y 2=1表示双曲线,q :函数f (x )=13x 3-mx 2+(2m +3)x 在(-∞,+∞)上是单调增函数.(1)若p 是真命题,求实数m 的取值范围;(2)若p 或q 是真命题,p 且q 是假命题,求实数m 的取值范围.17.(本题满分14分)如图,圆锥OO 1的体积为6π.设它的底面半径为x ,侧面积为S .(1)试写出S 关于x 的函数关系式;(2)当圆锥底面半径x 为多少时,圆锥的侧面积最小?18.(本题满分16分)在平面直角坐标系xOy 中,已知圆C 经过点A (1,3) ,B (4,2),且圆心在 直线l :x -y -1=0上.(1)求圆C 的方程;(2)设P 是圆M :x 2+y 2+8x -2y +16=0上任意一点,过点P 作圆C 的两条切线PM ,PN ,M ,N 为切点,试求四边形PMCN 面积S 的最小值及对应的点P 坐标.19.(本题满分16分)在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一条准线方程为x =433,离心率为32. (1)求椭圆C 的方程;(2)如图,设A 为椭圆的上顶点,过点A 作两条直线AM ,AN ,分别与椭圆C 相交于M ,N 两点,且直线MN 垂直于x 轴.① 设直线AM ,AN 的斜率分别是k 1, k 2,求k 1k 2的值;② 过M 作直线l 1⊥AM ,过N 作直线l 2⊥AN ,l 1与l 2相交于点Q .试问:点Q是否O 1(第17题图)在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.20.(本题满分16分)设函数f (x )=12ax 2-1-ln x ,其中a ∈R .(1)若a =0,求过点(0,-1)且与曲线y =f (x )相切的直线方程; (2)①求证:当x ∈(0,+∞)时,ln x ≤x -1恒成立;②若函数f (x )有两个零点x 1,x 2,求a 的取值范围.南京市2017-2018学年度第一学期期末检测卷 高二数学(文科)参考答案 2018.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,共70分) 1.“若b ≠0,则ab ≠0” 2.223.(1,0) 4.充分不必要 5.7 6.(-∞,-1)或(-∞,-1] 7.4 5 8.3(第19题图)9.3 10.3 3 11.(0,3) 12.313.55 14.[-12e2,e] 二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15.(本题满分14分)解(1)z =2+4m i 1-i =(2+4m i)(1+i)(1-i)(1+i)=1-2m +(2m +1)i . …………………… 3分 因为z 是纯虚数,所以1-2m =0且2m +1≠0,解得m =12. …………………… 6分(2)因为—z 是z 的共轭复数,所以—z =1-2m -(2m +1)i . ……………………8分所以—z +2z =1-2m -(2m +1)i +2[1-2m +(2m +1)i]=3-6m +(2m +1)i . …………………… 10分因为复数—z +2z 在复平面上对应的点在第一象限,所以⎩⎨⎧3-6m >0,2m +1>0,…………………… 12分解得-12<m <12,即实数m 的取值范围为(-12,12). …………………… 14分16.(本题满分14分)解(1)由题意知,曲线C :x 2+(m 2-6m )y 2=1是双曲线,所以 m 2-6m <0. …………………… 3分 解得0<m <6,即m 的取值范围为(0,6). …………………… 5分 (2)由函数f (x )=13x 3-mx 2+(2m +3)x 是单调增函数,可知f ′(x )=x 2-2mx +m +3≥0恒成立.故△=(-2m )2-4(2m +3)≤0,解得-1≤m ≤3. …………………… 8分 因为p 或q 是真命题,p 且q 是假命题,所以p 真q 假或者p 假q 真. …………………… 11分因此 ⎩⎨⎧0<m <6,m <-1或m >3;或者⎩⎨⎧m ≤0或m ≥6,-1≤m ≤3.故m 的取值范围是[-1,0]∪(3,6). …………………… 14分17.(本题满分14分)解(1)设圆锥OO 1的高为h ,母线长为l .因为圆锥的体积为6π,即 13πx 2h =6π,所以h =36x2.…………………… 2分因此 l =x 2+h 2=x 2+(36x2)2,从而S =πxl =πxx 2+(36x 2)2=πx 4+54x2,(x >0). …………………… 6分(2)令f (x )=x 4+54x 2,则f ′(x )=4x 3-108x3 ,(x >0). …………………… 8分由f ′(x )=0,解得x =3. …………………… 10分当0<x <3时,f ′(x )<0,即函数f (x )在区间(0,3)上单调递减;当x >3时,f ′(x )>0,即函数f (x )在区间(3,+∞)上单调递增.…………………… 12分所以当x =3时,f (x )取得极小值也是最小值.答:当圆锥底面半径为3时,圆锥的侧面积最小. ……………………… 14分18.(本题满分16分)解(1)设圆C 的方程为x 2+y 2+Dx +Ey +F =0,其圆心为(-D 2,-E2).因为圆C 经过点A (1,3) ,B (4,2),且圆心在直线l :x -y -1=0上, 所以 ⎩⎨⎧1+9+D +3E +F =0,16+4+4D +2E +F =0,-D 2+E2-1=0,…………………… 4分解得⎩⎪⎨⎪⎧D =-4,E =-2,F =0.所求圆C 的方程为x 2+y 2-4x -2y =0. …………………… 7分 (2)由(1)知,圆C 的方程为(x -2)2+(y -1)2=5.依题意,S =2S △PMC =PM ×MC = PC 2-5×5.所以当PC 最小时,S 最小. …………………… 10分 因为圆M :x 2+y 2+8x -2y +16=0,所以M (-4,1),半径为1. 因为C (2,1),所以两个圆的圆心距MC =6. 因为点P ∈M ,且圆M 的半径为1,所以PC min =6-1=5.所以S min =52-5×5=10. …………………… 14分此时直线MC :y =1,从而P (-3,1). …………………… 16分19.(本题满分16分)解(1)设椭圆C :x 2a 2+y 2b2=1的半焦距为c .由题意,得⎩⎨⎧a 2c =433,c a =32, 解得⎩⎨⎧a =2,c =3,从而b =1.所以椭圆C 的方程为x 24+y 2=1. …………………… 4分(2)①根据椭圆的性质,M ,N 两点关于x 轴对称,故可设M (x 0,y 0),N (x 0,-y 0)( x 0≠0,y 0≠0),从而 k 1k 2=y 0-1x 0·-y 0-1x 0=1-y 02x 02. …………………… 7分因为点M 在椭圆C 上,所以x 024+y 02=1,所以1-y 02=x 024,所以k 1k 2=1-y 02x 02=14. …………………… 10分②设Q (x 1,y 1),依题意A (0,1). 因为l 1⊥AM ,所以y 0-1x 0·y 1-y 0x 1-x 0=-1,即(y 0-1)(y 1-y 0)=-x 0 (x 1-x 0); 因为l 2⊥AN ,所以-y 0-1x 0·y 1+y 0x 1-x 0=-1,即(-y 0-1)(y 1+y 0)=-x 0 (x 1-x 0),故 (y 0-1)(y 1-y 0)-(-y 0-1)(y 1+y 0)=0,化得(y 1+1) y 0=0. …………………… 14分 从而必有y 1+1=0,即y 1=-1.即点Q 在一条定直线y =-1上. …………………… 16分20.(本题满分16分)解(1)当a =0时,f (x )=-1-ln x ,f ′(x )=-1x.设切点为T (x 0,-1-ln x 0),则切线方程为:y +1+ln x 0=-1x 0( x -x 0). …………………… 3分因为切线过点(0,-1),所以 -1+1+ln x 0=-1x 0(0-x 0),解得x 0=e .所以所求切线方程为y =-1e x -1. …………………… 5分(2)①考察函数g (x )=x -1-ln x .g′(x )=1-1x =x -1x.当x ∈(0,1)时,g′(x )<0,函数g (x )在(0,1)上单调递减; 当x ∈(1,+∞)时,g′(x )>0,函数g (x )在(1,+∞)上单调递增,所以g (x )≥g (1)=0,即当x ∈(0,+∞)时,ln x ≤x -1恒成立.……………… 8分 ② f ′(x )=ax -1x =ax 2-1x,x >0.(i) 若a ≤0,则f ′(x )<0,所以函数f (x )在(0,+∞)上单调递减,从而函数f (x )在(0,+∞)上至多有1个零点,不合题意. …………………… 10分 (ii)若a >0,由f ′(x )=0,解得x =1a. 当0<x <1a 时, f ′(x )<0,函数f (x )单调递减;当x >1a时, f ′(x )>0,f (x )单调递增, 所以f (x )min =f (1a )=12-ln 1a -1=-12-ln 1a.要使函数f (x )有两个零点,首先 -12-ln 1a <0,解得0<a <e . …………… 12分当0<a <e 时,1a >1e >1e. 因为f (1e )=a 2e 2>0,故f (1e )·f (1a )<0.又函数f (x )在(0,1a )上单调递减,且其图像在(0,1a)上不间断, 所以函数f (x )在区间(0,1a)内恰有1个零点. …………………… 14分 因为ln x ≤x -1,故f (2a )=2a -1-ln 2a≥0.因为2a -1a =2-a a >0,故2a >1a .因为f (1a )·f (2a )≤0,且f (x )在(1a ,+∞)上单调递增,其图像在(1a,+∞)上不间断,所以函数f (x )在区间(1a ,2a ] 上恰有1个零点,即在(1a,+∞)上恰有1个零点. 综上所述,a 的取值范围是(0,e). …………………… 16分。
【配套K12】江苏省南京市2017-2018学年高二数学上学期期末考试试题 理(含解析)

江苏省南京市2017-2018学年高二数学上学期期末考试试题理一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上.1. 命题“若ab=0,则b=0”的逆否命题是______.【答案】“若b≠0,则ab≠0”【解析】因为一个命题的逆否命题,是将原命题逆命题的条件与结论同时否定得到,所以命题“若ab=0,则b=0”的逆否命题是“若b≠0,则ab≠0”.故答案为:“若b≠0,则ab≠0”.2. 已知复数z满足z(1+i)=i,其中i是虚数单位,则 |z| 为______.【答案】【解析】复数z满足z(1+i)=i,所以.所以.故答案为:.3. 在平面直角坐标系xOy中,抛物线y2=4x的焦点坐标是______.【答案】(1,0)【解析】抛物线y2=4x,满足y2=2p x,其中p=2.所以抛物线y2=4x的焦点坐标是(1,0).故答案为:(1,0).4. “x2-3x+2<0”是“-1<x<2”成立的______条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).【答案】充分不必要【解析】由x2-3x+2<0,解得1<x<2,因为1<x<2是“-1<x<2”成立的充分不必要条件,所以“x2-3x+2<0”是“-1<x<2”成立的充分不必要条件.故答案为:充分不必要.5. 已知实数x,y满足条件则z=3x+y 的最大值是______.【答案】7【解析】作出不等式的可行域如图所示:作直线经过点A(2,1)时,z取最大值7.故答案为:7.点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.6. 函数f(x)=x e x 的单调减区间是______.【答案】(-∞,-1)或(-∞,-1]【解析】函数f(x)=x e x,求导得:.令,解得.所以函数f(x)=x e x 的单调减区间是(-∞,-1)( (-∞,-1]也可以).故答案为: (-∞,-1)或(-∞,-1].7. 如图,直线l经过点(0,1),且与曲线y=f(x) 相切于点(a,3).若f ′(a)=,则实数a的值是______.【解析】由导数的几何意义知f ′(a)=,即为切线斜率为.所以,解得.故答案为:3.8. 在平面直角坐标系xOy中,若圆 (x-a)2+(y-a)2=2 与圆x2+(y-6)2=8相外切,则实数a的值为______.【答案】3【解析】圆 (x-a)2+(y-a)2=2 与圆x2+(y-6)2=8相外切,则圆心距等于半径之和,即,解得.故答案为:3.点睛:这个题目考查的是两圆的位置关系;两圆的位置关系有相交,外切,内切,内含,外离这几种情况。
南京市数学高二上学期理数期末考试试卷A卷

南京市数学高二上学期理数期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)设集合,, 则A∩B=()A .B .C .D .2. (2分) (2018高二上·榆林期末) 曲线在处的切线的倾斜角是()A . -135°B . -45°C . 45°D . 135°3. (2分)已知双曲线C: =1(a>0,b>0)的离心率为,则C的渐近线方程为()A . y=± xB . y=± xC . y=± xD . y=±x4. (2分)向量(b.c)a-(a.c)b与向量c ()A . 一定平行但不相等B . 一定垂直C . 一定平行且相等D . 无法判定5. (2分) (2019高二上·郑州期中) 的内角,,的对边分别为,,,已知,,,则()A .B . 3C .D .6. (2分) (2016高二上·长沙开学考) 设{an}是等差数列,下列结论中正确的是()A . 若a1+a2>0,则a2+a3>0B . 若a1+a3<0,则a1+a2<0C . 若0<a1<a2 ,则a2D . 若a1<0,则(a2﹣a1)(a2﹣a3)>07. (2分)以下四个命题中,其中正确的个数为()①命题“若x2-3x+2=0,则x=1”的逆否命题为“若,则x2-3x+2=0”;②“”是“”的充分不必要条件;③若命题,则;④若为假,为真,则p,q有且仅有一个是真命题.A . 1B . 2C . 3D . 48. (2分) (2019高二上·兴宁期中) 如图,正方体中,两条异面直线与所成的角是()A .B .C .D .9. (2分) (2018高二上·双鸭山月考) 点为圆上的一个动点,点为线段的中点,则点的轨迹方程为()A .B .C .D .10. (2分) (2017高二上·湖南月考) 由不等式组确定的平面区域为,由不等式组确定的平面区域为,在内随机的取一点,则点落在区域内的概率为()A .B .C .D .11. (2分) (2017高一下·景德镇期末) 已知F1 , F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且|PF1|>|PF2|,椭圆的离心率为e1 ,双曲线的离心率为e2 ,若|PF2|=|F1F2|,则 + 的最小值为()A . 6+2B . 8C . 6+2D . 612. (2分)对于函数f(x)=x3﹣3x2 ,给出命题:①f(x)是增函数,无极值;②f(x)是减函数,无极值;③f(x)的递增区间为(﹣∞,0),(2,+∞),递减区间为(0,2);④f(0)=0是极大值,f(2)=﹣4是极小值.其中正确的命题有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共4题;共4分)13. (1分) (2016高一上·青浦期中) 已知a,b∈R,则“a>1,b>1”是“a+b>2”的________条件.14. (1分)(2018·成都模拟) 已知数列,若,则数列的前项和为________.15. (1分) (2019高二上·温州期中) 已知,记函数在的最大值为3,则实数的取值范围是________.16. (1分) (2016高二上·宝应期中) 短轴长为,离心率的椭圆两焦点为F1 , F2 ,过F1作直线交椭圆于A、B两点,则△ABF2的周长为________.三、解答题 (共6题;共60分)17. (10分) (2015高三上·房山期末) 在△ABC中,角A,B,C的对边分别为a,b,c,且a<b<c,.(1)求B的大小;(2)若a=2,,求c的值.18. (10分) (2018高二上·宁阳期中) 已知数列满足,.(1)求证:数列是等比数列;(2)求数列的通项公式和前项和.19. (10分) (2016高二上·黑龙江期中) 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC 的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′,连接EF,A′B.(1)求证:A′D⊥EF;(2)求二面角A′﹣EF﹣D的余弦值.20. (15分) (2015高二下·三门峡期中) 某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2﹣10x3(单位:万元),成本函数为C(x)=460x+5 000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)﹣f(x).(1)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值﹣成本)(2)问年造船量安排多少艘时,可使公司造船的年利润最大?(3)求边际利润函数MP(x)的单调递减区间,并说明单调递减在本题中的实际意义是什么?21. (10分) (2017高二上·如东月考) 已知椭圆:的左焦点为,离心率 .(1)求椭圆的标准方程;(2)已知直线交椭圆于,两点.(i)若直线经过椭圆的左焦点,交轴于点,且满足, .求证:为定值;(ii)若(为原点),求面积的取值范围.22. (5分)(2017·林芝模拟) 设函数f(x)=lnx+m(x2﹣x),m∈R.(Ⅰ)当m=﹣1时,求函数f(x)的最值;(Ⅱ)若函数f(x)有极值点,求m的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、20-3、21-1、21-2、22-1、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京市2017-2018学年度第一学期期末调研测试卷高二数学(理科) 2018.01注意事项:1.本试卷共3页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内.试题的答案写在答题卡...上对应题目的答案空格内.考试结束后,交回答题卡. 参考公式:圆锥的体积公式:V =13πr 2h ,侧面积公式:S =πrl ,其中r ,h 和l 分别为圆锥的底面半径,高和母线长.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上.1.命题“若ab =0,则b =0”的逆否命题是 ▲ .2.已知复数z 满足 z (1+i)=i ,其中i 是虚数单位,则 |z | 为 ▲ . 3.在平面直角坐标系xOy 中,抛物线y 2=4x 的焦点坐标是 ▲ .4.“x 2-3x +2<0”是“-1<x <2”成立的 ▲ 条件(在“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”中选一个填写).5.已知实数x ,y 满足条件 ⎩⎪⎨⎪⎧x ≥0,y ≥1,2x +y -5≤0,则z =3x +y 的最大值是 ▲ .6.函数 f (x )=x e x的单调减区间是 ▲ . 7.如图,直线l 经过点(0,1),且与曲线y =f (x ) 相切 于点(a ,3).若f ′(a )=23,则实数a 的值是 ▲ .8.在平面直角坐标系xOy 中,若圆 (x -a )2+(y -a )2=2 与圆 x 2+(y -6)2=8相外切,则实数a 的值为 ▲ .9.如图,在三棱锥P —ABC 中, M 是侧棱PC 的中点,且BM →=x AB →+y AC →+z AP →,则x +y +z 的值为 ▲ .10.在平面直角坐标系xOy 中,若双曲线 x 23-y 2=1的渐近线与 抛物线x 2=43y 的准线相交于A ,B 两点,则三角形OAB的面积为 ▲ .11.在平面直角坐标系xOy 中,若点A 到原点的距离为2,到直线3x +y -2=0的距离为1,则满足条件的点A 的个数为 ▲ .12.若函数f (x )=x 3-3x 2+mx 在区间 (0,3) 内有极值,则实数m 的取值范围是 ▲ . 13.在平面直角坐标系xOy 中,已知椭圆 x 2a 2+y 2b 2=1(a >b >0) 的左、右焦点分别为F 1,F 2,过F 1且与x 轴垂直的直线交椭圆于A ,B 两点,直线AF 2与椭圆的另一个交点为C . 若AF 2→=2F 2C →,则该椭圆的离心率为 ▲ .14.已知函数f (x )=x |x 2-3|.若存在实数m ,m ∈(0,5],使得当x ∈[0,m ] 时,f (x )的取值范围是[0,am ],则实数a 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)已知复数z =2+4m i1-i ,(m ∈R ,i 是虚数单位).(1)若z 是纯虚数,求m 的值;(2)设—z 是z 的共轭复数,复数—z +2z 在复平面上对应的点在第一象限,求m 的取值范围.16.(本题满分14分)如图,在正方体ABCD – A 1B 1C 1D 1中,点E ,F ,G 分别是棱BC ,A 1B 1,B 1C 1的中点. (1)求异面直线EF 与DG 所成角的余弦值; (2)设二面角A —BD —G 的大小为θ,B 1D CA 1C 1D 1FG求 |cos θ| 的值.17.(本题满分14分)如图,圆锥OO 1的体积为6π.设它的底面半径为x ,侧面积为S . (1)试写出S 关于x 的函数关系式;(2)当圆锥底面半径x 为多少时,圆锥的侧面积最小?18.(本题满分16分)在平面直角坐标系xOy 中,已知圆C 经过点A (1,3) ,B (4,2),且圆心在 直线l :x -y -1=0上.(1)求圆C 的方程;(2)设P 是圆D :x 2+y 2+8x -2y +16=0上任意一点,过点P 作圆C 的两条切线PM ,PN ,M ,N 为切点,试求四边形PMCN 面积S 的最小值及对应的点P 坐标.19.(本题满分16分)在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一条准线方程为x =433,离心率为32.(1)求椭圆C 的方程;(2)如图,设A 为椭圆的上顶点,过点A 作两条直线AM ,AN ,分别与椭圆C 相交于M ,N 两点,且直线MN 垂直于x 轴.① 设直线AM ,AN 的斜率分别是k 1, k 2,求k 1k 2的值;O 1(第17题图)② 过M 作直线l 1⊥AM ,过N 作直线l 2⊥AN ,l 1与l 2相交于点Q .试问:点Q 是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.20.(本题满分16分)设函数f (x )=12ax 2-1-ln x ,其中a ∈R .(1)若a =0,求过点(0,-1)且与曲线y =f (x )相切的直线方程; (2)若函数f (x )有两个零点x 1,x 2, ① 求a 的取值范围;② 求证:f ′(x 1)+f ′(x 2)<0.南京市2017-2018学年度第一学期期末检测卷 高二数学(理科)参考答案 2018.01说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,共70分)(第19题图)1.“若b ≠0,则ab ≠0” 2.223.(1,0) 4.充分不必要 5.7 6.(-∞,-1)或(-∞,-1] 7.3 8.3 9.0 10.3 3 11.3 12.(-9,3) 13.5514.[1,3) 二、解答题(本大题共6小题,共90分)15.(本题满分14分)解(1)z =2+4m i 1-i =(2+4m i)(1+i)(1-i)(1+i)=1-2m +(2m +1)i . …………………… 3分 因为z 是纯虚数,所以1-2m =0且2m +1≠0,解得m =12. …………………… 6分(2)因为—z 是z 的共轭复数,所以—z =1-2m -(2m +1)i . ……………………8分所以—z +2z =1-2m -(2m +1)i +2[1-2m +(2m +1)i]=3-6m +(2m +1)i . …………………… 10分因为复数—z +2z 在复平面上对应的点在第一象限,所以⎩⎨⎧3-6m >0,2m +1>0,…………………… 12分解得-12<m <12,即实数m 的取值范围为(-12,12). …………………… 14分16.(本题满分14分)解 如图,以{DA →,DC →,DD 1→}为正交基底建立坐标系D —xyz .设正方体的边长为2,则D (0,0,0),A (2,0,0), B (2,2,0),E (1,2,0),F (2,1,2),G (1,2,2)(1)因为EF →=(2,1,2)-(1,2,0)=(1,-1,2), DG →= (1,2,2), …………………… 2分 所以EF →·DG →=1×1+(-1)×2+2×2=3,|EF →|=1+(-1)2+22=6,|DG →|=3.…………………… 4分(第16题图)从而cos <EF →,DG →>=EF →·DG →|EF →||DG →|=36×3=66,即向量EF →与DG →的夹角的余弦为66,从而异面直线EF 与DG 所成角的余弦值为66. …………………… 7分 (2)DB →=(2,2,0),DG →= (1,2,2).设平面DBG 的一个法向量为n 1=(x ,y ,z ).由题意,得 ⎩⎪⎨⎪⎧DB →·n 1=2x +2y =0,DG →·n 1=x +2y +2z =0,取x =2,可得y =-2,z =1.所以n 1=(2,-2,1). …………………… 11分 又平面ABD 的一个法向量n 2=DD 1→=(0,0,2), 所以cos <n 1,n 2>=n 1·n 2|n 1||n 2|=23×2=13.因此 |cos θ|=13. …………………… 14分17.(本题满分14分)解(1)设圆锥OO 1的高为h ,母线长为l .因为圆锥的体积为6π,即 13πx 2h =6π,所以h =36x2.…………………… 2分因此 l =x 2+h 2=x 2+(36x2)2,从而S =πxl =πxx 2+(36x2)2=πx 4+54x2,(x >0). …………………… 6分(2)令f (x )=x 4+54x 2,则f ′(x )=4x 3-108x3 ,(x >0). …………………… 8分由f ′(x )=0,解得x =3. …………………… 10分当0<x <3时,f ′(x )<0,即函数f (x )在区间(0,3)上单调递减;当x >3时,f ′(x )>0,即函数f (x )在区间(3,+∞)上单调递增.…………………… 12分所以当x =3时,f (x )取得极小值也是最小值.答:当圆锥底面半径为3时,圆锥的侧面积最小. ……………………… 14分18.(本题满分16分)解(1)设圆C 的方程为x 2+y 2+Dx +Ey +F =0,其圆心为(-D 2,-E 2).因为圆C 经过点A (1,3) ,B (4,2),且圆心在直线l :x -y -1=0上,所以 ⎩⎨⎧1+9+D +3E +F =0,16+4+4D +2E +F =0,-D 2+E2-1=0,…………………… 4分解得⎩⎪⎨⎪⎧D =-4,E =-2,F =0.所求圆C 的方程为x 2+y 2-4x -2y =0. …………………… 7分 (2)由(1)知,圆C 的方程为(x -2)2+(y -1)2=5.依题意,S =2S △PMC =PM ×MC = PC 2-5×5.所以当PC 最小时,S 最小. …………………… 10分 因为圆M :x 2+y 2+8x -2y +16=0,所以M (-4,1),半径为1. 因为C (2,1),所以两个圆的圆心距MC =6. 因为点P ∈M ,且圆M 的半径为1, 所以PC min =6-1=5.所以S min =52-5×5=10. …………………… 14分此时直线MC :y =1,从而P (-3,1). …………………… 16分19.(本题满分16分)解(1)设椭圆C :x 2a 2+y 2b2=1的半焦距为c .由题意,得⎩⎨⎧a 2c =433,c a =32, 解得⎩⎨⎧a =2,c =3,从而b =1.所以椭圆C 的方程为x 24+y 2=1. …………………… 4分(2)①根据椭圆的性质,M ,N 两点关于x 轴对称,故可设M (x 0,y 0),N (x 0,-y 0)( x 0≠0,y 0≠0),从而 k 1k 2=y 0-1x 0·-y 0-1x 0=1-y 02x 02. …………………… 7分因为点M 在椭圆C 上,所以x 024+y 02=1,所以1-y 02=x 024,所以k 1k 2=1-y 02x 02=14. …………………… 10分②设Q (x 1,y 1),依题意A (0,1). 因为l 1⊥AM ,所以y 0-1x 0·y 1-y 0x 1-x 0=-1,即(y 0-1)(y 1-y 0)=-x 0 (x 1-x 0); 因为l 2⊥AN ,所以-y 0-1x 0·y 1+y 0x 1-x 0=-1,即(-y 0-1)(y 1+y 0)=-x 0 (x 1-x 0),故 (y 0-1)(y 1-y 0)-(-y 0-1)(y 1+y 0)=0,化得(y 1+1) y 0=0. …………………… 14分 从而必有y 1+1=0,即y 1=-1.即点Q 在一条定直线y =-1上. …………………… 16分20.(本题满分16分)解(1)当a =0时,f (x )=-1-ln x ,f ′(x )=-1x.设切点为T (x 0,-1-ln x 0),则切线方程为:y +1+ln x 0=-1x 0( x -x 0). …………………… 2分因为切线过点(0,-1),所以 -1+1+ln x 0=-1x 0(0-x 0),解得x 0=e .所以所求切线方程为y =-1ex -1. …………………… 4分(2)① f ′(x )=ax -1x =ax 2-1x,x >0.(i) 若a ≤0,则f ′(x )<0,所以函数f (x )在(0,+∞)上单调递减,从而函数f (x )在(0,+∞)上至多有1个零点,不合题意. …………………… 5分 (ii)若a >0,由f ′(x )=0,解得x =1a. 当0<x <1a 时, f ′(x )<0,函数f (x )单调递减;当x >1a时, f ′(x )>0,f (x )单调递增, 所以f (x )min =f (1a )=12-ln 1a -1=-12-ln 1a.要使函数f (x )有两个零点,首先 -12-ln 1a<0,解得0<a <e . …………… 7分当0<a <e 时,1a >1e >1e. 因为f (1e )=a 2e 2>0,故f (1e )·f (1a )<0.又函数f (x )在(0,1a )上单调递减,且其图像在(0,1a)上不间断, 所以函数f (x )在区间(0,1a)内恰有1个零点. …………………… 9分 考察函数g (x )=x -1-ln x ,则g′(x )=1-1x =x -1x .当x ∈(0,1)时,g′(x )<0,函数g (x )在(0,1)上单调递减; 当x ∈(1,+∞)时,g′(x )>0,函数g (x )在(1,+∞)上单调递增, 所以g (x )≥g (1)=0,故f (2a )=2a -1-ln 2a≥0.因为2a -1a =2-a a >0,故2a >1a .因为f (1a )·f (2a )≤0,且f (x )在(1a ,+∞)上单调递增,其图像在(1a,+∞)上不间断,所以函数f (x )在区间(1a ,2a ] 上恰有1个零点,即在(1a,+∞)上恰有1个零点. 综上所述,a 的取值范围是(0,e). …………………… 11分②由x 1,x 2是函数f (x )的两个零点(不妨设x 1<x 2),得 ⎩⎨⎧12ax 12-1-ln x 1=0,12ax 22-1-ln x 2=0, 两式相减,得 12a (x 12-x 22)-ln x 1x 2=0,即12a (x 1+x 2) (x 1-x 2)-ln x 1x 2=0,所以a (x 1+x 2)=2ln x 1x 2x 1-x 2. …………………… 13分f ′(x 1)+f ′(x 2)<0等价于ax 1-1x 1+ax 2-1x 2<0,即a (x 1+x 2)-1x 1-1x 2<0,即2ln x 1x 2 x 1-x 2-1x 1-1x 2<0,即2ln x 1x 2+x 2x 1-x 1x 2>0.设h (x )=2ln x +1x -x ,x ∈(0,1).则h′(x )=2x -1x 2-1=2x -1-x 2x 2=-(x -1)2x 2<0,所以函数h (x )在(0,1)单调递减,所以h (x )>h (1)=0. 因为x 1x 2∈(0,1),所以2ln x 1x 2+x 2x 1-x 1x 2>0,即f ′(x 1)+f ′(x 2)<0成立. …………………… 16分。
