题课一
工程流体力学习题课1-第2-3-4章-部分习题解答

2 2 d2
习题3-14解题示意图1
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
Fx1 =
y x
H1
D
H2
图 3-26 习题 3-11 附图
1 1 ρ gH1 × ( DL) = × 1000 × 9.8 × 4 × (4 × 10) = 784000 N=784kN 2 2 1 D 1 4 Fx 2 = ρ gH 2 × ( L) = × 1000 × 9.8 × 2 × × 10 = 196000 N=196kN 2 2 2 2
H
h
由此得: H ≥ 122mm + h ≥ 244mm (2) 结合以上正负压操作时结果有:
p / ρ g ≤ h ≤ H − | p| / ρ g
图 3-23 习题 3-8 附图
→ 122mm ≤ h ≤ 178mm
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
F1-6
习题 3-8 旋风除尘器如图 3-23 所示,其下端出灰口管段长 H,部分插入 水中,使旋风除尘器内部与外界大气隔开,称为水封;同时要求出灰管内液面 不得高于出灰管上部法兰位置。设除尘器内操作压力 ( 表 压 ) p = −1.2 kPa~ 1.2kPa。 净化空气 (1) 试问管段长 H 至少为多少 mm? (2) 若H=300mm,问其中插入水中的部分h应在 什么范围?(取水的密度 ρ =1000kg/m3) 含尘 解:(1) 正压操作时,出灰管内液面低于管外液 面,高差为 h′ = p / ρ g ;为实现水封,出灰管插入深 度 h 必须大于此高差,即
一题一课的教学模式

一题一课的教学模式简介一题一课的教学模式是一种针对学生个体特点的个性化教学方法。
它以学生的个别问题为起点,通过解析和解答一题一课的方式进行教学,从而让学生更深入地理解和掌握知识点。
这种教学模式注重对学生个体差异的关注和尊重,能够提升学生学习的效果和兴趣。
教学过程一题一课的教学模式可以通过以下几个步骤进行:1. 问题提出教师根据学生的学习情况和个体差异,选取一个适当的问题进行提出。
问题可以是与当前教学内容相关的,也可以是与学生生活经验和兴趣相关的,以激发学生的思考和兴趣。
2. 学生思考学生针对所提出的问题进行思考和回答。
学生可以自主思考,也可以与同伴一起合作探讨,激发彼此的思维。
学生可以提出各自的观点和答案,并进行讨论和辩论。
3. 教师解析教师通过对学生答案和观点的解析,引导学生思考,纠正错误观点,提供正确的知识和信息。
教师可以通过多种方式解析问题,例如通过实例、图表、实验等方式,帮助学生更加深入地理解和掌握知识点。
4. 学生练习教师提供相关的练习题或活动,让学生在解答问题的基础上进行深入练习。
学生可以通过练习巩固和应用所学知识,提高解决问题的能力。
5. 反馈与总结教师对学生的练习答案进行评价和反馈,指导学生进一步提升。
教师可以提出问题的其他解法或扩展问题,激发学生思考的深度和广度。
同时,教师还可以对本节课的内容进行总结,并引导学生从中得出经验和教训。
教学优势一题一课的教学模式具有以下几个优势:1. 个性化教学模式针对学生个体差异,注重对学生的差异化关注和教育。
每个学生都能得到针对自己问题的解答和指导,从而提高学习效果。
2. 激发兴趣通过提出有趣的问题,激发学生的思考和兴趣。
学生在思考和解答问题的过程中,能够主动参与和积极思考,提高学习的主动性。
3. 深入理解通过解析和讨论问题,学生能够深入地理解和掌握知识点。
学生通过自主思考和解答问题,能够更好地理解和应用知识,提高学习的深度。
4. 提高解决问题能力通过一题一课的教学模式,学生能够提高解决问题的能力。
09-习题课(一)

计算
f ( x ) ∗ h( x )
y
并作图
y
y
-3
-2
-1
1
2
3
x
-3
-2
-1
0
1
2
3
x
X-3
-3
-2
x X+1
-1 0
1
2
3
x
第一步
翻 转
第二步 平 移
17
第三步 乘 积
习 题 一 解 答
y y
求面积) 第四步 积 分(求面积)
y
?
X-3
f(x)*h(x)
3 2 1
-3
-2
-1
1
2
3
4
5
6
x
19
傅里叶光学
习 题 一 解 答
x x − a / 2 1 x 1.7 求证: rect + rect . 求证: ∗ comb = 1 b a − b a a
分析
0<x<a
y
x a2 − x2 1 1 f ( x ) Λh ( x ) = a − × x × = 2 2 a 2a
a/2
1
-a -3
-2
-1
1
2
3
a
x
25
习 题 一 解 答
• 同理
a2 − x2 2a h ( x ) Λf ( x ) = (a − x) 2 2a
可见, 可见,求相关不满足交换律
点的矩形函数, (1)第一项是宽度为 、中心在 点的矩形函数, )第一项是宽度为b、中心在0点的矩形函数 第二项是宽度为( - )、中心在a/2处的矩形函数 )、中心在 处的矩形函数, 第二项是宽度为(a-b)、中心在 处的矩形函数, 由图可见,两者相加得到一个宽度为a的矩形函数 的矩形函数。 由图可见,两者相加得到一个宽度为 的矩形函数。 (2)Comb函数由间隔为 的一系列δ函数组成 ) 函数由间隔为a的一系列 函数组成 函数由间隔为 的一系列 1 a x b/2 a-b/2 -2a -a 1 0 a x 2a
ARM嵌入式系统习题课1

(6) CMP指令是如何执行的?写一程序,判断R1的值是否大于0x30,是则 将R1减去0x30。 答:CMP指令是将寄存器Rn的值减去operand2的值,根据操作的结果更新 CPSR中的相应条件标志位,以便后面的指令根据相应的条件标志来判断是 否执行。 比如: CMP {cond} Rn,operand2 CMP R1,#0x30 ;将R1与常数0x30比较 LDRLE PC,LR;如果小于或等于0x30,则程序返回 SUB R1,R1,#0x30;大于0x30,则将R1减去0x30,结果存回 R1 (7)调用子程序是用B指令还是用BL指令?请写出返回子程序的指令。 答:调用子程序是用BL指令; MOV PC,LR 或 BX LR
• 2、定义R0 =0x12345678,假设使用存储指令将R0的值放在0x4000单元中。 如果存储器格式为大端格式,请写出在执行加载指令将存储器0x4000单元 内容取出存放到R2寄存器操作后所得R2的值。如果存储器改为小端格式, 所得的R2值又为多少?低地址0x4000单元的字节内容分别是多少?
PC,
第三章
ARM7TDMI(-S)指令系统
(1)ARM7TDMI(-S)有几种寻址方式?“LDR R1,[R0,#0x08]”属于哪种寻址 方式? 答:有8种寻址方式:1.寄存器寻址 2.立即寻址 3.寄存器移位寻址 4.寄存器 间接寻址 5.基址寻址 6.多寄存器寻址 7.堆栈寻址 8.相对寻址;“LDR R1,[R0,#0x08]”属于基址寻址。 (3) ARM指令中的第2个操作数有哪几种形式?列举5个8位图立即数。 答:a.常数表达式(8位图) b.寄存器方式 c.寄存器移位方式; 八位位图即常熟是由一个八位的常数循环移位偶数位得到的 0x3FC、0、0xF0000000、200、0xF0000001。 (5)请指出MOV指令与LDR加载指令的区别及用途? 答:MOV指令的源操作数是常数或(带偏移量的)寄存器,用于寄存器之 间的数据传送;LDR指令的源操作数是地址,用于存储器到寄存器的数据传 送。
三年级数学上册试题 一课一练《间隔排列》 -苏教版(含答案)

《间隔排列》1.小朋友们植树,先植一棵树,以后每隔3米植一棵,已经植了9棵。
问第一棵和第九棵之间相距多少米?2.在路的一侧插彩旗,每隔5米插一面,从起点到终点一共插了10面。
这条道路有多长?3.在学校的走廊两边,每隔4米放一盆菊花,从起点到终点一共放了18盆,这条走廊有多少米?4.在一条20米长的绳子上挂气球,从一端起,每隔5米挂一个气球。
一共挂了多少个气球?5.在一条长40米的大路两侧栽树,从起点到终点一共栽了22棵,已知相邻两棵树之间的距离都相等,问相邻两棵树之间的距离有多少米?6.在一条长32米的公路一侧插彩旗,从起点到终点一共栽插了5面,已知相邻两面彩旗之间的距离都相等,问相邻两面彩旗之间的距离有多少米?7.在公园一条长25米的小路两侧放椅子,从起点到终点等距离放了12把椅子,问相邻两把椅子之间相距有多少米?8.有一根木料,要锯成8段,每锯开一段需要2分钟,全部锯完需要多少分钟?9.把一根钢管锯成小段,一共锯了28分钟,已知每锯开一段需要4分钟,这根钢管锯成了多少段?10.有一根木料,要锯成4段,每锯开一处需要5分钟,全部锯完需要多少分钟?11.把一根圆木锯成2米长的小段,一共花了15分钟,已知每锯下一段需要3分钟,这根圆木长多少米?12.米德爬楼梯,每上一层要走12级台阶,一级台阶需走2秒,米德从一楼走到四楼共要多少时间?13.甲、乙两人比赛爬楼梯,甲跑到5楼,乙恰好跑到3楼,照这样计算,甲跑到17楼,乙跑到多少楼?14.有一个正方形水池,绕着它走一圈是200米,如果沿着这一圈每隔10米装一盏红灯,再在相邻的两盏红灯之间等距离地装4盏黄灯,水池周围一共装了几盏红灯?几盏黄灯?15.一条公路长480米,在两旁植树,两端都植。
每隔8米栽一棵杉树,两棵杉树之间又等距离栽了3棵柳树。
问杉树和柳树各栽了多少棵?答案1. 3×(9-1)=24(米)答:第一棵和第九棵之间相距24 米。
2.5×(10-1)=45(米)答:这条道路有45 米。
操作系统 习题课1 答案

(2) 用类Pascal语言和Wait, Signal操作写出这些进
程间的同步算法。
答:(1) 应编写1个程序;设置2个进程;
进程与程序间的对应关系是:多对1。
(2) begin
S1:=100 (有100个座位) S2:=0 (没有阅读者) mutex: =1 cobegin P1: repeat Wait(S1); wait(mutex); 登记信息; Signal(muetx); Signal(S2)
习题课1 答案
•习题课:
Wait.Signal 操作必须成对出现,有一个Wait 操作就一定有一个Signal 操作 当为互斥操作时,它们同处于同一进程 当为同步操作时,则不在同一进程中出现 如果Wait(S1) 和 Wait(S2)两个操作在一起, 那么Wait 操作的顺序至关重要,一个同步Wait 操作与一个互斥Wait 操作在一起时同步Wait 操作在互斥 Wait 操作前 而两个Signal 操作无关紧要
为防止死锁发生可采取的措施: • 最多允许4个哲学家同时就餐; • 仅当一个哲学家左右两边的筷子都可用时, 才允许他拿筷子(); • 给所有哲学家编号,奇数号的哲学家必须首 先拿左边的筷子,偶数号的哲学家则反之 为了避免死锁,把哲学家分为三种状态, 思考,饥饿,进食,并且一次拿到两只筷子, 否则不拿
129964189620781250习题课-1
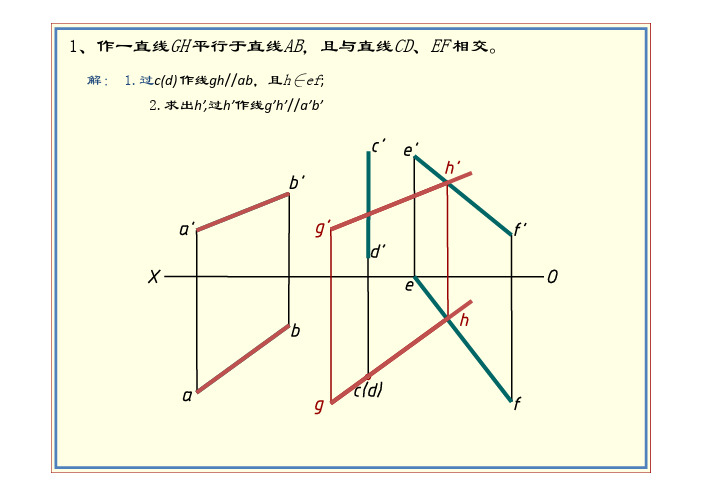
1、作一直线GH平行于直线AB,且与直线CD、EF相交。
解: 1.过c(d)作线gh//ab,且h∈ef;1过且2.求出h’,过h’作线g’h’//a’b’2、作一直线,使它与直线AB及CD均相交,且平行于OX轴。
解: 1.过c(d)作线ef//OX轴,且e∈ab;1过轴且2.求出e’,过e’作线e’f’// OX轴3、求作一直线MN ,使它与直线AB 平行,并与直线CD 相交于点K ,且CK :KD =1:2。
分析: 1.求出交点K 。
2.过交点K 求作AB解: 1.k’ 与c’(d’)重影。
2.用定比概念求k 。
的平行线MN 。
4.过k 作mn //ab 。
3.过k ’作m ’n ’//a’b’4、过点K作直线KF与直线CD正交。
解:CD是一般位置线,利用直角投影定理,过点K可作水平线KF、正平线KF均为所求;15、已知直线AB 与CD 垂直相交,求作c'd'。
空间分析:AB 为侧平线,故CD 为侧垂线。
解法一:2.CD 为侧垂线,故c’d’//OX 轴。
1.利用定比概念求出交点K 。
6、在直观图上标出各平面的位置(用相应的大写字母),在投影图上标出指定平面的其他两个投影。
并写出指定平面的名称。
一般位置平面面是面是水平面正平面面是铅垂面面是面是侧平面正垂面面是面是侧平面面是水平面7、已知下列平面上平面图形的一个投影,画出另一个投影。
解: 用面上取点、线的方法,即可完成水平投影。
8、作图判断直线AB 是否属于给定的平面。
解:1.在△ACD 上取线DI a’b’ d’1’ ab 不d1),故AB 不属于ACD ;2.判断AB 与DI 两面投影是否平行(//,//),△。
不属于9、求作五边形平面的水平投影。
解:三角形ABC可确定该平面,求出该平面上的点D、E的水平投影即可。
10、判别三条平行直线是否属于同一平面。
解:任取两直线组成一个平面,判别第三条直线是否属于该平面。
不属于答:11、给定一平面⊿ABC,作属于该平面的水平线,该线在H面上方,且距H面10mm;作属于该平面的正平线,该线在V面前方,且距V面;线,线,15mm。
工程光学 5 习题课 1
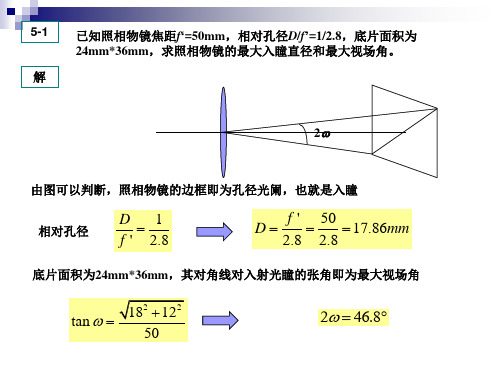
已知放大镜的焦距f'=25mm,通光口径D1=25mm,人眼的瞳孔D2=2mm, 位于放大镜后10mm处,物体位于放大镜前23mm处,求(1)该系统的孔 径光阑、入瞳和出瞳;(2)人眼通过放大镜所看到的最大物面范围。 (2)求人眼通过放大镜所看到的 最大物面范围 y
解
放大镜是视场光阑,最大物面范围,可 以定义为渐晕为0的最大视场 连接入瞳的下边缘点和透镜的上边缘 点,并延长至物面,视场角为
(1)求系统的孔径光阑、入瞳和出瞳 放大镜的共轭像就是其本身, 求瞳孔的物空间共轭像,将系统翻转 180,经透镜成像
解
1 1 1 l ' 16.67mm l ' 10 25 l ' 16.67 D2 ' D2 3.334mm 1.667 l 10
由物体向所有物空间的器件像做边缘连线
D1
D2
D2'
tan
最大物高
25 / 2 3.334 / 2 0.85 16.67
y (23 16.67) 0.85 3.334 / 2 32.05mm 2 y 64.1mm
人眼通过放大镜所看到的最大物面范围为64.1mm。
5-2
解
一个焦距为100mm的透镜与一个在其后方相隔20mm的光孔组成的系统对 无限远物体成像。设透镜的口径为15mm,光孔的口径为10mm。 (1)分别计算系统的入瞳和出瞳的位置和大小? (2)分别计算光线从左到右与从右到左入射时的系统相对孔径? (2)光线从左到右入射时,
光孔的共轭像是入瞳,故有相对孔径
2 43.6
5-4
有两个薄透镜组成的双光组组合系统,透镜1的焦距为f1'=100mm,透镜2 的焦距为f2'=50mm,两透镜间距d=50mm,两透镜的通光口径均为20mm。 物体距前透镜50mm。请分别用作图法和解析法求出光学系统的孔径光阑、 入瞳和出瞳的位置与大小。
大学物理 力学习题课1 哈尔滨工程大学

2
at = an
c b ct / R
哈尔滨工程大学理学院 孙秋华
t
R b c c
质点力学习题课 3.已知某些条件给出速度和运动方程 作业2.以初速度 v0 向上抛出一小球,小球在运动过程中
受到阻力,其大小为
f kv ,k为常数,求:小球任
意时刻的速度及达到的最大高度。
哈尔滨工程大学理学院
孙秋华
质点力学习题课 作业14. 质量为M=1.5kg的物体,用一根长为l=1.25m的 细绳悬挂在天花板上,今有一质量为m=10g的子弹以 v0=500m/s的速度射穿物体,刚穿出物体时子弹的速度 大小为v=30m/s, 设穿透时间极短,求(1)子弹刚穿出 时绳中张力的大小;(2)子弹在穿透过程中所受的冲 量。
哈尔滨工程大学理学院
孙秋华
质点力学习题课 1、力学中重要物理量的计算
作业4. 由楼窗口以水平初速度v 0射出一发子弹,求:(1) 子弹在任意时刻的位置及轨迹方程;(2)子弹在任意时 刻的速度、切向加速度和法向加速度;(3)任意时刻质 点所在轨迹的曲率半径。
作业11. 一物体按规律x=ct2作直线运动(c为常数)。设媒 质对物体的阻力正比于速度的平方,阻力系数为k,求: 物体由 x=0到 x=l过程中,阻力所作的功。
I p2 p1
(3)质点系的动量守恒定律
条件: F 0
f 内 F
m i v ix c 1 i m i v iy c 2 i m i v iz c 3 i
p2 p1 mi v i
哈尔滨工程大学理学院 孙秋华
哈尔滨工程大学理学院
孙秋华
质点力学习题课
一题一课的教学模式

一题一课的教学模式一题一课的教学模式是一种以问题为导向,以课程为载体的教学模式。
这种模式强调通过解决具体的问题来引导学生学习知识,提高学生的思维能力和解决问题的能力。
一题一课的教学模式的实施步骤如下:1. 提出问题:教师在课堂上提出一个具体的问题,这个问题应该是学生需要解决的问题,也是学生感兴趣的问题。
2. 分析问题:教师引导学生分析问题,找出问题的关键点和难点,帮助学生理解问题的本质。
3. 解决问题:教师引导学生运用所学的知识和方法来解决问题,教师在这个过程中起到引导和辅助的作用。
4. 总结反思:解决问题后,教师引导学生总结解决问题的过程和结果,反思自己的学习方法和策略,提高自己的学习能力。
一题一课的教学模式的优点如下:1. 提高学生的学习兴趣:这种模式以问题为导向,能够引起学生的学习兴趣,激发学生的学习动力。
2. 培养学生的思维能力:这种模式要求学生运用所学的知识和方法来解决问题,能够培养学生的思维能力和解决问题的能力。
3. 提高学生的自主学习能力:这种模式强调学生的主动参与和自主学习,能够提高学生的自主学习能力。
4. 提高教学效果:这种模式能够使学生在实践中学习和掌握知识,提高教学效果。
然而,一题一课的教学模式也存在一些问题,如:如果问题设置不当,可能会让学生感到困惑;如果教师引导不当,可能会影响学生的学习效果;如果学生基础薄弱,可能会难以理解和解决问题等。
因此,教师在使用这种教学模式时,需要注意合理设置问题,恰当引导,关注学生的学习情况,及时调整教学策略。
总的来说,一题一课的教学模式是一种有效的教学模式,它能够激发学生的学习兴趣,培养学生的思维能力和解决问题的能力,提高学生的自主学习能力和教学效果。
数据结构C++陈慧南习题课1

// O(1)
习题三(第50页) 习题三( 50页
五个元素依次进栈(进栈后可立即出栈) 3 .1 设A、B、C、D、E五个元素依次进栈(进栈后可立即出栈),问 能否得到下列序列。若能得到,则给出相应的push pop序列 push和 序列; 能否得到下列序列。若能得到,则给出相应的push和pop序列;若不 则说明理由。 能,则说明理由。 1) A,B,C,D,E 2) A,C,E,B,D 3) C,A,B,D,E 4) E,D,C,B,A 不能。 中的E 而言, 最先出栈则表明, 答:2)和3)不能。对2)中的E,B,D而言,E最先出栈则表明,此 均在栈中,由于, 先于D进栈,所以应有D先出栈。同理3 时 B 和 D 均在栈中 , 由于 , B 先于 D 进栈 , 所以应有 D 先出栈 。同理 3 ) 也不能。 也不能。 (1)能。 push,pop,push,pop,push,pop,push,pop,push,pop (4)能。 push,push,push,push,push,pop,pop,pop,pop,pop
设计共享栈。 3.2 设计共享栈。
0
n-1
↑ bottom1 bottom1
↑ top1 top1
↑ top2 top2
↑ bottom2 bot个足够大的栈空间 。 该空间的两端分别设为两个栈的 栈底, bottom1 bottom2 指示, 让两个栈的栈顶, top1 栈底 , 用 bottom1 和 bottom2 指示 , 让两个栈的栈顶 , 用 top1 和 top2 指示,都向中间伸展,直到两个栈的栈顶相遇, top2 指示 , 都向中间伸展 , 直到两个栈的栈顶相遇 , 才会发生 溢出。 溢出。 栈空,两栈均空:top1=0且 top2=n-1 栈空,两栈均空:top1 top2=n栈满:top1=top2 栈满:top1=top2-1
电路习题课(1-4)

Uoc= U1+ U2
U1= 456/9-45 2/10
b a
=30 - 9 = 21V
+
4
15A 4 2
U2 -
U2= (15 4/10) 2=12V Uoc= U1+ U2= 21+12 = 33V
b
3 6 4
a
求内阻Ri :
Ri 2 4
Ri=2+1.6=3.6
b
a
12V
U5
1
二、求电路中所有 的电压U 和 I 。
U1 a
U2
2 c
2 8V
d
40V
4
2
U3
I
1
U7 U6
b
2 U4
4 8 12 = = 0 .4 A I = 2 + 2 + 2 + 2 + 1 + 1 10 U 1 = U = 0.8V , U3 = U 4 = 0.8V , 2 = 0V U = 0.4V , U6 = 0.4V , U 7 5 Uab = U2 + 8 + U6 U4 = 0.8 + 8 + 0.4 + 0.8 = 10V
3
二、 求电流 I。
解: 用戴维南定理: 4
+ - 45V Is 15A 4 6 2 + 6 2
I
6.4
3 + - 45V Is 15A 4
a
Ri
a
4
Uoc -
+
Uoc -
b
b
3 + 4 - 45V 6 2 4 3 6
a 采用迭加定理求开路电压Uoc +
哈工程通信原理习题课(第5讲)_1

A
t -Ts/2 0 Ts/2
图P5-3
解答:(1)由图P5-3可以得到: 2 A(1 t ) Ts g (t ) 0
Ts t 2 其他
又 P(0) P(1) P
1 ,而且 g1 (t ) g (t ), g 2 (t ) 0 2
ATs 2 G( f ) S a ( fTs ) 2 2
该频率分量的功率为:
A2 4 A2 4 A2 A2 2 A2 Pv ( ) Sa ( ) Sa ( ) 4 4 4 16 2 16 2
5.5 设某二进制数字基带信号中,数字信息“1”和“0”分 g (t ) g (t ) 表示,且“1”与“0”出现的概率相等, g (t ) 及 别由 是升余弦频谱脉冲,即
0
t Ts/2
-Ts/2
-Ts/4
0
Ts/4
Ts/2
t
图P5-2(a)
图P5-2(b)
解答:(1)由随机基带序列的功率谱密度公式:
P ( ) P ( ) P ( ) s u v 2 f P(1 P) G1( f )G2 ( f ) f s PG1(mf s ) (1 P)G2 (mf s ) ( f mf ) s s m 2
将
P 带入上式整理得:
1 1 P ( ) f G ( mf ) (1 ) G ( mf ) v s g (t ) 1 s 2 s g ( t ) m 1 1 1 1 g (t ) g2 (t ) 2 因为 g1 ( t ) P 1 G1 ( mf s ) P 1 g2 ( t ) P G2 ( mf s ) P 得Pv ( ) 0 代入上式
第7讲 题课1模n剩余类加群

} 试证明 设 N {0,1,2,3,}, N {1,2,3,
( N , )与( N , ) 不同构.
证明:(反证法)如果 N N 设 (0) n N , (1) m,
0 1 1, m (1) (0) (1) n m
则
[a b] [a'b' ]
称此运算为模n剩余类加法,记 [a] [b] [a'b' ]
10/11/2018 09:21
模n剩余类集合 Z n 对于模n剩余类加法 构成一个群。 证明(定义法) 非空;封闭。
结合律 ([a] [b]) [c] [a b] [c] [(a b) c]
[c] [c' ] c ~ c' c c' (modn) q, c nq c'
模n剩余类集合 Z n
模n剩余类加法
设 [a] [a' ],[b] [b' ] q1 , q2 , a' nq1 a, b' nq2 b
a'b' n(q1 q2 ) a b
10/11/2018
09:21
[a (b c)] [a] [b c] [a] ([b] [c])
左单位元[0] [a]的左逆元[-a]
[0] [a] [0 a] [a] [a] [a] [a a] [0]
09:21
10/11/2018
模n剩余类集合 Z n 对于模n剩余类加法 构成一个群。 证明(同态法)
Z n {[r ] | r 0,1,, n 1}
概率统计习题课一

生产的概率? 解:(2)设Ai表示取到第i 个工厂产品,i=1,2,3,B表示取到次品,
由题意得: P(A1)=0.5,P(A2)=P(A3)=0.25
P(B|A1)=0.02,P(B|A2)=0.02,P(B|A3)=0.04 由Bayes公式得:
P( A1 | B)
P( A1 )P(B | A1 )
5
• P(A)=0.4,P(B)=0.3,P(A+B)=0.6, 求P(A-B).
• P(A)=0.7,P(A-B)=0.3,求P(s -AB)
• P(A) =P(B) = P(C) =1/4, P(AB)=0, P(AC)=P(BC)=1/6,求A、B、C都不出现的概率。
• A、B都出现的概率与 A、B 都不出现的概率相等, P(A)=p,求P(B).
(3)有利于事件C的基本事件数为62-2×2=32,P(C)=32/36=8/9
注意①若改为无放回地抽取两次呢? ②若改为一次抽取两个呢?
3
• AB=φ,P(A)=0.6,P(A+B)=0.8,求 B的逆事件 的概率。
解:由P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B) 得:P(B)=P(A+B)-P(A)=0.8-0.6=0.2,
P(B) P( A)P(B | A) P( A)P(B | A)
=(4/10)×(3/9)+(6/10)×(4/9)
= 6/15
12 市场上某种商品由三个厂家同时供获,其供应量为:甲
厂家是乙厂家的2倍,乙.丙两个厂家相等,且各厂产品的次品 率为2%,2%,4%, (1)求市场上该种商品的次品率.
=0.8×0.7×0.4=0.224
高等数学习题课(1)函数极限与连续性

连续,
证明 f (x) 对一切 x 都连续 .
提示:
lim f (x x) lim [ f (x) f (x)]
x0
x0
f (x) f (0)
f (x 0) f (x)
P73 题5. 证明: 若 f (x) 在 (, )内连续, lim f (x)
x
存在, 则 f (x) 必在 (, )内有界.
III.课堂训练题 1. 求数列极限
1 lim[ n n n n ] n
2 lim 1 a1 a2 1 a2n ,( a 1) n
2. 求下列极限
1 lim x0
1 tan x 1 sin x sin3 x
2 lim sin x 1 sin x x
公式:sin A sin B 2cos A B sin A B
xx0
f (x)
f
(x0 )
6. 连续函数的性质
1) 有限个连续函数的和、差、积、商(分母不为 零),仍为连续函数;
2) 单值单调连续函数的反函数在对应区间上也为 单值单调的连续函数;
3) 连续函数的复合函数也是连续函数; 4) 一切初等函数在其定义区间内都是连续函数。
7. 闭区间上连续函数的性质
有 y f (x0 x) f (x0 )
如 果 lim y 0
①
x0
或
lim
x0
f
( x0
x)
f
(x0 )
②
或
lim
x x0
f (x)
f (x0 )
③
则 称 函 数y f (x) 在 点 x0 处 连 续 。
命题:lim xx0
f
(x)
f
习题课1

u U ,
u 0 y
a sin b U ab cos b 0
u U sin
y 2
a U b 2
收缩管直径应限制在什么条件下,才能保证不出 现空化?(不考虑损失)
10m
解:水温40℃,汽化压强为7.38kPa 大气压强
pa 97.3 103 10m g 992.2 9.807
10m
汽化压强
pv 7.38103 0.76m g 992.2 9.807
1
1 10m
对液面V1=V2=0,p1=p2=0,由上式可得
l V2 H z1 z2 h f 1 h f 2 ( in v 2 b out ) d 2g
0.5 5.7 2
5.09m s 50 0.64 1.0 0.0173 0.1 2 9.81m s2
4
输油管道中安装一个收缩段以便测量流量Q ,管径从
d1 收缩到d2 。使用题图所示的缸套、活塞装置,活 塞直径 D,油的密度ρ ,如果固定活塞所要施加的力 F ,求管中油的体积流量 Q。
d1 260mm d 2 180mm D 300 mm 850kg / m3 F 75 N
t 0 1 x 0, y 0
C2
( x 1)( y 2) 2
例2:弦长为3m的机翼以300km/h的速度在温度为20℃、
压强为1at的静止空气中飞行,用λl=20的模型在风洞中 作试验:(1)如果风洞中空气的温度和压强不变,风 洞中空气速度应为多少? 解:风洞实验中粘性力是主要的——雷诺准则 υ相同
光学习题课1

几何光学习题课1基本知识在经典物理的范畴内,光是电磁播,其传播规律由麦克斯韦方程组来描述,但由于光的波长很短,在研究的问题中涉及到的尺度远大于光波波长时,光的波动性可以忽略,用光线来取代波线,由此建立起来的光传播理论就是所谓的几何光学。
几何光学在方法上是几何的,在物理上不涉及光的本质。
1. 折射率 几何光学的三个定律 全反射 折射率的定义:vc n =,c 是光在真空中的速度,v 是光在该种媒质中的传播速度;相对折射率的定义:1212n n n =。
光的直线传播定律:在均匀媒质中光沿直线传播。
光的反射和折射定律:(1)反射线和折射线都在入射面内,并分居在法线的两侧;(2)反射角等于入射角;(3)折射角与入射角的正弦比与入射角无关,是一个与媒质和光的波长有关的常数(相对折射率)。
(斯涅耳定律)全反射:当光线从光密媒质(2n )射向光疏媒质(21n n <)时,当入射角等于或大于某一角度时(临界角121/sin n n i C -=),折射光线消失,光线全部反射的现象。
2.棱镜与色散 偏向角:'11i i +=δ,1i :入射角,'1i :出射角;最小偏向角产生的充要条件:'11i i =或'22i i =作用:用来测透明介质的折射率:)2sin(/)2sin(minαδα+=n 。
色散产生的原因:介质的折射率n 是光束波长的函数,)(λn n =棱镜可以用做光谱仪,进行光谱分离。
3.光程 费马原理 光程:⎰=PQndlQP)(,光程可以理解为在相同的时间内光线在真空中传播的距离。
注意,光程是一个非常重要的一个概念,在后面的课程中研究光的干涉、衍射、位相延迟时要经常用到。
费马原理:QP 两点间光线的实际路径是光程)(QP为平稳的路径。
数学表达式为:0=⎰PQndl δ注意:费马原理的实质是揭示光线在媒质中沿什么路径传播。
4.光的可逆性原理当光线的方向反转时,光线将沿着同一路径传播。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.我
2.我国药典的英文缩写
A.BP B.CP C.JP D.ChP E.NF
3.英国国家处方集的缩写是
A.USP B.PDG C.BNF D.CA E.USN
4.药品的鉴别是证明
A.未知药物的真伪B.已知药物的真伪C.已知药物的疗效D.药物的纯度E.药物的稳定性
5.测定土霉素的效价时,需要
A.化学试剂(CP)B.分析试剂(AR)
C.对照品D.标准物质
E.标准品
6.中国药典(2000年版)规定称取2.0g药物时,系指称取
A.2.0g B.2.1g C.1.9g
D.1.95g~2.05g E.1.9g~2.1g
7.中国药典(2000年版)规定称取0.1g药物时,系指称取
5~8
A.附录B.正文C.凡例
D.通则E.一般信息
5.药品的质量标准应处在药典的———
6.对溶解度的解释应处在药典的———
7.通用检测方法应处在药典的———
8.制剂通则———
三、X型题(多项选择题)
1.检验报告应有以下内容
A.供试品名称
B.外观性状
C.检验结果、结论
D.送检人盖章
E.报告的日期
2.中国药典的内容应包括
A.正文B.性状C.凡例
D.索引E.附录
3.美国药典第25版的正文包括
A.品名、来源或化学名B.物理常数C.包装和贮藏D.参比物质要求E.化学文摘登录号。
