2012二模数学分析
2012年佛山二模理科数学试题以及解答(Word
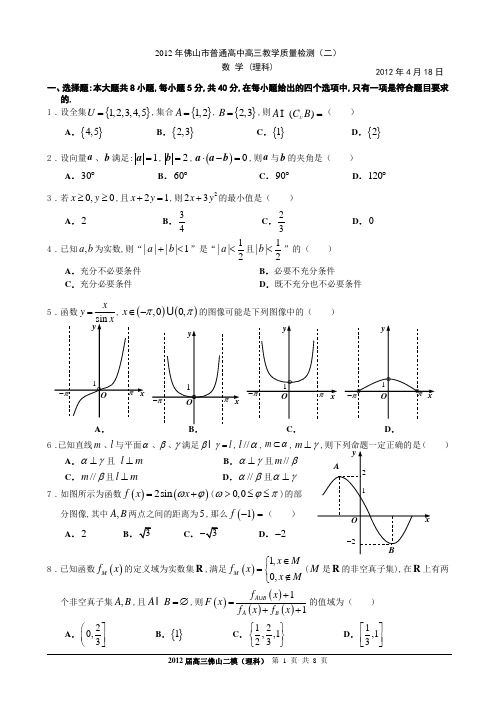
2012年佛山市普通高中高三教学质量检测(二)数 学 (理科)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集{}1,2,3,4,5U =,集合{}1,2A =,{}2,3B =,则=)(B C A U ( )A .{}4,5B .{}2,3C .{}1D .{}2 2.设向量a 、b 满足:1=a ,2=b ,()0⋅-=a a b ,则a 与b 的夹角是( )A .30︒B .60︒C .90︒D .120︒ 3.若0,0x y ≥≥,且21x y +=,则223x y +的最小值是( )A .2B .34 C .23D .0 4.已知,a b 为实数,则“||||1a b +<”是“1||2a <且1||2b <”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 5.函数xy =,()(),00,x ππ∈-的图像可能是下列图像中的( )A . C . D .6.已知直线m 、l 与平面α、β、γ满足l βγ=,//l α,m α⊂,m ⊥) A .αγ⊥且 l m ⊥ B .αγ⊥且//m β C .//m β且l m ⊥ D .//αβ且αγ⊥ 7.如图所示为函数()()2sin f x x ωϕ=+(0,0ωϕπ>≤≤)的部 分图像,其中,A B 两点之间的距离为5,那么()1f -=( ) A .2 B C . D .2-8.已知函数()M f x 的定义域为实数集R ,满足()1,0,M x Mf x x M∈⎧=⎨∉⎩(M 是R 的非空真子集),在R 上有两个非空真子集,A B ,且AB =∅,则()()()()11A B A B f x F x f x f x +=++的值域为( )A .20,3⎛⎤ ⎥⎝⎦B .{}1C .12,,123⎧⎫⎨⎬⎩⎭D .1,13⎡⎤⎢⎥⎣⎦2012年4月18日FAEDBC二、填空题:本题共7小题,考生作答6小题,每小题5分,共30分 (一)必做题(9~13题)9. 设i 为虚数单位,则()51i +的虚部为 .10. 设,x y 满足约束条件0201x x y x y ≥⎧⎪-≥⎨⎪-≤⎩,则2z x y =+的最大值是 .11. 抛掷一枚质地均匀的骰子,所得点数的样本空间为{}1,2,3,4,5,6S =,令事件{}2,3,5A =,事件{}1,2,4,5,6B =,则()|P A B 的值为 .12. 直线2y x =和圆221x y +=交于,A B 两点,以Ox 为始边,OA ,OB 为终边的角分别为,αβ,则()sin αβ+的值为 .13. 已知等比数列{}n a 的首项为2,公比为2,则1123n na a a a a a a a a a +=⋅⋅⋅⋅ .(二)选做题(14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分) 14.(坐标系与参数方程选做题)在极坐标系中,射线()03πθρ=≥与曲线1C :4sin ρθ=的异于极点的交点为A ,与曲线2C :8sin ρθ=的异于极点的交点为B ,则||AB =________. 15.(几何证明选做题)如图,已知圆中两条弦AB 与CD 相交于点F ,E 是AB 延长线上一点,且DF CF ==,:::4:2:1AF FB BE ,若CE与圆相切,则线段CE 的长为 .三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)在四边形ABCD 中,2AB =,4BC CD ==,6AD =,A C π∠+∠=. (Ⅰ)求AC 的长; (Ⅱ)求四边形ABCD 的面积.PCEFBA17.(本题满分12分)空气质量指数PM2.5(单位:3/g m μ)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:353575 75115 115150 150250一级 二级 三级四级五级 优良轻度污染 中度污染重度污染严重污染形图:(Ⅰ)估计该城市一个月内空气质量类别为良的概率;(Ⅱ)在上述30个监测数据中任取2个,设X 为空气质量类别为优的天数,求X 的分布列.18.(本题满分14分)如图所示四棱锥P ABCD -中,PA ⊥底面ABCD ,四边形ABCD 中,AB AD ⊥,//BC AD ,2PA AB BC ===,4AD =,E 为PD 的中 点,F 为PC 中点.(Ⅰ)求证:CD ⊥平面PAC ; (Ⅱ)求证://BF 平面ACE ;(Ⅲ)求直线PD 与平面PAC 所成的角的正弦值;19.(本题满分14分)已知椭圆E :()222210x y a b a b +=>>的一个交点为()1F ,而且过点12H ⎫⎪⎭.(Ⅱ)设椭圆E 的上下顶点分别为12,A A ,P 是椭圆上异于12,A A 的任一点,直线12,PA PA 分别交x 轴于点,N M ,若直线OT 与过点,M N 的圆G 相切,切点为T .证明:线段OT 的长为定值,并求出该定值.20.(本题满分14分)记函数()()()*112,nn f x x n n =+-≥∈N的导函数为()nf x ',函数()()ng x f x nx =-.(Ⅰ)讨论函数()g x 的单调区间和极值;(Ⅱ)若实数0x 和正数k 满足:()()()()0101n n n n f x f k f x f k ++'=',求证:00x k <<.21.(本题满分14分)设曲线C :221x y -=上的点P 到点()0,n n A a 的距离的最小值为n d ,若00a =,1n n a -=,*n ∈N(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求证:321212435214622n nn n a a a a a a a a a a a a -+++++<+++; (Ⅲ)是否存在常数M ,使得对*n ∀∈N ,都有不等式:33312111nM a a a +++<成立?请说明理由.2012年佛山市普通高中高三教学质量检测(二)参考答案数 学 (理科)二、填空题:本题共7小题,考生作答6小题,每小题5分,共30分2012年4月18日ABCDPCDEFB AOG PG9.4-; 10.5; 11.25; 12.45-; 13.4; 三、解答题:本大题共6小题,满分80分.解答应写出文字说明、证明过程和演算步骤 16.【解析】(Ⅰ)如图,连结AC ,依题意可知,B D π+=, 在ABC ∆中,由余弦定理得22224224cos AC B =+-⨯⨯ 2016cos B =-在ACD ∆中,由余弦定理得22264264cos AC D =+-⨯⨯ 5248cos 5248cos D B =-=+由2016cos 5248cos B B -=+,解得1cos 2B =-从而22016cos 28AC B =-=,即AC =6分(Ⅱ)由(Ⅰ)可知sin sin 2B D ==, 所以11sin sin 22ABCD ABC ACD S S S AB BC B AD CD D ∆∆=+=⋅+⋅==………12分 17.【解析】(Ⅰ)由条形统计图可知,空气质量类别为良的天数为16天, 所以此次监测结果中空气质量类别为良的概率为 1683015=.…………………4分 (Ⅱ)随机变量X 的可能取值为0,1,2,则()2222302310435C P X C ===,()118222301761435C C P X C ===,()28230282435C P X C === 所以X 的分布列为:18.【解析】(Ⅰ)因为PA ⊥底面ABCD ,CD ⊂面ABCD ,所以PA CD ⊥,又因为直角梯形面ABCD 中,AC CD == 所以222AC CD AD +=,即AC CD ⊥,又PAAC A =,所以CD ⊥平面PAC ;………4分(Ⅱ)解法一:如图,连接BD ,交AC 于O ,取PE 中点G , 连接,,BG FG EO ,则在PCE ∆中,//FG CE ,又EC ⊂平面ACE ,FG ⊄平面ACE ,所以//FG 平面ACE ,因为//BC AD ,所以BO GEOD ED=,则//OE BG , 又OE ⊂平面ACE ,BG ⊄平面ACE ,所以//BG 平面ACE , 又BG FG G =,所以平面//BFG 平面ACE ,因为BF ⊂平面BFG ,所以//BF 平面ACE .………10分……12分解法二:如图,连接BD ,交AC 于O ,取PE 中点G , 连接FD 交CE 于H ,连接OH ,则//FG CE ,在DFG ∆中,//HE FG ,则12GE FH ED HD ==, 在底面ABCD 中,//BC AD ,所以12BO BC OD AD ==,所以12FH BO HD OD ==,故//BF OH ,又OH ⊂平面ACE ,BF ⊄平面ACE ,所以//BF 平面ACE .………10分(Ⅲ)由(Ⅰ)可知,CD ⊥平面PAC ,所以DPC ∠为直线PD 与平面PAC 所成的角,在Rt PCD ∆中,CD PD ==所以sin CD DPC PD ∠===, 所以直线PD 与平面PAC.………14分 19.【解析】(Ⅰ)解法一:由题意得223a b -=,223114a b+=,解得224,1a b ==,所以椭圆E 的方程为2214x y +=.………………………………………………4分 解法二:椭圆的两个交点分别为())12,F F ,由椭圆的定义可得12712||||422a PF PF =+=+=,所以2a =,21b =, 所以椭圆E 的方程为2214x y +=.………………………………………………4分 (Ⅱ)解法一:由(Ⅰ)可知()()120,1,0,1A A -,设()00,P x y , 直线1PA :0011y y x x --=,令0y =,得001N x x y -=-; 直线2PA :0011y y x x ++=,令0y =,得001M x x y =+; 设圆G 的圆心为00001,211x x h y y ⎛⎫⎛⎫- ⎪ ⎪ ⎪+-⎝⎭⎝⎭,则2r =22220000000000112111411x x x x x h h y y y y y ⎡⎤⎛⎫⎛⎫--+=++⎢⎥ ⎪ ⎪+-++-⎝⎭⎝⎭⎣⎦,22200001411x x OG h y y ⎛⎫=-+ ⎪+-⎝⎭2222222200000200000114114111x x x x x OT OG r h h y y y y y ⎛⎫⎛⎫=-=++---= ⎪ ⎪+-+--⎝⎭⎝⎭ 而220014x y +=,所以()220041x y =-,所以()202204141y OT y -==-, 所以||2OT =,即线段OT 的长度为定值2.…………………………………………14分 解法二:由(Ⅰ)可知()()120,1,0,1A A -,设()00,P x y , 直线1PA :0011y y x x --=,令0y =,得001N x x y -=-;直线2PA :0011y y x x ++=,令0y =,得001M xx y =+; 则20002000||||111x x x OM ON y y y -⋅=⋅=-+-,而220014x y +=,所以()220041x y =-, 所以2020||||41x OM ON y ⋅==-,由切割线定理得2||||4OT OM ON =⋅= 所以||2OT =,即线段OT 的长度为定值2.…………………………………………14分 20.【解析】(Ⅰ)由已知得()()11ng x x nx =+--,所以()()111n g x n x -⎡⎤'=+-⎣⎦.………………2分① 当2n ≥且n 为偶数时,1n -是奇数,由()0g x '>得0x >;由()0g x '<得0x <.所以()g x 的递减区间为(),0-∞,递增区间为()0,+∞,极小值为()00g =.……………5分 ② 当2n ≥且n 为奇数时,1n -是偶数,由()0g x '>得2x <-或0x >;由()0g x '<得20x -<<. 所以()g x 的递减区间为()2,0-,递增区间为(),2-∞-和()0,+∞,此时()g x 的极大值为()222g n -=-,极小值为()00g =.……………8分(Ⅱ)由()()()()0101n n n n f x f k f x f k ++'='得()()()()()10101111111n nn n n x k n x k -+++-=+++-, 所以()()()10111111n n n k x n k +⎡⎤+-⎣⎦+=⎡⎤++-⎣⎦,()()()()0111111nnnk k x n k -++=⎡⎤++-⎣⎦……………10分 显然分母()()1110n n k ⎡⎤++->⎣⎦,设分子为()()()()1110nh k nk k k =-++>则()()()()()()11111110n n n h k n k n k nk n n k k --'=+++-=++>所以()h k 是()0,+∞上的增函数,所以()()00h k h >=,故00x >……………12分又()()()()10111111n nk n k x k n k +++-+-=⎡⎤++-⎣⎦,由(Ⅰ)知,()()11ng x x nx =+-- 是()0,+∞上的增函数,故当0x >时,()()00g x g >=,即()11nx nx +>+,所以()()1111n k n k +++>+所以00x k -<,从而0x k <. 综上,可知00x k <<.……………14分 21.【解析】(Ⅰ)设点(),P x y ,则221x y -=,所以||n PA == 因为y R ∈,所以当2n a y =时,||n PA 取得最小值n d ,且n d =,又1n n a -,所以1n n a +=,即1n n d +=将1n n d +=代入n d =1n +=两边平方得2212n n a a +-=,又00a =,212a =故数列{}2n a 是首项212a =,公差为2的等差数列,所以22n a n =,因为1n n a -0>,所以n a ………………………………………6分(Ⅱ)因为()()()222122120n n n n +--+=-<,所以()()()2221221n n n n +-<+所以2221212n n n n a a a a +-+<所以2122122n n n n a a a a -++<,所以321212434562122,,,n n n n a a aa a aa a a a a a -++<<< 以上n 个不等式相加得321212435214622n nn n a a a aa a a a a a a a -+++++<+++.…………………10分 (Ⅲ)因为31k a=,当2k≥时<==,=<=<=<2211nnkk ==<=<∑所以3111142nn i k ia ===<=+∑. 故存在常数142M =+,对*n ∀∈N ,都有不等式:33312111nM a a a +++<成立. …………14分。
2012年北京市各区二模试题分类解析【数学理】(10):平面向量.pdf

课题使用人编号07课型新授课课时1主备人石伟锋 备课 时间教 学 目 标(一)情感、态度、价值观:树立正确的资源环境意识和对自然环境的忧患意识。
以保护环境为荣,以破坏环境为耻,树立人与自然和谐共处的人生价值。
有意识的控制人对自然的破坏行为。
(二)能力:能从自我做起,珍爱和保护大自然的一切生命。
提高保护自然、保护环境的能力。
(三)知识:了解人与大自然的不和谐之音的表现,懂得人与大自然和谐相处的重要性。
重点 难点 教学难点:自然景观遭到人为的破坏教具多媒体 电子白板教法学法 讨论、欣赏、感悟、体验历年考点 展示 交流 自然物种在减少 自然景观遭到人为破坏 教师引导,PPT出示材料,阅读思考、讨论: 大自然物种不断减少、甚至灭绝的原因是什么? 如何保护物种,我们能做些什么? 教师引导,PPT出示材料, 这些自然景观为什么遭到人为破坏? 如何去改变这种状况? 教师引导归纳总结 结合本地实际,探讨如何保护自然景观 学生先阅读课本和PPT材料 ⑴、思考讨论,学生畅所欲言 ⑵讨论:如何保护物种,我们能做些什么? 分小组交流: 结合本地实际,探讨如何保护自然景观 15教 学 过 程环节知识点教师活动学生活动估时合作 探究 展示 交流3、环境状况 不容乐观教师:PPT出示,环境的一些恶化状况的图片, 然后让学生谈谈所知道的情况 在观察的基础上, 让学生总结,什么是环境问题?有什么危害? 并初步探讨如何解决这些问题? 老师对一些有创意的观点和看法做法及时鼓励和表扬,激发学生探究和参与环保的热情,进行有效的情感教育和升华。
积极思考 结合实际 总结归纳 建言献策 11强化 应用 形成 能力巩固训练投放课堂练习 限时规范训练 巩固学习成果 规范答题 反馈补偿12 构建 网络知识结构1、先由学生谈谈观点、收获、体会。
2、老师总结2教后反思 初中学习网,资料共分享!我们负责传递知识! 含义:是指人类不合理地开发利用自然资源所造成的环境污染与破坏。
2012年二模数学试卷分析

2012年二模数学试卷分析2012年二模数学试题在继承我省近几年中考命题整体思路的基础上,突出对基础知识、基本技能和基本数学思想的考查,关注学生的数学基础知识和能力、数学学习过程和数学创新意识的考查,整套试题充满着人文关怀。
一、总体评价本套试题的命制严格按照《课程标准》和《学科说明》的相关要求,充分体现和落实课改的理念和精神,整套试题覆盖面广,题量适当,结构合理,难度适中,内容新颖,表述科学。
在考查方向上,体现了突出基础,注重能力的思想;在考查内容上,体现了基础性、开放性、应用性、探究性和综合性。
能对我县的教学工作起到指导作用。
1、整体稳定,局部调整今年的数学试卷保持整体格局稳定,选择题12个;填空题8个小题减至6个;解答题依然是8个小题。
2、全面考查,突出重点整套试题覆盖了近百个知识点,所关注的内容是支撑学科的基本知识、基本技能和基本思想。
强调考查学生在这一学段所必须掌握的通法通则,淡化繁杂的运算和技巧性很强的方法。
试题重点考查了代数式、方程(组)与不等式(组)、函数、统计与概率、相交线与平行线、三角形与四边形等学科的核心内容,同时关注了函数与方程思想,分类讨论思想、统计与随机意识等数学思想,以及特殊与一般、运动与变化等数学观念。
试题突出了对学生研究问题的策略和运用数学知识解决实际问题能力的考查。
3、层次分明,确保试题合理的难度和区分度试题在结构上形成合理的层次,整套试题从易到难形成梯度。
其中第一、二大题分三个层次:第一层次(第1~7,13、14)考查基础知识、基本技能、判断、运算或操作方式单一,学生能直接上手;第二层次(第8~10、15~18小题)是范围的综合题,旨在考查最基本的数学方法和数学思想;第三层(第一阶段、12)更多的是关注数学思辨和思维过程。
第三大题注重数学能力,也分三个层次;第一层次(第19~22小题),考查代数式变形的运算的能力,图形变换的能力,对统计与概论知识的理解与应用,以及对函数的理解与应用的能力;第二层次(第23、24小题),考查学生的形成性学习方法与能力,以及逻辑思维能力。
2012年北京市各区高考二模试题分类解析【数学

一、集合〔必修一〕1.〔20####二模文〕设集合{0,1234,5}{12}U A ==,,,,,,{}2540B x x x =∈-+<Z ,则=⋃)(B A C U 〔 D 〕A .{0,1,2,3}B .{5}C .{124},,D .{0,4,5} 2.〔20##丰台二模文9〕已知集合A={x |2x-x 2>0},B={x |x>1},则AB =______. 答案:{}12x x <<。
3.〔20##昌平二模文1〕若集合}{0>=x |x A ,}4|{2<=x x B ,则=B A 〔 B 〕 A.{02<<-x |x } B. {20<<x |x } C. {22<<-x |x } D. {2->x |x }4.〔20##东城二模文1〕若集合{}0A x x =≥,且AB B =,则集合B 可能是〔 A 〕 A .{}1,2 B.{}1x x ≤ C.{}1,0,1- D.R六、不等式〔必修五〕1.〔20##西城二模 文12〕已知函数2()1f x x bx =++是R 上的偶函数,则实数 b =_____;不等式(1)f x x -<的解集为_____.答案:0,{|12}x x <<。
2.〔20##昌平二模文6〕 爬山是一种简单有趣的野外运动,有益于身心健康,但要注意安全,准备好必需物品,控制好速度.现有甲、乙两人相约爬山,若甲上山的速度为1v ,下山的速度为2v 〔21v v ≠〕,乙上下山的速度都是221v v +〔甲、乙两人中途不停歇〕,则甲、乙两人上下山所用的时间21,t t 的关系为〔 A 〕A .21t t > B. 21t t < C. 21t t = D. 不能确定七、常用逻辑用语〔选修2-1〕1.〔20####二模文3〕如果命题"p 且q 〞是假命题,"q ⌝〞也是假命题,则〔 C 〕A .命题"⌝p 或q 〞是假命题B .命题"p 或q 〞是假命题C .命题"⌝p 且q 〞是真命题D .命题"p 且q ⌝〞是真命题 2.〔20##昌平二模文2〕"1>x 〞 是"0lg >x 垂直〞的〔 C 〕A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件3.〔20##海淀二模文2〕已知命题p :x R ∃∈,x x 21sin <. 则p ⌝为〔 D 〕 A .x R ∃∈,x x 21sin =B.x ∀∈R ,x x 21sin <C.x R ∃∈,x x 21sin ≥D.x ∀∈R ,x x 21sin ≥。
2012北京西城高考二模数学理(含解析)

北京市西城区2012年高三二模试卷 数 学(理科)2012.5 第Ⅰ卷(选择题 共40分)一、选择题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合2{|log 1}A x x =<,{|0B x x c =<<,其中0}c >.若A B B =U ,则c 的取值范 围是( ).A .(0,1]B .[1,)+∞C .(0,2]D .[2,)+∞2.执行如图所示的程序框图,若输入如下四个函数: ①()e x f x =; ②()e x f x =-; ③1()f x x x -=+; ④1()f x x x -=- . 则输出函数的序号为( ).A .①B .②C .③D .④3.椭圆 3cos 5sin x y ϕϕ=⎧⎨=⎩(ϕ是参数)的离心率是( ).A .35B .45C .925D .16254.已知向量(,1)x =a ,(,4)x =-b ,其中x ∈R .则“2x =”是“⊥a b ”的( ). A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分又不必要条件 5.右图是1,2两组各7名同学体重(单位:kg )数据的茎叶图.设1,2两组数据的平均数依次 为1x 和2x ,标准差依次为1s 和2s ,那么( ).(注:标准差s =其中x 为12,,,n x x x L 的平均数)A .12x x >,12s s >B .12x x >,12s s <C .12x x <,12s s <D .12x x <,12s s >6.已知函数()1f x kx =+,其中实数k 随机选自区间[2,1]-.对[0,1]x ∀∈,()0f x ≥的概率是( ).A .13B .12C .23D .347.某大楼共有12层,有11人在第1层上了电梯,他们分别要去第2至第12层,每层1人.因 特殊原因,电梯只允许停1次,只可使1人如愿到达,其余10人都要步行到达所去的楼层.假设这10位乘客的初始“不满意度”均为0,乘客每向下步行1层的“不满意度”增量为1,每向上步行1层的“不满意度”增量为2,10人的“不满意度”之和记为S ,则S 的最小值是( ).A .42B .41C .40D .398.对数列{}n a ,如果*k ∃∈N 及12,,,k λλλ∈R L ,使1122n k n k n k k n a a a a λλλ++-+-=+++L 成立,其中*n ∈N ,则称{}n a 为k 阶递归数列.给出下列三个结论: ①若{}n a 是等比数列,则{}n a 为1阶递归数列; ②若{}n a 是等差数列,则{}n a 为2阶递归数列;③若数列{}n a 的通项公式为2n a n =,则{}n a 为3阶递归数列. 其中,正确结论的个数是( ). A .0 B .1 C .2 D .3第Ⅱ卷(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.在ABC △中,BC =AC π3A =,则B =_____.10.已知复数z 满足(1i)1z -⋅=,则z =_____.11.如图,ABC △是⊙O 的内接三角形,PA 是⊙O 的切线,PB 交AC 于点E ,交⊙O 于点D .若 PA PE =,60ABC ∠=o ,1PD =,9PB =,则PA =_____;EC =_____.12.已知函数2()1f x x bx =++是R 上的偶函数,则实数b =_____;不等式(1)||f x x -<的解集为_____.13.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是_____;若该几何体的所有顶点在同一球面上,则球的表面积是_____.14.曲线C 是平面内到定点(0,1)F 和定直线:1l y =-的距离之和等于4的点的轨迹,给出下列三个结论: ① 曲线C 关于y 轴对称;② 若点(,)P x y 在曲线C 上,则||2y ≤; ③ 若点P 在曲线C 上,则1||4PF ≤≤. 其中,所有正确结论的序号是____________.三、解答题共6小题,共80分. 解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)已知函数22π()cos ()sin 6f x x x =--.(Ⅰ)求π()12f 的值;(Ⅱ)若对于任意的π[0,]2x ∈,都有()f x c ≤,求实数c 的取值范围.如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB BC⊥,22AB CD BC==,EA EB⊥.(Ⅰ)求证:AB DE⊥;(Ⅱ)求直线EC与平面ABE所成角的正弦值;(Ⅲ)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出EFEA;若不存在,说明理由.甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是35,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.(Ⅰ)求乙得分的分布列和数学期望;(Ⅱ)求甲、乙两人中至少有一人入选的概率.已知抛物线24y x =的焦点为F ,过点F 的直线交抛物线于A ,B 两点. (Ⅰ)若2AF FB =uu u r uu r,求直线AB 的斜率;(Ⅱ)设点M 在线段AB 上运动,原点O 关于点M 的对称点为C ,求四边形OACB 面积的最小值.已知函数2221()1ax a f x x +-=+,其中a ∈R .(Ⅰ)当1a =时,求曲线()y f x =在原点处的切线方程;(Ⅱ)求()f x 的单调区间;(Ⅲ)若()f x 在[0,)+∞上存在最大值和最小值,求a 的取值范围.若12(0n n i A a a a a ==L 或1,1,2,,)i n =L ,则称n A 为0和1的一个n 位排列.对于n A ,将排列121n n a a a a -L 记为1()n R A ;将排列112n n n a a a a --L 记为2()n R A ;依此类推,直至()n n n R A A =.对于排列n A 和()i n R A (1,2,,1)i n =-L ,它们对应位置数字相同的个数减去对应位置数字不同的个数,叫做n A 和()i n R A 的相关值,记作(,())i n n t A R A .例如3110A =,则 13()011R A =,133(,())1t A R A =-.若(,())1(1,2,,1)i n n t A R A i n =-=-L ,则称n A 为最佳排列.(Ⅰ)写出所有的最佳排列3A ; (Ⅱ)证明:不存在最佳排列5A ;(Ⅲ)若某个21(k A k +是正整数)为最佳排列,求排列21k A +中1的个数.北京市西城区2012年高三二模试卷数学(理科)参考答案及评分标准2012.5一、选择题:本大题共8小题,每小题5分,共40分.1.D ; 2.D ; 3.B ; 4.A ; 5.C ; 6.C ; 7.C ; 8.D . 二、填空题:本大题共6小题,每小题5分,共30分. 9.π4; 10.1i22+; 11.3,4; 12.0,()1,2 13.13,3π; 14.① ② ③.注:11、12、13第一问2分,第二问3分;14题少填不给分. 三、解答题:本大题共6小题,共80分. 15.(本小题满分13分)(Ⅰ)解:22ππππ()cos ()sin cos 1212126f =--==. ………………5分(Ⅱ)解:1π1()[1cos(2)](1cos2)232f x x x =+--- ………………7分1π13[cos(2)cos 2]2cos 2)2322x x x x =-+=+ ………………8分π)3x =+. ………………9分 因为 π[0,]2x ∈,所以 ππ4π2[,]333x +∈, ………………10分所以当 ππ232x +=,即 π12x =时,()f x ……………11分所以 π[0,]2x ∀∈,()f x c ≤等价于c ≤.故当 π[0,]2x ∀∈,()f x c ≤时,c 的取值范围是)+∞. ……………13分16.(本小题满分14分)(Ⅰ)证明:取AB 中点O ,连结EO ,DO .因为EB EA =,所以EO AB ⊥. ……………1分 因为四边形ABCD 为直角梯形,22AB CD BC ==,AB BC ⊥, 所以四边形OBCD 为正方形,所以AB OD ⊥. …2分 所以AB ⊥平面EOD . ………………3分所以AB ED ⊥. ………………4分 (Ⅱ)解:因为平面ABE ⊥平面ABCD ,且 EO AB ⊥,所以EO ⊥平面ABCD ,所以EO OD ⊥. 由,,OB OD OE 两两垂直,建立如图所示的空间直角 坐标系O xyz -. …………5分因为三角形EAB 为等腰直角三角形,所以OA OB OD OE ===,设1OB =,所以 (0,0,0),(1,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,1)O A B C D E -.所以 (1,1,1)EC =-u u u r,平面ABE 的一个法向量为(0,1,0)OD =u u u r . ……………7分 设直线EC 与平面ABE 所成的角为θ,所以||sin |cos ,|||||EC OD EC OD EC OD θ⋅=〈〉==uu u r uuu ruu u r uuu r uu u r uuu r ,即直线EC 与平面ABE . …………9分 (Ⅲ)解:存在点F ,且13EF EA =时,有EC ∥平面FBD . ………10分 证明如下:由111(,0,)333EF EA ==--u u u r u u r ,12(,0,)33F -,所以42(,0,)33FB =-uu r .设平面FBD 的法向量为n (,,)a b c =,则有0,0.BD FB ⎧⋅=⎪⎨⋅=⎪⎩uuu r uurn n 所以 0,420.33a b a z -+=⎧⎪⎨-=⎪⎩取1a =,得(1,1,2)=n . ………………12分 因为 EC ⋅uu u rn (1,1,1)(1,1,2)0=-⋅=,且EC ⊄平面FBD ,所以EC ∥平面FBD . 即点F 满足13EF EA =时,有EC ∥平面FBD . ………………14分 17.(本小题满分13分)(Ⅰ)解:设乙答题所得分数为X ,则X 的可能取值为15,0,15,30-.………………1分35310C 1(15)C 12P X =-==; 2155310C C 5(0)C 12P X ===; 1255310C C 5(15)C 12P X ===; 35310C 1(30)C 12P X ===. ………………5分乙得分的分布列如下:分 155115(15)01530121212122EX =⨯-+⨯+⨯+⨯=. ………………7分 (Ⅱ)解:由已知甲、乙至少答对2题才能入选,记甲入选为事件A ,乙入选为事件B .则223332381()C ()()()555125P A =+=, ………………10分511()12122P B =+=. ………………11分故甲乙两人至少有一人入选的概率4411031()11252125P P A B =-⋅=-⨯=. ……13分 18.(本小题满分13分)(Ⅰ)解:依题意(1,0)F ,设直线AB 方程为1x my =+. ………………1分将直线AB 的方程与抛物线的方程联立,消去x 得2440y my --=. …………3分 设11(,)A x y ,22(,)B x y ,所以 124y y m +=,124y y =-. ① ………………4分 因为2AF FB =uu u r uu r ,所以122y y =-. ② ………………5分 联立①和②,消去12,yy ,得m = ………6分所以直线AB 的斜率是± ………………7分(Ⅱ)解:由点C 与原点O 关于点M 对称,得M 是线段OC 的中点,从而点O 与点C 到直线AB 的距离相等,所以四边形OACB 的面积等于2AOB S △. ……………… 9分 因为12122||||2ABC S OF y y =⨯⋅⋅-△………………10分, ………………12分所以0m =时,四边形OACB 的面积最小,最小值是4. ………………13分 19.(本小题满分14分) (Ⅰ)解:当1a =时,22()1x f x x =+,22(1)(1)()2(1)x x f x x +-'=-+. ………………2分由 (0)2f '=,得曲线()y f x =在原点处的切线方程是20x y -=.…………3分(Ⅱ)解:2()(1)()21x a ax f x x +-'=-+. ………………4分① 当0a =时,22()1xf x x '=+. 所以()f x 在(0,)+∞单调递增,在(,0)-∞单调递减. ………………5分 当0a ≠,21()()()21x a x a f x a x +-'=-+.② 当0a >时,令()0f x '=,得1x a =-,21x=,()f x 与()f x '的情况如下:故()f x 的单调减区间是(,)a -∞-,1(,)a +∞;单调增区间是1(,)a a-. ………7分③ 当0a <时,()f x 与()f x '的情况如下:所以()f x 的单调增区间是1(,)a-∞;单调减区间是1(,)a a --,(,)a -+∞.………………9分 (Ⅲ)解:由(Ⅱ)得, 0a =时不合题意. ………………10分 当0a >时,由(Ⅱ)得,()f x 在1(0,)a单调递增,在1(,)a +∞单调递减,所以()f x 在(0,)+∞上存在最大值21()0f a a=>.设0x 为()f x 的零点,易知2012ax a-=,且01x a <.从而0x x >时,()0f x >;0x x <时,()0f x <.若()f x 在[0,)+∞上存在最小值,必有(0)0f ≤,解得11a -≤≤.所以0a >时,若()f x 在[0,)+∞上存在最大值和最小值,a 的取值范围是(0,1]. ………………12分 当0a <时,由(Ⅱ)得,()f x 在(0,)a -单调递减,在(,)a -+∞单调递增,所以()f x在(0,)+∞上存在最小值()1f a -=-.若()f x 在[0,)+∞上存在最大值,必有(0)0f ≥,解得1a ≥,或1a ≤-.所以0a <时,若()f x 在[0,)+∞上存在最大值和最小值,a 的取值范围是(,1]-∞-. 综上,a 的取值范围是(,1](0,1]-∞-U . ………………14分 20.(本小题满分13分)(Ⅰ)解:最佳排列3A 为110,101,100,011,010,001. ………………3分 (Ⅱ)证明:设512345A a a a a a =,则1551234()R A a a a a a =,因为 155(,())1t A R A =-,所以15||a a -,21||a a -,32||a a -,43||a a -,54||a a -之中有2个0,3个1. 按512345a a a a a a →→→→→的顺序研究数码变化,由上述分析可知有2次数码不发生改变,有3次数码发生了改变. 但是5a 经过奇数次数码改变不能回到自身, 所以不存在5A ,使得155(,())1t A R A =-,从而不存在最佳排列5A . ………………7分 (Ⅲ)解:由211221(0k k i A a a a a ++==L 或1,1,2,,21)i k =+L ,得12121122()k k k R A a a a a ++=L , 2212211221()k k k k R A a a a a a ++-=L ,……2121342112()k k k R A a a a a a -++=L , 22123211()k k k R A a a a a ++=L .因为2121(,())1(1,2,,2)i k k t A R A i k ++=-=L ,所以21k A +与每个21()i k R A +有k 个对应位置数码相同,有1k +个对应位置数码不 同,因此有12121221212||||||||1k k k k k a a a a a a a a k +-+-+-++-+-=+L , 122212222121||||||||1k k k k k k a a a a a a a a k +-+--+-++-+-=+L ,……,132421212||||||||1k k a a a a a a a a k +-+-++-+-=+L , 1223221211||||||||1k k k a a a a a a a a k ++-+-++-+-=+L .以上各式求和得, (1)2S k k =+⨯. ………………10分 另一方面,S 还可以这样求和:设12221,,...,,k k a a a a +中有x 个0,y 个1,则2S xy =. ………………11分 所以21,22(1).x y k xy k k +=+⎧⎨=+⎩解得,1,x k y k =⎧⎨=+⎩或1,.x k y k =+⎧⎨=⎩ 所以排列21k A +中1的个数是k 或1k +. ………………13分北京市西城区高三二模试卷 数学(理科)选填解析一、 选择题 1.【答案】D【解析】解:当{}{}2|log 102A x x x =<=<<,A B B =Q U ,A B ∴⊆,即2c ≥.故选D .2.【答案】D【解析】解:由题可知输出的函数为存在零点的函数, 因为()e 0x f x =>,所以该函数不存在零点; 因为()e 0x f x =-<,所以该函数不存在零点;因为1()f x x x -=+为对勾函数且()2f x ≤-或()2f x ≥,所以该函数不存在零点; 因为当1x =时,1()0f x x x -=-=,所以该函数存在零点. 故选D .3.【答案】B【解析】解:由参数方程的知识可知椭圆方程为221259y x +=,故离心率45c e a ===. 故选B .4.【答案】A【解析】解:当⊥a b 时,()()2,1,440x x x ⋅=⋅-=-+=a b ,即2x =±,所以2x =是2x =±的充分不必要条件. 故选A .5.【答案】C【解析】解:可知()1153565758617072617x =⨯++++++=,()2154565860617273627x =⨯++++++=;1s ==2s =故选C .6.【答案】C【解析】解:由题可知()110f k =+≥,()010f =≥,故1k ≥-,所以概率()()112123p --==--.故选C .7.【答案】C【解析】解:由题可知,设在第()212n n ≤≤层下,S 达到最小值, 而()()23110S n n n =-+-++⨯+⨯⎡⎤⎣⎦L ()()111122n n +++-+-⨯⎡⎤⎣⎦L ()()()()1213122n n n n -⨯-=+-⨯-235315722n n =-+,可知函数的对称轴为536n =,由于n 为整数, 故当9n =时,min 40S =. 故选C .8.【答案】D【解析】解:① 正确.若数列{}n a 为等比数列, 且为1阶递归数列,只需存在1λ∈R , 使得111111n n n n a a a q a q λλ-+=+⇔=, 即1q λ=,满足题意;② 正确.若数列{}n a 为等差数列, 且为2阶递归数列,只需存在12,λλ∈R ,使得()[]()21121112111n n n a a a a n d a nd a n d λλλλ++=+⇔++=+++-⎡⎤⎣⎦, 即121λλ=+且()1221n n λλλ+=+-, 当122,1λλ==-时,满足题意;③ 正确.若数列{}n a 的通项公式为2n a n =, 且为3阶递归数列,只需存在123,,λλλ∈R ,使得()()()2222312213123321n n n n a a a a n n n n λλλλλλ+++=++⇔+=++++, 即1231212142649λλλλλλλ++=⎧⎪+=⎨⎪+=⎩, 当1233,3,1λλλ==-=时,满足题意. 故选D .二、 填空题 9.【答案】π4【解析】解:由正弦定理可知sin sin sin sin 3BC AC B A B =⇒=, 所以π4B =. 故答案为π4.10.【答案】1i 22+ 【解析】解:由题可知111i 1i 1i 1i 1i 2z ++==⋅=--+. 故答案为1i22+.11.【答案】3,4【解析】解:由切割线定理可知219PA PD PB =⋅=⨯,所以3PA =; 因为60PAC ABC ∠=∠=o ,且PA PE =,故3AE AP EP ===,则2D E PE PD =-=,6BE PB PE =-=,由相交弦定理可知312AE EC BE ED EC ⋅=⋅⇒=,所以4EC =. 故答案为3,4.12.【答案】0,()1,2【解析】解:由题可知002bb -=⇒=;当0x ≥,则不等式为()221132012x x x x x -+<⇒-+<⇒<<, 当0x <,则不等式为()221120x x x x -+<-⇒-+<, 因为180∆=-<,故方程无解. 故答案为0,()1,2.13.【答案】13,3π【解析】解:由题可知 ,,PA AB AD 两两垂直,所以1133V PA AB AD =⋅⋅⋅=;可知三棱锥P ABCD-的外接球的直径为PC =所以表面积2224π4π4π3π2PC S r ⎛⎫==⋅=⨯= ⎪⎝⎭⎝⎭. 故答案为13,3π.14.【答案】① ② ③【解析】解:设曲线C 上的动点为(),P x y ,则14y +=,整理的216481x y y =+-+,① 正确.显然()1,P x y -也满足曲线方程, 则曲线C 关于y 轴对称;② 正确.当1y ≥-时,2224xy =-≤,故12y -≤≤;当1y <-时,22212xy =-≥-,故21y -≤<-;综上,2y ≤;PDCBA③ 正确.由题可知41PF y =-+, 因为22y -≤≤,所以013y ≤+≤, 故14PF ≤≤. 故答案为① ② ③.。
2012年北京市各区二模试题分类解析【数学理】(1):集合.pdf

1、认识生态环境破坏对我们将来生活的影响并提高环保意识。
2、学习报告文学写作手法的运用;并以此写作倡导书。
教学难点: 1、真正意义上认识到环保的重要性。
2、认识到环保是我们每个公民的职责;并制止环境破坏者的行为。
过程和方法: 朗读课文后揣摩文章字里行间充盈的感情和中心的关系,体味文中所设置的悬念。
教学方法: 诵读法与讨论法 教学过程: 一、导入: 当我们眼见一个广阔、美丽、充满生机的地方变为荒漠;原本牛马成群,绿林环绕,河流清澈的生命绿洲,现在却是一片死寂,寸草不生,不见飞鸟,令人恐怖;我们会深思,这种生态的巨变,就发生在我们的身边,这就是我们今天要认识的一个地方——罗布泊。
二、初读课文:1、正确识读、理解文中生字: 萧瑟(sè)和煦(xù)干涸(hé)吞噬(shì)裸露(luǒ)戈壁(gē)荡漾(yàng)娱乐(yú) 2、词语释义: 萧瑟:①形容风吹树木的声音;②形容冷落,凄凉。
和煦:温暖,多指阳光、风等。
干涸:(河道、池塘等)没有水了。
吞噬:蚕食、并吞。
裸露:没有东西遮盖。
戈壁滩:蒙古或新疆人称沙漠地区,这种地区尽是沙子和石块,地面缺水,植物稀少。
沧海桑田:大海变成农田,农田变成大海。
比喻世事变化很大。
也说桑田沧海。
3、内容提要: 要比较具体地把握课文内容,可以做一份内容提要,就下面几个问题画出要点:①今日罗布泊是怎样的一个地方?关键词是“沙漠”“神秘”。
②过去罗布泊是怎样的一个地方?关键词是“绿洲”“仙湖”。
③罗布泊为什么会消亡?关键词是“改道”“四盲”。
④同样的悲剧还有哪些?关键词是“青海湖”“月牙泉”。
全文充满了痛惜之情,为罗布泊生态环境的破坏而痛惜,为人们的盲目性造成的悲剧而痛惜。
生态意识,环保意识,可持续发展意识,是课文的基本理念。
课文又涉及西部大开发战略问题,用历史的教训,说明生态环境保护的重要。
2012年佛山二模理科数学试题以及解答(Word超精美版)
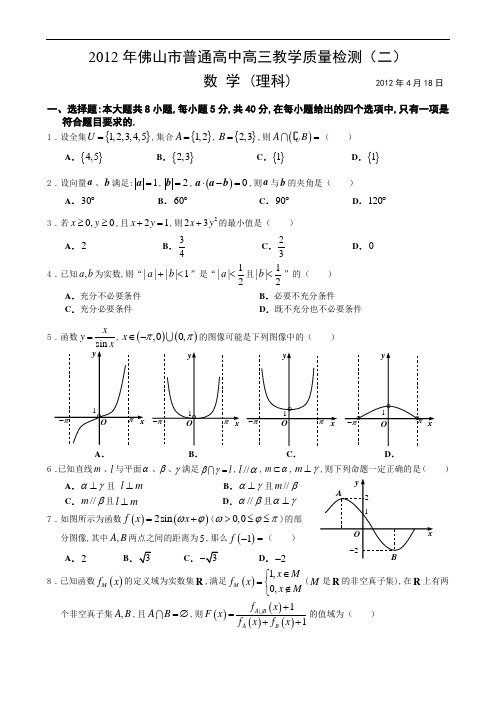
D. 0
4.已知 a, b 为实数,则“| a | | b |1”是“| a | 1 且| b | 1 ”的( )
2
2
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
5.函数 y x , x ,0 0, 的图像可能是下列图像中的( )
sin x
y
y
y
y
1。
O
x
1。
party, the party must follow t he Ge neral rule s. I n all the a ctivities of the party organizati on at all level s, will conti nue t o guide the br oad mas ses of party member s and cadre s, es peci ally leadi ng cadre s, cons cie ntiously study the party Constitution, a bide by the party Constitution, the im plementation of the party Constitution and maintaini ng party Constit ution, shoul d strengt hen party spirit, e nhance the consci ousnes s, purpose aware nes s, power aware ness, situati on aware ness , se nse of res ponsi bility, e arnestly s haring sorrow for the part y,
广州市2012年二模理科数学答案评分标准(内部woed)

2012年广州市普通高中毕业班综合测试(二) 数学(理科)试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.60 10.160- 11.1- 12.2- 13.⎤⎥⎣⎦14.23π⎛⎫⎪⎝⎭15说明:第14题的答案可以是22(3k k ππ⎛⎫+∈ ⎪⎝⎭Z ).三、解答题:16.( 12分) (本小题主要考查三角函数的图象和性质、二倍角的正弦与余弦、同角三角函数关系、两角差的正弦等知识, 考查化归与转化的数学思想方法和运算求解能力)(1) 解:∵函数()f x 的图象的最高点坐标为5,212π⎛⎫⎪⎝⎭, ∴2A =. … 1分 依题意,得函数()f x 的周期11521212T πππ⎛⎫=-= ⎪⎝⎭,…… 2分∴22T πω==. …… 3分 (2)解:由(1)得()2sin 23f x x π⎛⎫=- ⎪⎝⎭. … 4分∵0,2πα⎛⎫∈ ⎪⎝⎭,且4sin 5α=,∴3cos 5α==. …… 5分 ∴24sin 22sin cos 25ααα==, …… 7分 27cos 212sin 25αα=-=-.… 9分 ∴()2sin 23f παα⎛⎫=- ⎪⎝⎭ (10)分2sin 2cos cos 2sin 33ππαα⎛⎫=- ⎪⎝⎭…… 11分=… 12分 17. (12分)(本小题主要考查古典概型、离散型随机变量的分布列与数学期望等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1) 解: 从6条网线中随机任取三条网线共有3620C =种情况. ……… 1分∵1141236++=++=, ∴()1122361164C C P C ξ+===.…… 2分 ∵1242237++=++=∴()1122361174C C P C ξ+===.…… 3分∵1342248++=++=,Q 1P 1QPO N M D CBAC 1D 1∴()123613820C P C ξ+===.…… 4分∵2349++=, ∴()12361910C P C ξ===.……… 5分 ∴P ()()()()()66789P P P P ξξξξξ≥==+=+=+= 113134420104=+++=. 答: 线路信息畅通的概率为34.…… 6分 (2)解:ξ的取值为4,5,6,7,8,9.…… 7分 ∵1124++=, ∴()12361410C P C ξ===.… 8分∵1131225++=++=,∴()123613520C P C ξ+===. …… 9分∴ξ的的分布列为:…… 10分∴1311314567891020442010E ξ=⨯+⨯+⨯+⨯+⨯+⨯ … 11分 6.5=.…… 12分 18.(14分)(本小题主要考查空间线面关系、几何体的三视图、空间角、几何体的体积等知识, 考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)解法1:(1)作MO ⊥平面ABCD ,垂足为O ,连接AO ,则MA O ∠是直线AM 与平面ABCD 所成的角. …… 1分 由于平面ABCD //平面1111ABCD ,故MAO ∠是直线AM 与平面1111A B C D 所成的角.… 2分作MP AB ⊥,垂足为P ,连接PO , ∵AB ⊂平面ABCD ,∴MO AB ⊥. ∵,MO MP M MO =⊂ 平面MOP ,MP ⊂平面MOP ,∴AB ⊥平面MOP . …… 3分由题意知1,MO PO AP ===12,4AD AA ==,在R t △POM 中,PM 在R t △APM 中,AM R t △AOM 中,sin MO MAO AM ∠==∴直线AM 与平面1111A B C D …… 5分(2)延长PO 交CD 于点Q ,连接MQ ,由(1)知AB ⊥平面MOP ∵MQ ⊂平面MOP , ∴AB ⊥MQ .∵//MN AB ,∴,MN MP MN MQ ⊥⊥. …………… 6分11∴PMQ ∠是二面角A MN C --的平面角. …… 7分在△PMQ中,2MQ MP PQ ===,∵2224MP MQ PQ +==, ∴90PMQ ︒∠=. ……… 8分∴二面角A MN C --的余弦值为0. … 9分(3)作1//NP MP 交AB 于点1P ,作1//NQ MQ 交CD 于点1Q , 由题意知多面体MN ABCD -可分割为两个等体积的四棱锥M APQD -和 11N PBCQ -和一个直三棱柱11MPQ NPQ -. 四棱锥M APQD -的体积为113V AP AD MO = 1212133=⨯⨯⨯=, ………… 10分 直三棱柱11MPQ NPQ -的体积为2112222V MP MQ MN === ,…11分 ∴多面体MN ABCD -的体积为122V V V =+2102233=⨯+=. …………… 12分长方体1111ABCD A BC D -的体积为3142432V AB BC AA ==⨯⨯= . ……… 13分 ∴建筑物的体积为31063V V +=. …………… 14分 解法2:(1)以点D 为原点,DA 所在直线为x 轴,DC 所在直线为y 轴,1D D 所在直线为z 轴,建立空间直角坐标系D xyz -(如图),作MO ⊥平面ABCD ,垂足为O , 作OP AB ⊥,垂足为P ,依题意知1MO OP AP ===,12,4AD AA ==,则()()0,0,0,2,0,0,D A ()()1,1,1,1,3,1M N ,()12,0,4A -. …………… 1分∴()1,1,1AM =-. … 2分∵1AA ⊥平面1111A B C D , ∴平面1111A B C D 的一个法向量为()10,0,4AA =-.……… 3分设直线AM 与平面1111A B C D 所成角为θ,则sin θ=11AM AA AM AA == …… 4分 ∴直线AM 与平面1111A B C D.…………(2)由(1)知()()0,2,0,1,1,1MN DM ==,设平面ABNM 的法向量为1n (),,x y z =,由1n 0MN = ,1n 0AM = ,得0,20.x y z y -++=⎧⎨=⎩令1x =,则1,0z y ==.∴平面ABNM 的一个法向量为1n ()1,0,1=. …… 6分设平面CDMN 的法向量为2n (),,x y z =,由2n 0DM = ,2n 0MN = ,得0,20.x y z y ++=⎧⎨=⎩令1x =,则1,0z y =-=. ∴平面CDMN 的一个法向量为2n ()1,0,1=-.… 7分 ∵1n 2n ()110110=⨯++⨯-=,∴平面ABNM ⊥平面CDMN .…… 8分∴二面角A MN C --的余弦值为0. ……… 9分 (3)如图将多面体MN ABCD -补成一个直三棱柱1ADQ BCQ -,依题意知1111AQ DQ BQ CQ MQ NQ ======,2AD =,14AA =, 多面体MN ABCD -的体积等于直三棱柱1ADQ BCQ -的体积减去两个等体积的三 棱锥M ADQ -和1N BCQ -的体积.∵2224AQ DQ AD +==,∴90AQD ︒∠=. ∴直三棱柱1ADQ BCQ -的体积为1114422V AQ DQ AB === ,……… 10分三棱锥M ADQ -的体积为2V =11111132323AQ DQ MQ =⨯= .…… 11分∴多面体MN ABCD -的体积为V =122102433V V -=-=. …… 12分长方体1111ABCD A BC D -的体积为3142432V AB CD AA ==⨯⨯= . … 13分 ∴建筑物的体积为31063V V +=. …… 14分19. (14分)(本小题主要考查直线、椭圆、抛物线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力) (1)解法1:由22,4y x m x y=+⎧⎨=⎩消去y ,得2840x x m --=. …… 1分 ∵直线l 与抛物线2C 只有一个公共 ∴28440m ∆=+⨯=,解得4m =-. …… 3分 ∴直线l 的方程为24y x =-.…… 4分解法2:设直线l 与抛物线2C 的公共点坐标为()00,x y , 由214y x =,得'12y x =, ∴直线l 的斜率0'012x x k y x ===. …… 1分 依题意得0122x =,解得04x =.… 2分把04x =代入抛物线2C 的方程,得04y =. ∵点()00,x y 在直线l 上,∴424m =⨯+,解得4m =-. …… 3分 ∴直线l (2)解法1:∵抛物线2C 的焦点为()10,1F ,依题意知椭圆1C 的两个焦点的坐标为()()120,1,0,1F F -. 设点()10,1F 关于直线l 的对称点为()'100,Fx y , 则0000121,12 4.22y x y x -⎧⨯=-⎪⎪⎨+⎪=⨯-⎪⎩…… 7分解得004,1.x y =⎧⎨=-⎩∴点()'14,1F -. ……… 8分∴直线l 与直线'12:1F F y =-的交点为03,12P ⎛⎫-⎪⎝⎭. 由椭圆的定义及平面几何知识得:椭圆1C 的长轴长'12122a PF PF PF PF =+=+'1F ≥ 其中当点P 与点0P 重合时,上面不等式取等号. ∴2a ≥. ∴112e a =≤. 故当2a =时,max 12e =… 12分此时椭圆1C 的方程为22143y x +=,点P 的坐标为3,12⎛⎫- ⎪⎝⎭.… 14分解法2:∵抛物线2C 的焦点为()10,1F ,依题意知椭圆1C 的两个焦点的坐标为()()120,1,0,1F F - 5分设椭圆1C 的方程为()2222111y x a a a +=>-, … 6分 由222224,11y x y x aa =-⎧⎪⎨+=⎪-⎩消去y ,得()()()()22222541611160a x a x a a ---+--=.(*) … 7分 由()()()()222221614541160a a a a ⎡⎤∆=-----≥⎣⎦, …… 8分得425200a a -≥. ……… 9分 解得24a ≥.∴2a ≥. …………… 10分 ∴112e a =≤. …………… 11分 当2a =时,max12e =,此时椭圆1C 的方程为22143y x +=. …………… 12分把2a =代入方程(*),解得32x =,1y =-. …………… 13分 ∴点P 的坐标为3,12⎛⎫- ⎪⎝⎭. …………… 14分 20. (本小题满分14分)(本小题主要考查函数和方程、导数、函数的极值等知识, 考查函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力)(1)解:函数()f x 的定义域为()0,+∞. …………… 1分()2111ax x f x ax x x--'=-+=-. …………… 2分① 当0a =时,()1xf x x+'=,∵0,x > ∴()'0f x > ∴ 函数()f x 单调递增区间为()0,+∞. …………… 3分② 当0a ≠时,令()0f x '=得210ax x x---=, ∵0,x >∴210ax x --=. ∴14a ∆=+. (ⅰ)当0∆≤,即14a ≤-时,得210ax x --≤,故()0f x '≥, ∴ 函数()f x 的单调递增区间为()0,+∞. …………… 4分 (ⅱ)当0∆>,即14a >-时,方程210ax x --=的两个实根分别为1x =2x =. …………… 5分若104a -<<,则120,0x x <<,此时,当()0,x ∈+∞时,()0f x '>. ∴函数()f x 的单调递增区间为()0,+∞, …………… 6分 若0a >,则120,0x x <>,此时,当()20,x x ∈时,()0f x '>,当()2,x x ∈+∞时,()0,f x '<∴函数()f x 的单调递增区间为0,⎛ ⎝⎭,单调递减区间为⎫+∞⎪⎪⎝⎭.…………… 7分综上所述,当0a >时,函数()f x 的单调递增区间为10,2a ⎛⎫⎪ ⎪⎝⎭,单调递减区间为⎫+∞⎪⎪⎝⎭; 当0a ≤时,函数()f x 的单调递增区间为()0,+∞,无单调递减区间. ………… 8分(2)解:由(1)得当0a ≤时,函数()f x 在()0,+∞上单调递增,故函数()f x 无极值;…………… 9分当0a >时,函数()f x 的单调递增区间为⎛ ⎝⎭,单调递减区间为⎫+∞⎪⎪⎝⎭;则()f x 有极大值,其值为222221()ln 2f x x ax x =-+,其中212x a=. … 10分 而22210ax x --=,即2221ax x =+,∴2221()ln 2x f x x -=+. …………… 11分 设函数1()ln (0)2x h x x x -=+>,则'11()02h x x =+>, …………… 12分 则1()ln 2x h x x -=+在()0,+∞上为增函数.又(1)0h =,则()0h x >等价于1x >. ∴2()f x =221ln 2x x -+0>等价于21x >. …………… 13分 即在0a >时,方程210ax x --=的大根大于1,设2()1x ax x ϕ=--,由于()x ϕ的图象是开口向上的抛物线,且经过点(0,1)-,对称 轴102x a=>,则只需(1)0ϕ<,即110a --<,解得2a <,而0a >, 故实数a 的取值范围为()0,2. ……………… 14分说明:若采用下面的方法求出实数a 的取值范围的同样给1分.1.1122a a =++()0,+∞是减函数,而112a +=时,2a =,故112a>的解集为()0,2,从而实数a 的取值范围为()0,2.2.直接解不等式112a>,而0a >,通过分类讨论得出实数a 的取值范围为()0,2.21. (本小题满分14分)(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1)解:由于对任意(),1,1x y ∈-,都有()()1x y f x f y f xy ⎛⎫--=⎪-⎝⎭, 令0x y ==,得()()()00000100f f f f -⎛⎫-==⎪-⨯⎝⎭,解得()00f =. …………… 1分 令0x =,得()()()0010y f f y f f y y ⎛⎫--==- ⎪-⨯⎝⎭,∵()00f =,∴()()0f y f y -=-,即()()f y f y -=-. …………… 2分 ∴函数()f x 是奇函数. …………… 3分 (2)解:先用数学归纳法证明01n a <<.① 当1n =时,112a =,得101a <<, 结论成立. ② 假设n k =时, 结论成立, 即01k a <<, 当1n k =+时, 由于01k a <<, 12201kk ka a a +=>+,又1222121k kk kk a a a a a +=<==+. ∴101k a +<<.即1n k =+时, 结论也成立.由①②知对任意n ∈N *, 01n a <<. …………… 4分 求数列(){}n f a 的通项公式提供下面两种方法.法1:()()()12211n n n n n n n a a a f a f f a a a +⎛⎫--⎛⎫== ⎪ ⎪ ⎪+--⎝⎭⎝⎭ ()()n n f a f a =--.…………… 5分 ∵函数()f x 是奇函数, ∴()()n n f a f a -=-.∴()1n f a +()2n f a =. …………… 6分 ∴数列(){}n f a 是首项为()1112f a f ⎛⎫== ⎪⎝⎭,公比为2的等比数列. ∴数列(){}n f a 的通项公式为()12n n f a -=. …………… 7分法2: ∵()()1111n n n n n n a a f a f a f a a +++⎛⎫--=⎪-⎝⎭…………… 5分22221211n n n n n a a a f a a ⎛⎫- ⎪+ ⎪= ⎪- ⎪+⎝⎭321n n n a a f a ⎛⎫-= ⎪-⎝⎭ =()n f a , ∴()1n f a +()2n f a =. …………… 6分 ∴数列(){}n f a 是首项为()1112f a f ⎛⎫== ⎪⎝⎭,公比为2的等比数列. ∴数列(){}n f a 的通项公式为()12n n f a -=. …………… 7分(3)证法1:由(2)知01n a <<,∵1221nn n n na a a a a +-=-+()22101n n n a a a -=>+, ∴1n n a a +>. …………… 8分∴111,1(22n a a n =<<∈N *,且2)n ≥ ∴10(,2n m a a n m <-<∈N *,且)n m >. …………… 9分当2k ≥且k ∈ N *时,12kk k k a a a a A a k+++-=-()()()121k k k k a a a a a a k--+-++-= …………… 10分12k k -<…………… 11分 1122k =-12<.∴102k k a A <-<. …………… 12分∵110a A -=, ∴当2n ≥时,11102n niii i n a A ==-<-<∑∑. …………… 13分 ∴当2n ≥时,1112nni i i i n a A ==--<∑∑. …………… 14分 证法2:由(2)知01n a <<,∵1221nn n n na a a a a +-=-+()22101n n n a a a -=>+, ∴1n n a a +>. …………… 8分∴111,1(22n a a n =<<∈N *,且2)n ≥ ∴1(,2n m a a n m -<∈N *). …………… 9分下面用数学归纳法证明不等式1112n ni i i i n a A ==--<∑∑成立. ①当2n =时,左边1212121122a a a a a a a +⎛⎫=+-+=- ⎪⎝⎭111222<⨯<=右边. ∴2n =时,不等式成立. …………… 10分 ②假设(2,n k k k =≥∈N *)时,不等式成立,即1112k ki i i i k a A ==--<∑∑, 则1n k =+时, 左边=1111k k i i i i a A ++==-∑∑1211111k kk i k i i i a a a a a A k ++==+++=+--+∑∑ …………… 11分()()1121111k k k k i i i i k a a a a a A k +==+-+++⎛⎫=-+ ⎪+⎝⎭∑∑ ()()()111211111k ki i k k k k i i a A a a a a a a k +++==≤-+-+-++-+∑∑ ………… 12分 ()111211121k k k k k a a a a a a k +++-<+-+-++-+ 1111121222k k -⎛⎫<++++ ⎪+⎝⎭11212k k k -=+⨯+ ()1112221k k -=+-+ 1122k -<+ ()112k +-==右边. …………… 13分∴1n k =+时,不等式也成立.由①②知,当2n ≥时,1112n n ii i i n a A ==--<∑∑成立. …………… 14分 证法3:由(2)知()011,2,3,,k a k n <<= ,故对11k n ≤≤-,有110,0k n i i i i k ak a n k ==+<<<<-∑∑. …………… 8分由于对任意0,0x y >>,有{}max ,x y x y -<,其中{}max ,x y 表示x 与y 的较大值. 于是对11k n ≤≤-,有 11111kn n k i i i i k A A a a n k n ==+⎛⎫-=-- ⎪⎝⎭∑∑ …………… 9分 11111n ki i i k i a a n k n =+=⎛⎫=-- ⎪⎝⎭∑∑ 11111max ,n k i i i k i a a n k n =+=⎧⎫⎛⎫<-⎨⎬ ⎪⎝⎭⎩⎭∑∑ …………… 10分()111max ,n k k nk n ⎧⎫⎛⎫≤--⎨⎬ ⎪⎝⎭⎩⎭1(1,2,3,,1)k k n n=-=- . …………… 11分 故111n n nii n i i i i a A nA A ===-=-∑∑∑()()()121n n n n A A A A A A -=-+-++- …… 12分 121n n n n A A A A A A -≤-+-++-121111n n n n -⎛⎫⎛⎫⎛⎫<-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭…………… 13分 ()()12311n n n ++++-=--()()121n n n n -=--12n -=.…………… 14分。
高三二模数学科试卷质量分析

高三二模数学科试卷质量分析第一篇:高三二模数学科试卷质量分析高三二模数学科试卷质量分析选择题与填空题具有题小量大、适度、全面考查的特点。
呈现基础、全面、核心、人文、和谐的特征。
试题简约、凝练、直击核心,留有恰当的思维、探究、应用、操作空间,有一定的综合度、开放度和创新度。
呈现方式多样化,价值取向明确。
选择题是针对学生薄弱点设置干扰点,又适当设置提示项为学生灵活解题提供条件。
选择题中的大多数题具有多种解法。
为基础扎实、思维活跃的学生提供了充分发挥聪明才智、快速灵活解题的平台。
选择题这一题型在培养和发展学生的思维能力上有其独特和不可替代的教育功能和评价功能。
填空题作为基本题型,与选择题共同肩负起基础、全面、核心、简约、和谐评价功能的同时,从解题过程看,已兼具解答题的特征。
从某种意义上说,具有更大的思维空间和开放度。
关注填空题的命题特点及设计走向、分析解题思路、总结归纳常用的解法和技能很有必要。
其功能是比较全面地、高效地对学生基本核心的学段学习目标进行考查,同时,由试题的立意、定位、取材、背景、问题设置、呈现方式共同蕴含的题感,渲染着一种氛围,学生的心理情绪和思维状态都会渐入佳境,为顺利完成解答题做好了准备。
第11题,常规题,难度小,学生得分率高。
第12小题,难度较小,只是部分学生粗心大意,把把-写成了,导致失分。
第13小题也是一道常规题,学生得分率较高。
第14题是一个归纳推理题,部分学生的归纳总结能力较差,把1+ + +…+﹤弄成了1+ + +…+﹤,反映出他们没有明确对应关系。
第15小题,常规题,以考查学生的基础知识和基本技能为主。
学生失分率较小。
文科的填空题都是一些基础题,以考查学生的基础知识为主。
第16题,第一问得分较高,考查等差数列通项公式的简单运用,个别学生计算错误,大部分为全分6分。
第二小问考查分组组合法求数列和,部分学生与错位相减法和相混淆,且运算能力不太过关。
结论错误本题平均可达9分左右。
2012考研数学二真题及答案解析

dy
,所以
=
2x
dx ey +1
(10)计算
lim
x→∞
n
⎛ ⎜⎝
1
1 +n
2
+
22
1 +
n2
+…+
n2
1 +
n2
⎞ ⎟⎠
= ________。
3
π
【答案】:
4
∑ ∫ 【解析】:原式 = lim 1
n→∞ n
n
1
i=1
1
+
⎛ ⎜⎝
i n
⎞2 ⎟⎠
=
1 dx 0 1+ x2
=
arctan x 1 0
三、解答题:15—23 小题,共 94 分.请将解答写在答.题.纸.指定位置上.解答应写出文字说明、证明过程或 演算步骤. (15)(本题满分 10 分)
已知函数 f (x) = 1+ x − 1 ,记 a = lim f (x)
sin x x,
x→0
(1)求 a 的值
(2)若当 x → 0 时, f (x) − a 是 xk 的同阶无穷小,求 k
D
∫∫ ∫ ∫ 【解析】:
xydσ = π dθ 1+cosθ r cosθ ⋅ r sin θ ⋅ rdr
0
0
D
∫ = 1 π sin θ ⋅ cosθ ⋅ (1 + cosθ )4 dθ 40
6
∫ = 16
πθ sin
cos θ
(2 cos2
θ
− 1) cos8
θ
dθ
022
2
22
π
2012深圳二模理科数学含答案

2012年深圳市高三年级第二次调研考试数学(理科)2012.4本试卷共6页,21小题,满分150分.考试用时120分钟.一、选择题:本大题共8 个小题,每小题5 分,共40 分.1.集合{m i|*}(其中i是虚数单位)中元素的个数是n NA.1 B.2 C.4 D.无穷多个2.设随机变量,若,则c等于A.0 B.1 C.2 D.33.已知命题p:“存在正实数a,b,使得;lg(a+b)=lga+lgb”;命题q:“空间两条直线异面的充分必要条件是它们不同在任何一个平面内”.则它们的真假是A.p,q都是真命题B.p是真命题,q是假命题C.p,q都是假命题D.p是假命题,q是真命题4.在学校的一次演讲比赛中,高一、高二、高三分别有1名、2名、3名同学获奖,将这六名同学排成一排合影,要求同年级的同学相邻,那么不同的排法共有A.6种B.36种C.72种D.120种5.设,,,若a,1,b成等比数列,且c,1,d 成等差数列,则下列不等式恒成立的是6.设函数若f(x)的值域为R,则常数a的取值范围是7.如图1,直线l和圆c,当l从0 开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过900)时,它扫过的圆内阴影部分的面积S 是时间t的函数,这个函数的图象大致是8.如果函数y=|x|-1的图象与方程的曲线恰好有两个不同的公共点,则实数的取值范围是二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题:第9、10、11、12、13题为必做题.9.在实数范围内,方程|x |+|x +1|=1的解集是 . 10.某机器零件的俯视图是直径为24 mm 的圆(包括圆心),主 视图和侧视图完全相同,如图2所示.则该机器零件的体积是______mm 3(结果保留 ).11.已知平面向量a ,b 满足条件a +b =(0,1),a -b =(-1,2),则ab =_______12.执行图3中程序框图表示的算法,若输入m=5533,n=2012,则输出d =_____(注:框图中的赋值符号“=”也可以写成“←”或“:=”)13.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验. 根据收集到的数据(如下表),由最小二乘法求得回归方程.现发现表中有一个数据模糊看不清,请你推断出该数据的值为 . (二)选做题:第14、15题为选做题,考生只能从中选做一题. 14.(坐标系与参数方程选做题)在极坐标系中,已知直线把曲线所围成的区域分成面积相等的两部分,则常数a的值是 . 15.(几何证明选讲选做题)如图4,AB 是圆O 的直径, 弦AD 和BC 相交于点P ,连接CD .若∠APB =120°, 则C D A B等于 .三、解答题:本大题共 6 小题,满分80 分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知函数(1)求f(x)的最大值;(2)设△ABC中,角A、B的对边分别为a、b,若B=2A,且,求角C的大小.17.(本小题满分12分)深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3 个是旧球(即至少用过一次的球).每次训练,都从中任意取出2 个球,用完后放回.(1)设第一次训练时取到的新球个数为,求的分布列和数学期望;(2)求第二次训练时恰好取到一个新球的概率.18.(本小题满分14分)如图5,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形,其中A与A '重合,且BB'<DD'<CC'.(1)证明AD'//平面BB'C'C,并指出四边形AB'C'D’的形状;(2)如果四边形中AB'C'D’中,,正方形的边长为,求平面ABCD与平面AB'C'D’所成的锐二面角的余弦值.19.(本小题满分14分)已知数列满足:,且(1)求通项公式an(2)设的前n项和为S n,问:是否存在正整数m、n,使得若存在,请求出所有的符合条件的正整数对(m,n),若不存在,请说明理由.20.(本小题满分14分)如图6,已知动圆M过定点F(1,0)且与x轴相切,点F 关于圆心M 的对称点为F',动点F’的轨迹为C.(1)求曲线C的方程;(2)设是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P 、Q.①证明:直线PQ的斜率为定值;②记曲线C位于P 、Q两点之间的那一段为l.若点B在l上,且点B到直线PQ的距离最大,求点B的坐标.21.(本小题满分14分)已知函数f(x)=x-xlnx ,,其中表示函数f(x)在x=a处的导数,a为正常数.(1)求g(x)的单调区间;(2)对任意的正实数,且,证明:(3)对任意的2012年深圳市高三年级第二次调研考试数学(理科)参考答案及评分标准 2012.4一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 题号 1 2 3 4 5 6 7 8 答案CBACDADB二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题:第9、10、11、12、13题为必做题.9.]0,1[- 10.π2880 11.1- 12.503 13.68 (注:第9题答案也可以写成}01|{≤≤-x x ,如果写成01≤≤-x ,不扣分.) (二)选做题:第14、15题为选做题,考生只能从中选做一题. 14.(坐标系与参数方程选做题)1- 15.(几何证明选讲选做题)21三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数)6cos(sin )(π-+=x x x f ,R ∈x .(1)求)(x f 的最大值;(2)设△ABC 中,角A 、B 的对边分别为a 、b ,若A B 2=且)6(2π-=A f a b ,求角C 的大小.解:(1))6cos(sin )(π-+=x x x f x x x sin 21cos 23sin ++= ……………………2分⎪⎪⎭⎫ ⎝⎛+=x x cos 21sin 233)6sin(3π+=x .(注:也可以化为)3cos(3π-x ) …4分所以)(x f 的最大值为3. …………………………………………………………6分(注:没有化简或化简过程不全正确,但结论正确,给4分)(2)因为)6(2π-=A f a b ,由(1)和正弦定理,得A B 2sin32sin =.………………7分又A B 2=,所以A A 2sin 322sin =,即A A A 2sin3cos sin =, ………………9分而A 是三角形的内角,所以0sin ≠A ,故A A sin 3cos =,33tan =A , ………………11分所以6π=A ,32π==A B ,2ππ=--=B A C . ……………………………………12分17.(本小题满分12分)深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回. (1)设第一次训练时取到的新球个数为ξ,求ξ的分布列和数学期望; (2)求第二次训练时恰好取到一个新球的概率.解:(1)ξ的所有可能取值为0,1,2. ………………………………………1分设“第一次训练时取到i 个新球(即i =ξ)”为事件i A (=i 0,1,2).因为集训前共有6个篮球,其中3个是新球,3个是旧球,所以51)0()(26230====C C P A P ξ, ………………………………………3分53)1()(2613131====C C C P A P ξ, ………………………………………5分51)2()(26232====C C P A P ξ. ………………………………………7分所以ξ的分布列为(注:不列表,不扣分)ξ 012P515351ξ的数学期望为1512531510=⨯+⨯+⨯=ξE . ……………………………………8分(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B . 则“第二次训练时恰好取到一个新球”就是事件B A B A B A 210++.而事件B A 0、B A 1、B A 2互斥,所以,)()()()(210210B A P B A P B A P B A B A B A P ++=++.由条件概率公式,得253535151|()()(261313000=⨯=⨯==C C C A B P A P B A P ), …………………………………9分 2581585353|()()(261412111=⨯=⨯==C C C A B P A P B A P ), …………………………………10分 151315151|()()(261511222=⨯=⨯==C C C A B P A P B A P ). …………………………………11分所以,第二次训练时恰好取到一个新球的概率为7538151258253)(210=++=++B A B A B A P . …………………………………12分18.(本小题满分14分)如图5,已知正方形ABCD 在水平面上的正.投影(投影线垂直于投影面)是四边形''''D C B A ,其中A 与'A 重合,且'''CC DD BB <<.(1)证明//'AD 平面C C BB '',并指出四边形'''D C AB 的形状; (2)如果四边形'''D C AB 中,2'=AD ,5'=AB ,正方形ABCD 的边长为6,求平面ABCD 与平面'''D C AB 所成的锐二面角θ的余弦值. 证明:(1)依题意,⊥'BB 平面'''D C AB ,⊥'CC 平面'''D C AB , ⊥'DD 平面'''D C AB ,所以'//'//'DD CC BB . ……………2分(法1)在'CC 上取点E ,使得'DD CE =, 连结BE ,E D ',如图5-1.因为'//DD CE ,且'DD CE =,所以E CDD '是平行四边形,DC E D //',且DC E D ='.又ABCD 是正方形,AB DC //,且AB DC =,所以AB E D //',且AB E D =',故'ABED 是平行四边形, ………………………………4分从而BE AD //',又⊂BE 平面C C BB '',⊄'AD 平面C C BB '',所以//'AD 平面C C BB ''. ………………………………………………………………6分四边形'''D C AB 是平行四边形(注:只需指出四边形'''D C AB 的形状,不必证明).……7分 (法2)因为'//'CC DD ,⊂'CC 平面C C BB '',⊄'DD 平面C C BB '', 所以//'DD 平面C C BB ''.因为ABCD 是正方形,所以BC AD //,又⊂BC 平面C C BB '',⊄AD 平面C C BB '', 所以//AD 平面C C BB ''. ………………………………………………………………4分而⊂'DD 平面'ADD ,⊂AD 平面'ADD ,D AD DD = ',所以平面//'ADD 平面C C BB '',又⊂'AD 平面'ADD ,所以//'AD 平面C C BB ''. …………6分四边形'''D C AB 是平行四边形(注:只需指出四边形'''D C AB 的形状,不必证明).……7分 解:(2)依题意,在Rt △'ABB 中,1)5()6(''2222=-=-=AB ABBB ,在Rt △'ADD 中,2)2()6(''2222=-=-=AD ADDD ,所以3021''''=-+=-+=AA DD BB CC .15-图CD)'(A A B'C 'D 'B E(注:或312''''=+=+=+=BB DD EC CE CC ) ………………………………………8分 连结AC ,'AC ,如图5-2, 在Rt △'ACC 中,33)32(''2222=-=-=CC ACAC .所以222''''AB C B AC =+,故'''C B AC ⊥.……10分 (法1)延长CB ,''B C 相交于点F , 则31''''==CC BB FC FB ,而2''=C B ,所以223'=FC .连结AF ,则AF 是平面ABCD 与平面'''D C AB 的交线.在平面'''D C AB 内作AF G C ⊥',垂足为G , 连结CG .因为⊥'CC 平面'''D C AB ,⊂AF 平面'''D C AB ,所以AF CC ⊥'. 从而⊥AF 平面G CC ',AF CG ⊥.所以'CGC ∠是平面ABCD 与平面'''D C AB 所成的一个锐二面角. …………………………12分在Rt △F AC '中,553223)3(2233'''22=⎪⎭⎫⎝⎛+⨯=⨯=AFFC A C G C ,在Rt △G CC '中,53035533''2222=⎪⎪⎭⎫⎝⎛+=+=G C CC CG .所以66''cos cos ==∠=CGG C CGC θ,即平面ABCD 与平面'''D C AB 所成的锐二面角θ的余弦值为66.……………………14分(法2)以'C 为原点,A C '为x 轴,''B C 为y 轴,C C '为z 轴, 建立空间直角坐标系(如图5-3),则平面'''D C AB 的一个法向量)1,0,0(=n .设平面ABCD 的一个法向量为),,(z y x =m , 因为)0,0,3(A ,)1,2,0(B ,)3,0,0(C ,所以)1,2,3(-=AB ,)2,2,0(-=BC ,而AB ⊥m ,BC ⊥m , 所以0=∙AB m且0=∙BC m,25-图CD)'(A A B'C 'D 'B FG35-图CD)'(A A B'C 'D 'B yxz即⎪⎩⎪⎨⎧=+-=++-022023z y z y x ,取1=z ,则2=y ,3=x ,所以平面ABCD 的一个法向量为)1,2,3(=m .(注:法向量不唯一,可以是与)1,2,3(=m 共线的任一非零向量)……………………12分661001)2()3(|110203||||||,cos |cos 222222=++⨯++⨯+⨯+⨯==><=∙n m n mn m ||θ.所以平面ABCD 与平面'''D C AB 所成的锐二面角θ的余弦值为66. …………………14分(法3)由题意,正方形ABCD 在水平面上的正.投影是四边形''''D C B A , 所以平面ABCD 与平面'''D C AB 所成的锐二面角θ的余弦值ABCDD C AB S S '''=. …………………12分而6)6(2==ABCD S ,632''''''=⨯=⨯=AC C B S D C AB ,所以66cos =θ,所以平面ABCD 与平面'''D C AB 所成的锐二面角θ的余弦值为66. …………………14分19.(本小题满分14分)已知数列}{n a 满足:11=a ,22=a ,且3)1)(cos 2(2+-+=+n n a n a π,*N ∈n . (1)求通项公式n a ;(2)设}{n a 的前n 项和为n S ,问:是否存在正整数m 、n ,使得122-=n n mS S ?若存在,请求出所有的符合条件的正整数对),(n m ,若不存在,请说明理由. 解:(1)当n 是奇数时,1cos -=πn ;当n 是偶数时,1cos =πn .所以,当n 是奇数时,22+=+n n a a ;当n 是偶数时,n n a a 32=+. ……………………2分 又11=a ,22=a ,所以1a ,3a ,5a ,…,12-n a ,…是首项为1,公差为2的等差数列;2a ,4a ,6a ,…,n a 2,…是首项为2,公比为3的等比数列. ……………………4分所以,⎪⎩⎪⎨⎧⨯=-为偶数为奇数n n n a nn ,32,12. ………………………………………………6分(2)由(1),得)()(24212312n n n a a a a a a S +++++++=-)3262()]12(31[1-⨯++++-+++=n n132-+=n n,13321321122212-+=⨯--+=-=---n n a S S n n n n n n . ………………………8分所以,若存在正整数m 、n ,使得122-=n n mS S ,则133211313211212122-+⨯+=-+-+==----n n n S S m n n n n n n 3332111=⨯+≤--n n . ………………9分显然,当1=m 时,122122)13(113--=-+⨯≠-+=n n nn S n n S ;当2=m 时,由1222-=n n S S ,整理得1321-=-n n .显然,当1=n 时,11013211-=≠=-; 当2=n 时,1233212-==-,所以)2,2(是符合条件的一个解. ……………………………11分当3≥n 时, +⨯+⨯+=+=----2211111221)21(3n n n n C C2111421--++≥n n C C 3422+-=n n1)2(22-+-=n n12->n . …………………………12分当3=m 时,由1223-=n n S S ,整理得1=n , 所以)1,3(是符合条件的另一个解.综上所述,所有的符合条件的正整数对),(n m ,有且仅有)1,3(和)2,2(两对. ……14分 (注:如果仅写出符合条件的正整数对)1,3(和)2,2(,而没有叙述理由,每得到一组正确的解,给2分,共4分) 20.(本小题满分14分)如图6,已知动圆M 过定点)1,0(F 且与x 轴相切,点F 关于圆心M 的对称点为'F ,动点'F 的轨迹为C .(1)求曲线C 的方程;(2)设),(00y x A 是曲线C 上的一个定点,过点A 任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P 、Q .① 证明:直线PQ 的斜率为定值;② 记曲线C 位于P 、Q 两点之间的那一段为L .若点B 在L 上,且点B 到直线PQ 的距离最大,求点B 的坐标.解:(1)(法1)设),('y x F ,因为点)1,0(F 在圆M 上, 且点F 关于圆心M 的对称点为'F ,所以)21,2(+y x M , …………1分且圆M 的直径为22)1(|'|-+=y x FF .…………2分由题意,动圆M 与y 轴相切,16-图M∙'∙F xyOF∙NE所以2)1(2|1|22-+=+y x y ,两边平方整理得:y x 42=,所以曲线C 的方程为y x 42=. ………………………………………………5分 (法2)因为动圆M 过定点)1,0(F 且与x 轴相切,所以动圆M 在x 轴上方, 连结'FF ,因为点F 关于圆心M 的对称点为'F ,所以'FF 为圆M 的直径. 过点M 作x MN ⊥轴,垂足为N ,过点'F 作x E F ⊥'轴,垂足为E (如图6-1).在直角梯形'EOFF 中,1|'||||'|||2||2|'|+=+===E F FO E F MN MF F F ,即动点'F 到定点)1,0(F 的距离比到x 轴的距离大1. …………………………………………3分又动点'F 位于x 轴的上方(包括x 轴上),所以动点'F 到定点)1,0(F 的距离与到定直线1-=y 的距离相等.故动点'F 的轨迹是以点)1,0(F 为焦点,以直线1-=y 为准线的抛物线.所以曲线C 的方程为y x 42=. ………………………………………………5分 (2)①(法1)由题意,直线AP 的斜率存在且不为零,如图6-2.设直线AP 的斜率为k (0≠k ),则直线AQ 的斜率为k -. ……………………………6分 因为),(00y x A 是曲线C :y x 42=上的点, 所以4200x y =,直线AP 的方程为)(4020x x k x y -=-.由⎪⎩⎪⎨⎧-=-=)(440202x x k x y yx , 解之得⎪⎩⎪⎨⎧==4200x y x x 或⎪⎩⎪⎨⎧+-=+-=4)4(4200k x y k x x , 所以点P 的坐标为)4)4(,4(200k x k x +-+-, 以k -替换k ,得点Q 的坐标为)4)4(,4(200k x k x +--. ………………………………8分所以直线PQ 的斜率23216)4()4(4)4(4)4(00002020x k kx k x k x k x k x k PQ -=-=+----+--+=为定值.………………10分(法2)因为),(00y x A 是曲线C :y x 42=上的点,所以4200x y =,)4,(200x x A .又点P 、Q 在曲线C :y x 42=上,所以可设)4,(211x x P ,)4,(222x x Q , …………6分而直线AP ,AQ 的倾斜角互补,26-图M∙'∙F xyOF∙PQA所以它们的斜率互为相反数,即02222012214444x x x x x x x x ---=--,整理得0212x x x -=+. …………8分所以直线PQ 的斜率2424440021122122x x x x x x x x k PQ -=-=+=--=为定值. ………………10分 ②(法1)由①可知,P )4)4(,4(200k x k x +-+-,Q )4)4(,4(200k x k x +--,20x k PQ -=,所以直线PQ 的方程为)4(24)4(0020k x x x k x y -+-=+--,整理得016422200=-++k x y x x . ……………………………………11分设点)4,(2xx B 在曲线段L 上,因为P 、Q 两点的横坐标分别为k x 40+-和k x 40--,所以B 点的横坐标x 在k x 40+-和k x 40--之间,即||4||400k x x k x +-≤≤--, 所以||4||40k x x k ≤+≤-,从而22016)(k x x ≤+.点B 到直线PQ 的距离42|162|164|16442|20220022022020+-++=+-+⨯+=x k x x x x x k x xx x d4216)(42142|16)(|202202020220++++-=+-+=x k x x x x k x x . ………12分当0x x -=时,4216202max +=x k d .注意到||4||4000k x x k x +-≤-≤--,所以点)4,(200x x -在曲线段L 上.所以,点B 的坐标是)4,(200x x -. ……………………………………………………………14分(法2)由①可知,20x k PQ -=,结合图6-3可知,若点B 在曲线段L 上,且点B 到直线PQ 的距离最大, 则曲线C 在点B 处的切线PQ l //. ………………11分设l :b x x y +-=20,由方程组⎪⎩⎪⎨⎧=+-=yx b x x y 4220,消去y ,得04202=-+b x x x .令△0)4(14)2(20=-⨯⨯-=b x ,整理,得420x b -=.……12分36-图M∙'∙F xyOF∙PQABl代入方程组,解得0x x -=,420x y =.所以,点B 的坐标是)4,(200x x -. ……………………………………………………………14分(法3)因为抛物线C :y x 42=关于y 轴对称,由图6-4可知,当直线AP 的倾斜角大于︒0且趋近于︒0时,直线AQ 的倾斜角小于︒180且趋近于︒180,即当直线AP 的斜率大于0且趋近于0时,直线AQ 的斜率小于0且趋近于0.从而P 、Q 两点趋近于点)4,(200x x A 关于y 轴的对称点)4,('200x x A -. ………………11分由抛物线C 的方程y x 42=和①的结论, 得42xy =,PQ x x x x k x x y =-=='-=-=22|00.所以抛物线C 以点)4,('200x x A -为切点的切线PQ l //.……………………12分所以曲线段L 上到直线PQ 的距离最大的点就是点'A ,即点B 、点'A 重合. 所以,点B 的坐标是)4,(200x x -. ……………14分21.(本小题满分14分)已知函数x x x x f ln )(-=,)()()(a f x x f x g '-=,其中)(a f '表示函数)(x f 在a x =处的导数,a 为正常数.(1)求)(x g 的单调区间;(2)对任意的正实数21,x x ,且21x x <,证明:)()()()()()(11212212x f x x x f x f x f x x '-<-<'-;(3)对任意的*N ∈n ,且2≥n ,证明:nn f nln 2ln )1(1ln 13ln 12ln 1⋅+-<+++.解:(1)x x f ln )('-=,a x x x x x g ln ln )(+-=,xa a x a f x f x g lnln ln )()()(=+-='-'='. ……………………………………2分所以,),0(a x ∈时,0)('>x g ,)(x g 单调递增; ),(∞+∈a x 时,0)('<x g ,)(x g 单调递减.所以,)(x g 的单调递增区间为],0(a ,单调递减区间为),[∞+a . ……………………4分 (2)(法1)对任意的正实数21,x x ,且21x x <, 取1x a =,则),(12∞+∈x x ,由(1)得)()(21x g x g >,A 46-图M ∙'∙F xyOF∙1P 1Q B2P 3P 2Q 3Q l即)()()()()()(21221111x g x f x x f x f x x f x g ='->'-=,所以,)()()()(11212x f x x x f x f '-<-……①; ………………………6分取2x a =,则),0(21x x ∈,由(1)得)()(21x g x g <, 即)()()()()()(22222111x g x f x x f x f x x f x g ='-<'-=, 所以,)()()()(21212x f x x x f x f '->-……②.综合①②,得)()()()()()(11212212x f x x x f x f x f x x '-<-<'-. ………………………8分 (法2)因为x x f ln )('-=,所以,当)1,0(∈x 时,0)(>'x f ;当),1(∞+∈x 时,0)(<'x f .故)(x f 在]1,0(上单调递增,在),1[∞+上单调递减.所以,对任意的正实数21,x x ,且21x x <,有)1(21f x x f <⎪⎪⎭⎫ ⎝⎛,)1(12f x x f <⎪⎪⎭⎫⎝⎛. ……………6分 由)1(21f x x f <⎪⎪⎭⎫ ⎝⎛,得1ln 121212<-x xx x x x ,即0)ln (ln 12212<---x x x x x ,所以0)ln (ln )()()()(1221211212<---='---x x x x x x f x x x f x f . 故)()()()(11212x f x x x f x f '-<-.……①;由)1(12f x x f <⎪⎪⎭⎫⎝⎛,同理可证)()()()(21212x f x x x f x f '->-.……②. 综合①②,得)()()()()()(11212212x f x x x f x f x f x x '-<-<'-. ………………………8分 (3)对2,,2,1-=n k ,令xk x x k ln )ln()(+=ϕ(1>x ),则22))(ln ()ln()(ln )(ln )ln(ln )('x k x x k x k x x x x xk x kx xx k +++-=+-+=ϕ,显然k x x +<<1,)ln(ln 0k x x +<<,所以)ln()(ln k x k x x x ++<, 所以0)('<x k ϕ,)(x k ϕ在),1(∞+上单调递减.由2≥-k n ,得)2()(k k k n ϕϕ≤-,即2ln )2ln()ln(ln k k n n +≤-.所以)ln()2ln(ln 2ln k n k n -+≤,2,,2,1-=n k . ……………………………10分 所以⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛+++2ln 1ln 1)1ln(13ln 1ln 12ln 1ln 13ln 12ln 12n n n n 2ln ln ln 2ln )1ln(3ln 3ln )1ln(ln 2ln 2ln ln n n n n nn +++-+-++=nn nn nn ln 2ln ln 2ln ln 2ln 3ln )1ln(ln 2ln 2ln ln ++++-++≤⎪⎭⎫ ⎝⎛+++=n n ln 2ln ln 3ln 2ln 2 . ………………………………12分又由(2)知n n f n f n f ln )(')()1(-=<-+,所以)1()(ln +-<n f n f n .)1()()3()2()2()1(ln 2ln 1ln +-++-+-<+++n f n f f f f f n)1(1)1()1(+-=+-=n f n f f .所以,nn f nnnln 2ln )1(1ln 2ln ln 3ln 2ln ln 13ln 12ln 1+-<+++≤+++.……………………14分。
2012年北京市各区二模试题分类解析【数学文】(12):算法初步.pdf

结合时代背景,深层领会小说的思想意义。
教学过程 [教学步骤] 一、导语设计 同学们,作为中华民族20世纪的文化伟人,作为伟大的文学家、思想家和革命家的鲁迅,以文艺实现他改变“愚弱的国民”精神的启蒙主义抱负。
在他一生所创作的三十多篇小说中,他最喜欢的是收在小说集《呐喊》中的《孔乙己》。
巴金也说《孔乙己》写得好。
日本有一位作家说孔乙己是最完美的艺术典型,今天,我们就来认识一下孔乙己这个不朽的艺术形象。
(板书文题、作者) 三、诵读,整体感知文意 1.学生默读课文,初步感知文意,疏解下列字词。
(1)注音: (2)释义: 阔绰(chuò ) 羼(chàn) 绽出(zhàn) 拭(shì) 格局:布置的格式。
阔绰:阔气。
污人清白:毁坏人家的名誉。
2.学生自由诵读全文,找出反映下列内容的语句并揣摩其丰富含义。
(1)孔乙己的特殊身份 (2)孔乙己的地位 (3)孔乙己的结局 学生精彩回答,教师提示: (1)概括孔乙己特殊身份的语句:“孔乙已是站着喝酒而穿长衫的唯一的人” 句中“站着喝酒”表明孔乙己生活贫困,经济地位和社会地位都和短衣帮一样;“穿长衫”表明他不愿与“短衣帮”为伍,硬摆读书人的架子;“唯一的”点出了孔乙己的特殊性,他与上层人、下层人都有距离。
3.请学生理清小说情节结构,并概括孔乙己的六个生活片断。
学生回答,教师归结: 六个生活片断是: (1)众人取笑孔乙己脸上又添了新伤疤; (2)众人讥笑孔乙己考不中秀才;(3)孔乙己为偷书作辩解; (4)孔乙己教小伙计识字; (5)孔乙己给小孩子们分茴香豆; (6)侧面交代孔乙己被打断腿。
4.四人学习小组合作探究,分析孔乙己形象。
(1)填写下列句子,探究孔乙己性格中的矛盾表现。
孔乙己是站着喝酒但又_______的人。
孔乙已是穷得将要讨饭但又_______的人。
学生思考、交流,教师明确: 穿长衫 好喝懒做 把“半个秀才也没捞到”当作灵魂伤疤 偶有偷窃 从不拖欠酒钱屡遭冷遇 想和人交流无人关心、可有可无 (2)深入探因 学生合作探究孔乙己矛盾表现的思想原因和社会原因,深刻理解孔乙己形象。
2012年北京市各区二模试题分类解析【数学理】(13):排列、组合及二项式定理.pdf

4、背诵课文。
二、能力目标 1、复述课文,掌握作者求学的主要经历,理清行文思路,提高诵读能力。
2、理解本文对比手法的运用,体会其独特的表达效果。
三、情感目标 学习作者克服困难、勤心求学的精神和意志,树立正确的苦乐观,珍惜现有的优越条件,努力学习,早日成才。
四、教学重点 1、翻译课文,背诵课文,理解本文作者执著的求学之志和殷殷劝勉之情。
2、把握寓理于事的写作方法和对比的表现手法,学习形象说理的技巧。
五、教学难点 引导学生运用现代观念重新审视作品,理解文中作者的求学态度。
六、教学方法 诵读法 讨论点拨法 复述法 品读法 延伸拓展法 教学时间:二教时。
第一教时 一、导入新课 方法一:常言道:“自古雄才多磨难,从来纨绔少伟男。
”孟子也说:“夫天将降大任于斯人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为。
” 这些都说明了苦难并非全是坏事。
只要我们善于化苦难为动力,则苦难就会成为成功的垫脚石。
今天我们来学习宋濂的《送东阳马生序》。
(板书课文标题) 方法二:同学们,在五单元前面几篇课文里,我们学习了几种古代不同体裁的文章,如吴均的书信体山水小品文——《与朱元思书》、陶渊明的自传体文章——《五柳先生传》、韩愈的议论性文章——《马说》,今天我们一起来学习一篇体裁为赠序的文章——《送东阳马生序》,看看作者是怎样用自己的切身体会勉励马生勤奋学习的。
二、作者简介: 宋濂,明初文学家。
字景濂,号潜溪,浦江人(现渐江义乌人)。
他年少时受业于元末古文大家吴莱、柳贯、黄等。
元朝至正九年,召他为翰林院编修,因为身老不仕,隐居龙门山著书。
明初,征他作江南儒学提举,让他为太子讲经,修《元史》,官至翰林学士承旨、知制诰,朝廷的重要文书,大都由他参与撰写。
年老辞官,后因长孙宋慎犯罪,被流放到四川,途中病死。
他与刘基、高启为明初诗文三大家。
朱无璋称他为:开国文臣之首。
刘基称赞他为:当今文章第一。
四方学者称他为:太史公。
2012年北京市各区二模试题分类解析【数学文】(3):导数及其应用.pdf

三、导数及其应用(选修2-2) 1.(2012年西城二模 文18)已知函数,其中.(Ⅰ)当时,求曲线在原点处的切线方程;(Ⅱ)求的单调区间. 解:(Ⅰ)当时,,. ……2分 由 , 得曲线在原点处的切线方程是.……4分 (Ⅱ). ………6分 ① 当时,. 所以在单调递增,在单调递减. …7分 当,. ② 当时,令,得,,与的情况如下: 故的单调减区间是,;单调增区间是.……10分 ③ 当时,与的情况如下: 所以的单调增区间是;单调减区间是,. ……13分 综上,时在单调递减;在单调递增. 时,在单调递增,在单调递减;时在单调递增;在单调递减. 2.(2012年朝阳二模文18)设函数.(Ⅰ)已知曲线在点处的切线的斜率为,求的;(Ⅱ)讨论函数的单调性; (Ⅲ)在(Ⅰ)的条件下,求证:对于定义域内的一个,都有. 解:(Ⅰ)的定义域为 …1分 . ……2分 根据题意,,所以,即,解得 ………4分 (Ⅱ)(1)当时,因为,所以,, 所以,函数在上单调递减. ………6分 (2)当时, 若,则,,函数在上单调递减; 若,则,,函数在上单调递 综上,当时,函数在上单调递减;当时,函数在上单调递减在上单调递增………9分 (Ⅲ)由(Ⅰ)可知设,即. . …10分 当变化时,,的变化情况如下表: -0+极小值是在上的唯一极值点,且是极小值点,从而也是的最小值点. 可见 ……13分 所以,即,所以对于定义域内的每一个,都有. ……14分 ,两函数图象的交点在x轴上,且在该点处切线相同.(Ⅰ)求a,b的值;(Ⅱ)求证:当x>1时,f(x) 0可得x >2或x <1,由f ′ (x) < 0可得1< x <2. ∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ), 单调递减区间为 (1 , 2 ). …9分 (Ⅲ) 由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增. 且当x=1或x=2时,f ′ (x)=0. …10分 ∴ f (x) 的极大值为 ………11分 f (x)的极小值为 ……12分 则 ………14分 .(Ⅰ)若,求在处的切线方程;(Ⅱ)若在上是增函数,求实数的取值范围. 解:(Ⅰ)由,,, ……1分 所以. ……3分 又, 所以所求切线方程为即. ……5分 (Ⅱ)由已知,得. 因为函数在上是增函数, 所以恒成立,即不等式 恒成立. ………9分 整理得. 令 …11分 的变化情况如下表: +极小值 由此得的取值范围是. ……13分 6.(2012年海淀二模文18)已知函数(,).(Ⅰ)求函数的单调区间;(Ⅱ)当时,若对任意,有成立,求实数的最小值. 解:. 令,解得或. …2分 (Ⅰ)当时,,随着的变化如下表 极小值极大值函数的单调递增区间是,函数的单调递减区间是,. 当时,,随着的变化如下表 极小值极大值函数的单调递增区间是,函数的单调递减区间是,. (Ⅱ)当时,由(Ⅰ)得是上的增函数,是上的减函数. 又当时,. 所以 在上的最小值为,最大值为. 所以 对任意,. 所以 对任意,使恒成立的实数的最小值为.。
广东省汕头市2012年二模理科数学及详细答案

2012汕头二模理科数学参考答案一、选择题:二、填空题:9、 1 , 10、 3 , 11、222222(67)0(87)255s -+++-+==, 12、)2,1()1,0( ,13、 5 , 14、2 15、2=b , 三、解答题:16、解:(1)212cos22)46sin()(2-+-=xxx f πππ )112cos2(24sin6cos4cos6sin2-+-=xxxπππππ----------(1分)6cos26cos226sin22xxxπππ+-=---------------------(3分)6cos226sin22xxππ+=--------------------------------(4分))46sin(ππ+=x------------------------------------------(5分)12622===∴ππωπT ----------------------------------------(6分)(2)方法一:由题意知道:]4)2(6sin[)2()(ππ+-=-=x x f x g ------------------------------------------------(8分))1276sin()1276sin(ππππ--=+-=xx----------------------------(9分)31276127],211,0[ππππ≤-≤-∴∈x x --------------------------------------------------(10分) ,23)(min -=∴x g 此时,31276πππ=-x即211=x -------------------------------(12分)方法二:可以根据]211,0[∈x 关于1=x 的对称区间]2,27[-∈x 上函数)(x f 的最值。
17、证明:(1)⊥1AA 平面1111D C B A ,⊆11D B 平面1111D C B A --------------(1分)∴⊥1AA 11D B ,又 1111C A D B ⊥----------------------------------(2分) 1111C AA D B 平面⊥∴--------------------------------------------------(3分)又⊆11D B 平面11D AB1111C AA D AB 平面平面⊥∴---------------------------------------------(5分) (2)方法一:建立如图所示的空间直角坐标系,设h AA =1,那么 )0,0,0(1A ;),0,0(h A ;)0,0,1(1B ;)0,1,0(1D ;)0,1,1(1C ------(6分)),0,1(1h AB -=∴;),1,0(1h AD -=∴;)0,1,0(11=C B ;)0,0,1(11=C D -------(7分)假设平面11C AB 与平面11C AD 的法向量分别为),,(1111z y x n =;),,(2222z y x n =,那么 ,01111=-=∙hz x AB n ;0111111==-=∙y hz x C B n 令h x z ==11,1则∴)01,(),,(1111h z y x n ==-----------------------------------------------------------------(8分)同理可以求得: )1,,0(),,(2222h z y x n ==--------------------------------------(9分) |,cos |||||||212121><⨯=∙∴n n n n n n2111122⨯+⨯+=∴h h ,1,212==+∴h h -------------------------------(11分)此时,正四棱柱1111D C B A ABCD -是棱长为1的正方体,且 四棱锥1111D C B A A -的体积311131=⨯⨯=V ------------------------------(12分)方法二:过点1B 作11AC H B ⊥于H ,连接H D 1, 容易证得11AC H D ⊥,B 1=H D 1--------------------------------------(7分)所以011120=∠HD B ,且在11HD B ∆中,由余弦定理可得:2120cos 20112121211=⨯⨯-+=H D H B HD HB D B所以H B 1=H D 1=36,又可证得:------------(9分)111C B AB ⊥,所以在11C AB RT ∆,由等面积法:_D _B _ D _ D _1第17题图111C B AB ⨯=11AC H B ⨯,即2361122+⨯=⨯+h h ------------(9分)所以1=h ,---------------------------------------------(11分) 此时,正四棱柱1111D C B A ABCD -是棱长为1的正方体,且 四棱锥1111D C B A A -的体积311131=⨯⨯=V -------------------------------------------(12分)18、解法一:(1)设既会唱歌又会跳舞的有x 人,那么由题意可知: 只会唱歌的有(2-x )人,只会跳舞的有(5-x )人,文娱队中共有(7-x )人,那么只会一项的人数是(7-2 x )人.--------------------------(3分) 显然x 可以取得的值只有0,1,2① 当x=0时,0>ξ为不可能事件,显然不符合题意-------------------------------(4分)② 当x=1时,10==ξξ与是对立事件,且10731)1(P )0(P 261411≠=+===>CC C ξξ所以x=1时不符合题意---------------------------------------------------------------(6分) ③当x=2时,1071)0(P 1)1(P )0(P 2513=-==-=≥=>CC ξξξ符合题意。
2012年北京市各区二模试题分类解析【数学理】(3):导数及其应用.pdf

三、教学难点1、品读课文,体会本文写景的技巧,学习作者善于抓住景物特点生动传神地进行描写的方法。
2、理解“夫不能以游堕事,潇然于山石草木之间者,惟此官也”的丰富意蕴。
四、课时安排:1课时 五、教学过程:(一)导入:本文是一篇文字清新的记游小品。
满井是明、清两朝北京近郊的一个风景区。
文章用极精简的文字记游绘景、抒情谕理。
历历如画的景物描写,透出京郊早春的芬芳气息,勃勃生机,借景抒感,谕示读者以人生哲理。
(二)作者及背景简介 1、袁宏道(1568~1610),明朝文学家。
字中郎,号石公,明公安(今湖北人),万历年进士,官至吏部中郎,与兄宗道、弟中道并称“三袁”,为“公安派”的创始者。
作品真率自然、清新活泼,内容则多写闲情逸致,部分篇章反映民间疾苦,对当时政治现实有所批判。
有《袁中郎集》。
2、游记,散文的一种。
以轻快的笔调和生动的描写,记述旅途中的见闻,反映某地的山川景物、名胜古迹、风俗习惯和社会状况等,表达作者的思想感情。
本文属山水游记,又因其短小,称“山水小品”。
3、写作背景:万历二十七年(1599),袁宏道再次做官,任顺天府教授,终日又得和拜谒酬答打交道了,这使他颇为苦闷,更使他苦闷的是有政见却得不到申诉。
好在袁宏道所担任的职务比较清闲,有空暇就游览北京附近的名胜古迹。
《满井游记》就作于此时。
(三)朗读课文,整体感知文意。
1、下列加粗的字注音: 教师选四位同学回答,分四组。
(1)yān niàn zhāo huì (2)pù xiā jiā léi(3)liè qiàn jiǎn jì huán (4)huī lì wū 2、学生自由读课文,借助注释及工具书,理解文句,整体感知文意。
(1)学生自行翻译课文,画出疑难词句。
(2)同桌之间讨论交流,解决疑难问题。
教师巡视酌情指导。
(3)教师指导学生积累词语,理解文句。
2012年北京市各区二模试题分类解析【数学理】(4):定积分.pdf

2.理解蕴含在两文中的作者的观点。
难点:1.两篇短文都采用“逐层深入论证”的结构,这是学习本文的一个难点。
教学过程: 一、明确目标 疏通第一章大意,理解寓含其中的作者的观点,学生畅谈各自看法,以加深理解。
二、整体感知 《得道多助,失道寡助》选自《孟子·公孙丑》,标题是后来的编者加的。
此标题从内容上高度概括了本文的中心意即:凡讲仁义,行仁政的,就会得到广泛的支持与拥护;反之,就孤立,就会只有极少数人的支持与拥护。
孟子生活在各诸侯国互相攻伐,社会骚乱的战国时代。
因此,他提出“施仁政”,“行王道”的主张,反对武力兼并,这篇短论很能代表他的主张。
三、教学过程 1.投影习题,检测自学效果。
(1)下列句子朗读节奏划分有误的一句是() A.夫/环而攻之。
B.是/天时不如地利也。
C.威天下/不以/兵革之利。
D.故君子/有不战,战/必胜矣 (2)解释下句中加点词在文中的意思: ①池非不深也。
②域民不以封疆之界 2.讨论问题 (1)本文作者从作战入手,设举了两个战例,从中可以看出,作者把决定战争胜负的客观因素归结为哪几个?作者认为它们之间的关系如何? (2)本文借论战,深入阐述了怎样的政治主张?这一主张是如何逐层推进论证的? (3)画出第3、4节中的排比句,诵读体会,议论文说理运用排比句式的表达作用。
练习:请你紧扣强调“青少年时期要努力学习”这一内容写一组排比句,加深体会。
《生于忧患,死于安乐》一章选自《孟子·告子》,文题同样是编者所加,该标题也恰好概括了本章的中心意思——忧患激励人奋起,使人生存发展;安逸享乐使人萎靡,必将导致灭亡,即逆境能成才。
表明了孟子关于人才要在困难环境中磨炼造就的观点。
文章摆事实,讲道理,举例典型,观点与材料紧密结合,说理透彻,令人信服。
1.指导朗读。
听录音范读,学生跟读,自由诵读。
(1)读准下列加点字的音: 傅说 忍性 法家拂士 曾益 (2)正确划分下列句子的朗读节奏 ①必先/苦其/心志,劳其/筋骨,饿其/体肤,空乏/其身,行拂/乱其所为。
2012年北京市各区二模试题分类解析【数学理】(18):空间几何体.pdf

二、[教学重点] 1.了解作者留学日本的情况、与藤野先生的交往和本文的写作背景。
2.把握课文的组织结构,理解课文的思想内容。
三、[教学难点] 掌握本文通过典型事例突出人物品质的写法 五、[教学过程] 第一课时 [教学内容] 了解背景,学习并积累词语,初读课文。
[教学环节] 导入新课学过了《从百草园到三味书屋》这篇散文,我们了解到三味书屋中的老先生虽然施行的是封建书塾教育,但思想还算开明,因此,鲁迅对他“很恭敬”。
虽是“很恭敬”,但并不是很有感情。
藤野先生是鲁迅在日本仙台学医时的一位日本医专的教授,他是一位怎样的老师呢?鲁迅对他的感情又是如何呢?让我们一起走访《藤野先生》吧!二、简介作者、藤野先生和作品的写作背景。
联系旧知 三、学生默读课文,疏通有关阅读障碍 要求:1.标注出难字难词。
2.注意:文章变换了几个地点? 3.划分文章的段落层次,并说说各部分的大意。
学生默读后,讨论明确: 1.需要注意的字词列举如下: (多媒体展示) 绯(fēi)红:鲜红。
会馆:旧时同乡或同业的人在京城、省会或大商埠设立的寄寓和机构。
流言:流传的毫无根据的坏话。
瞥见:很快地看一下。
畸(jī)形:不正常的形状。
遗民:a.留下的在国外的人;b.改朝换代后仍效忠前一朝代的人;c.大乱后遗留下来的 人民。
不逊(Xùn):不客气;无礼貌;骄傲、蛮横。
美其名曰:(把不美的事物)美化它的名字叫。
四、学习课文第一部分 1.学生自由朗读第一部分内容。
2.思考:(1)请标出最能表现清国留学生丑态的词语和句子。
(2)对于这些清国留学生,“我”是持什么态度?哪些词语表明了“我”的态度? (3)从“我”的态度,可以看出作者的什么思想? 表达了作者对东京“清国留学生”的恶浊生活的憎恶、失望和不满,强有力地讽刺了这些顽固维护清王朝统治的“遗少”,强烈表达了作者对他们的极端憎恶的感情。
3.找出人物外貌、语言描写的语句,体现了人物什么特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从黄浦二模看高考捞分策略上海市向明中学(20020) 侯宝坤二模过了,高考复习的也接近尾声了,我们在二模中能得到什么启示?每个同学都有自己的关心方向。
今天,我们将结合2012年黄浦区的理科二模试题、高考改卷体会,和同学们谈谈,如何在现有的知识下尽量捞分的策略,希望对提高大家的高考分数有所帮助。
1.常规题得分在“稳”1.1基础是永远的灵魂近年上海高考试题在难度上稳中有降,高难度试题明显减少,基础题都在90分以上。
这次黄浦二模试卷明显为基础题的是1—12、14、15、19、20、21计96分,如果在加上22(1)、23(1)就共有106分的基本分,拿到这些基本分再略有突破就可以达到115分左右,就能达到或者超过一本的平均分了,因此,我们复习中基础永远是重中之重,是必胜的基石,必须拿全拿稳!要拿稳基本分,就要对考纲要求的知识点有一个全面的把握,概念必须清晰,对常见的错误要有一个清醒的认识。
如,(黄浦7).已知z ∈C ,z 为z 的共轭复数,若100110i 0z z z =(i 是虚数单位),则z = .对行列式的运算、复数概念只有最基本的要求,但考试中有很多同学认为复数不包括实数,正确答案是0,-i ,他漏写了0,白白浪费了4分!再如(黄浦11).若(12)n x +(*n ∈N )二项展开式中的各项系数和为n a ,其二项式系数和为n b ,则11lim n n n n nb a a b +→∞+-=+ . 这题也是考察二项式定理中的两个基本概念,有同学刚好混淆了,正确答案是13-,他写成了2,又白白浪费了4分!1.2计算是绕不开的关键数学除了考思维,就是考计算。
数学解题是一个连续化简的过程,计算是永远绕不开的湾。
在弄清题意、形成思路后剩下的只有计算。
上海同学平时过多的依赖计算器,对字母型的计算往往较为惧怕。
如(黄浦22)(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.已知定点(2,0)F ,直线:2l x =-,点P 为坐标平面上的动点,过点P 作直线l 的垂线,垂足为点Q ,且FQ PF PQ ⊥+ ().设动点P 的轨迹为曲线C . (1)求曲线C 的方程;(2)过点F 的直线1l 与曲线C 有两个不同的交点A 、B ,求证:111||||2AF BF +=; (3)记OA 与OB 的夹角为θ(O 为坐标原点,A 、B 为(2)中的两点),求cos θ的取值范围.对解析几何而言,这应当是个较为常规的问题,大家练习过不少这样的题,但那些平时怕算的同学考场上就更害怕了,裹足不前,犹豫不决,既浪费时间又得不到分数。
只有有耐心,我们用下列最基本的方法就可以得到答案。
解:(1)略(2)因为过点F 的直线1l 与曲线C 有两个不同的交点A 、B ,所以1l 的斜率不为零,故设直线1l 的方程为2x my =+. (已知横截距设这个形式比较方便计算,应当收集记忆)于是A 、B 的坐标11(,)x y 、22(,)x y 为方程组28,2,y x x my íï=ïìï=+ïî的实数解. 消x 并整理得28160y my --=.于是12128,16,y y m y y +=⎧⎨=-⎩进一步得21212221212484,4.88x x my my m y y x x ⎧+=++=+⎪⎨=⋅=⎪⎩(对抛物线计算12x x 用22y px =代人比用直线快点,但直线也可,应当有心收集)又因为曲线28y x =(0x ≥)的准线为2x =-, 所以12121212411111||||222()42x x FA FB x x x x x x +++=+==+++++,得证. (3)由(2)可知,11(,)OA x y =uu r ,22(,)OB x y =uu u r .于是cos ||||OA OB OA OB q ?===×uu r uu u r uu r uu u r ,不知道用2118y x =代人,创造使用韦达定理的条件,应当用心体会、学会)求得cos q =的取值范围为3,05轹÷ê-÷÷êøë. 近年,解析几何多从直线与圆锥曲线的关系入手,题型熟悉、套路明显,计算是决定成败的关键,只要大家针对性选上10道题练习练习,体会一下算法的选择、计算的技巧和套路,就会找到信心,提高得分机会。
2高.难题得分要“抢”2.1填选难题讲技巧每年高考填选题的最后两题,都具有把关的性质,以能力型问题为主,有一定的难度。
这些问题往往背景新颖,或较为抽象。
但这些题有很多时候不是死算得到的,而是以代人检验、特殊化、排除法等方法技巧性的求出,有些题甚至都不要动笔。
对背景新颖的题目,一定要淡定,按照题目的顺序依次操作,按部就班就能将问题解决得较好。
如(黄浦14).已知△FAB ,点F 的坐标为(1,0),点A 、B 分别在图中抛物线24y x =及圆22(1)4x y -+=的实线部分上运动,且AB 总是平行于x 轴,那么△FAB 的周长的取值范围为 .这题将圆与圆锥曲线融合,新但不难,我们只要将要计算的周长表达成||||||2||||AF BF AB AF AB ++=++,然后想到用抛物线的定义,只要求B 点到准线的距离范围即可,由图像易知B在(3,0)时B 点到准线的距离最大为4;B在(1,±2)时B 点到准线的距离最小为2,所以△FAB 的周长的取值范围为(4,6).对于抽象性较高的填选题,我们可以具体化,采用特殊值、特例法、排除法等技巧性性处理,这样既快又好,收效明显!如(黄浦17).已知△ABC 的三边分别是a b c 、、,且a b c ≤≤(*a b c ∈N 、、),若当b n =(*n ∈N )时,记满足条件的所有三角形的个数为n a ,则数列{}n a 的通项公式 【答】( ).A .21n a n =-B .(1)2n n n a +=C .21n a n =+D .n a n = 我们只要用1,2,3n =列举,代人即可得到正确答案B (事实上3n =即可)。
记住对与n 有关的问题,我们用列举、归纳、猜想的方法!这样又轻松得到5分! 再如(黄浦18).已知O 、A 、B 、C 是同一平面上不共线的四点,若存在一组正实数1λ、2λ、3λ,使得1230OA OB OC λλλ++= ,则三个角AOB ∠、BOC ∠、COA ∠【答】( ).A .都是钝角B .至少有两个钝角C .恰有两个钝角D .至多有两个钝角 这道题字母多,抽象度较高, 全区对分率36%.如果我们联想到三角形的重心,取1231λ=λ=λ=,再取特殊的正三角就知道三个角都为1200,排除C 、D 选项,再取含30的直角三角形就得到两个钝角、一个锐角,从而得到正确答案B 。
我问了答对的同学,他们也大部分用这种方法处理的,并不知一般性方法和问题的本质,但没关系,我们又在艰难的情况下,轻松地抢到了5分!这里提到的方法在上海对2011年高考13、14、17、18这几道较难的填选题都有非常好的抢分效果,同学用这种方法也可以检验一下今年各区新的二模试题,练练手、长长胆。
2.2领会暗示,各个击破攻压轴高考压轴题都有较高的抽象性、新颖性、字母多、问题多,很多同学拿到手就发懵、恐惧。
其实,压轴题的问题往往具有一定递进性,不是每个问题都难的;另外,在改卷时难题的尺度会适当放宽。
我们不指望得全分,但也要抱着抢几分算几分的心态,如果能结合题目间的相互暗示,采用猜想解答、缺步解答、跳步解答、高频知识试答等手段,很多时候反而能抢回许多分数。
那么如何能抢到分数呢?首先,我们将问题归类,弄清题型,是函数、方程、不等式,还是数列、解析几何类;是求值(以方程为主)、求范围(以转化成函数、不等式、数形结合为主),还是研究对象的性质(以证明、探究为主),这样会有熟悉感,以便确定解答的大方向,不为复杂的形式所囿。
如(黄埔23)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.对*n ∈N ,定义函数2()()n f x x n n =--+,1n x n -≤≤.(1)求证:()n y f x =图像的右端点与1()n y f x +=图像的左端点重合;并回答这些端点在哪条直线上.(2)若直线n y k x =与函数2()()n f x x n n =--+,1n x n -≤≤(2n ≥,*n ∈N )的图像有且仅有一个公共点,试将n k 表示成n 的函数.(3)对*n ∈N ,2n ≥,在区间[0,]n 上定义函数()y f x =,使得当1m x m-≤≤(*m ∈N ,且1m =,2,…,n )时,()()m f x f x =.试研究关于x 的方程()n f x k x =(0x n ≤≤,*n ∈N )的实数解的个数(这里的n k 是(2)中的n k ),并证明你的结论.这题大看是函数问题,(1)证明在直线上就是求直线方程,也就是看点的横纵坐标的关系,求出2()()n f n n n n n =--+=,即得坐标右端点(,)n n ,同理得1()n y f x +=图像的左端点(,)n n ,当然重合,并得直线y x =。
轻松抢到4分!(2)问具体来说是函数图象交点问题,也是方程2(),[1,]n k x x n n x n n =--+∈-根的分布问题,简单的可以解方程,复杂的用数形结合、参变量分离就可处理,(2)、(3)问都可以这样处理(下面再展示)。
其次,要善于利用问题问法的暗示、问题间的暗示帮我们寻找解题思路。
如利用图象结合(1)的暗示——图象的端点都在直线上,只能是相切时才只有一个交点,于是得到0∆=,即2n k n =4分!如果注意(2)提问:“将n k 表示成n 的函数”就在暗示我们应该是一个等式,所以只能0∆=,也可以抢到4分!如果在利用图象或特殊值检验,又可以帮我们肯定2n k n =,这样又多得2分,得6分已经很好了!如果回看定义域和韦达定理122[1,]2n n k x x n n -==∈-,即可得2n k n =,这样就可以得全8分。
如果用参变量分离22(),[1,],n n n k n x x n n x-=-+∈-利用大家熟知的“耐克“函数性质或图象易知,2()2(),[1,]n n g x n x x n n x-=-+∈-在[n -上递增,在]n 递减,且()(1)1g n g n =+=,所以2n k g n ==-8分。
对(3)只要大胆根据特殊值猜想解答:21n -,就可以得到2分,多么轻松!很多同学知道答案没敢写,浪费了机会,如果善于从答题过程中找出暗示——n k 的变化影响交点个数,就可以抓住解题的关键——研究n k 的单调性:当2n ≥时,2n k n =-=,可得12n k <<,且n k 单调递减.对于1i n -1≤≤,总有1n i k k <<,亦即直线n y k x =与函数()i f x 的图像总有两个不同的公共点(直线n y k x =在直线y x =与直线i y k x =之间).此时方程()n f x k x =(0x n ≤≤,*n ∈N )的实数解的个数为2(1)121n n -+=-.就能将题目解决得很好,如果你能写上单调性进行缺步解答,也可得到4分了,对压轴题这是很了不起的成绩了!高考要成绩,刻苦、坚韧、自信,必不可少;如果再重视上述答题的技巧,就可以达到准确、规范、快速,平均多10分的机会还是有的,真正达到高考必胜!。
