ansys拓扑优化形状优化实例1
拓扑优化简介及在ansys软件中的实现

件中的实现
ANSYS TRAINING
主要内容
1
2 3
拓扑优化概述 ANSYS中拓扑优化过程 实例讲解
ANSYS TRAINING
拓扑优化概述
ANSYS TRAINING
拓扑优化概述
工程结构优化
尺寸优化:以几何尺寸为设 计变量,而材料的性质,结构
的拓扑和几何形状保持不变
ANSYS TRAINING
实例讲解
实例二 力热载荷综合作用下的拓扑优化
3.3KN
换热系数 (Wm-2K)
在实例一中的模型上施加热边界条件如下:
位置 温度(K)
长×宽=160 ×120
1 2 3
1358.37 293 363
1092.36 105.3 13433
6.5MPa
ANSYS TRAINING
• GUI操作对应命令流的输出
– 单步查看 – 最终整体输出
Help is very helpful!
ANSYS TRAINING
实例讲解
实例一 力载荷下的拓扑优化
对一长正方形平板零件,底边中部受到均匀的压力6.5MPa,顶部两
侧受到集中载荷3.3KN。本问题的目标是在体积减少70%的条件下,
结构的柔顺度最小。 3.3KN
实例讲解
热-结构耦合分析
耦合方法
采用顺序耦合分析的方法,即首先进行整机温度场分析,然 后利用热分析结果即节点温度作为“体载荷”施加到随后的 结构分析中。
分析流程
温度场 边界条件 清除 物理环境 转换 单元 保存温度场 物理环境 转换 材料属性 温度场 计算 转换 接触算法 设置 参考温度 设置 边界条件
–PLNSOL,TOPO –or General Postproc > Plot Results > Nodal Solution… –红色表示要保留的材料 (pseudo-density 1.0); –蓝色表示可以去掉的材料 (pseudo-density 0.0)。
《Ansys拓扑优化》课件

优化飞机和航天器的结构,在减少重量的同时提高强度和刚度。
汽车工程
改进汽车结构以提高燃油效率和碰撞安全性。
建筑工程
优化建筑结构以提供更好的抗震性能和节能效果。
传统的结构优化与拓扑优化的 区别
• 传统的结构优化方法通常只考虑材料的分布,而拓扑优化还考虑了形 状的优化。
• 拓扑优化可以提供更自由的设计空间,允许非常复杂的结构形态。 • 拓扑优化能够更全面地优化结构的性能指标,如重量、刚度、疲劳寿
Ansys提供了先进的优化算法, 能够高效地进行拓扑优化。
集成的结构分析
Ansys可以直接对结构进行有 限元分析,提供准确的性能评 估。
与CAD软件的无缝集成
Ansys可以导入CAD模型,轻 松进行拓扑优化设计。
ቤተ መጻሕፍቲ ባይዱ
Ansys拓扑优化的输入数据要求
• 结构的几何形状和边界条件 • 设计的材料特性 • 优化目标和约束条件
命等。
拓扑优化的基本原理
拓扑优化基于有限元分析和优化算法,通过迭代地将材料从刚度较低的区域 转移到刚度较高的区域,以实现结构的最佳形态。
拓扑优化的流程
1
初始设计生成
2
根据设计要求生成初始设计。
3
优化迭代
4
通过重新分配材料进行优化迭代,直 到达到最优解。
设计空间定义
确定可调整材料的区域和边界条件。
有限元分析
使用有限元方法对结构进行力学分析, 评估性能。
拓扑优化在工程设计中的意义
1 降低成本
通过优化材料使用,减少了成本和浪费。
2 提高性能
优化后的结构能够提供更好的性能指标,如强度、刚度和疲劳寿命。
3 实现轻量化设计
《Ansys拓扑优化》课件

REPORTING
• 拓扑优化概述 • ANSYS拓扑优化的基本原理 • ANSYS拓扑优化的操作流程 • 拓扑优化案例分析 • 结论与展望
目录
PART 01
拓扑优化概述
REPORTING
拓扑优化的定义
拓扑优化是在给定设计空间、载荷和约束条件下,通过求解数学优化问题,确定 最优的材料分布方案,以达到结构轻量化、刚度最大化或柔度最小化的目的。
PART 05
结论与展望
REPORTING
拓扑优化在工程设计中的重要性
01
02
03
提高结构效率
通过优化材料的分布,减 少不必要的材料,降低重 量并提高结构的刚度和稳 定性。
降低制造成本
减少材料使用意味着减少 生产成本和资源消耗,同 时优化设计可降低加工难 度。
创新设计
拓扑优化能够发现传统设 计方法无法达到的全新设 计方案,为工程师提供更 多创新选择。
熟悉ANSYS软件
深入了解ANSYS拓扑优化的基本原理、操作 流程和参数设置。
建立合理的模型
根据实际工程问题,建立准确的数学模型, 并选择合适的优化算法。
迭代与调整
在优化过程中,根据收敛情况和结果反馈, 不断调整优化参数和方法。
结果验证与评估
对优化后的设计方案进行实验验证,确保其 在实际应用中的可行性和可靠性。
迭代与收敛
在优化过程中,迭代计算并检查收敛性,直 至达到预设的收敛准则或迭代次数。
结果后处理和评估
评估与验证
根据优化结果,评估设计的可行性和有效性 ,如有需要可进行实验验证。
结果后处理
查看拓扑优化结果,如等效应力、应变分布 等。
设计优化建议
(完整版)ANSYS拓扑优化原理讲解以及实例操作

拓扑优化是指形状优化,有时也称为外型优化。
拓扑优化的目标是寻找承受单载荷或多载荷的物体的最佳材料分配方案。
这种方案在拓扑优化中表现为“最大刚度”设计。
与传统的优化设计不同的是,拓扑优化不需要给出参数和优化变量的定义。
目标函数、状态变量和设计变量(参见“优化设计”一章)都是预定义好的。
用户只需要给出结构的参数(材料特性、模型、载荷等)和要省去的材料百分比。
给每个有限元的单元赋予内部伪密度来实现。
这些伪密度用PLNSOL ,TOPO 命令来绘出。
拓扑优化的目标——目标函数——是在满足结构的约束(V )情况下减少结构的变形能。
减小结构的变形能相当于提高结构的刚度。
这个技术通过使用设计变量。
结构拓扑优化的基本思想是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料分布的问题。
通过拓扑优化分析,设计人员可以全面了解产品的结构和功能特征,可以有针对性地对总体结构和具体结构进行设计。
特别在产品设计初期,仅凭经验和想象进行零部件的设计是不够的。
只有在适当的约束条件下,充分利用拓扑优化技术进行分析,并结合丰富的设计经验,才能设计出满足最佳技术条件和工艺条件的产品。
连续体结构拓扑优化的最大优点是能在不知道结构拓扑形状的前提下,根据已知边界条件和载荷条件确定出较合理的结构形式,它不涉及具体结构尺寸设计,但可以提出最佳设计方案。
拓扑优化技术可以为设计人员提供全新的设计和最优的材料分布方案。
拓扑优化基于概念设计的思想,作为结果的设计空间需要被反馈给设计人员并做出适当的修改。
最优的设计往往比概念设计的方案结构更轻,而性能更佳。
经过设计人员修改过的设计方案可以再经过形状和尺寸优化得到更好的方案。
5.1.2优化拓扑的数学模型优化拓扑的数学解释可以转换为寻求最优解的过程,对于他的描述是:给定系统描述和目标函数,选取一组设计变量及其范围,求设计变量的值,使得目标函数最小(或者最大)。
一种典型的数学表达式为:()()()12,,0,,0min ,g x x v g x x v f x v ⎧=⎪⎪≤⎨⎪⎪⎩式中,x -系统的状态变量;12g g 、-一等式和不等式的结束方程;(),f x v -目标函数;v -设计变量。
ansys优化方法简介以及实例

拓扑优化理论及在ANSYS软件中的实现一.拓扑优化概论:连续体结构的拓扑优化设计是继结构的尺寸优化设计和形状优化设计之后,在结构优化领域出现的一种富有挑战性的研究方向,它是一种比尺寸优化和形状优化更高层次的优化方法,也是结构优化问题中最为复杂的一类问题。
拓扑优化处于结构的概念设计阶段,其优化结果是一切后续设计的基础。
因而在初始设计阶段需要确定结构的最佳拓扑形式。
拓扑优化的目的是寻求结构的刚度在设计空间最佳的分布形式,或在设计域空间需求结构最佳的传力路线,以优化结构的某些性能或减轻结构的重量。
目前对于拓扑优化的研究主要集中在以下几个方面:结构拓扑描述方式和材料插值模型;拓扑优化中结构拓扑描述方式和材料的插值模型非常重要,是一切后续拓扑优化工作的基础。
常用的拓扑描述方式和材料插值模型有均匀化方法、密度法、变厚度法和拓扑函数描述法等。
拓扑优化求解数值算法,新型优化算法在拓扑优化中的应用;拓扑优化的数值计算方法主要包括有限元法和无网格法,基于成熟的有限元理论的拓扑优化格式简单,便于实现,但在优化过程中常因网格的重分和细化导致计算困难,结构中常出现中间密度材料、棋盘格现象和网格依赖性等问题。
无网格法是今年发展的一种新型数值求解技术,摆脱了有限元繁琐的网格生成过程,从理论上看比有限元法拥有更广阔的应用前景,但目前尚处于发展和完善中。
拓扑优化的特点是:设计变量多,计算规模大,目标函数和约束函数一般为设计变量的非线性、非单调函数。
目前应用于连续体结构拓扑优化计算的优化算法主要包括两类:优化准则法和序列凸规划法。
去除优化过程中数值计算不稳定的方法,优化结果的提取和重构;拓扑优化中经常出现的数值计算问题有:多孔材料、棋盘格现象、网格依赖性和局部极值问题。
优化结果的提取和应用主要考虑的是如何将优化的结果转化为可用的CAD模型问题,实现CAE和CAD之间的数据共享和交流。
随着拓扑优化理论研究的不断深入,拓扑优化在航空和汽车领域已开始得到初步的应用,主要是通过拓扑优化获得结构的最初拓扑形式,并在最初拓扑形式的基础上进行相关的后续优化设计。
[复习]ansys拓扑优化形状优化实例1
![[复习]ansys拓扑优化形状优化实例1](https://img.taocdn.com/s3/m/48322ed6e109581b6bd97f19227916888486b9e3.png)
[复习]ansys拓扑优化形状优化实例1 ansys拓扑优化形状优化实例1FINISH/CLEAR,START/TRIAD,OFF !关闭整体直角坐标系的三角符号 H=1000 !设置比例尺,采用iso TK16=6.35/H !设置参数变量并附初值 TK27=6.35/HTK38=6.35/HTK49=6.35/HTK50=4/H/PREP7ET,1,PLANE42MP,EX,1,6.89E10MP,NUXY,1,0.3K,1K,5,254/HKFILL ! 在第1至第5个关键点之间生成2,3,4关键点K,6,,TK16K,7,63.5/H,TK27K,8,127/H,TK38K,9,190.5/H,TK49K,10,254/H,TK50SPLINE,6,7,8,9,10L,1,6*REPEAT,5,1,1 !重复L命令,关键点编号自动加1,分别在2,7、3,8、4,9、5,10之间共生成4条线其中包含了、命令已生成的线,共5条LSEL,S,LINE,,5,9 !选择上述生成的5条线 LESIZE,ALL,,,1 !指定线在划分网格前的等分数为1 LSEL,ALLA,1,2,7,6*REPEAT,4,1,1,1,1 !重复上述命令,共生成4个面ESIZE,,4AMESH,ALLFINISH/SOLUNSEL,S,LOC,YDSYM,SYMM,X !对选择的节点施加x方向的对称约束NSEL,S,LOC,XDSYM,ASYM,Y !对选择的节点施加x方向的反对称约束NSEL,ALLFK,10,FX,66725*4 !在10号关键点施加集中载荷,实现弯矩DK,1,ALL,0 !在1号关键点施加全约束 SOLVEFINISH/POST1SET,LASTETABLE,EVOL,VOLU !建立单元表,并取出每个单元的体积EVOL=每个单元的体积PRNSOL,S,PRIN !列出节点的主应力 NSORT,S,1NSEL,U,LOC,X,0,230/H !选择介于0到230/H的节点*GET,STRS,SORT,,MAX !取出最大的应力值并赋给strsNSEL,ALLSSUM !体积相加*get,TVOL,ssum,,item,EVOL !取出结构总体积 TVOL=TVOL*2 !由于分析时只计算了结构的一半,总体积要乘2NSEL,U,LOC,X,250/H,265/H !选择介于250/H到265/H的节点PRNSOL,U,Y !列表显示出所选节点在y向的位移值 NSORT,U,Y,,1 !位移值升序排列PRNSOL,U,Y !列出排序后的结果*GET,DEFL,SORT,,MAX !取出最大的位移值赋给defl *STATUS,PARM !显示当前参数变量的状态值 DEFL=ABS(DEFL)DIF1=TK16-TK27 !设置参数值,以保证曲线的光滑性DIF2=TK27-TK38DIF3=TK38-TK49FINISHlgwrite,scratch,lgw/OPTopanl,scratch,lgw !指定分析文件 opvar,TVOL,Obj,,,1/H !定义优化目标函数,收敛误差为1,结构总体积TVOL为目标函数opvar,STRS,sv,,206E6 ! 定义状态变量即优化过程的约束条件opvar,DEFL,sv,,12.5/H opvar,DIF1,sv,,1/Hopvar,DIF2,sv,,1/Hopvar,DIF3,sv,,1/Hopvar,TK16,dv,4/H,7/H !定义第一个设计变量及其变化范围opvar,TK27,dv,4/H,7/Hopvar,TK38,dv,4/H,7/Hopvar,TK49,dv,4/H,7/Hopsave,INITIAL,opt !保存所有的优化数据到文件optp里optype,SUBP !设置优化方式,子问题逼近算法OPSUBP,30 !指定迭代次数opexe ! 执行优化 PARSAV,,RSET1 !将参数的值输出到文件中且文件名为rset1oplist,all,,1 !列表显示所有序列/AXLAB,Y,TVOL !设置曲线输出时y轴的说明 plvaropt,TVOL !绘图显示目标函数随优化次数的变化规律FINISH/POST1PLNSOL,U,SUM,0,1 !显示结构在优化后的总位移分布PLNSOL,S,EQV,0,1 !显示结构在优化后的应力分布 FINISH。
ANSYS拓扑优化实例

ANSYS拓扑优化实例如下图所示的长方体,受到一个1000N的集中载荷,四周为固定端,弹性模量为E=2e11,泊松比为0.3。
1.设定分析作业名从实用菜单中选择Utility Menu:File>Change Jobname 命令,将打开Change Jobname对话框,如图所示,输入example of topology单击OK。
2.设定分析标题从实用菜单中选择Utility Menu:File>Change Title 命令,将打开Change Title对话框,如图所示,输入single-load example of topo单击OK。
3.定义单元类型(1)从主菜单中依次选择Main Menu:Preprocessor-Element Type-Add/Edit/Delete命令将打开Element Type(单元类型)对话框。
(2)单击Add,将打开Library of Element Type ,选择Solid95,依次单击Apply、OK。
如下图所示,单元类型对话框将会出现两个单元类型(拓扑优化只优化单元类型为1(Type1)的部分)。
(3)单击Close,完成设置。
4.定义材料属性(1)从主菜单中选择Main Menu:Preprocessor-Material Props-Material Models将打开Define Material Model Behavior(定义材料属性)窗口,左窗口Material Model Number 1。
(2)依次在右窗口双击Structural>Linear>Elastic>Isotropic,给出弹性模量EX=2e11和泊松比PRXY=0.3。
(3)单击OK回到Define Material Model Behavior(定义材料属性)窗口,关闭窗口完成设置。
5.创建几何模型由于体的一部分不作优化,所以划分网格时,会要求不同部分选择不同的单元类型。
ANSYS命令流学习笔记7-多工况下的拓扑优化

!ANSYS命令流学习笔记7!多工况下的拓扑优化!学习重点:!1、何为拓扑优化!区分尺寸优化、形状优化、拓扑优化。
拓扑优化是形状优化的一种特殊形式。
网上资料和ansys help文件都有详细说明。
!2、单一工况载荷下的拓扑优化。
单一工况拓扑操作流程很简单,APDL命令也很简单。
Workbench也可以轻松实现。
!3、多工况下的拓扑优化。
需要apdl用到lswrite 命令。
目前不清楚如何完全由workbench 完成多工况的拓扑优化。
有可能在workbench中借助APDL命令来实现,按下不表,后期再做学习。
!案例如下:!平面应力问题。
一个100*100的平面。
左边固定,分别承受两种工况载荷情况。
两种载荷并不是同时作用,所以要进行多工况下的拓扑优化分析。
首先,对只有向上作用力fy=100时,或者只有向下作用力fy = -100时进行topo分析,结果如下图然后,对fy=100和fy=-100作为同一工况下加载,进行topo分析,结果如下图然后,对多工况进行topo分析,结果如下图上述结果可以证明,下列程序确实可以满足多工况的拓扑优化。
但是处理起来复杂模型,还是多有不便,所以如何将其应用到workbench,是下一次考虑的重点。
!APDL命令:finish/clear/prep7 !进入前处理et,1,plane82 !定义能进行topo分析的单元,将其编号为1,其他编号则不参与优化。
mp,ex,1,2e11mp,prxy,1,0.3 !定义材料属性rectng,0,100,0,100 !画个矩形面esize,2,0amesh,all !划分网格nsel,s,loc,x,0d,all,all !定义fix约束,第一个工况nsel,s,loc,y,100f,all,fy,-100 !施加节点力,第一个工况allsel,alllswrite,1 !写第一个工况文件ddele,allfdele,all !删除所有边界条件,以便于进行第二个工况的读写nsel,s,loc,x,0d,all,all ! 定义fix约束,第二个工况nsel,s,loc,y,0f,all,fy,100 !施加节点力,第二个工况allsel,alllswrite,2 !写第二个工况文件finish/solutocomp,mcomp,multiple,2 !两个工况的作用,定义目标函数名称为mcomp。
ansys优化方法简介以及实例

拓扑优化理论及在ANSYS软件中的实现一.拓扑优化概论:连续体结构的拓扑优化设计是继结构的尺寸优化设计和形状优化设计之后,在结构优化领域出现的一种富有挑战性的研究方向,它是一种比尺寸优化和形状优化更高层次的优化方法,也是结构优化问题中最为复杂的一类问题。
拓扑优化处于结构的概念设计阶段,其优化结果是一切后续设计的基础。
因而在初始设计阶段需要确定结构的最佳拓扑形式。
拓扑优化的目的是寻求结构的刚度在设计空间最佳的分布形式,或在设计域空间需求结构最佳的传力路线,以优化结构的某些性能或减轻结构的重量。
目前对于拓扑优化的研究主要集中在以下几个方面:结构拓扑描述方式和材料插值模型;拓扑优化中结构拓扑描述方式和材料的插值模型非常重要,是一切后续拓扑优化工作的基础。
常用的拓扑描述方式和材料插值模型有均匀化方法、密度法、变厚度法和拓扑函数描述法等。
拓扑优化求解数值算法,新型优化算法在拓扑优化中的应用;拓扑优化的数值计算方法主要包括有限元法和无网格法,基于成熟的有限元理论的拓扑优化格式简单,便于实现,但在优化过程中常因网格的重分和细化导致计算困难,结构中常出现中间密度材料、棋盘格现象和网格依赖性等问题。
无网格法是今年发展的一种新型数值求解技术,摆脱了有限元繁琐的网格生成过程,从理论上看比有限元法拥有更广阔的应用前景,但目前尚处于发展和完善中。
拓扑优化的特点是:设计变量多,计算规模大,目标函数和约束函数一般为设计变量的非线性、非单调函数。
目前应用于连续体结构拓扑优化计算的优化算法主要包括两类:优化准则法和序列凸规划法。
去除优化过程中数值计算不稳定的方法,优化结果的提取和重构;拓扑优化中经常出现的数值计算问题有:多孔材料、棋盘格现象、网格依赖性和局部极值问题。
优化结果的提取和应用主要考虑的是如何将优化的结果转化为可用的CAD模型问题,实现CAE和CAD之间的数据共享和交流。
随着拓扑优化理论研究的不断深入,拓扑优化在航空和汽车领域已开始得到初步的应用,主要是通过拓扑优化获得结构的最初拓扑形式,并在最初拓扑形式的基础上进行相关的后续优化设计。
ANSYS教程二---拓扑优化

ANSYS教程二---拓扑优化拓扑优化什么是拓扑优化?拓扑优化是指形状优化,有时也称为外型优化。
拓扑优化的目标是寻找承受单载荷或多载荷的物体的最佳材料分配方案。
这种方案在拓扑优化中表现为“最大刚度”设计。
与传统的优化设计不同的是,拓扑优化不需要给出参数和优化变量的定义。
目标函数、状态变量和设计变量(参见“优化设计”一章)都是预定义好的。
用户只需要给出结构的参数(材料特性、模型、载荷等)和要省去的材料百分比。
拓扑优化的目标――目标函数――是在满足结构的约束(V)情况下减少结构的变形能。
减小结构的变形能相当于提高结构的刚度。
这个技术通过使用设计变量(i)给每个有限元的单元赋予内部伪密度来实现。
这些伪密度用PLNSOL,TOPO命令来绘出。
例如,给定V=60表示在给定载荷并满足最大刚度准则要求的情况下省去60%的材料。
图2-1表示满足约束和载荷要求的拓扑优化结果。
图2-1a表示载荷和边界条件,图2-2b表示以密度云图形式绘制的拓扑结果。
图2-1 体积减少60%的拓扑优化示例如何做拓扑优化拓扑优化包括如下主要步骤:1.定义拓扑优化问题。
2.选择单元类型。
3.指定要优化和不优化的区域。
4.定义和控制载荷工况。
5.定义和控制优化过程。
6.查看结果。
拓扑优化的细节在下面给出。
关于批处理方式和图形菜单方式不同的做法也同样提及。
定义拓扑优化问题定义拓扑优化问题同定义其他线性,弹性结构问题做法一样。
用户需要定义材料特性(杨氏模量和泊松比),选择合适的单元类型生成有限元模型,施加载ANSYS教程二---拓扑优化荷和边界条件做单载荷步或多载荷步分析。
参见“ANSYS Analysis Procedures Guides”第一、二章。
选择单元类型拓扑优化功能可以使用二维平面单元,三维块单元和壳单元。
要使用这个功能,模型中只能有下列单元类型:二维实体单元:SOLID2和__三维实体单元:__和__壳单元:__二维单元用于平面应力问题。
ansys workbench拓扑优化实例

ansys workbench拓扑优化实例
拓扑优化(Topology Optimization)是一种结构优化的方法,通过在给定的设计空间内寻找最佳材料分布来实现结构的轻量化和性能优化。
在ANSYS Workbench 中,可以通过拓扑优化模块来进行这种优化分析。
以下是一个简单的ANSYS Workbench 拓扑优化实例的步骤:
1. 创建几何模型:首先,在ANSYS Workbench 中创建一个几何模型,可以是一个零件或者一个装配体。
2. 设定材料属性:为模型中的材料定义材料属性,包括弹性模量、泊松比等。
3. 设定加载和约束条件:定义模型的加载和约束条件,包括受力点、受力大小和方向,以及约束点和约束类型。
4. 添加拓扑优化模块:在Workbench 中选择拓扑优化模块,并将模型导入到拓扑优化模块中。
5. 设定优化目标和约束条件:定义优化的目标,比如最小化结构的重量或者最大化结构的刚度,同时设置一些约束条件,比如最大应力、最大变形等。
6. 设定优化参数:定义拓扑优化的参数,比如拓扑优化的迭代次数、网格分辨率等。
7. 运行优化分析:运行拓扑优化分析,软件会根据设定的优化目标和约束条件,在给定的设计空间内寻找最佳的材料分布。
8. 分析结果:分析优化结果,查看优化后的结构形态和性能指标,根据需要对设计进行进一步的调整和优化。
请注意,以上步骤是一个简化的示例,实际的拓扑优化分析可能涉及到更多的参数设定和分析步骤。
在实际应用中,建议根据具体的工程问题和软件版本进行详细的参数设定和分析。
ansys拓扑优化[整理版]
![ansys拓扑优化[整理版]](https://img.taocdn.com/s3/m/11d54a950912a21615792959.png)
ansys拓扑优化[整理版][ANSYS拓扑优化]注意点结果对载荷情况十分敏感。
很小的载荷变化将导致很大的优化结果差异。
结果对网格划分密度敏感。
一般来说,很细的网格可以产生“清晰”的拓扑结果,而较粗的网格会生成“混乱”的结果。
但是,较大的有限元模型需要更多的收敛时间。
,在一些情况下会得到珩架形状的拓扑结果。
这通常在用户指定很大的体积减少值和较细的网格划分时出现。
很大的体积减少值如80%或更大(TOPDEF命令)。
, 如果有多个载荷工况时,有多种方式将其联合进行拓扑优化求解。
例如,考虑有五个载荷工况的情况。
可以选择使用五个单独的拓扑优化分析过程,也可以使用包括这五个工况的一次拓扑优化分析。
还有,也可以将这五个工况合成为一个工况,然后做一次优化。
综合起来,可以有七个不同的拓扑优化求解:,5 独立的拓扑优化求解(每个工况一次)1 拓扑优化求解针对五个工况1 拓扑优化求解针对一个联合工况附加的结果或结果的组合都是可用的。
结果对泊松比敏感但对杨氏模量不敏感。
但是,随泊松比变化的效果不明显。
, TOPDEF和TOPITER命令中的指定值并不存储在ANSYS数据库中;因此,用户必须在每次拓扑优化时重新指定优化目标和定义。
[ANSYS拓扑优化]二维多载荷优化设计示例在本例中,对承受两个载荷工况的梁进行拓扑优化。
问题描述图2表示一个承载的弹性梁。
梁两端固定,承受两个载荷工况。
梁的一个面是用一号单元划分的,用于拓扑优化,另一个面是用二号单元划分的,不作优化。
最后的形状是单元1的体积减少50%。
图片2 承受两个载荷工况的梁图片3 拓扑优化结果——50%体积减少本问题是用下列的ANSYS命令流求解的。
两个载荷工况定义并用LSWRITE命令写入文件。
使用ANSYS选择功能,单元SOLID82通过类型号1和2分别指定优化和不优化的部分。
TOPDEF命令定义问题有两个载荷工况并要求50%体积减少。
TOPEXE命令在本例中没有使用,代之以用TOPITER宏命令指定最大迭代次数为12次。
拓扑优化简介和在ansys软件中的实现33页PPT

•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
现
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
拓扑优化简介和在ansys软件中的实
•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•Hale Waihona Puke 28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
ansys workbench拓扑优化实例

ansys workbench拓扑优化实例摘要:I.引言- 介绍ANSYS Workbench- 介绍拓扑优化II.ANSYS Workbench 拓扑优化实例- 实例一:某汽车零件拓扑优化- 背景介绍- 优化目标- 优化过程- 优化结果- 实例二:某飞机结构拓扑优化- 背景介绍- 优化目标- 优化过程- 优化结果III.拓扑优化在工程中的应用- 提高材料利用率- 减轻结构重量- 提高结构性能IV.总结- 总结ANSYS Workbench 拓扑优化实例- 展望拓扑优化在未来的发展正文:I.引言ANSYS Workbench 是一款集成的多物理场仿真工具,可以帮助工程师进行结构、热、流体、电磁等多种物理场的仿真分析。
在结构设计中,拓扑优化是一种重要的设计方法,可以有效地提高材料利用率、减轻结构重量、提高结构性能。
本文将通过两个实例,介绍如何在ANSYS Workbench 中进行拓扑优化分析。
II.ANSYS Workbench 拓扑优化实例实例一:某汽车零件拓扑优化背景介绍:在汽车制造领域,工程师们经常需要设计轻量化的零件,以提高汽车性能、降低油耗。
针对某汽车零件,我们需要在保持其功能不变的前提下,进行拓扑优化,以减轻其重量。
优化目标:在满足零件强度、刚度、耐疲劳等性能要求的前提下,降低零件重量。
优化过程:1.使用ANSYS DesignModeler 绘制零件的三维模型,并导出为IGS 格式文件。
2.在ANSYS Workbench 中,创建一个新的结构分析项目,并将模型导入到Workbench 中。
3.定义零件的材料属性、边界条件、载荷等。
4.运行拓扑优化分析,设置优化目标(如最小化零件质量)和约束条件(如保持零件的几何形状不变)。
5.查看优化结果,并使用DesignModeler 对优化后的零件进行可视化展示。
优化结果:经过拓扑优化,零件的质量减轻了约20%,同时保持了原有的强度、刚度和耐疲劳性能。
ANSYS16.0_____三角板的拓扑优化
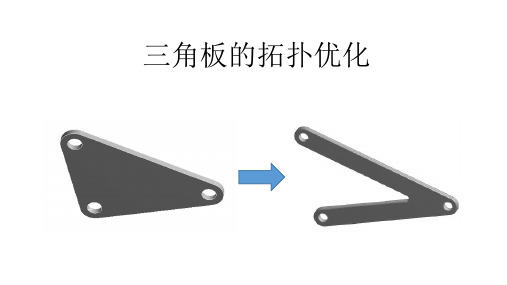
三角板的拓扑优化问题描述如图所示三角板,A和B两个圆孔的内表面施加固定约束,另一个圆孔的内表面施加力:FX=15N,FY=5,对其进行拓扑优化分析,使其质量减少45%,并做出拓扑优化分析后的新模型,进行应力的变形分析。
分析步骤•1.打开ANSYS workbench,双击左边工具栏中analysis system下的static structural选项,左键选中A3(geometry)栏,右键导入三角板模型;•2.双击A4(model)栏,进入DS模块;•3.材料默认为结构钢,单位选择Metric (mm, kg, N, s, mV, mA);4.右键单击mesh,弹出右键菜单选择insert>sizing,单击模型,并单击apply确认该项操作。
在element size栏中填入需要定义的尺寸2mm;5.右键单击mesh,弹出右键菜单选择insert>method,单击Sweep模型,并单击apply确认该项操作,生成网格高质量的六面体网格6.单击左侧的static structural,选择C 表面,鼠标右键选择insert>force,在左侧的工具栏中输入如图所示内容,再选择选择A、B表面,鼠标右键选择insert>fixed support约束条件:A:Force/B:Fixed Support7.求解计算后,单击solution,添加在弹出的工具条deformation下选择totall查看总变形,stress下选择equivalent stress查看Von Mises等效应力,查看位移和位移云图应力应力云图8.插入analysis systems中的shape optimization模块,用鼠标直接拖住toolbox中的shape optimization至A4栏中,双击B5(model),进入mechanical中9. 在左侧结构树中找到B5 Shape Optimization 并且对三角板施加与A5中完全一样的载荷和约束,保持与静力分析相同10.点击左侧结构树中的shape finder,选中确定模型后,在target reduction设置为45%,表明目标减少材料重量45%的使用10.求解查看拓扑优化之后的结构与对比位移和应力云图保留材料(灰色)去除材料(红色)结论通过以上表格和应力云图对比可知,更改设计后的模型质量(mass)比原来减少了44.35%(基本达到题目要求,由于更改几何模型的问题,没有达到题目所要求的45%),但应力和位移都有普遍的增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
opexe ! 执行优化
PARSAV,,RSET1 !将参数的值输出到文件中且文件名为rset1
oplist,all,,1 !列表显示所有序列
/AXLAB,Y,TVOL !设置曲线输出时y轴的说明
opvar,TK27,dv,4/H,7/H
opvar,TK38,dv,4/H,7/H
opvar,TK49,dv,4/H,7/H
opsave,INITIAL,opt !保存所有的优化数据到文件optp里
optype,SUBP !设置优化方式,子问题逼近算法
plvaropt,TVOL !绘图显示目标函数随优化次数的变化规律
FINISH
/POST1
PLNSOL,U,SUM,0,1 !显示结构在优化后的总位移分布
PLNSOL,S,EQV,0,1 !显示结构在优化后的应力分布
FINISH
MP,EX,1,6.89E10
MP,NUXY,1,0.3
K,1
K,5,254/H
KFILL ! 在第1至第5个关键点之间生成2,3,4关键点
K,6,,TK16
K,7,63.5/H,TK27
K,8,127/H,TK38
K,9,190.5/H,TK49
K,10,254/H,TK50
SPLINE,6,7,8,9,10
L,1,6
*REPEAT,5,1,1 !重复L命令,关键点编号自动加1,分别在2,7、3,8、4,9、5,10之间共生成4条线其中包含了、命令已生成的线,共5条
LSEL,S,LINE,,5,9 !选择上述生成的5条线
LESIZE,ALL,,,1 !指定线在划分网格前的等分数为1
TVOL=TVOL*2 !由于分析时只计算了结构的一半,总体积要乘2
NSEL,U,LOC,X,250/H,265/H !选择介于250/H到265/H的节点
PRNSOL,U,Y !列表显示出所选节点在y向的位移值
NSORT,U,Y,,1 !位移值升序排列
PRNSOL,U,Y !列出排序后的结果
opvar,DEFL,sv,,12.5/H
opvar,DIF1,sv,,1/H
opvar,DIF2,sv,,1/H
opvar,DIF3,sv,,1/H
op设计变量及其变化范围
FINISH
/CLEAR,START
/TRIAD,OFF !关闭整体直角坐标系的三角符号
H=1000 !设置比例尺,采用iso
TK16=6.35/H !设置参数变量并附初值
TK27=6.35/H
TK38=6.35/H
TK49=6.35/H
TK50=4/H
/PREP7
ET,1,PLANE42
*GET,DEFL,SORT,,MAX !取出最大的位移值赋给defl
*STATUS,PARM !显示当前参数变量的状态值
DEFL=ABS(DEFL)
DIF1=TK16-TK27 !设置参数值,以保证曲线的光滑性
DIF2=TK27-TK38
DIF3=TK38-TK49
FINISH
lgwrite,scratch,lgw
NSEL,ALL
FK,10,FX,66725*4 !在10号关键点施加集中载荷,实现弯矩
DK,1,ALL,0 !在1号关键点施加全约束
SOLVE
FINISH
/POST1
SET,LAST
ETABLE,EVOL,VOLU !建立单元表,并取出每个单元的体积EVOL=每个单元的体积
/OPT
opanl,scratch,lgw !指定分析文件
opvar,TVOL,Obj,,,1/H !定义优化目标函数,收敛误差为1,结构总体积TVOL为目标函数
opvar,STRS,sv,,206E6 ! 定义状态变量即优化过程的约束条件
PRNSOL,S,PRIN !列出节点的主应力
NSORT,S,1
NSEL,U,LOC,X,0,230/H !选择介于0到230/H的节点
*GET,STRS,SORT,,MAX !取出最大的应力值并赋给strs
NSEL,ALL
SSUM !体积相加
*get,TVOL,ssum,,item,EVOL !取出结构总体积
LSEL,ALL
A,1,2,7,6
*REPEAT,4,1,1,1,1 !重复上述命令,共生成4个面
ESIZE,,4
AMESH,ALL
FINISH
/SOLU
NSEL,S,LOC,Y
DSYM,SYMM,X !对选择的节点施加x方向的对称约束
NSEL,S,LOC,X
DSYM,ASYM,Y !对选择的节点施加x方向的反对称约束
