19.1.2函数的图象(二)
19.1.2函数图像(2)-画函数图像

函数的图象(1)知识技术目标1.掌握用描点法画出函数的图象;2.认识函数图像的性质 .过程性目标1.经过学生自己着手,领悟用描点法画函数的图象的步骤.2.结合画出的图形,教会学生看解析图形的性质,重点看什么。
授课过程一、复习引入问题 1 上节课的内容:函数的定义;定义域,值域;表达方式有三种:列表法,图形法,解析式法问题 2 提问:画函数图像的步骤是?列表——描点——连线二、研究归纳教师举例: p74 练习 1( 1)y x2 x0每个步骤都要有注意的地方。
1.列表:列表给出自变量与函数的一些对应值;2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;理论上点越多越好,不能够少于 5 个点,一般取 7 个点3.连线:依照自变量由小到大的序次,把所描各点用圆滑的曲线连结起来.描出的点越多,图象越精确.有时不能够把所有的点都描出,就用圆滑的曲线连结画出的点,从而获取函数的近似的图象.三、实践应用课堂让学生着手画三个函数图像:①y x 2②y 1 ③y 2x 1 x四、交流反思我们看图像看的是什么?1、定义域、值域2、对称性3、与坐标轴交点个数4、函数的单调性师生共同谈论:y x 2 图像定义域: x 可取任意实数 ,y >0;对称轴是 y 轴;与坐标轴交于( 0,0 )为什么 y >0,为什么以 y 轴为对称轴?; x<0 时, y 随着 x 的增大而减小, x>0 时, y 随着 x 的增大而增大。
师生共同谈论:y1 图像的定义域: x 0 , y 0 ;对称轴是 x 轴, y 轴, x=y ,x=-y ;与坐标轴没有交点 x为什么会有以上特色呢?x<0 时, y 随着 x 的增大而减小, x>0,y 随着 x 的增大而减小。
师生共同谈论:y2x 1 图像的定义域: x可取任意实数, y可取任意实数;与坐标轴交于两点,与x轴交于(1,0),与y轴交于(0,-1);y随着x的增大而增大2。
人教版数学八年级下册19.1.2《函数的图象—函数的图象及其画法》教学设计

人教版数学八年级下册19.1.2《函数的图象—函数的图象及其画法》教学设计一. 教材分析人教版数学八年级下册19.1.2《函数的图象—函数的图象及其画法》这一节,主要让学生了解函数图象的概念,学会如何画函数图象。
教材通过具体的例子,引导学生掌握函数图象的画法,并能够分析图象的性质。
本节内容是学生对函数知识体系的重要补充,也是后续学习函数性质的基础。
二. 学情分析学生在学习本节内容前,已经掌握了函数的基本概念,了解了函数的解析式。
但他们对函数图象的认识还比较模糊,可能只停留在图像的直观层面,对如何从解析式中得出函数图象的方法还不够清晰。
因此,在教学过程中,需要教师通过具体例子,引导学生理解函数图象的生成过程,以及如何从解析式中提取信息,画出函数图象。
三. 教学目标1.让学生了解函数图象的概念,理解函数图象与函数解析式之间的关系。
2.学会如何画函数图象,并能分析图象的性质。
3.培养学生的观察能力、动手能力以及逻辑思维能力。
四. 教学重难点1.重点:函数图象的概念,如何画函数图象。
2.难点:如何从解析式中提取信息,画出函数图象,并分析图象的性质。
五. 教学方法采用讲授法、引导法、实践法、讨论法等多种教学方法。
通过具体例子,引导学生动手实践,观察分析,理解函数图象的生成过程,以及如何从解析式中提取信息,画出函数图象。
六. 教学准备1.准备相关的教学PPT,包括函数图象的定义、生成过程、分析方法等内容。
2.准备一些具体的函数解析式,用于让学生实践画图。
3.准备一些函数图象的图片,用于让学生观察分析。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾函数的基本概念,然后引入函数图象的概念。
让学生思考:函数图象是什么?它与函数解析式有何关系?2.呈现(10分钟)教师通过PPT展示一些具体的函数图象,让学生观察并分析。
同时,教师引导学生思考:这些图象是如何生成的?从图象中我们可以得到哪些信息?3.操练(10分钟)教师给出一些函数解析式,让学生动手实践,尝试画出对应的函数图象。
人教版数学八年级下册19.1.2《函数的图象》说课稿2

人教版数学八年级下册19.1.2《函数的图象》说课稿2一. 教材分析《函数的图象》是人民教育出版社出版的初中数学八年级下册第19.1.2节的内容。
本节内容是在学生已经掌握了函数的概念、性质以及一些基本函数的基础上进行学习的,是函数知识体系中的重要组成部分。
通过本节的学习,使学生能够理解函数图象的意义,能够运用函数图象解决一些简单的实际问题。
二. 学情分析初中八年级的学生已经具备了一定的函数知识,对于函数的概念、性质有一定的了解。
但是,对于函数图象的理解和运用还比较薄弱,需要通过本节的学习,使学生能够将函数知识与实际问题相结合,提高解决问题的能力。
三. 说教学目标1.知识与技能目标:使学生能够理解函数图象的意义,掌握函数图象的绘制方法,能够通过函数图象解决一些简单的实际问题。
2.过程与方法目标:通过观察、分析、归纳等方法,使学生能够自主探究函数图象的性质,培养学生的动手操作能力和思维能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,增强学生对数学知识的应用意识,培养学生团结协作、积极进取的精神。
四. 说教学重难点1.教学重点:函数图象的意义,函数图象的绘制方法。
2.教学难点:函数图象的性质,如何通过函数图象解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组合作法等,引导学生主动探究,提高学生的问题解决能力。
2.教学手段:利用多媒体课件、函数图象软件等,直观展示函数图象,增强学生的直观感受。
六. 说教学过程1.导入:通过展示一些实际问题,引导学生思考如何通过函数图象来解决问题,激发学生的学习兴趣。
2.知识讲解:讲解函数图象的意义,介绍函数图象的绘制方法,引导学生通过实际操作来绘制函数图象。
3.案例分析:分析一些典型的实际问题,引导学生运用函数图象来解决问题,培养学生的应用能力。
4.小组讨论:学生进行小组讨论,分享彼此的学习心得和解决问题的方法,提高学生的合作能力。
八年级数学下册人教版课件:19.1.2 函数的图象2

19.1.2 函数的图象(2)
课件说明
• 本课是在学习函数概念和函数表示法的基础上,进 一步体会函数的三种表示方法的特点,学习综合运 用三种表示方法表示函数关系.
课件说明
• 学习目标: 1.了解函数的三种表示法及其优缺点; 2.能用适当的方式表示简单实际问题中的变量之间 的函数关系; 3.能对函数关系进行分析,对变量的变化情况进行 初步讨论.
(2)对于x 的值分别为1,2,3,4,5,6 时,想知 道其对应的函数值,用什么表示方法较好?
(3)想知道当x 的值增大时,函数值y 怎样变化,用 什么表示方法较好?
合作探究: 说说函数的三种表示方法各有什么优点和不足,分 小组讨论一下.
例 一水库的水位在最近5 h 内持续上涨,下表记录 了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表 示水位高度.
x
问题 如图,要做一个面积为12 m2的小花的图象吗?
y 40 35
x/m 1 2 3 4 5 6 y/m 26 16 14 14 14.8 16
30
25
20
15
10
5
O
5
10
x
思考
(1)对于每一个大于0 的自变量的值,想准确确定 对应的函数值,用什么表示法较好?
x
问题 如图,要做一个面积为12 m2的小花坛,该花 坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变 量的取值范围;
y 是 x 的函数,自变量 x 的取值范围是x>0.
x
问题 如图,要做一个面积为12 m2的小花坛,该花 坛的一边长为 x m,周长为 y m.
(2)能求出这个问题的函数解析式吗?
函数的图象(第2课时+函数的三种表示方法)+课件+2023-2024学年人教版数学八年级下册

A. B. C. D.
①当 时, 随 的增大而增大;②当 时, 有最小值,最小值为80(答案不唯一)
(3)数学应用:已知当潮水高度超过 时,货轮能够安全进出此港口,则当天什么时间段适合货轮进出此港口?
解:由图象,得当 时, 或 或 或 , 当 或 时, ,即当天 到 或 到 适合货轮进出此港口.
跟踪训练
1.(2023·萱花中学阶段练习)丽丽妈妈喜欢跳广场舞,某天她步行到离家较远的广场,跳了一会儿广场舞后跑步回家.下列能反映当天丽丽妈妈离家的距离 与时间 的函数关系的大致图象是( )
C
A. B. C. D.
解:用列表法表示该正方形的周长 关于边长 的函数如下:
0
1
2
3
4
...
0
4
8
12
16
...
用解析式法表示该正方形的周长 关于边长 的函数为 .
(2)用解析式法和图象法(在所给图中画出)表示该正方形的面积 关于边长 的函数.
解: 用解析式法表示该正方形的面积 关于边长 的函数为 .用图象法表示该正方形的面积 关于边长 的函数如图所示.
(3)结合函数图象,写出点 , 相距3个单位长度时 的值.
解: 当 时, ,即 ;当 时, ,即 ,解得 , 的值为3或4.5.
11.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发匀速行驶.两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续驶往乙
(3)当刺梨的销量为50千克时,销售额是_ _____元.
7.(教材P80例4变式)今年夏天,某地区由于持续高温和连日无雨,水库蓄水量普遍下降.某水库的蓄水量 (万立方米)与干旱持续时间 (天)之间的关系如图所示,请根据此图,回答下列问题:
人教版数学八年级下册19.1.2一次函数的图象和性质教学设计

2.对于一次函数中斜率k和截距b的理解,学生可能会存在困难。教师应结合实际情境,让学生在实际问题中感知k、b的意义,提高学生的理解程度。
3.在学习过程中,学生可能会对一次函数的性质产生混淆,如斜率的正负与函数图象的关系等。教师应通过对比、总结等方法,帮助学生梳理清楚这些关系。
2.引导学生思考:让学生尝试用数学语言描述上述问题中的关系,从而引出一次函数的定义。在此过程中,教师要注意引导学生从实际问题中抽象出数学模型,培养学生的建模意识。
(二)讲授新知
1.一次函数的标准形式:y=kx+b。详细讲解k、b分别代表的含义,以及在实际问题中的应用。
2.一次函数的图象:通过绘制一次函数的图象,让学生直观地认识一次函数的走势。同时,引导学生观察图象上任意两点的坐标,发现它们连线的斜率是定值k。
3.拓展作业:选择课本练习题19.1中的一道或两道拓展题进行思考,鼓励同学们挑战更高难度的题目,培养解决问题的创新思维。
-拓展题:结合一次函数的性质,探讨如何解决一些实际问题,例如最优化问题、行程问题等。
4.小组合作作业:布置一道需要小组合作的作业,要求同学们在课后分组讨论,共同完成。
-设计一道综合性的问题,涉及一次函数的多个知识点,要求小组合作,共同分析问题、建立模型、解决问题,并在下次课堂上进行展示和分享。
3.培养学生能够通过一次函数的图象,分析其性质,如单调性、截距等,并能够运用这些性质解决相关问题。
4.让学生学会运用数形结合的思想,将一次函数的图象和性质相互印证,提高解决问题的能力。
(二)过程与方法
1.通过直观的图象展示,引导学生观察、分析、总结一次函数的性质,培养学生的观察能力和逻辑思维能力。
人教版八年级数学(下)课件:19_1_2 函数的图象(第2课时)

19.1 函数 19.1.2 函数的图象
(第2课时)
导入新知 在计算器上按照下面的程序进行操作:
输入x(任意一个数)
按键
× 2 + 5=
填表:
显示y(计算结果)
x 1 3 -4 y 7 11 -3
0 101 5 207
显示的数y是输入的数x的函数吗?为什么? 如果是,写出它的解析式. 是, y = 2x+5.
27千克
探究新知
考点 2 利用函数表达式解答实际问题 如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m, 周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值 范围;
(2)能求出这个问题的函数解析式吗?
解:(1)y 是 x 的函数,自变量 x 的取
值范围是x>0.
答:是, y=8+2(x-3) =2x+2
用函数解析 式来表示.
这里是怎样表 示所付费用y与 所走路程x的 函数关系的?
探究新知 问题3 如图是某地某一天的气温变化图.
这里是怎样表示气温T与 时间t之间的函数关系的?
(1)指出其中的两个变量是 气温T , 时间t .
用平面直 角坐标系 中的一个 图象来表 示的.
探究新知
其函数的图象如下:
y/m
5
5
4
B
3
3A 2
1
O
O
1
2
3
4
5
6
7
5
8
t/h
探究新知
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度
将达到多少m.
解:如果水位的变化规律不变,按上述函数预测,再持续2小
2021年人教版数学八年级下册学案 19.1.2《 函数的图象 》(含答案)

19.1.2 函数的图象第1课时函数的图象学习目标①知道函数图象的意义.②学会用列表、描点、连线画函数图象.③学会观察、分析函数图象信息.④能利用函数的图象解决实际问题重点难点:函数图象的画法;观察、分析、概括图象中的信息.学习过程一、自主学习(阅读教材并完成下列活动)【活动1】思考:如图是某人体检时的心电图,图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,y与x之间的函数关系能用式子表达吗?显然有些函数问题用函数关系式表示出来,然而可以通过来直观反映.【活动2】正方形的边长x与面积S的函数关系式为;在这个函数中,自变量是、它的取值范围是,是的函数,请根据这个函数关x 0 0.5 1 2 3 ……S ……思考与探究:如果把自变量的值当作横坐标,函数S的值作为纵坐标,组成一对有序实数对(x、S),这样的实数对有多少对?请在下面的直角坐标系中描出这些点,你有什么发现?二、探究新知识①一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的、坐标,那么坐标平面内由这些点组成的图形,就是这个函数的。
②画函数图象的一般步骤是:、、。
③在坐标平面内,若点P(x,y)向右上方移动,则y随x的增大而;若点P(x,y)向右下方移动,则y随x的增大而。
第2课时函数的表示方法学习目标①进一步理解函数及其图像的意义.②学会根据自变量的值求函数值;或根据函数值求自变量的值,掌握函数的表示方法.③熟练掌握求函数中自变量的取值范围的方法.重点难点:①怎样根据自变量的值求函数值;②怎样求函数自变量的取值范围;③根据函数图象解决实际问题.学习过程一、自主学习(阅读教材)【活动1】分析并解决下列列问题:1.用解析法表示函数关系优点: . 缺点: . 2.用列表表示函数关系优点: . 缺点: . 3.用图象法表示函数关系优点: . 缺点: . 【活动2】请用原来所学的知识完成下列填空:1、若错误!未找到引用源。
有意义,则x的取值范围是 .2、若错误!未找到引用源。
人教版八下数学19-1-2函数的图象课时2

(3)据估计这种上涨规律还会持续 2 h,预测再过 2 h
水位高度将达到多少米?
如果水位的变化规律不变,则可利用上述函数预测,
再过 2 h,即 t=5+2=7(h) 时,水位高度
y=0.3×7+3=5.1(m).
把图中的函数图象(线段AB)向右延
伸到 t=7 所对应的位置,从图象也
能看出这时的水位高度约为 5.1 m.
新知探究 知识点2:列表法
列表法:通过列出自变量的值与对应函数值的表格来
表示函数关系的方法叫做列表法.
例2 以下式子,对于 x 的每一个确定的值,y 都有唯
一的对应值,即 y 是 x 的函数.从 x 的取值范围中选取
一些数值,算出 y 的对应值,列表.
y=2x+3
从式子 y=2x+3 可以看出,x 取任意实数时这个式子都
26
24
O 10 20 30 40 50 60 70
x
这个函数解析式是分段的,所以函数图象是折线段.
课堂小结
函
数
表
示
法
解析
式法
用数学式子表示函数关系的
方法叫做解析式法,其中的
等式叫做函数解析式.
列表法
通过列出自变量的值与对应
函数值的表格来表示函数关
系的方法叫做列表法.
图象法
用图象表示两个变量间的函
有意义,所以 x 的取值范围是全体实数.
从 x 的取值范围中选取一些数值,算出 y 的对应值,
列表:
x
……
-2
-1
0
1
2
……
y
……
-1
1
3
5
7
19.1.2函数的图像(正式稿)
1、列表 2、描点
3、连线
列出自变量与函数的对应值表。 注意:自变量的值(满足取值范围), 并取值要适当,以便画图.
建立直角坐标系,以自变量的值为横坐标, 相应的函数值为纵坐标,描出表格中数值 对应的各点 按照横坐标从小到大的顺序把描出的点用 平滑曲线依次连接起来
注:函数图象可能是曲线,也可能是直线,也可能是 线段或射线,函数图象的形状取决于函数关系和自 变量的取值范围。
【反思归纳】函数的三种表示法通常是相 互关联,可以相互转化(特殊的函数除外): (1)由函数解析式可以得到这个函数的列表 及图象; (2)由函数的图象可以得到其解析式及函数 的对应值表格; (3)由函数的表格可以得到函数的解析式及 图象.
(1)函数图象上的点的横纵坐标分别表示什么? (2)画函数图象时,怎样体现函数的自变量取值范围?
(1)判断下列各点是否在函数 y =x+ 0.5的图象上? ①(-4,-4.5); ②(4,4.5). 6 (2)判断下列各点是否在函数 y = (x>0) 的图象上? x ①(2,3);②(4,2).
2、函数 y=-2x-6的图象上,若点B(a,a+1)在这 个函数图象上,则a=________.
s/米
2.周末小明一家乘出租车前往离家8千米的公园, 出租车的收费标准如下:
里程 收费/元
t/秒
3千米以下(含3千米)
3千米以上,增加1千米
5.00
1.00
(1)写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系。 (2)小明带了10元钱,够不够付到公园的车费,为什么?
3. 已知某一函数的图象如图所示,根据图象回答下列问题 : (1)确定自变量的取值范围; (2)求当x=-4,-2,4时y的值是多少? (3)求当y=0,4时x的值是多少? (4)当x取何值时y的值最大?当x取 何值时y的值最小? (5)当x的值在什么范围内时y随x的增大而增大?当x的值在 什么范围内时y•随x的增大而减小?
19.1.2函数的图像(2)

请在9分钟内完成当堂检测题,看哪位同学完 成的又快又好。
当堂训练
必做题:
2、课本P83页第10题.
选做题:
课本P83页第12题.
8分钟内看哪些同学能又快又好的完成上述问题!
函数三种表示方法的优点
表示方法 全面性 准确性
× √ ×
直观性
√ × √
形象性
×
× √
列表法
解析式法 图象法
√
√ ×
从所填表中可以清楚看到三种表示方法各有优 缺点.在遇到实际问题时,就要要根据具体情况选 择适当的方法,有时为全面地认识问题,需要几种 方法同时使用.
学以致用
(1) 对于每一个大于0 的自变量的值,想准确 确定对应的函数值,用什么表示法较好? (2)对于x 的值分别为1,2,3,4,5,6 时, 想知道其对应的函数值,用什么表示方法较好? (3)想知道当x 的值增大时,函数值y 怎样变化, 用什么表示方法较好?
随堂检测
课本P81页的练习题1、2、3
19.1.2函数的图象
——第二课时
学习目标Biblioteka 1.理解并掌握函数的三种表示方法及各 自的优点; 2. 能够利用函数图象所提供的信息解题。
自学指导
1、阅读课本79页练习和思考中间的部分可知函数的 表示方法有几种?分别是什么? 2、例4的表19-6是函数的什么表示方法?这种表示方 法有什么优点? 3、例4(2)分别用了哪几种函数表示方法?它们分 别有什么优点? 4、例4(3)能否通过表19-6或者例4(2)的图象预测 ? (提示:函数不同表示方法的优点可以从全面、准确 、直观、形象四个角度分析)
人教版初中数学八年级下册《19.1.2函数的图像》教案

《19.1.2-函数的图象》教学设计1、教学目标(1)了解函数图象的意义;(2)会观察函数图象获取信息,能根据图象初步分析函数的对应关系和变化规律;(3)会用列表、描点、连线三步法画函数图象.经历函数图象的绘制过程,体会画函数图象的关键是分别用点的横、纵坐标表示自变量和对应的函数值.2、设计思路(1)借助简单实例,学生初步感知函数图象的意义,学会分析函数图象,能根据函数图象找出相关信息。
(2)从学生熟悉、感兴趣的实例引入课题,引领学生参与函数图象的形成过程,体验“发现、创造”数学知识的乐趣.学生初步感知实际生活蕴藏着丰富的数学知识,感知数学是有用、有趣的学科。
3、教学过程(一)导入【教师引导】我们在前面学习了函数意义,并掌握了函数关系式的确立。
但有些函数问题很难用函数关系式表示出来,然而可以通过图来直观反映。
例如用心电图表示心脏生物电流与时间的关系。
即使对于能列式表示的函数关系,如果也能画图表示则会使函数关系更清晰。
我们这节课就来解决如何画函数图象的问题及解读函数图象信息。
(二)新授课活动一:问题1 正方形的边长x与面积S的函数关系是什么?其中自变量x的取值范围是什么?计算并填写下表:x 0 0.5 1 1.5 2 2.5 3 3.5 …S【师生活动】函数关系式为S=x2,因为x代表正方形的边长,所以自变量x>0,将每个x的值代入函数式即可求出对应的S值.【教师引导】如果我们在直角坐标系中,将你所填表格中的自变量x及对应的函数值S当作一个点的横坐标与纵坐标,即可在坐标系中得到一些点.大家思考一下,表示x与S的对应关系的点有多少个?•如果全在坐标中指出的话是什么样子?可以讨论一下,然后发表你们的看法,建议大家不妨动手画画看.【师生活动】这样的点有无数多个,如果全描出来太麻烦,也不可能.我们只能描出其中一部分,然后想象出其他点的位置,用光滑曲线连接起来.这样我们就得到了一幅表示S与x关系的图.图中每个点都代表x的值与S的值的一种对应关系.如点(2,4)表示x=2时S=4.【归纳】一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.上图中的曲线即为函数S=x2(x>0)的图象.函数图象可以数形结合地研究函数,给我们带来便利.活动二:问题2 下图是自动测温仪记录的图象,它反映了北京春季某天气温T如何随时间t变化而变化,你从图象中得到了哪些信息?(气温T是时间t的函数)根据图象回答下列问题:(1)最低、最高温度分别是多少?(2)哪些时段温度呈下降状态?上升状态呢?(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少吗?【设计意图】通过图象进一步认识函数意义,体会图象的直观性、优越性,提高对图象的分析能力、认识水平,掌握函数变化规律.【教师引导】先考虑一个简单的问题:你是如何从图上找到各个时刻的气温的?【师生活动】图中,有一个直角坐标系,它的横轴是t轴,表示时间;它的纵轴是T轴,表示气温.这一气温曲线实质上给出了某日的气温T (℃)与时间t(时)的函数关系.例如,上午10时的气温是2℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10,2).实质上也就是说,当t=10时,对应的函数值T=2.气温曲线上每一个点的坐标(t,T),表示时间为t时的气温是T.【归纳】(1)这天中凌晨4时气温最低为-3℃,14时气温最高为8℃.(2)从0时至4时气温呈下降状态,即温度随时间的增加而下降.从4时至14•时气温呈上升状态,从14时至24时气温又呈下降状态.问题3 如图,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离他家的距离y与时间x之间的对应关系.根据图象回答下列问题:(1)食堂离小明家多远?小明从家到食堂用了多少时间?(2)小明吃早餐用了多少时间?(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?(4)小明读报用了多长时间?(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?【设计意图】按要求从图象中挖掘所需信息,并自理信息,进一步提高识图能力.【师生活动】引导学生分析图象、寻找图象信息,特别是图象中有两段平行于x轴的线段的意义.【归纳】(1)由纵坐标看出,菜地离小明家0.6千米;由横坐标看出,小明走到食堂用了8分钟.(2)由平行线段的横坐标可看出,小明吃早餐用了17分钟.(3)由纵坐标看出,食堂离图书馆0.2千米;从横坐标看,小明从食堂到图书馆用了3分钟.(4)由平行线段的横坐标可看出,小明读报用了30分钟.(5)由纵坐标看出,图书馆离小明家0.8千米.由横坐标看出,小明从图书馆回家的平均速度是回家的平均速度是2÷25=0.08(千米/分钟).【追问】我们通过两个活动已学会了如何观察分析图象信息,那么已知函数关系式,怎样画出函数图象呢?活动三:(1)画函数S=x2(x>0)的图象第一步:列表x 0 0.5 1 1.5 2 2.5 3 …S …第二步:描点:以x的值为坐标,相应的函数值为坐标,描出表格中数值对应的各点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
波峰中学初二数学作业A(课前)
编制:靳丽杰教研组长:备课组长:日期:
编号:班级小组姓名成绩
19.1.2函数的图象(二)
[学习目标]:1、总结函数三种表示方法.
2、了解三种表示方法的优缺点.
3、形成合作交流意识及独立思考习惯.
[学习重点]:认清函数的不同表示方法,知道各自优缺点.
[学习难点]:函数表示方法的应用.
[完成目标]
一、创设情境独立思考
1、阅读课本P80 ~81 页,思考下列问题:
1、函数的三种表示方法分别是什么?
2、课本P80-81页例4的解答你能理解吗?
3、课本P81页练习你能独立解答吗?
2、独立思考后我还有以下疑惑:(课前写在小组的小黑板上)
二、合作学习探索新知师生合作解决问题
(1)汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。
S = 60t这种表示函数的方法叫做解析式法解析式主要能反映数量关系
(2)下表是某种股票一周内周一至周五的收盘价。
这种表示函数的方法叫做列表法表格主要能反映对应关系
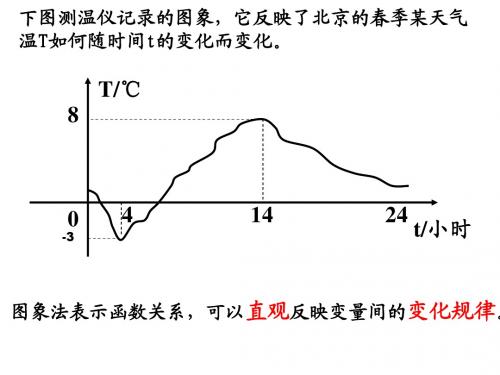
(3)下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。
这种表示函数的方法叫图象法图象主要能反映变化规律。
三、归纳总结
知识点的归纳总结:
(1)函数的表示方法:解析法、列表法、图象法
(2)优点:
①列表法比较直观、准确地表示出函数中两个变量的关系.
②解析式法则比较准确、全面地表示出了函数中两个变量的关系.
③图象法它则形象、直观地表示出函数中两个变量的关系.
(3)不足:
①列表法不如解析式法全面,也不如图象法形象;
②解析式法却不如列表法直观,不如图象法形象;
③图象法也不如列表法直观准确,不如解析式法全面.
波峰中学初二数学作业B(课后)
编制:靳丽杰备课组长:教研组长:日期:
编号:班级小组姓名成绩
一、运用新知解决问题:(重点例习题的强化训练)
一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度.
(1)由记录表推出这5小时中水位高度y(米)随时间t•(时)变化的函数解析式,并画出函数图象.
(2)据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
(3) 据估计这种上涨规律还会持续2小时,预测再过两小时水位高度将为多少米?
二、课堂小测(约5分钟)
1、已知点(-1,2)是函数y=kx的图象上的一点,则k= 。
2、下列各点中,在函数y=x图象上的是()
A、(—2,—4)
B、(4,4)
C、(—2,4)
D、(4,2)
3、点A(1,m)在函数y=2x的图象上,则点的坐标是()
A、(1,)
B、(1,2)
C、(1,1)
D、(2,1)
4、下列四个点中在函数y=2x—3的图象上有()个。
(1,2) , (3,3) , (—1, —1), (1.5,0)
A.1 B.2 C.3 D.4
三、反思与总结
满分共40 分,学生得分
【日期】月日
【批语】
相信自己,努力拼搏!。
