2-单个正态总体参数检验
单正态总体的参数假设检验

单正态总体的参数假设检验一、引言在统计学中,参数假设检验是一种常用的统计推断方法,用于对总体参数的假设进行验证。
在本文中,我们将讨论单正态总体的参数假设检验方法。
单正态总体是指样本来自一个服从正态分布的总体。
二、参数假设检验的基本步骤参数假设检验的基本步骤包括以下几个方面:1. 提出假设:在进行参数假设检验时,首先需要提出原假设和备择假设。
原假设(H0)是对总体参数的一个特定取值或一组取值的陈述,备择假设(H1)是对原假设的补充或对立假设。
2. 选择检验统计量:检验统计量是一个用于判断是否拒绝原假设的量。
在单正态总体的参数假设检验中,常用的检验统计量有样本均值、样本比例等。
3. 确定显著性水平:显著性水平是在进行假设检验时所允许的犯第一类错误的概率。
通常情况下,显著性水平取0.05或0.01。
4. 计算检验统计量的观察值:根据样本数据,计算检验统计量的观察值。
5. 确定拒绝域:拒绝域是一组检验统计量的取值,如果观察到的检验统计量的取值落在这个区域内,则拒绝原假设。
6. 做出决策:根据观察到的检验统计量的取值和拒绝域的关系,做出接受或拒绝原假设的决策。
三、单正态总体均值的参数假设检验在单正态总体均值的参数假设检验中,常用的检验方法有Z检验和t检验。
1. Z检验:当总体的标准差已知时,可以使用Z检验。
Z检验的检验统计量为样本均值与总体均值之差除以标准差的样本标准差。
根据中心极限定理,当样本容量较大时,检验统计量近似服从标准正态分布。
2. t检验:当总体的标准差未知时,使用t检验。
t检验的检验统计量为样本均值与总体均值之差除以标准误差的样本标准差。
根据学生t分布的性质,当样本容量较小时,检验统计量服从t分布。
四、实例分析为了更好地理解单正态总体的参数假设检验方法,我们以某电商平台的订单发货时间为例进行分析。
假设我们关注的是该电商平台订单的平均发货时间。
我们提出如下的原假设和备择假设:原假设(H0):订单的平均发货时间为3天。
正态总体参数的假设检验matlab处理

正态总体参数的检验1 总体标准差已知时的单个正态总体均值的U检验某切割机正常工作时,切割的金属棒的长度服从正态分布N(100,4)。
从该切割机切割的一批金属棒中随机抽取15根,测得长度为:97 102 105 112 99 103 102 94 100 95 105 98 102 100 103假设总体的方差不变,试检验该切割机工作是否正常,即检验总体均值是否等于100?,取显著性水平a=0.05。
分析:这是总体标准差已知时的单个正态总体均值的检验,根据题目要求可写出如下假设:H0:u=u0=100,H1=u /=u0(u不等于u0)H0称为原假设,H1称为被择假设(或对立假设)MATLAB统计工具箱中的ztest函数用来做总体标准差已知时的单个正态总体均值的检验调用格式ztest[h,p,muci,zval]=ztest(x,mu0,Sigma,Alpha,Tail)x:是输入的观测向量mu0:假设的均值Sigma:总体标准差Alpha:显著性水平,默认0.05Tail:尾部类型变量,‘both’双侧检验(默认),u不等于uo;‘right’右侧检验,u>u0; ‘left’左侧检验,u<u0;返回值:h:假设的结果(0,1),h=0时,接受假设H0;h=1,拒绝假设H0p:检验的p值,p>Alpha时,接受原假设H0;p<=Alpha 时,拒绝原假设H0.muci:总体均值u的置信水平为1-Alpha的置信区间zval:检验统计量的观测值%定义样本观测值向量x=[97 102 105 112 99 103 102 94 100 95 105 98 102 100 103];mu0=100; %原假设中的mu0sigma=2; %总体标准差Alpha=0.05; %显著性水平%调用ztest函数做总体均值的双侧检验(默认),%返回变量h,检验的p值,均值的置信区间muci,检验统计量的观测值zval[h,p,muci,zval]=ztest(x,mu0,sigma,Alpha)h =1p =0.0282muci =100.1212 102.1455zval =2.1947由ztest函数返回值可以看到,h=1,且p=0.0282<0.05,所以在显著性水平=0.05下拒绝的原假设H0:u=u0=100,因此认为该切割机不能正常工作,同时还返回了总体均值的置信水平为95%(1-0.05)的置信区间为[100.1212 102.1455]。
两个正态总体参数的假设检验 推导

两个正态总体参数的假设检验推导一、引言假设检验是统计学中常用的方法,用于检验两个正态总体参数是否具有显著差异。
本文将介绍两个正态总体参数的假设检验的推导过程,主要包括以下步骤:假设提出、样本收集、样本检验、推断结论、结果解释和误差分析。
二、假设提出假设检验的基本思想是通过样本数据对总体参数进行推断。
在这个过程中,首先需要提出假设,即对两个正态总体参数的关系做出假设。
通常,假设检验中包含两个假设:零假设(H0)和备择假设(H1)。
零假设通常表示两个总体参数无显著差异,备择假设则是与零假设相对的假设。
例如,我们可以在零假设中设定两个总体均数相等,备择假设则是均数不等。
三、样本收集在提出假设后,需要收集样本数据以进行检验。
样本收集应遵循随机抽样的原则,以确保样本的代表性。
在收集样本时,还需要注意样本量的大小,以保证推断结论的准确性。
四、样本检验样本检验是假设检验的核心步骤,包括计算样本统计量、确定临界值和做出推断结论等步骤。
样本统计量是根据样本数据计算出的量,用于推断总体参数。
临界值是用于判断样本统计量是否达到显著差异的标准。
在做出推断结论时,需要根据样本统计量和临界值进行比较,以确定零假设是否被拒绝。
五、推断结论根据样本检验的结果,可以做出推断结论。
如果样本统计量超过了临界值,则可以拒绝零假设,接受备择假设;否则,不能拒绝零假设。
推断结论是假设检验的关键步骤之一,要求谨慎和客观地做出判断。
六、结果解释推断结论做出后,需要对结果进行解释。
解释结果时需要关注以下几点:一是理解推断结论的含义,二是明确结果对于实践的意义,三是注意结果的局限性,即样本量和误差范围等因素对结果的影响。
结果解释要求清晰明了地传达结果的含义和应用范围。
七、误差分析误差分析是假设检验中不可或缺的一环。
误差分为两类:一类是随机误差,由随机抽样造成;另一类是系统误差,由样本设计和处理等环节造成。
误差分析的目的是评估结果的可靠性和精确性,从而确定结果在实际应用中的可信度。
正态总体参数的假设检验

578, 572, 570, 568, 572, 570, 570, 572, 596, 584 试判断新生产的铜丝的折断力有无提高(取α=0.05)?
解
H0 : 0 570 H1 : 0
用U检验法,这时拒绝条件为U u , 计算知 X 575.2,
U X 0 575.2 570 2.05 u u0.05 1.645
N (0,1) U u
| T | t / 2 T t T t
2法
2
2 0
2
2
2 0
2
2 0
2 0
2
(n 1)S 2
2 0
2
2 0
2
2 0
0
2
2 1
/
2
或
提出检验假设 H0 : p p 0 0.17 H1 : p 0
用大样本U 检验法,这时拒绝条件为|U| u / 2 将 n 400, x 56 / 400 0.14, p(1 p) 0.17(1 0.17) 0.376代入,得
| u |
U法
( 2已知)
0
0 0
0
T法
( 2未知)
0
0
假设H1
0 0 0
0 0 0
检验统计量
U X 0 / n
T X 0
S/ n
抽样分布 拒绝条件 A (P( A) )
9.2 正态总体参数的假设检验
一、一个正态总体参数的假设检验 二、非正态总体均值的假设检验 三、两个正态总体参数的假设检验 四、两个非正态总体均值的假设检验
单个正态总体均值假设检验(标准差已知,Z检验)

X
n
z 2
0
X
n
z
2
16
7
步骤1:提出检验假设
H0 : 1550, H1 : 1550
步骤2:确定检验规则
检验统计量为 Z X 1550. 取显著水平 0.05, n
由备择假设的形式知,这是左边检验,因此检验 规则为:当Z z z0.05 1.645时,拒绝H0.
8
步骤3:计算检验统计量的值
2
双边假设问题
H0 : 0, H1 : 0,
其中0是已知的常数.
2
拒绝域
接受域
2
检验统计量为 Z X 0
z 2
z 2
n
检验拒绝域W | Z |
X 0 n
z/2 .
3
P_值的计算
对给定的样本观察值x1,, xn,记检验统计量Z的取值
9
利用P_值进行假设检验
步骤3’:计算P_值
P_ P( X 1550 1530 1550 1550) n 120 225
P(Z 2.5) 0.006
步骤4’:根据显著水平作出判断
P_ 0.006 0.05,
同样做出拒绝原假设H0 : 1550的判断.
将样本均值x 1530, 120, n 225,
代入检验统计量,计算得
Z X 1550 1530 1550 2.5 1.645.
n 120 225
步骤4:根据实际情况作出判断
因此,根据检验规则,做出拒绝原假设H0的判断. 即认为A高校学生的生活水平低于B高校.
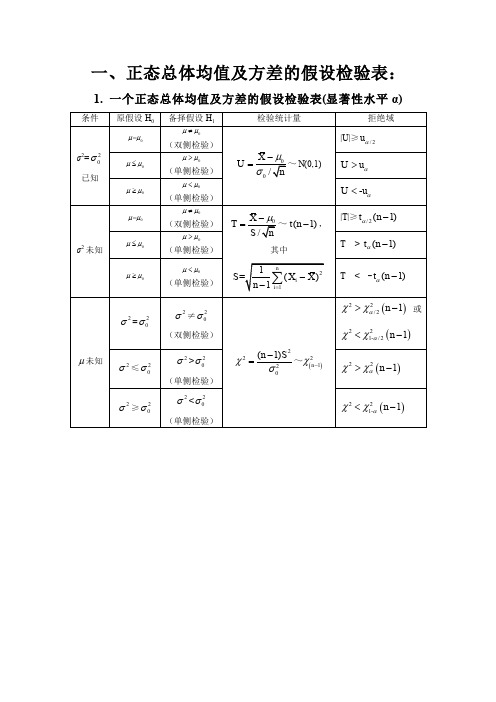
正态分布总体的区间估计与假设检验汇总表
(单侧检验)
2
(n
1)S 2
2 0
~2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
(单侧检验)
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
,
2 2
已知
1 =2 1 2 1 2
1 2
1 2
(单侧检验)
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1,2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
(双侧检验)
2 1
>
2 2
(单侧检验)
F
S12 S22
~
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ~ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
~2n1
(n 2 /
1)S 2
正态总体的参数检验

故拒绝域为
t / 2(n1 n2 2).
当两个正态总体的方差均为已知(不一定相 等)时,我们可用 Z 检验法来检验两正态总体均值 差的假设问题.
例4 在平炉上进行一项试验以确定改变操作方法 的建议是否会增加钢的得率, 试验是在同一只平 炉上进行的. 每炼一炉钢时除操作方法外, 其它条 件都尽可能做到相同.先采用标准方法炼一炉, 然 后用建议的新方法炼一炉, 以后交替进行, 各炼了 10炉, 其得率分别为(1)标准方法: 78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3; (2)新方法:
则 x 0 10.48 10.5 0.516, / n 0.15/ 15
查表得 z0.05 1.645,
于是
x
0
/n
0.516
z0.05
1.645,
故接受 H0, 认为该机工作正常.
设总体 X ~ N(, 2 ), 其中, 2 未知, 显著性水平为 . 求检验问题 H0 : 0, H1 : 0 的拒绝域.
X S
/
0
n
k
,
得 k t / 2(n 1),
上述利用 t 统计量得出的检验法称为t 检验法. 在实际中, 正态总体的方差常为未知, 所以
我们常用 t 检验法来检验关于正态总体均值的检 验问题.
例2 如果在例1中只假定切割的长度服从正态分 布, 问该机切割的金属棒的平均长度有无显著变
79.1, 81.0, 77.3, 79.1, 80.0, 78.1, 79.1, 77.3, 80.2, 82.1; 设这两个样本相互独立, 且分别来自正态总
体 N (1, 2 )和 N (2, 2 ), 1, 2, 2均为未知, 问建议的新操作方法能否提高得率? (取 0.05)
单个正态总体参数的假设检验

单个正态总体参数的假设检验1.提出假设:首先,我们需要提出关于总体参数的假设。
在单个正态总体参数的情况下,我们通常对总体的均值(μ)或标准差(σ)进行假设。
2.确定显著性水平:显著性水平(α)是一个事先设定的临界值。
根据显著性水平,我们可以决定接受还是拒绝原假设。
3.构建统计量:接下来,我们需要构建一个适当的统计量来判断总体参数的假设。
在单个正态总体参数的情况下,通常使用t统计量或z统计量。
4.计算统计量的值:根据样本数据,计算所选统计量的值。
如果使用t统计量,则需要计算样本均值和标准差;如果使用z统计量,则只需计算样本均值。
5.确定拒绝域:拒绝域是根据显著性水平和统计量的分布确定的。
根据统计量的值和拒绝域的临界值,我们可以决定是否拒绝原假设。
6.做出决策:根据统计量的值和拒绝域,我们可以做出决策:接受原假设或拒绝原假设。
下面以一个具体的例子来说明单个正态总体参数的假设检验。
假设我们要检验一些公司员工的平均工资是否等于5000元。
我们从公司中随机抽取了50个员工的工资数据,假设工资数据服从正态分布。
现在我们要进行假设检验。
1.假设提出:原假设(H0):员工的平均工资等于5000元;备择假设(H1):员工的平均工资不等于5000元。
2.显著性水平:我们设定显著性水平为0.053.构建统计量:由于样本量较大(n=50),我们可以使用z统计量。
z统计量的计算方法为(样本均值-总体均值)/(总体标准差/根号n)。
4.计算统计量的值:假设我们计算出样本均值为4950元,总体标准差为100元。
5.确定拒绝域:由于显著性水平为0.05,我们需要找出z值对应的临界值。
在标准正态分布表中查找z=1.96对应的值,并根据原假设的双侧检验找出拒绝域的范围。
6.做出决策:根据统计量的值和拒绝域的范围,我们可以判断是否拒绝原假设。
如果统计量的值落在拒绝域之外,我们将拒绝原假设,即认为员工的平均工资不等于5000元。
§8.2 正态总体参数的假设检验

已
知
202 2>02 2 i1
2 0
202 2<02
H0的拒绝域 2 2 2 (n)
或 2
2 1
2 (n)
2 2(n)
2 12(n)
2 检验
2 2 2(n1)
未
知
2=02 202
2
(n
1)S2
02
202 2>02
或2
2 1
2(n1)
22(n1)
202 2<02
212(n1)
例2.1 用热敏电阻测温仪间接测量地热,
检验法 条件 H0 H1 检验统计量
Z检 验
已
知
=0 0
0 >0
Z
X
0
0 <0
n
T检 验
未
知
=0
0 0
0 >0
<0
T
X 0
Sn
H0的拒绝域 |Z|z/2
Zz Z–z |T|t/2(n–1) Tt(n–1) T–t(n–1)
检验法 条件 H0 H1 检验统计量
2 检验
2=02 202
n
(Xi )2
故t 11.2811.26 0.46592.4469 1.13587
所以接受原假设, 认为用热敏电阻测温仪间接测量温度无系 统偏差。
例2.2 某厂生产的某种型号的电池, 其
寿命长期以来服从方差2=5000(小时2)的
正态分布。现有一批这种电池, 从它的生 产情况来看, 寿命的波动性有所改变。现 随机取26只电池, 测出其样本方差 s2=9200(小时2), 试根据这一数据能否推 断这批电池的寿命的波动性较以往的有
正态总体下参数的假设检验

正态分布的性质
1 2
3
集中性
正态分布的曲线关于均值$mu$对称。
均匀性
正态分布的曲线在均值附近最密集,向两侧逐渐扩散。
稳定性
正态分布的方差$sigma^2$决定了曲线的宽度,方差越大 ,曲线越宽。
正态分布在统计学中的应用
两个总体比例的比较案例
案例描述
某项调查显示,某地区支持甲政 策的居民占60%,支持乙政策的 居民占40%。现从该地区随机抽 取200名居民进行调查,得到支持 甲政策的居民有120名,支持乙政 策的居民有80名。
检验步骤
首先计算两组的样本比例和支持 率,然后根据正态分布的性质计 算临界值,最后根据临界值判断 两组之间是否存在显著差异。
检验步骤
首先计算两组的样本均值和标准差,然后根据正态分布的性质计算临界值,最后根据临界值判断两组之间是否存在显 著差异。
结论
如果两组之间的差异超过临界值,则可以认为两种药物治疗慢性胃炎的疗效存在显著差异;否则,不能 认为两种药物治疗慢性胃炎的疗效存在显著差异。
单个总体比例的假设检验案例
案例描述
检验步骤
03
正态总体下参数的假设检验 方法
单个总体均值的假设检验
总结词
单个总体均值的假设检验是统计学中常见的一种检验方法,用于检验单个正态总体均值 的假设。
详细描述
在假设检验中,我们通常会提出一个关于总体均值的假设,然后使用样本数据来检验这 个假设是否成立。对于单个总体均值的假设检验,我们首先需要确定样本数据和总体分 布的性质,然后选择合适的统计量进行计算,最后根据统计量的分布和临界值来判断假
单个正态总体参数的假设检验

单个正态总体参数的假设检验一、假设检验的基本概念假设检验是统计推断的一种方法,其基本思想是通过抽样来对总体参数进行推断,并判断总体参数是否满足其中一种假设。
在进行假设检验时,我们首先提出一个原假设(H0),这是一个既定的假设,表示总体参数满足其中一种特定的值或不满足其中一种特定的关系。
同时,我们还提出一个备择假设(H1),表示总体参数不满足原假设。
通过对样本数据的统计推断,我们可以对原假设进行拒绝或不拒绝的判断。
二、假设检验的步骤假设检验一般包括以下步骤:1.提出假设:根据问题的需求和背景条件,提出原假设和备择假设。
2.确定显著性水平:显著性水平(α)是指当原假设成立时,我们愿意犯第一类错误的概率。
一般情况下,我们常使用0.05作为显著性水平。
3.选择检验统计量:根据所需检验的问题,选择适当的检验统计量。
在单个正态总体参数的假设检验中,常用的检验统计量有Z检验和t检验。
4.计算检验统计量的观察值:根据样本数据计算出检验统计量的观察值。
5.根据显著性水平查找拒绝域:根据显著性水平和检验统计量的分布,查找拒绝域的临界值。
6.判断并作出结论:如果检验统计量的观察值落在拒绝域内,则拒绝原假设,否则不拒绝原假设。
三、应用领域1.药物临床试验:在新药物的临床试验中,可以通过对患者进行抽样,检验患者服用药物前后的药效差异是否显著,以判断药物的疗效。
2.市场调研:在市场调研中,可以通过对一定数量的顾客进行问卷调查,检验顾客对其中一种产品的满意度是否显著不同,以了解产品在市场中的竞争力。
3.品质控制:在生产过程中,可以通过抽样检验产品的质量是否符合设定的标准。
例如,食品加工厂可以通过抽样检验产品的营养成分是否达到设定的要求。
4.经济学研究:在经济学研究中,可以通过对一定数量的经济指标进行抽样,检验指标的差异是否显著,以判断宏观经济政策的有效性。
总结:单个正态总体参数的假设检验是统计学中一种重要的方法,通过对样本数据的统计推断,判断总体参数是否满足其中一种假设。
正态总体参数假设检验

计算得, x = 928, u = 928 − 950 = −6.6 ,此处 u 值落入拒绝域内,故拒绝原假设,可以判 10 3
断这批枪弹的初速有显著降低。
关于本题说明一点:本题中的一对假设 H0 : µ = µ0 vs H1 : µ < µ0 的检验与另一对假设
H0 : µ ≥ µ0 vs H1 : µ < µ0 的检验有完全相同的拒绝域,这是因为二者的拒绝域形式相同,
来就应接受原假设,所以在实用中对标准差的假定要慎重,若无把握,可考虑设总体标准差
未知,此时就应使用 t 检验。本题中,若假定总体标准差未知,则可由样本算得 s = 0.237 ,
于是 t =
6(19.9 −15) 0.237
=
−1.0379 ,而拒绝域为W
= {| t
|≥
t0.975 (5)} = {| t
这里 u 值没有落入拒绝域,故不能拒绝原假设,因而可以认为生产之铁水平均含碳量仍为
4.55。
3,由经验知某零件重量 X ~ N (15, 0.052 ) (单位:克),技术革新后,抽出 6 个零件,
测得重量为: 14.7 15.1 14.8 15.0 15.2 14.6
已知方差不变,问平均重量是否仍为 15 克?(取 α=005)
|≥
2.5706} ,故应
接受原假设。
4
4,化肥厂用自动包装机包装化肥,每包的重量服从正态分布,其平均重量为 100 千克, 标准差为 1.2 千克.某日开工后,为了确定这天包装机工作是否正常,随机抽取 9 袋化肥, 称得重量如下:
99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5 设方差稳定不变,问这一天包装机的工作是否正常? (取 α=005)
正态总体参数的假设检验

正态总体参数的假设检验 正态总体中有两个参数:正态均值与正态⽅差。
有关这两个参数的假设检验问题经常出现,现逐⼀叙述如下。
(⼀) 正态均值的假设检验 ( 已知情形) 建⽴⼀个检验法则,关键在于前三步l,2,3。
5.判断(同前) 注:这个检验法称为u检验。
(⼆) 正态均值的假设检验 ( 未知情形) 在未知场合,可⽤样本标准差s去替代总体标准差,这样⼀来,u统计量变为t统计量,具体操作如下: 1.关于正态均值常⽤的三对假设为 5.判断 (同前) 注:这个检验法称为t检验。
(三)正态⽅差的假设检验 检验正态⽅差有关命题成⽴与否,⾸先想到要⽤样本⽅差。
在基础上依据抽样分布特点可构造统计量作为检验之⽤。
具体操作如下: 1.关于正态⽅差常⽤的三对假设为 5.判断(同前) 注:这个检验法称为检验。
注:关于正态标准差的假设与上述三对假设等价,不另作讨论。
(四) ⼩结与例⼦ 上述三组有关正态总体参数的假设检验可综合在表1.5-1上,以供⽐较和查阅。
续表 [例1.5-2] 某电⼯器材⼚⽣产⼀种云母带,其厚度在正常⽣产下服从N(0.13,0.0152)。
某⽇在⽣产的产品中抽查了10次,发现平均厚度为0.136,如果标准差不变,试问⽣产是否正常?(取 =0.05)来源:考试通 解:①⽴假设:②由于已知,故选⽤u检验。
③~④根据显著性⽔平 =0.05及备择假设可确定拒绝域为{ >1.96}。
⑤由样本观测值,求得检验统计量: 由于u未落在拒绝域中,所以不能拒绝原假设,可以认为该天⽣产正常。
[例1.5-3] 根据某地环境保护法规定,倾⼊河流的废⽔中⼀种有毒化学物质的平均含量不得超过3ppm。
已知废⽔中该有毒化学物质的含量X服从正态分布。
该地区环保组织对沿河的⼀个⼯⼚进⾏检查,测定每⽇倾⼊河流的废⽔中该物质的含量,15天的记录如下(单位:ppm)3.2,3.2,3.3,2.9,3.5,3.4,2.5,4.3,2.9,3.6,3.2,3.0,2.7,3.5,2.9 试在⽔平上判断该⼚是否符合环保规定? 解:①如果符合环保规定,那么应该不超过3ppm,不符合的话应该⼤于3ppm。
单个正态总体参数假设检验

n
~ N (0,1)
(3)对于给定的显著水平,查正态分布双侧临界值 表,得到临界值 u / 2 ; (4)统计判断: u u / 2 , 拒绝H ,接受H ; 0 1
u u / 2,拒绝H1,接受H0。
双侧检验 (显著性水平与拒绝域 )
假设H0成立 抽样分布
拒绝域
医药数理统计方法
小概率事件还是会发生的
医药数理统计方法
2.两类错误及记号
(1)当原假设H0为真, 观察值却落入拒绝域, 而作出
了拒绝H0的判断, 称做第一类错误, 又叫弃真错 误。犯第一类错误的概率是显著性水平 。 (2)当原假设H0不真, 而观察值却落入接受域, 而作
出了接受H0的判断, 称做第二类错误, 又叫取伪
拒绝域
/2
1-
接受域
/2
临界值
临界值
样本统计量
医药数理统计方法
例6-2.某药厂正常情况下生产的某药膏含甘草酸量 X~N(4.45,0.1082).现随机抽查了5支药膏,其含 甘草酸量分别为: 4.40 4.25 4.21 4.33 4.46 若方差不变,问此时药膏的平均含甘草酸量 是否 有显著变化?(=0.05) 分析: 0 4.45, n 5, 0.108
X 64
解: 1.建立假设: H0 : 0 60 H1 : 0 60 2. 计算统计量:
u X 0
n
64 60 4 30
5.48
医药数理统计方法
3. 根据显著水平=0.01,查正态分布临界值表; 查附表4得: u0.01 2.33 4.做出统计判断
(1) X ~ N ( , / n)
2
第二节 正态总体参数的检验

2
9
二、两个正态总体参数的假设检验
2 设 有 两 个 相 互 独 立 的 正 态 总 体 X ~ N ( µ1,σ 1 ) ,
Y ~ N ( µ 2,σ ) , 分别抽取独立的样本 ( X1 , X2 ,⋯, Xn1 ) 和
2
µ 第六章证明, X = ( (− , ) 第六章证明,若 χ 2 ~ Nn−1σS 证明 (2) 检验统计量 2
2 2 H 下 O χ1−α / 2(n−1) 2 0 ), 2 则
x
( n − 1) S
~ χ (n −1) ,
(4) 由样本值算得
χ的值; 的值;
2
则拒绝H 否则 不能 若 χ 2 < λ1 或 χ 2 > λ2 ,则拒绝 0 ; 否则, 拒绝H 拒绝 0 .
− tα / 2 ( n − 1) O
tα / 2 (n − 1)
x
~
(4) 由样本值算得 t 的值; 的值; 则拒绝H 如果 | t |> tα 2 (n − 1) ,则拒绝 0 ; 否则, 不能拒绝H 否则 不能拒绝 0 .
5
两家生产同一类产品, 例2 两家生产同一类产品,其质量指标假定都服从正 态分布,标准规格为均值等于120.现从甲厂抽出5 120.现从甲厂抽出 态分布,标准规格为均值等于120.现从甲厂抽出5件 产品,测得其指标值为119,120,119.2,119.7,119.6; 产品,测得其指标值为119,120,119.2,119.7,119.6; 从乙厂也抽出5件产品,测得其指标值为110.5,106.3, 从乙厂也抽出5件产品,测得其指标值为110.5,106.3, 122.2,113.8,117.2。 122.2,113.8,117.2。试判断这两家厂的产品是否符 合标准. 合标准. (α = 0.05 )
正态总体的均值和方差的假设检验

2
(x)
2
2
O 12 /2(n 1) 2 / 2(n 1)
x
P{ χ 2
χ12α / 2(n 1)}
P{ χ 2
χα2/ 2n 1}
α, 2
拒绝域:
W 1 {( x1, x2, , xn ) : χ 2 χ12α / 2(n 1)}
U{( x1,
x2 , ,
xn )
:
2
2 /2
是否可以认为由新工艺炼出的铁水含碳质量分
数的方差仍为0.1082( = 0.05)?
解 检验假设
(1)H0 : 2 0.1082, H1: 2 0.1082 ,
(2)取检验统计量:
χ2
(n 1)Sn*2 σ02
~
χ 2(n 1),(当H0为真时)
由n = 5, = 0.05算得,
χα2/ 2n 1 χ02.0254 11.1, χ12α / 2n 1 χ02.9754 0.484.
问: 若总体的均值 已知,则如何设计假设检验?
n
( Xi μ)2
构造χ 2 i1 σ2
~ χ 2(n)可类似进行检验.
例3 某炼钢厂铁水含碳质量分数X在正常情况下
服从正态分布 N ( μ,σ 2 ),现对操作工艺进行了改 革又测量了5炉铁水,含碳质量分数分别为:
4.421,4.052,4.357,4.287,4.683
t/2 n1 n2 2 t0.025 18 2.10
由| t | 2.49 2.10 t0.025 18 W1,
故拒绝假设H0,认为物品处理前后含脂率的均值 有显著差异。
3. 两正态总体方差的检验
设总体
X
~
N
单个正态总体参数的假设检验

576.2 576 x 576 0.079 其中 | U | 8 / 10 8/ n
查表 z / 2 z0.025 1.96 0.079 故未落在拒绝域之内,故接受H0 ,即可以认为 576.
综合⑴与⑵,该生跳远成绩水平与鉴定成绩无显著差异.
X -0 取统计量 t ~ t (n 1) S/ n
x -0 拒绝域为 | t | t / 2 (n 1) s/ n 计算 | t | 2.6
| t | 2.6 t0.025 (35) 2.0301
故落在拒绝域之内,拒绝H0 ,接受H1 即不能认为全体考生的平均成绩为70分。 ⑵ μ的置信水平为0.95的置信区间为
2 2 2 双边假设检验 H 0 : 2 0 , H1 : 0
拒绝域为
(n 1) s 2
2 0
12 / 2 (n 1) 或 f y
2 2
(n 1) s 2
2 0
2 / 2 ( n 1)
2 12 / 2 (n 1) / 2 ( n 1)
观测5台压缩机的冷却用水的升高温的平均值为 x 5.34,
样本方差为 s 2 0.631. ⑴ 在显著水平α=0.05下是否可以
认为冷却用水升高温度的平均值不多于5°?(2)求σ2的
置信水平为0.95的置信区间。
解: ⑴ 先提出假设 H 0 : 0 5, H1 : 0
H1 : 0 ,拒绝域为
| x -0 | | u | z / 2 / n
2. σ2未知,检验μ (t 检验法)
n 1 2 可用样本方差 S 2 ( X X ) 代替σ2 k n 1 k 1
单正态总体的参数假设检验

单正态总体的参数假设检验在统计学中,假设检验是一种用于判断总体参数是否符合某种特定假设的方法。
而单正态总体的参数假设检验则是指对一个正态分布总体的参数进行假设检验。
单正态总体的参数假设检验通常涉及两个假设:原假设(H0)和备择假设(H1)。
原假设是我们想要进行检验的假设,而备择假设则是与原假设相反的假设。
在单正态总体的参数假设检验中,我们通常关注的参数有均值(μ)和标准差(σ)。
下面将分别介绍如何进行均值和标准差的参数假设检验。
1. 均值参数假设检验对于均值参数的假设检验,常用的方法有Z检验和T检验。
Z检验适用于总体的标准差已知的情况,而T检验适用于总体的标准差未知的情况。
假设我们要对一个正态分布总体的均值进行假设检验,原假设为均值等于某个特定值(H0: μ = μ0),备择假设为均值不等于特定值(H1: μ ≠ μ0)。
我们需要计算样本的均值(X̄)和标准差(S),然后根据样本量(n)和总体标准差(σ)的已知情况选择对应的检验方法。
如果总体标准差已知,可以使用Z检验。
计算Z统计量的公式为:Z = (X̄ - μ0) / (σ / √n)然后,根据显著性水平(α)选择临界值,比较计算得到的Z统计量与临界值的大小,以判断是否拒绝原假设。
如果Z统计量的绝对值大于临界值,则拒绝原假设;否则,接受原假设。
如果总体标准差未知,可以使用T检验。
计算T统计量的公式为:T = (X̄ - μ0) / (S / √n)同样地,根据显著性水平(α)选择临界值,比较计算得到的T统计量与临界值的大小,以判断是否拒绝原假设。
2. 标准差参数假设检验对于标准差参数的假设检验,常用的方法有卡方检验和F检验。
卡方检验适用于单个总体标准差的假设检验,而F检验适用于两个总体标准差的假设检验。
假设我们要对一个正态分布总体的标准差进行假设检验,原假设为标准差等于某个特定值(H0: σ = σ0),备择假设为标准差不等于特定值(H1: σ ≠ σ0)。
正态总体参数假设检验

嘉兴学院
第七章 假设检验
第18页
7.2.2 两个正态总体均值差的检验 检验 法 u检 验 t检 验 条 件 原假 设 备择 假设 检验统 计量 拒绝域
已 知
未 知
嘉兴学院
16 July 2012
第七章 假设检验
第19页
大样 本检 u验 近似 t检 验
未知 m,n充 分大 未知 m,n不 很大
16 July 2012
嘉兴学院
第七章 假设检验
第4页
(a)
16 July 2012
(b)
(c)
嘉兴学院
第七章 假设检验
第5页
该检验用 u 检验统计量,故称为u 检验。 下面以 由 为例说明: 可推出具体的拒绝域为
该检验的势函数是 的函数,它可用正态分布 写出,具体为
16 July 2012
16 July 2012
16.2 16.4 15.8 15.5 16.7 15.6 15.8 15.9 16.0 16.4 16.1 16.5 15.8 15.7 15.0
嘉兴学院
第七章 假设检验
第30页
这是两正态总体方差之比的双侧假设检验问题, 待检假设为 此处 m=7,n=8,经计算
于是 查表知 ,若取 =0.05,
通常 , 均未知,记 , 分别是由 算得的 的无偏估计和由 算得的 的无偏估计.
16 July 2012
嘉兴学院
第七章 假设检验
第28页
可建立检验统计量: 三种检验问题对应的拒绝域依次为
或
16 July 2012
}。
嘉兴学院
第七章 假设检验
第29页
例7.2.5 甲、乙两台机床加工某种零件,零件 的直径服从正态分布,总体方差反映了加工 精度,为比较两台机床的加工精度有无差别, 现从各自加工的零件中分别抽取7件产品和8 件产品,测得其直径为 X (机 床甲) Y (机 床乙)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§7.2
正态总体的参数检验
参数检验的常见三种基 本形式: 双侧检验 (1) H 0 : 0 vs H1 : 0
(2) H 0 : 0 vs H1 : 0 (3) H 0 : 0 vs H1 : 0
单侧检验
一个正态总体 N ( , )
注 1º 一般,作假设检验时,先控制犯第一类 错误的概率,在此基础上使 尽量地小.要 降低 一般要增大样本容量. 当H0不真时,参数值越接近真值, 越大.
注 2º 备择假设可以是单侧,也可以双侧.
引例2中的备择假设是双侧的.若根据以 往生产情况,0=68.现采用了新工艺,关 心的是新工艺能否提高螺钉强度,越大 越好.此时, 可作如下的假设检验:
例3 新设计的某种化学天平,其测量 误差服从正态分布, 现要求 99.7% 的测 量误差不超过 0.1mg , 即要求 3 0.1. 现拿它与标准天平相比,得10个误差数 据,其样本方差s2 =0.0009.
试问在 = 0.05 的水平上能否认为 满足设计要求? 解一
H0: 1/30 ; H1: 1/30
2= 02 2 02
接受域
(n 1) S 2 2 2 (n 1) S 2 2 2 ~ (n 1) 2 2 0 1 0 2 2 (未知)
待估参数
2
枢轴量及其分布
置信区间
(n 1) S 2 2 2 2 ~ (n 1) (n 1)s 2 (n 1)s 2 ( 2 , 2 ) 1 ( n 1) ( n 1) (未知)
设测量值
X ~ N ( , ) 0.00040
2
2
需考察改革后活塞直径的方差是否不 大于改革前的方差?故待检验假设可 设为: H0 : 2 0.00040 ; H1 : 2 > 0.00040.
此时可采用效果相同的单边假设检验 H0 : 2 =0.00040 ;H1 : 2> 0.00040.
(2)关于
2
的检验 检验法
2
原假设 备择假设 检验统计量及其在 H1 H0为真时的分布 H0
2= 02 2 02
2
拒绝域
( n 1)
2
2
2 2 0
2< 2 0
( n 1) S 2 0
2 2
2
或 2 12 ( n 1)
H0 : 0.8 ; H1 : > 0.8 未知, 故选检验统计量: X 0 T ~ t (15) S / 16 查表得 t0.95(15) = 1.753, 故拒绝域为
x 0.8 s/ n 1.753
0.32 0.94 x 0.8 1.753 4
现
x 0.92 0.94
(n 1) S 2 ~ (n 1) 取统计量 2 0
2 2
拒绝域 W:
2
2 0.05
(24) 36.415
0
2
24 0.00066 39.6 36.415 0.00040
落在W内, 故拒绝H0. 即改革后的方 差显著大于改革前, 因此下一步的改 革应朝相反方向进行.
未知, 故选检验统计量
2
9S
2
2 0
~ ( 9)
2
9S 2 0.95 (9) 16.919 拒绝域: 1 / 900
2
2
9S 7.29 16.919 现 1 / 900
2
2
故接受原假设, 即认为满足设计要求.
解二 2的单侧置信区间为
(n 1) S 0.0081 (0, 2 ) ( 0, ) ( 0 , 0.0024 ) 1 (n 1) 3.325
W U
U0
X 0
495 500 2 1.96 落在 W 内 25 / 100
/ n
u1 u0.975 1.96
2
故该天的产品不能投放市场.
T 检验法 (2 未知)
原假设 备择假设 检验统计量及其 H0 H1 H0为真时的分布 拒绝域
0 0 0
考虑检验的势函数 X ( X 1 ,, X n )
(1) H 0 : 0 vs H1 : 0 g( ) P ( X W ) P (| U | u1 / 2 )
P (| | u1 / 2 ) P (| X 0 | u1 / 2 ) / n / n 0 X P ( u1 / 2 ) / n / n 0 X P ( u1 / 2 ) / n / n 0 0 1 ( u1 / 2 ) (- u1 / 2 ) / n / n X 0
0 0
X 0 T ~ t ( n 1) S n
接受域
x 0 s n
t 1
( 2未知)
2
待估参数
枢轴量及其分布 置信区间
X T ~ t ( n 1) S n
( x t 1
s
2
( 2未知)
x t 1
s
n
,
2
n
)
原假设 备择假设 检验统计量及其在 H0为真时的分布 H0 H1
的解释 注 4º 关于假设检验判决结论
假设检验中给出的判决 结论是基于样本的, 具有随机性.
接受原假设相当于说通 过试验的样本,没有发 现 原假设不成立的证据; 拒绝原假设相当于说在 一定 程度上发现了原假设不 成立的证据.
定义 对检验问题 H 0 : 0 vs H1 : 1 如果一个检验满足对任 意的 0,都有 g( ) 则称该检验是显著性水 平为的显著性检验, 简称水平为 的检验.
2
~ ( n 1)
( 未知)
(n 1)
2 2
2 02 2>Βιβλιοθήκη 02 ( n 1)
2 2 1
例2 某汽车配件厂在新工艺下 对加工好的25个活塞的直径进行测量, 得样本方差S2=0.00066.已知老工艺生 产的活塞直径的方差为0.00040. 问 进一步改革的方向应如何? 解 一般进行工艺改革时, 若指标 的方差显著增大, 则改革需朝相反方 向进行以减少方差;若方差变化不显 著, 则需试行别的改革方案.
由例1可见: 对问题的提法不 同(把哪个假设作为原假设),统计 检验的结果也会不同.
上述两种解法的立场不同,因此 得到不同的结论.
第一种假设是不轻易否定厂方的结论; 第二种假设是不轻易相信厂方的结论.
由于假设检验是控制犯第一类错 误的概率, 使得拒绝原假设 H0 的决策 变得比较慎重, 也就是 H0 得到特别的 保护. 因而, 通常把有把握的, 经验的 结论作为原假设, 或者尽量使后果严 重的错误成为第一类错误.
假设检验基本步骤:
一、建立假设 根据实际问题所关心的 内容,建立H 0和H 1
二、选择检验统计量 能衡量原假设和备择假 设间的差异
三、给出拒绝域的形式
拒绝域的形式由 1确定 H 四、控制犯第一类的错 ,写出具体的拒绝域 误
P ( X W | H 0为真)
五、利用样本观测值进 行判断
2
1 0.0011 0.0024 H0中的 900
2 2 0
则H0 成立, 从而接受原假设 , 即认为
满足设计要求.
假设检验与区间估计的联系
同一函数 假 设 检 验 统计量 接受域 枢轴量 置信区间
1
对偶关系
区 间 估 计
假设检验与置信区间对照
原假设 备择假设 检验统计量及其在 H0为真时的分布 H1 H0 接受域
x 0 u1
0
0
待估参数
X 0 U ~ N (0 ,1) n ( 2 已知)
n
2
枢轴量及其分布
置信区间
X U ~ N (0,1) ( x u1 , x u1 ) 2 2 n n n ( 2 已知)
原假设 备择假设 检验统计量及其在 H0为真时的分布 H0 H1
2
(1)关于 的检验 拒绝域的推导 给定显著性水平与样本(x1,x2,…,xn )
设 X ~N ( 2),2 已知,需检验: H0 : 0 ; H1 : 0
X 0 ~ N (0 ,1) 构造统计量 U n
P(拒绝H0|H0为真)
P ( X 0 k 0 ) PH 0 ( X 0 k )
(2) H 0 : 0 vs H1 : 0 g( ) P ( X W ) P (U u )
/ n / n 0 0 X ) P ( u ) ( u / n / n / n
P ( X 0 u ) P (
故接受原假设, 即不能否定厂方断言.
解二
H0 : 0.8 ;
H1 : < 0.8
选用统计量:
X T ~ T (15) S / 16
查表得 t0.05(15) = 1.753, 故拒绝域 x 0.8 0.32 1.753 x 0.8 1.753 0.66 s/ n 4 现 x 0.92 0.66 故接受原假设, 即否定厂方断言.
X 0
u )
(3) H 0 : 0 vs H1 : 0 g( ) P ( X W ) P (U u1 )
P ( X 0
/ n
u1 ) 1 ( u1
