高考数学常见创新题型赏析
高考数学创新题型解读

高考数学创新题型解读1. 选择题:(1) 下列哪个函数的图像在x=1处取得最小值?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^5(2) 已知函数f(x) = ax^2 + bx + c,若f(x)在x=1时取得最大值,则a的取值范围是?A. a < 0B. a > 0C. a = 0D. a ≠ 0(3) 下列哪个函数的图像在y轴上截距为1?A. f(x) = x^2 + 2x + 1B. f(x) = x^2 - 2x + 1C. f(x) = x^2 + 2x - 1D. f(x) = x^2 - 2x - 1(4) 已知f(x) = ax^2 + bx + c,若f(x)的图像是开口向上的抛物线,则a的取值范围是?A. a > 0B. a < 0C. a = 0D. a ≠ 0(5) 下列哪个函数的图像在x=0时取得最大值?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^5(6) 已知函数f(x) = ax^2 + bx + c,若f(x)在x=2时取得最小值,则a的取值范围是?A. a < 0B. a > 0C. a = 0D. a ≠ 0(7) 下列哪个函数的图像在x=0时取得最小值?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^5(8) 已知f(x) = ax^2 + bx + c,若f(x)的图像是开口向下的抛物线,则a的取值范围是?A. a > 0B. a < 0C. a = 0D. a ≠ 0(9) 下列哪个函数的图像在y轴上截距为-1?A. f(x) = x^2 + 2x + 1B. f(x) = x^2 - 2x + 1C. f(x) = x^2 + 2x - 1D. f(x) = x^2 - 2x - 1(10) 已知函数f(x) = ax^2 + bx + c,若f(x)在x=3时取得最大值,则a的取值范围是?A. a < 0B. a > 0C. a = 0D. a ≠ 02. 填空题:(1) 已知函数f(x) = ax^2 + bx + c,若f(x)在x=1时取得最小值,则a的取值范围是________。
高考数学创新试题赏析

高考数学创新试题赏析1 定义新集合例 1 定义集合运算:{},,A B z z xy x A y B *==∈∈.设{}1,2A =,{}0,2B =,则集合A B * 的所有元素之和为 ( )A .0B .2C .3D .6 (江西省数学高考试题) 分析:由题意得,*{0,2,4}A B =,其所有元素和为6,故选D点评:利用集合描述法中的P 的性质,直接求出Z 的所有可能取值,注意不要遗漏,求解过程中运用了简单的分类讨论思想。
新集合在高考中常考常新,如曾经出现的差集、幂集等。
2定义新函数例2 设[x ]表示不超过x 的最大整数(如[2]=2, [54]=1),对于给定的n ∈N *,定义[][](1)(1)(1)(1)x n n n n x C x x x x --+=--+,x ∈[)1,+∞,则当x ∈3,32⎡⎫⎪⎢⎣⎭时,函数8x C 的值域是( )A.16,283⎡⎤⎢⎥⎣⎦B.16,563⎡⎫⎪⎢⎣⎭C.284,3⎛⎫⋃ ⎪⎝⎭[)28,56 D.16284,,2833⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦(湖南省数学高考试题)分析:依题意,当,2⎡⎫∈⎪⎢⎣⎭3x 2时,[]1x =,此时88164,3x c x ⎛⎤=∈ ⎥⎝⎦;[)2,3x ∈当时,[]2=x ,此时8875628,28(1)(1)3x c x x x x ⨯⎛⎤==∈ ⎥--⎝⎦。
因此,3,32x ⎡⎫∈⎪⎢⎣⎭当时,函数8x c 的值域是16284,,2833⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦,故选D 点评:本题是即时定义一个新函数,它是把组合数公式与高斯函数(取整函数)二者交汇而成,设计新颖,构思精妙,意味深长,从另一个方面也说明从课本中找原型、从竞赛课题中找启示成为高考命题的方向。
解此题的关键是理解符号函数[]x 的意义,把8x C 化为比较熟悉的函数从而求出其值域,它考查了学生对信息的接受、理解和运用的能力。
3 定义新数表例4 将全体正整数排成一个三角形数阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 。
高考数学创新题型思维方法归纳

高考数学创新题型思维方法归纳高考数学一直以来都是学生们最为关注的科目之一,也是决定着他们整体成绩的重要因素。
而面对着日益增多且不断创新的数学题型,学生们的压力也逐渐加大。
因此,为了更好地应对高考数学中的创新题型并提升自己的思维能力,本文将对一些常见的数学创新题型思维方法进行归纳总结。
1.解析式题型解析式题型是高考中常见的一种题型,特别是在数学选择题中。
对于此类问题,首先要考虑的是问题本身的语义。
有些问题看起来很抽象,但只要确立一个指导性的概念,就可以将问题解决。
例如,在求解某个极限的时候,若考生觉得难以通过微积分原理简化表达式,可以考虑将函数类型置于个别限制条件下。
此时,便于考生利用函数本身的特殊性质,直接进行简单的代入求解。
2.观察题型观察题型是考验学生思维能力的重要题型。
此类问题要求考生从已知信息中提取价值,并以此作为进一步进行推断的基础。
对于此类问题,建议学生采用尝试错误的方法,通过不停地试错来完善解法。
另外,需要注意的是,这类题目的结果可能是难以通过观察及分析得到的,必须通过多次尝试来得出正确结论。
3.计算便捷题型计算便捷题型主要是考察考生的计算能力。
此类题目特点是,计算量大且题目难度不高,但是考生需要完成大量重复的计算,并需要保证计算过程的准确性。
针对这类题目,学生需要掌握数学基本运算的规律,尤其是运算评分规则和公式的使用,可以采用逆算法等方式,将计算规模最小化。
4.逻辑推理题型逻辑推理题型是让学生思考问题解决过程的题型。
解决此类问题必须善于从问题条件中寻找因果关系,并通过运用逻辑推理的方式,将这种因果关系转化为可靠的推断结论。
在做这类问题时,考生需要充分利用其他科目的知识,建立一个概念框架,并根据问题提供的信息去规范自己的解析思路。
5.分数异化题型分数异化题型主要是考察考生的数学思维能力。
此类题目特点是对考生分数计算的运算规律进行改变,充分考察考生对分数的把握能力。
针对这类问题,学生需要将这种运算转换成为其他基本计算方法,例如,可以将所有分数收集再进行归并,最终得到答案。
高考数学模拟题中的创新题解法赏析

高考数学模拟题中的创新题解法赏析汪亚运 深圳市坪山高级中学近些年来高考数学中创新题精彩纷呈,所谓创新题是指在高中教材中不曾出现过的概念、定义,这类题型虽然表面看上去新颖别致,但是只要把表面那层面纱揭开,就会发现仍旧是用我们以前所学的知识迁移来解决。
创新题因为能够很好地考查学生的数学素养和创新能力,所以越来越受高考命题人的关注和重视,下面以2020年部分地区的模拟题为例来解读创新题,希望对大家有所启迪。
一、科赫曲线(山东省2020年高考模拟)科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到。
任意画一条线段,然后把它分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”,用同样的方法把每条小线段重复上述步骤得到16条更小的线段构成的折线称为“二次构造”,…,如此进行“n 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ) (lg30.4771≈,3010.02lg =)A.16B.17C.24D.25解析:记初始长度为a ,则一次构造后的折线长度是a 34,二次构造后的折线长度是a2)34(, , n 次构造后的折线长度是a n )34(,要使得到的折线长度达到原来的1000倍,应满足 a a n 100034≥⎪⎭⎫ ⎝⎛,两边同时取对数得到31000lg 34lg =≥n ,整理可得,3)3lg 2lg 2(≥-n 3lg 2lg 23-≥n ,把lg30.4771≈,3010.02lg =代入得02.244771.06020.03≈-≥n . 所以至少需要通过构造的次数是25次.故答案是D.点评:此题的背景是构造科赫曲线,同学们要能从复杂的背景中抽象出数学模型,列出不等式,再通过对数运算与估算得到答案。
主要考查同学们抽象概括能力和数学运算素养。
高考数学常见创新题型赏析

(原创、首发、专投稿,适合高二、高三年级11月份用,同意删改)高考数学创新题分类探究贵州省龙里中学 洪其强(551200)一、建构数列型:数列作为特殊的函数,在高考数学中占有相当重要的位置,主要涉及增长率、银行信贷等.解答这一类问题,要充分应用观察、归纳、猜想的手段,建立起等差、等比、或递推数列的模型来解题.例1 (2003年朝阳区高三统一练习(二))2002年底某县的绿化面积占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.(Ⅰ)设该县的总面积为1,2002年底绿化面积为1041=a ,经过n 年后绿化的面积为,1+n a 试用n a 表示1+n a ;(Ⅱ)求数列}{n a 的第1+n 项1+n a ;解析 (Ⅰ)设现有非绿化面积为1b ,经过n 年后非绿化面积为.1+n b 于是.1,111=+=+n n b a b a 依题意:1+n a 是由两部分组成,一部分是原有的绿化面积n a 减去被非绿化部分n a 1002后剩余的面积n a 10098,另一部分是新绿化的面积.1008n b 于 是1+n a =n a 10098+.1008n b =n a 10098+.252109)1(1008+=-n n a a (Ⅱ)1+n a =,252109+n a 1+n a -54=-).54(109-n a , 数列}54{-n a 是公比为,109首项5254104541-=-=-a 的等比数列. n n a )109)(52(541-+=∴+二、信息迁移型:信息迁移题指的是不便于直接运用所学数学知识解决问题,而需要从所给材料中获取信息,并用于新问题解决的一类问题.这一类问题,往往出现在一个较新的背景之下,题型新颖,形式多样,融综合性、应用性、开放性、创新性于一体.信息迁移型题可分为定义信息型、图表信息型、 图形图像信息型等. 1.定义信息型 例1 定义运算a c ad bcb d =-,复数z 满足11z ii i=+,则复数在的模为A .1+.1-解析 由11z i i i=+得1212izi i i z i i +-=+⇒==-,∴z ==,故选C 。
高中数学总结归纳点拨 古典概型创新题赏析

古典概型创新题赏析古典概型是一种重要的概率模型,也是高考命题的重点.近年来,在高考或各地模拟考试中出现了一些以古典概型为背景的创新题,考查了同学们的探究能力和创新能力.下面撷取几例,与同学们共赏析.一、信息迁移创新信息迁移题是近年高考命题改革的一个新的亮点.此类试题通过给出一个新概念,或定义一种新运算,或给出几个新模型等来创设新的问题情境,要求同学们在阅读理解的基础上,应用所学的知识和方法,实现信息的迁移,以达到灵活解题的目的.例1“渐升数”是指每个数字比其左边的数字大的自然数(如2578),在两位的“渐升数”中任取一个数比37大的概率是_____.解析:十位是1的“渐升数”有8个;十位是2的“渐升数”有7个;…;十位是8的“渐升数”有1个,所以两位的“渐升数”共有8+7+6+5+4+3+2+1=36个;以3为十位比37大的“渐升数”有2个,分别以4,5,6,7,8为十位数的“渐升数”均比37大,且共有5+4+3+2+1=15个,所以比37大的两位“渐升数”共有2+15=17个.故在两位的“渐升数”中任取一个比37大的概率是17 36.二、图表解读创新给出图表,要求同学们对图表进行观察,分析,并提炼,挖掘出图表所给予的有用信息,排除有关数据的干扰,进而抓住问题的实质,达到求解的目的.例2下表为某班英语及数学的成绩分布,全班共有学生50人,成绩分为1~5五个档次.例如表中所示英语成绩为4分,数学成绩为2分的学生共5人(设x,y分别表示英语成绩和数学成绩).(1)4x =的概率是多少?4x =且3y =的概率是多少?3x ≥的概率是多少?(2)2x =的概率是多少?a b +的值是多少?解析:(1)15717(4)5025P x +++===;7(43)50P x y ===,; 7(3)(3)(4)(5)10P x P x P x P x ==+=+==≥; (2)571(2)1(1)(3)150105P x P x P x ==-=-=--=≥; 又1601(2)505b a P x ++++===,则3a b +=.三、知识交汇创新 这类问题从学科知识的内在联系出发,在知识交汇点上做文章,一个题目往往包含多个知识点.例3 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1,2,3,4,5,6),骰子朝上的面的点数分别为X Y ,,则2log 1X Y =的概率为( )A.16 B.536 C.112 D.12解析:本题是古典概型与对数知识的交汇,可先根据对数性质得到Y与X的关系,进而求解.由题设知,骰子朝上的点数X ,Y 满足2Y X =,就是说朝上的面的点数只能是1,2;2,4;3,6,即所求概率为313612=.故选(C) 例4 设l 为平面上过点(01),的直线,l 的斜率等可能的取0-,则原点到l 的距离小于1的概率是 . 解析:本题是古典概型与解析几何知识的交汇,运用点到直线的距离公式分别求距离得解.原点到过点(01),且斜率分别为0-的直线的距离分别为1122111323323,,,,,,.故原点到l的距离小于1的概率为67.。
近年数学高考新颖试题赏析及启示

成都市教科院
二、新颖的情境
1.定义新概念 2.规定新运算 3.设定新规则 4.定义新性质
成都市教科院
例2 (2009 全国 II 卷理第 16 题)已知 AC, BD 为圆 O: x2+y2=4 的两条相互垂直的弦,垂足为 M(1, 2 ),则四边形 ABCD 面积的最大值为 .
解二:设圆心O到AC、BD的距离分别 为d1、d2,则d12 +d22=OM2=3.
1 2 2 S ABCD AC BD 2 (4 d1 )(4 d 2 ) 2 8 ( d12 d 22 ) 5
成都市教科院
这是一道加了包装 的均值不等式试题
例 1 (2006 年全国 I 理科第 11 题)用长度分别为 2,3、4,5、6(单位: cm)的 5 根细棒围成一个三角形(允许连接,但不允许折断),能够得 到的三角形的最大面积为 B (A) 8 5cm2 (B) 6 10cm 2 (C) 3 55cm 2 (D)20cm2
l 2 与 l3 间的距离是 2,正△ ABC 的三顶点分别在 l1 、 l 2 、 l3 上,则△ ABC 的边长是(
)
3 17 (C) 4
(A) 2 3
4 6 (B) 3
2 21 (D) 3
解:过 A、B 分别作 l3 的垂线 BD、AE,与 l 2 的交点为 F,设正三角 形边长为 a,则由勾股定理得:DC= CE=
成都市教科院
3.考查以数学思维能力为重点的五大能力
《考试大纲(理科)》的数学科指出,数学科考试着 重考查五大能力:思维能力,运算能力,空间想象 能力,实践能力和创新意识.在五大能力中以思维 能力为考查重点.高考数学创新型试题没有固定的 模式,难有现成的方法和套路,思维水平要求高, 思维容量大,运算量较小,能有效考查考生的思维 水平和创造意识,分析和解答这样的试题需要有较 高的能力与素质,依靠“死记硬背”、“题海战术” 和“强化训练”往往难以奏效.
829试析高考数学的创新题型

试析高考数学的创新题型摘要:高考数学在整个高考中居于至关重要的位置,尤其是江苏省以语数外来计算高考总成绩的高考数学,更是关系高考考生能否顺利考上大学的关键和核心。
本文以江苏省高考数学为例,对高考数学中的创新题型进行探究和分析。
关键字:高考数学 题型创新江苏省高考数学的题型在新课标的大背景下不断创新,旨在重视对考生基本能力与综合能力、创新意识与应用意识的考查。
近几年来,江苏省高考数学试题在题量、题型以及结构方面都基本趋于稳定,同时又有适当创新。
创新题型以其发散性思维的形式在高考数学中居凸显地位,它顺应了新课标的教学要求,对提高考生综合能力进行有效考查。
本文以近年来江苏省高考数学个别题为例来对创新题型进行分析。
1、对个别创新题型的解析以对2011年江苏省高考数学第19题的解析为例:已知a ,b 是实数,,)(,)(23bx x x g ax x x f +=+=)(x f '和)(x g '是)(),(x g x f 的导函数,若0)()(≥''x g x f 在区间I 上恒成立,则称)(x f 和)(x g 在区间I 上单调性一致.(1)设0>a ,若函数)(x f 和)(x g 在区间),1[+∞-上单调性一致,求实数b 的取值范围;(2)设,0<a 且b a ≠,若函数)(x f 和)(x g 在以a ,b 为端点的开区间上单调性一致,求|a-b|的最大值.解析:)(x f '=3x ²+a ,)(x g '=2x +b .(Ⅰ)由题意得0)()(≥''x g x f 在),1[+∞-上恒成立.因为a>0,故3x ²+a>0,进而2x+b ≥0,即b ≥-2x 在区间),1[+∞-上恒成立,所以b ≥2,因此b 的取值范围是[2,+∞).(Ⅱ)令)(x f '=0,解得x=±3a -,若b>0,由a<0得0∈(a,b ),又因为f ’(0)g ’(0)=ab <0,所以函数)(x f 和)(x g 在(a,b)上不是单调性一致的,因此b ≤0.现设b ≤0.当x ∈(-∞,0)时,)(x g <0;当x ∈(-∞,-3a -)时,)(x f '>0,)(x f ')(x g '<0,故由题设得a ≥-3a -且b ≥-3a -,从而-31≤a <0,于是-31≤b ≤0,因此,|a-b|≤31,且当a=-31,b=0时,等号成立,又当a=-31,b=0时,)(x f ')(x g '=6x(x ²-91),从而当x ∈(-31,0)时,)(x f ')(x g '>0,故函数)(x f 和)(x g 在(-31,0)上单调性一致的,因此|a-b|的最大值为31. 这道题不仅考查了函数的性质概念以及导数等方面的基础知识,重点对数形结合、转化与化归以及分类讨论等数学思想方法的灵活应用进行考查,由此可以看出考生能灵活应用所学数学思想方法来分析和解决问题的综合能力。
高考数学创新型试题的六种类型及评析

高考数学创新型试题的六种类型及评析数学是培养创新能力的重要途径.数学是研究数量关系和空间形式的学科,是思维的学科,对培养人的思辨能力、科学精神等方面有着重要的作用,而思辨能力和科学精神正是发展学生创造力的必备要素.数学中充满了创造,整个数学史就是一部创造史,可以说,没有创造就没有数学.[1]因此,数学对培养人的理性思维和创新能力具有巨大作用,正如《义务教育数学课程标准(2011年版)》(下文简称《课程标准》)所说“要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用.”[1]数学教育与创新密切相关.《课程标准》把“创新意识”确定为数学教学的十大核心概念之一,强调“创新意识的培养应该从义务教育阶段做起,贯穿数学教育的始终.”[2]《普通高中数学课程标准(2017年版)》(下文简称《标准》)指出:数学教育承载着培养学生创新意识的任务,要促进学生实践能力和创新意识的发展.[3] 创新意识表现为:对新颖的信息、情境的设问,能选择有效的方法和手段分析、处理信息,综合与灵活地应用所学的数学知识、思想和方法,进行独立的思考、探索和研究,提出解决问题的思路,并创造性地解决问题.[4]创新作为第一动力,高考命题也应体现这一导向.[5]高校要选拔具有创新潜质的人才,高考数学必须重视对学生创新意识的考查.[5]创新成为了历年高考新的热点和亮点.高考命题创新体现在四个方面:试题题型创新,试题内容创新、命题理念创新和问题解答方法创新.[5]由此,高考创新型试题成为评价学生创新能力的重要题型.所谓高考创新型试题是指从测量考生的发展性学力和创造性学力着手突出能力考查的试题.[6]本文重点评析近年高考创新型试题的六大类型:立德树人型、趣味逻辑型、公式证明型、问题推广型、高等背景型、活动经验型.一、立德树人型立德树人,简言之,即建立德行,为后人树立榜样,培养人才.党的十九大报告明确提出“落实立德树人根本任务.”在教育部制定的落实立德树人根本任务的配套文件《关于全面深化课程改革,落实立德树人根本任务的意见》中指出:“全面贯彻党的教育方针,坚持立德树人,加强社会主义核心价值体系教育,完善中华优秀传统文化教育,形成爱学习、爱劳动、爱祖国活动的有效形式和长效机制,增强学生社会责任感、创新精神、实践能力.”[1]数学教育应该而且可以发挥“数学教学具有的德育功能”.[6]通过德育渗透,培养人,塑造人.近年高考命题坚持立德树人的基本导向,命制了一系列立德树人型试题,意在通过德育渗透,培养学生良好的道德品行,可谓是高考命题中的独特创新.评析:本例以哥德巴赫猜想为载体,既凸显了我国在哥德巴赫猜想研究上的领先地位,更对普及数学家陈景润积极研究世界性难题并取得了巨大成就的故事有积极意义,这对育人有益:一方面,可以弘扬中华优秀文化,增强文化自信;另一方面,可以培养学生的爱国主义情怀,增强学生社会责任感,引导学生形成正确的世界观、人生观、价值观.本例借助数学文化,增强文化浸润,体现育人导向,育人于无声无息之中.二、趣味逻辑型《现代汉语词典》对逻辑的解释是思维的规律.《辞海》对逻辑的解释是研究思维形式及其规律的科学.逻辑是创造的起点.趣味逻辑型试题是指含有有趣情境、考查学生逻辑知识的试题.趣味逻辑型试题为考生营造轻松的氛围,给人的印象是推理有趣、推理好玩,推理的过程思维量大,思维品质要求高,但几乎不需要算,趣味逻辑涉及到的推理一般具有趣味性、逻辑性、思考性、挑战性和智慧性.[8]此类试题主要考查学生阅读能力、抽象能力和推理能力:阅读提取有用信息——抽象成图表或条件推理关系——推理得到结论.解答趣味逻辑型试题的常见方法有:代入法、假设法、排除法、找突破口法、图表法等等.试题涉及的常见题型有:真假型、排序型、匹配型等.趣味逻辑型试题是高考数学命题的一种创新,既为考生紧张的状态开辟了休憩的驿站,也拓宽了考生的视野,还让考生真切感受到逻辑就在身边,逻辑离我们的生活是那么近.例2(2017年全国II卷理科第7题)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩评析:本例为趣味逻辑型试题的经典案例:以学生询问成绩为素材,展示的情景贴近生活实际,与儿时的脑筋急转弯问题有较大的相似之处,呈现一定的趣味性和推理性,这在一定程度上使考生紧张的情绪得到放松,体现了命题者对考生的人文关怀.同时,老师和学生的对话看似平淡,实则蕴含思辩性和逻辑性,对学生的逻辑思维、推理能力等有所考查.三、公式证明型公式证明型试题是指直接将教材中公式证明设置为高考试题.该类试题是命题形式上的一大创新,旨在引导中学数学教学回归教材、重视教材.近20年来,2010年四川卷首次开发公式证明型试题,当然开发的过程中也经受了勇气和信心得考验.据四川命题组消息称,2010年四川卷命制公式证明型试题时引发了命题者们的激烈争论:绝大部分命题者认为命制公式证明型试题是命题创新,值得提倡;部分命题者认为此类题型从未考过(近20年未考过),不利于高考命题的稳定,经过激烈的辩论,最后还是决定选用公式证明型试题,但略有变化的是设置为两个小题:第一问证明公式,第二问设置为公式的应用.我们揣测,这样的设置是对该题型的一种试探与尝试.实践表明,公式证明型试题是一种成功的创新型试题,值得坚持,这从2011年高考陕西卷文理科第18题考“叙述并证明余弦定理.”、2012年高考陕西卷理科第18题考“三垂线定理及逆定理的证明”、2013年高考陕西卷理科第18题考“等比数列前m项和公式的推导”可以得到印证.评析: 本例要求证明教材中的两角和的正余弦公式,属于命题形式上的创新.这打破了一直以来不考书上命题、公式、法则等证明的命题模式.实际上,试题本身并不难,但这一“首发效应”使得许多考生手足无措,据阅卷场反馈的信息来看,2010年四川近50万考生仅有70人左右得满分,这让我们深刻反思教学中对教材的忽视,无疑对死记硬背、机械模仿的学习方式敲响了警钟.对改变教学活动重心,引导教学回归教材、关注知识的形成过程、发展过程、理解与内化过程有导向作用.从教学导向这一层面可以充分看出开发公式证明型试题的价值所在.四、问题推广型数学推广是指在一定范围内或一定层次上对数学概念、定理、法则进行拓展,使之在更大范围或更高层次上成立,此外,也指对条件、结论进行结构分析以后,进行适当变化,使得到的新命题为真.[9]张景中院士指出:“推广是数学研究中极其重要的手段之一,数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上,向未知的领域扩展,从实际的概念及问题推广出各式各样的新概念、新问题.”[10]问题推广型试题是指将已有问题的条件或结论推广到更一般情形的试题.从定义上看,问题推广型试题显然是一种典型的创新型试题.创新体现在两个方面:一是试题设置上打破了传统解答(或证明)已知问题的模式,二是推广的过程就是创新的过程.命题推广型试题有利于培养学生的问题意识,这对认识问题的本质有益、对培养学生完善的认知结构有利.同时,有利于学生体会研究的一般思路:研究特殊问题→提出一般问题→解决新问题.评析:本例第(Ⅲ)问打破了传统证明已知结论的模式,需要学生先提出猜想再证明,这在2012年前的高考命题和平常的模拟训练中几乎没有涉及,是一类典型的结论开放型试题,呈现高度的创新性.解答时,首先需要学生根据(Ⅱ)条件中变元的个数、非负性、和的特殊性及结论中变元的位置、运算的变化(幂的积到积的和),初步判断变元个数、变元和的值对结论的影响,进而模仿已有结论猜想更一般的命题,这对培养学生观察能力和提问意识尤为重要;其次,学生需要证明猜想的正确性,这一过程学生往往需要将已有特殊情形的证明方法迁移到一般的情形中,这对学生的迁移能力要求较高.总之,解答问题推广型试题的充满了创造的成分.无独有偶,2012福建卷理科17题要求学生将五个特殊的三角式子推广为三角恒等式并证明.特别指出,尽管2013年到2018年的高考命题中没有命制问题推广型试题,但是我们认为该题型必将成为未来高考命题创新点的焦点.五、高等背景型高等背景型试题是指以高等数学知识、方法和问题为素材命制的试题.该类试题的创新体现在三个方面:一是命题素材创新,即拓宽了命题素材选取范围,打破了源于教材的传统;二是试题背景创新,即试题含有丰富的高等数学背景;三是解答方法创新,即可用初等方法,也可以运用高等数学知识解答.实践表明,高等背景型试题具有积极作用:凸显能力立意的命题原则;强化中学数学与高数知识间的衔接;展示新颖的数学背景;丰富试题的内涵;拓宽试题解法;考查学生创新能力和创新意识.[11] 该类试题为学生个性发展、超前学习、创新创造提供了更为广阔的空间.是基于高等背景反向构造而来,具体设置过程可以参见文[5],这一过程充分展示了高等知识在命题中的指导性;二是解答层面,运用初等解法解答本例涉及多次构造,相当困难,高等解法体现了试题解答的多样性和创造性.据悉,某省理科近30万考生运用初等解法得满分的学生几乎没有,而运用高等解法得满分的学生不到20人,这表明高等背景型试题为学有余力的学生提供了创新、创造的空间.顺便指出,高考中高等背景型试题很多,比如:2018年全国Ⅰ卷理科21题以拉格朗日中值定理为背景,2017年全国Ⅲ卷理科21题以级数为背景;2016年四川卷理科21题以洛必达法则为背景,等等.六、活动经验型《课程标准》将“双基”扩展为“四基”,即“基础知识、基本技能、基本思想、基本活动经验”.[2]《标准》明确指出:“通过高中数学课程的学习,学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验.”[3]其中,基本活动经验是指数学基本活动经验,是学生在经历数学活动的过程中获得的数学体验和心理认知,既包含数学活动中获得的一般学科方法经验,也包含学生通过自我思考积累的个体感受.[12]具体来讲,基本数学活动经验包括基本的数学操作经验;基本的数学思维活动经验(归纳的经验,数据分析、统计推断的经验,几何推理的经验等);发现问题、提出问题、解决问题的经验.[13]基本数学活动经验具有个体性、情境性、内隐性、过程性、动态性、客观性、综合性、社会性等特征.[14]活动经验型试题是指以考查数学活动经验立意的试题.此类试题不仅是对传统命题考查“双基”这一定势的发展,而且对学生积累数学活动经验有导向功能.创新型试题作为高考的一种重要题型,在人才选拔、立德树人、思维发展、教学导向等方面具有积极功能.因此,我们相信在未来的高考命题中会开发更多类型的创新型试题.参考文献[1]赵思林,王婷.立德树人—高考数学命题的新亮点[J].数学通报,2017(4):39—43.[2]中华人民共和国教育部制定.《义务教育数学课程标准(2011年版)》[S].北京:人民教育出版社,2011.[3]中华人民共和国教育部制定.《普通高中数学课程标准(2017年版)》[S].北京:人民教育出版社,2017.[4]赵思林.高考数学创新型试题的几种类型[J].高中数学教与学(人大复印),2009(5):38-40.[5]胡琳,刘成龙.2018年高考命题创新的四个视角[J].中学数学,2018,9:15—19.[6]教育部考试中心.2017年普通高等学校招生全国统一考试大纲的说明:理科[M].北京:高等教育出版社,2017:206-276.[7]张奠宙,宋乃庆.数学教育概论[M].北京:高等教育出版社,2004.[8]李雪梅,赵思林.高考趣味逻辑性试题的几种常用解法[J].中学数学,2018(3):95—98.[9]郑隆昕.数学推广的类型与思想方法[J].武汉教育学院学报,1999,18(3):5—10.[10]朱华伟,张景中.论推广[J].数学通报,2005(4):55—57.[11]刘成龙,余小芬.高等数学背景下高考命题的问题及建议[J].中国数学教育,2017(11):53—56.[12]孔德鹏,端木彦.基于数学基本活动经验教学设计的整体分析—以“随机事件及其概率”为例[J].中国数学教育,2017(20):2—5.[13]徐斌艳.面向基本数学活动经验的教学设计[J].中学数学月刊,2011(2):1—4.[14]马文杰、鲍建生.论“数学活动经验”的基本特征[J].数学通报,2013(9):7—10.[15]余小芬,孙虹,刘成龙.2017高考数学全国卷Ⅲ理科21题的多角度分析[J].理科考试研究,2018(7):2-6.。
高考数学数列创新题的基本类型分析

高考数学数列创新题的基本类型分析Document number【980KGB-6898YT-769T8CB-246UT-18GG08】数列创新题的基本类型及求解策略高考创新题,向来是高考试题中最为亮丽的风景线。
这类问题着重考查观察发现,类比转化以及运用数学知识,分析和解决数学问题的能力。
当然数列创新题是高考创新题重点考查的一种类型。
下举例谈谈数列创新题的基本类型及求解策略。
一、 创新定义型例1、 已知数列)}({*N n a n ∈满足:)()2(log *1N n n a n n ∈+=+,定义使 ________]20051[)(......*321=∈⋅⋅⋅M ,,N k k a a a a k 内所有企盼数的和则区间叫做企盼数为整数的数解:)2(log )2(log ......4log 3log ......),()2(log 2132321*1+=+⋅=∴∈+=++k k a a a a N n n a k k n n要使)2(log 2+k 为正整数, 可设)(912005221)(22)(,22)(*1*11N n n ,N n n k n k n n n ∈≤≤⇒≤-≤∈-==++++令即2056,20561812)12(292)2.......222()22(.......)22()22()22()22()(]20051[92104321043291191==---=⨯+++++=-++-+-+-=-==∑∑=+=M n k M ,n n n 内所有企盼数的和则区间评析:准确理解企盼数的定义是求解关键。
解题时应将阅读信息与所学知识结合起来,侧重考查信息加工能力。
二、 性质探求型例2、 已知数列)}({*N n a n ∈满足:_________)7()65,4,3,2,1(2005*3=⎩⎨⎧∈≥-==+a ,N n n a ,n na n n 则且。
解:由,6,)6(636*3++++=≥=-=∈≥-=n n n n n n n a a n a a a N n n a a 时有从而知当知且于是知11163342005===+⨯a a a 。
立体几何创新题赏析

立体几何创新题赏析立体几何是数学中的一个重要分支,它研究的是三维空间中的图形和形体。
在学习立体几何的过程中,我们经常会遇到一些创新题目,这些题目不仅考验我们对基本概念的理解,还需要我们发挥想象力和创造力来解决问题。
本文将对一些立体几何创新题目进行赏析,探讨其中的数学原理和解题思路。
题目一,一个正方体的每个面上都有一个球,这些球的直径与正方体的边长相等,求这些球的体积之和。
解析,首先我们可以计算出正方体的体积,即边长的立方。
然后我们可以计算出一个球的体积,即4/3πr^3,其中r为球的半径,即正方体的边长的一半。
由于正方体有六个面,所以球的体积之和为64/3πr^3,即正方体体积的一半。
题目二,一个四棱锥的底面是边长为a的正方形,其侧面是等腰直角三角形,求这个四棱锥的体积。
解析,首先我们可以计算出正方形的面积,即a^2,然后我们可以计算出等腰直角三角形的面积,即1/2底边长高。
由于四棱锥的底面和侧面都可以用直角三角形拼接而成,所以四棱锥的体积为1/3底面积高,即1/3a^21/2底边长高。
题目三,一个圆锥的底面半径为r,高为h,另一个圆锥的底面半径为R,高为H,求这两个圆锥的体积之和。
解析,首先我们可以计算出两个圆锥的体积分别为1/3πr^2h和1/3πR^2H,然后将它们相加即可得到两个圆锥的体积之和。
通过以上的题目赏析,我们可以看到立体几何创新题目的解题过程中,需要我们熟练掌握基本的几何知识,例如计算立体图形的面积和体积的公式,以及对不同图形的分解和拼接。
同时,我们还需要具备一定的想象力和创造力,能够灵活运用数学原理解决问题。
这些创新题目的设计不仅能够锻炼我们的数学思维,还能够培养我们的逻辑推理能力和解决问题的能力。
在解决立体几何创新题目的过程中,我们还可以运用一些数学工具和方法,例如利用三角函数来计算三角形的面积,利用相似三角形来计算不规则图形的面积,利用积分来计算曲线围成的图形的面积等等。
高考数学创新题型精选(含解析)

高考数学创新题型精选一、选择题(共10小题,每小题3分,共30分)1.定义集合运算:A ⊙B ={z ︳z = xy (x+y ),z ∈A ,y ∈B },设集合A={0,1},B={2,3},则集合A ⊙B 的所有元素之和为A .0B .6C .12D .182.设○+是R 上的一个运算, A 是R 的非空子集,若对任意,a b A ∈有a ○+b A ∈,则称A 对运算○+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是A .自然数集B .整数集C .有理数集D .无理数集3.从集合{1,2,3,…,11}中的任意取两个元素作为椭圆22221x ym n +=方程中的m 和n ,则能组成落在矩形区域(){},|||11,||9B x y x y =<<内的椭圆的个数是A .43B .72C .86D .904.)(x f 是定义在R 上的以3为周期的偶函数,且0)2(=f ,则方程)(x f =0在区间(0,6)内解的个数的最小值是A . 5B . 4C . 3D . 25.如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。
在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是A .48B .18C .24D .366.点P 到点A (21,0),B (a ,2)及到直线x =-21的距离都相等,如果这样的点恰好只有一个,那么a 的值是A .21B .23C .21或23D .-21或21 7.如果二次方程 x 2-px-q=0(p,q ∈N*) 的正根小于3, 那么这样的二次方程有A .5个B .6个C .7个D .8个8.设四棱锥P-ABCD 的底面不是平行四边形, 用平面α去截此四棱锥(如右图),使得截面四边形是平行四边形, 则这样的平面 αA .不存在B .只有1个C .恰有4个D .有无数多个9.计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F 共16个记数符号;这些符号与十进制的数的对应关系如下表:例如,用十六进制表示:E+D=1B ,则A B ⨯=A .6EB .72C .5FD .B010.设P 是△ABC 内任意一点,S △ABC 表示△ABC 的面积,λ1=ABc PBC S S ∆∆, λ2=ABCPCA S S∆∆,λ3=ABCPAB S S ∆∆,定义f (P )=(λ1, λ, λ3),若G 是△ABC 的重心,f (Q )=(21,31,61),则A .点Q 在△GAB 内B .点Q 在△GBC 内C .点Q 在△GCA 内D .点Q 与点G 重合二、填空题(共6小题,每小题4分,共24分)11.在平面几何中有如下特性:从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。
高考数学创新型试题的若干类型与评析

㊀㊀㊀㊀㊀数学学习与研究㊀2022 2高考数学创新型试题的若干类型与评析高考数学创新型试题的若干类型与评析Һ谭业静㊀(深圳市高级中学,广东㊀深圳㊀518040)㊀㊀ʌ摘要ɔ近几年来,我国各地高考始终坚持综合能力题的立意,全面深入考查学生的基础数学知识,培养数学多维思想,积极探索试题的综合创新思维设计.创新型高考试题主要是以被动问题探索为探究核心,以问题探究为发现途径,以主动发现问题为探究目的,综合考查考生自主创新活动意识和综合创新能力,充分体现了高考的综合考查主体作用和选拔性的功能.ʌ关键词ɔ高考数学;创新型;题型评析引㊀言相较于一些传统综合试题来说,有着鲜明特点的创新型综合试题要求应试考生具备细致观察㊁认真分析㊁合理结构类比㊁准确推理归纳的综合能力.创新型高考试题的类型主要有:类比㊁归纳研究型,开放探索型,实用型,合情推理型,趣味逻辑型等.一㊁高考数学通过运用创新型试题考查考生的自主创新能力高考理科数学创新型试题主要是综合测量检查考生的自身发展性综合学习能力.高考理科数学考试十分重视对学生的创新思维意识的综合考查.考生的数学创新思维意识主要表现在以下方面:对新颖的数学信息﹑复杂情境,能主动选择有效的理论方法和科学手段进行分析㊁设问并处理,综合且灵活地应用自己所学的有关数学知识㊁思想和教学方法进行独立的问题思考﹑理论探索和问题研究,提出各种解决实际问题的具体思路方案﹐并能有创造性地通过分析和设计解决实际问题.从近几年的全国考题情况来看,创新型高考试题已逐渐成为当前全国各个重点高考院校命题组努力追求的一个理想考试目标之一.二㊁高考数学创新型试题的类型及其特点(一)类比㊁归纳研究型在学生学习数学的过程中,培养学生掌握解题思想的启发性研究方法,对学生今后的学习与工作都会有很大的促进作用.类比数学研究中的题型相较于传统信息化的迁移研究题型来得更直接,它在题目中会直接给出明确的命题方向,学生将学过的基础数学知识进行类比㊁归纳和应用就会得到更一般的数学结论.近些年,全国高考明显地加强了对广大高考生掌握归纳与发现类比知识能力的综合考查,即由考生通过猜想掌握类比知识到归纳发现科学新知,渗透了从局部到整体㊁从特殊到一般的多种思维表达方法.(二)开放探索型开放探索型数学题符合越来越开放的高中教育发展理念,从考查学生思维方面而言,它其实是为了提升高中学生敢于大胆尝试与自由猜想的思维能力.学生大胆演绎,自由联想,尝试探索并验证,将多种不同思维表达方式进行整合,寻求无固定解法的解题途径.开放探索题的解法别致㊁多样,进一步培养了学生的创造意识与思维,这是新的教育理念的具体体现.(三)实用型把数学带入学生切身体会的生活中去,是目前教学课程很关注的一个新理念.实用型数学试题是以社会生态环保㊁健康心理教育㊁经济社会发展等各种社会经济背景知识为主要载体而设立的社会相关综合数学试题,考查的是学生能否把握对现实社会问题的有效处理转化与有效运用的综合能力,能够提升学生的数学分析能力及理解能力.综合知识型高考试题类型主要包括高考学科内各章节知识㊁学科知识综合交汇及其他学科知识,考生要更快速地解答这一类考试题目,就得从题中构造数学模型着手,利用数学知识框架将与其相关的比如函数㊁数列㊁数轴㊁概率等知识点进行整合.高考综合考试教学模式正在日益深入改革创新中,教师在针对高三年级学生重点复习高中数学知识点的过程中,要指导学生去重视对数学知识中所蕴藏的思想进行探索,提升解题技巧.例1㊀(2018年全国Ⅱ卷理科第8题)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是 每个大于2的偶数可以表示为两个素数的和 ,如30=7+23.在不超过30的素数中,随机选取两个不All Rights Reserved.㊀㊀㊀㊀数学学习与研究㊀2022 2同的数,其和等于30的概率是(㊀㊀).A.112㊀㊀㊀B.114㊀㊀㊀C.115㊀㊀㊀D.118评析㊀该题充分弘扬我国中华优秀传统文化,可以不断增强学生的文化自觉和文化自信,引导学生形成独立的世界观.在讲解试题之前,教师可以让学生先发表对于该题的意见和解题思路并进行总结,写到黑板上,如果有错误,教师及时指出,这样能够让学生更加明确地了解习题中所运用到的知识,帮助学生巩固知识点.(四)合情推理型合情推理是根据已有的某种数学理论事实推理结论,或根据个人已有数学实践经验(包括数学理论实验或物理实践)和某种数学直观现象进行数学推测而直接得到某些数学结果的一种数学推理.我们通过观察现象,运用实验㊁归纳㊁类比等多种方法直接可以获得某种新的数学推理结论.从发现和掌握数学新知的角度来说﹐合情推理命题显得特别重要.因此,高考数学命题非常重视通过考查各个学生的合情理论推理思维能力水平来达到提高学生创新思维意识的基本目的.例2㊀古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5-12(5-12ʈ0.618,称为黄金分割比例),著名的 断臂维纳斯 便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5-12.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是(㊀㊀).A.165cm㊀㊀B.175cm㊀㊀C.185cm㊀㊀D.190cm评析㊀该题一出,引起社会各界的关注,更是有许多网友运用五花八门的方式进行解答.由此可以看出,重视演绎推理在古代是非常了不起的,因为古人往往处于一种需要努力维系生存的状态,因此需要考虑实际问题.比如罗马需要通过进攻维持帝国的强盛并且对征服的地区开展统治,因此高度重视军事武器的改良㊁法律的完善,而轻视那些似乎不着边际㊁没有实用性的纯数学理论.(五)趣味逻辑型逻辑学试题的研究对象主要是现代人们的逻辑思维活动形式及逻辑规律,在现代逻辑思维科学中,主要类型有形式逻辑﹑辩证主义逻辑和数理逻辑.其中趣味形式逻辑命题是一种形式逻辑,它从基本概念理解﹑逻辑命题㊁推理㊁逻辑数学基本规律等几个方面,通过通俗而有趣的经典故事形式介绍趣味逻辑学的基本知识及其实际应用.趣味逻辑命题展现了新的逻辑数学魅力,可以培养广大学生的逻辑创新思维意识,提高广大学生快速学习趣味逻辑数学的兴趣,帮助广大学生快速打开掌握逻辑数学知识的智慧宝库,培养学生掌握驾驭各种逻辑数学工具的技巧.趣味逻辑型数学试题主要是教育部考试中心近年来新开发的一种创新型数学试题,其主要特点之一是新颖有趣,突出了现代数学的逻辑思辨性﹑科学逻辑性和科学创新性.教师在教学过程中应让学生成为课堂的 主演 ,在讲解习题前,可以先让学生陈述自己的解题思路,然后总结几种解题思路写到黑板上.如果只讲解正确的解题思路,那么教师就先来用学生的解题思路,再把自己的解题思路讲解给学生;如果学生的解题思路是错误的,那么教师应该告诉学生解题思路错误的点与原因.这样学生就能够了解习题的题干㊁题眼,思考这道题用到哪些知识,从而巩固学过的知识点.三㊁针对创新题型的学习启示(一)复习巩固数学基础知识学生在考前基础学习和考后复习中要不断探索巩固所学基础知识,注重基础知识之间的相互联系,对这些基础知识需要有一个系统的知识认知体系结构,同时,学生对学习过程中可能出现的一些错误点也要加以重视,找出学习过程中所犯的错误并及时对其进行纠正.总之,学生应全面复习巩固数学基础知识,以不断提高分析数学问题和掌握解决实际问题的基本能力,并为不断提高综合数学能力水平打好坚实的基础.基础知识是非常重要的,一些同学在做题的过程中由于对公式运用不熟练导致解题思路不清晰,最终出现错误,所以应当在日常的练习中熟悉解题技巧,这样才能确保得到基本分.逻辑思维能力固然重要,但是公式是基础,要学会变通并熟练掌握,可通过反复练习不断巩固.当前学生存在的主要问题:第一,不会解题.一些学生因为想不到这个考点运用的是哪些知识点,分不清楚需要运用的公式,加上受到思维定式的影响,最终导致不会解题.第二,解题速度慢.解题速度慢的主要原因是对于公式和基础的解题思路不够熟All Rights Reserved.㊀㊀㊀㊀㊀数学学习与研究㊀2022 2练,对知识点的记忆较为模糊.第三,部分学生在做题的过程中不够细心,容易落入试题当中的陷阱,又或者是由于马虎出现错误,比如忘了加符号,忘了结果取整等.因此学生要在日常的练习过程中对重点公式反复记忆,掌握最基本的推理能力.(二)注重探索,提高理论综合应用能力在平常的教学过程中,教师要培养学生树立灵活的综合应用思维意识和自主创新实践意识,使他们在课间学习和集中复习时善于理性化地发散数学思维,将传统数学基础思想和方法合理有效地运用到日常数学理论学习中去,提高自己分析并解决数学问题的综合应用能力.例如,教师在讲解立体几何知识时,如果只让学生通过想象就练习,难度会很大.因此,教师可以利用多媒体教学设备帮助学生建立直观印象.例如,利用视频课件和PPT动画效果向学生展示几何变换,这样就会让学生对立体图形有更加系统的认识,能让学生更加有效地了解抽象的知识.虽然多媒体设备的使用课堂已经有较长的历史,但是如果在高中课堂当中不经常使用,就失去了多媒体设备教学的意义.教师不仅需要充分㊁正确地运用自己的知识多样性向学生解释抽象的数学知识,还需要不断增强学生在学习中的自信,这是教师在数学教学过程中培养学生核心素养的途径.(三)结合生活创新数学试题教师在教学中应培养学生对知识的运用能力,使得学生能够更加深入地理解知识,并且能够运用所学知识解决实际生活中的问题.比如,2021年数学试卷以 五育并举 教育方针为指引,通过情境创设引导考生关注生活,关注社会,关注劳动.第6题以北京冬奥会为背景宣传志愿者服务,第17题以芯片生产中的刻蚀速率为原型,设计了概率统计的应用问题,考查了考生对平均数㊁方差等知识的理解和应用,考查学生的运算能力,同时还让学生体会数学在实际生产生活中的学科价值.结合学生的生活设置数学问题已经较为常见,这类数学问题旨在对学生知识运用能力的考查,其源于学生的日常生活,却又高于学生的日常生活,能够有效地吸引学生的注意力,引导学生进入试题所创设的问题情境之中,引导学生的想象,增强学生对数学的亲切感,从而使得学生主动地将问题的思考与实际生活结合起来.例如,某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过十分钟的概率是(㊀㊀).A.13㊀㊀㊀B.12㊀㊀㊀C.23㊀㊀㊀D.34在解答此题时,教师要引导学生探究问题背后所蕴含的生活,代入几何概型概率计算公式,最终得到答案12.这样不仅对学生的知识运用能力进行了考查,也体现了数学源于生活的理念.(四)模型法解题万变不离其宗,学生在解题过程中要注重将多个知识点进行综合,了解题目中渗透的数学思想和数学方法.因此,教师要教会学生注意认真审题,了解命题人的意图.针对创新型的高考试题,我们只要在科学方法的引导下,就一定会有很大程度的提高,所以提出了利用模型法解决此类问题.创新型的题目虽然看起来较为新颖,但是最终的思想也是考查最基本的高中知识,所以我们解题的过程中需要熟悉题型,找到清晰的思路,然后将这个题目进行归类,最终把它归结为某一类考试题型.例如,将某一创新题型归结为考查圆锥曲线的知识点,掌握这一模型就知道圆锥曲线的考点,如求焦点问题等,有了一定的解题思路,解答题目时就不会出错.准确答题的关键就是仔细审题并进行深入思考和分析,谨防疏漏,要注意题型的变化,最终,利用模型法顺利解开谜题.结束语创新型试题已经成为高考一种重要的题型,在对于人才的选拔㊁立德树人理念的发展以及教学引领等各个方面都将起到积极的推动作用.因此,我们始终坚持在未来高考命题中研究和开发多种不同类型的创新型试题,对考生的综合素质和创新意识进行考查,这样可以有效地帮助广大考生积极备战自己的高考,以便顺利地考上理想的大学.ʌ参考文献ɔ[1]刘成龙,胡琳.高考数学创新试题的几种类型及评析[J].中学数学,2019(5):38-39,41.[2]叶国强,李世杰.2007年高考数学创新试题评析[J].上海中学数学,2008(1):26-28.[3]李恒.变中求新㊀新中出彩:2007年高考数学创新型试题评析[J].中学数学月刊,2007(8):3-5.All Rights Reserved.。
三、合情推理型——高考数学创新题型之赏析.doc

三、合情推理型图像的合情推理数量关系的合情推理规律探索型创新题给出了一个数学情景或一个数学命题,需要学生用发散思维去联想、类比、推广、转化,找出类似的命题,这是新课程较为重视的类比推理、归纳推理,主要考查学生的观察、分析、类比、归纳的能力,从不变中找规律、从不变中找变化。
(09福建文)16、五位同学围成一圈依序循环报数,规定:①第一位同学首次报出的数为1.第二位同学首次报出的数也为1, Z后每位同学所报出的数都是前两位同学所报出的数Z和;②若报出的是为3的倍数,则报该数的同学需拍手一次当第30个数被报出时,五位同学拍手的总次数为________________点评该题以历史上著名的数列"斐波那契数列”为背最,需要同学们从简单的计算,找出规律计算,用数列求解第n次、第n+1次、笫n+2次的报数关系。
寻找规律是解题的根本,否则费时费力。
解析首先求出这个数列的每一项除以3所得余数的变化规律,再求所求就比较简单了. 这个数列的变化规律是:从第三个数开始递增,且是前两项Z和,那么有1、1、2、3、5、8、13、21、34、55、89、144、233> 377、610、987……分别除以3 得余数分别是1、1、2、0、2、2、1、0、1、1、2、0、2、2、1、0……由此可见余数的变化规律是按1、1、2、0、2、2、1、0循坏,周期是8•在这一个周期内第四个数和第八个数都是3的倍数,所以在三个周期内共有6个报出的数是三的倍数,后面6个报出的数中余数是1、1、2、0、2、2, 只有一个是3的倍数,故3的倍数总共有7个,也就是说拍手的总次数为7次(10福建文)16.观察下列等式:®cos2a = 2cos「a-\;②COS4(7 =8cos4 6Z-8COS2 (7 + 1 :③cos6a = 32cos6(7-48cos4 a +18cos2a-l ;④cos 8a = 128 cos8a一256 cos6(7 + 160 cos4- 32 cos2 a +1 ;⑤cos 1 Oa = m cos10a-1280cos8(7 4-1120cos6a4-160cos4-32cos2 a +1 ;可以推测,m-n + p = __________ o16. 962解析(转换文字格式)分析因为 2 = 2\8 = 2\32 = 2\128 = 2\所以m = p = 50,所以m-n+p = 962・点评本题考查了观察发现能力、合情推理(归纳推理)能力(10 宁夏文)11.观察下列等式:13+23= ( 1 +2) 2, 13+25+33= ( 1+2 + 3) 2, 13+23+ 33+43= ( 1+2 + 3+4) 2,…,根据上述规律,箏四牛等氏为_________________ o解析p+23+33+43+53=(1+2 + 3+4 + 5)[(或15?).点评(08江苏)10、将全体正整数排成一个三角形数阵:18 9 10按照以上排列的规律,第〃行(心3)从左向右的第3个数为__________ 解析:点评:本题需要考生対信息迹行提炼、组织与加工,探索解题的思路。
高考数学复习点拨 立体几何创新问题常见类型探求
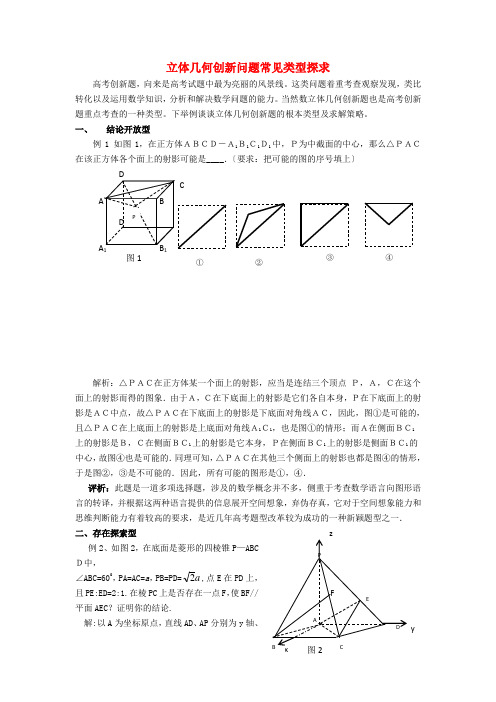
立体几何创新问题常见类型探求高考创新题,向来是高考试题中最为亮丽的风景线。
这类问题着重考查观察发现,类比转化以及运用数学知识,分析和解决数学问题的能力。
当然数立体几何创新题也是高考创新题重点考查的一种类型。
下举例谈谈立体几何创新题的根本类型及求解策略。
一、结论开放型例1 如图1,在正方体ABCD-A1B1C1D1中,P为中截面的中心,那么△PAC〔要求:把可能的图的序号填上〕解析:△PAC在正方体某一个面上的射影,应当是连结三个顶点P,A,C在这个面上的射影而得的图象.由于A,C在下底面上的射影是它们各自本身,P在下底面上的射影是AC中点,故△PAC在下底面上的射影是下底面对角线AC,因此,图①是可能的,且△PAC在上底面上的射影是上底面对角线A1C1,也是图①的情形;而A在侧面BC1上的射影是B,C在侧面BC1上的射影是它本身,P在侧面BC1上的射影是侧面BC1的中心,故图④也是可能的.同理可知,△PAC在其他三个侧面上的射影也都是图④的情形,于是图②,③是不可能的.因此,所有可能的图形是①,④.评析:此题是一道多项选择题,涉及的数学概念并不多,侧重于考查数学语言向图形语言的转译,并根据这两种语言提供的信息展开空间想象,弃伪存真,它对于空间想象能力和二、存在探索型例2、如图2,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=a2,点E在PD上,且PE:ED=2:1.在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.解:以A为坐标原点,直线AD、AP分别为y轴、②z 轴,过A 点垂直平面PAD 的直线为x 轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为所以 ).0,21,23(),31,32,0(a a AC a a AE ==).,21,23(),,0,0(a a a PC a AP -==设点F 是棱PC 上的点,,10),,21,23(<<-==λλλλλ其中a a a PC PF 那么 令 AE AC BF 21λλ+=得λ)λ,λλ,a(λ)a λa λ,λλλ,λ,λ,λ.a(λ)a λ.λλ.⎧-⎪-=⎪⎪⎪⎪+=++=+⇒==-=⎨⎨⎪⎪⎪⎪-=-=⎪⎪⎩⎩1112121222111124113112233222111133即 即 21=λ时,.2321AE AC BF +-=亦即,F 是PC 的中点时,BF 、AC 、AE 共面.又 BF ⊄平面AEC ,所以当F 是棱PC 的中点时,BF//平面AEC.评析:对于由给定结论,反溯应具备的条件的探索性问题,可执果索因,由给定的结论追溯应具备的条件。
高考数学创新题的思维分析

高考数学创新题的思维分析解析高考数学中创设xx题的思路(1)分析几何中的运动问题。
几何分析中创设xx小题是xx课程标准高考中X出现频率较高的题型。
2009年、2010年、2011年高考数学填空题的闭卷题都有动作题。
也就是xx课程标准高考的数学思维已经从传统的静态分析模型转变为动态分析模型。
因此考生在练习时需要把握变量和不变量,善于在练习时建立直接变量和间接变量之间的关系,总结特殊值的情况分析、存在的问题以及任意问题的解决方法。
在解决这类xx题时,往往需要综合生活中的很多想法,加上题中给出的信息。
在数学层面,考生要善于从各个角度思考问题,打开思路,同时要善于用数学思维将题目情境抽象成数学模型。
(2) xx距离近年来,坐标系中xx距离D=| X1-X2 ||| Y1-Y2 |的问题出现了。
考生需要知道坐标系中坐标差的原理,只需搞清楚两个对应点构成的矩形中坐标差的关系即可。
近两年来,xx距离已经介入高考,但高考考查的不再是xx距离本身,而是考生在建立xx的数学模型时,能否找出建立数学模型与数学思维的关系。
比如2011年大结局,对于一个序列的每个比特的绝对值之和,因为每个比特都有相同的值,所以只需要考虑一个比特。
笔者将在具体的解题中详细描述。
(三)xx名词对于题目中的xx名词xx,考生可以从xx自然本身的角度,从数学思维的角度充分理解xx所代表的数学意义。
这种xx题就像画一样描述一个数学模型,然后描述简洁透彻,让考生通过这种描述探索本质。
Xx课程标准数学追求对数学思维的自然描述,即不会给学生思维断层和非常规思维(2012年北京市海淀区高三期末考试的解析几何大题属于非常规思维)。
比如2009年的《北京卷艺》填空闭卷题,就是让学生直观形象地理解什么是孤立的元素,从而快速得到答案。
(四)知识点的组合。
这类题型主要结合函数性质、图像等知识点。
一般只要熟悉知识点的网络结构和思维模式就没问题。
比如2011年北京高考期末考试,考生需要掌握轨迹和方程的思想,以及方程和曲线关于变量和坐标的一一对应关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(原创、首发、专投稿,适合高二、高三年级11月份用,同意删改)高考数学创新题分类探究贵州省龙里中学 洪其强(551200)一、建构数列型:数列作为特殊的函数,在高考数学中占有相当重要的位置,主要涉及增长率、银行信贷等.解答这一类问题,要充分应用观察、归纳、猜想的手段,建立起等差、等比、或递推数列的模型来解题.例1 (2003年朝阳区高三统一练习(二))2002年底某县的绿化面积占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.(Ⅰ)设该县的总面积为1,2002年底绿化面积为1041=a ,经过n 年后绿化的面积为,1+n a 试用n a 表示1+n a ;(Ⅱ)求数列}{n a 的第1+n 项1+n a ;解析 (Ⅰ)设现有非绿化面积为1b ,经过n 年后非绿化面积为.1+n b 于是.1,111=+=+n n b a b a 依题意:1+n a 是由两部分组成,一部分是原有的绿化面积n a 减去被非绿化部分n a 1002后剩余的面积n a 10098,另一部分是新绿化的面积.1008n b 于 是1+n a =n a 10098+.1008n b =n a 10098+.252109)1(1008+=-n n a a (Ⅱ)1+n a =,252109+n a 1+n a -54=-).54(109-n a , 数列}54{-n a 是公比为,109首项5254104541-=-=-a 的等比数列. n n a )109)(52(541-+=∴+二、信息迁移型:信息迁移题指的是不便于直接运用所学数学知识解决问题,而需要从所给材料中获取信息,并用于新问题解决的一类问题.这一类问题,往往出现在一个较新的背景之下,题型新颖,形式多样,融综合性、应用性、开放性、创新性于一体.信息迁移型题可分为定义信息型、图表信息型、 图形图像信息型等. 1.定义信息型 例1 定义运算a c ad bcb d =-,复数z 满足11z ii i=+,则复数在的模为A .1+.1-解析 由11z i i i=+得1212izi i i z i i +-=+⇒==-,∴z ==,故选C 。
例2 (2001上海22)对任意函数f (x ), x ∈D ,可按图示构造一个数列发生器,其工作原理如下:①输入数据x 0∈D ,经数列发生器输出x 1=f (x 0);②若x 1∉D ,则数列发生器结束工作;若x 1∈D ,则将x 1反馈回输入端,再输出x 2=f (x 1),并依此规律继续下去.现定义124)(+-=x x x f (1)若输入x 0=6549,则由数列发生器产生数列{x n },请写出{x n }的所有项;(2)若要数列发生器产生一个无穷的常数列,试求输入的初始数据x 0的值;(3)若输入x 0时,产生的无穷数列{x n },满足对任意正整数n 均有x n <x n +1;求x 0的取值范围. 解析 (1)∵f (x )的定义域D =(–∞,–1)∪(–1,+∞) ∴数列{x n }只有三项,1,51,1911321-===x x x (2)∵x x x x f =+-=124)(,即x 2–3x +2=0 ∴x =1或x =2,即x 0=1或2时 n n n n x x x x =+-=+1241 ,故当x 0=1时,x n =1,当x 0=2时,x n =2(n ∈N *) (3)解不等式124+-<x x x ,得x <–1或1<x <2 要使x 1<x 2,则x 2<–1或1<x 1<2 对于函数164124)(+-=+-=x x x x f ,若x 1<–1,则x 2=f (x 1)>4,x 3=f (x 2)<x 2; 若1<x 1<2时,x 2=f (x 1)>x 1且1<x 2<2,依次类推可得数列{x n }的所有项均满足x n +1>x n (n ∈N *) 综上所述,x 1∈(1,2),由x 1=f (x 0),得x 0∈(1,2). 2.图表信息型例3 深夜,一辆出租车被牵涉进一起交通事故,该市有两家出租车公司——红色出租车公司和蓝色出租车公司,其中蓝色出租车公司和红色出租车公司分别占整个城市出租车的85%和15%。
据现场目击证人说,事故现场的出租车是红色,并对证人的辨别能力作了测试,测得他辨认的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑. 请问警察的认定对红色出租车公平吗?试说明理由.解析 设该城市有出租车1000辆,那么依题意可得如下信息:从表中可以看出,当证人说出租车是红色时,且它确实是红色的概率为41.0290120≈,而它是蓝色的概率为59.0290170≈. 在这种情况下,以证人的证词作为推断的依据对红色出租车显然是不公平的. 例4 已知某海滨浴场的海浪高度y (米)是时间t (0≤t ≤24,单位小时)的函数,记作y =f (t ),下表是某日各时的浪高数据经长期观测y =f (t )的曲线可近似地看成函数y =A cos ωt +b .(1)根据以上数据,求出函数y =A cos ωt +b 的最小正周期T ,振幅A 及函数表达式;(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多少时间可供冲浪者进行运动.解析 (1)由表中数据,知T =12,ω=62ππ=T . 由t =0,y =1.5得A +b =1.5.由t =3,y =1.0,得b =1.0.所以,A =0.5,b =1.振幅A =21, ∴y =16cos 21+t π(2)由题意知,当y >1时,才可对冲浪者开放.∴16cos 21+t π>1, t 6cos π>0.∴2k π–2262ππππ+<<k t ,即有12k –3<t <13k +3.由0≤t ≤24,故可令k =0,1,2,得0≤t <3或9<t <15或21<t ≤24. ∴在规定时间内有6个小时可供冲浪者运动即上午9:00至下午15:00. 3. 图形、图像信息型例5 一只小船以10 m/s 的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以20 m/s 的速度前进(如图),现在小船在水平P 点以南的40米处,汽车在桥上以西Q 点30米处(其中PQ ⊥水面),则小船与汽车间的最短距离为 .(不考虑汽车与小船本身的大小).解析:设经过时间t 汽车在A 点,船在B 点,(如图),则AQ =30–20t ,BP =40–10t ,PQ =20,且有AQ ⊥BP ,PQ ⊥AQ ,PQ ⊥PB ,设小船所在平面为α,AQ ,QP 确定平面为β,记α∩β=l ,由AQ ∥α,AQ ⊂β得AQ ∥l ,又AQ ⊥PQ ,得PQ ⊥l ,又PQ ⊥PB ,及l ∩PB =P 得PQ ⊥α.作AC ∥PQ ,则AC ⊥α.连CB ,则AC ⊥CB,进而AQ ⊥BP ,CP ∥AQ 得CP ⊥BP ,∴AB 2=AC 2+BC 2=PQ 2+PB 2+PC 2=202+(40–10t )2+(30–20t )2=100[5(t–2)2+9],t =2时AB 最短,最短距离为30 m.答案:30 m例6 某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系如下图1所示的一条件线表示;西红柿的种植成本与上市时间的关系用如下图2所示的抛物线段表示.(1)写出如图1所示市场售价与时间的函数关系式P=f(t);写出如下图2所示种植成本与时间的函数关系式Q=g(t).(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/102kg ,时间单位:天)图1图2解析 (1)f(t)=⎩⎨⎧≤<-≤≤-.300200,3002,2000,300t t t t ;g(t)=2001(t-150)2+100,0≤t ≤300. (2)设t 时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),即h(t)=⎪⎪⎩⎪⎪⎨⎧≤<-+-≤≤++-.300200,21025272001,2000,217521200122t t t t t t当0≤t ≤200时,配方整理得h(t)=-2001(t-50)2+100,所以,当t=50时,h(t)取得区间[0,200]上的最大值100;当200<t ≤300时,配方整理得h(t)=-2001(t-350)2+100所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从2月1日开始的第50天时,上市的西红柿纯收益最大.三、函 数 与 数列、不 等 式 证 明 的综合型:函 数 与 数列、不 等 式 证 明的 综 合 题 在 高 考 中 常 考 常 新 , 是 既 考 知 识 又 考 能 力 的 好 题型 , 在 高 考 备 考 中 有 较 高 的 训 练 价 值同时这类问题在高考中频频出现,是历年高考试题中不容忽视的一个考点。
例7 已知函数f (x )=aa a xx +(a>0,a≠1).(1) 证明函数f (x )的图象关于点P (21,21)对称.(2) 令a n =)1()(n f n f a -,对一切自然数n ,先猜想使a n >n2成立的最小自然数a ,并证明之.(3) 求证:n n n n )(!(lg 3lg )1(41>+∈N).解析 (1)关于函数的图象关于定点P 对称, 可采用解几中的坐标证法.设M (x ,y )是f (x )图象上任一点,则M 关于P (21,21)的对称点为M ’(1-x,1-y),yx f aa aaa ay a a a a a a a aa a xxxxxx x -=-∴+=+-=-+=⋅+=+--1)1(1111∴M′(1-x ,1-y )亦在f (x )的图象上,故函数f (x )的图象关于点P (21,21)对称.(2)将f (n )、f (1-n )的表达式代入a n 的表达式,化简可得a n =an猜a =3, 即3n>n2.下面用数学归纳法证明. 设n =k (k ≥2)时,3k>k2. 则n =k +1时,3k+1>3·3k>3k2 又3k 2-(k+1)2=2(k-21)2-23≥0(k≥2,k∈N)∴3n>n2.(3)∵3k>k2∴klg3>2lgk 令k =1,2,…,n ,得n 个同向不等式,并相加得:).!lg(3lg )1(4),21lg(23lg 2)1(n n nn n n >-⨯>+故 四、方案优化型寻找问题的最优解,是这一类题目的共同特点.解决问题的方法主要涉及线性规划、均值不等式、单调性等求最值的方法.例8 已知甲、乙、丙三种食物的维生素A 、B 含量及成本如下表,若用甲、乙、丙三种食物各x 千克,y 千克,z 千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A 和63000单位维生素B.(1)用x ,y 表示混合食物成本c 元; (2)确定x ,y ,z 的值,使成本最低.解析 (1)依题意得 100,4911=++++=z y x z y x c 又 y x c 57400++=∴.(2)由{y x z z y x z y x --=≥++≥++100,6300050040080056000400700600及 , 得{130332064≥-≥+y x y x , .45057≥+∴y x ,85045040057400=+≥++=∴y x c当且仅当{{2050,130332064==≥-=+y x y x y x 即时等号成立., ∴当x =50千克,y =20千克,z =30千克时,混合物成本最低为850元.五、是否存在型:给出一定的条件,让我们去证明在给定条件下,一些给定的结论一定存在或一定不存在,或者要求我们去判断在给定条件下的结论是否存在.例9 已知方向向量为v =(1,3)的直线l 过点(0,-23)和椭圆C :)0(12222>>=+b a by a x 的焦点,且椭圆C 的中心关于直线l 的对称点在椭圆C 的右准线上.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在过点E (-2,0)的直线m 交椭圆C 于点M 、N ,满足634=⋅OM , cot ∠MON ≠0(O 为原点).若存在,求直线m 的方程;若不存在,请说明理由.解析 (Ⅰ)由题意可得直线ι:y -①过原点垂直ι的方程为,y x =② 解①②得x=32.∵椭圆中心O(0,0)关于直线ι的对称点在椭圆C 的右准线上, ∴23232a c =⨯=.∵直线ι过椭圆焦点,∴该焦点坐标为(2,0). ∴a 2=6,c=2,b 2=2,故椭圆C 的方程为22162x y +=. ③ (Ⅱ)设M(x 1,y 1),N(x 2,y 2),当直线m 不垂直x 轴时,直线m :y=k(x+2)代入③,整理得(3k 2+1)x 2+12k 2x+12k 2-6=0,则x 1+x 2=221231k k -+,x 1x 2=2212631k k -+,==点O 到直线MN 的距离d=.∵OM ON ⋅=∠MON,即||||cos 0OM ON MON ⋅∠=≠ ,∴||||sin OM ON MON ⋅∠= ∴||OMN S MN d =∴⋅=即2|3)k k =+.整理得21,33k k =∴=±.当直线m 垂直x 轴时,也满足OMN S =故直线m 的方程为33y x =+或y=33x --或x=-2. 经检验上述直线均满足0OM ON ⋅≠.所在所求直线方程为y =或y=x -或x=-2.. 六、恒成立型例10 (2002年全国高考题)某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?解析 设2001年末汽车保有量为1b 万辆,以后各年末汽车保有量依次为2b 万辆,3b 万辆,……,每年新增汽车x 万辆,则301=b ,x b b n n +=+94.01所以,当2≥n 时,x b b n n +=-194.0,两式相减得:()1194.0-+-=-n n n n b b b b(1)显然,若012=-b b ,则011==-=--+ n n n n b b b b ,即301===b b n ,此时.8.194.03030=⨯-=x (2)若012≠-b b ,则数列{}n n b b -+1为以8.106.0112-=-=-x b x b b 为首项,以94.0为公比的等比数列,所以,()8.194.01-⋅=-+x b b n n n .(i )若012<-b b ,则对于任意正整数n ,均有01<-+n n b b ,所以,3011=<<<+b b b n n ,此时,.8.194.03030=⨯-<x(ii )当万8.1>x 时,012>-b b ,则对于任意正整数n ,均有01>-+n n b b ,所以,3011=>>>+b b b n n , 由()8.194.01-⋅=-+x b b n n n ,得()()()()()3094.0194.01112112211+---=+-++-+-=----n n n n n n b b b b b b b b b b()()3006.094.018.11+--=-n x ,要使对于任意正整数n ,均有60≤n b 恒成立,即()()603006.094.018.11≤+---n x对于任意正整数n 恒成立,解这个关于x 的一元一次不等式 , 得8.194.018.1+-≤nx , 上式恒成立的条件为:上的最小值在N n nx ∈⎪⎭⎫⎝⎛+-≤8.194.018.1,由于关于n 的函数()8.194.018.1+-=n n f 单调递减,所以,6.3≤x .七、环境保护型例11 有一个受到污染的湖泊,其湖水的容积为V 立方米,每天流出湖泊的水量都是r 立方米,现假设下雨和蒸发正好平衡,且污染物质与湖水能很好地混合,用g (t )表示某一时刻t 每立方米湖水所含污染物质的克数,我们称为在时刻t 时的湖水污染质量分数,已知目前污染源以每天p 克的污染物质污染湖水,湖水污染质量分数满足关系式g (t )=r p +[g (0)- rp]·e t v r-(p ≥0),其中,g (0)是湖水污染的初始质量分数.(1)当湖水污染质量分数为常数时,求湖水污染的初始质量分数; (2)求证:当g (0)<rp时,湖泊的污染程度将越来越严重;(3)如果政府加大治污力度,使得湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时污染水平的5%?解析 (1)∵g (t )为常数, 有g (0)-r p=0, ∴g (0)= rp .(2) 我们易证得0<t 1<t 2, 则g (t 1)-g (t 2)=[g (0)- rp ]e 1t vr --[g (0)-rp ]e 21t v r -=[g (0)-rp][e 1t vr --e21t v r -]=[g (0)-rp ])(2112)(t t vrt vr t vr ee e+-,∵g (0)·rp<0,t 1<t 2,e 21t v r>e 1t v r,∴g (t 1)<g (t 2) .故湖水污染质量分数随时间变化而增加,污染越来越严重.(3)污染停止即P =0,g (t )=g (0)·et vr-,设经过t 天能使湖水污染下降到初始污染水平5%即g (t )=5% g(0)∴201=e t v r-,∴t =rv ln20,故需要rvln20天才能使湖水的污染水平下降到开始时污染水平的5%.八、估测计算型例12 为促进个人住房商品化的进程,我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下:张先生家要购买一套商品房,计划贷款25万元,其中公积金贷款10万元,分十二年还清;商业贷款15万元,分十五年还清.每种贷款分别按月等额还款,问: (1)张先生家每月应还款多少元?(2)在第十二年底汪先生家还清了公积金贷款,如果他想把余下的商业贷款也一次性还清;那么他家在这个月的还款总数是多少?(参考数据:1.004455144=1.8966,1.005025144=2.0581,1.005025180=2.4651) 解析 设月利率为r ,每月还款数为a 元,总贷款数为A 元,还款期限为n 月 第1月末欠款数 A (1+r )-a第2月末欠款数 [A (1+r )-a ](1+r )-a = A (1+r )2-a (1+r )-a第3月末欠款数 [A (1+r )2-a (1+r )-a ](1+r )-a=A (1+r )3-a (1+r )2-a (1+r )-a ……第n 月末欠款数 0)1()1()1()1(21=-+--+-+-+--a r a r a r a r A n n n 得:1)1()1(-+⨯+=n n r rr A a对于12年期的10万元贷款,n =144,r =4.455‰ ∴37.9421004455.1004455.0004455.1100000144144=-⨯⨯=a对于15年期的15万元贷款,n =180,r =5.025‰ ∴22.12681005025.1005025.0005025.1150000180180=-⨯⨯=a由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.(2)至12年末,汪先生家按计划还款以后还欠商业贷款 a r a r a r a r A X -+--+-+-+=)1()1()1()1(142143144 其中A =150000,a =1268.22,r =5.025‰ ∴X =41669.53 再加上当月的计划还款数2210.59元,当月共还款43880.12元.九、类比归纳型:给出一个数学情景或一个数学命题,要求我们发散思维去联想、类比、推广、转化,找出类似的命题,或者根据一些特殊的数据,特殊的情况去归纳出一般的规律。
