元月调考圆复习一

合集下载

2022武汉市元月调考复习专题——测小灯泡电功率

2022武汉市元月调考专题——测小灯泡电功率例题讲解典例1：某同学利用图甲所示的电路测量小灯泡的电功率。

实验中电源电压保持不变，小灯泡的额定电压是2.5V；滑动变阻器的规格为“100Ω，0.5A”。

（1）该同学接错了一根导线，请你在这根导线上打“×”,并补画出正确的那根导线。

（2）该实验的原理是P = UI。

闭合开关前滑动变阻器移到阻值最大处，远离下接线柱电阻变大（3）连接电路时，开关应该断开。

将滑片P移到滑动变阻器的最左（选填“左”或“右”）端；（4）正确连接电路后，用开关进行试触，发现电流表指针不偏转，而电压表指针明显偏转。

故障原因可能是小灯泡（填“电流表”、“滑动变阻器”或“小灯泡”）断路。

移动滑片过程中，需要关注小灯泡两端电压是否达到额定电压（5）排除故障后，按正确的步骤进行实验。

在移动变阻器滑片的过程中，眼睛应注视的电压表的示数，直至灯泡正常发光，此时电流表的示数如图乙所示，则小灯泡的额定功率是0.65 W，此时小灯泡的电阻是9.62 (结果保留两位小数)Ω。

P额= U额I = 2.5V × 0.26A = 0.65W（6）使小灯泡两端的电压低于额定电压，观察小灯泡的亮度，测量它实际的电功率。

再使小灯泡两端的电压高于额定电压，一般不超过额定电压的 1.2 倍，观察小灯泡的亮度，测量它实际的电功率。

（7）实验表明：小灯泡的亮度是由它的实际功率决定的。

小灯泡实际功率越大，小灯泡越亮（8）将小灯泡换成发光二极管,测量加在它两端的电压和通过它的电流,计算它的电功率,将所得的电功率与小灯泡相比,发现它们在亮度相当的时候,发光二极管的电功率较小练习题1：(2019武汉元调)某同学利用图甲所示的电路测量小灯泡电功率。

已知待测小灯泡的额定电压为3.8V,滑动变阻器的规格为“20Ω 1.5A”。

（1）请在答题卡中的虚线框内画出与图甲相应的电路图。

（2）当电压表的示数为3.8V时,电流表示数如图乙所示,则小灯泡的额定电功率是W。

武汉市近五年元月调考《圆》专题

2014.1.14元月调考《圆》2．如图所示，点A ，B 和C 在⊙O 上，已知∠AOB ＝40°，则∠ACB 的度数是（） A ．10° B ．20° C ．30° D ．40°10．如图，扇形AOD 中，∠AOD ＝90°，OA ＝6，点P 为弧AD 上任意一点（不与点A 和D 重合），PQ ⊥OD 于Q ，点I 为△OPQ 的内心，过O ，I 和D 三点的圆的半径为r . 则当点P 在弧AD 上运动时，r 的值满足（）A ．30<<rB ．3=rC ．233<<rD ．23=r15．如图，P 为直径AB 上一点，点M 和N 在⊙O 上，且∠APM ＝∠NPB ＝30°，若 OP ＝2cm ，AB ＝16 cm ，则PN +PM ＝ cm ．16．已知圆锥的底面半径为1，全面积为4π，则圆锥的母线长为． 18．（本题6分）．如图，点A ，C 和B 都在⊙O 上，且四边形ACBO 为菱形．求证：点C 是弧AB的中点．22．（本题8分）如图，△ABC 中，AB ＝AC ，以AB 为直径的⊙O 分别与边BC 和AC 相交于点E 和F ，过E 作⊙O 的切线交边AC 于H ．（1）求证：CH ＝FH ；（2）如图2，连接OH ，若OH ＝7，HC ＝1，求⊙O 的半径．CA 图1图2第5题图25．（本题12分）如图1，⊙P 的直径AB 的长为16，E 为半圆的中点，F 为劣弧EB 上的一动点，EF 和AB 的延长线交于C ，过C 作AB 的垂线交AF 的延长线于点D ．（1）求证：BC ＝DC ；（2）以直线AB 为x 轴，线段PB 的中垂线为y 轴，建立如图2所示的平面直角坐标系xOy ，则点B 的坐标为（4，0）. 设点D 的坐标为（m ，n ），若m ，n 是方程082=+++p px x 的两根，求p 的值；（3）在（2）中的坐标系中，直线8+=kx y 上存在点H ，使△ABH 为直角三角形，若这样的H 点有且只有两个，请直接写出符合条件的k2015.1.28元月调考《圆》5．如图,在⊙O 中,弦AB 、AC 互相垂直,D 、E 分别为AB 、AC 的中点,则四边形OEAD 为A ．正方形B ．菱形C ．矩形D ．直角梯形7．圆的直径为13cm ，如果圆心与直线的距离是d ，则A ．当d=8cm 时，直线与圆相交B ．当d =4.5cm 时，直线与圆相离C ．当d =6.5cm 时，直线与圆相切D ．当d =13cm 时，直线与圆相切A图1D 图2图3A10．如图，在⊙O 中，弦AD 等于半径，B 为优弧AD 上的一动点，等腰△ABC 的底边BC 经过点D，若⊙O 的半径等于1，则OC 的长不可能为 A．2 B 1C ．2D 115．半径为3的圆内接正方形的边心距等于。

2022武汉市元月调考复习专题——探究物质的吸热能力

典例1：在“比较不同物质吸热的情况”的实验中，在两个相同的烧杯中分别装有质量为200g 的水和煤油，实验装置如图甲所示，反映该实验结果的图象如图乙所示。

1、本实验需要用到的测量仪器：托盘天平、温度计、停表本实验需要保证：①两种液体质量相同 ①使用相同规格的电加热器 2、①实验中应量取质量相同的甲、乙两种液体，分别倒入相同的烧杯中①实验中应该选择规格相同（填“规格相同”或“规格不同”的电加热器。

规格相同的电加热器指的是额定电压、额定电功率相同①相同规格的加热是为了保证在相同的加热时间内，液体吸收的热量相同本实验用加热时间来表示液体吸收热量的多少。

实验方法为转换法。

①加热10min ，水吸收的热量等于（填“大于”、“小于”或“等于”）煤油吸收的热量； 3、分析图象可知，对于质量相等的煤油和水，升温较快的是煤油；若使两者升高相同的温度，则水吸收的热量较多，由此可见，水的比热容较大。

4、实验结果：不同物质，质量相同，升高温度相同，吸收热量不同不同物质，质量相同，吸收热量相同，升高温度不同5、根据实验数据，小明作出了水和煤油的温度随加热时间变化的图象(如图乙)，由图象可知，水的沸点是 98 ℃，煤油的比热容是 2.1×103 J/（kg·①)【c 水=4.2×103J/（kg·①)】比热容之比等于升高相同温度的加热时间之比水与煤油都从68℃上升到98℃的加热时间分别为10min 、20min ，时间之比1：2c 水：c 煤油=1：2，所以煤油的比热容为 2.1×103 J/（kg·℃)2022武汉市元月调考专题——探究物质的吸热能力例题讲解练习题1：（2022武汉元调）某同学利用图甲所示的装置探究不同物质的吸热情况，他将质量相等的两种液体分别装在两个相同的烧杯中,用两个规格均为500W 的电加热器加热，并每隔2min 记录一次温度。

九年级元月调考考点复习

九年级元月调考考点复习³＝；
④
颗白棋子，随机摸出一颗是白棋子的概率为
C． D．
三、三角形的内切圆
三角形的内心和外心
1、：确定圆的条件：同一直线上的三个点确定一个圆．
四、垂径定理
垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．
推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧
五、圆心角、圆周角
（1）圆心角：顶点在圆心的角叫圆心角。

圆心角的度数等于它所对的弧的度数．
（2）圆周角：顶点在圆上，两边分别和圆相交的角，叫圆周角。

圆周角的度数等于它所对的弧的
七、扇形和弧长。

武汉元月调考电学复习

期末复习1Part 1、选择题1、如图所示，L 1和L 2是两只相同的小灯泡，a 、b 是电流表或电压表．闭合开关S 后，若两灯都能发光，则（）A 、a 、b 均为电流表B 、a 、b 均为电压表C 、a 为电流表，b 为电压表D 、为电压表，b 为电流表2、在探究“怎样用变阻器改变灯泡的亮度”时，连接的电路如图所示．闭合开关后，灯泡不亮，用电压表进行电路故障检测，测试结果如表所示，则电路中的故障可能是（）A 、开关断路B 、开关短路C 、变阻器断路D 、灯泡断路3、如图甲所示为一种调光型台灯，通过旋动下方连接碳膜电阻的旋钮，就可以调节灯的亮度．调节亮度的电路如图乙所示，P 为旋片，可随意转动从而改变在碳膜上的位置．要将图乙连在图丙所示的电路中，要求顺时针旋转旋片可以使灯泡亮度增加，下面接法正确的是（）A 、A 接M ，B 接N B 、A 接M ，C 接NC 、C 接M ，A 接ND 、C 接M ，B 接N4、家用电烙铁在长时间使用过程中：当暂时不使用时，如果断开电源，电烙铁会很快变冷，而再次使用时，温度就不能及时达到要求；如果长时间闭合电源，又浪费电能．为改变这种不足，小枫设计将电烙铁改成如图所示电路、其中R 0是适当的定值电阻，R 是电烙铁的电热丝，则（）A 、若暂不使用，应断开SB 、若再次使用，应断开SC 、若暂不使用，应闭合SD 、开关S 闭合时电烙铁消耗的电能小于开关S 断开时消耗的电能5、小枫同学设计了如图所示的电路：图中电源电压保持不变，R 是定值电阻，Rt 是热敏电阻，其阻值随温度的降低而增大，在该电路中，可以通过电流表或电压表示数的变化来判断温度的变化情况．小枫在连接好电路且闭合开关后做了以下的实验：往热敏电阻上擦一些酒精，然后观察电表示数的变化情况．他观察到的现象应该是（）A 、A 表和V 表示数均变小B 、 A 表示数变大，V 表示数变小C 、A 表示数变小，V 表示数变大D 、 A 表和V 表示数均变大6、将甲、乙两个定值电阻并联后接在电源两端，它们的电流与电压关系如图所示，若流过乙电阻的电流为1A ，则流过干路电流是（）A 、1AB 、2AC 、3AD 、4A7、如上右图所示，电源电压保持不变，R 1∶R 2 = 1∶2。

元月调考复习一圆的基本知识

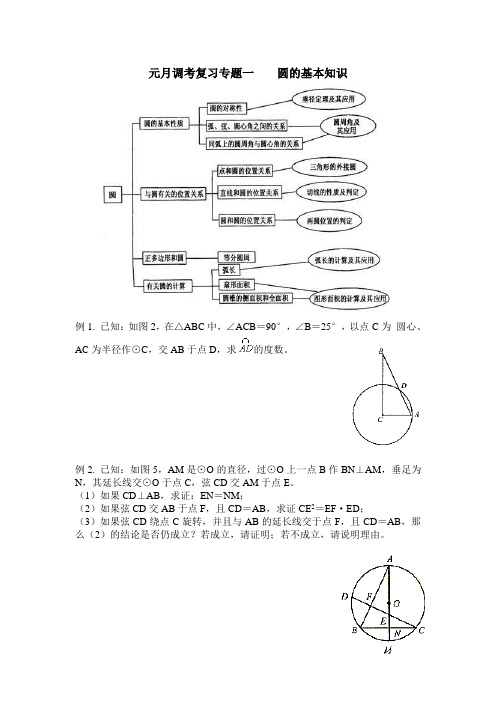
元月调考复习专题一圆的基本知识例1.已知：如图2，在△ABC中，∠ACB＝90°，∠B＝25°，以点C为圆心、AC为半径作⊙C，交AB于点D，求的度数。

例2. 已知：如图5，AM是⊙O的直径，过⊙O上一点B作BN⊥AM，垂足为N，其延长线交⊙O于点C，弦CD交AM于点E。

（1）如果CD⊥AB，求证：EN＝NM；（2）如果弦CD交AB于点F，且CD＝AB，求证CE2＝EF·ED；（3）如果弦CD绕点C旋转，并且与AB的延长线交于点F，且CD＝AB，那么（2）的结论是否仍成立？若成立，请证明；若不成立，请说明理由。

练习：1.已知：如图1，在⊙O中，半径OM⊥弦AB于点N。

①若AB＝，ON＝1，求MN的长；②若半径OM＝R，∠AOB＝120°，求MN的长。

2. （2014•甘谷县模拟）如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．（1）请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．（2）请在（1）的基础上，完成下列填空：①写出点的坐标：A、B、C、D；②⊙D的半径=（结果保留根号）；③求∠ADC的度数（写出解答过程）④若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面的半径．3. （2014•丹徒区）如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC=∠ABC，D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．（1）求证：MN是半圆的切线；（2）求证：FD=FG．（3）若△DFG的面积为4.5，且DG=3，GC=4，试求△BCG的面积．例3.在某张航海图上，标明了三个观测点的坐标，如图，O（0，0）、B（6，0）、C（6，8），由这三个观测点确定的圆形区域是海洋生物保护区．（1）画出圆形区域的中心位置P，并写出点P的坐标；（2）若在观测点O测得一艘渔船D的位置为（4，8.5），试问该渔船是否已进入海洋生物保护区？请通过计算回答．例5.如图1，Rt△ABC中，∠ACB=90°，AC=4，BA=5，点P是AC上的动点（P 不与A、C重合），设PC=x，点P到AB的距离为y．（1）求y与x的函数关系式；（2）试确定Rt△ABC内切圆I的半径，并探求x为何值时，直线PQ与这个内切圆I相切？例4. 已知：如图6，AB是⊙O的直径，C是AB延长线上一点，CG切⊙O于D，DE⊥AB于E。

武汉市元月调考数学复习要

元月调考过关训练（一） --------求自变量取值范围1、如果a -是二次根式，则有（）A 、a>0B 、a<0C 、a ≥0D 、a ≤02、（09年元月）要使式子2a -有意义，字母a 的取值必须满足A 、a ≠0B 、a ≥2C 、a ≠2D 、a ≤23、函数31y x =--中自变量的取值范围是（）A 、13x ≥B 、13x ≥-C 、13x ≤ D 、x ≥0 4、在函数12y x=-中，自变量x 的取值范围为（） A 、x>2 B 、x<2 C 、x>-2或x ≠0 D 、x ≥25、函数12x y x -=中自变量x 的取值范围是（） A 、12x ≤ 且x ≠0 B 、12x >- 且x ≠0 C 、x ≠0 D 、12x < 且x ≠0 6、（07年元月）要使式子21x x ++有意义，x 的取值范围是（） A 、x ≥-2 B 、x ≠-1 C 、x ≥-2且x ≠-1 D 、x ≥-17、如果5x -是二次根式，则x 的取值范围是（）A 、x ≠5B 、x=5C 、x ≥5D 、x ≤58、（08年元月）下列函数中，自变量x 的取值范围是x<3的函数是（）A 、3y x =-B 、3y x =-C 、13y x =-D 、13y x=- 9、若代数式1x x-在实数范围内有意义，则x 的取值范围为（） A 、x>0 B 、x ≥0 C 、x ≠1 D 、x ≥0x 且≠110、下列函数中，自变量x 的取值范围是x>2的函数是（）A 、2y x =-B 、2y x =-C 、12y x =-D 、12y x =-答案：1.D 2.B 3.A 4.B 5.A 6.C 7.D 8.D 9.A 10.C。

湖北省武汉市江岸区2023-2024学年高三上学期元月调考语文试卷

2023~2024学年度高三元月调考语文试卷一、现代文阅读(35分)(一)现代文阅读I (本题共5小题，19分)阅读下面的文字，完成1~5题。

清代常州词人张惠言曾指出，词是有比兴寄托的，“意内而言外”。

张惠言说温庭筠的词可比美，于屈子《离骚》，欧阳修的词反映了北宋初年政治上的党争，每句词都有深刻的含意。

王国维反对张惠言的这种比兴寄托的说法，可王国维自己的词里却也有许多比兴寄托。

他还在《人间词话》中以三首小词比喻古今成大事业大学问的三种境界。

他说“昨夜西凤凋碧树，独上高楼，望尽天涯路”(晏殊《堞恋花》词)为第一种境界，“衣带渐宽终不悔，为伊消得人憔悴”(柳永《凤栖梧》词)为第二种境界，“众里寻他千百度，蓦然回首，那人却在灯火阑珊处”(辛弃疾《青玉案》词)为第三种境界。

如果他认为张惠言说温庭筠和欧阳修等人的小词有比兴寄托是“深文罗织”，而他自己却又把晏殊、柳永、辛弃疾的三首小词说成是成大事业大学问的三种境界，对他的这种说法该如何看待呢？这就需要我们先将什么叫“比兴寄托”解释清楚。

比兴寄托有广义的解释，也有狭义的解释；有字面的解释，也有引中的解释；有就作者方面而言的说法，也有就读者方面而言的说法。

我们可以从不同的角度分析这个问题。

而对词这种形式，不论是张惠言还是王国维，为什么他们在写作或欣赏别人的词作的时候，都容易发生这种现象？而他们附加这些内容的时候使用的阐述方式又有什么不相同的地方？本来“比”“兴”二字是写诗的两种作法，如果换一种较新的说法，我以为比兴就是指心与物相结合的两种基本关系，“兴”是见物起兴，是由物及心。

见物起兴是说你看到一个物象，引起你内心的一种感发，以《诗经》来说，“关关雎鸠，在河之洲”是外在的物象，所谓“物象”是眼睛所能看见的，耳朵所能听见的，凡是感官所能感受的统称物象。

这在中国诗歌中有很久远的传统。

即如《诗品·序》中就说：“若乃春风春鸟，秋月秋蝉，夏云暑雨，冬月祁寒，斯四候之感诸诗者也。

元调综合复习(一)

九年级元调专题汇编（初数）-----综合篇课前检测1．如图，AB为⊙O的直径，CB、CD为⊙O的弦．若∠D＝35°，则∠ABC的度数是（）A．55°B．60°C．65°D．70°2．平面直角坐标系内一点P(2，－3)关于原点对称点的坐标是（）A．(－3，2)B．(－2，3)C．(－2，－3)D．(2，3)3．圆的直径为12 cm，如果圆心与直线的距离是d，则正确的是（）A．当d＝8 cm时，直线与圆相交B．当d＝4 cm时，直线与圆相离C．当d＝6 cm时，直线与圆相切D．当d＝12 cm时，直线与圆相切4．商场举行摸奖促销活动，对于“抽到一等奖的概率为0.1”，下列说法正确的是（）A．抽10次也可能没有抽到一等奖B．抽一次不可能抽到一等奖C．抽10次奖必有一次抽到一等奖D．抽了9次如果没有抽到一等奖，那么再抽一次肯定抽到一等奖5．抛物线y＝－x2＋2x＋6在直线y＝－2上截得的线段长度为（）A．6B．4C．2D．06.如图，⊙O的直径CD＝10 cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM⊥OC＝3⊥5，则AB的长为（）A．91cm B．8 cm C．6 cm D．4 cm模块一一元二次方程考点一一元二次方程判别式（注意：①二次项系数不等于0；②整式的公式和因式分解在方程中的应用。

）1.已知关于x的方程kx2＋(2k＋1)x＋2＝0(1) 求证：无论k为任何实数，方程总有实数根(2) 当抛物线y＝kx2＋(2k＋1)x＋2与x轴两个交点的横坐标均为整数，且k为正整数时，若P(a，y1)、Q(1，y2)是此抛物线上的两点，且y1＞y2，请结合函数图象确定实数a的取值范围(3) 已知抛物线y＝kx2＋(2k＋1)x＋2恒过定点，请直接写出定点坐标考点二一元二次方程根与系数的关系（注意：含参的一元二次方程首先要判断根与系数的关系（△是否大于0））2.已知关于x的方程x2－2(a－1)x＋a2＝0有两个实数根x1、x2(1) 求a的取值范围(2) 若x1＋x2＝1－x1x2，求a的值考点三一元二次方程应用题3.为迎接“2011李娜和朋友们国际网球精英赛”，某款桑普拉斯网球包原价168元，连续两次降价a%后售价为128元．下列所列方程中正确的是（）A．168(1＋a%)2＝128 B．168(1－a2%)＝128C．168(1－2a%)＝128 D．168(1－a%)2＝1284.2015年前三季度武汉市实际利用外资55.11亿元，其中2015年第一季度实际利用外资17.74亿美元．若实际利用外资平均每季度增长率为x，根据题意，所列方程为（）A．17.74(1＋x)2＝55.11B．17.74＋17.74(1＋x)＋17.74(1＋2x)＝55.11 C．17.74(1＋2x)＝55.11D．17.74＋17.74(1＋x)＋17.74(1＋x)2＝55.11模块二二次函数考点一二次函数图像和解析式（①a决定开口大小和方向；c决定图像与y轴交点；②a、b共同决定对称轴：对称轴在y轴左侧则a、b同号，在y轴右侧则a、b异号）1.已知抛物线y＝x2－(k＋2)x＋9的顶点在坐标轴上，则k的值是__________2.函数y＝ax2＋(a＋2)x＋2与x轴有且仅有一个交点，则a＝_________3.下图是二次函数y ＝ax 2＋bx ＋c 的图象，下列结论：① 顶点坐标为(－1，4)；② 4a －2b ＋c ＜0；③ 一元二次方程ax 2＋bx ＋c ＝1的两根之和为－1；④ 抛物线上有两点P (－2，y 1)和Q (q ，y 2)，若y 1≥y 2，则q ≤－2或q ≥0，其中正确的有（） A ．①② B ．①③ C ．①④ D ．③④考点二二次函数几何变换（①用顶点式y=a （x-h ）2+k 来解决几何变换问题；②也可记住“左加右减（变x ），上加下减（变c ）”）4.将抛物线y ＝－2(x ＋1)2－2向左平移2个单位，向下平移3个单位后的新抛物线解析式为（）A ．y ＝－2(x ＋1)2－2B ．y ＝－2(x ＋3)2－5C ．y ＝－2(x －1)2－5D ．y ＝－2(x ＋3)2＋1考点三二次函数与方程、不等式（函数与方程不等式综合，需要注意“数形结合”，计算考查较少）5.抛物线y ＝x 2－2x －3被直线y ＝x ＋1所截得的线段AB 长为_________6.已知点A (a ，m )、B (b ，m )、P (a ＋b ，n )为抛物线y ＝x 2－2x －2上的点，则n ＝__________7.抛物线y ＝(m ＋1)x 2＋2mx ＋3上有两点A (－3，y 1)、B (5，y 2)，C 点(x 0，y 0)为此抛物线顶点，且y 1＞y 2≥y 0，则m 的取值范围为（） A ．m ＞－1B ．m ＜21-C ．21-＜m ＜1 D ．－1＜m ＜21-8.二次函数y ＝－2x 2－3x ＋k 的图象在x 轴下方，则k 的取值范围是__________考点四二次函数应用题9.某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x 元（x为正整数），每个月的销售利润为y元(1) 求y与x的函数关系式并直接写出自变量x的取值范围(2) 每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？(3) 每件商品的售价定为多少元时，每个月的利润恰为2200元？根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元？模块三圆1.半径为2的正六边形的中心角为_________，边心距为_________，面积为_________2.圆内接等边三角形的边心距、半径、边长之比为（）A．1∶3∶2B．1∶2∶3C．1∶322∶2D．1∶2∶3 3.边心距为32的正六边形的面积为__________4.一个圆锥的侧面积是底面积的4倍，则此圆锥侧面展开图的扇形的圆心角是_________5.如图，圆内两条弦互相垂直，其中一条被分成长为4和3两段，另一条被分成长为2和6两段，则该圆的直径为（）A．64B．65C．9D．106.如图，在矩形ABCD 中，AB ＝4，AD ＝5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点．过点D 作⊙O 的切线切⊙O 于点N 且交BC 于点M ，则DM 的长为（） A ．313 B ．29 C ．3134 D ．527.如图，在平面直角坐标系中，⊙P 的圆心是(2，a )（a ＞2），半径为2，函数y ＝x 的图象被⊙P 截得的弦AB 的长为32，则a 的值是（） A ．22B ．22+C ．32D ．32+8.如图，AB 为⊙O 的直径，点C 在⊙O 上，点P 是直径AB 上的一点（不与A 、B 重合），过点P 作AB 的垂线交BC 的延长线于点Q(1) 在线段PQ 上取一点D ，使DQ ＝DC ，连接DC ，试判断CD 与⊙O 的位置关系，并说明理由(2) 若BP ＝6，AP ＝1，QP ＝8，求QC 的长。

初三数学元月调考专题圆

案例1 切线中常见基本图形[真题呈现]如图，AB为⊙O的直径，C为⊙O上一点，AD和过C的切线互相垂直，垂足为D，AD交⊙O于点E，连接A C．（1）求证：AC平分∠DAB；（2）若CE＝6，AC＝8，直接写出⊙O直径的长．【真题变式】1．例题中在（2）的前提下：①CD＝_________；②DE＝____________．2．在例题条件下，已知CD＝a，DE＝b．求⊙O的半径R．3．在例题条件下，已知R＝6，CE＝，则①R＝___________，②CD＝___________．4．在例题条件下，延长AB，DC相交于F，若∠F＝α，连接A C．（1）如图1，当α＝30°时，AFAC＝___________；（2）如图2，当α＝45°时，AFAO＝___________；（3）如图3，当α＝60°时，AFAO＝___________；图3图2图1FFFAAA案例2 图中几何变换【真题呈现】如图，△ABC 是等边三角形，O 为BC 的中垂线AH 上的动点，⊙O 经过B ，C 两点，D 为BC 上一点，D ，A 两点在BC 边异侧，连接AD ，BD ，C D ．（1）如图1，若⊙O 经过点A ，求证：BD ＋CD ＝ AD ；（2）如图2，圆心O 在BD 上，若∠BAD ＝ 45°，求∠ADB 的度数；（3）如图3，若 AH ＝OH ，求证：BD 2＋CD 2＝AD 2．D BCAA【真题变式】1．如图，AB 是⊙O 的直径，C 为圆上一点，△ACD 为等边三角形，D 在⊙O 外，已知∠ADB ＝45°，⊙O 的半径为4，则AD 的长为．ODBA2．如图，AB 是⊙O 的直径，C 为圆上一点，△ACD 为等边三角形，D 在⊙O 外，已知∠ABD ＝30°，则ADAB的值为．案例3 圆与等腰三角形（1）图1 图2 图3【真题呈现】如图1，已知⊙O中，BC是直径，D点为OB上任意一点（异于O，B），过D点作AD⊥BC，交O 于A点，=AB AF，连接BF交AD于E点．（1）探究AE与BE的大小关系并证明你的结；（2）当D为OC上任意一点（异于O，C），其他条件不变时，（1）中的结论是否仍然成立，画出图形并证明你的结论．CCFC图1图2图3解后反思其实第二问作出图形有两种情况，请试一试，如图3，但做法仍与图2一样．（回归双基）【真题变式】1．（回归双基）如图2，若OD＝5，AD＝12，则EG＝．2．如图（例题图3），已知OB＝5，CD＝2，则EG＝．3．（回归双基）如图1，连AF、AC交BF于M，已知BD＝4，DE＝3，则（1）AF＝．（2）BC＝．（3）AMFS△＝．案例4 圆与等腰三角形（2）真题呈现小明学习了垂径定理，做了下面的探究，根据题目要求帮小明完成探究．（1）更换定理的题设和结论可以得到许多真命题．如图1，在⊙O中，C是AB的中点，直线CD⊥AB于点E ，则AE ＝BE ．请证明此结论；（2）从圆上任意一点出发的两条弦所组成的折线，成为该圆的一条折弦．如图2，P A ，PB 组成⊙O 的一条折弦．C 是劣弧AB 的中点，直线CD ⊥P A 于点E ，则AE ＝PE ＋P B ．请证明此结论；（3）如图3，P A 、PB 组成⊙O 的一条折弦，若C 是优弧AB 的中点，直线CD ⊥P A 于点E ，则AE ，PE 与PB 之间存在怎样的数量关系？写出并证明你的结论．真题解读第一问：证△OAE ≌△OBE 即可；第二问：∵ ⌒CA ＝ ⌒CB ，∴AC ＝BC ，∵ ⌒CP ＝ ⌒CP ，∴∠CAP ＝∠CBP ，再从结论AE ＝PE ＋PB ，可考虑截长法，即在AP 上取AF ＝BP ，再证EF ＝EP 即可；第三问：用第二问的方法，可考虑补短法，即在P A 的延长线上截取AF ＝BP ，连接CF 、AC 、CP 、CB ，先证△AFC ≌△BPC ；再证EF ＝EP 即可．解后反思从条件看弧的中点可得到等弧，运用旋转可完成一些图形的变换，在运用旋转时，等角、等边是关键，圆内接四边形对角互补，外角等于内对角也是常见旋转的工具．【真题变式】1．BC 为⊙O 内一弦，A 为优弧 ⌒ BAC的中点，D 为劣弧 ⌒AB 上任意一点，过A 作AE ⊥BD 于E ，AF ⊥CD 于F ，则下列结论正确的有____________（填序号）．①∠ABD ＝∠ACD ，②∠EAF ＝∠BAC ，③∠BAC ＝2∠DEF ，④CD －BDED＝2．2．如图，在⊙O 中，直径AB ⊥弦CD ，点P 是 ⌒AD 上任一点，作AM ⊥DP 延长线于M ，则PC －PD PM＝____．（图3）C（图2）C（图1）3．如图，已知等边△ABC内接于⊙O，AB＝2，点D为弧AC上一点，∠ABD＝45°，AE⊥BD于点E，则△BDC的周长是________．A。

【武汉语文新题型】名校导练2023年中考语文元月调考模拟卷(一)

2023年中考语文元月调考模拟试卷一、现代文阅读(30分)(一)实用文本阅读(本题共3小题,10分)阅读下面的文字,完成1~3题。

一流的包袱¹①有人说,相声的笑点相对更“理性”,照我理解，这个“理性”就是大家常说的“意料之外,情理之中”的那个“情理之中”。

既在意料之外,也在情理之外,那就是如今所谓的无厘头。

意料之外情理之中则是人们推崇的一流包袱儿的标准。

②相声有没有不在情理之中的包袱?有。

老的新的都有。

有一些相声，表现的就是一些不符合常理的乖讹以及荒谬,是对现实中的荒谬的夸大。

比如康松广老师的代表作《颠三倒四》中那些完全不合情理、没有逻辑的大段台词,就是此类。

其他的不合常理的小包袱也多得很，甚至是越来越多，“于老师的父亲王老爷子”不就是最好的代表吗?悖于情理，正是很多此类小包袱逗笑观众的原因。

③但是,确实有更多的经典相声作品,表现的人物与事件、语言,是非常符合现实逻辑的。

那些语言和时间,是真实可能发生在一些人身上的,是与角色的性格行为相关联的,这尤其在一些有完整事件的单口相声里,表现得非常明确,比如说,可以去听听刘宝瑞的《金殿斗智》——可以先听一遍,记住自己会因为里面的哪些细节笑出声来,然后,再听一遍,琢磨琢磨,为什么你会因为那些地方发笑。

甚至你可以想想，如果那句话,脱离了整个的情节和人物,还是不是同样可笑?为什么?④一流的包袱儿是这样的:一句完全出乎你意料之外的对白或动作,会让你在那一瞬间感到巨大的荒谬可笑的感觉,但随后，你会发现,那句话语或行为,又是那么合情合理、恰如其分。

而这种“合情合理”带来的愉悦感,往往比刚开始的“爆笑”更有价值、更值得品味得多。

⑤我读过的一本电影编剧教材里说,纯靠“意料之外”抓人的包袱,也有个高下之分。

比方说，最简单的意料之外的包袱,是一个人趾高气扬地走在路上,没想到突然踩到香蕉皮滑倒了。

这种包袱在早年间的默片里到处都是。

但是高明一点儿的“意料之外”,会先让你看到一个趾高气扬走路的人，再让你看到地上有个香蕉皮,然后,这个人眼看就要踩上这个香蕉皮的时候，突然发现并成功地躲开了,没踩上。

元月调考攻略

元月调考攻略（一）一、选择题（共12小题，每小题3分，共36分）1、23）（-的平方根是（）A．3 B．-3 C．3±D．3±2、在函数xxy-=2中，自变量x的取值范围为（A．x＞-23m=( )A． 2 D．－14、）A B C D5、如图，将直角梯形ABCD的一角沿对角线AC折叠，D点刚好落在∠ACB的平分线上，若梯形的一个底角为72°，则∠ACD的度数为（）A．36°B．54°C．30°D．45°6、⊙O1、⊙O2相切且两圆半径分别为5和2，则O1O2=（）A、3B、7C、3或7D、87、如图，⊙O是△ABC的内切圆，切点分别是D、E、F，已知∠A=100º，∠C=30º,则∠DEF的度数是（）A．30ºB．50ºC．65ºD．80º第5题图第7题图8、正三角形外接圆的半径为2A．191cm C．4cm D．2cm105张形状、大小、质地均相同的卡片，正面分别印有北京奥运会的会徽、吉祥物（福娃）、火炬和奖牌等四种不同的图案，背面完全相同．现将这5张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面图案恰好是吉祥物（福娃）的概率是（）ABCD′A．15B．25C．12D．3511、近几年，某市在经济建设中取得突出成就，2004―2006年三年该市的国内生产总值的和为2200亿元。

图甲是这三年该市的国内生产总值的扇形统计图，图乙是这三年该市总人口折线统计图。

根据以上信息，下列判断：①2006年该市国内生产总值超过800亿元；②2006年该市人口的增长率比值增加2006年人口的年增长率相同那么2007年全市的国内生产总值将为2200451⨯）。

A．①②④B．①③④C．②③D．①③12、对于一元二次方程)0(02≠=++acbxax，下列说法：①当cab+=时，则方程02=++cbxax一定有一根为1-=x；②若ab＞0，bc＜0，则方程02=++cbxax一定有两个不相等的实数根；③若c 是方程02=++cbxax的一个根，则一定有01=++bac；④若cab32+=，则方程02=++cbxax有两个不相等的实数根。

武汉市元月调考总复习

元调总复习一、选择题1.市教育局明确要求全市所有中小学均为无烟学校，各学校会议室里均张贴了禁止吸烟标志，这主要是考虑到在空气不流通的房间里，只要有一个人吸烟，其他人都在被动吸烟，这是因为（）A．物质是由分子组成的B．分子之间有作用力C．分子之间有间隙D．分子在不停地运动2.关于温度、内能和热量，下列说法正确的（）A．物体温度越低，分子运动越剧烈B．物体温度越高，含有的热量越多C．水沸腾时吸收热量，温度保持不变D．物体的温度为0℃时，其内能为零3.为了安全，汽车行驶时驾驶员必须系好安全带．当系好安全带时，相当于闭合开关，指示灯不亮；未系好安全带时，相当于断开开关，指示灯发光．符合上述要求的学电路图是（）4. 如图所示的电路图，开关S接到a 时，电压表示数为9V，开关S接到b 时，电压表示数为4V 。

下列说法不正确的是（）A．电源电压为9V B．灯Ll两端的电压为4VC．灯L2 两端的电压为4V D．灯L1 和灯L2 的总电压为9V5. 如图所示，闭合开关，两灯并联，各电表都能正常工作．下列判断正确的是（）A．甲、乙、丙都是电流表B．甲、乙、丙都是电压表C．甲、乙是电压表，丙是电流表D．甲、丙是电流表，乙是电压表题4 题5 题76. 关于影响导体电阻大小的因素说法正确的是（）A．导体电阻大小取决于通过它电流的大小，电流越小的导体电阻越大B．导体电阻大小取决于加在它两端电压的大小，电压越大的导体电阻越大C．相同材料制成粗细相同的导线，长度越长电阻也越大D．相同材料制成长短，粗细相同的导线，其电阻一定随温度的升高而增加。

7. 在图所示的电路中，电源两端电压不变．闭合开关S，电压表V1与V2的示数之比为2：3，电流表A 的示数为1A．若将电压表V1换成电流表A1，则电流表A1的示数为2A．电阻R1 与电阻R3 的阻值之比为（）A．1：2 B．4：3 C．1：4 D．2：18.将两只额定电压相同的灯泡L1、L2 串联在电路中，闭合开关S 后，发现L1 亮，L2 不亮．对此有下列几种猜想，其中可能的是（）①L2 灯丝断了，灯座未短路；②灯泡L2 的电阻太小；③灯泡L2 两端电压较大；④通过灯泡L1、L2 电流不等；⑤灯泡L2 的灯座被短路；⑥灯泡L1、L2 的额定功率不同．A．①B．①③⑥C．③④D．②⑤⑥9. 如图电源电压不变，闭和开关S，当滑动变阻器滑片P 向右移动时（）A．电流表A1 示数变小，电压表V 示数变小B．电流表A2 示数变大，电压表V 示数变大C．电压表V 示数与电流表A1示数比值不变D．电压表V 示数与电流表A2示数比值不变10.如图表示阻值不等的两个电阻的电流随电压变化的I-U图线，从图中判断正确的是（）A．R1＞R2B．R1、R2串联后的总电阻的I﹣U 图线在区域ⅡC．R1、R2并联后的总电阻的I﹣U 图线在区域ⅢD．R1、R2并联后的总电阻的I﹣U 图线在区域Ⅰ题9 题10 二（题1）二、实验探究题1. 为了比较甲乙两种液体的吸热能力，某同学设计了以下实验：a．在两个同样的烧杯中，分别装入等体积的甲乙两种液体b．用温度计分别测出甲乙两种液体的初温c．在两个烧杯中分别装入功率相同的电热器，且加热时间相同d．用温度计分别测出甲乙两种液体的末温请解答下列问题：（1）在上述a、b、c、d 四个实验步骤中，存在错误的是步骤，该步骤中错误的内容应改为的两种液体；（2）步骤c 中“加热时间相同”是为了使甲乙两种液体；（3）图是甲乙两种液体的温度随时间变化的关系图像。

湖北省武汉市江岸区2024年元月质量检测高三英语试题参考答案

２０２３~２０２４学年度高三元月调考英语试卷参考答案第一部分㊀听力(共两节,满分３０分)１５．A A C A B㊀㊀６１０．C C B A C㊀㊀１１１５．A C B A B㊀㊀１６２０．B B A C CT E X T１W:J e n n y s a i d s h e p l a n n e d t o p l a y t e n n i sw i t h y o u y e s t e r d a y b u t y o uw e r en o t a t h o m e．M:Iw e n t t o t h eC i t y L i b r a r y t ob o r r o ws o m eb o o k s f o rm y r e s e a r c ho nm u s e u m s．T E X T２M:E x c u s em e,M r s．B r o w n．H e r e i s a p a c k a g e f o r y o u．W:T h a n k y o u,y o u n g m a n．M:A c t u a l l y,t h e d e l i v e r y m a n s e n t y o u r p a c k a g e t o o u r f l a t b y m i s t a k e．M o ma s k e dm e t o g i v e i t b a c k t o y o u．T E X T３W:G e o r g e,y o ua r e l a t e．W h a t h a p p e n e d?M:I ms o r r y,M s．G r e e n．Iw a s o nm y b i k ew h e n a b u s d r o v e b y a n d t h e n e x t s e c o n d t h e r ew a s m u d a l l o v e rm e．I h a d t o g ob a c ka n d g e t c h a n g e d．T E X T４M:T h e s h o r t v i d e oh a sm o r e t h a n２m i l l i o nv i e w s n o w．H a v e y o uw a t c h e d i t?W:Y o um e a n t h e o n e y o u s h a r e d y e s t e r d a y?Y e s．Iw a s e v e n t o u c h e d t o t e a r s．M:T o t e l l y o u t h e t r u t h,s ow a s I．T E X T５W:T h e p r i n t i n g m a c h i n e i sb r o k e n!M:C a l md o w n,L a u r a．J u s t p l u g i t i n,a n d p r e s s t h e r e db u t t o n t o t u r n i t o n．W:O h,l o o ka tm e!T h e p r o j e c t d r i v e sm em a d!M:Y o ud on e e da g o o d r e s t．T E X T６W:G o o dm o r n i n g,C r o w nH o t e l．C a n I h e l py o u?M:G o o dm o r n i n g．t h i s i sD a v i dC o o p e r．I b o o k e d a r o o mo n y o u r a p p a n d I mc a l l i n g t o c o n f i r m i t．W:S u r e,M r．C o o p e r．Ih a v es e e n y o u rr e s e r v a t i o nh e r e．O n er o o mf o rt o d a y a n dt o m o r r o w．W h e na r e y o u g o i n g t o c h e c k i nM:W e l l p r o b a b l y a r r i v e a t９p m．W i l l t h e s w i mm i n gp o o l b e o p e n t h e n?W:I ms o r r y．T h e p o o l i s c l o s e d e v e r y M o n d a y f o r c l e a n i n g．B u t o u r n e w l y d e c o r a t e d g y mo p e n s t i l lm i d n i g h t．W eh a v e s o m en e ws p o r t s e q u i p m e n t．１M:O K．Iw i l l h a v e a t r y．T E X T７W:I d o n t f e e l l i k e c o o k i n g t o d a y．L e t s j u s t g e t s o m e f o o dd e l i v e r e do n t h e p h o n e．H o wa b o u t s o m e f r i e d c h i c k e n t o n i g h tM:F r i e d c h i c k e n?Y o un e v e r l i k e d f r i e d f o o d!W h a t s g o i n g o n?W:I a ms t r e s s e do u t,a n d t h e y s a y f r i e d f o o d c a nb r i n g i n s t a n t j o y．M:N ow o n d e r．L i s t e n,y o u d o n t a c t u a l l y n e e d t h e f r i e d c h i c k e n．I k n o wa r e s t a u r a n t t h a t s e r v e s t h eb e s t I t a l i a nf o o d．I t t a s t e s l i k em yg r a n d m a sh o m e m a d ed i s h e s．W o u l d y o u l i k e t ot r y s o m eW:Y o um e a n r i g h t n o w?M:Y e s!I l l d r i v e．W:B u t I d o n tw a n t t om o v e a n i n c h．M:A l l r i g h t．W h a t a b o u t t h i s?Y o uh a v e an i c eb a t ha n d I l l d r i v e t h e r e t oo r d e r s o m e t a k e o u t．I t s q u i c k e r．W:O h,y o ua r e a l w a y s s o s w e e t,h o n e y．T E X T８W:D i d y o u g o t o s e e t h em o v i e A v a t a r２y e s t e r d a y?M:D o n tm e n t i o n i t!I t f e e l s l i k e a r e c y c l e dm o v i e．W:R e c y c l e d?W h a t d o y o um e a n?M:T h es e t t i n g,t h ec h a r a c t e r s,a n de v e nt h e p l o t w e r es i m i l a rt o A v a t a rI．T h ed i r e c t o r C a m e r o n s e e m s t oh a v e r e m a d e i t．W:Y o u c a n t b e s e r i o u s!T h e r eh a s t ob e s o m e t h i n g d i f f e r e n t．M:T h e o n l y d i f f e r e n c e i s t h e t i t l e,o t h e r w i s e Iw o u l d n t h a v e g o n e t o t h e c i n e m a．W:I t h o u g h t y o uw e r e a f a no f t h e d i r e c t o r．I s i t b e c a u s e y o ue x p e c t t o om u c ho f h i m?M:P r o b a b l y．T h e s p e c i a l e f f e c t so f A v a t a rI a r es o w o n d e r f u l t h a t Is a y w o w e v e r y t i m eI w a t c h i t．B u t t h i s t i m e,I d i d n t f e e l t h e e x c i t e m e n t I h a d e x p e c t e d．W:T h a t e x p l a i n s．N o t h i n g c a nc o m p a r et o A v a t a rI i n y o u r m i n d．W h y n o t g i v e A v a t a r２a s e c o n d c h a n c e T h e n p r o b a b l yy o uw i l l c h a n g e y o u rm i n d．T E X T９M:Y o u t o o k p a r t i n t h e a n n u a l c i t y m a r a t h o n l a s tw e e k!T h a t s a w e s o m e!Id i d n tk n o w y o u a r e a na t h l e t e!W:T h a n k y o u,b u t i t s j u s t ah o b b y．M a r a t h o n a l l o w sm e t o e s c a p e f r o m m y t i r i n g w o r k a t t h e l a wo f f i c e．M:W h a t a b o u t t h e r a c e?D i d y o u c o m p l e t e t h ew h o l e c o u r s e?W:I r a nah a l fm a r a t h o nＧa b o u t１３m i l e s a l t o g e t h e r．I t t o o km e a b o u t２h o u r s．M:O h,I c o u l d n t e v e n p i c t u r em y s e l f r u n n i n g t h a t l o n g,e s p e c i a l l y i n s u c hh o tw i n d l e s s d a y s．W:T h e r a c e s t a r t e d a t８o c l o c k,a n d l u c k i l y t h e r ew e r e e n o u g hc l o u d s t h ew h o l em o r n i n g．２M:D i d y o u c a r r y a n y s u p p l i e sw i t h y o u?W:N o,t h e v o l u n t e e r sw o u l d p r o v i d e u sw i t h e n o u g h s u p p l i e s a l o n g t h e p a t h．I tw a s n t a s t o u g h a s y o u t h i n k．W o u l d y o u l i k e t o j o i nm en e x t y e a rM:E r,I t h i n k I c a nh e l p d i s t r i b u t e t h e s u p p l i e s a n d c h e e r f o r t h e a t h l e t e s．W:T h a t s a g r e a t i d e a．T E X T１０I m K a t i e H a f n e r,h o s t o f a n e w w e e k l y r a d i o p r o g r a mc a l l e dL o s tW o m e n o f S c i e n c e c o m i n g n e x tN o v e m b e r．T h r o u g hh i s t o r y w o m e nh a v em a d eh u n d r e d so f s c i e n t i f i cb r e a k t h r o u g h s．T h e y h a v e a s i x t hs e n s e t h a t e n a b l e s t h e mt o p i c ko u tm o r e i m p o r t a n t c l u e s．B u tm a n y o f t h e f e m a l e s c i e n t i s t s a r e m i s s i n g f r o m p u b l i cv i e w．T h e m o r eId ot h i sr e s e a r c h,t h e m o r eIr e a l i z et h a t w o m e na r e a t t h eh e a r to f s o m eo f t h e m o s t i m p o r t a n td e v e l o p m e n t s i ns c i e n c e．F o re x a m p l e, R o s a l i n dF r a n k l i nc o n t r i b u t e dm u c h t o t h ed i s c o v e r y o f t h e s t r u c t u r eo fD N A．A n d t h ew o r ko f M a r g a r e tW i l c o x,a nA m e r i c a n e n g i n e e r,w a s c r u c i a l t o t h e d e v e l o p m e n t o f t h e a i r c o n d i t i o n e r i n c a r s．E a c hs e a s o n,w e l l e x p l o r e a n dc e l e b r a t e t h e l i f ea n dw o r ko f o n ew o m a nw h os h a p e do u r w o r l dv i e w．A n dw e l l e x p l o r e s o m e o f t h e r e a s o n sw h yy o um i g h t n o t k n o wh e r n a m e．W e l l b e l o o k i n g a t t h eb a r r i e r s t h e s ew o m e n f a c e d,a sw e l l a s t h e i r p a s s i o n a n d d r i v e．J o i nu s a sw e h o n o r t h e s e r e m a r k a b l e s t o r i e s y o um a y n o t k n o w．第二部分㊀阅读理解(共两节,满分５０分)第一节(共１５小题;每小题２．５分,满分３７．５分)２１２３．C D B㊀２４３１．B D A C㊀２８３１．C B D A㊀３２３５．B C A B第二节(共５小题:每小题２．５分,满分１２．５分)３６４０．B G E A D第三部分㊀语言运用(共两节,满分３０分)第一节㊀完形填空(共１５小题:每小题１分,满分１５分)４１４５．B A C D B㊀㊀４６５０．D A C B A㊀㊀５１５５．D C D B C第二节㊀短文填空(共１０小题:每小题１．５分,满分１５分)５６．t o p e r f e c t㊀㊀５７．a d d i n g㊀５８．m o r e f u n㊀㊀５９．e x c e p t㊀㊀６０．p o p u l a r i t y㊀６４．w h e r e㊀㊀６５．w a s l i s t e d６１．a㊀６２．p o w d e r e d㊀㊀６３．a s/w h e n/w h i l e㊀㊀第四部分㊀写作(共两节,满分４０分)第一节(满分１５分)D e a r J a c k,I m m o r et h a n g l a dt oh e a rf r o m y o u．Y e s,l i k e y o us a i d,Ih a v eb e e nl o n g i n g f o rt h e u p c o m i n g s u mm e r v a c a t i o na f t e r t h eC o l l e g eE n t r a n c eE x a m i n a t i o n,d u r i n g w h i c h I c a nd oa l o t o f a m a z i n g t h i n g s．T h i s t h r e eＧm o n t hv a c a t i o nw i l l u n d o u b t e d l y b em y l o n g e s t h o l i d a y e v e r．T h e r e f o r e,I d l i k e t om a k e i t a sm e a n i n g f u l a s p o s s i b l e．F i r s t l y,I l l t a k e a p a r t－t i m e j o bt oe a r ns o m em o n e y t o c o v e r p a r t o fm y c o l l e g e t u i t i o n．I n t h em e a n w h i l e,I c a nm e e tm a n y i n t e r e s t i n gp e o p l e a n d l e a r n３a b o u t s o c i e t y．B e s i d e s,I m p l a n n i n g t oe n r o l l i nad r i v i n g c o u r s ea n dt r y t o g e t m y d r i v e r s l i c e n s e a s d r i v i n g w i l l b e a n i m p o r t a n t a n d n e c e s s a r y s k i l l i nm o d e r n s o c i e t y．I f t i m e p e r m i t s,I m g o i n g t o l e a r n s o m eM u s i c a l I n s t r u m e n t s,w h i c h i s s o m e t h i n g I v e a l w a y sw a n t e d t od o．I h a v e a s t r o n g i n t e r e s t i n g u i t a r,s oIw a n t t o l e a r nh o wt o p l a yg u i t a r,w h i c hc a ne n r i c h m y h o b b y．I p r a c t i c e i nm y s p a r e t i m e i n t h e e v e n i n g,s o t h a t I c a ne n j o y t h e p e a c e o f t h e g u i t a rm e l o d y．B e s tw i s h e s!Y o u r s,L iH u a 第二节(满分２５分)参考范文T h i n g s s e e m e da l l r i g h t a t f i r s t．H o w e v e r,w i t h t i m e g o i n g b y,c o n f l i c t s e m e r g e d．A b i g a i l a l w a y s c o m p l a i n e d t h a t e v e r y t i m e I h u n g o u tw i t hA v a,s h ew a s l e f t a l o n e,w h i l eA v a s a i d t h a t I p a i d m o r e a t t e n t i o n t oA b i g a i l,w h i c hd r o v e h e r c r a z y,b e l i e v i n g t h a t o u r f r i e n d s h i p w a s n o tw h a t i t u s e d t ob e．T r a p p e d i nt h ed i l e mm a,I,e n v e l o p e db y t h e s e n s eo f s a d n e s s,s t i l l f e l t c o n f u s e d w h y t h i n g s t u r n e do u t t ob e t h a t c o m p l i c a t e d,n o tk n o w i n g h o wt ot a c k l e t h e p r o b l e m．W o r s e s t i l l,k a r a t e e v e nb e c a m e t h em o s t f r i g h t e n i n g t h i n g t om e．O n ed a y,Is i m p l y c o u l dn o t t a k e i ta n y m o r e．W i t ht e a r ss t r e a m i n g d o w n m y c h e e k s,I s t o p p e d t h e mf r o ma r g u i n g a n d s a i dw i t h a d e e p s i g h, W h y c a n t y o u g e t a l o n g w i t h e a c ho t h e r w e l l B o t ho f y o ua r c m y b e s t f r i e n d s．＂H e a r i n g m y w o r d s,t h e y d i d n tu t t e ras i n g l ew o r d, s i n k i n g i n t o ad e e p s i l e n c e．A f t e rw h a t s e e m e d l i k eac e n t u r y,A v a f i n a l l yp l a c e dh e ra r m w i t h a p p a r e n t l y u n a c c u s t o m e d a f f e c t i o na r o u n dA b i g a i l s s h o u l d e r s．S e e i n g t h i s s c e n e,I g a s p e dw i t h r e l i e f a n db u r s t i n t o l a u g h t e r．４。

元月调考模拟卷1(2011.1.1)

yxOCBA 元月调考模拟卷（一）一、选择题（12小题，每小题3分，共36分） 1.函数13y x =-中自变量x 的取值范围是（）. （A ）x ≥3（B ）x ≠ 3（C ）x ≠ 0（D ）x ＞32.下列算式中,由左到右计算正确的是( ) . ①1)1(222+=+aa； ②a a a =⋅)0(≥a ；③)0(≥=ab b aab ； ④11)1)(1(-+=-+x x x x ；（A ）①②（B ）②③ （C ）③④（D ）①3.如果2是方程20x c -=的一个根，那么另一个根是（）A.4B.-4C.2D.-24.已知两圆的半径为方程x 2-5x+6=0的两个实数根，圆心距为1，则两圆的位置关系是A.外离B.外切C.相交D.内切 5.下列事件中必然事件的个数（）.①如果a,b 都是实数，那么a+b=b+a ；②从一副扑克牌中任意抽出一张，得到“黑桃”； ③小伟掷六次骰子,每次向上的一面都是6点； ④某电话在一分钟内接到至少15次呼叫. （A ）1（B ）2（C ）3 （D ）46.有四张不透明的卡片为，除正面的数不同外，其余都相同．将它们背面朝上洗匀后，重新排列，第3张是无理数卡片的概率为（）．A.12B.13C.14D.347.在一次游戏当中，小明将下面前面的四张扑克牌中的某一张旋转180°后，得到后面四张牌的图示，小芳看了后，很快知道小明旋转的是哪一张扑克！应该是（）.(A)黑桃9 (B)方块J (C) 黑桃8 (D)梅花38.如图，AB 是⊙O 的直径，C 、D 是⊙O 上的两点，若∠AOC=116°，则∠D 的度数为（）.(A)64° (B) 58° (C)32° (D) 29° 9.若一人患了流感,经过两轮传染后共有121人感染了流感.按照这样的传染速度,若2人患了流感,第一轮传染后患流感的人数共有( ).（A ）20人（B ）22人（C ）121人（D ）242人10.下列说法：①若x 2=m 2，则x=m ；②若方程x 2=m 则方程的解为m x ±=；③若m 为方程01x x 2=--的根，则12m m 3+=；④若04ac b 2<+则方程0c bx ax 2=++和0a bx cx 2=+-都有两个不等的实数根. 其中正确的有（）A.①②③B.②④C.①③④D.③④11. 如图，冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是（） (A)20cm 2 (B)40cm 2 (C)20πcm 2 (D)40πcm 212.如图，△ABC 中，∠BAC=90º，点I 为△ABC 的内心，⊙O 为△ABC 的外接圆，延长AI 交B C 于D ，交⊙O 于E ，设△ABC 的内切圆半径为r.下列结论中：①2BCAC AB r -+=； ②∠BIA=90º-21∠BEA ；③ EI=EC ；④BD=BI, 其中正确的是（）A ．①④B ．②④C ．①②③D ．①②③④第Ⅱ卷（非选择题，共84分）二、填空题（4小题，每小题3分，共12分）13.已知一元二次方程290x mx ++=可以配方成()20x n +=的形式，则n = ．14.在一幅长8分米，宽6分米的矩形风景画（如图①）的四周镶宽度相同的金色纸边，制成一幅矩形挂图（如图②）．如果要使整个挂图的面积是80平方分米，则金色纸边的宽度为分米. ① ②15.在草稿纸上计算1121;1111211;1111112111.-⨯-⨯-⨯观察你计算的结果，用你发现的规律直接写出下面式子的值2111112111n n ⋅⋅⋅-⨯⋅⋅⋅=个个 . 16.在平面直角坐标系中，O 为原点，等腰梯形OBCD 的底边OB 在x 轴上，已知B （4，0），CD ＝2，∠DOB ＝60°，将梯形OBCD 绕点O 顺时针旋转90°，则旋转过程中线段DC 所扫过的图形的面积．三、解答题（9小题，共72分） 17.（本题满分6分）解方程013212=-+x x .18.（本题满分6分）化简：31462294x x xx+-，并将自己所喜欢的x 值代入化简结果进行计算.19.（本题满分6分）如图，平面直角坐标系中，Rt △ABC,∠C=90°,∠CAB=45°,点C （－4，2），先将△ABC 向右平移m 个单位到△A 1B 1C 1，且△ABC 和△A 1B 1C 1关于y 轴对称，使再将△A 1B 1C 1绕点1B 顺时针旋转90°，得到对应△A 2B 1C 2. (1)请在图中画出△A 1B 1C 1和△A 2B 1C 2；(2)填空：m= ；点C 1的坐标为__________，点C 2的坐标为__________. (3)经过这两次图象变换，求出C 点经过的路径长.20.(本题满分7分)星期天,小华和小明一起打乒乓球,他们决定用游戏的方式决定谁先开球,游戏规则为:两人随机地伸出手指,规定每人最多只能伸出3根手指.(1)用列举法求出手指根数之和为4的概率;(2)若手指根数之和为奇数,小华先开球;否则,小明先开球.谁先开球的可能性大?请判断并说明理由.π22272ODCBAxODCByB DCI AEO图 3B'A'DCBAB'A'图 2DCBA图 1B'A'DC BA21.(本题满分7分)沪市经过一段时间的“低迷”后近期“反弹”，某日A 股以每股81元成交，以后两个交易日连续“上扬”，达到每股100元，照这样“牛市”第四个交易日能否突破110元/每股的关口？22.（本题满分8分）已知，如图，AB 为半⊙O 直径，C 、D 为半圆上异于A 、B 的两点，且D 为AC 中点，AC 、BD 交于点G ，DE ⊥AB 于E 交AC 于F ，半径OD 交AC 于H ．（1）求证：F 为AG 中点；（2）若DF=10，CG=12，求AB 的长．22、（本小题满分10分）甲、乙做一个“配色”的游戏，如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色.同时转动两个转盘，如果转盘A 转出红色，转盘B 转出蓝色，或者转盘A 转出了蓝色，转盘B 转出了红色，则红色和蓝色在一起配成紫色，这种情况下乙获胜；同样，蓝色和黄色在一起配成绿色，这种情况下甲获胜；在其它情况下，则甲、乙不分胜负.(1)利用列表或画树状图的方法表示此游戏所有可能出现的结果； (2)此游戏的规则，对甲、乙公平吗？试说明理由； (3)你能设计并提供一种公平的游戏规则吗？24.（本题满分10分）△ABC 中，AB ＝AC.将△ABC 绕C 点旋转至△A ′B ′C ，连BB ′,以AB 、BB ′为邻边作平行四边形 ABB ′D ，连A ′D.⑴旋转后B 、C 、A ′在一条直线上.如图1，若∠BAC ＝60°，则∠ADA ′＝__________；如图2，若∠BAC ＝90°，则∠ADA ′＝__________；⑵如图3，旋转后B 、C 、A ′在一条直线上. 若∠BAC ＝α，则∠ADA ′＝__________(用含α的式子表示)；⑶分别将图1与图2中的△A ′B ′C 继续旋转至图4、图5，使B 、C 、A ′不在一条直线上，连AA ′，则图4中，△ADA ′ 的形状是__________；图5中，△ADA ′的形状是__________. 请你任选其中一个结论证明.25.（本题满分12分）已知等腰△ABC,AC=BC,D 是△ABC 外接圆⊙O 上的一点,直线CD 与直线AB 相交于点E,线段DE 的中垂线与直线OD 相交于P,以P 为圆心,PD 长为半径作⊙P.(1)当点D 在优弧AB 上运动时(如图1),点D 不与点A,B 重合,⊙P 与直线AB 存在怎样的位置关系?请写出你的结论,并说明理由;(2)当点D 在劣弧AB 上运动时(如图2),点D 不与点A,B,C 重合,(1)中的结论是否仍然成立.画出图形,并作出判断,不需说明理由;(3)若∠A=30°,CD 从CB 开始绕点C 顺时针旋转角度α(0°＜α＜120°).是否存在角度α,使随机投入⊙O 内部的点刚好落在⊙P 内部的概率为0.25.若存在,请求出此时α的值;若不存在,请说明理由.(图3供画图分析用)附加题：(本小题12分)如图1，已知在平面坐标系中，以第一象限点M 为圆心作⊙M 与x 轴交于点A （3,0）,交y 轴于点C ，且AC 恰好平分∠MCO ，直线MC 交x 轴于点B （—2,0）.（1）求证：⊙M 与x 轴相切. （2）求直线BC 的解析式（3）若点P 为y 轴负半轴上一动点，连AP ，以A 为圆心，AP 为半径作⊙A 交CB 的延长线于E 点，且∠APE ＝∠ACM ，当P 运动时，线段CP －CE 的值是否发生变化？若不变，求其值；若变化，求其变化范围.B'A'图 4DC BA图 5B'A'DC BAABCDO图2ABCO图3H G F ECDOBA转盘B转盘A 黄蓝红红蓝黄红OP MEDCBA图1。

2021-2022学年武汉市新动力初三数学元月调考数学试卷及解析(一)

2021-2022学年武汉市新动力初三数学元月调考数学试卷（一）一、选择题（共10小题，每小题3分，共30分）1．一元二次方程2320x x --=的二次项系数是3，它的一次项系数是( )A ．1-B ．2-C ．1D ．02．把“武汉加油”的首字母看成图形，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ．3．军运会射击运动中，运动员每次射击击中靶的环数为1到10，不考虑脱靶的情况下，下列事件为随机事件的是( )A ．某运动员两次射击总环数大于1B ．某运动员两次射击总环数等于1C ．某运动员两次射击总环数大于20D ．某运动员两次射击总环数等于204．直角ABC ∆，90BAC ∠=︒，8AB =，6AC =，以A 为圆心，4.8长度为半径的圆与直线BC 的公共点的个数为( )A ．0B ．1C ．2D ．不能确定5．用配方法解一元二次方程2640x x --=，下列变形正确的是( )A ．2(6)436x -=-+B ．2(6)436x -=+C ．2(3)49x -=-+D ．2(3)49x -=+6．二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象( )A ．向左移动1个单位，向上移动3个单位B ．向右移动1个单位，向上移动3个单位C ．向左移动1个单位，向下移动3个单位D ．向右移动1个单位，向下移动3个单位7．如图，在矩形ABCD 中，2AD =，将矩形ABCD 绕点A 逆时针旋转，得到矩形AEFG ，点B 的对应点E 落在CD 上，且DE EF =，则四边形ABCE 的面积为( )A ．22B ．824C ．422D ．2228．同时抛掷三枚质地均匀的硬币，至少有两枚硬币正面向上的概率是( )A ．38B ．58C ．23D ．129．如图，ABC ∆是等腰直角三角形，AC BC a ==，以斜边AB 上的点O 为圆心的圆分别与AC 、BC 相切于点E 、F ，与AB 分别相交于点G 、H ，且EH 的延长线与CB 的延长线交于点D ，则CD 的长为( )A ．2212a -B ．212a +C ．2aD ．1(2)4a - 10．已知二次函数222022y x x =--的图象上有两点(,1)A a -和(,1)Bb -，则223a b +-的值等于( )A ．2020B ．2021C ．2022D ．2023二、填空题（共6小题，每小题3分，共18分）11．已知点(2,3)P -关于原点对称的点的坐标是．12．如图，正方形ABCD 内的图形来自中国古代的太极图，现随机向正方形内掷一枚小针，则针尖落在黑色区域内的概率为．13．经过两年的连续治理，某城市的大气环境有了明显改善，其每月每平方公里的降尘量从50吨下降到40.5吨，则平均每年下降的百分率是 %．14．如图，在ABC ∆中，6AB =，以点A 为圆心，3为半径的圆与边BC 相切于点D ，与AC ，AB 分别交于点E 和点G ，点F 是O 上一点（不与G 、E 重合），18CDE ∠=︒，则GFE ∠的度数是．15．已知一个圆心角为270︒的扇形工件，没搬动前如图所示，A 、B 两点触地放置，滚动至点B 再次触地时停止，扇形工件直径为5m ，则圆心O 所经过的路线长是 m ．16．如图，二次函数2y ax bx c =++的图象经过点(1,0)A ，与y 轴的交点为C ，对称轴为直线1x =-，下列结论：①240ac b abc->；②若点2(2P t --，1)y 和2(3Q t +，2)y 是该抛物线上的两点，则12y y >；③不等式20cx bx a ++<的解集为113x -<<；④在对称轴上存在一点B ，使得ABC ∆是以AC 为斜边的直角三角形．其中一定正确的是（填序号即可）．三、解答题（共8小题，共72分）17．若关于x 的一元二次方程220x bx -+=有一个根是1x =，求b 的值及方程的另一个根．18．如图，将Rt AOB ∆绕直角顶点O 顺时针旋转得到Rt COD ∆，使点A 的对应点C 落在AB 边上，过点D 作//DE AB ，交AO 的延长线于点E ，求证：BCO E ∠=∠．19．一个不透明的袋子中有四个完全相同的小球，把它们分别标号为1，2，3，4．（1）随机摸出一个小球然后放回，再随机摸出一个小球．求第二次摸出的小球标号能整除第一次摸出的小球标号的概率．（2）随机摸出一个小球然后不放回，则两次摸出的小球标号之和为的概率最大，这个最大概率是．20．请用无刻度直尺完成下列作图，不写画法，保留画图痕迹（用虚线表示画图过程，实线表示画图结果）．（1）如图1，点E 是ABCD 边CD 上一点，在AB 边上取一点F ，使得DE BF =；（2）如图2，在33⨯正方形网格中，点A 、B 、C 在格点上，过点C 作CH AB ⊥于H ；（3）如图3，AB 是O 的直径，弦DE AB ⊥，点C 在O 外，过点C 作//CG DE 交AB 于G ；（4）如图4，点E 是正方形ABCD 边BC 上一点，连接AE ，将ABE ∆绕A 点逆时针旋转90︒得到ADG ∆，画出ADG ∆．21．如图，在正方形ABCD 中，以BC 为直径作半圆O ，以点D 为圆心、DA 为半径作圆弧交半圆O 于点P ．连接DP 并延长交AB 于点E ．（1）求证：DE 为半圆O 的切线；（2）求AE BE的值．22．个体户小陈新进一种时令水果，成本为20元/kg ，经过市场调研发现，这种水果在未来40天内的日销售量()m kg 与时间t （天)的关系如表：时间t （天)1 3 5 10 36 ⋯ 日销售量()m kg94 90 86 76 24 ⋯未来40天内，前20天每天的价格1y （元/)kg 与时间t （天)的函数关系式为1125(1204y t t =+且t 为整数），后20天每天的价格2y （元/)kg 与时间t （天)的函数关系式为2140(21402y t t =-+且t 为整数）．（1）直接写出()m kg 与时间t （天)之间的关系式；（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？（3）在实际销售的前20天中，个体户小陈决定每销售1kg 水果就捐赠a 元利润(4a <且a 为整数）给贫困户，通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t （天)的增大而增大，求前20天中个体户小陈共捐赠给贫困户多少钱？23．【问题背景】如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，则EF 、BE 、DF 之间的数量关系是EF BE DF =+，【迁移应用】如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E 、F 分别在边BC 、CD 上，45EAF ∠=︒，若B ∠、D ∠都不是直角，且180B D ∠+∠=︒，求证：EF BE DF =+．【联系拓展】如图3，在ABC ∆中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45DAE ∠=︒．猜想BD 、DE 、EC 应满足的等量关系是．24．在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于(1,0)A -、(B A 在B 的左边），与y 轴交于C ，且4OB OA =．（1）求抛物线的解析式；（2）如图1，直线y x =交抛物线于D 、E 两点，点F 在抛物线上，且在直线DE 下方，若以F 为圆心作F ，当F 与直线DE 相切时，求F 最大半径r 及此时F 坐标；（3）如图2，M 是抛物线上一点，连接AM 交y 轴于G ，作AM 关于x 轴对称的直线交抛物线于N ，连接AN 、MN ，点K 是MN 的中点，若G 、K 的纵坐标分别是t 、n ．求t ，n 的数量关系．参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）1．一元二次方程2--=的二次项系数是3，它的一次项系数是()x x320A．1-B．2-C．1D．0解：一次项系数为1-，故选：A．2．把“武汉加油”的首字母看成图形，既是轴对称图形又是中心对称图形的是()A．B．C．D．解：A．是轴对称图形，不是中心对称图形，故本选项不合题意；B．既是轴对称图形，也是中心对称图形，故本选项符合题意；C．不是轴对称图形，也不是中心对称图形，故本选项不合题意；D．是轴对称图形，不是中心对称图形，故本选项不合题意．故选：B．3．军运会射击运动中，运动员每次射击击中靶的环数为1到10，不考虑脱靶的情况下，下列事件为随机事件的是()A．某运动员两次射击总环数大于1B．某运动员两次射击总环数等于1C．某运动员两次射击总环数大于20D．某运动员两次射击总环数等于20解：A、某运动员两次射击总环数大于1，是必然事件，不合题意；B、某运动员两次射击总环数等于1，是不可能事件，不合题意；C、某运动员两次射击总环数大于20，是不可能事件，不合题意；D、某运动员两次射击总环数等于20，是随机事件．故选：D．4．直角ABCAB=，6AC=，以A为圆心，4.8长度为半径的圆与直线BC的公共点BAC∠=︒，8∆，90的个数为()A．0B．1C．2D．不能确定解：90AC=，AB=，6∠=︒，8BAC10BC ∴=，∴斜边上的高为： 4.8AB AC BC⋅=， 4.8 4.8d cm rcm cm ∴===，∴圆与该直线BC 的位置关系是相切，交点个数为1，故选：B ．5．用配方法解一元二次方程2640x x --=，下列变形正确的是( )A ．2(6)436x -=-+B ．2(6)436x -=+C ．2(3)49x -=-+D ．2(3)49x -=+ 解：2640x x --=，移项，得264x x -=，配方，得2(3)49x -=+．故选：D ．6．二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象( )A ．向左移动1个单位，向上移动3个单位B ．向右移动1个单位，向上移动3个单位C ．向左移动1个单位，向下移动3个单位D ．向右移动1个单位，向下移动3个单位解：二次函数2241y x x =-++的顶点坐标为(1,3)，22y x =-的顶点坐标为(0,0)，∴向左移动1个单位，向下移动3个单位．故选：C ．7．如图，在矩形ABCD 中，2AD =，将矩形ABCD 绕点A 逆时针旋转，得到矩形AEFG ，点B 的对应点E 落在CD 上，且DE EF =，则四边形ABCE 的面积为( )A ．22B ．824C ．422D ．222解：四边形ABCD 是矩形，AD BC ∴=，90ADC ∠=︒，由旋转得：BC EF =，AB AE =，DE EF =，2AD DE ∴==，即ADE ∆为等腰直角三角形，根据勾股定理得：22222222AE AD DE =+=+=，则22AB AE ==，∴四边形ABCE 的面积=矩形ABCD 的面积ADE -∆的面积14222AB AD AD DE =⋅-⋅=-，故选：C ．8．同时抛掷三枚质地均匀的硬币，至少有两枚硬币正面向上的概率是( )A ．38B ．58C ．23D ．12解：由题意可得，所有的可能性为：∴至少有两枚硬币正面向上的概率是：4182=，故选：D ．9．如图，ABC ∆是等腰直角三角形，AC BC a ==，以斜边AB 上的点O 为圆心的圆分别与AC 、BC 相切于点E 、F ，与AB 分别相交于点G 、H ，且EH 的延长线与CB 的延长线交于点D ，则CD 的长为( )A 221-B 21+C 2aD ．1(2)4a 解：ABC ∆是等腰直角三角形，AC BC a ==，以斜边AB 上的点O 为圆心的圆分别与AC 、BC 相切于点E 、F ，与AB 分别相交于点G 、H ，且EH 的延长线与CB 的延长线交于点D∴连接OE 、OF ，由切线的性质可得OE OF O ==的半径，90OEC OFC C ∠=∠=∠=︒OECF ∴是正方形由ABC ∆的面积可知111222AC BC AC OE BC OF ⨯⨯=⨯⨯+⨯⨯12OE OF a EC CF ∴====，0.5BF BC CF a =-=，2GH OE a ==由切割线定理可得2BF BH BG =∴21()4a BH BH a =+122BH a -+∴=或122BH a --=（舍去）//OE DB ，OE OH =OEH BDH ∴∆∆∽∴OEBDOH BH =BH BD ∴=，121222CD BC BD a a a -++=+=+=．故选：B ．10．已知二次函数222022y x x =--的图象上有两点(,1)A a -和(,1)B b -，则223a b +-的值等于()A ．2020B ．2021C ．2022D ．2023解：点(,1)A a -和(,1)B b -在二次函数222022y x x =--的图象上，a ∴、b 是方程2220221x x --=-的两个根，2a b ∴+=，将(,1)A a -代入222022y x x =--，2220221a a ∴--=-，222021a a ∴=+，22322021232()2018420182022a b a b a b ∴+-=++-=++=+=，故选：C ．二、填空题（共6小题，每小题3分，共18分）11．已知点(2,3)P -关于原点对称的点的坐标是 (2,3)- ．解：点(2,3)P -关于原点对称的点的坐标是(2,3)-，故答案为：(2,3)-．12．如图，正方形ABCD 内的图形来自中国古代的太极图，现随机向正方形内掷一枚小针，则针尖落在黑色区域内的概率为 8π ．解：设正方形的边长为2a ，则正方形的内切圆的半径为a ，所以针尖落在黑色区域内的概率221248a a ππ==．故答案为8π． 13．经过两年的连续治理，某城市的大气环境有了明显改善，其每月每平方公里的降尘量从50吨下降到40.5吨，则平均每年下降的百分率是 10 %．解：设平均每年下降的百分率是x ，根据题意得250(1)40.5x -=解得10.1x =，2 1.9x =（不合题意，舍去）所以平均每年下降的百分率是10%．14．如图，在ABC ∆中，6AB =，以点A 为圆心，3为半径的圆与边BC 相切于点D ，与AC ，AB 分别交于点E 和点G ，点F 是O 上一点（不与G 、E 重合），18CDE ∠=︒，则GFE ∠的度数是 48︒或132︒ ．解：如图，连接DG ，BC 与A 相切于点D ，90ADB ADC ∴∠=∠=︒，6AB =，3AG AD ==，3BG AG ∴==，12DG AB AG AD ∴===， ADG ∴∆是等边三角形， 60DAG ∴∠=︒，AD AE =， AED ADE ∴∠=∠，18CDE ∴∠=︒，901872AED ADE ∴∠=∠=︒-︒=︒， 180727236CAE ∴∠=︒-︒-︒=︒， 603696GAE ∴∠=︒+︒=︒，当点F 在O 上且在ABC ∆的外部时，则11964822GFE GAE ∠=∠=⨯︒=︒；当点F '在O 上且在ABC ∆的内部时，则180********GF E GFE ∠'=︒-∠=︒-︒=︒，故答案为：48︒或132︒．15．已知一个圆心角为270︒的扇形工件，没搬动前如图所示，A 、B 两点触地放置，滚动至点B 再次触地时停止，扇形工件直径为5m ，则圆心O 所经过的路线长是5πm ．解：36027090AOB ∠=︒-︒=︒， 45ABO ∴∠=︒，∴圆心O 旋转的长度为545522()1804m ππ⨯⨯⨯=，圆心O 移动的距离为5270152()1804m ππ⨯=， ∴圆心O 所经过的路线长是5155()44m πππ+=，故答案为：5π．16．如图，二次函数2y ax bx c =++的图象经过点(1,0)A ，与y 轴的交点为C ，对称轴为直线1x =-，下列结论：①240ac b abc->；②若点2(2P t --，1)y 和2(3Q t +，2)y 是该抛物线上的两点，则12y y >；③不等式20cx bx a ++<的解集为113x -<<；④在对称轴上存在一点B ，使得ABC ∆是以AC 为斜边的直角三角形．其中一定正确的是 ②③ （填序号即可）．解：开口向下， 0a ∴<，对称轴为直线1x =-， 20b a ∴=<，抛物线与y 轴的交点在y 轴正半轴， 0c ∴>， 0abc ∴>，图象与x 轴有两个不同的交点，∴△240b ac =->，∴240ac b abc-<，故①不正确；221(2)1t t ----=+，22314t t ++=+， 2241t t ∴+>+， 12y y ∴>，故②正确；函数经过(1,0)，0a b c ∴++=，即20a a c ++=， 3c a ∴=-，20cx bx a ∴++<可化为2320ax ax a -++<，23210x x ∴-++>，解得113x -<<，故③正确；过点C 作CM 垂直对称轴交于点M ，设BN m =，则3BM a m =--，当90ABC ∠=︒时，BAN CBM ∠=∠，∴123m a m=--， 2320m am ∴++=，△2980a =-时，m 存在，∴当223a -时，90ABC ∠=︒， ∴在对称轴上存在一点B ，使得ABC ∆是以AC 为斜边的直角三角形，故④不正确；故答案为：②③．三、解答题（共8小题，共72分）17．若关于x 的一元二次方程220x bx -+=有一个根是1x =，求b 的值及方程的另一个根．解：关于x 的一元二次方程220x bx -+=有一个根是1x =， 120b ∴-+=，解得：3b =，把3b =代入方程得：2320x x -+=，设另一根为m ，可得13m +=，解得：2m =，则b 的值为3，方程另一根为2x =．18．如图，将Rt AOB ∆绕直角顶点O 顺时针旋转得到Rt COD ∆，使点A 的对应点C 落在AB 边上，过点D 作//DE AB ，交AO 的延长线于点E ，求证：BCO E ∠=∠．证明：将Rt AOB∆绕直角顶点O顺时针旋转得到Rt COD∆，AO CO∴=，A ACO∴∠=∠，//AB DE，180A E∴∠+∠=︒，又180ACO BCO∠+∠=︒，BCO E∴∠=∠．19．一个不透明的袋子中有四个完全相同的小球，把它们分别标号为1，2，3，4．（1）随机摸出一个小球然后放回，再随机摸出一个小球．求第二次摸出的小球标号能整除第一次摸出的小球标号的概率．（2）随机摸出一个小球然后不放回，则两次摸出的小球标号之和为5的概率最大，这个最大概率是．解：（1）列表如下：12341(1,1)(2,1)(3,1)(4,1)2(1,2)(2,2)(3,2)(4,2)3(1,3)(2,3)(3,3)(4,3)4(1,4)(2,4)(3,4)(4,4)由表可知，共有16种等可能结果，其中第二次摸出的小球标号能整除第一次摸出的小球标号的有8种结果，∴第二次摸出的小球标号能整除第一次摸出的小球标号的概率为81 162=；（2）列表如下：1234 1345 235634574567由表知，共有12种等可能结果，其中两次摸出的小球标号之和为5的次数最多，有4次，所以两次摸出的小球标号之和为5的概率最大，最大概率为41 123=，故答案为：5、13．20．请用无刻度直尺完成下列作图，不写画法，保留画图痕迹（用虚线表示画图过程，实线表示画图结果）．（1）如图1，点E是ABCD边CD上一点，在AB边上取一点F，使得DE BF=；（2）如图2，在33⨯正方形网格中，点A、B、C在格点上，过点C作CH AB⊥于H；（3）如图3，AB是O的直径，弦DE AB⊥，点C在O外，过点C作//CG DE交AB于G；（4）如图4，点E是正方形ABCD边BC上一点，连接AE，将ABE∆绕A点逆时针旋转90︒得到ADG∆，画出ADG∆．解：（1）如图1中，点F即为所求；（2）如图2中，线段CH即为所求；（3）如图3中，直线CG即为所求；（4）如图4中，ADG ∆即为所求．21．如图，在正方形ABCD 中，以BC 为直径作半圆O ，以点D 为圆心、DA 为半径作圆弧交半圆O 于点P ．连接DP 并延长交AB 于点E ．（1）求证：DE 为半圆O 的切线；（2）求AEBE的值．（1）证明：连接OP ，OD ， BC 是O 的直径， OP OC ∴=，以点D 为圆心、DA 为半径作圆弧， PD CD ∴=，在ODP ∆和ODC ∆中， DP DC OD OD OP OC =⎧⎪=⎨⎪=⎩， ()ODP ODC SSS ∴∆≅∆， 90OPD OCD ∴∠=∠=︒，P 点在O 上， DE ∴为半圆O 的切线；（2）解：以点O 为圆心、OB 为半径作圆弧，四边形ABCD 是正方形，EB ∴是O 的切线， DE 为半圆O 的切线，EB EP ∴=，设正方形的边长为a ，EB EP x ==， AE a x ∴=-，DE a x =+，222AD AE DE +=，222()()a a x a x ∴+-=+，解得4a x =， 4a BE ∴=， 3AE EB ∴=，∴3AEBE=．22．个体户小陈新进一种时令水果，成本为20元/kg ，经过市场调研发现，这种水果在未来40天内的日销售量()m kg 与时间t （天)的关系如表：时间t （天) 1 3 5 10 36 ⋯ 日销售量()m kg9490867624⋯未来40天内，前20天每天的价格1y （元/)kg 与时间t （天)的函数关系式为1125(1204y t t =+且t 为整数），后20天每天的价格2y （元/)kg 与时间t （天)的函数关系式为2140(21402y t t =-+且t 为整数）．（1）直接写出()m kg 与时间t （天)之间的关系式；（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？（3）在实际销售的前20天中，个体户小陈决定每销售1kg 水果就捐赠a 元利润(4a <且a 为整数）给贫困户，通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t （天)的增大而增大，求前20天中个体户小陈共捐赠给贫困户多少钱？解：（1）设一次函数为m kt b =+，将194t m =⎧⎨=⎩和390t m =⎧⎨=⎩代入一次函数m kt b =+中，有94903k b k b =+⎧⎨=+⎩，∴?296k b =⎧⎨=⎩．296m t ∴=-+．经检验，其它点的坐标均适合以上解析式，故所求函数解析式为296m t =-+；（2）设前20天日销售利润为1p 元，后20天日销售利润为2p 元．由11(296)(2520)4p t t =-++-1(296)(5)4t t =-++21144802t t =-++21(14)5782t =--+，120t ，∴当14t =时，1p 有最大值578（元)．由21(296)(4020)2p t t =-+-+-1(296)(20)2t t =-+-+2881920t t =-+2(44)16t =--．2140t ，此函数对称轴是44t =，∴函数2p 在2140t 上，在对称轴左侧，随t 的增大而减小．∴当21t =时，2p 有最大值为2(2144)1652916513--=-=（元)．578513>，故第14天时，销售利润最大，为578元；（3）2111(296)(2520)(142)4809642p t t a t a t a =-++--=-+++-对称轴为142t a =+．120t ，∴当214t a +时，P 随t 的增大而增大，又每天扣除捐赠后的日利润随时间t 的增大而增大， 19.5214a ∴<+，2.754a ∴<<．又a 为整数， 3a ∴=，20天的总销量(120)20(2196)(2296)...(22096)2(12...20)962021920420192015002+⨯=-⨯++-⨯+++-⨯+=-⨯++++⨯=-⨯+=-+=， ∴小陈共捐赠给贫困户150034500=⨯=元．答：前20天中个体户小陈共捐赠给贫困户4500元．23．【问题背景】如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，则EF 、BE 、DF 之间的数量关系是EF BE DF =+，【迁移应用】如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E 、F 分别在边BC 、CD 上，45EAF ∠=︒，若B ∠、D ∠都不是直角，且180B D ∠+∠=︒，求证：EF BE DF =+．【联系拓展】如图3，在ABC ∆中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45DAE ∠=︒．猜想BD 、DE 、EC 应满足的等量关系是 222DE BD EC =+ ．【问题背景】证明：如图1，四边形ABCD 是正方形，AB AD ∴=，90B BAD ADC ∠=∠=∠=︒，把ABE ∆绕点A 逆时针旋转90︒到ADG ∆，则DAG BAE ∠=∠，AG AE =， 90ADG B ∠=∠=︒， 180ADC ADG ∴∠+∠=︒，∴点F 、D 、G 在同一条直线上；45EAF ∠=︒，904545GAF DAG DAF BAE DAF ∴∠=∠+∠=∠+∠=︒-︒=︒， GAF EAF ∴∠=∠，AF AF =，()AFG AFE SAS ∴∆≅∆，EF GF DG DF BE DF ∴==+=+，【迁移应用】证明：如图2，由题意得，AB AD=，90∠=︒，BAD把ABE∆绕点A逆时针旋转90︒到ADG=，∠=∠，AG AE∆，则DAG BAE∠=∠，ADG BB ADC∠+∠=︒，180∴∠+∠=︒，ADG ADC180∴点F、D、G在同一条直线上；∠=︒，EAF45∴∠=∠+∠=∠+∠=︒-︒=︒，GAF DAG DAF BAE DAF904545∴∠=∠，GAF EAFAF AF=，∴∆≅∆，()AFG AFE SAS∴==+=+，EF GF DG DF BE DF【联系拓展】222DE BD EC=+，证明：如图3，由题意得，AB ACBAC∠=︒，=，90B ACB∴∠=∠=︒；45把ABD∆绕点A逆时针旋转90︒到ACG=，CG BD=，∠=∠=︒，AG AD∆，则CAG BAD∠=∠，45ACG B∴∠=∠+∠=︒；ECG ACB ACG90∠=︒，DAE45∠=∠+∠=∠+∠=︒-︒=︒，GAE CAG CAE BAD CAE904545∴∠=∠，GAE DAE=，AE AE∴∆≅∆，AEG AED SAS()∴=，GE DE222=+，GE CG EC222∴=+．DE BD EC故答案为：222=+．DE BD EC24．在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于(1,0)A -、(B A 在B 的左边），与y 轴交于C ，且4OB OA =．（1）求抛物线的解析式；（2）如图1，直线y x =交抛物线于D 、E 两点，点F 在抛物线上，且在直线DE 下方，若以F 为圆心作F ，当F 与直线DE 相切时，求F 最大半径r 及此时F 坐标；（3）如图2，M 是抛物线上一点，连接AM 交y 轴于G ，作AM 关于x 轴对称的直线交抛物线于N ，连接AN 、MN ，点K 是MN 的中点，若G 、K 的纵坐标分别是t 、n ．求t ，n 的数量关系．解：（1）(1,0)A -，1OA ∴=，44OB OA ∴==， (4,0)B ∴，将点A 、点B 的坐标代入2y x bx c =++， ∴010164b c b c =-+⎧⎨=++⎩，解得34b c =-⎧⎨=-⎩， ∴抛物线的解析式为：234y x x =--；（2）联立234y x x y x ⎧=--⎨=⎩，解得222222x y ⎧=-⎪⎨=-⎪⎩或222222x y ⎧=+⎪⎨=+⎪⎩(222D ∴-，22)-，(22E +，222)+， 8DE ∴=，设F 与DE 相切于H ，连接FH ，FD ，FE ，过点F 作FG x ⊥轴交DE 于G ，设点F 的坐标为2(,34)x x x --，FH DE ∴⊥，(,)G x x ，22(34)44FG x x x x x ∴=---=-++， DE 为定值，142DEF S DE FH FH ∆=⋅=， ∴当DEF ∆的面积最大时，FH 最大，即r 最大，而1()2DEF E D S FG x x ∆=- 21(44)[(222)(222)]2x x =-+++-- 222(2)162x =--+，220-<，∴当2x =时，DEF S ∆最大，其最大值为162，此时42FH =，点F 的坐标为(2,6)-；（3）设AN 与y 轴交于点P ，由题意可知，点G 的坐标为(0,)t ，由对称的性质可知，点P 的坐标为(0,)t -，设直线AM 的解析式为：y kx a =+，将A 、G 的坐标代入，得0k a t a =-+⎧⎨=⎩，解得k t a t =⎧⎨=⎩， ∴直线AM 的解析为：y tx t =+，同理可求得，直线AN 的解析式为：y tx t =--，联立234y x x y tx t ⎧=--⎨=+⎩，解得10x y =-⎧⎨=⎩或245x t y t t =+⎧⎨=+⎩， ∴点M 的坐标为2(4,5)t t t ++，同理可得点N 的坐标为2(4,5)t t t --，∴点K 的纵坐标为222(5)(5)2t t t t n t ++-==，即2n t =．。

元月调考专题复习(1).docx

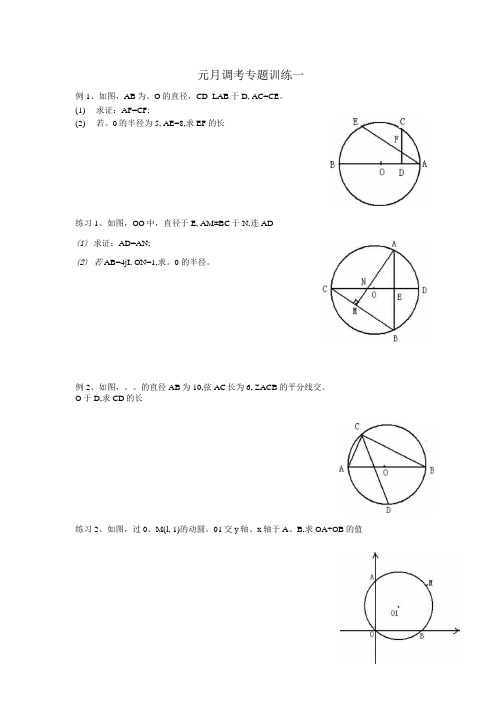
元月调考专题训练一例1、如图，AB为。

O的直径，CD_LAB于D, AC=CE。

(1)求证：AF=CF;(2)若。

0的半径为5, AE=8,求EF的长练习1、如图，OO中，直径于E, AM±BC于N,连AD(1)求证：AD=AN;(2)若 AB=4jI, ON=1,求。

0 的半径。

例2、如图，。

的直径AB为10,弦AC长为6, ZACB的平分线交。

O于D,求CD的长练习2、如图，过0、M(l, 1)的动圆。

01交y轴、x轴于A、B,求OA+OB的值例3、如图,OO为Z\ABC的外接圆，弦CP是与ZACB相邻的外角的平分线,ZACB=90°, 求证：(1) PA=PB;(2)AC-BC=V2PC.练习3、如图，A (4,0), B (0,4),。

经过A、B、O三点，点P为OA上一动点(异于0、A),则线段PA、PB、PO有什么数量关系，猜想并证明。

例4、已知：如图，AB为。

O的直径，C、D为。

O上两点，且AD=CD,过D点作直线BC的垂线交直线AB于E, F为垂足。

(1)求证：EF为。

O的切线；(2)若AC=6, BD=5,求CB 的长。

A0练习4、如图，AB为。

O的直径，BCJ_AB于点B,连接OC交OO于点E,弦AD〃OC, 弦DF1AB于点G(1)求证：CD是。

O的切线;(2)若竺=‘，。

的半径为5,求DF的长AD 5练习5、如图，过。

0上一点C作弦BA的垂线，交BA延长线于D点，连OA、CA,若AC 平分ZOAD.(1)求证:CD为。

0切线；(2)若AD=1,CD=2,求。

O 的半径.22、(本题8分)如图，在RtAABC中，匕(7=90°,蹄■平分匕交AC干点、E，点.D在边上且庞_L3£.(1)判断直^AC^ADBE外接圆的位置关系，并说明理由;⑵若AD=6, AE = 6^2,求△虚£外揆圆的半径1、一个圆锥的侧面积是底面积的3倍，这个圆锥的侧面展开图的圆心角为（）A 、60°B 、90°C 、120°D 、180°2、如果尸3是一元二次方程* =c 的一个根，则方程的另一根是（）A 、3B 、-3C 、0D 、1 3、中国象棋红方棋子按兵种不同分布如下：1个帅，5个兵，车、马、炮、士、将所有红子反面朝上放在棋盘中，任取一个不是兵和帅的概率是（1 口 5 厂 3 「5 16 16 8 8 4、如图，AABC 中，ZA=50°，以BC 为直径作©O,分别交 AB 、AC 于D 、E 两点，分别过D 、E 两点作。

2019年新观察九年级数学元月调考复习交流卷(一)(word版)

2017年新观察九年级数学元月调考复习交流卷（一）一、选择题（共10小题，每小题3分，共30分）1．将一元二次方程5x 2－1＝4x 化成一般形式后，二次项的系数和一次项系数分别是（）A ．5、－1B ．5、4C ．5、－4D ．5、12．下列四个图形中，既是轴对称图形又是中心对称图形的是（）3．袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球，下列事件是必然事件的是（）A ．摸出的三个球中至少有一个球是黑球B ．摸出的三个球中至少有一个球是白球C ．摸出的三个球中至少有两个球是黑球D ．摸出的三给球中至少有两个球是白球4．抛物线y ＝ax 2－2ax －3的对称轴为（）A ．直线x ＝2B ．直线x ＝－2C ．直线x ＝1D ．直线x ＝－1 5．如图，⊙O 中，弦AB 与CD 交于点M ，∠A ＝45°，∠AMD ＝75°，则∠B 的度数是（） A ．15°B ．25°C ．30°D ．75°6．在一个不透明的袋子里，有2个白球和2个红球，它们只有颜色上的区别，从袋子里随机摸出一个球记下颜色放回，再随机地摸出一个球，则两次都摸到白球的概率为（）A ．161B ．81C ．41D ．21 7．圆的直径为10 cm ，如果圆心与直线的距离是d ，则（）A ．当d ＝8 cm 时，直线与圆相交B ．当d ＝4.5 cm 时，直线与圆相离C ．当d ＝5 cm 时，直线与圆相切D ．当d ＝10 cm 时，直线与圆相切8．来自信息产业部的统计数字显示，今年1月至4月份我国手机产量为4000万台，相当于去年全年手机产量的80%，预计到明年年底手机产量达到9800万台．设则两年手机产量平均每年的增长率为x ，则可列方程为（）A ．4000×80%(1＋x )＝9800B ．4000×80%(1＋x )2＝9800C ．%804000(1＋x )＝9800D ．%804000(1＋x )2＝9800 9．定义运算：a ★b ＝a (1－b )，若a 、b 是方程x 2－x ＋41m ＝0（m ＜0）的两根，则b ★b －a ★a 的值为（）A ．0B ．1C ．2D ．与m 的值有关10．已知边长为4的等边△ABC ，E 、F 分别是AB 、BC 的中点，将△BEF 绕点B 顺时针旋转α，AE 与CF 交于P ．当α＝60°时，点P 运动的路径长是（）A ．π61 B ．π34 C ．932π D ．934π二、填空题（本大题共6个小题，每小题3分，共18分）11．第一象限的点(a ，b )绕(0，－1)顺时针旋转180°后所得点的坐标为___________12．把形状完全相同风景不同的两张图片全部从中剪断，再把四张形状相同的小图片混合在一起，从四张图片中随机摸取两张，则这两张小图片恰好合成一张完整图片的概率为___________13．方程025322=-+x x 的判别式的值等于___________ 14．如图，抛物线过点A (2，0)、B (6，0)、C (1，3)，平行于x 轴的直线CD 交抛物线于C 、D ，以AB 为直径的圆交直线CD 于点E 、F ，则CE ＋FD 的值是___________15．圆锥的底面周长是4πcm ，母线长9 cm ，则它的侧面展开图的圆心角的度数为_________度16．抛物线y ＝ax 2＋bx ＋2过B (－2，6)、C (2，2)两点，若直线x y 21-=向上平移m 个单位所得的直线与抛物线BC 段（包括端点B 、C ）部分有两个交点，则m 的取值范围是______________三、解答题（共8题，共72分）17．（本题8分）已知关于x 的一元二次方程2x 2－3kx ＋4＝0的一个根是1，求k 的值和方程的另一根18．（本题8分）不透明的袋子中装有大小、质地完全相同的2个白球和2个黑球(1) 先从袋中摸出1个球后放回，混合均匀后再摸出1个球，则第一次摸到白球，第二次摸到黑球的概率P 1为_________(2) 若第一次从袋子中摸出1个球后不放回，第二次再摸出1个球，则两次摸到的球中有1个白球和1个黑球的概率P 2是多少？（请用画树形图或列表法求出结果）19．（本题8分）如图，在△ABC 中，以AC 为边在外作正△ACD ，连接BD(1) 以点A 为中心，把△ADB 顺时针旋转60°，画出旋转后的图形（保留作图痕迹）(2) 若∠ABC ＝30°，BC ＝4，BD ＝6，求AB 的长20．（本题8分）如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF(1) 求证：∠1＝∠F2，求⊙O的半径长(2) 若CD＝3，EF＝521．（本题8分）一自动喷灌设备的喷流情况如图所示，设水管OA在高出地面1.5米的A处有一自动旋转的喷水头，一瞬间流出的水流是抛物线状，喷头A与水流最高点B连线与y轴成45°角，水流最高点B比喷头A高2米(1) 求水流落地点C到O点的距离(2) 若水流的水平位移s（米）（抛物线上两对称点之间的距离）与水流的运动时间（t秒）之间的函数关系为t＝0.8s．求共有几秒钟，水流高度不低于2米？22．（本题10分）某工艺品每件的成本是50元，在某段时间内若以每件x元出售，可卖出(200－2x)件，设这段时间内售出该工艺品的利润为y元(1) 直接写出利润y（元）与售价x（元）之间的函数关系式(2) 求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3) 如果要是利润不低于1200元，且成本不超过2500元，请直接写出x的范围为__________23．（本题10分）以C 为直角顶点的两个等腰直角△CAB 和△CDG ，E 为AB 的中点，F 为DG 的中点(1) 如图1，点A 、B 分别在边CD 、CG 上，则EF 与AD 的数量关系是_______________(2) 如图2，点A 、B 不在边CD 、CG 上，(1)中EF 与AD 的关系还成立吗？请证明你的结论(3) 如图3，若A 、B 、G 在同一直线上，且A 、C 、B 、F 在同一圆上，求△CDG 与△CAB 面积之比24．（本题12分）如图1，已知抛物线43412++=x x y 与x 轴交于A 、B 两点，以B 为直角顶点作等腰直角三角形ABP ，且P 在第三象限(1) 求点P 的坐标 (2) 若点Q 为抛物线上的动点，且S △P AQ ＝5，求点Q 的横坐标n 的值(3) 如图2，直线AC 交抛物线于C ，交y 轴于M ，连CP 交抛物线于E ，连AE 交y 轴于N ，求OM ·ON 的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第9课时元调专题《圆2》
专题一、选择题（42分）
1．如图OA=OB=OC且∠ACB=30°，则∠AOB的大小是（）
A．40°B．50°C．60°D．70°
2．如图，已知，AB是⊙O的直径，点C，D在⊙O上，∠ABC=50°，则∠D为（）
A．50°B．45°C．40°D．30°
3．同圆的内接正三角形与正六边形的边长之比为（）
A．1：2 B．1：1 C．√3：1 D．2：1
4．如图，在平面直角坐标系中，⊙M与y轴相切于原点O，平行于x轴的直线交⊙M于P，Q两点，点P在点Q的右方，若点P的
坐标是（-1，2），则点Q的坐标是（）
A．（-4，2）B．（-4.5，2）C．（-5，2）D．（-5.5，2）
5．在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作
BAC，如图所示．若AB=4，
A.
4π B.
4
π C.
11
4
π D.
5
4
π
6．如图．Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是 AB的中点，CD与AB的交点为E，则CE
DE
等于（）
A．4 B．3.5 C．3 D．2.8
A．2B．8 C．D．
9.如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（）
A.3
B.4-
C.4
D.6-
10.已知⊙O1和⊙O2的半径长分别是一元二次方程x2-6x+8=0的两个根，O1O2=2，则这两个圆的位置关系是（）
A．相离B．相交C．外切D．内切
11.如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2=8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现（）
A．3次B．5次C．6次D．7次
A. B. C.
3D.
2
A．点P在⊙O内B．点P在⊙O上C．点P在⊙O外D．无法确定
题型二、计算和证明
1．已知，如图：△ABC中，CH是高，∠ACH=2∠ABC，点O是AB上一点，以点O为圆心，OB为半径的⊙O经过点C，
（1）求证：AC是⊙O的切线；
（2）连接CO并延长交⊙0于点D，连接BD并延长与∠DCH的平分线CE相交于点E，若⊙O的半径为5cm，CH=4cm，求线段CE的长．
2．如图，AB是圆O的直径，AD、BC垂直于AB，AD=13，BC=16，DC=5，点P是动点，点P以1cm/s的速度由A向D运动，同时Q从C向B以2cm/s的速度运动，当一点到达时时，另一点同时停止运动．
（1）当P从A向Q运动t秒时，四边形PQCD的面积S与t的关系式．
（2）是否存在时间t，使得梯形PQCD是等腰梯形？若存在求出时间t，不存在说明
理由
题型三、综合和探究
2．如图1，在平面直角坐标系xoy中，M是x轴正半轴上一点，⊙M与x轴的正半轴交于A，B两点，A在B的左侧，且OA，OB 的长是方程x2-12x+27=0的两根，ON是⊙M的切线，N为切点，N在第四象限．
（1）求⊙M的直径的长．
（2）如图2，将△ONM沿ON翻转180°至△ONG，求证△OMG是等边三角形．
（3）求直线ON的解析式．
3．如图，平面直角坐标系中，A（-2，0），B（8，0），以AB为直径作半圆⊙P交y轴于M，以AB为一边作正方形ABCD．（1）求C、M两点的坐标；
（2）连CM，试判断直线CM是否与⊙P相切？说明你的理由．
（3）在x轴上是否存在一点Q，使△QMC周长最小？若存在，求出Q的坐标及△QMC最小周长；若不存在．请说明理由．
4．在直角坐标系中，M为x轴正半轴上一点，⊙M交x轴于A、B两点，交y轴于C、D两点，P为AB延长线上一
点（不含B点），连接PC交⊙M于Q，连接DQ，若A（-1，0），C（0
（1）求圆心M的坐标；
（2）过B点作BH⊥DQ于H，当P点运动时，线段CQ、QH、DH有何数量关系，证明你的结论；
（3）R为⊙M的直径DF延长线上的一个动点（不包括F点），过B、F、R三点作⊙N，CF交⊙N于T，当R点在DF 延长线上运动时，FT-FR的值是否变化？请说明理由．。