【恒心】2014年东北三省三校高三第二次联合模拟考试数学(理科)试题及参考答案
东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高三数学第二次联合模拟考试题 文(扫描版

东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)2014年高三数学第二次联合模拟考试题文(扫描版)新人教版二模文科数学参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A D C B B A D B A DC C13.22333(1)124n n n +++⋅⋅⋅+=14.1252π 15.3 16.①②④17.(Ⅰ)解:当1=n 时,111151,4=+∴=-a S a w.w.w.k.s.5.u.c.o.m………2分 又1151,51++=+=+Q n n n n a S a S115,n n n a a a ++∴-= ………4分114n n a a +=-即∴数列{}n a 是首项为114=-a ,公比为14=-q 的等比数列,∴1()4=-nn a ………6分 (Ⅱ)nb n n -=-=)41(log 4, ………8分 所以11111(1)1n n b b n n n n +==-++ ………10分 11111(1)()()22311n n T n n n ⎡⎤=-+-++-=⎢⎥++⎣⎦L ………12分 18.(Ⅰ)解:第三组的频率是0.150×2=0.3;第四组的频率是0.100×2=0.2;第五组的频率是0.050×2=0.1 ………3分 (Ⅱ)设“抽到的两个产品均来自第三组”为事件A ,由题意可知,分别抽取3个,2个,1个。
………6分 不妨设第三组抽到的是123,,A A A ;第四组抽到的是12,B B ;第五组抽到的是1C ,所含基本事件总数为:{}{}{}{}{}{}{}{}{}{}{}{}121323111211212221313231,,,,,,,,,,,,,,,,,,,,,,,A A A A A A A B A B A C A B A B A C A B A B A C {}{}{}121121,,,,,B B B C B C………10分所以31()155P A == (12)分 19.(Ⅰ)证明: 连结MO1111////A M MA MO AC AO OC MO BMD AC BMDAC BMD =⎫⎫⇒⎬⎪=⎭⎪⎪⊂⇒⎬⎪⊄⎪⎪⎭平面平面平面 ………4分(Ⅱ)设过1C 作1C H ⊥平面11BDD B 于H ,11BD AA BD AC BD A AC⊥⊥⊥,得面于是1BD A O⊥1111116022cos 60ABCDBAD AO AC AB AA A O AC A O ABCDA AC A O BD ⎫⎫⎫⎪⎪∠=⇒==⎬⎪⎪⎪⎪=⎭⎪⎪⎪⎪=⇒⊥⎬⎪⇒⊥⎬⎪∠=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪⊥⎪⎭o o 平面 (8)分又因为平面//ABCD 平面1111A B C D ,所以点B 到平面1111A B C D 的距离等于点1A到平面ABCD 的距离13A O = ………10分111111111111132232322B B C D C BB D V V AO C H C H --=⇔⋅⋅⨯=⋅⋅⨯⨯⇒= ………12分20.(Ⅰ)设(,)P x y2(1)18y x y =++⇒= ………4分 (Ⅱ)设直线AB :y kx b =+,1122(,),(,)A x yB x y将直线AB 代入到28x y =中得2880x kx b --=,所以12128,8x x k x x b +==-………6分又因为2221212121281664x x OA OB x x y y x x b b ⋅=+=+=-+=-u u u r u u u r 4b ⇒= (1)0分所以恒过定点(0,4) ………12分21.(Ⅰ)''(),()21bf xg x ax x ==-则''(1)(1)01(1)(1)1g f a g f b ===⎧⎧⇒⎨⎨==⎩⎩ ………3分 (Ⅱ) 设()2()()()ln 0u x g x f x x x x x =-=-->()()'211()x x u x x+-=………4分令'()01u x x =⇒=所以,()()10u x u ≥= 即()()g x f x ≥ ………7分(Ⅲ) 设()2()()()ln (1,)b h x f x g x x b x x x e =--=-∈,2'2()b x h x x -=,令'()0h x x =⇒=> ………8分所以,原问题()ln 1022b b h x h ⎛⎫==-> ⎪⎝⎭极大 ………10分又因为()()()()11,b b b h h e b e b e =-=-+设()xt x e x =-(()2,x e ∈+∞) '()10x t x e =->所以()t x 在()2,e +∞上单调递增,()()(2)00x b t x t e e x h e >>∴>∴<所以有两个交点 ………12分 22. (Ⅰ)2//AB CD PAB AQC AQC ACB ACB CQAPA O PAB ACB AQ O QAC CBA AC AB AC AB CQ CQ AC ⇒∠=∠⎫⎫⇒∠=∠⎬⎪⇒⇒∠=∠⎬⎭⎪⇒∠=∠⎭⇒=⇒=⋅V :V e e 为切线为切线………5分 (Ⅱ)//113622,AB CD BP AP AB AP PC PQ QCQC PC AQ BP AB ⎫⎫⎪⎪⇒===⎬⎪=⇒==⎬⎪⎭⎪⎪==⎭AP 为O e 切线212AP PB PC QA ⇒=⋅=⇒=又因为AQ 为O e 切线2AQ QC QD QD ⇒=⋅⇒= (10)分 23. (Ⅰ)221:22C x y +=,4l x += ………5分(Ⅱ)设),sin Qθθ,则点Q 到直线l 的距离d==≥………8分当且仅当242kππθπ+=+,即24kπθπ=+(k Z∈)时取等………10分24.解:(Ⅰ)由柯西不等式得,2222222()(111)()3a b c a b c++≤++++=∴a b c≤++≤所以a b c++的取值范围是[………5分(Ⅱ)同理,2222222()[111]()3a b c a b c-+≤+-+++=()………7分若不等式2|1|1()x x a b c-++≥-+对一切实数,,a b c恒成立,则311≥++-xx,解集为33(,][,)22-∞-⋃+∞………10分。
【2014大连市二模】辽宁省大连市2014届高三第二次模拟考试 数学理试题 Word版含答案
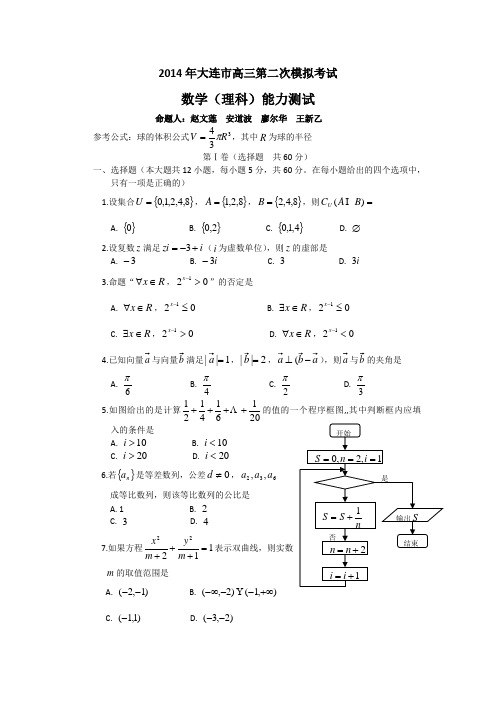
2014年大连市高三第二次模拟考试数学(理科)能力测试命题人:赵文莲 安道波 廖尔华 王新乙参考公式:球的体积公式334R V π=,其中R 为球的半径 第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是正确的) 1.设集合{}8,4,2,1,0=U ,{}8,2,1=A ,{}8,4,2=B ,则=)(B A C U A. {}0 B. {}2,0 C. {}4,1,0 D. ∅ 2.设复数z 满足i zi +-=3(i 为虚数单位),则z 的虚部是A. 3-B. i 3-C. 3D. i 3 3.命题“R x ∈∀,021>-x ”的否定是A. R x ∈∀,021≤-xB. R x ∈∃,021≤-x C. R x ∈∃,021>-x D. R x ∈∀,021<-x4.已知向量a 与向量b 满足1||=,2||=b ,a b a -⊥(),则a 与b 的夹角是A.6π B. 4π C. 2π D. 3π5.如图给出的是计算201614121++++ 的值的一个程序框图,,其中判断框内应填入的条件是A. 10>iB. 10<iC. 20>iD. 20<i6.若{}n a 是等差数列,公差0≠d ,632,,a a a 成等比数列,则该等比数列的公比是 A. 1 B. 2 C. 3 D. 47.如果方程11222=+++m y m x 表示双曲线,则实数 m 的取值范围是A. )1,2(--B. ),1()2,(+∞---∞C. )1,1(-D. )2,3(--8.函数)sin()(ϕω+=x A x f (其中0>A ,πϕ<||)的图象如图所示,则其中ω,ϕ分别为A. 2-=ω,3πϕ=B. 2=ω,3πϕ=C. 2=ω,32πϕ-= D. 2-=ω,3πϕ-=9.设141313114095)1()1()1()23()1(a x a x a x a x x +++++++=+- ,则=++++13210a a a aA. 93 B. 9532- C. 52 C. 5923-10.已知函数⎪⎩⎪⎨⎧-+---=3241|1|1)(2x x x x f )2()2(>≤x x ,如在区间),1(+∞上存在n (1≥n )个不同的数n x x x x ,,,,321 使得比值nn x x f x x f x x f )()()(2211=== 成立,则n 的取值集合是A. {}4,3,2,1B. {}3,2,1C. {}3,2D. {}4,3,211.沿边长为1的正方形ABCD 的对角线AC 进行折叠,使折后两部分所在的平面互相垂直,则折后形成的空间四边形ABCD 的内切球的半径为A.262-B. 261-C. 221- D. 1 12.设函数)(x f 是连续函数,且在1=x 处存在导数,如函数)(x f 及其导函数)(x f '满足xx f x x x f )(ln )(-=⋅',则函数)(x f A. 既有极大值,又有极小值 B. 有极大值,无极小值C. 有极小值,无极大值D. 既没有极大值,又没有极小值第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则y x z -=4的最小值为 .14.如图,网格纸是边长为1的小正方形,在其上用 粗线画出了某多面体的三视图,该多面体的体积 为 .15.过抛物线px y 22=(0>p )的焦点作斜率为3的直线与该抛物线交于B A ,两点,B A ,在y 轴上的正射影分别为D 、C ,若梯形ABCD 的面积为310,则=p .16.已知数列{}n a 满足:21=a ,121+-=+n n n na a a ,令11+⋅=n n n a a b ,则数列{}n b 的前n 项和=n S三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知函数x x x x x f 22cos 2cos sin 3sin )(+⋅+=(R x ∈). 在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,且2)(=A f . (1)求函数)(x f 的单调增区间及对称中心; (2)若3=a ,求ABC ∆面积的最大值.18. (本小题满分12分)如图,四棱锥ABCD P -中, 90=∠DAB ,CD BC ⊥,30=∠CDB ,且2=====AD AB PD PB PA .(1)求证:面⊥PBD 面ABCD ;(2)求平面PAB 与平面PBC所成锐二面角的余弦值.PACD19. (本小题满分12分)有6名员工,3男3女,平均分配到甲、乙、丙三个部门。
2014辽宁省大连市高三二模数学理试题和答案

2014年大连市高三第二次模拟考试数学(理科)参考答案与评分标准说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分. 一.选择题1.C2.C3.B4.D5.A6.C7.A8.B9.D 10.B 11.A 12.D 二、填空题: 13.225-14.3816π+ 15.3 16.2121+-n 三、解答题: 17、解:(I )x x x x f 2cos 12sin 2322cos 1)(+++-==23)62sin(++πx-----------2分 由226222πππππ+≤+≤-k x k ,解得函数的单调增区间为)](6,3[Z k k k ∈+-ππππ -----------4分由ππk x =+62,解得函数的对称中心为:))(23,122(Z k k ∈-ππ -----------6分 (II)由21)62sin(,223)62sin(,2)(=+∴=++∴=ππA A A f ,3,6562πππ=∴=+∴A A ------------------8分 又3=a ,由余弦定理:3,cos 222222=-+∴⋅-+=bc c b A bc c b a ,3≤∴bc ---------10分43343sin 21≤=⋅=bc A bc S ,当且仅当c b =时取等.-------12分18.(I )证明:取BD 中点O ,连PO 、AO.由PB=PD=2,BD=2可知DPB ∆为等腰直角三角形, 则,1==AO PO 而PA=2,故AO PO ⊥, -------3分又BD PO ⊥,则ABCD PO 面⊥,故面;ABCD PBD 面⊥ ------------6分(II )如图,按],,;[P B A O 建立坐标系,则)0,1,0(),0,0,1(B A ,)1,0,0(P ,),1,0,1(-=PA )1,1,0(-=PB ,设面PAB 的法向量为),,(z y x m =,由⎪⎩⎪⎨⎧=⋅=⋅00PB m m ,得: ⎩⎨⎧=-=-0z y z x , 令1=z ,则)1,1,1(=m-------7分又)0,21,23(-C , 则)1,21,23(--=设平面PBC 的法向量为),,(c b a n =,由⎪⎩⎪⎨⎧=⋅=⋅00n n,⎪⎩⎪⎨⎧=-+-=-⇒021230c b a c b , 令,1=c 则)1,1,33(-=n. --------9分则332-=⋅n m ,321||,3||==n m. -----------10分则212176|||||||,cos |-=⋅⋅=><n m n m n m. 故平面PAB 与平面PBC 所成锐二面角的余弦值为212176------12分注:利用几何法证明相应给分。
2014年东北三省三校高三第二次联合模拟考试理科综合

三校第二次模拟考试生物试题答案1.A 2.B 3.B 4.D 5.C 6.C29.(共10分)(1)5(1分)3(1分)(2)暗反应(1分)叶绿体基质(1分)(3)1(2分)5(2分)(4)暗反应(1分)暗反应需要多种酶参加催化(1分)30.(共10分)(1)增加(1分)(2)①将2株改为20株(或其它合理答案)(2分)②增加空白对照组,即蒸馏水处理(2分)(3)A(1分)是(1分)萘乙酸处理的组别中可溶性蛋白含量均高于对照组(2分)0--3.125mg/L(1分)31.(共9分)(1)致死(1分)(2)红眼(1分)染色体变异(缺失)(1分)红眼(1分)能(1分)不能(1分)(3)显微镜/显微/染色体(2分)32.(共10分)(1)J(1分)1(1分)无限环境(空间和资源充裕)(1分)理想条件(气候适宜,没有敌害等)(1分)(2)B(1分)(3)2(1分)1、2、3三个物种的营养级不同,营养级越高,能量越少,环境容纳量越小(其它合理答案也给分)(2分)(4)1→2→3(2分)39.(共15分)(1)①水中蒸馏/水蒸气蒸馏(2分)②NaCL(2分)③无水Na2SO4(2分)(2)石灰水(2分)原料易焦糊,有效成分易水解(2分)(3)石油醚(2分)纸层析(1分)萃取剂的选择、原料颗粒的大小、紧密程度、萃取温度、时间(2分)40.(15分)排卵(1分)受精(1分)2个极体(1分)透明带反应(1分)出生前(胎儿时期)(1分)精子获能(获能)(2分)(3)促性腺激素(2分)获能液(2分)(4)血清(2分)(5)BCFH(2分)三校第二次模拟考试化学试题答案物理试题参考答案题号14 15 16 17 18 19 20 21 答案 B C B D C ABD BD BD选择题每题6分,19—21部分正确3分,有错误的0分。
22、1.035 1.195(±0.002)(每空3分,共6分)23、乙(2分);22111U R N NR U =;(2分) (连线3分)N :V 1的总格数,N 1:V 1的读出格数,U 2:V 2的读数,R 1:待测表内阻,R 2:V 2表内阻。
2014沈阳高三第二次模拟数学试卷及答案(理科)

2014年沈阳市高中三年级教学质量监测(二)数 学(理科)命题:东北育才双语学校 王海涛 沈阳市第20中学 李蕾蕾 沈阳市第11中学 孟媛媛东北育才学校 侯雪晨 沈阳市第120中学 董贵臣 沈阳市第4中学 韩 娜主审:沈阳市教育研究院 王孝宇本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷2至4页。
满分150分,考试时间120分钟。
注意事项:1. 答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条形码粘贴在答题卡指定区域。
2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动用橡皮擦干净后,再选涂其他答案标号。
第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答,在本试题卷上作答无效。
3. 考试结束后,考生将答题卡交回。
第Ⅰ卷(共60分)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}1,2,3A =,集合{}2,3,4,5B =,则A.A B ⊆B.B A ⊆C.{}2,3A B =D.{}1,4,5A B = 2.设复数12iz +=(i 是虚数单位),则||z =A.2B.12C.13.下列命题中,真命题的是A.x ∀∈R ,20x > B.x ∀∈R ,1sin 1x -<<C.0x ∃∈R ,020x< D.0x ∃∈R ,0tan 2x =4.已知ABCD中,(2,8)AD = ,(3,4)AB =- ,对角线AC 与BD 相交于点M ,则AM的坐标为A. 1(,6)2--B.1(,6)2-C.1(,6)2-D.1(,6)25.若a ,b ,c 成等比数列,则函数c bx ax y ++=2的图象与x 轴的交点个数为A.0B.1C.2D.不能确定6.一次试验:向如图所示的正方形中随机撒一大把豆子. 经查数,落在正方形中的豆子的总数为N 粒,其中有m (m N <)粒豆子落在该正方形的内切圆内,以此估计圆周率π的值为 A.m N B.2m N C.3m N D.4m N7.已知中心在坐标原点,焦点在坐标轴上的双曲线的渐近线方程为x y 43±=,则此双曲线的离心率为 A.54 B.53 C.54或53 D.45或358.若[]x 表示不超过x 的最大整数,如[]2.12=,[]2.13-=-. 执行如图所示的程序框图,则输出的S 值为 A.2 B.3 C.4D.59.已知曲线()sin())f x x x ωω=(0ω>的距离为2π,且曲线关于点0(,0)x 成中心对称,若0[0,]2xπ∈,则0x =A.12πB.6πC.3πD.512π10.已知实数x ,y 满足26002x y x y x -+≥⎧⎪+≥⎨⎪≤⎩,若目标函数z mx y =-+210m -+,最小值为22m --,则实数m 的取值范围是A.[1,2]-B.[2,1]-C.[2,3]D.[1,3]- 11.四面体ABCD 的四个顶点都在球O 的球面上,AB BCD ⊥平面,BCD △是边长为3的等边三角形. 若2AB =,则球O 的表面积为A.323π B.12π C.16π D.32π 12.已知函数()f x 满足:①定义域为R ;②对任意x ∈R ,有(2)2()f x f x +=;③当[1,1]x ∈-时,()f x =若函数 (0)()ln (0)x e x g x x x ⎧≤=⎨>⎩,则函数()()y f x g x =-在区间[5,5]-上零点的个数是A.7B.8C.9D.10第Ⅱ卷 (共90分)二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题纸上.) 13.如图,某几何体的主视图和俯视图都是矩形,左视图是等腰直角三角形,则该几何体的体积为 . 14.6(2x -的二项展开式中的常数项为 . 15.已知函数()()()f x x x a x b =--的导函数为()f x ',且(0)4f '=,则222a b +的最小值为 .16.已知抛物线22y px =(0p >)的焦点为F ,ABC △的顶点都在抛物线上,且满足FA FB FC ++= 0, 则111AB BC CAk k k ++= . 俯视图主视图左视图三、解答题:(解答应写出文字说明,证明过程或演算步骤,解答过程书写在答题纸的对应位置.) 17.(本小题满分12分)在ABC △中,角A B C 、、的对边分别是a b c 、、,满足222b c bc a +=+. (Ⅰ)求角A 的大小;(Ⅱ)已知等差数列{}n a 的公差不为零,若1cos 1a A =,且2a ,4a ,8a 成等比数列. 求14n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n S .18.(本小题满分12分)为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程、20项民生类工程和10项产业建设类工程. 现有来沈的3名工人相互独立地从这60个项目中任选一个项目参与建设.(Ⅰ)求这3人选择的项目所属类别互异的概率;(Ⅱ)将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为X ,求X 的分布列和数学期望.19.(本小题满分12分)如图,BC 为圆O 的直径,D 为圆周上异于B 、C 的一点,AB 垂直于圆O 所在的平面,BE AC ⊥于点E ,BF AD ⊥于点F . (Ⅰ)求证:BF ⊥平面ACD ;(Ⅱ)若2AB BC ==,45CBD ∠=,求平面BEF 与平面所成锐角二面角的余弦值.20.(本小题满分12分)已知椭圆C 的方程是22221x y a b+=(0>>b a ),,且经过点. (Ⅰ)求椭圆C 的方程;(Ⅱ)圆O 的方程是2222x y a b +=+,过圆O 上任一点P 作椭圆C 的两条切线,若切线的斜率都存在,分别记为1k 、2k ,求12k k ⋅的值.C21.(本小题满分12分)已知函数()sin f x mx x =-,()cos 2sin g x ax x x =-(0a >). (Ⅰ)若过曲线()y f x =上任意相异两点的直线的斜率都大于0,求实数m 的最小值; (Ⅱ)若1m =,且对于任意[0,]2x π∈,都有不等式()()f x g x ≥成立,求实数a 的取值范围.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。
数学_2014年吉林省某校高考数学二模试卷(理科)(含答案)

2014年吉林省某校高考数学二模试卷(理科)一、选择题(每小题5分,共60分)1. 已知U =R ,M ={x|−l ≤x ≤2},N ={x|x ≤3},则(∁U M)∩N =( ) A {x|2≤x ≤3} B {x|2<x ≤3} C {x|x ≤−1, 或2≤x ≤3} D {x|x <−1, 或2<x ≤3}2. 复数z =2+i1+i 在复平面内对应的点在( )A 第一象限B 第二象限C 第三象限D 第四象限3. 在等差数列{a n }中,a 1+a 5=8,a 4=7,则a 5等于( ) A 3 B 7 C 10 D 114. 抛物线y 2=2px(p >0)的准线经过双曲线x 2−y 2=1的左焦点,则p =( ) A √22B √2C 2√2D 4√25. 将函数y =sin2x +cos2x 的图象向左平移π4个单位,所得图象的解析式是( ) A y =cos2x +sin2x B y =cos2x −sin2x C y =sin2x −cos2x D y =cosxsinx 6. 先后两次抛掷一枚骰子,在得到点数之和不大于6的条件下,先后出现的点数中有3的概率为( )A 16B 15C 13D 257. 一个棱锥的三视图如图所示,则它的体积为( )A 12 B 32 C 1 D 138. 执行如图所示的程序框图,则输出的结果是( )A 20B 30C 40D 509. 一个空间四边形ABCD 的四条边及对角线AC 的长均为√2,二面角D −AC −B 的余弦值为13,则下列论断正确的是( )A 空间四边形ABCD 的四个顶点在同一球面上且此球的表面积为3πB 空间四边形ABCD的四个顶点在同一球面上且此球的表面积为4π C 空间四边形ABCD 的四个顶点在同一球上且此球的表面积为3√3π D 不存在这样的球使得空间四边形ABCD 的四个顶点在此球面上10. 如图,在四面体OABC 中,AC =BC,|OA →|=3,|OB →|=1,则OC →⋅BA →=( )A 8B 6C 4D 311. 已知f(x)是定义在R 上的增函数,函数y =f(x −1)的图象关于点(1, 0)对称.若对任意的x ,y ∈R ,不等式f(x 2−6x +21)+f(y 2−8y)<0恒成立,则当x >3时,x 2+y 2的取值范围是( )A (3, 7)B (9, 25)C (13, 49)D (9, 49)12. 若2014=2a 1+2a 2+...+2a n ,其中a 1,a 2,…,a n 为两两不等的非负整数,令x =sin ∑a i n i=1,y =cos ∑a i n i=1,z =tan ∑a i ni=1,则x ,y ,z 的大小关系是( ) A x <y <z B z <x <y C x <z <y D y <z <x二、填空题(每小题5分,共20分)13. 将某班的60名学生编号为:01,02,…,60,采用系统抽样方法抽取一个容量为5的样本,且随机抽得的一个号码为04,则剩下的四个号码依次是________. 14. 设n =∫2#/DEL/#1#/DEL/#(3x 2−2)dx ,则(x +√x )n 的展开式中含x 2项的系数是________.15. 在△ABC 中,C =π3,AB =√3,AB 边上的高为43,则AC +BC =________.16. 若直角坐标平面内,A 、B 两点满足条件:①点A 、B 都在函数f(x)图象上;②点A 、B关于原点对称,则称点对(A 、B)是函数f(x)的一个“姐妹点对”(点对(A 、B)与点(B 、A)可看作同一个“姐妹对”).已知函数f(x)={x 2+2x 2e x (x <0)(x ≥0),则f(x)的“姐妹点对”有________个.三.解答题:(本大题共5小题,共60分)17. 已知α为锐角,且tanα=√2−1,函数f(x)=2xtan2a +sin(2a +π4),数列{a n }的首项a 1=1,a n+1=f(a n ). (1)求函数f(x)的表达式;(2)求数列{na n }的前n 项和S n .18. 如图,四棱锥A −BCDE 中,△ABC 是正三角形,四边形BCDE 是矩形,且平面ABC ⊥平面BCDE ,AB =2,AD =4. (1)若点G 是AE 的中点,求证:AC // 平面BDG ;(2)试问点F 在线段AB 上什么位置时,二面角B −CE −F 的余弦值为313√13.19. 某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的结果如下:(1)求表中a ,b 的值(2)若以上表频率作为概率,且每天的销售量相互独立, ①求5天中该种商品恰有2天销售量为1.5吨的概率;②已知每吨该商品的销售利润为2千元,X 表示该种商品两天销售利润的和(单位:千元),求X 的分布列和期望.20. 已知点F(0, 1),直线l:y =−1,P 为平面上的动点,过点P 作直线l 的垂线,垂足为Q ,且QP →⋅QF →=FP →⋅FQ →.(1)求动点P 的轨迹C 的方程;(2)已知圆M 过定点D(0, 2),圆心M 在轨迹C 上运动,且圆M 与x 轴交于A 、B 两点,设|DA|=l 1,|DB|=l 2,求l 1l 2+l2l 1的最大值.21. 已知函数f(x)=mxx 2+n (m, n ∈R)在x =1处取到极值2 (1)求f(x)的解析式;(2)设函数g(x)=ax −lnx .若对任意的x 1∈[12,2],总存在唯一的x 2∈[1e 2,1e ],使得g(x 2)=f(x 1),求实数a 的取值范围.选考题:(本小题满分10分)请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.22. 已知A 、B 、C 、D 为圆O 上的四点,直线DE 为圆O 的切线,AC // DE ,AC 与BD 相交于H 点.(Ⅰ)求证:BD 平分∠ABC ;(Ⅱ)若AB =4,AD =6,BD =8,求AH 的长.23. 已知某圆的极坐标方程为:ρ2−4√2ρcos(θ−π4)+6=0.(1)将极坐标方程化为直角坐标方程,并选择恰当的参数写出它的参数方程;(2)若点P(x, y)在该圆上,求x+y的最大值和最小值.24. 已知关于x的不等式|ax−1|+|ax−a|≥1(a>0).(1)当a=1时,解不等式;(2)若不等式的解集为R,求实数a的取值范围.2014年吉林省某校高考数学二模试卷(理科)答案1. D2. D3. C4. C5. B6. C7. A8. B9. A10. C11. C12. B13. 16、28、40、5214. 4015. √1116. 217. 解:(1)∵ tanα=√2−1,∴ tan2α=2tanα1−tan2α=√2−1)1−(√2−1)2=1,又α为锐角,∴ 2α=π4,∴ sin(2α+π4)=1,∴ f(x)=2x+1;(2)∵ a n+1=f(a n)=2a n+1,∴ a n+1+1=2(a n+1),∵ a1=1,∴ 数列{a n+1}是以2为首项,2为公比的等比数列,∴ a n+1=2⋅2n−1=2n,∴ a n=2n−1,∴ na n=n⋅2n−n,下面先求{n⋅2n}的前n项和T n:T n=1×2+2×22+3×23+...+(n−1)⋅2n−1+n⋅2n,2T n=1×22+2×23+...+(n−1)⋅2n+n⋅2n+1,两式相减得:−T n=2+22+23+...+2n−n⋅2n+1=2−2n+11−2−n ⋅2n+1=2n+1−2−n ⋅2n+1, ∴ T n =2+(n −1)⋅2n+1, ∴ S n =2+(n −1)⋅2n+1−(1+n)n 2.18. 解:(1)证明:连接CE 、BD ,设CE ∩BD =O ,连接OG , 由三角形的中位线定理可得:OG // AC , ∵ AC ⊄平面BDG ,OG ⊂平面BDG , ∴ AC // 平面BDG .(2)∵ 平面ABC ⊥平面BCDE ,DC ⊥BC , ∴ DC ⊥平面ABC ,∴ DC ⊥AC ,则△ACD 为直角三角形. ∵ △ABC 是正三角形,∴ 取BC 的中点M ,连结MO ,则MO // CD , ∴ MO ⊥面ABC ,以M 为坐标原点,以MB ,M0,MA 分别为x ,y ,z 轴,建立空间直角坐标系, ∵ AB =2,AD =4,∴ AM =√3,∴ B(1, 0, 0),C(−1, 0, 0),A(0, 0, √3),在Rt △ACD 中,CD =√AD 2−AC 2=√42−22=√12=2√3. ∴ BE =CD =2√3,即E(1, 2√3, 0) 则BA →=(−1,0,√3), ∵ 点F 在线段AB 上,∴ 设BF =xBA ,(0≤x ≤1) 则BF →=xBA →∴ F(1−x, 0, √3x),则CE →=(2,2√3,0),CF →=(2−x,0,√3x), 设面CEF 的法向量为n →=(a,b,c),则由{n →⋅CF →=0˙得,{2a +2√3b =0(2−x)a +√3xc =0,令a =√3,则b =−1,c =x−2x,即n →=(√3,−1,x−2x),平面BCE 的法向量为m →=(0,0,1), 二面角B −CE −F 的余弦值为|m →|⋅|n →|˙=3√1313,即|x−2x|√(√3)+1+(x−2x)=3√1313, ∴(x−2x)√4+(x−2x)2=3√1313,平方得(x−2x)24+(x−2x)2=913,解得:(x−2x)2=9,解得x =−1(舍去)或x =12.即F 是线段AB 的中点时,二面角B −CE −F 的余弦值为313√13.19. ∵ 100.2=50∴ a =2550=0.5,b =1550=0.3①依题意,随机选取一天,销售量为1.5吨的概率p =0.5 设5天中该种商品有X 天的销售量为1.5吨,则X ∼B(5, 0.5)P(X =2)=C 52×0.52×(1−0.5)3=0.3125 ②X 的可能取值为4,5,6,7,8,则 p(X =4)=0.22=0.04p(X =5)=2×0.2×0.5=0.2p(X =6)=0.52+2×0.2×0.3=0.37 p(X =7)=2×0.3×0.5=0.3 p(X =8)=0.32=0.09 所有X 的分布列为:EX =4×0.04+5×0.2+6×0.37+7×0.3+8×0.09=6.2. 20. (1)解:设P(x, y),则Q(x, −1), ∵ QP →⋅QF →=FP →⋅FQ →,∴ (0, y +1)⋅(−x, 2)=(x, y −1)⋅(x, −2). 即2(y +1)=x 2−2(y −1),即x 2=4y , 所以动点P 的轨迹C 的方程x 2=4y .(2)解:设圆M 的圆心坐标为M(a, b),则a 2=4b .① 圆M 的半径为|MD|=√a 2+(b −2)2.圆M 的方程为(x −a)2+(y −b)2=a 2+(b −2)2. 令y =0,则(x −a)2+b 2=a 2+(b −2)2, 整理得,x 2−2ax +4b −4=0.② 由①、②解得,x =a ±2.不妨设A(a −2, 0),B(a +2, 0),∴ l 1=√(a −2)2+4,l 2=√(a +2)2+4. ∴ l 1l 2+l2l 1=l 12+l 22l 1l 2=2√a 4+64=2√(a 2+8)2a 4+64=2√1+16a 2a 4+64,③当a ≠0时,由③得,l 1l 2+l 2l 1=2√1+16a 2+64a2≤2√1+162×8=2√2.当且仅当a =±2√2时,等号成立. 当a =0时,由③得,l1l 2+l 2l 1=2.故当a =±2√2时,l1l 2+l 2l 1的最大值为2√2.21. 解:(1)f′(x)=m(x 2+n)−2mx 2(x 2+n)2=m(n−x 2)(x 2+n)2f(x)在x =1处取到极值2,故f′(1)=0,f(1)=2即{mn−m (1+n)2=0m1+n=2,解得m =4,n =1,经检验,此时f(x)在x =1处取得极值.故f(x)=4xx 2+1(2)由(1)知f′(x)=4(1−x)(1+x)(x 2+1)2,故f(x)在(12,1)上单调递增,在(1, 2)上单调递减,由f(1)=2,f(2)=f(12)=85,故f(x)的值域为[85,2] 依题意g′(x)=a −1x =a(x−1a)x,记M =[1e 2,1e ],∵ x ∈M∴ e ≤1x ≤e 2(1)当a ≤e 时,g ′(x)≤0,g(x),依题意由{g(1e )≤85g(1e 2)≥2得0≤a ≤35e ,故此时0≤a ≤35e(2)当e <a ≤e 2时,1e>1a>1e 2当x ∈(1e2,1a)时,g′(x)<0,当x ∈(1a,1e)时,g′(x)>0.依题意由g(1a)≤85,得1−ln 1a≤85,即a ≤e 35.与a >e 矛盾(3)当a >e 2时,1a <1e 2,此时g′(x)>0,g(x).依题意得{a >e 2g(1e )≥2g(1e2≤85即{a >e 2a e +1≥2a e 2+2≤85此不等式组无解综上,所求a 取值范围为0<a ≤35e22. (1)∵ AC // DE ,直线DE 为圆O 的切线,∴ D 是弧AĈ的中点,即AD ̂=DC ̂ 又∠ABD ,∠DBC 与分别是两弧AD̂,DC ̂所对的圆周角,故有∠ABD =∠DBC , 所以BD 平分∠ABC(2)∵ 由图∠CAB =∠CDB 且∠ABD =∠DBC ∴ △ABH ∽△DBC ,∴ AHCD =ABBD 又AD̂=DC ̂ ∴ AD =DC ,∴AH AD=AB BD∵ AB =4,AD =6,BD =8 ∴ AH =323. 解:(1)ρ2−4√2ρcos(θ−π4)+6=0 ,即 ρ2−4√2( √22ρcosθ+√22ρsinθ )+6=0,即 x 2+y 2−4x −4y +6=0.配方为:(x −2)2+(y −2)2=2, 可得圆的参数方程为:{x =2+√2cosα,y =2+√2sinα.(2)圆的参数方程为 {x =2+√2cosα,y =2+√2sinα,∴ x +y =4+√2(sinα+cosα) =4+2sin(α+π4).由于−1≤sin(α+π4)≤1,∴ 2≤x +y ≤6,故x +y 的最大值为6,最小值为 2.24. 当a =1时,可得2|x −1|≥1,即|x −1|≥12,解得x ≥32x ≤12, ∴ 不等式的解集为(−∞,12]∪[32,+∞).∵ |ax −1|+|ax −a|≥|a −1|,不等式|ax −1|+|ax −a|≥1解集为R ,等价于|a −1|≥1.解得a ≥2,或a ≤0. 又∵ a >0,∴ a ≥2. ∴ 实数a 的取值范围为[2, +∞).。
黑龙江省哈三中2014届高三上学期第二次验收数学理试题

哈三中 2013-2014 学年度高三学年第二次验收考试数学试卷(理)考试说明:本试卷分第 I 卷(选择题)和第 II 卷(非选择题)两部分,满分 150 分,考试时间 120 分钟.(1)答题前,考生先将自己的姓名、准考证号码填写清楚;(2)选择题必须使用 2B 铅笔填涂,非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整,字迹清楚;(3)请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀. 第Ⅰ卷一、选择题(本题共有 12 小题,每小题 5 分, 共 60 分,在每小题给出的四个选项中, 只有一项是符合题目要求的.)1. 复数 z 满足 z(1 + i) = 1 - 2i ( i 为虚数单位),则复数 z 在复平面内所对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限2 xA. x | 0 x 2B.{x | 0 < x < 1} C. {x | 0 < x ≤ 1} D. {x | 0 < x ≤ 2} 3. 已知向量 a = (2,3), b = ( x,1) ,若 a ⊥ b ,则实数 x 的值为A. 3 2B. - 3 2C. 2 3D. - 234. 已知 A, B, C 三点共线,OC = a 1 OB + a 3 OA ,a 5 = 1,数列{a n }为等差数列,则a 6 =A.7 6B. 1C.3 2D.8 75. 若 cos α = -4 5 , α 是第二象限角,则 tan 2α =A.24 7B. - 24 7C.1 2 D. - 12数学试卷(理)第 1 页 共 4 页7. ∆ABC 中, BC = a , AC = b , a , b 是方程 x - 2 3x + 2 = 0 的两个根, C = 60︒,在数列 {a n }中, a n = 2n - 4λn ,若 {a n }为递增数列,则实数 λ 的取值范围为12. 已知函数 f ( x ) = ⎨6.已知向量 a , b ,若a =b = 1, | a - 2b |=3 ,则 a 与 b 的夹角为A.π6B.π3C.π 2D.2π32则 ∆ABC 的周长为A.6 + 2 3B.10 + 2 3C.6 + 2D. 10 + 28. 在等差数列 {a n }中,已知a 3 + a 5 + a 7 = 15,则 3a 4 + a 8 =A.14B.16C.18D. 209.2A. λ <32B. λ ≤ 1C. λ >32D. λ ≥ 110. 将函数 f (x ) = sin 2x - 3 cos 2x 的图象沿 x 轴向左平移 a 个单位 (a > 0) ,所得图象关于 y 轴对称,则 a 的最小值是A.π6B.π 3C.5π12 D.5π611. 给定下列命题:①在 ∆ABC 中, ∠A < ∠B 是 cos 2A > cos 2B 的充要条件; ② λ, μ为实数,若 λ a = μ b ,则 a 与 b 共线;③若向量a ,b 满足 a = b ,则 a = b 或 a = -b ;④ f (x ) =| sin x | + | cos x | ,则 f ( x ) 的最小正周期是 π其中真命题个数是 A.0 B.1 C.2 D.3⎧kx + 1, x ≤ 0 ⎩ln x , x > 0,则下列关于函数 y = f [ f (x )]的零点个数判断正确的是A.当 k > 0 时,有 3 个零点,当 k < 0 时,有 2 个零点B.当 k > 0 时,有 4 个零点,当 k < 0 时,有 2 个零点C.无论 k 为何值时,均有 2 个零点13. 函数 y = sin x + 2 cos x 的值域为, sin ) , b = (- 3,1) , f ( x) = a ⋅ b . (I )求 f ( x) 的最小正周期与单调减区间; D.无论 k 为何值时,均有 4 个零点第Ⅱ卷二、填空题(本题共 4 小题, 每小题 5 分)214. 设 O 是 ∆ABC 内部一点, + + = ,则 ∆ABC 和 ∆OBC 的面积之比为15. 设n P 1 + P 2 + P 3 + + P n为 n 个正数 P 1 , P 2 , P 3 , , P n 的“均倒数”.已知数列{a n }的前 n 项的“均倒数”为1 3n + 2,则1 a 1a2 1 a 2 a3 + +1a n a n +1= 16. 在平 行四 边形 ABCD 中 , AB = 2, AD = 1 , ∠BAD = 60︒ , 点 E, F 分 别 在线 段BD, AC 上,且 = λ = μ , λ + μ = 1,则 AE 的最小值为DECA三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(本小题满分 10 分)FB已知向量 a = (cosx2 x2.(II )求 f ( x) 在 [0,π ]上的最大值和最小值.18. (本小题满分 12 分)2a 2 =b 2 , a 5 = b 3 , a 14 = b 4 .*) , 数 列 {b n} 为 等 比 数 列 , 且已知函数 f (x) = log 2 (4 + 1) + kx (k∈ R) 是偶函数. (II )设函数 g ( x) = log 2 (2 - ) + log 2 a ,若函数 f ( x) 与 g (x) 的图象有且只有一 a n + ⎪⎪ , b n = n (Ⅱ)若对任意的 a ∈ (1 , 2 ) ,总存在 x 0, 1 ⎥ ,使不等式 f (x 0 ) > k (1- a 2 ) 成(I )求数列 {a n }和 {b n }的通项公式;(II )设数列 {c n }满足 c n =19. (本小题满分 12 分)a nb n,求数列 {c n }的前 n 项和 T n . 在 ∆ABC中 ,角A, B, C 的 对 边 分 别为 a, b, c ,且2b cos 2A +B 2- c cos B - b = - 2a cos A .(I )求 A ;(II )若a = 2 2 ,求 ∆ABC 面积的最大值.20. (本小题满分 12 分)x(I )求 k 的值;x43个交点,求 a 的取值范围.21. (本小题满分 12 分)若数列 {a n }和 {b n }有如下关系: a 1 = 2 , a n +1 =1 ⎛2 ⎝1 ⎫ a + 1(I )求证:数列 {log 3 b n }是等比数列;(II )当 n ≥ 2时,比较a n +1 - 1a n - 1 和110的大小.22. (本小题满分 12 分)已知函数 f ( x) = x 2 - ax + lnax +1 2. (a > 0)(Ⅰ)讨论函数 f ( x) 的单调性;⎡ 1 ⎣ 2⎤⎦立,求实数 k 的取值范围.。
2014年辽宁省沈阳市高三理科二模数学试卷

2014年辽宁省沈阳市高三理科二模数学试卷一、选择题(共12小题;共60分)1. 已知集合,集合,则A. B.C. D.2. 设复数(是虚数单位),则A. B. C. D.3. 下列命题中,真命题的是A. ,B. ,C. ,D. ,4. 已知在平行四边形中,,,对角线与相交于点,则A. B. C. D.5. 若,,成等比数列,则函数的图象与轴的交点个数为A. B. C. D. 或6. 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为粒,其中粒豆子落在该正方形的内切圆内,以此估计圆周率为A. B. C. D.7. 已知中心在坐标原点,焦点在坐标轴上的双曲线的渐近线方程为,则该双曲线的离心率为A. B. C. 或 D. 或8. 若表示不超过的最大整数,如,.执行如图所示的程序框图,则输出的值为A. B. C. D.9. 已知曲线的两条相邻的对称轴之间的距离为,且曲线关于点成中心对称,若,则A. B. C. D.10. 已知实数,满足若目标函数的最大值为,最小值为,则实数的取值范围为A. B. C. D.11. 四面体的四个顶点都在球的表面上,平面,是边长为的等边三角形.若,则球的表面积为A. B. C. D.12. 已知函数满足:定义域为;对任意的,有;③当时,,若函数则函数在区间上的零点的个数是A. B. C. D.二、填空题(共4小题;共20分)13. 如图,某几何体的主视图和俯视图都是矩形,左视图是等腰直角三角形,则该几何体的体积为______.14. 的二项展开式中的常数项为______(用数字作答).15. 函数的最小值为______.16. 已知抛物线的焦点为,的顶点都在抛物线上,且满足,则 ______.三、解答题(共8小题;共104分)17. 在中,角,,的对应边分别是,,满足.(1)求角的大小;(2)已知等差数列的公差不为零,若,且,,成等比数列,求的前项和.18. 为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是项基础设施类工程、项民生类工程和项产业建设类工程.现有来沈阳的名工人相互独立地从这个项目中任选一个项目参与建设.(1)求这人选择的项目所属类别互异的概率;(2)将此人中选择的项目属于基础设施类工程或产业建设类工程的人数记为,求的分布列和数学期望.19. 如图,为圆的直径,为圆周上异于,的一点,垂直于圆所在的平面,于点,于点.(1)求证:平面;(2)若,,求平面与平面所成锐角二面角的余弦值.20. 已知椭圆的方程式,离心率为,且经过点.(1)求椭圆的方程;(2)圆的方程是,过圆上任意一点作椭圆的两条切线,若切线的斜率都存在,分别记为,,求的值.21. 已知函数,.(1)若曲线上任意相异两点的直线的斜率都大于零,求实数的最小值;(2)若,且对任意,都有不等式成立,求实数的取值范围.22. 如图,内接圆,平分交圆于点,过点作圆的切线交直线于点.(1)求证:;(2)求证:.23. 在直角坐标平面内,以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,已知直线的参数方程为(为参数),圆的极坐标方程为.(1)将直线的参数方程化为普通方程,圆的极坐标方程化为直角坐标方程;(2)求圆上的点到直线的距离的最小值.24. 已知函数.(1)求不等式的解集;(2)若关于的不等式的解集非空,求实数的取值范围.答案第一部分1. C2. A3. D4. B5. A6. D7. C8. B9. C 10. A11. C 12. D第二部分13.14.15.16.第三部分17. (1)因为,所以,所以,因为,所以.(2)设的公差为,因为,且,,成等比数列,所以,且,所以,且,解得,所以,所以,所以18. (1)记第名工人选择的项目属于基础设施类、民生类和产业建设类分别为事件,,,.由题意知,,相互独立,,,相互独立,,,相互独立,且,,.他们选择的项目所属类别互不相同的概率.(2)记第名工人选择的项目属于基础工程或产业建设工程分别为事件,.,,相互独立,且,所以,即,所以的分布列是所以.19. (1)因为是圆的直径,所以,因为圆所在的平面,所以,且,所以平面,又因为平面,所以,又因为,且,所以平面.(2)如图,以为原点,建立空间直角坐标系,,,所以,,,,因为,所以,所以,所以点,设平面的法向量,所以即令,得,,所以,因为平面,所以平面的法向量为,所以,因为平面与平面所成二面角的平面角为锐角,所以平面与平面所成锐角二面角的余弦值为.20. (1)因为椭圆离心率为,且经过点,所以所以,所以椭圆的方程为.(2)设,过点的切线方程为,代入椭圆方程,可得,因为直线与椭圆相切,所以,所以,所以,因为点在圆上,所以,即,所以.21. (1)因为过曲线上任意相异两点的直线的斜率都大于,所以任取,且,则由,得.所以函数在上单调递增.所以恒成立,即,所以的最小值为.(2)因为,所以.因为,所以.对于任意的,令,则.(1)当,即时,,所以在上单调递增.所以,符合题意,所以.(2)当,即时,,,因为,所以,所以.所以在上单调递增,所以,即.所以.①当,即时,,所以在上为单调增函数,于是,符合题意.所以.②当,即时,存在,使得当时,有,此时在上为单调减函数,从而,不能使恒成立.综上所述,实数的取值范围为.22. (1)因为为圆的切线,所以,因为平分,所以,所以,因为,所以;(2)在和中,,,所以,所以,所以,因为平分,所以,所以.23. (1)直线的参数方程为(为参数),消去参数,得直线的普通方程为,,两边同乘以得,得的直角坐标方程为.(2)因为圆心为,所以点到直线的距离为,所以圆上的点到直线距离的最小值为.24. (1)原不等式为.当时,原不等式可化为,即;当时,原不等式可化为恒成立,即;当时,原不等式可化为,即,所以原不等式的解集为.(2)由函数,可得函数的最小值为.所以解得或.。
东北三省四市教研协作体2014届高三第二次模拟数学(理)试题(扫描版,答案文档版)

2014年数学二模答案(理科)1.B2.A3.A4.D5.D6. A7.C8.B9.A 10. A 11.C 12.B13. 2π14. -2 15. 3-6 16. ①②③17.解:(Ⅰ)由题意21=-+n n a a ,所以数列{}n a 为等差数列, 1 分n n na n n na S n -+=⨯-+=21122)1( 2 分729,306,124191614+=+=+=a S a S a S所以)729)(124()306(1121++=+a a a 解得11=a 4 分所以12-=n a n , 2n S n = 6 分(Ⅱ)由题意)156(2121562n n n n b n +=+=,*N n ∈ 7 分 令x x x x x f 156221)156(21)(⋅⋅≥+=,当且仅当x x 156=时取等 8 分当12=n 时,225)1215612(2112=+=b当13=n 时,225)1315613(2113=+=b 10 分所以12=n 或13=n 时,数列{}n b 的最小项是225。
12 分18.(1)设代表队共有n 人,则n 50165=,160=∴n 则季军队的男运动员人数为()203020303030160=++++-. …………2分 (2)ξ可以取的值为0,1,2 …………3分()()1061,10302512132523======C C C P C C P ξξ,()10122522===C C P ξ. …………5分所以ξ的分布列为…………6分8.0101210611030=⨯+⨯+⨯=ξE …………7分(3)试验的全部结果所构成的区域为()}{40,40,≤≤≤≤=Ωy x y x ,面积为1644=⨯=ΩS , …………8分 事件A 表示运动员获得奖品,所构成的区域为()⎭⎬⎫⎩⎨⎧≤≤≤≤≥=40,40,41,2y x x y y x A , …………9分 阴影面积为316341414342=⋅==⎰x dx x S 阴, …………11分所以()321631611=-=-=ΩS S A P 阴. …………12分19.(1)证明:取AD 中点O ,连接OG 、OE ,为等腰三角形ADE ∆ADOE ⊥∴……………1分ADE ,ABCD 平面平面又⊥AD ADE ABCD =平面平面 , AED OE 平面且⊂ABCD OE 平面⊥∴ ……………..3分CD EF AB //// , 且O 、G 分别是AD 、BC 的中点 EF OG EF ,OG ==∴3//且是平行四边形四边形OGFE ∴FG OE //∴ ……………..4分ABCD FG 平面⊥∴ . ……………..5分 (2)连接OB ,在602=∠==∆DAB ,AB ,AD ABD 中,是等边三角形ADB ∆∴,即AD OB ⊥.由(1)知,ABCD OE 平面⊥,分别以OA 、OB 、为轴轴轴、z 、y x 建立如图所示的空间直角坐标系,则()0,0,1A ,()0,3,0B ,C()0,0,1-D ,()1,0,0E ,利用2==及()0,32,3-C 、⎪⎪⎭⎫⎝⎛-1,233,23F , …………….6分 设平面BDF 的法向量()z y x n ,,=,则2323=++-=⋅z y x BF n03=--=⋅y x BD n ,令1=y ,则3-=x ,32-=z ,即()32,1,3--=4 ……………8分同理可求平面的BDE 法向量为()3,1,3-= ……………10分147,cos -< ……………11分14189的正弦值为二面角E BD F --∴. ……………12分20.解:(Ⅰ)如图,设221122(2)(2)A x x B x x ,,,,把22+=x y 代入22y x =得012=--x x . ……………1分由韦达定理得121=+x x . ……………2分∴21=M x , ……………3分N 点的坐标为)21,21(. ……………5分(Ⅱ)假设存在以为AB 直径的圆过点N .则有0=⋅把2y kx =+代入22y x =得2220x kx --=.由韦达定理得121212kx x x x +==-, . ……………6分∴1224N M x x k x x +===,∴N 点的坐标为248k k ⎛⎫ ⎪⎝⎭,. ……………7分22221122224848k k k k NA x x NB x x ⎛⎫⎛⎫=--=-- ⎪ ⎪⎝⎭⎝⎭,,,,则)82)(82()4)(4(22222121k x k x k x k x --+--=⋅222212124441616k k k k x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=--+-- ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=)]4)(4(41)[4)(4(2121k x k x k x k x +++-- 22313164k k ⎛⎫⎛⎫=---+ ⎪ ⎪⎝⎭⎝⎭=0 ……………8分 21016k --<,23304k ∴-+=,解得2=k . ……………9分则圆心M 点的坐标为(3,21) ……………10分 2122124)(1||x x x x k AB -++==555=⋅=R 2 ……………11分所以圆的方程为425)3()21(22=-+-y x ……………12分21. (1)=')(x h 211-++x e x , ……………1分令=)(x p 211-++x e x ,因为0≥x ,所以0)1(1)1()1(1)(222≥+-+=+-='x e x x e x p x x, ……………2分所以)(x p (即)(x h ')在),0[+∞上递增,所以0)0()(='≥'h x h ,所以)(x h 在),0[+∞上递增, ……………4分 所以1)0()(min ==h x h ……………5分 (2)设)(x g 的切点),(11y x ,)(x f 的切点),(22y x ,⎪⎩⎪⎨⎧==='111111)(x x e y x y e x g 解得⎪⎩⎪⎨⎧===e k e y x 111, ......7分所以⎪⎩⎪⎨⎧--===-=')1(ln 11)(2222222x a x y x y e a x x f ,∴2222)1(ln 1x x a x a x --=-,∴a x -=1ln 2,∴ae x -=12代入e a x 112=-得01=--ae e a ,令1)(--=ae e a p a e e a p a -=')(,)(a p 在)1,(-∞递减,在),1(+∞上递增 ......9分当)1,(-∞∈a 时,因为0)0(=p ,所以0=a ......10分当),1(+∞∈a 时,01)1(<-=p ,012)2(2>--=e e p ,所以21<<a , 综上0=a 或21<<a ......12分22.AC 是切线∴EACB ∠=∠又 DC 是ACB ∠的平分线,DCB ACD ∠=∠,AFD ADF ACD EAC DCB B ∠=∠∴∠+∠=∠+∠, ......3分BE 是圆O 的直径,︒=∠∴90BAE︒=∠45ADF ......5分(2)EAC ACB B AC AB ∠=∠=∠∴=,由(1)得︒=∠=∠+∠+∠=∠+∠∴︒=∠903,90B EAC ACE B AEB B BAE︒=∠∴30B......7分ACE ACB ACB EAC B ∆∴∠=∠∠=∠,,∽BCA ∆, ......9分3330tan =︒==AB AE BC AC ......10分23. (1)曲线C 的直角坐标方程为1422=+y x ......2分 所以参数方程为⎩⎨⎧==ααsin cos 2y x ,(α为参数) ......5分(2)2121ρρ=∆AOB S ,)cos 4sin )(sin 4cos (122222221θθθθρρ++= ......7分 4cos sin 16sin cos 174422θθθθ++=4sin cos 2)cos (sin 16sin cos 172222222θθθθθθ-++==]6425,41[41642sin 92∈+θ, ......9分当且仅当12sin =θ时即4πθ=时,54的最小值为AOB S ∆ ......10分24. 解:(Ⅰ)由题意0)3(416≥-+-a a43≤-+∴a a 1分当3≥a 时,43≤-+a a ,解得273≤≤a当30<<a 时,43≤-+a a ,解得30<<a当0≤a 时,43≤-+-a a ,解得021≤≤-a 4 分综上:}2721|{≤≤-=a a A 5 分(Ⅱ)由题意⎥⎦⎤⎢⎣⎡-∈27,21a令122)(2<-+-=t a t a g 恒成立 6 分)(a g 在⎥⎦⎤⎢⎣⎡-∈27,21a 单调递减)21(<-∴g 8 分 0122<-+∴t t33<<-∴t 10 分。
2014年东北三省三校高三第二次联合模拟考试理科综合试题及答案

2014年东北三省三校高三第二次联合模拟考试理科综合试题及答案可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 K 39 Mn 55 Fe 56一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1.下列有关生物体组成元素和化合物的叙述,正确的是 A.严重缺铁的人容易产生乳酸中毒B.一个DNA 分子彻底水解后能得到4种脱氧核苷酸C.蛋白质和DNA 分子的多样性都与它们的空间结构密切相关D.淀粉、糖原、纤维素和麦芽糖彻底水解后,得到的产物是不同的 2.下列关于实验条件或现象的描述,完全正确的是 A.使用双缩脲试剂鉴定蛋白质时,需要水浴加热B.纸层析法分离绿叶中色素时,滤纸条自上而下的第三条色素带最宽,颜色为蓝绿色C.用溴麝香草酚蓝水溶液检测CO 2时,颜色变化为蓝色→黄色→绿色D.观察细胞中的染色体数目,实验材料为人的口腔上皮细胞 3.据此,下列推测错误的是A.该病毒的遗传物质不是双链DNAB.该病毒的遗传信息流动过程不遵循中心法则C.以该病毒DNA 为模板,复制出的DNA 不是子代病毒的遗传物质D.该病毒DNA 的突变频率较高4.下图一是真核细胞DNA 复制过程的模式图,图二是大肠杆菌DNA 复制过程模式图,箭头表示复制方向。
对此描述错误的是A.真核细胞DNA 有多个复制起点,而大肠杆菌只有一个B.两者均具有双向复制的特点C.真核细胞DNA 复制时,在起点处不都是同时开始的D.两者的遗传物质均是环状的 5.下列关于下丘脑的叙述正确的是A.下丘脑通过释放促甲状腺激素来促进垂体分泌相关激素B.下丘脑控制生物节律,同时呼吸中枢也位于下丘脑C.出现尿量异常增大的可能原因是下丘脑或垂体受损D.下丘脑体温调节中枢可感受到寒冷或炎热6.如图是人类睾丸横切片示意图,其中①→⑤为精子发生过程中各阶段的细胞,下列有关说法正确的是 A.①为精原细胞,它只能进行减数分裂B.②为初级精母细胞,②所指细胞内有染色体92条C.③为次级精母细胞,细胞内可能有2条X 染色体D.同一精原细胞产生的④或⑤所含的遗传信息和染色体数完全相同图一 ① ②③④⑤图二 图二8.下列关于氯水的说法正确的是A.向氯水中通入少量二氧化硫,氯水的漂白性增强B.氯水中加入NaCl固体,对溶液的pH无影响C.常温下,pH=2的氯水中:c(Cl-)+c(ClO-)+c(OH-)=0.01mol/LD.向氯水中滴加少量NaHCO3溶液的离子反应方程式为:Cl2+2HCO3-2CO2↑+Cl-+ClO-+H2O9.相对分子质量为100的有机物A能与钠反应,且完全燃烧只生成CO2和H2O。
2014~2015学年度第二学期高三年级总复习质量检测(二)数学试卷(理工类)附答案

2014~2015学年度第二学期高三年级总复习质量检测(二)数学试卷(理工类) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至9页.祝各位考生考试顺利!第 Ⅰ 卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂在答题卡上;2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.3.本卷共8小题,每小题5分,共40分. 参考公式:·如果事件A ,B 互斥,那么 ·如果事件A ,B 相互独立,那么P (A ∪B )=P (A )+P (B ). P (AB )=P (A )•P (B ).·棱柱的体积公式V 柱体=Sh , ·球的体积公式V 球=34πR 3,其中S 表示棱柱的底面积, 其中R 表示球的半径. h 表示棱柱的高.一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设i 是虚数单位,则复数ii65-=( ). (A )6–5i (B )6+5i (C )–6+5i (D )–6–5i (2)已知命题p :x 1,x 2∈R ,(f (x 2)–f (x 1))(x 2–x 1)≥0,则⌝p 是( ).(A )x 1,x 2∈R ,(f (x 2)–f (x 1))(x 2–x 1)≤0 (B )x 1,x 2∈R ,(f (x 2)–f (x 1))(x 2–x 1)≤0 (C )x 1,x 2∈R ,(f (x 2)–f (x 1))(x 2–x 1)<0 (D )x 1,x 2∈R ,(f (x 2)–f (x 1))(x 2–x 1)<0(3)某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为( ).(A )10 (B )11(C )12(D )13(4)如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( ).(A )k <132? (B )k <70? (C )k <64? (D )k <63?(5)已知双曲线C :22x a –22y b=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( ).(A )220x –25y =1 (B )25x –220y =1(C )280x –220y =1 (D )220x –280y =1(6)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,已知8b=5c ,C=2B ,则cos C=( ). (A )725 (B )725- (C )725± (D )2425(7)由曲线y=x 2,y=x 围成的封闭图形的面积为( ). (A )61 (B )31(C )32(D )1(8)在△ABC 中,若|AB +|=|AB –|,AB=2,AC=1,E ,F 为BC 边的三等分点,则AE •AF =( ).(A )98 (B )910(C )925(D )926南开区2014~2015学年度第二学期高三年级总复习质量检测(二)答 题 纸(理工类)第 Ⅱ 卷注意事项:1.用黑色墨水的钢笔或签字笔答题; 2.本卷共12小题,共110分.二、填空题:本大题共6个小题,每小题5分,共30分.请将答案填在题中横线上。
2014届XXX等XXX高三第二次联合模拟考试理科数学试题(含答案解析)

2014届XXX等XXX高三第二次联合模拟考试理科数学试题(含答案解析)XXX2014年高三第二次联合模拟考试(XXX、XXX、XXX)数学理试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.若$U=\{1,2,3,4,5,6,7,8\}$,$A=\{1,2,3\}$,$B=\{5,6,7\}$,则$(C\cup A)\cap(C\cup B)$=A。
{4,8} B。
{2,4,6,8} C。
{1,3,5,7} D。
{1,2,3,5,6,7}2.已知复数$z=-\frac{1}{3}+i$,则$z+|z|$=A。
$-\frac{13}{22}-i$ B。
$-\frac{13}{22}+i$ C。
$\frac{3}{22}+i$ D。
$\frac{4}{22}-i$3.设随机变量$\xi$服从正态分布$N(2,9)$,若$P(\xi>c)=P(\xi<c-2)$,则$c$的值是A。
1 B。
2 C。
3 D。
44.已知$p:x\geq k$,$q:\frac{x+1}{3}<1$,如果$p$是$q$的充分不必要条件,则实数$k$的取值范围是A。
$(2,+\infty)$ B。
$(2,+\infty)$ C。
$[1,+\infty)$ D。
$(-\infty,-1]$5.已知$\triangle ABC$的内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$,且$\frac{c-b\sin A}{c\sin C+\sin B}$,则$\angle B=$A。
$\frac{\pi}{6}$ B。
$\frac{\pi}{4}$ C。
$\frac{\pi}{3}$ D。
$\frac{3\pi}{4}$6.已知函数$f(x)=\ln(x+1)$的值域为$\{y|y\leq 1\}$,则满足这样条件的函数的个数为A。
2014届高三上学期第二次联考理科数学试题含答案

2014届高三第二次联考理科数学试题(测试时间:120分钟 卷面总分:150分)一.选择题(每小题5分,共50分)1.设集合]}5,5[,sin 2|{-∈==x x y y M ,}lg |{)1(2-==x y x N ,则=N M ( )A . }51|{≤<x xB . }01|{≤<-x xC . }02|{≤≤-x xD . }21|{≤<x x 2.设5.03=a ,35log =b ,3cos =c ,则( )A .c b a <<B . b a c <<C .a b c <<D .a c b << 3.函数),(4sin )(322R b a bx x a x f ∈++=,若2013)20141(lg=f ,则=)(lg 2014f ( )A .2018B .-2009C .2013D .-2013 4.要得到函数)32cos(π+=x y 的图像,只需将函数x x y 2cos 232sin 21+=的图像( )A .向左平移4π B .向左平移8π C .向右平移2π D .向右平移3π5.在等差数列}{n a 中,首项a 1=0,公差d ≠0,若7321a a a a a k ++++= ,则k=( )A .22B .23C .24D .256.设R y x ∈,,向量)1,(x a =,),1(y b =,)4,2(-=c ,且c a ⊥,c b //,则=+||b a ( )A .5B .10C .52D .107.已知m 和n 是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m ⊥β的是( )A .α⊥β且α⊂mB .α⊥β且α//mC .n m //且n ⊥βD .m ⊥n 且βα//8.在ABC ∆中,若)sin()cos(21)sin(C A C B B A +++=-,则ABC ∆的形状一定是( )A .等边三角形B .不含60°的等腰三角形C .钝角三角形D .直角三角形第13题第14题9.定义域为R 的连续函数)(x f ,对任意x 都有)2()2(x f x f -=+,且其导函数)(x f '满足0)()2(>'-x f x ,则当42<<a 时,有( )A .)(log )2()2(2a a f f f <<B .)(log )2()2(2aa f f f << C .)2()2()(log 2f f f a a << D .)2()(log )2(2a a f f f <<10.已知函数,1log )10(sin )(2014⎪⎩⎪⎨⎧>≤≤=x x x x f xπ若a 、b 、c 互不相等,且)()()(c f b f a f ==,则a +b +c 的取值范围是( )A .(1,2014)B .(1,2015)C .(2,2015)D .[2,2015] 二.填空题(每小题5分,共25分)11.若x x x x f ln 42)(2--=,则0)(>'x f 的解集为 。
东北三省三校2014届高三第二次联合模拟考试 数学文 Word版含答案

东北三省三校2014年高三第二次联合模拟考试(哈师大附中、东北师大附中、辽宁实验中学)数学文试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 若{1,2,3,4,5,6,7,8},{1,2,3},{5,6,7}U A B ===,则()()U U C A C B = A. {4,8}B. {2,4,6,8}C. {1,3,5,7}D. {1,2,3,5,6,7}2. 已知复数12z =-+,则||z z +=A. 122-- B. 122-+ C.122i + D.122- 3. 已知数列{}n a 满足1220,1n n a a a ++==,则数列{}n a 的前10项和10S 为 A.104(21)3- B.104(21)3+ C.104(21)3-- D.104(21)3-+ 4. 已知1sin cos 3αα+=,则2sin ()4πα-=A.118B.1718C.89D.95. 已知:3:,:11p x k q x ≥<+,如果p 是q 的充分不必要条件,则k 的取值范围是 A. [2,)+∞B. (2,)+∞C. [1,)+∞D. (,1]-∞-6. 已知△ABC 的内角A ,B ,C 的对边分别为,,a b c ,若1cos ,sin 3sin 3A CB ==,且ABC S ∆b =A. 1B.C. D. 37. 已知△ABC 中,||10,16,BC AB AC D =⋅=- 为边BC 的中点,则||AD等于A. 6B. 5C. 4D. 38. 在某次测量中得到的A 样本数据如下:42,43,46,52,42,50,若B 样本数据恰好是A 样本数据每个都减5后所得数据,则A 、B 两样本的下列数字特征对应相同的是A. 平均数B. 标准差C. 众数D. 中位数9. 已知某算法的流程图如图所示,若输入7,6x y ==,则输出的有序数对为A. (13,14)B. (12,13)C. (14,13)D. (13,12)10. 将函数()2sin(2)4h x x π=+的图象向右平移4π个单位,再向上平移2个单位,得到函数()f x 的图象,则函数()f x 的图象与函数()h x 的图象A. 关于直线0x =对称B. 关于直线1x =对称C. 关于点(1,0)对称D. 关于点(0,1)对称11. 已知双曲线22221(0,0)x y a b a b-=>>的焦点1(,0)F c -、2(,0)F c (0)c >,过2F 的直线l 交双曲线于A ,D 两点,交渐近线于B ,C 两点。
【恒心】(2014哈三中二模)黑龙江省哈三中2014届高三下学期第二次高考模拟考试数学(理科)试题及参考答案

哈尔滨市第三中学二模考试数学(理)参考答案1-12 CDBBC,BCCBD,BA 13-16 6- 359 83 n109⨯17题(I )3)62sin(2)(+-=πx x f ………3分最大值为32+,x 集合为⎭⎬⎫⎩⎨⎧∈+=Z k k x x ,3ππ………6分 (II )⎥⎦⎤⎢⎣⎡-∈-65,662πππx ,若有两个零点,则[)32,31++∈m ………12分 18题(I )无论点F 运动到何处时,总有AE BF ⊥,则⊥AE 平面BCE ,………6分 所以平面⊥ADE 平面BCE(II )如图建立直角坐标系,)0,1,0(-A ,)2,1,0(-D ,)2,1,0(C ,)0,0,1(E , )0,2,0(=DC ,)2,1,1(--=CE ,)0,1,1(=AE平面EDC 的法向量为)1,0,2(=n ………..8分 平面EAC 的法向量为)1,1,1(-=m ………..10分515,cos >=<n m ………..12分 19题 (I )804800(100160)8000(160200)X X Y X -≤≤⎧=⎨≤≤⎩ ………..4分(II )120,(120)0.9X P X ≥∴≥= ………..6分 (III )根据题意得 获得利润Y 的分布列是 Y 4000 5600 7200 8000 P0.10.20.30.4所以数学期望为()6880E Y =(元)………..12分 20题ABCED FO x yz(I )设椭圆上点00(,)P x y 且点(,),(,)M m n N m n --在椭圆上22220022221,1,x y m n a b a b∴+=+=做差得22222220002222200,x m y n y n b a b x m a ---+=∴=-- 22222000222000144PM PNy n y n y n b k k a b x m x m x m a -+-∴⋅=⋅==-=-∴=-+- 又(),0F c 在直线230x y --=上,令0y =,得3c =,所以椭圆方程为2214x y +=…..4分 (II )21=y ()22222141612014y kx k x kx x y =+⎧⎪⇒+++=⎨+=⎪⎩ 1222122163140,,12414k x x k k x x k ⎧+=-⎪⎪+∆>∴>⎨⎪⋅=⎪+⎩取直线2y x =+与椭圆2214x y +=交于两点()64,,T 2,055S ⎛⎫-- ⎪⎝⎭直线1211:1,:162B S y x B T y x =+=--,两条直线的交点为113,2Q ⎛⎫- ⎪⎝⎭取直线2y x =-+与椭圆2214x y +=交于两点()64,,T 2,055S ⎛⎫⎪⎝⎭直线1211:1,:162B S y x B T y x =-+=-,两条直线的交点为213,2Q ⎛⎫⎪⎝⎭若交点在一条直线上则此直线只能为1:2l y = 验证对任意的33,,22k ⎛⎫⎛⎫∈-∞-+∞ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,直线1B S 与直线2B T 的交点Q 都在定直线1:2l y =上,设直线直线1B S 与直线1:2l y =交点为()000,Q x y ,直线2B T 与直线1:2l y =交点为()''000',Q x y ,设点()()1122,,T ,S x y x y 直线12121211:y 1,:1y y B S x B T y x x x -+=+=- 1111011:y 111,21212y B S x x x Q y y -⎧=+⎪⎛⎫⎪⇒⋅⎨ ⎪-⎝⎭⎪=⎪⎩;2121021:y 131',21212y B S x x Q y y +⎧=-⎪⎛⎫⎪⇒⋅⎨ ⎪+⎝⎭⎪=⎪⎩ ()()()()()22121200212112164343111414'0211211k k kx x x x k k x x y y y y -⋅+⋅++++-=⋅=⋅=+-+- 所以点()000,Q x y 与()''000',Q x y 重合,所以交点在直线1:2l y =上……12分 21题 解:(I )x e a ax x f ⋅+-=)2()(,xe ax xf ⋅+=)2()(',……………………1分当0≥a 时)('x f 在[]2,0上恒正,最大值为2)2()2(e a f += ……………………2分 当0<a 时,令0)('=x f ,得ax 2-= 所以当01<≤-a 时,仍有)(x f 在[]2,0上为增函数,最大值为2)2()2(e a f +=当1-<a 时,)(x f 在⎥⎦⎤⎢⎣⎡-a 2,0上为增函数,在⎥⎦⎤⎢⎣⎡-2,2a 上为减函数 最大值为=-)2(a f a ae 2-- 综上有,⎪⎩⎪⎨⎧-<--≥+=-1,1,)2()(22max a aea e a x f a ……………………6分 (II )3013)(22--=ax x a x g =)15)(2(-+ax ax所以只需要152->ax e x 即可,记=)(x h 152+-ax e x ,则=)('x h a e x -2故)(x h 在)2ln ,0(a 减,),2(ln +∞a 增,则152ln )(m in +-=a a a x h记152ln )(+-=x x x x k ,则2ln )('x x k -= 故)(x k 在)2,0(增,),2(+∞减在),2(+∞上取22e ,有0215)2(22>-=e e k 又0)215ln2(15)15(<-=k ,故存在0x ()15,22e ∈使0)(0=x k 而22e )15,14(∈,所以当14=a 时可保证0)(m in >x h ,有)()(2'x g x f >恒成立 当15=a 时0)(m in <x h ,不能有)()(2'x g x f >恒成立 所以a 所能取到的最大正整数为1422题(I )因为PB PE ,分别是⊙2O 割线,所以PB PD PE PA ⋅=⋅① 又PB PA ,分别是⊙1O 的切线和割线,所以PB PC PA ⋅=2② 由①②得PC PE PD PA ∙=∙ ………5分(II )连接DE AC ,,设DE 与AB 相交于点F ,因为BC 是⊙1O 的直径,所以︒=∠90CAB ,所以AC 是⊙2O 的切线,由(1)得DE AC //,所以DE AB ⊥,所以AE AD = ………10分 23解(I ))4cos(22πθρ-= ………5分(II )2=a 或23=a . ………10分24(I )⎩⎨⎧==∴⎩⎨⎧=+-=-∴≤≤-+≤≤-∴≤-32,5151,m a m a m a x m a x m a m a x ………5分(II )].22,2,0,2202,20,20,2222+∞-∴∴-≥+-<+≤≤∴≥+-<≤∴<≤≥+-≥≥+-∴=t x t x x t x x t x x t x t x x xt x a 解集为(成立时当成立时当舍去时,当 ………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【恒心】东北三省三校2014年高三第二次联合模拟考试数学(理科)参考答案【考前绝密】13.22333(1)124n n n +++⋅⋅⋅+= 14.315.23 16.①②④17.(Ⅰ)解:当1=n 时,111151,4=+∴=-a S a ………2分 又1151,51++=+=+ n n n n a S a S 115,n n n a a a ++∴-= ………4分114n n a a +=-即∴数列{}n a 是首项为114=-a ,公比为14=-q 的等比数列,∴1()4=-nn a ………6分(Ⅱ)n b nn -=-=)41(log 4, ………8分所以211111(2)22n n b b n n n n +⎛⎫==- ⎪++⎝⎭………10分 1111111111(1)()()1232422212n T n n n n ⎡⎤⎡⎤=-+-++-=+--⎢⎥⎢⎥+++⎣⎦⎣⎦………12分 18.(Ⅰ)解:第三组的频率是0.150×2=0.3;第四组的频率是0.100×2=0.2;第五组的频率是0.050×2=0.1 ………3分(Ⅱ)①由题意可知,在分层抽样的过程中第三组应抽到6×0.5=3个,而第三组共有100×0.3=30个,所以甲乙两产品同时被选中的概率为1283301145C P C == ………7分②第四组共有X 个产品被购买,所以X 的取值为0,1,21233266(0)15C C P X C +===;111322268(1)15C C C P X C +===;22261(2)15C P X C ===; 所以X 的分布列为01228151515XP………10分 812215153EX =+⨯= ………12分19.(Ⅰ)证明:连结MO1111////A M MA MO AC AO OC MO BMD AC BMD AC BMD =⎫⎫⇒⎬⎪=⎭⎪⎪⊂⇒⎬⎪⊄⎪⎪⎭平面平面平面 ………3分(Ⅱ)11BD AA BD AC BD A AC ⊥⊥⊥,得面于是1BD A O ⊥AC BD O ⋂=1111116022cos 60ABCD BAD AO AC AB AA AO AC AO ABCD A AC AO BD ⎫⎫⎫⎪⎪∠=⇒=⎬⎪⎪⎪⎪=⎭⎪⎪⎪⎪=⇒⊥⎬⎪⇒⊥⎬⎪∠=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪⊥⎪⎭平面 ………7分yxz(Ⅲ)如图建立直角坐标系,1(0,0,3)((0,1,0)(0,1,0)A A C B D -111((AC AC C ==-⇒-33()()2222M MB =--1(0,2,0)(1,3)DB BC ==--设平面1BC D 的法向量为(,,)n x y z =11200300y n DB n DB n y z n BC n BC ⎧⎧=⎧⊥⋅=⎪⎪⎪⇒⇒⇒=⎨⎨⎨-+=⊥⋅=⎪⎪⎪⎩⎩⎩………9分cos ,BM n <>= ………11分所以,直线BM 与平面1BC D………12分 20.解:(Ⅰ)设(,)P x y2(1)18y x y =++⇒= ………4分(Ⅱ)设直线BC :y kx b =+,1122(,),(,)B x y C x y将直线BC 代入到28x y =中得2880x kx b --=,所以12128,8x x k x x b +==-………5分又因为1122(4,2),(4,2)AB x y AC x y =--=--所以12121212221212(4)(4)(2)(2)(4)(4)(2)(2)(1)[(2)4]()(2)160AB AC x x y y x x kx b kx b k x x k b x x b ⋅=--+--=--++-+-=++--++-+=2222228(1)8[(2)4](2)160121632200(6)16(1)0b k k k b b b b k k b k ⇔-++--+-+=⇔---+=⇔--+=………8分410b k ⇒=+或42b k ⇒=-+ ………10分所以恒过定点(4,10)- ………12分21.解(Ⅰ)()()()()22'2222122()11a x x ax b ax bx af x xx+-++-==-++令'2()020f x ax bx a =⇒+-=224()0b a ∆=+> ………2分'()0f x ∴=有两实根不妨记为,αβ所以,()f x 有两个极值点 ,一个极大值点一个极小值点 ………4分(Ⅱ)220ax bx a +-=,由韦达定理得2baαβ+=-()()()()()2222110200110f a b a b f a b ααααβαβαβαββββ=-⎫⎧+++=⎪⇒⇒-+++=⇒+-=⎬⎨=--+=⎪⎩⎭ ………6分00,1,1b αβαβ∴+=⇒==-=,所以2a = ………7分(Ⅲ)因为22()01xxe g x e =>+,所以0m ≥ ………8分 又因为当0x =时,不等式恒成立所以,原问题22x x e e m x -+-⇔≤对一切()(),00,x ∈-∞+∞ 恒成立法一、设22()x x e e u x x -+-=(()(),00,x ∈-∞+∞ )()()()()2'432222()xx x x xx x x e e x x e e e e x e e u x x x ------+---+-==设()()()22x xx x h x e ex e e --=--+-,()()'()x x x x h x e e x e e --=+--,()''()x x h x e e x -=- 当0x >时,x xe e->,所以''()0h x >,当0x <时,xxe e-<,所以''()0h x >,所以'()h x 在R 上单调递增,又因为'(0)0h =所以当0x >时, '()0h x <,当0x <时, '()0h x >所以()h x 在(),0-∞上递减,()0,+∞递增,所以()(0)0h x h >= ………10分所以当0x >时, '()0u x <,当0x <时, '()0u x >所以()u x 在(),0-∞上递减,()0,+∞递增,所以0()lim ()1x h x h x →>=所以01m ≤≤ ………12分法二不妨设0x >()2()2x x h x e e mx -=+--()'()2x x h x e e mx -=--,()''()2x x h x e e m -=+-当1m ≤时,()22x xe em -+≥≥,''()0h x ≥,所以'()h x 在()0,+∞上单调递增,''()(0)0h x h >=所以()h x 在()0,+∞上单调递增, ()(0)0h x h >=,所以当1m ≤时成立………10分当1m >时''()0h x =得0ln(ln(x m x m ==+令当()x 0∈0,x 时''()0h x ≤所以'()h x 在()00,x 上单调递减,''()(0)0h x h <=所以()h x 在()00,x 上单调递减,()(0)0h x h <=,与条件矛盾,同理0x <时亦如此综上01m ≤≤ ……… 12分22.(Ⅰ)2//AB CD PAB AQCAQC ACB ACB CQAPA O PAB ACB AQ O QAC CBA AC ABAC AB CQ CQ AC⇒∠=∠⎫⎫⇒∠=∠⎬⎪⇒⇒∠=∠⎬⎭⎪⇒∠=∠⎭⇒=⇒=⋅ 为切线为切线 ………5分(Ⅱ)//113622,AB CD BP AP AB AP PC PQ QC QC PC AQ BP AB ⎫⎫⎪⎪⇒===⎬⎪=⇒==⎬⎪⎭⎪⎪==⎭ AP 为O切线212AP PB PC QA ⇒=⋅=⇒=又因为AQ 为O切线2AQ QC QD QD ⇒=⋅⇒=………10分 23.解:(Ⅰ)221:22C x y +=,4l x += ………5分 (Ⅱ)设),sin Q θθ,则点Q 到直线l 的距离d ==≥ ………8分 当且仅当242k ππθπ+=+,即24k πθπ=+(k Z ∈)时取等 ………10分24.解:(Ⅰ)由柯西不等式得,2222222()(111)()3a b c a b c ++≤++++=∴a b c ≤++ 所以a b c ++的取值范围是[ ………5分(Ⅱ)同理,2222222()[111]()3a b c a b c -+≤+-+++=() ………7分 若不等式2|1|1()x x a b c -++≥-+对一切实数,,a b c 恒成立, 则311≥++-x x ,解集为33(,][,)22-∞-⋃+∞ ………10分。
