热力学一般关系(热学高等数学偏微分)word版本
热力学一般关系

热力学一般关系本章提要及安排本章提要:1.工质的平衡热力性质是指工质状态参数间的函数关系,特别以可测参数为独立变量的热力学能、焓、熵函数在工程应用中尤为重要。
2.对热力学状态函数的研究通常从它们的偏微商着手。
在常用状态函数的偏微商中,有的是可以通过实验测定的,常将它们定义为各种热系数;有的则不能用实验的方法得出。
3.工质在准平衡变化中的热力学基本定律表达式同时也表达了热力学状态函数之间的基本关系,又称基本热力学关系式。
通过勒让德变换,基本热力学关系可以用不同的组合参数表达。
基本热力学关系的一阶偏微商和二阶混合偏微商给出状态函数偏微商之间的一般关系。
当然,与热力学基本定律一样这些一般关系对任何工质都是适用的。
4.按照基本热力学关系,可以用可测的状态参数和热系数来表达不能通过实验直接得出的偏微商,从而将各常用状态函数的全微分式用可测的参数及免系数表达出来。
这样,就为在实验测定数据的基础上得出工质的状态函数开辟了道路。
5.在工质热力性质研究中,并非所有热系数都是必需沤过实验测定的,应用热系数间的一般关系可以由少虽测得的热系数得到所需的其它热系数。
这样,可以大大减少研究中的实验工作量.同时减小由于有限的实验精确度带来的误差。
6.依据本章所导出的一般关系式,应用所讲述的推导方法,还可导得工程中需用的各种函数关系。
7.本章所导出的一般关系式只适用于简单可压缩系统。
本章要求:1.了解热力学一般关系的内容及其在工质热力性质研究中的地位和作用;2.掌握导出热力学一般关系的思路和推导方法;3.熟悉简单可压缩工质基本的和常用的热力学一般关系。
学习建议:本章学习时间建议共2学时:1.常用状态函数的偏微商;基本热力学关系; 1学时2.热力学能、焓和熵的微分式;热系数之间的一般关系; 1学时4.1 常用状态函数的偏微商本节知识点:状态方程的偏微商热力学能函数的偏微商焓函数的偏微商熵函数的偏微商本节参考图片:麦克斯韦汤姆逊汤姆逊实验本节疑问解答:思考题4.1.1 思考题4.1.2 思考题4.1.3本节基本概念:定温压缩系数压力的温度系数绝热压缩系数比定容热容比定压热容绝热节流系数工程中常用的状态函数有状态方程 F(p ,v ,T )=0,和以可测参数为独立变量的热力学能、焓、熵函数,通常热力学能函数u(T ,v ),焓函数h(T ,p),和熵函数s(T ,v),s(T ,p)的导得较为方便。
热力学基本关系式

)S
(V S
)
p
(Sp)T (VT)p
第17页,本讲稿共62页
4.7热力学关系式的应用
18
4.7.1材料热力学中一些常见的定义公式
U T
V
CV
H T
P
CP
CI
T S T I
S C p T p T
S CV T V T
恒压膨胀 V 系 V 1数 V TP
恒容压力 系 1数 P
U T p p V T T V
对理想气体而言:
U VT
Tp TV
pTTnVRTV
p
TnRppp0 V
由U=U(T,V),已证明理想气体的热力学能在定温下与 体积无关,所以U只是温度的函数。
第27页,本讲稿共62页
28
4.7.6理想气体的内能和焓
同理:
H p
T
T V T
p
V
对应系数关系式讲的是特性函数与其某一特征变
量的偏微商关系,脚标为该特性函数的另一特征变量 ,结果等于偏微特征变量的共轭变量。
U H T S V S p
U F p V S V T
H p
S
G p
T
V
F G S T V T p
第16页,本讲稿共62页
dG -SdT VdP
G S T P
G V P T
H G TS G T G T P
U H - PV G - T G P G T P P T
F G PV G P G P T
常用的特性函数与特征变量为:
G(T ,P ) F(T ,V ) U( S ,V )
和教材 P52的推导 进行比较
H p T G p T T T 2 G p V T T G p T p V T V T p
热力学函数的基本关系式

dG = -SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 :表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法:
T p
S
V S
p
① 对角乘积永远是pV,TS;
② 等式两边分母与外角标互换;
S p
T
V T
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习:由热力学基本方程出发证明,
H p
T
T
V T
p
V
证明:
dH=TdS+Vdp
定温下,等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程
热力学函数间的关系

计算结果说明,在给定条件下,298K时,合成氨反应可 以进行;而在1000K时,反应不能自发进行
再见!
H
U
TS
G
TS F
H U pV pV U H pV
G H TS F pV pV F U TS G pV
T1
T
T2 T1
H T2
dT
(1) 若温度变化范围不大,△H可近似为不随温度变化的常数
G T
T 2
G T
T 1
H
1 T2
1 T1
四、G与温度的关系—吉布斯-亥姆霍兹公式
25℃,反应 2SO3(g) 2SO2(g) O2(g)
rGm (298K) 1.400 10 5 J mol1 r Hm 1.966 105 J mol1
H T2
吉布斯-亥姆赫兹公式
G T
T
H T2
P
四、G与温度的关系—吉布斯-亥姆霍兹公式
吉布斯-亥姆赫兹方程式
Байду номын сангаас
G T
T
H T2
P
(微分形式)
应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T2时的rGm(T2)。
积分形式
T2 d ( G )
M 和N也是 x,y 的函数
二阶导数
M
2Z
( y )x xy ,
N
2Z
( x )y xy
所以
M N ( y )x ( x )y
三、Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,将上述
关系式用到四个基本公式中, 就得到Maxwell关系式:
热力学函数间的关系

r Gm ,2
1.400 × 105 1 1 5 ) = 1.966 × 10 ( 873 298 873 298
r Gm ,2 = 30820J mol -1
吉布斯- 吉布斯-亥姆赫兹方程式
G T = H T2 T P
(微分形式)
应用:在等压下若已知反应在 应用:在等压下若已知反应在T1的rGm(T1),则可求得该反 应在T 时的 应在 2时的rGm(T2)。 积分形式
∫
T2
T1
T2 G H ( ) = ∫ 2 dT T1 T T
( V V ) p dT = ( )T dp T p
1mol理想气体, PV = RT 理想气体, 理想气体 p T ( )p = , R V V V ( )T = , p p R p ( )V = V T 则 ( T ) p ( V )T ( p )V = 1
V p T
可写成
T V p ( )p( )T ( )V = 1 V p T
2010-8-2
三、Maxwell 关系式
证明: 例3证明:(
T V p )p( )T ( )V = 1 并以理想气体验证上式的正确。 并以理想气体验证上式的正确。 V p T
定量纯气体, 证: 定量纯气体, V = f (p,T)
dV = ( V V ) p dT + ( )T dp T p
当V恒定,dV = 0,则 恒定, , 恒定
dU = Td S pdV
U S 等温对V求偏微分 等温对 求偏微分 ( )T = T ( )T p V V
S p S 不易测定,根据Maxwell关系式 ( )T = ( ) V 关系式 ( )T 不易测定,根据 V T V
热力学函数间的普遍关系式

不可逆过程 可逆过程 不可能过程
此式热力学第二定律的数学表达式之一,其中δQ为微循环中系 统从外界吸收的热量,T为吸热时热源的温度。
孤立系统的熵增原理:
孤立系统所进行的一切实际过程都朝着系统熵增 加的方向进行,在有限的情况下,系统的熵维持 不变,任何使系统熵减小的过程都是不可逆的。
S iso
0 0 0
U P V S H V p S A P V T G V p T
下变量N常常省略
A S T V G S T
因为U、H、A和G为热力学函数,因此他们的微分式是全 微分,因全微分的二阶偏导数与求导次序无关,从而得 到下列麦克斯韦关系式:
U U (S ,V ) H H ( S , p) A A(T ,V ) G G(T , p)
上述热力学基本关系式仅适用于摩尔数不变的均匀 系,如果考虑单组元系统摩尔数的变化,系统的广 延参数将取决于其摩尔数,这样上式就可扩展为:
U U ( S ,V , N ) H H ( S , p, N ) A A(T ,V , N ) G G (T , p, N )
V , S p, T V , T V , T p, S p, T
S T T V S V pT
p
由于热熔:
CV T S
并有:
T
V
C p T S
dH d (U pV ) TdS Vdp
dG SdT Vdp
dA SdT pdV
这四个式子,是组成固定物质的热力学基本微分关系式。
5.一般关系式

从状态方程求得 ,V 与 p 的关系,就可求 ( S )T 或 S 。
Maxwell 关系式的应用
例如,对理想气体
pV nRT,
( S p )T
p2 p1
(
V T
) p V
nR p
nR p
S
nR p
dp nR ln
p1 p2
nR ln
所以 dA SdT pdV
(4) 因为
四个基本公式 dG SdT Vdp
G H TS dG dH TdS SdT
dH TdS Vdp
所以
dG SdT Vdp
从基本公式导出的关系式
(1) (2)
dU TdS pdV dH TdS Vdp
H U pV
H Q p
(dp 0,Wf 0)
(2)Helmholz 自由能定义式。在等温、可逆条件下, 它的降低值等于体系所作的最大功。
A U TS
A Wmax
(dT 0, 可逆)
几个函数的定义式
(3)Gibbs 自由能定义式。在等温、等压、可逆条件 下,它的降低值等于体系所作最大非膨胀功。
G H TS
或
G A pV
G Wf ,max (dT 0,dp 0, 可逆)
函数间关系的图示式
四个基本公式
(1)
dU TdS pdV
因为
dU Q pdV Q dS 代入上式即得。 T
这是热力学第一与第二定律的联合公式,适用 于组成恒定、不作非膨胀功的封闭体系。 虽然用到了Q TdS 的公式,但适用于任何可逆或 不可逆过程,因为式中的物理量皆是状态函数,其变 化值仅决定于始、终态。但只有在可逆过程中 TdS 才代 pdV 才代表 We 。 表 QR , 公式(1)是四个基本公式中最基本的一个。
第4章 热力学一般关系

第四章热力学一般关系4.1 常用状态函数的偏微商 (1)4.1.1 状态方程的偏微商 (1)4.1.2 热力学能函数u(T,v)的偏微商 (3)4.1.3 焓函数h(T , p )的偏微商 (4)4.1.4 熵函数的偏微商 (4)4.2 基本热力学关系 (5)4.2.1 基本热力学关系式 (5)4.2.2 特性函数 (6)4.2.3 麦克斯韦关系式 (6)4.3 热力学能、焓和熵的微分式 (7)4.3.1 热力学能、焓和熵的微分式 (7)4.3.2 偏微商关系的推导 (7)4.4 热系数之间的一般关系 (9)4.4.1 比热容的偏微商 (10)4.4.2 比热容差的一般关系 (10)4.4.3 绝热节流系数的一般关系式 (11)思考题及答案 (14)4.1 常用状态函数的偏微商工程中常用的状态函数有状态方程 F(p ,v ,T )=0,和以可测参数为独立变量的热力学能、焓、熵函数,通常热力学能函数u (T ,v ),焓函数h (T ,p ),和熵函数s(T ,v ),s(T ,p )的导得较为方便。
为导得这些状态函数,常常需要先得到它们的如下一些偏微商。
4.1.1 状态方程的偏微商由状态方程可得到、及、三个偏微商(还有三个分别是它们的倒数),常将它们定义成工质的三个热系数:热膨胀系数(4-1)热膨胀系数表征工质在定压下的热膨胀性质,单位是K-1。
定温压缩系数(4-2)定温压缩系数表征工质在恒定温度下的压缩性质。
对于所有物质恒为负值,故在定义式中引入负号,而使恒为正值。
的单位为Pa-1。
压力的温度系数(4-3)的单位为K-1按照二元函数偏微商的循环关系有=-1结合、及的定义式,整理可得= = (4-4)它表达了上述三个热系数之间的联系。
状态方程包含的是三个可测的基本状态参数,所以上述三个热系数是可以由实验直接测定的。
由实验测定出这些热系数数据,然后积分得出状态方程式,是由实验得出状态方程的一种基本方法。
热力学基本关系式
衡态) (不可逆) 例3:单纯pVT变化(仅研究均匀系统←→平衡系统)
纯pg,混合气体 由T1,p1→→T2,p2可用基本方程
dU Tds pdV -----最基本 dG sdT VdP ----最常用
3.由热力学基本方程计算纯物质pVT 变化过程的ΔA ,ΔG
①恒温过程dT= 0 dAT pdV
a. pg: PV=nRT
dGT Vdp
AT
V2 pdV
V1
nRT ln V2 V1
GT
p2Vdp nRT ln p2
p1
p1
b.凝聚相(S,l):等温压缩率很小,→体积可认为不变
AT
p
T
H p
S
V
dA SdT pdV
A S T V
A p V T
dG SdT Vdp
G S T p
G p
T
V
T U H
S V S p
U A p
V S V T
V
H p
S
G p
T
A G S
T V T p
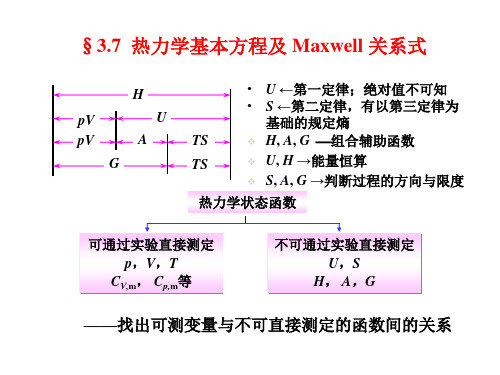
§3.7 热力学基本方程及 Maxwell 关系式
H
pV
U
pV
A
G
• U ←第一定律;绝对值不可知 • S ←第二定律,有以第三定律为
基础的规定熵
TS
❖ H, A, G 组合辅助函数
TS
❖ U, H →能量恒算
❖ S, A, G →判断过程的方向与限度
热力学状态函数
可通过实验直接测定 p,V,T
CV,m, Cp,m等
07_第七章 热力学一般关系式

Rg ∂p 例如理气 , = 代入上式则得理气热力学能计算公式 v ∂T V
Rg du = C V0 dT + T − p = C V0 dT v
如将第二、 方程代入 得到另外两个热力学能公式。 代入, 如将第二、第三 T · d S 方程代入,得到另外两个热力学能公式。 第二
第七章
热力学一般关系式
热力学一般关系式意义和作用
1 、热力学分析计算涉及到热力参数(du、dh、dS、 、热力学分析计算涉及到热力参数(du、dh、dS、 Cp、 Cv及P、V、T )计算。其中P、V、T,易 Cp、 Cv及 )计算。其中P 测得,而其余的不易测得。热力学一般关系式可以 建立这些易测与不易测参数间的联系,便于从易测 参数获取那些不易测参数。 2 、根据热力学一般关系式和状态方程可以推导出热力学 参数(热力学能、焓、熵、比热容)的普遍计算式。 3、 借助热力学一般关系式和实验数据(Cp、Cv)可以导 借助热力学一般关系式和实验数据(Cp、Cv)可以导 出实气状态方程。 4、 检验状态方程的准确性。 理想气体 — 实际气体性质 — 纯物质一般性质普遍关 系(适于理气、实气等)。
←
y不变
∂Z ∂Z = M ∂y = N x ∂x y
−→
比较系数
7 - 2 麦克斯韦关系式
↑ ↓ ∂T ∂P ∂U ∂U U = U( S,V) ⇒ dU= ⋅dS+ ⋅dV = T⋅dS−P⋅dV ∂V =− ∂S S V ∂S V ∂VS
∂T ∂v = ∂s p ∂p S
∂s ∂v = − ∂T p ∂p T
∂u ቤተ መጻሕፍቲ ባይዱ = −p ∂v S
热力学一般关系(热学高等数学偏微分).doc

第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能 U 、熵S)及其为某一研究方便而设的组合函数(如焓H 、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力 p 、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式全微分性质 +基本热力学关系式6.1状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数 z f ( x, y) 具有全微分性质z zdy ( 6-1)dz dxx y y x则必然有(1)互易关系令式( 6-1)中z zM ( x, y) ,N (x, y)x y y xM N( 6-2)则xy x y互易关系与 dz 0 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2)循环关系当保持 z 不变,即dz 0 时,由式(6-1),得zdx z zdy z 0x yy xzy x 则x z zy y xz y x1 ( 6-3)故有x zy x z y此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即循环就行了。
( 3)变换关系将式( 6-1)用于某第四个变量不变的情况,可有z zdz dx dyxy yx两边同除以 dx ,得z z z y( 6-4)x x y y x xz 是函数 z( x, y) 对x的偏导数;z 是以(x, ) 为式中:xx y独立变量时,函数z(x,) 对x的偏导数。
第4章热力学一般关系式1

p CV dS dT dV T T V
第一dS方程 第二dS方程
同理
Cp V dS dT dp T T p
dS C p p C V T d T dV T p V T V p
麦 克 斯 韦 关 系 式
T - P
V - S
T P
V S
图3.3.1 麦克斯韦关系助记图 一阶偏导关系和麦克斯韦关系式的用途: 麦克斯韦关系式可把热力学关系式推导过 程中,涉及熵S的函数关系,转变成只包含 可测参数p-v-T参数的热力学关系。
H T S p
此一阶偏导关 系代表焓商图 中的斜率
U CV T V
H Cp T p
定容热容和定压热容偏微分的推导
Cp CV 一阶偏导数 和 V p T T
∵
U T S V
U U S S CV T T V S V T V T V
概述
简单可压缩系统的容积变化功表示为:
此外还有:
W pdV
1
2
简单弹性系统,唯一的可逆功方式是弹性伸长; 简单磁系统,唯一的可逆功方式是磁化。 状态原理的假说 确定一个系统平衡状态所需要的独立参数的数目等于可能存在的可逆 功方式的数目加一。 简单可压缩系统的独立参数数目=1(容积变化功)+1=2 再“加一”是指系统除各种做功外还与外界交换热量。 独立参数——就是说这两个参数之间不存在关联关系 本章述热力学一般关系式是指简单可压缩系统的2参数原则下参数间的关系 两参数 法则
其中
z f ( x, y)
2.11热力学函数间的关系

dc = 0 d ( cv ) = cdv d ( u ± v ) = du ± dv d ( uv ) = vdu + udv
u vdu − udv d = 2 v v
c为常数; u、v 为变量 为常数; 为常数
不定积分公式
∫ du = u + C
u m +1 u m du = +C ∫ m +1 du ∫ u = ln u + C
一、热力学基本关系式
(2) 因为
dH = TdS + Vdp
H = U + pV
d H = d U + p d V + Vd p
dU = TdS − pdV dH = TdS + Vdp
所以
一、热力学基本关系式
(3)
dF = − SdT − pdV
F = U − TS dF = dU − TdS − SdT
式中:m为常数(指数); C为积分常数。
二、对应系数关系式
U = f ( S ,V )
可逆过程) (W’=0;可逆过程) 可逆过程
F = f (T , V )
dU = (
∂U ∂U )V dS + ( ) S dV ∂S ∂V ∂U p = −( )S ∂V
dU = T dS − pdV
∂F ∂F )V dT + ( )T d V ∂T ∂V dF = − SdT − pdV dF = ( S = −( ∂F )V ∂T p = −( ∂F θ )T ∂V
第十一节 热力学函数间的关系
H
H = U + pV pV
U
U = H − pV
TS TS
热力学四大基本关系式

热力学四大基本关系式嘿,朋友们!今天咱来聊聊热力学四大基本关系式,这可真是个超级有趣的玩意儿啊!你看啊,这热力学就像是一个神秘的魔法世界,而四大基本关系式就是打开这个魔法世界大门的钥匙。
就好像你要去一个陌生的地方探险,没有地图怎么行呢?内能,这可是个关键角色。
它就像是一个人的精力,有了足够的精力才能去做各种事情呀。
焓呢,就像是给这份精力加上了一些额外的助力,让它能发挥更大的作用。
熵,这个家伙有点特别哦!它就像是生活中的混乱度,有时候家里乱七八糟的,那就是熵在捣乱呢!但别小瞧它,它可有着大作用呢。
而吉布斯自由能,那就像是一个判断标准,告诉你这件事能不能干,值不值得去干。
想象一下,我们的生活中不也处处都有类似的情况吗?比如说,你想要去做一件事情,你得考虑自己有没有足够的能力和精力,这就是内能嘛;还得想想这件事做完了会有什么样的收获,是不是能让自己更上一层楼,这就像焓一样。
然后呢,还得看看这件事会不会把你的生活搞得一团糟,是不是会增加很多混乱,这就是熵啦。
最后呢,再判断一下做这件事到底划不划算,对自己有没有好处,这就是吉布斯自由能的作用呀!再比如说,你要装修房子。
你得先看看自己有多少钱和精力来搞,这就是内能;然后想想装修完了房子会变得多漂亮多舒适,这像焓;接着得考虑装修过程中会不会把家里弄得乱七八糟,这是熵;最后再衡量一下花这么多钱和精力装修值不值得,这就是吉布斯自由能呀!热力学四大基本关系式可不是只在书本里有用哦,它们在我们的生活中无处不在呢!它们就像一个个小精灵,在默默地影响着我们的一举一动。
咱再深入想想,这些关系式不就是在告诉我们要学会平衡吗?平衡自己的精力、收获、混乱和价值。
只有这样,我们才能在这个复杂的世界里游刃有余呀!我们不能只盯着一个方面看,得全面地考虑问题。
就像只关注内能,那可能会让自己累垮;只关注焓,可能会忽略了潜在的混乱;只关注熵,那可能什么都不敢做了;只关注吉布斯自由能,又可能会错过很多好机会。
热力学一般关系(热学 高等数学 偏微分)(完整资料).doc

【最新整理,下载后即可编辑】第二部分 工质的热力性质六 热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U 、熵S )及其为某一研究方便而设的组合函数(如焓H 、自由能F 、自由焓G 等)许多都是不可测量,必须将它们与可测量(如压力p 、体积V 、温度T 等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式←全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1)则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z 则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z xz x x y y z (6-3) 此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
2第二章_热力学函数与普遍关系式

第二章 热力学函数与普遍关系式在给出了热力系统的一段性描述之后,就可以根据热力学第一定律和第二定律建立的解桥式,推导出热力学参数的各种微分关系式。
这种推导过程只应用连续可微函数的数学性质,而不涉及系统的特殊情况,因此它们适用于状态连续变化的一切系统以及系统的全部状态,通常称之为热力学普遍关系式。
热力学普遍关系式是非常有用的,利用有关的式子,可以由可测量决定非可测量,或对实例量进行热力学一致性检验。
此外不论如何严密与细致的实验,所切得的数据总是有限的,在编制参数图表时,必须进行内插与外推,这时普遍关系式是导出有关公式的重要依据。
2-1 热力学一般关系式1 一般关系式热力学的普遍关系式热力学一般关系据热力学基本定律导出,因此是任何工质都必然遵循的关系;是研究工质热力性质的理论基础,适于主要对象有约束作用的复杂系统对复杂系统的热力学分析。
热力学分析的主要对象的限制包括以下几点:● 化学成分均匀不变 ● 纯物质● 不存在运动、毛细、固体变形效应● 不存在电场、磁场效应,忽略重力效应。
简单可压缩系统一种与外界只有热量及准静态容积变化的热力学系统,其中:简单表示只有一种可逆功方式、可压缩表示可逆过程中,以体积变化做功,p d v 确定系统状态所需的参数:热力学关系式中参数的个数是确定的,它们与能量相互作用方式数有相关关系。
一个系统平衡状态所需的独立参数个数,等于可能存在的可逆功方式数再加一。
其中,加一是因为系统中的热作用。
两参数法则:一个简单系统平衡状态可由二个独立状态参数表示,同时二个独立状态参数也确定了一个简单系统平衡状态,即简单系统平衡状态 2独立状态参数 [例] U ,V 非相互独立。
D ,M 非相互独立。
纯物质:液体 + 蒸汽混合物, T, P 非相互独立热力学普遍关系式的功能:●由可测参数及其它参数,计算不可测参数●使计算简化●对实测量进行热力学的一致性校验●数据的内插及外插,(由实测数制表时)2 热力学特征函数热力学特征函数所谓热力学特征函数是指由自然的或适当的独立变量对(对非简单系统则为独立变量组)所构成的一些显函数它们能够全面而确定地描述热力系统的平衡状态。
热力学函数的基本关系式

麦克斯韦关系式 S p V T T V
14
思考:定容或定压下S 随T 的变化率各等于什么?
S(T,p) S(T,V)
由定义式出发
1)由定义式出发
dS Qr C dT
定压
S Cp T p T
H p
T
T
V T
p
V
热力学状态方程,将U(或H)与p,V,T联系起来了。
—— 对实际气体,已知pVT状态方程式,代入,积分 可求ΔU、ΔH。
13
典型证明题:
证明: H T p V p V T T V V T
证:由热力学基本方程 dH = TdS + Vdp 定温下等式两边同除以dV,得
除了定义式外, 还可以导出四种类型的重要关系式
2
1. 热力学基本方程
封闭系统中, 微小可逆过程:dU=δQr+δWr
δWr ′=0时,
dS δ Qr T
δWr=-pdV,
dU=TdS-pdV
H=U+pV
dH=dU+pdV+Vdp
A=U-TS dA=dU-TdS-SdT
dH=TdS+Vdp
dA= - SdT - pdV
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V HS p源自H p SdA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
热力学文章

热力学一般关系式及其应用一. 热力学一般关系式热力学一般关系式是根据热力学第一定律、热力学第二定律以及某些状态参数的定义式而导得的一些微分方程式。
它们以微分的形式来表达各种热力学参数之间的关系,故也称热力学微分方程式.由于热力学一般关系式是从热力学的基本定律导得的.因此,具有普遍适用氏不仅适用于理想气体,也适用于实际气体,甚至还适用于固体和液体.1).闭口系统的四个基本关系式闭口系统热力学第一定律表达式为δQ=dU+δW对简单可压缩系统,当过程为可逆时,则上式变成δQ=dU+pdV根据热力学第二定律,对可逆过程则δQ=TdS根据上面的式子,再加上焓,自由能,自由焓的定义,可以得到简单可压缩系统状态参数间的四个基本关系式,如下:dU=TdS-pdVdH=Tds+VdpdF=-SdT-pdVdG=-SdT+Vdp这些式子可以用于闭口系统平衡态之间的如何热力工程,包括可逆过程和不可逆过程。
虽然推导的过程中用到了不可逆过程的关系式δQ=TdS 和δW=pdV ,但是应指出:一旦上述参数间的关系建立,它便纯粹是在平衡态下各参数之间的关系式了。
如果系统从一个平衡态转化到另一个平衡态,不论经历可你过程还是不可逆过程,只要初、终态相同,则状态参数之间的关系也应是相同的,这就是状态参数,即点函数的特性。
应用热力学一般关系式时,可以根据某些容易测定的某些偏导数及实验数据,确定内能、焓、熵以及物质的状态方程式,或者用以检验已有实际气体状态方程的难确性.热力学一般关系式是研究物质热力性质不可缺少的现论基础.2).麦克斯韦关系式VS S p V T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂ p SS V p Y ⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ VT T p V S ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ p TT V p S ⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ 上列四个关系式称为麦克斯韦关系式,这些关系式对计算热力学状态参数有极其重要的作用.我们知道熵、焓及内能等状态参数都是不能直接测量比但可通过实测比热及状态方程式,利用麦克斯韦关系式,方便地得出熵、焓及内能的计算式.由吉布斯方程,利用比较系数法,还可以导出八个非常游泳的偏导数,它们分别是: p v u T s u sv -=⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂, v p h T s h sp =⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂, s T f p v f vT -=⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂, s T g v p g p T-=⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂, 麦氏关系的重要性就在于通过它可以用少数的热力学量计算出其它的热力学量来.对这类问题的计算.最基本的是对熵S 的计算.因而,较熟练地掌握熵的计算是重要的二. 熵,焓在热力学第一定律和热力学第二定律的基础上引进了两个基本状态参数一内能和熵. 焓、熵是热力学中重要而且难懂的概念,又是常用的而且复杂的物理量.明确这些概念,掌握它们的计算公式,对理解热力学研究问题的方法,对了解关于态函数的物理意义及其数学特征等.都有非常重要的意义。
热力学函数的关系及应用

2.6 热力学函数间的关系及应用2.6.1. 定义式与热力学基本方程(公式)根据定义,在P,T,V,S,U,H,A,G 等热力学函数之间有如下关系:pV U H +=TS U A -=pV A TS pV U TS H G +=-+=-=上列均为定义式。
据热力学第一、第二定律,,有:pdV Q dU R -=δ和TdS Q R =δ,两式结合得:pdV TdS dU -= 根据pV U H +=,微分后代入上式可得:Vdp TdS dH +=pdV SdT dA --=Vdp SdT dG +-=上列四个公式称为热力学基本方程,其应用条件均相同。
pdV TdS dU -=是第一定律与第二定律的联合公式,是适用于组成不变且不做非体积功的封闭体系的热力学基本公式. 尽管在导出该式时,曾引用可逆条件的TdS Q R =δ,但该公式中各量均为状态函数,无论实际过程如何,上式的积分皆存在.但只有在可逆过程中,TdS 才代表体系所吸的热。
该式既适用于内部平衡的无相变化和化学变化的任意状态变化的单相封闭体系,也适用于已达相平衡和化学平衡的体系中同时发生pVT 变化及相变化和化学变化的可逆过程.从以四个热力学基本可导出一下微分关系式,如:p V SH S U T )()(∂∂=∂∂= ; T S V F V U p )()(∂∂-=∂∂-= T S pG T H V )()(∂∂=∂∂= ; p V T G T F S )()(∂∂-=∂∂-=2.6.2. 麦克斯韦(Maxwell )关系式若用z 代表体系的任一状态函数,且z 是两个变量x 和y 的函数.因其变化与过程无关,在数学上称z 具有全微分的性质.即若: ),(y x f z =则有: Ndy Mdx dy yz dx x z dz x y +=∂∂+∂∂=)()( M 对y 微分,N 对x 微分,得xy z y M x ∂∂∂=∂∂2)(及y x z x N y ∂∂∂=∂∂2)(显然: y x xN y M )()(∂∂=∂∂ 根据全微分函数性质,基于上述四个热力学基本方程可得到:S V TV p S )()(∂∂-=∂∂, S p T p V S )()(∂∂=∂∂,可以用容易从实验测定的偏微商代替那些不易直接测定的偏微商.2.6.3 .吉布斯-亥姆霍兹方程——温度对自由能变的影响在讨论化学反应问题时,常须自某一反应温度的)(0T G r ∆求另一个温度时的)(T G r ∆.因为: 2)(])([T G T G T T T G p p -∂∂=∂∂ 而: S T G p -=∂∂)( 故: 22)(](G/T)[T H T G S T T p -=--=∂∂ 由于体系的各个状态函数的绝对值均无法得到,故常将各状态函数写成相对值形式.因而,上式又可写成:2])([T H T T G p ∆-=∂∆∂ 上列二式均为吉布斯-亥姆霍兹方程式.因其推导过程中引入了等压的条件,故只能在等压下使用. 将其移项积分得:⎰∆-=∆-∆21)(21122T T dT TH T G T G 同理可得: 2])([T U T T A V -=∂∂ 及 2])([TU T T A V ∆-=∂∆∂ 上列均称吉布斯-亥姆霍兹方程或吉布斯-亥姆霍兹公式.2.6.4 克拉佩龙方程(1).克拉佩龙方程设在一定的压力和温度下,某物质的两个相呈平衡.若温度改变dT ,相应地压力也改变dp ,两相仍呈平衡.根据在等温等压下平衡的条件:0=∆G ,则有:p T, )()(βαB B −−→←平衡 )(αG )(βG)(αdG ↓ )(βdG ↓dp p ++dT,T )()(βαB B −−→←平衡)()(ααdG G + )()(ββdG G + 因)()(βG αG =,故)()(βdG αdG =,据Vdp SdT dG +-=得:dp V dT S dp V dT S ββαα+-=+-整理即得: VT H V S V V S S dT dp βαβαβαβααβαβ∆∆∆∆==--= 此式即称为克拉佩龙方程式.其对任何纯物质的两相平衡体系都可使用.(2).克拉佩龙方程对于固-液、固-固平衡的应用如液-固两相平衡有: VT H dT dp fus fus ∆∆= 对凝聚体系的相变过程研究可知,其m fus V ∆和m fus H ∆与温度和压力的关系不大,可近似视为常数.因而有:12ln T T V H p fus fus ∆∆∆= 近似地有: 1111ln T T V H T T V H T T V H p fus fus fus fus fus fus ∆∆∆∆∆∆∆∆∆∆⨯≈⨯≈+==)( (3).克拉佩龙方程对于液-气、固-气平衡的应用---克劳修斯-克拉佩龙方程 若为气-液两相平衡,则有: VT H dT dp vap vap ∆∆= 对于有气相参加的两相平衡,固体和液体的体积远较相同物质的量的的同类气体物质的气态要大,故常可忽略,并常令其气体符合理想气体状态方程.则:p/RT H p /nRT *T H TV H V T H dT dp m vapvap )g (vap vap vap 2∆∆∆∆∆==≈= 即: 2ln RTH dT p d m vap ∆= 该式称为克劳修斯-克拉佩龙方程式.若m vap H ∆与温度无关或在小的温度范围内可视为常数,则上式积分得:'ln C RT H p mvap +∆-= 或 C TB p +-=lg 上列二式最初是经验公式,在这里得到了热力学上的证明.若作定积分则:)11(ln 2112T T R H p p m vap -∆= 对于极性不太高,沸点在150K 以上,且分子没有缔合现象的液体,近似的有: 1188--⋅⋅≈=mol K J S T H m vap bmvap ∆∆ 该式称为楚顿(Trouton)规则.例: 已知θp 时水的沸点为100℃,蒸发热为42 kJ.mol -1.现将高压锅内的水加热,使其压力达到θp ⨯2.试求此时水的沸点.解: 由 )11(ln 2112T T R H p p m vap -∆= 得: 1212ln 11p p H R T T m vap ∆-= 代入已知数据得:)(10542722ln 1042314518153731ln 111331212--⨯=⨯⨯-=-=K .p p ..p p H R T T m vap θθ∆所以: C 120)(283931054272132︒≈≈⨯=-K ..T例 冰在273.15K 时的摩尔熔化热、水的摩尔体积和冰的摩尔体积分别为1mol kJ 025.6-⋅=∆f H132,mol dm 108018.1--⋅⨯=l m V 132,mol dm 109652.1--⋅⨯=s m V求在273.15K 时,使水的凝固点降低1K 需增加多大压强?解 由式(1)得1351molm 10)9652.1(1.8018K 15.273mol J 6025---⋅⨯-⨯⋅=∆∆=m f V T H dT dp 1K kPa 068.13499-⋅-=计算结果表明,使水的凝固点降低1K 需增加压强kPa 068.13499。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1) 则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z x z x x y y z (6-3)此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
(3) 变换关系将式(6-1)用于某第四个变量ω不变的情况,可有ωωωdy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 两边同除以ωdx ,得ωω⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂x y y z x z x z x y (6-4) 式中:yx z ⎪⎭⎫ ⎝⎛∂∂是函数),(y x z 对x 的偏导数;ω⎪⎭⎫ ⎝⎛∂∂x z 是以),(ωx 为独立变量时,函数),(ωx z 对x 的偏导数。
上面的关系可用于它们之间的变换。
这一关系式对于热力学公式的推导十分重要。
(4) 链式关系按照函数求导法则,可有下述关系:1=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂y y z x x z (6-5)1=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂yy y z x x z ωω (6-5a ) 这是在同一参数(如y )保持不变时,一些参数),,,(Λωx z 循环求导所得偏导数间的关系。
若将关系式中每个偏导数视为链的一环,则链式关系的环数可随所涉及参数的个数而增减。
以上这些关系式都是针对二元函数的,即以具有两个独立状态参数的简单系统为背景。
但对具有两个以上独立参数的系统即多元状态函数,其也有推广价值。
例题6-1 已知理想气体状态方程为RT pv =,试检验v 是否有全微分。
解 由状态方程得 pRT v =,故有 dp p v dT T v dv Tp ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=dp p RT dT p R 2-=于是p R p T M =),(, 2),(p RT p T N -= 而2p R p R p p M T T -=⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂22p R p RT T T N p -=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 二者相等,可见v 有全微分,即其为状态函数。
6.2 基本热力学关系式6.2.1 基本热力学关系式为简单计,以下推导全部采用比参数。
由热力学第一定律,得w du q δδ+= (3 -18d )对简单可压缩系统,若过程可逆,则pdv w =δ,故pdv du q +=δ而由热力学第二定律Tds q =δ (4-14b ) 二式联立,最后得pdv Tds du -= (6-6)式(6-6)表达了热力学基本定律对系统状态参数变化的限制,是导出其它热力学关系式的基本依据,称为基本热力学关系式。
需要指出的是:虽然式(6-6)是从可逆变化推导而来,但因为du 是状态函数的变化,它只与变化前后的状态有关,而与实际过程的可逆与否无关,所以对于不可逆变化仍然适用。
但若作为能量平衡方程,它只适用于可逆过程。
由焓的定义 pv u h += 得vdp pdv du pv d du dh ++=+=)(将式(6-6)代入上式,可得vdp Tds dh += (6-7)同样,由自由能的定义 Ts u f -= 可得pdv sdT df --= (6-8)由自由焓的定义 Ts h g -= 可得vdp sdT dg +-= (6-9) 以上式(6-7)~(6-9)为基本热力学关系式用组合参数表达的形式,故式(6-6)~(6-9)可统称为基本热力学关系式。
6.2.2 特性函数基本热力学关系式(6-6)~(6-9)分别为以特定参数为独立变量的状态函数),(v s u 、),(p s h 、),(v T f 、),(p T g 的全微分表达式。
这些函数有一个很重要的性质,就是它们的偏导数各给出一个状态函数。
对于函数),(v s u ,将其全微分解析式dv v u ds s u du sv ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=与式(6-6)作对比,即得T s u v=⎪⎭⎫⎝⎛∂∂(6-10) p v u s-=⎪⎭⎫⎝⎛∂∂(6-11) 同样,由于式(6-7)是函数),(p s h 的全微分,则有T s h p=⎪⎭⎫⎝⎛∂∂(6-12) v p h s=⎪⎪⎭⎫ ⎝⎛∂∂(6-13) 式(6-8)是函数),(v T f 的全微分,有s T f v-=⎪⎭⎫⎝⎛∂∂(6-14)p v f T -=⎪⎭⎫ ⎝⎛∂∂ (6-15)式(6-9)是函数),(p T g 的全微分,有s T g p-=⎪⎭⎫ ⎝⎛∂∂ (6-16) v p g T =⎪⎪⎭⎫ ⎝⎛∂∂ (6-17)正因为如此,只需知道上述函数中的任意一个函数,就可确定出所有的状态函数。
如已知),(v T f ,则由式(6-14)可得),(v T s ;由式(6-15)可得),(v T p 即状态方程;由自由能的定义Ts u f -=可得vT f T f v T u ⎪⎭⎫ ⎝⎛∂∂-=),( 由焓的定义pv u h +=可得v v f T f T f v T h Tv ⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=),( 由自由焓的定义pv f Ts h g +=-=可得v v f f v T g T⎪⎭⎫ ⎝⎛∂∂-=),(由此可见,若状态函数的独立参数选择适当,则可由这个函数及其偏导数得到所有的状态函数,从而将工质的平衡性质完全确定。
这样的函数称为特性函数。
特性函数包含了系统平衡状态的所有信息,它的自变量是特定的。
一经变换虽然还是状态函数,但由于信息丢失而不再是特性函数了,这一点需特别注意。
除了上面已给出的),(v s u 、),(p s h 、),(v T f 、),(p T g 这四个特性函数,还可通过基本热力学关系式寻找其它的特性函数。
如将式(6-6)写成dv T pdu T ds +=1(6-18)则可知 ),(v u s 也是特性函数;将式(6-7)写成dp Tv dh T ds -=1 (6-19) 则可知 ),(p h s 也是特性函数,等等。
特性函数为联系各热力学函数的枢纽。
在许多实际问题中,常采用v T ,或p T ,这些可测量作独立变量,所以),(v T f 和),(p T g 是两个最重要的特性函数。
6.2.3 麦克斯韦关系由于基本热力学关系式(6-6)~(6-9)是各特性函数的全微分表达式,故可对它们应用互易关系式(6-2),因此可得v s s p v T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂ (6-20)p s s v p T ⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-21) vT T p v s ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ (6-22) p TT v p s ⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ (6-23) 这四个关系式称为麦克斯韦关系。
借助它们可将包含不可测量熵s 的关系式代换成用可测量p 、v 、T 表达的关系式。
6.3 热系数状态函数的某些偏导数具有明确的物理意义,能表征工质的一定的热力性质,且可由实验测定,因而成为研究工质热力性质的重要数据,称为热系数。
常用的热系数有:热膨胀系数、定温压缩系数、绝热压缩系数、压力温度系数、定容比热、定压比热和绝热节流系数等。
1. 热膨胀系数pp T v v ⎪⎭⎫⎝⎛∂∂≡1α (6-24)热膨胀系数表征物质在定压下的体积随温度变化的性质,单位为1-K 。
2. 定温压缩系数TT p v v ⎪⎪⎭⎫⎝⎛∂∂-≡1κ (6-25)定温压缩系数表征物质在恒定温度下的体积随压力变化的性质。
由于所有物质的Tp v ⎪⎪⎭⎫⎝⎛∂∂均为负值,故在定义式中引入负号,而使T κ为正值。
其单位为1-Pa 。
3. 压力温度系数v v T p p ⎪⎭⎫⎝⎛∂∂≡1β (6-26)压力温度系数表征物质在定容下的压力随温度变化的性质,单位为1-K 。
由微分的循环关系式(6-3),有1-=⎪⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂Tp v p v v T T p因而,上面的三个热系数之间有如下关系v T p p βκα=(6-27)显然,如果有了工质的状态方程,就可计算出这三个热系数。
反之,如果由实验测出这些热系数数据,就可积分得到状态方程式。
4. 绝热压缩系数ss p v v ⎪⎪⎭⎫⎝⎛∂∂-≡1κ (6-28)绝热压缩系数表征工质在可逆绝热(定熵)变化中体积随压力变化的性质,单位为1-Pa 。
5. 定容比热vv dT q c ⎪⎪⎭⎫ ⎝⎛≡δ (6-29)定容比热表征物质在定容下的吸收热量的能力,单位为)/(K kg kJ ⋅。
根据热力学第一定律解析式w du q δδ+= (3-18d )对简单可压缩系统,定容下的体积功0=w δ,故du q =δ,因而vv T u c ⎪⎭⎫ ⎝⎛∂∂= (6-30)6. 定压比热pp dT q c ⎪⎭⎫⎝⎛≡δ (6-31)定压比热表征物质在定压下的吸收热量的能力,单位为)/(K kg kJ ⋅。
