一次函数的关系式

合集下载

怎样求一次函数关系式

怎样求一次函数关系式？广东林伟杰一次函数关系式)0(≠+=k b kx y 中有两个待定系数k 和b ，确定了它们就确定了一个一次函数，故一般需要两个条件才能确定一个一次函数.现结合实例介绍求一次函数关系式的方法，供同学们学习时参考.一、利用代入坐标法求一次函数关系式例1 已知一次函数的图象经过（1,5）和（3,9）两点，求此一次函数关系式. 分析：先设函数关系式为b kx y +=，然后代入坐标建立方程组，求出方程组的解后再代回所设关系式即可.解：设所求函数关系式为b kx y +=，则由题意，得⎩⎨⎧+=+=,39,5b k b k 故⎩⎨⎧==.3,2b k 故所求的函数关系式是32+=x y .点评：图象上每一点的横坐标和纵坐标都是此函数中自变量与函数的一对对应值，据此可通过建立二元一次方程组来求一次函数关系式.二、根据直线间的位置关系求一次函数关系式例2 某一次函数的图象过点（2,1）且与直线32+-=x y 相交于y 轴上的同一点，求此一次函数的关系式.分析：因直线32+-=x y 与y 轴的交点是（0,3），故设函数关系式为3+=kx y ，代入点（2,1）可求出k ，进而可得关系式.解：因直线32+-=x y 交y 轴于点（0,3），故某一次函数的图象也与y 轴相交于点（0,3），故设其关系式为3+=kx y ，代入点（2,1），得321+=k ，故1-=k ，故关系式为3+-=x y . 点评：由已知条件得出图象与y 轴的交点坐标，进而正确设出所求关系式是解本题的关键.三、根据表格信息求一次函数关系式例3 商店出售某商品时，在进价的基础上加一定的利润，其数量x 与售价y 的关系如下表所示，请根据表中提供的信息求出y 与x 的函数关系式，并求出当数量是2.5千克时的售价.分析：由表可知，当1=x 时， 4.08+=y ；当2=x 时，)4.08(28.016+=+=y ；当3=x 时，)4.08(32.124+=+=y ；当4=x 时，)4.08(46.132+=+=y ；…… 故x x y 4.8)4.08(=+=.解：由表中信息可求得函数关系式是x x y 4.8)4.08(=+=（正比例函数是一次函数的特例）.当5.2=x 千克时，214.85.2=⨯=y （元）.四、根据图象信息求一次函数关系式例4 长途汽车客运公司规定旅客可随身携带一定重量的行李，若超过规定，则要购买行李票，行李费用y （元）是行李重量x （千克）的一次函数，其图象如图所示，试求出y 与x 之间的函数关系式并求出自变量x 的取值范围.分析：由图象可知，直线过点（60,6）和（80,10）两点，据此即可求出y 与x 间的函数关系式.解：设函数关系式为b kx y +=，因为图象过点（60,6）和（80,10），则有⎩⎨⎧+=+=,8010,606b k b k 故⎪⎩⎪⎨⎧-==.6,51b k 故函数关系式是 651-=x y .令0=y ，得30=x ，故自变量x 的取值范围是x ≥30点评：直线与x 轴的交点的横坐标就是可免费携带行李的最大重量.解决本题的关键是读懂题意.此外，通过本题要注意掌握实际问题中自变量取值范围的确定方法，它包括：（1）使关系式有意义；（2）符合实际问题的需要.五、根据一次函数的性质求其关系式例5 一次函数b kx y +=的自变量的取值范围是-3≤x ≤6，相应函数值的取值范围是-5≤y ≤-2，求此一次函数的关系式.分析：对一次函数b kx y +=，若y 随x 的增大而增大，则由题意知其图象过点（-3,-5）和（6,-2），由此可求其关系式；若y 随x 的增大而减小，则由题意知其图象过点（-3,-2）和（6,-5），由此可求其关系式，故本题应分两种情况求解.略解：本题应分两种情况来解.设所求关系式为b kx y +=.（1）当y 随x 的增大而增大时，由题意知其图象过点（-3,-5）和（6,-2），由此可求得关系式是431-=x y (-3≤x ≤6)；（2）当y 随x 的增大而减小时，由题意知其图象过点（-3,-2）和（6,-5），由此可求得关系式是331--=x y (-3≤x ≤6). 点评：本题题设只给出了一次函数的自变量与函数值的取值范围，在这种情况下应根据一次函数的性质来求其关系式，否则极易造成漏解.x。

根据图象求一次函数关系式

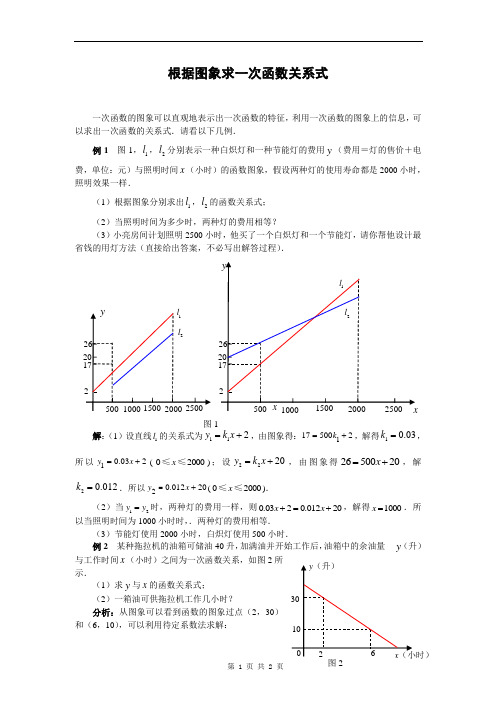
第 1 页共 2 页根据图象求一次函数关系式一次函数的图象可以直观地表示出一次函数的特征，利用一次函数的图象上的信息，可以求出一次函数的关系式．请看以下几例．例1 图1，1l ，2l 分别表示一种白炽灯和一种节能灯的费用y （费用＝灯的售价＋电费，单位：元）与照明时间x （小时）的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样．（1）根据图象分别求出1l ，2l 的函数关系式；（2）当照明时间为多少时，两种灯的费用相等？（3）小亮房间计划照明2500小时，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法（直接给出答案，不必写出解答过程）．解：（1）设直线1l 的关系式为112y k x =+，由图象得：1175002k =+，解得10.03k =，所以10.032y x =+(02000x ≤≤)；设2220y k x =+，由图象得2650020x =+，解20.012k =．所以20.01220y x =+(02000x ≤≤)．（2）当12y y =时，两种灯的费用一样，则0.0320.01220x x +=+，解得1000x =．所以当照明时间为1000小时时，．两种灯的费用相等．（3）节能灯使用2000小时，白炽灯使用500小时．例2 某种拖拉机的油箱可储油40升，加满油并开始工作后，油箱中的余油量 y （升）与工作时间x （小时）之间为一次函数关系，如图2所示．（1）求y 与x 的函数关系式；（2）一箱油可供拖拉机工作几小时？分析：从图象可以看到函数的图象过点（2，30）和（6，10），可以利用待定系数法求解：图1图2第 1 页共 2 页解：（1）设一次函数的关系式为y kx b =+，将条件代入，得230610.k b k b +=⎧⎨+=⎩，解得540.k b =-⎧⎨=⎩，所以此函数的关系式为540y x =-+．（2）当0y =时，即5400x -+=，所以8x =．即一箱油可供拖拉机工作8小时．例3某长途汽车客运站规定，乘客可以免费携带一定质量的行李，但超过该质量则需要购买行李票．且行李费y (元)是行李质量x (千克)的一次函数，如图3所示．（1）求y 与x 之间的函数关系式；（2）最多可免费携带多少质量的行李．解：（1）观察图象可知一次函数的图象经过（60，6），（80，10）两点，可设y kx b =+，将条件代入，得6068010.k b k b +=⎧⎨+=⎩，解得156k b ⎧=⎪⎨⎪=-⎩，．所以函数的关系式为165y x =-．（2）当0y =时，30x =．即最多可免费携带30千克的行李．图3。

一次函数关系式

一次函数关系式
一次函数，也称为线性函数，其关系式为y=ax+b，其中a和b都是常数，且a不等于0。

其中，a被称为斜率，表示函数图像在x轴的变化率；b被称为截距，表示函数图像与y轴的交点。

一次函数的图像是一条直线，其特点是斜率相等，截距不同。

当斜率为正数时，函数图像是向上的直线；斜率为负数时，函数图像是向下的直线。

一次函数在数学中应用广泛，例如在物理学中表示速度、加速度等；在经济学中表示成本、收益等；在金融学中表示股票的涨跌幅度等。

求一次函数的关系式_八年级初二数学课件

（1）求整齐摆放在桌面上的碗的高度y(cm)与碗的个数x(个) 之间的函数关系式；（y与x成一次函数关系）（2）把这两摞碗整齐地摆成一摞时，碗的高度是多少？
11cm
14cm
2.在弹性限度内，弹簧的长度 y（厘米）是
所挂物体质量 x（千克）的一次函数。一
根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米。请写出
V/(米/秒)
O
t/秒
利用点的坐标求函数关系式
1.已知一次函数y=kx+b，当x =0时， y =2；当x =4时，y =6.求这个一次函数的解析式． 2.已知一次函数的图象经过点(3,5)与（－4，－9）.求这个一次函数的解析式．
利用表格信息确定函数关系式
1.某型号汽车进行耗油实验，y(耗油量)是t(时间) 的一次函数，函数关系如下表，请确定函数表达式。
函数解析式和函数图象如何相互转化呢？
从数到形
函数解析式 y=kx+b(k ≠0)
选取满足条件的画出一次函数的
两点(x1,y1)
图象直线L
与(x2,y2)
解出
选取
从形到数
体现了“数形结合”的数学思想
利用图像求函数关系式
某物体沿一个斜坡下滑，它的速度 v （米/ 秒）与其下滑时间 t （秒）的关系如右图所示：请写出 v 与 t 的关系式；
若两个变量x,y间的关系式可以表示成 y=kx+b(k,b为常数,k不为零）的形式, 称y
是x的一次函数
一次函数的图象是直线
我们在画函数y=2x,y=3x-1时，至少应选取几个点？为什么？
前面我们学习了给定一次函数解析式，可以
说出它的性质，反过来给出有关的信息，能否求出解析式呢？

一次函数知识点大全

一次函数知识点大全一、一次函数和正比例函数的概念1．概念：若两个变量x，y间的关系式可以表示成y=kx+b（k，b为常数，k≠0）的形式，则称y是x的一次函数（x为自变量），特别地，当b=0时，称y 是x的正比例函数.（1）一次函数的自变量的取值范围是一切实数，但在实际问题中要根据函数的实际意义来确定.（2）一次函数y=kx+b（k，b为常数，k≠0）中的“一次”和一元一次方程、一元一次不等式中的“一次”意义相同，即自变量x的次数为1，一次项系数k必须是不为零的常数，b可为任意常数.★判断一个等式是否是一次函数先要化简（3）当b=0，k≠0时，y= kx仍是一次函数.(正比例函数)（4）当b=0，k=0时，它不是一次函数.二、函数的图象把一个函数的自变量x与所对应的y的值分别作为点的横坐标和纵坐标在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象．画函数图象一般分为三步：列表、描点、连线．一次函数的图象由于一次函数y=kx+b（k，b为常数，k≠0）的图象是一条直线，所以一次函数y=kx+b的图象也称为直线y=kx+b．由于两点确定一条直线，描出适合关系式的两点，再连成直线，一般选取两个特殊点：直线与y轴的交点（0，b），直线与x轴的交点（-，0）.画正比例函数y=kx的图象时，只要描出点（0，0），（1，k）即可.三、一次函数性质1. 一次函数y=kx+b（k，b为常数，k≠0）的性质（1）k的正、负决定直线的倾斜方向；①k＞0时，y的值随x值的增大而增大；②k﹤O时，y的值随x值的增大而减小．（2）|k|大小决定直线的倾斜程度，即|k|越大，直线与x轴相交的锐角度数越大（直线陡），|k|越小，直线与x轴相交的锐角度数越小（直线缓）；（3）b的正、负决定直线与y轴交点的位置；①当b＞0时，直线与y轴交于正半轴上；②当b＜0时，直线与y轴交于负半轴上；③当b=0时，直线经过原点，是正比例函数．（4）由于k，b的符号不同，直线所经过的象限也不同；（5）由于|k|决定直线与x轴相交的锐角的大小，k相同，说明这两个锐角的大小相等，且它们是同位角，因此，它们是平行的．另外，从平移的角度也可以分析，例如：直线y=x＋1可以看作是正比例函数y=x向上平移一个单位得到的．2. 正比例函数y=kx（k≠0）的性质（1）正比例函数y=kx的图象必经过原点；（2）当k＞0时，图象经过第一、三象限,y随x的增大而增大；（3）当k＜0时，图象经过第二、四象限,y随x的增大而减小．y=kx (k>0)y=kx (k<0)3.点P（x0，y0）与直线y=kx+b的图象的关系（1）如果点P（x0，y0）在直线y=kx+b的图象上，那么x0,y0的值必满足解析式y=kx+b；（2）如果x0，y0是满足函数解析式的一对对应值，那么以x0，y0为坐标的点P 必在函数的图象上．例如：点P（1，2）满足直线y=x+1，即x=1时，y=2，则点P（1，2）在直线y=x+l的图象上；点P′（2，1）不满足解析式y=x+1，因为当x=2时，y=3，所以点P′（2，1）不在直线y=x+l的图象上．确定正比例函数及一次函数表达式的条件（1）由于正比例函数y=kx（k≠0）中只有一个待定系数k，故只需一个条件（如一对x，y的值或一个点）就可求得k的值．（2）由于一次函数y=kx+b（k≠0）中有两个待定系数k，b，需要两个独立的条件确定两个关于k，b的方程，求得k，b的值，这两个条件通常是两个点或两对x，y的值．四、一次函数与方程1. 一元一次方程、一元一次不等式及一次函数的关系一次函数及其图像与一元一次方程及一元一次不等式有着密切的关系，函数y=ax+b（a≠0，a，b为常数）中，函数的值等于0时自变量x的值就是一元一次方程ax+b=0（a≠0）的解，所对应的坐标（－，0）是直线y=ax+b与x轴的交点坐标，反过来也成立；•直线y=ax+b在x轴的上方，也就是函数的值大于零，x 的值是不等式ax+b>0（a≠0）的解；在x轴的下方也就是函数的值小于零，x的值是不等式ax+b<0（a≠0）的解．2. 坐标轴的函数表达式函数关系式x=0的图像是y轴，反之，y轴可以用函数关系式x=0表示；•函数关系式y=0的图像是x轴，反之，x轴可以用函数关系式y=0表示．3. 一次函数与二元一次方程组的关系一般地，每个二元一次方程组，都对应着两个一次函数，于是也就是对应着两条直线，从“数”的角度看，解方程相当于考虑自变量为何值时两个函数的值相等，以及这两函数值是何值；从形的角度考虑，解方程组相当于确定两条直线的交点坐标，所以一次函数及其图像与二元一次方程组有着密切的联系．4. 两条直线的位置关系与二元一次方程组的解（1）二元一次方程组有唯一的解直线y=k1x+b1不平行于直线y=k2x+b2 k1≠k2．（2）二元一次方程组无解直线y=k1x+b1∥直线y=k2x+b2 k1=k2，b1≠b2．（3）二元一次方程组有无数多个解直线y=k1x+b1与y=k2x+b2重合k1=k2，b1=b2．5. 待定系数法先设待求函数关系式（其中含有未知常数系数），再根据条件列出方程（或方程组），求出未知系数，从而得到所求结果的方法，叫做待定系数法．其中未知系数也叫待定系数．例如：函数y=kx+b中，k，b就是待定系数．用待定系数法确定一次函数表达式的一般步骤：一设，二代，三解，四代入（1）设函数表达式为y=kx+b；（2）将已知点的坐标代入函数表达式，解方程（组）；（3）求出k与b的值；（4）将k、b的之带入y=kx+b，得到函数表达式。

知识点191 根据实际问题列一次函数关系式(解答题)

一、解答题1、已知等腰三角形的周长为12cm，若底边长为y cm，一腰长为x cm．（1）写出y与x的函数关系式；（2）求自变量x的取值范围．考点：根据实际问题列一次函数关系式；等腰三角形的性质。

专题：几何图形问题。

分析：（1）底边长=周长﹣2×腰长；（2）根据三角形三边关系定理：三角形任意两边之和大于第三边来进行解答．解答：解：（1）依题意有：y=12﹣2x，故y与x的函数关系式为：y=12﹣2x；（2）依题意有：，即，解得：3＜x＜6．故自变量x的取值范围为3＜x＜6．点评：本题的难点在于根据三角形三边关系定理得到自变量的取值范围．考点：根据实际问题列一次函数关系式。

专题：应用题。

分析：当摄氏温度每次增加10℃，华氏温度每次就增加18℉，由此判断是一次函数关系式，设一次函数解析式，用“两点法”求解．解答：解：根据表格可知，y与x是一次函数关系，设y=kx+b，把x=0，y=32和x=10，y=50代入函数关系式得：，解得：．所以：y=1.8x+32．点评：本题关键是根据表格确定函数关系式，再代值求函数关系式．3、某汽车加油站储油45000升，每天给汽车加油1500升，那么储油量y（升）与加油x（天）之间的关系式是什么？并指出自变量的取值范围．考点：根据实际问题列一次函数关系式。

专题：应用题。

分析：直接根据题意可求得储油量y（升）与加油x（天）之间的关系式是：储油量=45000﹣1500×加油天数．自变量根据1500x≤45000和天数是非负整数列不等式组即可求解．解答：解：根据题意得储油量y（升）与加油x（天）之间的关系式是：y=45000﹣1500x，∵1500x≤45000，x≥0，∴0≤x≤30，即y=45000﹣1500x（0≤x≤30）．点评：读懂题意，根据实际意义列出关于两个变量之间的等式是求得函数关系式的关键．自变量取值范围要结合实际意义列不等式求解．4、某商人进货时，进价已按原价a扣去了25%．他打算对此货订一新价销售，以便按新价让利20%销售后，还可获得售价的25%的利润．试写出此商人经销这种货物时按新价让利总额与货物售出件数之间的函数关系式．考点：根据实际问题列一次函数关系式。

如何求一次函数的关系式

所以把（２，１）代￣ｙ＝ｋｘ一３得２ｋ一３＝１，因
２，１），也是最简单的函数．掌握一个函数的最简点（
单的办法是求出函数关系式，有了函数式，
：２，就不难出其图像，从而获知其性质．本此所以这个一次函数的关系式为ｙ－＝２ｘ一３．文我们拟从几个表争方面总结一次函
示意图，注意考虑两种情况，因此方程中出
式为ｙ＝ｘ＋２．
ｋＩ，而不是ｋ．当ｋ＜Ｏ时，ｙ随着的增加而减少，因此现ｌ例７若直线Ｚ与直线ｍ：ｙ＝２ｘ一４关于ｙ当ｘ＝ｌ时，ｙ＝６；当ｘ＝４时，ｙ＝３．
可以把平行线 “ 数量化” ．
例４已知一次函－￣＆ｙ＝ｋｘ＋ｂ，当１ ≤ ≤ ４时，３ ≤ｙ ≤６，求这个一次函数的关系式．
例６已知直线ｙ＝ｋｘ一４与两坐标轴所
围成的三角形面积等于４，求直线关系式．
点的坐标是（１，４），（３，１）．
【点评】利用图像求解函数式的关键是，从图像上读出直线上的两点坐标，然后函数关系式的ｋ相等，但ｂ不相等．这个性质可以看做平行线的代数意义，利用ｋ，我们利用待定系数法求解．【点评】如果两条直线互相平行，那么

一次函数各类题型详解加练习

∴A的坐标为（0,2），B的坐标为（0，-3）
令 +2=-2 -3，解得 =
（提示：求两个函数之间的交点，令两个解析式相等即可得到交点横坐标）
将 = 带入y₁= +2
得：y₁= +2=
∴点C的坐标为（，）
（2）AB=2－（－3）=5（提示：AB与y轴重合，上y减下y求长度。）
（分析：以AB为底，点C到AB的距离为高，就可以求出△ABC的面积。）
求线段AB、CD的长度。
解：∵AB∥x轴
∴AB=6－(－3)= 9
（右x减左x，即可求得长度）
同理∵CD∥x轴
∴CD=5－2=3
③既不平行于x轴，也不平行于y轴：如：点A（x₁，y₁），点B（x₂，y₂），则使用求线段的通用公式AB=
例：点A的坐标为（3,3），点B的坐标为（-3，-5），
求线段AB的长度。
S△COP=
OC·OP= ×8×(2t-8)=8t－32（t≥4）
(上一问中刚求出)
－8t+32=2×16（0≤t＜4）
S△COP=2S△AOB，即或解，得：t=0或者t=8
8t－32=2×16（t≥4）
（4）思路：在△COP和△AOB中:∠COP=∠AOB=90°，OC =OA=8
还差一组条件就能证明两三角形全等了，因为整个题目并未有角度的信息，
解：AB中点的坐标为：（，）整理，得（，3）
∵直线AB的k₁=2，且k₁·k₂=－1
∴垂直于AB的直线的k₂=
设垂直平分线解析式为：y= +b，将（，3）代入解析式，
可得AB中垂线的解析式为y= +
把y=0代入解析式可得
点P的坐标为：（，0）
综上：符合要求的点P共有4个：

一次函数关系式的确定

一次函数关系式的确定
※知识要点
1．确定一次函数关系式
(1)基本方法：；源自(2)具体步骤：①设：；
②代：
；
③解：
；
④定：
；
2．确定直线交点
(1)理解交点：两条直线的交点坐标同时
两直线解析式；
(2)求解交点：解联立两直线解析式所形成的
；
※题型讲练【例 1】已知一次函数的图像经过点（3，5）与(－4，－9)， (1)求这个一次函数的解析式； (2)判断点（2，4）是否在该函数图像上？请说明理由．
(2)求当挂 5kg 重物时，弹簧的总长度是多少？
A．(0，－3) B．(－3，0) C．(0，3) D．(0，－3)
3．已知点(－4，y1)，(2，y2)都在直线 y 1 x 2 上，则 y1
和 y2 大小关系是(
)
2
A． y1＞y2
B． y1＝y2
C．y1＜y2 D．不确定
4．如果直线 y＝ax＋2 与直线 y＝bx＋3 的交点在 x 轴上，则
(3)已知直线与 y＝－x+7 交于 y 轴上一点 A，且过一次函数 y＝
14．直线 y＝kx＋b 过 A(－1，5)点且平行于 y＝－x．
(1)求这条直线的解析式；
(2)若点 B(m，2)在这条直线上，O 为坐标原点，求 m 及△AOB 的面积．
【例 4】两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给出的数据信息，解答问题：
(1)求整齐叠放在桌面上饭碗的高度 y(cm)与饭碗数 x (个)之间的一次函数解析式(不要求写出自变量 x 的取值范围)；
(2 )若桌面上有 12 个饭碗，整齐叠放成一摞，求出它的高度．
※课后练习 1．下列四个点中在 y＝3x＋2 的图象上的是( )

4.4.1一次函数的表达式

（２，５）
x/ 秒
练习
y=kx经过(4,2)这点则函数的表达式为
1 y= x 2
例：
已知一次函数的图象经过（0，-2）和（2，0）两点，求这个一次函数的表达式设这个一次函数的表达式：y=kx+b
∵这个一次函数图象过（0，-2）和（2，0）两点，
∴ -2=b 0=2k+b
① ② ∴k=1
∴b=2
∴原直线为y=-2x+2
4 直击中考
（1）、(陕西)若正比例函数的图象经过点 (-1, 2),则这个函数图象必经过点( D ) A.(1, 2) B.(-1, -2) C.(2, -1) D.(1, -2) （2）、(河南)图象经过点（2，6）的正比例函数的表达式是 y=3x ．（3）、已知函数y=(k-2)x+2k+1，若它是正比例函数, 求k的值. 若它是一次函数, 求k 值.
(3)当y=30时，x=______ 42 。
4 3 2 1 0 1 2 3 4 5
x
３. 已知直线l与直线y=-2x平行，且与y 轴交于点(0,2)，求直线l的解析式。
解：设直线l为y=kx+b, ∵l与直线y=-2x平行，∴k= -2 又直线过点（０，２）， ∴２＝－２×0+b,
解: (1) 把P(3, -6)代入正比例函数y=k1x得， -6=3k1，k1=-2，代入一次函数y=k2x-9得 k2=1，故两函数表达式分别为：y=-2x，y=x-9． (2) 由图象可知，S△OAP =1/2×9×6=27．
1.5
-3
0
x
2．（2010·清远中考）正比例函数y=kx和一次函数y=ax+b的图象都经过点A（1,2），

一次函数的关系式

mqx48jop
这，这是啥啊？”耿英尽量小声儿地说：“这还是俺想的法子呢！俺们大老远的带东西回来，路途难免不安全啊！还有，当时还不知道爹还在呢！唉，一两句话也说不清楚，等俺以后慢慢跟你说哇！”耿正第二个跑了出来，非常抱歉地轻轻抱住这个被吓傻了的好兄弟，连声说：“对不起了大壮！对不起，对不起，吓着你了！”耿老爹、耿直和尚武也出来了。看到这般光景，耿老爹和尚武都不由地一愣！耿直却笑了。见哥哥正抱着大壮在道歉呢，就说：“哥，你快拽拽大壮哥的耳朵哇，给他出出惊儿！”大壮拿下耿正拽他耳朵的手，不放心地问：“真没有事儿吗？”耿正肯定地说：“真没有！”看到耿英弯腰提起自己的两个鞋跟以后，又转身拾起了滚落在当院儿的那个大礼帽，耿老爹赶快说：“英子，你先别收拾！”说着话，他就稳稳地走到近前来。此时，被吓呆了的尚武也已经缓过来了，紧紧跟在耿老爹的身后过来看个究竟。耿老爹先认真地看看寿棺头上的彩绘、题词和挽联；再转着圈儿看看贴在寿棺外面那些三角形状的金纸和银纸；最后拿起了那个穿了一套寿衣闭目沉睡并且脏兮兮的模特儿，又从耿英手里拿过来大礼帽给它戴上，左看右看，忍不住哈哈大笑起来：“哈哈哈，哈哈哈，好哇，好哇，实在是好哇！岂之是好，实在是太妙了呀！”直笑得眼泪都流了出来，可把他的几个娃儿们给吓坏了！耿正瞪大眼睛问：“爹，你没事儿哇？”耿英说：“爹，都是俺出了这个馊主意，你可莫要怪俺哥啊！”耿直也说：“爹，你莫要生气！这不就好像人们做梦一样，正好反过来了嘛！咱们这就叫‘冲-喜’！”尚武也亲切地挽起耿老爹的胳膊说：“爹，二哥说得很对，这就叫‘冲喜’！咱们现在合家大团圆了，正是这个闭目沉睡的寿星老儿和它睡回来的这个大‘寿喜’，给咱们家冲来了天大的喜事啊！”耿老爹把脏兮兮的模特儿轻轻地放在杂乱的衣物上，又擦掉笑出来的眼泪，朗声说：“放心，娃儿们，爹没有事儿，高兴着呢，也清楚得很！”他说着，抬手轻轻拍一拍这个虽然板材很薄，但处置得相当完备的寿棺说：“这个‘寿喜’爹太喜欢了！虽然嘛，这挽联有些个受不起，但也不必修改了，原封不动地保存着哇，爹将来就用它了！”耿英说：“那咱把这个模特儿什么的处理掉哇„„”耿老爹又摇头又摆手，连声说：“不不不，全部保留，爹都要了！”耿正、耿英、耿直和尚武一起说：“模特儿也要？”耿老爹：“先让它给俺住着这个‘寿喜’哇！至于以后怎么安置这老兄，咱以后再说！”耿老爹吩咐完了以后，转身拍拍一直愣在一旁的大壮的肩膀，笑着说：“壮子，这都是他们三个鼓捣的，俺和武儿也是第一次看得这么仔细呢！既然是他们鼓捣的，就让他们自己收拾哇！走，咱们进屋里坐！”耿正也

一次函数的关系式

练习1：已知正比例函数y=kx,(k≠0)的图象经过点（-2，4）.求这个正比例函数的解析式．解：∵y=k x的图象过点（-2，4），∴4=-2k解得k=-2∴这个一次函数的解析式为y=-2x11.一次函数的一般形式是什么变式1：已知正比例函数y=kx,(k≠0),当x=-2时，y=4.求这个正比例函数的解析式．变式2：已知正比例函数y=kx,(k≠0),当x=-2时，y=4.求当x=5时的函数值．练习2：已知一次函数y=2x+b的图象过点(2,-1).求这个一次函数的解析式．解：∵y=2x+b的图象过点（2，-1）.∴-1=2×2 +b解得b=-5∴这个一次函数的解析式为y=2x-5确定正比例函数的表达式类型一：已知两点坐标求函数表达式1.已知一次函数的图象经过点(3,5)与（－4，－9）.求这个一次函数的解析式．类型二：根据定义求函数表达式1、已知y与x成正比例，且当x=-1时，y=-6，求y与x之间的函数关系式解：由题意可设y=kx(k≠0)∵当x=-1时，y=-6，∴-k=-6∴k=6∴y=6x2、已知y-2与x成正比例，当x=-2时，y=8，（1）写出y与x之间的函数关系式；（2）求当x＝－1时，y的值；（3）求当y＝0时，x的值。

解：根据题意设：y-2=kx(k≠0)∴-2k=8-2∴k=-3∴y-2=-3x∴y=-3x+21、已知直线l 与直线y=-2x 平行，且与y 轴交于点(0,2)，求直线l 的解析式。

类型五：根据图象之间的平行关系求解析式2.将函数y=x+2的图象平移，使它经过点(1，-3)，求平移后的直线所对应的函数表达式解：设y=kx+b （k ≠0）根据题意得：解得k=1k+b=-3k=1b=-4∴y=x-4写出一个一次函数，使它的图象过点（-1，2）解：设函数解析式为y=kx+b(k ≠0)由题意，得: -k+b=2∴b=2+k取k=1，则b=3，有y=x+3类型八：根据缺少的条件求表达式一次函数y=kx+b 的自变量的取值范围是-3≤x ≤6，相应函数值的取值范围是-5 ≤y ≤-2，求这个函数的解析式类型九：根据取值范围求表达式解：①若x=-3时，y=-5，x=6时，y=-2则-3k+b=-5；解得k=6k+b=-2，b=-413②若x=-3时，y=-2,有；x=6时，y=-5,则-3k+b=-2解得k=-6k+b=-5，b=-3故所求函数的解析式为：y= x-4或y=-x-3一次函数y=kx+b 的自变量的取值范围是-3≤x ≤6，相应函数值的取值范围是-5 ≤y ≤-2，求这个函数的解析式1313131.直线l 与直线y=1+2x 交点的横坐标为2，与直线y=-x+2的交点的纵坐标为1，求直线l 的解析式。

一次函数关系式的常见类型(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)

专题4.22一次函数关系式的常见类型（知识梳理与考点分类讲解）一次函数关系式常见类型目录：【类型1】定义型【类型2】一点型【类型3】两点型【类型4】图象型【类型5】斜截型【类型6】应用型【类型7】面积型【类型8】平移型【类型9】对称型【考点一】定义型【例1】（2023秋·八年级课时练习）已知函数()2324my m x n -=-++．（1）当,m n 为何值时，y 是x 的一次函数，并写出关系式；（2）当,m n 为何值时，y 是x 的正比例函数，并写出关系式．【答案】（1）当m=-2，n 为任意实数时，y 是x 的一次函数，关系式为44y x n =-++；（2）当m=-2，n=-4时，y 是x 的正比例函数，关系式为4y x=-【分析】（1）根据一次函数的定义即可求出结论；（2）根据正比例函数的定义即可求出结论．解：（1）由题意可得23120m m ⎧-=⎨-≠⎩，n 可以取任意实数解得：m=-2∴44y x n=-++∴当m=-2，n 为任意实数时，y 是x 的一次函数，关系式为44y x n =-++；（2）由题意可得2312040m m n ⎧-=⎪-≠⎨⎪+=⎩，解得：24m n =-⎧⎨=-⎩∴4y x=-∴当m=-2，n=-4时，y 是x 的正比例函数，关系式为4y x =-．【点拨】此题考查的是根据一次函数和正比例函数的定义，求参数问题，掌握一次函数和正比例函数的定义是解题关键．【举一反三】【变式1】（2022秋·八年级单元测试）在平面直角坐标系中，若一个正比例函数的图象经过A （5，b ），B （a ，4）两点，则a ，b 一定满足的关系式为（）A ．a ﹣b ＝1B ．a ＋b ＝9C ．a •b ＝20D ．a b ＝34【答案】C【分析】设该正比例函数是y ＝kx （k ≠0），将A 、B 两点的坐标分别代入，通过整理求得a ，b 一定满足的关系式．解：设该正比例函数是y ＝kx （k ≠0），则b ＝5k ，4＝ak ．∴4b ＝5a ，∴ab ＝20.故选：C ．【点拨】本题考查了正比例函数的概念，关键是清楚图象经过点，则点的坐标满足函数解析式．【变式2】（2022秋·安徽蚌埠·八年级校考阶段练习）已知2y -与3x +成正比,且当1x =时,y =-6，则y 与x 的关系式是.【答案】y=-2x-4【分析】由2y -与3x +成正比例可设2y -=k （3x +）（k≠0），代入1x =时,y =-6即可得出关于k 的一元一次方程，解之即可得出结论．解：∵2y -与3x +成正比，∴设2y -=k 3x +（）（k≠0）．∵当1x =时,y =-6，∴-6-2=k （1+3），解得：2k =-，∴22(3)y x -=-+∴y 与x 的关系式为y=-2x-4故答案为y=-2x-4.【点拨】本题考查了正比例的意义，根据正比例的定义正确设未知数是解题关键．【考点二】一点型【例2】（2023春·福建莆田·八年级校考期中）已知直线上l ：1y kx =-经过点()2,3A ．（1）求直线l 的解析式；（2）判断点(1,23)P m m --是否在直线l 上，请说明理由．【答案】（1）21y x =-；（2）在直线l 上，理由见详解【分析】（1）根据待定系数法可求解函数解析式；（2）把1x m =-代入（1）中解析式进行求解即可．（1）解：把点()2,3A 代入解析式1y kx =-得：213k -=，解得：2k =，∴直线l 的解析式为21y x =-；（2）解：由题意可把1x m =-代入21y x =-得：()21123m m --=-，∴点(1,23)P m m --在直线l 上．【点拨】本题主要考一次函数的图象与性质，熟练掌握利用待定系数法求解函数解析式是解题的关键．【举一反三】【变式1】（2021秋·广西梧州·八年级统考期中）已知一次函数5y kx =+的图象经过()12M -，，则k 的值是（）A ．3B ．3-C ．6D ．6-【答案】A【分析】把()12M -，代入一次函数5y kx =+求出k 的值即可．解：把()12M -，代入一次函数5y kx =+得：25k =-+，解得：3k =，故A 正确．故选：A ．【点拨】本题主要考查了求一次函数解析式，解题的关键是熟练掌握待定系数法．【变式2】（2023秋·重庆沙坪坝·八年级重庆八中校考阶段练习）已知一次函数2y x a =+与y x b =-+的图象都经过()2,0A ，且与y 轴分别交于B ，C ，则ABC 的面积为．【答案】6【分析】利用待定系数法求得a 、b 的值，求得点B ，C 的坐标，再利用三角形的面积公式计算即可．解：∵一次函数2y x a =+与y x b =-+的图象都经过()2,0A ，把()2,0A 代入2y x a =+得，40a +=，∴4a =-，∴一次函数解析式为24y x =-，∴()0,4B -，把()2,0A y x b =-+得，20b -+=，∴2b =，∴一次函数解析式为2y x =-+，∴()0,2C ，∴=42=6BC --，∴12662ABC S =⨯⨯= ，故答案为：6．【点拨】本题考查两直线的交点问题、一次函数的图象上点的特征，通过已知点的坐标求函数解析式是解题的关键．【考点三】两点型【例3】（2023春·吉林长春·八年级校考期中）已知某一次函数y kx b =+的图像经过点(1,3)，(1,7)-，求这个一次函数的解析式．【答案】25y x =-+【分析】将(1,3)，(1,7)-代入y kx b =+求出k 、b 的值，再将k 、b 的值反回代入y kx b =+中，即可得到一次函数的解析式．解：将(1,3)，(1,7)-代入y kx b =+，得37k b k b=+⎧⎨=-+⎩，解得25k b =-⎧⎨=⎩，∴一次函数的解析式为25y x =-+．【点拨】本题主要考查了利用待定系数法求一次函数的解析式，熟练掌握待定系数法是解题的关键．【举一反三】【变式1】（2023春·安徽池州·八年级统考开学考试）若弹簧的总长度()cm y 是所挂重物x （千克）的一次函数图象如图，则不挂重物时，弹簧的长度是（）A ．5cmB ．8cmC ．9cmD ．10cm【答案】B 【分析】先利用待定系数法求一次函数解析式，再令0x =，进行求解即可．解：设一次函数解析式为()0y kx b k =+≠，∵点()4,10、点()20,18在一次函数图象上，∴4102018k b k b +=⎧⎨+=⎩，解得128k b ⎧=⎪⎨⎪=⎩，∴一次函数解析式为182y x =+，当0x =时，1=08=82y ⨯+，∴不挂重物时，弹簧的长度是8cm ，故选：B ．【点拨】本题考查利用待定系数法求一次函数解析式、求函数值，熟练利用待定系数法求一次函数解析式是解题的关键．【变式2】（2023春·安徽宿州·八年级校考开学考试）如图，直线24y x =+与x 轴、y 轴交于点A 、B ，M 、N 分别是AB 、OA 的中点，点P 是y 轴上一个动点，则PM PN +的最小值为，此时点P 的坐标为．【答案】()0,1【分析】如图，作点M 关于y 轴对称的点M '，连接M N '，由PM PN PM PN '+=+，可知当点P 在M N '上时，PM PN +的值最小，当0x =时，2044y =⨯+=，即B ()0,4；当0y =时，240x +=，解得2x =-，即A ()2,0-，由M 、N 分别是AB 、OA 的中点，可得M ()1,2-，N ()1,0-，M '()1,2，即M N ='，进而可得PM PN +的最小值，待定系数法求得直线M N '的表达式为1y x =+，当0x =时，011y =+=，即点P 的坐标为()0,1．解：如图，作点M 关于y 轴对称的点M '，连接M N '，∵PM PN PM PN '+=+，∴当点P 在M N '上时，PM PN +的值最小，当0x =时，2044y =⨯+=，即B ()0,4；当0y =时，240x +=，解得2x =-，即A ()2,0-，∵M 、N 分别是AB 、OA 的中点，∴M ()1,2-，N ()1,0-，∴M '()1,2，∴MN ='∴PM PN +的最小值为设直线M N '的表达式为()0y kx b k =+≠，将()1,2M '，()1,0N -代入得20k b k b +=⎧⎨-+=⎩，解得11k b =⎧⎨=⎩，∴直线M N '的表达式为1y x =+，当0x =时，011y =+=，∴点P 的坐标为()0,1，故答案为：()0,1．【点拨】本题考查了一次函数解析式，对称的性质，勾股定理求两点之间的距离．解题的关键在于明确线段和最小的情况．【考点四】图像型【例4】（2023秋·贵州遵义·九年级校考阶段练习）如图，直线1l 的解析式为33y x =-+，且1l 与x 轴交于点D ，直线2l 经过点A 、B ，直线1l 、2l 交于点C ．（1）求ADC △的面积；（2）在直线2l 上存在异于点C 的另一点P ，使得ADP △与ADC △的面积相等，请求出点P 的坐标．【答案】（1）92；（2）()6,3【分析】（1）已知1l 的解析式，令0y =求出x 的值即可求出()1,0D ，设2l 的解析式为y kx b =+，由图联立方程组求出k ，b 的值，即可得直线2l 的解析表达式为362y x =-；联立方程组，求出交点C 的坐标，继而可求出ADC S △；（2）ADP △与ADC △底边都是AD ，面积相等所以高相等，ADC △高就是点C 到AD 的距离．解：（1）由33y x =-+，令0y =，得330x -+=，∴1x =，∴()1,0D ；设直线2l 的解析表达式为y kx b =+，由图象知：403x y x ===，；，32y =-，代入表达式y kx b =+，∴40332k b k b +=⎧⎪⎨+=-⎪⎩，∴326k b ⎧=⎪⎨⎪=-⎩，∴直线2l 的解析表达式为362y x =-；由33362y x y x =-+⎧⎪⎨=-⎪⎩，解得23x y =⎧⎨=-⎩，∴()2,3C -，∵3AD =，∴193322ADC S =⨯⨯-=△；（2）ADP △与ADC △底边都是AD ，面积相等所以高相等，ADC △高就是点C 到直线AD 的距离，即C 纵坐标的绝对值33=-=，则P 到AD 距离3=，∴P 纵坐标的绝对值3=，点P 不是点C ，∴点P 纵坐标是3，∵ 1.563y x y =-=，，，1.563x ∴-=，6x =，即()6,3P ．【点拨】本题考查的是一次函数的图象与性质，二元一次方程组，以及三角形面积的计算等有关知识，难度中等．掌握一次函数的图象与性质，是解答本题的关键．【举一反三】【变式1】（2023·河南郑州·河南省实验中学校考模拟预测）如图是y 关于x 的一个函数图象，根据图象，下列说法正确的是（）A ．该函数的最小值为3-B ．当0x ≥时，y 随x 的增大而增大C ．当0x =时，对应的函数值12y =D ．当12x =和32x =时，对应的函数值相等【答案】C 【分析】分别求出1x ≥和1x ≤时的函数解析式，结合图象，逐一进行判断即可．解：A 、由图象可知，函数的最小值为2-；故该选项错误；B 、当1x ≥时，y 随x 的增大而增大，故该选项错误；C 、设1x ≤时，函数的解析式为y kx b =+，由图可知，点()()1,3,1,2--，在直线上，∴32k b k b =-+⎧⎨-=+⎩，解得：5212k b ⎧=-⎪⎪⎨⎪=⎪⎩，∴5122y x =-+，∴当0x =时，12y =，故该选项正确；D 、当12x =时，51132224y =-⨯+=-，设1x ≥时，函数的解析式为y mx n =+，由图可知，点()()3,1,1,2-在直线上，∴132m n m n =+⎧⎨-=+⎩，解得：3272m n ⎧=⎪⎪⎨⎪=-⎪⎩，∴3722y x =-，∴当32x =时，975424y =-=-；∴当12x =和32x =时，对应的函数值不相等；故该选项错误；故选C ．【点拨】本题考查一次函数的图象和性质，解题的关键是正确的求出函数的解析式，利用数形结合的思想进行求解．【变式2】（2023秋·山东泰安·七年级统考期末）如图，已知一次函数y kx b =+的图象与x 轴，y 轴分别交于点()1,0，点()0,2，有下列结论：①图象经过点()2,3；②关于x 的方程0kx b +=的解为1x =；③当1x >时，0y <．其是正确的是．【答案】②③【分析】待定系数法求出函数解析式，根据图象法解方程，增减性判断函数值的变化情况，逐一进行判断即可．解：∵一次函数y kx b =+的图象与x 轴，y 轴分别交于点()1,0，点()0,2，∴02k b b =+⎧⎨=⎩，解得：22k b =-⎧⎨=⎩，∴22y x =-+，当2x =时，222y =-⨯+，=2y -；∴图象不经过点()2,3；故①错误；一次函数y kx b =+的图象与x 轴交于点()1,0，∴关于x 的方程0kx b +=的解为1x =；故②正确；由图象可知，y 随x 的增大而减小，∴当1x >时，0y <；故③正确；故答案为：②③【点拨】本题考查一次函数的图象和性质，待定系数法求出函数解析式，利用函数的性质和图象法求解，是解题的关键．【考点五】斜截型【例5】（2019秋·安徽合肥·八年级校联考阶段练习）已知一次函数的图象平行于y ＝﹣13x ，且截距为1．（1）求这个函数的解析式；（2）判断点P （﹣2，13）是否在这个函数的图象上．【答案】（1）y ＝﹣13x +1；（2）不在．【分析】（1）根据两平行直线的解析式的k 值相等可求出k ，再由截距为1求出b 值，即可得解；（2）把点1(2,3P -代入函数解析式检验即可.解：（1）设这个函数的解析式为y kx b =+，∵一次函数的图象平行于13y x =-，且截距为1，1,13k b ∴=-=∴这个函数的解析式为113y x =-+；（2）当2x =-时，151((2)1333y =-⨯-+=≠，故点1(2,)3P -不在这个函数的图象上.【点拨】本题考查了一次函数的定义和性质，如果两条直线平行，则他们的函数解析式的k 值相等，这条性质常常用来解题，需熟记.【举一反三】【变式1】（2021秋·安徽六安·八年级校考阶段练习）若y 关于x 的一次函数y =（2m +1）x -m +3，y 随x 的增大而增大，且截距不大于1，则m 的取值范围是（）A ．m >-12B ．m ≥4C ．-12＜m ≤2D ．m ≥2【答案】D 【分析】根据题意，可得一次函数的0k >，1b ≤，据此列出不等式组，即可求得m 的取值范围．解：依题意，21031m m +>⎧⎨-+≤⎩解得2m ≥故选D ．【点拨】本题考查了一次函数的性质，解一元一次不等式组，掌握一次函数的性质是解题的关键．【变式2】（2023春·上海闵行·八年级统考期末）直线y kx b =+在y 轴上的截距为3-，且平行于l ：y x =-，那么直线的表达式为．【答案】3y x =--/3y x=--【分析】根据互相平行的直线的解析式k 的值相等确定出k ，根据“在y 轴上的截距是3-”求出b 值，即可得解．解：∵直线y kx b =+平行于直线y x =-，∴1k =-．又∵直线y kx b =+在y 轴上的截距是3-，∴3b =-，∴这条直线的解析式是3y x =--．故答案为：3y x =--．【点拨】本题考查了两直线平行的问题，熟记并利用平行直线的解析式的k 值相等是解题的关键．【考点六】应用型【例6】（2022春·湖南怀化·八年级统考期末）一辆轿车在高速公路上匀速行驶，油箱存油量Q （升）与行驶的路程S （km ）成一次函数关系．若行驶100km 时，油箱存油43.5升，当行驶300km 时，油箱存油30.5升，请求出这个一次函数关系式，并写出自变量S 的取值范围．【答案】1350200Q S =-+，自变量S 的取值范围为3076913S ≤≤【分析】根据题目意思设出函数关系式，根据已知条件用待定系数法解出函数关系式中的参数，可得函数关系式，当0Q =时，此时的S 为最大值，最小值为0，即可写出S 的取值范围．解：设：Q mS n =+，根据题意的方程组43.510030.5300m n m n=⨯+⎧⎨=⨯+⎩，解得1320050m n ⎧=-⎪⎨⎪=⎩，则该一次函数解析式为：1350200Q S =-+，当0Q =时，13500200S -+=，∴3769km 13S =，∴自变量S 的取值范围为3076913S ≤≤．【点拨】本题考查一次函数的应用，利用待定系数法确定函数解析式，注意函数自变量的取值范围应符合实际问题有意义是解答本题的关键．【举一反三】【变式1】（2023春·全国·八年级专题练习）某商场为了增加销售额，推出“七月销售大酬宾”活动，其活动内容为：“凡七月份在该商场一次性购物超过100元以上者，超过100元的部分按9折优惠．”在大酬宾活动中，小王到该商场为单位购买单价为60元的办公用品x 件（x ＞2），则应付货款y （元）与商品件数x 的函数关系式是（）A ．y ＝54x （x ＞2）B ．y ＝54x ＋10（x ＞2）C ．y ＝54x ＋90（x ＞2）D ．y ＝54x ＋100（x ＞2）【答案】B【分析】由题意得2x >，则销售价超过100元，超过的部分为60x −100，即可得．解：∵2x >，∴销售价超过100元，超过部分为60x ﹣100，∴y ＝100+（60x ﹣100）×0.9＝54x +10（2x >，且x 为整数），故选：B ．【点拨】本题考查了一次函数的应用，解题的关键是理解题意，找出等量关系．【变式2】（2023春·湖南永州·八年级统考期末）小胜参加2023年的高考，到达考点时发现没有带身份证，求助交警后，交警驱车载小胜迅速回到离考点2千米的家取身份证，并立即返回考场，小胜离考点行驶路程y （米）与时间x （分钟）之间的变化关系如右图所示，根据图像中的数据，写出y 与()06x x ≤≤之间的函数表达式．【答案】()1000306y x x =≤≤【分析】根据待定系数法求解析式即可求解．解：设y 与()06x x ≤≤之间的函数表达式为y kx =，将点()6,2000代入得，20006k =，解得：10003k =，∴y 与()06x x ≤≤之间的函数表达式为()1000306y x x =≤≤，故答案为：()1000306y x x =≤≤．【点拨】本题考查了待定系数法求解析式，数形结合是解题的关键．【考点七】面积型【例7】（2023春·八年级单元测试）如图1，在四边形ABCD 中，90B Ð=°，AD BC ∥，4AB =，6AD =．若动点P 从点B 出发，以每秒2个单位的速度沿着BC CD DA →→的路线向终点A 运动．设点P 的运动时间为t 秒，图2是点P 出发t 秒后，ABP 的面积S 与t 的函数图像．（1）a =______，b =______；（2）求MN 所在直线对应的函数表达式；（3）运动几秒后，ABP 的面积为14？【答案】（1）92，7；（2）1214455S t =-+；（3）72秒或376秒【分析】（1）结合四边形ABCD 的形状、S 与t 的函数图像，判断出t a =，t b =，10t =时，点P 的位置，利用时间、速度、路程的关系即可求解；（2）求出点M ，N 的坐标，利用待定系数法求解；（3）ABP 的面积为14时，对应的点在线段OM 或MN 上，将14S =代入对应直线的函数解析式即可求解．（1）解：由图可知，当t a =时，点P 运动到点C ，当t b =时，点P 运动到点D ，当10t =时，点P 运动到点A ，∴2BC a =，()210CD DA a +=-由图可知，点P 运动到点C 时，18ABP S = ，∴1141822BC AB BC ⋅=⋅=，解得9BC =，∴922BC a ==，∴9210112CD DA ⎛⎫+=⨯-= ⎪⎝⎭，∴111165CD DA =-=-=，∴957222CD b a =+=+=，故答案为：92，7；（2）解：由（1）知点M 的坐标为9,182⎛⎫ ⎪⎝⎭，当t b =时，点P 运动到点D ，∴当t b =时，11461222ABP S AB AD =⋅=⨯⨯= ，∴点M 的坐标为()7,12，设MN 所在直线对应的函数表达式为S mt n =+，将9,182M ⎛⎫ ⎪⎝⎭，()7,12N 代入，得：9182127m n m n ⎧=+⎪⎨⎪=+⎩，解得1251445m n ⎧=-⎪⎪⎨⎪=⎪⎩，∴1214455S t =-+；（3）解：由题意知，ABP 的面积为14时，对应的点在线段OM 或MN 上，当对应的点在线段OM 上时，设OM 的函数解析式为=S kt ，将9,182M ⎛⎫ ⎪⎝⎭代入，得：9182k =，解得4k =，∴OM 的函数解析式为4S t =，当14S =时，14742t ==；当对应的点在线段MN 上时，当14S =时，121441455t =-+，解得376t =，综上可知，运动72秒或376秒后，ABP 的面积为14．【点拨】本题考查一次函数的实际应用，涉及三角形面积公式、求一次函数解析式及自变量的值等，解题的关键是根据图形判断出不同时间段内点P 的位置．【举一反三】【变式1】（2023春·河南商丘·八年级统考期末）如图，已知直线1:24l y x =-+与坐标轴分别交于A 、B 两点，那么过原点O 且将AOB 的面积平分的直线2l 的解析式为（）A ．y x=B ．2y x =C ．3y x =D ． 1.5y x=【答案】B 【分析】根据直线与坐标轴的交点坐标求法得到A 、B 两点坐标，再由AOB 的面积被中线平分得到AB 中点坐标，利用待定系数法即可求出过原点O 且将AOB 的面积平分的直线2l 的解析式．解：直线1:24l y x =-+与坐标轴分别交于A 、B 两点，∴当0x =时，4y =，即()0,4B ；当0y =时，024x =-+，解得2x =，即()2,0A ；由三角形中线平分三角形面积可知，过原点O 且将AOB 的面积平分的直线2l 过AB 中点，∴AB 中点为0240,22++⎛⎫ ⎪⎝⎭，即()1,2，设直线2l 的解析式为2:l y kx =，将()1,2代入2:l y kx =得到2k =，则2y x =，故选：B ．【点拨】本题考查待定系数法求直线解析式，涉及求直线与坐标轴交点坐标、中线平分三角形面积、中点坐标求法等知识，熟练掌握一次函数图像与性质是解决问题的关键．【变式2】（2023春·上海·八年级专题练习）已知直线()0y kx b k =+≠与坐标轴围成的三角形面积是6，且经过()2,0，则这条直线的表达式是．【答案】36y x =-+或36y x =-【分析】先根据面积求出三角形在y 轴上边的长度，再分正半轴和负半轴两种情况讨论求解．解：根据题意，设与y 轴交点坐标为()0b ，则1262b ⨯⨯=，解得6b =，6b ∴=±，①当6b =时，与y 轴交点为()06，∴206k b b +=⎧⎨=⎩，解得36k b =-⎧⎨=⎩，∴函数解析式为36y x =-+；②当6b =-时，与y 轴的交点为()06-，∴206k b b +=⎧⎨=-⎩解得36k b =⎧⎨=-⎩，∴函数解析式为36y x =-．∴这个一次函数的解析式是36y x =-+或36y x =-．故答案为：36y x =-+或36y x =-．【点拨】本题考查的是待定系数法求一次函数的解析式，先根据三角形面积求出与y 轴的交点，再利用待定系数法求函数解析式，本题需要注意有两种情况．【考点八】平移型【例8】（2022春·湖北武汉·八年级校考阶段练习）已知直线1l 经过()0,3A -、()2,0B ．（1）求直线1l 的解析式及1l 与坐标轴围成的图形的面积；（2）将1l 向下平移3个单位长度，再向左平移1个单位长度，得到直线2l ，直接写出2l 的解析式______．【答案】（1）332y x =-；3；（2）3922y x =-【分析】（1）用待定系数法求出直线1l 的解析式，根据三角形面积公式求出与坐标轴围成的图形的面积即可；（2）根据平移的规律求出直线2l 的解析式即可．（1）解：设直线1l 的解析式为()0y kx b k =+≠，把()0,3A -、()2,0B 代入得：320b k b =-⎧⎨+=⎩，解得：323k b ⎧=⎪⎨⎪=-⎩，∴直线1l 的解析式为332y x =-；直线1l 与坐标轴围成的图形的面积为13232S =创=．（2）解：将1l 向下平移3个单位长度，再向左平移1个单位长度后得出的直线2l 的解析式为：()31332y x =+--，即3922y x =-，故答案为：3922y x =-．【点拨】本题主要考查了求一次函数解析式，直线与坐标轴围成的图形面积，一次函数的平移，解题的关键是熟练掌握待定系数法和平移规律．【举一反三】【变式1】（2023春·云南昆明·八年级统考期末）把直线6y x =向上平移后得到直线AB ，若直线AB 经过点(),m n ，且64n m -=，则直线AB 的表达式为（）A ．64y x =-+B ．64y x =--C ．64y x =-D ．64y x =+【答案】D【分析】设向上平移d 个单位，则平移后的直线AB 的解析式为6y x d =+，根据题意直线AB 经过点(),m n ，得出6d n m =-，结合已知条件，即可求解．解：设向上平移d 个单位，则平移后的直线AB 的解析式为6y x d =+，∵直线AB 经过点(),m n ，∴6n m d =+，即6d n m =-，又64n m -=，∴4d =，∴直线AB 的解析式为64y x =+，故选：D ．【点拨】本题考查了一次函数的平移，熟练掌握一次函数的平移规律是解题的关键．【变式2】（2022·江苏苏州·统考一模）如图，已知()1,6A 为直线:2l y x b =-+上一点，先将点A 向下平移a 个单位长度，再向右平移4个单位长度至点B ，再将点B 向下平移a 个单位长度至点C ．若点C 恰好落在直线l 上，则a 的值为．【答案】4【分析】先将点A 代入y =-2x +b 求得b 的值，得到直线的解析式，然后用含有a 的式子表示点C ，再将点C 的坐标代入直线的解析式求得a 的值．解：点A （1，6）代入y =-2x +b 得，-2×1+b =6，解得：b =8，∴直线l 的解析式为y =-2x +8，∵点A 向下平移a 个单位长度，再向右平移4个单位长度至点B ，再将点B 向下平移a 个单位长度至点C ，∴点C 的坐标为（5，6-2a ），将点C 的坐标代入直线的解析式y =-2x +8得，-2×5+8=6-2a ，解得：a =4，故答案为：4．【点拨】本题考查了一次函数图象上点的坐标特征，解题的关键用待定系数法求得一次函数的解析式．【考点九】对称型【例9】（2023春·河南洛阳·八年级统考期末）如图，在矩形ABCO 中，点C 在x 轴上，点A 在y 轴上，点B 的坐标是(68)，，ABD △与EBD △关于直线BF 对称，且点E 在对角线OB 上．（1）求线段OB 的长；（2）求点D 的坐标及直线BF 的函数表达式．【答案】（1）10；；（2）13(0,3，1113183y x =+．【分析】（1）根据点B 的坐标，利用勾股定理直接计算出OB 长；（2）设DE x =，则AD x =，8=-OD x ，4OE =，利用勾股定理可求出OD 长，点的坐标可求，根据B 、D 坐标，待定系数法可求直线BF 解析式．解：（1）∵点B 的坐标是(68)，，∴6OC =，8BC =，在Rt BOC 中，由勾股定理得：10OB ===；（2）∵ABD △与EBD △关于直线BF 对称，∴90DEO DEB BAO ∠=∠=∠=︒，AD DE =，6AB BE ==，在Rt DEO △中，设DE x =，则AD x =，8=-OD x ，4OE OB BE =-=，由勾股定理得222DE OE OD +=得，()22246x x +=-，解得53x =，∴513633OD =-=，∴1303D ⎛⎫ ⎪⎝⎭，，设BF 的解析式为133y kx =+，∵(68)B ，在直线BF 上，∴13863k =+，∴1118k =，∴BF 的解析式为1113183y x =+．【点拨】本题考查了坐标与图形的性质，勾股定理，轴对称的性质，待定系数法求函数解析式，根据条件灵活设解析式便于简化计算．【举一反三】【变式1】（2023秋·全国·八年级专题练习）在平面直角坐标系中，直线3y x b =-+与直线1y kx =-关于直线2x =对称，则k ，b 的值分别为（）A ．3k =-，11b =B ．3k =，11b =C ．13k =，1b =D ．13k =-，1b =【答案】B【分析】根据直线y =－3x ＋b 与直线y =kx －1关于直线x =2对称，可知这两条直线上的点也关于直线x =2对称，然后根据直线y =kx －1上的定点（0，－1）关于直线x =2的对称点（4，－1）可以求出b 的值，然后根据直线y =－3x ＋11与直线x =2的交点为：（2，5）也在直线y =kx －1，即可求出k 的值．解：∵直线y =－3x ＋b 与直线y =kx －1关于直线x =2对称，∴这两条直线上的点也关于直线x =2对称，∵直线y =kx －1必过点（0，－1），∴点（0，－1）关于直线x =2的对称点（4，－1）在直线y =－3x ＋b 上，∴－1=－3×4＋b ，解得：b =11，∴直线y =－3x ＋b 即为：y =－3x ＋11，∵直线y =－3x ＋11与直线x =2的交点为：（2，5），∴点（2，5）一定在直线y =kx －1上，∴5=2k －1，解得：k =3．故选：B ．【点拨】本题主要考查用待定系数法一次函数的解析式和轴对称的性质，熟练掌握一次函数的图像、轴对称的性质以及利用数形结合思想是解题关键．【变式2】（2021·山东临沂·统考一模）定义：若两个函数的图象关于直线y =x 对称，则称这两个函数互为反函数．请写出函数y =-2x +1的反函数的解析式．【答案】y =-12x +12【分析】首先可求得函数y =-2x +1与x 轴和y 轴的交点坐标，再求得它们关于直线y =x 对称点的坐标，据此即可求得函数y =-2x +1的反函数的解析式．解：在y =-2x +1中，当x =0时，y =1，当y =0时，x =12，即函数和x 轴的交点为（12,0），和y 轴的交点坐标为（0,1），所以两点关于直线y =x 对称的点的坐标分别为（0,12）和（1,0），设函数y =-2x +1的反函数的解析式为y =kx +b （k ≠0），把（0,12）和（1,0）代入，可得：120b k b ⎧=⎪⎨⎪+=⎩，解得：1212k b ⎧=-⎪⎪⎨⎪=⎪⎩，∴函数y =-2x +1的反函数的解析式为y =-12x +12，故答案为：y =-12x +12．【点拨】本题考查了利用待定系数法求一次函数的解析式，理解新定义，求出已知点关于直线y =x 对称点的坐标是解决本题的关键．。

17.3.4 求一次函数的关系式

3
一次函数y=kx+b的自变量的取值范围是-3≤x ≤6，相应函数值的取值范围是-5 ≤y ≤-2，求这个函数的解析式 ②若x=-3时，y=-2,有-3k+b=-2； x=6时，y=-5,有6k+b=-5，联立上面两式，解得k=- 1 ，b=-3 故所求函数的解析式为：
3
1 1 y= x-4或y=x-3 3 3
-17 所以当x=5时，函数y的值是__________
一次函数y=kx+b表示的直线经过点A(1，2)、B(-1，-4)，
试求直线AB的解析式解：由题意，得： k+b=2 k=3 解得： -k+b=-4 b=-1 ∴直线AB的解析式为y=3x-1
4、根据图象之间的平行关系求解析式
四、5、将函数y=x+2的图象平移，使它经过点(1，-3)，求平移后的直线所对应的函数解析式解：设所求直线的解析式为y=kx+b k=1 根据题意得： k+b=-3 k=1 ∴y=x-4 b=-4
∴k+b=0
解 k=-2
k+b=0
b=±2
或
得： k=2
b=2
b=-2
B
1 o A
∴y=-2x+2或y=2x-2
12、弹簧总长 y y(cm)与所挂 22 物体质量x(kg) 之间是一次函 14.5 数关系，则该弹簧不挂物体时的长度为多少？
6、应用
5
20
x
解：设函数解析式为y=kx+b(k≠0) 5k+b=14.5 由题意，得： k=0.5 解得： b=12 20k+b=22 y
例：已知弹簧的长度y(cm)在一定的限度内是所挂重物质量x（千克）的一次函数，现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米。求这个一次函数的关系式 y＝kx+b(k≠0) 解：设这个一次函数的关系是为_______________, 由题意得： 0+b __________ ＝6 4k+b ＝7.2 __________ 解得, 0.3 k＝_____ 6 b＝_____

17.3.4求一次函数的关系式

一、根据定义求解析式
已知y与x成正比例，且当x=-1时， y=-6，求y与x之间的函数关系式
解：由题意可设y=kx(k≠0) ∵当x=-1时，y=-6， ∴-k=-6 ∴k=6 ∴y=6x
像这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定数法．
变式训练
y=0.5x+12 当x=0时，y=12(cm) 5 所以，弹簧不挂物体时的长度为12cm 20
x
2、已知点Ａ(-4，1)，B(-2，5) 在x轴上求一点P，使PA+PB的和最小
B.
A
y
o
.
x
3、某气象研究中心观测一场沙尘暴从发生到结束的全过程，开始时风速平均每小时增加2千米/小时后，沙尘暴经过开阔漠地，风速保持不变，当沙尘暴遇到绿色植被区时，其风速成平均每小时减少4千米/小时，最终停止。结合风速与时间的图像如图，回答下列问题：（1）在图象的（）内填入相应的数值；（2）沙尘暴从发生到结束，共经过多少小时？（3）求出风速(千米/小时)与时间(小时)之间的函数关系式.
七、根据取值范围求解析式
例7、一次函数y=kx+b的自变量的取值范围是-3≤x ≤6，相应函数值的取值范围是-5 ≤y ≤-2，求这个函数的解析式解：要确定函数的解析式，从已知条件出发，可分两种情形讨论： ①若x=-3时，y=-5；若x=6时，y=-2，则有 3k b 5 6 k b 2
∴直线AB的解析式为y=3x-1
三、根据图象求解析式例3：一次函数的图象如图所示，求这个一次函数的解析式 y 解：设一次函数解析式为y=kx+b 根据题意得： -3k+b=0
2 k 解得： 3 b2

一次函数关系式的求解途径

式预测该水库今年Ｉ２月１日的水位吗？
【例４】（２０１７・荆州）将直线ｙ＝＋６沿轴向下
平移３个单位长度，点Ａ（一１，２）关于ｙ轴的对称点
【分析】（１）州衷ｒ｝］的数据，日期每增『Ｊｌ】１，，Ｋ，、增』Ｊｕ（）．５米，昕以１是的 … 玖函数．
ｍｌ：（６＞０）平移或向下（６＜０）移个Ｆｆ长嚏
５２Ｉ策略方法
／
初学习・策略方法
僻剑．五、利用一次函数的图像求解
注意的世：【｝１的．
衷，Ｊ段ｉ＜＝．必
ｉ
线段长正（如本题中线段ＯＢ长为ｌ４ｆ）．这１
一
落在平移后的直线上，则ｂ的值为— — ．
【分析】将直线＋厶沿、轴向下、ｇ３１、单长嘘．忻得直线的函数天系式为ｒ＋ｂ－３．再将
・＿Ａ（一１，２）芙丁Ｙ轴的对称』、、（１，２）标代人直
解途径
利用一次函数的定义求解用所建、的函数模型远离已知数据，作预测
一
、
【例１】已知函数 ’ ＝（，ｎ＋２） … 。。＋６是关于．１７的不可靠的．
一
次函数，试求一；欠函数关系式．
、＝Ｏ．５．ｒ＋ｌ９．５．（２）ｔ＝６代入（１）Ｌ卜Ｉ求僻函教关系

求一次函数的关系式二

（2）你能确定该关系所在直线的函数解析式吗？
y(元)
30 20 30 40
y=x-10
(x≥10)
（3）当货物少于
x(千克)
10
千克，可约用水，
采取分段收费标准。居民每月应交水费y（元）是用水量x（吨）的函数，其图象如图所示： (1)分别写出0＜x≤5和x＞5时， y与x的函数解析式； 6.3
(2)若某用户居民该月用水3.5吨， 3.6 问应交水费多少元？ (3)若该月交水费9元，则用水多少
●
●
吨? 5
8
例4、已知一次函数y=kx+b的图象过点（0，-2），与两坐标轴围成的三角形面积为2，求此一次函数的解析式
表格型
例2、小明根据某个一次函数关系式填写了下表:
x y … … -1 0 1 1 0
其中有一格不慎被墨汁遮住了,想想看，该空格里原来填的数是多少？说明你的理由。
根据表格，得到两点的坐标，再用待定系数法，求出一次函数的解析式；最后再代入
图象型
例3、火车站托运行李费用与托运行李的重量关系如图所示。 20 40 （1）当x=30时，y=_______; 当x=_______,y=30 。
1、用待定系数法求函数表达式
2、实际问题中求一次函数的表达式
定义型
例1、已知y＋5与3x＋4成正比例，且x=1时，y=2; (1)求y与x之间的函数关系式 (2)求当x＝－1的函数值； (3)如果x的取值为0≤x≤3，求y的最大值. 变式：如果y的取值为0≤y≤5，求x的取值范围.
练习：已知y=y1+y2,y1与x2成正比例，y2与x-2 成正比例，当x=1时，y=0；当x=-3时，y=4. (1)求y与x之间的函数关系式; (2)当x=3时,求y的值.

一次函数简单计算-解析式

一次函数简单计算-解析式定义：一般地，形如y=kx+b (k，b 为常数，k 不等于0)的函数，叫做一次函数。

当b=0时，y=kx+b 即为y=kx，所以正比例函数是特殊的一次函数。

因此，学好一次函数的前提是学好正比例函数，一次函数是通过正比例函数上下移动得到的。

其中k 值表示的是一次函数的斜率，当k>0时，y 是随着x 值的增大而增大的，当k<0时，y 是随着x 值的增大而减小的，b 值代表的是一次函数图像与y 轴交点的纵坐标，当b>0时，一次函数与y 轴的正半轴相交，当b=0时，一次函数与原点相交，此时一次函数便是正比例函数，当b<0时，一次函数与y 轴的负半轴相交，因此，学好一次函数解析式必须要理解其中的k 值，b 值的含义。

例题赏析一、用待定系数法求一次函数的解析式：1.已知一次函数y kx b =+的图象经过点(2,4)--，且与正比例函数12y x =的图象相交于点(4,)a ，求：一次函数的解析式 2.某一次函数的图象经过点(1,3)-，且函数y 随x 的增大而减小，请你写出一个符合条件的函数解析式_ _ _ _ _ _ _ _ ．3.（2020•东营市中考）已知一次函数(0)y kx b k =+≠的图象经过(1,1)A -、(1,3)B -两点，则k _ _ _ _ _ _ _ _ 0（填“>”或“<”)．二、用面积法求一次函数的解析式：例题赏析1.如图，直线y kx b =+与x 轴相交于点A ，与y 轴相交于点B ，且1OA =，AB =（1）求直线AB 的解析式；2.如图1，在平面直角坐标系中，O 是坐标原点，长方形OACB 的顶点A 、B 分别在x 轴与y 轴上，已知6OA =，10OB =．点D 为y 轴上一点，其坐标为(0,2)，点P 从点A 出发以每秒2个单位的速度沿线段AC CB -的方向运动，当点P 与点B 重合时停止运动，运动时间为t 秒．当点P 经过点C 时，直线DP 的函数解析式()．A．423y x =+B．223y x =+C．423y x =-D．423y x =-+3.如图，四边形ABCD 的顶点坐标分别为(4,0)A -，(2,1)B --，(3,0)C ，(0,3)D ，当过点B 的直线l 将四边形ABCD 分成面积相等的两部分时，直线l 所表示的函数表达式为()．A．116105y x =+B．2133y x =+C．1y x =+D．5342y x =+参考答案一、用待定系数法求一次函数的解析式：1.将点(4,)a 代入正比例函数12y x =，解得2a =；将点(4,2)、(2,4)--分别代入y kx b =+得：4224k b k b +=⎧⎨-+=-⎩解得12k b =⎧⎨=-⎩，所以一次函数表达式为y=x-2.2.该一次函数的解析式为(0)y kx b k =+<，一次函数的图象经过点(1,3)-，3k b ∴-+=，∴当1k =-时，2b =，∴符合条件的函数关系式可以是：2y x =-+（答案不唯一）．故答案为：2y x =-+（答案不唯一）．3.设直线AB 的解析式为：(0)y kx b k =+≠，把(1,1)A -，(1,3)B -代入y kx b =+得，13k b k b-=+⎧⎨=-+⎩，解得：2k =-，1b =，0k ∴<，故答案为：<．二、用面积法求一次函数的解析式：1.在Rt AOB 中， 1OA =，AB =90AOB ∠=︒，∴2OB ==，∴(1,0)A -，(0,2)B ，把A ，B 两点坐标代入y kx b =+，则有20b k b =⎧⎨-+=⎩解得22k b =⎧⎨=⎩∴直线AB 的解析式为22y x =+．2. 6OA =，10OB =，四边形OACB 为长方形，∴(6,10)C ．设此时直线DP 解析式为y kx b =+，把(0,2)，(6,10)C 分别代入，得2610b k b =⎧⎨+=⎩，解得432k b ⎧=⎪⎨⎪=⎩则此时直线DP 解析式为423y x =+．故选：A ．3.解：由(4,0)A -，(2,1)B --，(3,0)C ，(0,3)D ，∴7AC =，3DO =，∴四边形ABCD 分成面积11(||3)741422B AC y =⨯⨯+=⨯⨯=，可求CD 的直线解析式为3y x =-+，设过B 的直线l 为y kx b =+，将点B 代入解析式得21y kx k =+-，∴直线CD 与该直线的交点为4251,11k k k k --⎛⎫ ⎪++⎝⎭，直线21y kx k =+-与x 轴的交点为12,0k k -⎛⎫ ⎪⎝⎭，∴1125173121k k k k --⎛⎫⎛⎫=⨯-⨯+ ⎪ ⎪+⎝⎭⎝⎭，∴54k =或0k =，∴54k =，∴直线解析式为5342y x =+．故选D。