高中数学2投影画与射影几何试题880

合集下载

投影和射影的区别高中数学

投影和射影的区别高中数学
《投影和射影的区别——高中数学》
一、投影和射影的定义
投影：在三维空间中，将一个物体投射至另一个平面上，投射的时候物体各点和其对应位置图像之间的关系可以用一个函数描述，这个函数叫投影。

射影：在三维空间中，将一个物体投射至另一个平面上，投射的过程，物体各顶点和其对应点图像之间的关系可以用线段表示，这种投射过程叫射影。

二、投影和射影的区别
1、形式不同：投影通过将三维物体投射到一个二维平面上，将物体各点映射到平面上的点之间的关系用函数来描述，而射影则是将三维物体投射到另一个平面上，将物体各点映射到另一个平面上的点之间的关系用线段表示。

2、效果不同：投影能够准确记录物体在三维空间中的构造，可以用来绘制三维物体的投影图，而射影则是将三维物体“折叠”成一个二维物体，它把物体在三维空间中的几何形状「变形」成为二维物体，因此二维物体的几何形状不能够反应物体在三维空间中的几何形状。

3、作用不同：投影的作用主要是为了准确的保存三维物体的形状，常用于绘制三维物体的投影图；而射影可以将三维物体折叠成一个二维物体，因此也常常用于绘制平面地图、建筑图纸等。

画法几何与阴影透视模拟试题

画法几何与阴影透视模拟试题
2.补画V、H面投影中所漏线条。

3.画出被截三棱柱的侧面投影，并补全水平投影。

7.根据V、W面投影画出
8.根据V、W面投影画出
12.试画出立体的阴影。

（题目和答案在一起）
13.根据H、W面投影画出V面投影14.根据V、W面投影画出H面投影15.画出被截四棱住的侧面投影，并画全水平投影16.画出四棱住与原球表面的交线17.作出形体的透视度18.画出立体的阴影
19.根据两面投影画出第三面投影20.根据两面投影画出第三面投影
21.补画圆柱上截交线的H、W投影22.根据立体的V、W投影画出H投影23.试画出形体的透视图24.求平面立体的阴影
豆丁致力于构建全球领先的文档发布与销售平台，面向世界范围提供便捷、安全、专业、有效的
文档营销服务。

包括中国、日本、韩国、北美、欧洲等在内的豆丁全球分站，将面向全球各地的文档拥有者和代理商提供服务，帮助他们把文档发行到世界的每一个角落。

豆丁正在全球各地建立便捷、安全、高效的支付与兑换渠道，为每一位用户提供优质的文档交易和账务服务。

人教课标版高中数学必修2《中心投影与平行投影、空间几何体的三视图》基础训练

《中心投影与平行投影、空间几何体的三视图》基础训练一、选择题1.[2018江西新余一中高一月考]下列关于投影的说法不正确的是( )A.平行投影的投影线是互相平行的B.中心投影的投影线是互相垂直的C.线段上的点在中心投影下仍然在线段上D.平行的直线在中心投影中可能平行2.[2018广东中山模考]下列几何体各自的三视图中，有且仅有两个视图相同的是（）A.B.C.D.①②②③①④②④3.如图所示的三棱柱111ABC A B C 的三视图为( )4.[2018湖南岳阳一中高一月考]一个几何体的正视图、侧视图和俯视图形状、大小都相同，则这个几何体不可能是( )A.球B.三棱锥C.正方体D.圆柱5.[2017河北冀州校级月考]如图，在正方体1111ABCD A B C D 中，E 为棱1BB 的中点，用过点1,,A E C 的平面截去该正方体的上部分，则剩余几何体的正视图为( )6.[2018陕西宝鸡中学高一月考]沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的侧视图为（）7.已知一个几何体的二视图如图所示，则此几何体的组成为（）A. 上面为棱台，下面为棱柱B. 上面为圆台，下面为棱柱C. 上面为圆台，下面为圆柱D. 上面为棱台，下面为圆柱8.在一个几何体的三视图中，正视图和侧视图是两个完全相同的图形，如图所示，则相应的俯视图可以为（）A.B.C.D.①②②③③④②④二、填空题9.[2017东北育才学校高一（上）第一次月考]如图，,E F 分别是正方体1111ABCD A B C D -的面11ADD A 和面11BCC B 的中心，则四边形1BFD E 在该正方体的面上的正投影可能是_____(把所有可能图形的序号都填上）.10.[2018重庆九校联盟高三（上）联考]半径为R 的球O 放置在水平平面α上，点P 位于球O 的正上方，且到球O 表面的最小距离为R ,则从点P 发出的光线在平面α上形成的球O 的中心投影的面积等于_____.11.如图是一个空间几何体的三视图，则该几何体为_____.12.如图()1、()2、()3为三个几何体的三视图，根据三视图可以判断这三个几何体依次为_____、_____、_____.13.若一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_____(填序号).①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱.14.[2018山东枣庄三中高一月考]已知三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形.若三棱柱的正视图（如图所示）的面积为8，则侧视图的面积为_____.三、解答题15.如图，螺栓是棱柱和圆柱的组合体，画出它的视图.参考答案一、选择题1.答案：B解析：中心投影是由一点向外散射形成的投影，它的光线之间的关系不确定，故B 说法不正确2.答案：D解析：①的三个视图都相同，都是正方形;②的正视图与侧视图相同，都是等腰三角形，俯视图不同；③的三个视图都不相同；④的正视图与侧视图相同,都是等腰三角形,俯视图不同.故选D.3.答案：A解析：其正视图为矩形，侧视图为三角形，俯视图为矩形（其中棱1CC 可见，为实线），只有A 符合.4.答案：D解析：球的正视图、侧视图和俯视图是三个全等的圆；如图所示，在正方体1111ABCD A B C D -中，三棱锥1D ACD -的正视图、侧视图和俯视图都是全等的等腰直角三角形；正方体的正视图、侧视图和俯视图可以都是全等的正方形.故选D.5.答案：C解析：设过点1,,A E C 的截面与棱1DD 相交于点F ,则F 是棱1DD 的中点,截去正方体的上部分,剩余几何体的直观图如图所示,则其正视图为C .6.答案：A解析:由已知中几何体的直观图，我们可得侧视图首先应该是一个正方形,故D 不正确；左面的面对角线在侧视图中对应一条对角线,且对角线的方向应该从左上到右下，故B,C 不正确，故选A.7.答案：C解析：结合三视图，易知该几何体上面为圆台,下面为圆柱.8.答案：D解析：若俯视图为图①,则该几何体的正视图的上方三角形应该没有高线,故俯视图不可能为图①，排除选项A ；若俯视图为图③,则该几何体的侧视图的上方应该没有左边小三角形,故俯视图不可能为图③，排除选项B,C ；若俯视图为图②，则该几何体是由上面是正四棱锥，下面是正方体组合而成的简单组合体；若俯视图为图④，则该几何体是由上面是正四棱锥，下面是圆柱组合而成的简单组合体.故选D.二、填空题9.答案：()()23解析：图()2是在面11DCC D 或面ABCD 上的正投影;图()3是在面11BCC B 上的正投影.图()()14均不符合.10.答案：23R π解析：轴截面如图所示,分析题意可知3MN NT TP R ===,所以中心投影的面积为23R π11.答案：六棱台解析：由正视图、侧视图得几何体为台体，结合俯视图，得该几何体为六棱台. 12.答案：四棱锥圆锥圆台解析：图()1的三视图对应的几何体是四棱锥；图()2的三视图对应的几何体是圆锥；图()3的三视图对应的几何体是圆台.13. 答案：①②③⑤解析：三棱锥、四棱锥和圆锥的正视图都可能是三角形.当三棱柱的一个侧面平行于水平面，底面对着观测者时，其正视图是三角形.四棱柱、圆柱无论怎样放置，其正视图都不可能是三角形.14.答案：3解析：设该三棱柱的侧棱长为a ，则28a =，所以4a =.该三棱柱的侧视图是一个矩形，一边长为43视图的面积为3三、解答题15.答案：见解析解析：螺栓的三视图如图所示.。

苏教版必修2第1章第一节空间几何体3中心投影、平行投影和直观图画法(习题+解析)

高中数学中心投影、平行投影和直观图画法（答题时间： 40 分钟）*1. 以下说法：① 从投影角度看，三视图是在平行投影下画出的；②平行投影的投射线相互平行，中心投影的投射线交于一点；③空间图形经过投影后，直线变为直线，但平行线有可能变为订交线了；④空间几何体在平行投影与中心投影下有不一样的表现形式。

此中正确的说法有。

（填序号）**2.（梅州检测）以下图，一个水平搁置的正方形ABCD ，它在直角坐标系xOy 中，点 B 的坐标为（ 2， 2），则在用斜二测画法画出的正方形的直观图A′B′C′D′中，极点B′到x′轴的距离为 ________。

*3.以下图，在正方体ABCD A'B'C 'D ' 中， E 、 F 分别是 A'A 、 C 'C 的中点，则以下判断正确的选项是。

（填序号）①四边形 BFD ' E 在底面ABCD内的投影是正方形；②四边形 BFD ' E 在面 A ' D ' DA 内的投影是菱形；③四边形 BFD 'E 在面 A' D ' DA 内的投影与在面 ABB ' A ' 内的投影是全等的平行四边形。

**4.以下图，在四边形OABC 中， OA＝ BC＝ 1 cm，AB＝OC＝ 3 cm，OB⊥ BC， OB⊥ OA，那么，用斜二测画法画出的直观图是______（填四边形的种类），其周长为 ______cm。

*5.一个几何体由几个同样的小正方体组合而成，它的主视图、左视图、俯视图以下图，则这个组合体包括的小正方体的个数是________。

**6.如图为水平搁置的△ABO 的直观图△ A′ B′O′，由图判断在△ABO 中 AB、 BO、BD 、 OD 的大小关系是 ________。

**7. 用斜二测画法画出长、宽、高分别是 3 cm、3 cm、2 cm 的长方体 ABCD －A B C D的直观图。

画法几何与阴影透视习题集与参考答案

画法几何与阴影透视习题集与参考答案
• 几何基础知识 • 画法几何 • 阴影透视 • 习题集 • 参考答案
目录
01
几何基础知识
平面几何
01
02
03
定义与性质
平面几何研究二维空间中的图形，如直线、圆、三角形等，以及它们的性质和关系。
基本定理
包括平行线定理、三角形全等定理、勾股定理等，这些定理是解决平面几何问题的基础。
阴影和透视的高级技巧探讨一些特殊的阴影和透视效果，如动态阴影、反射效果等，以及如何利用特殊技巧提高绘图的真实感。
感谢观看
THANKS
阴影的基本概念
阴影的绘制技巧
阴影是物体在光源照射下产生的暗部区域。
掌握阴影的形状、大小、方向和深浅变化，利用阴影表现物体的立体感和空间感。
阴影的分类
根据光源与观察者的相对位置，阴影可以分为正面阴影、侧面阴影和顶面阴影。
透视的原理
透视的基本概念
透视是物体在观察者视线方向上产生的近大远小、近清晰远模糊的视觉效果。
应用
平面几何在日常生活和工程领域中有着广泛的应用，如建筑设计、地图绘制等。
立体几何
定义与性质
立体几何研究三维空间中的图形，如球、圆锥、圆柱等，以及它们的性质和关系。
基本定理
包括空间中两点间最短距离的定理、平行六面体的性质等，这些定理是解决立体几何问题的基础。
应用
立体几何在建筑学、机械工程等领域中有着广泛的应用，如建筑设计、机械零件的制造等。
透视的类型
透视可以分为线性透视和大气透视两种类型。线性透视主要表现物体在视线方向上的大小变化，大气透视主要表现物体在视
线方向理可以帮助我们更好地表现物体的空间感和立体感，增强画面的真实感和深度感。

高中数学2投影画与射影几何试题860

高中数学2投影画与射影几何试题 2019.091,过点A （4，8）且与点B （1，2）距离为3的直线方程为 .2,点A 、B 在抛物线 213y x =上，且其横坐标是方程20x px q ++=的两根，则直线AB 的方程为 .3,抛物线过直线 0x y += 与圆 2240x y y ++= 的交点，且关于y 轴对称，则此抛物线的方程为 .4,双曲线222222b x a y a b -= (0)b a >> 的两条渐进线的夹角为 2α，则其离心率等于 .5,已知定点 A （0，6）、B （0，3），点C 为x 轴正半轴上的点，当∠ACB 最大时，求点C 的坐标。

6,点（4，0）关于直线54210x y ++=的对称点的坐标是（） A. （－6，8） B. （－8，6） C. （6，8） D. （－6，－8）7,若直线20ax y -+=与30x y b --=关于直线y x =对称，则（）A. 1,63a b ==B. 1,63a b ==- C. 3,2a b ==- D. 3,6a b ==8,直线2360x y +-=关于点（1，－1）对称的直线方程为（） A. 3220x y -+= B. 2370x y ++= C. 32120x y --= D.9,若,x y 满足22240x y x y +-+=，则2x y -的最大值为（）A. B. 10 C. 9 D.5+10,与圆22420x y y +-+=相切，且在,x y 轴上的截距相等的直线有（）条A. 3B. 4C. 5D.611,过圆O 外一点P 且与该圆外切的圆的圆心轨迹的形状为（） A. 双曲线的一支 B. 直线 C. 椭圆 D 圆12,由点P （－1，4）向圆 2246120x y x y +--+= 所引的切线长等于（）A. B. 3 C. D. 613,通过椭圆22143x y +=的焦点且垂直于x 轴的直线l 被该椭圆截得的弦长等于（）A. B. 3 C. D. 614,曲线221259x y +=与221259x y k k +=--有（）A. 相等的长轴和短轴B. 相等的焦距C. 相等的离心率D. 相同的准线15,曲线1(22)y x =-≤≤与直线(2)4y k x =-+有两个不同的交点时，实数k 的取值范围是（）A. 53,124⎛⎤ ⎥⎝⎦B. 5(,)12+∞C. 13,34⎛⎤ ⎥⎝⎦D.5(0,)1216,从点(,3)P x 向圆22(2)(2)1x y +++=所引切线长的最小值为（）A. 4B. 11217,与定圆2222()()4()x a y b a b -+-=+及2222()()4()x a y b a b +++=+都相切）个A. 2B. 3C. 5D. 18,平面直角坐标系有点)cos ,1(x P ，)1,(cos x Q ， ∈x [4,4ππ-]；（1）求向量OP 和的夹角θ的余弦用x 表示的函数)(x f ；（2）求θ的最值。

画法几何及阴影透视练习题

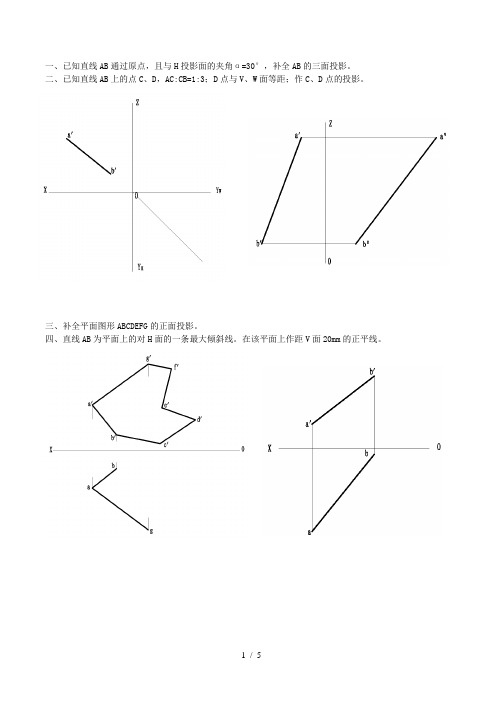
一、已知直线AB通过原点，且与H投影面的夹角α=30°，补全AB的三面投影。

二、已知直线AB上的点C、D，AC:CB=1:3；D点与V、W面等距；作C、D点的投影。

三、补全平面图形ABCDEFG的正面投影。

四、直线AB为平面上的对H面的一条最大倾斜线。

在该平面上作距V面20mm的正平线。

五、求两平面的交线，并表明可见性。

六、过点B作三角形ABC对正投影面（V面）的最大倾斜线及三角形ABC对V面的倾角β。

七、左旋圆柱螺旋线的直径D及导程S如图所示，求作该螺旋线的投影。

八、补全正五棱锥切割后的立体的投影。

九、补全正四棱柱切割后的投影。

十、补全立体的投影。

十一、补全立体的投影。

十二、作直线与立体的贯穿点。

十三、作两立体的相贯线。

阴影与透视习题与答案

2-2 求下列房屋轮廓落于地面、墙面和屋面上的影子。
2-3 求下列房屋轮廓落于地面、墙面和屋面上的影子。
2-4 求下列房屋轮廓落于地面、墙面和屋面上的影子。
2-5 求下列房屋轮廓落于地面、墙面和屋面上的影子。
2-6 求镜框及绳子落于墙面上的影子。
2-7 求阳台轮廓落于墙面上的影子。
”
2-8 求四棱柱落于墙面上的影子。
单击此处添加副标题
市场汇报
点击此处添加正文，文字是您思想的提炼，请言简意赅的阐述您的观点。
汇报人姓名
a'
X
a' a
O
1-1 求A点落于投影面上影子Ao及假影的H面和V面的投影。
a
a'
a
a'
a
a'
a
1-2 求A点落X于投影面上影子AOo的投影ao、 ao '和ao"。 a
a
a
30 1-3 设A点离开W面平行面P为30mm，已知a"，求A点落于P面上影
b0'
c0'
X 1-22 求下列正方形ABCD的阴影。
b
a0 c
d0
a
d
b' c'
b' c'
c'd'
c'0
a' d' c'0 a'd'
a' b'
c'0
b'0
d'0
b'0
b'0
d'0
1-23 求下列正方d'形0 ABCD的阴影。
a'0

高一数学暑假作业必修二第一部分立体几何4.投影与直观图含答案

4.投影与直观图A 组1、下列四个命题： 1）过三点确定一个平面 2）矩形是平面图形 3）四边相等的四边形是平面图形 4）三条直线两两相交则确定一个平面， 5）三角形的平行投影只能得到三角形，其中正确命题的个数是A ．1个B ．2个C ．3个D ．4个 2、哪个实例不是中心投影A ．工程图纸B ．小孔成像C ．相片D ．人的视觉 3、利用斜二测画法得到的①三角形的直观图一定是三角形；②正方形的直观图一定是菱形； ③等腰梯形的直观图可以是平行四边形；④菱形的直观图一定是菱形. 以上结论正确的是（）A ．①②B ． ①C ．③④D ． ①②③④ 4、利用斜二测画法得到的结论正确的是①三角形的直观图一定是三角形；②正方形的直观图一定是菱形；③等腰梯形的直观图可以是平行四边形；④菱形的直观图一定是菱形.A ．①②B ． ①C ．③④D ． ①②③④5、关于斜二测画法画直观图说法不正确的是 A ．在实物图中取坐标系不同，所得的直观图有可能不同 B ．平行于坐标轴的线段在直观图中仍然平行于坐标轴 C ．平行于坐标轴的线段长度在直观图中仍然保持不变D ．斜二测坐标系取的角可能是135°6、一个水平放置的三角形的斜二测直观图是等腰直角三角形'''A B O ，若''1O B =，那么原∆ABO 的面积是 A ．12 B ．2C D ． 7、下列几种说法正确的个数是①相等的角在直观图中对应的角仍然相等 ②相等的线段在直观图中对应的线段仍然相等 ③平行的线段在直观图中对应的线段仍然平行④线段的中点在直观图中仍然是线段的中点 A ．1 B ．2 C ．3D ．48、等腰梯形ABCD ,上底边CD =1, 腰AD =CB =2 , 下底AB=3，按平行于上、下底边取x 轴，则直观图A ′B ′C ′D ′的面积为________．B 组9、关于直角AOB 在水平面的正投影有如下判断：①可能是00角②可能是锐角③可能是直角④可能是钝角⑤可能是1800的角，其中正确判断的序号是C 组10、两条相交直线的平行投影是（）A.两条相交直线B.一条直线C.两条平行直线D.两条相交直线或一条直线 11、下列说法正确的是A ．互相垂直的两条直线的直观图一定是互相垂直的两条直线B ．梯形的直观图可能是平行四边形C ．矩形的直观图可能是梯形D ．正方形的直观图可能是平行四边形 12、一个梯形采用斜二测画法作出其直观图，则其直观图的面积是原来梯形面积的A.42倍 B. 21倍 C. 22倍 D. 2倍13、一个三角形在其直观图中对应一个边长为1正三角形，原三角形的面积为A ．46B ．43 C ．23D ．2614、如图甲所示，在正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AA 1、C 1D 1的中点，G 是正方形BCC 1B 1的中心，则四边形AGFE 在该正方体的各个面上的投影可能是图12乙中的____________.4．投影与直观图1、A2、A3、B4、B5、C6、C7、B8、9、①③④②⑤10、D 11.D 12、A 13、D 14．（1）（2）（3）。

高中数学 3.2投影画与射影几何同步精练北师大版选修3-1-北师大版高二选修3-1数学试题

投影画与射影几何练习1．“做一个合格的画家首先要精通几何学”，是由《绘画》一书的作者提出的，他的重要功绩是大量地应用了欧几里得几何学的原理，抓住了透视学的关键，提出了“没影点”的思想．这位伟大人物是( )A．达·芬奇B．阿尔贝蒂C．拉斐尔D．丢勒2．下图所示的作品利用了______原理．( )A．射影几何学 B．素描C．透视学 D．平面几何学3．“欣赏我的作品的人，没有一个不是数学家”，这句名言的作者对透视学作出了最大贡献，他是( )A．达·芬奇 B．阿尔贝蒂C．拉斐尔 D．丢勒4．下面的作图方法利用了______原理．( )A．平面几何学B．透视学C．素描D．射影几何学5．利用透视学原理画自己的房间．6．利用射影几何的基本思想画一个正四棱柱．7．阅读下面有关达·芬奇的资料，欣赏他的作品体会透视学的原理，简述透视学的发展与数学的联系．达·芬奇(Leonardo Da Vinci,1452—1519)作为文艺复兴时期最卓越的代表人物，他的成就和贡献是多方面的．达·芬奇出生在佛罗伦萨附近的一个小镇——芬奇镇．他是一位天才，他一面热心于艺术创作和理论研究，他研究如何用线条与立体造型去表现形体的各种问题；另一方面他也同时研究自然科学．达·芬奇是意大利文艺复兴时期最伟大、最著名的巨匠，他不仅是一位天才的画家，并且是大数学家、科学家、力学家和工程师，是一位多才多艺、全面发展的人．他有着多方面的才能，对人类作出过多方面的贡献．他不仅会画画、雕塑、建筑房屋，还会发明武器，设计过世界上第一架飞行机，他又是一个医学家、音乐家和戏剧家，而且在物理学、地理学和植物学等其他科学的研究上也很有成就．他道德高尚，举止文雅，且体格健壮，力量过人，据说他一只手就能轻易地折断马蹄铁．他左右手都会写字、作画，他用左手写的字是反向的，人们只有在镜子里才能看懂．人们一般认为，艺术不是科学．但是按照达·芬奇的界定，艺术，尤其是绘画，不但是一种科学，甚至是“所有科学之后”．达·芬奇既能发现事物表面迷人的美感，又不丧失物理学者与解剖学者的视角．他同时具有科学家的观察力与艺术家的表现力，是艺术史上第一位对人体和动物的比例做过系统研究的艺术家．他研究解剖长达40年之久，还亲自解剖了三十几具各种年龄的尸体．他不但熟悉人体外部的比例，而且了解人体的内部构造，因此笔下人物的比例、结构、动态都十分准确，无懈可击．达·芬奇对几何比例与构图十分着迷．《蒙娜丽莎》除了那永恒的神秘微笑外，还创造性地解决了半身肖像的构图问题．此后，西方那些卓越的半身像无一不受这幅画的影响．他还丰富和发展了前人的金字塔形构图，《岩间圣母》中群像以圣母的头部为顶点，形成的等腰三角形，如金字塔般稳定而和谐．与其他作品一样，《最后的晚餐》以几何图形为基础设计画面，体现出数学的对称美．有人评价这幅画是科学与艺术成了婚，而哲学又在这种完美的结合上留下了亲吻．达·芬奇最大的艺术贡献是运用明暗法使平的画面呈现出空间感和立体感．在文艺复兴初期，画家一般都用线条来表现透视，单线平涂，色彩较单调．而达·芬奇研究光影学，首创明暗渐进法，用光线和阴影的技巧来描绘人物、景致，使之呈现逼真的立体感．一直到印象派出现的几百年内，无人能够逾越达·芬奇建立的三度空间绘画体系．由他首创的明暗法使这一时期的绘画为之一变，艺术史家普遍认为它是绘画艺术的一个转折点．他的艺术成就直接影响了后来的米开朗琪罗、拉斐尔等艺术大师．从《最后的晚餐》起，西方绘画才真正进入了文艺复兴的鼎盛时期．达·芬奇还进一步归纳整理了解剖、透视、明暗和构图等零碎的技法知识，并从科学的角度进行审视．在他的《论绘画》手稿中，最初是想记录下对物理世界的客观描述，但不久就转而注意到透视、比例、几何与光学，之后是解剖学与机械学，最后则是探索宇宙本身的机械功能问题．《论绘画》是后人从达·芬奇十八本笔记中抽取出来编撰而成的，有人称它是整个艺术史上最珍贵的文献．尽管有的时候，对科学的兴趣浓厚到使他不愿提笔作画，但绘画毕竟是他最初的事业．达·芬奇就像研究别的学问一样，努力把绘画当成一种科学，终其一生都在孜孜不倦的探索中．参考答案1．答案：B2．答案：C3．答案：A4．答案：D5．答案：略6．答案：略7．答：由于绘画、制图的刺激而导致了富有文艺复兴特色的学科——透视学的兴起，人们渴望描述真实的世界，数学成为了反映世界和描述艺术的工具，借助数学的帮助，自然界将变得更加真实．。

高中数学空间几何中的面体积与射影问题解析

高中数学空间几何中的面体积与射影问题解析在高中数学的学习中，空间几何是一个重要的部分，其中面体积与射影问题是常见的考点。

本文将通过具体的题目举例，分析解题思路和方法，帮助高中学生或者他们的父母更好地理解和应用这些知识。

一、面积问题1. 题目：已知一个正方体的一个面的面积为16平方厘米，求这个正方体的体积。

解析：首先，我们知道正方体的六个面都是正方形，所以每个面的面积都相等。

设正方体的边长为a，则一个面的面积为a^2，根据题目可知a^2=16，解得a=4。

因此，正方体的体积为a^3=4^3=64立方厘米。

这道题考察了正方体的面积和体积的关系，通过解方程求解可以得到正确答案。

2. 题目：一个长方体的长、宽、高分别为3cm、4cm、5cm，求它的表面积和体积。

解析：长方体的表面积由六个面的面积之和组成。

设长方体的长、宽、高分别为a、b、c，则它的表面积为2(ab+ac+bc)。

代入题目中的数据，可得表面积为2(3×4+3×5+4×5)=94平方厘米。

长方体的体积由长、宽、高的乘积得到，即体积为abc。

代入题目中的数据，可得体积为3×4×5=60立方厘米。

这道题考察了长方体的表面积和体积的计算方法，通过代入数值计算可以得到正确答案。

二、射影问题1. 题目：已知一个正方体的边长为6cm，一条直线垂直于正方体的一面，并与这个面的一条边相交于点P，求点P到正方体的另一面的距离。

解析：在这道题中，我们可以利用射影的概念来解决。

首先，我们需要确定正方体的几何特征。

正方体的六个面都是正方形，所以任意两个相对的面平行，并且正方体的对角线互相垂直。

设正方体的边长为a，点P到正方体的另一面的距离为h。

由于点P在直线上，所以点P到直线上的任意一点的距离都相等。

我们可以选取正方体的对角线上的两个点，分别设为A和B，连接点P和点A、B，得到两个直角三角形。

根据勾股定理，可得PA^2+PB^2=AB^2。

高中数学2投影画与射影几何试题

高中数学2投影画与射影几何试题 2019.091,实数y x ,满足,2)1()1(=++-y i x i 则.________=xy2,用0,1,2,3,4,5六个数字组成无重复数字的三位数,其中能被3整除的有_______个(用数字作答).3,设B A ,都是n 阶方阵，且0≠A ，证明AB 与BA 相似．4,求下列矩阵的特征值和特征向量:(1)⎪⎪⎭⎫ ⎝⎛-4211; (2)⎪⎪⎪⎭⎫ ⎝⎛633312321; (3)())0(,12121≠⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a a a a a a a n n .并问它们的特征向量是否两两正交?5,下列矩阵是不是正交阵:(1) ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---121312112131211; (2) ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------979494949198949891．6,试求一个正交的相似变换矩阵,将下列对称矩阵化为对角矩阵:(1)⎪⎪⎪⎭⎫⎝⎛----020212022; (2)⎪⎪⎪⎭⎫ ⎝⎛----542452222．7,设U 为可逆矩阵,U U A T=,证明Ax x f T =为正定二次型．8,设对称矩阵A 为正定矩阵，证明：存在可逆矩阵U ，使U U A T=． 9,求一个正交变换将下列二次型化成标准形:(1)322322214332x x x x x f +++=; (2)43324121242322212222x x x x x x x x x x x x f +--++++=．10,已知函数的图象)0,,,()(22≠∈++=a R c b a c bx ax x f )2,1(-P 过点，且在点P 处的切线与直线.03垂直=-y x（Ⅰ）若0=c ，试求函数)(x f 的单调区间；（Ⅱ）若)(),(),,(0,0x f n m b a 是且+∞-∞>>的单调递增区间，试求m n -的范围.11,一个几何的三视图如图所示：其中，正视图中△ABC 的边长是2的正三角形，俯视图为正六边形，那么该几何体几的体积为 .12,在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：.222b a c +=设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN ，如果用321,,s s s 表示三个侧面面积，4s 表示截面面积，那么你类比得到的结论是 .13,已知点)0,2()4,0(),(-B A y x P 和到的距离相等，则yx 42+的最小值为（）A ．2B ．4C ．28D ．2414,如图是一个长方体ABCD-A 1B 1C 1D 1截去一个角后的多面体的三视图，在这个多面体中，AB=4,BC=6,CC 1=3.则这个多面体的体积为 .15,已知[0,]απ∈，讨论方程22cos sin 1x y αα+=所表示的曲线的类型，当它表示圆锥曲线时，试求其离心率.16,从平面上取6点，从平面上取4点，这10个点最多可以确定多少个三棱锥？17,过点P 3)-且以坐标轴为对称轴的等轴双曲线的方程为（）A. 221x y -=B. 221y x -=C.2217x y -= D. 2217y x -=18,曲线 1xy x y +=+ 所围成图形的面积等于（）A. 4B. 1C. 2D. π19,已知曲线21244::log log 0C y C x y =-=，3:2C xy =，这三条曲线中，与直线 y x = 恰有两个公共点的是（）A. 1CB. 2CC. 3CD. 2C和 3C20,直线 1x y += 与圆224x y += 交于 A 、B 两点，则 AB =（）A.试题答案1, 1 2, 363, 证明 0≠A 则A 可逆BA BA A A A AB A ==--))(()(11 则AB 与BA 相似． 4, 解 (1) ①)3)(2(4211--=---=-λλλλλE A故A 的特征值为3,221==λλ．② 当21=λ时,解方程0)2(=-x E A ,由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--=-00112211)2(~E A 得基础解系⎪⎪⎭⎫⎝⎛-=111P 所以)0(111≠k P k 是对应于21=λ的全部特征值向量．当32=λ时,解方程0)3(=-x E A ,由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--=-00121212)3(~E A 得基础解系⎪⎪⎭⎫⎝⎛-=1212P 所以)0(222≠k P k 是对应于33=λ的全部特征向量．③ 023121)1,1(],[2121≠=⎪⎪⎭⎫ ⎝⎛--==P P P P T 故21,P P 不正交．(2) ①)9)(1(633312321-+-=---=-λλλλλλλE A故A 的特征值为9,1,0321=-==λλλ． ② 当01=λ时，解方程0=Ax ，由⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=000110321633312321~A 得基础解系⎪⎪⎪⎭⎫⎝⎛--=1111P故)0(111≠k P k 是对应于01=λ的全部特征值向量. 当12-=λ时,解方程0)(=+x E A ，由⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=+000100322733322322~E A 得基础解系⎪⎪⎪⎭⎫⎝⎛-=0112P故)0(222≠k P k 是对应于12-=λ的全部特征值向量当93=λ时，解方程0)9(=-x E A ，由⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---=-00021101113333823289~E A 得基础解系⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=121213P 故)0(333≠k P k 是对应于93=λ的全部特征值向量．③ 0011)1,1,1(],[2121=⎪⎪⎪⎭⎫⎝⎛---==P P P P T，12121)0,1,1(],[3232=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-==P P P P T ， 012121)1,1,1(],[3131=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--==P P P P T ，所以321,,P P P 两两正交．(3)λλλλ---=-2212221212121n n n n n a a a a a a a a a a a a a a a E A=)(222211n n n a a a +++-- λλ[])(222211n n a a a +++-=- λλ ∑==+++=∴ni i na a a a 12222211 λ, 032====n λλλ当∑==ni i a 121λ时，()E A λ-⎪⎪⎪⎪⎪⎭⎫⎝⎛------------=-212221212223211212122322n n n n nnn a a a a a a a a a a a a a a a a a a a a a初等行变换~⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----00000000121n nn na a a a a a取n x 为自由未知量，并令n n a x =，设112211,,--===n n a x a x a x .故基础解系为⎪⎪⎪⎪⎪⎭⎫⎝⎛=n a a a P 211 当032====n λλλ 时，()⎪⎪⎪⎪⎪⎭⎫⎝⎛=⋅-22122212121210n n n n n a a a a a a a a a a a a a a a E A⎪⎪⎪⎪⎪⎭⎫⎝⎛000000~21n a a a 初等行变换可得基础解系⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=112312200,,00,00a a P a a P a a P n n 综上所述可知原矩阵的特征向量为()⎪⎪⎪⎪⎪⎭⎫⎝⎛--=112212100,,,a a a a a a a P P P nn n5, 解 (1) 第一个行向量非单位向量,故不是正交阵．(2) 该方阵每一个行向量均是单位向量，且两两正交，故为正交阵．6, 解 (1)λλλλ-------=-2212022E A )2)(4)(1(+--=λλλ故得特征值为4,1,2321==-=λλλ．当21-=λ时，由0220232024321=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----x x x 解得⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛2211321k x x x单位特征向量可取:⎪⎪⎪⎭⎫ ⎝⎛=3232311P当12=λ时,由0120202021321=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----x x x 解得⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛2122321k x x x 单位特征向量可取:⎪⎪⎪⎭⎫⎝⎛-=3231322P 当43=λ时,由0420232022321=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-------x x x 解得⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛1223321k x x x ．单位特征向量可取: ⎪⎪⎪⎭⎫⎝⎛-=3132323P得正交阵⎪⎪⎪⎭⎫⎝⎛--==12221222131),,(321P P P P ⎪⎪⎪⎭⎫⎝⎛-=-4000100021AP P(2)⎪⎪⎪⎭⎫⎝⎛-------=-λλλλ542452222E A )10()1(2---=λλ，故得特征值为10,1321===λλλ 当121==λλ时，由⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----000442442221321x x x 解得⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10201221321k k x x x此二个向量正交,单位化后,得两个单位正交的特征向量⎪⎪⎪⎭⎫⎝⎛-=012511P⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=*15452012540122P 单位化得⎪⎪⎪⎭⎫ ⎝⎛=15452352P当103=λ时,由⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-------000542452228321x x x 解得⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛2213321k x x x单位化⎪⎪⎪⎭⎫⎝⎛--=221313P :得正交阵),,(321P P P⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=323503215545131155252⎪⎪⎪⎭⎫⎝⎛=-1000100011AP P ．7, 证明设),,,(212111211n nn n n n a a a a a a a a a U=⎪⎪⎪⎭⎫ ⎝⎛=，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n x x x x11，Ux U x Ax x f T T T ==)()(Ux Ux T =),,,(1121211111n nn n n n n n x a x a x a x a x a x a ++++++=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛++++++⋅n nn n n n n n x a x a x a x a x a x a 1121211111 2212121111)()(n n n n x a x a x a x a +++++= 0)(211≥++++n nn n x a x a ．若“0=”成立，则⎪⎩⎪⎨⎧=++=++00111111n nn n n n x a x a x a x a 成立．即对任意⎪⎪⎪⎪⎪⎭⎫⎝⎛=n x x x x 11使02211=+++n n x x x ααα 成立．则n ααα,,,21 线性相关,U 的秩小于n ，则U 不可逆，与题意产生矛盾．于是0>f 成立．故Ax x f T=为正定二次型．8, 证明 A 正定，则矩阵A 满秩，且其特征值全为正．不妨设n λλ,,1 为其特征值，n i i ,,10 =>λ 由定理8知，存在一正交矩阵P使⎪⎪⎪⎪⎪⎭⎝=Λ=n TAP P λλ21⎪⎪⎪⎪⎪⎭⎫⎝⎛⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n λλλλλλ2121又因P 为正交矩阵，则P 可逆，P PT =-1．所以)(PQ PQ P Q PQ A TTT⋅==．令U PQ T=)(，U 可逆,则U U A T=.9, 解 (1) 二次型的矩阵为⎪⎪⎪⎭⎫⎝⎛=320230002A λλλλ---=-32230002E A )1)(5)(2(λλλ---=故A 的特征值为1,5,2321===λλλ．当21=λ时, 解方程0)2(=-x E A ，由⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=-0001002101202100002~E A得基础解系⎪⎪⎪⎭⎝=001ξ. 取⎪⎪⎪⎭⎝=001P当52=λ时，解方程0)5(=-x E A ，由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---=-0001100012202200035~E A得基础解系⎪⎪⎪⎭⎫⎝⎛=1102ξ取⎪⎪⎪⎭⎫ ⎝⎛=212102P ．当13=λ时，解方程0)(=-x E A ，由⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=-000110001220220001~E A得基础解系⎪⎪⎪⎭⎫⎝⎛-=1103ξ取⎪⎪⎪⎭⎫ ⎝⎛-=212103P ，于是正交变换为⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛3213212121021210001y y y x x x且有23222152y y y f ++=．(2)二次型矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛----=1101111001111011A λλλλλ--------=-111111001111011E A 2)1)(3)(1(--+=λλλ，故A 的特征值为1,3,14321===-=λλλλ当11-=λ时，可得单位特征向量⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=212121211P ，当32=λ时，可得单位特征向量⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=212121212P ，当143==λλ时，可得单位特征向量⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=0210213P ，⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2102104P ．于是正交变换为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛432143212102121021212121021210212121y y y y x x x x且有242322213y y y y f +++-=．10, 解：（1）由2)2,1()(23=++--++=c b a P c bx ax x f 知的图象过点① 又.23)('2bx ax x f += 相互垂直处的切线与在点03)2,1()(=--∴y x P x f ， 323-=-∴b a ②又,0=c ①、②联立得：.3,1==b a .63)(2x x x f +=∴ 2,0:0)('21-===x x x f 得令)()0,2.()(,20x f x f x x 是的单调递增区间时或当--<>∴的单调递减区间.（2）令.32,0,023)('212a bx x bx ax x f -===+=得又,0,0>>b a .0)(',320>-<>∴x f a bx x 时或当即)(),0(),32,(x f a b是+∞--∞单调递增区间..32)32(0a ba b m n =--≥-∴由（1）知：,3232-=-=++-b a c b a 且033,021>-=>-=∴c b c a21<∴cc c c c c a b m n 211121)1(2)21(3)33(232-+=--=--=≥-∴由,02121>-<c c 知12111,0221>-+>-∴c c1>-∴m n另解：由323-=-b a 得：3a 3b 2+=b 0> a 1a 0∴>->又.0>∴a11133332>+=+=≥-∴a a a a b m n注：若用b 表示a ，酌情给分.11, 2312, 24232221S S S S =++13, D 14, 6015, 解：①当0α=时，sin 0α=，cos 1α=，方程表示两条直线1x =±； ②当04πα<<时，0sin cos αα<<，方程表示焦点在y 轴上的椭圆，③当4πα=时，sin cos 2αα==，方程表示中心在原点的圆；④当42ππα<<时，0cos sin αα<<，方程表示焦点在x 轴上的椭圆，⑤当2πα=时，cos 0α=，sin 1α=，方程表示两条直线1y =±；⑥当2παπ<<，sin 0,cos 0αα><，方程表示焦点在y 轴上的双曲线,其离心率为αtan 1-⑦当απ=时，cos 1α=-，sin 0α=，方程变为21x =-，它不表示任何曲线. 16, 解：从平面α上6个点中任取一个与平面β上4个点中任取3个构成三棱锥，有3416C C 个从平面上6个点中任取2个与平面β上4个点中任取2个构成三棱锥，有2426C C 个从平面α上6个点中任取3个与平面上4个点中任取1个构成三棱锥，有1436C C 个根据加法原理最多有143624263416C C C C C C ++=194（个）三棱锥17, B [将点P 坐标代入22x y k -= 得 1k =-] 18, A [ 原方程即 (1)(1)0x y --=，画图即知 ]19, C20, B [ <1> 联立得 22230x x --= ，∴ AB ===<2> 计算可知，圆心到直线距，由勾股定理得，122AB AB =⇒=。

中心投影和平行投影作业高中数学必修二苏教版含答案

中心投影和平行投影练习1．下列命题不正确的是__________．(只填序号)①若长方体的长、宽、高各不相同，则长方体的三视图中不可能有正方形(以长×高所在的平面表示观察视角的正面)；②照片是三视图中的一种；③若三视图中有圆，则原几何体中一定有球体；④圆锥的三视图都是等腰三角形．2．根据几何体的三视图画法规则，能判断几何体的宽度与高度的应是三视图中的__________视图．3．若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是__________cm3.4．下列几何体各自的三视图中，有且仅有两个视图相同的序号是__________．5．一个几何体由几个相同的小正方体组合而成，它的主视图、左视图、俯视图如下图所示，这个组合体包含的小正方体个数是__________．6．若某几何体的三视图如图所示，则这个几何体可以是__________．(只填序号)7．画出下列几何体的三视图．8．在下图中补全左图所示物体的三视图．9．已知某个几何体的三视图如图所示，根据图中的尺寸(单位：cm)，可得这个几何体的底面积和高分别是多少？参考答案1.解析：由三视图的定义可判断．答案：②③④2.解析：主视图主要刻画物体的长与高，左视图则描述物体的宽与高，俯视图描述的是物体的长与宽．答案：左3.解析：由三视图可知原几何体由两个长方体叠加而成，V＝1×3×3＋1×3×3＝18(cm3)．答案：184.解析：②与④的三视图中只有俯视图不同，其主视图、左视图都是等腰三角形．答案：②④5.解析：根据几何体的三视图可知，该几何体底层有4个小正方体，上层只有1个，共5个．答案：56.解析：由主视图来看符合条件的只有③④.由俯视图来看，只有④中的几何体符合．答案：④7.解：图(1)，(2)的三视图分别如图(3)，(4)所示．(3)(4)8.解：左视图中有一条看不见的轮廓线，故应改为：；俯视图中应还有两条看得见的轮廓线和两条看不见的轮廓线，故应改为：.9.解：由俯视图和左视图可知底面是边长为20 cm的正方形，∴底面积为20×20＝400(cm2)．由主视图可知该几何体的高为20 cm.。

高中数学2投影画与射影几何专项测试同步训练

高中数学2投影画与射影几何专项测试同步训练2020.031,过点A （4，8）且与点B （1，2）距离为3的直线方程为 .2,平面//α平面β，α∈A 、β∈B ，A 、B 为定点，32=AB ，AB 与β成60°的角，C 为β上的动点，且满足AC AB ⊥，则AC 长的取值范围是。

3,过圆O 外一点P 且与该圆外切的圆的圆心轨迹的形状为（） A. 双曲线的一支 B. 直线 C. 椭圆 D 圆4,从点(,3)P x 向圆22(2)(2)1x y +++=所引切线长的最小值为（） A. 4 B. 26 C. 5 D. 1125,长方体ABCD-A 1B 1C 1D 1中，AB=5，AD=4，AA 1=3，则从A 沿着长方体的表面到C 1的最短距离为。

6,如图是一个长方体ABCD-A 1B 1C 1D 1截去一个角后的多面体的三视图，在这个多面体中，AB=4,BC=6,CC 1=3.则这个多面体的体积为 .7,若,x y 满足22240x y x y +-+=，则2x y -的最大值为（）A. 5B. 10C. 9D.525+8,已知过球面上A 、B 、C 三点的截面到球心的距离等于球的半径的一半，且AB=BC=CA=2，则球的表面积是（）A ．π916B ．π38 C ．π4 D ．π9649,分别在已知两个平面内的两条直线的位置关系是（）A ．相交或异面B ．平行或相交C ．异面或平行D ．非以上答案10,从平面上取6点，从平面上取4点，这10个点最多可以确定多少个三棱锥？11,如图所示，在正方体AC 1中，点P 在侧面BCC 1B 1及其边界上运动，并且始终保持1BD AP ⊥，则动点P 的轨迹是。

12,α，β表示平面，m 、n 表示直线，则α//m 的一个充分条件是（） A ．βα⊥且β⊥m B ．n a =⋂β且n m // C ．n m //且α//n D ．βα//且β⊂m13,双曲线 222222b x a y a b -= (0)b a >> 的两条渐进线的夹角为 2α，则其离心率等于 .14,已知曲线221244:4:log log 0C y x C x y =--=，3:2C xy =，这三条曲线中，与直线 y x = 恰有两个公共点的是（）A. 1CB. 2CC. 3CD. 2C 和 3C15,空间四边形ABCD 的各边与两条对角线的长都为1，点P 在边AB 上运动，点Q 在边CD 上运动，则点P 与点Q 的最短距离为（）A ．21B ．22 C ．43 D ．23答案1, 24200x y -+= 和 4x = 2, ),6[∞+3, A [设定圆半径为r ，动圆圆心为M ，由MO MP r -=即知]4, B [l ==≥=5, 746, 607, B [<解1>令2t x y =-，则2x t y =+，代入得225420y ty t t ++-=，由0≥V ，得010t ≤≤；<解2>用线性规划方法：令圆心（1，－2）到直线20x y t --=，得010t ≤≤]8, D 9, D 10, 解：从平面α上6个点中任取一个与平面β上4个点中任取3个构成三棱锥，有3416C C 个从平面上6个点中任取2个与平面β上4个点中任取2个构成三棱锥，有2426C C 个从平面α上6个点中任取3个与平面上4个点中任取1个构成三棱锥，有1436C C 个根据加法原理最多有143624263416C C C C C C ++=194（个）三棱锥11, 线段B 1C 12, D13, 1sin α14, C 15, B。

2021届高中数学必修二中心投影与平行投影含解析

A级基础巩固一、选择题1．以下关于投影的叙述不正确的是()A．手影就是一种投影B．中心投影的投影线相交于点光源C．斜投影的投影线不平行D．正投影的投影线和投影面垂直解析：平行投影的投影线互相平行，分为正投影和斜投影两种，故C错．答案：C2．如图所示的三视图表示的几何体可能是()A．圆台B．四棱台C．四棱锥D．三棱台解析：由三视图知，该几何体是四棱台．答案：B3．如图所示，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是()A．三棱锥B．三棱柱C．四棱锥D．四棱柱解析：由三视图可知，该几何体是一个放倒的直三棱柱．答案：B4．某空间几何体的正视图是三角形，则该几何体不可能是() A．圆柱B．圆锥C．四面体D．三棱柱解析：圆柱的正视图不可能为三角形．答案：A5．若某几何体的三视图如图所示，则这个几何体的直观图可以是()解析：所给选项中，A、C选项的俯视图不符合题意，D选项的侧视图不符合题意，只有选项B符合题意．答案：B二、填空题6．下列几何体各自的三视图中，有且仅有两个视图相同的是________(填序号)．①正方体②圆锥③三棱台④正四棱锥解析：在各自的三视图中，①正方体的三个视图都相同；②圆锥有两个视图相同；③三棱台的三个视图都不同；④正四棱锥有两个视图相同．所以满足仅有两个视图相同的是②④.答案：②④7.一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为：①长方形；②正方形；③圆．其中满足条件的序号是________．答案：②③8．下图中的三视图表示的几何体是________．解析：根据三视图的生成可知，该几何体为三棱柱．答案：三棱柱三、解答题9．下图是一个棱柱的三视图，请根据三视图的作图原则，求出x 、y 的值．解：棱柱的底面是一个直角三角形，根据“长对正、高平齐、宽相等”的原则可知两直角边长分别为x ＋y －2(或8)和x －y ＋5(或3y )，则⎩⎪⎨⎪⎧x ＋y －2＝8，x －y ＋5＝3y ，即⎩⎪⎨⎪⎧x ＋y ＝10，x －4y ＝－5，解得⎩⎪⎨⎪⎧x ＝7，y ＝3.10．画出图中3个图形的指定视图．解：如图所示．B级能力提升1．如图所示，画出四面体AB1CD1三视图中的正视图，以面AA1D1D为投影面，则得到的正视图可以为()解析：显然AB1、AC、B1D1、CD1分别投影得到正视图的外轮廓为正方形，B1C为可见轮廓线，其投影画成实线，且是从左下到右上，AD1为不可见轮廓线，其投影画成虚线，且是从左上到右下，故A正确．答案：A2.若一个正三棱柱(底面为等边三角形，侧面为矩形的棱柱)的三视图如图所示，则这个正三棱柱的侧棱长和底面边长分别为________，________．解析：侧视图中尺寸2为正三棱柱的侧棱长，尺寸23为俯视图等边三角形的高，所以正三棱柱的底面边长为4.答案：2 43．(2017·山东卷改编)由一个长方体和两个14圆柱体构成的几何体的三视图如下图，试作出该几何体的直观图，并分析数据．解：由三视图可知，此几何体的左、右两侧为14圆柱，中间部分为长方体，该几何体的直观图如图．其中，长方体的长，宽，高分别为2，1，1，圆柱体的底面半径为1，高为1.。

高等几何射影几何练习题分析与答案

一、选择题（共15分，每小题3分）1、下列关于射影平面的论述正确的是 ――――――――――――――――― （）A,无穷远直线视为普通的直线； B,所有直线都是封闭的； C,任意两直线必相交于一点； D,一条直线分射影平面为两部分。

2、下列到直线自身的射影对应属于双曲型对合的是 ―――――――――――（） A, 21λλλ+'=-；B, 40λλλλ''--+=； C, 21λλλ+'=- D, 230λλλ'+-=；3、下列哪个几何性质或图形不属于仿射几何的研究范围――――――――――（）A, 平行四边形； B,简比； C, 三角形的垂心； D,接合性；4、二次曲线2212121323320x x x x x x x x --+-=在射影观点下的基本类型是――（）A ，虚的常态二阶曲线；B,实的常态二阶曲线；C,两条虚直线； D,两条实直线5、由几对对应元素可以确定平面上任意的一个射影变换――――――――――（）A, 1 B, 2 C, 3 D, 4 二、填空题（共15 分，每小题 3分） 1、复点（9，3i,5-i ）对应的实直线的线坐标为。

2，对合42027μμμ+'=+的基本范式为。

3、求坐标三角形123A A A 的一边12A A 在坐标变换 112321233123x x x x x x x x x x x xρρρ'=-++⎧⎪'=-+⎨⎪'=+-⎩下的方程。

4、求由两个射影线束1213()0x x x x λ-++=与312()0,x x x λ'-+=()2λλλ'=-所决定的二阶曲线的齐次方程。

5、双曲线22221,x y ab-=的两条斜率分别为,λλ'直径成为共轭的条件是。

三、作图题（共20分，每小题 4 分）1、给定椭圆E 的短轴A A '和长轴B B '，试作出已知直线l 和E 的两个交点C 1 ，C 2。

空间几何的投影模拟试题

空间几何的投影模拟试题在学习空间几何的过程中，投影是一个非常重要的概念。

通过投影，我们可以将一个三维图形映射到二维平面上，使得我们更加清晰地观察和分析图形的性质。

为了帮助大家更好地理解和掌握空间几何的投影，下面编排了一些模拟试题。

试题一：已知直线AB在XYZ坐标系中的方程为：x - 2 = (y - 1)/2 = (z + 4)/3，点C坐标为(3, 2, -1)，求点C在直线AB上的投影C'的坐标。

解答：首先，我们可以通过方向向量来确定直线AB的方向。

由方程可得，直线的方向向量为(1, 2, 3)。

接下来，我们需要找到直线AB上的一点D，使得向量CD与直线AB的方向向量平行。

由于直线AB的方向向量为(1, 2, 3)，我们可以取D坐标为(4, 4, 5)。

接下来，我们可以通过向量CD和直线AB的方向向量的点乘来求得投影C'的坐标。

向量CD为(3-4, 2-4, -1-5)，即(-1, -2, -6)，直线AB的方向向量为(1, 2, 3)，则有：AC' = AC - (AC·AB/|AB|^2)·AB= (-1, -2, -6) - [(-1, -2, -6)·(1, 2, 3)/|(1, 2, 3)|^2]·(1, 2, 3)= (-1, -2, -6) - (-1/14, -1/7, -2/7)·(1, 2, 3)= (-1, -2, -6) + (1/14, 1/7, 2/7)= (-14/14 + 1/14, -28/14 + 1/7, -84/14 + 2/7)= (-13/14, -26/14, -80/14)= (-13/14, -13/7, -40/7)故点C'的坐标为(-13/14, -13/7, -40/7)。

试题二：已知平面α的法向量为(1, -2, 1)，直线l: x = 2 + t，y = -1 + t，z = 4 - t，其中t为实数。

投影点练习题大全

投影点练习题大全投影点是几何学中的重要概念之一，在平面几何和空间几何中都有广泛的应用。

为了帮助读者更好地理解和掌握投影点的相关知识，本文整理了一系列的投影点练习题，供读者练习和巩固所学知识。

1. 平面投影点练习题1.1 已知平面上一点P(x,y)及直线L: ax + by + c = 0，求P点在直线L上的投影点Q的坐标。

1.2 已知平面上两点A(x1,y1)和B(x2,y2)，以及直线L: ax + by + c = 0，求线段AB在直线L上的投影点。

1.3 已知平面上一点P(x,y)及直线L: ax + by + c = 0，求P点到直线L的距离。

2. 空间投影点练习题2.1 已知空间中一点P(x,y,z)及直线L: ax + by + cz + d = 0，求P点在直线L上的投影点Q的坐标。

2.2 已知空间中两点A(x1,y1,z1)和B(x2,y2,z2)，以及直线L: ax + by + cz + d = 0，求线段AB在直线L上的投影点。

2.3 已知空间中一点P(x,y,z)及平面π: Ax + By + Cz + D = 0，求P点在平面π上的投影点Q的坐标。

3. 综合应用练习题3.1 在平面上，已知点A(1,2)、B(3,4)和直线L: 2x - y + 3 = 0，求线段AB在直线L上的投影点。

3.2 在空间中，已知点A(1,2,3)、B(4,5,6)和直线L: 3x + y - 2z + 5 = 0，求线段AB在直线L上的投影点。

3.3 在空间中，已知点A(1,2,3)和平面π: 2x + y - 3z + 6 = 0，求点A在平面π上的投影点。

以上就是关于投影点的练习题大全。

通过练习这些题目，读者可以提高对投影点的理解和运用能力，有助于解决实际问题中涉及投影点的计算和推导。

希望读者能够通过不断的练习和思考，掌握投影点的相关知识，为解决几何学问题提供有力的支持。

本文所涉及的练习题仅是一部分，读者可以进一步扩展和深化练习内容，提升自己的几何学水平。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学2投影画与射影几何试题 2019.09
1,在△ABC 中，已知角A ，B ，C 的对边分别为a ，b ，c ，且bcosB ＋ccosC ＝acosA ，
试判断△ABC 的形状． 2,方程
22
141x y t t -=--表示曲线C ，给出以下命题：①曲线C 不可能是圆。

②若曲线C 为椭圆，则有1<t<4。

③若曲线C 为双曲线，则t<1或t>4 ④若曲线C 为焦点在X 轴上的椭圆，则1<t<2.5 其中正确的是_________________________。

3, 已知函数
3cos 33cos 3sin )(2
x
x x x f +=；
（1）求)(x f 的对称轴和对称中心；
（2）如果ABC ∆的三边a 、b 、c 满足ac b =2
，且边b 所对的角为x ，试求x
的范围及此时函数)(x f 的值域。

4,如图，在直三棱柱ABC-A 1B 1C 1中，AC=BC=A 1A=2，︒=∠90ACB ，E 为BB 1的中点，︒=∠901DE A 。

（1）求证：⊥CD 平面11ABB A （2）求证：平面⊥CDE 平面11ABB A
5,已知四棱锥P-ABCD的底面是边长为4的正方形，⊥
PD平面ABCD，且PD=6，M、N分别是PB、AB的中点。

MN⊥
（1）求证：CD
（2）求三棱锥P-DMN的体积
（3）求二面角M-DN-C的平面角的正切值
6,分别在已知两个平面内的两条直线的位置关系是（）
A．相交或异面 B．平行或相交 C．异面或平行 D．非以上答案
7,有下列命题：①平行于同一条直线的两条直线平行；②垂直于同一条直线的两条直线平行；③平行于同一条直线的两个平面平行；④垂直于同一平面的两个平面平行，其中，正确的命题的个数是（）A．1个 B．2个 C．3个 D．4个
8,把正方形ABCD沿对角线AC折成直二面角后，AB与CD所成的角等于（）
A ．30°
B ．45°
C ．60°
D ．90°
9,α，β表示平面，m 、n 表示直线，则α//m 的一个充分条件是（） A ．βα⊥且β⊥m B ．n a =⋂β且n m //
C ．n m //且α//n
D ．βα//且β⊂m
10,空间四边形ABCD 的各边与两条对角线的长都为1，点P 在边AB 上运动，点Q 在边CD 上运动，则点P 与点Q 的最短距离为（）
A ．21
B ．2
2 C ．4
3 D ．23
11,直线a 是平面α的一条斜线，α⊂b ，当a 与b 成60°的角，且b 与a 在α内的射影所成的角为45°时，则直线a 与α所成的角的大小为（） A ．60° B ．45° C ．90° D ．135°
12,设α，β表示两个平面，l 表示不在α和β内的直线，现有三点：①
α⊥l ；② βα⊥；③ β
//l 。

若以其中的两个作为条件，另一个作为结论，
则所构成的三个命题中，正确的命题的个数是（）
A ．0个
B ．1个
C ．2个
D ．3个
13,如图所示，三棱锥的三条侧棱OA 、OB 、OC 两两垂直，底面ABC ∆内有一点P ，OP 与经过O 的各侧面所成的角分别为α、β、γ，则
γ
βα222cos cos cos ++的值等于（）
A ．0
B ．1
C ．2
D ．其它值
14,已知过球面上A 、B 、C 三点的截面到球心的距离等于球的半径的一半，且AB=BC=CA=2，则球的表面积是（）
A ．π916
B ．π3
8 C ．π4 D ．π
9
64
15,如图，直三棱柱ABC-A 1B 1C 1的体积为V ，P 、Q 分别是侧棱AA 1、CC 1上的点，且AP=C 1Q ，则四棱柱B-APQC 的体积是（）
A ．V 32
B ．V 3
1 C ．V 73 D ．V
72
16,已知地球的半径为R ，A 、B 分别在北纬20度，东经60度和南纬60度，西经120度的位置上，则AB 两点的球面距离等于。

17,长方体ABCD-A 1B 1C 1D 1中，AB=5，AD=4，AA 1=3，则从A 沿着长方体的表面到C 1的最短距离为。

18,如图所示，在正方体AC 1中，点P 在侧面BCC 1B 1及其边界上运动，并且始终保持1BD AP ⊥，则动点P 的轨迹是。

19,正四棱锥的底面边长为4cm ，侧棱长为cm 52，则它的侧面与底面所
成的二面角是。

20,平面//α平面β，α∈A 、β∈B ，A 、B 为定点，32=AB ，AB 与β成60°的角，C 为β上的动点，且满足AC AB ⊥，则AC 长的取值范围是。

试题答案
1, 解：∵ bcosB ＋ccosC ＝acosA ，由正弦定理得：sinBcosB ＋sinCcosC ＝sinAcosA ，
即sin2B ＋sin2C ＝2sinAcosA ，∴2sin(B ＋C)cos （B －C ）＝2sinAcosA ∵ A ＋B ＋C ＝π，∴sin （B ＋C ）＝sinA 而sinA ≠0 ∴ cos （B －C ）＝cosA ，即cos （B －C ）＋cos （B ＋C ）＝0 ∴ 2cosBcosC ＝0 ∵ 0＜B ＜π，0＜C ＜π，∴B ＝2π或C ＝2π
即△ABC 是直角三角形
2, ① 3, 解：（1）
2
3)332sin(2332cos 2332sin 21)32cos 1(2332sin 21)(++=++=++=
πx x x x x x f
令22333
2ππππ-
=⇒=+k x k x
∴ 对称中心为)23
,223(ππ-k （Z
k ∈）
令423233
2π
ππππ+
=⇒+=+k x k x
∴ 对称轴为
4
23π
π+=
k x （Z k ∈）
（2）由已知ac b =2
21
2222cos 22222=
-≥-+=-+=ac ac ac ac ac c a ac b c a x ∴
9
53323
3
01cos 21
π
ππ
π
≤+<
≤
<<≤x x x
∴
1)3
32sin(
3
sin
≤+<π
π
x ∴
2
3123)332sin(
3+≤++<πx
即)(x f 的值域为
]231,3(+
4,
（1）由直三棱柱知AB A 1∠︒=∠=901BA B ，又︒=∠901DE A ∴ ︒=∠+∠901EDB DA A 又 ︒=∠+∠9011D AA DA A ∴ EDB D AA ∠=∠1 ∴ AD A Rt 1∆∽DBE Rt ∆ ∴
BE DB
AD A A =1 又︒=∠90ACB ，2==BC AC ，21=A A ，E 为BB 1中点
∴ 22=AB ，BE=1，DB AD BE A A ⋅=⋅1 ∴ DB DB DB AD ⋅-=⇒⋅=⨯)22
(2212=
⇒DB ，即D 为AB 的中点
∴ AB CD ⊥ 又由直三棱柱知平面⊥11ABB A 平面ABC ∴ ⊥CD 平面A 1ABB 1
（2）由（1）⊥CD 平面A 1ABB 1、⊂CD 平面CDE
∴ 平面⊥CDE 平面A 1ABB 1
5, （1）连结AC ，BD 。

设O BD AC =⋂，连结MO ，NO ，则PD MO //。

又⊥
PD
平面ABCD ，所以⊥MO 平面ABCD ，易证NO CD ⊥，所以CD MN ⊥（三垂线
定理）
（2）4
61621
31414141=⨯⨯⨯⨯====----ADB P PAB D PMN D DMN P V V V V
（3）由（1）⊥MO 平面ABCD ，过O 作DN
OH
⊥，垂足为H ，连结MH ，则DN
MH
⊥（三垂线定理）所以MHO ∠为所求二面角的平面角在MHO Rt ∆中，3=MO ，5
5
2=
OH
所以：
2
5
3tan ==
∠OH MO MHO
所以MHO ∠为所求二面角的平面角的正切值为2/53
6, D 7, A 8, C 9, D 10, B 11, B 12, C 13, C 14, D 15, B 16, 9/7R π 17, 74
18, 线段B 1C 19, 60° 20, ),6[∞+。