九年级数学专题复习函数综合
2023年九年级中考数学专题训练:二次函数综合(含简单答案)

2023年九年级中考数学专题训练:二次函数综合一、单选题1.已知抛物线()2330y x x c x =++-≤≤与直线2y x =-有且只有一个交点,若c 为整数,则c 的值有( ) A .1个B .2个C .3个D .4个2.方程231x x +=的根可视为函数3y x的图象与函数1y x=的图象交点的横坐标,那么用此方法可推断出方程321x x +=-的实数根x 所在的范围是( ) A .112x -<<-B .1123x -<<-C .1134x -<<-D .104x -<<3.如图,已知二次函数()()5144y x x =-+-的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,Р为该二次函数在第一象限内的一点,连接AP ,交BC 于点K ,则APPK的最小值为( )A .94B .2C .74D .544.如图.抛物线y =ax 2+c 与直线y =mx +n 交于A (﹣1,p ),B (3,q )两点,则不等式ax 2+mx +c >n 的解集为( )A .x >﹣1B .x <3C .x <﹣3或x >1D .﹣1<x <35.如图,抛物线y =12-x 2+7x ﹣452与x 轴交于点A ,B ,把抛物线在x 轴及共上方的部分记作C 1将C 1向左平移得到C 2,C 2与x 轴交于点B ,D ,若直线y =12-x +m 与C 1,C 2共3个不同的交点,则m 的取值范是( )A .52928m << B .12928m << C .54528m << D .14528m <<6.在平面直角坐标系中,对图形F 给出如下定义:若图形F 上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形ABCD 的坐标角度是90°.现将二次函数()213y ax a =≤≤的图象在直线1y =下方的部分沿直线1y =向上:翻折,则所得图形的坐标角度α的取值范围是( )A .3060α︒≤≤︒B .120150α︒≤≤︒C .90120α︒≤≤︒D .6090α︒≤≤︒7.二次函数y =2x 2﹣2x +m (0<m < 12),如果当x =a 时,y <0,那么当x =a ﹣1时,函数值y 的取值范围为( ) A .y <0B .0<y <mC .m <y <m +4D .y >m8.如图,抛物线21322y x x =-++的图象与坐标轴交于点A ,B ,D ,顶点为E ,以AB为直径画半圆交y 负半轴交于点C ,圆心为M ,P 是半圆上的一动点,连接EP . ①点E 在①M 的内部;①CD 的长为32①若P 与C 重合,则①DPE =15°;①在P 的运动过程中,若AP =PE =①N 是PE 的中点,当P 沿半圆从点A 运动至点B 时,点N 运动的路径长是π.则正确的选项为( )A .①①①B .①①①C .①①①D .①①①二、填空题9.如图,已知抛物线24y x x c =-+的顶点为D ,与y 轴交于点C ,过点C 作x 轴的平行线AC 交抛物线于点A ,过点A 作y 轴的平行线AB 交射线OD 于点B ,若OA OB =,则c 的值为_____________.10.已知抛物线()2123y x m x m =-+++以及平面直角坐标系中的点()1,1E --、()3,7F ,若该抛物线与线段EF 只有一个交点,则m 的取值范围是________.11.在平面直角坐标系中,抛物线215y x bx c =-+(0b >,b 、c 为常数)的顶点为A ,与y 轴交于点B ,点B 关于抛物线对称轴的对称点为C .若ABC 是等腰直角三角形,则BC 的长为________.12.如图,2=23y x x --与x 轴交于A ,B 两点(A 在左边)与y 轴交于C 点,P 是线段AC 上的一点,连结BP 交y 轴于点Q ,连结OP ,当OAP △和PQC △的面积之和与OBQ △的面积相等时,点P 的坐标为______.13.如图,在平面直角坐标系中,抛物线214y x mx =-+与x 轴正半轴交于点A ,点B是y 轴负半轴上一点,点A 关于点B 的对称点C 恰好落在抛物线上,过点C 作//CD x 轴,交抛物线于点D ,连结OC 、AD .若点C 的横坐标为4-,则四边形OCDA 的面积为___________.14.若243P m m m ++(,)是一个动点(m 为实数),点Q 是直线4y x =-上的另一个动点,则PQ 长度的最小值为_____.15.已知抛物线2=23y x x --与x 轴交于A ,B 两点(点A 在点B 的左侧)与y 轴交于点C ,点(6,)D y 在抛物线上,E 是该抛物线对称轴上一动点,当BE 十DE 的值最小时,ACE △的面积为是____16.已知:如图,抛物线的顶点为M ,平行于x 轴的直线与该抛物线交于点A ,B (点A 在点B 左侧),我们规定:当AMB 为直角三角形时,就称AMB 为该抛物线的“优美三角形”.若抛物线26y ax bx =++的“优美三角形”的斜边长为4,求a 的值______.三、解答题17.抛物线23y ax bx =++顶点为点(1,4)D ,与x 轴交于点A 、B ,与y 轴交于点C ,点P 是抛物线对称轴上的一个动点.(1)求a 和b 的值;(2)是否存在点P ,使得以P 、D 、B 为顶点的三角形中有两个内角的和等于45°?若存在,求出点P 的坐标;若不存在,说明理由.18.如图,已知直线443y x =+与x 轴交于点A ,与y 轴交于点C ,抛物线2y ax bx c =++经过A ,C 两点,且与x 轴的另一个交点为B ,对称轴为直线=1x -.(1)求抛物线的表达式;(2)已知点M 是抛物线对称轴上一点,当MB MC +的值最小时,点M 的坐标是___________;(3)若点P 在抛物线对称轴上,是否存在点P ,使以点B ,C ,P 为顶点的三角形是等腰三角形?若存在,请求出P 点的坐标;若不存在,请说明理由.19.如图,已知抛物线233384y x x =--与x 轴的交点为点A 、D (点A 在点D 的右侧),与y 轴的交点为点C .(1)直接写出A 、D 、C 三点的坐标;(2)在抛物线的对称轴上找一点M ,使得MD MC +的值最小,并求出点M 的坐标; (3)设点C 关于抛物线对称轴的对称点为点B ,在抛物线上是否存在点P ,使得以A 、B 、C 、P 四点为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由.20.如图,已知抛物线223y ax ax =++中,当=1x -时,4y =.(1)求此抛物线的解析式;(2)点E 是抛物线上且位于直线AB 上方的一个动点,不与点A ,B 重合,求ABE 的面积最大时,点E 的坐标.(3)若1t x ≤≤时,y 的取值范围是04y ≤≤,请直接写出t 的取值范围.参考答案:1.D 2.B 3.A 4.C 5.A 6.D 7.C 8.D 9.8310.2m <-或m>2或1m = 11.6 12.2,13⎛⎫-- ⎪⎝⎭13.641415.616.12±17.(1)1a =-,2b = (2)存在,(1,2)或(1,6)-18.(1)248433y x x =--+(2)8(1,)3M -(3)存在,P 点的坐标为(1,0)-或(-或(1,-或13(1,)8-19.(1)()4,0A ,()2,0D -,()0,3C -(2)连接AC 交对称轴于点M ,点M 即为所求,91,4M ⎛⎫- ⎪⎝⎭(3)()2,0-或()6,6.20.(1)223y x x =--+(2)315()24-,(3)31t -≤≤-。
2021年九年级数学中考复习专题:反比例函数综合(考察坐标、取值范围、面积等)(四)

2021年九年级数学中考复习专题:反比例函数综合(考察坐标、取值范围、面积等)(四)1.如图1,在平面直角坐标系中,已知△ABC,∠ABC=90°,∠ACB=30°,顶点A 在第二象限,B,C两点在x轴的负半轴上(点C在点B的右侧),BC=2,△ACD与△ABC关于AC所在的直线对称.(1)当OC=2时,求点D的坐标;(2)若点A和点D在同一个反比例函数的图象上,求OC的长;(3)如图2,将第(2)题中的四边形ABCD向左平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=(k≠0)的图象与BA的延长线交于点P,问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.2.如图1,A(1,0)、B(0,2),双曲线y=(x>0)(1)若将线段AB绕A点顺时针旋转90°后B的对应点恰好落在双曲线y=(x>0)上①则k的值为;②将直线AB平移与双曲线y=(x>0)交于E、F,EF的中点为M(a,b),求的值;(2)将直线AB平移与双曲线y=(x>0)交于E、F,连接AE.若AB⊥AE,且EF =2AB,如图2,直接写出k的值.3.如图1,在平面直角坐标系xOy中,函数y=(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点.(1)求∠OCD的度数;(2)如图2,连接OQ、OP,当∠DOQ=∠OCD﹣∠POC时,求此时m的值;(3)如图3,点A,点B分别在x轴和y轴正半轴上的动点.再以OA、OB为邻边作矩形OAMB.若点M恰好在函数y=(m为常数,m>1,x>0)的图象上,且四边形BAPQ为平行四边形,求此时OA、OB的长度.4.如图,在四边形ABCD中,AB=BC=5,AD=DC=8,对角线BD=3+4,点B在y轴上,BD与x轴平行,点C在x轴上.(1)求∠ADC的度数.(2)点P在对角线BD上,点Q在四边形ABCD内且在点P的右边,连接AP、PQ、QC,已知AP=AQ,∠APQ=60°,设BP=m.①求CQ的长(用含m的代数式表示);②若某一反比例函数图象同时经过点A、Q,求m的值.5.已知一次函数y1=kx+n(n<0)和反比例函数y2=(m>0,x>0).(1)如图1,若n=﹣2,且函数y1、y2的图象都经过点A(3,4).①求m,k的值;②直接写出当y1>y2时x的范围;(2)如图2,过点P(1,0)作y轴的平行线l与函数y2的图象相交于点B,与反比例函数y3=(x>0)的图象相交于点C.①若k=2,直线l与函数y1的图象相交点D.当点B、C、D中的一点到另外两点的距离相等时,求m﹣n的值;②过点B作x轴的平行线与函数y1的图象相交于点E.当m﹣n的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.6.如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F 在第一象限内,OF的长度不变,且反比例函数y=经过点F.(1)如图1,当F在直线y=x上时,函数图象过点B,求线段OF的长.(2)如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.①求证:CD=2AE.②若AE+CD=DE,求k.③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.7.如图,二次函数与反比例函数的图象有公共点A(﹣2,5),▱ABCD的顶点B(﹣5,p)在双曲线上,C、D两点在抛物线上(点C在y轴负半轴,点D在x轴正半轴)(1)求直线AB的表达式及C、D两点的坐标;(2)第四象限的抛物线上是否存在点E,使得四边形ACED的面积最大,若存在,求出点E的坐标和面积的最大值,不存在,说明理由.8.如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0)、D(﹣7,3),点B、C在第二象限内.(1)点B的坐标;(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.9.如图所示,在平面直角坐标系Oxy中,等腰△OAB的边OB与反比例函数y=(m >0)的图象相交于点C,其中OB=AB,点A在x轴的正半轴上,点B的坐标为(2,4),过点C作CH⊥x轴于点H.(1)已知一次函数的图象过点O,B,求该一次函数的表达式;(2)若点P是线段AB上的一点,满足OC=AP,过点P作PQ⊥x轴于点Q,连结OP,记△OPQ的面积为S△OPQ,设AQ=t,T=OH2﹣S△OPQ①用t表示T(不需要写出t的取值范围);②当T取最小值时,求m的值.10.如图,点P在曲线上,PA⊥x轴于点A,点B在y轴正半轴上,PA=PB,OA、OB的长是方程t2﹣8t+12=0的两个实数根,且OA>OB,点C是线段PB延长线上的一个动点,△ABC的外接圆⊙M与y轴的另一个交点是D.(1)填空:OA=;OB=;k=;(2)设点Q是⊙M上一动点,若圆心M在y轴上且点P、Q之间的距离达到最大值,则点Q的坐标是;(3)试问:在点C运动的过程中,BD﹣BC的值是否为定值?若是,请求出该定值;若不是,请给出合理的解释.参考答案1.解:(1)∵△ADC与△ABC关于AC所在的直线对称,∴CD=BC=2,∠ACD=∠ACB=30°,如图1,过点D作DE⊥BC于点E,∵∠DCE=60°,∴,∵OC=2,∴OE=3,∴;(2)设OC=m,则OE=m+1,OB=m+2在Rt△ABC中,∠ACB=30°,BC=2,∴,∴,∵A,D在同一反比例函数上,∴,解得:m=1,∴OC=1;(3)由(2)得:∴,∵四边形A1B1C1D1由四边形ABCD平移得到,∴,∵D1在反比例函数上,∴同理:,,∴,∴,∵x P=x A=﹣3,P在反比例函数上,∴,①若P为直角顶点,则A1P⊥DP,过点P作l1⊥y轴,过点A1作A1F⊥l1,过点D作DG⊥l1,则△A1PF∽△PDG,,解得:;②若D为直角顶点,则A1D⊥DP,过点D作l2⊥x轴,过点A1作A1H⊥l2,则△A1DH∽△DPG,,,解得:k=0(舍),综上:存在.2.解:(1)设旋转后点B的对应点为点C,过点C作CD⊥x轴于点D,如图所示∵∠BAC=90°,∴∠BAO+∠CAD=90°,∵∠BAO+∠ABO=90°,∴∠ABO=∠CAD,在△OAB和△DCA中,,∴△OAB≌△DCA(AAS),∴CD=OA=1,AD=OB=2,∴OD=OA+AD=3,∴C(3,1),把C(3,1)代入y=中,得k=3,故答案为:3;(2)直线AB表达式中的k值为﹣2,AB∥EF,则直线EF表达式中的k值为﹣2,设点E(m,n),mn=3,直线EF的表达式为:y=﹣2x+t,将点E坐标代入上式并解得,直线EF的表达式为y=﹣2x+2m+n,将直线EF表达式与反比例函数表达式联立并整理得:2x2﹣(2m+n)x+3=0,x1+x2=,x1x2=,则点F(n,),则a=(),b=(n+),===2;(3)故点E作EH⊥x轴交于点H,由(1)知:△ABO∽△EHA,∴,设EH=m,则AH=2m,则点E(2m+1,m),且k=m(2m+1)=2m2+m,直线AB表达式中的k值为﹣2,AB∥EF,则直线EF表达式中的k值为﹣2,设直线EF的表达式为:y=﹣2x+b,将点E坐标代入并求解得:b=5m+2,故直线EF的表达式为:y=﹣2x+5m+2,将上式与反比例函数表达式联立并整理得:2x2﹣(5m+2)x+3=0,用韦达定理解得:x F+x E=,则x F=,则点F(m,4m+2),则EF==2AB=2×,整理得:3m2+4m﹣4=0,解得:m=或﹣2(舍去负值),k=m(2m+1)=2m2+m=.3.解:(1)设直线PQ的解析式为y=kx+b,则有,解得,∴y=﹣x+m+1,令x=0,得到y=m+1,∴D(0,m+1),令y=0,得到x=m+1,∴C(m+1,0),∴OC=OD,∵∠COD=90°,∴∠OCD=45°.(2)如图2,过Q作QM⊥y轴于M,过P作PN⊥OC于N,过O作OH⊥CD于H,∵P(m,1)和Q(1,m),∴MQ=PN=1,OM=ON=m,∵∠OMQ=∠ONP=90°,∴△OMQ≌△ONP(SAS),∴OQ=OP,∠DOQ=∠POC,∵∠DOQ=∠OCD﹣∠POC,∠OCD=45°,∴∠DOQ=∠POC=∠QOH=∠POH=22.5°,∴MQ=QH=PH=PN=1,∵∠OCD=∠ODC=45°,∴△DMQ和△CNP都是等腰直角三角形,∴DQ=PC=,∵OC=OD=m+1,∴CD=OC=,∵CD=DQ+PQ+PC,∴=2+2,∴m=+1;(3)如图3,∵四边形BAPQ为平行四边形,∴AB∥PQ,AB=PQ,∴∠OAB=45°,∵∠AOB=90°,∴OA=OB,∴矩形OAMB是正方形,∵点M恰好在函数y=(m为常数,m>1,x>0)的图象上,∴M(,),即OA=OB=,∵AB=PQ,∴,解得:m=或(舍),∴OA=OB====.4.解:(1)连接AC交BD于点H,∵AB=BC,AD=DC,BD=BD,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,∴BH是等腰三角形ABC的高,即BH⊥AC,即BD是AC的中垂线,设HD=x,则BH=4+3﹣x,AH2=AB2﹣BH2=AD2﹣DH2,即82﹣x2=52﹣(3+4﹣x)2,解得:x=,cos∠ADB===,故∠ADB=30°BD是AC的中垂线,则∠ADB=30°=∠CDB,故∠ADC=2∠ADB=60°;(2)①连接AQ、QD、PC,∵∠APQ=60°,AP=AQ,∴△APQ为等边三角形,故∠PAQ=60°=∠PAC+∠HAQ,同理△ACD是边长为8的等边三角形,∴∠CAD=60°=∠HAQ+∠QAD,∴∠PAC=∠QAD,而AP=AQ,AD=AC,∴△ACP≌△ADQ(SAS),∵BD是AC的中垂线,故PA=PC,则△ACP为等腰三角形,∴△AQD也为等腰三角形,即AQ=QD,而AC=CD(△ACD为等边三角形),CQ=CQ,∴△ACQ≌△DCQ(SSS),故∠ACQ=∠DCQ,在△CAD中,延长CQ交AD于点K,∵AC=CD,则CK⊥AD,∴∠AKQ=90°∵∠AKQ=90°=∠AHP,∠QAK=∠PAH,PA=AQ,∴△AKQ≌△QHP(AAS),∴QK=PH,过点D作DR⊥x轴交于点R,BD∥x轴,故∠BDC=∠DCR=30°,DR=CD=8×=4=CH=OB,而BC=5,故OC=3=BH,故点C(3,0),PH=BH=BP=3﹣m=QK,在等边三角形ACD中,AD边上的高CK=CD sin∠CDA=8×sin60°=4,则CQ=CK﹣QK=4﹣3+m;②过点Q分别作x、y轴的垂线,垂足为M、N,∵AK是等边三角形CDA的高,则∠KCD=30°,而∠DCR=30°,故∠QCR=60°,QM=CQ sin∠QCM=CQ sin60°=CQ,CM=CQ,故点Q(3+CQ,CQ),点C(3,0),CH=4,故点A(3,8),反比例函数图象同时经过点A、Q,则3×8=(3+CQ)×CQ,而CQ=4﹣3+m,即m2+24m+39﹣96=0,解得:m=﹣4(不合题意值已舍去).5.解:(1)①将点A的坐标代入一次函数表达式并解得:k=2,将点A的坐标代入反比例函数得:m=3×4=12;②由图象可以看出x>3时,y1>y2;(2)①当x=1时,点D、B、C的坐标分别为(1,2+n)、(1,m)、(1,n),则BD=|2+n﹣m|,BC=m﹣n,DC=2+n﹣n=2则BD=BC或BD=DC或BC=CD,即:|2+n﹣m|=m﹣n或|2+n﹣m|=2或m﹣n=2,即:m﹣n=1或0或2或4,当m﹣n=0时,m=n与题意不符,点D不能在C的下方,即BC=CD也不存在,n+2>n,当B、D重合时,m﹣n=2成立,故m﹣n=1或4或2;②点E的横坐标为:,当点E在点B左侧时,d=BC+BE=m﹣n+(1﹣)=1+(m﹣n)(1﹣),m﹣n的值取不大于1的任意数时,d始终是一个定值,当1﹣=0时,此时k=1,从而d=1.当点E在点B右侧时,同理BC+BE=(m﹣n)(1+)﹣1,当1+=0,k=﹣1时,(不合题意舍去)故k=1,d=1.6.解:(1)∵F在直线y=x上∴设F(m,m)∵y=经过点B(2,4).∴k=8.∵F(m,m)在反比例函数的图象上,∴m2=8∴m=2(负值已舍去).∴由两点间的距离公式可知:OF==4.(2)①∵函数y=的图象经过点D,E∴OC•CD=OA•AE=k.∵OC=2,OA=4,∴CD=2AE.②由①得:CD=2AE∴可设:CD=2n,AE=n∴DE=CD+AE=3n,BD=4﹣2n,BE=2﹣n在Rt△EBD,由勾股定理得:DE2=BD2+BE2,∴9n2=(4﹣2n)2+(2﹣n)2.解得n=,∴k=4n=6﹣10.③CD=2c,AE=c当OD=DE时,22+4c2=(4﹣2c)2+(2﹣c)2,∴c=10﹣2,∴k=4c=40﹣8.(a+b)2=a2+b2+2ab=16+2k=96﹣16.当若OE=DE时,16+c2=(4﹣2c)2+(2﹣c)2,∴c=.∴k=4c=10﹣2.∴(a+b)2=a2+b2+2ab=16+2k=36﹣4.当OE=OD时,4+4c2=16+c2,解得c=2.此时点D与点E重合,故此种情况不存在.综上所述,(a+b)2的值为96﹣16或36﹣4.7.解:(1)设反比例函数的解析式为y=.∵它图象经过点A(﹣2,5)和点B(﹣5,p),∴5=,∴k=﹣10,∴反比例函数的解析式为y=﹣,∴P=﹣=2,∴点B的坐标为(﹣5,2),设直线AB的表达式为y=mx+n,则,∴,∴直线AB的表达式为y=x+7.由▱ABCD中,AB∥CD,设CD的表达式为y=x+c,∴C(0,c),D(﹣c,0),∵CD=AB,∴CD2=AB2,∴c2+c2=(﹣5+2)2+(2﹣5)2,∴c=﹣3,∴点C、D的坐标分别是(0,﹣3)、(3,0).(2)设二次函数的解析式为y=ax2+bx﹣3,,∴,∴二次函数的解析式为y=x2﹣2x﹣3,假设第四象限的抛物线上存在点E,使得△CDE的面积最大.设E(k,k2﹣2k﹣3),则F(k,k﹣3),过点E作x轴的垂线交CD于点F,则S△CDE=S△EFC+S△EFD=•EF•OD=•[(k﹣3)﹣(k2﹣2k﹣3)]=﹣(k2﹣3k)=﹣(k﹣)2+,所以,当k=时,△CDE的面积最大值为,此时点E的坐标为(,﹣).∵A(﹣2,5),C(0,﹣3),D(3,0),∴△ACD的面积为定值,∵直线AD的解析式为y=﹣x+3,∴直线AD交y轴于K(0,3),∴S△ACD=S△ACK+S△CKD=×6×2+×6×3=15,∴四边形ACED的面积的最大值为15+=.8.解:(1)过点B、D分别作BE⊥x轴、DF⊥x轴交于点E、F,∵∠DAF+∠BAE=90°,∠DAF+∠FDA=90°,∴∠FDA=∠BAE,又∠DFA=∠AEB=90°,AD=AB,∴△DFA≌△AEB(AAS),∴DF=AE=3,BE=AF=1,∴点B坐标为(﹣3,1),故答案为(﹣3,1);(2)t秒后,点D′(﹣7+2t,3)、B′(﹣3+2t,1),则k=(﹣7+2t)×3=(﹣3+2t)×1,解得:t=,则k=6,则点D′(2,3)、B′(6,1);(3)存在,理由:设:点Q(m,n),点P(0,s),mn=6,①当BD为平行四边形一条边时,图示平行四边形B′D′QP,点B′向左平移4个单位、向上平移2个单位得到点D′,同理点Q(m,n)向左平移4个单位、向上平移2个单位为(m﹣4,n+2)得到点P (0,s),即:m﹣4=0,n+2=s,mn=6,解得:m=4,n=,s=,故点Q(4,)、点P(0,);②当BD为平行四边形对角线时,图示平行四边形D′Q′B′P′,B′、D′中点坐标为(4,2),该中点也是P′Q′的中点,即:4=,=2,mm=6,解得:m=8,n=,s=,故点Q′(8,)、P′(0,);故点Q的坐标为:Q(4,)或(8,),点P的坐标为P(0,)(0,).9.解:(1)将点O、B的坐标代入一次函数表达式:y=kx得:4=2k,解得:k=2,故一次函数表达式为:y=2x,(2)①过点B作BM⊥OA,则∠OCH=∠QPA=∠OAB=∠ABM=α,则tanα=,sinα=,∵OB=AB,则OM=AM=2,则点A(4,0),设:AP=a,则OC=a,在△APQ中,sin∠APQ===sinα=,同理PQ==2t,则PA=a=t,OC=t,则点C(t,2t),T=OH2﹣S△OPQ=(OC•sinα)2﹣×(4﹣t)×2t=4t2﹣4t,②∵4>0,∴T有最小值,当t=时,T取得最小值,而点C(t,2t),故:m=t×2t=.10.解:(1)t2﹣8t+12=0,解得:t=2或6,∵OA、OB的长是方程t2﹣8t+12=0的两个实数根,且OA>OB,即OA=6,OB=2,即点A、B的坐标为(﹣6,0)、(0,2),设点P(﹣6,),由PA=PB得:36+(2+)2=()2,解得:k=﹣60,故点P(﹣6,10),故答案为:6,2,﹣60;(2)当PQ过圆心M时,点P、Q之间的距离达到最大值,tan∠ACO=,线段AB中点的坐标为(﹣3,1),则过AB的中点与直线AB垂直的直线PQ的表达式为:y=mx+n=﹣3x+n,将点(﹣3,1)的坐标代入上式并解得:n=﹣8,即点M的坐标为(0,﹣8),则圆的半径r=MB=2+8=10=MQ,过点Q作QG⊥y轴于点G,tan∠QMG=tan∠HMP===,则sin∠QMG=故GQ=MQ sin∠QMG=,MG=3,故点Q(,﹣8﹣3);故答案为:(,﹣8﹣3).(3)是定值,理由:延长PA交圆M于E,过点E作EH⊥BD于H,连接CE,DE,∵PA=PB,∴∠PAB=∠PBA,∵四边形ABCE是圆的内接四边形,∴∠PAB=∠PCE,∠PBA=∠PEC,∴∠PEC=∠PCE,∴PE=PC,∴AE=BC,∵AO⊥BD,EH⊥BD,PA⊥OA,∴四边形AOHE是矩形,∴AO=EH,AE=OH=BC,∵PA∥BD,∴=,∴,∴∠ABD=∠BDE,且∠AOB=∠EHD=90°,AO=EH,∴△AOB≌△EHD(AAS)∴OB=DH=2,∴BD﹣BC=BD﹣OH=OB+DH=4.。
北师大版数学九年级上册期末复习压轴专题:反比例函数综合(四)

北师大版数学九年级上期末复习压轴专题:反比例函数综合(四)1.如图,点A 是反比例图数y =(x <0)图象上一点,AC ⊥x 轴于点C ,与反比例函数y =(x <0)图象交于点B ,AB =2BC ,连接OA 、OB ,若△OAB 的面积为2,则m +n =( )A .﹣3B .﹣4C .﹣6D .﹣82.如图,点A ,B 在反比例函数y =﹣(x <0)的图象上,连结OA ,AB ,以OA ,AB 为边作▱OABC ,若点C 恰好落在反比例函数y =(x >0)的图象上,此时▱OABC 的面积是( )A .3B .C .2D .6 3.如图,是反比例函数y 1=和y 2=(k 1<k 2)在第一象限的图象,直线AB ∥x 轴,并分别交两条曲于A 、B 两点,若S △AOB =3,则k 2﹣k 1的值是( )A.8 B.6 C.4 D.24.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于()A.B.6 C.3 D.125.如图,A、B是双曲线y=(k>0)上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=3.则k的值为()A.2 B.1.5 C.4 D.66.如图,在平面直角坐标系中,反比例函数y=(k≠0)经过▱ABCD的顶点B、D,点A 的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),▱ABCD的面积是18,则点D的坐标是()A.(﹣2,2)B.(3,2)C.(﹣3,2)D.(﹣6,1)7.已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=.反比例函数y=,则k=()=在第一象限图象经过点A,与BC交于点F.S△AOFA.15 B.13 C.12 D.58.正方形ABCD的顶点A(2,2),B(﹣2,2),C(﹣2,﹣2),反比例函数y=与y =﹣的图象均与正方形ABCD的边相交,如图,则图中的阴影部分的面积是()A.2 B.4 C.8 D.69.如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在第一象限,点C在线段AB 上,点D在AB的右侧,△OAB和△BCD都是等腰直角三角形,∠OAB=∠BCD=90°,若函数y=(x>0)的图象经过点D,则△OAB与△BCD的面积之差为()A.12 B.6 C.3 D.210.双曲线与在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为()A.1 B.2 C.3 D.411.如图,反比例函数的图象经过矩形OABC对角线的交点M,分别与AB、BC 相交于点D、E.若四边形ODBE的面积为6,则k的值为()A.1 B.2 C.3 D.412.如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x 上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为()A.3 B.C.﹣1 D.+113.如图所示,正方形ABCD的边长为2,AB∥x轴,AD∥y轴,顶点A在双曲线y=上,边CD,BC分别交双曲线于E,F,线段AB,CD分别交y轴于G,H,且线段AE恰好经过原点,下列结论:=,其中①E是CD中点:②点F坐标为(,);③△AEF是直角三角形;④S△AEF 正确结论的个数是()A.1个B.2个C.3个D.4个14.如图,平面直角坐标系中,O为原点,点A,B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,且点P在反比例函数y=的图象上.PA,PB的延长线分别交x轴、y轴于点C,D,连结CD.则△OCD的面积是()A.8 B.8C.16 D.1615.如图,平行四边形AOBC中,对角线交于点E,双曲线y=(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k的值是()A.2 B.4 C.6 D.816.如图,△AOB的内心在x轴上,顶点A在函数y=(k1>0,x>0)的图象上,顶点B在函数y=(k2<0,x>0)的图象上,若△AOB的面积为4,则k1•k2的值为()A.﹣8 B.﹣12 C.﹣14 D.﹣1617.如图,已知三角形的顶点C在反比例函数y=位于第一象限的图象上,顶点A在x的负半轴上,顶点B在反比例函数y=(k≠0)位于第四象限的图象上,BC边与x轴交于点D,CD=2BD,AC边与y轴交于点E,AE=CE,若△ABD面积为,则k=()A.﹣4 B.﹣C.﹣2D.318.如图:A,B是函数y=的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于x轴于点D,设四边形ADBC的面积为S,则()A.S=2 B.2<S<4 C.S=4 D.S>419.如图,已知点A(m,m+3),点B(n,n﹣3)是反比例函数y=(k>0)在第一象限的图象上的两点,连接AB.将直线AB向下平移3个单位得到直线l,在直线l上任取一点C,则△ABC的面积为()A.B.6 C.D.920.如图,四边形OABC为平行四边形,A在x轴上,且∠AOC=60°,反比例函数y=(k >0)在第一象限内过点C,且与AB交于点E.若E为AB的中点,且S=8,则OC△OCE 的长为()A.8 B.4 C.D.参考答案1.解:设B(a,),A(a,)∵AB=2BC,∴=,∴m=3n,∵△OAB的面积为2,∴根据反比例函数k的几何意义可知:△AOC的面积为﹣,△BOC的面积为﹣,∴△AOB的面积为﹣+=2,∴n﹣m=4,∴n﹣3n=4,∴n=﹣2,∴m=﹣6,∴m+n=﹣8故选:D.2.解:如图,连接AC,BO交于点E,作AG⊥x轴,CF⊥x轴,设点A(a,﹣),点C(m,)(a<0,m>0)∵四边形ABCO是平行四边形∴AC与BO互相平分∴点E()∵点O坐标(0,0)∴点B[(a+m),(﹣)]∵点B在反比例函数y=﹣(x<0)的图象上,∴﹣+=﹣∴a=﹣2m,a=m(不合题意舍去)∴点A(﹣2m,)∴S△AOC=()(m+2m)﹣﹣1=∴▱OABC的面积=2×S△AOC=3故选:A.3.解:由反比例函数比例系数k的几何意义可知,S△BOC=S△AOC=∵S△BOC ﹣S△AOC=S△AOB=3∴﹣=3∴k2﹣k1=6故选:B.4.解:如图,将C2及直线y=x绕点O逆时针旋转45°,则得到双曲线C3,直线l与y轴重合.双曲线C3,的解析式为y=﹣过点P作PB⊥y轴于点B∵PA=PO∴B为OA中点.∴S△PAB =S△POB由反比例函数比例系数k的性质,S△POB=3∴△POA的面积是6故选:B.5.解:如图,分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x 轴于点E,∵k>0,点A是反比例函数图象上的点,∴S△AOD =S△AOF=|k|,∵A、B两点的横坐标分别是a、3a,∴AD=3BE,∴点B是AC的三等分点,∴DE=2a,CE=a,∴S△AOC =S梯形ACOF﹣S△AOF=(OE+CE+AF)×OF﹣|k|=×5a×﹣|k|=3,解得k=1.5.故选:B.6.解:如图,∵点A的坐标为(0,﹣1),AB∥x轴,反比例函数y=(k≠0)经过▱ABCD 的顶点B,∴点B的坐标为(﹣k,﹣1),即AB=﹣k,又∵点E(0,2),∴AE=2+1=3,又∵平行四边形ABCD的面积是18,∴AB×AE=18,∴﹣k×3=18,∴k=﹣6,∴y=﹣,∵CD经过点(0,2),∴令y=2,可得x=﹣3,∴点D的坐标为(﹣3,2),故选:C.7.解:过点A作AM⊥x轴于点M,如图所示.设OA=a=OB,则在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=,∴AM=OA•sin∠AOB=a,OM=a,∴点A的坐标为(a,a).=,∵四边形OACB是菱形,S△AOF∴OB×AM=,即×a×a=39,解得a=±,而a>0,∴a=,即A(,6),∵点A在反比例函数y=的图象上,∴k=×6=15.故选:A.8.解:根据对称性可知,阴影部分的面积=正方形ABCD的面积的=×4×4=8,故选:C.9.解:∵△OAB和△BCD都是等腰直角三角形,∴OA=AB,CD=BC.设OA=a,CD=b,则点D的坐标为(a+b,a﹣b),∵反比例函数y=在第一象限的图象经过点D,∴(a+b)(a﹣b)=a2﹣b2=6,∴△OAB与△BCD的面积之差=a2﹣b2=×6=3.故选:C.10.解:设直线AB与x轴交于点C.∵AB∥y轴,∴AC⊥x轴,BC⊥x轴.∵点A在双曲线y=的图象上,∴△AOC的面积=×5=.点B在双曲线y=的图象上,∴△COB的面积=×3=.∴△AOB的面积=△AOC的面积﹣△COB的面积=﹣=1.故选:A.11.解:由题意得:E、M、D位于反比例函数图象上,则S△OCE =,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则++6=4k,k=2.故选:B.12.解:因为AO∥BC,上底边OA在直线y=x上,则可设BE的解析式为y=x+b,将E(2,0)代入上式得,b=﹣2,BE的解析式为y=x﹣2.把y=1代入y=x﹣2,得x=3,C点坐标为(3,1),则反比例函数解析式为y=,将它与y=x组成方程组得:,解得x=,x=﹣(负值舍去).代入y=x得,y=.A点坐标为(,),OA==,BC==3,∵B(0,﹣2),E(2,0),∴BE=2,∴BE边上的高为,∴梯形AOBC高为:,梯形AOBC面积为:×(3+)×=3+,△OBE的面积为:×2×2=2,则四边形AOEC的面积为3+﹣2=1+.故选:D.13.解:①∵线段AE过原点,且点A、E均在双曲线y=上,∴点A、E关于原点对称,∵正方形ABCD边长为2,∴点A的坐标为(﹣,﹣1),点E的坐标为(,1),∴AG=DH=EH=,∵CD=2,∴CE=DE=1,∴E是CD中点;故①正确;②∵CH=,∴F(,),故②正确;③∵点A的坐标为(﹣,﹣1),点E的坐标为(,1),F(,),∴AE2==5,AF2==,EF2==1,∴AE2+EF2≠AF2,∴△AEF不是直角三角形;故③不正确;=2×2﹣﹣﹣=,④∵S△AEF故④正确;故选:C.14.解:如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.∴∠PMA=∠PHA=90°,∵∠PAM=∠PAH,PA=PA,∴△PAM≌△PAH(AAS),∴PM=PH,∠APM=∠APH,同理可证:△BPN≌△BPH,∴PH=PN,∠BPN=∠BPH,∴PM=PN,∵∠PMO=∠MON=∠PNO=90°,∴四边形PMON是矩形,∵PM=PN,∴可以假设P(m,m),∵P(m,m)在y=上,∴m2=16,∵m>0,∴m=4,∴P(4,4).设OA=a,OB=b,则AM=AH=4﹣a,BN=BH=4﹣b,∴AB=AH+BH=8﹣a﹣b,∵AB2=OA2+OB2,∴a2+b2=(8﹣a﹣b)2,可得ab=8a+8b﹣32,∴4a+4b﹣16=ab,∵PM∥OC,∴,∴,∴OC=,同法可得OD=,=•OC•DO=•=•=•=16.∴S△COD故选:C.15.解:过A作AD⊥OB于D,过E作EF⊥OB于F,如图,设A(x,y=),B(a,0),∵四边形AOBC为平行四边形,∴AE=BE,∴EF为△BAD的中位线,∴EF=AD=,∴DF=(a﹣x),OF=OD+DF=,∴E(,),∵E点在双曲线上,∴•=k,∴a=3x,∵平行四边形的面积是12,∴AD•OB=12,即•a=12,∴•3x=12,∴k=4.故选:B.16.解:∵△AOB的内心在x轴上,∴∠AOE=∠BOE,∴∠AOC=∠BOD,过作AC⊥y轴于C,BD⊥y轴于D,∴△ACO∽△BDO,∴=,设A(a,b),B(c,d),∴AC=a,OC=b,BD=c,OD=﹣d,∴=,∴bc=﹣ad,∴S△AOB =S梯形ACDB﹣S△AOC﹣S△BDO=(BD+AC)(OC+OD)﹣AC•OC﹣BD•OD=(a+c)(b﹣d)﹣ab+cd=4,∴bc﹣ad=8,∴bc=4,∴c=,d=,∴点B(,),∴•=k2,∴k2•ab=﹣16又∵ab=k1,∴k2•k1=﹣16.故选:D.17.解:如图,过点C,点B分别作x轴的垂线,垂足分别为M,N,则EO∥CM,∴△AEO∽△ACM,∴,设AO=OM=a,OE=b,CM=2b,∴点C的坐标为(a,2b),∵顶点C 在反比例函数y =位于第一象限的图象上,∴2ab =4,即ab =2,∵CM ∥BN ,∴△CMD ∽△BND ,∴,设DN =m ,则MD =2m ,BN =b ,∴点B 的坐标为(a +3m ,﹣b ),∵顶点B 在反比例函数y =(k ≠0)位于第四象限的图象上,∴﹣b (a +3m )=k ,∵△ABD 面积为,∴,即ab +mb =,∴mb =0.5,∴k =﹣b (a +3m )=﹣ab ﹣3mb =﹣2﹣1.5=﹣3.5,故选:B .18.解:∵A ,B 是函数y =的图象上关于原点O 对称的任意两点,且AC 垂直于x 轴于点C ,BD 垂直于x 轴于点D ,∴S △AOC =S △BOD =×2=1,假设A 点坐标为(x ,y ),则B 点坐标为(﹣x ,﹣y ),则OC =OD =x ,∴S △AOD =S △AOC =1,S △BOC =S △BOD =1,∴四边形ADBC 面积=S △AOD +S △AOC +S △BOC +S △BOD =4.故选:C .19.解:∵点A(m,m+3),点B(n,n﹣3)在反比例函数y=(k>0)第一象限的图象上,∴k=m(m+3)=n(n﹣3),即:(m+n)(m﹣n+3)=0,∵m+n>0,∴m﹣n+3=0,即:m﹣n=﹣3,过点A、B分别作x轴、y轴的平行线相交于点D,∴BD=x B﹣x A=n﹣m=3,AD=y A﹣y B=m+3﹣(n﹣3)=m﹣n+6=3,又∵直线l是由直线AB向下平移3个单位得到的,∴平移后点A与点D重合,因此,点D在直线l上,∴S△ACB =S△ADB=AD•BD=,故选:A.20.解:过点C作CD⊥x轴于点D,过点E作EF⊥x轴于点F,如图:∵四边形OABC为平行四边形,∴OC=AB,OC∥AB,∴∠EAF=∠AOC=60°,在Rt△COD中,∵∠DOC=60°,∴∠DOC=30°,设OD=t,则CD=t,OC=AB=2t,在Rt △EAF 中,∵∠EAF =60°,AE =AB =t , ∴AF =,EF =AF =t ,∵点C 与点E 都在反比例函数y =的图象上, ∴OD ×CD =OF ×EF ,∴OF ==2t ,∴OA =2t ﹣=t ,∴S 四边形OABC =2S △OCE ,∴t ×t =2×8,∴解得:t =(舍负), ∴OC =. 故选:D .。
2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(一)

2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(一)1.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.(1)求抛物线的解析式;(2)求点P在运动的过程中线段PD长度的最大值;(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.2.如图1,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点B坐标为(3,0),点C坐标为(0,3).(1)求抛物线的表达式;(2)点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)如图2,点M为该抛物线的顶点,直线MD⊥x轴于点D,在直线MD上是否存在点N,使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.3.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.已知点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,连接AP、PC、CD.(1)求这个抛物线的表达式.(2)当四边形ADCP面积等于4时,求点P的坐标.(3)①点M在平面内,当△CDM是以CM为斜边的等腰直角三角形时,直接写出满足条件的所有点M的坐标;②在①的条件下,点N在抛物线对称轴上,当∠MNC=45°时,直接写出满足条件的所有点N的坐标.4.如图,抛物线y=x2+bx+c与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为C,D,BC=CD.(1)求b,c的值;(2)求直线BD的函数解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.5.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).(1)求抛物线的解析式;(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.①求S与m之间的函数关系式,并写出自变量m的取值范围;②当S取得最值时,求点P的坐标.(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.6.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C(0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.7.如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数解析式;(2)点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;(3)如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.8.已知二次函数图象过点A(﹣2,0),B(4,0),C(0,4).(1)求二次函数的解析式.(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标;若不存在,请说明理由.(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角θ,且tanθ=,求点K的坐标.9.如图,在平面直角坐标系中,抛物线y=x2+bx+c与y轴交于点A(0,2),与x轴交于B(﹣3,0)、C两点(点B在点C的左侧),抛物线的顶点为D.(1)求抛物线的表达式;(2)用配方法求点D的坐标;(3)点P是线段OB上的动点.①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;③若点Q是射线OA上的动点,且始终满足OQ=OP,连接AP,DQ,请直接写出AP+DQ的最小值.10.如图1,已知:抛物线y=a(x+1)(x﹣3)交x轴于A,C两点,交y轴于点B,且OB =2CO.(1)求二次函数解析式;(2)在二次函数图象(如图2)位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;(3)抛物线对称轴上是否存在点P,使得△ABP为直角三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.参考答案1.解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴,解得,∴抛物线解析式为y=x2﹣4x+3;(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3),∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,∵a=﹣1<0,∴当x=时,线段PD的长度有最大值;(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1),∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1),综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.2.解:(1)∵点B(3,0),点C(0,3)在抛物线y=﹣x2+bx+c图象上,∴,解得:,∴抛物线解析式为:y=﹣x2+2x+3;(2)∵点B(3,0),点C(0,3),∴直线BC解析式为:y=﹣x+3,如图,过点P作PH⊥x轴于H,交BC于点G,设点P(m,﹣m2+2m+3),则点G(m,﹣m+3),∴PG=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m,=×PG×OB=×3×(﹣m2+3m)=﹣(m﹣)2+,∵S△PBC有最大值,∴当m=时,S△PBC∴点P(,);(3)存在N满足条件,理由如下:∵抛物线y=﹣x2+2x+3与x轴交于A、B两点,∴点A(﹣1,0),∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点M为(1,4),∵点M为(1,4),点C(0,3),∴直线MC的解析式为:y=x+3,如图,设直线MC与x轴交于点E,过点N作NQ⊥MC于Q,∴DE=4=MD,∴∠NMQ=45°,∵NQ⊥MC,∴∠NMQ=∠MNQ=45°,∴MQ=NQ,∴MQ=NQ=MN,设点N(1,n),∵点N到直线MC的距离等于点N到点A的距离,∴NQ=AN,∴NQ2=AN2,∴(MN)2=AN2,∴(|4﹣n|)2=4+n2,∴n2+8n﹣8=0,∴n=﹣4±2,∴存在点N满足要求,点N坐标为(1,﹣4+2)或(1,﹣4﹣2).3.解:(1)∵抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),∴抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,即﹣3a=2,解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+2;(2)连接OP,设点P(x,﹣x2﹣x+2),∵抛物线y=﹣x2﹣x+2交y轴于点C,∵S =S 四边形ADCP =S △APO +S △CPO ﹣S △ODC =×AO ×y P +×OC ×|x P |﹣×CO ×OD =4,∴×3×(﹣x 2﹣x +2)+×2×(﹣x )﹣×1×2=4,∴x 1=﹣1,x 2=﹣2, ∴点P (﹣1,)或(﹣2,2);(3)①如图2,若点M 在CD 左侧,连接AM ,∵∠MDC =90°,∴∠MDA +∠CDO =90°,且∠CDO +∠DCO =90°, ∴∠MDA =∠DCO ,且AD =CO =2,MD =CD , ∴△MAD ≌△DOC (SAS )∴AM =DO ,∠MAD =∠DOC =90°, ∴点M 坐标(﹣3,1),若点M 在CD 右侧,同理可求点M '(1,﹣1); ②如图3,∵抛物线的表达式为:y =﹣x 2﹣x +2=﹣(x +1)2+;∴对称轴为:直线x =﹣1,∴点D在对称轴上,∵MD=CD=M'D,∠MDC=∠M'DC=90°,∴点D是MM'的中点,∵∠MCD=∠M'CD=45°,∴∠MCM'=90°,∴点M,点C,点M'在以MM'为直径的圆上,当点N在以MM'为直径的圆上时,∠M'NC=∠M'MC=45°,符合题意,∵点C(0,2),点D(﹣1,0)∴DC=,∴DN=DN'=,且点N在抛物线对称轴上,∴点N(﹣1,),点N'(﹣1,﹣)延长M'C交对称轴与N'',∵点M'(1,﹣1),点C(0,2),∴直线M'C解析式为:y=﹣3x+2,∴当x=﹣1时,y=5,∴点N''的坐标(﹣1,5),∵点N''的坐标(﹣1,5),点M'(1,﹣1),点C(0,2),∴N''C==M'C,且∠MCM'=90°,∴MM'=MN'',∴∠MM'C=∠MN''C=45°∴点N''(﹣1,5)符合题意,综上所述:点N的坐标为:(﹣1,)或(﹣1,﹣)或(﹣1,5).4.解:(1)∵BO=3AO=3,∴点B(3,0),点A(﹣1,0),∴抛物线解析式为:y=(x+1)(x﹣3)=x2﹣x﹣,∴b=﹣,c=﹣;(2)如图1,过点D作DE⊥AB于E,∴CO∥DE,∴,∵BC=CD,BO=3,∴=,∴OE=,∴点D横坐标为﹣,∴点D坐标为(﹣,+1),设直线BD的函数解析式为:y=kx+b,由题意可得:,解得:,∴直线BD的函数解析式为y=﹣x+;(3)∵点B(3,0),点A(﹣1,0),点D(﹣,+1),∴AB=4,AD=2,BD=2+2,对称轴为直线x=1,∵直线BD:y=﹣x+与y轴交于点C,∴点C(0,),∴OC=,∵tan∠CBO==,∴∠CBO=30°,如图2,过点A作AK⊥BD于K,∴AK=AB=2,∴DK===2,∴DK=AK,∴∠ADB=45°,如图,设对称轴与x轴的交点为N,即点N(1,0),若∠CBO=∠PBO=30°,∴BN=PN=2,BP=2PN,∴PN=,BP=,当△BAD∽△BPQ,∴,∴BQ==2+,∴点Q(1﹣,0);当△BAD∽△BQP,∴,∴BQ==4﹣,∴点Q(﹣1+,0);若∠PBO=∠ADB=45°,∴BN=PN=2,BP=BN=2,当△DAB∽△BPQ,∴,∴,∴BQ=2+2∴点Q(1﹣2,0);当△BAD∽△PQB,∴,∴BQ==2﹣2,∴点Q(5﹣2,0);综上所述:满足条件的点Q的坐标为(1﹣,0)或(﹣1+,0)或(1﹣2,0)或(5﹣2,0).5.解:(1)∵直线x=1是抛物线的对称轴,且点C的坐标为(0,3),∴c=3,﹣=1,∴b=2,∴抛物线的解析式为:y=﹣x2+2x+3;(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点M(1,4),∵抛物线的解析式为:y=﹣x2+2x+3与x轴相交于A,B两点(点A位于点B的左侧),∴0=﹣x2+2x+3∴x1=3,x2=﹣1,∴点A(﹣1,0),点B(3,0),∵点M(1,4),点B(3,0)∴直线BM解析式为y=﹣2x+6,∵点P在直线BM上,且PD⊥x轴于点D,PD=m,∴点P(3﹣,m),∴S△PCD=×PD×OD=m×(3﹣)=﹣m2+m,∵点P在线段BM上,且点M(1,4),点B(3,0),∴0<m≤4∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4)②∵S=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,S有最大值为,∴点P(,3)∵0<m≤4时,S没有最小值,综上所述:当m=3时,S有最大值为,此时点P(,3);(3)存在,若PC=PD=m时,∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6);若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,∴m3=﹣2﹣2(舍去),m4=﹣2+2,∴点P(4﹣,﹣2+2);若DC=PC时,∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,∴m5=0(舍去),m6=6(舍去)综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.6.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,∴直线AC的解析式为y=﹣3x+3,又∵抛物线对称轴为直线x=﹣=2,∴x=2时,y=﹣3×2+3=﹣3,故,点M的坐标为(2,﹣3);(3))∵OB=OC=3,OB⊥OC,∴△BOC是等腰直角三角形,∵EF∥y轴,直线BC的解析式为y=﹣x+3,∴△DEF只要是直角三角形即可与△BOC相似,∵D(2,1),A(1,0),B(3,0),∴点D垂直平分AB且到点AB的距离等于AB,∴△ABD是等腰直角三角形,∴∠ADB =90°,如图,①点F 是直角顶点时,点F 的纵坐标与点D 的纵坐标相同,是1,∴x 2﹣4x +3=1,整理得x 2﹣4x +2=0,解得x =2±, 当x =2﹣时,y =﹣(2﹣)+3=1+, 当x =2+时,y =﹣(2+)+3=1﹣, ∴点E 1(2﹣,1+)E 2(2+,1﹣), ②点D 是直角顶点时,易求直线AD 的解析式为y =x ﹣1,联立,解得,,当x =1时,y =﹣1+3=2,当x =4时,y =﹣4+3=﹣1,∴点E 3(1,2),E 4(4,﹣1),综上所述,存在点E 1(2﹣,1+)或E 2(2+,1﹣)或E 3(1,2)或E 4(4,﹣1),使以D 、E 、F 为顶点的三角形与△BCO 相似.7.解:(1)∵抛物线y =x 2+bx +c 交x 轴于点A (1,0),与y 轴交于点C (0,﹣3),∴,解得:,∴抛物线解析式为:y=x2+2x﹣3;(2)∵抛物线y=x2+2x﹣3与x轴于A,B两点,∴点B(﹣3,0),∵点B(﹣3,0),点C(0,﹣3),∴OB=OC=3,∴∠OBC=∠OCB=45°,如图1,当点D在点C上方时,∵∠DBC=15°,∴∠OBD=30°,∴tan∠DBO==,∴OD=×3=,∴CD=3﹣;若点D在点C下方时,∵∠DBC=15°,∴∠OBD=60°,∴tan∠DBO==,∴OD=3,∴DC=3﹣3,综上所述:线段CD的长度为3﹣或3﹣3;(3)如图2,在BO上截取OE=OA,连接CE,过点E作EF⊥AC,∵点A(1,0),点C(0,﹣3),∴OA=1,OC=3,∴AC===,∵OE=OA,∠COE=∠COA=90°,OC=OC,∴△OCE≌△OCA(SAS),∴∠ACO=∠ECO,CE=AC=,∴∠ECA=2∠ACO,∵∠PAB=2∠ACO,∴∠PAB=∠ECA,=AE×OC=AC×EF,∵S△AEC∴EF==,∴CF===,∴tan∠ECA==,如图2,当点P在AB的下方时,设AP与y轴交于点N,∵∠PAB=∠ECA,∴tan∠ECA=tan∠PAB==,∴ON=,∴点N(0,﹣),又∵点A(1,0),∴直线AP解析式为:y=x﹣,联立方程组得:,解得:或,∴点P坐标为:(﹣,﹣),当点P在AB的上方时,同理可求直线AP解析式为:y=﹣x+,联立方程组得:,解得:或,∴点P坐标为:(﹣,),综上所述:点P的坐标为(﹣,),(﹣,﹣).8.解:(1)∵二次函数图象过点B(4,0),点A(﹣2,0),∴设二次函数的解析式为y=a(x+2)(x﹣4),∵二次函数图象过点C(0,4),∴4=a(0+2)(0﹣4),∴a=﹣,∴二次函数的解析式为y=﹣(x+2)(x﹣4)=﹣x2+x+4;(2)存在,理由如下:如图1,取BC中点Q,连接MQ,∵点A(﹣2,0),B(4,0),C(0,4),点P是AC中点,点Q是BC中点,∴P(﹣1,2),点Q(2,2),BC==4,设直线BP解析式为:y=kx+b,由题意可得:,解得:∴直线BP的解析式为:y=﹣x+,∵∠BMC=90°∴点M在以BC为直径的圆上,∴设点M(c,﹣c+),∵点Q是Rt△BCM的中点,∴MQ=BC=2,∴MQ2=8,∴(c﹣2)2+(﹣c+﹣2)2=8,∴c=4或﹣,当c=4时,点B,点M重合,即c=4,不合题意舍去,∴c=﹣,则点M坐标(﹣,),故线段PB上存在点M(﹣,),使得∠BMC=90°;(3)如图2,过点D作DE⊥BC于点E,设直线DK与BC交于点N,∵点A(﹣2,0),B(4,0),C(0,4),点D是AB中点,∴点D(1,0),OB=OC=4,AB=6,BD=3,∴∠OBC=45°,∵DE⊥BC,∴∠EDB=∠EBD=45°,∴DE=BE==,∵点B(4,0),C(0,4),∴直线BC解析式为:y=﹣x+4,设点E(n,﹣n+4),∴﹣n+4=,∴n=,∴点E(,),在Rt△DNE中,NE===,①若DK与射线EC交于点N(m,4﹣m),∵NE=BN﹣BE,∴=(4﹣m)﹣,∴m=,∴点N(,),∴直线DK解析式为:y=4x﹣4,联立方程组可得:,解得:或,∴点K坐标为(2,4)或(﹣8,﹣36);②若DK与射线EB交于N(m,4﹣m),∵NE=BE﹣BN,∴=﹣(4﹣m),∴m=,∴点N(,),∴直线DK解析式为:y=x﹣,联立方程组可得:,解得:或,∴点K坐标为(,)或(,),综上所述:点K的坐标为(2,4)或(﹣8,﹣36)或(,)或(,).9.解:(1)∵抛物线y=x2+bx+c与y轴交于点A(0,2),与x轴交于B(﹣3,0),∴∴∴抛物线解析式为:y=x2﹣x+2;(2)∵y=x2﹣x+2=﹣(x+1)2+,∴顶点D坐标(﹣1,);(3)①∵抛物线y=x2﹣x+2与x轴交于B(﹣3,0)、C两点,∴点C(1,0)设点E(m,m2﹣m+2),则点P(m,0),∵PE=PC,∴m2﹣m+2=1﹣m,∴m=1(舍去),m=﹣,∴点E(﹣,)②如图,连接AE交对称轴于点N,连接DE,作EH⊥DN于H,交y轴于点F,∵点A(0,2),点E(﹣,),∴直线AE解析式为y=﹣x+2,∴点N坐标(﹣1,)∴DH==,HN==,∴DH=NH,且EH⊥DN,∴∠DEH=∠NEH,∴点F到AE,DE的距离相等,∴DN∥y轴,EH⊥DN,∴EH⊥y轴,∴EF=;③在x轴正半轴取点H,使OH=OA=2,∵OH=OA,∠AOP=∠QOH=90°,OP=OQ,∴△AOP≌△HOQ(SAS)∴AP=QH,∴AP+DQ=DQ+QH≥DH,∴点Q在DH上时,DQ+AP有最小值,最小值为DH的长,∴AP+DQ的最小值==.10.解:(1)对于抛物线y=a(x+1)(x﹣3),令y=0,得到a(x+1)(x﹣3)=0,解得x=﹣1或3,∴C(﹣1,0),A(3,0),∴OC=1,∵OB=2OC=2,∴B(0,2),把B(0,2)代入y=a(x+1)(x﹣3)中得:2=﹣3a,a=﹣∴二次函数解析式为=;(2)设点M的坐标为(m,),则点N的坐标为(2﹣m,),MN=m﹣2+m=2m﹣2,GM=矩形MNHG的周长C=2MN+2GM=2(2m﹣2)+2()==∴当时,C有最大值,最大值为;(3)∵A(3,0),B(0,2),∴OA=3,OB=2,由对称得:抛物线的对称轴是:x=1,∴AE=3﹣1=2,设抛物线的对称轴与x轴相交于点E,当△ABP为直角三角形时,存在以下三种情况:①如图1,当∠BAP=90°时,点P在AB的下方,∵∠PAE+∠BAO=∠BAO+∠ABO=90°,∴∠PAE=∠ABO,∵∠AOB=∠AEP,∴△ABO∽△PAE,∴,即,∴PE=3,∴P(1,﹣3);②如图2,当∠PBA=90°时,点P在AB的上方,过P作PF⊥y轴于F,同理得:△PFB∽△BOA,∴,即,∴BF=,∴OF=2+=,∴P(1,);③如图3,以AB为直径作圆与对称轴交于P1、P2,则∠AP1B=∠AP2B=90°,设P1(1,y),∵AB2=22+32=13,由勾股定理得:AB2=P1B2+P1A2,∴12+(y﹣2)2+(3﹣1)2+y2=13,解得:y=1±,∴P(1,1+)或(1,1﹣),综上所述,点P的坐标为(1,﹣3)或(1,)或(1,1+)或(1,1﹣)。
2023年九年级中考数学专题专练--反比例函数与一次函数的综合【含答案】

2023年九年级中考数学专题专练--反比例函数与一次函数的综合1.如图,在平面直角坐标系中,点A(m ,n)(m >0)在双曲线y = 上.4x (1)如图1,m =1,∠AOB =45°,点B 正好在y = (x >0)上,求B 点坐标; 4x (2)如图2,线段OA 绕O 点旋转至OC ,且C 点正好落在y = 上,C(a ,b),试求m 与a4x 的数量关系.2.如图,一次函数y=kx+3的图象与反比例函数y= 的图象交于P 、Q 两点,PA ⊥x 轴于点A ,mx 一次函数的图象分别交x 轴、y 轴于点C ,点B,其中OA=6,且 .12OC CA(1)求一次函数和反比例函数的表达式; (2)求△APQ 的面积;(3)根据图象写出当x 取何值时,一次函数的值小于反比例函数的值.3.如图,已知一次函数y 1=k 1x+b (k 1为常数,且k 1≠0)的图象与反比例函数y 2= (k 2为常数,2k x 且k 2≠0)的图象相交于A (1,2),B (m ,﹣1)两点.(1)求一次函数和反比例函数的解析式;(2)若A 1(m 1,n 1),A (m 2,n 2),A 3(m 3,n 3)为反比例函数图象上的三点,且m 1<m 2<0<m 3,请直接写出n 1、n 2、n 3的大小关系式;(3)结合图象,请直接写出关于x 的不等式k 1x+b > 的解集.2k x 4.如图,在平面直角坐标系xOy 中,直线y=x﹣2与双曲线y= (k≠0)相交于A,B 两点,且点Akx 的横坐标是3.(1)求k 的值;(2)过点P(0,n)作直线,使直线与x 轴平行,直线与直线y=x﹣2交于点M ,与双曲线y=kx (k≠0)交于点N ,若点M 在N 右边,求n 的取值范围.5.已知双曲线y= 和直线y=kx+4.6x (1)若直线y=kx+4与双曲线y= 有唯一公共点,求k 的值.6x(2)若直线y=kx+4与双曲线交于点M (x 1,y 1),N (x 2,y 2).当x 1>x 2,请借助图象比较y 1与y 2的大小.6.如图,已知A (﹣2,﹣2),B (1,4)是一次函数y =kx+b (k≠0)的图象和反比例函数(m≠0)的图象的两个交点,直线AB 与y 轴交于点C.my x =(1)求一次函数和反比例函数的解析式;(2)求△AOC 的面积;(3)结合图象直接写出不等式的解集.mkx b x +<7.如图,在平面直角坐标系系中,一次函数y 1=kx+b(k0)与反比例函数y 2= (m≠0)的图象交mx 于第二、第四象限A ,B 两点,过点A 作AD ⊥x 轴,垂足为D ,AD=4,sin ∠AOD= ,且点B 的45坐标为(n ,-2).(1)求一次函数与反比例函数的表达式;(2)将一次函数y 1=kx+b(k0)向下移动2个单位的函数记为y 3,当y 3<y 2时,求x 的取值范围。
2023年九年级中考数学专项训练——二次函数与一次函数的综合运用

2023年中考数学专项训练——二次函数与一次函数的综合运用一、综合题1.已知:二次函数y =ax 2+bx+12(a >0,b <0)的图象与x 轴只有一个公共点A . (1)当a =12时,求点A 的坐标; (2)求A 点的坐标(只含b 的代数式来表示);(3)过点A 的直线y =x+k 与二次函数的图象相交于另一点B ,当b≥﹣1时,求点B 的横坐标m 的取值范围.2.已知二次函数图象的顶点在原点 O ,对称轴为 y 轴.直线 1:l y kx b =+ 的图象与二次函数的图象交于点 (3,2)A - 和点 3(,)2B m (点 A 在点 B 的左侧)(1)求 m 的值及直线 1l 解析式;(2)若过点 (0,)P n 的直线 2l 平行于直线 1l 且直线 2l 与二次函数图象只有一个交点 Q ,求交点Q 的坐标.3.如图,已知抛物线 212y x bx =+ 与直线 2y x = 交于点O (0,0),A (a ,12),点B 是抛物线上O 、A 之间的一个动点,过点B 分别作x 轴和y 轴的平行线与直线OA 交于点C 、E ,(1)求抛物线的函数解析式;(2)若点C 为OA 的中点,求BC 的长;(3)以BC 、BE 为边构造矩形BCDE ,设点D 的坐标为(m ,n ),求出m 、n 之间的关系式.4.已知,直线 23y x =-+ 与抛物线 2y ax = 相交于 A 、 B 两点,且 A 的坐标是 (3,)m -(1)求 a , m 的值;(2)抛物线的表达式及其对称轴和顶点坐标.5.已知抛物线的解析式为 ()2221.y x m x m m =--+-(1)求证:此抛物线与x 轴必有两个不同的交点;(2)若此抛物线与直线 34y x m =-+ 的一个交点在y 轴上,求m 的值.6.如图,二次函数的图象与x 轴交于A (-3,0)和B (1,0)两点,交y 轴于点C (0,3),点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D.(1)求点D 坐标及二次函数的解析式;(2)根据图象直接写出使一次函数值大于二次函数值的x 的取值范围.7.如图,已知抛物线y=ax 2+bx+c (a≠0)经过点A (3,0),B (﹣1,0),C (0,﹣3).(1)求该抛物线的解析式;(2)若以点A 为圆心的圆与直线BC 相切于点M ,求切点M 的坐标;(3)若点Q 在x 轴上,点P 在抛物线上,是否存在以点B ,C ,Q ,P 为顶点的四边形是平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.8.抛物线y=﹣23 x 2+ 73x ﹣1与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,其顶点为D .将抛物线位于直线l :y=t (t < 2524)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.(1)点A ,B ,D 的坐标分别为 , , ; (2)如图①,抛物线翻折后,点D 落在点E 处.当点E 在△ABC 内(含边界)时,求t 的取值范围; (3)如图②,当t=0时,若Q 是“M”形新图象上一动点,是否存在以CQ 为直径的圆与x 轴相切于点P ?若存在,求出点P 的坐标;若不存在,请说明理由.9.如图,已知抛物线与 x 轴交于 (1,0)A - 、 (3,0)B 两点,与 y 轴交于点 (0,3)C .(1)求抛物线的解析式;(2)点 D 是第一象限内抛物线上的一个动点(与点 C 、 B 不重合),过点 D 作 DF x ⊥ 轴于点F ,交直线 BC 于点 E ,连接 BD 、 CD .设点 D 的横坐标为 m , BCD 的面积为 S .求 S关于 m 的函数解析式及自变量 m 的取值范围,并求出 S 的最大值; (3)已知 M 为抛物线对称轴上一动点,若MBC 是以 BC 为直角边的直角三角形,请直接写出点M 的坐标.10.如图,直线 12y kx =+ 与 x 轴交于点 ( 0)A m , ( 4m > ),与 y 轴交于点 B ,抛物线 224y ax ax c =-+ ( 0a < )经过 A , B 两点, P 为线段 AB 上一点,过点 P 作 //PQ y 轴交抛物线于点 Q .(1)当 5m = 时, ①求抛物线的关系式;②设点 P 的横坐标为 x ,用含 x 的代数式表示 PQ 的长,并求当 x 为何值时, 85PQ =? (2)若 PQ 长的最大值为16,试讨论关于 x 的一元二次方程 24ax ax kx h --= 的解的个数与 h 的取值范围的关系.11.如图,抛物线y=ax 2+bx 经过点A(7,0),B(-1,4),经过点B 的直线与抛物线的另一个交点C 在第四象限.已知△ABC 的面积为14.(1)求抛物线的函数关系式; (2)求点C 的坐标#(3)设P 是线段BC 延长线上的点,作直线PD△x 轴,交抛物线于点D 、E(点D 在点E 的左侧).若DE=PE ,求点P 的横坐标.12.如图,若b 是正数,直线l :y=b 与y 轴交于点A ;直线a :y=x ﹣b 与y 轴交于点B ;抛物线L :y=﹣x 2+bx 的顶点为C ,且L 与x 轴右交点为D .(1)若AB=8,求b 的值,并求此时L 的对称轴与a 的交点坐标; (2)当点C 在l 下方时,求点C 与l 距离的最大值;(3)设x 0≠0,点(x 0,y 1),(x 0,y 2),(x 0,y 3)分别在l ,a 和L 上,且y 3是y 1,y 2的平均数,求点(x 0,0)与点D 间的距离;(4)在L 和a 所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.13.在平面直角坐标系中,正方形ABCD 的四个顶点坐标分别为A(-2,4),B(-2,-2),C(4,-2),D(4,4).(1)填空:正方形的面积为 ;当双曲线 ky x= (k≠0)与正方形ABCD 有四个交点时,k 的取值范围是 .(2)已知抛物线L : 2()y a x m n =-+ (a>0)顶点P 在边BC 上,与边AB ,DC 分别相交于点E ,F ,过点B 的双曲线 ky x=(k≠0)与边DC 交于点N. ①点Q(m ,-m 2-2m+3)是平面内一动点,在抛物线L 的运动过程中,点Q 随m 运动,分别求运动过程中点Q 在最高位置和最低位置时的坐标.②当点F 在点N 下方,AE=NF ,点P 不与B ,C 两点重合时,求 BE CFBP CP- 的值. ③求证:抛物线L 与直线的交点M 始终位于轴下方.14.如图,抛物线2y ax bx c =++与x 轴交于点(10)A -,,点(30)B ,,与y 轴交于点C ,且过点(23)D -,.点P 、Q 是抛物线2y ax bx c =++上的动点.(1)求抛物线的解析式;(2)当点P 在直线OD 下方时,求POD ∆面积的最大值.(3)直线OQ 与线段BC 相交于点E ,当ΔOBE 与ΔABC 相似时,求点Q 的坐标.15.如图,在平面直角坐标系中,抛物线y=-x 2+4x+m(m 为常数)与y 轴的交点为A ,M(4,0)与N(0,-3) 分别是x 轴、y 轴上的点。
2024学年九年级中考数学专题复习:行程问题(一次函数的综合实际应用)(提升篇)(含答案)

2024学年九年级中考数学专题复习:行程问题(一次函数的综合实际应用)姓名:___________班级:___________考号:___________1.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,图中的折线表示两车之间距离()kmy与慢车行驶时间()h x之间的函数关系图象,请根据图象提供的信息回答:(1)快车的速度是______km/h.(2)求线段BC所表示的函数关系式.(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同,直接写出第二列快车出发多长时间与慢车相距200km.2.A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中12,分别表示甲、乙l l两人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.(1)求点A的坐标,并说明其实际意义;(2)甲出发多少时间,两人之间的距离恰好相距5km;(3)若用y3(km)表示甲、乙两人之间的距离,请在坐标系(图3)中画出y3(km)关于时间x(h)的函数关系图象,注明关键点的数据.3.快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.下图表示的是两车之间的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息.解答下列问题:(1)直接写出快、慢两车的速度及A、B两站间的距离;(2)求快车从B返回A站时,y与x之间的函数关系式;(3)出发几小时,两车相距200千米?请直接写出答案.4.甲、乙两人从相距4千米的两地同时、同向出发,乙每小时走4千米,小狗随甲一起同向出发,小狗追上乙的时候它就往甲这边跑,遇到甲时又往乙这边跑,遇到乙的时候再往甲这边跑…就这样一直匀速跑下去.如图,折线A B C--,A D E--分别表示甲、小狗在行进过程中,y与甲行进时间x(h)之间的部分函数图象.离乙的路程()km(1)求AB所在直线的函数解析式;(2)小狗的速度为______km/h;求点E的坐标;(3) 小狗从出发到它折返后第一次与甲相遇的过程中,求x为何值时,它离乙的路程与离甲的路程相等?5.甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米).图中的折线表示y与x之间的函数关系图像.求:(1)甲、乙两地相距______千米;(2)求动车和普通列车的速度;(3)求C点坐标和直线CD解析式;(4)求普通列车行驶多少小时后,两车相距1000千米.6.甲、乙两车分别从A,B两地同时出发,匀速行驶,先相向而行.途中乙车因故停留1小时,然后以原速继续向A地行驶,甲车到达B地后,立即按原路原速返回A地(甲车掉头的时间忽略不计),到达A地后停止行驶,原地休息;甲、乙两车距B地的路程y(千米)与所用时间x (时)之间的函数图象如图,请结合图象信息解答下列问题:(1)乙车的速度为千米/时,在图中的()内应填上的数是.(2)求甲车从B地返回A地的过程中,y与x的函数关系式.(3)两车出发后几小时相距120千米,请直接写出答案:时.7.甲、乙两人从A地前往B地,先到终点的人在原地休息.已知甲先出发30s后,乙才出发.在运动过程中,甲、乙两人离A地的距离分别为1y(单位:m)、2y(单位:m),都是甲出发时间x(单位:s)的函数,它们的图象如图①.设甲的速度为1v m/s,乙的速度为2v m/s.(1)12:v v=______,=a______;(2)求2y与x之间的函数表达式;(3)在图②中画出甲、乙两人之间的距离s(单位:m)与甲出发时间x(单位:s)之间的函数图象.8.小明从学校出发,匀速骑行前往距离学校2400米的图书馆,小明出发的同时,同学小阳以每分钟80米的速度从图书馆沿同一条道路步行回学校,两人距离学校的路程y(单位:米)与小明从学校出发的时间x(单位:分钟)的函数图象如图所示.(1)点C的坐标为_________;(2)求直线BC的表达式;(3)若小明在图书馆停留7分钟后沿原路按原速返回,请补全小明距离学校的路程y与x的函数图象;(4)在(3)的基础上,小明能否在返校途中追上小阳?若能,请计算此时两人与学校之间的距离;若不能,请说明理由.9.如图,已知:平面直角坐标系中,正比例函数y=kx(k≠0)的图象经过点A(﹣2,﹣2),点B是第二象限内一点,且点B的横、纵坐标分别是一元二次方程x2﹣36=0的两个根.过点B作BC⊥x轴于点C.(1)直接写出k的值和点B的坐标:k=;B(,);(2)点P从点C出发,以每秒1个单位长度的速度沿x轴向右运动,设运动时间为t,若△BPO 的面积是S,试求出S关于t的函数解析式(直接写出t的取值范围)(3)在(2)的条件下,当S=6时,以PQ为一边向直线PQ下方作正方形PQRS,求点R 的坐标.10.甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.根据图像回答下列问题:(1)乙车行驶小时追上了甲车.(2)乙车的速度是;(3)m=;(4)点H的坐标是;(5)n=.11.已知矩形ABCD中,AB=4米,BC=6米,E为BC中点,动点P以2米/秒的速度从A 出发,沿着△AED的边,按照A→E→D→A顺序环行一周,设P从A出发经过x秒后,△ABP 的面积为y(平方米),求y与x间的函数关系式.12.某兴趣小组利用计算机进行电子虫运动实验.如图1,在相距100个单位长度的线段AB 上,电子虫甲从端点A出发,匀速往返于端点A、B之间,电子虫乙同时从端点B出发,设定不低于甲的速度匀速往返于端点B、A之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员重点探究了甲、乙迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.设甲、乙第一次迎面相遇时,相遇地点与点A之间的距离为x个单位长度,他们第二次迎面相遇时,相遇地点与点A之间的距离为y个单位长度.(1)请直接写出:当x=20时,y的值为_________;当x=40时,y的值为________;(2)兴趣小组成员发现了y与x的函数关系,并画出了部分函数图像(如图2中的线段OM,但不包括点O,因此点O用空心画出)①请直接写出:a=_______;②分别求出各部分图像对应的函数解析式,并在图2中补全函数图像,标出关键点的坐标;(2)小黄在距离学校多少米处遭遇堵车?从小黄遇到堵车到小吴追上小黄用了多少时间?(3)小吴和小黄何时相距520m?15.甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示.(1)点A的实际意义是什么?(2)求甲、乙两人的速度;(3)求OC和BD的函数关系式;(4)求学校和博物馆之间的距离.16.甲乙两人沿相同的路线同时登山甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲距地面的高度y(米)与登山时间x(分)之间的函数关系式为:y 甲.(2)若乙提速后,乙的速度是甲登山速度的3倍,登山多长时间时,乙追上了甲?此时乙距A 地的高度为多少米?答案:21200 430v=15 6v∴=⨯30 a∴=⨯。
最新九年级中考数学复习:二次函数综合题(特殊三角形问题)

2023年九年级中考数学复习:二次函数综合题(特殊三角形问题)1.抛物线y=ax2+c交x轴于A、B(1,0)两点,且经过(2,3).(1)求抛物线的解析式;(2)如图1,直线y=kx+3交y轴于点G,交抛物线y=ax2+c于点E和F,F在y轴右侧,若△GOF的面积为△GOE面积的2倍,求k值;(3)如图2,点P是第二象限的动点,分别连接P A、PB,并延长交直线y=-2于M、N 两点. 若M、N两点的横坐标分别为m、n,试探究m、n之间的数量关系.2.如图,已知抛物线2=++与直线y=0.5x+3相交于A,B两点,交△轴于C,0.5y x bx cD两点,连接AC,BC,已知A(0,3),C(-3,0).(1)求抛物线的表达式;(2)在抛物线对称轴l上找一点M,使|MB一MD|的值最大,并求出这个最大值;(3)点P为y轴右侧抛物线上的一动点,连接P A,过点P作PQ△P A交y轴于点Q,是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.3.如图,抛物线与x轴交于A和B两点(点B位于点A右侧),与y轴交于点C,对称轴是直线x=2,且OA=1,OC=3,连接AC,BC.(1)求此抛物线的函数解析式;(2)设抛物线的顶点为点P,请在x轴上找到一个点D,使以点P、B、D为顶点的三角形与△ABC相似?(3)此抛物线的对称轴和以AC为直径的圆是什么位置关系?如果是相切或相交,请直接写出切点或交点的坐标(不必写演推过程);如果是相离,请简要说明理由.4.如图1,已知抛物线y=ax2+bx+3与x轴分别交于A(−3,0),B(1,0)两点,与y轴交于点C,点D为抛物线的顶点,连接AD、CD、AC、BC.(1)请直接写出抛物线的表达式及顶点D的坐标;(2)求证:△ACD是直角三角形;(3)判断△ACB和△OAD的数量关系,并说明理由;(4)如图2,点F是线段AD上一个动点,以A,F,O为顶点的三角形是否与△ABC相似?若相似,请直接写出点F的坐标;若不相似,请说明理由.5.抛物线y=ax2﹣2x+c经过点A(3,0),点C(0,﹣3),直线y=﹣x+b经过点A,交抛物线于点E.抛物线的对称轴交AE于点B,交x轴于点D,交直线AC于点F.(1)求抛物线的解析式;(2)如图△,点P 为直线AC 下方抛物线上的点,连接P A ,PC ,△BAF 的面积记为S 1,△P AC 的面积记为S 2,当S 2=38S 1时.求点P 的横坐标;(3)如图△,连接CD ,点Q 为平面内直线AE 下方的点,以点Q ,A ,E 为顶点的三角形与△CDF 相似时(AE 与CD 不是对应边),请直接写出符合条件的点Q 的坐标. 6.如图,抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ,与y 轴交于点C ,联结AC 、BC .(1)求该抛物线的表达式及顶点D 的坐标;(2)如果点P 在抛物线上,CB 平分ACP ∠,求点P 的坐标:(3)如果点Q 在抛物线的对称轴上,DBQ 与ABC 相似.求点Q 的坐标.7.如图1,已知二次函数y =ax2+bx +c (a ≠0)的图象与x 轴交于A (﹣1,0),B (3,0)两点,与y 轴交于点C (0,﹣2),顶点为D ,对称轴交x 轴于点E .(1)求该二次函数的解析式;(2)设M 为该抛物线上直线BC 下方一点,过点M 作x 轴的垂线,交线段BC 于点N ,线段MN 是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;(3)连接CE (如图2),设点P 是位于对称轴右侧该抛物线上一点,过点P 作PQ △x 轴,垂足为Q .连接PE ,请求出当△PQE 与△COE 相似时点P 的横坐标.8.如图,直线y kx b =+与x 轴、y 轴分别交于A ,B 两点,抛物线2y ax bx c =++经过A ,B 两点,点C 的坐标为()1,0-,3AO CO ==,点C 关于点B 的对称点M 刚好落在抛物线上,连接AM .(1)求点M 的坐标;(2)求抛物线的解析式;(3)过点M 作MD 平行于y 轴交AB 于点D ,若点E 为抛物线上的一点,点F 在x 轴上,连接AE ,AF ,EF .是否存在点F 使得△ADM 与△AEF 相似?若存在,请直接写出点F 的坐标;若不存在,请说明理由.9.如图1,已知在平面直角坐标系xOy 中,四边形OABC 是边长为3的正方形,其中顶点A ,C 分别在x 轴的正半轴和y 轴的正半轴上,抛物线2y x bx c =-++经过A ,C 两点,与x 轴交于另一个点D .(1)△求点A ,B ,C 的坐标;△求b ,c 的值.(2)若点P 是边BC 上的一个动点,连结AP ,过点P 作PM △AP ,交y 轴于点M (如图2所示).当点P 在BC 上运动时,点M 也随之运动.设BP =m ,CM =n ,试用含m 的代数式表示n ,并求出n 的最大值.10.平面直角坐标系中,已知抛物线1C :()21y x m x m =-++-(m 为常数)与x 轴交于点A ,B 两点(点A 在点B 左边),与y 轴交于点C .(1)若4m =,求点A ,B ,C 的坐标;(2)如图1,在(1)的条件下,D 为抛物线x 轴上方一点,连接BD ,若90DBA ACB ∠∠+=︒,求点D 的坐标;(3)如图2,将抛物线1C 向左平移n 个单位长度(0n >)与直线AC 交于M ,N (点M 在点N 右边),若2AM CN =,求m ,n 之间的数量关系.11.如图,直线y x n =-+与x 轴交于点()3,0A ,与y 轴交于点B ,抛物线2y x bx c =-++经过点A ,B .(1)求n 的值及抛物线的解析式;(2)(),0E m 为x 轴上一动点,过点E 作ED x ⊥轴,交直线AB 于点D ,交抛物线于点P ,连接BP .△点E 在线段OA 上运动,若BPD △与ADE 相似,求点E 的坐标;△若抛物线的顶点为Q ,AQ 与CB 的延长线交于点H ,点E 在x 轴的正半轴上运动,若PBD CBO H ∠+∠=∠.请求写出m 的值.12.如图1,平面直角坐标系xOy 中,直线y =-12x -2与x 轴交于点A ,与y 轴交于点C .抛物线y =14x 2+bx +c 经过点A 、点C ,且与x 轴交于另一点B ,连接BC .(1)求抛物线的解析式;(2)点P 是抛物线上一动点.△当点P 在直线AC 下方的抛物线上运动时,如图2,连接AP ,CP .求四边形ABCP 面积的最大值及此时点P 的坐标;△当点P 在x 轴上方的抛物线上运动时,过点P 作PM △x 轴于点M ,连接BP .是否存在点P ,使△PMB 与△AOC 相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.13.如图,抛物线y 2b c x ++与x 轴交于点A 、B ,点A 、B 分别位于原点的左、右两侧,BO =3AO =3,过点B 的直线与y 轴正半轴和抛物线的交点分别为C 、D ,BC.(1)求b、c的值;(2)求直线BD的直线解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.14.如图,抛物线23(0)y ax bx a=+-≠的顶点E的横坐标为1,与x轴交于A、B两点,与y轴交于点C,直线113y x=-+过点B,与y轴交于点D.(1)求抛物线的解析式;(2)证明:ABD CBE∠=∠;(3)是否存在点1O,使点1O到A,B,C,D的距离都相等,若存在,求出点1O坐标,若不存在,请说明理由.(4)设抛物线与直线DB另一交点为Q,F为线段BQ上一点(不含端点),连接AF,一动点P从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FQ个单位的速度运动到Q后停止,当点F的坐标是多少时,点P在整个运动过程中用时最少?(直接写出答案)15.如图,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A 、B ,与y 轴交于点C ,且OC =2OB =6OA =6,点P 是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC 与OP ,交于点D ,当PD :OD 的值最大时,求点P 的坐标;(3)点P 在抛物线上运动,点N 在y 轴上运动,是否存在点P 、点N .使△CPN =90°,且△CPN 与△BOC 相似,若存在,请直接写出点P 的坐标,若不存在,说明理由.16.在平面直角坐标系xOy 中,抛物线y =﹣x 2+bx +c 与x 轴分别交于点A ,点B (3,0),与y 轴交于点C (0,3).(1)求抛物线的解析式;(2)如图1,连接BC ,点D 是直线BC 上方抛物线上一动点,连接AD 交BC 于点E ,若AE =2ED ,求点D 的坐标;(3)直线y =kx ﹣2k +1与抛物线交于M ,N 两点,取点P (2,0),连接PM ,PN ,求△PMN 面积的最小值.17.综合与探究如图,直线3y x =-+与x 轴,y 轴分别交于B ,C 两点,抛物线2y x bx c =-++经过点B ,C ,与x 轴的另一交点为A ,顶点为D .(1)求抛物线的解析式及顶点D的坐标.(2)连接CD,BD,求点D到BC的距离h.(3)P为对称轴上一点,在抛物线上是否存在点Q,使得PDQ与BOC相似?若存在,请直接写出Q点坐标;若不存在,请说明理由.18.如图,已知直线223y x=-与x轴交于点A,与y轴交于点B,抛物线226y x bx=-++经过点A,与x轴的另一个交点为C,交y轴于点D.(1)求抛物线的函数表达式及点D的坐标;(2)点M是y轴上的点,在y轴右侧的抛物线上是否存在点P,使得PMD△与BOC相似,且点M与点O为对应点,若存在,请求出点P的坐标,若不存在,请说明理由.19.如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交点C,抛物线y=-2x2+bx+c过A,C两点,与x轴交于另点B.(1)求抛物线的解析式.(2)在直线AC 上方的抛物线上有一动点E ,连接BE ,与直线AC 相交于点F ,当EF =12BF 时,求sin△EBA 的值.(3)点N 是抛物线对称轴上一点,在(2)的条件下,若点E 位于对称轴左侧,在抛物线上是否存在一点M ,使以M ,N ,E ,B 为顶点的四边形是平行四边形?若存在,直接写出点M 的坐标;若不存在,请说明理由.20.如图,一次函数3y x =-+的图象与x 轴和y 轴分别交于点B 和点C ,二次函数2y x bx c =-++的图象经过B ,C 两点,并与x 轴交于点A .点(),0M m 是线段OB 上一个动点(不与点O 、B 重合),过点M 作x 轴的垂线,分别与二次函数图象和直线BC 相交于点D 和点E ,连接CD .(1)求这个二次函数的解析式.(2)△求DE 、CE 的值(用含m 的代数式表示).△当以C ,D ,E 为顶点的三角形与△ABC 相似时,求m 的值.(3)点F 是平面内一点,是否存在以C ,D ,E ,F 为顶点的四边形为菱形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.参考答案:1.(1)21y x =- (2)k =(3) 1.-2.(1)215322y x x =++(3)在点P (1,6)3.(1)y =x 2-4x +3(2)点D 的坐标是(0,0)或(73,0) (3)相交,交点的坐标是(2,1)或(2,2)4.(1)抛物线解析式为y =-x 2-2x +3;顶点D 的坐标为(-1,4);(2)见解析(3)△OAD =△ACB(4)相似,F 点的坐标为(-65,185)或(-2,2).5.(1)y =x 2﹣2x ﹣3(2)P 352(3)Q 点坐标为(﹣7,5)或(﹣12,5)或(3,﹣10)或(3,﹣5)6.(1)2=+43y x x --,(21)D , (2)111639⎛⎫ ⎪⎝⎭,- (3)(2,−2)或12,3⎛⎫ ⎪⎝⎭7.(1)224233y x x =--(2)线段MN 存在最大值,最大值为32(3)点P 的横坐标为5或28.(1)(M(2)2y x x =(3)存在,()()()()()11,0,3,0,,0,5,0,7,0,13,03⎛⎫-- ⎪⎝⎭9.(1)△A (3,0),B (3,3),C (0,3);△23b c =⎧⎨=⎩ (2)2133324n m ⎛⎫=--+ ⎪⎝⎭(0≤m ≤3);3410.(1)A (1,0),B (4,0),C (0,﹣4)(2)D (83,209) (3)93m n =-11.(1)n =3,y =-x 2+2x +3.(2)△(1,0)或(2,0).△m =5或73.12.(1)211242y x x =+- (2)△四边形ABCP 面积的最大值为8,此时点P 为(-2,-2);△存在符合条件的点P ,点P 坐标为(-6,4)或(-12,28)或(4,4)13.(1)132b c ⎧=-⎪⎪⎨⎪=-⎪⎩(2)y=+(3)Q 1(,0)、Q 2(0)、Q 3,0)、Q 4(,0) 14.(1)2 2 3y x x =--(2)见解析(3)存在点()111O -,,使点P 到A ,B ,C ,D 的距离都相等(4)F 的坐标为41,3⎛⎫- ⎪⎝⎭时,点P 在整个运动过程中用时最少15.(1)y =﹣2x 2+4x +6(2)点P 的坐标为315(,)22(3)存在,点P 的坐标分别为(3,0)或(1,8)或939(,)48或755(,)4816.(1)y =﹣x 2+2x +3(2)(1,4)或(2,3)17.(1)223y x x =-++,顶点D (1,4)(2)h =(3)Q (0,3)或(2,3)18.(1)2246y x x =-++;(0,6)D(2)存在,点P 的坐标为755,48⎛⎫ ⎪⎝⎭或939,48⎛⎫ ⎪⎝⎭或(1,8)或(3,0)19.(1)抛物线的解析式为y =-2x 2-4x +6;(2)sin△EBA ; (3)M 的坐标为(2,-10)或(-4,-10)或(0,6).20.(1)223y x x =-++(2)△23DE m m =-,CE ;△m 的值为32或53(3)存在以C ,D ,E ,F 为顶点的四边形为菱形,点M 的坐标为(1,0)或(2,0)或(3,0).。
部编数学九年级上册专题22.4二次函数的综合(压轴题专项讲练)(人教版)(解析版)含答案

专题22.4 二次函数的综合【典例1】如图,平面直角坐标系中,正方形ABCD的顶点A,B在x轴上,抛物线y=﹣x2+bx+c经过A,C(4,﹣5)两点,且与直线DC交于另一点E.(1)求抛物线的解析式;(2)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为Q,连接EQ,AP.试求EQ+PQ+AP的最小值;(3)N为平面内一点,在抛物线对称轴上是否存在点M,使得以点M,N,E,A为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.(1)求出A点坐标后,将点A、C代入y=﹣x2+bx+c,即可求解;(2)连接OC,交对称x=1于点Q,此时EQ+OQ的值最小,最小值为线段OC长,再求解即可;(3)分三种情况讨论:①以AE为菱形对角线,此时AM=ME;②以AM为菱形对角线,此时AE=EM;③以AN为菱形对角线,此时AE=AM;再利用中点坐标公式和两点间距离公式求解即可.解:(1)∵四边形ABCD为正方形,C(4,﹣5),∴AD=AB=5,B(4,0),∴OA=1,∴A(﹣1,0),将点A,C代入y=﹣x2+bx+c,∴−16+4b+c=−5−1−b+c=0,解得b=2 c=3,∴抛物线的解析式为y=﹣x2+2x+3;(2)连接OC,交对称轴x=1于点Q,∵PQ⊥y轴,∴AO∥PQ,∵AO=PQ=1,∴四边形AOQP是平行四边形,∴AP=OQ,∴EQ+PQ+AP=EQ+1+OQ若使EQ+PQ+AP值为最小,则EQ+OQ的值为最小,∵E,C关于对称轴x=1对称,∴EQ=CQ,∴EQ+OQ=CQ+OQ,此时EQ+OQ的值最小,最小值为线段OC长,∵C(4,﹣5),∴OC∴EQ+PQ+AP,即EQ+PQ+AP+1;(3)存在点M,使得以点M,N,E,A为顶点的四边形是菱形,理由如下:①以AE为菱形对角线,此时AM=ME,∴−1−2=1+x−5=m+y4+m2=9+(m+5)2,解得x=−4y=−2m=−3,∴M(1,﹣3);②以AM为菱形对角线,此时AE=EM,∴−1+1=−2+xm=y−51+25=9+(m+5)2,解得x=y=m=−5+x=2y=m=∴M(1,﹣51,﹣5③以AN为菱形对角线,此时AE=AM,∴−1+x=−2+1 y=m−51+25=4+m2,解得x=y=m或x=0y=m=∴M(11,综上所述:M点坐标为(1,﹣3),(1,(1,,(1,−5+,(1,.1.(2022•新化县模拟)如图,已知点A(﹣1,0)和点B(1,1),若抛物线y=x2+c与线段AB有公共点,则c的取值范围是( )A.﹣1≤c≤0B.﹣1≤c≤12C.﹣1≤c≤916D.0≤c≤916【思路点拨】先通过待定系数法将AB所在直线解析式求出,然后通过数形结合方法,求出抛物线与直线相切及抛物线经过点A时c的值求解.【解题过程】解:设AB所在直线为y=kx+b,将(﹣1,0),(1,1)代入y=kx+b得k=12 b=12,∴y=12x+12,如图,当抛物线与线段AB相切时,令12x+12=x2+c,整理得x2−12x−12+c=0,∴Δ=(−12)2﹣4(−12+c)=0,解得c=9 16,c减小,抛物线向下移动,当抛物线经过点A(﹣1,0)时,将(﹣1,0)代入y=x2+c得0=1+c,解得c=﹣1,∴﹣1≤c≤916满足题意.故选:C.2.(2022•新河县一模)如图,已知抛物线经过点B(﹣1,0),A(4,0),与y轴交于点C(0,2),P为AC上的一个动点,则有以下结论:①抛物线的对称轴为直线x=32;②抛物线的最大值为98;③∠ACB=90°;④OPA.①②④B.①②C.①②③D.①③④【思路点拨】用待定系数法求出函数的解析式即可对①②进行判断;利用勾股定理对③进行判断即可;求出直线AC的解析式,设P(t,−12t+2),再利用两点间距离公式求出OP的最大值即可.【解题过程】解:设抛物线的解析式为y=ax2+bx+c,将B(﹣1,0),A(4,0),C(0,2)代入,∴a−b+c=016a+4b+c=0 c=2,解得a=−12 b=32c=2,∴y=−12x2+32x+2,∵y=−12x2+32x+2=−12(x−32)2+258,∴抛物线的对称轴为直线x=3 2,故①正确;当x=32时,抛物线有最大值258,故②不正确;∵B (﹣1,0),A (4,0),C (0,2),∴AB =5,AC =BC ∵AC 2=AB 2+BC 2,∴△ABC 是直角三角形,∴∠ACB =90°,故③正确;设直线AC 的解析式为y =kx +m ,∴m =24k +m =0,解得k =−12m =2,∴y =−12x +2,设P (t ,−12t +2),∴OP∴当t =45时,OP 故④正确;故选:D .3.(2022•市中区二模)定义:对于已知的两个函数,任取自变量x 的一个值,当x ≥0时,它们对应的函数值相等;当x <0时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数y =x ,它的相关函数为y =x(x ≥0)−x(x <0).已知点M ,N 的坐标分别为(−12,1),(92,1),连结MN ,若线段MN 与二次函数y =﹣x 2+4x +n 的相关函数的图象有两个公共点,则n 的取值范围为( )A .﹣3≤n ≤﹣1或1<n ≤54B .﹣3<n <﹣1或1<n ≤54C .﹣3<n ≤﹣1或1≤n ≤54D .﹣3≤n ≤﹣1或1≤n ≤54【思路点拨】首先确定出二次函数y =﹣x 2+4x +n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值,然后结合函数图象可确定出n 的取值范围.【解题过程】解:如图1所示:线段MN 与二次函数y =﹣x 2+4x +n 的相关函数的图象恰有1个公共点,∵二次函数y=﹣x2+4x+n的对称轴为x=−42×(−1)=2,∴当x=2时,y=1,即﹣4+8+n=1,解得n=﹣3,如图2所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰好3个公共点.∵抛物线y=x2﹣4x﹣n与y轴交点纵坐标为1,∴﹣n=1,解得:n=﹣1;∴当﹣3<n≤﹣1时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点,如图3所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点.∵抛物线y=﹣x2+4x+n经过点(0,1),∴n=1,如图4所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.∵抛物线y=x2﹣4x﹣n经过点M(−12,1),∴14+2﹣n=1,解得:n=54,∴1≤n≤54时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.综上所述,n的取值范围是﹣3<n≤﹣1或1≤n≤5 4,故选:C.4.(2022•江阴市校级一模)如图,抛物线y=ax2−103x+4与直线y=43x+b经过点A(2,0),且相交于另一点B;抛物线与y轴交于点C,与x轴交于另一点E;点N在线段AB上,过点N的直线交抛物线于点M,且MN∥y轴,连接AM、BM、BC、AC;当点N在线段AB上移动时(不与A、B重合),下列结论中正确的是( )A.MN+BN<AB B.∠BAC=∠BAEC.∠ACB﹣∠ANM=12∠ABC D.四边形ACBM的最大面积为13【思路点拨】(1)当MN过对称轴的直线时,解得:BN=256,而MN=56,BN+MN=5=AB;(2)由BC∥x轴(B、C两点y坐标相同)推知∠BAE=∠CBA,而△ABC是等腰三角形,∠CBA≠∠BCA,故∠BAC=∠BAE错误;(3)如上图,过点A作AD⊥BC、BE⊥AC,由△ABC是等腰三角形得到:EB是∠ABC的平分线,∠ACB﹣∠ANM=∠CAD =12∠ABC ;(4)S 四边形ACBM =S △ABC +S △ABM ,其最大值为94.【解题过程】解:将点A (2,0)代入抛物线y =ax 2−103x +4与直线y =43x +b解得:a =23,b =−83,设:M 点横坐标为m ,则M (m ,23m 2−103m +4)、N (m ,43m −83),其它点坐标为A (2,0)、B (5,4)、C (0,4),则AB =BC =5,则∠CAB =∠ACB ,∴△ABC 是等腰三角形.A 、当MN 过对称轴的直线时,此时点M 、N 的坐标分别为(52,−16)、(52,23),由勾股定理得:BN =256,而MN =56,BN +MN =5=AB ,故本选项错误;B 、∵BC ∥x 轴(B 、C 两点y 坐标相同),∴∠BAE =∠CBA ,而△ABC 是等腰三角形不是等边三角形,∠CBA ≠∠BCA ,∴∠BAC =∠BAE 不成立,故本选项错误;C 、如上图,过点A 作AD ⊥BC 、BF ⊥AC ,∵△ABC 是等腰三角形,∴BF 是∠ABC 的平分线,易证:∠CAD =∠ABF =12∠ABC ,而∠ACB ﹣∠ANM =∠CAD =12∠ABC ,故本选项正确;D 、S 四边形ACBM =S △ABC +S △ABM ,S △ABC =10,S △ABM =12MN •(x B ﹣x A )=﹣m 2+7m ﹣10,其最大值为94,故S 四边形ACBM 的最大值为10+94=12.25,故本选项错误.故选:C .5.(2022•高青县一模)已知点A (2,4),B (0,1),点M 在抛物线y =14x 2上运动,则AM +BM 的最小值为 5 .【思路点拨】设点M (m ,14m 2),用含m 代数式表示BM =14m 2+1,可得点M 到点B 的距离与点M 到直线y =﹣1的距离相等,进而求解.【解题过程】解:设点M (m ,14m 2),则点M 到x 轴距离为14m 2,BM 14m 2+1,∴点M 到点B 的距离与点M 到直线y =﹣1的距离相等,∵点A 横坐标为x =2,∴点M 为直线x =2与抛物线交点,如图,设直线x =2与直线y =﹣1交点B '(2,﹣1),∴AB '为AM +BM 最小值,AB '=4﹣(﹣1)=5,故答案为:5.6.(2022•广西模拟)如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(﹣2,0)和(﹣1,0)之间(包括这两点),顶点C是矩形DEFG上(包括边界和内部)的一个动点,则a的取值范围是 .【思路点拨】分两种情况分别求得a的取值范围,再取两者的公共部分即可:当顶点C与D点重合时,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3;当顶点C与F点重合时,顶点坐标为(3,2),则抛物线解析式y =a(x﹣3)2+2.【解题过程】解:∵顶点C是矩形DEFG上(包括边界和内部)的一个动点,∴当顶点C与D点重合时,顶点坐标为(1,3),则抛物线解析式y=a(x﹣1)2+3,∴a(−2−1)2+3≤0 a(−1−1)2+3≥0,解得−34≤a≤−13;当顶点C与F点重合时,顶点坐标为(3,2),则抛物线解析式y=a(x﹣3)2+2,∴a(−2−3)2+2≤0 a(−1−3)2+2≥0,解得−18≤a≤−225;∵顶点可以在矩形内部,∴−34≤a≤−225.故答案为:−34≤a≤−225.7.(2022•包河区校级三模)函数y=2mx 2−4mx−3(x≥0)−2mx2−4mx−3(x<0),其中m是常数且m≠0,该函数的图象记为G.(1)当m=12时,图象G与x轴的交点坐标为 (3,0) .(2)若直线y=m与该函数图象G恰好只有两个交点,则m的取值为 3或﹣1 .【思路点拨】(1)m=12,从而两个解析式是已知的,令y=0,解方程即可;(2)分m>0,m<0两种情况,画出草图,令y=m与二次函数联列得方程组,求解即可.【解题过程】解:(1)当x≥0时,对称轴为直线x=−−4m2×2m=1,当x<0时,对称轴为直线x=−−4m2×(−2m)=−1,又当m=12时,函数y=x2−2x−3(x≥0)−x2−2x−3(x<0),当x≥0时,令x2﹣2x﹣3=0,∴(x﹣3)(x+1)=0,∴x1=3或x2=﹣1(舍去),∴x≥0时,x=3;当x<0时,令﹣x2﹣2x﹣3=0,∴x2+2x+3=0,∵Δ=9﹣12<0,∴x<0,无解,∴与x轴的交点坐标为(3,0);(2)当m>0时,图象大致如图1所示,当y=m经过顶点时,恰有2个交点,∴当x=﹣1时,y=﹣2m+4m﹣3=2m﹣3=m,∴m=3;∴当x=1时,y=2m﹣4m﹣3=﹣2m﹣3=m,∴m=﹣1(舍去),当m<0时,图象大致如图2所示,当y=m经过顶点时,恰有2个交点,当x=﹣1时,y=﹣2m+4m﹣3=2m﹣3=m,∴m=3(舍去),当x=1时,y=2m﹣4m﹣3=﹣2m﹣3=m,∴m=﹣1,综上所述,m取值为3或﹣1.8.(2022•安顺模拟)如图,抛物线y=ax2+2x+c.与x轴交于A,B两点,与y轴交于C(0,3),直线y =﹣x﹣1经过点A且与抛物线交于另一点D.(1)求抛物线的解析式;(2)若P是位于直线AD上方的抛物线上的一个动点,连接PA,PD,求△PAD的面积的最大值.【思路点拨】(1)根据y=﹣x﹣1经过点A,可求出点A的坐标,将点A、C的坐标代入y=ax2+2x+c即可求出抛物线的解析;(2)联立抛物线和一次函数y=﹣x﹣1的解析式列方程解出可得点D的坐标,过点P作PE∥y轴,交AD 于E,设P(t,﹣t2+2t+3),则E(t,﹣t﹣1),表示PE的长,根据三角形面积公式可得△APD的面积,配方后可得结论.【解题过程】解:(1)∵直线y=﹣x﹣1经过点A,∴令y=0,则0=﹣x﹣1,∴x=﹣1,∴A(﹣1,0),将A(﹣1,0),C(0,3)代入y=ax2+2x+c得:a−2+c=0c=3,解得:a=−1 c=3,∴抛物线的解析式为:y=﹣x2+2x+3;(2)﹣x2+2x+3=﹣x﹣1,解得:x1=﹣1,x2=4,∴D(4,﹣5),过点P作PE∥y轴,交AD于E,设P(t,﹣t2+2t+3),则E(t,﹣t﹣1),∴PE=(﹣t2+2t+3)﹣(﹣t﹣1)=﹣t2+3t+4,∴△PAD 的面积=12•PE •(4+1)=52(﹣t 2+3t +4)=−52(t −32)2+1258,当t =52时,△PAD 的面积最大,且最大值是1258.9.(2022•平桂区 一模)如图,抛物线y =x 2+bx +c 与x 轴交于A (﹣1,0)、B 两点,与y 轴交于点C (0,﹣3),顶点为D .(1)求该抛物线的解析式和顶点D 的坐标;(2)在第四象限内抛物线上存在一点M ,使S △MAB =S △CAB ,请求出点M 的坐标;(3)点N 在该抛物线上且到对称轴的距离为3个单位,点P 为点M ,N 之间(含点M 、N )抛物线上的一个动点.求点P 纵坐标y P 的取值范围.【思路点拨】(1)直接利用待定系数法求出抛物线解析式进而得出答案即可;(2)设点M 的纵坐标为t (t <0),根据S △MAB =S △CAB ,可得12AB •OC =12AB •(﹣t ),求出t 的值,即可得M 点坐标;(3)利用点N 到对称轴的距离为3个单位求出点N 的横坐标,即可得点N 的坐标,再结合M 、D 两点的坐标即可求解.【解题过程】解:(1)∵二次函数y =x 2+bx +c 的图象经过A (﹣1,0)、C (0,﹣3),∴1−b +c =0c =−3,解得:b =−2c =−3,∴抛物线解析式为:y =x 2﹣2x ﹣3,把y =x 2﹣2x ﹣3配方,得y =(x ﹣1)2﹣4∴顶点D 的坐标为(1,﹣4);(2)设点M的纵坐标为t(t<0),∵S△MAB=S△CAB,∴12AB•OC=12AB•(﹣t),∵抛物线解析式为:y=x2﹣2x﹣3,令y=0,则x2﹣2x﹣3=0,解得x1=3,x2=﹣1,∴A(﹣1,0)、B(3,0),∵点C(0,﹣3),∴AB=4,OC=3.∴﹣t=3,得t=﹣3.当t=﹣3时,x2﹣2x﹣3=﹣3,解得x1=0,x=2,∴点M的坐标为(2,﹣3);(3)∵顶点D的坐标为(1,﹣4),∴抛物线的对称轴为x=1,∵点N到对称轴的距离为3个单位,∴点N的横坐标为﹣2或4,∴点N纵坐标为42﹣2×4﹣3=5.∴点N的坐标为(﹣2,5)或(4,5).∵点M的坐标为(2,﹣3),顶点D的坐标为(1,﹣4),当N在对称轴的右侧时,﹣3≤y P≤5;当N在对称轴的左侧时,﹣4≤y P≤5;10.(2022春•浦江县期末)如图,已知二次函数图象的顶点坐标为A(1,9),与坐标轴交于B、C、D 三点,且B点的坐标为(﹣2,0).(1)求二次函数的解析式;(2)在二次函数图象位于x轴上方部分有两个动点M、M,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;(3)在(2)中的矩形周长最大时,连接BM,已知点P是x轴上一动点,过点P作PQ∥y轴,交直线BM 于点Q,是否存在这样的点P,使直线PQ把△BCM分成面积为1:2的两部分?若存在,求出该点的坐标;若不存在,请说明理由.【思路点拨】(1)设抛物线的解析式为y=a(x﹣1)2+9,将点B代入即可;(2)设M(m,﹣m2+2m+8),则N(2﹣m,﹣m2+2m+8),则矩形MNHG的周长=﹣2(m﹣2)2+20,可求当m=2时,矩形MNHG的周长有最大值20;(3)求出S△BCM=24,设P(t,0),则Q(t,2t+4),分两种情况讨论:当S△BPQ=8时,P(2,0);当S△BPQ=16时,P(2,0).【解题过程】解:(1)设抛物线的解析式为y=a(x﹣1)2+9,将点B(﹣2,0)代入,∴9a+9=0,∴a=﹣1,∴y=﹣(x﹣1)2+9=﹣x2+2x+8;(2)设M(m,﹣m2+2m+8),则N(2﹣m,﹣m2+2m+8),∴MN=2m﹣2,MG=﹣m2+2m+8,∴矩形MNHG的周长=2(MN+MG)=2(﹣m2+4m+6)=﹣2(m﹣2)2+20,∴当m=2时,矩形MNHG的周长有最大值20;(3)存在点P,使直线PQ把△BCM分成面积为1:2的两部分,理由如下:当m=2时,M(2,8),设直线BM的解析式为y=kx+b,∴−2k+b=0 2k+b=8,解得k=2 b=4,∴y=2x+4,令y=0,则﹣x2+2x+8=0,解得x=﹣2或x=4,∴C(4,0),∴BC=6,∴S△BCM=12×6×8=24,设P(t,0),则Q(t,2t+4),当S△BPQ=8时,12×(t+2)×(2t+4)=8,解得t=2或t=﹣2(舍),∴P(2,0);当S△BPQ=16时,12×(t+2)×(2t+4)=16,解得t=2或t=﹣6(舍),∴P(2,0);综上所述,P点坐标为(2,0)或(2,0).11.(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB 上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E 处.(1)求抛物线解析式;(2)连接BE,求△BCE的面积;(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.【思路点拨】(1)由点A的坐标可得出点E的坐标,由点A,E的坐标,利用待定系数法即可求出抛物线的解析式;(2)利用二次函数图象上点的坐标特征可求出点B的坐标,由点A,B的坐标,利用待定系数法可求出直线AB的解析式,利用一次函数图象上点的坐标特征可求出点C的坐标,再利用三角形的面积计算公式,结合S△BCE=S△ABE﹣S△ACE,即可求出△BCE的面积;(3)存在,由点A,B的坐标可得出OA=OB,结合∠AOB=90°可得出∠BAE=45°,设点P的坐标为(m,﹣m2+2m+3),分点P在x轴上方及点P在x轴下方两种情况考虑:①当点P在x轴上方时记为P1,过点P1作P1M⊥x轴于点M,则EM=P1M,进而可得出关于m的一元二次方程,解之即可得出m的值,将符合题意的m值代入点P的坐标中即可求出点P1的坐标;②当点P在x轴下方时记为P2,过点P2作P2N⊥x 轴于点N,则EN=P2N,进而可得出关于m的一元二次方程,解之即可得出m的值,将符合题意的m值代入点P的坐标中即可求出点P2的坐标.【解题过程】解:(1)∵将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处,点A的坐标为(3,0),点D的坐标为(1,0),∴点E的坐标为(﹣1,0).将A(3,0),E(﹣1,0)代入y=ax2+bx+3,得:9a+3b+3=0a−b+3=0,解得:a=−1b=2,∴抛物线的解析式为y=﹣x2+2x+3.(2)当x=0时,y=﹣1×(0)2+2×0+3=3,∴点B的坐标为(0,3).设直线AB的解析式为y=mx+n(m≠0),将A(3,0),B(0,3)代入y=mx+n,得:3m+n=0n=3,解得:m=−1n=3,∴直线AB的解析式为y=﹣x+3.∵点C在直线AB上,CD⊥x轴于点D(1,0),当x=1时,y=﹣1×1+3=2,∴点C的坐标为(1,2).∵点A的坐标为(3,0),点B的坐标为(0,3),点C的坐标为(1,2),点E的坐标为(﹣1,0),∴AE=4,OB=3,CD=2,∴S△BCE=S△ABE﹣S△ACE=12AE•OB−12AE•CD=12×4×3−12×4×2=2,∴△BCE的面积为2.(3)存在,理由如下:∵点A的坐标为(3,0),点B的坐标为(0,3),∴OA=OB=3.在Rt△AOB中,∠AOB=90°,OA=OB,∴∠BAE=45°.∵点P在抛物线上,∴设点P的坐标为(m,﹣m2+2m+3).①当点P在x轴上方时记为P1,过点P1作P1M⊥x轴于点M,在Rt△EMP1中,∠P1EA=45°,∠P1ME=90°,∴EM=P1M,即m﹣(﹣1)=﹣m2+2m+3,解得:m1=﹣1(不合题意,舍去),m2=2,∴点P1的坐标为(2,3);②当点P在x轴下方时记为P2,过点P2作P2N⊥x轴于点N,在Rt△ENP2中,∠P2EN=45°,∠P2NE=90°,∴EN=P2N,即m﹣(﹣1)=﹣(﹣m2+2m+3),解得:m1=﹣1(不合题意,舍去),m2=4,∴点P2的坐标为(4,﹣5).综上所述,抛物线上存在一点P,使∠PEA=∠BAE,点P的坐标为(2,3)或(4,﹣5).12.(2022•太原一模)综合与实践如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.点D在直线AC 下方的抛物线上运动,过点D作y轴的平行线交AC于点E.(1)求直线AC的函数表达式;(2)求线段DE的最大值;(3)当点F在抛物线的对称轴上运动,以点A,C,F为顶点的三角形是直角三角形时,直接写出点F的坐标.【思路点拨】(1)分别令x=0,y=0,求得点C、A的坐标,再运用待定系数法即可求得答案;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),可得DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,运用二次函数的性质即可求得线段DE的最大值;(3)设F(﹣1,n),根据两点间距离公式可得:AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,分三种情况:①当∠AFC=90°时,②当∠CAF=90°时,③当∠ACF=90°时,分别建立方程求解即可.【解题过程】解:(1)在y=x2+2x﹣8中,令x=0,得y=﹣8,∴C(0,﹣8),令y=0,得x2+2x﹣8=0,解得:x1=﹣4,x2=2,∴A(﹣4,0),B(2,0),设直线AC的解析式为y=kx+b,则−4k+b=0 b=−8,解得:k=−2 b=−8,∴直线AC的解析式为y=﹣2x﹣8;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),∵点D在点E的下方,∴DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,∵﹣1<0,∴当m=﹣2时,线段DE最大值为4;(3)∵y=x2+2x﹣8=(x+1)2﹣9,∴抛物线的对称轴为直线x=﹣1,设F(﹣1,n),又A(﹣4,0),C(0,﹣8),∴AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,①当∠AFC=90°时,∵AF2+CF2=AC2,∴n2+9+n2+16n+65=80,解得:n1=﹣4n2=﹣4+∴F(﹣1,﹣4﹣1,﹣4②当∠CAF=90°时,∵AF2+AC2=CF2,∴n2+9+80=n2+16n+65,解得:n=3 2,∴F(﹣1,32);③当∠ACF=90°时,∵CF2+AC2=AF2,∴n2+16n+65+80=n2+9,解得:n=−17 2,∴F(﹣1,−172);综上所述,点F的坐标为(﹣1,﹣4﹣1,﹣4+﹣1,32)或(﹣1,−172).13.(2022•将乐县模拟)抛物线y=ax2+bx+c与直线y=−12有唯一的公共点A,与直线y=32交于点B,C(C在B的右侧),且△ABC是等腰直角三角形.过C作x轴的垂线,垂足为D(3,0).(1)求抛物线的解析式;(2)直线y=2x与抛物线的交点为P,Q,且P在Q的左侧.(ⅰ)求P,Q两点的坐标;(ⅱ)设直线y=2x+m(m>0)与抛物线的交点为M,N,求证:直线PM,QN,CD交于一点.【思路点拨】(1)过点A作AM⊥BC交于M,由等腰直角三角形的性质求出AM=BM=2,从而求出M(1,32),A(1,−12),B(﹣1,32),再用待定系数法求解析式即可;(2)(ⅰ)联立方程组y=2xy=12x2−x,即可求P、Q点的坐标;(ⅱ)设M(x1,y1),N(x2,y2),联立方程组y=2x+my=12x2−x,可得x1+x2=6,y1=2x1+m,y2=2=﹣2x1+m+12,求出直线PM的解析式后,求直线PM与CD的交点为(3,6+3mx1),求出QN的解析式后,求直线QN与CD的交点为(3,6+3mx1),从而所求得证.【解题过程】(1)解:过点A作AM⊥BC交于M,∵△ABC是等腰直角三角形,∴AM=BM=32−(−12)=2,∵CD⊥x轴,D(3,0),∴C(3,32),∴M(1,32),A(1,−12),B(﹣1,32),设y=ax2+bx+c(a≠0),∴a+b+c=−12a−b+c=329a+3b+c=32,解得a=12 b=−1 c=0,∴y=12x2﹣x;(2)(ⅰ)解:联立方程组y=2xy=12x2−x,解得x=0y=0或x=6y=12,∵P在Q的左侧,∴P(0,0),Q(6,12);(ⅱ)证明:设M(x1,y1),N(x2,y2),联立方程组y=2x+m y=12x2−x,整理得x2﹣6x﹣2m=0,∴x1+x2=6,∴y1=2x1+m,y2=2=﹣2x1+m+12,设直线PM的解析式为y=k1x,∴2x1+m=k1x1,∴k1=2+mx1,∴y=(2+mx1)x,∴直线PM与CD的交点为(3,6+3mx1),设QN的解析式为y=k2x+b2,∴6k2+b2=12(6−x1)k2+b2=−2x1+m+12,解得k2=2−mx1b2=6mx1,∴y=(2−mx1)x+6mx1,∴直线QN与CD的交点为(3,6+3mx1),∴直线PM,QN,CD交于一点.14.(2022春•兴宁区校级期末)如图,抛物线y=x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,连接AC,BC,点P是直线AC下方抛物线上的一个动点.(1)求抛物线的解析式;(2)连接AP,CP,设P点的横坐标为m,△ACP的面积为S,求S与m的函数关系式;(3)试探究:过点P作BC的平行线1,交线段AC于点D,在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,请直接写出点E的坐标,若不存在,请说明理由.【思路点拨】(1)将A(﹣3,0),B(1,0)代入y=x2+bx+c即可得到答案;(2)过点P作PM∥y轴交直线AC于点M,则P的坐标是(m,m2+2m﹣3),利用待定系数法求AC的解析式,表示M的坐标,用m的代数式表示PM的长度,根据三角形面积公式即可得到答案;(3)分两种情况:①如图2,四边形CDEB是菱形,②如图3,四边形CBDE是菱形,根据两点的距离公式和菱形的边长相等列方程可解答.【解题过程】解:(1)将A(﹣3,0),B(1,0)代入y=x2+bx+c得:9−3b+c=0 1+b+c=0,解得:b=2c=−3,∴y=x2+2x﹣3;(2)如图1,过点P作PM∥y轴交直线AC于点M,∵A(﹣3,0),C(0,﹣3),设直线AC的解析式为:y=kx+n,∴−3k+n=0 n=−3,∴k=−1 n=−3,∴AC的解析式为:y=﹣x﹣3,∵P点的横坐标为m,∴P的坐标是(m,m2+2m﹣3),则M的坐标是(m,﹣m﹣3),∴PM=﹣m﹣3﹣(m2+2m﹣3)=﹣m2﹣3m,∵点P是直线AC下方抛物线上的一个动点,∴﹣3<m<0,∴S=12•PM•OA=32(﹣m2﹣3m)=−32m2−92m(﹣3<m<0);(3)分两种情况:①如图2,四边形CDEB是菱形,设D(t,﹣t﹣3),则E(t+1,﹣t),∵四边形CDEB是菱形,∴CD=BC,∴(t﹣0)2+(﹣t﹣3+3)2=12+32,∴t=∵t<0,∴t=∴E(+1②如图3,四边形CBDE是菱形,设D(t,﹣t﹣3),则E(t﹣1,﹣t﹣6),∵四边形CBDE是菱形,∴CE=BC,∴(t﹣1﹣0)2+(﹣t﹣6+3)2=12+32,∴t=0(舍)或﹣2,∴E(﹣3,﹣4);综上所述,点E的坐标为(1﹣3,﹣4).15.(2022春•兴宁区期末)如图,已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(3,﹣2),点C(0,﹣5),顶点为点M,过点A作AB∥x轴,交y轴于点D,交二次函数y=x2+bx+c的图象于点B,连接BC.(1)求该二次函数的表达式及点M的坐标;(2)若将该二次函数图象向上平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)若E为线段AB上一点,且BE:EA=3:1,P为直线AC上一点,在抛物线上是否存在一点Q,使以B、P、E、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的横坐标;若不存在,请说明理由.【思路点拨】(1)将点A(3,﹣2),点C(0,﹣5)代入y=x2+bx+c,即可求解;(2)平移后的顶点坐标为(1,m﹣6),求出直线AC的解析式,由题意可知﹣4<m﹣6<﹣2,求出m的取值即可;(3)设P(t,t﹣5),Q(x,x2﹣2x﹣5),根据对角线分三种情况求解即可.【解题过程】解:(1)将点A(3,﹣2),点C(0,﹣5)代入y=x2+bx+c,∴9+3b+c=−2 c=−5,解得b=−2 c=−5,∴y=x2﹣2x﹣5,∴M(1,﹣6);(2)平移后的函数解析式为y=(x﹣1)2﹣6+m,∴平移后的顶点坐标为(1,m﹣6),∴抛物线的顶点在x=1的直线上,设直线CA的解析式为y=kx+b,∴3k+b=−2 b=−5,∴k=1b=−5,∴y=x﹣5,当x=1时,y=﹣4,∴﹣4<m﹣6<﹣2,解得2<m<4;(3)存在一点Q,使以B、P、E、Q为顶点的四边形是平行四边形,理由如下:当y=﹣2时,x2﹣2x﹣5=﹣2,解得x=﹣1或x=3,∴B(﹣1,﹣2),∴AB=4,∵BE:EA=3:1,∴AE=1,∴E (2,﹣2),设P (t ,t ﹣5),Q (x ,x 2﹣2x ﹣5),①当BE 为平行四边形的对角线时,2−1=t +x −2−2=t−5+x 2−2x−5,解得t =x =或t =x =,∴Q ②当BP 为平行四边形的对角线时,−1+t =2+x −2+t−5=−2+x 2−2x−5,解得x =t =或x =y =∴Q ③当BQ 为平行四边形的对角线时,−1+x =2+t −2+x 2−2x−5=−2+t−5,此时无解;综上所述:Q16.(2022•肃州区模拟)如图,已知抛物线y =﹣x 2+bx +c 与x 轴交于A 、B 两点,AB =4,交y 轴于点C ,对称轴是直线x =1.(1)求抛物线的关系式;(2)请在抛物线的对称轴上找一点P ,使△ACP 的周长最小,并求此时点P 的坐标.(3)动点M 从点O 出发,以每秒2个单位长度的速度向点B 运动(到点B 停止),过M 作x 轴的垂线交抛物线于点N ,交线段BC 于点Q .设运动时间为t (t >0)秒.△BOQ 能否为等腰三角形?若能,求出t 的值;若不能,请说明理由.【思路点拨】(1)根据x轴上的点A、B关于直线x=1对称,AB=4,求得点A、B的坐标,再代入抛物线解析式,解方程组即可得出答案;(2)点B与点A关于抛物线的对称轴对称,根据两点之间,线段最短可知,抛物线的对称轴与BC的交点就是△ACP的周长最小时点P的位置,先求出直线BC的解析式,再求出点P的坐标;(3)分OQ=BQ或OB=BQ或OQ=OB三种情况,分别求解即可.【解题过程】解:(1)∵x轴上的点A、B关于直线x=1对称,AB=4,∴A(﹣1,0),B(3,0),把A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,得:−9+3b+c=0−1−b+c=0,解得b=2 c=3,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图1,点A关于对称轴的对称点是点B,连接BC,交对称轴直线x=1于点P.点P就是使△ACP 的周长最小的点.在y=﹣x2+2x+3中,令x=0,得y=3,∴C(0,3),设直线BC的解析式为y=mx+n,则:n=33m+n=0,解得:m=−1 n=3,∴直线BC的解析式为y=﹣x+3,当x=1时,y=2.∴P(1,2).(3)如图2,∵动点M从点O出发,以每秒2个单位长度的速度向点B运动(到点B停止),运动时间为t(t>0)秒,∴OM=2t,且0<t≤3 2,∴M(2t,0),∵MN⊥x轴,∴点Q的横坐标为2t,当x=2t时,y=﹣x+3=﹣2t+3=3﹣2t,∴Q(2t,3﹣2t),∴QM=3﹣2t,BM=3﹣2t,∴BM=QM,∵△BOQ为等腰三角形,∴OQ=BQ或OB=BQ或OQ=OB:①当OQ=BQ时,∵QM⊥OB,∴OM=BM,∴2t=3﹣2t,解得:t=3 4;②当OB=BQ时,在Rt△BMQ中,∵BM=QM,∠BMQ=9°,∴△BQM是等腰直角三角形,∴∠OBQ=45°,BQ=,∴OB,即3=3﹣2t),解得:t=③当OQ=OB时,则点Q、C重合,此时t=0,而t>0,故不符合题意,综上述,当t=34秒或△BOQ为等腰三角形.17.(2022•鄂尔多斯)如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A(−12,0),B(3,72)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【思路点拨】(1)根据待定系数法,将点A,点B代入抛物线解析式,解关于b,c的二元一次方程组,即可求得抛物线的解析式;(2)设出点P的坐标,确定出PD∥CO,由PD=CO,列出方程求解即可;(3)过点D 作DF ⊥CP 交CP 的延长线于点F ,过点F 作y 轴的平行线EF ,过点D 作DE ⊥EF 于点E ,过点C 作CG ⊥EF 于点G ,证明△DEF ≌△FGC (AAS ),由全等三角形的性质得出DE =FG ,EF =CG ,求出F 点的坐标,由待定系数法求出直线CF 的解析式,联立直线CF 和抛物线解析式即可得出点P 的坐标.【解题过程】解:(1)将点A (−12,0),B (3,72)代入到y =ax 2+bx +2中得:a−12b +2=0+3b +2=72,解得:a =−1b =72,∴抛物线的解析式为y =﹣x 2+72x +2;(2)设点P (m ,﹣m 2+72m +2),∵y =﹣x 2+72x +2,∴C (0,2),设直线BC 的解析式为y =kx +c ,∴3k +c =72c =2,解得k =12c =2,∴直线BC 的解析式为y =12x +2,∴D (m ,12m +2),∴PD =|﹣m 2+72m +2−12m ﹣2|=|m 2﹣3m |,∵PD ⊥x 轴,OC ⊥x 轴,∴PD ∥CO ,∴当PD =CO 时,以P 、D 、O 、C 为顶点的四边形是平行四边形,∴|m 2﹣3m |=2,解得m =1或2∴点P 的横坐标为1或2(3)①当Q 在BC 下方时,如图,过B 作BH ⊥CQ 于H ,过H 作MN ⊥y 轴,交y 轴于M ,过B 作BN ⊥MH 于N ,∴∠BHC=∠CMH=∠HNB=90°,∵∠QCB=45°,∴△BHC是等腰直角三角形,∴CH=HB,∴∠CHM+∠BHN=∠HBN+∠BHN=90°,∴∠CHM=∠HBN,∴△CHM≌△HBN(AAS),∴CM=HN,MH=BN,∵H(m,n),∵C(0,2),B(3,72),=3−m−n=m,解得m=94n=54,∴H(94,54),设直线CH的解析式为y=px+q,p+q=542,解得p=−13q=2,∴直线CH的解析式为y=−13x+2,联立直线CF与抛物线解析式得y=−x2+72x+2y=−13x+2,解得x=0y=2或x=236y=1318,∴Q(236,1318);②当Q在BC上方时,如图,过B作BH⊥CQ于H,过H作MN⊥y轴,交y轴于M,过B作BN⊥MH于N,同理得Q(12,72).综上,存在,点Q的坐标为(236,1318)或(12,72).18.(2022•武汉模拟)点P(﹣3,a)在抛物线y=x2﹣6上,过点P的直线l1:y=k1x+b1与抛物线交于另一点F.(1)直接写出a的值;(2)如图(1),当点F在第四象限时,若PF交x轴的负半轴于点S,交y轴的负半轴于点T,且PS+FT=ST,求点F的坐标;(3)如图(2),过点P的另一条直线l2:y=k2x+b2与抛物线交于另一点H,M,N分别为线段PF,PH 的中点,且k1+k2=﹣4,求证:直线MN与经过原点的一条定直线平行.【思路点拨】(1)利用待定系数法解答即可;(2)设F(m,m2﹣6),利用待定系数法可得到直线PF的解析式为y=(m﹣3)x+3m﹣6,利用已知条件可求得点S的坐标,将点S的坐标代入直线PF的解析式y=(m﹣3)x+3m﹣6,即可求得m的值,则结论可求;(3)利用待定系数法可得直线PF的解析式为y=k1x+3k1+3,与抛物线解析式联立,则得点P,点F的横坐标是方程x2﹣k1x﹣3k1﹣9=0的两根,利用一元二次方程的根与系数的关系和中点坐标的特征可得点M 的坐标,同理可求得点N坐标,利用待定系数法求得直线MN的解析式,利用直线平行的特征可得直线MN 与直线y=2x平行,则结论可得.【解题过程】(1)解:∵点P(﹣3,a)在抛物线y=x2﹣6上,∴a=(﹣3)2﹣6,∴a=3.(2)解:设F(m,m2﹣6),直线PF的解析式为y=k1x+b1,∴−3k1+b1=3mk1+b1=m2−6,解得:k1=m−3b1=3m−6,∴直线PF的解析式为y=(m﹣3)x+3m﹣6.∵PS+FT=ST,∴PF=2ST.∴x F﹣x P=2(x T﹣x S),∴m+3=2(0﹣x S),∴x S=−m3 2.∴S(−m32,0).将S(−m32,0)代入PF的解析式得:(m﹣3)(−m32)+3m﹣6=0,解得:m=33∵当点F在第四象限,∴m2﹣6<0.当m=3+m2﹣6=0,不合题意,舍去,当m=3m2﹣6=9﹣0,∴F(39﹣(3)证明:∵直线y=k1x+b1经过点P(﹣3,3),∴﹣3k1+b1=3,∴b1=3k1+3,∴直线PF的解析式为y=k1x+3k1+3,联立:y=x2−6y=k1x+3k1+3,∴x2﹣k1x﹣3k1﹣9=0.∴点P,点F的横坐标是方程x2﹣k1x﹣3k1﹣9=0的两根,∴x P+x F=k1.∵M为线段PF的中点,∴x M=x P x F2=k12,∴M(k12,k212+3k1+3),∵直线y=k2x+b2经过点P(﹣3,3),∴﹣3k2+b2=3,∴b2=3k2+3,∴直线PH的解析式为y=k2x+3k2+3,联立:y=k2x+3k2+3 y=x2−6,∴x2﹣k2x﹣3k2﹣9=0.∴点P,点H的横坐标是方程x2﹣k1x﹣3k1﹣9=0的两根,∴x P+x H=k2,∵N为线段PH的中点,∴x N=x P x H2=k22,∴N(k22,k222+3k2+3),设直线MN的解析式为y=kx+n,k+n=k212+3k1+3k+n=k222+3k2+3,解得:k=k1+k2+6 n=3−k1k22,∴直线MN的解析式为y=(k1+k2+6)x+3−k1k2 2.∵k1+k2=﹣4,∴直线MN的解析式为y=2x+3−k1k2 2,∴直线MN与直线y=2x平行,∵直线y=2x是一条经过原点的直线,∴直线MN与经过原点的一条定直线平行.19.(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【思路点拨】(1)利用待定系数法可得抛物线的解析式;(2)过P作PG∥y轴,交OE于点G,设P(m,m2﹣4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得△OPE的面积,利用二次函数的最值可得其最大值;(3)求出原抛物线的对称轴和顶点坐标以及对称轴与OE的交点坐标、与AE的交点坐标,用含h的代数式表示平移后的抛物线的顶点坐标,列出不等式组求出h的取值范围;(4)存在四种情况:作辅助线,构建全等三角形,证明△OMP≌△PNF,根据|OM|=|PN|,列方程可得点P 的坐标;同理可得其他图形中点P的坐标.【解题过程】解:(1)∵抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),∴1+b+c=0c=3,解得b=−4c=3,∴抛物线的解析式为:y=x2﹣4x+3;(2)如图,过P作PG∥y轴,交OE于点G,设P(m,m2﹣4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),∴直线OE的解析式为:y=x,∴G(m,m),∴PG=m﹣(m2﹣4m+3)=﹣m2+5m﹣3,∴S△OPE=S△OPG+S△EPG=12 PG•AE=12×3×(﹣m2+5m﹣3)=−32(m2﹣5m+3)=−32(m−52)2+398,∵−32<0,∴当m =52时,△OPE 面积最大,此时,P 点坐标为(52,−34);(3)由y =x 2﹣4x +3=(x ﹣2)2﹣1,得抛物线l 的对称轴为直线x =2,顶点为(2,﹣1),抛物线L 向上平移h 个单位长度后顶点为F (2,﹣1+h ).设直线x =2交OE 于点DM ,交AE 于点N ,则E (2,3),∵直线OE 的解析式为:y =x ,∴M (2,2),∵点F 在△OAE 内(包括△OAE 的边界),∴2≤﹣1+h ≤3,解得3≤h ≤4;(4)设P (m ,m 2﹣4m +3),分四种情况:①当P 在对称轴的左边,且在x 轴下方时,如图,过P 作MN ⊥y 轴,交y 轴于M ,交l 于N ,∴∠OMP =∠PNF =90°,∵△OPF 是等腰直角三角形,∴OP=PF,∠OPF=90°,∴∠OPM+∠NPF=∠PFN+∠NPF=90°,∴∠OPM=∠PFN,∴△OMP≌△PNF(AAS),∴OM=PN,∵P(m,m2﹣4m+3),则﹣m2+4m﹣3=2﹣m,解得:m=∴P②当P在对称轴的左边,且在x轴上方时,同理得:2﹣m=m2﹣4m+3,解得:m1=m2∴P③当P在对称轴的右边,且在x轴下方时,如图,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:m=m2=P ④当P 在对称轴的右边,且在x 轴上方时,如图,同理得m 2﹣4m +3=m ﹣2,解得:m =P综上所述,点P20.(2022•大方县二模)如图,抛物线y =ax 2+bx +2与x 轴相交于A 、B 两点,与y 轴相交于点C ,已知B点的坐标为(4,0),抛物线的对称轴为直线x =32,点D 是BC 上方抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当△BCD 的面积为74时,求点D 的坐标;(3)过点D 作DE ⊥BC ,垂足为点E ,是否存在点D ,使得△CDE 中的某个角等于∠ABC 的2倍?若存在,请直接写出点D 的横坐标;若不存在,请说明理由.【思路点拨】。
2021年九年级数学中考复习专题 一次函数综合(考察坐标、长度、面积等)(四)【解析】

中考复习专题:一次函数综合(考察坐标、长度、面积等)(四)1.如图1,在平面直角坐标系xOy中,直线y=2x+2分别与x轴、y轴交于A、B两点,直线分别与x轴、y轴交于D、B两点,点C(﹣3,m)是BD上一点.(1)b=,m=.(2)试判断线段CA与线段BA之间的关系,并说明理由;(3)如图2,若点Q(0,﹣1)是y轴上一点,点M是直线AB上一动点,点N是直线BD 上一动点,当△MNQ是以点Q为直角顶点的等腰三角形时,请直接写出相应的点M、N的坐标.2.如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,3),直线1经过点B且与x轴平行.(1)直线AB的函数解析式.(2)在直线l上找到一点P,△PAO为等腰三角形,请直接写出点P的坐标;(3)点C在第一象限内,若∠BAC=90°,AB=AC,直线BC交x轴于点D.①求点C的坐标;②点E(2,t)是线段AB上一点,点F是线段AD上一点,若直线EF将△ABD平分为面积相等的两部分,请直接写出点F的坐标.3.(1)如图1,Rt△ABC中,∠ACD=90°,CD⊥AB于D.①此图中有对相似三角形,(直接写出答案)②求证:=.(2)如图2,直线y=2x+4与x轴交于点B,与y轴交于点A,作OC⊥AB于点C,直接写出点C的坐标.(3)如图2,如图2,直线y=2x+4与x轴交于点B,与y轴交于点A,作点O关于AB 的对称点D,直接写出点D的坐标.(4)如图2,直线y=2x+4与x轴交于点B,与y轴交于点A,△ABO绕点B逆时针旋转得到△A′BO′,旋转角小于180°,当旋转到∠BAO=∠BOO′时,直接写出O′的坐标.4.如图,在平面直角坐标系中,直线l的解析式为y=﹣x+4,与x轴交于点C,直线l上有一点B的横坐标为,点A是OC的中点.(1)求直线AB的函数表达式;(2)在直线BC上有两点P、Q,且PQ=4,使四边形OAPQ的周长最小,求周长的最小值;(3)直线AB与y轴交于点H,将△OBH沿AB翻折得到△HBG,M为直线AB上一动点,N 为平面内一点,是否存在这样的点M、N,使得以H、M、N、G为顶点的四边形是菱形,若存在,直接写出点M的坐标,若不存在,说明理由.5.如图,在平面直角坐标系中,矩形OABC 的三个顶点A ,O ,C 在坐标轴上,矩形的面积为12,对角线AC 所在直线的解析式为y =kx ﹣4k (k ≠0).(1)求A ,C 的坐标;(2)若D 为AC 中点,过D 的直线交y 轴负半轴于E ,交BC 于F ,且OE =1,求直线EF 的解析式;(3)在(2)的条件下,在坐标平面内是否存在一点G ,使以C ,D ,F ,G 为顶点的四边形为平行四边形?若存在,请直接写出点G 的坐标;若不存在,请说明理由.6.如图,直线l 1:y =2x +4与x 轴交于点A ,与y 轴交于点B ,将直线l 1关于坐标原点中心对称后得到直线l 2,l 2与x 轴交于点C ,与y 轴交于点D .(1)求直线l 2的表达式;(2)求证:四边形ABCD 为菱形;(3)除菱形ABCD 外,是否在直线l 1上还存在点P ,在直线l 2上还存在点Q ,使得以点B 、C 、P 、Q 为顶点的四边形为菱形?若存在,求出符合条件的所有点P 坐标,若不存在,说明理由.7.综合与探究如图,在平面直角坐标系中,直线l 1:y =3x ,直线l 2交x 轴于点A ,交y 轴于点B ,点A 的坐标为(4,0),直线l 1与直线l 2交于点C ,点C 的横坐标为1.(1)求直线l 2的解析式;(2)求△OBC 的面积;(3)点M 是直线AB 上的一个动点,在平面内是否存在点N ,使以O 、A 、M 、N 为顶点的四边形是菱形?若存在,直接写出符合条件的点N 的坐标,若不存在,说明理由.8.如图1,在平面直角坐标系中,正方形OABC 的边OA ,OC 分别在x 轴,y 轴的正半轴上,直线y =2x ﹣4经过线段OA 的中点D ,与y 轴交于点G ,E 是射线CG 上一点,作点E 关于直线DG 的对称点F ,连结BE ,BF ,FG .设点E 的坐标为(0,m ).(1)求点B 的坐标是( , ).(2)如图2,当点F 落在线段BA 的延长线上时,求证:四边形BEGF 为菱形.(3)在点E 的整个运动过程中,①当S △BEG =S 正方形OABC 时,求线段CE 的长.②N 为平面内任意一点,当B ,E ,F ,N 四点构成的四边形为矩形时,则m 的值为 .(请直接写出答案)9.如图,在平面直角坐标系xOy中,直线分别交x轴,y轴于A、B两点,点A 关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.(1)在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;(2)动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q 从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.①若△POQ的面积为3,求t的值;②点O关于B点的对称点为M,点C关于x轴的对称点为N,过点P作PH⊥x轴,问MP+PH+NH是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.10.如图A(﹣10,0),B(﹣8,6),将△ABO沿AB折叠,点O落在点C处.(1)直接写出四边形BOAC是一个什么样的图形..(2)在y轴上找点P使PA+PB的值最小,直接写出点P的坐标.(3)在直线y=x+4上找点D,使点D到CA和CB的距离相等,则点D的坐标为.参考答案1.解:(1)对于y=2x+2,令x=0,则y=2,令y=0,即y=2x+2=0,解得x=﹣1,故点A、B的坐标分别为(﹣1,0)、(0,2),∵直线过点B,将点B坐标代入上式并解得:故b=2,则该直线的表达式为y=x+2,当x=﹣3时,y=x+2=1=m,即点C(﹣3,1);故答案为:2,1;(2)由(1)知,点A、B、C的坐标分别为(﹣1,0)、(0,2)、(﹣3,1),则AB==,同理AC=,BC=,则AB2+AC2=BC2,故∠BAC为直角,且AC=BC,故线段CA与线段BA之间的关系为垂直且相等;(3)当△MNQ是以点Q为直角顶点的等腰三角形时,∠MQN=90°,QM=QN,设点M、N的坐标分别为(s,2s+2)、(t,t+2),过点Q作x轴的平行线交过点M与y轴的平行线于点H,交过点N与y轴的平行线于点G,∵∠NQG+∠MQH=90°,∠NQG+∠QNG=90°,∴∠MQH=∠QNG,∵∠MHQ=∠QGN=90°,MQ=NQ,∴△MHQ≌△QGN(AAS),∴MH=GQ,NG=QH,即2s+2﹣(﹣1)=﹣t(或﹣1﹣2s﹣2=﹣t),s=t+2﹣(﹣1)(或﹣s=t+2+1),解得:或,故点M、N的坐标分别为(﹣,)、(﹣,)或(﹣,﹣)、(﹣,).2.解:(1)设直线AB的表达式为y=kx+b,则,解得,故直线AB的表达式为y=﹣x+3,故答案为y=﹣x+3;(2)设点P(m,3),则PA2=(m﹣4)2+9,PO2=m2+9,AO2=16,当PA=PO时,即(m﹣4)2+9=m2+9,解得m=2;当PA=AO时,同理可得m=4±;当PO=AO时,同理可得m=±;故点P的坐标为(2,3)或(2,4+)或(2,4﹣)或(2,)或(2,﹣);(3)①过点C作CH⊥x轴于点H,∵∠BAO+∠CAH=90°,∠BAO+∠ABO=90°,∴∠CAH=∠ABO,∵∠BOA=∠AHC=90°,AB=AC,∴△BOA≌△AHC(AAS),∴OB=AH=3,CH=OA=4,故点C(7,4);②当x=2时,y=﹣x+3=,故点E(2,),由点B、C的坐标同理可得,直线BC的表达式为y=x+3,当y=0,即y=x+3=0,解得x=﹣21,故点D(﹣21,0),S=×AD×OB=×(4+21)×3=,△ABDS=×AF×y E=×AF×==×,△AEF解得AF=25,故点F(﹣21,0).3.解:(1)①∵∠ACD+∠BCD=90°,∠A+∠ACD=90°,∴∠A=∠BCD,∵∠CDA=∠BDC=90°,∴△CDB∽△ADC,同理可证△ACD∽△ABC,故△ACB∽△ADC∽△CDB,故相似三角形有3对,故答案为3;②由△CDB∽△ADC得:=;(2)对于y=2x+4,令x=0,则y=4,令y=0,则x=﹣2,故点A、B的坐标分别为(0,4)、(﹣2,0),即OA=4,OB=2,则AB===,如图,过点C作CR⊥OB于点R,。
微专题4 反比例函数的综合应用++课件+2025年九年级中考数学总复习人教版(山东)

①当AC,BO为对角线时,AC,BO的中点重合,∴
,
+4=0+0
=
解得
,
= −
经检验,t=4,k=-16符合题意,
此时点C的坐标为(4,-4);
25
②当CB,AO为对角线时,CB,AO的中点重合,
+=+
∴
,
+0=4+0
= −
解得
,
= −
经检验,t=-4,k=-16符合题意,
所以S△AOB=S△AOM+S△BOM= ×2×3+ ×2×1=4.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中
心,
所以点B和点C关于点O成中心对称,所以BO=CO,所以S△ABC=2S△AOB=8.
17
类型2
求特殊三角形或特殊四边形
【思维切入】
1.动点三角形的形状问题:
∵点A(m,4)在y=2x+2上,
∴2m+2=4,∴m=1,
∴点A的坐标为(1,4),
∵点A(1,4)在y= 上,∴4= ,∴k2=4,∴y= .
8
(2)如图,连接DE,过点B作BF垂直于y轴,垂足为F,
联立
= +
=
= 1 = −2
,解得
,
,
= 4 = −2
3.动点四边形的问题转化为动点三角形问题:
动点菱形问题转化为动点等腰三角形问题;
动点矩形问题转化为动点直角三角形问题.
2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(四)

2021年九年级数学中考复习专题:二次函数综合(考察动点坐标、长度、面积等)(四)1.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于点A,点B,与y轴交于点C,其中A(﹣4,0),B(2,0),C(0,﹣4).(1)求该抛物线的函数表达式;(2)点P为直线AC下方抛物线上一点,PD⊥AC,当线段PD的长度最大时,求点P的坐标;(3)将△BOC沿直线BC平移,平移后的三角形为△B'O'C'(其中点O'与点O不重合),点S是坐标平面内一点,若以A,C,O',S为顶点的四边形是菱形,请直接写出所有符合条件的点O'的坐标.2.如图,已知抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A (1,0)和点B (﹣3,0),与y 轴交于点C ,且OC =OB .(1)求点C 的坐标和此抛物线的解析式;(2)若点E 为第二象限抛物线上一动点,连接BE ,CE ,BC ,求△BCE 面积的最大值; (3)点P 在抛物线的对称轴上,若线段PA 绕点P 逆时针旋转90°后,点A 的对应点A ′恰好也落在此抛物线上,求点P 的坐标.3.抛物线y =ax 2+bx ﹣5的图象与x 轴交于A 、B 两点,与y 轴交于点C ,其中点A 坐标为(﹣1,0),一次函数y =x +k 的图象经过点B 、C . (1)试求二次函数及一次函数的解析式;(2)如图1,点D (2,0)为x 轴上一点,P 为抛物线上的动点,过点P 、D 作直线PD 交线段CB 于点Q ,连接PC 、DC ,若S △CPD =3S △CQD ,求点P 的坐标;(3)如图2,点E 为抛物线位于直线BC 下方图象上的一个动点,过点E 作直线EG ⊥x 轴于点G ,交直线BC 于点F ,当EF +CF 的值最大时,求点E 的坐标.4.如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的表达式;(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.5.如图,已知抛物线y=ax2过点A(﹣3,).(1)求抛物线的解析式;(2)已知直线l过点A,M(,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MA•MB;(3)若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.6.如图,在平面直角坐标系中,点O 为坐标原点,抛物线y =ax 2+bx +c 的顶点是A (1,3),将OA 绕点O 顺时针旋转90°后得到OB ,点B 恰好在抛物线上,OB 与抛物线的对称轴交于点C .(1)求抛物线的解析式;(2)P 是线段AC 上一动点,且不与点A ,C 重合,过点P 作平行于x 轴的直线,与△OAB 的边分别交于M ,N 两点,将△AMN 以直线MN 为对称轴翻折,得到△A ′MN ,设点P 的纵坐标为m .①当△A ′MN 在△OAB 内部时,求m 的取值范围; ②是否存在点P ,使S △A ′MN =S △OA ′B ,若存在,求出满足条件m 的值;若不存在,请说明理由.7.如图,在平面直角坐标系中,已知二次函数y =﹣(x ﹣m )2+4图象的顶点为A ,与y轴交于点B ,异于顶点A 的点C (1,n )在该函数图象上. (1)当m =5时,求n 的值.(2)当n =2时,若点A 在第一象限内,结合图象,求当y ≥2时,自变量x 的取值范围. (3)作直线AC 与y 轴相交于点D .当点B 在x 轴上方,且在线段OD 上时,求m 的取值范围.8.已知二次函数y=ax2+2x+c(a≠0)的图象与x轴的交于A、B(1,0)两点,与y轴交于点C(0,﹣3),(1)求二次函数的表达式及A点坐标;(2)D是二次函数图象上位于第三象限内的点,求点D到直线AC的距离取得最大值时点D的坐标;(3)M是二次函数图象对称轴上的点,在二次函数图象上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请写出点N的坐标(不写求解过程).9.在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.(1)求抛物线的函数解析式;(2)若直线l:线y=﹣x+m与该抛物线交于D、E两点,如图.①连接CD、CE、BE,当S△BCE =3S△CDE时,求m的值;②是否存在m的值,使得原点O关于直线l的对称点P刚好落在该抛物线上?如果存在,请直接写出m的值;如果不存在,请说明理由.10.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.(1)求抛物线的解析式及顶点D的坐标;(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;(3)若点Q为线段OC上的一动点,问:AQ+QC是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.参考答案1.解:(1)设抛物线解析式为y=a(x+4)(x﹣2),∵抛物线过C(0,﹣4),∴﹣8a=﹣4,∴,∴此抛物线解析式为;(2)过点P作PE∥y轴交AC于点E,如下图所示,∵A(﹣4,0),C(0,﹣4),∴AC解析式为y=﹣x﹣4,设P(),E(m,﹣m﹣4),则PE=,∵,∴当时,PE最大,此时PD最大,∴P(﹣2,﹣4);(3)∵A(﹣4,0),C(0,﹣4),O′(a,2a),∴AC2=32,CO'2=5a2+16a+16,AO'2=5a2+8a+16,①CA2=CO′2即5a2+16a+16=32,∴,∴O′(﹣4,﹣8),,1②AC2=AO′2即5a2+8a+16=32,∴,∴,,③CO'2=AO'2即5a2+8a+16=5a2+16a+16,∴a=0,∴O5′(0,0)(舍),综上所述,满足条件的点O'坐标有O1′(﹣4,﹣8),,,.答:(1)此抛物线解析式为;(2)P(﹣2,﹣4);(3)点O'坐标有O1′(﹣4,﹣8),,,.2.解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),∴OB=3,∵OC=OB,∴OC=3,∴c=3,∴,解得:,∴所求抛物线解析式为:y=﹣x2﹣2x+3,C(0,3).(2)如图2,连接BC,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0),∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,∴S△BEC =S四边形BOCE﹣S△BOC=BF•EF+(OC+EF)•OF﹣•OB•OC=(a+3)•(﹣a2﹣2a+3)+(﹣a2﹣2a+6)•(﹣a)﹣=﹣a2﹣a=﹣(a +)2+,∴当a =﹣时,S △BEC 最大,且最大值为.(3)∵抛物线y =﹣x 2﹣2x +3的对称轴为x =﹣1,点P 在抛物线的对称轴上, ∴设P (﹣1,m ),∵线段PA 绕点P 逆时针旋转90°后,点A 的对应点A 1恰好也落在此抛物线上, ①当m ≥0时,∴PA =PA 1,∠APA 1=90°,如图3,过A 1作A 1N ⊥对称轴于N ,设对称轴于x 轴交于点M , ∴∠NPA 1+∠MPA =∠NA 1P +∠NPA 1=90°, ∴∠NA 1P =∠NPA , 在△A 1NP 与△PMA 中,,∴△A 1NP ≌△PMA (AAS ), ∴A 1N =PM =m ,PN =AM =2, ∴A 1(m ﹣1,m +2),代入y =﹣x 2﹣2x +3得:m +2=﹣(m ﹣1)2﹣2(m ﹣1)+3, 解得:m =1,m =﹣2(舍去),②当m <0时,要使P 2A =P 2A 2,由图可知A 2点与B 点重合, ∵∠AP 2A 2=90°, ∴MP 2=MA =2, ∴P 2(﹣1,﹣2),∴满足条件的点P 的坐标为P (﹣1,1)或(﹣1,﹣2).3.解:(1)∵抛物线y=ax2+bx﹣5的图象与y轴交于点C,∴C(0,﹣5),∵一次函数y=x+k的图象经过点B、C,∴k=﹣5,∴B(5,0),设抛物线的解析式为y=a(x+1)(x﹣5)=ax2﹣4ax﹣5a,∴﹣5a=﹣5,∴a=1,∴二次函数的解析式为y=x2﹣4x﹣5,一次函数的解析式为y=x﹣5.(2)①当点P在直线BC的上方时,如图2﹣1中,作DH∥BC交y轴于H,过点D作直线DT交y轴于T,交BC于K,作PT∥BC交抛物线于P,直线PD交抛物线于Q.∵S△CPD =3S△CQD,∴PD=3DQ,∵PT∥DH∥BC,∴===3,∵D(2,0),B(5,0),C(﹣5,0),∴OA=OB=5,OD=OH=2,∴HC=3,∴TH=9,OT=7,∴直线PT的解析式为y=x+7,由,解得或,∴P(,)或(,),②当点P在直线BC的下方时,如图2﹣2中,当点P与抛物线的顶点(2,﹣9)重合时,PD=9.DQ=3,∴PQ=3DQ,∴S△CPD =3S△CQD,过点P作PP′∥BC,此时点P′也满足条件,∵直线PP′的解析式为y=x﹣11,由,解得或,∴P′(3,﹣8),综上所述,满足条件的点P的坐标为(,)或(,)或(2,﹣9)或(3,﹣8).(3)设E(m,m2﹣4m﹣5),则F(m,m﹣5),∴EF=(m﹣5)﹣(m2﹣4m﹣5)=5m﹣m2,CF=m,∴EF+CF=﹣m2+6m=﹣(m﹣3)2+9,∵﹣1<0,∴m=3时,EF+CF的值最大,此时E(3,﹣8).4.解:(1)把A(﹣3,0),B(1,0)代入y=x2+bx+c中,得,解得,∴y=x2+2x﹣3.(2)①设直线AC的表达式为y=kx+b,把A(﹣3,0),C(0,﹣3)代入y=kx+b.得,解得,∴y=﹣x﹣3,∵点P(m,0)是x轴上的一动点,且PM⊥x轴.∴M(m,﹣m﹣3),N(m,m2+2m﹣3),∴MN=(﹣m﹣3)﹣(m2+2m﹣3)=﹣m2﹣3m=﹣(m+)2+,∵a=﹣1<0,∴此函数有最大值.又∵点P在线段OA上运动,且﹣3<﹣<0,∴当m=﹣时,MN有最大值.②如图2﹣1中,当点M在线段AC上,MN=MC,四边形MNQC是菱形时.∵MN=﹣m2﹣3m,MC=﹣m,∴﹣m2﹣3m=﹣m,解得m=﹣3+或0(舍弃)∴MN=3﹣2,∴CQ=MN=3﹣2,∴OQ=3+1,∴Q(0,﹣3﹣1).如图2﹣2中,当MC是菱形的对角线时,四边形MNCQ是正方形,此时CN=MN=CQ=2,可得Q(0,﹣1).如图2﹣3中,当点M在CA延长线上时,MN=CM,四边形MNQC是菱形时,则有,m 2+3m =﹣m , 解得m =﹣3﹣或0(舍弃), ∴MN =CQ =3+2,∴OQ =CQ ﹣OC =3﹣1, ∴Q (0,3﹣1).综上所述,满足条件的点Q 的坐标为(0,﹣3﹣1)或(0,﹣1)或(0,3﹣1). 5.解:(1)把点A (﹣3,)代入y =ax 2,得到=9a , ∴a =, ∴抛物线的解析式为y =x 2.(2)设直线l 的解析式为y =kx +b ,则有,解得,∴直线l 的解析式为y =﹣x +,令x =0,得到y =, ∴C (0,), 由,解得或,∴B (1,),如图1中,过点A 作AA 1⊥x 轴于A 1,过B 作BB 1⊥x 轴于B 1,则BB 1∥OC ∥AA 1,∴===,===,∴=,即MC2=MA•MB.(3)如图2中,设P(t,t2)∵OC为一边且顶点为O,C,P,D的四边形是平行四边形,∴PD∥OC,PD=OC,∴D(t,﹣t+),∴|t2﹣(﹣t+)|=,整理得:t2+2t﹣6=0或t2+2t=0,解得t=﹣1﹣或﹣1+或﹣2或0(舍弃),∴P(﹣1﹣,2+)或(﹣1+,2﹣)或(﹣2,1).6.解:(1)∵抛物线y=ax2+bx+c的顶点是A(1,3),∴抛物线的解析式为y=a(x﹣1)2+3,∵OA绕点O顺时针旋转90°后得到OB,∴B(3,﹣1),把B(3,﹣1)代入y=a(x﹣1)2+3可得a=﹣1,∴抛物线的解析式为y=﹣(x﹣1)2+3,即y=﹣x2+2x+2,(2)①如图1中,连接OA′,A′B.∵B(3,﹣1),∴直线OB的解析式为y=﹣x,∵A(1,3),∴C(1,﹣),∵P(1,m),AP=PA′,∴A′(1,2m﹣3),由题意3>2m﹣3>﹣,∴3>m>.②当点P在x轴上方时,∵直线OA的解析式为y=3x,直线AB的解析式为y=﹣2x+5,∵P(1,m),∴M(,m),N(,m),∴MN=﹣=,∵S△A′MN =S△OA′B,∴•(m﹣2m+3)•=××|2m﹣3+|×3,整理得m2﹣6m+9=|6m﹣8|解得m=6+(舍去)或6﹣,当点P在x轴下方时,同法可得•(3﹣m)•(+3m)=××[﹣﹣(2m﹣3)]×3,整理得:3m2﹣12m﹣1=0,解得m=或(舍去),∴满足条件的m的值为6﹣或.7.解:(1)当m=5时,y=﹣(x﹣5)2+4,当x=1时,n=﹣×42+4=﹣4.(2)当n=2时,将C(1,2)代入函数表达式y=﹣(x﹣m)2+4,得2=﹣(1﹣m)2+4,解得m=3或﹣1(舍去),∴此时抛物线的对称轴x=3,根据抛物线的对称性可知,当y=2时,x=1或5,∴x的取值范围为1≤x≤5.(3)∵点A与点C不重合,∴m≠1,∵抛物线的顶点A的坐标是(m,4),∴抛物线的顶点在直线y=4上,当x=0时,y=﹣m2+4,∴点B的坐标为(0,﹣m2+4),抛物线从图1的位置向左平移到图2的位置前,m逐渐减小,点B沿y轴向上移动,当点B与O重合时,﹣m2+4=0,解得m=2或﹣2(不合题意舍去),当点B与点D重合时,如图2,顶点A也与B,D重合,点B到达最高点,∴点B(0,4),∴﹣m2+4=4,解得m=0,当抛物线从图2的位置继续向左平移时,如图3点B不在线段OD上,∴B点在线段OD上时,m的取值范围是:0≤m<1或1<m<2.8.解:(1)把B(1,0),C(0,﹣3)代入y=ax2+2x+c 则有,解得,∴二次函数的解析式为y=x2+2x﹣3,令y=0,得到x2+2x﹣3=0,解得x=﹣3或1,∴A(﹣3,0).(2)如图1中连接AD,CD.∵点D到直线AC的距离取得最大,∴此时△DAC的面积最大,设直线AC解析式为:y=kx+b,∵A(﹣3,0),C(0,﹣3),∴,解得,,∴直线AC的解析式为y=﹣x﹣3,过点D作x轴的垂线交AC于点G,设点D的坐标为(x,x2+2x﹣3),则G(x,﹣x﹣3),∵点D在第三象限,∴DG=﹣x﹣3﹣(x2+2x﹣3)=﹣x﹣3﹣x2﹣2x+3=﹣x2﹣3x,∴S=•DG•OA=(﹣x2﹣3x)×3=﹣x2﹣x=﹣(x+)2+,△ACD=,点D(﹣,﹣),∴当x=﹣时,S最大∴点D到直线AC的距离取得最大时,D(﹣,﹣).(3如图2中,当OB是平行四边形的边时,OB=MN=1,OB∥MN,可得N(﹣2,﹣3)或N′(0,﹣3),当OB为对角线时,点N″的横坐标为2,x=2时,y=4+4﹣3=5,∴N″(2,5).综上所述,满足条件的点N的坐标为(﹣2,﹣3)或(0,﹣3)或(2,5).9.解:(1)把A(﹣1,0)、B(3,0)两点代入y=﹣x2+bx+c可得:,解得:,∴抛物线的解析式为y=﹣x2+x+.(2)①如图1中,对于y═﹣x2+x+,令x=0,可得y=,∴C(0,),∵B(3,0),∴OC=,OB=3,∴tan∠CBO=,∴∠CBO=30°,∵直线l:y=﹣x+m与x轴交于N(m,0)与y轴交于M(0,m),∴tan∠MNO==,∴∠MNO=30°=∠CBO,∴l∥BC,∵S△BCE =3S△CDE,∴BC=3DE,∴直线l应该在BC的上方,在BC上取一点F,使得BC=3BF,∴BF=DE,∴四边形BEDF是平行四边形,∵C(0,),B(3,0),BC=3BF,∴F(2,),设D(n,﹣n+m),则E(n+1,﹣(n+1)+m),将它们代入抛物线的解析式得到:,解得,∴m的值为.②如图2中,过点O作OM⊥BC交抛物线于M或M′.则直线OM的解析式为y=x,由,解得或,∴M(,),M′(,),由题意直线l经过OM或OM′的中点,∴=﹣×+m或=﹣×+m,解得m=.10.解:(1)函数的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),即:3a=3,解得:a=1,故抛物线的表达式为:y=x2﹣4x+3,则顶点D(2,﹣1).(2)将点B、C的坐标代入一次函数表达式:y=mx+n并解得:直线BC的表达式为:y=﹣x+3,过点P作y轴的平行线交BC于点H,设点P(x,x2﹣4x+3),则点H(x,﹣x+3),=•PH×OB=(﹣x+3﹣x2+4x﹣3)=(﹣x2+3x),则S△PBC∵﹣<0,故S有最大值,此时x=,△PBC故点P(,﹣).(3)存在,理由:如上图,过点C作与y轴夹角为30°的直线CH,作QH⊥CH,垂足为H,则HQ=CQ,AQ+QC最小值=AQ+HQ=AH,直线HC所在表达式中的k值为,直线HC的表达式为:y=x+3…①,则直线AH所在表达式中的k值为﹣,则直线AH的表达式为:y=﹣x+s,将点A的坐标代入y=﹣x+s并解得:s=,则直线AH的表达式为:y=﹣x+…②,联立①②并解得:x=,故点H(,),而点A(1,0),则AH=,即:AQ+QC的最小值为.。
2024学年九年级中考数学专题复习:分配方案问题(一次函数实际综合应用)(含答案)

2024 学年九年级中考数学专题复习:分配方案问题(一次函数实际综合应用)1.春天来了,学校计划用两种花卉对校园进行美化.已知用600元购买A 种花卉与用900元购买B 种花卉的数量相等,且B 种花卉每盆的价格比A 种花卉每盆的价格多0.5元.(1)求A ,B 两种花卉每盆的价格各是多少元;(2)学校计划购买A ,B 两种花卉共6000盆,其中A 种花卉的数量不超过B 种花卉数量的13,请你给出购买这批花卉费用最低的方案,并求出最低费用. 2.某市的A 县和B 县春季育苗,急需化肥分别为90t 和60t ,该市的C 县和D 县分别储存化肥100t 和50t ,全部调配给A 县和B 县.已知从C 县运化肥到A 县的运费为35元/t ,从C 县运化肥到B 县的运费为30元/t ,从D 县运化肥到A 县的运费为40元/t ,从D 县运化肥到B 县的运费为45元/t .(1)设C 县运到A 县的化肥为x t ,求总运费W (单位:元)关于x (单位:t )的函数解析式,并写出自变量x 的取值范围;(2)求最低总运费,并说明总运费最低时的运送方案.3.为加强学生的劳动教育,某校准备开展以“种下希望,共建美好家园”为主题的义务植树活动. 经了解,购买2棵枣树和3棵石榴树共需44元;购买5棵枣树和6棵石榴树共需98元,该校决定购买(0)m m 棵枣树和50棵石榴树.(1)求枣树和石榴树的单价;(2)实际购买时,商家给出了如下优惠方案:方案一:均按原价的九折销售;方案二:如果购买的枣树不超过50棵,按原价销售. 如果购买的枣树超过50棵,则超出的部分按原价的八折销售,石榴树始终按原价销售.分别求出两种方案的费用1W ,2W 关于m 的函数解析式.4.“一骑红尘妃子笑,无人知是荔枝来”,夏季是盛产荔枝的季节,某县城为尽快打开市场,对本地的荔枝品种妃子笑进行线上和线下销售相结合的模式,具体费用标准如下:线上销售模式:不超过6千克时,按原价出售,超过6千克时,超出部分每千克再让利3.5元;线下销售模式:一律九折出售.购买妃子笑x 千克,所需费用为y 元,y 与x 之间的函数关系如图所示.根据以上信息回答下列问题:(1)请问妃子笑的标价为多少?(2)请求出线上销售模式所需费用y关于x的函数解析式;(3)若想购买妃子笑40千克,请问选择哪种模式购买最省钱?5.某公司为改善办公条件,计划采购一批A,B两种型号的电脑,已知1台A型电脑比1台B型电脑的便宜1200元;采购4台A型电脑与采购3台B型电脑的费用一样多.(1)求A型电脑和B型电脑每台各需多少元;(2)若公司计划采购A、B两种型号电脑共50台,且A型电脑的台数不超过B型电脑的4倍,两种型号电脑的采购总费用不超过200000元,该公司共有几种采购方案?哪种采购方案可使总费用最低,最低费用是多少元?6.希望艺术团准备采购甲,乙两种道具,某经销商知道了活动的方案后,主动联系希望艺术团,对甲种道具的出售价格根据购买量给予优惠,对乙种道具按25元/件的价格出售.设希望艺术团购买甲种道具x件,付款y元,y与x之间的函数关系如图所示.(1)直接写出当0≤x≤50和x>50时,y与x之间的函数关系式;(2)若希望艺术团计划一次性购买甲,乙两种道具共100件,且甲种道具不少于40件,但又不超过60件.如何分配甲,乙两种道具的购买量,才能使希望艺术团付款总金额w(元)最少?(3)若甲、乙两种道具的进货价格分别为22元/件和18元/件.经销商按(2)中甲,乙两种道具购买量的分配比例卖出两种道具共a件,且销售完a件道具获得的利润不少于1050元,求a的最小值.7.我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买A,B两种奖品.已知2件A种奖品和3件B种奖品共需41元,5件A种奖品和2件B种奖品共需53元.(1)这两种奖品的单价各是多少元?(2)学校准备购进这两种奖品共90件,且B种奖品的数量不少于A种奖品数量的13,请设计出最省钱的购买方案,并求出最少费用.8.我市是福建省茶叶的主要产区,清明过后就是春茶的采摘季节.已知熟练采茶工人每天采茶的数量是新手采茶工人的3倍,每个熟练采茶工人采摘600斤鲜叶比新手采茶工人采摘450斤鲜叶少用25天.(1)求熟练采茶工人和新手采茶工人一天分别能采摘鲜叶的斤数;(2)某茶厂计划一天采摘鲜叶600斤,该茶厂有20名熟练采茶工人和15名新手采茶工人,按点工制度付给熟练采茶工人每人每天的工资为300元,付给新手采茶工人每人每天的工资为80元,应如何安排熟练采茶工人和新手采茶工人能使费用最少?9.为了方便老师工作,某中学决定购进一批教学用具,在购买教学用具时,该校从甲、乙、丙三家商场了解到同一种型号教学用具的优惠条件如下:甲:定价为90元,超过5个,超过的部分每个优惠20%;乙:定价为90元,每个优惠10% ;丙:购会员卡100元,每个教学用具70元.(1)设该校购买x个教学用具,选择甲商场时,所需费用为y1元;选择乙商场时,所需费用为y2元;选择丙商场时,所需费用为y3元;请分别求出y1,y2,y3与x之间的函数关系式;(2)当购买教学用具数量大于多少件时,y2>y3?10.某年级430名师生秋游,计划租用8辆客车,现有甲、乙两种型号客车,它们的载客量和租金如下表:(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?11.目前,全国各地都在积极开展新冠肺炎疫苗接种工作,某生物公司接到批量生产疫苗任务,要求5天内加工完成22万支疫苗,该公司安排甲,乙两车间共同完成加工任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止,设甲,乙两车间各自生产疫苗y (万支)与甲车间加工时间x (天)之间的关系如图1所示;两车间未生产疫苗w (万支)与甲车间加工时间x (天)之间的关系如图2所示,请结合图象回答下列问题:(1)甲车间每天生产疫苗 万支,第一天甲、乙两车间共生产疫苗 万支,=a ;(2)当3x =时,求甲、乙车间生产的疫苗数(万支)之差12y y -;(3)若5.5万支疫苗恰好装满一辆货车,那么加工多长时间装满第一辆货车?再加工多长时间恰好装满第三辆货车?12.某校准备在健康大药房购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)求每盒口罩和每盒水银体温计的价格各是多少元?(2)如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m 盒(m 为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m 的代数式表示.(3)在健康大药房累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付w 元,求w 关于m 的函数关系式.若该校九年级有1000名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元? 13.某商场销售一种夹克和衬衣,夹克每件定价100元,衬衣每件定价50元,商场在开展促销活动期间,向顾客提供两种优惠方案.方案一:买一件夹克送一件衬衣方案二:夹克和衬衣均按定价的80%付款现有顾客要到该商场购买夹克30件,衬衣x件(x>30)(1)用含x的代数式表示方案一购买共需付款y1元和方案二购买共需付款y2元;(2)通过计算说明,购买衬衣多少件时,两种方案付款一样多?(3)当x=40时,哪种方案更省钱?请说明理由.14.灵宝寺河山被誉为“亚洲第一高山果园”,海拔800﹣1200米,土质肥沃,雨量充沛,日照充足,昼夜温差大,气候条件得天独厚,是苹果的最佳适生地.寺河山苹果,是三门峡市灵宝苹果的龙头品牌,素有“天下苹果属灵宝,灵宝苹果属寺河”之说.在苹果收获季节,为了保证苹果的新鲜度,需要将苹果运送至冷库进行保存,现有A,B两个果园,若A果园有苹果120吨,B果园有苹果60吨.现将A,B两个果园的苹果全部运往C,D两个冷库进行冷藏保存,已知C仓库可储存100吨,D仓库可储存80吨,A,B 两个果园到C,D两个冷藏仓库的运费如下表:设从A果园运往C仓库的苹果重量为x吨.(1)用含x(吨)的代数式表示总运费W(元),并写出自变量x的取值范围;(2)如何进行运送才能使总运费最少?求出最低总运费.15.学习贯彻习近平总书记关于生态文明建设系列重要讲话精神,牢固树立“绿水青山就是金山银山”理念,把生态文明建设融入经济建设、政治建设、文化建设、社会建设各个方面和全过程.在建设美丽中国的活动中,某学校计划组织全校1450名师生到相关部门规划的林区植树,经过研究,决定在当地租车公司租用62辆A、B两种型号的客车作为交通工具.下表是租车公司提供给学校有关A、B两种型号客车的载客量和租金信息:注:载客量指的是每辆客车最多可载该校师生的人数;(1)设租用A型号客车x辆,租车总费用为y元,求y与x之间的函数表达式,并通过计算求出x的取值范围;(2)若要使租车总费用不超过13460元,则共有几种租车方案?哪种租车方案最省钱?参考答案:1.(1)A 种花卉每盆1元,B 种花卉每盆1.5元(2)当购买A 种花卉1500盆,B 种花卉4500盆时购买这批花卉总费用最低,最低费用为8250元.2.(1)W =10x +4800(40≤x ≤90)(2)最低总运费为5200元,此时的运送方案是:C 县的100t 化肥40t 运往A 县,60t 运往B 县,D 县的50t 化肥全部运往A 县3.(1)枣树的单价为10元,石榴树的单价为8元(2)19360W m =+,210400(050),8500(50).m m W m m +<≤⎧=⎨+>⎩4.(1)25元/千克(2)()()250621.5216x x y x x ⎧≤<⎪=⎨+>⎪⎩(3)线上购买5.(1)购买1台A 型电脑需要3600元,购买1台B 型电脑需要4800元.(2)该公司共有7种采购方案. 购买A 型电脑40台,B 型电脑10台方案可使总费用最低,最低费用是192000元6.(1)30(050)24300(50)x x y x x ≤≤⎧=⎨+>⎩ (2)购进甲道具40件,乙道具60件时,才能使希望艺术团付款总金额w (元)最少;(3)a 的最小值为2107.(1)A :7元,B :9元(2)购进A 种奖品67件,购进B 种奖品23件;676元8.(1)每名熟练的采茶工人一天能采摘鲜叶30斤,每名新手采茶工人一天能采摘鲜叶10斤(2)茶厂应安排15名熟练的采茶工人采摘鲜叶,15名新手采茶工人采摘鲜叶能使得费用最少9.(1)190(05)7290(5)x x y x x <≤⎧=⎨+>⎩;290(110%)81y x x =⨯-=;370100y x =+ (2)1010.(1)y =100x +3600(2)当甲种客车有5辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是4100元11.(1)2,3.5,1.5(2)1(3)2天,2天12.(1)每盒口罩和每盒水银体温计的价格各是200元,50元(2)5m(3)当m ≤4时,则w=450m ;当m >4时,w =360m +360,需要购买口罩20盒,水银体温计100盒,所需总费用为7560元13.(1)12501500402400y x y x =+⎧⎨=+⎩;(2)当90x =时12y y =;(3)当x =40时,方案一更省钱. 14.(1)43400W x =+,40100x ≤≤;(2)运送方案为A 果园将40吨苹果运往C 仓库,80吨运往D 仓库,B 果园的60吨苹果全部运往C 仓库,此时总运费最低,最低是3560元 15.(1)y =100x +11160(21≤x ≤62且x 为整数);(2)3种,租用A 型号客车21辆。
2021年九年级数学中考复习专题:一次函数综合(考察坐标、长度、面积等)(五)

中考复习专题:一次函数综合(考察坐标、长度、面积等)(五)1.如图,在平面直角坐标系xOy中,点A是一次函数y=3x﹣20与y=﹣x+12的交点,过点A分别作x,y轴的垂线段,垂足分别是B和C,动点P和Q以1个单位/秒的速度,分别从点C和B出发,沿线段CA和BO方向,向终点A和O运动,设运动时间为t秒.(1)证明:无论运动时间t(0<t<8)取何值,四边形OPAQ始终为平行四边形;(2)当四边形OPAQ为菱形时,请求出此时PQ的长及直线PQ的函数解析式;(3)当OP满足2≤OP≤5时,连接PQ,直线PQ与y轴交于点M,取线段AC的中点N,试确定三角形MNP的面积S与运动时间t之间的函数关系,并求出S的取值范围.2.如图所示,在平面直角坐标系中,矩形OABC的边AB=5,边OA=4,直线l:y=2x+b 与矩形OABC的边OC和AB都有交点,交点分别是点D与点E.(1)请用含b的代数式分别表示点D和点E的坐标:D,E;(2)当四边形ADCE为平行四边形时,求b的值;(3)若要使在平面内存在点F,使以点C、D、E、F这四点为顶点的四边形为菱形,是否存在满足条件的b的值?若存在,求出b的值;若不存在,请说明理由.3.在平面直角坐标系xOy中,点A在直线l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E.给出如下定义:若在线段OE,⊙A和直线l上分别存在点B、点C和点D,使得四边形ABCD是矩形(点A,B,C,D顺时针排列),则称矩形ABCD为直线l的“理想矩形”.例如,图①中的矩形ABCD为直线l的“理想矩形”.(1)如图②,已知点A(﹣1,2)在直线x=﹣1上,四边形ABCD为直线x=﹣1的“理想矩形”,直接写出点D的坐标;(2)如图③,已知一次函数y=kx+1(k≠0)的图象是直线l,点A(1,2)在直线l 上,求直线l的“理想矩形”ABCD的面积;(3)已知点A(1,3)在直线l上,若直线l的“理想矩形”ABCD是正方形,求点D的坐标.4.如图,▱ABCD的顶点A、B在x轴上,顶点D在y轴上,已知OA=3,OB=5,OD=4.(1)▱ABCD的面积为;(2)如图1,点E是BC边上的一点,若△ABE的面积是▱ABCD面积的,求点E的坐标.(提示:可通过求直线BC的解析式,得出E点坐标)5.如图,平面直角坐标系中,一次函数y=x+b的图象交x轴负半轴于点A,交y轴正半轴于点B,且△AOB的面积为32.(1)求一次函数的解析式;(2)动点P从点A出发,以每秒个单位长度的速度向终点B运动,点P出发的同时,动点Q从点O出发,以每秒2个单位长度的速度沿y轴正半轴运动,当点P停止运动时,动点Q也随之停止运动,连接PQ,设点P的运动时间为t,△BPQ的面积为S.求S与t 的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,D为AB中点,连接OD,交直线PQ于点F,若OF=3DF,求线段QF的长.6.如图,直线l1的解析式为y=x+1,且l1与x轴交于点D,直线l2经过定点A、B,直线l1与l2交于点C.(1)求直线l2的解析式;(2)求△ADC的面积;(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.7.如图1,平面直角坐标系中,直线与x轴、y轴分别交于点A,B,直线y=﹣x+b经过点A,并与y轴交于点C.(1)求A,B两点的坐标及b的值;(2)如图2,动点P从原点O出发,以每秒1个单位长度的速度沿x轴正方向运动.过点P作x轴的垂线,分别交直线AC,AB于点D,E.设点P运动的时间为t.①点D的坐标为.点E的坐标为;(均用含t的式子表示)②请从下面A、B两题中任选一题作答我选择题.A.当点P在线段OA上时,探究是否存在某一时刻,使DE=OB?若存在,求出此时△ADE 的面积;若不存在说明理由.B.点Q是线段OA上一点.当点P在射线OA上时,探究是否存在某一时刻使?若存在、求出此时t的值,并直接写出此时△DEQ为等腰三角形时点Q的坐标;若不存在,说明理由.8.平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于点B、A.(1)直接写出直线AB关于x轴对称的直线BC的解析式;(2)如图1,直线BC与直线y=x交于E点,点P为y轴上一点,PE=PB,求P点坐标;(3)如图2,点P为y轴上一点,∠OEB=∠PEA,直线EP与直线AB交于点M,求M点的坐标.9.如图,在平面直角坐标系中,直线BC:y=﹣x+3交x轴于点B,交y轴于点C,直线AD 与直线BC互相垂直,垂足为点E,且CD=1.(1)求直线AD解析式.(2)点P从点B出发沿线段BO方向以1个单位/秒的速度向终点O运动,设△AEP的面积为S,运动时间为t,求S与t的函数关系式,并直接写出自变量t的取值范围.(3)在(2)的条件下,点P运动的同时点Q从C点出发沿射线CO方向以3个单位/秒的速度运动,当点P到达终点时,点Q也停止运动,过点P作x轴垂线交BC于点F,连接FQ和EQ,平面内是否存在一点M,使得以点E,Q,F,M为顶点且以EQ为边的四边形是菱形?若存在,求出此时t值和M点坐标;若不存在,说明理由.10.如图,在平面直角坐标系中,直线y=﹣x+m分别与x轴、y轴交于点B、A.其中B 点坐标为(12,0),直线y=x与直线AB相交于点C.(1)求点A的坐标.(2)求△BOC的面积.(3)点D为直线AB上的一个动点,过点D作y轴的平行线DE,DE与直线OC交于点E (点D与点E不重合).设点D的横坐标为t,线段DE长度为d.①求d与t的函数解析式(写出自变量的取值范围).②当动点D在线段AC上运动时,以DE为边在DE的左侧作正方形DEPQ,若以点H(,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点时,请直接写出t的取值范围.参考答案1.解:(1)联立y=3x﹣20与y=﹣x+12并解得:x=8,故点A(8,4),则PA=8﹣t,OQ=8﹣t=PA,而PA∥OQ,故四边形OPAQ始终为平行四边形;(2)点P(t,4),点Q(8﹣t,0),OC=4,四边形OPAQ为菱形时,OP=OQ,即:42+t2=(8﹣t)2,解得:t=3,故点P、Q的坐标分别为(3,4)、Q(5,0),则PQ==2;将点P、Q的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线PQ的表达式为:y=﹣2x+10;(3)当OP=2时,OC=4,则CP=2,即t=2,同理当OP=5时,t=3,即:2≤t≤3,点P(t,4),点Q(8﹣t,0),同理可得直线PQ的表达式为:y=+,故点M(0,),S=PN×MC=×(4﹣t)(﹣4)=t,故2≤S≤3.2.解:(1)AB=5,边OA=4,则点A、B、C的坐标分别为:(0,4)、(5,4)、(5,0),直线l:y=2x+b,令y=0,则x=﹣b,当y=4时,x=,故点D、E的坐标分别为:(﹣b,0)、(,4);故答案为:(﹣b,0);(,4);(2)由(1)知点D、E的坐标分别为:(﹣b,0)、(,4);点A、C的坐标分别为:(0,4)、(5,0);则AE=,CD=5+b,四边形ADCE为平行四边形时,则AE=CD,即=5+b,解得:b=﹣3;(3)①当DE是菱形的边时,点F对应的点为:F′或F″,在菱形DEF′C中,DE=DC,即(﹣b﹣)2+(4﹣0)2=(5+b)2,解得:b=﹣10±4,当b=﹣10﹣4时,点E(7+,4)不在AB边上,故该b值舍去,故b=﹣10+4;当四边形F′′DEC为菱形时;同理可得:b=﹣2;②当DE是菱形的对角线时,AECD为菱形,点F点与点A重合,则AD=AE,即16+(﹣b)2=()2,解得:b=﹣6,综上:b=﹣10+4或﹣6或﹣2.3.解:(1)如图1,点D的坐标为(﹣1,0).故答案为:(﹣1,0);(2)过点A作AF⊥y轴于点F,连接AO、AC,如图2.∵点A的坐标为(1,2),∴AC=AO=,AF=1,OF=2.∵点A(1,2)在直线y=kx+1上,∴k+1=2,解得k=1.设直线y=x+1与y轴相交于点G,当x=0时,y=1,点G(0,1),OG=1,∴FG=OF﹣OG=2﹣1=1=AF,∴∠FGA=45°,AG=.在Rt△GAB中,AB=AG•tan45°=.在Rt△ABC中,BC==.∴所求“位置矩形”ABCD面积为AB•BC=;(3)设“位置矩形”的一组邻边长分别为x、y,则有x2+y2=AC2=AO2=12+32=10.∵(x﹣y)2=x2+y2﹣2xy=10﹣2xy≥0,∴xy≤5.当且仅当x=y时,xy取最大值是5,此时“位置矩形”是正方形.①当点D在第四象限时,如图3,过点A作x轴的平行线,交y轴于点M,交过点D平行于y轴的直线于点N,∵∠BAM+∠DAN=90°,∠BAM+∠ABM=90°,∴∠ABM=∠DAN,在RtAMB和Rt△DNA中,∠AMB=∠DNA,∠ABM=∠DAN,AB=AD,∴Rt△AMB≌Rt△DNA(AAS),则有AN=BM=2,DN=AM=1,∴点D的坐标为(1+2,﹣3+1),即(3,﹣2).②当点D在第三象限时,如图4,过点A作x轴的平行线,交y轴于点N,交过点D平行于y轴的直线于点M,同①的方法得:Rt△ANB≌Rt△DMA(AAS),则有DM=AN=1,AM=BN=2,∴点D的坐标为(1﹣2,﹣3+1)即(﹣1,﹣2).故答案为:5、(3,﹣2)或(﹣1,﹣2).4.解:(1)∵OA=3,OB=5,OD=4,∴AB=8,∴▱ABCD的面积=4×8=32,故答案为:32;(2)过点E作EF⊥AB于F,∵△ABE的面积是▱ABCD面积的,∴×AB×EF=×AB×OD,∴EF=2,∵OA=3,OB=5,OD=4,∴点B(5,0),点C(8,4),设BC解析式:y=kx+b,∴,解得:,∴BC的解析式:y=x﹣,当y=2时,x=,∴E(,2).5.解:(1)对于y=x+b,令x=0,则y=b,令y=0,则x+b=0,解得x=﹣b,故点A、B的坐标分别为(﹣b,0)、(0,b),则AO=OB=b,△AOB的面积=×AO×BO=b2=32,解得b=8,故点A、B的坐标分别为(﹣8,0)、(0,8),故一次函数的表达式为y=x+8;(2)点D是A、B的中点,则点D(﹣4,4),如图,过点P作PK⊥x轴于点K,连接BQ,∵OA=OB=8,故∠BAO=45°,t秒时,AP=t,OQ=2t,则AK=PK=t=yP,故点P的坐标为(﹣8+t,t),点Q(2t,0),S=S△AQB ﹣S△AQP=×AQ×(y B﹣y P)=×(2t+8)×(8﹣t)=﹣t2+4t+32(0≤t≤8);(3)由(2)知,点P的坐标为(﹣8+t,t),点Q(2t,0),设直线PQ的表达式为y=mx+n,则,解得,故直线PQ的表达式为y=﹣x+,∵OF=3DF,则OF:OD=3:4,如上图,分别过点D、F作x轴的垂线,垂足分别为M、N,∴△OFN∽△ODM,则=,而DM=4,故FN=3,由O、D的坐标知,直线OD的表达式为y=﹣x,当y=3时,则x=﹣3,故点F(﹣3,3),将点F的坐标代入y=﹣x+得,3=+,解得t=(舍去负值),故t=2,则点Q(4,0),由点QF的坐标得,QF==.的解析式是y=kx+b,6.解:(1)设l2根据题意得:,解得,则函数的解析式是:y=﹣x+4;(2)在y=x+1中令y=0,即y=x+1=0,解得:x=﹣2,则D的坐标是(﹣2,0).解方程组,解得,则C的坐标是(2,2).则S=×AD×y C=×6×2=6;△ADC(3)存在,理由:设C(2,2)关于x轴的对称点C′(2,﹣2),连接BC′交x轴于点E,则点E为所求点,△BCE的周长=BC+BE+CE=BC+BE+C′E=BC+BC′为最小,设经过(2,﹣2)和B的函数解析式是y=mx+n,则,解得:,则直线的解析式是y=﹣x+,令y=0,则y=﹣x+=0,解得:x=.则E的坐标是(,0).7.解:(1)将y=0代入得,解得:x=4,∴点A的坐标为(4,0).将x=0代入,并解得:y=﹣2,∴点B的坐标为(0,﹣2).将A(4,0)代入y=﹣x+b,得0=﹣4+b,解得b=4;(2)①由(1)知,直线的表达式为y=﹣x+4,∵点P(t,0),∴当x=t时,y=﹣x+4=﹣t+4,即D(t,﹣t+4);同理可得:,故答案为(t,﹣t+4)、(t,t﹣2);②A.存在,理由:由①得D(t,﹣t+4),,∵点P在线段OA上,∴,∵B(0,﹣2),∴OB=2.∵DE=OB,∴,解得:.∴,∴;B.存在,理由:由①得D(t,﹣t+4),.∵OP=t,.当点P在线段OA上时,,∴,解得t=3,故点D、E的坐标分别为(3,1)、(3,﹣),设点Q(m,0),则DE2=,DQ2=(m﹣3)2+1,DE2=(m﹣3)2+,当DE=DQ时,即=(m﹣3)2+1,解得m=3±(舍去3+);当DE=QE时,同理可得:m=3(舍去3+);点Q的坐标为或.当点P在线段OA的延长线上时,,∴,解得t=6,同理可得:点Q的坐标为或;综上所述,点Q的坐标为或或或.8.解:(1)∵直线y=2x+4与x轴、y轴分别交于点B、A.∴A(0,4),B(﹣2,0),∵直线AB与直线BC关于x轴对称,∴C(0,﹣4),设直线BC的解析式为y=kx+b,∴,解得,;∴直线BC的解析式为y=﹣2x﹣4;故答案为:y=﹣2x﹣4;(2)∵,∴,∴E(﹣4,4),∴AE⊥AO,设OP=a,AP=4﹣a,在Rt△BOP和Rt△EAP中,BP2=4+a2,PE2=16+(4﹣a)2,∵PE=PB,∴4+a2=16+(4﹣a)2,解得a=3.5.∴P(0,3.5).(3)①如图,当点P在点A的下方,∵∠OEB=∠PEA,∠AEO=45°,∴∠PEB=45°,过点B作BN⊥BE交直线EP于点N,过点N作NQ⊥OB于Q,过点E作EH⊥OB于点H,∴△EBN为等腰直角三角形,∴EB=BN,∵∠BEH+∠EBH=90°,∠EBH+∠NBQ=90°,∴∠BEH=∠NBQ,又∵∠EHB=∠BQN=90°,∴△EHB≌△BQN(AAS),∴NQ=BH=2,BQ=EH=4,∴N(2,2),设直线EN的解析式为y=kx+b,∴,解得,∴直线EN的解析式为y=﹣x+,∴,解得,即M(﹣,);②P点在A点的上方,由①知图1中OP=,则AP=,∴OP=,设直线EP的解析式为y=mx+,∵E(﹣4,4),∴﹣4m+=4,解得m=,∴直线EP的解析式为y=x+,∴,解得,∴M(0.8,5.6).综合以上可得点M的坐标为(﹣,)或(0.8,5.6).9.解:(1)∵直线BC:y=﹣x+3 交x轴于点B,交y轴于点C,∴B(3,0),C(0,3),∵CD=1,∴OD=4,D(0,4),∵AD⊥BC,∴直线AD的解析式为y=x+4.(2)如图所示,由y=﹣x+3和y=x+4可得点E的坐标为(﹣,),∵P(3﹣t,0),A(﹣4,0),△AEP的高是,=×AP×=×(4+3﹣t)×=﹣t+(0<t≤3);∴S△AEP(3)如图所示,则E(﹣,),Q(0,3﹣3t),F(3﹣t,t),①当EQ=EF时,使得以点E、Q、F、M为顶点且以EQ为边的四边形是菱形;则()2+(+3t)2=(﹣t)2+(t﹣)2,解得:t=1或﹣(舍去),∴Q(0,0),F(2,1),E(﹣,),设M(m,n),则有,解得,∴M(,﹣);②当EQ=QF时,使得以点E、Q、F、M为顶点且以EQ为边的四边形是菱形,则()2+(+3t)2=(3﹣t)2+(4t﹣3)2,解得:t=或﹣(舍去),同法可得点M的坐标为(,3).综上所述,t1=1,M1(,﹣);t2=1,M2(,3).10.解:(1)∵直线y=﹣x+m与y轴交于点B(12,0),∴0=﹣×12+m,∴m=9,∴直线AB的解析式为:y=﹣x+9,当x=0时,y=9,∴点A坐标为(0,9);(2)由题意可得:,解得:,∴点C(8,3),∴△BOC的面积=×12×3=18;(3)①如图,21 /21∵点D 的横坐标为t ,∴点D (t ,﹣t +9),点E (t ,t ),当t <8时,d =﹣t +9﹣t =﹣t +9,当t >8时,d =t +t ﹣9=t ﹣9;②∵以点H (,t )、G (1,t )为端点的线段与正方形DEPQ 的边只有一个交点, ∴≤t ≤1或, ∴≤t ≤1或≤t ≤.。
九年级中考数学专题复习:二次函数综合题(特殊三角形问题)含答案

中考数学专题复习:二次函数综合题(特殊三角形问题)1.如图,已知抛物线经过点A (-1,0),B (4,0),C (0,2)三点,点D 与点C 关于x 轴对称,点P 是线段AB 上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q ,交直线BD 于点M .(1)求该抛物线所表示的二次函数的表达式;(2)在点P 运动过程中,是否存在点Q ,使得△BQM 是直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由;(3)连接AC ,将△AOC 绕平面内某点H 顺时针旋转90°,得到111A O C △,点A 、O 、C 的对应点分别是点1A 、1O 、1C 、若111A O C △的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点1A 的横坐标.2.如图,已知A (﹣2,0)、B (3,0),抛物线y =ax 2+bx +4经过A 、B 两点,交y 轴于点C .点P 是第一象限内抛物线上的一动点,点P 的横坐标为m .过点P 作PM ⊥x 轴,垂足为点M ,PM 交BC 于点Q .过点P 作PN ⊥BC ,垂足为点N .(1)直接写出抛物线的函数关系式 ;(2)请用含m 的代数式表示线段PN 的长 ;(3)连接PC ,在第一象限的抛物线上是否存在点P ,使得⊥BCO +2⊥PCN =90°?若存在,请求出m 的值;若不存在,请说明理由;(4)连接AQ ,若△ACQ 为等腰三角形,请直接写出m 的值 .3.如图,抛物线2y ax bx =+过()4,0A ,()1,3B 两点,点C 、B 关于抛物线的对称轴对称,过点B 作直线BH x ⊥轴,交x 轴于点H .(1)求抛物线的表达式;(2)求ABC 的面积;(3)若点M 在直线BH 上运动,点N 在x 轴上运动,当CMN △为等腰直角三角形时,点N 的坐标为______.4.如图,已知二次函数的图象经过点()3,3A 、()4,0B 和原点O .P 为二次函数图象上的一个动点,过点P 作x 轴的垂线,垂足为(),0D m ,并与直线OA 交于点C .(1)求出二次函数的解析式;(2)当点P 在直线OA 的上方时,求线段PC 的最大值;(3)当0m >时,探索是否存在点P ,使得PCO △为等腰三角形,如果存在,求出P 的坐标;如果不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线2y ax x m =++(a ≠0)的图象与x 轴交于A 、C 两点,与y 轴交于点B ,其中点B 坐标为(0,-4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D 是直线AB 下方抛物线上一个动点,连接AD 、BD ,探究是否存在点D ,使得⊥ABD 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点P 为该抛物线对称轴上的动点,使得⊥P AB 为直角三角形,请求出点P 的坐标.6.如图,在平面直角坐标系xOy 中,抛物线26y ax bx =++与x 轴交于点()2,0A -和点()6,0B ,与y 轴交于点C ,顶点为D ,连接BC 交抛物线的对称轴l 于点E .(1)求抛物线的表达式;(2)连接CD 、BD ,点P 是射线DE 上的一点,如果PDB CDB S S =△△,求点P 的坐标;(3)点M 是线段BE 上的一点,点N 是对称轴l 右侧抛物线上的一点,如果EMN 是以EM 为腰的等腰直角三角形,求点M 的坐标.7.已知抛物线经过A (-1,0)、B (0、3)、 C (3,0)三点,O 为坐标原点,抛物线交正方形OBDC 的边BD 于点E ,点M 为射线BD 上一动点,连接OM ,交BC 于点F(1)求抛物线的表达式;(2)求证:⊥BOF =⊥BDF :(3)是否存在点M 使⊥MDF 为等腰三角形?若不存在,请说明理由;若存在,求ME 的长8.如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45︒得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式;(2)当点D 在第二象限且34DE EO =时,求点D 的坐标; (3)当ODF △为直角三角形时,请直接写出点D 的坐标.9.已知二次函数214y x bx c =-++图像的对称轴与x 轴交于点A (1,0),图像与y 轴交于点B (0,3),C 、D 为该二次函数图像上的两个动点(点C 在点D 的左侧),且90CAD ∠=.(1)求该二次函数的表达式;(2)若点C 与点B 重合,求tan⊥CDA 的值;(3)点C 是否存在其他的位置,使得tan⊥CDA 的值与(2)中所求的值相等?若存在,请求出点C 的坐标;若不存在,请说明理由.10.如图1,抛物线y =-x 2+bx +c 交x 轴于A ,B 两点,交y 轴于C 点,D 是抛物线上的动点,已知A 的坐标为(-3,0),C 的坐标为(0,3).(1)求该抛物线的函数表达式以及B 点的坐标;(2)在第二象限内是否存在点D 使得⊥ACD 是直角三角形且⊥ADC=90°,若存在请求出D 点的坐标,若不存在请说明理由;(3)如图2,连接AC ,BC ,当⊥ACD=⊥BCO ,求D 点的坐标.11.如图,在平面直角坐标系中,抛物线C 1:y =ax 2+bx ﹣1经过点A (﹣1,﹣2)和点B (﹣2,1),抛物线C 2:y =3x 2+3x +1,动直线x =t 与抛物线C 1交于点N ,与抛物线C 2交于点M .(1)求抛物线C 1的表达式;(2)求线段MN 的长(用含t 的代数式表达);(3)当⊥BMN 是以MN 为直角边的等腰直角三角形时,求t 的值.12.如图,二次函数23y ax bx =++的图象经过点A (-1,0),B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)第一象限内的二次函数23y ax bx =++图象上有一动点P ,x 轴正半轴上有一点D ,且OD =2,当S △PCD =3时,求出点P 的坐标;(3)若点M 在第一象限内二次函数图象上,是否存在以CD 为直角边的Rt MCD ,若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线23y ax bx =+-与x 轴交于()2,0A -,()6,0B 两点,与y 轴交于点C .直线l 与抛物线交于A ,D 两点,与y 轴交于点E ,点D 的坐标为()4,3-.(1)求抛物线的解析式;(2)若点P 是抛物线上的点,点P 的横坐标为()0m m ≥,过点P 作PM x ⊥轴,垂足为M .PM 与直线l 交于点N ,当点N 是线段PM 的三等分点时,求点P 的坐标;(3)若点Q 是y 轴上的点,且45ADQ ∠=︒,求点Q 的坐标.14.如图,抛物线23y ax bx =+-与x 轴交于()30A -,,()1,0B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)若点E 是线段AC 上一动点,过点E 的直线EF 平行于y 轴并交抛物线于点F ,当线段EF 取得最大值时,在x 轴上是否存在这样的点P ,使得以点E 、B 、P 为顶点的三角形是以EB 为腰的等腰三角形?若存在,请求出所有点P 的坐标;若不存在,请说明理由.15.如图,抛物线2y x bx c =-++与x 轴相交于A ,B 两点(点A 位于点B 的左侧),与y 轴相交于点C ,M 是抛物线的顶点,直线1x =是抛物线的对称轴,且点C 的坐标为(0,3).(1)求抛物线的解析式;(2)已知P 为线段MB 上一个动点,过点P 作PD x ⊥轴于点D .若,PD m PCD =△的面积为S .⊥求S 与m 之间的函数关系式,并写出自变量m 的取值范围;⊥当S 取得最大值时,求点P 的坐标.(3)在(2)的条件下,在线段MB 上是否存在点P ,使PCD 为等腰三角形?如果存在,直接写出满足条件的点P 的坐标;如果不存在,请说明理由.16.如图,在平面直角坐标系中,已知抛物线y =ax 2+4x +c 与直线AB 相交于点A (0,1)和点B (3,4).(1)求该抛物线的解析式;(2)设C 为直线AB 上方的抛物线上一点,连接AC ,BC ,以AC ,BC 为邻边作平行四边形ACBP ,求四边形ACBP 面积的最大值;(3)将该抛物线向左平移2个单位长度得到抛物线y =a 1x 2+b 1x +c 1(a 1≠0),平移后的抛物线与原抛物线相交于点D ,是否存在点E 使得△ADE 是以AD 为腰的等腰直角三角形?若存在,直接写出....点E 的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系中,抛物线223y x x =--与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴相交于点C ,连接,AC BC .(1)求线段AC 的长;(2)若点Р为该抛物线对称轴上的一个动点,当PA PC =时,求点P 的坐标;(3)若点M 为该抛物线上的一个动点,当BCM 为直角三角形时,求点M 的坐标.18.如图,已知抛物线212y x bx c =++经过点B (4,0)和点C (0,-2),与x 轴的另一个交点为点A ,其对称轴l 与x 轴交于点E ,过点C 且平行x 轴的直线交抛物线于点D ,连接AD .(1)求该抛物线的解析式;(2)判断⊥ABD 的形状,并说明理由;(3)P 为线段AD 上一点,连接PE ,若△APE 是直角三角形,求点P 的坐标;(4)抛物线的对称轴上是否存在一点P ,使△APD 是直角三角形,若存在,求出P 点坐标;若不存在,请说明理由.19.如图,抛物线22y ax x c =-+与x 轴相交于A ,B 两点,与y 轴相交于点C ,点A 在点B 的左侧,()1,0A -,()0,3C -,点E 是抛物线的顶点,P 是抛物线对称轴上的点.(1)求抛物线的函数表达式;(2)当点P 关于直线BC 的对称点Q 落在抛物线上时,求点Q 的横坐标;(3)若点D 是抛物线上的动点,是否存在以点B ,C ,P ,D 为顶点的四边形是平行四边形.若存在,直接写出点D 的坐标__________;若不存在,请说明理由;(4)直线CE 交x 轴于点F ,若点G 是线段EF 上的一个动点,是否存在以点O ,F ,G 为顶点的三角形与ABC 相似,若存在,请直接写出点G 的坐标__________;若不存在,请说明理由.20.如图1,抛物线23y ax bx =++与x 轴交于点()3,0A 、()1,0B -,与y 轴交于点C ,点P 为x 轴上方抛物线上的动点,点F 为y 轴上的动点,连接PA ,PF ,AF .(1)求该抛物线所对应的函数解析式;(2)如图1,当点F 的坐标为()0,4-,求出此时AFP 面积的最大值;(3)如图2,是否存在点F ,使得AFP 是以AP 为腰的等腰直角三角形?若存在,求出所有点F 的坐标;若不存在,请说明理由.参考答案:1.(1)213222y x x =-++ (2)存在,Q (3,2)或Q (-1,0)(3)两个“和谐点”,1A 的横坐标是1或122.(1)222433y x x =-++ (2)22655PN m m =-+ (3)存在,741253.(1)24y x x =-+(2)3(3)(2,0)或(﹣4,0)或(﹣2,0)或(4,0).4.(1)y =-x 2+4x (2)94(3)存在,点P 的坐标为(3+或(3-或(5,-5)或(4,0)5.(1)2142y x x =+- (2)(-2,-4)(3)P 点坐标为:(-1,3),(-1,-5),(12--+,,(12--, 6.(1)21262y x x =-++ (2)()2,2(3)()4,2或(27.(1)2y x 2x 3=-++(2)见解析(3)存在,2或28.(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)()3,4-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭9.(1)211342y x x =-++(2)1(3)()2,1-,()32,(12--10.(1)y =-x 2-2x +3,B (1,0)(2)存在,D (-2,3) (3)D (-52,74)或(-4,-5)11.(1)y =2x 2+3x ﹣1(2)t 2+2(3)t =012.(1)2+23y x x =-+(2)P 1(32,154),P 2(2,3)(3)存在点M 其坐标为1M 43539(,)或2M13.(1)y =14x 2−x −3 (2)(3,−154)或(0,−3) (3)(0,−133)或(0,9)14.(1)223y x x =+-(2)()4,-0,或10⎛⎫ ⎪ ⎪⎝⎭,或10⎛⎫ ⎪ ⎪⎝⎭15.(1)2y x 2x 3=-++ (2)⊥213(04)42S m m m =-+<≤;⊥S 有最大值为94,此时3,32P ⎛⎫ ⎪⎝⎭(3)存在,(6-+-或(42-+16.(1)241y x x =-++ (2)274(3)存在,E (4,3)或(-2,5)或(-3,2)或(3,0).17.(2)()11,-(3)()14-,或()25-,或⎝⎭或⎝⎭18.(1)213222y x x =-- (2)直角三角形,见解析(3)(1,-1)或(32,-54)(4)存在,( 32,-1+2 ),( 32,-1- 2,( 32,5),( 32,-5) 19.(1)223y x x =-- (2)11(3)存在,()2,3-或()4,5或()2,5-(4)存在,39,44⎛⎫-- ⎪⎝⎭或()1,2--20.(1)2y x 2x 3=-++ (2)323(3)存在,12(0,3),(0,1)F F --,32)F。
最新九年级中考数学专题: 二次函数综合题(相似三角形问题)含答案
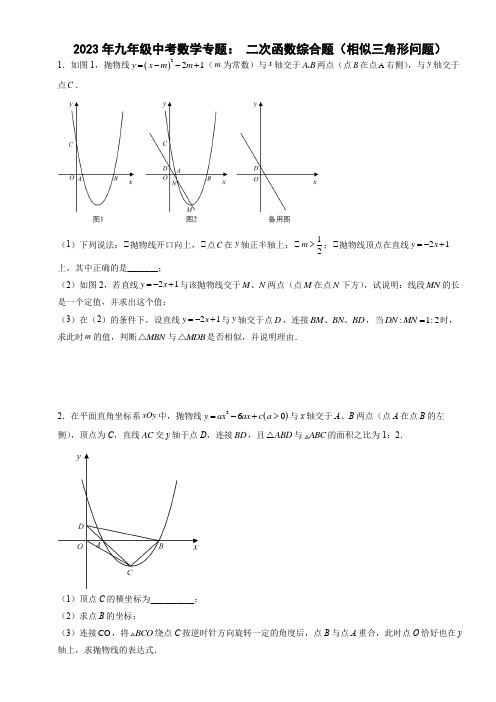
2023年九年级中考数学专题: 二次函数综合题(相似三角形问题)1.如图1,抛物线()221y x m m =--+(m 为常数)与x 轴交于A B 、两点(点B 在点A 右侧),与y 轴交于点C .(1)下列说法:①抛物线开口向上,①点C 在y 轴正半轴上;①12m >;①抛物线顶点在直线21y x =-+上,其中正确的是_______;(2)如图2,若直线21y x =-+与该抛物线交于M N 、两点(点M 在点N 下方),试说明:线段MN 的长是一个定值,并求出这个值;(3)在(2)的条件下,设直线21y x =-+与y 轴交于点D ,连接BM BN BD 、、,当:1:2DN MN =时,求此时m 的值,判断MBN △与MDB △是否相似,并说明理由.2.在平面直角坐标系xOy 中,抛物线()260y ax ax c a =-+>与x 轴交于A 、B 两点(点A 在点B 的左侧),顶点为C ,直线AC 交y 轴于点D ,连接BD ,且ABD △与ABC 的面积之比为1:2.(1)顶点C 的横坐标为__________; (2)求点B 的坐标;(3)连接CO ,将BCO 绕点C 按逆时针方向旋转一定的角度后,点B 与点A 重合,此时点O 恰好也在y 轴上,求抛物线的表达式.3.如图,抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B ,与y 轴交于点C ,点D 是直线BC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,过点D 作DE x ⊥轴于点E ,交直线BC 于点M .当2DM ME =时,求点D 的坐标; (3)如图2,设AB 的中点为点N ,过点D 作DF BC ⊥于点F ,连接CD 、CN ,使得以C 、D 、F 三点为顶点的三角形与CNO 相似,请直接写出点D 的坐标.4.如图,在平面直角坐标系xOy 中,抛物线()2y a x h k =-+与x 轴相交于O ,A 两点,顶点P 的坐标为()2,1-.点B 为抛物线上一动点,连接,AP AB ,过点B 的直线与抛物线交于另一点C .(1)求抛物线的函数表达式;(2)若点B 的横坐标与纵坐标相等,ABC OAP ∠=∠,且点C 位于x 轴上方,求点C 的坐标; (3)若点B 的横坐标为t ,90ABC ∠=︒,请用含t 的代数式表示点C 的横坐标,并求出当0t <时,点C 的横坐标的取值范围.5.如图,在平面直角坐标系xOy 中,抛物线213442y x x =-++与两坐标轴分别相交于A ,B ,C 三点(1)求证:①ACB =90°(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F . ①求DE +BF 的最大值;①点G 是AC 的中点,若以点C ,D ,E 为顶点的三角形与AOG 相似,求点D 的坐标.6.在平面直角坐标系xOy 中,已知抛物线L 与x 轴交于,A B 两点,且经过点(0,2)C -,抛物线的顶点D 的坐标为325,28⎛⎫- ⎪⎝⎭.(1)求抛物线L 的函数表达式;(2)如图1,点E 为第四象限抛物线L 上一动点,过点E 作EG BC ⊥于点G ,求EG 的最大值,及此时点E 的坐标;(3)如图2,连接,AC BC ,过点O 作直线//l BC ,点,P Q 分别为直线l 和抛物线L 上的点.试探究:在第一象限是否存在这样的点,P Q ,使PQB CAB ∽.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.7.如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C .(1)求A 、B 、C 三点的坐标;(2)过点A 作AP ①CB 交抛物线于点P ,求四边形ACBP 的面积;(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ①x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与①PCA 相似?若存在,请求出M 点的坐标;否则,请说明理由.8.如图,在同一直角坐标系中,抛物线1L :28y ax bx =++与x 轴交于()8,0A -和点C ,且经过点()2,12B -,若抛物线1L 与抛物线2L 关于y 轴对称,点A 的对应点为'A ,点B 的对应点为'B .(1)求抛物线2L 的表达式;(2)现将抛物线2L 向下平移后得到抛物线3L ,抛物线3L 的顶点为M ,抛物线3L 的对称轴与x 轴交于点N ,试问:在x 轴的下方是否存在一点M ,使MNA '与ACB '△相似?若存在,请求出抛物线的3L 表达式;若不存在,说明理由.9.如图,在平面直角坐标系中,抛物线26y ax bx =++与x 轴交于点(1,0),(3,0)A B -,与y 轴交于点C ,点P 是第一象限内抛物线上的动点. (1)求抛物线的解析式;(2)连接BC 与OP ,交于点D ,当:PD OD 的值最大时,求点P 的坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使90CMN ∠=︒,且CMN △与BOC 相似,若存在,请直接写出点M 的坐标.10.如图,已知抛物线23y ax bx =+-与x 轴交于()2,0A -、()6,0B 两点,与y 轴交于C 点,设抛物线的顶点为D .过点D 作DE x ⊥轴,垂足为E .P 为线段DE 上一动点,(),0F m 为x 轴上一点,且PC PF ⊥.(1)求抛物线的解析式:(2)①当点P 与点D 重合时,求m 的值;①在①的条件下,将COF 绕原点按逆时针方向旋转90︒并平移,得到111C O F △,点C ,O ,F 的对应点分别是点1C ,1O ,1F ,若COF 的两个顶点恰好落在抛物线上,直接写出点1F 的坐标; (3)当点P 在线段DE 上运动时,求m 的变化范围.11.综合与实践如图1,抛物线y =﹣83x 2﹣94x +6与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .(1)求直线AC 的表达式;(2)点E 在抛物线的对称轴上,在平面内是否存在点F ,使得以点A ,C ,E ,F 为顶点的四边形是矩形?若存在,请直接写出点E 的坐标;若不存在,请说明理由;(3)如图2,设点P 从点O 出发以1个单位长度/秒的速度向终点A 运动,同时点Q 从点A 出发以54个单位长度/秒的速度向终点C 运动,运动时间为t 秒,当①OPQ 的平分线恰好经过OC 的中点时,求t 的值.12.抛物线23y x bx =-++与x 轴交于(3,0),(1,0)A B -两点,与y 轴交于点C ,点D 为抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标; (2)在直线AC 上方的抛物线上找一点P ,使12ACPACDSS =,求点P 的坐标;(3)在坐标轴上找一点M ,使以点B ,C ,M 为顶点的三角形与ACD △相似,直接写出点M 的坐标.13.如图,将抛物线2443y x =-+平移后,新抛物线经过原抛物线的顶点C ,新抛物线与x 轴正半轴交于点B ,联结BC ,tanB 4=,设新抛物线与x 轴的另一交点是A ,新抛物线的顶点是D .(1)求点D 的坐标;(2)设点E 在新抛物线上,联结,AC DC ,如果CE 平分DCA ∠,求点E 的坐标;(3)在(2)的条件下,将抛物线2443y x =-+沿x 轴左右平移,点C 的对应点为F ,当DEF 和ABC 相似时,请直接写出平移后得到抛物线的表达式.14.在平面直角坐标系xOy 中,已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A B ,两点(点A 在点B 的左边),与y 轴交于点C ,其顶点的横坐标为1,且过点(2)3,和(312)--,. (1)求此二次函数的表达式;(2)若直线:(0)l y kx k =≠与线段BC 交于点D (不与点B C ,重合),则是否存在这样的直线l ,使得以B O D ,,为顶点的三角形与BAC 相似?若存在,求出该直线的函数表达式及点D 的坐标;若不存在,请说明理由;(3)若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角PCO ∠与ACO ∠的大小(不必证明),并写出此时点P 的横坐标p x 的取值范围.15.如图1,在平面直角坐标系中,抛物线2y x bx c =-++经过点A 和点()10B ,,交y 轴于点()0,3C .(1)求抛物线的解析式及顶点D 的坐标;(2)点P 是抛物线上A 、D 之间的一点,过点P 作PE x ⊥轴于点E ,PG y ⊥轴,交抛物线于点G ,过点G 作GF x ⊥轴于点F ,当矩形PEFG 的周长最大时,求点P 的坐标;(3)如图2,连接AD 、BD ,点M 在线段AB 上(不与A 、B 重合),作直线MN x ⊥轴交抛物线于点N ,是否存在点M ,使得AMN 与OBC 相似?若存在,求出点M 的坐标;若不存在,请说明理由.16.在平面直角坐标系xOy 中,已知抛物线2y ax bx c =++与x 轴交于()1,0A -,()4,0B 两点,与y 轴交于点()0,2C -.(1)求抛物线的函数表达式;(2)如图1,点D 为第四象限抛物线上一点,连接AD ,BC 交于点E ,求DEAE的最大值; (3)如图2,连接AC ,BC ,过点O 作直线//l BC ,点P ,Q 分别为直线l 和抛物线上的点,试探究:在第一象限是否存在这样的点P ,Q ,使PQB CAB ∽.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.17.如图1,在平面直角坐标xoy 系中,已知抛物线y =-12x 2+bx +c 与x 轴交于点A (﹣4,0)、B(2,0),与y 轴交于点C . (1)求抛物线的解析式;(2)如图2,沿直线AC 平移抛物线y =-12x 2+bx +c ,使得A 、C 两点的对应点E 、F 始终在直线AC上.①设在平移过程中抛物线与y 轴交于点M ,求点M 纵坐标的最大值;①试探究抛物线在平移过程中,是否存在这样的点E ,使得以A 、E 、B 为顶点的三角形与①ABF 相似.若存在,请求出此时点E 的坐标;若不存在,请说明理由.18.如图,已知二次函数y =ax 2+bx +c 的图象经过点A (﹣1,0),B (4,0),E (1,3),与y 轴交于点C .(1)求该二次函数表达式;(2)判断△ABC 的形状,并说明理由;(3)P 为第一象限内该二次函数图象上一动点,过P 作PQ ∥AC ,交直线BC 于点Q ,作PM ∥y 轴交BC 于M .①求证:△PQM ∽△COA ; ②求线段PQ 的长度的最大值.19.如图,直线y x n =-+与x 轴交于点(4,0)A ,与y 轴交于点B ,抛物线2y x bx c =-++经过点A ,B .(1)求抛物线的解析式;(2)(m,0)E 为x 轴上一动点,过点E 作ED x ⊥轴,交直线AB 于点D ,交抛物线于点P ,连接BP . ①点E 在线段OA 上运动,若BPD ∆直角三角形,求点E 的坐标;①点E 在x 轴的正半轴上运动,若45PBD CBO ∠+∠=︒.请直接写出m 的值.20.如图,点A ,B 都在x 轴上,过点A 作x 轴的垂线交抛物线24y x x =-+于点C ,过点B 作x 轴的垂线交该抛物线于点D ,点C ,D 都在第一象限,点D 在点C 的右侧,DE AC ⊥于点E ,连结CD ,BE ,//CD EB .(1)若2OA =,求AB 的长.(2)若点A 是线段OB 的中点,求点E 的坐标.(3)根据(2)的条件,连结OD ,动点P 在线段OB 上,作PQ OD ⊥交OD 于点Q ,当PDQ 与CDE △相似时,求OQOD的值.答案1.(1)①①①;(3)m =3,相似;m =1,不相似2.(1)3;(2)(5,0);(3)2y 3.(1)2y x 2x 3=-++;(2)()2,3D ;(3)57,24D ⎛⎫ ⎪⎝⎭或315,24⎛⎫ ⎪⎝⎭4.(1)214y x x =-或21(2)14y x =--;(2)点C 的坐标为(6,3)或51,4⎛⎫- ⎪⎝⎭;(3)164t t --+;12C x ≥ 5.(1)(2)①9;①(4,6)D 或25(3,)4D .6.(1)213222y x x =--;(2)max ()=EG E 的坐标为(2,3)-;(3)存在,点P 的坐标为6834,99⎛⎫ ⎪⎝⎭或⎝⎭. 7.(1)A (-1,0),B (1,0),C (0,-1);(2)四边形ACBP 的面积为4;(3)M 点的坐标为(-2,3)或(43,79)或(4,15). 8.(1)抛物线2L 的解析式为21382y x x =-++.(2)函数3L 的解析式为:2121322y x x =-+-或2126323y x x =-+-. 9.(1)2 246y x x =-++;(2)点P 的坐标为315,22⎛⎫ ⎪⎝⎭;(3)存在,点M 的坐标为939,48⎛⎫ ⎪⎝⎭. 10.(1)2134y x x =--;(2)①4;①1(2,9)16或13(6-,49)144;(3)748m ≤≤ 11.(1)直线AC 的表达式为364y x =+;(2)点E 1的坐标为20(3,)3--;点E 2的坐标为(3,10)-;点E 3的坐标为(3,3-+;点E 4的坐标为(3,3--;(3)t 的值为5.12.(1)223y x x =--+;(1,4)D -;(2)⎝⎭P 或⎝⎭;(3)点M 的坐标为(0,0)或(9,0)-,或10,3⎛⎫- ⎪⎝⎭. 13.(1)16(1,)3-;(2)(2,4)-;(3)242()433y x =-++或241()4312y x =--+ 14.(1)2y x 2x 3=-++;(2)存在,点D 的坐标分别为3944⎛⎫ ⎪⎝⎭,或(12),; (3)当5p x >时,锐角PCO ACO ∠<∠;当5p x =时,锐角PCO ACO ∠=∠;当25p x <<时,锐角PCO ACO ∠>∠.15.(1)223y x x =--+,()1,4-;(2)()2,3P -;(3)存在,()2,0-或2,03⎛⎫ ⎪⎝⎭16.(1)213222y x x =--;(2)45;(3)存在,点P 的坐标为6834,99⎛⎫ ⎪⎝⎭或⎝⎭17.(1)2142y x x =--+;(2)①6;①存在,E (62--或(62--18.(1)二次函数表达式为:213222y x x =-++ ;(2)△ABC 为直角三角形;(3); 19.(1)234y x x =-++;(2)①(2,0)或(3,0);①7m =或134.20.(1;(2)1296,749E ⎛⎫ ⎪⎝⎭;(3)2或4932。
2023年九年级中考数学专题复习:二次函数综合题(角度问题)含答案

2023年九年级中考数学专题复习: 二次函数综合题(角度问题)1.已知抛物线2y x bx c =++经过点()1,0A -和点()0,3C -,与x 轴交于另一点B .(1)求抛物线的解析式;(2)点P 为第四象限内抛物线上的点,连接,,CP AP AC ,如图1,当CP AC ⊥时,求P 点坐标;(3)设点M 为抛物线上的一点,若2MAB ACO ∠=∠时,求M 点坐标.2.如图,已知抛物线213y x bx c =-++交x 轴于()30A -,,()4,0B 两点,交y 轴于点C ,点P 是抛物线上一点,连接AC 、BC .(1)求抛物线的表达式;(2)连接OP ,BP ,若2BOP AOC S S =△△,求点P 的坐标;(3)在抛物线的对称轴上是否存在点Q ,使得∠QBA =75°?若存在,直接写出点Q 的坐3.已知抛物线y=ax2+2x+c过A(﹣1,0),C(0,3),交x轴于另一点B.点P是抛物线上一动点(不与点C重合),直线CP交抛物线对称轴于点N.(1)求抛物线的解析式;(2)连接AN,当∠ANC=45°时,求P点的横坐标;(3)如图2,过点N作NM∠y轴于点M,连接AM,当AM+MN+CN的值最小时,直接写出N点的坐标.4.如图,抛物线y=34x2+bx+c交x轴于A,B两点,交轴于点C,点A,B的坐标分别为(-1,0),(4,0).(1)求抛物线的解析式;(2)点P是直线BC下方的抛物线上一动点,求∠CPB的面积最大时点P的坐标;(3)若M是抛物线上一点,且∠MCB=∠ABC,请直接写出点M的坐标.5.如图,抛物线y 14=x 2+bx +c 与直线y 12=-x +3分别交于x 轴,y 轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为A ,顶点为D ,连接CD 交x 轴于点E .(1)求该抛物线的解析式;(2)点F ,G 是对称轴上两个动点,且FG =2,点F 在点G 的上方,请求出四边形ACFG 的周长的最小值;(3)连接BD ,若P 在y 轴上,且∠PBC =∠DBA +∠DCB ,请直接写出点P 的坐标.6.如图∠,二次函数2y ax bx c =++(a ≠0)的图象经过点A (1-,0),并且与直线122y x =-相交于坐标轴上的B 、C 两点,动点P 在直线BC 下方的二次函数的图象上. (1)求此二次函数的表达式;(2)如图∠,连接PC ,PB ,设∠PCB 的面积为S ,求S 的最大值; (3)如图∠,过点A ,C 作直线,求证AC ∠BC ;(4)如图∠,抛物线上是否存在点Q ,使得∠ABQ =2∠ABC ?若存在,则求出直线BQ 的解析式;若不存在,请说明理由.7.如图,在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于(1,0)A ,(4,0)B 两点,与y 轴交于点(0,2)C .(1)求抛物线的表达式; (2)求证:CAO BCO ∠=∠;(3)若点P 是抛物线上的一点,且PCB ACB BCO ∠+∠=∠,求直线CP 的表达式.8.如图,已知抛物线(2)(4)y a x x =+-(a 为常数,且a >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B 的直线34y x b =-+与抛物线的另一交点为D .(1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)若在第一象限的抛物线上有点P ,使得以A ,B ,P 为顶点的三角形与∠ABC 相似,求a 的值;(3)在(1)的条件下,直线BD 上是否存在点E ,使∠AEC =45°?若存在,请直接写出点E 的横坐标;若不存在,请说明理由.9.如图,直线y =﹣x +3与x 轴、y 轴分别交于B 、C 两点,抛物线y =﹣x 2+bx +c 经过B 、C 两点,与x 轴另一交点为A ,顶点为D . (1)求抛物线的解析式.(2)如果一个圆经过点O 、点B 、点C 三点,并交于抛物线AC 段于点E ,求∠OEB 的(3)在抛物线的对称轴上是否存在点P ,使∠PCD 为等腰三角形,如果存在,直接写出点P 的坐标,如果不存在,请说明理由.(4)在抛物线的对称轴上是否存在一点P ,使∠APB =∠OCB ?若存在,求出PB 2的值;若不存在,请说明理由.10.在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线212y x bx c =-++经过A ,B 两点且与x 轴负半轴交于点C .(1)求该抛物线的解析式;(2)若点D 为直线AB 上方抛物线上的一个动点,当2ABD BAC ∠=∠时,求点D 的坐标;(3)已知E 是x 轴上的点,F 是抛物线上的动点,当B ,C ,E ,F 为顶点的四边形是平行四边形时,求出所有符合条件的E 的坐标.11.如图,在平面直角坐标系中,直线122y x =-+与x 轴交于点A ,与y 轴交于点B ,抛物线212y x bx c =-++经过A ,B 两点且与x 轴的负半轴交于点C .(1)求该抛物线的解析式;(2)若点D 为直线AB 上方抛物线上的一个动点,当2ABD BAC ∠=∠时,求点D 的坐(3)已知E是x轴上的点,F是抛物线上的动点,当B,C,E,F为顶点的四边形是平行四边形时,求出所有符合条件的E点的坐标,12.如图1,抛物线2=-+与x轴交于A(-2,0)、B(4,0)两点,与y轴交于y ax x c点C,直线l与抛物线交于A、D两点,其中D点的横坐标为2.(1)求抛物线的解析式以及直线AD的解析式;(2)点P是抛物线上位于直线AD下方的动点,过点P作x轴,y轴的平行线,交AD 于点E、F,当PE+PF取最大值时,求点P的坐标;(3)如图2,连接AC,点Q在抛物线上,且满足∠QAB=2∠ACO,求点Q的坐标.13.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).(1)求该抛物线的表达式及顶点坐标;(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P 的坐标;(3)在(2)的条件下,在对称轴上是否存在一点Q,连接PQ,将线段PQ绕点Q顺时针旋转90°,使点P恰好落在抛物线上?若存在,请求出点Q的坐标;若不存在,请14.抛物线2y x bx c =-++与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴正半轴交于点C .(1)如图1,若()1,0A -,()3,0B , ∠求抛物线2y x bx c =-++的解析式;∠Р为抛物线上一点,连接AC 、PC ,若AC PC ⊥,求点P 的坐标;(2)如图2,D 为x 轴下方抛物线上一点,连DA ,DB ,若290BDA BAD ∠+∠=︒,求点D 的纵坐标.(1)如图1,抛物线21y ax bx =++与x 轴交于点A 和点()3,0B ,对称轴为直线1x =; ∠求抛物线的解析式;∠点P 为抛物线上一动点,PN BC ⊥,垂点为N ,当PCN △与BOC 相似时,直接写出P 点坐标;(2)点D 为抛物线顶点,若抛物线上有且只有一个点Q 的横坐标是纵坐标的2倍,且45DCO ∠=︒,求a 的值.16.如图,点B ,C 分别在x 轴和y 轴的正半轴上,OB ,OC 的长分别为28120x x -+=的两个根()OC OB >,点A 在x 轴的负半轴上,且3OA OC OB ==,连接AC .(1)求过A ,B ,C 三点的抛物线的函数解析式;(2)点P 从点C 出发,以每秒2个单位长度的速度沿CA 运动到点A ,点Q 从点O 出发,以每秒1个单位长度的速度沿OC 运动到点C ,连接PQ ,当点P 到达点A 时,点Q 停止运动,求CPQ S △的最大值;(3)M 是抛物线上一点,是否存在点M ,使得15ACM ∠=︒?若存在,请求出点M 的坐标;若不存在,请说明理由.17.如图,已知二次函数2y x bx c =-++的图象经过点()()1,0,3,0A B -,与y 轴交于点C .(1)求抛物线的解析式;(2)点D 为抛物线的顶点,求BCD △的面积;(3)抛物线上是否存在点P ,使PAB ABC ∠=∠,若存在,请直接写出点P 的坐标;若不存在,请说明理由.18.已知直线43y x n =-+交x 轴于点A ,交y 轴于点C (0,4),抛物线223y x bx c =++经过点A ,交y 轴于点B (0,-2),点P 为抛物线上一个动点,设P 的横坐标为m (m >0),过点P 作x 轴的垂线PD ,过点B 作BD ∠PD 于点D ,联结PB . (1)求抛物线的解析式;(2)当△BDP 为等腰直角三角形时,求线段PD 的长;(3)将△BDP 绕点B 旋转得到△BD P '',且旋转角∠PB P '=∠OAC ,当点P 对应点P '落在y 轴上时,求点P 的坐标.19.如图,顶点为(),P m m (0m >)的二次函数图象与x 轴交于点()2,0A m ,点B 在该图象上,直线OB 交二次函数图象对称轴l 于点M ,点M 、N 关于点P 对称,连接BN 、(1)求该二次函数的关系式(用含m 的式子表示).(2)若点B 在对称轴l 右侧的二次函数图象上运动,请解答下列问题: ∠连接OP ,当12OP MN =时,请判断NOB 的形状,并说明理由. ∠求证:BNM ONM ∠=∠.20.如图1,已知抛物线21y x =-与x 轴交于A ,B 两点,与y 轴交于点D . (1)求直线BD 的解析式;(2)P 为抛物线上一点,当点Р到直线BD 的距离为P 的坐标; (3)如图2,直线y t =交抛物线与M ,N 两点,C 为抛物线上一点,当90MCN ∠=︒时,请探究点C 到MN 的距离是否为定值.参考答案:1.(1)223y x x =--(2)(73,209-) (3)点M 的坐标为939,416⎛⎫- ⎪⎝⎭或1557,416⎛⎫ ⎪⎝⎭2.(1)211433y x x =-++(2)(﹣5,﹣6)或(6,﹣6)(3)存在,Q 的坐标为(12,(123.(1)2y x 2x 3=-++(2)44(3)(1,32)4.(1)239344y x x =-- (2)92,2P ⎛⎫- ⎪⎝⎭ (3)M 的坐标为()3,3-或531125,749⎛⎫ ⎪⎝⎭5.(1)抛物线的解析式为:21234y x x =-+(2)四边形ACFG 2(3)点P 的坐标为(0,﹣2)或(0,18)6.(1)213222y x x =--;(2)4;(4)存在,41633y x =-和41633y x =-+. 7.(1)215222y x x =-+;(3)直线CP 的解析式为423y x =-+或2y =8.(1):y =14x 2-12x -2;(2)a (3)在直线BD 上不存在点E ,使∠AEC =45°.理由见解析9.(1)y =﹣x 2+2x +3;(2)45°;(3)存在,点P (1,2)、(1,3)、(1,4)、(1,、(1,4;(4)存在,.10.(1)213222y x x =-++;(2)(2,3);(3)()3,2或2⎫-⎪⎪⎝⎭. 11.(1)抛物线得解析式为213222y x x =-++;(2)点D 的坐标为()2,3;(3)E 点的坐标为(2,0)或(52,0)或(52,0)或(-4,0). 12.(1)2142y x x =--,2y x =--;(2)P (0,-4);(3)点Q 的坐标为440(,)39-,20104(,)39. 13.(1)y =x 2-4x +3,顶点(2,-1);(2)(113,169);(3)(2,109)或(2,319) 14.(1)∠2–23y x x =++;∠720(,)39P ;(2)1- 15.(1)∠212133y x x =-++;∠()2,1,1735,416⎛⎫- ⎪⎝⎭,52,3⎛⎫-- ⎪⎝⎭;(2)1916a =或22516a =16.(1)21262y x x =--+;(2(3)存在,M 4⎡-⎢⎣⎦或(4--- 17.(1)2y x 2x 3=-++;(2)3;(3)存在,P 1(2,3),P 2(4,-5) 18.(1)224233y x x =--;(2)72或12;(3)P (258,1132)或(7255,896-) 19.(1)()12y x x m m =--;(2)∠等腰直角三角形20.(1)1y x =-;(2)P ⎝⎭或P ⎝⎭;(3)C 到MN 的距离为定值1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考总复习函数综合【考纲要求】1.平面直角坐标系的有关知识平面直角坐标系中各象限和坐标轴上的点的坐标的特征,求点关于坐标轴、坐标原点的对称点的坐标,求线段的长度,几何图形的面积,求某些点的坐标等.2.函数的有关概念求函数自变量的取值范围,求函数值、函数的图象、函数的表示方法.3.函数的图象和性质常见的题目是确定图象的位置,利用函数的图象确定某些字母的取值,利用函数的性质解决某些问题.利用数形结合思想来说明函数值的变化趋势,又能反过来判定函数图象的位置.4.函数的解析式求函数的解析式,求抛物线的顶点坐标、对称轴方程,利用函数的解析式来求某些字母或代数式的值.一次函数、反比例函数和二次函数常与一元一次方程、一元二次方程、三角形的面积、边角关系、圆的切线、圆的有关线段组成综合题.【知识网络】【考点梳理】考点一、平面直角坐标系 1.相关概念(1)平面直角坐标系 (2)象限 (3)点的坐标2.各象限内点的坐标的符号特征3.特殊位置点的坐标 (1)坐标轴上的点(2)一三或二四象限角平分线上的点的坐标 (3)平行于坐标轴的直线上的点的坐标 (4)关于x 轴、y 轴、原点对称的点的坐标 4.距离(1)平面上一点到x 轴、y 轴、原点的距离(2)坐标轴或平行于坐标轴的直线上两点间的距离 (3)平面上任意两点间的距离 5.坐标方法的简单应用(1)利用坐标表示地理位置 (2)利用坐标表示平移 要点进阶:点P(x,y)到坐标轴及原点的距离:(1)点P(x,y)到x 轴的距离等于y ; (2)点P(x,y)到y 轴的距离等于x ; (3)点P(x,y)到原点的距离等于22y x .考点二、函数及其图象 1.变量与常量 2.函数的概念3.函数的自变量的取值范围4.函数值5.函数的表示方法(解析法、列表法、图象法)6.函数图象 要点进阶:由函数解析式画其图像的一般步骤:(1)列表:列表给出自变量与函数的一些对应值;(2)描点:以表中每对对应值为坐标,在坐标平面内描出相应的点;(3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来.考点三、一次函数1.正比例函数的意义2.一次函数的意义3.正比例函数与一次函数的性质4. 一次函数的图象与二元一次方程组的关系5.利用一次函数解决实际问题 要点进阶:确定一个正比例函数,就是要确定正比例函数定义式kx y =(k ≠0)中的常数k ;确定一个一次函数,需要确定一次函数定义式b kx y +=(k ≠0)中的常数k 和b.解这类问题的一般方法是待定系数法.考点四、反比例函数 1.反比例函数的概念2.反比例函数的图象及性质3.利用反比例函数解决实际问题 要点进阶:反比例函数中反比例系数的几何意义,如下图,过反比例函数)0(≠=k xky 图像上任一点),(y x P 作x 轴、y 轴的垂线PM ,PN ,垂足为M 、N ,则所得的矩形PMON 的面积S=PM •PN=xy x y =•.,y xk=∴||k S k xy ==,.考点五、二次函数 1.二次函数的概念2.二次函数的图象及性质3.二次函数与一元二次方程的关系4.利用二次函数解决实际问题 要点进阶:1、两点间距离公式(当遇到没有思路的问题时,可用此方法拓展思路,以寻求解题方法) 如图:点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则AB 间的距离,即线段AB 的长度为()()221221y y x x -+-.2、函数平移规律:左加右减、上加下减.3、二次函数的最值如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当abx 2-=时,ab ac y 442-=最值.如果自变量的取值范围是21x x x ≤≤,那么,首先要看ab2-是否在自变量取值范围21x x x ≤≤内,若在此范围内,则当x=ab2-时,a b ac y 442-=最值;若不在此范围内,则需要考虑函数在21x x x ≤≤范围内的增减性,如果在此范围内,y 随x 的增大而增大,则当2x x =时,c bx ax y ++=222最大,当1x x =时,c bx ax y ++=121最小;如果在此范围内,y 随x 的增大而减小,则当1x x =时,c bx ax y ++=121最大,当2x x =时,c bx ax y ++=222最小.4、抛物线的对称变换 ①关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---.②关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++.③关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-. ④关于顶点对称2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.⑤关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-.根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a永远不变.求抛物线的对称图象的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.考点六、函数的应用1.一次函数的实际应用2. 反比例函数的实际应用3. 二次函数的实际应用要点进阶:分段函数是指自变量在不同的取值范围内,其关系式(或图象)也不同的函数,分段函数的应用题多设计成两种情况以上,解答时需分段讨论.在现实生活中存在着很多需分段计费的实际问题,因此,分段计算的应用题成了近几年中考应用题的一种重要题型.【典型例题】类型一、用函数的概念与性质解题例1.在平面直角坐标系中,点A的坐标是(4,0),点P是第一象限内的直线y=6-x上的点,O 是坐标原点(如图所示):(1)P点坐标设为(x, y) ,写出ΔOPA的面积S的关系式;(2)S与y具有怎样的函数关系,写出这函数中自变量y的取值范围;(3)S与x具有怎样的函数关系?写出自变量x的取值范围;(4)如果把x看作S的函数时,求这个函数解析式,并写出这函数中自变量取值范围;(5)当S=10时,求P的坐标;(6)在直线y=6-x上,求一点P,使ΔPOA是以OA为底的等腰三角形.举一反三:2x+4x+k-1=0有实数根,k为正整数.【变式】已知关于x的一元二次方程2(1)求k的值;y=2x+4x+k-1的图象向下平移8个单位,(2)当此方程有两个非零的整数根时,将关于x的二次函数2求平移后的图象的解析式;(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线1y=x+b(b<k)2与此图象有两公共点时,b的取值范围.2.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )(A) (B) (C) (D)举一反三:【变式】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快骑车速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合这个同学行驶情况的图象大致是( ).类型二、函数的综合题例3.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为()A.4 B.8 C.16 D.82举一反三:【变式】在坐标系中,二次函数2(3)3(0)y mx m x m=+-->的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A的坐标;(2)当45ABC∠=︒时,求m的值;(3)已知一次函数y kx b=+,点P(n,0)是x轴上的一个动点,在(2)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数2(3)3(0)y mx m x m=+-->的图象于N. 若只有当22n-<<时,点M位于点N的上方,求这个一次函数的解析式.A BCOyx例4.函数y=和y=在第一象限内的图象如图,点P是y=的图象上一动点,PC⊥x轴于点C ,交y=的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=AP.其中所有正确结论的序号是()举一反三:【变式】如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t)秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是(类型三、函数与几何综合题例5.如图,将—矩形OABC 放在直角坐际系中,O 为坐标原点.点A 在y 轴正半轴上.点E 是边AB 上的—个动点(不与点A 、B 重合),过点E 的反比例函数(0)ky x x=>的图象与边BC 交于点F. (1)若△OAE、△OCF 的而积分别为S 1、S 2.且S 1+S 2=2,求k 的值;(2)若OA=2.0C=4.问当点E 运动到什么位置时,四边形OAEF 的面积最大.其最大值为多少?例6.如图,在平面直角坐标系中,已知点A (8,1),B (0,﹣3),反比例函数 y=(x >0)的图象经过点A ,动直线x=t (0<t <8)与反比例函数的图象交于点M ,与直线AB 交于 点N .(1)求k 的值;(2)求△BMN 面积的最大值; (3)若MA⊥AB,求t 的值.例7.如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线y=﹣x2+bx+c经过坐标原点O和x轴上另一点E(4,0)(1)当x取何值时,该抛物线取最大值?该抛物线的最大值是多少?(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).①当t=时,判断点P是否在直线ME上,并说明理由;②以P、N、C、D为顶点的多边形面积是否可能为5?若有可能,求出此时N点的坐标;若无可能,请说明理由.【巩固练习】一、选择题1.函数31xyx+=-中自变量x的取值范围是( )A.x≥-3 B.x≥-3且x≠1 C.x≠1 D.x≠-3且x≠12.如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )A. a+b=-1 B.a-b=-1 C.b<2a D.ac<03.设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α、β,则α、β满足( ) A.1<α<β<2 B.1<α<2 <β C.α<1<β<2 D.α<1且β>24.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )A B C D5.如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A .B .C . 3D .46.如图,一次函数y =-12x +2的图象上有两点A 、B ,A 点的横坐标为2,B 点的横坐标为a(0<a <4且a ≠2),过点A 、B 分别作x 的垂线,垂足为C 、D ,△AOC 、△BOD 的面积分别为S 1、S 2,则S 1、S 2的大小关系是( )A .S 1>S 2B .S 1=S 2C .S 1<S 2D .无法确定二、填空题7.抛物线2222y ax ax a =+++的一部分如图所示,那么该抛物线在y 轴右侧与x 轴交点的坐标 是________.8.在直角坐标系中,有如图所示的Rt△ABO,AB⊥x 轴于点B ,斜边AO =10,sin∠AOB=35,反比例函数k y x= (k >0)的图象经过AO 的中点C ,且与AB 交于点D ,则点D 的坐标为_______________.第7题 第8题 第9题9.如图,点A 在双曲线k y x=上,AB⊥x 轴于B ,且△AOB 的面积S △AOB =2,则k =______.10.如图,已知二次函数y1=x2﹣x的图象与正比例函数y2=x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是 .11.如图所示,直线OP经过点P (4, 4 3),过x轴上的点1、3、5、7、9、11……分别作x轴的垂线,与直线OP相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为S1、S2、S3……S n则S n关于n 的函数关系式是________.第11题第12题12.在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、A3B3C3C2、…、A n B n C n C n-1按如图所示的方式放置,其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上,点C1、C2、C3、…、C n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为____________.三、解答题13.已知,如图所示,正方形ABCD的边长为4 cm,点P是BC边上不与点B、C重合的任意一点,连结AP,过点P作PQ⊥AP交DC于点Q,设BP的长为x cm,CQ的长为y cm.(1)求点P在BC上运动的过程中y的最大值;(2)当14y cm时,求x的值.14.大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).(1)直接写出y与x之间的函数关系式;(2)如何确定销售价格才能使月利润最大?求最大月利润;(3)为了使每月利润不少于6000元应如何控制销售价格?15.已知关于x的二次函数2212my x mx+=-+与2222my x mx+=--,这两个二次函数的图象中的一条与x轴交于A、B两个不同的点.(1)试判断哪个二次函数的图象经过A、B两点;(2)若A点坐标为(-l,0),试求B点坐标;(3)在(2)的条件下,对于经过A、B两点的二次函数,当x取何值时,y的值随x值的增大而减小?16. 探究 (1)在下图中,已知线段AB,CD,其中点分别为E,F.①若A(-1,0),B(3,0),则E点坐标为________;②若C(-2,2),D(-2,-1),则F点坐标为________;(2)在下图中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程.归纳无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y)时,x=________,y=_______.(不必证明)运用在下图中,一次函数y=x-2与反比例函数3yx的图象交点为A,B.①求出交点A,B的坐标;②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标.。
