决策树练习题[精品文档]

合集下载

(完整word版)管理学决策树习题及答案.docx

注意答卷要求：1．统一代号： P 为利润， C 为成本， Q为收入， EP为期望利润2．画决策树时一定按照标准的决策树图形画，不要自创图形3．决策点和状态点做好数字编号4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I 开发新产品 A ，需要追加投资 180 万元，经营期限为 5 年。

此间，产品销路好可获利 170 万元；销路一般可获利 90 万元；销路差可获利 -6 万元。

三种情况的概率分别为 30%，50%， 20%。

II.开发新产品 B，需要追加投资 60 万元，经营期限为 4 年。

此间，产品销路好可获利100 万元；销路一般可获利50 万元；销路差可获利20 万元。

三种情况的概率分别为 60%，30%， 10%。

（ 1）画出决策树销路好0.3170销路一般0.5290销路差0.1-6开发产品A1销路好0.6100开发产品B销路一般0.3350销路差0.120（ 2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案 A=170×0.3 ×5+90×0.5 ×5+(-6) ×0.2×5=770(万元 ) 方案 B=100×0.6 ×4+50×0.3×4+20×0.1 ×4=308(万元 ) 求出各方案的净收益值：方案 A=770-180=590(万元 )方案 B=308-60=248(万元 )因为 590 大于 248 大于 0所以方案 A 最优。

某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（ 1）公司组织技术人员逐渐改进技术，使用期是 10 年；（ 2）购买先进技术，这样前期投入相对较大，使用期是 10 年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

决策树练习题

决策树作业题公司拟建一预制构件厂,一个方案就是建大厂,需投资300万元,建成后如销路好每年可获利100万元,如销路差,每年要亏损20万元,该方案的使用期均为10年;另一个方案就是建小厂,需投资170万元,建成后如销路好,每年可获利40万元,如销路差每年可获利30万元;若建小厂,则考虑在销路好的情况下三年以后再扩建,扩建投资130万元,可使用七年,每年盈利85万元。

假设前3年销路好的概率就是0、7,销路差的概率就是0、3,后7年的销路情况完全取决于前3年;为了适应市场的变化,投资者又提出了第三个方案,即先小规模投资160万元,生产3年后,如果销路差,则不再投资,继续生产7年;如果销路好,则再作决策就是否再投资140万元扩建至大规模(总投资300万元),生产7年。

前3年与后7年销售状态的概率见表16,大小规模投资的年损益值同习题58。

试用决策树法选择最优方案。

表16 销售概率表项目前3年销售状态概率后7年销售状态概率好差好差销路差0、7 0、3 0、9 0、1决策树例题1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。

两个方案的生产期均为10年,其每年的损益值及销售状态的规律见下表。

试用决策树法选择最优方案。

(2)计算各状态点的期望收益值节点②:[100*0、7+(-20)*0、3]*10-300=340;节点③:[60*0、7+20*0、3]*10-160=320;将各状态点的期望收益值标在圆圈上方。

(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。

2.某项目有两个备选方案A与B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。

A方案的投资额度为500万元,其年净收益在产品销售好时为150万元,销售差时为50万元;B方案的投资额度为300万元,其年净收益在产品销售好时为100万元,销售差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比较。

决策树习题练习(答案)

决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。

试用决策树法选择最优方案。

【解】（1）绘制决策树，见图1；（2）计算各状态点的期望收益值节点②：[]10300340()⨯⨯⨯-=1000.7+(-20)0.3万元节点③：[]10160320()⨯⨯⨯-=600.7+200.3万元将各状态点的期望收益值标在圆圈上方。

（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案，用符号“//”在决策树上“剪去”被淘汰的方案。

表1 各年损益值及销售状态2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。

A方案的投资额为500万元，其年净收益在产品销售好时为150万元，，销售差时为50万元；B方案的投资额为300万元，其年净收益在产品销路好时为100万元，销路差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%,销路差的可能性为30％，试根据以上资料对方案进行比选。

已知标准折现率i c=10%。

【解】（1）首先画出决策树此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。

（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元)机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元)最后计算各个备选方案净现值的期望值。

方案A的净现值的期望值＝533-500＝33（万元）方案B的净现值的期望值＝448.5-300＝148.5（万元）因此，应该优先选择方案B。

决策树练习题

决策树练习题决策树练习题决策树是一种常用的机器学习算法，它通过对数据集进行分割和判断，最终得出决策结果。

在实际应用中，决策树可以帮助我们解决各种问题，如分类、回归和聚类等。

为了更好地理解和掌握决策树算法，下面将给出一些练习题，供读者进行实践和思考。

1. 假设有一个数据集，包含了学生的年龄、性别和成绩等信息。

我们想要根据这些信息判断学生是否会通过考试。

请问，在构建决策树时，应该如何选择最佳的划分属性？答案：在构建决策树时，我们需要选择最佳的划分属性，以使得每个子节点的纯度最高。

常用的划分属性选择方法有信息增益、信息增益比和基尼系数等。

其中，信息增益是一种常用的选择方法，它通过计算划分前后的信息熵差异来衡量划分的好坏。

选择信息增益最大的属性作为划分属性即可。

2. 假设有一个数据集，包含了某个地区的天气信息和人们是否出门的记录。

我们想要构建一个决策树模型，来预测某一天是否适合出门。

请问，在构建决策树时，应该如何处理连续型特征？答案：在处理连续型特征时，我们可以将其转化为离散型特征。

一种常用的方法是通过设定阈值，将连续型特征划分为多个离散的取值。

例如，对于温度这一连续型特征，我们可以设定一个阈值，如25摄氏度，将其划分为“高温”和“低温”两个离散的取值。

然后，我们可以将离散化后的特征作为划分属性，继续构建决策树。

3. 假设有一个数据集，包含了某个电商网站的用户信息和购买记录。

我们想要根据用户的特征来预测其购买意向。

请问，在构建决策树时，应该如何处理缺失值？答案：在处理缺失值时，我们可以选择忽略带有缺失值的样本，或者使用合适的方法进行填充。

常用的填充方法有均值填充、中位数填充和众数填充等。

如果缺失值较少，可以考虑使用均值或中位数填充；如果缺失值较多，可以考虑使用众数填充。

另外，我们还可以将缺失值作为一个特殊的取值，单独作为一类进行处理。

4. 假设有一个数据集，包含了某个电商网站的用户信息和购买记录。

我们想要构建一个决策树模型，来预测用户的购买类别。

(完整版)决策树决策表练习题与参考答案

1.某厂对一部分职工重新分配工作，分配原则是：⑴年龄不满20岁，文化程度是小学者脱产学习，文化程度是中学者当电工；⑵年龄满20岁但不足50岁，文化程度是小学或中学者，男性当钳工，女性当车工；文化程度是大专者，当技术员。

⑶年龄满50岁及50岁以上，文化程度是小学或中学者当材料员，文化程度是大专者当技术员。

要求：做出决策表。

123456789101112条件及行动说明年龄≤20≤20≤20≤20≤20≤20(20,50](20,50](20,50](20,50](20,50](20,50]文化程度小学小学中学中学大专大专小学小学中学中学大专大专性别男女男女男女男女男女男女脱产学习√√电工√√钳工√√车工√√材料员技术员√√131415161718条件及行动说明年龄≥50≥50≥50≥50≥50≥50文化程度小学小学中学中学大专大专性别男女男女男女脱产学习电工钳工车工材料员√√√√技术员√√优化后的决策表如下：12345789101112条件及行动说明年龄≤20≤20(20,50](20,50](20,50](20,50](20,50](20,50]≥50≥50≥50文化程度小学中学小学小学中学中学大专大专小学中学大专性别--男女男女男女---脱产学习√√电工钳工√√车工√√材料员√√技术员√√√2、试画出某企业库存量监控处理的判断树。

若库存量≤0，按缺货处理；若库存量≤库存下限，按下限报警处理；若库存量＞库存下限，而又≤储备定额，则按订货处理；若库存量＞库存下限，而又＞储备定额，则按正常处理；若库存量≥库存上限，又＞储备定额，则按上限报警处理。

3某货运站收费标准如下：若收件地点在本省，则快件6元／公斤，慢件4元／公斤；若收件地点在外省，则在25公斤以内（包括25公斤），快件8元／公斤，慢件6元／公斤；而超过25公斤时，快件10元／公斤，慢件8元／公斤；画出决策表和决策树：决策表：条件组合条件活动说明12345678地点本省本省本省本省外省外省外省外省重量25公斤以内25公斤以内25公斤以外25公斤以外25公斤以内25公斤以内25公斤以外25公斤以外邮寄方式快件慢件快件慢件快件慢件快件慢件4元/公斤√√6元/公斤√√√8元/公斤√√10元/公斤√优化后的结果如下所示：条件组合条件活动说明123456地点本省本省外省外省外省外省重量--25公斤以内25公斤以内25公斤以外25公斤以外邮寄方式快件慢件快件慢件快件慢件4元/公斤√6元/公斤√√8元/公斤√√10元/公斤√决策树：收费本省外省快件慢件快件慢件≤25斤>25斤≤25斤>25斤6元4元8元10元6元8元地点规格重量收费金额。

决策树练习题-多级决策树

3
E（5）=1.0×（-30）×7= -210 （万元）
4
前三年的期望收入=0.7×100×3+0.3×（-30）×3=183（万元）
5
E（1）=183+0.7×609+0.3×（-210）-300=246.3 （万元）
6
02
03
对于节点2即改建车间
E（6）=0.9×40×7+0.1×10×7=259 （万元）
Hale Waihona Puke 01通过比较各期望收益，选择方案。
03
方案3为最佳方案。
02
E（3）=302.3> E（1）246.3 > E（2）155.3
销路好0.7
销路好0.7
销路差0.3
销路差0.3
销路差0.3
销路差1.0
销路差0.1
销路差0.1
销路差1.0
销路差0.1
销路差0.1
销路差1.0
销路好0.9
销路好0.9
销路好0.9
销路好0.9
100
-30
-30
40
10
10
10
10
100
-30
40
前三年
后七年
扩建
不扩建
E（4）=0.9×100×7+0.1×（-30）×7=609
E（5）=1.0×（-30）×7= -210
前三年的期望收入= 0.7×100×3+0.3×（-30）×3=183
E（1）=183+0.7×609+0.3×（-210）-300=246.3
决策树计算题
某工厂为生产一种新产品，制定三个基建方案。一是新建车间生产；二是改建原有车间进行生产；三是先改建，生产3年后当产品销路好时再进行扩建。新建和改建车间所需投资分别是300万元和140万元，若要在改建的基础上扩建车间，还需要追加投资140万元，产品生产期定为10年。

管理学决策树习题及答案

注意答卷要求：1．统一代号：P为利润，C为成本，Q为收入，EP为期望利润2．画决策树时一定按照标准的决策树图形画，不要自创图形3．决策点和状态点做好数字编号4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I开发新产品A，需要追加投资180万元，经营期限为5年。

此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。

三种情况的概率分别为30%，50%，20%。

II.开发新产品B，需要追加投资60万元，经营期限为4年。

此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。

三种情况的概率分别为60%，30%，10%。

（1）画出决策树（2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A 最优。

销路好 0.3170 90 -6 100 50 20某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。

如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。

决策树习题练习(答案)

决策树习题练习（答案）决策树习题练习答案1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。

试用决策树法选择最优方案。

表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7100 60 销路差 0.3 -2020【解】（1）绘制决策树，见图1；100×10 -20×10 60×1020×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 3202 31 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。

2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。

已知标准折现率ic=10%。

【解】（1）首先画出决策树150 5010010 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -3002 31 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。

（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。

【决策树习题练习(答案)】

【决策树习题练习（答案）】决策树习题练习答案 1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元；②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见表15。

试用决策树法选择最优方案。

表1 各年损益值及销售状态销售状态概率损益值（万元/年）大规模投资小规模投资销路好 0.7 100 60 销路差 0.3 -20 20 【解】（1）绘制决策树，见图1；100×10 -20×10 60×10 20×10 销路好0.7 销路差（0.3）销路好0.7 销路差（0.3）大规模小规模 340 340 320 2 3 1 图1 习题1决策树图（2）计算各状态点的期望收益值节点②：节点③：将各状态点的期望收益值标在圆圈上方。

2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。

已知标准折现率ic=10%。

【解】（1）首先画出决策树 150 50 100 10 销路好0.7 销路差0.3 销路好0.7 销路差0.3 -500 -300 2 3 1 图2 决策树结构图此题中有一个决策点，两个备用方案，每个方案又面临着两种状态，因此可以画出其决策树如图18。

（2）然后计算各个机会点的期望值机会点②的期望值＝150（P/A,10%,10）×0.7+(-50)（P/A,10%,10）×0.3=533(万元) 机会点③的期望值＝100（P/A,10%,10）×0.7+10（P/A,10%,10）×0.3=448.5(万元) 最后计算各个备选方案净现值的期望值。

[复习]决策树决策表练习题与参考答案

1.某厂对一部分职工重新分配工作，分配原则是：
⑴年龄不满20岁，文化程度是小学者脱产学习，文化程度是中学者当电工；
⑵年龄满20岁但不足50岁，文化程度是小学或中学者，男性当钳工，女性当车工；文化程度是大专者，当技术员。

⑶年龄满50岁及50岁以上，文化程度是小学或中学者当材料员，文化程度是大专者当技术员。

要求：做出决策表。

2、试画出某企业库存量监控处理的判断树。

3某货运站收费标准如下：
若收件地点在本省，则快件6元／公斤，慢件4元／公斤；
若收件地点在外省，则在25公斤以内（包括25公斤），快件8元／公斤，慢件6元／公斤；而超过25公斤时，快件10元／公斤，慢件8元／公斤；
画出决策表和决策树：
决策表：
优化后的结果如下所示：
决策树：
收费
本省
外省快件
慢件
快件
慢件
≤25斤
>25斤
≤25斤
>25斤
6元
4元
8元
10元
6元
8元
地点规格重量收费金额。

决策树练习题

设有某石油钻探队，在一片估计能出油的荒田钻探。可以先做地震试验，然后决定钻井与否。或不做地震试验，只凭经验决定钻井与否。做地震试验的费用每次3000元，钻井费用为10000元。假设钻井后出油，这井队可收入40000元，假设不出油就没
有任何收入。在试验效果好的条件〔概率为〕下钻井出油的概率为〔不出油〕，试验效果不好的条件〔概率为〕下钻井出油的概率为；假设不做试验，钻井出油的概率为〔不出油〕。问：钻井队的决策者如何作出决策使收入的期望值最大？
14
14
14
14
有些复杂的决策问题不可能或很难一次弄清全部自然信息状态情况，而只能先作一个简单决策〔又称一级决策〕，决策后根据产生的新情况再补充信息作出一个新的决策。如此有二级〔阶段〕或更多级决策，称为多阶段序列决策。
多阶段序列决策可以分为两种：一种是在一级决策之后通过通过补充信息再扩展为二级、三级决策；另一种是贝叶斯多级决策。
某公司为了生产某种新产品，考虑三个方案：第一个方案是建大厂，需投资300万元，建成后假设销路好，每个可得利润100万元，假设销路差，每年亏损20万元；第二个方案是建小厂，需投资约180 万元，建成后假设销路好，每年可得利润40万元，销路差，每年可得利润30万元。假设大厂和小厂的使用期限都是10年，考虑第三个方案，先建小厂，试销3年，假设销路好，再投资100万元，加以扩建，扩建后可再使用7年，后7年中每年的利润增至 95万元。问：应该采取何种方案，对公司最有利？〔销路好的概率，销路差的概率〕
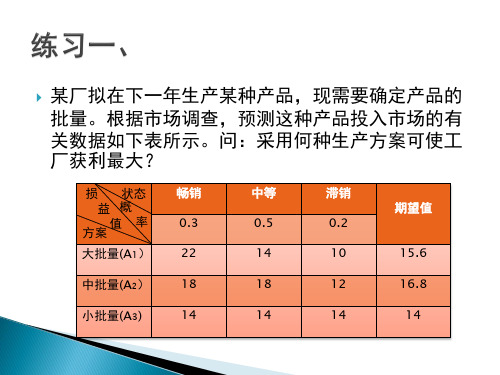
某厂拟在下一年生产某种产品，现需要确定产品的
批量。根据市场调查，预测这种产品投入市场的有
关数据如下表所示。问：采用何种生产方案可使工厂获利最大？
损状态益概

决策树练习题

决策树练习题一、问题描述假设你是某个电子商务平台的数据分析师，你接到了一个任务：利用决策树算法对该平台的用户行为数据进行分析，以预测用户是否会购买特定的产品。

下面是给定的数据集：用户ID | 年龄 | 性别 | 浏览网页数 | 购买产品-------|-----|------|-----------|--------1 | 青年 | 男 | 30 | 否2 | 中年 | 女 | 50 | 否3 | 老年 | 男 | 10 | 否4 | 老年 | 女 | 30 | 是5 | 中年 | 男 | 40 | 是6 | 青年 | 女 | 20 | 否请根据给定的数据集，构建一个决策树模型，以预测用户是否会购买特定的产品。

二、决策树模型构建决策树是一种用于决策分析的机器学习算法，通过构建一棵树状结构来对数据进行分类。

在构建决策树模型之前，我们需要先确定决策树的分裂规则。

根据给定的数据集，我们可以选择以下特征来进行分裂：- 年龄：- 青年- 中年- 老年- 性别：- 男- 女- 浏览网页数：选择特征进行分裂时，我们需要衡量它的划分能力。

常用的衡量指标有信息增益、信息增益比和基尼指数。

在这里，我们选择使用信息增益作为划分标准。

首先，我们计算每个特征的信息增益：- 对于年龄特征：- 青年：信息熵为0- 中年：信息熵为0.971- 老年：信息熵为1信息增益为原始数据集的信息熵减去年龄特征的加权信息熵。

- 对于性别特征：- 男：信息熵为1- 女：信息熵为0.971信息增益为原始数据集的信息熵减去性别特征的加权信息熵。

- 对于浏览网页数特征：- 10：信息熵为1- 20：信息熵为0.918- 30：信息熵为0.918- 40：信息熵为1- 50：信息熵为0信息增益为原始数据集的信息熵减去浏览网页数特征的加权信息熵。

根据计算得到的信息增益，我们选择信息增益最大的特征进行分裂。

在这里，浏览网页数的信息增益最大，因此我们选择浏览网页数作为根节点，并以它进行分裂。

决策树练习题【范本模板】

决策树作业题公司拟建一预制构件厂，一个方案是建大厂，需投资300万元，建成后如销路好每年可获利100万元，如销路差,每年要亏损20万元，该方案的使用期均为10年;另一个方案是建小厂，需投资170万元，建成后如销路好，每年可获利40万元，如销路差每年可获利30万元；若建小厂,则考虑在销路好的情况下三年以后再扩建，扩建投资130万元，可使用七年，每年盈利85万元。

假设前3年销路好的概率是0。

7，销路差的概率是0。

3,后7年的销路情况完全取决于前3年；为了适应市场的变化,投资者又提出了第三个方案,即先小规模投资160万元，生产3年后，如果销路差，则不再投资，继续生产7年;如果销路好，则再作决策是否再投资140万元扩建至大规模（总投资300万元），生产7年。

前3年和后7年销售状态的概率见表16，大小规模投资的年损益值同习题58。

试用决策树法选择最优方案。

表16 销售概率表决策树例题1.某投资者预投资兴建一工厂，建设方案有两种：①大规模投资300万元;②小规模投资160万元。

两个方案的生产期均为10年，其每年的损益值及销售状态的规律见下表。

试用决策树法选择最优方案。

(2）计算各状态点的期望收益值节点②：[100＊0.7+（-20）*0。

3]＊10-300=340;节点③：［60*0。

7+20*0.3]＊10—160=320；将各状态点的期望收益值标在圆圈上方.（3）决策比较节点②与节点③的期望收益值可知，大规模投资方案优于小规模投资方案，故应选择大规模投资方案,用符号“//"在决策树上“剪去”被淘汰的方案。

2.某项目有两个备选方案A和B，两个方案的寿命期均为10年，生产的产品也完全相同，但投资额及年净收益均不相同。

A方案的投资额度为500万元，其年净收益在产品销售好时为150万元，销售差时为50万元；B方案的投资额度为300万元,其年净收益在产品销售好时为100万元,销售差时为10万元，根据市场预测，在项目寿命期内，产品销路好时的可能性为70%，销路差的可能性为30％,试根据以上资料对方案进行比较。

决策树复习题

1、假设某大学要从学生中挑选男子篮球队队员。

基本条件是：各门课程的平均分在70分以
上；身高超过1.8米；体重超过75千克。

需要从学生登记表中挑选出符合上述条件的男同
学，以便进一步选拔。

请根据要求画出判定树。

选拨男子篮球队员
2、某学生选课系统根据学生本学期选课学分的不同，采取不同的处理：
(1)学分总数小于等于0分，则进行“异常”处理：
(2)学分总数大于0分，小于或等于4分，则直接进行“补选课”处理；
(3)学分总数大于20分，则进行“调选课”处理；
(4)其他情况为正常，选课结束。

请用决策树表示该决策过程。

第 1 页共1 页。

管理学决策树习题及答案

注意答卷要求：1．统一代号：P 为利润，C 为成本，Q 为收入，EP 为期望利润 2．画决策树时一定按照标准的决策树图形画，不要自创图形 3．决策点和状态点做好数字编号 4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I 开发新产品A ，需要追加投资180万元，经营期限为5年。

此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。

三种情况的概率分别为30%，50%，20%。

B ，需要追加投资60万元，经营期限为4年。

此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。

三种情况的概率分别为60%，30%，10%。

（1）画出决策树（2）计算各点的期望值，并做出最优决策销路好17090 -61005020求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。

某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。

如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。

管理学决策树习题及答案

注意答卷要求：1．统一代号：P为利润，C为成本，Q为收入，EP为期望利润2．画决策树时一定按照标准的决策树图形画，不要自创图形3．决策点和状态点做好数字编号4．决策树上要标出损益值某企业似开发新产品，现在有两个可行性方案需要决策。

I开发新产品A，需要追加投资180万元，经营期限为5年。

此间，产品销路好可获利170万元；销路一般可获利90万元；销路差可获利-6万元。

三种情况的概率分别为30%，50%，20%。

II.开发新产品B，需要追加投资60万元，经营期限为4年。

此间，产品销路好可获利100万元；销路一般可获利50万元；销路差可获利20万元。

三种情况的概率分别为60%，30%，10%。

（1）画出决策树17090-61005020（2）计算各点的期望值，并做出最优决策求出各方案的期望值：方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值：方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。

某企业为提高其产品在市场上的竞争力，现拟定三种改革方案：（1）公司组织技术人员逐渐改进技术，使用期是10年；（2）购买先进技术，这样前期投入相对较大，使用期是10年；（3）前四年先组织技术人员逐渐改进，四年后再决定是否需要购买先进技术，四年后买入技术相对第一年便宜一些，收益与前四年一样。

预计该种产品前四年畅销的概率为0.7，滞销的概率为0.3。

如果前四年畅销，后六年畅销的概率为0.9；若前四年滞销，后六年滞销的概率为0.1。