广东2010年高考数学(文)B卷试题及参考答案(估分)-中大网校

合集下载

2010年广东高考试卷和答案(包含_语文_文理数_英语_文综_理综_全)

2010年普通高等学校招生全国统一考试（广东卷）语文本试卷共8页，24小题，满分150分。

考试用时150分钟注意事项：1.答卷前，考生务必用黑色字迹的铅笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型（A）填涂在答题卡相应位置上，将条形号码贴在答题卡右上角“条形码粘贴处”。

选择题每小题选出答案后，用2B铅笔把答题卡上对应的题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再填涂其他答案。

答案不能答在试卷上。

3.非选择题必须用黑色字迹的铅笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案，不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.作答选做题时，请先用2B铅笔填涂选做题的题级号的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、本大题四小题，每小题3分，共12分。

1.下列词语中加点的字，每对读音都不相同．．．的一组是A．皎洁/打搅业绩．/污渍．纤．维/纤夫．．B．效．仿/发酵．空旷．/粗犷．盛．开/盛．饭C．隐瞒．/蛮．横挑衅．/抚恤．埋．伏/埋．怨D．市侩．/反馈．濒．临/频．繁辟．谣/精辟．2．下面语段中画线的词语，使用不恰当的一项是中国历代文人视为至宝的笔、墨、纸、砚，是中国传统文化的代表性符号。

它们虽然有着不同的发展轨迹，但殊途同归。

它们在艺术创作中淋漓尽致地表现了中国古代书画艺术的神韵，记录了岁月的斗转星移，体现了古代文人的生活情趣。

今天他们并没有因为现在高科技手段的甚嚣尘上而销声匿迹，而是继续在书画艺术中展示着华夏民族的质朴和灵动。

A．殊途同归 B.斗转星移 C.甚嚣尘上 D.销声匿迹3.下列句子中，没有语病．．．．的一项是A.以“城市，让生活更美好”为主题的上海世博会，让肤色不同、语言不同的人们在这样一个巨大的平台上共同寻找答案。

2010年高考题(答案)

第一部分函数的概念及表示方法函数的定义域、值域1．（2010广东文数）2.函数)1lg()(-=x x f 的定义域是A.),2(+∞B. ),1(+∞C. ),1[+∞D. ),2[+∞解：01>-x ，得1>x ，选B.2．（2010湖北文数）5.函数y =的定义域为 A.( 34,1) B(34,∞) C （1，+∞） D. ( 34,1)∪（1，+∞）3．（2010湖北文数）3.已知函数3log ,0()2,0x x x f x x >⎧=⎨≤⎩，则1(())9f f = A.4 B. 14 C.-4 D-14【答案】B 【解析】根据分段函数可得311()log 299f ==-，则211(())(2)294f f f -=-==，所以B 正确.4．（2010重庆文数）（4）函数y =（A ）[0,)+∞ （B ）[0,4]（C ）[0,4) （D ）(0,4)解析：[)40,0164160,4x x >∴≤-< 5．（2010山东文数）(3)函数()()2log 31x f x =+的值域为 A. ()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 答案：A6．（2010天津文数）（10）设函数2()2()g x xx R =-∈，()4,(),(),().(){g x x x g x g x x x g x f x ++<-≥=则()f x 的值域是（A ）9,0(1,)4⎡⎤-⋃+∞⎢⎥⎣⎦ （B ）[0,)+∞ （C ）9[,)4-+∞（D ）9,0(2,)4⎡⎤-⋃+∞⎢⎥⎣⎦【答案】D【解析】本题主要考查函数分类函数值域的基本求法，属于难题。

依题意知22222(4),2()2,2x x x x f x x x x x ⎧-++<-⎪⎨--≥-⎪⎩，222,12()2,12x x x f x x x x ⎧+<->⎪⎨---≤≤⎪⎩或7．（2010浙江理数）（10）设函数的集合211()log (),0,,1;1,0,122P f x x a b a b ⎧⎫==++=-=-⎨⎬⎩⎭，平面上点的集合11(,),0,,1;1,0,122Q x y x y ⎧⎫==-=-⎨⎬⎩⎭，则在同一直角坐标系中，P 中函数()f x 的图象恰好．．经过Q 中两个点的函数的个数是（A ）4 （B ）6 （C ）8 （D ）10解析：当a=0,b=0;a=0,b=1;a=21,b=0; a=21,b=1;a=1,b=-1;a=1,b=1时满足题意，故答案选B ，本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点，对数学素养有较高要求，体现了对能力的考察，属中档题8．（2010陕西文数）13.已知函数f （x ）＝232,1,,1,x x x ax x +<⎧⎨+≥⎩若f （f （0））＝4a ，则实数a＝ 2 .解析：f （0）=2，f （f （0））=f(2)=4+2a=4a ，所以a=29．（2010重庆文数）(12)已知0t >，则函数241t t y t-+=的最小值为____________ . 解析：241142(0)t t y t t t t-+==+-≥-> ，当且仅当1t =时，min 2y =- 10．（2010天津文数）（16）设函数f(x)=x-1x,对任意x [1,∈+∞），f(mx)+mf(x)<0恒成立，则实数m 的取值范围是________【答案】m<-1【解析】本题主要考查了恒成立问题的基本解法及分类讨论思想，属于难题。

2010广东高考文科数学 (4)

2010广东高考文科数学一、概述2010年广东高考文科数学试卷是广东省教育厅于2010年组织的一次高中毕业生综合评价考试。

本文将对该试卷的题目进行详细分析和解答。

二、试题分析1. 选填题选填题是广东高考文科数学试卷中的一部分，共有若干道题目。

这些题目的特点是答案具有多样性，考生可以根据自己的方法和计算结果进行填写。

举例来说，试题可能是给出了一个方程，考生需要求出方程的根或解。

对于这类题目，考生可以采用因式分解、配方法、求根公式等不同的方法进行计算，最终填写答案。

2. 解答题解答题是广东高考文科数学试卷中的主要部分，包括选择题、填空题和证明题。

2.1 选择题选择题是广东高考文科数学试卷中一道典型的题目。

该类型的题目给出了一些选项，考生需要选择符合要求的选项作为答案。

通常情况下，选择题包括单选题和多选题。

对于选择题，考生需要认真阅读题干和选项，并结合自己的数学知识进行推理和判断，最终选择正确的答案。

2.2 填空题填空题是广东高考文科数学试卷中的一类题目。

该类型的题目通常给出了一些未知数或变量，考生需要根据所给的条件进行计算，并填写答案。

填空题对考生的计算能力和逻辑思维能力有一定的要求，考生需要熟练掌握数学计算方法，并能够合理推理和运用所学知识。

2.3 证明题证明题是广东高考文科数学试卷中的一类题目。

该类型的题目要求考生根据所给的条件和已知的数学知识进行推理和证明，最终得出结论。

对于证明题，考生需要熟悉各种证明方法和数学定理，并能够运用这些知识进行推理和证明。

证明题对考生的逻辑思维能力、分析问题的能力和数学知识的整合能力有较高的要求。

三、题目解答1. 选填题题目一已知方程x2−2x+1=0的两个解之和是？解析：这是一个二次方程求解的问题，考生可以采用求根公式进行计算。

根据求根公式，对于二次方程xx2+xx+x=0，其解为 $x = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a}$。

广东高考文科数学B卷参考答案

2088年普通岛考广东卷数学（文科）（B 卷）参考答案: CCBBD CAAAD二填窖JS I 11. J3_ 12. 祁 13.12 1 11 2J1 —（心16解,1）农題意如A-l4?r T ；如 /(x)=$in(x+f»,sin a = ・血"丄5 13 /(a-//)=cos(a-/l)=i»sacofi/?+siiia5iri/? = ”x 扫十；x 右=善i7 IF ： a««*平方米的平均综合費为f (x )无.a...“ .2160x10000弘)屮如燃)+飞顾一当x>i5 r. /V)>o » 当 o<x<istf. <(x)<o因此卅“5E ・rg 取最小位/（15卜2W0；符；为^灿8料平方米的平均惊台剜妙，洙仗席应也古15'Z- 18*； Cl ） V BD 是圆的R 径•・• ZA4£> = 90B 又 CMQPPRML3…12 ⑵丫 /(a)・Escr* ■13皿+48卄罟■(加O."Z ・),旦巴・刖上竺二竺竺欢拥 ADM («DMn30J 彳心丨M 略2(2)在 RlUIiCD 中・ CD = HDcas45*= &R•/ PD' +CDQ9RG2R'“IR— PC’1?^(1> V —=0192000・・・*380(2) 切三年级人数为 y+z=2000 —〈373 + 377+卿+3加)=500，现用分曲样的方法在全怨抽取48 乂锲，便在梅三鏗经摘欧的人戡为：—x500=12 4 2000(3) 改切三毎级女生比男生多的妙件为A • M 三邙级女生男生数记为(y ・臥棊本事件左同包含的甚本事件有；C245. 2S5). < 346. 254、( 347. 253、••…(255. 345)共 11 个>■件 A 包含的茎本D 件冇以⑸，249X ( 252 . 248)*(253. 247X (2H246)v(255.245)共 5 个^M ； (I)由H = 8(F -町俗丘* ■ t 曲曲•血(Q+朋•卜:.PD 丄 CD 又 ZPfMoWh 円)丄融磁D二枝绘P-MC 的体税为由 di fal 尸+二=500 .且 yj F V ,8当丿・巾+2时.x = ±4. 为2. b+2)卩冷八/|x-<=lWS G 的瞰力甲为>,-(^+2}=x-4 .即F=X+b・ 2.令y.0 H x = 2-b ■点的坐标为<2-k OX由柄髦力程目斥点的坐标为（b.叽A 2-b=b 即 b=l.<2> VilA 作K 轻的聆级与检物钱只育一牛交点RAW SIE 为小的RQ1BP 只有一牛.同驭为曲的RfQ 砂財「f ；匕以厶1/呂为it 积哎P 点的坐拆为（X 丄F+i ）・則A ・B 坐斥分別&为（』0）・（近斯由屈 1诵=蛊'一2+（丄蛊‘+1〉' = 0S 64 4好疋的一元二次方用育一堺•小有*瞩L 山PB 为nA 的&卫抄有二个.Eifcmwili 上曲存在4个AttO.W 为直用三師帝・ 21 «：（ 1 > 由a. =%-q2A W｛也-a.｝魅S •项为I 公㉛的和:；IW • 1当 n JWWf ・1总 nIE 此 bjWifcO 的柯列万程及他掰戈方程分别为「亍（S ・％）（沦3）£ -Hi+f-jyf 2 丫■ - *•••+ 2■ «■f =l -!f£ul 3丿 J 丿3 丿出5・ ISA+^G-ISb 冋S 】由-l£Z>,Sl得 ^ = -1由・20 »b.wZ'b*丰 0力血严又 Q t -flg« I* 0 •P!理可n 为佻敷时.A F »-I ：当n 为奇炽• 4 = 1：wq+q+q+G + ・TC.当n为奇洞譽也4—23 | g （卄3）（2 J 4»+27 9（门+3）卩丫5 5 UJ-J （34 f!）3・•• H"）闫。

da2010年高考数学广东(文)

π 3 ． 6 2
π ， 2
2π 4． π 2
π ． 5
∴ f ( x) 3sin 4 x
（3）由 f ∴ cos
π π 9 π 3sin 3cos ， 3 6 5 4 12
3 ． 5
x ≥ 0，y ≥ 0， x ≥ 0，y ≥ 0， 12 x 8 y ≥ 64， 3 x 2 y ≥ 16，即 6 x 6 y ≥ 42， x y ≥ 7， 6 x 10 y ≥ 54. 3 x 5 y ≥ 27.
0) ， B(4， 3) ， C (2， 5) ， D(0， 8) 处的值分别是 z 在可行域的四个顶点 A(9，
设 A 表示随机事件“5 名观众中任取 2 名，恰有 1 名观众年龄为 20 至 40 岁” ，则 A 中的基本事件有 6 种：
Y1 A1，Y1 A2，Y1 A3，Y2 A1，Y2 A2，Y2 A3 ，
故所求概率为 P ( A)
6 3 ． 10 5
F
18．（本小题满分 14 分）（1）证明： ∵点 E 为 AC 的中点，且 AB BC，AC 为直径， ∴ EB ⊥ AC ． ∵ EC ⊥ 平面 BED ，且 BE 平面 BED ， ∴ FC ⊥ EB ． ∵ FC∩ AC C ， A ∴ EB ⊥ 平面 BDF ． ∵ FD 平面 BDF ， ∴ EB ⊥ FD ．（2）解：∵ FC ⊥ 平面 BED ，且 BD 平面 BED ， ∴ FC ⊥ BD ．又∵ BC DC ， ∴ FD FB 5a ． ∴ VE FBD
2
∴ sin 1 cos
4 ． 5
17．（本小题满分 12 分）解：（1）因为在 20 至 40 岁的 58 名观众中有 18 名观众收看新闻节目，而大于 40 岁的 42

2010广东高考文科数学答案

2010广东高考文科数学答案【篇一：2010广东高考数学(文科b卷)试卷及详细解答】统一考试(广东卷) 数学(文科)本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2b铅笔将试卷类型（b）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题每小题选出答案后，用2b铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时。

请先用2b铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

1参考公式：锥体的体积公式v=3sh，其中s是锥体的底面积，h是锥体的高。

一、选择题：本大题共10小题，每小题5分，满分50分。

在每小题给出的四个选项中，只有一项是符合题目要求的．1．若集合a=｛0，1，2，3｝，b=｛1，2，4｝，则集合a?b= ( a )a．｛0，1，2，3，4｝b．｛1，2，3，4｝c．｛1，2｝ d．｛0｝2．函数，f(x)?lg(x?1)的定义域是 ( b )a．(2，??)b．(1,??)c．[1，??)d．[2，??)3．若函数f(x)?3?3与g(x)?3?3的定义域均为r，则 ( d )a．f(x)与g(x)均为偶函数b．f(x)为奇函数，g(x)为偶函数c．f(x)与g(x)均为奇函数d．f(x)为偶函数，g(x)为奇函数x?xx?x5w_w*w.k_s_5 u.c*o*ma．35 b．33 c．31d．29??????a．6 b．5c．4d．36．若圆心在x轴上、o位于y轴左侧,且与直线x?2y?0相切,则圆o的方程是( d ) o*m2222(x?y?5(x?y?5 a．b．2222(x?5)?y?5 (x?5)?y?5 c． d．7．若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 ( b )4321a． 5b．5c．5 d．58．“x0”成立的 (a )a．充分非必要条件 b．必要非充分条件w_w*w.k_s_5u.c*o*mc．非充分非必要条件d．充要条件3cc?平面abc且3aa?bb?cc?ab29．如图1，vabc为正三角形，aa//bb//cc，，则多面体abc?abc的正视图(也称主视图)是 ( d )10．在集合{a，b，c，d}上定义两种运算?和?如下: ( a )那么d ?(a?c)?a．a b．b c．cd．d二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题(11～13题)11．某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中4位居民的月均用水量分别为程序框图，若x1，…，x4 (单位：吨)．根据图2所示的x1，x2，x3，x4分别为1，1.5，1.5，2，则输出的结果s为 1.5 .12．某市居民2005～2009年家庭年平均收入x（单位：万元）与年平均支出y（单位：万元）的统计资料如下表所示：w_w w.k#s5_u.c o*m根据数是有13．已统计资料，居民家庭年平均收入的中位13 ，家庭年平均收入与年平均支出正线性相关关系.知a,b,c分别是△abc的三个内角a,b,c1所对的边，若则sina= 2 . w_w w. k#s5_u.c o*m（二）选做题（14、15题，考生只能从中选做一题） 14．（几何证明选讲选做题）如图3，在直角梯形abcd中，dc∥ab，acb⊥ab，ab=ad=a，cd=2，点e，f分别为线段ab，ad的中点，则aef= 2 .(1,)??cos??sin???1??sin??cos???12 . 中，曲线与的交点的极坐标为三、解答题：本大题共6小题，满分80分。

2010年普通高等学校招生全国统一考试高考数学教师精校版含详解广东文

2010年广东文一、选择题（共10小题；共50分）1. 若集合A=0,1,2,3，B=1,2,4，则集合A∪B= A. 0,1,2,3,4B. 1,2,3,4C. 1,2D. 02. 函数f x=lg x−1的定义域是 A. 2,+∞B. 1,+∞C. 1,+∞D. 2,+∞3. 若函数f x=3x+3−x与g x=3x−3−x的定义域均为R，则 A. f x与g x均为偶函数B. f x为奇函数，g x为偶函数C. f x与g x均为奇函数D. f x为偶函数，g x为奇函数4. 已知数列a n为等比数列，S n是它的前n项和，若a2⋅a3=2a1，且a4与2a7的等差中项为54，则S5= A. 35B. 33C. 31D. 295. 若向量a=1,1，b=2,5，c=3,x满足条件8a−b⋅c=30，则x = A. 6B. 5C. 4D. 36. 若圆心在x轴上、半径为5的圆O位于y轴左侧，且与直线x+2y=0相切，则圆O的方程是 A. x−2+y2=5 B. x+52+y2=5C. x−52+y2=5D. x+52+y2=57. 若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 A. 45B. 35C. 25D. 158. " x>0 " 是 " x23>0 " 成立的 A. 充分非必要条件B. 必要非充分条件C. 非充分非必要条件D. 充要条件9. 如图，△ABC为正三角形，AAʹ∥BBʹ∥CCʹ，CCʹ⊥平面ABC，且3AAʹ=32BBʹ=CCʹ=AB，则多面体ABC−AʹBʹCʹ的正视图（也称主视图）是 A. B.C. D.10. 在集合a,b,c,d上定义两种运算⊕和⊗如下：⊕a b c da abc db b b b bc c b c bd d b b d ⊗a b c da a a a ab a bc dc a c c ad a d a d那么d⊗a⊕c= A. aB. bC. cD. d二、填空题（共5小题；共25分）11. 某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中4位居民的月均用水量分别为x1,x2,x3,x4（单位：吨）．根据如图所示的程序框图，若x1、x2、x3、x4分别为1、1.5、1.5、2，则输出的结果s为．12. 某市居民2005−2009年家庭年平均收入x（单位：万元）与年平均支出Y（单位：万元）的统计资料如下表所示：年份20052006200720082009收入x11.512.11313.315支出Y 6.88.89.81012根据统计资料，居民家庭年平均收入的中位数是，家庭年平均收入与年平均支出有（填“正”或“负”）线性相关关系．13. 已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=3，A+C=2B，则sin A=．14. 如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=a2，点E，F分别为线段AB，AD的中点，则EF=．15. 在极坐标系ρ,θ（0≤θ≤2π）中，曲线ρcosθ+sinθ=1与ρsinθ−cosθ=1的交点的极坐标为．三、解答题（共6小题；共78分）16.设函数f x=3sin ωx+π6，ω>0，x∈−∞,+∞，且以π2为最小正周期．（1）求f0；（2）求f x的解析式；（3）已知fα4+π12=95，求sinα的值．17. 某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：文艺节目新闻节目总计20到40岁401858大于40岁152742总计5545100（1）由表中数据直观分析，收看新闻节目的观众是否与年龄有关?（2）用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名?（3）在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率．18. 如图，AEC是半径为a的半圆，AC为直径，点E为AC的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FC⊥平面BED，FB=a．（1）证明：EB⊥FD；（2）求点B到平面FED的距离．19. 已知函数f x对任意实数x均有f x=kf x+2，其中常数k为负数，且f x在区间0,2上有表达式f x=x x−2．（1）求f−1，f2.5的值；（2）写出f x在−3,3上的表达式，并讨论函数f x在−3,3上的单调性；（3）求出f x在−3,3上的最小值与最大值，并求出相应的自变量的取值．20. 已知曲线C n:y=nx2，点P n x n,y n x n>0,y n>0是曲线C n上的点n=1,2,⋯．（1）试写出曲线C n在点P n处的切线l n的方程，并求出l n与y轴的交点Q n的坐标；（2）若原点O0,0到l n的距离与线段P n Q n的长度之比取得最大值，试求点P n的坐标x n,y n；（3）设m与k为两个给定的不同的正整数，x n与y n是满足（2）中条件的点P n的坐标，证明：m+1x n2−k+1y nsn=1<ms−ks s=1,2,…．21. 某营养师要为某个儿童预定午餐和晚餐．已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C．另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素C．如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐?答案第一部分 1. A2. B3. D4. C【解析】a 2⋅a 3=a 1q ⋅a 1q 2=2a 1，a 1q 3=2，即a 4=2．又a 4与2a 7的等差中项为54，即a 4+2a 7=52，得a 7=14．所以q =12，a 1=16．所以S 5=16 1−1251−12=31．5. C6. D【解析】由题意设圆的方程为 x −a 2+y 2=5 a <0 ，由于与直线x +2y =0相切，则5= 5得a =−5，∴圆的方程为 x +5 2+y 2=5．7. B【解析】由题意知，2⋅2b =2a +2c ，即2b =a +c ，即4 a 2−c 2 =4b 2= a +c 2，即5c 2+2ac −3a 2=0，即 5c −3a c +a =0，所以e =35． 8. A【解析】当x >0时，x 2>0，有 x 23>0，所以" x 2>0 "是" x 23>0 "成立的充分条件；x 23>0则x 2>0，所以x ≠0，所以" x >0 "是" x 23>0 "的不必要条件．综上" x >0 "是" x 23>0 "成立的充分非必要条件． 9. D 10. A【解析】由表易知，a ⊕c =c ，d ⊗c =a ．第二部分 11. 1.5 12. 13，正 13. 12【解析】因为A +C =2B ，所以B =60∘，又由正弦定理得：asin A=b sin B，所以sin A =a sin B b=323=12．14. a2【解析】在直角梯形中，连结DE ，易知△ADE 为直角三角形，而F 为中点，则EF 为斜边AD 的一半，故EF =a2． 15. 1,π2【解析】 ρ cos θ+sin θ =1ρ sin θ−cos θ =1，整理得cos θ+sin θ=sin θ−cos θ，即cos θ=0．得θ=π2或32π．当θ=π2时，ρ=1cos θ+sin θ=1sin θ=1 .因为ρ>0，所以当θ=3π2时，极坐标也是 1,π2 . 第三部分16. （1）因为函数f x =3sin ωx +π6 ,所以f 0 =3sin ω×0+π6 =3sin π6=32.（2）因为函数f x=3sin ωx+π6，ω>0，x∈−∞,+∞，且以π2为最小正周期．所以ω=4，所以f x=3sin4x+π6．（3）因为fα4+π12=95，所以3sin4α4+π12+π6=95，所以sin α+π2=35，所以cosα=35，所以1−sin2α=925，所以sin2α=1625，所以sinα=±45．17. （1）由表中数据，年龄在20至40岁间收看新闻节目的观众所占的比例为1858，而年龄大于40岁的收看新闻节目的观众所占的比例为2742，这两个比例值相差比较大，所以收看新闻节目的观众与年龄有关．（2）根据分层抽样的特点，大于40岁的观众应抽取27×545=3（名）．（3）由题意抽取的5名观众有3名大于40岁，用A，B，C表示，有2名年龄为20至40岁的，用a，b表示．在5名观众中任取2名共构成10个基本事件A,B，A,C，A,a，A,b，B,C，B,a，B,b，C,a，C,b，a,b．其中恰有1名观众的年龄为20岁至40岁的基本事件有6个．设“恰有1名观众的年龄为20岁至40岁”为事件D，根据古典概型的概率计算公式P D=610=35．18. （1）∵点E为AC的中点，且AB=BC，AC为直径，∴EB⊥AC．∵FC⊥平面BED，且BE⊂平面BED，∴FC⊥BE．∵FC∩AC=C，∴BE⊥平面FBD，∵FD⊂平面FBD，∴EB⊥FD．（2）∵FC⊥平面BED，且BD⊂平面BED，∴FC⊥BD，又∵BC=DC，∴FD=FB=5a，所以V F−EBD=1×S△FBD×EB=1×1×2a×5a2−a2×a=2a3 3,∵EB⊥平面BDF，且FB⊂平面BDF，所以EF=EB+FB=a+5a=6a,又因为EB⊥BD，所以ED=EB2+BD2=a2+4a2=5a,所以S△FED=1×6a×5a 2−6a =21a2,所以点B到平面FED的距离d=V F−EBD13×S△FED=421a.19. （1）由已知得f−1=kf−1+2=kf1=k×1×1−2=−k,又因为f0.5=kf2.5，所以f2.5=1kf0.5=1k−34=−34k.（2）设−2≤x<0，则0≤x+2<2，所以f x=kf x+2=k x+2x+2−2=kx x+2.设−3≤x<−2，则−1≤x+2<0，所以f x=kf x+2=k2x+2x+4.设2<x≤3，则0<x−2≤1，又因为f x−2=kf x，所以f x=1f x−2=1x−2x−4.由此f x=k2x+2x+4,−3≤x<−2, kx x+2,−2≤x<0, x x−2,0≤x≤2,1kx−2x−4,2<x≤3.因为k<0，所以由二次函数知识得f x在−3,−2上是增函数，在−2,−1上是增函数，在−1,0上是减函数，在0,1上是减函数，在1,2上是增函数，在2,3上是增函数．（3）由函数f x在−3,3上的单调性可知，f x在x=−3或x=1处取得最小值f−3=−k2 或 f1=−1,而在x=−1或x=3处取得最大值f−1=−k 或 f3=−1 .①k<−1时，而f x在x=−3处取得最小值f−3=−k2,在x=−1处取得最大值f−1=−k;②k=−1时，f x在x=−3与x=1处取得最小值f−3=f1=−1,在x=−1与x=3处取得最大值f−1=f3=1;③−1<k <0时，f x 在x =1处取得最小值f 1 =−1.在x =3处取得最大值f 3 =−1.20. （1）因为y =nx 2，所以yʹ=2nx ．又P n x n ,nx n 2 ，所以曲线C n 在点P n x n ,nx n 2 处的切线l n 为y −nx n 2=2nx n x −x n ,即y =2nx n x −nx n 2.令x =0，得Q n 0,−nx n 2 ．（2）直线l n 的一般式方程为y −2nx n x +nx n 2=0,原点到l n 的距离为d 1=n 21+4n 2x n2,线段P n Q n 的长度为d 2= x n 22n 4=x n 2n2. 所以d 1d 2=nx n 2x n 1+4n 2x n 2 =nx n1+4n 2x n2=n 1x n+4n 2x n ≤n 4n =14.当且仅当1x n=4n 2x n ，即x n =12n 时取等号，此时P n 12n ,14n ．（3）由（2）知x n =12n，y n =14n，于是m +1 x n 2− k nsn =1= m +1− k +12 n s n =1=2 n m +1+ k +1 sn =1< m −k2 n m + k sn =1= m − k 12 n sn =1现证明： 2 ns n < s s =1,2,3,⋯ ．因为12 n sn =1<1n + n −1sn =1= n − n −1sn =1=1+ 2−1 + 3− 2 +⋯+ s − s −1 = s ,故问题得证．21. 设为该儿童分别预订x 、y 个单位的午餐和晚餐，共花费z 元，则z =2.5x +4y ，且满足以下条件12x +8y ≥64,6x +6y ≥42,6x +10y ≥54,x ,y ≥0,化简得3x +2y ≥16,x +y ≥7,3x +5y ≥27,x ,y ≥0,作出可行域如图，则z 在可行域的四个顶点A 9,0 ，B 4,3 ，C 2,5 ，D 0,8 处的值分别为z A =2.5×9+4×0=22.5,z B =2.5×4+4×3=22,z C =2.5×2+4×5=25,z D =2.5×0+4×8=32.比较之，z B 最小，因此应当为该儿童预定4个单位的午餐和3个单位的晚餐，就可以满足要求．。

2010年广东、福建、北京的数学高考试卷

绝密?使用完毕前
2010年普通高等学校招生全国统一考试
数学（文）（北京卷）
本试卷分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷1至2页、第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效，考试结束后，将本试卷和答题卡。

第Ⅰ卷（选择题共140分）
一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合
题目要求的一项。

2⑴集合P?{x?Z0?x?3},M?{x?Zx?9}，则PIM=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}
⑵在复平面内，复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点，则点C对应的复数是
（A）4+8i (B)8+2i （C）2+4i (D)4+i
⑶从{1,2,3,4,5}中随机选取一个数为a，从{1,2,3}中随机选取一个数为b，则b>a的概率是
（A）4321 (B) （C） (D) 5555
⑷若
a,b
是非零向量，且a?b，a?b，则函数f(x)?(xa?b)?(xb?a)是（A）一次函数且是奇函数（B）一次函数但不是奇函数（C）二次函数且是偶函数（D）二次函数但不是偶函数（5）一个长方体去掉一个小长方体，所得几何体的
正视图与侧（左）视图分别如右图所示，则该集合体
的俯视图为：
(6)给定函数①y?x，②y?log1(x?1)，③y?|x?1|，④y?2
212x?1，期中在区间（0，
1）上单调递减的函数序号是
中国校长网资源频道。

2010年全国统一高考数学试卷(文科)(新课标)及答案(分析解答)

2010年全国统一高考数学试卷（文科）（新课标）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x||x|≤2，x∈R}，B={x|≤4，x∈Z}，则A∩B=（）A．（0，2） B．[0，2]C．{0，2}D．{0，1，2}2．（5分）平面向量，已知=（4，3），=（3，18），则夹角的余弦值等于（）A．B．C．D．3．（5分）已知复数Z=，则|z|=（）A．B．C．1 D．24．（5分）曲线y=x3﹣2x+1在点（1，0）处的切线方程为（）A．y=x﹣1 B．y=﹣x+1 C．y=2x﹣2 D．y=﹣2x+25．（5分）中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4，2），则它的离心率为（）A．B．C．D．6．（5分）如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（）A．B．C．D．7．（5分）设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（）A．3πa2B．6πa2C．12πa2D．24πa28．（5分）如果执行右面的框图，输入N=5，则输出的数等于（）A．B．C．D．9．（5分）设偶函数f（x）满足f（x）=2x﹣4（x≥0），则{x|f（x﹣2）＞0}=（）A．{x|x＜﹣2或x＞4}B．{x|x＜0或x＞4}C．{x|x＜0或x＞6}D．{x|x ＜﹣2或x＞2}10．（5分）若cos α=﹣，α是第三象限的角，则sin（α+）=（）A．B．C．D．11．（5分）已知▱ABCD的三个顶点为A（﹣1，2），B（3，4），C（4，﹣2），点（x，y）在▱ABCD的内部，则z=2x﹣5y的取值范围是（）A．（﹣14，16）B．（﹣14，20）C．（﹣12，18）D．（﹣12，20）12．（5分）已知函数，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（）A．（1，10）B．（5，6） C．（10，12）D．（20，24）二、填空题：本大题共4小题，每小题5分．13．（5分）圆心在原点上与直线x+y﹣2=0相切的圆的方程为．14．（5分）设函数y=f（x）为区间（0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法计算由曲线y=f（x）及直线x=0，x=1，y=0所围成部分的面积S，先产生两组（每组N个），区间（0，1]上的均匀随机数x1，x2，…，x n和y1，y2，…，y n，由此得到N个点（x，y）（i﹣1，2…，N）．再数出其中满足y1≤f（x）（i=1，2…，N）的点数N1，那么由随机模拟方法可得S 的近似值为．15．（5分）一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的（填入所有可能的几何体前的编号）①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱．16．（5分）在△ABC中，D为BC边上一点，BC=3BD，AD=，∠ADB=135°．若AC=AB，则BD=．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（10分）设等差数列{a n}满足a3=5，a10=﹣9．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{a n}的前n项和S n及使得S n最大的序号n的值．18．（10分）如图，已知四棱锥P﹣ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．（Ⅰ）证明：平面PAC⊥平面PBD；（Ⅱ）若AB=，∠APB=∠ADB=60°，求四棱锥P﹣ABCD的体积．19．（10分）为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如表：（1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；（2）能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（3）根据（2）的结论，能否提供更好的调查方法来估计该地区老年人中，需要志愿帮助的老年人的比例？说明理由．附：20．（10分）设F1，F2分别是椭圆E：x2+=1（0＜b＜1）的左、右焦点，过F1的直线l与E相交于A、B两点，且|AF2|，|AB|，|BF2|成等差数列．（Ⅰ）求|AB|；（Ⅱ）若直线l的斜率为1，求b的值．21．设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．22．（10分）如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于E点，证明：（Ⅰ）∠ACE=∠BCD．（Ⅱ）BC2=BE•CD．23．（10分）已知直线C1（t为参数），C2（θ为参数），（Ⅰ）当α=时，求C1与C2的交点坐标；（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P 点的轨迹的参数方程，并指出它是什么曲线．24．（10分）设函数f（x）=|2x﹣4|+1．（Ⅰ）画出函数y=f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．2010年全国统一高考数学试卷（文科）（新课标）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2010•新课标）已知集合A={x||x|≤2，x∈R}，B={x|≤4，x∈Z}，则A∩B=（）A．（0，2） B．[0，2]C．{0，2}D．{0，1，2}【分析】由题意可得A={x|﹣2≤x≤2}，B={0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}，从而可求【解答】解：∵A={x||x|≤2}={x|﹣2≤x≤2}B={x|≤4，x∈Z}={0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}则A∩B={0，1，2}故选D2．（5分）（2010•新课标）平面向量，已知=（4，3），=（3，18），则夹角的余弦值等于（）A．B．C．D．【分析】先设出的坐标，根据a=（4，3），2a+b=（3，18），求出坐标，根据数量积的坐标公式的变形公式，求出两个向量的夹角的余弦【解答】解：设=（x，y），∵a=（4，3），2a+b=（3，18），∴∴cosθ==，故选C．3．（5分）（2010•新课标）已知复数Z=，则|z|=（）A．B．C．1 D．2【分析】由复数的代数形式的乘除运算化简可得Z=，由复数的模长公式可得答案．【解答】解：化简得Z===•=•=•=，故|z|==，故选B4．（5分）（2010•新课标）曲线y=x3﹣2x+1在点（1，0）处的切线方程为（）A．y=x﹣1 B．y=﹣x+1 C．y=2x﹣2 D．y=﹣2x+2【分析】欲求在点（1，0）处的切线方程，只须求出其斜率的值即可，故先利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．【解答】解：验证知，点（1，0）在曲线上∵y=x3﹣2x+1，y′=3x2﹣2，所以k=y′|x﹣1=1，得切线的斜率为1，所以k=1；所以曲线y=f（x）在点（1，0）处的切线方程为：y﹣0=1×（x﹣1），即y=x﹣1．故选A．5．（5分）（2010•新课标）中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4，2），则它的离心率为（）A．B．C．D．【分析】先求渐近线斜率，再用c2=a2+b2求离心率．【解答】解：∵渐近线的方程是y=±x，∴2=•4，=，a=2b，c==a，e==，即它的离心率为．故答案选D．6．（5分）（2010•新课标）如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（）A．B．C．D．【分析】本题的求解可以利用排除法，根据某具体时刻点P的位置到到x轴距离来确定答案．【解答】解：通过分析可知当t=0时，点P到x轴距离d为，于是可以排除答案A，D，再根据当时，可知点P在x轴上此时点P到x轴距离d为0，排除答案B，故应选C．7．（5分）（2010•新课标）设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（）A．3πa2B．6πa2C．12πa2D．24πa2【分析】本题考查的知识点是球的体积和表面积公式，由长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则长方体的对角线即为球的直径，即球的半径R满足（2R）2=6a2，代入球的表面积公式，S球=4πR2，即可得到答案．【解答】解：根据题意球的半径R满足（2R）2=6a2，=4πR2=6πa2．所以S球故选B8．（5分）（2010•新课标）如果执行右面的框图，输入N=5，则输出的数等于（）A．B．C．D．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=的值．【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=的值．∵S==1﹣=故选D．9．（5分）（2010•新课标）设偶函数f（x）满足f（x）=2x﹣4（x≥0），则{x|f（x ﹣2）＞0}=（）A．{x|x＜﹣2或x＞4}B．{x|x＜0或x＞4}C．{x|x＜0或x＞6}D．{x|x ＜﹣2或x＞2}【分析】由偶函数f（x）满足f（x）=2x﹣4（x≥0），可得f（x）=f（|x|）=2|x|﹣4，根据偶函数的性质将函数转化为绝对值函数，再求解不等式，可得答案．【解答】解：由偶函数f（x）满足f（x）=2x﹣4（x≥0），可得f（x）=f（|x|）=2|x|﹣4，则f（x﹣2）=f（|x﹣2|）=2|x﹣2|﹣4，要使f（|x﹣2|）＞0，只需2|x﹣2|﹣4＞0，|x﹣2|＞2解得x＞4，或x＜0．应选：B．10．（5分）（2010•新课标）若cos α=﹣，α是第三象限的角，则sin（α+）=（）A．B．C．D．【分析】根据α的所在的象限以及同角三角函数的基本关系求得sinα的值，进而利用两角和与差的正弦函数求得答案．【解答】解：∵α是第三象限的角∴sinα=﹣=﹣，所以sin（α+）=sinαcos+cosαsin=﹣=﹣．故选A11．（5分）（2010•新课标）已知▱ABCD的三个顶点为A（﹣1，2），B（3，4），C（4，﹣2），点（x，y）在▱ABCD的内部，则z=2x﹣5y的取值范围是（）A．（﹣14，16）B．（﹣14，20）C．（﹣12，18）D．（﹣12，20）【分析】根据点坐标与向量坐标之间的关系，利用向量相等求出顶点D的坐标是解决问题的关键．结合线性规划的知识平移直线求出目标函数的取值范围．【解答】解：由已知条件得⇒D（0，﹣4），由z=2x﹣5y得y=，平移直线当直线经过点B（3，4）时，﹣最大，即z取最小为﹣14；当直线经过点D（0，﹣4）时，﹣最小，即z取最大为20，又由于点（x，y）在四边形的内部，故z∈（﹣14，20）．如图：故选B．12．（5分）（2010•新课标）已知函数，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（）A．（1，10）B．（5，6） C．（10，12）D．（20，24）【分析】画出函数的图象，根据f（a）=f（b）=f（c），不妨a＜b＜c，求出abc的范围即可．【解答】解：作出函数f（x）的图象如图，不妨设a＜b＜c，则ab=1，则abc=c∈（10，12）．故选C．二、填空题：本大题共4小题，每小题5分．13．（5分）（2010•新课标）圆心在原点上与直线x+y﹣2=0相切的圆的方程为x2+y2=2．【分析】可求圆的圆心到直线的距离，就是半径，写出圆的方程．【解答】解：圆心到直线的距离：r=，所求圆的方程为x2+y2=2．故答案为：x2+y2=214．（5分）（2010•新课标）设函数y=f（x）为区间（0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法计算由曲线y=f（x）及直线x=0，x=1，y=0所围成部分的面积S，先产生两组（每组N个），区间（0，1]上的均匀随机数x1，x2，…，x n和y1，y2，…，y n，由此得到N个点（x，y）（i ﹣1，2…，N）．再数出其中满足y1≤f（x）（i=1，2…，N）的点数N1，那么由随机模拟方法可得S的近似值为．【分析】由题意知本题是求∫01f（x）dx，而它的几何意义是函数f（x）（其中0≤f（x）≤1）的图象与x轴、直线x=0和直线x=1所围成图形的面积，积分得到结果．【解答】解：∵∫01f（x）dx的几何意义是函数f（x）（其中0≤f（x）≤1）的图象与x轴、直线x=0和直线x=1所围成图形的面积，∴根据几何概型易知∫01f（x）dx≈．故答案为：．15．（5分）（2010•新课标）一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的①②③⑤（填入所有可能的几何体前的编号）①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱．【分析】一个几何体的正视图为一个三角形，由三视图的正视图的作法判断选项．【解答】解：一个几何体的正视图为一个三角形，显然①②⑤正确；③是三棱柱放倒时也正确；④⑥不论怎样放置正视图都不会是三角形；故答案为：①②③⑤16．（5分）（2010•新课标）在△ABC中，D为BC边上一点，BC=3BD，AD=，∠ADB=135°．若AC=AB，则BD=2+．【分析】先利用余弦定理可分别表示出AB，AC，把已知条件代入整理，根据BC=3BD推断出CD=2BD，进而整理AC2=CD2+2﹣2CD 得AC2=4BD2+2﹣4BD把AC=AB，代入整理，最后联立方程消去AB求得BD的方程求得BD．【解答】用余弦定理求得AB2=BD2+AD2﹣2AD•BDcos135°AC2=CD2+AD2﹣2AD•CDcos45°即AB2=BD2+2+2BD ①AC2=CD2+2﹣2CD ②又BC=3BD所以CD=2BD所以由（2）得AC2=4BD2+2﹣4BD（3）因为AC=AB所以由（3）得2AB2=4BD2+2﹣4BD （4）（4）﹣2（1）BD2﹣4BD﹣1=0求得BD=2+故答案为：2+三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（10分）（2010•新课标）设等差数列{a n}满足a3=5，a10=﹣9．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{a n}的前n项和S n及使得S n最大的序号n的值．【分析】（1）设出首项和公差，根据a3=5，a10=﹣9，列出关于首项和公差的二元一次方程组，解方程组得到首项和公差，写出通项．（2）由上面得到的首项和公差，写出数列{a n}的前n项和，整理成关于n的一元二次函数，二次项为负数求出最值．【解答】解：（1）由a n=a1+（n﹣1）d及a3=5，a10=﹣9得a1+9d=﹣9，a1+2d=5解得d=﹣2，a1=9，数列{a n}的通项公式为a n=11﹣2n（2）由（1）知S n=na1+d=10n﹣n2．因为S n=﹣（n﹣5）2+25．所以n=5时，S n取得最大值．18．（10分）（2010•新课标）如图，已知四棱锥P﹣ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．（Ⅰ）证明：平面PAC⊥平面PBD；（Ⅱ）若AB=，∠APB=∠ADB=60°，求四棱锥P﹣ABCD的体积．【分析】（Ⅰ）要证平面PAC⊥平面PBD，只需证明平面PAC内的直线AC，垂直平面PBD内的两条相交直线PH，BD即可．（Ⅱ），∠APB=∠ADB=60°，计算等腰梯形ABCD的面积，PH是棱锥的高，然后求四棱锥P﹣ABCD的体积．【解答】解：（1）因为PH是四棱锥P﹣ABCD的高．所以AC⊥PH，又AC⊥BD，PH，BD都在平PHD内，且PH∩BD=H．所以AC⊥平面PBD．故平面PAC⊥平面PBD（6分）（2）因为ABCD为等腰梯形，AB∥CD，AC⊥BD，AB=．所以HA=HB=．因为∠APB=∠ADB=60°所以PA=PB=，HD=HC=1．可得PH=．等腰梯形ABCD的面积为S=ACxBD=2+（9分）所以四棱锥的体积为V=×（2+）×=．（12分）19．（10分）（2010•新课标）为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如表：（1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；（2）能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（3）根据（2）的结论，能否提供更好的调查方法来估计该地区老年人中，需要志愿帮助的老年人的比例？说明理由．附：【分析】（1）由列联表可知调查的500位老年人中有40+30=70位需要志愿者提供帮助，两个数据求比值得到该地区老年人中需要帮助的老年人的比例的估算值．（2）根据列联表所给的数据，代入随机变量的观测值公式，得到观测值的结果，把观测值的结果与临界值进行比较，看出有多大把握说该地区的老年人是否需要帮助与性别有关．（3）从样本数据老年人中需要帮助的比例有明显差异，调查时，可以先确定该地区老年人中男、女的比例，再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好．【解答】解：（1）∵调查的500位老年人中有40+30=70位需要志愿者提供帮助， ∴该地区老年人中需要帮助的老年人的比例的估算值为．（2）根据列联表所给的数据，代入随机变量的观测值公式，．∵9.967＞6.635，∴有99%的把握认为该地区的老年人是否需要帮助与性别有关．（3）由（2）的结论知，该地区老年人是否需要帮助与性别有关，并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异，因此在调查时，先确定该地区老年人中男、女的比例，再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好．20．（10分）（2010•新课标）设F1，F2分别是椭圆E：x2+=1（0＜b＜1）的左、右焦点，过F1的直线l与E相交于A、B两点，且|AF2|，|AB|，|BF2|成等差数列．（Ⅰ）求|AB|；（Ⅱ）若直线l的斜率为1，求b的值．【分析】（1）由椭圆定义知|AF2|+|AB|+|BF2|=4，再由|AF2|，|AB|，|BF2|成等差数列，能够求出|AB|的值．（2）L的方程式为y=x+c，其中，设A（x1，y1），B（x1，y1），则A，B两点坐标满足方程组，化简得（1+b2）x2+2cx+1﹣2b2=0．然后结合题设条件和根与系数的关系能够求出b的大小．【解答】解：（1）由椭圆定义知|AF2|+|AB|+|BF2|=4又2|AB|=|AF2|+|BF2|，得（2）L的方程式为y=x+c，其中设A（x1，y1），B（x2，y2），则A，B两点坐标满足方程组．，化简得（1+b2）x2+2cx+1﹣2b2=0．则．因为直线AB的斜率为1，所以即．则．解得．21．（2010•新课标）设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．【分析】（I）求导函数，由导数的正负可得函数的单调区间；（II）f（x）=x（e x﹣1﹣ax），令g（x）=e x﹣1﹣ax，分类讨论，确定g（x）的正负，即可求得a的取值范围．【解答】解：（I）a=时，f（x）=x（e x﹣1）﹣x2，=（e x﹣1）（x+1）令f′（x）＞0，可得x＜﹣1或x＞0；令f′（x）＜0，可得﹣1＜x＜0；∴函数的单调增区间是（﹣∞，﹣1），（0，+∞）；单调减区间为（﹣1，0）；（II）f（x）=x（e x﹣1﹣ax）．令g（x）=e x﹣1﹣ax，则g'（x）=e x﹣a．若a≤1，则当x∈（0，+∞）时，g'（x）＞0，g（x）为增函数，而g（0）=0，从而当x≥0时g（x）≥0，即f（x）≥0．若a＞1，则当x∈（0，lna）时，g'（x）＜0，g（x）为减函数，而g（0）=0，从而当x∈（0，lna）时，g（x）＜0，即f（x）＜0．综合得a的取值范围为（﹣∞，1]．22．（10分）（2010•新课标）如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于E点，证明：（Ⅰ）∠ACE=∠BCD．（Ⅱ）BC2=BE•CD．【分析】（I）先根据题中条件：“”，得∠BCD=∠ABC．再根据EC是圆的切线，得到∠ACE=∠ABC，从而即可得出结论．（II）欲证BC2=BE x CD．即证．故只须证明△BDC～△ECB即可．【解答】解：（Ⅰ）因为，所以∠BCD=∠ABC．又因为EC与圆相切于点C，故∠ACE=∠ABC所以∠ACE=∠BCD．（5分）（Ⅱ）因为∠ECB=∠CDB，∠EBC=∠BCD，所以△BDC～△ECB，故．即BC2=BE×CD．（10分）23．（10分）（2010•新课标）已知直线C1（t为参数），C2（θ为参数），（Ⅰ）当α=时，求C1与C2的交点坐标；（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P 点的轨迹的参数方程，并指出它是什么曲线．【分析】（I）先消去参数将曲线C1与C2的参数方程化成普通方程，再联立方程组求出交点坐标即可，（II）设P（x，y），利用中点坐标公式得P点轨迹的参数方程，消去参数即得普通方程，由普通方程即可看出其是什么类型的曲线．【解答】解：（Ⅰ）当α=时，C1的普通方程为，C2的普通方程为x2+y2=1．联立方程组，解得C1与C2的交点为（1，0）．（Ⅱ）C1的普通方程为xsinα﹣ycosα﹣sinα=0①．则OA的方程为xcosα+ysinα=0②，联立①②可得x=sin2α，y=﹣cosαsinα；A点坐标为（sin2α，﹣cosαsinα），故当α变化时，P点轨迹的参数方程为：，P点轨迹的普通方程．故P点轨迹是圆心为，半径为的圆．24．（10分）（2010•新课标）设函数f（x）=|2x﹣4|+1．（Ⅰ）画出函数y=f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．【分析】（I）先讨论x的范围，将函数f（x）写成分段函数，然后根据分段函数分段画出函数的图象即可；（II）根据函数y=f（x）与函数y=ax的图象可知先寻找满足f（x）≤ax的零界情况，从而求出a的范围．【解答】解：（Ⅰ）由于f（x）=，函数y=f（x）的图象如图所示．（Ⅱ）由函数y=f（x）与函数y=ax的图象可知，极小值在点（2，1）当且仅当a＜﹣2或a≥时，函数y=f（x）与函数y=ax的图象有交点．故不等式f（x）≤ax的解集非空时，a的取值范围为（﹣∞，﹣2）∪[，+∞）．。

2010年全国统一高考数学试卷(文科)(新课标)(带答案)

2010年全国统一高考数学试卷（文科）（新课标）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x||x|≤2，x∈R}，B={x|≤4，x∈Z}，则A∩B=（）A．（0，2）B．[0，2]C．{0，2}D．{0，1，2} 2．（5分）平面向量，已知=（4，3），=（3，18），则夹角的余弦值等于（）A．B．C．D．3．（5分）已知复数Z=，则|z|=（）A．B．C．1D．24．（5分）曲线y=x3﹣2x+1在点（1，0）处的切线方程为（）A．y=x﹣1B．y=﹣x+1C．y=2x﹣2D．y=﹣2x+2 5．（5分）中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4，2），则它的离心率为（）A．B．C．D．6．（5分）如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（）A．B．C．D．7．（5分）设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（）A．3πa2B．6πa2C．12πa2D．24πa28．（5分）如果执行如图的框图，输入N=5，则输出的数等于（）A．B．C．D．9．（5分）设偶函数f（x）满足f（x）=2x﹣4（x≥0），则{x|f（x﹣2）＞0}=（）A．{x|x＜﹣2或x＞4}B．{x|x＜0或x＞4}C．{x|x＜0或x ＞6}D．{x|x＜﹣2或x＞2}10．（5分）若cos α=﹣，α是第三象限的角，则sin（α+）=（）A．B．C．D．11．（5分）已知▱ABCD的三个顶点为A（﹣1，2），B（3，4），C（4，﹣2），点（x，y）在▱ABCD的内部，则z=2x﹣5y的取值范围是（）A．（﹣14，16）B．（﹣14，20）C．（﹣12，18）D．（﹣12，20）12．（5分）已知函数，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（）A．（1，10）B．（5，6）C．（10，12）D．（20，24）二、填空题：本大题共4小题，每小题5分．13．（5分）圆心在原点上与直线x+y﹣2=0相切的圆的方程为．14．（5分）设函数y=f（x）为区间（0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法计算由曲线y=f（x）及直线x=0，x=1，y=0所围成部分的面积S，先产生两组（每组N个），区间（0，1]上的均匀随机数x1，x2，…，x n和y1，y2，…，y n，由此得到N个点（x，y）（i﹣1，2…，N）．再数出其中满足y1≤f（x）（i=1，2…，N）的点数N1，那么由随机模拟方法可得S的近似值为．15．（5分）一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的（填入所有可能的几何体前的编号）①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱．16．（5分）在△ABC中，D为BC边上一点，BC=3BD，AD=，∠ADB=135°．若AC=AB，则BD=．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（10分）设等差数列{a n}满足a3=5，a10=﹣9．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{a n}的前n项和S n及使得S n最大的序号n的值．18．（10分）如图，已知四棱锥P﹣ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．（Ⅰ）证明：平面PAC⊥平面PBD；（Ⅱ）若AB=，∠APB=∠ADB=60°，求四棱锥P﹣ABCD的体积．19．（10分）为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如表：性别男女是否需要志愿者需要4030不需要160270（1）估计该地区老年人中，需要志愿者提供帮助的比例；（2）能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（3）根据（2）的结论，能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人比例？说明理由．P（K2≥k）0.0500.0100.0013.841 6.63510.828附：K2=．20．（10分）设F1，F2分别是椭圆E：x2+=1（0＜b＜1）的左、右焦点，过F1的直线l与E相交于A、B两点，且|AF2|，|AB|，|BF2|成等差数列．（Ⅰ）求|AB|；（Ⅱ）若直线l的斜率为1，求b的值．21．设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．22．（10分）如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于E点，证明：（Ⅰ）∠ACE=∠BCD．（Ⅱ）BC2=BE•CD．23．（10分）已知直线C1（t为参数），C2（θ为参数），（Ⅰ）当α=时，求C1与C2的交点坐标；（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P 点的轨迹的参数方程，并指出它是什么曲线．24．（10分）设函数f（x）=|2x﹣4|+1．（Ⅰ）画出函数y=f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．2010年全国统一高考数学试卷（文科）（新课标）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x||x|≤2，x∈R}，B={x|≤4，x∈Z}，则A∩B=（）A．（0，2）B．[0，2]C．{0，2}D．{0，1，2}【考点】1E：交集及其运算．【专题】11：计算题．【分析】由题意可得A={x|﹣2≤x≤2}，B={0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}，从而可求【解答】解：∵A={x||x|≤2}={x|﹣2≤x≤2}B={x|≤4，x∈Z}={0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}则A∩B={0，1，2}故选：D．【点评】本题主要考查了集合的交集的求解，解题的关键是准确求解A，B，属于基础试题2．（5分）平面向量，已知=（4，3），=（3，18），则夹角的余弦值等于（）A．B．C．D．【考点】9S：数量积表示两个向量的夹角．【分析】先设出的坐标，根据a=（4，3），2a+b=（3，18），求出坐标，根据数量积的坐标公式的变形公式，求出两个向量的夹角的余弦【解答】解：设=（x，y），∵a=（4，3），2a+b=（3，18），∴∴cosθ==，故选：C．【点评】本题是用数量积的变形公式求向量夹角的余弦值，数量积的主要应用：①求模长；②求夹角；③判垂直，实际上在数量积公式中可以做到知三求一．3．（5分）已知复数Z=，则|z|=（）A．B．C．1D．2【考点】A5：复数的运算．【专题】11：计算题．【分析】由复数的代数形式的乘除运算化简可得Z=，由复数的模长公式可得答案．【解答】解：化简得Z===•=•=•=，故|z|==，故选：B．【点评】本题考查复数的代数形式的乘除运算，涉及复数的模长，属基础题．4．（5分）曲线y=x3﹣2x+1在点（1，0）处的切线方程为（）A．y=x﹣1B．y=﹣x+1C．y=2x﹣2D．y=﹣2x+2【考点】6H：利用导数研究曲线上某点切线方程．【专题】1：常规题型；11：计算题．【分析】欲求在点（1，0）处的切线方程，只须求出其斜率的值即可，故先利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．【解答】解：验证知，点（1，0）在曲线上∵y=x3﹣2x+1，y′=3x2﹣2，所以k=y′|x﹣1=1，得切线的斜率为1，所以k=1；所以曲线y=f（x）在点（1，0）处的切线方程为：y﹣0=1×（x﹣1），即y=x﹣1．故选：A．【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．5．（5分）中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4，2），则它的离心率为（）A．B．C．D．【考点】KC：双曲线的性质．【专题】11：计算题．【分析】先求渐近线斜率，再用c2=a2+b2求离心率．【解答】解：∵渐近线的方程是y=±x，∴2=•4，=，a=2b，c==a，e==，即它的离心率为．故选：D．【点评】本题考查双曲线的几何性质．6．（5分）如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（）A．B．C．D．【考点】3A：函数的图象与图象的变换．【分析】本题的求解可以利用排除法，根据某具体时刻点P的位置到到x轴距离来确定答案．【解答】解：通过分析可知当t=0时，点P到x轴距离d为，于是可以排除答案A，D，再根据当时，可知点P在x轴上此时点P到x轴距离d为0，排除答案B，故选：C．【点评】本题主要考查了函数的图象，以及排除法的应用和数形结合的思想，属于基础题．7．（5分）设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（）A．3πa2B．6πa2C．12πa2D．24πa2【考点】LG：球的体积和表面积．【专题】11：计算题．【分析】本题考查的知识点是球的体积和表面积公式，由长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则长方体的对角线即为球的直径，即球的半径R满足（2R）2=6a2，代入球的表面积公式，S球=4πR2，即可得到答案．【解答】解：根据题意球的半径R满足（2R）2=6a2，=4πR2=6πa2．所以S球故选：B．【点评】长方体的外接球直径等于长方体的对角线长．8．（5分）如果执行如图的框图，输入N=5，则输出的数等于（）A．B．C．D．【考点】EF：程序框图．【专题】28：操作型．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=的值．【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S=的值．∵S==1﹣=故选：D．【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．9．（5分）设偶函数f（x）满足f（x）=2x﹣4（x≥0），则{x|f（x﹣2）＞0}=（）A．{x|x＜﹣2或x＞4}B．{x|x＜0或x＞4}C．{x|x＜0或x ＞6}D．{x|x＜﹣2或x＞2}【考点】3K：函数奇偶性的性质与判断．【专题】11：计算题．【分析】由偶函数f（x）满足f（x）=2x﹣4（x≥0），可得f（x）=f（|x|）=2|x|﹣4，根据偶函数的性质将函数转化为绝对值函数，再求解不等式，可得答案．【解答】解：由偶函数f（x）满足f（x）=2x﹣4（x≥0），可得f（x）=f（|x|）=2|x|﹣4，则f（x﹣2）=f（|x﹣2|）=2|x﹣2|﹣4，要使f（|x﹣2|）＞0，只需2|x﹣2|﹣4＞0，|x﹣2|＞2解得x＞4，或x＜0．应选：B．【点评】本题主要考查偶函数性质、不等式的解法以及相应的运算能力，解答本题的关键是利用偶函数的性质将函数转化为绝对值函数，从而简化计算．10．（5分）若cos α=﹣，α是第三象限的角，则sin（α+）=（）A．B．C．D．【考点】GG：同角三角函数间的基本关系；GP：两角和与差的三角函数．【专题】11：计算题．【分析】根据α的所在的象限以及同角三角函数的基本关系求得sinα的值，进而利用两角和与差的正弦函数求得答案．【解答】解：∵α是第三象限的角∴sinα=﹣=﹣，所以sin（α+）=sinαcos+cosαsin=﹣=﹣．故选：A．【点评】本题主要考查了两角和与差的正弦函数，以及同角三角函数的基本关系的应用．根据角所在的象限判断三角函数值的正负是做题过程中需要注意的．11．（5分）已知▱ABCD的三个顶点为A（﹣1，2），B（3，4），C（4，﹣2），点（x，y）在▱ABCD的内部，则z=2x﹣5y的取值范围是（）A．（﹣14，16）B．（﹣14，20）C．（﹣12，18）D．（﹣12，20）【考点】7C：简单线性规划．【专题】11：计算题；16：压轴题．【分析】根据点坐标与向量坐标之间的关系，利用向量相等求出顶点D的坐标是解决问题的关键．结合线性规划的知识平移直线求出目标函数的取值范围．【解答】解：由已知条件得⇒D（0，﹣4），由z=2x﹣5y得y=，平移直线当直线经过点B（3，4）时，﹣最大，即z取最小为﹣14；当直线经过点D（0，﹣4）时，﹣最小，即z取最大为20，又由于点（x，y）在四边形的内部，故z∈（﹣14，20）．如图：故选B．【点评】本题考查平行四边形的顶点之间的关系，用到向量坐标与点坐标之间的关系，体现了向量的工具作用，考查学生线性规划的理解和认识，考查学生的数形结合思想．属于基本题型．12．（5分）已知函数，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（）A．（1，10）B．（5，6）C．（10，12）D．（20，24）【考点】3A：函数的图象与图象的变换；3B：分段函数的解析式求法及其图象的作法；4H：对数的运算性质；4N：对数函数的图象与性质．【专题】13：作图题；16：压轴题；31：数形结合．【分析】画出函数的图象，根据f（a）=f（b）=f（c），不妨a＜b＜c，求出abc 的范围即可．【解答】解：作出函数f（x）的图象如图，不妨设a＜b＜c，则ab=1，则abc=c∈（10，12）．故选：C．【点评】本题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力．二、填空题：本大题共4小题，每小题5分．13．（5分）圆心在原点上与直线x+y﹣2=0相切的圆的方程为x2+y2=2．【考点】J1：圆的标准方程；J9：直线与圆的位置关系．【分析】可求圆的圆心到直线的距离，就是半径，写出圆的方程．【解答】解：圆心到直线的距离：r=，所求圆的方程为x2+y2=2．故答案为：x2+y2=2【点评】本题考查圆的标准方程，直线与圆的位置关系，是基础题．14．（5分）设函数y=f（x）为区间（0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法计算由曲线y=f（x）及直线x=0，x=1，y=0所围成部分的面积S，先产生两组（每组N个），区间（0，1]上的均匀随机数x1，x2，…，x n和y1，y2，…，y n，由此得到N个点（x，y）（i﹣1，2…，N）．再数出其中满足y1≤f（x）（i=1，2…，N）的点数N1，那么由随机模拟方法可得S的近似值为．【考点】CE：模拟方法估计概率；CF：几何概型．【分析】由题意知本题是求∫01f（x）dx，而它的几何意义是函数f（x）（其中0≤f（x）≤1）的图象与x轴、直线x=0和直线x=1所围成图形的面积，积分得到结果．【解答】解：∵∫01f（x）dx的几何意义是函数f（x）（其中0≤f（x）≤1）的图象与x轴、直线x=0和直线x=1所围成图形的面积，∴根据几何概型易知∫01f（x）dx≈．故答案为：．【点评】古典概型和几何概型是我们学习的两大概型，古典概型要求能够列举出所有事件和发生事件的个数，而不能列举的就是几何概型，几何概型的概率的值是通过长度、面积和体积的比值得到．15．（5分）一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的①②③⑤（填入所有可能的几何体前的编号）①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱．【考点】L7：简单空间图形的三视图．【专题】15：综合题；16：压轴题．【分析】一个几何体的正视图为一个三角形，由三视图的正视图的作法判断选项．【解答】解：一个几何体的正视图为一个三角形，显然①②⑤正确；③是三棱柱放倒时也正确；④⑥不论怎样放置正视图都不会是三角形；故答案为：①②③⑤【点评】本题考查简单几何体的三视图，考查空间想象能力，是基础题．16．（5分）在△ABC中，D为BC边上一点，BC=3BD，AD=，∠ADB=135°．若AC=AB，则BD=2+．【考点】HR：余弦定理．【专题】11：计算题；16：压轴题．【分析】先利用余弦定理可分别表示出AB，AC，把已知条件代入整理，根据BC=3BD推断出CD=2BD，进而整理AC2=CD2+2﹣2CD 得AC2=4BD2+2﹣4BD把AC=AB，代入整理，最后联立方程消去AB求得BD的方程求得BD．【解答】用余弦定理求得AB2=BD2+AD2﹣2AD•BDcos135°AC2=CD2+AD2﹣2AD•CDcos45°即AB2=BD2+2+2BD ①AC2=CD2+2﹣2CD ②又BC=3BD所以CD=2BD所以由（2）得AC2=4BD2+2﹣4BD（3）因为AC=AB所以由（3）得2AB2=4BD2+2﹣4BD （4）（4）﹣2（1）BD2﹣4BD﹣1=0求得BD=2+故答案为：2+【点评】本题主要考查了余弦定理的应用．考查了学生创造性思维能力和基本的推理能力．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（10分）设等差数列{a n}满足a3=5，a10=﹣9．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{a n}的前n项和S n及使得S n最大的序号n的值．【考点】84：等差数列的通项公式；85：等差数列的前n项和．【分析】（1）设出首项和公差，根据a3=5，a10=﹣9，列出关于首项和公差的二元一次方程组，解方程组得到首项和公差，写出通项．（2）由上面得到的首项和公差，写出数列{a n}的前n项和，整理成关于n的一元二次函数，二次项为负数求出最值．【解答】解：（1）由a n=a1+（n﹣1）d及a3=5，a10=﹣9得a1+9d=﹣9，a1+2d=5解得d=﹣2，a1=9，数列{a n}的通项公式为a n=11﹣2n（2）由（1）知S n=na1+d=10n﹣n2．因为S n=﹣（n﹣5）2+25．所以n=5时，S n取得最大值．【点评】数列可看作一个定义域是正整数集或它的有限子集的函数，当自变量从小到大依次取值对应的一列函数值，因此它具备函数的特性．18．（10分）如图，已知四棱锥P﹣ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．（Ⅰ）证明：平面PAC⊥平面PBD；（Ⅱ）若AB=，∠APB=∠ADB=60°，求四棱锥P﹣ABCD的体积．【考点】LF：棱柱、棱锥、棱台的体积；LY：平面与平面垂直．【专题】11：计算题；14：证明题；35：转化思想．【分析】（Ⅰ）要证平面PAC⊥平面PBD，只需证明平面PAC内的直线AC，垂直平面PBD内的两条相交直线PH，BD即可．（Ⅱ），∠APB=∠ADB=60°，计算等腰梯形ABCD的面积，PH是棱锥的高，然后求四棱锥P﹣ABCD的体积．【解答】解：（1）因为PH是四棱锥P﹣ABCD的高．所以AC⊥PH，又AC⊥BD，PH，BD都在平PHD内，且PH∩BD=H．所以AC⊥平面PBD．故平面PAC⊥平面PBD（6分）（2）因为ABCD为等腰梯形，AB∥CD，AC⊥BD，AB=．所以HA=HB=．因为∠APB=∠ADB=60°所以PA=PB=，HD=HC=1．可得PH=．等腰梯形ABCD的面积为S=ACxBD=2+（9分）所以四棱锥的体积为V=×（2+）×=．（12分）【点评】本题考查平面与平面垂直的判定，棱柱、棱锥、棱台的体积，考查空间想象能力，计算能力，推理能力，是中档题．19．（10分）为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如表：男女性别是否需要志愿者需要4030不需要160270（1）估计该地区老年人中，需要志愿者提供帮助的比例；（2）能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（3）根据（2）的结论，能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人比例？说明理由．P（K2≥k）0.0500.0100.0013.841 6.63510.828附：K2=．【考点】BL：独立性检验．【专题】11：计算题；5I：概率与统计．【分析】（1）由样本的频率率估计总体的概率，（2）求K2的观测值查表，下结论；（3）由99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关，则可按性别分层抽样．【解答】解：（1）调查的500位老年人中有70位需要志愿者提供帮助，因此在该地区老年人中，需要帮助的老年人的比例的估计值为（2）K2的观测值因为9.967＞6.635，且P（K2≥6.635）=0.01，所以有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关．（3）根据（2）的结论可知，该地区的老年人是否需要志愿者提供帮助与性别有关，并且从样本数据能够看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异，因此在调查时，先确定该地区老年人中男、女的比例，再把老年人分成男女两层，并采取分层抽样方法比简单随机抽样方法更好．【点评】本题考查了抽样的目的，独立性检验的方法及抽样的方法选取，属于基础题．20．（10分）设F1，F2分别是椭圆E：x2+=1（0＜b＜1）的左、右焦点，过F1的直线l与E相交于A、B两点，且|AF2|，|AB|，|BF2|成等差数列．（Ⅰ）求|AB|；（Ⅱ）若直线l的斜率为1，求b的值．【考点】K4：椭圆的性质．【专题】15：综合题．【分析】（1）由椭圆定义知|AF2|+|AB|+|BF2|=4，再由|AF2|，|AB|，|BF2|成等差数列，能够求出|AB|的值．（2）L的方程式为y=x+c，其中，设A（x1，y1），B（x1，y1），则A，B 两点坐标满足方程组，化简得（1+b2）x2+2cx+1﹣2b2=0．然后结合题设条件和根与系数的关系能够求出b的大小．【解答】解：（1）由椭圆定义知|AF2|+|AB|+|BF2|=4又2|AB|=|AF2|+|BF2|，得（2）L的方程式为y=x+c，其中设A（x1，y1），B（x2，y2），则A，B两点坐标满足方程组．，化简得（1+b2）x2+2cx+1﹣2b2=0．则．因为直线AB的斜率为1，所以即．则．解得．【点评】本题综合考查椭圆的性质及其运用和直线与椭圆的位置关系，解题时要注意公式的灵活运用．21．设函数f（x）=x（e x﹣1）﹣ax2（Ⅰ）若a=，求f（x）的单调区间；（Ⅱ）若当x≥0时f（x）≥0，求a的取值范围．【考点】6B：利用导数研究函数的单调性．【专题】15：综合题；53：导数的综合应用．【分析】（I）求导函数，由导数的正负可得函数的单调区间；（II）f（x）=x（e x﹣1﹣ax），令g（x）=e x﹣1﹣ax，分类讨论，确定g（x）的正负，即可求得a的取值范围．【解答】解：（I）a=时，f（x）=x（e x﹣1）﹣x2，=（e x ﹣1）（x+1）令f′（x）＞0，可得x＜﹣1或x＞0；令f′（x）＜0，可得﹣1＜x＜0；∴函数的单调增区间是（﹣∞，﹣1），（0，+∞）；单调减区间为（﹣1，0）；（II）f（x）=x（e x﹣1﹣ax）．令g（x）=e x﹣1﹣ax，则g'（x）=e x﹣a．若a≤1，则当x∈（0，+∞）时，g'（x）＞0，g（x）为增函数，而g（0）=0，从而当x≥0时g（x）≥0，即f（x）≥0．若a＞1，则当x∈（0，lna）时，g'（x）＜0，g（x）为减函数，而g（0）=0，从而当x∈（0，lna）时，g（x）＜0，即f（x）＜0．综合得a的取值范围为（﹣∞，1]．另解：当x=0时，f（x）=0成立；当x＞0，可得e x﹣1﹣ax≥0，即有a≤的最小值，由y=e x﹣x﹣1的导数为y′=e x﹣1，当x＞0时，函数y递增；x＜0时，函数递减，可得函数y取得最小值0，即e x﹣x﹣1≥0，x＞0时，可得≥1，则a≤1．【点评】本题考查导数知识的运用，考查函数的单调性，考查分类讨论的数学思想，属于中档题．22．（10分）如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于E点，证明：（Ⅰ）∠ACE=∠BCD．（Ⅱ）BC2=BE•CD．【考点】N9：圆的切线的判定定理的证明；NB：弦切角．【专题】14：证明题．【分析】（I）先根据题中条件：“”，得∠BCD=∠ABC．再根据EC是圆的切线，得到∠ACE=∠ABC，从而即可得出结论．（II）欲证BC2=BE x CD．即证．故只须证明△BDC～△ECB即可．【解答】解：（Ⅰ）因为，所以∠BCD=∠ABC．又因为EC与圆相切于点C，故∠ACE=∠ABC所以∠ACE=∠BCD．（5分）（Ⅱ）因为∠ECB=∠CDB，∠EBC=∠BCD，所以△BDC～△ECB，故．即BC2=BE×CD．（10分）【点评】本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识，考查运化归与转化思想．属于基础题．23．（10分）已知直线C1（t为参数），C2（θ为参数），（Ⅰ）当α=时，求C1与C2的交点坐标；（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P 点的轨迹的参数方程，并指出它是什么曲线．【考点】J3：轨迹方程；JE：直线和圆的方程的应用；Q4：简单曲线的极坐标方程；QJ：直线的参数方程；QK：圆的参数方程．【专题】15：综合题；16：压轴题．【分析】（I）先消去参数将曲线C1与C2的参数方程化成普通方程，再联立方程组求出交点坐标即可，（II）设P（x，y），利用中点坐标公式得P点轨迹的参数方程，消去参数即得普通方程，由普通方程即可看出其是什么类型的曲线．【解答】解：（Ⅰ）当α=时，C1的普通方程为，C2的普通方程为x2+y2=1．联立方程组，解得C1与C2的交点为（1，0）．（Ⅱ）C1的普通方程为xsinα﹣ycosα﹣sinα=0①．则OA的方程为xcosα+ysinα=0②，联立①②可得x=sin2α，y=﹣cosαsinα；A点坐标为（sin2α，﹣cosαsinα），故当α变化时，P点轨迹的参数方程为：，P点轨迹的普通方程．故P点轨迹是圆心为，半径为的圆．【点评】本题主要考查直线与圆的参数方程，参数方程与普通方程的互化，利用参数方程研究轨迹问题的能力．24．（10分）设函数f（x）=|2x﹣4|+1．（Ⅰ）画出函数y=f（x）的图象：（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围．【考点】3A：函数的图象与图象的变换；7E：其他不等式的解法；R5：绝对值不等式的解法．【专题】11：计算题；13：作图题；16：压轴题．【分析】（I）先讨论x的范围，将函数f（x）写成分段函数，然后根据分段函数分段画出函数的图象即可；（II）根据函数y=f（x）与函数y=ax的图象可知先寻找满足f（x）≤ax的零界情况，从而求出a的范围．【解答】解：（Ⅰ）由于f（x）=，函数y=f（x）的图象如图所示．（Ⅱ）由函数y=f（x）与函数y=ax的图象可知，极小值在点（2，1）当且仅当a＜﹣2或a≥时，函数y=f（x）与函数y=ax的图象有交点．故不等式f（x）≤ax的解集非空时，a的取值范围为（﹣∞，﹣2）∪[，+∞）．【点评】本题主要考查了函数的图象，以及利用函数图象解不等式，同时考查了数形结合的数学思想，属于基础题．。

数学(文科)试题参考答案及评分标准

2m 8
令d
2 ，解得 m 1．
16 (m 4)2
综上所述，当 m 1时，直线 AK 与圆 x2 ( y 2)2 4 相交；
当 m 1时，直线 AK 与圆 x2 ( y 2)2 4 相切；
当 m 1时，直线 AK 与圆 x2 ( y 2)2 4 相离．………………………………14 分
2
3
3
3
所以
f
x 在区间
1,
2 3
a
上是减函数，在区间
2 3
a, 2
上是增函数．
所以 h a
f

2 3
a

4 27
a3
．
……………………………………………………………8 分
④若 a 3 ，即 2 a 2 ，则当1 x 2 时， f ' x 0 ，所以 f x 在区间1, 2上是减函数．
21．（本小题满分 14 分）
（1）解：∵ f x x3 ax2 ，∴ f ' x 3x2 2ax . ……………………………………1 分
∵函数
f
x
在区间

0,
2 3
内是减函数，∴
f
'x

3x2

2ax

0
在

0,
2 3
上恒成立．……2
分
即
a

3x 2
在

0,
2 3

上恒成立，…………………………………………………………………3
分
5
3x 3 2 1，∴ a 1 ． 2 23

广东2010年高考文科综合(B卷)试题及参考答案(估分)-中大网校

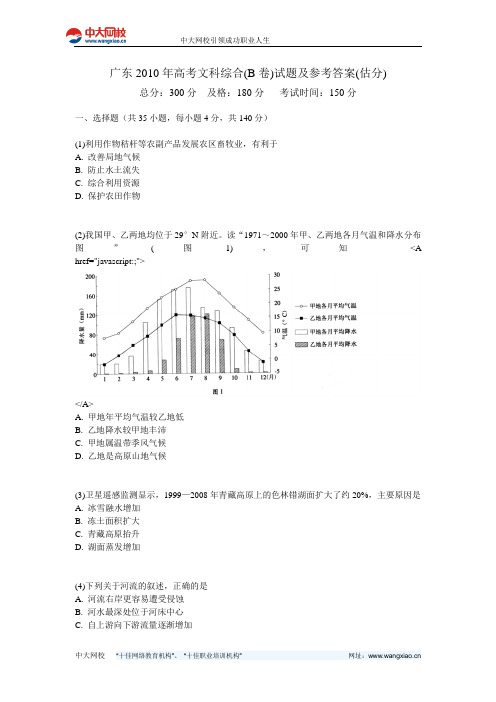
广东2010年高考文科综合(B卷)试题及参考答案(估分)总分：300分及格：180分考试时间：150分一、选择题（共35小题，每小题4分，共140分）(1)利用作物秸杆等农副产品发展农区畜牧业，有利于A. 改善局地气候B. 防止水土流失C. 综合利用资源D. 保护农田作物(2)我国甲、乙两地均位于29°N附近。

读“1971～2000年甲、乙两地各月气温和降水分布图”(图1)，可知<A href="javascript:;"></A>A. 甲地年平均气温较乙地低B. 乙地降水较甲地丰沛C. 甲地属温带季风气候D. 乙地是高原山地气候(3)卫星遥感监测显示，1999—2008年青藏高原上的色林错湖面扩大了约20%，主要原因是A. 冰雪融水增加B. 冻土面积扩大C. 青藏高原抬升D. 湖面蒸发增加(4)下列关于河流的叙述，正确的是A. 河流右岸更容易遭受侵蚀B. 河水最深处位于河床中心C. 自上游向下游流量逐渐增加D. 水面宽度一年中洪水期最大(5)读“2006年我国水资源、人口、耕地和经济总量区域比重图”(图2)，完成{TSE}题。

(6)水资源与人口、耕地、经济发展匹配较差的区域是A. 北方区和西南区B. 北方区和南方区C. 西北区和西南区D. 西北区和南方区(7)三峡大坝下游附近河床某测点，沉积物粒径的平均值比建坝前大(如图3示意)，其成因是<Ahref="javascript:;"></A>A. 风化一侵蚀作用B. 搬运一堆积作用C. 侵蚀一搬运作用D. 沉积一固结成岩作用(8)下列关于无霜期的叙述，正确的是A. 同一海拔，纬度越高无霜期越长B. 同一纬度，海拔越低无霜期越短C. 同一山地，阳坡无霜期短于阴坡D. 同一地段，开阔地无霜期长于低洼地(9)沙尘暴对地理环境的影响是多方面的。

华北地区沙尘暴的降尘会A. 导致气候变暖B. 增加土壤肥力C. 引起地表水体酸化D. 引发草场退化(10)读“2005年我国东部沿海某市各圈层间人口净迁移模式图”(图4)，完成{TSE}题。

2010广东高考文科数学

2010广东高考文科数学引言文科数学是广东高考中的一门重要科目，考查学生在数学方面的基础知识和解题能力。

本篇文档将对2010年广东高考文科数学试题进行分析和解答，帮助考生更好地理解和应对考试。

题目解析题目一题目：已知函数f(x) = sin(x)，g(x) = cos(x)，h(x) =f(x)·g(x)，求h(x)在[0, π]上的最大值和最小值。

解析：首先，我们需要计算h(x)在[0, π]上的导数。

利用链式法则，我们可以得到h’(x) = f’(x)g(x) + f(x)g’(x) = cos^2(x) - sin^2(x)。

因为h’(x) = 0时，h(x)取得极值，所以我们需要求解方程cos^2(x) - sin^2(x) = 0。

化简得到cos(2x) = 0，即2x = π/2或2x = 3π/2。

由于x的范围是[0, π]，所以当x = π/4或x = 3π/4时，h(x)取得最小值0。

当x = π/2时，h(x)取得最大值1。

题目二题目：一元二次方程x^2 - (a + 3)x + 2a = 0有两个实数解x1和x2。

已知x1 + x2 = 7，求a的值。

解析：根据一元二次方程的基本知识，我们知道二次方程的两个根的和等于系数b的相反数除以系数a。

所以，根据题目给出的信息，我们可以得到下列等式：x1 + x2 = a + 3 = 7。

解方程得到a = 4。

解答步骤问题一解答步骤1.计算h(x)在[0, π]上的导数。

h’(x) = cos^2(x) - sin^2(x)2.求解方程cos^2(x) - sin^2(x) = 0。

化简得到cos(2x) = 0，即2x = π/2或2x = 3π/2。

3.计算h(x)在[0, π]上的最大值和最小值。

当x = π/4或x = 3π/4时，h(x)取得最小值0。

当x = π/2时，h(x)取得最大值1。

问题二解答步骤1.根据一元二次方程的基本知识，我们知道二次方程的两个根的和等于系数b的相反数除以系数a。

新课标2010年高考数学(文)试题及参考答案(估分)-中大网校

新课标2010年高考数学(文)试题及参考答案(估分)总分：150分及格：90分考试时间：120分本大题共12题，每小题5分，在每小题给出的四个选项中，中有一项是符合题目要求的。

(1)<Ahref="javascript:;"></A>(2)<Ahref="javascript:;"></A>(3)(4)<Ahref="javascript:;"></A> (5)(6)<Ahref="javascript:;"></A>(7)<Ahref="javascript:;"></A>(8)<Ahref="javascript:;"></A>(9)<Ahref="javascript:;"></ A>(10)<Ahref="javascript:;"></A>(11)(12)<Ahref="javascript:;"></A>本大题共4小题，每小题5分。

(1)<Ahref="javascript:;"></A>(2)<Ahref="javascript:;"></A>(3)<Ahref="javascript:;"></A>(4)<Ahref="javascript:;"></A>解答应写出文字说明，证明过程或演算步骤。

第(22题)~第(24)题为选考题，考生根据要求做答。

2010年普通高等学校招生全国统一考试预测卷(广东卷)数学(文科)

广东省2010届高考文科数学预测第一部分选择题本试卷共21小题，满分150分。

考试用时120分钟。

一、选择题：本大题共10小题，每小题5分，满分50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

请将答案填在答题卷上。

1. 已知全集合{},3,2,1,0=I 集合{}2,1,0=M ,{}3,2,0=N ,则()=⋂N C M I （）A.{}1 B.{}3,2 C.{}2,1,0 D. φ 2. 已知复数z=1－2i ，则 z +1z －1=（） (A) 1+i(B) 1－i(C) －1+i(D) －1－i3. 已知正方形ABCD 的边长为1, 则AB BC AC ++=（） A. 0 B. 2 C. 2 D. 224. 曲线34y x x =-在点()1,3--处的切线方程是（）（A ）74y x =+ （B ）72y x =+ （C ）4y x =- （D ）2y x =-5. 已知等差数列{}n a 中, 315,a a 是方程2610x x --=的两根, 则7891011a a a a a ++++等于（）A. 18B. 18-C. 15D. 126. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为（） A ．2- B ．2 C ．4- D ．4 7. 已知：┓p 且q 为真，则下列命题中的假命题是：（） ①p ；②p 或q ； ③p 且q ； ④┓qA ．①④B ．①②③C ．①③④D ．②③④8. 两座灯塔A 和B 与海洋观察站C 的距离都等于a km , 灯塔A 在观察站C 的北偏东20, 灯塔B 在观察站C 的南偏东40，则灯塔A 与灯塔B 的距离为（）km A. a B. a 2 C. a 2 D. a 39. 设,m n 是两条不同的直线，,αβ是两个不同的平面，下列命题正确的是 A.若,,//,m n m n αβ⊥⊥则//αβ B.若//,//,//m n αβαβ，则//m n图5C.若,//,//m n αβαβ⊥，则m n ⊥D.若//,//,//,m n m n αβ则//αβ 10. 若函数)(x f y =的图象如右下图所示, 则函数)1(x f y -=的图象大致为（）第Ⅱ卷二、填空题(本大题共5小题，考生做答4小题，每小题5分，共20分) (一)必做题(11～13题)11．某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布图如图所示，若130—140分数段的人数为90人，则90—100分数段的人数为_______12. 设实数x 、y 满足约束条件：0,,23,x x y x y ≥⎧⎪≤⎨⎪+≤⎩则2z x y =-的最大值是_______13.如图所示，这是计算111124620++++的值的一个程序框图，其中判断框内应填入的条件是_______(二)选做题(14～15题考生只能从中选作一题)14.（坐标系与参数方程选做题）若直线340x y m ++=与圆⎩⎨⎧+-=+=θθsin 2cos 1y x （θ为参数）相切,则实数m 的值是_______D.C.A. B.ACD 图2BACD图115.（几何证明选讲选做题）如图5, AB 为⊙O 的直径, AC 切⊙O 于点A ,且cm AC 22=,过C 的割线CMN 交AB 的延长线于点D ,CM=MN=ND.AD 的长等于_______cm .三.解答题(本大题共有6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.) 16．（本小题满分12分）已知：A 、B 、C 是ABC ∆的内角，c b a ,,分别是其对边长，向量()1cos ,3+=A m ，()1,sin -=A ，⊥.（Ⅰ）求角A 的大小；（Ⅱ）若,33cos ,2==B a 求b 的长.17．（本小题满分12分）设AB=6，在线段AB 上任取两点（端点A ，B 除外），将线段AB 分成三条线段， (Ⅰ)若分成三条线段的长度均为正整数，求这三条线段可以构成三角形的概率；（Ⅱ）若分成三条线段的长度均为正实数，求这三条线段可以构成三角形的概率；18．（本小题满分14分）如图，在直角梯形ABCD 中,90ADC ∠=︒,//CD AB ,4,2AB AD CD ===.将ADE ∆沿AC 折起,使平面ADE ⊥平面ABC ,得到几何体D ABC -,如图2所示. (Ⅰ) 求证:BC ⊥平面ACD ；(Ⅱ) 求几何体D ABC -的体积.19．（本小题满分14分）某商店预备在一个月内分批购入每张价值为20元的书桌共36台，每批都购入x 台（x 是正整数）,且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费. （1）求该月需用去的运费和保管费的总费用()x f ;（2）能否恰当地安排每批进货的数量,使资金够用?写出你的结论,并说明理由. 20．（本小题满分14分）已知长方形ABCD, AB=22,BC=1.以AB 的中点O 为原点建立如图8所示的平面直角坐标系xoy .(Ⅰ)求以A 、B 为焦点，且过C 、D 两点的椭圆的标准方程;(Ⅱ)过点P(0,2)的直线l 交(Ⅰ)中椭圆于M,N 两点,是否存在直线l ,使得以弦MN 为直径的圆恰好过原点?若存在,求出直线l 的方程;若不存在,说明理由.21．（本小题满分14分）已知数列｛n a ｝中，11122n n a n a a +=-、点（、）在直线y=x 上，其中n=1,2,3…. (Ⅰ)令{}是等比数列；求证数列n n n n b a a b ,31--=-(Ⅱ)求数列{}的通项；n a图8(Ⅲ)设分别为数列、n n T S {}、n a {}n b 的前n 项和,是否存在实数λ，使得数列n n S T n λ+⎧⎫⎨⎬⎩⎭为等差数列？若存在，试求出λ.若不存在,则说明理由。

广东卷高中数学题

2010年普通高等学校招生全国统一考试·文科数学(广东卷)第Ⅰ卷一、选择题:本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.(2010广东，文1)若集合A ={0，1，2，3}，B ={1，2，4}，则集合A ∪B =( ) A.{0，1，2，3，4} B.{1，2，3，4} C.{1，2} D.{0} 答案:A2.(2010广东，文2)函数f (x )=lg(x －1)的定义域是( ) A.(2，+∞) B.(1，+∞) C.\[1，+∞) D.\[2，+∞)答案:B3.(2010广东，文3)若函数f (x )=3x +3-x 与g (x )=3x －3-x 的定义域均为R ，则( ) A.f (x )与g (x )均为偶函数 B.f (x )为奇函数，g (x )为偶函数 C.f (x )与g (x )均为奇函数 D.f (x )为偶函数，g (x )为奇函数答案:D4.(2010广东，文4)已知数列{a n }为等比数列，S n 是它的前n 项和.若a 2·a 3=2a 1，且a 4与2a 7的等差中项为45，则S 5=( )A.35B.33C.31D.29 答案:C5.(2010广东，文5)若向量a =(1，1)，b =(2，5)，c =(3，x )满足条件(8a －b )·c =30，则x =( )A.6B.5C.4D.3答案:C6.(2010广东，文6)若圆心在x 轴上、半径为5的圆O 位于y 轴左侧，且与直线x +2y =0相切，则圆O 的方程是( )A.(x －5)2+y 2=5B.(x +5)2+y 2=5C.(x －5)2+y 2=5D.(x +5)2+y 2=5答案:D7.(2010广东，文7)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是( )A.54 B.53 C.52 D.51答案:B8.(2010广东，文8)“x >0”是“32x >0”成立的( )A.充分非必要条件B.必要非充分条件C.非充分非必要条件D.充要条件答案:A9.(2010广东，文9)如图，△ABC 为正三角形，AA ′∥BB ′∥CC ′，CC ′⊥平面ABC 且3AA ′=23BB ′=CC ′=AB ，则多面体ABC —A ′B ′C ′的正视图(也称主视图)是( )'A B CD 答案:D10.(2010广东，文10)在集合{a ，b ，c ，d }上定义两种运算⊕和⊗如下:a b c d a b c d b b b b c b c b d b b d+a b c d a b c da a a a abcd a c c a a d a d+a b c d 那么d ⊗(a ⊕c )=( ) A.aB.bC.cD.d答案:A第Ⅱ卷二、填空题:本大题共5小题，考生作答4小题，每小题5分，满分20分.把答案填在答题卡的相应位置.(一)必做题(11~13题)11.(2010广东，文11)某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中4位居民的月均用水量分别为x 1，…，x 4(单位:吨).根据如图所示的程序框图，若x 1，x 2，x 3，x 4分别为1，1.5，1.5，2，则输出的结果s 为________________.答案:2312.(2010广东，文12)某市居民2005～2009年家庭年平均收入x (单位:万元)与年平均支出Y (单位:万元)的统计资料如下表所示:年平均支出有________________线性相关关系.答案:13 正13.(2010广东，文13)已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边，若a =1，b =3，A +C =2B ，则sin A =________________.答案:21(二)选做题(14、15题，考生只能从中选做一题) 14.(2010广东，文14)(几何证明选讲选做题)如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB =AD =a ，CD =2a ，点E ，F 分别为线段AB ，AD 的中点，则EF =________________.ABCD EF答案:2a15.(2010广东，文15)(坐标系与参数方程选做题)在极坐标系(ρ，θ)(0≤θ<2π)中，曲线ρ(cos θ+sin θ)=1与ρ(sin θ－cos θ)=1的交点的极坐标为________________.答案:(1，2π)三、解答题:本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.写在答题卡上的指定区域内.16.(2010广东，文16)设函数f (x )=3sin(ωx +6π)，ω＞0，x ∈(－∞，+∞)，且以2π为最小正周期.(1)求f (0);(2)求f (x )的解析式;(3)已知f (4α+12π)=59，求sin α的值.解:(1)由题设可知f (0)=3sin 6π=23.(2)∵f (x )的最小正周期为2π，∴ω=22ππ=4.∴f (x )=3sin(4x +3π).(3)由f (4α+12π)=3sin(α+3π+6π)=3cos α=59，∴cos α=53.∴sin α=±α2cos 1-=±54.17.(2010广东，文17)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示:(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？(3)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率. 解:(1)因为在20至40岁的58名观众中有18名观众收看新闻节目，而大于40岁的42名观众中有27名观众收看新闻节目.所以，经直观分析，收看新闻节目的观众与年龄是有关的.(2)应抽取大于40岁的观众人数为4527×5=53×5=3(名) .(3)用分层抽样方法抽取的5名观众中，20至40岁有2名(记为Y 1，Y 2)，大于40岁有3名(记为A 1，A 2，A 3)，5名观众中任取2名，共有10种不同取法:Y 1Y 2，Y 1A 1，Y 1A 2，Y 1A 3，Y 2A 1，Y 2A 2，Y 2A 3，A 1A 2，A 1A 3，A 2A 3.设A 表示随机事件“5名观众中任取2名，恰有1名观众年龄为20至40岁”.则A 中的基本事件有6种:Y 1A 1，Y 1A 2，Y 1A 3，Y 2A 1，Y 2A 2，Y 2A 3，故所求概率为P (A )=106=53.18.(2010广东，文18)如图，是半径为a 的半圆，AC 为直径，点E 为的中点，点B 和点C 为线段AD 的三等分点，平面AEC 外一点F 满足FC ⊥平面BED ，FB =5a..(1)证明:EB ⊥FD ;(2)求点B 到平面FED 的距离. (1)证明:∵点E 为的中点，且AB =BC ，AC 为直径，∴EB ⊥AC .∵FC ⊥平面BED ，且BE ⊂平面BED ， ∴FC ⊥EB .∵FC ∩AC =C ，∴EB ⊥平面BDF .∵FD ⊂平面BDF ，∴EB ⊥FD .(2)解:∵FC ⊥平面BED ，且BD ⊂平面BED ， ∴FC ⊥BD .又∵BC =DC ，∴FD =FB =5a .∴V E —FBD =31·S △FBD ·EB =31·21·2a ·225a a -·a =323a .∵EB ⊥平面BDF ，且FB ⊂平面BDF ，∴EF =22EB FB +=225a a +=6a .∵EB ⊥BD ，∴ED =22BD EB +=224a a +=5a .S △FED =21·6a ·22)26()5(a a -=221a 2.∴点B 到平面FED 的距离d =FEDFBD E S V Δ31⋅-=21214a .19.(2010广东，文19)某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐?解:法(一):设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位，所花的费用为z 元，则依题意得z =2.5x +4y ，且x ，y 满足⎪⎪⎩⎪⎪⎨⎧≥+≥+≥+≥≥,54106,4266,64812,0,0y x y x y x y x 即⎪⎪⎩⎪⎪⎨⎧≥+≥+≥+≥≥.2753,7,1623,0,0y x y x y x y xz 在可行域的四个顶点A (9，0)，B (4，3)，C (2，6)，D (0，8)处的值分别是z A =2.5×9+4×0=22.5，z B =2.5×4+4×3=22，z C =2.5×2+4×5=25，z D =2.5×0+4×8=32.比较之，z B 最小，因此，应当为该儿童预订4个单位的午餐和3个单位的晚餐，就可满足要求.法(二):设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位，所花的费用为z 元，则依题意得z =2.5x +4y ，且x ，y 满足⎪⎪⎩⎪⎪⎨⎧≥+≥+≥+≥≥,54106,4266,64812,0,0y x y x y x y x即⎪⎪⎩⎪⎪⎨⎧≥+≥+≥+≥≥.2753,7,1623,0,0y x y x y x y x 让目标函数表示的直线2.5x +4y =z 在可行域上平移，由此可知z =2.5x +4y 在B (4，3)处取得最小值.因此，应该为该儿童预订4个单位的午餐和3个单位的晚餐，就可满足要求.20.(2010广东，文20)已知函数f (x )对任意实数x 均有f (x )=kf (x +2)，其中常数k 为负数，且f (x )在区间［0，2］上有表达式f (x )=x (x －2).(1)求f (－1)，f (2.5)的值;(2)写出f (x )在［－3，3］上的表达式，并讨论函数f (x )在［－3，3］上的单调性; (3)求出f (x )在［－3，3］上的最小值与最大值，并求出相应的自变量的取值. 解:(1)f (－1)=kf (1)=－k ，∵f (0.5)=kf (2.5)， ∴f (2.5)=k1f (0.5)=k1(0.5－2)×0.5=－k43.(2)∵对任意实数x ，f (x )=kf (x +2)， ∴f (x －2)=kf (x ).∴f (x )=k1f (x －2).当－3≤x <0时，0≤x +2<2， f (x )=kf (x +2)=kx (x +2);当－3≤x <－2时，－1≤x +2<0， f (x )=kf (x +2)=k 2(x －2)(x +4); 当2≤x ≤3时，0≤x －2≤1， f (x )=k1f (x －2)=k1(x －2)(x －4).故f (x )=⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤--<≤-<≤-+-<≤-++.32),4)(2(1,20),2(,02),2(,23),4)(2(2x x x kx x x x x kx x x x k∵k <0，∴f (x )在［－3，－1］与［1，3］上为增函数，在［－1，1］上为减函数. (3)由函数f (x )在［－3，3］上的单调性可知，f (x )在x =－3或x =1处取得最小值f (－3)=－k 2或f (1)=－1，而在x =－1或x =3处取得最大值f (－1)=－k 或f (3)=－k1.故有①k <－1时，f (x )在x =－3处取得最小值f (－3)=－k 2，在x =－1处取得最大值f (－1)=－k .②k =－1时，f (x )在x =－3与x =1处取得最小值f (－3)=f (1)=－1，在x =－1与x =3处取得最大值f (－1)=f (3)=1.③－1<k <0时，f (x )在x =1处取得最小值f (1)=－1，在x =3处取得最大值f (3)=－k1.21.(2010广东，文21)已知曲线C n :y =nx 2，点P n (x n ，y n )(x n >0，y n >0)是曲线C n 上的点(n =1，2，…).(1)试写出曲线C n 在点P n 处的切线l n 的方程，并求出l n 与y 轴的交点Q n 的坐标; (2)若原点O (0，0)到l n 的距离与线段P n Q n 的长度之比取得最大值，试求点P n 的坐标(x n ，y n );(3)设m 与k 为两个给定的不同的正整数，x n 与y n 是满足(2)中条件的点P n 的坐标，证明:∑=+sn nx m 12)1(|－n y k )1(+|<|ms －ks |(s =1，2，…).解:(1)∵(nx 2)′=2nx ，∴曲线C n 过点P n (x n ，y n )的切线l n 的方程为y －nx n 2=2nx n (x －x n )，即2nx n x －y －nx n 2=0. 令x =0，得y =－nx n 2， ∴Q n 的坐标为(0，－nx n 2). (2)原点O (0，0)到l n 的距离为d (x n )=23241nnx n nx +，|P n Q n |=42224x n x n +. 2241||)(nn n n n x n nx Q P x d +==nnx n x n 241+，∴nx 1=4n 2x n ，即x n =n21时，||)(n n n Q P x d 取得最大值41.故所求P n 的坐标为(n 21，n41).(3)证明:由(2)知，x n =n21，y n =n41，于是∑=+-+kn n ny k x m 1|)1(2)1(|=∑=+-+kn nk m 1|211|=∑=+++-kn k m n k m 1)11(2||<∑∑==-=+-kn kn nk m k m n k m 1121||)(2||.现证明∑=kn n121<s (s =1，2，…).∑=kn n121<∑=-+kn n n 111=∑=--kn n n 1)1(=1+(2－1)+( 3－2)+…+(s －1-s )=s .故问题得证.。