分数小数的列式计算
常见分数小数及百分数互化 常用平方数立方数及各种计算方法
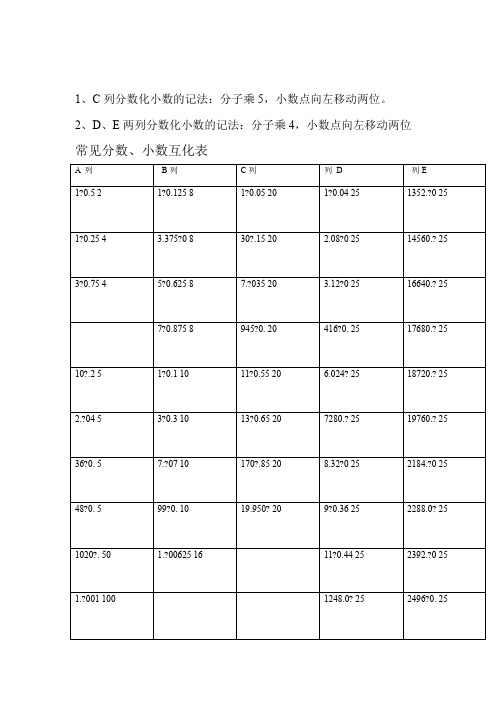
1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表1 / 12常见的分数、小数及百分数的互化常用平方数2 / 12常见立方数减错位相加/ ;9= A×10-A×9型速算技巧:A×A10-743=7430-743=6687 ×743×9=743例:;÷10A×9.9= A×10+AA×9.9型速算技巧:10=7430-74.3=7355.7 ÷×10-743例:743×9.9=74310+A;11= A型速算技巧:A××A×1110+743=7430+743=8173 11=743×例:743×100+A;×101= A×AA×101型速算技巧:100+743=75043 101=743×例:743×的速算技巧:25、125除以乘/5、;5=10A÷2×5型速算技巧:A×A2=43697.25 ÷÷2=87394.58739.45×5=8739.45×10例:2;A÷5=0.1A×5A÷型速算技巧:2=7.3686 ×2=3.6843×0.1×例:36.843÷5=36.843;÷4A×25型速算技巧:×25=100AA4=180850 4=723400÷25=7234×100÷7234例:×4;25=0.01A25÷型速算技巧:A÷×A4=148.564=37.140.0125=37143714例:÷×××3 / 12A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:×(头+1);积的尾=尾×尾头=积的头例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
五年级数学上册列式计算

五年级数学上册列式计算一、加法与减法运算在五年级数学上册中,学生将进一步巩固加法和减法的基本运算。
这包括整数、小数和分数的加法与减法。
例如:1.计算 32 + 17 =2.计算 5.6 -3.2 =3. 计算 1/2 + 2/5 =二、乘法与除法运算在掌握了基本的加法和减法后,学生将学习乘法和除法。
乘法部分会涉及到简单的乘法表,而除法则更注重于平均分配的概念。
例如:1.计算 6 × 8 =2.计算 15 ÷ 3 =3. 计算 6/7 × 21/8 =三、分数与小数运算分数和小数的运算是一个重要的概念,它要求学生将两者进行转换,并理解其背后的数学意义。
例如:1. 计算 2/3 + 3/4 = (将分数转换为小数进行运算)2. 将 0.8 转换为分数形式 =3. 计算 1.5 × 7/3 = (小数与分数的混合运算)四、综合运算(加、减、乘、除混合)综合运算要求学生能够按照正确的顺序(先乘除后加减)进行混合运算。
例如:1.计算 (10 + 5) × 2 - 4 =2. 计算 (7/8) × (4/9) + (1/2) = (分数和小数的混合运算)3. (4 × (15 - 9)) + (3 × 6) = (综合的加减乘除运算)五、分数与小数的互化学生需要掌握将分数和小数互化的技能,这有助于他们更清晰地理解两者的关系。
例如:1.将分数 3/8 转换为小数 =2.将小数 0.75 转换为分数 =3. 将分数 7/12 转换为最简形式 =六、应用题列式计算应用题是帮助学生理解数学概念在实际问题中的应用的关键题型。
例如:1. 一个果园里有400棵苹果树,其中1/4是红富士品种。
红富士品种的苹果树有多少棵?2. 小明有6本书,其中3本是故事书,3本是科普书。
他从书架上随机取出一本书,取到故事书的概率是多少?3. 一个长方形的长是6cm,宽是4cm。
分数乘法(小数乘分数、分数综合计算

分数乘法三:小数乘分数一、小数乘分数:1、把下面的小数化成分数,分数化成小数。
1.2 0.4 3.5 1.25 85 54 41 2512、小数乘分数:例题:甲数是3.6,乙数是甲数的45,乙数是多少? 列式:思考:这个算式和我们前面学习的分数乘法有什么不同?该如何进行计算?方法1、可以把小数化成分数:3.6=1036,3.6×45 = 1036×45 = 29 方法2、可以把分数化成小数:45= 1.25, 3.6×1.25 =4.5 小结:这两种方法都适用,主要还是要根据题目的事情情况来选择运用哪种方法。
二、练习巩固: 1、计算。
1.2×532.5×53 1.4×65 2.4×652、列式计算。
(1)2.4的 52是多少?(2)1.2的 43是多少?(3)甲数占乙数的 87,已知乙数是5.6,甲数是多少?(4)16.4吨的 41是多少吨?3、解决问题。
(1)一列火车每小时行87.9千米,从甲站到乙站行了31小时,甲乙两站间的铁路长多少千米?(2)一面墙的面积是27.8平方米,已经刷完了整面墙的 21。
已经刷完的面积是多少平方米?(3)一包茶叶重10.5克,用去 53,用去多少克?(4)一水果店,上午卖出苹果28.4千克,下午卖出的是上午的 43,下午卖出多少千克?(5)一根钢管长8.7米,用去一部分,还剩下全长的 31,还剩下多少米?分数乘法四:分数乘法混合运算积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a ×b=c,当b >1时,c>a 。
一个数(0除外)乘小于1的数,积小于这个数。
a ×b=c,当b <1时,c<a (b ≠0)。
一个数(0除外)乘等于1的数,积等于这个数。
a ×b=c,当b =1时,c=a 。
注意:在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
分数化小数表

分数化小数表一、介绍分数化小数是将分数表示成小数形式的一种方式。
在数学中,分数是指两个整数之间的比值,通常由一个分子和一个分母组成。
而小数是指不完全是整数的数,可以用有限或无限的十进制表示。
在实际问题中,我们常常需要把分数转化为小数,以便更方便地进行计算和比较。
本文将介绍如何将分数转化为小数,并给出一份分数化小数表。
二、分数化小数的方法将分数化小数的方法主要有两种:长除法和分数除法。
1.长除法法长除法是将分数除以一个整数,得到一个小数的过程。
具体步骤如下:(1)将分子写在除号上面,分母写在除号下面,画一条横线。
(2)从左往右,将分子的第一位数与分母进行相除,得到商和余数。
(3)将商写在横线上方,将余数写在横线下方。
(4)将余数乘以10,得到一个新的被除数。
(5)将新的被除数与分母进行相除,得到新的商和余数。
(6)继续按照上述步骤进行操作,直到出现重复的余数或者得到指定位数的小数为止。
2.分数除法法分数除法是将分数除以一个小数,得到一个无限循环小数的过程。
具体步骤如下:(1)将分子写在除号上面,分母写在除号下面,画一条横线。
(2)判断分母是否能整除10,如果不能,则在分母的末尾加上一个0,得到新的分母。
(3)将新的分母与分子进行相乘,并将结果写在横线上方。
(4)将新的被除数写在横线下方,得到一个新的被除数。
(5)重复上述步骤,直到出现相同的被除数为止。
出现相同的被除数时,将出现重复的商,说明小数是无限循环的。
三、分数化小数表下面是一个分数化小数表,将常见的分数表示成小数形式。
1/2 = 0.51/3 ≈ 0.33331/4 = 0.251/5 = 0.21/6 ≈ 0.16661/7 ≈ 0.1428571/8 = 0.1251/9 ≈ 0.11111/10 = 0.12/3 ≈ 0.66662/5 = 0.42/8 = 0.253/4 = 0.753/5 = 0.63/8 ≈ 0.3754/5 = 0.84/7 = 0.5714285/6 ≈ 0.83335/8 = 0.6256/7 ≈ 0.8571427/8 = 0.875四、总结分数化小数是将分数转化为小数的一种方法,能够使我们更方便地进行计算和比较。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C 列分数化小数的记法:分子乘 5,小数点向左挪动两位。
2、D 、E 两列分数化小数的记法:分子乘4,小数点向左挪动两位常有分数、小数互化表A 列B 列C 列D 列E 列11 1 1 0.0413 20.50.1250.050.52820252513 3 2 14 0.250.3750.150.080.564820252535 7 3 16 0.75 0.625 0.35 0.12 0.6448 20 25 2579 4 17 0.875 0.45 0.16 0.68820252511 11 6 18 0.20.10.550.240.7251020252523 13 7 19 0.4 0.3 0.65 0.28 0.765 10 20 25 2537 17 8 21 0.6 0.7 0.85 0.32 0.8451020252549 19 9 22 0.80.90.950.360.8851020252511 11 23 0.02 0.0625 0.44 0.9250 1625 251 12 24 0.01 0.48 0.961002525常有的分数、小数及百分数的互化除法除不尽(按四舍五入计算)除法比分数小数百分除法比分数小数百分1÷ 21:21/250%1÷ 31:31/333% 1÷ 41:41/425%2÷ 32:32/367% 1÷ 51:51/520%1÷ 61:61/617% 2÷ 52:52/540%5÷ 65:65/683% 3÷ 53:53/560%1÷ 71:71/714% 4÷ 54:54/580%2÷ 72:72/729% 1÷ 81:81/8%3÷ 73:73/743% 3÷ 83:83/8%4÷ 74:74/757% 5÷ 85:85/8%5÷ 75:75/771% 7÷ 87:87/8%6÷ 76:76/786% 1÷ 101:101/1010%1÷ 91:91/911% 3÷ 103:103/1030%2÷ 92:92/922% 7÷ 107:107/1070%4÷ 94:94/944% 9÷ 109:109/1090%5÷ 95:95/956% 3÷ 23:23/2150%7÷ 97:97/978% 5÷ 45:45/4125%8÷ 98:98/989% 7÷ 57:57/5140%4÷ 34:34/3133%备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无穷循环)小数;除不尽与除尽相反,是无穷循环小数。
六年级分数、小数四则混合运算

六年级分数、小数四则混合运算分数、小数四则运算是小学数学中的一项重要内容,它对于培养同学们的计算能力起着十分重要的作用,对于培养同学们的计算能力起着十分重要的作用,要想掌握要想掌握好分数、小数的四则混合运算,一要牢记分数、小数的基本运算法则,二要掌握分数与小数的互化。
运算法则,二要掌握分数与小数的互化。
分析与解 当题目中出现分数的个数大于出现的小数的个数时,可考虑将小数化为分数进行运算可考虑将小数化为分数进行运算..注意分数作为除数时,分子与分母的位置要互换后作乘数。
分子与分母的位置要互换后作乘数。
分析与解 此题目属于形式较复杂型题目此题目属于形式较复杂型题目..与例1不同的是,分数与小数在题目中出现的个数基本相同分数与小数在题目中出现的个数基本相同..因此在计算时先不要急于进行分数与小数的互换,而要考虑寻找题目的特点,争取用简便方法计算。
点,争取用简便方法计算。
=(10+1010+10)×1+0×6.04)×1+0×6.04)×1+0×6.04 =20+0 =20分析与解 当题目出现括号时,告诉我们要注意运算的先后顺序顺序..同时还要注意乘法分配律的应用。
同时还要注意乘法分配律的应用。
=48+1 =49分析与解 因为题目中有分数、小数还有百分数,因此要考虑它们之间的互化虑它们之间的互化..对于这道题目而言,将分数和百分数都化为小数比较容易计化为小数比较容易计=23.3×1.25+14×5+1.25×28.7=23.3×1.25+14×5+1.25×28.7 =1.25=1.25((23.3+28.723.3+28.7))+70 =1.25×52+70=1.25×52+70 =65+70 =135例5 某小学五年级四班为希望工程捐款,五(某小学五年级四班为希望工程捐款,五(11)班捐款150.25元,五(元,五(22)班比五()班比五(11)班多捐了)班多捐了 15.45 15.45元,五(元,五(33)班捐款是五(班捐款是五(22)元?元?分析与解 这是一道应用题,要根据题目中所给的条件列出算式,计算时还会遇到分数小数的四则混合运算,所以计算时不但要细心,还要尽量使用简便算法。
常见分数、小数及百分数互化-常用平方数、立方数及各种计算方法
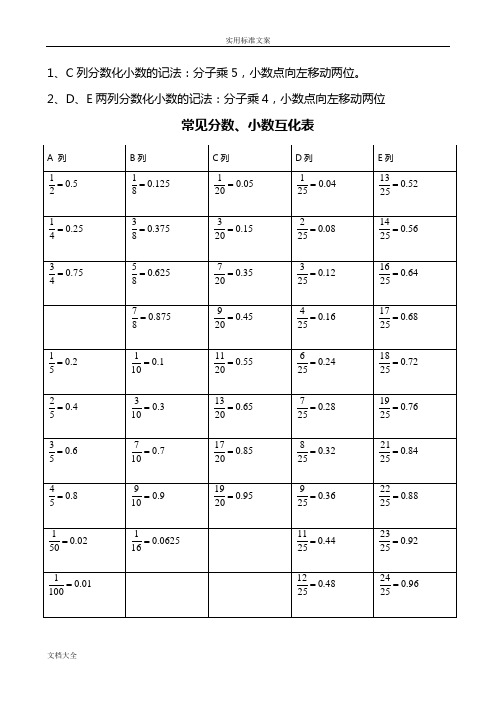
1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化常用平方数常见立方数常见特殊数的乘积错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
分数乘以小数

复习巩固
1.将下列小数化为分数,分数化为小数。
3 4
12 5
0.48
1.5
= 0.75 = 2.4
= 12 25
=
3 2
复习巩固
2.判断下列是否合理。
3 4
×
5
=
3 20
应该是整数乘以分数的分子
7 4
×
5 7
=
35 28
没有约分
新知探索 (教材第8页例5)
5
松鼠的尾巴长度约占身体长度的
新知探索
(2)松鼠乐乐的尾巴有多长?
松鼠的尾巴长度约占身体的长度的
3 4
。
平均分成 4 份, 我身体长2.4dm。
取其中的 3 份。
乐乐
新知探索
画一画!
2.4dm 尾?巴
乐乐身体长度 自己试着 计算一下。
列式:
2.4 3 4
(dm)
2.4 3
4
=
0.6
2.4
3 41
=1.8(dm)
这样约分计算更简便。
新知探索
分数乘小数的三种计算方法: (1)分数化成小数; (2)小数化成分数; (3)分数的分母与小数约分后再计算。
课堂练习 (教材第8页“做一做”)
1.
1.2×
3 5
=
18 25
1.4×
5 6
=
7 6
2.5×
3 5
=
3 2
2.4×56 = 2
课堂练习
2.美国人均淡水资源约为1.38万立方米,我
3 2.1×
4
=
_1_.5_7__5(dm)
1.转化成小数乘小数:
常见分数、小数及百分数互化-常用平方数、立方数及各种计算方法

1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
分数与小数四则混合运算(教师)

学科教师辅导讲义(2)3843488853454310313715777151515⎛⎫⎛⎫++=++=+= ⎪ ⎪⎝⎭⎝⎭; (3)3154351485218251117485858855⎛⎫⎛⎫⎛⎫⎛⎫-+-=+-+=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭;(4)()3434129.38129.38 2.7911.77777⎛⎫⎛⎫--+=-++=+= ⎪ ⎪⎝⎭⎝⎭.【方法总结】计算时,要认真审题,看清运算符号和数的特点,灵活选择合理的计算方法,数学中的运算性质、运算律方面有较大的作用.通常在分数的计算中,两个分散相加、减时,能“凑整”的可以先算. 【例3】计算:(1)2326138⨯⨯;(2)37.61421÷⨯;(3)1310.7545⨯÷; 【答案】(1)238112616223838⨯⨯=⨯⨯=; (2).(3)1353410.75145453⨯÷=⨯⨯=. 【方法总结】乘、除运算属同级运算,一般情况下应当依次计算,否则容易发生差错.避免这类差错最好的办法是把乘、除混合运算转化为连乘运算.在计算过程中能约分的先约分. 【例4】(1)16125925÷⨯;(2)0.320.250.125⨯⨯; 【解析】 (1)()()1611611252525162525425425925999÷⨯=⨯⨯=⨯⨯⨯=⨯⨯⨯⨯ 100001111199==;(2)0.320.250.1250.01480.250.1250.01(40.25)(80.125)⨯⨯=⨯⨯⨯⨯=⨯⨯⨯⨯0.01=;【方法总结】计算时,要认真审题,看清运算符号和数的特点,灵活选择合理的计算方法,数学中的运算性质、运算律方面有较大的作用.通常在分数乘法计算中可用交换律的则先用交换律.总之,要根据题中具体数字来考虑如何使运算过程简便,要能运用各种运算律来进行计算. 【例5】计算:(1)164133534÷-⨯;(2)157.25 1.47-⨯;(3)22 3.6 6.83⨯-; (4)52552634÷-⨯;(5)11811169322÷+÷;(6)111112233-÷⨯÷. 【答案】略【例6】计算:【例1】某化工厂第一天生产酒精3455吨,第二天生产酒精1484吨,第三天比前两天的总和少43.7吨,那么第三天生产了多少吨酒精?【例2】已知梯形的上底、下底和高分别是23厘米、56厘米和0.6厘米,求这个梯形的面积.【例3】化肥厂第一季度生产化肥425吨,比第二季度产量少465吨,第三季度的产量是第二季度产量的1117倍,求第三季度生产化肥多少吨?【解析】第二季度产量是(425+465)吨,第三季度产量是(425+465)的1117倍.【解】答:第三季度生产化肥1 4575吨,【例4】小刚两天看了一本书的30页,第一天看了比全书的310多8页,第二天看了10页,求这本书共有多少页.【解析】第一天看书20页,比全书的斋多8页,即,全书页数的310+8=20.方法一:设全书共有x页.根据题意得方程3810x+=30-1031210x=31210x=÷10123x=⨯40x=(页)方法二(20-8)310÷10123=⨯=40(页)答:全书共有40页.【借题发挥】1.列式计算:(1)229的910除以1.85与14的差,商是多少?(2)78比一个数的23少6,求这个数2.一个工程队必须住三天内完成一项,第一天完成了工程总量的14,第二天完成了工程总量的25,问两天一共完成了工程总量的几分之几?第三天应该完成工程总量的几分之几?3.某电影院放映电影《阿凡达》.上午卖出全部电影票的47后,下午又卖出48张,这时剩下的张数正好是全部电影票的314,那么全部电影票有多少张?现在还剩多少张?4.一幢高楼A的高度是80米.。
小数乘分数

下面下面各题。
×7.8×0.36
2.4×2.5×
B类题(选做题):
+++++
我的收获有:
学科
数学
年级
六年级
主备人
段宗义
课题
小数乘分数
上课教师
课时数
1课时
学习内容
教材第8页内容及练习。
学习目标
我会根据数的特点正确的计算小数乘分数。
学习流程
学习导航
学习笔记
预习质疑
生成问题
1.复习:整数乘加,乘减混合运算的运算顺序。
2.预习课本第8页的内容。
我想提出的问题:
自主学习
探究问题
自学指导:
学一学:
想一想:
比较2.1×与2.4×的算法:说一说小数乘分数在什么情况下选择哪种方法计算更简便?完成学习笔记三。
想一想:
你能想出几道能运用小数乘分数的计算题吗?并算一算,完成学习笔记四。
说一说:你还有不明白的问题吗?如果有,请写在“我的困惑”中。
学习笔记一:
列式为:2.1×
算法一×
算法二2.1x0.75
学习笔记二:
列式为2.4×
笔记三:
比较2.1×与2.4×的算法,我认为小数乘分数在()情况下选择()算法更简便些。
:笔记四:我想出的小数乘分数的题目是:
我的困惑:
合作学习
研讨问题
对学指导:
对子间就自学情况进行评定,用双色笔更正学习笔记。
群学指导:
组长负责组织本组成员针对展示的主题中的要求进行交流。
小组学习:
1.1.对学。
自学课本第8页例5.
想一想:例5中松鼠欢欢的尾巴有多长?应怎样列式计算?完成学习笔记一。
小数乘分数

先说下列各算式表示的意义,再口算出得数。
4
312××2152列式计算。
(1)20的是多少?是多少?(2)6的5143求一个数的几分之几是多少,
用乘法计算
2、把下面的小数化成分数。
1.2 0.4 3.5
3、把下面的分数化成小数。
8554
41
例5:松鼠的尾巴长度约占身体长度的
4
3
欢欢我身长2.1dm.
我身长2.4dm.
乐乐
(1)松鼠欢欢的尾巴有多长?(2)松鼠乐乐的尾巴有多长?
小数乘分数的计算方法•小数乘分数,可以先把小数化成分数再计算。
•小数乘分数,如果这个分数可以化成有限小数,也可以先把分数化成小数再计算。
•小数乘分数,如果这个小数能和分数的分母约分,那么先约分再计算比较简便。
计算下面各题:
•2.5×49
54×3.61.6×4127
×2.3
解决问题:
•在一次跳远比赛中小军跳了2.4米,王浩跳的距离是小军的,王浩跳
了多少米?
•成人头长大约是身高的,王老师的身高是1.8米,他的头长大约是多少米?1211152。
分数化成小数

分数化成小数:直接用分子除以分母。
例:1120.52=÷= 4450.85=÷= 992 4.52=÷= 292512 2.4212=÷= 小数化成分数:把小数化成分母是10, 100, 1000的分数,小数直接把小数点去掉当分子,一位小数对应的分母是10,两位小数对应的分母是100,三位小数对应的分母是1000.例:210.2105== 2510.251004== 12510.12510008== 1261.2105== 12551.251004==练一练1. 填空题。
0.1表示( )分之( ),写作( );0.4表示( )分之( ),写作( );0.25表示( )分之( ),写作( );0.126表示( )分之( ),写作( );2. 判断下面的分数与小数互化是否正确。
5 7 0.5 = — ( ) — = 0.7 ( ) 10 10107 21 1.07 = —— ( ) 1—— = 0.21 ( ) 100 100100 111 0.65 = —— ( ) ——— = 0.111 ( ) 65 100003. 把下列每个小数和相等的分数用线连起来。
0.5 1.8 3.07 0.65 7.25 0.904113 13 4 1 1 1 —— — 1— — — 7— 125 20 5 5 2 44. 把下列的各数化成小数(不能化成有限小数的,保留三位小数)4 33 29 — = — = —— = 7 40 100 115 — = — =0.27= 1.52= 0.5= 0.08=3.28= 0.86= 0.005=6. 判断各组数的大小。
3 1 19 2—( )2.375 0.009( )—— 0.91( )— 8 100 20 17. A 超市中一盒伊利牛奶要1.75元,B 超市中一盒伊利牛奶要1—元,那你认为在那里买比较合适呢? 48. 小兔和小猴进行跑步比赛,跑完同一段路程,小兔用12分之11分钟,小猴用了0.65分钟,求谁花的时间多?谁的速度快?带分数:非零整数+真分数=带分数,一般读作几又几分之几。
整数,分数,小数,百分数四则混合运算

技术资料整数、分数、小数、百分数四则混合运算答案知识梳理教学重、难点作业完成情况典题探究例1.一个数,减去它的20%,再加上5,还比原来小3.那么,这个数是40 .考点:整数、分数、小数、百分数四则混合运算.分析:把这个数看做单位“1”,减去它的20%为1﹣20%=80%,再加上5,还比原来小3,也就是(5+3)是原来的20%,列式为:(5+3)÷20%,计算即可.解答:解:(5+3)÷20%,=8÷0.2,=40.知识共享答:这个数是40.故答案为:40.点评:此题也可这样解答,设这个数为x,由题意得:(1﹣20%)x+5=x﹣3,解方程即可.例2.求值:1.2×[7﹣4÷(+)+2÷1]= 4 .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:按照先算小括号里面的,再同时算中括号里面的除法,然后算中括号里面的减法,以及中括号里面的加法,最后算括号外面的乘法顺序计算即可解答.解答:解:1.2×[7﹣4÷(+)+2÷1]=1.2×[7﹣4÷+2÷1]=1.2×[7﹣5+1]=1.2×3=4故答案为:4.点评:依据四则运算计算方法正确进行计算,是本题考查知识点.例3.用简便方法计算.×﹣÷133.5×98+35×0.2.考点:整数、分数、小数、百分数四则混合运算;运算定律与简便运算;小数四则混合运算.专题:运算顺序及法则;运算定律及简算.分析:①运用乘法的分配律进行计算即可.②把3.5×98化成35×9.8,然后运用乘法的分配律进行计算即可.解答:解:①×﹣÷13=×﹣×=(﹣)×=×=②3.5×98+35×0.2=35×9.8+35×0.2=35×(9.8+0.2)=35×10=350点评:考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.例4.只列式不计算.(1)12.5的比1.3除52的商少多少?(2)一种混凝土把石子、沙和水泥按6:2:1的比调配而成,要配制这种混凝土27吨,需要水泥多少吨?考点:整数、分数、小数、百分数四则混合运算;按比例分配应用题.专题:文字题;压轴题;比和比例应用题.分析:(1)先求出12.5×的积,再求出52÷1.3的商,最后用求得的商﹣求得的积即可解答,(2)根据一种混凝土把石子、沙和水泥按6:2:1的比调配而成,求出混凝土中石子、沙和水泥的总份数,再依据按比例分配方法即可解答.解答:解:(1)52÷1.3﹣12.5×,=40﹣10,=30,答:少30;(2)×27,=27,=3(吨),答:需要水泥3吨.点评:解答本题的关键是明确解决问题需要的数量间的等量关系,以及解决问题所用的方法.演练方阵A档(巩固专练)一.选择题(共13小题)1.某数减少它的后是50,这个数是()A.B.125 C.160 D.70考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:把这个数看作单位“1”,求单位“1”用除法计算,数量50除以对应的分率(1﹣).解答:解:50÷(1﹣),=50÷,=125.答:这个数是125.故选:B.点评:本题关键是对题意的理解,找出先算什么,再算什么,根据计算的顺序列出算式求解.2.(2010•湖北模拟)30比()少20%.A.36 B.24 C.37.5考点:整数、分数、小数、百分数四则混合运算.分析:30比一个数少20%,将这个数当做单位“1”则30是这个数的1﹣20%,已知一个数的几分之几是多少,求这个数用除法:30÷(1﹣20%).解答:解:30÷(1﹣20%),=30÷80%,,=37.5.故选:C.点评:本题是根据分数除法的意义即已知一个数的几分之几是多少,求这个数用除法,进行分析解答的.3.(2014•湘潭模拟)12加上一个数的,和是18,这个数是()A.12 B.15 C.18 D.20考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题意数量间的相等关系:12+一个数×=18,设这个数为x,列并解方程即可.解答:解:设这个数为x,12+x=18,,12+x﹣12=18﹣12,x=6,x÷=6÷,x=15.答:这个数是15.故选:B.点评:解答这类题目,分清题里的数量关系,确定先算什么,在算什么,找清列式的顺序,列出算式或方程解答.4.的值是多少.()A.8B.18 C.6D.26考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:通过观察,此题把百分数和分数化为小数计算比较简单,然后运用乘法分配律简算.解答:解:3.5×0.8+5.5×80%+,=3.5×0.8+5.5×0.8+0.8,=(3.5+5.5+1)×0.8,=10×8,=8;故选:A.点评:此题解答的关键是注意数字转化,运用所学的运算定律灵活简算.5.的值是多少.()A.B.C.5D.考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先算小括号内的,再算中括号内的乘法,然后算中括号内的加法,最后算括号外的除法.解答:解:1.8÷[3.6+(1﹣)×32],=1.8÷[3.6+×32],=1.8÷[3.6+12],=1.8÷15.6,=;故选:B.点评:此题考查了四则混合运算,注意运算顺序和运算法则,是完成此题的关键.6.的倒数的3倍减去的一半,差为()A.B.C.D.考点:整数、分数、小数、百分数四则混合运算;倒数的认识.专题:文字叙述题.分析:根据题意,的倒数是,那么可用与3的积减去与的积,列式解答后再选择即可得到答案.解答:解:×3﹣×=4﹣,=3.故选:C.点评:解答此题的关键是根据题干的叙述确定算式的运算顺序,然后再列式计算即可.7.1.5加上22.5的所得的和,再除以4.5,商是()A.B.2C.考点:整数、分数、小数、百分数四则混合运算.分析:本题先要求出1.5+22.5×的和,然后再去除以4.5,即可解得.解答:解:(1.5+22.5×)÷4.5,=(1.5+7.5)÷4.5,=9÷4.5,=2;故选:B.点评:本题考查了四则混合运算的顺序,特别是括号的使用,文字题要注意运用“缩句法”弄清文字题的主干.8.1+2﹣3×4÷5+6﹣7×8÷9的计算结果是()A.B.C.D.考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:因为3×4÷5和7×8÷9的计算结果都除不尽,因此可把这两项的结果写成分数形式,运用加法交换与结合律简算即可.解答:解:1+2﹣3×4÷5+6﹣7×8÷9=3﹣+6﹣=(3+6)﹣(+)=9﹣=故选:A.点评:此题通过转化的数学思想,运用运算定律进行简算.9.算式等于()A.1020 B.204 C.273 D.747考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:把带分数化成小数,先算乘法、再算加法.解答:解:2×19.5+7.2×20,=2.8×19.5+7.2×20.75,=54.6+149.4,=204.故应选:B.点评:既有加减、又有乘除法,先算乘除法、再算加减.10.如果甲数的3倍是48,那么甲数的是()A.16 B.4C.12 D.30考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:先用48除以3求出甲数,再把甲数看成单位“1”,用乘法求出它的即可.解答:解:48÷3×,=16×,=4;答:甲数的是4.故选:B.点评:本题先根据倍数关系求出甲数,再找出单位“1”,根据已知单位“1”的量求它的几分之几是多少用乘法求解.11.(2010•白云区模拟)甲数的60%等于乙数的,那么()(甲、乙不为0).A.甲=乙B.甲>乙C.甲<乙考点:整数、分数、小数、百分数四则混合运算;分数大小的比较.分析:由甲数的60%等于乙数的可得:甲数×60%=乙数×.两两相乘数的积相等,乘较小数的那个数较大,比较60%与的大小,则可判定甲乙两数的大小.解答:解:甲数×60%=乙数×,60%=<,所以甲数>乙数.故选:B.点评:根据“两两相乘数的积相等,乘较小数的那个数较大”来判定甲乙两数的大小.12.的值是多少.()A.5B.12 C.1D.10考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则;运算定律及简算.分析:我们运用乘法的分配律进行计算即可,然后再进行正确的选择.解答:解:7.5×+2.5×+10×,=×(7.5+2.5)+10×,=+10×,=10×(),=10;故选:D.点评:本题先把题干的算式进行计算,再与答案进行对比在进行选择即可.13.(2008•淳安县)下面算式中,结果最小的是()A.7÷0.16 B.7×1.6 C.7×16% D.7÷160%考点:整数、分数、小数、百分数四则混合运算.专题:计算题;压轴题.分析:把算式7÷0.16改写成7×6.25,把算式7×16%改写成7×0.16,把算式7÷160%改写成7×0.625,再根据一个因数7相同,看另一个因数的大小即可断定结果最小的算式.解答:解:A、7÷0.16=7×6.25;B、7×1.6;C、7×16%=7×0.16;D、7÷160%=7×0.625;因为一个因数7相同,另一个因数0.16<0.625<1.6<6.25,所以7×0.16的积最小,即结果最小的算式是7×16%.故选:C.点评:解决此题关键是把每个选项中的算式分别改写成7乘一个数的形式,再根据另一个因数最小,则积就最小解答即可.二.填空题(共14小题)14.甲数的40%是乙数的,如果乙数是20,那么甲数是16.考点:整数、分数、小数、百分数四则混合运算.专题:文字题.分析:根据题意数量间的相等关系,乙数×=甲数×40%,设甲数为x,列并解方程即可.解答:解;设甲数为x,x×40%=20×,x=,x÷=÷,x=16.答:甲数是16.故答案为:16.点评:此题考查列方程解答的列式计算题,找出数量间的相等关系设未知数x,列并解方程.15.10﹣1.2+5﹣3.4+3﹣5.6+2﹣7.8= 2 .考点:整数、分数、小数、百分数四则混合运算;运算定律与简便运算.分析:根据小数加减法的法则进行计算即可得到答案.解答:解:10﹣1.2+5﹣3.4+3﹣5.6+2﹣7.8=10+5+3+2﹣{(1.2+7.8)+(3.4+5.6)}=20﹣{9+9}=20﹣18=2;故答案为:2.点评:此题主要考查的是在小数加减法中简便运算的使用.16.[2﹣(5.55×﹣÷0.4)]÷0.135= 10 .考点:整数、分数、小数、百分数四则混合运算.分析:按四则混合运算的顺序解答即可.解答:解:[2﹣(5.55×﹣÷0.4)]÷0.135=[2﹣(×﹣÷)]÷0.135=[2﹣(﹣×)]÷0.135=[2﹣(﹣)]÷0.135=[2﹣]÷0.135=÷0.135=1.35÷0.135=10.故答案为:10.点评:此题考查分数与小数四则混合运算,计算中注意小数和分数的互化.17.脱式计算,能简算的要简算(1)(2)(3)12.87+3.65+1.35(4)74.6×19+19×25.4(5)(6)168.1÷(4.5×2﹣0.8)考点:整数、分数、小数、百分数四则混合运算;运算定律与简便运算;分数的简便计算.分析:不能简算的题,要先算乘除法,再算加减法;能简算的题,运用运算定律进行简算,要有择优意识.解答:解:(1)×=××==;(2)()×15=×15=14;(3)12.87+3.65+1.35=12.87+(3.65+1.35)=12.87+5=17.87;(4)74.6×19+19×25.4=(74.6+25.4)×19=100×19=1900;(5)【1﹣()】=【1﹣】×=×=;(6)168.1÷(4.5×2﹣0.8)=168.1÷8.2=20.5;点评:属于数的四则运算,灵活运算.18.直接写得数.×10= ﹣= ÷=0.75+=÷4=考点:整数、分数、小数、百分数四则混合运算.专题:计算题.分析:①分数乘法注意分母和分子约分,②﹣先通分,再计算,③变成×,④0.75+看做0.75+0.25,⑤÷4变成×.解答:解:×10=8 ﹣=÷=0.75+=1 ÷4=点评:此题考查同学们快算计算的能力,注意选择合适的方法计算,能用简便方法的用简便方法计算.19.(2012•楚州区模拟)用计算器计算“364÷7”,如果你的计算器的键“6”坏了,你怎么计算?用算式表示出过程:364÷7=(280+84)÷7=280÷7+84÷7=40+12=52;.考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:我们可以把364分成280与84的和,然后用280除以7加上84除以7,把商相加在一起即可.解答:解:364÷7,=(280+84)÷7,=280÷7+84÷7,=40+12,=52;故答案为:364÷7=(280+84)÷7=280÷7+84÷7=40+12=52.点评:本题运用两个数的和除以一个数,可以运用这两个数分别除以这个数.20.(13.5﹣8﹣4.75)÷[5×(x+1)÷1]=,则x= .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先化简方程,根据等式的性质,两边同时乘以[x+],再两边同时减去,然后两边同时除以求解即可.解答:解:(13.5﹣8﹣4.75)÷[5×(x+1)÷1]=[13.5﹣(8+4.75)]÷[5×(x+1)÷1]=[(13.5﹣13]÷[5×(x+1)÷1]=0.5÷[×(x+1)]=0.5÷[x+]=0.5÷[x+]×[x+]=×[x+]0.5=x+0.5﹣=x+﹣0.275=x0.275=xx=;故答案为:.点评:此题考查的目的是理解方程的意义,掌握利用等式的性质解方程的方法步骤.21.一个数的和20的40%相等,这个数是28 .考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据分数乘法的意义,20的40%是20×40%,又一个数的和20的40%相等,根据分数除法的意义,用20的40%除以即得这个数是多少.解答:解:20×40%=8=28答:这个数是28.故答案为:28.点评:已知一个数的几分之几是多少,求这个数,用除法.求一个数的几分之几是多少,用乘法.22.[240﹣(0.125×76+12.5%×24)×8]÷14= 10 .考点:整数、分数、小数、百分数四则混合运算.分析:按照四则混算的运算顺序计算,在小括号内(0.125×76+12.5%×24)把12.5%变成0.125后可以运用乘法分配律进行简算.解答:解:[240﹣(0.125×76+12.5%×24)×8]÷14,=[240﹣(0.125×76+0.125×24)×8]÷14,=[240﹣(76+24)×0.125×8]÷14,=[240﹣12.5×8]÷14,=[240﹣100]÷14,=140÷14,=10.点评:按计算顺序和计算法则计算,同时注意运用定律进行简算.23.计算2.25÷[﹣(+0.45)÷1]= 6 .考点:整数、分数、小数、百分数四则混合运算.分析:此题按运算顺序进行计算,先算小括号内的加法,把0.45化成分数再计算;然后算小括号外的除法,把除法改为乘法;再算中括号内的减法,最后算括号外的除法.解答:解:2.25÷[﹣(+0.45)÷1],=2.25÷[﹣(+)÷1],=2.25÷[﹣(+)÷1],=2.25÷[﹣÷1],=2.25÷[﹣×],=2.25÷[﹣],=2.25÷,=2.25×,=6.点评:此题考查了学生对四则混合运算顺序的掌握,以及综合计算能力.24.+(0.875×+1+6.5÷8)×1= .考点:整数、分数、小数、百分数四则混合运算.分析:把小数化为分数,原式变为+(×+1+)×,在计算中,可以运用乘法分配律简算.解答:解:+(0.875×+1+6.5÷8)×1,=+(×+1+)×,=+××+×,=++,=,=.点评:此题计算量较大,需要仔细认真,最后注意通分.25.计算:8.5= 17 .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先算小括号里的乘法,再算小括号里的减法,再算中括号里的除法,最后算括号外的除法.解答:解:8.5,=8.5÷[(4﹣3.5)÷1],=8.5÷[÷1],=8.5÷,=17;故答案为:17.点评:考查了整数、小数、分数的四则混合运算的顺序,有小括号先算小括号里的,再算中括号里的,最后算括号外的.26.5个减去2个,还剩 3 个,就是.考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题意,求结果相同的加数和的简便运算用乘法,再由同分母分数减法的计算方法进行解答即可.解答:解:根据题意,由同分母分数减法的计算方法可得:5×﹣2×==答:5个减去2个,还剩3个,就是.故答案为:3,.点评:本题主要考查同分母分数的减法的计算方法,然后再根据题意进一步解答即可.27.(2012•中山市模拟)计算[(10.75﹣4)×2]÷[(1.125+)÷(2.25÷10]= .考点:整数、分数、小数、百分数四则混合运算.分析:本题有两个中括号,两个中括号同时进行计算,都要先算小括号内的,再算中括号内的,在运算过程中,可以运用除法的性质,进行简算.解答:解:[(10.75﹣4)×2]÷[(1.125+)÷(2.25÷10],=[(10﹣4)×2]÷[(1+)÷(2÷10],=[(10﹣4)×2]÷[(1+)÷(×],=×÷[÷],=×÷[×],=×××,=.故答案为:.点评:此题计算量较大,应按运算顺序一步步进行.重点考查学生对运算顺序的掌握,以及仔细计算的能力.三.解答题(共1小题)28.(2014•海安县模拟)脱式计算.6760÷13+17×25 4.82﹣5.2÷0.8×0.6 35÷×1﹣.考点:整数、分数、小数、百分数四则混合运算.分析:(1)根据整数的四则混合运算进行计算即可;(2)根据小数的四则混合运算进行计算即可;(3)根据分数的四则混合晕进行计算即可.解答:解:(1)6760÷13+17×25,=520+425,=945;(2)4.82﹣5.2÷0.8×0.6,=4.82﹣6.5×0.6,=4.82﹣3.9,=0.92;(3)35÷×1﹣=40×1﹣,=40﹣,=39.点评:此题主要考查的是整数、分数和小数的四则混合运算,要注意运算顺序.B档(提升精练)一.选择题(共15小题)1.(2010•湖北模拟)30比()少20%.A.36 B.24 C.37.5考点:整数、分数、小数、百分数四则混合运算.分析:30比一个数少20%,将这个数当做单位“1”则30是这个数的1﹣20%,已知一个数的几分之几是多少,求这个数用除法:30÷(1﹣20%).解答:解:30÷(1﹣20%),=30÷80%,,=37.5.故选:C.点评:本题是根据分数除法的意义即已知一个数的几分之几是多少,求这个数用除法,进行分析解答的.2.(2014•湘潭模拟)7.8减去1.8的所得的差,除3.4,商是()A.2B.4C.D.考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:先列出1.8的,用7.8减去1.8的,再用3.4除以差即可.解答:接:3.4÷(7.8﹣1.8×),=3.4÷6.8,=.答:商是.故选:D.点评:解答这类题目,分清题里的数量关系,确定先算什么,在算什么,找清列式的顺序,列出算式解答.3.的倒数的3倍减去的一半,差为()A.B.C.D.考点:整数、分数、小数、百分数四则混合运算;倒数的认识.专题:文字叙述题.分析:根据题意,的倒数是,那么可用与3的积减去与的积,列式解答后再选择即可得到答案.解答:解:×3﹣×=4﹣,=3.故选:C.点评:解答此题的关键是根据题干的叙述确定算式的运算顺序,然后再列式计算即可.4.的值是多少.()A.12 B.7C.10 D.5考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:根据整数、分数、小数的四则混合运算的计算方法进行计算即可得到答案.解答:解:=2×[3.8÷(3﹣)],=2×[3.8÷],=2×5,=12.故答案为:A.点评:此题主要考查的是整数、小数、分数的四则混合运算的计算方法的应用.5.甲数的等于乙数的60%,那么()A.甲数>乙数B.乙数>甲数C.甲数=乙数D.无法确定考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:由题意可知:甲数×=乙数×60%,分两种情况进行解答,(1)逆运用比例的基本性质,得出甲数与乙数的比,即可进行判断;(2)当甲数和乙数都等于0时,等式仍然成立,此时甲数等于乙数,据此解答即可.解答:解:甲数×=乙数×60%,(1)甲数:乙数=60%:=9:10所以甲数<乙数;(2)当甲数和乙数都等于0时,等式仍然成立,此时甲数等于乙数,故选:D.点评:此类题目,若没注明取值范围,则要分两种情况进行解答.6.一个数的30%减去15,结果是95,求这个数的算式是()A.90÷30%﹣15 B.90÷30%+15 C.(90+15)÷30% D.(90+15)×30%考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:用结果95加上15,就是这个数的30%,所得的和再除以30%,就是这个数.解答:解:(90+15)÷30%,=105÷30%,=350.故选:C.点评:本题的关键是找出单位“1”,并找出单位“1”的百分之几对应的数量,用除法就可以求出单位“1”的量.7.计算+0.25+时,正确简便的方法是()A.把分数化成小数B.把小数化成分数C.两种方法都可以考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:因和不能化成有限小数,所以要把小数化成分数,再进行计算.据此解答.解答:解:+0.25+=++=(+)+==.故选:B.点评:本题主要考查了学生根据题目特点采用合适的方法进行简便计算的能力.8.一个数的40%加80是700的,如果设这个数为X,根据题意可列方程()A.40%X+700=80×B.40%X﹣700×=80 C.700×﹣80=40%XD.80+700×=40%X考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题意,设这个数为X,这个数的40%是40%X,40%X加80是700×,也就是700×﹣80等于40%X,由此列方程为700×﹣80=40%X,解决问题.解答:解:设这个数为X,得:40%X+80=700×即700×﹣80=40%X40%X=340X=850故选:C.点评:此题考查了学生根据等量关系列方程的能力.9.一个最简分数,如果分子加上3,就可以变成100%;如果分子减去1,就可以约简成,这个最简分数是()A.B.C.考点:整数、分数、小数、百分数四则混合运算.分析:根据条件“如果分子加上3,就可以变成100%”,因为100%=1==,又因为“如果分子减去1,就可以约简成”,==;→≠1,排除选项A;→=1,→=,符合要求,以此作出选择.解答:解:→==1,→==,故答案选B.点评:此题可用排除法,并运用分数的基本性质将分数化简,作出选择.10.(2010•河池)一个数的比它的25%少5,这个数是()A.99 B.100 C.25考点:整数、分数、小数、百分数四则混合运算.专题:压轴题.分析:一个数的比它的25%少5,即5占这个数的25%﹣,根据分数除法的意义可知,这个数为5÷(25%﹣).解答:解:5÷(25%﹣)=5÷,=100.答:这个数是100.故选:B.点评:根据分数减法意义求出5占总数的分率是完成本题的关键.11.(2010•白云区模拟)甲数的60%等于乙数的,那么()(甲、乙不为0).A.甲=乙B.甲>乙C.甲<乙考点:整数、分数、小数、百分数四则混合运算;分数大小的比较.分析:由甲数的60%等于乙数的可得:甲数×60%=乙数×.两两相乘数的积相等,乘较小数的那个数较大,比较60%与的大小,则可判定甲乙两数的大小.解答:解:甲数×60%=乙数×,60%=<,所以甲数>乙数.故选:B.点评:根据“两两相乘数的积相等,乘较小数的那个数较大”来判定甲乙两数的大小.12.的值是多少.()A.5B.12 C.1D.10考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则;运算定律及简算.分析:我们运用乘法的分配律进行计算即可,然后再进行正确的选择.解答:解:7.5×+2.5×+10×,=×(7.5+2.5)+10×,=+10×,=10×(),=10;故选:D.点评:本题先把题干的算式进行计算,再与答案进行对比在进行选择即可.13.的值是多少.()A.5B.C.D.考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先计算中括号里面的小括号,再计算中括号外面的小括号最后计算除法.进一步找出正确的答案.解答:解:[3(0.2+)×4.5]÷(7.05+6),=[3﹣()×4.5]÷(7.05+6.45),=[3.75﹣2.4]÷13.5,=1.35÷13.5,=0.1,=;故选:D.点评:考查了四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算律简便计算.14.的值是多少.()A.8.75 B.0.0875 C.0.8 D.0.875考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先依据四则运算计算方法,求出第一个括号的里面算式的得数,再运用除法性质即可解答.解答:解:(12﹣4 2.3)÷(100.875),=(12﹣2)÷(100.875),=1010×0.875,=1×0.875,=0.875,故答案为:D.点评:本题考查知识点:(1)四则运算计算方法,(2)除法性质的正确运用.15.下面的式子中()的结果最大.A.246÷6 B.246×0.6 C.24.6÷0.06考点:整数、分数、小数、百分数四则混合运算.专题:计算题.分析:我们通过对每一个选项进行计算,然后作出选择即可.注意小数点的位置的移动,以免出错.解答:解:A.246÷6=41;B.246×0.6=147.6;C.24.6÷0.06=410;故选:C.点评:本题运用计算方法选择出正确答案,计算时要认真计算.二.填空题(共14小题)16.(2013•北京模拟)= .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先进行小括号中的加法和减法运算,进而进行乘法和除法运算,最后进行减法运算,据此解答即可.解答:解:10﹣3.125×(1.6+)÷(2﹣0.625),=10﹣3.125×÷,=10﹣×,=10﹣,=.故答案为:.点评:此题主要考查整数、分数、小数、百分数四则混合运算的顺序的方法的灵活应用.17.(2013•永昌县模拟)列式计算:一个数的25%比它的少1.2.这个数是多少?考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题意,把这个数看作单位“1”,那么这个数的25%比它的少它的(﹣25%),正好少了1.2,也就是说1.2站这个数的(﹣25%),因此,这个数是1.2÷(﹣25%),解决问题.解答:解:1.2÷(﹣25%)=1.2÷(﹣)=1.2÷=1.2×12=14.4答:这个数是14.4.点评:此题解答的关键是把这个数看作单位“1”,找准数量与对应分率,列式解答.18.(2014•长沙模拟)已知:,那么□= .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:根据题意设□的数为x,将所给的式子转化成含未知数的等式(即方程),根据加,减,乘,除,各部分的关系,利用逆推的方法,解答即可.解答:解:设□的数为x,则:,{13.5÷[11+]﹣1÷7}×1=1,13.5÷[11+﹣1×=1÷1,13.5÷[11+]﹣=,13.5÷[11+]=,11+=13.5÷1,=13.5﹣11,=2.5,×=,10﹣10x=9,x=,故答案为:.点评:解答此题的关键是,把所给的式子转化为方程,运用加,减,乘,除,各部分的关系,利用逆推的方法,解方程即可.19.(2014•岚山区模拟)a的与b的50%一定相等.(a、b均为自然数)×.(判断对错)考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题干,假设a是8,b是12,据此分别求出它们的50%和是多少,再比较即可判断.解答:解:假设a是8,b是12,则a的是:8×=4,b的50%是:12×50%=6;4≠6,所以原题说法错误.故答案为:×.点评:本题中两分率对应的单位“1”不一定相同,单位“1”的大小不确定,它们分率所对应的大小就不能确定.20.(2013•黎平县)500克的相当于 1 千克的30%.考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:把要填的数看作单位“1”,单位“1”是未知的,用除法计算,数量500克的,500×=300克,300克=0.3千克,0.3除以对应分率30%.解答:解:500×=300(克),300克=0.3千克,0.3÷30%,=0.3÷0.3,=1(千克).答:500克的相当于1千克的30%.故答案为:1.点评:解决此题的关键是单位“1”确定和统一单位,把克统一成千克.21.(2013•广州模拟)我会列式,我会算乘的积减去1.5,再除以0.5,商是多少?考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:根据题意,用乘的积减去1.5,再用所得到的差除以0.5即可,列式解答即可得到答案.解答:解:(×﹣1.5)÷0.5=(3﹣1.5)=1.5×2=3答:商是3.点评:解答此题的关键是根据题干确定算式的运算顺序,然后再列式解答即可.22.(2013•青羊区模拟)19.8千克比22 千克轻10%,7.5 米比5米长.考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:(1)把()应填写的数看做单位“1”,单位“1”不知道用除法进行解答即可.(2)把5米看做单位“1”,也就是求5米的(1+)是多少.用乘法进行解答.解答:解:(1)19.8÷(1﹣10%),=19.8×,=22(千克);(2)5×(1+),=5×1.5,=7.5(米);故答案为:22,7.5.点评:此题属于分数乘法应用题的基本类型:找准单位“1”,弄清谁比谁多或少几分之几,列式解答即可.23.(2013•北京模拟)×23=16×+×= .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:(1)此题若转化成×(23+)或×(24﹣)再计算,因为不能约分,又牵扯到通分,反而使计算量加大,所以最好的办法是把带分数转化为假分数,再用分数乘法法则进行即可;(2)根据混合运算的顺序,先算两边的乘法,最后算加法即可.解答:解:(1)×23,=×,=;(2)16×+×,=+,=+,=.点评:本题考查了分数的乘法及混合运算,应用分数乘法法则及混合运算的顺序进行,计算时要细心,很容易出错.24.(2013•华亭县模拟)比24 少它的的数是18.×.考点:整数、分数、小数、百分数四则混合运算.专题:文字叙述题.分析:先求出24的,再用24减去24的,据此判断即可.解答:解:24﹣24×,=24﹣8,=16.故答案为:×点评:解决此题的关键是先求出24的,再用24减去得数,25.(2014•长沙模拟)17.5+17.5×1÷(﹣0.06)= 148.75 ;1÷= 1;1﹣= .考点:整数、分数、小数、百分数四则混合运算;繁分数的化简.专题:运算顺序及法则.分析:(1)按照先算括号里面的减法,再算乘法,然后算除法,最后算加法顺序计算即可解答,(2)先求出2减的差,再用1除以求得的差,最后用1除以求得的商即可解答,(3)先求出2加的和,再用1除以所得的和,最后用1减求得的商即可解答.解答:解:(1)17.5+17.5×1÷(﹣0.06)=17.5+17.5×1÷0.24=17.5+31.5÷0.24=17.5+131.25=148.75;(2)1÷=1÷=1=1;(3)1﹣=1﹣=1﹣=.故答案为:148.75,1,.点评:针对不同的题型,采用不同的方法正确进行计算,是本题考查知识点.26.(2014•长沙模拟)(1.5﹣)÷[×(0.4+2)]= 11.考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:按照先算小括号里面的,再算中括号里面的顺序计算即可解答.解答:解:(1.5﹣)÷[×(0.4+2)]=1÷[×2.5]=1÷=11故答案为:11.点评:依据四则运算计算方法正确进行计算,是本题考查知识点.27.(2014•台湾模拟)计算:= .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:先把算式中的带小数和带分数化成假分数,再把除以一个数改写成乘这个数的倒数,进而先约分,再计算得解.解答:解:,=×÷(×)×,=×××××,=;故答案为:.点评:解决此题要根据数据和运算符号的特点,灵活运用所学的简便方法进行计算.28.(2014•长沙模拟)计算:1×[6﹣4÷(+)+2÷1.5]= 3 .考点:整数、分数、小数、百分数四则混合运算.专题:运算顺序及法则.分析:按照先算小括号里面的加法,再同时计算中括号里面的除法,然后算中括号里面的减。
沪教版六年级数学讲义 第10讲 分数、小数的四则混合运算

第10讲 分数、小数的四则混合运算【学习目标】分数、小数的四则混合运算是六年级数学上学期第二章第2节中的内容.分数、小数的四则运算对于培养同学们的计算能力起着十分重要的作用,要想掌握好分数、小数的四则混合运算:一要牢记分数、小数的基本运算法则:基本运算法则是运算的基础;二要掌握分数与小数的互化:分数与小数的互化在它们的四则运算中是十分重要的一环,我们需要根据题目的需要将分数化成小数或将小数化成分数;三要有意识地观查并灵活地分析题目的特征,充分利用乘法分配律等技巧进行速算和巧算.【基础知识】一:分数、小数的混合运算1.混合运算的一般原则(1)加减混合运算时,只需将题目中的数同时化成小数或分数后再运算;但当分数不能化成有限小数时,则应同时化成分数后再运算.(2)乘除运算中,一般将除法先转化为乘法,小数转化为分数,然后遵循先约分再运算的原则进行计算. (3)一般的运算顺序:先乘除,后加减;若有括号,则先算括号内.二:分数、小数的速算与巧算1.常见的分数与小数的互化在分数与小数的混合运算中,要非常熟练的掌握一些简单的分数和小数之间的互化,做到一看便知,从而有效地提高运算的简便性和正确性.如:10.52=,10.25=,10.110=,10.0520=,10.0425=,10.0250=, 10.254=,30.754=,10.1258=,30.3758=,50.6258=,70.8758=.2.凑整的思想(1)加法凑整:若几个数相加的和是一个整数,那么可将这几个数作为一组进行计算,如:30.2514+=;减法亦然.(2)乘法凑整:若几个数相乘的积是一个整数,那么可将这几个数作为一组进行计算,如:0.2541⨯=;除法亦然.3.乘法分配律的逆运用乘法分配律:()a b c a c b c +⨯=⨯+⨯,将等号的左边和右边调换位置后得到()a c b c a b c ⨯+⨯=+⨯: .这一运用,在速算和巧算中是很常用也很重要的方法,例如:29290.90.90.90.9 11111111⎛⎫⨯+⨯=+⨯=⎪⎝⎭.【考点剖析】考点一:分数、小数的混合运算例1.计算:(1)30.24+;(2)40.255-;(3)20.57+;(4)10.453-.【难度】★【答案】(1)1920;(2)1120;(3)1114;(4)760.【解析】第(1)(2)小题也可以统一为小数进行加减运算,30.20.750.20.954+=+=,40.250.80.250.555-=-=.【总结】考查分数与小数互化运用于基础加减运算.例2.计算:(1)40.35⨯;(2)40.35÷;(3)30.67⨯;(4)30.67÷.【难度】★【答案】(1)0.24;(2)83;(3)935;(4)57.【解析】分数与小数的乘、除法运算法则需要熟练掌握. 【总结】考查分数与小数互化运用于基础乘除运算.例3.计算:(1)120.5523++;(2)710.384--;(3)230.3358+-;(4)110.7532-+.【难度】★【答案】(1)10360;(2)130.32540或;(3)710.355200或;(4)112.【解析】分数与小数混合运算,能化为有限小数的分数可以化为小数进行计算,比如第(2)小题和第(3)小题.【总结】考查分数与小数加减混合运算.例4.计算:(1)3160.7421⨯⨯;(2)820.8253÷÷;(3)30.37534÷⨯;(4)790.81910⨯÷.【难度】★【答案】(1)25;(2)35;(3)332;(4)710.【解析】分数与小数乘除法混合运算,一般要求学生将小数化为分数进行运算. 【总结】考查分数与小数乘除混合运算.例5.计算:(1)12150.35234⨯-÷;(2)315.2 4.625585⨯+⨯.【难度】★★【答案】(1)8942;(2)26.【解析】值得一提的是第(2)小题可以巧算:31355.2+4.6255 5.2(4) 5.25268588⨯⨯=⨯+=⨯=.【总结】考查分数与小数的四则混合运算,注意可以简便运算的时候要简便运算.例6.计算:(1)51.20.712⎛⎫-+⎪⎝⎭;(2)120.7523⎛⎫--⎪⎝⎭;(3)2120.153⎛⎫⨯+⎪⎝⎭;(4)510.7534⎛⎫÷-⎪⎝⎭.【难度】★★【答案】(1)112;(2)512;(3)495;(4)103.【解析】需要学生熟练掌握小数化分数的方法,并且注意结果的最简性,运算结果是假分数的可以化为带分数,也可保留假分数.【总结】考查分数与小数四则混合运算.例7.下列运算过程中,正确的是()A.22121133232⎛⎫÷+=+÷⎪⎝⎭B.732237÷⨯=C.33633751375136⎛⎫÷÷=⨯⨯⎪⎝⎭D.33213153157515721521⎛⎫+÷=⨯+⨯⎪⎝⎭【难度】★★【答案】D【解析】A选项,错误原因在于除法没有分配律,而D选项将2115÷化为1521⨯就可以利用乘法分配律,所以计算正确,B选项因为运算顺序出错,C选项的错因是去括号法则不清楚正确的解法是336336()51375137÷÷=÷⨯.【总结】考查学生对运算顺序及去括号法则的掌握.例8.甲数是1403,乙数比甲数多它的211,乙数是________.【难度】★★【答案】乙数是14324733或.【解析】列式:1121212113143 404040133113113113+⨯=⨯=⨯=.【总结】考查学生对“比一个数多几分之几”的理解运用.例9.比215米多2.5分米是______米.【难度】★★【答案】1.65米.【解析】首先,注意统一题目中的单位为米,列式:210.25 1.40.25 1.655+=+=米.【总结】考查“比一个数多几分之几(带单位)”的理解运用.例10.某数的2倍与153的差是4.25,求这个数.【难度】★★【答案】115 24.【解析】设这个数为x,125 4.253x-=,解得11524x=.【总结】考查列方程解文字题及分数小数混合运算.例11.六(2)班组织去苏州春游,上午7:30从学校坐大巴出发,用了56个小时到达目的地,中午利用了0.5个小时吃了午饭,下午回上海时用了45分钟,在17:15回到学校,则他们实际游玩的时间是多少小时?【难度】★★【答案】实际游玩时间273小时.【解析】上午7:30到下午17:15历时9小时45分即394小时,减去来回的乘车时间和午餐时间,列式:351329746243---=小时.【总结】考查分数与小数混合运算的应用.例12。
分数、小数的四则运算

分数、小数四则混合运算一、基础知识熟练掌握分数、小数四则运算是小学数学中的一项重要内容,它对于培养同学们的计算能力起着十分重要的作用,要想掌握好分数、小数的四则混合运算,一要牢记分数、小数的基本运算法则,二要掌握分数与小数的互化。
运算法则有:1.小数加、减法的计算法则:把各数的小数点对齐,按照整数的加、减法的法则计算,在得数里对齐横线上的小数点,点上小数点。
2.小数乘、除法的计算法则:按照整数乘法(或除法)的法则计算出积(或商),对于乘法要看乘数和被乘数里共有几位小数,就从积的右边数出几位,点上小数点,不够时补零.对于除法,商里的小数点要和被除数的小数点对齐。
3.分数的加、减法运算法则:同分母的分数相加减,只要把分子相加减,分母不变;异分母的分数相加减,要先通分(找出分母的最小公倍数,分子分母同时扩大相同的倍数,使不同的分母变成同分母,然后按同分母分数进行运算;带分数相加减,把分数部分和整数部分分别相加减,然后将所得结果合并。
4.分数的乘法运算法则:用分子相乘积作分子,分母相乘积作分母.带分数相乘时,先将带分数化成假分数,然后相乘。
5.分数的除法运算法则:将作为除数的分数的分子、分母相互换位,化成乘法来做。
在分数运算中,约分是重要的步骤,通过约分可以简化运算及得到最简分数.约分的过程,是找出分子、分母的公约数,然后利用分数基本性质:分子分母同时乘以或除以同一个不为零的数,分数的值不变.消去公约数,得到所需的分数或最简分数。
分数与小数的互化在它们的四则运算中是十分重要的一环,根据题目的需要将分数化成小数或小数化成分数.互化一般原则是:(1)分数能化成有限小数的,化成小数计算比较简单,分数不能化成有限小数时,则把小数化成分数再计算。
(2)在进行分数、小数混合计算时,题目含分数或小数的哪个个数多,就保留哪个,把个数少的转化成个数多的那种形式.特别是一些简单的分数和小数,要非常熟练地掌握它们的互化,做到一看便知。
五年级上册的列式计算

五年级上册的列式计算一、小数乘法的列式计算。
1. 简单的小数乘法。
- 例如:0.5×3 =?- 列式:- 按照整数乘法计算:5×3 = 15。
- 因数0.5有一位小数,从积的右边起数出一位点上小数点,所以结果是1.5。
- 再如:1.2×2.5 =?- 列式:- 先按照整数乘法计算:12×25 = 300。
- 因数1.2有一位小数,2.5有一位小数,共两位小数,从积的右边起数出两位点上小数点,结果是3.00,化简后为3。
2. 小数乘整数与整数乘法意义的联系。
- 例如:一支铅笔0.8元,买5支铅笔多少钱?- 列式:0.8×5 = 4(元)- 这里的0.8×5表示5个0.8相加的和是多少,这与整数乘法中求几个相同加数的和的意义相同。
3. 积的近似数。
- 例如:0.38×2.5(得数保留一位小数)- 列式:- 先计算0.38×2.5 = 0.95。
- 保留一位小数,看百分位上的数,百分位是5,根据四舍五入法,向十分位进1,所以0.95≈1.0。
二、小数除法的列式计算。
1. 除数是整数的小数除法。
- 例如:3.6÷3 =?- 列式:- 按照整数除法的方法除:3÷3 = 1,6÷3 = 2。
- 商的小数点要和被除数的小数点对齐,所以结果是1.2。
- 再如:5.6÷7 =?- 列式:- 5除以7不够除,商0占位,56÷7 = 8。
- 商是0.8。
2. 除数是小数的小数除法。
- 例如:1.26÷0.3 =?- 列式:- 除数0.3变为整数,小数点向右移动一位,被除数1.26的小数点也向右移动一位变成12.6。
- 然后计算12.6÷3 = 4.2。
- 又如:2.4÷0.12 =?- 列式:- 把0.12变为12,小数点向右移动两位,2.4的小数点也向右移动两位变为240。
分数小数四则混算

一、分数、小数四则混合运算分数、小数四则运算是小学数学中的一项重要内容,它对于培养同学们的计算能力起着十分重要的作用,要想掌握好分数、小数的四则混合运算,一要牢记分数、小数的基本运算法则,二要掌握分数与小数的互化。
运算法则有:1.小数加、减法的计算法则:把各数的小数点对齐,按照整数的加、减法的法则计算,在得数里对齐横线上的小数点,点上小数点。
2.小数乘、除法的计算法则:按照整数乘法(或除法)的法则计算出积(或商),对于乘法要看乘数和被乘数里共有几位小数,就从积的右边数出几位,点上小数点,不够时补零.对于除法,商里的小数点要和被除数的小数点对齐。
3.分数的加、减法运算法则:同分母的分数相加减,只要把分子相加减,分母不变;异分母的分数相加减,要先通分(找出分母的最小公倍数,分子分母同时扩大相同的倍数,使不同的分母变成同分母,然后按同分母分数进行运算;带分数相加减,把分数部分和整数部分分别相加减,然后将所得结果合并。
4.分数的乘法运算法则:用分子相乘积作分子,分母相乘积作分母.带分数相乘时,先将带分数化成假分数,然后相乘。
5.分数的除法运算法则:将作为除数的分数的分子、分母相互换位,化成乘法来做。
在分数运算中,约分是重要的步骤,通过约分可以简化运算及得到最简分数.约分的过程,是找出分子、分母的公约数,然后利用分数基本性质:分子分母同时乘以或除以同一个不为零的数,分数的值不变.消去公约数,得到所需的分数或最简分数。
分数与小数的互化在它们的四则运算中是十分重要的一环,根据题目的需要将分数化成小数或小数化成分数.互化一般原则是:(1)分数能化成有限小数的,化成小数计算比较简单,分数不能化成有限小数时,则把小数化成分数再计算。
(2)在进行分数、小数混合计算时,题目含分数或小数的哪个个数多,就保留哪个,把个数少的转化成个数多的那种形式.特别是一些简单的分数和小数,要非常熟练地掌握它们的互化,做到一看便知。
对于一般的分数化小数,用分子除以分母即可得到结果.小数化分数,只需把原小数去掉小数点儿以后作为分子,原小数的小数点后有几位,就在1后面添几个零,作为分母,然后通分化成最简结果即可.在互化时要细心,互化的错误会导致整个题目的错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列式计算加强训练
1 、从3
8的倒数里减去
1
4的
2
3,差是多少?
2、2
3与
1
4的差等于一个数的
5
6,这个数是多少?
3、甲数是5的1
5,乙数的
1
5是5,两数相差多少?
4、一个数的3
比180的
1
多24,求这个数。
5、从30里减去48的1
2,所得的差去除3,商是多少?
6、一个数比4.5的1.6倍小0.72,求这个数。
7、一个数的7倍比13多7.4,求这个数。
(列方程)
8、用2除10
7的商,减去7的倒数,差是多少?
9、甲数的3
4等于乙数的
3
5,如果乙数是15,甲数是多少?
10、0.8与0.4的差,乘除1.25的商,积是多少?
11、3.4与5.6的和除以它们的差,商是多少?
12、 2除1.6的商加上5.4乘以5
的积,和是多少?
13、4
5的倒数除
5
3与
1
3的和,商是多少?
14、一个数的3倍加上5除以5
8的商,和是32.6,求这个数。
(方程解答)
15、某数的1
5比4.5的1.6倍少3.2,求这个数?。
