预应力混凝土斜拉桥肋板式主梁施工过程中的剪力滞效应研究

合集下载

铁路肋板式槽型连续梁剪力滞效用试验研究

Value Engineering0引言槽型梁是一种新型桥梁结构，主要运用于铁路桥梁、城市轨道交通中。

肋板式槽型梁由腹板、底板、肋板、设置在支座处的横隔板组成，属于下承式开口薄壁构件。

轨道及列车直接作用在底板上，底板将荷载传递至腹板下缘，腹板将荷载传递给支座。

槽型梁具有以下特点：列车直接作用在底板上，能够有效解决空间受限问题；桥梁结构高度减小，结构体量较小，显得轻巧、美观；腹板结构承受荷载、隔音降噪。

因截面为开口薄壁截面，截面受力和变形较复杂，特殊的传力路径导致底板与腹板连接位置受力较复杂，易出现开裂等问题，国内外学者对简支槽型梁的力学特性和试验研究较多，但对铁路肋板式槽型连续梁实桥试验却研究较少。

为此，本文以沪通铁路（40+64+40）m 铁路肋板式槽型连续梁进行实桥足尺静载试验，分析研究了槽型连续梁底板剪力滞分布规律，该研究成果可为铁路预应力混凝土槽型连续梁桥的设计、建造、维护提供参考。

1工程概况试验梁为沪通铁路黄封联络线特大桥（40+64+40）m 预应力混凝土槽型连续梁桥采用盘扣支架法施工。

桥梁各跨计算跨径分别为4000cm 、6400cm 、4000cm ，在边支点和中支点设置4道横隔板，跨中共设置15道板肋。

横隔板截面高500cm ，腹板厚200cm ，底板宽1120cm ，底板厚110cm ；板肋截面高450cm ，腹板厚65cm ，底板宽1050cm ，底板厚60cm ；板肋截面高450cm ，板肋厚200cm ，底板宽1050cm ，底板厚60cm 。

梁体设2%横坡，曲线半径为1500m 。

梁体采用C55高性能混凝土，预应力筋采用抗拉强度标准值为f pk =1860MPa 、弹性模量为E p =195GPa 、公称直径为15.20mm 高强度钢绞线。

2施工方法2.1支架设置支架采用盘扣支架，根据力学计算确定支架布设。

2.2支架加载预压安照0->40%->60%->110%->60%->40%->0每级加载、分级卸载并测量测点数据。

宽幅脊骨梁矮塔斜拉桥剪力滞效应分析及试验研究

宽幅脊骨梁矮塔斜拉桥剪力滞效应分析及试验研究刘傲;林文强;宋军【摘要】以江肇高速公路西江特大桥为背景,研究宽幅脊骨梁矮塔斜拉桥截面正应力分布规律.通过理论计算并结合实桥试验验证,得出了各关键断面应力不均匀系数,为优化预应力钢束设计及改善宽幅截面受力性能提供了依据.【期刊名称】《城市道桥与防洪》【年(卷),期】2016(000)005【总页数】3页(P78-80)【关键词】矮塔斜拉桥;剪力滞;效应分析【作者】刘傲;林文强;宋军【作者单位】广东省南粤交通投资建设有限公司,广东广州510101;广东省南粤交通投资建设有限公司,广东广州510101;同济大学,上海市200092【正文语种】中文【中图分类】U448.27江肇高速公路是珠江三角洲经济区外环公路的西环段，位于珠江三角洲西部地区。

路线起于江门市杜阮镇，终于肇庆市四会市东城区。

西江特大桥是江肇高速公路建设难度最大的控制性工程，也是江肇高速公路的标志性工程。

大桥位于永安镇与沙浦镇之间，桥位跨越西江主干流，主桥为四塔五跨单索面脊骨梁预应力混凝土矮塔斜拉桥，跨径布置为128 m+3×210 m+128 m=886 m，采用墩、塔、梁固结刚构体系，见图1。

大桥主梁为预应力混凝土结构，采用变高度斜腹板单箱三室宽幅脊梁断面。

顶板宽38.3 m，悬臂长8.15 m，两侧设5.15 m宽后浇带，在同类型桥梁中，桥面宽度和挑臂长度均较大，故剪力滞效应明显，应对其顶底板纵向剪力滞效应进行研究。

箱梁纵向受力不均匀性主要受剪力滞效应以及偏载效应影响。

关于剪力滞理论以及翼缘板有效工作宽度的研究，早在20世纪20年代就开始了，虽然对剪力滞问题提出了较多的理论，如弹性理论解法、比拟杆法、能量变分法、数值分析法等进行分析和求解，但这些方法大多依赖于假定位移函数，计算结果偏理想化，新结构以及分节段受力特性使得传统算法存在较多的不足之处[1-4]，在西江特大桥中，主梁体系具有如下特点：（1）主梁为宽幅脊梁，顶底板普遍较薄，悬臂较长，首先会会加剧剪力滞效应，其次边载偏心距增大，也会加剧扭转和偏载效应；（2）主梁悬臂分次浇筑，后浇段受力时机及纵向受力特征与一次浇筑构件存在本质区别；（3）单索面矮塔斜拉桥体系，索力传递不均匀，成为纵向受力不均匀原因之一；（4）悬臂施工，各截面剪力滞效应随各阶段荷载及边界的变化产生变化，不加以验算配筋，可能导致施工阶段主梁局部开裂或破坏，目前剪力滞研究中较少涉及。

箱形梁的剪力滞效应分析

箱形梁的剪力滞效应分析摘要: 针对某100m+192m+100m预应力混凝土连续刚构桥的箱梁受力特征，以现有的剪力滞效应理论为基础，并利用三维通用有限元分析软件ANSYS，建立本桥在运营阶段的三维有限元实体模型，分析了该桥在恒载、恒载与预应力荷载组合下的箱梁顶底板的应力分布情况，同时根据相关公式计算了各截面的剪力滞系数。

关键词：箱梁有限元实体模型剪力滞系数0引言箱梁剪力滞效应是指在箱形梁中,产生弯曲的横向力通过肋板传递给翼板,而剪应力在翼板上的分布是不均匀的,在肋板与翼板的交接处最大,随着离开肋板的距离增加而逐渐减小,因此,剪切变形沿翼板的分布是不均匀的。

由于翼板剪切变形的不均匀性,引起弯曲时远离肋板的翼板之纵向位移滞后于近肋板的翼板之纵向位移,因此弯曲应力的横向分布呈曲线形状,这种弯曲应力分布不均匀的现象,称作剪力滞效应。

剪力滞效应常用剪力滞系数λ来衡量,λ的经典定义为:当λ值大于1时称为正剪力滞效应:而当λ值小于1时称为负剪力滞效应混凝土箱梁桥虽然是空间结构，但通常按平面梁单元进行简化分析，这种计算能够把握桥梁结构纵向抗弯、抗剪的主要规律，在一般情况下，能够较好地保证结构的安全度。

然而，在大跨度、宽箱体及曲线梁桥中，结构的空间效应比较显著，难以通过平面计算解决，在这些情况下，考虑箱梁桥的空间弯曲、剪滞、扭转、畸变等效应就显得十分重要。

为考虑箱梁在偏载作用下的扭转、畸变等效应，在工程设计中，经常引入偏载增大系数用以修正按平面杆系计算的截面应力值。

有关箱梁剪力滞的相关成果已纳入规范标准之中，例如德国工业规范（DIN1075）、美国公路桥梁设计规范（(AASHTO—LRFD)、中国《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）、中国《高速铁路设计规范》（试行）（TB 10621-2009）。

笔者通过对某特大桥进行空间有限元分析，讨论该桥在不同荷载下的剪力滞效应，为今后的桥梁设计提供一定的参考。

斜拉桥索塔与索梁锚固区局部应力分析

索塔、梁锚固区受力十分复杂。针对索塔、梁锚固区的受力状况进行研究，优化锚固区细部索索对
构造及预应力钢束的布置均有重要意义。以一座独塔混凝土斜拉桥为例＇用有限元方法对索 ’ 运塔、梁锚固区进行了空间应力分析，索总结了锚固区的受力特点。
结果表明．工艺与传统工艺相比具有明显的先进性，的独到之处是使繁琐的转体施工工艺变本它
得简单、速、全、控。快安易关键词转体施工工艺钢球铰牵引索连续牵引
桥梁转体施工是指将桥梁结构在非设计轴线位置制作成形后，通过转体就位的一种施工方法。转体施工与以往悬臂拼装、臂浇筑、悬原位现浇等施工工艺相比，有几乎完全不干扰交通的特点，具特别适用于具有繁忙运输要求线路的跨线桥。且施工快速、合经济效益高。桥梁转体施工根据综
ａ）立面
图２索塔锚固端构造图（位：ｍ）单ｃ
固区，为单箱双室截面。斜拉索锚固端布置于中
隔板两侧，点横向间距１６ｉ直接锚于混凝土锚．ｎ，
图３索粱锚固端构造图（位：ｍ）单ｃ
收稿日期：０ｌ６１２１－ —３０
向２横坡。斜拉索布置为扇形密索体系，索双面，采用低松弛镀锌高强钢丝，每个主塔布有１４

箱梁的剪力滞效应研究综述

科技信息
。建筑与工程ｏ
ＳＩＮＥ＆ＴＣＮＯＧＯＭＡＩＣＥＣＥＨＯＬＹＩＲＴＯＮＮＦ
２１００年
第２期３
箱梁的剪力滞效应研究综述
胡欣（汉交通职业学院湖北武汉武
【摘
４０６３０５）
要】本文介绍国内外研究箱梁剪力滞效应的方法原理和研究成果，比较其适用性和优缺点，为今后开展箱梁剪力滞效应研究提供了
衡条件和变形协调条件建立一组微分方程。一般情况下．带悬臂翼２箱梁剪力滞效应研究的展望不板的单室矩形箱梁取５根杆来计算．精度足可。１９其９０年，士铎教张综上所述。内外学者研究薄壁箱梁剪力滞问题所提出的理论和国授等人将三杆比拟法用在求解变截面连续箱梁中去。比拟杆法不仅解方法各有特点，也都受到一定的限制，存在着一些共同的问题。但并笔决了受弯构件的剪力滞问题，还解决了受轴向力作用构件的剪力滞问者对今后薄壁箱梁剪力滞研究方向提出几点建议。题，于在压、荷载共同作用下加劲梁的剪力滞问题可用叠加法求至弯２１研究理论目前剪力滞的研究理论基本停留在传统的弹性力学．得。方法上，已不能适应复杂结构分析的要求。为半解析法的有限段法．作１３弹性理论解法弹性理论的解法是建立在经典弹性理论基础之．尽管能将二维位移场按一维离散，而降低离散的自由度，降低了从亦上的，括正交异性板法、包折板理论和板壳理论等。待求方程组的阶数。但由于有限段法是沿着横断面中线的方向离散．瑞斯纳ｆ．ｅｓｎｅ）上下板为波纹状的悬臂矩形箱梁截面的剪ＥＲｉｅｒｓ把按一般的有限单元技术，段单元间的搭接处理造成困难。此，改梁因需力滞问题比拟成一正交异性板进行了分析与研究，作了近似简化处进有限段法的单元模型．用广义协调法、糊广义参数法及样条函并利模理。马尔可ｆｌｏｉ等人进一步用此法分析了加劲箱梁的剪力滞效Ｍａｃｌ）ｎ数法等理论完善剪力滞的单元模型．以提高计算精度。应。正交异性板法所考虑的是整个箱梁，施加的荷载要用傅立叶级所桥梁结构大部分采用钢筋混凝土作为主要材料，际上钢筋混凝实数表达，因而比较繁琐，应用上也受到一定限制。弹性折板理论由在土受力时呈现出弹塑性状态，所谓的非线性。目前剪力滞研究仅停即Ｇｌ．ｅｇ和ＬｖｏｄＢｒｅｅ提出．定板平面内与平面外的性能是完全独立的，假留在弹性范围．于材料非线性方面几乎还未涉及到，展材料非线至开板端在平面外位移和转角以及平面内横向位移都是受到约束的，对但性剪力滞理论研究是有必要的。翘曲则为自由。．．ｉｓｎ和Ｍ．Ｈｉａｌ９６年提出了用板壳理论ＪＧｂｏＥＨ．ｔｎｔ１７ｗｙ２２荷载形式目前剪力滞理论研究的荷载形式基本上停留在静载．分析箱梁的剪力滞效应。们认为各种截面形状的箱梁都可看作是板他范围的竖向集中荷载和分布荷载。际上大跨径桥梁大多数采用预应实单元和筒壳单元的组合体，因而，引用板的理论和筒壳理论加以处力混凝土结构或斜拉桥等压弯体系，们都处于轴向和横向荷载共同可它理，种理论的前提对板厚要求相同。这作用下的受力状态。因此，进一步研究压弯薄壁结构的剪力滞问题，需国内的宋启根教授曾用弹性平面应力理论求解了Ｔ形、形和箱Ｉ尤其要探索考虑剪力滞的二阶稳定理论。外有关动荷载的剪力滞研另形粱在压、荷载共同作用下，用于简支、臂、续梁的简化公式。弯适悬连究几无涉及．待进一步开展。有蔡松柏、存权等在利用程翔云教授研究成果的基础上，出了对称２３结构形式当前剪力滞研究的结构形式大多数局限于简支梁、李导．挠曲荷载作用下简支箱梁的剪力滞公式的精确解ｌｌｌ。悬臂梁，对于变高度连续梁、平曲线连续梁、拉桥和吊桥等研究而水斜１数值分析法数值分析法主要是指有限元法、有限条法及有限．４得较少。开展大跨径桥梁的剪力滞研究，当前工程设计部门亟待解是

(完整版)桥梁工程简答题

五、问答题1) 桥梁有哪些基本类型？按照结构体系分类，各种类型的受力特点是什么？答: 梁桥、拱桥、斜拉桥、悬索桥。

按结构体系划分，有梁式桥、拱桥、钢架桥、缆索承重桥(即悬索桥、斜拉桥)等四种基本体系。

梁式桥：梁作为承重结构是以它的抗弯能力来承受荷载的。

拱桥：主要承重结构是拱肋或拱圈，以承压为主。

刚架桥：由于梁与柱的刚性连接，梁因柱的抗弯刚度而得到卸载作用，整个体系是压弯构件，也是有推力的结构。

缆索桥：它是以承压的塔、受拉的索与承弯的梁体组合起来的一种结构体系。

2) 桥梁按哪两种指标划分桥梁的大小？具体有哪些规定？答：按多孔跨径总L 和单孔跨径划分。

3) 各种体系桥梁的常用跨径范围是多少？各种桥梁目前最大跨径是多少，代表性的桥梁名称？答：梁桥常用跨径在20米以下，采用预应力混凝土结构时跨度一般不超过40 米。

代表性的桥梁有丫髻沙。

拱桥一般跨径在500 米以内。

目前最大跨径552 米的重庆朝天门大桥。

钢构桥一般跨径为40-50 米之间。

目前最大跨径为4) 桥梁的基本组成部分有哪些？各组成部分的作用如何？答：有五大件和五小件组成。

具体有桥跨结构、支座系统、桥墩、桥台、基础、桥面铺装、排水防水系统、栏杆、伸缩缝和灯光照明。

桥跨结构是线路遇到障碍时，跨越这类障碍的主要承载结构。

支座系统式支承上部结构并传递荷载于桥梁墩台上，应满足上部结构在荷载、温度或其他因素所预计的位移功能。

桥墩是支承两侧桥跨上部结构的建筑物。

桥台位于河道两岸，一端与路堤相接防止路堤滑塌，另一端支承桥跨上部结构。

基础保证墩台安全并将荷载传至地基的结构部分。

桥面铺装、排水防水系统、栏杆、伸缩缝、灯光照明与桥梁的服务功能有关。

5) 桥梁规划设计的基本原则是什么？答：桥梁工程建设必须遵照“安全、经济、适用、美观”的基本原则，设计时要充分考虑建造技术的先进性以及环境保护和可持续发展的要求。

6) 桥梁设计必须考虑的基本要求有哪些？设计资料需勘测、调查哪些内容？答: 要考虑桥梁的具体任务，桥位，桥位附近的地形，桥位的地质情况，河流的水文情况。

顶板_底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响

第24卷第2期长沙交通学院学报V o.l 24N o .22008年6月J OURNAL O F CHANG SHA COMMUNICAT I ONS UNIVERSITY J un .2008 文章编号:1000-9779(2008)02-0023-06顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响张玉平,李传习(长沙理工大学土木与建筑学院,湖南长沙 410076)摘要:以株洲建宁大桥斜拉桥为工程背景,用板壳单元模拟箱梁,研究了顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响,通过计算结果的分析和比较,对影响斜拉桥箱形主梁剪力滞效应的顶板、底板和斜腹板厚度进行了参数分析.计算结果表明:在斜拉桥单箱三室主梁中,顶板、底板和斜腹板厚度对顶板剪力滞效应的影响大于对底板剪力滞效应的影响;底板和斜腹板厚度增加均会使顶板剪力滞效应趋于不均匀;在顶板、底板和斜腹板厚度三者变化中,斜腹板厚度变化对于剪力滞效应的影响最为显著.关键词:斜拉桥;剪力滞效应;有限元法;参数分析中图分类号:U 448.23 文献标识码:A收稿日期:2008-03-07作者简介:张玉平(1976-),男,长沙理工大学讲师,博士生.Influence of top flange ,botto m fl ange and w eb thicknesson the shear lag effect of box girder used i n cable -stayed bri dgeZ HANG Yu -ping ,LI Chuan -x i(Schoo l of C i v il and Constructi on ,Changsha U n i ve rsity o f Sc ience &T echnology ,Changsha 410076,Chi na)Abst ract :M any different di m ensional finite e le m entary m ode ls ,in w hich the top flange ,botto m flange and w eb o f box gir der are si m u lated w ith shell ele m en,t w ere estab lished on t h e background of Jiann i n g bri d ge i n Zhuzhou .Para m eter analysis of the t h ickness change of the top flange ,botto m flange and w eb on shear lag effect of box g irder w as based on the ana lysis and co m parson o f the ca lculated results .The resu lts sho w tha t t h e t h ickness change of the top flange ,bo tto m flange and w eb have m o re influence on the shear lag effect o f top flange than that of botto m flange ,thickness increase of bo tto m flange and w eb can m ake the shear lag effect in -tensified obviousl y ,and th ickness change ofw eb hasm ost si g nifican t i n fluence on the shear lag e ffect a m ong t h e m for box g irder w it h si n g le box and t h ree r oo m s used in cable -stayed bridges .K ey w ords :cable -stayed bridge ;shear lag e ffec;t finite e le m entm ethod ;para m eter ana lysis在对称荷载作用下,箱梁结构由于剪切变形的影响使得翼板内的正应力沿截面宽度方向呈现不均匀分布的现象,称为/剪力滞效应0.随着桥梁宽度的加大和安全储备的降低,在设计计算和施工控制计算时,准确分析其剪力滞效应很有必要.剪力滞效应引起应力不均匀分布程度通常用剪力滞系数K 进行度量.其经典定义:剪力滞系数K =R / R .式中:R 表示考虑剪力滞效应后求得的翼板正应力; R 表示按初等梁理论计算出的翼板正应力,即空间分析得到的正应力沿梁宽方向的平均值.靠近腹板处翼板的纵向应力若大于翼板中点或悬臂板边缘点处的纵向应力,称为/正剪力滞0;而翼板中点或悬臂板边缘点处的纵向应力若大于靠近腹板处翼板的纵向应力,称为/负剪力滞0.箱梁剪力滞效应的影响因素较多,主要有宽跨比、结构尺寸、翼缘板悬臂长度、腹板高厚比、有无横隔梁、梁的支承条件和荷载形式等.目前,这些因素对梁桥的影响研究得较多,也得到了许多规律性的结论[1-6],而对于斜拉桥箱形主梁剪力滞效应的影响因素分析还不多[7-9].本研究以株洲建宁大桥斜拉桥为工程背景,对影响斜拉桥箱形主梁剪力滞效应的主要结构尺寸(顶板、底板和斜腹板厚度)进行参数分析,得到一些可供借鉴的结论.1 空间有限元计算模型作者采用软件ANSYS,应用参数化程序设计语言APDL ,建立了株洲建宁大桥斜拉桥成桥状态的多个空间有限元模型.1.1 工程背景株洲建宁大桥是株洲市城市快速环道上的一座特大型桥梁,于2005年12月建成通车.主桥为独塔单索面混凝土箱梁斜拉桥,其跨径布置为240+134+42+41.7m (见图1),为塔、梁、墩固结体系,目前为国内同类型桥梁的最大跨径.建宁大桥斜拉桥设计为双向6车道,桥宽30m .主梁采用单箱三室箱梁断面形式,见图2.主塔由上、中、下塔柱及横梁组成,横桥向为钻石型,顺桥向为I 字型.斜拉索采用扇形布置,梁上斜拉索布置在中央分隔带,横向布置两排,两排索索面距为1.2m.锚固在中室横隔梁处索锚区,梁上基本索距为7m (边跨有8根斜拉索索距为4m ),塔上基本索距为1.5m,全桥共有2@31对索.横隔梁每3.5m 设一道,其中斜拉索索锚区的横隔梁厚度为40c m,两索锚区之间的横隔梁厚度为22c m.1.2 单元选取与有限元模型斜拉桥箱梁单元划分通常有3种类型:板壳单元、块体单元和梁单元[10].用梁单元模拟箱梁无法得到其纵向应力沿横截面的分布;用块体单元模拟主梁进行分析会导致有限元模型求解规模过大;使用板壳单元建模相对简单,修改较为方便,而且求解规模适中.因此,本研究采用板壳单元(She ll 63)模拟箱24 长沙交通学院学报第24卷梁的顶板、底板、斜腹板和横隔板.此外,用杆单元(L i n k10)模拟斜拉索,用弹性梁单元(B ea m 44)模拟桥塔和基础;用杆单元(L i n k8)模拟预应力筋;用刚臂单元模拟斜拉索与主梁、主塔的连接.为了提高计算效率,本研究用约束模拟了边墩和辅助墩对箱梁的支承作用.在建宁大桥斜拉桥成桥状态计算模型中,箱梁共划分了32923个Shell 63单元,主塔和基础划分794个Bea m44单元,斜拉索采用L i n k10单元,共计124个,预应力筋划分了12026个L i n k8单元.其空间有限元模型如图3所示.图3 株洲建宁大桥斜拉桥空间有限元模型1.3 结构荷载的模拟和索力的确定在成桥状态下,斜拉桥承受恒载主要有结构自重和桥面铺装及附属设施重量等.有限元计算时,结构自重以体积力形式加以考虑;桥面铺装和附属设施等重量以面力的形式均布施加在主梁顶板单元.斜拉索成桥索力值取自用平面杆系有限元分析程序BR-C AL V 1.0进行的施工控制仿真计算结果[11].2 顶板、底板和斜腹板厚度的影响2.1 顶板厚度的影响为了考查斜拉桥箱形主梁顶板厚度变化对剪力滞效应的影响,分别建立顶板厚度为16,20,22(设计值),24和28c m 5种尺寸(其他结构尺寸均取设计值)的全桥有限元模型.对5种有限元模型的应力结果分别进行分析整理,由于篇幅所限,选择了有代表性的主跨L /2和主跨靠近主塔根部箱梁(均为标准断面)截面,分别绘制其顶板和底板纵向应力沿横截面分布曲线见图4,5(由于对称性只绘制了1/2箱梁断面分布曲线,均以y 轴为箱梁中心线;图中应力值为负表示为压应力).由图4,5可以看出,两个箱梁截面顶板的应力分布曲线走向有一定的差别,顶板厚度改变对顶板剪力滞效应有较大影响;顶板厚度改变对箱梁不同位置截面顶板剪力滞效应的影响程度不同;和顶板相比,顶板厚度改变对箱梁底板剪力滞效应影响不大,5条应力曲线走向基本重合.主塔根部箱梁截面顶板剪力滞效应引成的应力不均匀程度较大,剪力滞效应显著;而且主塔根部箱梁截面翼缘板端部的应力较截面的其他位置顶板应力大的现象应引起重视(见图5(a)).图4 不同顶板厚度主跨L /2箱梁截面顶板和底板纵向应力沿横截面分布曲线25 第2期张玉平,等:顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响图5 不同顶板厚度主跨主塔根部箱梁截面顶板和底板纵向应力沿横截面分布曲线2.2 底板厚度的影响分别建立底板厚度为24,28,30(设计值),32和36c m 5种尺寸的全桥有限元模型,考查斜拉桥箱形主梁底板厚度变化对剪力滞效应的影响.对5种有限元模型的应力结果分别进行分析整理,选择有代表性的主跨靠近主塔根部箱梁截面和主跨靠近L /2的无横梁箱梁截面,分别绘制其顶板和底板纵向应力沿横截面分布曲线见图6,7.通过对图6,7比较分析可以得出结论:底板厚度变化对箱梁不同截面顶板和底板剪力滞效应的影响程度不同,在所选择的两个截面中,对主跨主塔根部箱梁截面顶板和底板的应力分布影响较大.底板厚度变化对顶板剪力滞效应的影响大于对底板剪力滞效应的影响,底板厚度由24c m 变为36c m 时,顶板剪力滞系数(可通过图中所示的应力值计算出来)最大变化量达到0.086(在主跨L /2截面顶板),底板剪力滞系数最大变化量达到0.024(主跨主塔根部).在5种有限元模型中,底板厚度增加,底板剪力26 长沙交通学院学报第24卷滞效应趋于均匀(即纵向应力分布曲线趋于缓和),顶板剪力滞效应趋于不均匀(即纵向应力分布曲线变陡).2.3 斜腹板厚度的影响分别建立斜腹板厚度为16,20,22(设计值),24和28c m 5种尺寸的全桥有限元模型,考查斜拉桥箱形主梁斜腹板厚度变化对剪力滞效应的影响.对5种有限元模型的应力结果分别进行分析整理,选择有代表性的主跨L /2箱梁截面和主跨L /4箱梁截面,分别绘制其顶板和底板纵向应力沿横截面分布曲线(见图8,9).由图8,9可以看出:斜腹板厚度变化对不同截面顶板和底板的剪力滞效应影响程度不同,在所选择的两个代表性截面中,斜腹板厚度变化对主跨主塔根部箱梁截面顶板和底板的应力分布影响较大;但共同之处是:斜腹板厚度增加,箱梁顶板和底板的剪力滞效应均趋于不均匀;斜腹板厚度变化对顶板剪力滞效应影响大于对底板剪力滞效应影响,斜腹板厚度由16c m 变为28c m 时,顶板剪力滞系数最大变化值达到0.186(主跨L /2箱梁截面),底板剪力滞系数最大变化值达到0.043(主跨主塔根部箱梁截面).3 结论应用ANSYS 软件,本研究建立了株洲建宁大桥斜拉桥成桥状态的多种有限元计算模型,对斜拉桥单箱三室主梁主要结构尺寸(顶板、底板和斜腹板厚度在一定量值范围的变化)对箱梁剪力滞效应的影响进行了参数分析.得到了一些初步结论,可供同类型的桥梁设计和施工参考.1)在斜拉桥单箱三室主梁中,顶板、底板和斜腹板厚度改变对箱梁顶板剪力滞效应影响较大,对底27 第2期张玉平,等:顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响28长沙交通学院学报第24卷板剪力滞效应影响不大.2)在斜拉桥单箱三室主梁中,底板厚度增加,底板剪力滞效应趋于均匀,顶板剪力滞效应趋于不均匀;斜腹板厚度增加,箱梁顶板和底板的剪力滞效应均趋于不均匀.3)在斜拉桥单箱三室主梁中,顶板、底板和斜腹板厚度三者变化相比较,斜腹板厚度变化对顶板和底板剪力滞效应的影响较为显著;顶板、底板和斜腹板厚度变化对不同位置箱梁截面的纵向应力沿横截面分布的影响不同,其中,主塔根部附近主梁截面应力分布变化幅度最为明显;此外,主塔根部箱梁截面翼缘板端部的应力较截面上其他位置顶板应力大的现象(负剪力滞现象)也应引起重视.4)如果只考虑箱梁剪力滞效应的影响,可以对箱梁顶板、底板和斜腹板厚度进行适当优化(比如:厚度减薄2c m),但是控制箱梁顶板、底板和斜腹板厚度的主要因素还有预应力筋布置、桥面板受力和施工临时荷载等诸多因素,因此,须综合考虑.参考文献:[1]张士铎,邓小华,王文州.箱形薄壁梁剪力滞效应[M].北京:人民交通出版社,1998.[2]罗旗帜.基于能量原理的薄壁箱梁剪力滞理论与试验研究[D].长沙:湖南大学,2005.[3]曹国辉,方志,周先雁,等.影响薄壁箱梁剪力滞系数的几何参数分析[J].中外公路,2003,23(1):39-41.[4]文国华,程翔云.横向预应力对箱梁正应力的影响[J].公路,1997(11):34-36.[5]陈菁菁,姚永丁,陶舍辉,等.三跨变截面预应力混凝土双箱双室并联连续箱梁桥的空间受力分析研究[J].公路交通科技,2003,20(5):36-39.[6]罗旗帜,娄亦红,杜嘉斌,等.变高度连续曲线箱梁的剪力滞效应[J].铁道学报,2007,10(5):79-84.[7]杨霞林.斜拉桥双箱单室箱形主梁的空间应力分析[D].成都:西南交通大学,2002.[8]杨霞林,周洁华.斜拉桥主梁底板厚度的参数分析[J].兰州铁道学院学报(自然科学版),2003,22(6):84-87.[9]万臻,李乔.现代斜拉桥不同截面形式的剪力滞效应分析[J].公路交通科技,2007,24(2):61-64.[10]龚曙光,谢桂兰.Ansy s操作命令与参数化编程[M].北京:机械工业出版社,2004.[11]李传习,夏桂云.大跨度桥梁结构计算理论[M].北京:人民交通出版社,2002.(上接第15页)通过螺旋群桩基础沉降实测值与计算值的对比,本研究所提出的沉降计算值较等代墩式基础沉降法计算值更接近于群桩基础的沉降实测值,说明建立在M indlin应力解基础上的桩端压力相互影响极限深度判定条件较好地反映了桩端地基沿深度方向的应力叠加问题,所建议的沉降计算方法对螺旋桩基础沉降计算有一定的指导意义.参考文献:[1]Lee I K,W h ite W,Ing les O G.岩土工程[M].俞调梅,叶书麟译.北京:中国建筑工业出版社,1986.[2]G eddes J D.Stress i n f oundati on so ils due to verti ca l subsurface l oad[J].G eotechn i que,1966,16:231-255.[3]刘金砺.桩基础设计与计算[M].北京:中国建筑工业出版社,1990.[4]赵明华,邹丹,邹新军.群桩沉降计算的荷载传递法[J].工程力学,2006,23(7):119-123.[5]O ttav i an iM.T hree di m ensi onal fi n ite ele m en t analysis of vertica ll y l oaded p ile g roups[J].G eotechn i que,1975,25(2):159-174.[6]陈云敏,陈仁朋,凌道盛.考虑相互作用的桩筏基础简化分析法[J].岩土工程学报,2001,23(6):686-691.[7]孙晓立,杨敏.大规模桩筏基础非线性共同作用简化分析方法[J].土木工程学报,2006,39(9):91-97.[8]B A弗洛林.土力学原理(第一卷)[M].同济大学土力学及地基基础教研室译.北京:中国工业出版社,1965.[9]辽宁省电力勘测设计院.螺旋锚基础试验研究[R].沈阳:辽宁电力勘测设计院,2002.[10]GB50007-2002,建筑地基基础设计规范[S].[11]J G J-94-94,建筑桩基技术规范[S].[12]DB21-907-96,建筑地基基础技术规范[S].。

预应力混凝土斜拉桥考虑剪力滞效应的主梁应力监控

预应力混凝土斜拉桥考虑剪力滞效应的主梁应力监控武志军【摘要】During construction control for long span pre-stressed concrete bridge, stress monitoring on the main gird is the main method to ensure the construction security and the consistency between the finished bridge's stress and the design stress. The theoretical stress of the main girder can better accord with the actual stress by considering the shear lag effects. The finite element theory considering two shear lag freedom degrees per joints was applied during construction control in a cable-stayed bridge. Practice proves that the result based on this theory can be better accordance with the actual result. Carrying out the research on the shear lag effects not only can enrich the shear lag theory application but also can perform more accurately the monitoring and controlling for the main gird of the bridge during long span pre-stressed concrete bridge construction.%大跨度预应力混凝土桥梁在施工过程中,对主梁的应力进行监测,是确保主梁施工安全及成桥应力与设计一致的主要方法.在主梁应力监测过程中,考虑剪力滞效应,则主梁的实测应力与理论应力更为合理.采用每节点两剪力滞自由度的剪力滞有限元理论,考虑剪力滞效应,在某预应力混凝土斜拉桥主梁的施工监控中,对主梁混凝土的应力进行了监测与控制.研究结果表明,基于每节点两自由的剪力滞有限梁段理论而得出的理论应力与实际应力较为符合.在大跨度预应力混凝土桥梁的施工过程中开展剪力滞效应研究,既丰富了剪力滞效应的研究内容,且较为准确地对主梁应力进行监测与控制.【期刊名称】《铁道标准设计》【年(卷),期】2012(000)009【总页数】4页(P73-76)【关键词】预应力混凝土;斜拉桥;施工控制;剪力滞效应;应力监测【作者】武志军【作者单位】中铁十局集团有限公司,济南250000【正文语种】中文【中图分类】U448.271 概述大跨度桥梁的建造,为保证施工质量和安全,使桥梁的线形与内力达到设计的理想状态,对整个施工过程进行监控,是不可缺少的措施之一。

箱梁的剪力滞效应分析

箱梁的剪力滞效应分析文章类型：论述文剪力滞效应是指箱梁在承受剪力作用时，剪切力和剪切变形之间的关系出现滞后现象。

这种现象对箱梁的承载能力和正常使用有着重要影响。

本文将介绍箱梁剪力滞效应的基本概念和分析方法，并探讨如何采取有效的措施应对剪力滞效应的影响。

一、箱梁剪力滞效应概述箱梁是一种常见的桥梁结构形式，具有结构强度高、刚度大等特点，被广泛应用于公路、铁路、城市轨道交通等领域。

箱梁在承受剪力作用时，剪切力和剪切变形之间的关系通常应该是线性的，但在某些情况下，剪切力与剪切变形之间的关系会出现滞后现象，即所谓的剪力滞效应。

剪力滞效应会对箱梁的结构性能产生不利影响，降低桥梁的承载能力和使用性能。

当剪力滞效应较严重时，可能导致桥梁出现裂缝、变形过大等现象，影响行车安全和桥梁寿命。

因此，对箱梁剪力滞效应进行分析和研究，采取有效的应对措施，具有重要意义。

二、箱梁剪力滞效应分析方法1、有限元法有限元法是一种常用的结构分析方法，通过将结构离散成多个小的单元，利用数学方法近似求解结构整体的力学行为。

对于箱梁的剪力滞效应分析，可以采用有限元法进行数值模拟，通过调整箱梁的几何尺寸、材料参数等因素，模拟剪力滞效应的产生和变化规律。

2、解析法解析法是通过理论建模和推导，得出结构的力学响应的解析解。

对于箱梁的剪力滞效应分析，可以采用解析法建立简化的力学模型，从而得到剪力滞效应的近似解。

解析法具有计算速度快、成本低等优点，但精度较有限元法低。

三、箱梁剪力滞效应应对措施1、优化结构设计通过优化箱梁的结构设计，可以降低剪力滞效应的影响。

例如，可以合理布置箱梁的横隔板和竖向肋板，增加结构的整体性和抗扭刚度；同时，可以通过选用高强度材料，提高结构的强度和稳定性。

2、增加配筋率增加箱梁的配筋率可以增强结构的抗剪能力，降低剪力滞效应引起的变形和裂缝等问题。

同时，合理的配筋设计还可以提高箱梁的承载能力和使用寿命。

3、采用新型材料采用新型材料如高性能混凝土、纤维增强混凝土等，可以提高箱梁的抗剪性能和耐久性，降低剪力滞效应的影响。

个人整理-同济大学高等桥梁结构知识点

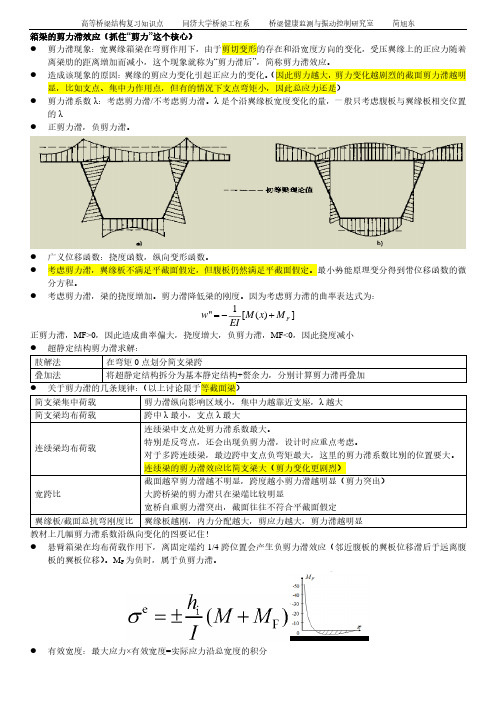
箱梁的剪力滞效应（抓住“剪力”这个核心）● 剪力滞现象：宽翼缘箱梁在弯剪作用下，由于剪切变形的存在和沿宽度方向的变化，受压翼缘上的正应力随着离梁肋的距离增加而减小，这个现象就称为“剪力滞后”，简称剪力滞效应。

● 造成该现象的原因：翼缘的剪应力变化引起正应力的变化。

（因此剪力越大，剪力变化越剧烈的截面剪力滞越明显，比如支点、集中力作用点，但有的情况下支点弯矩小，因此总应力还是）● 剪力滞系数λ：考虑剪力滞/不考虑剪力滞。

λ是个沿翼缘板宽度变化的量，一般只考虑腹板与翼缘板相交位置的λ● 正剪力滞，负剪力滞。

● 广义位移函数：挠度函数，纵向变形函数。

● 考虑剪力滞，翼缘板不满足平截面假定，但腹板仍然满足平截面假定。

最小势能原理变分得到带位移函数的微分方程。

● 考虑剪力滞，梁的挠度增加。

剪力滞降低梁的刚度。

因为考虑剪力滞的曲率表达式为：1''[()]F w M x M EI=-+ 正剪力滞，MF>0，因此造成曲率偏大，挠度增大，负剪力滞，MF<0，因此挠度减小● 悬臂箱梁在均布荷载作用下，离固定端约1/4跨位置会产生负剪力滞效应（邻近腹板的翼板位移滞后于远离腹板的翼板位移）。

M F 为负时，属于负剪力滞。

● 有效宽度：最大应力×有效宽度=实际应力沿总宽度的积分●规范规定，结构整体分析采用全截面，截面应力验算，采用有效宽度。

●承受纯弯曲荷载的箱梁截面，是否也存在剪力滞现象？材料进入塑性状态后，箱梁截面剪力滞将如何变化？●本节主要介绍剪弯状态下剪力滞问题，如果是压弯状态下（如预应力筋直线布置）截面是否存在剪力滞现象?箱梁的扭转效应（抓住关键：扭转=偏载×偏心距）●自由扭转：纵向不受约束，不产生纵向正应力。

公式推导：（闭口截面抗扭性能强的原因：剪力流的力臂大）q=τk t●自由扭转剪切变形：（综合考虑纵向变形和扭转角变形）●自由扭转惯矩：与截面包围面积、壁厚有关。

箱梁的结构与受力特点

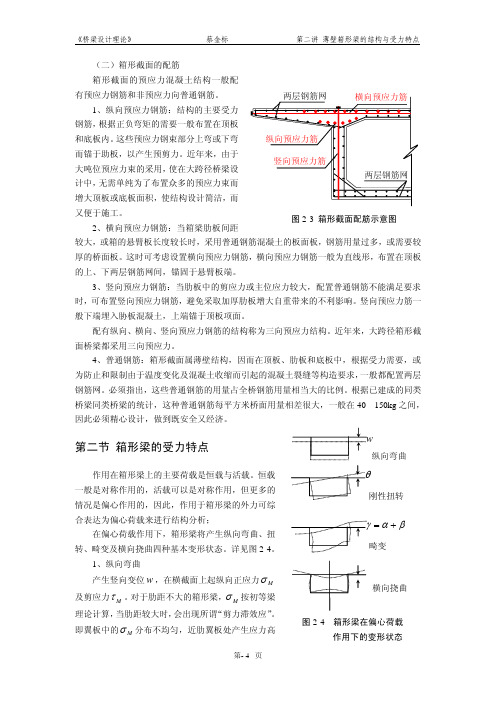
（二）箱形截面的配筋箱形截面的预应力混凝土结构一般配有预应力钢筋和非预应力向普通钢筋。

1、纵向预应力钢筋：结构的主要受力钢筋，根据正负弯矩的需要一般布置在顶板和底板内。

这些预应力钢束部分上弯或下弯而锚于助板，以产生预剪力。

近年来，由于大吨位预应力束的采用，使在大跨径桥梁设计中，无需单纯为了布置众多的预应力束而增大顶板或底板面积，使结构设计简洁，而又便于施工。

2、横向预应力钢筋：当箱梁肋板间距厚的桥面板。

的上、下两层钢筋网间，锚固于悬臂板端。

3时，可布置竖向预应力钢筋，面桥梁都采用三向预应力。

4钢筋网。

必须指出，因此必须精心设计，做到既安全又经济。

第二节箱形梁的受力特点作用在箱形梁上的主要荷载是恒载与活载。

恒载一般是对称作用的，活载可以是对称作用，但更多的情况是偏心作用的，因此，作用于箱形梁的外力可综合表达为偏心荷载来进行结构分析；在偏心荷载作用下，箱形梁将产生纵向弯曲、扭转、畸变及横向挠曲四种基本变形状态。

详见图2-4。

1、纵向弯曲产生竖向变位w ，在横截面上起纵向正应力Mσ及剪应力M τ。

对于肋距不大的箱形梁，M σ按初等梁理论计算，当肋距较大时，会出现所谓“剪力滞效应”。

即翼板中的M σ分布不均匀，近肋翼板处产生应力高βα+= 刚性扭转横向挠曲图2-4 箱形梁在偏心荷载作用下的变形状态峰，而远肋翼板处则产生应力低谷，这称为“正剪力滞”；反之，如果近肋翼板处产生应力低谷，而远肋翼板处则产生应力高峰，则为“负剪力滞”。

对于肋距较大的宽箱梁，这种应力高峰可达相当大比例，必须引起重视。

2、刚性扭转刚性扭转即受扭时箱形的周边不变形。

扭转产生扭转角θ。

分自由扭转与约束扭转。

（1）自由扭转：箱形梁受扭时，截面各纤维的纵向变形是自由的，杆件端面虽出现凹凸，但纵向纵维无伸长缩短，能自由翘曲，因而不产生纵向正应力，只产生自由扭转剪应力K τ。

（2）约束扭转：受扭时纵向纤维变形不自由，受到拉伸或压缩，截面不能自由翘曲。

叠合梁斜拉桥混凝土桥面板湿接缝浇筑工序研究

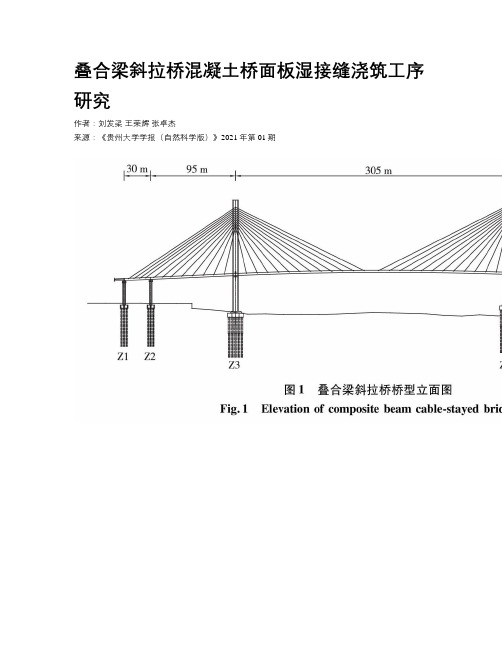
叠合梁斜拉桥混凝土桥面板湿接缝浇筑工序研究作者：刘发梁王荣辉张卓杰来源：《贵州大学学报（自然科学版）》2021年第01期摘要：叠合梁斜拉桥的施工工序繁多，施工过程会影响最终的成桥状态。

以洛溪大桥为背景，在保证施工和成桥运营阶段结构受力安全的前提下，利用Midas civil有限元软件对该桥建立模型进行计算分析，开展桥面板滞后浇筑湿接缝和双节段循环施工对主桥结构受力影响的研究。

研究表明，双节段循环施工每个标准节段至少可以节省3.5 d，并且主梁内力在几个不同方案当中处于最优状态，可以满足现场的实际需要，结构内力也可得到保障，并且施工周期也可以得到大幅度缩短。

关键词：叠合梁;斜拉桥;施工工序中图分类号：U448.27文献标志码：A叠合梁斜拉桥的施工内容多，施工工序繁杂，施工工序对最终的成桥的线型及内力密切相关。

不同的施工工序决定了主梁的内力分配，若施工考虑不充分，则可能会导致桥面板在施工或运营中开裂现象的发生，影响结构的安全耐久性。

所以确保结构安全、保证施工及成桥合理状态、保证工期合理的前提下，如何确定主梁的最优施工工序是确保叠合梁斜拉桥质量的关键。

由于计算机技术的快速发展、超静定结构分析理论以及斜拉桥结构本身具有跨越能力大、结构性能好、外形美观、造价相对便宜等优点，拉桥得到了迅速发展[1-2]，国外学者MACORINI[3]等针对组合梁桥面板方法进行了研究，国内学者朱力等[4]对组合梁桥剪力滞效应进行了研究，伍彦斌等[5]对叠合梁斜拉桥的主梁钢混结合段传力机理进行了研究。

张健[6]针对叠合梁斜拉桥桥面板湿接缝浇筑时间的合理性和双节段循环施工可行性进行了研究。

祝海燕、易云焜[7-8]等对叠合梁斜拉桥的主梁的施工工序进行了详细的比选。

胡俊等[9]对桥面板滞后浇筑湿接缝的工序进行了研究。

王梓龙[10]对叠合梁斜拉桥滞后浇筑湿接缝的工序进行了解读分析。

洪丽娟等[11]对组合梁斜拉桥的主梁双节段循环安装施工技术进行了研究。

斜拉桥施工要点

1．拉索的模拟 2．截面的处理和应力计算 3．预应力钢束的处理 4. 温度次内力计算 5. 徐变次内力计算
第三章斜拉桥的计算
1．拉索的模拟只需将单元抗弯惯矩取小。如果需考虑索单元的非线性，在计算中采用Ernst公式计入缆索垂度的影响。
2．截面的处理和应力计算对于箱形主梁，程序将各种不同的构件截面等效为工字型截面。主梁剪力滞后效应较明显，计算应力时应该考虑截面面积和惯性矩的折减；采用全截面计算应力是偏于不安全。
P A E A E A L / L E A T L / L E A T
第三章斜拉桥的计算
4. 温度次内力计算温度效应可归结为两种情况：年温差；日照温差 1）年温差：计算时以合龙温度为起点，考虑年最高气温和最低气温两种不利情况影响。 2）日照温差：主梁上、下缘，索塔左、右侧及拉索温度变化量均是不同的，一般情况下，索塔左右侧的日照温差均取±5℃，其间温度梯度按线性分布。拉索与主梁、索塔间的温差取±10℃～±15℃。
第三章斜拉桥的计算
斜拉桥静力分析分为三步： 1）确定成桥的理想状态，即确定成桥阶段的索力、主梁内力、位移和桥塔内力。 2）按照施工过程、方法和计算需要划分施工阶段。 3）确定施工阶段的理想状态，经过多次反复调试、计算，才可达到成桥阶段的理想状态。
第三章斜拉桥的计算
2．动力方面斜拉桥扭转和弯曲振型耦合在一起，动力分析时宜采用空间计算模型。地震频繁地区在初设阶段就考虑地震作用。
某大跨度斜拉桥离散后的结构计算模型
第六节斜拉桥的抗震分析
斜拉桥的动力分析主要包括抗震和抗风两方面。斜拉桥的动力特性分析是研究斜拉桥动力行为基础，其自振特性决定其动力反应特性。由于空间斜拉索的存在，对斜拉桥的动力分析必须采用三维空间模型。

本科生毕业设计（论文）原创性及知识产权声明[合集五篇]

本科生毕业设计（论文）原创性及知识产权声明[合集五篇]第一篇：本科生毕业设计(论文)原创性及知识产权声明北华航天工业学院本科生毕业设计（论文）原创性及知识产权声明本人郑重声明：所呈交的毕业设计（论文）是本人在指导教师的指导下，独立进行研究工作取得的成果。

除文中已经注明引用的内容外，本设计（论文）不含任何其他个人或集体已经发表或撰写过的作品或成果。

对本设计（论文）的研究做出重要贡献的个人和集体，均已在文中以明确方式标明。

因本毕业设计（论文）引起的法律结果完全由本人承担。

本毕业设计（论文）成果归北华航天工业学院所有。

本人遵循北华航天工业学院有关毕业设计（论文）的相关规定，提交毕业设计（论文）的印刷本和电子版本。

本人同意北华航天工业学院有权保存毕业设计（论文）的印刷本和电子版，并提供目录检索与阅览服务；可以采用影印、缩印、数字化或其它复制手段保存论文；在不以营利为目的的前提下，可以公布非涉密毕业设计（论文）的部分或全部内容。

特此声明毕业设计（论文）作者：指导教师：****年**月**日****年**月**日第二篇：论文原创性声明格式（精选）论文原创性声明←黑体，二号，居中本人以信誉声明：所呈交的毕业论文是在导师的指导下进行的设计（研究）工作及取得的成果，论文中引用他（她）人的文献、数据、图件、资料均已明确标注出，论文中的结论和结果为本人独立完成，不包含他人成果及为获得重庆科技学院或其它教育机构的学位或证书而使用其材料。

与我一同工作的同志对本设计（研究）所做的任何贡献均已在论文中作了明确的说明并表示了谢意。

↑宋体，四号毕业论文作者（签字）：签字日期：年月日第三篇：论文原创性声明论文/设计/报告原创性声明本人郑重声明：所呈交的论文/设计/报告时本人在导师的指导下独立进行研究所取得的研究成果。

除了论文/设计/报告中特别加以标注引用的内容外，本论文/设计/报告不包含任何其他个人或集体已经发表或撰写的成果作品。

薄壁箱梁剪力滞效应研究

西南交通大学硕士学位论文薄壁箱梁剪力滞效应研究姓名：王子健申请学位级别：硕士专业：桥梁与隧道工程指导教师：强士中20040201西南交通大学硕士学位论文摘要剪力滞（应力分散）问题很早就有学者对其进行研究，最初是在航空工程上，后来应用到土建工程当中，经过２０多年的发展，对剪力滞的研究也取得了一些成果，解决了一些实际工程问题，但许多问题并没有得到完全的解决，随着我国交通事业的发展，有关剪力滞的新问题也在不断出现，需要进一步的研究，本文就剪力滞的问题进行了如下的一些工作：１．对于箱形截面主梁，本文考虑剪力滞效应的变形特点，根据箱梁纵向位移函数，采用基于能量变分法基础上的最小势能原理推导出系统的总势能表达式，然后通过变分法得到带有不同边界条件的一组微分方程，并写出轴向应力的解析表达式。

结合实际的算例研究了等截面简支梁的剪力滞效应。

采用截面当量法研究了变截面连续梁的剪力滞效应。

２．就悬臂梁的负剪力滞现象进行理论分析和推导，并结合实际算例来对悬臂梁负剪力滞现象进行参数分析。

３．阐述了宜宾中坝金沙江斜拉桥的模型试验，并结合该桥的模型试验数据，研究该斜拉桥的剪力滞效应。

通过本论文的工作，箱形截面梁桥的设计、分析提供更安全、合理的设计依据。

【关键词】剪力滞负剪力滞有限元最小势能原理能量变分法西南交通大学硕士学位论文１１ＡＢＳＴＲＣＴＳｈｅａｒｌａｇｐｈｅｎｏｍｅｎａｏｒｔｈｅｎｏｎｕｎｉｆｏｍｄｉｓｔｒｉｂｕｔｉｏｎｏｆｂｅｎｄｉｎｇｓｔｒｅｓｓａｃｒｏｓｓｗｉｄｅｆｌａｎｇｅｓｏｆｂｅａｍｃｒｏｓｓｓｅｃｔｉｏｎｈａｖｅ１０ｎｇｂｅｅｎｒｅｃｏｇｎｉｚｅｄａｎｄｓｔｕｄｉｅｄ。

ＦｉｒｓｔｓｔｕｄｉｅｓｗｅｒｅｗｉｔｈｓｔｉｆｆｅｎｂｅａｍｏｆＩｓｈａｐｅｉｎａｖｉａｔｉｏｎｅｎｇｉｎｅｅｒｉｎｇ．ｗｈｉｌｅ１ａｔｃｒｍａｉｎｌｙｃｏｎｃｅｒｎｅｄｃｏｎｃｅｒｎｅｄｗｉｔｈｃｉｖｉｌｅｎｇｉｎｅｅｒｉｎｇ．Ｓｏｍｅｒｅｓｅａｒｃｈｏｕｔｃｏｍｅｓａｂｏｕｔｓｈｅａｒｌａｇｐｒｏｂｌｅｍｓｗｅｒｅａａａｉｎｅｄａｎｄｐａｒｔｏｆｐｒｏｊｅｃｔｐｒｏｂｌｅｍｓｗｅｒｅｓｏｌｖｅｄｄ嘶ｎｇｔｈｅＰ．ｖｅｎｔｙｙｅａｒｓ．ｗ｛ｔｌｌｔｈｅｄｅｖｅｌｏｐｍｅｎｔｏｆｃｏｍｍｕｎｉｃａｔｉｏｎｔｈｅｒｅａｒｅｓｔｉｌｌｍａｎｙｐｒｏｂｌｅｍｓｗｈｉｃｈｎｅｅｄｆａｒｔｈｅｒｒｅｓｅａｒｃｈ．Ｉｎｔｈｉｓｄｉｓｓｅｒｔａｔｉｏｎ．ｓｈｅａｒｌａｇｅｆｆｅｅｔｉｓｓｔｕｄｉｅｄ．Ｔｈｅｍａｉｎｃｏｎｔｅｎｔｓａｒｅｔｈｅｆｏｌｌｏｗｉｎｇｓ．１．Ａｇｅｎｅｒａｌｐｏｔｅｎｔｉａｌｅｎｅｒｇｙｅｑｕａｔｉｏｎｉｓｄｅｒｉｖｅｄａｃｃｏｒｄｉｎｇｔｏｔｈｅｐｒｉｎｃｉｐｌｅｏｆｍｉｎｉｍｕｍｐｏｔｅｎｔｉａｌｅｎｅｒｇｙａｎｄａｓｅｔｏｆｄｉｆｆｅｒｅｎｔｉａｌｅｑｕａｔｉｏｎｓ、ｖｉｔｌｌｄｉｆｆｅｒｅｎｔｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎｓａｒｅｄｅｒｉｖｅｄａｃｃｏｒｄｉｎｇｔｏｖａｒｉａｔｉｏｎａｌｐｒｉｎｃｉｐｌｅｍｅｔｈｏｄｃｏｎｓｉｄｅｒｉｎｇｔｈｅｄｅｆｏｒｍｍｉｏｎｐｒｏｐｅｒｔｉｅｓａｎｄｌｏｎｇｉｔｕｄｉｎａｌｄｉｓｐｌａｃｅｍｅｎｔｆｕｎｃｔｉｏｎｓｏｆｃｏｎｓｔａｎｔｄｅｐｍｂｏｘｂｅａｍｗｉｌｌｂｅｓｔｕｄｉｅｄｗｉｔｈａｎｇｉｒｄｅｒｓ．Ｔｈｅｓｈｅａｒｌａｇｅｆｒｃｃｔｏｆｓｉｍｐｌｅｓｕｐｐｏｒｔｅｄｅｘａｍｐｌｅ．Ｔ１１ｅｍｅｔｈｏｄｏｆｓｕｂｓｔｉｔｕｔｅｖａｒｉａｂｌｅｉｓａｐｐｌｉｅｄｔｏｓｔｕｄｙｔｈｅｓｈｅａｒ１ａｇｅｆｆｅｃｔｏｆｃｏｎｔｉｎｕｏｕｓｂｏｘ２ｉｒｄｅｒｓｗｉｔｈｖａｒｉａｂｌｅｄｅｐｔｈ．２．Ｔｈｅｎｅｇａｔｉｖｅｓｈｅａｒｌａｇｅｆｆｅｃｔｏｆｔｈｅｃａｎｔｉｌｅｖｅｒａｎｄｃｏｎｔｉｎｕｏｕｓｇｉｒｄｅｒｓｉｓｓｔｕｄｉｅｄａｎｄｔｈｅｐａｒａｍｅｔｅｒｓｗｈｉｃｈｉｎｆｌｕｅｎｃｅｔｈｅｓｈｅａｒｌａｇｅｆｆｅｃｔｉｓａｎａｌｙｓｅｄ．３．ＣｏｍｂｉｎｉｎｇｗｉｔｈｔｈｅｅｘｐｅｒｉｍｅｎｔｏｆＹｉｂｉｎＺｈｏｎｇｂａＪｉｎｓｈａｊｉａｎｇｃａｂｌｅ・ｓｔａｙｅｄｂｒｉｄｇｅｃｏｎｃｒｅｔｅｍｏｄｅｌ，ｔｈｉｓｄｉｓｓｅｒｔａｔｉｏｎａｎａｌｙｓｅｓｔｈｅｓｈｅａｒｌａｇｅｆｆｅｃｔｏｆｔｈｅｃａｂｌｅ－ｓｔａｙｅｄｂｒｉｄｇｅ．Ｂｙｔｈｅｗｏｒｋｏｆｔｈｉｓｄｉｓｓｅｒｔａｔｉｏｎ，ｍｏｒｅｓａｆｅｒａｎｄｍｏｒｅｒｅａｓｏｎａｂｌｅｄｅｓｉｇｎａｎｄａｎａｌｙｓｉｓｍｅｔｈｏｄｆｏｒｂｏｘｇｅｒｄｅｒｈａｖｅｂｅｅｎｏｆｆｅｒｅｄ．［ｋｅｙｗｏｒｄｓ］ｓｈｅａｒｌａｇ，ｎｅｇａｔｉｖｅｓｈｅａｒｌａｇ，ｆｉｎｉｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄ，ｈｅｐｒｉｎｃｉｐｌｅｏｆｍｉｎｉｍｕｍｐｏｔｅｎｔｉａｌｅｎｅｒｇｙ，ｅｎｅｒｇｙｖａｒｉａｔｉｏｎａｌｐｒｉｎｃｉｐｌｅｍｅｔｈｏｄ．＋第１章绪论１．１选题背景随着交通事业的发展以及城市化速度的加快，桥梁在日益繁忙的公路和城市交通中显得越来越来重要。

考虑梗腋影响的箱形梁剪力滞效应分析

考虑梗腋影响的箱形梁剪力滞效应分析箱形梁的剪力滞效应是翼板产生纵向位移时，由于面内不均匀剪切变形引起弯曲正应力沿横向呈曲线分布的一种力学现象[1-3]。

在设计计算时，该效应引起的应力峰值应得到足够重视，否则将无法保证结构的抗裂性能，甚至引发安全事故。

为此，国内外学者基于能量变分法[4-12]开展了大量研究，这些研究工作主要体现在：改进的剪力滞翘曲位移模式分析[5-8]、剪力滞剪切效应的联合求解方法[9]、考虑剪切变形影响的翘曲位移修正模式研究[10]、基于弹性力学方法的翘曲位移函数合理形式探讨[11]、考虑翼板变厚度影响的剪力滞效应变分解析方法[12]等，但这些研究均未考虑箱形梁梗腋加劲的影响。

箱形梁设计时为改善截面的受力特性，在翼板和腹板的连接处均设有梗腋。

已有文献对考虑梗腋加劲影响的剪力滞效应分析很少。

文献[13]通过建立MIDAS模型，分析了梗腋对波形钢腹板预应力混凝土刚构桥剪力滞效应的影响。

文献[14-15]运用ANSYS有限元法分析了梗腋对直线和曲线箱形梁静力特性的影响。

可见，梗腋对箱梁剪力滞效应的理论分析还较缺乏，需要进一步研究和完善。

本文在引入梗腋特性参数的基础上，选取剪力滞效应引起的挠度变化为广义位移，运用能量变分法建立考虑梗腋影响的剪力滞效应控制微分方程，导出集中和均布荷载作用下简支箱梁的剪力滞效应解析解。

基于某一预应力混凝土简支箱梁算例，进一步揭示梗腋及其参数变化对箱梁剪力滞效应的影响规律。

1 考虑梗腋的剪力滞控制微分方程如图1所示，考虑梗腋影响时箱形梁在任意竖向分布荷载q(z)作用下发生挠曲变形，其横截面上任一点的纵向位移u(x,y,z)表达为u(x,y,z)=u0(x,y,z)+uω(x,y,z)=( 1 )式中：为对应于附加挠曲转角f′(z)的剪力滞广义翘曲位移函数；η为与翘曲正应力有关的弯矩自平衡修正系数；ω为各翼板的基本翘曲位移函数；ω0为与翘曲正应力有关的轴力自平衡修正系数；u0为初等梁纵向位移；uω为翘曲纵向位移；为初等梁挠度；f为剪力滞引起的挠度变化。

斜拉桥面内竖向固有振动模型及特性影响的有限差分分析

第50 卷第 7 期2023年7 月Vol.50，No.7Jul. 2023湖南大学学报（自然科学版）Journal of Hunan University（Natural Sciences）斜拉桥面内竖向固有振动模型及特性影响的有限差分分析陈柯帆1，李源1，2†，贺拴海1，2，王康1，殷怡萍1，宋一凡1，2（1.长安大学公路学院，陕西西安 710064；2.旧桥检测与加固技术交通行业重点实验室（长安大学），陕西西安 710064）摘要：为研究精确且方便的斜拉桥面内竖向模态频率及振型计算方法，建立了用于模拟斜拉桥面内竖向固有振动行为的主梁集中质量参数体系动力学模型. 该模型考虑了拉索对主梁的竖向弹性支承作用及对主梁不同截面的水平索力投影，通过引入微梁段两侧剪力以模拟主梁弯曲刚度、拉索间运动耦合作用. 基于微梁段间的弯矩平衡和有限差分法，得到了不同体系斜拉桥面内竖向固有振动的频率方程和振型函数，编制了求解程序. 通过分别代入相关研究中算例参数、某斜拉桥参数并对比模态参数理论计算结果、实测频率值，验证了本文建模方法及公式的精确度、适用性. 参数分析结果表明：斜拉桥低阶面内竖向频率受主梁轴力影响较大，轴力增大后会发生低阶频率的跃迁现象；发生断索对各阶频率值的影响效应与拉索锚固处主梁质点的对应阶次振型参与系数相关.关键词：斜拉桥；固有振动；动力学模型；有限差分法；模态分析中图分类号：U441.3 文献标志码：AInfluence Analysis on In-plane Vertical Natural Vibration Model ofCable-stayed Bridges Based on Finite Difference MethodCHEN Kefan1，LI Yuan1，2†，HE Shuanhai1，2，WANG Kang1，YIN Yiping1，SONG Yifan1，2（1.School of Highway， Chang’an University， Xi’an 710064， China；2.Key Laboratory of Transport Industry of Bridge Detection & Reinforcement Technology （Chang’an University）， Xi’an 710064， China）Abstract：To propose a precise and convenient solution method for in-plane vertical modes of cable-stayed bridges， a new dynamic model comprised of lumped mass beam segments was established in this paper， which was used to simulate the in-plane vertical natural vibration behavior of cable-stayed bridges. In the model， the cables were reduced to vertical elastic supports and external forces on the girder in the horizontal direction. Additionally，the shear forces on both sides of the micro beam-segment were introduced to simulate the actions of the beam’s bending stiffness and the coupled interaction between the cables. Based on the moment equilibrium between the beam segments and the finite difference method， the solutions of the in-plane vertical modal frequencies and shapes∗收稿日期：2022-06-15基金项目：国家自然科学基金资助项目（51978062）， National Natural Science Foundation of China（51978062）；陕西省自然科学基础研究计划资助项目（2020JQ-377，2021JM-174，2022JQ-415），Natural Science Basic Research Program of Shaanxi Province（2020JQ-377，2021JM-174， 2022JQ-415）作者简介：陈柯帆（1995―），男，四川洪雅人，长安大学博士研究生† 通信联系人，E-mail：**************.cn文章编号：1674-2974（2023）07-0033-11DOI：10.16339/ki.hdxbzkb.2023077湖南大学学报（自然科学版）2023 年of cable-stayed bridges of different systems can be obtained. A computational solution program was also developed. The theoretical solutions were compared to field-test results from an actual bridge， confirming that the model and method proposed in this paper can accurately calculate the modal properties of in-plane vertical modes of cable-stayed bridges. The results through parametric analysis showed that the effect of the beam’s axial force was more significant on the low-order modal. The phenomenon of a transition on the low-order mode was observed when the axial force was increased to a high value. Moreover， when the cable is broken， the influence on each mode is related to the corresponding mode participation coefficient of the beam segment anchored with the cable.Key words：cable-stayed bridges；natural vibration；dynamic model；finite difference method；modal analysis斜拉桥美观、经济、跨越能力强，近年来备受桥梁工程师青睐［1］. 与此同时，斜拉桥整体结构复杂，柔度大、阻尼低、刚度不足导致其非线性行为极为突出［2］. 尤其当拉索局部模态与斜拉桥整体模态频率比处于“1∶2”或“1∶1”等固定比例区间时［3-6］，容易在环境激励下，引发拉索剧烈振动，给桥梁安全运营带来了极大隐患. 因此，除了目前仅有的有限元方法外［7-9］，如何建立准确的斜拉桥整体动力模型来便捷而又准确地计算斜拉桥竖向整体模态参数，对推动斜拉桥应用与发展至关重要［10］.近年来，国内外学者围绕斜拉桥整体动力学建模方法，尤其对于斜拉桥主梁在多点弹性支撑作用下的力学行为模拟与分析做了大量研究工作. 吴庆雄等［11］进行了单索-梁结构和二索-梁结构模型固有振动试验，建立了多索-梁结构动力学模型，讨论了斜拉索对索梁结构面内固有振动特性的影响；Cao 等［12］和李专干等［13］通过建立主梁的分段函数，将主梁和拉索等效为若干独立梁段，基于拉索锚固处的边界条件得到了刚塔柔梁斜拉桥整体动力学建模的运动方程，讨论了结构对称性对动力特性的影响；赵文忠等［14］通过分段函数求解了三索结构的动力方程，研究了拉索一阶和二阶频率比条件对共振的影响； Cong等［15］、Kang等［16-18］、苏潇阳等［19］建立了多梁弹簧动力学模型，运用传递矩阵法给出了不同体系下斜拉桥整体动力学模型动力学微分控制方程，提出了不同体系斜拉桥竖向刚度评估方法. 在此基础上，该课题组还对索拱结构［20-21］、悬索结构［22］的面内外固有振动模态参数进行了系统分析与研究.受限于现有动力学建模方法与整体模态参数计算过程的烦冗，目前关于斜拉桥整体竖向模态的理论计算方法大多高度简化甚至忽略索力水平投影、振动时拉索间的耦合影响作用、主梁弯曲刚度等因素对结构振动特性的影响，或是迭代解析方法烦琐、复杂，不利于在实际斜拉桥工程中推广与应用.针对此问题，本文通过离散斜拉桥多点弹性支承梁的集中质量参数体系，建立了一种新的斜拉桥面内竖向整体动力学模型. 该模型考虑了斜拉索对主梁的竖向弹性支承作用与对水平梁截面的轴力影响，引入微梁段两侧的剪力以模拟主梁弯曲刚度、拉索间振动耦合等影响作用，通过微梁段间的弯矩平衡和有限差分法，修正了不同结构体系斜拉桥面内竖向整体动力学模型的运动方程，结合特征值法给出了斜拉桥面内竖向模态频率及振型计算方法. 通过对比参考文献中动力学模型算法案例分析结果与某斜拉桥的实测值，进一步验证了本文关于斜拉桥面内竖向运动参数体系建模方法的适用性和正确性. 本文计算方法无须建立大量细化的有限元模型，运用MATLAB、Excel等软件按编码流程即可准确、快速地估算斜拉桥面内竖向模态频率及振型，简化了计算过程，便于工程应用.1 多点弹性支撑梁的离散模型约定下标“B”和“C”分别表示梁和索；下标“i”和“j”分别表示索和梁序号（i∈[1，I]，j∈[1，J]）. 为便于区别有索区梁段与无索区梁段，对于C i#拉索锚固处的有索区梁段表示为B j i#梁段. 建立如图1（a）所示的多索-主梁模型. 由于桥面质量远大于拉索质量，本文忽略了拉索振动对主梁振动的影响，将C i#拉索竖向视为B j i#梁段的弹性支承k BC i［7，10，23-24］，水平向的索力投影等效为B j i#梁段的轴向荷载H BC i，定义H e为支座水平力，如图1（b）所示. 为了精确模拟和34第 7 期陈柯帆等：斜拉桥面内竖向固有振动模型及特性影响的有限差分分析求解具有分布质量、荷载和多点弹性支撑作用下斜拉桥主梁的动力行为，不考虑主梁的纵向运动，本文将主梁进一步简化为J 个间距d 相同、彼此铰接、带有I 个竖向弹力支承和I 个不同轴力的集中质量参数体系，主梁的质量和荷载均被视为作用在这些集中质量点之上，独立梁段间彼此通过理想铰连接，如图1（c ）所示.图1（b ）中，C i #拉索对B j i #梁段竖向弹性支承系数k BC i 为［7，10，23-24］：k BC i =E C i A C i sin 2θC il C i.（1）式中：E C i 、A C i 分别为C i #拉索的弹性模量及截面积；θC i 表示C i #拉索轴线与主梁大里程方向夹角；l C i 表示 C i #拉索上下端锚固点轴向距离. 由于拉索振动中的索力增量远小于拉索初始索力，对于拉索索力的水平投影本文仅考虑初始索力［25-26］. 因此，主梁上水平轴力H BC i 和支座水平力H Be （下标e 表示边界）满足：H BC i =S C i cos θC i ，（2）H Be +∑i =1I S C i cos θC i =0.（3）式中：S C i 表示C i #拉索初始索力. 图1（c ）中，独立梁段彼此铰接，通过引入离散梁段的左右侧剪力以模拟具有分布质量的主梁竖向弯曲刚度、拉索间振动耦合作用在振动过程中的相互影响.梁段间的受力如图2（a ）所示，梁段处的受力如图2（b ）和（c ）所示.图2中，F B （j -1，j ）、F B （j ，j +1）表示梁段左右两侧的剪力；N B （j-1，j ）、N B （j ，j +1）表示梁段左右两侧的轴力；-M B j -1、-M B j 表示相邻梁段间的节段左右两侧受到的弯矩作用；γB ()j -1，j 、γB ()j ，j +1表示相邻梁段运动夹角； a B j 表示梁段运动加速度. 考虑系统初始为平衡状态，基于D ’Alembert 原理可以得到B j #梁段在竖向的动力平衡方程：-M B j V ..B j (t )-c B j V B j (t )-F B(j -1，j )cos γB(j -1，j )+F B(j ，j +1)cos γB(j ，j +1)-N B(j -1，j )sin γB(j -1，j )+N B(j ，j +1)sin γB(j ，j +1)-k BC i ⋅V B j ⋅δ(j -j i )-k T ⋅V B j ⋅δ(j -j T )=0.（4）式中：V B j （t ）表示B j #梁段与时间相关的竖向振动位移变化因子，后文中简写为V B j ；k T 表示斜拉桥主塔对主梁面内竖向自由运动的刚度弹簧系数，需依据图纸和规范，以及不同结构体系下塔-梁处的边界条件进行取值. δ(j -j i )为狄拉克（Dirac ）函数，由式（5）~式（6）定义：δ(j -j i )=0，j ≠j i ，（5）δ(j -j i )=1，j =j i .（6）值得注意的是，靠近边界的梁段需根据结构体（a ）斜拉桥主梁简化模型（b ）弹性支撑主梁简化模型（c ）斜拉桥主梁的集中质量参数体系图1 斜拉桥主梁离散模型的简化流程Fig.1 The reduction process of main beamof cable-stayed bridges（a ）微梁段间弯矩平衡（b ）B j #梁段振动形态（c ）t 1时刻B j #梁段受力示意图图2 微梁段受力示意图Fig.2 The force schematic of the micro-beam segment35湖南大学学报（自然科学版）2023 年系边界条件进行求解运算，如附表1所示.2 数学表达与验证2.1 基于有限差分法的方程优化假设质量体系分布较密，梁段间相对位移较小，则其振动的几何关系满足以下关系式：cos γB(j -1，j )≈1，（7）sin γB(j -1，j )≈γB(j -1，j )，（8）γB(j -1，j )≈tan γB(j -1，j )=V B j -V B j -1d.（9）参考弹性力学基本知识，B j #梁段处竖向位移w B j的二阶微分——曲率(1ρ)B j可近似用二阶中心差分表示［27］：(1ρ)B j=(d 2w B j d x 2)B j≈éëêêêê()V B j +1-V B j d -()VB j-V B j -1dùûúúúú/d .（10）因此，B j #梁段处弯矩表达式为：MˉB j =-E B j I B j (1ρ)B j≈-E B j I B jd 2(V B j -1-2V B j +V B j +1).（11）图2（a ）中，显然梁段间存在剪力与弯矩平衡：M ˉB j -1+F B(j -1，j )⋅d =M ˉB j .（12）由上式可得梁段间剪力、弯矩与振动位移间关系：F B(j -1，j )=MˉB j -M ˉB j -1d .（13）对于无索区梁段（即j ≠j i ），左右侧截面受到同一方向常轴力影响，可以得到：N B(j -1，j )=-N B(j ，j +1).（14）对于有索区梁段（即j =j i ），左右侧截面轴力突变量为拉力的水平投影：N B(ji-1，j i )=∑i =1I -1S C i ， N B(j i，j i+1)=∑i =1IS C i .（15）整合式（7）~式（15）并代入式（4）后，可以得到B j #梁段的振动方程：M B j V B j (t )+c B j V B j (t )-E B j -1I B j -1d 3(-V B j -2+2V B j -1-V B j )+E B j I B jd 3(-2V B j -1+4V B j -2V B j +1)-E B j +1I B j +1d 3(-V B j +2V B j +1-V B j +1)-∑i =1I -1H BC i ⋅2V B j -V B j +1-V B j -1d -(H BC i ⋅V B j i-V B ji+1d-k BC i V B j i)⋅δ(j -j i )+k T V B j i⋅δ(j -j T )=0.（16）整合B1#~B J #梁段方程后可以得到斜拉桥面内竖向固有振动方程：V B j +ψB j ⋅V B j +1M B j d 3⋅Γ⋅V B j +1M B j d⋅Ξ⋅V B j =0.（17）式中：Γ为等效剪力效应系数矩阵，表征了剪力效应对主梁运动的影响，与斜拉桥边界条件有关；Ξ为等效轴力效应系数矩阵，表征了轴力效应对主梁运动的影响，与拉索数量和锚固位置有关，矩阵具体形式如附录1所示；V B j 、V B j 皆为相同形式的J 维列向量. 为避免赘述，在此仅展示V B j 形式：V B j ={V B1，V B2，⋯，V B j ，⋯，V B J }T.（18）ψB j 为形式相同的J 阶系数对角矩阵：ψB j =éëêêêêêêêêêêùûúúúúúúúúúúψB1ψB2⋱ψB j⋱ψB J -1ψB J ，（19）ψB j =κD j +κC i +κS j +κT ，（20）κD j =-∑i =1I -12H BC i M B j d -HBC i M B j d ⋅δ(j -j i )，（21）κC i =k BC iM B j⋅δ(j -j i ).（22）κS j =ìíîïïïïïï()E B j -1I B j -1+λj E B j I B j +E B j +1I B j +1/M B j d 3，1<j <J ；()λj E B j I B j +E B j +1I B j +1/M B j d 3，j =1；()E B j -1I B j -1+λj E B j I B j /M B j d 3，j =J .（23）36第 7 期陈柯帆等：斜拉桥面内竖向固有振动模型及特性影响的有限差分分析κT=k T M B j⋅δ(j-j T).（24）式（20）中：ψB j单位与频率一致，是B j#梁段的局部模态频率方程，表征了B j#梁段参与整体模态的模态频率，由κD j、κC i、κS j、κT构成. κD j表示索力水平投影，即主梁轴力对B j#梁段局部模态频率的影响；κC i表示拉索竖向弹性支承作用的影响；κS j表示主梁轴力的影响，系数λj与斜拉桥边界条件有关，具体形式如附表1所示；κT表征了不同结构体系主塔的影响.2.2 基于特征值法的结构模态分析参数体系的自由振动方程组——式（17）实际上是一个J维的齐次方程组，方程有解的前提是系数矩阵行列式为0. 因此，不计结构阻尼，根据式（17）构造结构特征矩阵形式如下：M B j⋅V B j+K B j⋅V B j=0.（25）式中：M B j表示质量对角矩阵；K B j表示主梁的等效刚度矩阵. 根据简谐振动理论，构造频率表达式：Δ=K B j-ωV2⋅M B j= (Γ+Ξ+κC i+κT)-ωV2⋅M B j.（26）式中：Γ、Ξ分别为主梁轴力及剪力的等效系数矩阵，其具体形式如附录2所示. 特征方程式（25）的齐次解是斜拉桥面内固有振动频率ωV的函数，将满足各阶方程的频率值代入式（26）可以解得J个一维向量ϕV，对应即为该阶竖向振型下各个梁段对应的形状变化坐标，按序依次相连即为该阶斜拉桥面内竖向固有振型，由式（27）定义：[ϕV，ωV]=eig(ΚB j⋅ΜB j-1).（27）式中：eig表示求解矩阵特征值与特征向量. 采用以上计算公式和流程求解斜拉桥的面内竖向固有振动模态参数，在确定质量矩阵并根据相应结构边界条件选择和编辑相应轴力与剪力系数矩阵后，仅需借助MATLAB、Excel等工具就能简单地计算和求解固有振动频率和振型，无须进行大量细化的有限元建模分析. 本文依托MATLAB编制了运行算法程序，其流程如图3所示.2.3 参考文献算例验证以2020年Cong团队的双索-梁结构理论解析研究结果为对比对象［14，28］，该研究通过简化斜拉桥为多索-梁动力学模型，考虑结构构件间的几何非线性边界条件，基于传递矩阵法研究了多索斜拉结构的固有振动特性与面内外振动响应. 其研究模型如图4所示.本文代入了文献［14，28］参数，选取主梁划分节段参数d=1 m，即J=300，I=2，运用MATLAB软件根据图3计算流程编写计算程序，讨论和对比多索斜拉结构的面内固有振动频率及以主梁为主要振型的前五阶振动模态，如表1所示.图3 斜拉桥面内竖向固有振动模态参数计算流程Fig.3 The computation solution process of a cable-stayed bridge’s in-plane vertical natural vibration modal properties图4 文献［14，28］双索-梁结构示意图Fig.4 Schematic of a double-cable-beam structurein the references ［14，28］表1 两索-梁结构面内竖向固有振动频率Tab.1 In-pane vertical natural vibration frequencies of the two-cable-beam structure Hz数据来源文献［14，28］有限元解文献［14，28］解析解本文解析解（d=1）与文献有限元解误差/‰一阶（V1）0.136 00.135 50.136 00.00二阶（V2）0.230 70.230 70.230 80.43三阶（V3）0.434 90.435 40.435 00.23四阶（V4）0.784 00.784 80.783 90.13五阶（V5）1.214 71.216 21.214 40.2537湖南大学学报（自然科学版）2023 年根据表1，本文解析法得到的频率数值平均绝对误差仅为0.2‰，精确度超过了原文解析方法绝对误差1.4%.分别按照本文有限元数值模拟与解析法求解该结构以主梁为主的前五阶固有振型，如图5所示.图5显示两种方法得到的结构振型一致性良好，进一步验证了本文计算方法的有效性和准确性.3 斜拉桥固有振动特性及影响性分析3.1 斜拉桥模态分析以我国西北地区某混凝土斜拉桥为对象开展固有振动特性及其影响参数分析. 该桥全长166.8 m （39 m+88.8 m+39 m ），采用三跨双台、双塔、双索面对称布置，墩塔处固结，为半漂浮支承体系，其立面图如图6所示. 钢筋混凝土主梁由节段预制双箱梁和预制行车道板组合形成，箱梁高1.2 m ，桥面净宽8.5 m. 在两箱梁间锚固板处设横系梁一道，纵向长约0.22 m ，为方便引用，汇总主梁各截面参数设置如表2所示；全桥现有48根斜拉索，从小里程边跨至大里程边跨方向以C1#~C24#对单索面拉索依次编号，参数如表3所示（仅示出一侧，另一侧参数与之相近，斜拉索弹性模量经恩斯特公式修正后取200 GPa ）.根据桥梁结构形式，采用商业有限元软件对该桥进行动力特性分析，得到该结构前三阶自振频率、振型特征，如图7所示.为进一步对比和验证本文解析公式的正确性，采用实桥实测、有限元分析、本文解析三种方法对该桥3 9008 8803 90017 328全桥长1#墩2#墩图6 桥梁立面图（单位：cm ）Fig.6 Bridge elevation drawing （unit ： mm ）（ⅰ）ωV (1)（ⅱ） ωV (2)（ⅲ） ωV（ⅳ） ωV （ⅴ）ωV （a ）文献［14，28］有限元计算结果1d =10d =50d =（Ⅰ）ωV (1)=0.136 0 Hz1d =10d =50d =（Ⅱ） ωV (2)=0.230 8 Hz 1d =10d =50d =（Ⅲ） ωV(3)=0.435 0 Hz1d =10d =50d =（Ⅳ） ωV (4)=0.783 9 Hz 1d =10d =50d =（Ⅴ）ωV (5)=1.214 4 Hz （b ）本文解析结果图5 两索-梁结构的竖向振型Fig.5 Vertical modal shapes of the two cable-beam structure表2 主梁参数设置表Tab.2 Parameters of the beam截面位置边跨横系梁边跨主梁中跨横系梁中跨主梁弹性模量/GPa28.028.031.531.5惯性矩/m 40.411.150.321.09截面面积/m 22.408.751.928.2738第 7 期陈柯帆等：斜拉桥面内竖向固有振动模型及特性影响的有限差分分析进行自振特性分析. 设置参考算例参数详情如下所示：1#算例（Referred Case 1#， RC1），实体结构有限元法：根据实际桥梁结构形式，采用商业有限元软件对该桥进行动力特性分析，识别该结构自振频率、振型特征等.2#算例（Referred Case 2#， RC2），现场实测法：在桥梁边跨0.4L（L表示跨径）截面及中跨跨中截面布设加速度传感器，应用脉动激励法进行桥梁结构的振动试验，识别大桥前3阶整体模态的动力特性参数，采用DHSAS频谱分析及模态分析软件对其进行快速傅里叶变换得到相应的功率谱图，再对其作进一步的频谱分析可得到桥梁结构的自振频率、阻尼比. 现场动载试验布置如图8所示.3#算例（Referred Case 3#， RC3），简化模型解析法：根据本文动力简化模型及振动方程，塔梁连接处按照图纸取k T=5.3×109 N/m，大小里程结合墩采用简支边界条件，位于主梁同一截面的双索考虑为动力弹簧的并联关系，基于式（17）采取微梁段长度d1=0.1 m，运用MATLAB软件根据图3计算流程编写计算程序，对该结构的面内竖向模态频率和振型进行了计算和分析.汇总以上工况下得到的该桥以主梁面内竖向为主要振型的前三阶自振频率，如表4所示.表4中，若以实桥测得的模态参数为标准，有限元法得到的结果的绝对误差平均值为3.3%，而本文解析法得到的结果的绝对误差平均值为2.7%. 此外，相较于其他两种结果，实测频率值整体偏小，这是由于该桥建设时间较长，结构刚度在通行运营中有所下降. 汇总RC1和RC3工况下得到的该斜拉桥前三阶竖向固有振型，如图9所示.图9中两种工况下结构面内竖向前三阶振型一致性良好，上述情况进一步说明了本文方法计算斜表3 斜拉索参数设置表Tab.3 Parameters of stay cables编号LC1# LC2# LC3# LC4# LC5# LC6# LC7# LC8# LC9# LC10# LC11# LC12#索力/kN828.8756.5601.4532.4424.5416.7428.0452.5510.8614.2771.2794.5面积/m20.001 70.001 40.001 20.001 20.001 20.001 20.001 20.001 20.001 20.001 40.001 40.001 4索长/m44.8237.2931.1224.9118.6512.2912.1218.7525.3831.9938.5945.27编号LC13#LC14#LC15#LC16#LC17#LC18#LC19#LC20#LC21#LC22#LC23#LC24#索力/kN749.0749.0614.2490.1449.9409.2416.7444.7585.8616.0799.7743.7面积/m20.001 40.001 40.001 40.001 20.001 20.001 20.001 20.001 20.001 20.001 20.001 40.001 7索长/m45.2638.5931.9925.3818.7512.1112.2918.6524.9131.1237.2944.82（a）现场测试基频（b）进行动载试验图8 现场动载试验Fig.8 On-site dynamic load test表4 斜拉桥面内竖向固有振动频率Tab.4 In-plane vertical natural vibration frequenciesof the cable-stayed bridge Hz工况RC1RC2RC3一阶（V1）0.9030.8790.882二阶（V2）1.4411.5361.492三阶（V3）1.9731.9531.860（a）第一阶振型（f1=0.903 Hz ）（b）第二阶振型（f2=1.441 Hz ）（c）第三阶振型（f3=1.973 Hz）图7 有限元法得到的斜拉桥前三阶固有振动模态参数Fig.7 The first-three order natural modes of the cable-stayedbridge by the finite element model39湖南大学学报（自然科学版）2023 年拉桥面内竖向固有振动模态参数的精确性和适用性.3.2 梁轴力对斜拉桥竖向模态的影响为研究索力水平投影为梁提供的轴向力对斜拉桥面内竖向振动模态参数的影响，引入μa表示轴向力对B j#梁段动平衡方程的放大系数，由式（28）定义：K B=Γ+μa⋅Ξ+κC i+κT.（28）按照本文解析法研究成果，基于RC3参数设置，图10展示了轴力对斜拉桥固有振型的影响，图11展示了轴力对斜拉桥固有振动频率的影响.由图10可知轴力对结构振型影响不大. 图11引入k V（n）表示对应第n阶的斜拉桥面内竖向频率ωV(n)和μa的一阶线性拟合斜率，k V（n）值越大，表明频率受到轴力的影响越明显. 因此，由图11可得，轴力对结构面内竖向基频影响效应较弱，而后随着阶次增加，轴力影响效应递减.这进一步表明轴力对结构面内低阶频率变化影响较明显. 此外，梁轴向力的增加将进一步降低结构频率，表明轴向力增加将降低结构整体的等效刚度，这与文献［29］结论一致. 可见当轴力增大到一定程度时，结构整体刚度将降低至0，此时结构失稳. 为进一步研究这个问题，继续增大μa，汇总其与结构前五阶关系，如图12所示.图12显示，μa<28时，V1~V5随轴力增大而呈现线性缓慢下降. 当μa达到30左右时，V1发生频率跃迁现象，此时尽管V2频率数值低于V1，但V1的振型是结构的一阶振型. 当μa达到34.4时，V1~V3值产生共轭对称解，其频域信号值幅值相同而相位不同，图9 RC1、RC3工况下的斜拉桥前三阶面内竖向振型Fig.9 The first three order modes of cable-stayed bridgeunder the conditions of RC1 and RC3图10 轴力对斜拉桥竖向固有振型的影响Fig.10 Influence of the axial force on the vertical natural modesof the cable-stayed bridgew(n)/w(1)拟合系数(n)图11 梁轴力对斜拉桥面内竖向频率的影响Fig.11 Influence trends of the beam’s axial force on the in-plane vertical frequencies of the cable-stayed bridge图12 μa与结构前五阶频率关系Fig.12 Relation between the first-five order in-plane verticalfrequencies with μa40第 7 期陈柯帆等：斜拉桥面内竖向固有振动模型及特性影响的有限差分分析而V2在μa 接近38.7时急速下降为0，此时斜拉桥一阶固有振动频率为0，结构整体失稳. 表明从轴力角度考虑，该桥目前暂无整体失稳风险，只有当轴力达到现有轴力38倍以后会出现整体失稳现象. 此外，随着结构轴力的增大，结构基频将发生跃迁，结构体系内易产生非线性内共振，需进行更深入的研究.3.3 断索对斜拉桥面内竖向模态的影响从式（20）与式（22）中可发现，斜拉桥拉索为主梁提供了轴力与弹性支撑作用（k BC i ），为结构提供了有效刚度. 因此，结构的固有振动模态频率与每一根拉索息息相关. 以此实体结构为背景，模拟单拉索出现断裂的极端情况对结构固有振动频率及振型的影响，图13显示了该工况下低阶频率变化规律.拉索的索力水平投影对主梁产生的轴压力降低了整体刚度，而其竖向弹性支承作用则增大了整体刚度，两者作用下使得断索对结构基频影响较小，如图13所示. 此外，左右侧索面断索后影响效应变化规律基本一致，其中中跨拉索断裂对V1、V2和V5影响较大，而边跨拉索对V3和V4影响较大，对比图10中结构前五阶面内竖向振型，表明断索后的影响效应与该拉索对应的主梁质点的振型参与系数相关. 拉索发生损伤甚至断裂会改变结构整体频率，因此，当此情况发生时需进一步考虑结构因局部-整体模态耦合发生非线性共振的问题.4 结论1）本文方法考虑了主梁截面的变刚度、变轴力作用，建立的斜拉桥整体模态动力学模型更贴近工程实际结构. 通过代入已有文献中理论模型算例参数并对比其理论计算结果，本文方法计算结果平均误差率为0.2‰；代入某斜拉桥参数并对比其面内竖向固有振动频率实测值，本文方法计算结果误差率为2.7%，进一步说明本文解析方法具有较高的精确度和较好的适用性.2）斜拉桥低阶面内竖向固有振动频率随着轴力增加而降低，振型基本无变化，当轴力增加到一定值后，结构的低阶面内竖向整体模态频率将发生频率跃迁、分叉现象.3）斜拉桥发生断索对整体结构固有振动频率影响较小，断索对各阶频率值影响效应与拉索锚固处主梁的对应阶次振型参与系数相关.4）本文方法为快速计算斜拉桥整体模态频率以避免斜拉桥整体-局部模态耦合而发生非线性内共振问题提供了有效帮助. 下一步将考虑拉索、主塔与主梁间几何非线性边界条件，通过建立更加细化的斜拉桥整体动力学模型开展斜拉桥的相关非线性共振研究.参考文献［1］赵跃宇，蒋丽忠，王连华，等．索-梁组合结构的动力学建模理论及其内共振分析［J ］．土木工程学报，2004，37（3）：69-72．ZHAO Y Y ，JIANG L Z ，WANG L H ，et al ．The dynamical modelling theory and internal resonance of cable-beam composite structure ［J ］．China Civil Engineering Journal ，2004，37（3）：69-72．（in Chinese ）［2］吴庆雄，罗秋芳，王文平，等．振动松弛对斜索参数振动的影响分析［J ］．工程力学，2014，31（S1）：182-188．WU Q X ，LUO Q F ，WANG W P ，et al ．Influence analysis of vibration loosening on nonlinear parametric vibrations of inclined cables ［J ］．Engineering Mechanics ，2014，31（S1）：182-188．（inChinese ）［3］WEBER B. Nonlinear stay cable –bridge deck interaction ［C ］//Proceedings of International Conference on Experimental Vibration Analysis for Civil Engineering Structures. Cham ：Springer ， 2017.［4］孙测世．大跨度斜拉桥非线性振动试验研究［D ］．长沙：湖南大学，2015．SUN C S ．Experimental study of nonlinear vibrations of long-span cable-stayed bridge ［D ］．Changsha ：Hunan University ，2015．（in Chinese ）［5］CAETANO E. Cable vibrations in cable-stayed bridges ［M ］. Zurich ： IABSE ， 2007.［6］赵跃宇，王涛，康厚军，等．斜拉桥双索与桥面耦合的非线性参数振动特性分析［J ］．湖南大学学报（自然科学版），2008，35（10）：1-5．图13 不同位置的拉索断裂对结构V1～V5频率的影响Fig.13 Influence on the V1~V5-order modal frequencies whencables of different positions broke down41湖南大学学报（自然科学版）2023 年ZHAO Y Y，WANG T，KANG H J，et al．Performance study ofthe nonlinear parametric vibration of coupled bridge decks and twocables［J］．Journal of Hunan University （Natural Sciences），2008，35（10）：1-5．（in Chinese）［7］LOU P，ZENG Q Y．Formulation of equations of motion of finite element form for vehicle-track-bridge interaction system with twotypes of vehicle model［J］．International Journal for NumericalMethods in Engineering，2005，62（3）：435-474．［8］吴庆雄，王文平，陈宝春．索梁结构非线性振动有限元分析［J］．工程力学，2013，30（3）：347-354．WU Q X，WANG W P，CHEN B C．Finite element analysis fornonlinear vibration of cable-beam structure［J］．EngineeringMechanics，2013，30（3）：347-354．（in Chinese）［9］胡建华，王连华，赵跃宇．索结构几何非线性分析的悬链线索单元法［J］．湖南大学学报（自然科学版），2007，34（11）：29-32．HU J H，WANG L H，ZHAO Y Y．A catenary cable element forthe nonlinear analysis of cable structures［J］．Journal of HunanUniversity （Natural Sciences），2007，34（11）：29-32．（inChinese）［10］龚平，苏潇阳，蔡向阳，等．拉索对斜拉桥竖向频率的影响研究［J］．振动工程学报，2018，31（6）：957-965．GONG P，SU X Y，CAI X Y，et al．The influence of cables onvertical frequency of cable-stayed bridge［J］. Journal of VibrationEngineering，2018，31（6）：957-965．（in Chinese）［11］吴庆雄，王文平，陈宝春．多索-梁结构固有振动特性分析［J］．工程力学，2017，34（1）：109-116．WU Q X，WANG W P，CHEN B C．Natural vibration analysis ofmulti-cables-stayed beam structures［J］. Engineering Mechanics，2017，34（1）：109-116．（in Chinese）［12］CAO D Q，SONG M T，ZHU W D，et al．Modeling and analysis of the in-plane vibration of a complex cable-stayed bridge［J］．Journal of Sound and Vibration，2012，331（26）：5685-5714．［13］李专干，宋敉淘，曹登庆，等．一类单塔斜拉桥固有频率及模态的计算与分析［J］．应用力学学报，2016，33（6）：1038-1044．LI Z G，SONG M T，CAO D Q，et al．Calculation and analysis ofnatural frequencies and mode shapes of a cable-stayed bridge witha single rigid tower［J］．Chinese Journal of Applied Mechanics，2016，33（6）：1038-1044．（in Chinese）［14］赵文忠，康健，梁栋．索梁结构面内耦合振动机理研究［J］．重庆交通大学学报（自然科学版），2019，38（8）：20-26．ZHAO W Z，KANG J，LIANG D．In-plane coupled vibrationmechanism of cable-beam structure［J］．Journal of ChongqingJiaotong University （Natural Science），2019，38（8）：20-26．（inChinese）［15］CONG Y Y，KANG H J，YAN G R，et al．Modeling，dynamics，and parametric studies of a multi-cable-stayed beam model［J］．Acta Mechanica，2020，231（12）：4947-4970．［16］KANG H J，SU X Y，PI Z H．Planar nonlinear dynamic analysis of cable-stayed bridge considering support stiffness［J］．Nonlinear Dynamics，2022，107（2）：1545-1568．［17］康厚军，解维东，郭铁丁．CFRP索斜拉梁面内自由振动建模及参数分析［J］．湖南大学学报（自然科学版），2016，43（9）：18-25．KANG H J，XIE W D，GUO T D．Modeling and parametersanalysis on in-plane free vibration of cable-stayed beam［J］．Journal of Hunan University （Natural Sciences），2016，43（9）：18-25．（in Chinese）［18］康厚军，苏潇阳，龚平，等．漂浮式独塔斜拉桥竖弯刚度评估新方法［J］．湖南大学学报（自然科学版），2017，44（11）：126-134．KANG H J，SU X Y，GONG P，et al．A new method for verticalbending stiffness evaluation of floating single-tower cable-stayedbridge［J］．Journal of Hunan University （Natural Sciences），2017，44（11）：126-134．（in Chinese）［19］苏潇阳，康厚军，丛云跃．混合体系多塔斜拉桥竖弯刚度评估动力学理论［J］．动力学与控制学报，2020，18（4）：26-32．SU X Y，KANG H J，CONG Y Y．Dynamic theory for evaluationon vertical bending stiffness of multi-tower cable-stayed bridgewith hybrid system［J］．Journal of Dynamics and Control，2020，18（4）：26-32．（in Chinese）［20］KANG H J，XIE W D，GUO T D．Modeling and parametric analysis of arch bridge with transfer matrix method［J］．AppliedMathematical Modelling，2016，40（23/24）：10578-10595．［21］苏潇阳，康厚军，皮梓豪，等．斜拉桥多索-浅拱-弹性约束模型及面内自由振动［J］．湖南大学学报（自然科学版），2021，48（7）：138-144．SU X Y，KANG H J，PI Z H，et al．Elastically constrained multi-cable-stayed shallow-arch model in cable-stayed bridge and itsin-plane free vibration research［J］．Journal of Hunan University （Natural Sciences），2021，48（7）：138-144．（in Chinese）［22］WANG Z Q，KANG H J，SUN C S，et al．Modeling and parameter analysis of in-plane dynamics of a suspension bridge with transfermatrix method［J］．Acta Mechanica，2014，225（12）：3423-3435．［23］赵跃宇，杨相展，刘伟长，等.索-梁组合结构中拉索的非线性响应［J］.工程力学，2006，23（11）：153-158.ZHAO Y Y. YANG X Z， LIU W Z， et al. Non-linear response ofcables in cable-stayed beam structure［J］. EngineeringMechanics， 2006，23（11）：153-158. （in Chinese）［24］康厚军，赵跃宇，蒋丽忠．参数振动和强迫振动激励下超长拉索的面内非线性振动［J］．中南大学学报（自然科学版），2011，42（8）：2439-2445．KANG H J，ZHAO Y Y，JIANG L Z．In-plane nonlinear vibrationof super long stay cables under parametric and forcied excitations［J］．Journal of Central South University （Science andTechnology），2011，42（8）：2439-2445．（in Chinese）［25］PENG J，XIANG M J，WANG L H，et al．Nonlinear primary resonance in vibration control of cable-stayed beam with timedelay feedback［J］．Mechanical Systems and Signal Processing，2020，137：106488．［26］唐艺玮，彭剑，符翔，等．多输入时滞反馈控制下的斜拉梁主共振响应［J］．动力学与控制学报，2020，18（5）：92-96．TANG Y W，PENG J，FU X，et al．Primary resonance response ofcable-stayed beam under multi-input time-delayed feedback42。

预应力混凝土箱梁质量通病及解决措施的分析夏国锋

预应力混凝土箱梁质量通病及解决措施的分析夏国锋摘要：近年来随着经济的不断发展，我国公路、桥梁等的建造工作也在有条不紊的开展，而预应力混凝土箱梁的施工好坏直接影响到所对应的城市公路的桥梁工程的质量，因此在工程开展过程中需要格外注意。

本文将对在预应力混凝土箱梁施工中常见的质量问题进行针对性分析，结合这些容易出现的问题介绍预应力混凝土箱梁施工中的质量通病并分析其原因，从而能够得到较为有效的措施加以预防及改善。

关键词：预应力混凝土箱梁；质量问题；解决措施在城市公路以及桥梁的建造过程中，预应力混凝土箱梁的应用是十分广泛的，这主要是因为这一结构的桥型受力性能好、抗震能力、维护工程量小。

但与此同时，预应力混凝土箱梁桥的结构较其他桥型而言更加复杂，工程质量容易受到很多因素的影响，这样在工程设计以及施工中就会要很多的要求需要严格把控。

我们对预应力混凝土箱梁桥施工过程中的质量通病进行分析并提出相应的措施加以预防，这对于提高桥梁安全性，促进工程发展是有很大意义的。

一、预应力混凝土箱梁桥施工过程中的质量通病1.1 顶底板横向裂缝顶底板出现横向裂缝是预应力混凝土箱梁过程中常见的质量问题，这一问题的出现意味着预应力混凝土箱梁桥正截面的抗裂能力存在明显的不足。

造成该现象的主要原因是实际提供的有效预应力小于纵向预应力的损失，另外在预应力混凝土箱梁桥使用过程中发生的实际收缩徐变变形值超过了桥梁设计时的理论预测也会导致顶底板横向裂缝的出现，除此之外，在工程建设过程中对剪力滞效应考虑不足使得截面收到的应力峰值在平均值以上也会导致顶底板横向裂缝这一质量问题的出现。

1.2 顶底板纵向裂缝顶底板纵向裂缝这一质量问题的出现主要代表的是预应力混凝土箱梁桥横向抗裂能力较差。

造成这一问题的原因有多种：一是横向预应力的损失超过了实际提供的有效预应力；二是实际横向预应力与预测的位置发生了偏差；三是在进行纵向预应力横向平弯的径向力的预测值小于实际值；四是顺桥向预应力过大导致的正交向产生横向拉应变，从而导致在波纹管的方向上出现纵向雷锋，值得注意的是这样的纵向裂缝容易导致积水对钢束的锈蚀作用，危害性较其他纵向裂缝更加严重；最后，由于施工过程中会经过水化热过程导致的温度自应力变化，最终引起纵向裂缝的产生。

预应力混凝土桥梁施工质量控制及张拉过程中所出现质量问题的原因分析

预应力混凝土桥梁施工质量控制及张拉过程中所出现质量问题的原因分析桥梁预应力混凝土结构是充分利用材料的高强度性能，有效防止混凝土裂缝，减轻结构自重，增大桥梁跨径、刚度，同时有行车舒适等优点，为了保证安全可靠的建好每座桥梁，桥梁的施工控制将变得非常重要，而桥梁预应力施工作为预应力桥梁施工中极为重要的一环，无论是从设计、施工等环节都应该进行严格的控制，因为其直接影响今后的运营安全、桥梁使用寿命等问题，在桥梁施工中是一项极为重要的工序。

第二章预应力混凝土施工工序预应力混凝土施工流程：锚具及钢绞线检验合格预应力梁底模安装非预应力钢筋安装按设计坐标及高程焊接波纹管定位支架安装波纹管及排气管安装锚垫板及螺旋筋预应力工程隐蔽验收浇筑混凝土并养护钢绞线下料编束预应力钢绞线穿束拆除模板张拉设备及仪表配套校验安装锚板及夹片安装千斤顶预应力筋张拉锚固张拉质量检验预应力孔道压浆切除多余长钢绞线封堵锚具孔转入下道工序施工。

其中预应力孔道压浆宜在预应力束张拉完毕后尽早进行，一般预应力混凝土构件，在张拉完毕，停10小时左右，观察预应力钢材和锚具稳定后，即可进行。

第三章施工质量控制内容及影响因素预应力混凝土桥梁的施工控制包括结构变形控制、结构应力控制和结构稳定性控制。

线形控制就是严格控制每一节段的竖向挠度及其横向位移，保证成桥后的线形趋于设计线形；内力控制则是控制主梁在施工过程中以及成桥后的应力，尤其是合龙时的控制，使其不致过大而偏于不安全，并符合设计要求；桥梁的稳定性不仅包括桥梁的稳定计算，还包括施工各阶段结构构件的局部和整体稳定。

3.1预应力材料的质量控制严把材料质量关，采用信誉好质量好的厂家产品。

产品要有出厂合格证，质量检测报告，对到场材料进行检验，其强度、刚度、严密性及螺旋压接缝咬合牢度等各项指标均达到质量标准方可使用。

加强对波纹管的保护减少对其损伤。

减少电焊作业。

在普通钢筋骨架成型后再铺设波纹管，用振捣棒振捣混凝土时，要避开波纹管，波纹管接头。

桥梁结构中的剪力滞效应赖良建

桥梁结构中的剪力滞效应赖良建发布时间：2022-06-30T09:52:12.480Z 来源：《建筑模拟》2022年第4期作者：赖良建[导读] 国内针对混凝土箱梁结构的剪力滞效应研究已经颇为成熟，而对钢箱梁剪力滞效应的研究还不够全面。

国内外均建造了大量的箱形薄壁梁桥，对高跨比较大、宽高比较突出的箱形梁桥，其剪力滞效应相当严重，如果忽略剪力滞的影响，势必导致结构失稳或破坏。

设计上分析剪力滞效应的常用分析方法多采用平面梁格模型、单梁模型、实体模型等。

本文介绍了薄壁箱梁剪力滞效应及常用求解方法，以及T梁剪力滞的分布规律。

阐述了剪力滞现象的存在，并为桥梁的精细化设计作出了思考。

重庆交通大学土木工程学院重庆 400041摘要：在桥梁结构中，剪力滞效应问题不可忽略。

目前而言，国内针对混凝土箱梁结构的剪力滞效应研究已经颇为成熟，而对钢箱梁剪力滞效应的研究还不够全面。