相交线、垂线习题及解析
相交线和垂线的练习题

相交线、垂线练习题
一、选择题:(每题2分,共24分)
1、下列语句正确的是().
A、相等的角是对顶角
B、相等的两个角是邻补角
C、对顶角相等
D、邻补角不一定互补,但可能相等
2、平面上三条直线两两相交最多能构成对顶角的对数是().
A、7
B、6
C、5
D、4
3、下列语句错误的有()个.
(1)两个角的两边分别在同一条直线上,这两个角互为对顶角
(2)有公共顶点并且相等的两个角是对顶角
(3)如果两个角相等,那么这两个角互补
(4)如果两个角不相等,那么这两个角不是对顶角
A、1
B、2
C、3
D、4
4、如果两个角的平分线相交成90°的角,那么这两个角一定是().
A、对顶角
B、互补的两个角
C、互为邻补角
D、以上答案都不对
5、已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是().
A、对顶角
B、相等但不是对顶角
C、邻补角
D、互补但不是邻补角
6、下列说法正确的是().
A、有公共顶点的两个角是对顶角
B、两条直线相交所成的两个角是对顶角
C、有公共顶点且有一条公共边的两个角是邻补角
D、两条直线相交所成的无公共边的两个角是对顶角
7、如图1所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB;
B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段;
D.线段BD是点B到AD的垂线段
D C
B A
D
C
B
A
O D
C
B
A
(1) (2) (3)
8、如图1所示,能表示点到直线(线段)的距离的线段有( )
A.2条
B.3条
C.4条
D.5条
9、下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
相交线和垂线的练习题

相交线、垂线练习题
一、选择题:
1、下列语句正确的是( ).
A 、相等的角是对顶角
B 、相等的两个角是邻补角
C 、对顶角相等
D 、邻补角不一定互补,但可能相等 2、平面上三条直线两两相交最多能构成对顶角的对数是( ).
A 、7
B 、6
C 、5
D 、4 3、下列语句错误的有( )个.
(1)两个角的两边分别在同一条直线上,这两个角互为对顶角 (2)有公共顶点并且相等的两个角是对顶角 (3)如果两个角相等,那么这两个角互补 (4)如果两个角不相等,那么这两个角不是对顶角
A 、1
B 、2
C 、3
D 、4 4、如果两个角的平分线相交成90°的角,那么这两个角一定是( ).
A 、对顶角
B 、互补的两个角
C 、互为邻补角
D 、以上答案都不对 5、已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( ).
A 、对顶角
B 、相等但不是对顶角
C 、邻补角
D 、互补但不是邻补角 6、如图1所示,下列说法不正确的是( )
A.点B 到AC 的垂线段是线段AB;
B.点C 到AB 的垂线段是线段AC
C.线段AD 是点D 到BC 的垂线段;
D.线段BD 是点B 到AD 的垂线段
D
C
B
A
(1) (2) (3) 7、如图1所示,能表示点到直线(线段)的距离的线段有( )
A.2条
B.3条
C.4条
D.5条
8、如图2所示,AD ⊥BD,BC ⊥CD,AB=a cm, BC=b cm,则BD 的范围是( ) A.大于a cm B.小于b cm
C.大于a cm 或小于b cm
D.大于b cm 且小于a cm 9、到直线L 的距离等于2cm 的点有( )
相交线与垂线(两线四角)练习题
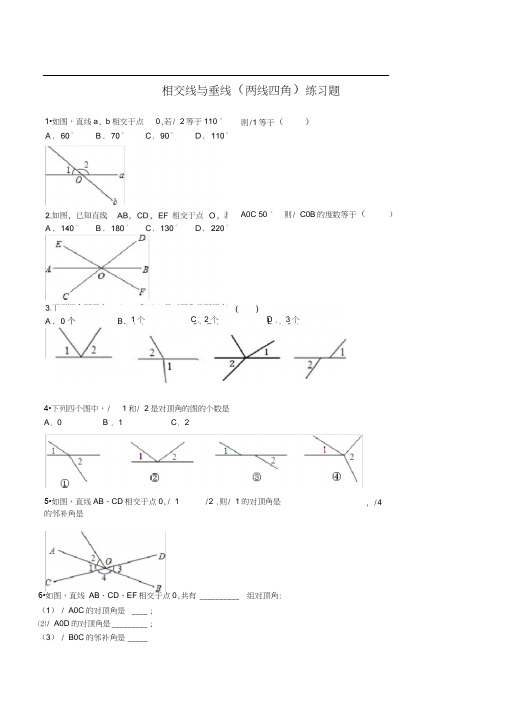
相交线与垂线(两线四角)练习题
4•下列四个图中,/ 1和/ 2是对顶角的图的个数是
A . 0
B . 1
C . 2
, /
4的邻补角是
6•如图,直线 AB 、CD 、EF 相交于点0,共有 __________ 组对顶角:
(1) / A0C 的对顶角是 ____ ;
⑵/ A0D 的对顶角是 _________ ;
(3) / B0C 的邻补角是 _____
0,若/ 2等于110 ° 则/1等于( )
则/ C0B 的度数等于(
)
1•如图,直线a , b 相交于点 A0C 50 ° C . 2个 D . 1个 3个
5•如图,直线AB 、CD 相交于点0,/ 1 /2 .则/ 1的对顶角是
7•下列说法正确的有()
①相等的角是对顶角
②一个角的两个邻补角是对顶角
③若两个角不是对顶角,则这两个角不相等
④凡直角皆相等
A . 1个
B . 2个
C . 3个
D . 4个
8•对两条直线相交所得的四个角中,下面说法正确的是()
①没有公共边的两个角是对顶角②有公共边的两个角是对顶角
③没有公共边的两个角是邻补角④有公共边的两个角是邻补角.
A .①②B.①③ C .①④ D .以上都不对
9•如图,直线AB、CD相交于O, 0E丄CD,且/ B0D的度数是/ A0D的4倍. 求:(1)/ A0D、/ B0D 的度数;(2)/ B0E的度数.
参考答案:
1. B .(理由:由图形可得7 1与7 2互为邻补角,从而可得7 1 180° / 2 70°故选B.)
2. C.(理由:丁7 A0C 50° /-7 C0B 180° 7 A0C 180° 50° 130° 故选C.)
沪科版七年级下册数学《10.1相交线》同步练习含答案解析

沪科版七年级下册数学10.1相交线同步练习
一、选择题(本大题共8小题)
1. 下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
2. 如图,同位角是( )
A.∠1和∠2 B.∠3和∠4 C.∠2和∠4 D.∠1和∠4
3. 如图,图中∠α的度数等于( )
A. 135°B.125°C.115°D.105°
4.如图所示,直线AB和CD相交于点O,OE、OF是过点O的射线,其中构成对顶角的是()
A.∠AOF和∠DOE
B.∠EOF和∠BOE
C.∠COF和∠BOD
D.∠BOC和∠AOD
5. 如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°;
B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
6. 如图7,AB,CD相交于点O,AC⊥CD与点C,若∠BOD=38°,则∠A等于______°。
A.52
B.46
C. 48
D. 50
7. 如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是( )
A.平行
B.相交
C.垂直
D.不能确定
8. 下列说法中正确的是()
A.有且只有一条直线垂直于已知直线
B.互相垂直的两条线段一定相交
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短的线段长是3cm,则点A到直线c的距离是3cm.
相交线、垂线及三线八角练习题

相交线、垂线及三线八角练习题
一、选择题:
1.下列说法正确的是(
).
A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条.
B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线.
C.作出点P 到直线的距离
D.连结直线外一点和直线上任一点的线段长是点到直线的距离. 2.已知OA ⊥OC ,∠AOB :∠AOC=2:3,则∠BOC 的度数是( ).
A.30°
B.150°
C.30°或150°
D.以上答案都不对
3.如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是( ).
A.
2
1
(∠1+∠2) B.
2
1
∠1 C.
21(∠1–∠2) D. 2
1
∠2 4.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ).
A.1
B.2
C.3或2
D.1或2或3
5.下列语句正确的是( ). A.相等的角为对顶角
B.不相等的角一定不是对顶角
C.不是对顶角的角都不相等
D.有公共顶点且和为180°的两角是邻补角
6.下列说法正确的是( ).
A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.
B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.
C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.
D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直. 7.直线a 、b 、c 相交于点O ,则图中对顶角共有( )
A .6对
B .5对
C .4对
D .3对 8.下列结论中,错误的是( )
A .同一个角的两个邻补角是对顶角
B .对顶角相等,相等的两个角也是对顶角
七年级下册相交线与垂直线练习题及答案

七年级下册相交线与垂直线练习题及答案第一部分相交线与垂直线的基础知识
1. 请为以下图形标出所有的垂线和水平线。
2. 以下哪条直线是垂直线?
A. 直线AB
B. 直线CD
C. 直线EF
D. 直线GH
3. 若线段AB ⊥线段BC,且角ABC = 78°,则角ABD 等于多少度?
第二部分题目练
1. 见以下图形,若线段AB ⊥线段CD,EF 与 GH 垂直,且角AED = 58°,则角FHB 等于多少度?
2. 见以下图形,线段AB ⊥线段CD,EF 垂直 BC 于点G,且角AED = 46°,则角ABF 等于多少度?
3. 见以下图形,若线段AB ⊥线段CD,角ABC = 50°,角EFG = 68°,则角EDF 等于多少度?
第三部分答案
第一部分
1. 垂线:AD, BC, FE 水平线:BE, DG
2. 直线CD 是垂直线
3. 角ABD = 12°
第二部分
1. 角FHB = 32°
2. 角ABF = 34°
3. 角EDF = 62°
希望以上内容能帮助您顺利完成七年级下册相交线与垂直线部分的练习题。
5.1相交线垂线习题精选

5.1相交线垂线习题精选
一.解答题(共10小题)
1.有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的东南方向,
(1)试确定C地的位置;
(2)画射线CA;
(3)画出点C到AB的垂线段CD.
2.如图,已知直线AB,OC⊥AB,OD⊥OE,若∠COE=∠BOD,则求∠COE,∠BOD,∠AOE的度数.
3.如图,AO⊥OB,直线CD过点O,且∠BOD=130°,求∠AOD的大小.
4.如图:AB,CD,EF相交于O点,AB⊥CD,OG平分∠AOE,∠FOD=30°,求∠BOE及∠AOG的度数.
5.如图,AB、CD相交于O点,若∠EOD=40°,∠BOC=130°,猜想射线OE与直线AB的位置关系,并求证.
6.如图,直线AB、CD相交于点O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE.请你求∠DOB的度数.
7.如图,直线AB,CD相交于O点,OM⊥AB于O.
(1)若∠1=∠2,求∠NOD;
(2)若∠BOC=4∠1,求∠AOC与∠MOD.
8.如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF 的度数.
9.如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一
起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?
答:_________(填写“是”或“否”);
(2)如图1,若∠DCE=35°,则∠ACB=_________°;
【相交线,垂线】之专题—能力提升训练与解析

【相交线,垂线】之专题—能力提升训练与解析
【学习目标】
1.了解两直线相交所成的角的位置和大小关系,理解邻补角和对顶角概念,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,掌握垂直的定义及性质;
3.理解点到直线的距离的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质,进行简单的计算.
【要点梳理】
知识点一、邻补角与对顶角
1.邻补角:如果两个角有一条公共边,并且它们的另一边互为反向延长线,那么具有这种关系的两个角叫做互为邻补角.
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的是位置相邻,“补”指的是两个角的和为180°.
(2)邻补角是成对出现的,而且是“互为”邻补角.
(3)互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角.
(4)邻补角满足的条件:①有公共顶点;②有一条公共边;另一边互为反向延长线.
2.对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点没有公共边(相对)的两个角,互为对顶角.
(2)性质:对顶角相等.
要点诠释:
(1)由定义可知只有两条直线相交时,才能产生对顶角.
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线.
3
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.
要点诠释:
(1)记法:直线a 与b 垂直,记作:a b ⊥;
直线AB 和CD 垂直于点O ,记作:AB⊥CD 于点O.
相交线,垂线(基础)知识点及典型例题举一反三讲解,总结升华

相交线,垂线(基础)知识讲解
【学习目标】
1.了解两直线相交所成的角的位置和大小关系,理解邻补角和对顶角概念,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,掌握垂直的定义及性质;
3.理解点到直线的距离的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质,进行简单的计算.
【要点梳理】
知识点一、邻补角与对顶角
1.邻补角:如果两个角有一条公共边,并且它们的另一边互为反向延长线,那么具有这种关系的两个角叫做互为邻补角.
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的是位置相邻,“补”指的是两个角的和为180°.
(2)邻补角是成对出现的,而且是“互为”邻补角.
(3)互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角.
(4)邻补角满足的条件:①有公共顶点;②有一条公共边,另一边互为反向延长线.
2.对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点没有公共边(相对)的两个角,互为对顶角.
(2)性质:对顶角相等.
要点诠释:
(1)由定义可知只有两条直线相交时,才能产生对顶角.
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线.
【高清课堂:相交线两条直线垂直】
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.
要点诠释:
⊥;
(1)记法:直线a与b垂直,记作:a b
直线AB和CD垂直于点O,记作:AB⊥CD于点O.
相交线与垂线(两线四角)练习题
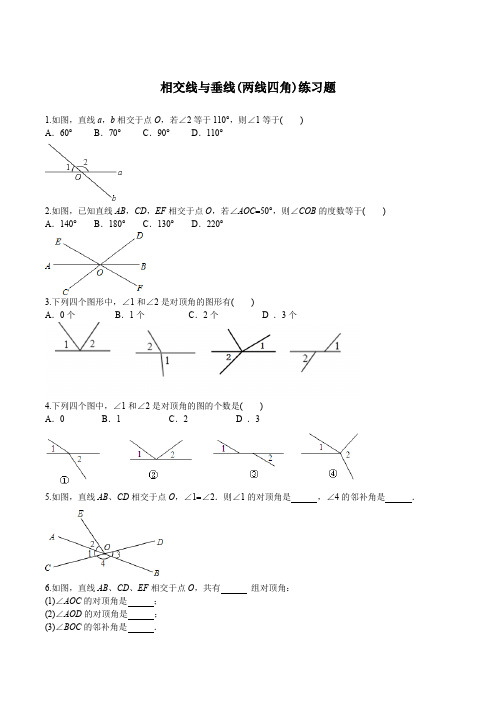
相交线与垂线(两线四角)练习题
1.如图,直线a,b相交于点O,若∠2等于110°,则∠1等于()
A.60° B.70° C.90° D.110°
2.如图,已知直线AB,CD,EF相交于点O,若∠AOC=50°,则∠COB的度数等于() A.140° B.180° C.130° D.220°
3.下列四个图形中,∠1和∠2是对顶角的图形有()
A.0个B.1个C.2个 D .3个
4.下列四个图中,∠1和∠2是对顶角的图的个数是()
A.0B.1 C.2 D .3
5.如图,直线AB、CD相交于点O,∠1=∠2.则∠1的对顶角是,∠4的邻补角是.
6.如图,直线AB、CD、EF相交于点O,共有组对顶角:
(1)∠AOC的对顶角是;
(2)∠AOD的对顶角是;
(3)∠BOC的邻补角是.
7.下列说法正确的有()
①相等的角是对顶角
②一个角的两个邻补角是对顶角
③若两个角不是对顶角,则这两个角不相等
④凡直角皆相等
A.1个B.2个C.3个D.4个
8.对两条直线相交所得的四个角中,下面说法正确的是()
①没有公共边的两个角是对顶角②有公共边的两个角是对顶角
③没有公共边的两个角是邻补角④有公共边的两个角是邻补角.
A.①②B.①③C.①④D.以上都不对
9.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的4倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
10.如图,直线a,b,c相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
参考答案:
1.B.(理由:由图形可得∠1与∠2互为邻补角,从而可得∠1=180° -∠2=70°.故选B.)
相交线计算题

相交线计算题
1.如图所示,在长方形的台球桌桌面上,选择适当的方法击打白球,可以使白球经过两次反弹后将黑球直接撞入中洞,此时∠1=∠2,∠3=∠4,且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口连线和台球桌面边缘的夹角为∠5=40°,那么∠1应等于多少度才能保证黑球进入中洞?
2.取一张正方形纸片ABCD,如图
(1)折叠∠A,设顶点A落在点A′的位置,折痕为EF;如图(2)折叠∠B,使EB沿EA′的方向落下,折痕为EG.试判断∠FEG的度数是否是定值,并说明理由.
3.如图所示,直线AB,CD,EF相交于点O,∠AOF=3∠FOB,∠AOC=90°,求∠EOC的度数.
10.如图所示,已知l 1,l 2,l 3相交于点O ,∠1
=∠2,∠3︰∠1=8︰1,求∠4的度数.
11.如图所示,三条直线相交于一点,求∠1+∠2+∠3的度数.
12.如图,直线AB 与CD 相交于点E ,∠1=∠2,EF 平分∠AED ,且∠1=50°,求∠AEC 的度数.
13.如图所示,直线AB 截直线CD 和EF ,构成8个角,指出图中的同位角、内错角、同旁内角.
14.如图所示,AO⊥BO于O,CO⊥DO于O,∠BOD =30°,求∠AOC的度数.
15.如图所示,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.方案一:分别过C,D作AB的垂线,垂足分别为E,F,沿CE,DF铺设管道;方案二:连接CD交AB于点P,沿PC、PD铺设管道.问:这两种铺设管道的方案中哪一种更节省材料,为什么?
人教版初一数学7年级下册 第5章(相交线与平行线)垂线 课后练习(含解析)

垂线课后练习
一、选择题
1.如图所示,下列说法不正确的是( )
A. 线段BD是点B到AD的垂线段
B. 线段AD是点D到BC的垂线段
C. 点C到AB的垂线段是线段AC
D. 点B到AC的垂线段是线段AB
2.如图,把河AB中的水引到C,拟修水渠中最短的是( )
A. CM
B. CN
C. CP
D. CQ
3.如图,E是直线CA上一点,∠FEA=40°,射线EB平分
∠CEF,GE⊥EF.则∠GEB=( )
A. 10°
B. 20°
C. 30°
D. 40°
4.如图,直线AB、CD相交于点O,EO⊥CD.下列说法错误
的是( )
A. ∠AOD=∠BOC
B. ∠AOE+∠BOD=90°
C. ∠AOC=∠AOE
D. ∠AOD+∠BOD=180°
5.点P为直线l外一点,点A,B在直线l上,若PA=5 cm,PB=7 cm,则点P到
直线l的距离( )
A. 等于5 cm
B. 小于5 cm
C. 不大于5 cm
D. 等于6 cm
6.如下图,在平面内过点P作已知直线m的垂线,可作垂线
的条数有( )
A. 0条
B. 1条
C. 2条
D. 无数条
7.如图,∠1=15°,AO⊥OC,点B,O,D在同一直线上,
则∠2的度数为()
A. 75°
B. 15°
C. 105°
D. 165°
8.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,
PC=6 cm,则点P到直线m的距离()
A. 等于5 cm
B. 等于4 cm
C. 小于4 cm
D. 不大于4 cm
9.如图,OA⊥OB,若∠1=55°,则∠2的度数是()
A. 35°
《5.1相交线》练习题

(D)(C)
(B)
(A)
2
2
2
1
1
121
《5.1相交线》练习题一
1、下列各图中,∠1和∠2是对顶角的是( )
2、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有 ( ) A 、1个 B 、2个 C 、3个 D 、4个
3、如图,三条直线两两相交,其中对顶角共有 ( ) A 、3对 B 、4对 C 、5对 D 、6对
4、如图,直线AB 、CD 交于点O ,OE 、OF 是过O 点的两条射线,其中构
成对顶角的是 ( )
A 、∠AOF 与 ∠DOE
B 、∠EOF 与∠BOE
C 、∠BOC 与∠AO
D D 、∠COF 与∠BOD
5、下列说法错误的是 ( )
A 、对顶角的平分线成一个平角
B 、对顶角相等
C 、相等的角是对顶角
D 、对顶角的余角相等 6、如图,直线AB 与CD 相交于点O ,∠AOD+∠BOC=236度,则∠AOC 的度数为 ( )
A 、72度
B 、62度
C 、124度
D 、144度 7、如图,点A 到直线CD 的距离是指哪条线段长 ( )
A 、AC
B 、CD
C 、A
D D 、BD 8、在“同一平面内,过一点有且只有一条直线与已知直线垂直”中这一点的位置 ( )
A 、在直线的上方
B 、在直线的下方
C 、在直线上
D 、可以任意位置
9、下列说法中正确的个数有 ( ) (1)直线外一点与直线上各点连接的所有线中垂线段最短。 (2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。 (4)从直线外一点到这条直线的垂线段叫做点到直线的距离。 A 、1个 B 、2个 C 、3个 D 、4个
相交线和垂线的练习题

《相交线、垂线,三线八角》练习题
姓名家长签字
一、选择题:(每题3分,共33分)
1、下列语句:(1)两个角的两边分别在同一条直线上,这两个角互为对顶角(2)有公共顶点并且相等的两个角是对顶角(3)如果两个角相等,那么这两个角互补(4)如果两个角不相等,那么这两个角不是对顶角,错误的有()个.矚慫润厲钐瘗睞枥庑赖賃軔朧碍鳝绢。
A、1
B、2
C、3
D、4聞創沟燴鐺險爱氇谴净祸測樅锯鳗鲮。
2、如果两个角的平分线相交成90°的角,那么这两个角一定是().
A、对顶角
B、互补的两个角
C、互为邻补角
D、以上答案都不对
3、已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是().
A、对顶角
B、相等但不是对顶角
C、邻补角
D、互补但不是邻补角
4、如下图所示,能表示点到直线(线段)的距离的线段有( )
A.2条
B.3条
C.4条
D.5条
D C
B A
D
C
B
A
5、如上图所示,AD⊥BD,BC⊥CD,AB=a cm, BC=b cm,则BD的范围是( )
A.大于a cm
B.小于b cm
C.大于a cm或小于b cm
D.大于b cm 且小于a cm残骛楼諍锩瀨濟溆塹籟婭骒東戇鳖納。
6、下列说法:①在平面内,过直线上一点有且只有一条直线垂直于已知直线。②在平面内,过直线外一点有且只有一条直线垂直于已知直线。
③在平面内,过一点可以任意画一条直线垂直于已知直线。④在平面内,有且只有一条直线垂直于已知直线.正确的有( )个酽锕极額閉镇桧猪訣锥顧荭钯詢鳕驄。
A.1个
B.2个
C.3个
D.4个
7、到直线L的距离等于2cm的点有( )
相交线练习题(含答案)

第五章相交线与平行线
5.1 相交线
1.邻补角是
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.如图,经过直线l外一点A画l的垂线,能画出
A.1条B.2条C.3条D.4条3.如图,OA⊥OB,∠1=35°,则∠2的度数是
A.35°B.45°C.55°D.70°4.如图,下列说法不正确的是
A.∠1和∠2是同旁内角B.∠1和∠3是对顶角
C.∠3和∠4是同位角D.∠1和∠4是内错角
5.下列说法正确的是
A.一个角的补角一定比这个角大
B.一个角的余角一定比这个角小
C.一对对顶角的两条角平分线必在同一条直线上
D.有公共顶点并且相等的两个角是对顶角
6.如图,三条直线a,b,c相交于点O,则∠1+∠2+∠3等于
A.90°B.120°C.180°D.360°
7.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是
A.两点确定一条直线
B.同一平面内,经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一直线
D.垂线段最短
8.如图,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC–∠COD=∠BOC.
A.①②③B.①②④
C.①③④D.②③④
9.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是__________.
10.如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为
相交线、垂线的练习题

相交线、垂线练习题
一、选择题:
1、平面上三条直线两两相交最多能构成对顶角的对数是( ).
A 、7
B 、6
C 、5
D 、4
2、下列语句错误的有( )个.
(1)两个角的两边分别在同一条直线上,这两个角互为对顶角
(2)有公共顶点并且相等的两个角是对顶角
(3)如果两个角相等,那么这两个角互补
(4)如果两个角不相等,那么这两个角不是对顶角
A 、1
B 、2
C 、3
D 、4
3、如果两个角的平分线相交成90°的角,那么这两个角一定是( ).
A 、对顶角
B 、互补的两个角
C 、互为邻补角
D 、以上答案都不对
4、已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( ).
A 、对顶角
B 、相等但不是对顶角
C 、邻补角
D 、互补但不是邻补角
5、如图1所示,下列说法不正确的是( )
A.点B 到AC 的垂线段是线段AB;
B.点C 到AB 的垂线段是线段AC
C.线段AD 是点D 到BC 的垂线段;
D.线段BD 是点B 到AD 的垂线段
6、如右图所示,能表示点到直线(线段)的距离的线段有( )
A.2条
B.3条
C.4条
D.5条
7、下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个
B.2个
C.3个
D.4个
8、到直线L 的距离等于2cm 的点有( )
A.0个
B.1个
C.无数个
D.无法确定
9、点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到直线m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1. 在一个平面内,任意四条直线相交,交点的个数最多有()
A.7个
B.6个
C.5个
D.4个
2. 已知点A、B、C是直线a上有三点,P是直线a外的一点,且PA=6,PB=7,PC=8,则点P到直线a 的距离是()
A.6
B.7
C.8
D.不大于6
3. 下列说法中正确的个数有()
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(2)画一条直线的垂线段可以画无数条.
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个
B.2个
C.3个
D.4个
4. 如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120∘,那么∠COB的度数为()
A.80∘
B.70∘
C.60∘
D.50∘
5. 点到直线的距离是指这点到这条直线的()的长度.
A.垂线
B.垂线段
C.线段
D.垂段
6. 如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是()
A.∠BOE
B.∠BOD
C.∠DOE
D.∠BOC
6题图 8题图 9题图 10题图
7. 直线l外有一点A,点A到l的距离是5cm,点P是直线l上任意一点,则()
A.AP>5cm
B.AP≥5cm
C.AP=5cm
D.AP<5cm
8. 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是()
A.OA
B.OB
C.OC
D.OD
9. 如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=36∘,则∠DOE等于()
A.73∘
B.90∘
C.107∘
D.108∘
10. 如图,直线AB、CD相交于点O,OF⊥CO,∠AOF与∠BOD的度数之比为3:2,则∠AOC的度数是()
A.18∘
B.45∘
C.36∘
D.30∘
11. 下列几何语言描述正确的是()
A.直线mn与直线ab相交于点D
B.点A在直线M上
C.点A在直线AB上
D.延长直线AB
12. 如图,在△ABC中,∠C=90∘,D是边BC上一点,且∠ADC=60∘,那么下列说法中错误的是()
A.直线AD与直线BC的夹角为60∘
B.直线AC与直线BC的夹角为90∘
C.线段CD的长是点D到直线AC的距离
D.线段AB的长是点B到直线AD的距离
13. 如图是小明同学在体育课上跳远后留下的脚印,则表示他的跳远成绩是()
A.线段AC的长
B.线段BC的长
C.线段AD的长
D.线段BD的长
二、填空题
14. 如图,直线AB、CD相交于点O,EO⊥CD,∠AOD=4∠BOD,则∠AOE=________∘.
14题图 15题图 16题图 17题图
15. 如图,直线AB、CD相交于O,且∠AOD=50∘,则∠BOC的度数为________.
16. 如图,AC⊥BC,D在AB上,∠CDA=90∘,则线段________的长度是点C到直线AB的距离,线段BC
的长度是点B到直线________的距离.
17. 如图点B到直线a的距离是线段________的长度.
18. 如图,要从小河引水到村庄A,请设计并作出一最佳路线,理由是________.
19. 如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,
则∠COP与∠BOP的比为________.
20. 在直角三角形ABC中,∠B=90∘,则它的三条边AB,AC,BC中,最长的边是________.
21. 已知,∠α=50∘,且∠α的两边与∠β的两边互相垂直,则∠β=________.
22. 如图,AC⊥BC于点C,CD⊥AB于点D,DE⊥BC于点E,能表示点到直线(或线段)的距离的线段
有________条.
三、解答题
23. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90∘,∠1=30∘.求∠2和∠3的度数.
24. 如图,在△ABC中,AC⊥BC,CD⊥AB垂足为D.
(1)AB,AC,CD之间的大小关系为________(用“<”号连接起来).
(2)若AC=4,BC=3,AB=5,求点C到直线AB的距离.
25. 如图,直线EF、BC相交于点O,∠AOC是直角,∠AOE=115∘,求∠COF的度数.
26. 直线AB,CD,EF相交于点O,且∠AOD=100∘,∠1=30∘,求∠2的度数.
27. 如图,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
参考答案与试题解析
一、选择题(本题共计 13 小题,每题 3 分,共计39分)
1.【解答】故选B.
2.【解答】故选D.
3.【解答】故选C.
4.【解答】故选C.
5.【解答】故选B.
6.【解答】故选B.
7.【解答】故选B.
8.【解答】故选:B.
9.【解答】故选:D.
10.【解答】故选:C.
11.【解答】故选C.
12.【解答】故选D.
13.【解答】故选:D.
二、填空题
14.【解答】故答案为:54∘
15.【解答】故答案为:50∘.
16.【解答】故答案为:CD,AC.
17.【解答】故答案为:BC.
18.【解答】解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短,∴过点A作河岸的垂线段,理由是垂线段最短.
19.【解答】故答案为:3:2.
20.【解答】解:如图,最长的边是AC.故答案为:AC.
21.【解答】解:①如图1,∵∠a+∠β=180∘−90∘−90∘=180∘,∠α=50∘,
∴∠β=140∘,
②如图2,若∠a的两边分别与∠β的两边在同一条直线上,∴∠a=∠β=50∘,
综上所述,∠β=140∘或50∘.故答案是:140∘或50∘.
22.【解答】故答案为:9.
三、解答题(本题共计 5 小题,每题 10 分,共计50分)
23.【解答】
