2020届湖南省长沙市雅礼中学高三下学期第七次月考数学(文)试题(解析版)

合集下载

2024届湖南省长沙雅礼中学高三下学期月考(七)语文试题及答案

雅礼中学2024届高三月考试卷(七)语文注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

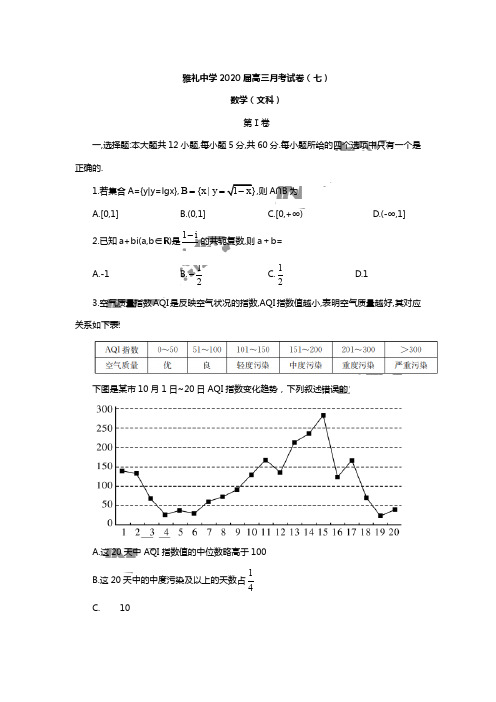
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读I(本题共5小题，19分)阅读下面的文字，完成1～5题。

乡土文学内涵丰富多彩，既可书写乡土历史，也可关注乡村现实，或写实，或象征，或抒情。

但无论如何，乡土小说在未来要有所突破，更具审美价值，能对中国乡村历史、现实与未来前景作出更具梯度与广度的思考，须摆脱传统叙事范式的限度，“接通”乡村现实的巨变，在多方面进行更新。

一是更新对乡土文明的价值认知。

也就是说，充分尊重乡村的本体地位与独立价值，重构乡土文明的正向价值。

长期以来，由于对现代性的某种迷思，乡土文明通常被预设、框定为传统、落后的文化形态，与现代化构成一种悖论与张力，总是遭到无情的批判与碾压，中国百年来的乡土文学基本上是在此方向上惯性地书写。

事实上，中华文明本质上是一种农耕文明，而乡村则是农耕文明的实体载体与存在空间。

可以说，乡村文化不仅是建构中华民族心理认同感的重要精神源泉，还滋育着中华文明的根脉。

“乡村文明是中华民族文明史的主体，村庄是这种文明的载体，耕读文明是我们的软实力。

”因此，悠久、灿烂的农耕文明支撑了古代中国的生存与繁荣，也为当代中国积淀了文化基因与根脉。

乡土文明有其独立存在的价值，并非仅仅是评判现代性的参照坐标，亦不是城市文明的附庸，它同样有着现代文明的价值指向。

因此现代化并非是完全要抛弃传统，现代化也可以说是植根于传统的一种转型与生长，与传统一脉相承。

未来的乡土小说不必再视乡村为一种话语批判的武器，实有必要以平视的姿态去看待农耕文化中那些悠远的传统元素，通过对乡村固有的风俗、风情、风景的展示，建构乡村自身之美，从而彰显乡村文化的丰盈，赋予乡土以中华民族的文化记忆功能。

长沙雅礼中学2020届高三月考试卷(七)文科数学试题及答案解析

S9 S5
___.
14.曲线 y=xlnx 在点(1,0)处的切线的方程为___
15.设函数 f (x) sin(x )( 0, 0 ) 的图象与 y 轴交点的纵坐标为 3 , 轴
2
2
右侧第一个最低点的横坐标为 ,则 ω 的值为____. 6
16.如图,在边长为 2 的正方形 AP 1 P 2 P 3 中,边 P 1 P 2 ,P 2 P 3
(2)若 P 是线段 AC 上一点, AD
3 ,AB=BC=2,三棱锥 A 1 -PBC 的体积为
3 ，求 AP 3 PC
的值
20.(本小题满分 12 分)
设中心在原点,焦点在 x 轴上的椭圆 E 过点( (1, 3 ) .且离心率为 3 ,F 为 E 的右焦点,P
2
雅礼中学 2020 届高三月考试卷（七）
数学（文科）
第Ⅰ卷
一,选择题:本大题共 12 小题,每小题 5 分,共 60 分.每小题所给的四个选项中只有一个是
正确的.
1.若集合 A={y|y=lgx}, B {x | y 1 x},则 A∩B 为
A.[0,1]
B.(0,1]
C.[0,+∞)
2.已知 a+bi(a,b∈R)是 1 i 分)
△ABC 的内角 A,B,C 的对边分别为 a,b,c,已知 2cos A(b cosC c cos B) 3a
(1)求角 A;
(2)若 a=1,△ABC 的周长为 5 1 求△ABC 的面积.
19.(本小题满分 12 分)
如图,在直三棱柱 ABC-A 1 B 1C 1 中,AD⊥平面 A 1 BC ,其垂足 D 落在直线 A 1 B 上. (1)求证:BC⊥A 1 B :

7.湖南省长沙市雅礼中学2020届高三月考作文题解含范文

湖南省长沙市雅礼中学2020届高三月考作文题阅读下面的材料，根据要求写作。

大疫之时，很多标语引发了网民的关注和热议。

乡间标语：口罩还是呼吸机，您老看着二选一。

老实在家防感染，丈人来了也得撵。

街头标语：武汉人，不服输，疫情面前不低头。

你加油，我加油，战胜病毒有盼头。

众志成城齐努力，誓把病毒全抗击。

日本援华物资标语：青山一道同云雨，明月何曾是两乡。

（盛唐•王昌龄）山川异域，日月同天。

（盛唐•日本大臣赠中国僧人语）岂曰无衣，与子同袍。

（先秦《诗经•无衣》）这些语言承自先民，馈自邻邦，萌于热土，其中蕴含着人们的情感和智慧，给与大疫抗争的中国人以鼓舞和力量。

乡间百姓富有生活气息的标语和日本人对传统中国诗文的运用，更给我们对于如何传承、创造和运用民族语言带来诸多思考。

请你选择一个角度，就此谈谈你的感触和思考。

自拟标题，不少于800字。

【审题精析】（一）感受真实情境。

材料由大疫之时三组不同风格的抗疫标语切入情境，这些标语引发了网民的关注和热议：国内乡间街头的标语富有生活气息；日本援华物资标语则恰当地运用了传统中国诗文。

导语部分依次交代这些语言的来源、内涵与作用，点明这些语言“承自先民，馈自邻邦，萌于热土，其中蕴含着人们的情感和智慧，给与大疫抗争的中国人以鼓舞和力量”。

材料真实鲜活，情境直面现实。

考生写作不得脱离材料。

（二）明确典型任务。

可供选择的角度有三：一是抗疫标语为什么引发了网民的关注和热议；二是抗疫标语的用语比较与作用分析；三是由如何传承、创造和运用民族语言带来的诸多思考。

“此”规定了写作的范围，“感触和思考”点明了写作的重心。

考生写作时必须把抗疫标语的使用分析和民族语言的传承发展结合起来，不能顾此失彼。

（三）坚定价值判断。

本题考查考生的文化自信与理性思辨能力，在网民的关注和热议中，既要保持高度的文化自信，又要合理吸收他人的长处。

我们先民的语言异彩纷呈，各种方式的表达，共同汇聚战“疫”的力量。

虽然文辞各异，但心意相通，目的相同。

2020年湖南省雅礼中学高三1-6次月考理科数学、文科数学(含答案)

预计去年消费金额在!$$!'$$(内的消费者今年都将会申请办理普通会员$消费金额在 !!'$$$1#$$(内的消费者都将会申请办理银卡会员$消费金额在!1#$$$2"$$(内的消费者都将会申请办理金卡会员! 消费者在申请办理会员时$需一次性缴清相应等级的消费金额! 该健身机构在今年底将针对这些消费者举办消费返利活动$现有如下两种预设方案# 方案!#按分层抽样从普通会员$银卡会员$金卡会员中总共抽取 #& 位-幸运之星.给予奖励#普通会员中的-幸运之星.每人奖励&$$元1 银卡会员中的-幸运之星.每人奖励'$$元1金卡会员中的 -幸运之星.每人奖励"$$元! 方案##每位会员均可参加摸奖游戏$游戏规则如下#从一个装有1个白球%#个红球!球只有颜色不同"的箱子中$有放回地摸三次球$每次只能摸一个球!若摸到红球的总数为#$则可获得#$$元奖励金1若摸到红球的总数为1$则可获得1$$元奖励金1其他情况不给予奖励!规定每位普通会员均可参加!次摸奖游戏1每位银卡会员均可参加#次摸奖游戏1每位金卡会员均可参加1次摸奖游戏!每次摸奖的结果相互独立"! 以方案#的奖励金的数学期望为依据$请你预测哪一种方案投资较少0 并说明理由!
时&()!%"*$&当%)
槡##&#
时&()!%"-$&所以(!%",(
槡# #
1#槡#&则'#槡#&故选 /!
+!/!$解析%设轴截面的中心角为#&由条件可知-

湖南省长沙市长郡中学2020年高三第七次月考文科数学试题(含解析)

2019-2020学年高三第二学期月考（文科）数学试卷一、选择题（共12小题）1.若集合{||2|2}A x x x =+=+，{}2|9=<B x x ，则A B =I （） A. ()3,3-B. (2,3)-C. (3,2]-D. [2,3)- 2.已知实数a ，b 满足11a bi i =+-（i 为虚数单位）则复数z a bi =+的共轭复数为（） A. 12i - B. 2i - C. 2i + D. 12i +3.设曲线C 为双曲线，则“C 的方程为221x y -=”是“C 的渐近线方程为y x =±”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件4.如果函数()f x 的图象与函数()x g x e =的图象关于直线y x =对称，则2(4)f x x -的单调递增区间为（）A. (0,)+∞B. (2,)+∞C. (0,2)D. (2,4)5.下边的茎叶图记录的是甲、乙两个班级各5名同学在一次数学小题训练测试中的成绩（单位：分，每题5分，共16题）．已知两组数据的平均数相等，则x 、y 的值分别为（）A. 0，0B. 0，5C. 5，0D. 5，56.《九章算术》是中国古代张苍，耿寿昌所撰写的一部数学专著，成书于公元一世纪左右，内容十分丰富．书中有如下问题：“今有圆堢瑽，周四丈八尺，高一丈一尺，问积几何？答曰：二千一百一十二尺．术曰：周自相乘，以高乘之，十二而一．”这里所说的圆堢瑽就是圆柱体，它的体积112V =⨯（底面的圆周长的平方⨯高），则该问题中的体积为估算值，其实际体积（单位：立方尺）应为（）A. 528πB. 6336πC. 704πD.2112π7.已知向量(1,1)a=-r，OA a b=-u u u r rr，OB a b=+u u u r rr，若OABV是以O为直角顶点的等腰直角三角形，则OABV的面积为（）．A. 1B. 2C. 2D. 228.如图所示，在平面直角坐标系中，角α和角β均以Ox为始边，终边分别为射线OA和OB，射线OA，OC与单位圆的交点分别为34,55A⎛⎫⎪⎝⎭，(1,0)C-．若6BOCπ∠=，则cos()βα-的值是（）A.343-B.34310+C.433-D.43310+9.在棱长为1的正方体1111ABCD A B C D-中，E，F分别为线段CD和11A B上的动点，且满足1CE A F=，则四边形1D FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A. 有最小值32B. 有最大值52C. 为定值3D. 为定值210.为了解学生课外使用手机的情况，某研究学习小组为研究学校学生一个月使用手机的总时间，收集了500名学生2019年12月课余使用手机的总时间（单位：小时）的数据．从中随机抽取了50名学生，将数据进行整理，得到如图所示的频率分布直方图．已知这50人中，恰有2名女生的课余使用手机总时间在[18,20]区间，现在从课余使用手总时间在[18,20]样本对应的学生中随机抽取2人，则至少抽到1名女生的概率为（）A. 25B. 710C. 815D. 71511.已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为A. 16B. 14C. 12D. 1012.如图，函数sin f x A x ωϕ=+（）（）（其中00||2A ωϕπ≤＞，＞，）与坐标轴的三个交点P Q R 、、满足204P PQR M π∠=(，)，，为QR 的中点，25PM =，则A 的值为（）A. 1633B. 833C. 8D. 16二、填空题13.已知数列{}n a 满足1(1)n n na n a +=+，且612a =，则12a =__________．14.已知直线3450x y ++=与圆222:()0O x y r r +=>相交于A ，B 两点，且120AOB ∠=︒，则r =__________．15.在平行四边形ABCD 中，BD CD ⊥，AB BD ⊥，2AB CD ==，22BD =．沿BD 把ABD △翻折起来，形成三棱锥A BCD -，且平面ABD ⊥平面BCD ，则该三棱锥外接球的体积为__________．16.设函数eln ,0()2020,0x x f x x x x ⎧>⎪=⎨⎪-⎩…，函数2()[()]()2g x f x mf x =-+，若函数()g x 恰有4个零点，则整数m 的最小取值为__________．三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.第17〜21题为必考题，每个试题考生都必须作答.第22，23题为选考题，考生根据要求作答.（一）必考题：共60分.17.已知公差不为零的等差数列{}n a ，满足37a =，且11a -，21a -，41a -成等比数列．（1）求{}n a 的通项公式；（2）在平面直角坐标系中，设(),k k A k a ，(,0)k B k ，*k N ∈，记以k A ，k 1A +，k B ，1k B +四点为顶点的四边形面积为k S ，求1321n S S S -+++…．18.如图所示，四棱柱1111ABCD A B C D -中，底面ABCD 为直角梯形，AB CD ∥，AB BC ⊥，平面ABCD ⊥平面11ABB A ，160BAA ∠=︒，1236AB AA BC CD ====．（1）求该四棱柱的体积；（2）在线段1DB 上是否存在点M ，使得CM ∥平面11DAA D ？若存在，求1DM DB 的值；若不存在，说明理由．19.已知ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，且满足tan 2tan C B =-．（1）证明：2223a c b =-；（2）若cos 9A =，且ABC V的，求c ．20.已知函数21()2x f x ax e b =-+．（1）若该函数在(1,(1))f 处的切线为y ex =，求,a b 的值；（2）若该函数在1x ，2x 处取得极值()120x x <<，且213x x …，求实数a 的取值范围． 21.已知椭圆2222:1(0)x y C a b a b +=>>的x 轴交于点1A ，2A ，过x 轴上一点Q 引x 轴的垂线，交椭圆C 于点1P ，2P ，当Q 与椭圆右焦点重合时，121PP =．（1）求椭圆C 的方程；（2）设直线11A P 与直线22A P 交于点P ，是否存在定点M 和N ，使||PM PN ||-||为定值．若存在，求M 、N 点的坐标；若不存在，说明理由．（二）选考题：共10分.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分.选修4-4：坐标系与参数方程22.已知过点()0,0P x 的直线l 的倾斜角为6π，以平面直角坐标系的原点为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos p θ=．（1）求曲线C 的直角坐标方程并写出直线l 的一个参数方程；（2）若直线l 和曲线C 交于A 、B 两点，且||||2PA PB ⋅=，求实数0x 的值．选修4-5：不等式选讲23.设函数()|21|f x x =-．（1）若函数()()F x f x ax =+有最小值，求a 的取值范围；（2）若关于x 的不等式()|21|||f x x x m +-+„的解集为A ，且3,24A ⎡⎤⊆⎢⎥⎣⎦，求实数m 的取值范围．一、选择题（共12小题）1.若集合{||2|2}A x x x =+=+，{}2|9=<B x x ，则A B =I （） A. ()3,3-B. (2,3)-C. (3,2]-D. [2,3)-【答案】D【解析】【分析】首先确定集合,A B 中的元素，再由交集定义求解．【详解】由题意{|2}A x x =-…，{|33}B x x =-<<，∴[2,3)A B ⋂=-，故选：D ．【点睛】本题考查集合的交集运算，解题关键是确定集合中的元素． 2.已知实数a ，b 满足11a bi i =+-（i 为虚数单位）则复数z a bi =+的共轭复数为（） A. 12i - B. 2i -C. 2i +D. 12i + 【答案】B【解析】【分析】已知等式变形为两个复数相等，由复数相等的定义求出,a b ，得z 后可得其共轭复数．【详解】由题意,a b ∈R ，且(1)(1)(1)(1)a i bi b b i =-+=++-，则11a b b =+⎧⎨=⎩，21a b =⎧⎨=⎩， ∴2z i =+，2z i =-，故选：B ．【点睛】本题考查复数的乘除法的定义，考查复数相等的共轭复数的概念，掌握复数相关的定义是解题基础．3.设曲线C 为双曲线，则“C 的方程为221x y -=”是“C 的渐近线方程为y x =±”的（） A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件【答案】A【解析】【分析】根据充分必要条件的定义判断．【详解】221x y -=的渐近线方程为y x =±，而渐近线为y x =±时，C 方程不一定为221x y -=，故选：A ．【点睛】本题考查充分必要条件的判断，考查双曲线的渐近线，掌握双曲线的渐近线的概念是解题关键．4.如果函数()f x 的图象与函数()x g x e =的图象关于直线y x =对称，则2(4)f x x -的单调递增区间为（）A. (0,)+∞B. (2,)+∞C. (0,2)D. (2,4)【答案】C【解析】【分析】根据反函数知识求出()f x ，得复合函数2(4)f x x -，由对数型复合函数的性质可求得增区间．【详解】由題知，()ln f x x =，故()()224ln 4f x xx x -=-，定义域为(0,4)，(0,4)x ∈时，24y x x =-在(0,2)是递增，∴2(4)f x x -的单调递增区间为(0,2)．故选：C ．【点睛】本题考查反函数的概念，考查对数型复合函数的单调性，掌握对数函数性质是解题关键． 5.下边的茎叶图记录的是甲、乙两个班级各5名同学在一次数学小题训练测试中的成绩（单位：分，每题5分，共16题）．已知两组数据的平均数相等，则x 、y 的值分别为（）A. 0，0B. 0，5C. 5，0D. 5，5【答案】B【解析】【分析】由茎叶图得各个数据，由平均数相等可得,x y 的关系5x y +=，从而可得结论【详解】两组数据和相等，则802757065807027570x y ⨯++++=+⨯+++，即5x y +=，则0x =，5y =．只有B 适合．故选：B ．【点睛】本题考查茎叶图，考查平均数，正确认识茎叶图是解题关键．6.《九章算术》是中国古代张苍，耿寿昌所撰写的一部数学专著，成书于公元一世纪左右，内容十分丰富．书中有如下问题：“今有圆堢瑽，周四丈八尺，高一丈一尺，问积几何？答曰：二千一百一十二尺．术曰：周自相乘，以高乘之，十二而一．”这里所说的圆堢瑽就是圆柱体，它的体积112V =⨯（底面的圆周长的平方⨯高），则该问题中的体积为估算值，其实际体积（单位：立方尺）应为（）A. 528πB. 6336πC. 704πD. 2112π 【答案】B【解析】【分析】求出底面半径，由圆柱体积公式计算，【详解】设r 为底面半径，则248r π=，24r π=，又11h =， ∴22246336()11V r h ππππ==⨯⨯=．故选：B ．【点睛】本题考查圆柱的体积，解题关键是求出底面半径，得底面面积，再由体积公式可得．7.已知向量(1,1)a =-r ，OA a b =-u u u r r r ，OB a b =+u u u r r r ，若OAB V 是以O 为直角顶点的等腰直角三角形，则OAB V 的面积为（）．A. 1B. 2 D. 【答案】B【解析】【分析】OAB V 为等腰直角三角形，则有||||OA OB =u u u r u u u r 及OA OB ⋅u u u r u u u r ，【详解】由题知，||||0OA OB a b a b a b =⇒+=-⇒⋅=u u u r u u u r r r r r r r ，220||||OA OB a b a b ⋅=-=⇒=u u u r u u u r r r r r ，故||||2==u u u r u u u r OA OB ，则2OAB S =△，故选：B ．【点睛】本题考查向量的数量积，掌握向量的模、向量的垂直与数量积的关系是解题关键．8.如图所示，在平面直角坐标系中，角α和角β均以Ox 为始边，终边分别为射线OA 和OB ，射线OA ，OC 与单位圆的交点分别为34,55A ⎛⎫ ⎪⎝⎭，(1,0)C -．若6BOC π∠=，则cos()βα-的值是（）343- B. 34310+ 433- D. 43310+ 【答案】C【解析】【分析】由三角函数定义得cos ,sin αα，由诱导公式得cos ,sin ββ，再由两角差的余弦公式可求值．【详解】由题知，3cos 5α=，4sin 5α=，cos 32β=-，1sin 2β=，则334cos()cos cos sin sin 10βαβαβα-=+=433-= 故选：C ．【点睛】本题考查三角函数的定义，考查诱导公式和两角差的余弦公式，解题关键是掌握两角差的余弦公式．9.在棱长为1的正方体1111ABCD A B C D -中，E ，F 分别为线段CD 和11A B 上的动点，且满足1CE A F =，则四边形1D FBE 所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A. 有最小值32B. 有最大值52C. 为定值3D. 为定值2【答案】D【解析】【分析】分别在后，上，左三个平面得到该四边形的投影，求其面积和即可．【详解】依题意，设四边形D1FBE的四个顶点在后面，上面，左面的投影点分别为D'，F'，B'，E'，则四边形D1FBE 在上面，后面，左面的投影分别如上图．所以在后面的投影的面积为S后=1×1=1，在上面的投影面积S上=D'E'×1=DE×1=DE，在左面的投影面积S左=B'E'×1=CE×1=CE，所以四边形D1FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和S=S后+S上+S左=1+DE+CE=1+CD=2．故选D．【点睛】本题考查了正方体中四边形的投影问题，考查空间想象能力．属于中档题．10.为了解学生课外使用手机的情况，某研究学习小组为研究学校学生一个月使用手机的总时间，收集了500名学生2019年12月课余使用手机的总时间（单位：小时）的数据．从中随机抽取了50名学生，将数据进行整理，得到如图所示的频率分布直方图．已知这50人中，恰有2名女生的课余使用手机总时间在[18,20]区间，现在从课余使用手总时间在[18,20]样本对应的学生中随机抽取2人，则至少抽到1名女生的概率为（）A.25B.710C.815D.715【答案】B 【解析】【分析】由频率分布直方图求出在[18,20]区间的学生人数，然后求出抽取2人的总方法数和至少有1名女生的方法数，从而计算出概率．【详解】500.105⨯=，则[18,20]样本对应的学生为5人，即2名女生，3名男生，从中抽取2人有25C =10种方法，至少抽到一名女生有2253C C -=7种方法，概率为710．【点睛】本题考查频率分布直方图，考查古典概型，正确理解频率分布直方图是解题基础，求出至少抽到1名女生所含有的基本事件的数量是解题关键．11.已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A. 16 B. 14C. 12D. 10【答案】A 【解析】设11223344(,),(,),(,),(,)A x y B x y D x y E x y ，直线1l 的方程为1(1)y k x =-，联立方程214(1)y xy k x ⎧=⎨=-⎩，得2222111240k x k x x k --+=，∴21122124k x x k --+=-212124k k +=，同理直线2l 与抛物线的交点满足22342224k x x k ++=，由抛物线定义可知12342AB DE x x x x p +=++++=221222222212121224244416482816k k k k k k k k ++++=++≥+=，当且仅当121k k =-=（或1-）时，取等号. 点睛:对于抛物线弦长问题，要重点抓住抛物线定义，到定点的距离要想到转化到准线上，另外，直线与抛物线联立，求判别式，利用根与系数的关系是通法，需要重点掌握.考查最值问题时要能想到用函数方法和基本不等式进行解决.此题还可以利用弦长的倾斜角表示，设直线的倾斜角为α，则22||sin p AB α=，则2222||πcos sin (+)2p pDE αα==，所以222221||||4(cos sin cos p p AB DE ααα+=+=+ 222222222111sin cos )4()(cos sin )4(2)4(22)16sin cos sin cos sin ααααααααα=++=++≥⨯+=. 12.如图，函数sin f x A x ωϕ=+（）（）（其中00||2A ωϕπ≤＞，＞，）与坐标轴的三个交点P Q R 、、满足204P PQR M π∠=(，)，，为QR 的中点，25PM =，则A 的值为（）1633833C. 8D. 16【答案】A 【解析】【分析】由题意设出(20)0Q a a ,＞，用a 表示出R 点坐标以及M 点坐标，根据25PM =利用距离公式求出Q 坐标，通过五点法求出函数的解析式，即可求出A ．【详解】解：设(2,0),0Q a a >，Q 函数()sin(x+)f x A ϖϕ=（其中0,0,||2A πωφ>>≤）与坐标轴的三个交点P Q R 、、满足4PQR π∠=，∴(0,2a)R -，Q M 为QR 的中点，∴(,)M a a -，PM =Q ，=解得4a =，80Q ∴（，），又20P （，）， 18262T ∴=-=， 2T 12πω∴==，解得6π=ω． Q 函数经过(20)(08)P R -，，，，∴sin 206 sin086A A πϕπϕ⎧⎛⎫⨯+= ⎪⎪⎪⎝⎭⎨⎛⎫⎪⨯+=- ⎪⎪⎝⎭⎩，||2πϕ≤Q ，,3πϕ∴=-，解得A =，故选A ．【点睛】本题考查由sin x y A ωϕ=+（）的部分图象确定其解析式，求得Q 点与P 点的坐标是关键，考查识图、运算与求解能力，属于中档题．二、填空题13.已知数列{}n a 满足1(1)n n na n a +=+，且612a =，则12a =__________．【答案】24 【解析】【分析】已知式变形为11n n a a n n +=+，得一常数列{}n an，从而易得n a ，得12a【详解】由题知11n n a a n n +=+，故626n a an ==，故1224a =．故答案为：24．【点睛】本题考查求数列的通项公式，解题关键是已知等式变形后构造出一个常数列．14.已知直线3450x y ++=与圆222:()0O x y r r +=>相交于A ，B 两点，且120AOB ∠=︒，则r =__________．【答案】2 【解析】【分析】求出圆心到弦的距离，在等腰三角形中易求得半径．【详解】直线到圆心距离1d ==，由120AOB ∠=︒，故22r d ==．故答案为：2．【点睛】本题考查直线与圆相交问题．解题关键是掌握垂径定理．15.在平行四边形ABCD 中，BD CD ⊥，AB BD ⊥，2AB CD ==，BD =．沿BD 把ABD △翻折起来，形成三棱锥A BCD -，且平面ABD ⊥平面BCD ，则该三棱锥外接球的体积为__________．【答案】323π【解析】【分析】由于题中的垂直及折叠后的平面垂直，因此把三棱锥可补形为长、宽、高分别为2，2的长方体，其外接圆直径易得，即半径易得．由此可求得体积．【详解】该三棱锥可补形为长、宽、高分别为，2，2的长方体，故其外接圆直径为24R ==，2R =，故体积为343233V R ππ==．故答案为：323π．【点睛】本题考查求球的体积，解题关键是把几何体补成一个长方体，长方体的对角线就是外接球直径．16.设函数eln,0 ()2020,0xxf x xx x⎧>⎪=⎨⎪-⎩…，函数2()[()]()2g x f x mf x=-+，若函数()g x恰有4个零点，则整数m的最小取值为__________．【答案】4【解析】【分析】作出()f x的图象，结合已知条件得方程2()20g t t mt=-+=有两正根1t，2t，且1(0,1)t∈，212(2,)tt=∈+∞，可得m的取值范围．【详解】作出()f x的图象，易知要使()0g t=有两正根1t，2t，且1(0,1)t∈，212(2,)tt=∈+∞，故112(3,)m tt=+∈+∞，故m的最小整数值为4．故答案为：4．【点睛】本题考查函数零点个数，考查转化思想，通过作出函数图象，问题转化二次方程根的分布问题，由此可得m的取值范围．三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.第17〜21题为必考题，每个试题考生都必须作答.第22，23题为选考题，考生根据要求作答.（一）必考题：共60分.17.已知公差不为零的等差数列{}n a ，满足37a =，且11a -，21a -，41a -成等比数列．（1）求{}n a 的通项公式；（2）在平面直角坐标系中，设(),k k A k a ，(,0)k B k ，*k N ∈，记以k A ，k 1A +，k B ，1k B +四点为顶点的四边形面积为k S ，求1321n S S S -+++…．【答案】（1）21n a n =+（2）()213212n S S S n n -+++=+…【解析】【分析】（1）由11a -，21a -，41a -成等比数列求得公差d ，可得通项公式；（2）求出四边形面积k S ，可得()132112212n n S S S a a a -+++=+++L …，由等差数列前n 项和公式可得．【详解】（1）设{}n a 的公差为d ，则1312162a a d d -=--=-，216a d -=-，416a d -=+，依题意，()()()2214111a a a -=--，即2(6)(62)(6)d d d -=-+，化简得：220d d -=，又0d ≠，故2d =．3(3)21n a a n d n =+-=+．（2）由题知，四边形11k k k k A A B B ++为直角梯形，故()111122k k k k k a a S a a +++=+⋅=，故()()2132112211(341)22222n n n nS S S a a a n n -++⋅+++=+++=⋅=+L …．【点睛】本题考查等差数列的通项公式，考查等差数列前n 项和公式，及等比数列的性质．掌握等差数列通项公式和前n 项和公式是解题基础．18.如图所示，四棱柱1111ABCD A B C D -中，底面ABCD 为直角梯形，AB CD ∥，AB BC ⊥，平面ABCD ⊥平面11ABB A ，160BAA ∠=︒，1236AB AA BC CD ====．（1）求该四棱柱的体积；（2）在线段1DB 上是否存在点M ，使得CM ∥平面11DAA D ？若存在，求1DMDB 的值；若不存在，说明理由．【答案】（1）363（2）存在，113DM DB = 【解析】【分析】（1）过1A 作1A H AB ⊥于点H ，由面面垂直求出棱柱的高，然后由体积公式计算体积；（2）连结1DA ，在1DB 上取113DM DB =，在1DA 上取113DN DA =，连接MN ．可证得DNMC 是平行四边形，从而得线线平行后得线面平行．【详解】（1）过1A 作1A H AB ⊥于点H ,由平面ABCD ⊥平面1ABB A 知，1A H ⊥平面ABCD ，133A H =故1111-=ABCD A B D C V S 梯形11(26)3333632⋅=⨯+⨯⨯=ABCD A H （2）当113DM DB =时，CM ∥平面11DAA D ，证明：连结1DA ，在1DB 上取113DM DB =，在1DA 上取113DN DA =，连接MN ．则11MN A B ∥，且2MN =．则MN DC =∥，故四边形CMND 为平行四边形．故CM DN ∥，CM ⊄平面11AA D D ，DN ⊂平面11AA D D ．故CM ∥平面11AA D D ．【点睛】本题考查求棱柱的体积，考查线面平行和证明．求体积时，利用面面垂直得线面垂直，从而得棱柱的高．19.已知ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，且满足tan 2tan CB=-．（1）证明：2223a c b =-；（2）若cos 9A =，且ABC V，求c ．【答案】（1）见解析（2）c =或【解析】【分析】（1）已知等式切化弦后应用正弦定理和余弦定理化角为边，进行翴的恒等变形可得；（2）由余弦定理及（1）的结论得b =或b =，由面积可得bc ，然后可求得c ．【详解】（1）证明：由题知，tan 2tan C B =-，即sin cos 2sin cos C B B C ⋅=-⋅，由正弦定理和余弦定理知，222222222a c b a b c c b ac ba+-+-⋅=-⋅，即222222222a c b a b c +-=--+，即2223a c b =-．（2）由余弦定理知：2222cos b c a bc A +-=，又2223a c b =-，代入消去a得，22203b c-+=，即(2)03b b⎛⎫--=⎪⎪⎝⎭．即b=或3b c=．又sin(0,))A Aπ=∈，且1sin2ABCS bc A==△，ⅰ．当2b c=时，则2182⋅=c=；ⅱ．当3b c=时，2183c⋅=c=．故c=或【点睛】本题考查正弦定理和余弦定理，考查三角形面积公式．属于中档题．20.已知函数21()2xf x ax e b=-+．（1）若该函数在(1,(1))f处的切线为y ex=，求,a b的值；（2）若该函数在1x，2x处取得极值()120x x<<，且213xx…，求实数a的取值范围．【答案】（1）2a e=，b e=．（2）ln3⎡⎫+∞⎪⎢⎪⎣⎭【解析】【分析】（1）求出导函数，由导数几何意义可得,a b；（2）由极值点得1212x xe eax x==，研究()xeh xx=的性质得1201x x<<<，结合213x x…．分类：113x<≤和1113x<<．前者由()h x的单调性可得a的最小值，后者转化为1213x x<<，则由单调性121(3)()()h x h x h x <=，这样可得1x 的取值范围，然后可求得a 的范围．最后总结可得结论．【详解】（1）由题知：()x f x ax e '=-，故()f x 在(1,(1))f 处的切线方程为：()(1)2a y a e x e b =--+-+，即()2a y a e xb =--+．易知：2a e =，b e =．（2）由题知：1x ，2x 为()f x 的极值点，则12120x x ax e ax e -=-=．即1212x x e e a x x ==．令()xe h x x=，2(1)()x e x h x x '-=．故()h x 在(0,1)上单调递减，在(1,)+∞上单调递增．则1201x x <<<，且213x x …． ⅰ．若1103x <„，由2(1,)x ∈+∞，故123x x >， ()h x 在(0,1)单调递减，故13a h ⎛⎫= ⎪⎝⎭…． ⅱ．若1113x <<，此时1213x x <„，()h x 在(1,)+∞单调递增，故()1213112133x x x e e e h x x x x ==„，即123x e „，11ln32x „．此时，ln 32ln 3ln 322e a h ⎛⎫== ⎪⎝⎭… 故实数a的取值范围为⎫+∞⎪⎪⎣⎭．【点睛】本题考查导数的几何意义，考查用导数研究函数的单调性、函数的极值．由不等式恒成立转化为求函数的最小值．解题时注意极值点到a 的关系．21.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2，与x 轴交于点1A ，2A ，过x 轴上一点Q 引x 轴的垂线，交椭圆C 于点1P ，2P ，当Q 与椭圆右焦点重合时，121PP =．（1）求椭圆C 的方程；（2）设直线11A P 与直线22A P 交于点P ，是否存在定点M 和N ，使||PM PN ||-||为定值．若存在，求M 、N 点的坐标；若不存在，说明理由．【答案】（1）2214x y +=（2）存在，M为(0)，N ．【解析】【分析】（1）12PP 是椭圆的通径，由此已知条件可表示为,,a b c 的两个等式，结合222a b c =+可求得,a b ，得椭圆方程；（2）设P 点坐标为(),P P x y ，()100,P x y ，()200,P x y -，不妨设1(2,0)A-，2(2,0)A ．P 在直线11A P 可得00,,,P P x y x y 的关系，同理由P 在直线22A P 又得一关系式，消去00,x y 可得P 点轨迹方程，轨迹是双曲线，由双曲线定义可作答．【详解】（1）由题知：2221c a b a⎧=⎪⎪⎨⎪=⎪⎩，解得21a b c ⎧=⎪=⎨⎪=⎩，故椭圆C 的方程为2214x y +=．（2）设P 点坐标为(),P P x y ，()100,P x y ，()200,P x y -，不妨设1(2,0)A -，2(2,0)A ．则P ，1P ，1A 三点共线，0022P P y y x x =++，① 同理：0022P P y y x x -=--，② ⨯①②得：22022044P P y y x x -=--，又1P 在椭圆上，()2200144y x =-，代入整理得：2214P P x y -=．即P 点的轨迹为双曲线2214x y -=，取M 、N 为该双曲线的左、右焦点．即(M，N ．此时||||||4PM PN -=为定值，故M为(0)，N ．【点睛】本题考查求椭圆的标准方程，考查直线与椭圆相交的定值问题．本题解法是求出动点P 的轨迹方程，由轨迹方程确定图形为双曲线，由双曲线定义可得结论．（二）选考题：共10分.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分.选修4-4：坐标系与参数方程22.已知过点()0,0P x 的直线l 的倾斜角为6π，以平面直角坐标系的原点为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos p θ=．（1）求曲线C 的直角坐标方程并写出直线l 的一个参数方程；（2）若直线l 和曲线C 交于A 、B 两点，且||||2PA PB ⋅=，求实数0x 的值．【答案】（1）2220x x y -+=．012x x y t ⎧=+⎪⎪⎨⎪=⎪⎩，（t 为参数）．（2）01x =±【解析】【分析】（1）由公式cos sin x y ρθρθ=⎧⎨=⎩可得C 的直角坐标方程，由一点的坐标及倾斜角可得直线的参数方程；（2）由（1）中参数方程几何意义，把直线参数方程代入曲线C 的直角坐标方程可得12t t ，12t t PA PB =，由此再求得0x【详解】（1）由2cos ρθ=，22cos ρρθ=．得曲线C 的方程为：222x y x +=，即2220x x y -+=．直线l的参数方程可为：012x x y t ⎧=⎪⎪⎨⎪=⎪⎩，（t 为参数）．（2）把直线l 的参数方程代入2220x x y -+=得：2200020t t x x ++-=．由>0∆，得013x -<<．设A 、B 两点对应的参数分别为1t 、2t ，则12||||2t t PA PB =⋅=．即20022x x -=，即20022x x -=±．解得：01x =±又0(1,3)x ∈-，故01x =【点睛】本题考查极坐标方程与直角坐标方程的互化，考查直线的参数方程．掌握直线的标准参数方程中参数t 的几何意义是解题关键．选修4-5：不等式选讲23.设函数()|21|f x x =-．（1）若函数()()F x f x ax =+有最小值，求a 的取值范围；（2）若关于x 的不等式()|21|||f x x x m +-+„的解集为A ，且3,24A ⎡⎤⊆⎢⎥⎣⎦，求实数m 的取值范围．【答案】（1）[2,2]a ∈-（2）11,04⎡⎤-⎢⎥⎣⎦【解析】【分析】（1）分类讨论去绝对值符号得()F x ，分析其有最小值的条件是左减右增，于是可得a 的范围．（2）由不等式在3[,2]4上恒成立得||2x m +„在3,24x ⎡⎤∈⎢⎥⎣⎦上恒成立．转化为22x m -+剟．max min (2)(2)x m x ---+剟，即可得结论．【详解】（1）1(2)1,2()()1(2)1,2a x x F x f x ax a x x ⎧+-⎪⎪=+=⎨⎪-+<⎪⎩…，使()F x 有最小值的充要条件为2020a a +⎧⎨-⎩…„．即[2,2]a ∈-．（2）由题知：|21||21|||x x x m -+-+„在3,24⎡⎤⎢⎥⎣⎦上恒成立．即||21(21)x m x x ++--„．即||2x m +„3,24x ⎡⎤∈⎢⎥⎣⎦上恒成立．则22x m -+剟．故max min (2)(2)x m x ---+剟．得1104m -剟．故实数m 的取值范围为11,04⎡⎤-⎢⎥⎣⎦．【点睛】本题考查含绝对值的函数与不等式，解题时可根据绝对值的定义分类去绝对值符号后再分析求解．。

湖南省雅礼中学2020届高三第七次月考(理数PDF版)理数试题

雅礼中学2020届高三月考试卷（七）数学（理科）第I 卷一、选择题:本大题共12个小题，每小题5分,共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1.设集合{|1},A y y x B ==-={x|(x+1)(x-2)<0},则A∩B= A.[1,2)B.(-1,1]C.[0,2)D.(-1,2)2.已知复数z 满足0,z z -=且4z z ⋅=，则z= A.2B.2iC.±2iD.±23.下列说法正确的是 A."若,6πα=则1sin 2α=的否命题是“若6πα=，则1sin 2α≠” B.若命题p,¬q 均为真命题，则命题p ∧q 为真命题C.命题p:“2000,50x x x ∃∈-->R ”的否定为¬p:“2,50x x x ∀∈--≤R ”D.在△ABC 中“2C π=”是"sinA=cosB”的充要条件4.已知向量a 、b 满足|a |1,||2,|2|3|2|==+=-b a b a b ,则a 与b 夹角为 A.30°B.45°C.60°D.120°5.已知3cos()63πα+=,则sin(2)6πα-的值为 1.3A1.3B -22.3C22.3D -6.已知函数1(),ln 1f x x x =--则y=f(x)的图象大致为7.如果将函数55y x =x 的图象向右平移(0)2πθθ<<)个单位得到函数y=3sinx+acosx(a<0)的图象,则tanθ的值为1.3A1.2B C.2 D.38.现有10名学生排成一-排,其中4名男生,6名女生,若有且只有3名男生相邻排在一起，则不同的排法共有()种.2267.A A A3247.B A A322367.C A A A362467.D A A A9.已知△ABC 外接圆的半径R=2,且2sin .2AA =，则△ABC 周长的取值范围为.4]A.(4,B4C +.(4D +10.已知双曲线C 2222:1(0,0)x y a b a b-=>>的左、右焦点分别为12,,F F 过原点的直线与双曲线C 交于A,B 两点,若2260,AF B ABF ︒∠=∆2,，则双曲线的离心率为.2A.3B C.2D11.已知()f x '是函数f(x)的导函数,且对任意的实数x 都有()(21)xf x e x '=++f(x),f(0)=-2,则不等式()4x f x e <的解集为A.(-2,3)B.(-3,2)C.(-∞,-3)∪(2,+∞)D.(-∞,-2)∪(3,+∞)12.在三棱锥S-ABC 中,AB ⊥BC,2,AB BC SA SC ====二面角S-AC-B 的余弦值是3-,若S,A,B,C 都在同一球面上，则该球的表面积是A.6πB.8πC.12πD.18π第II 卷本卷包括必考题和选考题两部分.第13~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.二、填空题:本大题共4小题，每小题分,共20分.13.设随机变量2~(3,)N ξσ,若P(ξ≥7)=0.16,则P(-1≤ξ≤7)=___.14.向曲线22|||x y x y +=+|所围成的区域内任投一点,这点正好落在21y x =-与两坐标轴非负半轴所围成区域内的概率为___.15.过直线l:x+y=3上任一点P 向圆22:1C x y +=作两条切线,切点分别为A,B,线段AB 的中点为Q,则点Q 到直线l 的距离的取值范围为___.16.定义在实数集R 上的偶函数f(x)满足(2)2f x +=f(2021)=___.三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)设等差数列{}n a 的前n 项和为,n S ,首项11,a =，且202020173.20202017S S -=数列{}n b 的前n 项和为,n T 且满足*2().n n T b n =-∈N(1)求数列{}n a 和{}n b 的通项公式; (2)求数列{}2n na b 的前m 项和.'n S18. (本小题满分12分)如图,三棱锥P-ABC 中,平面PAB ⊥平面ABC, PA=PB,∠APB=∠ACB=90° ,点E,F 分别是棱AB,PB 的中点,点G 是△BCE 的重心.(1)证明:GF//平面PAC;(2)若GF 与平面ABC 所成的角为60°,求二面角B-AP-C 的余弦值.19. (本小题满分12分)在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶某村100户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标x.将指标x 按照[0,0.2),[0.2,0.4),[0.4,0.6),[0.6,0.8),[0.8,1.0]分成五组，得到如图所示的频率分布直方图.规定若0≤x<06,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”;当0≤x<0.2时,认定该户为"亟待帮住户”.工作组又对这100户家庭的受教育水平进行评测,家庭受教育水平记为“良好”与“不好”两种.(1)完成下面的列联表,并判断是否有95%的把握认为绝对贫困户数与受教育水平不好有关:(2)上级部门为了调查这个村的特困户分布情况,在贫困指标处于[0,0.4)的贫困户中,随机选取两户,用X 表示所选两户中“亟待帮助户”的户数,求X的分布列和数学期望EX.20. (本小题满分12分)已知椭圆2222:1(0)x yC a ba b+=>>的离x3点2)M在椭圆C上,焦点为12,,F F圆O的直径为12.F F(1)求椭圆C及圆O的标准方程;(2)设直线l与圆O相切于第一象限内的点P, 且直线l与椭圆C交于A,B两点.记△OAB的面积为S,证明: 3.S<21.(本小题满分12分) 已知函数f(x)=1+x-2sinx,x ＞0. (1)求f(x)的最小值; (2)证明:2().xf x e ->请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做，则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C的参数方程为,x y αα⎧=⎪⎨=⎪⎩(α为参数),以坐标原点O 为极点,以x 轴正半轴为极轴，建立极坐标系，直线l 的极坐标方程为cos() 2.3πρθ+=(1)求C 的普通方程和l 的直角坐标方程;(2)直线l 与x 轴的交点为P,经过点P 的直线m 与曲线C 交于A,B 两点,若|PA ||PB +=求直线m 的倾斜角.23.(本小题满分10分)选修4-5:不等式选讲已知函数f(x)=2|x+1|+|x-m|(m>--1). (1)若m=3,求不等式f(x)>7的解集;(2)若0,x ∃∈R 使得0()2f x <成立,求实数m 的取值范围.。

湖南省长沙市雅礼中学高三数学月考试题(七)文(含解析)

湖南省长沙市雅礼中学高三数学月考试题（七）文（含解析）数学（文科）注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2. 回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3. 回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4. 考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{1,2,3,4}A =，{}0,1,2,4,5B =，全集B A U ⋃=，则集合)(B A C U 中的元素共有（） A. 3个 B. 4个 C. 5个 D. 6个【答案】A 【解析】【分析】利用交集与并集定义先求B A 与B A ，再利用补集定义求)(B A C U .【详解】由题意得{}0,1,2,3,4,5A B ⋃=，{}1,2,4A B ⋂=，所以(){}0,3,5U C A B ⋂= 故选A.【点睛】理解交集、并集、补集的概念，确定A 、B 中的公共元素、所有元素、B A 的补集中的元素，本题考查集合的基本运算.2.若复数12iz i+=，则z 等于（） A. 2i -- B. 2i -+C. 2i -D. 2i +【答案】D 【解析】【分析】由复数的四则运算，将复数化成bi a z +=的形式，再利用共轭复数的定义可得答案. 【详解】∵()121221i ii z i i ++===--，∴2z i =+. 故选D.【点睛】本题考查复数的计算，同时考查实部和虚部以及共轭复数，当两个复数的实部相等且虚部为相反数时称一个复数是另一个复数的共轭复数，意在考查学生对这一部分知识的掌握水平.3.已知p ：12x +>，q ：x a >，且p ⌝是q ⌝的充分不必要条件，则a 的取值范围是（） A. 1a ≥ B. 1a ≤C. 3a ≥-D. 3a -≤【答案】A 【解析】【分析】首先解不等式x 12+>，求出p ⌝和q ⌝对应的不等式，再根据p ⌝是q ⌝的充分不必要条件，得到二者之间的关系，建立不等关系进而求解.【详解】p ⌝是q ⌝的充分不必要条件的等价命题为q 是p 的充分不必要条件，即q p ⇒，而p ⇒q ，p 化简为1x >或3x <-，所以当1a ≥时，q p ⇒. 故选A.【点睛】本题考查了不等式和充分不必要条件的应用，对于充分不必要条件的考查，首先要根据题设写出命题所表示的不等式的解集，其次根据条件列出不等关系，再解不等式即可.4.在一次数学实验中，运用图形计算器采集到如下一组数据：则x 、y 的函数关系与下列哪类函数最接近？（其中a 、b 为待定系数）（）A. y a bx =+B. xy a b =+ C. b ax y +=2D. b y a x=+【答案】B 【解析】【分析】可以逐一验证,若选A ，则y 的值增加幅度应比较接近；若选C ，则x=1,-1的值应比较接近；若选D ，则x=0不可取.【详解】∵对应数据显示该函数是增函数，且增幅越来越快，∴A 不成立； ∵C 是偶函数，∴1x =±的函数值应该相等，∴C 不成立； ∵0x =时，bx无意义，∴D 不成立；对于B ，当0x =时，1y =，∴11a +=，0a =；当1x =时， 2.02y b ==，经验证它与各教据比较接近. 故选B.【点睛】函数模型的选择应充分利用函数的性质，函数的性质主要有函数的定义域、值域、单调性、奇偶性、周期性、图像的对称性等方面.5.若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值为A. 2-B. 2C. 4-D. 4【答案】D 【解析】解：椭圆22162x y +=的右焦点为(2,0)，所以抛物线22y px =的焦点为(2,0)，则4p =，故选D 。

湖南省长沙市雅礼中学2024届高三下学期月考(七)数学试题(含答案与解析)_4591

雅礼中学2024届高三月考试卷（七）数学（时量120分钟，满分150分）注意事项：1.答卷前，考生务必将自己的姓名､考生号､考场号､座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集{}2,4,6,8,10,12U =，{}4,6,8M =，{}8,10N =，则集合{}2,12=（）A. M N ⋃B. M N ⋂C. ()U C M N ⋃D. ()U C M N2. 下列命题正确的是（）A. “ln ln m n <”是“e e m n <”的充分不必要条件B. 命题：0,ln 1x x x ∀>≤-的否定是：0000,ln 1x x x ∃>≥-C. 5πsin cos 2x x ⎛⎫+=- ⎪⎝⎭D. 函数21x y x +=+在()(),11,-∞--+∞ 上是减函数 3. 若复数z 满足|2i ||2i |8z z ++-=，则复数z 在复平面内所对应点的轨迹是（） A 椭圆B. 双曲线C. 圆D. 线段4. 已知D 是ABC 所在平面内一点，3255AD AB AC =+，则（）A. 25BD BC =B. 35BD BC = C. 32BD BC =D. 23BD BC =5. 我们把由0和1组成的数列称为01-数列，01-数列在计算机科学和信息技术领域有着广泛应用，把斐波那契数列{}()12211,n n n n F F F F F F ++===+中的奇数换成0，偶数换成1可得到01-数列{}n a ，记.数列{}n a 的前n 项和为n S ，则100S 的值为（） A. 32B. 33C. 34D. 356. 我国元代瓷器元青花团菊花纹小盏如图所示，撇口，深弧壁，圈足微微外撇，底心有一小乳突.器身施白釉，以青花为装饰，釉质润泽，底足露胎，胎质致密.碗内口沿饰有一周回纹，内底心书有一文字，碗外壁绘有一周缠枝团菊纹，下笔流畅，纹饰洒脱.该元青花团菊花纹小盏口径8.4厘米，底径2.8厘米，高4厘米，它的形状可近似看作圆台，则其侧面积约为（单位：平方厘米）（）12.2≈）A. 34πB. 27πC. 20πD. 18π7. 已知椭圆22221(0)x y a b a b +=>>与双曲线22221(0,0)x y m n m n-=>>有共同的焦点1F ，2F ，且在第一象限内相交于点P ，椭圆与双曲线的离心率分别为1e ，2e ．若123F PF π∠=，则12e e ⋅的最小值是A.12B.C.D.328. 求值：2cos40cos80sin80+=（）A.B.C. D. 二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 某市7天国庆节假期期间的楼房日认购量（单位：套）与日成交量（单位：套）的折线图如下图所示，小明同学根据折线图对这7天的日认购量与日成交量作出如下判断，则下列结论正确的是（）A. 日认购量与日期正相关B. 日成交量的中位数是26C. 日成交量超过日平均成交量的有2天D. 10月7日日认购量的增量大于10月7日日成交量的增量10. 抛物线的弦与弦的端点处的两条切线形成的三角形称为阿基米德三角形，该三角形以其深刻的背景､丰富的性质产生了无穷的魅力.设,A B 是抛物线2:4C x y =上两个不同的点，以()()1122,,,A x y B x y 为切点的切线交于P 点.若弦AB 过点()0,1F ，则下列说法正确的有（） A. 124x x =-B. 若12x =，则A 点处的切线方程为10x y --=C. 存在点P ，使得0PA PB ⋅>D. PAB 面积的最小值为411. 已知函数()()()1e 1xf x x x =+--，则下列说法正确的有A. ()f x 有唯一零点B. ()f x 无最大值C. ()f x 在区间()1,+∞上单调递增D. 0x =为()f x 的一个极小值点三､填空题：本题共3小题，每小题5分，共15分.12. 雅礼中学将5名学生志愿者分配到街舞社､戏剧社､魔术社及动漫社4个社团参加志愿活动，每名志愿者只分配到1个社团､每个社团至少分配1名志愿者，则不同分配方案共有__________种13. 已知圆221:(2)1C x y +-=与圆222:(2)(1)4C x y -+-=相交于,A B 两点，则()1211C C C A C B =⋅+__________.的14. 某同学在学习和探索三角形相关知识时，发现了一个有趣性质：将锐角三角形三条边所对的外接圆的三条圆弧（劣弧）沿着三角形的边进行翻折，则三条圆弧交于该三角形内部一点，且此交点为该三角形的垂心（即三角形三条高线的交点）.如图，已知锐角ABC 外接圆的半径为2，且三条圆弧沿ABC 三边翻折后交于点P .若3AB =，则sin PAC ∠=___________；若::6:5:4AC AB BC =，则PA PB PC ++的值为___________.四､解答题：本题共5小题，共77分.请在答题卡指定区域内作答.解答时应写出文字说明､证明过程或演算步骤.15. 人工智能正在改变我们的世界，由OpenAI 开发的人工智能划时代标志的ChatGPT 能更好地理解人类的意图，并且可以更好地回答人类的问题，被人们称为人类的第四次工业革命.它渗透人类社会的方方面面，让人类更高效地生活.现对130人的样本使用ChatGPT 对服务业劳动力市场的潜在影响进行调查，其数据的统计结果如下表所示：服务业就业人数的ChatGPT 应用的广泛性减少增加合计广泛应用 60 10 70 没广泛应用 40 20 60 合计 10030130（1）根据小概率值0.01α=独立性检验，是否有99%的把握认为ChatGPT 应用的广泛性与服务业就业人数的增减有关？（2）现从“服务业就业人数会减少”的100人中按分层随机抽样的方法抽取5人，再从这5人中随机抽取3人，记抽取的3人中有X 人认为人工智能会在服务业中广泛应用，求X 的分布列和均值.的的附：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α 0.10.05 0.01x α 2.706 3841 6.63516. 如图，在四棱锥P ABCD -中，PA ⊥平面,2,,120ABCD PA AB BC AD CD ABC ∠===== .（1）求证：平面PAC ⊥平面PBD；（2）若点M 为PB 的中点，线段PC 上是否存在点N ，使得直线MN 与平面PAC 所成角的正弦值为.若存在，求PN PC 的值；若不存在，请说明理由.17. 如图，圆C 与x 轴相切于点()2,0T ，与y 轴正半轴相交于,M N 两点（点M 在点N 的下方），且3MN =．(1)求圆C 的方程；(2)过点M 任作一条直线与椭圆22184x y +=相交于两点A B 、，连接AN BN 、，求证：ANM BNM ∠=∠．18. 已知函数()()2ln 3f x x x ax x a =--∈R ..（1）若1x =是函数()f x 的一个极值点，求实数a 的值；（2）若函数()f x 有两个极值点12,x x ，其中12x x <， ①求实数a 的取值范围；②若不等式122ln 31ax k x k +>+恒成立，求实数k 的取值范围.19. 对于无穷数列{}n c ，若对任意*,m n ∈N ，且m n ≠，存在*k ∈N ，使得m n k c c c +=成立，则称{}n c 为“G 数列”.（1）若数列{}n b 的通项公式为2n b n =，试判断数列{}n b 是否为“G 数列”，并说明理由；（2）已知数列{}n a 为等差数列，①若{}n a 是“G 数列”，*128,a a =∈N ，且21a a >，求2a 所有可能的取值；②若对任意*n ∈N ，存在*k ∈N ，使得k n a S =成立，求证：数列{}n a 为“G 数列”.参考答案一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集{}2,4,6,8,10,12U =，{}4,6,8M =，{}8,10N =，则集合{}2,12=（）A. M N ⋃B. M N ⋂C. ()U C M N ⋃D. ()U C M N【答案】C 【解析】【分析】根据交集、并集、补集的定义分别计算各选项对应的集合，从而可得正确的选项. 【详解】{}4,6,810M N = ，而{}8M N = ，故(){}U 2,12M N =U ð，(){}U 2,4,6,10,12M N = ð，故选：C.2. 下列命题正确的是（）A. “ln ln m n <”是“e e m n <”的充分不必要条件B. 命题：0,ln 1x x x ∀>≤-的否定是：0000,ln 1x x x ∃>≥-C. 5πsin cos 2x x ⎛⎫+=- ⎪⎝⎭D. 函数21x y x +=+在()(),11,-∞--+∞ 上是减函数【答案】A 【解析】【分析】根据充分条件、必要条件的定义判断A ，根据全称量词命题的否定为特称量词命题判断B ，利用诱导公式判断C ，利用特殊值判断D.【详解】对于A ：由函数ln y x =为定义在()0,∞+上单调递增函数，因为ln ln m n <，可得0m n <<，又因为函数e x y =为单调递增函数，可得e e m n <，即充分性成立；反之：由e e m n <，可得m n <，当,m n 小于0时，此时ln ,ln m n 没意义，即必要性不成立，所以“ln ln m n <”是“e e m n <”的充分不必要条件，故A 正确；对于B ：命题：0,ln 1x x x ∀>≤-的否定是：0000,ln 1x x x ∃>>-，故B 不正确；对于C ：5ππsin sin cos 22x x x ⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭，故C 不正确；对于D ：当2x =-时0y =，当0x =时2y =，但20-<，可得02<，所以函数21x y x +=+在()(),11,-∞--+∞ 上不是减函数，故D 不正确；故选：A.3. 若复数z 满足|2i ||2i |8z z ++-=，则复数z 在复平面内所对应点的轨迹是（） A. 椭圆 B. 双曲线C. 圆D. 线段【答案】A 【解析】【分析】根据题意，利用复数的几何意义，以及椭圆的定义，即可求解. 【详解】设()()()12,,0,2,0,2P x y F F -，复数z 对应点P ，因为复数z 满足|2i ||2i |8z z ++-=，由复数的几何意义，可得21128242PF PF a F F c +==>==，的所以复数z 对应的点满足椭圆的定义，复数z 在复平面内所对应点的轨迹是椭圆. 故选：A.4. 已知D 是ABC 所在平面内一点，3255AD AB AC =+，则（）A. 25BD BC =B. 35BD BC = C. 32BD BC =D. 23BD BC =【答案】A 【解析】【分析】由平面向量线性运算可得.【详解】由3255AD AB AC =+ ，得3255AB BD AB AC +=+得2255BD AB AC =-+，得()2255BD AB AC BC =-+= ，故选：A5. 我们把由0和1组成的数列称为01-数列，01-数列在计算机科学和信息技术领域有着广泛应用，把斐波那契数列{}()12211,n n n n F F F F F F ++===+中的奇数换成0，偶数换成1可得到01-数列{}n a ，记数列{}n a 的前n 项和为n S ，则100S 的值为（） A. 32 B. 33C. 34D. 35【答案】B 【解析】【分析】根据题意求得数列的前9项，通过观察找到规律，继而可求. 【详解】因为12211,n n n F F F F F ++===+，所以34567892,3,5,8,13,21,34,F F F F F F F ======= ，所以数列{}n a 的前若干项为：1231567890,1,0,0,1,0,0,1,a a a a a a a a a ========= ，则1234567891a a a a a a a a a ++=++=++== ，所以100331033S =⨯+=. 故选:B.6. 我国元代瓷器元青花团菊花纹小盏如图所示，撇口，深弧壁，圈足微微外撇，底心有一小乳突.器身施白釉，以青花为装饰，釉质润泽，底足露胎，胎质致密.碗内口沿饰有一周回纹，内底心书有一文字，碗外壁绘有一周缠枝团菊纹，下笔流畅，纹饰洒脱.该元青花团菊花纹小盏口径8.4厘米，底径2.8厘米，高4厘米，它的形状可近似看作圆台，则其侧面积约为（单位：平方厘米）（）12.2≈）A. 34πB. 27πC. 20πD. 18π【答案】B 【解析】【分析】根据题意结合圆台的侧面积公式分析求解. 【详解】设该圆台的上底面､下底面的半径分别为,R r ，由题意可知： 4.2, 1.4R r ==，则圆台的母线长l ==所以其侧面积为()()π 4.2 1.4π 4.2 1.44 1.2227π⨯+⨯≈⨯+⨯⨯≈. 故选：B.7. 已知椭圆22221(0)x y a b a b +=>>与双曲线22221(0,0)x y m n m n-=>>有共同的焦点1F ，2F ，且在第一象限内相交于点P ，椭圆与双曲线的离心率分别为1e ，2e ．若123F PF π∠=，则12e e ⋅的最小值是A.12B.C.D.32【答案】C 【解析】【分析】设共同的焦点为(,0)c -，(,0)c ，设1PF s =，2PF t =，运用椭圆和双曲线的定义，以及三角形的余弦定理和基本不等式，即可得到所求最小值．【详解】解：设共同的焦点为(,0)c -，(,0)c ，设1PF s =，2PF t =，由椭圆和双曲线的定义可得2s t a +=，2s t m -=，解得s a m =+，t a m =-，在12PF F ∆中，123F PF π∠=，可得222121212122cos F F PF PF PF PF F PF =+-⋅⋅∠，即为222224()()()()3c a m a m a m a m a m =++--+-=+，即有222234a m c c+=，即为2221314e e +=，由221213e e +≥，可得12e e ⋅≥，当且仅当21e =，故选C ．【点睛】本题考查椭圆和双曲线的定义、方程和性质，考查方程思想和运算能力，属于中档题．8. 求值：2cos40cos80sin80+=（）A.B.C.D. 【答案】A 【解析】【分析】易知()cos40=cos 12080-，再利用两角差的余弦公式计算可得结果.【详解】()2cos 12080cos802cos40cos80sin80sin80-++=()2cos120cos80sin120sin80cos80sin80++===故选：A.二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 某市7天国庆节假期期间的楼房日认购量（单位：套）与日成交量（单位：套）的折线图如下图所示，小明同学根据折线图对这7天的日认购量与日成交量作出如下判断，则下列结论正确的是（）A. 日认购量与日期正相关B. 日成交量的中位数是26C. 日成交量超过日平均成交量的有2天D. 10月7日日认购量的增量大于10月7日日成交量的增量【答案】BD 【解析】【分析】根据正相关的定义结合图象即可判断A ；根据中位数的定义结合图象即可判断B ；根据图中数据进行计算即可求得平均数，即可判断C ；根据图中数据进行计算即可判断D . 【详解】由题图可以看出，数据点并不是从左下至右上分布，所以A 错；将成交量数据按大小顺序排列，中位数为26，所以B 对；日平均成交量为1383216263816642.77++++++≈，超过42.7的只有一天，所以C 错；10月7日认购量的增量为276112164-=，成交量的增量为16638128-=，所以D 对，故选:BD.10. 抛物线的弦与弦的端点处的两条切线形成的三角形称为阿基米德三角形，该三角形以其深刻的背景､丰富的性质产生了无穷的魅力.设,A B 是抛物线2:4C x y =上两个不同的点，以()()1122,,,A x y B x y 为切点的切线交于P 点.若弦AB 过点()0,1F ，则下列说法正确的有（） A. 124x x =-B. 若12x =，则A 点处的切线方程为10x y --=C. 存在点P ，使得0PA PB ⋅>D. PAB 面积的最小值为4 【答案】ABD 【解析】【分析】联立方程组，结合韦达定理，可判定A 正确；求得12y x '=，得到切点坐标2111,4A x x ⎛⎫⎪⎝⎭，得出切线方程2111124y x x x =-，进而可判定B 正确；由直线AP 的斜率为112x ，直线BP 的斜率为212x ，得到12114x x =-，可判定C 错误；由过点B 的切线方程为2221124y x x x =-，结合弦长公式，得到()32241ABP S k=+ ，可D 正确.【详解】对于A 中，设直线:1AB y kx =+，联立方程组214y kx x y=+⎧⎨=⎩，整理得2440x kx --=，再设()()1122,,,A x y B x y ，则12124,4x x k x x +=⋅=-，所以A 正确；对于B 中，由抛物线24x y =.可得214y x =，则12y x '=，则过点A 的切线斜率为112x ，且21114y x =，即2111,4A x x ⎛⎫⎪⎝⎭，则切线方程为：()21111142y x x x x -=-，即2111124y x x x =-，若12x =时，则过点A 的切线方程为：10x y --=，所以B 正确；对于C 中，由选项B 可得：直线AP 的斜率为112x ，直线BP 的斜率为212x ，因为12121111224x x x x ⋅==-，所以AP BP ⊥，即0PA PB ⋅= ，所以C 错误；对于D 中，由选项B 可知，过点B 的切线方程为2221124y x x x =-，联立直线,PA PB 的方程可得()12,1,,1,PF PF AB P k k k k PF AB k-=-⋅=-⊥，所以12ABP S AB PF =⋅ ，()2241AB x k =-===+，PF ===则()32241ABPSk=+ ，当0k =时，ABP S △有最小值为4，所以D 正确.故选：ABD.11. 已知函数()()()1e 1xf x x x =+--，则下列说法正确的有A. ()f x 有唯一零点B. ()f x 无最大值C. ()f x 在区间()1,+∞上单调递增D. 0x =为()f x 的一个极小值点【答案】BCD 【解析】【分析】求出函数的零点判断A ；利用导数探讨函数()f x 在(2,)+∞上的取值情况判断B ；利用导数探讨单调性及极值情况判断CD.【详解】对于A ，依题意，()()100f f -==，即=1x -和0x =是函数()()()1e 1xf x x x =+--的零点，A 错误；对于B ，当0x >时，令()e 1xu x x =--，求导得()e 10xu x =->'，函数()u x 在()0,∞+上递增，当2x ≥时，()2e 31u x ≥->，而1y x =+在()0,∞+上递增，值域为()1,+∞，因此当2x ≥时，()1f x x >+，则()f x 无最大值，B 正确；对于C ，()()2e 22xf x x x '=+--，令()()2e 22xg x x x =+--，求导得()()3e 2xg x x =+-'，当0x >时，令()()3e 2xh x x =+-，则()()4e 0xh x x '=+>，即()()g x h x '=在()0,∞+上递增，()()010g x g '='>>，则()()f x g x '=在()0,∞+上递增，()()00f x f ''>=，因此()f x 在()0,∞+上递增，即()f x 在()1,+∞上单调递增，C 正确；对于D ，当10x -<<时，()22e 2xx x x ϕ+=-+，求导得()22e (2)xx x ϕ=-+'，显然函数()x ϕ'在()1,0-上递增，而()()11120,00e 2ϕϕ'-'=-<=>，则存在()01,0x ∈-，使得()00x ϕ'=，当()0,0x x ∈时，()0x ϕ'>，函数()x ϕ在()0,0x 上单调递增，则()()00x ϕϕ<=，即当()0,0x x ∈时，22e 2xx x +<+，则()()2e 220xf x x x '=+--<，又()00f '=，因此0x =为()f x 的一个极小值点，D 正确. 故选：BCD【点睛】方法点睛：函数零点的求解与判断方法：①直接求零点：令()0f x =，如果能求出解，则有几个解就有几个零点．②零点存在性定理：利用定理不仅要函数在区间[,]a b 上是连续不断的曲线，且()()0f a f b ⋅＜，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．③利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．三､填空题：本题共3小题，每小题5分，共15分.12. 雅礼中学将5名学生志愿者分配到街舞社､戏剧社､魔术社及动漫社4个社团参加志愿活动，每名志愿者只分配到1个社团､每个社团至少分配1名志愿者，则不同的分配方案共有__________种【答案】240 【解析】【分析】根据题意，先将5名学生志愿者分为4组，再将分好4组安排参加4个社团参加志愿活动，结合分步计数原理，即可求解.【详解】根据题意，分2步进行分析：①将5名学生志愿者分为4组，有25C 10=种分组方法，②将分好的4组安排参加4个社团参加志愿活动，有44A 24=种情况，的则有1024240⨯=种分配方案. 故答案为：240.13. 已知圆221:(2)1C x y +-=与圆222:(2)(1)4C x y -+-=相交于,A B 两点，则()1211C C C A C B =⋅+__________. 【答案】2 【解析】【分析】易知两圆公共弦AB 所在的直线方程为()()12210,0,2,2,1x y C C -+=，由点到直线距离公式可得向量1C A 在向量12C C 方向上的投影为d = 2.【详解】由题意可知两圆公共弦AB 所在的直线方程为()()12210,0,2,2,1x y C C -+=，如下图所示：所以点1C 到直线210x y -+=的距离为2d C ==，又易知12C C AB ⊥，所以向量1C A 在向量12C C 方向上的投影为d =所以1211C C C A ⋅== ，同理可得1211C C C B ⋅= ，所以()12112C C C A C B ⋅+=.故答案为：214. 某同学在学习和探索三角形相关知识时，发现了一个有趣的性质：将锐角三角形三条边所对的外接圆的三条圆弧（劣弧）沿着三角形的边进行翻折，则三条圆弧交于该三角形内部一点，且此交点为该三角形的垂心（即三角形三条高线的交点）.如图，已知锐角ABC 外接圆的半径为2，且三条圆弧沿ABC 三边翻折后交于点P .若3AB =，则sin PAC ∠=___________；若::6:5:4AC AB BC =，则PA PB PC ++的值为___________.【答案】 ①.②. 234##5.75【解析】【分析】第一空，由正弦定理求得3sin 4ACB ∠=，可得cos ACB ∠=角形诱导公式推得sin cos PAC ACB ∠∠=，即得答案；第二空，设,,CAB CBA ACB ∠θ∠α∠β===，由余弦定理求得它们的余弦值，然后由垂心性质结合正弦定理表示出()4cos cos cos PA PB PC θαβ++=++，即可求得答案. 【详解】设外接圆半径为R ，则2R =，由正弦定理，可知324sin sin AB R ACB ACB∠∠===，即3sin 4ACB ∠=，由于ACB ∠是锐角，故cos ACB ∠= 又由题意可知P 为三角形ABC 的垂心，即⊥AP BC ,故π2PAC ACB ∠∠=-，所以sin cos PAC ACB ∠∠==；设,,CAB CBA ACB ∠θ∠α∠β===，则πππ,,222PAC PBA PAB ∠β∠θ∠α=-=-=-，由于::6:5:4AC AB BC =，不妨假设6,5,4AC AB BC ===，由余弦定理知222222222654345614659cos ,cos ,cos 2654245824616θαβ+-+-+-======⨯⨯⨯⨯⨯⨯，设AD,CE,BF 为三角形的三条高，由于ππ,22ECB EBC PCD CPD ∠+∠=∠+∠= , 故EBC CPD ∠=∠ ,则得πππAPC CPD EBC ABC ∠∠∠=-∠=-=-，所以24ππsin sin sin sin 22PC PA AC ACR APC ABC∠∠βθ=====⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，同理可得24πsin sin sin 2PB AB ABR APB ACB∠∠α====⎛⎫- ⎪⎝⎭，所以()319234cos cos cos 448164PA PB PC θαβ⎛⎫++=++=++=⎪⎝⎭,；234 【点睛】本题重要考查了正余弦定理在解三角形中的应用，涉及到三角形垂心的性质的应用，解答时要能灵活地结合垂心性质寻找角之间的关系，应用正余弦定理，解决问题.四､解答题：本题共5小题，共77分.请在答题卡指定区域内作答.解答时应写出文字说明､证明过程或演算步骤.15. 人工智能正在改变我们的世界，由OpenAI 开发的人工智能划时代标志的ChatGPT 能更好地理解人类的意图，并且可以更好地回答人类的问题，被人们称为人类的第四次工业革命.它渗透人类社会的方方面面，让人类更高效地生活.现对130人的样本使用ChatGPT 对服务业劳动力市场的潜在影响进行调查，其数据的统计结果如下表所示：服务业就业人数的ChatGPT 应用的广泛性减少增加合计广泛应用601070没广泛应用 40 20 60 合计 10030130（1）根据小概率值0.01α=的独立性检验，是否有99%的把握认为ChatGPT 应用的广泛性与服务业就业人数的增减有关？（2）现从“服务业就业人数会减少”的100人中按分层随机抽样的方法抽取5人，再从这5人中随机抽取3人，记抽取的3人中有X 人认为人工智能会在服务业中广泛应用，求X 的分布列和均值.附：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α 0.10.05 0.01x α 2.706 3.841 6.635【答案】（1）没有（2）分布列见解析，95【解析】【分析】（1）根据题意求2χ，并与临界值对比判断；（2）根据分层抽样求各层人数，结合超几何分布求分布列和期望. 【小问1详解】零假设为0H ：ChatGPT 对服务业就业人数的增减无关.根据表中数据得220.01130(60204010) 6.603 6.635706010030x ⨯⨯-⨯=≈<=⨯⨯⨯χ，所以根据小概率值0.01α=的独立性检验，没有充分证据推断0H 不成立，因此可以认为无关. 【小问2详解】由题意得，采用分层抽样抽取出的5人中，有6053100⨯=人认为人工智能会在服务业中广泛应用，有4052100⨯=人认为人工智能不会在服务业中广泛应用，则X 的可能取值为1,2,3，又()()()1231332323335355C C C C C 3311,2,3C 10C 5C 10P X P X P X =========，所以X 的分布列为X1 2 3P310 35 110所以()3319123105105E X =⨯+⨯+⨯= 16. 如图，在四棱锥P ABCD -中，PA ⊥平面,2,,120ABCD PA AB BC AD CD ABC ∠===== .（1）求证：平面PAC ⊥平面PBD ；（2）若点M 为PB 的中点，线段PC 上是否存在点N ，使得直线MN 与平面PAC 所成角的正弦值为.若存在，求PN PC 的值；若不存在，请说明理由.【答案】（1）证明见解析（2）存在，14PN PC =或38PN PC = 【解析】【分析】（1）设AC 的中点为O ，根据题意证得BD AC ⊥和BD PA ⊥，证得BD ⊥平面PAC ，进而证得平面PAC ⊥平面PBD .（2）以,OCOD 所在的直线为x 轴和y轴，建立空间直角坐标系，设()01PN PC λλ=≤≤，分别求得平面PAC和1,122MN λ⎛⎫=-- ⎪ ⎪⎝⎭，结合向量的夹角公式，列出方程，即可求解..【小问1详解】设AC 的中点为O ，因为AB BC =，所以BO AC ⊥，因为AD CD =，所以DO AC ⊥，所以,,B O D 三点共线，所以BD AC ⊥，因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD PA ⊥，因为PA AC A = ，PA ⊂平面PAC ，AC ⊂平面PAC ，所以BD ⊥平面PAC ，因为BD ⊂平面PBD ，所以平面PAC ⊥平面PBD . 【小问2详解】以,OC OD 所在的直线为x 轴和y 轴，过O 点作平行于AP 的直线为z 轴，建立空间直角坐标系，如图所示，则)()(),2,0,1,0CP B -，因为M 为PB的中点，所以1,12M ⎛⎫- ⎪ ⎪⎝⎭，设()01PN PC λλ=≤≤，所以()22N λ--，所以1,122MN λ⎛⎫=- ⎪ ⎪⎝⎭，由（1）知BD ⊥平面PAC ，所以平面PAC 的一个法向量为()0,1,0n =，设直线MN 与平面PAC 所成角为θ，则sin cos ,MN n MN n MN n θ⋅====，即当14PN PC =或38PN PC =时，直线MN 与平面PAC.17. 如图，圆C 与x 轴相切于点()2,0T ，与y 轴正半轴相交于,M N 两点（点M 在点N 的下方），且3MN =．(1)求圆C 的方程；(2)过点M 任作一条直线与椭圆22184x y +=相交于两点A B 、，连接AN BN 、，求证：ANM BNM ∠=∠．【答案】（Ⅰ）()22525224x y ⎛⎫-+-= ⎪⎝⎭；（Ⅱ）见解析【解析】【详解】分析：(1)设圆心坐标为()2,r ，根据3MN =.可由勾股定理求出r ，求得圆的方程． (2)讨论当斜率不存在时0ANM BNM ∠=∠= ；当斜率存在时，设出直线1y kx =+方程，联立椭圆方程，利用韦达定理表示出1212246,1212k x x x x k k+=-=-++，表示出AN BN k k 、，即可判定ANM BNM ∠=∠．详解：(1)由题可知圆心的坐标为()2,.r ∵22232553,2,242MN r r ⎛⎫=∴=+== ⎪⎝⎭∴圆C 方程为:()22525224x y ⎛⎫-+-=⎪⎝⎭ (2) 由圆C 方程可得()()0,1,0,4M N①当AB 斜率不存在时，0ANM BNM ∠=∠=②当AB 斜率存在时，设AB 直线方程为:1y kx =+. 设()()1122,,,A x y B x y()2222112460184y kx k x kx x y =+⎧⎪⇒++-=⎨+=⎪⎩ 1212246,1212k x x x x k k +=-=-++∴()22121212121226423234412120612AN BN k k kx x x x y y k k k k x x x x k ⎛⎫⎛⎫--- ⎪ ⎪-+--++⎝⎭⎝⎭+=+===-+∴0AN BN k k +=综上所述ANM BNM ∠=∠点睛：本题考查了求圆标准方程，直线与椭圆的关系，通过韦达定理解决相交弦问题，也是高考的常考点，属于难点．18. 已知函数()()2ln 3f x x x ax x a =--∈R .（1）若1x =是函数()f x 的一个极值点，求实数a 的值；（2）若函数()f x 有两个极值点12,x x ，其中12x x <， ①求实数a 的取值范围；②若不等式122ln 31ax k x k +>+恒成立，求实数k 的取值范围. 【答案】18. 1-19. ①310,2e ⎛⎫⎪⎝⎭，②[)1,+∞ 【解析】【分析】（1）对函数求导，依题意可得()10f '=，解得1a =-，经检验符合题意；（2）①将函数()f x 有两个极值点转化为方程ln 220x ax --=有两个不同的正数根，再由函数与方程的思想可知函数()ln 2x g x x-=与函数2y a =的图象在()0,∞+上有两个不同交点，利用数形结合可得310,2e a ⎛⎫∈ ⎪⎝⎭；②由两极值点的关系通过构造函数可将不等式恒成立问题转化为函数()()ln 11ln 0F t t t t k t t =-+---<对任意的01t <<恒成立，利用导数并对实数k 的取值分类讨论即可求得[)1,k ∞∈+. 【小问1详解】易知()ln 123ln 22f x x ax x ax =+--=--'，又1x =是函数()f x 的一个极值点，()10f ∴'=，即220,1a a --=∴=-.此时()ln 22f x x x +'=-，令()()1ln 22,20h x x x h x x+='=-+>， ()()f x h x ∴'=在()0,∞+上单调递增，且()10f '=，当()()0,1,0x f x ∈'<，当()()1,,0x f x '∈+∞>，()f x ∴在()0,1上单调递减，在()1,∞+上单调递增，所以1x =是()f x 的极小值点，即1a =-符合题意；因此实数a 的值为1-. 【小问2详解】①因为()ln 22f x x ax -'=-，且()()2ln 3f x x x ax x a =--∈R 有两个极值点12,x x ，所以方程()0f x '=在()0,∞+上有两个不同的根，即方程ln 220x ax --=有两个不同的正数根，将问题转化为函数()ln 2x g x x-=与函数2y a =的图象在()0,∞+上有两个不同交点，则()23ln x g x x -'=，令()23ln 0xg x x'-==，解得3e x =，当3e x >时，()()0,g x g x '<单调递减，当30e x <<时，()()0,g x g x '>单调递增，且当2e x >时，()()20,e0g x g >=，故作出()g x 的图象如下：由图象可得3120,e a ⎛⎫∈ ⎪⎝⎭满足题意，即310,2e a ⎛⎫∈ ⎪⎝⎭. 即实数a 的取值范围为310,2e a ⎛⎫∈ ⎪⎝⎭； ②由①知12,x x 是ln 220x ax --=的两个根，故11222ln 20,2ln 20x ax x ax -+-=-+-=，则1212ln ln 2x x a x x -=-，不妨设12x t x =，又120x x <<，所以()120,1x t x =∈可得21tx x =，可得122212ln ln 2ln 0x x x x x x --+-=-，即122122ln2ln 0x x x x x x -+-=-，所以2ln ln 21tx t =+-；故由122ln 31ax k x k +>+可得121212ln ln ln 31x x x k x k x x -+>+-，即2222ln ln 31t tx k x k tx x +>+-，所以2ln ln 311t tk x k t +>+-；也即ln ln 23111t t t k k t t ⎛⎫++>+ ⎪--⎝⎭，化简得ln 11ln 11t t t t t k t t -+--⎛⎫> ⎪--⎝⎭，由于01t <<，所以等价于()ln 11ln 0t t t k t t -+---<对任意的01t <<恒成立，令()()ln 11ln F t t t t k t t =-+---，故()0F t <对任意01t <<恒成立，则()ln kF t t k t '=-+，设()ln k m t t k t =-+，则()221k t km t t t t='-=-，（i ）当0k ≤时，()()()20,t km t m t F t t-=>'='单调递增，故()()()10,F t F F t '='<单调递减，故()()10F t F >=，不满足，舍去；（ii ）当1k ≥时，()()()20,t km t m t F t t -=<'='单调递减，故()()()10,F t F F t '='>单调递增，故()()10F t F <=，故()0F t <恒成立，符合题意；（iii ）当01k <<时，令()20t km t t-'==，则t k =，当1k t <<时，()()()0,m x m x F t >'='单调递增，当0t k <<时，()()()0,m x m t F t <'='单调递减，又()10F '=，故1k t <<时，()()10F t F ''<=，此时()F t 单调递减，故()()10F t F >=，的因此当1k t <<时，()0F t >，不符合题意，舍去. 综上，实数k 的取值范围为[)1,+∞.【点睛】关键点点睛：本题关键在于利用两极值点关系可得1212ln ln 2x x a x x -=-，并通过构造函数将不等式问题转化为函数在指定区间上恒成立问题，利用导函数求出函数最值即可求得实数k 的取值范围. 19. 对于无穷数列{}n c ，若对任意*,m n ∈N ，且m n ≠，存在*k ∈N ，使得m n k c c c +=成立，则称{}n c 为“G 数列”.（1）若数列{}n b 的通项公式为2n b n =，试判断数列{}n b 是否为“G 数列”，并说明理由；（2）已知数列{}n a 为等差数列，①若{}n a 是“G 数列”，*128,a a =∈N ，且21a a >，求2a 所有可能取值；②若对任意*n ∈N ，存在*k ∈N ，使得k n a S =成立，求证：数列{}n a 为“G 数列”. 【答案】（1）是，理由见解析（2）①2a 的可能值为9,10,12,16.②证明见解析【解析】【分析】（1）根据题意，推得()222m n b b m n m n +=+=+，取k m n =+，得到m n k b b b +=，即可求解；（2）若{}n a 是“G 数列”，且为等差数列，得到()81n a n d =+-，进而得到存在*k ∈N ，使得m n k a a a +=，求得()18k m n d --+=，得到d 的值，进而求得2a 的可能值；②设数列{}n a 公差为d ，得到()3n a t n d =+-，求得()26m n a a t m n d +=++-，鸡儿推得k m n a a a =+，得到答案.【小问1详解】解：数列{}n b 的通项公式为2n b n =，对任意的*,,m n m n ∈≠N ，都有()2,2,222m n m n b m b n b b m n m n ==+=+=+，取k m n =+，则m n k b b b +=，所以 {}n b 是“G 数列”.的【小问2详解】解：数列{}n a 为等差数列，①若{}n a 是“G 数列”，*128,a a =∈N ，且*2121,0,a a d a a d >=->∈N ，则()81n a n d =+-，对任意的()()*,,,81,81m n m n m n a m d a n d ∈≠=+-=+-N ，()882m n a a m n d +=+++-，由题意存在*k ∈N ，使得m n k a a a +=，即()()88281m n d k d +++-=+-，显然k m n ≥+，所以()()281m n d k d +-+=-，即()18k m n d --+=，*1k m n --+∈N .所以d 是8的正约数，即1,2,4,8d =，1d =时，29,7a k m n ==++； 2d =时2,10,3a k m n ==++；4d =时2,12,1a k m n ==++；8d =时2,16,a k m n ==+.综上，2a 的可能值为9,10,12,16.②若对任意*n ∈N ，存在*k ∈N ，使得k n a S =成立，所以存在*122,,3t t a a S a t ∈+==≥N ，设数列{}n a 公差为d ，则()()11121,2a d a t d a t d +=+-=-，可得()()()213n a t d n d t n d =-+-=+-，对任意()()*,,,3,3m n m n m n a m d a n d ιι∈≠=+-=+-N ，则()26m n a a t m n d +=++-，取*3k t m n =++-∈N ，可得()()326k m n a t k d t m n d a a =-+=++-=+，所以数列{}n a 是“G 数列”.。

2020届湖南省雅礼中学高三第七次模拟考试数学(文)试题

2020届湖南省雅礼中学高三第七次模拟考试文科数学★祝考试顺利★ 注意事项：1、考试范围：高考范围。

2、试题卷启封下发后，如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况，应当立马报告监考老师，否则一切后果自负。

3、答题卡启封下发后，如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象，应当马上报告监考老师，否则一切后果自负。

4、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

5、选择题的作答：每个小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

6、主观题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。

如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

7、保持答题卡卡面清洁，不折叠，不破损，不得使用涂改液、胶带纸、修正带等。

8、考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合要求的。

1．已知集合{}9,7,5,4,3,1=U ，{}5,4,1=A ，则U A =ð A ．{}9,3B ．{}9,7C ．{}9,7,5D ．{}9,7,32．已知i 是虚数单位，复数1(2)i m m ++-在复平面内对应的点在第二象限，则实数m 的取值范围是A ．()1,-∞-B ．()2,1-C ．()+∞,2D ．()(),12,-∞-+∞3．已知向量()()1,,2,1m ==-a b ，且()b b a ⊥-，则实数=mA ．3B ．12C ．12-D ．3-4．某车间生产C B A ,,三种不同型号的产品，产量之比分别为3::5k ，为检验产品的质量,现用分层抽样的方法抽取一个容量为120的样本进行检验，已知B 种型号的产品共抽取了24件，则C 种型号的产品抽取的件数为A ． 12B ．24C ．36D ．605．要得到函数πcos(2)4y x =+的图象，只需要将函数cos y x =的图象A ．向左平行移动π8个单位长度，横坐标缩短为原来的21倍，纵坐标不变.B ．向左平行移动π4个单位长度，横坐标缩短为原来的21倍，纵坐标不变.C ．向右平行移动π8个单位长度，横坐标伸长为原来的2倍，纵坐标不变.D ．向右平行移动π4个单位长度，横坐标伸长为原来的2倍，纵坐标不变.6．设直线,m n 是两条不同的直线,αβ,是两个不同的平面,下列命题中正确的是A ．,m n m n αα⇒∥∥∥B ．,,m n m n αβαβ⊥⊥⊥⇒⊥C ．,m m αβαβ⇒∥∥∥D ．,m m αβαβ⊥⇒⊥∥7．已知412ln33332,e ,3a bc===，则A ．a b c <<B ．c a b <<C ．b a c <<D ．a c b <<8．执行如图所示的程序框图，输出的k 值为A ．4B ．5C ．6D ．79．函数1ln )(+=x xx f 的图像大致是A. B. C. D. A. B. C. D. 10．已知π(0,)2α∈，且02sin cos 5sin 322=+-ααα，则sin2cos2αα+=A ． 1B ．2317-C ．2317-或1 D ．1- 11．如图,在ABC ∆Rt 中，π2C ∠=，π6B ∠=， 4AC =，D 在AC 上且:3:1AD DC =，当AED ∠最大时，AED ∆的面积为A ．32B.2C.3 D ．12．已知函数()4ln 3,f x a x x =-且不等式(1)43e ,x f x ax +-≥在(0,)+∞上恒成立,则实数a 的取值范围A ．3(,)4-∞B ．3(,]4-∞ C ．(,0)-∞ D ．(,0]-∞第11题图D二、填空题：本大题共4个小题，每小题5分，共20分。

2019-2020学年湖南省长沙市雅礼中学高三(下)月考数学试卷(文科)(六)

2019-2020学年湖南省长沙市雅礼中学高三（下）月考数学试卷（文科）（六）一、选择题：本大题共12小题，每小题5分，共60分.每小题所给的四个选项中只有一个是正确的.1．（5分）集合A＝{x|1＜x＜3}，集合B＝{y|y＝x﹣2，x∈A}，则集合A∩B＝（）A．{x|1＜x＜3}B．{x|﹣1＜x＜3}C．{x|﹣1＜x＜1}D．∅2．（5分）复数z＝1﹣2i的虚部是（）A．﹣2B．2C．﹣2i D．2i3．（5分）已知f（x）是定义在R上的偶函数，且在（﹣∞，0]上是减函数，设a＝f（0.32），b＝f（log25），c＝f（20.3），则a，b，c的大小关系是（）A．b＜c＜a B．a＜b＜c C．c＜b＜a D．a＜c＜b4．（5分）若实数x，y满足x+y＞0，则“x＞0”是“x2＞y2”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件5．（5分）在长方形ABCD中，AB＝2，AD＝1，点E为BC的中点，点F为CD的中点，则•＝（）A．﹣1B．﹣C．﹣2D．﹣6．（5分）一只小虫在边长为2的正方形内部爬行，到各顶点的距离不小于1时为安全区域，则小虫在安全区域内爬行的概率是（）A．B．C．D．7．（5分）已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，若将f （x）的图象向左平移个单位后得到函数g（x）的图象关于y轴对称，则函数f（x）的图象（）A．关于直线对称B．关于直线对称C．关于点对称D．关于点对称8．（5分）已知实数x，y满足，若直线kx﹣y+1＝0经过该可行域，则实数k的最大值是（）A．1B．C．2D．39．（5分）两个等差数列{a n}和{b n}，其前n项和分别为S n，T n，且，则等于（）A．B．C．D．10．（5分）已知三个实数2，a，8成等比数列，则双曲线的渐近线方程为（）A．3x±4y＝0B．4x±3y＝0C．x±2y＝0D．9x±16y＝0 11．（5分）定义在R上的偶函数f（x）在[0，+∞）单调递增，且f（﹣2）＝1，则f（x﹣2）≤1的x取值范围是（）A．[0，4]B．（﹣∞，﹣2]∪[2，+∞）C．（﹣∞，0]∪[4，+∞）D．[﹣2，2]12．（5分）已知函数f（x）＝e x﹣e，g（x）＝lnx+1，若对于∀x1∈R，∃x2∈（0，+∞），使得f（x1）＝g（x2），则x1﹣x2的最大值为（）A．e B．1﹣e C．1D．二、填空题：本大题共4小题，每小题5分，共20分.13．（5分）若，则＝．14．（5分）已知向量，的夹角为，＝（﹣3，4），＝﹣10，则的模长是．15．（5分）△ABC的三个顶点都在球O的球面上，若∠BAC＝90°，AB＝AC＝2，若球O 的表面积为12π，则球心O到平面ABC的距离等于．16．（5分）设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周期为2，且f（x）是奇函数．当x∈（0，2]时，f（x）＝，g（x）＝其中k＞0．若在区间（0，9]上，关于x的方程f（x）＝g（x）有8个不同的实数根，则k 的取值范围是．三、解答题：本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17．（12分）在△ABC中，a，b，c分别为角A ，B，C的对边，且满足4cos2﹣cos2（B+C）＝，（Ⅰ）求角A的大小；（Ⅱ）若b+c＝3，求a的最小值．18．（12分）2019年2月13日《烟台市全民阅读促进条例》全文发布，旨在保障全民阅读权利，培养全民阅读习惯，提高全民阅读能力，推动文明城市和文化强市建设．某高校为了解条例发布以来全校学生的阅读情况，随机调查了200名学生每周阅读时间X（单位：小时）并绘制如图所示的频率分布直方图．（1）求这200名学生每周阅读时间的样本平均数和中位数a（a的值精确到0.01）；（2）为查找影响学生阅读时间的因素，学校团委决定从每周阅读时间为[6.5，7，5），[7.5，8.5）的学生中抽取9名参加座谈会．（i）你认为9个名额应该怎么分配？并说明理由；（ii）座谈中发现9名学生中理工类专业的较多．请根据200名学生的调研数据，填写下面的列联表，并判断是否有95%的把握认为学生阅读时间不足（每周阅读时间不足8.5小时）与“是否理工类专业”有关？阅读时间不足8.5小时阅读时间超过8.5小时理工类专业4060非理工类专业附：．临界值表：0.150.100.050.0250.0100.0050.001P（K2≥k0）k0 2.072 2.706 3.841 5.024 6.6357.87910.82819．（12分）如图1，等腰梯形ABCD中，AD∥BC，AB＝AE＝BE＝CD＝2，BC＝ED＝4，O为BE中点，F为BC中点．将△ABE沿BE折起到△A'BE的位置，如图2．（1）证明：CD⊥平面A'OF；（2）若平面A'BE⊥平面BCDE，求点F到平面A'EC的距离．20．（12分）已知椭圆C：+＝l（a＞b＞0）过点（2，1），且离心率e＝．（l）求椭圆C的方程；（2）已知斜率为的直线l与椭圆C交于两个不同点A，B，点P的坐标为（2，1），设直线P A与PB的倾斜角分别为α，β，证明：α+β＝π．21．（12分）已知f（x）＝e x﹣alnx（a∈R）．（1）求函数f（x）在点（1，f（1））处的切线方程；（2）当a＝﹣1时，若不等式f（x）＞e+m（x﹣1）对任意x∈（1，+∞）恒成立，求实数m的取值范围．（二）选考题：共10分.请考生在22、23两题中任选-题作答，如果多做，则按所做的第--题记分.[选修4--4：坐标系与参数方程.]22．（10分）在平面直角坐标系xOy中，曲线C的参数方程为（r＞0，φ为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为，若直线l与曲线C相切；（Ⅰ）求曲线C的极坐标方程；（Ⅱ）在曲线C上取两点M，N与原点O构成△MON，且满足，求面积△MON的最大值．[选修4-5：不等式选讲]23．设函数f（x）＝k|x|﹣|2x﹣1|．（1）当k＝1时，求不等式f（x）＞0的解集；（2）当x∈（0，+∞）时，f（x）+b＞0恒成立，求k+b的最小值．2019-2020学年湖南省长沙市雅礼中学高三（下）月考数学试卷（文科）（六）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.每小题所给的四个选项中只有一个是正确的.1．（5分）集合A＝{x|1＜x＜3}，集合B＝{y|y＝x﹣2，x∈A}，则集合A∩B＝（）A．{x|1＜x＜3}B．{x|﹣1＜x＜3}C．{x|﹣1＜x＜1}D．∅【解答】解：∵集合A＝{x|1＜x＜3}，集合B＝{y|y＝x﹣2，x∈A}＝{x|﹣1＜x＜1}，∴集合A∩B＝∅．故选：D．2．（5分）复数z＝1﹣2i的虚部是（）A．﹣2B．2C．﹣2i D．2i【解答】解：复数z＝1﹣2i的虚部是﹣2．故选：A．3．（5分）已知f（x）是定义在R上的偶函数，且在（﹣∞，0]上是减函数，设a＝f（0.32），b＝f（log25），c＝f（20.3），则a，b，c的大小关系是（）A．b＜c＜a B．a＜b＜c C．c＜b＜a D．a＜c＜b【解答】解：根据题意，f（x）是定义在R上的偶函数，且在（﹣∞，0]上是减函数，则f（x）在[0，+∞）上为增函数，又由0＜0.32＜1＜20.3＜2＜log25，则a＜c＜b；故选：D．4．（5分）若实数x，y满足x+y＞0，则“x＞0”是“x2＞y2”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：∵实数x，y满足x+y＞0，若x＞0，则未必有x2＞y2；例如x＝1，y＝2时，有x2＜y2；反之，若x2＞y2，则x2﹣y2＞0，即（x+y）（x﹣y）＞0；由于x+y＞0，故x﹣y＞0，∴x＞y且x＞﹣y，∴x＞0；∴当x+y＞0时，“x＞0”推不出“x2＞y2”，“x2＞y2”⇒“x＞0”；∴“x＞0”是“x2＞y2”的必要不充分条件．故选：B．5．（5分）在长方形ABCD中，AB＝2，AD＝1，点E为BC的中点，点F为CD的中点，则•＝（）A．﹣1B．﹣C．﹣2D．﹣【解答】解：由条件得，||＝2，||＝1，•＝0；＝+＝+；＝+＝﹣；∴•＝（+）•（﹣）＝+＝．故选：B．6．（5分）一只小虫在边长为2的正方形内部爬行，到各顶点的距离不小于1时为安全区域，则小虫在安全区域内爬行的概率是（）A．B．C．D．【解答】解：安全区域为图中阴影部分，其面积S＝2×2﹣π×12＝4﹣π，故小虫在安全区域内爬行的概率，故选：A．7．（5分）已知函数f（x）＝2sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，若将f （x）的图象向左平移个单位后得到函数g（x）的图象关于y轴对称，则函数f（x）的图象（）A．关于直线对称B．关于直线对称C．关于点对称D．关于点对称【解答】解：∵函数周期T＝π，即T＝＝π，即ω＝2，即f（x）＝2sin（2x+φ），若将函数f（x）的图象向左平移个单位长度后，得f（x）＝2sin[2（x+）+φ）]＝2sin（2x++φ），若图象关于y轴对称．则+φ＝+kπ，即φ＝kπ﹣，k∈Z，∵0＜φ＜π，∴当k＝1时，φ＝，即f（x）＝2sin（2x+），令2x+＝kπ+，k∈Z，可得：x＝﹣，k∈Z，可得：A错误；B正确．令2x+＝kπ，k∈Z，可得：x＝﹣，k∈Z，可得函数f（x）的图象的对称点为（﹣，0），k∈Z，可得：C，D均错误．故选：B．8．（5分）已知实数x，y满足，若直线kx﹣y+1＝0经过该可行域，则实数k的最大值是（）A．1B．C．2D．3【解答】解：直线kx﹣y+2＝0过定点（0，1），作可行域如图所示，，由，得B（2，4）．当定点（0，1）和B点连接时，斜率最大，此时k＝＝，则k的最大值为：故选：B．9．（5分）两个等差数列{a n}和{b n}，其前n项和分别为S n，T n，且，则等于（）A．B．C．D．【解答】解：因为：＝＝＝＝＝．故选：D．10．（5分）已知三个实数2，a，8成等比数列，则双曲线的渐近线方程为（）A．3x±4y＝0B．4x±3y＝0C．x±2y＝0D．9x±16y＝0【解答】解：三个实数2，a，8成等比数列，可得a2＝16，双曲线的渐近线方程为：3x±4y＝0，故选：A．11．（5分）定义在R上的偶函数f（x）在[0，+∞）单调递增，且f（﹣2）＝1，则f（x﹣2）≤1的x取值范围是（）A．[0，4]B．（﹣∞，﹣2]∪[2，+∞）C．（﹣∞，0]∪[4，+∞）D．[﹣2，2]【解答】解：定义在R上的偶函数f（x）在[0，+∞）单调递增，且f（﹣2）＝1，可得f（2）＝f（﹣2）＝1，f（x﹣2）≤1，即为f（|x﹣2|）≤f（2），可得|x﹣2|≤2，即﹣2≤x﹣2≤2，解得0≤x≤4，即x的取值范围是[0，4]．故选：A．12．（5分）已知函数f（x）＝e x﹣e，g（x）＝lnx+1，若对于∀x1∈R，∃x2∈（0，+∞），使得f（x1）＝g（x2），则x1﹣x2的最大值为（）A．e B．1﹣e C．1D．【解答】解：令f（x1）＝g（x2）＝t＞﹣e，则e﹣e＝t，lnx2+1＝t，x1＝ln（e+t），x2＝e t﹣1，令h（t）＝x1﹣x2＝ln（e+t）﹣e t﹣1，（t＞﹣e），∴h′（t）＝﹣e t﹣1，h″（t）＝﹣﹣e t﹣1＜0在（﹣e，+∞）上恒成立，∴h′（t）为（﹣e，+∞）上的减函数，又h′（0）＝﹣e﹣1＝0，∴﹣e＜t＜0时，h′（t）＞h′（0）＝0，x＞0时，h′（t）＞h′（0）＝0，∴h（t）在（﹣e，0）上递增，在（0，+∞）上递减，∴t＝0时，h（t）取得最大值h（0）＝ln（e+0）﹣e0﹣1＝1﹣．即x1﹣x2的最大值为1﹣．故选：D．二、填空题：本大题共4小题，每小题5分，共20分.13．（5分）若，则＝．【解答】解：∵，∴．故答案为：．14．（5分）已知向量，的夹角为，＝（﹣3，4），＝﹣10，则的模长是．【解答】解：由向量，的夹角为，＝（﹣3，4），＝﹣10，得＝||||cos＝﹣10，即||＝＝2，故答案为：2．15．（5分）△ABC的三个顶点都在球O的球面上，若∠BAC＝90°，AB＝AC＝2，若球O 的表面积为12π，则球心O到平面ABC的距离等于1．【解答】解：△ABC的三个顶点都在球O的球面上，若∠BAC＝90°，AB＝AC＝2，三角形的外心D在BC的中点，球O的表面积为12π，可得球的半径为：＝OB＝OA＝OC，BD＝OD＝＝1．故答案为：1．16．（5分）设f（x），g（x）是定义在R上的两个周期函数，f（x）的周期为4，g（x）的周期为2，且f（x）是奇函数．当x∈（0，2]时，f（x）＝，g（x）＝其中k＞0．若在区间（0，9]上，关于x的方程f（x）＝g（x）有8个不同的实数根，则k的取值范围是[，）．【解答】解：作出函数f（x）与g（x）的图象如图，由图可知，函数f（x）与g（x）＝﹣（1＜x≤2，3＜x≤4，5＜x≤6，7＜x≤8）仅有2个实数根；要使关于x的方程f（x）＝g（x）有8个不同的实数根，则f（x）＝，x∈（0，2]与g（x）＝k（x+2），x∈（0，1]的图象有2个不同交点，由（1，0）到直线kx﹣y+2k＝0的距离为1，得，解得k＝（k＞0），∵两点（﹣2，0），（1，1）连线的斜率k＝，∴≤k＜．即k的取值范围为[，）．故答案为：[，）．三、解答题：本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17．（12分）在△ABC中，a，b，c分别为角A，B，C的对边，且满足4cos2﹣cos2（B+C）＝，（Ⅰ）求角A的大小；（Ⅱ）若b+c＝3，求a的最小值．【解答】解：（Ⅰ）∵A+B+C＝π，即B+C＝π﹣A，∴4cos2﹣cos2（B+C）＝2（1+cos A）﹣cos2A＝﹣2cos2A+2cos A+3＝，∴2cos2A﹣2cos A+＝0，∴cos A＝，又0＜A＜π，∴A＝60°；（Ⅱ）由余弦定理cos A＝得：bc＝b2+c2﹣a2，∴a2＝（b+c）2﹣3bc＝9﹣3bc≥9﹣3（）2＝，∴a≥，则a的最小值为，当且仅当b＝c＝时取等号．18．（12分）2019年2月13日《烟台市全民阅读促进条例》全文发布，旨在保障全民阅读权利，培养全民阅读习惯，提高全民阅读能力，推动文明城市和文化强市建设．某高校为了解条例发布以来全校学生的阅读情况，随机调查了200名学生每周阅读时间X（单位：小时）并绘制如图所示的频率分布直方图．（1）求这200名学生每周阅读时间的样本平均数和中位数a（a的值精确到0.01）；（2）为查找影响学生阅读时间的因素，学校团委决定从每周阅读时间为[6.5，7，5），[7.5，8.5）的学生中抽取9名参加座谈会．（i）你认为9个名额应该怎么分配？并说明理由；（ii）座谈中发现9名学生中理工类专业的较多．请根据200名学生的调研数据，填写下面的列联表，并判断是否有95%的把握认为学生阅读时间不足（每周阅读时间不足8.5小时）与“是否理工类专业”有关？阅读时间不足8.5小时阅读时间超过8.5小时理工类专业4060非理工类专业附：．临界值表：0.150.100.050.0250.0100.0050.001P（K2≥k0）k0 2.072 2.706 3.841 5.024 6.6357.87910.828【解答】解：（1）该组数据的平均数……………………（2分）因为0.03+0.1+0.2+0.35＝0.68＞0.5，所以中位数a∈[8.5，9.5），由0.03+0.1+0.2+（a﹣8.5）×0.35＝0.5，解得；…（4分）（2）（i）每周阅读时间为[6，5，7.5）的学生中抽取3名，每周阅读时间为[7.5，8.5）的学生中抽取6名．…………………………………（5分）理由：每周阅读时间为[6，5，7.5）与每周阅读时间为[7.5，8.5）是差异明显的两层，为保持样本结构与总体结构的一致性，提高样本的代表性，宜采用分层抽样的方法抽取样本；因为两者频率分别为0.1，0.2，所以按照1：2进行名额分配．………………………（7分）（ii）由频率分布直方图可知，阅读时间不足8.5小时的学生共有200×（0.03+0.1+0.2）＝66人，超过8.5小时的共有200﹣66＝134人．于是列联表为：阅读时间不足8.5小时阅读时间超过8.5小时理工类专业4060非理工类专业2674……………（9分）K2的观测值，………（11分）所以有95%的把握认为学生阅读时间不足与“是否理工类专业”有关．……（12分）19．（12分）如图1，等腰梯形ABCD中，AD∥BC，AB＝AE＝BE＝CD＝2，BC＝ED＝4，O为BE中点，F为BC中点．将△ABE沿BE折起到△A'BE的位置，如图2．（1）证明：CD⊥平面A'OF；（2）若平面A'BE⊥平面BCDE，求点F到平面A'EC的距离．【解答】（1）证明：图1中，可得△ABF为等边三角形，∴∠EBF＝∠AEB＝60°，∴BF＝BE＝EF＝2，∴四边形ABCE为菱形，∴AO⊥BE，FO⊥BE，∴在图2中，A′O⊥BE，FO⊥BE，又A′O∩FO＝O，∴BE⊥面A′OF．∵BC＝ED＝4，BC∥DE，∴四边形BCDE为平行四边形．∴BE∥CD，∴CD⊥A′OF；（2）解：由（1）可知A′O⊥BE，∵平面A'BE⊥平面BCDE，平面A'BE∩平面BCDE＝BE．A′O⊂面A'BE．A′O⊥面BCDE，由余弦定理可得EC＝．A＝＝4，∴A′C2＝EC2+A′E2，∴∠A′EC＝900．∴S△A′EC＝3，设B到面A′EC的距离为d，∵V B﹣A′EC＝V A′﹣BEC．∴，∴3d＝，∴d＝2，因此，F到平面A'EC的距离为．20．（12分）已知椭圆C：+＝l（a＞b＞0）过点（2，1），且离心率e＝．（l）求椭圆C的方程；（2）已知斜率为的直线l与椭圆C交于两个不同点A，B，点P的坐标为（2，1），设直线P A与PB的倾斜角分别为α，β，证明：α+β＝π．【解答】解：（1）因为椭圆C：+＝l（a＞b＞0）过点（2，1），且离心率e＝．所以，，a2＝b2+c2，解得a2＝8，b2＝2，所以椭圆C的方程．（2）设直线l的方程为y＝x+m，A（x1，y1），B（x2，y2），联立直线l与椭圆的方程得2x2+4mx+4m2﹣8＝0，x1+x2＝﹣2m，x1x2＝2m2﹣4，k P A+k PB＝＝，＝，＝，＝，所以k P A+k PB＝0，∴α+β＝π．21．（12分）已知f（x）＝e x﹣alnx（a∈R）．（1）求函数f（x）在点（1，f（1））处的切线方程；（2）当a＝﹣1时，若不等式f（x）＞e+m（x﹣1）对任意x∈（1，+∞）恒成立，求实数m的取值范围．【解答】解：（1）由f（x）＝e x﹣alnx，则，切点为（1，e），所求切线方程为y﹣e＝（e﹣a）（x﹣1），即（e﹣a）x﹣y+a＝0．（2）由f（x）＝e x﹣alnx，原不等式即为e x+lnx﹣e﹣m（x﹣1）＞0，记F（x）＝e x+lnx﹣e﹣m（x﹣1），F（1）＝0，依题意有F（x）＞0对任意x∈[1，+∞）恒成立，求导得，当x＞1时，F''（x）＞0，则F'（x）在（1，+∞）上单调递增，有F'（x）＞F'（1）＝e x+1﹣m，若m≤e+1，则F'（x）＞0，若F（x）在（1，+∞）上单调递增，且F（x）＞F（1）＝0，适合题意；若m＞e+1，则F'（1）＜0，又，故存在x1∈（1，lnm）使F'（x）＝0，当1＜x＜x1时，F'（x）＜0，得F（x）在（1，x1）上单调递减，在F（x）＜F（1）＝0，舍去，综上，实数m的取值范围是m≤e+1．（二）选考题：共10分.请考生在22、23两题中任选-题作答，如果多做，则按所做的第--题记分.[选修4--4：坐标系与参数方程.]22．（10分）在平面直角坐标系xOy中，曲线C的参数方程为（r＞0，φ为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为，若直线l与曲线C相切；（Ⅰ）求曲线C的极坐标方程；（Ⅱ）在曲线C上取两点M，N与原点O构成△MON，且满足，求面积△MON的最大值．【解答】解：（Ⅰ）∵直线l的极坐标方程为，∴由题意可知直线l的直角坐标方程为y＝+2，曲线C是圆心为（，1），半径为r的圆，直线l与曲线C相切，可得r＝＝2，∵曲线C的参数方程为（r＞0，φ为参数），∴曲线C的普通方程为（x﹣）2+（y﹣1）2＝4，所以曲线C的极坐标方程为ρ2﹣2ρcosθ﹣2ρsinθ＝0，即．（Ⅱ）由（Ⅰ）不妨设M（ρ1，θ），N（ρ2，），（ρ1＞0，ρ2＞0），＝＝4sin（）sin（）＝2sinθcosθ+2＝sin2θ+＝2sin（2）+，当时，，所以△MON面积的最大值为2+．[选修4-5：不等式选讲]23．设函数f（x）＝k|x|﹣|2x﹣1|．（1）当k＝1时，求不等式f（x）＞0的解集；（2）当x∈（0，+∞）时，f（x）+b＞0恒成立，求k+b的最小值．【解答】解（1）当k＝1时，不等式化为|x|﹣|2x﹣1|＞0，即，或，或；……………（3分）解得x∈∅，或＜x＜，或≤x＜1；综上，原不等式的解集为（，1）；……………（5分）（2）x∈（0，+∞）时，不等式f（x）+b＞0恒成立，可化为k|x|+b＞|2x﹣1恒成立；画出y＝|2x﹣1|与y＝k|x|+b的图象，如图所示；由图象知当k≥2，且b≥1时，y＝k|x|+b的图象始终在y＝|2x﹣1|的上方，……………（8分）∴k+b≥3，即k+b的最小值为3（这时k＝2，b＝1）．……………（10分）。

湖南省长沙市雅礼中学2021届高三下学期月考(七)数学试题

雅礼中学2021届高三月考试卷（七）数学第Ⅰ卷一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集为实数集，集合{}3|6A x x =-<<，{}2|9140B x x x +-=<，则()U A B ⋂=A ．(2,6)B ．(2,7)C ．(]3,2-D ．()3,2-2．若3112i z i i+=⋅-，则z 的虚部为 A ．15B ．15C ．35D ．353．函数2()()1x x x e e f x x --=-的图象大致是 A ． B ．C ．D ．4．某新晋网红一线城市鹅城人口模型近似为0.012250024t P e =，其中0t =表示2020年的人口数量，则鹅城人口数量达到320000的年份大约是（ln20.693≈，ln3 1.099≈，ln5 1.609≈） A ．2040年B ．2045年C ．2030年D ．2050年5．我们打印用的A4，之所以是这个比值，是因为把纸张对折，得到纸张的形状不变．已知圆柱的母线长小于底面圆的直径长（如图所示），它的轴截面ABCD 为一张A4纸，若点E 为上底面圆上弧AB 的中点，则异面直线DE 与AB 所成的角约为A ．6π B ．4π C ．3π D ．23π 6．十二生肖，又称十二属相，与中国传统文化中的十二地支呈现一一对应关系，分别为子鼠、丑牛、寅虎、卯兔、辰龙、巳蛇、午马、未羊、申猴、西鸡、戌狗、亥猪．现有十二生肖吉祥物各一件，甲、乙、丙三位同学分别随机抽取一件作为礼物．甲同学喜欢马、牛，乙同学喜欢马、龙、狗，丙同学除了鼠不喜欢外其他的都喜欢，则这三位同学恰好都抽到各自喜欢的礼物的概率是 A ．388B ．344C ．120D ．9447．唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为221x y +≤，若将军从点(2,0)A 处出发，河岸线所在直线方程为3x y +=，并假定将军只要到达军营所在区域即回到军营，则“将军饮马”的最短总路程为A ．1B ．1-C ．D ．8．将函数()4sin()22f x x ππ=-和直线()1g x x =-的所有交点从左到右依次记为1A ，2A ，⋅⋅⋅，n A 若P 点坐标为(，则12||n PA PA PA +++=A ．0B ．2C ．6D ．10二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分． 9．某调查机构对全国互联网行业进行调查统计，得到如下整个互联网行业从业者年龄分布饼状图、“90后”从事互联网行业闵位分布条形图，则下列结论中正确的是注：“90后”指1990年及以后出生的人，“80后”指1980—1989年之间出生的人，“80前”指1979年及以前出生的人．A ．互联网行业从业人员中“90后”占一半以上B ．互联网行业中从事技术岗位的人数超过总人数的20%C ．互联网行业中从事运营岗位的人数“90后”比“80前”多D ．互联网行业中从事技术闵位的人数“90后”比“80后”多 10．设1a b >>，01c <<，则下列不等式中，成立的是A ．c c a b <B ．b c a b >C ．log log b a c c <D ． log log c c b a <11．已知等比数列{}n a 首项11a >，公比为q ，前n 项和为n S ，前n 项积为n T ，函数127()()()()f x x x a x a x a =+++，若(0)1f '=，则A ．{lg }n a 为单调递增的等差数列B ．01q <<C ．11n a S q --⎧⎫⎨⎬⎩⎭为单调递增的等比数列D ．使得1n T >成立的n 的最大值为612．已知直线l ：220kx y kp --=与抛物线2:2(0)C y px p =>相交于A ，B 两点，点(1,1)M --是抛物线C 的准线与以AB 为直径的圆的公共点，则下列结论正确的是 A ．2p =B ．2k =-C ．MAB 的面积为D ．5AB = 第Ⅱ卷三、填空题：本大题共4小题，每小题5分，共20分． 13．曲线21y x x=+在点(1,2)处的切线方程为_____． 14．在5(12)(2)x x -+展开式中，4x 的系数为_____．15．农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子”，古称“角黍”，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原．如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为_____．16．设双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ，2F ，过1F 直线l 分别与双曲线左、右两支交于M ，N 两点，且22F M F N ⊥，22F M F N =，则双曲线C 的离心率为_____．四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）从条件①2(1)n n S n a =+(2)n a n =≥，③0n a >，2=2nn n a a S +中任选一个，补充到下面问题中，并给出解答．已知数列{}n a 的前n 项和为n S ，11a =，___．若1a ，k a ，2k S +成等比数列，求k 的值． 18．（本小题满分12分）如图，四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，底面ABCD 为梯形，AB CD ∥，2AB DC ==，AC BD F ⋂=且PAD 与ABD 均为正三角形，G 为PAD 的重心．（1）求证：GF ∥平面PDC ；（2）求平面PAD 与平面PBC 所成锐二面角的余弦值． 19．（本小题满分12分）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．已知(sin cos )0b a C C +-=．（1）求A ；（2）若D 为BC 边上一点，且AD BC ⊥，2)BC AD =，求sin2B ． 20．（本小题满分12分）设椭圆22221(0)x y a b a b +=>>离心率12e =，椭圆上的点到左焦点1F 的距离的最大值为3．（1）求椭圆C 的方程；（2）求椭圆C 的外切矩形（即矩形的四边所在的直线均与椭圆相切）ABCD 的面积S 的取值范围．21．（本小题满分12分）随着中美贸易战的不断升级，越来越多的国内科技巨头加大了科技研发投入的力度．某科技公司拟对“麒麟”手机芯片进行科技升级，根据市场调研与模拟，得到科技升级投入x （亿元）与科技升级直接收益y （亿元）的数据统计如下模型①：ˆ 4.111.8yx =+；模型②：ˆ14.4y =．当17x >时，确定y 与x 满足的线性回归方程为ˆ0.7yx a =-+．（1）根据下列表格中的数据，比较当017x <≤时模型①、②的相关指数2R 的大小，并选择拟合精度更高、更可靠的模型，预测对“麒麟”手机芯片科技升级的投入为17亿元时的直接收益．（附：刻画回归效果的相关指数22121ˆ()1()ii i n ii yyR yy ==-=--∑∑ 4.1≈）（2）为鼓励科技创新，当科技升级的投入不少于20亿元时，国家给予公司补贴5亿元，以回归方程为预测依据，比较科技升级投入17亿元与20亿元时公司实际收益的大小．（附：用最小二乘法求线性回归方程ˆˆˆybx a =+的系数ˆb =1122211()()ˆ()nni iii i i nniii i x ynx yxx y y bxnx xx ====-⋅--==--∑∑∑∑，ˆˆay bx =-）（3）科技升级后，“麒麟”芯片效率X 大幅提高，经实际试验得X 大致服从正态分布20.52,0.01)(N ,公司对科技升级团队的奖励方案如下：若芯片的效率不超过50%，不予奖励；若芯片的效率超过50%，但不超过53%，每部芯片奖励2元；若芯片的效率超过53%，每部芯片奖励4元，记Y 为每部芯片获得的奖励，求(Y)E （精确到0.01）．（附：若随机变量）2~(,)(0)P N μσσ>，则()0.6827P X μσμσ-<≤+=，(22)0.9545P X μσμσ-<≤+=．22．（本小题满分12分）已知函数()x f x e ax =-，()ln g x x ax =-，a ∈R ．（1）当a e <时，讨论函数()f x 的零点个数；（2）记函数()()()F x f x g x =-的最小值为m ，求()ln 2x m G x e e =-的最小值．雅礼中学2021届高三月考试卷（七）数学参考答案一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．C ∵29140{27}B xx x x x =-+<=<<∣∣，∴ 2 7UB x x x =≤≥∣或，∴(){}32(3,2]U A B x x ⋂=-<≤=-∣．故选C ．2．A 因为3111(1)(12)331()121212(12)(12)555i i i i i i z i i i i i i i i ++--++=⋅=⋅-====+----+，所以z 的虚部为15，故选A ．3．D ()()22e e e e ()()11x x x x x x f x f x x x ------===--，()f x 是偶函数，排除A ，0x >时，e e x x ->，即e e 0x x-->，当1x >时，又有210x ->，因此()0f x >，排除B ，C ，故选D ．4．A 由已知，得0.012320000ln ln e250024t⎛⎫= ⎪⎝⎭，则320000ln 2500240.012t ⎛⎫ ⎪⎝⎭=，近似于5ln 22ln 520.5830.012-≈，过20年或21年，结合选项选A ，故选A ．5．C ∵//AB CD ，∴EDC ∠（或补角）为异面直线DE 与AB 所成的角，设CD 的中点为O ，过E 作EF ⊥底面⊙O ，连接OE ，OF ， ∵E 是弧AB 的中点，∴F 是弧CD 的中点，∴CD OF ⊥，又EF ⊥平面⊙O ，∴EF CD ⊥，EF OF F ⋂=， ∴CD ⊥平面OEF ，∴OD OE ⊥．设1AD =，则CD =2OF =，1EF =，于是OE ==∴tan2OEEDOOD∠===，∴3EDOπ∠=．故选C．6．A 依题意可分类：①甲同学选马，则有112918C C=种情况符合要求；②甲同学选牛，则有113927C C=种情况符合要求；三位同学抽取礼物的所有情况有312A种，则这三位同学恰好都抽到各自喜欢的礼物的概率3121827388PA+==．故选A．7．A 设点A关于直线3x y+=的对称点(,)A a b'，AA'的中点为2,22a b+⎛⎫⎪⎝⎭，2AAbka'=-，故(1)1,223,22baa b⎧⋅-=-⎪⎪-⎨+⎪+=⎪⎩解得3,1,ab=⎧⎨=⎩，要使从点A到军营总路程最短，即为点A'到军营最短的距离，1，故选A．8．D 函数()4cos2f x xπ=与()1g x x=-的所有交点从左往右依次记为1A、2A、3A、4A和5A，且1A和5A，2A和4A都关于点3A对称，如图所示：则125355(1,PA PA PA PA +++==，所以1210n PA PA PA +++=．故选D ．二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9．互联网行业从业人员中“90后”从事技术岗位的人数占总人数的56%39.6%22.176%⨯=，超过20%，所以互联网行业从业人员（包括“90后”“80后”“80前”）从事技术岗位的人数超过总人数的20%，B 正确；互联网行业从业人员中“90后”从事运营岗位的人数占总人数的56%17%9.52%⨯=，超过“80前”的人数占总人数的比例，且“80前”中从事运营岗位的比例未知，C 正确；互联网行业从业人员中“90后”从事技术岗位的人数占总人数的56%39.6%22.176%⨯=，小于“80后”的人数占总人数的比例，但“80后”中从事技术岗位的比例未知，D 不一定正确．故选ABC ．10．BC 01c c c a b <<⇒>，故A 错误；因为1a b >>，01c <<，所以b b c a b b >>，故B 正确；由对数函数的单调性可得log log c c b a >，故D 错误；因为1log log b c c b =，1log log a a c a=，0log log c c b a >>，所以log log a b c c <，故C 正确．故选BC ．11．BCD 令()()()127()g x x a x a x a =+++，则()()f x xg x =，∴()()()f x g x xg x ''=+，∴127(0)(0)1f g a a a '===，因为{}n a 是等比数列，所以712741a a a a ==，即3411a a q ==，∵11a >，∴01q <<，B 正确； ∵()111lg lg lg (1)lg n n a a q a n q -==+-，∴{}lg n a 是公差为1gq 的递减等差数列，A 错误； ∵()111111111n n n a a a qS q q q q q --=--=⋅---， ∴11n a S q ⎧⎫-⎨⎬-⎩⎭是首项为101a qq <-，公比为q 的递增等比数列，C 正确； ∵11a >，01q <<，41a =，∴3n ≤时，1n a >，5n ≥时，01n a <<， ∴4n ≤时，1n T >， ∵7712741T a a a a ===，∴8n ≥，78971n n T T a a a T =<=，又75671T T a a =>，7671TT a =>，所以使得1n T >成立的n 的最大值为6，D 正确．故选BCD ．12．ABD 由题意知，抛物线C 的准线为1x =-，即12p=，解得2p =，故选项A 正确；因为2p =，所以抛物线C 的方程为：24y x =，其焦点为(1,0)F ，又直线l ：220kx y kp -=一，即(1)y k x =-，所以直线l 恒过抛物线的焦点(1,0)F ，设点()11,A x y ，()22,B x y ，因为A ，B 两点在抛物线C 上，联立方程21122244,,y x y x ⎧=⎨=⎩，两式相减可得，1212124y y k x x y y -==-+，设AB 的中点为()00,Q x y ，则02y k=，因为点()00,Q x y 在直线l 上，解得0221x k=+，所以点2221,Q kk ⎛⎫+ ⎪⎝⎭是以AB 为直径的圆的圆心，由抛物线的定义知，圆Q 的半径012222222222x x x AB r k+++====+，因为2222222||21QM r k k ⎛⎫⎛⎫=+++= ⎪ ⎪⎝⎭⎝⎭，所以22222222212k k k ⎛⎫⎛⎫⎛⎫+++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得2k =-，故选项B 正确；因为2k =-，所以直线l 为2(1)0y x +-=，由点到直线的距离公式可得，点M 到直线l 的距离为22512d ==+，所以11||522MABSd AB =⋅⋅==，故选项C 错误；因为2k =-，所以弦长222||2222254AB r k ⎛⎫⎛⎫==+=+= ⎪ ⎪⎝⎭⎝⎭，故选项D 正确；故选ABD ．三、填空题：本大题共4小题，每小题5分，共20分． 13．1y x =+设()y f x =，则21()2f x x x '=-，所以(1)211f '=-=，所以曲线21y x x=+在点(1,2)处的切线方程为21(1)y x -=⨯-，即1y x =+． 14．80555(12)(2)2(12)(12)x x x x x -+=-+-，二项式5(12)x -的展开式的第1r +项为15(2)r r r r T C x +=-，令3r =，则333345(2)80T C x x =-=-，令4r =，则444455(2)80T C x x =-=，则5(12)(2)x x -+展开式中，4x 的系数为2808080⨯-=．15．6每个三角形面积是112S =⨯=由对称性可知该六面体是由两个正四面体合成的，可求出该四面体的高为=，故四面体体积1312=，因此该六面体体积是正四面体的2．16如图，作2F D MN ⊥于D ，根据双曲线定义212MF MF a -=，122NF NF a -=，所以12||22NF NF MN a a -=-=，所以||4MN a =，所以22MF NF ==，12)MF a =，22F D a =，1F D =．在12Rt F F D 中，2224)(2)c a =+，化简得223c a =，所以c e a==四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．若选择①，因为2(1)n n S n a =+，*n ∈N ，所以112(2)n n S n a ++=+，*n ∈N ，两式相减得112(2)(1)n n n a n a n a ++=+-+，整理得1(1)n n na n a +=+．即11n n a a n n +=+，*n ∈N ，所以n a n ⎧⎫⎨⎬⎩⎭为常数列． 111n a a n ==，所以n a n =．（或由11n n a n a n++=，利用相乘相消法，求得n a n =）所以k a k =，2(2)(12)(2)(3)22k k k k k S ++++++==，又1a ，k a ，2k S +成等比数列，所以2(2)(3)2k k k ++=，所以2560k k --=，解得6k =或1k =-（舍），所以6k =．若选择②，(2)n a n =≥1n n S S -=-，=，易知0n S >1=，所以为等差数列．1==n =，2n S n =， ∴121(2)n n n a S S n n -=-=-≥，又1n =时，11a =也满足上式，所以21n a n =-．因为1a ，k a ，2k S +成等比数列，∴22(2)(21)k k +=-，∴3k =或13k =-，又*k ∈N ，∴3k =．若选择③，因为()2*2n n n a a S n +=∈N ，所以21112(2)n n n a a S n ---+=≥，两式相减得22111222(2)n n n n n n n a a a a S S a n ----+-=-=≥，整理得()()111(2)n n n n n n a a a a a a n ----+=+≥，因为0n a >，∴11(2)n n a a n --=≥，所以{}n a 是等差数列，所以1(1)1n a n n =+-⨯=．2(2)(12)(2)(3)22k k k k k S ++++++==．又1a ，k a ，2k S +成等比数列，∴2(2)(3)2k k k ++=， ∴6k =或1k =-，又*k ∈N ，∴6k =．18．（1）设PD 的中点为E ，连接AE ，CE ，GF ．∵//AB CD，=2 AB DC ，=AC BD F ⋂，∴==2AF AB FC CD．又∵G 为PAD 的重心G ， ∴2AGGE=，∴//GF CE ．又∵GF ⊄面PDC ，CE ⊂面PDC ， ∴//GF 平面PDC ．（2）设O 为AD 的中点，PAD 为正三角形，则PO AD ⊥． ∵平面PAD ⊥平面ABCD ，平面PAD ⋂平面ABCD AD =， ∴PO ⊥平面ABCD ．过O 分别作BC ，AB 的平行线，建系如图.∵(0,0,3)P，32B ⎛⎫ ⎪ ⎪⎝⎭，32C ⎛⎫- ⎪ ⎪⎝⎭，易知平面PAD 的法向量1(1,3,0)n =．设平面PBC 的法向量为()2222,,n x y z =，∴3,322PB ⎛⎫=- ⎪ ⎪⎝⎭，(3,0,0)BC =-，∴222222330,230,PB n x y z BC n x ⎧⋅=+-=⎪⎨⎪⋅=-=⎩得232n ⎛⎫= ⎪⎝⎭，121212cos ,721n nn n n n ⋅===，从而，平面PAD 与平面PBC ．19．（1）因为(sincos )0b a C C +-=，所以sin sin (sin cos )0B A C C +-=，所以sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=，即cos sin sin sin 0A C A C +=．因为0C π<<，所以sin 0C ≠，所以sin cos 0A A +=，则tan 1A =-．因为0A π<<，所以34A π=…6分（2）因为AD BC ⊥，所以11sin 22ABCSbc A a AD ==⋅，即2a AD =⋅．因为2)BC AD =，所以AD =，所以2(2a bc =+．由余弦定理得2222cos a b c bc A =+-，则22(2bc b c +=++，整理得2()0b c -=，即b c =，故B C =．因为34A π=，所以8B π=，所以sin 2sin 42B π==…12分20．（1）由题设条件可得12c a =，3a c +=，解得2a =，1c =，∴2223b a c =-=，所以椭圆C 的方程为22143x y +=．…4分（2）当矩形ABCD 的一组对边斜率不存在时，得矩形ABCD的面积S =当矩形ABCD 四边斜率都存在时，不妨设AB ，CD 所在直线斜率为k ，则BC ，AD 斜率为1k-，设直线AB 方程为y kx m =+，与椭圆联立22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩，可得()2224384120kx kmx m +++-=，由()()222(8)4434120km k m ∆=-+-=，得2243m k =+．由对称性知直线CD 的直线方程为y kx m =-，直线AB ，CD间的距离1d === 同理可求得BC ，AD间的距离为2d == 所以四边形ABCD 面积为12ABCD S d d ====14=≤=（等号当且仅当1k =±时成立）．又ABCD S >=故由以上可得外切矩形面积的取值范围是．…12分21．（1）由表格中的数据，182.479.2>，所以()()772211182.479.2iii i y y y y ==>--∑∑，所以()()772211182.479.211iii i y y y y ==-<---∑∑．可见模型①的相关指数21R 小于模型②的相关指数22R ．所以回归模型②的拟合效果更好．所以当17x =亿元时，科技升级直接收益的预测值为ˆ21.314.421.3 4.114.472.93y=≈⨯-=（亿元）．…4分（2）当17x >时，由已知可得2122232425235x ++++==，68.56867.5666667.25y ++++==．所以0.767.20.72383.3a y x =+=+⨯=．所以当17x >时，y 与x 满足的线性回归方程为ˆ0.783.3yx =-+．当20x =时，科技升级直接收益的预测值为ˆ0.72083.369.3y=-⨯+=亿元．当20x =亿元时，实际收益的预测值为69.3574.3+=亿元72.93>亿元，所以技术升级投入20亿元时，公司的实际收益更大．…8分（3）因为20.50μσ-=，0.53μσ+=，所以(0.500.53)(2)P X P X μσμσ<≤=-<≤+(2)()P X P X μσμσμσμσ=-<≤-+-<≤+ 0.95450.68270.68270.81862-=+=；10.6827(0.53)()2P X P X μσ->=>+=．所以10.6827()020.81864 2.2718 2.272E Y -=+⨯+⨯=≈（元）．…12分 22．（1）()f x 的定义域为(,)-∞+∞，()e x f x a '=-．①当0a <时，()e 0x f x a '=->，()f x 单调递增，又(0)1f =，11e 10a f a ⎛⎫=-< ⎪⎝⎭，所以函数()f x 有唯一零点；②当0a =时，()e 0x f x =>恒成立，所以函数()f x 无零点； ③当0a e <<时，令()e 0x f x a '=-=，得ln x a =．当ln x a <时，()0f x '<，()f x 单调递减；当ln x a >时，()0f x '>，()f x 单调递增．所以ln min ()(ln )e ln (1ln )a f x f a a a a a ==-=-，故当0a e <<时，(ln )0f a >，所以函数()f x 无零点．综上所述，当0a e ≤<时函数()f x 无零点；当0a <，函数()f x 有一个零点．…4分（2）由题意得，()ln x F x e x =-，则1()e x F x x'=-，令1()e x h x x =-，则21()e 0x h x x'=+>，所以()h x 在(0,)+∞上为增函数，即()F x '在(0,)+∞上为增函数．又(1)e 10F '=->，1202F ⎛⎫'=< ⎪⎝⎭，所以()F x '在(0,)+∞上存在唯一零点0x ，且01,12x ⎛⎫∈ ⎪⎝⎭，()0001e 0x F x x '=-=，即001e x x =．当()00,x x ∈时，()0F x '<，()F x 在()00,x 上为减函数，当()0,x x ∈+∞时，()0F x '>，()F x 在()0,x +∞上为增函数，()F x 的最小值()000e ln x m F x x ==-．因为001e x x =，所以00ln x x =-，所以0012m x x =+>．由()e e ln xmG x x =-得e ()e mxG x x'=-，易知()G x '在(0,)+∞上为增函数．因为2m >，所以(1)e e 0m G '=-<，e 1()e e 10m mm G m m m '⎛⎫=-=-> ⎪⎝⎭，所以()G x '在(0,)+∞上存在唯一零点1x ，且1(1,)x m ∈，()111e e 0mx G x x '=-=，当()10,x 时，()0G x '<，()G x 在()10,x 上为减函数，当()1,x x ∈+∞时，()0G x '>，()G x 在()1,x +∞上为增函数，所以()G x 的最小值为()11e e ln x m G x x =-，因为11e e mx x =，所以11ln x m x =-，所以11ln m x x =+，又000011e ln ln x m x x x =-=+，所以110011ln ln x x x x +=+，又函数ln y x x =+在(0,)+∞上为增函数，所以101x x =， ()000000111111ln 1000001111e e ln e e ln e e ln x x x x x x mG x x x x x +=-⋅=-⋅=-⋅⋅()0011000000111e ln e ln x x x x x x x x ⎛⎫=⋅⋅-=⋅⋅+ ⎪⎝⎭．因为00ln 0x x +=，所以()10G x =，即()G x 在(0,)+∞上的最小值为0．…12分。