矩形定义及性质的应用
矩形的判定和性质
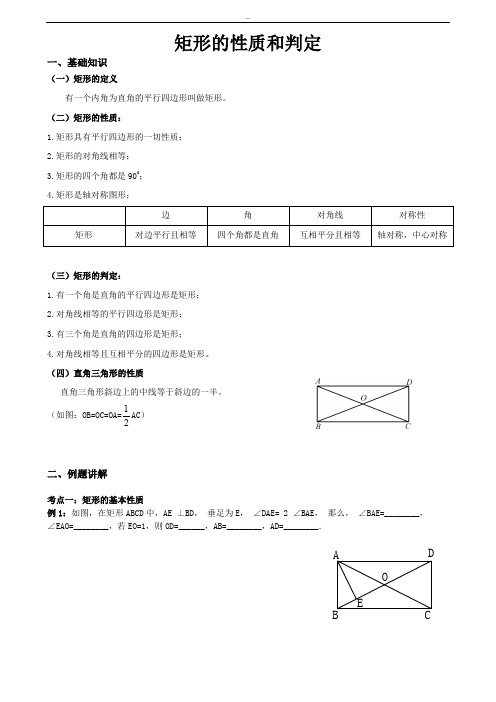
矩形的性质和判定一、基础知识(一)矩形的定义有一个内角为直角的平行四边形叫做矩形。
(二)矩形的性质:1.矩形具有平行四边形的一切性质;2.矩形的对角线相等;3.矩形的四个角都是900; 4.矩形是轴对称图形;边 角 对角线 对称性 矩形对边平行且相等四个角都是直角互相平分且相等轴对称,中心对称(三)矩形的判定:1.有一个角是直角的平行四边形是矩形;2.对角线相等的平行四边形是矩形;3.有三个角是直角的四边形是矩形;4.对角线相等且互相平分的四边形是矩形。
(四)直角三角形的性质直角三角形斜边上的中线等于斜边的一半。
(如图:OB=OC=OA=21AC )二、例题讲解考点一:矩形的基本性质例1:如图,在矩形ABCD 中,AE•⊥BD ,•垂足为E ,•∠DAE=•2•∠BAE ,•那么,•∠BAE=________, ∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.AEDCBO练习 1:矩形ABCD中, ,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.练习2:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?练习1:矩形ABCD中, ,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长。
例3:如图,在矩形ABCD 中,相邻两边AB 、BC 分别长15cm 和25cm ,内角∠BAD 的角平分线与边BC 交于点E .试求BE 与CE 的长度.练习1:如图,在矩形ABCD 中,E 是边AD 上的一点.试说明△BCE 的面积与矩形ABCD 的面积之间的关系.例4:(2009年广西钦州)已知:如图1,在矩形ABCD 中,AF =BE .求证:DE =CF ;ADCB 图1F E练习1:如图,矩形ABCD 中,E 为AD 中点,∠BEC 为直角,矩形ABCD 的周长是20,求AD 、AB 的长。
矩形的性质与计算方法

矩形的性质与计算方法矩形是一种具有特殊性质和计算方法的几何图形,拥有广泛的应用领域和实际价值。
本文将详细介绍矩形的性质和计算方法,并探讨其在数学和实际生活中的应用。
一、矩形的性质1. 边长性质:矩形的四条边长度相等,对应边两两平行。
2. 角性质:矩形的四个角都是直角。
3. 对角线性质:矩形的对角线相等,且相互平分。
二、矩形的计算方法1. 周长计算:矩形的周长等于两条相邻边的长度之和的两倍。
即,周长C = 2 × (a + b),其中a和b分别表示相邻边的长度。
2. 面积计算:矩形的面积等于两条相邻边的长度相乘。
即,面积A = a × b,其中a和b分别表示相邻边的长度。
3. 对角线计算:矩形的对角线长度可以通过勾股定理计算。
即,对角线d = √(a² + b²),其中a和b分别表示相邻边的长度。
三、矩形的应用1. 数学领域应用:矩形是数学中的基本几何图形,它在数学的各个分支中都有重要的应用,如代数、几何、概率等。
矩形的性质和计算方法是解决各类与矩形相关问题的基础。
2. 建筑领域应用:矩形是建筑设计和施工中常见的形状,比如房屋的平面图通常是矩形。
矩形的性质和计算方法可以帮助建筑师和工程师计算房屋的面积、周长,从而更好地规划和布置建筑空间。
3. 器物设计应用:矩形形状的器物在生活中随处可见,如桌子、书架、电视等。
矩形的性质和计算方法可以帮助设计师确定正确的比例,确保产品的美观和功能性。
4. 地理测量应用:矩形的性质和计算方法在地理测量中也有重要应用,如测算土地面积、建筑用地面积等。
通过测量边长和角度,可以精确计算各类地理空间和物体的尺寸和形状。
结语:矩形作为一种特殊的几何图形,具有独特的性质和重要的计算方法。
理解矩形的性质和熟悉计算方法对于数学学习和实际应用都很重要。
通过学习矩形的相关知识,我们可以更好地理解和应用几何学,同时也有助于我们更好地规划和设计生活、工作和学习中的各类场景。
矩形的性质及应用

矩形的性质及应用矩形是一种常见的几何形状,具有一些独特的性质和广泛的应用。
本文将介绍矩形的性质及其在日常生活和工程领域中的应用。
一、矩形的定义和性质矩形是一种四边形,具有以下性质:1. 边长相等:矩形的对边两两相等,即AB = CD,BC = AD。
2. 对角线相等:矩形的对角线相等,即AC = BD。
3. 内角为直角:矩形的四个内角均为直角(90度角),即∠A = ∠B = ∠C = ∠D = 90°。
4. 互相平行:矩形的对边互相平行,即AB∥CD,AD∥BC。
5. 对边垂直:矩形的对边互相垂直,即AB⊥BC,AD⊥DC。
二、矩形的应用1. 建筑设计:矩形是建筑设计中常用的几何形状之一。
例如,在房屋平面设计中,矩形可以表示房间的墙壁,屋顶的平面形状等。
使用矩形结构可以简化建筑设计过程,使结构更稳定。
2. 产品设计:许多产品的外观设计都使用了矩形的形状。
例如,电视、手机、书桌等产品的外形通常是矩形,因为矩形有较大的空间利用率和良好的稳定性,便于制造和使用。
3. 数学推导:矩形的性质在数学推导中经常被应用。
例如,利用矩形的对角线相等性质,可以推导出勾股定理;利用矩形的内角为直角性质,可以推导出平行线之间的角度关系等。
4. 图像处理:在图像处理和计算机图形学中,矩形常被用作图像的基本单元。
图像可以被划分成一个个矩形像素块,利用矩形的性质和坐标系统进行处理和显示。
5. 地理测量:在地理测量中,矩形常被用来表示土地的边界、建筑物的平面布局等。
通过测量矩形的边长和角度,可以计算土地的面积和建筑物的体积。
6. 电路布局:在电路设计中,矩形的形状可以用来表示电路板的外形和内部布局。
矩形的边界可以作为电路板的导线和器件的连接点,方便电路布线和组装。
7. 几何推理:利用矩形的性质,可以进行一些几何推理和证明。
例如,通过对矩形的两个对角线进行分析,可以证明一个四边形是矩形。
三、总结矩形是一种重要的几何形状,具有明确的性质和广泛的应用。
矩形的性质和判定

矩形的性质和判定基础知识点1、矩形的性质和判定:定 义矩 形有一个内角是直角的平行四边形。
性质边对边平行,对边相等。
角 四个角相等,都是直角。
对角线互相平分,相等。
判定有一个角是直角的平行四边形是矩形。
有三个角是直角的四边形是矩形。
对角线相等的平行四边形是矩形。
2、在直角三角形中,斜边的中线等于斜边的一半。
3、矩形是轴对称图形,对称轴是对边中点的连线所在的直线。
例题剖析例1、 已知矩形ABCD 中,AB=2BC ,点E 在边DC 上,且AE=AB ,求∠EBC 的度数.【变式练习】矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F ,•求证:BE=CF .【变式练习】在矩形ABCD 中,AC ,BD 是对角线,过顶点C 作BD•的平行线与AB 的延长线相交于点E ,求证:△ACE 是等腰三角形.例2、折叠矩形ABCD 纸片,先折出折痕BD ,再折叠使A 落在对角线BD 上A ′位置上,折痕为DG ,AB=2,BC=1。
求AG 的长。
GA`DCBA【变式练习】如图,将矩形ABCD 沿对角线BD 折叠,使点C 落在F 的位置,BF 交AD 于E ,AD=8,AB=4,求△BED 的面积。
EDC BAF例3、在△ABC中,∠ABC=90°,BD是△ABC的中线,延长BD到E,•使DE=BD,连结AE,CE,求证:四边形ABCE是矩形.【变式练习】在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形。
求证:四边形ADCE是矩形。
例4、已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.【变式练习】(2011•青岛)在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC ,当CA=CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论【变式练习】E 为□ABCD 外一点,AE ⊥CE,BE ⊥DE ,求证:□ABCD 为矩形例5、□ABCD 中,AE 、BF 、CG 、DH 分别是各内角的平分线,E 、F 、G 、H 为它们的交点, 求证:四边形EFGH 的矩形。
矩形的性质和用途

矩形的性质和用途矩形是几何学中最基本的形状之一,具有许多独特的性质和广泛的应用。
本文将就矩形的性质和常见用途展开讨论。
一、性质1. 边长关系:矩形的两对相邻边长相等,对角线长度相等。
这个性质使得矩形有较好的对称性,可以方便地进行计算和推导。
2. 角度特性:矩形的四个角均为直角,即90度。
这使得矩形在建筑、绘图、设计等领域中应用广泛。
3. 面积计算:矩形的面积可以通过长度乘以宽度来计算,公式为A=长×宽。
这个简单的计算公式方便了矩形面积的求解,在测量、工程设计等方面具有重要作用。
4. 对角线性质:矩形的对角线相互垂直且相互平分。
这个性质使得矩形可以用于工程测量、图形构建以及装饰设计等方面。
二、用途1. 建筑和土木工程:矩形在建筑和土木工程中扮演重要角色。
例如,在房屋建设中,房间的墙壁往往是矩形的,矩形的角度特性使得房间更稳定和对称。
此外,建筑平面图中的墙壁、窗户、门等也常常利用矩形的性质来进行设计。
2. 绘图和设计:矩形在绘图和设计中常被使用。
绘制平面图、制作建筑物的模型、设计网页布局等都需要利用矩形的性质和对称性。
矩形还可以用于绘制地图、棋盘等。
3. 数学和几何学:矩形是几何学中最经典的形状之一,形成了许多数学定律和公式。
矩形的性质被广泛应用于数学问题的解决过程中,如计算面积、周长等。
4. 家居和室内设计:矩形的简单性质使得它在家居和室内设计领域中得到广泛运用。
例如,家具的设计往往以矩形为基础,包括桌子、座椅、柜子等。
墙壁、地板、天花板等室内元素也可以利用矩形的性质进行设计和布局。
5. 电子设备:矩形在电子设备中也有重要的应用。
例如,电视屏幕、电脑显示器、手机屏幕等都采用了矩形的形状。
此外,电子电路板的设计和制造也需要矩形的性质来进行布局和连接。
6. 艺术和装饰:矩形在艺术和装饰方面具有重要的地位。
矩形的简洁性和对称性使得它适合于许多装饰设计和艺术创作。
例如,画框、相框、墙画等的形状常常是矩形的。
矩形的性质与判定知识点

矩形的性质与判定知识点矩形是我们日常生活中最常见的几何形状之一,因为它有很多明显的性质和特点,所以在数学、物理等领域中也被广泛应用。
本文旨在介绍矩形的性质与判定知识点,以帮助读者更好地理解和应用矩形。
一、矩形的基本定义和性质在几何学中,矩形是一个四边形,其中对角线相等,且所有内角均为直角。
它的两条对边平行且长度相等,两条相邻边的内角均为90度。
由此可以得到矩形的以下基本性质:1. 对角线相等设矩形的两条对角线为AC和BD,则AC=BD,即对角线相等。
2. 边角关系设矩形的边长为a和b,则它的周长为C=2a+2b,面积为S=ab。
3. 内角和由于矩形的内角均为90度,因此它的任意两个内角的和均为180度。
4. 三角函数关系设矩形的一条边长为a,另一条边长为b,则其对角线长为D=sqrt(a^2+b^2)。
根据三角函数关系,可得矩形各角的正切值和余切值:tanA=a/b,tanB=b/a,cotA=b/a,cotB=a/b。
二、矩形的性质扩展除了以上基本性质外,矩形还有一些特殊的性质,它们在具体的数学问题中往往会有实际的应用。
下面介绍一些常见的扩展性质。
1. 中线定理设矩形ABCD的对角线AC和BD相交于点O,线段AB与线段CD交于点E,线段AD与线段BC交于点F。
则OE、OF为矩形的中线,且OE=OF=1/2AC。
证明:由于AC=BD,因此OC=OD。
又由于AB∥CD,因此∠OAB=∠OCD,∠OBA=∠OCB。
因此三角形OAB和OCD,三角形OBA和OCB均为全等三角形,故OA=OC,OB=OD。
又因为OE是线段AB上的中线,OF是线段AD上的中线,因此OE=1/2AB=1/2CD,OF=1/2AD=1/2BC。
因此OE=OF=1/2AC。
2. 对称性质设矩形ABCD的对角线AC和BD相交于点O,则AO=CO,BO=DO。
由此可知,点O是矩形的对称中心。
证明:因为AC=BD,所以OC=OD,且三角形AOC和COD的第一边、第三边、第五边相等,因此它们一定全等。
矩形总结归纳

矩形总结归纳矩形是一个常见而重要的几何形状,具有多个特点和应用。
在本文中,我们将对矩形的性质和用途进行全面的总结和归纳,以便更好地理解和应用矩形。
一、矩形的定义矩形是指具有四条边,其中相对的边相等且平行的四边形。
矩形的特点是四个内角都是直角(90度),对角线长度相等。
二、矩形的性质1. 直角性质:矩形的四个内角都是直角,即都等于90度。
2. 边性质:矩形的相对边相等且平行,可以表示为AB=CD,AB∥CD, BC=AD, BC∥AD。
3. 对角线性质:矩形的对角线相等,可以表示为AC=BD,且对角线互相平分。
4. 对边性质:矩形的对边相等,可以表示为AB=CD, AD=BC。
5. 相等性质:在一个矩形中,如果两个相邻边相等,那么这个矩形就是正方形(特殊的矩形)。
三、矩形的计算方法1. 周长:矩形的周长等于两倍的宽加两倍的长,可以表示为周长=2(宽+长)。
2. 面积:矩形的面积等于宽乘以长,可以表示为面积=宽×长。
3. 对角线长度:根据矩形的对角线性质,我们可以通过已知的宽和长来计算对角线的长度,可以使用勾股定理计算。
四、矩形的应用1. 建筑领域:矩形平面图在建筑设计过程中经常使用,例如绘制房屋平面布局图、办公室布局图等。
2. 数学几何学:矩形是平面几何中的重要基本概念,可以应用于解决多边形的性质和计算问题。
3. 计算机图形学:矩形是计算机屏幕的基本显示单位之一,图形界面中的窗口、按钮等元素通常都以矩形的形式呈现。
4. 地理测量:在地图制作和测量工作中,使用矩形网格划分地图区域,方便进行度量和定位。
5. 其他领域:矩形也可以应用于纺织品、家具设计、装饰艺术等众多领域,具有广泛的实际应用。
综上所述,矩形是一个常见且重要的几何形状,具有多种性质和应用。
通过对矩形的定义、性质、计算方法以及应用领域的总结和归纳,我们能更好地理解和应用矩形。
在日常生活和工作中,矩形的概念和特点能够帮助我们解决问题和进行创造性的思考。
矩形的认识与分类

矩形的认识与分类矩形是几何学中常见的形状之一,具有许多重要的性质和用途。
本文将对矩形的基本定义、特点以及不同类型的矩形进行详细介绍。
一、基本定义矩形是一种有四个直角的四边形,其对边长度相等且相对平行。
也就是说,一条边和和其相邻的两条边构成一个直角。
二、性质和特点1. 对角线相等:矩形的对角线相等,而且相互平分。
2. 相对边平行:矩形的相对边是平行的。
3. 内角和为180度:矩形的内角和等于180度,每个角都是直角。
根据以上性质和特点,我们可以通过测量边长和角度来判断是否是矩形。
三、不同类型的矩形1. 正矩形:正矩形是一种特殊的矩形,其四个内角都是直角,并且所有边长相等。
正矩形常见于建筑物中的窗户、门框等。
2. 长方形:长方形也是一种矩形,其相邻两条边长度不同,但仍然保持直角。
长方形在日常生活中非常常见,例如书、手机、电视等。
3. 菱形:菱形是矩形的一种特殊情况,其对边长度相等,但相邻两边不平行。
菱形在宝石、纹身等领域中常见。
四、矩形的应用矩形在日常生活和工作中有着广泛的应用。
以下是一些常见的应用场景:1. 建筑设计:矩形常用于建筑设计中的墙壁、门窗等构造物的规划和设计。
2. 统计学:矩形常用于绘制柱状图,用于表示数据的分布情况和比较。
3. 地理学:地理学中常用矩形来表示地图上的区域。
总结:矩形是一种重要的几何形状,具有许多独特的性质和特点。
我们可以通过测量边长和角度来判断是否是矩形,并进一步分类为正矩形、长方形和菱形。
矩形在我们的日常生活和工作中有着广泛的应用,需要我们对其进行深入的认识和理解。
注:以上内容为文章的主要部分,字数仅为500字,如需增加字数可适当拓展各小节的内容,提供更多实际应用和相关案例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C
★ ★★3.如图在矩形 ABCD 中,P 是 AD 上的一个动点, PE⊥ AC 于 E,PF⊥ BD 于 F,AG⊥ BD 于 G. 试问,PE+PF 与 AG 有什么关系?证明你的结论.
【交流总结,有哪些收获】
学生自主学习学案
Hale Waihona Puke 审核人: 矩形的性质的应用
科目 设计人 学习 目标 重难点
初二数学
课题 沈正江
授课时间 姓名
12 月 5 序号 16
日
班级
八1
1、利用矩形的性质进行有关的论证和计算. 2.解决与矩形有关的实际问题. 3.会解决折纸问题中的折叠矩形纸片问题. 矩形的性质的理解和掌握
【课前自练】 (10 分钟) 1._____________________的平行四边形叫做矩形. 2.如图,平行四边形 ABCD 中,∠BAD=90°,对角线 AC、 BD 相交于点 O, 则∠BAD=___________=_________=_________ =90 ° , △ ABC ≌ __________ ( 只 需 写 出 一 个 ) ,所以 AC=___________, 即矩形的四角都是________,矩形的对角线_______. 3. 如第 2 题图, 在矩形 ABCD 中, AB=3, BC=4, 对角线 AC、 BD 相交于点 O, 则 AC=______, OD=________. 如∠AOD=120°,AB=5cm,则 AC=______ cm. 4.像平行四边形一样, 矩形的两条对角线将矩形分成了____组全等的三角形,其中每一个小 三角形都是____三角形且面积相等,每一个大三角形是____三角形. 5.如图,用 8 块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别 是( ) A.48cm,12cm B.48cm,16cm C.44cm,16cm D.45cm,15cm.
6 0
60cm
【动动脑,挑战自我】 : ★1、如图,矩形 ABCD 中,AC、BD 相交于点 O,AE 平分 ∠BAD 交 BC 于 E,若 c ∠CAE=15°,求:∠BOE 的度数.
mA
O B E
D
C
★★2、 如图, 将矩形 ABCD 沿着直线 BD 折叠使点 C 落在点 C' 处, BC' 交 AD 于 E, AD=8, AB=4,求△BED 的面积。
