二模四边形专题
专题02特殊平行四边形中的折叠问题教师版

专题02 特殊平行四边形中的折叠问题【典型例题】1.(2020·河北定州初三二模)如图,正方形ABCD 中,AB =6,G 是BC 的中点.将△ABG 沿AG 对折至△AFG ,延长GF 交DC 于点E ,则DE 的长是 ( )A .1B .1.5C .2D .2.5【解析】连接AE ,∵AB =AD =AF ,∠D =∠AFE =90°,由折叠的性质得:Rt △ABG ≌Rt △AFG ,在△AFE 和△ADE 中,∵AE =AE ,AD =AF ,∠D =∠AFE ,∴Rt △AFE ≌Rt △ADE ,∴EF =DE ,设DE =FE =x ,则CG =3,EC =6−x .在直角△ECG 中,根据勾股定理,得:(6−x )2+9=(x +3)2,解得x =2.则DE =2. 2.(2019·全国初三单元测试)如图,在菱形ABCD 中,AE ⊥BC 于E ,将△ABE 沿AE 所在直线翻折得△AEF ,若AB =2,∠B =45°,则△AEF 与菱形ABCD 重叠部分(阴影部分)的面积为( ).A .2B .C .D .【解析】∵在边长为2的菱形ABCD 中,∠B =45°,AE 为BC 边上的高,∴AE ,由折叠的性质可知,△ABF 为等腰直角三角形,∴S △ABF =12AB •AF =2,S △ABE =1,∴CF =BF -BC =-2,∵AB ∥CD ,∴∠GCF =∠B =45°,又由折叠的性质知,∠F =∠B =45°,∴CG =GF =2∴S △CGF =12GC •GF =3-,∴重叠部分的面积为:2-1-(3-)=2,故选D . 3.(2020·全国)如图,把矩形纸片ABCD 沿EF 折叠后,使得点D 与点B 重合,点C 落在点C ′的位置上.(1)折叠后,DC 的对应线段是 ,CF 的对应线段是 ;(2)若∠1=50°,求∠2、∠3的度数;(3)若AB =8,DE =10,求CF 的长度.【答案】(1)由折叠的性质可得:折叠后,DC 的对应线段是BC ′,CF 的对应线段是C ′F ;故答案为:BC ′,C ′F . (2)由折叠的性质可得:∠2=∠BEF ,∵AD ∥BC ,∴∠1=∠2=50°.∴∠2=∠BEF =50°,∴∠3=180°﹣50°﹣50°=80°; 故答案为:50°,80°(3)∵AB =8,DE =10,∴BE =10,∴AE 6,∴AD =BC =6+10=16,∵∠1=∠BEF =50°,∴BF =BE =10, ∴CF =BC ﹣BF =16﹣10=6.故答案为:6【专题训练】一、选择题1.(2020·海南临高)如图,在矩形纸片ABCD 中,AB =3,点E 在边BC 上,将△ABE 沿直线AE 折叠,点B 恰好落在对角线AC 上的点F 处,若∠EAC =∠ECA ,则AC 的长是( )A .B .6C .4D .5【解析】∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,∴AF=AB,∠AFE=∠B=90°,∴EF⊥AC,∵∠EAC=∠ECA,∴AE=CE,∴AF=CF,∴AC=2AB=6,选B.2.(2020·全国)如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )A.6B.8C.10D.12【解析】解:∵长方形纸片ABCD按图中那样折叠,∴∠1=∠2,而∠1=∠3,∴∠2=∠3,∴ED=EB=5,∵矩形ABCD中,∠A=90°∴重叠部分△BDE的面积=12DE×AB=12×5×4=10.故选:C..3.(2020·全国)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为()A.3B.4C.6D.8【解析】解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中,∴△BAE≌△BC′F(ASA),∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,△ABE和△BC′F的周长=2△ABE的周长=2×3=6.故选C.4.(2020·新疆昌吉初三一模)如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是()A.3cm B.4cm C.5cm D.6cm【解析】设CN=xcm,则DN=(8﹣x)cm,由折叠的性质知EN=DN=(8﹣x)cm,而EC=12BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8﹣x)2=16+x2,整理得16x=48,所以x=3.故选:A.5.(2019·河北遵化初三一模)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()A.78°B.75°C.60°D.45°【解析】试题分析:连接BD,∵四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.∵P为AB的中点,∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°.∴∠PDC=90°.∴由折叠的性质得到∠CDE=∠PDE=45°.在△DEC中,.故选B.6.(2020·全国)如图,已知四边形ABCD 是边长为6的菱形,且∠BAD =120°,点E ,F 分别在AB ,BC 边上,将菱形沿EF 折叠,点B 正好落在AD 边的点G 处.若EG ⊥AC ,则FG 的长为( )A .3B .6C .D .【解析】如图,设AC 与EG 交于点O ,FG 交AC 于点H .∵ 四边形ABCD 是菱形,∠BAD =120°,∴60B D ∠=∠=︒, ∴ABC ACD 、是等边三角形.∴60CAD B ∠=∠=︒.∵EG AC ⊥,∴90GOH ∠=︒.∵60EGF B ∠=∠=︒,∴30OHG ∠=︒,∴18090AGH CAD OHG ∠=︒-∠-∠=︒,∴FG AD ⊥,∴FG 是菱形ABCD 的高,即为等边三角形ABC 的高,∴ =C .7.(2020·兴仁市真武山街道办事处黔龙学校)如图,把一个矩形纸片ABCD 沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB =65°,则∠AED ′为( )。
2023年山东省中考数学模拟题知识点分类汇编:四边形(附答案解析)

等于( )
第 1页(共 58页)
A.75°
B.72°
C.60°
D.45°
5.(2022•槐荫区二模)如图,在平面直角坐标系中,四边形 ABCD 是边长为 2 的正方形,
点 A 在 y 轴上运动,点 B 在 x 轴上运动,点 E 为对角线的交点,在运动过程中点 E 到 y
轴的最大距离是( )
A.
B.1
A.
B.
C.3
D.
3.(2022•烟台模拟)如图,点 M 是正方形 ABCD 边 CD 上一点,连接 AM,过 D 作 DE⊥ AM 于点 E,过 B 作 BF⊥AM 于点 F,连接 BE.若 AF=1,四边形 ABED 的面积为 10, 则 BF 的长为( )
A.10
B.
C.4
D.3
4.(2022•沂水县二模)如图,在正六边形 ABCDEF 内作正方形 BCGH,连接 AH,则∠FAH
角线 BD 相交于点 N,F 是线段 CE 的中点,则下列结论中正确的有( )个.
①OF= ;②ON= ;③S△CON= ;④sin∠ACE= .
A.1
B.2
C.3
D.4
19.(2020•聊城一模)如图,在菱形 ABCD 中,∠BAD=80°,AB 的垂直平分线交对角线
AC 于点 F,垂足为 E.连接 DF,则∠DFE 等于( )
A.2
B.3
C.4
D.5
17.(2020•乳山市模拟)如图,▱ ABCD 的周长为 36,对角线 AC、BD 相交于点 O,点 E
是 CD 的中点,BD=12,则△DOE 的周长为( )
A.15
B.18
C.21
D.24
18.(2020•市北区二模)如图,在矩形 ABCD 中,AB=3,AD=4,CE 平分∠ACB,与对
北京市各城区中考二模数学——四边形的证明与计算题19题汇总

DCBAADCB 北京市各城区中考二模数学——四边形的证明与计算题19题汇总1、(门头沟二模)19. 如图,在平行四边形ABCD 中,点E ,F 分别是AB ,CD 的中点.(1)求证:四边形AEFD 是平行四边形; (2)若∠A =60°,AB =6,AD =4,求BD 的长.2、(丰台二模)19.如图,在四边形ABCD 中,AD∥BC ,CA 是∠BCD 的平分线,且AB ⊥AC ,AB=4,AD=6,求AC 的长.3、(平谷二模)19.如图,在四边形ABCD 中,对角线BD 平分∠ABC ,∠A =120°, ∠C =60°,AB =5,AD =3. (1)求证:AD =DC ;(2)求四边形ABCD 的周长.4、(顺义二模) 19.如图,在ABC △中,D 、E 分别是AB 、AC 的中点,BE =2DE ,过点C 作CF ∥BE 交DE 的延长线于F . (1)求证:四边形BCFE 是菱形;(2)若4CE =,120BCF ∠=°,求菱形BCFE 的面积.5、(石景山二模)19.如图1,在△OAB 中,∠OAB =90°,∠AOB =30°,BA =2.以OB 为边,向外作等边△OBC ,D 是OB 的中点,连接AD 并延长交OC 于E . (1)求证:四边形ABCE 是平行四边形;(2)如图2,将图1中的四边形ABCO 折叠,使点C 与点A 重合,折痕为FG ,求OG 的长.6、(海淀二模)19.如图,在△ABC 中,点D 、E 分别是边BC 、AC 的中点,过点A 作AF∥BC 交DE 的延长线于F 点,连接CF . (1)求证:四边形ABDF 是平行四边形;(2)若∠CAF =45°,BC=4,CF=10,求△CAF 的面积.7、(西城二模)19.如图,在四边形ABCD 中,AB ∥DC , DB 平分∠ADC , E 是CD 的延长线上一点,且12AEC ADC ∠=∠.(1)求证:四边形ABDE 是平行四边形.(2)若DB ⊥CB ,∠BCD =60°,CD =12,作AH ⊥BD 于H ,求四边形AEDH 的周长.FEDCBAEADCBOG A BCFD E C B A O 图1 F GCBO A图2GDC BAEF8、(通州二模)20.如图,在平行四边形ABCD 中,E 为BC 边上的一点,连接AE 、BD 交于点F ,AE =AB .(1)若∠AEB =2∠ADB ,求证:四边形ABCD 是菱形. (2)若AB =10,BE =2EC ,求EF 的长.9、(东城二模)19.在平行四边形ABCD 中,AB =6,AD =9,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE 于点G ,42BG ,求EFC 的周长.10、(朝阳二模)19.如图,在四边形ABCD 中,AB =34,∠DAB =90°,∠B =60°,AC ⊥BC .(1)求AC的长.(2)若AD=2,求CD 的长.11、(密云二模)19.如图,在平行四边形ABCD 中,AB=4,∠BAD 的平分线与BC 的延长线交于点E ,与DC 交于点F,且点F 为边DC 的中点,DG ⊥AE ,垂足为G ,若DG=1,求AE 的长.12、(延庆二模)13、(房山二模) 19. 已知:如图,梯形ABCD 中,AD=BC ,F 为BC 的中点,AB=2,∠A =120°,过点F 作EF⊥BC 交DC 于点E ,且EF = 3 ,求DC 的长.14、(昌平二模)18.如图,已知□ABCD ,E ,F 是对角线BD 上的两点,且BE =DF .(1)求证:四边形AECF 是平行四边形;(2)当AE 垂直平分BC 且四边形AECF 为菱形时,直接写出AE ∶AB 的值.15、(怀柔二模)19.如图,已知△ABC 是等边三角形,点D 、F 分别在线段BC 、AB 上,∠EFB=60°,DC=EF . (1)求证:四边形EFCD 是平行四边形; (2)若BF=EF ,求证:AE=AD .16、(大兴二模)19.已知: 如图,在平行四边形ABCD 中,点E 、F 分别是AB 、CD 的中点 .(1)求证:四边形AEFD 是平行四边形; (2)若∠A =60°,AB=8,AD=4,求BD 的长 .FDCEABFE DCBA17、(燕山二模)19. 如图,在四边形ABCD中,BC AD //,25=AB ,4=BC ,连接BD ,BAD ∠的平分线交BD 于点E ,且CD AE //. (1)求AD 的长;(2)若︒=∠30C ,求四边形ABCD 的周长.ED CBA。
初中数学专题《四边形中的最值问题》专项训练30道含答案解析

专题18.8 四边形中的最值问题专项训练(30道)【人教版】考卷信息:本套训练卷共30题,选择10题,填空10题,解答10题,题型针对性较高,覆盖面广,选题有深度,可强化学生对四边形中最值问题模型的记忆与理解!一.选择题(共10小题)1.(2022春•重庆期末)如图,矩形ABCD中,AB=23,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )A.43+3B.221C.23+6D.45【分析】将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.【解答】解:将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE 的长即为所求.由旋转的性质可知:△PFC是等边三角形,∴PC=PF,∵PB=EF,∴PA+PB+PC=PA+PF+EF,∴当A、P、F、E共线时,PA+PB+PC的值最小,∵四边形ABCD是矩形,∴∠ABC=90°,∴AC=AB2+BC2=43,∴AC=2AB,∴∠ACB=30°,AC=2AB=43,∵∠BCE=60°,∴∠ACE=90°,∴AE=(43)2+62=221,故选:B.2.(2022•灞桥区校级模拟)如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是( )2 A.5B.7C.72D.72【分析】如图将△BDA绕点D顺时针旋转90°得到△CDM.由旋转不变性可知:AB=AM,CM=4,DA=DM.∠ADM=90°,推出△ADM是等腰直角三角形,推出AD=22推出当AM的值最大时,AD的值最大,利用三角形的三边关系求出AM的最大值即可解决问题;【解答】解:如图将△BDA绕点D顺时针旋转90°得到△CDM.由旋转不变性可知:AB=CM=4,DA=DM.∠ADM=90°,∴△ADM是等腰直角三角形,AM,∴AD=22∴当AM的值最大时,AD的值最大,∵AM≤AC+CM,∴AM≤7,∴AM的最大值为7,,∴AD的最大值为722故选:D .3.(2022春•中山市期末)如图,在边长为a 的正方形ABCD 中,E 是对角线BD 上一点,且BE =BC ,点P 是CE 上一动点,则点P 到边BD ,BC 的距离之和PM +PN 的值( )A .有最大值aB .有最小值22a C .是定值a D .是定值22a 【分析】连接BP ,作EF ⊥BC 于点F ,由正方形的性质可知△BEF 为等腰直角三角形,BE =a ,可求EF ,利用面积法得S △BPE +S △BPC =S △BEC ,将面积公式代入即可.【解答】解:如图,连接BP ,作EF ⊥BC 于点F ,则∠EFB =90°,∵正方形的性质可知∠EBF =45°,∴△BEF 为等腰直角三角形,∵正方形的边长为a ,∴BE =BC =a ,∴BF =EF =22BE =22a ,∵PM ⊥BD ,PN ⊥BC ,∴S △BPE +S △BPC =S △BEC ,∴12BE ×PM +12BC ×PN =12BC ×EF ,∵BE =BC ,∴PM +PN =EF =22a .则点P 到边BD ,BC 的距离之和PM +PN 的值是定值22a .故选:D .4.(2022春•三门峡期末)如图,在矩形ABCD 中,AB =2,AD =1,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点,连接PB ,则PB 的最小值是( )A.2B.4C.2D.22【分析】根据中位线定理可得出点点P的运动轨迹是线段P1P2,再根据垂线段最短可得当BP⊥P1P2时,PB取得最小值;由矩形的性质以及已知的数据即可知BP1⊥P1P2,故BP 的最小值为BP1的长,由勾股定理求解即可.【解答】解:如图:当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,CE.∴P1P2∥CE且P1P2=12当点F在EC上除点C、E的位置处时,有DP=FP.CF.由中位线定理可知:P1P∥CE且P1P=12∴点P的运动轨迹是线段P1P2,∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB=2,AD=1,E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角BCP1中,CP1=BC=1.∴BP1=2.∴PB的最小值是2.故选:C.5.(2022春•滨湖区期末)如图,已知菱形ABCD的面积为20,边长为5,点P、Q分别是边BC、CD上的动点,且PC=CQ,连接PD、AQ,则PD+AQ的最小值为( )A.45B.89C.10D.72【分析】过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,根据菱形的性质和勾股定理可得BM=3,以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,可得B(0,0),A(3,4),C(5,0),D(8,4),A′(3,﹣4),然后证明△ABP≌△ADQ(SAS),可得AP=AQ=A′P,连接A′D,AP,A′P,由A′P+PD>A′D,可得A′,P,D三点共线时,PD+A′P取最小值,所以PD+AQ 的最小值=PD+A′P的最小值=A′D,利用勾股定理即可解决问题.【解答】解:如图,过点A作AM⊥BC于点M,延长AM到点A′,使A′M=AM,∵四边形ABCD是菱形,∴AB=BC=AD=5,∠ABC=∠ADC,∵菱形ABCD的面积为20,边长为5,∴AM=4,在Rt△ABM中,根据勾股定理得:BM=AB2−AM2=3,以点B为原点,BC为x轴,垂直于BC方向为y轴,建立平面直角坐标系,∴B(0,0),A(3,4),C(5,0),D(8,4),A′(3,﹣4),∵PC=CQ,BC=CD,∴BP=DQ,在△ABP和△ADQ中,AB=AD∠ABC=∠ADC,BP=DQ∴△ABP≌△ADQ(SAS),∴AP=AQ=A′P,连接A′D,AP,A′P,∵A′P+PD>A′D,∴A′,P,D三点共线时,PD+A′P取最小值,∴PD+AQ的最小值=PD+A′P的最小值=A′D=(8−3)2+(4+4)2=89.故选:B.6.(2022•泰山区一模)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF的最小值是( )A.2B.1C.5−1D.5−2【分析】根据正方形的性质可得AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,然后利用“HL”证明Rt△ADM和Rt△BCN全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△DCE和△BCE全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AFD=90°,取AD的中点O,连接OF、OC,根据直角AD=1,利用勾股定理列式求出OC,然三角形斜边上的中线等于斜边的一半可得OF=12后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.【解答】解:在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,在Rt△ADM和Rt△BCN中,AD=BCAM=BN,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2,在△DCE和△BCE中,BC=CD∠DCE=∠BCE,CE=CE∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3,∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,AD=1,则OF=DO=12在Rt△ODC中,OC=DO2+DC2=12+22=5,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=5−1.故选:C.7.(2022•龙华区二模)如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为13−2.其中正确的有( )A.1个B.2个C.3个D.4个【分析】连接AE,过E作EH⊥AB于H,则EH=BC,根据全等三角形的判定和性质定理即可得到AF=EG,故①正确;根据平行线的性质和等腰三角形的判定和性质即可得到PE=PC;故②正确;连接EF,推出点E、P、F、C四点共圆,根据圆周角定理得到∠FEC=∠FPC=45°,于是得到BF=DE=1,同理当F运动到C点右侧时,此时∠FPC=45°,且EPCF四点共圆,EC=FC=3,故此时BF=BC+CF=4+3=7.因此BF=1或7,故③错误;取AE的中点O,连接PO,CO,根据直角三角形的性质得到AO=PO =1AE,推出点P在以O为圆心,AE为直径的圆上,当OC最小时,CP的值最小,根2据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.【解答】解:连接AE,过E作EH⊥AB于H,则EH=BC,∵AB=BC,∴EH=AB,∵EG⊥AF,∴∠BAF+∠AGP=∠BAF+∠AFB=90°,∴∠EGH=∠AFB,∵∠B=∠EHG=90°,∴△HEG≌△ABF(AAS),∴AF=EG,故①正确;∵AB∥CD,∴∠AGE=∠CEG,∵∠BAF+∠AGP=90°,∠PCF+∠PCE=90°,∵∠BAF=∠PCF,∴∠AGE=∠PCE,∴∠PEC=∠PCE,∴PE=PC;故②正确;连接EF,∵∠EPF=∠FCE=90°,∴点E、P、F、C四点共圆,∴∠FEC=∠FPC=45°,∴EC=FC,∴BF=DE=1,同理当F运动到C点右侧时,此时∠FPC=45°,且E、P、C、F四点共圆,EC=FC=3,故此时BF=BC+CF=4+3=7.因此BF=1或7,故③错误;取AE的中点O,连接PO,CO,AE,∴AO=PO=12∵∠APE=90°,∴点P在以O为圆心,AE为直径的圆上,∴当OC最小时,CP的值最小,∵PC ≥OC ﹣OP ,∴PC 的最小值=OC ﹣OP =OC −12AE ,∵OC =22+(72)2=652,在Rt △ADE 中,AE =42+12=17,∴PC 的最小值为652−172,故④错误,故选:B .8.(2022•南平校级自主招生)如图,在△ABC 中,AB =6,AC =8,BC =10,P 为边BC 上一动点(且点P 不与点B 、C 重合),PE ⊥AB 于E ,PF ⊥AC 于F .则EF 的最小值为( )A .4B .4.8C .5.2D .6【分析】先由矩形的判定定理推知四边形PEAF 是矩形;连接PA ,则PA =EF ,所以要使EF ,即PA 最短,只需PA ⊥CB 即可;然后根据三角形的等积转换即可求得PA 的值.【解答】解:如图,连接PA .∵在△ABC 中,AB =6,AC =8,BC =10,∴BC 2=AB 2+AC 2,∴∠A =90°.又∵PE ⊥AB 于点E ,PF ⊥AC 于点F .∴∠AEP =∠AFP =90°,∴四边形PEAF 是矩形.∴AP =EF .∴当PA 最小时,EF 也最小,即当AP ⊥CB 时,PA 最小,∵12AB •AC =12BC •AP ,即AP =AB ⋅AC BC =6×810=4.8,∴线段EF 长的最小值为4.8;故选:B .9.(2022春•崇川区期末)如图,正方形ABCD 边长为1,点E ,F 分别是边BC ,CD 上的两个动点,且BE =CF ,连接BF ,DE ,则BF +DE 的最小值为( )A .2B .3C .5D .6【分析】连接AE ,利用△ABE ≌△BCF 转化线段BF 得到BF +DE =AE +DE ,则通过作A 点关于BC 对称点H ,连接DH 交BC 于E 点,利用勾股定理求出DH 长即可.【解答】解:连接AE ,如图1,∵四边形ABCD 是正方形,∴AB =BC ,∠ABE =∠BCF =90°.又BE =CF ,∴△ABE ≌△BCF (SAS ).∴AE =BF .所以BF +DE 最小值等于AE +DE 最小值.作点A 关于BC 的对称点H 点,如图2,连接BH ,则A 、B 、H 三点共线,连接DH ,DH 与BC 的交点即为所求的E 点.根据对称性可知AE =HE ,所以AE +DE =DH .在Rt △ADH 中,AD =1,AH =2,∴DH =AH 2+AD 2=5,∴BF +DE 最小值为5.故选:C .10.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )A.2B.2C.22D.4【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.【解答】解:如图,连接AE,∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=EF+CF+AE,∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,连接AC,∴d1+d2+d3最小值为AC,在Rt△ABC中,AC=2AB=22,∴d1+d2+d3最小=AC=22,故选:C.二.填空题(共10小题)11.(2022春•江城区期末)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=2.运动过程中点D到点O的最大距离是 3+13 .【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于的一半可得OE=12第三边可得OD过点E时最大.【解答】解:如图:取线段AB的中点E,连接OE,DE,OD,∵AB=6,点E是AB的中点,∠AOB=90°,∴AE=BE=3=OE,∵四边形ABCD是矩形,∴AD=BC=2,∠DAB=90°,∴DE=AE2+AD2=13,∵OD≤OE+DE,∴当点D,点E,点O共线时,OD的长度最大.∴点D到点O的最大距离=OE+DE=3+13,故答案为:3+13.12.(2022•东莞市校级一模)如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+DQ的最小值为 13 .【分析】连接BP,在BA的延长线上截取AE=AB=6,连接PE,CE,PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=6,则PC+QD=PC+PB=PC+PE≥CE,根据勾股定理可得结果.【解答】解:如图,连接BP,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵AP=CQ,∴AD﹣AP=BC﹣CQ,∴DP=QB,DP∥BQ,∴四边形DPBQ是平行四边形,∴PB∥DQ,PB=DQ,∴PC+QD=PC+PB,∴PC+QD的最小值转化为PC+PB的最小值,如图,在BA的延长线上截取AE=AB=6,连接PE,CE,∵PA⊥BE,∴PA是BE的垂直平分线,∴PB=PE,∴PC+PB=PC+PE,∴PC+QD=PC+PB=PC+PE≥CE,∵BE=2AB=12,BC=AD=5,∴CE=BE2+BC2=13.∴PC+DQ的最小值为13.故答案为:13.13.(2022•钱塘区一模)如图,在矩形ABCD中,线段EF在AB边上,以EF为边在矩形ABCD内部作正方形EFGH,连结AH,CG.若AB=10,AD=6,EF=4,则AH+CG的最小值为 62 .【分析】方法一:延长DA至A′,使A′A=EH=EF=4,连接A′E,EG,可得四边形AA′EH是平行四边形,所以A′E=AH,则AH+CG的最小值即为A′E+CG的最小值,根据勾股定理即可解决问题.方法二:过点G作GA′∥AH交AF于点A′,可得四边形AHGA′是平行四边形,进而可以解决问题.【解答】解:方法一:如图,延长DA至A′,使A′A=EH=EF=4,连接A′E,EG,∵HE⊥AB,AA′⊥AB,∴AA′∥EH,∵A′A=EH,∴四边形AA′EH是平行四边形,∴A′E=AH,则AH+CG的最小值即为A′E+CG的最小值,∵四边形EFGH是正方形,∴EF=FG=4,∴EG=42,∵A′D=AD+AA′=6+4=10,在Rt△A′DC中,DC=AB=10,∴A′C=A′D2+DC2=102,∴A′E+CG=A′C﹣EG=62.方法二:如图,过点G作GA′∥AH交AF于点A′,∴四边形AHGA′是平行四边形,∴AA′=HG=4,A′G=AH,∴A′B=AB﹣AA′=6,∵BC=6,∴A′C=62,∴AH+CG=A′G+CG≥A′C,则AH+CG的最小值为62.故答案为:62.14.(2022春•东城区期中)在正方形ABCD中,AB=5,点E、F分别为AD、AB上一点,且AE=AF,连接BE、CF,则BE+CF的最小值是 55 .【分析】连接DF,根据正方形的性质证明△ADF≌△ABE(SAS),可得DF=BE,作点D关于AB的对称点D′,连接CD′交AB于点F′,连接D′F,则DF=D′F,可得BE+CF=DF+CF=D′F+CF≥CD′,所以当点F与点F′重合时,D′F+CF最小,最小值为CD′的长,然后根据勾股定理即可解决问题.【解答】解:如图,连接DF,∵四边形ABCD是正方形,∴AD=AB,∠BAE=∠DAF=90°,在△ADF 和△ABE 中,AD =AB ∠FAD =∠EAB AF =AE,∴△ADF ≌△ABE (SAS ),∴DF =BE ,作点D 关于AB 的对称点D ′,连接CD ′交AB 于点F ′,连接D ′F ,则DF =D ′F ,∴BE +CF =DF +CF =D ′F +CF ≥CD ′,∴当点F 与点F ′重合时,D ′F +CF 最小,最小值为CD ′的长,在Rt △CDD ′中,根据勾股定理得:CD ′=CD 2+DD′2=52+102=55,∴BE +CF 的最小值是55.故答案为:55.15.(2022春•虎林市期末)如图,在Rt △ABC 中,∠BAC =90°,且BA =12,AC =16,点D 是斜边BC 上的一个动点,过点D 分别作DE ⊥AB 于点E ,DF ⊥AC 于点F ,点G 为四边形DEAF 对角线交点,则线段GF 的最小值为 245 .【分析】由勾股定理求出BC 的长,再证明四边形DEAF 是矩形,可得EF =AD ,根据垂线段最短和三角形面积即可解决问题.【解答】解:连接AD 、EF ,∵∠BAC =90°,且BA =9,AC =12,∴BC =AB 2+AC 2=122+162=20,∵DE ⊥AB ,DF ⊥AC ,∴∠DEA =∠DFA =∠BAC =90°,∴四边形DEAF 是矩形,∴EF =AD ,∴当AD ⊥BC 时,AD 的值最小,此时,△ABC 的面积=12AB ×AC =12BC ×AD ,∴12×16=20AD ,∴AD =485∴EF 的最小值为485,∵点G 为四边形DEAF 对角线交点,∴GF =12EF =245;故答案为:245.。
备战中考数学二模试题分类汇编——平行四边形综合含答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.问题发现:(1)如图①,点P 为平行四边形ABCD 内一点,请过点P 画一条直线l ,使其同时平分平行四边形ABCD 的面积和周长.问题探究:(2)如图②,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在x 轴、y 轴正半轴上,点B 坐标为(8,6).已知点(6,7)P 为矩形外一点,请过点P 画一条同时平分矩形OABC 面积和周长的直线l ,说明理由并求出直线l ,说明理由并求出直线l 被矩形ABCD 截得线段的长度.问题解决:(3)如图③,在平面直角坐标系xOy 中,矩形OABCD 的边OA 、OD 分别在x 轴、y 轴正半轴上,DC x ∥轴,AB y ∥轴,且8OA OD ==,2AB CD ==,点(1052,1052)P --为五边形内一点.请问:是否存在过点P 的直线l ,分别与边OA 与BC 交于点E 、F ,且同时平分五边形OABCD 的面积和周长?若存在,请求出点E 和点F 的坐标:若不存在,请说明理由.【答案】(1)作图见解析;(2)25y x =-,353)(0,0)E ,(5,5)F .【解析】试题分析:(1)连接AC 、BD 交于点O ,作直线PO ,直线PO 将平行四边形ABCD 的面积和周长分别相等的两部分.(2)连接AC ,BD 交于点O ',过O '、P 点的直线将矩形ABCD 的面积和周长分为分别相等的两部分.(3)存在,直线y x =平分五边形OABCD 面积、周长.试题解析:(1)作图如下:(2)∵(6,7)P ,(4,3)O ',∴设:6PO y kx =+',67{43k b k b +=+=,2{5k b ==-, ∴25y x =-,交x 轴于5,02N ⎛⎫ ⎪⎝⎭, 交BC 于11,62M ⎛⎫ ⎪⎝⎭, 2211563522MN ⎛⎫=+-= ⎪⎝⎭.(3)存在,直线y x =平分五边形OABCD 面积、周长.∵(1052,102)P --在直线y x =上,∴连OP 交OA 、BC 于点E 、F ,设:BC y kx b =+,(8,2)(2,8)B C ,82{28k b k +=+=,1{10k b =-=, ∴直线:10BC y x =-+,联立10{y x y x =-+=,得55x y =⎧⎨=⎩, ∴(0,0)E ,(5,5)F .2.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到到B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′(2)若AB = 8,DE = 3,点P为线段AC上任意一点,PG⊥AE于G,PH⊥BC于H.求PG + PH的值.【答案】(1)证明见解析;(2).【解析】【分析】(1)由折叠的性质知,,,,则由得到;(2)由,可得,又由,即可求得的长,然后在中,利用勾股定理即可求得的长,再过点作于,由角平分线的性质,可得,易证得四边形是矩形,继而可求得答案.【详解】(1)四边形为矩形,,,又,;(2),,,,在中,,过点作于,,,,,,,、、共线,,四边形是矩形,,.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作法,注意数形结合思想的应用.3.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.4.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD和△FOB中,∴△DOE≌△BOF(ASA);(2)当∠DOE=90°时,四边形BFDE为菱形,理由:∵△DOE≌△BOF,∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,∵∠EOD=90°,∴EF⊥BD,∴四边形BFDE为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.5.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222106DF CF-=-8.∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH 的值为8;迁移拓展:如图,由题意得:A (0,8),B (6,0),C (﹣4,0)∴AB 2268+10,BC =10.∴AB =BC ,(1)由结论得:P 1D 1+P 1E 1=OA =8∵P 1D 1=1=2,∴P 1E 1=6 即点P 1的纵坐标为6又点P 1在直线l 2上,∴y =2x+8=6,∴x =﹣1,即点P 1的坐标为(﹣1,6);(2)由结论得:P 2E 2﹣P 2D 2=OA =8∵P 2D 2=2,∴P 2E 2=10 即点P 1的纵坐标为10又点P 1在直线l 2上,∴y =2x+8=10,∴x =1,即点P 1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.6.在ABC 中,AD BC ⊥于点D ,点E 为AC 边的中点,过点A 作//AF BC ,交DE 的延长线于点F ,连接CF .()1如图1,求证:四边形ADCF 是矩形;()2如图2,当AB AC =时,取AB 的中点G ,连接DG 、EG ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF ).【答案】(1) 证明见解析;(2)四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【解析】【分析】(1)由△AEF ≌△CED ,推出EF=DE ,又AE=EC ,推出四边形ADCF 是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF 是矩形.(2)四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【详解】()1证明:∵//AF BC ,∴AFE EDC ∠=∠,∵E 是AC 中点,∴AE EC =,在AEF 和CED 中,AFE CDE AEF CED AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AEF CED ≅,∴EF DE =,∵AE EC =,∴四边形ADCF 是平行四边形,∵AD BC ⊥, ∴90ADC ∠=,∴四边形ADCF 是矩形.()2∵线段DG 、线段GE 、线段DE 都是ABC 的中位线,又//AF BC ,∴//AB DE ,//DG AC ,//EG BC , ∴四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【点睛】考查平行四边形的判定、矩形的判定、三角形的中位线定理、全等三角形的判定和性质等知识,正确寻找全等三角形解决问题是解题的关键.7.△ABC 为等边三角形,AF AB =.BCD BDC AEC ∠=∠=∠.(1)求证:四边形ABDF 是菱形.(2)若BD 是ABC ∠的角平分线,连接AD ,找出图中所有的等腰三角形.【答案】(1)证明见解析;(2)图中等腰三角形有△ABC ,△BDC ,△ABD ,△ADF ,△ADC ,△ADE .【解析】【分析】(1)先求证BD ∥AF ,证明四边形ABDF 是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD 平分∠ABC ,得到BD 垂直平分线段AC ,进而证明△DAC 是等腰三角形,根据BD ⊥AC,AF ⊥AC ,找到角度之间的关系,证明△DAE 是等腰三角形,进而得到BC =BD =BA =AF =DF ,即可解题,见详解.【详解】(1)如图1中,∵∠BCD =∠BDC ,∴BC =BD ,∵△ABC 是等边三角形,∴AB =BC ,∵AB =AF ,∴BD =AF ,∵∠BDC =∠AEC ,∴BD ∥AF ,∴四边形ABDF 是平行四边形,∵AB =AF ,∴四边形ABDF 是菱形.(2)解:如图2中,∵BA =BC ,BD 平分∠ABC ,∴BD 垂直平分线段AC ,∴DA =DC ,∴△DAC 是等腰三角形,∵AF ∥BD ,BD ⊥AC∴AF ⊥AC ,∴∠EAC =90°,∵∠DAC =∠DCA ,∠DAC +∠DAE =90°,∠DCA +∠AEC =90°,∴∠DAE=∠DEA,∴DA=DE,∴△DAE是等腰三角形,∵BC=BD=BA=AF=DF,∴△BCD,△ABD,△ADF都是等腰三角形,综上所述,图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.【点睛】本题考查菱形的判定,等边三角形的性质,等腰三角形的判定等知识,属于中考常考题型,熟练掌握等腰三角形的性质是解题的关键.8.正方形ABCD的边长为1,对角线AC与BD相交于点O,点E是AB边上的一个动点(点E不与点A、B重合),CE与BD相交于点F,设线段BE的长度为x.(1)如图1,当AD=2OF时,求出x的值;(2)如图2,把线段CE绕点E顺时针旋转90°,使点C落在点P处,连接AP,设△APE 的面积为S,试求S与x的函数关系式并求出S的最大值.【答案】(1)x=﹣1;(2)S=﹣(x﹣)2+(0<x<1),当x=时,S的值最大,最大值为,.【解析】试题分析:(1)过O作OM∥AB交CE于点M,如图1,由平行线等分线段定理得到CM=ME,根据三角形的中位线定理得到AE=2OM=2OF,得到OM=OF,于是得到BF=BE=x,求得OF=OM=解方程,即可得到结果;(2)过P作PG⊥AB交AB的延长线于G,如图2,根据已知条件得到∠ECB=∠PEG,根据全等三角形的性质得到EB=PG=x,由三角形的面积公式得到S=(1﹣x)•x,根据二次函数的性质即可得到结论.试题解析:(1)过O作OM∥AB交CE于点M,如图1,∵OA=OC,∴CM=ME,∴AE=2OM=2OF,∴OM=OF,∴,∴BF=BE=x,∴OF=OM=,∵AB=1,∴OB=,∴,∴x=﹣1;(2)过P作PG⊥AB交AB的延长线于G,如图2,∵∠CEP=∠EBC=90°,∴∠ECB=∠PEG,∵PE=EC,∠EGP=∠CBE=90°,在△EPG与△CEB中,,∴△EPG≌△CEB,∴EB=PG=x,∴AE=1﹣x,∴S=(1﹣x)•x=﹣x2+x=﹣(x﹣)2+,(0<x<1),∵﹣<0,∴当x=时,S的值最大,最大值为,.考点:四边形综合题9.如图①,在△ABC中,AB=7,tanA=,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动(不与点A、B重合),过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t(秒),正方形PQMN 与△ABC重叠部分图形的面积为S(平方单位).(1)直接写出正方形PQMN的边PQ的长(用含t的代数式表示).(2)当点M落在边BC上时,求t的值.(3)求S与t之间的函数关系式.(4)如图②,点P运动的同时,点H从点B出发,沿B-A-B的方向做一次往返运动,在B-A上的速度为每秒2个单位长度,在A-B上的速度为每秒4个单位长度,当点H停止运动时,点P也随之停止,连结MH.设MH将正方形PQMN分成的两部分图形面积分别为S1、S2(平方单位)(0<S1<S2),直接写出当S2≥3S1时t的取值范围.【答案】(1) PQ=7-t.(2) t=.(3) 当0<t≤时,S=.当<t≤4,.当4<t<7时,.(4)或或.【解析】试题分析:(1)分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时.(2)根据AP+PN+NB=AB,列出关于t的方程即可解答;(3)当0<t≤时,当<t≤4,当4<t<7时;(4)或或.试题解析:(1)当点Q在线段AC上时,PQ=tanAAP=t.当点Q在线段BC上时,PQ=7-t.(2)当点M落在边BC上时,如图③,由题意得:t+t+t=7,解得:t=.∴当点M落在边BC上时,求t的值为.(3)当0<t≤时,如图④,S=.当<t≤4,如图⑤,.当4<t<7时,如图⑥,.(4)或或..考点:四边形综合题.10.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.∴∠E′AF=90°-45°=45°=∠EAF,又∵AE′=AE,AF=AF∴△AE′F≌△AEF(SAS)∴EF=E′F=DE′+DF=BE+DF.类比猜想:(1)请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?请说明理由.(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF吗?请说明理由.【答案】证明见解析.【解析】试题分析:(1)把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,根据菱形和旋转的性质得到AE=AE′,∠EAF=∠E′AF,利用“SAS”证明△AEF≌△AE′F,得到EF=E′F;由于∠ADE′+∠ADC=120°,则点F、D、E′不共线,所以DE′+DF>EF,即由BE+DF>EF;(2)把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),根据旋转的性质得到AE′=AE,∠EAF=∠E′AF,然后利用“SAS”证明△AEF≌△AE′F,得到EF=E′F,由于∠ADE′+∠ADC=180°,知F、D、E′共线,因此有EF=DE′+DF=BE+DF;根据前面的条件和结论可归纳出结论.试题解析:(1)当∠BAD=120°,∠EAF=60°时,EF=BE+DF不成立,EF<BE+DF.理由如下:∵在菱形ABCD中,∠BAD=120°,∠EAF=60°,∴AB=AD,∠1+∠2=60°,∠B=∠ADC=60°,∴把△ABE绕点A逆时针旋转120°至△ADE′,如图(2),连结E′F,∴∠EAE′=120°,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B=60°,∴∠2+∠3=60°,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴EF=E′F,∵∠ADE′+∠ADC=120°,即点F、D、E′不共线,∴DE′+DF>EF∴BE+DF>EF;(2)当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF成立.理由如下:如图(3),∵AB=AD,∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′,如图(3),∴∠EAE′=∠BAD,∠1=∠3,AE′=AE,DE′=BE,∠ADE′=∠B,∵∠B+∠D=180°,∴∠ADE′+∠D=180°,∴点F、D、E′共线,∵∠EAF=∠BAD,∴∠1+∠2=∠BAD,∴∠2+∠3=∠BAD,∴∠EAF=∠E′AF,在△AEF和△AE′F中,∴△AEF≌△AE′F(SAS),∴E F=E′F,∴EF=DE′+DF=BE+DF;归纳:在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=∠BAD时,EF=BE+DF.考点:四边形综合题.。
2011二模四边形、圆答案
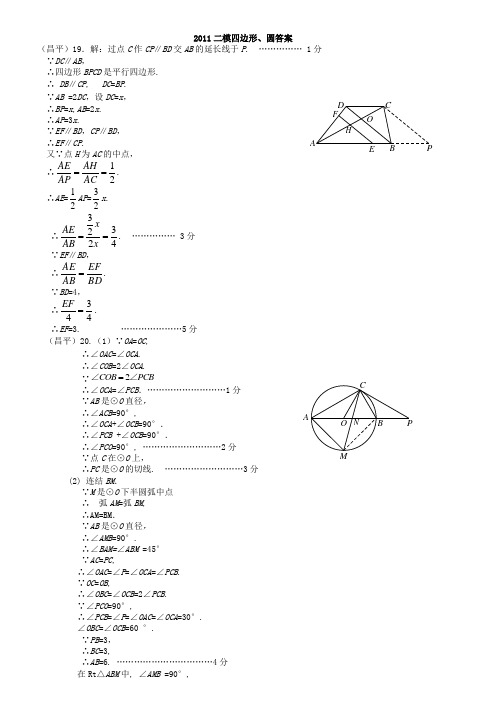
2011二模四边形、圆答案(昌平)19.解:过点C 作CP ∥BD 交AB 的延长线于P . …………… 1分 ∵DC ∥AB ,∴四边形BPCD 是平行四边形. ∴ DB ∥CP , DC =BP . ∵AB =2DC ,设DC =x ,∴BP =x ,AB =2x .∴AP =3x .∵EF ∥BD ,CP ∥BD ,∴EF ∥CP .又∵点H 为AC 的中点, ∴12A E A H A PA C ==.∴AE =21AP =32x .∴33224xAEAB x ==. …………… 3分 ∵EF ∥BD , ∴BD EFAB AE =. ∵BD =4, ∴344EF =.∴EF =3. …………………5分(昌20.(1)∵OA =OC ,∴∠OAC =∠OCA .∴∠COB =2∠OCA .∵2C O B P C B =∠∠∴∠OCA =∠PCB .………………………1分∵AB 是⊙O 直径,∴∠ACB =90°,∴∠OCA +∠OCB =90°.∴∠PCB +∠OCB =90°.∴∠PCO =90°, ………………………2分∵点C 在⊙O 上,∴PC 是⊙O 的切线. ………………………3分 (2) 连结BM .∵M 是⊙O 下半圆弧中点 ∴ 弧AM =弧BM , ∴AM=BM .∵AB 是⊙O 直径, ∴∠AMB =90°.∴∠BAM=∠ABM =45° ∵AC =PC ,∴∠OAC =∠P =∠OCA =∠PCB . ∵OC =OB ,∴∠OBC =∠OCB =2∠PCB . ∵∠PCO =90°,∴∠PCB =∠P =∠OAC =∠OCA =30°. ∠OBC =∠OCB =60 °. ∵PB =3, ∴BC =3,∴AB =6. ……………………………4分 在Rt △ABM 中, ∠AMB =90°,PH O FED C BA N MO PCB A根据勾股定理,得AM =23 . ……………………………5分(朝阳)19.解:(1)连接OA ,∵AD 为⊙O 切线, ∴ ∠OAD=90°.…… 1分 ∵sinD=12, ∴∠D=30°.……………… 2分 ∴∠AOC=60°.∴∠ABC=12∠AOC=30°. ……………… 3分(2)在Rt △OAD 中,∠D=30°,OD=20.∴OA=12OD=10. ∵OE ⊥AC ,OA=OC , ∴∠AOE=30°,AE=12OA=5.∴AC=2AE=10.∵BC 是⊙O 的直径, ∴∠BAC=90°.在Rt △BAC 中,AB=103tan A C A B C=∠, ………………………… 4分在Rt △ABE 中,BE=22513AB AE +=. ………………………… 5分(东城)19.(本小题满分5分) 解:(1)证明:∵BD 是∠ABC 的平分线,∴ ∠1=∠2.∵ AD //BC ,∴∠2=∠3. ∴ ∠1=∠3.∴AB=AD . ---------------------2分(2)作AE ⊥BC 于E ,DF ⊥BC 于F .∴ EF=AD=AB .∵ ∠ABC =60°,BC =3AB , ∴ ∠BAE =30°. ∴ BE =21AB . ∴ BF =23AB=21BC .∴ BD=DC .∴ ∠C =∠2.∵ BD 是∠ABD 的平分线, ∴ ∠1=∠2=30°.∴ ∠C =30°. -------------------------5分(东城)20.(本小题满分5分) 解:(1)CD 与圆O 相切. …………………1分 证明:连接OD ,则∠AOD =2∠AED =2⨯45︒=90︒. …………………2分 ∵四边形ABCD 是平行四边形,∴AB //DC .∴∠CDO =∠AOD =90︒.∴OD ⊥CD . …………………3分 ∴CD 与圆O 相切.(2)连接BE ,则∠ADE =∠ABE .∴sin ∠ADE =sin ∠ABE =65. …………………4分EB CAO DEB CAO DAB CDEOABCD 123E F∵AB 是圆O 的直径,∴∠AEB =90︒,AB =2⨯3=6. 在Rt △ABE 中,sin ∠ABE =ABAE =65.∴AE =5 .(房山)19.解:过点B 作BE ⊥AC 交CD 于E ,过点A 作AF ⊥CB 于F ∵CD ∥AB ,AB=AC , ∴四边形ABEC 是菱形---------------------------------------1分 ∴BE=CE=AB ∵∠BAC=120°∴∠ABC=30°,∠ABE=60°,∠BED=60° ∵CD=2AB ,BD=2∴△ABC 是等边三角形 ,AB=2--------------------------------------------------------------------2分 在△ABF 中,∠AFB=90°, ∠ABC=30°,AB =2∴BF=3,AF=1---------------------------------------------------------------------------3分 ∴BC=23-------------------------------------------------------------------------------4分 ∴△ABC 的面积为3-------------------------------------------------------------------------------5分 (房山)20.解:(1)直线BD 与O 相切.------------------------------------------------------------------1分证明:如图1,连结O D .O A O D = , ∴A A D O ∠=∠. 90C ∠= , ∴90CBD CDB ∠+∠=. 又C B D A ∠=∠ , ∴90ADO CDB ∠+∠=.∴90ODB ∠= .∴直线BD 与O 相切-------------------------------------2分(2)解法一:如图1,连结D E .90C ∠=, 2B C =,B D =52∴4cos 5B C C B D B D∠==----------------------------------------------------3分AE 是O 的直径, ∴90ADE ∠=.∴cos A DA A E=.∵C B D A ∠=∠,∴A DA E =BCBD =45.-------------------4分∵AE=2AO ∴A D A O =85------------------------------------------------------5分解法二:如图2,过点O 作O H A D ⊥于点H . ∴12A H D H A D ==.∴cos A H A A O= F E ABC D(图1)CB AO DE(图2)HCBAO DE3310sin .1010∠==A E A B C =A B231DCBAOE90C ∠=, 2B C =,B D =52∴4cos 5B C C B D B D∠==.------------------------- 3分∵C B D A ∠=∠, ∴A H A O =BC BD =45.---------------------------------4分 ∴A D A O =85----------------------------------------5分 (丰台)19. 解:如图,分别过点、A D 作AE BC ⊥于点E ,D F B C ⊥于点F .………………………………1分∴AE D F ∥.又AD BC ∥,∴四边形A E F D 是矩形.2EF AD ∴==.…………………………………2分 ,⊥= BD DC BD DC ,6B C =,∴△BDC 是等腰直角三角形,……………………3分 132∴====D F B F A E B C .3D F B F ∴==,1BE BF EF =-=.………………………………4分在R t △A B E 中,90ABE ∠= , 2210AB AE BE∴=+=,∴ .5分 …………5分(丰台)20. (1)证明:联结OD , ∴OD =OA , ∴∠1=∠2,∵BC 为⊙O 的切线,∴∠ODB =90°,…………1分 ∵∠C =90°,∴∠ODB =∠C , ∴OD ∥AC ,∴∠3=∠2,………………………2分 ∴∠1=∠3 ,∴AD 是∠BAC 的平分线. ……3分(2)解:在Rt △ABC 中,∠C =90°, tan B =34, AC = 3, ∴BC =4,AB =5,………………………………………………………4分在Rt △ODB 中, tan B =34O D BD =,设一份为x ,则OD=OA=3x ,则BD=4x ,OB=5x , ∴AB =8x ,∴8x=5,解得x=58,∴半径OA =158. …………………………………………………………5分(海淀)19.解:作DE //AC ,交BC 的延长线于点E ,作DF ⊥BE,垂足为F. …………..1分∵AD //BC ,∴四边形ACED 为平行四边形.∴AD=CE=3,BE=BC+CE=8. .……………………..2分F EOD CB A∵AC ⊥BD , ∴DE ⊥BD.∴△BDE 为直角三角形 ,90.BD E ∠=︒ ∵∠DBC =30°,BE =8,∴4,4 3.DE BD == …….……………………..4分 在直角三角形BDF 中∠DBC =30°,∴23DF =. …….……………………..5分 (海淀)20.(1)证明:连结OC .∵CD 是O ⊙的切线,∴OC ⊥CD.∴90O C M ∠=︒. …….……………………..1分 ∵//C D AB ,∴180O C M C O A ∠+∠=︒. ∵AM ⊥CD,∴90AM C ∠=︒.∴在四边形OAMC 中90O AM ∠=︒ .∵OA 为O ⊙的半径,∴AM 是O ⊙的切线 .…….……………………..2分 (2)连结OC ,BC .∵CD 是O ⊙的切线, ∴OC ⊥CD . ∴90O C M ∠=︒. ∵AM ⊥CD , ∴90AM C ∠=︒. ∴//O C AM .∴12∠=∠.∵OA= OC ,∴32∠=∠. 即BAC C AM ∠=∠. …….……………………..3分 易知90AC B ∠=︒,∴BAC C AM △∽△. …….……………………..4分 ∴AB AC ACAM=.即224AC AB AM =⋅=.∴26AC =. …….……………………..5分(怀柔)19. (1)证法一:如图,连接O D .22.52DAB DOC DAB ∠=∠=∠, 45DOC ∴∠= 1分又45ACD ∠=,18090ODC ACD DOC ∴∠=-∠-∠=,2分 即O D C D ⊥.C D ∴是O 的切线. 3分(2)解:由(1)可得:O D C △是等腰直角三角形.4分22AB = ,A B 是直径, 2OD OB ∴==.5分22OC OD ∴==.22BC OC OB ∴=-=-.6分 (怀柔)20.解:(1)∵四边形 ABCD 是正方形∴∠BCF+∠FCD=900BC=CD 1分∵△ECF 是等腰直角三角形,DBMAOC1图2图OABDMC123B A DC EF21E A CBD ∴∠ECD+∠FCD=900. CF=CE 2分 ∴∠BCF=∠ECD.∴△BCF ≌△DCE 3分(2)在△BFC 中,BC=5,CF=3,∠BFC=900.∴BF=2222534BC CF -=-=. 4分∵△BCF ≌△DCE ,∴DE=BF=4,∠BFC=∠DEC=∠FCE=900.∴DE ∥FC ∴△DGE ∽△CGF 5分 ∴DG :GC=DE :CF=4:3. 6分(门头沟)19. 解:如图,分别过点A 、D 作AE ⊥BC 于点E ,DF ⊥BC 于点F . ……………………1分∴ AE // DF . 又∵ AD // BC ,∴ 四边形AEFD 是矩形.∴ EF =AD =3. ……………………………………… 2分 ∵ BD ⊥CD ,∠C =60°,BC =43, ∴ DC =BC ·cos60°=143232⨯=.∴ CF =DC ·cos60°=12332⨯=.∴ AE =DF = DC ·sin60°=32332⨯=. …………………………………………… 3分∴23BE BC EF CF =--=. ………………………………………………………… 4分 在Rt △ABE 中,∠AEB =90°,∴ AB =22223(23)21AE BE +=+=. ………………………………………… 5分(门头沟)20.解:(1)由直径A B 平分 CD , 可证A B C D ⊥. ······················ 1分 BF 与O ⊙相切,A B 是O ⊙的直径,AB BF ∴⊥.···························2分 C D B F ∴∥. ·························· 3分 (2)连结B D . A B 是O ⊙的直径, 90A D B ∴∠=°.在R t AD B △中,3cos cos 4A C == ,428AB =⨯=,3cos 864A D A B A ∴=⋅=⨯=. ··················· 4分 在R t AED △中,39cos 642A E A D A =⋅=⨯=,∴ DE =2222937622AD AE⎛⎫-=-=⎪⎝⎭.由直径A B 平分 CD , 可求237C D DE ==. ····················· 5分(平谷)19.解:(1)∵ AC =BC , AD = BE , ∠CAD =∠CBE , ∴ △ADC ≌△BEC ……………………………………..1分∴ DC =EC ,∠1=∠2. ……………………………………2分 ∵ ∠1+∠BCD =90°, ∴ ∠2+∠BCD =90°. 所以 △DCE 是等腰直角三角形…………………………..3分 (2) ∵ △DCE 是等腰直角三角形. ∴ ∠CDE =45°. ∵ ∠BDC =135°,∴ ∠BDE =90°……………………………………….4分 ∵ BD :CD =1:2,设BD =x ,则CD =2x ,DE =x 22,BE =3x.FE DC B A AD F BCO EOE B D A CH O F EDCBA∴.31sin ==∠BEBD BED (5)(平谷)20.(1)证明:连接OD .………………………….1分 ∵ OD = OB , ∴ ∠B =∠ODB . ∵ A B A C =,∴ B C ∠=∠. ∴ ∠ODB =∠C .∴ OD ∥AC .………………………………………2分∵ DE ⊥ AC , ∴ OD ⊥DE .∴DE 是O ⊙的切线.………………………………………………………………………3分 (2) 解:连接AD , ∵ AB 为直径, ∴ ∠ADB =90°.∵120AB AC BAC =∠=,°, ∴ 30B C ∠=∠=°. ∴ AD =121=AB .∵ 在Rt △AED 中,DE ⊥ AC ,∠DAE =60°, ∴ AE =2121=AD ,DE =23.…………………………………………………………….4分∴ EC =.23212=-∴ .833232321S =⨯⨯=∆DEC ……………………………………………………………..5分(石景山)19.解:(1)作出线段C D ' ………………………………… 1分 过点D 作BC DF ⊥于F ,过点A 作BC AH ⊥于H ∵四边形ABCD 是等腰梯形,AD ∥BC 易证()22-621===BH FC︒=∠=∠90ADF EDF过点'C 作E C '垂直于AD 的延长线于点E ∴︒=∠='∠90DFC C DE∵线段DC 绕点D 逆时针旋转90°,得到线段C D ' ∴︒='∠90C CD ,C D DC '=∴︒=∠+∠9031,︒=∠+∠9032 ∴21∠=∠∴CFD ∆≌ED C '∆ ………………………… 2分 ∴2=='FC C E ∴=∆'ADC S 2222121'=⨯⨯=⋅E C AD …………………… 3分(2)在'AEC Rt ∆中,52tan ='∠C DA ,2='C E∴5=EA ∵2=AD∴3=ED …………………………… 4分由CFD ∆≌ED C '∆得: 3==ED DF在DFC Rt ∆中,由勾股定理得:13=CD∴13==CD AB ……………………………5分(石景山)20.解:(1)证明:联结BE ………………………………1分321H EFC 'ABCD∵ BC 为直径 ∴E ∠=90°∴︒=∠+∠90EHB EBH∵ AC AH =, ABC AF 为△的角平分线 ∴ACH AHC ∠=∠ ∵EHB AHC ∠=∠ ∴ACH EHB ∠=∠ ∵E 点为弧BD 的中点 ∴DBE ECB ∠=∠∴︒=∠+∠90ACH ECB ……………2分 ∴ AC 是⊙O 的切线(2) ∵ AC 是⊙O 的切线 ∴︒=∠90ACB∵10,6==AB AC ∴8=BC∵AC AH = ∴4=BH …………………………………………3分 又∵DBE ECB ∠=∠,E ∠为公共角 ∴BEH △∽CEB △∴2184===CBBH ECBE …………………………………………4分∴在EBC Rt △中,可得222)21(BC EC EC =+,5516=EC ………………………………5分(顺义)19. 解:(1)∵四边形A B C D 是矩形,∴90A D ∠=∠=︒,7,4AD BC DC AB ====.∴ 90APE AEP ∠+∠=︒ ∵P E P C ⊥ ∴90E P C ∠=︒∴90APE D PC ∠+∠=︒∴A E P D P C ∠=∠--------------------------------------1分 ∴A E P D P C ∆∆∴P EA PC PD C= -------------------------------------------2分∵P E C ∆是等腰三角形,90E P C ∠=︒∴ P E C P = ∴ 4AP D C ==∴ 3P D A D A P =-= ------------------------------3分 (2)设P D x =, 则7A P x =-∵P E A PC PD C = ∴74P E xC P -= -------------------------------------------4分 在C P E ∆中, 90E P C ∠=︒, 30P E C ∠=︒∴3tan 303C PPE =︒=∴3P EC P = ∴734x -=∴743x =-∴43AP = ---------------------------------------------5分(顺义)20. (1)证明:连结O C由D C 是切线得O C D C ⊥-------------------------------1分 又AD D C ⊥ AD O C ∥DCBOAE∴D A C A C O ∠=∠又由O A O C =得BAC AC O ∠=∠ D AC BAC ∴∠=∠∴ ECBC = ∴B C E C = --------------------------------------------2分 (2)解:A B 为直径∴90A C B ∠=° 又B A C B E C ∠=∠∴ cos cos 8AC AB BAC AB BEC =⋅∠=⋅∠= 226BC AB AC∴=-=--------------------------3分∴ 3sin 5B AC ∠= ----------------------------------4分又D AC BAC BEC ∠=∠=∠ 且AD D C ⊥24sin sin 5C D A C D A C A C B A C ∴=∠=∠=·· --------5分(西城)20.解:(1)作DM ⊥AB 于点M ,CN ⊥AB 于点N .(如图3)∵ AB ∥D C ,DM ⊥AB ,CN ⊥AB ,∴ ∠DMN =∠CNM =∠MDC =90︒. ∴ 四边形MNCD 是矩形. ∵4C D =,∴ MN =CD = 4.∵ 在梯形ABC D 中,AB ∥D C ,5AD BC ==, ∴ ∠DAB =∠CBA ,DM=CN . ∴ △ADM ≌△BCN . 又∵10AB =, ∴ AM =BN =()11(104)322AB M N -=⨯-=.∴ MB =BN +MN =7.……………………………………………………………2分∵ 在Rt △AMD 中,∠AMD =90︒,AD =5,AM =3, ∴ 224D M AD AM=-=.∴ 4tan 7D M ABD BM∠==.……………………………………………………3分(2)∵ EF AB ⊥,∴ ∠F =90︒.∵∠DMN =90︒, ∴ ∠F =∠DMN .∴ DM ∥EF .∴ △BDM ∽△BEF . ∵ D E BD =,∴12BM BD BFBE==.∴ BF =2BM =14. ……………………………………………………………4分 ∴ AF =BF -AB =14-10=4. …………………………………………………5分(西城)21.(1)证明:如图4.∵ 点A 是劣弧BC 的中点,∴ ∠ABC =∠ADB .………………………1分 又∵ ∠BAD =∠EAB ,图 4E COFADB 图3M N QP(图2)DCBAHGPBA∴ △ABE ∽△ADB .………………………2分∴ABADAE AB=.∴ 2A B A E A D =⋅.………………………………………………………3分(2)解:∵ AE =2,ED =4,∴()22612AB AE AD AE AE ED =⋅=+=⨯=.∴23AB =(舍负).………………………………………………………4分∵ BD 为⊙O 的直径,∴ ∠A =90︒.又∵ DF 是⊙O 的切线,∴ DF ⊥BD.∴ ∠BDF =90︒.在Rt △ABD 中,233tan 63A B A D B A D∠===,∴ ∠ADB =30︒.∴ ∠ABC =∠ADB =30︒. ∴∠DEF=∠AEB=60︒,903060ED F BD F AD B ∠=∠-∠=︒-︒=︒.∴ ∠F =18060D EF ED F ︒-∠-∠=︒. ∴ △DEF 是等边三角形.∴ EF = DE =4.………………………………………………………………5分(延庆)19.解:(1)如图过B 点作BE ⊥CD ,垂足为E 在Rt ∆BEC 中,∠BEC=90度, tanC=34,AD=BE=4∴ tanC=34CEBE=,CE=3由勾股定理可得BC=5AB=DE=2∴CD=5 ∴ S 梯形ABCD=144)52(21=⨯+ (2)解法一:如图过点P 作PN ⊥CD ,交CD 于点N ,交AB 的延长线于M 已知条件可知点P 是点D 沿AQ 翻折而得到的,推得AP=4 梯形ABCD ∴AB ∥CD ∴∠MBP=∠C在Rt ∆BMP 中,∠BMP=90度,BP=x ,tan ∠BMP=tan ∠C=34可推得MP=x 54,BM=x 53在Rt ∆AMP 中,利用勾股定理可推得222AP MPAM=+ 即16)54()532(22=++x x整理方程得0601252=--x x 解之满足条件的52146+-==x BP 。
2023年中考数学压轴题专题32 四边形与新定义综合问题【含答案】

专题32四边形与新定义综合问题【例1】(2022•汇川区模拟)定义:有一组对角互补的四边形叫做“对补四边形”,例如:四边形ABCD中,若∠A+∠C=180°或∠B+∠D=180°,则四边形ABCD是“对补四边形”.【概念理解】(1)如图1,四边形ABCD是“对补四边形”.①若∠A:∠B:∠C=3:2:1,则∠D=度.②若∠B=90°.且AB=3,AD=2时.则CD2﹣CB2=.【类比应用】(2)如图2,在四边形ABCD中,AB=CB,BD平分∠ADC.求证:四边形ABCD是“对补四边形”.【例2】.(2022•赣州模拟)我们定义:有一组邻角相等的凸四边形做“等邻角四边形”,例如:如图1,∠B=∠C,则四边形ABCD为等邻角四边形.(1)定义理解:已知四边形ABCD为等邻角四边形,且∠A=130°,∠B=120°,则∠D =度.(2)变式应用:如图2,在五边形ABCDE中,ED∥BC,对角线BD平分∠ABC.①求证:四边形ABDE为等邻角四边形;②若∠A+∠C+∠E=300°,∠BDC=∠C,请判断△BCD的形状,并明理由.(3)深入探究:如图3,在等邻角四边形ABCD中,∠B=∠BCD,CE⊥AB,垂足为E,点P为边BC上的一动点,过点P作PM⊥AB,PN⊥CD,垂足分别为M,N.在点P的运动过程中,判断PM+PN与CE的数量关系?请说明理由.(4)迁移拓展:如图4,是一个航模的截面示意图.四边形ABCD是等邻角四边形,∠A =∠ABC,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,AB=2dm,AD=3dm,BD=dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.【例3】(2022•常州二模)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图I,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上;(3)如图3,已知四边形ABCD是以AB为邻余线的邻余四边形,AB=15,AD=6,BC=3,∠ADC=135°,求CD的长度.【例4】(2022•工业园区模拟)【理解概念】如果一个矩形的一条边与一个三角形的一条边能够重合,且三角形的这条边所对的顶点恰好落在矩形这条边的对边上,则称这样的矩形为这个三角形的“矩形框”.如图①,矩形ABDE 即为△ABC的“矩形框”.(1)三角形面积等于它的“矩形框”面积的;(2)钝角三角形的“矩形框”有个;【巩固新知】(3)如图①,△ABC的“矩形框”ABDE的边AB=6cm,AE=2cm,则△ABC周长的最小值为cm;(4)如图②,已知△ABC中,∠C=90°,AC=4cm,BC=3cm,求△ABC的“矩形框”的周长;【解决问题】(5)如图③,锐角三角形木板ABC的边AB=14cm,AC=15cm,BC=13cm,求出该木板的“矩形框”周长的最小值.一.解答题(共20题)1.(2022•罗湖区模拟)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:(1)如图1,正方形ABCD中E是CD上的点,将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点F在DA的延长线上,则四边形BEDF(填“是”或“不是”)“直等补”四边形;(2)如图2,已知四边形ABCD是“直等补”四边形,AB=BC=10,CD=2,AD>AB,过点B作BE⊥AD于E.①过C作CF⊥BF于点F,试证明:BE=DE,并求BE的长;②若M是AD边上的动点,求△BCM周长的最小值.2.(2022•越秀区校级模拟)有一组对边平行,一个内角是它对角的两倍的四边形叫做倍角梯形.(1)已知四边形ABCD是倍角梯形,AD∥BC,∠A=100°,请直接写出所有满足条件的∠D的度数;(2)如图1,在四边形ABCD中,∠BAD+∠B=180°,BC=AD+CD.求证:四边形ABCD 是倍角梯形;(3)如图2,在(2)的条件下,连结AC,当AB=AC=AD=2时,求BC的长.3.(2022•嘉祥县一模)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)如图2,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF 交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.4.(2021•任城区校级三模)我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”(1)概念理解:请你根据上述定义举一个等邻角四边形的例子:;(2)问题探究;如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;(3)应用拓展;如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt△ABD 绕着点A顺时针旋转角α(0°<∠α<∠BAC)得到Rt△AB′D′(如图3),当凸四边形AD′BC为等邻角四边形时,求出它的面积.5.(2022春•曾都区期末)定义:我们把对角线相等的凸四边形叫做“等角线四边形”.(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,一定是“等角线四边形”的是(填序号);(2)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,且EC=DF,连接EF,AF,求证:四边形ABEF是等角线四边形;(3)如图2,已知在△ABC中,∠ABC=90°,AB=4,BC=3,D为线段AB的垂直平分线上一点,若以点A,B,C,D为顶点的四边形是等角线四边形,求这个等角线四边形的面积.6.(2022春•南浔区期末)定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形.【性质初探】如图1,已知,▱ABCD,∠B=80°,点E是边AD上一点,连结CE,四边形ABCE恰为等腰梯形.求∠BCE的度数;【性质再探】如图2,已知四边形ABCD是矩形,以BC为一边作等腰梯形BCEF,BF=CE,连结BE、CF.求证:BE=CF;【拓展应用】如图3,▱ABCD的对角线AC、BD交于点O,AB=2,∠ABC=45°,过点O作AC的垂线交BC的延长线于点G,连结DG.若∠CDG=90°,求BC的长.7.(2022春•长汀县期末)在平面直角坐标系中,如果点p(a,b)满足a+1>b且b+1>a,则称点p为“自大点”:如果一个图形的边界及其内部的所有点都不是“自大点”,则称这个图形为“自大忘形”.(1)判断下列点中,哪些点是“自大点”,直接写出点名称;p 1(1,0),,.(2)如果点N(2x+3,2)不是“自大点”,求出x的取值范围.(3)如图,正方形ABCD的初始位置是A(0,6),B(0,4),C(2,4),D(2,6),现在正方形开始以每秒1个单位长的速度向下(y轴负方向)平移,设运动时间为t秒(t>0),当正方形成为“自大忘形”时,求t的取值范围.8.(2022春•江北区期末)定义:对于一个四边形,我们把依次连结它的各边中点得到的新四边形叫做原四边形的“中点四边形”.如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”.概念理解:下列四边形中一定是“中方四边形”的是.A.平行四边形B.矩形C.菱形D.正方形性质探究:如图1,四边形ABCD是“中方四边形”,观察图形,写出关于四边形ABCD的两条结论:;.问题解决:如图2,以锐角△ABC的两边AB,AC为边长,分别向外侧作正方形ABDE和正方形ACFG,连结BE,EG,GC.求证:四边形BCGE是“中方四边形”;拓展应用:如图3,已知四边形ABCD是“中方四边形”,M,N分别是AB,CD的中点,(1)试探索AC与MN的数量关系,并说明理由.(2)若AC=2,求AB+CD的最小值.9.(2022春•铜山区期末)新定义;若四边形的一组对角均为直角,则称该四边形为对直四边形.(1)下列四边形为对直四边形的是(写出所有正确的序号);①平行四边形;②矩形;③菱形,④正方形.(2)如图,在对直四边形ABCD中,已知∠ABC=90°,O为AC的中点.①求证:BD的垂直平分线经过点O;②若AB=6,BC=8,请在备用图中补全四边形ABCD,使四边形ABCD的面积取得最大值,并求此时BD的长度.10.(2022春•盐田区校级期末)给出如下定义:有两个相邻内角互余的四边形称为“邻余四边形”,这两个角的夹边称为“邻余线”.(1)如图1,格点四边形ABCD是“邻余四边形”,指出它的“邻余线”;(2)如图2,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是“邻余四边形”;(3)如图3,四边形ABCD是“邻余四边形”,AB为“邻余线”,E,F分别是AB,CD的中点,连接EF,AD=4,BC=6.求EF的长.11.(2022春•玄武区期末)【概念认识】在四边形ABCD中,∠A=∠B.如果在四边形ABCD内部或边AB上存在一点P,满足∠DPC=∠A,那么称点P是四边形ABCD的“映角点”.【初步思考】(1)如图①,在四边形ABCD中,∠A=∠B,点P在边AB上且是四边形ABCD的“映角点”.若DA∥CP,DP∥CB,则∠DPC的度数为°;(2)如图②,在四边形ABCD中,∠A=∠B,点P在四边形ABCD内部且是四边形ABCD 的“映角点”,延长CP交边AB于点E.求证:∠ADP=∠CEB.【综合运用】在四边形ABCD中,∠A=∠B=α,点P是四边形ABCD的“映角点”,DE、CF分别平分∠ADP、∠BCP,当DE和CF所在直线相交于点Q时,请直接写出∠CQD与α满足的关系及对应α的取值范围.12.(2022春•北仑区期末)定义:对角线相等的四边形称为对美四边形.(1)我们学过的对美四边形有、.(写出两个)(2)如图1,D为等腰△ABC底边AB上的一点,连结CD,过C作CF∥AB,以B为顶点作∠CBE=∠ACD交CF于点E,求证:四边形CDBE为对美四边形.(3)如图2,对美四边形ABCD中,对角线AC、BD交于点O,AC=BD,DC∥AB.①若∠AOB=120°,AB+CD=6,求四边形ABCD的面积.②若AB⋅CD=6,设AD=x,BD=y,试求出y与x的关系式.13.(2022春•玄武区校级期中)如图1,∠A=∠B=∠C=∠D=∠E=∠F=90°,AB、EF、CD为铅直方向的边,AF、DE、BC为水平方向的边,点E在AB、CD之间,且在AF、BC之间,我们称这样的图形为“L图形”,若一条直线将该图形的面积分为面积相等的两部分,则称此直线为该“L图形”的等积线.(1)如图2所示四幅图中,直线L是该“L图形”等积线的是(填写序号).(2)如图3,直线m是该“L图形”的等积线,与边BC、AF分别交于点M、N,过MN 中点O的直线分别交边BC、AF于点P、Q,则直线PQ(填“是”或“不是”)该图形的等积线.(3)在图4所示的“L图形”中,AB=6,BC=10,AF=2.①若CD=2,在图中画出与AB平行的等积线l(在图中标明数据);②在①的条件下,该图形的等积线与水平的两条边DE、BC分别交于P、Q,求PQ的最大值;③如果存在与水平方向的两条边DE、BC相交的等积线,则CD的取值范围为.14.(2022•姑苏区一模)定义:有两个内角分别是它们对角的一半的四边形叫做半对角四边形.(1)如图1,在半对角四边形ABCD中,∠B=∠D,∠C=∠A,则∠B+∠C=°;(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,在OA上取点E,使得DE=OE,连接DE并延长交AC于点F,∠AED=3∠EAF.求证:四边形BCFD 是半对角四边形;(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,OH=2,DH =6.①连接OC,若将扇形OBC围成一个圆锥的侧面,则该圆锥的底面半径为;②求△ABC的面积.15.(2022•江北区开学)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上.(3)如图3,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,CD=3BE,QB=6,求邻余线AB的长.16.(2022春•西城区校级期中)平面直角坐标系xOy中,正方形ABCD的四个顶点坐标分别为:A(﹣,),B(﹣,﹣),C(,﹣),D(,),P、Q是这个正方形外两点,且PQ=1.给出如下定义:记线段PQ的中点为T,平移线段PQ得到线段P'Q'(其中P',Q'分别是点P,Q的对应点),记线段P'Q'的中点为T.若点P'和Q'分别落在正方形ABCD的一组邻边上,或线段P'Q'与正方形ABCD的一边重合,则称线段TT'长度的最小值为线段PQ到正方形ABCD的“回归距离”,称此时的点T'为线段PQ到正方形ABCD 的“回归点”.(1)如图1,平移线段PQ,得到正方形ABCD内两条长度为1的线段P1Q1和P2Q2,这两条线段的位置关系为;若T1,T2分别为P1Q1和P2Q2的中点,则点(填T1或T2)为线段PQ到正方形ABCD的“回归点”;(2)若线段PQ的中点T的坐标为(1,1),记线段PQ到正方形ABCD的“回归距离”为d1,请直接写出d1的最小值:,并在图2中画出此时线段PQ到正方形ABCD的“回归点”T'(画出一种情况即可);(3)请在图3中画出所有符合题意的线段PQ到正方形ABCD的“回归点”组成的图形.17.(2022秋•福田区期中)定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图1,∠ABC=∠ADC=90°,四边形ABCD 是损矩形,则该损矩形的直径是线段AC.同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC.(1)请在图1中再找出一对这样的角来:=;(2)如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF,D为菱形ACEF 对角线的交点,连接BD.①四边形ABCD损矩形(填“是”或“不是”);②当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由;③若∠ACE=60°,AB=4,BD=5,求BC的长.18.(2022春•江阴市校级月考)定义:长宽比为:1(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图a所示.操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为矩形.(1)证明:四边形ABCD为矩形;(2)在题(1)的矩形ABCD中,点M是边AB上一动点.①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN 的值;②若AM=AD,点N在边BC上,当△DMN的周长最小时,求的值;③连接CM,作BR⊥CM,垂足为R.若AB=4,则DR的最小值=.19.(2022春•柯桥区月考)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.(1)阅读与理解:如图1,四边形内接于⊙O,点A为弧BD的中点.四边形ABCD(填“是”或“不是”)等补四边形.(2)探究与运用:①如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由;②如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,若CD=10,AF=5,求DF的长.(3)思考与延伸:在等补四边形ABCD中,AB=AD=3,∠BAD=120°,当对角线AC长度最大时,以AC 为斜边作等腰直角三角形ACP,直接写出线段DP的长度.20.(2021秋•荔湾区期末)如图,共顶点的两个三角形△ABC,△AB′C′,若AB=AB',AC=AC',且∠BAC+∠B′AC′=180°,我们称△ABC与△AB′C'互为“顶补三角形”.(1)如图2,△ABC是等腰三角形,△ABE,△ACD是等腰直角三角形,连接DE;求证:△ABC与△ADE互为顶补三角形.(2)在(1)的条件下,BE与CD交于点F,连接AF并延长交BC于点G.判断DE与AG 的数量关系,并证明你的结论.(3)如图3,四边形ABCD中,∠B=40°,∠C=50°.在平面内是否存在点P,使△PAD 与△PBC互为顶补三角形,若存在,请画出图形,并证明;若不存在,请说明理由.【例1】2022•汇川区模拟)定义:有一组对角互补的四边形叫做“对补四边形”,例如:四边形ABCD中,若∠A+∠C=180°或∠B+∠D=180°,则四边形ABCD是“对补四边形”.【概念理解】(1)如图1,四边形ABCD是“对补四边形”.①若∠A:∠B:∠C=3:2:1,则∠D=90度.②若∠B=90°.且AB=3,AD=2时.则CD2﹣CB2=5.【类比应用】(2)如图2,在四边形ABCD中,AB=CB,BD平分∠ADC.求证:四边形ABCD是“对补四边形”.【分析】(1)①设∠A=3x°,则∠B=2x°,∠C=x°,利用“对补四边形”的定义列出方程,解方程即可求得结论;②连接AC,利用“对补四边形”的定义和勾股定理解答即可得出结论;(2)在DC上截取DE=DA,连接BE,利用全等三角形的判定与性质,等腰三角形的性质和“对补四边形”的定义解答即可.【解答】(1)解:①∵∠A:∠B:∠C=3:2:1,∴设∠A=3x°,则∠B=2x°,∠C=x°,∵四边形ABCD是“对补四边形”,∴∠A+∠C=180°,∴3x+x=180,∴x=45°.∴∠B=2x=90°.∵四边形ABCD是“对补四边形”,∴∠B+∠D=180°,∴∠D=90°.故答案为:90;②连接AC,如图,∵∠B=90°,∴AB2+BC2=AC2.∵四边形ABCD是“对补四边形”,∴∠B+∠D=180°.∴∠D=90°.∴AD2+CD2=AC2.∴AB2+BC2=AD2+CD2,∴CD2﹣CB2=AB2﹣AD2,∵AB=3,AD=2,∴CD2﹣CB2=32﹣22=5.故答案为:5;(2)证明:在DC上截取DE=DA,连接BE,如图,∵BD平分∠ADC,∴∠ADB=∠EDB.在△ADB和△EDB中,,∴△ADB≌△EDB(SAS),∴∠A=∠DEB,AB=BE,∵AB=CB,∴BE=BC,∴∠BEC=∠C.∵∠DEB+∠BEC=180°,∴∠DEB+∠C=180°,∴∠A+∠C=180°,∴四边形ABCD是“对补四边形”.【例2】(2022•赣州模拟)我们定义:有一组邻角相等的凸四边形做“等邻角四边形”,例如:如图1,∠B=∠C,则四边形ABCD为等邻角四边形.(1)定义理解:已知四边形ABCD为等邻角四边形,且∠A=130°,∠B=120°,则∠D =55度.(2)变式应用:如图2,在五边形ABCDE中,ED∥BC,对角线BD平分∠ABC.①求证:四边形ABDE为等邻角四边形;②若∠A+∠C+∠E=300°,∠BDC=∠C,请判断△BCD的形状,并明理由.(3)深入探究:如图3,在等邻角四边形ABCD中,∠B=∠BCD,CE⊥AB,垂足为E,点P为边BC上的一动点,过点P作PM⊥AB,PN⊥CD,垂足分别为M,N.在点P的运动过程中,判断PM+PN与CE的数量关系?请说明理由.(4)迁移拓展:如图4,是一个航模的截面示意图.四边形ABCD是等邻角四边形,∠A =∠ABC,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,AB=2dm,AD=3dm,BD=dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.【分析】(1)由等邻角四边形的定义和四边形内角和定理可求解;(2)①由角平分线的性质和平行线的性质可得∠EDB=∠ABD,可得结论;②由三角形内角和定理和四边形内角和定理可求∠C=60°,即可求解;(3)由面积关系可求解;(4)由直角三角形的性质可得AM=DM=ME,EN=NB=CN,由勾股定理可求DG=1,BG=6,即可求解.【解答】(1)解:∵四边形ABCD为等邻角四边形,∠A=130°,∠B=120°,∴∠C=∠D,∴∠D=55°,故答案为:55;(2)①证明:∵BD平分∠ABC,∴∠ABD=∠DBC,∵ED∥BC,∴∠EDB=∠DBC,∴∠EDB=∠ABD,∴四边形ABDE为等邻角四边形;②解:△BDC是等边三角形,理由如下:∵∠BDC=∠C,∴BD=BC,∠DBC=180°﹣2∠C,∵∠A+∠E+∠ABD+∠BDE=360°,∴∠A+∠E=360°﹣2∠ABD,∵∠A+∠C+∠E=300°,∴300°﹣∠C=360°﹣2(180°﹣2∠C),∴∠C=60°,又∵BD=BC,∴△BDC是等边三角形;(3)解:PM+PN=CE,理由如下:如图,延长BA,CD交于点H,连接HP,∵∠B=∠BCD,∴HB=HC,=S△BPH+S△CPH,∵S△BCH∴×BH×CE=×BH×PM+×CH×PN,∴CE=PM+PN;(4)解:如图,延长AD,BC交于点H,过点B作BG⊥AH于G,∵ED⊥AD,EC⊥CB,M、N分别为AE、BE的中点,∴AM=DM=ME,EN=NB=CN,∵AB2=BG2+AG2,BD2=BG2+DG2,∴52﹣(3+DG)2=37﹣DG2,∴DG=1,∴BG==6,由(3)可得DE+EC=BG=6,∴△DEM与△CEN的周长之和=ME+DM+DE+EC+EN+CN=AE+BE+BG=AB+BG=(6+2)dm.【例3】(2022•常州二模)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图I,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形;(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上;(3)如图3,已知四边形ABCD是以AB为邻余线的邻余四边形,AB=15,AD=6,BC=3,∠ADC=135°,求CD的长度.【分析】(1)根据邻余四边形的定义证明结论即可;(2)连接AB,在∠A+∠B=90°的基础上选择合适的E点和F点连接作图即可;(3)邻余四边形的定义可得∠H=90°,由勾股定理可求解.【解答】(1)证明:∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴∠DAB+∠DBA=90°,∴∠FAB与∠EBA互余,∴四边形ABEF是邻余四边形;(2)解:如图所示(答案不唯一),(3)解:如图3,延长AD,CB交于点H,∵四边形ABCD是以AB为邻余线的邻余四边形,∴∠A+∠B=90°,∵∠ADC=135°,∴∠HDC=45°,∴∠HDC=∠HCD=45°,∴CH=DH,∵AB2=AH2+BH2,∴225=(6+DH)2+(3+DH)2,∴DH=6(负值舍去),∴CD=6.【例4】(2022•工业园区模拟)【理解概念】如果一个矩形的一条边与一个三角形的一条边能够重合,且三角形的这条边所对的顶点恰好落在矩形这条边的对边上,则称这样的矩形为这个三角形的“矩形框”.如图①,矩形ABDE 即为△ABC的“矩形框”.(1)三角形面积等于它的“矩形框”面积的;(2)钝角三角形的“矩形框”有1个;【巩固新知】(3)如图①,△ABC的“矩形框”ABDE的边AB=6cm,AE=2cm,则△ABC周长的最小值为(6+2)cm;(4)如图②,已知△ABC中,∠C=90°,AC=4cm,BC=3cm,求△ABC的“矩形框”的周长;【解决问题】(5)如图③,锐角三角形木板ABC的边AB=14cm,AC=15cm,BC=13cm,求出该木板的“矩形框”周长的最小值.【分析】(1)利用同底等高的面积关系求解即可;(2)根据钝角三角形垂线的特点进行判断即可;(3)作A点关于DE的对称点F,连接BF,则△ABC周长≥AC+BF,求出BF+AC即可求解;(4)以三角形三边分别为矩形的一边作“矩形框”,分别求出周长即可;(5)以三角形三边分别为矩形的一边作“矩形框”,分别求出周长,取最小值即可.=×AB×AE,S矩形ABDE=AB×AE,【解答】解:(1)∵S△ABC=S矩形ABDE,∴S△ABC故答案为:;(2)由定义可知,钝角三角形以钝角所对的边为矩形一边,能够构造出一个“矩形框”,故答案为:1;(3)如图①,作A点关于DE的对称点F,连接BF,∴CF=AC,∴AC+BC≥BF,∴△ABC周长=AB+AC+BC≥AC+BF,∵AB=6cm,AE=2cm,在Rt△ABF中,BF=2,∴△ABC周长的最小值(6+2)cm,故答案为:(6+2);(4)如图②﹣1,以AB边为矩形一边时,作“矩形框”ABDE,∵∠C=90°,AC=4cm,BC=3cm,∴AB=5cm,=×3×4=×5×AE,∵S△ABC∴AE=,∴矩形ABDE的周长=2×(5+)=(cm);如图②﹣2,以BC边为矩形一边时,作“矩形框”BCAF,∴矩形BCAF的周长=2×(3+4)=14(cm);同理,以AB为矩形一边时,“矩形框”的周长为14cm;综上所述:△ABC的“矩形框”的周长为cm或14cm;(5)如图③﹣1,以AB为一边作“矩形框”ABDE,过点C作CG⊥AB交于G,∴CG2=AC2﹣AG2=BC2﹣BG2,AG+BG=AB,又∵AB=14cm,AC=15cm,BC=13cm,∴AG=9cm,BG=5cm,∴CG=12cm,∴“矩形框”ABDE的周长=2×(14+12)=52cm;如图③﹣2,以BC为一边作“矩形框”BCNM,过点A作AH⊥CB交于H,=×CG×AB=×12×14=×AH×BC,∵S△ABC∴AH=cm,∴“矩形框”BCNM的周长=2×(13+)=cm;如图③﹣3,以AC为矩形一边,作“矩形框”ACTS,过点B作BK⊥AC交于点K,=×CG×AB=×12×14=×BK×AC,∵S△ABC∴BK=cm,∴“矩形框”ACTS的周长=2×(15+)=cm;∵<52<,∴该木板的“矩形框”周长的最小值为cm.一.解答题(共20题)1.(2022•罗湖区模拟)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:(1)如图1,正方形ABCD中E是CD上的点,将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点F在DA的延长线上,则四边形BEDF是(填“是”或“不是”)“直等补”四边形;(2)如图2,已知四边形ABCD是“直等补”四边形,AB=BC=10,CD=2,AD>AB,过点B作BE⊥AD于E.①过C作CF⊥BF于点F,试证明:BE=DE,并求BE的长;②若M是AD边上的动点,求△BCM周长的最小值.【分析】(1)由旋转的性质可得∠ABF=∠CBE,BF=BE,根据正方形的性质得∠ABC=∠D=90°,可得出∠EBF=∠D=90°,即可得出答案;(2)①首先证明四边形CDEF是矩形,则DE=CF,EF=CD=2,再证△ABE≌△BCF,根据全等三角形的判定和性质可得BE=CF,AE=BF,等量代换即可得BE=DE;由AE=BF,EF=CD=2可得AE=BE﹣2,设BE=x,根据勾股定理求出x的值即可;②延长CD到点G,使DG=CD,连接BG交AD于点M′,过点G作GH⊥BC,交BC的延长线于点H,证明△ABE∽△CGH,根据相似三角形的性质求出CH、HG的值,在Rt△BHG中,根据勾股定理求出BG,即可求解.【解答】解:(1)∵将△BCE绕B点旋转,BC与BA重合,点E的对应点F在DA的延长线上,∴∠ABF=∠CBE,BF=BE,∵四边形ABCD是正方形,∴∠ABC=∠D=90°,∴∠ABE+∠CBE=90°,∴∠ABE+∠ABF=90°,即∠EBF=∠D=90°,∴∠EBF+∠D=180°,∵∠EBF=90°,BF=BE,∴四边形BEDF是“直等补”四边形.故答案为:是;(2)①证明:∵四边形ABCD是“直等补”四边形,AB=BC=10,CD=2,AD>AB,∴∠ABC=90°,∠ABC+∠D=180°,∴∠D=90°,∵BE⊥AD,CF⊥BE,∴∠DEF=90°,∠CFE=90°,∴四边形CDEF是矩形,∴DE=CF,EF=CD=2,∵∠ABE+∠A=90°,∠ABE+∠CBE=90°,∴∠A=∠CBF,∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF(AAS),∴BE=CF,AE=BF,∵DE=CF,∴BE=DE;∵四边形CDEF是矩形,∴EF=CD=2,∵△ABE≌△BCF,∴AE=BF,∴AE=BE﹣2,设BE=x,则AE=x﹣2,在Rt△ABE中,x2+(x﹣2)2=102,解得:x=8或x=﹣6(舍去),∴BE的长是8;②∵△BCM周长=BC+BM+CM,∴当BM+CM的值最小时,△BCM的周长最小,如图,延长CD到点G,使DG=CD,连接BG交AD于点M′,过点G作GH⊥BC,交BC的延长线于点H,∵∠ADC=90°,∴点C与点G关于AD对称,∴BM+CM=BM+MG≥BG,即BM+CM≥BM′+M′C,∴当点M与M′重合时,BM′+M′C的值最小,即△BCM的周长最小,在Rt△ABE中,AE===6,∵四边形ABCD是“直等补”四边形,∴∠A+∠BCD=180°,∵∠BCD+∠GCH=180°,∴∠A=∠GCH,∵∠AEB=∠H=90°,∴△ABE∽△CGH,∴===,即=,∴GH=,CH=,∴BH=BC+CH=10+=,∴BG===2,∴△BCM周长的最小值为2+10.2.(2022•越秀区校级模拟)有一组对边平行,一个内角是它对角的两倍的四边形叫做倍角梯形.(1)已知四边形ABCD是倍角梯形,AD∥BC,∠A=100°,请直接写出所有满足条件的∠D的度数;(2)如图1,在四边形ABCD中,∠BAD+∠B=180°,BC=AD+CD.求证:四边形ABCD 是倍角梯形;(3)如图2,在(2)的条件下,连结AC,当AB=AC=AD=2时,求BC的长.【分析】(1)由题意得出∠D=2∠B或∠B=2∠D或∠A=2∠C,根据梯形的性质可得出答案;(2)过点D作DE∥AB,交BC于点E,证明四边形ABED为平行四边形,得出AD=BE,∠B=∠DEC=∠ADE,证出∠ADC=2∠B,则可得出结论;(3)过点E作AE∥DC交BC于点E,由等腰三角形的性质求出∠B=∠ACB=36°,证明△ABE∽△CBA,由相似三角形的性质得出,设AE=BE=CD=x,得出方程22=x (x+2),求出x=﹣1,则可得出答案.【解答】解:(1)∵AD∥BC,∴∠A+∠B=180°,∵∠A=100°,∴∠B=80°,∵四边形ABCD是倍角梯形,∴∠D=2∠B或∠B=2∠D或∠A=2∠C,若∠D=2∠B,则∠D=160°;若∠B=2∠D,则∠D=40°,若∠A=2∠C,则∠C=50°,∴∠D=130°,故所有满足条件的∠D的度数为160°或40°或130°;(2)证明:过点D作DE∥AB,交BC于点E,∵∠BAD+∠B=180°,∴AD∥BC,∵DE∥AB,∴四边形ABED为平行四边形,∴AD=BE,∠B=∠DEC=∠ADE,∵BC=BE+CE,∴BC=AD+CE,又∵BC=AD+CD,∴CE=CD,BC>AD,∴∠CDE=∠DEC,∴∠ADC=∠ADE+∠CDE=2∠B,∴四边形ABCD是倍角梯形;(3)过点E作AE∥DC交BC于点E,∵AB=AC,∴∠B=∠ACB,∵AD=AC,∴∠ACD=∠D,∵AD∥BC,∴∠ACB=∠DAC,设∠B=α,则∠D=2α,∵∠DAC+∠D+∠ACD=180°,∴α+2α+2α=180°,∴α=36°,∴∠B=∠ACB=36°,∴∠BAC=∠AEB=108°,∵∠B=∠B,∴△ABE∽△CBA,∴,设AE=BE=CD=x,则BC=2+x,∴22=x(x+2),∴x=﹣1(负值舍去),∴CD=﹣1.∴BC=AD+CD=2+﹣1=+1.3.(2022•嘉祥县一模)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.(2)如图2,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF 交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长.【分析】(1)由等腰三角形的三线合一定理先证AD⊥BC,再证∠DAB+∠DBA=90°,由邻余四边形定义即可判定;(2)由等腰三角形的三线合一定理先证BD=CD,推出CE=5BE,再证明△DBQ∽△ECN,推出==,即可求出NC,AC,AB的长度.【解答】(1)证明:∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴∠DAB+∠DBA=90°,∴∠FBA与∠EBA互余,∴四边形ABEF是邻余四边形;(2)解:∵AB=AC,AD是△ABC的角平分线,∴BD=CD,∵DE=2BE,∴BD=CD=3BE,∴CE=CD+DE=5BE,∵∠EDF=90°,点M是EF的中点,∴DM=ME,∴∠MDE=∠MED,∵AB=AC,∴∠B=∠C,∴△DBQ∽△ECN,∴==,∵QB =3,∴NC =5,∵AN =CN ,∴AC =2CN =10,∴AB =AC =10.4.(2021•任城区校级三模)我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”(1)概念理解:请你根据上述定义举一个等邻角四边形的例子:矩形或正方形;(2)问题探究;如图1,在等邻角四边形ABCD 中,∠DAB =∠ABC ,AD ,BC 的中垂线恰好交于AB 边上一点P ,连结AC ,BD ,试探究AC 与BD 的数量关系,并说明理由;(3)应用拓展;如图2,在Rt △ABC 与Rt △ABD 中,∠C =∠D =90°,BC =BD =3,AB =5,将Rt △ABD 绕着点A 顺时针旋转角α(0°<∠α<∠BAC )得到Rt △AB ′D ′(如图3),当凸四边形AD ′BC 为等邻角四边形时,求出它的面积.【分析】(1)矩形或正方形邻角相等,满足“等邻角四边形”条件;(2)结论:AC =BD ,证明△APC ≌△DPB (SAS );(3)分两种情况考虑:Ⅰ、当∠AD ′B =∠D ′BC 时,延长AD ′,CB 交于点E ,如图1,由S 四边形ACBD ′=S △ACE ﹣S △BED ′,求出四边形ACBD ′面积;Ⅱ、当∠D ′BC =∠ACB =90°时,过点D ′作D ′E ⊥AC 于点E ,如图2,由S 四边形ACBD ′=S △AED ′+S 矩形ECBD ′,求出四边形ACBD ′面积即可.【解答】解:(1)矩形或正方形是一个等邻角四边形.故答案为:矩形,正方形;(2)结论:AC=BD,理由:连接PD,PC,如图1所示:∵PE是AD的垂直平分线,PF是BC的垂直平分线,∴PA=PD,PC=PB,∴∠PAD=∠PDA,∠PBC=∠PCB,∴∠DPB=2∠PAD,∠APC=2∠PBC,即∠PAD=∠PBC,∴∠APC=∠DPB,∴△APC≌△DPB(SAS),∴AC=BD;(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,如图3(i)所示,∴∠ED′B=∠EBD′,∴EB=ED′,设EB=ED′=x,由勾股定理得:42+(3+x)2=(4+x)2,解得:x=4.5,过点D′作D′F⊥CE于F,∴D′F∥AC,∴△ED′F∽△EAC,∴=,即=,解得:D′F=,∴S △ACE =AC ×EC =×4×(3+4.5)=15;S △BED ′=×BE ×D ′F =××4.5×=,则S 四边形ACBD ′=S △ACE ﹣S △BED ′=15﹣=;(ii )当∠D ′BC =∠ACB =90°时,过点D ′作D ′E ⊥AC 于点E ,如图3(ii )所示,∴四边形ECBD ′是矩形,∴ED ′=BC =3,在Rt △AED ′中,根据勾股定理得:AE ==,∴S △AED ′=×AE ×ED ′=××3=,S 矩形ECBD ′=CE ×CB =(4﹣)×3=12﹣3,则S 四边形ACBD ′=S △AED ′+S 矩形ECBD ′=+12﹣3=12﹣.5.(2022春•曾都区期末)定义:我们把对角线相等的凸四边形叫做“等角线四边形”.(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,一定是“等角线四边形”的是②④(填序号);(2)如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,且EC =DF ,连接EF ,AF ,求证:四边形ABEF 是等角线四边形;(3)如图2,已知在△ABC 中,∠ABC =90°,AB =4,BC =3,D 为线段AB 的垂直平分线上一点,若以点A ,B ,C ,D 为顶点的四边形是等角线四边形,求这个等角线四边形的面积.。
2021北京各区中考二模分类汇编-专题15 四边形有关计算与证明(教师版)

专题15 四边形有关计算与证明1. (2021·东城二模) 如图,在菱形ABCD中,点E是CD的中点,连接AE,交BD于点F.(1)求BF:DF的值;(2)若AB=2,AE=√3,求BD的长.【解答】1. 解:(1)∵四边形ABCD是菱形,∴AB∥CD,AB=CD.∴△ABF∽△DEF.∴BF:DF=AB:ED.∵点E是CD的中点,∴AB=CD=2DE.∴BF:DF=2:1.(2) ∵四边形ABCD是菱形,∴AB=AD.∵AB=2,∴AD=2,DE=1.∵AE=√3,∴AD2=AE2+DE2。
∴∠AED=90°.∵ sin∠ADE=2,∴∠ADE=60°.在菱形ABCD中,BD为对角线,∴∠ADB=12∠ADE=30°.连接AC,交BD于点O .∵四边形ABCD是菱形,∴AC⊥BD,OB=OD.∴AO=12AD=1.在Rt△AOD中,由勾股定理,得OD.∴BD=2OD=2√3.【分析】(1)根据菱形性质可知AB∥CD,AB=CD.再根据点E是CD的中点和8字形相似即可求出结果。
(2)连接AC,由勾股定理逆定理可知△AED为直角三角形,根据三角函数可求得∠ADE=60°,∠ADB=12∠ADE=30°,在Rt△AOD中易求OD,由BD=2OD即可求出结果。
2.(2021·西城二模)如图,在△ABC中,AC BC=,CD为△ABC的角平分线,//AE DC AE DC=,,连接CE.(1)求证:四边形ADCE为矩形:(2)连接DE,若1012AB CD==,,求DE的长.【解答】2.(本小题满分 5 分)(1)证明:∵AE∥DC,AE=DC,∴四边形A DCE 为平行四边形.∵在△ABC 中,AC=BC,CD 为△ABC 的角平分线,∴CD⊥AB.∴∠ADC=90°.∴四边形A DCE 为矩形.(2) ∵AC=BC,CD 为△ABC 的角平分线,AB=10,AB=5∴AD=12在Rt△ACD 中,∠ADC =90°,AD=5,CD=12,∴根据勾股定理得AC=13∵四边形ADCE 为矩形,∴DE=AC=13.【分析】(1)根据AE∥DC,AE=DC可知四边形A DCE为平行四边形,再根据三线合一可得结果。
2021年北京市各区中考数学模拟真题专练:四边形综合

2021年北京市各区中考数学模拟真题专练:四边形综合1.(2021•房山区二模)如图,已知AC是矩形ABCD的对角线,∠BAC=30°,点M 是DC延长线上一点,∠BAC的平分线与∠BCM的平分线交于点E,将线段CA绕点C逆时针旋转,得到线段CF,使点F在射线CB上,连接EF.(1)依题意补全图形;(2)求∠AEC的度数;(3)用等式表示线段AE,CE,EF之间的数量关系,并证明.2.(2021•房山区二模)如图,已知△ACB中,∠ACB=90°,E是AB的中点,连接CE,分别过点A,C作CE和AB的平行线相交于点D.(1)求证:四边形ADCE是菱形;(2)若AB=4,∠DAE=60°,求△ACB的面积.3.(2021•平谷区二模)如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.(1)求证:四边形CFBD是菱形;(2)连接AE,若CF=,DF=2,求AE的长.4.(2021•门头沟区二模)已知,如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E,连接DE交AB于点O.(1)求证:四边形ADBE是矩形;(2)若BC=8,AO=,求四边形AEBC的面积.5.(2021•北京二模)如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠A=120°,求△DCE的底边CE上的高及DE的长.6.(2021•朝阳区二模)如图,在菱形ABCD中,AC,BD相交于点O,过B,C两点分别作AC,BD的平行线,相交于点E.(1)求证:四边形BOCE是矩形;(2)连接EO交BC于点F,连接AF,若∠ABC=60°,AB=2,求AF的长.7.(2021•丰台区二模)如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,AE∥BC,CE∥AD.(1)求证:四边形ADCE是菱形;(2)连接BE,若∠ABC=30°,AC=2,求BE的长.8.(2021•顺义区二模)如图,平行四边形ABCD的对角线AC,BD交于点O,AE⊥BC于点E,点F在BC延长线上,且CF=BE.(1)求证:四边形AEFD是矩形;(2)连接AF,若tan∠ABC=2,BE=1,AD=3,求AF的长.9.(2021•朝阳区二模)在平面直角坐标系xOy中,对于图形Q和∠P,给出如下定义:若图形Q上的所有的点都在∠P的内部或∠P的边上,则∠P的最小值称为点P对图形Q的可视度.如图1,∠AOB的度数为点O对线段AB的可视度.(1)已知点N(2,0),在点M1(0,),M2(1,),M3(2,3)中,对线段ON的可视度为60°的点是.(2)如图2,已知点A(﹣2,2),B(﹣2,﹣2),C(2,﹣2),D(2,2),E (0,4).①直接写出点E对四边形ABCD的可视度为°;②已知点F(a,4),若点F对四边形ABCD的可视度为45°,求a的值.10.(2021•西城区二模)如图,在△ABC中,AC=BC,CD为△ABC的角平分线,AE ∥DC,AE=DC,连接CE.(1)求证:四边形ADCE为矩形;(2)连接DE,若AB=10,CD=12,求DE的长.11.(2021•石景山区二模)如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA 至点F,使得EF=DA,连接BF,CF.(1)求证:四边形BCEF是矩形;(2)若AB=3,CF=4,DF=5,求EF的长.12.(2021•东城区二模)对于平面直角坐标系xOy中的图形W,给出如下定义:点P是图形W上任意一点,若存在点Q,使得∠OQP是直角,则称点Q是图形W的“直角点”.(1)已知点A(6,8),在点Q1(0,8),Q2(﹣4,2),Q3(8,4)中,是点A的“直角点”;(2)已知点B(﹣3,4),C(4,4),若点Q是线段BC的“直角点”,求点Q的横坐标n的取值范围;(3)在(2)的条件下,已知点D(t,0),E(t+1,0),以线段DE为边在x轴上方作正方形DEFG.若正方形DEFG上的所有点均为线段BC的“直角点”,直接写出t的取值范围.13.(2021•西城区校级模拟)如图,在四边形ABCD中,AB∥CD,AB=AD,AC平分∠BAD.(1)求证:四边形ABCD是菱形;(2)若菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长,与AB的延长线相交于点G,求EG的长.14.(2021春•海淀区校级月考)对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离”,记作d(M,N).如图,已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2),D(6,6).(1)d(点O,CD)=,d(点B,AC)=;(2)记线段BC,AD组成图形G已知点T(4,m),若d(点T,G)≤2,求m的取值范围;(3)若E(t,0),F(t+1,0),d(EF,四边形ABCD)=2,直接写出t的取值范围.参考答案1.(1)补全图形如图所示:(2)∵AC是矩形ABCD的对角线,延长DC至M,∴∠ABC=∠BCD=∠BCM=90°.∵将线段CA绕点C逆时针旋转,得到线段CF,使线段CF在射线CB上,∠BAC=30°,∴∠ACF=60°,∵∠BAC的平分线与∠BCM的平分线交于点E,∴∠BAE=∠CAE=15°,∠ECF=45°,∴∠ACE=∠ACF+∠ECF=60°+45°=105°,∴∠AEC=180°﹣∠ACE﹣∠CAE=180°﹣105°﹣15°=60°;(3)答:AE=CE+EF.证明:在EA上截取EH=EC,连接CH,∵∠AEC=60°,∴△ECH是等边三角形,∴∠EHC=∠ECH=60°,CE=CH=EH.∴∠ECF+∠FCH=∠FCH+∠HCA=60°,∴∠ECF=∠HCA,∵将线段CA绕点C逆时针旋转,得到线段CF,∴CF=CA.在△ECF与△HCA中,,∴△ECF≌△HCA(SAS).∴EF=HA.∵AE=EH+HA,∴AE=CE+EF.2.(1)证明:∵AD∥CE,CD∥AE,∴四边形ADCE是平行四边形,∵∠ACB=90°,E是AB的中点,∴CE=AE,∴四边形ADCE是菱形;(2)解:∵AB=4,AE=CE=EB,∴CE=AE=2.∵四边形ADCE是菱形,∠DAE=60°,∴∠CAE=30°.在Rt△ABC中,∠ACB=90°,∠CAE=30°,AB=4,∴,∴.∴S△ACB=AC•BC=2.3.证明:(1)∵点E为BC的中点,∴CE=BE,又∵EF=DE,∴四边形CFBD是平行四边形,∵D,E分别是边AB,BC的中点,∠ACB=90°,∴DE∥AC,∴∠DEB=∠ACB=90°,即DF⊥CB,∴四边形CFBD是菱形;(2)∵D,E分别是边AB,BC的中点,∴AC=2DE,∵DF=2DE=2EF,DF=2,∴AC=2,EF=1,∵CF=,四边形CFDB是菱形,∴∠CEF=90°,∴CE===3,∵∠ACE=90°,∴AE===,即AE的长是.4.解:(1)∵AE∥BC,BE∥AD,∴四边形ADBE是平行四边形,∵AB=AC,AD是BC边的中线,∴AD⊥BC,即∠ADB=90°.∴四边形ADBE为矩形.(2)∵在矩形ADBE中,AO=,∴DE=AB=5,∵D是BC的中点,∴AE=DB=4,∴AB=2AO=5,∵∠ADB=90°,根据勾股定理,∴S△ABC=×BC×AD=×8×3=12,∴S△ABE=×AE×BE=×4×3=6,∴S四边形AEBC=S△ABC+S△ABE=12+6=18,即S四边形AEBC为18.5.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵F是AD的中点,∴FD=AD,∵CE=BC,∴FD=CE,∵FD∥CE,∴四边形CEDF是平行四边形;(2)过点D作DG⊥CE于点G,∵四边形ABCD是平行四边形,∴AB∥CD,CD=AB=4,∠A=120°,BC=AD=6,∴∠DCE=∠B=60°,在Rt△DGC中,∠DGC=90°,∴CG=CD•cos∠DCE=2,DG=CD•sin∠DCE=2,∵CE=BC=3,∴GE=1,在Rt△DGE中,∠DGE=90°,∴DE==.6.(1)证明:∵BE∥AC,EC∥BD,∴四边形BOCE是平行四边形,∵四边形ABCD是菱形,∴AC⊥BD,∴∠BOC=90°,∴平行四边形BOCE是矩形;(2)解:如图,∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴BC=AB=2,∠BAC=60°,∵四边形BOCE是矩形,∴BF=CF=BC=1,∴AF⊥BC,∠BAF=∠BAC=30°,∴∠AFB=90°,∴AF=BF=.7.解:(1)证明:∵AE∥BC,CE∥AD.∴四边形ADCE是平行四边形.∵∠BAC=90°,AD是斜边BC边上的中线.∴AD=CD.∴四边形ADCE是菱形.(2)连接BE,过点E作EF垂直BA,垂足为F,如图:∵∠ABC=30°,AC=2.∴BC=4,AB=.∵∠BAC=90°,AD是斜边BC边上的中线.∴AD=BD=CD.∴∠DAB=∠DBA.∵∠ABC=30°.∴∠CDA=60°.∴△ADC的等边三角形.∵AC=2.∴AD=AE=2∵四边形ADCE是菱形.∴∠ECA=∠CAD=60°.∴∠EAF=30°.∴=1.∴AF==.∴BF=3.∴BE=.8.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵CF=BE,∴CF+EC=BE+EC,即BC=EF,∴AD=EF,且AD∥EF,∴四边形AEFD是平行四边形,∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;(2)解:在Rt△ABE中,∠AEB=90°,BE=1,∵tan∠ABC=,∴AE=2BE=2,∵四边形AEFD为矩形,∴FD=AE=2,∠ADF=90°,∵AD=3,∴AF===.9.解:(1)如图1,连结M1N、M2O、M2N、M3O、M3N,作M2G⊥x轴于点G,则G (1,0),OG=ON=1,∴OM2=NM2,∴∠OM2G=∠NM2G.∵tan∠OM1N===,∴∠OM1N=60°,∴点M1对线段ON的可视度为60°;∵tan∠OM2G===,∴∠OM2G=∠NM2G=30°,∴∠OM2N=60°,∴点M2对线段ON的可视度为60°;∵tan∠OM3N=<1,∴∠OM3N<45°,∴点M3对线段ON的可视度不是60°.故答案为:M1,M2.(2)①∵A(﹣2,2),B(﹣2,﹣2),C(2,﹣2),D(2,2),∴四边形ABCD是正方形,且各边与坐标轴垂直(或平行).如图2,设AD交y轴于点I,则∠AIE=∠DIE=90°.∵E(0,4),∴AI=EI=DI=2,∴∠IEA=∠IED=45°,∴∠AED=90°,∴点E对四边形ABCD的可视度为90°.故答案为:90.②由题意可知,点F在直线y=4上.延长CD交直线y=4于点H,以点D为圆心、DA长为半径作⊙D,则点C在⊙D上;∵DH与直线y=4垂直,且DH<DA,∴直线y=4与⊙D有两个交点.设⊙D与直线y=4在直线CD右侧的交点为点F,连结AF、CF、DF.∵∠AFC=∠ADC=45°,∴点F对四边形ABCD的可视度为45°.∵∠DHF=90°,DH=2,DF=DA=4,∴sin∠DFH=,∴∠DFH=30°,∴FH=DF•cos30°=4×=2,∴F(2+2,4),∴a=2+2;同理,如图4,以点A为圆心、AD长为半径作⊙A,交直线y=4于点F,点F在直线AB左侧,此时,F(,4),∴a=.综上所述,a=2+2或a=.10.(1)证明:∵AE∥DC,AE=DC,∴四边形ADCE是平行四边形,∵AC=BC,CD为△ABC的角平分线,∴CD⊥AB,∴∠ADC=90°,∴平行四边形ADCE为矩形;(2)解:∵AC=BC,CD为△ABC的角平分线,∴BD=AD=AB=5,CD⊥AB,∴∠BDC=90°,∴AC===13,由(1)得:四边形ADCE为矩形,∴DE=AC=13.11.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵EF=DA,∴EF=BC,EF∥BC,∴四边形BCEF是平行四边形,又∵CE⊥AD,∴∠CEF=90°,∴平行四边形BCEF是矩形;(2)解:∵四边形ABCD是平行四边形,∴CD=AB=3,∵CF=4,DF=5,∴CD2+CF2=DF2,∴△CDF是直角三角形,∠DCF=90°,∴△CDF的面积=DF×CE=CF×CD,∴CE===,由(1)得:EF=BC,四边形BCEF是矩形,∴∠FBC=90°,BF=CE=,∴BC===,∴EF=.12.解:(1)∵点Q1(0,8),Q2(﹣4,2),Q3(8,4),点A(6,8),∴OQ1==8,OQ==,2OQ===,3OA==10,AQ==6,1AQ===,2AQ===,3∴OQ12+AQ12=OA2,OQ32+AQ32=OA2,OQ22+AQ22≠OA2,∴∠OQ1A=90°,∠OQ3A=90°,∴Q1和Q3是点A的直角点;故答案为:Q1和Q3;(2)如图所示,连接OB,OC,取BO的中点M,OC的中点N,分别以M,N为圆心,OB,OC为直径作圆,由图可知,Q1,Q2为两个临界点,则=x M﹣Q2M=﹣﹣=﹣4,同理,=2+2,∴﹣4≤n≤2+2;(3)如图2,⊙M、⊙N分别与x轴交于B′(﹣3,0),C′(4,0),∴,解得:﹣3≤t≤3,∵D(t,0),E(t+1,0),∴DE=1,由(2)可知,Q为BC的“直角点”,Q的横坐标n的取值范围为﹣4≤n≤2+2,∴,解得:﹣3≤t≤3,综上所述,﹣3≤t≤3.13.解:(1)∵AC平分∠BAD,AB∥CD.∴∠DAC=∠BAC,∠DCA=∠BAC.∴∠DAC=∠DCA.∴AD=DC.又∵AB∥CD,AB=AD.∴AB∥CD且AB=CD∴四边形ABCD是平行四边形.∵AB=AD.∴四边形ABCD是菱形.(2)连接BD,交AC于点O,如图:∵菱形ABCD的边长为13,对角线AC=24.∴CD=13,AO=CO=12.∵点E、F分别是边CD、BC的中点.∴EF∥BD(中位线).∵AC、BD是菱形的对角线.∴AC⊥BD,OB=OD.又∵AB∥CD,EF∥BD.∴DE∥BG,BD∥EG.∴四边形BDEG是平行四边形.∴BD=EG.在△COD中.∵OC⊥OD,CD=13,CO=12.∴.∴EG=BD=10.14.解(1)设CD交x轴于M,连接AC,过B作BN⊥AC,如图:∵A(﹣2,6),B(﹣2,﹣2),C(6,﹣2),D(6,6).∴O到CD的距离CM=6,AB=8,BC=8,AC=8,∴根据“闭距离”定义得:d(点O,CD)=6,∵S△ABC=AB•BC=AC•BN,∴B到AC的距离BN==4,∴d(点B,AC)=4,故答案为:6,4;(2)作直线x=4,取E(4,8)、F(4,4)、G(4,0)、H(4,﹣4),如图:在直线x=4上,E(4,8)、F(4,4)到AD距离为2,线段EF上的点到AD距离都小于2,同理G(4,0)、H(4,﹣4)到BC的距离为2,线段GH上的点到BC的距离都小于2,∴记线段BC,AD组成图形G已知点T(4,m),若d(点T,G)≤2,则4≤m≤8或﹣4≤m≤0;(3)取G(﹣5,0)、H(﹣4,0)、M(4,0)、N(8,0),如图:∵E(t,0),F(t+1,0),∴线段EF在x轴上,F在E右侧1个单位,①EF在AB左侧时,∵H到AB距离为2,∴F与H重合,此时EF上的点F到AB的距离最小为2,故d(EF,四边形ABCD)=2,∴t+1=﹣4,可得t=﹣5,②EF在正方形ABCD内时,当EF在线段OM上,则EF的点到BC的距离都为2,故d(EF,四边形ABCD)=2,此时,∴0≤t≤3,③EF在AB右侧时,E与N重合,此时EF上的点E到AB的距离最小为2,故d(EF,四边形ABCD)=2,∴t=8,综上所述,d(EF,四边形ABCD)=2,t=﹣5或0≤t≤3或t=8.。
2024年上海市16区中考二模数学分类汇编 专题12 解答题23题(几何证明题15题)(练习版)

专题12解答题23题(几何证明题15题)(16区二模新题速递)(原卷版)学校:___________姓名:___________班级:___________考号:___________一、解答题1.(2024·上海奉贤·二模)如图,在四边形ABCD 中,AB DC ∥,B ADC ∠=∠,点E 、F 分别在边AB 、BC 上,且ADE CDF ∠=∠.(1)求证:CF CB AE AB ⋅=⋅;(2)连接AC 、EF ,如果EF AC ∥,求证:四边形ABCD 是菱形.2.(2024·上海嘉定·二模)如图,在梯形ABCD 中,AD BC ∥,AB DC =,点P 在四边形ABCD 内部,PB PC =,连接PA 、PD .(1)求证:APD △是等腰三角形;(2)已知点Q 在AB 上,连接PQ ,如果AP CD ∥,AQ AP =,求证:四边形AQPD 是平行四边形.3.(2024·上海长宁·二模)已知:在梯形ABCD 中,AD BC BD AD ⊥∥,,点E 在边AD 上(点E 不与点A 、D 重合),点F 在边CD 上,且ABD EBF C ∠=∠=∠.(1)求证:AB BE BD BF=;(2)连接EF ,与BD 交于点G ,如果BG EG =,求证:四边形BEDF 为等腰梯形.4.(2024·上海浦东新·二模)已知:如图,在菱形ABCD 中,点E 是边DC 上的任意一点(不与点D 、C 重合),AE 交对角线BD 于F ,过点E 作EG BC ∥交BD 于点G .(1)求证:2=⋅DF FG BF ;(2)当2⋅=⋅BD DF AD DE 时,求证:AE DC ⊥.5.(23-24九年级下·上海宝山·期中)如图,在O 中,直径AB 垂直于弦CD ,垂足为点E ,连接AC 、DO ,延长DO 交AC 于点F .(1)求证:2AF OF DF =⋅;(2)如果82CD BE ==,,求OF 的长.6.(2024·上海虹口·二模)如图,在Rt ABC △中,90C ∠=︒,延长CB 至点D ,使得DB CB =,过点A 、D 分别作AE BC ∥,DE BA ∥,AE 与DE 相交于点E ,连接BE .(1)求证:BE CD ⊥;(2)连接AD 交BE 于点F ,连接CE 交AD 于点G .如果FBA ADB ∠=∠,求证:23AG AB =.7.(2024·上海静安·二模)已知:如图,直线EF 经过矩形ABCD 顶点D ,分别过顶点A 、C 作EF 的垂线,垂足分别为点E 和点F ,且DE DF =,连接AC .(1)求证:2AD AE AC =⋅;(2)连接BE 和BF ,求证:BE BF =.8.(2024·上海金山·二模)如图,已知:D 是ABC 的边BC 上一点,点E 在ABC 外部,且BAE CAD ∠=∠,ACD ADC ADE ∠=∠=∠,DE 交AB 于点F .(1)求证:AB AE =;(2)如果AD AF =,求证:2EF BF AB =⋅.9.(2024·上海黄浦·二模)如图,M 、N 分别是平行四边形ABCD 边AD 、BC 的中点,对角线BD 交AN 、CM 分别于点P 、Q .(1)求证:13PQ BD =;(2)当四边形ANCM 是正方形时,试从内角大小和邻边的数量关系的角度探究平行四边形ABCD 的形状特征.10.(2024·上海青浦·二模)已知:如图,在四边形ABCD 中,AD BC ∥,点E 是对角线AC 上一点,EA ED =,且DAB DEC DCB ∠=∠=∠.(1)求证:四边形ABCD 是菱形;(2)延长DE 分别交线段AB CB 、的延长线于点F G 、,如果GB BC =,求证:22AD EF GD =⋅.11.(2024·上海普陀·二模)已知:如图,四边形ABCD 中,AB CD ∥,点E 在边AD 上,CE 与BA 的延长线交于点F ,FA AE AB ED=.(1)求证:四边形ABCD 为平行四边形;(2)联结FD ,分别延长FD 、BC 交于点G ,如果2FC FD FG =⋅,求证:AD CG BF CD ⋅=⋅.12.(2024·上海徐汇·二模)如图,在菱形ABCD 中,点E 、G 、H 、F 分别在边AB 、BC 、CD 、DA 上,AE AF =,CG CH =,CG AE ≠.(1)求证:EF GH ∥;(2)分别连接EG 、FH ,求证:四边形EGHF 是等腰梯形.13.(2024·上海松江·二模)如图,已知AB 是1O 与2O 的公共弦,12O O 与AB 交于点C ,12O O 的延长线与2O 交于点P ,连接PA 并延长,交1O 于点D .(1)连接12,O A O A 、如果AB AD AP ==.求证:12O A O A ⊥;(2)如果123PO PO =,求证:PA AD =.14.(23-24九年级下·上海崇明·期中)如图,已知在四边形ABCD 中,AB CD ∥,对角线AC 平分DAB ∠,点O 是AC 上一点,以OA 为半径的O 过B D 、两点.(1)求证:四边形ABCD 是菱形;(2)设O 与AC 交于点E ,连接DE 并延长,交AB 的延长线于点F ,若2AB AC EC =⋅,求证:AE EF =.15.(2024·上海闵行·二模)沪教版九年级第二学期的教材给出了正多边形的定义.......:各边相等、各角也相等的多边形叫做正多边形.同时还提到了一种用直尺和圆规作圆的内接正六边形和圆的内接正五边形的方法,但课本上并未证明.我们现开展下列探究活动.活动一:如图1,展示了一种用尺规作O 的内接正六边形的方法.①在O 上任取一点A ,以A 为圆心、AO 为半径作弧,在O 上截得一点B ;②以B 为圆心,AO 为半径作弧,在O 上截得一点C ;再如此从点C 逐次截得点D 、E 、F ;③顺次连接AB 、BC 、CD 、DE 、EF 、FA .(1)根据正多边形的定义.........,我们只需要证明__________,________(请用符号语言表示,不需要说明理由),就可证明六边形ABCDEF是正六边形.的内接正五边形的方法.活动二:如图2,展示了一种用尺规作O的两条互相垂直的直径PQ和AF;①作O②取半径OP的中点M;再以M为圆心、MA为半径作弧,和半径OQ相交于点N;相截,得交点B.③以点A为圆心,以AN的长为半径作弧,与O如此连续截取3次,依次得分点C、D、E,顺次连接AB、BC、CD、DE、EA,那么五边形ABCDE是正五边形.的半径为2,求边AB的长,并证明五边形ABCDE是正五边形.(2)已知O(参考数据:sin22.5︒cos22.5︒=sin36=︒cos36︒=sin72=︒)。
2020年浙江中考数学一模二模——三角形、四边形

2020年浙江中考数学一模二模——三角形、四边形一.选择题(共20小题)1.(2020•富阳区一模)如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB运动到点B停止,过点E作EF⊥PE交射线BC于点F,联结PF,设M是线段PF的中点,则点P运动的整个过程中,线段DM长的最小值为()A.B.C.3D.2.(2020•拱墅区一模)如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为()A.B.C.D.3.(2020•余杭区一模)如图,在正方形ABCD中,E是BC边上的点,AE的垂直平分线交CD,AB与点F,G.若BG=2BE,则DF:CF的值为()A.B.C.D.4.(2020•上城区一模)如图,在菱形ABCD中,∠ABC=60°,点P在对角线BD上(不与点B,D重合),PE∥BC,PF∥DC.设AB=m,AP=a,PF=b,PE=c,下列表述正确的是()A.c2+b2=a2B.a+b=c+mC.c2+b2﹣bc=a2D.a+b+c≥2m5.(2020•西湖区一模)在菱形ABCD中,∠ADC=120°,点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,连结EG.若AE=1,AB=4,则EG=()A.2B.2C.3D.6.(2020•上城区一模)如图,在▱ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是()A.B.2 C.D.37.(2020•拱墅区模拟)如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是()A.α=βB.α=γC.α+β+2γ=90°D.2α+γ=90°8.(2020•萧山区一模)如图,▱ABCD的周长为22cm,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为()A.8cm B.9cm C.10cm D.11cm9.(2020•上城区校级三模)如图,已知在△ABC中,AB=AC,∠ABC=70°,点P是∠BAC的平分线AP 和∠CBD的平分线BP的交点,射线CP交AB的延长线于点D,则∠D的度数为()A.15°B.17.5°C.20°D.22.5°10.(2020•上城区二模)若等腰三角形的一个外角度数为100°,则该等腰三角形顶角的度数为()A.80°B.100°C.20°或100°D.20°或80°11.(2020•上城区二模)如图,四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D 作DE⊥BC,垂足为E,若BD=4,BC=6,则AB=()A.B.2 C.2D.312.(2020•江干区模拟)如图,直l1∥l2,点A、B固定在直线l2上,点C是直线11上一动点,若点E、F 分别为CA、CB中点,对于下列各值:①线段EF的长;②△CEF的周长;③△CEF的面积;④∠ECF 的度数,其中不随点C的移动而改变的是()A.①②B.①③C.②④D.③④13.(2020•上城区一模)如图,在△ABC中,AB=AC,BE⊥AC,D是AB的中点,且DE=BE,则∠C的度数是()A.65°B.70°C.75°D.80°14.(2020•江干区模拟)已知⊙O的半径为3,A为圆内一定点,AO=1,P为圆上一动点,以AP为边作等腰△APQ,AP=PQ,∠APQ=120°,则OQ的最大值为()A.1+3B.1+2C.3+D.315.(2020•拱墅区一模)如图,在△ABC中,∠C=90°,D是BC边上一点,∠ADC=3∠BAD,BD=4,DC=3.则AB的值为()A.5+3B.2+2C.7D.16.(2020•上城区模拟)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是()A.S1=2 B.S2=3 C.S3=6 D.S1+S3=817.(2020•拱墅区一模)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=36°,∠C=44°,则∠EAC的度数为()A.18°B.28°C.36°D.38°18.(2020•拱墅区四模)如图,△ABC的两条中线BE、CD交于点O,则下列结论不正确的是()A.=B.=C.S△DOE:S△BOC=1:2 D.△ADE∽△ABC19.(2020•西湖区模拟)如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC 的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为()A.50°B.60°C.70°D.80°20.(2020•西湖区校级模拟)在△ABC中,2(∠A+∠B)=3∠C,则∠C的补角等于()A.36°B.72°C.108°D.144°二.填空题(共10小题)21.(2020•上城区二模)已知平行四边形ABCD的对角线AC,BD相交于直角坐标系的原点O,点A,B 的坐标分别为(﹣1,3),(1,2),则点C的坐标为.22.(2020•西湖区校级模拟)如图,在菱形ABCD中,边AB=5,E,F分别在BC和AD上,若DF=1,BE=3,且此时BF=DE,则BF的长为23.(2020•江干区一模)如图,已知正方形ABCD的边长为2,延长BC至E点,使CE=BC,连结AE交CD于点F,连结BF并延长与线段DE交于点G,则FG的长是.24.(2020•上城区校级三模)若周长为12的等腰三角形的腰长为x,则x的取值范围是.25.(2020•萧山区模拟)如图,△P AB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD 的面积之和为10,则△P AB与△PCD的面积之差为.26.(2020•富阳区一模)如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=.27.(2020•萧山区模拟)如图,在△ABC中,AB=AC,点D,点E分别是BC,AC上一点,且DE⊥AD,若∠BAD=55°,∠B=50°,则∠DEC的度数为.28.(2020•余杭区一模)如图,在△ABC中,∠ACB=90°,CD是△ABC的中线,若∠DCB=40°,则∠A的度数为°.29.(2020•萧山区一模)如图,CE、BF分别是△ABC的高线,连接EF,EF=6,BC=10,D、G分别是EF、BC的中点,则DG的长为.30.(2020•上城区模拟)等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是.三.解答题(共20小题)31.(2020•西湖区校级模拟)如图,点E、G是矩形ABCD边AB上的两点,F是边DC上的点,AB=8且CG=EF.(1)如图1,若BE=2,DF=1,此时点E在点G右侧,求EG的长;(2)在(1)的条件下,连结CE,若CE平分∠BCG,求BC的长;(3)如图2,若EB=1,DF=k,tan∠EFC=k,且满足AB≤DF+EB≤AB,求tan∠AFD的范围.32.(2020•江干区一模)如图,点O是矩形ABCD对角线的交点,过点O的两条互相垂直的直线分别交矩形于点E、F、G、H,点E在线段AB上运动,AD=4,AB=2,设AE=x,AH=y.(1)四边形EFGH是什么特殊四边形?请说明理由;(2)写出y关于x的关系式,并写出y的取值范围;(3)求四边形EFGH的面积及其最值.33.(2020•下城区一模)如图,在正方形ABCD中,点E在DC边上(不与点C,点D重合),点G在AB 的延长线上,连结EG,交边BC于点F,且EG=AG,连结AE,AF,设∠AED=α,∠GFB=β.(1)求α,β之间等量关系;(2)若△ADE≌△ABF,AB=2,求BG的长.34.(2020•下城区一模)如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.(1)求证:四边形BPEQ为平行四边形;(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.35.(2020•下城区模拟)如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.(1)判断DG与BE的位置关系,并说明理由:(2)若正方形ABCD的边长为2,正方形AEFG的边长为2,求BE的长.36.(2020•萧山区模拟)如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE.连接DE并延长交射线AP于点F,连接BF.(1)若∠BAP=α,直接写出∠ADF的大小(用含α的式子表示);(2)求证:BF⊥DF;(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.37.(2020•萧山区一模)如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若AB=2,求△OEC的面积.38.(2020•西湖区模拟)如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC 于点F.(1)求证:四边形BEDF为菱形;(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.39.(2020•杭州模拟)如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.(1)求DE:CG的值;(2)设AE=x,S△BEG=y.①求y关于x的函数表达式及x的取值范围.②当图中点E、M关于对角线BD成轴对称时,求y的值.40.(2020•江干区一模)已知:如图,在△ABC中,AB>AC,∠B=45°,点D是BC边上一点,且AD =AC,过点C作CF⊥AD于点E,与AB交于点F.(1)若∠CAD=α,求:①∠BCA的大小;②∠BCF的大小;(用含α的式子表示)(2)求证:AC=FC.41.(2020•上城区二模)如图,在边长为6的菱形ABCD中,对角线AC,BD交于点O,点P是△ADO的重心.(1)当菱形ABCD是正方形时,则P A=,PD=,PO=.(2)线段P A,PD,PO中,是否存在长度保持不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.(3)求线段PD,DO满足的等量关系,并说明理由.42.(2020•上城区一模)如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E.(1)在图中找出与∠EPC始终相等的角,并说明理由;(2)若△PDE为正三角形时,求BD+CE的值;(3)当DE∥BC时,请用BP表示BD,并求出BD的最大值.43.(2020•西湖区校级模拟)如图,AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于E,DF⊥EF 于F,BE=DF.(1)求证:Rt△BCE≌Rt△DCF;(2)若BE=2,EC=4,求四边形ABCD的面积.44.(2020•江干区模拟)已知:如图,在Rt△ABC和Rt△ABD中,∠ACB=90°,∠ABD=90°,AB=BD,BC=4,(点A、D分别在直线BC的上下两侧),点G是Rt△ABD的重心,射线BG交边AD于点E,射线BC交边AD于点F.(1)求证:∠CAF=∠CBE;(2)当点F在边BC上,AC=1时,求BF的长;(3)若△BGC是以BG为腰的等腰三角形,试求AC的长.45.(2020•余杭区一模)如图,在△ABC中,AB<AC<BC,以点A为圆心,线段AB的长为半径画弧,与BC边交于点D,连接AD过点D作DE⊥AD,交AC于点E.(1)若∠B=50°,∠C=28°,求∠AED度数;(2)若点F是BD的中点,连接AF,求证:∠BAF=∠EDC.46.(2020•拱墅区一模)在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.47.(2020•拱墅区模拟)如图,在Rt△ABC中,∠CAB=90°,AF为BC边上的中线,DE经过△ABC的重心G,且∠ADE=∠C.(1)问:线段AG是△ADE的高线还是中线?请说明理由.(2)若AB=6,AC=8,求AD的长.48.(2020•拱墅区模拟)已知两直角边和为12的Rt△ABC,且∠C=90°.(1)当Rt△ABC为等腰直角三角形,求斜边的长.(2)若过锐角顶点的直线把Rt△ABC分成两个等腰三角形,求Rt△ABC的两条直角边长.(3)设Rt△ABC的斜边长为x,面积为y,求y关于x的函数表达式,并写出自变量的取值范围.49.(2020•江干区模拟)在等腰三角形ABC中,底边BC为y,腰长AB长为x,若三角形ABC的周长为12,(1)求y关于x的函数表达式;(2)当腰长比底边的2倍多1时,求x的值.50.(2020•上城区模拟)如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).(1)若点P在AC上,且满足P A=PB时,求出此时t的值;(2)若点P恰好在∠BAC的角平分线上,求t的值;(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.2020年浙江中考数学一模二模考试试题分类(杭州专版)(5)——三角形、四边形参考答案与试题解析一.选择题(共20小题)1.(2020•富阳区一模)如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB运动到点B停止,过点E作EF⊥PE交射线BC于点F,联结PF,设M是线段PF的中点,则点P运动的整个过程中,线段DM长的最小值为()A.B.C.3D.【答案】A【解答】解:连接BE、EM、BM,作BE的垂直平分线GH分别与DA的延长线、BC的延长线交于点G、H,过D作DN⊥GH于点N,连接EH,过H作HK⊥AD,与AD的延长线交于点K,∵∠ABC=∠PEF=90°,M是PF的中点,∴BM=EM,∴无论P点运动到什么位置时,M点始终在BE的垂直平分线上,∴M点在GH上,当M与N点重合时,DM=DN的值最小,设EH=x,∵GH是BE的垂直平分线,∴BH=EH=x,∴∠EHG=∠BHG,∵GD∥BH,∴∠EHG=∠BHG=∠G,∴EG=EH=x,∵∠ABH=∠BAK=∠K=90°,∴四边形ABHK为矩形,∴AK=BH=x,AB=KH=6,∵AD=8,点E在边AD上,且AE:ED=1:3,∴AE=2,ED=6,∴EK=AK﹣AE=x﹣2,∵EH2﹣EK2=KH2,∴x2﹣(x﹣2)2=62,解得,x=10,∴GE=x=10,GD=EG+DE=x+6=10+6=16,∵OE∥DN,∴△GEO∽△GDN,∴,∴DN=EO,∵,∴EO=BE=,∴,即线段DM长的最小值为,故选:A.2.(2020•拱墅区一模)如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为()A.B.C.D.【答案】A【解答】解:作GM⊥CD交CD于点M,连接GE,设BE=a,则BG=2a,则GE=a,∵四边形ABCD是正方形∴∠B=∠C=90°,∵GM⊥CD,∴∠CMG=90°,∴四边形BCMG是矩形,∴BG=CM=2a,GM=BC,∵FG垂直AE,并且平分AE,∴AG=GE=,∴AB=2a+,∵∠FGM+∠AGF=90°,∠AGF+∠GAE=90°,∴∠F AM=∠EAB,在△ABE和△GMF中,∴△ABE≌△GMF(ASA),∴BE=MF,∴MF=a,∵DF=CD﹣CM﹣MF,AB=CD=2a+,CF=CM+MF=2a+a=3a,∴DF=2a+﹣2a﹣a=﹣a,∴DF:CF=(﹣a):(3a)=,故选:A.3.(2020•余杭区一模)如图,在正方形ABCD中,E是BC边上的点,AE的垂直平分线交CD,AB与点F,G.若BG=2BE,则DF:CF的值为()A.B.C.D.【答案】A【解答】解:连接GE,延长GF交AD的延长线于H点,∵BG=2BE,设BE=x,BG=2x,则:;又∵FG垂直平分AE,则AG=GE=,故正方形的边长;在Rt△ABE中,;∵∠H=∠BAE,,∴,则,∴,∵,∴,∴,故;故选:A.4.(2020•上城区一模)如图,在菱形ABCD中,∠ABC=60°,点P在对角线BD上(不与点B,D重合),PE∥BC,PF∥DC.设AB=m,AP=a,PF=b,PE=c,下列表述正确的是()A.c2+b2=a2B.a+b=c+mC.c2+b2﹣bc=a2D.a+b+c≥2m【答案】C【解答】解:如图,连接PC,过点P作PH⊥BC,交BC延长线于点H,∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP,且PD=PD,∴△APD≌△CPD(SAS),∴AP=CP=a,∵PE∥BC,PF∥DC,∴四边形PECF是平行四边形,∴PE=CF=c,∵PF∥DC∥AB,∴∠PFC=∠ABC=60°,∵PH⊥BC,∴∠FPH=30°,∴FH=,PH=FH=b,∴CH=﹣c,∵PC2=CH2+PH2,∴a2=(﹣c)2+(b)2,∴c2+b2﹣bc=a2,故选:C.5.(2020•西湖区一模)在菱形ABCD中,∠ADC=120°,点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,连结EG.若AE=1,AB=4,则EG=()A.2B.2C.3D.【答案】B【解答】解:连接FG,∵菱形ABCD,∠ADC=120°,∴∠A=60°,∠ABC=120°,∵点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,∴AE=AF,BF=BG,∴△AEF是等边三角形,∴∠AFE=60°,∵BF=BG,∴△BFG是等腰三角形,∴∠GFB=,∴∠EFG=180°﹣60°﹣30°=90°,∵BF=4﹣1=3,∴FG=2,∴EG=,故选:B.6.(2020•上城区一模)如图,在▱ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是()A.B.2 C.D.3【答案】B【解答】解:∵四边形ABCD为平行四边形,∴AB∥CD,CD=AB=6,∴∠ABE=∠CEB,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠CBE=∠CEB,∴CE=BC=4,∴DE=CD﹣CE=6﹣4=2.故选:B.7.(2020•拱墅区模拟)如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是()A.α=βB.α=γC.α+β+2γ=90°D.2α+γ=90°【答案】B【解答】解:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,∵∠ADE=α,∠EDF=β,∠FDC=γ,∴α+β+γ=90°,∵∠AED+α=90°,∠AED=α+β,∴2α+β=90°,∴α+β+γ=2α+β,∴α=γ,故选:B.8.(2020•萧山区一模)如图,▱ABCD的周长为22cm,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为()A.8cm B.9cm C.10cm D.11cm【答案】D【解答】解:∵四边形ABCD是平行四边形∴AB=CD,AD=BC,AO=CO,又∵EO⊥AC,∴AE=CE,∵▱ABCD的周长为22cm,∴2(AD+CD)=22cm∴AD+CD=11cm∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm故选:D.9.(2020•上城区校级三模)如图,已知在△ABC中,AB=AC,∠ABC=70°,点P是∠BAC的平分线AP 和∠CBD的平分线BP的交点,射线CP交AB的延长线于点D,则∠D的度数为()A.15°B.17.5°C.20°D.22.5°【答案】见试题解答内容【解答】解:如图,AP与BC相交于点O,∵AB=AC,∴∠ABC=∠ACB=70°,∴∠CAB=40°,∵点P是△ABC内角和外角角平分线的交点,∴∠APB=∠ACB=35°,∵AB=AC,AP是∠BAC的平分线,∴AP⊥BC,OB=OC,∴CP=BP,∴∠APC=∠APB=35°,∴∠BPC=70°,∵BP是△ABC的外角的平分线,∴∠PBD=∠CBD=55°,∴∠D=∠BPC﹣∠PBD=70°﹣55°=15°.故选:A.10.(2020•上城区二模)若等腰三角形的一个外角度数为100°,则该等腰三角形顶角的度数为()A.80°B.100°C.20°或100°D.20°或80°【答案】D【解答】解:当100°的角是顶角的外角时,顶角的度数为180°﹣100°=80°;当100°的角是底角的外角时,底角的度数为180°﹣100°=80°,所以顶角的度数为180°﹣2×80°=20°;故顶角的度数为80°或20°.故选:D.11.(2020•上城区二模)如图,四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D 作DE⊥BC,垂足为E,若BD=4,BC=6,则AB=()A.B.2 C.2D.3【答案】B【解答】解:如图,过点D作DH⊥AB,交BA的延长线于H,∵∠ABC=∠ADC=90°,DH⊥AB,DE⊥BC,∴四边形BEDH是矩形,∵BD平分∠ABC,∴∠DBE=45°,∴∠DBE=∠BDE=45°,∴BE=DE,∴四边形BEDH是正方形,∴BD=BE,DE=HD,∠HDE=∠ADC=90°,∴HD=DE=HB=BE=4,∠HDA=∠CDE,又∵∠H=∠DEC=90°,∴△ADH≌△CDE(ASA),∴CE=AH=BC﹣BE=6﹣4=2,∴AB=BH﹣AH=4﹣2=2,故选:B.12.(2020•江干区模拟)如图,直l1∥l2,点A、B固定在直线l2上,点C是直线11上一动点,若点E、F 分别为CA、CB中点,对于下列各值:①线段EF的长;②△CEF的周长;③△CEF的面积;④∠ECF 的度数,其中不随点C的移动而改变的是()A.①②B.①③C.②④D.③④【答案】B【解答】解:∵A、B为定点,∴AB长为定值,∵点E,F分别为CA,CB的中点,∴EF是△CAB的中位线,∴EF=AB为定值,故①正确;∵点A,B为直线l2上定点,直线l1∥l2,∴C到l2的距离为定值,∵EF是△CAB的中位线,∴EF∥l1∥l2,∴C到EF的距离为定值,又∵EF为定值,∴△CEF的面积为定值,故③正确;当C点移动时,CA+CB的长发生变化,则CE+CF的长发生变化,∴△CEF的周长发生变化,故②错误;当C点移动时,∠ACB发生变化,则∠ECF发生变化,故④错误;故选:B.13.(2020•上城区一模)如图,在△ABC中,AB=AC,BE⊥AC,D是AB的中点,且DE=BE,则∠C的度数是()A.65°B.70°C.75°D.80°【答案】C【解答】解:∵BE⊥AC,∴∠AEB=90°,∵D是AB的中点,∴DE=AB=BD=AD,∵DE=BE,∴DE=BE=BD,∴△BDE为等边三角形,∴∠ABE=60°,∴∠A=90°﹣60°=30°,∵AB=AC,∴∠C=×(180°﹣30°)=75°,故选:C.14.(2020•江干区模拟)已知⊙O的半径为3,A为圆内一定点,AO=1,P为圆上一动点,以AP为边作等腰△APQ,AP=PQ,∠APQ=120°,则OQ的最大值为()A.1+3B.1+2C.3+D.3【答案】A【解答】解:如图,以点P为顶点作等腰三角形OPM,OP=PM,∠OPM=120,∵∠APQ=120°,∴∠OPM=∠APQ,∵∠OP A+∠APM=∠MPQ+∠APM,∴∠OP A=∠MPQ,∵AP=PQ,OM=PM,∴△AOP≌△QMP(SAS),∴MQ=OA=1,∵∠POM=30°,∴OM=2×OP•cos30°=3,∴OQ≤OM+MQ=3+1,当且仅当M在OQ上时,取等号,则OQ的最大值为1+3.故选:A.15.(2020•拱墅区一模)如图,在△ABC中,∠C=90°,D是BC边上一点,∠ADC=3∠BAD,BD=4,DC=3.则AB的值为()A.5+3B.2+2C.7D.【答案】B【解答】解:如图,延长CB到E,使得BE=BA.设BE=AB=a.∵BE=BA,∴∠E=∠BAE,∵∠ADC=∠ABD+∠BAD=2∠E+∠BAD=3∠BAD,∴∠BAD=∠E,∵∠ADB=∠EDA,∴△ADB∽△EDA,∴,∴AD2=4(4+a)=16+4a,∵AC2=AD2﹣CD2=AB2﹣BC2,∴16+4a﹣32=a2﹣72,解得a=2+2或2﹣2(舍弃).∴AB=2+2,故选:B.16.(2020•上城区模拟)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是()A.S1=2 B.S2=3 C.S3=6 D.S1+S3=8【答案】D【解答】解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,∴CG=NG,CF=DG=NF,∴S1=(CG+DG)2,=CG2+DG2+2CG•DG,=GF2+2CG•DG,S2=GF2,S3=(NG﹣NF)2=NG2+NF2﹣2NG•NF,∴S1+S2+S3=GF2+2CG•DG+GF2+NG2+NF2﹣2NG•NF=3GF2=12,∴GF2=4,∴S2=4,∵S1+S2+S3=12,∴S1+S3=8,故选:D.17.(2020•拱墅区一模)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=36°,∠C=44°,则∠EAC的度数为()A.18°B.28°C.36°D.38°【答案】B【解答】解:∵∠ABC=36°,∠C=44°,∴∠BAC=180°﹣36°﹣44°=100°,∵BD平分∠ABC,∴∠ABD=∠ABC=18°,∵AE⊥BD,∴∠BF A=90°,∴∠BAF=90°﹣18°=72°,∴∠EAC=∠BAC﹣∠BAF=100°﹣72°=28°,故选:B.18.(2020•拱墅区四模)如图,△ABC的两条中线BE、CD交于点O,则下列结论不正确的是()A.=B.=C.S△DOE:S△BOC=1:2 D.△ADE∽△ABC【答案】C【解答】解:∵BE和CD是△ABC的中线,∴DE是△ABC的中位线,∴DE=BC,DE∥BC,∴=,故A选项正确;∵DE∥BC,∴=,故B选项正确;∵DE∥BC,∴△DOE∽△COB,∴=()2=()2=,故C选项错误;∵DE∥BC,∴△ADE∽△ABC,故D选项正确;故选:C.19.(2020•西湖区模拟)如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于AC 的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为()A.50°B.60°C.70°D.80°【答案】C【解答】解:在△ABC中,∵∠B=50°,∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=100°,由作图可知MN为AC的中垂线,∴DA=DC,∴∠DAC=∠C=30°,∴∠BAD=∠BAC﹣∠DAC=70°,故选:C.20.(2020•西湖区校级模拟)在△ABC中,2(∠A+∠B)=3∠C,则∠C的补角等于()A.36°B.72°C.108°D.144°【答案】C【解答】解:∵2(∠A+∠B)=3∠C,∠A+∠B=180°﹣∠C,∴2(180°﹣∠C)=3∠C,∴∠C=72°,∴∠C的补角等于108°,故选:C.二.填空题(共10小题)21.(2020•上城区二模)已知平行四边形ABCD的对角线AC,BD相交于直角坐标系的原点O,点A,B 的坐标分别为(﹣1,3),(1,2),则点C的坐标为(1,﹣3).【答案】见试题解答内容【解答】解:由题意知:点A与点C、点B与点D关于原点对称,∵点A的坐标分别为(﹣1,3),∴点C的坐标分别是(1,﹣3),故答案为:(1,﹣3).22.(2020•西湖区校级模拟)如图,在菱形ABCD中,边AB=5,E,F分别在BC和AD上,若DF=1,BE=3,且此时BF=DE,则BF的长为【答案】见试题解答内容【解答】解:∵在菱形ABCD中,边AB=5,DF=1,BE=3,∴CE=2,AF=4,如图,在AF上截取AG=CE=2,过点B作BH⊥FG于点H,则FG=AF﹣AG=2,∵菱形ABCD中,∠A=∠C,AB=DC,∴在△BAG和△DCE中,∴△BAG≌△DCE(SAS).∴BG=DE,∵BF=DE,∴BG=BF.过点B作BH⊥FG于点H,则FH=HG=FG=1,∴AH=AG+GH=2+1=3,∵AB=5,∴在Rt△ABH中,由勾股定理得:BH=4,∴在Rt△BHF中,由勾股定理得:BF===.故答案为:.23.(2020•江干区一模)如图,已知正方形ABCD的边长为2,延长BC至E点,使CE=BC,连结AE交CD于点F,连结BF并延长与线段DE交于点G,则FG的长是.【答案】见试题解答内容【解答】解:如图,过点C作CP∥BG,交DE于点P.∵BC=CE=2,∴CP是△BEG的中位线,∴P为EG的中点.又∵AD=CE=2,AD∥CE,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴CF=DF,又CP∥FG,∴FG是△DCP的中位线,∴G为DP的中点.∵CD=CE=2,∴DE=2,因此DG=GP=PE=DE=.连接BD,易知∠BDC=∠EDC=45°,所以∠BDE=90°.又∵BD=2,∴BG=.∴FG=,故答案为:.24.(2020•上城区校级三模)若周长为12的等腰三角形的腰长为x,则x的取值范围是3<x<6.【答案】3<x<6.【解答】解:∵腰长为x,且等腰三角形的周长为12∴底边为12﹣2x,并且12﹣2x>0,得x<6.又∵x+x>12﹣2x,解得x>3.∴x的取值范围是3<x<6.故答案为:3<x<6.25.(2020•萧山区模拟)如图,△P AB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD 的面积之和为10,则△P AB与△PCD的面积之差为10.【答案】见试题解答内容【解答】解:∵△P AB与△PCD均为等腰直角三角形,∴PC=PD,∠APB=∠CPD=90°,AP=BP,∴△APC≌△BPD(SAS),∴S△APC=S△BPD,∵S△APB﹣S△PCD=S△APC+S△ABC﹣(S△BPD﹣S△BCD),∴S△APB﹣S△PCD=S△BCD+S△ABC=10,故答案为:10.26.(2020•富阳区一模)如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=230°.【答案】见试题解答内容【解答】解:∵∠A=50°,∴△ABC中,∠B+∠C=130°,又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,∴∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=360°﹣130°=230°,故答案为:230°.27.(2020•萧山区模拟)如图,在△ABC中,AB=AC,点D,点E分别是BC,AC上一点,且DE⊥AD,若∠BAD=55°,∠B=50°,则∠DEC的度数为115°.【答案】见试题解答内容【解答】解:∵AB=AC,∴∠B=∠C,∵∠B=50°,∴∠C=50°,∴∠BAC=180°﹣50°﹣50°=80°,∵∠BAD=55°,∴∠DAE=25°,∵DE⊥AD,∴∠ADE=90°,∴∠DEC=∠DAE+∠ADE=115°.故答案为:115°.28.(2020•余杭区一模)如图,在△ABC中,∠ACB=90°,CD是△ABC的中线,若∠DCB=40°,则∠A的度数为50°.【答案】见试题解答内容【解答】解:∵在△ABC中,∠ACB=90°,CD是△ABC的中线,∵BD=CD=AB,∴∠B=∠DCB=40°,∴∠A=90°﹣∠B=50°,故答案为:50.29.(2020•萧山区一模)如图,CE、BF分别是△ABC的高线,连接EF,EF=6,BC=10,D、G分别是EF、BC的中点,则DG的长为4.【答案】见试题解答内容【解答】解:连接EG、FG,∵CE,BF分别是△ABC的高线,∴∠BEC=90°,∠BFC=90°,∵G是BC的中点,∴EG=FG=BC=5,∵D是EF的中点,∴ED=EF=3,GD⊥EF,由勾股定理得,DG==4,故答案为:4.30.(2020•上城区模拟)等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是62°或118°.【答案】见试题解答内容【解答】解:分两种情况:①当高在三角形内部时(如图1),∵∠ABD=28°,∴顶角∠A=90°﹣28°=62°;②当高在三角形外部时(如图2),∵∠ABD=28°,∴顶角∠CAB=90°+28°=118°.故答案为:62°或118°.三.解答题(共20小题)31.(2020•西湖区校级模拟)如图,点E、G是矩形ABCD边AB上的两点,F是边DC上的点,AB=8且CG=EF.(1)如图1,若BE=2,DF=1,此时点E在点G右侧,求EG的长;(2)在(1)的条件下,连结CE,若CE平分∠BCG,求BC的长;(3)如图2,若EB=1,DF=k,tan∠EFC=k,且满足AB≤DF+EB≤AB,求tan∠AFD的范围.【答案】(1)3;(2)2;(3).【解答】解:(1)过F作FH⊥AB于点H,如图1,则AH=DF=1,FH=BC,∵EF=CG,∴Rt△EFH≌Rt△GCB(HL),∴EH=GB,∴HG=BE=2,∴EG=AB﹣AH﹣HG﹣BE=8﹣1﹣2﹣2=3;(2)过E作EM⊥CG于M,如图1,则EM=EB=2,∴GM=∵CE=CE,∴Rt△CEM≌Rt△CEB(HL),∴CM=CB,设BC=x,则CG=,∵CM+GM=CG,∴x+=,解得,x=2,∴BC=2;(3)如图2,过点E作EN⊥CD于点N,则EN=AD,BE=CN=1,∴FN=CD﹣DF﹣CN=8﹣k﹣1=7﹣k,∵tan∠EFC=k,∴,即,∴EN=k(7﹣k),∴tan∠AFD=,∵AB≤DF+EB≤AB,∴,解得,,∴,∴.32.(2020•江干区一模)如图,点O是矩形ABCD对角线的交点,过点O的两条互相垂直的直线分别交矩形于点E、F、G、H,点E在线段AB上运动,AD=4,AB=2,设AE=x,AH=y.(1)四边形EFGH是什么特殊四边形?请说明理由;(2)写出y关于x的关系式,并写出y的取值范围;(3)求四边形EFGH的面积及其最值.【答案】见试题解答内容【解答】解:(1)四边形EHGF是菱形,理由如下:∵四边形ABCD是矩形,∴AO=CO,BO=DO,AB∥CD,AD∥BC,∴∠BAO=∠DCO,∠AEO=∠CGO,∴△AEO≌△CGO(AAS),∴EO=GO,AE=CG,同理:可证:△DHO≌△BFO(AAS),∴HO=FO,BF=DH,∴四边形EHGF是平行四边形,∵EG⊥HF,∴四边形EHGF是菱形;(2)∵四边形EHGF是菱形,∴EH=EF,∵EH2=AE2+AH2,EF2=BE2+BF2,∴AE2+AH2=BE2+BF2,∴x2+y2=(2﹣x)2+(4﹣y)2,∴y=﹣+,∵0≤x≤2,∴≤y≤;(3)∵四边形EFGH的面积=S矩形ABCD﹣S△AEH﹣S△DHG﹣S△GFC﹣S△BEF,∴四边形EFGH的面积=8﹣2×[xy+(2﹣x)(4﹣y)]=2y+4x﹣2xy=x2﹣2x+5=(x﹣1)2+4,∴当x=1时,四边形EFGH的面积的最小值为4,当x=0或2时,四边形EFGH的面积的最大值为5.33.(2020•下城区一模)如图,在正方形ABCD中,点E在DC边上(不与点C,点D重合),点G在AB 的延长线上,连结EG,交边BC于点F,且EG=AG,连结AE,AF,设∠AED=α,∠GFB=β.(1)求α,β之间等量关系;(2)若△ADE≌△ABF,AB=2,求BG的长.【答案】见试题解答内容【解答】解:(1)∵四边形ABCD是正方形,∴DC∥AB,∠CBG=∠ABC=90°,∴∠AED=∠GAE,∵EG=AG,∴∠GAE=∠GEA,∴∠AED=∠AEG=α,∴∠G=180°﹣2α,∵∠BFG+∠G=90°,∴180°﹣2α+β=90°,∴2α﹣β=90°;(2)如图,连接AF,∵四边形ABCD是正方形,∴AB=BC=CD=AD=2,∠C=∠ABC=∠CBG=90°,设BF=x,∵△ADE≌△ABF,∴DE=BF,∴CE=CF=2﹣x,∴EF=2x,∠CFE=∠BFG=45°,∴BG=BF=x,∴FG==x,∵AG=EG,∴2+x=2x+x,解得,x=2﹣2,∴.34.(2020•下城区一模)如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.(1)求证:四边形BPEQ为平行四边形;(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.【答案】见试题解答内容【解答】证明:(1)∵AC∥DF,AB=EF,BC=DE,∴四边形ABFE和四边形BCED是平行四边形,∴AE=BF,AE∥BF,BD∥CE,∴四边形BPEQ为平行四边形;(2)由(1)得:四边形ABFE、四边形BCED和四边形BPEQ为平行四边形,∴AE=BF=3,BD=CE=6,∵DP=2BP,∴QE=BP=BD=2,∵AC∥DF,∴△APB∽△EPD,∴==,∴EP=AE=2,∴BP=EP,∴四边形BPEQ为菱形.35.(2020•下城区模拟)如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.(1)判断DG与BE的位置关系,并说明理由:(2)若正方形ABCD的边长为2,正方形AEFG的边长为2,求BE的长.【答案】见试题解答内容【解答】解:(1)DG⊥BE,理由如下:∵四边形ABCD,四边形AEFG是正方形,∴AB=AD,∠DAB=∠GAE,AE=AG,∠ADB=∠ABD=45°,∴∠DAG=∠BAE,在△DAG和△BAE中∴△DAG≌△BAE(SAS).∴DG=BE,∠ADG=∠ABE=45°,∴∠ABD+∠ABE=90°,即∠GBE=90°.∴DG⊥BE;(2)连接GE,∵正方形ABCD的边长为2,正方形AEFG的边长为2,∴BD=2,GE=4,设BE=x,则BG=x﹣2,在Rt△BGE中,利用勾股定理可得x2+(x﹣2)2=42,∴x=+∴BE的长为+.36.(2020•萧山区模拟)如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE.连接DE并延长交射线AP于点F,连接BF.(1)若∠BAP=α,直接写出∠ADF的大小(用含α的式子表示);(2)求证:BF⊥DF;(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.【答案】见试题解答内容【解答】(1)解:由轴对称的性质得:∠EAP=∠BAP=α,AE=AB,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠DAE=90°﹣2α,AD=AE,∴∠ADF=∠AED=(180°﹣∠DAE)=(90°+2α)=45°+α;(2)证明:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵点E与点B关于直线AP对称,∴∠AEF=∠ABF,AE=AB.∴AE=AD.∴∠ADE=∠AED.∵∠AED+∠AEF=180°,∴在四边形ABFD中,∠ADE+∠ABF=180°,∴∠BFD+∠BAD=180°,∴∠BFD=90°∴BF⊥DF;(3)解:线段AF,BF,CF之间的数量关系为AF=BF+CF,理由如下:过点B作BM⊥BF交AF于点M,如图所示:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABM=∠CBF,∵点E与点B关于直线AP对称,∠BFD=90°,∴∠MFB=∠MFE=45°,∴△BMF是等腰直角三角形,∴BM=BF,FM=BF,在△AMB和△CFB中,,∴△AMB≌△CFB(SAS),∴AM=CF,∵AF=FM+AM,∴AF=BF+CF.37.(2020•萧山区一模)如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若AB=2,求△OEC的面积.【答案】见试题解答内容【解答】(1)证明:∵AD∥BC,∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,∵∠ABC=∠ADC,∴∠BAD=∠BCD,∴四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴四边形ABCD是矩形.(2)解:作OF⊥BC于F,如图所示.∵四边形ABCD是矩形,∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,∴AO=BO=CO=DO,∴BF=FC,∴OF=CD=1,∵DE平分∠ADC,∠ADC=90°,∴∠EDC=45°,在Rt△EDC中,EC=CD=2,∴△OEC的面积=•EC•OF=1.38.(2020•西湖区模拟)如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC 于点F.(1)求证:四边形BEDF为菱形;(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.【答案】见试题解答内容【解答】证明:(1)∵DE∥BC,DF∥AB,∴四边形BFDE是平行四边形,∵BD是△ABC的角平分线,∴∠EBD=∠DBF,∵DE∥BC,∴∠EDB=∠DBF,∴∠EBD=∠EDB,∴BE=ED,∴平行四边形BFDE是菱形;(2)连接EF,交BD于O,∵∠BAC=90°,∠C=30°,∴∠ABC=60°,∵BD平分∠ABC,∴∠DBC=30°,∴BD=DC=12,∵DF∥AB,∴∠FDC=∠A=90°,∴DF=,在Rt△DOF中,OF=,∴菱形BFDE的面积=.39.(2020•杭州模拟)如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.(1)求DE:CG的值;(2)设AE=x,S△BEG=y.①求y关于x的函数表达式及x的取值范围.②当图中点E、M关于对角线BD成轴对称时,求y的值.【答案】见试题解答内容【解答】解:(1)∵四边形ABCD是正方形,∴∠BDE=∠BCG=∠CBD=45°,BD=BC,∵∠EBM=45°,∴∠DBE=∠CBG,∴△BDE∽△BCG,∴DE:CG=BD:BC=:1;(2)①∵四边形ABCD是正方形,且△BDE∽△BCG,∴BE:BG=BD:BC=BD:AB=:1,∴△BEG∽△BAD,∴△BEG为等腰直角三角形,∴y=S△BEG=x2+9(0<x<6);②若E、M关于对角线BD成轴对称,连接EM,交BD于点H,∴BD垂直平分EM,BE平分∠ABD,∴AE=HE=DH,DE=HE,∴6﹣x=x,即x=6﹣6,则y=×(6﹣6)2+9=36﹣18.40.(2020•江干区一模)已知:如图,在△ABC中,AB>AC,∠B=45°,点D是BC边上一点,且AD =AC,过点C作CF⊥AD于点E,与AB交于点F.(1)若∠CAD=α,求:①∠BCA的大小;②∠BCF的大小;(用含α的式子表示)(2)求证:AC=FC.【答案】(1)①90°﹣;②α;(2)见解析.【解答】(1)解:①∵AD=AC,∠CAD=α,∴∠BCA=(180°﹣α)=90°﹣,②过点A作AG⊥BC于点G,如图所示:∴∠DAG+∠ADG=90°,∴∠CAG=∠DAG=∠CAD=α,∵CF⊥AD于点E,∴∠DCE+∠ADG=90°,∴∠DCE=∠DAG=∠CAD=α,即∠BCF=α;(2)证明:∵∠B=45°,AG⊥BC,∴∠BAG=45°,∵∠BAC=45°+∠CAG,∠AFC=45°+∠DCE,∠DCE=∠DAG,∠CAG=∠DAG,∴∠BAC=∠AFC,∴AC=FC.41.(2020•上城区二模)如图,在边长为6的菱形ABCD中,对角线AC,BD交于点O,点P是△ADO的重心.(1)当菱形ABCD是正方形时,则P A=,PD=,PO=2.(2)线段P A,PD,PO中,是否存在长度保持不变的线段?若存在,请求出该线段的长度;若不存在,请说明理由.(3)求线段PD,DO满足的等量关系,并说明理由.【答案】见试题解答内容【解答】解:(1)如图1中,连接P A,PD,PO,延长OP交AD于T.∵四边形ABCD是正方形,∴△AOD是等腰直角三角形,∵P是△AOD的重心,∴OT是△AOD的中线,∴OT=AD=3.AT=DT=3,∵OP=OT=2,∴PT=1,∴P A=PD===.故答案为,,2.(2)如图2中,结论:OP的长度不变.理由:延长OP交AD于E.∵四边形ABCD是菱形,∴AC⊥BD,∵P是△AOD的重心,∴OE=AD=3,∴OP=OE=2.(3)结论:3DP2﹣OD2=12.理由:延长DP交AO于F.∵P是△AOD的重心,∴PF=PD,∵∠DOF=90°,∴DF2=OD2+OF2,∴(DP)2=OD2+OF2,∵AD2=OD2+AO2,∴62=OD2+4OF2,∴3DP2﹣OD2=12.42.(2020•上城区一模)如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E.(1)在图中找出与∠EPC始终相等的角,并说明理由;(2)若△PDE为正三角形时,求BD+CE的值;(3)当DE∥BC时,请用BP表示BD,并求出BD的最大值.【答案】见试题解答内容【解答】解:(1)∠BDP=∠EPC,理由如下:∵△ABC为等边三角形,∴∠B=60°,∵∠DPE=60°,∴∠DPE=∠B,∵∠DPC是△BDP的外角,∴∠DPE+∠EPC=∠B+∠BDP,∴∠EPC=∠BDP;(2)∵△PDE为正三角形,∴PD=PE,在△BDP和△CPE中,,∴△BDP≌△CPE(AAS),∴BD=CP,BP=CE,∴BD+CE=CP+BP=BC=8;(3)∵DE∥BC,△ABC为等边三角形,∴△ADE为等边三角形,∴AD=AE,∴BD=CE,∵∠B=∠C,∠EPC=∠BDP,∴△BDP∽△CPE,∴=,即=,整理得,BD=,﹣BP2+8BP=﹣(BP﹣4)2+16,∴BD的最大值为4.43.(2020•西湖区校级模拟)如图,AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于E,DF⊥EF 于F,BE=DF.(1)求证:Rt△BCE≌Rt△DCF;(2)若BE=2,EC=4,求四边形ABCD的面积.。
2011各区县二模(四边形、圆)
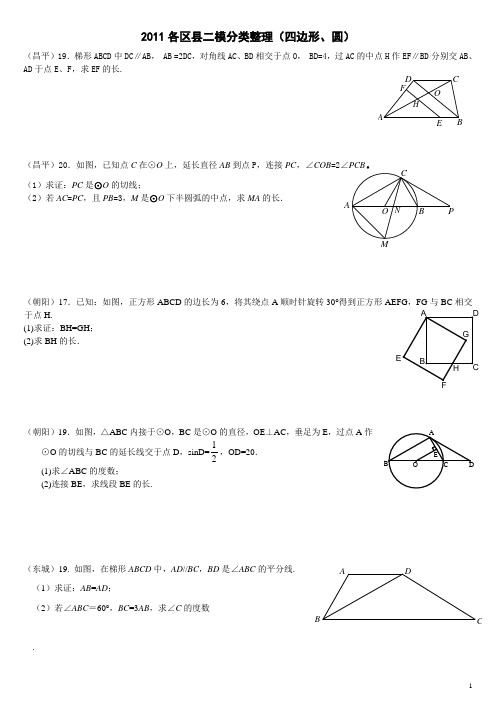
2011各区县二模分类整理(四边形、圆)(昌平)19.梯形ABCD 中DC ∥AB , AB =2DC ,对角线AC 、BD 相交于点O , BD=4,过AC 的中点H 作EF ∥BD 分别交AB 、AD 于点E 、F ,求EF 的长.(昌平)20.如图,已知点C 在⊙O 上,延长直径AB 到点P ,连接PC ,∠COB =2∠PCB . (1)求证:PC 是⊙O 的切线;(2)若AC =PC ,且PB =3,M 是⊙O 下半圆弧的中点,求MA 的长.(朝阳)17.已知:如图,正方形ABCD 的边长为6,将其绕点A 顺时针旋转30°得到正方形AEFG ,FG 与BC 相交于点H.(1)求证:BH=GH ; (2)求BH 的长.(朝阳)19.如图,△ABC 内接于⊙O ,BC 是⊙O 的直径,OE ⊥AC ,垂足为E ,过点A 作⊙O 的切线与BC 的延长线交于点D ,sinD=21,OD=20.(1)求∠ABC 的度数; (2)连接BE ,求线段BE 的长.(东城)19. 如图,在梯形ABCD 中,AD //BC ,BD 是∠ABC 的平分线. (1)求证:AB =AD ;(2)若∠ABC =60°,BC =3AB ,求∠C 的度数 .ABC D EFO HAB CPO MN HEGFBD CA EBCA ODA BCDO D C B A E O ABC D (东城)20. 如图,四边形ABCD 是平行四边形,以AB 为直径的⊙O 经过点D ,E 是⊙O 上一点,且∠AED =45︒. (1) 试判断CD 与⊙O 的位置关系,并证明你的结论; (2) 若⊙O 的半径为3,sin ∠ADE =65,求AE 的值.(房山)19.(本小题满分5分)在△ABC 中,AB=AC ,∠BAC=120°,过点C 作CD ∥AB ,且CD=2AB ,联结BD ,BD=2.求△ABC 的面积.(房山)20.(本小题满分5分)已知:如图,在R t ABC △中,90C ∠= ,点O 在A B 上,以O 为圆心,O A 长为半径的圆与A C A B ,分别交于点D E ,,且C B D A ∠=∠. (1)判断直线B D 与O 的位置关系,并证明你的结论;(2)若2B C =,B D =52,求ADAO的值.(丰台)19. 已知:如图,在梯形ABCD 中,AD ∥BC ,BD =CD ,BD ⊥CD ,AD =2,BC =6.求sin ∠ABC 的值.(丰台)20. 已知:如图,在Rt △ABC 中,∠C =90°,点E 在斜边AB 上,以AE 为直径的⊙O 与BC 边相切于点D ,联结AD.(1)求证:AD 是∠BAC 的平分线; (2)若AC = 3,tan B =34,求⊙O 的半径.DCBA EDO ABC(海淀)19.如图,梯形ABCD 中,AD //BC ,BC =5,AD =3,对角线AC ⊥BD ,且∠DBC =30°,求梯形ABCD 的高.(海淀)20.已知AB 是O ⊙的直径,C 是O ⊙上一点(不与A 、B 重合),过点C 作O ⊙的切线CD ,过A 作CD 的垂线,垂足是点M .(1)如图1,若//C D AB ,求证:AM 是O ⊙的切线; (2)如图2,若AB =6,AM =4,求AC 的长.(怀柔)20.如图,四边形ABCD 是正方形,△ECF 是等腰直角三角形,其中CE=CF ,G 是CD 与EF 的交点. (1)求证:△BCF ≌△DCE.(2)若BC=5,CF=3,∠BFC=900,求DG :GC 的值.(怀柔)19. 如图,已知AB 是⊙O 的直径,AD 是弦,∠DAB =22.5º,延长AB 到点C ,使得∠ACD =45º. (1)求证:CD 是⊙O 的切线; (2)若AB =22,求BC 的长.(门头沟)19.如图,在梯形ABCD 中,AD //BC ,BD ⊥CD ,∠C =60°,AD =3,BC =43,求AB 的长.B A DC OAB DMCOABDMC1图2图ABCDOEBDACEACBD(门头沟)20.已知:如图,O ⊙的直径AB 与弦CD 相交于点E , BCBD =,O ⊙的切线BF 与弦AD 的延长线相交于点F .(1)求证:C D B F ∥;(2)连结BC ,若O ⊙的半径为4,3cos 4B C D ∠=,求线段AD 、CD 的长.(平谷)19. 已知:如图,∠ACB =90°,AC =BC , AD = BE , ∠CAD =∠CBE . (1)判断△DCE 的形状,并说明你的理由;(2)当BD :CD =1:2时,∠BDC =135°时,求sin ∠BED 的值.(平谷)20.如图,在A B C △中,A B A C =,以AB 为直径的O ⊙交BC 于点D ,DE ⊥AC 于点E . (1)求证DE 是O ⊙的切线;(2)若∠BAC =120°,AB =2,求△DEC 的面积.(石景山)19.已知:等腰梯形ABCD 中,AD ∥BC ,2=AD ,6=BC ,将线段DC 绕点D 逆.时针旋转︒90,得到线段C D '.(1)求△C AD '的面积; (2)若52tan ='∠C DA ,求AB 的长.AD FBCO EDCBAABCDEFOH(石景山)20.已知:如图,ABC AF 为△的角平分线,以BC 为直径的圆与边AB 交于点,D E 点为弧BD 的中点,联结CE 交AB 于H ,AC AH =. (1)求证:AC 与⊙O 相切;(2)若6=AC ,10=AB ,求EC 的长.(顺义)19.已知:如图,矩形ABCD 中, 4A B =,7B C =,点P 是AD 边上一个动点,P E P C ⊥, P E 交A B 于点E ,对应点E 也随之在A B 上运动,连结E C . (1)若P E C ∆是等腰三角形,求P D 的长; (2)当30P E C ∠=︒时,求A P 的长.(顺义)20. 已知:如图,A B 是O ⊙的直径,10A B =, D C 切O ⊙于点C A D D C ⊥,,垂足为D ,A D 交O ⊙于点E . (1)求证:B C E C =; (2)若4cos 5B EC ∠=, 求D C 的长.(西城)20.如图,在梯形ABC D 中,AB ∥D C ,5AD BC ==,10AB =,4C D =,连结并延长BD 到E ,使D E B D=,作EF AB ⊥,交BA 的延长线于点F . (1)求tan ABD ∠的值; (2)求AF 的长.DCBOAEE P DCBA DCBABC=BE (西城)21.已知:如图,BD 为⊙O 的直径,点A 是劣弧BC 的中点,AD 交BC 于点E ,连结AB . (1)求证:2A BA E A D =⋅;(2)过点D 作⊙O 的切线,与BC 的延长线交于点F ,若AE =2,ED =4,求EF 的长.(延庆)19.如图,在梯形ABCD 中,AB//CD,2=AB ,4=AD ,=C tan 34, 90=∠=∠DAB ADC ,P 是腰BC 上一个动点(不含点C 、B ),作A P PQ ⊥交CD 于点Q (图1) (1)求BC 的长与梯形ABCD 的面积; (2)当DQ PQ =时,求BP 的长;(图2)(延庆)20.如图,A B 为O ⊙的直径,劣弧 ,CE //BD ,连接A E 并延长交B D 于D .求证:(1)B D 是O ⊙的切线;(2)若O ⊙的半径为cm 2,cm AC 3=,求的长B D .(燕山)18.已知:如图,AB 是半圆的直径,AB=10,梯形ABCD 内接于半圆,CE ∥AD 交AB 于E ,BE=2, 求∠A 的余弦值.(燕山)21.已知:如图,AB 是⊙O 的直径,点C 在⊙O 上,△ABC 的外角平分线BD 交⊙O 于D ,DE 与⊙O相切,交CB 的延长线于E.⑴ 判断直线AC 和DE 是否平行,并说明理由;⑵ 若∠A=30°,BE=1cm ,分别求线段DE 和 BD ⌒ 的长(直接写出最后结果).OE DCBA 第20题图第19题图2QPD CBAQPD CBA第19题图1DE A O BC· ·D CEA EB。
中考数学备考一轮训练:四边形综合问题-试卷
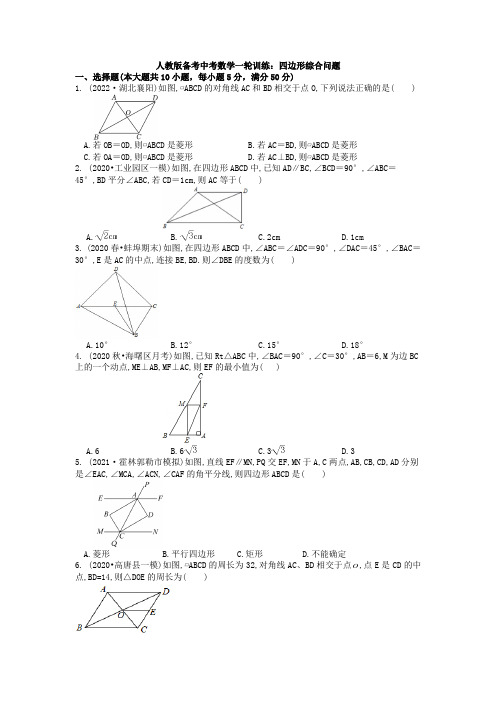
人教版备考中考数学一轮训练:四边形综合问题一、选择题(本大题共10小题,每小题5分,满分50分)1. (2022·湖北襄阳)如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )A.若OB=OD,则▱ABCD是菱形B.若AC=BD,则▱ABCD是菱形C.若OA=OD,则▱ABCD是菱形D.若AC⊥BD,则▱ABCD是菱形2. (2020•工业园区一模)如图,在四边形ABCD中,已知AD∥BC,∠BCD=90°,∠ABC=45°,BD平分∠ABC,若CD=1cm,则AC等于( )A. B. C.2cm D.1cm3. (2020春•蚌埠期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠DAC=45°,∠BAC=30°,E是AC的中点,连接BE,BD.则∠DBE的度数为( )A.10°B.12°C.15°D.18°4. (2020秋•海曙区月考)如图,已知Rt△ABC中,∠BAC=90°,∠C=30°,AB=6,M为边BC 上的一个动点,ME⊥AB,MF⊥AC,则EF的最小值为( )A.6B.6C.3D.35. (2021·霍林郭勒市模拟)如图,直线EF∥MN,PQ交EF,MN于A,C两点,AB,CB,CD,AD分别是∠EAC,∠MCA,∠ACN,∠CAF的角平分线,则四边形ABCD是( )A.菱形B.平行四边形C.矩形D.不能确定6. (2020•高唐县一模)如图,▱ABCD的周长为32,对角线AC、BD相交于点O,点E是CD的中点,BD=14,则△DOE的周长为( )A.14B.15C.18D.217. (2020·四川眉山中考)如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①∠EAB=∠GAD;②△AFC∽△AGD;③2AE2=AH•AC;④DG⊥AC其中正确的个数为( )A.1个B.2个C.3个D.4个8. (2020•绥化)如图,在Rt△ABC中,CD为斜边AB的中线,过点D作DE⊥AC于点E,延长DE 至点F,使EF=DE,连接AF,CF,点G在线段CF上,连接EG,且∠CDE+∠EGC=180°,FG=2,GC =3.下列结论:①DE BC;②四边形DBCF是平行四边形;③EF=EG;④BC=2.其中正确结论的个数是( )A.1个B.2个C.3个D.4个9. (2020•龙华区二模)如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DF=1,F 为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45o时,BF=1;④PC的最小值为-2.其中正确的有( )A.1个B.2个C.3个D.4个10. (2021•河北)如图1,▱ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )A.甲、乙、丙都是B.只有甲、乙才是C.只有甲、丙才是D.只有乙、丙才是二、填空题(本大共6小题,每小题5分,满分30分)11. (2020·四川中考真题)如图,在平行四边形ABCD中,BE平分∠ABC,CF⊥BE,连接AE,G是AB的中点,连接GF,若AE=4,则GF=_____.12. (2020•顺德区三模)如图,分别以△ABC的边AB、AC为一边向外做正方形ABDE和正方形ACFG,连结CE、BG交于点P,连结AP和EG.在不添加任何辅助线和字母的前提下,写出四个不同类型的结论__________.13. (2020•温州模拟)如图,四边形ABCD,CEFG均为菱形,A F∠=∠,连结BE,EG,EG//BC,EB ⊥BC,若sin∠EGD=,菱形ABCD的周长为12,则菱形CEFG的周长为__________.14. (2020·河南中考真题)如图,在边长为22的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD点G,H分别是EC,FD的中点,连接GH,则GH的长度为__________.15. (2020·江苏连云港·中考真题)如图,正六边形A1A2A3A4A5A6内部有一个正五形B1B2B3B4B5,且A3A4//B3B4,直线l经过B2、B3,则直线l与A1A2的夹角a=________︒.16. (2020•安徽)在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点Q处.折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,此时点C,D落在AP上的同一点R处.请完成下列探究:(1)∠PAQ的大小为°;(2)当四边形APCD是平行四边形时,的值为.三、解答题(本大题共5道小题,每小题6-12分)17. (6分)(2022北京东直门中学)如图,在平行四边形ABCD中,BC=BD,BE平分∠CBD交CD 于O,交AD延长线于E,连接CE.(1)求证:四边形BCED是菱形;(2)若OD=2,1tan2AEB∠=,求△ABE的面积.18. (6分)(2020春•海陵区)如图,O为∠BAC内一点,E、F、G、H分别为AB,AC,OC,OB的中点.(1)求证:四边形EFGH为平行四边形;(2)当AB=AC,AO平分∠BAC时,求证:四边形EFGH为矩形.19. (6分)(2020春•中山市校级月考)一张矩形纸ABCD,将点B翻折到对角线AC上的点M处,折痕CE交AB于点E.将点D翻折到对角线AC上的点H处,折痕AF交DC于点F,折叠出四边形AECF.(1)求证:AF∥CE;(2)当∠BAC=度时,四边形AECF是菱形?说明理由.20. (10分)(2022·河北唐山)问题提出(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为 ;问题探究(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.问题解决(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交AB于点E,又测得DE=8m.请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)21. (12分)(2021•交城县二模)综合与实践问题背景在综合实践课上,同学们以“图形的平移与旋转”为主题开展数学活动,如图(1),先将一张等边三角形纸片ABC对折后剪开,得到两个互相重合的△ABD和△EFD,点E与点A重合,点B 与点F重合,然后将△EFD绕点D顺时针旋转,使点F落在边AB上,如图(2),连接EC.操作发现(1)判断四边形BFEC的形状,并说明理由;实践探究(2)聪聪提出疑问:若等边三角形的边长为8,将图(2)中的△EFD沿射线BC的方向平移a个单位长度,得到△E′F′D′,连接BF′,CE′,若四边形BF′E′C为菱形,如图(3),则a的值为多少?请你帮聪聪解决这个问题,求出a的值;(3)如果将(2)中聪聪所提问题的平移方向改为:沿射线CB的方向平移a个单位长度,其余条件都不变,则是否还存在四边形BF′E′C为菱形?若存在,直接写出平移距离a的值,若不存在,请说明理由;(4)老师提出问题:请参照聪聪的思路,若等边三角形的边长为8,将图(2)中的△EFD在平面内进行一次平移,得到△E″F″D″,请在图(4)中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的一个结论,不必证明.。
初中数学专题《四边形中的最值问题》专项训练30道原卷

点,且 BM=CN,连 AM 和 BN,交于点 P.猜想 AM 与 BN 的位置关系,并证明你的结论. (2)如图②,已知正方形 ABCD 的边长为 4.点 M 和 N 分别从点 B、C 同时出发,以相同的速度沿 BC、CD 方向向终点 C 和 D 运动,连接 AM 和 BN,交于点 P.求△APB 周长的最大值.
BN 于点 E,连接 DE 交 AM 于点 F,连接 CF,若正方形的边长为 2,则线段 CF 的最小值是( )
A.2
B.1
C. 5−1
D. 5−2
7.(2022•龙华区二模)如图,已知四边形 ABCD 是边长为 4 的正方形,E 为 CD 上一点,且 DE=1,F 为
射线 BC 上一动点,过点 E 作 EG⊥AF 于点 P,交直线 AB 于点 G.则下列结论中:①AF=EG;②若∠BAF
25.(2022•宁德)如图,四边形 ABCD 是正方形,△ABE 是等边三角形,M 为对角线 BD(不含 B 点)上 任意一点,将 BM 绕点 B 逆时针旋转 60°得到 BN,连接 EN、AM、CM. (1)求证:△AMB≌△ENB; (2)①当 M 点在何处时,AM+CM 的值最小; ②当 M 点在何处时,AM+BM+CM 的值最小,并说明理由; (3)当 AM+BM+CM 的最小值为 3 +1时,求正方形的边长.
=∠PCF,则 PC=PE;③当∠CPF=45°时,BF=1;④PC 的最小值为 13−2.其中正确的有( )
A.1 个
B.2 个
C.3 个
2023年湖北省中考数学模拟题知识点分类汇编:四边形(附答案解析)

2023年湖北省中考数学模拟题知识点分类汇编:四边形一.选择题(共19小题)
1.(2022•武汉模拟)如图,在平行四边形ABCD中,∠BAD=45°,AD=4,CD=2,若用半径为r的圆形纸片完全覆盖平行四边形ABCD,则r的最小值是()
A .B.2C.2D .
2.(2022•南漳县模拟)如图,在菱形ABCD中,M,N分别为AB,AC的中点,若MN=2,则菱形ABCD的周长为()
A.8B.12C.16D.24 3.(2022•老河口市模拟)如图,四边形ABCD是矩形,E,F,G,H分别为各边的中点,则四边形EFGH一定是()
A.菱形B.矩形
C.正方形D.对角线相等的四边形
4.(2022•谷城县模拟)如图,已知点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到四边形EFGH,我们把四边形EFGH叫做四边形ABCD的“中点四边形”.若四边形ABCD是矩形,则矩形ABCD的“中点四边形”
一定是()
第1页(共50页)。
河北省各市各区2021年中考模拟数学试题汇编:四边形解答

河北省各市各区2021年中考模拟数学试题汇编:四边形解答1.(2021•长安区二模)如图,正方形ABCD和正方形BEFG有公共顶点B,且顶点A,G,F三点共线,顶点C,F,E三点共线,DM⊥AG于点M,AB=15,BE=9.(1)求证:△ABG≌△DAM;(2)连接DG,求DG的长;(3)直接写出△ABH与△CFH的面积差.2.(2021•竞秀区一模)如图,平行四边形ABCD中,AB=9,AD=13,tan A=,点P在射线AD上运动,连接PB,沿PB将△APB折叠,得△A'PB.(1)如图1,点P在线段AD上,当∠DPA′=20°时,∠APB=度;(2)如图2,当PA'⊥BC时,求线段PA的长度;(3)当点A′落在平行四边形ABCD的边所在的直线上时,求线段PA的长度;(4)直接写出:在点P沿射线AD运动过程中,DA′的最小值是多少?3.(2021•石家庄一模)如图,在边长为6的正方形ABCD中,点M为对角线BD上任意一点(可与B,D重合),连接AM,将线段AM绕点A逆时针旋转90°得到线段AN,连接MN,DN,设BM=x.(1)求证:△ABM≌△ADN;(2)当时,求MN的长;(3)嘉淇同学在完成(1)后有个想法:“△ABM与△MND也会存在全等的情况”,请判断嘉淇的想法是否正确,若正确,请直接写出△ABM与△MND全等时x的值;若不正确,请说明理由.4.(2021•新华区模拟)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.动点P从点A出发,以每秒3个单位长度的速度沿AC﹣CB﹣BA方向绕行△ABC一周,动直线l从AC开始,以每秒1个单位长度的速度向右平移,分别交AB、BC于D、E 两点.当点P运动到点A时,直线l也停止运动.(1)求点P到AB的最大距离;(2)当点P在AC上运动时,①求tan∠PDE的值;②把△PDE绕点E顺时针方向旋转,当点P的对应点P′落在ED上时,ED的对应线段ED′恰好与AB垂直,求此时t的值.(3)当点P关于直线DE的对称点为F时,四边形PEFD能否成为菱形?若能,直接写出t的值;若不能,请说明理由.5.(2021•裕华区模拟)如图,在矩形ABCD中,AB=8,BC=12,点E在AB上,AE=5,P是AD上一点,将矩形沿PE折叠,点A落在点A'处.连接AC,与PE相交于点F,设AP=x.(1)AC=;(2)若点A'在∠BAC的平分线上,求FC的长;(3)求点A',D距离的最小值,并求此时tan∠APE的值;(4)若点A'在△ABC的内部,直接写出x的取值范围.6.(2021•新华区模拟)已知:如图,▱ABCD中,E为DC的中点,连接AE并延长交BC的延长线于点F,连接AC、DF.(1)求证:AD=CF;(2)嘉琪说:“添加一个条件,能使四边形ACFD是矩形”,你是否同意嘉琪的观点?如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.7.(2021•邯郸模拟)如图1,图2中,正方形ABCD的边长为6,点P从点B出发沿边BC﹣CD以每秒2个单位长的速度向点D匀速运动,以BP为边作等边三角形BPQ,使点Q在正方形ABCD内或边上,当点Q恰好运动到AD边上时,点P停止运动.设运动时间为t秒(t≥0).(1)当t=2时,点Q到BC的距离=;(2)当点P在BC边上运动时,求CQ的最小值及此时t的值;(3)若点Q在AD边上时,如图2,求出t的值;(4)直接写出点Q运动路线的长.8.(2021•长安区二模)如图1,矩形ABCD中,AB=8,BC=16,对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O,连接BE,DF.(1)求BE的长;(2)如图2,动点M,N分别从B,D两点同时出发,分别沿B→E→A→B和D→C →F→D匀速运动,其中一点到达终点时另一点也随之停止运动.①若点M的运动速度为每秒5个单位长度,点N的运动速度为每秒4个单位长度,运动时间为t秒(t>0),则当t=1时,MN=;当t为何值时,以B,M,D,N四点为顶点的四边形是平行四边形?②若点M,N两点的运动路程分别为m,n(m,n≠0),当B,M,D,N四点为顶点的四边形是平行四边形,请直接写出m,n所满足的数量关系.9.(2021•石家庄模拟)在正方形ABCD中,点P是射线CB上一个动点,连接PA,PD,点M,N分别为BC,AP的中点,连接MN交PD于点Q.(1)当点P在线段CB的延长线上时,如图2.①依题意补全图2;②判断△QPM的形状并加以证明;(2)点P'与点P关于直线AB对称,且点P'在线段BC上.连接AP',若点Q恰好在直线AP'上,正方形ABCD的边长为2,请写出求此时BP长的思路.(可以不写出计算结果)10.(2021•承德二模)如图,在正方形ABCD中,E是AB边上任意一点(不与点A,B重合),BG⊥CE,垂足为点O,交AC于点F,交AD于点G,连接EF.(1)①BE与AG的数量关系是;②当△AGF为等腰三角形时,∠ABF=°;(2)当点E为AB的中点时,求证:∠AEF=∠CEB.11.(2021•石家庄一模)如图1,在▱ABCD中,AB<BC.把▱ABCD沿对角线AC所在的直线折叠,使点B落在点E处,CE交AD于点F,连接DE.(1)求证:△ADE≌△CED;(2)求证:△DEF为等腰三角形;(3)将图1中的△AEC沿射线CA方向平移得到△A′E′C′(如图2所示).若在▱ABCD中,AB=AC=2,BC=2,当BA′=BC时,直接写出△AEC平移的距离.12.(2021•新华区一模)如图,在等腰△ABC中,AB=BC,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△ADE,连接BE.(1)求证:BE=BC.(2)四边形ABED是什么形状的四边形?并说明理由.(3)直接写出:当α分别是多少度时,①BE⊥AC;②BE∥AC.13.(2021•邢台模拟)已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.(1)求证:△BAD≌△CAE;(2)若∠ABC=30°,求∠MEC的度数;(3)求证:四边形MBDE是平行四边形.14.(2021•唐山一模)如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A 按逆时针方向旋转α°.得到△ADE,连接BD,CE交于点F.(1)求证:△ABD≌△ACE;(2)用α表示∠ACE的度数;(3)若使四边形ABFE是菱形,求α的度数.15.(2021•唐山二模)实践操作如图1,将矩形纸ABCD沿对角线AC翻折,使B′落在矩形ABCD所在平面内,B′C和AD相交于E,连接B′D.解决问题(1)在图1中,①B′D和AC的位置关系为;②△AEC剪下后展开,得到的图形是;(2)若图1中的矩形变为平行四边形(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;拓展应用(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为.16.(2021•开平区一模)如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与点A,O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.(1)求证:PE=PB;(2)如图2,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由;(3)用等式表示线段PC,PA,CE之间的数量关系.参考答案1.【分析】(1)由四边形ABCD和四边形BEFG是正方形以及DM⊥AG证明△ABG ≌△DAM即可;(2)先在在Rt△ABG中求出AG=12,再由△ABG≌△DAM得DM=AG=12,AM =BG=9,故MG=AG﹣AM=3,再在Rt△DMG中求出DG即可;(3)先证明△ABG≌△CBE,由此得S△ABG=S△CBE,再由S△ABH﹣S△CHF=S△ABH+S﹣(S△CHF+S四边形HFEB)=S△ABG+S正方形GBFE﹣S△CBE=S正方形BGFE求出即四边形BHFE可.【解答】(1)证明:∵四边形ABCD和四边形BEFG是正方形,∴∠BAD=∠FGB=90°,AB=AD,∵DM⊥AG,∴∠DMA=∠AGB=90°,∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,∴∠ADM=∠GAB,∴△ABG≌△DAM(AAS);(2)解:在Rt△ABG中,AG==12,∵△ABG≌△DAM,∴DM=AG=12,AM=BG=9,∴MG=AG﹣AM=3,在Rt△DMG中,DG==3;(3)解:∵四边形ABCD和四边形BEFG是正方形,∴∠ABC=∠GBE=90°,AB=BC,∴∠ABG=∠CBE,∴△ABG≌△CBE(SAS),∴S△ABG=S△CBE,∵S△ABH﹣S△CHF=S△ABH+S四边形BHFE﹣(S△CHF+S四边形HFEB)=S△ABG+S正方形GBFE﹣S△CBE=S正方形BGFE=92=81,∴△ABH与△CFH的面积差为81.2.【分析】(1)分两种情形根据折叠的性质求解即可;(2)作BH⊥AD于H,由tan A=,设AH=5x,BH=12x,可得AB==13x=9,求出x即可解决问题;(3)分三种情形:①当点A′在AD上时,②当A′在BC上时,③当A′在AB的延长线上时,分别求解即可;(4)作DH⊥AB于H,连接BD,求出BD,BA′,根据三角形的三边关系即可解决问题.【解答】解:(1)当PA′在直线AD的右侧时,∠APB=∠A′PB=(180°﹣20°)=80°,当PA′在直线AD的左侧时,∠APB=∠A′PB=(180°+20°)=100°,故答案为:80或100;(2)如图,作BH⊥AD于H,∵四边形ABCD是平行四边形,∴AD∥BC,∵PA′⊥BC,∴PA′⊥AD,∴∠APA′=90°,∴∠APB=∠A′PB=45°,∵tan A=,∴设AH=5x,BH=12x∴AB==13x=9,∴x=,∴AH=,BH=,在Rt△BHP中,∠BPH=45°,∴BH=PH=,∴AP=AH+PH=;(3)①当点A′在AD上时,∵AB=A′B,PA=PA′,∴BP⊥AD,∵tan A=,∴AP=AB=;②当A′在BC上时,由折叠可知,AB=BA′,AP=PA′,又∵AD∥BC,∴∠APB=∠PBA′=∠ABP,∴AB=PA,∴四边形ABA′P为菱形,∴AP=9;③当A′在AB的延长线上时,∠ABP=∠ABA′=90°,∴AP=AB=.综上,线段PA的长度为或9或;(4)如图,作DH⊥AB于H,连接BD.∵AD=13,tan A==,∴DH=12,AH=5,BH=9﹣5=4,∴BD==4,∵DA′≤BD﹣BA′,∴DA′≤BD﹣A′B,∵A′B=AB=9,∴DA′的最小值是4﹣9.3.【分析】(1)由全等三角形的判定定理SAS证得结论;(2)由△ABM≌△AND得:,∠ADN=∠ABM=45°,推导出△MDN 是直角三角形,利用勾股定理求得MN的长度;(3)正确,抓住全等特征分析出AM⊥BD,得△ABM和△ADN是全等的等腰直角三角形,即可得出结论.【解答】(1)证明:在正方形ABCD中,AB=AD,由旋转的性质知:AM=AN,∵∠BAD=∠MAN=90°,∴∠BAM=∠DAN,在△ABM和△ADN中,,∴△ABM≌△ADN(SAS).解:(2)∵BD是正方形ABCD的对角线,且AB=6,∴,∠ADB=45°,∴,由△ABM≌△AND得:,∠ADN=∠ABM=45°,∴∠MDN=∠ADB+∠ADN=45°+45°=90°,在Rt△MDN中,.(3)正确;.理由如下:如图:当AM⊥BD,易得△ABM和△ADN是全等的等腰直角三角形,∴∠NDA=∠ABM=45°,AN=AM,∵正方形ABCD中,∠ADB=∠ABD=45°,∴∠NDM=90°,∵∠NAM=∠AMD=∠NDM=90°,∴四边形AMDN为矩形,又∵AN=AM,∴矩形AMDN为正方形,∴△NMD≌△DAN(SAS),∴△NMD≌△ABM(全等传递性),此时AM===3.当△ABM与△MND全等时x=3.4.【分析】(1)当点P与点C重合时,点P到AB的距离最大,由三角形面积求解即可;(2)①当点P在AC上运动时,设运动时间为ts,则有AP=3t,CE=t,由平行线的性质得∠PDE=∠APD,过点D作DG⊥AC于点G,则四边形CEDG是矩形,得DG =CE=t,PG=AP﹣AG=3t﹣AG,再由锐角三角函数定义求出PG=t,即可求解;②证出∠BED'=∠A,∠CEP=∠BED',再证△CEP∽△CAB,得,即可求解;(3)当PF也垂直平分DE时,四边形PEFD为菱形.证△DBE∽△ABC,得=,求出,再分情况讨论即可.【解答】解:(1)当点P与点C重合时,点P到AB的距离最大,设Rt△ABC斜边AB上的高h,∵∠ACB=90°,AC=3,BC=4,∴AB===5,∵△ABC的面积=AB•h=AC•BC,∴h===,即点P到AB的最大距离是;(2)①当点P在AC上运动时,设运动时间为ts,则有AP=3t,CE=t,∵直线l∥AC,∴∠PDE=∠APD,如图1,过点D作DG⊥AC于点G,则四边形CEDG是矩形,∴DG=CE=t,PG=AP﹣AG=3t﹣AG,∵tan A==,∴=,∴AG=t,∴PG=3t﹣t=t,∴,即;②∵ED'⊥AB,∴∠BED'+∠B=90°,∵∠A+∠B=90°,∴∠BED'=∠A,∵直线l∥AC,∴直线l⊥BC,∴∠CEP+∠PED=90°,∠P'ED'+∠BED'=90°,由旋转的性质,得:∠PED=∠P'ED',∴∠CEP=∠BED',∴∠CEP=∠A,又∵∠ECP=∠ACB,∴△CEP∽△CAB,∴,即,解得:;(3)四边形PEFD能成为菱形,理由如下:∵点F是点P关于直线DE的对称点,∴DE垂直平分PF,∴当PF也垂直平分DE时,四边形PEFD为菱形.∵直线l∥AC,∴△DBE∽△ABC,∴=,即,∴,①当点P在AC上时,连接PF,如图2所示:若PF垂直平分DE,则有DE=3﹣3t,∴(4﹣t)=3﹣3t,解得:;②当点P在BC上时,P、F、E三点都在x轴上,构不成四边形;③当点P在BA上时,若点P在直线l的右侧,连接PF,如图3所示:类比①可得:,解得:;若点P在直线l的左侧,P、E、F、D四点构不成凸四边形;综上所述,当t为或时,四边形PEFD为菱形.5.【分析】(1)利用勾股定理求解即可.(2)证明AE=AF=5,可得结论.(3)利用勾股定理求出DE,根据DA′≥DE﹣EA′,可得结论.(4)如图3﹣1中,当点A′落在AC上时,求出AP的长,如图3﹣2中,当点A′落在BC上时,求出AP,可得结论.【解答】解:(1)如图1中,∵四边形ABCD是矩形,∴∠B=90°,∵AB=8,BC=12,∴AC===4.故答案为:4.(2)如图1中,∵AA′平分∠BAC,∴∠EAA′=∠FAA′,由翻折可知,AA′⊥EF,∴∠EAA′+∠AEF=90°,∠AFE+∠FAA′=90°,∴∠AEF=∠AFE,∴AE=AF=5,∴CF=AC﹣AF=4﹣5.(3)如图2中,连接DE,DA′.在Rt△ADE中,∠EAD=90°,AE=5,AD=BC=12,∴DE===13,∵EA=EA′=5,∴DA′≥DE﹣EA′=8,∴DA′的最小值为8,此时E,A′,D共线,设PA=PA′=x,则有(12﹣x)2=x2+82,解得x=,∴tan∠APE===.(4)如图3﹣1中,当点A′落在AC上时,∵∠AEP+∠EAC=90′,∠ACB+∠EAC=90°,∴∠AEP=∠ACB,∴tan∠AEP=tan∠ACB,∴=,∴=,∴PA=.如图3﹣2中,当点A′落在BC上时,过点P作PH⊥BC于H,则PH=AB=8,PA =BH.在Rt△BEA′中,BE=3,EA′=EA=5,∴BA′===4,∵∠B=∠EA′P=∠PHA′=90°,∴∠BA′E+∠PA′H=90°,∠PA′H+∠A′PH=90°,∴∠BA′E=∠A′PH,∴△BA′E∽△HPA′,∴=,∴=,∴A′H=6,∴AP=BH=BA′+A′H=10.观察图像可知当<x<10时,点A'在△ABC的内部.6.【分析】(1)根据平行四边形的性质和全等三角形的判定和性质得出AD=CF即可;(2)根据矩形的判定解答即可.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠DAE=∠CFE,∠ADE=∠FCE,∵E为DC的中点,∴ED=EC.∴△ADE≌△FCE(AAS),∴AD=CF.(2)答:同意.当DC=AF时,四边形ACFD是矩形.理由如下:∵AD∥CF,AD=CF,∴四边形ACFD是平行四边形.∵DC=AF,∴四边形ACFD是矩形.7.【分析】(1)先求出BP=4,∠PBQ=60°,即可得出结论;(2)先判断出CQ⊥BQ时,CQ最小,再用含30°角的直角三角形的性质即可得出结论;(3)先判断出Rt△BAQ≌Rt△BCP(HL),再由勾股定理建立方程即可得出结论;(4)判断出点Q的运动路线长等于点P的路线长即可得出结论.【解答】解:(1)如图1,由运动知,BQ=2t=4,过点Q作QH⊥BC于H,∵△BPQ是等边三角形,∴BP=BQ=4,∠PBQ=60°,在Rt△BPH中,PH=BP•sin∠PBQ=4×=2,故答案为2;解:(2)点P在BC边上运动时,有∠QBC=60°,根据垂线段最短,当CQ⊥BQ时,CQ最小.如图,在直角三角形BCQ中,∠QBC=60°,∴∠BCQ=30°∴BQ=∴BP=BQ=3,∴t=∴CQ=BQ•tan∠QBC=;(3)若点Q在AD边上,则CP=2t﹣6,∵BA=BC,BQ=BP,∠A=∠C=90°,∴Rt△BAQ≌Rt△BCP(HL)∴AQ=CP=2t﹣6,∴DQ=DP=12﹣2t,∵BP=PQ,在Rt△PDQ和Rt△BCP中,由勾股定理可得,DQ2+DP2=QP2,BC2+CP2=BP2∴2(12﹣2t)2=62+(2t﹣6)2解得:(不合题意,舍去),∴;(4)如图,当点P在BC上从点B运动到点C时,点Q从点B运动到点Q,∵△PBQ是等边三角形,∴BQ=BC,∠QBC=60°当点P在CD上从点C运动到如图所示的点P时,点Q从如图所示的点Q运动到Q',∵△BPQ'是等边三角形,∴BP=BQ',∠PBQ'=60°=∠QBC,∴∠PBC=∠Q'BQ,∵BQ=BC,∴△BQQ'≌△BCP,∴QQ'=CP,∴点Q的运动路线长等于点P的运动路线长,由(3)知,t=9﹣3,∴点Q的运动路线长等于2(9﹣3)=8.【分析】(1)设BE=DE=x,则AE=16﹣x,依据勾股定理进行计算,即可得到BE 的长;(2)①根据MN是梯形BCDE的中位线,即可得到MN的长;依据以B,M,D,N 四点为顶点的四边形是平行四边形,分四种情况讨论,即可得出当t=秒时,以B,M,D,N四点为顶点的四边形是平行四边形;②分三种情况讨论,即可得出当B,M,D,N四点为顶点的四边形是平行四边形,m,n所满足的数量关系为m+n=24.【解答】解:(1)∵四边形ABCD是矩形,∴AD=BC=16,∵EF垂直平分BD,∴BE=DE,设BE=DE=x,则AE=16﹣x,在Rt△ABF中,由勾股定理得:82+(16﹣x)2=x2,解得x=10,∴BE=10.(2)①当t=1时,DN=4,BM=5,∴M,N分别是BE,DC的中点,∴MN是梯形BCDE的中位线,∴MN==(10+16)=13,故答案为:13;若以B,M,D,N四点为顶点的四边形是平行四边形,分四种情况讨论:第一种:当N在CD上,M在BE上时,以B,M,D,N四点为顶点的四边形不可能是平行四边形;第二种:如图2,当N在CF上,M在AE上时,以B,M,D,N四点为顶点的四边形可能是平行四边形;∵DM∥BN,∴当DM=BN时,四边形BMDN是平行四边形,∵BE+EM=5t,DE=BE,∴DM=DE+EM=5t,∵BC+CD=24,DC+CN=4t,∴BN=24﹣4t,当DM=BN时,5t=24﹣4t,解得t=,∴当t=秒时,四边形BMDN是平行四边形;第三种:当N在CF上,M在BA上时,以B,M,D,N四点为顶点的四边形不可能是平行四边形;第四种:当N在DF上,M在AB上时,以B,M,D,N四点为顶点的四边形不可能是平行四边形.综上所述,当t=秒时,以B,M,D,N四点为顶点的四边形是平行四边形;②如图3,当M在BE上,N在DF上时,BM=DN,即m=24﹣n,故m+n=24;如图4,当M在AE上,N在CF上时,DM=BN,即m=24﹣n,故m+n=24;如图5,当M在AB上,N在CD上时,BM=DN,即24﹣m=n,m+n=24;综上所述,当B,M,D,N四点为顶点的四边形是平行四边形,m,n所满足的数量关系为m+n=24.9.【分析】(1)①根据题意补充图形即可;②△QPM的形状是等腰三角形,延长BC至E,使CE=BP,连接AE,证明△DCP≌△ABE,得到∠DPC=∠E,再证明MN∥AE,得到∠NMP=∠E,通过等量代换得到∠DPC=∠NMP,根据等角对等边得到QM=QP,即可解答.(2)利用相似三角形的性质定理和判定定理、对称的性质,写出解题思路.【解答】解:(1)①如图2,②△QPM的形状是等腰三角形,如图3,延长BC至E,使CE=BP,连接AE,∵PB=CE,∴PB+BC=CE+BC,即CP=BE,∵四边形ABCD是正方形,∴AB=DC,∠ABC=∠DCB=90°,在△DCP和△ABE中,,∴△DCP≌△ABE(SAS),∴∠DPC=∠E,∵M为BC的中点,∴MB=MC,∴MB+BP=MC+CE,即MP=ME,∴M为PE的中点,∵N为AP的中点,∴MN∥AE,∴∠NMP=∠E,∴∠DPC=∠NMP,∴QM=QP,∴△QPM是等腰三角形.(2)求解思路如下:由题意画出图形,并延长BC至E,使CE=BP,连接AE,如图4.由②可得QM∥AE,可.由PP′∥AD,可证△P′PQ∽△ADQ,从而.可得.再由点P′与点P关于直线AB对称,得到BP′=BP=CE,设BP′=BP=CE=x,由AD=BC=2,可分别表示P′M,ME,P′P,可求BP的长.P′M=1﹣x,ME=1+x,P′P=2x,所以,解得:x=或(负值舍去).10.【分析】(1)①根据正方形的性质利用ASA判定△GAB≌△EBC,根据全等三角形的对应边相等可得到AG=BE;②根据等腰三角形的性质得到∠AGF=∠AFG,根据平行线的性质得到∠AGB=∠3,根据全等三角形的性质得到∠2=∠4,于是得到结论;(2)利用SAS判定△GAF≌△EAF,从而得到∠AGF=∠AEF,由△GAB≌△EBC 可得到∠AGF=∠CEB;所以∠AEF=∠CEB.【解答】解:(1)①BE=AG,理由:∵四边形ABCD是正方形,∴∠ABC=90°,∴∠1+∠3=90°,∵BG⊥CE,∠BOC=90°,∴∠2+∠3=90°,∴∠1=∠2,在△GAB和△EBC中,∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2,∴△GAB≌△EBC(ASA),∴BE=AG;②方法一:当△AGF为等腰三角形时,只有AG=AF这种情况存在,∴∠AGF=∠AFG,∵AD∥BC,∴∠AGB=∠3,∵∠AFG=∠CFO,∴△COF≌△COB(AAS),∴∠2=∠4,∵∠ACB=45°,∴∠2=22.5°,∴∠1=∠2=22.5°,即∠ABF=22.5°,方法二:当△AGF为等腰三角形时,只有AG=AF这种情况存在,∴∠AGF=∠AFG,∵四边形ABCD是正方形,∴∠GAF=45°=∠BAF,∴∠AFG=67.5°,∵∠AFG=∠ABF+∠BAF,∴∠ABF=∠AGF﹣∠BAF=67.5°﹣45°=22.5°,故答案为:BE=AG,22.5;(2)解:当点E位于线段AB中点时,∠AEF=∠CEB.理由如下:当点E位于线段AB中点时,AE=BE,由(1)知,∵AG=BE,∴AG=AE,∵四边形ABCD是正方形,∴∠GAF=∠EAF=45°,又∵AF=AF,∴△GAF≌△EAF(SAS),∴∠AGF=∠AEF,由(1)知,△GAB≌△EBC,∴∠AGF=∠CEB,∴∠AEF=∠CEB.11.【分析】(1)由平行四边形的性质可得AB=CD,BC=AD,由折叠的性质可得AE =AB=CD,BC=CE=AD,由“SSS”可知△ADE≌△CED;(2)由全等三角形的性质可得∠ADE=∠CED,可得DF=EF,可得结论;(3)过点A作AH⊥BC于H,过点B作BM⊥AC于M,由锐角三角函数可求∠ACB =30°,由等腰三角形的性质和直角三角形的性质可求A'M=MC=3,即可求解.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,BC=AD,∵把▱ABCD沿对角线AC所在的直线折叠,使点B落在点E处,∴AE=AB,BC=CE,∴AE=CD,AD=CE,又∵DE=DE,∴△ADE≌△CED(SSS);(2)∵△ADE≌△CED,∴∠ADE=∠CED,∴DF=EF,∴△DEF为等腰三角形;(3)如图2,过点A作AH⊥BC于H,过点B作BM⊥AC于M,∵AB=AC=2,BC=2,AH⊥BC,∴BH=CH=,∵cos∠ACB==,∴∠ACB=30°,又∵BM⊥AC,∴BM=BC=,CM=BM=3,∵BA'=BC,BM⊥A'C,∴A'M=MC=3,∴AA'=3+3﹣2=4,∴△AEC平移的距离为4.12.【分析】(1)由旋转的性质可得∠EAC=2α,∠DAE=∠BAC=α,由“SAS”可证△ABE≌△ABC,可得BE=BC;(2)由旋转的性质可得AD=AB,BC=DE,且AB=BC,BE=BC,可证四边形ABED 是菱形;(3)由菱形的性质可求解.【解答】(1)证明:∵将△ABC绕点A逆时针旋转2α,∴∠EAC=2α,∠DAE=∠BAC=α,AD=AB,∵∠BAC=α,∴∠BAE=∠EAC﹣∠BAC=2α﹣α=α,∴∠BAE=∠BAC.∵AE=AC,AB=AB,∴△ABE≌△ABC(SAS),∴BE=BC;(2)答:四边形ABED是菱形.理由如下:∵将△ABC绕点A逆时针旋转2α,∴AD=AB,BC=DE,∵AB=BC,BE=BC,∴AD=AB=BE=DE.∴四边形ABED是菱形;(3)如图,当BE⊥AC时,延长EB交AC于H,∵四边形ABED是菱形,∴AD∥BE,∵BE⊥AC,∴AD⊥AC,∴∠DAC=90°,∵∠DAE=∠BAC=α,∠EAC=2α,∴α+2α=90°,∴α=30°;如图,当BE∥AC,∵四边形ABED是菱形,∴AD∥BE,又∵BE∥AC,∴AD与AC共线,∴∠DAE+∠EAC=180°,∴α+2α=180°,∴α=60°.13.【分析】(1)证明∠BAC=∠DAE,得出∠BAD=∠CAE,由SAS即可得出结论;(2)求出∠ACB=∠ACE=30°,由平行线的性质得出∠MEC+∠ECD=180°,即可得出结果;(3)由△BAD≌△CAE,得出DB=CE,再证明∠ACE=∠EMC,得出ME=EC,推出DB=ME,即可得出结论.【解答】(1)证明:∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°﹣2∠ABC,∵以AD、AE为腰做等腰三角形ADE,∴AD=AE,∴∠ADE=∠AED,∴∠DAE=180°﹣2∠ADE,∵∠ADE=∠ABC,∴∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS);(2)解:∵AB=AC,∴∠ACB=∠ABC=30°,∵△BAD≌△CAE,∴∠ABD=∠ACE=30°,∴∠ACB=∠ACE=30°,∴∠ECB=∠ACB+∠ACE=60°,∵EM∥BC,∴∠MEC+∠ECD=180°,∴∠MEC=180°﹣60°=120°;(3)证明:∵△BAD≌△CAE,∴DB=CE,∠ABD=∠ACE,∵AB=AC,∴∠ABD=∠ACB,∴∠ACB=∠ACE,∵EM∥BC,∴∠EMC=∠ACB,∴∠ACE=∠EMC,∴ME=EC,∴DB=ME,又∵EM∥BD,∴四边形MBDE是平行四边形.14.【分析】(1)根据旋转角求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等;(2)根据等腰三角形的性质得到结论;(3)根据等腰三角形的性质得到∠ABD=∠ADB=∠ACE=∠AEC=90°﹣,求得∠BFE=150°,若使四边形ABFE是菱形,只要四边形ABFE是平行四边形即可,得到∠BAE=∠BFE,于是得到结论.【解答】(1)证明:∵ABC绕点A按逆时针方向旋转α°,∴∠BAC=∠DAE=30°,∴∠BAD=∠CAE=α°,又∵AB=AC,∴AB=AC=AD=AE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵∠CAE=α°,AC=AE,∴∠ACE=(180°﹣∠CAE)=(180°﹣α°)=90°﹣;(3)解:∵∠BAD=∠CAE=α°,AB=AC=AD=AE,∴∠ABD=∠ADB=∠ACE=∠AEC=90°﹣,∵∠BAE=∠BAD+∠DAE=α°+30°=(α+30)°,∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=360°﹣(α+30)°﹣2(90°﹣α°)=150°,∵AB=AE,∴若使四边形ABFE是菱形,只要四边形ABFE是平行四边形即可,∵∠ABD=∠AEC,∴只要∠BAE=∠BFE,即(30+α)°=150°,解得:α°=120°,即当α°=120°时,四边形ABFE是菱形.15.【分析】(1)由平行线的性质和折叠的性质可得∠DAC=∠ACE,证得ED=EB',可得∠ADB'=∠ACE=∠DAC,可得AC∥B'D;由菱形的定义可求解;(2)证明∠ADB'=∠DAC,可证得结论①,证明△AEC是等腰三角形,可得出结论②;(3)①当AB:AD=1:1时,符合题意.②当AD:AB=时,也符合题意.【解答】解:(1)∵四边形ABCD是矩形,∴AD∥BC,∠B=∠ADC=90°,∴∠DAC=∠ACB,∵将矩形纸片ABCD沿对角线AC翻折,∴∠AB'C=∠B=90°,∠ACB=∠ACE,BC=CB',∴∠DAC=∠ACE,∴AE=EC,∵AD=BC,∴CB'=AD,∴ED=EB',∴∠EDB'=∠EB'D,∵∠AEC=∠DEB',∴∠ADB'=∠DAC,∴B'D∥AC,∵将△AEC剪下后展开,AE=EC,∴展开图形是四边相等的四边形,∴展开图形是菱形,故答案为:B'D∥AC;菱形;(2)结论①,②都成立,若选择①,证明如下:∵四边形ABCD是平行四边形,∴AD=BC,∵将△ABC沿AC翻折至△AB'C,∴B'C=BC,∴B'C=AD,∴B'E=DE,∴∠CB'D=∠ADB',∵∠AEC=∠B'ED,∠ACB'=∠CAD,∴∠ADB'=∠DAC,∴B'D∥AC;若选择②,证明如下:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACB,∵将△ABC沿AC翻折至△AB'C,∴∠ACB'=∠ACB,∴∠DAC=∠ACB',∴AE=CE,∴△AEC是等腰三角形;∴将△AEC剪下后展开,得到的图形四边相等,∴将△AEC剪下后展开,得到的图形是菱形.(3)如图,①当AB:AD=1:1时,四边形ABCD是正方形,此时,点B',E,D重合,∴AF=CF=DF,且∠AFD=90°,此时△ADF是轴对称图形,符合题意.②如图,当AD:AB=时,也符合题意,∵此时∠DAC=30°,∴AC=2CD,∴AF=FC=CD=AB=AB′,∴此时四边形AFEB′是轴对称图形,符合题意.综上,矩形纸片ABCD的长宽之比是1:1或:1.故答案为:1:1或:1.16.【分析】(1)作辅助线,构建全等三角形,根据ASA证明△BMP≌△PNE可得结论;(2)如图2,连接OB,通过证明△OBP≌△FPE,得PF=OB,则PF为定值是;(3)根据△AMP和△PCN是等腰直角三角形,得PA=PM,PC=NC,整理可得结论.【解答】(1)证明:如图①,过点P作MN∥AD,交AB于点M,交CD于点N.∵PB⊥PE,∴∠BPE=90°,∴∠MPB+∠EPN=90°.∵四边形ABCD是正方形,∴∠BAD=∠D=90°.∵AD∥MN,∴∠BMP=∠BAD=∠PNE=∠D=90,∵∠MPB+∠MBP=90°,∴∠EPN=∠MBP.在Rt△PNC中,∠PCN=45°,∴△PNC是等腰直角三角形,∴PN=CN,∴BM=CN=PN,∴△BMP≌△PNE(ASA),∴PB=PE.(2)解:在P点运动的过程中,PF的长度不发生变化.理由:如图2,连接OB.∵点O是正方形ABCD对角线AC的中点,∴OB⊥AC,∴∠AOB=90°,∴∠AOB=∠EFP=90°,∴∠OBP+∠BPO=90°.∴∠BPE=90°,∴∠BPO+∠OPE=90°,∴∠OBP=∠OPE.由(1)得PB=PE,∴△OBP≌△FPE(AAS),∴PF=OB.∵AB=2,△ABO是等腰直角三角形,∴.∴PF的长为定值.(3)解:.理由:如图1,∵∠BAC=45°,∴△AMP是等腰直角三角形,∴.由(1)知PM=NE,∴.∵△PCN是等腰直角三角形,∴.。
回归教材重难点03 四边形与特殊四边形(原卷版)

回归教材重难点03 四边形与特殊四边形本考点是中考五星高频考点,难度中等及中等偏上,在全国各地市的中考试卷中都有考查。
(2022年天津市中考数学试卷第17题)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于.【分析】如图,过点F作FH∥CD,交DE于H,过点C作CM⊥AB,交AB的延长线于M,连接FB,先证明FH是△CDE的中位线,得FH=1,再证明△AEG≌△FHG(AAS),得AG=FG,在Rt△CBM 中计算BM和CM的长,再证明BF是中位线,可得BF的长,由勾股定理可得AF的长,从而得结论.【解答】解:如图,过点F作FH∥CD,交DE于H,过点C作CM⊥AB,交AB的延长线于M,连接FB,∵四边形ABCD是菱形,∴AB=CD=BC=2,AB∥CD,∴FH∥AB,∴∠FHG=∠AEG,∵F是CE的中点,FH∥CD,∴H是DE的中点,∴FH是△CDE的中位线,∴FH=CD=1,∵E是AB的中点,∴AE=BE=1,∴AE=FH,∵∠AGE=∠FGH,∴△AEG≌△FHG(AAS),∴AG=FG,∵AD∥BC,∴∠CBM=∠DAB=60°,Rt△CBM中,∠BCM=30°,∴BM=BC=1,CM==,∴BE=BM,∵F是CE的中点,∴FB是△CEM的中位线,∴BF=CM=,FB∥CM,∴∠EBF=∠M=90°,Rt△AFB中,由勾股定理得:AF===,∴GF=AF=.故答案为:.【点评】此题考查的是菱形的性质,三角形中位线定理,全等三角形的判定与性质,掌握其性质定理是解决此题的关键.四边形在初中数学教材中分《平行四边形》与《特殊平行四边形》两大部分,因为其考点多,性质及判定各有特点的同时又兼具相似点,解题中大部分还需要转化思想、归纳思想、分类讨论思想等,所以考察难度通常较大,题目也比较综合,在中考中常以压轴题形式出现本考点是中考五星高频考点,难度较大,个别还会以压轴题出现,在全国各地市的中考试卷中均有考查。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
朝阳二模19.如图,在平行四边形ABCD 中,AD = 4,∠B =105º,E 是BC 边的中点,∠BAE =30º,将△ABE 沿AE 翻折,点B 落在点F 处,连接FC ,求四边形ABCF 的周长.
东城二模20. 已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF 与对角线AC 交于点
M ,过M 作ME ⊥CD 于点E . (1)求证:AM =2CM ;
(2)若12∠=∠,23CD =,求ME 的值.
海淀二模19.如图,
ABCD 中,E 为BC 中点,过点E 作AB 的垂线交AB 于点G ,交
DC 的延长线于点H ,连接DG .若10BC =,45GDH ∠=︒,DG 82=,求CH
的长及
ABCD 的周长.
怀柔二模19. 已知如图:在菱形ABCD 中,O 是对角线BD 上
的一点.连结AO 并延长,与DC 交于点R ,与BC 的延长线交于点S .若
460,10
A D D C
B B S ===
,∠. (1)求AS 的长度; (2)求OR 的长度. 解:
门头沟二模19.如图,在四边形ABCD 中,∠DAB =60º,AC 平分
∠DAB ,BC ⊥AC ,AC 与BD 交于点E ,AD =6, CE =437,7tan 33
BEC ∠=,求BC 、DE 的长及
四边形ABCD 的面积.
D
F C
E
B
A
19题图
A
B
C D
E
O
石景山二模19.如图,四边形ABFE 中,延长FE 至点P ,∠AEP =74°,∠BEF =30°,∠EFB
=120°, AF 平分∠EFB ,EF =2. 求A B 长(结果精确到0.1).(参考数据:3≈1.73,
2≈1.41,sin74°≈0.6,cos74°≈0.28,
tan74°≈3.49, sin76°≈0.97,cos76°≈0.24)
西城二模20.如图,四边形ABCD 中,∠BAD=135°,∠BCD=90°,AB=BC=2, tan ∠BDC=
6
3
. (1) 求BD 的长; (2) 求AD 的长.
大兴二模21.如图,将□ABCD 的边DC 延长到点E ,使CE=DC ,连接AE , 交BC 于点F .若∠AFC=2∠D ,连结AC 、BE. 求证:四边形ABEC 是矩形.
顺义二模19.已知:如图,四边形ABCD 中,对角线AC 、BD 相交于点E ,
90ABC ACD ∠=∠=︒,62AB BC ==,2
tan 3
CDE ∠=
. 求对角线BD 的长和ABD ∆的面积.
F E
D C
B
A E
D
C
B
A
昌平二模21. 如图所示,等腰梯形ABCD 中,AB ∥CD ,AB =15,AD =20,∠C =30°.点M 、N 同时以相同的速度分别从点A 、点D 开始在AB 、DA 上向点B 、点A 运动. (1)设ND 的长为x ,用x 表示出点N 到AB 的距离;
(2)当五边形BCDNM 面积最小时,请判断△AMN 的形状.
房山二模19.如图,四边形ABCD 中,AB ∥CD ,AB =13,CD =4,点E 在边AB 上,
DE ∥BC .若CB CE =,且3tan =∠B ,求四边形ABCD 的面积.
丰台二模19.如图,四边形ABCD 中, CD=2, 90=∠BCD , 60=∠B ,
30,45=∠=∠CAD ACB ,求AB 的长.
密云二模19.已知:平行四边形ABCD 的对角线交点为O ,点E 、
F 分别在边AB 、CD 上,分别沿DE 、BF 折叠四边 形ABCD ,A 、C 两点恰好都落在O 点处,且四边 形DEBF 为菱形(如图).
(1)求证:四边形ABCD 是矩形; (2)在四边形ABCD 中,求的值.
N M
D
C
B
A
第19题图
A
B
C
D E
D
A
B
C。
