上海市罗泾中学七年级数学上册 9.14 公式法(第1课时)教案 沪教版五四制
上海市罗泾中学七年级数学上册 9.14 公式法(第1课时)教案 沪教版五四制

9.14 公式法(第1课时)教学目标:认知目标:理解整式乘法公式中的平方差公式在因式分解中的作用。
理解平方差公式的意义,弄清公式的形式和特点,并运用对比的方法弄清两种“平方差公式”的区别与联系。
能力目标:掌握运用平方差公式分解因式。
情感目标:形成全面地观察问题、分析问题和逆向思维的能力。
渗透类比思想,使学生学会举一反三。
教学重点和难点正确运用平方差公式分解因式。
教学过程设计一、复习提问:1.什么叫因式分解?我们已学过什么因式分解的方法?2.因式分解与整式乘法有什么区别和联系?3.我们学过哪些乘法公式?二、学习新课:1、观察思考:提问:整式乘法与因式分解是互逆关系,那么乘法公式除了可以进行整式乘法外,还有其它什么用途?教师总结:如果把乘法公式从右向左用,就可以用来把某些符合条件的多项式分解因式.我们把这种多项式的分解方法叫做运用公式法.引出因式分解的平方差公式:a2-b2=(a+b)(a-b),总结该公式的特征:公式左边是两个数的平方差,右边是两个因式积的形式,这两个因式分别为这两个数的积及这两个数的差。
利用这个公式,可以把具有平方差特征的多项式分解因式.2、例题分析:利用平方差公式因式分解:1)x2-16;2)9m2-4n2练习1.填空4x2=( )2 25m2=( )2 36a4=( )2 0.49b2=( )281n6=( )2 64x2y2=( )2 100p4q2=( )22.下列多项式可不可以可不可以用平方差公式?如果可以,应分解成什么式子?如果不可以,说明为什么?(书后练习)x2+y2 -x2+y2 x2+y2 -x2-y2 a4-b2总结出能用平方差公式分解因式的多项式应满足的条件:。
上海市罗泾中学七年级数学上册 分式的复习(第1课时)教案 沪教版五四制

例1:当m取何值时,分式 (1)有意义? (2)值为零?
例2:不改变分式的值,使 的分子、分母的最高次项的系数为整数.
例3:计算:
练习:计算:
例4:当x=2005时,求 的值.
练习:已知分Biblioteka 的复习(第1课时)教学目标:
了解分式的概念,会确定使分式有意义的分式中字母的取值X围。掌握分式的基本性质,会约分,通分。会进行分式的加减乘除乘方的运算。会进行繁分式的化简。
教学重难点:
重 点:熟练而准确地掌握分式四则运算.
难 点:四则混合运算中的去括号及符号问题.
教学方法:查缺补漏,引导法.
教学手段:点拨式、纠正错误法、多练习.
教学过程:
一、基础知识
1.分式的有关概念
设A、B表示两个整式.如果B中含有字母,式子 就叫做分式.注意分母B的值不能为零,否则分式没有意义
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简
2、分式的基本性质
(M为不等于零的整式)
3.分式的运算
(分式的运算法则与分数的运算法则类似). (异分母相加,先通分);
上海市罗泾中学七年级数学上册 9.4 整式(第1课时)教案 沪教版五四制

教学目标:知识与技能:1、理解单项式、多项式和整式中有关概念。
2、知道单项式、多项式和整式之间的从属关系。
3、知道“指数”与“次数”的区别,能准确迅速地写出单项式中的系数和次数及多项式的次数。
过程与方法:通过观察、比较、归纳,经历单项式、多项式的概念发生过程。
情感态度与价值观:教学重难点:重点:正确理解单项式、多项式和整式中有关概念难点:能准确迅速地写出单项式中的系数和次数及多项式的次数。
教学过程:教学环节教师活动学生活动引入观察:根据运算将下列代数式分成两类32x3yx+122+-aa22yx-yx394-32ba322333babbaa-+-分类:1、32x yx394-32ba2、3yx+122+-aa22yx-322333babbaa-+-概念讲述:像第一类这几个代数式我们称为单项式。
那何为单项式呢?单项式:由数与字母的积或字母与字母的积所组成的代数式叫做单项式注意:单独一个数也是单项式,如1、31、52-提问:第二类代数式我们可以看做是由几个单项式相加组合而成的,例如122+-aa是由哪几个单项式相加的?多项式:像这样由几个单项式的和组成的代数式叫做多项式。
不含字母的项叫做常数项。
整式:单项式和多项式统称为整式回答:是由单项式2a、a2-、+1相加而成的。
例题解 ab2、-4a2b4都是数与字母或字母与字母的积,所以它们是单项式。
2a+3b、2a-5b7都是由两个单项式的和组成,所以它们是多项式。
单项式的系数与次数讲述:对于项其实我们并不陌生,在六年级学习方程的时候已接触过。
提问:例如:02173=-x中,x21-这一项的系数和次数分别是多少?讲述:单项式的系数也一样单项式的系数:单项式中的数字因数叫做这个单项式的系数。
注意:符号也是系数的一部分例如:2ab-的系数是多少?单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
注意:区分指数与次数提问:2ab-的次数是多少?练一练:请分别说出下列各单项式的系数与次数单项式25x-27xy-26abx2yz-系数x21-的系数是21-,这一项的次数是12ab-的系数是-12ab-的次数是3学生独立完成表格次数多项式的项数与次数提问:1、多项式3422563xxxx+---有几个单项式相加而成的?分别是哪几个单项式?2、-5这一项叫什么项?设问:单项式有次数,多项式有没有次数呢?讲述:我们规定次数最高项的次数就是这个多项式的次数。
上海市罗泾中学七年级数学上册 9.14.1 公式法分解因式-平方差教案 沪教版五四制

提问:如何分解因式?(1)能否直接利用平方差公式?
解:(1)
注意:先提公因式在用公式法,分解一定要彻底
(2) 先让学生独立完成
提问:分解彻底了吗?
(3)
(4)
可以,将 、 看作一个整体
(1)不能直接利用平方差公式可以先提取公因式3x
预估学生的解题过程:
没有
课堂练习
1、分解因式:
(1)36b4x8-9c6y10
公式法分解因式-平方差
教学目标:
知识与技能:掌握使用平方差公式进行因式分解的方法,并能熟练使用平方差公式进行因式分解;
过程与方法:1、通过知识的迁移经历运用平方差公式分解因式的过程,发展逆向思维;
2、在应用平方差公式分解因式的过程中体验换元思想,同时增强观察能力和归纳总结的能力。
情感态度与价值观:
教学重难点:
(7)(x+5)(x-5)=
(8)(3a+1)(3a-1)=
引入
比一比:看谁算得快
提问:说一说你的依据?
试一试:因式分解
提问:当一个多项式具有什么特点时可用平方差公式因式分解?
练一练:下列多项式可以用平方差公式分解因式吗?
(1) a2+4b2; (2)4a2-b2; (3) a2-(-b)2; (4)–4+a2; (5)–4-a2; (6) x2- ; (7) x2n+2-x2n
(2)(x+2y)2-(x-2y)2
(3)
(4)81
(5)(3a+2b)2-(2a+3b)2
2、若 , ,则代数 的值
小结
1、分解因式平方差公式
a2-b2=(a+b)(a-b)
上海市罗泾中学七年级数学上册 9.14.3 公式法完全平方公式教案 沪教版五四制
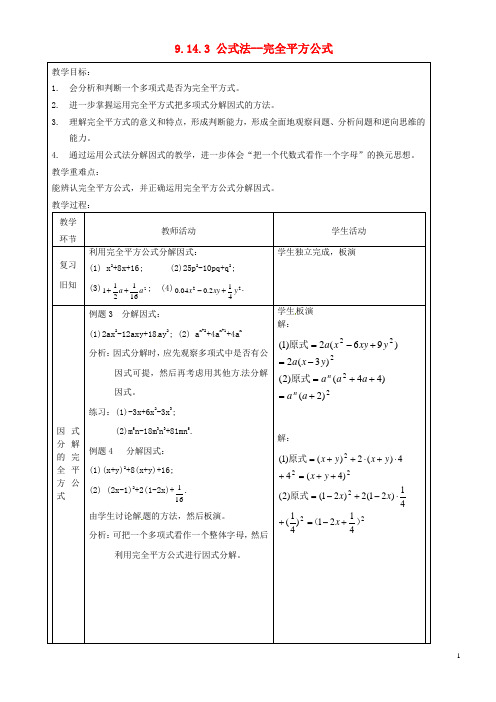
9.14.3 公式法--完全平方公式教学目标:1.会分析和判断一个多项式是否为完全平方式。
2.进一步掌握运用完全平方式把多项式分解因式的方法。
3.理解完全平方式的意义和特点,形成判断能力,形成全面地观察问题、分析问题和逆向思维的能力。
4.通过运用公式法分解因式的教学,进一步体会“把一个代数式看作一个字母”的换元思想。
教学重难点:能辨认完全平方公式,并正确运用完全平方公式分解因式。
教学过程:教学环节教师活动学生活动复习旧知利用完全平方公式分解因式:(1) x2+8x+16; (2)25p2-10pq+q2;(3)2161211aa++; (4)22412.004.0yxyx+-.学生独立完成,板演因式分解的完全平方公式例题3 分解因式:(1)2ax2-12axy+18ay2; (2) a n+2+4a n+1+4a n分析:因式分解时,应先观察多项式中是否有公因式可提,然后再考虑用其他方法分解因式。
练习:(1)-3x+6x2-3x3;(2)m5n-18m3n3+81mn5.例题4 分解因式:(1)(x+y)2+8(x+y)+16;(2) (2x-1)2+2(1-2x)+161.由学生讨论解题的方法,然后板演。
分析:可把一个多项式看作一个整体字母,然后利用完全平方公式进行因式分解。
学生板演解:22222)2()44()2()3(2)96(2)1(+=++=-=+-=aaaaayxayxyxann原式原式解:2222224121)41(41)21(2)21()2()4(44)(2)()1()(原式原式+-=+⋅-+-=++=+⋅+⋅++=xxxyxyxyx学生板演: 解:2222222222222)2()2()]2)(2[()4(13)2()()()2)(2()1(x x x x x x y x y x xy y x xy y x -+=-+=-=+-=-+=-+++=)(原式原式作业 同步练习同步练习: 一、因式分解: 1、7a m+1-14a m+7a m -12、-a 2-8ab -16b 23、a 5+a 4+41a 3 4、xy 3-2x 2y 2+x 3y 5、(x 2+4y 2)2-16x 2y 26、(x+2y )2-2(x+2y )+1 7、(a+b )2-4(a+b-1) 8、(x -y)2-6(x -y)+9 9、(a +b)2+4(a +b)c +4c 210、a 3+2a 2b +ab 211、x 2(m -n)-4x(n -m)-4(n -m) 12、(x 2-y 2)(x +y)-(x -y)313、x 5-18x 3y 2+81xy 4二、利用因式分解计算 1.39.82-2×39.8×49.8+49.822.152+15×10+52二、已知正方形的面积是4x 2+4xy +y 2,求正方形的周长。
上海市罗泾中学七年级数学上册 9122 完全平方公式教案 沪教版五四制

教学环节
教师活动
学生活动
复习
1、平方差公式
2、完全平方公式
3、指出下列个体分别用什么公式计算并且计算下列各题。
(1) (2)
(3) (4)
4、在括号内填入适 当的项,使等号成立
(1)a+b-c=a+( )(2)a-b+c=a+( )
(3)a-b+c=a-( ) (4)a-b-c=a-( )
分析:
提问:请写出乙商店11月份的销售额
解:
规律:
等于每一项的平方和加上每两项乘积的2倍.
解:课堂练习练习册 Nhomakorabea课堂小结
乘法公式的综合运用
添括号 法则
作业
课课练9.12.2
提问:你能说一说天括号的法则吗?
(1)a+b-c=a+( b-c )
(2)a-b+c=a+(-b+c )
(3)a-b+c=a-( b-c )
(4)a-b-c=a-( b+c )
添括号时,如果括号前面是“+”号,括到括号里的各项都不变号
如果括号前面是“-”号括到括号 里的各项都变号。
例题分析
例2:计算
解:
试一试:
提问:观察
从左到右的变化,你能找到结果的 规律吗?
练一练:
例3:计算
提问:此题能否直接利用乘法公式?
应该如何变形?
练一练:
(1)
(2)
例4:甲乙两家商店9月份的销售额为a万元,在10月份和11月份这两个月份中,甲商店的销售额平均每月增长x%,乙商店的销售额平均每月减少x%,11月份甲商店的销售额比乙商店的销售额多多少万元?
七年级数学上册9.14公式法(1)平方差公式教案沪教版五四制

平方差公式第(1)课时课题:书法---写字基本知识课型:新授课教学目标:1、初步掌握书写的姿势,了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点:基本笔画的书写。
难点:运笔的技法。
教学过程:一、了解书法的发展史及字体的分类:1、介绍我国书法的发展的历史。
2、介绍基本书体:颜、柳、赵、欧体,分类出示范本,边欣赏边讲解。
二、讲解书写的基本知识和要求:1、书写姿势:做到“三个一”:一拳、一尺、一寸(师及时指正)2、了解钢笔的性能:笔头富有弹性;选择出水顺畅的钢笔;及时地清洗钢笔;选择易溶解的钢笔墨水,一般要固定使用,不能参合使用。
换用墨水时,要清洗干净;不能将钢笔摔到地上,以免笔头折断。
三、基本笔画书写1、基本笔画包括:横、撇、竖、捺、点等。
2、教师边书写边讲解。
3、学生练习,教师指导。
(姿势正确)4、运笔的技法:起笔按,后稍提笔,在运笔的过程中要求做到平稳、流畅,末尾处回锋收笔或轻轻提笔,一个笔画的书写要求一气呵成。
在运笔中靠指力的轻重达到笔画粗细变化的效果,以求字的美观、大气。
5、学生练习,教师指导。
(发现问题及时指正)四、作业:完成一张基本笔画的练习。
板书设计:写字基本知识、一拳、一尺、一寸我的思考:通过导入让学生了解我国悠久的历史文化,激发学生学习兴趣。
这是书写的起步,让学生了解书写工具及保养的基本常识。
基本笔画书写是整个字书写的基础,必须认真书写。
课后反思:学生书写的姿势还有待进一步提高,要加强训练,基本笔画也要加强训练。
总第(2)课时课题:书写练习1课型:新授课教学目标:1、教会学生正确书写“杏花春雨江南”6个字。
2、使学生理解“杏花春雨江南”的意思,并用钢笔写出符合要求的的字。
重点:正确书写6个字。
难点:注意字的结构和笔画的书写。
教学过程:一、小结课堂内容,评价上次作业。
二、讲解新课:1、检查学生书写姿势和执笔动作(要求做到“三个一”)。
2、书写方法是:写一个字看一眼黑板。
上海市罗泾中学七年级数学上册-整式的复习(第1课时)教案-沪教版五四制

整式的复习(第1课时) 教学目标:
1.使学生对本章内容的认识更全面、更系统化。
2.进一步加深学生对本章基础知识的理解以及基本技能(主要是计算)的掌握。
3.经历复习回顾知识过程,培养学生合作交流,归纳总结的能力。
重点:本章基础知识的归纳、总结;基础知识的运用;整式的加减运算。
难点:本章基础知识的归纳、总结;基础知识的运用;整式的加减运算。
教学过程
2.主要法则:
①提问:在本章中,我们学习了哪几个重要的法则?分别如何叙述?
②在学生回答的基础上,进行归纳总结:
整式的加减
二、讲授新课:
1.例题:例1:找出下列代数式中的单项式、多项式和整式。
3z
y x ++,4x y ,a 1,22n m ,x2+x+x 1,0,x x 212-,m ,―2.01×105
例2:指出下列单项式的系数、次数:
ab ,―x2,53xy5,
353z y x -。
⎩⎨⎧合并同类项。
去(添)括号。
例3:化简,并将结果按x 的降幂排列:
(1)(2x4―5x2―4x+1)―(3x3―5x2―3x);
(2)―[―(―x+21)]―(x ―1);
(3)―3(21x2―2x y+y2)+ 21(2x2―xy ―2y2)。
三、 课堂练习:
课本p76―77:1,2, 3⑴⑶⑸,4⑴⑶⑸⑺,5,7.
四、小结 引导学生小结
五 作业布置课本76―77:3⑵⑷⑹,4⑵⑷⑹⑻,6,8,9。
上海市罗泾中学七年级数学上册 9.12 完全平方公式(第1课时)教案 沪教版五四制

9.12 完全平方公式(第1课时)教学目标认知目标:知道完全平方公式与多项式乘法的关系,理解完全平方公式的意义。
能力目标:熟悉完全平方公式的特征,并且能运用公式进行简单计算。
情感目标:经历探索完全平方公式的过程,进一步提高观察力、发展符号感;在合作、交流和讨论中发掘知识,体会学习的乐趣。
教学重点及难点体会公式的发现和推导过程,理解公式的本质,并会运用公式进行简单的计算。
从广泛意义上理解公式中的字母含义。
教学过程设计1.观察与思考思考1计算下列各题,并观察下列乘式与结果的特征:(1) ()=+2b a(2) ()=+232b a通过计算你发现了什么规律?学生活动:同学先相互观察,然后以四人一小组相互交流,统一意见后举手回答.(比较等号左边的代数式的特点,等号右边的代数式的特点,等号左右两边的联系) 教师:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们积的两倍. 教师:请同学把语言归纳的规律用数学的符号来表示.学生:()2222b ab a b a ++=+教师板书课题与公式 【教法说明】通过观察和归纳,顺利得到完全平方公式.2、完全平方的几何背景思考: 你能根据下图中图形的面积关系来说明平方差公式吗?学生活动:同桌间相互交流意见,互相纠正补充.达成一致后,举手回答,其他学生思考,准备更正或补充.【教法说明】通过学生自己概括总结,既培养了学生的图形理解能力,又训练了他们归纳及口头表达能力.3、运用新知,体会成功例1 学一学:利用完全平方公式进行计算:(1)2)32(y x +(2)2)2(b a +-a+bIII II II I ba+baa b解:(1) 222229124)3(322)2()32(y xy x y y x x y x ++=+••+=+()2222b ab a b a ++=+4.综合尝试,巩固知识练习1 计算(1)222224422)2()2(y xy x y y x x y x ++=+••+=+(2)222224131912121312312131n mn m n n m m n m ++=⎪⎭⎫ ⎝⎛+••+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+学生活动:每一题目均由学生说出完整的解题过程.【教法说明】学生已具备运用已学知识解决问题的能力,同时,在学生“说”,教师“写”的过程中,教师可随时发现并及时纠正学生解题中出现的问题.5、总结、扩展这节课我们学习了完全平方公式及应用,请同学们谈一下你对本节课学习的体会. 学生活动:谈这节课的主要内容或注意问题等等.【教法说明】课堂归纳总结由学生来说,可以使学生上课听讲精神集中,还可以训练学生归纳总结的能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总结出能用平方差公式分解因式的多项式应满足的条件:
教师总结:如果把乘法公式从右向左用,就可以用来把某些符合条件的多项式分解因式.我们把这种多项式的分解方法叫做运用公式法.
引出因式分解的平方差公式:a2-b2=(a+b)(a-b),
总结该公式的特征:公式左边是两个数的平方差,右边是两个因式积的形式,这两个因式分别为这两个数的积及这两个数的差。
利用这个公式,可以把具有平方差特征的多项式分解因式.
2Байду номын сангаас例题分析:
利用平方差公式因式分解:1)x2-16;2)9m2-4n2
练习
1.填空
4x2=( )225m2=( )236a4=( )20.49b2=( )2
81n6=( )264x2y2=( )2100p4q2=( )2
2.下列多项式可不可以可不可以用平方差公式?如果可以,应分解成什么式子?如果不可以,说明为什么?(书后练习)
教学重点和难点
正确运用平方差公式分解因式。
教学过程设计
一、复习提问:
1.什么叫因式分解?我们已学过什么因式分解的方法?
2.因式分解与整式乘法有什么区别和联系?
3.我们学过哪些乘法公式?
二、学习新课:
1、观察思考:
提问:整式乘法与因式分解是互逆关系,那么乘法公式除了可以进行整式乘法外,还有其它什么用途?
9.14公式法(第1课时)
教学目标:
认知目标:理解整式乘法公式中的平方差公式在因式分解中的作用。
理解平方差公式的意义,弄清公式的形式和特点,并运用对比的方法弄清两种“平方差公式”的区别与联系。
能力目标:掌握运用平方差公式分解因式。
情感目标:形成全面地观察问题、分析问题和逆向思维的能力。
渗透类比思想,使学生学会举一反三。
