江苏省第二十一届初中数学竞赛
江苏省历年初中数学竞赛试题及解答(23份)

第十五届江苏省初中数学竞赛试题初一年级第一试 (1)第十五届江苏省初中数学竞赛试卷初一年级 第二试 (3)江苏省第十五届初中数学竞赛初二第1试试题 (6)江苏省第十五届初中数学竞赛初二年级 第二试 (8)江苏省第十五届初中数学竞赛初三年级 (14)2001年第十六届江苏省初中数学竞赛A 卷 (19)2001年第十六届江苏省初中数学竞赛B 卷 (24)第十六届江苏省初中数学竞赛试题(C 卷)初三年级 (29)江苏省第十七届初中数学竞赛 初一年级 第l 试 (33)江苏省第十七届初中数学竞赛试卷 初一年级(第2试) (35)江苏省第十七届初中数学竞赛 初二年级 第l 试 (38)江苏省第十七届初中数学竞赛试卷 初二年级(第2试) (40)江苏省第十七届初中数学竞赛试卷 初三年级 (43)江苏省第十八届初中数学竞赛初一年级第1试 (45)2003年江苏省第十八届初中数学竞赛初中一年级 第2试 (48)2003年江苏省第十八届初中数学竞赛初中二年级 第2试 (52)2003年江苏省第十八届初中数学竞赛初中三年级 (57)江苏省第十九届初中数学竞赛初一年级 第1试 (60)江苏省第十九届初中数学竞赛初二年级第1试 (62)江苏省第十九届初中数学竞赛试卷初二年级第2试 (65)江苏省第十九届初中数学竞赛初三年级(第1试) (71)江苏省第十九届初中数学竞赛(保留)初三年级第l 试 (73)江苏省第十九届初中数学竞赛试题与答案初三年级(第2试) (80)第十五届江苏省初中数学竞赛试题初一年级第一试一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( ).(A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2 (c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)2 3.若a 是负数,则a+|-a|( ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ).(A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ).(A)A 、B 两点的距离 (B)A 、C 两点的距离(C)A 、B 两点到原点的距离之和(D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ).(A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba (b+1)得( ). (A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)= 10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)= ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 . 16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月.18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中a 1=6×2+l ;a 2=6×3+2;a 3=6×4+3;a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = .20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a +1 06. 10.一43.6. 11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-151 1 6.1. 1 7.1988;1.18.1022.5;101 8.1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).第十五届江苏省初中数学竞赛试卷初一年级 第二试一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( )(A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c =2001,且a+b+c=2001k ,那么k 的值为( )。
2021年江苏省徐州市中考数学联赛试题附解析

2021年江苏省徐州市中考数学联赛试题 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.上午九时,阳光灿烂,小李在地面上同时摆弄两根长度不相等的竹竿,若它们的影子长度相等,则这两根竹竿的相对位置可能是( )A .两根都垂直于地面B .两根都倒在地面上C .两根不平行斜竖在地面上D .两根平行斜竖在地面上 2.如图,小芳和爸爸正在散步,爸爸身高1.8m ,他在地面上的影长为2.1m .若小芳比爸爸矮0.3m ,则她的影长为( )A .1.3mB .1.65mC .1.75mD .1.8m3.如图,是由一些相同的小正方形构成的几何体的三视图.这几个几何体中相同的小正方体的个数有( )A .4 个B .5 个C .6 个D .7 个 4.如图,请你在正方形地板上涂上阴影部分,使得小猫在地板上自由地走来走去,它最终停留在地板上的概率是 41.( ) 5.若 3x=4y ,则x :y 等于( )A .3 : 4B .4 : 3C .11:34 D .11:436.如图,△ABC 中,E ,D 分别是AB .AC 上的点,AB=AC ,BD=BC ,AD=DE=EB ,那么∠A 等于( )A .30°B .36°C .45°D .54°7.下列命题中,是假命题的为( )A .两条直线相交,只有一个交点B .全等三角形对应边上的中线相等C .全等三角形对应边上的高相等D .三角形一边上的中线把这个三角形分成两个全等的小三角形8.在共有15人参加的的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的 ( )A .中位数B .众数C .平均数D .方差9.当我国发现H1N1流感第一个确诊病例时,卫生部要求全国各地做好流感预防工作. 一个立方体玩具的每个面上都有一个汉字,其表面展开图如图所示,那么在该立方体中和“毒”字相对的字是( )A . 卫B .防C .讲D .生10.下列算式正确的是( )A .-30=1B .(-3)-1=31C .3-1= -31D .(π-2)0=111.公因式是23ax -的多项式是( )A .2225ax a --B .22236a x ax --C .2223612ax a x ax --+D .3261224ax ax a x ---12.赵师傅透过平举的放大镜从正上方看到水平桌面上的菱形图案的一角(如图所示),那么∠A 与放大镜中的∠C 的大小关系是( )A .∠A=∠CB .∠A >∠CC .∠A <∠CD .∠A 与∠C 的大小无法比较13.由图,可知销售量最大的一年是( )A . 2005年B . 2006年C .2007年D .无法确定14.如图,数轴上一动点A 向左移动2个单位长度到达点B ,再向右移动5个单位长度到达点C .若点C 表示的数为1,则点A 表示的数为( )A .7B .3C .3-D .2-二、填空题15.小明与父母从广州乘火车回梅州参观叶帅纪念馆,他们买到的火车票是同一排相邻的三个座位,那么小明恰好坐在父母中间的概率是 .16.如图,在Rt △ABC 中,∠ACB= 90°,CD ⊥AB 于D ,DE ∥BC ,交 AC 于E ,则图中与△ABC 相似的三角形有 个.17. 若代数式(2)(1)x x -+的值为零,则 x= . 18.已知反比例函数8y x=-的图象经过点P (a+1,4),则a=__ __. 19.下列事件中,哪些是必然事件?哪些是不确定事件?哪些是不可能事件?(1)掷一枚硬币,有国徽的一面朝上: .(2)随意翻一下日历,翻到的号数是奇数: .(3)杭州每年春季都会下雨: .20.已知点A 、B 、C 三个点在同一条直线上,若线段AB=8,BC=5,则线段AC=_______. 解答题21.若温度上升10℃记作+10℃,那么-8℃表示 .22.如果正数m 的平方根为1x +和3x -,则m 的值是 .23.用“<”号连结 0,( 1.5)--,|3|--,123,132-是 . 三、解答题24.为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米(结果精确到1米.732.13≈,414.12≈)?水平线 A BCD 30° 新 楼 1米 40米 旧 楼 E25.在电视台举行的某选秀比赛中,甲、乙、丙三位评委对选手的综合表现,分别给出“待定”或“通过”的结论.(1)写出三位评委给出 A 选手的所有可能的结论;(2)对于选手 A,只有甲、乙两位评委给出相同结论的概率是多少?26.为了了解学生的身高情况,抽测了某校17岁学生中50名男生的身高,数据如下:将数据分成7组,组距为3,填写频数分布表,并回答下列问题:(1)样本数据中,17岁男生身高的众数、中位数分别是多少?(2)依据样本数据,估计该校17岁男生身高不低于165cm,且不高于170cm的学生所占比例;(3)指出该校17岁男生中,身高在哪个范围内的频率最大?若该校17岁男生共500人,那么在这个范围内的人数估计是多少人?分组频数频率1.565~1.5951.625~1.6551.685~1.7151.745~1.775合计27.某中学为美化校园,准备在长32 m,宽20m的长方形场地上,修筑若干条道路(道路的宽要求相同),余下部分作草坪,并请全校学生参与图纸设计.现有三位学生各设计了一种方案(图纸如图所示),问三种设计方案中道路的宽分别为多少?(1)甲方案图纸为①,设计草坪总面积540 m2;(2)乙方案图纸为②,设计草坪总面积540 m2;(3)丙方案图纸为③,设计草坪总面积570 m2.28.如图,已知CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?并说明理由.29.计算: (用简便方法)(1) (+1.3) +(-0.8)+2.7+(-0. 6);(2)13( 2.25)(3)(3)(0.125)84-+-+-++(3)4( 6.74)(1)( 1.74)( 1.8)5++++-+-30.现在各学校都采用政府统一采购行为,教育局对各个学校的校服征订也采用了统一征订的办法.在教育局的样品室里摆放着12个样品,有l2种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元.现要对全校1500名学生统一征订校服,由于价格相差甚远,学校于是采取征求家长意见,制作了一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表格(要求家长用打“√”的形式来表达).【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.C3.B4.任意4块染成红色都可以.5.B6.C7.D8.A9.B10.D11.B12.A13.C14.D二、填空题15.1316. 417.2或一118.-319.(1)不确定事件;(2)不确定事件;(3)必然事件20.3和1321.温度下降8℃22.423.113|3|0( 1.5)223-<--<<--<三、解答题24.过点C 作CE ⊥BD 于E ,由于AB = 40米,即CE = 40米,而阳光入射角为︒30,所以∠DCE =︒30,在Rt △DCE 中,CE DE DCE =∠tan ,所以3340=DE ,即233340≈⨯=DE ,而AC = BE = 1米,则DB = BE + ED =24231=+米.即新建楼房最高约24米.25.(1)评委给出 A选手的所有可能结果如下:由上可知评委给出 A 选手所有可能的结果有8种.(2)对于 A 选手,“只有甲、乙两住评委给出相同的结论”有 2 种,即“通过一通过一待定”、“待定一待定一通过”,所以对于 A选手“只有甲、乙两位评委给出相同结论”的概率是1 426.⑴169cm,169cm;⑵54%;⑶该校17岁男生身高在168.5~171.5cm范围内频率最大,约为0.34,若该校17岁男生共有500人,估计此身高范围内人数为170人.27.(1)1 m;(2)2 m;(3)1m28.EF∥AB,理由略29.(1)2.6 (2)-9 (3)530.校服价格(单位:元)5060708090100110120130140150160在您认可的价格下打“√”。
江苏省第二十一届初中数学竞赛
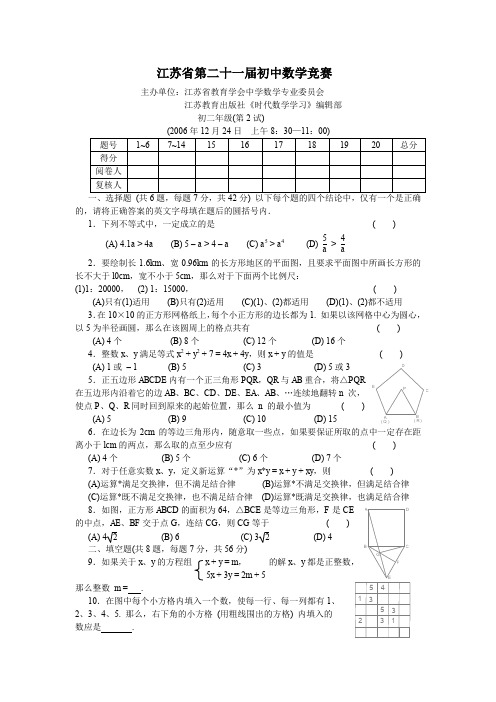
江苏省第二十一届初中数学竞赛主办单位:江苏省教育学会中学数学专业委员会江苏教育出版社《时代数学学习》编辑部初二年级(第2试)一、选择题(共6题,每题7分,共42分) 以下每个题的四个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.1.下列不等式中,一定成立的是( )(A) 4.1a > 4a(B) 5 –a > 4 –a(C) a5 > a4(D) 5a>4a2.要绘制长1.6km、宽0.96km的长方形地区的平面图,且要求平面图中所画长方形的长不大于l0cm,宽不小于5cm,那么对于下面两个比例尺:(1)1:20000,(2) 1:15000,( )(A)只有(1)适用(B)只有(2)适用(C)(1)、(2)都适用(D)(1)、(2)都不适用3.在10×10的正方形网格纸上,每个小正方形的边长都为1. 如果以该网格中心为圆心,以5为半径画圆,那么在该圆周上的格点共有( )(A) 4个(B) 8个(C) 12个(D) 16个4.整数x、y满足等式x2 + y2 + 7 = 4x + 4y,则x + y的值是( )(A) 1或– 1 (B) 5 (C) 3 (D) 5或35.正五边形ABCDE内有一个正三角形PQR,QR与AB重合,将△PQR在五边形内沿着它的边AB、BC、CD、DE、EA、AB、…连续地翻转n次,使点P、Q、R同时回到原来的起始位置,那么n 的最小值为( )(A) 5 (B) 9 (C) 10 (D) 156.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于lcm的两点,那么取的点至少应有( )(A) 4个(B) 5个(C) 6个(D) 7个7.对于任意实数x、y,定义新运算“*”为x*y = x + y + xy,则( )(A)运算*满足交换律,但不满足结合律(B)运算*不满足交换律,但满足结合律(C)运算*既不满足交换律,也不满足结合律(D)运算*既满足交换律,也满足结合律8.如图,正方形ABCD的面积为64,△BCE是等边三角形,F是CE的中点,AE、BF交于点G,连结CG,则CG等于( )(A) 4 2 (B) 6 (C) 3 2 (D) 4二、填空题(共8题,每题7分,共56分)9.如果关于x、y的方程组x + y = m,的解x、y都是正整数,5x + 3y = 2m + 5那么整数m = .10.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5. 那么,右下角的小方格(用粗线围出的方格) 内填入的数应是.132353145DCBAGFE( R )( Q )EDCBAP11.在如图的算式中,“美、好、末、来、祥、和、谐”七个不同的汉 字,代表0~9这十个数字中的某七个数字,相同的汉字代表相同的数字, 不同的汉字代表不同的数字.这里“美好未来”是一个四位数,那么“祥 和和谐”代表的四位数最小是 .12.观察图(1)中“蝴蝶”的画法,在图(2)的8×8正方形网格中,画两只与图(1)形状、大小都相同的蝴蝶(二者可以有部分重叠),组成一幅对称图案,并标出对称轴l 或对称中心O .(1 ) (2 )13.2006除以正整数n ,余数为6,这样的正整数n 共有 个.14.如图(1),一个正方体的三个面上分别写有1、2、3,与它们相对的三个面上依次写有6、5、4.这个正方体的每一条棱处各嵌有一根金属条, 每根金属条的质量数(单位:克)等于过该棱的两个面上所 写数的平均数.(1)这个正方体各棱上所嵌金属条的质量 总和为 克.(2)沿这个正方体的某些棱(连同嵌条) 剪开,得到图(2)所示的展开图,其周边棱上金属条质 量之和的最小值为 克.在图(2)中把这个正方体的六个面上原有的数字写出来(注:写字的这一面是原正方体的外表面).15.如图,△ABC 、中,AB = AC ,点D 、E 分别在BC 和AC 上,且AD = AE .设∠DAB = α,∠B = β,∠CDE = γ,∠DAC = θ.(1) 写一个含有上面四个角度的等式: ; (等式中若有同类项应予合并,使形式简明)(2)写一个仅含有上述两个角度的等式: .16,一个直角三角形三边的长a 、b 、c 都是整数,且满足a < b < c ,a + c = 49.则这个直角三角形的面积为 .三、解答题(共4题,每题12分,共48分)17.有两只同样的杯子,甲杯盛满了水,乙杯是空杯.第一次操作是将甲杯中水的一半倒入乙杯,第二次操作是将乙杯中水的一半倒入甲杯,如此反复上述过程.操作三次后两杯(2) 对于n >1的情况,比较 a n 与 b n 的大小;美未来来好未来和谐和祥来未好+(3) 对于n >1的情况,求a n与a n – 1的关系(用a n – 1表示a n ).18.河岸l同侧的两个居民小区A、B到河岸的距离分别为a米、b米(即图(1)中所示AA′ = a米,BB′ = b米),A′B′ = c米. 现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.(1) 在图(2)中画出绿化带的位置,并写出画图过程;(2) 求AC + BD的最小值.19. 甲、乙、丙三支乒乓球队,人数都不相同,每队不少于2人,甲队最少,丙队最多. 同一球队的队员互相不比赛,不同球队的队员之间都要比赛一场. 统计员作了记录:参加比赛的共有13人,进行的比赛共有54场. 求甲、乙、丙三支球队的队员数,并说明理由.20.为了培养学生的理财能力,初二(1)班创办了一个“小银行”.王华打算将一张存单上的钱全部取出,“银行出纳员”匆忙中把存单金额的整数部分(元数)与小数部分正好错位(即把小数部分当成整数部分,而把整数部分当成小数部分)付给了王华.王华没有清点即回家,回家途中他购物用了3.50元,购物后却惊奇地发现所剩的钱数是应取钱数的2倍.便立即与出纳员联系.问王华应取多少钱?。
江苏省第二十一届初中数学竞赛

江苏省如皋中学语文第1、2册考试(总分:150 分)一、判断题。
(共41 分)1. ( 8分)判断下列各项正误。
A.人类的血战前行的历史,正如煤的形成,当时用大量的木材,如果却只是一小块,但请愿是不在其中的,更何况是徒手。
这段话表明鲁迅先生对请愿持否定态度,他认为刘和珍等人的牺牲是无意义的。
( )B.鲁迅先生说:“我将深味这非人间的浓黑的悲凉,以我的最大哀痛显示于非人间,使它们快意于我的苦痛,……”表明鲁迅与反动政府和反动文人势不两立的立场和态度。
( )C.“时间永是流驶,街市依旧太平”,此句中“依旧太平”意在说明徒手请愿对社会“触动”不大。
( )D.看见鱼翅,并不就抛在路上以显其“平民化”,只要有养料,也和朋友们像萝卜、白菜一样的吃掉。
此中的“鱼翅”喻事物中的精华,“萝卜白菜”喻民间俗气的事物。
( )2. ( 8分)判断下列说法的正误,正确的打“T”,错误的打“F”。
A.《劝学》篇在《荀子》32篇之首,足见荀子对教育的重视。
“学不可以已”包括两方面的意思:一方面是学习有重要意义,所以“不可以已”;另一方面是学习应有“学不可已”的态度。
()B.韩愈在《师说》一文中针对上层“士大夫之族”的门第观念,明确提出“无贵无贱,无长无少,道之所存,师之所存也”。
这种思想闪耀着民主、进步的光芒,提出了全新的师道观念。
()C.《鸿门宴》语言精炼主动,寥寥数语,突出地刻画出项羽、刘邦、范增、张良等人物的个性。
难怪南宋词人刘辰翁称赞为:“历历如目睹,无毫发渗漉,非十分笔力,模写不出”,这评语毫不夸张。
()D.《五人墓碑记》是明初政治活动家和文学家张溥写的。
他字天如,号西铭,书房命名为“七录斋”。
课文中心是歌颂五位平民“激于义而死”的精神和群众斗争的巨大力量。
()3. ( 12分)下列说法,你认为对的,就在其后的括号里画“T”;你认为错的,就在其后的括号里画“F”。
1.项脊轩,归有光的书斋名。
此名的由来有两种解释:一说归有光的祖父曾住在太仓项脊泾,用此以纪念祖先;一说是形容书房的狭小。
江苏省历年初中数学竞赛试题及解答(23份)

第十五届江苏省初中数学竞赛试题初一年级第一试 (1)第十五届江苏省初中数学竞赛试卷初一年级 第二试 (3)江苏省第十五届初中数学竞赛初二第1试试题 (6)江苏省第十五届初中数学竞赛初二年级 第二试 (8)江苏省第十五届初中数学竞赛初三年级 (14)2001年第十六届江苏省初中数学竞赛A 卷 (19)2001年第十六届江苏省初中数学竞赛B 卷 (24)第十六届江苏省初中数学竞赛试题(C 卷)初三年级 (29)江苏省第十七届初中数学竞赛 初一年级 第l 试 (33)江苏省第十七届初中数学竞赛试卷 初一年级(第2试) (35)江苏省第十七届初中数学竞赛 初二年级 第l 试 (38)江苏省第十七届初中数学竞赛试卷 初二年级(第2试) (40)江苏省第十七届初中数学竞赛试卷 初三年级 (43)江苏省第十八届初中数学竞赛初一年级第1试 (46)2003年江苏省第十八届初中数学竞赛初中一年级 第2试 (48)2003年江苏省第十八届初中数学竞赛初中二年级 第2试 (52)2003年江苏省第十八届初中数学竞赛初中三年级 (57)江苏省第十九届初中数学竞赛初一年级 第1试 (60)江苏省第十九届初中数学竞赛初二年级第1试 (62)江苏省第十九届初中数学竞赛试卷初二年级第2试 (65)江苏省第十九届初中数学竞赛初三年级(第1试) (71)江苏省第十九届初中数学竞赛(保留)初三年级第l 试 (73)江苏省第十九届初中数学竞赛试题与答案初三年级(第2试) (80)第十五届江苏省初中数学竞赛试题初一年级第一试一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( ).(A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2 (c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)2 3.若a 是负数,则a+|-a|( ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ).(A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ).(A)A 、B 两点的距离 (B)A 、C 两点的距离(C)A 、B 两点到原点的距离之和(D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ).(A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba (b+1)得( ). (A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)= 10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)= ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 . 16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月.18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中a 1=6×2+l ;a 2=6×3+2;a 3=6×4+3;a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = .20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a +1 06. 10.一43.6. 11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-151 1 6.1. 1 7.1988;1.18.1022.5;101 8.1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).第十五届江苏省初中数学竞赛试卷初一年级 第二试一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( )(A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c =2001,且a+b+c=2001k ,那么k 的值为( )。
2021年江苏省扬州市中考数学联赛试卷附解析

2021年江苏省扬州市中考数学联赛试卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.上午九时,阳光灿烂,小李在地面上同时摆弄两根长度不相等的竹竿,若它们的影子长度相等,则这两根竹竿的相对位置可能是( )A .两根都垂直于地面B .两根都倒在地面上C .两根不平行斜竖在地面上D .两根平行斜竖在地面上 2.如图,直线2=y x 与双曲线x k y =的图象的一个交点坐标为(2,4).则它们的另一个交点坐标是( )A .(-2,-4)B .(-2,4)C .(-4,-2)D .(2,-4)3.下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同一个圆中,相等的圆周角所对的弦相等;④三个点确定一个圆. 其中正确命题的个数为( )A .1 个B .2 个C .3 个D .4 个4.圆锥的底面半径为 1,全面积为4π,则圆锥的母线长为( )A .4B .3C .22D .325.已知函数y =12x 2-x +4,当函数值 y 随 x 的增大而减小时,则x 的取值范围是( ) A .x ≤1 B .x ≥1 C .x>-2 D .-2<x<46.下列等式成立的是( ) A . 22a b a b +=+ B . b a ab a -=-- C .a ab b = D . 22a b ab -=-7.若直线l 与已知直线y=2x+1关于y 轴对称,则直线l 的解析式为( )A .y=-2x 一1B .y=-2x+1C .y=2x-1D .112y x =-+ 8.如图所示,是一个几何体的三视图,这个几何体是( )A .圆锥B .圆柱C .长方体D .直三棱柱9.如图是用直尺和圆规作一个角的平分线的示意图,则说明 OC 平分∠AOB 的依据是( )A . SASB .SSSC .ASAD . AAS10.平面上有三点A 、B 、C ,如果AB=8,AC=5,BC=3,则( )A .点C 在线段AB 上 B .点C 在线段AB 的延长线上C .点C 在直线AB 外D .点C 可能在直线AB 上,也可能在直线AB 外11.近似数5.60所表示的准确数的范围是( )A .5.595至5.605之间B .5.50至5.70之间C .5.55至5.64之间D .5.600至5.605之间12.北京奥组委从4月15日起分三个阶段向境内公众销售门票,开幕式门票分为五个档次,票价分别为人民币5000元、3000元、1500元、800元和200元.某网点第一周内开幕式门票的销售情况见统计图,那么第一周售出的门票票价..的众数是( ) A .1500元 B .11张 C .5张 D .200元二、填空题13.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长),⊙A 的半径为1,⊙B 的半径为2,要使⊙A 与静止的⊙B 内切,那么⊙A 由图示位置需向右平移个单位长. 14.一只口袋里有相同的红、绿、蓝三种颜色的小球,其中有6个红球,5个绿球.若任意摸出一个绿球的概率是14,则任意摸出一个蓝球的概率是 . 15.某学生推铅球,铅球的飞行高度 y(m)与水平距离 x(m)之间的函数关系式是211315302y x x =-++,则铅球落地的水平距离为 m . 16.不等式3(1)53x x +≥-的正整数解是 .17.如图,AC 、BD 相交于点O ,∠A=∠D ,,请你再补充一个条件,使得△AOB ≌△DOC ,你补充的条件是 .18.如图,数轴上两点A,B,在线段AB上任取一点,则点C到表示1的点的距离不大于2的概率是.19.a5÷(a7÷a4)=________.三、解答题20..如图,△ABO 中,OA = OB,以 0为圆心的圆经过 AB 的中点 C,且分别交OA、OB 于点E、F.(1)求证:AB 是⊙O的切线;(2)若∠A=30°,且43AB ,求⌒ECF的长.21.观察图,图①是面积为 1 的等边三角形,连结它的各边中点,挖去中间的三角形得到如图②所示,再分别连结剩下的三角形各边中点,挖去中间的三角形得到如图③所示,继续用同样方法将得到图④,图⑤,图⑥…图n.(1)图②中空自部分面积为 , 图③中空白部分面积为,图④中空白部分面积为.(2)猜想:图③中空白部分面积为;(3)根据以上结论可推知,图n中空白部分面积为.22.已知抛物线y =12x 2+x -52. (1)用配方法求出它的顶点坐标和对称轴;(2)若抛物线与x 轴的两个交点为A 、B ,求线段AB 的长.23.如图,在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F .(1)求证:CF AB =;(2)当BC 与AF 满足什么数量关系时,四边形ABFC 是矩形,并说明理由.24.如图,P 是正方形ABCD 对角线BD 上一点,PE ⊥DC ,PF ⊥BC ,E ,F 分别是垂足,求证:AP=EF .25.在同一直角坐标系中画出一次函数121y x =-+与223y x =+的图象,并根据图象解答下 列问题:FE D C B A(1)直线121y x=-+、223y x=+与y轴分别交于A、B.求A、B两点的坐标;(2)求直线121y x=-+与223y x=+的交点P的坐标;(3)△PAB的面积为多少?26.已知:如图,在△ABC中,AD是么BAC的平分线,AD的垂直平分线交BC的延长线于F.试说明∠BAF=∠ACF成立的理由.27.如图,已知∠ABC、∠ADC都是直角,BC=DC.说明:DE=BE.28.如图所示为由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G是小正方形的顶点,以这7个点中的任意三个点为顶点,可组成多少个面积为1的三角形?请写出所有满足条件的三角形.29.(1)用如下图所示的两种正方形纸片甲、乙各 1 张,长方形纸片丙 2 张拼成一个大长方形(画出图示),并运用面积之间的关系,将一个多项式分解因式,并写出这个因式分解的过程.(2)请运用上面的方法将多项式2244a ab b ++分解因式,则需要正方形纸片甲 张,正方形纸片乙 张,长方形纸片丙 张拼成一个大的正方形. 画出图形并写出这个因式分解的过程.(3)假若要将多项式2254a ab b ++分解因式,你将利用什么样的图形的面积关系将它分解因式?30.一个多项式加上2532x x +-的2倍得213x x -+,求这个多项式.21355x x --+【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.A3.C4.B5.A6.D7.B8.D9.B10.A11.A12.A二、填空题13.4或614.92015. 516.1,2,317.AO = DO 或AB = DC 或BO=CO18.2319. a 2三、解答题20.(1)连结 OC.∵C 为 AB 中点,∴AC=BC ,∵OA=OB ,∴OC ⊥AB ,∴AB 是⊙O 的切线(2)由题意得:∠A=30°,AC =,∴OC=2,∵AO=BO ,∴∠OBC=∠A=30°,∴∠AOB= 120°,∴⌒ECF 的长=120241803ππ⋅⋅=. 21. (1) 34,916,2764;(2)81256;(3)13()4n - 22.(1)抛物线的顶点坐标为(-1,-3),对称轴是直线x=-1;(2)AB=26 .. 23.(1)证明:∵四边形ABCD 是平行四边形,∴CD AB CD AB =,//, ∴FCE ABE CFE BAE ∠=∠∠=∠,.∵E 为BC 的中点,∴EC EB =,∴FCE ABE ∆≅∆∴CF AB =.(2)解:当AF BC =时,四边形ABFC 是矩形.理由如下: ∵CF AB CF AB =,//, ∴四边形ABFC 是平行四边形.∵AF BC =,∴四边形ABFC 是矩形24.连结PC ,证△APD ≌△CPD25.图象略.(1)A(0,1),B(0,3); (2)P(12-,2);(3)111(31)222⨯-⨯-= . 26.略27.先说明Rt △ADC ≌Rt △ABC ,再说明△DCE ≌△BCE28.共l4个三角形,具体表示略29.(1)如图 1. 2222()a ab b a b ++=+(2)1,4,4(如图 2);22244(2)a ab b a b ++=+(3)需要 1张正方形纸片甲,4张正方形纸片乙,5张长方形纸片丙拼成一个大的长方形(如图 3)30.2--+x x1355。
江苏省第21届初中数学竞赛成绩揭晓.

江苏省第21届初中数学竞赛成绩揭晓初三年级江苏省一等奖:学校名称姓名学校名称姓名木渎中学陆吉余江苏外校钱宇斌江苏外校吕紫慧木渎中学严祎祎江苏外校吴羚琦光福中学府晓宗东山中学俞佳斌木渎中学吴煜昊碧波中学李佳智碧波中学樊崚崎江苏外校钱晓兰迎春中学陆慰卿江苏外校李克迎春中学顾晗江苏外校宗思思江苏外校陈宇悦江苏外校花仲萱浦庄中学刘俊豪木渎中学高原木渎中学陆晗华木渎中学陆赟怡东山中学宋松东山中学顾晨杰江苏外校张玉婷木渎中学丁彦碧波中学周祥江苏外校叶秋君江苏外校王鼎文东山中学许文俊江苏外校袁方舟江苏省二等奖:学校名称姓名学校名称姓名石公中学曹纪平木渎中学吴佳俊光福中学马雪强蓝缨学校濮敏斐碧波中学王媛江苏外校徐晓强江苏外校盛燕飞江苏外校殷梦祎木渎中学孙梦园木渎中学黄佳江苏外校周冰言江苏外校赵伟炜浦庄中学沈剑木渎实中邱益健长桥中学吴越木渎中学郭利城西中学陈昱昊浦庄中学王俊江苏外校潭曦悦木渎中学叶兰木渎中学张俊磊迎春中学刘司墨木渎中学钱东旭江苏外校罗恺天长桥中学马家琪碧波中学莫其凡甪直中学顾圆横泾中学任浩杰横泾中学沈佳杰初二年级江苏省一等奖:学校名称姓名学校名称姓名木渎中学濮希夷木渎中学陈一鸣木渎中学王凯宏木渎中学范世元木渎中学朱苏君迎春中学张何晨江苏外校杨晓宇渡村中学柳仁杰甪直中学潘志杰东山中学施怡浩江苏外校许佳林江苏省二等奖:学校名称姓名学校名称姓名迎春中学姚戈丰城西中学戴喆辰木渎中学石雨馨浦庄中学尤东林浦庄中学尤东江苏外校周子涵石公中学郑喜伟渡村中学孔顺凯江苏外校李雯君木渎中学叶晌江苏外校席晴横泾中学张文哲江苏外校马淑雯江苏外校王颜江苏外校李文倩城西中学支酉星胥口中学严晟曦木渎实中徐晨鸿木渎实中黄一枫横泾中学周华木渎实中周亮羽香山中学顾浩亮渡村中学潘蕾江苏外校吕岚胥口中学陶杰江苏外校邬录健胥口中学严政长桥中学朱国平东山中学王圣杰江苏外校陆一丹长桥中学王冠峰江苏外校胡飞横泾中学马艳木渎实中尤琦琦碧波中学倪雅群横泾中学施玉萍木渎中学邵晨宇甪直中学周振华木渎实中蒋子健横泾中学查任翔东山中学侯征远胥口中学徐燕云甪直中学周励婕渡村中学李佳萍胥口中学蔡丽君各年级江苏省三等奖名单见获奖证书。
第二十一届“五羊杯”初中数学竞赛初二试题+答案

第二十一届“五羊杯”初中数学竞赛初二试题(考试时间90分钟,满分100分)一、选择题(4选1型,共10小题,每小题选对得5分,否则得O 分.本题满分50分).1.计算:()=--+137137A .2/23;B .2;C .2D .222.己知x ,y ,z 是正整数,且222z y x =+,则下列结论正确的是( ).A .茗是4的倍数,y 不是4的倍数;B .x 不是4的倍数,y 是4的倍数;C .x 和y 都不是4的倍数;D .工和y 至少有一个是4的倍数,3.若02223=+++x x x ,则 ++--20062008x x2009200720053241x x x x x x x +++++++++-- 的值为( )A.1;B.0;C. -1;D.2.4.若有一个公共角的两个三角形被称为一对“共角三角形”,则图1中以角曰为公共角的“共角三角形”有( )对.A.6;B.9;C.12;D.15.5.己知三角形的三条边a ,b ,c 的长都为整数,且a ≤b <c .如果b=8,则这样的三角形有( )个.A .21;B .28;C .49;D .54.6.设a ,b ,c 均为正数,若a cbc b a b a c +<+<+则a ,b ,c 三个数的大小关系是( ). A .c <a <b ; B .b <c <a ; C .a <b <c ; D.c <b <a .7.晚会上,工作人员在礼堂四周挂了一串彩色的气球,个数超过5000个,其排列的规则如下:红黄黄蓝绿红蓝绿红黄黄蓝绿红蓝绿红黄黄蓝绿红蓝绿红黄黄……那么第2009个气球的颜色为( ).A .红;B .黄;C .蓝;D .绿.8.己知方程组⎪⎩⎪⎨⎧=+=+n x y mn x n 2720092,(其中m 是偶数,n 是奇数)有两组整数解⎩⎨⎧==⎩⎨⎧==q y p x b y a x 2211,,若令M =a+b ,N=p+q ,那么下列说法正确的是( ).A .M ,N 中有一个是偶数,一个是奇数;B .M ,N 两个都是偶数; C. M ,N 两个都是奇数; D .M ,N 的奇偶性不能确定.9.假设△表示运算符号并定义a △b =axb-2b ,如果c △d =X ,d △c=Y ,e △c=Z ,且有O <c <d <e ,则( ).A .X=Y <Z ;B .X >Y >Z ; C.X <Y <Z ; D .X >Y ,Y <Z10.有一摞208张的卡片,贝贝拿着它,从最上面的一张开始,按如下的顺序进行操作:把上面的第一张卡片拿掉,把下一张卡片放到这摞卡片的最下面;再把原来第三张卡片拿掉,把下一张卡片放到最下面,反复这样地做,直到手中只剩下一张卡片.那么剩下的这张卡片是原来那一摞卡片中的第( )张?A.208;B.128;C.104;D.160.二、填空题(共10小题,每小题答对得5分,否则得O 分,本题满分50分).11.分解因式:=-+---333)()()(z y z x y x __________________________________。
2021年江苏省盐城市中考数学联赛试卷附解析

2021年江苏省盐城市中考数学联赛试卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.如图,EB 为半圆O 的直径,点A 在EB 的延长线上,AD 切半圆O 于点D ,BC ⊥AD 于点C ,AB =2,半圆O 的半径为2,则BC 的长为( )A .2B .1C .1.5D .0.52. 当锐角∠A>300 时,cosA 的值( )A .小于12B . 大于12C . 小于32D . 大于323.一个滑轮起重装置如图所示,滑轮的半径是10cm,当重物上升10cm 时, 滑轮的一条半径OA 绕轴心O 按逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动, 取3.14,结果精确到1°)( )A .115°B .60°C .57°D .29°滑轮重物O A4.如图,在△ABC 中,M 是BC 的中点,AN 平分∠BAC ,BN ⊥AN .若AB=14,AC=19,则MN 的长为( )A .2B .2.5C .3D .3.5 5.某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( ) A .9cm B .12cm C .15cm D .12cm 或15cm6.如图,在下列给出的条件中,不能判定AB ∥DF 的是( ) A .∠A +∠2 = 180° B .∠A=∠3 C .∠1 = ∠AD .∠1 =∠47.三角形的一个外角小于与它相邻的内角,这个三角形是( )A . 直角三角形B . 锐角三角形C . 钝角三角形D .属于哪一类不能确定8.若关于x 的方程652m x =-的根为 1,则m 等于( ) A . 1 B . 8 C .18 D . 429.在下面四个图形中,既包含图形的旋转,又有图形的轴对称设计的是( )A .B .C .D .10. 已知下列条件,不能作出三角形的是( )A .两边及其夹角B 两角及其夹边C .三边D .两边及除夹角外的另一个角11.暗箱中有大小质量都相同的红色、黑色小球若干个,随机摸出一个球是红球的概率是 0.6,已知黑色小球有12个,则红球的数量为( )A .30B .20C .18D .10 12.计算(18x 4-48x 3+6x )÷(-6x )的结果是( ) A .3x 3-8x 2B .-3x 3+8x 2C .-3x 3+8x 2-1D .3x 3-8x 2-1 13.用字母表示数,下列书写规范的是( ) A .2×a ×bB . ax ÷2C .a2bD .2ab 14.与 cos70°值相等的是( )A .sin70°B .cos20°C .sin20°D .tan70° 二、填空题15.如图1,先将一矩形ABCD 置于直角坐标系中,使点A 与坐标系的原点重合,边AB 、AD 分别落在x 轴、y 轴上,再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图2),若AB =4,BC =3,则图1和图2中点B 点的坐标为 ;点C 的坐标 . 解答题16.若两圆外切,圆心距为8cm ,一个圆的半径为3 cm ,则另一个圆的半径为 cm .17.函数22y x x =+-的图象如图所示,当 y>0时,x 的取值范围是 当 y<0 时,x 的取值范围是 .18.把命题“两个奇数的和必为偶数”改写成“如果…那么…”的形式为___________________.19.已知一个样本容量为40的样本,把它分成七组,•第一组到第五组的频数分别为5,12,8,5,6,第六组的频率为0.05,第七组的频率为______.20.化简:1180= .21.平行四边形的周长为30 cm,两条邻边不等,其中较长一边为y(cm),较短一边为x(cm),则y与x的函数解析式为,自变量x的取值范围为.22.已知3a x-1b y+1与-12a2-y b x是同类项,则x-y-1=______.223.观察下列图形:其中既是轴对称图形又是旋转变换图形的为 (填序号) .三、解答题24.如图所示,水坝的横断面为梯形 ABCD,迎水坡 AD 的坡角为 30°,背水坡 BC 的坡度为1:1.2,坝顶 AB 的宽为 3 m,坝高为5m,求:(1)坝底 CD 的长;(2)迎水坡 AD 的坡度.25.如图,E是□ABCD外一点,∠AEC=∠BED=90°.求证:□ABCD是矩形.26.如图,如果∠2+ 3 = 180∠,那么a与b平行吗?请说明理由.①②③④⑤⑥27.用平方差公式计算:(1)2(2)(2)(4)x x x -++;(2)99810029991001⨯-⨯;(3)22222210099989721-+-+-; (4) 2222211111(1){1)(1)(1)(1)234910-----28.如图所示,画出△ABC 的角平分线BD ,AB 边上的高CE ,BC 边上的中线AF .29.一家奶制品厂现有鲜奶9 t ,若将这批鲜奶制成酸奶销售,则加工l t 鲜奶可获利1200元;若制成奶粉销售,则加工1 t 鲜奶可获利2000元.该厂的生产能力是:若专门生产酸奶,则每天可用去鲜奶3 t ,若专门生产奶粉,则每天可能用去l t ,由于受人员和设备的限制,酸奶和奶粉两种产品不可能同时生产,为了保证产品的质量,这批鲜奶必须在不超过4天内加工完毕.假如你是厂长,你将如何设计生产方案,才能使工厂获利最大,最大利润是多少?30.滴水成河,若20滴水流在一起为1cm 3,现有一条河流总体积为l 万m 3.试求该河流相当于多少滴具有相同体积的水滴?【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.B2.C3.C4.B5.C6.C7.C8.C9.D10.D11.C12.C13.D14.C二、填空题15.B (4,0)、(32,2),C (4,3)、( 2334- ,2433+) 16.517.x<-2 或 x>1,-2<x<1.18.如果两个数是奇数,那么它们的和必为偶数.19.0.0520.. y=15-x ,O<x<7.522.23.②③⑥三、解答题24.(1)过 B 作BH ⊥CD 于点 H ,AE ⊥CD 于点E ,∠D=30°,11.2BH CH = ,AB=3 ,BH= 5 ,AE=5,∴.CH=6,DE =∴639CD CH HE DE =++=++=+m(2)AE DE ==,∴AD 的坡度是.25.连结AC,BD交于O,连结OE,证AC=BD26.平行.理由:∵∠2+∠3=180°,∠2=∠4,∴∠4+∠3=180°,∴a∥b.27.(1)416x ;(2)-3;(3)5050;(4)11 2028.略29.用2.5天生产酸奶,用1.5天生产奶粉,即方案三可获最大利润为l2000元,且不浪费.30.2×1O11滴。
2006年江苏省第二十一届初三数学竞赛获奖名单(江阴市级)

高烨昶
江阴高中初中部
138
夏诚
江阴市夏港中学
90
陆亚
江阴高中初中部
139
牟怡珺
江阴市夏港中学
91
王超元
江阴高中初中部
140
金磊
江阴市周庄中学
92
于佳莹
江阴市南闸中学
141
陈彦希
江阴高中初中部
93
王静贤
江阴市南闸中学
142
倪文杰
江阴高中初中部
94
蒋乔瑜
江阴市暨阳中学
143
刘磊
江阴市暨阳中学
95
周佳能
肖迪丁健季科孙枫顾俭伟杨志超薛标彬
徐霞客中学
李玮波
峭岐中学
刘晓春陈泽强
桐岐中学
陆晓磊姚焱宏
长寿中学
龚凯
华士实验
胡艳红张奇李学辉巫佳翔夏爱军王洁查凌云
周庄中学
卞敏杰张琛亚任梦蕾沈珍珠陆勇徐淳
陆桥中学
费宇杰费洋徐昕张盼盼费天昊龚凯强钱梦娇刘超王颖杰
新桥中学
孙卉朱哲文
瓠岱中学
刘念
文林中学
王江
祝塘中学
薛强
长泾中学
2006年江苏省第二十一届初三数学竞赛获奖名单(江阴市级)
一等奖2006.12
序号
姓名
学校
序号
姓名
学校
1
沈煜杰
江苏省南菁中学
28
张坚鹏
江阴市璜塘实验学校
2
朱衍吉
江苏省南菁超
江苏省南菁中学
30
钱晓瑞
江阴市第二中学
4
陶壮
江阴高中初中部
31
肖翔宇
江阴高中初中部
2021年江苏省中考数学竞赛试卷附解析

2021年江苏省中考数学竞赛试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.如图,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF .若CD =6,则AF 等于 ( ) A .34B .33C .24D .82.下列特征中,菱形具有而矩形不一定具有的特征是( )A .对边平行且相等B .对角线互相平分C .内角和等于外角和D .每一条对角线所在直线都是它的对称轴3.已知22222()3()40a b a b +-+-=,则22a b +=( ) A .-lB .4C .4或-lD .任意实数4.下列条件中,不能判定两个直角三角形全等的是 ( ) A .一条直角边和一个锐角分别相等 B .两条直角边对应相等 C .斜边和一条直角边对应相等 D .斜边和一个锐角对应相等 5. 用加减法解方程组2333211x y x y +=⎧⎨-=⎩时,有下列四种变形,其中正确的是( )A .4639611x y x y +=⎧⎨-=⎩B .6396222x y x y +=⎧⎨-=⎩C .4669633x y x y +=⎧⎨-=⎩D .6936411x y x y +=⎧⎨-=⎩6.把图形(1)进行平移,能得到的图形是( )7.把0.000295用科学计数法表示并保留两个有效数字的结果是( ) A .43.010-⨯ B .53010-⨯ C .42.910-⨯D .53.010-⨯8.如图,将四边形AEFG 变换到四边形ABCD,其中E 、G 分别是AB 、AD 的中点.下列叙述不正确的是( ) A .这种变换是相似变换 B .对应边扩大原来的2倍 C .各对应角度不变D .面积扩大到原来的2倍9.如图所示,△ABC 平移至△DEF ,下列关于平移的方向和移动距离叙述正确的是( )A.方向是沿BC方向,大小等于BC的长B.方向是沿BC方向,大小等于CF的长C.方向是沿BA方向,大小等于BE的长D.方向是沿AD方向,大小等于BF的长10.一个两位数,若十位上的数字为x,个位上的数字比十位上的数字小1,则这个两位数为()A.21x-B.111x-C.1110x-29x+11.巴广高速路的设计者准备在西华山再设计修建一个隧道,以缩短两地之间的里程,其主要依据是()A.垂线段最短B.两点之间线段最短C.两点确定一条直线D.过直线外一点有且只有一条直线平行于已知直线12.长方形的周长是36(cm),长是宽的2倍,设长为x(cm),则下列方程正确的是()A.x+2 x =36 B.1362x x+=C.2(x +2x)=36 D.12()362x x+=二、填空题13.二次根式32a-中,a的取值范围是.14.已知点A(-1,2),将它先向左平移2个单位,再向上平移3个单位后得到点B,则点B的坐标是______.15.如图,直线a、b被直线c 截. 若要 a∥b,则需增加条件 (填一个条件即可).16.如图,∠1=75°,∠2 =75°,∠3 = 105°,那么∠4 = ,可推出的平行关系有 .17.如图所示,数学课中,老师让两个同学在黑板上做游戏,老师发给两个同学每人一个一模一样的圆形纸片,让他们想办法在黑板上的甲,乙两个长方形外部画一个圆 ( 即圆形纸上覆盖整个长方形),请问谁获胜的可能性要大?理由:.18.∠α的补角为125°,∠β的余角为37°,则∠α、∠β的大小关系为∠α∠β(填“>”、“<”或“=”).19.方程434x x=-的解是x= .20.3227xy z-的次数是,系数是.21.当 x= 0.5 时,||23xx-= .22.如图,为测量学校旗杆的高度,小丽用长为3.2m的竹竿做测量工具.移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22米,则旗杆的高为________m.三、解答题23.画出下列几何体的三种视图.24.如图,在等边△ABC中,D、E分别是AB、AC上的一点,AD=CE,CD、BE交于点F.(1)试说明∠CBE=∠ACD;(2)求∠CFE的度数.25.根据下图提供的信息,求出每只网球拍和每只乒乓球拍的单价. 26.填表,使上、下每对x和y 的值满足方程35x y+=.x-20252y12-0327.如下表,“谢氏三角”是波兰著名数学家谢尔宾斯基在1915年~l916年期间提出的,它的作法是:第一步:取一个等边三角形(记为P1),连结各边的中点,得到完全相同的小正三角形,挖掉中间的一个;第二步:将剩下的三个小正三角形(记为P2),按上述办法各自取中点,各自分成4个小三角形,去掉各自中间的一个小正三角形;依次类推,不断划分出小的正三角形,同时去掉中间的一个小正三角形.试求P4的“黑”三角形的个数,“黑”三角形的总边数,边长,周长和面积,并将结果填入下表中.28.如图所示,点E在△ABC的边AB上,点D在CA的延长线上,点F在BC的延长线上.试问:∠ACF与∠AED的关系如何?请说明理由.29.如图所示,在Rt △ABC中,∠ACB为直角,∠CAD的平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.30.2008年西宁市中考体育测试中,1分钟跳绳为自选项目.某中学九年级共有50名女同学选考1分钟跳绳,根据测试评分标准,将她们的成绩进行统计后分为A ,B ,C ,D 四等,并绘制成下面的频数分布表(注:6~7的意义为大于等于6分且小于7分,其余类似)和扇形统计图(如图1). 频数分布表(1(2)在抽取的这个样本中,请说明哪个分数段的学生最多?请你帮助老师计算这次1分钟跳绳测试的及格率(6分以上含6分为及格).图1扇形统计图【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.A2.D3.B4.A5.C6.C7.A8.D9.B10.B11.BD二、填空题 13.32a ≤14.(-3,5)15.答案不唯一.如∠l+∠2=180°16.105°;1l ∥2l 、3l ∥4l17.乙;从大小看,甲大于乙,所以覆盖的机会小18.>19.-420.4,87-21.-122.12三、解答题 23.24.(1)说明△ACD ≌△CBE ;(2)60°25.每只网球拍单价为 80 元,每只乒乓球拍的单价为 40 元116,53,23;11,5,195,-1 27.27,81,118a ,1818a ,12764S28.∠ACF>∠AED ,理由略29.∠E=27.5°,∠BAF=117.5°30.解:(1)根据题意,得50(412171)16m n +=-+++=;171006450m+⨯=%%. 则161732m n m +=⎧⎨+=⎩①②,解之,得151m n =⎧⎨=⎩.(2)7~8分数段的学生最多.及格人数412171548=+++=(人),及格率481009650=⨯=%%.答:这次1分钟跳绳测试的及格率为96%.。
江苏省第二十一届初中数学竞赛

江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第一试)(2006年12月3日上午8:30—10:30)一、选择题(每小题8分,共64分)以下每个题的四个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内. 1.化简9x 2 – 6x + 1 – (3x – 5 )2,结果是( ).(A)6x – 6 (B) – 6x + 6 (C) – 4 (D) 42.使得关于x 的一元二次方程2x (kx –4)–x 2+6=0无实数根的最小整数k 为( ).(A) – 1 (B) 2 (C)3 (D)4个3.在正方形ABCD 的边AB 、BC 、CD 、DA 上分别任意取点E 、F 、G 、H . 这样得到的四边形EFGH 中,是正方形的有( ).(A)1个 (B)2个 (C)4个 (D)无穷多个4.如图,四边形ABCD 的对角线AC 与BD 互相垂直,若AB =3,BC =4,CD =5,则AD 的长为( ).(A)3 2 (B) 4 (C)2 3 (D)4 25.已知x ,y ,z 为实数,若x 2 + y 2 = 1,y 2 + z 2 = 2,z 2 + x 2 = 2,则xy + yz + zx 的最小值为( ).(A) 52 (B) 12 + 3 (C) – 12 (D) 12– 3 6.在三角形ABC 中,∠BAC =90°,AC = 3 ,AB =4,D 为边BC 上一点,∠CAD =30°,则AD 的长为( ).(A) 65 (B) 75 (C) 85 (D) 957.如图,MN 是⊙O 的直径,若∠E =25°,∠PMQ =35°,则∠MQP =( ).(A)30° (B)35° (C)40° (D )50°8.如图,点A ,B 分别在一次函数y =x ,y =8x 的图象上,其横坐标分别为a ,b (a >0,b >0).若直线AB 为一次函数y = kx + m 的图象,则当b a是整数时,满足条件的整数k 的 值共有( ).(A )1个 (B)2个(C )3个 (D)4个二、填空题(每小题8分,共96分)9.在2006的中间嵌入一个数字得到五位数20口06,若此五位数能被7整除,则嵌入的数字口为 .10.设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为 .11.若 a 4 + b 4 = a 2 – 2a 2b 2 + b 2 + 6,则a 2 + b 2 = .12.如图,在四边形ABCD 中,AB =AC =AD ,若∠BAC =25°,∠CAD = 75°,则∠BDC = ,∠DBC = .13.若实数x ,y 满足70,3392;xy x y x y xy ì+++=ïïíï+=+ïî则x 2y + xy 2= . 14.如图,正六边形ABCDEF 的边长为2 3 cm ,点P 为六边形内任一点.则点P 到各边距离之和为 cm .15.某人5次上班所用时间(单位:分钟)分别为a ,b ,8,9,10.已知这组数据的平均数为9,方差为2,则| a – b | 的值为 .16.若整数m 使方程x 2 – mx + m + 2006 = 0 的根为非零整数,则这样的整数m 的个数为 .17.某次数学测验共有20题,每题答对得5分,不答得0分,答错得 –2分.若小丽这次测验得分是质数,则小丽这次最多答对 题.18.设5×4×3cm 3长方体的一个表面展开图的周长为n cm ,则n 的最小值是 .19.一个人把四根绳子紧握在手中,仅在两端露出它们的头和尾,然后随机地把一端的四个头中的某两个相接,另两个相接,把另一端的四个尾中的某两个相接,另两个相接,则放开手后四根绳子恰好连成一个圈的概率是 .20.有一个五边形ABCDE ,若把顶点A ,B ,C ,D ,E 涂上红、黄、绿三种颜色中的一种,使得相邻的顶点所涂的颜色不同,则共有 种不同的涂色方法.江苏省第二十一届初中数学竞赛(初三年级第一试)参考答案与评分标准一、选择题:题号1 2 3 4 5 6 7 8 答案 D B D A D C C B二、填空题:(9.0或7;10.10;11.3;12.12.5°;37.5°;13.6;.18;15.4;16.5个;17.17;18.50;19.23;20.30.说明:第9题与第12题填对一个得4分. 江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第二试)(2006年12月24日 上午8:30—11:00)一、选择题(共6题,每题7分,共42分)以下每题的四个结论中,有且仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.1.若n n x 221+=+,2122--+=n n y ,其中n 为整数,则x 与y 的数量关系为( )(A )y x 4= (B )x y 4= (C )y x 12= (D )x y 12=2.如图,AB 为半圆O 的直径,C 为半圆上一点,且∠COA =60°;设扇形AOC 、△COB 、弓形B m C 的面积分别为1S ,2S ,3S ,则它们之间的大小关系是( ).(A ) 1S <2S <3S (B ) 2S <1S <3S(C ) 1S <3S <2S (D ) 3S <2S <1S3.设1x ,2x 是方程042=-+x x 的两个实数根,则1052231+-x x =( ).(A )-29 (B )-19 (C )-15 (D )-94.如图,正方形ABCD 中,E 为CD 的中点,EF ⊥AE ,交BC 于点F ,则∠1与∠2的大小关系为( ).(A )∠1>∠2 (B )∠1<∠2(C )∠1=∠2 (D )无法确定5.方程y x y xy x 23322-=++的非负整数解(x ,y )的组数为( ).(A )0 (B )1 (C )2 (D )36.图示某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A 、B 、 C 的机动车辆数如图所示,图中1x ,2x ,3x 分别表示该时段单位时间通过路段AB⌒,BC ⌒,CA ⌒的机动车辆数 (假设单位时间内,在上述路段中,同一路段上驶入与驶出的机动车辆数相等),则1x ,2x ,3x 的大小关系为( ).(A )1x >2x >3x (B )1x >3x >2x(C )2x >3x >1x (D )3x >2x >1x二、填空题(共8题,每题7分,共56分)7.若p 和q 为质数,且9135=+q p ,则p = ,q = .8.设x 、y 均为实数,代数式4284522++-+x xy y x 的最小值为 .9.某工件的形状如图所示,圆弧BC⌒的度数为60°,AB =6cm , 点B 与点C 的距离等于AB ,∠BAC =30°,则此工件的面积为 .10.设关于x 的一元二次方程04122=-++k kx x 有两个实数 根,则k 的取值范围为 .11.在平行四边形ABCD 中,AM ⊥BC ,AN ⊥CD ,M 、N 为垂足,若AB =13,BM =5,MC =9,则MN 的长度为 .12.如图,用红,蓝,黄三色将图中区域A 、B 、C 、D 着色,要求有公共边界的相邻区域不能涂相同的颜色,满足恰好A 涂蓝色的概率为 .13.如图,在直角三角形ABC 中,AB =3,BC =4,∠ABC =90°,过B 作BA 1⊥AC ,过A 1作A 1B 1⊥BC ,得阴影直角三角形A 1B 1B ;再过B 1作B 1A 2⊥AC ,过A 2作A 2B 2⊥BC ,得阴影直角三角形A 2B 2B 1;…,如此无限下去,请猜测这样得到的所有阴影三角形的面积之和为 .14.在一个3×3的方格表中填有1~9这9个数字,现将每行中数字最大的那个格子涂红色,数字最小的那个格子涂绿色.设M为三个红色方格中数字最小的那个数,m 是三个绿色方格中数字最大的那个数,则m M -可以有 个不同的值.三、解答题(共4题,每题13分,共52分).15.如图,直线OB 是一次函数x y 2=的图象,点A 的坐标为(0,2),在直线 OB 上找点C ,使得△AOC 为等腰三角形,求点C 的坐标.16.如图,ABCD 为正方形,⊙O 过正方形的顶点A 和对角线的交点P ,分别 交AB 、AD 于点F 、E .(1)求证:DE =AF .(2)若⊙O 的半径为23,AB =12+, 求ED AE 的值.17.在7×7的单位正方形的网格中,共有64个格点,有许多以这些格点为顶 点的正方形.这些正方形的面积有多少不同的值?18.k ,a ,b 为正整数,k 被2a 、2b 整除所得的商分别为m ,116+m .(1)若a ,b 互质,证明22b a -与2a 、2b 都互质;(2)当a ,b 互质时,求k 的值;(3)若a ,b 的最大公约数为5,求k 的值.江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第二试)参考答案1.A ;2.B ;3.B ;4.C ;5.C ;6.C ;7.17,2;8.3;9.6π2cm ; 10.212212+≤-≥k k 或;11.13180;12.31;13.4196;14.8; 15.四个点),)、(,)、,)、,121554552(554552(51658(--; 16.(1)略;(2)222或. 17.18个不同的面积,边长19种但有两种面积是一样的25;18.(1)略;(2)k =176400;(3) k =4410000.。
江苏省第二十一届初中数学竞赛

江苏省第二十一届初中数学竞赛主办单位:江苏省教育学会中学数学专业委员会江苏教育出版社《时代数学学习》编辑部初二年级(第2试)一、选择题(共6题,每题7分,共42分) 以下每个题的四个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.1.下列不等式中,一定成立的是( )(A) 4.1a > 4a(B) 5 –a > 4 –a(C) a5 > a4(D) 5a>4a2.要绘制长1.6km、宽0.96km的长方形地区的平面图,且要求平面图中所画长方形的长不大于l0cm,宽不小于5cm,那么对于下面两个比例尺:(1)1:20000,(2) 1:15000,( )(A)只有(1)适用(B)只有(2)适用(C)(1)、(2)都适用(D)(1)、(2)都不适用3.在10×10的正方形网格纸上,每个小正方形的边长都为1. 如果以该网格中心为圆心,以5为半径画圆,那么在该圆周上的格点共有( )(A) 4个(B) 8个(C) 12个(D) 16个4.整数x、y满足等式x2 + y2 + 7 = 4x + 4y,则x + y的值是( )(A) 1或– 1 (B) 5 (C) 3 (D) 5或35.正五边形ABCDE内有一个正三角形PQR,QR与AB重合,将△PQR在五边形内沿着它的边AB、BC、CD、DE、EA、AB、…连续地翻转n次,使点P、Q、R同时回到原来的起始位置,那么n 的最小值为( )(A) 5 (B) 9 (C) 10 (D) 156.在边长为2cm的等边三角形内,随意取一些点,如果要保证所取的点中一定存在距离小于lcm的两点,那么取的点至少应有( )(A) 4个(B) 5个(C) 6个(D) 7个7.对于任意实数x、y,定义新运算“*”为x*y = x + y + xy,则( )(A)运算*满足交换律,但不满足结合律(B)运算*不满足交换律,但满足结合律(C)运算*既不满足交换律,也不满足结合律(D)运算*既满足交换律,也满足结合律8.如图,正方形ABCD的面积为64,△BCE是等边三角形,F是CE的中点,AE、BF交于点G,连结CG,则CG等于( )(A) 4 2 (B) 6 (C) 3 2 (D) 4二、填空题(共8题,每题7分,共56分)9.如果关于x、y的方程组x + y = m,的解x、y都是正整数,5x + 3y = 2m + 5那么整数m = .10.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5. 那么,右下角的小方格(用粗线围出的方格) 内填入的数应是.132353145DCBAGFE( R )( Q )EDCBAP11.在如图的算式中,“美、好、末、来、祥、和、谐”七个不同的汉 字,代表0~9这十个数字中的某七个数字,相同的汉字代表相同的数字, 不同的汉字代表不同的数字.这里“美好未来”是一个四位数,那么“祥 和和谐”代表的四位数最小是 .12.观察图(1)中“蝴蝶”的画法,在图(2)的8×8正方形网格中,画两只与图(1)形状、大小都相同的蝴蝶(二者可以有部分重叠),组成一幅对称图案,并标出对称轴l 或对称中心O .(1 ) (2 )13.2006除以正整数n ,余数为6,这样的正整数n 共有 个.14.如图(1),一个正方体的三个面上分别写有1、2、3,与它们相对的三个面上依次写有6、5、4.这个正方体的每一条棱处各嵌有一根金属条, 每根金属条的质量数(单位:克)等于过该棱的两个面上所 写数的平均数.(1)这个正方体各棱上所嵌金属条的质量 总和为 克.(2)沿这个正方体的某些棱(连同嵌条) 剪开,得到图(2)所示的展开图,其周边棱上金属条质 量之和的最小值为 克.在图(2)中把这个正方体的六个面上原有的数字写出来(注:写字的这一面是原正方体的外表面).15.如图,△ABC 、中,AB = AC ,点D 、E 分别在BC 和AC 上,且AD = AE .设∠DAB = α,∠B = β,∠CDE = γ,∠DAC = θ.(1) 写一个含有上面四个角度的等式: ; (等式中若有同类项应予合并,使形式简明)(2)写一个仅含有上述两个角度的等式: .16,一个直角三角形三边的长a 、b 、c 都是整数,且满足a < b < c ,a + c = 49.则这个直角三角形的面积为 .三、解答题(共4题,每题12分,共48分)17.有两只同样的杯子,甲杯盛满了水,乙杯是空杯.第一次操作是将甲杯中水的一半倒入乙杯,第二次操作是将乙杯中水的一半倒入甲杯,如此反复上述过程.操作三次后两杯(2) 对于n >1的情况,比较 a n 与 b n 的大小;美未来来好未来和谐和祥来未好+(3) 对于n >1的情况,求a n与a n – 1的关系(用a n – 1表示a n ).18.河岸l同侧的两个居民小区A、B到河岸的距离分别为a米、b米(即图(1)中所示AA′ = a米,BB′ = b米),A′B′ = c米. 现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.(1) 在图(2)中画出绿化带的位置,并写出画图过程;(2) 求AC + BD的最小值.19. 甲、乙、丙三支乒乓球队,人数都不相同,每队不少于2人,甲队最少,丙队最多. 同一球队的队员互相不比赛,不同球队的队员之间都要比赛一场. 统计员作了记录:参加比赛的共有13人,进行的比赛共有54场. 求甲、乙、丙三支球队的队员数,并说明理由.20.为了培养学生的理财能力,初二(1)班创办了一个“小银行”.王华打算将一张存单上的钱全部取出,“银行出纳员”匆忙中把存单金额的整数部分(元数)与小数部分正好错位(即把小数部分当成整数部分,而把整数部分当成小数部分)付给了王华.王华没有清点即回家,回家途中他购物用了3.50元,购物后却惊奇地发现所剩的钱数是应取钱数的2倍.便立即与出纳员联系.问王华应取多少钱?。
第15-19届江苏省初中数学竞赛试卷

第十五届江苏省初中数学竞赛试题初一年级第一试 ...................第十五届江苏省初中数学竞赛试卷初一年级 第二试 ..................江苏省第十五届初中数学竞赛初二第1试试题 ........................江苏省第十五届初中数学竞赛初二年级 第二试 ...................... 江苏省第十五届初中数学竞赛初三年级 ..............................2001年第十六届江苏省初中数学竞赛A 卷 ...........................2001年第十六届江苏省初中数学竞赛B 卷 ...........................第十六届江苏省初中数学竞赛试题(C 卷)初三年级 ....................江苏省第十七届初中数学竞赛 初一年级 第l 试 ....................江苏省第十七届初中数学竞赛试卷 初一年级(第2试) ................江苏省第十七届初中数学竞赛 初二年级 第l 试 ..................江苏省第十七届初中数学竞赛试卷 初二年级(第2试) ................江苏省第十七届初中数学竞赛试卷 初三年级 ........................江苏省第十八届初中数学竞赛初一年级第1试 ........................2003年江苏省第十八届初中数学竞赛初中一年级 第2试 .............2003年江苏省第十八届初中数学竞赛初中二年级 第2试 .............2003年江苏省第十八届初中数学竞赛初中三年级 .....................江苏省第十九届初中数学竞赛初一年级 第1试 ......................江苏省第十九届初中数学竞赛初二年级第1试 ........................江苏省第十九届初中数学竞赛试卷初二年级第2试 ....................江苏省第十九届初中数学竞赛初三年级(第1试) ......................江苏省第十九届初中数学竞赛(保留)初三年级第l 试 ..................江苏省第十九届初中数学竞赛试题与答案初三年级(第2试) ............第十五届江苏省初中数学竞赛试题初一年级第一试一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( ).(A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2 (c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)2 3.若a 是负数,则a+|-a|( ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ).(A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ).(A)A 、B 两点的距离 (B)A 、C 两点的距离(C)A 、B 两点到原点的距离之和(D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ).(A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba (b+1)得( ). (A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn二、填空题(每小题分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)= 10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)= ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 . 16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月.18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中a 1=6×2+l ;a 2=6×3+2;a 3=6×4+3;a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = .20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a +1 06. 10.一43.6. 11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-1511 6.1. 1 7.1988;1.18.1022.5;101 8.1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).第十五届江苏省初中数学竞赛试卷初一年级 第二试一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( )(A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c =2001,且a+b+c=2001k ,那么k 的值为( )。
初中数学培优专题之-数据的集中程度

初中数学培优专题之-数据的集中程度当代信息社会,人们需要对纷繁的信息作出适当的判断、选择与处理.生活中,我们离不开数据.在数据中,我们常要根据有些具有代表性的数据进行判断,比如平均数、众数、中位数就是有代表性的数据,它们从不同侧面反映了数据的集中程度.一、知识链接透彻理解数学概念,提升你的数学内涵!1、平均数(1)定义:一般地,对于n个数某1,某2,,某n,我们把某某1某2某n(公式n①)叫做这n个数的算术平均数,简称为平均数.简要的说:若干个数的平均数就是这若干个数的总和除以这些数的总个数的商.可以类推到有关实际问题中,比如:平均速度等于总路程除以总时间的商,班级数学考试成绩的平均分等于全班同学数学考试成绩的总分除以班级人数的商,若干件某种商品的平均价格等于总价钱除以总件数的商,等等.我们把样本中所有个体的平均数称为样本平均数,把总体中所有个体的平均数称为总体平均数,我们常用样本平均数去估计总体平均数.(2)平均数的简便计算方法:若n个数某1,某2,,某n都在常数a附近波动,那么'我们可以将原来的每一个数都减去a,得到一组新数某1,某2,,某n,先求出这组新数据''''的平均数某,从而就能得到原来那组数据的平均数为某某a(公式②),公式②称为平均数的简化计算公式.(3)加权平均数:在实际问题中,一组数据中各个数据的重要程度并平总是相同的,有时有些数据比其它数据更重要。
所以,我们在计算这组数据时,往往给每个数据一个“权”,这样计算得来的平均数称为加权平均数.如果在n个数中,某1出现f1次,某2出现f2次,,某k出现fk次,其中f1+f2+f某k,则这n个数的平均数为某1f1某2f2某kfk(公式③),其中f1、f2、、fk分别叫做某1、某2、、某kn的权.“权”字含义有权衡轻重之意.fk越大,某k就越多,越重要.在计算加权平均数时,“权”还可以表示总体中的各种成分所占的比例,因此加权平均数中“权”通常有下列三种表现形式:整数的形式、比的形式、百分比的形式.请分别参照下面例题中的例2、3、4,体会加权平均数的计算方法.2.中位数一般地,将n个数据按大小(从小到大或从大到小)顺序排列,如果数据的个数为奇数,处于最中间位置的一个数据叫做这组数据的中位数;如果数据的个数为偶数,最中间的数据有两个,这两个最中间数据的平均数叫做这组数据的中位数.应注意:(1)中位数是一组数据的\分水岭\,它可能在这组数据中,也可能不在这组数据中.(2)在统计数据的个数时,相同的数据不能算作一个数据;(3)求一组数据的中位数时,一定要先按从小到大(或从大到小)的顺序将这组数据排列起来,并且注意这组数据的个数的奇偶性.3.众数一般地,一组数据中出现次数最多的那个数据叫做这组数据的众数.应注意:(1)一组数据可以有不止一个的众数,也可以没有众数:若一组数据中,有两个或两个以上(少于数据总数)个数据出现的次数最多,则这两个或两个以上数据都是这组数据的众数;如果一组数据中所有数据出现的次数相同,则这组数据没有众数.(2)一组数据可以有多个众数,但若一组数据若存在众数,则众数必在这组数据中.中位数、众数都能用来描述一组数据的集中程度,但是描述的角度不同.在特殊情况下,平均数、中位数、众数有可能是同一个数据.我们应当注意平均数、中位数、众数的合理选用,避免误用.三者的区别有:(1)平均数的大小与一组数据里每个数据都有关系,其中任何数据的变动都会相应引起平均数的变动.因此,平均数能较充分地反映一组数据的\平均水平\,但它容易受极端值的影响.当一组数据没有极端值时,一般选用平均数来描述\平均水平\.(2)中位数的大小仅与数据的排列位置有关,部分数据变动对中位数没有影响。
2021年江苏省常州市中考数学联赛试卷附解析

2021年江苏省常州市中考数学联赛试卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.已知抛物线21(4)33y x =--的部分图象如图所示,图象再次与x 轴相交时的坐标是( ) A .(5,0) B .(6,0) C .(7,0) D .(8,0)2. 如图,小红同学要用纸板制作一个高4cm ,底面周长是6πcm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )A .12πcm 2B .15πcm 2C .18πcm 2D .24πcm 2 3.某厂计划用两年的时间把某种型号的电视机成本降低36%,若每年下降的百分比相同,则这个百分比为( )A .16%B .18%C .20%D .22% 4.如图,在△ABC 中,AB =AC ,BC =BD ,AD =DE =EB ,则∠A 的度数是( )A .30°B .36°C .45°D .54° 5.在菱形ABCD 中,若∠ADC=120°,则BD :AC 等于( )A 2B 3C .1:2D :16.在□ABCD 中,对角线AC ,BD 的长分别为6和8,则边AB 的取值范围为( )A .2<AB<14B .1<AB<7C .1<AB<5D .2<AB<10 7.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根,那么k 的取值范围是( )A .k >14-B .k >14-且0k ≠C .k <14- D .14k ≥-且0k ≠ 8.已知(x -3)(x 2+mx+n )的乘积项中不含x 2和x 项,则m ,n 的值分别为( ) A .m=3,n=9 B .m=3,n=6 C .m=-3,n=-9 D .m=-3,n=9 9.游泳池里,男孩戴蓝游泳帽,女孩戴红游泳帽,在每个男孩看来,蓝帽与红帽一样多;在每个女孩看来,蓝帽是红帽的两倍,则男孩,女孩的人数分别为( )A .4 人,3 人B .3 人,4 人C .3 人,3 人D .4人,2人 10.如图所示,△DEF 是由边长为2 cm 的等边△ABC 平移3cm 得到的,则AD 为( )A .1 cmB .2 cmC .3 cmD .无法确定二、填空题11.一副象棋(共 32 个),全部正面朝下,小明任意模一颗,取到“车”的概率是 . 12.如图所示,一人拿着一把刻有厘米刻度的小尺,他站在距电线杆 30m 的地方,把手臂向前伸直,小尺竖直看到尺上 12 cm 恰好遮住电线杆,已知臂长 60 cm ,则电线杆的高为 .13.如图,∠E=∠F=90°,∠B=∠C ,AE=AF ,给出下列结论:①∠l=∠2;②BE=CF ;③△CAN ≌△ABM ;④CD=DN .其中正确的结论是 (将你认为正确的结论的序号都填上).14.如果把一根l00cm 长的铁丝折成一个面积为525cm 2的长方形,那么长方形的长为 ,宽为 .15.分解因式:=-a a 3 .16.在同一平面内直线m ,n 都和直线l 垂直,则直线m 与n 的位置关系是 .17.买6千克苹果,付出10元,找回3元4角,则每千克苹果的价格是_______元.18.地球上的海洋面积约为3.6×108 km 2 ,则这个数为 km 2.三、解答题19.如图,AB 、CD 是⊙O 的两条直径,过点A 作AE ∥CD 交⊙O 于点 E ,连结 BD 、DE ,求证:BD=DE .20.在四边形ABCD 中,∠A =∠B ,∠C =∠D ,且∠A ∶∠C =1∶2,求四边形ABCD 各内角的度数.21.如图所示,在□ABCD 中,对角线AC ,BD 交于点0,BD=2AD ,E ,F ,G 分别是OA ,OB ,DC 的中点.求证:(1)DE ⊥AC ;(2)EF=EG .22.已知43x a +=,274x b -=,并且22b b a ≤≤,求x 的取值范围,并把解集在数轴上表示出来.1126322x -≤≤23.用小数表示下列各数:(1)210-;(2)53.7510--⨯24.用科学记数法表示下列各数:(1)0.0000007;(2)0.000l006-25.先化简,再求值:(4)(2)(1)(3)x x x x ----+,其中52x =-.26.把大小为4×4的正方形方格图形分割成两个全等图形,如右图所示,请在下图中,沿着虚线再画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形27.如图直线AB 和CD 相交于点0,OE ⊥CD 于点0,OD 平分∠BOF ,∠BOE=50°,求∠AOC 、∠EOF 、∠AOF 的度数.28.丽水市为打造“浙江绿谷”品牌,决定在省城举办农副产品展销活动.某外贸公司推出品牌产品“山山牌”香菇、“奇尔”惠明茶共10 t 前往参展,用6辆汽车装运,每辆汽车规定满载,且只能装运一种产品;因包装限制,每辆汽车满载时能装香菇l .5 t 或茶叶2 t .问装运香菇、茶叶的汽车各需多少辆?29.如图,OD是∠AOB 的平分线,∠AOC=2∠BOC,∠COD=21°30′,求∠AOB的度数.30.将- 8 ,- 6 ,-4 , 0 , -2 ,2,4,6,8 这 9 个数分别填入右图的 9 个空格中,使得每行的 3 个数,每列的3 个数,斜对角线的 3 个数相加均为 0.【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.B3.C4.C5.B6.B7.B8.A9.A10.C二、填空题1812. 6 cm13.①②③14.35 cm ,15 cm15.)1)(1(-+a a a 16.平行17.1.118.360000000三、解答题19.∵AE ∥CD ,∴⌒AC = ⌒DE ,∵∠AOC=∠BOD ,∴⌒AC = ⌒BD ,DE=BD .20.60°,60°,120°,120°.21.(1)证明DO=AD ,E 是OA 的中点,则DE ⊥AC ;(2)由EF=12AB ,EG=12CD ,证明EF=EG 22.1126322x -≤≤23.(1) 0.01;(2)0.0000375-24.(1)7710-⨯;(2)41.00610--⨯25.811x -+,3126.略∠ADC=40°,∠EDF=130°,∠ADF=100°28.装运香菇、茶叶的汽车分别需要 4辆、2辆.29.设∠BOC=x,则∠AOC=2∠BOC=2x.因为 OD是∠AOB的平分线,∠COD= 21°30′,∴∠AOC-21°30′=∠BOC+21°30′,即2x-21°30′=x+21°30′,∴x=43°,∴∠AOB=3x=129°30.填法不唯一。
2021年江苏省徐州市中考数学联赛试卷附解析

2021年江苏省徐州市中考数学联赛试卷 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.下列图形中的角是圆周角的是( )2.若a 、b 分别表示圆中的弦和直径的长,则( )A .a>bB .a<bC . a=bD .a ≤b3.点A 、C 是反比例函数(0)k y k x=>图象上的两点,AB ⊥x 轴于点 B ,CD ⊥x 轴于点D. 若设 Rt △AOB 和 Rt △GOD 的面积分别为 S 1、S 2, 则( )A . S 1>S 2B . S 1=S 2C .S 1<S 2D .无法确定 4.小明3min 共投篮80次,进了50个球,则小明进球的频率是( )A .80B .50C .1.6D .0.625 5.如图,长方体的长为 15、为 10、高为 20,点B 离点 C 的距离为 5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是( )A . 5215B .25C . 1055+D .356.某种商品在降价x %后,单价为a 元,则降价前它的单价为( )A .%a xB .%a x ⋅C .1%a x -D .(1%)a x -7.如图,∠AOB=∠COD=90°,则∠AOC=∠B0D ,这是根据 ( )A .同角的余角相等B .直角都相等C .同角的补角相等D .互为余角的两个角相等8.下列各类项目中,所使用的“球”不属于球体的是( )A .足球B .乒乓球C .羽毛球D .篮球 9.下列方程中属于一元一次方程的是( ) A .x-y=3 B .-x+1=1 C .11x x += D .2210x x -+= 10.数a 没有平方根,则 a 的取值范围是( ) A .0a > B .0a ≥ C .0a < D .0a =二、填空题11. 掷一枚质地均匀的小正方体,它的六个面上分别标有数宇 1、2、3、4、5、6,则朝上一面的数字是小于 6 的概率是 .12.小明将一把钥匙放进自己家中的抽屉中,他记不清到底放进三个抽屉中的哪个抽屉里了,那么他一次选对的抽屉的概率是 . 13.二次函数y=x2+x-5取最小值时,自变量x的值是 . 14.如图,在正方形网格交点上找一点C ,使由A 、B 、C 三点构成的三角形与⊿ABO 相似,但不全等,则点C 的坐标是 .15.比较大小:65 73.(填“>、“=”或“<”)16.一个三角形的两边长分别为2、3,第三边长为x ,则周长y 与x 之何的函数解析式为 ,自变量x 的取值范围为 . 17.为美化校园,某班三个劳动小组在劳动课上栽花的株数分别为:10、x ,8. 已知这组数据只有一个众数且众数等于中位数,那么这组数据的平均数是 .18.如图,已知a ∥b ,∠1=70°,∠2=40°,则∠3= __________.19.12= ,12的相反数是 .三、解答题20.如图,PA 为⊙O 的切线,A 为切点,PBC 为过圆心0 的割线,PA=10cm ,PB =5cm ,求⊙11xy BA OO 的直径.21.已知抛物线2=++的图象经过A(0,1)、B(2,一1)两点.y x px q(1)求p、q的值;(2)试判断点 P(—1,2)是否在此函数图象上?22.画出如图所示的几何体的三视图.23.已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x轴交于点B(3,0).(1)求这两个函数的解析式;(2)画出它们图象.24.如图是斜拉桥的剖面图.BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB= AC.大桥建成以后,工程技术人员要对大桥质量进行验收,由于桥墩AD很高,无法直接测量钢绳AB、AC的长度.请你用两种方法检验AB、AC的长度是否相等,并说明理由.25.取出一张长方形的纸,沿一条对角线折叠,如图所示,问:重叠部分是一个什么三角形?并说明理由.26.一个三角形有两条边相等,它的最长的边比最短的边多2,已知这个三角形的周长为8,求它的三条边长.27.如图,射线OC和OD把平角AOB三等分,OE平分∠AOC,OF平分∠BOD.(1)求∠COD的度数;(2)写出图中所有的直角;(3)写出∠COD的所有余角和补角.28.已知某工厂从1997年到2002年每年的年产值和利润依次分别为(单位:万元):80,8;95,10;100,15;100,20;95,15;110,20列出该工厂从l997年到2002年产值和利润统计表.29.根据图给出的信息,求每件T恤衫和每瓶矿泉水的价格.30.四人做传数游戏,甲任报一个数给乙,乙把这个数加1 传给丙,丙再把接到的数平方后传给丁,丁把所接到的数减 1 后报出答案.(1)如泉甲所报的数为x,请把丁最后所报的答案用代数式表示出来;(2)若甲报的数为 9,则丁的答案是多少?(3)若丁报出的答案是 15,则甲传给乙的数是多少?【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.B2.D3.B4.D5.B6.C7.A8.C9.B10.C二、填空题5612. 1313. -1214.(2,5),(4,4)15.>16.y=x+5,l<x<517.283株或263株 18.70°19.21-,21-三、解答题20.连结 OA .设⊙O 的半径为r ,∵PA 为⊙O 的切线,PA=10 cm ,PB=5 cm.∴∠OPA=90°, OP= (r+5) cm ,∵22210(5)r r +=+,r=7.5 cm ,2r=15cm ,∴⊙O 的直径是 15.21.(1)p=-3,q=1(2)∵231y x x =-+,当1x =-时,13152y =+++≠,∴P 不在函数图象上.22.略(1)y=4x ,y=-2x+6;(2)图略24.方法一:测量BD 、ED 的长度,看是否相等;方法二:测量∠B 、∠C 的度数,看是否相等25.等腰三角形,说明∠ABD=∠C ′DB=∠BDC26.103,103,4327.(1)60° (2)∠DOE 与∠COF (2)∠COD 的余角:∠AOE 、∠EOC 、∠DOF 、∠FOB ;∠COD 的补角:∠AOD 、∠EOF 、∠BOC28.1997~2002年产值和利润统计表 单位:万元29.T 恤衫每件 20 元,矿泉水每瓶 2 元30.(1)2(1)1x +-;(2)若甲报的数为 9,则22(1)1(91)199x +-=+-=,即丁的答案是99;(3)若丁报出的答案是 15,则有2(1)115x +-=,2(1)16x +=,∴14x +=或14x +=-. ∴3x =或5x =-,故甲传给乙的数是3或-5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第一试)(2006年12月3日上午8:30—10:30)一、选择题(每小题8分,共64分)以下每个题的四个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.1.化简9x2– 6x + 1 – (3x– 5 )2,结果是( ).(A)6x– 6 (B) – 6x + 6 (C) – 4 (D) 42.使得关于x的一元二次方程2x(kx–4)–x2+6=0无实数根的最小整数k为( ).(A) – 1 (B) 2 (C)3 (D)4个3.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有().(A)1个(B)2个(C)4个(D)无穷多个4.如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为( ).(A)3 2 (B) 4 (C)2 3 (D)4 25.已知x,y,z为实数,若x2 + y2 = 1,y2 + z2 = 2,z2 + x2 = 2,则xy + yz + zx的最小值为( ).(A) 52(B)12+ 3 (C) –12(D)12– 36.在三角形ABC中,∠BAC=90°,AC= 3 ,AB=4,D为边BC上一点,∠CAD=30°,则AD的长为( ).(A) 65(B)75(C)85(D)957.如图,MN是⊙O的直径,若∠E=25°,∠PMQ=35°,则∠MQP=( ).(A)30°(B)35°(C)40°(D)50°8.如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b(a>0,b>0).若直线AB为一次函数y = kx + m的图象,则当ba是整数时,满足条件的整数k的值共有().(A)1个(B)2个(C)3个(D)4个二、填空题(每小题8分,共96分)9.在2006的中间嵌入一个数字得到五位数20口06,若此五位数能被7整除,则嵌入的数字口为.10.设有四个数,其中每三个数的和分别为24,36,28,32.则这四个数的平均数为.11.若a4 + b4 = a2– 2a2b2 + b2 + 6,则a2 + b2 = .12.如图,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD = 75°,则∠BDC = ,∠DBC = .13.若实数x,y满足70,3392;xy x yx y xyì+++=ïïíï+=+ïî则x2y + xy2= .14.如图,正六边形ABCDEF的边长为2 3 cm,点P为六边形内任一点.则点P 到各边距离之和为 cm .15.某人5次上班所用时间(单位:分钟)分别为a ,b ,8,9,10. 已知这组数据的平均数为9,方差为2,则| a – b | 的值为 .16.若整数m 使方程x 2 – mx + m + 2006 = 0 的根为非零整数,则这样的整数m 的个数为 .17.某次数学测验共有20题,每题答对得5分,不答得0分,答错得 –2分.若小丽这次测验得分是质数,则小丽这次最多答对 题.18.设5×4×3cm 3长方体的一个表面展开图的周长为n cm ,则n 的最小值是 .19.一个人把四根绳子紧握在手中,仅在两端露出它们的头和尾,然后随机地把一端的四个头中的某两个相接,另两个相接,把另一端的四个尾中的某两个相接,另两个相接,则放开手后四根绳子恰好连成一个圈的概率是 .20.有一个五边形ABCDE ,若把顶点A ,B ,C ,D ,E 涂上红、黄、绿三种颜色中的一种,使得相邻的顶点所涂的颜色不同,则共有 种不同的涂色方法.江苏省第二十一届初中数学竞赛(初三年级第一试)参考答案与评分标准一、选择题:(每题8分,共64分)题号 1 2 3 4 5 6 7 8 答案DBDADCCB二、填空题:(每题8分,共96分)9.0或7;10.10;11.3;12.12.5°;37.5°;13.6;.18;15.4;16.5个;17.17;18.50;19.23;20.30.说明:第9题与第12题填对一个得4分.江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第二试)(2006年12月24日 上午8:30—11:00)一、选择题(共6题,每题7分,共42分)以下每题的四个结论中,有且仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.1.若n n x 221+=+,2122--+=n n y ,其中n 为整数,则x 与y 的数量关系为( )(A )y x 4= (B )x y 4= (C )y x 12= (D )x y 12= 2.如图,AB 为半圆O 的直径,C 为半圆上一点,且∠COA =60°; 设扇形AOC 、△COB 、弓形B m C 的面积分别为1S ,2S ,3S , 则它们之间的大小关系是( ).(A ) 1S <2S <3S (B ) 2S <1S <3S (C ) 1S <3S <2S (D ) 3S <2S <1S3.设1x ,2x 是方程042=-+x x 的两个实数根,则1052231+-x x =( ). (A )-29 (B )-19 (C )-15 (D )-94.如图,正方形ABCD 中,E 为CD 的中点,EF ⊥AE , 交BC 于点F ,则∠1与∠2的大小关系为( ).(A )∠1>∠2 (B )∠1<∠2 (C )∠1=∠2 (D )无法确定5.方程y x y xy x 23322-=++的非负整数解(x ,y )的组数为( ).(A )0 (B )1 (C )2 (D )36.图示某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A 、B 、C 的机动车辆数如图所示,图中1x ,2x ,3x 分别表示该时段单位时间通过路段AB ⌒,BC ⌒,CA ⌒的机动车辆数 (假设单位时间内,在上述路段中,同一路段上驶入 与驶出的机动车辆数相等),则1x ,2x ,3x 的大小 关系为( ).(A )1x >2x >3x (B )1x >3x >2x(C )2x >3x >1x (D )3x >2x >1x二、填空题(共8题,每题7分,共56分)7.若p 和q 为质数,且9135=+q p ,则p = ,q = . 8.设x 、y 均为实数,代数式4284522++-+x xy y x 的最小值为 .9.某工件的形状如图所示,圆弧BC ⌒的度数为60°,AB =6cm , 点B 与点C 的距离等于AB ,∠BAC =30°,则此工件的面积 为 .10.设关于x 的一元二次方程04122=-++k kx x 有两个实数根,则k 的取值范围为 .11.在平行四边形ABCD 中,AM ⊥BC ,AN ⊥CD ,M 、N 为 垂足,若AB =13,BM =5,MC =9,则MN 的长度为 . 12.如图,用红,蓝,黄三色将图中区域A 、B 、C 、D 着色, 要求有公共边界的相邻区域不能涂相同的颜色,满足恰好A 涂蓝色的概率为 .13.如图,在直角三角形ABC 中,AB =3,BC =4,∠ABC =90°, 过B 作BA 1⊥AC ,过A 1作A 1B 1⊥BC ,得阴影直角三角形A 1B 1B ; 再过B 1作B 1A 2⊥AC ,过A 2作A 2B 2⊥BC ,得阴影直角三角形A 2B 2B 1; …,如此无限下去,请猜测这样得到的所有阴影三角形的面积之和 为 .14.在一个3×3的方格表中填有1~9这9个数字,现将每行中 数字最大的那个格子涂红色,数字最小的那个格子涂绿色.设M 为三个红色方格中数字最小的那个数,m 是三个绿色方格中数字 最大的那个数,则m M -可以有 个不同的值.三、解答题(共4题,每题13分,共52分).15.如图,直线OB 是一次函数x y 2=的图象,点A 的坐标为(0,2),在直线 OB 上找点C ,使得△AOC 为等腰三角形,求点C 的坐标.16.如图,ABCD 为正方形,⊙O 过正方形的顶点A 和对角线的交点P ,分别 交AB 、AD 于点F 、E .(1)求证:DE =AF .(2)若⊙O 的半径为23,AB =12+,求EDAE的值.17.在7×7的单位正方形的网格中,共有64个格点,有许多以这些格点为顶 点的正方形.这些正方形的面积有多少不同的值?18.k ,a ,b 为正整数,k 被2a 、2b 整除所得的商分别为m ,116+m . (1)若a ,b 互质,证明22b a -与2a 、2b 都互质; (2)当a ,b 互质时,求k 的值;(3)若a ,b 的最大公约数为5,求k 的值.江苏省第二十一届初中数学竞赛江苏省教育学会中学数学专业委员会主办单位:江苏教育出版社《时代数学学习》编辑部初三年级(第二试)参考答案1.A ;2.B ;3.B ;4.C ;5.C ;6.C ;7.17,2;8.3;9.6π2cm ;10.212212+≤-≥k k或;11.13180;12.31;13.4196;14.8; 15.四个点),)、(,)、,)、,121554552(554552(51658(--;16.(1)略;(2)222或.17.18个不同的面积,边长19种但有两种面积是一样的25; 18.(1)略;(2)k =176400;(3) k =4410000.。
