江苏省第十六届初中数学竞赛试题(初三年级)及答案
第十六届江苏省初中数学竞赛(C卷)
,
方 l x8 鬟 x7 解 程 + += x +的 是
-
。,_。_______。 。__。_。_一
1 . 使 2 +2 O要 6 +2 为 完 全 平 方 数 , 么 , 负 那 非
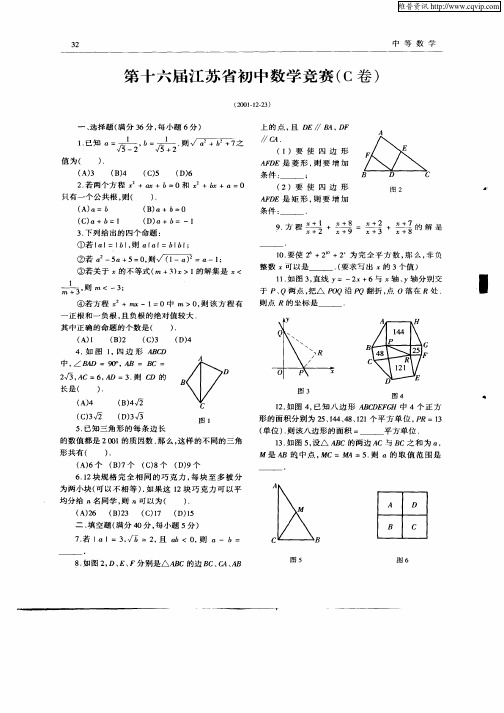
整数 可 以是— — .要求 写 出 的 3 值 ) ( 个 1 . 图 3 直线 Y=一2 1如 , x+6与 轴 、 Y轴 分 别交 于 P、 Q两 点 , △ t p沿 把 o
则 点 尺 的 坐 标 是
则 m< 一3 ;
翻折 , O落 在 R处 . 点
④若 方程 +眦 一1 =0中 m >0, 该 方 程 有 则
一
正 根 和一负 根 , 负根 的绝 对值 较 大 . 且 ) .
( 4 D)
G
其 中正确 的命 题 的个数 是 (
( ) AI ( ) B2 ( ) C3
( ) 三( ) 共 5 1初 1班 7人 , 人 需 要 1本 A种 练 习 每
本, 则该 班集 体去 买 时 , 最少 需付 多 少元 ?
( ) 三年 级 共 2 7人 , 人需 要 1本 A种 练 习 2初 2 每
8 ( ) D平 分 B C, A .1A A 或 D上 E 或 ・ ・ F. ・ ; … ( ) B C: 0 , … … . 2 A 9  ̄ 或
4. 图 I 四 边 形 A C 如 , BD 中 , B D = 9 ̄ 仙 = A 0, =
D
F。
2 3, C:6 A =3 则 C 的 4 A , D - D
长是( ) . ( 4 B) ( 33 D) √
曰
图 3
图
4
( 4 A) ( ) √ C3 2
块小的.
第十六届江苏省初中数学竞赛(C卷)

第十六届江苏省初中数学竞赛(C卷)
佚名
【期刊名称】《《中等数学》》
【年(卷),期】2002(000)004
【摘要】一、选择题 (满分 36分 ,每小题 6分 )1.已知a =15 - 2 ,b =15 + 2 .则a2 +b2 + 7之值为 ( ) .(A) 3 (B) 4 (C) 5 (D) 62 .若两个方程x2 +ax +b =0和x2 +bx +a =0只有一个公共根 ,则 ( ) .(A)a =b (B)a +b
=0(C)a +b =1(D)a +b =- 13.
【总页数】3页(P32-34)
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.第十届江苏省高等数学竞赛专科试题评析 [J], 陆健
2.江苏省初中数学竞赛系列培训:浅谈数学竞赛中选择题的解法 [J], 周立元
3.第十六届“五羊杯”初中数学竞赛试题解答 [J], 吴康;尤利华
4.第十六届“五羊杯”初中数学竞赛获奖名单 [J], 无
5.第十届江苏省初中数学竞赛试题及参考解答 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
江苏数学竞赛试题及答案

江苏数学竞赛试题及答案【试题一】题目:求证:对于任意正整数\( n \),\( 1^2 + 2^2 + 3^2 +\ldots + n^2 = \frac{n(n + 1)(2n + 1)}{6} \)。
【答案】证明:我们使用数学归纳法来证明这个等式。
1. 当\( n = 1 \)时,左边为\( 1^2 = 1 \),右边为\( \frac{1\cdot 2 \cdot 3}{6} = 1 \),等式成立。
2. 假设当\( n = k \)时等式成立,即\( 1^2 + 2^2 + 3^2 + \ldots + k^2 = \frac{k(k + 1)(2k + 1)}{6} \)。
3. 当\( n = k + 1 \)时,我们需要证明\( 1^2 + 2^2 + 3^2 +\ldots + k^2 + (k + 1)^2 = \frac{(k + 1)(k + 2)(2k + 3)}{6} \)。
4. 根据假设,将\( k \)的和代入,得到\( \frac{k(k + 1)(2k + 1)}{6} + (k + 1)^2 \)。
5. 简化上述表达式,我们得到\( \frac{(k + 1)(k + 2)(2k + 3)}{6} \),这正是我们需要证明的等式。
6. 因此,根据数学归纳法,对于任意正整数\( n \),等式成立。
【试题二】题目:已知函数\( f(x) = x^3 - 3x^2 + 2 \),求\( f(x) \)的极值。
【答案】解:首先求导得到\( f'(x) = 3x^2 - 6x \)。
令\( f'(x) = 0 \),解得\( x = 0 \)或\( x = 2 \)。
1. 当\( x < 0 \)或\( x > 2 \)时,\( f'(x) > 0 \),函数\( f(x) \)在此区间单调递增。
2. 当\( 0 < x < 2 \)时,\( f'(x) < 0 \),函数\( f(x) \)在此区间单调递减。
初三数学竞赛考试试题及答案

初三数学竞赛考试试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.14159B. 0.333...C. πD. √22. 如果一个直角三角形的两个直角边分别为3和4,那么斜边的长度是多少?A. 5B. 6C. 7D. 83. 一个数的立方根是2,这个数是多少?A. 2B. 4C. 8D. 164. 一个圆的半径是5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π5. 一个数的相反数是-3,这个数是多少?A. 3B. -3C. 6D. -66. 一个数的绝对值是5,这个数可能是?A. 5B. -5C. 5或-5D. 07. 如果一个二次方程的解是x1=2和x2=3,那么这个方程可以表示为?A. x^2 - 5x + 6 = 0B. x^2 - 5x + 4 = 0C. x^2 + 5x - 6 = 0D. x^2 + 5x + 4 = 08. 一个数列的前三项是2, 4, 6,这是一个什么数列?A. 等差数列B. 等比数列C. 等比数列D. 既不是等差也不是等比数列9. 一个长方体的长、宽、高分别是2, 3, 4,那么它的体积是多少?A. 24B. 26C. 28D. 3210. 一个分数的分子是3,分母是6,化简后是多少?A. 1/2B. 2/3C. 3/6D. 1/3二、填空题(每题4分,共20分)11. 一个数的平方根是4,这个数是_________。
12. 一个数的平方是16,这个数是_________。
13. 一个数的立方是27,这个数是_________。
14. 一个数的倒数是2/3,这个数是_________。
15. 一个数的对数(以10为底)是2,这个数是_________。
三、解答题(每题10分,共50分)16. 解一个一元二次方程:x^2 - 7x + 10 = 0。
17. 证明:对于任意实数a和b,(a + b)^2 ≤ 2(a^2 + b^2)。
江苏省历年初中数学竞赛试题及解答(23份)

第十五届江苏省初中数学竞赛试题初一年级第一试 (1)第十五届江苏省初中数学竞赛试卷初一年级 第二试 (3)江苏省第十五届初中数学竞赛初二第1试试题 (6)江苏省第十五届初中数学竞赛初二年级 第二试 (8)江苏省第十五届初中数学竞赛初三年级 (14)2001年第十六届江苏省初中数学竞赛A 卷 (19)2001年第十六届江苏省初中数学竞赛B 卷 (24)第十六届江苏省初中数学竞赛试题(C 卷)初三年级 (29)江苏省第十七届初中数学竞赛 初一年级 第l 试 (33)江苏省第十七届初中数学竞赛试卷 初一年级(第2试) (35)江苏省第十七届初中数学竞赛 初二年级 第l 试 (38)江苏省第十七届初中数学竞赛试卷 初二年级(第2试) (40)江苏省第十七届初中数学竞赛试卷 初三年级 (43)江苏省第十八届初中数学竞赛初一年级第1试 (46)2003年江苏省第十八届初中数学竞赛初中一年级 第2试 (48)2003年江苏省第十八届初中数学竞赛初中二年级 第2试 (52)2003年江苏省第十八届初中数学竞赛初中三年级 (57)江苏省第十九届初中数学竞赛初一年级 第1试 (60)江苏省第十九届初中数学竞赛初二年级第1试 (62)江苏省第十九届初中数学竞赛试卷初二年级第2试 (65)江苏省第十九届初中数学竞赛初三年级(第1试) (71)江苏省第十九届初中数学竞赛(保留)初三年级第l 试 (73)江苏省第十九届初中数学竞赛试题与答案初三年级(第2试) (80)第十五届江苏省初中数学竞赛试题初一年级第一试一、选择题(每小题7分,共56分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内)1.在-|-3|3,-(-3)3,(-3)3,-33中,最大的是( ).(A)-|-3|3 (B)-(-3)3 (C)(-3)3 (D)-332. “a 的2倍与b 的一半之和的平方,减去a 、b 两数平方和的4倍”用代数式表示应为( )(A)2a+(21b 2)-4(a+b)2 (B)(2a+21b)2-a+4b 2 (c)(2a+21b)2-4(a 2+b 2) (D)(2a+21b)2-4(a 2+b 2)2 3.若a 是负数,则a+|-a|( ),(A)是负数 (B)是正数 (C)是零 (D)可能是正数,也可能是负数4.如果n 是正整数,那么表示“任意负奇数”的代数式是( ).(A)2n+l (B)2n-l (C)-2n+l (D)-2n-l5.已知数轴上的三点A 、B 、C 分别表示有理数a 、1、-l ,那么|a+1|表示( ).(A)A 、B 两点的距离 (B)A 、C 两点的距离(C)A 、B 两点到原点的距离之和(D)A 、C 两点到原点的距离之和6.如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且d-2a =10,那么数轴的原点应是( ).(A)A 点 (B)B 点 (C)C 点 (D)D 点7.已知a+b =0,a≠b ,则化简a b (a+1)+ba (b+1)得( ). (A)2a (B)2b (C)+2 (D)-28.已知m<0,-l<n<0,则m ,mn ,mn 2由小到大排列的顺序是 ( ).(A)m ,mn ,mn 2 (B)mn ,mn 2,m (C)mn 2,mn ,m (D)m ,mn 2,mn二、填空题(每小题?分,共84分)9.计算:31a -(21a -4b -6c)+3(-2c+2b)= 10.计算:0.7×194+243×(-15)+0.7×95+41×(-15)= ll.某班有男生a(a>20)人,女生20人,a-20表示的实际意义是12.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是13.下表中每种水果的重量是不变的,表的左边或下面的数是所在行或所在列水果的总重量,0.25,则正确结果应是 .15.在数轴上,点A 、B 分别表示-31和51,则线段AB 的中点所表示的数是 . 16.已知2a x b n-1与-3a 2b 2m (m 是正整数)是同类项,那么(2m-n)x =17.王恒同学出生于20世纪,他把他出生的月份乘以2后加上5,把所得的结果乘以50后加上出生年份,再减去250,最后得到2 088,则王恒出生在 年 月.18.银行整存整取一年期的定期存款年利率是2.25%,某人1999年12月3日存入1 000元,2000年12月3日支取时本息和是 元,国家利息税税率是20%,交纳利息税后还有 元.19.有一列数a 1,a 2,a 3,a 4,…,a n ,其中a 1=6×2+l ;a 2=6×3+2;a 3=6×4+3;a 4=6×5+4;则第n 个数a n = ;当a n =2001时,n = .20.已知三角形的三个内角的和是180°,如果一个三角形的三个内角的度数都是小于120的质数,则这个三角形三个内角的度数分别是第十五届江苏省初中数学竞赛参考答案初一年级第一试一、1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.D二、9.一6a +1 06. 10.一43.6. 11.男生比女生多的人数.1 2.90. 1 3.1 6. 1 4.0.1 2 5. 1 5.-151 1 6.1. 1 7.1988;1.18.1022.5;101 8.1 9.7n+6;2 8 5.2 O .2,8 9,8 9或2,7 1,1 07(每填错一组另扣2分).第十五届江苏省初中数学竞赛试卷初一年级 第二试一、选择题1.已知x=2是关于x 的方程3x-2m=4的根,则m 的值是( )(A)5 (B)-5 (C)1 (D)-12.已知a+2=b-2=2c =2001,且a+b+c=2001k ,那么k 的值为( )。
初中数学竞赛试题及答案doc

初中数学竞赛试题及答案doc一、选择题(每题3分,共15分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个数的平方等于16,那么这个数是多少?A. 4B. -4C. 4 或 -4D. 2答案:C3. 一个直角三角形的两条直角边分别为3和4,斜边的长度是多少?A. 5B. 6C. 7D. 8答案:A4. 一个数的立方等于-27,这个数是多少?A. -3B. 3C. -27D. 27答案:A5. 一个数的倒数等于它自身,这个数是?A. 1B. -1C. 0D. 都不是答案:B二、填空题(每题2分,共10分)6. 一个数的绝对值是5,这个数可能是_________。
答案:±57. 如果一个数的平方根是2,那么这个数是_________。
答案:48. 一个数的立方根是3,那么这个数是_________。
答案:279. 一个分数的分子是7,分母是14,化简后是_________。
答案:1/210. 一个数的相反数是-5,那么这个数是_________。
答案:5三、解答题(每题5分,共20分)11. 证明:如果一个三角形的两边之和大于第三边,那么这个三角形是存在的。
证明:根据三角形不等式定理,对于任意三角形ABC,有AB + BC > AC,AC + BC > AB,AB + AC > BC。
如果已知AB + BC > AC,则满足三角形的构造条件,因此这样的三角形是存在的。
12. 计算:(2x - 3)(x + 4)。
解:根据多项式乘法法则,我们有(2x - 3)(x + 4) = 2x^2 + 8x - 3x - 12 = 2x^2 + 5x - 12。
13. 解方程:2x + 5 = 11。
解:首先将5移到等式右边,得到2x = 11 - 5,即2x = 6。
然后将2除到等式右边,得到x = 6 / 2,即x = 3。
14. 一个长方形的长是宽的两倍,如果长增加2米,宽增加1米,面积增加了15平方米,求原长方形的长和宽。
江苏数学竞赛初中试题及答案

江苏数学竞赛初中试题及答案试题一:代数基础题题目:已知 \( a \) 和 \( b \) 是两个正整数,且 \( a^2 - b^2 = 21 \),求 \( a \) 和 \( b \) 的值。
答案:根据差平方公式,\( a^2 - b^2 = (a+b)(a-b) \)。
已知\( a^2 - b^2 = 21 \),我们可以将21分解为两个因数的乘积,即\( 21 = 3 \times 7 \)。
考虑到 \( a \) 和 \( b \) 是正整数,我们可以得出 \( a = 7 \),\( b = 3 \)。
试题二:几何题题目:在一个直角三角形中,如果一个锐角是另一个锐角的两倍,求这个三角形的三个角度数。
答案:设较小的锐角为 \( x \) 度,则较大的锐角为 \( 2x \) 度。
根据直角三角形的性质,三个角的和为180度,因此有 \( x + 2x + 90 = 180 \)。
解这个方程,我们得到 \( 3x = 90 \),所以 \( x = 30 \)。
因此,较小的锐角是30度,较大的锐角是60度,直角是90度。
试题三:数列题题目:一个数列的前三项为 \( 2, 4, 7 \),从第四项开始,每一项都是前三项的和。
求第10项的值。
答案:根据题意,数列的前几项为:2, 4, 7, (2+4+7), (4+7+13), ...即:2, 4, 7, 13, 24, 41, 75, 130, 231, ...第10项的值为 \( 231 \)。
试题四:逻辑推理题题目:有5个盒子,每个盒子里都装有不同数量的球,分别是1个,2个,3个,4个和5个。
现在有5个人,每个人从每个盒子里都拿了一个球,但没有人拿到两个相同数量的球。
每个人拿的球的总数都是6个。
问每个人分别从哪些盒子里拿球?答案:设5个人分别为A、B、C、D、E。
根据题意,每个人拿的球的总数都是6个,且没有人拿到两个相同数量的球。
我们可以列出以下可能的组合:- A: 1, 2, 3- B: 1, 3, 4- C: 1, 4, 5- D: 2, 3, 5- E: 2, 4由于每个人拿的球的总数都是6个,我们可以排除E的组合,因为2+4=6,没有第三个球。
初三数学竟赛试题及答案

初三数学竟赛试题及答案初三数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2B. πC. 0.5D. √42. 一个数的立方等于它本身,这个数是:A. 0B. 1C. -1D. 0, 1, -13. 如果一个三角形的两边长分别为3和4,第三边长x满足的条件是:A. 1 < x < 7B. 0 < x < 7C. 1 < x < 5D. 0 < x < 54. 一个圆的直径是10cm,那么它的半径是:A. 5cmB. 10cmC. 20cmD. 15cm5. 一个数的相反数是它本身,这个数是:A. 0B. 1C. -1D. 任意数6. 一个数的绝对值是它本身,这个数是:A. 0B. 正数C. 负数D. 0或正数7. 一个数的倒数是它本身,这个数是:A. 1B. -1C. 0D. 1或-18. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 0, 1, -19. 一个数的立方根是它本身,这个数是:A. 0B. 1C. -1D. 0, 1, -110. 一个数的平方是它本身,这个数是:A. 0B. 1C. -1D. 0, 1二、填空题(每题4分,共20分)11. 如果一个数的平方是25,那么这个数是______。
12. 一个数的绝对值是5,那么这个数是______。
13. 一个数的倒数是1/2,那么这个数是______。
14. 一个数的平方根是3,那么这个数是______。
15. 一个数的立方根是2,那么这个数是______。
三、解答题(每题10分,共50分)16. 计算:(3+2√2)(3-2√2)。
17. 证明:对于任意实数a和b,(a+b)^2 = a^2 + 2ab + b^2。
18. 已知一个等腰三角形的两边长分别为5和8,求第三边的长度。
19. 一个圆的面积是π,求这个圆的半径。
20. 解方程:x^2 - 5x + 6 = 0。
江苏省第十六届初中数学竞赛试题(初三年级)及答案

1 / 4江苏省第十六届初中数学竞赛试题(初三年级)一、选择题(6×6=36分)1. 已知5252a b ==-+227a b ++的值为 (A )3 (B )4 (C )5 (D )62. 若两个方程20x ax b ++=和20x bx a ++=,则( )(A )a b = (B )0a b += (C )1a b += (D )1a b +=-3. 下列给出四个命题:命题1 若||||a b =,则||||a a b b =;命题2 若2550a a -+=2(1)1a a -=-;命题3 若关于x 的不等式(3)1m x +>的解集是13x m <+,则3m <-; 命题4 若方程210x mx +-=中0m >,则该方程有一正根和一负根,且负根的绝对值较大。
其中正确的命题个数是( )(A )1 (B )2 (C )3 (D )44. 如图,四边形ABCD 中,∠BAD=90°,AB=BC=23AC=6,AD=3,则CD 的长是( )(A )4 (B )42(C )32(D ) 335.已知三角形的每条边长的数值都是2001的质因数那么这样的三角形共有( )(A )6个 (B )7个 (C )8个 (D )9个6.12块规格完全相同的巧克力,每块至多被分为两小块(可以不相等)。
如果 这12 块巧克力可以平均分给n 名同学,则n 可以为( )(A )26 (B )23 (C )17 (D )15二、填空题(5×8=40分)7.若||2a b ==,且0ab <,则a b -= .8.如图,D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点且DE ∥BA ,DF ∥CA 。
(1) 要使四边形AFDE 是菱形,则要增加条件:____________________________(2) 要使四边形AFDE 是矩形,则要增加条件:____________________________第4题 第8题2 / 49.方程18272938x x x x x x x x +++++=+++++的解是 . 10.要使610222x ++为完全平方数,那么非负数x 可以是____________。
数学竞赛试卷初三答案

一、选择题(每题5分,共20分)1. 下列各数中,不是有理数的是()A. -√2B. 1/2C. √9D. 0.25答案:A2. 下列方程中,解集为全体实数的是()A. x^2 + 1 = 0B. x^2 - 1 = 0C. x^2 + 2x + 1 = 0D. x^2 - 2x + 1 = 0答案:D3. 若a,b,c成等差数列,且a + b + c = 0,则b的值是()A. 0B. 1C. -1D. 不存在答案:C4. 已知正方形的对角线长为√2,则它的面积是()A. 1B. 2C. √2D. 2√2答案:B5. 下列函数中,是奇函数的是()A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^4答案:C二、填空题(每题5分,共25分)6. 若a,b,c成等差数列,且a + b + c = 12,则b的值是______。
答案:47. 已知等差数列{an}的首项为a1,公差为d,若a1 + a2 + a3 = 9,则a4 + a5 + a6 =______。
答案:278. 若a,b,c成等比数列,且a + b + c = 12,ab + bc + ca = 36,则b的值是______。
答案:49. 已知正方形的对角线长为√10,则它的面积是______。
答案:2510. 若函数f(x) = ax^2 + bx + c在x = 1时取得最小值,则a的值是______。
答案:-1三、解答题(每题10分,共30分)11. 已知等差数列{an}的首项为a1,公差为d,若a1 + a2 + a3 = 9,求a4 + a5 + a6的值。
解:由等差数列的性质可知,a2 = a1 + d,a3 = a1 + 2d。
将a1 + a2 + a3 = 9代入,得a1 + (a1 + d) + (a1 + 2d) = 9,即3a1 + 3d = 9。
化简得a1 + d = 3。
初中数学竞赛试题及答案pdf

初中数学竞赛试题及答案pdf一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333...(3无限循环)B. √2C. 3.14D. 1/32. 一个数的平方等于它本身,这个数是?A. 0B. 1C. -1D. 0或13. 如果一个等腰三角形的底边长为6,高为4,那么它的周长是多少?A. 12B. 14C. 16D. 184. 一个数列的前三项是2,4,8,那么第四项是多少?A. 16B. 32C. 64D. 1285. 一个圆的半径是5,那么它的面积是多少?A. 25πC. 75πD. 100π6. 下列哪个图形的面积是最大的?A. 边长为4的正方形B. 半径为4的圆C. 长为6,宽为4的矩形D. 底边为6,高为4的等腰三角形7. 如果一个数的绝对值是5,那么这个数可能是?A. 5B. -5C. 5或-5D. 08. 一个数的相反数是-3,那么这个数是?A. 3B. -3C. 0D. 69. 一个数的倒数是1/4,那么这个数是?A. 4B. 1/4C. 1/2D. 210. 下列哪个表达式的值是最小的?A. 5 - 3B. 5 + 3D. 5 ÷ 3二、填空题(每题4分,共20分)11. 一个数的立方等于-8,这个数是______。
12. 如果一个直角三角形的两条直角边长分别是3和4,那么它的斜边长是______。
13. 一个数的平方根是2,那么这个数是______。
14. 如果一个数除以3的商是5,那么这个数是______。
15. 一个圆的直径是10,那么它的周长是______。
三、解答题(每题10分,共50分)16. 一个等差数列的前三项分别是3,7,11,求这个数列的第10项。
17. 一个长方形的长是宽的两倍,且周长是24,求这个长方形的面积。
18. 一个三角形的内角和是多少?19. 一个数的平方加上这个数本身等于0,求这个数。
20. 一个圆的半径增加2,那么它的面积增加了多少?答案一、选择题1. B2. D3. C4. B5. C6. B7. C8. A9. A 10. A二、填空题11. -2 12. 5 13. 4 14. 15 15. 31.4三、解答题16. 第10项是31。
初三数学竞赛试题及答案

初三数学竞赛试题及答案一、选择题(每题5分,共30分)1. 下列哪个数是无理数?A. 2.5B. πC. 0.33333...D. -12. 若a、b、c是三角形的三边长,且满足a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定3. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 以上都不是4. 某工厂生产的产品数量y与时间x(小时)成正比,已知2小时生产了40个产品,那么4小时生产的产品数量是:A. 80B. 100B. 120D. 1605. 一个圆的半径是5,那么这个圆的面积是:A. 25πB. 50πC. 75πD. 100π6. 下列哪个是二次根式的化简结果?A. \(\sqrt{48}\)B. \(\sqrt{64}\)C. \(\sqrt{81}\)D. \(\sqrt{144}\)二、填空题(每题4分,共20分)1. 一个数的立方根是2,这个数是________。
2. 若一个等差数列的第3项是10,第5项是14,那么这个等差数列的公差是________。
3. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么这个长方体的体积是________cm³。
4. 一个多项式\(ax^2 + bx + c\)的系数a、b、c满足\(a + b + c = 6\),且\(a - b + c = 0\),那么\(2a - 2b + 2c\)的值是________。
5. 若一个二次方程\(x^2 - 4x + 4 = 0\),那么这个方程的判别式Δ是________。
三、解答题(每题15分,共50分)1. 已知一个直角三角形的两条直角边分别为3和4,求这个直角三角形的斜边长。
2. 一个水池的底部有一个排水口,水池的容积是100立方米。
如果打开排水口,水池的水在2小时内可以排完。
现在同时打开排水口和进水口,进水口每小时可以注入20立方米的水。
江苏省第十六届初中数学竞赛试题(初三)(有答案)-初中三年级数学试题练习、期中期末试卷-初中数学试卷

江苏省第十六届初中数学竞赛试题(初三)(有答案)-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载江苏省第十六届初中数学竞赛试题(初三年级)一、选择题(6×6=36分)1.已知,则的值为(A)3(B)4(C)5(D)62. 若两个方程和,则()(A)(B)(C)(D)3.下列给出四个命题:命题1若,则;命题2若,则;命题3若关于的不等式的解集是,则;命题4若方程中,则该方程有一正根和一负根,且负根的绝对值较大。
其中正确的命题个数是()(A)1(B)2(C)3(D)44.如图,四边形ABCD中,∠BAD=90°,AB=BC=,AC=6,AD=3,则CD的长是()(A)4(B)(C)(D)5.已知三角形的每条边长的数值都是2001的质因数那么这样的三角形共有()(A)6个(B)7个(C)8个(D)9个6.12块规格完全相同的巧克力,每块至多被分为两小块(可以不相等)。
如果这12 块巧克力可以平均分给名同学,则可以为()(A)26(B)23(C)17(D)15二、填空题(5×8=40分)7.若,且,则.8.如图,D、E、F分别是∠ABC的边BC、CA、AB上的点且DE∠BA,DF∠CA。
(1)要使四边形AFDE是菱形,则要增加条件:____________________________(2)要使四边形AFDE是矩形,则要增加条件:____________________________9.方程的解是.10.要使为完全平方数,那么非负数可以是____________。
(要求写出的3个值)11.如图,直线与轴、轴分别交于P、Q两点,把∠POQ沿PQ翻折,点O落在R处,则点R 的坐标是_____________。
12.如图,已知八边形ABCDEFGH中4个正方形的面积分别为25、144、48、121平方单位,PR=13(单位),则该形的面积=___________平方单位。
江苏中学竞赛试题答案

江苏中学竞赛试题答案江苏省中学数学竞赛试题一、选择题(每题4分,共40分)1. 若一个等差数列的首项为3,公差为5,那么它的第10项是多少?A. 53B. 55C. 57D. 592. 已知一个圆的半径为7cm,求这个圆的面积(圆周率取3.14)。
A. 153.86平方厘米B. 149.96平方厘米C. 154.96平方厘米D. 150.86平方厘米3. 下列哪个分数是最简分数?A. 六分之四B. 三分之二C. 九分之三D. 十一分之五4. 若a、b、c是等比数列,且a+b+c=6,abc=8,则b的值为:A. 2B. 1C. 4D. 无法确定5. 一个长方体的长、宽、高分别是5cm、3cm、2cm,求它的体积。
A. 30立方厘米B. 15立方厘米C. 10立方厘米D. 20立方厘米6. 已知函数f(x) = x^2 - 3x + 2,求f(4)的值。
A. 8B. 10C. 6D. 27. 一个等腰三角形的底边长为6cm,两腰边长相等,且周长为18cm,求腰边的长度。
A. 6cmB. 4.5cmC. 3cmD. 无法确定8. 已知一个二次函数y = ax^2 + bx + c的顶点坐标为(2, -3),且经过点(0, 1),求a、b、c的值。
A. a=1, b=-5, c=1B. a=1, b=-3, c=-1C. a=-1, b=5, c=1D. a=-1, b=3, c=-19. 一个圆的直径是14cm,求这个圆的周长(圆周率取3.14)。
A. 43.96厘米B. 28.26厘米C. 43.98厘米D. 28.28厘米10. 若a、b、c是等差数列,且a+b+c=9,a^2+b^2+c^2=29,求b的值。
A. 2B. 3C. 4D. 无法确定二、填空题(每题5分,共20分)11. 一个等比数列的前三项分别是2,6,_______,求它的公比。
12. 已知一个三角形的三个内角分别是60°、45°、_______°。
初三数学竞赛试题及答案

初三数学竞赛试题及答案一、选择题1. 已知平面内一直线L的倾斜角为α,斜率为k,若点A(-1,2)在L 上,则直线L的方程为:A. y-2 = k(x+1)B. y+2 = k(x-1)C. y-2 = k(x-1)D. y+2 = k(x+1)答案:A2. 若函数f(x) = ax^2 + bx + c 是一个减函数,那么a, b, c的关系是:A. a > 0, b > 0, c > 0B. a > 0, b < 0, c < 0C. a < 0, b < 0, c < 0D. a < 0, b > 0, c > 0答案:D3. 已知等差数列{an}的公差为d,首项为a1,末项为an,且an =3a1,若a4 = 7,则d的值是:A. 1B. 2C. 3D. 4答案:B4. 在ΔABC中,∠A=60°,AC=2AB,则∠B的度数为:A. 40°B. 50°C. 60°D. 70°答案:D5. 若直角三角形的两直角边分别为3和4,求斜边的长度是:A. 5B. 6C. 7D. 8答案:A二、填空题1. 已知ABC是一个等边三角形,AB的边长为5,则三角形ABC 的面积为______。
答案:(25√3)/42. 若一组数据中50%的数据小于等于10,25%的数据大于15,中位数为12,则这组数据的总个数为______。
答案:83. 若甲数是乙数的8倍,且甲数减去乙数等于30,则甲数的绝对值为______。
答案:404. 已知某数的60%等于120,这个数是______。
答案:2005. 若甲数是乙数的1/5,乙数是丙数的1/3,则甲数与丙数之和的三倍为______。
答案:28三、解答题1. 一条细长导线的电阻率R为ρ,长度为l,截面积为A。
如果将导线的长度翻倍,截面积减半,则新的导线的电阻率是多少?答:R2. 已知函数f(x)满足f(x+1) = 2f(x) - 1,且f(2) = 3,求f(5)的值。
初三数学竞赛试题及答案

初三数学竞赛试题及答案一、选择题(每题5分,共30分)1. 下列哪个数是无理数?A. 3.14159B. √2C. 0.33333D. π答案:B2. 一个数的立方等于该数本身,这个数是?A. 1B. -1C. 0D. 1或-1或0答案:D3. 如果一个三角形的两边长分别为3和4,那么第三边的长可能是?A. 1B. 7C. 5D. 以上都有可能答案:C4. 一个数列的前三项是2,4,8,那么第四项是?A. 16B. 32C. 64D. 128答案:A5. 一个圆的直径是10,那么它的面积是?A. 25πB. 50πC. 100πD. 200π答案:C6. 一个等腰三角形的底边长为6,腰长为5,那么它的高是?A. 4B. 3C. 2D. 1答案:B二、填空题(每题5分,共30分)1. 一个数的平方等于9,这个数是______。
答案:±32. 一个矩形的长是宽的两倍,如果宽是4,那么面积是______。
答案:323. 一个等差数列的前三项是2,5,8,那么第10项是______。
答案:274. 一个二次函数的顶点是(0, -1),且通过点(1, 2),那么它的解析式是______。
答案:y = x^2 - x - 15. 一个圆的半径是5,那么它的周长是______。
答案:10π6. 一个直角三角形的两条直角边长分别为3和4,那么斜边长是______。
答案:5三、解答题(每题10分,共40分)1. 已知一个等比数列的前三项分别是1,2,4,求该数列的第10项。
答案:第10项是1024。
2. 一个矩形的长是宽的三倍,如果宽是5,求矩形的面积。
答案:矩形的面积是75。
3. 一个二次函数的图像通过点(-2, 10)和(1, 5),且顶点在y轴上,求该二次函数的解析式。
答案:二次函数的解析式为y = -x^2 + 4x + 6。
4. 一个直角三角形的两条直角边长分别为6和8,求该三角形的斜边长和面积。
初三竞赛数学试题及答案

初三竞赛数学试题及答案一、选择题(每题5分,共30分)1. 若a,b,c是三角形的三边长,且满足a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定2. 已知x^2 - 5x + 6 = 0,求x的值:A. 2, 3B. -2, 3C. -3, 2D. 1, 43. 一个圆的半径为r,若圆的周长为2πr,则圆的面积是:A. πr^2B. 2πrC. πrD. r^24. 函数y = 3x - 2的图象与x轴交点的坐标是:A. (0, -2)B. (2/3, 0)C. (0, 0)D. (2, -3)5. 若一个数的平方根等于它本身,那么这个数是:A. 0B. 1C. -1D. 0或16. 已知一个长方体的长、宽、高分别是a、b、c,那么它的对角线的长度是:A. √(a^2 + b^2)B. √(a^2 + b^2 + c^2)C. √(a^2 + b^2 + c)D. √(a + b + c)二、填空题(每题5分,共20分)1. 一个数的立方根是它本身,这个数可以是______。
2. 一个数的绝对值是它本身,这个数是______。
3. 一个数的相反数是它本身,这个数是______。
4. 一个数的倒数是它本身,这个数是______。
三、解答题(每题10分,共50分)1. 已知一个等差数列的首项a1=2,公差d=3,求这个数列的前10项的和。
2. 解不等式:2x - 5 > 3x - 1。
3. 证明:对于任意正整数n,n^3 - n^2 - n + 1能被6整除。
4. 已知一个直角三角形的两条直角边长分别是6和8,求斜边的长度。
5. 一个圆的半径为5,求圆的内接正六边形的边长。
答案:一、选择题1. B2. A3. A4. B5. A6. B二、填空题1. 0, 1, -12. 非负数3. 04. ±1三、解答题1. 等差数列前n项和公式为S_n = n/2 * (a1 + an),其中an = a1 + (n-1)d。
初三数学竞赛选拔试题(含答案)

初三数学竞赛选拔试题(含答案)初三数学竞赛选拔试题(含答案)一、选择题1. 若 3x + 2 = 17,则 x 的值是A. 5B. 7C. 9D. 112. 在一个几何图形中,有一个正方形,边长为 x 厘米,另有一个等腰直角三角形,直角边的长为 y 厘米。
已知正方形的面积是等腰直角三角形面积的 20 倍,下列等式成立的是A. x² = 20y²B. x² + y² = 20C. 20x² = y²D. x + y = 203. 若 a² - b² = 15 且 a + b = 5,则 a 的值是A. 10B. 5C. 3D. -104. 某校参加比赛的男女生比例为 5:3 ,男生比女生多 48 人,那么该校一共有多少学生?A. 320B. 480C. 800D. 9605. 以下各数中,最小的是A. -0.5B. -1/2C. -50%D. 1/-2二、填空题6. 将 120 分钟化为小时的形式,填入空白:____小时。
7. 三个角相加是 180°,如果有两个角是 50°和 80°,那么第三个角的度数是____°。
8. 分数 7/10 是小数____。
9. 甲、乙两地相距 150 公里,有两辆车同时相向而行,如果两车速度一样,则若干小时后两车相遇,填入空白:____小时。
10. (-a) ×(-a) ×(-a) ×(-a) ×(-a) ×(-a)表示的结果是____。
三、解答题11. 某衣服打对折后价格为 420 元,原价是多少元?12. 小丽拥有一些小球,其中有红球、蓝球和绿球。
红球比蓝球的 3 倍多 2 个,蓝球比绿球的 2 倍少 4 个。
如果小丽总共有 51 个球,求小丽拥有的绿球数量。
13. 若 a + b = 5 ,a - b = 3 ,求 a 和 b 的值。
江苏省第十六届初中数学竞赛试题(B卷)及参考答案

江苏省第十六届初中数学竞赛试题(B 卷)及参考答案一、选择题(每题8分,共48分.以下每题的4个结论中,仅有一个是正确的,请将正确答案的英文字母填在题后的圆括号内.)1.已知b>a>0,a 2+b 2=4ab ,则b a b a -+等于( ). A .-21B . 3C .2D .-32.已知xB x A x x x ++=+-1322,其中A 、B 为常数,则A-B 的值为( ). A .-8 B8C .-1D .43.1 O 个棱长为l 的小正方体木块,堆成如图所示的形状,则它的表面积为( ).A .30B .34C .36D .484.如图所示.△ABC 中,∠B=∠C,D 在BC 上,∠BA D=50°,AE=AD ,则∠EDC 的度数为( ).A .15° B.25° C.30°D.50°5.将一个正方形分割成n 个小正方形(n>1),则n 不可能取( ).A .4B .5C .8D .96.如图所示,在一条笔直的公路上有7个村庄,其中A 、B 、C 、D 、E 、F 离城市的距离分别为4,10,15,17,l9,20 km ,而村庄G 正好是AF 的中点.现要在某个村庄建一个活动中心,使各村到活动中心的路程之和最短,则活动中心应建在( ).A .A 处B .C 处 C .G 处D .E 处二、填空题(每题8分,共48分)7.一列数71,72,73,…,72001,其中末位数是3的有 个.8.已知对任意有理数a 、b ,关于x 、y 的二元一次方程(a -b)x -(a+b)y=a+b 有一组公共解,则公共解为 .9.数a 比数b 与c 的和大于16,a 的平方比b 与c 的和的平方大1664.那么,a 、b 、c 的和等于10.数的集合X由1,2,3,…,600组成,将集合X中是3的倍数,或4的倍数,或既是3的倍数又是4的倍数的所有数,组成一个新的集合y,则集合y中所有数的和为.11.若a1=5,a5=8,并且对所有正整数n,有a n+a n+1+a n+2=7,则a2001=12.三条线段能构成三角形的条件是:任意两条线段长度的和大于第三条线段的长度.现有长为144 cm的铁丝,要截成n小段(n>2),每段的长度不小于1 cm,如果其中任意三小段都不能拼成三角形,则n的最大值为三、解答题(每题16分,共64分)13.中国第三届京剧艺术节在南京举行,某场京剧演出的票价由2元到100元多种,某团体需购买票价为6元和10元的票共140张,其中票价为10元的票数不少于票价为6元的票数的2倍,问这两种票各购买多少张所需的钱最少?最少需要多少钱?14.如图所示,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP= AC,点Q在CE上,CQ=AB.求证:(1)AP=AQ;(2)AP⊥AQ.15.有五个数,每两个数的和分别为2,3,4,5,6,7,8,6,5,4(未按顺序排列).求这5个数的值.16.如图所示,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD、QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省第十六届初中数学竞赛试题(初三年级)
一、选择题(6×6=36分)
1.
已知a b ==
的值为 (A )3 (B )4 (C )5 (D )6
2. 若两个方程20x ax b ++=和2
0x bx a ++=,则( )
(A )a b = (B )0a b += (C )1a b += (D )1a b +=-
3. 下列给出四个命题:
命题1 若||||a b =,则||||a a b b =;
命题2 若2550a a -+=
1a =-; 命题3 若关于x 的不等式(3)1m x +>的解集是13x m <
+,则3m <-; 命题4 若方程210x mx +-=中0m >,则该方程有一正根和一负根,且负根的绝
对值较大。
其中正确的命题个数是( )
(A )1 (B )2 (C )3 (D )4
4. 如图,四边形ABCD 中,∠BAD=90°,
AB=BC=AC=6,AD=3,
则CD 的长是( )
(A )4 (B
)(C
)(D )
5.已知三角形的每条边长的数值都是2001的质因数那么这样的三角形共有( )
(A )6个 (B )7个 (C )8个 (D )9个
6.12块规格完全相同的巧克力,每块至多被分为两小块(可以不相等)。
如果 这12 块巧克力可以平均分给n 名同学,则n 可以为( )
(A )26 (B )23 (C )17 (D )15
二、填空题(5×8=40分)
7.
若||2a ==,且0ab <,则a b -= .
8.如图,D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点且DE ∥BA ,
DF ∥CA 。
(1) 要使四边形AFDE 是菱形,则要增加条件:____________________________
(2) 要使四边形AFDE 是矩形,则要增加条件:
____________________________ 第4题
第8题
9.方程18272938
x x x x x x x x +++++=+++++的解是 . 10.要使610222x ++为完全平方数,那么非负数x 可以是____________。
(要求写出x 的3个值)
11.如图,直线26y x =-+与x 轴、y 轴分别交于P 、Q 两点,把△POQ 沿PQ 翻折,点O 落在R 处,则点R 的坐标是_____________。
12.如图,已知八边形ABCDEFGH 中4个正方形的面积分别为25、144、48、121平方单位,PR=13(单位),则该形的面积=___________平方单位。
13.如图,设△ABC 的两边AC 与BC 之和为a ,M 是AB 的中点,MC=MA=5,则a 的取值范围是_____________。
14.如图,一个田字形的区域A 、B 、C 、D 载种观赏植物,要求同一个区域种同一种植物,相邻的两块种不同的植物。
现有4种不同的植物可供选择,那么有__________种载种方案。
三、解答题(16×4=64分)
15.某商店有A 种练习本出售,每本零售价为0.30元,一打(12本)售价为3.00元,买10打以上的,每打还可以按2.70元付款。
(1) 初三(1)班共57人,每人需要1本A 种练习本,则该班集体去买时,最少需付多
少元?
(2) 初三年级共227人,每人需要1本A 种练习本,则该年级集体去买时,最少需付
多少元?
16.设12,x x 是方程22242320x mx m m -++-=的两个实根,当m 为何值时,2212x x +有
最小值?并求这个最小值。
17.(1)已知:如图,在四边形ABCD 中,BC ⊥CD ,∠ACD=∠ADC 。
求证:
(2) 已知:如图,在△ABC 中,AB 上的高为CD 。
试判断
(AC+BC)2与BA 2+4CD 2之间的大小关系,并证明你的结论。
第12题
第13题
第14题
第17题
(1) 第17题(2)
18.编号为1到25的25个弹珠被分在两个篮子A 和B 中,15号弹珠在篮子A 中,把这个弹珠从篮子A 中移到篮子B 中,这时篮子A 中的弹珠号码的平均数等于原平均数加14,篮子B 中的弹珠号码的平均数也等于原平均数加14
,问原来篮子A 中有多少个弹珠?
答案:
一、1.C 2.D 3.C 4.D 5.B 6.D
二、7.7,-7 8.(1)AD 平分∠BAC ,或AD ⊥EF ,或……;(2)∠BAC =90°,或…… 9.112- 11.2412,55⎛⎫ ⎪⎝
⎭
12.428+
13.10a <≤14.84 三、15.(1)可买5打或4打加9本,前者需付款3.00×5=15.00(元),后者只需付款
3.00×4+0.3×9=1
4.70(元).故该班集体去买时,最少需付14.70元。
(2)可买19打或18打加11本,前者需付款2.70×19=51.30(元),后者需付款2.70×18+0.3×11=51.90(元),比前者还要多付0.60元,故该年级集体去买,最少需付51.30元。
16.由题意知方程有实根,Δ≥0. 有2416m -+≥0,则m ≤23
. 又由根与系数关系,得2221237248
x x m ⎛⎫+=-+ ⎪⎝⎭. 2332,03443m m ≤∴-≥->.从而,22332443m ⎛⎫⎛⎫-≥- ⎪ ⎪⎝⎭⎝⎭. 于是,当23m =时,2212x x +取得最小值,且最小值为2
327824389
⎛⎫⨯-+= ⎪⎝⎭. 17.(1)连结BD 即可证明。
(2)大小关系是()2224AC BC AB CD +≥+. 如图,作EB ⊥AB ,EB =2CD. 应用(1)的结论,易证。
18.设原来篮子A 中有弹珠x 个,则篮子B 中有弹珠(25-x )个. 又记原来A 中弹珠号码数的平均数为a ,B 中
弹珠号码数的平均数为b. 则由题意得
B
D A C E
()()2512253251511
425151264ax x b ax a x b x b x ⎧⎪+-=+++=⎪-⎪-=⎨-⎪⎪-+-=⎪-⎩
,解得9x =.即原来篮子中有9个弹珠。
