做一做1_圆柱的体积-优质公开课-人教6下精品
人教版六年级下数学_三_1_第3课时《圆柱的体积》教学课件
ห้องสมุดไป่ตู้
答:因为502.4大于498,所以杯子能装下这袋牛 奶。
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
分成的扇形越多,拼成的立体图形就越接近于长方 体。
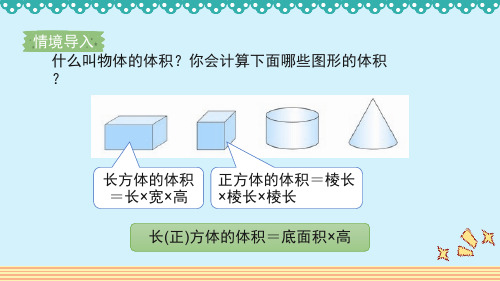
情境导入 什么叫物体的体积?你会计算下面哪些图形的体积 ?
长方体的体积 正方体的体积=棱长 =长×宽×高 ×棱长×棱长
长(正)方体的体积=底面积×高
复习旧知 还记得圆的面积的推导吗?
复习旧知
复习旧知
探究新知 圆柱体积怎样计算呢?能不能将圆柱转化成我们学过的立体图 形,计算出它的体积呢?
探究新知
探究新知
长方体的底面积=圆柱的底面积 V=Sh
长方体的高=圆柱的高 圆柱体积=底面积×高
V= πr2h
探究新知
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得
10cm
到的。)
8cm
牛奶
498mL
杯子的底面积: 3.14×(8÷2)2 =3.14×42 =3.14×16 =50.24(cm2)
六年级数学下册圆柱的体积优质课公开课教案

圆柱的体积教学目标知识技能学生经历用切割拼合的方法推导出圆柱体积公式的过程,理解圆柱体积公式的推导过程,掌握圆柱体体积的计算方法。
数学思考与问题解决在自主探究的过程中,运用圆柱的体积解决简单的实际问题,培养学生独立思考及解题的能力。
情感态度在体积公式的推学过程中渗透极限思想。
教学重点理解圆柱体积公式的推导过程。
教学难点在自主探究的过程中,运用圆柱的体积解决简单的实际问题。
教学过程一、导入。
师:家人的生日快到了,老师打算买一个蛋糕,到了蛋糕店我发现有两款蛋糕比较不错,而且价格相同。
这时我犹豫了,买哪款蛋糕更划算呢?你们能帮我选一选吗?提问:要解决这个问题,你打算怎么办?找学生回答。
(分别求出两款蛋糕的体积再比较大小就可以了。
)设置疑问:我们会求长方体的体积,关键是圆柱的体积怎样求呢?导出课题:圆柱的体积。
(板书)二、探究新知。
1、大胆猜想师:前几节课我们学习了圆柱的表面积,知道了圆柱的表面积与它的底面半径和高有关系,那么圆柱的体积又可能与哪些量有关系呢?学生说猜想。
引导学生利用圆的面积公式推导方法验证猜想。
2、复习圆的面积公式的推导。
找学生说一说,回答好的同学奖励小红花。
师小结:我们在推导圆的面积公式时,是把它转化成近似的长方形,然后找到这个长方形与圆各部分之间的联系,由长方形的面积公式推导出圆的面积公式:S=πr2。
3、小组合作,探究圆柱的体积公式。
师:结合圆的面积公式推导过程,小组合作讨论,怎么样才能将圆柱转化成我们熟悉的图形,进而推出圆柱的体积计算方法。
小组讨论。
找小组汇报,表现积极的小组奖励红花。
小结:把圆柱转化成长方体后,形状变了,体积不变,长方体的底面积等于圆柱的底面积,高等于圆柱的高,因为长方体的体积等于底面积乘高,所以圆柱的体积也等于底面积乘高。
用字母表示是V=Sh(板书)。
如果我们知道的是底面圆的半径,那么公式还可以表示为:V=πr2h(板书)。
验证了猜想。
4、回顾导入,解决问题。
人教版六下数学第3课时圆柱的体积公开课教案课件

三人行,必有我师焉。 择其善者而从之,其不善者而改之。
人外有人,天外有天。 取人之长,补己之短。 自满人十事九空,虚心人万事可成。 谦受益,满招损。
骄傲自满是我们的一座可怕的陷阱;而且,这个陷阱是我们自己亲 手挖掘的。 —— 老舍
尺有所短;寸有所长。物有避短, • 2、正视自己的缺点,知错能改, • 3谦虚使人进步, • 4、人应有一技之长, • 5、自信是走向成功的第一步, • 6强中更有强中手,一山还比一山高, • 7艺无止境 • 8、宝剑锋从磨砺出,梅花香自苦寒来,刻苦训练才能有所收获,取得
解题指导:先把60cm化成0.6m,然后根据V圆柱 =Sh=π×(d÷2)²×h 求出机井的体积,再与6m³进行比较。
4.明明要把一罐可乐倒入杯中,请你帮他算一算,下面这个杯子 能装下这罐可乐吗?(杯子的厚度忽略不计)
3.14×(7÷2)2×8=307.72(cm³) 307.72 cm³=307.72 mL 307.72>245 能装下。
2.计算下列圆柱的体积。 28.26×8=226.08(cm³) 3.14×2²×10=125.6(dm³)
3.一口废弃的机井,从里面量井底直径是60 cm,井深20 m,为了
避免意外事故的发生,要用三合土把它填平,现在有6 m³的三合
土,能把这口井填平吗? 60 cm=0.6 m 3.14×(0.6÷2)2×20=5.652(m³) 5.652<6 能。
3 圆柱与圆锥
1.圆柱 第第1课3课时时分数圆乘柱整的数体积
1.仔细想,认真填。 (1)圆柱的底面周长是6.28 cm,高是4 cm,这个圆柱的表面积是 ( 31.4 )cm²,体积是( 12.56 )cm³。 (2)把一个圆柱的侧面沿高展开,得到一个正方形,圆柱的底面半 径是10 dm,这个圆柱的高是( 62.8)dm,体积是( 19719.2)dm³。 (3)一个圆柱的体积是750 cm³,底面积是150 cm²,它的高是 ( 5 )cm。 (4)把一根2 m长的圆柱形木料截成3段小圆柱,表面积增加了12 dm²,这根木料原来的体积是( 60 )dm³。
人教版六年级数学下册《圆柱的体积》课件课件

# 人教版六年级数学下册《圆柱的体积》课件PPT大纲
引入
今天我们要学习《圆柱的体积》这个重要数学概念,通过本节课的学习,我们将了解圆柱的结构特点以 及计算方法。
知识点讲解
圆柱是一个常见的几何体,它具有底面、高度和侧面。我们将学习如何计算 圆柱的底面积、高度以及体积。
例题讲解
让我们通过数道练习题来巩固所学知识。这些例题将帮助我们更好地理解和应用圆柱的体积公式。
课堂练习
是时候进行一些实际的课堂练习了。我将提供一些问题供你们自主思考和解 答,然后我们一起进行讨论和分析。
总结
经过本节课的学习,我们已经掌握了计算圆柱体积的方法。别忘了继续巩固 和深化所学知识,以便在数学学习中取得更好的成绩。
课后作业
为了巩固所学知识,我将布置一些相应的课后作业。请合理安排时间完成作 业,并牢记作业的重要性。
课堂回顾
在开始新的课程内容之前,让我们先回顾一下上一课堂所学的内容,解决可能存在的问题,确保大家都 掌握了基础知识。
结束语
非常感谢大家的积极参与和表现,你们做得很好!下一课堂,我们将继续学习其他有趣的数学知识。
新课标人教版六下圆柱的体积课件市公开课一等奖百校联赛特等奖课件

圆柱体积
第2页
第3页
第4页
第5页
第6页
第7页
长方形体积= 长×宽×高 正方形体积= 棱长×棱长 ×棱长
V= S × h
大胆猜测圆柱体体积等于?? 因为变换成长方体后,底面积 和 高大小是不变,所以圆柱体积也 等于底面积×高
第8页
直柱体体积 = 底面积×高
V =s h
第9页
试一试
1、填表。
底面积 (平方米)
高 (米)
圆柱体积
(立方米)
15
3
45
6.4
4
25.6
第34页
2、求圆柱体积。(单位:厘米)
2 10 3.14 ×(10÷2)2×2=157(立方厘米)
第35页
3、判断正误,正确画“√”,错误画“×”。
(1)圆柱体底面积越大,它体积越大。 (×)
(2)圆柱体高越长,它体积越大。 (×)
想
你会计算它们体积吗?
一
想
8 米
16平方米
15平方米
9 米
第10页
图1:
h=h
甲
乙
讨论题:
1、甲圆柱与乙圆柱谁体积大?
2、它们什么条件是相同?
3、圆柱体积大小与什么相关?
第11页
图1:
h=h
甲
乙
讨论题:
1、甲圆柱与乙圆柱谁体积大?
2、它们什么条件是相同?
3、圆柱体积大小与什么相关?
第12页
图1:
C、2.1米=210厘米 50×210=10500(立方厘米)
D、50平方厘米=0.005平方米 0.005×2.1=0.0105(立方米)
上面哪些答案正确,请选择。
人教版六年级下册 圆柱的体积 公开课课件

正方体的体积=棱长×棱长×棱长
底面积×高
圆柱体积的大小与哪些条件有关?
图1:
h=h
甲
乙
讨论题:
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
图1:
h=h
甲
乙
讨论题:
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
3、圆柱的体积大小与什么有关?
图1:
h=h
甲
乙
讨论题:
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
图1:
h=h
பைடு நூலகம்
甲
乙
讨论题: 1、甲圆柱与乙圆柱谁的体积大? 2、它们的什么条件是相同的? 3、圆柱的体积大小与什么有关?
图2 将一个圆柱截成不相等的两段,哪个圆柱体积大?
把圆柱体切割拼成近似( ),它们
的( )相等。长方体的高就是圆柱体的
( ),长方体的底面积就是圆柱体的
(
),因为长方体的体积=( 底面积×高
),所以圆柱体的体积=(底面积×高)。用
字母“V”表示( ),“S”表示
(
),“h”表示( ),那么,圆柱
体体积用字母表示为( )
讨论
(1)已知圆的半径和高: V=∏r2h (2)已知圆的直径和高: V=∏(d2)2h
(3)已知圆的周长和高: V=∏(C÷d÷2 )2h
只列式,不计算。
① 底面积12平方分米,高6分米。 ② 底面半径3厘米,高7厘米。 ③ 底面直径6米,高8米。 ④ 底面周长314毫米,高20毫米。
人教版六年级数学下册《圆柱与圆锥 圆柱 圆柱的体积》公开课课件_10

智慧城堡
加油啊!圆柱体的底面积越大,它的体积越大。(×) (2)圆柱体的高越长,它的体积越大。(×) (3)圆柱体的体积与长方体的体积相等。(×) (4)圆柱体的底面直径和高可以相等。( √ )
2. 小明和妈妈出去游玩,带了一个圆柱形
保温杯,从里面量底面直径是8cm,高是15cm。 如果两人游玩期间要喝1L水,带这杯水够喝吗?
保温杯的底面积:3.14×(8÷2)2 = 3.14×4 2 = 3.14×16 = 50.24 (cm2)
保温杯的容积:50.24×15 =753.6 (cm³) =0.7536(L)
答:因为0.7536小于1,所以带这杯水不够喝。
3. 一个圆柱形粮囤,从里面量得底面半径是 1.5m,高2m。如果每立方米玉米约重750kg, 这个粮囤能装多少吨玉米?
答:这个粮囤能装10.5975吨。
直柱体的体积 = 底面积×高
V =s h
想 一
试 (1)你会计算它们的体积吗? 一
想
试 (2)试写出它们的体积公式。
8 米
16平方米
15平方米
9 米
75×90=6750(立方厘米)
答:它的体积是6750立方厘米。
看图列式,并写出相应的公式。
12平方分米 6 分 米
12×6
V=s h
(1)
7分米
.
3 分 米
3.14 ×32 ×7
V= 兀r 2× h
(2)
3.14 ×(6÷2)2 ×8 V=兀(d÷2)2 ×h
(3)
10cm
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测 量得到的。)
圆柱的体积
高 宽
长
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
六年级下册数学第4课时 圆柱的体积公开课教案教学设计课件公开课教案课件

第3单元 圆柱与圆锥第4课时 圆柱的体积【学习目标】1.能够根据割、拼等方法推导出圆柱的体积公式,能理解圆柱体积的推导过程。
2.能运用圆柱的体积公式解决实际问题。
【学习过程】一、知识铺垫1.计算长8cm ,宽5cm ,高3cm 的长方体的体积。
长方体的体积=( )×( )2.回忆圆的面积公式的推导过程,用自己的话简单说一说。
二、自主探究1.探究圆柱的体积计算方法。
(1)圆柱的体积可以用这种转化的方法进行推导,你想把圆柱转化成( )形状?(2)合作探索。
我的发现:转化后的长方体的体积和圆柱的体积( ),长方体的底面积与圆柱的底面积( ),长方体的高和圆柱的( )相等。
(3)填一填,并小组交流你的结论。
长方体的体积 = 底面积 × 高圆柱的体积 =( )× ( )(4)你会用字母表示圆柱的体积公式吗?我的收获: 。
我的困惑: 。
2.练一练。
你能照样子拼一拼,并说一说你的发现吗?三、课堂达标1.下面的长方体和圆柱,哪个体积大?6cm5cm 8cm6cm6cm2.一个圆柱形水池,底面半径是10米,深1.5米。
这个水池占地面积是多少平方米?如果把水池蓄满水,这个水池可装水多少方?四、拓展练习将长、宽、高分别为18cm、18cm、16cm的长方体木块,削成一个最大的圆柱,圆柱的体积是多少立方厘米?“节约用水,人人有责”,课后,我们一起召开一节主题班会课,学习一下“节水”精神吧!可以根据班级需要展开这个活动哦!目的:教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的,每个人都要保护它,做到节约每一滴水,造福子孙万代。
活动过程:1.主持人上场,神秘地说:“我让大家猜个谜语,你们愿意吗?”大家回答:“愿意!”主持人口述谜语:“双手抓不起,一刀劈不开,煮饭和洗衣,都要请它来。
”主持人问:“谁知道这是什么?”生答:“水!”一生戴上水的头饰上场说:“我就是同学们猜到的水。
听大家说,我的用处可大了,是真的吗?”主持人:我宣布:“水”是万物之源主题班会现在开始。
人教版小学数学六年级下册《圆柱的体积》教学设计公开课教案

六年级下册《圆柱的体积》教学设计教学目标:1、使学生理解和掌握圆柱体积的计算方法,在推导圆柱体积计算公式的过程中培养学生初步的空间观念和动手操作的技能。
2、使学生能够通过观察,大胆猜想和验证获得新知识,在教学活动过程中发展学生的推理能力,渗透转化极限思想。
3、引导学生积极参与数学学习活动,培养学生的数学意识和合作意识。
教学重点:理解并掌握圆柱体积计算公式,并能应用公式计算圆柱的体积。
教学难点:掌握圆柱体积公式的推导过程。
教学准备:多媒体课件、圆柱学具。
教学过程:一、创设情境,引入课题。
1、(1)出示长方体和正方体求出体积(2)猜测底面是平行四边形的立体图形的体积(3)猜测底面是三角形的立体图形的体积(4)如果底面是圆形,又要怎样计算体积2、揭题二、探索交流,解决问题(一)调动经验,初步验证1、师:这只是我们的猜测,是否正确还要加以验证。
怎样才能验证我们的猜测是否正确呢?把你的想法在小组里交流下。
2、学生汇报(二)实验探究,再次验证(1)动手操作,合作探究学生边操作边思考大屏幕上的问题,把答案填写在学习单上。
①把圆柱转化为长方体,什么变了,什么没有变?②转化后的长方体的底面积与圆柱的底面积有什么关系?它们的高有什么关系?③由此,你能得出怎样的结论?(2)整合思路,汇报成果①形状变了,体积没变。
表面积也变了,表面积增加了左右两个长方形的面积。
②圆柱的底面积和长方体底面积相等,圆柱的高与长方体的高相等③长方体的长、宽、高相当于圆柱的什么?④因为长方体的体积=底面积X高,长方体的体积等于圆柱的体积,长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,所以圆柱的体积=底面积X高。
(3)课件演示,深化认知①课件呈现操作过程,思考:为什么拼成的只是一个近似的长方体呢?②依次呈现把圆柱的底面平均分成32份,64份……让学生感受极限思想。
③小结,板书(4)课堂小结,适度拓展(5)首尾呼应,构建知识网络三、巩固应用,内化提高1、联系生活,拓展思维①理解底面积相等,高越大,体积越大。
六年级【下】册数学-3.圆柱的体积人教版(26张ppt)公开课课件

计算下面立体图形的体积
底面积: 20平方厘米 高: 5厘米
底面积: 10平方厘米 高: 8厘米
体积=底面积×高
V=s h
如何计算圆柱的体积?
?
圆柱的体积
人教版数学六年级下册第三单元第三课
回顾圆的面积推导过程
转化
S=πr2
r πr
把圆柱的底面分成16等份
把圆柱的底面分成32等份
先要计算出杯子的容积.
3.14×(8÷2)2×10 =3.14×16×10 =3.14×160 =502.4(cm3) =502.4(ml)
502.4 ml>498ml 答:能装下这袋奶。
(名师示范课)六年级【下】册数学- 3.1.3 圆柱的体积 人教版(26张ppt)公开课课件 (名师示范课)六年级【下】册数学- 3.1.3 圆柱的体积 人教版(26张ppt)公开课课件
第3关
努 力 吧 !
(名师示范课)六年级【下】册数学- 3.1.3 圆柱的体积 人教版(26张ppt)公开课课件
第一关
(名师示范课)六年级【下】册数学- 3.1.3 圆柱的体积 人教版(26张ppt)公开课课件
圆柱体积=底面积×高
1.5米=150厘米 50×150=7500(立方厘米)
答:它的体积是7500立方厘米。
(名师示范课)六年级【下】册数学- Байду номын сангаас.1.3 圆柱的体积 人教版(26张ppt)公开课课件
第2关
(名师示范课)六年级【下】册数学- 3.1.3 圆柱的体积 人教版(26张ppt)公开课课件
(1)、压路机的前轮
半径是1米,前轮宽2米。
3.14×1 2 ×2
(2)、铅笔
直径是0.8厘米,长是20厘米。
新人教版六年级数学下册 第4课时 圆柱的体积-优质教案.doc

第三单元 圆柱与圆锥
第4课时 圆柱的体积
【学习目标】
1.能够根据割、拼等方法推导出圆柱的体积公式,能理解圆柱体积的推导过程。
2.能运用圆柱的体积公式解决实际问题。
【学习过程】
一、知识铺垫
1.计算长8cm ,宽5cm ,高3cm 的长方体的体积。
长方体的体积=( )×( )
2.回忆圆的面积公式的推导过程,用自己的话简单说一说。
二、自主探究
1.探究圆柱的体积计算方法。
(1)圆柱的体积可以用这种转化的方法进行推导,你想把圆柱转化成( )形状?
(2)合作探索。
我的发现:转化后的长方体的体积和圆柱的体积( ),长方体的底面积与圆柱的底面积( ),长方体的高和圆柱的( )相等。
(3)填一填,并小组交流你的结论。
长方体的体积 = 底面积 × 高
圆柱的体积 =( )× ( )
(4)你会用字母表示圆柱的体积公式吗?
我的收获: 。
我的困惑: 。
2.练一练。
你能照样子拼一拼,并说一说你的发
现吗?
三、课堂达标
1.下面的长方体和圆柱,哪个体积大?
6cm
5cm 8cm
6cm
6cm
2.一个圆柱形水池,底面半径是10米,深1.5米。
这个水池占地面积是多少平方米?如果把水池蓄满水,这个水池可装水多少方?
四、拓展练习
将长、宽、高分别为18cm、18cm、16cm的长方体木块,削成一个最大的圆柱,圆柱的体积是多少立方厘米?。
