江西省宜春市上2016-2017学年高二中2016-2017学年高一(下)第六次月考数学试卷(理科)(1)(解析版)
2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(文科)(解析版)
)
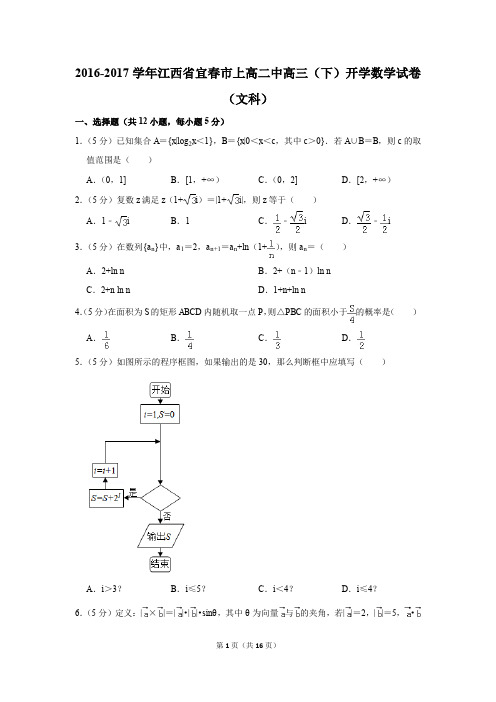
5. (5 分)如图所示的程序框图,如果输出的是 30,那么判断框中应填写(
A.i>3?
B.i≤5?
C.i<4?
D.i≤4?
6. (5 分)定义:| × |=| |•| |•sinθ,其中 θ 为向量 与 的夹角,若| |=2,| |=5, •
第 1 页(共 16 页)
=﹣6,则| × |=( A.8
2016-2017 学年江西省宜春市上高二中高三(下)开学数学试卷 (文科)
一、选择题(共 12 小题,每小题 5 分) 1. (5 分)已知集合 A={x|log2x<1},B={x|0<x<c,其中 c>0}.若 A∪B=B,则 c 的取 值范围是( A. (0,1] ) B.[1,+∞) i)=|1+ C. (0,2] i|,则 z 等于( C. ﹣ i ) D. ) ﹣ i D.[2,+∞)
第 2 页(共 16 页)
A.
B.
C.
D. |=| |,则 的最
11. (5 分)已知 A,B,C 是单位圆上互不相同的三点,且满足| 小值为( A.﹣ ) B.﹣ C.﹣
D.﹣1
12. (5 分)在平面直角坐标系中,定义 d(P,Q)=|x1﹣x2|+|y1﹣y2|为两点 P(x1,y1) ,Q (x2,y2)之间的“折线距离” .在这个定义下,给出下列命题: ①到原点的“折线距离”等于 1 的点的集合是一个正方形; ②到原点的“折线距离”等于 1 的点的集合是一个圆; ③到 M(﹣1,0) ,N(1,0)两点的“折线距离”相等的点的轨迹方程是 x=0; ④到 M(﹣1,0) ,N(1,0)两点的“折线距离”差的绝对值为 1 的点的集合是两条平 行线. 其中正确的命题有( A.1 个 ) B.2 个 C.3 个 D.4 个
江西省宜春中学2016-2017学年高一2月月考英语试题 Word版含答案

江西省宜春中学2016-2017学年度高一下学期2月月考英语试卷(时间:120分钟分值150分)本试卷分第I卷和第II卷两部分,考试用时120分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
2.全部答案在答题卡上完成,答在本试卷上无效。
第I卷 (选择题共100分)第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5个小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从每题所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是 C。
1. What time is it now?A. 9:10.B. 9:50.C. 10:00.2. What does the woman think of the weather?A. It's nice.B. It's warm.C. It's cold.3. What will the man do?A. Attend a meeting.B. Give a lecture.C. Leave his office.4. What is the woman's opinion about the course?A. Too hard.B. Worth taking.C. Very easy.5. What does the woman want the man to do?A. Speak louder.B. Apologize to her.C. Turn off the radio.第二节(共15小题;每小题1. 5分,满分22.5分)听下面5段对话。
2016-2017年江西省宜春市上高二中高二(下)期末物理试卷及参考答案

2016-2017学年江西省宜春市上高二中高二(下)期末物理试卷一、选择题(本大题共10小题,每小题4分,共40分)1.(4分)下列说法正确的是()A.布朗运动反映了悬浮颗粒在永不停息地做无规则运动B.气体分子的平均动能增大,压强也一定增大C.不同温度下,水的饱和汽压都是相同的D.完全失重状态下悬浮的水滴呈球状是液体表面张力作用的结果2.(4分)核电站核泄漏的污染物中含有碘131和铯137.碘131的半衰期约为8天,会释放β射线;铯137是铯133的同位素,半衰期约为30年,发生衰变期时会辐射γ射线.下列说法正确的是()A.碘131释放的β射线由氦核组成,β衰变的方程是I→Xe+eB.碘131释放的β射线是电子流,β衰变的方程是I→Xe+eC.与铯137相比,碘131衰变更慢,且铯133和铯137含有相同的质子数D.铯137衰变时辐射处的γ光子能量大于可见光光子能量3.(4分)如图所示,一束可见光射向半圆形玻璃砖的圆心O,经折射后分为两束单色光a 和b.下列判断正确的是()A.玻璃对a光的折射率小于对b光的折射率B.a光的频率大于b光的频率C.在真空中a光的波长大于b光的波长D.a光光子能量小于b光光子能量4.(4分)如图甲所示,50匝矩形闭合导线框.ABCD处于磁感应强度大小B=T的水平匀强磁场中,线框电阻不计.线框匀速转动时所产生的正弦交流电压图象如图乙所示.把该交流电压加在图丙中理想变压器的P、Q两端.已知变压器的原线圈I和副线圈Ⅱ的匝数比为5:1,交流电流表为理想电表,电阻R=1Ω,其他各处电阻不计,以下说法正确的是()A.t=0.1s时,电流表的示数为0B.副线圈中交流电的频率为50HzC.线框面积为m2D.0.05s线圈位于图甲所示位置5.(4分)实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与电子恰在纸面内做匀速圆周运动,运动方向和轨迹示意如图.则()A.轨迹1是电子的,磁场方向垂直纸面向外B.轨迹2是电子的,磁场方向垂直纸面向外C.轨迹1是新核的,磁场方向垂直纸面向里D.轨迹2是新核的,磁场方向垂直纸面向里6.(4分)在进行光电效应实验时,用黄光照射某金属表面时发生光电效应现象,并产生了光电流,则()A.若增大黄光的照射强度,光电子的最大初动能将增大B.若增大黄光的照射强度,单位时间内出射的电子数目将增多C.若改用红光照射该金属,一定能产生电效应现象D.若改用蓝光照射该金属,饱和光电流一定增大7.(4分)如图所示,甲分子固定在坐标原点O,乙分子位于x轴上,甲分子对乙分子的作用力与两分子间距离的关系如图中曲线所示.F>0表示斥力,F<0表示引力,a,b,c,d为x轴上四个特定的位置.现把乙分子从a处由静止释放,则()A.乙分子由a到b做加速运动,由b到d做减速运动B.乙分子由a到c做加速运动,由c到d做减速运动C.乙分子由a到b的过程中,两分子的分子势能一直增加D.乙分子由b到d的过程中,两分子的分子势能一直减小8.(4分)如图所示,弧形轨道置于足够长的水平轨道上,弧形轨道与水平轨道平滑连接,水平轨道上静置一小球B和C,小球A从弧形轨道上离地高h处由静止释放,小球A沿轨道下滑后与小球B发生弹性正碰,碰后小球A被弹回,B球与C球碰撞后粘在一起,A球弹同后再从弧形轨道上滚下,已知所有接触面均光滑,A、C两球的质量相等,B球的质量为A球质量的2倍,如果让小球A从h=0.2m处静止释放,则下列说法正确的是(重力加速度为g=10m/s2)()A.A球从h处由静止释放则最后不会与B球冉相碰B.A球从h处由静止释放则最后会与B球再相碰C.A球从h=0.2m处由静止释放则C球的最后速度为m/sD.A球从h=0.2m处由静止释放则C球的最后速度为m/s9.(4分)某原子的部分能级图如图所示,大量处于某激发态的该原子向低能级跃迁时,发出三种波长的光如图所示,它们的波长分别为λa、λb、λc.下列说法正确的是()A.在同种均匀介质中传播时,b光的速度最大B.用同一套装置做双缝干涉实验,a光相邻亮纹的间距最大C.若b光照射某种金属能发生光电效应,c光照射该金属也能发生光电效应D.三种光的波长关系为=10.(4分)如图所示,在水平面内的直角坐标系xOy中有一光滑金属导轨AOC,其中曲线导轨OA满足方程y=Lsin kx,长度为的直导轨OC与x轴重合,整个导轨处于垂直纸面向外的匀强磁场中。
2016-2017年江西省宜春市高安中学高一(下)期末数学试卷(理科)(解析版)

2016-2017学年江西省宜春市高安中学高一(下)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若tanα<0,cosα<0,则α的终边所有的象限为()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)计算sin45°cos15°+cos45°sin15°=()A.B.C.D.3.(5分)若点(sin,cos)在角α的终边上,则sinα的值为()A.B.C.D.4.(5分)若tanα=3,则的值等于()A.2B.3C.4D.65.(5分)在数列{a n}中,若为定值,且a4=2,则a2a6等于()A.32B.4C.8D.166.(5分)在等差数列{a n}中,已知a1+a5+a9=3,则数列{a n}的前9项和S9=()A.9B.15C.18D.247.(5分)已知a,b,c为△ABC的三个角A,B,C所对的边,若3b cos C=c(1﹣3cos B),则=()A.2:3B.4:3C.3:1D.3:28.(5分)等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=()A.29B.31C.33D.369.(5分)若在△ABC中,2cos B sin A=sin C,则△ABC的形状一定是()A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形10.(5分)数列{a n}满足a n+a n+1=(n∈N*),a2=2,S n是数列{a n}的前n项和,则S21为()A.5B.C.D.11.(5分)在等比数列{a n}中,a1=2,前n项和为S n,若数列{a n+1}也是等比数列,则S n 等于()A.2n+1﹣2B.3n C.2n D.3n﹣112.(5分)已知实数a>0,b>0,若是4a与2b的等比中项,则下列不对的说法是()A.B.0<b<1C.D.二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上)13.(5分)sin15°cos165°=.14.(5分)已知实数1<a<2,3<b<4,则的取值范围是.15.(5分)已知数列{a n}的通项公式,则数列{a n}的项取最大值时,n =.16.(5分)若不等式﹣2≤x2﹣2ax+a≤0有唯一解,则a的值为.三、解答题(17题10分,其他题12分,解答应写出文字说明,证明过程或演算步骤)17.(10分)已知,.(1)求tanα的值;(2)求的值.18.(12分)在等差数列{a n}中,a2=4,a4+a7=15.(1)求数列{a n}的通项公式;(2)设,求b1+b2+b3+…+b10的值.19.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知a cos B+b cos A=2c cos C.(1)求角C的大小;(2)若a=5,b=8,求边c的长.20.(12分)在△ABC中,A,B,C所对的边分别为a,b,c,.(1)求角C的大小;(2)若c=2,求△ABC面积的最大值.21.(12分)在数列{a n}中,a1=,a n+1=(Ⅰ)证明{}是等比数列,并求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n.22.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且2a cos C+c=2b.(1)求角A的大小;(2)若a2=3bc,求tan B的值.2016-2017学年江西省宜春市高安中学高一(下)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若tanα<0,cosα<0,则α的终边所有的象限为()A.第一象限B.第二象限C.第三象限D.第四象限【考点】GC:三角函数值的符号.【解答】解:根据题意,若tanα<0,角α的终边在第二、四象限;cosα<0,角α的终边在第二、三象限,以及x负半轴.所以角α的终边在第二象限;故选:B.2.(5分)计算sin45°cos15°+cos45°sin15°=()A.B.C.D.【考点】GP:两角和与差的三角函数.【解答】解:sin45°cos15°+cos45°sin15°=sin(45°+15°)=sin60°=,故选:D.3.(5分)若点(sin,cos)在角α的终边上,则sinα的值为()A.B.C.D.【考点】G9:任意角的三角函数的定义.【解答】解:角α的终边上一点的坐标为(sin,cos)即(,),则由任意角的三角函数的定义,可得sinα=,故选:A.4.(5分)若tanα=3,则的值等于()A.2B.3C.4D.6【考点】GF:三角函数的恒等变换及化简求值;GS:二倍角的三角函数.【解答】解:==2tanα=6故选:D.5.(5分)在数列{a n}中,若为定值,且a4=2,则a2a6等于()A.32B.4C.8D.16【考点】88:等比数列的通项公式.【解答】解:由为定值,得数列{a n}是等比数列,∵a4=2,∴a2a6=a42=4,故选:B.6.(5分)在等差数列{a n}中,已知a1+a5+a9=3,则数列{a n}的前9项和S9=()A.9B.15C.18D.24【考点】85:等差数列的前n项和.【解答】解:∵a1+a5+a9=3=3a5,∴a5=1.则数列{a n}的前9项和S9==9a5=9.故选:A.7.(5分)已知a,b,c为△ABC的三个角A,B,C所对的边,若3b cos C=c(1﹣3cos B),则=()A.2:3B.4:3C.3:1D.3:2【考点】HP:正弦定理.【解答】解:∵3b cos C=c(1﹣3cos B),∴由正弦定理可得:3sin B cos C=sin C﹣3sin C cos B,∴3sin B cos C+3sin C cos B=3sin(B+C)=3sin A=sin C,∴3a=c,即:=3:1.故选:C.8.(5分)等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=()A.29B.31C.33D.36【考点】89:等比数列的前n项和.【解答】解:∵数列{a n}是等比数列,a2•a3=2a1=a1q•=a1•a4,∴a4=2.∵a4与2a7的等差中项为,∴a4 +2a7 =,故有a7 =.∴q3==,∴q=,∴a1==16.∴S5==31.故选:B.9.(5分)若在△ABC中,2cos B sin A=sin C,则△ABC的形状一定是()A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形【考点】GZ:三角形的形状判断.【解答】解:∵在△ABC中2cos B sin A=sin C,∴2cos B sin A=sin C=sin(A+B),∴2cos B sin A=sin A cos B+cos A sin B,∴sin A cos B﹣cos A sin B=0,∴sin(A﹣B)=0,∴A﹣B=0,即A=B,∴△ABC为等腰三角形,故选:C.10.(5分)数列{a n}满足a n+a n+1=(n∈N*),a2=2,S n是数列{a n}的前n项和,则S21为()A.5B.C.D.【考点】8H:数列递推式.【解答】解:由a n+a n+1=(n∈N*),a2=2,得,…,∴数列{a n}的所有奇数项项为,所有偶数项为2,∴.故选:B.11.(5分)在等比数列{a n}中,a1=2,前n项和为S n,若数列{a n+1}也是等比数列,则S n 等于()A.2n+1﹣2B.3n C.2n D.3n﹣1【考点】89:等比数列的前n项和.【解答】解:因数列{a n}为等比,则a n=2q n﹣1,因数列{a n+1}也是等比数列,则(a n+1+1)2=(a n+1)(a n+2+1)∴a n+12+2a n+1=a n a n+2+a n+a n+2∴a n+a n+2=2a n+1∴a n(1+q2﹣2q)=0∴q=1即a n=2,所以s n=2n,故选:C.12.(5分)已知实数a>0,b>0,若是4a与2b的等比中项,则下列不对的说法是()A.B.0<b<1C.D.【考点】88:等比数列的通项公式.【解答】解:∵实数a>0,b>0,是4a与2b的等比中项,∴4a•2b=2,∴2a+b=1,∴0<a<,0<b<1,,3a+b=a+(2a+b)=a+1∈(1,),故A,B,C均正确,D错误.故选:D.二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上)13.(5分)sin15°cos165°=.【考点】GS:二倍角的三角函数.【解答】解:sin15°cos165°=﹣sin15°cos15°=﹣sin30°=.故答案为:.14.(5分)已知实数1<a<2,3<b<4,则的取值范围是.【考点】7C:简单线性规划.【解答】解:实数1<a<2,3<b<4,表示的可行域如图:的几何意义是:可行域内的点与坐标原点连线的斜率,由图形可知:OA的斜率最大,OB的斜率最小,k OA=,k OB=,则的取值范围是:.故答案为:.15.(5分)已知数列{a n}的通项公式,则数列{a n}的项取最大值时,n=1或2.【考点】82:数列的函数特性.【解答】解:∵,∴a n+1=(n+3)•()n+1,∴===(1+)≥1,解得n≤1,∵单调递减,∴当n=1或2时,a n取得最大值.故答案为:1或216.(5分)若不等式﹣2≤x2﹣2ax+a≤0有唯一解,则a的值为0或1.【考点】7E:其他不等式的解法.【解答】解:∵不等式﹣2≤x2﹣2ax+a≤﹣1有唯一解,∴x2﹣2ax+a=0有唯一解,即△=(﹣2a)2﹣4a=0;即a2﹣a=0;解得,a=0或1;故答案为:0或1.三、解答题(17题10分,其他题12分,解答应写出文字说明,证明过程或演算步骤)17.(10分)已知,.(1)求tanα的值;(2)求的值.【考点】GF:三角函数的恒等变换及化简求值.【解答】(本题满分为12分)解:(1)∵,∴,…(3分)∴;…(6分)(2)原式==,…(9分)=…(12分)18.(12分)在等差数列{a n}中,a2=4,a4+a7=15.(1)求数列{a n}的通项公式;(2)设,求b1+b2+b3+…+b10的值.【考点】8E:数列的求和.【解答】解:(1)设等差数列{a n}的公差为d,由已知得,解得…(3分)∴a n=3+(n﹣1)×1,即a n=n+2.…(5分)(2)由(1)知,∴b1+b2+b3+…+b10=21+22+…+210==2046.…(10分)19.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知a cos B+b cos A=2c cos C.(1)求角C的大小;(2)若a=5,b=8,求边c的长.【考点】HP:正弦定理;HR:余弦定理.【解答】解:(1)a cos B+b cos A=2c cos C,∴sin A cos B+sin B cos A=2sin C cos C∴sin(A+B)=sin C=2sin C cos C,sin C≠0,解得cos C=,C∈(0,π),∴C=.(2)由余弦定理可得:c2=52+82﹣2×5×8cos=49,解得c=7.20.(12分)在△ABC中,A,B,C所对的边分别为a,b,c,.(1)求角C的大小;(2)若c=2,求△ABC面积的最大值.【考点】HT:三角形中的几何计算.【解答】解:(1)∵在△ABC中,A,B,C所对的边分别为a,b,c,.∴+=,∴+=,,,=,,故cos C=,∵0<C<π,∴C=.(2)由c2=a2+b2﹣2ab cos C,得即,∵∴△ABC面积的最大值.21.(12分)在数列{a n}中,a1=,a n+1=(Ⅰ)证明{}是等比数列,并求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n.【考点】87:等比数列的性质;8E:数列的求和.【解答】解:(Ⅰ)∵a1=,a n+1=,∴a n>0,∴,又,∴{}为首项为,公比为的等比数列,∴,∴;(Ⅱ)S n=…①,∴=…②,①﹣②得:﹣=﹣,∴﹣,∴.22.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且2a cos C+c=2b.(1)求角A的大小;(2)若a2=3bc,求tan B的值.【考点】HT:三角形中的几何计算.【解答】解:(1)∵2a cos C+c=2b,∴由正弦定理得2sin A cos C+sin C=2sin B=2sin(A+C)=2(sin A cos C+cos A sin C),即sin C(2cos A﹣1)=0.∵sin C≠0,∴cos A=,从而得A=;(2)由A=及余弦定理得b2+c2﹣bc=a2=3bc,即b2+c2﹣4bc=0,∴=2±,当=2+时,又sin C=sin(﹣B)=cos B+sin B,故===2+,∴tan B=﹣2﹣,当=2﹣时,同理得tan B=2﹣,综上所述,tan B=﹣2﹣或2﹣.。
2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)(解析版)

2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)一、选择题1.(5分)已知复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)若“0<x<1”是“(x﹣a)[x﹣(a+2)]≤0”的充分不必要条件,则a的取值范围是()A.(﹣∞,0]∪[1,+∞)B.(﹣1,0)C.[﹣1,0]D.(﹣∞,﹣1]∪[0,+∞)3.(5分)已知集合A={(x+1)≥﹣2},B={x|≥2},则A∩B=()A.(﹣1,1)B.[0,1)C.[0,3]D.∅4.(5分)若平面内共线的A、B、P三点满足条件,,其中{a n}为等差数列,则a2008等于()A.1B.﹣1C.D.5.(5分)函数y=A sin(ωx+φ)(ω>0,|φ|<,x∈R)的部分图象如图所示,则函数表达式为()A.y=﹣4sin()B.y=4sin()C.y=﹣4sin()D.y=4sin()6.(5分)若y=(m﹣1)x2+2mx+3是偶函数,则f(﹣1),f(﹣),f()的大小关系为()A.f()>f()>f(﹣1)B.f()<f(﹣)<f(﹣1)C.f(﹣)<f()<f(﹣1)D.f(﹣1)<f()<f(﹣)7.(5分)过双曲线﹣=1(a>0,b>0)的右焦点F作直线y=﹣x的垂线,垂足为A,交双曲线左支于B点,若=2,则该双曲线的离心率为()A.B.2C.D.8.(5分)若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm39.(5分)已知实数x,y满足:,则3x+9y的最小值为()A.82B.4C.D.10.(5分)已知向量,满足,且关于x的函数在实数集R上单调递增,则向量,的夹角的取值范围是()A.B.C.D.11.(5分)设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0,f(x0)),其中x0满足f″(x0)=0.已知f(x)=x3﹣x2+3x﹣,则f()+f()+f()+…+f()=()A.2013B.2014C.2015D.201612.(5分)已知点列A n(a n,b n)(n∈N*)均为函数y=a x(a>0,a≠1)的图象上,点列B n(n,0)满足|A n B n|=|A n B n+1|,若数列{b n}中任意连续三项能构成三角形的三边,则a的取值范围为()A.(0,)∪(,+∞)B.(,1)∪(1,)C.(0,)∪(,+∞)D.(,1)∪(1,)二.填空题13.(5分)已知双曲线﹣=1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.14.(5分)函数f(x)=,则f(x)dx的值为.15.(5分)已知三棱锥O﹣ABC,A、B、C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O﹣ABC的体积为,则球O的体积是.16.(5分)在△ABC中,•=16,sin A=sin B cos C,D是线段AB上的动点(含端点),则•的取值范围是.三.解答题17.(10分)已知数列{a n}满足a1=0,a n+1=a n+2+1(1)求证数列{}是等差数列,并求出a n的通项公式;(2)若b n=,求数列{b}的前n项的和T n.18.(12分)某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.(1)求N和[30,35)这组的参加者人数N1;(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.19.(12分)如图1所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接P A,PB,PD,得到如图2所示五棱锥P﹣ABFED,且AP=,(1)求证:BD⊥平面POA;(2)求二面角B﹣AP﹣O的正切值.20.(12分)如图,椭圆C:+=1(a>b>0)的离心率是,且过点(,).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过点A1,B1引椭圆C的两条弦A1E、B1F.(1)求椭圆C的方程;(2)若直线A1E与B1F的斜率是互为相反数.①求直线EF的斜率k0②设直线EF的方程为y=k0x+b(﹣1≤b≤1)设△A1EF、△B1EF的面积分别为S1和S2,求S1+S2的取值范围.21.(14分)已知函数f(x)=x++lnx,a∈R.(Ⅰ)若f(x)在x=1处取得极值,求a的值;(Ⅱ)若f(x)在区间(1,2)上单调递增,求a的取值范围;(Ⅲ)讨论函数g(x)=f'(x)﹣x的零点个数.请考生在第22、23题中任选一题作答,如果多做,则按所做第一题记分.22.(10分)在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为(,),直线l的极坐标方程为ρcos(θ﹣)=a,且点A在直线l上,(1)求a的值及直线l的直角坐标方程;(2)圆C的参数方程为(α为参数),试判断直线l与圆C的位置关系.23.设f(x)=|x﹣3|+|x﹣4|.(1)解不等式f(x)≤2;(2)若存在实数x满足f(x)≤ax﹣1,试求实数a的取值范围.2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)参考答案与试题解析一、选择题1.【解答】解:由,得=.∴z在复平面内对应的点的坐标为,是第一象限的点.故选:A.2.【解答】解:∵(x﹣a)[x﹣(a+2)]≤0,∴a≤x≤a+2,若“0<x<1”是“(x﹣a)[x﹣(a+2)]≤0”的充分不必要条件,则,即﹣1≤a≤0,故选:C.3.【解答】解:∵集合A={(x+1)≥﹣2}={x|﹣1<x≤3},B={x|≥2}={x|0≤x<1},∴A∩B={x|0≤x<1}=[0,1).故选:B.4.【解答】解:∵A、B、P三点共线∴∴∴∵∴a1+a4015=1∵{a n}为等差数列∴2a2008=1∴a2008=故选:C.5.【解答】解:由图象得A=±4,=8,∴T=16,∵ω>0,∴ω==,①若A>0时,y=4sin(x+φ),当x=6时,φ=2kπ,φ=2kπ﹣,k∈Z;又|φ|<,∴φ∈∅;②若A<0时,y=﹣4sin(x+φ),当x=﹣2时,φ=2kπ,φ=2kπ+,k∈z;又|φ|<,∴φ=.综合①②该函数解析式为y=﹣4sin().故选:A.6.【解答】解:因为函数y=(m﹣1)x2+2mx+3是偶函数,所以2m=0,即m=0.所以函数y=(m﹣1)x2+2mx+3=﹣x2+3,函数在(0,+∞)上单调递减.又f(﹣1)=f(1),f(﹣)=f(),所以f(1)>f()>f(),即f()<f(﹣)<f(﹣1),故选:B.7.【解答】解:设F(c,0),则直线AB的方程为y=(x﹣c)代入双曲线渐近线方程y =﹣x得A(,﹣),由=2,可得B(﹣,﹣),把B点坐标代入双曲线方程﹣=1,即=1,整理可得c=a,即离心率e==.故选:C.8.【解答】解:由几何体的三视图可知,该几何体为底面是直角梯形,高为的四棱锥,其中直角梯形两底长分别为1和2,高是2.故这个几何体的体积是×[(1+2)×2]×=(cm3).故选:B.9.【解答】解:由约束条件作出可行域如图,令z=x+2y,化为y=﹣,由图可知,当直线y=﹣过A(﹣2,﹣2)时直线y轴上的截距最小为z=﹣4,∴3x+9y≥=.故选:C.10.【解答】解:求导数可得f′(x)=6x2+6||x+6,则由函数f(x)=2x3+3|a|x2+6a•bx+7在实数集R上单调递增,可得f′(x)=6x2+6||x+6≥0恒成立,即x2+||x+≥0恒成立,故判别式△=2﹣4≤0 恒成立,再由,可得8||2≤8||2cos<,>,∴cos<,>≥,∴<,>∈[0,],故选:C.11.【解答】解:∵f(x)=x3﹣x2+3x﹣,∴f′(x)=x2﹣x+3,∴f″(x)=2x﹣1,令f″(x)=2x﹣1=0解得,x=,f()=1,由题意知,(,1)是f(x)=x3﹣x2+3x﹣的对称中心;故f()+f()=2,f()+f()=2,…,故f()+f()+f()+…+f()=2016,故选:D.12.【解答】解:由题意得,点B n(n,0),A n(a n,b n)满足|A n B n|=|A n B n+1|,由中点坐标公式,可得B n B n+1的中点为(n+,0),即a n=n+,b n=;当a>1时,以b n﹣1,b n,b n+1为边长能构成一个三角形,只需b n﹣1+b n>b n+1,b n﹣1<b n<b n+1,即+>,即有1+a<a2,解得1<a<;同理,0<a<1时,解得<a<1;综上,a的取值范围是1<a<或<a<1,故选:B.二.填空题13.【解答】解:由题意,一条渐近线方程为2x﹣y=0,圆(x+1)2+(y﹣2)2=4的圆心坐标为(﹣1,2),半径为2,∴圆心到渐近线的距离d==,∴渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为2=.故答案为:.14.【解答】解:函数f(x)=,则f(x)dx=(4﹣x)dx+dx,其中(4﹣x)dx=(4x﹣x2)=0﹣(﹣8﹣2)=10,dx表示以原点为圆心以2为半径的圆的面积的四分之一,即dx =π,故f(x)dx=(4﹣x)dx+dx=π+10,故答案为:π+1015.【解答】解:三棱锥O﹣ABC,A、B、C三点均在球心O的表面上,且AB=BC=1,∠ABC=120°,AC=,∴S△ABC=×1×1×sin120°=,∵三棱锥O﹣ABC的体积为,△ABC的外接圆的圆心为G,∴OG⊥⊙G,外接圆的半径为:GA==1,∴S△ABC•OG=,即OG=,∴OG=,球的半径为:=4.球的体积:π•43=π.故答案为:π.16.【解答】解:由sin A=sin B cos C,得a=b,即a2+c2=b2,∴△ABC是以B为直接的直角三角形,如图,∵•=16,∴bc cos A=16,即c2=16,c=4.以BC所在直线为x轴,以BA所在直线为y轴建系,则A(0,4),D(0,t)(0≤t≤4),C(a,0),∴,∴=t2﹣4t=(t﹣2)2﹣4∈[﹣4,0].故答案为:[﹣4,0].三.解答题17.【解答】(1)证明:由a n+1=a n+2+1=﹣1,∴﹣=1,故数列{}是等差数列,首项为1,公差为1的等差数列.∴=1+(n﹣1)=n,∴a n=n2﹣1.(2)解:b n==(n+1)•2n,∴数列{b}的前n项的和T n=2×2+3×22+4×23+…+(n+1)•2n,2T n=2×22+3×23+…+n•2n+(n+1)•2n+1,∴﹣T n=4+22+23+…+2n﹣(n+1)•2n+1=2+﹣(n+1)•2n+1,可得T n=n•2n+1.18.【解答】解:(1)∵年龄在[35,40)内的频率为0.04×5=0.2,∴总人数N==40人.∵[30,35)这组的频率为:1﹣(0.01×2+0.02+0.03×2+0.04)×5=0.3,[30,35)这组的参加者人数N1为:40×0.3=12人.(2)记事件B为“从年龄在[30,35]之间选出的人中至少有2名数学教师”,∵年龄在[30,35)之间的人数为12,∴P(B)=1﹣=,记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,∵年龄在[35,40)之间的人数为8,∴P(C)=1﹣=,∴两组选出的人中都至少有1名数学老师的概率P(BC)==.(3)年龄在[45,55)之间的人数为6人,其中女教师4人,∴ξ的可能取值为1,2,3,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:Eξ==2.19.【解答】证明:(1)PO⊥EF,AO⊥EF,所以EF⊥平面POA,因为BD∥EF ∴BD⊥平面POA则PO⊥BD,又AO⊥BD,AO∩PO=O,AO⊂平面APO,PO⊂平面APO,∴BD⊥平面APO,(2)因为AP=,可证PO⊥AO,所以EF,PO,AO互相垂直以O为原点,OA为x轴,OF为y轴,OP为z轴,建立坐标系,则O(0,0,0),A(3,0,0),P(0,0,),B(,2,0),设=(x,y,z)为平面OAP的一个法向量,则=(0,1,0),=(x,y,z)为平面ABP的一个法向量,=(﹣2,2,0),=(﹣3,0,),则,令x=1,则y=,z=3,则=(1,,3)….cosθ==,∴tanθ=∴二面角B﹣AP﹣O的正切值为20.【解答】解:(1)由题意可知:椭圆的离心率e==,则3a2=4c2,b2=a2﹣c2=a2,即a2=4b2,将(,)代入椭圆方程:,则,解得:b2=1,a2=4,椭圆C的方程;(2)①设点E(x1,y1),F(x2,y2),直线A1E,y=k(x﹣2),直线B1E:y=﹣kx+1,(4k2+1)x2﹣16k2x+16k2﹣4=0,则2x1=,x1=,则,消去y得:y1=k(x1﹣2)=,则E(,),联立,消去y整理得:(4k2+1)x2﹣8kx=0,x2=,y2=﹣kx2+1=,F(,),则k EF==,②设直线EF:y=x+b,联立方程组,消去y得:x2+2bx+2b2﹣2=0,△=(﹣2b)2﹣4(2b2﹣2)=8﹣4b2>0,解得:﹣<b<,x1+x2=﹣2b,x1x2=2b2﹣2,丨EF丨=•=,设d1,d2分别为点A1,B1到直线EF的距离,则d1=,d2=,则S1+S2=•(d1+d2)丨EF丨=(丨b+1丨+丨b﹣1丨),∵﹣1≤b≤1时,∴S1+S2=2,由2∈[2,2],S1+S2∈[2,2],S1+S2的取值范围[2,2].21.【解答】解:(Ⅰ)函数f(x)=x++lnx(x>0),f′(x)=1﹣+=,f(x)在x=1处取得极小值,即有f′(1)=0,解得a=2,经检验,a=2时,f(x)在x=1处取得极小值.则有a=2;(Ⅱ)f′(x)=1﹣+=,x>0,f(x)在区间(1,2)上单调递增,即为f′(x)≥0在区间(1,2)上恒成立,即a≤x2+x在区间(1,2)上恒成立,由x2+x∈(2,6),则a≤2;(Ⅲ)g(x)=f′(x)﹣x=1﹣+﹣x,x>0,令g(x)=0,则a=﹣x3+x2+x,令h(x)=﹣x3+x2+x,x>0,则h′(x)=﹣3x2+2x+1=﹣(3x+1)(x﹣1),当x∈(0,1),h′(x)>0,h(x)在(0,1)递增;当x∈(1,+∞),h′(x)<0,h(x)在(1,+∞)递减.即有h(x)的最大值为h(1)=1,则当a>1时,函数g(x)无零点;当a=1或a≤0时,函数g(x)有一个零点;当0<a<1时,函数g(x)有两个零点.请考生在第22、23题中任选一题作答,如果多做,则按所做第一题记分.22.【解答】解:(1)点A(,)在直线l上,得cos(θ﹣)=a,∴a=,故直线l的方程可化为:ρsinθ+ρcosθ=2,得直线l的直角坐标方程为x+y﹣2=0;(2)消去参数α,得圆C的普通方程为(x﹣1)2+y2=1圆心C到直线l的距离d=<1,所以直线l和⊙C相交.23.【解答】解(1),由图象可得f(x)≤2的解集为﹣(5分)(2)函数y=ax﹣1,的图象是经过点(0,﹣1)的直线,由图象可得﹣﹣﹣﹣﹣(10分)。
江西省宜春市上高二中2016-2017学年高二下学期第五次月考数学试卷(文科)Word版含解析

2016-2017学年江西省宜春市上高二中高二(下)第五次月考数学试卷(文科)一、选择题(12×5=60分)1.某学校高一、高二、高三年级分别有720、720、800人,现从全校随机抽取56人参加防火防灾问卷调查.先采用分层抽样确定各年级参加调查的人数,再在各年级内采用系统抽样确定参加调查的同学,若将高三年级的同学依次编号为001,002,...,800,则高三年级抽取的同学的编号不可能为()A.001,041,...761B.031,071,...791C.027,067,...787D.055,095, (795)2.若f(x)=xcosx,则函数f(x)的导函数f'(x)等于()A.1﹣sinx B.x﹣sinx C.sinx+xcosx D.cosx﹣xsinx3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是()A.①③B.①④C.②③D.①②4.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.15.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是()A.B.C.D.6.一组数据的平均数是4.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是()A.55.2,3.6 B.55.2,56.4 C.64.8,63.6 D.64.8,3.67.已知双曲线=1(a>0,b>0)的一条渐近线与函数y=lnx+ln2+1的图象相切,则双曲线的离心率等于()A.B.C.D.8.如图是某四面体ABCD水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD外接球的表面积为()A.20πB.C.25πD.100π9.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式e x f (x)>e x+3(其中e为自然对数的底数)的解集为()A.(0,+∞)B.(﹣∞,0)∪(3,+∞)C.(﹣∞,0)∪(0,+∞)D.(3,+∞)10.已知a为常数,函数f(x)=ax3﹣3ax2﹣(x﹣3)e x+1在(0,2)内有两个极值点,则实数a的取值范围为()A.B.C.D.11.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足f'(x1)=,f'(x2)=,则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)=2x3﹣x2+m是[0,2a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,)C.(,)D.(,1)12.已知f(x)是定义在区间(0,+∞)上的函数,其导函数为f'(x),且不等式xf'(x)<2f(x)恒成立,则()A.4f(1)<f(2)B.4f(1)>f(2)C.f(1)<4f(2)D.f(1)<2f'(2)二、填空题(5×4=20分)13.如表是某厂1﹣4月份用水量(单位:百吨)的一组数据:由散点可知,用水量y与月份x之间由较好的线性相关关系,其线性回归方程是=0.7x+a,则a等于.14.已知函数y=f(x)(x∈R)的图象如图所示,则不等式xf′(x)<0的解集为.15.若曲线y=在点P(a,)处的切线与两坐标轴围成的三角形的面积为2,则实数a的值是.16.已知f(x)=﹣(x﹣1)2+m,g(x)=xe x,若∃x1,x2∈R,使得f(x1)≥g (x2)成立,则实数m的取值范围是.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00~12:00间各自的车流量(单位:百辆),得如图所示的统计图,试求:(1)甲、乙两个交通站的车流量的极差分别是多少?(2)甲交通站的车流量在[10,60]间的频率是多少?(3)甲、乙两个交通站哪个站更繁忙?并说明理由.18.已知函数f(x)=.(1)若函数f(x)的曲线上一条切线经过点M(0,0),求该切线方程;(2)求函数f(x)在区间[﹣3,+∞)上的最大值与最小值.19.如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC∥平面DEF;(Ⅲ)求三棱锥C﹣DEF的体积.20.据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量y(升)与行驶速度y(千米∕时)之间有如下函数关系:.已知甲、乙两地相距100千米.(Ⅰ)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?21.已知椭圆的焦距为,短半轴长为2,过点P(﹣2,1)斜率为1的直线l与椭圆C交于A,B点.(1)求椭圆C的标准方程;(2)求弦AB的长.22.已知函数f(x)=x+,g(x)=x+lnx,其中a≠0.(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值及h(x)的单调区间;(2)若对任意的x1,x2∈[1,2],f(x1)≥g(x2)恒成立,且﹣2<a<0,求实数a的取值范围.2016-2017学年江西省宜春市上高二中高二(下)第五次月考数学试卷(文科)参考答案与试题解析一、选择题(12×5=60分)1.某学校高一、高二、高三年级分别有720、720、800人,现从全校随机抽取56人参加防火防灾问卷调查.先采用分层抽样确定各年级参加调查的人数,再在各年级内采用系统抽样确定参加调查的同学,若将高三年级的同学依次编号为001,002,...,800,则高三年级抽取的同学的编号不可能为()A.001,041,...761B.031,071,...791C.027,067,...787D.055,095, (795)【考点】系统抽样方法.【分析】由系统抽样得到的数据特征应成等差数列,经计算答案中的数据795﹣055=740不是40的整数倍,即可得出结论.【解答】解:由系统抽样得到的数据特征应成等差数列,经计算答案中的数据795﹣055=740不是40的整数倍,因此这组数据不合系统抽样得到的,故选D.2.若f(x)=xcosx,则函数f(x)的导函数f'(x)等于()A.1﹣sinx B.x﹣sinx C.sinx+xcosx D.cosx﹣xsinx【考点】导数的运算.【分析】根据题意,由导数乘积的运算法则求f(x)=xcosx求导,即可得答案.【解答】解:根据题意,f(x)=xcosx,其导数f′(x)=x′cosx+x•(cosx)′=cosx﹣xsinx,即f'(x)=cosx﹣xsinx,故选:D.3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是()A.①③B.①④C.②③D.①②【考点】变量间的相关关系.【分析】观察两个变量的散点图,若样本点成带状分布,则两个变量具有线性相关关系,若带状越细说明相关关系越强,得到两个变量具有线性相关关系的图是①和④.【解答】解:∵两个变量的散点图,若样本点成带状分布,则两个变量具有线性相关关系,∴两个变量具有线性相关关系的图是①和④.故选B.4.已知函数f(x)=ln(ax﹣1)的导函数是f'(x),且f'(2)=2,则实数a的值为()A.B.C.D.1【考点】导数的运算.【分析】利用导数的运算法则即可得出.【解答】解:由f(x)=ln(ax﹣1)可得,由f'(2)=2,可得,解之得.故选:B.5.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是()A.B.C.D.【考点】函数的单调性与导数的关系.【分析】先根据导函数的图象确定导函数大于0 的范围和小于0的x的范围,进而根据当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减确定原函数的单调增减区间.【解答】解:由y=f'(x)的图象易得当x<0或x>2时,f'(x)>0,故函数y=f(x)在区间(﹣∞,0)和(2,+∞)上单调递增;当0<x<2时,f'(x)<0,故函数y=f(x)在区间(0,2)上单调递减;故选C.6.一组数据的平均数是4.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是()A.55.2,3.6 B.55.2,56.4 C.64.8,63.6 D.64.8,3.6【考点】极差、方差与标准差;众数、中位数、平均数.【分析】首先写出原来数据的平均数表示式和方差的表示式,把数据都加上60以后,再表示出新数据的平均数和方差的表示式,两部分进行比较,得到结果【解答】解:设这组数据分别为x1,x2,…,x n,若其平均数是4.8,方差是3.6,则有1=(x1+x2+…+x n)=4.8,方差S12= [(x1﹣)2+…+(x n﹣)2]=3.6;若将这组数据中的每一个数据都加上60,则数据为60+x 1,60+x 2,…,60+x n ,则平均数2= [(60+x 1)+)60+x 2)+…+(60+x n )]=60+4.8=64.8,方差S 22= [(60+x 1﹣64.8)2+…+(60+x n ﹣64.8)2]=3.6;故选:D .7.已知双曲线=1(a >0,b >0)的一条渐近线与函数y=lnx +ln2+1的图象相切,则双曲线的离心率等于( )A .B .C .D .【考点】双曲线的简单性质.【分析】由函数的导数的几何意义可知:则渐近线的斜率为k==,则=,解得:x 0=,即可求得b=2a ,双曲线的离心率e===.【解答】解:由函数y=lnx +ln2+1,(x >0),求导y′=,设渐近线与函数的切点为P (x 0,y 0),则渐近线的斜率为k==,∴=,解得:x 0=,∴==2,b=2a ,双曲线的离心率e===,故选D .8.如图是某四面体ABCD 水平放置时的三视图(图中网格纸的小正方形的边长为1,则四面体ABCD 外接球的表面积为( )A.20πB.C.25πD.100π【考点】由三视图求面积、体积.【分析】还原三视图成直观图,得到如图所示的三棱锥P﹣ABC,其中AC⊥BC,PA⊥平面ABC,AB=BC=2且PA=3.利用线面垂直的判定与性质,证出PB是Rt △PAB与Rt△PBC公共的斜边,从而得到PB的中点O就是多面体的外接球的球心.再根据勾股定理和球的表面积公式加以计算,可得答案.【解答】解:根据三视图的形状,将该多面体还原成直观图,得到如图所示的三棱锥P﹣ABC.其中△ABC中,AC=4,AB=BC=2,PA⊥平面ABC,PA=3∵PA⊥平面ABC,BC⊂平面ABC,∴PA⊥BC.∵BC⊥AC,PA∩AC=C,∴BC⊥平面PAC结合PC⊂平面PAC,得BC⊥PC因此,PB是Rt△PAB与Rt△PBC公共的斜边,设PB的中点为0,则OA=OB=OC=OP=PB.∴PB的中点O就是多面体的外接球的球心∵Rt△ABC中,AC⊥BC,AC=BC=2,∴AB=2.又∵Rt△PAB中,PA=3,∴PB==,所以外接球表面积为S=4πR2=25π.故选:C.9.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式e x f (x)>e x+3(其中e为自然对数的底数)的解集为()A.(0,+∞)B.(﹣∞,0)∪(3,+∞)C.(﹣∞,0)∪(0,+∞)D.(3,+∞)【考点】利用导数研究函数的单调性;导数的运算.【分析】构造函数g(x)=e x f(x)﹣e x,(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解【解答】解:设g(x)=e x f(x)﹣e x,(x∈R),则g′(x)=e x f(x)+e x f′(x)﹣e x=e x[f(x)+f′(x)﹣1],∵f(x)+f′(x)>1,∴f(x)+f′(x)﹣1>0,∴g′(x)>0,∴y=g(x)在定义域上单调递增,∵e x f(x)>e x+3,∴g(x)>3,又∵g(0)═e0f(0)﹣e0=4﹣1=3,∴g(x)>g(0),∴x>0故选:A.10.已知a为常数,函数f(x)=ax3﹣3ax2﹣(x﹣3)e x+1在(0,2)内有两个极值点,则实数a的取值范围为()A.B.C.D.【考点】利用导数研究函数的极值.【分析】求出函数f(x)的导数,问题转化为y=a和g(x)在(0,2)有2个交点,根据函数的单调性求出a的范围即可.【解答】解:f′(x)=(x﹣2)(3ax﹣e x),若f(x)在(0,2)内有两个极值点,即a=在(0,2)有2个解,令g(x)=,x∈(0,2),问题转化为y=a和g(x)在(0,2)有2个交点,则g′(x)=,令g′(x)>0,解得:1<x<2,令g′(x)<0,解得:0<x<1,故g(x)在(0,1)递减,在(1,2)递增,故g(x)min=g(1)=,而f(2)=,x→0时,f(x)→+∞,故a∈(,),故选:C.11.定义:如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足f'(x1)=,f'(x2)=,则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)=2x3﹣x2+m是[0,2a]上“双中值函数”,则实数a的取值范围是()A.(,)B.(,)C.(,)D.(,1)【考点】函数与方程的综合运用.【分析】根据定义得出=8a2﹣2a,相当于6x2﹣2x=8a2﹣2a在[0,2a]上有两个根,利用二次函数的性质解出a的范围即可.【解答】解:f(x)=2x3﹣x2+m是[0,2a]上的“双中值函数”,∴=8a2﹣2a,∵f'(x)=6x2﹣2x,∴6x2﹣2x=8a2﹣2a在[0,2a]上有两个根,令g(x)=6x2﹣2x﹣8a2+2a,∴△=4+24(8a2﹣2a)>0,g(0)>0,g(2a)>0,2a>,∴<a<.故选A.12.已知f(x)是定义在区间(0,+∞)上的函数,其导函数为f'(x),且不等式xf'(x)<2f(x)恒成立,则()A.4f(1)<f(2)B.4f(1)>f(2)C.f(1)<4f(2)D.f(1)<2f'(2)【考点】函数的单调性与导数的关系.【分析】令g(x)=,(x>0),求出函数的导数,得到函数的单调性,求出g(1)>g(2),从而求出答案.【解答】解:令g(x)=,(x>0),则g′(x)=,∵不等式xf'(x)<2f(x)恒成立,∴xf'(x)﹣2f(x)<0,即g′(x)<0,g(x)在(0,+∞)递减,故g(1)>g(2),故4f(1)>f(2),故选:B.二、填空题(5×4=20分)13.如表是某厂1﹣4月份用水量(单位:百吨)的一组数据:由散点可知,用水量y与月份x之间由较好的线性相关关系,其线性回归方程是=0.7x+a,则a等于 5.25.【考点】线性回归方程.【分析】首先求出x,y的平均数,根据所给的线性回归方程知道b的值,根据样本中心点满足线性回归方程,把样本中心点代入,得到关于a的一元一次方程,解方程即可.【解答】解:=(1+2+3+4)=2.5,=(4.5+4+3+2.5)=3.5,将(2.5,3.5)代入线性回归直线方程是=﹣0.7x+a,可得3.5=﹣1.75+a,故a=5.25.故答案为:5.25.14.已知函数y=f(x)(x∈R)的图象如图所示,则不等式xf′(x)<0的解集为(﹣∞,0)∪(,2).【考点】函数的单调性与导数的关系.【分析】由函数y=f(x)(x∈R)的图象可得函数的单调性,根据单调性与导数的关系得导数的符号,进而得不等式xf′(x)<0的解集.【解答】解:由f(x)图象特征可得,f′(x)在(﹣∞,)∪(2,+∞)上大于0,在(,2)上小于0,∴xf′(x)<0⇔⇔⇔x<0或<x <2,所以xf′(x )<0的解集为(﹣∞,0)∪(,2).故答案为:(﹣∞,0)∪(,2).15.若曲线y=在点P (a ,)处的切线与两坐标轴围成的三角形的面积为2,则实数a 的值是 4 .【考点】利用导数研究曲线上某点切线方程;直线的截距式方程.【分析】求导数可得切线的斜率,进而可得切线的方程,可得其截距,由面积为2可得a 的方程,解方程可得.【解答】解:对y=求导数可得y′=,∴曲线在P (a ,)处的切线斜率为k=,∴切线方程为:y ﹣=(x ﹣a ),令x=0,可得y=,即直线的纵截距为, 令y=0,可得x=﹣a ,即直线的横截距为﹣a , ∴切线与两坐标轴围成的三角形的面积为:S=|||﹣a |=2,解得a=4故答案为:416.已知f (x )=﹣(x ﹣1)2+m ,g (x )=xe x ,若∃x 1,x 2∈R ,使得f (x 1)≥g(x 2)成立,则实数m 的取值范围是 [﹣,+∞) . 【考点】函数最值的应用.【分析】∃x 1,x 2∈R ,使得f (x 1)≥g (x 2)成立,等价于f (x )max ≥g (x )min ,分别求出最值,即可得出结论.【解答】解:∃x 1,x 2∈R ,使得f (x 1)≥g (x 2)成立,等价于f (x )max ≥g (x )min ,∵g (x )=xe x ,∴g′(x)=(1+x)e x,x<﹣1时,g′(x)<0,x>﹣1时,g′(x)>0,∴x=﹣1时,g(x)min=﹣,∵f(x)=﹣(x﹣1)2+m,∴f(x)max=m,∴m≥﹣,∴实数m的取值范围是[﹣,+∞).故答案为:[﹣,+∞).三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8:00~12:00间各自的车流量(单位:百辆),得如图所示的统计图,试求:(1)甲、乙两个交通站的车流量的极差分别是多少?(2)甲交通站的车流量在[10,60]间的频率是多少?(3)甲、乙两个交通站哪个站更繁忙?并说明理由.【考点】茎叶图;古典概型及其概率计算公式.【分析】(1)由各组数据的最大值减去最小值就是这组数据的极差;(2)用甲交通站的车流量在[10,60]间天数除以14就得到甲交通站的车流量在[10,60]间的频率;(3)通过茎叶图中的数据对甲乙两个交通站比对,明显甲交通站集中在60百辆附近,乙较分散.【解答】解:(1)甲交通站的车流量的极差为73﹣8=65(百辆),乙交通站的车流量的极差为71﹣5=66(百辆);(2)甲交通站的车流量在[10,60]间的频率为.(3)甲交通站的车流量集中在茎叶图的下方,而乙交通站的车流量集中在茎叶图的上方,从数据的分布情况来看,甲交通站更繁忙.18.已知函数f(x)=.(1)若函数f(x)的曲线上一条切线经过点M(0,0),求该切线方程;(2)求函数f(x)在区间[﹣3,+∞)上的最大值与最小值.【考点】利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,设切点是(a,),求出a的值,从而求出切线方程即可;(2)求出函数f(x)的单调区间,从而求出f(x)的最值即可.【解答】解:(1)f′(x)=,设切点是(a,),则k=f′(a)=,故切线方程是:y﹣=(x﹣a)(*),将(0,0)带入(*)得:a=1,故切点是(1,),k=,故切线方程是:y﹣=(x﹣1),整理得:y=x;(2)f′(x)=,令f′(x)>0,解得:0<x<2,令f′(x)<0,解得:x>2或x<0,故f(x)在[﹣3,0)递减,在(0,2)递增,在(2,+∞)递减,而f(﹣3)=9e3,f(0)=0,f(2)=,x→+∞时,f(x)→0,故f(x)的最小值是0,最大值是f(﹣3)=9e3.19.如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC∥平面DEF;(Ⅲ)求三棱锥C﹣DEF的体积.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.【分析】(Ⅰ)推导出BE⊥AC,AC⊥BD.由此能证明AC⊥平面BDE.(Ⅱ)设AC∩BD=O,设G为DE的中点,连结OG,FG,推导出四边形AOGF为平行四边形,从而AO∥FG,即AC∥FG,由此能证明AC∥平面DEF.=V A (Ⅲ)推导出点C到平面DEF的距离等于A点到平面DEF的距离,由V C﹣DEF,能求出三棱锥C﹣DEF的体积.﹣DEF【解答】(本小题满分14分)证明:(Ⅰ)因为平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,且AB⊥BE,所以BE⊥平面ABCD.因为AC⊂平面ABCD,所以BE⊥AC.又因为四边形ABCD为正方形,所以AC⊥BD.因为BD∩BE=B,所以AC⊥平面BDE.…(Ⅱ)设AC∩BD=O,因为四边形ABCD为正方形,所以O为BD中点.设G 为DE 的中点,连结OG ,FG ,则OG ∥BE ,且.由已知AF ∥BE ,且,则AF ∥OG ,且AF=OG .所以四边形AOGF 为平行四边形. 所以AO ∥FG ,即AC ∥FG .因为AC ⊄平面DEF ,FG ⊂平面DEF , 所以AC ∥平面DEF .…解:(Ⅲ)由(Ⅰ)可知BE ⊥平面ABCD ,因为AF ∥BE ,所以AF ⊥平面ABCD ,所以AF ⊥AB ,AF ⊥AD . 又因为四边形ABCD 为正方形,所以AB ⊥AD , 所以AD ⊥平面ABEF .由(Ⅱ)可知,AC ∥平面DEF ,所以,点C 到平面DEF 的距离等于A 点到平面DEF 的距离, 所以 V C ﹣DEF =V A ﹣DEF . 因为AB=AD=2AF=2.所以=.故三棱锥C ﹣DEF 的体积为.…20.据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量y (升)与行驶速度y (千米∕时)之间有如下函数关系:.已知甲、乙两地相距100千米.(Ⅰ)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?【考点】利用导数求闭区间上函数的最值;函数模型的选择与应用.【分析】(Ⅰ)求出汽车从甲地到乙地行驶的时间,即可求得需耗油的升数;(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶小时,列出耗油函数关系式,利用导数可得最值.【解答】解:(Ⅰ)当x=40千米∕时时,汽车从甲地到乙地行驶了(小时),需耗油(升).所以,汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油17.5升….(Ⅱ)当汽车的行驶速度为x千米∕时时,从甲地到乙地需行驶小时.设耗油量为h(x)升,依题意,得,其中,0<x≤120.…即(0<x≤120).令h′(x)=0,得x=80当x∈(0,80)时,h′(x)<0,函数单调递减;当x∈(80,120)时,h′(x)>0,函数单调递增∴x=80时,从甲地到乙地耗油最少,最少为11.25升∴所以当汽车以80千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为11.25升.…21.已知椭圆的焦距为,短半轴长为2,过点P(﹣2,1)斜率为1的直线l与椭圆C交于A,B点.(1)求椭圆C的标准方程;(2)求弦AB的长.【考点】直线与椭圆的位置关系;椭圆的标准方程.【分析】(1)由已知可得:2c=4,b=2,a2=b2+c2,联立解得即可得出.(2)直线l的方程为:y﹣1=x+2,即y=x+3.设A(x1,y1),B(x2,y2).与题意方程联立化为:4x2+18x+15=0,利用弦长公式|AB|=即可得出.【解答】解:(1)由已知可得:2c=4,b=2,a2=b2+c2,联立解得:c=2,b=2,a2=12.∴椭圆C的标准方程为=1.(2)直线l的方程为:y﹣1=x+2,即y=x+3.设A(x1,y1),B(x2,y2).联立,化为:4x2+18x+15=0,∴x1+x2=﹣,x1•x2=,∴|AB|===.22.已知函数f(x)=x+,g(x)=x+lnx,其中a≠0.(1)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值及h(x)的单调区间;(2)若对任意的x1,x2∈[1,2],f(x1)≥g(x2)恒成立,且﹣2<a<0,求实数a的取值范围.【考点】利用导数研究函数的极值;利用导数求闭区间上函数的最值.【分析】(1)对h(x)求导数,利用h′(x)=0时存在极值点,求出a的值,再利用导数讨论h(x)的单调性;(2)设存在实数a,对任意的x1,x2∈[1,2]都有f(x1)≥g(x2)成立,等价于对任意的x1,x2∈[1,2]时,都有[f(x)]min≥[g(x)]max,分别求出函数f(x)在区间[1,2]的最小值与g(x)在[1,2]上的最大值,列出不等式求出实数a的取值范围.【解答】解:(1)∵h(x)=f(x)+g(x)=2x++lnx,其定义域为(0,+∞),∴h′(x)=2﹣+;又x=1是函数h(x)的极值点,∴h'(1)=0,即3﹣a2=0,∵a>0,∴a=;经检验,a=时,x=1是函数h(x)的极值点,∴a=;又h′(x)==,∴当0<x<1时,h′(x)<0,h(x)是单调减函数,x>1时,h′(x)>0,h(x)是单调增函数;∴h(x)的单调减区间为(0,1),增区间为(1,+∞);(2)假设存在实数a,对任意的x1,x2∈[1,2]都有f(x1)≥g(x2)成立,等价于对任意的x1,x2∈[1,2]时,都有[f(x)]min≥[g(x)]max,当x∈[1,2]时,g′(x)=1+>0.∴函数g(x)=x+lnx在[1,2]上是增函数.∴[g(x)]max=g(2)=2+ln2.∵f′(x)=1﹣=,且x∈[1,2],﹣2<a<0,①当﹣1<a<0且x∈[1,2]时,f′(x)=>0,∴函数f(x)=x+在[1,2]上是增函数.∴[f(x)]min=f(1)=1+a2.由1+a2≥2+ln2,得a≤﹣,又﹣1<a<0,∴a≤﹣不合题意.②当﹣<≤a≤﹣1时,若1≤x<﹣a,则f′(x)=<0,若﹣a<x≤2,则f′(x)=>0,∴函数f(x)=x+在[1,﹣a)上是减函数,在(﹣a,2]上是增函数.∴[f(x)]min=f(﹣a)=﹣2a﹣2a≥2+ln2,得a≤﹣1﹣ln2,∴﹣2<a≤﹣1﹣ln2.综上,存在实数a的取值范围为(﹣2,﹣1﹣ln2).2017年4月29日。
江西省宜春市上高二中2016-2017学年高二(下)第七次月考数学试卷(文科)

2016-2017学年江西省宜春市上高二中高二(下)第七次月考数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.用反证法证明命题:“a,b,c,d∈R,a+b=1,c+d=1,且ac+bd>1,则a,b,c,d 中至少有一个负数”时的假设为()A.a,b,c,d全都大于等于0 B.a,b,c,d全为正数C.a,b,c,d中至少有一个正数D.a,b,c,d中至多有一个负数2.甲、乙两人练习射击,命中目标的概率分别为和,甲、乙两人各射击一次,目标被命中的概率为()A.B.C.D.3.一个多面体的三视图和直观图如图所示,M是AB的中点,一只蜻蜓在几何体ADF ﹣BCE内自由飞翔,则它飞入几何体F﹣AMCD内的概率为()A.B.C.D.4.设样本数据x1,x2,…,x20的均值和方差分别为1和8,若y i=2x i+3(i=1,2,…,20),则y1,y2,…,y20的均值和方差分别是()A.5,32 B.5,19 C.1,32 D.4,355.两个变量x,y与其线性相关系数r有下列说法(1)若r>0,则x增大时,y也相应增大;(2)若r<0,则x增大时,y也相应增大;(3)若r=1或r=﹣1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.其中正确的有()A.①②B.②③C.①③D.①②③6.如图所示的茎叶图(图一)为高三某班50名学生的化学考试成绩,图(二)的算法框图中输入的a i为茎叶图中的学生成绩,则输出的m,n分别是()A.m=38,n=12 B.m=26,n=12 C.m=12,n=12 D.m=24,n=107.已知函数y=f(x=2)是偶函数,且当x≠2时其导函数f′(x)满足(x﹣2)f′(x)>0,若2<a<3,则下列不等式式成立的是()A.f(2a)<f(3)<f(log2a)B.f(3)<f(log2a)<f(2a)C.f(log2a)<f(3)<f(2a)D.f(log2a)<f(2a)<f(3)8.假设有两个分类变量X和Y的2×2列联表:y1y2总计YXx1a10a+10x2c30c+30总计6040100对同一样本,以下数据能说明X与Y有关系的可能性最大的一组为()A.a=45,c=15 B.a=40,c=20 C.a=35,c=25 D.a=30,c=309.如图所示是一个容量为200的样本的重量频率分布直方图,则由图可估计该样本重量的平均数为()A.11 B.11.5 C.12 D.12.510.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间的人做问卷A,编号落入区间的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为()A.7 B.9 C.10 D.1511.已知函数y=x+1+lnx在点A(1,2)处的切线l,若l与二次函数y=ax2+(a+2)x+1的图象也相切,则实数a的取值为()A.12 B.8 C.0 D.412.函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式e x•f(x)>e x+1的解集为()A.{x|x>0}B.{x|x<0}C.{x|x<﹣1,或x>1}D.{x|x<﹣1,或0<x<1}二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在等差数列{a n}中,我们有=,则在正项等比数列{b n}中,我们可以得到类似的结论是.14.按如图所示的程序框图运算,若输出k=2,则输入x的取值范围是.15.为促进抚州市精神文明建设,评选省级文明城市,现省检查组决定在未来连续5天中随机选取2天对抚州的各项文明建设进行暗访,则这两天恰好为连续两天的概率.16.已知函数f(x)=2lnx﹣x2,若方程f(x)+m=0在内有两个不等的实根,则实数m的取值范围是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:分数区间甲班频率乙班频率hslx3y3h0,30)0.10.2hslx3y3h30,60)0.20.2hslx3y3h60,90)0.30.3hslx3y3h90,120)0.20.2hslx3y3h120,150)0.20.1(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?优秀不优秀总计甲班乙班总计k0 2.072 2.706 3.841 5.024 6.6357.87910.828P(K2≥k0)0.150.100.050.0250.0100.0050.001,其中n=a+b+c+d.18.从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组160,165);…;第八组.如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数及平均身高;(2)求第六组、第七组的频率并补充完整频率分布直方图;(3)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x、y,求满足“|x﹣y|≤5”的事件的概率.19.如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.(Ⅰ)求证:BF∥平面ADE;(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;(Ⅲ)若AC=4,求几何体C﹣BDF的体积.20.某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.(1)求出f(5)的值;(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你的关系式求出f(n)的解析式.21.已知函数f(x)=x3+x2f'(1).(1)求f'(1)和函数x的极值;(2)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围;(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.22.已知圆O:x2+y2=1过椭圆C:(a>b>0)的短轴端点,P,Q分别是圆O与椭圆C上任意两点,且线段PQ长度的最大值为3.(Ⅰ)求椭圆C的方程;(Ⅱ)过点(0,t)作圆O的一条切线交椭圆C于M,N两点,求△OMN的面积的最大值.2016-2017学年江西省宜春市上高二中高二(下)第七次月考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.用反证法证明命题:“a,b,c,d∈R,a+b=1,c+d=1,且ac+bd>1,则a,b,c,d 中至少有一个负数”时的假设为()A.a,b,c,d全都大于等于0 B.a,b,c,d全为正数C.a,b,c,d中至少有一个正数D.a,b,c,d中至多有一个负数【考点】FC:反证法.【分析】用反证法证明数学命题时,应先假设结论的否定成立.【解答】解:“a,b,c,d中至少有一个负数”的否定为“a,b,c,d全都大于等于0”,由用反证法证明数学命题的方法可得,应假设“a,b,c,d全都大于等于0”,故选:A.2.甲、乙两人练习射击,命中目标的概率分别为和,甲、乙两人各射击一次,目标被命中的概率为()A.B.C.D.【考点】C5:互斥事件的概率加法公式;C9:相互独立事件的概率乘法公式.【分析】对立事件的概率之和为1,相互独立事件的概率用乘法法则.【解答】解:∵甲、乙两人各射击一次,目标没被命中的概率为(1﹣)×(1﹣)=,∴甲、乙两人各射击一次,目标被命中的概率为1﹣=.故选A.3.一个多面体的三视图和直观图如图所示,M 是AB 的中点,一只蜻蜓在几何体ADF ﹣BCE 内自由飞翔,则它飞入几何体F ﹣AMCD 内的概率为( )A .B .C .D . 【考点】CF :几何概型.【分析】先根据三棱锥的体积公式求出F ﹣AMCD 的体积与三棱锥的体积公式求出ADF ﹣BCE 的体积,最后根据几何概型的概率公式解之即可. 【解答】解:因为V F ﹣AMCD ==,V ADF ﹣BCE =,所以它飞入几何体F ﹣AMCD 内的概率为=,故选:D .4.设样本数据x 1,x 2,…,x 20的均值和方差分别为1和8,若y i =2x i +3(i=1,2,…,20),则y 1,y 2,…,y 20的均值和方差分别是( ) A .5,32 B .5,19 C .1,32 D .4,35【考点】BB :众数、中位数、平均数;BC :极差、方差与标准差. 【分析】方法1:根据变量之间均值和方差的关系直接代入即可得到结论. 方法2:根据均值和方差的公式计算即可得到结论. 【解答】解:方法1:∵y i =2x i +3, ∴E (y i )=2E (x i )+E (3)=2×1+3=5, 方差D (y i )=22×D (x i )+E (3)=4×8+0=32. 方法2:由题意知y i =2x i +3,则=(x1+x2+…+x20+20×3)=(x1+x2+…+x20)+3=+3=1+3=4,方差s2==22×=4s2=4×8=32.故选:A.5.两个变量x,y与其线性相关系数r有下列说法(1)若r>0,则x增大时,y也相应增大;(2)若r<0,则x增大时,y也相应增大;(3)若r=1或r=﹣1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.其中正确的有()A.①②B.②③C.①③D.①②③【考点】BS:相关系数.【分析】处理本题时可根据线性回归中,相关系数的定义,利用相关系数r进行判断:而且|r|越接近于1,相关程度越强;|r|越接近于0,相关程度越弱,当r为正数时,表示变量x,y正相关,说明一变量随另一变量增减而增减,方向相同;当r为负数时,表示两个变量x,y负相关,即可得答案.【解答】解:根据相关系数的定义,变量之间的相关关系可利用相关系数r进行判断:当r为正数时,表示变量x,y正相关,说明一变量随另一变量增减而增减,方向相同;当r为负数时,表示两个变量x,y负相关,|r|越接近于1,相关程度越强;|r|越接近于0,相关程度越弱,故可知①③正确.故选C.6.如图所示的茎叶图(图一)为高三某班50名学生的化学考试成绩,图(二)的算法框图中输入的a i为茎叶图中的学生成绩,则输出的m,n分别是()A.m=38,n=12 B.m=26,n=12 C.m=12,n=12 D.m=24,n=10【考点】BA:茎叶图;E7:循环结构.【分析】算法的功能是计算学生在50名学生的化学考试成绩中,成绩大于等于80的人数,和成绩小于80且大于等于60的人数,根据茎叶图可得【解答】解:由程序框图知:算法的功能是计算学生在50名学生的化学考试成绩中,成绩大于等于80的人数,和成绩小于80且大于等于60的人数,由茎叶图得,在50名学生的成绩中,成绩大于等于80的人数有80,80,81,84,84,85,86,89,90,91,96,98,共12人,故n=12,由茎叶图得,在50名学生的成绩中,成绩小于60的人数有43,46,47,48,50,51,52,53,53,56,58,59,共12人,则在50名学生的成绩中,成绩小于80且大于等于60的人数有50﹣12﹣12=26,故m=26故选:B.7.已知函数y=f(x=2)是偶函数,且当x≠2时其导函数f′(x)满足(x﹣2)f′(x)>0,若2<a<3,则下列不等式式成立的是()A.f(2a)<f(3)<f(log2a)B.f(3)<f(log2a)<f(2a)C.f(log2a)<f(3)<f(2a)D.f(log2a)<f(2a)<f(3)【考点】6A:函数的单调性与导数的关系.【分析】由函数y=f(x+2)是偶函数可知,函数y=f(x)关于直线x=2对称,又(x﹣2)f′(x)>0,故函数y=f(x)在(﹣∞,2)上单调递减,在(2,+∞)上单调递增,确定变量的大小关系,即可得出结论.【解答】解:由函数y=f(x+2)是偶函数可知,函数y=f(x)关于直线x=2对称,又(x﹣2)f′(x)>0,故函数y=f(x)在(﹣∞,2)上单调递减,在(2,+∞)上单调递增,又2<a<3,所以1<log2a<2,4<2a<8,所以f(log2a)<f(3)<f(2a),故选C.8.假设有两个分类变量X和Y的2×2列联表:Yy1y2总计Xx1a10a+10x2c30c+30总计6040100对同一样本,以下数据能说明X与Y有关系的可能性最大的一组为()A.a=45,c=15 B.a=40,c=20 C.a=35,c=25 D.a=30,c=30【考点】BO:独立性检验的应用.【分析】根据题意,a、c 相差越大,与相差就越大,由此得出X与Y有关系的可能性越大.【解答】解:根据2×2列联表与独立性检验的应用问题,当与相差越大,X与Y有关系的可能性越大;即a、c 相差越大,与相差越大;故选:A.9.如图所示是一个容量为200的样本的重量频率分布直方图,则由图可估计该样本重量的平均数为()A.11 B.11.5 C.12 D.12.5【考点】B8:频率分布直方图.【分析】利用组中值,即可求出该样本重量的平均数.【解答】解:平均值为:7.5×5×0.06+12.5×5×0.1+17.5×(1﹣5×0.06﹣5×0.1)=12,故选C.10.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间的人做问卷A,编号落入区间的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为()A.7 B.9 C.10 D.15【考点】B4:系统抽样方法.【分析】由题意可得抽到的号码构成以9为首项、以30为公差的等差数列,求得此等差数列的通项公式为a n=9+(n﹣1)30=30n﹣21,由451≤30n﹣21≤750 求得正整数n 的个数.【解答】解:960÷32=30,故由题意可得抽到的号码构成以9为首项、以30为公差的等差数列,且此等差数列的通项公式为a n=9+(n﹣1)30=30n﹣21.由451≤30n﹣21≤750 解得15.7≤n≤25.7.再由n为正整数可得16≤n≤25,且n∈z,故做问卷B的人数为10,故选:C.11.已知函数y=x+1+lnx在点A(1,2)处的切线l,若l与二次函数y=ax2+(a+2)x+1的图象也相切,则实数a的取值为()A.12 B.8 C.0 D.4【考点】6H:利用导数研究曲线上某点切线方程.【分析】求出y=x+1+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.【解答】解:y=x+1+lnx的导数为y′=1+,曲线y=x+1+lnx在x=1处的切线斜率为k=2,则曲线y=x+1+lnx在x=1处的切线方程为y﹣2=2x﹣2,即y=2x.由于切线与曲线y=ax2+(a+2)x+1相切,y=ax2+(a+2)x+1可联立y=2x,得ax2+ax+1=0,又a≠0,两线相切有一切点,所以有△=a2﹣4a=0,解得a=4.故选:D.12.函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式e x•f(x)>e x+1的解集为()A.{x|x>0}B.{x|x<0}C.{x|x<﹣1,或x>1}D.{x|x<﹣1,或0<x<1}【考点】3F:函数单调性的性质;63:导数的运算.【分析】构造函数g(x)=e x•f(x)﹣e x,结合已知可分析出函数g(x)的单调性,结合g(0)=1,可得不等式e x•f(x)>e x+1的解集.【解答】解:令g(x)=e x•f(x)﹣e x,则g′(x)=e x•∵对任意x∈R,f(x)+f′(x)>1,∴g′(x)>0恒成立即g(x)=e x•f(x)﹣e x在R上为增函数又∵f(0)=2,∴g(0)=1故g(x)=e x•f(x)﹣e x>1的解集为{x|x>0}即不等式e x•f(x)>e x+1的解集为{x|x>0}故选A二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在等差数列{a n}中,我们有=,则在正项等比数列{b n}中,我们可以得到类似的结论是.【考点】F3:类比推理.【分析】由题意,本题用类比推理由等差数列的性质得到等比数列的性质,其运算关系由加类比乘,故结论易得.【解答】解:由题意,等差数列{a n}中,我们有=,.类比得:在正项等比数列{b n}中.故答案为:.14.按如图所示的程序框图运算,若输出k=2,则输入x的取值范围是19≤x<200.【考点】E7:循环结构.【分析】由框图知,此程序输出的是循环次数,K值等于次循环数,循环退出的条件是x≥2010,由此关系得出不等式,求出x的取值范围,由题意得【解答】解:依题意可知19≤x<200故答案为:19≤x<200.15.为促进抚州市精神文明建设,评选省级文明城市,现省检查组决定在未来连续5天中随机选取2天对抚州的各项文明建设进行暗访,则这两天恰好为连续两天的概率.【考点】CB:古典概型及其概率计算公式.【分析】先求出基本事件总数,再用列举法求出这两天恰好为连续两天包含怕基本事件个数,由此能求出这两天恰好为连续两天的概率.【解答】解:在未来连续5天中随机选取2天,基本事件总数为n==10,这两天恰好为连续两天包含的基本事件为(12),(23),(34),(45),共有4个基本事件,∴这两天恰好为连续两天的概率p=.故答案为:.16.已知函数f(x)=2lnx﹣x2,若方程f(x)+m=0在内有两个不等的实根,则实数m的取值范围是.【考点】6K:导数在最大值、最小值问题中的应用;54:根的存在性及根的个数判断.【分析】转化方程为函数,通过求解函数的最值,转化求解m的范围即可.【解答】解:函数f(x)=2lnx﹣x2,若方程f(x)+m=0在内有两个不等的实根,即函数f(x)=2lnx﹣x2,与y=﹣m在内有两个不相同的交点,f′(x)=﹣2x,令﹣2x=0可得x=±1,当x∈hslx3y3h,1)时f′(x)>0,函数是增函数,当x∈(1,e)时,f′(x)<0,函数是减函数,函数的最大值为:f(1)=﹣1,f()=﹣2﹣,f(e)=2﹣e2.函数的最小值为:2﹣e2.方程f(x)+m=0在内有两个不等的实根,只需:﹣2﹣,解得m∈.故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:分数区间甲班频率乙班频率hslx3y3h0,30)0.10.2hslx3y3h30,60)0.20.2hslx3y3h60,90)0.30.3hslx3y3h90,120)0.20.2hslx3y3h120,150)0.20.1(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?优秀不优秀总计甲班乙班总计k0 2.072 2.706 3.841 5.024 6.6357.87910.828P(K2≥k0)0.150.100.050.0250.0100.0050.001,其中n=a+b+c+d.【考点】BO:独立性检验的应用.【分析】(I)计算乙班参加测试的90(分)以上的同学人数,以及120分以人数,利用列举法求出对应事件数,求出对应的概率值;(II)计算甲、乙两班优秀与不优秀的人数,填写列联表,计算K2,对照数表得出概率结论.【解答】解:(I)乙班参加测试的90(分)以上的同学有20×(0.2+0.1)=6人,记为A、B、C、D、E、F;其中成绩优秀120分以上有20×0.1=2人,记为A、B;从这6名学生随机抽取两名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个…设事件G表示恰有一位学生成绩优秀,符合要求的事件有{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共8个;…所以;…(II)计算甲班优秀的人数为20×0.2=4,不优秀的人数为16,乙班优秀人数为2,不优秀的人数为18,填写列联表,如下;优秀不优秀总计甲班41620乙班21820总计63440…计算K2=≈0.7843<2.706;…所以在犯错概率小于0.1的前提下,没有足够的把握说明学生的数学成绩是否优秀与班级有关系.…18.从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组160,165);…;第八组.如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数及平均身高;(2)求第六组、第七组的频率并补充完整频率分布直方图;(3)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x、y,求满足“|x﹣y|≤5”的事件的概率.【考点】CS:概率的应用;B8:频率分布直方图;CC:列举法计算基本事件数及事件发生的概率.【分析】(1)由频率分布直方图可得前五组频率,进而可得后三组频率和人数,又可得后三组的人数,可得平均身高;(2)易得后三组的,可得频率分布直方图;(3)身高在190,195180,185)内的人数为4,设为a、b、c、d,身高在内的人数为2,设为A、B,若x,y∈190,195180,185)和内时,有aA、bA、cA、dA、aB、bB、cB、dB,共8种情况.∴基本事件总数为6+1+8=15,事件“|x﹣y|≤5”所包含的基本事件个数有6+1=7,∴P(|x﹣y|≤5)=.19.如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.(Ⅰ)求证:BF∥平面ADE;(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;(Ⅲ)若AC=4,求几何体C﹣BDF的体积.【考点】LY:平面与平面垂直的判定;LF:棱柱、棱锥、棱台的体积.【分析】(Ⅰ)取DA的中点G连结FG,GE,推导出四边形BFGE为平行四边形,从而BF∥EG,由此能证明BF∥平面ADE.(Ⅱ)取DE的中点H,连AH,CH,推导出AH⊥DE,AH⊥HC,从而AH⊥平面BCDE,由此能证明平面ADE⊥BCDE.(Ⅲ)几何体C﹣BDF的体积,由此能求出结果.【解答】证明:(Ⅰ)取DA的中点G连结FG,GE,∵F为AC的中点,∴,又∵DC∥BE,CD=2BE,∴EB∥GF,且EB=GF,∴四边形BFGE为平行四边形,∴BF∥EG,∵EG⊂平面ADE,BF⊄平面ADE,∴BF∥平面ADE…解:(Ⅱ)取DE的中点H,连AH,CH,∵△ADE为等边三角形,∴AH⊥DE,且,在△DHC中,DH=1,DC=4,HDC=60°,∴,∴AC2=AH2+HC2,即AH⊥HC,∵DE∩HC=H,∴AH⊥平面BCDE,∵AH⊂平面ADE,∴平面ADE⊥BCDE…(Ⅲ)==2,∵F是AC中点,∴几何体C﹣BDF的体积.…20.某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.(1)求出f(5)的值;(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你的关系式求出f(n)的解析式.【考点】F1:归纳推理.【分析】(1)先分别观察给出正方体的个数为:1,1+4,1+4+8,…从而得出f(5);(2)将(1)总结一般性的规律:f(n+1)与f(n)的关系式,再从总结出来的一般性的规律转化为特殊的数列再求解即得【解答】解:(1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴f(2)﹣f(1)=4=4×1.f(3)﹣f(2)=8=4×2,f(4)﹣f(3)=12=4×3,f(5)﹣f(4)=16=4×4∴f(5)=25+4×4=41.(2)由上式规律得出f(n+1)﹣f(n)=4n.∴f(2)﹣f(1)=4×1,f(3)﹣f(2)=4×2,f(4)﹣f(3)=4×3,…f(n﹣1)﹣f(n﹣2)=4•(n﹣2),f(n)﹣f(n﹣1)=4•(n﹣1)∴f(n)﹣f(1)=4=2(n﹣1)•n,∴f(n)=2n2﹣2n+1.21.已知函数f(x)=x3+x2f'(1).(1)求f'(1)和函数x的极值;(2)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围;(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.【考点】6D:利用导数研究函数的极值;6H:利用导数研究曲线上某点切线方程.【分析】(1)求导f′(x)=3x2+2f'(1)x,f′(1)=3+2f'(1),解得:f′(1)=﹣3,则f′(x)=3x(x﹣2),令f′(x)=0,解得:x=0,x=2,由函数的单调性与导数的关系,即可求得f(x)的极值;(2)由题意可知:y=a与f(x)有三个不同的交点,利用函数的图象即可求得实数a 的取值范围;(3)设切点(x0,x03﹣3x02),斜线斜率k=3x02﹣6x0,求得切线方程,由函数过(0,0),即可求得x0,即可求得直线l的方程.【解答】解:(1)由f(x)=x3+x2f'(1),求导f′(x)=3x2+2f'(1)x,则f′(1)=3+2f'(1),解得:f′(1)=﹣3,∴f(x)=x3﹣3x2,f′(x)=3x(x﹣2),令f′(x)=0,解得:x=0,x=2,由x,f′(x),f(x)变化,x(﹣∞,0)0(0,2) 2 (2,+∞)f′(x)+0﹣0+f(x)↑ 极大值0↓极小值﹣4↑则当x=0,f(x)取极大值0,当x=2时,取极小值﹣4;(2)由题意可知:y=a与f(x)有三个不同的交点,由函数图象可知:∴﹣4<a<0,(3)设切点(x0,x03﹣3x02),切线斜率k=3x02﹣6x0,则切线方程y﹣(x03﹣3x02)=(3x02﹣6x0)(x﹣x0),由切线过(0,0),则﹣x03+3x02=﹣x0(3x02﹣6x0),解得:x0=0,或x0=,当x0=0,切线k=0,切线方程y=0,当x0=,切点(,﹣),切线k=﹣,切线方程y=﹣x,直线l的方程y=0或y=﹣x.22.已知圆O:x2+y2=1过椭圆C:(a>b>0)的短轴端点,P,Q分别是圆O与椭圆C上任意两点,且线段PQ长度的最大值为3.(Ⅰ)求椭圆C的方程;(Ⅱ)过点(0,t)作圆O的一条切线交椭圆C于M,N两点,求△OMN的面积的最大值.【考点】K4:椭圆的简单性质.【分析】(Ⅰ)由圆O过椭圆C的短轴端点b=1,线段PQ长度的最大值为3,a+1=3,a=2,即可求得椭圆方程;(Ⅱ)设直线MN的方程,由点到直线的距离公式,求得k2=t2﹣1,代入椭圆方程,由韦达定理及弦长公式求得丨MN丨,利用三角形的面积公式及基本不等式的性质,即可求得△OMN的面积的最大值.【解答】解:(Ⅰ)∵圆O过椭圆C的短轴端点,∴b=1,又∵线段PQ长度的最大值为3,∴a+1=3,即a=2,∴椭圆C的标准方程为.(Ⅱ)由题意可设切线MN的方程为y=kx+t,即kx﹣y+t=0,则,得k2=t2﹣1.①联立得方程组,消去y整理得(k2+4)x2+2ktx+t2﹣4=0.其中△=(2kt)2﹣4(k2+4)(t2﹣4)=﹣16t2+16k2+64=48>0,设M(x1,y1),N(x2,y2),则,,则.②将①代入②得,∴,而,等号成立当且仅当,即.)max=1.综上可知:(S△OMN2017年6月14日。
【全国市级联考】江西省宜春市2016-2017学年高一下学期期末统考语文试题

绝密★启用前【全国市级联考】江西省宜春市2016-2017学年高一下学期期末统考语文试题试卷副标题考试范围:xxx ;考试时间:36分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、填入下面文段处空白处的词语,最恰当的一组是当然,表面的公正不等于公正。
①,②表面功夫都不做足,内在的真诚性③是值得怀疑的。
④,议员在议会中打架,⑤只是作秀,但也有可能是全力为选民争取利益;⑥ 假如他们只顾着打呼噜,连表现一下的念头都没有,那就一定是置选民利益于不顾。
① ② ③ ④ ⑤ ⑥ A 然而试卷第2页,共13页如果 一定 那么 虽然 / B 可是 / 肯定 也许 即使 那么 C / 一旦 似乎 也许 那么 可是 D 但是 如果 大概 比如 也许 而2、下列各句中,没有语病的一句是A .十八届五中全会公报提出推动义务教育均衡发展和普及高中阶段教育的目标,正是顺应了经济社会发展对全民素质乃至劳动力素质提升的新需求。
B .滞后的燃油标准,低劣的燃油质量才是造成我国机动车污染排放的“罪魁祸首”,当务之急应该把燃油改善上去。
C.群众评价扶贫工作的成效如何,不会以开了多少会、发了多少文件作为标准,只会以做了多少工作、取得多少实效、脱贫不够稳定来衡量。
D.生态文明建设是建设美丽中国的必然要求。
对于满足人民群众对良好生态环境的期待,形成人与自然和谐发展的现代化建设新格局,具有十分重要的意义。
3、下列各句中加点成语的使用,全部正确的一项是①科技巨头三星电子在硬件上一直处于世界领先的位置,但是在软件上一直是该公司的薄弱之处。
近日三星认为公司内部只有1%-2%的员工可以在谷歌任职,登高自卑之感油然而生。
②中国和本地区国家就解决南海分歧达成了有效共识,希望域外国家支持而不是干扰中国和东盟国家的努力,不要横生枝节,不要试图破坏这个局面。
2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)

2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)一、选择题1.(5分)已知复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)若“0<x<1”是“(x﹣a)[x﹣(a+2)]≤0”的充分不必要条件,则a 的取值范围是()A.(﹣∞,0]∪[1,+∞)B.(﹣1,0)C.[﹣1,0]D.(﹣∞,﹣1]∪[0,+∞)3.(5分)已知集合A={x|log(x+1)≥﹣2},B={x|≥2},则A∩B=()A.(﹣1,1)B.[0,1) C.[0,3]D.∅4.(5分)若平面内共线的A、B、P三点满足条件,,其中{a n}为等差数列,则a2008等于()A.1 B.﹣1 C.D.5.(5分)函数y=Asin(ωx+φ)(ω>0,|ϕ|<,x∈R)的部分图象如图所示,则函数表达式为()A.y=﹣4sin()B.y=4sin()C.y=﹣4sin()D.y=4sin()6.(5分)若y=(m﹣1)x2+2mx+3是偶函数,则f(﹣1),f(﹣),f()的大小关系为()A.f()>f()>f(﹣1)B.f()<f(﹣)<f(﹣1) C.f(﹣)<f()<f(﹣1)D.f(﹣1)<f()<f(﹣)7.(5分)过双曲线﹣=1(a>0,b>0)的右焦点F作直线y=﹣x的垂线,垂足为A,交双曲线左支于B点,若=2,则该双曲线的离心率为()A.B.2 C.D.8.(5分)若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm39.(5分)已知实数x,y满足:,则3x+9y的最小值为()A.82 B.4 C.D.10.(5分)已知向量,满足,且关于x的函数在实数集R上单调递增,则向量,的夹角的取值范围是()A.B.C.D.11.(5分)设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0,f(x0)),其中x0满足f″(x0)=0.已知f(x)=x3﹣x2+3x﹣,则f()+f()+f()+…+f()=()A.2013 B.2014 C.2015 D.201612.(5分)已知点列A n(a n,b n)(n∈N*)均为函数y=a x(a>0,a≠1)的图象上,点列B n(n,0)满足|A n B n|=|A n B n+1|,若数列{b n}中任意连续三项能构成三角形的三边,则a的取值范围为()A.(0,)∪(,+∞)B.(,1)∪(1,)C.(0,)∪(,+∞)D.(,1)∪(1,)二.填空题13.(5分)已知双曲线﹣=1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.14.(5分)函数f(x)=,则f(x)dx的值为.15.(5分)已知三棱锥O﹣ABC,A、B、C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O﹣ABC的体积为,则球O的体积是.16.(5分)在△ABC中,•=16,sinA=sinBcosC,D是线段AB上的动点(含端点),则•的取值范围是.三.解答题17.(10分)已知数列{a n}满足a1=0,a n+1=a n+2+1(1)求证数列{}是等差数列,并求出a n的通项公式;(2)若b n=,求数列{b}的前n项的和T n.18.(12分)某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.(1)求N和[30,35)这组的参加者人数N1;(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.19.(12分)如图1所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图2所示五棱锥P﹣ABFED,且AP=,(1)求证:BD⊥平面POA;(2)求二面角B﹣AP﹣O的正切值.20.(12分)如图,椭圆C:+=1(a>b>0)的离心率是,且过点(,).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过点A1,B1引椭圆C 的两条弦A1E、B1F.(1)求椭圆C的方程;(2)若直线A1E与B1F的斜率是互为相反数.①求直线EF的斜率k0②设直线EF的方程为y=k0x+b(﹣1≤b≤1)设△A1EF、△B1EF的面积分别为S1和S2,求S1+S2的取值范围.21.(14分)已知函数f(x)=x++lnx,a∈R.(Ⅰ)若f(x)在x=1处取得极值,求a的值;(Ⅱ)若f(x)在区间(1,2)上单调递增,求a的取值范围;(Ⅲ)讨论函数g(x)=f'(x)﹣x的零点个数.请考生在第22、23题中任选一题作答,如果多做,则按所做第一题记分.22.(10分)在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为(,),直线l的极坐标方程为ρcos (θ﹣)=a,且点A在直线l上,(1)求a的值及直线l的直角坐标方程;(2)圆C的参数方程为(α为参数),试判断直线l与圆C的位置关系.23.设f(x)=|x﹣3|+|x﹣4|.(1)解不等式f(x)≤2;(2)若存在实数x满足f(x)≤ax﹣1,试求实数a的取值范围.2016-2017学年江西省宜春市上高二中高三(下)开学数学试卷(理科)参考答案与试题解析一、选择题1.(5分)(2016•安徽二模)已知复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:由,得=.∴z在复平面内对应的点的坐标为,是第一象限的点.故选:A.2.(5分)(2014秋•越城区校级期末)若“0<x<1”是“(x﹣a)[x﹣(a+2)]≤0”的充分不必要条件,则a的取值范围是()A.(﹣∞,0]∪[1,+∞)B.(﹣1,0)C.[﹣1,0]D.(﹣∞,﹣1]∪[0,+∞)【解答】解:∵(x﹣a)[x﹣(a+2)]≤0,∴a≤x≤a+2,若“0<x<1”是“(x﹣a)[x﹣(a+2)]≤0”的充分不必要条件,则,即﹣1≤a≤0,故选:C.3.(5分)(2017春•上高县校级月考)已知集合A={x|log(x+1)≥﹣2},B={x|≥2},则A∩B=()A.(﹣1,1)B.[0,1) C.[0,3]D.∅【解答】解:∵集合A={x|log(x+1)≥﹣2}={x|﹣1<x≤3},B={x|≥2}={x|0≤x<1},∴A∩B={x|0≤x<1}=[0,1).故选:B.4.(5分)(2010秋•金牛区校级期中)若平面内共线的A、B、P三点满足条件,,其中{a n}为等差数列,则a2008等于()A.1 B.﹣1 C.D.【解答】解:∵A、B、P三点共线∴∴∴∵∴a1+a4015=1∵{a n}为等差数列∴2a2008=1∴a2008=故选C.5.(5分)(2005•天津)函数y=Asin(ωx+φ)(ω>0,|ϕ|<,x∈R)的部分图象如图所示,则函数表达式为()A.y=﹣4sin()B.y=4sin()C.y=﹣4sin()D.y=4sin()【解答】解:由图象得A=±4,=8,∴T=16,∵ω>0,∴ω==,①若A>0时,y=4sin(x+φ),当x=6时,φ=2kπ,φ=2kπ﹣,k∈Z;又|φ|<,∴φ∈∅;②若A<0时,y=﹣4sin(x+φ),当x=﹣2时,φ=2kπ,φ=2kπ+,k∈z;又|φ|<,∴φ=.综合①②该函数解析式为y=﹣4sin().故选A.6.(5分)(2010秋•让胡路区校级期末)若y=(m﹣1)x2+2mx+3是偶函数,则f(﹣1),f(﹣),f()的大小关系为()A.f()>f()>f(﹣1)B.f()<f(﹣)<f(﹣1) C.f(﹣)<f()<f(﹣1)D.f(﹣1)<f()<f(﹣)【解答】解:因为函数y=(m﹣1)x2+2mx+3是偶函数,所以2m=0,即m=0.所以函数y=(m﹣1)x2+2mx+3=﹣x2+3,函数在(0,+∞)上单调递减.又f(﹣1)=f(1),f(﹣)=f(),所以f(1)>f()>f(),即f()<f(﹣)<f(﹣1),故选B.7.(5分)(2017•平顶山一模)过双曲线﹣=1(a>0,b>0)的右焦点F 作直线y=﹣x的垂线,垂足为A,交双曲线左支于B点,若=2,则该双曲线的离心率为()A.B.2 C.D.【解答】解:设F(c,0),则直线AB的方程为y=(x﹣c)代入双曲线渐近线方程y=﹣x得A(,﹣),由=2,可得B(﹣,﹣),把B点坐标代入双曲线方程﹣=1,即=1,整理可得c=a,即离心率e==.故选:C.8.(5分)(2016•湖南模拟)若某几何体的三视图(单位:cm)如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是()A.2cm2B.cm3C.3cm3D.3cm3【解答】解:由几何体的三视图可知,该几何体为底面是直角梯形,高为的四棱锥,其中直角梯形两底长分别为1和2,高是2.故这个几何体的体积是×[(1+2)×2]×=(cm3).故选:B.9.(5分)(2016秋•杭州期中)已知实数x,y满足:,则3x+9y的最小值为()A.82 B.4 C.D.【解答】解:由约束条件作出可行域如图,令z=x+2y,化为y=﹣,由图可知,当直线y=﹣过A(﹣2,﹣2)时直线y轴上的截距最小为z=﹣4,∴3x+9y≥=.故选:C.10.(5分)(2015秋•福建校级期中)已知向量,满足,且关于x的函数在实数集R上单调递增,则向量,的夹角的取值范围是()A.B.C.D.【解答】解:求导数可得f′(x)=6x2+6||x+6,则由函数f(x)=2x3+3|a|x2+6a•bx+7在实数集R上单调递增,可得f′(x)=6x2+6||x+6≥0恒成立,即x2+||x+≥0恒成立,故判别式△=2﹣4≤0 恒成立,再由,可得8||2≤8||2cos<,>,∴cos<,>≥,∴<,>∈[0,],故选:C.11.(5分)(2016春•晋中校级期中)设y=f″(x)是y=f′(x)的导数.某同学经过探究发现,任意一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心(x0,f(x0)),其中x0满足f″(x0)=0.已知f(x)=x3﹣x2+3x﹣,则f()+f()+f()+…+f()=()A.2013 B.2014 C.2015 D.2016【解答】解:∵f(x)=x3﹣x2+3x﹣,∴f′(x)=x2﹣x+3,∴f″(x)=2x﹣1,令f″(x)=2x﹣1=0解得,x=,f()=1,由题意知,(,1)是f(x)=x3﹣x2+3x﹣的对称中心;故f()+f()=2,f()+f()=2,…,故f()+f()+f()+…+f()=2016,故选D.12.(5分)(2016•虹口区二模)已知点列A n(a n,b n)(n∈N*)均为函数y=a x (a>0,a≠1)的图象上,点列B n(n,0)满足|A n B n|=|A n B n+1|,若数列{b n}中任意连续三项能构成三角形的三边,则a的取值范围为()A.(0,)∪(,+∞)B.(,1)∪(1,)C.(0,)∪(,+∞)D.(,1)∪(1,)【解答】解:由题意得,点B n(n,0),A n(a n,b n)满足|A n B n|=|A n B n+1|,由中点坐标公式,可得B n B n+1的中点为(n+,0),即a n=n+,b n=;当a>1时,以b n﹣1,b n,b n+1为边长能构成一个三角形,只需b n﹣1+b n+1>b n,b n﹣1<b n<b n+1,即+>,即有1+a2<a,解得1<a<;同理,0<a<1时,解得<a<1;综上,a的取值范围是1<a<或<a<1,故选:B.二.填空题13.(5分)(2016•朔州校级模拟)已知双曲线﹣=1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.【解答】解:由题意,一条渐近线方程为2x﹣y=0,圆(x+1)2+(y﹣2)2=4的圆心坐标为(﹣1,2),半径为2,∴圆心到渐近线的距离d==,∴渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为2=.故答案为:.14.(5分)(2016秋•让胡路区校级期末)函数f(x)=,则f(x)dx的值为π+10.【解答】解:函数f(x)=,则f(x)dx=(4﹣x)dx+dx,其中(4﹣x)dx=(4x﹣x2)|=0﹣(﹣8﹣2)=10,dx表示以原点为圆心以2为半径的圆的面积的四分之一,即dx=π,故f(x)dx=(4﹣x)dx+dx=π+10,故答案为:π+1015.(5分)(2017春•上高县校级月考)已知三棱锥O﹣ABC,A、B、C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O﹣ABC的体积为,则球O的体积是π.【解答】解:三棱锥O﹣ABC,A、B、C三点均在球心O的表面上,且AB=BC=1,∠ABC=120°,AC=,=×1×1×sin120°=,∴S△ABC∵三棱锥O﹣ABC的体积为,△ABC的外接圆的圆心为G,∴OG⊥⊙G,外接圆的半径为:GA==1,•OG=,即OG=,∴S△ABC∴OG=,球的半径为:=4.球的体积:π•43=π.故答案为:π.16.(5分)(2017春•上高县校级月考)在△ABC中,•=16,sinA=sinBcosC,D是线段AB上的动点(含端点),则•的取值范围是[﹣4,0] .【解答】解:由sinA=sinBcosC,得a=b,即a2+c2=b2,∴△ABC是以B为直接的直角三角形,如图,∵•=16,∴bccosA=16,即c2=16,c=4.以BC所在直线为x轴,以BA所在直线为y轴建系,则A(0,4),D(0,t)(0≤t≤4),C(a,0),∴,∴=t2﹣4t=(t﹣2)2﹣4∈[﹣4,0].故答案为:[﹣4,0].三.解答题17.(10分)(2016秋•闽侯县校级期中)已知数列{a n}满足a1=0,a n+1=a n+2+1(1)求证数列{}是等差数列,并求出a n的通项公式;(2)若b n=,求数列{b}的前n项的和T n.=a n+2+1=﹣1,【解答】(1)证明:由a n+1∴﹣=1,故数列{}是等差数列,首项为1,公差为1的等差数列.∴=1+(n﹣1)=n,∴a n=n2﹣1.(2)解:b n==(n+1)•2n,∴数列{b}的前n项的和T n=2×2+3×22+4×23+…+(n+1)•2n,2T n=2×22+3×23+…+n•2n+(n+1)•2n+1,∴﹣T n=4+22+23+…+2n﹣(n+1)•2n+1=2+﹣(n+1)•2n+1,可得T n=n•2n+1.18.(12分)(2016•陕西一模)某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.(1)求N和[30,35)这组的参加者人数N1;(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.【解答】解:(1)∵年龄在[35,40)内的频率为0.04×5=0.2,∴总人数N==40人.∵[30,35)这组的频率为:1﹣(0.01×2+0.02+0.03×2+0.04)×5=0.3,[30,35)这组的参加者人数N1为:40×0.3=12人.(2)记事件B为“从年龄在[30,35]之间选出的人中至少有2名数学教师”,∵年龄在[30,35)之间的人数为12,∴P(B)=1﹣=,记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,∵年龄在[35,40)之间的人数为8,∴P(C)=1﹣=,∴两组选出的人中都至少有1名数学老师的概率P(BC)==.(3)年龄在[45,55)之间的人数为6人,其中女教师4人,∴ξ的可能取值为1,2,3,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:Eξ==2.19.(12分)(2017春•宾阳县校级月考)如图1所示,在边长为4的菱形ABCD 中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF 翻折到△PEF,连接PA,PB,PD,得到如图2所示五棱锥P﹣ABFED,且AP=,(1)求证:BD⊥平面POA;(2)求二面角B﹣AP﹣O的正切值.【解答】证明:(1)PO⊥EF,AO⊥EF,所以EF⊥平面POA,因为BD∥EF∴BD⊥平面POA则PO⊥BD,又AO⊥BD,AO∩PO=O,AO⊂平面APO,PO⊂平面APO,∴BD⊥平面APO,(2)因为AP=,可证PO⊥AO,所以EF,PO,AO互相垂直以O为原点,OA为x轴,OF为y轴,OP为z轴,建立坐标系,则O(0,0,0),A(3,0,0),P(0,0,),B(,2,0),设=(x,y,z)为平面OAP的一个法向量,则=(0,1,0),=(x,y,z)为平面ABP的一个法向量,=(﹣2,2,0),=(﹣3,0,),则,令x=1,则y=,z=3,则=(1,,3)….cosθ==,∴tanθ=∴二面角B﹣AP﹣O的正切值为20.(12分)(2017春•上高县校级月考)如图,椭圆C:+=1(a>b>0)的离心率是,且过点(,).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过点A1,B1引椭圆C的两条弦A1E、B1F.(1)求椭圆C的方程;(2)若直线A1E与B1F的斜率是互为相反数.①求直线EF的斜率k0②设直线EF的方程为y=k0x+b(﹣1≤b≤1)设△A1EF、△B1EF的面积分别为S1和S2,求S1+S2的取值范围.【解答】解:(1)由题意可知:椭圆的离心率e==,则3a2=4c2,b2=a2﹣c2=a2,即a2=4b2,将(,)代入椭圆方程:,则,解得:b2=1,a2=4,椭圆C的方程;(2)①设点E(x1,y1),F(x2,y2),直线A1E,y=k(x﹣2),直线B1E:y=﹣kx+1,则,消去y得:(4k2+1)x2﹣16k2x+16k2﹣4=0,则2x1=,x1=,y1=k(x1﹣2)=,则E(,),联立,消去y整理得:(4k2+1)x2﹣8kx=0,x2=,y2=﹣kx2+1=,F(,),则k EF==,②设直线EF:y=x+b,联立方程组,消去y得:x2+2bx+2b2﹣2=0,△=(﹣2b)2﹣4(2b2﹣2)=8﹣4b2>0,解得:﹣<b<,x1+x2=﹣2b,x1x2=2b2﹣2,丨EF丨=•=,设d1,d2分别为点A1,B1到直线EF的距离,则d1=,d2=,则S1+S2=•(d1+d2)丨EF丨=(丨b+1丨+丨b﹣1丨),∵﹣1≤b≤1时,∴S1+S2=2,由2∈[2,2],S1+S2∈[2,2],S1+S2的取值范围[2,2].21.(14分)(2015•东城区一模)已知函数f(x)=x++lnx,a∈R.(Ⅰ)若f(x)在x=1处取得极值,求a的值;(Ⅱ)若f(x)在区间(1,2)上单调递增,求a的取值范围;(Ⅲ)讨论函数g(x)=f'(x)﹣x的零点个数.【解答】解:(Ⅰ)函数f(x)=x++lnx(x>0),f′(x)=1﹣+=,f(x)在x=1处取得极小值,即有f′(1)=0,解得a=2,经检验,a=2时,f(x)在x=1处取得极小值.则有a=2;(Ⅱ)f′(x)=1﹣+=,x>0,f(x)在区间(1,2)上单调递增,即为f′(x)≥0在区间(1,2)上恒成立,即a≤x2+x在区间(1,2)上恒成立,由x2+x∈(2,6),则a≤2;(Ⅲ)g(x)=f′(x)﹣x=1﹣+﹣x,x>0,令g(x)=0,则a=﹣x3+x2+x,令h(x)=﹣x3+x2+x,x>0,则h′(x)=﹣3x2+2x+1=﹣(3x+1)(x﹣1),当x∈(0,1),h′(x)>0,h(x)在(0,1)递增;当x∈(1,+∞),h′(x)<0,h(x)在(1,+∞)递减.即有h(x)的最大值为h(1)=1,则当a>1时,函数g(x)无零点;当a=1或a≤0时,函数g(x)有一个零点;当0<a<1时,函数g(x)有两个零点.请考生在第22、23题中任选一题作答,如果多做,则按所做第一题记分.22.(10分)(2015•铜仁市模拟)在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为(,),直线l 的极坐标方程为ρcos(θ﹣)=a,且点A在直线l上,(1)求a的值及直线l的直角坐标方程;(2)圆C的参数方程为(α为参数),试判断直线l与圆C的位置关系.【解答】解:(1)点A(,)在直线l上,得cos(θ﹣)=a,∴a=,故直线l的方程可化为:ρsinθ+ρcosθ=2,得直线l的直角坐标方程为x+y﹣2=0;(2)消去参数α,得圆C的普通方程为(x﹣1)2+y2=1圆心C到直线l的距离d=<1,所以直线l和⊙C相交.23.(2017•广元模拟)设f(x)=|x﹣3|+|x﹣4|.(1)解不等式f(x)≤2;(2)若存在实数x满足f(x)≤ax﹣1,试求实数a的取值范围.【解答】解(1),由图象可得f(x)≤2的解集为﹣(5分)(2)函数y=ax﹣1,的图象是经过点(0,﹣1)的直线,由图象可得﹣﹣﹣﹣﹣(10分)参与本试卷答题和审题的老师有:sxs123;maths;zlzhan;刘长柏;wzj123;qiss;炫晨;刘老师;lcb001;whgcn;沂蒙松;陈远才;铭灏2016;双曲线(排名不分先后)胡雯2017年4月12日。
江西省宜春市2016-2017学年高二上学期期末物理试卷

2016-2017学年江西省宜春市高二(上)期末物理试卷一、选择题:共48分,在每小题给出的四个选项中,1-7小题只有一个选项正确,8-12小题有多个选项正确,每小题4分,全部选对的得4分,选不全的得2分,有选错或不答的得0分.1.在物理学发展的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是()A.安培首先提出了磁场对运动电荷的作用力公式B.法拉第根据小磁针在通电导线周围的偏转而发现了电流的磁效应C.法国物理学家库仑利用扭秤实验发现了电荷之间的相互作用规律﹣﹣库仑定律D.楞次发现了电磁感应现象,并研究得出了判断感应电流方向的方法﹣﹣楞次定律2.神经纤维可分为有髓鞘和无髓鞘两大类,现代生物学认为,髓鞘是由多层类脂物质﹣﹣髓质累积而成,具有很大的电阻,经实验测得髓质的电阻率为ρ=8×106Ω•m.某生物体中某段髓质神经纤维可看做长为20cm,半径为4cm的圆柱体,在其两端加上逐渐升高的电压,当电压U=100V时,该髓质神经纤维发生反应,则引起该髓质神经纤维产生感觉的最小电流为()A.0.15μA B.0.31μA C.0.43μA D.0.62μA3.已知北京地区地磁场的水平分量为3.0×10﹣5T.若北京市一高层建筑安装了高100m的金属杆作为避雷针,在某次雷雨天气中,当带有正电的乌云经过避雷针的上方时,避雷针开始放电,某一时刻的放电电流为1×105A,此时金属杆所受安培力的方向和大小分别为()A.方向向东,大小为300 N B.方向向东,大小为30 NC.方向向西,大小为300 N D.方向向西,大小为30 N4.从太阳或其它星体上放射出的宇宙射线中含有大量的高能带电粒子.这些高能带电粒子到达地球会对地球上的生命带来危害,但由于地球周围存在地磁场,地磁场能改变宇宙射线中带电粒子的运动方向,如图所示,对地球上的生命起到保护作用.假设所有的宇宙射线从各个方向垂直射向地球表面,那么以下说法正确的是()A.地磁场对宇宙射线的阻挡作用各处都相同B.由于南北极磁场最强,因此阻挡作用最强C.沿地球赤道平面射来的高能正电荷向东偏转D.沿地球赤道平面射来的高能负电荷向南偏转5.如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是()A.电流表读数变下,电压表读数变大B.电容器C上电荷量减小C.小电炮L变暗D.电源的总功率变小6.如图为探究平行板电容器电容大小决定因素的实验.给电容器充电后与电源断开,即保持电量Q不变,那么若保持板间距离d不变,正对面积S变小,则()A.电容C变小,两板电势差U变大B.电容C变小,两板电势差U变小C.电容C变大,两板电势差U变小D.电容C变大,两板电势差U变大7.真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断正确的是()A.x=2a处的电势一定为零B.点电荷M、N一定为异种电荷C.点电荷M、N所带电荷量的绝对值之比为1:1D.点电荷M、N所带电荷量的绝对值之比为4:18.如图所示是高频焊接原理示意图.线圈中通以高频变化的电流时,待焊接的金属工件中就产生感应电流,感应电流通过焊缝产生大量热量,将金属融化,把工件焊接在一起,而工件其他部分发热很少,以下说法正确的是()A.电流变化的频率越高,焊缝处的温度升高的越快B.电流变化的频率越低,焊缝处的温度升高的越快C.工件上只有焊缝处温度升的很高是因为焊缝处的电阻小D.工件上只有焊缝处温度升的很高是因为焊缝处的电阻大9.如图所示,a、b是两个带有同种电荷的小球,用绝缘丝线悬挂于同一点,两球静止时,它们距水平面的高度相等,绳与竖直方向的夹角分别为α、β,且β>α.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则()A.a球的质量比b球的大B.a、b两球同时落地C.a球的电荷量比b球的大D.a、b两球飞行的水平距离相等10.关于对楞次定律的理解,下面说法中正确的是()A.感应电流的方向总是要使它的磁场阻碍原来的磁通量的变化B.感应电流的磁场方向,总是跟原磁场方向相同C.感应电流的磁场方向,总是跟原磁砀方向相反D.感应电流的磁场方向可以跟原磁场方向相同,也可以相反11.如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是()A.电路中电源电动势为3.6VB.变阻器向右滑动时,V2读数逐渐减小C.变阻器的最大阻值为30ΩD.此电路中,电动机的最大输出功率为0.9W12.某一学习小组在研究电磁感应现象时,利用一根粗细均匀的金属丝弯成导轨abcd,=3.导体棒ef的电阻是bc段电阻的两倍,如图所示,匀强磁场垂直于导轨平面,当用平行于导轨的外力F将导体棒ef由靠近bc位置匀速向右移动时,则()A.导体棒ef两端的电压不变B.导体棒ef中的电流变大C.拉力F的瞬时功率变小D.导轨abcd消耗的电功率先变大后变小二、填空题(本题共2小题,每空2分,共12分)13.用螺旋测微器测圆柱体的直径时,示数如图甲所示,此示数为mm,用20分度的游标卡尺测量某物体的厚度时,示数如图乙所示,此示数为mm.14.在实验室用“伏安法”测定电源的电动势和内阻,现备有如下实验器材:被测电源(一节干电池)、电压表、电流表、滑动变阻器、开关、导线等.①画出实验电路图(图1),补充完实物连线图(图3).②根据实验作出U﹣I图象如图2所示,则由图象可确定:该电源的电动势为V,电源的内电阻为Ω.三、计算题:本题有4小题,8+9+9+14=40分,解答要写出必要的文字说明、方程式和重要演算步骤.只写出最后答案的不得分.有数值计算的,答案中必须明确写出数值和单位.15.如图所示为等离子体发电机原理的示意图,平行金属板间距为d,有足够的长度跟宽度,其间有匀强磁场,磁感应强度为B,方向如图,等离子体的流速为v,发电机等效内阻为r,负载电阻为R,等离子体从一侧沿着垂直磁场且与极板平行的方向射入极板间.已知电子电量为e,忽略金属板边缘效应,求:(1)打在上极板上的离子的带电性质;(2)闭合开关后等离子发电机能提供的最大功率.16.长为L的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,一个带电量为+q、质量为m的带电粒子,以初速度v0紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与下极板成30°角,如图所示,不计粒子重力,求:(1)粒子末速度的大小;(2)匀强电场的场强;(3)两板间的距离.17.如图所示,有界匀强磁场的磁感应强度B=2×10﹣3T;磁场右边是宽度L=0.2m、场强E=40V/m、方向向左的匀强电场.一带电粒子电荷量q=﹣3.2×10﹣19C,质量m=6.4×10﹣27kg,以v=4×104m/s的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出.求:(1)大致画出带电粒子的运动轨迹;(画在答题纸上给出的图中)(2)带电粒子在磁场中运动的轨道半径;(3)带电粒子飞出电场时的动能E K.18.如图所示,质量m1=0.1kg,电阻R1=0.3Ω,长度l=0.4m的导体棒ab横放在U型金属框架上.框架质量m2=0.2kg,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2,相距0.4m的MM′、NN′相互平行,电阻不计且足够长.电阻R2=0.1Ω的MN垂直于MM′.整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5T.垂直于ab施加F=2N的水平恒力,ab从静止开始无摩擦地运动,始终与MM′、NN′保持良好接触,当ab运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,g取10m/s2.(1)求框架开始运动时ab速度v的大小;(2)从ab开始运动到框架开始运动的过程中,MN上产生的热量Q=0.1J,求该过程ab位移x的大小.2016-2017学年江西省宜春市高二(上)期末物理试卷参考答案与试题解析一、选择题:共48分,在每小题给出的四个选项中,1-7小题只有一个选项正确,8-12小题有多个选项正确,每小题4分,全部选对的得4分,选不全的得2分,有选错或不答的得0分.1.在物理学发展的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是()A.安培首先提出了磁场对运动电荷的作用力公式B.法拉第根据小磁针在通电导线周围的偏转而发现了电流的磁效应C.法国物理学家库仑利用扭秤实验发现了电荷之间的相互作用规律﹣﹣库仑定律D.楞次发现了电磁感应现象,并研究得出了判断感应电流方向的方法﹣﹣楞次定律【考点】1U:物理学史.【分析】本题根据涉及的相关物理学家,如洛伦兹、安培、奥斯特、库仑、法拉第等人的物理学贡献进行解答.【解答】解:A、洛伦兹首先提出了磁场对运动电荷的作用力公式,故A错误.B、奥斯特根据小磁针在通电导线周围的偏转而发现了电流的磁效应,故B错误.C、法国物理学家库仑利用扭秤实验,发现了电荷之间的相互作用规律﹣﹣库仑定律,故C正确.D、法拉第发现了电磁感应现象,楞次研究得出了判断感应电流方向的方法﹣﹣楞次定律,故D错误.故选:C2.神经纤维可分为有髓鞘和无髓鞘两大类,现代生物学认为,髓鞘是由多层类脂物质﹣﹣髓质累积而成,具有很大的电阻,经实验测得髓质的电阻率为ρ=8×106Ω•m.某生物体中某段髓质神经纤维可看做长为20cm,半径为4cm的圆柱体,在其两端加上逐渐升高的电压,当电压U=100V时,该髓质神经纤维发生反应,则引起该髓质神经纤维产生感觉的最小电流为()A.0.15μA B.0.31μA C.0.43μA D.0.62μA【考点】B7:电阻定律;B2:欧姆定律.【分析】已知电阻率、导体长度以及半径,由电阻定义式可得电阻值,进而再由欧姆定律可得电流.【解答】解:由电阻定义式可得:R=ρ=8×106×Ω=3.18×108Ω故电流为:I==A=0.31μA故B正确,ACD错误故选:B3.已知北京地区地磁场的水平分量为3.0×10﹣5T.若北京市一高层建筑安装了高100m的金属杆作为避雷针,在某次雷雨天气中,当带有正电的乌云经过避雷针的上方时,避雷针开始放电,某一时刻的放电电流为1×105A,此时金属杆所受安培力的方向和大小分别为()A.方向向东,大小为300 N B.方向向东,大小为30 NC.方向向西,大小为300 N D.方向向西,大小为30 N【考点】CE:安培力的计算.【分析】金属杆竖直,与地磁场水平分量垂直,受到地磁场的安培力,根据安培力公式F=BIL,求出金属杆所受磁场力.地磁场水平分量向北,根据左手定则判断安培力方向.【解答】解:当带有正电的乌云经避雷针放电时,放电电流方向沿避雷针向下,若面向北方而立,则空间水平磁场均为“×”,若右方为东方,左方为西方向,如图,由左手定则判定可知金属杆所受安培力的方向向东,大小为F=BIL=3.0×10﹣5×1×105×100N=300N故选A4.从太阳或其它星体上放射出的宇宙射线中含有大量的高能带电粒子.这些高能带电粒子到达地球会对地球上的生命带来危害,但由于地球周围存在地磁场,地磁场能改变宇宙射线中带电粒子的运动方向,如图所示,对地球上的生命起到保护作用.假设所有的宇宙射线从各个方向垂直射向地球表面,那么以下说法正确的是()A.地磁场对宇宙射线的阻挡作用各处都相同B.由于南北极磁场最强,因此阻挡作用最强C.沿地球赤道平面射来的高能正电荷向东偏转D.沿地球赤道平面射来的高能负电荷向南偏转【考点】CD:左手定则;C5:地磁场.【分析】根据地球磁场的分布,由左手定则可以判断粒子的受力的方向,从而可以判断粒子的运动的方向.【解答】解:A、高能带电粒子到达地球受到地磁场的洛伦兹力作用,发生偏转.不同的磁场,所受到的洛伦兹力大小不一,所以在南、北两极最强赤道附近最弱,故A错误;B、高能带电粒子到达地球受到地磁场的洛伦兹力作用,发生偏转.不同的磁场,所受到的洛伦兹力大小不一,而磁场在南、北两极最强赤道附近最弱,则地磁场对垂直射向地球表面的宇宙射线的阻挡作用在南、北两极最弱,赤道附近最强,故B错误;C、地磁场会使沿地球赤道平面内射来的宇宙射线中的带电粒子在洛伦兹力作用下向东偏转,偏向面与赤道平面平行,故C正确;D错误;故选:C.5.如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是()A.电流表读数变下,电压表读数变大B.电容器C上电荷量减小C.小电炮L变暗D.电源的总功率变小【考点】BB:闭合电路的欧姆定律.【分析】把滑动变阻器滑片P向右移动时,变阻器接入电路的电阻减小,根据闭合电路欧姆定律分析电路中总电流的变化,判断灯泡L亮度的变化.电路稳定时电容器的电压等于路端电压,分析路端电压的变化,判断电容器充电或放电;根据总电流的变化分析电源总功率的变化.【解答】解:AC、把滑动变阻器的滑片向右移动时,变阻器接入电路的电阻减小,外电路总电阻减小,根据闭合电路欧姆定律分析得知:电路中总电流I增大,电流表读数变大.通过灯泡的电流增大,则灯泡L变亮;电源的内电压增大,则路端电压减小,电压表读数变小,故A、C错误B、电容器与滑动变阻器并联,它们两端的电压相等,电容器两端的电压U C=U ﹣IR L,由于I增大,U减小,所以电容器端电压U C减小,电容器C上电荷量减小.故B正确.D、总电流I增大,据P=EI知,电源的总功率变大,故D错误.故选:B6.如图为探究平行板电容器电容大小决定因素的实验.给电容器充电后与电源断开,即保持电量Q不变,那么若保持板间距离d不变,正对面积S变小,则()A.电容C变小,两板电势差U变大B.电容C变小,两板电势差U变小C.电容C变大,两板电势差U变小D.电容C变大,两板电势差U变大【考点】AS:电容器的动态分析.【分析】平行板电容器充电后与电源断开,其电量保持不变.将两极板间距离减小,由电容的决定式分析电容如何变化,由电容的定义式确定电量的变化.【解答】解:平行板电容器充电后与电源断开,电量Q保持不变.若保持板间距离d不变,正对面积S变小,由电容的决定式C=分析得知,电容C变小,由C=,知Q不变,C变小,则U变大.故A正确,BCD错误.故选:A.7.真空中相距为3a的两个点电荷M、N,分别固定于x轴上x1=0和x2=3a的两点上,在它们连线上各点场强E随x变化关系如图所示,以下判断正确的是()A.x=2a处的电势一定为零B.点电荷M、N一定为异种电荷C.点电荷M、N所带电荷量的绝对值之比为1:1D.点电荷M、N所带电荷量的绝对值之比为4:1【考点】AD:电势差与电场强度的关系;AC:电势.【分析】场强为零的地方电势不一定为零,电势零点是人为选取的.场强先正方向减少到零又反方向增加,必为同种电荷,由点电荷公式判断电荷量之比.【解答】解:A、x=2a处的场强为零,由于电势与场强无关,则场强为零的地方电势不一定为零,故A错误;B、x从0到3a,场强先正方向减少到零又反方向增加,必为同种电荷,故B错误;CD、x=2a处的合场强为0,由E=k得:k=k,得Q M:Q N=4:1,故C错误,D正确.故选:D8.如图所示是高频焊接原理示意图.线圈中通以高频变化的电流时,待焊接的金属工件中就产生感应电流,感应电流通过焊缝产生大量热量,将金属融化,把工件焊接在一起,而工件其他部分发热很少,以下说法正确的是()A.电流变化的频率越高,焊缝处的温度升高的越快B.电流变化的频率越低,焊缝处的温度升高的越快C.工件上只有焊缝处温度升的很高是因为焊缝处的电阻小D.工件上只有焊缝处温度升的很高是因为焊缝处的电阻大【考点】D6:电磁感应在生活和生产中的应用.【分析】高频焊接利用高频交变电流产生高频交变磁场,在焊接的金属工件中就产生感应电流,根据法拉第电磁感应定律分析电流变化的频率与焊缝处的温度升高的关系.焊缝处横截面积小,电阻大,电流相同,焊缝处热功率大,温度升的很高.【解答】解:A、B高频焊接利用高频交变电流产生高频交变磁场,在焊接的金属工件中就产生感应电流,根据法拉第电磁感应定律分析可知,电流变化的频率越高,磁通量变化频率越高,产生的感应电动势越大,感应电流越大,焊缝处的温度升高的越快.故A正确,B错误.C、D焊缝处横截面积小,电阻大,电流相同,焊缝处热功率大,温度升的很高.故C错误,D正确.故选AD9.如图所示,a、b是两个带有同种电荷的小球,用绝缘丝线悬挂于同一点,两球静止时,它们距水平面的高度相等,绳与竖直方向的夹角分别为α、β,且β>α.若同时剪断两根细线,空气阻力不计,两球带电荷量不变,则()A.a球的质量比b球的大B.a、b两球同时落地C.a球的电荷量比b球的大D.a、b两球飞行的水平距离相等【考点】A4:库仑定律;AD:电势差与电场强度的关系.【分析】同时剪断两根细线时,小球受水平方向的库仑力和竖直方向的重力作用,然后根据水平方向和竖直方向运动的独立性可正确求解.【解答】解:A、对小球受力分析,根据平衡条件有:m a g=m b g=,由于β>α,所以m a>m b,故A正确B、m a>m b,因此水平方向上,a的加速度小于b的加速度.竖直方向上作自由落体运动,根据运动的独立性可知,两球同时落地,故B正确C、a球的电荷量和b球的电量大小无法判断,故C错误D、由于a的加速度小于b的加速度,因此a球水平飞行的距离比b球小,故D 错误.故选AB.10.关于对楞次定律的理解,下面说法中正确的是()A.感应电流的方向总是要使它的磁场阻碍原来的磁通量的变化B.感应电流的磁场方向,总是跟原磁场方向相同C.感应电流的磁场方向,总是跟原磁砀方向相反D.感应电流的磁场方向可以跟原磁场方向相同,也可以相反【考点】D8:法拉第电磁感应定律;DB:楞次定律.【分析】根据楞次定律知,感应电流的磁场总是阻碍引起感应电流的磁通量的变化.当磁通量增大时,感应电流的磁场与它相反,当磁通量减小时,感应电流的磁场与它相同.【解答】解:A、感应电流的方向总是要使它的磁场阻碍原来的磁通量的变化.故A正确.B、C、D、感应电流的磁场方向阻碍原磁场磁通量的变化,方向可能与原磁场方向相同,可能相反.故B、C错误,D正确.故选:AD.11.如图所示,图甲中M为一电动机,当滑动变阻器R的触头从一端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是()A.电路中电源电动势为3.6VB.变阻器向右滑动时,V2读数逐渐减小C.变阻器的最大阻值为30ΩD.此电路中,电动机的最大输出功率为0.9W【考点】BB:闭合电路的欧姆定律;BG:电功、电功率.【分析】先确定U﹣I图线与电压表示数对应的关系.再根据图线求出电源的电动势,并判断V2读数的变化情况.变阻器的全部接入电路时,电路中电流最小.由欧姆定律求解变阻器的最大阻值.当I=0.3A时,电动机输出功率最大.由电动机的总功率UI与发热功率I2R之差求解电动机的最大输出功率.【解答】解:A、由电路图甲知,电压表V2测量路端电压,电路中电流增大时,内电压增大,路端电压减小,所以图乙中最上面的图线表示V2的电压与电流的关系.此图线的斜率大小等于电源的内阻,为r=Ω=2Ω当电流I=0.1A时,U=3.4V,则电源的电动势E=U+Ir=3.4+0.1×2V=3.6V,故A正确:B、变阻器向右滑动时,R阻值变大,总电流减小,内电压减小,路端电压增大,则V2读数逐渐增大,故B错误;C、当I=0.1A时,电路中电流最小,变阻器的电阻为最大值,所以R=﹣r﹣r M=(﹣2﹣4)Ω=30Ω,故C正确.由图可知,电动机的电阻r M=Ω=4Ω.D、当I=0.3A时,U=3V,电动机输出功率最大,最大值为P=UI﹣I2r M=3V×0.3A ﹣(0.3A)2×4Ω=0.54W,故D错误;故选:AC12.某一学习小组在研究电磁感应现象时,利用一根粗细均匀的金属丝弯成导轨abcd,=3.导体棒ef的电阻是bc段电阻的两倍,如图所示,匀强磁场垂直于导轨平面,当用平行于导轨的外力F将导体棒ef由靠近bc位置匀速向右移动时,则()A.导体棒ef两端的电压不变B.导体棒ef中的电流变大C.拉力F的瞬时功率变小D.导轨abcd消耗的电功率先变大后变小【考点】D9:导体切割磁感线时的感应电动势;BB:闭合电路的欧姆定律;BG:电功、电功率.【分析】导体棒ef向右切割磁感线产生感应电动势,相当于电源,ef两端的电压是外电压,根据法拉第电磁感应定律和欧姆定律列式分析ef两端电压的变化;由欧姆定律分析电流的变化.导体棒匀速运动时拉力F的功率等于回路中的电功率;abcd消耗的功率是电源的输出功率,根据电源的内外电阻越接近,电源的输出功率越大进行分析.【解答】解:A、设ef的电阻为r,ebcf的电阻为R,ef长为L,速度为v,磁感应强度为B,则导体棒ef产生的感应电动势为:E=BLvef两端的电压为:U=E,E、r不变,R变大,可知U变大.故A错误.B、ef中的电流为:I=,E、r不变,R变大,I变小,故B错误.C、导体棒匀速运动时拉力F的功率等于回路中的电功率,为P=,R增大,则P减小,故C正确.D、abcd消耗的功率是电源ef的输出功率,根据条件:=3.ef的电阻是bc段电阻的两倍,可知ebcf的电阻先小于ef的电阻,再等于ef的电阻,后大于ef的电阻,所以导轨abcd消耗的电功率先增大后减小,故D正确.故选:CD.二、填空题(本题共2小题,每空2分,共12分)13.用螺旋测微器测圆柱体的直径时,示数如图甲所示,此示数为 6.125mm,用20分度的游标卡尺测量某物体的厚度时,示数如图乙所示,此示数为63.60 mm.【考点】L3:刻度尺、游标卡尺的使用;L4:螺旋测微器的使用.【分析】解决本题的关键掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读.螺旋测微器的读数方法是固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读.【解答】解:螺旋测微器的固定刻度为6mm,可动刻度为12.5×0.01mm=0.125mm,所以最终读数为6mm+0.125mm=6.125mm.20分度的游标卡尺,精确度是0.05mm,游标卡尺的主尺读数为63mm,游标尺上第12个刻度和主尺上某一刻度对齐,所以游标读数为12×0.05mm=0.60mm,所以最终读数为:63mm+0.60mm=63.60mm.故答案为:6.125 63.6014.在实验室用“伏安法”测定电源的电动势和内阻,现备有如下实验器材:被测电源(一节干电池)、电压表、电流表、滑动变阻器、开关、导线等.①画出实验电路图(图1),补充完实物连线图(图3).②根据实验作出U﹣I图象如图2所示,则由图象可确定:该电源的电动势为1.40V,电源的内电阻为0.57Ω.【考点】N5:描绘小电珠的伏安特性曲线.【分析】(1)由实验原理可得出对应的图象,根据原理图可得出实物图;(2)由闭合电路欧姆定律可得出函数关系,结合数学公式及图象可明确电动势和内电阻;【解答】解:(1)采用伏安法测电源的电动势和内电阻的实验,只需将滑动变阻器与电源串联即可;由于电流表内阻接近电源内阻;故采用电流表相对电源的外接法;故原理图如图所示;根据原理图连接实物图如图;(2)由U=E﹣Ir可知:U﹣I图象中图象与纵坐标的交点为电源的电动势;故E=1.40V;。
江西省宜春市上高二中2016-2017学年高一下学期第六次

2016-2017学年江西省宜春市上高二中高一(下)第六次月考数学试卷(文科)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有四个命题:①数列是自变量为正整数的一类函数;②数列,,,,…的通项公式是a n=;③数列的图象是一群孤立的点;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列.其中正确的是()A.①②③B.①③C.②③④D.②④2.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=.求sin(B+C)的值()A.B.﹣ C.0 D.3.△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=4,且C=60°,则ab的值为()A.B.C.1 D.4.在△ABC中,已知D是AB边上一点,若=2,=,则λ=()A.B.C.﹣ D.﹣5.若=(cos,cos),||=2||,且(+)•=﹣2,则向量,的夹角为()A.B. C. D.6.y=cos(x+1)图象上相邻的最高点和最低点之间的距离是()A. B.πC.2 D.7.如图,在△ABC中,=,DE∥BC交AC于E,BC边上的中线AM交DE于N,设=,=,用,表示向量.则等于()A.(+)B.(+)C.(+)D.(+)8.已知函数f(x)=sinωx(ω>0)在[0,]上的最大值为,当把f(x)的图象上所有的点向右平移φ个单位,得到函数g(x),且g(x)满足g(π+x)=g(π﹣x),则正数φ的最小值为()A.B.C.D.9.如图,圆O与x轴的正半轴的交点为A,点B,C在圆O上,点B的坐标为(﹣1,2),点C位于第一象限,∠AOC=α.若|BC|=,则sin cos+cos2﹣=()A.﹣B.﹣C.D.10.已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量在方向上的投影为()A.﹣B.﹣1 C.﹣ D.11.将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.12.设O为△ABC的外心,且,则△ABC的内角C=()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.在等差数列{a n}中,若a2=4,a4=2,则a6=.14.已知向量,如果(3+4)∥(﹣2),则t=.15.在△ABC,三内角A,B,C的对边分别为a,b,c,已知A=30°,,则c=.16.已知向量,为两个互相垂直的单位向量,向量满足=0,则=.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,(1)求函数f(x)的解析式;(2)求f(﹣)的值.18.已知=(2,1),(1)如果||=,且向量与共线,求的坐标表示;(2)如果||=,且向量与夹角为,求的坐标表示.19.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA(Ⅰ)求B的大小;(Ⅱ)若,c=5,求b.20.在△ABC中,内角A,B,C的对边分别为a,b,c,已知=.(1)求的值(2)若cosB=,b=2,求△ABC的面积S.21.如图,在△ABC中,BC=3.AC=,B=,∠BAC,AE,AF是∠BAC 的三等分角平分线,分别交BC于点E,F.(1)求角C的大小;(2)求线段EF的长.22.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,且f()=0,将函数f(x)图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移个单位长度后得到函数g(x)的图象.(1)求函数f(x)与g(x)的解析式;(2)是否存在x0∈(,),使得f(x0),g(x0),f()按照某种顺序成等差数列?若存在,请求出x0的值,若不存在,说明理由;(3)求实数a,使得F(x)=f(x)+ag(x)在(0,2π)内恰有3个零点.2016-2017学年江西省宜春市上高二中高一(下)第六次月考数学试卷(文科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有四个命题:①数列是自变量为正整数的一类函数;②数列,,,,…的通项公式是a n=;③数列的图象是一群孤立的点;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列.其中正确的是()A.①②③B.①③C.②③④D.②④【考点】2K:命题的真假判断与应用;81:数列的概念及简单表示法.【分析】根据数列的定义可判断①,根据通项公式可判断②,根据数列各项与元素性质的差别,可以判断③,根据数列相同的判定方法,可以判断④的真假,进而得到答案.【解答】解:①数列是自变量为正整数的一类函数,正确②数列,,,,…的通项公式是a n=,而不是a n=;③数列的图象是一群孤立的点,正确;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…不是同一数列.综上可得:只有①③正确.故选:B.2.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=.求sin(B+C)的值()A.B.﹣ C.0 D.【考点】GQ:两角和与差的正弦函数.【分析】根据同角的三角函数的关系和诱导公式计算即可.【解答】解:∵cosA=,∴sinA=∴sin(B+C)=sinA=,故选:A.3.△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=4,且C=60°,则ab的值为()A.B.C.1 D.【考点】HR:余弦定理.【分析】将(a+b)2﹣c2=4化为c2=(a+b)2﹣4=a2+b2+2ab﹣4,又C=60°,再利用余弦定理得c2=a2+b2﹣2abcosC=a2+b2﹣ab即可求得答案.【解答】解:∵△ABC的边a、b、c满足(a+b)2﹣c2=4,∴c2=(a+b)2﹣4=a2+b2+2ab﹣4,又C=60°,由余弦定理得c2=a2+b2﹣2abcosC=a2+b2﹣ab,∴2ab﹣4=﹣ab,∴ab=.故选:A.4.在△ABC中,已知D是AB边上一点,若=2,=,则λ=()A.B.C.﹣ D.﹣【考点】9B:向量加减混合运算及其几何意义.【分析】本题要求字母系数,办法是把表示出来,表示时所用的基底要和题目中所给的一致,即用和表示,画图观察,从要求向量的起点出发,沿着三角形的边走到终点,把求出的结果和给的条件比较,写出λ.【解答】解:在△ABC中,已知D是AB边上一点∵=2,=,∴=,∴λ=,故选A.5.若=(cos,cos),||=2||,且(+)•=﹣2,则向量,的夹角为()A.B. C. D.【考点】9R:平面向量数量积的运算.【分析】根据平面向量的坐标运算与模长公式,数量积运算以及夹角公式,即可求出向量,的夹角.【解答】解:=(cos,cos)=(cos,sin),∴||==1,∴||=2||=2,∴(+)•=•+=×2×1×cosθ+12=﹣2,∴cosθ=﹣;又∵θ∈[0,π],∴向量,的夹角为.故选:C.6.y=cos(x+1)图象上相邻的最高点和最低点之间的距离是()A. B.πC.2 D.【考点】H7:余弦函数的图象.【分析】y=cos(x+1)的周期是2π,最大值为1,最小值为﹣1,即可求出y=cos (x+1)图象上相邻的最高点和最低点之间的距离.【解答】解:y=cos(x+1)的周期是2π,最大值为1,最小值为﹣1,∴y=cos(x+1)图象上相邻的最高点和最低点之间的距离是=,故选:A.7.如图,在△ABC中,=,DE∥BC交AC于E,BC边上的中线AM交DE于N,设=,=,用,表示向量.则等于()A.(+)B.(+)C.(+)D.(+)【考点】9H:平面向量的基本定理及其意义.【分析】利用平行线的性质、向量的平行四边形法则、向量共线定理即可得出.【解答】解:由题意可得:==.故选:C.8.已知函数f(x)=sinωx(ω>0)在[0,]上的最大值为,当把f(x)的图象上所有的点向右平移φ个单位,得到函数g(x),且g(x)满足g(π+x)=g(π﹣x),则正数φ的最小值为()A.B.C.D.【考点】H2:正弦函数的图象.【分析】由函数的最大值求得ω的值,由正弦函数图象变换,求得g(x)的解析式,由函数的对称性求得g(x)的对称轴,可知2×π﹣2φ=kπ+,k∈Z,解得φ=﹣+,k∈Z,当k=0时,即可求得正数φ的最小值.【解答】解:由题意,函数f(x)在区间[0,]上单调递增,∴sin(ω)=,∴ω=,∴ω=2,由f(x)的图象上所有的点向右平移φ个单位,∴g(x)=sin(2x﹣2φ),又g(π+x)=g(π﹣x),所以x=π是函数g(x)的一条对称轴,故2×π﹣2φ=kπ+,k∈Z,∴φ=﹣+,k∈Z,当k=0时,正数φ取最小值.故答案选:C.9.如图,圆O与x轴的正半轴的交点为A,点B,C在圆O上,点B的坐标为(﹣1,2),点C位于第一象限,∠AOC=α.若|BC|=,则sin cos+cos2﹣=()A.﹣B.﹣C.D.【考点】G9:任意角的三角函数的定义.【分析】根据三角函数的倍角公式将函数式进行化简,结合三角函数的定义即可得到结论.【解答】解:∵点B的坐标为(﹣1,2),∴|OB|=|OC|=,∵|BC|=,∴△OBC是等边三角形,则∠AOB=α+.则sin(α+)==,cos(α+)==﹣,则sin cos+cos2﹣=sinα+cosα=sin(α+)=,故选:D.10.已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量在方向上的投影为()A.﹣B.﹣1 C.﹣ D.【考点】9R:平面向量数量积的运算.【分析】建立如图所示平面直角坐标系,求出A、D、B的坐标,得到的坐标,代入投影公式求解.【解答】解:建立如图所示平面直角坐标系,则A(0,0),B(4,2),D(﹣2,3).∴,.∴,.∴向量在方向上的投影为.故选:A.11.将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.另解:f(x)=sin2x,g(x)=sin(2x﹣2φ),设2x1=2kπ+,k∈Z,2x2﹣2φ=﹣+2mπ,m∈Z,x1﹣x2=﹣φ+(k﹣m)π,由|x1﹣x2|min=,可得﹣φ=,解得φ=,故选:D.12.设O为△ABC的外心,且,则△ABC的内角C=()A.B.C.D.【考点】9V:向量在几何中的应用.【分析】由,移项得,再平方得到=0,从而,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C 值.【解答】解:设外接圆的半径为R,∵,∴,∴,∴2R2+2=2R2,∴=0,∴,根据圆心角等于同弧所对的圆周的两倍得:△ABC中的内角C值为=.故选B.二、填空题(本大题共4小题,每小题5分,共20分)13.在等差数列{a n}中,若a2=4,a4=2,则a6=0.【考点】84:等差数列的通项公式.【分析】由已知结合等差数列的性质列式计算.【解答】解:在等差数列{a n}中,由a2=4,a4=2,且a2+a6=2a4,∴a6=2a4﹣a2=2×2﹣4=0.故答案为:0.14.已知向量,如果(3+4)∥(﹣2),则t=.【考点】9K:平面向量共线(平行)的坐标表示.【分析】利用平面向量坐标运算法则先分别求出和,由此利用(3 +4)∥(﹣2),能求出t的值.【解答】解:∵向量,∴=(6,﹣3)+(﹣12,4t)=(﹣6,4t﹣3),=(8,﹣1﹣2t),∵(3+4)∥(﹣2),∴,解得t=.故答案为:.15.在△ABC,三内角A,B,C的对边分别为a,b,c,已知A=30°,,则c=1或2.【考点】HP:正弦定理.【分析】利用余弦定理列出关系式,把A=30°,值代入计算即可求出c的值【解答】解:∵A=30°,,∴由余弦定理得A2=b2+c2﹣2bccosB,即1=3+c2﹣2××c×,即c2﹣3c+2=0解得:c=1或c=2;故答案为:1或2.16.已知向量,为两个互相垂直的单位向量,向量满足=0,则=.【考点】9R:平面向量数量积的运算.【分析】作出图形,根据向量垂直得出的终点的轨迹,从而得出||的最大模长.【解答】解:设,,,则OA=OB=1,延长OB到D,使得OD=2OB,则=2,∴=,=2,∵=0,∴CA⊥CD,即C在以AD为直径的圆M上,又OA⊥OD,∴OC的最大值为圆M的直径AD=.故答案为:.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,(1)求函数f(x)的解析式;(2)求f(﹣)的值.【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式;H2:正弦函数的图象.【分析】(1)根据图象的最高点坐标,最高点横坐标与零点距离等求出A,φ,ω;(2)利用(1)的解析式代入求值【解答】解:(1)由图象可知A=2,并且T=()=π,所以ω=2,又f()=2,0<φ<π,得到φ=,所以;(2)由(1)得到f(﹣)=2sin(﹣)=﹣2sin=1.18.已知=(2,1),(1)如果||=,且向量与共线,求的坐标表示;(2)如果||=,且向量与夹角为,求的坐标表示.【考点】9R:平面向量数量积的运算;9J:平面向量的坐标运算.【分析】(1)设,由向量的模及斜率共线列关于x,y的方程组求解;(2)设,由向量的模及斜率夹角列关于x,y的方程组求解.【解答】解:(1)设,由||=,且向量与共线,得,解得或.∴或;(2)设,由||=,且向量与夹角为,得,解得或.∴或.19.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA(Ⅰ)求B的大小;(Ⅱ)若,c=5,求b.【考点】HQ:正弦定理的应用;HS:余弦定理的应用.【分析】(1)根据正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由△ABC为锐角三角形可得答案.(2)根据(1)中所求角B的值,和余弦定理直接可求b的值.【解答】解:(Ⅰ)由a=2bsinA,根据正弦定理得sinA=2sinBsinA,所以,由△ABC为锐角三角形得.(Ⅱ)根据余弦定理,得b2=a2+c2﹣2accosB=27+25﹣45=7.所以,.20.在△ABC中,内角A,B,C的对边分别为a,b,c,已知=.(1)求的值(2)若cosB=,b=2,求△ABC的面积S.【考点】HR:余弦定理;HP:正弦定理.【分析】(1)由正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知可得sinC=2sinA,即可得解=2.(2)由正弦定理可求c=2a,由余弦定理解得a=1,从而c=2.利用同角三角函数基本关系式可求sinB的值,进而利用三角形面积公式即可计算得解.【解答】(本题满分为12分)解:(1)由正弦定理,则=,所以=,即(cosA ﹣2cosC )sinB=(2sinC ﹣sinA )cosB ,化简可得sin (A +B )=2sin (B +C ).因为A +B +C=π,所以sinC=2sinA .因此=2.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)由=2,得c=2a ,由余弦定理b 2=a 2+c 2﹣2accosB ,及cosB=,b=2,得4=a 2+4a 2﹣4a 2×.解得a=1,从而c=2.因为cosB=,且sinB==,因此S=acsinB=×1×2×=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣21.如图,在△ABC 中,BC=3.AC=,B=,∠BAC,AE ,AF 是∠BAC的三等分角平分线,分别交BC 于点E ,F . (1)求角C 的大小; (2)求线段EF 的长.【考点】HT :三角形中的几何计算.【分析】(1)设∠BAE=α,则∠C=150°﹣3α,利用正弦定理可得角C 的大小; (2)利用正弦定理可得BE ,CF ,即可求线段EF 的长. 【解答】解:(1)设∠BAE=α,则∠C=150°﹣3α,∴由正弦定理可得==,∴sin3α=,∵∠BAC,∴3α=135°, ∴C=150°﹣3α=15°;(2)在△ABC中,=,∴AB=,△ABE中,=,∴BE=6﹣3.△AFC中,,∴CF=,∴EF=3﹣6+3﹣=2﹣3.22.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,且f()=0,将函数f(x)图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移个单位长度后得到函数g(x)的图象.(1)求函数f(x)与g(x)的解析式;(2)是否存在x0∈(,),使得f(x0),g(x0),f()按照某种顺序成等差数列?若存在,请求出x0的值,若不存在,说明理由;(3)求实数a,使得F(x)=f(x)+ag(x)在(0,2π)内恰有3个零点.【考点】8I:数列与函数的综合;54:根的存在性及根的个数判断.【分析】(1)由周期公式可得ω,ω>0,再由对称中心可得φ值,可得f(x)解析式,由函数图象变换和诱导公式化简可得;(2)根据x的范围,求出sinx0+cos2x0=1,继而求出sinx0的值,即可判断,(3)根据函数零点存在定理可得cos2x+asinx=0,再分类讨论即可求出答案【解答】解:(1)∵函数f(x)=sin(ωx+φ)的周期为π,ω>0,∴ω==2,又曲线y=f(x)的一个对称中心为(,0),φ∈(0,π),∴sin(2×+φ)=0,可得φ=,∴f(x)=cos2x,将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,再将y=cosx的图象向右平移个单位长度后得到函数g(x)=cos(x﹣)的图象,由诱导公式化简可得g(x)=sinx;(2)当x∈(,),<sinx<,0<cos2x<,∵f()=,则g(x0)>f()>f(x0),∴g(x0)+f(x0)=2f(),即sinx0+cos2x0=1,化简得sinx0=0或sinx0=与<sinx0<矛盾,所以不存在x0∈(,),使得f(x0),g(x0),f()按照某种顺序成等差数列.(3)F(x)=f(x)+ag(x)=0,即cos2x+asinx=0,当sinx=0,显然不成立,当sinx≠0时,a=﹣=2sinx﹣,令t=sinx,则当x∈[0,2π]时,t∈[﹣1,1],由函数a=2t﹣,t∈[﹣1,1],以及t=sinx,x∈[0,2π]的图象可知,当a=±1时,a=2sinx﹣在[0,2π]内恰有3个零点.综上所述,a=±12017年6月28日。
2016-2017年江西省宜春市奉新一中高二(下)第一次月考数学试卷(文科)(解析版)

第 3 页(共 14 页)
(2)设 max{A}表示数集 A 中的最大数,且
21.(12 分)设函数 f(x)=|x﹣1|+|2x﹣1|. (Ⅰ)求不等式 f(x)≥2 的解集; (Ⅱ)若∀x∈R,不等式 f(x)≥a|x|恒成立,求实数 a 的取值范围. 22.(12 分)已知 b=a3+ ,a∈[0,1]. 证明: (1)b≥1﹣a+a2. (2) <b≤ .
A.π
B.4
C.4π
D.16
【解答】解:将原极坐标方程为 ρ=4cosθ,化成: ρ2=4ρcosθ,其直角坐标方程为: ∴x2+y2=4x,是一个半径为 2 的圆,其面积为 4π.
故选:C.
2.(5 分)在极坐标系中,已知点 P(2, ),则过点 P 且平行于极轴的直线的方程是( )
A.ρsinθ=1
B.ρsinθ=
C.ρcosθ=1
D.ρcosθ=
【解答】解:∵点 P(2, )的直角坐标为( ,1),此点到 x 轴的距离为 1,
故经过此点到 x 轴的距离为 1 的直线的方程是 y=1, 故过点 P 且平行于极轴的直线的方程是 ρsinθ=1, 故选:A.
3.(5 分)如图,在复平面内,复数 z1,z2 对应的向量分别是 , ,则|z1+z2|=( )
12.(5 分)将自然数 0,1,2,…按照如下形式进行摆列:
根据以上规律判定,从 2016 到 2018 的箭头方向是( )
A.
B.
C.
D.
第 2 页(共 14 页)
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分
13.(5 分)设平面上的伸缩变换的坐标表达式为
江西省宜春市上高二中2016-2017学年高一(下)第五次月考数学试卷

2016-2017学年江西省宜春市上高二中高一(下)第五次月考数学试卷一、选择题(每小题5分,共60分)1.设集合A={x|2x≤4},集合B={x|y=lg(x﹣1)},则A∩B等于()A.(1,2)B.C.2.函数f(x)=3x﹣﹣a的一个零点在区间(1,2)内,则实数a的取值范围()A.(﹣2,7) B.(﹣1,6) C.(﹣1,7) D.(﹣2,6)3.sin(﹣690°)的值为()A.B.C.D.4.已知幂函数y=f(x)的图象过点,则log2f(2)的值为()A.B.﹣C.2 D.﹣25.已知函数f(x)的定义域为(﹣1,0),则函数f(2x+1)的定义域为()A.(﹣1,1) B.C.(﹣1,0) D.6.函数f(x)=sin(2x﹣)在区间上的最小值是()A.﹣1 B.﹣C.D.07.设向量=(1,2),=(2,1),若向量﹣λ与向量=(5,﹣2)共线,则λ的值为()A.B.C.﹣D.48.已知点A(1,3),B(4,﹣1),则与向量反方向的单位向量的坐标为()A.B.C.D.9.如图,已知=,=,=4,=3,则=()A.﹣B.﹣C.﹣D.﹣10.O为△ABC内一点,且2++=,=t,若B,O,D三点共线,则t的值为()A.B.C.D.11.已知,则cos2α=()A.1 B.﹣1 C.D.012.已知函数f(x)=,若f(f(m))≥0,则实数m的取值范围是()A.B.∪﹣2,2+﹣2,2+4,+∞)二、填空题(本大题共4个小题,每小题5分,共20分)13.已知f(x)=x5+ax3+bx﹣8,若f(﹣2)=10,则f(2)=.14.函数f(x)=3x﹣1,若f=2x+3,则g(x)=.15.已知与是两个不共线向量,=3+2,=2﹣5,=λ﹣,若三点A、B、D共线,则λ=.16.如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC 于不同的两点M,N,若=,=m,则m的值为.三、解答题(共6个小题,共70分)17.已知集合A={x|a≤x≤a+8},B={x|x<﹣1或x>5},(1)当a=0时,求A∩B,A∪(C R B);(2)若A∪B=B,求实数a的取值范围.18.已知点A(﹣1,2),B(2,8)以及,=﹣13,求点C、D的坐标和的坐标.19.(1)已知角α终边上一点P(﹣4,3),求的值.(2)若sinx=,cosx=,x∈(,π),求tanx.20.设函数x+1(1)求f(x)的最小正周期及其图象的对称中心;(2)求函数f(x)的单调递增区间.21.在△ABC中,E为AC中点,D为BC靠近C的三等分点,记=.(1)用表示;(2)求BP:PE,并用表示.22.已知函数是奇函数,f(x)=lg(10x+1)+bx是偶函数.(1)求a+b的值.(2)若对任意的t∈,使不等式g(x)>h成立,求实数a的取值范围.2016-2017学年江西省宜春市上高二中高一(下)第五次月考数学试卷参考答案与试题解析一、选择题(每小题5分,共60分)1.设集合A={x|2x≤4},集合B={x|y=lg(x﹣1)},则A∩B等于()A.(1,2)B.C.【考点】对数函数的定义域;交集及其运算.【分析】解指数不等式求出集合A,求出对数函数的定义域即求出集合B,然后求解它们的交集.【解答】解:A={x|2x≤4}={x|x≤2},由x﹣1>0得x>1∴B={x|y=lg(x﹣1)}={x|x>1}∴A∩B={x|1<x≤2}故选D.2.函数f(x)=3x﹣﹣a的一个零点在区间(1,2)内,则实数a的取值范围()A.(﹣2,7) B.(﹣1,6) C.(﹣1,7) D.(﹣2,6)【考点】二分法的定义.【分析】由题意可得f(1)f(2)=(a+1)(a﹣7)<0,解不等式求得实数a的取值范围.【解答】解:由题意可得f(1)f(2)=(3﹣4﹣a)(9﹣2﹣a)<0,即(a+1)(a﹣7)<0,解得:﹣1<a<7,故实数a的取值范围是(﹣1,7),故选:C.3.sin(﹣690°)的值为()A.B.C.D.【考点】运用诱导公式化简求值.【分析】由条件利用诱导公式化简所给的三角函数式,可得结果.【解答】解:sin(﹣690°)=sin(﹣720°+30°)=sin30°=,故选:C.4.已知幂函数y=f(x)的图象过点,则log2f(2)的值为()A.B.﹣C.2 D.﹣2【考点】对数的运算性质;幂函数的性质.【分析】先设log2f(2)=n,求出函数f(x)的解析式,然后将点代入解析式,即可求出结果.【解答】解:设log2f(2)=n,则f(2)=2n∴f(x)=x n又∵由幂函数y=f(x)的图象过点∴,故选A.5.已知函数f(x)的定义域为(﹣1,0),则函数f(2x+1)的定义域为()A.(﹣1,1) B.C.(﹣1,0) D.【考点】函数的定义域及其求法.【分析】原函数的定义域,即为2x+1的范围,解不等式组即可得解.【解答】解:∵原函数的定义域为(﹣1,0),∴﹣1<2x+1<0,解得﹣1<x<﹣.∴则函数f(2x+1)的定义域为.故选B.6.函数f(x)=sin(2x﹣)在区间上的最小值是()A.﹣1 B.﹣C.D.0【考点】三角函数的最值.【分析】由题意,可先求出2x取值范围,再由正弦函数的性质即可求出所求的最小值.【解答】解:由题意x∈,得2x∈,∴∈hslx3y3h,1﹣2,2﹣2,24,+∞)C.D.∪﹣2,2+4,+∞).故选:D.二、填空题(本大题共4个小题,每小题5分,共20分)13.已知f(x)=x5+ax3+bx﹣8,若f(﹣2)=10,则f(2)=﹣26.【考点】函数奇偶性的性质;函数的值.【分析】把f(x)=x5+ax3+bx﹣8,转化为令g(x)=f(x)+8=x5+ax3+bx是一个奇函数,即可计算出.【解答】解:由f(x)=x5+ax3+bx﹣8,可令g(x)=f(x)+8=x5+ax3+bx,可知:g(﹣x)=f(﹣x)+8=﹣g(x),∴f(﹣2)+8=﹣,∴f(2)=﹣16﹣10=﹣26.故答案为﹣26.14.函数f(x)=3x﹣1,若f=2x+3,则g(x)=.【考点】函数解析式的求解及常用方法.【分析】直接利用函数的解析式,求解即可.【解答】解:函数f(x)=3x﹣1,若f=2x+3,可得3g(x)﹣1=2x+3,解得g(x)=.故答案为:.15.已知与是两个不共线向量,=3+2,=2﹣5,=λ﹣,若三点A、B、D共线,则λ=8.【考点】平行向量与共线向量.【分析】由于三点A、B、D共线,因此存在实数k使得,利用向量的运算和共面向量基本定理即可得出.【解答】解:=,∵三点A、B、D共线,∴存在实数k使得,∴3+2=k hslx3y3h kπ﹣,kπ+0,+∞),不等式g(t2﹣2t)+g (2t2﹣k)>0恒成立,求实数k的取值范围.(3)设,若存在x∈(﹣∞,1lg(10a+9)0,+∞)恒成立,求得3t2﹣2t的最小值,可得k的范围.(3)由题意可得存在x∈(﹣∞,10,+∞)恒成立,即3t2﹣2t>k,t∈0,+∞)上F(x)的最小值为,∴.(3)h(x)=lg(10x+1),h(lg(10a+9))=lg=lg(10a+10),则由已知得,存在x∈(﹣∞,1单增,∴,∴,∴.又,∵,∴,∴.2017年5月14日。
江西省宜春市高一数学下学期期中试题

江西省宜春2016—2017学年度高一下学期期中考试数学试卷一、选择题:(共12小题,每小题5分,共60分)1.若角α=﹣4,则α的终边在()A.第四象限B.第三象限C.第二象限D.第一象限2.数轴上点A,B分别对应﹣1、2,则向量的长度是( )A.﹣1 B.2 C.1 D.33.若角α的终边过点P(3,﹣4),则cosα等于()A. B.C.D.4.已知向量,满足||=1,⊥,则向量﹣2在向量﹣方向上的投影为()A.0 B.1 C.2 D.﹣15.已知α是第四象限角,tanα=﹣,则sinα=()A. B.C.D.6.化简y=( )A.tanαB.tan2αC.2tanαD.2tan2α7.设向量=(2,m),=(1,﹣1),若⊥(+2),则实数m等于()A.2 B.4 C.6 D.﹣38.在△ABC中,AB=3,AC=2,BC=,则•=()A. B.C. D.9.已知函数y=2sinωx(ω>0)的图象与直线y=﹣2的相邻的两个公共点之间的距离为,则ω的值为()A. B. C.3 D.10.要得到函数y=2cos(2x﹣)的图象,只需将函数y=2cos2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位11.如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若=m,=n,则m+n的值为()A.1 B.2 C.﹣2 D.12.在平面直角坐标系xoy中,动点P关于x轴的对称点为Q,且•=2,已知点A(﹣2,0),B(2,0),则(|PA|﹣|PB|)2()A.为定值8 B.为定值4 C.为定值2 D.不是定值二、填空题:(本大题共4小题,每小题5分,共20分)13.的值是.14.已知向量,的夹角为,且|=1,,|= .15.的部分图象如图所示,则函数f(x)的解析式为16.已知直角梯形ABCD中,AB∥CD,∠BCD=60°,E是线段AD上靠近A的三等分点,F是线段DC的中点,若AB=2,AD=,则= .三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤)17.已知函数,(1)求f(x)的最小正周期T;(2)求f(x)的单调递增区间.18.已知向量=(sinx,cosx),=,x∈R,函数f(x)=•.(1)求f(x)的最大值;(2)解关于x的不等式f(x)≥.19.(1)已知tanα=﹣,且α为第四象限角,求sinα,cosα;(2)计算sin.20.(Ⅰ)已知在△ABC中,AB=1,BC=2,∠B=,=,=求(2﹣3)•(4+);(Ⅱ)已知向量=(2,1),=(﹣1,3),且向量t+与向量﹣平行,求t的值.21.已知函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).(1)求函数f(x)的最小正周期和单调递增区间;(2)若x∈[,],且F(x)=﹣4λf(x)﹣cos(4x﹣)的最小值是﹣,求实数λ的值.22.已知向量,,函数f(x)=cos2x.(1)求函数f(x)的解析式及其单调递增区间;(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若c=且f(C)=0,求△ABC周长的取值范围.参考答案123456789101112 C D A D C C C C C D B A14。
【数学】江西省宜春市高安中学2016-2017学年高一(下)期末试卷(文)(解析版)

江西省宜春市高安中学2016-2017学年高一(下)期末数学试卷(文科)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)不等式<x的解集是()A.(1,+∞)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)2.(5分)若tanα=3,则的值等于()A.2 B.3 C.4 D.63.(5分)函数f(x)=cos2x+6cos(﹣x)的最大值为()A.4 B.5 C.6 D.74.(5分)在数列{a n}中,若为定值,且a4=2,则a2a6等于()A.32 B.4 C.8 D.165.(5分)在等差数列{a n}中,已知a1+a5+a9=3,则数列{a n}的前9项和S9=()A.9 B.15 C.18 D.246.(5分)已知a,b,c为△ABC的三个角A,B,C所对的边,若3b cos C=c(1﹣3cos B),则=()A.2:3 B.4:3 C.3:1 D.3:27.(5分)等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=()A.29 B.31 C.33 D.368.(5分)在△ABC中,若2cos B•sin A=sin C,则△ABC的形状一定是()A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形9.(5分)若α,β都是锐角,且,则cosβ=()A.B.C.或D.或10.(5分)有一长为1千米的斜坡,它的倾斜角为20°,现要将倾斜角改为10°(坡高不变),则斜坡长为________千米.()A.1 B.2sin10°C.2cos10°D.cos20°11.(5分)数列{a n}满足a n+a n+1=(n∈N*),a2=2,S n是数列{a n}的前n项和,则S21为()A.5 B.C.D.12.(5分)在等比数列{a n}中,a1=2,前n项和为S n,若数列{a n+1}也是等比数列,则S n=()A.2n+1﹣2 B.3n C.2n D.3n﹣1二.填空题:(本大题共4个小题,每小题5分,共20分)13.(5分)化简2sin15°sin75°的值为.14.(5分)若sin(α﹣)=,则cos(α+)=.15.(5分)=.16.(5分)数列{a n}的通项公式,其前n项和为S n,则S35=.三、解答题(17题10分,其他题12分,解答应写出文字说明,证明过程或演算步骤)17.(10分)解不等式0<x2﹣x﹣2≤4.18.(12分)已知函数f(x)=2sinωx cosωx+cos2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)的单调递增区间.19.(12分)在等差数列{a n}中,a2=4,a4+a7=15.(1)求数列{a n}的通项公式;(2)设,求b1+b2+b3+…+b10的值.20.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知a cos B+b cos A=2c cos C.(1)求角C的大小;(2)若a=5,b=8,求边c的长.21.(12分)在△ABC中,角A、B、C所对的边分别为a、b、c,已知a=,cos A=,B=A+(1)求b的值;(2)求△ABC的面积.22.(12分)已知函数f(x)=,数列{a n}满足a1=1,a n+1=f(),n∈N*.(1)求数列{a n}的通项公式;(2)令b n=(n≥2),b1=3,S n=b1+b2+…+b n,若S n<对一切n∈N*成立,求最小正整数m.【参考答案】一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.C【解析】不等式<x可化为:>0即x(x﹣1)(x+1)>0,利用标根法(如图所示),可知﹣1<x<0或x>1.所以原不等式的解集是:(﹣1,0)∪(1,+∞).故选C.2.D【解析】==2tanα=6故选D.3.B【解析】函数f(x)=cos2x+6cos(﹣x)=1﹣2sin2x+6sin x,令t=sin x(﹣1≤t≤1),可得函数y=﹣2t2+6t+1=﹣2(t﹣)2+,由∉[﹣1,1],可得函数在[﹣1,1]递增,即有t=1即x=2kπ+,k∈Z时,函数取得最大值5.故选B.4.B【解析】由为定值,得数列{a n}是等比数列,∵a4=2,∴a2a6=a42=4,故选B.5.A【解析】∵a1+a5+a9=3=3a5,∴a5=1.则数列{a n}的前9项和S9==9a5=9.故选A.6.C【解析】∵3b cos C=c(1﹣3cos B),∴由正弦定理可得:3sin B cos C=sin C﹣3sin C cos B,∴3sin B cos C+3sin C cos B=3sin(B+C)=3sin A=sin C,∴3a=c,即:=3:1.故选C.7.B【解析】∵数列{a n}是等比数列,a2•a3=2a1=a1q•=a1•a4,∴a4=2.∵a4与2a7的等差中项为,∴a4 +2a7 =,故有a7 =.∴q3==,∴q=,∴a1==16.∴S5==31.故选B.8.C【解答】解析:∵2cos B•sin A=sin C=sin(A+B)⇒sin(A﹣B)=0,又B、A为三角形的内角,∴A=B.故选C.9.A【解析】∵α,β都是锐角,且,∴cosα==,cos(α﹣β)==,则cosβ=cos[α﹣(α﹣β)]=cosαcos(α﹣β)+sinαsin(α﹣β)=+ =,故选A.10.C【解析】设颇高为h,则h=1•sin20°=sin20°,设新斜坡长为x,则x•sin10°=h=sin20°,∴x==2cos10°,故选C.11.B【解析】由a n+a n+1=(n∈N*),a2=2,得,…,∴数列{a n}的所有奇数项项为,所有偶数项为2,∴.故选B.12.C【解析】设等比数列{a n}的公比为q,∵a1=2,数列{a n+1}也是等比数列,∴=(a1+1)(a3+1),即(2q+1)2=3(2q2+1),化为:(q﹣1)2=0,解得q=1.则S n=2n.故选C.二.填空题:(本大题共4个小题,每小题5分,共20分)13.【解析】2sin15°sin75°=2sin15°sin(90°﹣15°)=2sin15°cos15°=sin30°=.故答案为.14.【解析】cos(α+)=cos(α﹣+)=﹣sin(α﹣)=﹣.故答案为.15.【解析】∴,若A为锐角,则A<,∴cos A=,sin B=此时cos C=cos(π﹣A﹣B)=﹣cos(A+B)=﹣cos A cos B+sin A sin B=若A为钝角,则A,A+B>π,不合要求故答案为16.630【解析】由,得,,,…,,∴S35=a1+a2+…+a33+a34+a35=﹣(3+7+11+15+…+67)+352=﹣=630.故答案为630.三、解答题(17题10分,其他题12分,解答应写出文字说明,证明过程或演算步骤)17.解:不等式0<x2﹣x﹣2≤4等价于,即,可化为,解得,如图所示;所以原不等式的解集为{x|﹣2≤x<﹣1或2<x≤3}.18.解:(1)f(x)=2sinωx cosωx+cos2ωx=sin2ωx+cos2ωx==.由T=,得ω=1;(2)由(1)得,f(x)=.再由,得.∴f(x)的单调递增区间为[](k∈Z).19.解:(1)设等差数列{a n}的公差为d,由已知得,解得∴a n=3+(n﹣1)×1,即a n=n+2.(2)由(1)知,∴b1+b2+b3+…+b10=21+22+…+210==2046.20.解:(1)a cos B+b cos A=2c cos C,∴sin A cos B+sin B cos A=2sin C cos C∴sin(A+B)=sin C=2sin C cos C,sin C≠0,解得cos C=,C∈(0,π),∴C=.(2)由余弦定理可得:c2=52+82﹣2×5×8cos=49,解得c=7.21.解:(1)在△ABC中,∵0<A<π,cos A=,B=A+,∴sin A==,sin B=sin(A+)=cos A=,又a=,由得,b===;(2)由(1)得,cos B=cos(A+)=﹣sin A=﹣,∵A+B+C=π,∴C=π﹣(A+B),∴sin C=sin(A+B)=sin A cos B+cos A sin B=×(﹣)+×=,∴△ABC的面积S===.22.解:(1)∵f(x)=,数列{a n}满足a1=1,∴=,∴{a n}是首项为1,公差为的等差数列,∴.(2)当n≥2时,b n===,当n=1时,b1=3,代入上式成立,∴S n=b1+b2+…+b n==,∵S n<,∴对一切n∈N*成立,又沿n递增,且,∴,∴m≥2013,∴最小正整数m为2013.。
江西省宜春市奉新一中2016-2017学年高一(下)第一次月考数学试卷(理科)

2016-2017学年江西省宜春市奉新一中高一(下)第一次月考数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分)1.已知等差数列{a n}中,a7+a9=16,a4=1,则a12的值是()A.64 B.31 C.30 D.15=f(a n),n=1,2,…,则a2012等于()2.对于数列{a n},a1=4,a n+1x12345 f(x)54312A.2 B.3 C.4 D.53.已知,则tan2α=()A.B.C.D.4.平面向量,已知=(4,3),=(3,18),则夹角的余弦值等于()A.B.C.D.5.△ABC的三个内角A、B、C成等差数列,,则△ABC一定是()A.直角三角形 B.等边三角形 C.锐角三角形 D.钝角三角形6.已知P1(2,﹣1),P2(0,5)且点P在P1P2的延长线上,||=2||,则点P 的坐标为()A.(2,11)B.C.D.(﹣2,11)7.已知函数f(x)=x2+2bx过(1,2)点,若数列的前n项和为S n,则S2012的值为()A.B.C.D.8.函数y=sin(ωx+φ)的部分图象如图,则φ、ω可以取的一组值是()A.ω=,φ=B.ω=,φ=C.ω=,φ=D.ω=,φ=9.已知向量=(a n,2),=(a n,),且a1=1,若数列{a n}的前n项和为S n,且+1∥,则S n=()A.B.C.D.10.已知A、B、C是直线l上不同的三个点,点O不在直线l上,则使等式x2+x+=成立的实数x的取值集合为()A.{﹣1}B.∅C.{0} D.{0,﹣1}11.已知A,B,C 是平面上不共线的三点,O是△ABC的重心,动点P满足=(++2),则点P一定为三角形ABC的()A.AB边中线的中点B.AB边中线的三等分点(非重心)C.重心D.AB边的中点12.在△ABC中,tanA,tanB,tanC依次成等差数列,则B的取值范围是()A.(0,B.(0,C.,)二、填空题(本大题共4小题,每小题5分,共20分)13.已知向量,满足||=1,||=2,与的夹角为60°,则|﹣|=.14.已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|+3|的最小值为.15.某科研单位欲拿出一定的经费奖励科研人员,第1名得全部资金的一半多一万元,第二名得剩下的一半多一万元,以名次类推得到剩下的一半多一万元,到第10名恰好资金分完,求此科研单位共拿出多少万元资金进行奖励.16.已知S n是等差数列{a n}(n∈N*)的前n项和,且S6>S7>S5,有下列四个命题:①d<0;②S11>0;③S12<0;④数列{S n}中的最大项为S11,其中正确命题的序号是.三、解答题(本大题共6小题,共10+12+12+12+12+12=70分)17.已知向量,,.(1)若,求θ;(2)求的最大值.18.如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设.(1)用表示向量,.(2)若,求实数λ的值.19.已知等差数列{a n}前三项的和为﹣3,前三项的积为8.(1)求等差数列{a n}的通项公式;(2)若a2,a3,a1成等比数列,求数列{|a n|}的前n项和.20.已知A、B、C的坐标分别为A(4,0),B(0,4),C(3cosα,3sinα).(1)若α∈(﹣π,0),且||=||,求角α的大小;(2)若⊥,求的值.21.已知O为坐标原点,向量,点P满足(1)记函数,讨论函数f(α)的单调性,并求其值域;(2)若O,P,C三点共线,求的值.22.已知数列{a n}的前三项与数列{b n}的前三项对应相等,且a1+2a2+22a3+…+2n﹣1a n=8n 对任意的n∈N*都成立,数列{b n﹣b n}是等差数列.+1(1)求数列{a n}与{b n}的通项公式;(2)是否存在k∈N*,使得b k﹣a k∈(0,1)?请说明理由.2016-2017学年江西省宜春市奉新一中高一(下)第一次月考数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.已知等差数列{a n}中,a7+a9=16,a4=1,则a12的值是()A.64 B.31 C.30 D.15【考点】84:等差数列的通项公式.【分析】利用等差数列的通项公式即可得出.【解答】解:设等差数列{a n}的公差为d,∵a7+a9=16,a4=1,∴,解得a1=﹣,d=则a12=+×11=15.故选:D.2.对于数列{a n},a1=4,a n+1=f(a n),n=1,2,…,则a2012等于()x12345 f(x)54312A.2 B.3 C.4 D.5【考点】82:数列的函数特性.【分析】由表格可知:f(1)=5,f(5)=2,f(2)=4,f(4)=1,f(3)=3.又a1=4,a n+1=f(a n),n=1,2,…,可得a n+4=a n.即可得出.【解答】解:由表格可知:f(1)=5,f(5)=2,f(2)=4,f(4)=1,f(3)=3.又a1=4,a n+1=f(a n),n=1,2,…,∴a2=f(a1)=f(4)=1,a3=f(a2)=f(1)=5,a4=f(a3)=f(5)=2,a5=f(a4)=f(2)=4,a6=f(a5)=f(4)=1.….∴a n+4=a n.=a4=2.∴a2012=a4×502+4故选:A.3.已知,则tan2α=()A.B.C.D.【考点】GU:二倍角的正切;GG:同角三角函数间的基本关系.【分析】由题意结合sin2α+cos2α=1可解得sinα,和cosα,进而可得tanα,再代入二倍角的正切公式可得答案.【解答】解:∵,又sin2α+cos2α=1,联立解得,或故tanα==,或tanα=3,代入可得tan2α===﹣,或tan2α===故选C4.平面向量,已知=(4,3),=(3,18),则夹角的余弦值等于()A.B.C.D.【考点】9S:数量积表示两个向量的夹角.【分析】先设出的坐标,根据a=(4,3),2a+b=(3,18),求出坐标,根据数量积的坐标公式的变形公式,求出两个向量的夹角的余弦【解答】解:设=(x,y),∵a=(4,3),2a+b=(3,18),∴∴cosθ==,故选C.5.△ABC的三个内角A、B、C成等差数列,,则△ABC一定是()A.直角三角形 B.等边三角形 C.锐角三角形 D.钝角三角形【考点】9R:平面向量数量积的运算;8F:等差数列的性质.【分析】由,结合等腰三角形三线合一的性质,我们易判断△ABC为等腰三角形,又由△ABC的三个内角A、B、C成等差数列,我们易求出B=60°,综合两个结论,即可得到答案.【解答】解:∵△ABC的三个内角A、B、C成等差数列∴2B=A+C又∵A+B+C=180°∴B=60°设D为BC边上的中点则=2又∵∴=0∴即△ABC为等腰三角形,故△ABC为等边三角形,故选:B6.已知P1(2,﹣1),P2(0,5)且点P在P1P2的延长线上,||=2||,则点P 的坐标为()A.(2,11)B.C.D.(﹣2,11)【考点】9K:平面向量共线(平行)的坐标表示.【分析】利用已知:点P在P1P2的延长线上,||=2||,因此点P2是线段P1P的中点,利用中点坐标公式即可得出.【解答】解:∵点P在P1P2的延长线上,||=2||,∴点P2是线段P1P的中点.∴,.解得x P=﹣2,y P=11.∴P(﹣2,11).故选D.7.已知函数f(x)=x2+2bx过(1,2)点,若数列的前n项和为S n,则S2012的值为()A.B.C.D.【考点】8E:数列的求和.【分析】先由f(x)=x2+2bx过(1,2)点求得b值,从而得到f(x),进而求得,利用裂项相消法即可求得S n,再把n=2012代入S n即可求得.【解答】解:由f(x)=x2+2bx过(1,2)点,得f(1)=2,即1+2b=2,解得b=,所以f(x)=x2+x,则==,所以S n=(1﹣)+(﹣)+(﹣)+…+()=1﹣=,所以S2012=.故选D.8.函数y=sin(ωx+φ)的部分图象如图,则φ、ω可以取的一组值是()A.ω=,φ=B.ω=,φ=C.ω=,φ=D.ω=,φ=【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】由图象观察可知周期的值,由周期公式即可求ω的值.又因为图象过点(1,1),即可解得φ的值,从而得解.【解答】解:由图象观察可知:3﹣1=,可解得:T=8=,从而有ω=.又因为图象过点(1,1),所以有:sin(φ)=1,故可得:φ=2k,k∈Z,可解得:φ=2kπ,k∈Z当k=0时,有φ=.故选:B.9.已知向量=(a n,2),=(a n,),且a1=1,若数列{a n}的前n项和为S n,且+1∥,则S n=()A.B.C.D.【考点】8H:数列递推式;96:平行向量与共线向量.=×a n,即=,【分析】根据题意,由∥结合向量平行的坐标表示方法可得2a n+1由等比数列的定义可得数列{a n}为首项a1=1,公比为的等比数列,由等比数列前n项和公式计算可得答案.,),【解答】解:根据题意,向量=(a n,2),=(a n+1=×a n,即=,若∥,则有2a n+1则数列{a n}为首项a1=1,公比为的等比数列,则其前n项和为S n==,故选:A.10.已知A、B、C是直线l上不同的三个点,点O不在直线l上,则使等式x2+x+=成立的实数x的取值集合为()A.{﹣1}B.∅C.{0} D.{0,﹣1}【考点】9H:平面向量的基本定理及其意义.【分析】利用向量的运算法则将等式中的向量都用以o为起点的向量表示,利用三点共线的条件列出方程求出x.【解答】解:,即即∵A,B,C共线,∴﹣x2+1﹣x=1,解得x=0,﹣1当x=0时,,此时B,C两点重合,不合题意故选A.11.已知A,B,C 是平面上不共线的三点,O是△ABC的重心,动点P满足=(++2),则点P一定为三角形ABC的()A.AB边中线的中点B.AB边中线的三等分点(非重心)C.重心D.AB边的中点【考点】98:向量的加法及其几何意义.【分析】根据O是三角形的重心,得到三条中线上对应的向量的模长之间的关系,根据向量加法的平行四边形法则,求出向量的和,根据共线的向量的加减,得到结果.【解答】解:设AB 的中点是E,∵O是三角形ABC的重心,动点P满足=(++2),∴=(+2)∵=2,∴=()==,∴P在AB边的中线上,是中线的三等分点,不是重心.故选:B.12.在△ABC中,tanA,tanB,tanC依次成等差数列,则B的取值范围是()A.(0,B.(0,C.,)【考点】8F:等差数列的性质;GH:同角三角函数基本关系的运用;GR:两角和与差的正切函数.【分析】由已知先求出2tanB=tanA+tanC>0,tanAtanC=3.再由(2tanB)2=(tanA+tanC)2=tan2A+tan2C+2tanAtanC≥4tanAtanC=12,求出,从而得到B的取值范围.【解答】解:由已知得2tanB=tanA+tanC>0(显然tanB≠0,若tanB<0,因为tanA>0且tanC>0,tanA+tanC>0,这与tanB<0矛盾),又tanB=﹣tan(A+C)=,所以tanAtanC=3.又(2tanB)2=(tanA+tanC)2=tan2A+tan2C+2tanAtanC≥4tanAtanC=12,因此tan2B≥3,又tanB>0,所以,,即B的取值范围是hslx3y3h),故选D.二、填空题(本大题共4小题,每小题5分,共20分)13.已知向量,满足||=1,||=2,与的夹角为60°,则|﹣|=.【考点】93:向量的模.【分析】根据题意和根据向量的减法几何意义画出图形,再由余弦定理求出||的长度.【解答】解:如图,由余弦定理得:||===故答案为:.14.已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|+3|的最小值为5.【考点】93:向量的模.【分析】根据题意,利用解析法求解,以直线DA,DC分别为x,y轴建立平面直角坐标系,则A(2,0),B(1,a),C(0,a),D(0,0),设P(0,b)(0≤b≤a),求出,根据向量模的计算公式,即可求得,利用完全平方式非负,即可求得其最小值.【解答】解:如图,以直线DA,DC分别为x,y轴建立平面直角坐标系,则A(2,0),B(1,a),C(0,a),D(0,0)设P(0,b)(0≤b≤a)则=(2,﹣b),=(1,a﹣b),∴=(5,3a﹣4b)∴=≥5.故答案为5.15.某科研单位欲拿出一定的经费奖励科研人员,第1名得全部资金的一半多一万元,第二名得剩下的一半多一万元,以名次类推得到剩下的一半多一万元,到第10名恰好资金分完,求此科研单位共拿出多少万元资金进行奖励.【考点】89:等比数列的前n项和.【分析】设第十名到第一名得到的奖金分别是a1,a2,…,a10,则a n=S n+1,可证奖金数组成一个以2为首项,公比为2的等比数列,由等比数列的求和公式可得.【解答】解:设第十名到第一名得到的奖金分别是a1,a2,…,a10,则a n=S n+1,∴a1=2,a n﹣a n﹣1=a n,∴a n=2a n﹣1∴每人所得奖金数组成一个以2为首项,公比为2的等比数列,∴S10==2046∴此科研单位共拿出2046万元资金进行奖励.16.已知S n是等差数列{a n}(n∈N*)的前n项和,且S6>S7>S5,有下列四个命题:①d<0;②S11>0;③S12<0;④数列{S n}中的最大项为S11,其中正确命题的序号是①②.【考点】8F:等差数列的性质.【分析】先由条件确定第六项和第七项的正负,进而确定公差的正负,再将S11,S12由第六项和第七项的正负判定.【解答】解:由题可知等差数列为a n=a1+(n﹣1)ds6>s7有s6﹣s7>0即a7<0s6>s5同理可知a6>0a1+6d<0,a1+5d>0由此可知d<0 且﹣5d<a1<﹣6d∵s11=11a1+55d=11(a1+5d)>0s12=12a1+66d=6(a1+a12)=6(a6+a7)>0,s13=13a1+78d=13(a1+6d)<0即①②是正确的,③是错误的故答案是①②三、解答题(本大题共6小题,共10+12+12+12+12+12=70分)17.已知向量,,.(1)若,求θ;(2)求的最大值.【考点】9T:数量积判断两个平面向量的垂直关系;93:向量的模.【分析】(1)利用向量垂直的充要条件列出方程,利用三角函数的商数关系求出正切,求出角.(2)利用向量模的平方等于向量的平方,利用三角函数的平方关系及公式,化简,利用三角函数的有界性求出范围.【解答】解:(1)因为,所以得又,所以θ=(2)因为=所以当θ=时,的最大值为5+4=9故的最大值为318.如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设.(1)用表示向量,.(2)若,求实数λ的值.【考点】9B:向量加减混合运算及其几何意义.【分析】(1)根据平行四边形的法则结合向量的基本定理即可用表示向量,.(2)根据向量关系的条件建立方程关系,求实数λ的值.【解答】解:(1)由题意知A是BC的中点,且=,由平行四边形法则得+=2,则=2﹣=2﹣,则=﹣=2﹣﹣=2﹣.(2)由图知∥,∵=﹣=2﹣﹣λ=(2﹣λ)﹣,,∴,解得.19.已知等差数列{a n}前三项的和为﹣3,前三项的积为8.(1)求等差数列{a n}的通项公式;(2)若a2,a3,a1成等比数列,求数列{|a n|}的前n项和.【考点】8E:数列的求和;84:等差数列的通项公式;8G:等比数列的性质.【分析】(I)设等差数列的公差为d,由题意可得,,解方程可求a1,d,进而可求通项(II)由(I)的通项可求满足条件a2,a3,a1成等比的通项为a n=3n﹣7,则|a n|=|3n﹣7|=,根据等差数列的求和公式可求【解答】解:(I)设等差数列的公差为d,则a2=a1+d,a3=a1+2d由题意可得,解得或由等差数列的通项公式可得,a n=2﹣3(n﹣1)=﹣3n+5或a n=﹣4+3(n﹣1)=3n﹣7(II)当a n=﹣3n+5时,a2,a3,a1分别为﹣1,﹣4,2不成等比当a n=3n﹣7时,a2,a3,a1分别为﹣1,2,﹣4成等比数列,满足条件故|a n|=|3n﹣7|=设数列{|a n|}的前n项和为S n当n=1时,S1=4,当n=2时,S2=5当n≥3时,S n=|a1|+|a2|+…+|a n|=5+(3×3﹣7)+(3×4﹣7)+…+(3n﹣7)=5+=,当n=2时,满足此式综上可得20.已知A、B、C的坐标分别为A(4,0),B(0,4),C(3cosα,3sinα).(1)若α∈(﹣π,0),且||=||,求角α的大小;(2)若⊥,求的值.【考点】9R:平面向量数量积的运算;93:向量的模;GK:弦切互化;GS:二倍角的正弦;GT:二倍角的余弦.【分析】(1)利用点的坐标求出向量的坐标,根据向量模的平方等于向量的平方得到三角函数的关系,据角的范围求出角.(2)利用向量垂直的充要条件列出方程利用三角函数的二倍角公式、切化弦公式化简三角函数,利用三角函数的平方关系求出值.【解答】解:(1),,∵∴25﹣24cosα=25﹣24sinα∴sinα=cosα又α∈(﹣π,0),∴α=.(2)∵∴即(3cosα﹣4)×3cosα+3sinα×(3sinα﹣4)=0解得所以1+2∴故==2sinαcosα=21.已知O为坐标原点,向量,点P满足(1)记函数,讨论函数f(α)的单调性,并求其值域;(2)若O,P,C三点共线,求的值.【考点】9R:平面向量数量积的运算.【分析】(1)可求出的坐标,并设,从而写出的坐标,这样根据条件即可求出x,y,从而求出,并且,进行向量数量积的坐标运算,并根据二倍角的正余弦公式,两角和的正弦公式得出,根据α的范围可求出的范围,进而判断出f(α)的单调性,并求出其值域;(2)可写出的坐标,根据O,P,C三点共线便可得出的坐标关系,从而得出,进而求出,可求出,从而,这样便可求出的值.【解答】解:(1),设,则;∴由得,;∴x=2cosα﹣sinα,y=﹣1;∴,;∴=(sinα﹣cosα,1)•(2sinα,﹣1)=﹣(sin2α+cos2α)=;∵,∴;∴当,即时,f(α)单调递减;当,即时,f(α)单调递增;∴函数f(α)的单调递增区间为,单调递减区间为;∵;∴f(α)的值域为;(2),;∴由O,P,C三点共线得,(2cosα﹣sinα)•2﹣(﹣sinα)•(﹣1)=0;∴,带入sin2α+cos2α=1得:;∴====.22.已知数列{a n}的前三项与数列{b n}的前三项对应相等,且a1+2a2+22a3+…+2n﹣1a n=8n﹣b n}是等差数列.对任意的n∈N*都成立,数列{b n+1(1)求数列{a n}与{b n}的通项公式;(2)是否存在k∈N*,使得b k﹣a k∈(0,1)?请说明理由.【考点】8H:数列递推式;8F:等差数列的性质.【分析】(1)利用a1+2a2+22a3+…+2n﹣1a n=8n推出n﹣1时的表达式,然后作差求出数列﹣b n}是等差数列利用累加法求出{b n}的通项公式;{a n}的通项公式,利用数列{b n+1(2)化简b k﹣a k=k2﹣7k+14﹣24﹣k,通过k≥4时,f(k)=(k﹣)2+﹣24﹣k单调递增,且f(4)=1,所以k≥4时,f(k)≥1,结合f(1)=f(2)=f(3)=0,说明不存在k∈N*,使得b k﹣a k∈(0,1).【解答】解:(1)已知a1+2a2+22a3+…+2n﹣1a n=8n(n∈N*)①=8(n﹣1)(n∈N*)②n≥2时,a1+2a2+22a3+…+2n﹣2a n﹣1①﹣②得2n﹣1a n=8,解得a n=24﹣n,在①中令n=1,可得a1=8=24﹣1,所以a n=24﹣n(n∈N*)由题意b1=8,b2=4,b3=2,所以b2﹣b1=﹣4,b3﹣b2=﹣2,﹣b n}的公差为﹣2﹣(﹣4)=2,∴数列{b n+1﹣b n=﹣4+(n﹣1)×2=2n﹣6,∴b n+1b n=b1+(b2﹣b1)+(b3﹣b2)+…+(b n﹣b n)﹣1=8+(﹣4)+(﹣2)+…+(2n﹣8)=n2﹣7n+14(n∈N*)、(2)b k﹣a k=k2﹣7k+14﹣24﹣k,当k≥4时,f(k)=(k﹣)2+﹣24﹣k单调递增,且f(4)=1,所以k≥4时,f(k)=k2﹣7k+14﹣24﹣k≥1又f(1)=f(2)=f(3)=0,所以,不存在k∈N*,使得b k﹣a k∈(0,1)2017年6月12日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年江西省宜春市上高二中高一(下)第六次月考数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有四个命题:①数列是自变量为正整数的一类函数;②数列,,,,…的通项公式是a n=;③数列的图象是一群孤立的点;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列.其中正确的是()A.①②③B.①③C.②③④D.②④2.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=.求sin(B+C)的值()A.B.﹣ C.0 D.3.△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=4,且C=60°,则ab的值为()A.B.C.1 D.4.在△ABC中,已知D是AB边上一点,若=2,=,则λ=()A.B.C.﹣ D.﹣5.若=(cos,cos),||=2||,且(+)•=﹣2,则向量,的夹角为()A.B. C. D.6.y=cos(x+1)图象上相邻的最高点和最低点之间的距离是()A. B.πC.2 D.7.如图,在△ABC中,=,DE∥BC交AC于E,BC边上的中线AM交DE于N,设=,=,用,表示向量.则等于()A.(+)B.(+)C.(+)D.(+)8.已知函数f(x)=sinωx(ω>0)在[0,]上的最大值为,当把f(x)的图象上所有的点向右平移φ个单位,得到函数g(x),且g(x)满足g(π+x)=g(π﹣x),则正数φ的最小值为()A.B.C.D.9.如图,圆O与x轴的正半轴的交点为A,点B,C在圆O上,点B的坐标为(﹣1,2),点C位于第一象限,∠AOC=α.若|BC|=,则sin cos+cos2﹣=()A.﹣B.﹣C.D.10.已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量在方向上的投影为()A.﹣B.﹣1 C.﹣ D.11.设O为△ABC的外心,且,则△ABC的内角C=()A.B.C.D.12.设向量=(cos25°,sin25°),=(sin20°,cos20°),若t是实数,且=+t,则||的最小值为()A.B.1 C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=|sin2x|,则此函数的最小正周期为.14.已知向量,如果(3+4)∥(﹣2),则t=.15.在△ABC,三内角A,B,C的对边分别为a,b,c,已知A=30°,,则c=.16.已知向量,为两个互相垂直的单位向量,向量满足=0,则=.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,(1)求函数f(x)的解析式;(2)求f(﹣)的值.18.已知=(2,1),(1)如果||=,且向量与共线,求的坐标表示;(2)如果||=,且向量与夹角为,求的坐标表示.19.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA(Ⅰ)求B的大小;(Ⅱ)若,c=5,求b.20.在△ABC中,内角A,B,C的对边分别为a,b,c,已知=.(1)求的值(2)若cosB=,b=2,求△ABC的面积S.21.已知函数f(x)=2cos2x﹣2sin(x+π)cos(x﹣)﹣.(1)求函数f(x)的单调递减区间;(2)将函数f(x)的图象向右平移个单位长度,再向上平移个单位长度,得到函数g(x)的图象,求当x∈[0,]时,函数g(x)的值域.22.如图,在△A BC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,,S为△A BC的面积,圆O是△A BC的外接圆,P是圆O上一动点,(1)求取得最大值;(2)当B=30°时,求的最大值.2016-2017学年江西省宜春市上高二中高一(下)第六次月考数学试卷(理科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有四个命题:①数列是自变量为正整数的一类函数;②数列,,,,…的通项公式是a n=;③数列的图象是一群孤立的点;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…是同一数列.其中正确的是()A.①②③B.①③C.②③④D.②④【考点】2K:命题的真假判断与应用;81:数列的概念及简单表示法.【分析】根据数列的定义可判断①,根据通项公式可判断②,根据数列各项与元素性质的差别,可以判断③,根据数列相同的判定方法,可以判断④的真假,进而得到答案.【解答】解:①数列是自变量为正整数的一类函数,正确②数列,,,,…的通项公式是a n=,而不是a n=;③数列的图象是一群孤立的点,正确;④数列1,﹣1,1,﹣1,…与数列﹣1,1,﹣1,1,…不是同一数列.综上可得:只有①③正确.故选:B.2.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=.求sin(B+C)的值()A.B.﹣ C.0 D.【考点】GQ:两角和与差的正弦函数.【分析】根据同角的三角函数的关系和诱导公式计算即可.【解答】解:∵cosA=,∴sinA=∴sin(B+C)=sinA=,故选:A.3.△ABC的内角A,B,C所对的边a,b,c满足(a+b)2﹣c2=4,且C=60°,则ab的值为()A.B.C.1 D.【考点】HR:余弦定理.【分析】将(a+b)2﹣c2=4化为c2=(a+b)2﹣4=a2+b2+2ab﹣4,又C=60°,再利用余弦定理得c2=a2+b2﹣2abcosC=a2+b2﹣ab即可求得答案.【解答】解:∵△ABC的边a、b、c满足(a+b)2﹣c2=4,∴c2=(a+b)2﹣4=a2+b2+2ab﹣4,又C=60°,由余弦定理得c2=a2+b2﹣2abcosC=a2+b2﹣ab,∴2ab﹣4=﹣ab,∴ab=.故选:A.4.在△ABC中,已知D是AB边上一点,若=2,=,则λ=()A.B.C.﹣ D.﹣【考点】9B:向量加减混合运算及其几何意义.【分析】本题要求字母系数,办法是把表示出来,表示时所用的基底要和题目中所给的一致,即用和表示,画图观察,从要求向量的起点出发,沿着三角形的边走到终点,把求出的结果和给的条件比较,写出λ.【解答】解:在△ABC中,已知D是AB边上一点∵=2,=,∴=,∴λ=,故选A.5.若=(cos,cos),||=2||,且(+)•=﹣2,则向量,的夹角为()A.B. C. D.【考点】9R:平面向量数量积的运算.【分析】根据平面向量的坐标运算与模长公式,数量积运算以及夹角公式,即可求出向量,的夹角.【解答】解:=(cos,cos)=(cos,sin),∴||==1,∴||=2||=2,∴(+)•=•+=×2×1×cosθ+12=﹣2,∴cosθ=﹣;又∵θ∈[0,π],∴向量,的夹角为.故选:C.6.y=cos(x+1)图象上相邻的最高点和最低点之间的距离是()A. B.πC.2 D.【考点】H7:余弦函数的图象.【分析】y=cos(x+1)的周期是2π,最大值为1,最小值为﹣1,即可求出y=cos (x+1)图象上相邻的最高点和最低点之间的距离.【解答】解:y=cos(x+1)的周期是2π,最大值为1,最小值为﹣1,∴y=cos(x+1)图象上相邻的最高点和最低点之间的距离是=,故选:A.7.如图,在△ABC中,=,DE∥BC交AC于E,BC边上的中线AM交DE于N,设=,=,用,表示向量.则等于()A.(+)B.(+)C.(+)D.(+)【考点】9H:平面向量的基本定理及其意义.【分析】利用平行线的性质、向量的平行四边形法则、向量共线定理即可得出.【解答】解:由题意可得:==.故选:C.8.已知函数f(x)=sinωx(ω>0)在[0,]上的最大值为,当把f(x)的图象上所有的点向右平移φ个单位,得到函数g(x),且g(x)满足g(π+x)=g(π﹣x),则正数φ的最小值为()A.B.C.D.【考点】H2:正弦函数的图象.【分析】由函数的最大值求得ω的值,由正弦函数图象变换,求得g(x)的解析式,由函数的对称性求得g(x)的对称轴,可知2×π﹣2φ=kπ+,k∈Z,解得φ=﹣+,k∈Z,当k=0时,即可求得正数φ的最小值.【解答】解:由题意,函数f(x)在区间[0,]上单调递增,∴sin(ω)=,∴ω=,∴ω=2,由f(x)的图象上所有的点向右平移φ个单位,∴g(x)=sin(2x﹣2φ),又g(π+x)=g(π﹣x),所以x=π是函数g(x)的一条对称轴,故2×π﹣2φ=kπ+,k∈Z,∴φ=﹣+,k∈Z,当k=0时,正数φ取最小值.故答案选:C.9.如图,圆O与x轴的正半轴的交点为A,点B,C在圆O上,点B的坐标为(﹣1,2),点C位于第一象限,∠AOC=α.若|BC|=,则sin cos+cos2﹣=()A.﹣B.﹣C.D.【考点】G9:任意角的三角函数的定义.【分析】根据三角函数的倍角公式将函数式进行化简,结合三角函数的定义即可得到结论.【解答】解:∵点B的坐标为(﹣1,2),∴|OB|=|OC|=,∵|BC|=,∴△OBC是等边三角形,则∠AOB=α+.则sin(α+)==,cos(α+)==﹣,则sin cos+cos2﹣=sinα+cosα=sin(α+)=,故选:D.10.已知点A,B,C,D在边长为1的方格点图的位置如图所示,则向量在方向上的投影为()A.﹣B.﹣1 C.﹣ D.【考点】9R:平面向量数量积的运算.【分析】建立如图所示平面直角坐标系,求出A、D、B的坐标,得到的坐标,代入投影公式求解.【解答】解:建立如图所示平面直角坐标系,则A(0,0),B(4,2),D(﹣2,3).∴,.∴,.∴向量在方向上的投影为.故选:A.11.设O为△ABC的外心,且,则△ABC的内角C=()A.B.C.D.【考点】9V:向量在几何中的应用.【分析】由,移项得,再平方得到=0,从而,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C 值.【解答】解:设外接圆的半径为R,∵,∴,∴,∴2R2+2=2R2,∴=0,∴,根据圆心角等于同弧所对的圆周的两倍得:△ABC中的内角C值为=.故选B.12.设向量=(cos25°,sin25°),=(sin20°,cos20°),若t是实数,且=+t,则||的最小值为()A.B.1 C.D.【考点】9P:平面向量数量积的坐标表示、模、夹角;HW:三角函数的最值.【分析】由题意先进行坐标运算,求出向量的坐标,再用求模公式求出模,然后根据条件求最值即可.【解答】解:由题设=(cos25°+tsin20°,sin25°+tcos20°)∴===t是实数,由二次函数的性质知当t=﹣时,取到最小值最小值为故选C二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=|sin2x|,则此函数的最小正周期为.【考点】H1:三角函数的周期性及其求法.【分析】利用函数y=|Asin(ωx+φ)|的周期为•,得出结论.【解答】解:∵y=sin2x的最小正周期为=π,∴函数f(x)=|sin2x|的最小正周期为,故答案为:.14.已知向量,如果(3+4)∥(﹣2),则t=.【考点】9K:平面向量共线(平行)的坐标表示.【分析】利用平面向量坐标运算法则先分别求出和,由此利用(3 +4)∥(﹣2),能求出t的值.【解答】解:∵向量,∴=(6,﹣3)+(﹣12,4t)=(﹣6,4t﹣3),=(8,﹣1﹣2t),∵(3+4)∥(﹣2),∴,解得t=.故答案为:.15.在△ABC,三内角A,B,C的对边分别为a,b,c,已知A=30°,,则c=1或2.【考点】HP:正弦定理.【分析】利用余弦定理列出关系式,把A=30°,值代入计算即可求出c的值【解答】解:∵A=30°,,∴由余弦定理得A2=b2+c2﹣2bccosB,即1=3+c2﹣2××c×,即c2﹣3c+2=0解得:c=1或c=2;故答案为:1或2.16.已知向量,为两个互相垂直的单位向量,向量满足=0,则=.【考点】9R:平面向量数量积的运算.【分析】设与的夹角为θ,则与的夹角为+θ,设||=x,根据题意可得x=cos(θ+φ),利用三角函数的性质即可求出最大值【解答】解:∵向量,为两个互相垂直的单位向量,设与的夹角为θ,则与的夹角为+θ,设||=x,∴•=0,∴•=||•||=xcosθ,•=||•||=xcos(θ+)=﹣xsinθ,∵=0∴•﹣2﹣•+2=2x2﹣2xcosθ+xsinθ=0,∴x=cosθ﹣sinθ=cos(θ+φ),其中cosφ=,sinφ=,∴0≤x≤,若设与的夹角为﹣θ,同理可得0≤x≤,故=,故答案为:.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,(1)求函数f(x)的解析式;(2)求f(﹣)的值.【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式;H2:正弦函数的图象.【分析】(1)根据图象的最高点坐标,最高点横坐标与零点距离等求出A,φ,ω;(2)利用(1)的解析式代入求值【解答】解:(1)由图象可知A=2,并且T=()=π,所以ω=2,又f()=2,0<φ<π,得到φ=,所以;(2)由(1)得到f(﹣)=2sin(﹣)=﹣2sin=1.18.已知=(2,1),(1)如果||=,且向量与共线,求的坐标表示;(2)如果||=,且向量与夹角为,求的坐标表示.【考点】9R:平面向量数量积的运算;9J:平面向量的坐标运算.【分析】(1)设,由向量的模及斜率共线列关于x,y的方程组求解;(2)设,由向量的模及斜率夹角列关于x,y的方程组求解.【解答】解:(1)设,由||=,且向量与共线,得,解得或.∴或;(2)设,由||=,且向量与夹角为,得,解得或.∴或.19.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA (Ⅰ)求B的大小;(Ⅱ)若,c=5,求b.【考点】HQ:正弦定理的应用;HS:余弦定理的应用.【分析】(1)根据正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由△ABC为锐角三角形可得答案.(2)根据(1)中所求角B的值,和余弦定理直接可求b的值.【解答】解:(Ⅰ)由a=2bsinA,根据正弦定理得sinA=2sinBsinA,所以,由△ABC为锐角三角形得.(Ⅱ)根据余弦定理,得b2=a2+c2﹣2accosB=27+25﹣45=7.所以,.20.在△ABC中,内角A,B,C的对边分别为a,b,c,已知=.(1)求的值(2)若cosB=,b=2,求△ABC的面积S.【考点】HR:余弦定理;HP:正弦定理.【分析】(1)由正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知可得sinC=2sinA,即可得解=2.(2)由正弦定理可求c=2a,由余弦定理解得a=1,从而c=2.利用同角三角函数基本关系式可求sinB的值,进而利用三角形面积公式即可计算得解.【解答】(本题满分为12分)解:(1)由正弦定理,则=,所以=,即(cosA﹣2cosC)sinB=(2sinC﹣sinA)cosB,化简可得sin(A+B)=2sin(B+C).因为A+B+C=π,所以sinC=2sinA.因此=2.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)由=2,得c=2a,由余弦定理b2=a2+c2﹣2accosB,及cosB=,b=2,得4=a2+4a2﹣4a2×.解得a=1,从而c=2.因为cosB=,且sinB==,因此S=acsinB=×1×2×=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣21.已知函数f(x)=2cos2x﹣2sin(x+π)cos(x﹣)﹣.(1)求函数f(x)的单调递减区间;(2)将函数f(x)的图象向右平移个单位长度,再向上平移个单位长度,得到函数g(x)的图象,求当x∈[0,]时,函数g(x)的值域.【考点】H5:正弦函数的单调性;HJ:函数y=Asin(ωx+φ)的图象变换.【分析】(1)化函数f(x)为正弦型函数,根据正弦函数的图象与性质求出函数f(x);(2)根据函数图象平移法则,得出函数g(x)的解析式,求出x∈[0,]时函数g(x)的值域即可.【解答】解:(1)函数f(x)=2cos2x﹣2sin(x+π)cos(x﹣)﹣=2•+2cosx(cosxcos+sinxsin)﹣=1+cos2x+cos2x+sinxcosx﹣=1+cos2x++sin2x﹣=cos2x+sin2x=(sin2x+cos2x)=sin(2x+);令+2kπ≤2x+≤+2kπ,k∈Z,解得+kπ≤x≤+kπ,k∈Z,∴函数f(x)的单调递减区间是[+kπ, +kπ],k∈Z;(2)将函数f(x)的图象向右平移个单位长度,得y=sin[2(x﹣)+]=sin(2x﹣)的图象;再向上平移个单位长度,得y=sin(2x﹣)+的图象;∴函数g(x)=sin(2x﹣)+;当x∈[0,]时,2x﹣∈[﹣,],∴sin(2x﹣)∈[﹣,1];∴sin(2x﹣)∈[﹣,],∴sin(2x﹣)+∈[,],即函数g(x)的值域是[,].22.如图,在△A BC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,,S为△A BC的面积,圆O是△A BC的外接圆,P是圆O上一动点,(1)求取得最大值;(2)当B=30°时,求的最大值.【考点】9R:平面向量数量积的运算.【分析】(1)根据余弦定理和和正弦定理以及两角差的余弦公式和三角函数的性质即可求出,(2)方法一:利用向量的数量积以及三角函数的性质即可求出,方法二,建立坐标系,利用向量的坐标运算即可求出【解答】解:(1)由a2=b2+c2+bc,∴cosA==﹣,∵0°<A<180°,∴A=120°由正弦定理:⇒b=2sinB,c=2sinC∴===cos(B ﹣C)≤,当且仅当B=C时取等号,∴最大值为;(2)方法一:当B=30°时,△A BC为等腰三角形,═=1+2+(其中D 为AB的中点)=≤法二:以O为原点,OA为半轴,建立平面直角坐标系,则,设P(cosθ,sinθ),则=(﹣cosθ,1﹣sinθ),=(﹣﹣cosθ,﹣sinθ),∴•=cos2θ+cosθ+sin2θ﹣sinθ+=(cosθ﹣sinθ)+=cos(θ+)+≤+当且仅当θ=时取等号,∴的最大值为+.2017年6月30日。
