运筹学胡运权第五版第三章
《运筹学教程》胡云权-第五版-运筹学复习

x6
10
[2]
-5
1
0
-1
1
5
3M+2
3-4M
2M-5
0
-M
0
-z
-M
x4
2
0
[7/2 ]
1/2
1
1/2
-1/2
4/7
2
x1
5
1
-5/2
1/2
0
-1/2
1/2
-
0
7M/2+8
M/2-6
0
M/2+1
-3M/2-1
-z
3
x2
4/7
0
1
1/7
2/7
1/7
-1/7
2
x1
45/7
1
0
6/7
5/7
-1/7
1/7
✓ 右端项非负
解的重要概念
可行解(或可行点):满足所有约束条件的向量 x ( x1 , x 2 , x n )
可行域:所有的可行解的全体
D { x Ax b, x 0}
最优解:在可行域中目标函数值最大(或最小)的可行解,最优解的全体
称为最优解集合
O {x D c x c y, y D }
0
x3
0
x4
0
x5
9
4
3
4
5
[ 10 ]
1
0
0
0
1
0
0
0
1
90
40
30
7
12
0
0
0
1
90
bi
360
《运筹学(胡运权)》第五版课后习题答案
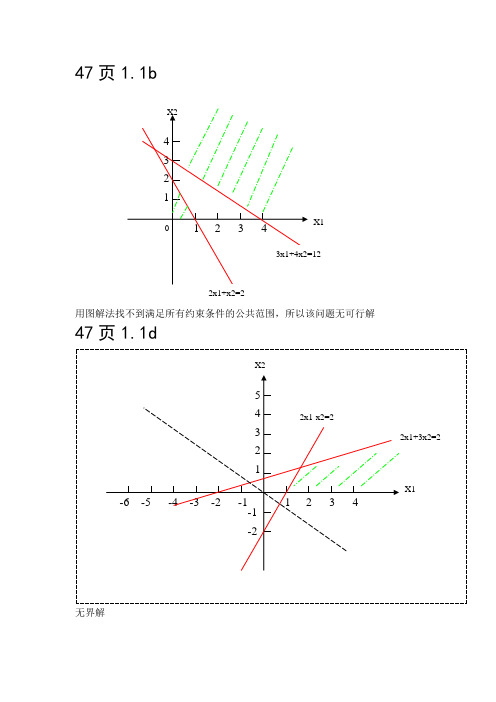
可知购进原材料15个单位为宜。
4.1
a)设yi= 1第i组条件起作用
0第i组条件不起作用
x1+x2≤2-(1-y1)M M—充分大正数
2x1+3x2≥5+(1-y2)M
y1+y2=1
y1,y2=0或1
b)设yi= 1第i组条件起作用
0第i组条件不起作用
x=0y1
x=3y2
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
0.03(a2+b2+c1)-0.06(a3+b3)-0.11(a4+c1)-0.05a5
=0.95a1+0.97a2+0.94a3+1.5b3+2.1c1-0.05b1-0.11a4-0.05a5
s.t.
5a1+10b1≤6000
7a2+b2+12c1≤10000
6a3+8a3≤4000
4a4+11c1≤7000
5.3c
因为使mind1-,故在x1+x2=40的右侧,若使mind4+,则在x1+x2=50的左侧,即阴影区域,因为在阴影部分无法使2d2-+d3-最小,故比较E(20,30),F(24,26),E点:d2-=4,d3-=0 min2d2-+d3-=8,F点:d2-=0,d3-=4, min2d2-+d3-=4,故选F点
胡运权《运筹学教程》(第5版)配套题库-考研真题精选及课后习题(第一~三章)【圣才出品】

2.μ是关于可行流 f 的一条增广链,则在μ上有:对一切(i,j)∈μ-,有 fij>0。( ) [暨南大学 2019 研]
【答案】√ 【解析】由增广链定义可知,当边(i,j)属于μ的反向边集时,该条边的流量大于 0。
3.事件 j 的最早时间 TE(j)是指以事件 j 为开工事件的工序最迟必须开工时间。( ) [暨南大学 2019 研]
零元素的最少直线数目的集合。结果如下:
4 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)在未被覆盖的元素中找最小元素,未被覆盖的行分别减去该最小元素,在出现负
数的列上整列加上最小元素,得到新矩阵 C′:
0 2 6 1 0 0 4
表 1-1-1
解:(1)先对各行减去本行的最小元素,再对各列减去本列最小元素,得到矩阵 C 如
下:
0 2 6 9
C 1 4 4 0 1 0 0 3 2 3 6 0
(2)确定独立零元素,对 C 加圈,得到
◎ 2 6 9
C
1
1
4 ◎
4
◎ 3
2
3
6
(3)由于只有 3 个独立零元素,少于系数矩阵阶数 n=4,故需要确定能够覆盖所有
A.没有无穷多最优解 B.没有最优解 C.有无界解 D.有最优解 【答案】B 【解析】有最优解的前提是有可行解,该题无可行解,则也无最优解。
2.如果某种资源的影子价格大于其市场价格,则说明( )。[暨南大学 2019 研] A.该资源稀缺 B.该资源过剩 C.企业应尽快处理该资源 D.企业应充分利用该资源,开辟新的生产途径 【答案】A 【解析】当资源的影子价格不为 0 时,表明该种资源在生产中已耗费完毕;且若影子 价格大于其市场价格,说明企业应买进该种资源,该种资源稀缺。
运筹学基础及应用第五版 胡运权第三章

例3
设有三个化肥厂供应四个地区的农用化肥,假
定等量的化肥在这些地区使用效果相同,已知各化肥厂 年产量,各地区年需要量及从各化肥厂到各地区单位化 肥的运价表如下,试决定使总的运费最节省的化肥调拨 方案。
解:这是一个产销不平衡的运输问题,总产量为
160万t,四个地区最低需求为110万t ,最高需求为无限。 当其它地区都是满足最低需求时,第Ⅳ地区每年最多能 分配到60万t ,这样最高需求就是210万t,大于产量。 为建立产销平衡表,在表中增加一假想化肥厂D , 其年产量为50万t 。并把各地区的最低需求和额外需求 区分开来,建立产销平衡表。
例1
现在把问题概括一下,在线性规划中我们研究这样 一类运输问题:有某种物资需要调运,这种物资的计量
单位可以是重量、包装单位或其他。已知有m个地点可以
供应该种物资(以后通称产地,用 i 1,, m 表示),有 n个地点需要该种物资(以后通称销地,用 j 1,, n 表示),又知这m个产地的可供量(以后通称产量)为 (可通写为 a i ),n个销地的需要量(以后 a1 , a2 ,, am
第三章 运输问题
§1.运输问题的典例和数学模型
§ 2.表上作业法
§ 3.产销不平衡的运输问题及其应用
§1.运输问题的典例和数学模型
某食品公司经销主要产品之一是糖果,它下面 设有三个加工厂,每天的糖果生产量分别为: A1 7t , A3 9t。该公司把这些糖果分别运往四个地区 A2 4t , 的门市部销售,各地区每天的销售量: B1 3t , B2 6t, B4 6t 。已知从每个加工厂到各销售门市部每 B3 5t, 吨糖果的运价如下表: 单位:元/t
产 销 平 衡 表
当一个产地的产量不能运往某一个销地的时候,认为 运价为M(表示任意大正数)。额外需求部分的销量,由于 是否满足都可以,所以假想厂运往这些销地的运价定为 0。
《运筹学教程》胡云权 第五版 第三章 整数规划

人出国留学打点行李,现有三个旅行包,容积大小分别 为1000毫升、1500毫升和2000毫升,根据需要列出需带物品清单, 其中一些物品是必带物品共有7件,其体积大小分别为400、300、 150、250、450、760、190、(单位毫升)。尚有10件可带可不带 物品,如果不带将在目的地购买,通过网络查询可以得知其在目的 地的价格(单位美元)。这些物品的容量及价格分别见下表,试给 出一个合理的安排方案把物品放在三个旅行包里。 物品 2 3 4 5 6 7 8 9 10 1
割平面法
纯整数线性规划
max z c j x j
j 1 n
松弛问题
(3.1a)
max z c j x j
j 1
n
(3.1a)
aij x j bi
j 1
n
(i 1, 2, , m) (3.1b) ( j 1, 2, , n) (3.1c) ( j 1, 2, , n)(3.1d)
整数规划数学模型解的特点
• 不考虑x1、x2取整数的约束,称为上述 规划的松弛问题,可行域如图; • B为最优解:X=(3.57,7.14),Z= 35.7。 • 由于x1 、 x2必须取整数值,可行解集 只是图中可行域内的那些整数点;
• 凑整法:比较四种组合,但(4,7)、 (4,8)(3,8)都不是可行解,(3, 7)虽属可行解,但代入目标函数得 Z=33;
m个约束方程可表示为 CB CN
xi aij x j bi
jK
i Q
(3.2)
XB
CB XB cj-zj B-1b I 0
XN
B-1N ≤0
若其中的 不是整数, 则式(3.2)中相应的约束方程为
运筹学胡运权第五版课件(第3章)分析

B3
B4
ai
11 ④
3 ③
10 7
1
9
2
③
①
7
4
⑥
10 ③
84 59
3
6
5
6 20
24 (8 3) (2 10) 1
表示新方案的费用要减少1元
综上,得到检验数表如下: B1 B2 B3 B4
A1 1 2 0 0 A2 0 1 0 -1 A3 10 0 12 0 注意:有数字格(基变量)的检验数为0。
3
B2 11 9 4
6
B3 3 2
10
5
B4
ai
10 7
84
59
6 20
3、运输问题的数学模型
对于m产n销运输问题,设xij表示产地 i 运往销地 j 的物资 数量,则其数学模型如下:
mn
min z
cij xij
i1 j 1
n
xij ai
i 1,2,, m (产量约束)
s.t.
1
9① 2
③
7
4
⑥
10 ③
84 59
3
6
5
6 20
22 (9 5 3) (4 10 2) 1
表示新方案的费用要增加1元
空格(A1,B2)的闭回路
销地 产地
A1
B1 3
B2
B3
B4
ai
11 ④④ 3③ ③ 10 7
A2
③③ 1
9 ①① 2
84
A3
7 ⑥⑥ 4
10③ ③ 5 9
bj
3
6
5
2、表上作业法的步骤
(1)分析问题,列出产销平衡表和单位运价表。 (2)利用最小元素法或沃格尔法求初始调运方案。
运筹学教程 胡运权 第5版

运筹学教程胡运权第5版1. 简介《运筹学教程》是一本经典的运筹学教材,由胡运权教授编写,已经出版了第5版。
本教程旨在介绍运筹学的基本概念、方法和应用,帮助读者掌握运筹学的基本原理和技巧。
2. 内容概述本教程分为十个章节,涵盖了运筹学的主要内容。
第一章:运筹学概述本章介绍了运筹学的基本概念和发展历程,阐述了运筹学在现代管理决策中的重要作用。
第二章:线性规划本章介绍线性规划的基本概念、模型和求解方法,包括单纯形法和对偶理论等内容。
第三章:整数规划本章介绍整数规划的基本概念和求解方法,包括分枝定界法和割平面法等内容。
第四章:非线性规划本章介绍非线性规划的基本概念和求解方法,包括梯度法和牛顿法等内容。
第五章:动态规划本章介绍动态规划的基本概念和求解方法,包括最优子结构和状态转移方程等内容。
第六章:网络优化本章介绍网络优化的基本概念和求解方法,包括最小生成树和最短路问题等内容。
第七章:多目标规划本章介绍多目标规划的基本概念和求解方法,包括帕累托最优解和权衡法等内容。
第八章:排队论本章介绍排队论的基本概念和模型,包括利用泊松分布和指数分布建模等内容。
第九章:库存管理本章介绍库存管理的基本概念和模型,包括经济订货量和安全库存等内容。
第十章:决策分析本章介绍决策分析的基本概念和方法,包括决策树和期望值法等内容。
3. 学习目标通过学习本教程,读者可以掌握以下技能:•理解运筹学的基本概念和方法;•掌握线性规划、整数规划、非线性规划等方法的应用;•学会运用动态规划、网络优化、多目标规划等方法解决实际问题;•掌握排队论、库存管理、决策分析等方法的应用。
4. 使用说明读者可以将本教程作为自学资料,按照章节顺序逐步学习。
每个章节都包括基本概念的讲解、求解方法的介绍和案例分析。
在阅读本教程时,读者可以使用Markdown文本格式进行标注和整理笔记。
Markdown具有简单易学、格式清晰的特点,适合用于文档编写和批注。
5. 结语《运筹学教程》是一本经典的运筹学教材,适合作为运筹学的入门教材或者参考资料。
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)

城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
运筹学(胡运权)第五版课后答案,运筹作业
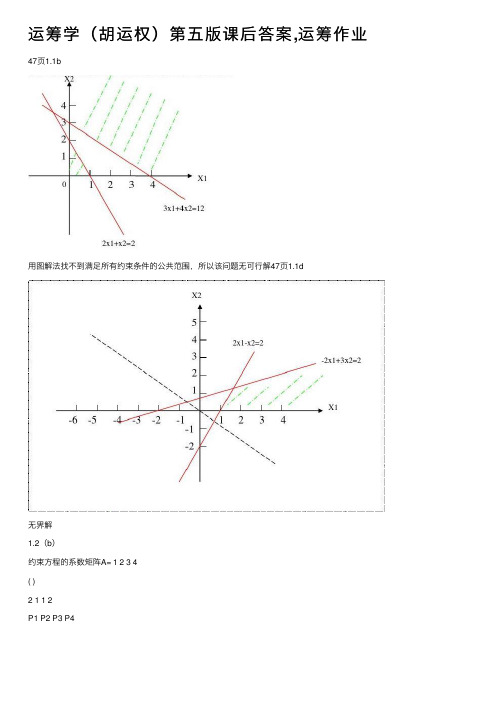
运筹学(胡运权)第五版课后答案,运筹作业47页1.1b⽤图解法找不到满⾜所有约束条件的公共范围,所以该问题⽆可⾏解47页1.1d⽆界解1.2(b)约束⽅程的系数矩阵A= 1 2 3 4( )2 1 1 2P1 P2 P3 P4最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i⽉租j个⽉的⾯积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0⽤excel求解为:⽤LINDO求解:LP OPTIMUM FOUND A T STEP 3OBJECTIVE FUNCTION V ALUE1) 118400.0VARIABLE V ALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.000000 1500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费⽤最⼩,需第⼀个⽉租⼀个⽉租期300平⽅⽶,租四个⽉租期1200平⽅⽶,第三个⽉租⼀个⽉租期800平⽅⽶,50页14题设a1,a2,a3, a4, a5分别为在A1, A2, B1, B2, B3加⼯的Ⅰ产品数量,b1,b2,b3分别为在A1, A2, B1加⼯的Ⅱ产品数量,c1为在A2,B2上加⼯的Ⅲ产品数量。
运筹学(胡运权版)第三章运输问题课后习题答案
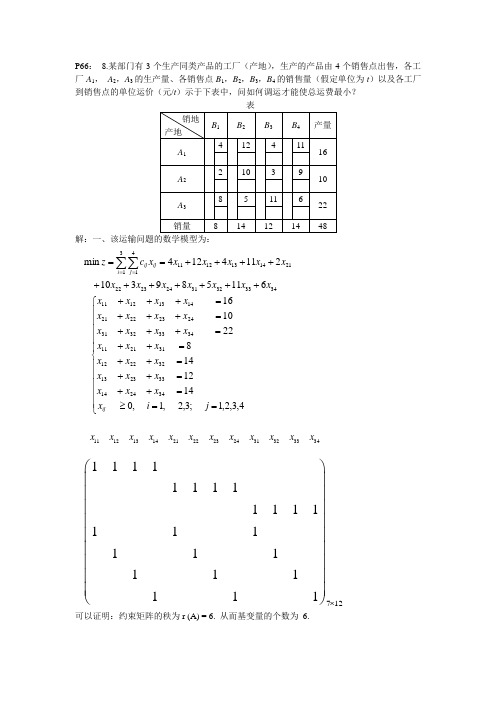
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
(完整word版)运筹学(胡运权)第五版课后答案,运筹作业
47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解薅47页1。
1d蒂无界解(b)衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=(01/220)T和(0011)T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为:薁用LINDO求解:羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。
000000虿X113.0000000。
000000螇X210。
0000002800。
000000莃X318。
0000000.000000肁X410.0000001100。
000000莈X120.0000001700.000000袆X220.0000001700。
000000螄X320.0000000。
000000蕿X130.000000400.000000膇X230。
0000001500。
000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。
000000—2800。
000000羆3)2.0000000.000000羆4)0。
000000—2800.000000节5)0。
000000-1700.000000蝿NO。
ITERATIONS=3罿答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,页14题肆50蚃设a1,a2,a3,a4,a5分别为在A1,A2,B1,B2,B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1,A2,B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。
《运筹学教程》胡云权第五版运筹学-线性规划-3excel线性规划及应用PPT课件

x3
4000
x1 3000
x2
3000
x3 3000
xi
0, i
1, 2, 3
2021/2/12
第 3第3 页33 页
3、人员分配问题
上海财经大学
《运筹学》
某昼夜服务的公交线路每天各时间区段内所需四
级和乘务人员数如下表所示。问该公交线路至少配备 多少名司机和乘务人员?
班次 1 2 3 4 5 6
开始上班,则
min Z x1 x2 x3 x4 x5 x6
x1 x6 60
x1
x2
70
x2
x3
60
x3 x4 50
x4
x5
20
x5 xi
x6 30 0, i 1, 2,
,6
2021/2/12
第 3第5 页35 页
4、运输问题
上海财经大学
《运筹学》
设有A1,A2,A3三个产地,生产某种物质,其产 量分别为7,5,7,B1,B2,B3,B4四个销地,需要该 物资,销量分别为2,3,4,6,又已知各产销地之间 的运价如下表,确定总运费最少的调运方案。
2021/2/12
第 2第9 页29 页
1、材料利用问题
上海财经大学
《运筹学》
现要做100 套钢架,每套用长为2.9m , 2.1m 和1.5m 的元钢各一根制成。已知原料长7.4米,问应如何下料, 使用的原材料最省?
2021/2/12
30
第 3第0 页30 页
1、材料利用问题
上海财经大学
《运筹学》
第18页运筹学第18页2019117上海财经大学?在工作表的顶部输入数据?确定每个决策变量所对应的单元格位置?选择单元格输入公式找到目标函数的值?选择一个单元格输入公式计算每个约束条件左边的值?选择一个单元格输入公式计算每个约束条件右边的值图中规定b12c12为可变单元格可变单元格存放决策变量的取值可变单元格数目等于决策变量个数建立数学公式步骤二第19页运筹学第19页2019117上海财经大学?在工作表的顶部输入数据?确定每个决策变量所对应的单元格位置?选择单元格输入公式找到目标函数的值?确定约束单元格输入公式计算每个约束条件左边的值?确定约束单元格输入公式计算每个约束条件右边的值在目标单元格中需要填入计算目标函数值的公式
运筹学胡运权第五版课件(第3章)分析

B1 3 1 7
3
B2 11 9 4
6
B3 3 2
10
5
B4
ai
10 7
84
59
6 20
3、运输问题的数学模型
对于m产n销运输问题,设xij表示产地 i 运往销地 j 的物资 数量,则其数学模型如下:
mn
min z
cij xij
i1 j1
n
xij ai
空格(A3,B1)的闭回路
Ïú µØ ²ú µØ
A1 A2 A3 bj
B1 3
③1
B2
B3
B4
ai
11 ④
3 ③
10 7
9
2
①
84
7
4
⑥
3
6
10 ③
59
5
6 20
31 (7 10 2) (5 3 1) 10
表示新方案的费用要增加10元
空格(A3,B3)的闭回路
Ïú µØ ²ú µØ
x24 1, x23 0, x13 5, x14 2
此时x23=0,可看成非基变量。
得到新的调运方案:
Ïú µØ ²ú µØ
A1
B1 3
B2
B3
B4
ai
11 ⑤
3 ②
10 7
1
A2
③
9
2 ①
84
A3
7
4
⑥
10 ③
59
bj
3
6
5
6 20
该方案就是用沃格尔法得到的初始方案。
其检验数表为
2 - 12 2-1-
《运筹学(胡运权)》第五版课后习题答案

VARIABLE VALUE REDUCED COST
Z 0.000000 1.000000
X11 3.000000 0.000000
X21 0.000000 2800.000000
X31 8.000000 0.000000
X41 0.000000 1100.000000
X12 0.000000 1700.000000
程序法
6.4a
破圈法
避圈法
最小部分树16
6.4b
最小部分树32
172页6.11
红色曲线为使用一年卖出
蓝色曲线为使用两年卖出
绿色曲线为使用三年卖出
紫色曲线为使用四年卖出
最短路程为3.7万元,路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4
三种方案分别为:第一年年初买新车,年末卖掉再买新车,一直用到第四年年末卖掉;
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
d)
maxz=3x1+x2+4x3-0.4y
s.t.
6x1+3x2+5x3≤45
3x1+4x2+5x3-y≤30
x1,x2,x3,y≥0
用lomdo求解为
LP OPTIMUM FOUND AT STEP 0
OBJECTIVE FUNCTION VALUE
运筹学胡运权第五版课件

则依次引入松弛变量或剩余变量(统称为松弛变量),
转化为等式约束条件。
约束为≥不等式,减去松弛变量,化为等式约束条件;
多 退
约束为≤不等式,加上松弛变量,化为等式约束条件。 少
补
注意:松弛变量在目标函数中系数全为0。
例:max z=2 x1+3 x2
s.t.
2 x1+2 x2 12 标准化
4x1
16
z=2 x1+3 x2
2 x1+2 x2 12
4x1
16
5 x2
1x510, x2 0
此为有约束极值问题
h
9
1-2 线性规划问题的数学模型
1、原型:现实世界中人们关心、研究的实际对象。 模型:将某一部分信息简缩、提炼而构造的原型替代物。 数学模型:对现实世界的一个特定对象,为达到一定目的,
根据内在规律做出必要的简化假设,并运用适当数学工具得到 的一个数学结构。
应如何裁剪可使做成的容器的容积最大?
解:如图设四个角上减去的小正方形边
x 长为x,则容器体积为:
a
Va2x2x (0 x a) 2
由 dV 0 dx
有 xa 6
时,容积最大
此为无约束的极值问题
h
7
例2 常山机器厂生产 I、II 两型产品。这两型 产品都分别要在A、B、C三种不同设备上加工。按 工艺规定,生产每件产品的单位利润、消耗三种设 备的工时以及各种设备工时的限额如下表:
2x1 2x2 x3
12
s.t.
4 x1
5 x2
x4 16 x5 15
x1, x2, x3, x4, x5 0
h
28
P1 P2 P3 P4 P5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 课后题答案
33.4 答案: (a) 最优方案不变,最优值z'=z+kar (b) 最优方案不变,最优值z'=z+kbp,同理与(a) (c) 最优方案不变,最优值z'=kz
➢ 课后题答案
3.5 答案:
(a)Δc22∈[-4,3] 即:c22∈[3,10]
(b)c24=17,举例调整x24,使0≤x≤10即可
销地 产地
A1 A2 A3
销量
B1
B2 B3
B4 产 量
3 5 16 10 15
0 10 15 4
25
5 17 17 12
5
5 15 15 10 45
用Vogel法确定的近似运输方案解如下: (可在下表中所示行或列任一位置添加一个0)
销地 产地
A1 A2 A3
B1 B2 B3 B4
5
10
10 15
5
销地 产地
A1 A2 A3
B1
B2
B3
B4
4 5 17 10 0 10 15 3 5 17 17 11
销量
5 15 15 10
产量 15 25 5
产量 15 25 5
➢ 课后题答案
3.6答案 设Xij表示在第i季度生产的在第j季度销售的柴油机数 。由于生产数为100,而合同数为70,供大于销, 故增加第Ⅴ季度作为库存,转化为供销平衡的运输 问题如下:
习题讲解
课程:运筹学 内容:第三章课后习题解
LOGO
表上作业法的步骤
1.将运输问题化为产销平衡的问题 ✓供过于求:增加假设销地; ✓供不应求:增加假设产地; 2.确定初始调运方案 ✓(最小元素法,西北角法,vogel法) 3.最优性检验(闭回路法,位势法) 若所有非基变量的检验数都有σij ≥0,则得最优方案,结 束计算。否则,转4; 4.调整方案(闭回路法),转3。
1
M
M 620 0
3
3
3
4
7 17
➢ 课后题答案
最优方案为:
销 供
期初贮存 第1年正常生产数 第1年加班生产数 第2年正常生产数 第2年加班生产数 第3年正常生产数 第3年加班生产数
第1年 2 1
第2年 1 2
第3年 0
1 3
多余
3 2 2
➢ 课后题答案
3.10(a)答案
产销平衡及单价表如下:
煤矿 销量
➢ 课后题答案
销供 Ⅰ
Ⅱ
Ⅲ
Ⅳ 库存
Ⅰ
10
15 0
0
0.15
Ⅱ
M-10.95 0
0
5
30
Ⅲ
M-10.7 M-10.85 25
5
0.25
Ⅳ
M-10.85 M-11 M-11.15 10
0.1
此方案即该厂全年生产、贮存和维护费用最小的方案 且,min Z=773
➢ 课后题答案
3.7答案 设xij为第i年生产于第j年交货的货轮数,cij为相应的 货轮成本(生产费+存贮费),则该问题可列出如 下的产销平衡表与单位运价表:
产量
15 25 5
销量
5 15 16 10
45
➢ 课后题答案
3.1 表3-36 最终表如下:
销地 产地
A1 A2 A3
B1
B2 B3 B4 B5
5 3 7 13 9 5 13 4 3 1 10 1 15 1
销量
10 10 20 15 3
产量
7 25 26
注:黑色数字表最优解,红色表示对应非基变量的 检验数。 即:最优值Z*=193. 用Vogel法确定的近似运输方案解同上。
销地 产地
Ⅰ Ⅱ Ⅲ Ⅳ
销量
Ⅰ Ⅱ Ⅲ ⅣⅤ
10.8 10.95 11.1 11.25 0 M 11.1 11.25 11.4 0 M M 11.0 11.15 0 M M M 11.3 0 10 15 25 20 30
产量
25 35 30 10 100
注:此题中有非基变量检验数为0,故有无穷多最优 解,此处只写一个最优方案为参考,如下:
➢ 课后题答案
3.1 表3-35 最终表如下:
销地 产地
A1 A2 A3
销量
B1
B2 B3 B4 产 量
15 5 16 10 15
12 10 15 4
25
5 5 50
5
5 15 15 10 45
注:黑色数字表最优解,红色表示对应非基变量的 检验数。即:最优值Z*=335. 亦或是:
➢ 课后题答案
5
0
5
50 3
注:有非基变量检验数为0,故有无穷多最优解. 此题答案不唯一,以上最优解仅作参考。
且,min Z=1390
谢谢观看
城市
Ⅰ Ⅱ Ⅲ Ⅳ
12 3 4 5 87 5 5 2 52 1 1 3 64 3 3 5 MMM 0 0 110 150 70 50 50
产量
120 160 100 50 430
最优方案为:
➢ 课后题答案
销 供
Ⅰ Ⅱ Ⅲ Ⅳ
1
10 1 100 M-3
2
3
1
60
150 10
0
0
M-1 M
4
5
0
50
0
第1年 第2年 第3年 多余 产量
期初贮存 第1年正常生产数 第1年加班生产数 第2年正常生产数 第2年加班生产数 第3年正常生产数 第3年加班生产数 需要量
40
80 120 0
2
500 540 580 0
2
570 610 650 0
3
M 600 640 0
4
M 670 710 0
2
M
M 550 0
销地 产地
A1 A2 A3
B1
B2
B3
B4 产 量
5+x 0 10-x 15 5
10-x 15
x
25
5
销量
5 15 15 10
(c)c31=M,最优解为:
➢ 课后题答案
销地 产地
A1 A2 A3
B1
B2
B3
B4
4 10 17 5
5 5 15 3
M-13 6 6
5
销量
5 15 15 10
(d)单纯行表根据下表完成
