中考总复习数学竞赛辅导讲义及习题解答 第24讲 几何的定值与最值
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
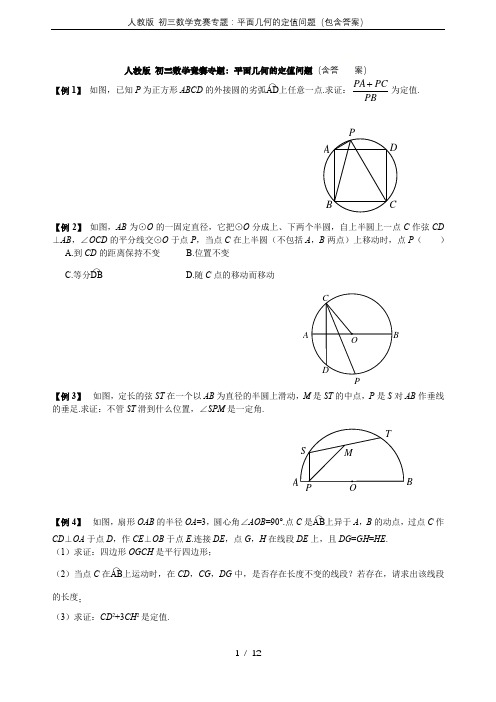
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
中考数学复习研讨会几何中的最值与定值问题公开课PPT课件

在圆中
变式2.定平方和:
如图,⊙O的半径为R,AB、CD是⊙O的任意两条弦且 ABCD于M。求证:+为定值。
C
B
AM
D
如图,内接于⊙O的四边形ABCD的对角线AC与BD垂直相 交于点K,设⊙O的半径为R。求证:
变式3.定倒数和:
如图,过⊙O内定点P作任意弦AB,又过A、B作两切线,自点P作 两切线的垂线PQ、PR,垂足为Q、R。
练习
1. △ABC中,AB=AC=2,BC边有100个不同点P1, P2,……,P100, 记mi=APi2+Bpi×PiC (i=1,2,3,……,100). 则m1+m2+……+m100=___.
2. 如图,以G(0,1)为圆心,半径为 2的圆与轴交于A,B两点,与y轴交于C, D两点,点E为⊙G上一动点,于F.当 点E从点B出发顺时针运动到点D时,求 点F所经过的路径长。
如图,已知A是定角的平分线上一个定点,过 A任作一条直线与
N
变式4.定角:
如图,定长的弦ST在一个以AB为直径的半圆上滑动,M是ST的中 点,P是S对AB作垂线的垂足。求证:不管ST滑到什么位置,是一 定角。
T M S
AP
O
B
4.坐标系中
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半 轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线 PM交AB的延长线于点D. (1)求点D的坐标(用含m的代数式表示); (2)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线 ME的垂线,垂足为H(如图2). 当点P从O向C运动时, 点H也随之运动. 请直接写出点H 所经过的路长
等边三角形中的定值问题:
中考试题几何中的最值问题(讲义)

几何中的最值问题(讲义)一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解; 求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理. 一般处理方法:常用定理:两点之间,线段最短(两个定点) 垂线段最短(一个定点、一条定直线)三角形三边关系(两边长固定或其和、差固定)lB'BAPlB'ABP线段和差、 周长最值 几何变换、 等线段转移 构建三角形线段最值 ① 折转直;②集中线段长; ③目标线段转化为相关线段. 转化 P A +PB 最小, 需要点在异侧|P A -PB |最大, 需要点在同侧1. 如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm .蜂蜜蚂蚁ACQP ED CBA第1题图 第2题图2. 如图,正方形ABCD 的边长是4,∠DAC 的平分线交DC 于点E ,若点P ,Q 分别是AD 和AE 上的动点,则DQ +PQ 的最小值为 .3. 如图,在锐角△ABC 中,42AB ,∠BAC =45°,∠BAC 的平分线交BC于点D ,点M ,N 分别是AD 和AB 上的动点,则BM +MN 的最小值为___________.NMABDCQPKDCBA第3题图 第4题图 4. 如图,在菱形ABCD 中,AB =2,∠A =120°,点P 、Q 、K 分别为线段BC 、CD 、BD 上的任意一点,则PK +QK 的最小值为 .5. 如图,当四边形P ABN 的周长最小时,a = .N (a +2,0)P (a ,0)B (4,-1)A (1,-3)OyxP ABDCD'C'B'第5题图 第6题图6. 如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与点B 或点C 重合),分别过点B 、C 、D 作射线AP 的垂线,垂足分别是B ′、C ′、D ′,则BB ′+CC ′+DD ′的最大值为 ,最小值为 .7. 如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC =8,B 到MN 的距离BD =5,CD =4,P 在直线MN 上运动,则PA PB -的最大值等于 .ABCDPMNxOABy第7题图 第8题图8. 点A 、B 均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P 是x 轴上使得PA PB -的值最大的点,Q 是y 轴上使得QA +QB 的值最小的点,则OP OQ ⋅= .9. 如图,在△ABC 中,AB =6,AC =8,BC =10,P 为边BC 上一动点,PE ⊥AB于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为_________.ABCE FPM ABCDP第9题图 第10题图10. 如图,已知AB =10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 . 11. 如图,点P 在第一象限,△ABP 是边长为2的等边三角形,当点A 在x 轴的正半轴上运动时,点B 随之在y 轴的正半轴上运动,运动过程中,点P 到原点的最大距离是________.A BO PxyA DCB PQ A'第11题图 第12题图12. 动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示,折叠纸片,使点A 落在BC 边上的A ′处,折痕为PQ ,当点A ′在BC 边上移动时,折痕的端点P 、Q 也随之移动.若限定点P 、Q 分别在AB 、AD 边上移动,则点A ′在BC 边上可移动的最大距离为 .13. 如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF 沿EF 翻折,点A 的落点记为P . (1)当P 落在线段CD 上时,PD 的取值范围为 ; (2)当P 落在直角梯形ABCD 内部时,PD 的最小值等于多少?AB C D P FE D CBAA BCD EFP14. 如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM .(1)当M 点在何处时,AM +CM 的值最小; (2)当M 点在何处时,AM +BM +CM 的值最小,并说明理由.15. 如图,已知平面直角坐标系中A ,B 两点的坐标分别为A (2,-3),B (4,-1). (1)若P (p ,0)是x 轴上的一个动点,则当p =________时,△P AB 的周长最短;(2)若C (a ,0),D (a +3,0)是x 轴上的两个动点,则当a =________时,四边形ABDC 的周长最短;(3)设M ,N 分别为x 轴和y 轴上的动点,请问:是否存在这样的点M (m ,0),N (0,n ),使四边形ABMN 的周长最短?若存在,请写出m 和n 的值;若不存在,请说明理由.BA Ox y(3)BA Ox y(2)(1)yx OA BABCDEM N1. 15 2.22 3.4 4.3 5.74 6.2,27.58.39.12510.5 11. 3+112.213.(1)8434-≤≤PD ;(2) 458-14.(1)点M 在BD 的中点时,AM+CM 的值最小;(2)点M 在EC 与BD 的交点处时,AM+BM +CM 的值最小15.(1)72;(2)54;(3)55,23==-m n初中数学试卷灿若寒星制作。
第二十四讲几何的定值与最值(2014年初中数学培优提高)[1]
![第二十四讲几何的定值与最值(2014年初中数学培优提高)[1]](https://img.taocdn.com/s3/m/1cc963f21a37f111f1855bf5.png)
第二十四讲 几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法;2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法.【例题就解】【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD,则CD 长度的最小值为 .思路点拨 如图,作CC ′⊥AB 于C,DD ′⊥AB 于D ′,DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=21AB 一常数,当CQ 越小,CD 越小,本例也可设AP=x ,则PB=x -10,从代数角度探求CD 的最小值.注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指:(1)中点处、垂直位置关系等;(2)端点处、临界位置等.【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T,圆交AC 、BC 于M 、N,则对于所有可能的圆的位置而言, MTN 为的度数( )A.从30°到60°变动B.从60°到90°变动C.保持30°不变D.保持60°不变思路点拨 先考虑当圆心在正三角形的顶点C 时,其弧的度数,再证明一般情形,从而作出判断.注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得定值与最值.【例3】 如图,已知平行四边形ABCD,AB=a ,BC=b (a >b ),P 为AB 边上的一动点,直线DP 交CB 的延长线于Q,求AP+BQ 的最小值.思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+(当且仅当b a =时取等号)来求最小值.【例4】 如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A 、B 的点M,设直线AC 与BM 相交于K,直线CB 与AM 相交于点N,证明:线段AK 和BN 的乘积与M 点的选择无关. 思路点拨 即要证AK ·BN 是一个定值,在图形中△ABC 的边长是一个定值,说明AK ·BN与AB 有关,从图知AB 为△ABM 与△ANB 的公共边,作一个大胆的猜想,AK ·BN=AB 2,从而我们的证明目标更加明确.⌒ ⌒注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.【例5】 已知△XYZ 是直角边长为1的等腰直角三角形(∠Z=90°),它的三个顶点分别在等腰Rt △ABC(∠C=90°)的三边上,求△ABC 直角边长的最大可能值.思路点拨 顶点Z 在斜边上或直角边CA(或CB)上,当顶点Z 在斜边AB 上时,取xy 的中点,通过几何不等关系求出直角边的最大值,当顶点Z 在(AC 或CB)上时,设CX=x ,CZ=y ,建立x ,y 的关系式,运用代数的方法求直角边的最大值.注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值;(2)构造二次函数求几何最值.学力训练1.如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B ′、C ′、D ′,则BB ′+CC ′+DD ′的最大值为 ,最小值为 .2.如图,∠AOB=45°,角内有一点P ,PO=10,在角的两边上有两点Q,R(均不同于点O),则△PQR 的周长的最小值为 .3.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=5,CD=4,P 在直线MN 上运动,则PB PA -的最大值等于 .4.如图,A 点是半圆上一个三等分点,B 点是弧AN 的中点,P 点是直径MN 上一动点,⊙O 的半径为1,则AP+BP的最小值为( )A.1B.22 C.2 D.13- 5.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( ) A.212π+ B.2412π+ C.214π+ D.242π+6.如图、已知矩形ABCD,R,P 户分别是DC 、BC 上的点,E,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A.线段EF 的长逐渐增大B.线段EF 的长逐渐减小C.线段EF 的长不改变D.线段EF 的长不能确定7.如图,点C 是线段AB 上的任意一点(C 点不与A 、B 点重合),分别以AC 、BC 为边在直线AB 的同侧作等边三角形ACD 和等边三角形BCE,AE 与CD 相交于点M,BD 与CE 相交于点N.(1)求证:MN ∥AB;(2)若AB 的长为l0cm,当点C 在线段AB 上移动时,是否存在这样的一点C,使线段MN 的长度最长?若存在,请确定C 点的位置并求出MN 的长;若不存在,请说明理由.(2002年云南省中考题)8.如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足,求证:不管ST 滑到什么位置,∠SPM 是一定角.(加拿大数学奥林匹克试题)9.已知△ABC 是⊙O 的内接三角形,BT 为⊙O 的切线,B 为切点,P 为直线AB 上一点,过点P 作BC 的平行线交直线BT 于点E,交直线AC 于点F.(1)当点P 在线段AB 上时(如图),求证:PA ·PB=PE ·PF;(2)当点P 为线段BA 延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果不成立,请说明理由.10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=l,在AB 上的一点P ,使矩形PNDM 有最大面积,则矩形PNDM 的面积最大值是( )A.8B.12C.225D.1411.如图,AB 是半圆的直径,线段CA 上AB 于点A,线段DB 上AB 于点B,AB=2;AC=1,BD=3,P 是半圆上的一个动点,则封闭图形ACPDB 的最大面积是( )A.22+B.21+C.23+D.23+12.如图,在△ABC 中,BC=5,AC=12,AB=13,在边AB 、AC 上分别取点D 、E,使线段DE 将△ABC 分成面积相等的两部分,试求这样线段的最小长度.(全国初中数学联赛试题)13.如图,ABCD 是一个边长为1的正方形,U 、V 分别是AB 、CD 上的点,AV 与DU 相交于点P ,BV 与CU 相交于点Q.求四边形PUQV 面积的最大值.“弘晟杯”上海市竞赛题14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?(河南省竞赛题)15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形MNPQ 与四个相同矩形(图中阴影部分)的面积的和为800平方米.(1)设矩形的边AB=x (米),AM=y (米),用含x 的代数式表示y 为 .(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.①设该工程的总造价为S(元),求S 关于工的函数关系式.②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?若能,请列出所有可能的设计方案;若不能,请说明理由.(镇江市中考题)16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).(北京市数学知识应用竞赛试题)。
九年级数学竞赛培优专题及答案 24 平面几何的定值问题

专题24 平面几何的定值问题【阅读与思考】所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变).几何定值问题的基本特点是:题设条件中都包含着变动元素和固定元素,变动元素是指可变化运动的元素,固定元素也就是“不变量”,有的是明显的,有的是隐含的,在运动变化中始终没有发生变化的元素,也就是我们要探求的定值. 解答定值问题的一般步骤是: 1.探求定值; 2.给出证明.【例题与求解】【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值. 解题思路:线段的和差倍分考虑截长补短,利用圆的基本性质,证明三角形全等.P AB CD【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A .到CD 的距离保持不变 B .位置不变C .等分DB⌒ D .随C 点的移动而移动 (济南市中考试题)解题思路:添出圆中相关辅助线,运用圆的基本性质,用排除法得出结论.A【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.(加拿大数学奥林匹克试题)解题思路:不管ST 滑到什么位置,∠SOT 的度数是定值.从探寻∠SPM 与∠SOT 的关系入手.B【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值. (广州市中考试题)解题思路:延长OG 交CD 于N ,利用题中的三等分点、平行四边形和三角形中位线的性质,实现把线段ON 转化成线段CH 的倍分关系,再以Rt △OND 为基础,通过勾股定理,使问题得以解决.BOACE HGD 【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发 生变化?若不变,求出比值;若变化,说明变化规律. (深圳市中考试题)解题思路:对于(3)从动点F 达到的特殊位置时入手探求定值.(图1) (图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.解题思路:当点P 与C 点重合时,P A 2+PB 2+PC 2=2BC 2为定值,就一般情形证明.A【能力训练】A 级1.如图,点A ,B 是双曲线xy 3=上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则=+21S S _______.(牡丹江市中考试题)AABCDEF(第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.(全国初中数学联赛试题)3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A .30°B .40°C .50°D .60°(武汉市竞赛试题)5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( )A .在平分AB 的某直线上移动 B .在垂直AB 的某直线上移动C .在弧AMB 上移动D .保持固定不移动(荆门市中考试题)AB'B(第5题图) (第6题图)6.如图,A ,B 是函数xky图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A .3 B .6 C .9 D .12(海南省竞赛试题))7.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.⑥⑤④③②①)P (B )PB(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.(济南市中考试题)8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.(济宁市中考试题)9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(江苏省竞赛试题)(第9题图) (第10题图) (第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O的半径为R .求证:(1)2222DK CK BK AK +++是定值;(2)2222DA CD BC AB +++是定值.PD CB A A11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.(克罗地亚数学奥林匹克试题)B 级1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).(福州市中考试题) 折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D +∠E +∠F =α,则下列结论一定正确的是( )A . ∠1+∠2=900°-2αB . ∠1+∠2=1080°-2αC . ∠1+∠2=720°-αD . ∠1+∠2=360°-21α (武汉市竞赛试题)(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则12GF ED CHBAA .在0°到30°变化B .在30°到60°变化C .保持30°不变D .保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A .5B .6C .7D .8(黄石市中考试题)(第5题图)6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.(株洲市中考试题)7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(湖北省选拔赛试题)(第7题图) (第8题图)B NKMB AC HCBA离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.(全国初中数学联赛试题)9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程. (黄冈市中考试题)(第9题图) (第10题图)10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变.(四川省竞赛试题)专题24平面几何的定值问题例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故2PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN=DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM=CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP=163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OF PF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •PA +PC •AB ,而AB =BC =AC ,∴PA =PB +PC ,从而PA 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×23=6.故PA 2+PB 2+PC 2为定值.A 级 1.4 提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273提示:1+3+5=9是等边三角形的高. 3.r 2 提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A ′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P 在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP 2a ,DP •a =BP •a +AP 2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a 2a ),从而21AP BPCP DP++为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设FA 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD 2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN =3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PM EC PC=,即()2112x x EC --=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989) ⑵若四边形PQCA 为平行四边形,由于QC ∥PA ,故只要QC =PA 即可,而PA =18-4t ,CQ =t ,故18-4t =t ,得t =185. ⑶设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P 在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =PA +AF =PA +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +224441425=.∴t = 4142. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4142时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB 的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP⊥AB,OP=12(EM+G N)=12(AH+BH)=12AB.∴无论点C在AB同一侧的位置如何,E G中点P的位置不变.。
初中数学竞赛 知识点和真题 第24讲 几何极值

第24讲 几何极值代数不过是书写的几何,而几何不过是图形的代数。
——索菲娅·格梅茵 知识方法扫描求几何量(如线段的长度,角的度数,平面图形的面积,立体图形的体积)的最大最小值的问题,或确定某些几何元素(如点)的位置,几何量有最大最小的问题称为几何极值问题。
处理几何极值问题一般有两种方法:几何方法和代数方法。
1.几何方法:利用几何量之间的不等关系如两点之间线段最短;过直线外一点向直线引的线段中、垂线段最短;三角形任何两边之和大于第三边, 两边之差小于第三边;三角形中大角对大边;同一圆中, 弦心距越小, 它所对的弦越大等结论来求几何极值的方法。
另外,在用几何方法求几何极值时,几何变换是重要的方法。
2.代数方法:先将几何图形中量的计算转化为代数的问题, 然后通过代数式的恒等变形, 利用一次函数、二次函数的有关性质或构造二次方程, 利用根的判别式, 或利用不等式的性质来处理等方法。
数形结合是一种重要的数学解题策略。
经典例题解析例1(1998年北京市竞赛试题)如图, 矩形ABCD 中, AB =20cm, BC =10cm, 若在AC 、AB 上各取一点M 、N, 使BM +MN 的值最小, 求这个最小值.解 取B 点关于AC 的对称点B′, 连结AB′, AB′交CD 于P, 则N 点关于AC 的对称点N′必在AB′上, 连结MN′, 则MN′=MN, 问题转化为求BM +MN′的最小值.自B 作BH ⊥AB′于H, 则BH 为BM +MN′的最小值, 也即BM +MN 的最小值.连结PB, 则S △PAB =21S 矩形ABCD =100.∵∠1=∠2, ∠2=∠3, ∴∠1=∠3, AP =PC.设AP =x, 则DP =20-x.由勾股定理, 得 x 2=102+(20-x)2.A ∴x =225, 即AP =225. ∴S △PAB =21AP·BH =21×225·BH =100. ∴BH =16. 即BM +MN 的最小值是16cm.例2(1984年西安市初中数学竞赛试题)在圆弧DE 上求一点P (如图),使P 点对小圆C 有最大视角(在P 点看小圆看得最清楚),并证明你的结论。
几何最值问题(讲义及答案)

4
11. (2020 扬州)如图,在□ABCD 中,∠B=60°,AB=10, BC=8,点 E 为边 AB 上的一个动点,连接 ED 并延长至点 F,使得 DF= 1 DE,以 EC,EF 为邻边构造□EFGC,连接 4 EG,则 EG 的最小值为__________.
A E
DF
G
B
C
12. 如图,在△A1B1C1 中,A1B1=8,∠A1B1C1=60°,∠B1A1C1=75°, P 是 B1C1 上的任意点,连接 A1P,将 A1P 绕点 A1 按顺时针方 向旋转 75°,得到线段 A1Q,连接 B1Q.则线段 B1Q 长度的最 小值为__________.
在∠AOB 内有一点 P(4,3),M,N 分别是 OA,OB 边上的动
点,连接 PM,PN,MN,则△PMN 周长的最小值是_______.
y A
M
P
O
N Bx
6. 如图,在正方形 ABCD 中,AB=8,AC 与 BD 交于点 O,N
是 AO 的中点,点 M 在 BC 边上,且 BM=6,P 为对角线 BD
几何最值问题(讲义)
知识点睛
1. 解决几何最值问题的理论依据: 两点之间,线段最短(已知两个定点) 垂线段最短(已知一个定点、一条定直线) 三角形三边关系(已知两边长固定或其和、差固定) 过圆内一点,最长的弦为直径,最短的弦为垂直于直径的弦
2. 解决几何最值问题的处理思路 ①分析定点、动点,寻找不变特征; ②若属于常见模型、结构,调用模型、结构解决问题; 若不属于常见模型,要结合所求目标,根据不变特征转化为 基本定理或表达为函数解决问题. 转化原则: 尽量减少变量,向定点、定线段、定图形靠拢,或使用同一 变量表达所求目标.
中考几何中的最值问题讲义及答案

几何中的最值问题一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理. 一般处理方法:常用定理:两点之间,线段最短(已知两个定点时) 垂线段最短(已知一个定点、一条定直线时)三角形三边关系(已知两边长固定或其和、差固定时)llBPA +PB 最小,需转化,使点在线异侧|PA -PB |最大, 需转化,使点在线同侧二、精讲精练1. 如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm .蜂蜜蚂蚁CNO第1题图 第2题图2.3. 如图,正方形ABCD 的边长是4,∠DAC 的平分线交DC 于点E ,若点P ,Q 分别是AD 和AE上的动点,则DQ +PQ 的最小值为 .QP ED CBAQPKDCBA第3题图 第4题图 4. 如图,在菱形ABCD 中,AB =2,∠A =120°,点P 、Q 、K 分别为线段BC 、CD 、BD 上的任意一点,则PK +QK 的最小值为.5. 如图,当四边形PABN 的周长最小时,a = .第5题图 第6题图6. 在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点. 若E 、F 为边OA 上的两个动点,且EF =2,当四边形CDEF 的周长最小时,则点F 的坐标为 .7. 如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC =8,B 到MN 的距离BD =5,CD =4,P 在直线MN 上运动,则PA PB -的最大值等于 .ABCDPMN第7题图 第8题图 8. 点A 、B 均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P 是x 轴上使得PA PB -的值最大的点,Q 是y 轴上使得QA +QB 的值最小的点,则OP OQ ⋅= .9. 如图,在△ABC 中,AB =6,AC =8,BC =10,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M为EF 中点,则AM 的最小值为_________.ABCE FPM ABCDP第9题图 第10题图10. 如图,已知AB =10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC和等边△BPD ,则CD 长度的最小值为 .11. 如图,点P 在第一象限,△ABP 是边长为2的等边三角形,当点A 在x 轴的正半轴上运动时,点B 随之在y 轴的正半轴上运动,运动过程中,点P 到原点的最大距离是________.若将△ABP 中边PA 的长度改为22,另两边长度不变,则点P 到原点的最大距离变为_________.A DCB PQ A'第11题图 第12题图12. 动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示,折叠纸片,使点A 落在BC 边上的A ′处,折痕为PQ ,当点A ′在BC 边上移动时,折痕的端点P 、Q 也随之移动.若限定点P 、Q 分别在AB 、AD 边上移动,则点A ′在BC 边上可移动的最大距离为 .13. 如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF沿EF 翻折,点A 的落点记为P .(1)当P 落在线段CD 上时,PD 的取值范围为 ; (2)当P 落在直角梯形ABCD 内部时,PD 的最小值等于 .14. 在△ABC 中,∠BAC =120°,AB=AC =4,M 、N 两点分别是边AB 、AC 上的动点,将△AMN 沿MN翻折,A 点的对应点为A ′,连接BA ′,则BA ′的最小值是_________.A'NMCBAA B CDP FE D CBA A BCD EFP【参考答案】1. 152.63.45.74 6.(73,0) 7.5 8.39.12510.5 11. 12.213.(1)84-≤PD ;(2) 814. 4。
初中数学联赛讲义几何最值
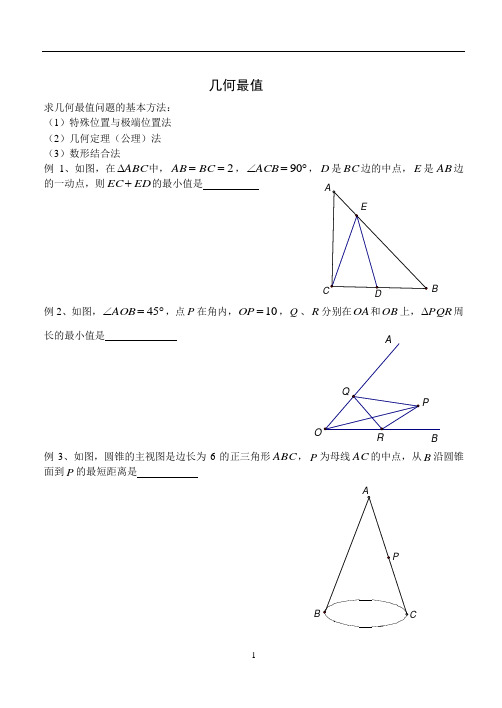
BO BR B 几何最值求几何最值问题的基本方法: (1)特殊位置与极端位置法 (2)几何定理(公理)法 (3)数形结合法例1、如图,在ABC ∆中,2==BC AB ,︒=∠90ACB ,D 是BC 边的中点,E 是AB 边的一动点,则ED EC +的最小值是例2、如图,︒=∠45AOB ,点P 在角内,10=OP ,Q 、R 分别在OA 和OB 上,PQR ∆周长的最小值是例3、如图,圆锥的主视图是边长为6的正三角形ABC ,P 为母线AC 的中点,从B 沿圆锥面到P 的最短距离是APAQ例4、如图,两圆内切于A ,大圆直径为48厘米,小圆直径为30厘米,两只甲虫同时从A 点出发,沿逆时针方向以相同的速度分别沿两个圆爬行,当小圆上的甲虫爬了 圈时,两只甲虫相距最远。
例5、如图,10=AB ,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边APC ∆和等边BPD ∆,求CD 长度的最小值。
例6、设正三角形ABC 边长为2,M 是AB 边上的中点,P 是BC 边上任意一点,求PM PA +的最大值和最小值。
例7、如图,已知平行四边形ABCD 中,a AB =,b BC =(b a >),P 为AB 边上一动点,直线DP 交CB 的延长线于Q ,求BQ AP +的最小值M例8、如图,已知边长为4的正方形钢板。
有一个角锈蚀,其中2=AF ,1=BF ,在五边形EABCD 内截取一个矩形MDNP ,使点P 在AB 上,且要求面积最大,求钢板的最大利用率。
例9、在有定角A 和定半径r 的内切圆的一切三角形中,确定一个有最小周长的三角形。
例10、已知点A 、B 是圆O 外的两定点,点P 是圆O 上的动点,求22PB PA +的最大值和最小值。
例11、在锐角ABC ∆的AB 边取一点M ,作BC MP ⊥于点P ,AC MQ ⊥于点Q ,求点M 的位置,使线段PQ 最短例12、如图,边长为2的正三角形ABC 内有一点P ,它到三边的距离分别为PD 、PE 、PF ,求:(1)222PF PE PD ++的最小值(2)DEF ∆面积的最大值例13、在ABC ∆中,5=BC ,12=AC ,13=AB 。
中考总复习数学竞赛辅导讲义及习题解答 第24讲 几何的定值与最值

第二十四讲 几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有: 1.特殊位置与极端位置法; 2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、 逻辑推理与合情想象相结合等思想方法. 【例题就解】【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 .思路点拨 如图,作CC ′⊥AB 于C ,DD ′⊥AB 于D ′,DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=21AB 一常数,当CQ 越小,CD 越小,本例也可设AP=x ,则PB=x 10,从代数角度探求CD 的最小值.注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指: (1)中点处、垂直位置关系等; (2)端点处、临界位置等.【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T ,圆交AC 、BC 于M 、N ,则对于所有可能的圆的位置而言, MTN 为的度数( ) A .从30°到60°变动 B .从60°到90°变动C .保持30°不变D .保持60°不变思路点拨 先考虑当圆心在正三角形的顶点C 时,其弧的度数,再证明一般情形,从而作出判断.注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得定值与最值.【例3】 如图,已知平行四边形ABCD ,AB=a ,BC=b (a >b ),P 为AB 边上的一动点,⌒直线DP 交CB 的延长线于Q ,求AP+BQ 的最小值.思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+ (当且仅当b a =时取等号)求最小值.【例4】 如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A 、B 的点M ,设直线AC 与BM 相交于,直线CB 与AM 相交于点N ,证明:线段A 和BN 的乘积与M 点的选择无关.思路点拨 即要证A ·BN 是一个定值,在图形中△ABC 的边长是一个定值,说明A ·BN 与AB 有关,从图知AB 为△ABM 与△ANB 的公共边,作一个大胆的猜想,A ·BN=AB 2,从而我们的证明目标更加明确.注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.【例5】 已知△Y 是直角边长为1的等腰直角三角形(∠=90°),它的三个顶点分别在等腰Rt △ABC(∠C=90°)的三边上,求△ABC 直角边长的最大可能值.思路点拨 顶点在斜边上或直角边CA(或CB)上,当顶点在斜边AB 上时,取xy 的中点,通过几何不等关系求出直角边的最大值,当顶点在(AC 或CB)上时,设C=x ,C=y ,建立x ,y 的关系式,运用代数的方法求直角边的最大值.注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值; (2)构造二次函数求几何最值.学力训练1.如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B ′、C ′、D ′,则BB ′+CC ′+DD ′的最大值为 ,最小值为 .2.如图,∠AOB=45°,角内有一点P ,PO=10,在角的两边上有两点Q ,R(均不同于点O),则△PQR 的周长的最小值为 .⌒3.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=5,CD=4,P 在直线MN 上运动,则PB PA -的最大值等于 .4.如图,A 点是半圆上一个三等分点,B 点是弧AN 的中点,P 点是直径MN 上一动点,⊙O 的半径为1,则AP+BP 的最小值为( ) A .1 B .22C .2D .13-5.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( )A .212π+B .2412π+C .214π+D .242π+6.如图、已知矩形ABCD ,R ,P 户分别是DC 、BC 上的点,E ,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减小C .线段EF 的长不改变D .线段EF 的长不能确定7.如图,点C 是线段AB 上的任意一点(C 点不与A 、B 点重合),分别以AC 、BC 为边在直线AB 的同侧作等边三角形ACD 和等边三角形BCE ,AE 与CD 相交于点M ,BD 与CE 相交于点N . (1)求证:MN ∥AB ;(2)若AB 的长为l0cm ,当点C 在线段AB 上移动时,是否存在这样的一点C ,使线段MN 的长度最长?若存在,请确定C 点的位置并求出MN 的长;若不存在,请说明理由. (2002年云南省中考题)8.如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足,求证:不管ST 滑到什么位置,∠SPM 是一定角.9.已知△ABC 是⊙O 的内接三角形,BT 为⊙O 的切线,B 为切点,P 为直线AB 上一点,过点P 作BC 的平行线交直线BT 于点E ,交直线AC 于点F .(1)当点P 在线段AB 上时(如图),求证:PA ·PB=PE ·PF ;(2)当点P 为线段BA 延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果不成立,请说明理由.10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE ,其中AF=2,BF=l ,在AB 上的一点P ,使矩形PNDM 有最大面积,则矩形PNDM 的面积最大值是( )A .8B .12C .225D .1411.如图,AB 是半圆的直径,线段CA 上AB 于点A ,线段DB 上AB 于点B ,AB=2;AC=1,BD=3,P 是半圆上的一个动点,则封闭图形ACPDB 的最大面积是( ) A .22+ B .21+ C .23+ D .23+12.如图,在△ABC 中,BC=5,AC=12,AB=13,在边AB 、AC 上分别取点D 、E ,使线段DE 将△ABC 分成面积相等的两部分,试求这样线段的最小长度.13.如图,ABCD 是一个边长为1的正方形,U 、V 分别是AB 、CD 上的点,AV 与DU 相交于点P ,BV 与CU 相交于点Q .求四边形PUQV 面积的最大值.14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.(1)设矩形的边AB=x(米),AM=y(米),用含x的代数式表示y为.(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.①设该工程的总造价为S(元),求S关于工的函数关系式.②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?若能,请列出所有可能的设计方案;若不能,请说明理由.16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).参考答案。
中考复习 几何最值问题(讲义和答案)

几何最值问题课前预习本内容全部需要在做讲义题目之前进行 一、 读一读下面的内容,想一想 1. 解决几何最值问题的理论依据①两点之间,线段最短(已知两个定点);②_______________(已知一个定点、一条定直线); ③三角形三边关系(已知两边长固定或其和、差固定). 2. 几何最值问题常见的基本结构①利用几何变换进行转化——在右侧一栏中画出相关分析的辅助线,找到最终时刻点P 的位置ll求min ()PA PB +,异侧和最小llMN 为固定线段长,求min ()AM BN +ll求max PB PA -,同侧差最大 ②利用图形性质进行转化DCAB O NM求max OD不变特征:Rt △AOB 中,直角与斜边长均不变,取斜边中点进行分析.二、 还原自己做最值问题的过程(从拿到题目读题开始),与下面小明的动作对标,补充或调整与自己不一样的地方.①研究背景图形,相关信息进行标注;②分析考查目标中的定点、动点及图形特征,利用几何变换或图形性质对问题进行分析; ③封装常见的几何结构,当成一个整体处理,后期直接调用分析.三、 根据最值问题做题的思考过程,思考最值问题跟存在性问题、动点问题在分析过程中有什么样的区别和联系,简要写一写你的看法. 答:下面是小明的看法:①都需要分层对问题分析,一层层,一步步进行分析;②都需要研究基本图形,目标,条件,相关信息都需要有标注;③在画图分析时,都会使用与之有关的性质,判定,定理及公理.如存在性问题需要用四边形的判定;最值问题需要回到问题处理的理论依据.四、借助对上述问题的思考,做讲义的题目.几何最值问题(讲义)一、知识点睛解决几何最值问题的通常思路:1.分析定点、动点,寻找不变特征.2.若属于常见模型、结构,调用模型、结构解决问题;若不属于常见模型,结合所求目标,依据不变特征转化,借助基本定理解决问题.转化原则:尽量减少变量,向定点、定线段、定图形靠拢.二、精讲精练1.如图,在△ABC中,AB=6,AC=8,BC=10,P为BC边上一动点,PE⊥AB于点E,PF⊥AC于点F.若M为EF的中点,则AM长度的最小值为____________.M FE PCBAOED CBA第1题图 第2题图2. 如图,在Rt △ABC 中,∠B =90°,AB =3,BC =4,点D 在BC 边上,则以AC 为对角线的所有□ADCE 中,DE 长度的最小值为_____________.3. 若点D 与点A (8,0),B (0,6),C (a ,a )是一平行四边形的四个顶点,则CD 长度的最小值为_____________.4. 如图,已知AB =2,C 是线段AB 上任一点,分别以AC ,BC 为斜边,在AB 的同侧作等腰直角三角形ACD 和等腰直角三角形BCE ,则DE 长度的最小值为_____________.ED B CA第4题图 第5题图5. 如图,已知AB =10,C 是线段AB 上任一点,分别以AC ,BC 为边,在AB 的同侧作等边三角形ACP 和等边三角形BCQ ,则PQ 长度的最小值为_____________.6. 动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示,折叠纸片,使点A 落在BC边上的A ′处,折痕为PQ ,当点A ′在BC 边上移动时,折痕的端点P ,Q 也随之移动.若限定点P ,Q 分别在AB ,AD 边上移动,则点A ′在BC 边上可移动的最大距离为________________.QPA'D CB AD CBA7. 如图,在直角梯形纸片ABCD 中,AD ⊥AB ,AB =8,AD =CD =4,点E ,F 分别在线段AB ,AD 上,将△AEF 沿EF 翻折,点A 的对应点记为P .QPCBA(1)当点P 落在线段CD 上时,PD 的取值范围是_______.(2)当点P 落在直角梯形ABCD 内部时,PD 长度的最小值为_____________.P F ED CB APFE DCBADCBADCBA8. 如图,在Rt △ABC 中,∠ACB =90°,∠A =30°,AC =BC 的中点为D .将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ,EF 的中点为G ,连接DG ,则在旋转过程中,DG 长度的最大值为____________.9. 如图,已知△ABC 是边长为2的等边三角形,顶点A 的坐标为(0,6),BC 的中点D 在点A下方的y 轴上,E 是边长为2且中心在坐标原点的正六边形的一个顶点,把这个正六边形绕其中心旋转一周,则在旋转过程中DE 长度的最小值为_________.10. 探究:如图1,在等边三角形ABC 中,AB =6,AH ⊥BC 于点H ,则AH =_______,△ABC的面积ABC S △__________.发现:如图2,在等边三角形ABC 中,AB =6,点D 在AC 边上(可与点A ,C 重合),分别过点A ,C 作直线BD 的垂线,垂足分别为点E ,F ,设BD =x ,AE =m ,CF =n .DGFECB A图1 图2(1)用含x ,m ,n 的代数式表示ABD S △及CBD S △;(2)求(m n +)与x 之间的函数关系式,并求出(m n +)的最大值和最小值.应用:如图,已知正方形ABCD 的边长为1,P 是BC 边上的任一点(可与点B ,C 重合),分别过点B ,C ,D 作射线AP 的垂线,垂足分别为点B′,C′,D′,则BB′+CC′+DD′的最大值为______,最小值为______.三、回顾与思考________________________________________________ ________________________________________________ ________________________________________________ 【参考答案】精讲精练 1.1252.3HBAD'B'C'P D CBA3. 4.1 5.5 6.27.(1)84PD -≤;(2)8 8.69.410.探究:发现:(1)12ABD S xm =△,12CBD S xn =△(2)m n x+=;m +n 的最大值为6,最小值为应用:2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四讲 几何的定值与最值
几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明. 几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有: 1.特殊位置与极端位置法; 2.几何定理(公理)法;
3.数形结合法等.
注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、 逻辑推理与合情想象相结合等思想方法. 【例题就解】
【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 .
思路点拨 如图,作CC ′⊥AB 于C ,DD ′⊥AB 于D ′,DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=
2
1
AB 一常数,当CQ 越小,CD 越小,本例也可设AP=x ,则PB=x 10,从代数角度探求CD 的最小值.
注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指:
(1)中点处、垂直位置关系等; (2)端点处、临界位置等.
【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T ,圆
交AC 、BC 于M 、N ,则对于所有可能的圆的位置而言, MTN 为的度数( ) A .从30°到60°变动 B .从60°到90°变动
C .保持30°不变
D .保持60°不变
思路点拨 先考虑当圆心在正三角形的顶点C 时,其弧的度数,再证明一般情形,从而作出判断.
⌒
注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得定值与最值.
【例3】 如图,已知平行四边形ABCD ,AB=a ,BC=b (a >b ),P 为AB 边上的一动点, 直线DP 交CB 的延长线于Q ,求AP+BQ 的最小值.
思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+ (当且仅当b a =时取等号)求最小值.
【例4】 如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A 、B 的点M ,设直线AC
与BM 相交于,直线CB 与AM 相交于点N ,证明:线段A 和BN 的乘积与M 点的选择无关.
思路点拨 即要证A ·BN 是一个定值,在图形中△ABC 的边长是一个定值,说明A ·BN 与AB 有关,从图知AB 为△ABM 与△ANB 的公共边,作一个大胆的猜想,A ·BN=AB 2,从而我们的证明目标更加明确.
注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.
【例5】 已知△Y 是直角边长为1的等腰直角三角形(∠=90°),它的三个顶点分别在等腰Rt △ABC(∠C=90°)的三边上,求△ABC 直角边长的最大可能值.
思路点拨 顶点在斜边上或直角边CA(或CB)上,当顶点在斜边AB 上时,取xy 的中点,通过几何不等关系求出直角边的最大值,当顶点在(AC 或CB)上时,设C=x ,C=y ,建立x ,y 的关系式,运用代数的方法求直角边的最大值.
注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:
(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值; (2)构造二次函数求几何最值.
⌒
学力训练
1.如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B ′、C ′、D ′,则BB ′+CC ′+DD ′的最大值为 ,最小值为 .
2.如图,∠AOB=45°,角内有一点P ,PO=10,在角的两边上有两点Q ,R(均不同于点O),则△PQR 的周长的最小值为 .
3.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=5,CD=4,P 在直线MN 上运动,则PB PA -的最大值等于 .
4.如图,A 点是半圆上一个三等分点,B 点是弧AN 的中点,P 点是直径MN 上一动点,⊙O 的半径为1,则AP+BP 的最小值为( )
A .1
B .
2
2
C .2
D .13-
5.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( )
A .212π+
B .2412π+
C .214π+
D .242π+
6.如图、已知矩形ABCD ,R ,P 户分别是DC 、BC 上的点,E ,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减小
C .线段EF 的长不改变
D .线段EF 的长不能确定
7.如图,点C 是线段AB 上的任意一点(C 点不与A 、B 点重合),分别以AC 、BC 为边在直线AB 的同侧作等边三角形ACD 和等边三角形BCE ,AE 与CD 相交于点M ,BD 与CE 相交于点N .
(1)求证:MN ∥AB ;
(2)若AB 的长为l0cm ,当点C 在线段AB 上移动时,是否存在这样的一点C ,使线段MN 的长度最长?若存在,请确定C 点的位置并求出MN 的长;若不存在,请说明理由. (2002年云南省中考题)
8.如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足,求证:不管ST 滑到什么位置,∠SPM 是一定角.
9.已知△ABC 是⊙O 的内接三角形,BT 为⊙O 的切线,B 为切点,P 为直线AB 上一点,过点P 作BC 的平行线交直线BT 于点E ,交直线AC 于点F . (1)当点P 在线段AB 上时(如图),求证:PA ·PB=PE ·PF ;
(2)当点P 为线段BA 延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果
不成立,请说明理由.
10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE ,其中AF=2,BF=l ,在AB 上的一点P ,使矩形PNDM 有最大面积,则矩形PNDM 的面积最大值是( )
A .8
B .12
C .
2
25
D .14
11.如图,AB 是半圆的直径,线段CA 上AB 于点A ,线段DB 上AB 于点B ,AB=2;AC=1,BD=3,P 是半圆上的一个动点,则封闭图形ACPDB 的最大面积是( ) A .22+ B .21+ C .23+ D .23+
12.如图,在△ABC 中,BC=5,AC=12,AB=13,在边AB 、AC 上分别取点D 、E ,使线段DE 将△ABC 分成面积相等的两部分,试求这样线段的最小长度.
13.如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?
15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.
(1)设矩形的边AB=x(米),AM=y(米),用含x的代数式表示y为.
(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.
①设该工程的总造价为S(元),求S关于工的函数关系式.
②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,
请列出设计方案;若不能,请说明理由.
③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?
若能,请列出所有可能的设计方案;若不能,请说明理由.
16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).
参考答案。
