自动控制理论 第三版 课后答案
自动控制理论 (刘丁 著) 机械工业出版社 课后答案--习题三

习题31. 答案:t K >=0.32. 此温度计的时间常数T= t/4=15秒3. 答案: ()10.11s s φ=+4. 答案:b 变大系统阶跃响应的延迟时间、上升时间和调节时间都加长。
5. )1)(2(22++-=s s s X Y 6. 略7. 答案: (1)2600()70600G s s s =++,(2)24.5n w =,ζ=1.43 8. 答案: 1.24p t =,%9.5%σ= 1.58(5%)s t =∆=或 2.11(2%)s t =∆= 9. 1)开环零点-2.5 开环极点-0.52)闭环零点-2.5 闭环极点-0.4500 ± 0.8930i3)1=n ω ζ=0.454)38.1=r t 96.7=s t %6.22%=ο10. 答案:H K =0.9,0K =1011. 答案:47,0.1K τ≈≈12. 答案:313. 答案:(1)不稳定,右半S 平面有2个根;(2)不稳定,右半S 平面有2个根;(3)不稳定,右半S 平面有1个根;14. 略15. 答案:系统的参数(),K ξ的稳定域为0020K ξξ><<,。
16. 答案:51499K << 17. 答案:(1)由()D s 表达式可见,当0β=时系统结构不稳定;当0β>时系统总是稳定的。
(2)由ξ=可见2%3.57s n t K ξσβξωβ⎧↑→↓⎪↑⇒⎨==↓⎪⎩(3) 1ss ss a a e e K K ββ==∴↑→↑。
18. 答案:a T 、M T 与K 均大于0且10z K T <<时闭环系统是稳定的。
19. 答案:121ssn K e K =-+ 20. 证明:是I 型系统;21.B K K v = KB e ss = 与K 成反比,与B 成正比 22.G=tf(80,[1 2 0]);GB=feedback(G,1);t=0:0.01:1;[y,t]=step(GB);e=1-y;m=length(t);subplot(2,1,1),plot(t,y,'k',t,ones(m,1),'k-.') %draw unit step response curve title('unit step response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -0.21],'FontSize',8)ylabel('Amplitude','FontSize',8)axis([0 6 0 2])subplot(2,1,2), plot(t,e,'k',t,zeros(m,1),'k-.') %draw error response curve title('error response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -1.21],'FontSize',8)ylabel('Amplitude','FontSize',8)12unit step responseTime(sec.)A m p l i t u d e-101error response Time(sec.)A m p l i t u d e ()()1()k B k G s s G s φ=+()()1()B k B s G s s φφ=-2()()Ks b G s s a k s +=+-0lim ()V s b K sG s a K →==-1ss v a k e K b-==23 clearnum=1;den=conv([0.5 1 0],[4 1]);rangek=[0.2,0.8,1.2];t=linspace(1,60,300)';for j=1:3s1=tf(num*rangek(j),den);sys=feedback(s1,1);y(:,j)=step(sys,t);endplot(t,y(:,1),'k',t,y(:,2),'r',t,y(:,3),'b')title('unit step response under different k','FontSize',8) xlabel('Time(sec.)','Position',[50 -1.8],'FontSize',8) ylabel('Amplitude','FontSize',8)axis([0 60 -1.5 3.5])gtext('k=0.2'),gtext('k=0.8'),gtext('k=1.2')Time(sec.)A m p l i t u d e 求当k =0.8时系统的性能指标clearnum=1;den=conv([0.5 1 0],[4 1]);k=0.8;num=num*k;s1=tf(num,den);sys=feedback(s1,1);t=0:0.005:50;y=step(sys,t);r=1;while y(r)<1.0001r=r+1;endrise_time=(r-1)*0.005[ymax,tp]=max(y);peak_time=(tp-1)*0.005max_overshoot=ymax-1s=length(t);while y(s)>0.98 & y(s)<1.02s=s-1;endsettling_time=(s+1)*0.005运行结果:rise_time =4.5350peak_time =7.7950max_overshoot =0.5710settling_time =46.855024 num=[6.3223 18 12.811]den=[1 6 11.3223 18 12.811]step(num,den)25 num=1for kesi=0:0.2:1sys=tf(num,[1 2*kesi 1]);step(sys)hold onend。
自动控制理论基础答案

图E2.7 题2.8图
G n (s) K4 R (s) + K1 K2 s
N(s)
-
K3 Ts+ 1
C (s)
图E2.7 题2.8图
解:1)令N(s)=0,则 2)令R(s)=0,则
K1 K 2 K 3 C ( s) R( s) s(Ts 1) K1 K 2 K 3
C ( s ) K 1 K 2 K 3 Gn K 3 K 4 S N ( s) s(Ts 1) K1 K 2 K 3
2-6 试画出图E2.5所示系统的动态结构图,并求 传递函数 U c ( s ) 。
U r (s)
R1 C1 ur R0 R0 +
C2 R2 +
R4 R3 +
uc
图E2.5 题2-6图
R1 C1 ur R0 R0 +
C2 R2 +
R4 R3 +
uc
Ur -
R1 R0 ( R1Cs 1)
1 R2C2 s
要消除干扰对输出的影响,令C(s)/N(s)=0
K4s 则 Gn ( s ) K1 K 2
2.9 简化图E2.8中各系统结构图,并求出传递函 数C(s)/R(s)。
R (s) + G1 G2 + G3 + + C(s)
R (s) +
G1 G2 G3
+
C (s)
(a)
G4
(b)
R (s)+ G1 C (s)
G2 1 G2
2.10 系统结构如图E2.9所示,试求出系统的 传递函数。
+
K1 K 2 K4s
-1
(完整版)自动控制原理谢克明第三版部分习题答案

《自动控制原理(第3版)》部分习题答案第2章C2-1(a) 21211()(1)()()(1)R sL R Cs G s R sL R Cs R ++=+++C2-221114232233342526()()(1)(1)()()()()()()()()()()()()()m a a a a a e ma a L a a a a e m f fR G s K R R G s R Cs K T s R G s K c s G s U s JL s L f JR s fR c c L s R s G s M s JL s L f JR s fR c c U s G s K s =-=-=-+=-+=-Ω==++++-+Ω==++++==Ω 123412346512346()()()()()()1()()()()()()()()1()()()()()r L G s G s G s G s s U s G s G s G s G s G s G s s M s G s G s G s G s G s Ω=+Ω=+C2-4(a) 3123123()()()R LsG s R R R Ls R R R =++++C2-4(b) 323123()()()R LsG s R R Ls R R R =+++C2-5321122211212311(1)(1)(),(),(),()()1a b c d R Cs R Cs R C s R C s RG s RCs G s G s G s R Cs R C s R R R Cs ++++=-=-=-=-++ C2-612314512123214342123312341232233344()()()()()()()1()()()()()()()()()()()()()()()()()()()()1()()()()()()()()()()a b G s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s +=++++++=+++-12341()()()()()G s G s G s G s H sC2-713241761113241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ 283261213241762851324()()()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +=+++++ 24132852213241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ 17413152113241762851324()()()[1()()]()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ C2-812341123243123312312()()()()()1()()()()()()()()()()()()()()()()G s G s G s G s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s H s H s +=+++++C2-9 12345214561111452145145124561112322()()()[1()()()]()()()()()()()1()()()()()()()()()()()()()()()()[1()()]()()(()()()G s G s G s G s G s H s G s G s G s G s C s s R s G s H s G s G s H s G s G s G s G s G s G s H s H s G s G s G s G s H s G s G s G C s s R s --Φ==+-+-++Φ==4511452145145121122)()()1()()()()()()()()()()()()()()()()()()s G s G s G s H s G s G s H s G s G s G s G s G s G s H s H s C s s R s s R s +-+-=Φ+Φ C2-1013453564256313421356253431342535643535123561434523345624()()[1()()]()[1()()]()()1()()()()()()()()()a G s G G G s G H s G G H s G G G s G H s G G H s G G G G s G G G G s G H s G G H s G H s G G H s G G s G G H H s G G G H H s G G G H H s G G G G H H s =++++++-+++++++++12353241212131223123()()()()()[1()]()[1()()2()()]()1()()2()()()()2()()()b G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++++++=+++++第3章C3-1 21()Ts TsK e Tse G s T s ----=C3-2 220.910()1110s s s s s ++Φ=++C3-3105050()10.283sin(545)()1 1.4sin(545)t t tc t e e t c t et ---=--+=-+精近C3-422*0.23()(0.5)2*0.23()0.50.23G s s s s s s =+Φ=++C3-51212T T bK T T ε+<<C3-6 阶跃信号作用下稳态误差为零,要求n m a b =加速度信号作用下稳态误差为零,要求1122,,n m n m n m a b a b a b ----=== C3-7 21()(1)c sG s K T s =+C3-8 24()(46)G s s s s =++C3-9 250()(1225)G s s s s =++ C3-100.243τ=C3-11 (1)06,(2)303,(4)010/3K K K <<<<<<结构不稳()C3-12 (1)015,(2)0.72 6.24K K <<<< C3-13(1)(2)34系统稳定系统不稳定,有两个右根,()系统稳定()系统不稳定,有三个右根C3-14 3,K ω==C3-1533231()()1()()()()()n r G s G s G s H s G s G s G s =-+=第4章C4-1 图略C4-2 (1)图略 (2) 2233()24x y ++=C4-3 (1)图略 (2) 0.40.5K <<C4-4 分会点和渐近线123=0,,2,22a a d d d a πδϕ-+==±12320,2a d d d ====-(1)当时,图略 123180,6a d d d ====-(2)当时,图略 120,0a a d σ<=>(3)当0<时,图略 1180,0a a d δ<=<(4)当2<时,图略12318,,0a a d d d δ><(5)当时,三个不同实数分会点,图略C4-5(1) 图略,原系统不稳定;(2)增加零点且选择合适位置,可是系统稳定,零点05z << C4-6图略,系统稳定34K > C4-7 (1) 图略(2)当0.8629.14K <<,系统为欠阻尼状态,且 1.87K =阻尼比最小,系统地闭环极点为3 2.8j -±(3)试探求得 2,4 2.8K j =-±闭环极点, 1.06,0.75~1P s M t == C4-8 (1)等效开环传递函数为: (1)()(2)K s G s s s --=+正反馈系统根轨迹, 图略(2)系统稳定02K <<(3) 2,K ω==C4-9等效开环传递函数为: 22()===10)(44)(4410)Ka K G s K a s s s K s s s ''++++等(,图略 C4-10(1) 图略(2) 64,K ω==(3)1,20.5,1s ζ==-±C4-11(1) 图略 (2) 不在根轨迹上; (3) ()1cos 4c t t =-C4-12等效开环传递函数为: 322()=(4416)(4)(4)K KG s s s s s s s s =+++++等,K=8时试探求第5章C5-1(1)C5-1(2)C5-1(3)C5-2000(1)()0.83sin(30 4.76)(2)()0.83sin( 4.76) 1.64cos(2459.46)c t t c t t t =+-=----C5-3当12T T <,系统稳定当12T T >,系统不稳定. C5-4 2100()10100G s s s =++ C5-5(a) 0110(1)300(),4111(1)(1)510s G s s s γ+==++ (b) 00.1(),2581(1)50sG s s γ==+(c) 032(),141(1)2G s s s γ==+(d) 025(), 1.66(1001)(0.11)G s s s s γ==-++(e) 020.5(21)(),36.8(0.51)s G s s s γ+==+ (f) 0231.62(),9.860.010.0981G s s s γ==++ C5-6 (1) K=1(2)K=25(3)K=2.56(或精确求K=3.1) C5-7()()()a g i 稳定,(b)不稳定,(c)稳定,(d)稳定,(e)不稳定,(f)稳定,不稳定,(h)不稳定,不稳定,(j)不稳定,C5-8 102510000K K <<<和 C5-9(1)(2)闭环系统稳定; (3)078.5,g K γ==∞(4)K 增大10倍,对数幅值上升,但相频特性不变,系统的快速性提高,平稳性降低,系统地抗干扰性降低。
自动控制原理(第三版)试题及答案

2012年6月23日星期六课程名称: 自动控制理论 (A/B 卷 闭卷)一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
自动控制理论习题答案

习题参考答案2-1 已知R -L -C 网络如图所示,试列写以u i 为输入,u o 为输出的微分方程模型。
解: 电感方程:i o u i R u ti L =++113d d ...(1) 电容方程:2d d i tu Cc=...(2) 有6个变量,列出微分方程模型时保留2个,因此要消掉4个变量,还需要列出3个方程:由KVL :i c u i R u i R =++2211...(3) 由KCL :321i i i +=...(4) 在输出端:o u i R =33 (5)将(5)代入(1)(4)可消去3i ,然后将(4)代入(1)(3)消去1i 得到: ⎪⎪⎩⎪⎪⎨⎧=+++=+++)7()()6()(d d 223213213 i c oi o o ou i R u R u i R u R u i R u t u R L 用方程(2)消去c u :将(7)整理为i c o u i R R u u R R =+++22131)(后取时间的导数,再将(2)代入,得到: tut i R R C i t u R R i o d d d d )(d d 221231=+++ tuC R t i C R R R i R t u CR i o d d d d )(d d 32213231=+++...(8) 最后,将(6)整理为])(d d [133231o oi u R R tu Lu R i R R ++-=,代入1)8(R ⨯得到t u CR R t u R R t u L t u R C R R u R R t uL u R t u CR io o i o o i o d d ]}d d )(d d [d d {)(]})(d d [{d d 31132232113321=++-++++-+经整理,可得到系统的微分方程模型为i i ooo u R R R t u R R C R R u t u R R L C R R C R R C R R t u R R LC R R 313313231323121223121d d d d d d )(+++=++++++++ 2-2 已知机械系统如图所示,其中位移i x 为输入,位移o x 为输出。
自动控制理论第三版课后习题详细解答答案(夏德钤翁贻方版)

1 U i ( s) I1 ( s) R1[ I1 ( s) I 2 ( s)] C1s 1 U o ( s) I 2 ( s) C2 s
并且有
1 1 I1 (s) ( R2 ) I 2 ( s) C1s C2 s
2
2-2 假设图 2-T-2 的运算放大器均为理想放大器,试写出以 ui 为输入, uo 为输出的传递函 数。 (a)由运算放大器虚短、虚断特性可知: 对上式进行拉氏变换得到
ui du du C i C 0 , uc ui u0 , R dt dt
U i ( s) sU i (s) sU 0 (s) RC
(s) (考虑温度计有贮存热的热容 C 和限制热流的热阻 R) 。 i (s)
解:根据能量守恒定律可列出如下方程:
C
对上式进行拉氏变换得到
d i dt R i (s) (s) R
Cs(s)
则传递函数为
( s) 1 i ( s) RCs 1
2-8 试简化图 2-T-8 所示的系统框图,并求系统的传递函数
CR1 dui 2u0 2ui 0 2R dt R1 R
对该式进行拉氏变换得到
CR1 2 2 sU i (s) U 0 ( s) U i (s) 0 2R R1 R
故此传递函数为
U 0 ( s) R ( R Cs 4) 1 1 U i ( s) 4R
2-3 试求图 2-T-3 中以电枢电压 ua 为输入量, 以电动机的转角 为输出量的微分方程式和传 递函数。 解:设激磁磁通 K f i f 恒定
《自动控制理论》习题答案详解

C s C s 1i 《自动控制理论》习题答案详解第二章2-11 试求图2- T - 1所示 RC 网络的传递函数。
(a) z 1 = R 1 ⋅ Cs 1 = R 1 , z = R ,则传递函数为: R Cs + 1 2 2R 1 + Cs1U o (s ) = U i (s ) z 2 z 1 + z 2 =R 1R 2Cs + R 2R 1R 2Cs + R 1 + R 2(b) 设流过C 1 、C 2的电流分别为I 1、 I 2 ,根据电路图列出电压方程:⎧U (s ) = 1I (s ) + R [I (s ) + I (s )]⎪ C 1s ⎨ 1 并且有⎪ U o (s ) = ⎩C 2s I 2(s ) 1C 1sI 1(s ) = (R 2 +1 C 2s )I2 (s ) 联立三式可消去I 1 (s ) 与 I 2 (s ) ,则传递函数为:U o (s ) =U (s )1 C 2s⎛ 1⎫⎛ 1⎫ = R R C Cs 2 + (R C1 + R C + R C)s +1iR 1 + C 1s ⎝ 1 + R 1 ÷ ⎭⎝ 2 + R 2 ÷⎭1 2 1 21 11 22 22-2 2 假设图 2- T - 2 的运算放大器均为理想放大器,试写出u 以i 为输入,u o 为输出的传递函 数。
(a)u i du i du 0 由运算放大器虚短、虚断特性可知: R 对上式进行拉氏变换得到 = -C + C dt dt, u c = u i - u 0 ,故传递函数为U i (s )= -sU RC i(s ) + sU 0 (s ) U 0(s ) =RCs +111 12⎪(b)由运放虚短、虚断特性有:Cdu cU i (s )- u i - u c RCs+ - u c= 0 ,uc+ u 0= 0 ,dt R 2R 2R 2 R 1iU R 0 cU R 0 U 联立两式消去u c 得到CR ⋅ du 0 + 2u + 2 u = 0对该式进行拉氏变换得2R 1 dtRR 1故此传递函数为CR sU 2R 1 (s ) + 2 U R i (s ) +2(s ) = 0 1U 0(s ) = -U i (s ) 4R 1 R (RCs + 4)(c)Cdu c + u c - u 0 + u c = 0 ,且 u i = - uc ,联立两式可消去u 得到 dtR 1 / 2R 1 / 2RR 1 2CR 1 ⋅ du i + 2u 0 + 2u i = 0对该式进行拉氏变换得到2R dt R 1 R故此传递函数为CR 1⋅ sU 2R i (s ) + 2 (s ) + 12 (s ) = 0 R i U 0(s ) = - R 1( R 1Cs + 4)U i (s ) 4R2-3 3 试求图2- T - 3中以电枢电压u a 为输入量,以电动机的转角θ 为输出量的微分方程式和传递函数。
自动控制原理与系统部分课后答案孔凡才 第3版 机械工业出版社

课后吧
于是可画出对数幅频特性
如下图所示
课后吧
课后吧
图 ( 4-1)
由于
其中惯性环节的作用占主导地位,因此它是一个相位滞后的环节。
3、题 4-13[解] 由图 4-42 可见,系统的固有部分的传递函数为
图11稳压电源电路的框图及自动调节过程由以上分析可知此系统的输出量为给定值取决于稳压管的稳压值检测元件为构成的分压电路反馈信号为电压负反馈执行元件为调压管放大元件为动量为整流输出电压的波动
课后吧
第 1 章 [疑难问题解答] 思 考 题 : 1-1 开环控制与闭环控制的特征、优缺点和应用场合 (1)对于开环控制,系统的输出量不被引回来对系统的控制部分产生影响。
在如图 1-17 所示的电路中,被控量是负载(电阻 )上的电压 (输出电压)。若不采用稳压
电 源 ,将 负 载 直 接 接 到 整 流 电 路( 图 中 未 画 出 )的 输 出 电 压 上 ,则 当 负 载 电 流 增 加( 减 小)时,整流电源的等效内阻上的电压降落将增加,使整流输出电压 (此时即为负载上的电 压)降低。当然,若电网电压波动,也会使整流输出电压产生波动。设整流输出电压的波动为 △ ,它是造成负载上电压不稳定的主要原因。
如今增设了稳压电路,此时负载上的电压不再是整流电压 ,而是整流电压在经调整管 的调节后输出的电压 。 导通程度愈大,则输出电压 大些,反之将小些。由图可见,调
整管 的导通程度将取决于放大管 的导通程度。 管的发射极电位由电阻 和稳压管 构 成的稳压电路提供恒定的电位。 管基极电位 取决于负载电压 (由 和 构成的分压电 路 提 供 输 出 的 负 载 电 压 的 采 样 信 号 )。
电阻分压后的 。 由图可见:
自动控制原理课后答案

自动控制原理课后答案1. 根据反馈控制原理,系统的控制目标是通过比较输出信号与参考信号之间的差异,对系统的输入进行调整,使系统达到期望的状态或行为。
2. 控制系统一般包括传感器、执行器和控制器三个基本组成部分。
传感器用于收集系统的实时数据,执行器用于执行调整系统输入的指令,控制器则根据传感器采集的数据来计算和调整控制信号。
3. 反馈控制系统中,控制器根据系统的输出信号和参考信号之间的差异进行调整。
比例控制器(P控制器)只根据差异的大小,线性比例地调整控制信号;积分控制器(I控制器)不仅考虑差异的大小,还考虑差异的累积量;微分控制器(D控制器)则考虑差异的变化率。
4. P控制器适用于稳态差异较大的系统,可以快速调整系统输出至参考信号附近,但容易产生超调现象;I控制器适用于存在稳态差异的系统,可以逐渐消除稳态差异,但容易产生震荡现象;D控制器适用于存在瞬态差异的系统,可以抑制系统的瞬态响应,但无法消除稳态差异。
5. 比例积分微分控制器(PID控制器)是一种综合了P、I和D控制器的控制器。
通过合理地调整比例、积分和微分系数,可以实现系统的快速响应和稳定。
6. 开环控制系统和闭环控制系统都可以实现对系统的控制,但闭环控制系统更加稳定和鲁棒。
开环控制系统中,控制器不根据系统的反馈信号来调整控制信号,容易受到外部干扰和参数变化的影响。
7. 可以使用根据控制对象的动态特性设计的控制器来提高系统的控制性能。
常见的控制器设计方法包括根据稳态误差的允许范围来选取比例、积分和微分系数,以及根据系统传递函数进行校正和补偿。
8. 多变量控制系统可以同时控制多个输入和多个输出。
常见的多变量控制系统包括串级控制、并联控制和内模控制等。
9. 控制系统的稳定性是指当系统接受一定的输入时,输出是否趋于稳定。
稳定性的判断可以通过判断系统的传递函数的极点位置来确定。
10. 控制系统的仿真和实验可以通过使用计算机软件进行模拟仿真,或搭建实际的物理实验平台进行。
自动控制理论 (刘丁 著) 机械工业出版社 课后答案--习题五
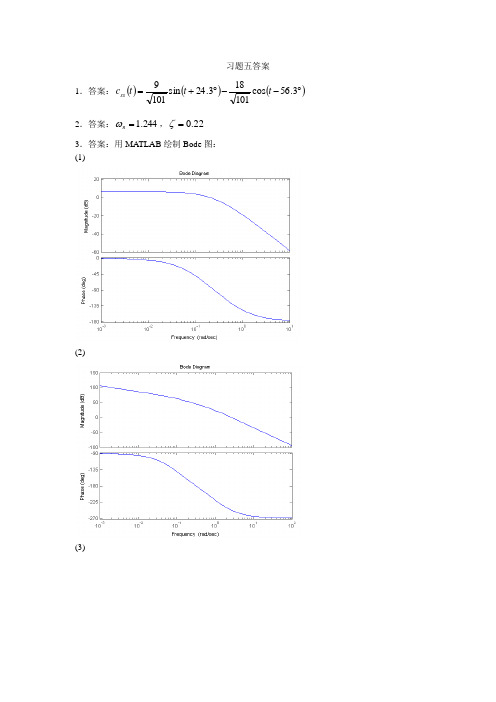
习题五答案1.答案:()()()︒--︒+=3.56cos 101183.24sin 1019t t t c ss2.答案:244.1=n ω,22.0=ζ3.答案:用MATLAB 绘制Bode 图: (1)(2)(3)4.答案: a) ()10100+=s s G ; b) ()505+=s s s G ; c) ()()1005000+=s s s Gd) ()()()120101.0100++=s s s s Ge) ()17493826.02749102+⨯⨯+⎪⎭⎫ ⎝⎛=s s s Gf) ()⎪⎪⎭⎫ ⎝⎛+⨯⨯+⎪⎭⎫ ⎝⎛=1503.02501002s s s s G5.答案:(1)(2)(3)6.答案:()()()125105.010++-=s s s s G7.答案:T >τ稳定,T <τ不稳定,T =τ临界稳定选取K=1τ=10,T=2时的幅相频率特性曲线: τ=2,T=10时的幅相频率特性曲线:8.答案:a) 稳定b) 不稳定,不稳定极点2个c) 稳定d) 稳定e) 不稳定,不稳定极点2个f) 不稳定,不稳定极点2个g) 稳定h) 不稳定,不稳定极点2个i) 稳定j) 不稳定,不稳定极点2个9.答案:1)23<K ;2)91<T ;3)11<+T KT;10.答案:44.2=g ω,63.2<K11.答案:707.0=a12.答案:︒=2.65γ,s rad c /95.1=ω13.答案:︒=52γ,s rad c /58.1=ω14.答案:2121T T K T T K g +=16.答案:1)()()()()125.0110152+++=s s s s s G ;2)系统稳定;3)5.0=ss e ;4)↑c ω,快速性变好;γ不变,平稳性相当;高频特性基本不变;开环增益变大,稳态误差变小。
17.答案:1.0=h K18.答案:(1)6<K ;(2)K 值无限制;19.答案:K=5时的奈氏图:相角裕量13.6 幅值裕量6.85K=20时的奈氏图:不稳定。
自动控制原理第三版课后答案

自动控制原理第三版课后答案 1. 课后习题答案。
1.1 第一章。
1.1.1 选择题。
1. A。
2. C。
3. B。
4. A。
5. D。
1.1.2 填空题。
1. 系统。
2. 控制。
3. 输入。
4. 输出。
5. 误差。
1.1.3 简答题。
1. 控制系统是指能够对某一对象进行控制的系统,包括反馈控制系统和前馈控制系统两种类型。
2. 控制系统的基本组成包括输入端、输出端、控制器和执行器四个部分。
3. 控制系统的闭环和开环是指系统是否具有反馈环节,闭环系统具有反馈环节,开环系统则没有。
1.2 第二章。
1.2.1 选择题。
1. B。
2. A。
3. D。
4. C。
5. B。
1.2.2 填空题。
1. 传递函数。
2. 时域。
3. 频域。
4. 线性。
5. 时不变。
1.2.3 简答题。
1. 传递函数是描述系统输入输出关系的函数,通常用H(s)表示。
2. 时域分析是指通过对系统的状态方程进行求解,得到系统的时域响应。
3. 频域分析是指通过对系统的传递函数进行频域分析,得到系统的频域特性。
2. 综合题。
2.1 第三章。
2.1.1 选择题。
1. D。
2. A。
3. B。
4. C。
5. D。
2.1.2 填空题。
1. 稳定。
2. 系统。
3. 极点。
4. 零点。
5. 阶跃响应。
2.1.3 简答题。
1. 稳定性是指系统在受到干扰或参数变化时,能够保持稳定的特性。
2. 极点和零点是描述系统传递函数特性的重要参数,极点决定系统的稳定性,零点则影响系统的动态响应特性。
2.2 第四章。
2.2.1 选择题。
1. B。
2. C。
3. A。
4. D。
5. B。
2.2.2 填空题。
1. PID。
2. 比例。
3. 积分。
4. 微分。
5. 控制。
2.2.3 简答题。
1. PID控制器是一种常用的控制器,由比例、积分和微分三部分组成,能够实现对系统的稳定控制。
2. 比例控制器的作用是根据当前误差的大小来调节控制量,积分控制器的作用是根据误差的历史累积值来调节控制量,微分控制器的作用是根据误差变化速度来调节控制量。
最新自动控制原理精品资料控制电机(第三版)考试简答题及答案

《控制电机》一、简答题(每小题6分,共30分)1.直流伺服电动机在不带负载时,其调节特性有无死区?若有,为什么?调节特性死区的大小与哪些因素有关?2.直流电动机为什么不能直接起动?如果直接起动会引起什么后果?答: 起动瞬间转速n=0,电动势E a =C e Φn=0,最初起动电流a N N R U I =。
若直接起动,由于R a 很小,I st 会达到十几倍 甚至几十倍的额定电流,造成电机无法换向,同时也会过热,因此不能直接起动。
3.要得到圆形旋转磁场,加在励磁绕组和控制绕组上的电压应符合什么条件?答:当励磁绕组有效匝数和控制绕组有效匝数相等时,要求两相电压幅值相等,相位相差90度;当励磁绕组有效匝数和控制绕组有效匝数不相等时,要求两相电压相位相差90度,电压幅值应与匝数成正比。
4. 直流电动机的启动性能要求是什么?答:(1)启动时电磁转矩要大,以利于克服启动时的阻转矩;(2)启动时电枢电流不要太大;(3)要求电动机有较小的转动惯量和在加速过程中保持足够大的电磁转矩以利于缩短启动时间。
5.答: 因为电动机轴上总带有机械负载,即使在空载下,电机本身也会存在阻转矩。
为了克服机械负载的阻力矩,转子绕组中必须要有一定大小的电流以产生足够的电磁转矩,而转子绕组中的电流是由旋转磁场切割转子导条产生的,那末要产生一定数量的电流,转子转速必须要低于旋转磁场的转速。
四、计算题(每小题10分,共30分)1. 设一台直流电动机原来运行情况为:电机端电压U a =220V ,E a =100V ,R a =20Ω,I a =1A ,n=1500r/min 。
如果电源电压降低一半,而负载转矩不变,试计算转速将降低到原来的百分之几?1. 解:当负载转矩不变时,电磁转矩a T I C T φ=不变,又由φ不变可知,a I 不变。
若电压降低到一半后的感应电势、转速、电流用'a E 、'n 、'a I 表示,则'a U =110V 时的转速对原来的转速之比为:45.010211010255//'''''=⨯-⨯-=--===a a a a a a a a e a e a R I U R I U E E C E C E n n φφ,即转速降低到原来的45%。
自动控制理论 (刘丁 著) 课后习题二~八答案

习题22-1. (1)线性,时变,动态(2)非线性,时变,动态 (3)非线性,定常,动态 (4)非线性,定常,静态 (5)非线性,定常,动态 (6)非线性,定常,静态 2-2. (a )1212)(st e ss s F -+=(b )211)1(1)(sst e s t s F -+-=(c )2121)1)(1()(1st e s t s F s t --+= 2-3.1212221332121(1)(),lim(1),lim(3)134324321111()[],2132s s t tc c s s F s c s c s s s s s s s F s f t e e s s →-→---++=+=+==+=++++++∴=+=+++得到:()()()()1023(2)()1+cos(t)-5*sin(t)111(3)sin cos 222119(4)()8181(5)()12131(6)()()32412t t t tt t t f t f t e t e t t f t e ef t t e f t t e e -------==--+=-==+=-++(4) syms s FF=ilaplace(1/(s^3+21*s^2+120*s+100))运行结果:F =1/81*exp(-t)-1/9*t*exp(-10*t)-1/81*exp(-10*t) (5) syms s FF=ilaplace((s^2+2*s+3)/(s+1)^3) 运行结果:F =t^2*exp(-t)+exp(-t) (6) F=ilaplace((s+2)/(s*(s+3)*(s+1)^2))运行结果:F = 2/3+1/12*exp(-3*t)-1/2*t*exp(-t)-3/4*exp(-t)2-4.(1) ()1()1()tTx t e r t t -=-= ()(1)tT x t t T e r t-=--=(2) 2()tx t - (3) ()1(1)t x t t e -=-+2-5.(a )21212=++crU R U R R R R s(b )1221212+=++crU R R cs R U R R R R cs2-6 (a )211crU R Cs U R Cs+=-,实际上是一个PI 控制器。
自动控制原理课后练习答案(潘丰)

∑ p −∑z
i
j
σa =
5) 根轨迹的分离点
i =1
j =1
n−m
=
0 + (−1) + (−1) 2 =− 3 3
根据等效开环传递函数的表达式,有 A( s ) = s 3 + 2s 2 + s , B ( s ) = 1 ,于是
A( s ) B '( s) − A '( s ) B( s ) = −3s 2 − 4s − 1 = 0
K∗ = s +1 ⋅ s + 2 ⋅ s + 4
于是,可得 K ∗ = 12 。 (2) 系统的特征方程为 D( s) = ( s + 1)( s + 2)( s + 4) + K ∗ = 0 ,由劳斯表
1
s3 s2 s1 s0
1 7 90 − K ∗ 7 8 + K∗
14 8 + K∗ 0
易得使闭环系统稳定的 K*值的范围为-8 < K* < 90。 4-6【答案】
图 4-13 题 4-7(3)系统的根轨迹图 4-8【证】设 s 为系统根轨迹上的一点,则根据相角条件有 ∠( s + 6) − ∠s − ∠( s + 4) = ±(2k + 1)π , k = 0, 1, 2, ⋯ 然后,将 s=σ+jω 代入上式,得到
4
∠(σ + 6 + jω ) − ∠(σ + jω ) − ∠(σ + 4 + jω ) = ±(2k + 1)π , k = 0, 1, 2, ⋯
2
由系统的开环传递函数,可得对应的闭环特征方程为
自动控制理论(夏德钤)第3版 课后答案
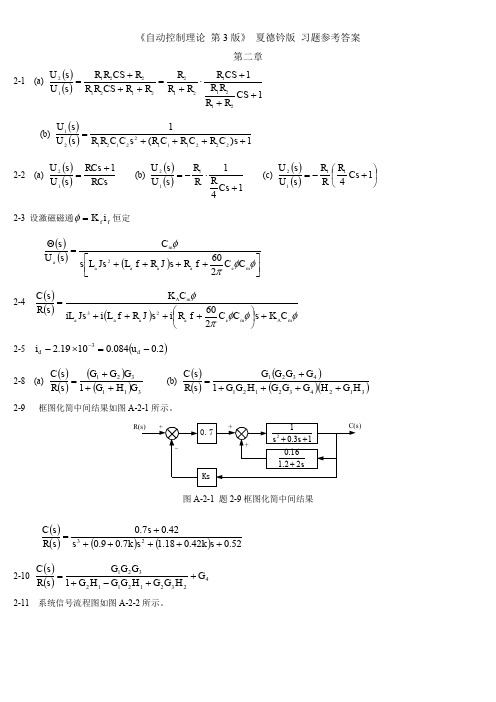
框图化简中间结果如图 A-2-1 所示。
0.7
_ + +
1 s 0.3s 1
2
C(s)
0.16 1 .2 2 s
Ks
图 A-2-1 题 2-9 框图化简中间结果
C s 0.7 s 0.42 3 Rs s 0.9 0.7k s 2 1.18 0.42k s 0.52
2 1 n t 2 1 nt e e ct t 2 2 2 2 2 n 2 1 n 1 1
2
1
(b) 当 0 1 时
s 0 s 0
C 2 lim
s 0
d2 2(0.1s 2 s 10) 20(0.2s 1) 2 s lim 0 e s 0 ds 2 (0.1s 2 s 10) 3
(1)
s (t ) r (t ) R0 ,此时有 rs (t ) R0 , r r (t ) 0 ,于是稳态误差级数为 s esr t C0 rs (t ) 0 , t 0
, t 0
1 2 n 比较上述两种情况, 可见有 z 1 零点时, 单位脉冲响应的振幅较无零点时小, 而且产生相移, 相移角为 arctg 。 1 n
自动控制原理课后练习答案(潘丰)

A( s ) B '( s ) − A '( s ) B ( s) = 0 ,整理得到 s 2 + 4s − 6 = 0
求解上述方程,得到
s1 = −5.1623 , s2 = 1.1623
由于 s1 在根轨迹(-∞,-2]上,故取分离点坐标为 d = −5.1623 。 6) 确定根轨迹的出射角。 由零、极点分布位置及出射角计算公式,得到点 p1 处的出射角为
A( s ) B '( s ) − A '( s ) B ( s) = 0 ,整理得到 2s 3 + 20s 2 + 50s + 30 = 0
求解上述方程,得到
s1 = −6.5171 , s2 = −2.5964 , s3 = −0.8865
由于 s3 在根轨迹[-2,0]上,故取分离点坐标为 d = −0.8865 。 系统的完整根轨迹如图 4-13 所示。
2
由系统的开环传递函数,可得对应的闭环特征方程为
s 3 + 1.7 s 2 + 0.8s + 0.1 + K ∗ = 0
将 s=jω 代入上式,整理得到
−1.7ω 2 + 0.1 + K ∗ + j(−ω 3 + 0.8ω ) = 0
分别令上式中的实部和虚部为零,即
2 ∗ −1.7ω + 0.1 + K = 0 3 −ω + 0.8ω = 0
ω σ +6 σ = ω ω ω σ +4 1+ ⋅ σ +6 σ
−
整理可得
ω
(σ + 6) 2 + ω 2 = (2 3) 2
自动控制理论_(刘丁_著)_机械工业出版社_课后答案

习题31. 答案:t K >=0.32. 此温度计的时间常数T= t/4=15秒3. 答案: ()10.11s s φ=+4. 答案:b 变大系统阶跃响应的延迟时间、上升时间和调节时间都加长。
5.)1)(2(22++-=s s s X Y 6. 略7. 答案: (1)2600()70600G s s s =++,(2)24.5n w =,ζ=1.438. 答案: 1.24p t =,%9.5%σ= 1.58(5%)s t =∆=或 2.11(2%)s t =∆=9. 1)开环零点-2.5 开环极点-0.52)闭环零点-2.5 闭环极点-0.4500 ± 0.8930i 3)1=n ω ζ=0.45 4)38.1=r t 96.7=s t %6.22%=ο10. 答案:H K =0.9,0K =10 11. 答案:47,0.1K τ≈≈ 12. 答案:3 13. 答案:(1)不稳定,右半S 平面有2个根; (2)不稳定,右半S 平面有2个根; (3)不稳定,右半S 平面有1个根;14. 略15. 答案:系统的参数(),K ξ的稳定域为0020K ξξ><<,。
16. 答案:51499K << 17. 答案:(1)由()D s 表达式可见,当0β=时系统结构不稳定;当0β>时系统总是稳定的。
(2)由ξ=可见2%3.57s n t K ξσβξωβ⎧↑→↓⎪↑⇒⎨==↓⎪⎩(3) 1ss ss a a e e K K ββ==∴↑→↑。
18. 答案:a T 、M T 与K 均大于0且10zK T <<时闭环系统是稳定的。
19. 答案:121ssn K e K =-+20. 证明:是I 型系统;21.B K K v =KBe ss = 与K 成反比,与B 成正比 22.G=tf(80,[1 2 0]); GB=feedback(G,1); t=0:0.01:1; [y,t]=step(GB); e=1-y;m=length(t);subplot(2,1,1),plot(t,y,'k',t,ones(m,1),'k-.') %draw unit step response curve title('unit step response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -0.21],'FontSize',8) ylabel('Amplitude','FontSize',8) axis([0 6 0 2])subplot(2,1,2), plot(t,e,'k',t,zeros(m,1),'k-.') %draw error response curve title('error response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -1.21],'FontSize',8) ylabel('Amplitude','FontSize',8)012unit step responseTime(sec.)A m p l i t u d e-11error responseTime(sec.)A m p l i t u d e()()1()k B k G s s G s φ=+()()1()B k B s G s s φφ=-2()()Ks bG s s a k s+=+-0lim ()V s bK sG s a K →==-1ss v a k e K b-==23 clearnum=1;den=conv([0.5 1 0],[4 1]); rangek=[0.2,0.8,1.2]; t=linspace(1,60,300)'; for j=1:3s1=tf(num*rangek(j),den); sys=feedback(s1,1); y(:,j)=step(sys,t); endplot(t,y(:,1),'k',t,y(:,2),'r',t,y(:,3),'b')title('unit step response under different k','FontSize',8) xlabel('Time(sec.)','Position',[50 -1.8],'FontSize',8) ylabel('Amplitude','FontSize',8) axis([0 60 -1.5 3.5])gtext('k=0.2'),gtext('k=0.8'),gtext('k=1.2')Time(sec.)A m p l i t u d e求当k =0.8时系统的性能指标 clear num=1;den=conv([0.5 1 0],[4 1]); k=0.8;num=num*k; s1=tf(num,den); sys=feedback(s1,1); t=0:0.005:50; y=step(sys,t); r=1;while y(r)<1.0001 r=r+1; endrise_time=(r-1)*0.005 [ymax,tp]=max(y);peak_time=(tp-1)*0.005 max_overshoot=ymax-1 s=length(t);while y(s)>0.98 & y(s)<1.02s=s-1;endsettling_time=(s+1)*0.005运行结果:rise_time =4.5350peak_time =7.7950max_overshoot =0.5710settling_time =46.855024 num=[6.3223 18 12.811]den=[1 6 11.3223 18 12.811]step(num,den)25 num=1for kesi=0:0.2:1sys=tf(num,[1 2*kesi 1]);step(sys)hold onend习题41.(a) (b) (c)(d) (e) (f) 2.(1)(2)证明:s j σω=+代入1+G(s)H(s)=0*()()0s s b k s a +++=*()(())(())0jw jw b k jw a σσσ++++++=*2()()0k a b σσσω+++-=*20k b a ++=消去*k 得:222()a a ab σω++=-所以根轨迹是以(-a,0) 3.答案:(1)(2)(3)(4)4.答案:(1)分离点: 3.854d =-渐近线 25,a a πσϕ=-=±,* 1.37K =,闭环系统稳定的*K 值的范围是*04K <<。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《自动控制理论 第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 26022-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i 2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。
0.7C(s)++_R(s)113.02++s s s22.116.0+Ks+图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。
图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdh s R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C 2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(limlim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =,此时有0)()(,)(0===t r t r R t r ss s ,于是稳态误差级数为 ()0)(0==t r C t e s sr ,0≥t(2) t R R t r 10)(+=,此时有0)(,)(,)(110==+=t r R t r t R R t r ss s ,于是稳态误差级数为 ()1101.0)()(R t rC t r C t e s s sr =+= ,0≥t (3) 221021)(t R t R R t r ++=,此时有t R R t r t R t R R t r s s 212210)(,21)(+=++= ,2)(R t r s= ,于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ,0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件(1)~(4)确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。
图A-3-1 二阶系统极点在s 平面上的分布区域3-6 系统在单位斜坡输入下的稳态误差为 nsr e ωζ2=加入比例—微分环节后()()()()[]()()()()()()()()()()()()()()()nns sr nn nnnnna s sE im e s s R s R s s sa s s C s R s E s R s s as s R s G s G as s C s G s C as s R s C ωωζωζωωωζωζωω-===++-+=-=+++=++=-+=→21222111102222222可见取na ωζ2=,可使0=sr e3-7588.19,598.0==n ωζ3-8 ()()6442++=s s s s G 3-9 按照条件(2)可写出系统的特征方程2)22()2())(22())(1)(1(232=+++++=+++=+++-+a s a s a s a s s s a s j s j s将上式与0)(1=+s G 比较,可得系统的开环传递函数[])22()2(2)(2a s a s s as G ++++=根据条件(1),可得aae K sr v 2225.01+===解得1=a ,于是由系统的开环传递函数为[]432)(2++=s s s s G 3-10()()()())5.0,/1(,%28%,3.162)24.0,/12.2(,%299.7%,6.461========ζωζωs rad s t Ms rad s t M n s pn s p()s ts153=)25.1,/4.0(,==ζωs rad n ,过阻尼系统,无超调。
3-11 (1)当a = 0时,22,354.0==n ωζ。
(2)n ω不变,要求7.0=ζ,求得a = 0.25 3-12 1. 单位脉冲响应 (a) 无零点时()()0,1s i n 122≥--=-t t e t c n t nn ωζζωζω(b )有零点1-=z 时()()0,111sin 1212222≥⎪⎪⎭⎫⎝⎛--+--⋅+-=-t arctg t et c n n n tnn n n ζωωζωζζωωζωζω 比较上述两种情况,可见有1-=z 零点时,单位脉冲响应的振幅较无零点时小,而且产生相移,相移角为nnarctg ζωωζ--112。
2.单位阶跃响应 (a) 无零点时()()0,11sin 111222≥⎪⎪⎭⎫⎝⎛-+---=-t arctg t et c n tn ζζωζζζω (b )有零点1-=z 时()()0,11sin 12112222≥⎪⎪⎭⎫⎝⎛-----+-+=-t arctg t et c n n tnn n ζωζωζζωζωζω 加了1-=z 的零点之后,超调量p M 和超调时间p t 都小于没有零点的情况。
3-13 系统中存在比例-积分环节()ss K 111+τ,当误差信号()0=t e 时,由于积分作用,该环节的输出保持不变,故系统输出继续增长,知道出现()0<t e 时,比例-积分环节的输出才出现减小的趋势。
因此,系统的响应必然存在超调现象。
3-14 在()t r 为常量的情况下,考虑扰动()t n 对系统的影响,可将框图重画如下()122+s s K τ()s s K 111+τ()122+s s K τ()ss K 111+τ+_N(s)C(s)图A-3-2 题3-14系统框图等效变换()()()()s N s K K s s sK s C 11121222+++=ττ根据终值定理,可求得()t n 为单位阶跃函数时,系统的稳态误差为0,()t n 为单位斜坡函数时,系统的稳态误差为11K 。
